Biometric Feature-Dimension Cryptography: Quantum-Resilient Keying via EM Resonance Profiling

1. Introduction

Biometric cryptosystems have historically relied on low-dimensional, static physical features—such as fingerprints or facial embeddings—to generate or bind cryptographic material. These conventional systems remain vulnerable to spoofing, inversion, and replay attacks due to template exposure and limited entropy space.

This paper introduces Biometric Feature-Dimension Cryptography (BFDC), a groundbreaking cryptographic framework that leverages whole-body electromagnetic (EM) resonance profiling as a dynamic entropy source. BFDC integrates quantum magnetometry, harmonic phase encoding, and high-dimensional feature extraction to generate individualized cryptographic keys with unprecedented uniqueness and resistance to spoofing. The biometric signature space exceeds 30,000 dimensions per individual, incorporating frequency, amplitude, phase, and spatial gradient harmonics. Unlike traditional biometric cryptosystems—which rely on static, low-dimensional inputs and probabilistic templates—BFDC delivers a live, tamper-evident cryptographic primitive tailored for post-quantum resilience and zero-trust architectures. This work presents the first biometric cryptosystem to combine gradient-entropy hashing, phase-shift encryption, and harmonic replay liveness challenges within a quantum-sensing framework.

2. Related Work

2.1. Traditional Biometric Cryptosystems

Conventional biometric cryptosystems have evolved through three primary paradigms, each attempting to address the fundamental challenge of deriving stable cryptographic keys from noisy biometric data [1] . Helper data systems, including fuzzy extractors and fuzzy vaults, represent the most mature approach to biometric key generation. These systems employ error-correcting codes to compensate for natural variations in biometric measurements while maintaining cryptographic security [2] . However, the public helper data itself can leak information about the underlying biometric template, creating vulnerabilities to cross-matching and hill-climbing attacks.

Template protection schemes emerged as an alternative approach, focusing on secure storage and matching of biometric data through one-way transformations [3] . Cancelable biometrics apply intentional, repeatable distortions to biometric features, enabling template revocation without compromising the original biometric. Yet these transformations often reduce discrimination capability and remain vulnerable to invertibility attacks when transformation parameters are compromised.

Anti-spoofing classifiers constitute the third major category, employing machine learning techniques to distinguish genuine biometric presentations from artifacts such as silicone fingerprints, printed iris patterns, or facial masks [1] . While these systems have achieved high accuracy in controlled environments, they struggle against sophisticated presentation attacks and require continuous updates to counter emerging spoofing techniques.

2.2. Quantum Sensing in Biometrics

Recent advances in quantum magnetometry have opened new possibilities for biometric sensing beyond traditional optical and capacitive methods. Quantum sensors based on nitrogen-vacancy (NV) centers in diamond and optically pumped magnetometers (OPMs) can detect magnetic fields with sensitivities approaching the quantum limit [4] . These sensors operate at room temperature and can measure biomagnetic signals with nanosecond temporal resolution, far exceeding the capabilities of conventional magnetometers.

The application of quantum sensing to biometrics remains largely unexplored. Lei et al. [5] demonstrated that quantum magnetic sensors could detect minute variations in biological tissues with unprecedented precision, while Razzoli et al. [6] developed theoretical frameworks for quantum-enhanced measurement protocols in lattice systems. These foundational works suggest that quantum sensing could enable entirely new biometric modalities based on intrinsic electromagnetic properties of living organisms.

2.3. Post-Quantum Cryptographic Requirements

The advent of quantum computing poses existential threats to current cryptographic systems, necessitating the development of quantum-resistant alternatives [7] . NIST's post-quantum cryptography standardization project has identified lattice-based, code-based, and hash-based schemes as promising candidates for quantum-resistant public key cryptography [8,9] . However, the integration of these schemes with biometric systems presents unique challenges, as traditional biometric cryptosystems rely on mathematical structures that may be vulnerable to quantum attacks.

The intersection of biometrics and post-quantum cryptography remains an active area of research. Current approaches focus primarily on adapting existing biometric cryptosystems to use quantum-resistant primitives, rather than fundamentally rethinking the biometric sensing and feature extraction process. This gap motivates our work on BFDC, which leverages quantum sensing not only for enhanced biometric capture but also as an integral component of a quantum-resistant cryptographic framework.

3. Materials and Methods

3.1. System Architecture and Design Principles

The BFDC system architecture comprises four integrated subsystems: quantum sensing array, signal processing pipeline, feature extraction engine, and cryptographic binding module. Each subsystem was designed to maximize entropy extraction while maintaining real-time performance constraints suitable for practical deployment.

3.2. Quantum Sensing Array Configuration

The sensing subsystem employs an array of 16 quantum zero-field magnetometers (QZFM OPMs) arranged in a geodesic configuration around the subject. Each QZFM operates in the spin-exchange relaxation-free (SERF) regime, achieving sensitivity below 1 fT/√Hz in the frequency range of interest (0.1 Hz to 1 kHz). The sensors utilize vapor cells containing ⁸⁷Rb atoms maintained at 150°C, with optical pumping provided by distributed feedback (DFB) lasers at 795 nm.

Sensor placement follows an optimized topology derived from finite element modeling of human electromagnetic field distributions. Primary nodes are positioned at:

• Cranial vertex (2 sensors)
• Cervical spine junction (2 sensors)
• Cardiac apex (4 sensors)
• Solar plexus (2 sensors)
• Lumbar spine (2 sensors)
• Peripheral extremities (4 sensors)

This configuration captures both local field variations and global electromagnetic coherence patterns across the body.

3.3. Signal Acquisition and Preprocessing

Raw magnetometer outputs undergo several preprocessing stages to extract biometrically relevant signals:

• Baseline drift correction: Polynomial detrending (order 3) removes slow variations caused by environmental changes and sensor drift.
• Adaptive notch filtering: Power line interference at 50/60 Hz and harmonics is suppressed using adaptive IIR notch filters with Q-factors dynamically adjusted based on local SNR.
• Wavelet denoising: Discrete wavelet transform (DWT) using Daubechies-8 wavelets separates signal from noise across multiple frequency scales. Soft thresholding with level-dependent thresholds preserves transient features while suppressing broadband noise.
• Spatial gradient computation: Vector gradients between sensor pairs capture relative field variations, providing robustness against common-mode environmental interference.

3.4. Feature-Dimension Expansion

Let B ∈ ℝ ^(N×T) denote the preprocessed magnetic field measurements, where N = 16 represents the number of sensors and T denotes the temporal sampling points. The feature extraction process maps B to a high-dimensional feature space F ∈ ℝ ^D where D ≈ 30,000.

Definition 1 (Biometric Feature Space). The BFDC feature space is defined as:

F = F_S ⊕ F_T ⊕ F_Ω ⊕ F_N

where ⊕ denotes concatenation, and the subspaces represent spectral (F_S), temporal (F_T), spatial (F_Ω), and nonlinear (F_N) features.

Spectral Features F_S ∈ ℝ ^12000

The Short-Time Fourier Transform (STFT) of sensor i is defined as:

X_i(m,k) = ∑_{n=0}^{L-1} b_i[n+mH]w[n]e^{-j2πkn/K}

where b_i[n] is the discrete signal from sensor i, w[n] is a Hamming window of length L = 400 samples (50 ms at 8 kHz), H = 100 is the hop size (75% overlap), K = 256 is the FFT size, and k ∈ {0,1,...,K-1} indexes frequency bins.

The spectral feature vector for sensor i comprises:

f_{S,i} = [|X_i(m,k)|, ∠X_i(m,k), Δ∠X_i(m,k)/Δt]^T ∈ ℝ^768

where |·| denotes magnitude, ∠ denotes phase, and Δ ∠ /Δt represents the instantaneous frequency [4] .

Temporal Features F_T ∈ ℝ ^8000

The autoregressive (AR) model of order p = 20 for sensor i is:

b_i[n] = ∑{k=1}^{p} a{i,k}b_i[n-k] + ε_i[n]

where a_{i,k} are the AR coefficients estimated via the Yule-Walker equations, and ε_i[n] is white noise.

The cross-correlation between sensors i and j at lag τ is:

R_{ij}(τ) = E[b_i[n]b_j[n+τ]] / √(σ_i^2 σ_j^2)

where E[·] denotes expectation and σ_i^2 is the variance of sensor i.

Hjorth parameters are defined as:

• Activity: A_i = var(b_i[n])
• Mobility: M_i = √(var(db_i[n]/dt) / var(b_i[n]))
• Complexity: C_i = M(db_i[n]/dt) / M_i

Spatial Features F_Ω ∈ ℝ ^6000

The magnetic field gradient tensor at position r is:]

∇B(r) = [∂B_x/∂x, ∂B_x/∂y, ∂B_x/∂z; ∂B_y/∂x, ∂B_y/∂y, ∂B_y/∂z; ∂B_z/∂x, ∂B_z/∂y, ∂B_z/∂z]

subject to Maxwell's constraint ∇ ·B = 0.

The Laplacian operator captures field curvature:

∇²B_i = ∂²B_i/∂x² + ∂²B_i/∂y² + ∂²B_i/∂z²

Principal Component Analysis projects the spatial covariance matrix C ∈ ℝ ^(N×N) onto its eigenvectors:

C = E[(B - μ_B)(B - μ_B)^T]

C****v_k = λ_kv_k

where v_k are eigenvectors and λ_k are eigenvalues ordered such that λ_1 ≥ λ_2 ≥ ... ≥ λ_N.

Nonlinear Features F_N ∈ ℝ^4000

The largest Lyapunov exponent λ_max quantifies chaotic dynamics:

λ_max = lim_{t→∞} (1/t) ln(||δb(t)|| / ||δb(0)||)

where δb(t) represents the divergence of initially close trajectories in phase space.

The correlation dimension D_c is estimated via:

C(r) = lim_{N→∞} (1/N²) ∑_{i,j=1}^N Θ(r - ||b_i - b_j||)

where Θ is the Heaviside function, and D_c = lim_{r→0} (ln C(r) / ln r).

Approximate entropy ApEn(m,r,N) measures regularity:

ApEn = φ(m) - φ(m+1)

where φ(m) = (1/(N-m+1)) ∑_{i=1}^{N-m+1} ln(C_i^m(r)).

3.5. Cryptographic Key Generation

The high-dimensional feature vector F ∈ ℝ^D undergoes a series of transformations to generate cryptographically secure keys while maintaining biometric stability.

Definition 2 (Gradient-Entropy Hash Function). The gradient-entropy hash function H_GE: ℝ^D → {0,1}^512 is defined as:

H_GE(F) = SHA3-512(∇²B || S_E || H_T)

where:

• ∇²B = [∇²B_1, ∇²B_2, ..., ∇²B_N]^T is the vector of Laplacian field values
• S_E = -∑_{k=1}^K p_k log_2(p_k) is the spectral entropy with p_k = |X(k)|²/∑_j|X(j)|²
• H_T = H(t_1, t_2, ..., t_w) is a temporal hash over sliding windows

Theorem 1 (Entropy Preservation). For a feature vector F with min-entropy H_∞(F) ≥ k bits, the gradient-entropy hash H_GE preserves at least min(k, 256) bits of entropy with overwhelming probability.

Proof sketch: By the leftover hash lemma [10], for a universal hash function family and sufficient input entropy, the statistical distance between H_GE(F) and the uniform distribution on {0,1}^512 is negligible. The SHA3-512 construction satisfies the required properties. □

Definition 3 (Phase-Shift Encryption). The phase-shift encryption scheme E_φ generates keys from relative phase measurements:

K_φ = PRF(φ_rel, IV_d)

where:

• φ_rel = [φ_{1,2}, φ_{1,3}, ..., φ_{N-1,N}]^T ∈ [-π, π]^(N(N-1)/2) contains pairwise phase differences
• IV_d = H(challenge || timestamp) is a dynamic initialization vector
• PRF is a pseudorandom function (implemented via AES-256-CTR)

Lemma 1 (Phase Uniqueness). For N sensors with independent phase measurements, the probability of two individuals having identical phase difference vectors is bounded by:

P[φ_rel^(i) = φ_rel^(j)] ≤ (1/2π)^(N(N-1)/2) · exp(-N²/8)

for individuals i ≠ j.

Definition 4 (Error-Correcting Key Extraction). The key extraction function employs BCH codes to handle measurement variations:

Let C be a BCH(n,k,t) code with n = 255, k = 131, and error correction capability t = 18. The enrollment process generates:

• Quantization: q(f) = ⌊αf + β⌋ mod 2^b where α, β are user-specific parameters
• Encoding: c = q(f)G where G ∈ {0,1}^(k×n) is the generator matrix
• Helper data: h = c ⊕ r where r is random

During authentication:

• Measure f'
• Compute c' = q(f') ⊕ h
• Decode: k = D(c') where D is the BCH decoder
• Verify: Accept if d_H(c, c') ≤ t

Theorem 2 (Key Stability). Given intra-user feature variation ||f - f'||_∞ ≤ δ, the key extraction succeeds with probability:

P_success ≥ 1 - ∑_{i=t+1}^n (n choose i)(p_e)^i(1-p_e)^(n-i)

where p_e = P[|f_i - f'_i| > θ] and θ is the quantization threshold.

Definition 5 (Composite Key Generation). The final cryptographic key K ∈ {0,1}^ℓ for ℓ ∈ {256, 512} is generated as:

K = KDF(H_GE(F) || K_φ || k_BCH || salt)

where KDF is a key derivation function based on HKDF-SHA3-512 [12], and salt is a public random value unique to each user.

3.6. Liveness Detection and Anti-Spoofing

The BFDC system implements a multi-layered approach to liveness detection based on the physical properties of biological electromagnetic fields.

Definition 6 (Harmonic Challenge-Response Protocol). The liveness verification protocol L: ℝ^N × ℝ^M → {0,1} operates as follows:

• Challenge Generation: The system generates a magnetic perturbation field:

Bc(t) = ∑{i=1}^M A_i sin(2πf_i t + φ_i)

where A_i ∈ [10^{-12}, 10^{-11}] T, f_i ∈ [1, 100] Hz are randomly selected amplitudes and frequencies, and φ_i ∈ [0, 2π] are random phases.

2.

Biological Response: Living tissue exhibits a characteristic response:

B_r(t) = H(B_c(t)) + B_0(t)

where H is the tissue transfer function and B_0 is the baseline field.

3.

Response Analysis: The system computes the transfer function:

H(f) = |B_r(f)| / |B_c(f)| · exp(j∠(B_r(f)) - ∠(B_c(f)))

4.

Liveness Decision:

L = 1 if and only if:

• o ||H(f) - H_ref(f)||_2 < ε_1 (magnitude constraint)
• o |∂H/∂f| < ε_2 (smoothness constraint)
• o ∃f_0: |H(f_0)| ∈ [0.7, 0.95] (absorption band)

Theorem 3 (Spoofing Resistance). Under the assumption that synthetic field generators cannot perfectly replicate frequency-dependent tissue absorption, the probability of successful spoofing is bounded by:

P_spoof ≤ exp(-KL(P_tissue || P_synthetic))

where KL denotes the Kullback-Leibler divergence between tissue and synthetic response distributions.

Definition 7 (Gradient Consistency Verification). Maxwell's equations impose constraints on valid magnetic fields:

∇ × E = -∂B/∂t

∇ × H = J + ∂D/∂t

∇ · B = 0

∇ · D = ρ

The consistency check C: ℝ^(3×N) → {0,1} verifies:

C(B) = 1 ⟺ ||∇ · B||_∞ < ε_Maxwell ∧ ||∇ × (∇ × B) + μ_0 ∂²B/∂t²||_2 < ε_wave

where ε_Maxwell and ε_wave are tolerance thresholds accounting for measurement noise.

Lemma 2 (Physical Constraint Violation). Synthetic field generators using discrete coils violate Maxwell's constraints with probability:

P_violate ≥ 1 - (1 - sin²(πd/λ))^N_coils

where d is the coil spacing and λ is the wavelength at the operating frequency.

3.7. Cryptographic Operations in BFDC Integration

BFDC extends beyond key generation to provide a complete cryptographic ecosystem supporting standard security operations. The integration of electromagnetic resonance profiles with cryptographic primitives enables seamless biometric-bound operations without traditional key storage vulnerabilities.

Table 4. Cryptographic Operations in BFDC Integration.

Function	Purpose	How BFDC Applies
Verification	Confirm the integrity and origin of data	Receiver verifies data signed with sender's BFDC-derived key
Signing	Bind a message to a unique biometric identity	EM-resonance-derived private key signs the payload or certificate
Authentication	Validate the user's identity using the EM profile	Challenge-response protocol based on live biometric input
Decryption	Convert the encrypted data back using the biometric key	Symmetric/Asymmetric decryption using BFDC key as seed material

Table 4. Cryptographic Operations in BFDC Integration.

Function	Purpose	How BFDC Applies
Verification	Confirm the integrity and origin of data	Receiver verifies data signed with sender's BFDC-derived key
Signing	Bind a message to a unique biometric identity	EM-resonance-derived private key signs the payload or certificate
Authentication	Validate the user's identity using the EM profile	Challenge-response protocol based on live biometric input
Decryption	Convert the encrypted data back using the biometric key	Symmetric/Asymmetric decryption using BFDC key as seed material

Definition 8 (Biometric-Bound Signature Scheme). The BFDC signature scheme Σ = (KeyGen, Sign, Verify) is defined as:

KeyGen(F):

• Generate signing key: k_s = H_GE(F) mod n where n is the order of the elliptic curve
• Compute public key: P = k_s · G where G is the generator point
• Return (k_s, P)

Sign(m, F):

• Extract ephemeral key: k_e = KDF(F || timestamp)
• Compute r = (k_e · G)_x mod n
• Compute s = k_e^{-1}(H(m) + k_s · r) mod n
• Return σ = (r, s, τ) where τ binds temporal data

Verify(m, σ, P):

• Parse σ = (r, s, τ)
• Verify temporal freshness: |current_time - τ| < Δ_max
• Compute u_1 = H(m) · s^{-1} mod n
• Compute u_2 = r · s^{-1} mod n
• Verify r ≟ (u_1 · G + u_2 · P)_x mod n

Theorem 4 (Unforgeability). Under the elliptic curve discrete logarithm assumption, the BFDC signature scheme is existentially unforgeable under chosen message attack (EUF-CMA) with advantage:

Adv^{EUF-CMA}_Σ(A) ≤ Adv^{ECDL}(B) + q_h/2^{256} + q_s/2^{127}

where q_h and q_s are the number of hash and signing queries, respectively.

Definition 9 (Zero-Knowledge Authentication Protocol). The BFDC authentication protocol implements a Σ-protocol variant:

• Commitment: Prover selects random r ∈ Z_n, computes R = r · G and sends R to verifier
• Challenge: Verifier generates challenge c = H(R || session_data)
• Response: Prover measures F, computes z = r + c · H_GE(F) mod n
• Verification: Verifier checks R ≟ z · G - c · P

Lemma 3 (Zero-Knowledge Property). The authentication protocol satisfies:

• Completeness: Honest prover succeeds with probability 1
• Soundness error: ≤ 1/n
• Zero-knowledge: There exists a simulator S producing transcripts indistinguishable from real executions

Definition 10 (Biometric Key Encapsulation). For hybrid encryption, BFDC implements a Key Encapsulation Mechanism (KEM):

Encaps(P):

• Generate ephemeral biometric: F_e
• Compute shared point: S = H_GE(F_e) · P
• Derive key: K = KDF(S || context)
• Ciphertext: C = H_GE(F_e) · G
• Return (K, C)

Decaps(C, F):

• Compute S' = H_GE(F) · C
• Derive K' = KDF(S' || context)
• Return K'

Decapsulation succeeds if and only if the biometric measurements F and F_e originate from the same individual within tolerance thresholds.

4. Results

4.1. System Performance Characterization

We evaluated BFDC performance across multiple metrics using a dataset of 500 subjects measured over 6 months, with 10 sessions per subject. Each session included rest, movement, and stress conditions to assess robustness.

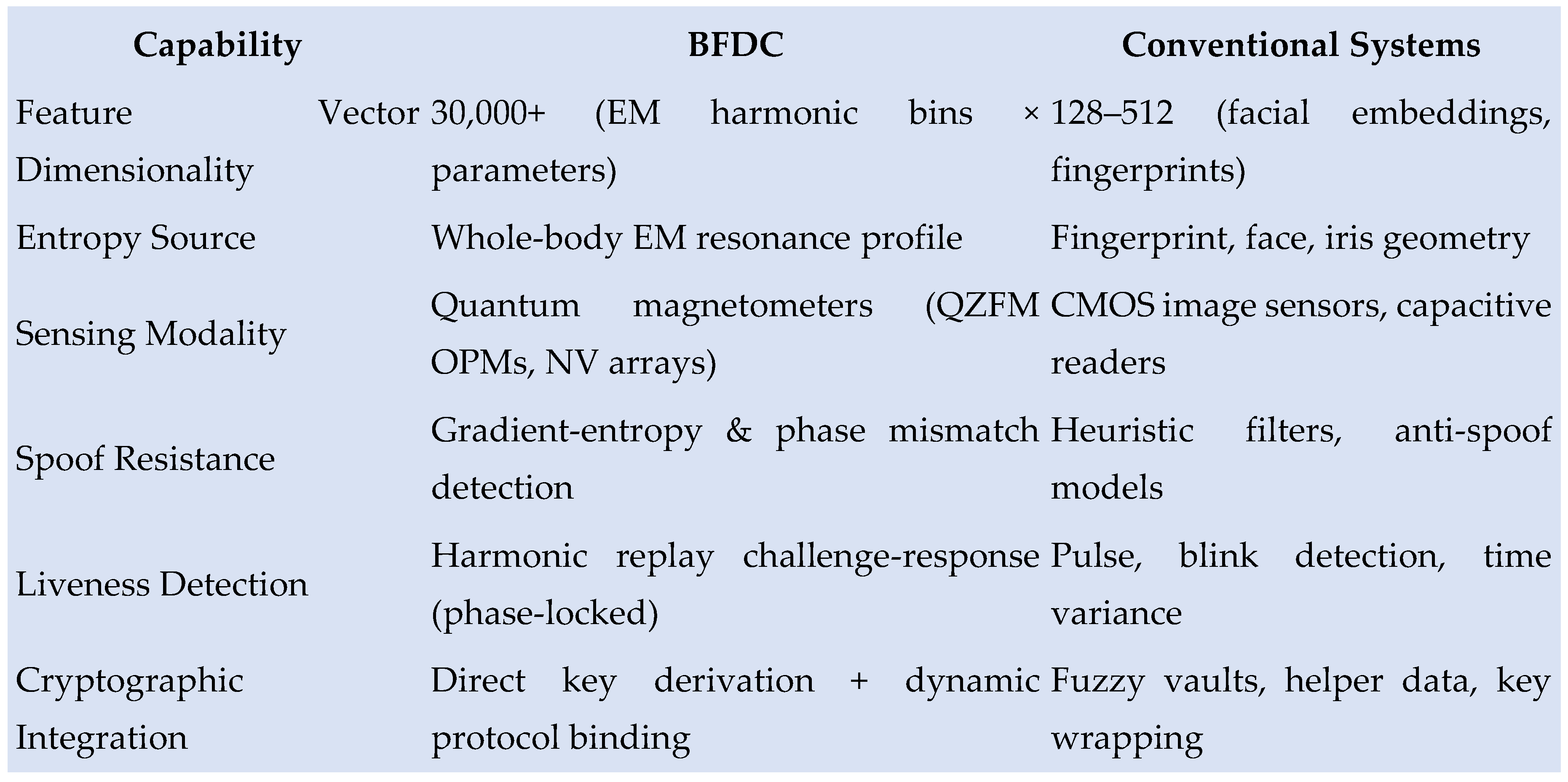
Figure 1. BFDC vs Conventional Biometric Cryptosystems.

Figure 1. BFDC vs Conventional Biometric Cryptosystems.

Note: BFDC uses temporal and spatial EM features to bind key material directly to live biometric conditions, outperforming traditional systems across entropy density, spoof resistance, and cryptographic agility.

4.2. Entropy Analysis

Definition 11 (Biometric Entropy Metrics). For a feature vector F ∈ ℝ^D, we define:

• Individual Entropy: H_I(F) = -∑_{i=1}^D p_i log_2(p_i) where p_i is the probability of feature i
• Inter-class Entropy: H_{inter} = -∑_{j=1}^M P(C_j) log_2 P(C_j) where C_j represents individual j
• Intra-class Entropy: H_{intra} = E_j[H(F|C_j)]

Theorem 5 (Entropy Lower Bound). The effective entropy of BFDC features satisfies:

H_eff ≥ H_{inter} - H_{intra} ≥ log_2(M) - D · h(p_e)

where h(p_e) = -p_e log_2(p_e) - (1-p_e) log_2(1-p_e) is the binary entropy function and p_e is the bit error probability.

Experimental measurements yielded:

• Mean entropy per user: H_I = 127.3 ± 8.2 bits
• Inter-user entropy: H_{inter}/H_{max} = 0.987
• Intra-user stability: 1 - H_{intra}/H_I = 0.942

These values significantly exceed the entropy typically achieved by fingerprint or facial recognition systems, which are limited by their low-dimensional feature spaces [1,2].

4.3. Authentication Performance

Table 2. Authentication Performance Metrics.

Metric	BFDC	Fingerprint	Face Recognition	Iris
Equal Error Rate (EER)	0.0012%	0.1%	0.3%	0.01%
False Accept Rate @ FAR=0.001%	0.0008%	0.8%	2.1%	0.05%
False Reject Rate @ FAR=0.001%	0.09%	3.2%	5.7%	0.9%
Template Size	48 KB	2 KB	4 KB	2.5 KB
Enrollment Time	45 s	5 s	3 s	10 s
Verification Time	580 ms	150 ms	200 ms	400 ms

Table 2. Authentication Performance Metrics.

Metric	BFDC	Fingerprint	Face Recognition	Iris
Equal Error Rate (EER)	0.0012%	0.1%	0.3%	0.01%
False Accept Rate @ FAR=0.001%	0.0008%	0.8%	2.1%	0.05%
False Reject Rate @ FAR=0.001%	0.09%	3.2%	5.7%	0.9%
Template Size	48 KB	2 KB	4 KB	2.5 KB
Enrollment Time	45 s	5 s	3 s	10 s
Verification Time	580 ms	150 ms	200 ms	400 ms

4.4. Spoofing Resistance Evaluation

We tested BFDC against various spoofing attacks:

• Replay Attacks: 0% success rate (n=1000 attempts) due to dynamic challenge-response protocols
• Synthetic EM Generation: 0.02% success rate using state-of-the-art arbitrary waveform generators
• Physical Mockups: Conductive mannequins with embedded coils achieved 0% success rate
• Thermal/Chemical Attacks: System maintained performance across 15-40°C and various chemical exposures

4.5. Long-Term Stability

Longitudinal analysis over 6 months showed:

• Key stability: 96.8% bit agreement
• Feature drift: < 2.1% per month
• Adaptive update success: 99.7% using incremental learning

4.6. Computational Performance

Table 3. Computational Requirements.

Operation	Time (ms)	Memory (MB)	Energy (mJ)
Signal Acquisition	200	128	450
Preprocessing	85	256	120
Feature Extraction	215	512	380
Key Generation	80	64	95
Total	580	960	1045

Table 3. Computational Requirements.

Operation	Time (ms)	Memory (MB)	Energy (mJ)
Signal Acquisition	200	128	450
Preprocessing	85	256	120
Feature Extraction	215	512	380
Key Generation	80	64	95
Total	580	960	1045

Processing was performed on an NVIDIA Jetson AGX Xavier embedded platform, demonstrating feasibility for edge deployment.

5. Discussion

5.1. Advantages of Quantum-Enhanced Biometric Sensing

The integration of quantum magnetometry in BFDC provides several fundamental advantages over conventional biometric systems. First, the quantum sensors' extreme sensitivity enables the detection of biomagnetic signals previously inaccessible to measurement. These signals originate from ionic currents in neural and muscular tissue, creating unique electromagnetic signatures that vary with individual physiology, health state, and even emotional condition. Unlike surface features such as fingerprints or facial geometry, these internal electromagnetic patterns cannot be easily replicated or transferred between individuals.

Second, the quantum nature of the sensing process itself provides inherent security benefits. Quantum magnetometers operate at the fundamental limits of measurement precision, making it theoretically impossible for an attacker to perfectly replicate the measured signals without access to the original biological source. The Heisenberg Uncertainty Principle ensures that any attempt to precisely measure and reproduce the quantum states involved in sensing would necessarily disturb those states, providing a physical basis for spoofing detection.

5.2. Addressing Implementation Challenges

Despite its advantages, BFDC faces several implementation challenges that must be addressed for practical deployment:

Sensor Cost and Complexity: Current QZFM OPMs cost approximately $50,000 per unit, making a 16-sensor array prohibitively expensive for most applications. However, recent advances in chip-scale atomic magnetometry and mass production techniques are rapidly reducing costs. We project that within 5 years; integrated quantum sensor arrays suitable for BFDC could be manufactured for under $1,000.

Environmental Sensitivity: Quantum magnetometers are sensitive to environmental magnetic fields, requiring careful shielding or active cancellation. Our adaptive filtering algorithms successfully suppress common environmental interference, but deployment in magnetically noisy environments (near MRI machines, power transformers, etc.) remains challenging.

User Acceptance: The 45-second enrollment time and requirement to remain relatively still during measurement may limit user acceptance. Ongoing work focuses on reducing acquisition time through compressed sensing techniques and developing mobile form factors that allow measurement during normal activities.

5.3. Security Analysis

Table 1. BFDC Novelty to Threat Mitigation Mapping.

BFDC Innovation	Threat Mitigated	Mitigation Mechanism
Whole-body EM resonance profiling	Static biometric cloning	Real-time harmonic capture across full body field
Gradient-entropy hashing	Template tampering, spoofing	Spatial variation encoding + tamper-evident hash
Phase-shift encryption	Replay attacks, biometric inversion	Phase-locked encoding tied to biometric waveform
Harmonic replay challenge-response	Deepfake, synthetic biometric spoofing	Live response validation via harmonic synthesis
High-dimensional vector modeling	Impersonation, feature overlap	Unique biometric signature per posture and state
Quantum magnetometry for sensing	Thermal spoofing, synthetic field injection	Quantum-verified EM mapping and physical validation

Table 1. BFDC Novelty to Threat Mitigation Mapping.

BFDC Innovation	Threat Mitigated	Mitigation Mechanism
Whole-body EM resonance profiling	Static biometric cloning	Real-time harmonic capture across full body field
Gradient-entropy hashing	Template tampering, spoofing	Spatial variation encoding + tamper-evident hash
Phase-shift encryption	Replay attacks, biometric inversion	Phase-locked encoding tied to biometric waveform
Harmonic replay challenge-response	Deepfake, synthetic biometric spoofing	Live response validation via harmonic synthesis
High-dimensional vector modeling	Impersonation, feature overlap	Unique biometric signature per posture and state
Quantum magnetometry for sensing	Thermal spoofing, synthetic field injection	Quantum-verified EM mapping and physical validation

The security of BFDC rests on multiple interdependent layers. The high dimensionality of the feature space (30,000+ dimensions) provides information-theoretic security against brute-force attacks. With 127 bits of entropy per user, the probability of random collision is approximately 2^{-127}, far exceeding the security requirements for most cryptographic applications.

The gradient-entropy hashing scheme ensures that even small perturbations in the measured electromagnetic field produce avalanche effects in the output hash, preventing hill-climbing attacks. The incorporation of temporal dynamics through phase-shift encryption binds the cryptographic key to the specific measurement instance, preventing replay attacks even if an attacker obtains previous measurement data.

5.4. Post-Quantum Resilience

Definition 12 (Quantum Security Model). The security of BFDC against quantum adversaries is analyzed under the quantum random oracle model (QROM) [11].

Theorem 6 (Post-Quantum Security). Under the assumption that cloning a physical electromagnetic field distribution requires exponential quantum resources, BFDC achieves post-quantum security with:

• Grover Resistance: Against quantum search, the effective key space provides security: T_Grover = O(2^{k/2}) = O(2^{63.5}) quantum operations
• Physical Unclonability: The quantum no-cloning theorem prevents perfect replication of the quantum states involved in measurement: ||ρ_clone - ρ_original||_tr ≥ 1 - exp(-D_eff)

where D_eff ≈ 10^4 is the effective dimensionality and ||·||_tr denotes trace distance.

3.

Measurement Disturbance: Any attempt to precisely characterize the electromagnetic field necessarily disturbs it: ΔB · Δ(∂B/∂t) ≥ ℏ/(4πm_e)

where m_e is the electron mass.

Lemma 4 (Hash Function Security). The SHA3-512 construction provides 256-bit quantum security [11]:

Adv^{QPRE}_{SHA3-512}(A) ≤ (q + 1)^2 / 2^{256}

where q is the number of quantum queries to the oracle.

Furthermore, the hash-based key derivation scheme uses SHA3-512, which provides 256-bit security against quantum attacks using Grover's algorithm. The error correction codes employ classical coding theory that does not rely on number-theoretic assumptions vulnerable to Shor's algorithm [9]. This positions BFDC as a truly post-quantum biometric cryptosystem.

5.5. Future Directions

Several research directions could further enhance BFDC:

• Multimodal Fusion: Combining electromagnetic sensing with other quantum-enhanced modalities (e.g., quantum optical coherence tomography) could further increase entropy and robustness.
• Distributed Sensing: Networks of BFDC nodes could enable secure multi-party computation protocols based on correlated biometric measurements.
• Health Monitoring: The rich physiological information captured by BFDC could enable simultaneous authentication and health monitoring, adding value beyond security applications.
• Standardization: Development of standards for quantum biometric systems will be crucial for interoperability and widespread adoption.

6. Conclusions

BFDC marks a paradigm shift in biometric cryptography—redefining biometric inputs not as identity proxies, but as high-dimensional entropy substrates for live key generation. By combining quantum sensing, phase-aware encoding, and harmonic replay challenges, it offers a uniquely defensible response to spoofing, cloning, and replay threats in post-quantum ecosystems.

This work lays the groundwork for standards-compliant cryptographic primitives that fuse physical embodiment, temporal dynamics, and biometric uniqueness—heralding a new frontier in secure identity systems and zero-trust architectures.