An Observation on the Use of Integral Transform to Solve Fractional SIR and SIS Epidemic Models

1. Introduction

In mathematics and mathematical modeling, the integral transform has various applications. DEs, IEs, and IDEs can all be resolved using equation solving (ET). This method is unsuitable for solving nonlinear DEs due to the nonlinear variables. Nonlinear DEs can be solved with ET aid using the differential transform method, homotopy approach, or any other method. In the present era, nonlinear equations have grown in importance. There are many uses for nonlinear phenomena in engineering, physics, and applied mathematics. It requires inventiveness to find novel exact or approximate solutions to nonlinear PDEs, which is difficult even in fields like applied mathematics and physics where exact solutions are essential.

Many writers have focused on studying the solutions of nonlinear PDEs with different methods in the past few years. Many techniques have been tried, such as ET, Laplace; double Laplace, homotopy perturbation, variantal iteration, differential transform, Laplace variational iteration, and ET transforms [1,2,3,4,5,6,7,8,9,10,11,12]. Numerous analytical and numerical techniques, including the local fractional Fourier method and the local fractional variational iteration approach, have been developed to solve nonlinear PDEs with FDs.

Although FDs have a long history in mathematics, the scientific community did not use them for a very long period. One reason why FDs are so despised could be the predominance of non-equivalent definitions. Another problem is that it is difficult to interpret the geometric significance of FDs because they are nonlocal. But in the last 20 years, mathematicians and engineers have started to focus significantly more on fractional calculus. It was found that FDs are a useful tool for simulating many different applications, especially multidisciplinary ones. For instance, FDs can be used to resolve the issue resulting from the fluid-dynamic traffic model's assumption of continuous traffic flow and to explain the nonlinear oscillation of earthquakes.

Based on actual data, a number of studies suggest fractional PDEs and DEs features for seepage flow in porous media. Over the last ten years, scientists have found that the most comprehensive explanation for a variety of physical phenomena, including dumping laws and diffusion processes, comes from non-integer order derivatives. These findings stimulated research on fractional calculus in many fields, such as natural philosophy, technology, and alchemy.

Epidemiology is a branch of biology that focuses on statistical modeling of disease spread. The initial step in characterizing physical real-world problems that emerge in epidemiology is to employ differential equations. To the best of our knowledge, the earliest mathematical model of epidemiology was created and solved in 1760 by Daniel Bernoulli. Since the work of Kermack and McKendrick [13], the subject of mathematical epidemiology has grown greatly, and a variety of models have been created and applied to the study of infectious diseases [14,15].

The biological discipline of epidemiology examines the statistics the issue with epidemiological models is that, even in the simplest mathematical models of real phenomena, which are composed of sets of first-order DEs, they are not necessarily integrable. Nucci and Leach [16], who developed an integrable SIS model via Lie analysis, have detailed these features in accordance with Leach and Nucci [5].

According to Khan [6], the homotopy analysis method yields the convergent series solutions for the SIR and SIS models, despite the model's apparent poor performance in mathematics. The index, topological concepts, Poincar´e-Bendixson type theorems, stability, bifurcation theory, and Lyapunov method have all been heavily utilized by a number of writers to analyze these models [14].

To understand the meaning of SIS and SIR, consider the following: given a constant population, divide it into three groups: susceptible (S) = capable of contracting the disease; infective (I) = infected and capable of spreading the disease to susceptible; and removed (R) = either recovered from the disease, died, developed immunity, or was isolated from other components. In the SIR model, all three classes are present; however, in the SIS model, since the sickness does not confer immunity against reinfection, the infectious agent returns to the susceptible class upon recovery.

In fact, closed-form solutions to mathematical models are crucial for a thorough understanding of the qualitative components of natural science. The effects of disease on a population are described by mathematical models in epidemiology; hence, careful examination of these models is required. Given this, the main goal of this work is to obtain an exact, pure analytical solution for the SIS and SIR epidemic model, a particular application of the model put forth by McKendrick and Kermack [13], ET was used to study a few technical and biological challenges in [20,21,22], and it showed high efficacy in identifying exact solutions, and in [23,24,25], finally the conformable ET was studied.

Fractional calculus is an extension of classical calculus that deals with integrals and derivatives of non-integer orders. The concept has evolved significantly since it was first proposed more than three centuries ago, impacting several disciplines such as viscoelasticity, control theory, and anomalous diffusion.

This study presents a detailed demonstration of the unique method, which is based on the Elzaki transform (ET). We additionally explore in this study the potential application of this new transform to the newly proposed F SIR and F SIS EM solution approach. Both impulsive and discontinuous functions respond well to this strategy.

The document is structured as follows: Section 2 provides the fundamental definitions, theorems, and Caputo FDs of ET. Section 3 contains a convergence study, several instances, and a formula for resolving FSIR & FSIS EMs. A debate wrapped up Section 4.

Definition 1: 

It is claimed that one has a real function. $R\left(\lambda \right) , \lambda > 0,$ in the space $C_{\mu }, \mu \in \Re$ if a real number $p > \mu ,$ exists such that $R\left(\lambda \right) = {\lambda }^p{R}_1\left(\lambda \right),$ where $R_1\left(\lambda \right) \in C\left(0, \infty \right)$ , in addition to being stated to be in the space $C_{\mu }^n$ if and only if $R^n\in C_{\mu }, n \in N.$

Definition 2: 

The Riemann–Liouville integral operator, of the order $\alpha > 0,$ of a function $R \in C_{\mu }, \mu \ge -1,$ is,

$$\begin{array}{l}{J}^{\alpha }R\left(\lambda \right)={\displaystyle \frac{1}{\mathsf{\Gamma }\left(\alpha \right)}}{\displaystyle \underset{0}{\overset{\lambda }{\int }}{\left(\lambda -v\right)}^{\alpha - 1}R\left(v\right) dv, \alpha >0}.\\ J^0 R\left(\lambda \right) = R\left(\lambda \right),\end{array}$$

(1)

Among the essential characteristics of the operator $J^{\alpha },$ are the subsequent ones:

For $R^n \in C_{\mu }, n \in N,$ $\alpha , \beta \ge 0$ and $\gamma \ge -1:$

$$\begin{array}{l}1. J^{\alpha }{J}^{\beta }R\left(\lambda \right) = J^{\alpha + \beta }R\left(\lambda \right),\\ 2. J^{\alpha } {\lambda }^{\gamma } = {\displaystyle \frac{\mathsf{\Gamma }\left(\gamma + 1\right)}{\mathsf{\Gamma }\left(\gamma + \alpha + 1\right)}} {\lambda }^{\alpha + \gamma },\end{array}$$

Definition 3: 

According to Caputo, the FDs of $R\left(\lambda \right)$ are: $D^{\alpha }R\left(\lambda \right) = J^{m - \alpha }{D}^{m}R\left(\lambda \right)$

Or,

$${}_a{}^{C}D_{\lambda }^{\alpha }R(\lambda )={\displaystyle \frac{1}{\mathsf{\Gamma }(m-\alpha )}}{\displaystyle \underset{a}{\overset{\lambda }{\int }}{(\lambda -\tau )}^{m-\alpha -1}{R}^{(m)}(\tau )d\tau ,}$$

(2)

For $m - 1 < \alpha \le m , m \in N, \lambda > 0,$ and $R \in C_{-1}^m.$

The fundamental characteristics of the operator ${}_a{}^{C}D_{\lambda }^{\alpha }$ are as follows:

$$\begin{array}{l}1. {}_a{}^{c}D_{\lambda }^{\alpha }\left[c\right]=0, \\ 2. {}_a{}^{c}D_{\lambda }^{\alpha }{I}_{\lambda }^{\alpha }\left[R(\lambda )\right]=R(\lambda ), \\ 3. {}_a{}^{c}D_{\lambda }^{\alpha }\left[{\lambda }^{\beta }\right]={\displaystyle \frac{\mathsf{\Gamma }(\beta +1)}{\mathsf{\Gamma }(\beta -\alpha +1)}}{\lambda }^{\beta -\alpha },\\ 4. {}_a{}^{c}D_{\lambda }^{\alpha }{}_a{}^{c}D_{\lambda }^{\sigma }\left[R(\lambda )\right]{=}_a^C{D}_{\lambda }^{\alpha +\sigma }R(\lambda ){=}_a^C{D}_{\lambda }^{\sigma }{}_a{}^{c}D_{\lambda }^{\alpha }R(\lambda ),\\ 5. I^{\alpha }{}_a{}^{c}D_{\lambda }^{\alpha }\left[R(\lambda )\right]=R(\lambda )-{\displaystyle \sum _{k=0}^{m-1}{R}^{(k)}(0)\frac{{\lambda }^k}{k!}},\end{array}$$

Where $c,\beta ,\sigma ,\delta$ are constants.

2. Elzaki Transform

To solve PDEs, ODEs, and systems of ODEs, Tarig M. Elzaki has provided examples of how to apply the modified Sumudu transform, or ET. For DEs with variable coefficients that cannot be solved by Sumudu and Laplace transforms, ET is a helpful technique [18]. The use of ET is powerful in applied mathematics and engineering. An overview of the main ideas behind this shift is provided below:

The ET of $R(\lambda )$ is,

$$E\left[R(\lambda )\right]=v{\displaystyle \underset{0}{\overset{\infty }{\int }}R(\lambda ) e^{-\frac{\lambda }{v}}}d\lambda =T(v) , \lambda >0.$$

(3)

Definition 4:

Let $T^{\prime }(v)$ be the ET of the derivatives of $R\left(\lambda \right)$. Then:

$$\begin{gathered} (a) T^{\prime }(v) = {\displaystyle \frac{T(v)}{v}} -vR(0) \\ \left(b\right) T^{\left(n\right)}\left(v\right)={\displaystyle \frac{T\left(v\right)}{v^n}}-{\displaystyle \sum _{k=0}^{n-1}{v}^{2-n+k}}{R}^{\left(k\right)}\left(0\right), n\ge 1. \end{gathered}$$

Where $T^n\left(v\right)$ is ET of the nth derivative of the function, $R\left(\lambda \right).$ see [9].

Some useful ETs utilized in this paper are listed below:

Let: $E\left[R\left(\lambda \right)\right] = T\left(v\right)$ and, $E\left[H\left(\lambda \right)\right] = H_1\left(v\right),$

Then;

$$\begin{array}{l}1. E\left[R\left(\lambda \right) \mp H\left(\lambda \right)\right] = E\left(R\left(\lambda \right)\right) \mp E\left(H\left(\lambda \right)\right)=T(v)\mp H_1(v)\\ 2. E\left[{\lambda }^{\alpha }\right] = v^{\alpha +2} \mathsf{\Gamma }\left(\alpha + 1\right), \alpha > -1,\\ 3. E\left[R^{\left(n\right)}\left(\lambda \right)\right] = {\displaystyle \frac{T\left(v\right)}{v^n}} - {\displaystyle \frac{R\left(0\right)}{v^{n-2}}} - {\displaystyle \frac{R^{\prime }\left(0\right)}{v^{n - 3}}} - \cdot \cdot \cdot - v R^{\left(n - 1\right)}\left(0\right)\end{array},$$

Let: $E\left[R(\zeta ,\lambda )\right] = T\left(\zeta ,v\right),$ then:

$$\begin{array}{l}E\left[{\displaystyle \frac{\partial R(\zeta ,\lambda )}{\partial \lambda }}\right]={\displaystyle \frac{1}{v}}T(\zeta ,v)-vR(\zeta ,0), \\ E\left[{\displaystyle \frac{{\partial }^{2}R(\zeta ,\lambda )}{\partial {\lambda }^2}}\right]={\displaystyle \frac{1}{v^2}}T(\zeta ,v)-R(\zeta ,0)-v{\displaystyle \frac{\partial R(\zeta ,0)}{\partial \lambda }},\\ {\rm E}\left[{\displaystyle \frac{\partial R(\zeta ,\lambda )}{\partial \zeta }}\right]={\displaystyle \frac{d}{d\zeta }}\left[T\left(\zeta ,v\right)\right] , {\rm E}\left[{\displaystyle \frac{{\partial }^{2}R(\zeta ,\lambda )}{\partial {\zeta }^2}}\right]={\displaystyle \frac{d^2}{d{\zeta }^2}}\left[T\left(\zeta ,v\right)\right] .\\ E\left[{\displaystyle \frac{{\partial }^{n}R(\zeta ,\lambda )}{\partial {\lambda }^n}}\right]={\displaystyle \frac{T\left(\zeta ,v\right)}{v^n}}-{\displaystyle \sum _{k=0}^{n-1}{v}^{2-n+k}}{R}^{\left(k\right)}\left(\zeta ,0\right), n\ge 1.\end{array}$$

Lemma 1: 

The R-L operator of order $\alpha > 0$ has the following expression for its ET:

$$E\left[J^{\alpha } R\left(\lambda \right)\right] = v^{\alpha } T\left(v\right).$$

(4)

Proof: 

ET of R-L FIO of order $\alpha > 0$ is:

$$\begin{array}{l}E\left[J^{\alpha } R\left(\lambda \right)\right] = E\left[{\displaystyle \frac{1}{\mathsf{\Gamma }\left(\alpha \right)}} {\displaystyle \underset{0}{\overset{\lambda }{\int }}{\left(\lambda - \alpha \right)}^{\alpha - 1}R\left(\lambda \right) d\lambda }\right] \\ = {\displaystyle \frac{1}{\mathsf{\Gamma }\left(\alpha \right)}} {\displaystyle \frac{1}{v}} T\left(v\right) G\left(v\right)=v^{\alpha } T\left(v\right)\end{array},$$

Where,

$$G\left(v\right) = E\left[{\lambda }^{\alpha - 1}\right] = v^{\alpha + 1}\mathsf{\Gamma }\left(\alpha \right)$$

Lemma 2: 

ET of Caputo FDs for $\alpha >0, m - 1 < \alpha \le m, m \in N$ is;

$$E\left[{}^{c}D_{\lambda }^{\alpha }R\left(\lambda \right)\right] = v^{m-\alpha }\left[{\displaystyle \frac{T\left(v\right)}{v^m}} - {\displaystyle \frac{R\left(0\right)}{v^{m-2}}} - {\displaystyle \frac{R^{\prime }\left(0\right)}{v^{m - 3}}} - \cdot \cdot \cdot - v R^{\left(m - 1\right)}\left(0\right)\right]$$

(5)

Proof: 

  $E\left[{}^{c}D_{\lambda }^{\alpha }R\left(\lambda \right)\right] = E\left[J^{m - \alpha } R^{\left(m\right)}\left(\lambda \right)\right] = v^{m - \alpha }E\left[R^{\left(m\right)}\left(\lambda \right)\right]$ .

Equation (4) enables us to determine the outcome. Equation (5) is expressed as:

$$E\left[{}^{c}D_{\lambda }^{\alpha }R\left(\lambda \right)\right] = {\displaystyle \frac{1}{v^{\alpha }}}E\left[R\left(\lambda \right)\right]-{\displaystyle \sum _{k=0}^{m-1}{R}^{(k)}\left(0\right)v^{2-\alpha +k}},$$

(6)

Also we have: $E\left[{\lambda }^{\alpha }\right]=\mathsf{\Gamma }(\alpha +1)v^{\alpha +2} \Rightarrow E^{-1}\left[v^{\alpha +2}\right]={\displaystyle \frac{{\lambda }^{\alpha }}{\mathsf{\Gamma }(\alpha +1)}}, \alpha \ge 0.$ Now, in order to extract the function $R(\lambda )$ from its ET, we prove the following lemma.

Lemma 3:

If $\alpha , \beta > 0,$ $a \in C$ and ${\displaystyle \frac{1}{v^{\alpha }}} > \left|a\right|,$ then:

$$E^{- 1}\left[{\displaystyle \frac{v^{\beta + 1}}{1 + a v^{\alpha }}}\right] = {\lambda }^{\beta - 1} {\in }_{\alpha , \beta }\left(- a {\lambda }^{\alpha }\right).$$

(7)

Proof: 

$${\displaystyle \frac{v^{\beta + 1}}{1 + a v^{\alpha }}} = v^{\beta + 1} {\displaystyle \frac{1}{1 + a v^{\alpha } }} = v^{\beta + 1} {\displaystyle \sum _{n = 0}^{\infty }{\left(- a\right)}^n{\left(v^{\alpha }\right)}^n} ={\displaystyle \sum _{n = 0}^{\infty }{\left(- a\right)}^n v^{n \alpha + \beta + 1}},$$

Then;

$$\begin{array}{l}{E}^{- 1}\left[{\displaystyle \frac{v^{\beta + 1}}{1 + a v^{\alpha }}}\right] = E^{-1}\left[{\displaystyle \sum _{n = 0}^{\infty }{\left(- a\right)}^n v^{n \alpha + \beta + 1}}\right] ={\displaystyle \sum _{n = 0}^{\infty }\frac{{\left(- a\right)}^n{\lambda }^{n\alpha +\beta - 1}}{\mathsf{\Gamma }\left(n\alpha +\beta \right)}}=\\ {\lambda }^{\beta - 1}{\displaystyle \sum _{n = 0}^{\infty }\frac{{\left(- a{\lambda }^{\alpha }\right)}^n}{\mathsf{\Gamma }\left(n\alpha +\beta \right)}}={\lambda }^{\beta - 1}{\in }_{\alpha , \beta }\left(- a {\lambda }^{\alpha }\right)\end{array}$$

3. Analysis of Proposed Scheme

Fractional-order DEs describes a system having a memory kernel or memory function that depends on both the current and earlier states of the system. However, a system's current state is the only thing that an IDEs can explain. When ET is applied to nonlinear FSIR & FSIS EMs in this study, the equations are converted into straightforward algebraic equations that are easily solved repeatedly. The solutions are then found by using the inverse of the ET.

Using the following initial conditions and nonlinear FSIR & FSIS EMs, we demonstrate the basic principle of this approach:

First, consider the nonlinear FSIR EM,

$$\begin{array}{l}{}^{c}D_t^{\alpha }S(t)=-rS(t)I(t)-\mu S(t)+\mu , S(0)=s_0, 0<\alpha \le 1,\\ {}^{c}D_t^{\alpha }I(t)=rS(t)I(t)-\mu I(t) , I(0)=i_0,\end{array}$$

(8)

Where $r>0, s_0>0, i_0>0.$ Here $r$ is the infectivity coefficient of the typical Lotka-Volterra interaction term, $s_0, i_0$ are given constants, $S(t)$ is the susceptible population, $I(t)$ is the infected population, and $\mu$ the recovery coefficient.

By using ET to Eqs (8), we get:

$$\begin{array}{l}E\left[{}^{c}D_t^{\alpha }S(t)\right]=E\left[-rS(t)I(t)-\mu S(t)+\mu \right], \\ E\left[{}^{c}D_t^{\alpha }I(t)\right]=E\left[rS(t)I(t)-\mu I(t)\right], \end{array}$$

By using ET's property, we can obtain:

$$\begin{array}{l}{\displaystyle \frac{1}{v^{\alpha }}}E\left[{}^{c}D_t^{\alpha }S(t)\right]-v^{2-\alpha }{s}_0=E\left[-rS(t)I(t)-\mu S(t)+\mu \right],\\ {\displaystyle \frac{1}{v^{\alpha }}}E\left[{}^{c}D_t^{\alpha }I(t)\right]-v^{2-\alpha }{i}_0=E\left[rS(t)I(t)-\mu I(t)\right],\end{array}$$

(9)

Equation (9), after treating each of the two sides as the Elzaki inverse, get the following result:

$$\begin{array}{l}S(t)=s_0+E^{-1}\left\{v^{\alpha }E\left[-rS(t)I(t)-\mu S(t)+\mu \right]\right\} ,\\ I(t)=i_0+E^{-1}\left\{v^{\alpha }E\left[rS(t)I(t)-\mu I(t)\right]\right\} ,\end{array}$$

Utilize these relationships to find iterative solutions to the problem:

$$\begin{array}{l}{S}_{n+1}(t)=E^{-1}\left\{v^{\alpha }E\left[-r{S}_n(t)I_n(t)-\mu S_n(t)+\mu \right]\right\} , S_0(t)=s_0,\\ I_{n+1}(t)=E^{-1}\left\{v^{\alpha }E\left[r{S}_n(t)I_n(t)-\mu I_n(t)\right]\right\} , I_0(t)=i_0,\end{array}$$

(10)

Equation (8), are believed to have the following series form solutions:

$$S(t)={\displaystyle \sum _{n=0}^{\infty }{S}_n(t)} , I(t)={\displaystyle \sum _{n=0}^{\infty }{I}_n(t)} .$$

(11)

The following $S_0\left(t\right), S_1\left(t\right), S_2\left(t\right) , \mathrm{...} , I_0\left(t\right), I_1\left(t\right), I_2\left(t\right) , \mathrm{...} ,$ can be inferred from Equation (10), the solutions can then be found using Equation (11).

Second, consider the nonlinear F SIS EM,

$$\begin{array}{l}{}^{c}D_t^{\alpha }S(t)=-rS(t)I(t)+\mu S(t) , S(0)=s_0, 0<\alpha \le 1,\\ {}^{c}D_t^{\alpha }I(t)=rS(t)I(t)-\mu I(t) , I(0)=i_0,\end{array}$$

(12)

Where $r>0, s_0>0, i_0>0.$ Here $r$ is the infectivity coefficient of the typical Lotka-Volterra interaction term, $s_0, i_0$ are given constants, $S(t)$ is the susceptible population, $I(t)$ is the infected population, and $\mu$ the recovery coefficient.

From Equation (12), we see that $S(t)+I(t)=k$ , where $k$ is total population.

Using ET in Equation (12), to get:

$$\begin{array}{l}E\left[{}^{c}D_t^{\alpha }S(t)\right]=E\left[-rS(t)I(t)+\mu S(t) \right], \\ E\left[{}^{c}D_t^{\alpha }I(t)\right]=E\left[rS(t)I(t)-\mu I(t)\right], \end{array}$$

Then:

$$\begin{array}{l}{\displaystyle \frac{1}{v^{\alpha }}}E\left[{}^{c}D_t^{\alpha }S(t)\right]-v^{2-\alpha }{s}_0=E\left[-rS(t)I(t)+\mu S(t) \right],\\ {\displaystyle \frac{1}{v^{\alpha }}}E\left[{}^{c}D_t^{\alpha }I(t)\right]-v^{2-\alpha }{i}_0=E\left[rS(t)I(t)-\mu I(t)\right],\end{array}$$

(13)

Take the inverse of ET to find:

$$\begin{array}{l}S(t)=s_0+E^{-1}\left\{v^{\alpha }E\left[-rS(t)I(t)+\mu S(t)\right]\right\} ,\\ I(t)=i_0+E^{-1}\left\{v^{\alpha }E\left[rS(t)I(t)-\mu I(t)\right]\right\} ,\end{array}$$

Make use of these relationships to solve the problem repeatedly:

$$\begin{array}{l}{S}_{n+1}(t)=E^{-1}\left\{v^{\alpha }E\left[-r{S}_n(t)I_n(t)+\mu S_n(t)\right]\right\} , S_0(t)=s_0,\\ I_{n+1}(t)=E^{-1}\left\{v^{\alpha }E\left[r{S}_n(t)I_n(t)-\mu I_n(t)\right]\right\} , I_0(t)=i_0,\end{array}$$

(14)

As of right now, the series form solutions to Equation (12) are as follows:

$$S(t)={\displaystyle \sum _{n=0}^{\infty }{S}_n(t)} , I(t)={\displaystyle \sum _{n=0}^{\infty }{I}_n(t)} .$$

(15)

The following $S_0\left(t\right), S_1\left(t\right), S_2\left(t\right) , \mathrm{...} , I_0\left(t\right), I_1\left(t\right), I_2\left(t\right) , \mathrm{...} ,$ can be deduced from Equation (14). After that, Equation (15), can be used to find the solutions.

From Equation (14), the following $S_0\left(t\right), S_1\left(t\right), S_2\left(t\right) , \mathrm{...} , I_0\left(t\right), I_1\left(t\right), I_2\left(t\right) , \mathrm{...} ,$ can be inferred. The solutions can then be found using Equation (15).

3.1. Convergence Analysis

The convergence of the ET technique to the FSIR & FSIS EM solutions is covered in this section.

Theorem 1: 

if $B$ is a Banach space then, ${\displaystyle \sum _{n=0}^{\infty }{S}_n},$ in Equation (11) and (15) is convergence to $a\in B$ if $\exists \left(0\le \eta <1\right)$ , s.t. $\forall \tau \in \mathbb{N} \Rightarrow ‖S_{\tau }‖\le \eta ‖S_{\tau -1}‖.$

Proof: 

It is said that the partial sum sequence ${\left\{a_{\tau }\right\}}_{\tau =0}^{\infty }$ is,

$$\begin{array}{c}{a}_0=S_0\\ a_1=S_0+S_1\\ a_2=S_0+S_1+S_2\\ ⋮\\ a_{\tau }=S_0+S_1+\dots +S_{\tau }.\end{array}$$

The next task is to demonstrate that ${\left\{a_{\tau }\right\}}_{\tau =0}^{\infty }$ in Banach space is a Cauchy series.

$$‖a_{\tau +1}-a_{\tau }‖=‖{\displaystyle \sum _{n=0}^{\tau +1}{S}_n}-{\displaystyle \sum _{n=0}^{\tau }{S}_n}‖=‖S_{\tau +1}‖\le \eta ‖S_{\tau }‖\le \dots \le {\eta }^{\tau +1}‖S_n‖,$$

for all $\tau ,\lambda \in \mathbb{N} as\tau \ge \lambda ,$

$$\begin{array}{l}‖a_{\tau }-a_{\lambda }‖=‖\left(a_{\tau }-a_{\tau -1}\right)+\left(a_{\tau -1}-a_{\tau -2}\right)+\dots +\left(a_{\lambda +1}-a_{\lambda }\right)‖\le \\ ‖a_{\tau }-a_{\tau -1}‖+‖a_{\tau -1}-a_{\tau -2}‖+\mathrm{....}+‖\left(a_{\lambda +1}-a_{\lambda }\right)‖\le {\eta }^{\tau }‖S_0‖+{\eta }^{\tau -1}‖S_0‖+\mathrm{...}+{\eta }^{\lambda +1}‖S_0‖\\ \le {\eta }^{\lambda +1}‖S_0‖\left({\eta }^{\tau -\lambda -1}+{\eta }^{\tau -\lambda -2}+\mathrm{....}+\eta \right)={\displaystyle \frac{1-{\eta }^{\tau -\lambda }}{1-\eta }}{\eta }^{\lambda +1}‖S_0‖.\end{array}$$

Then, $\left({\eta }^{\tau -\lambda -1}+{\eta }^{\tau -\lambda -2}+\mathrm{....}+\eta \right)$ is a geometric series and $0\le \eta <1,$ and $\underset{\tau ,\lambda \to \infty }{\lim }{a}_{\tau }-a_{\lambda }=0,$

That is to say, if the sequence solution $S={\displaystyle \sum _{n=0}^{\infty }{S}_n},$ converges, then ${\left\{a_{\tau }\right\}}_{\tau =0}^{\infty }$ is a Cauchy in Banach space.

4. Numerical Applications

This section presents a numerical application to show how the suggested method is very accurate, straightforward, and applicable. The numerical results are very encouraging.

Example 1. 

Consider the FSIR EM linking the Caputo FDs

$$\begin{array}{l}{}^{c}D_t^{\alpha }S(t)=-2S(t)I(t)-S(t)+1 , S(0)=0.3, 0<\alpha \le 1,\\ {}^{c}D_t^{\alpha }I(t)=2S(t)I(t)-I(t) , I(0)=0.7,\end{array}$$

(16)

For $\alpha =1$ ; the exact solutions of Eqs (16) are (See. [19]),

$$S(t)=1-{\displaystyle \frac{1}{2-\frac{4}{7}{e}^{-t}}}, I(t)={\displaystyle \frac{1}{2-\frac{4}{7}{e}^{-t}}},$$

We can get the following recurrence connection by taking the same earlier steps:

$$\begin{array}{l}{S}_{n+1}(t)=E^{-1}\left\{v^{\alpha }E\left[1-2S_n(t)I_n(t)-S_n(t)\right]\right\} , S_0(t)=0.3,\\ I_{n+1}(t)=E^{-1}\left\{v^{\alpha }E\left[2S_n(t)I_n(t)-I_n(t)\right]\right\} , I_0(t)=0.7,\end{array}$$

(17)

Equation (17), give:

$$\begin{array}{l}{S}_1(t)=E^{-1}\left[v^{\alpha }E\left[1-0.3-0.42 \right]\right] =E^{-1}\left[0.28v^{\alpha +2}\right]={\displaystyle \frac{0.28t^{\alpha }}{\mathsf{\Gamma }(\alpha +1)}}, \\ I_1(t)=E^{-1}\left[v^{\alpha }E\left[0.42-0.7 \right]\right] =E^{-1}\left[-0.28v^{\alpha +2}\right]=-{\displaystyle \frac{0.28t^{\alpha }}{\mathsf{\Gamma }(\alpha +1)}}, \\ S_2(t)={\displaystyle \frac{t^{\alpha }}{\mathsf{\Gamma }(\alpha +1)}}-{\displaystyle \frac{0.28}{\mathsf{\Gamma }(2\alpha +1)}}{t}^{2\alpha }+{\displaystyle \frac{2{\left(0.28\right)}^2\mathsf{\Gamma }(2\alpha +1)}{{\left[\mathsf{\Gamma }(\alpha +1)\right]}^2\mathsf{\Gamma }(3\alpha +1)}}{t}^{3\alpha },\mathrm{.....},\\ I_2(t)={\displaystyle \frac{0.28}{\mathsf{\Gamma }(2\alpha +1)}}{t}^{2\alpha }-{\displaystyle \frac{2{\left(0.28\right)}^2\mathsf{\Gamma }(2\alpha +1)}{{\left[\mathsf{\Gamma }(\alpha +1)\right]}^2\mathsf{\Gamma }(3\alpha +1)}}{t}^{3\alpha },\mathrm{.....},\end{array}$$

Then the solutions are,

$$\begin{array}{l}S(t)=0.3+{\displaystyle \frac{1.28}{\mathsf{\Gamma }(\alpha +1)}}{t}^{\alpha }-{\displaystyle \frac{0.28}{\mathsf{\Gamma }(2\alpha +1)}}{t}^{2\alpha }+{\displaystyle \frac{2{\left(0.28\right)}^2\mathsf{\Gamma }(2\alpha +1)}{{\left[\mathsf{\Gamma }(\alpha +1)\right]}^2\mathsf{\Gamma }(3\alpha +1)}}{t}^{3\alpha }+\mathrm{....}, \\ I(t)=0.7-{\displaystyle \frac{0.28}{\mathsf{\Gamma }(\alpha +1)}}{t}^{\alpha }+{\displaystyle \frac{0.28}{\mathsf{\Gamma }(2\alpha +1)}}{t}^{2\alpha }-{\displaystyle \frac{2{\left(0.28\right)}^2\mathsf{\Gamma }(2\alpha +1)}{{\left[\mathsf{\Gamma }(\alpha +1)\right]}^2\mathsf{\Gamma }(3\alpha +1)}}{t}^{3\alpha }+\mathrm{....},\end{array}$$

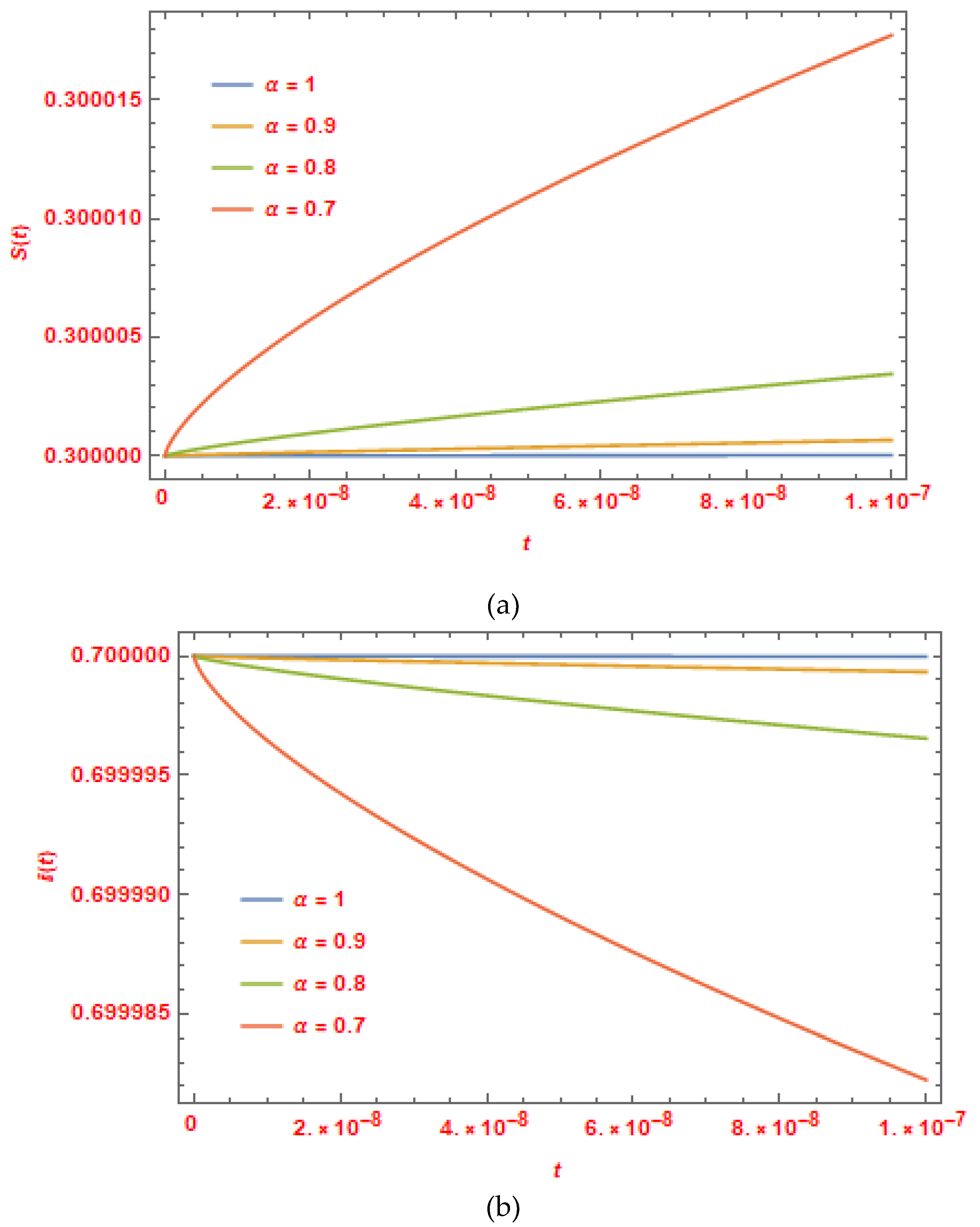
Figure 1. (a) and (b): Plots of solutions of example 1 produced with the current methods.

Figure 1. (a) and (b): Plots of solutions of example 1 produced with the current methods.

Example2. 

Consider the FSIS EM pertaining to the Caputo FDs,

$$\begin{array}{l}{}^{c}D_t^{\alpha }S(t)=-2S(t)I(t)-I(t) , S(0)=0.6, 0<\alpha \le 1,\\ {}^{c}D_t^{\alpha }I(t)=2S(t)I(t)-I(t) , I(0)=0.4,\end{array}$$

(18)

For $\alpha =1$ ; the exact solutions of Eqs (18) are, $S(t)=1-{\displaystyle \frac{2}{4+e^{-t}}}, I(t)={\displaystyle \frac{2}{4+e^{-t}}},$

By following the same previous procedures, we may obtain the following recurrence connection:

$$\begin{array}{l}{S}_{n+1}(t)=E^{-1}\left\{v^{\alpha }E\left[I_n(t)-2S_n(t)I_n(t)\right]\right\} , S_0(t)=0.6,\\ I_{n+1}(t)=E^{-1}\left\{v^{\alpha }E\left[2S_n(t)I_n(t)-I_n(t)\right]\right\} , I_0(t)=0.4,\end{array}$$

(19)

Then we obtain:

$$\begin{array}{l}{S}_1(t)=E^{-1}\left[v^{\alpha }E\left[0.4-0.48 \right]\right] =E^{-1}\left[-0.08v^{\alpha +2}\right]=-{\displaystyle \frac{0.08}{\mathsf{\Gamma }(\alpha +1)}}{t}^{\alpha }, \\ I_1(t)=E^{-1}\left[v^{\alpha }E\left[0.48-0.4 \right]\right] =E^{-1}\left[0.08v^{\alpha +2}\right]=-{\displaystyle \frac{0.08}{\mathsf{\Gamma }(\alpha +1)}}{t}^{\alpha }, \\ S_2(t)=-{\displaystyle \frac{0.08}{\mathsf{\Gamma }(2\alpha +1)}}{t}^{2\alpha }+{\displaystyle \frac{0.0128\mathsf{\Gamma }(2\alpha +1)}{{\left[\mathsf{\Gamma }(\alpha +1)\right]}^2\mathsf{\Gamma }(3\alpha +1)}}{t}^{3\alpha },\mathrm{.......},\\ I_2(t)=-{\displaystyle \frac{0.08}{\mathsf{\Gamma }(2\alpha +1)}}{t}^{2\alpha }-{\displaystyle \frac{0.0128\mathsf{\Gamma }(2\alpha +1)}{{\left[\mathsf{\Gamma }(\alpha +1)\right]}^2\mathsf{\Gamma }(3\alpha +1)}}{t}^{3\alpha },\mathrm{........},\end{array}$$

Therefore:

$$\begin{array}{l}S(t)=0.6-{\displaystyle \frac{0.08}{\mathsf{\Gamma }(\alpha +1)}}{t}^{\alpha }-{\displaystyle \frac{0.08}{\mathsf{\Gamma }(2\alpha +1)}}{t}^{2\alpha }+{\displaystyle \frac{0.0128\mathsf{\Gamma }(2\alpha +1)}{{\left[\mathsf{\Gamma }(\alpha +1)\right]}^2\mathsf{\Gamma }(3\alpha +1)}}{t}^{3\alpha },\mathrm{.......}, \\ I(t)=0.4+{\displaystyle \frac{0.08}{\mathsf{\Gamma }(\alpha +1)}}{t}^{\alpha }-{\displaystyle \frac{0.08}{\mathsf{\Gamma }(2\alpha +1)}}{t}^{2\alpha }-{\displaystyle \frac{0.0128\mathsf{\Gamma }(2\alpha +1)}{{\left[\mathsf{\Gamma }(\alpha +1)\right]}^2\mathsf{\Gamma }(3\alpha +1)}}{t}^{3\alpha },\mathrm{........}, \end{array}$$

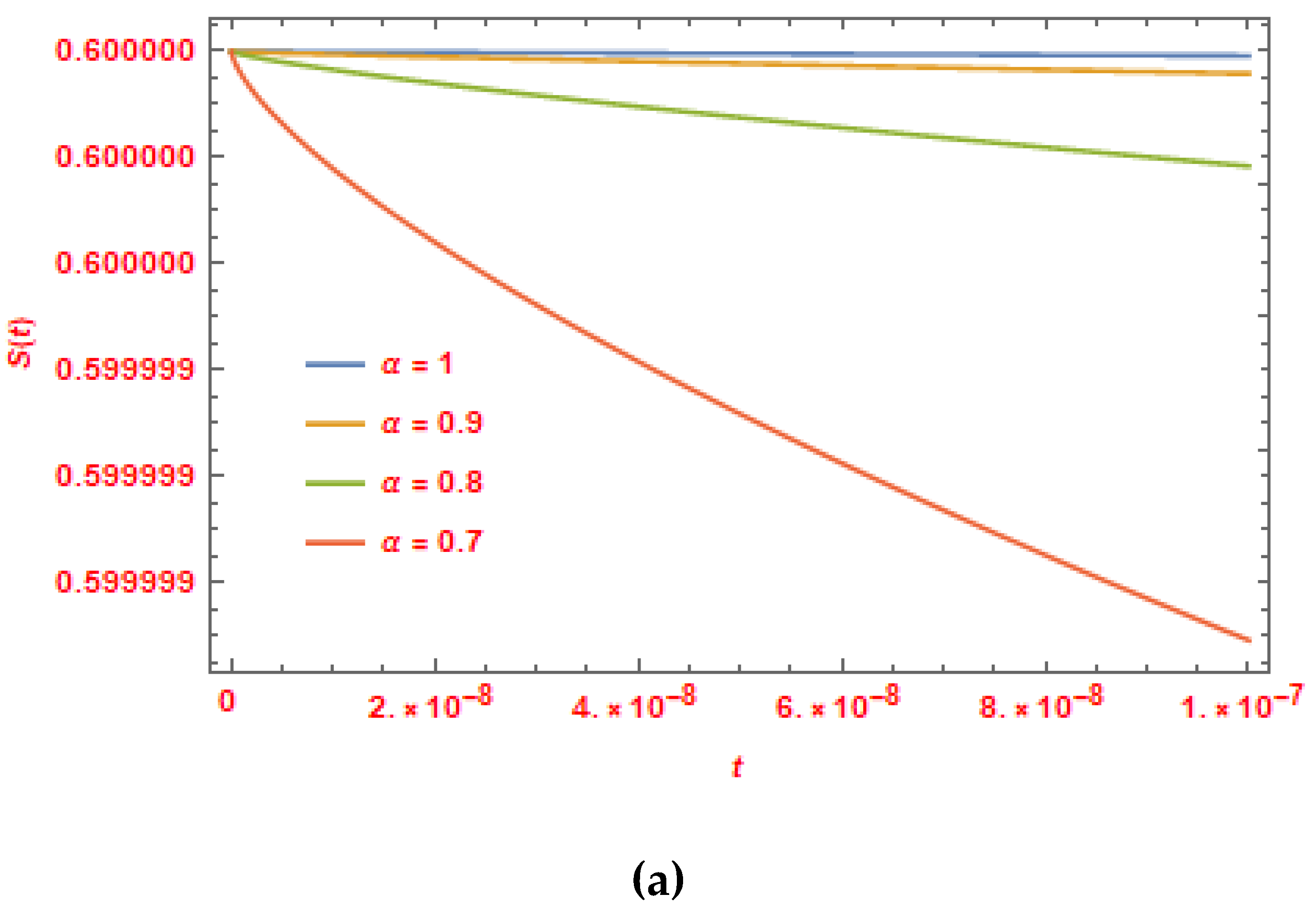
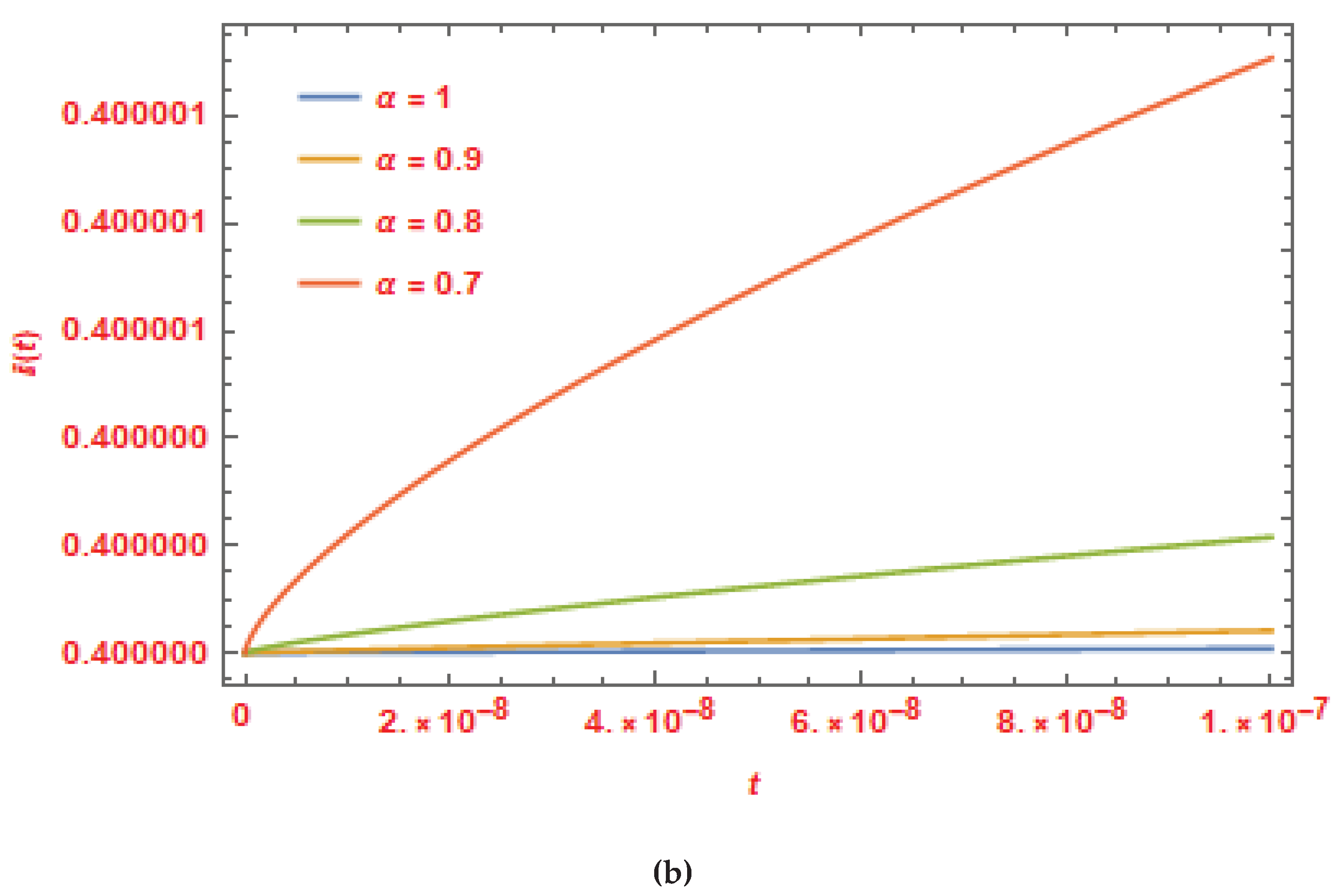
Figure 2. (a) and (b): Plots of solutions of example 2 produced with the current methods.

Figure 2. (a) and (b): Plots of solutions of example 2 produced with the current methods.

5. Results and Simulations

Graphs show the physical behavior of the FSIR & FSIS EM solution obtained by applying the suggested technique combining the Caputo FDs and the ET. When the fractional order $\alpha ,$ of the derivative changes, it also changes the value of the solution that is produced in series form using the approach that is being provided.

The line graphs in Figure 1(a) and (b) illustrate how the solution to Example 1 behaves. To illustrate the similarity, the line graph is colored differently for various $\alpha ,$ values. Plots of outcome at, $\alpha =0.7, \alpha =0.8, \alpha =0.9$ , and $\alpha =1$ were denoted by the red, green, yellow, and blue lines, respectively.

Figure 2 (a) and (b) show lines plots of the solution for $\alpha =0.7, \alpha =0.8, \alpha =0.9$ , and $\alpha =1$ , visually illustrating the impact of $\alpha ,$ on the solution of Example 2.

The graphs for various fractional order $\alpha ,$ values show that the suggested method uses a limited number of computed terms to get results with excellent accuracy. The correctness of the obtained findings is confirmed by comparing them with the actual solutions at $\alpha =1$ , which are summarized in Figure 1 and Figure 2.

From the foregoing, it can be inferred that the suggested method may be used to accurately and efficiently find the solution of FSIR & FSIS EMs with initial conditions. The practical uses of FDs have not yet been thoroughly investigated since fractional calculus theory and fractional order models are still developing. Nonetheless, we can see that when the value of fractional order $\alpha ,$ increases, the solution for the FSIR & FSIS EMs continually changes. In the end, it is confirmed that Caputo FDs is an extension of the classical integer order derivative as the solution at $\alpha =1$ agrees with the solution of the classical integer order FSIR & FSIS EMs.

6. Conclusions

This work proposes a novel computational method for solving the FSIR & FSIS EMs using the Caputo FDs. The ET technique is the name of this procedure. This study presents a numerical example that illustrates the simplicity, precision, and efficiency of the proposed method. Moreover, this method yields solutions in the form of infinite series that converge fast to the exact solutions. The investigation also demonstrated that the figures in this work attest to the method's efficacy in resolving the FSIR & FSIS EMs. Lastly, drawing from this study, we conclude that the proposed method is a powerful and practical mathematical tool for investigating a range of real-world problems that occur in engineering and the natural sciences that may be represented by fractional DE.

Our results show that the current method is efficient for FDEs based on an integral transform, which allows it to be used for additional linear and non-linear FPDEs in the future. Furthermore, expanding this approach's applicability or integrating it with other numerical approaches or symbolic computing software is one of our key goals moving ahead in order to create a more developed application that can be employed in a range of applied sciences.