Submitted:
23 May 2023
Posted:
25 May 2023
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Preliminaries and Basic Concepts
- .
- .
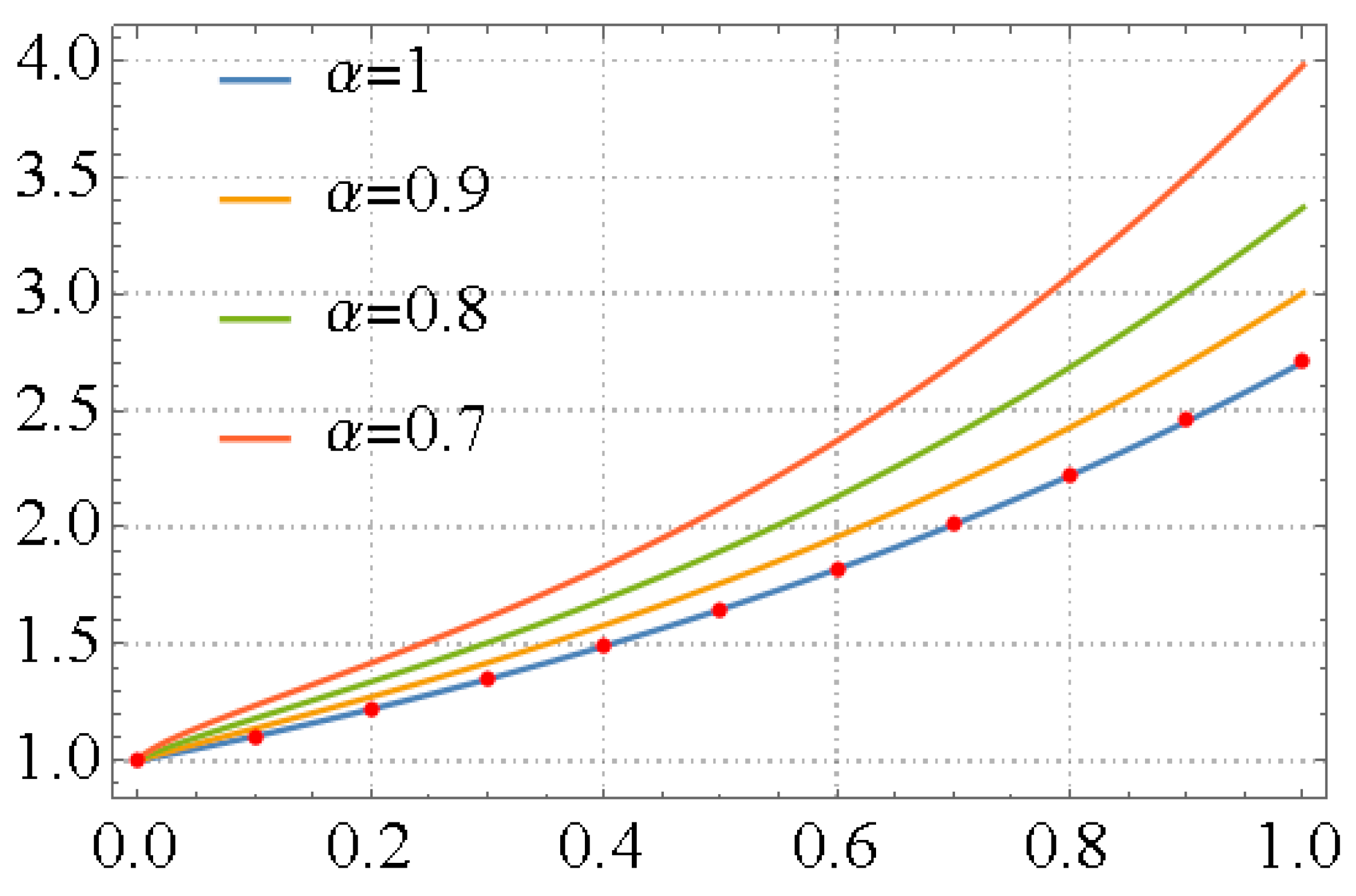
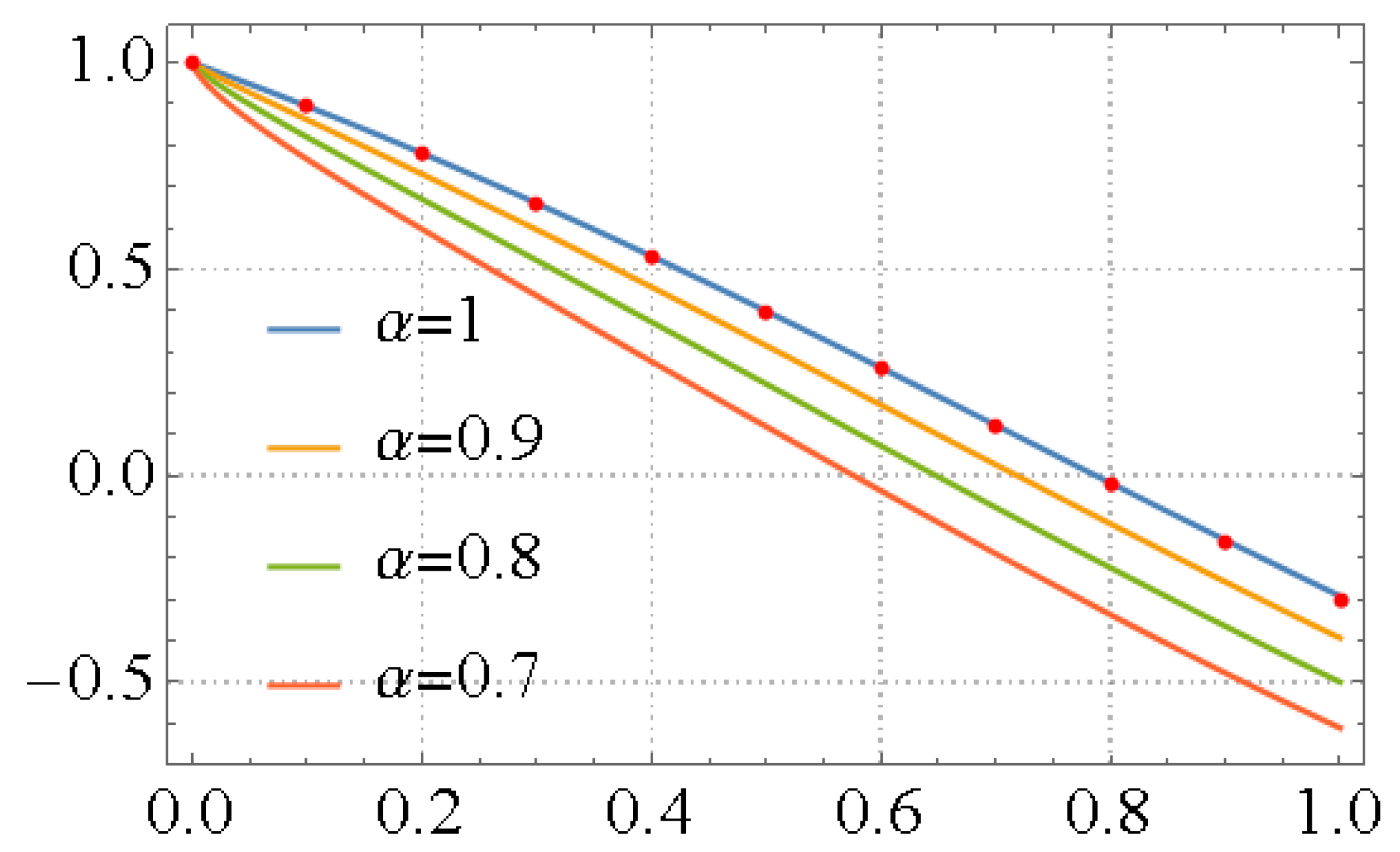
3. Principle of the LFPS Algorithm
4. Illustrated Examples
- If is odd, then
- If is even, then
- The non-linear term
5. Conclusions
Author Contributions
Data Availability Statement
Conflicts of Interest
References
- Loverro, A. Fractional calculus: history, definitions and applications for the engineer, Rapport technique, Univeristy of Notre Dame: Department of Aerospace and Mechanical Engineering, 2004.
- Mainardi, F. Fractional calculus and waves in linear viscoelasticity: an introduction to mathematical models. World Scientific, 2022.
- Yang, X. J. General fractional derivatives: theory, methods and applications. CRC press, 2019.
- Kilbas, A. A., Srivastava, H. M., & Trujillo, J. J.” Theory and applications of fractional differential equations”, 2006, 204, elsevier.
- Inc, M. Yusuf, A. Aliyu, A. I. and Baleanu, D. Soliton solutions and stability analysis for some conformable nonlinear partial differential equations in mathematical physics, Optical and Quantum Electronics,Volume 50, article 190, 2018. [CrossRef]
- Akdemir, A. O., Dutta, H., Atangana, A. “Fractional order analysis: theory, methods and applications”. John Wiley & Sons, 2020.
- Bagley R. L. and Torvik, P. J. “Fractional calculus in the transient analysis of viscoelastically damped structures”, AIAA Journal, 1985, 23(6), 918–925, 1985. [CrossRef]
- Al-Smadi, M.; Djeddi, N.; Momani, S. Al-Omari, S; Araci, S. “An attractive numerical algorithm for solving nonlinear Caputo–Fabrizio fractional Abel differential equation in a Hilbert space”, Advances in Difference Equations, Volume 2021, Article ID 271, 2021. [CrossRef]
- Ragb, O. Wazwaz, A. M. Mohamed, M. Matbuly, M. S. Salah, M. “Fractional differential quadrature techniques for fractional order Cauchy reaction--diffusion equations”. Mathematical Methods in the Applied Sciences, 2023. [CrossRef]
- Hashim, I.; Sharadga, M.; Syam, M.I.; Al-Refai, M. A Reliable Approach for Solving Delay Fractional Differential Equations. Fractal Fract. 2022, 6, 124. [CrossRef]
- Bataineh M.; Alaroud M, Al-Omari S, Agarwal P. “Series Representations for Uncertain Fractional IVPs in the Fuzzy Conformable Fractional Sense”. Entropy. 2021; 23(12):1646. [CrossRef]
- Syam, M.; Al-Refai, M. “First order delay equations Implicit hybrid method”. Alex. Eng. J. 2020, 59, 2677–2681.
- Al-qudah, Y.; Alaroud, M.; Qoqazeh, H.; Jaradat, A.; Alhazmi, S.E.; Al-Omari, S. Approximate Analytic–Numeric Fuzzy Solutions of Fuzzy Fractional Equations Using a Residual Power Series Approach. Symmetry 2022, 14, 804. [CrossRef]
- Hengamian Asl, E., Saberi-Nadjafi, J., Gachpazan, M. “Numerical Solution of Fractional-Order Population Growth Model Using Fractional-Order Muntz–Legender Collocation Method and Pade–Approximations”, Jordan Journal of Mathematics and Statistics, (2022),15.
- Hartley,T. T., Lorenzo, C. F. and Killory Qammer, H. “Chaos in a fractional order Chua's system”, IEEE Transactions on Circuits and Systems I: Fundamental Theory and Applications, 1995, 42(8), 485–490.
- Oldham, K. B. “The reformulation of an infinite sum via semiintegration”, SIAM Journal on Mathematical Analysis, 1983, 14, (5), 974–981.
- Povstenko, Y. Z, “Thermoelasticity that uses fractional heat conduction equation”, Journal of Mathematical Sciences, 2009, 162 (2), 296–305.
- Baskin, E. and Iomin, A. Electro-chemical manifestation of nanoplasmonics in fractal media, Central European Journal of Physics, 2013, 11(6), 676–684.
- Bapna, I. B. and Mathur, N. Application of fractional calculus in statistics, International Journal of Contemporary Mathematical Sciences, 2012, 7(17-20), 849–856.
- Goncalves E. and Zeidan,D, “Numerical simulation of unsteady cavitation in liquid hydrogen flows”, Journal of Engineering Systems Modelling and Simulation, 2017, 9(1)pp. 41–51, 2017.
- Kulish V. V. and Lage, J. L, “Application of fractional calculus to fluid mechanics”, Journal of Fluids Engineering, 2002, 124, (3), 803–806.
- Derdar, N. “Nonlinear Implicit Caputo-Hadamard Fractional Differential Equation with Fractional Boundary Conditions”. Jordan Journal of Mathematics and Statistics (JJMS), 2022, 15(4B), 999-1014.
- Bendouma, B. “Monotone Iterative Technique for a Coupled System of Nonlinear Conformable Fractional Dynamic Equations on Time Scales”. Jordan J. Math. Stat. JJMS, 2023, 16, 41–55.
- Al-Smadi, M., Al-Omari, S., Karaca, Y., and Momani, S. Effective Analytical Computational Technique for Conformable Time-Fractional Nonlinear Gardner Equation and Cahn-Hilliard Equations of Fourth and Sixth Order Emerging in Dispersive Media, Journal of Function Spaces, 2022.
- Alaroud, M.; Alomari, A.-K.; Tahat, N.; Al-Omari, S.; Ishak, A. “A Novel Solution Approach for Time-Fractional Hyperbolic Telegraph Differential Equation with Caputo Time Differentiation”. Mathematics 2023, 11, 2181. [CrossRef]
- Alaroud, M.; Al-Smadi, M.; Rozita Ahmad, R.; Salma Din, U.K. “An Analytical Numerical Method for Solving Fuzzy Fractional Volterra Integro-Differential Equations”. Symmetry 2019, 11, 205. [CrossRef]
- Ma, C. “A Novel Computational Technique for Impulsive Fractional Differential Equations”. Symmetry 2019, 11, 216. [CrossRef]
- Mahmood, S.; Shah, R.; khan, H.; Arif, M. “Laplace Adomian Decomposition Method for Multi Dimensional Time Fractional Model of Navier-Stokes Equation. Symmetry 2019, 11, 149. [CrossRef]
- Youbi, F.; Momani, S.; Hasan, S.; Al-Smadi, M. “Effective numerical technique for nonlinear Caputo-Fabrizio systems of fractional Volterra integro-differential equations in Hilbert space”. Alex. Eng. J. 61(3), 1778-1786, 2022.
- Zedan, H. A.; Alaidarous, E., “Haar wavelet method for the system of integral equations”, Abstract and Applied Analysis, vol. 2014, Article ID 418909, 9 pages, 2014.
- Biazar, J. “Solution of systems of integral-differential equations by Adomian decomposition method”, Applied Mathematics and Computation, vol. 168, no. 2, pp. 1232–1238, 2005.
- S. Abbasbandy, M. S. Hashemi, and I. Hashim, “On convergence of homotopy analysis method and its application to fractional integro-differential equations”, Quaestiones Mathematicae, vol. 36, no. 1, pp. 93–105, 2013.
- D. Baleanu, S. Zibaei, M. Namjoo, and A. Jajarmi, “A nonstandard finite difference scheme for the modeling and non-identical synchronization of a novel fractional chaotic system”, Advances in Difference Equations, vol. 2021, no. 1, pp. 1–19, 2021.
- K. Maleknejad, N. Aghazadeh, and M. Rabbani, Numerical solution of second kind Fredholm integral equations system by using a Taylor-series expansion method, Applied Mathematics and Computation, vol. 175, no. 2, pp. 1229–1234, 2006.
- N. Sahin, S. Yuzbasi, and M. Gulsu, A collocation approach for solving systems of linear Volterra integral equations with variable coefficients, Computers & Mathematics with Applications, vol. 62, no. 2, pp. 755–769, 2011.
- M. Alaroud, M. Al-smadi, R. R. Ahmad, and U. K. S. Din, “Numerical computation of fractional Fredholm integro-differential equation of order 2β arising in natural sciences”. In Journal of Physics: Conference Series (Vol. 1212, No. 1, p. 012022). IOP Publishing, (2019, April).
- H. Aljarrah, M. Alaroud, A. Ishak, M. Darus, “Adaptation of Residual-Error Series Algorithm to Handle Fractional System of Partial Differential Equations”. Mathematics 2021, 9, 2868. [CrossRef]
- M. A. Hammad, M. Alaroud, O. A. Arqub, R. Edwan, M. Al-Smadi and S. Momani, “Solving Fuzzy Fractional IVPs of order 2β by Residual Power Series Algorithm”, 2019 IEEE Jordan International Joint Conference on Electrical Engineering and Information Technology (JEEIT), Amman, Jordan, 2019, pp. 52–57. [CrossRef]
- M. I. Liaqat, A. Khan, M. Alam, and M. K. Pandit, “A highly accurate technique to obtain exact solutions to time-fractional quantum mechanics problems with zero and nonzero trapping potential”, Journal of Mathematics, vol. 2022, Article ID 9999070, 20 pages, 2022.
- Alaroud, M., Tahat, N., Al-Omari, S., Suthar, D. L., & Gulyaz-Ozyurt, S. , “An Attractive Approach Associated with Transform Functions for Solving Certain Fractional Swift-Hohenberg Equation”, Journal of Function Spaces, vol. 2021, Article ID 3230272, 14 pages, 2021. [CrossRef]
- Liaqat, M. I., and Okyere, E. “Comparative Analysis of the Time-Fractional Black–Scholes Option Pricing Equations (BSOPE) by the Laplace Residual Power Series Method (LRPSM)”. Journal of Mathematics, 2023.
- Aljarrah, H.; Alaroud, M.; Ishak, A.; Darus, M. Approximate Solution of Nonlinear Time-Fractional PDEs by Laplace Residual Power Series Method. Mathematics 2022, 10, 1980. [CrossRef]
- Alaroud, M.; Ababneh, O.; Tahat, N.; Al-Omari, S. “Analytic technique for solving temporal time-fractional gas dynamics equations with Caputo fractional derivative”. AIMS Math 2022, 7, 17647–17669.
- Alaroud, M.; Alomari, A.-K.; Tahat, N.; Ishak, A. “Analytical Computational Scheme for Multivariate Nonlinear Time-Fractional Generalized Biological Population Model”. Fractal Fract. 2023, 7, 176. [CrossRef]
- Oqielat, M.A.N.; Eriqat, T.; Al-Zhour, Z.; Ogilat, O.; El-Ajou, A.; Hashim, I. “Construction of fractional series solutions to nonlinear fractional reaction–diffusion for bacteria growth model via Laplace residual power series method”. Int. J. Dyn. Control 2023, 11, 520–527.
- Wazwaz, A. M. “The combined Laplace transform–Adomian decomposition method for handling nonlinear Volterra integro–differential equations. Applied Mathematics and Computation”, 2010), 216(4), 1304-1309.
- Moa’ath, N. O., El-Ajou, A., Al-Zhour, Z., Eriqat, T., and Al-Smadi, M. A new approach to solving fuzzy quadratic Riccati differential equations. International Journal of Fuzzy Logic and Intelligent Systems, 2022, 22(1), 23-47.
| 20 | 40 | 60 | 80 | ||
| 0.1 | |||||
| 0.2 | |||||
| 0.3 | |||||
| 0.4 | |||||
| 20 | 40 | 60 | 80 | ||
|---|---|---|---|---|---|
| 0.1 | |||||
| 0.2 | |||||
| 0.3 | |||||
| 0.4 | |||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





