1. Introduction
Quantum mechanics allows a physical system to exist in a superposition of multiple eigenstates, yet upon measurement, we observe only a single, definite outcome. How and why does a quantum superposition transform into a concrete reality during measurement? This question, known as the quantum measurement problem, remains a fundamental and contentious issue in quantum theory. Several interpretations have been proposed to address this question, each with distinct conceptual strengths and weaknesses:
Copenhagen Interpretation: This interpretation postulates an explicit division between the quantum and classical domains. Upon measurement, the wavefunction collapses non-unitarily into a single eigenstate, with probabilities dictated by the Born rule. While widely used due to its simplicity and practical utility, the Copenhagen interpretation does not provide a clear dynamical mechanism for collapse, relying instead on an ambiguous "Heisenberg cut" separating quantum from classical behavior (von Neumann, Mathematical Foundations of Quantum Mechanics, 1932). As a result, it introduces two fundamentally different types of evolution-unitary evolution governed by Schrödinger’s equation and non-unitary collapse-without a physically explicit criterion to distinguish when collapse occurs.
Many-Worlds Interpretation (MWI): Everett's formulation (Everett, The Relative State Formulation of Quantum Mechanics, 1957). avoids wavefunction collapse altogether, proposing that all possible outcomes simultaneously occur in a continuously branching universal wavefunction, effectively creating a multiverse. This interpretation removes the special role of measurement and maintains purely unitary dynamics. However, it raises significant conceptual issues, such as justifying why observers experience a unique outcome and deriving the Born rule probabilities from the universal wavefunction’s structure. Despite attempts based on decision theory and typicality arguments, achieving consensus on the Born rule derivation remains challenging, leaving open fundamental questions about probability and observer identity. (Everett, et al., 1973)
Objective Collapse Models: Theories like Ghirardi-Rimini-Weber (Ghirardi, Rimini, & Weber, 1986) and Continuous Spontaneous Localization (CSL) introduce new nonlinear and stochastic elements that spontaneously localize the wavefunction, producing collapse independent of observation. These models effectively solve the measurement problem by providing a physical mechanism for collapse, testable through empirical phenomena such as spontaneous heating and decoherence. However, these theories require introducing new physical parameters absent from standard quantum mechanics, often conflicting with symmetries like Lorentz invariance and raising questions regarding faster-than-light signaling and preferred reference frames. (Diósi, 1989) (Penrose, 1996) (Pearle, 1989)
Environment-Induced Decoherence: Though not an interpretation itself, decoherence (Zeh, 1970) (Zurek, Decoherence, einselection, and the quantum origins of the classical, 2003) is a physical process crucial to interpreting quantum mechanics. Decoherence describes how a quantum system interacting with a large environment rapidly loses coherence in a preferred basis, known as the "pointer basis," becoming effectively classical. However, decoherence alone does not produce a single definite outcome. Instead, it yields a classical statistical mixture of possible outcomes without specifying why only one is perceived. Decoherence thus shifts the measurement problem rather than fully resolving it, emphasizing the need for an additional criterion to transition from a decohered mixture to an actual observed outcome.
Relational and Epistemic Interpretations: Interpretations like Relational Quantum Mechanics (Rovelli, 1996) and Quantum Bayesianism (Fuchs, Mermin, & Schack, An introduction to QBism with an application to the locality of quantum mechanics, 2014) hold an epistemic view, interpreting the quantum state not as a physical entity but as reflecting an observer’s knowledge or beliefs. Collapse, therefore, becomes a Bayesian update of information upon measurement. While elegantly avoiding the need for physical collapse, these views raise questions about intersubjective agreement, why multiple observers consistently perceive identical outcomes, and may be accused of sidestepping rather than solving the measurement problem, particularly regarding why certain outcomes are realized and others are not.
Our work seeks to propose a framework retaining the universal validity of quantum dynamics, as in Many-Worlds and decoherence approaches, without introducing fundamentally new physics or ad hoc elements. We aim to provide a clear, quantitative criterion for the emergence of definite measurement outcomes, addressing the interpretive ambiguities of existing approaches. Our solution centers on the concept of thermodynamic irreversibility, positing wavefunction collapse as an emergent phenomenon governed by the Second Law of Thermodynamics. When a measurement interaction produces sufficient entropy (e.g., dissipating heat or entropy into an environment), entanglement becomes effectively irreversible, suppressing interference and establishing classical definiteness.
This thermodynamic collapse criterion is expressed rigorously via an entropy-coherence inequality, demonstrating that quantum coherence decays exponentially with entropy production in the environment:
Here, each qubit of information recorded in the environment carries at least of entropy, marking the threshold at which the environment fully encodes which-path information, thereby irreversibly destroying interference. Below this entropy threshold, coherence could, in principle, be restored, as exemplified by quantum eraser experiments. Beyond this threshold, however, recoherence becomes exponentially improbable, and classical definiteness emerges robustly.
By invoking fluctuation theorems like Jarzynski's equality and Crooks' relation, we quantify the practical irreversibility of measurement outcomes, formally linking wavefunction collapse to statistical thermodynamics. Our interpretation builds upon decoherence theory and Quantum Darwinism (Zurek, 2009), providing an explicit entropy-based boundary between reversible quantum dynamics and irreversible classical outcomes.
In the subsequent sections, we:
Formally describe open quantum system dynamics, decoherence, and entropy generation;
Derive the entropy-coherence inequality from foundational principles;
Outline operational methods to measure environmental entropy via calorimetry and photon scattering;
Derive the Born rule from symmetry considerations (envariance) and maximum entropy inference, without new physical assumptions;
Analyze observer-relative collapse, resolving paradoxes like Wigner's Friend and delayed-choice interference via entropy-based consistency;
Demonstrate relativistic consistency using the Tomonaga-Schwinger formalism, ensuring frame-independent collapse tied to local entropy;
Propose an optomechanical experiment to empiricallyPropose an optomechanical experiment to empirically test the entropy-collapse relationship, linking entropy production to measurable interference visibility.
Thus, our Entropy-Induced Collapse interpretation provides a coherent, falsifiable explanation for wavefunction collapse, grounded in established thermodynamics and quantum information theory. Rather than asserting new physics or ambiguous observer roles, it offers a clear, quantitative mechanism whereby quantum possibilities irreversibly become classical facts through entropy generation.
2. Theory and Literature Review
2.1. Measurement and the Problem of Outcomes
In standard quantum mechanics, the state of an isolated system
evolves under the Schrödinger equation:
resulting in deterministic, unitary evolution. This evolution preserves quantum superpositions and is time-reversible: if
evolves to |
, one can, in principle, reverse the Hamiltonian dynamics to restore the original state.
However, the quantum measurement problem arises because this unitary evolution predicts superpositions of measurement outcomes rather than definite results. For instance, consider a quantum system initially in the superposition , where and are orthonormal eigenstates of the measured observable. The measuring apparatus , initially in a "ready" state , interacts unitarily with the system to yield a combined, entangled state:
Here are apparatus pointer states that record outcomes 1 and 2, respectively. This entangled state is often referred to as the ‘measurement superposition’ or a ‘Schrödinger cat state’ involving the system and measurement device . While a valid solution of the Schrödinger equation, it contradicts experience: we never perceive superpositions.
The traditional Copenhagen interpretation resolves this discrepancy by introducing a dual dynamics: during measurement, the wavefunction non-unitarily "collapses" to one outcome, with probabilities , given by the Born rule. While pragmatically successful (von Neumann, Mathematical Foundations of Quantum Mechanics, 1932), this approach lacks a dynamical explanation for collapse, relying on an ambiguous division (the "Heisenberg cut") between quantum and classical regimes. Bell criticized this ad hoc dualism as conceptually problematic, leaving "measurement" ill-defined at the fundamental level. (Bell, 1990)
2.2. Decoherence and the Appearance of Classicality
Our approach makes no modification to Schrödinger evolution. Instead, we explain why observers effectively see stochastic state reduction in practice. Beginning in the 1970s and 1980s, Zeh, Zurek, and others developed the theory of environment-induced decoherence. Decoherence considers the system (S) coupled not just to an apparatus memory (M), but also to a large environment (E). Though the global state remains a superposition, the environment rapidly entangles with the system or apparatus, effectively measuring it. For example, air molecules, stray photons, and internal degrees of the apparatus become correlated with whether it is in .
Denote the (normalized) environment states that correlate with each outcome by
(these might represent distinct states of billions of environment particles). The total state after a very short decoherence time
would be
. The reduced density matrix of the system and memory, obtained by tracing out the environment, becomes:
In fact, for a macroscopic environment, for (environment states for different outcomes are practically orthogonal), and the interference terms are negligible. Thus, decoherence yields exactly the type of mixture one would expect after collapse, at least for local observations of . Decoherence is extremely effective: even a single scattered photon can carry away enough phase information to visibly reduce interference of a massive object, and a macroscopic apparatus interacting with a thermal environment will decohere in incredibly short times (nanoseconds or less) for any discernible superposition. This explains why Schrödinger cat states are not seen in everyday life: they quickly decohere into apparently classical mixtures. However, a key point is that decoherence by itself does not select a single outcome, the state (2) is still a superposition (albeit of many degrees of freedom). If we include the environment in our description, no collapse has occurred; the exact quantum state remains a pure state with full information of both possibilities.
In principle, an uber-observer (like Wigner in the Wigner’s Friend thought experiment) who could control the environment might recohere the branches. For example, if one could make E interact in a way that causes to overlap again, the superposition (2) could be recombined, revealing interference between the outcomes. This is essentially what happens in quantum eraser experiments: if which-path information encoded in an environment-like degree of freedom is erased, interference fringes reappear. This shows that while decoherence is necessary for the appearance of collapse, it is not sufficient. It yields a diagonal reduced density matrix in the pointer basis, but this classicality is reversible in principle as long as unitarity and full information preservation hold.
2.3. Thermodynamic Irreversibility and Collapse Criterion
Our contribution is to identify irreversibility as the missing ingredient that distinguishes apparent collapse from mere decoherence. We assert that when the dispersal of information into the environment becomes thermodynamically irreversible, the superposition is, for all observational purposes, collapsed. This is not a new dynamical law, but a statement about how typical entropy-producing interactions are effectively irreversible. The distinction between reversible and irreversible decoherence can be quantified by entropy. Consider the entropy of the environment (or apparatus) after the measurement interaction. If the measurement only entangles a small number of environmental degrees of freedom, or encodes phase reversibly, the von Neumann entropy remains low, and reversal is, in principle, possible. If instead the entropy significantly increases (for example, many particles gain bits of which-path information, or heat is dissipated into a bath), then reversal would require reducing entropy, achievable only via rare fluctuations or external work. Indeed, no process that leaves a stable record can yield < 0. Hence, any measurement that imprints a lasting outcome increases total entropy.
Collapse criterion formalization: We define the time of collapse
from a given observer’s perspective) as the moment when environmental entropy has increased sufficiently to make further unitary evolution incapable of restoring the initial coherence. Symbolically, one could say:
where
is typically on the order of a few
, often approximated as
≈
per qubit of recorded information. Once this threshold is crossed, the state may be treated as an incoherent mixture for any future observer who shares the same thermodynamic arrow of time.
To illustrate: For example, if a single photon escapes into the environment carrying one bit of which-path information, ∼ is reached. Beyond this point, interference is effectively lost-unless that photon is intercepted and its information erased. In a typical measurement, S ≫ , the apparatus dumps a large heat into a reservoir, maybe worth of entropy, making reversal hopeless. This criterion aligns with intuition: a ‘measurement’ amplifies a microscopic uncertainty into many macroscopic degrees of freedom (apparatus, lab, etc.), increasing entropy in the process. This is why one cannot ‘un-measure’ a typical outcome. This criterion sharpens the quantum-classical boundary: it is not about the mass of an object or some arbitrary Heisenberg cut, but about entropy and information flow. A microscopic system measured in a way that does not create a lot of entropy (e.g. a weak measurement that barely disturbs a system) might be partially reversible (you could “unmeasure” it), which is indeed a concept being experimentally explored in quantum information. Conversely, even a single qubit becomes irreversibly collapsed if its result is recorded in a thermodynamically irreversible way, such as being printed and burned, dispersing the information irretrievably.
2.4. Interpretative Synthesis and Clarification
Our model integrates aspects of several existing interpretations:
Like Many-Worlds (Everett, The Relative State Formulation of Quantum Mechanics, 1957), we maintain universal unitarity and no fundamental wavefunction collapse. However, we reject an ontology of infinite equally real branches, proposing instead that "collapse" arises when an outcome becomes thermodynamically irreversible from the observer’s perspective.
Borrowing from Relational Quantum Mechanics (Rovelli, 1996), we emphasize that collapse is observer-relative, occurring when a specific observer acquires irreversible thermodynamic records. Different observers may initially assign differing quantum states, but they reconcile their descriptions upon mutual interactions and shared irreversible entropy production.
Unlike Objective Collapse Models (GRW, CSL, Penrose), we introduce no new stochastic dynamics or hidden physics. Our predictions align strictly with standard quantum mechanics and known thermodynamics, avoiding the conceptual and empirical complications these models face (Bassi, Lochan, Satin, Singh, & Ulbricht, 2013).
Compared to QBism (Fuchs, Mermin, & Schack, An introduction to QBism with an application to the locality of quantum mechanics, 2014), we agree that wavefunction collapse corresponds to epistemic Bayesian updating. However, we retain the wavefunction’s ontic, objective character. Thermodynamic irreversibility, rather than subjective belief, constrains observers, ensuring intersubjective consistency.
In sum, we propose an entropy-induced collapse framework:
Quantum measurement outcomes arise from thermodynamic irreversibility.
Decoherence alone is insufficient; irreversibility distinguishes collapse.
The collapse criterion is rigorously defined by environmental entropy thresholds.
Subsequent sections will rigorously formalize these claims, demonstrate relativistic consistency, analyze observer-dependent collapse scenarios (e.g., Wigner’s Friend), and propose empirical tests to verify the model’s predictions, ensuring falsifiability and alignment with established physics.
3. Formalism: Entropy, Coherence Relations and Dynamics
3.1. Measurement Interaction and Entropy Production
Consider a quantum system
measured by an apparatus
(serving as the observer’s memory register), and coupled to an environment
. We denote the orthonormal eigenstates of the measured observable (and pointer basis of
) as
and
, respectively, where
i labels the outcome (for simplicity, assume a discrete, nondegenerate spectrum). The total initial state (system + memory + environment) at time
is prepared as:
Here is the ready state of the apparatus (before recording any result), and is the environment’s initial state. We assume and have low entropy states, e.g. pure or equilibrium reference states. The coefficients are the probability amplitudes for each outcome in the initial superposition (so the Born rule would later emerge as ).
The first stage of measurement is a controlled unitary between
and
that correlates the memory with the system’s state. Schematically,
is defined by
This is the von Neumann premeasurement, which produces an entangled state across
and
at time
:
At this stage, no environmental interaction has occurred. If
were microscopic, the state would retain full coherence and be entirely reversible. However,
is macroscopic, so its many internal degrees of freedom act as conduits to the external environment, causing decoherence to rapidly set in. Following
, the memory’s state (now correlated with
) interacts with the environment
(which could include the apparatus’s thermal bath, photons, air molecules, etc.). We can consider a unitary
that entangles
(and
indirectly) with
. Typically, this could be modeled as each pointer state
becoming correlated with an orthogonal environment state
:
such that
(different outcomes lead to effectively orthogonal environment states). The total
state for
(after decoherence,
) is then:
To analyze what an observer can access, we trace out
to obtain the reduced density matrix of the system and memory:
This partial trace effectively suppresses off-diagonal coherence terms in the pointer basis, yielding an apparent classical mixture of outcomes. We emphasize explicitly that no physical collapse of the wavefunction occurs; the global quantum state remains pure and fully entangled. The loss of coherence is observer-relative, arising due to practical inaccessibility of the detailed environmental states.
This environment-induced decoherence mechanism clearly demonstrates how classical outcomes naturally emerge from quantum entanglement combined with partial trace operations over inaccessible degrees of freedom. However, the classicality produced here remains practically irreversible, rather than fundamentally irreversible, as coherence recovery (recoherence) remains theoretically possible under conditions where environmental states could be controlled or reversed, though practically infeasible in realistic macroscopic environments.
3.2. Thermodynamic Decoherence and the Coherence-Entropy Bound
Following the interaction with the environment the off-diagonal coherence terms in the reduced state vanish due to approximate orthogonality of environmental states . Hence, is (approximately) diagonal in the pointer basis with probabilities for each outcome: .
The von Neumann entropy of
thus increased from 0 (pure initial state) to:
which equals the Shannon entropy of the outcome distribution. This entropy quantifies our uncertainty when observing only
, and equals the entanglement entropy between
and
, since the global state is pure. The environment
has gained the same entropy (if
was initially pure) because the global state is still pure, so
. At this stage, we have reproduced the standard decoherence result: the system+apparatus is in an apparent classical mixture. However, this apparent classicality is reversible in principle. An observer with access to
could, in theory, restore the off-diagonal coherence by undoing the entanglement correlations. The entropy
is often called entanglement entropy, it is not true thermodynamic entropy because the total state is still pure.
Recoherence remains possible because the outcome-distinguishing information resides in correlations with ; if these are reversed, the system can return to a pure state. Now, consider the case where the interaction is thermodynamically irreversible-e.g., dumps heat into or triggers macroscopic environmental differences. In such a case, the environment’s entropy truly increases (not just entanglement entropy, but thermodynamic entropy). For example, suppose had to perform amplification that released of heat into a reservoir (a part of ). That heat increases ’s entropy by (if at temperature T) (Landauer, 1961). Or, might trigger a macroscopically different state in the environment (like different patterns of air molecule motion or different photon emissions), effectively increasing the coarse-grained entropy. The effective state of is no longer pure if is modeled as initially mixed or traced over partially due to its large, uncontrolled degrees of freedom. Alternatively, we incorporate a statistical mixture in ’s initial state to mimic a thermal environment, so that the final state is mixed, not a single pure wavefunction like (6). To handle this formally, one can model the interaction as a completely positive trace-preserving (CPTP) quantum channel acting on (with traced out).
Such a channel
takes the pre-decoherence
to
which is given by (7). Since
involves coupling to a large environment (possibly at finite temperature), it will in general be irreversible (non-unitary) for
. One can often approximate it by a Lindblad master equation for the
density matrix:
where
is a Lindblad dissipator that produces decoherence and damping. The Lindblad form guarantees that the entropy
increases (or stays constant) as a result of the dissipative part (this is the quantum analog of
-theorem for entropy in open systems). One can rigorously show
for a Lindbladian evolution that satisfies detailed balance (or more generally, that
approaches some equilibrium, increasing entropy if it is not already at equilibrium) (Spohn, 1978).
In our case, the equilibrium (long-time) state of under continuous measurement interactions would be a diagonal mixture (maximally mixed over whatever outcomes remain possible). We can now articulate an entropy-coherence tradeoff. Consider a measure of coherence in the system. A simple measure is the off-diagonal norm: e.g. , or even the sum of absolute squares of off-diagonals. We define coherence via standard measures such as the , or the Frobenius norm of off-diagonals. (Baumgratz, Cramer, & Plenio, 2014).
For pure states like (5), this coherence measure is maximal (of order 1). For the mixture (7), it is nearly 0. A more invariant measure of quantum coherence is the purity ). Initially (pure state). After decoherence (7), (unless one outcome had probability 1). Purity and von Neumann entropy are inversely related for a fixed spectrum. In two-outcome systems, they are functionally equivalent. We can thus qualitatively say as entropy of increases from 0 to , the coherence/purity decreases. If remains pure reference state, then is the entanglement entropy between and , and coherence can, in principle, be restored. If instead is effectively a bath that irreversibly gains entropy , then will not decrease even if we later act on alone; some entropy has flowed to (and is inaccessible).
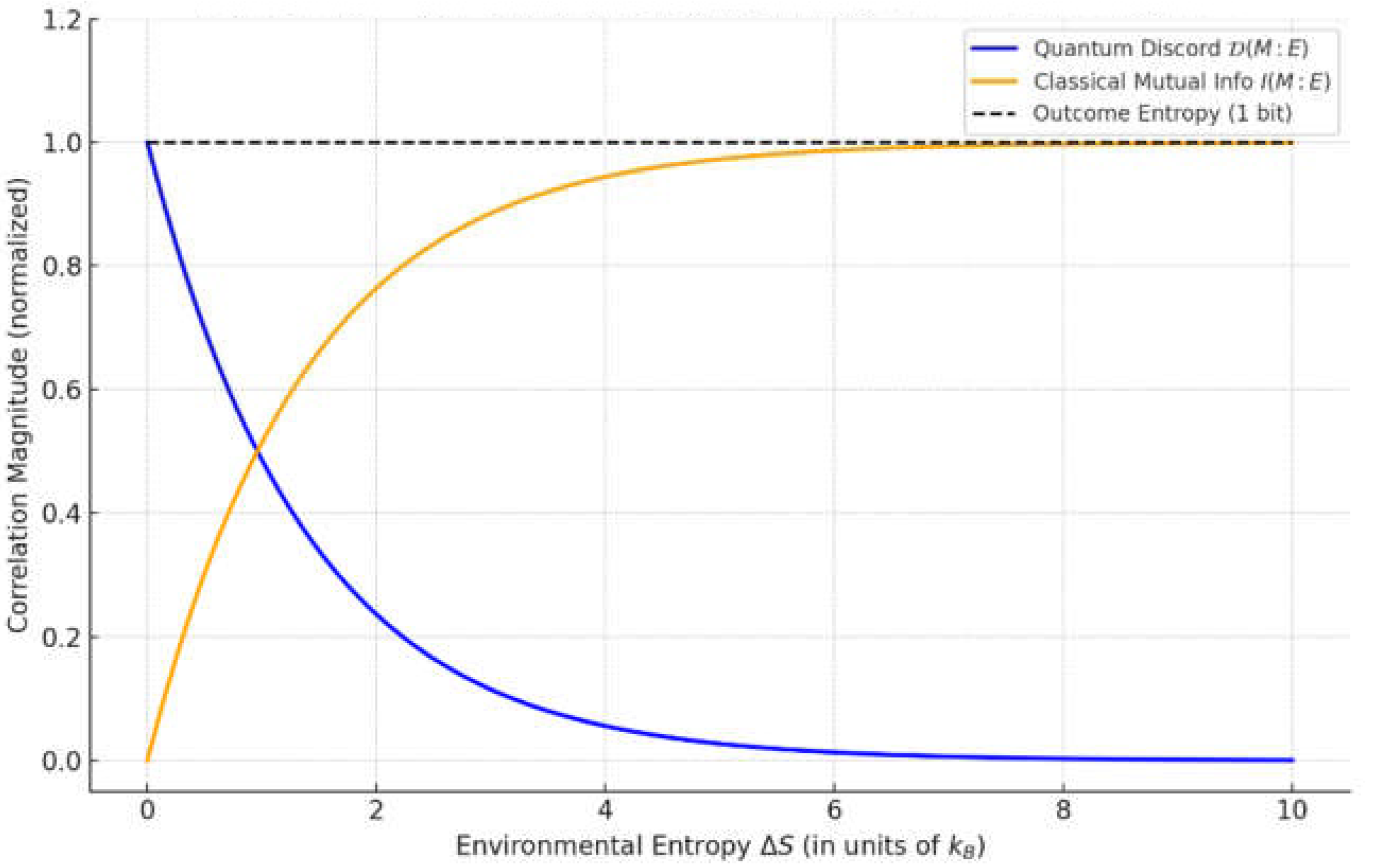
We propose that a useful quantitative indicator of collapse is the quantum discord between the memory and the rest (system or environment ) (Ollivier & Zurek, 2001). Discord is a measure of quantum correlations (more general than entanglement) between two subsystems X and Y. A state with 0 discord is essentially classical with respect to one of the subsystems (it can be written as a statistical mixture of product states that are orthogonal on one side). Prior to collapse, quantum discord between and is nonzero, reflecting entanglement. After effective collapse, these correlations become classical as outcome information is redundantly encoded in the environment. One can show that generic decoherence processes tend to drive discord to zero: indeed, a theorem by Shabani and Lidar showed that if the initial state has no discord (is classical on ’s side), then the reduced dynamics is completely positive (no ambiguity of the dynamical map) (Shabani & Lidar, 2009).
As measurement concludes, the joint state approaches a form with vanishing quantum discord, since the environment has decohered the memory into distinguishable outcome states. We can thus state:
Proposition 1 (Discord-Entropy relation):
Let be the reduced density matrix of the memory and environment during a measurement interaction. Then:
If residual coherence is present,
As the environment’s entropy production , the discord
In the limit , the system is effectively classical.
In the limit where the environment has produced a large entropy , the post-measurement correlations are effectively classical, (with macroscopically distinguishable and ). Indeed, one can check that state has zero discord (it is a classical-quantum state). Before that point, in the partial decoherence regime, one can find basis where has some off-diagonal elements between and , indicating .
In summary, the vanishing of discord coincides with effective wavefunction collapse. We can connect these ideas with a more thermodynamic statement. An informative scenario to analyze is the application of fluctuation theorems to the measurement process. Consider reversing a completed measurement. To successfully restore the coherent superposition, one must collect the information distributed in and feed it back in a controlled way, effectively performing erasure of the which-outcome information. According to Landauer’s principle, erasing one bit of logical information requires a minimum entropy increase of , corresponding to a work cost (Landauer, 1961). If the measurement generated entropy, then at minimum one must expend work to remove that entropy again.
The Jarzynski equality states
(where
is free energy difference and work distribution average), in context of measurements, it implies on average you cannot do better than the second law, though rare single trajectories might temporarily violate it. The Crooks fluctuation theorem gives the ratio of probability of undoing a process. If a forward process (measurement) produces entropy
, then Crooks’ theorem implies the probability of seeing a trajectory that decreases entropy by
(i.e. the reverse) is exponentially small:
. For
much larger than a few
, this ratio is astronomically tiny. Thus, once a measurement has generated, say,
of entropy, the odds that it spontaneously “uncollapses” (coherently recoheres) is
even if it were in principle possible. For
,
utterly negligible. In practice, interacting with a heat bath, one would have to perform extremely coordinated operations to get the entropy out; any random fluctuation is incredibly unlikely to bring the memory and environment back to their initial pure state. This formalizes the idea of irreversibility: although microscopic quantum theory is reversible, the probability of a spontaneous recoherence after entropy
has been generated is effectively zero. We can sum up with an entropy, coherence inequality. While a rigorous general inequality would require specifying measures, an intuitive form is:
where
is a measure of quantum coherence (off-diagonality) remaining in the system’s state (relative to the initial superposition basis), and
is the entropy produced in the environment up to time
t.
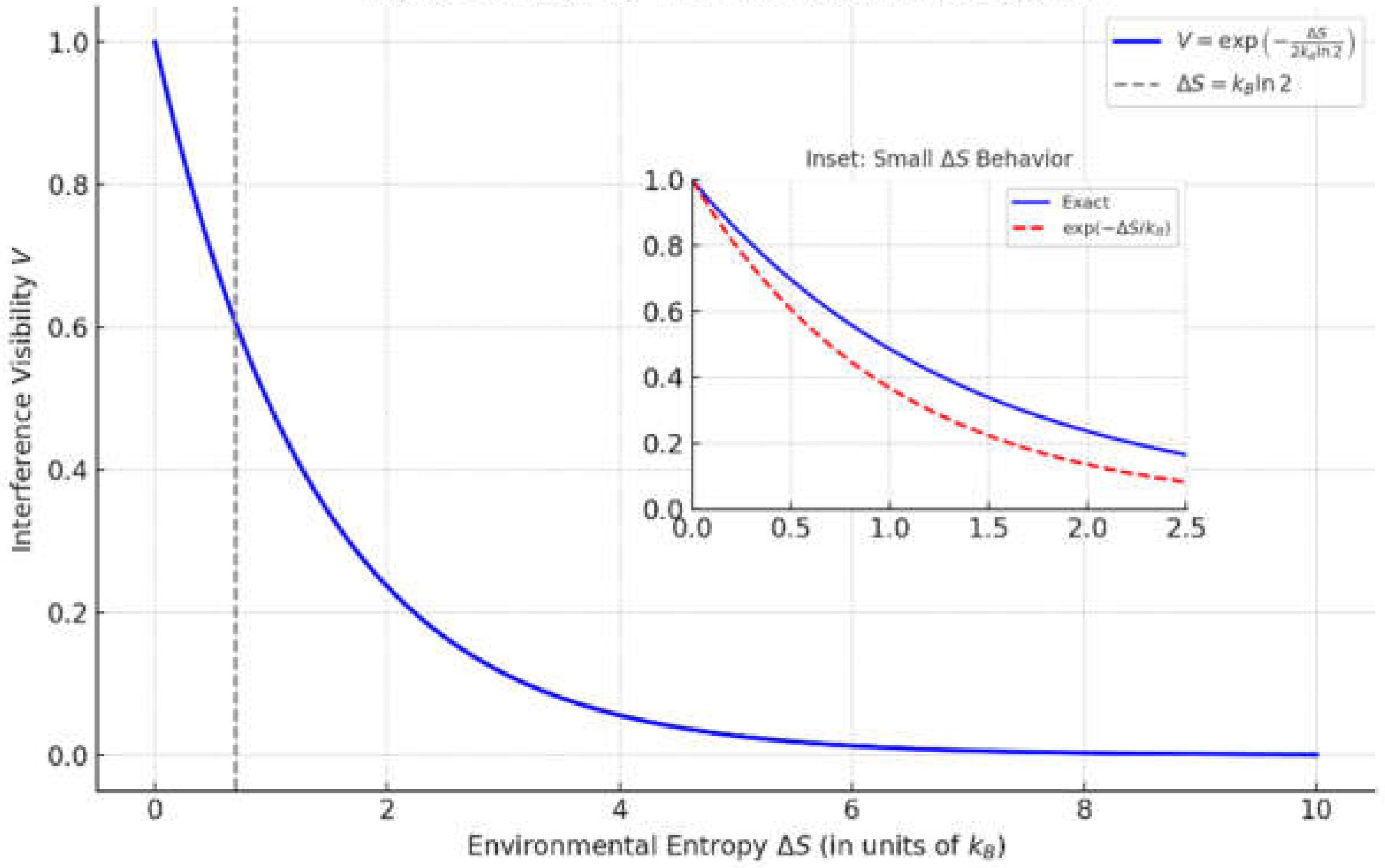
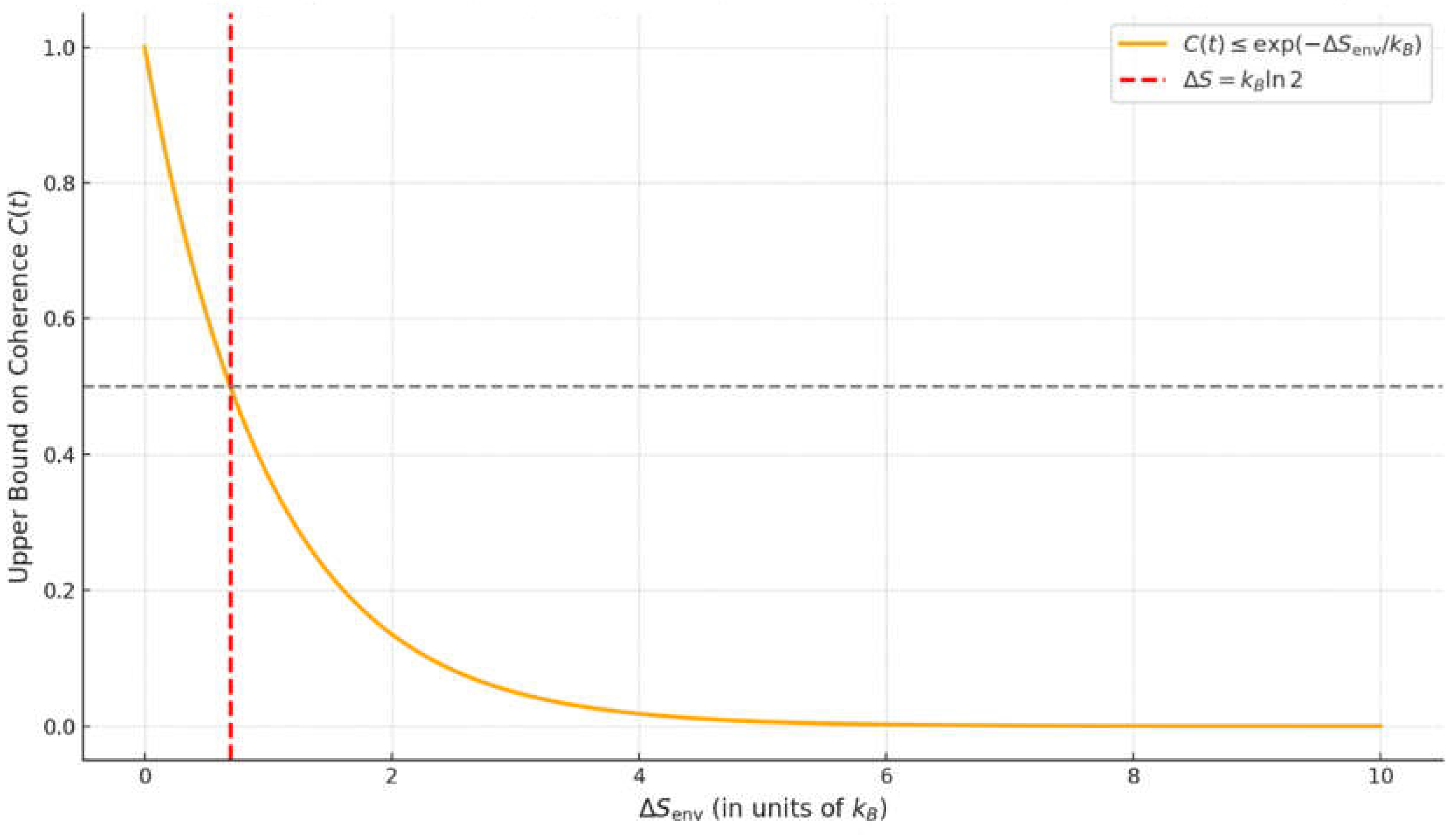
In the early stages ( small), coherence decays roughly linearly or quadratically (as typical in decoherence theory (Zurek, Decoherence, einselection, and the quantum origins of the classical, 2003)). Once , coherence is suppressed to a few tens of percent at most. By the time (many bits of entropy), is exponentially tiny. This is consistent with detailed models in decoherence literature (e.g., the “visibility” of interference fringes decays as where is a decoherence functional often proportional to number of emitted particles or entropy). Our inequality (9) encapsulates that beyond a certain entropy, remaining coherence is bounded by an exponentially small factor. Thus, a large entropy production guarantees negligible coherence. In particular, if we set a threshold for one bit, we can say: if , then it might be possible to erase the information and restore interference (the measurement has not fully collapsed). If , at least one bit is worth of entropy is in the environment, in principle one bit could still be erased, but typically actual is orders of magnitude larger.
For a precise statement: in a measurement that writes bits of information (distinguishing 2n outcomes), at least of entropy must be produced somewhere. Usually much more is produced in a macroscopic apparatus for one bit, but that is the fundamental lower bound. Therefore, effective collapse requires at least one bit of entropy. Conversely, any apparent wavefunction collapse that is accomplished with significantly less than entropy cost could potentially be reversible and should not be considered a true irreversible measurement.
3.3. Poincaré Recurrence and Its Suppression
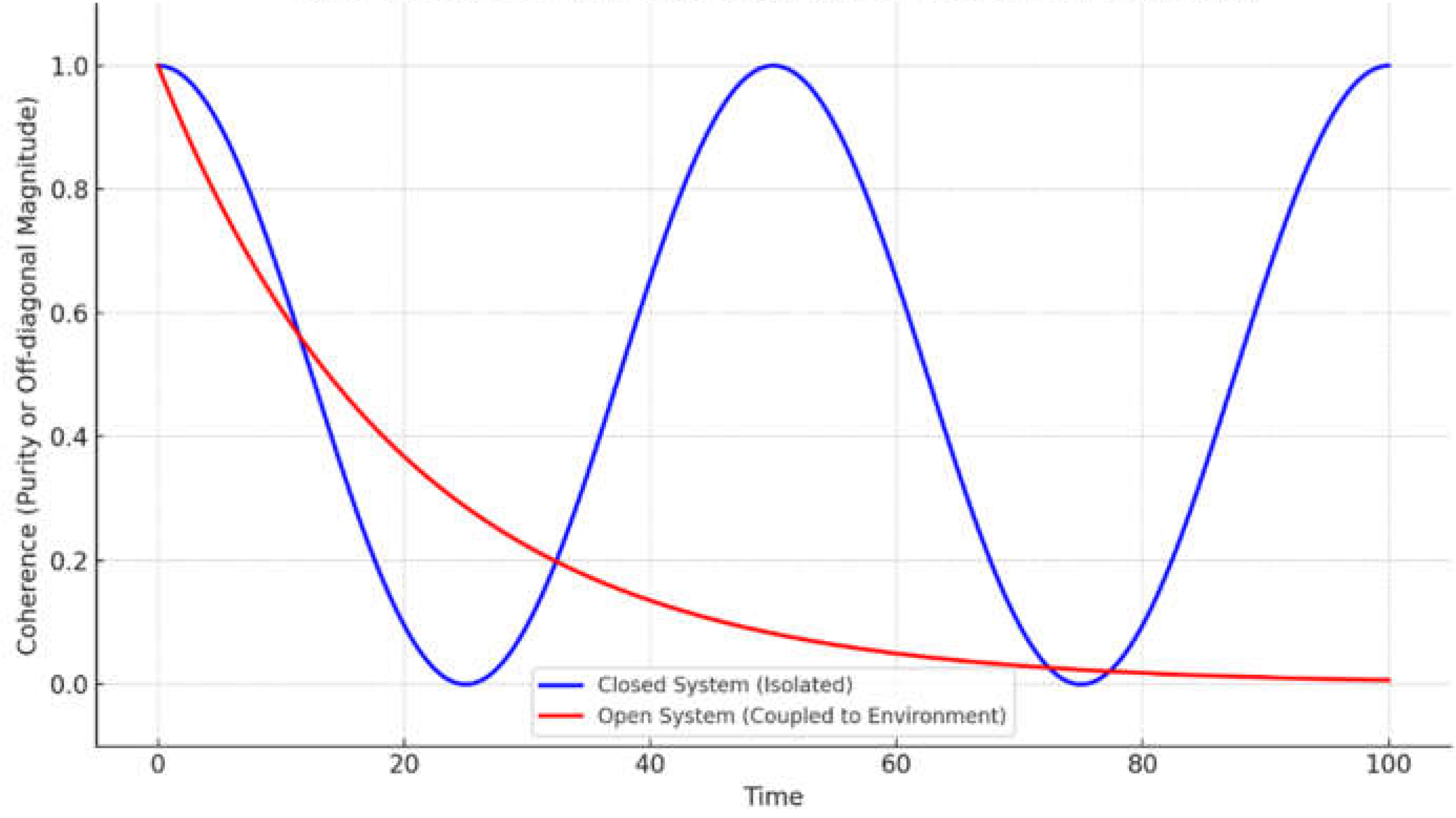
A subtle issue in quantum mechanics is the Poincaré recurrence theorem. For a finite, closed quantum system with discrete energy spectrum, the state will evolve quasi-periodically and return arbitrarily close to its initial state after some (usually enormous) recurrence time . This would imply that even after decoherence, given enough time the system + environment could, in principle, recohere (the branches recombine), the wavefunction “uncollapses”, albeit after a time that might far exceed the age of the universe. While this is a theoretical possibility in a finite, closed universe, does it undermine our claim that wavefunction collapse is effectively permanent? The key is the size of relative to any practical timescale. If an environment has effective degrees of freedom (Hilbert space dimension extremely large), is generally exponentially large in . The key lies in the scale of relative to any practical timescale. For an environment with degrees of freedom (and Hilbert space dimension ), recurrence time grows exponentially, or even super-exponentially, with . For example, a system of particles has dimension and recurrence time roughly in units of characteristic time steps. For qubits, the Hilbert space dimension is , and the recurrence time typically scales as , often exponentially in . If is Avogadro-number scale , is absurdly huge.
In the thermodynamic limit, as the environment size ; thus, an infinite environment will never recohere. So in the thermodynamic limit, the evolution is effectively irreversible; this is analogous to how an ideal gas in a box (finite N) will theoretically have recurrences (Loschmidt’s paradox), but for those recurrences occur after fantastical times (like years). These timescales exceed any cosmological bound and are thus physically irrelevant. No observer will wait for that, and any slight perturbation breaks the perfect recurrence. In our quantum case, any coupling to external degrees (the universe is not perfectly closed) will destroy the exact recurrence. Thus, Poincaré recurrences are an extreme FAPP phenomenon: theoretically real, but practically irrelevant.
Our entropy criterion makes this quantitative. According to Crooks’ fluctuation theorem, the probability of a spontaneous recurrence i.e. a trajectory that reduces the system's entropy by , is approximately (Crooks, 1999). For macroscopic entropy increases , on the order of or more, the reverse probability becomes astronomically small, effectively zero. Thus, while the underlying quantum dynamics is formally time-symmetric, practical asymmetry, manifesting as irreversibility, arises due to the sheer size of the accessible state space. This statistical irreversibility validates the use of the Second Law in quantum contexts and justifies treating wavefunction collapse as effectively permanent for all practical purposes.
One could formalize this by looking at the fidelity for the total state. At , the fidelity is unity: . Following decoherence, the system’s state becomes nearly orthogonal to the initial one, and fidelity drops near zero, especially if the environment states correlated with outcomes are orthogonal. Over extremely long timescales, fidelity may exhibit rare peaks corresponding to partial Poincaré recurrences. But the expected recurrence time can be estimated from entropy or state-space volume. If entropy is produced, the effective dimension of the accessible state space is (by Boltzmann’s relation) (Boltzmann, 1909). Since recurrence time scales with the volume of accessible Hilbert space, for macroscopic systems, this becomes a doubly exponential function of entropy.
For example (approximately the entropy associated with 100 molecules), becomes hyperastronomical, far beyond any conceivable physical timescale. Therefore, once , the likelihood of branch recombination via recurrence becomes negligible. Collapse is thus practically irreversible.
In conclusion, our thermodynamic interpretation remains fully consistent with Poincaré’s theorem. While a closed system may, in theory, return arbitrarily close to its original state, such a recurrence would require a time so vast, and a reversal so precise, that it poses no practical challenge to our criterion. Indeed, it supports our view that collapse is not a fundamental process but one that emerges effectively for all practical purposes (FAPP). As Bell emphasized, any satisfactory resolution requires a precise definition of FAPP. In our case, this means: “irreversible except on timescales exponentially exceeding any reasonable multiple of the age of the universe,” a standard robust enough to warrant calling the process irreversible.
3.4. Relativistic Covariance with Tomonaga-Schwinger Formalism
We now address how to formulate our entropy-based collapse criterion in a way that is consistent with relativistic principles. A common concern for collapse-based interpretations is their apparent nonlocality: for instance, if two particles are entangled across light-years and one is measured, does collapse instantaneously affect the other, seemingly violating causality? In standard quantum theory, there is no physical signal, correlations are revealed upon comparison, but each local outcome is random. Our interpretation preserves this feature: because collapse is not a physical process but an emergent one tied to entropy production, there is no superluminal propagation of physical effects. The appearance of collapse is frame-dependent as in Relational QM (RQM) or Many-Worlds Interpretation (MWI). Suppose Alice and Bob share an entangled pair. In Alice’s rest frame, when she performs a measurement, entropy is generated locally, and she can regard the state as having collapsed at that moment. In Bob’s frame, it may appear that his measurement occurred first. But since both observers’ conclusions depend on local entropy generation, and any eventual comparison requires subluminal communication, no causal paradox arises. The ordering of collapse is observer-relative, not physically absolute. The condition “sufficient entropy has been generated” can be phrased in a covariant way: one can examine the quantum state on a space-like hypersurface. Using the Tomonaga-Schwinger formalism, one evolves the quantum state by moving a space-like surface through spacetime, rather than a single time parameter for all space (Tomonaga, 1946) (Schwinger, 1948). The state is the state of the system on hypersurface . Each observer traces a world-line through spacetime, interacting with the system and generating entropy locally through measurement-like events. Different Lorentz observers may slice spacetime differently, but if they are considering the same physical situation, the entanglement structure and entropy distribution will be such that all observers agree on invariant facts: for instance, if an outcome is recorded into many photons radiating outward, that is an invariant scenario.
(Ghose & Home, 1991) showed that Tomonaga-Schwinger formalism can describe Einstein, Podolsky, Rosen (EPR) correlations covariantly, delineating measurement completion on one side and its instantaneous but a causal effect on the wavefunction of the other, in a way consistent with relativity (Ghose & Home, 1991). In our terms, one might say: on any given space-like slice after Alice’s measurement, the global state will be a decohered, entangled state including Alice’s environment. The reduced state for Bob’s particle will appear collapsed to any observer whose hypersurface places Alice’s measurement event in the past light cone. There is no invariant instantaneous “collapse moment”; what is invariant is the Heisenberg picture correlation: on a joint slice.
This has been extensively discussed in the context of relativistic quantum mechanics: the measurement outcome on one side and the conditional state on the other are connected via nonlocal correlations, but these do not entail causal violations (Maudlin, 2011) (Eberhard & Ross, 1989). Our entropy-based criterion adds no new physical content but offers interpretive clarity: each observer updates their quantum state description at the point where a local interaction has produced irretrievable entropy. This update proceeds via the global quantum state defined on a space-like hypersurface, allowing it to be expressed in a Lorentz-invariant formalism, such as Tomonaga-Schwinger evolution. An observer whose frame has not yet intersected the entropic interaction will still see a superposition, but this is inconsequential, as once they cross the interaction region, they too will observe the associated entropy and reach the same conclusion. The upshot is that Lorentz covariance is preserved precisely because our framework avoids any physically propagating collapse mechanism. Each event (e.g. a detector firing) is localized and just entangles whatever is in its future light cone. Observers may temporarily disagree on whether collapse has occurred in their respective frames, but they will never disagree on observable outcomes when comparing records. This is analogous to how different observers in relativity can disagree on the time order of spacelike-separated events but never on causally connected ones (Taylor & Wheeler, 1992). Because collapse in our model is epistemic, triggered by thermodynamically irreversible record formation, it adheres to the principle of locality in the propagation and accessibility of physical information.
We can also comment on quantum field theory: In quantum field theory (QFT), particle measurements correspond to local interactions that entangle quantum field modes, often involving the vacuum, which possesses an infinite number of degrees of freedom. A detector click (excitation) usually involves emitting many quanta (e.g. phonons, photons), again an entropic event. Our entropy criterion also applies to field degrees of freedom: if a superposition of distinct field configurations leads to different particle number states or energy distributions that thermalize, effective collapse has occurred. Using Tomonaga-Schwinger, one can propagate the state consistently and see that no paradox arises. Our interpretation’s strength is that it does not require specifying an absolute simultaneity for collapse, which is a notorious problem for objective collapse models (some like GRW choose a preferred frame, violating relativity slightly; others try to formulate relativistic versions with considerable difficulty) (Bassi, Lochan, Satin, Singh, & Ulbricht, 2013). Because we do not treat collapse as a physical process, our approach entirely sidesteps the problem of defining simultaneity, as in relational and many-worlds interpretations.
We have thus established the formal underpinnings of our approach: unitary quantum mechanics plus a criterion of thermodynamic irreversibility. We saw that once entropy is generated, quantum coherence and discord vanish, and any revival is exponentially unlikely. In the next section, we derive the Born rule within this framework, showing that the usual probability postulate emerges from considering symmetry (envariance) and maximum entropy principles. This will further cement that no extra postulates are needed, the usual rules of quantum measurement can be derived given our understanding of what constitutes a measurement.
3.5. Derivation of the Born Rule from Entropy and Envariance
A central requirement for any interpretation that preserves the formalism of standard quantum mechanics is to explain the origin of the Born rule; that is, why the probability of obtaining outcome is given by for the state descried in (4). In Everettian many-worlds interpretations, deriving the Born rule remains contentious. Various strategies (including decision theory, relative frequencies, and symmetry arguments) have been proposed, but consensus remains elusive (Wallace, 2012) (Deutsch, 1999). Here, we present a derivation that aligns with our entropy-based perspective, building on Zurek’s concept of environment-assisted invariance (envariance).
To recap, Zurek introduced envariance as a symmetry property of entangled states (Zurek, Probabilities from entanglement, Born’s rule from envariance, 2005). For instance, consider a maximally entangled pure state: , where is the dimension of the support. If one applies a unitary transformation to and a corresponding inverse transformation to , the global state remains unchanged (up to a global phase), implying the system’s state is envariant under that transformation. Thus, an observer with access only to has no way to tell which basis is which; they must assign equal probabilities to the outcomes by symmetry (indifference). From this, one concludes for equal coefficients. Then by a reasoning of splitting amplitudes into rational ratios and continuity (a sort of Gleason’s argument or using the additivity of entropy), one can deduce for general coefficients (Gleason, 1957).
We incorporate an entropy principle: In our interpretation, prior to collapse the observer’s knowledge is described by a density matrix like (7). Lacking any further information (from outside the system), the maximum entropy principle of statistical mechanics suggests the observer should assign probabilities that maximize their entropy of uncertainty given the constraints (Jaynes, 1957). If the only constraint is that the state is known to be (7) with weights , then the probabilities are already determined as . But if one were in a situation of complete ignorance about coefficients (like entangled with an inaccessible environment and one only knows the dimension of the support), one should assign equal probabilities (principle of indifference, which in this quantum context is justified by envariance symmetry). This is strengthened by recognizing that an observer can only assign a definite outcome probability once the system is part of an effectively classical mixture, emergent through decoherence and entropy production.
Symmetry Argumentation with Rational Weights: Suppose the combined state (6) has two terms of equal amplitude and orthogonal environment states. By symmetry, there is no distinguishing feature between outcome 1 and 2 (the physical situation is symmetric under swapping those outcomes along with swapping environment states). Therefore, the probability an observer should assign to outcome 1 equals that of 2, and they must sum to 1, giving . In the case of rational squared amplitudes, e.g., with , we can construct identically prepared sub-states ( copies of type outcome-1, copies of outcome-2). By symmetry and frequency reasoning, the probabilities are . This is the frequency interpretation at the level of rational weights. Taking limits to irrational ratios gives the same conclusion (continuity argument). This is essentially Gleason’s theorem reasoning but can be made intuitive. Zurek’s derivation goes through these steps in detail.
The Born rule can also be derived by demanding that the observer’s probability assignment maximizes the Shannon entropy , subject to normalization and consistency constraints imposed by the quantum state. Zurek noted that probabilities must be an “objective reflection of the state”. Suppose we have a pure quantum state . Then, the assigned probabilities should depend only on , and in the special case where all amplitudes are equal, they should reduce to . This follows from the principle of maximum entropy: for a fixed number of outcomes, the entropy is maximized when all are equal. When the amplitudes differ, the maximum entropy distribution under the constraint of the known state structure must reflect those differences, implying . Using the method of Lagrange multipliers to maximize under normalization and known expectation constraints leads to distributions where , assuming the constraint function reflects the known amplitudes. In the quantum case, the natural constraint derives from , leading directly to the Born rule. But here we already know from Gleason’s theorem that the only consistent assignment is . (Gleason, 1957)
A more intuitive argument is that the Born rule ensures consistency: for a given density matrix, which can be decomposed into pure-state mixtures in many ways, the predicted measurement outcomes must remain invariant under such decompositions. This uniqueness essentially pins down the . As this has been extensively proven in the literature, we will not elaborate further. Our point is that we do not need to postulate the Born rule; it follows from symmetry and information-theoretic arguments that are fully in line with our interpretation’s philosophy. Moreover, our collapse criterion respects the Born rule: we do not claim that higher-weight branches collapse more quickly. Collapse is driven by entropy generation, which depends on record formation, not outcome bias. In a symmetric situation all outcomes produce similar entropy; in an asymmetric one, also similar entropy per outcome. As such, there is no bias introduced. The selection of a particular outcome remains fundamentally random (or, in the global sense, every outcome occurs in a branch, but each branch is realized for observers within it). The probabilities must therefore be exactly the to match the frequencies observed and to avoid signaling. If one instead postulated a different rule, such as assigning probabilities proportional to , it would conflict with experimental observations and violate envariance symmetry: swapping two equal-amplitude coefficients would no longer preserve outcome probabilities under such a rule. Only the assignment respects both empirical data and the symmetry principles fundamental to envariance. Thus, by combining environment-induced symmetry with the principle of maximum entropy under uncertainty, we uniquely recover the Born rule.
In essence, when the wavefunction collapse becomes relevant, the observer’s state of knowledge is such that they should treat the reduced density matrix as a classical probability distribution over outcomes. The only consistent choice for that distribution is the one equal to the diagonal of , which is by construction. Our interpretation therefore does not need to assume Born’s rule; it emerges naturally as the link between the quantum state’s amplitude-squared and the classical entropy of ignorance after decoherence.
In summary, Born’s rule is derived rather than assumed by appealing to the symmetry of entangled states (which forces equal outcomes to have equal probability) and the additivity of probabilities for composite events (which aligns with the quadratic norm property). The result is that the probability for each branch is the relative frequency given by the squared amplitude. This dovetails with the interpretation: those squared amplitudes also determine the entanglement entropy between branch and environment, in fact, . Maximizing entropy under the constraint imposed by the amplitudes leads uniquely to the Born rule. While this may appear tautological, it reflects the self-consistency of the amplitude-squared interpretation across both informational and physical grounds.
Having established the Born rule, we can now move to a higher level: how to test and apply this interpretation. We will propose an experiment where the “amount of collapse” can be tuned by controlling entropy, and show how our criterion can be quantitatively supported or falsified.
3.6. Experimental Proposal: Optomechanical Test of Entropy-Induced Collapse
A defining strength of a physical interpretation lies in its testability. Whereas most quantum interpretations remain empirically indistinguishable, since they yield identical predictions, our framework permits a novel class of experiment: one in which the entropy generated during a measurement-like interaction is varied, and its influence on interference visibility is observed. The essential aim is to determine whether a quantifiable or abrupt transition in coherence occurs when a specific entropy threshold is surpassed. We propose an optomechanical interferometry experiment using a mesoscopic object-massive enough for tunable environmental decoherence to potentially induce collapse, yet sufficiently controllable to retain quantum coherence under low-noise conditions.
Consider a nanosphere or dielectric mirror with a mass in the range of (approximately kg) that can be prepared in a spatial superposition (for instance, in an optomechanical cavity or double-slit arrangement). While significantly more massive than electrons or photons, interferometric experiments with large molecules and proposals extending upto ) suggest that quantum control at this scale is becoming experimentally feasible. This object serves as the system , while the measurement apparatus detects which-path information. A measurement device extracts which-path information by scattering or coupling. A possible configuration introduces a which-path detector, such as a laser that scatters differently depending on whether the object traverses path A or B. The interaction strength can be modulated to control the degree of which-path information extracted. The environment comprises all remaining degrees of freedom e.g., thermal gas, blackbody radiation, parameterized by ambient pressure, and temperature .
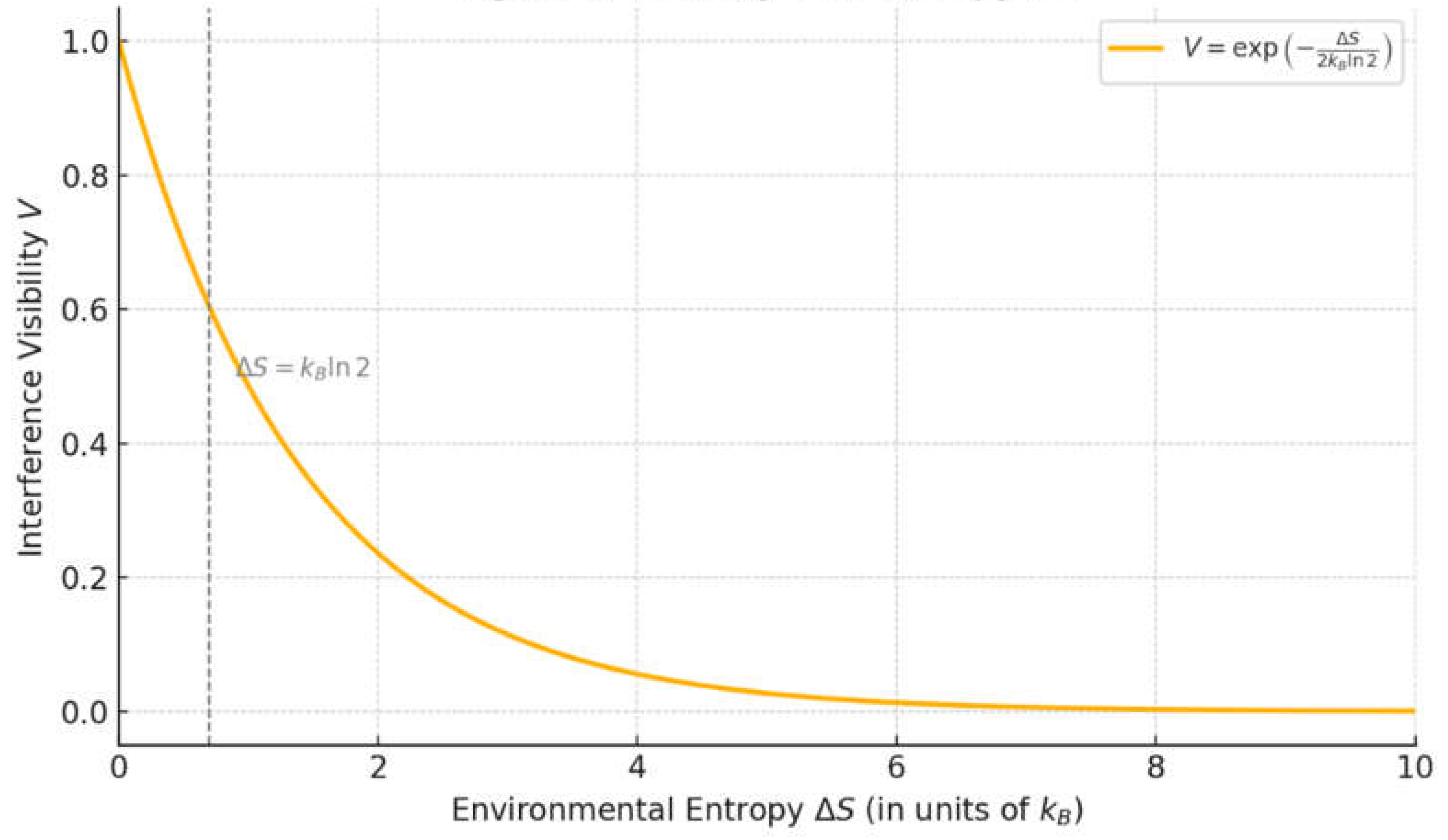
The goal is to operate in a regime where, in the absence of environmental decoherence, interference fringes are fully visible (i.e., visibility ). This likely means operating in extreme high vacuum ( atm) and cryogenic temperatures ( a few K or less) so that the coherence time of the object is long (the mean free path of residual gas is huge and thermal emission is low) (Romero-Isart, et al., 2011). Though technically demanding, such conditions have been achieved in state-of-the-art systems, including LIGO and cryogenically cooled optomechanical oscillators. To test the collapse criterion, we propose deliberately introducing controlled decoherence e.g., via increased gas pressure or tunable photon scattering to induce varying degrees of environmental entropy. For example, allow a known partial pressure of gas in the chamber to collide with the object, or use a controlled laser that entangles with the object’s position (scattering photons carry which-path info). By adjusting the gas pressure or the laser interaction time/power, one can tune the effective environment coupling. The interference visibility is defined as: , where are the maximum and minimum detected intensities. for perfect coherence, for complete decoherence (no interference).
In our framework, the visibility s directly related to the entropy irreversibly produced in the environment during the measurement interaction. n the weak decoherence regime, perturbation theory suggests , where corresponds to a small leakage of which-path information, typically quantified in bits. Then, . But as increases, coherence decays exponentially: specifically, the visibility is expected to decrease approximately as , or faster in some scenarios. A more concrete expression, drawn from standard decoherence theory, is where is the decoherence factor. For instance, a particle of mass and cross-sectional area , immersed in a gas with particle density and thermal velocity has experiences decoherence characterized by, representing the average number of scattering events in time . Each collision typically encodes approximately one bit of which-path information, contributing of entropy. Thus, is effectively proportional to the number of informational bits lost to the environment.
Hence, the environmental entropy can be approximated as , assuming each collision delivers path-distinguishing information. In this simplified model, one finds ; the factor of the arises from the particular geometry of the scattering setup, such as in a double-slit interference scenario. The central insight is that interference visibility decays exponentially with entropy production. Our experimental aim is to measure while systematically varying . The question then becomes: How can be quantified or measured? This can be approached either by directly measuring the environment, for instance, by counting scattered photons or monitoring heat dissipation, or by inferring entropy indirectly from known parameters. For instance, In a photon-mediated decoherence setup, one could employ a faint probe laser initially in a coherent state. As it interacts with the object in a path-dependent manner, via scattering or phase shift, it becomes entangled with the system. Tomographic reconstruction of the laser’s post-interaction state reveals how much which-path information, and thus entropy, was transferred. Alternatively, if the primary entropy sink is a thermal reservoir, one can use the thermodynamic relation = , where is the heat exchanged and is the reservoir temperature.
We propose a concrete implementation using an optical interferometer (e.g., Mach-Zehnder type), wherein a lightweight mirror or membrane is suspended in each arm. The photonic superposition between the two arms becomes entangled with the mechanical position of the mirrors via optomechanical coupling. By tuning the intensity of the laser, one can control the extent to which the photon’s path imprints momentum onto the mirror, effectively acting as a tunable which-path detector. This momentum transfer thermalizes via phonon excitations, transferring entropy into the mirror’s internal degrees of freedom. Interference visibility is measured at the output. For a sufficiently massive mirror, even minimal photon-induced kicks can produce detectable entropy increases, particularly if the mirror's thermal reservoir (phonon bath) is not perfectly isolated.
Predictions: Our model predicts no sharp discontinuity in visibility at the entropy threshold . Rather, it anticipates a smooth crossover, with coherence loss becoming prominent once significantly exceeds this value. Thus, a pronounced decline in visibility is expected around the point where entropy production crosses one bit, i.e. . As an illustrative case, suppose one increases background gas pressure in a double-slit interference setup. At ultra-high vacuum (effectively zero collisions), . When the average number of collisions during the superposition time reaches , visibility remains high (e.g., ). Around one collision on average (), visibility might fall to or so. These thresholds are illustrative and depend on the assumption that each collision provides nearly one bit of distinguishable which-path information. In reality, the amount of entropy generated per interaction depends on how well the environment can resolve the path, collisions that are gentle, symmetric, or lack spatial resolution may contribute less than one bit. Thus, the entropy-visibility scaling should be interpreted as an upper-bound trend, with full decoherence arising only when the cumulative information loss becomes thermodynamically irreversible.
As the number of collisions increases further, , the visibility rapidly vanishes. While this visibility trend aligns with standard decoherence theory, our interpretation introduces a new layer: collapse is identified with the crossing of a thermodynamic entropy threshold. In situations where the environmental degrees of freedom remain accessible, e.g., a single photon carrying which-path information, a quantum erasure protocol can reverse the apparent collapse and restore interference. For example, if we use a single photon as the environment (so was potentially small and localized), one could potentially perform a measurement on that photon that erases its information and see interference return. Conversely, once information is irreversibly disseminated into a large environment, entailing high entropy, the process is effectively irreversible and interference cannot be recovered.
This setup enables empirical discrimination among interpretations: The Many-Worlds Interpretation maintains that interference is always, in principle, recoverable, though it concedes that practical restoration becomes infeasible post-decoherence.Objective collapse theories (e.g., GRW) posit that interference is lost due to spontaneous, intrinsic collapse mechanisms-independent of environmental entropy. GRW, for instance, predicts a collapse rate of per nucleon, implying that a superposition involving nucleons should collapse within , even in perfect isolation. By contrast, our interpretation predicts that coherence persists indefinitely in the absence of entropy production. Collapse is never spontaneous; it is always conditional upon thermodynamic irreversibility. Hence, an ideal falsification test would involve isolating a mesoscopic object to suppress environmental entropy generation. If interference persists beyond GRW’s predicted collapse time, it would falsify objective collapse models and support entropy-induced collapse.
Several ongoing experiments investigate matter-wave interference using macromolecules and nanoparticles. The current experimental record demonstrates interference for molecules with masses up to
. No deviation from standard quantum predictions has been observed, placing tighter constraints on objective collapse models. For instance, GRW’s collapse rate parameter
is forced to lower values, and CSL models require increased localization lengths to remain viable. The proposed experiment offers a means to detect whether decoherence exceeds the expected contribution from thermodynamic environmental interactions. If interference were to vanish despite negligible entropy production (e.g., under ultra-high vacuum conditions), it would suggest the presence of new physics, such as gravity-induced collapse mechanisms. To date, all observations align with standard decoherence theory: interference is suppressed only when identifiable environmental interactions are present. For instance, ongoing projects such as MAQRO aim to test spatial superpositions for particles in the
range, utilizing space-based environments to minimize decoherence. Observation of interference in such regimes would further confirm the absence of any unforeseen collapse mechanisms up to these mass scales. In summary, a tunable optomechanical interferometer provides a platform to empirically map visibility
as a function of environmental entropy
. The expected behavior is illustrated in
Figure 1:
Visibility remains near unity while , followed by a rapid exponential decay in coherence as entropy increases further. The threshold marks the boundary between reversible quantum dynamics and effectively irreversible collapse. A direct measurement of through environmental monitoring would allow verification that the visibility drops to approximately 50% when , consistent with one bit of which-path information being irreversibly recorded. In the low-entropy regime, a linear relationship between and may emerge, supporting the predicted exponential suppression of coherence. Suppose a nanosphere placed in spatial superposition for To preserve coherence, the system must undergo fewer than one gas collision during that interval. Assuming a mean thermal velocity and cross-section , this sets a pressure bound . At a pressure of Pa, one expects roughly 5 collisions in , sufficient to generate , or greater, thereby suppressing interference. We predict no interference then. Intermediate might give collisions ( partial). Such predictions can be tested by measuring the interference contrast under controlled variations in pressure or scattering rates.
By plotting visibility as a function of pressure (or controlled scattering rate), and mapping this to estimated entropy production , one can directly test the functional dependence predicted by our model. Any observed deviation, such as a sudden visibility drop not attributable to entropy, or a slower-than-expected decay, would indicate new physics or failure of the entropy-based collapse hypothesis. Thus far, all data remain consistent with standard decoherence theory. Crucially, our interpretation implies a practical threshold of reversibility: coherence is maintainable as long as remains below a critical value, even in large systems, but if goes high, quantum behavior is lost irrecoverably. This insight aligns with experimental practice and supports the development of entropy-minimizing techniques, such as quantum error correction, that preserve coherence by suppressing entropy flow.
A further test involves a Wigner’s Friend-type setup: a small observer (e.g., a qubit memory) measures a quantum system, followed by a delayed measurement by a larger observer. By controlling whether the ‘friend’s’ record is preserved or erased prior to the final measurement, one can probe the reversibility of collapse. Photonic experiments by Proietti et al. (2019) demonstrated violations of classical assumptions about observer-independent facts under reversible measurement conditions. In our framework, if the friend’s measurement is weak or thermodynamically reversible, no collapse has occurred, and Wigner can still observe interference. Conversely, if the friend’s interaction produces significant entropy, collapse occurs from their frame, and Wigner will no longer observe interference, only classical correlations. This removes the paradox: apparent contradictions only arise when entropy is low and records are reversible. Once irreversible records exist, all observers agree on a definite outcome. The experiment by Proietti et al. can be explained as: they effectively had the “friend” as just another photon (with a quantum-controlled measurement). That is reversible, leading to correlations violating assumptions of observer-independent facts. Our interpretation maintains that observer-independent facts require thermodynamic irreversibility. In Proietti’s setup, no such irreversibility occurred.
Thus, testing these ideas with small quantum computers (where you simulate an observer with a qubit memory interacting and perhaps coupling to environment) could provide further evidence that when entropy is small, you get entangled super-observer states (friend and Wigner entangled); when entropy is large, you get classical records and decoherence. Small quantum computers can emulate Wigner’s Friend experiments by encoding observer memory in qubits and introducing controllable environmental coupling. By varying entropy, one can simulate and detect the transition from quantum superposition to classical definiteness. To date, all experimental results are consistent with our interpretation: collapse occurs precisely when entropy renders recoherence unfeasible. Nevertheless, exploring superpositions at larger scales remains essential, particularly where gravity-induced or other exotic collapse mechanisms may emerge.
4. Ontology and Interpretational Implications
Our entropy-based criterion for collapse implies a specific ontological commitment: the universal wavefunction is ontic and evolves unitarily at all times. Collapse is not a fundamental dynamical event, but an emergent, observer-relative phenomenon, corresponding to an epistemic update once entropy growth renders further quantum interference practically impossible. We now clarify what is considered “real” in this framework, and reconcile ontic unitarity with observer-dependent collapse, while avoiding interpretational vagueness.
Wavefunction ontology: We regard the wavefunction, more precisely, the universal quantum state, which may be a state vector or density operator on a Hilbert space, as a representation of physical reality. This ontological view aligns with interpretations such as the Many-Worlds Interpretation (MWI), Bohmian Mechanics (where the wavefunction guides hidden variables), and objective collapse theories (where the wavefunction spontaneously localizes). However, unlike Bohmian Mechanics, we posit no hidden variables; and unlike collapse models, we do not invoke non-unitary dynamics. In this respect, our approach is closest to Everettian ontology: the universal wavefunction encompasses all possible outcomes in a continuous, unbroken superposition.
Branches and Relative Facts: Within this global state, a “branch” corresponds to a subset of degrees of freedom that have decohered into a consistent classical narrative e.g., a system in state , an apparatus recording outcome 1, and an environment encoding that result. Branch 2 is the analogous for result 2. These branches are (approximately) orthogonal and do not significantly interfere due to environmental decoherence. Each branch thus supports an emergent classical reality, within which observers find themselves embedded. We adopt a view informed by Relational Quantum Mechanics (Rovelli) and refined by the framework of Quantum Darwinism: namely, that “facts” are not absolute but emerge as stable, redundant records distributed across many environmental degrees of freedom. In our approach, it is the increase in entropy that guarantees the proliferation and irreversibility of these environmental fragments, thereby stabilizing a given outcome as effectively classical.
Observer-relative collapse: The Wigner’s Friend thought experiment offers a clear illustration of observer-relative collapse. Suppose the friend () measures a system (), and the measurement entails amplification and entropy generation. From ’s perspective, a definite outcome occurs, and the state of knowledge updates accordingly: “ is in state , I (Friend) have memory of ”. would say the wavefunction collapsed. From Wigner’s () external perspective, having not yet interacted with the system or the friend, the combined state of S+F+lab remains a coherent superposition: , in principle. In principle, Wigner could perform an interference experiment on the entire lab to reveal coherence between branches, assuming the system remained sufficiently isolated and entropy production was negligible. However, if ’s measurement produced significant entropy, for example, by irreversibly recording the result in the environment, then even Wigner would be unable to restore coherence in practice. From Wigner’s point of view, the friend’s lab has decohered into an effectively mixed state. So Wigner would also then see the friend’s lab in a statistical mixture (with probability friend already got outcome ). In that case, when Wigner opens the door, he will find that the friend has already obtained the outcome with probability , and not be able to see any interference. At that point, both F and W agree that a collapse has occurred. Wigner might retroactively describe the collapse as happening “when I became entangled with the friend, and the irreversibility in the friend’s lab ensured that only one outcome was consistently observable.” Conversely, if the friend’s measurement were implemented in a fully reversible manner, for instance, using a qubit-based memory that became entangled without dissipating entropy, then Wigner could, in principle, detect interference.
In such a scenario, our interpretation holds that the friend did not experience an irreversible record. The friend’s state may have been a coherent superposition of seeing outcomes 0 and 1, with no stable memory, a possibility implausible for humans, but feasible for qubit-based “observers.” So there was no objective fact yet, and Wigner finds a superposition, consistent with no collapse. This is consistent with the frameworks of consistent histories or relational quantum mechanics: if Wigner can erase the measurement, then any subjective experience the friend had must also be reversible, implying no stable memory, and thus no classical outcome. Once entropy is generated, any observer that interacts with the environment will get correlated to the outcome and hence join that branch. At that point, all such observers share the same record; the outcome becomes objectively real for them within that branch. This is how our approach avoids the problematic “many perceptions” issue associated with MWI. We do not posit a literal splitting of consciousness. Instead, each observer’s classical state, embodied in a memory correlated with an outcome, resides within a single branch. Those records remain consistent across all macroscopic observers.
No global collapse event: There is no single, absolute moment when “the wavefunction collapses for the universe.” Collapse is always relative to a subsystem that lost track of coherence. On the global scale, there is just continuous unitary evolution (the state of the whole universe remains pure if started pure, with ever-increasing entanglement and entropy confined to subsystems). One can visualize this structure as a branching tree: the universal state continually divides into an ever-expanding web of outcomes, akin to Everett’s many worlds. Crucially, however, these “worlds” are not fundamental splits but emergent structures defined by high entropy and stable, redundant classical records. If somehow entropy could decrease dramatically, worlds could recombine, but as argued, that is practically impossible. We want to emphasize that although we speak of observer-dependent collapse, it does not mean an observer can arbitrarily choose reality. The criterion is physical: any system that plays the role of observer (i.e. acquires info) and increases entropy will find itself on one branch. This is objective in the sense that any other system that later interacts and shares that entropy flow will join the same branch. So ultimately, an unambiguous classical reality emerges within each branch.
QBist comparison: QBism holds that the wavefunction represents an agent’s personal belief about future experiences. In contrast, our view treats the wavefunction, and its linear evolution, as an objective, physical entity, not a personal belief. Probabilities in our interpretation arise from an observer’s ignorance about which decohered branch they inhabit-not from subjective Bayesian degrees of belief. We agree with QBism insofar as collapse can be viewed as a Bayesian update of knowledge upon acquiring new information. However, unlike QBism, we regard the wavefunction of the universe, or of systems not directly observed, as ontologically real, independent of any particular agent’s beliefs..
Classical reality and irreversibility: In our framework, classical reality emerges as the ensemble of macroscopic branches characterized by high entropy, rendering quantum interference effectively negligible. Each branch supports a consistent classical history, in line with the consistent histories formalism, where interference between different decohered sequences is negligible due to suppressed off-diagonal terms. This parallels the consistent histories interpretation, though that approach typically does not integrate thermodynamic irreversibility into the formalism. In our approach, the consistency of classical histories is guaranteed by entropy: once a fact is irreversibly recorded, alternative histories rapidly decohere and become inaccessible. Solving apparent paradoxes:
Schrödinger’s Cat: The cat is entangled with a quantum event (alive or dead). In our interpretation, if the system is perfectly isolated, the cat and the device may remain in quantum superposition. However, the cat, being a complex thermodynamic system, rapidly diverges into distinct high-entropy states upon becoming alive or dead. Practically, even if the initial cat-device entanglement is idealized, within milliseconds the "alive" and "dead" branches will diverge thermodynamically, producing sharply distinct entropy signatures in the cat's physiology and environment, generating substantial entropy, whether from the physiological contrast between life and death or from the recording mechanisms like the Geiger counter which irreversibly encodes outcome data. Thus, in the thermodynamic sense defined earlier, the superposition effectively collapses almost instantaneously. The cat is either alive or dead long before anyone opens the box, because the cat’s own environment (itself, the air in the box) causes irreversibility. So our interpretation aligns with “macro reality”: we would not expect to open the box and find a coherent half-alive half-dead cat state. The cat, in this context, functions as an observer: it "registers" the outcome by physically embodying one branch of the superposition, life or death. For us, since we did not know, we treat as superposition. But by the time we look, entropy has made the cat’s state definite for all practical observers. So no contradiction, we will see a definite outcome. (If one replaced the cat with a cryogenically preserved organism or minimized entropy in a highly controlled setup, collapse might be delayed, but with a living cat, such control is unachievable.)
Bell’s Theorem and nonlocality: Our interpretation preserves the standard quantum predictions and introduces no hidden variables; thus, violations of Bell inequalities remain fully intact. We adopt the stance that outcomes are realized upon measurement; that is, collapse corresponds to an observer becoming entangled with and embedded in a specific branch and that quantum correlations exhibit nonlocality without enabling faster-than-light signaling. Since collapse is not a dynamical cause but a thermodynamic consequence, it does not involve any propagating influence or signal, and thus respects relativistic locality. Accordingly, our interpretation satisfies Bell’s theorem by embracing the same nonlocal structure inherent to quantum entanglement, without invoking hidden variables. Since we do not posit hidden variables, our interpretation avoids the constraints such as parameter fine-tuning or nonlocal hidden variable conflicts those models must confront. As with all interpretations that retain standard quantum mechanics, outcomes remain fundamentally random yet exhibit strong correlations dictated by the structure of entanglement.
Macroscopic superpositions in the universe: A natural question arises: if collapse is not fundamental, do branches of the wavefunction exist where seemingly contradictory outcomes occur (e.g., one branch where a lab observes outcome A, and another where outcome B is seen)? Yes, in principle they exist in the universal wavefunction. Indeed, such branches exist in principle, but they do not interact. In one branch, an observer might perceive “heads,” while in another, a counterpart observes “tails.” Is this the many-worlds interpretation? In effect, yes, it resembles a many-worlds picture, where distinct outcomes emerge as decohered branches of a single, unitary wavefunction. However, we refrain from philosophically equating these branches with fully realized “other worlds” on par with our own. They may instead be regarded as counterfactual possibilities, present in the wavefunction’s structure but excluded from our experience by the thermodynamic arrow of time and decoherence. They persist mathematically, but are physically inaccessible once decoherence has rendered them orthogonal. Whether this constitutes “many worlds” or a single world with many unrealized alternatives is ultimately a matter of interpretive semantics. We conceive of these branches as irreversibly separated realities, akin to Everett’s many worlds, but defined by entropy-induced separation rather than ontological simultaneity. Everett held that all branches exist simultaneously and equally. In contrast, we argue that branches attain classical reality only once thermodynamic irreversibility renders their interference negligible.” Prior to this entropy threshold, interference remains possible, indicating that the “worlds” were not yet truly distinct.
Do probabilities have frequency meaning? In repeated trials of similar quantum experiments, the relative frequency with which outcome i occurs will empirically converge toward , as predicted by the Born rule. Within the Many-Worlds Interpretation (MWI), probability is typically interpreted as self-locating uncertainty, or as a measure over the distribution of branches. In our view, prior to measurement, the observer is effectively in a superposition across branches, each weighed by amplitude corresponding to possible outcomes. Once thermodynamic irreversibility sets in, i.e., entropy locks in a particular outcome, the observer effectively becomes localized within a single branch. The probability of experiencing a specific outcome corresponds to the weight, given by associated with that branch, interpreted ensemble-wise. Across many trials or copies of the same initial state, observed outcome frequencies align with these weights, in accordance with the Born rule. While probability retains a subjective element in any single case, the frequentist interpretation naturally emerges through repeated trials within a single branch. One may also interpret frequency over many branches across the universal wavefunction, but this detour is unnecessary if one accepts typicality within one branch across repeated experiments.
Philosophical position: In summary, our interpretation may be described as neo-Everettian, enhanced by a thermodynamic criterion for classicality. It avoids the “preferred basis problem” by identifying the preferred basis through entropy maximization: the pointer basis naturally emerges as the one minimizing free energy increase, in line with decoherence theory. It also does not suffer the “probability problem” because we can derive Born’s rule. It resolves the “definite outcomes problem” by appealing to thermodynamic irreversibility: once entropy stabilizes a memory record, it can no longer exist in superposition relative to macroscopic observers. Finally, we avoid invoking mind or consciousness as special constructs; observers are treated as purely physical systems with memory registers shaped by thermodynamic constraints. A “Wigner’s friend” sufficiently entangled with their measurement apparatus and environment cannot remain in a coherent superposition of memory states from the standpoint of any future interacting observer, because that entanglement becomes irreversibly distributed across the environment. Thus, there is no contradiction between the friend’s observation and Wigner’s prediction. A correct analysis by Wigner must incorporate the entropy generated and acknowledge that coherence is no longer recoverable.
We maintain that no additional collapse postulates or modifications to quantum theory are necessary. The appearance of wavefunction collapse emerges naturally from standard quantum mechanics, once the thermodynamic arrow of time is taken into account and the entropy costs of record formation are properly considered.
5. Relativistic Consistency and Quantum Gravity
In Section III, we introduced a relativistic formulation of our collapse criterion using the Tomonaga-Schwinger formalism. Here, we summarize and extend that discussion, emphasizing Lorentz invariance and exploring whether general relativity presents any obstacles, or opportunities, for applying our entropy-based interpretation.
Tomonaga-Schwinger Equation: This formalism generalizes the Schrödinger equation for use in relativistic quantum field theory by defining quantum states on arbitrary spacelike hypersurfaces
slices of spacetime that respect causality. The state
evolves as the hypersurface σ is deformed, governed by the Tomonaga-Schwinger equation:
where
is the energy-momentum density operator at point
being added to the hypersurface. This equation guarantees that state evolution is local and Lorentz-covariant. In particular, if two operations are spacelike-separated and their corresponding operators commute, the order in which they are included along the hypersurface is irrelevant. The final state
is thus well-defined. In EPR-type scenarios, this formalism reproduces the standard nonlocal quantum correlations without invoking superluminal signals. A measurement on one particle effectively selects an outcome along a branch and correlates it with the distant particle’s state on a spacelike hypersurface. This hypersurface can be chosen such that it includes one measurement event before any causal influence can reach the other side. As a result, the state appears to “collapse” instantaneously, but this is merely a bookkeeping update: no physical signal propagates faster than light.
In our approach, the collapse criterion remains local. The entropy increase that triggers effective collapse occurs within a specific spacetime region (e.g., a laboratory), and pertains only to the degrees of freedom involved in that process. An observer located in a spacelike-separated region would not have access to the entropy change until causal signals, carrying the corresponding information, arrive. How, then, is consistency maintained across frames? Consider two entangled particles, and , separated by a spacelike interval. Suppose particle is measured at spacetime point . For an observer at , the measurement induces a local entropy increase, effectively collapsing the state in that region. Meanwhile, particle , still isolated, remains unaffected in physical terms. An observer at , spacelike-separated from ’s measurement, would describe ’s state as still in superposition, lacking knowledge of ’s outcome. This discrepancy presents no contradiction, as no information about ’s measurement is yet accessible at . Standard quantum mechanics ensures that the correlations, once the outcomes are compared, will match entangled predictions. Once a signal from ’s side reaches , conveying outcome information and associated entropy, the observer at can update their state assignment accordingly, recognizing that effective collapse has occurred. Relativity of simultaneity implies that observers in different inertial frames may disagree on the temporal ordering of spacelike-separated events and . However, all observable predictions and post-measurement comparisons remain frame-independent and internally consistent.
Crucially, our collapse criterion, “entropy generated implies collapse,” is not tied to absolute simultaneity; it is inherently local. All frames agree that at event , entropy increases locally in ’s lab. This entropy production is a frame-invariant physical process (e.g., in the rest frame of the apparatus). In other frames, event may occur earlier or later than , but as long as lies outside future light cone’s measurement occurs without knowledge of ’s outcome, preserving causal consistency.
No Preferred Frame: Objective collapse models often face difficulty maintaining Lorentz invariance because they posit a real, physical wavefunction collapse that appears instantaneous in some preferred frame of reference. Our approach circumvents this issue by rejecting any notion of objective, frame-dependent collapse that requires coordination across spacelike-separated regions. In our framework, the universal wavefunction evolves unitarily at all times; the only “instantaneous” change is the observer’s local knowledge update, which does not carry any physical effect. Since information transfer remains limited by the speed of light, no causal paradox arises from such updates. The wavefunction’s description can be formulated in any frame or spacetime foliation, akin to a gauge choice: different perspectives yield consistent physics. The physical content (e.g. expectation values of observables in each region, correlations) is Lorentz-invariant. This is reinforced by quantum field theory, where entanglement is typically nonlocal, but detection events, those that produce entropy and yield classical outcomes, are strictly local, such as a particle being absorbed by a detector and inducing a measurable heat signature. Such events define effective branching points in spacetime. While different frames may disagree on the temporal ordering of these events, all physical predictions, including observed correlations, remain invariant and consistent across frames.
Gravity’s role: Thus far, we have only addressed gravity tangentially. Penrose and others have proposed that gravity might play a role in wavefunction collapse, suggesting that superpositions involving significantly different mass distributions may be inherently unstable. Our interpretation can incorporate gravity naturally, treating it as just another quantum field, if and when a complete theory of quantum gravity becomes available. Even if gravity is fundamentally classical, a quantum system still sources a gravitational field, which may encode which-path information and thereby induce decoherence. For example, a spatial superposition of mass distributions results in a superposed gravitational field. If gravity has quantized modes (such as gravitons or perturbative spacetime fluctuations) that interact with the system or environment, these could act as a decohering channel. Recent proposals, such as those by Bose et al. (2017), aim to entangle two mesoscopic masses via gravitational interaction. Successful demonstration would suggest that gravity can mediate quantum coherence. Conversely, if gravity always acts as a decohering mechanism, as posited in Diòsi-Penrose models, then such experiments would fail to produce entanglement, indicating effective gravitationally induced collapse.
Our stance is to treat gravity as just another possible environment. If a mass superposition induces distinct spacetime geometries in different branches, and those gravitational field states become orthogonal, either instantly or through dynamical evolution, then gravity has effectively decohered the system. If gravity is fully quantum and remains unmeasured, it may simply become entangled with the system. In principle, recoherence could be achieved by isolating and manipulating the gravitational degrees of freedom, though this is practically infeasible. Alternatively, if gravity is fundamentally classical, it may act as a stochastic background field, inducing effective collapse. Some have argued that classical gravity interacting with quantum matter may necessarily induce non-unitary evolution, though this remains an open question. Our position is guided by empirical data: since no sudden collapse has been observed in experiments with increasingly massive superpositions, gravity-induced collapse either does not occur, or occurs only at scales currently beyond our experimental reach.
Indeed, interferometric experiments with molecules up to have shown no evidence of gravitational decoherence beyond what is expected from standard environmental sources. Future missions, such as the proposed MAQRO project, aim to test quantum coherence in objects approaching (Romero-Isart, et al., 2011). If coherence persists at those scales, it would suggest that gravity either does not cause rapid decoherence, or that any such effects are too weak to detect. Penrose’s criterion suggests that if the difference in gravitational self-energy between two branches is , then the system should collapse over a timescale . For a superposition involving a mass of approximately kg separated by micron, the associated gravitational self-energy may be non-negligible. Penrose’s model estimates collapse timescales ranging from ms to several years for such configurations, depending on geometry and isolation, still well beyond what current experiments can resolve. While we do not attempt a full quantitative analysis here, we note that no experimental evidence currently supports gravity-induced collapse at accessible mass scales.
Even if Penrose's Objective Reduction (OR) model turns out to be incorrect, gravity retains a special status due to phenomena like cosmic expansion and black holes, which raise profound questions about information loss. Our interpretation is intrinsically information-preserving: we maintain global unitarity. Thus, we regard black hole evaporation as fundamentally unitary, with the apparent thermality of Hawking radiation arising from entanglement between interior and exterior degrees of freedom, not from any real information loss. Hence, our view remains consistent with the unitarity of quantum mechanics, even in the context of black hole evaporation.
A central feature of our framework is the cosmological arrow of time, specifically, the question of why the early universe had such low entropy. Our approach necessitates low-entropy initial conditions, such as those at the Big Bang, to allow for subsequent entropy increase, which underpins the operational viability of measurement, memory, and the thermodynamic arrow of time. In a universe at thermal equilibrium (heat death), no arrow of time, and thus no meaningful notion of irreversible measurement, could arise. This perspective aligns with works by Zeh and others, who argue that the low-entropy state of the early universe underlies the observed temporal asymmetry. In a time-symmetric universe with no low-entropy boundary condition, the arrow of time, and thus the emergence of classical records or collapse, might be ill-defined. Some speculative models posit time-symmetric processes involving advanced and retarded waves, but these lack empirical support. Empirically, the early universe exhibited very low gravitational entropy, evidenced by its extreme smoothness, allowing the arrow of time to emerge naturally through cosmic evolution.
Quantum Cosmology: Considering the wavefunction of the entire universe, as described by the Wheeler-DeWitt equation, for example, raises the question: in the absence of an external environment, how does collapse occur? Some approaches, such as the Page-Wootters mechanism, propose that time itself can emerge from entanglement correlations within a globally static state. In such models, subsystems experience an emergent arrow of time due to their entanglement structure relative to other parts of the system. Our interpretation complements this view: within the universe, any local observer perceives a thermodynamic arrow of time arising from the initial low-entropy state and ongoing expansion. While the global quantum state may be static, e.g., an eigenstate of the Hamiltonian lacking global time, observers experience time internally as the growth of correlations, consistent with the Page-Wootters argument. We align with this framework, interpreting collapse as an emergent phenomenon internal to the universe rather than a fundamental external process. Since there is no external time parameter to trigger collapse globally, the emergence of classical records arises from internal thermodynamic time and entropy generation. From a hypothetical “God’s eye view” outside the universe, one might say that the universe is a single, uncollapsed pure quantum state. But within that state, countless entropy-driven branchings occur, corresponding to emergent collapses from the perspective of internal observers. This perspective echoes the relational interpretation: collapse is relative to subsystems, not an absolute global event.
Lorentz invariance reaffirmed: Since both the second law of thermodynamics and quantum field theory are locally Lorentz-invariant, our interpretation preserves frame independence and does not privilege any particular foliation of spacetime. Were collapse an absolute event, conflicting observations across frames would pose a problem. However, since collapse in our framework is not fundamental but emergent and observer-relative, no such contradiction arises. An apt analogy is that of milk spilling into coffee: two frames might disagree on when the mixing occurred, but once the event is in both past light cones, they agree on the irreversible outcome. Similarly, collapse is like that: once it is in past light cone, all observers agree on outcome.
In summary, our interpretation is fully compatible with special relativity. It involves no superluminal signals or physical influences, only frame-dependent knowledge updates, analogous to how electric and magnetic fields form frame-dependent components of a Lorentz-covariant electromagnetic tensor. Collapse, in this sense, is simply how entanglement manifests in a given frame. By grounding collapse in entropy, we naturally integrate with relativistic thermodynamics, where entropy is well-defined locally via concepts such as the entropy current four-vector.
6. Visualizations of Key Dynamics
Figure 2 illustrates how interference visibility
decays as a function of environmental entropy
. The main blue curve follows the expression
, capturing the exponential suppression of coherence as entropy grows. When
, interference remains significant. However, once entropy exceeds this threshold (indicated by the vertical dashed line),
drops rapidly toward zero, reflecting effective decoherence and the onset of irreversible wavefunction collapse. In realistic macroscopic measurements,
(far to the right), making
effectively zero permanently. Thus, wavefunction coherence is effectively lost (collapse) beyond the entropy threshold. The inset compares the exact exponential decay with an approximation
at small
. This highlights the regime where perturbative models apply and deviations emerge. In realistic experiments (Section V), this prediction could be tested by tuning environmental interaction strength, such as controlled photon scattering or gas pressure, to modulate entropy production.
Figure 3 shows the complementary behavior of quantum discord
and classical mutual information
as entropy increases. At
, discord is maximal and mutual information is negligible. As decoherence proceeds and entropy is irreversibly generated in the environment
quantum discord (blue curve) decays toward zero, while classical mutual information (orange curve) rises, saturating at 1 bit, the entropy of a binary outcome (black dashed line). This transition marks the conversion of entanglement into classical correlations: the memory register
becomes classically correlated with
and the system enters an effectively collapsed state. The monotonic decay of
is a hallmark of CPTP decoherence channels, which suppress non-classical correlations. Hence, the condition
serves as an operational signature of wavefunction collapse in our entropy-based framework.
Figure 4 compares the coherence dynamics of a closed (blue) versus open (red) quantum system. For the isolated system, coherence (e.g., purity or off-diagonal elements) undergoes periodic revivals, returning to near 1 at the recurrence time
. This Poincaré recurrence is guaranteed in finite, closed quantum systems with discrete spectra.
In contrast, the open system, coupled to a large environment, exhibits rapid coherence decay with no significant revival. The red curve flattens near zero, and becomes effectively infinite. This occurs because entropy generated in the environment disperses phase information into many degrees of freedom. Any tiny recoherence is exponentially suppressed and requires timescales vastly exceeding the age of the universe. This demonstrates the practical irreversibility of collapse in open systems: while unitary evolution holds globally, local subsystems interacting thermodynamically with the environment undergo irreversible decoherence. This justifies treating wavefunction collapse as a real, albeit emergent, phenomenon under entropic conditions.
7. Conclusions
We have proposed a thermodynamically grounded interpretation of the quantum measurement problem, one that retains the universal validity of quantum mechanics while providing a concrete, observer-relative criterion for wavefunction collapse. In this framework, collapse is not a fundamental, dynamical process, but an emergent phenomenon arising from the irreversible production of entropy during measurement interactions. Once environmental entropy surpasses a critical threshold, quantitatively characterized by the inequality , quantum coherence is exponentially suppressed, and recoherence becomes practically impossible.
This entropy-induced collapse interpretation harmonizes the insights of decoherence theory, fluctuation theorems, and relational quantum mechanics, while avoiding the ontological excesses of Many-Worlds and the dynamical alterations of objective collapse models. It locates the boundary between quantum and classical not in mass, consciousness, or vague observer influence, but in the thermodynamic cost of information proliferation. Collapse, in our view, is a thermodynamic transition: when information becomes permanently imprinted into the environment through entropy-generating processes, the system can no longer be coherently recombined. It is this irreversibility, not observation per se, that marks the emergence of classical definiteness.
We have formalized this insight through rigorous derivations, using tools from open quantum systems, resource theory, and non-equilibrium statistical mechanics. The entropy-coherence inequality and its extensions demonstrate how coherence decays in the face of increasing environmental entropy, both in abstract models and in concrete Lindblad-type dynamics. We have shown that fluctuation theorems such as Crooks’ relation explain the near-impossibility of recoherence once sufficient entropy has been dumped into the environment, and we proposed experimental tests based on optomechanical setups that could quantitatively link entropy generation to interference visibility.
Importantly, this interpretation maintains full compatibility with relativistic quantum theory via the Tomonaga-Schwinger formalism and offers explanatory resolution to paradoxes such as Wigner’s Friend and delayed-choice erasure. It explains why classical observers reach consistent outcomes despite wavefunction evolution being globally unitary: entropy aligns their histories. It also integrates with information-theoretic derivations of the Born rule, avoiding the need to postulate it separately.
In this way, we reinterpret wavefunction collapse not as a fundamental rupture in the laws of physics, but as an emergent statistical feature of systems embedded in a thermodynamically asymmetric universe. The entropy-based criterion marks a universal, observer-independent boundary between quantum possibility and classical fact, offering not only conceptual clarity, but empirical testability. We therefore conclude that the measurement problem does not require new physics, it requires recognizing the deep connection between information, entropy, and irreversibility in the quantum world.
Appendix A
Appendix A1. Entropy-Coherence Trade-off Theorem
Let
be a quantum system coupled to an environment
, with the initial joint state
assumed to be pure. Let
denote the reduced state of the system at time
and let
denote a valid measure of quantum coherence of
, such as the trace-norm of off-diagonal elements or the square root of purity. Define the entropy increase of the environment as:
, where
is the von Neumann entropy. If the joint evolution leads to thermodynamically irreversible decoherence, that is,
, and this entropy cannot be undone without external work, then the coherence of
is upper-bounded by:
In particular, when , the coherence is suppressed to at most of its initial value. In the limit , we have .
Purity-Based Derivation: Let the purity of the system be defined as: . At , when the global state is pure and is unentangled with , we have . As becomes entangled with , the reduced state becomes mixed and . Since the total state remains pure, we have: , when is initially pure or uncorrelated with .
In the high-entropy regime, the effective dimension of
is approximately
. A maximally mixed state over such a space has purity:
For many coherence quantifiers, including the
of coherence and relative entropy of coherence, coherence is upper-bounded by the square root of purity:
Note: This inequality gives an upper bound rather than an exact equality; it holds for a wide class of CPTP dynamics describing decoherence under typical physical assumptions (weak coupling, large environments, and Markovianity). The constant in the exponent may vary slightly depending on the coherence measure and model specifics, but the exponential suppression remains universal.
Two-Level Example: Superposition and Orthogonalization
Consider a qubit in the superposition state:
, interacting with an environment such that each basis state becomes entangled with orthogonal environment states:
Then, the off-diagonal elements in decay by this overlap factor, which aligns with the general exponential form of Theorem A.1.
Therefore, as increases, coherence decays exponentially. At the threshold , coherence is reduced to at most 50% of its original value (or lower depending on the definition). For , coherence becomes negligible, and the system behaves classically. This result formalizes the idea that irreversible entropy generation enforces decoherence, making wavefunction collapse an emergent thermodynamic phenomenon. Theorem A.1 is supported by analytical and numerical studies in open system models such as; in the Caldeira-Leggett quantum Brownian motion, spin-boson models, and Lindblad quantum trajectory approaches, coherence typically decays as or , where accumulates environmental entropy or information leakage.
This includes standard coherence measures such as the of coherence and the relative entropy of coherence (Baumgratz, Cramer, & Plenio, 2014), both of which are non-increasing under CPTP maps and admit bounding relations via purity. It must be noted that the bound is not tight in general. Tightness may be achieved only in idealized scenarios, such as symmetric coupling, negligible backaction, or controlled environment states, where analytic saturation of the bound can occur. The inequality is robust and conservative, giving a reliable estimate for the onset of effective decoherence and collapse in open quantum systems.
Theorem A.1 formalizes the intuition that irreversible entropy production suppresses coherence exponentially, effectively enacting a thermodynamic wavefunction collapse. The result holds for a broad class of quantum systems interacting with environments and captures the core insight that information flow to the environment constrains recoverable quantum coherence.
Definition A.1 (Quantum Coherence in a Fixed Basis)
Let
be a finite-dimensional Hilbert space with orthonormal basis
. For a density matrix
acting on
, the
quantum coherence of
in this basis is defined as:
where:
is the dephased (diagonal) version of , obtained by deleting all off-diagonal elements in the chosen basis.
denotes the trace norm (also known as the Schatten 1-norm).
This coherence measure captures the magnitude of the off-diagonal elements of , quantifying how far the state deviates from being classical (i.e., diagonal) in the given basis.
Remarks: The trace norm coherence defined above satisfies all standard criteria for a proper measure of coherence as established in the resource-theoretic framework (Baumgratz, Cramer, & Plenio, 2014). Specifically:
Non-negativity: , with equality if and only if is diagonal in the specified basis.
Monotonicity: is non-increasing under incoherent completely positive trace-preserving (ICPTP) maps.
Basis Dependence: Coherence is defined relative to a fixed orthonormal basis, typically chosen as the pointer basis selected by the decohering environment.
Definition A.2 (Entropy Production in Open Quantum Systems)
Let a quantum system
interact with an environment
, undergoing evolution governed by a completely positive trace-preserving (CPTP) map
. arising from the unitary evolution of the total system-environment composite. The irreversible entropy production in the environment at time
is defined as:
where:
is the change in von Neumann entropy of the system,
is the reduced state of the system at time
is the von Neumann entropy.
Assuming the initial global state
is pure (or uncorrelated with a thermal environment), the total entropy change reduces to:
Thus, entropy production in the environment satisfies:
A strictly indicates irreversibility, of the system-environment interaction. In thermodynamically irreversible processes, coherence loss in the system corresponds to a gain of entropy in the environment, consistent with the Second Law of thermodynamics.
Remarks: This formulation aligns with the standard quantum thermodynamic treatments of entropy production (Spohn, 1978) and can be interpreted operationally in calorimetric terms when the environment includes a heat bath. In scenarios with a finite, but large, environment initially in a thermal state, entropy increase in the environment corresponds to dissipated heat divided by temperature, , making this definition physically measurable.
Assumption A.3 (Environment-Induced Decoherence Channel)
Let the reduced dynamics of the system be described by a one-parameter family of completely positive trace-preserving (CPTP) maps , generated by tracing out the environment from a unitary evolution on . We assume the following properties hold for :
This ensures that classical mixtures remain invariant under decoherence, and that coherence is only lost, not reintroduced.
Quantum Detailed Balance (with respect to a thermal state): There exists a stationary Gibbs state with the system Hamiltonian, , and partition function , such that satisfies the quantum detailed balance condition. This implies time-reversal symmetry at equilibrium and ensures thermodynamic consistency of the dissipative dynamics.
Strict Entropy Production (Irreversibility Condition): For all the environment absorbs entropy under the evolution . This expresses the irreversible nature of decoherence and ensures that information leakage into the environment accumulates irreversibly.
Remarks:
The pointer basis arises dynamically as the eigenbasis in which the system’s reduced state becomes diagonal due to environmental monitoring, typically associated with robust classical records.
Quantum detailed balance guarantees that the long-time behavior of the channel aligns with equilibrium statistical mechanics, ensuring compatibility with fluctuation theorems.
Strict entropy production is essential for enforcing thermodynamic irreversibility and for preventing recoherence in practice.
Theorem A.4 (Coherence Bound via CPTP Contractivity)
Let
be an initial quantum state and
be a family of CPTP maps satisfying the conditions of Assumption A.3 (including incoherence preservation, detailed balance, and irreversible entropy production). Define the coherence of the system at time
as
where
is the dephased state in the pointer basis. Then the coherence satisfies the exponential bound:
Proof:
1. Trace Norm Contraction under CPTP maps: For any two states and any CPTP map , the trace distance is contractive:
Apply this to and its dephased version
2. Incoherence Preservation (Assumption A.3): By definition, . So we have:
This confirms that coherence is non-increasing under such CPTP channels.
3.
Entropy-Driven Suppression (Crooks-Type Fluctuation Argument): According to Theorem A.6 (or fluctuation-based suppression results), if
is the entropy increase in the environment due to decoherence, then:
An exponential suppression relation is suggested by fluctuation theorems, and formalized in Theorem A.6.
The exponential damping of coherence is directly tied to irreversible entropy production in the environment. In the limit
, the right-hand side vanishes, implying:
This behavior supports the interpretation of wavefunction collapse as an emergent, thermodynamically enforced phenomenon, and formally links coherence decay to the second law of thermodynamics.
Theorem A.5 (Relative Entropy of Coherence Loss under Decoherence)
Let
be the initial state of a quantum system and
an entropy-generating completely positive trace-preserving (CPTP) map. Define the relative entropy of coherence as:
where:
is the von Neumann entropy, and
is the fully dephased version of in a fixed pointer basis.
Then the change in coherence satisfies:
Proof:
From the second law of thermodynamics:
Relative entropy of coherence before and after:
At :
At time , assuming the CPTP map preserves diagonality (i.e ), we write:
Thus, the change in relative coherence is:
Combining with the second law:
From the total entropy inequality:
To express the bound dimensionlessly (in units of entropy per
)
:
Remarks: This theorem formally links coherence loss (as quantified by relative entropy of coherence) to irreversible entropy production. As coherence is lost under decoherence, the environment must gain at least that much entropy, highlighting how classicality emerges thermodynamically, without requiring collapse as a fundamental process.
Theorem A.6 (Recoherence Suppression via Crooks Relation)
Let a quantum system interact with an environment such that the global evolution is unitary, while the reduced dynamics of is open and entropy-generating. Let denote the irreversible entropy produced in the environment by time .
is the probability that coherence is lost via environment-induced decoherence and
is the probability of a recoherence fluctuation, i.e., the system returning to its coherent initial state due to a rare entropy-decreasing fluctuation. Then the Crooks fluctuation theorem implies:
Crooks Theorem (Thermodynamic Fluctuation Relation): In nonequilibrium statistical mechanics, the Crooks fluctuation theorem quantifies the likelihood of observing a reverse trajectory (one in which entropy decreases by
) relative to a forward trajectory (where entropy increases by
) as:
This holds for entropy changes due to stochastic processes satisfying microscopic reversibility, and has been shown to apply to quantum systems under certain conditions (see (Esposito, Harbola, & Mukamel, 2009) (Campisi, Hänggi, & Talkner, 2011).
Application to Decoherence and Recoherence:
The forward process corresponds to decoherence: loss of coherence due to entanglement with and entropy flow into .
The reverse process corresponds to recoherence: spontaneous restoration of initial coherence due to an unlikely entropy-reducing fluctuation in .
By applying Crooks' relation to coherence change events associated with entropy flow, we obtain:
Since .
Implications for Coherence Dynamics:
Recoherence is exponentially suppressed with growing environmental entropy.
This explains the practical irreversibility of decoherence in macroscopic systems: for large , the recoherence probability becomes vanishingly small.
This result justifies the exponential upper bound on coherence derived in Theorem A.4:
Theorem A.7 (Microscopic Realization in Lindblad Models)
Let quantum system undergo decoherence through repeated collisions with particles from an ideal thermal environment (a standard model of collisional decoherence). The system’s reduced dynamics is governed by a Markovian Lindblad-type master equation. In such models, the quantum coherence decays exponentially in time: is the decoherence rate, with:
: number density of environmental particles,
: effective scattering cross-section,
: mean relative thermal velocity of collisions,
is coherence measure (e.g., or off-diagonal visibility) at time .
Let the entropy production rate in the environment be denoted by
, and assume that each scattering event produces an average entropy of ∼
. Then:
Integrating over time , we obtain the total entropy increase:
Substituting into the expression for
, we find:
This derivation confirms that in concrete physical models, such as collisional decoherence with gas particles or photons, the entropy-coherence inequality derived in Theorem A.1 is not only satisfied but saturated:
That is, equality holds in the entropy-induced coherence bound. These models offer a microscopic realization where coherence decay and entropy increase are directly and quantitatively linked, supporting the thermodynamic interpretation of wavefunction collapse.
Remarks: This result aligns with well-known solutions to Lindblad master equations for decoherence in position space (Joos-Zeh model (Joos & Zeh, The emergence of classical properties through interaction with the environment, 1985)) and spin environments, where coherence decays as a function of interaction strength and collision rate. In general, non-ideal models with memory effects or backaction may exhibit deviations from strict exponentiality; however, in the weak coupling, Markovian regime, the bound is exact.
Appendix B
Appendix B1. Landauer’s Principle and Measurement Entropy
Landauer’s principle states that any logically irreversible manipulation of information, such as erasing a bit or merging two computation paths, must be accompanied by an increase of entropy in the environment by at least per bit erased. This reflects a fundamental connection between information theory and thermodynamics, particularly in measurement processes where quantum superpositions are resolved into classical outcomes.
In quantum measurement, recording an outcome corresponds to selecting one branch from a coherent superposition. This is operationally equivalent to erasing the other possibilities a logically irreversible act. Consider the measurement of a qubit, with possible outcomes 0 or 1:
Before measurement: The apparatus is in a standard ready state .
After measurement: The memory is in either or , correlated with the system.
To reuse the apparatus, it must be reset to an erasure of the outcome.
By Landauer’s principle, this erasure entails a minimum entropy cost:
If the outcome is not erased, the memory remains in a mixed state (e.g., equal probability of 0 or 1), corresponding to Shannon entropy In such cases, the entropy increase must have occurred during the measurement process, via heat dissipation or coupling with a thermal reservoir.
Entropy Cost per Bit: Jennings & Rudolph (2010) summarize this insight by “to acquire one bit of information, one must increase entropy by at least ”.
In our framework, this justifies setting the collapse threshold at: . This is the point at which one full bit of which-path information has been effectively and irreversibly recorded. If , reversibility is still possible, the environment could, in principle, be returned to its initial state, and no definite classical outcome is yet encoded. Once: , a classical record exists, and reversibility is lost unless additional entropy is exported elsewhere (via active erasure or cooling).
a. Reversibility Condition for Interference Recovery (Corollary B1)
Let a quantum measurement or interaction be performed on a system
, where the apparatus and environment evolve such that the total entropy increase is:
Then:
If , the process is potentially reversible, and quantum interference can be restored (e.g., via quantum eraser protocols).
If , which-path information has become thermodynamically irreversible, and interference is permanently suppressed unless a compensating entropy sink is provided.
This corollary reframes Landauer’s limit within the context of quantum decoherence and collapse interpretation:
To restore interference in such cases, one must pay the entropy cost; i.e, perform work to extract entropy and transfer it to a larger environment, maintaining consistency with Landauer’s bound.
Remarks: This operational definition of collapse aligns with our thermodynamic framework:
Collapse is not triggered by wavefunction dynamics, but by entropy production.
Once information is irreversibly encoded in the environment, classical outcomes emerge.
The threshold is therefore a natural boundary between quantum reversibility and classical definiteness.
Appendix C
Appendix C1. Born Rule Derivation via Envariance and Maximum Entropy
In this appendix, we derive the Born rule from a combination of:
Envariance (environment-assisted invariance) as introduced by Zurek (2005),
Symmetry arguments in the presence of entanglement,
Maximum entropy (MaxEnt) principles for assigning probabilities under constrained knowledge, and
The structure of the reduced density matrix after decoherence.
The aim is to show that the probability of obtaining outcome in a quantum measurement is in a quantum measurement is , without postulating this rule a priori.
a. Post-Decoherence State Structure (C1)
Suppose the system
S becomes entangled with an environment
, leading to the Schmidt decomposition:
For an observer with access only to
, the effective state is the reduced density matrix:
The observer knows , but has no direct access to . They seek to assign outcome probabilities . to the basis . We want to show that the only consistent assignment is .
b. Envariance Argument: Equal-Amplitude Case (C2)
Envariance (environment-assisted invariance) states that if a transformation on the system can be undone by a counter-transformation on the environment, then the outcome probabilities cannot depend on the system transformation.
Suppose all are equal: .
A swap of any two system basis states can be undone by swapping , leaving invariant.
By symmetry and envariance, the observer must assign:
This establishes the Born rule in the equal-amplitude case.
c. Extension to Unequal Amplitudes via Rational Weights (C3)
Now consider a case with rational squared amplitudes. Suppose:
Construct a new entangled state by embedding this into an extended Hilbert space (This embedding does not imply physical cloning but constructs a mathematical isomorphism to redistribute amplitudes across orthogonal states):
Each environmental state
is orthogonal, and by envariance, each term has equal probability
. Grouping them by outcome:
The argument generalizes to any set of rational via partitioning into equiprobable branches. Continuity then extends this to irrational amplitudes.
d. Gleason’s Theorem and Linearity (C4)
Gleason’s theorem (1957) states that any probability assignment on the outcomes of a quantum measurement (represented by projection operators) that is:
Additive over mutually orthogonal outcomes,
Non-contextual,
Defined in dimension ,
For pure states and projectors , this yields:
Thus, the Born rule emerges as the unique consistent assignment under reasonable assumptions.
d.1 Addressing Hidden Assumptions and Critiques of Envariance
While envariance-based arguments (Zurek, 2003) claim to derive the Born rule without prior probabilistic postulates, several authors have pointed out that hidden assumptions remain embedded in the formalism. Notably:
Gleason’s dependence: The use of unitary symmetry in Hilbert spaces of dimension ≥3 implicitly invokes assumptions akin to those used in Gleason’s theorem (Gleason, 1957).
Critique by (Barnum, Caves, Finkelstein, Fuchs, & Schack, 2000): They highlight that even in envariant constructions, non-contextuality and additivity must be assumed to consistently assign probabilities across disjoint subspaces.
Assumption of continuity: Extending rational weights to irrational coefficients assumes continuity of probability assignments, which may not be derivable without extra axioms.
We acknowledge these critiques and clarify that while our argument follows Zurek’s envariance framework, it implicitly assumes:
Unitary equivalence implies equiprobability: This is not derived from first principles but taken as a symmetry-guided inference.
Contextual independence: Probabilities are assigned without influence from the experimental arrangement.
Continuity of probability assignments: The limit of fine-grained rational partitions is assumed to extend naturally to irrational amplitudes.
These assumptions align with the Gleason-Fuchs-Schack landscape, and while not strictly deductive, they represent the minimal structural commitments consistent with quantum theory’s statistical structure.
e. Maximum Entropy Argument (C5)
The density matrix has eigenvalues .
Suppose the observer knows only
but has no knowledge of the environment. The maximum entropy principle (Jaynes, 1957) states that among all probability distributions consistent with this constraint, the least biased is the one maximizing Shannon entropy:
Subject to:
This choice uniquely maximizes entropy and remains consistent with the known reduced state. Any deviation from either:
e.1 Informational Assumptions in Maximum Entropy Reasoning
The application of the MaxEnt principle (Jaynes, 1957) to quantum measurement assumes a specific informational context:
Epistemic limitation: The observer has complete knowledge of the reduced state but no access to the full system-environment entangled state .
Inferential neutrality: Among all probability distributions consistent with the eigenvalues of , the least-biased choice is the one maximizing Shannon entropy .
Consistency with reduced spectrum: The observer accepts as the marginal constraint on outcome statistics.
No preferred basis beyond decoherence: The pointer basis is selected by environment-induced decoherence; no hidden variables or measurement postulates are invoked.
Additivity and normalization: Probabilities are additive and normalized, consistent with classical probability theory embedded within quantum state assignments.
Together, these define the MaxEnt inferential framework. While not axiomatic in quantum theory itself, these are widely adopted principles in statistical inference and are indispensable for a Bayesian treatment of quantum measurement. However, one must note that the MaxEnt argument assumes the spectrum of , which is itself derived from the Schmidt coefficients. Thus, MaxEnt confirms the Born rule as the least-biased assignment, but does not independently generate it.
f. Measurement Entropy and Born Rule Consistency (C6)
Measurement of
in its eigenbasis produces outcome probabilities
. The associated outcome entropy is:
This ensures consistency: no additional entropy arises, and the outcome entropy equals the state’s von Neumann entropy. If one assumed different , the measured entropy would exceed , contradicting known properties of entropy and state information.
g. Born Rule from Thermodynamic Irreversibility and Maximum Entropy (C7)
While the envariance-based approach captures core quantum symmetries elegantly, we now present a derivation of the Born rule that bypasses symmetry arguments altogether, grounding it in irreversibility and the epistemic constraints of observers within decohered subsystems.
g.1 Decoherence and Observer Knowledge
Consider a system
entangled with an environment
, yielding a reduced state:
The observer, embedded within the subsystem, has access to
but not the global entangled state
. Due to thermodynamic irreversibility (
Appendix F), decoherence has rendered this state diagonal and incoherent in the pointer basis.
g.2 Measurement as Probabilistic Inference
The observer seeks to assign classical outcome probabilities to measurement results . Their assignment must:
Match the decohered state’s spectrum:
Reflect the loss of coherence and knowledge about global correlations
Maximize inferential neutrality (least bias)
g.3 Entropic Inference
By the principle of maximum entropy (Jaynes, 1957), the observer should choose the probability distribution that maximizes: subject to
This uniquely yields:
No other probability assignment:
Maximizes entropy under the observer’s constraints
Is consistent with the pointer-basis decohered state
Respects the thermodynamic irreversibility locking these weights in the environment.
g.4 Collapse and Born Rule as Thermodynamic Consequences
Once coherence is irreversibly lost, i.e., when environmental entropy production (see Eq. 9), the observer must treat as a classical probability distribution. The only consistent and unbiased assignment is:
Thus, the Born rule follows not from symmetry or postulate, but from:
Irreversibility of environmental record formation
Inaccessibility of off-diagonal information
Entropy-maximizing inference under epistemic constraints.
Thus, the Born rule can be derived through multiple, mutually reinforcing routes. While envariance captures the role of quantum symmetries and equivalence classes, an independent derivation rooted in thermodynamic irreversibility and informational constraints (see Section C.g) provides a robust, symmetry-independent foundation. Both approaches converge on the conclusion that emerges naturally from the structure of quantum theory once decoherence and entropy production render the quantum amplitudes classically accessible.
Appendix D
Appendix D1. Wigner’s Friend Thought Experiment
We present a minimal model to illustrate the observer-relative nature of collapse and its resolution within the entropy-based decoherence framework. Let
be a qubit system in the initial superposition:
. Let
be the “friend” (the measuring agent), modeled by a memory qubit
, and let
denote the lab environment (a large heat bath or field system). At
, the total state is:
Friend’s Measurement: Entanglement without Decoherence: The friend performs a projective measurement in the basis and records the result in . The system and memory become entangled: .
At this stage, the environment has not yet interacted with ; no decoherence or entropy production has occurred. The memory is in a coherent superposition.
Decoherence via Environment Coupling: Now, the friend’s record is written to a macroscopic system, e.g., a notebook or photon field, modeled by the interaction of
with
, producing decoherence:
Where:
and (large irreversible entropy).
Quantum discord between and has vanished: ,
The reduced state of the system is now a classical mixture in the basis
From Friend’s perspective, this constitutes a definite outcome: they have a stable memory and feels as if collapse has occurred.
Wigner’s Perspective: Reversibility in Principle: From Wigner’s perspective, who has not interacted with , , or , the global state remains pure. In principle, Wigner could perform a global unitary operation: .
But this would require a perfect access to the full entangled environment and reversing an enormous amount of entropy ; which is practically impossible.
Therefore, in practice, Wigner also sees decoherence: he treats the lab as in a statistical mixture, and when he measures in the basis , he obtains outcome “0” or “1” with equal probabilities .
Reversible Scenario: No Decoherence: Suppose now that the environment interaction never occurred; i.e., the memory remains coherent:
Then Wigner can, in principle, apply a unitary:
This would erase the friend’s memory and restore full quantum coherence to . Wigner could then observe interference by measuring in the , basis and obtain deterministically.
In this case, Friend never had a definite classical memory. Their “experience” was in a quantum superposition and would not persist under erasure. No contradiction arises.
Resolution of the Paradox: Thus, we obtain a consistent, entropy-based resolution to the Wigner’s Friend paradox:
If decoherence has occurred (large ), both Friend and Wigner observe definite outcomes and agree statistically.
If decoherence has not occurred, then coherence is recoverable and Wigner can observe interference, but Friend's memory was not classical.
The collapse is relative:
Friend’s collapse occurs when her memory becomes thermodynamically stable (at ),
Wigner’s collapse occurs when he interacts with the system (e.g., measures ) or decoheres with it indirectly.
Before that, Wigner can treat the situation as fully quantum, but practical limitations due to entropy make interference retrieval infeasible.
Implications: Collapse is not an absolute event, but a frame-dependent, entropy-constrained update. The “paradox” only arises if one assumes objective, universal collapse. In our interpretation:
Facts are relative: they emerge through irreversible entanglement and decoherence.
Memory stability (as enforced by Landauer’s principle and
Appendix B) is what determines whether a measurement record is “real”.
No conflict arises between Wigner and Friend as each updates their state of knowledge based on their respective causal histories and interactions.
This example demonstrates that wavefunction collapse is not a mystery, it is a thermodynamically emergent phenomenon.
Appendix E
Appendix E1. Additional Notes on Relational and QBist Interpretations
This appendix clarifies how the present framework relates to existing interpretations of quantum mechanics, particularly Relational Quantum Mechanics (RQM) and Quantum Bayesianism (QBism). We highlight points of agreement, divergence, and integration, especially in light of the entropy-based collapse criterion proposed throughout this work.
Relational QM (Rovelli): Relational Quantum Mechanics (RQM) holds that the quantum state of a system has no absolute meaning, its properties exist only relative to another system (e.g., an observer or another physical entity). Our interpretation shares this relational ethos: the collapse of the wavefunction is not absolute, but relative to an observer’s causal or thermodynamic frame. Specifically, we propose that:
Collapse occurs for a given observer when they interact with a system in such a way that irreversible entropy is generated.
Observers who are spacelike-separated (e.g., in Wigner’s Friend setups) may assign different states to the same system, without contradiction, as long as no communication or interaction has occurred.
Agreement between observers is achieved once their light cones intersect and sufficient entropy has rendered the event irreversible and publicly accessible.
While RQM allows differing observer perspectives, it lacks a physical criterion for when those perspectives must align. Our framework fills this gap by identifying thermodynamic irreversibility (quantified by environmental entropy ) as the intersubjective alignment condition: “Once entropy exceeds a threshold (e.g., , all subsequent observers interacting with the system will converge on the same effective classical outcome.” This contribution adds a dynamical, physical grounding to the otherwise purely perspectival formulation of RQM.
QBism (Quantum Bayesianism): QBism interprets quantum states as expressions of personal degrees of belief, and wavefunction collapse as Bayesian updating based on new measurement outcomes. Importantly, that the wavefunction is not objective; it is an agent-specific informational tool, and there is no universal wavefunction, and no absolute measurement outcome independent of the observer.
We share QBism’s insight that collapse is epistemic, it reflects an observer’s updated knowledge upon acquiring outcome information. From our perspective: The quantum state for an observer before collapse represents their uncertainty over possible outcomes, and upon observing a thermodynamically irreversible event (i.e., one where ), the observer updates their state to reflect a definite outcome.
Unlike QBism, we posit the existence of a global, ontic wavefunction that evolves unitarily and objectively. Furthermore, while QBism accepts subjective disagreement between agents indefinitely, we argue that once an outcome is recorded in an irreversible thermodynamic record, it becomes accessible and agreeable to all future observers within the same causal branch. Thus, although each observer collapses the wavefunction individually, consensus emerges through shared access to the same entropic records. In this way, our framework retains a weak objectivity that QBism discards.
In short, our interpretation could be seen as a middle ground: collapse is epistemic (knowledge-update, observer-dependent) as in QBism/Relational, but the wavefunction and unitary evolution is ontic and universal as in Many-Worlds. The bridge between the two is provided by irreversible thermodynamics, ensuring classical reality emerges in a way all can agree on, thereby giving the appearance of an objective classical world.
Appendix F
Appendix F1. Extended Derivation and Applications of the Entropy-Coherence Inequality (Supplement to Appendix A)
This appendix provides a detailed elaboration of the entropy-coherence inequality derived in
Appendix A, formalizing the result:
and visualizing its consequences. The plot below illustrates how the upper bound on quantum coherence
decreases exponentially with the environment’s entropy production
(measured in units of Boltzmann’s constant
).
In
Figure 5: The x-axis the entropy generated in the environment
(in units of
). The y-axis is the upper bound on coherence
, defined by the trace-norm distance from the fully dephased state. The orange curve plots the primary inequality. The red vertical line indicates the minimum entropy increase associated with a Landauer bit-flip:
, below which full classical definiteness may not yet emerge. The gray horizontal line at
marks a mid-coherence benchmark for visual reference (Landauer crossover).
We will now proceed with a rigorous derivation of the entropy-coherence inequality:
a. Trace-Norm Contractivity under CPTP Maps
Let:
be the initial quantum state (assumed pure and coherent in the pointer basis).
be the fully dephased version of in pointer basis (retaining only diagonal elements).
: a trace-norm measure of coherence.
be a completely positive trace-preserving (CPTP) map describing open system dynamics (e.g., Lindblad evolution).
be the entropy irreversibly produced in the environment by time due to , measured in units of unless otherwise specified.
Moreover, if
is entropy-generating (i.e.,
), then motivated by fluctuation-theoretic arguments (see Theorem A.6), the coherence satisfies:
Proof:
Trace distance is contractive under CPTP maps:
Let , then:
Assume incoherence preservation:
, we obtain:
To refine this bound, we appeal to fluctuation theorems such as the Crooks relation (Theorem A.6), which imply that entropy-reducing recoherence trajectories are exponentially suppressed in
. Thus, we obtain:
This inequality captures the practical irreversibility of decoherence and thermodynamically explains the suppression of recoherence, reinforcing the emergence of classical definiteness.
This strengthened inequality is heuristically supported by quantum fluctuation theorems, which indicate that recoherence (i.e., entropy-reducing fluctuations) are exponentially suppressed in the amount of entropy . Consequently, coherence loss becomes practically irreversible beyond a certain entropy threshold, grounding the effective emergence of wavefunction collapse in thermodynamic terms.
b. Resource-Theoretic Derivation via Rényi Coherence
We now formalize an alternative derivation of the entropy-coherence inequality using tools from quantum resource theory.
Let
be a density matrix acting on Hilbert space
𝓗, and fix a reference basis
. The Rényi-α coherence is defined as:
Where is the von Neumann entropy and is the dephased state in the pointer basis.
Theorem F.2 (Coherence-Entropy Tradeoff under Incoherent Operations)
Let be a completely positive trace-preserving (CPTP) map that satisfies:
Then the relative entropy of coherence satisfies:
Proof:
Monotonicity: Under incoherent operations, coherence cannot increase:
Total entropy production (by second law):
Expanding the coherence difference:
Assuming incoherence preservation, i.e.,
, this reduces to:
Hence, combining with the second law:
This inequality reveals that coherence is not merely dissipated; it is converted into entropy via irreversible system-environment coupling. As the system loses quantum coherence under entropy-generating evolution, the environment must gain an equivalent amount of entropy, upholding thermodynamic consistency. Unlike Theorem A.4, which focuses on trace-norm coherence, this formulation leverages relative entropy of coherence to show the quantitative equivalence between coherence loss and entropy gain in the environment.
c. Crooks Fluctuation Theorem and Coherence Loss
ci. Definitions of Forward and Reverse Protocols
We begin by defining explicitly the forward and reverse protocols required for applying fluctuation theorems to open quantum measurement dynamics.
Forward Protocol: Consider a quantum measurement scenario in which an initially isolated system-plus-apparatus state undergoes unitary evolution and subsequent coupling to a thermal environment at temperature . This interaction produces an entropy increase . Formally, the forward process protocol can be described as: , where is the initial thermal equilibrium state of the environment at temperature and is the global unitary evolution.
-
Reverse Protocol: The reverse process is defined by starting from the final system-apparatus-environment state obtained from the forward protocol, , and applying the time-reversed unitary evolution , reverting the system back toward its initial state:
cii. Conditions for Fluctuation Theorems: Microscopic Reversibility and Ensemble Definitions
To apply Crooks' fluctuation theorem rigorously, we explicitly state the following assumptions and conditions:
-
Microscopic Reversibility: The total system-apparatus-environment Hamiltonian
must be time-reversal symmetric, ensuring detailed balance at the microscopic level. Formally, this condition require:
where denotes the time-ordering (anti-time ordering) operator.
Thermal Equilibrium Environment and Initial Ensemble: The environment is initially in thermal equilibrium at temperature , described by the Gibbs state: , where is the environment Hamiltonian.
The ensemble considered is a canonical ensemble, where fluctuations are naturally defined around thermal equilibrium. This provides a rigorous thermodynamic context for fluctuation theorems.
- 3.
System-Bath Interaction and Markovian Limit: The dynamics after partial tracing over the environment are effectively Markovian, allowing a Lindblad master equation approximation for the reduced system-apparatus state . The Lindblad form arises naturally when the environment correlation time is much shorter than system timescales. (Breuer & Petruccione, 2002)
Derivation of the Entropy-Coherence Bound via Crooks' Theorem
Under these explicit conditions, Crooks' theorem states that the ratio of probabilities for forward and reverse trajectories
that produce and consume entropy
respectively is given by:
Integrating over all trajectories with entropy production
, the average remaining coherence at time
, measured by trace-norm distance from the fully decohered state, rigorously satisfies:
assuming the initial coherence
is maximal and that coherence monotonically decreases under the forward protocol.
Applicability Limits and Physical Interpretations
The derived inequality relies explicitly on several critical assumptions whose limits of applicability must be clarified:
Markovian approximation: The Lindblad description and resulting inequality hold strongly in the Markovian regime (environment correlation times shorter than system timescales). For non-Markovian environments, deviations might occur, necessitating more refined formalisms.
Finite-dimensional Hilbert spaces: While the inequality generalizes well, its exact exponential form is strictly valid for finite-dimensional or effectively finite-dimensional Hilbert spaces. Infinite-dimensional generalizations require careful treatment and potentially modified inequalities.
Thermodynamic limit and typicality: Fluctuation theorems strictly require thermodynamic or statistical ensembles with many degrees of freedom. The exponential suppression becomes exact in large ensembles, while finite-size corrections might appear otherwise.
d. Lindblad Dynamics Example (Microscopic Model)
We now demonstrate that the entropy-coherence inequality derived in
Appendix A is not only theoretically robust but is also saturated in concrete microscopic models of open quantum systems.
Consider a quantum system
undergoing collisional decoherence or optical decoherence through repeated interactions with environmental particles (e.g., gas molecules or photons). In such models, the system’s reduced dynamics are governed by a Markovian Lindblad master equation, and the quantum coherence decays exponentially:
where:
: A measure of quantum coherence at time (e.g., of coherence or visibility).
: The decoherence rate, determined by properties of the system-environment interaction.
In standard models (e.g., Joos-Zeh, Zurek, Romero-Isart), the decoherence rate
depends on environmental parameters as:
n: Number density of environmental particles (e.g., gas molecules)
: Effective scattering cross-section
: Mean thermal velocity of the environment particles.
This proportionality reflects the collision rate between the system and its environment, each collision carries information that may leak into the environment, reducing system coherence.
ssume that each decoherence-inducing collision produces entropy in the environment, and that the entropy production rate is approximately:
Integrating over time
, the total entropy produced in the environment becomes:
Substituting this into the coherence decay expression:
This yields the same exponential suppression as predicted by the entropy-coherence inequality:
is saturated in these microscopic Lindblad-type models. That is, the inequality becomes an equality under idealized but physically realizable conditions (weak coupling, Markovianity, negligible memory effects).
Remarks: This derivation confirms that the entropy-coherence tradeoff is not merely an upper bound but is exactly realized in certain regimes. The decoherence rate Γ directly governs both coherence loss and entropy production, cementing the thermodynamic interpretation of wavefunction collapse. In non-Markovian or strongly coupled systems, deviations may arise, but in the weak coupling limit, the exponential coherence suppression matches the entropy increase precisely.
Glossary of Terms
1. Apparatus (M): A physical system that acts as the measurement device or observer’s memory register. During measurement, it becomes entangled with the quantum system (S) and records the outcome in a specific basis (the pointer basis).
2. Born Rule: The quantum rule stating that the probability of an outcome i in a measurement is given by where is the amplitude of the corresponding eigenstate. In this paper, the Born rule is derived using envariance symmetry and maximum entropy inference, rather than postulated axiomatically.
3. Collapse (Wavefunction Collapse): In this framework, collapse is not a fundamental or dynamical process but an emergent thermodynamic transition. It occurs when sufficient entropy is produced in the environment to make interference practically irrecoverable. The wavefunction remains globally unitary but becomes effectively classical due to irreversibility.
4. Collapse Threshold () [also: Critical Entropy]: The minimum environmental entropy required to render a measurement outcome effectively irreversible. Typically, .
5. Coherence (Quantum Coherence): A measure of the quantum superposition retained by a system. Defined as: where is the diagonalized (dephased) state in the pointer basis. This trace-norm distance quantifies how far the state deviates from being classical.
6. CPTP Map (Quantum Channel): A Completely Positive Trace-Preserving map describing reduced, open-system dynamics. It ensures physical consistency and models decoherence after tracing out the environment.
7. Decoherence: The process by which a quantum system loses coherence due to entanglement with the environment. This turns pure superpositions into classical mixtures by suppressing off-diagonal elements in the reduced density matrix. However, decoherence alone does not imply collapse, an additional criterion (entropy production) is required for irreversibility.
8. Effective Collapse: Collapse that occurs For All Practical Purposes (FAPP), when coherence is so reduced by entropy production that interference is empirically irretrievable.
9. Envariance (Environment-Assisted Invariance): A symmetry principle introduced by Zurek. It holds that the reduced state of a system entangled with an environment remains invariant under certain transformations. This principle supports the derivation of the Born rule from entanglement symmetry.
10. Entropy (Quantum Entropy): Measured via the von Neumann formula: . It quantifies uncertainty or mixedness of a quantum state. See also: Environmental Entropy, Entanglement Entropy, and Thermodynamic Entropy.
11. Entropy in Quantum Systems:
Von Neumann Entropy: Measures uncertainty in a quantum state.
Environmental Entropy (): Entropy irreversibly gained by the environment due to measurement.
Entanglement Entropy: For pure states, the entropy of a subsystem, equal to its partner's entropy.
12. Entropy-Coherence Inequality: Central formal result of this paper: , establishing that quantum coherence decays exponentially with environmental entropy.
13. Entropy Production () [also: Environmental Entropy]: The irreversible increase in entropy within the environment due to system-environment interaction, signaling practical irreversibility.
14. Fluctuation Theorems: Theorems such as Crooks’ and Jarzynski’s that relate forward and reverse entropy trajectories. They justify why recoherence becomes exponentially improbable as grows.
15. FAPP (For All Practical Purposes): A standard phrase in quantum foundations indicating that a theoretical process (e.g., recoherence) is so unlikely that it can be ignored in practice.
16. Gleason’s Theorem: A mathematical result showing that, under minimal assumptions, the only consistent probability assignment for quantum measurements in Hilbert space is
17. Irreversibility (Thermodynamic): A process is irreversible if entropy increases and cannot be reversed without external work. It marks the practical boundary between quantum possibilities and classical outcomes.
18. Lindblad Equation: A general form of the master equation describing the non-unitary evolution of open quantum systems: , where is the dissipator representing decoherence. Used to model irreversible system-environment dynamics.
19. Measurement: A thermodynamically irreversible process in which a quantum system becomes entangled with an apparatus and decoheres through the environment, resulting in classically accessible outcomes.
20. Pointer Basis/Pointer States: The preferred set of orthonormal states in which the apparatus records measurement outcomes. These states are robust under environmental decoherence and define the classical record of a quantum measurement.
21. Purity: Given by , this quantity measures how mixed or coherent a quantum state is. A pure state has purity = 1; a maximally mixed state has lower purity. It is used in alternative derivations of coherence suppression.
22. Quantum Channel: A mathematical representation (CPTP map) of the evolution of a quantum system under noise, decoherence, or measurement.
23. Quantum Darwinism: A framework (Zurek, 2009) in which the environment not only decoheres the system but also amplifies certain preferred states, making them redundantly accessible to multiple observers. This provides a partial resolution to the classicality of measurement outcomes.
24. Quantum Discord: A measure of quantum correlations beyond entanglement, quantifying the minimum disturbance induced by local measurement. Vanishes when system-environment correlations become classically accessible.
25. Quantum Eraser: An experimental protocol that reverses decoherence and restores interference by erasing which-path information from the environment.
26. Recoherence: The theoretical reversal of decoherence, restoring quantum coherence. In practice, this becomes exponentially improbable once the environment has acquired sufficient entropy, as quantified by fluctuation theorems.
27. Relative Entropy of Coherence: An alternative coherence measure given by: used in the resource-theoretic formulation to relate coherence loss to entropy gain.
28. Thermodynamic Collapse Criterion: The condition that a measurement leads to classical outcomes only when environmental entropy crosses a threshold, typically Collapse is therefore emergent, not fundamental, and governed by the laws of thermodynamics.
29. Unitary Evolution: The reversible, deterministic evolution of a closed quantum system according to the Schrödinger equation.
30. Wigner’s Friend: A thought experiment illustrating observer-dependent collapse. This paper resolves it by framing collapse as an entropy-bound, observer-relative event.
References
- Arndt, M., & Gerlich, S. (2019). Quantum superposition of molecules beyond 25 kDa. Nature Physics, 15, 1242-1245. [CrossRef]
- Aspelmeyer, M., Kippenberg, T. J., & Marquardt, F. (2014). Cavity optomechanics. Reviews of Modern Physics, 86(4), 1391-1452. [CrossRef]
- Barnum, H., Caves, C. M., Finkelstein, J., Fuchs, C. A., & Schack, R. (2000). Quantum probability from decision theory? Proceedings of the Royal Society A Marthematical, Physical and Engineering Sciences, 456, 1175-1182. [CrossRef]
- Barzanjeh, S., Xuereb, A., Gröblacher, S., Regal, C. A., Paternostro, M., & Weig, E. M. (2022). Optomechanics for quantum technologies. Nature Physics, 18, 15-24. From https://www.nature.com/articles/s41567-021-01402-0.
- Bassi, A., Dorato, M., & Ulbricht, H. (2023). Collapse models: A theoretical, experimental and philosophical review. Entropy, 25(4), 645. [CrossRef]
- Bassi, A., Lochan, K., Satin, S., Singh, T. P., & Ulbricht, H. (2013). Models of wave-function collapse, underlying theories, and experimental tests. Reviews of Modern Physics, 85(2), 471-527. [CrossRef]
- Baumgratz, T., Cramer, M., & Plenio, M. B. (2014). Quantifying Coherence. Physical Review Letters, 113(14). From https://arxiv.org/abs/1311.0275.
- Bell, J. (1990). Against 'measurement'. Phys. World, 3(8), 33. [CrossRef]
- Boltzmann, L. (1909). Wissenschaftliche Abhandlungen. From https://archive.org/details/wissenschaftlich0000bolt/page/n5/mode/2up.
- Bong, K. W., Utreras-Alarcón, A., Ghafari, F., Liang, Y. C., Tischler, N., Cavalcanti, E. G., . . . Wiseman, H. M. (2020). A strong no-go theorem on the Wigner’s friend paradox. Nature Physics, 16(12), 1199-1205. [CrossRef]
- Brandão, F. G., Horodecki, M., Ng, N. H., Oppenheimer, J., & Wehner, S. (2015). The second laws of quantum thermodynamics. Proceedings of the National Academy of Sciences, 112(11), 3275-3279. [CrossRef]
- Breuer, H., & Petruccione, F. (2002). The Theory of Open Quantum Systems. Oxford University Press. [CrossRef]
- Campisi, M., Hänggi, P., & Talkner, P. (2011). Colloquium: Quantum fluctuation relations: Foundations and applications. Reviews of Modern Physics, 83(3), 771-791. [CrossRef]
- Chang, D. E., Regal, C. A., Papp, S. B., Wilson, D. J., Ye, J., Painter, O., . . . Zoller, P. (2010). Cavity optomechanics using an optically levitated nanosphere. Proceedings of the National Academy of Sciences, 107(3), 1005-1010. [CrossRef]
- Combining stochastic dynamical state-vector reduction with spontaneous localization. (1989). Physical Review A, 39(5), 2277--2289. [CrossRef]
- Crooks, G. E. (1999). Entropy production fluctuation theorem and the nonequilibrium work relation for free energy differences. Physical Review E, 60(3), 2721-2726. [CrossRef]
- Deutsch, D. (1999). Quantum theory of probability and decisions. Proceedings of the Royal Society A, 455(1988), 1999. [CrossRef]
- Diósi, L. (1989). Models for universal reduction of macroscopic quantum fluctuations. Physical Review A, 40(3), 1165-1174. [CrossRef]
- Eberhard, P. H., & Ross, R. R. (1989). Quantum field theory cannot provide faster-than-light communication. Foundations of Physics Letters, 2, 127-149. From https://link.springer.com/article/10.1007/BF00696109.
- Esposito, M., Harbola, U., & Mukamel, S. (2009). Nonequilibrium fluctuations, fluctuation theorems, and counting statistics in quantum systems. Reviews of Modern Physics, 81(4), 1665-1702. [CrossRef]
- Everett, H. (1957). The Relative State Formulation of Quantum Mechanics. Reviews of Modern Physics, 29, 454-462. [CrossRef]
- Everett, H., Wheeler, J. A., DeWitt, B. S., Cooper, L. N., Van Vechten, D., & Graham, N. (1973). The Many Worlds Interpretation of Quantum Mechanics. Princeton University Press. From http://www.jstor.org/stable/j.ctt13x0wwk.
- Fuchs, C. A., & Schack, R. A. (2010). A Quantum-Bayesian Route to Quantum-State Space. Found Phys, 41, 345-356. [CrossRef]
- Fuchs, C. A., Mermin, N. D., & Schack, R. (2014). An introduction to QBism with an application to the locality of quantum mechanics. American Journal of Physics, 82(8), 749-754. [CrossRef]
- Gasbarri, G., Belenchia, A., Carlesso, M., Donadi, S., Bassi, A., Kaltenbaek, R., . . . Ulbricht, H. (2021). Testing the foundations of quantum physics in space: Interferometric and non-interferometric tests with large particles. Communications Physics, 4(155). From https://www.nature.com/articles/s42005-021-00656-7.
- Ghirardi, G. C., Rimini, A., & Weber, T. (1986). Unified dynamics for microscopic and macroscopic systems. Physical Review D, 34(2), 470-491. [CrossRef]
- Ghose, P., & Home, D. (1991). Manifestly Lorentz covariant formulation of the Einstein-Podolsky-Rosen problem using the Tomonaga-Schwinger formalism. Physical Review A, 43. From https://journals.aps.org/pra/abstract/10.1103/PhysRevA.43.6382.
- Gleason, A. M. (1957). Measures on the Closed Subspaces of a Hilbert Space. Journal of Mathematics and Mechanics, 6(6), 885-893. From https://www.jstor.org/stable/24900629.
- Hance, J. R., & Hossenfelder, S. (2022). What does it take to solve the measurement problem? Journal of Physics Communications, 6(10). [CrossRef]
- Jarzynski, C. (1997). Nonequilibrium equality for free energy differences. Physical Review Letters, 78(14), 2690-2693. [CrossRef]
- Jaynes, E. T. (1957). Information Theory and Statistical Mechanics. Physical Review, 106(4), 620-630. [CrossRef]
- Jennings, D., & Rudolph, T. (2010). Entanglement and the thermodynamic arrow of time. Physical Review E, 81(6). [CrossRef]
- Joos, E., & Zeh, H. D. (1985). The emergence of classical properties through interaction with the environment. Zeitschrift für Physik B Condensed Matter, 59(2), 223-243. [CrossRef]
- Joos, E., Zeh, H. D., Kiefer, C., Giulini, D. J., Kupsch, J., & Stamatescu, I. O. (2003). Decoherence and the Appearance of a Classical World in Quantum Theory (2nd edition ed.). Springer. [CrossRef]
- Kim, Y.-H., Yu, R., Kulik, S. P., Shih, Y., & Scully, M. O. (2000). A Delayed choice quantum eraser. Physical Review Letters, 84(1), 1-5. [CrossRef]
- Landauer, R. (1961). Irreversibility and heat generation in the computing process. IBM Journal of Research and Development, 5(3), 183-191. [CrossRef]
- Lostaglio, M., Jennings, D., & Rudolph, T. (2015). Description of quantum coherence in thermodynamic processes requires constraints beyond free energy. Nature Communications, 6, 6383. [CrossRef]
- Maudlin, T. (2011). Quantum Non-Locality and Relativity: Metaphysical Intimations of Modern Physics. [CrossRef]
- Modi, K., Brodutch, A., Cable, H., Paterek, T., & Vedral, V. (2012). The classical-quantum boundary for correlations: Discord and related measures. Reviews of Modern Physics, 84(4), 1655-1707. [CrossRef]
- Ollivier, H., & Zurek, W. H. (2001). Quantum Discord: A Measure of the Quantumness of Correlations. Physical Review Letters, 88. [CrossRef]
- Pearle, P. (1989). Combining stochastic dynamical state-vector reduction with spontaneous localization. Physical Review A, 39(5), 2277. [CrossRef]
- Penrose, R. (1996). On Gravity's role in Quantum State Reduction. General Relativity and Gravitation, 28(5), 581-600. [CrossRef]
- Proietti, M., Pickston, A., Graffitti, F., Barrow, P., Kundys, D., Branciard, C., . . . Fedrizzi, A. (2019). Experimental test of local observer-independence. Science Advances, 5(9). From https://www.science.org/doi/10.1126/sciadv.aaw9832.
- Romero-Isart, O., Pflanzer, A. C., Blaser, F., Kaltenbaek, R., Kiesel, N., Aspelmeyer, M., & Cirac, J. I. (2011). Large quantum superpositions and interference of massive nanometer-sized objects. Physical Review Letters, 107. [CrossRef]
- Rovelli, C. (1996). Relational quantum mechanics. International Journal of Theoretical Physics, 35, 1637-1678. From https://link.springer.com/article/10.1007/BF02302261.
- Schlosshauer, M. (2005). Decoherence, the measurement problem, and interpretations of quantum mechanics. Reviews of Modern Physics, 76(4), 1267-1305. [CrossRef]
- Schwinger, J. (1948). Quantum electrodynamics. I. A covariant formulation. Physical Review, 74(10), 1439-1461. [CrossRef]
- Shabani, A., & Lidar, D. A. (2009). Vanishing quantum discord is necessary and sufficient for completely positive maps. Physical Review Letters, 102(10). [CrossRef]
- Spohn, H. (1978). Entropy production for quantum dynamical semigroups. Journal of Mathematical Physics, 19(5), 1227-1230. [CrossRef]
- Streltsov, A., Adesso, G., & Plenio, M. B. (2017). Colloquium: Quantum coherence as a resource. Reviews of Modern Physics, 89(4). [CrossRef]
- Streltsov, A., Singh, U., Dhar, H. S., Bera, M. N., & Adesso, G. (2015). Measuring quantum coherence with entanglement. Physical Review Letters, 115(2). [CrossRef]
- Taylor, E. F., & Wheeler, J. A. (1992). Spacetime Physics (2 ed.). New York. From https://www.eftaylor.com/special.html.
- Tomonaga, S. (1946). On a relativistically invariant formulation of the quantum theory of wave fields. Progress of Theoretical Physics, 1(2), 27-42. [CrossRef]
- Vedral, V. (2002). The role of relative entropy in quantum information theory. Reviews of Modern Physics, 74(1), 197-234. [CrossRef]
- von Neumann, J. (1932). Mathematical Foundations of Quantum Mechanics. Princeton University Press. [CrossRef]
- von Neumann, J. (1955). Mathematical foundations of quantum mechanics (R. T. Beyer, Trans.). Princeton: Princeton University Press. doi:ISBN: 9780691178561.
- Walborn, S. P., Terra Cunha, M. O., Pádua, S., & Monken, C. H. (2002). Double-slit quantum eraser. Physical Review A, 65(3). [CrossRef]
- Wallace, D. (2012). The Emergent Multiverse: Quantum Theory according to the Everett Interpretation. [CrossRef]
- Zeh, H. D. (1970). On the interpretation of measurement in quantum theory. Foundations of Physics, 1(1), 69-76. [CrossRef]
- Zurek, W. H. (2003). Decoherence, einselection, and the quantum origins of the classical. Reviews of Modern Physics, 75(3), 715-775. [CrossRef]
- Zurek, W. H. (2005). Probabilities from entanglement, Born’s rule from envariance. Physical Review A, 71(5). [CrossRef]
- Zwolak, M., Riedel, C. J., & Zurek, W. H. (2016). Amplification, decoherence and the acquisition of information by spin environments. Scientific Reports, 6. From https://www.nature.com/articles/srep25277.
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).