Theoretical Modeling and Geometric Optimization of Flat Sieves for Grain Mixture Separation

1. Introduction

From a physical standpoint, the grain separation process in mechanical separators occurs in the same manner—the grain first passes through the spatial grid of the separation layer and then through the planar grid of the separator. This provides grounds to assume that separation in such separators can be described by the same relationship, which several studies have established to be of an exponential nature [1,2,3,4,5].

This type of relationship highlights the high sensitivity of the separation process to the length of the separators. In reality, the process occurs across the entire working surface of the separator, justifying the need to find a relationship that simultaneously describes the process along both the length and width of the separator. Determining such a relationship will enable the optimization of the separator's geometric dimensions so that its separation capability and operational quality are as high as possible under given conditions.

Optimizing the working process of any machine is a prerequisite for increasing its efficiency. In this regard, the separation process of grain mixtures heavily depends on the geometric dimensions and shape of the separator. The aforementioned factors are decisive for the grain mixture separation process and the associated separation coefficient along the length (μₓ) and separation coefficient over the area (μₓᵧ).

The possible interrelation between the two coefficients would enable either one to be used with equal precision in determining the allowable grain losses from the separator.

2. Materials and Methods

The separation coefficient μ(x), which defines the performance of a separator, is inherently variable along its length under identical operating conditions [1,4]. Physically, μ(x) quantifies the probability of an individual grain particle being sieved over a unit-length segment, as given by the formula:

$$\mu \left(x\right)={\displaystyle \frac{q}{y.∆x}}=-{\displaystyle \frac{∆y}{y.∆x}},$$

(1)

where, the ratio ${\displaystyle \frac{q}{y}}$ represents the statistical (experimental) probability of a single grain being sieved through a section of length $∆x$

$q$ is the quantity of grain sieved in a section of length $∆x$;

$y$ is the quantity of unsieved but separable grain.

From equation (1), the differential equation of the sieving process along the length of mechanical separators is derived [1,3]:

$${\displaystyle \frac{dy}{dx}}=-\mu \left(x\right).y,$$

(2)

After integration, it takes the form:

$$y=e^{-\int \mu \left(\mathrm{х}\right).dx},$$

(3)

Taking into account the initial condition (y = a, where a is the quantity of separable grain at the beginning of the separator, i.e., x = 0), equation (3) becomes:

$$y=a.e^{-\phi \left(x\right)},$$

(4)

where $\phi \left(x\right)$ is a function related to the separation coefficient $\mu \left(x\right)$.

The presented relationships demonstrate that as the length of the separator increases and its separation efficiency improves, grain losses decrease significantly. This enhances the separation effect and, consequently, the operational quality of the separator.

However, the separation process must also be evaluated in terms of the geometric dimensions defining the separator's working area. This assertion is supported by the fact that separators of equal length may exhibit different separation coefficients due to variations in their widths, i.e., changes in the experimental probability of grain sieving.

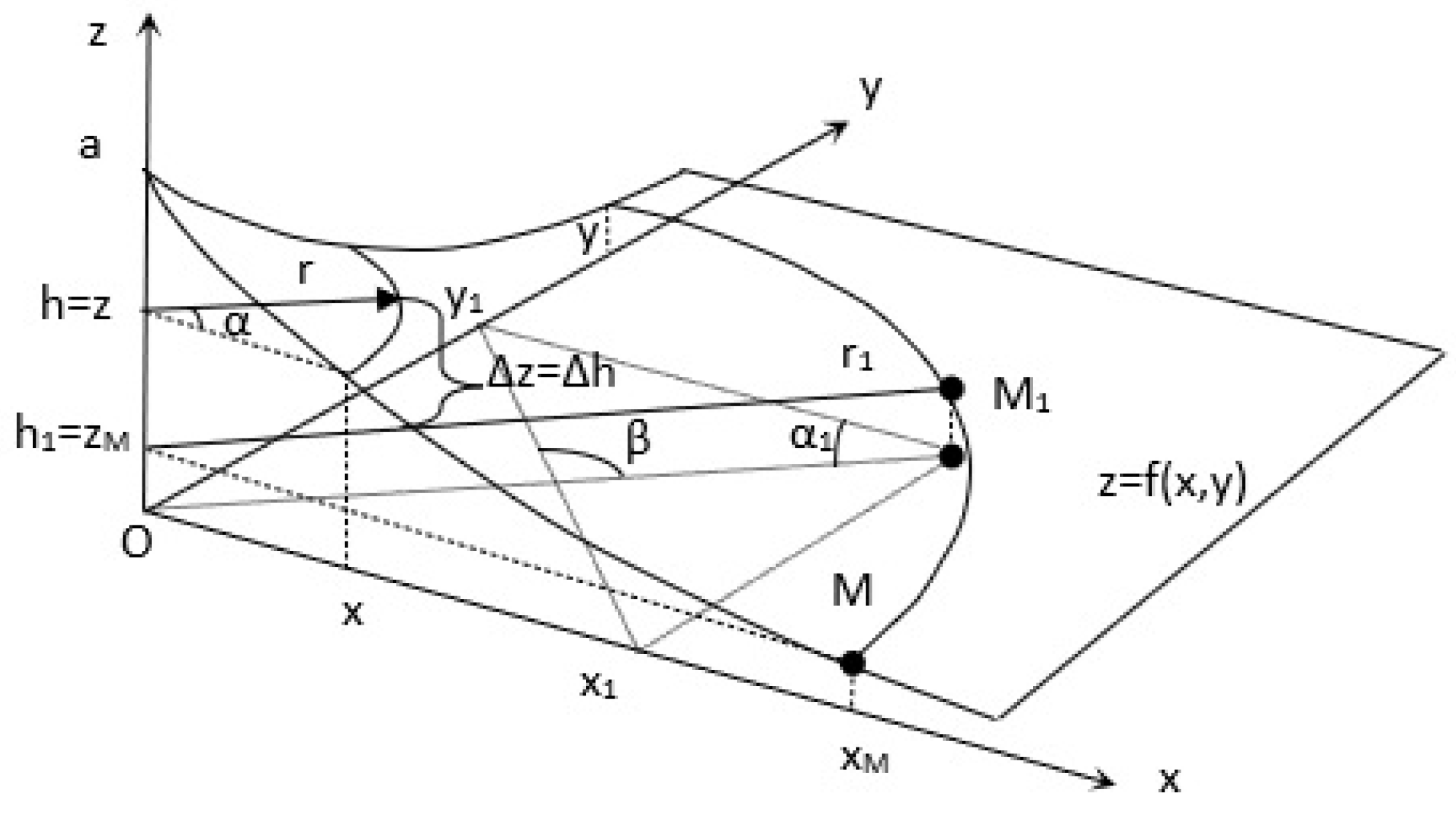
In three-dimensional space, the separation process can be represented by the nonlinear surface shown in Figure 1.

where:

x is the distance from the separator's inlet to any of its cross-sections;

y is the distance from the separator's inlet to any of its longitudinal sections;

z is the quantity of separable grain that has not been sieved through a section of length x;

x₁ and y₁ are Cartesian coordinates of point M₁;

r, α, h are cylindrical coordinates of a point on the surface with the function z = f(x, y);

r₁, α₁, h₁ are cylindrical coordinates of point M₁;

a is the quantity of separable grain fed at the separator's inlet (x = 0).

The curve z = f(x), lying in the Oxz plane, is described by a dependency of the form (4) and is considered the generatrix of the curvilinear surface representing the target function z = f(x, y).

An arbitrarily chosen point (M) on the generatrix, when rotated around the z-axis by an angle α = π/2, describes a circular arc. The position of a given point (M₁) along this arc can be determined using its cylindrical coordinates:

$$\left.\begin{array}{c}{r}_1=\sqrt{x_1^2+y_1^2}\\ \tan {\alpha }_1={\displaystyle \frac{y_1}{x_1}}\\ h_1=z_M\end{array}\right\}$$

(5)

The equality between coordinates $z_M$ and $h_1$ indicates that, regardless of the rotation angle α of the generatrix, the quantity of unsieved grain remains constant. This justifies the following equation:

$$\left.\begin{array}{c}\mu \left(x\right)=\mu \left(r\right)\\ -{\displaystyle \frac{∆z}{z.∆x}}=-{\displaystyle \frac{∆h}{h.∆r}}\end{array}\right\}$$

(6)

Therefore, for point M₁, expression (4) takes the form:

$$h_1=a.e^{-\phi \left(r\right)},$$

(7)

where $\phi \left(r\right)$ is a function related to the areal separation coefficient $\mu \left(r\right)$.

Let the Cartesian coordinates of the projection of point M₁ onto the Oxy plane define the geometric dimensions of the separator. The resulting figure has equal diagonals, each matching the cylindrical coordinate $r_1$. The sieving area of the separator is given by:

$$S={\displaystyle \frac{r_1^2}{2}}.\sin \beta ,$$

(8)

where $\beta$ is the angle between the diagonals.

Equation (7) justifies the conclusion that if changes in coordinates $x_1$ and $y_1$ y₁ do not alter coordinate $r_1$, the quantity of unsieved grain through the separator will remain constant. However, this will be accompanied by a change in the separator's working area, which according to equation (8) will be maximized at $\beta ={\displaystyle \frac{\pi }{2}}$. Therefore, a separator with a square-shaped working area will operate at maximum capacity while maintaining unchanged grain losses.

The presented relationships (5, 6, 7 and 8) demonstrate that the separation process in mechanical separators should be determined based on their working area, using the expression:

$$z=a.e^{-\mu \left(r\right).r}=a.e^{-\mu \left(xy\right).\sqrt{x^2+y^2}}$$

(9)

In this relationship, the coefficient $\mu \left(xy\right)$ remains constant under specific conditions ($r=\sqrt{x^2+y^2}=const$), while the coefficient $\mu \left(x\right)$ has been proven [4] to vary under these same conditions depending on $x$.

The determination of $\mu \left(xy\right)$ should be performed at the separator's maximum operating capacity, where grain losses do not exceed permissible limits. When determined this way, this coefficient enables optimization of the separator's geometric parameters.

The performance of mechanical separators is primarily characterized by grain losses at maximum productivity. It has been established that under conditions of constant specific area loading, a separator with a larger sieving area will be more productive. Among separators with equal diagonals, the one with a square shape will have the largest sieving area. The use of square-shaped separators is therefore recommended, with their dimensions considered optimal for quality separation of grain mixtures.

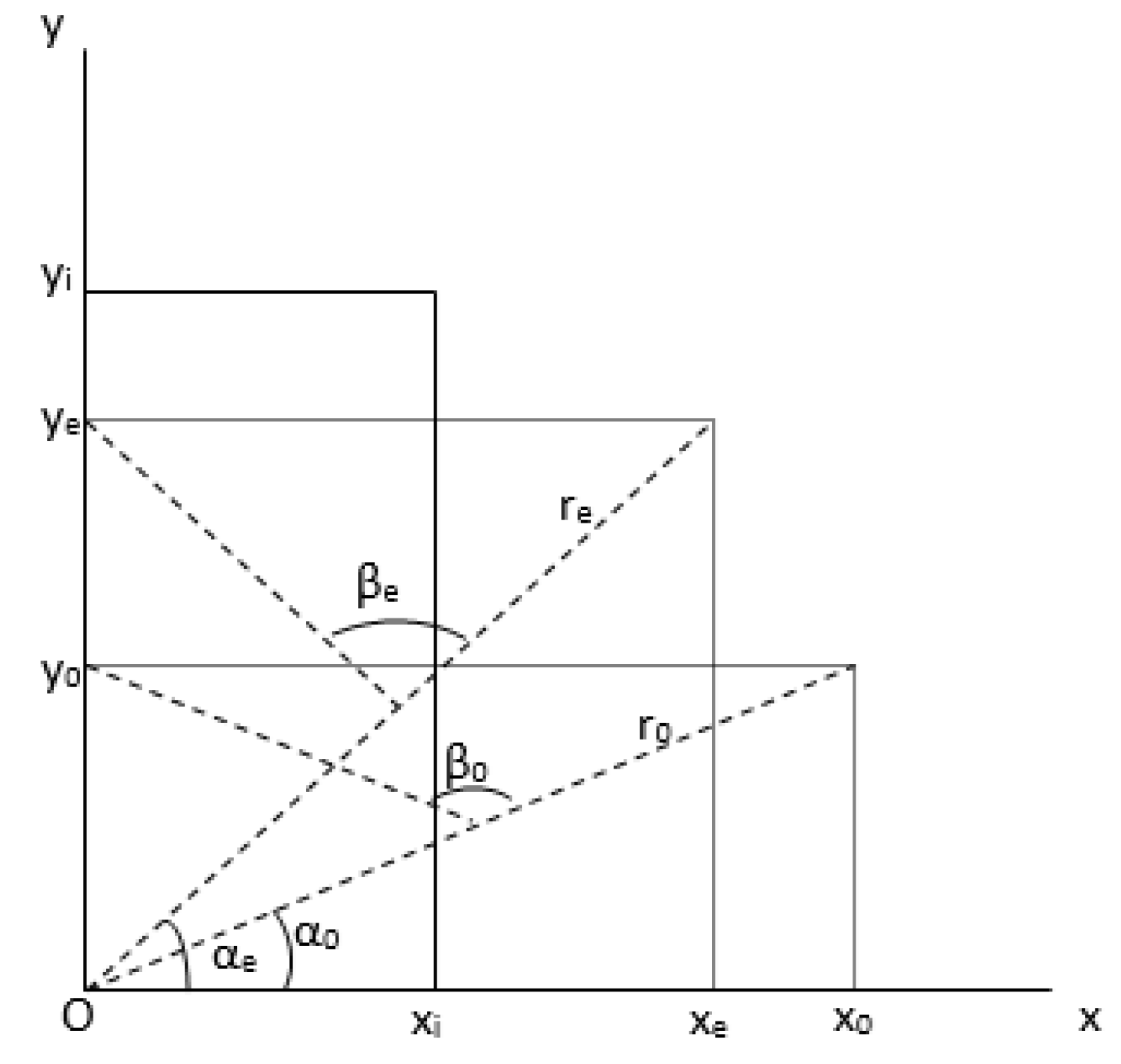
During the sieving process, the grain material moves toward the separator's end as a layer covering its entire working surface. Theoretically, it is reasonable to expect that grain losses would be identical whether determined by the length-based separation coefficient $\mu \left(x\right)$ or the area-based separation coefficient $\mu \left(xy\right)$. To verify this hypothesis, an approach comparing two flat sieves with different working surface shapes operating under identical conditions was used. One had a rectangular shape with dimensions x₀ and y₀, while the other was square-shaped with dimensions $x_{\mathrm{е}}$ and $y_{\mathrm{е}}$ (Figure 2).

Under specified initial operating conditions, the fundamental equation of the lengthwise sieving process for the rectangular sieve takes the form:

$$z_0=a.e^{-{\mu \left(x\right)}_0.x_0},$$

(10)

where:

${\mu \left(x\right)}_0$ is the length-based separation coefficient of the rectangular sieve (m⁻¹)

$x_0$ is the sieve length (m)

An identical structure applies to the fundamental sieving process equation expressed through the area-based separation coefficient. For the square sieve with dimensions $x_{\mathrm{е}}$ and $y_{\mathrm{е}}$, equation (10) becomes:

$$z_{\mathrm{е}}=a.e^{-{\mu \left(xy\right)}_e.r_{\mathrm{е}}},$$

(11)

where:

${\mu \left(xy\right)}_e$ is the area-based separation coefficient of the square sieve (m⁻¹)

$r_{\mathrm{е}}$ is the sieve diagonal (m)

When both sieves achieve identical grain losses under equal (technological and kinematic) conditions, their operational similarity can be established [6]. Here, the relative grain losses serve as the similarity criterion:

$${\pi }_1={\displaystyle \frac{z}{a}}=idem,$$

(12)

with the similarity indicator:

$${∆}_1=e^{-{\mu }_c.l_c}=1,$$

(13)

where:

${\mu }_c$ is the ratio of the sieves' separation coefficients

$l_c$ is the ratio of their linear dimensions (length to diagonal)

From these follows the equality:

$${\mu \left(x\right)}_0.x_0={\mu \left(xy\right)}_e.r_e$$

(14)

For both sides of this expression, the following similarity criterion applies:

$${\pi }_2=\mu .l=idem$$

(15)

with the similarity indicator:

$${∆}_2={\mu }_c.l_c=1$$

(16)

Consequently, for the right-hand side of equation (14), the following expression holds:

$${\mu \left(xy\right)}_0.r_0={\mu \left(xy\right)}_e.r_e,$$

(17)

where:

${\mu \left(xy\right)}_0$ is the area-based separation coefficient of the rectangular sieve (m⁻¹)

$r_0$ is the diagonal of the rectangular sieve (m)

By expressing the diagonal $r_0$ through the working surface area of the rectangular sieve, we obtain a relationship between its separation coefficients (length-based and area-based) in the general form:

$${\mu \left(x\right)}_0.x_0={\mu \left(xy\right)}_0.\sqrt{{\displaystyle \frac{2.S_0}{sin{\beta }_0}}},$$

(18)

where ${\beta }_0$ is the angle between the diagonals of the rectangular sieve. After algebraic transformations, this expression simplifies to:

$${\mu \left(x\right)}_0={\mu \left(xy\right)}_0.\sqrt{1+{tg}^2\left({\alpha }_0\right)},$$

(19)

where ${\mathsf{\alpha }}_0$ is the angle between the diagonal ${\mathrm{r}}_0$ and the sieve length ${\mathrm{x}}_0$ . The angle ${\mathsf{\alpha }}_0$ belongs to the interval $0÷{\displaystyle \frac{\mathsf{\pi }}{2}}$.

From equation (19), it is evident that across the entire range of angle ${\mathsf{\alpha }}_0$ variation, the coefficient ${\mu \left(xy\right)}_0$ will have a smaller value than coefficient ${\mu \left(x\right)}_0$.

After applying the similarity criterion π₂ to the left-hand side of equation (14) and performing transformations analogous to those for the rectangular sieve, we arrive at a similar relationship (19) but for the square sieve:

$${\mu \left(x\right)}_e={\mu \left(xy\right)}_e.\sqrt{1+{tg}^2\left({\alpha }_e\right)},$$

(20)

where:

${\mu \left(x\right)}_e$ is the length-based separation coefficient of the square sieve (m⁻¹)

${\alpha }_{\mathrm{е}}$ is the angle between the sieve's diagonal and its length (in degrees)

For sieves with equal diagonals, the relationship between their working areas is given by:

$${\displaystyle \frac{S_0}{S_e}}={\displaystyle \frac{\frac{r_0^2}{2}.\sin {\mathsf{\beta }}_0}{\frac{r_e^2}{2}.\sin {\beta }_e}}={\displaystyle \frac{\sin {\beta }_0}{\sin {\beta }_e}},$$

(21)

where ${\beta }_{\mathrm{е}}$ is the angle between the diagonals of the square sieve (in degrees).

The assumption that both sieves operate under equal loading conditions implies that the reciprocal of expression (21) represents the ratio of their specific area loadings:

$${\displaystyle \frac{q_{F0}}{q_{Fe}}}={\displaystyle \frac{\sin {\beta }_e}{\sin {\beta }_0}},$$

(22)

where:

$q_{F0}$ and $q_{Fe}$ are the specific area loadings of the rectangular and square sieves, respectively (kg/(s·m²))

${\beta }_0$ and ${\beta }_{\mathrm{е}}$ are the angles between the diagonals of the rectangular and square sieves, respectively

Expanding the left-hand side of (22) yields:

$${\displaystyle \frac{{\rho }_0.V_0.h_0.y_0.x_e.y_e}{{\rho }_e.V_e.h_e.y_e.x_0.y_0}}={\displaystyle \frac{\sin {\beta }_e}{\sin {\beta }_0}},$$

(23)

where:

${\rho }_0$ (${\rho }_{\mathrm{е}}$) = bulk density of the grain material on the rectangular (square) sieve (kg/m³)

$V_0$ ($V_e$) = material flow velocity across the rectangular (square) sieve (m/s)

$h_0$ ($h_e$) = grain layer height on the rectangular (square) sieve (m)

$x_0$ ($x_e$) = length of the rectangular (square) sieve (m)

$y_0$ ($y_e$) = width of the rectangular (square) sieve (m)

Since both sieves operate under identical conditions, the final form of equation (23) becomes:

$${\displaystyle \frac{h_0.x_e}{h_e.x_0}}={\displaystyle \frac{\sin {\beta }_e}{\sin {\beta }_0}}$$

(24)

This expression demonstrates how the grain layer height varies with changes in the sieve's working area and consequently with changes in their specific loading. Clearly, as the specific loading decreases, the layer height on the separator also decreases. This relationship can be expressed using the similarity criterion from literature [6]:

$${\pi }_3=\mu \left(x\right).h=idem$$

(25)

with the similarity indicator:

$${∆}_3={\displaystyle \frac{{\mu \left(x\right)}_0.h_0}{{\mu \left(x\right)}_e.h_e}}=1$$

(26)

(26)

Substituting equation (24) into the similarity indicator Δ₃ yields the relationship between the length-based separation coefficients of the two differently-shaped sieves:

$${\displaystyle \frac{{\mu \left(x\right)}_0.x_0.\sin {\beta }_e}{x_e.\sin {\beta }_0}}={\mu \left(x\right)}_e$$

(27)

By substituting this equality into (20), we obtain:

$${\displaystyle \frac{{\mu \left(x\right)}_0.x_0.\sin {\beta }_e}{x_e.\sin {\beta }_0}}={\mu \left(xy\right)}_e.\sqrt{1+{tg}^2\left({\alpha }_e\right)}$$

(28)

Given that for the square sieve ${\beta }_e={\displaystyle \frac{\pi }{2}}$ and ${\alpha }_{\mathrm{е}}={\displaystyle \frac{\pi }{4}}$ , the final form of equation (28) becomes:

$${\displaystyle \frac{{\mu \left(x\right)}_0.x_0}{x_e.\sin {\beta }_0}}={\mu \left(xy\right)}_e.\sqrt{2}$$

(29)

Analysis of the derived relationships (19), (20), and (28) reveals that under identical operating conditions, modifying the shape of the separator's working surface leads to increased values of both separation coefficients ($\mu \left(x\right)$ and $\mu \left(xy\right)$). However, this trend persists only until the rectangular sieve with dimensions $x_0$ and $y_0$ transforms into a square sieve with dimensions $x_{\mathrm{е}}$ and $y_{\mathrm{е}}$. If a rectangular sieve is converted to another rectangular sieve with the same diagonal but with length ($x_i$) smaller than its width ($y_i$) (Fig. 2), the aforementioned trend will continue only for the length-based separation coefficient, while the area-based separation coefficient will decrease. This implies that under identical operating conditions, the lowest grain losses will occur with a flat sieve having a square-shaped working surface, due to its higher area-based separation coefficient and increased working area.

Equation (29) enables the conversion of the length-based separation coefficient of a rectangular sieve to the area-based separation coefficient of a square sieve with an identical diagonal length. This demonstrates that by altering the shape and geometric dimensions of the sieve, the operational quality of such mechanical separators can be enhanced.

It is recommended to use an expression of the form (2) when determining grain losses in flat sieves. The same expression is also suitable for calculating losses in rotary mechanical separators.

3. Discussion

The performance of all types of mechanical separators depends significantly on their geometric dimensions. Despite the proven strong influence of length, the separation process should be considered in terms of the working area of the separator. In such cases, when determining grain losses, it is appropriate to use an expression of the form (9). As the parameter $r$ (i.e., the area of the separator) increases, grain losses decrease exponentially. Under certain conditions, the area-based separation coefficient $\mu \left(xy\right)$ should be considered constant, while the coefficient $\mu \left(x\right)$ varies under the same conditions depending on $x$. The geometric parameters at which the area-based separation coefficient is determined are optimal for the separator, and its working area has a square shape.

The key difference between these coefficients lies in how they change when the factors determining them vary. The distinctive feature in the behavior of the length-based separation coefficient is that it maintains the direction in which its values change when the length of the separator is altered. This is not the case with the ${\mu }_{xy}$ coefficient. From this difference arises the variation in separation intensity. Notably, these changes indicate that not only the dimensions but also the shape of the separator's screening area are of significant importance.

The performance of all types of mechanical separators is strongly influenced by their geometric dimensions. It is generally accepted that changing the length of the separator plays a crucial role in its separation capability. However, the proven strong influence of length should not be considered independently of the separator's working area. This conclusion stems from the analysis of dependence (20). According to it, when examining a single flat sieve, the relationship between the length-based separation coefficient and the area-based separation coefficient of the sieve is a function of the angle ${\alpha }_{\mathrm{е}}$. The values of this angle depend on the ratio between the length and width of the sieve, i.e., the shape of the separator's working area. Although the similarity criterion π₁ leads to the same grain losses, transforming expression (20) into the form (28) shows that, under given working conditions, the experimental probability of grain screening per unit area is highest for a square-shaped sieve. Additionally, expression (28) allows the length-based separation coefficient of a sieve to be adjusted to this highest experimental screening probability per unit area.

For flat sieves with equal diagonals, the trend is that as the angle ${\alpha }_{\mathrm{е}}$ increases, the values of the length-based separation coefficient also increase. However, for the area-based separation coefficient, this increase continues only until the angle reaches ${\displaystyle \frac{\pi }{4}}$ . Beyond this value of ${\alpha }_{\mathrm{е}}$, the area-based separation coefficient decreases. This, combined with the fact that the largest area (for sieves with equal diagonals) is achieved with a square sieve, results in the smallest grain losses under otherwise equal conditions among sieves.

The conclusions drawn regarding the relationship between the length-based and area-based separation coefficients of mechanical separators, as well as the process of separating grain mixtures across the surface of mechanical separators, should be further verified experimentally.