A Preliminary Study on the Reasons Why Planets Rotate Synchronously

1. Introduction

In 1609, Kepler [1] published the first and second laws of planetary motion. The first law points out that the orbit of a planet is an ellipse, and the sun is located at a focal point of the ellipse; the second law points out that the connection between the planet and the sun swept through equal areas within equal time intervals. The essence of Kepler’s second law is the law of conservation of angular momentum for planetary operations [2]. In 1687, Isaac Newton expounded the law of universal gravitation in “Mathematical Principles of Natural Philosophy” [3]. The law of universal gravitation pointed out that there is gravity between any two objects in the universe, and its size is proportional to their mass and inversely proportional to the square of their distance. Newtonian gravity provides the centripetal force of planets, explaining the source of power for planets to operate in elliptical orbits.

Many scholars have expressed their views on the synchronous rotation of the moon [4,5,6,7]. Scholars generally believe that the reason for the synchronous rotation of the moon is mainly the result of the tidal locking effect. The earth’s gravity on the moon is stronger at one end close to the earth than the one far away from the earth. This gravitational difference causes the moon’s shell to bulge, and the continuous pulling ultimately slows down the moon’s rotation speed until it reaches a state that is synchronized with the orbital period. Is the tidal locking effect really such a big effect? This view is debatable.

2. The Equivalent Radius of the Planet’s Gravitons

“Graining, gravitational field and graviton - inference about the frequency of gravitational energy waves” [8] believes that the most basic unit of matter is nucleons (collective name of protons and neutrons). All nucleons emit gravitons. The energy carried by gravitons is the Planck constant h, and the value is 6.626×10^ (-34) J·s. Gravitators propagate in space with gravitational energy waves. The gravitational energy wave resonates with other nucleons, transmitting energy to form gravity. For planets [9], gravitons emitted by nucleons inside the planet interact with other nucleons inside the planet to form the cohesion of the planet. The gravitons emitted by nucleons near the outside of the planet are partially emitted outside the sphere and propagate in space with gravitational energy waves. The gravitational energy waves encounter nucleons from other planets and resonate with them to form gravitational force between the planets.

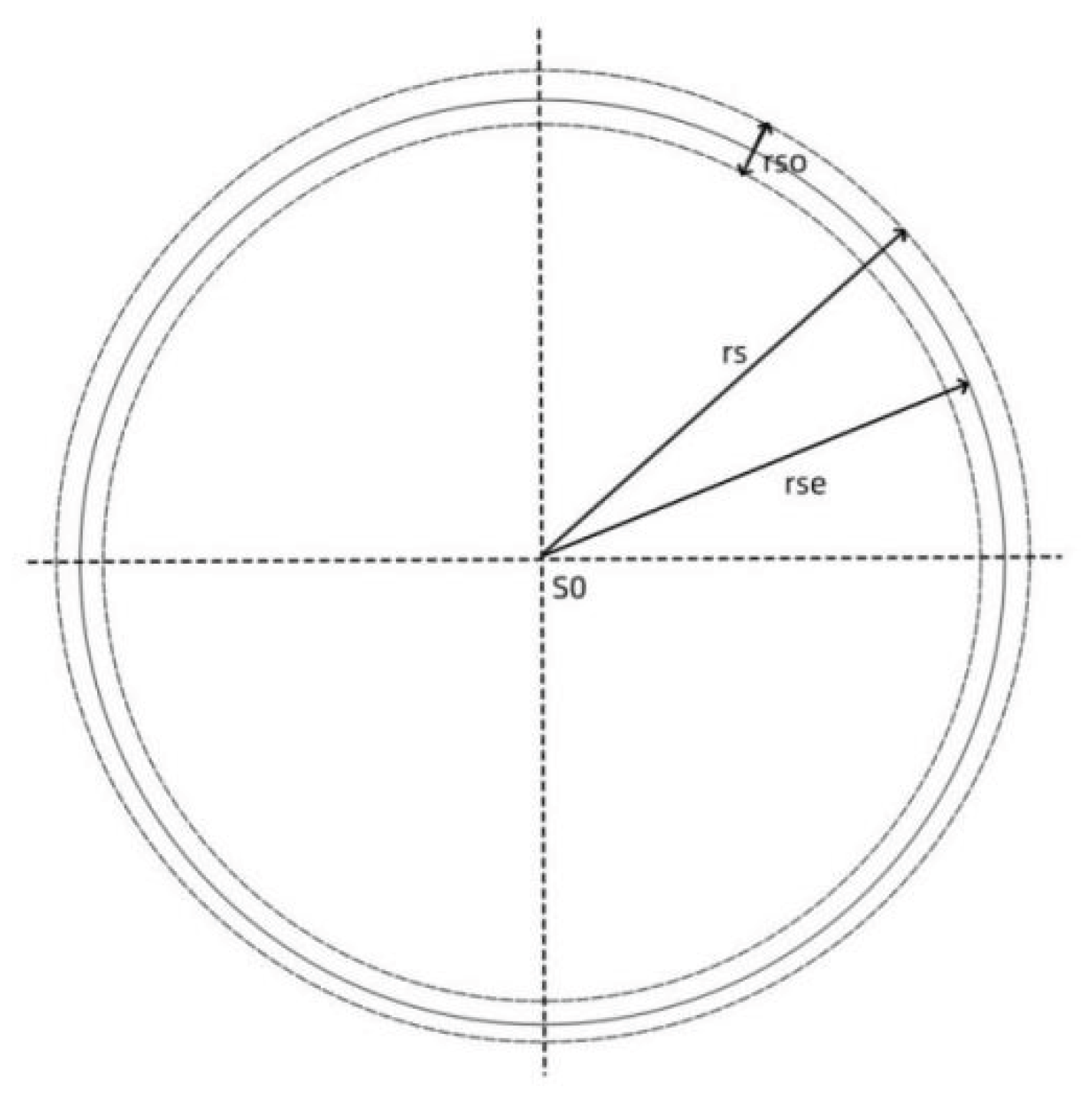
Figure 1 is a schematic diagram of the equivalent spherical surface of a planet’s graviton emitted. In the figure, rs is the planet’s radius, and rso is the thickness of the graviton shell sent to the outside of the sphere. There should be a spherical layer rse in the middle. It can be considered that all gravitons on the planet are emitted by this spherical layer. If this spherical layer is used as the equivalent spherical layer emitted by the planet’s gravitons, for general circumstances, it can be considered that this spherical layer is in the middle of the planet’s graviton emission shell.

“The attempt to correct the universal gravitational formula from the proportion of the planet emitted to the outside of the ball - the ratio of the outside of the ball graviton in the deflection gravitational theory” [10] article calculates the number of gravitons sent to the outside of the ball. The thickness of the outer layer where the planet can emit gravitons outside the ball is:

$$r_{so}={\displaystyle \frac{6m_0}{k_{ng}{r}_0^2{\rho }_s}}={\displaystyle \frac{k_{s\rho }}{{\rho }_s}}={\displaystyle \frac{41540}{{\rho }_s}}$$

(1)

In the formula, kng is the ratio in which gravitons passing through the nucleus can be absorbed by the nucleus, m0 is the mass of the nucleus, r0 is the radius of the nucleus, and ρs is the density of the shell matter of the planet.

The number of gravitons sent by the planet to the outside of the ball is approximately:

$$n_{go}\approx {\mathrm{k}}_{\mathrm{gr}}{r_s}^2=1.599\times {10}^{55}{r_s}^2$$

(2)

Through calculations, it can be seen that the thickness of the shell of the planet emitting gravitons outward is too small relative to the planet’s radius and can be ignored. Therefore, the equivalent shell radius of the planet’s emitting gravitons is approximately equal to the planet’s radius.

$$r_{se}=r_s-{\displaystyle \frac{1}{2}}{r}_{so}\approx r_s$$

(3)

3. The center of Mass and Gravity of the Planet

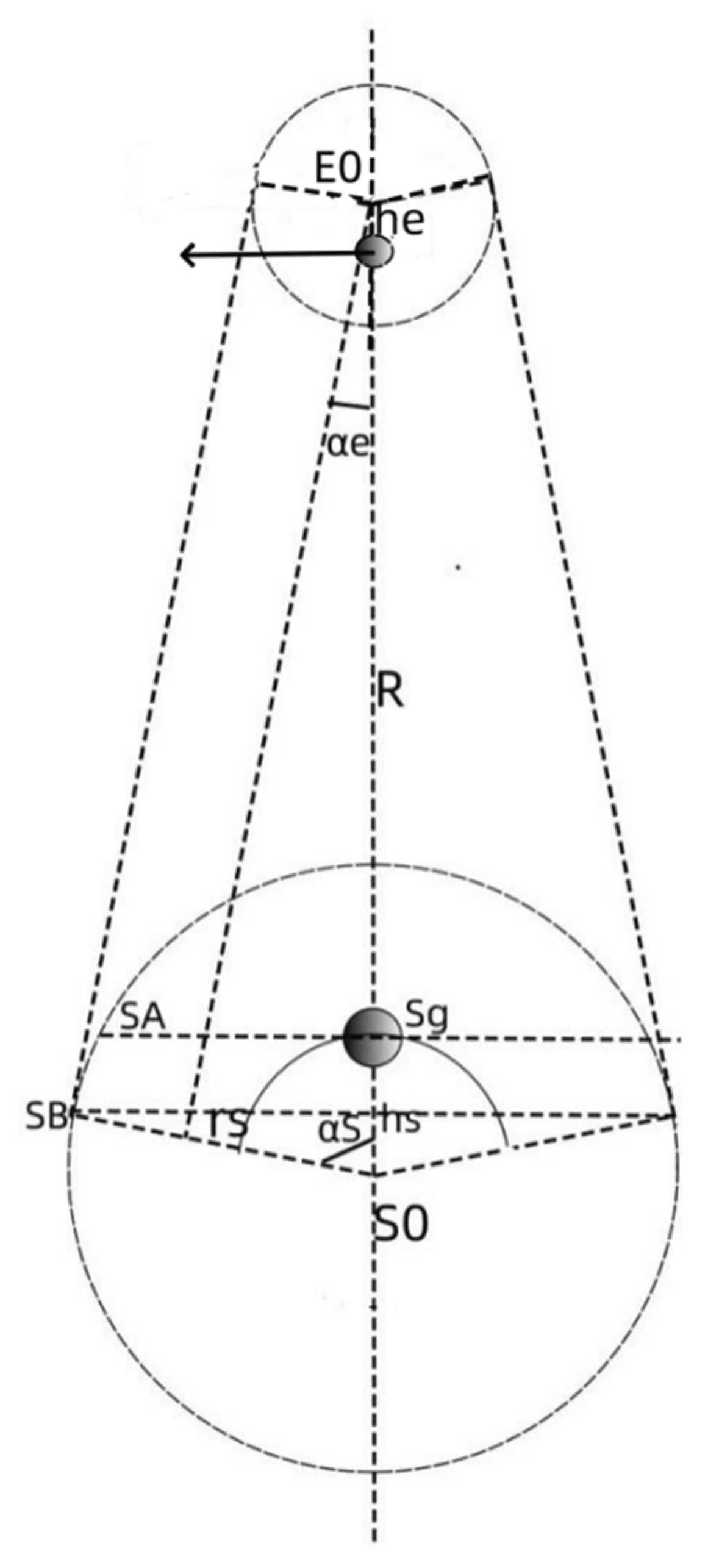
Figure 2 is an analysis diagram of the gravity effect between two planets. In the picture, the planet E rotates around the planet S. The center of mass of the central planet S is S0, the radius is rs, the mass is ms, the center of mass of the planet E is E0, the radius is re, the mass is me, and the center of mass distance between the planets is R0. Now, the effect of planet S on planet E is analyzed. In the figure, only the gravitons emitted by planet S facing the nucleons on the sphere of planet E can form gravity on planet E’s shell nucleons facing planet S. This phenomenon can be proved by the gravity double valley phenomenon during the solar eclipse [11]. Before the solar eclipse, objects on the ground are subjected to the dual gravity of the sun and the moon, and the gravity of the earth that the object receives will decrease; during the solar eclipse, the gravity of objects on the ground is measured, and the results show that the gravity of objects on the ground is the same as the gravity when there is only the sun, which means that the gravitons received by the sun on the ground are blocked by the moon; when the solar eclipse ends, the sun is no longer blocked by the moon, and the objects on the ground are superimposed by the gravity of the sun and the moon, and the gravity decreases again, which forms the gravity double valley phenomenon during the solar eclipse.

To accurately calculate the effect of gravitons emitted by planet S on planet E, we should calculate the gravity of each surface element on planet S on planet E. When the distance between planets is much greater than the planet’s radius, it can be approximately believed that the energy transmitted between the surface elements of the two planets is equal, so that the energy transmitted from planet S to planet E is proportional to the area of the spherical surface.

In the figure, the nucleus equivalent center of the planet S ball affecting planet E is obviously on the connection between the centers of mass of the two planets. As shown in the figure, it is assumed that the gravity is

The distance between the center of mass S of the planet S is hs,

$$h_s={\displaystyle \frac{R_0+r_s-r_e}{2R_0}}{r}_s\approx {\displaystyle \frac{1}{2}}{r}_s$$

(4)

For planet E, the area affected by planet S is greater than half the sphere. Therefore, the equivalent center of gravity action is closer to the center of mass of planet E. As shown in the figure, let the distance between the center of gravity and the center of mass is he, and there are:

$$h_e={\displaystyle \frac{1-\sin {\alpha }_e}{2}}{r}_e={\displaystyle \frac{R_0-r_s+r_e}{2R_0}}{r}_e\approx {\displaystyle \frac{1}{2}}{r}_e$$

(5)

The energy transmitted by planet S to planet E is the ratio of the area of the sphere occupied by planet E from planet S distance R0 to the total number of gravitons emitted by planet S:

$$F_{se}={\displaystyle \frac{\pi r_e^2}{4\pi R_0^2}}{n}_{sg}h={\displaystyle \frac{r_e^2}{4R_0^2}}{k}_{gr}{r}_s^{2}h={\displaystyle \frac{k_{gr}h{r}_e^2{r}_s^2}{4R_0^2}}=G_i{\displaystyle \frac{r_e^2{r}_s^2}{R_0^2}}$$

(6)

$$G_i={\displaystyle \frac{1}{4}}{k}_{gr}h$$

(7)

Here Gi is the gravitational coefficient, kgr is the proportional coefficient of the graviton sent to the outside of the ball by the planet, and h is the Planck constant. From the above analysis, we can find that the energy (gravity) transmitted by nucleons between planets is proportional to the planet’s surface area, rather than to the planet’s mass.

4. Analysis of the Effect of Gravity on Planetary Movement

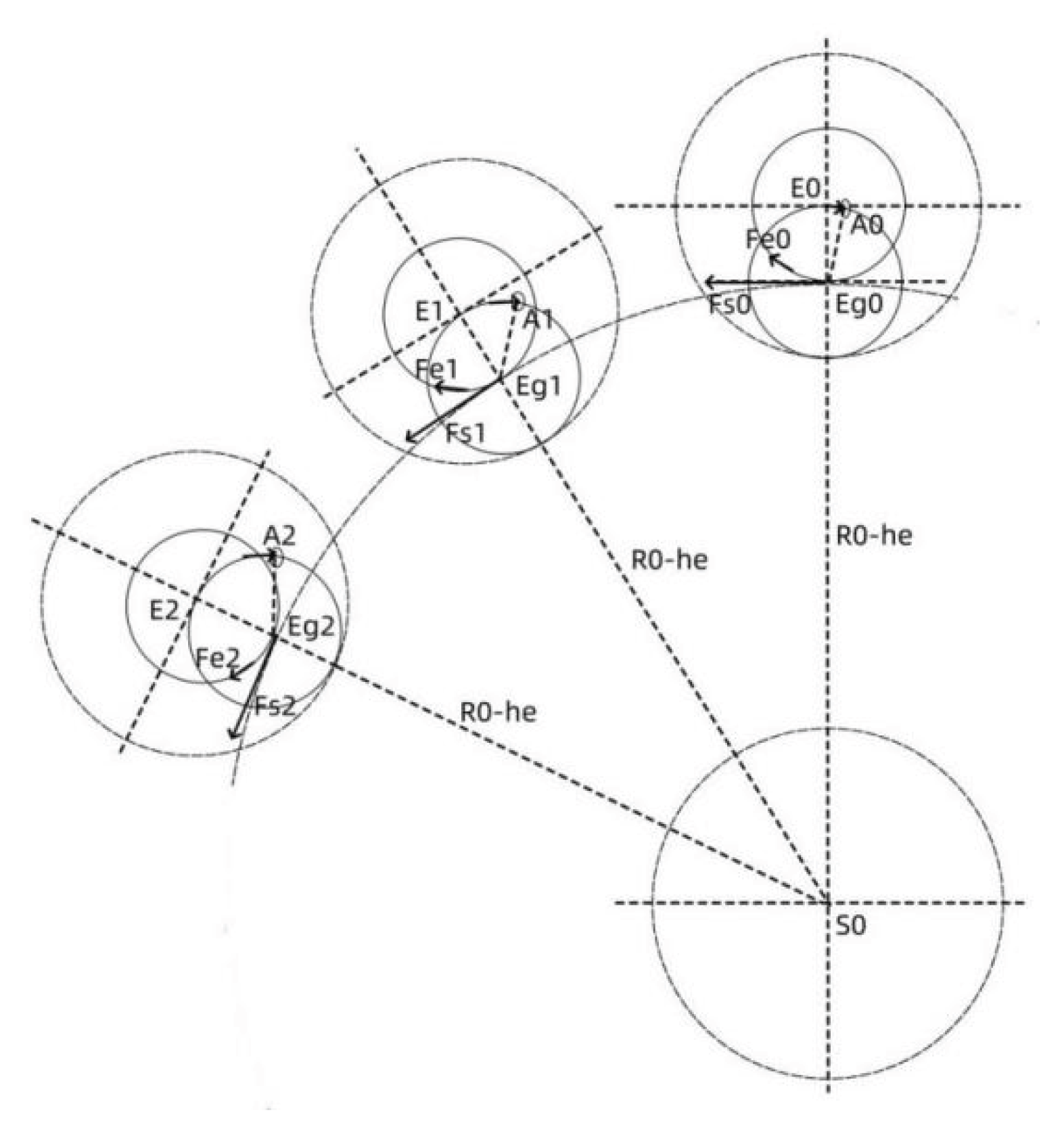
Figure 3 is an analysis diagram of the planet’s revolution and rotation caused by planet gravity. In the figure, S0 is the center of mass of the central planet S. E is the planet orbiting the central planet S. When the planet E is at the E0 position, the gravitational action point of planet S on planet E is Eg0. Since the gravitational action point is separated from the planet center of mass, gravity is divided into Fs0 related to the center planet S and Fe0 related to the planet E. When the same planet E is at position E1, gravity is divided into Fs1 related to the center planet S and Fe1 related to the planet E. When the planet E is at position E2, gravity is divided into Fs2 related to the center planet S and Fe2 related to the planet E. It can be seen that Fs0, Fs1, and Fs2 related to the center planet S act on the gravitational action point E, forming the driving force for the planet E to orbit the planet S. From the effect, Fs forms the centripetal force of planet E orbiting the planet S.

Since the gravitational action point Eg is separated from the planet’s center of mass, another effect of gravity received by the gravitational action point Eg is to drag the planet E to run. Generally, external forces rotate around the center of the sphere. Without considering the planet E orbiting the central planet S, it can be considered that the planet E has always been affected by a gravitational Fe, and this point of action is fixed at the gravitational action point Eg. Therefore, this is not an external force rotates around the planet, but the center of mass of the planet rotates around the gravitational action point Eg. At the initial position E0, the planet’s center of mass tends to run towards A0. With the increase of time, the angle of rotation of the planet’s center of mass increases. Under the combined action of the two components of gravity, when the planet is at position E1, the center of mass moves to point A1, and when the planet is at position E2, the center of mass moves to point A2.

According to the above analysis, the total gravity Fse of the planet is:

$$F_{se}=F_s+F_e$$

(8)

The components related to the E-region of the planet are:

$$F_s=m_e{\displaystyle \frac{v_s^2}{R_0}}=m_e{\Omega }_s^2{R}_0$$

(9)

In the formula, gravity causes the linear velocity of the planet E to orbit the central planet S to be vs, unit m/s, the angular velocity of the revolution to be Ωs, unit radian/s, and me is the mass of the object (unit kg).

The moment of inertia of the sphere rotating around the gravitational action point Eg is:

$$I_e={\displaystyle \frac{2}{5}}{m}_e{r}_e^2+m_e{h}_e^2$$

(10)

where me is the mass of the planet E, re is the radius of the planet E, and he is the distance between the gravitational action point Eg and the center of mass of the planet E.

According to the rotation law of rigid body fixed axis:

$$M_Z=I\alpha$$

(11)

where Mz represents the external torque for a certain fixed axis, I represents the moment of inertia of the rigid body about a given axis, and α represents the angular acceleration. Here the torque is the component force of gravity and the rotation of the planet. The force arm is the distance he between the gravitational action point Eg and the center of mass of the planet. According to the definition of angular acceleration, there are:

$$\alpha ={\displaystyle \frac{d^2{\theta }_e}{d^{2}t}}={\displaystyle \frac{{\Delta }^{2}t{\omega }_e^2}{{\Delta }^{2}t}}={\omega }_e^2$$

(12)

At this time, the law of rotation of the rigid body fixed axis can be written as:

$$F_e{h}_e=I{\omega }_e^2$$

(13)

$$F_e={\displaystyle \frac{I{\omega }_e^2}{h_e}}=\left({\displaystyle \frac{2}{5}}{m}_e{r}_e^2+m_e{h}_e^2\right){\displaystyle \frac{{\omega }_e^2}{h_e}}$$

(14)

For the rotation of a planet, it refers to the component of rotation in the planet’s rotation plane, which is generally not on the same plane as the actual rotation of the planet. Therefore, the angular velocity of the planet here is not the planet’s rotation angular velocity that is usually observed.

For objects that move in a circular motion, the relationship between linear velocity and angular velocity is as follows:

$$v_0=R_0{\Omega }_s$$

(15)

$$v_0\Delta t\sin {\beta }_0={\theta }_s$$

(16)

According to the law of conservation of momentum, momentum cannot be generated and disappeared out of thin air. For planet E, the planet’s revolution generates a positive momentum, and planet E rotates around the center of mass Eg to produce a reverse momentum, and these two should be equal:

$$p=m_e{v}_s=m_e{\Omega }_s{R}_0=m_e{v}_e=m_e{\omega }_e{h}_e$$

(17)

$${\Omega }_s{R}_0={\omega }_e{h}_e$$

(18)

$${\Omega }_s={\displaystyle \frac{h_e}{R_0}}{\omega }_e$$

(19)

Bring the above result into formula 27:

$$F_{se}=m_e{\Omega }_s^2{R}_0+\left({\displaystyle \frac{2}{5}}{m}_e{r}_e^2+m_e{h}_e^2\right){\displaystyle \frac{{\omega }_e^2}{h_e}}$$

(20)

$$F_{se}=m_e{R}_0{\left({\displaystyle \frac{{\omega }_e{h}_e}{R_0}}\right)}^2+\left({\displaystyle \frac{2}{5}}{m}_e{r}_e^2+m_e{h}_e^2\right){\displaystyle \frac{{\omega }_e^2}{h_e}}$$

(21)

$${\omega }_e=\sqrt{{\displaystyle \frac{F_{se}}{m_e\left[\frac{h_e^2{R}_0}{R_0^2}+\frac{1}{h_e}\left(\frac{2}{5}{r}_e^2+h_e^2\right)\right]}}}=\sqrt{{\displaystyle \frac{F_{se}}{m_e\left(\frac{h_e^2}{R_0}+\frac{2r_e^2}{5h_e}+h_e\right)}}}$$

(22)

The ratio of component force used for planet rotation to the entire gravity is:

$$\begin{array}{l}{k}_F={\displaystyle \frac{F_e}{F_{se}}}={\displaystyle \frac{\left(\frac{2}{5}{m}_e{r}_e^2+m_e{h}_e^2\right)\frac{{\omega }_e^2}{h_e}}{m_e{R}_0{\left(\frac{{\omega }_e{h}_e}{R_0}\right)}^2+\left(\frac{2}{5}{m}_e{r}_e^2+m_e{h}_e^2\right)\frac{{\omega }_e^2}{h_e}}}\\ ={\displaystyle \frac{\left(\frac{2}{5}{r}_e^2+h_e^2\right)}{\frac{h_e^3}{R_0}+\left(\frac{2}{5}{r}_e^2+h_e^2\right)}}\approx {\displaystyle \frac{\left(\frac{2}{5}{r}_e^2+\frac{1}{4}{r}_e^2\right)}{\frac{r_e^3}{8R_0}+\left(\frac{2}{5}{r}_e^2+\frac{1}{4}{r}_e^2\right)}}={\displaystyle \frac{26R_0}{5r_e+26R_0}}\approx 1\end{array}$$

(23)

From this we can see that almost all the gravity of the planet is used for the rotation of the planet, and only a little bit is left for the rotation of the planet. Here, it can also be considered that at the point of gravity, the torque of the planet’s revolution is equal to the moment of the planet’s rotation. Since the force arm of the planet’s revolution is much larger than the force arm of the planet’s rotation, the force used for the planet’s revolution is much smaller than the force of the planet’s rotation.

The movement of a planet is not a simple unforced system, it is subject to gravity at any time. Therefore, the angular momentum of a planet at any point includes: the angular momentum of the initial velocity of the planet relative to the angular momentum of the central planet, gravity forms the angular momentum of the planet’s revolution, and gravity forms the angular momentum of the planet’s rotation reflected to the sphere of the revolution:

$$L_0=m_e{R}_0{v}_0\sin {\beta }_0+m_e{R}_0{v}_s-m_e{R}_0{v}_e$$

(24)

Since vs is equal to ve, after the above formula is included

$$L_0=m_e{R}_0{v}_0\sin {\beta }_0$$

(25)

The angular momentum of the planet’s revolution is only the angular momentum caused by the initial velocity. It can be seen that the offset of the angular momentum of the planet’s revolution generated by gravity is the fundamental reason for the conservation of angular momentum in the planet’s revolution system.

For different positions, according to the law of conservation of angular momentum, there are:

$$L=R_0{m}_e{v}_0\sin {\beta }_0=R_1{m}_e{v}_1\sin {\beta }_1$$

(26)

In the formula, L is the angular momentum, R0, v0, and β0 are the distance between the planet and the central planet at its initial position, the linear velocity of the planet, the angle between the gravity line and the linear velocity, R1, v1, and β1 are the distance between the central planet after the change in the position of the planet, the linear velocity of the planet, the angle between the gravity line and the linear velocity. From the above formula:

$$v_1={\displaystyle \frac{R_0{v}_0\sin {\beta }_0}{R_1\sin {\beta }_1}}$$

(27)

At present, the minimum orbital speed and maximum orbital speed of the moon have not been found. Kepler’s area law is used to estimate the minimum speed of the moon’s apogee. Assuming that the semi-major axis of the orbit of the planet E is a and the semi-major axis is b, then the elliptical area of the orbit of the planet E is:

$$S=\pi ab$$

(28)

According to Kepler’s law of area, when the planet E moves in an elliptical orbit, the area it swepts through with the sun’s line within an equal time. If the planet E runs into n parts, the ellipse area is also divided into n parts. Assuming the unit area is Sn, assuming the linear velocity of planet E running is v0, the angle between planet E and the gravitational line is β0, the distance between planet E and the central planet S is R0, and the time interval is Δt:

$$S_n={\displaystyle \frac{S}{n}}={\displaystyle \frac{1}{2}}{R}_0{v}_0{\displaystyle \frac{T}{n}}\sin {\beta }_0$$

(29)

When the moon is at an apogee, the direction of the moon’s velocity is at an angle of 90° with the direction of gravity line. The above formula is simplified to:

$$S={\displaystyle \frac{1}{2}}{R}_0{v}_{0}T$$

(30)

The initial linear velocity of the moon’s apogee is:

$$v_0={\displaystyle \frac{2S}{R_{0}T}}$$

(31)

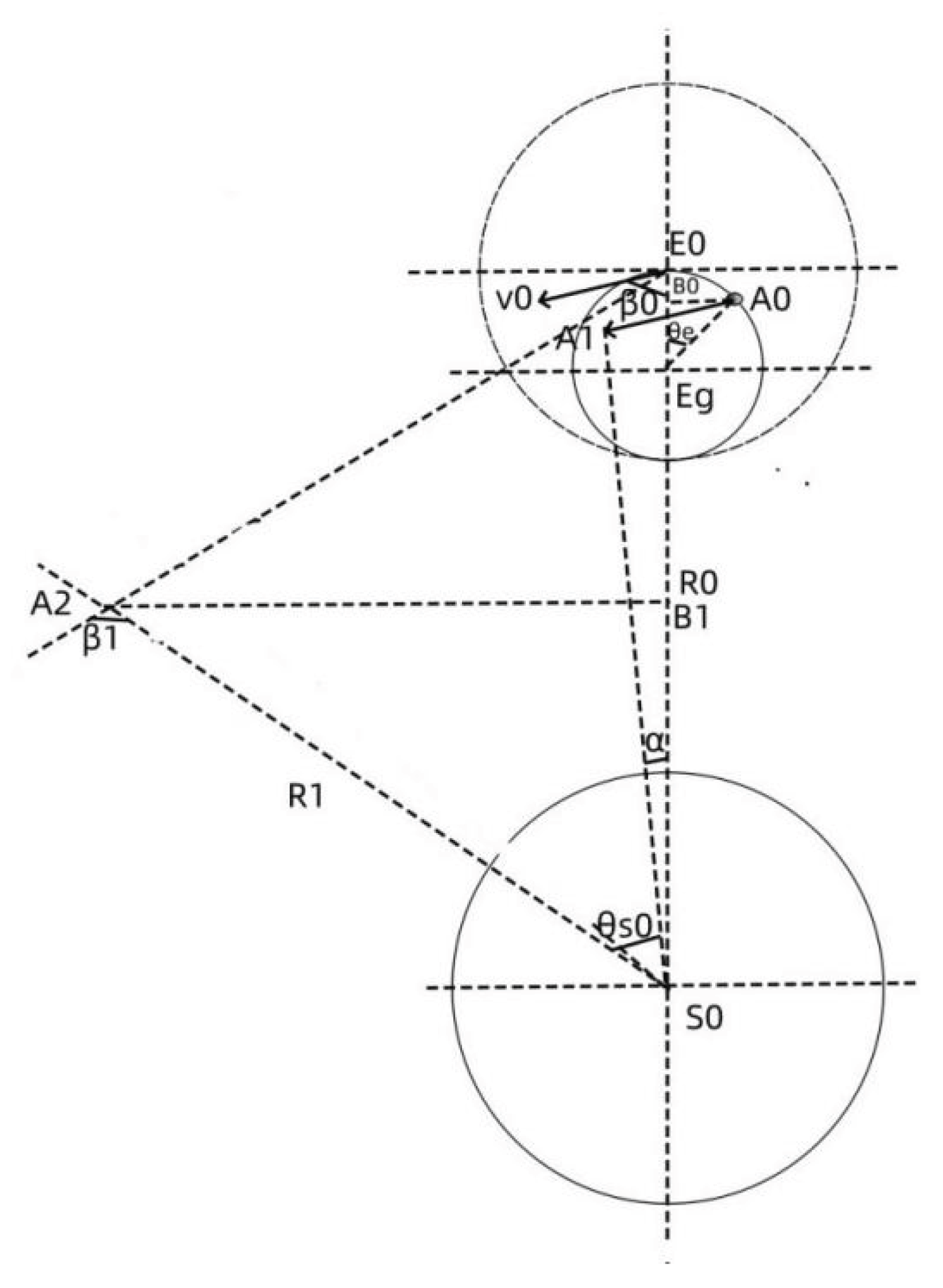
Figure 4 is a planet operation analysis diagram. Here, the operation cycle of planet E is divided into n parts by time, and the unit time is Δt. In the figure, the center S0 of the central planet S is the coordinate origin, R0 is the distance between the initial position of the planet and S0, v0 is the initial speed of planet E, β0 is the angle between the initial direction of the planet and the gravitational line, θe is the angle at which the center of mass of planet E rotates around the gravitational action point Eg in unit time, θs is the angle at which the planet E rotates around the central planet S under the action of gravitational component, and translates v0 to point A0, and its end point is A1, and then rotates A1 to the angle of θs to position A2, A2 is the end point of the center of mass of planet E through Δt time. here:

The coordinates of point A1 are:

$$x_{a1}=v_0\Delta t\sin {\beta }_0-h_e\sin {\theta }_e$$

(32)

$$y_{a1}=R_0-v_0\Delta t\cos {\beta }_0-h_e+h_e\cos {\theta }_e$$

(33)

The distance from point A1 to S0 is:

$$R_1=\sqrt{x_{a1}^2+y_{a1}^2}=\sqrt{{\left(v_0\Delta t\sin {\beta }_0-h_e\sin {\theta }_e\right)}^2+{\left(R_0-v_0\Delta t\cos {\beta }_0-h_e+h_e\cos {\theta }_e\right)}^2}$$

(34)

The angle α between point A1 and the initial position of planet E satisfies:

$$\tan \alpha ={\displaystyle \frac{v_0\Delta t\sin {\beta }_0-h_e\sin {\theta }_e}{R_0-v_0\Delta t\cos {\beta }_0-h_e+h_e\cos {\theta }_e}}$$

(35)

When the planet E rotates through Δt time to the A2 position under the action of the gravitational component Fs, the distance between planet E and S0 remains unchanged to R1, and the angle between the position A2 of planet E and the initial position increases to:

$${\theta }_c={\theta }_s+\alpha ={\Omega }_s\Delta t+\alpha$$

(36)

It can be seen that the planet’s rotation is inertia when it is running on the equilibrium planet.

5. Simulation of the Elliptical Orbit of the Planet

The relevant parameters of the moon and the earth [12] are as follows: the average radius of the moon is about 1737.10km, the mass is 7.342×10^22kg, the average radius of the earth is 6371.393km, the perigee distance of the moon: 363300km; the apogee distance is 405696km; the average revolution period is 27.32 days; the average revolution speed is 1.023 kilometers/second; the rotation period is: 27 days, 7 hours, 43 minutes, 11.559 seconds (27.32 days, synchronous rotation); the inclination angle of the rotation axis varies between 3.60° and 6.69°, the semi-major axis of the moon orbit orbit is 384403km, and the criterion rate is 0.0549.

Based on the above derivation, the moon’s orbit can be simulated. Table 1 is a partial screenshot of the simulation data table of the moon’s orbit around the earth. The most column in the table is the correlation constant, re is the radius of the moon, me is the mass of the moon, rs is the radius of the earth, and Gr is the gravitational coefficient for the application of the planet’s semi-compassage to calculate gravity. Unlike the commonly used gravitational coefficient G that uses the mass of the planet to calculate gravity, T is the orbital period, which refers to the time when the moon orbits the earth, unit seconds, n is the number of equal parts of the period. Here is 10,000, and Table 1 above is just a few of the data. Δt is unit time, S is the orbital area calculated based on the moon’s semi-major axis and eccentricity, and is used to calculate the initial velocity of the moon’s apogee. The first column R in Table 2 shows the distance between the moon and the earth when the moon is at different positions. The initial value is the apogee. The second column he is the distance between the gravitational action point Eg, which acts on the moon and the center of mass. The third column is the angle between the direction of the moon and the gravitational line. The fourth column is the velocity of the moon. The calculation of the initial velocity of the apogee uses Kepler’s area law. The fifth column is the gravity of the earth to the moon. Here the earth and the radius of the moon are used to calculate the gravity of the earth to the moon. The sixth column ωe is the angular velocity generated by gravity to cause the moon to be autobiography. The seventh column Ωs is the angular velocity generated by the force used for the moon’s revolution to cause the moon to be produced. The eighth column α is the angle in which the initial inertia v0 of the moon and the combined motion of the moon’s rotation caused the moon to deflect. The tenth column θc is the angular displacement actually generated by the moon unit time. It is the sum of θs and α. Column 11 θ is the accumulation of angular displacement per unit time, and columns 12-13 are the rectangular coordinates used when plotting simulated data.

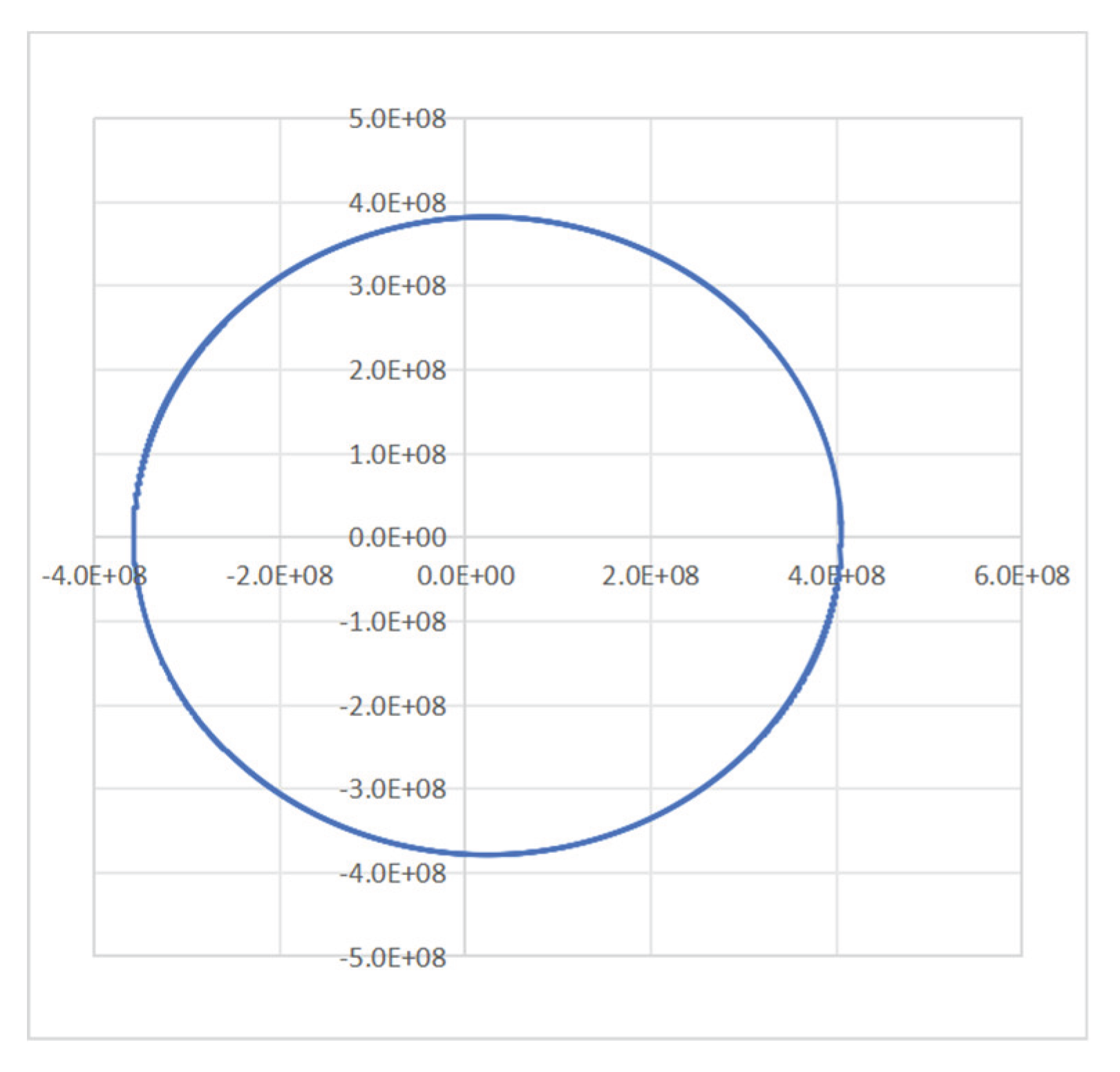
Figure 5 is a simulation diagram of the moon orbit directly generated in Table 2. The apogee is 4.056960E+08m,

Given by the initial simulation value, and the perigee is 3.5547541E+8m. Returns the ariel point 4.051655E+08m, where E is the commonly used power base in the table, 4.056960E+08m is the same as 4.056960×10^8m, and it can be seen from the parameters that it is an ellipse. The angle between the moon’s running direction and the gravitational line is at a given value of 1.57080 radians at the aurora point. As the moon moves from avera to perigee, this angle gradually decreases. After decreasing to the minimum value of 1.5056601 radians, it begins to gradually increase. After passing through 1.57080, it continues to increase. When it increases to the maximum value of 1.6359258, it begins to gradually decrease, and finally returns to the aurora, with the return value of 1.5711103 radians. The velocity value of the moon’s apogee is 968.061m/s, the perigee velocity is 1107.073m/s, and the return value of the apogee is 969.329m/s. Under the action of the earth’s gravity, the minimum rotation angular velocity of the moon on the white path is 7.355E-5 radian/s, the maximum angular displacement is 8.409E-5 radian/s, and the average angular velocity of the revolution is 2.662E-6 radian/s.

The simulation average is 2.725E-6 radians/s, and the angular velocity of the moon caused by the earth’s gravity is 29.49 times greater than the angular velocity of the revolution. More than 99.9% of the earth’s gravity is used for the rotation of the moon.

Although the above simulation process is generally consistent with the actual situation, there are still many inconsistencies in the details, and the simulation data of the moon and the earth need to be further carefully adjusted.

6. Synchronous Rotation of the Moon

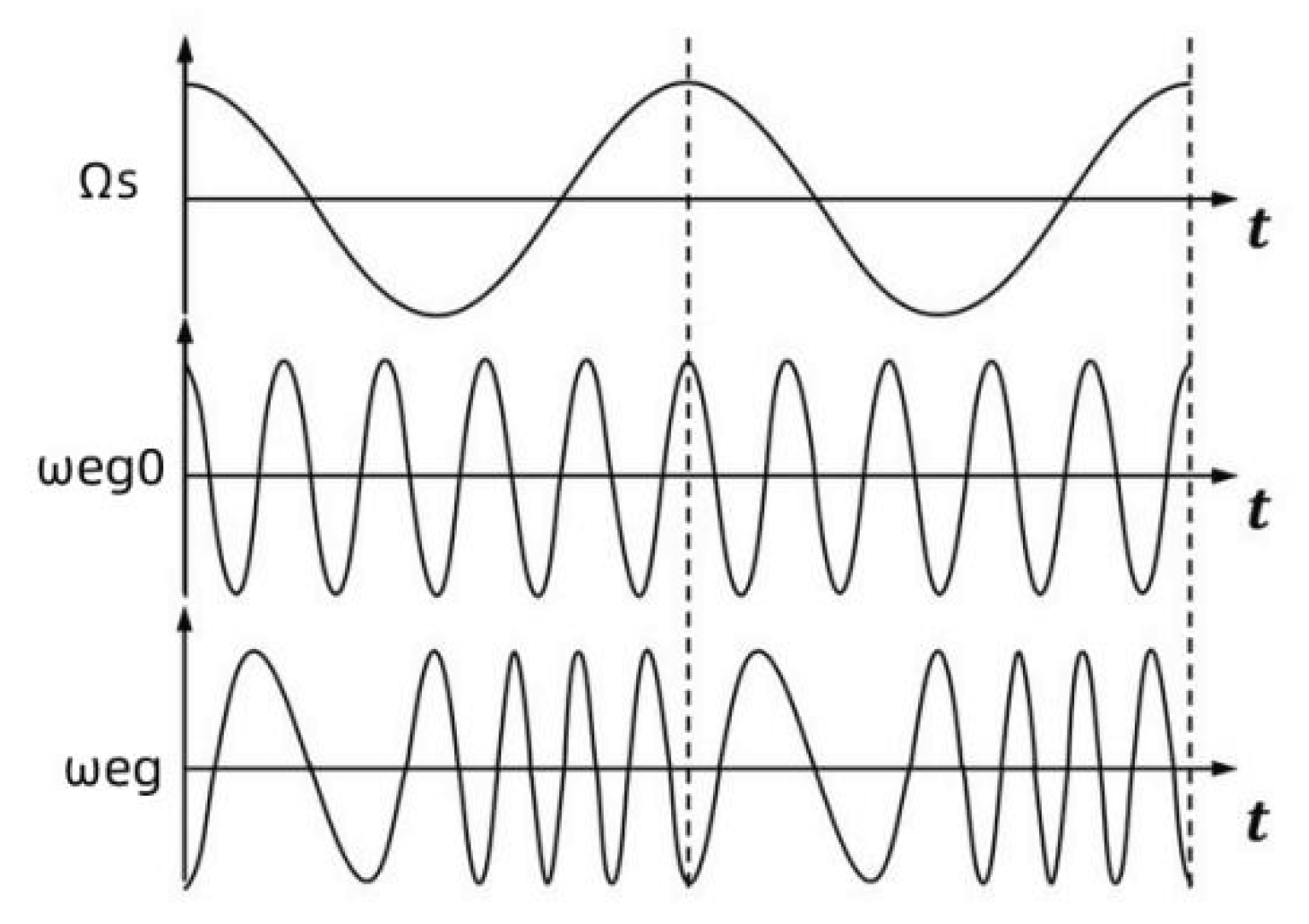
From the analysis in Section 6, it can be seen that the moon is subject to gravity of the earth, and it will form a rotation opposite to the direction of the revolution on the white path surface, and its rotation angular speed will be The degree is ωe. The moon is subject to the gravity of the earth in accordance with the above formula (25). The angular velocity of the moon’s rotation conforms to the above formula (43). From the elliptical orbit simulation table of the moon’s revolution, it can be seen that the angular velocity of the moon caused by the gravity of the earth and the moon is about 30 times the actual angular velocity of the moon. At the same time, ωe is affected by the distance between the earth and the moon, and its size is proportional to the angular velocity of the moon. Therefore, the angular velocity of the moon caused by the gravity of the earth and the moon can be seen as the angular velocity of the moon’s revolution velocity of the moon and a relatively high-speed angular velocity of ωeg0. That is to say, the angular velocity of the moon’s revolution velocity of the moon is modulated at the angular velocity of the angular velocity of the moon modulated by the angular velocity of the moon. As shown in Figure 6.

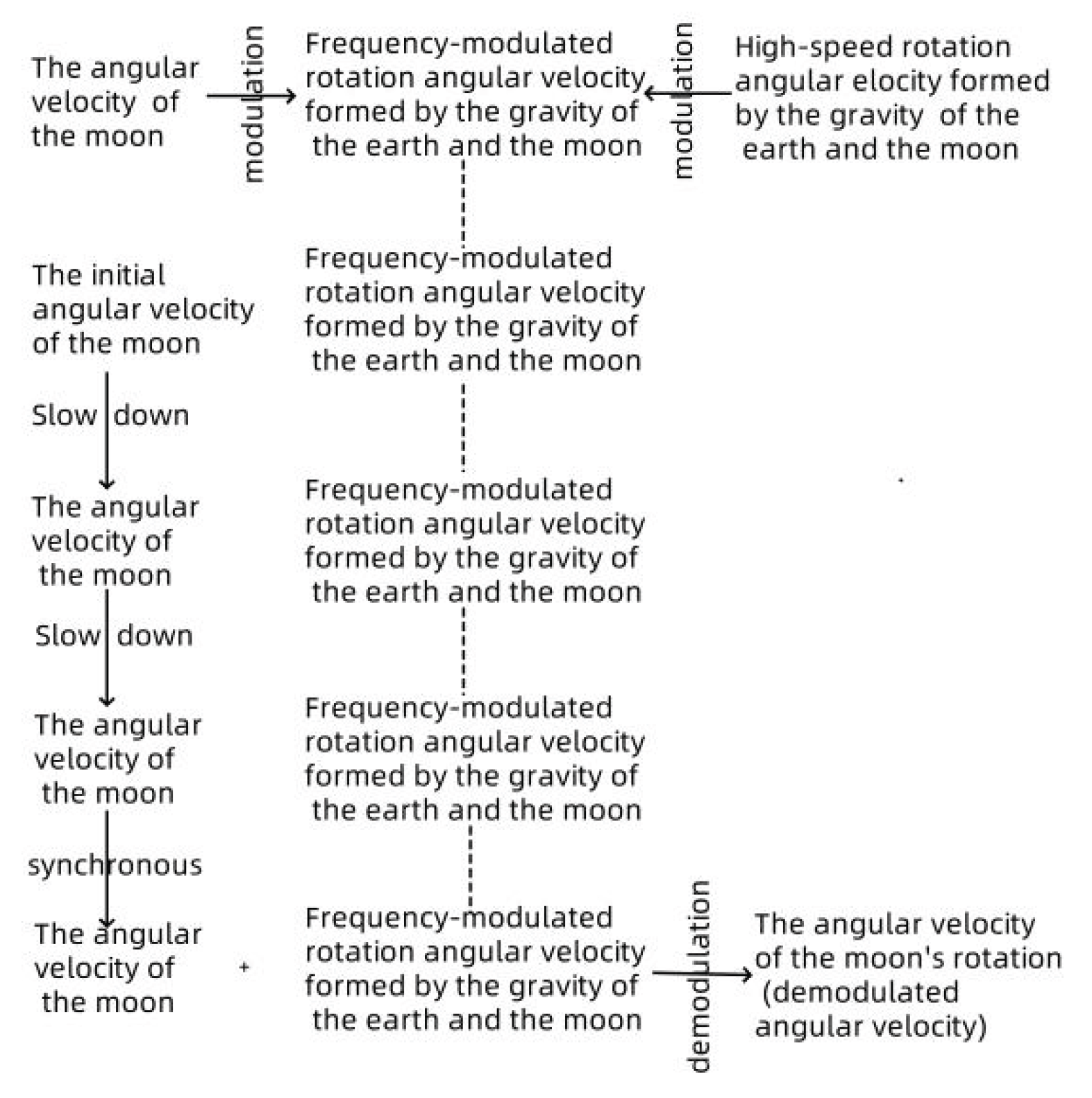
The moon is affected by the angular velocity ωeg generated by the earth’s gravity. The moon’s initial rotation angular velocity ωc0 will be superimposed into the new moon’s rotation angular velocity ωc1. The moon’s initial rotation angular velocity is superimposed with the moon’s rotation map velocity ωeg caused by the earth-moon gravity. The moon’s initial rotation angular velocity will gradually decrease, and the moon’s rotation angular velocity and the white-dao plane will also change. Due to the long-term existence of earth-moon gravity, the moon’s initial rotation angular velocity will gradually converge with the moon’s rotation angular velocity caused by the sun-to-earth gravity. The moon’s initial rotation angular velocity will eventually be the same as the moon’s rotation angular velocity caused by the earth-moon gravity. At this time, this rotation angular velocity is superimposed with the moon’s rotation angular velocity caused by the earth-moon gravity, which is equivalent to the demodulation process of frequency modulation waves. The demodulated waveform is the angular velocity waveform of the moon’s rotation angular velocity caused by the earth-moon gravity. This rotation angular velocity is the final angular velocity of the moon. It is the same as the angular velocity of the moon’s rotation. Judging from the results, the moon is rotating synchronously. It can be seen from the wave superimposed data simulation diagram that when the frequencies of the two waves are close, a straight curve of extremely small amplitude will appear. At this time, the moon’s rotation plane is perpendicular to the moon’s white path plane. The entire modem and demodulation process of the moon’s rotation is shown in Figure 7.

7. Changes in the Angle Between the Equatorial Plane and the White Path Surface of the Moon

After the moon achieves synchronous rotation, regardless of the influence of other factors, the moon’s rotation surface and the white path surface will be at an angle of 90°. The rotation speed of the moon is the demodulated Ωme of the moon orbiting the earth. The minimum value is 2.386E-06 radians/s, the average value is 2.662E-06 radians/s, and the maximum value is 2.979E-06 radians/s. The average radius of the moon is 1737.10km and the rotation period is 27.32 days (rotating counterclockwise from west to east). The angle between the moon’s rotation axis and the white path surface will also vary between 6.69° (i.e., 5.15°+1.54°) and 3.60° (i.e., 5.15°-1.54°).

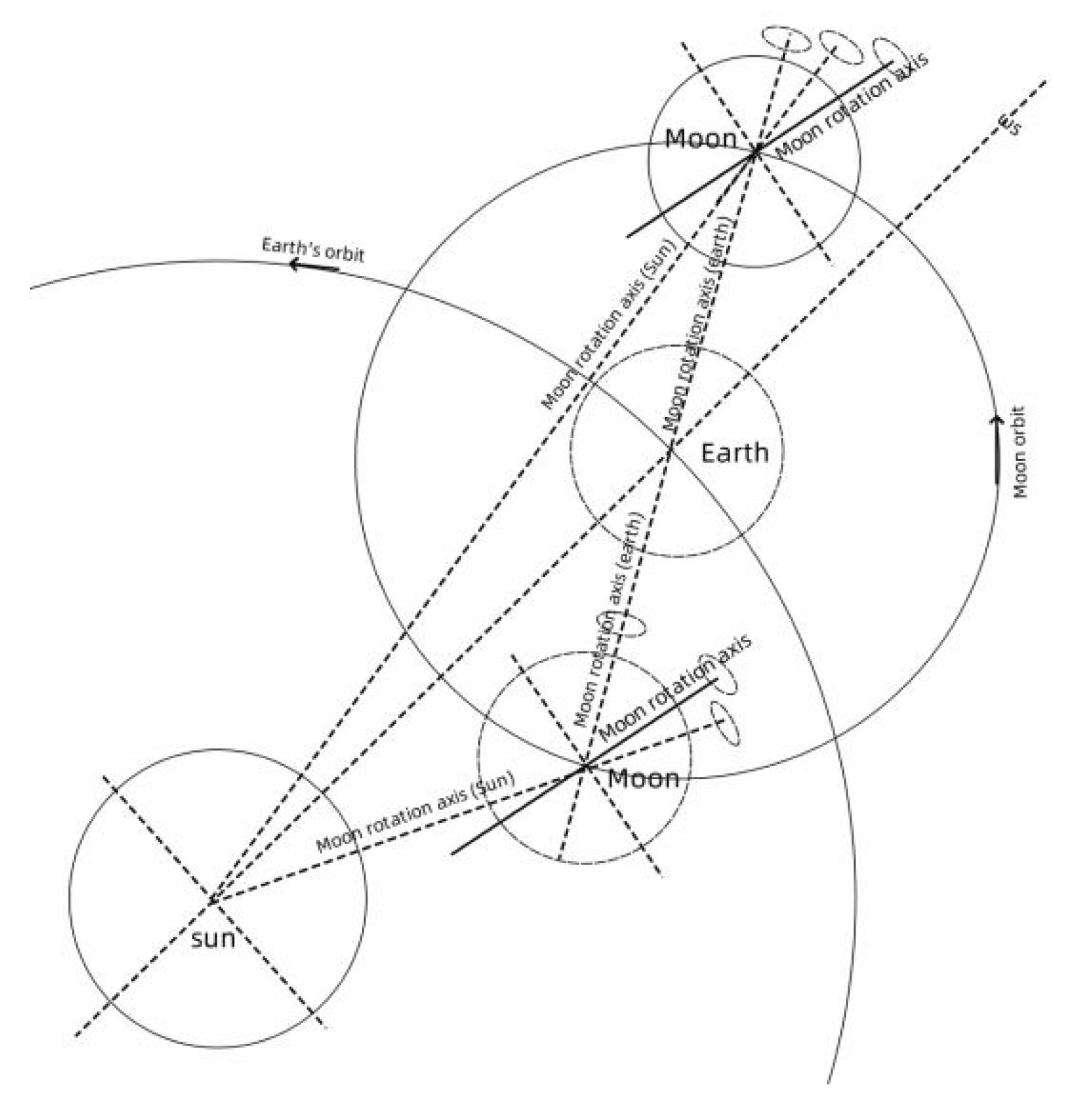
The moon is the Earth’s satellite. While the moon orbits the earth, it also orbits the sun with the earth. Figure 8 shows the moon and the earth orbits the sun.

Running diagram. In the figure, S0 is the center of mass of the sun, E0 is the center of mass of the earth, and M0 is the center of mass of the moon. The connection of S0E0 is the rotation axis of the earth rotating in the ecliptic plane under the gravitational force of the sun, which is opposite to the direction of the earth’s revolution. The connection of E0M0 is the rotation axis of the moon rotating in the white path under the gravitational force of the earth, which is Opposite to the direction of the moon rotating in the white path. The connection of S0M0 is the rotation axis of the moon rotating in the gravitational force of the sun. When the moon and the earth achieve synchronous rotation, the moon’s rotation plane is perpendicular to the white path plane, the rotation plane of the moon’s rotation formed by the sun’s gravity is perpendicular to the connection line of S0M0. The synchronous rotation angular velocity between the moon and the earth and the angular velocity of the moon’s rotation formed by the sun’s gravity are finally superimposed to form the observable rotation angular velocity of the moon. The observable angular velocity plane finally formed by the moon forms an angle α with the white path plane.

Suppose the synchronous rotation angular velocity ωme between the moon and the earth, the angular velocity ωms of the moon formed by the gravity of the sun, and the angle between the earth and the line connecting the sun and the moon is δ, then the synchronized angular velocity ωm of the moon is:

$${\omega }_m=\sqrt{{\omega }_{me}^2+{\omega }_{ms}^2-2{\omega }_{me}{\omega }_{ms}\cos \left[\pi -\left({\displaystyle \frac{\pi }{2}}-\delta \right)\right]}=\sqrt{{\omega }_{me}^2+{\omega }_{ms}^2+2{\omega }_{me}{\omega }_{ms}\sin \delta }$$

(37)

$${\displaystyle \frac{{\omega }_{ms}}{\sin \left(\frac{\pi }{2}-\alpha \right)}}={\displaystyle \frac{{\omega }_{me}}{\sin \left[\left(\frac{\pi }{2}-\delta \right)-\left(\frac{\pi }{2}-\alpha \right)\right]}}$$

(38)

$${\displaystyle \frac{{\omega }_{ms}}{\cos \alpha }}={\displaystyle \frac{{\omega }_{me}}{\sin \left(\alpha -\delta \right)}}$$

(39)

Here, the synchronous rotation angular velocity ωg of the moon and the earth is the demodulated velocity Ωs of the moon orbiting the earth. The minimum value is 2.386E-06 radians/s, the average value is 2.662E-06 radians/s, and the maximum value is 2.979E-06 radians/s.

Since the distance between the moon and the earth is much smaller than the distance between the sun and the earth, the orbit of the moon orbits the sun can be approximately regarded as the orbit of the earth orbits the sun. The angular velocity of the moon caused by the sun’s gravity is:

$$h_{ms}={\displaystyle \frac{R_{sm}-r_s+r_m}{2R_{sm}}}{r}_m$$

(40)

$${\omega }_{ms}={\displaystyle \frac{r_m{r}_s}{R_{sm}}}\sqrt{{\displaystyle \frac{G_r}{m_m\left(\frac{h_{ms}^2}{R_{sm}}+\frac{2r_m^2}{5h_{ms}}+h_{ms}\right)}}}$$

(41)

The minimum distance between the earth and the moon is 3.631E+08m, the maximum distance is 4.057E+08m, the minimum distance between the sun and the earth is 1.471E+11m, the maximum distance between the sun and the earth is 1.521E+11m, the minimum distance between the sun and the moon is 1.467E+11m, the maximum distance between the sun and the moon is 1.525E+11m, the maximum distance between the sun and the moon is 1.525E+11m, the maximum distance between the sun and the moon is 1.525E+11m, the gravitational coefficient Gr takes the constant of the earth and the gravitational simulation of the earth and the moon is 1.210E+12N/m^2, bringing other constants to:

$$h_{ms\min }={\displaystyle \frac{\left(1.467E+11\right)-\left(6.955E+8\right)+\left(7.637E+6\right)}{2\times \left(1.467E+11\right)}}\times \left(7.637E+6\right)=8.644E+5m$$

(42)

$$h_{ms\max }={\displaystyle \frac{\left(1.525E+11\right)-\left(6.955E+8\right)+\left(7.637E+6\right)}{2\times \left(1.525E+11\right)}}\times \left(7.637E+6\right)=8.646E+5m$$

(43)

$${\omega }_{ms\max }={\displaystyle \frac{r_m{r}_s}{R_{sm\min }}}\sqrt{{\displaystyle \frac{G_r}{m_m\left(\frac{h_{ms}^2}{R_{sm\min }}+\frac{2r_m^2}{5h_{ms}}+h_{ms}\right)}}}=3.593E-05/s$$

(44)

$${\omega }_{ms\min }={\displaystyle \frac{r_m{r}_s}{R_{sm\max }}}\sqrt{{\displaystyle \frac{G_r}{m_m\left(\frac{h_{ms}^2}{R_{sm\max }}+\frac{2r_m^2}{5h_{ms}}+h_{ms}\right)}}}=3.458E-05/s$$

(45)

The angle δ between the earth and the moon and the sun and the moon is the minimum value of the sun, the earth and the moon on a line (solar eclipse or lunar eclipse). At this time, the angle δ=0 is the maximum that the earth and the moon are on the eclipse. At this time, the angle δ=0 is the situation where the earth and the moon are on the eclipse. At this time, δ meets:

$${\delta }_{\max }={\displaystyle \frac{R_{em\max }}{R_{se\min }}}={\displaystyle \frac{4.057E+08}{1.471E+11}}=2.758E-03$$

(46)

The angle α between the lunar equatorial plane and the white path plane can be calculated from the above data.Since the moon is subject to the gravity of the sun, it is related to the problem of three-body problems, which is relatively complicated. Here, ωms can also be inversely deduced by the angle between the moon’s equatorial plane and the white path plane.

$${\displaystyle \frac{{\omega }_{ms}}{\cos \alpha }}={\displaystyle \frac{{\omega }_{me}}{\sin \left(\alpha -\delta \right)}}$$

(47)

$${\omega }_{ms}={\displaystyle \frac{{\omega }_{me}\cos \alpha }{\sin \left(\alpha -\delta \right)}}$$

(48)

$${\omega }_{ms\max }={\displaystyle \frac{{\omega }_{me\max }\cos {\alpha }_{\min }}{\sin \left({\alpha }_{\min }-{\delta }_{\max }\right)}}={\displaystyle \frac{\left(2.979E-06\right)\times \cos 0.06283}{\sin \left(0.06283-2.758E-03\right)}}=4.952E-05/s$$

(49)

$${\omega }_{ms\min }={\displaystyle \frac{{\omega }_{me\min }\cos {\alpha }_{\max }}{\sin \left({\alpha }_{\max }-{\delta }_{\min }\right)}}={\displaystyle \frac{\left(2.386E-06\right)\times \cos 0.11676}{\sin \left(0.11676-0\right)}}=2.034E-05/s$$

(50)

The angular velocity ωms of the reverse thrust moon caused by the gravity of the sun are on the same order of magnitude as the angular velocity ωms of the moon caused by the gravity of the sun, and the calculated angular velocity falls within the angular velocity range of the reverse thrust, but the calculated estimation range is small, and the calculated thrust calculation range is large. This should be related to the frequency broadening after modulation and demodulation of the angular velocity calculated by the moon’s revolution. The specific calculation needs further calculation and research.

8. In conclusion

Gravity is the process in which nucleons emit gravitons and gravitons propagate in space with gravitational energy waves, and gravitational energy waves resonate with other nucleons and form energy transfer. For planets, gravitons emitted by nucleons inside the planet interact with other nucleons inside the planet, forming the cohesion of the planet. Gravitationaltons emitted by nucleons on the surface of the planet are partially emitted outside the ball. These gravitons emitted outside the ball meet the nucleons of other planets and resonate with them to form energy transfer. These transferred energy will cause the resonant nucleons to produce a vertical gravity line displacement, forming a vertical and gravitational line action force. The planets orbiting the central planet S, only spherical nucleons facing the central planet S can be received The gravitons emitted by the central planet S, the nucleus of the central planet S, will not receive the gravitons of the central planet S. In this way, for the entire planet, the equivalent gravitational action point Eg is not in the center of mass of the planet, but on the spherical surface of about 0.5 radius near the center of mass S. In this way, the central planet S will have two effects on the planet E that rotates around it. One is the centripetal force that rotates around the central planet S, and the other is the rotational force that rotates around the center of mass of the planet around the gravitational action point Eg. Within a certain time Δt, the initial velocity of planet E will cause the planet to move a uniform linear displacement. Planet E is subjected to the component force Fs of the gravity of the center planet S, which will cause the planet E to move for a distance in the arc. Planet E is subjected to another component force Fe of the gravity of the center planet S, which will cause the center of mass of planet E to move backwards on the arc for a distance around the gravitational point. Under the combined action of these three, planet E will form a standard elliptical orbit. After derivation calculation and data simulation, more than 99.9% of the gravity of the central planet is used for the rotation of the planet. It can also be said that at the balanced inertia of the planet’s movement, it can also be considered that at the point of gravity, the moment of the planet’s revolution is equal to the moment of the planet’s rotation. Since the force arm of the planet’s revolution is much larger than the force arm of the planet’s rotation, the force used for the rotation of the planet is much smaller than the force of the planet’s rotation. For the moon, the rotation speed of the moon generated by the earth’s gravity is much faster than the actual rotation speed, and this speed is affected by the moon’s revolution speed. Therefore, it can be considered that the rotation speed generated by the earth’s gravity on the moon is a frequency modulated wave modulated by the moon’s revolution speed. The initial rotation speed of the moon is constantly superimposed with the rotation speed of the earth’s gravity. The initial rotation speed of the moon will approach the rotation speed of the moon caused by the earth’s gravity. When the velocities of the two are similar, the superposition of the two velocities will demodulate the revolution speed modulated on the rotation speed of the moon caused by the earth’s gravity. From the results, the demodulated speed is the same as the revolution speed of the moon, which means that the moon is rotating synchronously. The moon orbits the earth and revolves around the sun at the same time. While the moon is subject to the gravity of the earth, it is also subject to the gravity of the sun. The gravity of the sun will cause the moon to rotate in the orbit of the moon that is opposite to the direction of the revolution. When the moon rotates synchronously with the earth, the demodulated rotation plane is perpendicular to the white path surface of the moon. The angular velocity of the moon generated by the gravity of the sun is superimposed to the angular velocity of the earth and the moon, forming the observable rotation angular velocity of the moon, and the angle between the rotation plane of the moon and the white path surface of the moon will change within a certain range. Through the above analysis, we can see that the solid structure of the planet’s radius 0.5 to the spherical surface is a necessary condition for the planet’s synchronous rotation. The planet’s synchronous rotation is the final return of the planet’s operation.