Submitted:
19 May 2025
Posted:
19 May 2025
You are already at the latest version
Abstract
Keywords:
1. Introduction
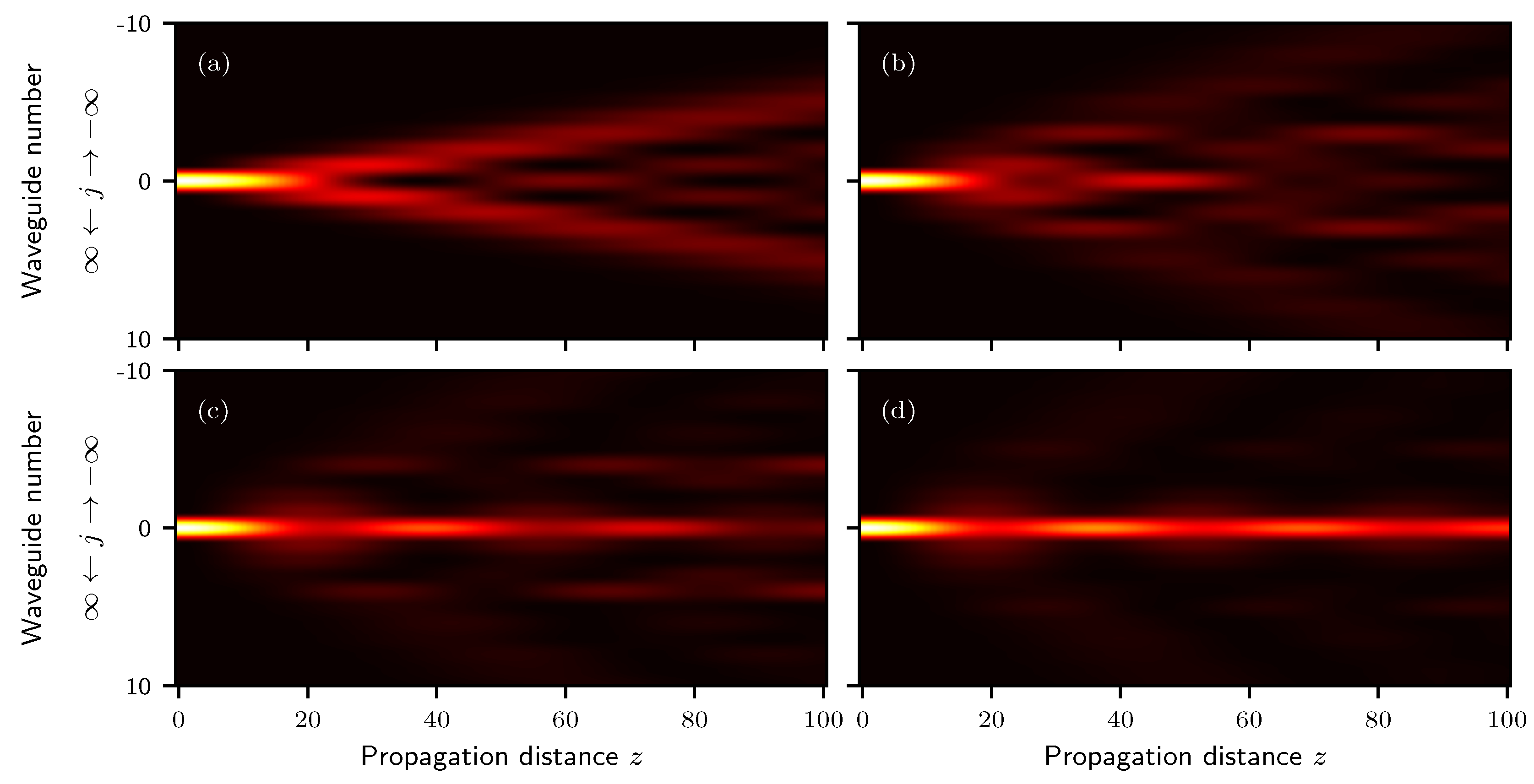
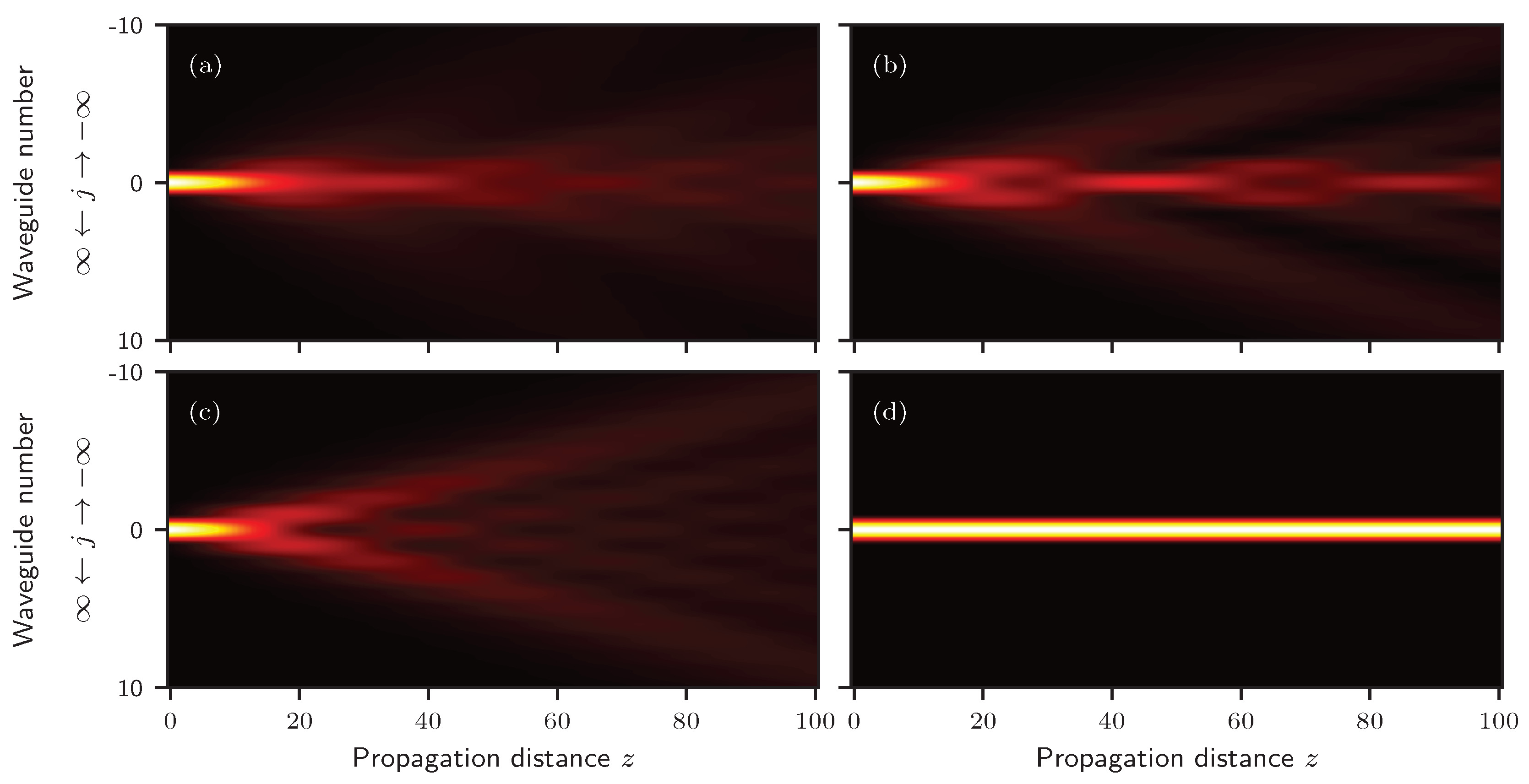
2. Interaction with N Neighbors
3. Interaction with N Neighbors Using the Generating Function of the Generalized Bessel Functions of N Variables and N − 1 Parameters
4. From Discrete to Continuous Models
4.1. Natural Logarithm Function
4.2. Exponential Function
4.3. Polylogarithm Function
4.4. Quadratic Polynomial
4.5. Geometric Series
5. Conclusions
References
- Heitler, W. The Quantum Theory of Radiation; Dover Books on Physics, Dover Publications, 1984. [Google Scholar]
- Gyongyosi, L.; Imre, S. A Survey on quantum computing technology. Computer Science Review 2019, 31, 51–71. [Google Scholar] [CrossRef]
- Fedida, S.; Serafini, A. Tree-level entanglement in quantum electrodynamics. Phys. Rev. D 2023, 107, 116007. [Google Scholar] [CrossRef]
- Vidal, G. Efficient Classical Simulation of Slightly Entangled Quantum Computations. Phys. Rev. Lett. 2003, 91, 147902. [Google Scholar] [CrossRef] [PubMed]
- Feynman, R.P. Simulating physics with computers. In Feynman and computation; CRC Press, 2018; pp. 133–153. [Google Scholar]
- Blatt, R.; Wineland, D. Entangled states of trapped atomic ions. Nature 2008, 453, 1008–1015. [Google Scholar] [CrossRef] [PubMed]
- Monroe, C.; Campbell, W.C.; Duan, L.M.; Gong, Z.X.; Gorshkov, A.V.; Hess, P.W.; Islam, R.; Kim, K.; Linke, N.M.; Pagano, G.; et al. Programmable quantum simulations of spin systems with trapped ions. Rev. Mod. Phys. 2021, 93, 025001. [Google Scholar] [CrossRef]
- Bloch, I.; Dalibard, J.; Zwerger, W. Many-body physics with ultracold gases. Rev. Mod. Phys. 2008, 80, 885–964. [Google Scholar] [CrossRef]
- Mivehvar, F.; Piazza, F.; Donner, T.; and, H.R. Cavity QED with quantum gases: new paradigms in many-body physics. Advances in Physics 2021, 70, 1–153. [Google Scholar] [CrossRef]
- Bohrdt, A.; Homeier, L.; Reinmoser, C.; Demler, E.; Grusdt, F. Exploration of doped quantum magnets with ultracold atoms. Annals of Physics 2021, 435, 168651. [Google Scholar] [CrossRef]
- Christodoulides, D.N.; Lederer, F.; Silberberg, Y. Discretizing light behaviour in linear and nonlinear waveguide lattices. Nature 2003, 424, 817–823. [Google Scholar] [CrossRef]
- Barral, D.; Walschaers, M.; Bencheikh, K.; Parigi, V.; Levenson, J.A.; Treps, N.; Belabas, N. Quantum state engineering in arrays of nonlinear waveguides. Phys. Rev. A 2020, 102, 043706. [Google Scholar] [CrossRef]
- Urzúa, A.R.; Ramos-Prieto, I.; Moya-Cessa, H.M. Integrated optical wave analyzer using the discrete fractional Fourier transform. J. Opt. Soc. Am. B 2024, 41, 2358–2365. [Google Scholar] [CrossRef]
- Rai, A.; Das, S.; Agarwal, G. Quantum entanglement in coupled lossy waveguides. Opt. Express 2010, 18, 6241–6254. [Google Scholar] [CrossRef] [PubMed]
- Perez-Leija, A.; Szameit, A.; Ramos-Prieto, I.; Moya-Cessa, H.; Christodoulides, D.N. Generalized Schrödinger cat states and their classical emulation. Phys. Rev. A 2016, 93, 053815. [Google Scholar] [CrossRef]
- Perets, H.B.; Lahini, Y.; Pozzi, F.; Sorel, M.; Morandotti, R.; Silberberg, Y. Realization of quantum walks with negligible decoherence in waveguide lattices. Phys. Rev. Lett. 2008, 100, 170506. [Google Scholar] [CrossRef]
- Peruzzo, A.; Lobino, M.; Matthews, J.C.; Matsuda, N.; Politi, A.; Poulios, K.; Zhou, X.Q.; Lahini, Y.; Ismail, N.; Wörhoff, K.; et al. Quantum walks of correlated photons. Science 2010, 329, 1500–1503. [Google Scholar] [CrossRef]
- Biggerstaff, D.N.; Heilmann, R.; Zecevik, A.A.; Gräfe, M.; Broome, M.A.; Fedrizzi, A.; Nolte, S.; Szameit, A.; White, A.G.; Kassal, I. Enhancing coherent transport in a photonic network using controllable decoherence. Nat Commun 2016, 7, 11282. [Google Scholar] [CrossRef]
- Lahini, Y.; Avidan, A.; Pozzi, F.; Sorel, M.; Morandotti, R.; Christodoulides, f.D.N.; Silberberg, Y. Anderson localization and nonlinearity in one-dimensional disordered photonic lattices. Phys. Rev. Lett. 2008, 100, 013906. [Google Scholar] [CrossRef]
- Keil, R.; Perez-Leija, A.; Dreisow, F.; Heinrich, M.; Moya-Cessa, H.; Nolte, S.; Christodoulides, D.N.; Szameit, A. Classical Analogue of Displaced Fock States and Quantum Correlations in Glauber-Fock Photonic Lattices. Phys. Rev. Lett. 2011, 107, 103601. [Google Scholar] [CrossRef] [PubMed]
- Keil, R.; Perez-Leija, A.; Aleahmad, P.; Moya-Cessa, H.; Nolte, S.; Christodoulides, D.N.; Szameit, A. Observation of Bloch-like revivals in semi-infinite Glauber-Fock photonic lattices. Opt. Lett. 2012, 37, 3801–3803. [Google Scholar] [CrossRef]
- Efremidis, N.K.; Christodoulides, D.N. Discrete solitons in nonlinear zigzag optical waveguide arrays with tailored diffraction properties. Phys. Rev. E 2002, 65, 056607. [Google Scholar] [CrossRef]
- Szameit, A.; Pertsch, T.; Nolte, S.; Tünnermann, A.; Lederer, F. Long-range interaction in waveguide lattices. Phys. Rev. A 2008, 77, 043804. [Google Scholar] [CrossRef]
- Tapia-Valerdi, M.A.; Ramos-Prieto, I.; Soto-Eguibar, F.; Moya-Cessa, H.M. Waveguide arrays interaction to second neighbors: Exact solution. arXiv preprint 2025. [Google Scholar]
- Stockhofe, J.; Schmelcher, P. Bloch dynamics in lattices with long-range hopping. Phys. Rev. A 2015, 91, 023606. [Google Scholar] [CrossRef]
- Longhi, S.; Marangoni, M.; Lobino, M.; Ramponi, R.; Laporta, P.; Cianci, E.; Foglietti, V. Observation of Dynamic Localization in Periodically Curved Waveguide Arrays. Phys. Rev. Lett. 2006, 96, 243901. [Google Scholar] [CrossRef]
- Anuradha, T.; Patra, A.; Gupta, R.; Rai, A.; Sen(De), A. Production of genuine multimode entanglement in circular waveguides with long-range coupling. Phys. Rev. A 2024, 109, 032411. [Google Scholar] [CrossRef]
- Wang, G.; Huang, J.P.; Yu, K.W. Nontrivial Bloch oscillations in waveguide arrays with second-order coupling. Opt. Lett. 2010, 35, 1908–1910. [Google Scholar] [CrossRef] [PubMed]
- Qi, F.; Feng, Z.; Wang, Y.; Xu, P.; Zhu, S.; Zheng, W. Photon-number correlations in waveguide lattices with second order coupling. J. Opt. 2014, 16, 125007. [Google Scholar] [CrossRef]
- Román-Ancheyta, R.; Ramos-Prieto, I.; Perez-Leija, A.; Busch, K.; León-Montiel, R.d.J. Dynamical Casimir effect in stochastic systems: Photon harvesting through noise. Phys. Rev. A 2017, 96, 032501. [Google Scholar] [CrossRef]
- Villegas-Martínez, B.; Moya-Cessa, H.; Soto-Eguibar, F. Modeling displaced squeezed number states in waveguide arrays. Physica A: Statistical Mechanics and its applications 2022, 608, 128265. [Google Scholar] [CrossRef]
- Dreisow, F.; Wang, G.; Heinrich, M.; Keil, R.; Tünnermann, A.; Nolte, S.; Szameit, A. Observation of anharmonic Bloch oscillations. Opt. Lett. 2011, 36, 3963–3965. [Google Scholar] [CrossRef]
- Ramos-Prieto, I.; Uriostegui, K.; Récamier, J.; Soto-Eguibar, F.; Moya-Cessa, H.M. Kapitza–Dirac photonic lattices. Opt. Lett. 2021, 46, 4690–4693. [Google Scholar] [CrossRef]
- London, F. Über die Jacobischen transformationen der quantenmechanik. Z. Physik 1926, 37, 915–925. [Google Scholar] [CrossRef]
- Susskind, L.; Glogower, J. Quantum mechanical phase and time operator. Physics Physique Fizika 1964, 1, 49–61. [Google Scholar] [CrossRef]
- Carruthers, P.; Nieto, M.M. Phase and Angle Variables in Quantum Mechanics. Rev. Mod. Phys. 1968, 40, 411–440. [Google Scholar] [CrossRef]
- Perez-Leija, A.; Andrade-Morales, L.A.; Soto-Eguibar, F.; Szameit, A.; Moya-Cessa, H.M. The Pegg–Barnett phase operator and the discrete Fourier transform. Physica Scripta 2016, 91, 043008. [Google Scholar] [CrossRef]
- Dattoli, G.; Torre, A.; Lorenzutta, S.; Maino, G.; Chiccoli, C. Theory of generalized Bessel functions.-ii. Il Nuovo Cimento B (1971-1996) 1991, 106, 21–51. [Google Scholar] [CrossRef]
- Dattoli, G.; Chiccoli, C.; Lorenzutta, S.; Maino, G.; Richetta, M.; Torre, A. Generating functions of multivariable generalized Bessel functions and Jacobi-elliptic functions. Journal of Mathematical Physics 1992, 33, 25–36. [Google Scholar] [CrossRef]
- Szameit, A.; Dreisow, F.; Pertsch, T.; Nolte, S.; Tünnermann, A. Control of directional evanescent coupling in fs laser written waveguides. Opt. Express 2007, 15, 1579–1587. [Google Scholar] [CrossRef]
- Szameit, A.; Blömer, D.; Burghoff, J.; Pertsch, T.; Nolte, S.; Tünnermann, A. Hexagonal waveguide arrays written with fs-laser pulses. Appl. Phys. B 2006, 82, 507–512. [Google Scholar] [CrossRef]
- Gradshteyn, I.; Ryzhik, I. Table of Integrals, Series, and Products; Academic Press, 2014. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).




