Analysis of Common Phenomena and Causes of Changes in the Earth’s Rotation Speed

1. Introduction

In recent years, earthquake science has developed rapidly. Through the study of the mutation interface of seismic wave propagation velocity, it was confirmed that the earth consists of crust, mantle, and core [1], as shown in Table 1.

Crust: The crust is the outermost solid lithosphere on the earth, with an average thickness of about 17 kilometers, but it is unevenly distributed. The continental crust is thicker (average 33 kilometers, and the Qinghai-Tibet Plateau can reach 60-70 kilometers), mainly composed of granite (silicon-aluminum layer) and basalt (silicon-maximum layer); the oceanic crust is thin (average 6 kilometers), almost no granite, mainly basalt.

Mantle: It is divided into the upper mantle and the lower mantle, with a total thickness of about 2,900 kilometers. There is a soft-spheric layer on the top of the upper mantle (deep about 60-250 kilometers), which is the birthplace of magma; the material in the lower mantle is in a plastic solid state, and the density and pressure increase with depth. The upper mantle is mainly peridotite, and the part close to the core contains iron and nickel oxides.

Earth core: divided into external core and internal core. The outer core (depth 2900-5100 kilometers) is a liquid iron-nickel alloy, and the inner core (5100 kilometers to the center of the earth) is a solid iron-nickel alloy. ‌Seismic wave evidence‌: The transverse wave (S wave) cannot pass through the external core, confirming its liquid properties.

In recent years, Chinese-American scientists Song Xiaodong and others have discovered through observation and research on seismic waves [2,3,4,5,6,7,8,9,10] that the rotation direction of the earth’s core is opposite to the rotation direction of the earth, with an angle of 10° to the rotation axis, and the rotation speed of the core is about 1.1° faster than the rotation speed of the earth itself every year.

In recent years, scientific researchers have shown through long-term observations [11,12,13] that the earth’s rotation speed slows down in spring and accelerates in autumn, and the annual cycle amplitude is about 20-25 milliseconds. The traditional view believes that the reason is mainly related to the seasonal changes in atmospheric circulation, especially the redistribution of the Earth’s angular momentum due to wind system activities.

In recent years, scientific researchers have shown through long-term observations [14] that the Earth’s rotation speed is gradually slowing down, causing the day length to grow by about 12 milliseconds every century. Traditionally, the tidal friction of the Earth is the main reason for the long-term changes in the rotation speed.

In recent years, scientific researchers have shown through long-term observations [15]: “The correlation between solar orbital motion and the change in the earth’s rotation rate reaches 0.9994.”

Through in-depth research on quantum gravity theory, the author believes that the above phenomena are related to the point of gravity of the sun on the earth and the phenomenon of the separation of the center of mass of the earth, and is related to the fact that 99.99% of the sun’s gravity on the earth are used for the rotation of the earth.

2. Gravity Analysis Between Planets and Simulation of Elliptical Orbits

2.1. The Equivalent Radius of the Planet’s Graviton Emission

“Graining, gravitational field and graviton—inference about the frequency of gravitational energy waves” [16] believes that the most basic unit of matter is a nucleon (a collective name for protons and neutrons). All nucleons emit gravitons. The energy carried by gravitons is the Planck constant h, and the value is 6.626×10^ (-34) J·s. Gravitators propagate in space with gravitational energy waves. The gravitational energy wave resonates with other nucleons, transmitting energy to form gravity. For planets [17], gravitons emitted by nucleons inside the planet interact with other nucleons inside the planet to form the cohesion of the planet. The gravitons emitted by nucleons near the outside of the planet are partially emitted outside the sphere and propagate in space with gravitational energy waves. The gravitational energy waves encounter nucleons from other planets and resonate with them to form gravitational force between the planets.

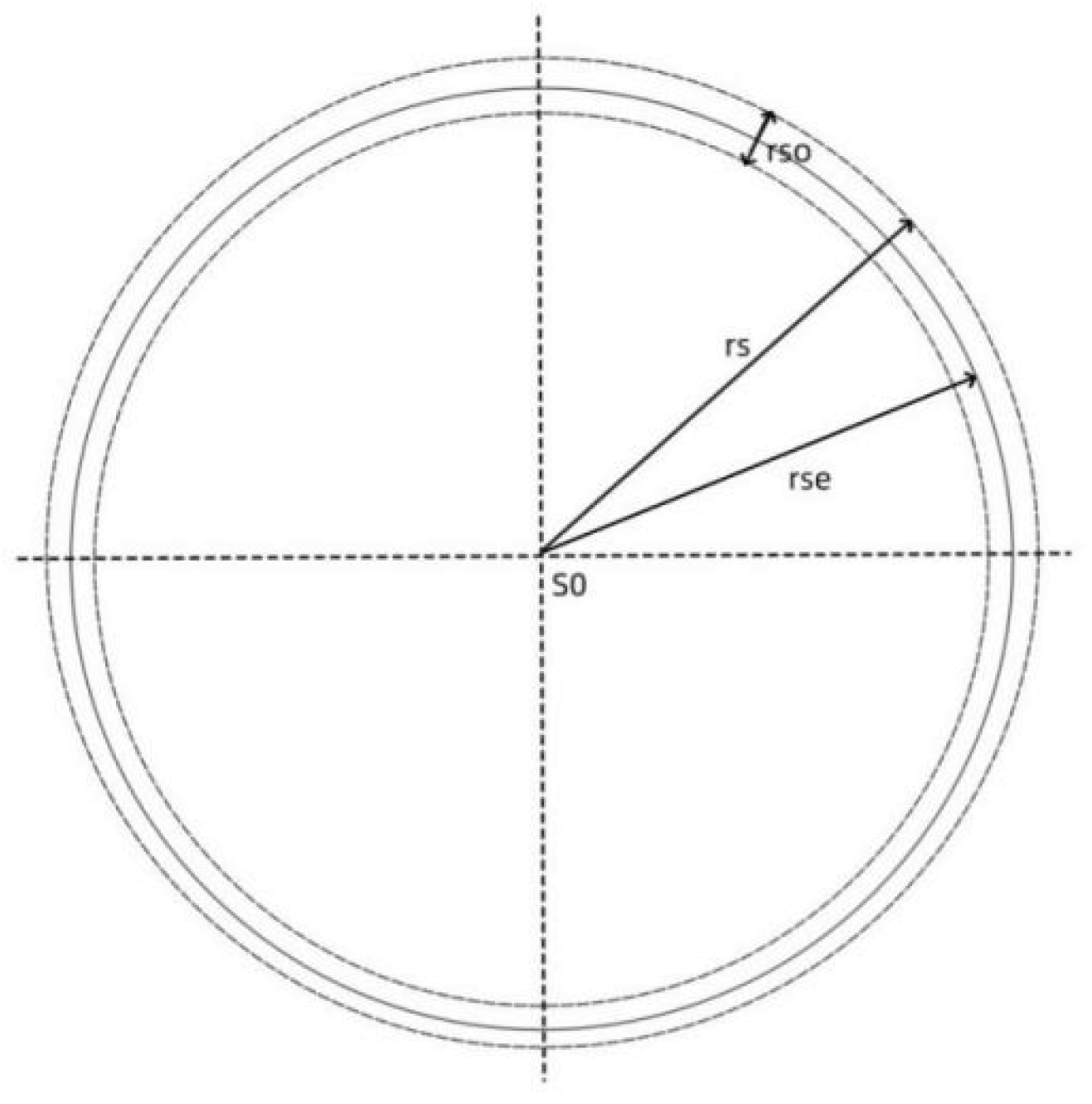
Figure 1 is a schematic diagram of the equivalent spherical surface of a planet’s graviton emitted.In the figure, rs is the planet’s radius, and rso is the thickness of the graviton shell sent to the outside of the sphere. There should be a spherical layer rse in the middle. It can be considered that all gravitons on the planet are emitted by this spherical layer. If this spherical layer is used as the equivalent spherical layer emitted by the planet’s gravitons, for general circumstances, it can be considered that this spherical layer is in the middle of the planet’s graviton emission shell.

“The attempt to correct the universal gravitational formula from the proportion of the planet emitted to the outside of the ball—the ratio of the outside of the ball graviton in the deflection gravitational theory” [18] article calculates the number of gravitons sent to the outside of the ball. The thickness of the outer layer where the planet can emit gravitons outside the ball is:

$$r_{so}={\displaystyle \frac{6m_0}{k_{ng}{r}_0^2{\rho }_s}}={\displaystyle \frac{k_{s\rho }}{{\rho }_s}}={\displaystyle \frac{41540}{{\rho }_s}}$$

(1)

In the formula, kng is the ratio in which gravitons passing through the nucleus can be absorbed by the nucleus, m0 is the mass of the nucleus, r0 is the radius of the nucleus, and ρ is the density of the shell matter of the planet. From the above analysis and calculation, it can be seen that the thickness of the shell of the planet emitting gravitons outward is too small relative to the planet’s radius and can be ignored. Therefore, the equivalent shell radius of the planet’s emitting gravitons is approximately equal to the planet’s radius.

$$r_{se}=r_s-{\displaystyle \frac{1}{2}}{r}_{so}\approx r_s$$

(2)

The number of gravitons sent by the planet to the outside of the ball is approximately:

$$n_{go}\approx {\mathrm{k}}_{\mathrm{gr}}{r}_s^2=1.599\times {10}^{55}{r}_s^2$$

(3)

In the formula, kgr is the constant and rs is the planet’s radius.

2.2. The Gravitational Point and Sphere of the Planet

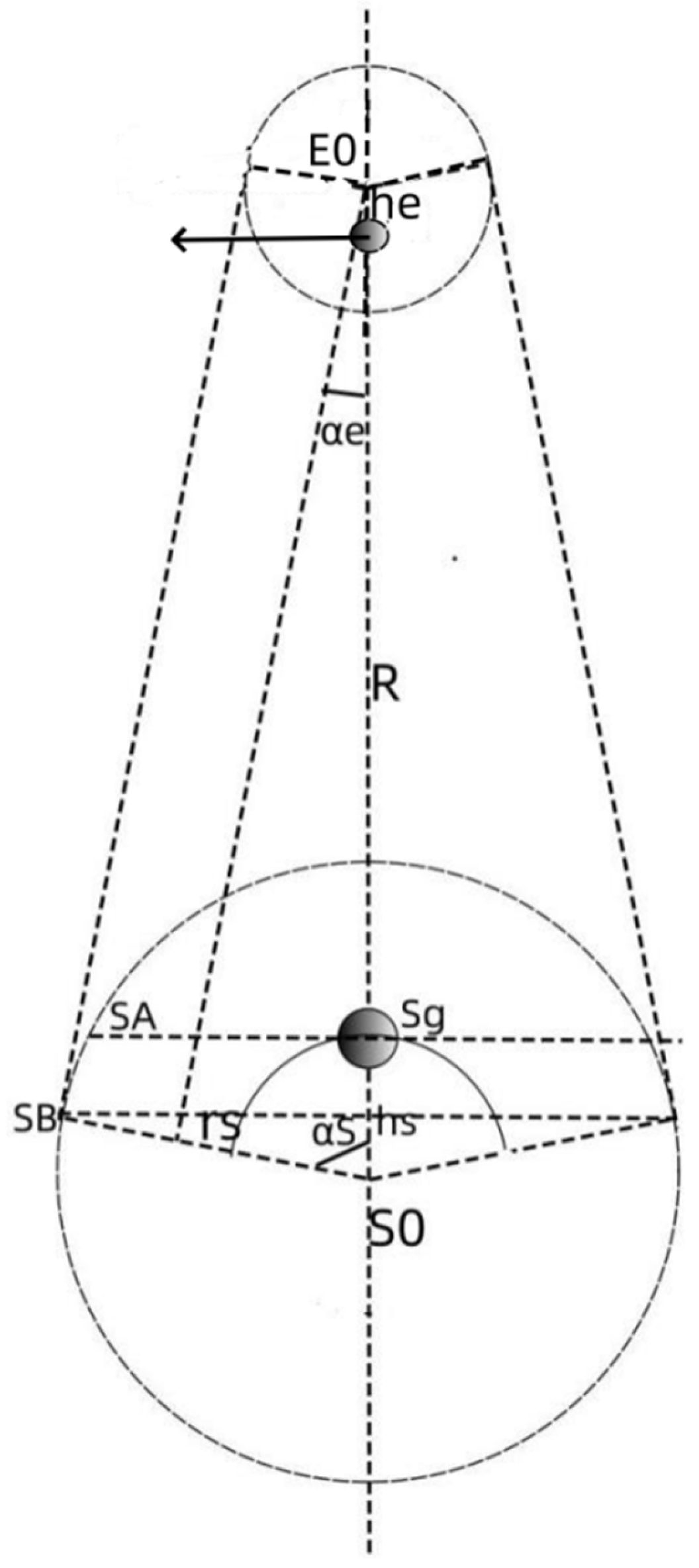
Figure 2 is an analysis diagram of the gravity effect between two planets. In the picture, the planet E rotates around the planet S. The center of mass of the central planet S is S0, the radius is rs, the mass is ms, the center of mass of the planet E is E0, the radius is re, the mass is me, and the center of mass distance between the planets is R0. Now, the effect of planet S on planet E is analyzed. In the figure, only the gravitons emitted by planet S facing the nucleons on the sphere of planet E can form gravity on planet E’s shell nucleons facing planet S. This phenomenon can be proved by the gravity double valley phenomenon during the solar eclipse [19]. Before the solar eclipse occurs, objects on the ground are subjected to the dual gravity of the sun and the moon, and the gravity of the earth that the object receives will decrease; during the solar eclipse, the gravity of objects on the ground is measured, and the results show that the gravity of objects on the ground is the same as the gravity when there is only the sun, which means that the gravitons received by the sun on the ground are blocked by the moon; when the solar eclipse ends, the sun is no longer blocked by the moon, and the objects on the ground are superimposed by the gravity of the sun and the moon, and the gravity decreases again, which forms the gravity double valley phenomenon during the solar eclipse.

To accurately calculate the effect of gravitons emitted by planet S on planet E, we should calculate the gravity of each surface element on planet S on planet E. When the distance between planets is much greater than the planet’s radius, it can be approximately believed that the energy transmitted between the surface elements of the two planets is equal, so that the energy transmitted from planet S to planet E is proportional to the area of the spherical surface.

Obviously, the equivalent center of the nuclear nucleus that the planet S ball works against the planet E is on the connection between the center of mass of the two planets. As shown in the figure, the distance between the center of gravity action of the center of mass of the planet S is hs, and there is

$$h_s={\displaystyle \frac{R_0+r_s-r_e}{2R_0}}{r}_s\approx {\displaystyle \frac{1}{2}}{r}_s$$

(4)

For planet E, the equivalent center of gravity is closer to the center of mass of planet E. As shown in the figure, let the distance between the center of gravity and the center of mass is he,

$$h_e={\displaystyle \frac{R_0-r_s+r_e}{2R_0}}{r}_e\approx {\displaystyle \frac{1}{2}}{r}_e$$

(5)

The energy transmitted by planet S to planet E is the ratio of the area of the sphere occupied by planet E from planet S distance R0 to the total number of gravitons emitted by planet S:

$$F_{se}={\displaystyle \frac{\pi r_e^2}{4\pi R_0^2}}{n}_{sg}h=G_i{\displaystyle \frac{r_e^2{r}_s^2}{R_0^2}}$$

(6)

$$G_i={\displaystyle \frac{1}{4}}{k}_{gr}h$$

(7)

Here Gi is the gravitational coefficient, kgr is the proportional coefficient of the graviton sent to the outside of the ball by the planet, and h is the Planck constant. From the above analysis, we can find that the energy (gravity) transmitted by nucleons between planets is proportional to the planet’s surface area, rather than to the planet’s mass.

2.3. Analysis of the Effect of Gravity on Planetary Movement

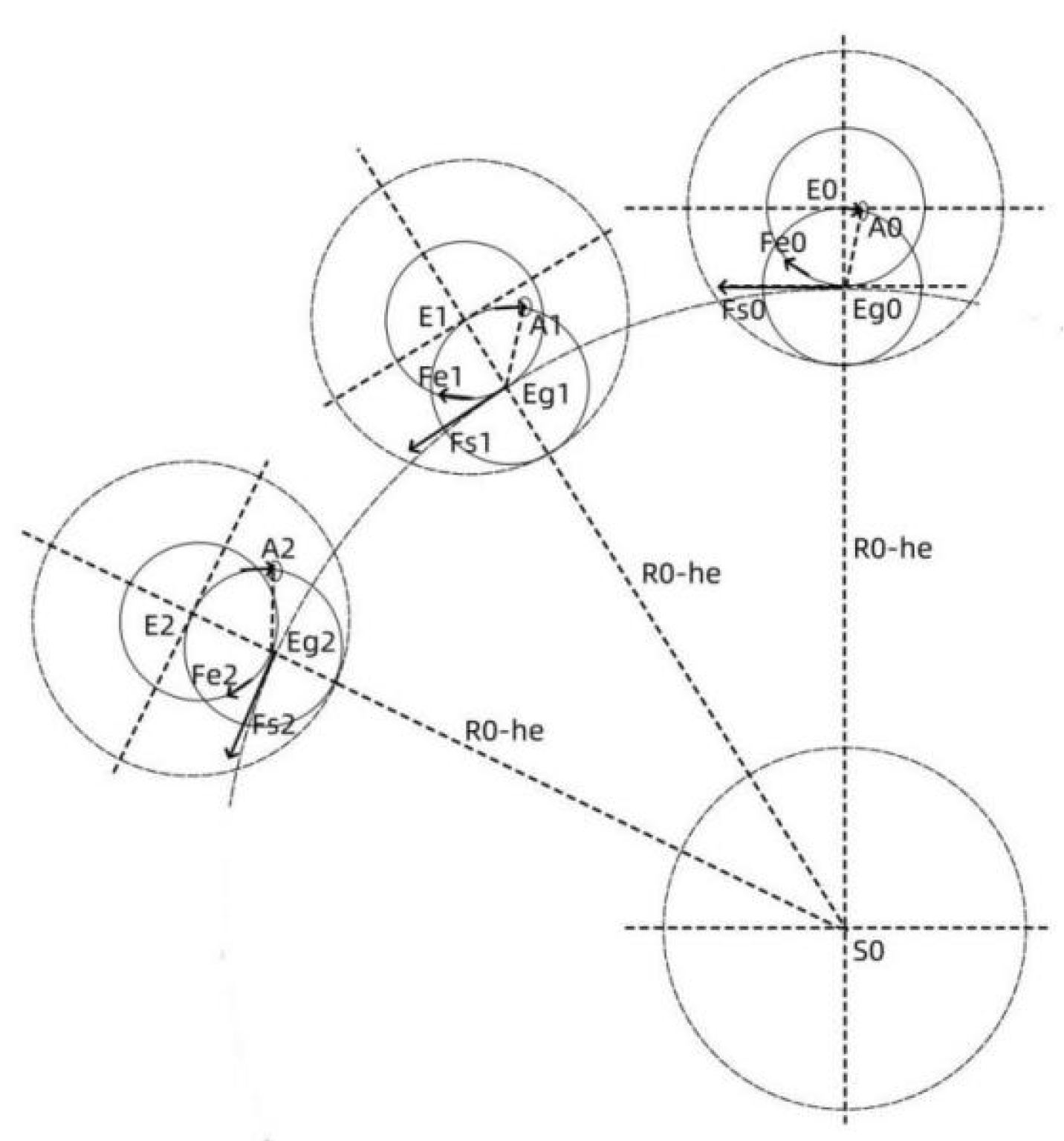
Figure 3 is an analysis diagram of the planet’s revolution and rotation caused by planet gravity. In the figure, S0 is the center of mass of the central planet S. E is the planet orbiting the central planet S. When the planet E is at the E0 position, the gravitational action point of planet S on planet E is Eg0. Since the gravitational action point is separated from the planet center of mass, gravity is divided into Fs0 related to the center planet S and Fe0 related to the planet E. When the same planet E is at position E1, gravity is divided into Fs1 related to the center planet S and Fe1 related to the planet E. When the planet E is at position E2, gravity is divided into Fs2 related to the center planet S and Fe2 related to the planet E. It can be seen that Fs0, Fs1, and Fs2 related to the center planet S act on the gravitational action point E, forming the driving force for the planet E to orbit the planet S. From the effect, Fs forms the centripetal force of planet E orbiting the planet S.

Since the gravitational action point Eg is separated from the planet’s center of mass, another effect of gravity received by the gravitational action point Eg is to drag the planet E to run. Generally,external forces rotate around the center of the sphere. Without considering the planet E Orbiting the central planet S, it can be considered that the planet E has always been affected by a gravitational Fe, and this point of action is fixed at the gravitational action point Eg. Therefore, this is not an external force rotates around the planet, but the center of mass of the planet rotates around the gravitational action point Eg. At the initial position E0, the planet’s center of mass tends to run towards A0. With the increase of time, the angle of rotation of the planet’s center of mass increases. Under the combined action of the two components of gravity, when the planet is at position E1, the center of mass moves to point A1, and when the planet is at position E2, the center of mass moves to point A2.

According to the above analysis, the total gravity Fse of the planet is:

$$F_{se}=F_s+F_e$$

(8)

The components related to the E-region of the planet are:

$$F_s=m_e{\displaystyle \frac{v_s^2}{R_0}}=m_e{\Omega }_s^2{R}_0$$

(9)

In the formula, gravity causes the linear velocity of the planet E to orbit the central planet S to be vs, unit m/s, the angular velocity of the revolution to be Ωs, unit radian/s, and me is the mass of the object (unit kg).

For the planet E that rotates around the gravitational action point Eg, its moment of inertia is:

$$I_e=k_I{m}_e{r}_e^2+m_e{h}_e^2$$

(10)

where me is the mass of the planet E, re is the radius of the planet E, and he is the distance between the gravitational action point Eg and the center of mass of the planet E. kI is the rotational moment of inertia coefficient, and for the earth kI=0.3307.

According to the rotation law of rigid body fixed axis:

$$M_Z=I\alpha$$

(11)

where Mz represents the external torque for a certain fixed axis, I represents the moment of inertia of the rigid body about a given axis, and α represents the angular acceleration. Here the torque is the component force of gravity and the rotation of the planet. The force arm is the distance he between the gravitational action point Eg and the center of mass of the planet. According to the definition of angular acceleration, there are:

$$\alpha ={\displaystyle \frac{d^2{\theta }_e}{d^{2}t}}={\displaystyle \frac{{\Delta }^{2}t{\omega }_e^2}{{\Delta }^{2}t}}={\omega }_e^2$$

(12)

At this time, the law of rotation of the rigid body fixed axis can be written as:

$$F_e{h}_e=I{\omega }_e^2$$

(13)

$$F_e={\displaystyle \frac{I{\omega }_e^2}{h_e}}=\left(k_I{m}_e{r}_e^2+m_e{h}_e^2\right){\displaystyle \frac{{\omega }_e^2}{h_e}}$$

(14)

For the rotation of a planet, it refers to the component of rotation in the planet’s rotation plane, which is generally not on the same plane as the actual rotation of the planet. Therefore, the angular velocity of the planet here is not the planet’s rotation angular velocity that is usually observed.

For objects that move in a circular motion, the relationship between linear velocity and angular velocity is as follows:

$$v_0=R_0{\Omega }_s$$

(15)

$$v_0\Delta t\sin {\beta }_0={\theta }_s$$

(16)

According to the law of conservation of momentum, momentum cannot be generated and disappeared out of thin air. For planet E, the planet’s revolution generates a positive momentum, and planet E rotates around the center of mass Eg to produce a reverse momentum, and these two should be equal:

$$p=m_e{v}_s=m_e{\Omega }_s{R}_0=m_e{v}_e=m_e{\omega }_e{h}_e$$

(17)

$${\Omega }_s{R}_0={\omega }_e{h}_e$$

(18)

$${\Omega }_s={\displaystyle \frac{h_e}{R_0}}{\omega }_e$$

(19)

Bring the above result into Formula (8):

$$F_{se}=m_e{\Omega }_s^2{R}_0+\left(k_I{m}_e{r}_e^2+m_e{h}_e^2\right){\displaystyle \frac{{\omega }_e^2}{h_e}}$$

(20)

$$F_{se}=m_e{R}_0{\left({\displaystyle \frac{{\omega }_e{h}_e}{R_0}}\right)}^2+\left(k_I{m}_e{r}_e^2+m_e{h}_e^2\right){\displaystyle \frac{{\omega }_e^2}{h_e}}$$

(21)

$${\omega }_e=\sqrt{{\displaystyle \frac{F_{se}}{m_e\left[\frac{h_e^2{R}_0}{R_0^2}+\frac{1}{h_e}\left(k_I{r}_e^2+h_e^2\right)\right]}}}=\sqrt{{\displaystyle \frac{F_{se}}{m_e\left(\frac{h_e^2}{R_0}+k_I\frac{r_e^2}{h_e}+h_e\right)}}}$$

(22)

The ratio of component force used for planet rotation to the entire gravity is:

$$\begin{array}{l}{k}_F={\displaystyle \frac{F_e}{F_{se}}}={\displaystyle \frac{\left(k_I{m}_e{r}_e^2+m_e{h}_e^2\right)\frac{{\omega }_e^2}{h_e}}{m_e{R}_0{\left(\frac{{\omega }_e{h}_e}{R_0}\right)}^2+\left(k_I{m}_e{r}_e^2+m_e{h}_e^2\right)\frac{{\omega }_e^2}{h_e}}}={\displaystyle \frac{\left(k_I{r}_e^2+h_e^2\right)}{\frac{h_e^3}{R_0}+\left(k_I{r}_e^2+h_e^2\right)}}\\ \approx {\displaystyle \frac{\left(0.33r_e^2+0.25r_e^2\right)}{\frac{r_e^3}{8R_0}+\left(0.33r_e^2+0.25r_e^2\right)}}={\displaystyle \frac{4.64R_0}{r_e+4.64R_0}}\approx 1\end{array}$$

(23)

From this we can see that almost all the gravity of the planet is used for the rotation of the planet, and only a little bit is left for the rotation of the planet. Here, it can also be considered that at the point of gravity, the torque of the planet’s revolution is equal to the moment of the planet’s rotation. Since the force arm of the planet’s revolution is much larger than the force arm of the planet’s rotation, the force used for the planet’s revolution is much smaller than the force of the planet’s rotation.

The movement of a planet is not a simple unforced system, it is subject to gravity at any time. Therefore, the angular momentum of a planet at any point includes: the angular momentum of the initial velocity of the planet relative to the angular momentum of the central planet, gravity forms the angular momentum of the planet’s revolution, and gravity forms the angular momentum of the planet’s rotation reflected to the sphere of the revolution:

$$L_0=m_e{R}_0{v}_0\sin {\beta }_0+m_e{R}_0{v}_s-m_e{R}_0{v}_e$$

(24)

Since vs is equal to ve, after the above formula is included

$$L_0=m_e{R}_0{v}_0\sin {\beta }_0$$

(25)

The angular momentum of the planet’s revolution is only the angular momentum caused by the initial velocity. It can be seen that the offset of the angular momentum of the planet’s revolution generated by gravity is the fundamental reason for the conservation of angular momentum in the planet’s revolution system.

For different positions, according to the law of conservation of angular momentum, there are:

$$L=R_0{m}_e{v}_0\sin {\beta }_0=R_1{m}_e{v}_1\sin {\beta }_1$$

(26)

In the formula, L is the angular momentum, R0, v0, and β0 are the distance between the planet and the central planet at its initial position, the linear velocity of the planet, the angle between the gravity line and the linear velocity, R1, v1, and β1 are the distance between the central planet after the change in the position of the planet, the linear velocity of the planet, the angle between the gravity line and the linear velocity. From the above formula:

$$v_1={\displaystyle \frac{R_0{v}_0\sin {\beta }_0}{R_1\sin {\beta }_1}}$$

(27)

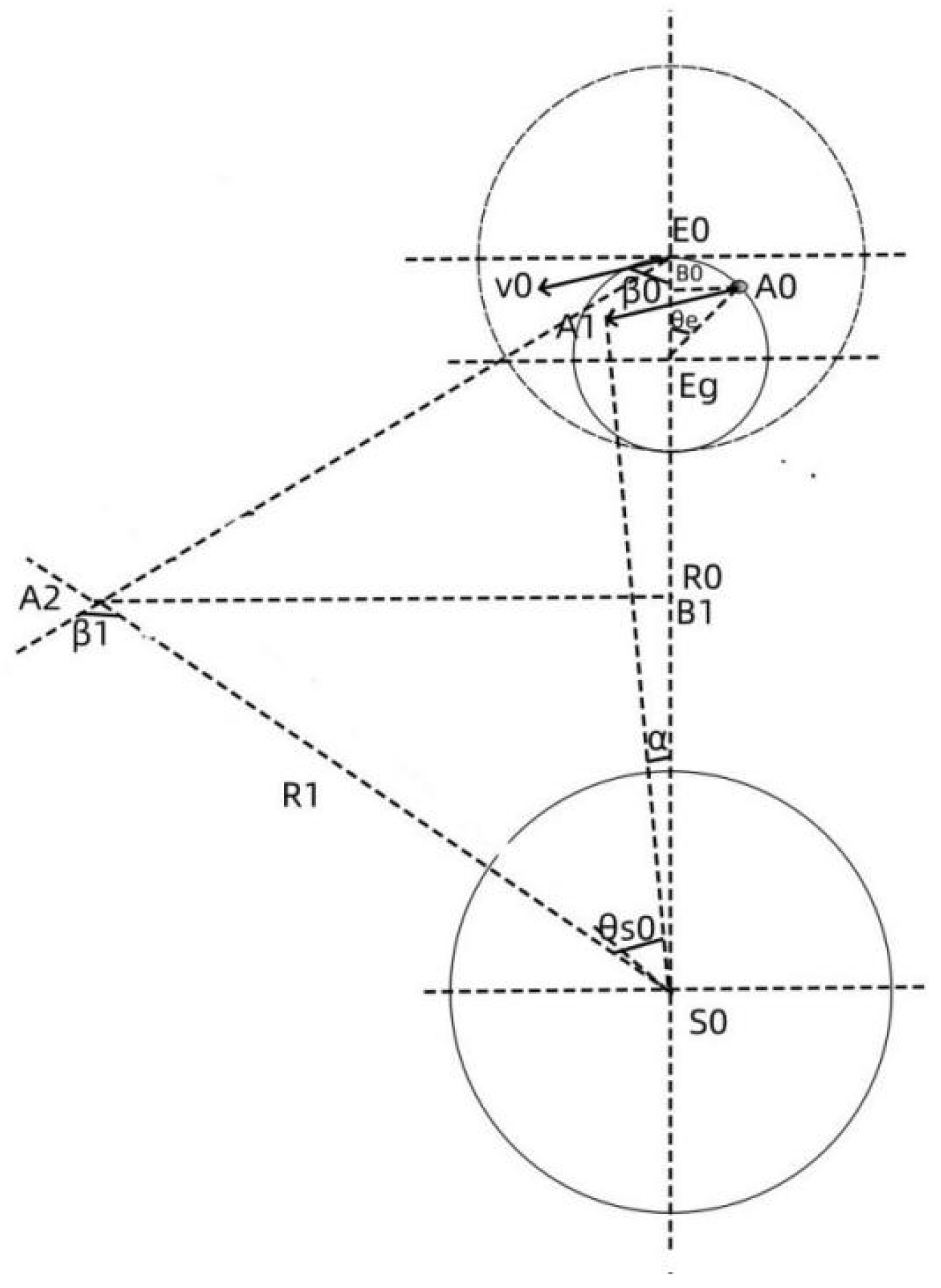
Figure 4 is a planet operation analysis diagram. Here, the operation cycle of planet E is divided into n parts by time, and the unit time is Δt. In the figure, the center S0 of the central planet S is the coordinate origin, R0 is the distance between the initial position of the planet and S0, v0 is the initial speed of planet E, β0 is the angle between the initial direction of the planet and the gravitational line, θe is the angle at which the center of mass of planet E rotates around the gravitational action point Eg in unit time, θs is the angle at which the planet E rotates around the central planet S under the action of gravitational component, and translates v0 to point A0, and its end point is A1, and then rotates A1 to the angle of θs to position A2, A2 is the end point of the center of mass of planet E through Δt time. Taking S0 as the coordinate origin, the coordinates of point A1 are:

$$x_{a1}=v_0\Delta t\sin {\beta }_0-h_e\sin {\theta }_e$$

(28)

$$y_{a1}=R_0-v_0\Delta t\cos {\beta }_0-h_e+h_e\cos {\theta }_e$$

(29)

The distance from point A1 to S0 is:

$$R_1=\sqrt{x_{a1}^2+y_{a1}^2}=\sqrt{{\left(v_0\Delta t\sin {\beta }_0-h_e\sin {\theta }_e\right)}^2+{\left(R_0-v_0\Delta t\cos {\beta }_0-h_e+h_e\cos {\theta }_e\right)}^2}$$

(30)

The angle α between point A1 and the initial position of planet E satisfies:

$$\tan \alpha ={\displaystyle \frac{v_0\Delta t\sin {\beta }_0-h_e\sin {\theta }_e}{R_0-v_0\Delta t\cos {\beta }_0-h_e+h_e\cos {\theta }_e}}$$

(31)

When the planet E rotates through Δt time to the A2 position under the action of the gravitational component Fs, the distance between planet E and S0 remains unchanged to R1, and the angle between the position A2 of planet E and the initial position increases to:

$${\theta }_c={\theta }_s+\alpha ={\Omega }_s\Delta t+\alpha$$

(32)

It can be seen that the planet’s rotation is inertia when it is running on the equilibrium planet.

2.4. Simulation of the Earth’s Elliptical Orbit

The relevant parameters of the Earth [20] are as follows: the average radius of the earth is 6.371×10^6m, the earth’s mass is 5.972×10^24kg, the sun’s radius is 6.955×10^8m, the earth’s orbital period is 365.256363 days (stellar day), 23:56:4.100 seconds (stellar hour) (stellar day), averule point distance is 1.52097597×10^11m, perihelion distance is

1.4709845×10^11m, the average revolution speed is 29783 m/s, the maximum revolution speed is 30287 m/s, the minimum revolution speed is 29291 m/s, the calculated value is 29277m/s, and the earth’s rotational moment of inertia coefficient is 0.3307.

Based on the above derivation, the Earth’s orbit can be simulated. Table 2 is a partial screenshot of the simulation data table for the Earth’s orbit around the sun.

The most column in the table is the correlation constant, re is the radius of the earth, me is the mass of the earth, rs is the radius of the sun, and Gr is the gravitational coefficient for the application of the planet’s semi-compassage to calculate gravity. Unlike the commonly used gravitational coefficient G that uses the mass of the planet to calculate gravity, T is the revolution period, which refers to the time when the earth orbits the sun, unit seconds, n is the number of equal parts of the period. Here is 10,000, and Table 3 above is only a small part of the data. Δt is unit time. The first column R in Table 3 shows the distance between the earth and the sun when the earth is at different positions. The initial value is the apogee. The second column he is the distance between the gravitational action point Eg, the center of mass of the earth, the third column is the angle between the earth’s direction of movement and the gravitational line, the fourth column is the speed of the earth, the initial velocity of the apogee is 29.291km/s, the fifth column is the gravity of the sun on the earth, here the sun and the radius of the earth are used to calculate the gravity of the sun on the earth, the sixth column ωe is the angular velocity generated by gravity to cause the earth’s autobiography, the seventh column Ωs is the angular velocity generated by the force used for the earth’s revolution to cause the earth to produce, the eighth column α is the angle in which the earth’s initial inertia v0 and gravity causes the earth’s rotation to cause the earth to deflect, and the tenth column θc is the angular displacement actually generated by the earth’s unit time, which is the sum of θs and α. Column 11 θ is the accumulation of angular displacement per unit time, and columns 12-13 are the rectangular coordinates used when plotting simulated data.

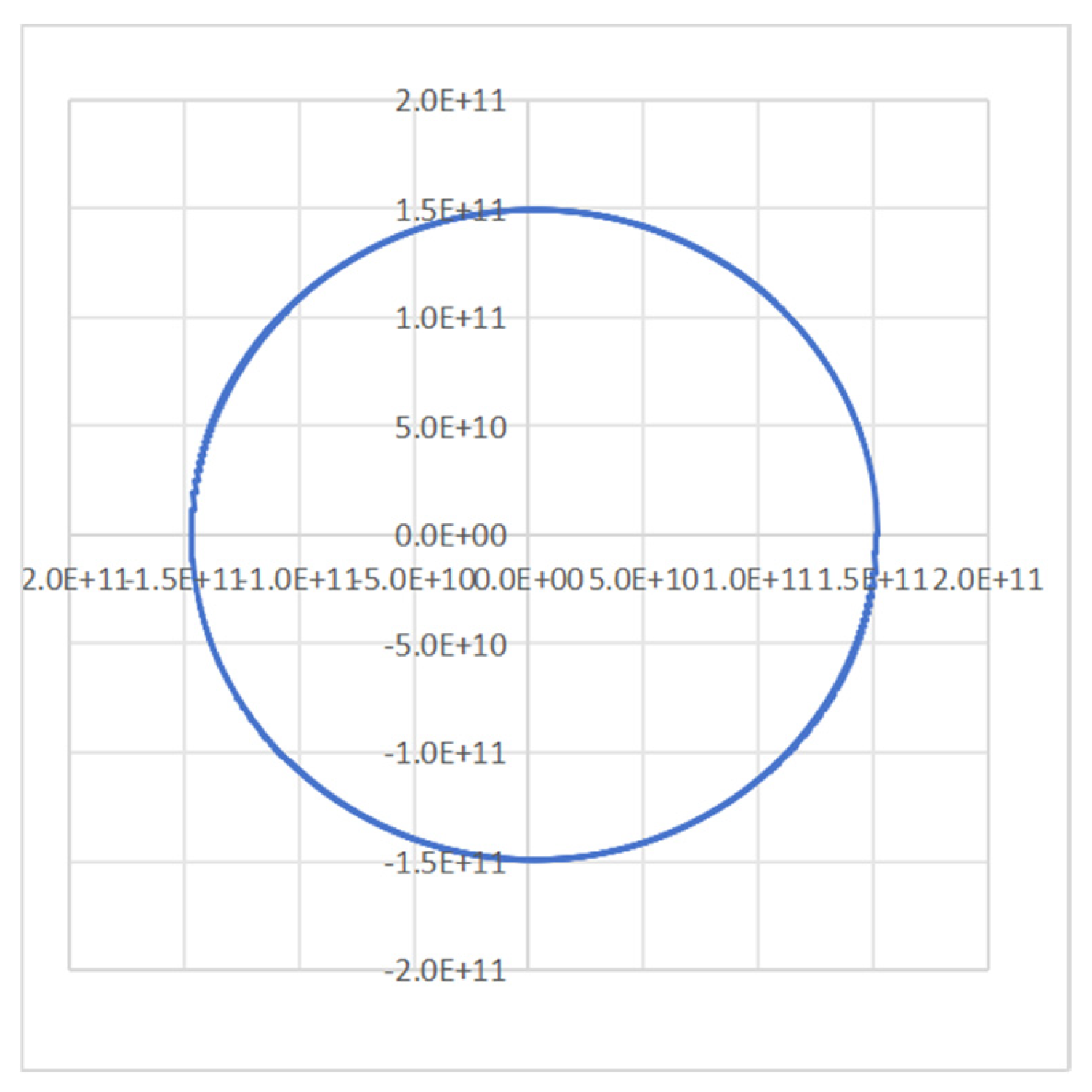
Figure 5 is the Earth orbit simulation diagram directly generated by the solar orbit data simulation table. The aphrodisiac point is1. 520976E+11m, given by the simulation initial value.

The perihelion point is 1.469384E+11m, and the arihelion point is 1.515900E+11m. It can be seen from the parameters that it is an ellipse. The angle between the earth’s direction of movement and the gravitational line: At the arising point, the given value is 1.57080 radians. As the earth moves from the arising point to the perihelion, this angle gradually decreases. After decreasing to the minimum value of 1.55381 radians, it begins to gradually increase. After passing through 1.57080 radians, it continues to increase. When it increases to the maximum value of 1.58673 radians, it begins to gradually decrease, and finally returns to the arising point, with the return value of 1.57066 radians. The velocity value of the Earth’s ahelion point is 29291 m/s, the perihelion velocity is 30319m/s, and the return value of the ahelion point is 29389 m/s. The minimum rotation angular velocity of the Earth on the ecliptic surface produced by gravity is 6.010E-05 radian/s, the maximum value is 6.221E-05 radian/s, the return value is 6.030E-05 radian/s, and the average value is 6.118E-05 radian/s. The average radius of the spherical surface acting on the gravitational force is 3.171E+06m. More than 99.99% of the sun’s gravity on the earth is used for the earth’s rotation.

Although the above simulation process is generally consistent with the actual situation, there are still many inconsistencies in the details, and the simulation data of the earth needs to be further carefully adjusted.

3. The Rotation of the Earth

For the entire earth, the gravitational action point of the sun forms a circle, with a radius of 3.171E+06m. It can be seen from Table 1 that the gravitational action point of the sun on the earth (circle) falls into the liquid layer. In the circle of the gravitational force of the sun, the average rotation angular velocity of the earth generated by the sun’s gravity is 6.118E-05 radians/s, and the linear velocity is: 194m/s.

3.1. Reverse Rotation of the Core

Since the earth is affected by the gravity of the sun, it is difficult to calculate the speed of the inner sphere rotation caused by gravity from the sphere acting on the gravitational surface. Only qualitative inference can be made here: there is a rotation opposite to the earth’s rotation around the sun. Since the distance between the gravitational circle and the inner sphere of solid body is small and the density of liquid matter is high, the rotation speed of the earth caused by the gravity of the gravitational circle will drive the rotation of the inner sphere to be greater than the rotation speed of the earth’s crust.

3.2. Causes of Earth’s Rotation Slowing Down

From the circle of gravity to the sun, the earth’s rotation speed caused by gravity quickly decays until the solid matter in the crust stops decay. At this time, on the earth’s rotation plane (ecliptic plane), gravity will produce a rotation speed opposite to the earth’s rotation speed on the crust. This can only be a qualitative inference. It is difficult to calculate the speed of the crust rotation caused by gravity from the sphere of gravity. Here, the proportional coefficient of the rotation speed of the earth’s rotation on the circle can be used to drive the rotation of the crust.

The earth revolves around the sun in a counterclockwise direction, and its orbital plane (ecliptic plane) and the earth’s equator show an angle of 23.439281° (0.40909 radians).

$${\alpha }_0=23.439°=0.40909rad/s$$

(33)

This angle is also the angle between the rotation axis and the rotation axis, as shown in Figure 6. The Earth’s rotation period is: 23 hours, 56 minutes, 04 seconds (stellar day). The average angular velocity is:

$${\omega }_0={\displaystyle \frac{2\pi }{23h56\prime 4.1″}}=7.292\mathrm{E}-05$$

(34)

The equatorial line speed is about 465 meters per second.

According to data, the Earth’s rotation speed slows down by about 0.00015 seconds per year on average. ‌Average daily slowdown:

$$\Delta t={\displaystyle \frac{0.00015}{365.256363}}=4.107\mathrm{E}-07\mathrm{s}$$

(35)

Suppose the rotation angular velocity generated by gravity is ωg, and the angular velocity after the earth rotates for one round is ω1.

$${\omega }_1^2={\omega }_0^2+{\omega }_g^2-2{\omega }_0{\omega }_g\cos \alpha$$

(36)

$${\omega }_g^2-2{\omega }_0{\omega }_g\cos \alpha +\left({\omega }_0^2-{\omega }_1^2\right)=0$$

(37)

$${\omega }_g={\displaystyle \frac{2{\omega }_0\cos \alpha \pm \sqrt{{\left(2{\omega }_0\cos \alpha \right)}^2-4\left({\omega }_0^2-{\omega }_1^2\right)}}{2}}={\omega }_0\cos \alpha \pm \sqrt{{\left({\omega }_0\cos \alpha \right)}^2-\left({\omega }_0^2-{\omega }_1^2\right)}$$

Bring in the value and take the reasonable value as:

$${\omega }_g={\omega }_0\cos \alpha -\sqrt{{\omega }_1^2-{\omega }_0^2{\sin }^2\alpha }=3.788\mathrm{E}-16$$

(39)

The ratio of the angular velocity of the crust formed by gravity to the angular velocity of the crust on the gravitational circle is:

$$k_{\omega }={\displaystyle \frac{3.788\mathrm{E}-16}{6.118\mathrm{E}-05}}=6.192\mathrm{E}-12$$

(40)

It can be seen that since the gravitational action point falls into the liquid layer, the angular velocity of the earth’s rotation caused by gravity has been greatly reduced.

3.3. Seasonal and Periodic Changes in the Earth’s Rotation

The seasonal and periodic changes in the earth’s rotation are related to the position of the earth on the orbit, and the position of the earth on the orbit is reflected in the gravity of the earth under the sun. The earth is subject to the gravity of the sun, in accordance with Formula (6), and the earth’s reverse rotation angular velocity formed by the sun’s gravity on the ecliptic plane conforms to Formula (22), and the earth’s rotation angular velocity formed by the sun’s gravity on the ecliptic plane is:

$${\omega }_e=\sqrt{{\displaystyle \frac{G_i\frac{r_e^2{r}_s^2}{R_0^2}}{m_e\left(\frac{h_e^2}{R_0}+k_I\frac{r_e^2}{h_e}+h_e\right)}}}={\displaystyle \frac{r_e{r}_s}{R_0}}\sqrt{{\displaystyle \frac{G_i}{m_e\left(\frac{h_e^2}{R_0}+k_I\frac{r_e^2}{h_e}+h_e\right)}}}\approx {\displaystyle \frac{r_e{r}_s}{R_0}}\sqrt{{\displaystyle \frac{G_i}{m_e\left(k_I\frac{r_e^2}{h_e}+h_e\right)}}}$$

(41)

In the formula, ωe is the reverse rotation angular velocity of the earth formed by the ecliptic sun’s gravitational action point, re is the earth’s radius, rs is the sun’s radius, R0 is the distance between the sun and the earth, Gi is the gravitational constant, me is the earth’s mass, he is the distance between the gravitational action point and the center of the earth, because he<.

Suppose the angular velocity of the gravitational action point coupled to the crust forming the coupling coefficient of the rotation of the crust is kω, and the angular velocity of the reverse rotation of the crust forming the crust is:

$${\omega }_g=k_{\omega }{\omega }_e$$

(42)

From this we can see that if the distance between the sun and the earth changes by 5%, the angular velocity of the earth’s rotation formed by gravity will change approximately 5%, which will change to 5%. In other words, the change in the distance between the sun and the earth (gravity) can be reflected 100% in the earth’s rotation speed formed by the gravity of the earth’s ecliptic.

The angular velocity of the earth’s rotation formed by gravity and the angular velocity of the earth itself are superimposed to form a new angular velocity of the earth’s rotation according to Formula (36). Therefore, the angular velocity of the crust caused by ωg1 is:

$${\omega }_1^2={\omega }_0^2+{\omega }_{g1}^2-2{\omega }_0{\omega }_{g1}\cos \alpha$$

(43)

The angular velocity of the crust caused by ωg2 is:

$${\omega }_2^2={\omega }_0^2+{\omega }_{g2}^2-2{\omega }_0{\omega }_{g2}\cos \alpha$$

(44)

The change in the crust rotation speed caused by the change in ωg2-ωg1 is:

$${\omega }_2^2-{\omega }_1^2={\omega }_{g2}^2-{\omega }_{g1}^2-2{\omega }_0\left({\omega }_{g2}-{\omega }_{g1}\right)\cos \alpha$$

(45)

The change in the rotation speed of the earth’s crust caused by gravity determines the change in the rotation speed of the earth. To sum up: The position of the earth on the orbit changes seasonally, with half a year and annual cycles. Therefore, the gravity of the sun and the earth will undergo seasonal changes in the cycles of half a year and the year, and the changes in the sun and the earth’s gravity determine the changes in the rotation of the earth’s crust. Finally, it must be manifested as the change in the earth’s rotation speed changes seasonally, with half a year and year cycles.

3.4. Changes in Earth’s Rotation Speed Are Related to the Strong Gravitational Force of the Sun

According to many years of research by scholars such as Teng Yongfu, Liu Fugang, Luo Jinming, and Berlin, the School of Science, Qiqihar University, the correlation between solar orbital motion and the changes in the earth’s rotation rate reached 0.9994. The orbital motion of the sun actually reflects the changes in the distance between the sun and the earth. The changes in the distance between the sun and the earth determine the changes in the gravity of the sun and the earth. According to the deduction and calculation in the previous section, the changes in the gravity of the sun and the earth determine the changes in the rotation of the earth. Therefore, it is inevitable that the change in the rotation speed of the earth is strongly related to the movement of the sun and the orbital motion.

3.5. The Influence of the Moon, Jupiter and Saturn on the Changes in the Rotation Speed of the Earth

In the solar system, due to the gravity of the sun on the earth, the earth revolves around the sun; due to the gravity of the earth on the moon, the moon revolves around the earth; while the earth forms gravity of the moon on the moon, the moon will also form gravity on the earth. The gravity of the moon on the earth will also cause the earth to produce a reverse rotation angular velocity at the point of the gravitational force of the earth, causing the earth’s rotation to be affected by the changes in the distance (gravity). Jupiter and Saturn are larger in size and will also form a certain gravity on the earth. As the distance between Jupiter and Saturn changes, their gravity on the earth will change. These changes in gravity will also affect the rotation speed of the earth, but the impact will be different in size.

4. Discuss

The effect (coupling) coefficients of the power from the earth’s liquid layer (on the gravitational circle) drive the rotation of the earth’s crust and core need to be further studied and determined.

5. In Conclusions

Gravity is the process in which nucleons emit gravitons and gravitons propagate in space with gravitational energy waves, and gravitational energy waves resonate with other nucleons and form energy transfer. For planets, gravitons emitted by nucleons inside the planet interact with other nucleons inside the planet to form the cohesion of the planet. The gravitons emitted by nucleons on the surface of the planet are partially emitted outside the ball. These gravitons emitted outside the ball meet the nucleons of other planets and resonate with them to form energy transfer. These transferred energy will cause the resonant nucleon to produce a vertical gravity line displacement, forming a vertical and gravitational line action force. Only spherical nucleons facing the sun can receive gravitons emitted by the sun. Spherical nucleons facing the sun will not receive gravitons from the sun. In this way, for the entire earth, the equivalent gravitational action point Eg does not coincide with the center of mass of the earth, but is at a radius of about 0.5 near the side of the sun. In this way, the sun’s gravity on the earth will have two effects, one is the centripetal force of the earth’s rotation around the sun, and the other is the rotational force of the earth’s centripetal rotation around the gravitational action point Eg. Within a certain time Δt, the initial velocity of the earth will cause the planet to move at a uniform speed and linear displacement. The earth is subjected to the component force of the sun’s gravity, which will cause the earth to rotate at a certain angle in the orbit of rotation. The earth is subjected to another component force of the sun’s gravity, which will cause the earth’s center of mass to rotate backwards in the arc around the gravitational point. Under the combined action of these three, the earth will form a standard elliptical orbit. According to the law of conservation of momentum, the linear velocity of the earth’s rotation around the sun formed by gravity is equal to the linear velocity of the earth’s rotation and opposite direction. The angular velocity of the earth’s rotation around the sun is equal to the angular velocity of the earth’s rotation reflected to the earth’s rotation. At this time, for the earth’s revolution, the angular momentum generated by the sun’s gravity cancels each other, leaving only the angular momentum formed by the earth’s initial velocity, which is the fundamental reason for the conservation of the earth’s revolution under the action of gravity. After derivation calculation and data simulation, more than 99.99% of the sun’s gravity is used for the rotation of the earth. It can also be said to balance the inertia of the earth’s movement. It can also be considered that at the point of gravity, the moment of the earth’s revolution is equal to the moment of the earth’s rotation. Since the force arm of the earth’s revolution is much larger than the force arm of the earth’s rotation, the force used for the earth’s revolution is much smaller than the force used for the earth’s rotation. For the earth, the rotation speed of the solar gravitational circle is reflected in the earth’s crust, superimposed with the earth’s initial rotation angular velocity, forming a phenomenon that the earth’s rotation angular velocity is slowly decreasing. This speed is reflected in the earth’s core, causing the earth’s core to produce a rotation opposite to the current direction of the earth’s rotation, and this rotation speed is greater than the rotation speed of the earth’s crust. The changes in the four seasons of the earth are closely related to the position of the earth on the orbit, and the position of the earth on the orbit reflects the changes in the earth being subjected to the sun’s gravity. 99.99% of the sun’s gravity is used for the earth’s rotation. Therefore, the changes in the sun’s gravity determine the change of the earth’s rotation speed on the gravitational circle, and determine the change of the earth’s rotation speed on the gravitational circle coupled to the earth’s crust forming a crust, and also determine the actual earth’s rotation speed after the superposition of the earth’s rotation speed formed by gravity and the earth’s own rotation speed. To sum up, the seasonal periodic changes of the earth’s rotation and slowing down for a long time are related to the changes in the solar orbit and the rapid rotation of the earth’s core in reverse are all related to the separation between the action point of the sun’s gravitational force and the center of the earth. They are all inevitable results of almost all the sun’s gravity used for the earth’s rotation.