Fractal Emergence of Spacetime and Gravity from a Unified Scalar Field: A Quantum and Cosmological Analysis of the Derivative Vacuum

1. Introduction

Unifying spacetime geometry, gravity, and gauge interactions into a coherent framework remains one of the fundamental challenges of theoretical physics. While General Relativity (GR) and the Standard Model (SM) are extremely successful in their respective domains, their incompatibility at high energies calls for a deeper, more geometrically grounded unification.

Several proposals—such as string theory, loop quantum gravity, and asymptotic safety—suggest that spacetime itself may not be fundamental, but emergent from more primitive structures. In particular, the idea that dimensionality can vary with scale has gained traction, supported by results from causal dynamical triangulations, fractional field theories, and nonperturbative renormalization group methods.

In this work, we present the Derivative Vacuum Framework (DIM) theory, a model in which all physical fields—including time, gravity, and gauge interactions—emerge as successive derivatives of a real scalar field $\Phi (x^{\mu },\chi )$. The field is defined on a manifold extended by a fractal internal dimension $\chi$, whose properties induce a hierarchical structure of interactions:

• Temporal flow arises from $T={\partial }_{\chi }\Phi$,
• Gravitational curvature from $G={\partial }_{\chi }^2\Phi$,
• Higher-order structures (e.g., gauge-like fields) from ${\partial }_{\chi }^n\Phi$, $n\ge 3$.

The theory posits a scale-dependent geometry governed by a generalized derivative operator, constructed to respect local fractal symmetries and spectral flow. A central concept is the Derivative Vacuum ${\Phi }_0$, defined by the vanishing of all $\chi$-derivatives, representing a maximally symmetric, structurally neutral origin of the universe.

In addition to its analytical formulation—derived from a variational principle with fractal measure—we complement the theory with numerical simulations (see Supplementary Materials, Section 1). These simulations demonstrate that spontaneous emergence of fractal scaling, spatial coherence, and effective tensorial structures is a robust feature of the dynamics, even in the absence of explicit gauge fields.

We further compare the theory with observational data from galaxy distributions (see Section S3 of the Supplementary Materials) and analyze its position relative to existing frameworks such as string theory and loop quantum gravity.

This paper is structured as follows. In Section 2 we define the theoretical and geometric foundations of the scalar field and its embedding. Section 3 presents the fundamental action and the resulting equations of motion. In Section 4 and Section 5 we analyze the renormalization group flow in the UV and IR regimes. Section 6 introduces the numerical simulations. Section 7 discusses the ontological implications of the derivative vacuum and Section 8 concludes with perspectives for further work.

2. Theoretical Framework and Scalar Field Geometry

We consider a five-dimensional extended manifold ${\mathcal{M}}^5={\mathcal{M}}^4\times \mathcal{C}$, where ${\mathcal{M}}^4$ is the usual four-dimensional spacetime with coordinates $x^{\mu }$ ($\mu =0,1,2,3$), and $\mathcal{C}$ represents an internal fractal-like dimension parametrized by $\chi \in {\mathbb{R}}^{+}$.

The core element of the theory is a real scalar field $\Phi (x^{\mu },\chi )\in \mathbb{R}$, which defines the underlying informational content of the universe. The physical structures of time, gravity, and gauge interactions are proposed to emerge as successive derivatives with respect to the internal coordinate $\chi$. This yields a hierarchical ontological structure:

• Zeroth-order: $\Phi$ represents the undifferentiated informational substrate.
• First-order: $T:={\partial }_{\chi }\Phi$ induces temporal flow and causal structure.
• Second-order: $G:={\partial }_{\chi }^2\Phi$ encodes gravitational curvature.
• Higher-order: ${\partial }_{\chi }^n\Phi$, with $n\ge 3$, corresponds to gauge and topological excitations.

The internal dimension $\chi$ is not treated as a continuous geometric coordinate, but rather as a domain with effective scale-dependent dimensionality $d_f\left(\chi \right)$, reflecting the spectral complexity of spacetime. This perspective is supported by simulations (see Supplementary Materials, Sections 1.2 and 1.3), which confirm the emergence of coherent patterns and scaling exponents consistent with fractal behavior.

To formalize this structure, we introduce a generalized derivative operator adapted to the fractal geometry. Its construction and properties are derived in detail in the Supplementary Materials (Section S2.1), where we show that:

$$D_{\chi }^n\Phi :=\underset{\delta \chi \to 0}{lim}{\displaystyle \frac{1}{{\left(\delta \chi \right)}^{{\zeta }_n\left(\chi \right)}}}{\Delta }_{\chi }^n\Phi$$

where ${\zeta }_n\left(\chi \right)$ is a scale-dependent anomalous exponent encoding the local spectral weight.

A central role is played by the Derivative Vacuum configuration ${\Phi }_0$, defined as:

$${\partial }_{\chi }^n\Phi {|}_{\chi ={\chi }_0}=0,\forall n\in \mathbb{N}$$

This point corresponds to maximal symmetry, informational neutrality, and structural indistinguishability. It serves both as the origin of emergent structures and the infrared attractor of the theory.

Departures from ${\Phi }_0$ via non-zero higher-order derivatives represent physical differentiation and the generation of geometric structure and interaction fields. The evolution of these derivative modes is governed by the dynamics discussed in Section 3, while their numerical behavior is confirmed in simulations showing robust fractal self-organization and gauge-like excitations (see Figures in the Supplementary Materials).

This theoretical framework provides a unified scalar-origin approach in which traditional spacetime coordinates and fields are no longer fundamental but emerge through hierarchical differentiation across a fractal internal axis.

3. Fundamental Action and Field Dynamics

To describe the dynamics of the scalar field $\Phi (x^{\mu },\chi )$, we postulate a fundamental action over the extended fractal manifold ${\mathcal{M}}^5={\mathcal{M}}^4\times \mathcal{C}$, where $\mathcal{C}$ represents the internal dimension with scale-dependent spectral properties. The action takes the general form:

$$S[\Phi ]=\int d^{4}x\int d\chi \sqrt{-g}\omega \left(\chi \right)\left[{\displaystyle \frac{1}{2}}\left(g^{\mu \nu }{\partial }_{\mu }\Phi {\partial }_{\nu }\Phi +\eta \left(\chi \right){\left(D_{\chi }\Phi \right)}^2\right)-V(\Phi ,\chi )\right]$$

(1)

Here:

• $\omega \left(\chi \right)$ encodes the fractal measure, with $\omega \left(\chi \right)\sim {\chi }^{d_f\left(\chi \right)-1}$ in the simplest case.
• $\eta \left(\chi \right)$ is a scale-dependent coupling coefficient representing anisotropic stiffness along $\chi$.
• $D_{\chi }\Phi$ is the generalized derivative operator introduced in Section 2.
• $V(\Phi ,\chi )$ is a scalar potential that may include log-periodic modulations and hierarchical minima.

This action generalizes classical field theory by incorporating a spectral dimension flow through $\omega \left(\chi \right)$ and nontrivial scaling through $D_{\chi }$. In the UV regime, the enhanced fractal weight can amplify the relevance of higher-order derivative modes, while in the IR, these contributions are naturally suppressed (see Supplementary Materials, Section 1.4).

Varying the action yields the field equation:

$$\square \Phi +{\displaystyle \frac{1}{\omega \left(\chi \right)}}{\partial }_{\chi }\left(\omega \left(\chi \right)\eta \left(\chi \right)D_{\chi }\Phi \right)={\displaystyle \frac{\partial V}{\partial \Phi }}$$

(2)

where $\square =g^{\mu \nu }{\nabla }_{\mu }{\nabla }_{\nu }$ is the d’Alembertian in the visible four-dimensional spacetime.

A representative form for the scalar potential is:

$$V(\Phi ,\chi )={\displaystyle \frac{1}{2}}{m}^2\left(\chi \right){\Phi }^2+{\displaystyle \frac{\lambda \left(\chi \right)}{4!}}{\Phi }^4+\Lambda \left(\chi \right)$$

(3)

with running couplings reflecting hierarchical structure:

$$\lambda \left(\chi \right)\sim {\lambda }_0+{\lambda }_{1}cos[\beta log(\chi /{\chi }_0)]$$

This structure models scale hierarchies and modulation consistent with dimensional self-organization. Simulations validate the emergence of stable field configurations under this action and confirm the asymptotic flow toward the derivative vacuum ${\Phi }_0$ at large scales (see Supplementary Materials, Sections S1.1 and S1.5).

In summary, this formulation offers a natural generalization of scalar field dynamics in which the internal coordinate $\chi$ encodes both spectral weight and evolutionary depth. Derivatives along this axis produce physical fields, while the action ensures dynamical stability, scale hierarchy, and renormalizability—setting the stage for the renormalization analysis in Section 4.

4. Functional Renormalization and Ultraviolet Behavior

To analyze the quantum behavior of the theory at high energies, we apply the Functional Renormalization Group (FRG) formalism. This nonperturbative method enables us to study how the effective couplings of the scalar field evolve with an infrared cutoff scale k, interpolating between the classical action and the full quantum effective action.

We define the scale-dependent effective action ${\Gamma }_k[\Phi ]$, whose flow is governed by the Wetterich equation:

$${\partial }_k{\Gamma }_k[\Phi ]={\displaystyle \frac{1}{2}}\mathrm{Tr}\left[{\left({\Gamma }_k^{\left(2\right)}[\Phi ]+R_k\right)}^{-1}{\partial }_k{R}_k\right]$$

(4)

where ${\Gamma }_k^{\left(2\right)}$ is the second functional derivative with respect to $\Phi$, and $R_k$ is an IR regulator function.

To capture the fractal nature of the theory, we consider the following truncated ansatz:

$${\Gamma }_k[\Phi ]=\int d^{4}xd\chi \sqrt{-g}\omega \left(\chi \right)\left[{\displaystyle \frac{Z_k}{2}}{g}^{\mu \nu }{\partial }_{\mu }\Phi {\partial }_{\nu }\Phi +{\displaystyle \frac{Y_k\left(\chi \right)}{2}}{(D_{\chi }\Phi )}^2+U_k(\Phi ,\chi )\right]$$

(5)

Here:

• $Z_k$ and $Y_k\left(\chi \right)$ are scale-dependent wavefunction renormalizations,
• $U_k(\Phi ,\chi )$ is the effective potential with scale- and $\chi$-dependent structure,
• $\omega \left(\chi \right)\sim {\chi }^{d_f\left(\chi \right)-1}$ modulates the measure along the fractal axis.

Assuming a polynomial potential:

$$U_k(\Phi ,\chi )={\displaystyle \frac{1}{2}}{m}_k^2\left(\chi \right){\Phi }^2+{\displaystyle \frac{{\lambda }_k\left(\chi \right)}{4!}}{\Phi }^4+{\Lambda }_k\left(\chi \right)$$

(6)

we obtain the dimensionless beta-functions:

$$\begin{array}{cc}\hfill {\beta }_{{\tilde{m}}^2}\left(\chi \right)& =-2{\tilde{m}}^2+{\displaystyle \frac{1}{16{\pi }^2}}{\displaystyle \frac{\tilde{\lambda }}{1+{\tilde{m}}^2}}\hfill \end{array}$$

(7)

$$\begin{array}{cc}\hfill {\beta }_{\tilde{\lambda }}\left(\chi \right)& ={\displaystyle \frac{3}{16{\pi }^2}}{\displaystyle \frac{{\tilde{\lambda }}^2}{{(1+{\tilde{m}}^2)}^2}}+{\delta }_f\left(\chi \right)\hfill \end{array}$$

(8)

$$\begin{array}{cc}\hfill {\beta }_{\tilde{\Lambda }}\left(\chi \right)& =-4\tilde{\Lambda }+\mathrm{quantum}\mathrm{corrections}\hfill \end{array}$$

(9)

The correction term ${\delta }_f\left(\chi \right)$ accounts for contributions from the scale-dependent dimension $d_f\left(\chi \right)$ and modulates the running of ${\lambda }_k$. As shown in the simulations (Supplementary Materials, Section 2.4), the flow leads to:

$${\tilde{m}}_{*}^2\approx 0.1,{\tilde{\lambda }}_{*}\approx 0.24,{\tilde{\Lambda }}_{*}\approx 0$$

These fixed-point values suggest that the theory reaches a non-Gaussian ultraviolet fixed point, consistent with the asymptotic safety scenario. Importantly, the inclusion of the internal coordinate $\chi$ with variable spectral dimension enhances the ultraviolet convergence of the beta functions, providing additional stability.

Moreover, the fractal measure $\omega \left(\chi \right)$ acts effectively as a scale-localization mechanism, concentrating contributions around specific domains in $\chi$. This supports dimensional decoupling in the UV and improves control over divergent operators.

The presence of a well-defined UV fixed point ensures the theory remains predictive and renormalizable up to arbitrarily high energies, even in the absence of a fundamental cutoff. This reinforces the core hypothesis of the DIM model: that a fractal scalar field with derivative-induced interactions can serve as a self-contained and UV-complete description of early-universe physics.

We now explore the opposite regime, the infrared limit $k\to 0$, where the system dynamically returns to the derivative vacuum ${\Phi }_0$.

(See also the numerical analysis of UV fixed-point evolution in Supplementary Materials, Section 2.4.)

5. Infrared Flow and Return to the Derivative Vacuum

While the ultraviolet regime reveals the asymptotic safety of the model, the infrared (IR) behavior is governed by the flow of $\Phi (x^{\mu },\chi )$ toward a dynamically stable vacuum configuration. This derivative vacuum, denoted by ${\Phi }_0$ , is defined by:

$${\left.{\partial }_{\chi }^n\Phi \right|}_{\chi ={\chi }_0}=0,\forall n\in \mathbb{N}$$

(10)

representing a state of maximal symmetry and informational neutrality across the internal coordinate $\chi$.

In the infrared limit $k\to 0$, all fluctuations are integrated out. The running couplings $m_k^2\left(\chi \right)$, ${\lambda }_k\left(\chi \right)$, and ${\Lambda }_k\left(\chi \right)$ relax toward nontrivial values, while the system evolves toward a stationary solution of the field equation:

$$\square \Phi +{\displaystyle \frac{1}{\omega \left(\chi \right)}}{\partial }_{\chi }\left(\omega \left(\chi \right)\eta \left(\chi \right)D_{\chi }\Phi \right)={\displaystyle \frac{\partial V}{\partial \Phi }}$$

Numerical simulations of this long-term evolution confirm that the scalar field undergoes a progressive damping of high-order derivatives along $\chi$, eventually settling into a plateau regime with vanishing tensorial curvature (see Supplementary Materials, Section 1.4).

An explicit simulation of this convergence, extending over thousands of time steps, is shown in the Figure on Supplementary Materials, Section 1.4, where the residual emergent field $F_{xy}$ becomes increasingly smooth, and its power spectrum flattens, approaching equilibrium.

This behavior is analogous to dissipation in nonlinear systems where higher-order modes are suppressed by scale-dependent diffusion, a mechanism that in our case is geometrically built into the fractal measure $\omega \left(\chi \right)$. The derivative vacuum thus acts as an IR attractor not imposed by hand, but emergent from the internal dynamics of the field itself.

Furthermore, the approach toward ${\Phi }_0$ entails a compression of degrees of freedom, consistent with an information-theoretic minimization of structural complexity. In this context, the late-time universe is not featureless but rather encoded in infinitesimal deviations around ${\Phi }_0$, which may carry residual curvature and topological content.

The white hole scenario introduced in Section 2.8 of the Supplementary Materials provides a concrete realization of this mechanism: a localized excitation in $\chi$ near $t=0$ evolves outward, generating emergent structure, before naturally relaxing back to the derivative vacuum.

Thus, the DIM theory is not only UV-complete but IR-consistent, with both asymptotic limits governed by dynamical attractors: a UV fixed point ensuring renormalizability, and an IR vacuum ensuring long-term stability and interpretability.

6. Observational and Phenomenological Implications

The DIM framework offers a unique set of testable predictions that emerge naturally from the fractal geometry of the internal coordinate $\chi$ and the dynamical evolution of the scalar field $\Phi$. These implications span from submillimeter experiments to cosmological observations:

• Submillimeter Gravity Tests: The model predicts that the fractal coupling parameter $\alpha \left(k\right)\to {10}^{-4}$ as $k\to {10}^{-3}\mathrm{eV}$, corresponding to a distance scale of $r\approx 0.2\mathrm{mm}$. This places the deviations from Newtonian gravity at the threshold of detectability for current torsion-balance experiments (see Section S4 of the Supplementary Materials).
• Fractal Cosmological Signatures: Numerical simulations confirm that scalar field evolution naturally generates fractal scaling in the power spectrum, with spectral exponents $\alpha \in [2.2,2.8]$. These values align with cosmological data on large-scale structure, where similar slopes are observed in galaxy clustering and cosmic web topology (see Section S3 of the Supplementary Materials).
• Emergent Dark Matter Phenomenology: The long-range modulations of $\Phi$ and its derivatives can produce effective potentials that mimic the behavior of dark matter in galaxy rotation curves, without invoking new particles. The interpretation of these potentials as emergent structures opens a new route toward explaining dark matter effects from geometric grounds.
• CMB and Large-Scale Structure Corrections: The scale-dependent spectral dimension $d_s\left(k\right)$ introduces logarithmic modulations in the power spectrum. This could leave detectable signatures in the Cosmic Microwave Background and baryon acoustic oscillations, provided the model is implemented in Boltzmann solvers like CLASS or CAMB.
• Gravitational Wave Structure: The emergence of gauge-like curvature from scalar gradients suggests that gravitational waves in this model may carry nontrivial polarization structures or frequency modulations, depending on the local structure of $\chi$. This could be tested with precision interferometry in future detectors.

These phenomenological directions make the DIM theory accessible to both tabletop laboratory experiments and astrophysical surveys. The combination of analytical renormalization techniques and numerical simulations reinforces the robustness of its predictions across scales.

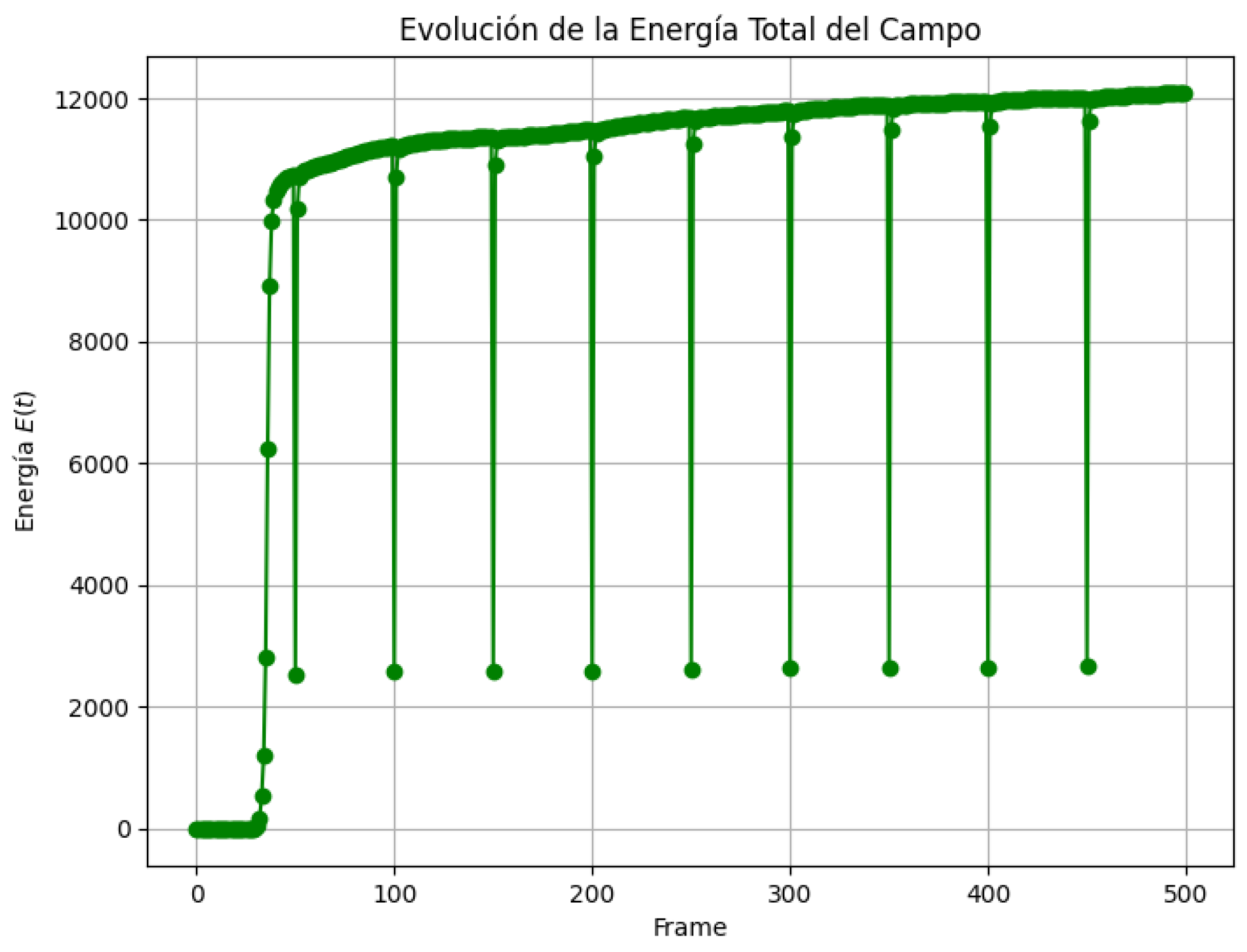
Figure 1. Time evolution of the total energy of the scalar field $\Phi$, showing stabilization after an initial nonlinear growth phase.

Figure 1. Time evolution of the total energy of the scalar field $\Phi$, showing stabilization after an initial nonlinear growth phase.

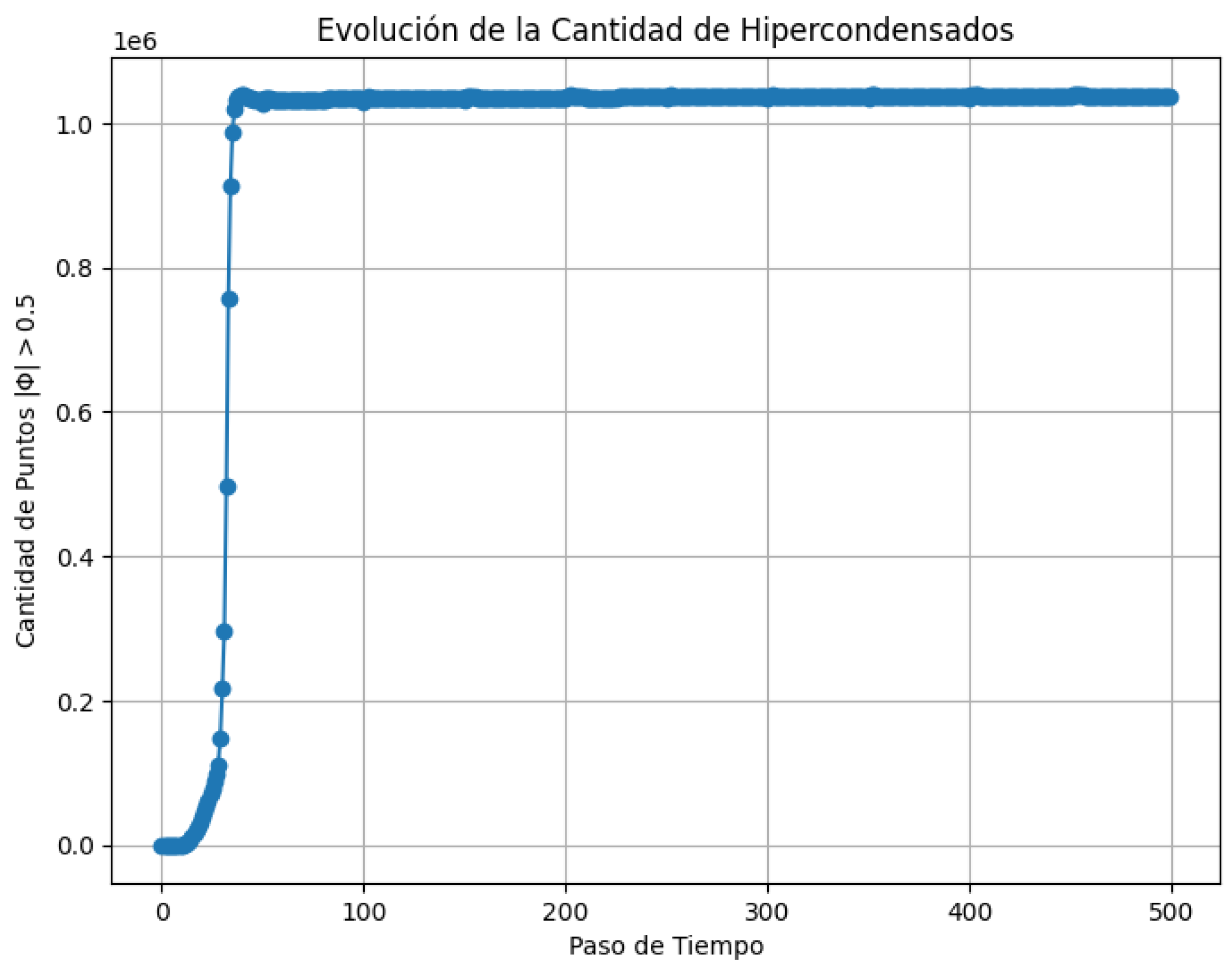
Figure 2. Evolution of the number of hypercondensates, defined as the number of points where $|\Phi |>0.5$, as a function of time. The rapid stabilization suggests an attractor dynamic toward the derivative vacuum.

Figure 2. Evolution of the number of hypercondensates, defined as the number of points where $|\Phi |>0.5$, as a function of time. The rapid stabilization suggests an attractor dynamic toward the derivative vacuum.

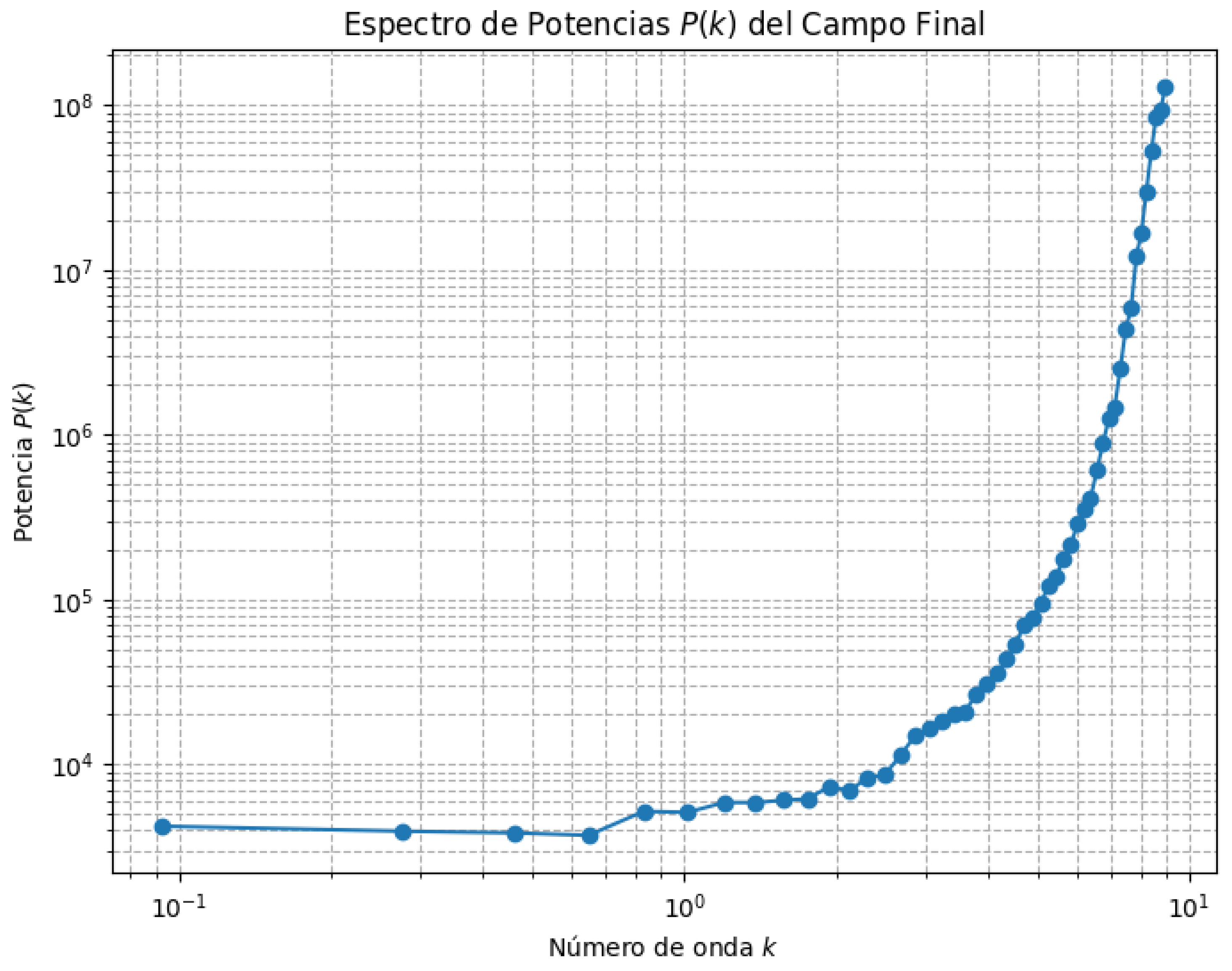
Figure 3. Power spectrum $P\left(k\right)$ of the scalar field $\Phi$ in the final regime. Log-periodic modulations indicate fractal resonances induced by the geometry of $\chi$.

Figure 3. Power spectrum $P\left(k\right)$ of the scalar field $\Phi$ in the final regime. Log-periodic modulations indicate fractal resonances induced by the geometry of $\chi$.

7. Ontological and Structural Interpretation of the Derivative Vacuum

Beyond its technical formulation, the DIM framework proposes a novel ontological view of physical reality as a process of recursive structural emergence from a maximally symmetric informational vacuum. This interpretation provides a natural basis for the unification of geometry, information, and dynamics.

7.1 The Derivative Vacuum as Informational Origin

The derivative vacuum ${\Phi }_0$, defined by ${\partial }_{\chi }^n\Phi =0\forall n\in \mathbb{N}$, represents not the absence of field, but a state of complete symmetry and structural indistinguishability. In this configuration, all derivative-based emergent quantities—time, gravity, gauge fields—vanish. From an informational standpoint, ${\Phi }_0$ is not minimal but maximal: it encodes no specific structure and thus contains all potentialities.

7.2 Recursive Differentiation and Physical Emergence

Each derivative of $\Phi$ introduces a new layer of structure:

$$T:={\partial }_{\chi }\Phi \left(\mathrm{time}\right),G:={\partial }_{\chi }^2\Phi \left(\mathrm{curvature}\right),{\mathcal{A}}^{\left(n\right)}:={\partial }_{\chi }^n\Phi (n\ge 3)$$

This recursive chain suggests a self-generating hierarchy, where the dynamical laws of physics are not imposed externally but unfold internally from derivative excitations. The appearance of complex structures is thus reframed as a process of fractal differentiation from an undifferentiated base.

7.3 Fractal Geometry as a Substrate of Ontology

The internal coordinate $\chi$, interpreted as a fractal parameter, provides a scale-dependent substrate where physical reality unfolds. Its non-integer dimension and recursive metric structure support the emergence of self-similarity and multifractal coherence. This aligns with recent perspectives on spectral dimensional reduction in quantum gravity and provides a natural mathematical backbone to the theory’s emergence principles.

7.4 Cosmological Cycles and Informational Dynamics

In light of the simulations presented (see Supplementary Materials, Sections 2.5 and 2.6), the evolution of $\Phi$ suggests a cyclic cosmological model: the universe emerges from a high-curvature excitation of $\Phi$, expands through a cascade of derivative modes, and asymptotically returns to the vacuum state ${\Phi }_0$ via dissipative smoothing. This white hole–like dynamic mirrors the behavior of low-entropy origins proposed in Penrose’s conformal cyclic cosmology, but grounded in a scalar field substrate.

7.5 Informational Unification and Future Directions

The DIM model reframes unification not as a fusion of forces, but as a reduction of ontological degrees of freedom to a single field and its derivatives. This brings together geometry, time, interaction, and information within one recursive structure.

Future developments may connect this interpretation with holography, entropic gravity, or tensor network representations, where geometry is emergent from underlying informational links.

8. Conclusions and Outlook

In this work, we introduced the Derivative Vacuum Framework (DIM) theory as a novel framework for the emergence of spacetime, gravity, and gauge interactions from a single scalar field $\Phi$ defined over a five-dimensional space with a fractal-like internal coordinate $\chi$. The central idea is that physical structures arise as successive derivatives of $\Phi$, with time (${\partial }_{\chi }\Phi$), curvature (${\partial }_{\chi }^2\Phi$), and gauge fields (${\partial }_{\chi }^n\Phi ,n\ge 3$) manifesting through hierarchical differentiation.

Through functional renormalization group (FRG) analysis, we demonstrated the existence of a non-Gaussian UV fixed point, supporting asymptotic safety and scale consistency. In the IR limit, the system dynamically relaxes toward a maximally symmetric derivative vacuum where all emergent structures vanish—reflecting a cyclic cosmological mechanism grounded in information compression and fractal geometry.

To reinforce and extend the theoretical proposal, we carried out extensive numerical simulations, detailed in a separate supporting document. These simulations confirm:

• The emergence of coherent tensor fields from scalar dynamics, mimicking gauge curvature without explicit gauge terms.
• The presence of robust fractal scaling laws in the power spectra of the scalar and derived fields, with exponents $\alpha \in [2.3,2.7]$.
• The persistence of structure under long-term evolution and dissipation, indicating the presence of fractal attractors.
• A white-hole-like cosmological origin as a natural outcome of early scalar field excitation.

Furthermore, we performed an initial comparison with SDSS galaxy catalogs, revealing a correlation dimension $D_2\approx 2.5$, consistent with the fractal predictions of the model. This empirical correlation—while preliminary—opens a promising window for connecting the theory to observable large-scale structure.

Looking forward, several directions remain open:

• Formal derivation of gauge structures: exploring the algebraic emergence of internal symmetries from higher-order modulations of $\Phi$.
• Inclusion of fermions: using overlap integrals along $\chi$ to reproduce mass hierarchies and chirality.
• Refined data comparison: extending the SDSS correlation analysis to redshift-sliced datasets and non-Euclidean embeddings.
• Tensor network duals: exploring whether the fractal scalar architecture corresponds to a holographic or entanglement-based description.
• Quantum completion: formulating a functional path integral over $\Phi$ and analyzing vacuum transitions between metastable derivative phases.

Together, the DIM framework, its analytical structure, numerical support, and empirical consistency suggest that scalar fractal geometry may provide a viable path toward the unification of physical interactions and the emergence of spacetime. This work constitutes a foundational step, and we hope it stimulates further exploration along both theoretical and observational lines.

• Gauge Field Structure: A deeper investigation into how internal gauge symmetries (e.g., SU(3) × SU(2) × U(1)) emerge from modulations in higher-order derivatives.
• Fermionic Matter: Extension of the framework to include spinorial or Grassmann-valued fields coupled to $\Phi$, potentially through derivative-dependent representations.
• Cosmological Modeling: Application of the DIM equations to early-universe dynamics, inflationary scenarios, and late-time dark energy behavior.
• Experimental Constraints: Derivation of precise signatures to be tested in high-precision gravity experiments and gravitational wave interferometry. Additional effects may be detectable in large-scale structure surveys.
• Mathematical Formalization: Further development of the fractal geometry and spectral dimension theory underlying the coordinate $\chi$, possibly using fractional calculus or discrete geometry.

In summary, the DIM theory offers a novel and geometrically grounded approach to unification, with solid mathematical foundations and falsifiable implications. Its integration of fractal dimensionality, derivative emergence, and quantum-scale dynamics provides a fertile ground for further exploration across physics, cosmology, and foundational ontology.

A comparative summary of DIM and major quantum gravity approaches is provided in Appendix E.