Improved Electrochemical-Mechanical Parameters Estimation Technique for Lithium-Ion Batteries Models

1. Introduction

Lithium-ion batteries (LIBs) have become the dominant energy storage technology for various applications, ranging from consumer electronics to grid storage and electric vehicles, also in the working vehicle industry [1,2]. Accurate modeling of LIBs is essential for predicting performance, optimizing efficiency, and ensuring safe operation. Battery models can be broadly categorized into empirical, equivalent circuit models (ECMs) [3] and physics-based models. The latter offer a more comprehensive representation of the multiphysics processes occurring in batteries; however, this increased accuracy comes at the cost of higher computational complexity due to the coupling of Partial Differential Equations (PDEs). Among physics-based models, the Doyle-Fuller-Newman (DFN) model [4] stands out as the most prominent due to its ability to accurately describe lithium-ion transport, charge transfer, and electrochemical reactions within the battery. It serves as a fundamental reference for advanced battery simulations and optimization studies, making it a cornerstone in battery modeling research. However, this requires precise estimation of electrochemical and mechanical parameters, which influence battery behavior under operating conditions.

When it comes to battery modeling, it is important to distinguish between the manufacturer perspective and the end user or system integrator one. Manufacturers typically have access to comprehensive internal data, including detailed material properties, geometric specifications, and electrochemical parameters obtained through dedicated design, optimization and characterization campaigns. In contrast, end users – such as developers of battery management systems or integrators of battery packs – often have limited access to such internal information. Therefore, parameter identification plays a crucial role in battery modeling, ensuring that simulation results aligned with actual behavior. Some parameters can be directly measured using experimental setups, while others are more challenging or expensive to determine, requiring estimation methods.

Many studies performed battery parameter estimation through voltage curve fitting [5,6], where experimental discharge and charge curves are matched to the simulated ones. This method is widely used due to its simplicity and effectiveness in capturing electrochemical characteristics. The drawback is the reduced accuracy when dealing with a large number of parameters that are not strictly sensitive to voltage profile – called "voltage-insensitive" after a dedicated sensitivity analysis [7]. Other works leverage on multi-objective approach in order to capture a larger number of sensitive parameters. COBRAPRO [8] is a MATLAB-based open-source toolbox with an integrated parameter estimation routine for physics-based battery models. It minimizes a multi-objective cost function considering the voltage profile and SOC depending on the concentration of lithium-ions in the electrodes. PyBOP [9] is a Python library designed to work with PyBaMM, offering a flexible framework for parameter estimation. It uses both gradient-based and free derivative optimization methods to fit model parameters to experimental data, supporting custom objective functions. Zhang et al. [10] propose a coupled electro-thermal model using Genetic Algorithms (GAs) and minimizing the multi-objective function through Pareto fronts.

Recently, significant focus has been placed on the mechanical response of LIBs during operation, leading to the development of various techniques to measure and model the battery deformation induced by the electrochemical processes [11,12,13,14,15] . However, existing parameter estimation methods largely overlook this mechanical behavior. In this work, the effect of the mechanical measurements of the battery deformation on parameter estimation is deeply investigated through an optimization model developed in COMSOL Multiphysics. Particularly focusing on LFP/graphite batteries, a comparison between the electrochemical and the electro-chemo-mechanical approach is then presented to highlight the differences.

2. Materials and Methods

Optimization is an engineering challenge based on identifying the set of parameters ${\mathit{\theta }}_{\mathit{0}}=\{{\theta }_1,...,{\theta }_i,...,{\theta }_n\}$ that minimize an objective function $f\left(\mathit{\theta }\right)$ while ensuring the constraints of the physical phenomenon ($g_i\left(\mathit{\theta }\right)$ and $h_j\left(\mathit{\theta }\right)$). Each parameter ${\theta }_i$ can vary in a range defined between a lower bound $a_i$ and an upper bound $b_i$ in accordance to the parameters constraints. Therefore, an optimization problem is generally expressed with the mathematical formulation shown in Equation (1).

$$\left\{\begin{array}{c}Find{\mathit{\theta }}_{\mathit{0}}:\hfill \\ f\left({\mathit{\theta }}_{\mathit{0}}\right)\le f\left(\mathit{\theta }\right)\forall \mathit{\theta }\hfill \\ g_i\left(\mathit{\theta }\right)\le 0,i=1,...,m\hfill \\ h_j\left(\mathit{\theta }\right)=0,j=1,...,p\hfill \\ a_i\le {\theta }_i\le b_i\hfill \end{array}\right.$$

(1)

The aim of this work is the introduction of a novel battery parameter estimation approach based on a multi-objective function that also integrates the mechanical deformation of the battery during its operating conditions. To achieve this goal, it is necessary to develop an appropriate model that accurately describes the battery behavior and to properly asses the optimization problem defining objective functions, parameters and constraints as deeply described in this work. The optimization is performed using the BOBYQA algorithm [16], which is especially useful when the first derivative of the objective function is not available and each simulation is computationally expensive, requiring an efficient optimization strategy. A more detailed overview of the electro-chemo-mechanical model and the optimization algorithm is provided in the following sections.

2.1. Doyle-Fuller-Newman Model

The DFN model provides a physics-based framework that captures the coupled electrical and chemical species transport phenomena that occur within the battery. Based on the porous electrode and concentrated solution theories, the model accounts for key processes such as lithium-ion diffusion in the solid and electrolyte phases and charge transfer kinetics at the electrode-electrolyte interface. It also captures the multiscale behavior arising from lithium diffusion within the active material particles. The DFN model is also referred to as the Pseudo-Two-Dimensional (P2D) model. This name arises from its formulation: it resolves a one-dimensional spatial domain along the electrode thickness, and at each position within this domain, it incorporates a second dimension representing lithium diffusion within spherical particles. The P2D governing equations and the corresponding boundary conditions are listed in Table 1.

The superscript eff refers to the correction applied to the diffusion coefficients, conductivities, and reaction rates, accounting for porosity and tortuosity in each domain [17], as well as thermal dependence when the temperature differs from the reference value [18].

2.2. Mechanical Deformation

The electrodes of lithium-ion batteries are composed of porous composite structures that include active material particles, conductive additives, and a polymeric binder. The active material serves as a host for lithium ions, which are reversibly inserted and extracted during charge and discharge. These processes are called intercalation and deintercalation, respectively. As lithium ions intercalate into or deintercalate from the host structure, they cause lattice configuration changes, leading to microscopic volume expansion or contraction.

The lattice structure strain can be characterized through XRD techniques by measuring the variation of the lattice parameters as a function of the corresponding state of lithiation of the electrode. The state of lithiation is the ratio between the actual and the maximum amount of lithium concentration that can be hosted from the active material (y is the cathode state of lithiation while x is the anode one as reported in Equation (2)).

$$y={\displaystyle \frac{c_{s,p}}{c_{s,p}^{max}}};x={\displaystyle \frac{c_{s,n}}{c_{s,n}^{max}}}$$

(2)

The maximum lithium concentration depends on the lithiated active material crystal’s density ${\rho }^{crystal}$ and molar mass $M_m$ as shown in Equation (3) [19].

$$c_s^{max}={\displaystyle \frac{{\rho }^{crystal}}{M_m}}$$

(3)

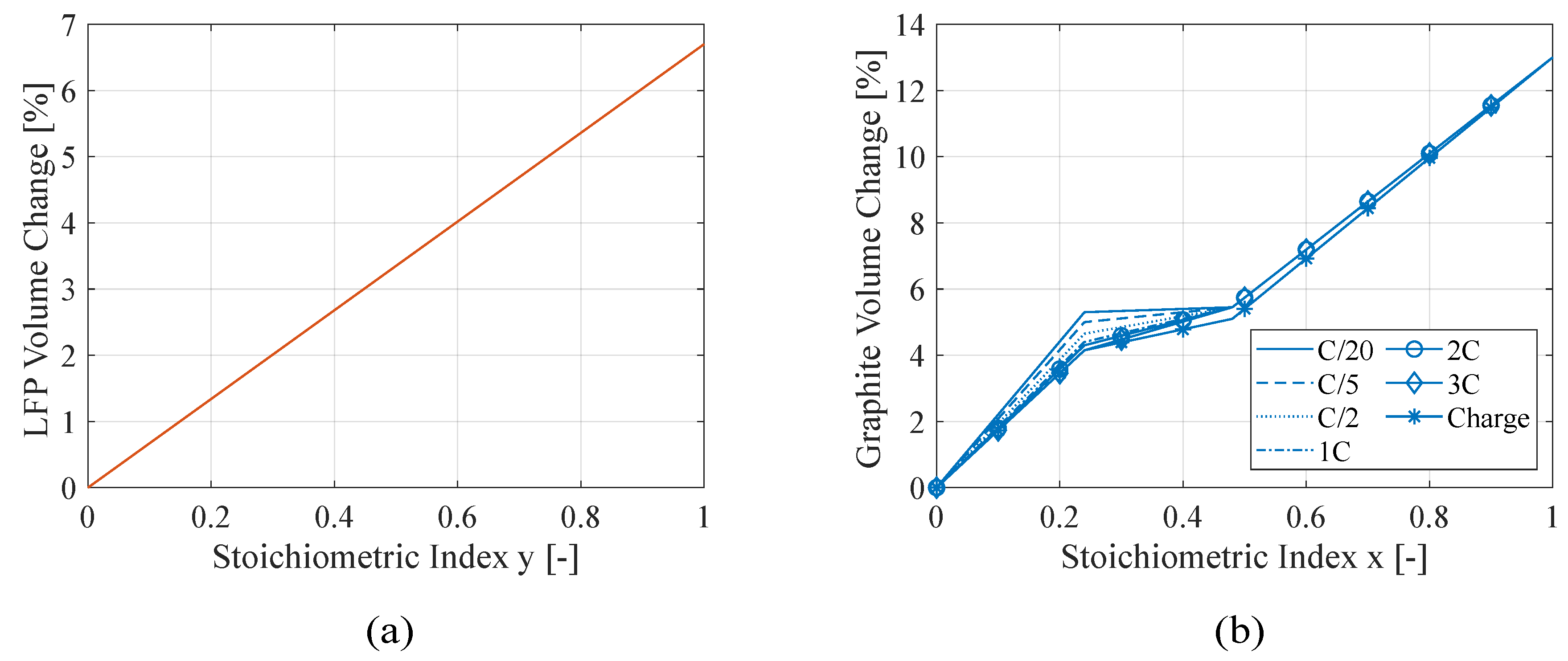
During lithiation, active materials exhibit phase transitions from their delithiated configuration to the fully lithiated one. LFP undergoes through a single phase transition from $FeP{O}_4$ to $LiFeP{O}_4$. Instead, graphite ($C_6$) manifests multiple phase transitions before reaching its fully lithiated stage $Li{C}_6$ [11,20]. In addition, graphite stage transition is not symmetric during its lithiation-delithiation cycle. This is mainly due to the presence of the stage IIL during lithium extraction. In fact, this stage is only present at low discharge current rates and gradually fades increasing the discharge current. Therefore, there is a lithiation window where stages II, IIL and III coexist; lower discharge rates increase the stage IIL volume fraction and smooth the volume change from stage II to III, due to the lower density of stage IIL. From the XRD measurement on LFP [21] and graphite [20,22], the crystal volume change as function of the state of lithiation are shown in Figure 1.

The lattice parameters exhibit directional dependence in their deformation due to the intrinsic anisotropy of the lattice structure. Although, this anisotropic nature is mitigated by the random orientation of the crystals within the particle. Thus, considering the volumetric strain, the active material particle deforms consistently with its crystal lattice.

Then, at the upper scale the electrode volume change $\Delta V^e$ depends on the $n^p$ particles volumetric deformation $\Delta V^p$ and on a possible reduction in porosity accounted through a volumetric expansion parameter g [23] as shown in Equation (4). In addition, the volume of the $n^p$ particles constitute the overall active material volume leading to Equation (5).

$$\Delta V^e=g{n}^p\Delta V^p$$

(4)

$$n^p{V}_0^p=\zeta V_0^e$$

(5)

Therefore, the volumetric strain of the electrode is obtained dividing the Equation (4) by the initial volume of the single particle $V_0^p$ and accounting for Equation (5) as reported in Equation (6). Since the battery is assumed to be free to expand, the reduction in porosity is considered negligible adopting the assumption of $g=1$ [11].

$${\epsilon }_v^e\left(t\right)={\displaystyle \frac{\Delta V^e}{V_0^e}}=\zeta {\displaystyle \frac{\Delta V^p}{V_0^p}}=\zeta {\epsilon }_v^p\left(t\right)$$

(6)

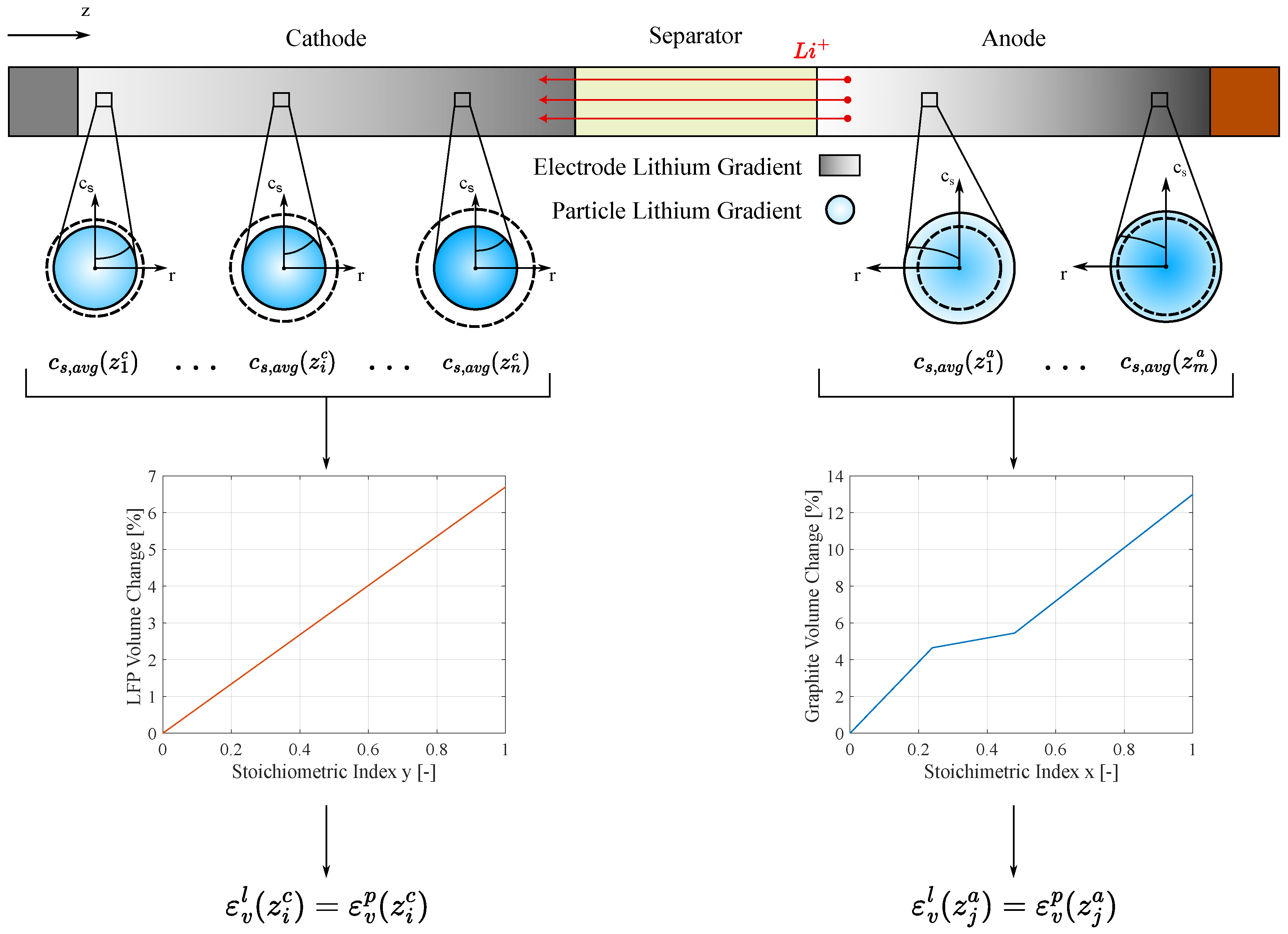
The previous equations hold under the assumption that all $n^p$ particles deform uniformly. However, this is not entirely accurate due to lithium diffusion along the electrode thickness. In reality, during battery operation, the lithiated electrode has more lithium content near the separator while the delithiated one has higher lithium concentration near the current collector. In fact, the lithium-ions diffusion is less constrained in the separator area (Figure 2).

Equation (6) remains valid if ${\epsilon }_v^p\left(t\right)$ represents the average deformation of the particles across the electrode thickness. To achieve this, the P2D model is used to extract the lithium concentration $c_s(z,r,t)$ at different positions along this direction. The concentration is then averaged over the particle radius ($c_{s,avg}(z,t)$) to determine the crystal lattice strain of the material, thus the particle strain ${\epsilon }_v^p\left(c_{s,avg}(z,t)\right)$ as shown in Figure 2. Finally, the particle strain is averaged across the electrode thickness to obtain the overall mean particle deformation ${\epsilon }_v^p\left(t\right)$.

The volumetric strain propagates across the battery scales, resulting in a macroscopic thickness change that is evaluated accounting for the deformation of both the electrodes and the presence of N layers [24,25]. Due to the small thickness of the electrode with respect to the in-plane geometry, the volumetric strain of the electrode is assumed to be responsible just of the out-of-plane strain (${\epsilon }_z^e={\epsilon }_v^e$) [11] resulting in the overall battery thickness change modeled as presented in Equation (7).

$$\Delta t_{bat}\left(t\right)=N(t_p{\epsilon }_{z,p}^e\left(t\right)+t_n{\epsilon }_{z,n}^e\left(t\right))$$

(7)

2.3. Objective Function

Once the electro-chemo-mechanical behavior of the battery is modeled, the objective function for the parameter estimation can be set. Least-Square Objective Function ($LSOF$) has been used to measure and minimize the difference between observed data points and the model’s predicted values. This approach is very useful for curve fitting since it evaluates the sum of squared errors, computed over all data points, preventing positive and negative errors from canceling out and ensuring that larger deviations are penalized more heavily, improving convergence.

In a time-dependent curve fitting, considering $y_i$ the variable at the i-th time step, the $LSOF$ is computed as presented in Equation (8).

$$LSOF\left(\mathit{\theta }\right)=\sum _{i=0}^n{(y_i^m\left(\mathit{\theta }\right)-y_i^e)}^2$$

(8)

A multi-objective function approach is needed to evaluate the integration of the battery deformation in parameters estimation. Therefore, two LSOFs need to be computed in order to account both the electrochemical measurements of the voltage profile and the mechanical measurements of the battery deformation.

$$LSO{F}_{ec}\left(\mathit{\theta }\right)=\sum _{i=0}^n{(V_i^m\left(\mathit{\theta }\right)-V_i^e)}^2$$

(9)

$$LSO{F}_m\left(\mathit{\theta }\right)=\sum _{i=0}^n{(\Delta t_{bat,i}^m\left(\mathit{\theta }\right)-\Delta t_{bat,i}^e)}^2$$

(10)

Due to the different scales of the electrochemical objective function $LSO{F}_{ec}$ and the mechanical one $LSO{F}_m$, Equations (9) and (10) have been normalized with respect to the square of the minimum voltage and maximum deformation – measured at the end of the test – respectively. Additionally, also the battery capacity C is controlled with the same quadratic approach obtaining the objective functions reported in Equations (11)–(13) which constitute the multi-objective problem statement presented in Equation (14) as a vector of objective functions.

$$f_{LSO{F}_{ec}}\left(\mathit{\theta }\right)={\displaystyle \frac{LSO{F}_{ec}\left(\mathit{\theta }\right)}{V_{min}^2}}$$

(11)

$$f_{LSO{F}_m}\left(\mathit{\theta }\right)={\displaystyle \frac{LSO{F}_{ec}\left(\mathit{\theta }\right)}{\Delta t_{max}^2}}$$

(12)

$$f_C\left(\mathit{\theta }\right)={\displaystyle \frac{{(C^m\left(\mathit{\theta }\right)-C^e)}^2}{{\left(C^e\right)}^2}}$$

(13)

$$\mathit{F}\left(\mathit{\theta }\right)=\left\{\begin{array}{c}{f}_{LSO{F}_{ec}}\left(\mathit{\theta }\right)\\ f_{LSO{F}_m}\left(\mathit{\theta }\right)\\ f_C\left(\mathit{\theta }\right)\end{array}\right\}$$

(14)

Depending on the same set of parameters $\mathit{\theta }$ coming from the same multiphysics modeling, the objective functions cannot be minimized at the same time and independently. Therefore, the multi-objective problem is solved using a scalarization approach to reduce computational complexity and enable variations in the weighting of the objective functions with respect to the Pareto technique [26,27]. Thus, a single objective function is obtained in Equations (15) and (16) where $\mathit{w}$ is the weights vector of the objective functions. Weighting factors are eventually applied to prioritize certain objective functions over others. During the electrochemical-only parameter estimation $w_2=0$ to ignore the mechanical objective function.

$$f\left(\mathit{\theta }\right)={\mathit{w}}^T·\mathit{F}\left(\mathit{\theta }\right)$$

(15)

$$f\left(\mathit{\theta }\right)=w_1{f}_{LSO{F}_{ec}}\left(\mathit{\theta }\right)+w_2{f}_{LSO{F}_m}\left(\mathit{\theta }\right)+w_3{f}_C\left(\mathit{\theta }\right)$$

(16)

2.4. Optimization Algorithm

Since the optimization problem involves multiple objectives, the derivative of $f\left(\mathit{\theta }\right)$ with respect to the control variables is not easily obtainable: the presence of several objectives complicates the calculation of a unique and continuous gradient, making gradient-based algorithms unsuitable. In addition, changes in geometry often lead to remeshing, which may introduce discontinuities or non-differentiable behavior in the objective function. As a result, the computed gradients may be inaccurate or undefined. Therefore, a derivative-free algorithm is more appropriate for addressing this type of problem. The drawback is the slower convergence of the optimization process.

Among the derivative-free algorithm implemented in COMSOL Multiphysics, BOBYQA (Bound Optimization BY Quadratic Approximation) is the only one that uses a quadrative interpolation model to approximate the objective function. Unlike gradient-based methods, BOBYQA constructs and updates a local quadratic model $Q\left(\mathit{\theta }\right)$ using only objective function evaluations. In particular, the quadratic model is built to interpolate the objective function at a set of m points $\{{\mathit{\theta }}_{\mathit{1}},{\mathit{\theta }}_{\mathit{2}},...,{\mathit{\theta }}_{\mathit{m}}\}$, with $m\ge n+1$ as shown in Equation (17). The interpolation points ${\mathit{\theta }}_{\mathit{j}}$ are strategically chosen and updated as stated by Powell in his work [16].

$$Q\left({\mathit{\theta }}_{\mathit{j}}\right)=f\left({\mathit{\theta }}_{\mathit{j}}\right),\forall i=1,...,m$$

(17)

Then, the quadratic approximation of the objective function has the form presented in Equation (18) where c is a scalar constant, g is the estimated gradient, H is an approximated Hessian matrix and ${\mathit{\theta }}_{\mathit{k}}$ is the evaluation point at the k-th iteration.

$$Q\left(\mathit{\theta }\right)=c+g(\mathit{\theta }-{\mathit{\theta }}_{\mathit{k}})+{\displaystyle \frac{1}{2}}{(\mathit{\theta }-{\mathit{\theta }}_{\mathit{k}})}^{T}H(\mathit{\theta }-{\mathit{\theta }}_{\mathit{k}})$$

(18)

To determine the next point to evaluate, BOBYQA minimizes the quadratic model $Q\left(\mathit{\theta }\right)$ within a neighborhood of the current point ${\mathit{\theta }}_{\mathit{k}}$, known as the trust region. This area is defined by a radius ${\Delta }_k$, which bounds the maximum allowed step from the current iteration. The trust-region subproblem is expressed in Equation (19).

$$\underset{\mathit{\theta }\in {\Omega }_k}{min}Q\left(\mathit{\theta }\right){\Omega }_k=\{\mathit{\theta }\in {\mathbb{R}}^n,\parallel \mathit{\theta }-{\mathit{\theta }}_{\mathit{k}}\parallel \le {\Delta }_k\}$$

(19)

After evaluating the objective function at the new candidate point, the radius ${\Delta }_k$ is updated depending on the agreement between the predicted decrease in $Q\left(\mathit{\theta }\right)$ and the actual decrease in $f\left(\mathit{\theta }\right)$. If the model prediction is sufficiently accurate, ${\Delta }_k$ is expanded to allow broader exploration; otherwise, it is reduced to focus on a more local region, enhancing model reliability but risking to miss the global minimum.

In parallel, the quadratic model itself is updated to maintain interpolation accuracy: whenever a new function evaluation is accepted and one of the existing interpolation points is replaced, the curvature of the model – represented by the Hessian approximation H – must also be updated. This update ensures that the new model still satisfies the interpolation conditions at the updated set of points.

2.5. Error Analysis and Models Comparison

Once the parameters are estimated using the least squares method, the Root Mean Square Errors (RMSEs) of the fitted curves is computed and the reliability of the parameters estimates is evaluated using the covariance matrix. For n parameters ${\theta }_1,{\theta }_2,...,{\theta }_n$, the covariance matrix C is expressed as shown in Equation (20).

$$C=\left(\begin{array}{cccc}Var\left({\theta }_1\right)& Cov({\theta }_1,{\theta }_2)& \dots & Cov({\theta }_1,{\theta }_n)\\ Cov({\theta }_2,{\theta }_1)& Var\left({\theta }_2\right)& \dots & Cov({\theta }_2,{\theta }_n)\\ ⋮& ⋮& \ddots & ⋮\\ Cov({\theta }_n,{\theta }_1)& Cov({\theta }_n,{\theta }_2)& \dots & Var\left({\theta }_n\right)\end{array}\right)$$

(20)

The diagonal elements $Var\left({\theta }_i\right)$ represent the variances of the individual parameter estimates, indicating the variability in each estimation. The off-diagonal elements $Cov({\theta }_i,{\theta }_j)$ represent the covariance between pairs of parameters, reflecting their linear relationship.

In this model, during the optimization process, each iteration produces a set of parameters that typically improves or maintains the objective function value. These intermediate estimates can be interpreted as a set of plausible solutions within the parameter space. By treating them as empirical samples, it is possible to compute a covariance matrix that captures the spread and correlation of the parameters across iterations. The empirical covariance matrix can then be used to construct confidence (or error) ellipses for selected pairs of parameters. These ellipses are derived from the $2x2$ submatrices of the covariance matrix $C\in {\mathbb{R}}^{nxn}$, which are symmetric and positive definite. The rescaling of the parameters is needed because of the difference in order of magnitude and units of measures of the estimated parameters.

The orientation of the ellipse is determined by the covariance between the two parameters. Specifically, the orientation of the ellipse can be described by an angle $\alpha$, measured with respect to the x-axis: the closer $\alpha$ is to $\pm 45$°, the stronger the correlation between the parameters, while $\alpha =0$° or $\pm 90$° indicates no correlation. On the other hand, larger ellipse indicates higher variances in the estimated parameters across iterations, suggesting that the algorithm has explored a broader region of the parameter space. While this may reflect a more thorough search of the objective function landscape, it can also be a sign of reduced convergence toward stable parameter values. For this reason, the confidence ellipses – which provide a qualitative representation of the parameter uncertainty and correlation given by the optimization model – should be considered together with the RMSE values to enable a more comprehensive comparison between the electrochemical and the electro-chemo-mechanical approach.

3. Experiment

Three commercial LFP/graphite prismatic LIB samples undergo electrical, thermal, and mechanical characterization to evaluate their performance. The tests consist of measuring voltage, temperature, and deformation responses under different charge and discharge currents. Charge rates vary from C/20 to C/2, while discharge rates range from C/20 to 3C, in accordance with manufacturer specifications. Each charge/discharge test is conducted within a state of charge (SOC) range of 0%–100% and repeated five times on the same battery sample. A dedicated testing setup with laser sensors is used to monitor battery deformation during operation by measuring thickness variations, as reported in a previous study by the authors [28]. The measured voltage and thickness change, averaged over the tested samples, constitute the dataset used for parameter estimation through the optimization algorithm.

4. Results

4.1. Parameters and Constraints

Certain battery parameters can be measured or evaluated experimentally with relatively simple tests and can therefore be considered known or fixed during the estimation procedure, which helps to reduce the complexity of the simulation. In contrast, some electrochemical parameters – such as diffusion coefficients and reaction rates – require more advanced and complex experimental procedures for accurate identification, and their values reported in the literature often span a wide range. Other physical parameters, such as electrode thickness and the number of electrode layers, can only be determined after battery teardown.

Therefore, alongside the comparison between electrochemical and electro-chemo-mechanical parameter estimation, two distinct scenarios are analyzed:

• Battery Teardown – the battery has been disassembled and parameters such as electrode thickness and the number of layers are known. In this case, the set of parameters to be estimated comprises the diffusion coefficients, the reaction rates and the active material fractions of the two electrodes as shown in Equation (21)

  $${\mathit{\theta }}_{\mathit{1}}=\left\{\begin{array}{cccccc}{D}_{s,p}& D_{s,n}& k_p& k_n& {\zeta }_p& {\zeta }_n\end{array}\right\}$$

  (21)
• No Battery Teardown – the battery has not been disassembled and also the thickness of the electrodes and the number of layers are unknown. The extended set of parameters is presented in Equation (22).

  $${\mathit{\theta }}_{\mathit{2}}=\left\{\begin{array}{cccc}{\mathit{\theta }}_{\mathit{1}}& t_p& t_n& N\end{array}\right\}$$

  (22)
  In this case, it is necessary to constrain the overall battery thickness computed by the model $t_{bat}^m$ – accounting also for the separator thickness $t_s$ and the current collectors ones $t_p^{cc}$ and $t_n^{cc}$ (Equation (23)) – to remain within a specified tolerance range around the experimental value $t_{bat}^e$ as shown in Equation (24).

  $$t_{bat}^m=N(t_p+t_s+t_n)+{\displaystyle \frac{N}{2}}(t_p^{cc}+t_n^{cc})+2t_{case}$$

  (23)

  $${\displaystyle \frac{|t_{bat}^m-t_{bat}^e|}{t_{bat}^e}}\le to{l}_{thick}$$

  (24)

Then, the parameters sets ${\mathit{\theta }}_{\mathit{1}}$ and ${\mathit{\theta }}_{\mathit{2}}$ are estimated by fitting experimental curves obtained from constant current cycles with 100% depth of discharge (DOD) at $C/2$ current rate. In both scenarios, the stoichiometric windows are calculated with differential voltage analysis (DVA) at low current rates. The stoichiometric indexes corresponding to $SOC=100\%$ ($x_{100}$ and $y_{100}$) are imposed as fixed initial values during discharge while $x_0$ and $y_0$ are constrained around their corresponding experimental value with a certain tolerance ($to{l}_{x_0}$ and $to{l}_{y_0}$ respectively) as shown in Equation (25).

$${\displaystyle \frac{|x_0^m-x_0^e|}{x_o^e}}\le to{l}_{x_0}{\displaystyle \frac{|y_0^m-y_0^e|}{y_o^e}}\le to{l}_{y_0}$$

(25)

However, the estimation cannot be considered complete: the diffusion coefficients are current-dependent [18] and the contact resistance $R_c$ – which is another challenging parameter to assess – is voltage-insensitive at low current rates, namely its value does not influence the voltage when the current is low. Therefore, the experimental data at $3C$ discharge current rate are then used to assess $R_c$ and extrapolate the diffusion coefficient behavior $D_{s,k}\left(i\right)$ by linearly fitting the estimated $D_{s,k}\left(i_{C/2}\right)$ and $D_{s,k}\left(i_{3C}\right)$.

Among the other parameters – considered fixed in the optimization process – there are material properties like the molar mass $M_m$ and the crystal density ${\rho }^{crystal}$ of the active materials lattice structure, the corresponding maximum lithium concentration that can be obtained as stated in Equation (3), electrolyte properties, solid-phase conductivity and the active material particle radius. Electrolyte parameters have low influence on the results, thus are taken from literature. The influence of the active material particle radius on the results is correlated with the diffusion coefficient, making trivial the estimation of both parameters. The fixed parameters are reported in Table 2.

4.2. Teardown Configuration

In this configuration, the electrode thickness and the number of layers are known through SEM analysis conducted after battery teardown as shown in an authors previous work [11]. The estimation procedure need initial guess values as starting point for the parameters to be estimated. The initial values of the diffusion coefficients and reaction rates are chosen from common values reported in literature while their lower bound is one order of magnitude lower and their upper bound is one order of magnitude higher. On the other hand, the initial value of the active material fraction is evaluated from the electrode capacity at low discharge rates – in which the stoichiometric window is known – from the relation expressed in Equation (26). The parameters ranges and their final estimated values with the electrochemical (EC) and the electro-chemo-mechanical (ECM) approaches are reported in Table 3.

$$C_p={\displaystyle \frac{c_{s,p}^{max}\Delta yFNA{t}_p{\zeta }_p}{3600}}{C}_n={\displaystyle \frac{c_{s,n}^{max}\Delta xFNA{t}_n{\zeta }_n}{3600}}$$

(26)

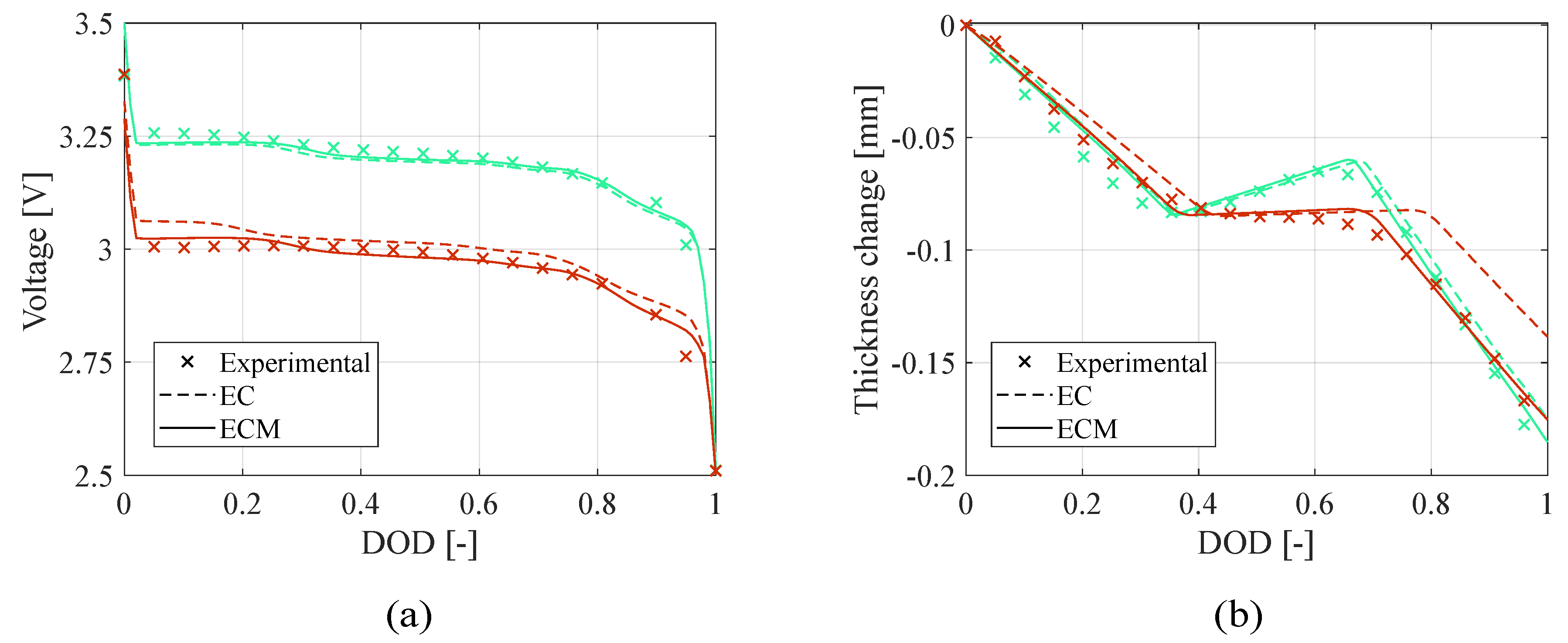
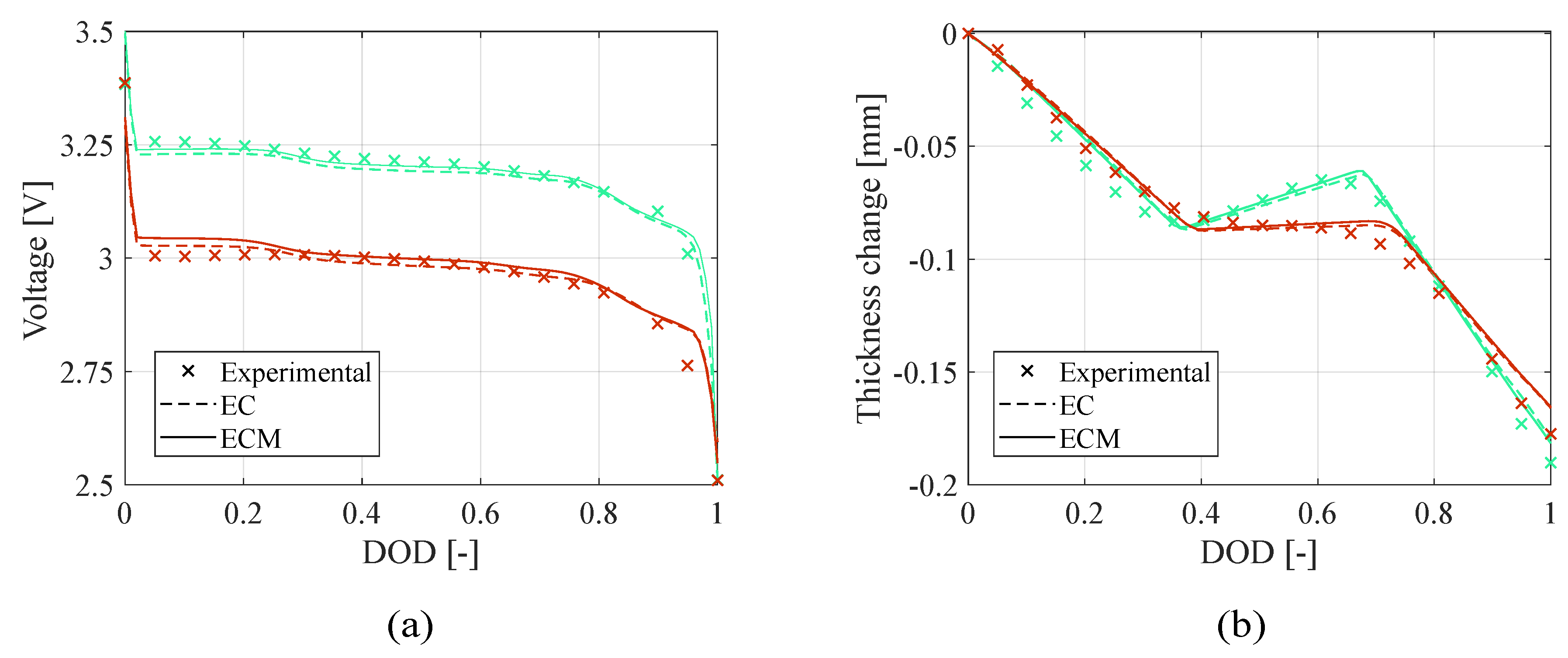
Figure 3 shows the voltage profile and the thickness change obtained at the end of the optimization process with the two estimation approaches in teardown scenario. Furthermore, in Table 4 are reported the corresponding Root Mean Square Errors (RMSEs) as sum of the RMSEs computed at $C/2$ and at $3C$: the electro-chemo-mechanical (ECM) approach leads to more accurate prediction of the battery behavior presenting significantly lower errors; in fact, the electrochemical (EC) approach converges faster due to the simplicity of the objective function but leads to less accurate estimate. 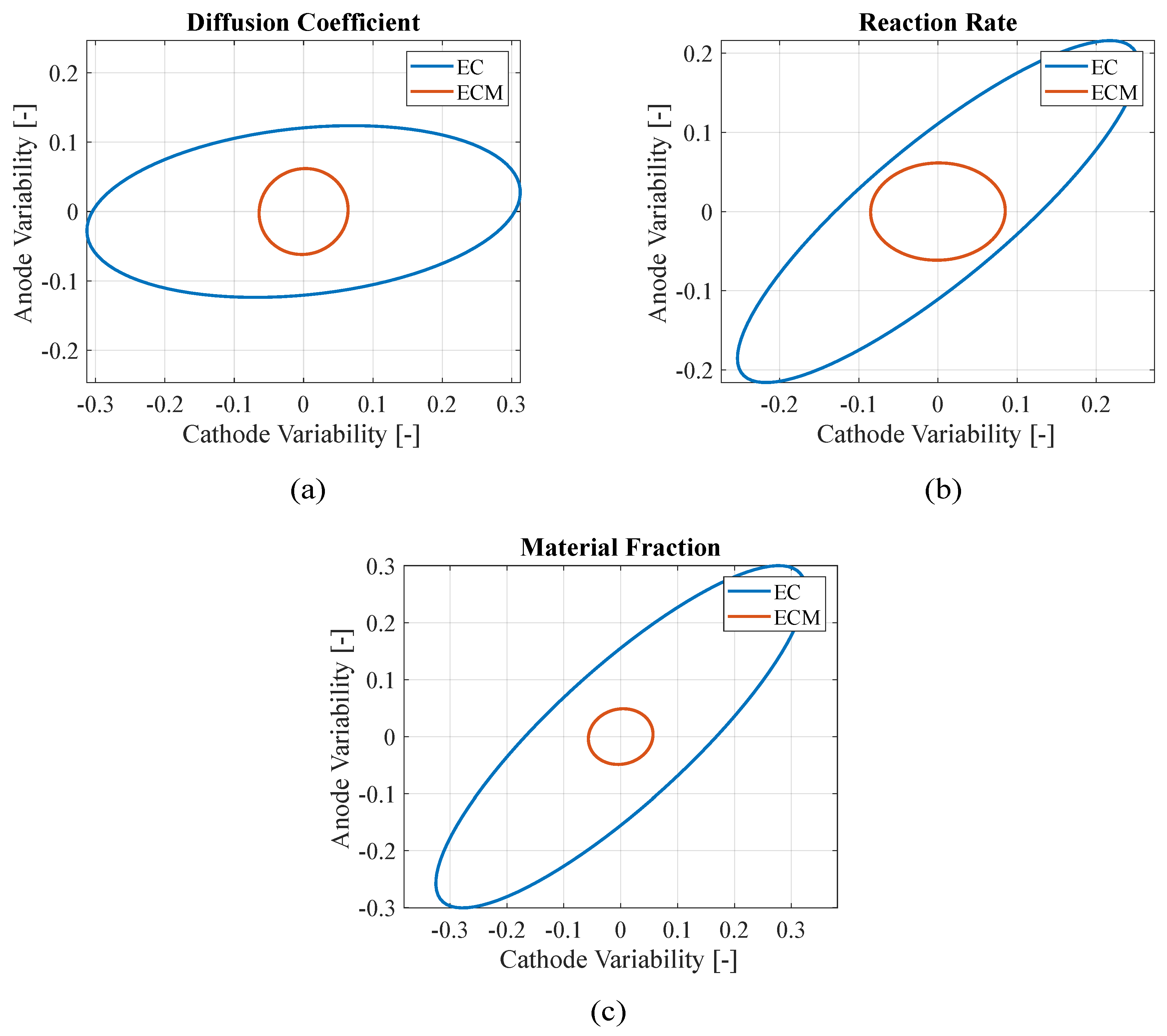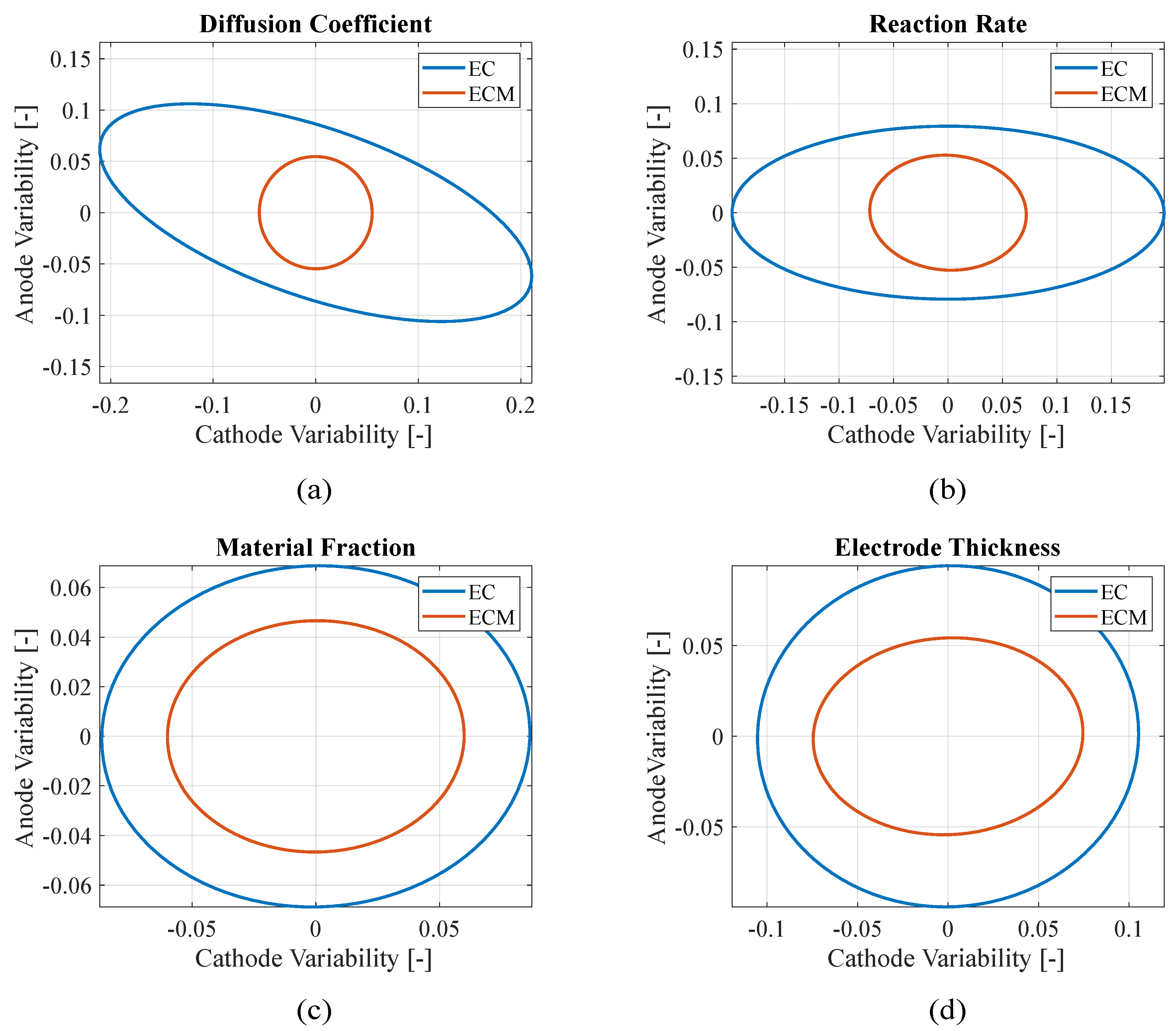In addition, Figure 4 presents the confidence ellipses of paired parameters to compare the stability of the two approaches: adding the mechanical constraints makes the algorithm more reliable reducing the parameters variability with respect to using just electrochemical objective functions. In fact, smaller ellipses indicate that the parameters present lower variances through the iterations, which is a sign of improved convergence toward the final value. However, small ellipses may also result from the algorithm converging rapidly to a local minimum of the objective function without exploring a wide range of the possible parameters. For this reason, the confidence ellipses should be interpreted alongside the RMSEs to better assess the overall quality and reliability of the model. In this case, the electrochemical-only approach lead both to higher RMSEs and larger ellipses with respect to the electrochemical-mechanical approach, making the parameters identification with the latter approach more reliable.

4.3. No Teardown Configuration

In this configuration, even the electrode thickness and the number of layers must be estimated. While this increases the computational complexity, it also enables the estimation of such parameters without the need of the battery teardown. To assess the robustness of the model, the initial values for the electrode thickness are deliberately set slightly different from the measured ones. However, as shown in Table 5, the end values of these parameters are strictly close to the one imposed in the teardown condition.

Figure 5 shows the voltage profile and the thickness change obtained at the end of the optimization process while Table 6 reports the corresponding RMSEs in the configuration without battery teardown. In this scenario, the difference between the two model is negligible both in the estimation and therefore in the committed error: adding new capacity-sensitive parameters to be estimated avoids the wrong convergence reached in the previous scenario. However, in this case, the main difference between the two models stands in their capability of generating reliable solutions. In fact, even in this scenario, the electro-chemo-mechanical approach is able to increase the reliability of the estimation as presented in Figure 6 comparing the area of the error ellipses between the two models.

4.4. Validation

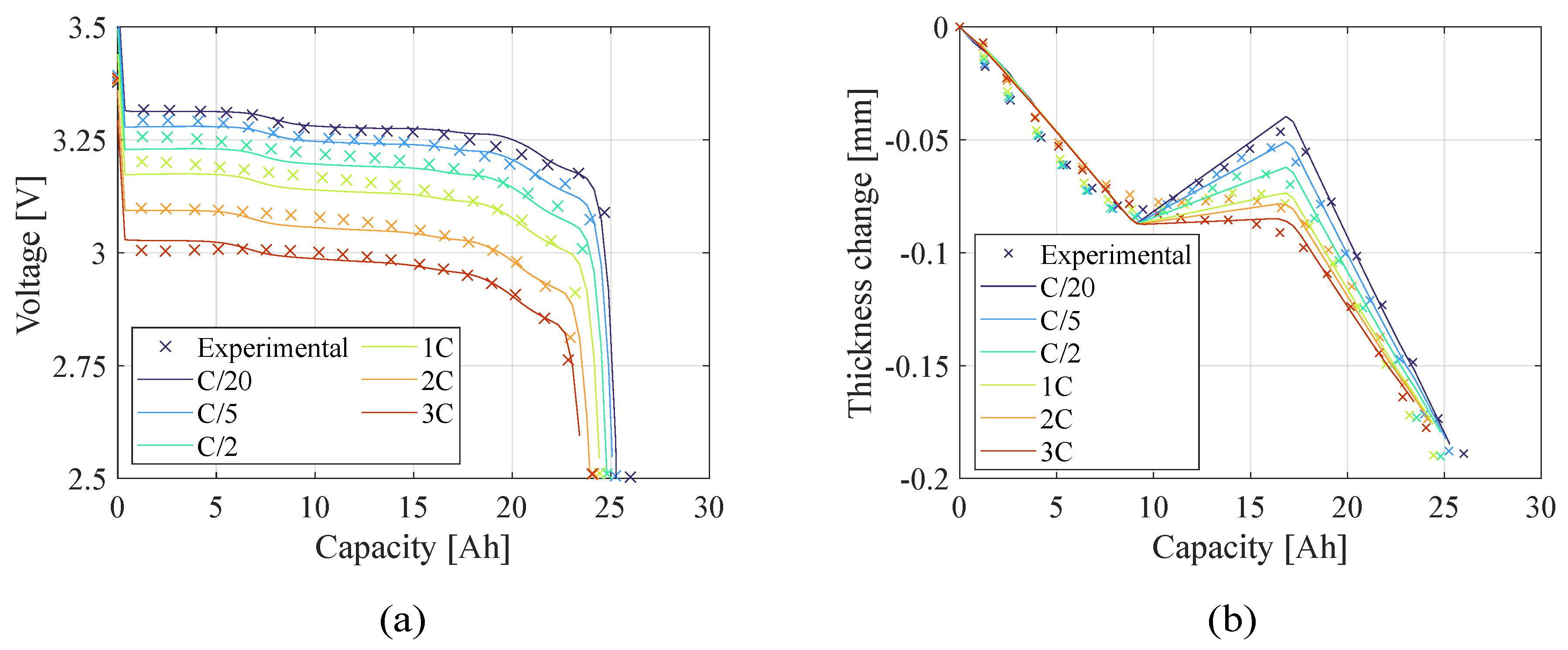
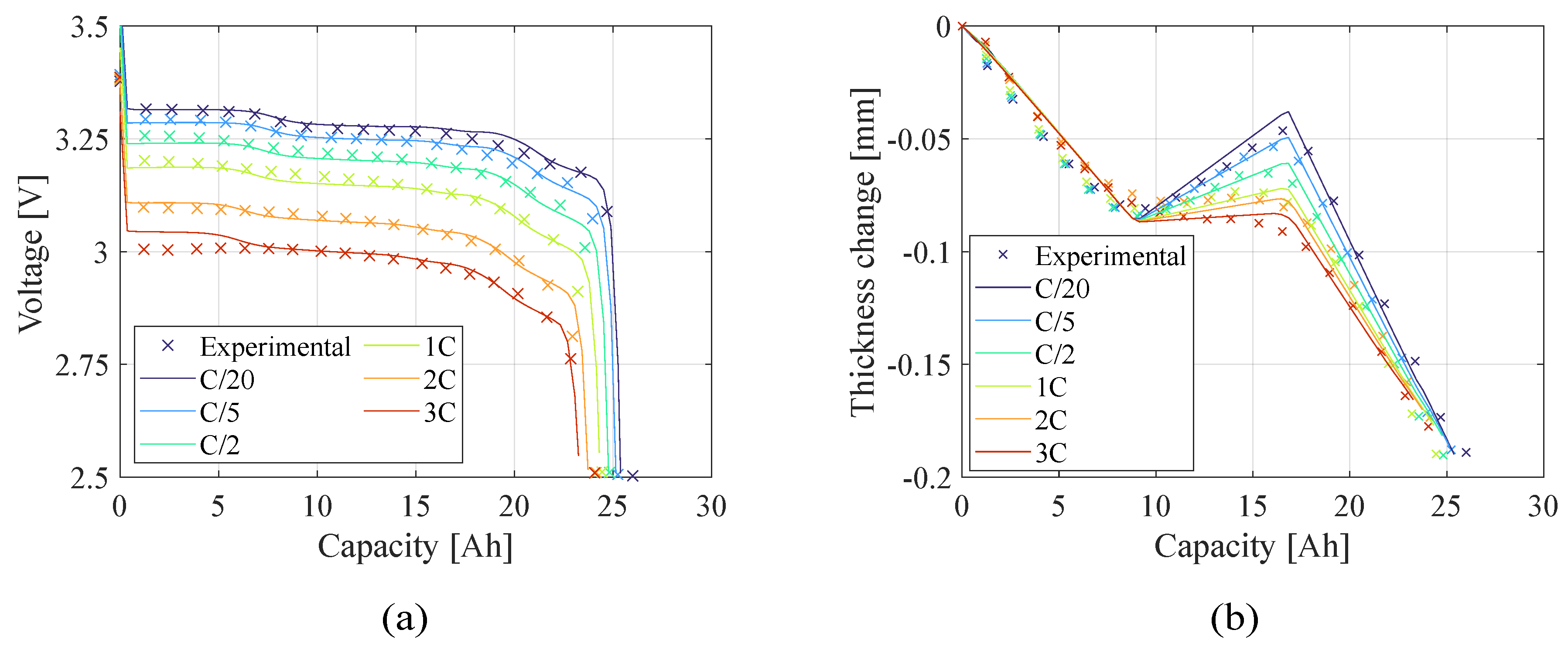
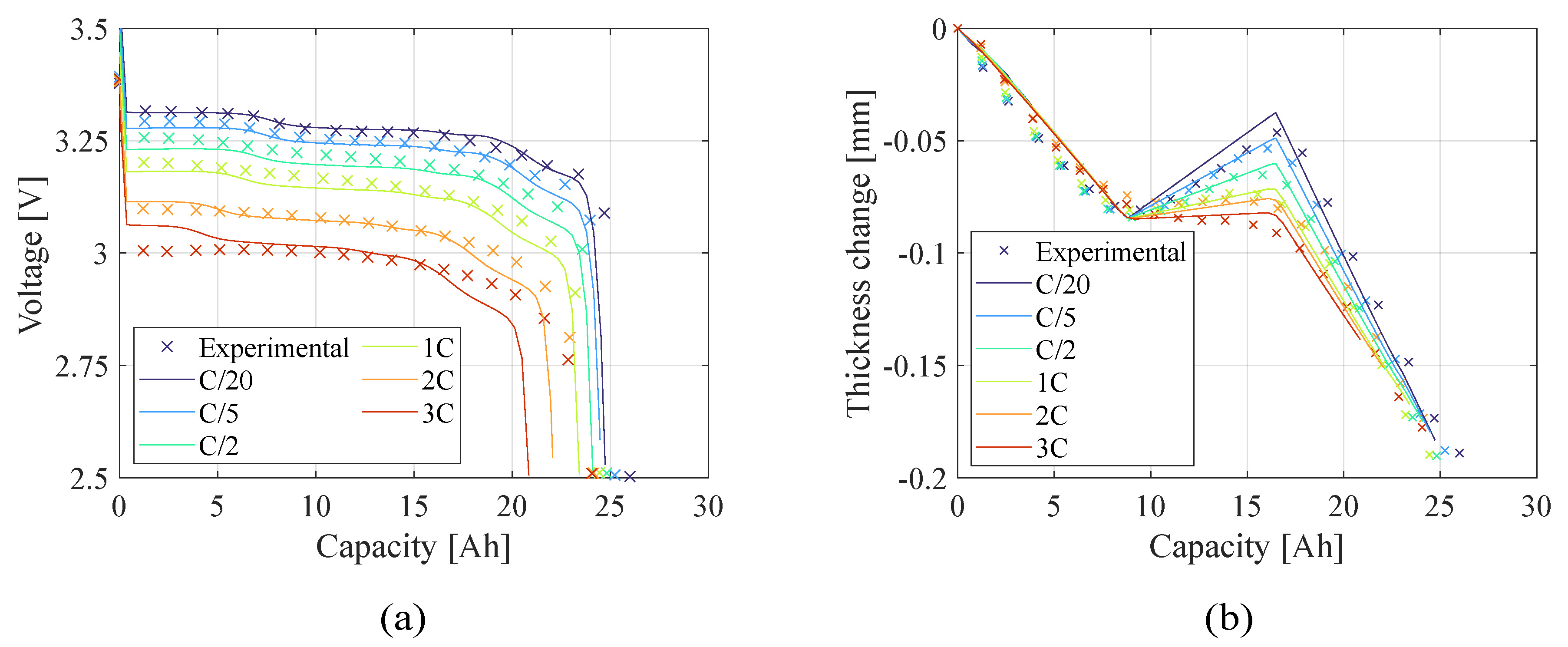
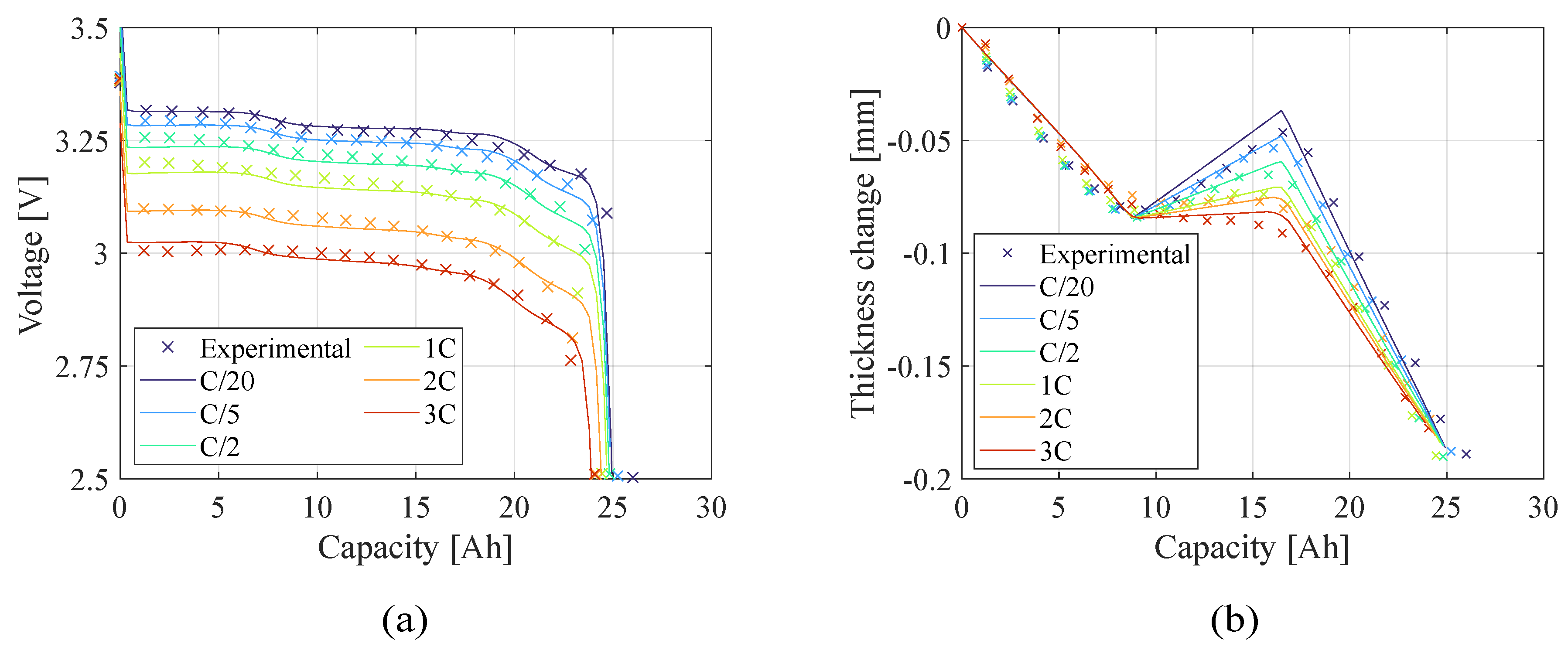
The obtained parameters are then used to validate the reliability of the estimation computing the model at different discharge current rates and comparing the results with the experimental values. Figure 7 and Figure 8 present the teardown scenario with the electrochemical and electro-chemo-mechanical estimated parameters, respectively. In the teardown scenario, as shown in Section 4.2, the electrochemical-only approach converged to less accurate parameters resulting in a less accurate prediction of the battery behavior at different current rates. Conversely, with the same initial conditions, the electro-chemo-mechanical approach reaches better results. In the no-teardown scenario (Figure 9 and Figure 10.), there is no significant difference in representing the battery behavior between the two estimation models because the number of the capacity sensitive parameters increased. The advantage of using the electro-chemo-mechanical approach stands in the reliability of its estimates.

5. Conclusion

In this work, a parameter estimation framework has been developed by integrating both electrochemical and mechanical measurements into the parameter estimation process. The inclusion of mechanical data, such as the battery thickness change, introduces additional constraints that significantly enhance the identifiability of key parameters, particularly those related to diffusion and reaction kinetics.

Two scenarios were considered: one where the battery underwent teardown to measure electrode thicknesses and the number of layers, and one without teardown. In the first case, the electrochemical-only estimation, constrained by fewer free parameters, converged to incorrect solutions while the electro-chemo-mechanical approach reached satisfying estimates with lower RMSEs and parameter variability. In the second case, when teardown was not performed and more parameters could be varied, the electrochemical approach yielded better estimates but still showed higher uncertainty compared to the electro-chemo-mechanical method. Integrating mechanical data consistently improve accuracy and robustness, reducing parameter variability.