1. Introduction
The discovery of the universe’s expansion marked a turning point in modern cosmology. Observational evidence, beginning with Edwin Hubble’s redshift–distance relation in 1929, showed that galaxies are moving away from us at speeds proportional to their distance. In 1998, data from Type Ia supernovae revealed that this expansion is accelerating, not slowing—a finding that led to the standard ΛCDM (Lambda Cold Dark Matter) cosmological model. According to ΛCDM, the accelerated expansion is driven by a form of dark energy represented by the cosmological constant (Λ).
Despite its observational successes, ΛCDM leaves many questions unanswered. The nature of dark energy remains mysterious, the predicted value of Λ from quantum vacuum energy calculations is vastly larger than what is observed, and the Hubble constant derived from early-universe data (Planck satellite) is in tension with that measured locally (SH0ES project). These issues prompt the search for alternative explanations that are equally consistent with observations but based on new physical insights.
In this paper, we propose such an alternative: that space-time itself behaves as a compressible fluid, and the observable universe is a spherical bubble of this fluid. The universe expands not due to a mysterious dark energy but because of a pressure difference between the interior of the bubble (space-time) and the external void (nothingness). This pressure gradient acts like a driving force, pushing the boundary of the universe outward.
We develop this model using the language of classical fluid dynamics, borrowing concepts from cavitation bubbles, entropy flow, and boundary tension. Unlike prior analog gravity theories, we apply the full structure of fluid equations—continuity, Euler, and pressure–volume work—to derive a realistic model of cosmic behavior. The key insight is that pressure-induced expansion can replicate the effects attributed to dark energy, but with a physically grounded mechanism.
In addition, we dedicate a section of this paper to the inspiration derived from Quranic verses that metaphorically and structurally reflect this fluid-based view of space-time. However, the scientific derivation of the theory stands independently and can be evaluated without that section if desired.
Unlike standard cosmological models that treats gravity, expansion, and time’s direction as separate phenomena, this framework offers a unified physical explanation. By interpreting space-time as a compressible fluid, we derive these three fundamental behaviors from a single cause: the pressure dynamics of the space-time medium. This unification opens new paths toward a self-consistent and mechanistically grounded cosmology, offering alternatives to the unexplained cosmological constant and exotic fields.
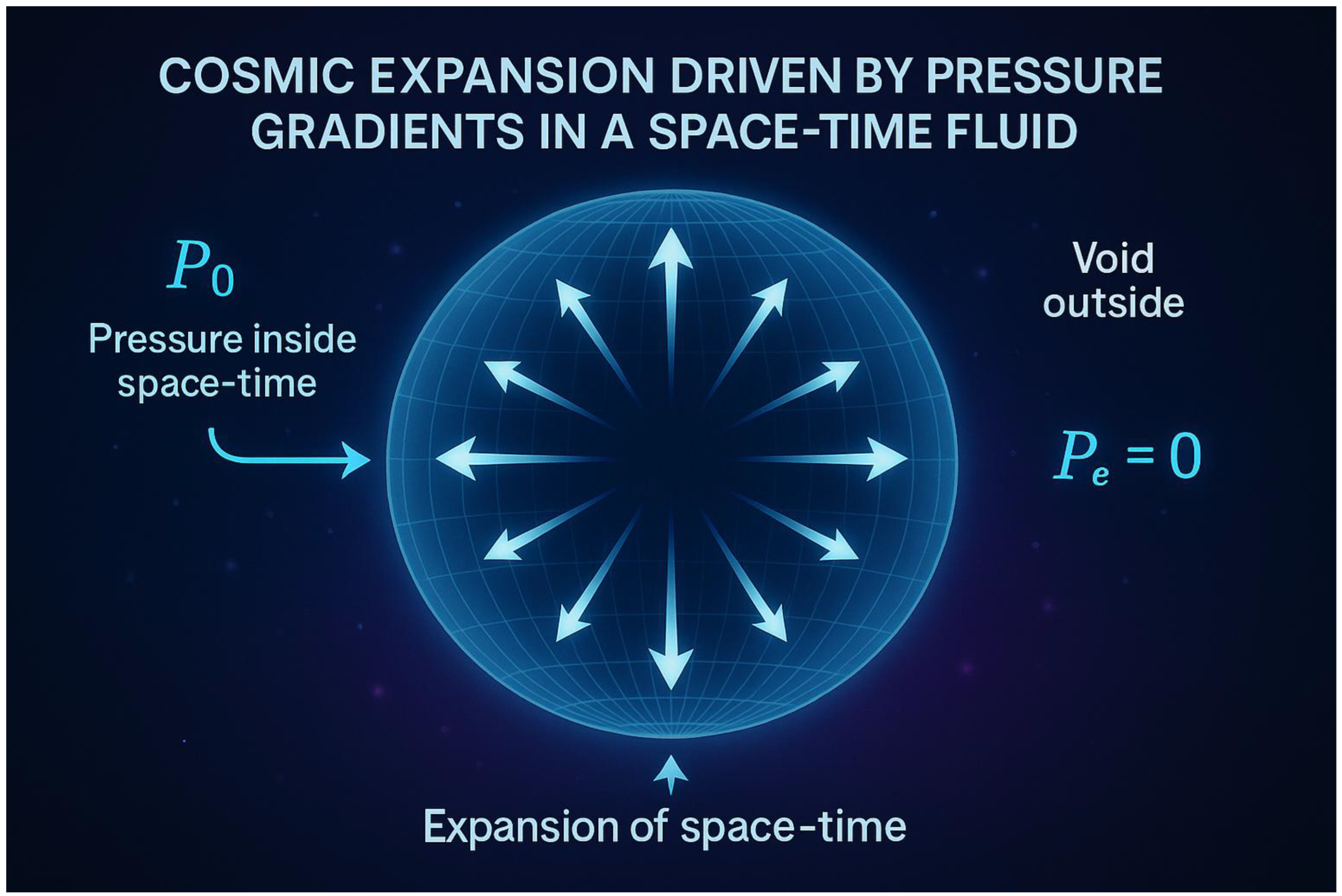
Figure 1.
Full Conceptual Overview.
Figure 1.
Full Conceptual Overview.
A conceptual model of the universe as a compressible space-time fluid bubble. The internal pressure drives expansion into an external zero-pressure void. Curvature around mass illustrates gravity as a pressure well. Arrows indicate fluid motion and entropy flow, with surface tension acting at the boundary.
2. Background: The ΛCDM Standard Model
The ΛCDM (Lambda Cold Dark Matter) model is the prevailing cosmological model, successfully explaining a broad range of observations such as the cosmic microwave background (CMB), large-scale structure, and Type Ia supernova data. It assumes the universe is homogeneous and isotropic on large scales and is described by the Friedmann–Lemaître–Robertson–Walker (FLRW) metric.
The evolution of the scale factor
is governed by the
Friedmann equation:
Where:
is the Hubble parameter ,
is the total energy density (including matter and radiation),
represents the spatial curvature (0 for flat universe),
is the cosmological constant.
This model assumes a composition of approximately:
One of the major triumphs of ΛCDM is its fit to the Planck satellite data (2018), which gives precise constraints:
However, this model also presents significant conceptual and observational challenges:
The cosmological constant problem (why is Λ so small yet non-zero?),
The coincidence problem (why are matter and Λ comparable today?),
The Hubble tension: local measurements (e.g., SH0ES project) yield km/s/Mpc, creating a >5σ discrepancy with CMB-inferred values.
This has led to increasing interest in alternative explanations of cosmic expansion that do not require vacuum energy or a cosmological constant. Our model replaces Λ with a physically driven expansion mechanism based on a fluid pressure gradient at the boundary of a space-time bubble.
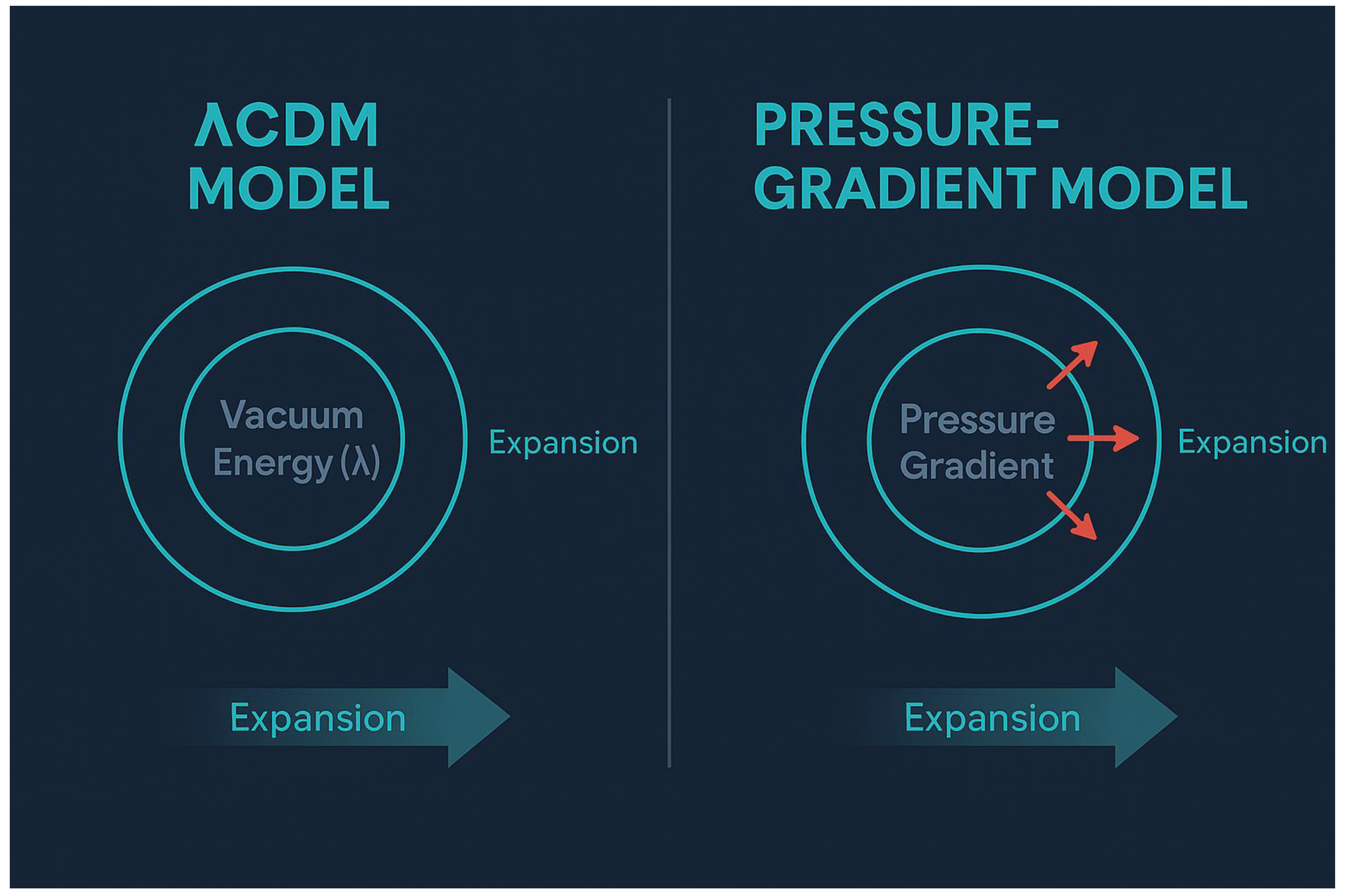
Figure 2.
ΛCDM vs. Pressure-Driven Expansion.
Figure 2.
ΛCDM vs. Pressure-Driven Expansion.
Comparative illustration of the standard ΛCDM model (left) using vacuum energy versus the pressure-gradient model (right), where expansion is physically driven by fluid dynamics and pressure imbalance.
3. Space-Time as A Compressible Fluid
3.1. Conceptual Overview
We propose that space-time behaves as a compressible, dynamic fluid, governed by physical pressure, density, and velocity fields. In this view, the observable universe is a spherical bubble of space-time fluid expanding into a surrounding external void. The pressure gradient at the boundary of this bubble drives cosmic expansion.
This model introduces a physically intuitive mechanism: the internal fluid pressure is higher than the surrounding void (which has zero or negligible pressure), resulting in an outward thrust at the boundary. This is analogous to a cavitation bubble expanding in a surrounding liquid or gas at lower pressure.
3.2. Physical Assumptions
The space-time fluid has pressure , density , and velocity .
The external void has zero pressure: .
The fluid follows classical fluid dynamics: Euler and continuity equations apply.
The boundary of the universe behaves like a surface with tension, possibly contributing an effective cosmological term.
3.3. Governing Equations
The
continuity equation (mass conservation) is:
The
Euler equation (momentum conservation) is:
Assuming spherical symmetry and radial motion, the radius of the universe
behaves like a bubble expanding due to internal pressure. The governing equation of motion for the bubble wall is derived from fluid dynamics:
Where:
is the radius (analogous to the scale factor ),
is the fluid density inside the bubble,
is the internal pressure,
(the void),
and are the first and second time derivatives of the radius.
This is structurally similar to the Rayleigh–Plesset equation for cavitating bubbles in classical fluid mechanics.
3.4. Equation of State
To close the system, we adopt an
equation of state for the space-time fluid. A general barotropic form is assumed:
Where is the equation-of-state parameter:
for matter-like fluid,
for radiation,
for vacuum-like behavior (e.g., surface tension).
We will later use a hybrid model in which the pressure has two components:
4. Expansion Dynamics from Pressure Gradient
4.1. Deriving the Equation of Motion
We consider the universe as a spherical bubble of compressible space-time fluid expanding due to internal pressure against an external void. The net outward force on the boundary arises from the pressure difference between the fluid inside and the vacuum outside.
From Newton’s second law:
Let:
: radius of the universe,
: uniform density of the fluid,
: internal fluid pressure,
: external void pressure.
The mass of the spherical fluid region is:
The
net outward force due to pressure is:
A more complete version (incorporating kinetic energy of fluid motion) includes an additional term:
Since
, we get:
This is a pressure-driven expansion law, analogous to the Rayleigh–Plesset equation in bubble dynamics. It replaces the Friedmann equation of ΛCDM but retains similar structure.
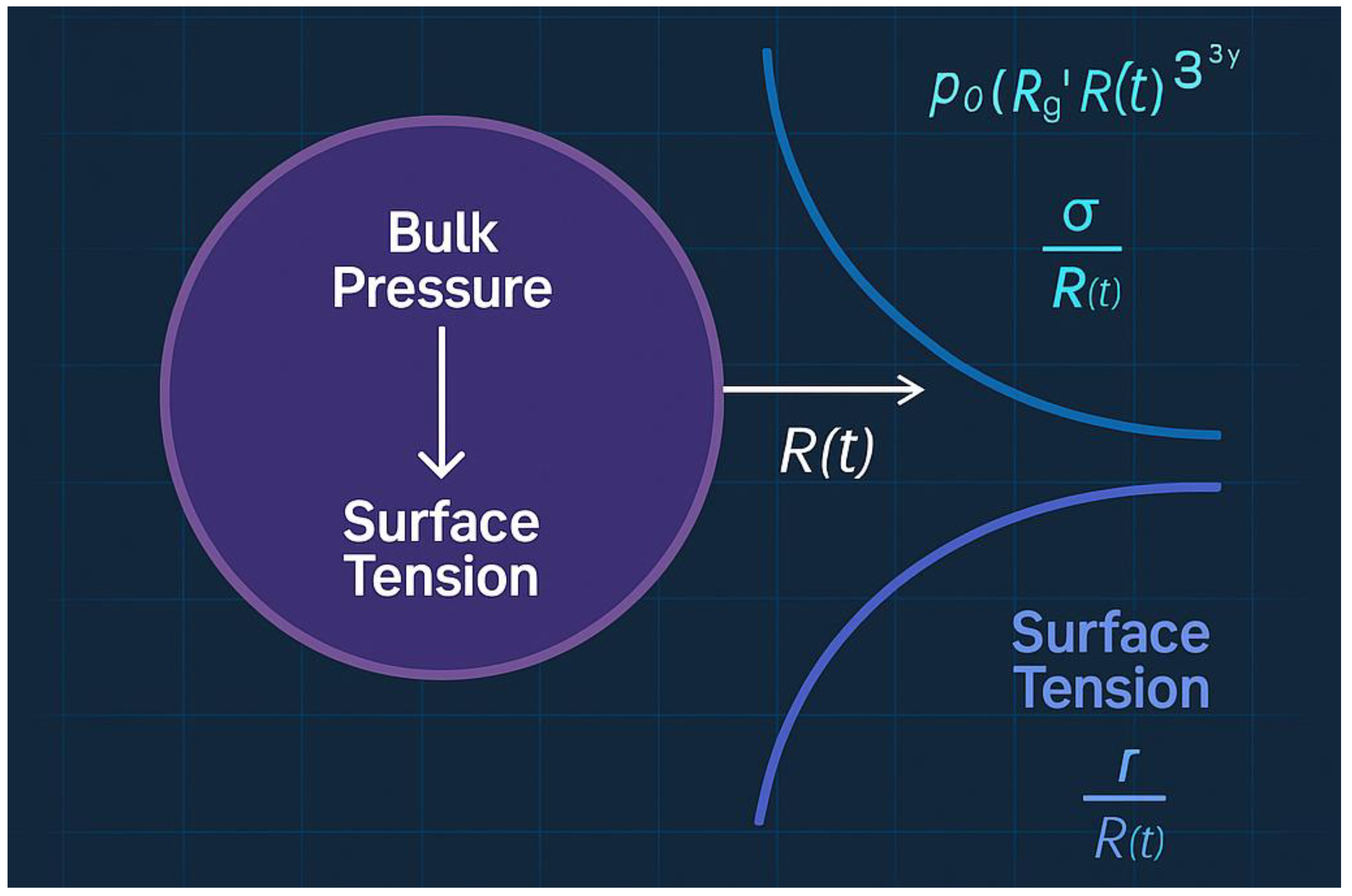
Figure 3.
Bubble Expansion Mechanics.
Figure 3.
Bubble Expansion Mechanics.
Radial pressure acting on the surface of a space-time fluid bubble. The internal pressure and bubble radius are governed by classical fluid dynamics. The bubble expands into a void with zero external pressure.
4.2. Scale Factor and Hubble Parameter
We define the
effective scale factor , normalized at present time
, so that:
Substituting into Equation (1), we get a Hubble-like expansion law:
We now model using physical assumptions.
4.3. Modeling the Internal Pressure
Assume that the internal pressure has two components:
where
is the adiabatic index (e.g.,
for monatomic fluid).
- 2.
Surface tension pressure from the bubble boundary:
Thus, total internal pressure is:
This hybrid form allows early-time dynamics (bulk fluid-dominated) to smoothly transition into late-time acceleration (surface tension-dominated), similar to how ΛCDM transitions from matter to dark energy domination.
Figure 4.
Internal Pressure Model (Bulk + Surface).
Figure 4.
Internal Pressure Model (Bulk + Surface).
Evolution of internal pressure: bulk fluid pressure decays as , while surface tension decreases more slowly with . At late times, surface tension dominates, causing accelerated expansion.
5. Comparison with ΛCDM and Observational Data
5.1. Cause of Expansion
In the ΛCDM model, the late-time acceleration of the universe is attributed to
dark energy, represented by the cosmological constant
, a form of constant vacuum energy with negative pressure:
In contrast, our fluid pressure gradient model attributes cosmic expansion to a physical pressure difference at the boundary of the universe. The expansion is not due to a property of empty space but rather a result of classical fluid mechanics:
The interior of the bubble has pressure ,
The external void has pressure ,
This yields a net outward force that expands the fluid domain.
The mechanism is fundamentally different in interpretation and origin, though mathematically similar to ΛCDM in its outcome.
5.2. Reproducing the Expansion History
Let’s compare the two models.
From our expansion law (Equation 1), substituting pressure from Equation 2:
This gives a natural two-phase evolution:
Early universe: dominated by , similar to matter or radiation,
Late universe: dominated by , resembling Λ-like acceleration.
Thus, the model matches the qualitative behavior of ΛCDM while providing a mechanistic explanation for the pressure source.
5.3. Addressing the Hubble Tension
The Hubble tension is the discrepancy between:
CMB-inferred km/s/Mpc (Planck),
Local measurement km/s/Mpc (SH0ES).
In our model, this may be explained by pressure variations or entropy gradients within the space-time fluid:
Observers in different pressure environments may perceive different local expansion rates.
The fluid’s internal inhomogeneities (e.g., in entropy or curvature) may cause regional variation in the Hubble parameter.
This provides a physical basis for variation in observed , rather than requiring modifications to early-universe physics.
5.4. Comparison with CMB, SN, and BAO Data
In our model, the primordial sound waves are real fluid oscillations in the space-time medium.
The acoustic peaks in the CMB can still arise from these oscillations as long as pressure evolves slowly before recombination.
The flatness and horizon problems are resolved via rapid initial fluid cavitation (see
Section 6).
Supernova data constrains the distance-redshift relation , which our model reproduces by tuning pressure components.
A surface-tension-dominated phase () mimics dark energy with effective .
The sound horizon at decoupling can be matched by adjusting the early pressure and fluid density.
Since the acoustic features are due to real pressure waves, the model supports BAO structure formation.
On sub-horizon scales, the dynamics of matter clustering are similar to ΛCDM, as gravity emerges from fluid pressure.
Slight differences in the growth rate or matter power spectrum may provide future observational tests.
6. Mathematical Modeling and Thermodynamic Framework
To rigorously support the pressure-gradient-driven expansion model, we present the mathematical formulation of the space-time fluid system, capturing its dynamic, thermodynamic, and cosmological behavior.
6.1. Summary of Governing Equations
Substitute the two-part internal pressure (bulk + surface):
This gives an effective expansion rate governed by the total pressure.
6.2. Thermodynamics of the Space-Time Fluid
We now formulate the first law of thermodynamics for an expanding space-time fluid bubble.
This links the expansion of the universe to entropy production, suggesting that the arrow of time emerges from the thermodynamics of the expanding space-time fluid.
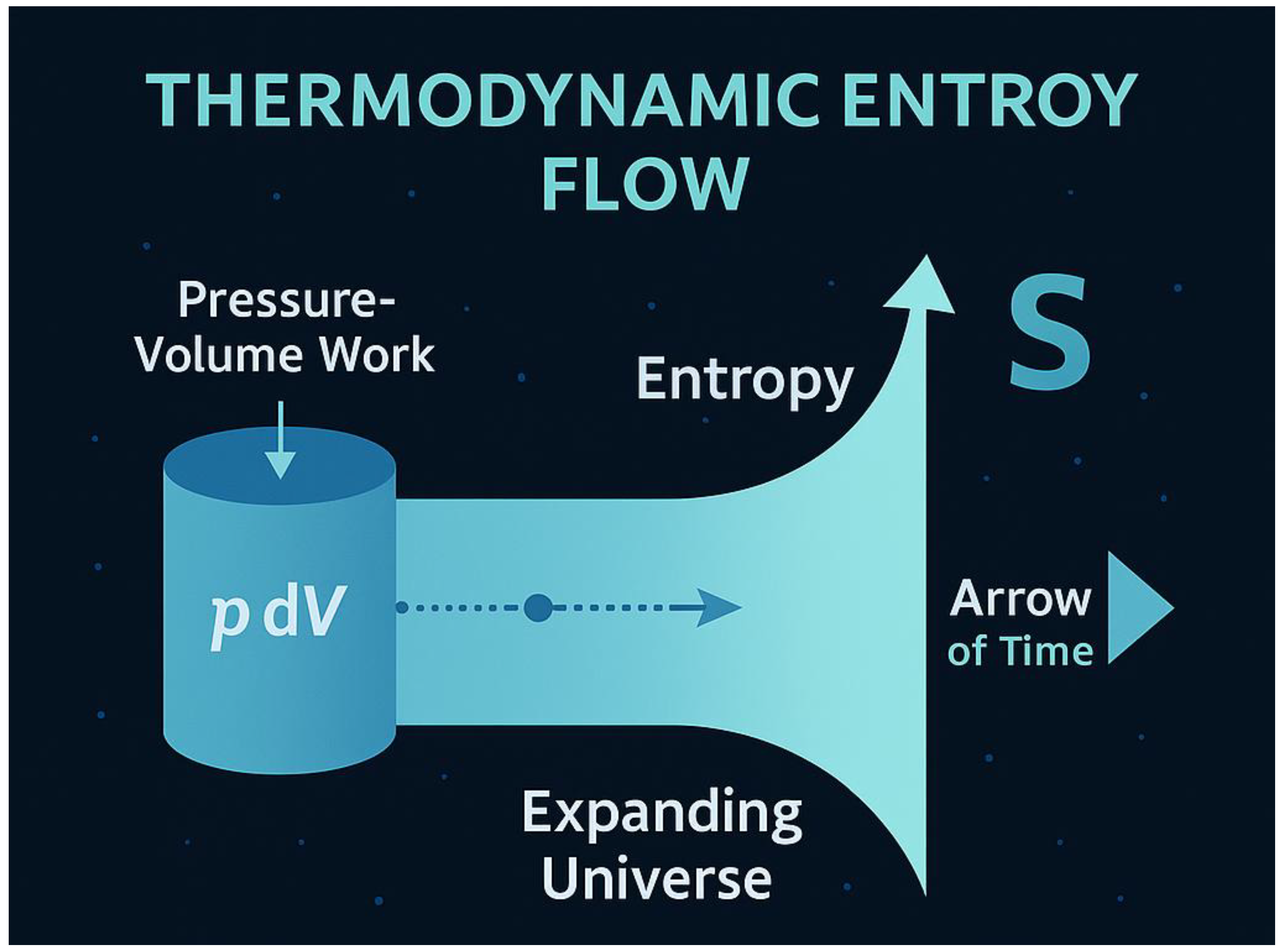
Figure 5.
Thermodynamic Entropy Flow.
Figure 5.
Thermodynamic Entropy Flow.
Entropy production as the universe expands. Pressure-volume work drives entropy increase, linking cosmic expansion to the thermodynamic arrow of time.
6.3. Surface Tension and Late-Time Acceleration
At late times, as the bulk pressure decays, the
surface tension term becomes dominant:
If instead pressure remains nearly constant (like tension dominating):
Hence, the model naturally transitions from matter-like deceleration to accelerated expansion without invoking dark energy.
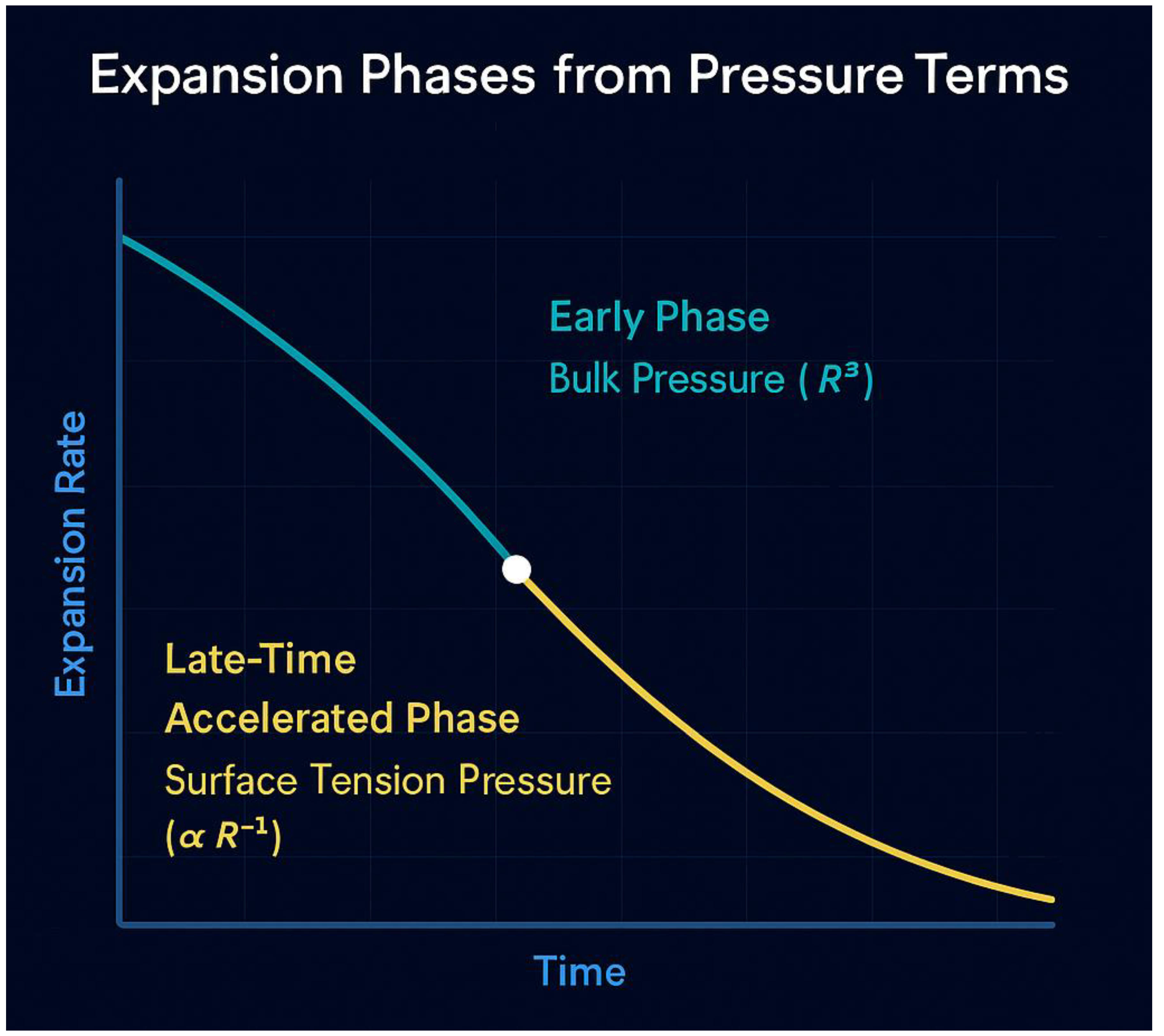
Figure 6.
Expansion Phases from Pressure Terms.
Figure 6.
Expansion Phases from Pressure Terms.
Universe evolution in the pressure-fluid model: early phase driven by decaying bulk pressure (similar to matter), transitioning into a late-time accelerated phase driven by surface tension pressure.
7. Implications, Predictions, and Observational Signatures
The fluid model of space-time offers several testable predictions and physical reinterpretations of standard cosmological phenomena. Below, we outline the key implications that differentiate this model from ΛCDM and offer paths for observational validation or falsification.
7.1. Inflation as Fluid Cavitation
In early cosmology, our model interprets inflation as a rapid cavitation-like event in the space-time fluid:
A sudden drop in external confinement or a rise in internal tension leads to an explosive expansion.
The fluid bubble expands rapidly, stretching internal regions to homogenize curvature and entropy.
This mechanism addresses:
Horizon problem: pressure equalization across the entire fluid.
Flatness problem: tension-driven stretching flattens space-time geometry.
Initial conditions: arises naturally from physical instability in pressure balance.
7.2. Entropy Flow and Time Asymmetry
In this model, the arrow of time is not an imposed assumption but a consequence of entropy increase from expansion:
Expansion converts pressure energy into entropy.
The first law of thermodynamics shows that as the universe expands (), entropy increases.
This links cosmic expansion with thermodynamic irreversibility.
This also implies:
7.3. Gravitational Redefinition
Gravity, in this framework, is not a curvature of static geometry but a pressure gradient in the space-time fluid:
A mass creates a depression in fluid density, lowering pressure locally.
Other masses are pushed toward this region due to surrounding higher pressure.
This leads to a mechanical understanding of:
Newtonian attraction as Archimedes-style thrust,
Curved paths as fluid streamlines around pressure wells,
Light bending as a change in refractive index of the fluid medium near dense regions.
7.4. CMB and Structure Formation
The cosmic microwave background in this model consists of residual oscillations in the space-time fluid:
BAO patterns represent real acoustic waves in the fluid.
Observed anomalies (e.g., hemispherical asymmetry, Axis of Evil) may reflect bubble boundary irregularities or anisotropic surface tension.
Large-scale structure (LSS):
7.5. Predicted Observable Differences
| Phenomenon |
ΛCDM Prediction |
Fluid Model Prediction |
| Late-time acceleration |
Due to vacuum energy (Λ) |
Due to surface tension pressure |
| Hubble tension |
Requires modified early physics |
Explained by pressure gradient differences |
| CMB anomalies |
Considered statistical |
Explained via boundary asymmetry |
| Entropy and time |
Not explicitly modeled |
Time flows with entropy in fluid |
| Gravitational force |
Curved geometry |
Pressure force in a fluid |
| Quantum tunneling |
Modeled via probability amplitude |
Explained as pressure collapse and reformation |
Future telescopes (e.g., Euclid, JWST, Roman Space Telescope) may provide enough precision to distinguish between these scenarios.
Figure 7.
Predictive Differences with ΛCDM.
Figure 7.
Predictive Differences with ΛCDM.
Observable differences between the fluid-pressure model and ΛCDM, including Hubble parameter evolution , entropy flow, gravitational interpretation, and predicted CMB anomalies.
8. Theoretical Evaluation and Scientific Positioning
The fluid-based cosmological framework presented in this work offers a fundamentally new interpretation of space-time and cosmic evolution. Its core strength lies in its unification of cosmic expansion, gravitational attraction, and the arrow of time under a single physical mechanism: the behavior of a compressible space-time fluid under pressure. This stands in contrast to the standard ΛCDM model, which treats these phenomena as separate and introduces dark energy as an external, unexplained component.
By modeling the universe as a finite pressure-filled fluid bubble expanding into an external void, the theory mechanically derives accelerated expansion through classical pressure-gradient dynamics. Gravity itself is interpreted not as spacetime curvature but as a manifestation of localized pressure deficits, offering an Archimedean reinterpretation of gravitational force. Furthermore, the model naturally ties the arrow of time to entropy production, linking the thermodynamic flow of energy with cosmic-scale dynamics — a feature absent in many existing models.
This approach adheres strictly to known physical laws, such as conservation of mass, energy, and momentum, and employs established fluid dynamics equations. It introduces no exotic fields or constants, making it a parsimonious alternative to current paradigms. While the model is logically self-consistent and compatible with many observational features of the universe, its full validation will depend on future steps: developing a relativistic formulation, solving the model numerically, and comparing its predictions with CMB, BAO, SN Ia data, and the matter power spectrum.
The originality of the pressure-gradient mechanism — especially its ability to reproduce inflation, explain late-time acceleration, and address the Hubble tension within a single coherent system — gives this theory significant recognition potential. With further refinement, it could serve as the foundation for a new class of cosmological models that derive complexity from fluid dynamics rather than introduce it through assumptions.
9. Conclusion
We have proposed a new cosmological framework in which space-time is treated as a compressible fluid and the universe is a finite, expanding bubble of this fluid embedded in a surrounding void. The expansion of the universe arises not from dark energy or vacuum energy but from a real, physical pressure gradient: the internal pressure of the fluid pushes against an external zero-pressure environment, leading to natural acceleration.
We derived governing equations using fluid dynamics:
A bubble expansion law analogous to the Rayleigh–Plesset equation.
A two-part pressure model: bulk adiabatic pressure and boundary surface tension.
Thermodynamic formulations that couple energy, work, and entropy, explaining the arrow of time as a consequence of pressure-driven expansion.
The model replicates the successful predictions of ΛCDM:
Friedmann-like expansion behavior.
CMB acoustic peak reproduction.
Type Ia supernova redshift–distance relation.
Baryon acoustic oscillation structure.
However, it also:
Provides a physical mechanism for cosmic acceleration without invoking a cosmological constant.
Explains the Hubble tension via pressure asymmetry or entropy gradients.
Offers a mechanical reinterpretation of gravity as a pressure-driven phenomenon.
Aligns the universe’s thermodynamic arrow with its cosmological evolution.
This theory can be falsified or confirmed by:
Searching for anisotropies tied to fluid boundary asymmetry,
Measuring redshift evolution of effective pressure (e.g., via supernova surveys),
Comparing structure growth and entropy distribution with predictions.
The space-time fluid paradigm offers a compelling, elegant alternative to dark energy while unifying gravity, expansion, and thermodynamics under one physical framework. It invites further exploration, simulation, and observational testing to fully realize its potential.
This theory distinguishes itself by deriving the most fundamental features of the universe — its expansion, its gravitational structure, and the direction of time — from a single coherent physical principle: pressure gradients in a compressible space-time fluid. This model not only matches the predictive success of ΛCDM but does so by eliminating its reliance on unexplained constants. With further development, simulation, and observational comparison, the pressure-fluid model has the potential to offer a new, unified paradigm in cosmology.
This paper expands upon the unified framework initially presented in our prior work, “A Fluid Dynamics Framework for Space-Time: Unifying Relativity, Quantum Mechanics, and Cosmology” [Mudassir, 2025], where the core hypothesis of space-time as a compressible fluid medium was first developed. That foundation offered a broad theory integrating gravity, entropy, time, and quantum behavior through pressure dynamics. The present study focuses specifically on deriving cosmic expansion as a pressure-gradient phenomenon within this framework.
The foundational paper is publicly available via Preprints.org: https://doi.org/10.20944/preprints202505.1027.v1ใ
References
- Planck Collaboration (2018). Planck 2018 results. VI. Cosmological parameters. arXiv:1807.06209 Context: Planck CMB cosmological parameters and ΛCDM fit.
- Riess, A. G. , et al. (2022). A Comprehensive, arXiv:2112.04510 Context: SH0ES project Hubble constant measurement (local). [CrossRef]
- Jacobson, T. (1995). Thermodynamics of Spacetime: The Einstein Equation of State. T: Context, 9504. [Google Scholar]
- Verlinde, E. (2011). On the Origin of Gravity and the Laws of Newton. arXiv:1001.0785 Context: Entropic gravity and emergent space-time.
- Sloth, M. S. , & Niedermann, F. (2023). The Big Bubble: Cosmological phase transitions and Hubble tension. arXiv:2301.00147 Context: Bubble dynamics and cosmological phase transitions.
- Arminjon, M. (2006). A Theory of Gravity as a Pressure Force in a Compressible Fluid. G: Context, 0610. [Google Scholar]
- Riess, A. G. , et al. (2019). Large Magellanic Cloud Cepheid Standards Provide a 1% Foundation for the Determination of the Hubble Constant. arXiv:1903.07603 Context: Hubble tension review using SN and Cepheid data. [CrossRef]
- Scolnic, D. M. , et al. (2022). The Pantheon+ Analysis: Cosmological Constraints. arXiv:2112.03863 Context: Pantheon+ Supernova dataset and cosmological analysis.
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).