Submitted:
09 May 2025
Posted:
12 May 2025
You are already at the latest version
Abstract
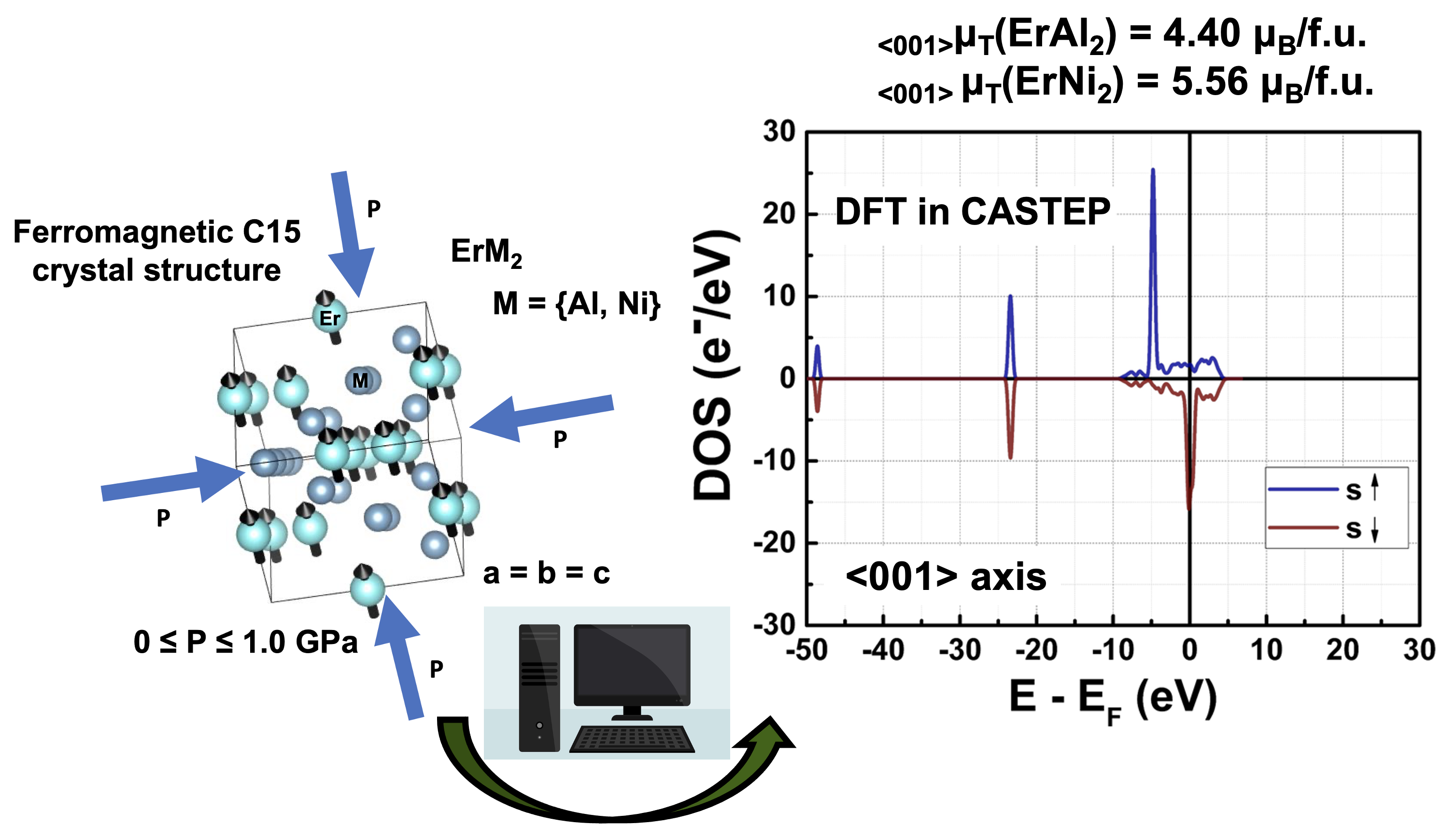
Keywords:
1. Introduction
2. Computational Method
3. Results and Discussion
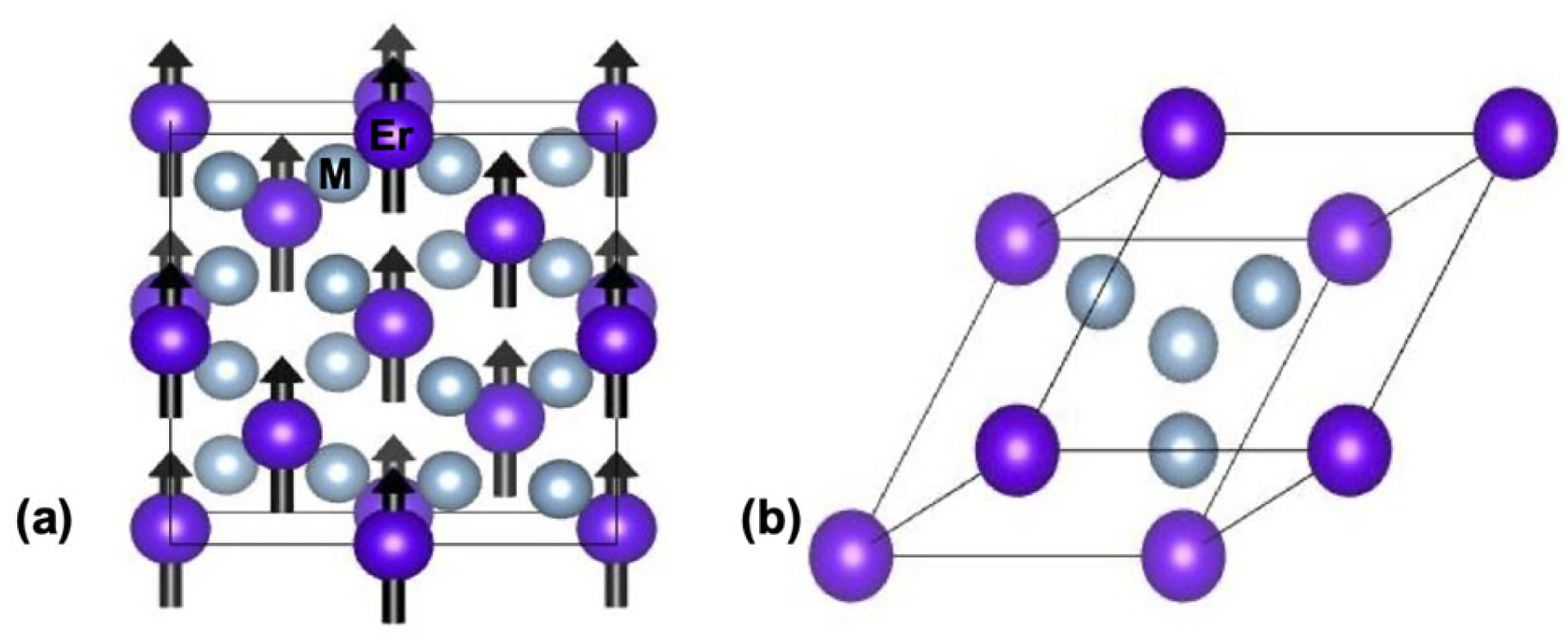
3.1. Electronic Structure at Normal Pressure
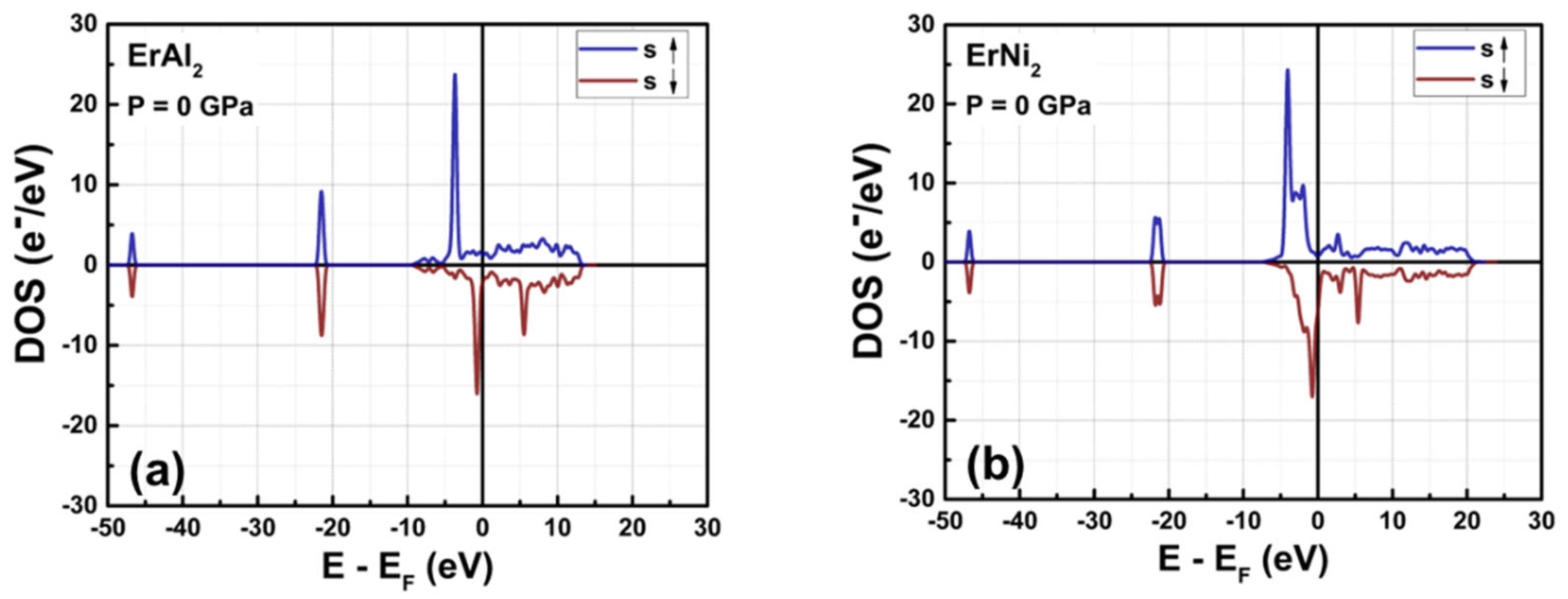
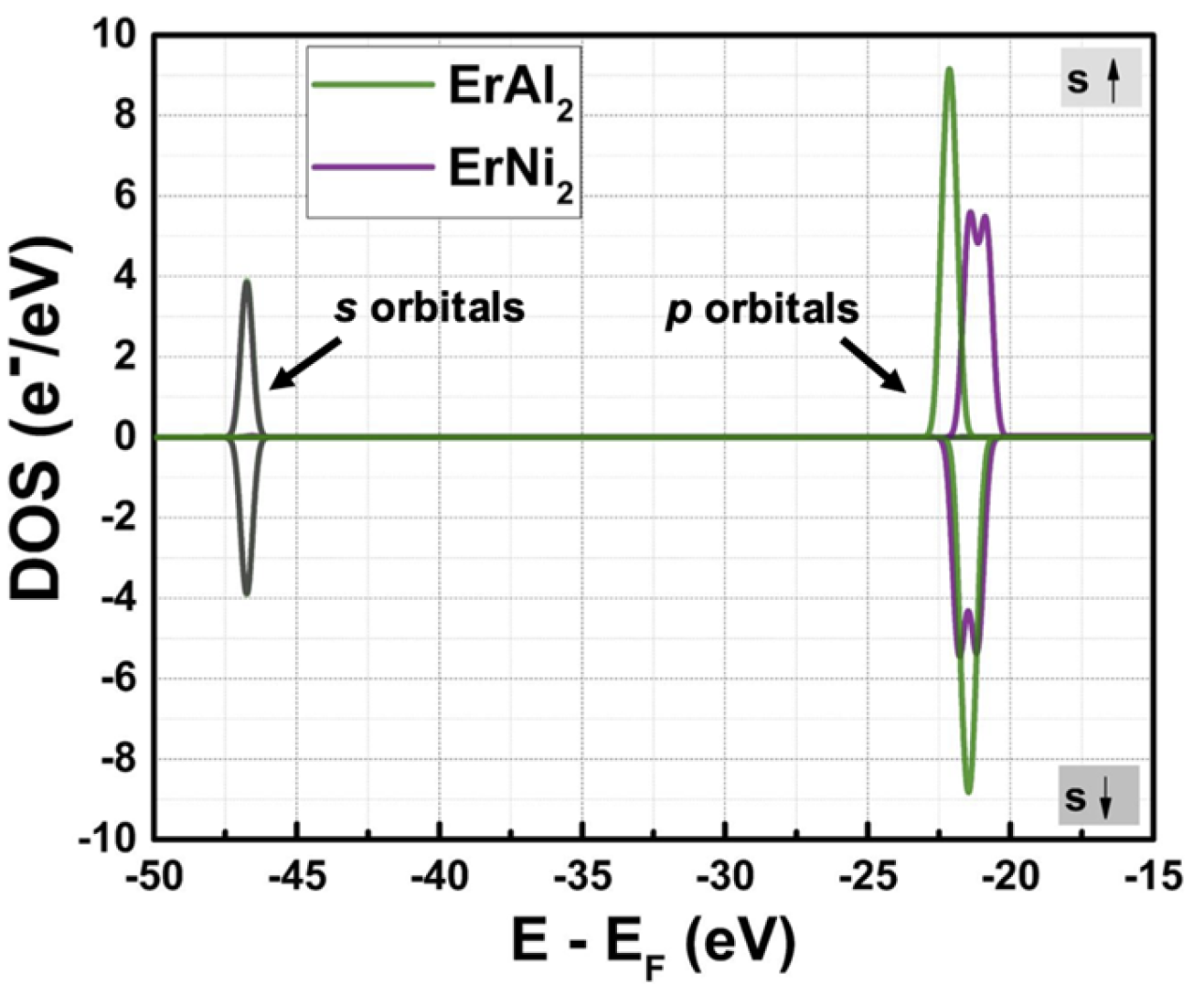
| Compound |
nS↑ (EF) (e–/eV) |
nS↓ (EF) (e–/eV) |
Δn(EF) (e–/eV) |
(µB/f.u.)[15,16 | (µB/f.u.) | (µB/f.u.) | (µB/f.u.) |
Magnetization axis |
reference |
| ErAl2 | 1.31 | – 2.24 | – 0.93 | 30.19 | – 25.80 | 4.40 |
4.40 4.75 † |
hard | [40] [26] |
| ErNi2 | 0.78 | – 6.20 | – 5.42 | 36.46 | – 30.40 | 5.56 |
5.30‡ 6.23 |
easy | [27] [40] |
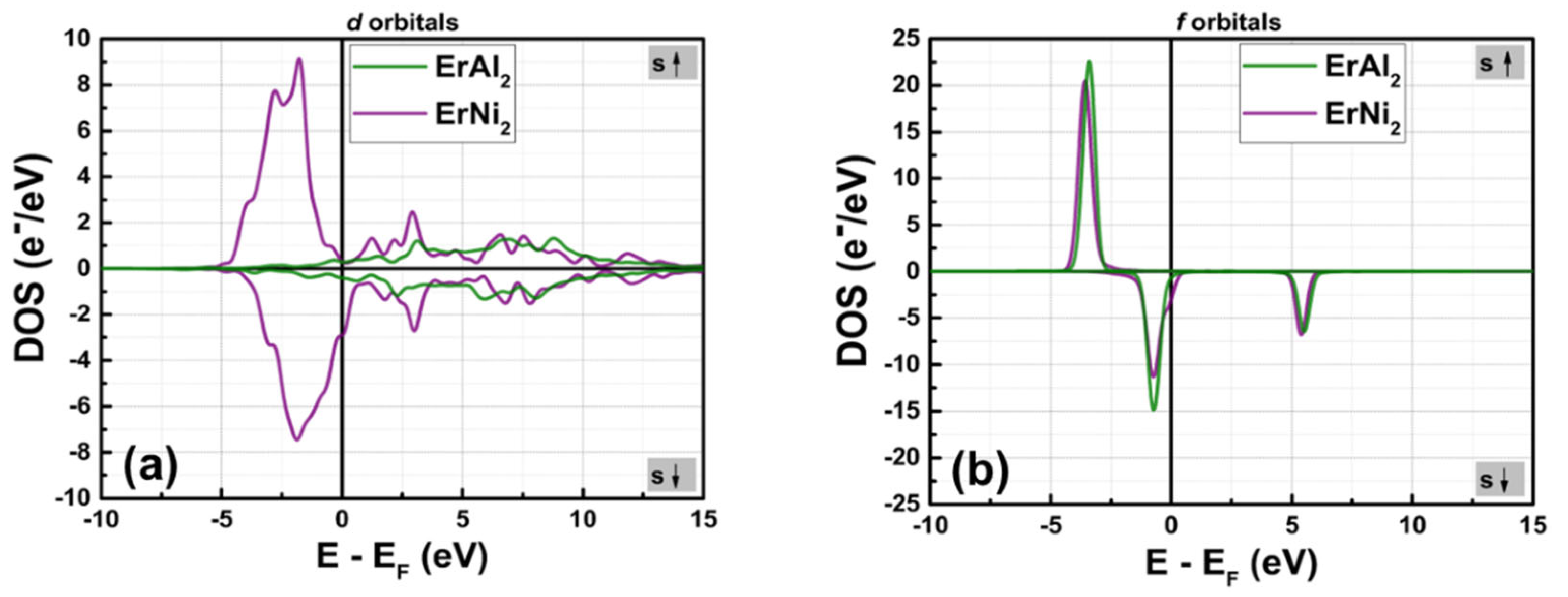
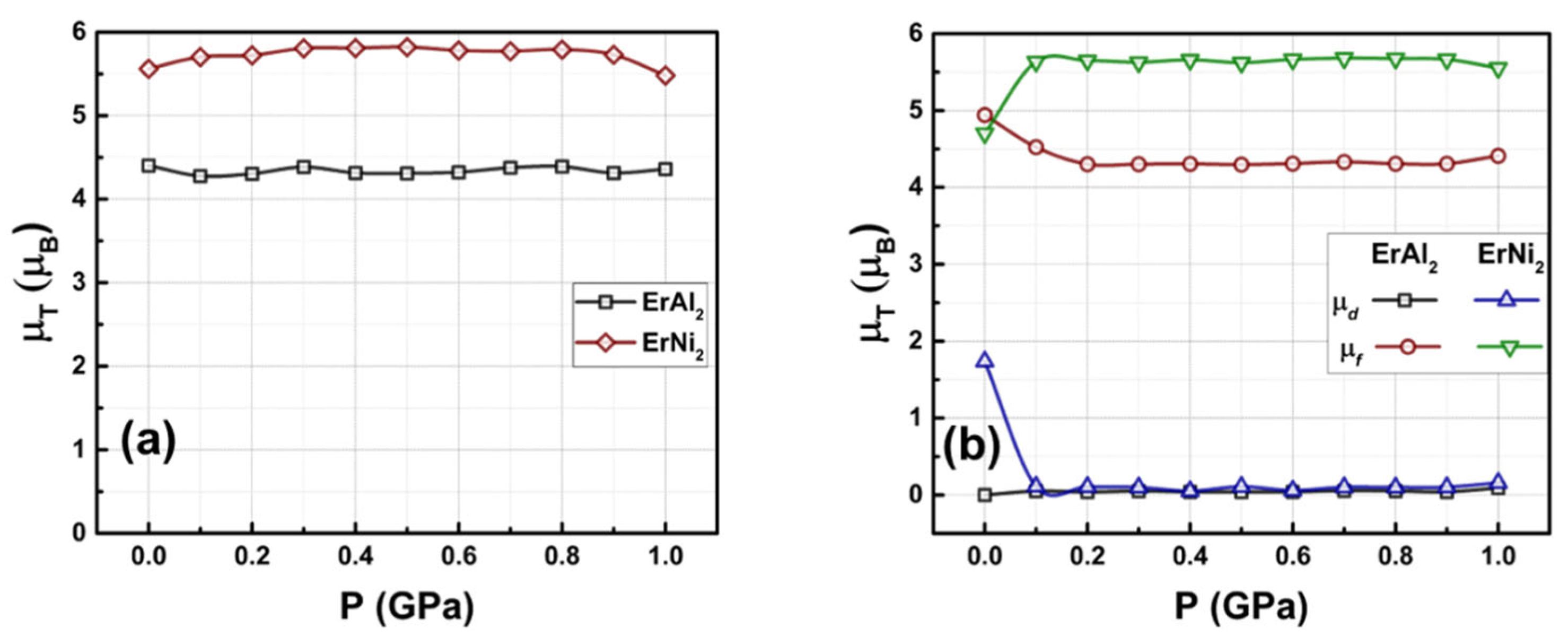
| Laves phase | μs(μB/f.u.) | μp (μB/f.u.) | μd(μB/f.u.) | μf(μB/f.u.) | μT(μB/f.u.) |
| ErAl2 | – 0.005 | – 0.002 | – 0.001 | 4.940 | 4.932 |
| ErNi2 | – 0.058 | – 0.249 | 1.737 | 4.701 | 6.131 |
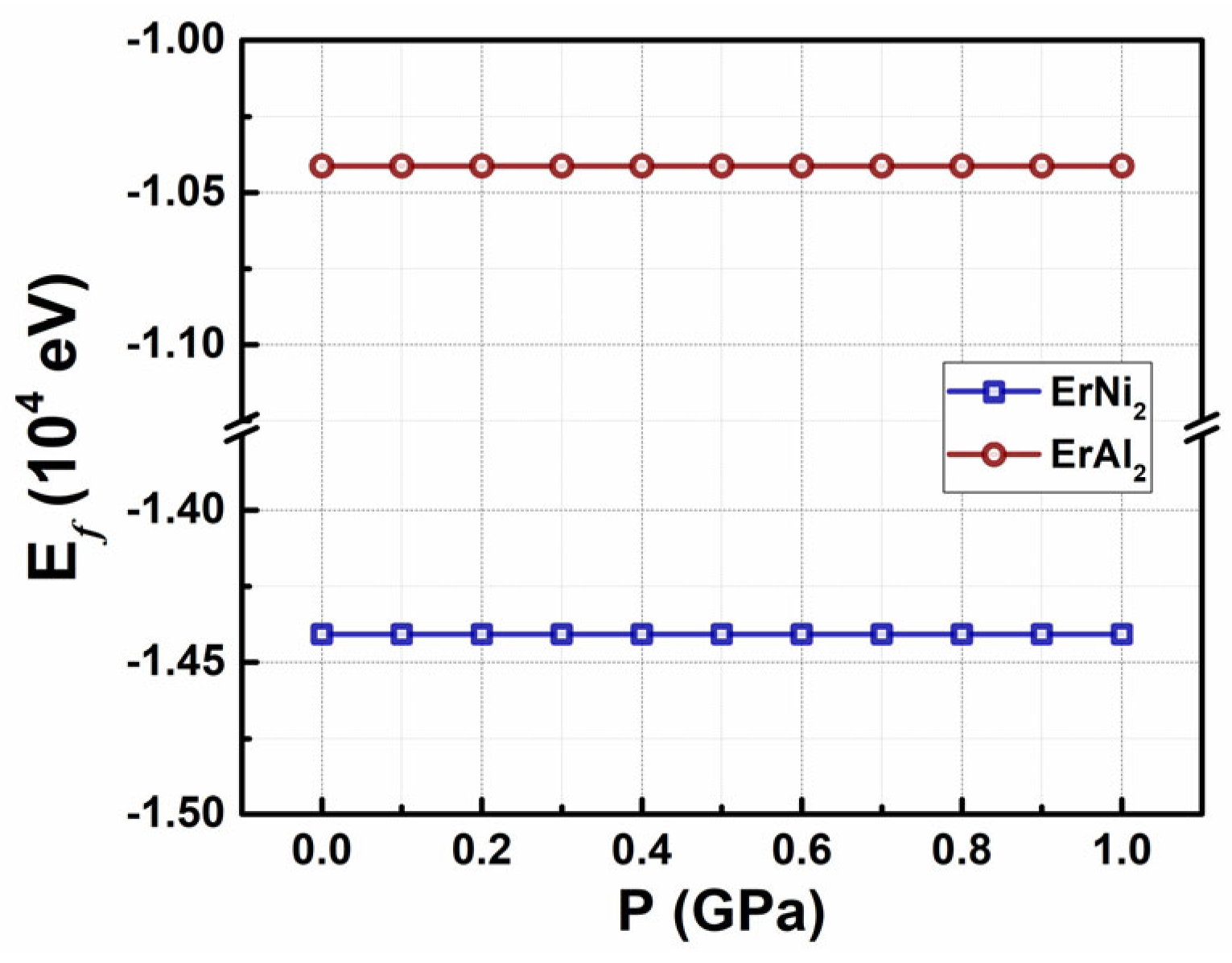
3.2. Electronic Structure at Moderate Hydrostatic Pressures
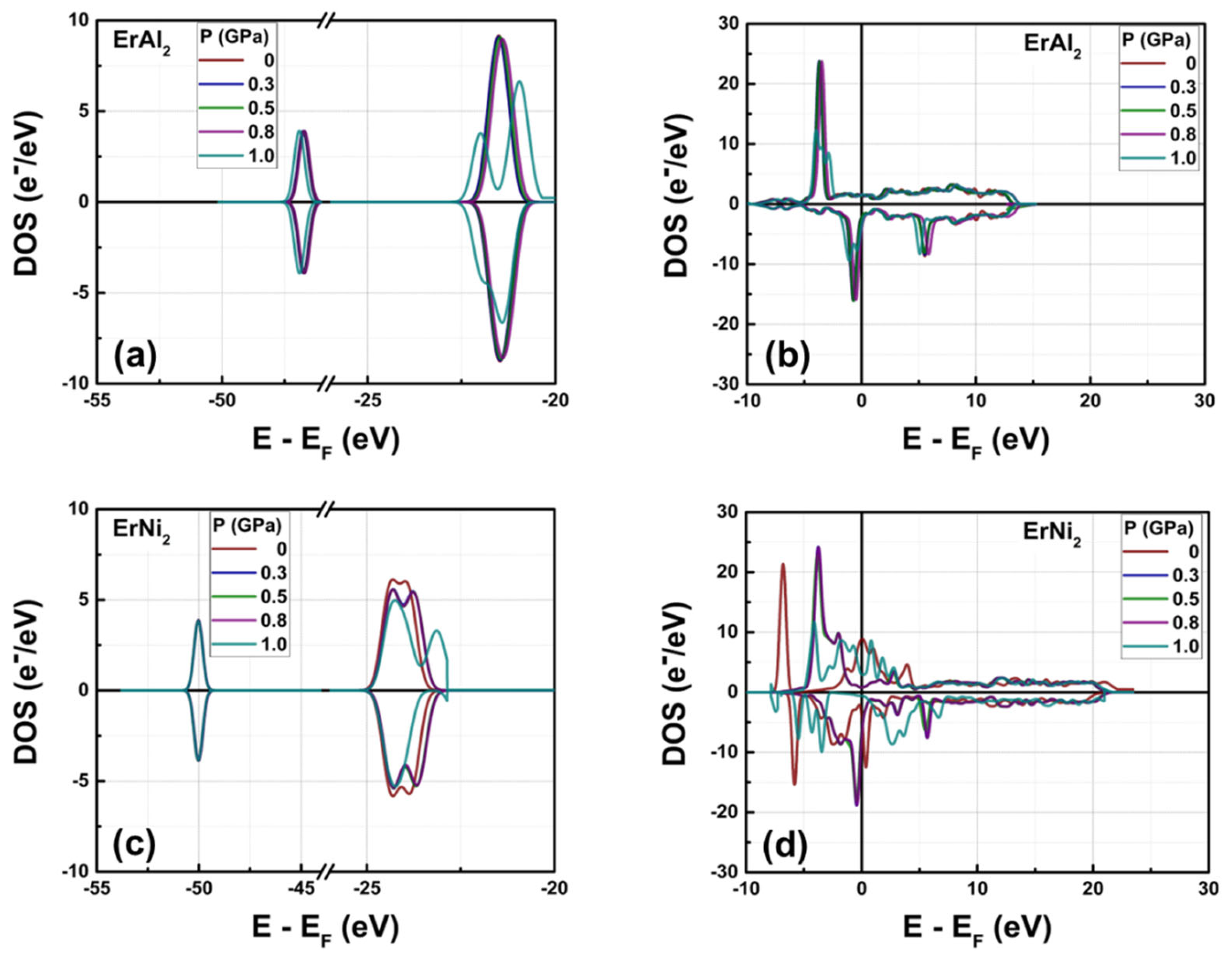
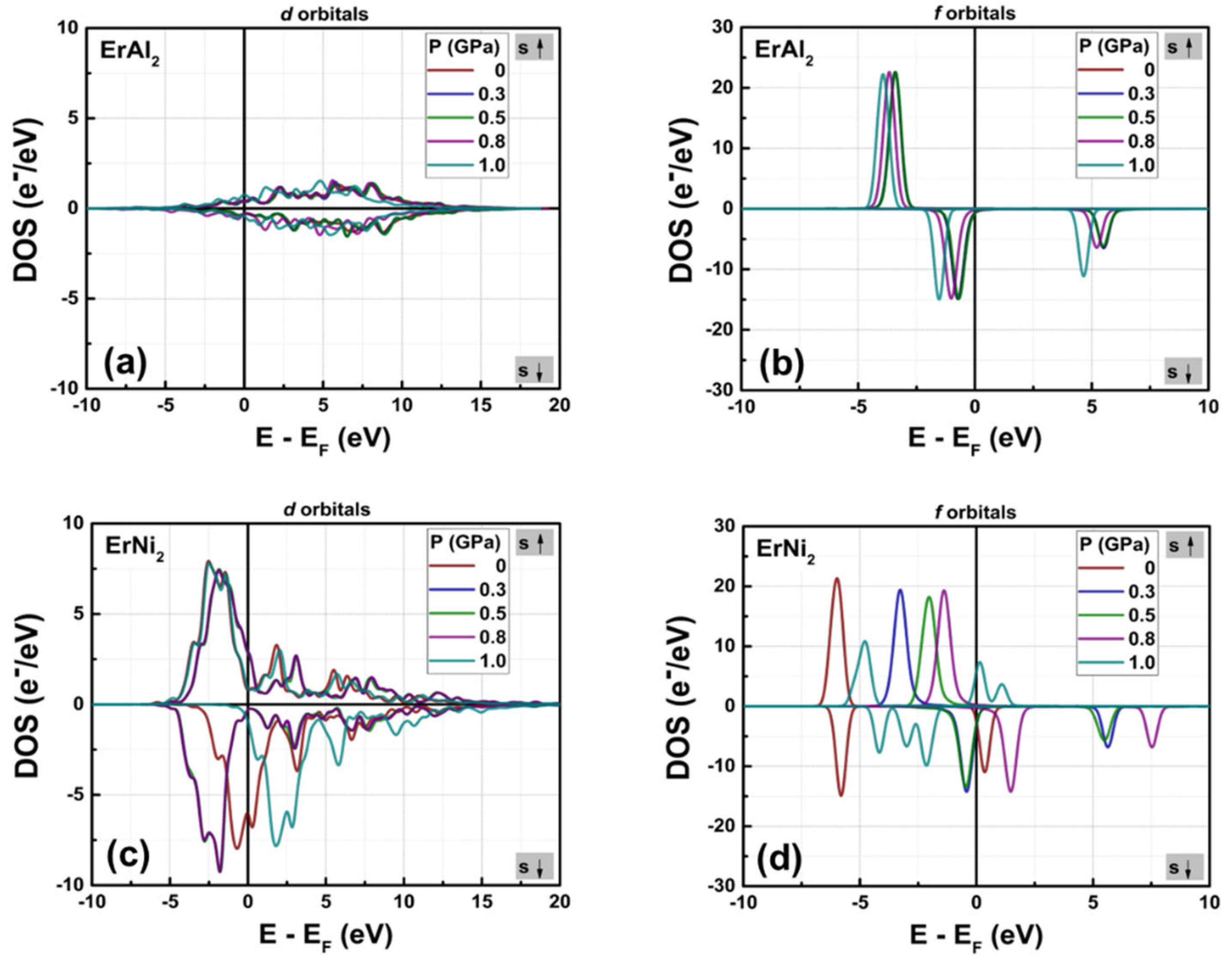
| Alloy | ErAl2 | ErNi2 | ||||||||||||
| P (GPa) | a (Å) | dAl-Al (Å) | dEr-Al (Å) | VP (Å3) | Δ (%) | B (GPa) | σij (GPa) | a (Å) | dNi-Ni (Å) | dEr-Ni (Å) | VP (Å3) | Δ (%) | B (GPa) | σij (GPa) |
| 0.0 | 5.5551 | 2.777 | 3.257 | 121.218 | 0.000 | 63.76 | – 0.00184 | 5.1030 | 2.551 | 2.991 | 93.949 | 0.000 | 128.13 | – 0.00631 |
| 0.1 | 5.5530 | 2.776 | 3.256 | 121.090 | – 0.105 | 64.53 | – 0.06960 | 5.1023 | 2.550 | 2.990 | 93.853 | – 0.101 | 128.56 | – 0.10767 |
| 0.2 | 5.5503 | 2.775 | 3.254 | 120.908 | – 0.255 | 64.87 | – 0.16420 | 5.1010 | 2.549 | 2.989 | 93.737 | – 0.225 | 129.90 | – 0.22623 |
| 0.3 | 5.5455 | 2.772 | 3.251 | 120.590 | – 0.517 | 65.76 | – 0.31888 | 5.0999 | 2.548 | 2.988 | 93.653 | – 0.314 | 129.89 | – 0.31054 |
| 0.4 | 5.5434 | 2.771 | 3.250 | 120.456 | – 0.628 | 65.96 | – 0.38991 | 5.0973 | 2.547 | 2.987 | 93.560 | – 0.413 | 130.11 | – 0.40776 |
| 0.5 | 5.5412 | 2.770 | 3.249 | 120.310 | – 0.748 | 66.14 | – 0.47108 | 5.0956 | 2.546 | 2.986 | 93.464 | – 0.516 | 130.82 | – 0.50732 |
| 0.6 | 5.5374 | 2.768 | 3.247 | 120.062 | – 0.953 | 66.98 | – 0.59076 | 5.0939 | 2.546 | 2.985 | 93.366 | – 0.620 | 131.39 | – 0.61002 |
| 0.7 | 5.5345 | 2.767 | 3.245 | 119.873 | – 1.108 | 67.08 | – 0.69311 | 5.0921 | 2.545 | 2.984 | 93.270 | – 0.722 | 131.91 | – 0.71256 |
| 0.8 | 5.5315 | 2.765 | 3.243 | 119.677 | – 1.270 | 67.56 | – 0.79821 | 5.0904 | 2.544 | 2.983 | 93.182 | – 0.816 | 132.08 | – 0.80705 |
| 0.9 | 5.5275 | 2.763 | 3.242 | 119.324 | – 1.561 | 67.96 | – 0.88224 | 5.0888 | 2.543 | 2.982 | 93.102 | – 0.901 | 132.88 | – 0.89113 |
| 1.0 | 5.5259 | 2.762 | 3.240 | 119.318 | – 1.566 | 68.04 | – 0.99389 | 5.0853 | 2.542 | 2.981 | 92.994 | – 1.015 | 133.12 | – 1.00668 |
3.3. Determination of Electronic Coefficient in Specific Heat Capacity
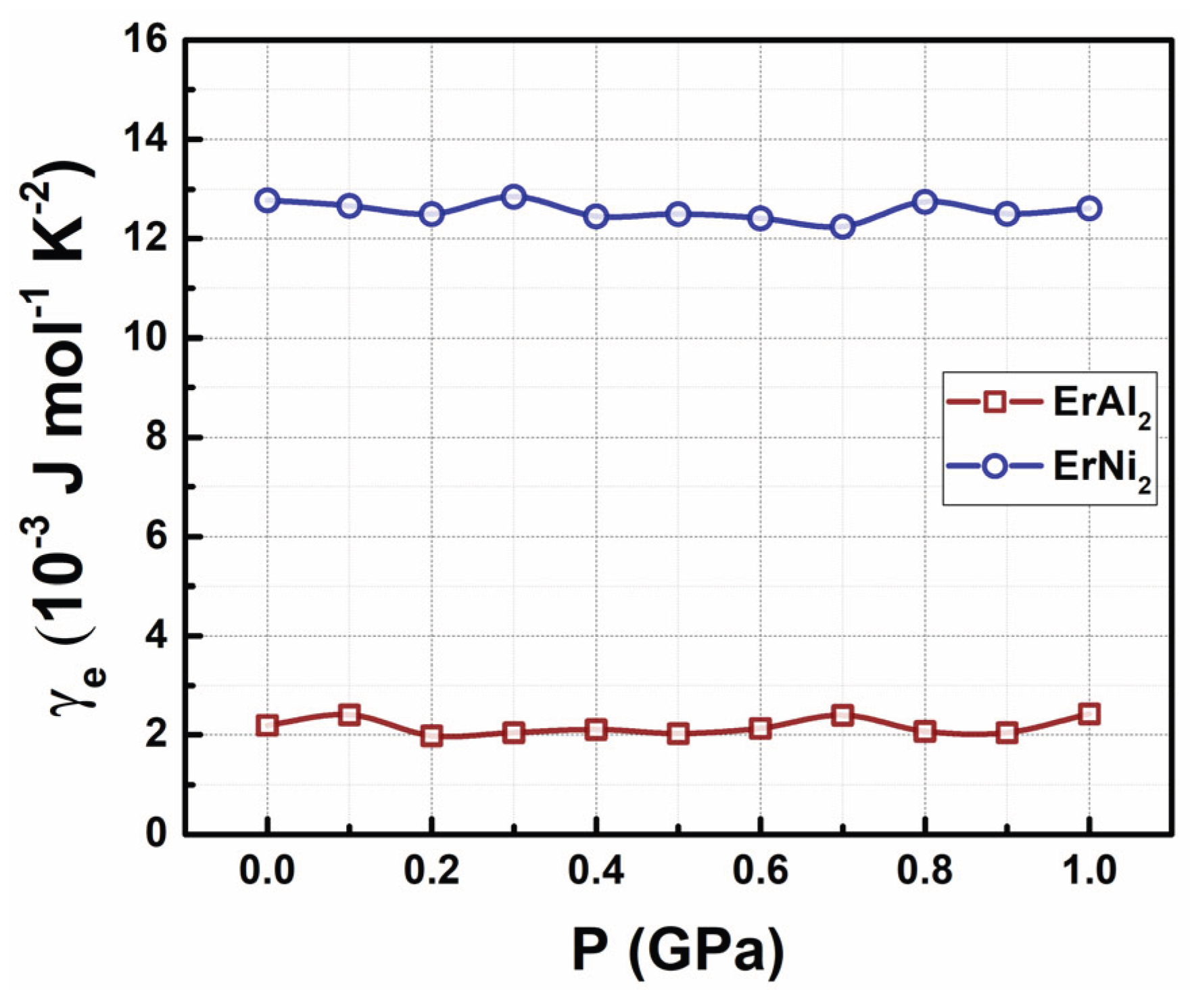
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pecharsky, V.K.; Gschneider Jr., K.A. Magnetocaloric effect and magnetic refrigeration. J. Magn. Magn. Mater. 1999, 200, 044–56. [Google Scholar] [CrossRef]
- Moya, X.; Mathur, N.D. Caloric materials for cooling and heating. Science. 2020, 370, 797–803. [Google Scholar] [CrossRef] [PubMed]
- Moya, X.; Kar-Narayan, S.; Mathur, N.D. Caloric materials near ferroic phase transitions. Nature Mater. 2014; 14, 439-450. [CrossRef]
- Franco, V.; Blázquez, J.S.; Ipus, J.J.; Law, J.Y.; Moreno-Ramírez, L.M.; Conde, A. Magnetocaloric effect: From materials research to refrigeration devices. Prog. Mater. Sci. 2018, 93, 112–232. [Google Scholar] [CrossRef]
- Tang, X.; Sepehri-Amin, H.; Terada, N.; Martin-Cid, A.; Kurniawan, I.; Kobayashi, S.; Kotani, Y.; Takeya, H.; Lai, J.; Matsushita, Y.; Ohkubo, T.; Miura, Y.; Nakamura, T.; Hono, K. Magnetic refrigeration material operating at a full temperature range required for hydrogen liquefaction. Nature Comm. 2022, 13, 1817. [Google Scholar] [CrossRef]
- Smith, A.; Bahl, C.R.H.; Bjørk, R.; Engelbrecht, K.; Nielsen, K.K.; Pryds, N. Materials challenges for high performance magnetocaloric refrigeration devices. Adv. Energy Mater. 2012, 2, 1288–1318. [Google Scholar] [CrossRef]
- Pecharsky, V.K.; Gschneidner Jr., K.A. Giant magnetocaloric effect in Gd5(Si2Ge2). Phys. Rev. Lett. 1997, 78, 4494. [Google Scholar] [CrossRef]
- Kitanovski, A. Energy applications of magnetocaloric materials. Advanced Energy Mater. 2020, 10, 1903741. [Google Scholar] [CrossRef]
- Lyubina, J. Magnetocaloric materials for energy efficient cooling. J. Phys. D. Appl. Phys. 2017, 50, 053002. [Google Scholar] [CrossRef]
- Gschneidner Jr., K.A.; Pecharsky, V.K. Binary rare earth Laves phases - an overview. Z. Kristallogr. 2006, 221, 375–38. [Google Scholar] [CrossRef]
- Stein, F.; Leineweber, A. Laves phases: a review of their functional and structural applications and an improved fundamental understanding of stability and properties. J. Mater. Sci. 2021, 56, 5321–5427. [Google Scholar] [CrossRef]
- Liu, W.; Bykov, E.; Taskaev, S.; Bogush, M.; Khovaylo, V.; Fortunato, N.; Aubert, A.; Zhang, H.; Gottschall, T.; Wosnitza, J.; et al. A study on rare-earth Laves phases for magnetocaloric liquefaction of hydrogen. Appl. Mat. Today. 2022, 29, 101624. [Google Scholar] [CrossRef]
- Gschneidner, K.A. Jr; Pecharsky, V.K.; Tsokol, A.O. Recent developments in magnetocaloric materials. Rep. Prog. Phys. 2005, 68, 1479. [Google Scholar] [CrossRef]
- Kumar, K.S.; Hazzledine, P. M. Polytypic transformations in Laves phases. Intermetallics. 2004, 12, 763–770. [Google Scholar] [CrossRef]
- Sánchez Llamazares, J.L.; Zamora, J.; Sánchez-Valdés, C.F.; Álvarez-Alonso, P. Design and fabrication of a cryogenic magnetocaloric composite by spark plasma sintering based on the RAl2 Laves phases (R = Ho, Er). J. Alloys Compd. 2020, 831, 154779. [Google Scholar] [CrossRef]
- Sánchez Llamazares, J.L.; Ibarra-Gaytán, P.; Sánchez-Valdés, C.F.; Ríos-Jara, D.; Álvarez-Alonso, P. Magnetocaloric effect in ErNi2 melt-spun ribbons. J. Rare Earths. 2020, 38, 612–616. [Google Scholar] [CrossRef]
- Biswas, A.; Pathak, A.K.; Zarkevich, N.A.; Liu, X.; Mudryk, Y.; Balema, V.; Johnson, D.D.; Pecharsky, V.K. Designed materials with the giant magnetocaloric effect near room temperature. Acta Materialia. 2019, 180, 341–348. [Google Scholar] [CrossRef]
- Hafner, J.; Wolverton, C.; Ceder, G. Toward computational materials design: the impact of density functional theory on materials research. MRS Bulletin. 2006, 31, 659–668. [Google Scholar] [CrossRef]
- Pan F.-Ch., Lin, X.-l.; Li J., Ma, L.; Ma, L.-C., Cheng H.M. The electronic structures and Ferromagnetism of Cu-Doped ZnO: the first-principle calculation Study. J. Supercond. Nov. Magn. 2018, 31, 2103-2110. [CrossRef]
- Patel, P.D.; Shinde, S.; Gupta, S.D. First principle calculation of structural, electronic and magnetic properties of Mn2RhSi Heusler alloy. AIP Conf. Proc. 2018, 2005, 040004. [Google Scholar] [CrossRef]
- Wang, S. First-principles prediction of ferromagnetism in transition-metal doped monolayer AlN. Superlattices Microstruct. 2019, 122, 171–180. [Google Scholar] [CrossRef]
- Odkhuu, D.; Tsevelmaa, T.; Sangaa, D.; Tsogbadrakh, N.; Rhim, S.H.; Hong, S.C. First-principles study of magnetization reorientation and perpendicular magnetic anisotropy in CuFe2O4/MgO heterostructures. Phys. Rev. B. 2018, 98, 094408. [Google Scholar] [CrossRef]
- Kanomata, T.; Endo, H.; Mori, S.; Okajima, H.; Hihara, T.; Sumiyama, K.; Kaneko, T.; Suzuki, K. Specific heat of MnAlGe, MnGaGe and MnZnSb. J. Magn. Magn. Mater. 1995, 140-144 Part 1, 133-134. [CrossRef]
- Aschauer, U.; Braddell, R.; Brechbuhl, S.A; Derlet, P.M.; Spaldin, N.A. Strain-induced structural instability in FeRh. Phys. Rev. B. 2016, 94, 014109. [Google Scholar] [CrossRef]
- He, L.; Zhu, J.; Zhang, L. First-principles study of Structural phase transition, electronic, elastic and thermodynamic properties of C15-type Laves phases TiCr2 under pressure. Physica B: Condensed Matter. 2018, 531, 79–84. [Google Scholar] [CrossRef]
- Purwins, H.G.; Walker, E.; Barbara, B.; Rossignol, M.F.; Furrer, A. Single crystal magnetization of ErAl2 and interpretation in terms of the crystalline field. J. Phys. C: Solid State Phys. 1976, 9, 1025-1030. [CrossRef]
- Gignoux, D.; Givord, F. Quadrupolar interactions in ErNi2. J. Magn. Magn. Mater. 1983, 31-34, 217-218. [CrossRef]
- Ibarra-Gaytán, P.J.; Sánchez Llamazares, J.L.; Álvarez-Alonso, P.; Sánchez-Valdés, C. F.; Gorria, P.; Blanco, J.A. Magnetic entropy table-like shape in RNi2 composites for cryogenic refrigeration. J. Appl. Phys. 2015, 117, 17C116. [Google Scholar] [CrossRef]
- Eyert, V. A comparative study on methods for convergence acceleration of iterative vector sequences. J. Comput. Phys. 1996, 124, 271–285. [Google Scholar] [CrossRef]
- Pfrommer, B. G.; Côté, M.; Louie, S.G.; Cohen, M.L. Relaxation of crystals with the quasi-Newton method. J. Comput. Phys. 1997, 131, 233–240. [Google Scholar] [CrossRef]
- Lewars, E. Computational chemistry: introduction to the theory and applications of molecular and quantum mechanics. First edition, 2004. ISBN: 0-306-48391-2, Print ISBN: 1-4020-7285-6.
- Clark, S.J.; Seagall, M.D.; Pickard, C.J.; Hasnip, P.J.; Probert, M.I.J.; Refson, K.; Payne, M.C. First principles methods using CASTEP. Z. Kristallogr. 2005, 220, 567–570. [Google Scholar] [CrossRef]
- Bader, R.F.W. The density in density functional theory. J. Molec. Struct.: THEOCHEM. 2010, 943, 2–18. [Google Scholar] [CrossRef]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations, Phys. Rev. B. 1976, 13, 5188. [Google Scholar] [CrossRef]
- Cococcioni, M.; de Gironcoli, S. Linear response approach to the calculation of the effective interaction parameters in the LDA+U method. Phys. Rev. B. 2005, 71, 035105. [Google Scholar] [CrossRef]
- Anisimov, V.I.; Zaanen, J.; Andersen; O.K. Band theory and Mott insulators: Hubbard U instead of Stoner I. Phys. Rev. B. 1991, 44, 943. [CrossRef]
- Moroni, E.G.; Kresse, G.; Hafner, J.; Furthmüller, J. Ultrasoft pseudopotentials applied to magnetic Fe, Co, and Ni: From atoms to solids. Phys. Rev. B. 1997, 56, 15629. [Google Scholar] [CrossRef]
- Staroverov, V. N.; Scuseria, G. E.; Tao, J.; Perdew, J. P. Test of the ladder of density functionals for bulk solids and surfaces. Phys. Rev. B. 2004, 69, 075102. [Google Scholar] [CrossRef]
- Cyrot, M.; Lavagna, M. Density of states and magnetic properties of the rare-earth compounds RFe2, RCo2 and RNi2. Le Journal de Physique. 1979, 40, 763. [Google Scholar] [CrossRef]
- Taylor, K.N.R. Intermetallic rare-earth compounds. Advances in Physics. 1971, 20, 551–660. [Google Scholar] [CrossRef]
- Harris, I.R.; Mansey, R.C.; Raynor, G.V. Rare earth intermediate phases: III. The cubic laves phases formed with aluminium and cobalt. J. Less-Common Met. 1965, 9, 270–280. [Google Scholar] [CrossRef]
- Gschneidner Jr., K. A.; L. Eyring. Handbook on the Physics and Chemistry of Rare Earths. Vol. 2 – Alloys and Intermetallics, North-Holland, 1978. ISBN: 0444850228, 9780444850225.
- Tipler, P.A.; Llewellyn, R. Modern Physics, Fifth Edition, 2008. ISBN-13: 978-0-7167-7550-8, ISBN-10: 0-7167-7550-6.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





