Event-Based Control Approach to Cyber-Security for Complex Discrete-time Networked Systems

1. Introduction

Advances in mathematics, physics, computer science, and engineering over the last twenty years have enabled the development of novel stabilization and monitoring techniques for complex systems [1,2,3,4,5,6,7]. This progress has significantly increased the importance and sophistication of Control-Supervision Systems, particularly in communication networks [8,9,10]. Given the growing need for safety and resilience, research has increasingly focused on Fault-Tolerant and FTA systems [11,12,13,14]. Ensuring resilience in FTA design is critical for maintaining operational efficiency under abnormal conditions, a necessity for modern industrial supervision systems [15,16]. Unlike conventional systems, where cyber-security primarily safeguards data, NCSs face threats from CA that manipulate physical processes via feedback mechanisms [17]. This distinction highlights the importance of integrating control approaches to improve NCS security by analyzing the interplay between CA and control algorithms, particularly their physical impacts [18,19,20].

Extensive research has explored CA detection and mitigation, with particular attention to false data injection and physical attack models. These studies emphasize mathematical modeling of CA and their disruptive effects on controlled processes. Using dynamic process models and control algorithms, CAs can be effectively identified. Among the most studied attack vectors are physical intrusions, which remain key considerations in NCS security analysis [21]. For instance, numerous methodologies have been proposed to detect and assess such attacks in CPS:

• Graph-Theoretic Analysis: Using graph theory [22] to model complex system structures and pinpoint vulnerabilities in network control systems.
• Secure Set Theory: Employ maximal robustly controlled invariant sets [23] to strengthen the resilience of the system against external disturbances and uncertainties.
• Frequency-Domain Attack Analysis: Investigating the effects of CA on control inputs and outputs using frequency domain techniques [24,25].
• Distributed Consensus Control: Applying discontinuous observation-based control consensus principles to linear multi-agent systems [26] for enhanced reliability in distributed architectures.
• Event-Triggered-State Feedback: Implement consensus control via event-triggered state feedback [27] to reduce network congestion while maintaining system performance.
• Adaptive Fault-Tolerant Control: Design of controllers that depend on the state in time [28] to improve robustness against faults and dynamic uncertainties.
• Observer-Based Protocol Synthesis: Developing topology-dependent Lyapunov functions for observer-based protocols with nonlinear Lipschitz dynamics [29], ensuring stability in large-scale networked systems.
• Sampled-Data Observers: Utilizing programmable sampled-data observers [30,31] for real-time CA detection and mitigation.

While extensive research has addressed continuous-time systems, complex discrete-time systems have received comparatively limited attention in the literature [32,33]. Furthermore, existing observer-based approaches predominantly utilize state feedback mechanisms rather than output feedback strategies. To bridge these research gaps, this study introduces novel security measures employing observer-based output feedback controls specifically designed for discrete-time systems. The proposed framework simultaneously addresses both safety and security considerations through model-based attack detection using observers. By comparing estimated process outputs with actual measurements, the method identifies discrepancies and triggers appropriate corrective actions, enabling effective attack and fault detection.

The key contributions of this work include:

• Developments of an innovative Event-Triggered with output feedback control strategy for cyber-physical discrete-time systems, contrasting with conventional continuous-time approaches. The proposed method specifically resolves the technical challenges of implementing output feedback in faulty system models, advancing beyond traditional state feedback limitations.
• Significant generalization capabilities, being successfully adapted to both nonlinear Lipschitz systems and decentralized architectures. This extension substantially broadens the method’s potential applications in complex networked environments.
• The introduction of supplementary decision variables enhances the convex optimization formulation, providing greater design flexibility. Through innovative slack variable techniques, the linearization of complex bilinear terms in the BMI formulation is formulated, yielding more computationally tractable solutions.
• Simulation studies validate the proposed approach’s effectiveness, with results indicating strong potential for real-time implementation using digital signal processing platforms. These findings demonstrate practical feasibility for industrial applications.

The paper is organized as follows: preliminary concepts and the problem statement are presented, followed by the synthesis of an attack-tolerant controller. Numerical validation on an example is then provided, concluding with insights for future research directions.

Notation: The following notation will be used throughout this paper:

• In a matrix, the notation (🟉) is used for the blocks induced by symmetry.
• ${\overline{Q}}^T$ is the transposed matrix of $\overline{Q}$, if $\overline{Q}$ is a square matrix then the notation $\overline{Q}>0$$(\overline{Q}<0$ ) means that $\overline{Q}$ is positive definite (negative definite).
• The set $Co(x,y)=\{\lambda x+(1-\lambda )y,0\le \lambda \le 1\}$ is the convex hull of $\mathrm{x},\mathrm{y}$.

2. Problem Statement and Preliminaries

This section outlines a modeling framework to address various types of attacks with event trigged control systems. The cyber-physical system can be represented by:

$$\begin{array}{cc}\hfill & x_{k+1}^i=\underline{A_i}{x}_k^i+\underline{B_i}{\tilde{u}}_k^i+\underline{F_i}\overline{f_k^i}\hfill \\ \hfill & y_k^i=\underline{C_i}{x}_k^i\hfill \end{array}$$

(1)

The global system is :

$$\begin{array}{cc}\hfill & x_{k+1}=\underline{A}{x}_k+\underline{B}{\tilde{u}}_k+\underline{F}\overline{f_k}\hfill \\ \hfill & y_k=\underline{C}{x}_k\hfill \end{array}$$

(2)

Where $x_k\left(t\right)\in R^{n_x}$ represent the sate vector, $y_k\left(t\right)\in R^{n_y}$ is the output vector, ${\tilde{u}}_k\in R^{n_u}$ is the control vector, $\overline{f_k}\in R^{n_f}$ is the unknown inputs represents the effect of faults, $\underline{A}=$$diag\left\{\underline{A_i}\right\},\underline{B}=diag\left\{\underline{B_i}\right\},\underline{C}=diag\left\{\underline{C_i}\right\},\underline{F}=diag\left\{\underline{F_i}\right\}$are constant matrices of appropriate dimensions.

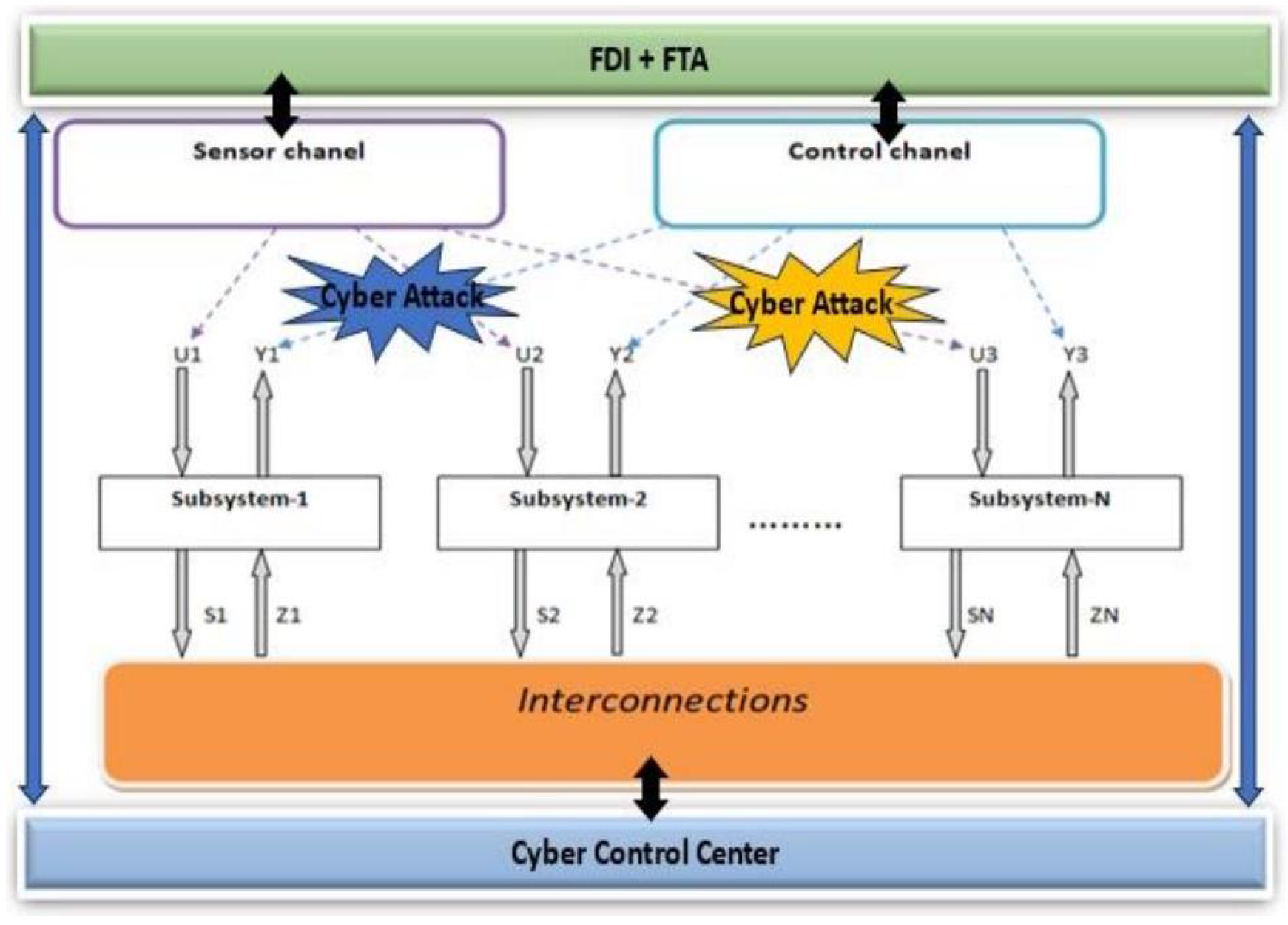
In this particular system, our focus lies in exploring a method for detecting and identifying attacks primarily through a model designed to detect and estimate attack signals within two communication channels. The diagram in Figure 1 provides an overview of the general control/supervision structure of interconnected cyber-physical systems.

Cyber-attacks can simultaneously impact control and/or observation communication chains, as well as interconnection functions. The latter will be modeled in the following by: $\underline{b_{k^u}}$ and ${\underline{b}}_{k^y}$ which represent the data corruption / modification on the control sequences and measurements respectively. Following this, the FDI function will be executed through the synthesized observers. This will furnish the Cyber Control Center with crucial information regarding the nature and location of the cyber-attack, thereby enabling it to compute or update the command via a event-trigged strategy.

For this, the designed Luenberger observer is :

$$\begin{array}{cc}\hfill & {\widehat{x}}_k=\underline{A}{\widehat{x}}_k+\underline{B}{u}_k+\overline{L}\left({\tilde{y}}_k-{\widehat{y}}_k\right)\hfill \\ \hfill & {\widehat{y}}_k=\underline{C}{\widehat{x}}_k\hfill \end{array}$$

(3)

The control signal, by principle of output feedback, is designed with the following form:

$$\begin{array}{cc}\hfill & u_k=\overline{K_1}{\widehat{y}}_k+\overline{K_2}{\tilde{y}}_k\hfill \end{array}$$

(4)

The faults and attacks are modeled as follows:

-

$\overline{f_k}$ simulates errors modeling, faults, unknown input, disturbances.

-

Since data corruption / modification can change the control sequences and measurements provided by the different sensors from their actual calculations or values $u_k$, $y_k$ to corrupted signals ${\tilde{u}}_k$ and ${\tilde{y}}_k$ .

False attacks are modelled by:

$$\begin{array}{cc}\hfill & {\tilde{u}}_k=u_k+\underline{{\Gamma }^u}\overline{b_k^u}\hfill \\ \hfill & {\tilde{y}}_k=y_k+\underline{{\Gamma }^y}\overline{b_k^y}\hfill \end{array}$$

(5)

With $\overline{b_k^u}$ and $\overline{b_k^y}$ represents the pirated data. $\underline{{\Gamma }^u}$ and $\underline{{\Gamma }^y}$ are the binary impact matrices indicating which data strings can be accessed by the ‘hacker’.

Now we define a new variable $\overline{{\alpha }_k}$, group the fault/attack signals as follows: $\overline{{\alpha }_k}={\left[\begin{array}{ccccccc}\overline{f_k}& & & \overline{b_k^u}& & & \overline{b_k^y}\end{array}\right]}^T$. This allows us to rewrite the augmented system (system + observer) as follows:

$$\begin{array}{cc}\hfill & {\eta }_{k+1}=\underline{A_{\alpha }}\overline{{\eta }_k}+\underline{B_{\alpha }}\overline{{\alpha }_k}\hfill \\ \hfill & y_{\alpha }=\underline{C_{\alpha }}\overline{{\eta }_k}\hfill \end{array}$$

(6)

With $\overline{{\eta }_k}=\left[\begin{array}{c}{x}_k\hfill \\ {\widehat{x}}_k\hfill \end{array}\right],\overline{y_{\alpha }}=\left[\begin{array}{c}{y}_k\hfill \\ {\widehat{y}}_k\hfill \end{array}\right]$

$$\underline{A_{\alpha }}=\left[\begin{array}{ccccc}\underline{A}+\underline{B}\overline{K_2}\underline{C}& & & & \underline{B}\overline{K_1}\underline{C}\\ \overline{L}\underline{C}+\underline{B}\overline{K_2}\underline{C}& & & & \underline{A}-\overline{L}\underline{C}+\underline{B}\overline{K_1}\underline{C}\end{array}\right]$$

$$\underline{B_{\alpha }}=\left[\begin{array}{ccccc}\underline{F}& & \underline{B}\underline{{\Gamma }^u}& & \underline{B}\overline{K_2}\underline{{\Gamma }^y}\\ 0& & 0& & \left(\overline{L}+\underline{B}\overline{K_2}\right)\underline{{\Gamma }^y}\end{array}\right],\underline{C_{\alpha }}=\left[\begin{array}{ccc}\underline{C}& & 0\\ 0& & \underline{C}\end{array}\right]$$

Then the following lemmas are considered:

Lemma 1:

[34] Given two matrices $\underline{M},\underline{N}$, of appropriate dimensions, then the following inequality holds for any constant $\underline{\beta }>0$

$$\begin{array}{c}\hfill {\underline{M}}^T\underline{N}+{\underline{N}}^T\underline{M}\le \underline{\beta }{\underline{M}}^T\underline{M}+{\underline{\beta }}^{-1}{\underline{N}}^T\underline{N}\end{array}$$

(7)

Lemma 2:

[34] Consider a nonlinear function $h:{\mathbb{R}}^n\to {\mathbb{R}}^n$, the following two items are equivalent: h is globally Lipschitz with respect to its argument, i.e.,

$$\begin{array}{c}\hfill \parallel h\left(a\right)-h\left(b\right)\parallel \le \underline{l}\parallel a-b\parallel \end{array}$$

(8)

There exist constants $\underline{h_{ij}}$ and $\overline{h_{ij}}$ so that for all $\forall a,b\in {\mathbb{R}}^n$ there exist $r_i\in Co(a,b),r_i\ne$$a,r_i\ne b$ and functions $h_{ij}:{\mathbb{R}}^n\ast {\mathbb{R}}^n$ satisfying the following equality:

$$\begin{array}{c}\hfill h\left(a\right)-h\left(b\right)=\sum _{i,j=1}^{q,n}{h}_{ij}\left(r_i\right)H_{ij}(a-b)\end{array}$$

(9)

And $\underline{h_{ij}}\le h_{ij}\left(r_i\right)\le \overline{h_{ij}}$ where $h_{ij}\left(r_i\right)={\displaystyle \frac{\partial h_i}{\partial h_j}}\left(r_i\right)$ and $H_{ij}=e_q\left(i\right)e_n^T\left(j\right)$

3. FTA Control Synthesis

This section is dedicated to the development of the new FTA synthesis. The main result is given by the following Theorem:

Theorem 1:

There exists an asymptotic stable observer of the form (3) and an event-based fault-attack tolerant controller (4), with a triggering condition ${∥\overline{{\alpha }_k}∥}^2\le \underline{\sigma }{∥\overline{{\eta }_k}∥}^2$, for the system (2), if there exist positive symmetric matrices $\overline{P}=\left[\begin{array}{ccc}\overline{P_1}& & 0\\ 0& & \overline{P_2}\end{array}\right]$, matrices $R=\overline{P_2}\overline{L}$, $\overline{K_1}$, $\overline{K_2}$ and a positive scalar $\underline{\beta }$, solution if the following BMI is feasible:

$$\left[\begin{array}{ccccc}\underline{A_{\alpha }^T}\overline{P}\underline{A_{\alpha }}-\overline{P}& & {\underline{A_{\alpha }}}^T\overline{P}\underline{B_{\alpha }}& & 0\\ 🟉& & {\left({\underline{\beta }}^{-1}I\right)}^{-1}& & 0\\ 🟉& & 🟉& & \underline{B_{\alpha }^T}\overline{P}\underline{B_{\alpha }}+\underline{\sigma }\underline{\beta }I\end{array}\right]<0$$

(10)

With: $\overline{P_2}=\underline{\mu }\overline{P_1},\overline{L}={\left(\underline{\mu }\overline{P_1}\right)}^{-1}R,\overline{K_1}={\underline{B}}^{+}{\overline{P_1}}^{-1}{Z}_1,\overline{K_2}={\underline{B}}^{+}{\overline{P_1}}^{-1}Z.$

Proof

To determine the different control and observer gains, a stability analysis is based on the Lyapunov function:

$$\begin{array}{c}\hfill \overline{\Delta V}={\overline{V}}_{k+1}-{\overline{V}}_k<0\end{array}$$

(11)

With ${\overline{V}}_k=\overline{{\eta }_k^T}\overline{P}\overline{{\eta }_k},{\overline{V}}_{k+1}=\overline{{\eta }_{k+1}^T}\overline{P}\overline{{\eta }_{k+1}}$.

Now using lemma 1 on $\overline{\Delta V}$, the latter becomes:

$$\begin{array}{cc}\hfill & \overline{\Delta V}=\overline{{\eta }_k^T}\left[\underline{A_{\alpha }^T}\overline{P}\underline{A_{\alpha }}+{\underline{\beta }}^{-1}\underline{A_{\alpha }^T}\overline{P}\underline{B_{\alpha }{B}_{\alpha }^T}\overline{P}\underline{A_{\alpha }}-\overline{P}\right]\overline{{\eta }_k}\hfill \\ \hfill & +\overline{{\alpha }_k^T}\left[\underline{B_{\alpha }^T}\overline{P}\underline{B_{\alpha }}+\underline{\sigma }\underline{\beta }I\right]\overline{{\alpha }_k}<0\hfill \end{array}$$

(12)

Thus, the stability condition can be given by

$$\begin{array}{c}\hfill \overline{\Delta V}<0\equiv \overline{Q}<0\end{array}$$

(13)

We apply Schur’s complement using ${∥\overline{{\alpha }_k}∥}^2\le \underline{\sigma }{∥\overline{{\eta }_k}∥}^2$, we obtain:

$$\overline{Q}=\left[\begin{array}{ccccc}\underline{A_{\alpha }^T}\overline{P}{\underline{A}}_{\alpha }-\overline{P}& & \underline{A_{\alpha }^T}\overline{P}\underline{B_{\alpha }}& & 0\\ 🟉& & {\left({\underline{\beta }}^{-1}I\right)}^{-1}& & 0\\ 🟉& & 🟉& & \underline{B_{\alpha }^T}\overline{P}\underline{B_{\alpha }}+\underline{\sigma }\underline{\beta }I\end{array}\right]$$

(14)

Where:

•$\underline{A_{\alpha }^T}\overline{P}\underline{A_{\alpha }}-\overline{P}=\left[\begin{array}{ccccccc}& & \overline{R_{11}}& & \overline{R_{12}}& & \\ & & \overline{R_{21}}& & \overline{R_{22}}& \end{array}\right]$

with:

$\overline{R_{11}}={\underline{A}}^T\overline{P_1}\underline{A}+{\underline{A}}^T\overline{P_1}\underline{B}\overline{K_2}\underline{C}+{\underline{C}}^T{\overline{K_2}}^T{\underline{B}}^T\overline{P_1}\underline{A}+{\underline{C}}^T{\overline{K_2}}^T{\underline{B}}^T\overline{P_1}\underline{B}\overline{K_2}\underline{C}+{\underline{C}}^T{\overline{K_2}}^T{\underline{B}}^T\overline{P_2}\underline{B}\overline{K_2}\underline{C}+{\underline{C}}^T{\overline{K_2}}^T{\underline{B}}^T\overline{P_{2}L}\underline{C}+{\underline{C}}^T{\overline{L}}^T\overline{P_2}\underline{B}\overline{K_2}\underline{C}+{\underline{C}}^T{\overline{L}}^T\overline{P_2}\overline{L}\underline{C}-\overline{P_1}$

$\overline{R_{12}}={\underline{A}}^T\overline{P_1}\underline{B}\overline{K_1}\underline{C}+{\underline{C}}^T{\overline{K_2}}^T{\underline{B}}^T\overline{P_1}\underline{B}\overline{K_1}\underline{C}+{\underline{C}}^T{\overline{K_2}}^T{\underline{B}}^T\overline{P_2}\underline{A}-{\underline{C}}^T{\overline{K_2}}^T{\underline{B}}^T\overline{P_2}\overline{L}\underline{C}+{\underline{C}}^T{\overline{K_2}}^T{\underline{B}}^T\overline{P_2}\underline{B}\overline{K_1}\underline{C}+{\underline{C}}^T{\overline{L}}^T\overline{P_2}\underline{A}-{\underline{C}}^T{\overline{L}}^T\overline{P_2}\overline{L}\underline{C}+{\underline{C}}^T{\overline{L}}^T\overline{P_2}\underline{B}\overline{K_1}\underline{C}$

$\overline{R_{21}}={\underline{C}}^T{\overline{K_1}}^T{\underline{B}}^T\overline{P_1}\underline{A}+{\underline{C}}^T{\overline{K_1}}^T{\underline{B}}^T\overline{P_1}\underline{B}\overline{K_2}\underline{C}+{\underline{A}}^T\overline{P_2}\underline{B}\overline{K_2}\underline{C}+{\underline{A}}^T\overline{P_2}\overline{L}\underline{C}-{\underline{C}}^T{\overline{L}}^T\overline{P_2}\underline{B}\overline{K_2}\underline{C}-{\underline{C}}^T{\overline{L}}^T\overline{P_2}\overline{L}\underline{C}+{\underline{C}}^T{\overline{K}}_1^T{\underline{B}}^T\overline{P_2}\underline{B}\overline{K_2}\underline{C}+{\underline{C}}^T{\overline{K_1}}^T{\underline{B}}^T\overline{P_2}\overline{L}\underline{C}$

$\overline{R_{22}}={\underline{C}}^T{\overline{K}}_1^T{\underline{B}}^T\overline{P_1}\underline{B}\overline{K_1}\underline{C}+{\underline{A}}^T\overline{P_2}\underline{A}-{\underline{A}}^T\overline{P_{2}L}\underline{C}+{\underline{A}}^T\overline{P_2}\underline{B}\overline{K_1}\underline{C}-{\underline{C}}^T{\overline{L}}^T\overline{P_2}\underline{A}+{\underline{C}}^T{\overline{L}}^T\overline{P_2}\overline{L}\underline{C}-{\underline{C}}^T{\overline{L}}^T\overline{P_2}\underline{B}\overline{K_1}\underline{C}+{\underline{C}}^T{\overline{K_1}}^T{\underline{B}}^T\overline{P_2}\underline{A}-{\underline{C}}^T{\overline{K_1}}^T{\underline{B}}^T\overline{P_2}\overline{L}\underline{C}+{\underline{C}}^T{\overline{K_1}}^T{\underline{B}}^T\overline{P_2}\underline{B}\overline{K_1}\underline{C}-\overline{P_2}$

and:

•$\underline{A_{\alpha }^T}\overline{P}\underline{B_{\alpha }}=\left[\begin{array}{ccccccccc}& & \overline{S_{11}}& & \overline{S_{12}}& & \overline{S_{13}}& & \\ & & \overline{S_{21}}& & \overline{S_{22}}& & \overline{S_{23}}& & \end{array}\right]$

With:

$\begin{array}{cc}& \overline{S_{11}}={\underline{A}}^T\overline{P_1}\underline{F}+{\underline{C}}^T{\overline{K_2}}^T{\underline{B}}^T\overline{P_1}\underline{F}\hfill \\ & \overline{S_{12}}={\underline{A}}^T{\overline{P}}_1\underline{B}\underline{{\Gamma }^u}+{\underline{C}}^T{\overline{K_2}}^T{\underline{B}}^T\overline{P_1}\underline{B}\underline{{\Gamma }^u}\hfill \\ & \overline{S_{13}}={\underline{A}}^T\overline{P_1}\underline{B}\overline{K_2}\underline{{\Gamma }^y}+{\underline{C}}^T{\overline{K_2}}^T{\underline{B}}^T\overline{P_1}\underline{B}\overline{K_2}\underline{{\Gamma }^y}+{\underline{C}}^T{\overline{K_2}}^T{\underline{B}}^T\overline{P_{2}L}\underline{{\Gamma }^y}\hfill \\ & +{\underline{C}}^T{\overline{K_2}}^T{\underline{B}}^T\overline{P_2}\underline{B}\overline{K_2}\underline{{\Gamma }^y}+{\underline{C}}^T{\overline{L}}^T\overline{P_{2}L}{\underline{\Gamma }}^y+{\underline{C}}^T{\overline{L}}^T\overline{P_2}\underline{B}\overline{K_2}\underline{{\Gamma }^y}\hfill \\ & \overline{S_{21}}={\underline{C}}^T{\overline{K_1}}^T{\underline{B}}^T\overline{P_1}\underline{F},\overline{A_{22}}={\underline{C}}^T{\overline{K_1}}^T{\underline{B}}^T\overline{P_1}\underline{B}\underline{{\Gamma }^u}\hfill \\ & \overline{S_{23}}={\underline{C}}^T{\overline{K_1}}^T{\underline{B}}^T\overline{P_1}\underline{B}\overline{K_2}\underline{{\Gamma }^y}+{\underline{A}}^T\overline{P_{2}L}\underline{{\Gamma }^y}+{\underline{A}}^T\overline{P_2}\underline{B}\overline{K_2}\underline{{\Gamma }^y}\hfill & \\ & -{\underline{C}}^T{\overline{L}}^T\overline{P_{2}L}\underline{{\Gamma }^y}-{\underline{C}}^T{\overline{L}}^T\overline{P_2}\underline{B}\overline{K_2}\underline{{\Gamma }^y}+{\underline{C}}^T{\overline{K_1}}^T{\underline{B}}^T\overline{P_2}\overline{L}\underline{{\Gamma }^y}\hfill & \\ & +{\underline{C}}^T{\overline{K_1}}^T{\underline{B}}^T\overline{P_2}\underline{B}\overline{K_2}{\underline{\Gamma }}^y\hfill \end{array}$•$\begin{array}{c}\hfill \underline{B_{\alpha }^T}\overline{P}\underline{B_{\alpha }}=\left[\begin{array}{ccccccccc}{\underline{F}}^T\overline{P_1}\underline{F}& & & {\underline{F}}^T\overline{P_1}\underline{B}\underline{{\Gamma }^u}& & & & & {\underline{F}}^T\overline{P_1}\underline{B}\overline{K_2}\underline{{\Gamma }^y}\\ 🟉& & & {\underline{{\Gamma }^u}}^T{\underline{B}}^T\overline{P_1}\underline{B}\underline{{\Gamma }^u}& & & & & {\underline{{\Gamma }^u}}^T{\underline{B}}^T\overline{P_1}\underline{B}\overline{K_2}\underline{{\Gamma }^y}\\ 🟉& & & 🟉& & & & & \overline{M_{33}}\end{array}\right]\end{array}$

$$\begin{gathered} \overline{M_{33}}={\underline{{\Gamma }^y}}^T{\overline{K_2}}^T{\underline{B}}^T\overline{P_1}\underline{B}\overline{K_2}\underline{{\Gamma }^y}+{\underline{\Gamma }}^{y^T}{\overline{L}}^T\overline{P_2}\overline{L}\underline{{\Gamma }^y}+{\underline{{\Gamma }^y}}^T{\overline{L}}^T\overline{P_2}\underline{B}\overline{K_2}\underline{{\Gamma }^y}+{\underline{{\Gamma }^y}}^T{\overline{K_2}}^T{\underline{B}}^T\overline{P_{2}L}\underline{{\Gamma }^y} \\ +\underline{{\Gamma }^y}{\overline{K_2}}^T{\underline{B}}^T\overline{P_2}\underline{B}\overline{K_2}\underline{{\Gamma }^y} \end{gathered}$$

Then, contrary to the various synthesis approaches considered in the literature and to give more degrees of freedom to the optimization problem, we propose the following form of the matrix $\overline{P}$ :

$$\begin{array}{c}\hfill \overline{P}=\left[\begin{array}{cc}\overline{P_1}& 0\\ 0& \overline{P_2}\end{array}\right]=\left[\begin{array}{cc}\overline{P_1}& 0\\ 0& \underline{\mu }\overline{P_1}\end{array}\right]\end{array}$$

(15)

Where $\underline{\mu }>0.$

The final step, let’s consider the following proposed variables changes:

$$\begin{array}{cc}& Z=\overline{P_1}\underline{B}\overline{K_2},Z_1=\overline{P_1}\underline{B}\overline{K_1},X={\overline{L}}^{T}R,Y=Z^T\overline{L},Y_1=Z_1^T\overline{L},\hfill \\ & W=Z^T\underline{B}\overline{K_2},W_1=Z_1^T\underline{B}\overline{K_1},W_2=Z_1^T\underline{B}\overline{K_2}\hfill \end{array}$$

Then, inequality (10) is easily obtained.

4. Event-Triggered Mechanisms

To implement Event-based control [35], it’s necessary to recompute the control gains and update the signal whenever (10) nears a violation. To express this equality conveniently, we assume that the input remains constant between successive recomputation of the FTA. This practice is commonly known in the literature as ‘sample and hold’.

$$u_k=u_{k_i}\forall k\in \left[k_i,k_{i+1}[,k\in N\right.$$

(16)

Or the sequence $\left\{k_i\right\}i\in N$ represents the moment when the command is recalculated. Subsequently, we introduce the error $e_1\left(k\right)$ defined by:

$$\begin{array}{cc}\hfill & e_1\left(k\right)=u_{k_i}-{\tilde{u}}_k\hfill \\ \hfill & e_1\left(k\right)=u_k-{\tilde{u}}_k+u_{k_i}-u_k\hfill \\ \hfill & e_1\left(k\right)=\left(\begin{array}{cccc}0& & \underline{{\Gamma }^u}& 0\end{array}\right)\left(\overline{{\alpha }_{k_i}}-\overline{{\alpha }_k}\right)\hfill \end{array}$$

(17)

which means that

$$\begin{array}{c}\hfill \overline{{\alpha }_{k_i}}-\overline{{\alpha }_k}={\overline{C_1}}^{+}{e}_1\left(k\right)+\left(I-{\overline{C_1}}^{+}\overline{C_1}\right)\overline{w_k}\end{array}$$

(18)

Such as: $\overline{C_1}=\left(\begin{array}{cccccc}0& & & \underline{{\Gamma }^u}& & 0\end{array}\right),{\overline{C_1}}^{+}$: is the pseudo-inverse of $\overline{C_1},\overline{w_k}$ : Arbitrary vector represents the disturbances.

From equation (6), the dynamics of the system in the interval $\left[k_i,k_{i+1}\right.$ [ is given by:

$$\begin{array}{cc}\hfill & \overline{{\dot{\eta }}_k}=A_{\alpha }\overline{{\eta }_k}+\underline{B_{\alpha }}\overline{{\alpha }_{k_i}}\hfill \\ \hfill & \overline{{\dot{\eta }}_k}=\overline{A_{\alpha }}\overline{{\eta }_k}+\underline{B_{\alpha }}\overline{{\alpha }_{k_i}}+\underline{B_{\alpha }}\left(\overline{{\alpha }_k}-\overline{{\alpha }_k}\right)\hfill \\ \hfill & \overline{{\dot{\eta }}_k}=\underline{A_{\alpha }}\overline{{\eta }_k}+\underline{B_{\alpha }}\overline{{\alpha }_k}+\underline{B_{\alpha }}{\overline{C_1}}^{+}{e}_1\left(k\right)+\underline{B_{\alpha }}\left(I-{\overline{C_1}}^{+}\overline{C_1}\right)\overline{w_k}\hfill \end{array}$$

(19)

Using (13) and (19), held to:

$$\begin{array}{c}\hfill J_k^T\left[\begin{array}{ccccccccc}\overline{Q}& & & & \overline{P}\underline{B_{\alpha }}{\overline{C_1}}^{+}& & & & \overline{P}\underline{B_{\alpha }}\left(I-{\overline{C_1}}^{+}\overline{C_1}\right)\\ 🟉& & & & 0& & & & 0\\ 🟉& & & & 0& & & & 0\end{array}\right]J_k\le 0\end{array}$$

(20)

With $J_k^T={\left[\begin{array}{c}\overline{{\eta }_k}\\ e_1\left(k\right)\\ \overline{w_k}\end{array}\right]}^T$

Subsequently, the $k_i$ trigger time can now be defined as the moment that this equality is satisfied:

$$\begin{array}{c}\hfill J_{k_i}^T{\rm Y}{J}_{k_i}=0\end{array}$$

(21)

With ${\rm Y}=\left[\begin{array}{ccccccc}\overline{Q}& & & \overline{P}\underline{B_{\alpha }}{\overline{C_1}}^{+}& & & \overline{P}{\underline{B}}_{\alpha }\left(I-{\overline{C_1}}^{+}\overline{C_1}\right)\\ & & & 0& & & 0\\ & & & 0& & & 0\end{array}\right]$

5. Discussion and Comments

• This article examines the closed-loop system dynamics, which can be extended and generalized to accommodate the case of (by adjusting the matrix dimensions):
  • Lipschitz nonlinear discrete-time systems where the basic idea is to use the DMVT on the nonlinear function [34] to transform the global nonlinear system to LPV system using Lemma 2. Then, if the nonlinear function verify $h(k,0)=0$, the dynamic matrix $\underline{A}$ becomes $\underline{\mathcal{A}}\left(\varphi \right)$ where the parameter $\varphi$ lies inside the bounded convex set of $h(k,x_k)$ variation.
  • Decentralized systems with the consideration of the nonlinear interconnection function in the synthesis of the proposed control.
• In this work, two gains ( $\overline{K_1}$ and $\overline{K_2}$ ) have been synthesized separately to stabilize the overall system during cyber-attacks on the two communications chains of control and observation (representing the interconnections). To reduce the complexity of the BMI to be solved, a proposal can ensure this by admitting that $\overline{K_2}=\theta \overline{K_1}$ (like the proposed form of the $\overline{P}$ matrix where $\theta >0$ ). This will make it possible to linearize several expressions in the BMI while guaranteeing a more optimal solution (scalar variables to be searched instead of matrices).

6. Numerical Simulation and Results

This section presents an application on a pilot system comprising three tanks. A plant model is introduced, and the proposed control design is implemented on the system. Numerical findings are provided to demonstrate the effectiveness of the developed methodology.

The dynamic equation for the system is given as:

$$\underline{A}=\left[\begin{array}{ccccc}1& & 0& & 0\\ 0& & 1& & 0\\ 0& & 0& & 1\end{array}\right];\underline{B}=\left[\begin{array}{cc}0.0649& 0\\ 0& 0.0649\\ 0& 0\end{array}\right];\underline{C}=I_3$$

${\overline{f}}_k$ simulates errors modeling, faults, unknown input, disturbances, where the weighing matrix $\underline{F}$ is defined as: $\underline{F}=\left[\begin{array}{c}0\\ 0\\ 0.2626\end{array}\right]$

$\underline{{\Gamma }^u}$ and $\underline{{\Gamma }^y}$ is equal to the identity matrix I. The event condition $\underline{\sigma }$ rate was chosen to be equal to $5\%$. The initial conditions of the system and the observer are: ${\left[\begin{array}{cccccccc}& & 0.4& & 0.2& & 0.3& \end{array}\right]}^T$ with $T_e=0.001\mathrm{s}$ By solving (10) with (15)using YALMIP^®, an optimal solution is found such that the gains found are as follows:

$\begin{array}{c}\overline{L}=\left[\begin{array}{ccccccc}0.19005& & & 0.071893& & & 0.10582\\ 0.72594& & & 0.81695& & & 0.51331\\ -0.014559& & & -0.069732& & & 0.017343\end{array}\right]\\ \overline{K_1}=\left[\begin{array}{ccccccc}-80.4016& & & -6.7935& & & 0.0647\\ -6.7955& & & -70.8443& & & -0.0177\end{array}\right]\\ \overline{K_2}=\left[\begin{array}{ccccccc}-15.3423& & & 0.0114& & & 2.3703\\ 0.0117& & & -15.3609& & & 1.1387\end{array}\right]\\ \underline{\mu }=2.4052\end{array}$

6.1. No-Attacks Case:

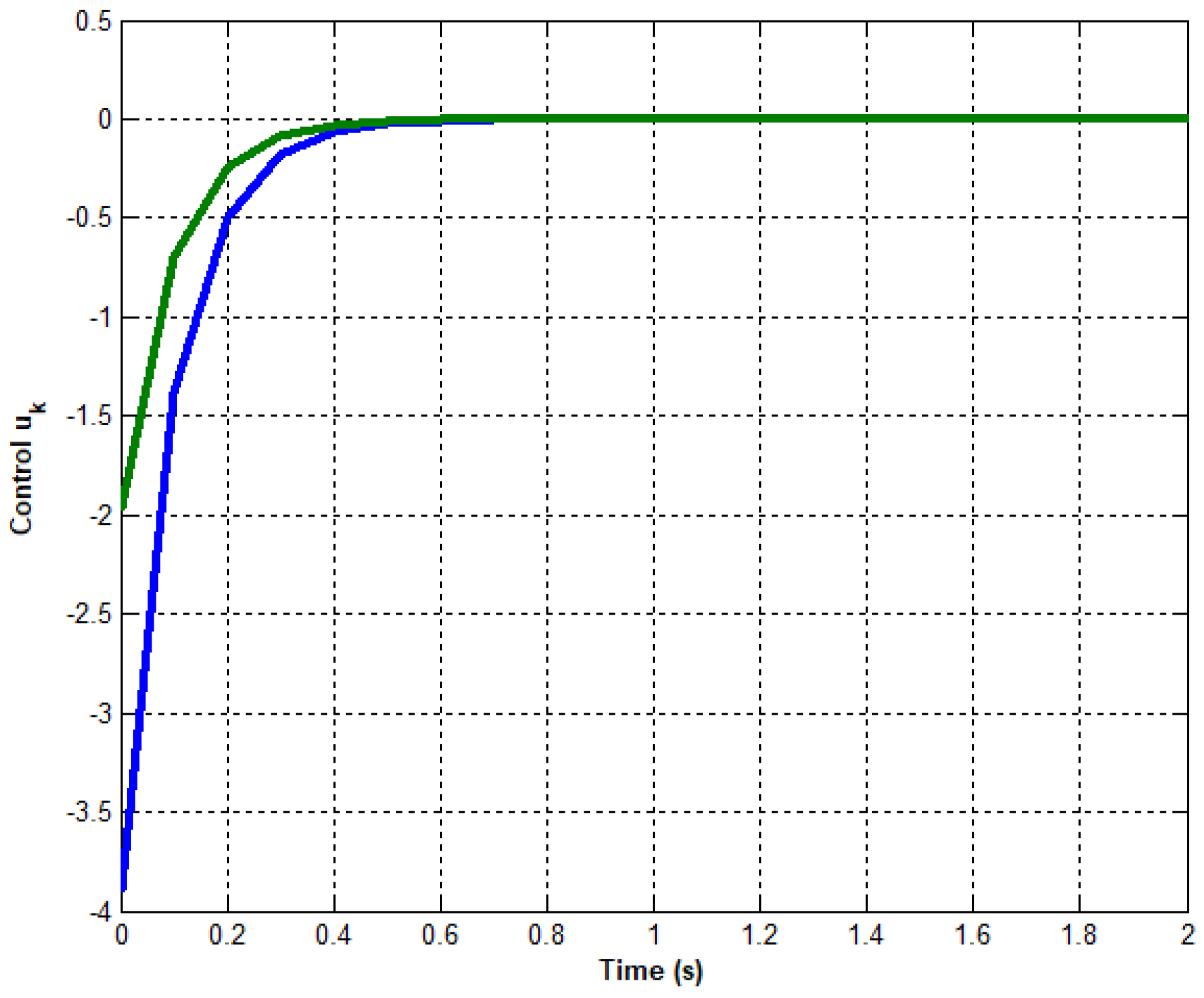
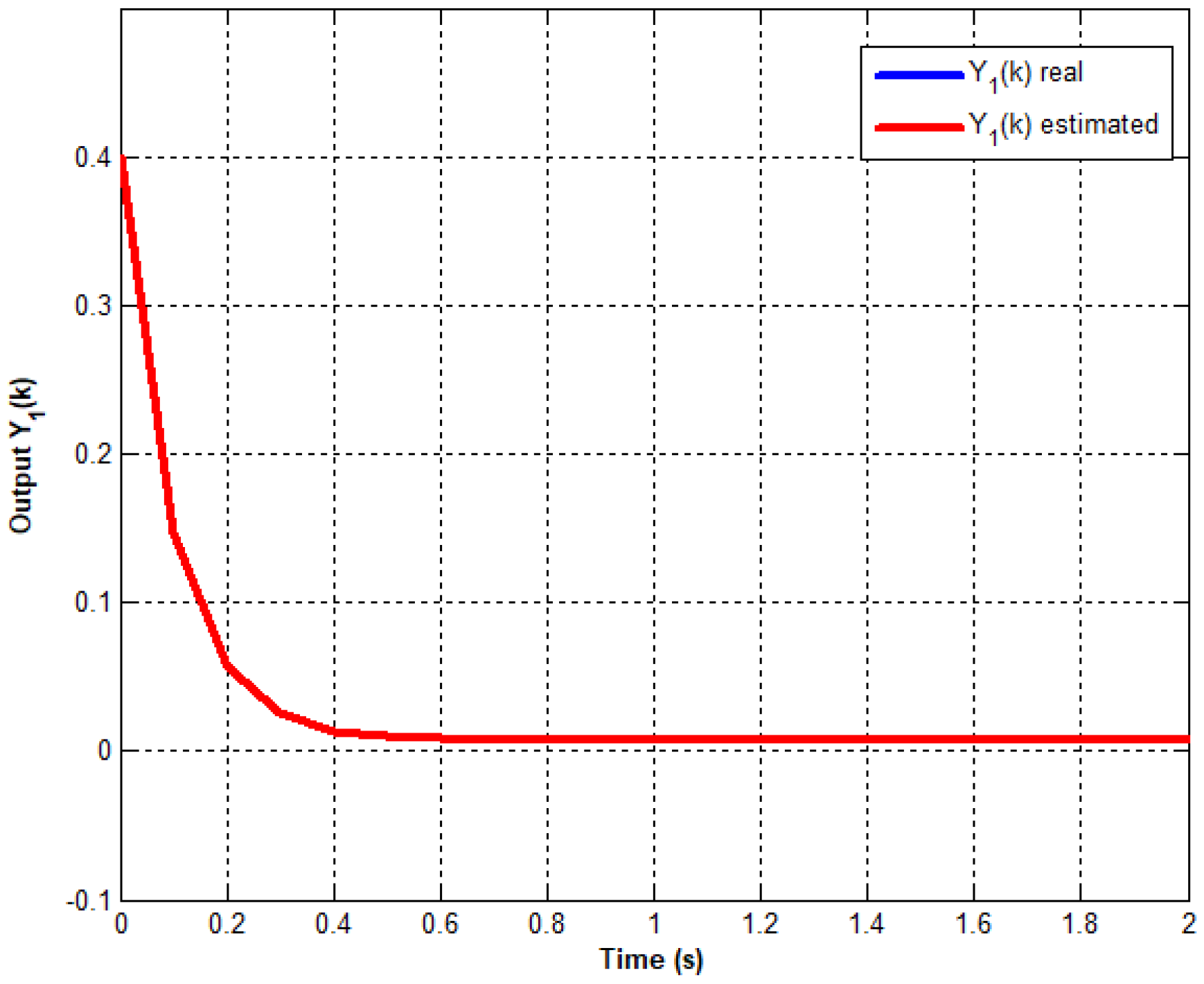
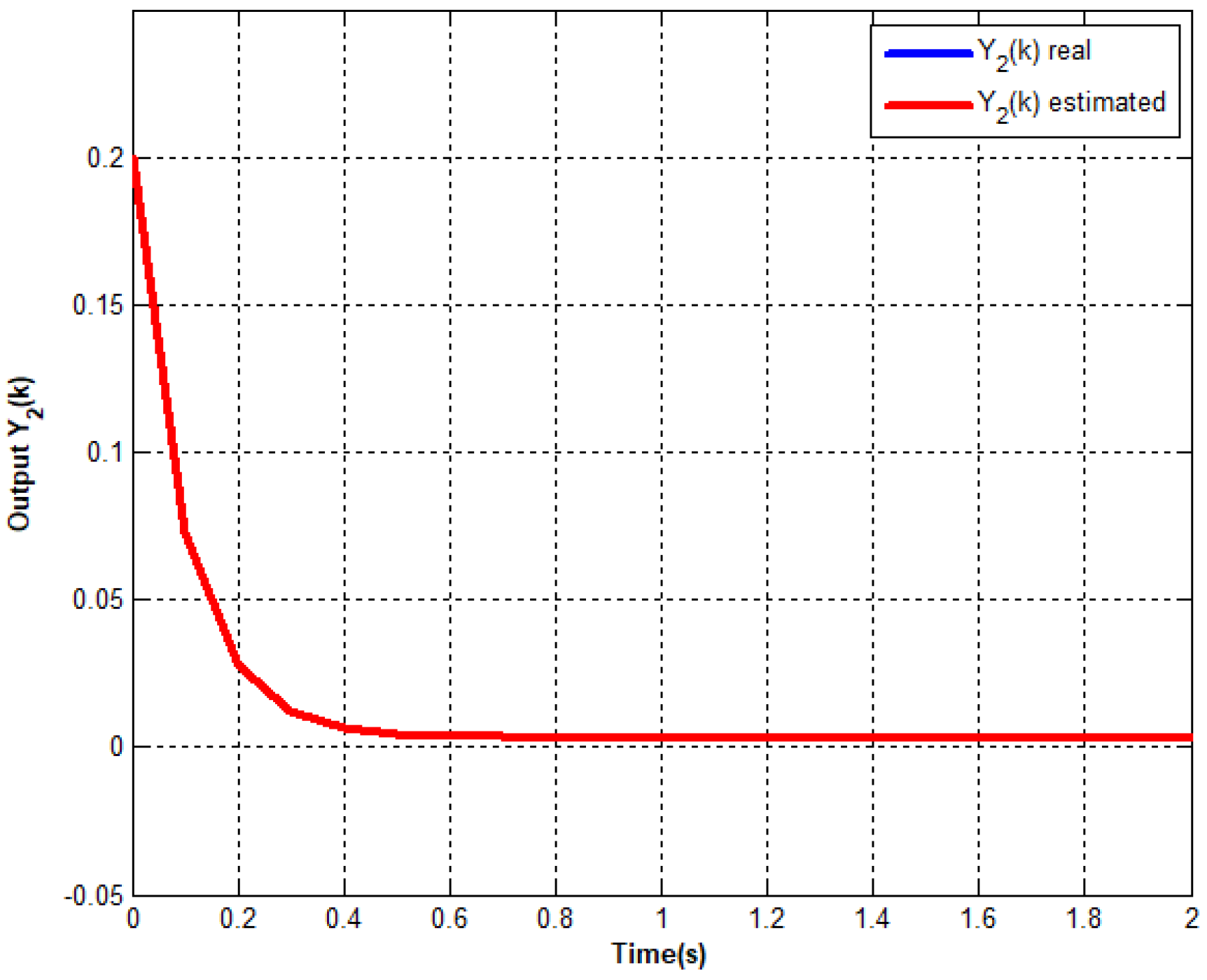
First, during the implementation phase, noise was introduced into the system in the form of sinusoidal signals characterized by a random varying frequencies (between 02 and 42 Hz) and amplitudes $(\pm 0.15\%y(k\left)\right)$. Now, Figure 2, Figure 3 and Figure 4 show the evolution of the control $u_k$ and various outputs $\left(y_1\left(k\right),y_2\left(k\right)\right)$ without attacks:

From Figure 2, Figure 3 and Figure 4, it is clear that the proposed output feedback control ensures the stabilization despite injected disturbances. Effectively, According to Figure 3 and Figure 4, the estimated states converge to the real ones around the equilibrium point, despite the injection of random perturbations on the system dynamics and output. This is also validated through the variation of the control signals Figure 2, which show the convergence of the control without amplitude variation and even in terms of convergence time.

Remark 3:

In the dynamics of the proposed system, the eigenvalues are on the stability limit $\left({\lambda }_i=1\right)$. The output feedback control strategy (even without cyber-attacks on the control/observation chains) guarantees the overall stability of the system towards the equilibrium point despite injected disturbances such as ${\lambda }_i=\{0.0046;0.0027;0.0038\}$.

6.2. Case With Attacks

For this case, we apply the attack on the actuator chain and then on the sensor chain such as $\underline{b_k^u}={\left[\begin{array}{cccc}& 0.001& & 0\end{array}\right]}^T$ and $\underline{b_k^y}={\left[\begin{array}{cccccccc}& 0.3& & & 0& & & 0\end{array}\right]}^T$. Now, the cyber-attacks will be applied to the control chain and the sensor chain in the time interval $\left[\begin{array}{ccccc}& 16\mathrm{s}& & & 26\mathrm{s}\end{array}\right]$.

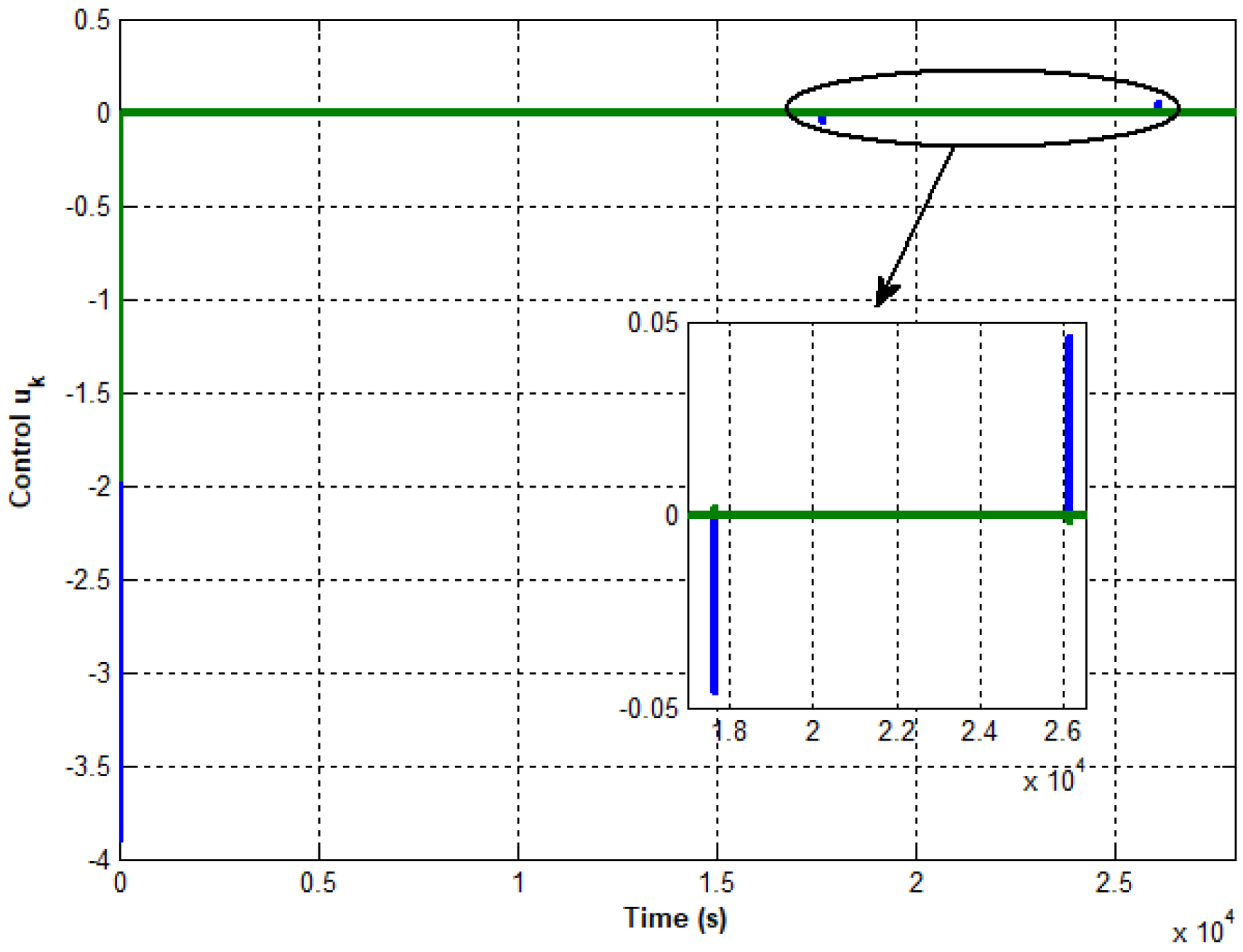
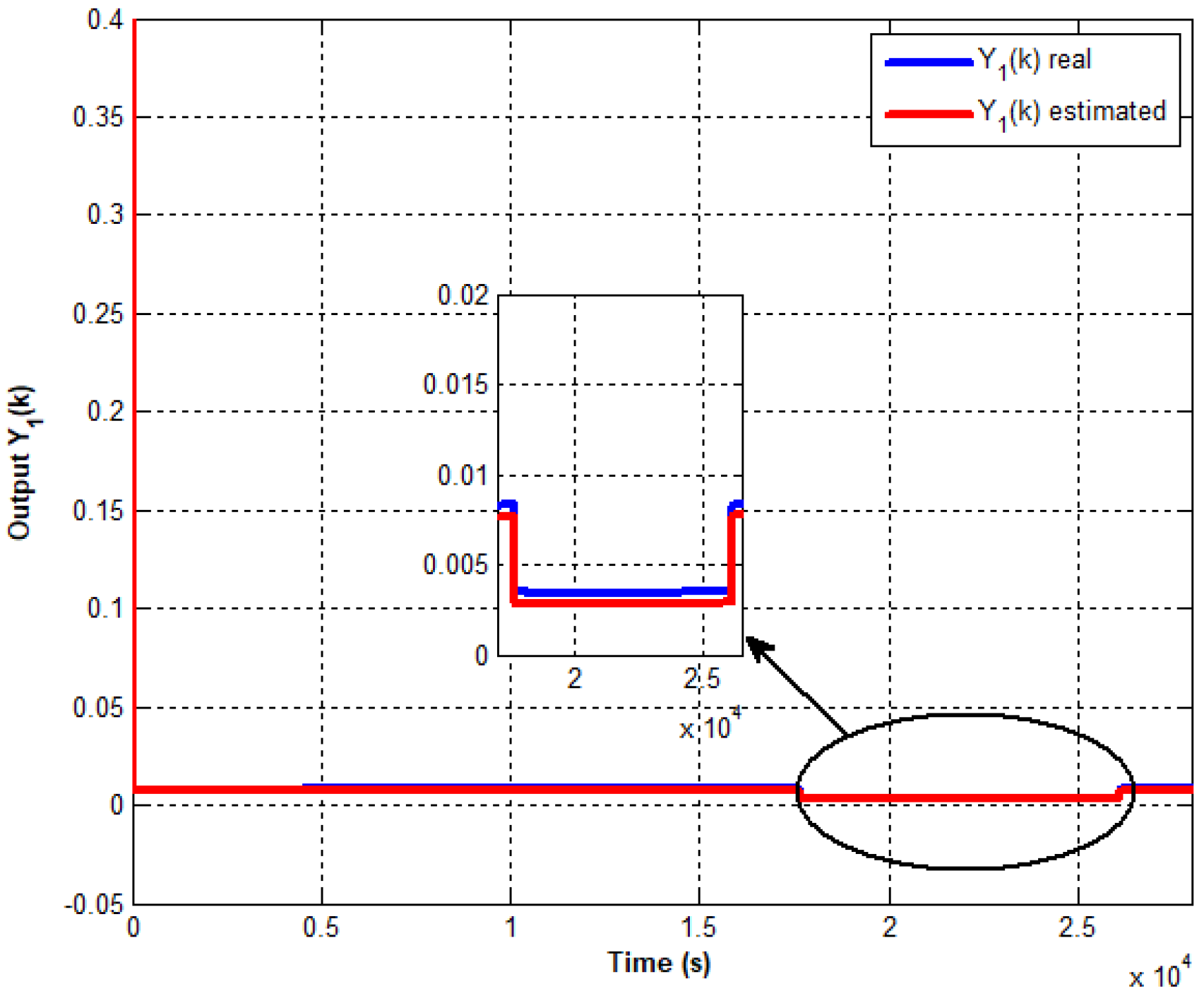
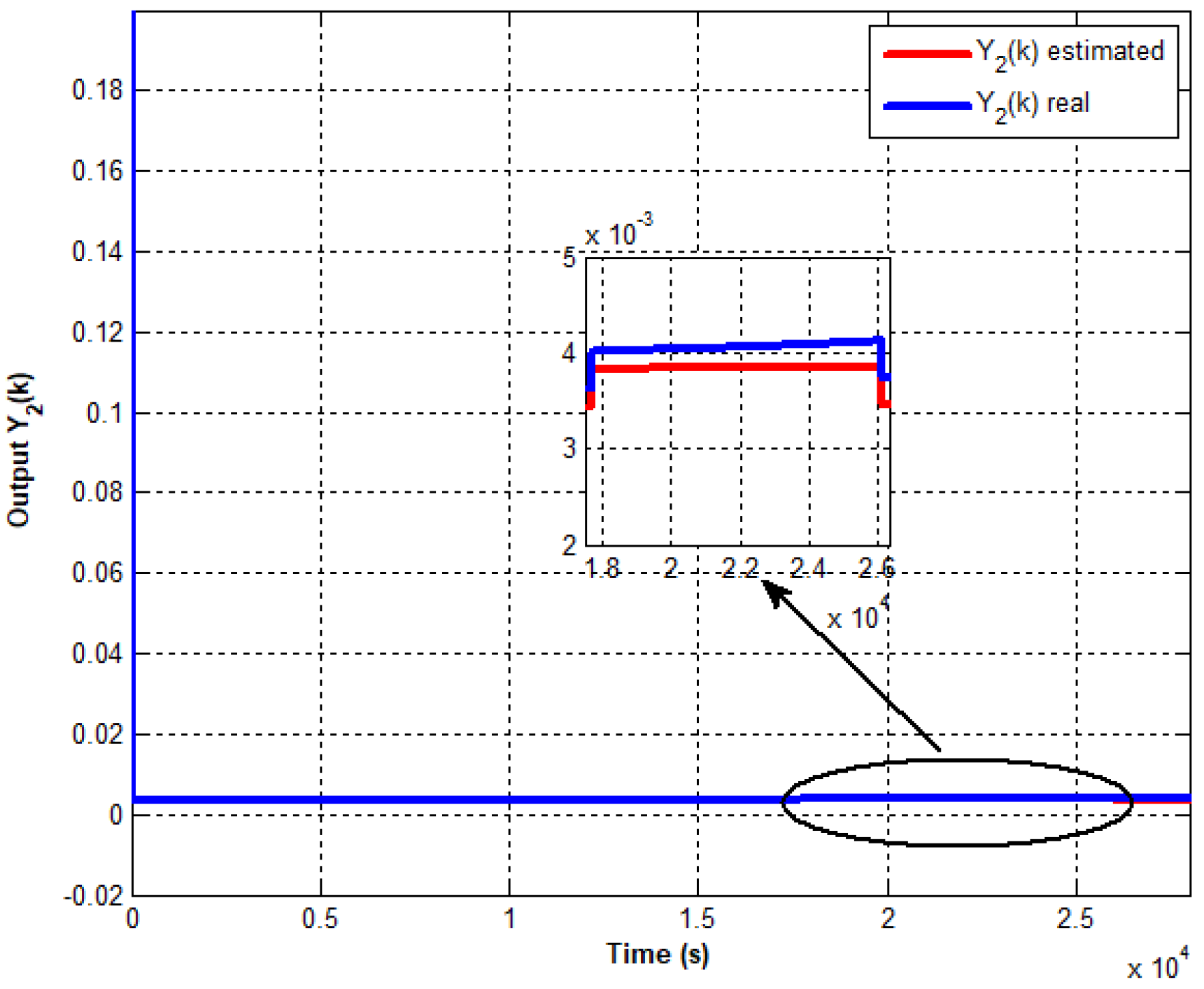
Figure 5, Figure 6 and Figure 7 illustrate the evolution of the control $u_k$ to reduce the impact of cyber-attacks on control and observer chains and the various outputs $\left(y_1\left(k\right),y_2\left(k\right)\right)$ using the trigger condition ( ${∥\overline{{\alpha }_k}∥}^2\le 0.05{∥\overline{{\eta }_k}∥}^2$ ).

Figure 5, Figure 6 and Figure 7 depict the progression of control and different outputs utilizing the event-triggered approach. This strategy aims to minimize the effects of attacks on sensors and actuators while ensuring the stabilization of the interconnected system around its equilibrium point. Thus, it is evident that the initial phase of attack detection and identification has been successfully achieved Figure 6 and Figure 7. Moreover, the impact of attacks on both communication chains (control/observation) in terms of amplitude spikes and even control signal Figure 5 has been reduced through the proposed approach while avoiding a very important parameter which is the switching phenomenon in actuators.

Another point related to convergence speed/time is shown in the presented figures. Effectively, comparing the convergence times $\left(t_c\right)$ of an approach that handles the continuous-time case [8] such that $t_c=220$ s while the proposed discrete version converges to only 0.189 s for the same example system.

A comparison of convergence times with approaches dealing with the discrete case is as follows:

• Unamed Ground Vehicle [33] with $t_c=1.087s$ where the proposed approach converges in 0.9824 s.

• Modular Servo System [32] with $t_c=0.63s$ where the proposed approach converges in 0.5771 s.

7. Conclusion

This paper introduces an attack/fault-tolerant control system based on an event-triggered control framework. Through an examination of stability using the BMIs framework and the design of an observer, a feedback controller is derived to compute control inputs. The triggering mechanism for control input activation is determined based on a predefined threshold for error occurrence. A numerical validation is conducted using a three-tank system subjected to disturbances and attempts at sensor and actuator data falsification, yielding satisfactory results. Additionally, fault detection and attack isolation are facilitated through the utilization of a residual generator and observer. Future studies may explore extending the proposed synthesis methods to accommodate nonlinear output and generalizing the approach for robust schemes.