Reinforced Design and Temperature-Varying Compressive Performance Investigation of Aperiodic Honeycomb Metamaterials

1. Introduction

In recent years, inspired by disordered microstructures in biological materials (e.g., spider silk, bone, etc.), researchers have begun exploring the mechanical performance advantages of aperiodic metamaterials. Aperiodicity (disorder) is gradually revolutionizing the traditional design paradigm of ordered structures. This paradigm shift traces back to Shechtman’s 1984 discovery of quasicrystals (non-periodic atomic arrays) [1] and Gong et al.’s 2006 theoretical analysis using group theory, which revealed that quasicrystals exhibit superior isotropy compared to conventional crystals (periodic atomic arrays) [2]. These findings established a foundation for subsequent studies, demonstrating the inherent advantages of aperiodic (disordered) structural configurations in material design [3,4]. Subsequently, Hanifpour et al. [5] investigated the effects of disorder on the mechanical properties of auxetic materials, demonstrating that rationally controlled disorder could optimize their mechanical performance. Moat et al. [6] designed an aperiodic P3-based honeycomb structure inspired by non-periodic Penrose tiling [7], showing that aperiodic honeycombs outperform periodic square and hexagonal counterparts in reducing anisotropy while exhibiting more stable deformation during plastic stages. Recently, Choukir et al. [8] achieved a breakthrough by innovatively introducing disorder to overcome the traditional strength-toughness trade-off. In their study, 50,000 Voronoi networks with varying disorder levels were generated and evaluated through high-throughput finite-element simulations. Remarkably, some disordered networks demonstrated 20% higher strength and 100% greater toughness than regular hexagonal honeycombs. This breakthrough not only confirms the immense potential of aperiodic structures for mechanical optimization but also challenges the previous assumption that "only quasi-order enables superior performance". The study highlights that meticulous design of local geometric features enables exceptional strength and toughness across all disorder levels, significantly expanding the application prospects of aperiodic structures in material design.

Notably, aperiodic (disordered) structures cannot be constructed through periodic tiling of a single cell unit, requiring instead diverse cell configurations. This poses significant challenges for practical implementation. Consequently, researchers had long sought a single tile shape capable of continuously tiling infinite planes in an aperiodic manner. This quest was resolved in 2023 by mathematicians Smith et al. [9], who discovered the ‘einstein’ monotile. This monotile enables aperiodic tiling of infinite planes without symmetry or translational repetition. Subsequent work revealed that the ‘hat’ monotile belongs to an infinite family: by modifying the relative edge lengths of the ‘hat’ monotile, various monotiles could be derived, with only three specific cases (coordinates (0,1), (1,1), and (1,0)) failing to exhibit aperiodicity. This discovery sparked global interest in applying ‘einstein’ monotile to aperiodic metamaterial exploration.

Clarke and Moat et al. [10,11] pioneered the application of ‘einstein’ monotiles in aperiodic honeycomb metamaterial design. Initially, they designed an aperiodic honeycomb structure based on the ‘hat’ monotile, discovering that within the relative density range of 0.2-0.4, the structure exhibits near-zero Poisson’s ratio during elastic deformation, functioning as an isotropic zero-Poisson’s-ratio material. Subsequent studies with the ‘hat’ family demonstrated independent regulation of Poisson’s ratio and elastic modulus through geometric parameter adjustments while maintaining isotropic mechanical properties. Recently, Clarke et al. [12] combined numerical simulations and experimental testing to quantify specimen size effects on the predictability of mechanical properties in aperiodic honeycombs, establishing crucial theoretical foundations for their design and application. Jung et al. [13] investigated the fracture behavior of ‘hat’-based aperiodic composites through combined experiments and simulations, revealing superior stiffness, strength, and toughness compared to periodic structures. Wang et al. [14] developed a 3D microlattice structure based on the ‘hat’ monotile, experimentally verifying exceptional strength, toughness, and damage resistance. They further designed an aperiodic interpenetrating phase composite (IPC) [15] demonstrating unprecedented improvements in compressive strength and energy absorption. Rieger et al. [16] analyzed the macroscopic elastic behavior of ‘hat’ monotile through simulations and theoretical methods, confirming their isotropic elastic properties. Naji et al. [17] numerically estimated the effective elastic properties of novel 2D aperiodic lattice metamaterials derived from monotiles, revealing density-independent isotropic elastic behavior. Guo et al. [18] further demonstrated the mechanical superiority of aperiodic honeycombs over periodic counterparts through structural entropy analysis.

Later, Imediegwu et al. [19] generated diverse aperiodic lattice structures through mathematical substitution rules, comparative studies showing their mechanical advantages over periodic lattices in specific isotropy-driven scenarios. Liu et al. [20] proposed a node-based self-organizing method for generating novel disordered metamaterials, employing 34 structural descriptors to characterize morphological diversity and establish descriptor-property correlations, thereby providing a systematic framework for innovative structural design.

Honeycomb metamaterials [21,22,23], by emulating cellular organization patterns in biological tissues to construct periodic or aperiodic microstructural units, exhibit exceptional mechanical properties including high strength-to-weight ratio, ultralow density, and superior energy absorption capacity [24,25,26,27]. These remarkable characteristics have enabled broad applications in aerospace engineering [28], biomedical devices [29], impact-resistant structures [30], and flexible sensing systems [31].

Despite significant progress in disordered design of honeycomb metamaterials, current research remains constrained by critical limitations: most studies focus on macroscopic disorder in cell arrangement patterns while neglecting microscopic cell-internal design. Biological materials inspire us that multi-scale disordered synergy (e.g., glass-sponge-inspired lattice optimization [32], cuttlebone-inspired array structures [33], ironclad beetle’s jigsaw-like connections [34]) often produces extraordinary mechanical properties. Local cell design may influence metamaterial strength and toughness through micro-mechanisms like stress redistribution and energy dissipation pathways, necessitating further investigation.

Inspired by the ‘einstein’ monotile, this study designed four distinct aperiodic honeycomb unit cells through internal cell design optimization and fabricated corresponding aperiodically tiled honeycomb metamaterials using 3D printing technology. Compression experiments were conducted under varying temperature conditions to successfully obtain the equivalent stress-strain curves of these metamaterials at different temperatures. In parallel, quasi-static compression simulations were performed using the finite element analysis software ABAQUS to comparatively analyze the mechanical properties and energy absorption characteristics of the four metamaterials under thermal variations. This systematic evaluation revealed performance differences among the structures and uncovered temperature-dependent patterns in compressive modulus and compressive strength. Additionally, a focused comparative analysis of deformation characteristics was conducted between ambient temperature conditions and the vicinity of the glass transition temperature (Tg).

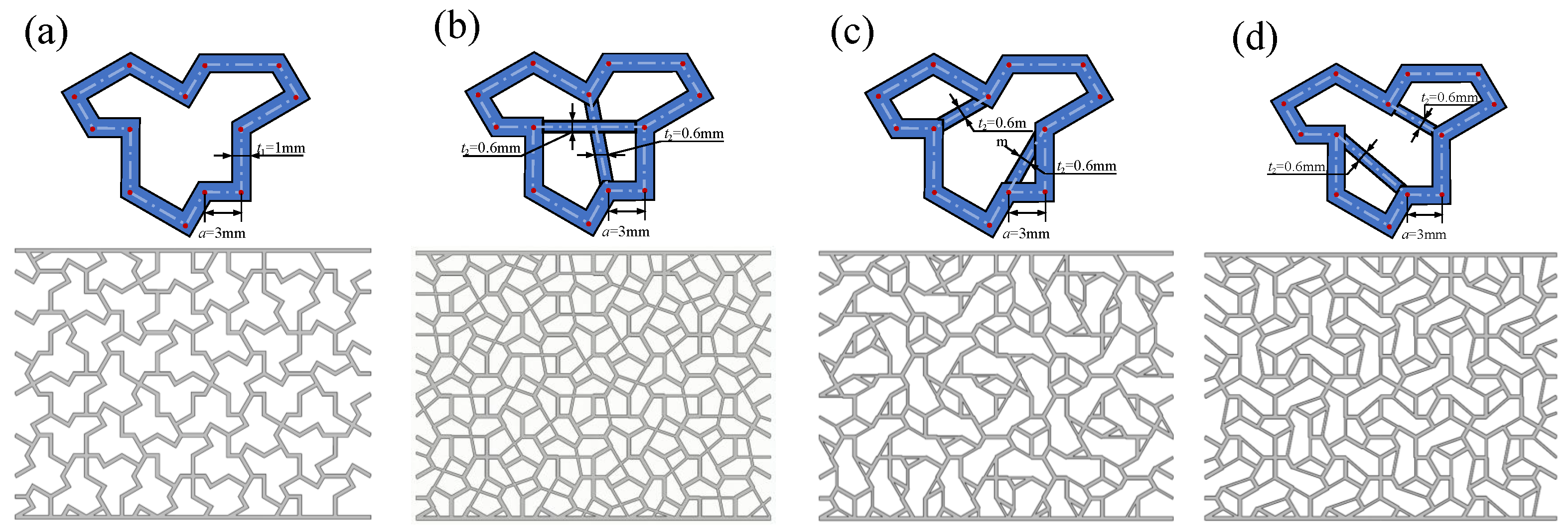
2. Design and Manufacturing

Based on the aperiodic tiling of the ‘einstein’ monotile in space, the ‘hat’ family is used as a unit cell for aperiodic tiling in metamaterial design, which exhibits superior mechanical properties compared to traditional periodic honeycomb structures. Therefore, this study takes the aperiodic ‘hat’ monotile as the basis, and connects the concave nodes of two ‘hat’ monomers to design three enhanced ‘hat’ unit cells, as shown in Figure 1. The four concave points of the ‘hat’ monotile are named and marked as A, B, C, and D. The ‘hat’-ACBD monomer is designed by connecting the diagonal concave points of the ‘hat’ monotile, while the ‘hat’-ADCB and ‘hat’-ABDC monomers are designed by connecting the concave points on one side of the ‘hat’ monotile. The four monomers in Figure 1 are designed into four types of honeycomb unit cells and aperiodically tiled to form four types of honeycomb metamaterials. A series of geometric parameters are established, with the side length of the ‘hat’ monotile $a=3$ mm, wall thickness $t_1=1$ mm, and the thickness of the concave point connection support $t_2=0.6$ mm, as shown in Figure 2.

This study fabricated the four honeycomb metamaterials using 3D printing technology based on the fused deposition modeling (FDM) principle, with acrylonitrile butadiene styrene (ABS) filament as the printing material. The material density is $1.05{\mathrm{g}/\mathrm{cm}}^3$, with a layer height of $0.2\mathrm{mm}$ and a printing speed of $30\mathrm{mm}/\mathrm{s}$ to ensure interlayer adhesion and detail resolution. The ABS material exhibits high strength, ease of processing, good dimensional stability, and recyclability. Figure 3 shows the specimens of the four honeycomb metamaterials, all with envelope dimensions of $90\mathrm{mm}\times 39\sqrt{3}\mathrm{mm}\times 16\mathrm{mm}$ (cell wall thicknesses as shown in Figure 2). All specimens were weighed to calculate the relative density and specific energy absorption, where the reference “hat” honeycomb metamaterial has a relative density of $0.2$.

3. Experimental

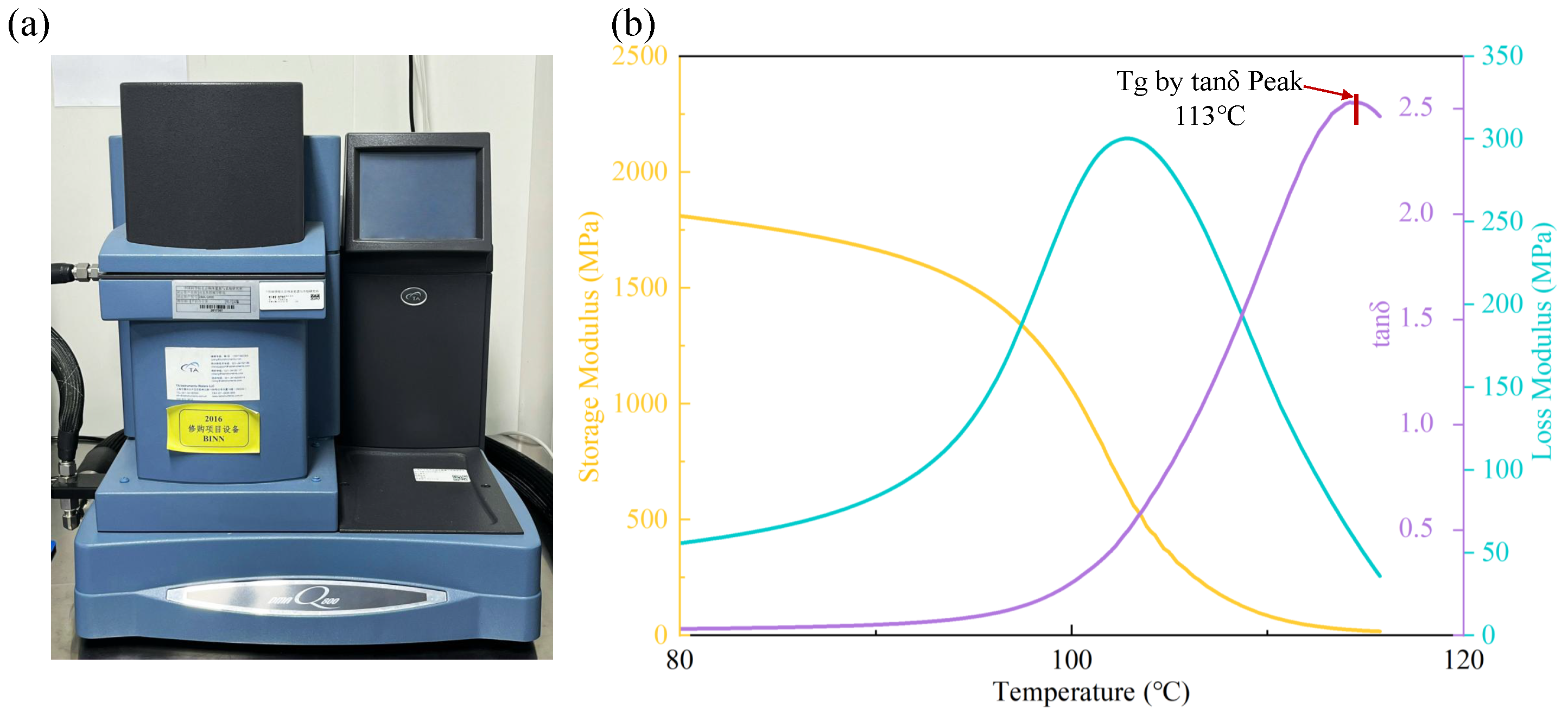
3.1. Material Characterization

Material characterization of the honeycomb metamaterials was conducted, with the obtained properties implemented into finite element simulations to simulate their quasi-static compressive deformation behavior.

The glass transition temperature ($T_g$) [35] is the temperature at which a material transitions from a glassy state to a highly elastic state, directly influencing its serviceability and processability. ABS exhibits elastoplastic behavior at room temperature but transforms into a softer, more elastic rubbery state at elevated temperatures. While the $T_g$ of ABS typically approximates ${105}^{\circ }\mathrm{C}$, variations may occur due to formulation differences, processing conditions, or additives. To determine the $T_g$ of the ABS material used in this study, tensile specimens ($30\mathrm{mm}\times 8\mathrm{mm}\times 0.5\mathrm{mm}$) were fabricated via fused deposition modeling (FDM). Dynamic mechanical analysis (DMA Q800) was conducted across a temperature range spanning from ${80}^{\circ }\mathrm{C}$ to ${120}^{\circ }\mathrm{C}$, applying cyclic stress/strain to measure temperature-dependent storage modulus ($E^{\prime }$), loss modulus ($E^{\prime \prime }$), and loss factor ($tan\delta ={\displaystyle \frac{E^{\prime \prime }}{E^{\prime }}}$), as shown in Figure 4. The $T_g$ was identified as ${113}^{\circ }\mathrm{C}$ based on the peak of the loss factor ($tan\delta$).

In accordance with ISO 527-2, ABS dogbone specimens were fabricated via fused deposition modeling (FDM), with tensile specimens printed along the loading direction. The experimental setup and specimen dimensions are shown Figure 5(a). Quasi-static isothermal tensile tests were conducted using a universal testing machine (MTS) coupled with a temperature-controlled chamber (SanDu) at ${25}^{\circ }\mathrm{C}$, ${60}^{\circ }\mathrm{C}$, ${105}^{\circ }\mathrm{C}$, and ${115}^{\circ }\mathrm{C}$, with a crosshead speed of $2\mathrm{mm}/\min$. Figure 5(b) presents the nominal stress-strain curves, which were converted to true stress-strain relationships to extract fundamental material properties. The results indicate that the elastic modulus of ABS at ${60}^{\circ }\mathrm{C}$ remains comparable to room-temperature values, retaining elastoplastic behavior. However, near the $T_g$, the elastic modulus decreases significantly due to activation of polymer chain mobility: molecular segments gain sufficient energy to overcome thermal barriers, enabling relative motion and reducing overall rigidity.

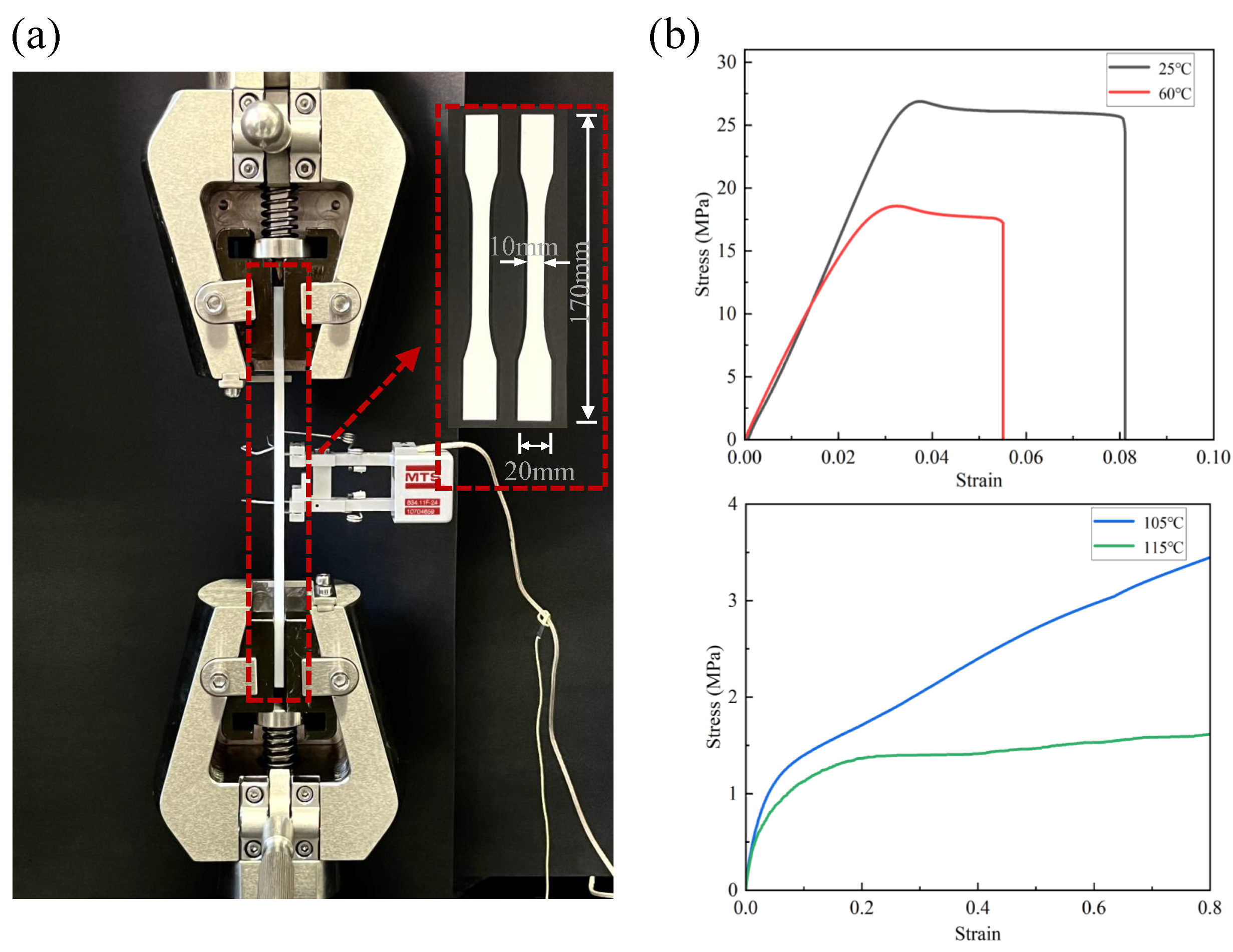
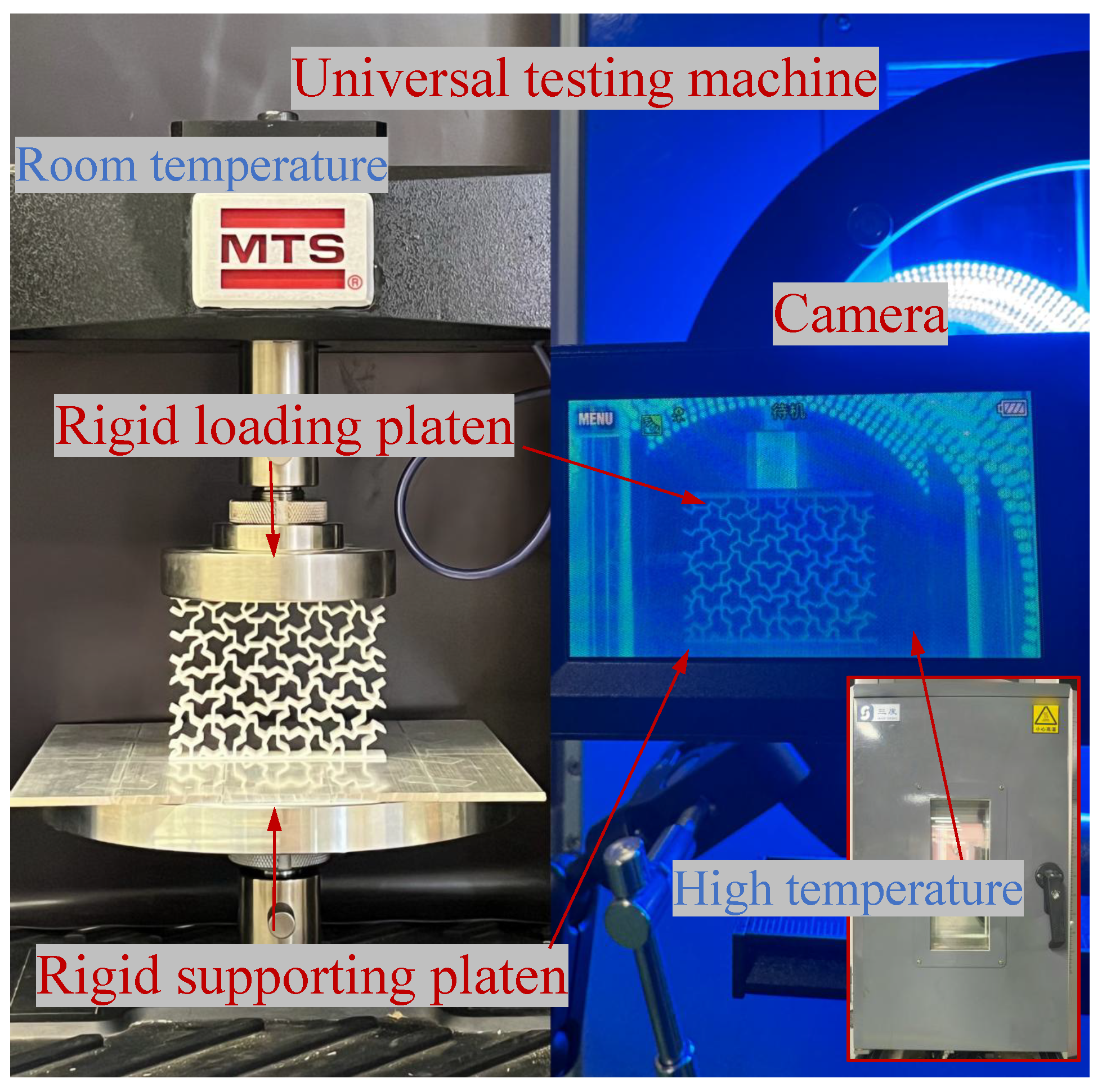
3.2. Compression Test

The unit cell design of honeycomb metamaterial structures determines their mechanical properties and energy absorption capabilities. To evaluate the mechanical properties and energy absorption capabilities of four types of honeycomb metamaterials under variable temperatures, quasi-static compression tests were conducted using a universal testing machine (MTS) integrated with a temperature-controlled chamber (SanDu) at variable temperatures, as shown in Figure 6. Four temperature conditions were selected: ${25}^{\circ }\mathrm{C}$, ${60}^{\circ }\mathrm{C}$, ${105}^{\circ }\mathrm{C}$, and ${115}^{\circ }\mathrm{C}$, which allows for a better investigation of the mechanical properties and energy absorption performance of honeycomb metamaterials at different temperatures. The specimens were loaded using a displacement-controlled method with a loading rate of $4\mathrm{mm}/\min$, and the loading process continued until the densification stage of the specimens was reached. To ensure the reliability of the experiments, three parallel tests were conducted for the same type of specimen under identical conditions, and the data acquisition system of the equipment accurately recorded the entire testing process. A camera was used to document the deformation of the specimens during the compression process. To clearly record the compression of the specimens inside the temperature chamber, blue light illumination was employed for photography.

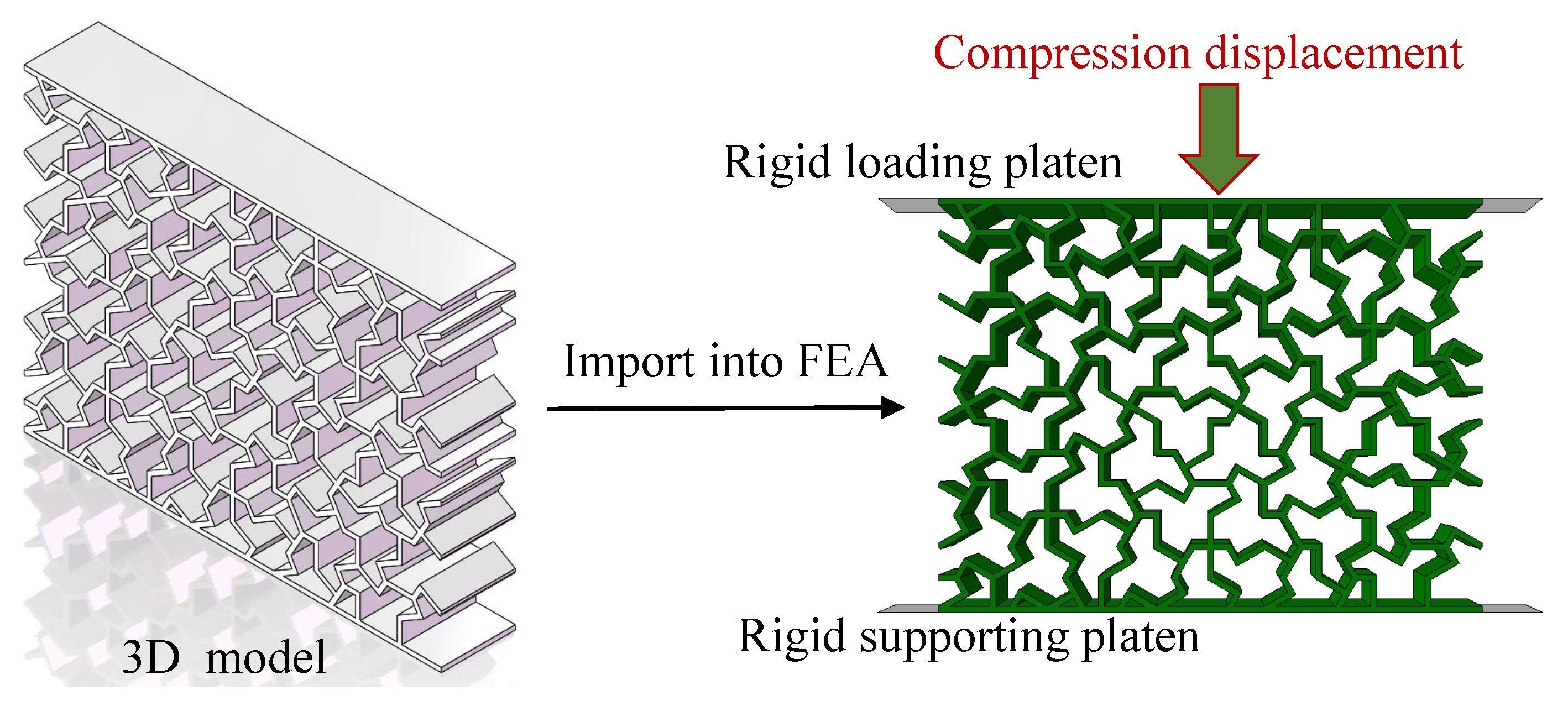
4. Numerical Simulation

The compressive mechanical properties and deformation characteristics of four types of honeycomb metamaterials at different temperatures were studied by ABAQUS/EXPLICIT numerical simulation. The explicit dynamics of this software can effectively address issues such as the nonlinearity of the structure, large deformations, and complex contact interactions. The finite element modeling process is shown in Figure 7. First, models of the four types of honeycomb metamaterials were established using a 3D modeling software and then imported into the finite element software. The setup of the finite element model reflects the experimental apparatus. To simulate the compressive testing state of the structure, rigid plates were placed on the upper and lower surfaces of the structure. The in-plane longitudinal direction of the finite element model is the Y direction, and the in-plane transverse direction is the X direction. Throughout the simulation, the bottom support plate was fully constrained, while the top loading plate moved at a constant velocity in the Y direction, with all other degrees of freedom restricted. A ductile damage model was employed to simulate the damage and fracture behavior of the honeycomb metamaterials during compressive deformation. To prevent interpenetration between unit cells, the contact settings were defined as general contact with “hard” normal behavior. The 3D model utilized 8-node C3D8R solid elements, and hexahedral meshes were generated through free meshing. A global element size of $0.8\mathrm{mm}$ was selected for numerical simulation after mesh convergence validation.

5. Results and Discussion

5.1. Compressive Mechanical Properties

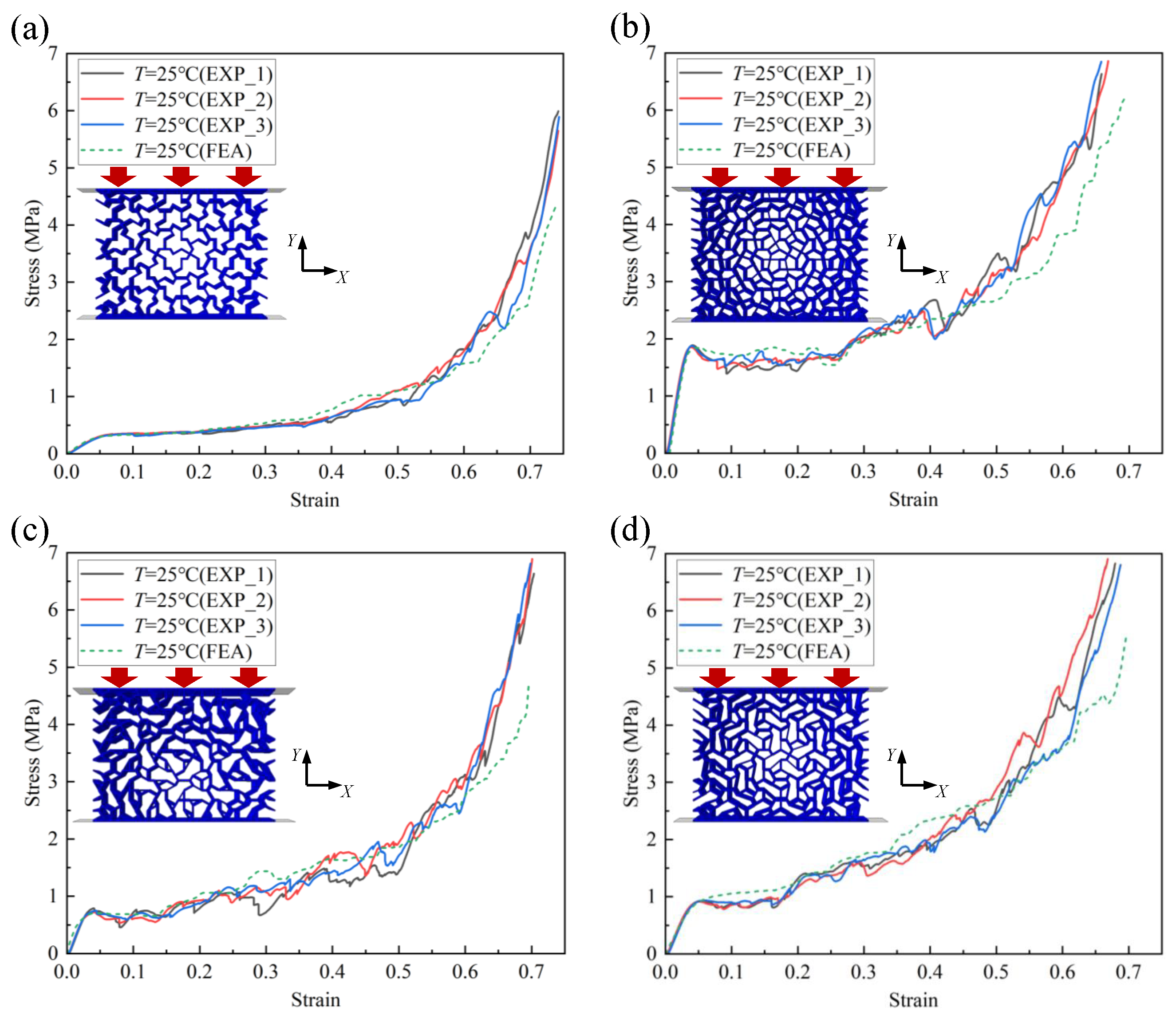
5.1.1. Quasi-Static Compressive Mechanical Properties at Room Temperature

The experimental results were compared and validated with the finite element simulation results. The experimental data of the four types of honeycomb metamaterials at room temperature (${25}^{\circ }\mathrm{C}$) were processed, and the force-displacement (F-S) curves were converted into equivalent stress and strain curves, as shown in the following formulas:

$${\sigma }_{eq}={\displaystyle \frac{F}{Lb}},{\epsilon }_{eq}={\displaystyle \frac{S}{H}},$$

(1)

where L, b, and H represent the length, width, and height of the honeycomb metamaterial specimen.

As shown in Figure 8, the experimental data and simulation results of the four honeycomb metamaterials demonstrate strong consistency, validating the accuracy of the finite element simulation methodology. During the initial elastic phase, the stress of all four metamaterials increases quasi-linearly to their compressive strengths. The unit cell of the ‘hat’ honeycomb metamaterial, lacking internal support, exhibits a relatively low initial peak stress. However, the aperiodic arrangement of the concave corners in the unit cell effectively suppresses significant lateral deformation of the structure. As a result, the stress remains stable during the plateau stage without any significant stress drop. This further demonstrates that the stress distribution in aperiodically arranged metamaterial structures is uniform. The compressive strength of the three honeycomb metamaterials with added internal support in the unit cell is significantly enhanced, among which the ‘hat’-ACBD honeycomb metamaterial shows a more pronounced improvement. After the elastic stage, due to the local failure of the internal support structure of the unit cell in the early stage of the plastic phase, the ‘hat’-ADCB honeycomb metamaterial exhibits a significant stress drop following the initial peak stress. In contrast, the other two types of honeycomb metamaterials experience only a slight stress decrease after reaching the initial peak stress and maintain a relatively high plateau stress. When the equivalent compressive strain of the honeycomb metamaterials exceeds $0.6$ at room temperature, the structure enters the densification stage, which marks the end of the effective compression process. Experimental results indicate that the three enhanced ‘hat’ honeycomb metamaterial structures demonstrate a higher stress response compared to the basic ‘hat’ honeycomb metamaterial.

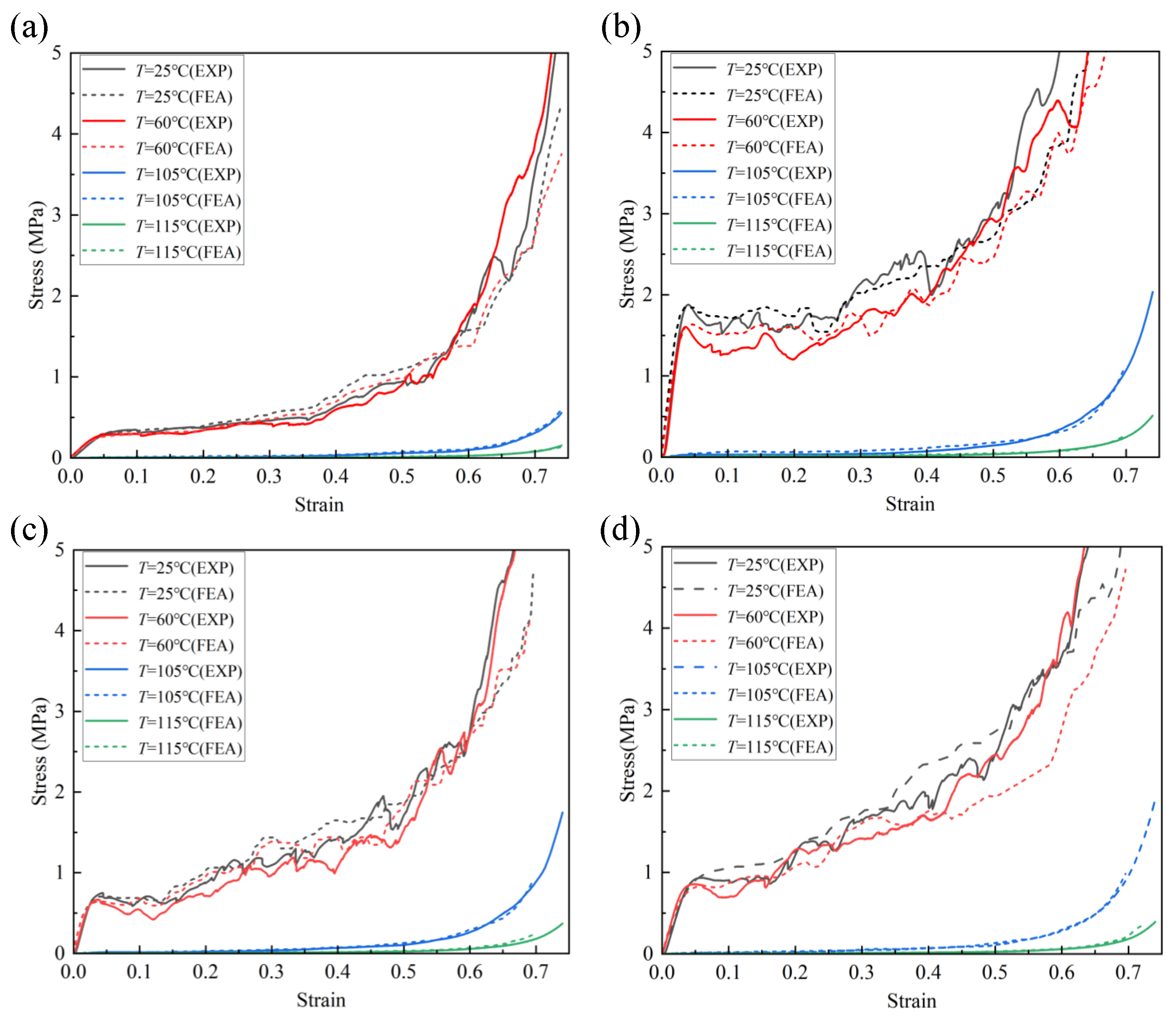
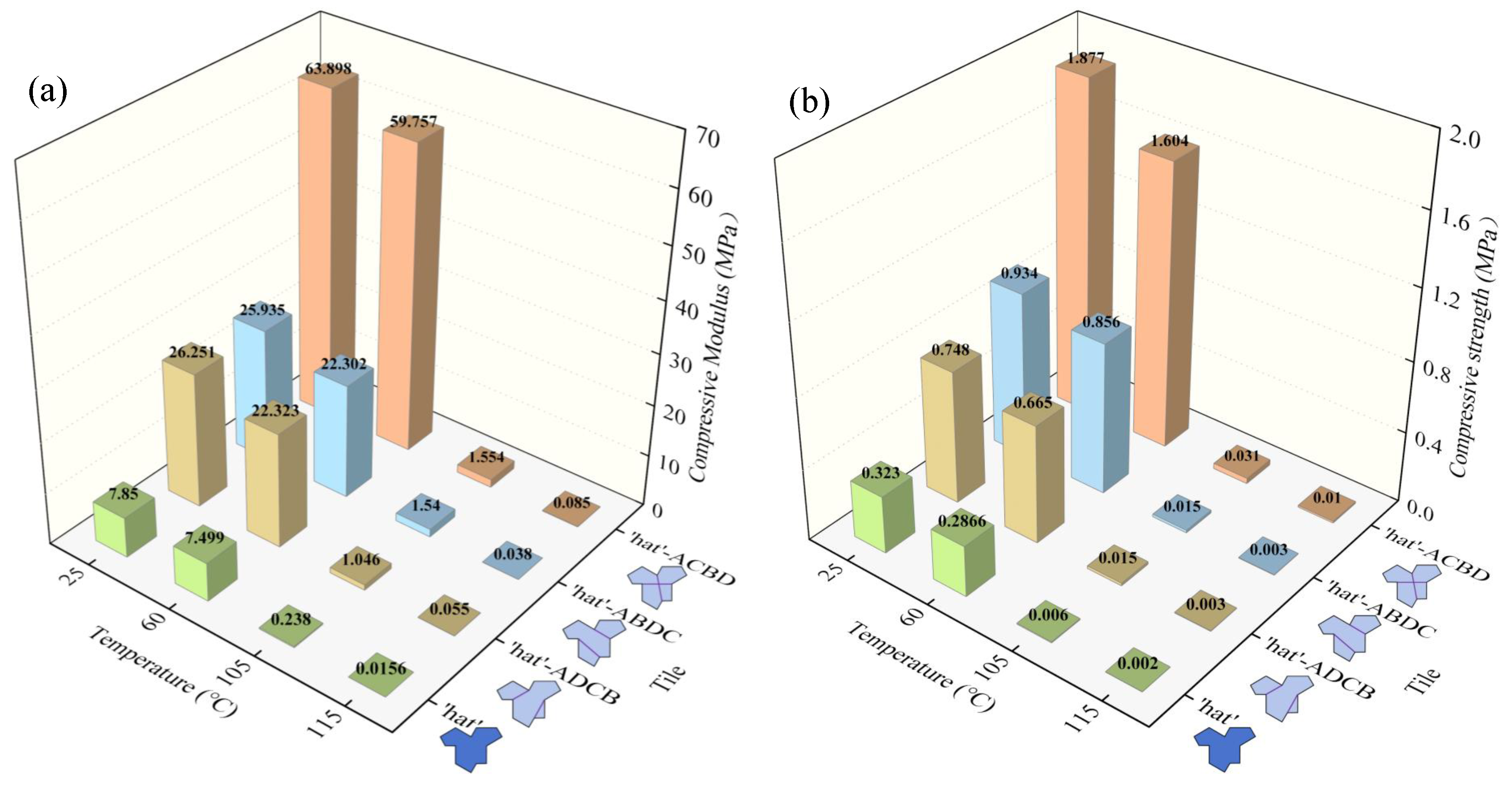
5.1.2. Quasi-Static Compressive Mechanical Properties at Variable Temperatures

ABS resin is a thermoplastic material whose mechanical properties are highly influenced by temperature. The $T_g$ of the material used is approximately ${113}^{\circ }\mathrm{C}$. To investigate the effect of temperature changes on the mechanical properties of four types of honeycomb metamaterials, we conducted compression tests at temperatures of ${25}^{\circ }\mathrm{C}$, ${60}^{\circ }\mathrm{C}$, ${105}^{\circ }\mathrm{C}$, and ${115}^{\circ }\mathrm{C}$ and established corresponding finite element simulations. Figure 9 shows the equivalent stress-strain curves of the four honeycomb metamaterials at different temperatures. It can be seen that as the temperature increases, the stress response of the honeycomb metamaterials gradually decreases until the temperature approaches their $T_g$. Since ${60}^{\circ }\mathrm{C}$ is still below the $T_g$ of ABS material, the molecular activity within the material is not significant in the temperature range of ${25}^{\circ }\mathrm{C}$ to ${60}^{\circ }\mathrm{C}$, and thus the difference in elastic modulus at these two temperatures is small. This makes the equivalent stress-strain curves of the honeycomb metamaterials at these two temperatures relatively close, which is consistent with the results obtained from our material property experiments. When the temperature reaches ${105}^{\circ }\mathrm{C}$, the material has already undergone significant softening. Therefore, when the temperature approaches or exceeds $T_g$ ($T_g={113}^{\circ }\mathrm{C}$), the fluctuations in stress response are no longer obvious. Finally, as the temperature increases further, the stiffness of the material decreases, causing the compressive stress response curves of the honeycomb metamaterials to become smoother. There are slight differences between the finite element simulation results and the experimental data, which may be attributed to minor dimensional errors that may occur during the 3D printing process and the complexity of material molecular behavior at high temperatures. Overall, the experimental data and simulation results at different temperatures show good consistency.

The compressive modulus of the structures was obtained by linearly fitting the initial elastic stage of the equivalent stress-strain curves. The relationship between the compressive modulus of the four honeycomb metamaterials and temperature changes is shown in Figure 10(a). It can be clearly seen that the compressive modulus decreases with increasing temperature, with a relatively smooth decline between ${25}^{\circ }\mathrm{C}$ and ${60}^{\circ }\mathrm{C}$, and a sharp drop between ${60}^{\circ }\mathrm{C}$ and ${105}^{\circ }\mathrm{C}$. The initial peak stress of the equivalent stress-strain curve was taken as the compressive strength of the structure. The relationship between the compressive strength of the four honeycomb metamaterials and temperature changes is shown in Figure 10(b), which is consistent with the trend of the compressive modulus with temperature. These four honeycomb metamaterials exhibit similar trends with temperature changes. By comparing the compressive modulus and compressive strength of the four honeycomb metamaterials at different temperatures, it can be seen that adding internal support to the unit cells effectively improves the mechanical properties of the structures between ${25}^{\circ }\mathrm{C}$ and ${60}^{\circ }\mathrm{C}$, with the compressive modulus and compressive strength increasing by approximately 3 to 8 times. However, near the $T_g$ (between ${105}^{\circ }\mathrm{C}$ and ${115}^{\circ }\mathrm{C}$), the strength of the structures drops sharply. Notably, the ‘hat’-ACBD honeycomb metamaterial retains relatively superior strength and stiffness even under these conditions. Since the error in the initial linear elastic stage of the three parallel tests for each structure was less than 5%, the average values were taken for presentation.

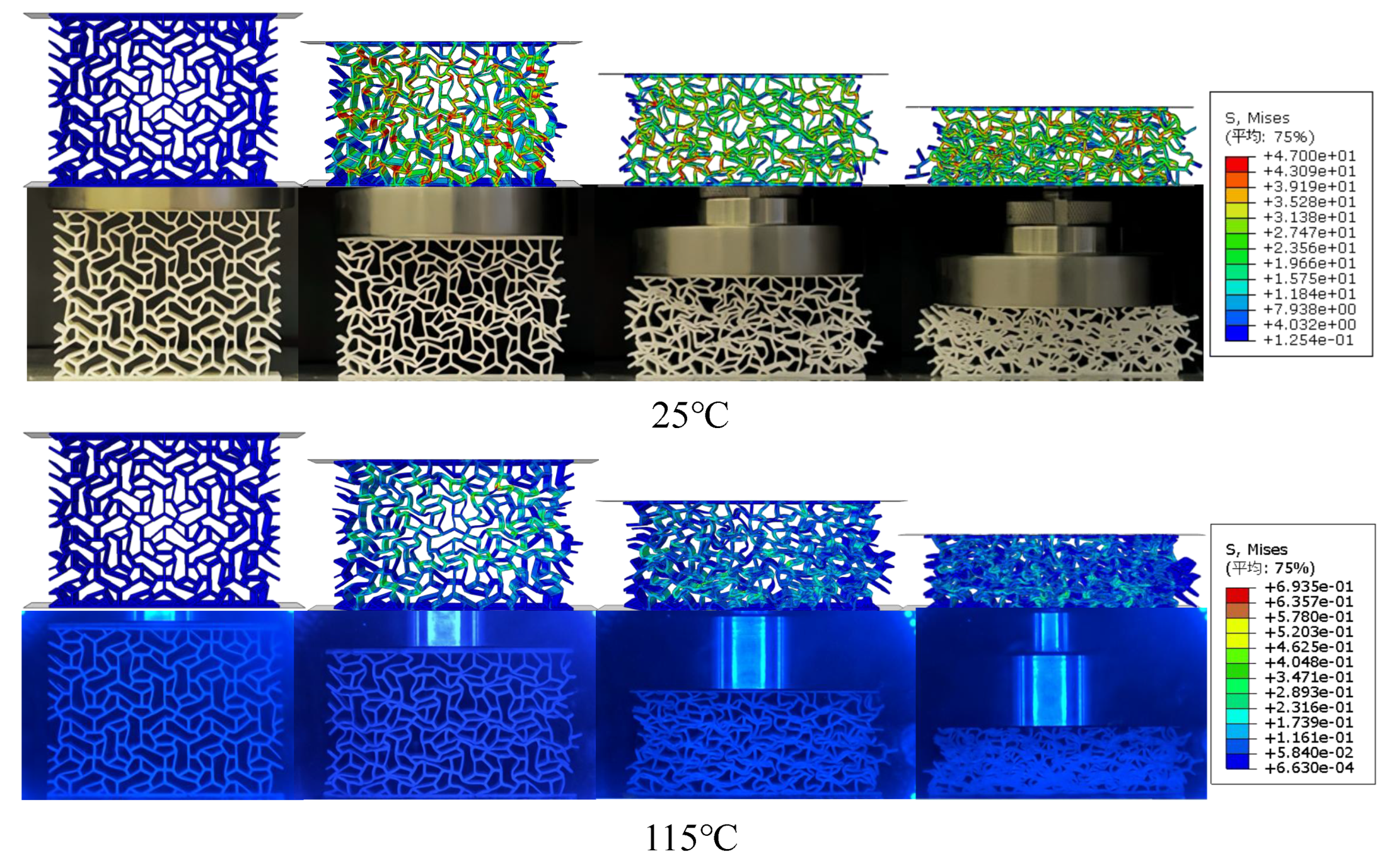
5.2. Compressive Deformation Characteristics

5.2.1. Macrostructural Compressive Deformation Characteristics

The mechanical properties and damage mechanisms of honeycomb metamaterials can be effectively assessed by studying their deformation modes. Given that ABS material exhibits elastoplastic behavior between ${25}^{\circ }\mathrm{C}$ and ${60}^{\circ }\mathrm{C}$ and shows a highly elastic state between ${105}^{\circ }\mathrm{C}$ and ${115}^{\circ }\mathrm{C}$ (near the $T_g$), this study selected the deformation processes of honeycomb metamaterials at ${25}^{\circ }\mathrm{C}$ and ${115}^{\circ }\mathrm{C}$ for analysis. Specifically, the deformations of the four types of honeycomb metamaterials at equivalent strains of approximately 0, $0.2$, $0.44$, and $0.32$ were captured, and the experimental results were compared with the finite element simulation results. The relevant results are shown in in Figure 11, Figure 12, Figure 13 and Figure 14.

Figure 11 shows the experimental and simulated deformation processes of the ‘hat’ honeycomb metamaterial at different temperatures. According to the Mises stress diagram output by the finite element simulation, it is evident that the structure has a higher stiffness at ${25}^{\circ }\mathrm{C}$. At an equivalent strain of approximately $0.2$, the stress distribution indicates that the structure undergoes lateral band-like deformation. However, due to the aperiodic arrangement, the movement of adjacent ‘hat’ unit cells is not in the same direction. Instead, the concave corners of the unit cells resist each other, thereby suppressing excessive lateral deformation. This phenomenon is consistent with the research results of Moat et al. [9]. We also agree with their description of the flexibility of the interstitial struts of the ‘hat’ unit cells (similar to a spring assembly of three struts). These “springs” can adapt to large deformations through wrinkling, hinging, and a certain degree of correction, and they are more effective in resisting deformation than continuous struts. Throughout the compression process, the structure maintains a stable deformation mode, which corresponds to the stable stress in the plateau stage after the initial peak stress in Figure 8(a). When the temperature reaches ${115}^{\circ }\mathrm{C}$, higher than the material’s $T_g$, the stiffness of the structure significantly decreases, and it is more prone to deformation under load. However, the stress distribution and deformation mode throughout the process remain consistent with those at ${25}^{\circ }\mathrm{C}$. Under continuous compressive strain, the structure exhibits a progressive collapse behavior until it is fully densified. The finite element deformation model is consistent with the experimental results.

Figure 12 shows the experimental and simulated deformation processes of the ‘hat’-ACBD honeycomb metamaterial at different temperatures. The Mises stress diagram output from the finite element simulation indicates that during compression, the ‘hat’-ACBD honeycomb metamaterial exhibits uniform deformation without significant localized premature failure or instability. By adding supports through connecting the diagonal concave points of the ‘hat’ cells, a bidirectional bending-resistant mechanism is formed within the cells, where the supports resist external stresses through bending deformation. Although the addition of supports increases the mass of the specimen, the compressive strength is approximately six times higher than that of the traditional ‘hat’ honeycomb metamaterial, as shown in Figure 10(b), which also has a significant impact on the specific energy absorption of the structure. As the temperature rises, the stiffness of the structure decreases, but the deformation process remains stable. The overall design enables more uniform stress distribution, resulting in higher stress levels on the macroscopic equivalent stress-strain curves, consistent with the results shown in Figure 9(b). Under continuous compressive strain, the structure exhibits a progressive collapse behavior until it is fully densified. The finite element deformation model is highly consistent with the experimental results.

Figure 13 shows the experimental and simulated deformation processes of the ‘hat’-ADCB honeycomb metamaterial at different temperatures. The Mises stress diagram output from the finite element simulation indicates that during compression, the ‘hat’-ADCB honeycomb metamaterial initially exhibits localized diagonal band-like deformation with relatively non-uniform stress distribution. This phenomenon likely stems from the introduced supports modifying stress transfer pathways, thereby concentrating higher stresses in specific regions. However, as the compressive strain increases, at an equivalent strain of approximately $0.44$, the structure gradually homogenizes its stress distribution through coordinated deformation of the internal unit cells until full densification is achieved. Under high-temperature conditions, the structure’s stiffness decreases, leading to localized buckling. The ‘hat’-ADCB honeycomb metamaterial enhances its compressive strength by adding supports through the connection of the concave points on one side of the unit cells, compared to ‘hat’ honeycomb metamaterials. However, the overall stability of the structure is not significantly improved. The finite element deformation model is consistent with the experimental results.

Figure 14 shows the experimental and simulated deformation processes of the ‘hat’-ABDC honeycomb metamaterial at different temperatures. The Mises stress diagram output from the finite element simulation indicates that during compression, the ‘hat’-ABDC honeycomb metamaterial exhibits uniform deformation with relatively uniform stress distribution. Even under high-temperature conditions, although the stiffness of the structure decreases, only slight local deformation occurs, and the overall stability remains good. The finite element deformation model is consistent with the experimental results. The ‘hat’-ABDC honeycomb metamaterial also enhances its mechanical properties by adding supports through the connection of the concave points on one side of the unit cells, but its mechanical performance is significantly better than that of the ‘hat’-ADCB honeycomb metamaterial. This suggests that the supports added through different concave point connections within the unit cells have significantly different effects on the mechanical properties of the structure. The finite element deformation model is consistent with the experimental results.

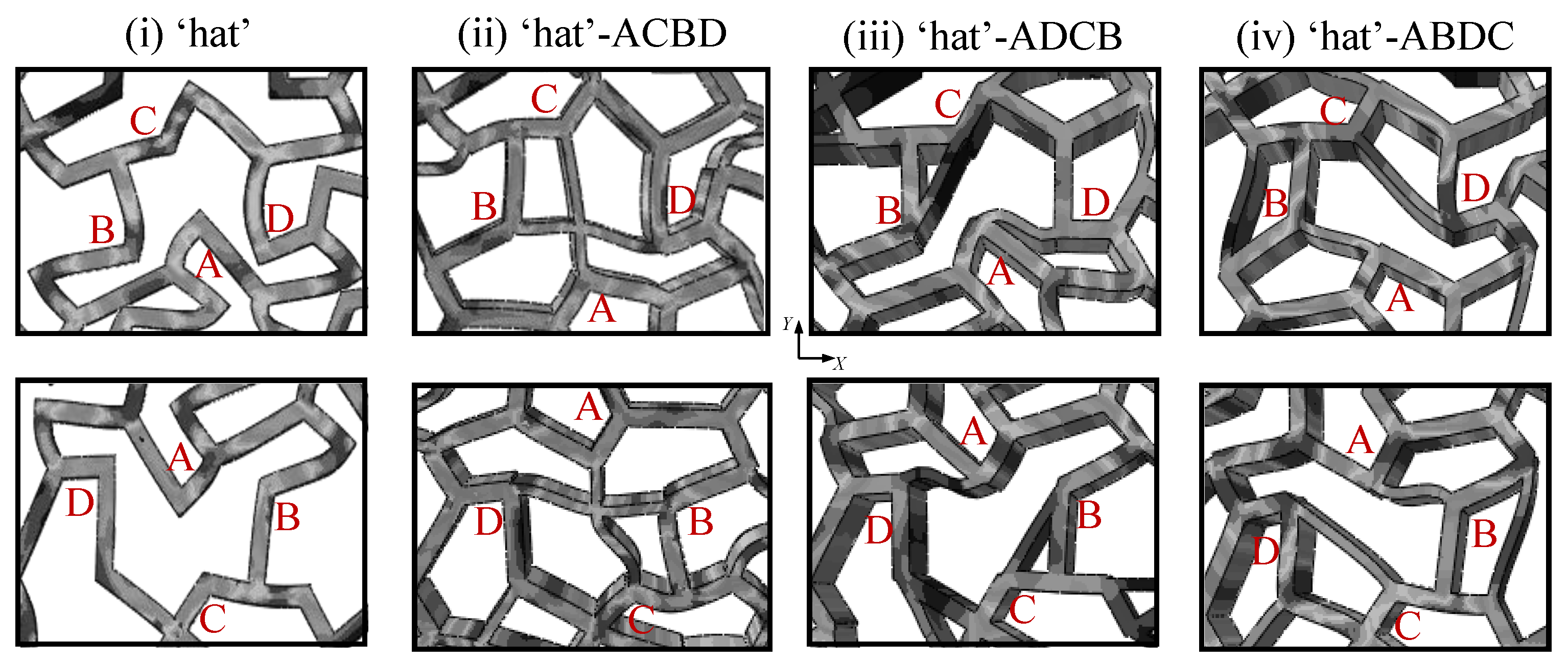
5.2.2. Microscale Unit Cell Deformation Characteristics

Investigating the unit cell deformation of honeycomb metamaterials helps to establish the correlation system of “microstructure-deformation mechanism-macroscopic properties,” which can provide a more comprehensive understanding of the structural deformation characteristics and thereby offer theoretical basis and guidance for structural design and optimization. In the four sets of finite element models, two representative unit cells with consistent geometric positions were selected to conduct comparative analyses on the deformation of the single cells of the four types of honeycomb metamaterials, as shown in Figure 15. Under compressive stress, the concave corners of the ‘hat’ unit cells move inward. However, due to the characteristic of aperiodic arrangement, the movement directions of each unit cell are inconsistent. In this way, the unit cells can coordinate bending deformation through their concave corners to suppress lateral deformation. Meanwhile, the convex corners of the unit cells sometimes coincide with the concave corners of the surrounding unit cells, which can effectively resist the lateral deformation of the structure. However, the concave angles of unit cells are prone to stress concentration, compromising load transfer and structural stiffness. Thus, rational incorporation of internal supports within unit cells helps optimize stress distribution while enhancing structural stability and reliability. The ‘hat’-ACBD unit cells add supports by connecting the diagonal concave points, forming a bidirectional anti-bending mechanism within the unit cells. The supports resist external stress through bending deformation, which can significantly increase the stiffness of the structure. As can be seen from Figure 15, both the ‘hat’-ADCB and ‘hat’-ABDC unit cells add supports by connecting the concave points on one side. The AD support beam of the ‘hat’-ADCB unit cells fails prematurely due to buckling, and the effective span of the BC support beam within the unit cells is relatively small, resulting in a reduced load-bearing contribution. Although the AB support beam of the ‘hat’-ABDC unit cells also fails relatively early, the DC support beam spans across the interior of the unit cells and can better resist internal deformation.

The analysis of the microscopic deformation of the four types of honeycomb unit cells and the macroscopic deformation of the four types of honeycomb metamaterials revealed that the results are highly consistent with each other and are in agreement with the stress response curves of the structures.

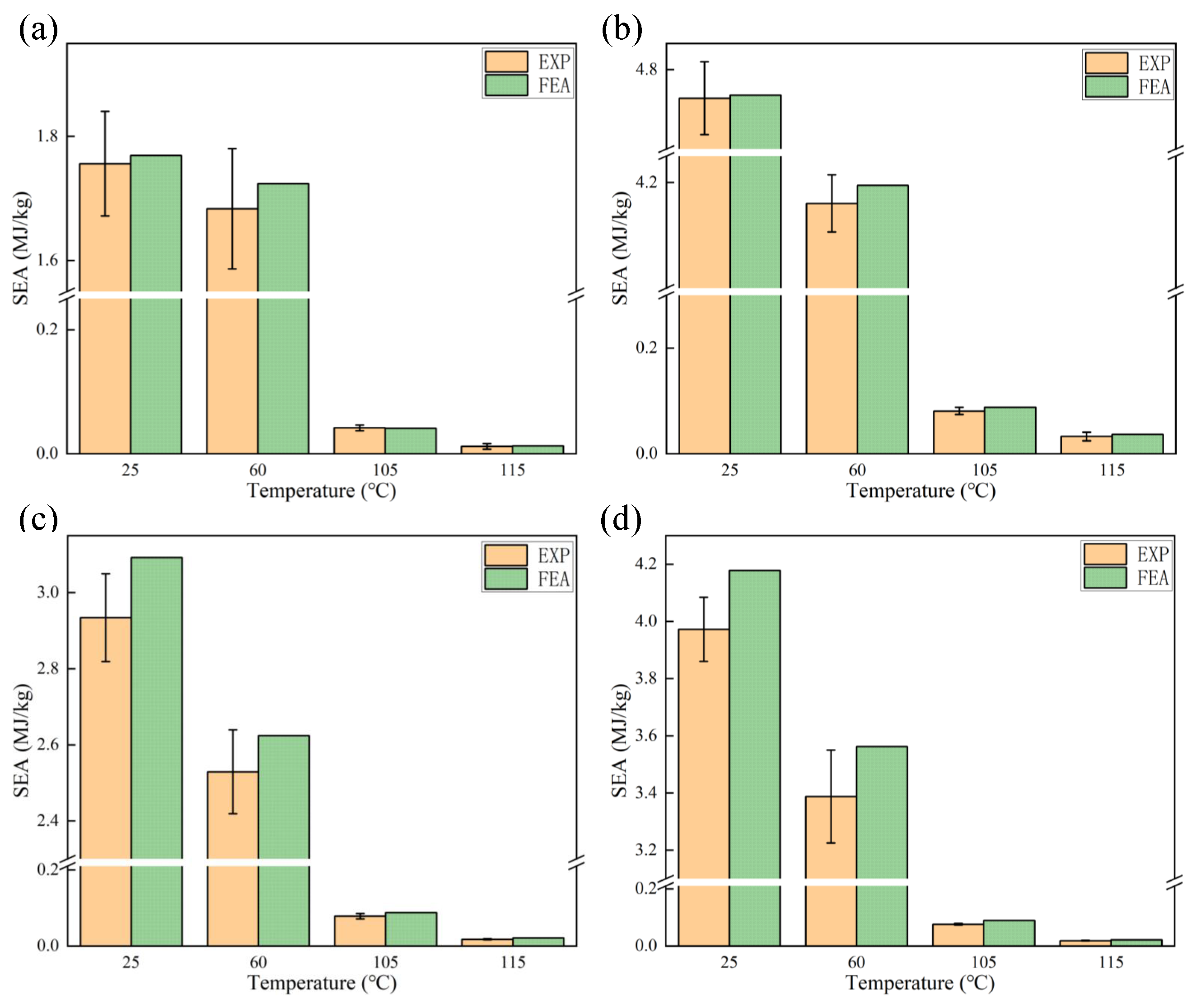
5.3. Absorption Performance Analysis

Energy absorption (EA) and specific energy absorption (SEA) can quantitatively assess a structure’s energy absorption capability, with the values of EA and SEA being directly proportional to the structure’s energy absorption capability. Since different structures have different masses, to fairly compare the energy absorption performance among various structures, we adopt SEA as the measure. It is defined as the ratio of energy absorption to mass, as given by Equation (2):

$$SEA={\displaystyle \frac{EA}{M}},$$

(2)

Where M represents the mass of the energy-absorbing structure, and EA denotes the energy absorbed under a specific compressive strain. EA is obtained by integrating the stress-strain curve under the specific compressive strain, with the calculation method given by Equation (3):

$$EA={\int }_0^{\epsilon }\sigma \left(\epsilon \right)d\epsilon$$

(3)

We take the compaction strain ${\epsilon }_D$ of the structure. During the compaction process of the structure, the strain gradually increases with the increase of stress until it reaches a relatively stable plateau region. This plateau region typically corresponds to the densification stage of the structure, during which the pores or voids within the structure undergo significant compression. As the strain continues to increase, the stress rises sharply, indicating that the material has reached its compaction strain point. At this point, the pores or voids are compressed to the maximum extent, and the density of the material reaches its peak.

Based on the variation patterns of the stress-strain curves of the structures, we determined the compaction strains of the four types of honeycomb metamaterials at different temperatures. Under the conditions of ${25}^{\circ }\mathrm{C}$, ${60}^{\circ }\mathrm{C}$, ${105}^{\circ }\mathrm{C}$, and ${115}^{\circ }\mathrm{C}$, the compaction strains of these four honeycomb metamaterials are approximately $0.6$, $0.6$, $0.5$, and $0.5$, respectively. The experimental data and finite element simulation data of the SEA of the four honeycomb metamaterials at different temperatures are compared in Figure 16. It can be seen that as the temperature increases, the SEA of the four honeycomb metamaterials all show a downward trend. When the temperature exceeds the $T_g$ of the material, the molecular motion of the material intensifies and its viscoelastic behavior gradually becomes dominant, which may mask the performance differences caused by different structural designs. Therefore, the SEA of the four honeycomb metamaterials tends to stabilize.

As can be seen from Figure 16, at ${25}^{\circ }\mathrm{C}$ and ${60}^{\circ }\mathrm{C}$, the SEA of the ‘hat’-ACBD honeycomb metamaterial is higher than that of the other three types of honeycomb metamaterials. This is mainly attributed to the fact that the ‘hat’-ACBD honeycomb metamaterial exhibits the highest stiffness and strength at different temperatures and shows good stability during the compaction process. Although both the ‘hat’-ADCB and ‘hat’-ABDC honeycomb metamaterials increase support by connecting the concave points on one side of the unit cells, the ‘hat’-ABDC honeycomb metamaterial demonstrates superior energy absorption capability, which is consistent with the analysis of structural mechanical properties and deformation characteristics. At ${105}^{\circ }\mathrm{C}$, the SEA of the ‘hat’-ACBD, ‘hat’-ADCB, and ‘hat’-ABDC honeycomb metamaterials is essentially the same, while the SEA of the ‘hat’ honeycomb metamaterial is relatively lower. When the temperature rises to ${115}^{\circ }\mathrm{C}$, the SEA of the ‘hat’-ACBD honeycomb metamaterial reaches the maximum value, the SEA of the ‘hat’-ADCB and ‘hat’-ABDC honeycomb metamaterials is basically the same, and the SEA of the ‘hat’ honeycomb metamaterial remains the smallest. The total energy absorption results obtained from finite element simulation are basically consistent with the experimental data.

6. Conclusions

This study utilized the aperiodic tiling principle of the ‘einstein’ monotile to design four types of honeycomb metamaterials with aperiodically unit cell arrangements, fabricated via 3D printing technology. Comprehensive evaluations of their compressive mechanical properties, deformation characteristics, and energy absorption capacities under varying temperatures were conducted through finite element simulations and quasi-static compression experiments. The key conclusions are summarized as follows:

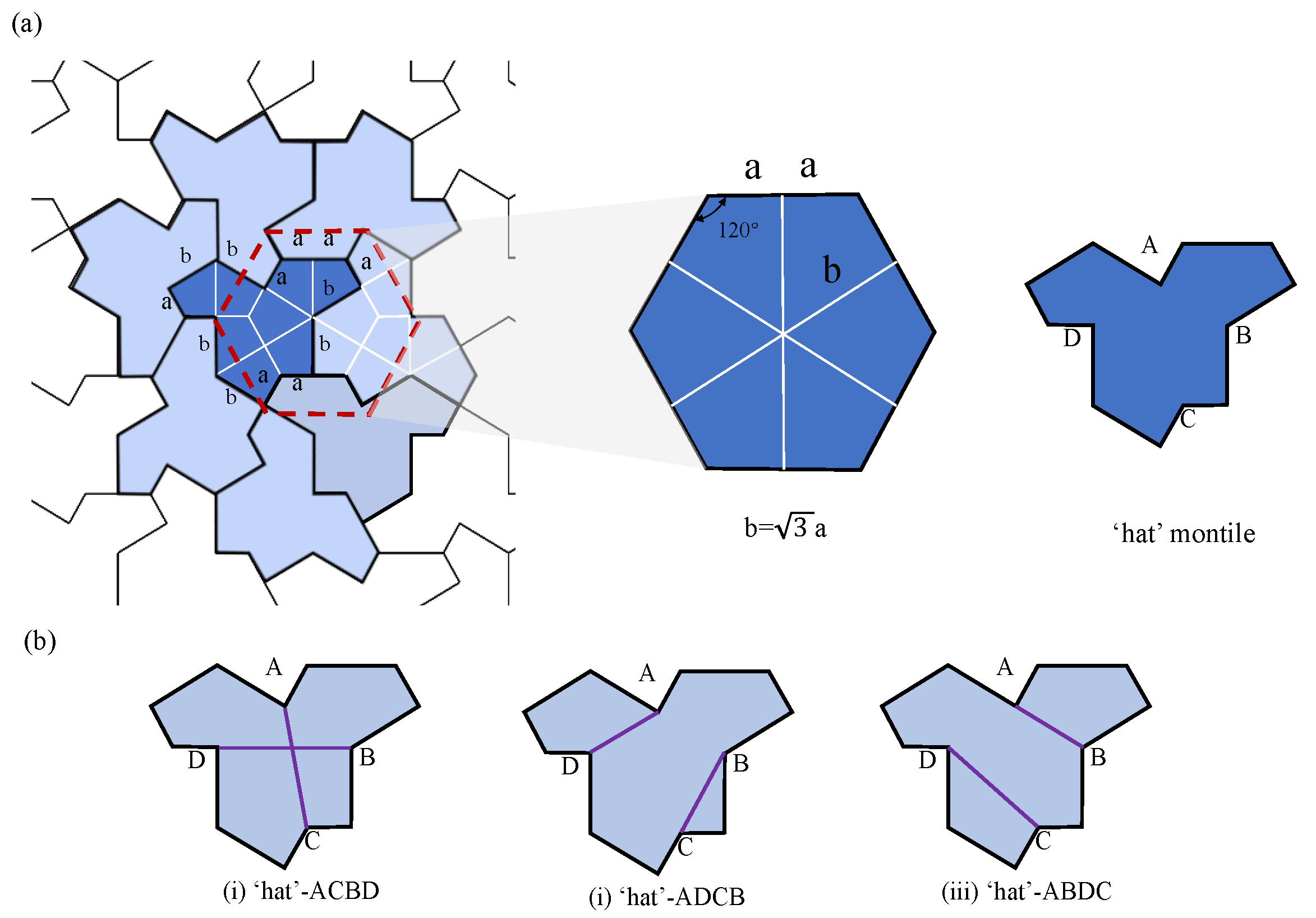
• The aperiodically arranged honeycomb metamaterial structures inspired by the ‘einstein’ monotile exhibit exceptional mechanical properties. The coordinated bending deformation between the concave corners of the unit cells effectively suppresses the lateral displacement of the structure. Compared with traditional periodically arranged honeycomb structures, the aperiodically arranged honeycomb structures show greater stability during overall deformation.
• By connecting the concave points of the “hat” unit cells to create supporting beams, the rigidity of the unit cells is significantly enhanced, thereby effectively improving the structure’s strength, stiffness, and energy absorption capacity. According to experimental data, the compressive modulus and compressive strength increased by approximately 3 to 8 times, and the energy absorption capacity increased by about 2 to 3 times. Therefore, the “hat” honeycomb metamaterial without added supporting beams performs relatively weaker in mechanical properties and energy absorption characteristics.
• A comparative analysis of the compressive mechanical responses of the four types of honeycomb metamaterials at different temperatures revealed that temperature variations significantly affect parameters such as the structure’s strength and modulus. Among them, the ‘hat’-ACBD honeycomb metamaterial forms a bidirectional anti-bending mechanism within the unit cells, which significantly enhances the structure’s strength and stiffness, resulting in excellent mechanical performance across different temperatures. The ‘hat’-ADCB and ‘hat’-ABDC honeycomb metamaterials show a noticeable increase in strength compared to the ‘hat’ honeycomb metamaterial at low temperatures, but this enhancement effect is no longer evident when the temperature exceeds $T_g$.
• A comparison of the deformation characteristics of the four types of honeycomb metamaterials at different temperatures showed that the aperiodically arranged honeycomb structures all have good overall stability at low temperatures. However, when the temperature exceeds $T_g$, only the “hat”-ACBD honeycomb metamaterial does not exhibit significant buckling, while the other three types of honeycomb metamaterials all show varying degrees of buckling.
• A comparative analysis of the energy absorption capacities of the four types of honeycomb metamaterials at different temperatures revealed that at low temperatures, the ‘hat’-ACBD honeycomb metamaterial has the best energy absorption capacity, followed by the ‘hat’-ABDC honeycomb metamaterial. When the temperature approaches $T_g$, the differences in energy absorption capacity among the ‘hat’-ACBD, ‘hat’-ADCB, and ‘hat’-ABDC honeycomb metamaterials are not significant. However, when the temperature exceeds $T_g$, the “hat”-ACBD honeycomb metamaterial still has the best energy absorption capacity.