CFD Analysis on Mars Entry Vehicle Using a 5-Species Model

1. Introduction

The possibility of actual or past life on Mars is an open subject due to the planet’s proximity and similarities to Earth. For this reason, Mars is the most visited planet to search for extraterrestrial life. Unfortunately, the landing on Mars’ surface is a very complicated and risky mission. For example, the last attempt of European Space Agency (ESA) to send the Schiaparelli lander on Mars’ surface was a complete failure because it crashed on the planet’s surface.

The National Institute for Aerospace Research (INCAS) “Elie Carafoli” has studied the reentry of capsules and meteors on Earth’s atmosphere in projects founded by ESA and Romanian Research Ministry using in-house codes and Ansys Fluent [1,2,3].

There are some available papers, which deal with hypersonic aerodynamics of Mars entry vehicles but they have especially used in-house CFD codes [4,5,6,7], which are available to a small number of researchers. For this reason, the present paper focuses to find an affordable numerical approach using Ansys Fluent [8], which is a very popular and appreciate CFD code by both academic and industrial communities.

2. Governing Equations

Because CO₂ is the dominant species of Martian atmosphere and its relaxation time is very short compared with the characteristic time of flow field, the level of thermal nonequilibrium in the flow field is minor [7]. Therefore, in the current study, one temperature model is employed and the vibrational-electronic energy conservation is not presented [7].

The classic governing equations for axisymmetric reacting laminar hypersonic gas dynamics in thermal equilibrium are [2,8]:

$${\displaystyle \frac{\partial \left(\mathrm{r}\mathrm{U}\right)}{\partial \mathrm{t}}}+{\displaystyle \frac{\partial \left[\mathrm{r}\left({\mathrm{F}}_{\mathrm{x}}-{\mathrm{G}}_{\mathrm{x}}\right)\right]}{\partial \mathrm{x}}}+{\displaystyle \frac{\partial \left[\mathrm{r}\left({\mathrm{F}}_{\mathrm{r}}-{\mathrm{G}}_{\mathrm{r}}\right)\right]}{\partial \mathrm{r}}}=\mathrm{S}$$

(1)

where

$$\mathrm{U}=\left(\begin{array}{c}\begin{array}{c}\mathrm{\rho }\\ \mathrm{\rho }\mathrm{u}\\ \mathrm{\rho }\mathrm{v}\end{array}\\ \mathrm{\rho }E\\ \mathrm{\rho }{\mathrm{Y}}_{\mathrm{i}}\end{array}\right)-\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{s}\mathrm{e}\mathrm{r}\mathrm{v}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{v}\mathrm{e}\mathrm{ }\mathrm{v}\mathrm{a}\mathrm{r}\mathrm{i}\mathrm{a}\mathrm{b}\mathrm{l}\mathrm{e}\mathrm{s}$$

(2)

Y_i is the mass fraction of species I,

$${\mathrm{F}}_{\mathrm{x}}=\left(\begin{array}{c}\begin{array}{c}\mathrm{\rho }\mathrm{u}\\ \mathrm{\rho }{\mathrm{u}}^2+\mathrm{p}\\ \mathrm{\rho }\mathrm{u}\mathrm{v}\end{array}\\ \mathrm{\rho }uH\\ \mathrm{\rho }{\mathrm{u}\mathrm{Y}}_{\mathrm{I}}\end{array}\right),\mathrm{ }{\mathrm{F}}_{\mathrm{r}}=\left(\begin{array}{c}\begin{array}{c}\mathrm{\rho }\mathrm{v}\\ \mathrm{\rho }\mathrm{v}\mathrm{u}\\ \mathrm{\rho }{\mathrm{v}}^2+\mathrm{p}\end{array}\\ \mathrm{\rho }vH\\ \mathrm{\rho }{\mathrm{v}\mathrm{Y}}_{\mathrm{i}}\end{array}\right)-\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{v}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{v}\mathrm{e}\mathrm{ }\mathrm{f}\mathrm{l}\mathrm{u}\mathrm{x}\mathrm{e}\mathrm{s}$$

(3)

$${\mathrm{G}}_{\mathrm{x}}=\left(\begin{array}{c}\begin{array}{c}0\\ {\mathrm{\tau }}_{\mathrm{x}\mathrm{x}}\\ {\mathrm{\tau }}_{\mathrm{x}\mathrm{r}}\end{array}\\ u{\mathrm{\tau }}_{\mathrm{x}\mathrm{x}}+v{\mathrm{\tau }}_{\mathrm{x}\mathrm{r}}+k{\displaystyle \frac{\partial \mathrm{T}}{\partial \mathrm{x}}}+\mathrm{\rho }{\displaystyle \sum _{\mathrm{i}=1}^{\mathrm{N}}}{\mathrm{h}}_{\mathrm{i}}{\mathrm{D}}_{\mathrm{I}\mathrm{ }\mathrm{m}\mathrm{i}\mathrm{x}\mathrm{t}\mathrm{u}\mathrm{r}\mathrm{e}}{\displaystyle \frac{\partial {\mathrm{Y}}_{\mathrm{i}}}{\partial \mathrm{x}}}\\ \mathrm{\rho }{\mathrm{D}}_{\mathrm{I}\mathrm{ }\mathrm{m}\mathrm{i}\mathrm{x}\mathrm{t}\mathrm{u}\mathrm{r}\mathrm{e}}{\displaystyle \frac{\partial {\mathrm{Y}}_{\mathrm{i}}}{\partial \mathrm{x}}}\end{array}\right)-\mathrm{d}\mathrm{i}\mathrm{f}\mathrm{f}\mathrm{u}\mathrm{s}\mathrm{i}\mathrm{v}\mathrm{e}\mathrm{ }\mathrm{f}\mathrm{l}\mathrm{u}\mathrm{x}\mathrm{ }\mathrm{i}\mathrm{n}\mathrm{ }\mathrm{a}\mathrm{x}\mathrm{i}\mathrm{a}\mathrm{l}\mathrm{ }\mathrm{d}\mathrm{i}\mathrm{r}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}$$

(4)

$${\mathrm{G}}_{\mathrm{r}}=\left(\begin{array}{c}\begin{array}{c}0\\ {\mathrm{\tau }}_{\mathrm{r}\mathrm{x}}\\ {\mathrm{\tau }}_{\mathrm{r}\mathrm{r}}\end{array}\\ u{\mathrm{\tau }}_{\mathrm{r}\mathrm{x}}+v{\mathrm{\tau }}_{\mathrm{r}\mathrm{r}}+k{\displaystyle \frac{\partial \mathrm{T}}{\partial \mathrm{r}}}+\mathrm{\rho }{\displaystyle \sum _{\mathrm{i}=1}^{\mathrm{N}}}{\mathrm{h}}_{\mathrm{i}}{\mathrm{D}}_{\mathrm{I}\mathrm{ }\mathrm{m}\mathrm{i}\mathrm{x}\mathrm{t}\mathrm{u}\mathrm{r}\mathrm{e}}{\displaystyle \frac{\partial {\mathrm{Y}}_{\mathrm{i}}}{\partial \mathrm{r}}}\\ \mathrm{\rho }{\mathrm{D}}_{\mathrm{I}\mathrm{ }\mathrm{m}\mathrm{i}\mathrm{x}\mathrm{t}\mathrm{u}\mathrm{r}\mathrm{e}}{\displaystyle \frac{\partial {\mathrm{Y}}_{\mathrm{i}}}{\partial \mathrm{r}}}\end{array}\right)-\mathrm{d}\mathrm{i}\mathrm{f}\mathrm{f}\mathrm{u}\mathrm{s}\mathrm{i}\mathrm{v}\mathrm{e}\mathrm{ }\mathrm{f}\mathrm{l}\mathrm{u}\mathrm{x}\mathrm{ }\mathrm{i}\mathrm{n}\mathrm{ }\mathrm{r}\mathrm{a}\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{l}\mathrm{ }\mathrm{d}\mathrm{i}\mathrm{r}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}$$

(5)

$$\mathrm{S}=\left(\begin{array}{c}\begin{array}{c}0\\ 0\\ \mathrm{p}-{\mathrm{\tau }}_{\mathrm{\theta }\mathrm{\theta }}\end{array}\\ -r{\displaystyle \sum _{\mathrm{i}=1}^{\mathrm{N}}}\left[{\mathrm{h}}_{\mathrm{i}}^{\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{m}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}\mathrm{ }{\mathrm{T}}_{\mathrm{r}\mathrm{e}\mathrm{f}}}-{\mathrm{c}}_{\mathrm{p}\mathrm{i}}\left({\mathrm{T}}_{\mathrm{r}\mathrm{e}\mathrm{f}}\right){\mathrm{T}}_{\mathrm{r}\mathrm{e}\mathrm{f}}\right]{\mathrm{\omega }}_{\mathrm{i}}\\ r{\mathrm{\omega }}_{\mathrm{i}}\end{array}\right)-\mathrm{s}\mathrm{o}\mathrm{u}\mathrm{r}\mathrm{c}\mathrm{e}\mathrm{ }\mathrm{t}\mathrm{e}\mathrm{r}\mathrm{m}$$

(6)

where ω_I is the rate of formation/destruction of species I, N signifies the number of chemical species,

$${\mathrm{\tau }}_{\mathrm{\theta }\mathrm{\theta }}={\displaystyle \frac{2}{3}}\mathrm{\mu }\left(2{\displaystyle \frac{\mathrm{v}}{\mathrm{r}}}-{\displaystyle \frac{\partial \mathrm{u}}{\partial \mathrm{x}}}-{\displaystyle \frac{\partial \mathrm{v}}{\partial \mathrm{r}}}\right)-\mathrm{c}\mathrm{r}\mathrm{o}\mathrm{s}\mathrm{s}\mathrm{ }\mathrm{v}\mathrm{i}\mathrm{s}\mathrm{c}\mathrm{o}\mathrm{u}\mathrm{s}\mathrm{ }\mathrm{s}\mathrm{t}\mathrm{r}\mathrm{e}\mathrm{s}\mathrm{s}$$

(7)

$${\mathrm{\tau }}_{\mathrm{x}\mathrm{x}}={\displaystyle \frac{2}{3}}\mathrm{\mu }\left(2{\displaystyle \frac{\partial \mathrm{u}}{\partial \mathrm{x}}}-{\displaystyle \frac{\partial \mathrm{v}}{\partial \mathrm{r}}}-{\displaystyle \frac{\mathbf{v}}{\mathbf{r}}}\right)-\mathrm{a}\mathrm{x}\mathrm{i}\mathrm{a}\mathrm{l}\mathrm{ }\mathrm{v}\mathrm{i}\mathrm{s}\mathrm{c}\mathrm{o}\mathrm{u}\mathrm{s}\mathrm{ }\mathrm{s}\mathrm{t}\mathrm{r}\mathrm{e}\mathrm{s}\mathrm{s}$$

(8)

$${\mathrm{\tau }}_{\mathrm{r}\mathrm{r}}={\displaystyle \frac{2}{3}}\mathrm{\mu }\left(2{\displaystyle \frac{\partial \mathrm{v}}{\partial \mathrm{r}}}-{\displaystyle \frac{\partial \mathrm{u}}{\partial \mathrm{x}}}-{\displaystyle \frac{\mathbf{v}}{\mathbf{r}}}\right)-\mathrm{r}\mathrm{a}\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{l}\mathrm{ }\mathrm{v}\mathrm{i}\mathrm{s}\mathrm{c}\mathrm{o}\mathrm{u}\mathrm{s}\mathrm{ }\mathrm{s}\mathrm{t}\mathrm{r}\mathrm{e}\mathrm{s}\mathrm{s}$$

(9)

$${\mathrm{\tau }}_{\mathrm{x}\mathrm{r}}={\mathrm{\tau }}_{\mathrm{r}\mathrm{x}}=\mathrm{\mu }\left({\displaystyle \frac{\partial \mathrm{u}}{\partial \mathrm{r}}}+{\displaystyle \frac{\partial \mathrm{v}}{\partial \mathrm{x}}}\right)-\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{s}\mathrm{v}\mathrm{e}\mathrm{r}\mathrm{s}\mathrm{a}\mathrm{l}\mathrm{ }\mathrm{v}\mathrm{i}\mathrm{s}\mathrm{c}\mathrm{o}\mathrm{u}\mathrm{s}\mathrm{ }\mathrm{s}\mathrm{t}\mathrm{r}\mathrm{e}\mathrm{s}\mathrm{s}\mathrm{ }\left(\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{ }\mathrm{s}\mathrm{a}\mathrm{m}\mathrm{e}\mathrm{ }\mathrm{a}\mathrm{s}\mathrm{ }\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{ }2\mathrm{D}\mathrm{ }\mathrm{p}\mathrm{l}\mathrm{a}\mathrm{n}\mathrm{a}\mathrm{r}\mathrm{ }\mathrm{f}\mathrm{l}\mathrm{o}\mathrm{w}\mathrm{s}\right)$$

(10)

$$\mathrm{p}=\mathrm{\rho }{\mathrm{R}}^0\mathrm{T}{\displaystyle \sum _{\mathrm{i}=1}^{\mathrm{N}}}{\displaystyle \frac{{\mathrm{Y}}_{\mathrm{i}}}{{\mathrm{W}}_{\mathrm{i}}}}-\mathrm{e}\mathrm{q}\mathrm{u}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}\mathrm{ }\mathrm{o}\mathrm{f}\mathrm{ }\mathrm{i}\mathrm{d}\mathrm{e}\mathrm{a}\mathrm{l}\mathrm{ }\mathrm{g}\mathrm{a}\mathrm{s}\mathrm{e}\mathrm{s},\mathrm{ }\mathrm{ }\mathrm{ }{\mathrm{R}}^0=8314.5{\displaystyle \frac{\mathrm{J}}{\mathrm{k}\mathrm{m}\mathrm{o}\mathrm{l}·\mathrm{K}}}$$

(11)

where W_i represents the molecular weight of species I,

$${\mathrm{h}}_{\mathrm{i}}={\mathrm{h}}_{\mathrm{i}}\left(\mathrm{T}\right)={\mathrm{c}}_{\mathrm{p}\mathrm{i}}\left(\mathrm{T}\right)\mathrm{T}-\mathrm{h}\mathrm{y}\mathrm{p}\mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{s}\mathrm{i}\mathrm{s}\mathrm{ }\mathrm{o}\mathrm{f}\mathrm{ }\mathrm{a}\mathrm{ }\mathrm{c}\mathrm{a}\mathrm{l}\mathrm{o}\mathrm{r}\mathrm{i}\mathrm{c}\mathrm{a}\mathrm{l}\mathrm{l}\mathrm{y}\mathrm{ }\mathrm{p}\mathrm{e}\mathrm{r}\mathrm{f}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{ }\mathrm{g}\mathrm{a}\mathrm{s}\mathrm{e}\mathrm{s}\mathrm{ }\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{ }\mathrm{c}\mathrm{h}\mathrm{e}\mathrm{m}\mathrm{i}\mathrm{c}\mathrm{a}\mathrm{l}\mathrm{ }\mathrm{s}\mathrm{p}\mathrm{e}\mathrm{c}\mathrm{i}\mathrm{e}\mathrm{s}$$

(12)

In this paper, the authors have used the NASA-piecewise-polynomial to compute the specific heats of chemical species at constant pressure [9]:

$${\mathrm{c}}_{\mathrm{p}}\left(\mathrm{T}\right)={\mathrm{A}}_1{\mathrm{T}}^{-2}+{\mathrm{A}}_2{\mathrm{T}}^{-1}+{\mathrm{A}}_3+{\mathrm{A}}_4\mathrm{T}+{\mathrm{A}}_5{\mathrm{T}}^2+{\mathrm{A}}_6{\mathrm{T}}^3+{\mathrm{A}}_7{\mathrm{T}}^4$$

(13)

where the coefficients A_i are constant over a range of temperature.

In the hypersonic flows, there are huge variations of temperature. Unfortunately, there are very few available experimental data at very high temperatures for viscosity and thermal conductivity of gases. For this reason, one prefers the kinetic theory of gases to compute their viscosity and thermal conductivity at very high temperatures [10,11].

The flow is assumed laminar; therefore, the speed of chemical reactions is governed by the modified Arrhenius equation [12]:

$${\displaystyle \sum _{\mathrm{i}=1}^{\mathrm{N}}}{\mathrm{\nu }}_{\mathrm{i}\mathrm{j}}^{\mathrm{\text{'}}}{\mathrm{M}}_{\mathrm{i}}\stackrel{{\mathrm{k}}_{\mathrm{f}}}{\to }{\displaystyle \sum _{\mathrm{i}=1}^{\mathrm{N}}}{\mathrm{\nu }}_{\mathrm{i}\mathrm{j}}^{\mathrm{”}}{\mathrm{M}}_{\mathrm{i}}$$

(14)

where j is the number of chemical reactions,

$${\mathrm{\omega }}_{\mathrm{i}}={\mathrm{W}}_{\mathrm{i}}{\displaystyle \sum _{\mathrm{j}=1}^{\mathrm{n}\mathrm{u}\mathrm{m}\mathrm{b}\mathrm{e}\mathrm{r}\mathrm{ }\mathrm{o}\mathrm{f}\mathrm{ }\mathrm{r}\mathrm{e}\mathrm{a}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}\mathrm{s}}}\left[\left({\mathrm{\nu }}_{\mathrm{i}\mathrm{j}}^{\mathrm{”}}-{\mathrm{\nu }}_{\mathrm{i}\mathrm{j}}^{\mathrm{\text{'}}}\right){\mathrm{\Gamma }}_{\mathrm{j}}{\mathrm{k}}_{{\mathrm{f}}_{\mathrm{j}}}{\displaystyle \prod _{\mathrm{i}=1}^{\mathrm{N}}}{\left({\displaystyle \frac{{\mathrm{X}}_{\mathrm{i}}\mathrm{p}}{{\mathrm{R}}^0\mathrm{T}}}\right)}^{{\mathrm{n}}_{\mathrm{i}\mathrm{j}}^{\mathrm{\text{'}}}}\right]$$

(15)

$${\mathrm{X}}_{\mathrm{i}}={\mathrm{Y}}_{\mathrm{i}}{\displaystyle \frac{\mathrm{W}}{{\mathrm{W}}_{\mathrm{I}}}},\mathrm{ }\mathrm{ }{\displaystyle \frac{1}{\mathrm{W}}}={\displaystyle \sum _{\mathrm{i}=1}^{\mathrm{N}}}{\displaystyle \frac{{\mathrm{Y}}_{\mathrm{i}}}{{\mathrm{W}}_{\mathrm{I}}}}\mathrm{ }$$

(16)

$${\mathrm{k}}_{{\mathrm{f}}_{\mathrm{j}}}={\mathrm{A}}_{\mathrm{j}}{\mathrm{T}}^{{\mathrm{\beta }}_{\mathrm{j}}}{\mathrm{e}}^{-{\displaystyle \frac{{\mathrm{E}\mathrm{a}}_{\mathrm{j}}}{{\mathrm{R}}^0\mathrm{T}}}}-\mathrm{m}\mathrm{o}\mathrm{d}\mathrm{i}\mathrm{f}\mathrm{i}\mathrm{e}\mathrm{d}\mathrm{ }\mathrm{A}\mathrm{r}\mathrm{r}\mathrm{h}\mathrm{e}\mathrm{n}\mathrm{i}\mathrm{u}\mathrm{s}\mathrm{ }\mathrm{e}\mathrm{q}\mathrm{u}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}$$

(17)

where Γ_j is the third body efficiency, X_i is the volume (molar) fraction of species I, W represents the molecular weight of gas mixture, k_fj signifies the rate of forward chemical reaction j and Ea_j is the activation energy of reaction j.

For entry velocities below 8 km/s, the level of ionization will be small [6]. As the Martian atmosphere is a mixture of 95.7% CO₂, 2.7% N₂ by volume and some other gases [5], it is possible to assume it contains only CO₂, in a first approximation. Therefore, the Mars 5-species McKenzie model [13] described in Table 1 is suitable for the purpose of this paper.

It Is worth to mention that In the hypersonic gas dynamics, one prefers to use the kinetic theory of gases as much as possible. For this reason, the rate exponents n’_ij are the stoichiometric coefficients of reactants ν’_ij (see Table 1) while for the common applications (for example for the burning of hydrocarbons), the rate exponents are determined experimentally [3].

3. Numerical Simulations

The Mars Pathfinder entry vehicle was launched in 1996 and entered the atmosphere of Mars in the following year [14]. This vehicle whose geometry is given in [14] is used as a test case in this paper. At altitude of 41.204 km, the maximum stagnation heat convective flux occurs. For this reason, the paper focuses to study the flow at this altitude.

The freestream conditions for the Pathfinder vehicle at this altitude are given in Table 2.

The flow is supersonic; therefore, on inlet boundary, all conservative variables are imposed while on outlet boundary, these variables are extrapolated. On Pathfinder wall, one imposes isothermal surface of 1693 K, which is the temperature on Pathfinder surface at stagnation point [12], the non-slip condition for velocity (V_w = 0), and zero wall normal gradients of pressure (∂p_w/∂n = 0) and species (∂Y_iw/∂n = 0, non-catalytic wall).

Three multiblock structured meshes clustered near Pathfinder’s wall were generated using the commercial meshing tool Beta CAE ANSA 25 [15] to study the grid sensitivity as shown in Table 3. The drag coefficient is the most important coefficient to study the entry of Mars vehicles. The Table 3 clearly shows that the values of this parameter obtained with medium and fine grids are extremely close.

The convective flux (see Equation 3) was discretized by AUSM⁺-p scheme [16,17,18], which was developed continuously by Liou over a period of about 15 years and it is suitable for hypersonic regime [3].

4. Numerical Results and Discussions

As it follows, the given numerical results are obtained with fine grid.

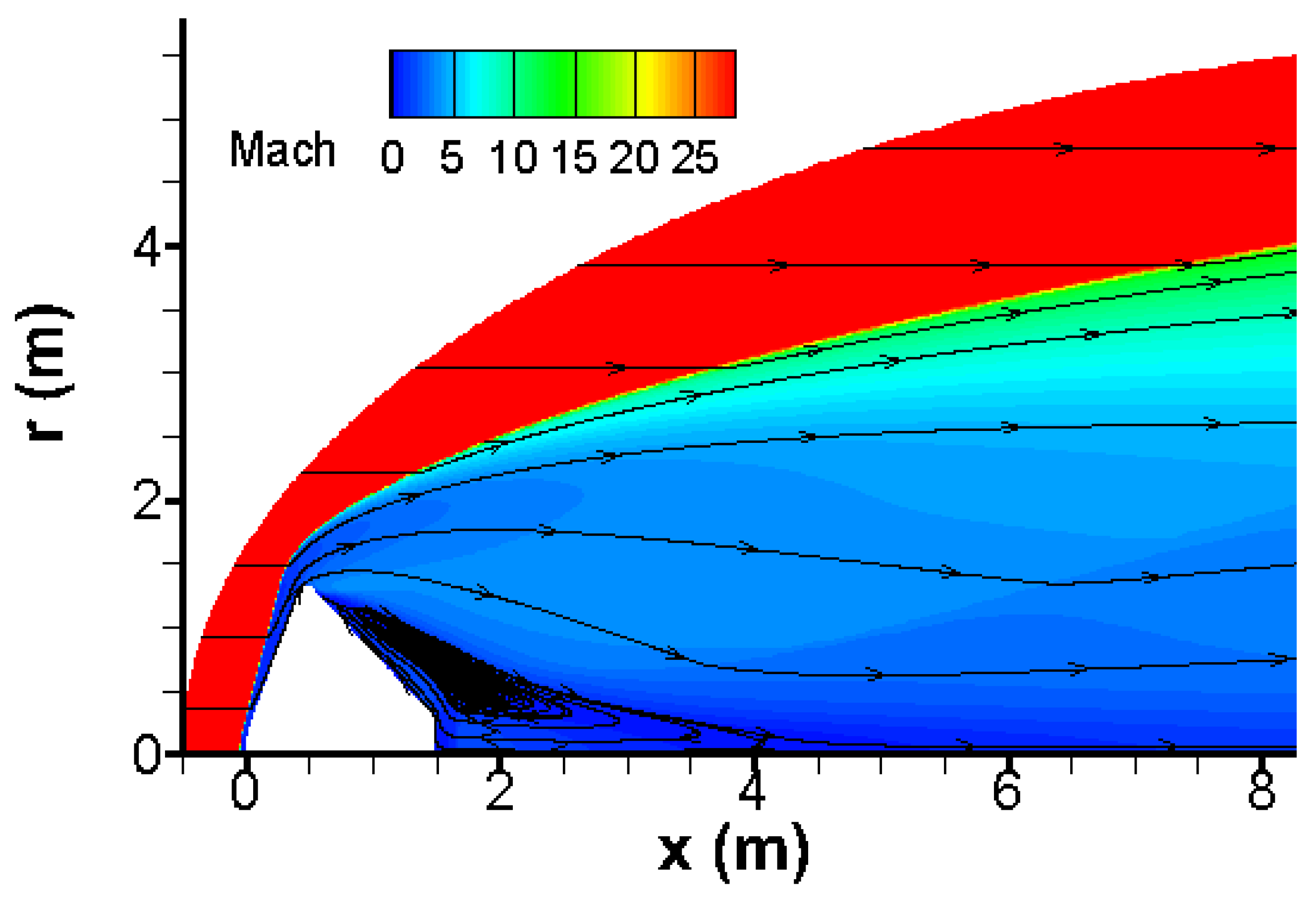
The velocity field over Pathfinder vehicle is shown in Figure 1. One clearly observes the very strong bow shock in front of vehicle, the recirculation region and neck behind Pathfinder. Furthermore, this velocity distribution is very close to that given in [14], which was obtained with a two-temperature model and an 8-species finite rate chemical reaction model proposed by Micheltree and Gnoffo [19]. This model is reduced from the 18-species reaction model of Park et al. [20], neglecting ionization reactions.

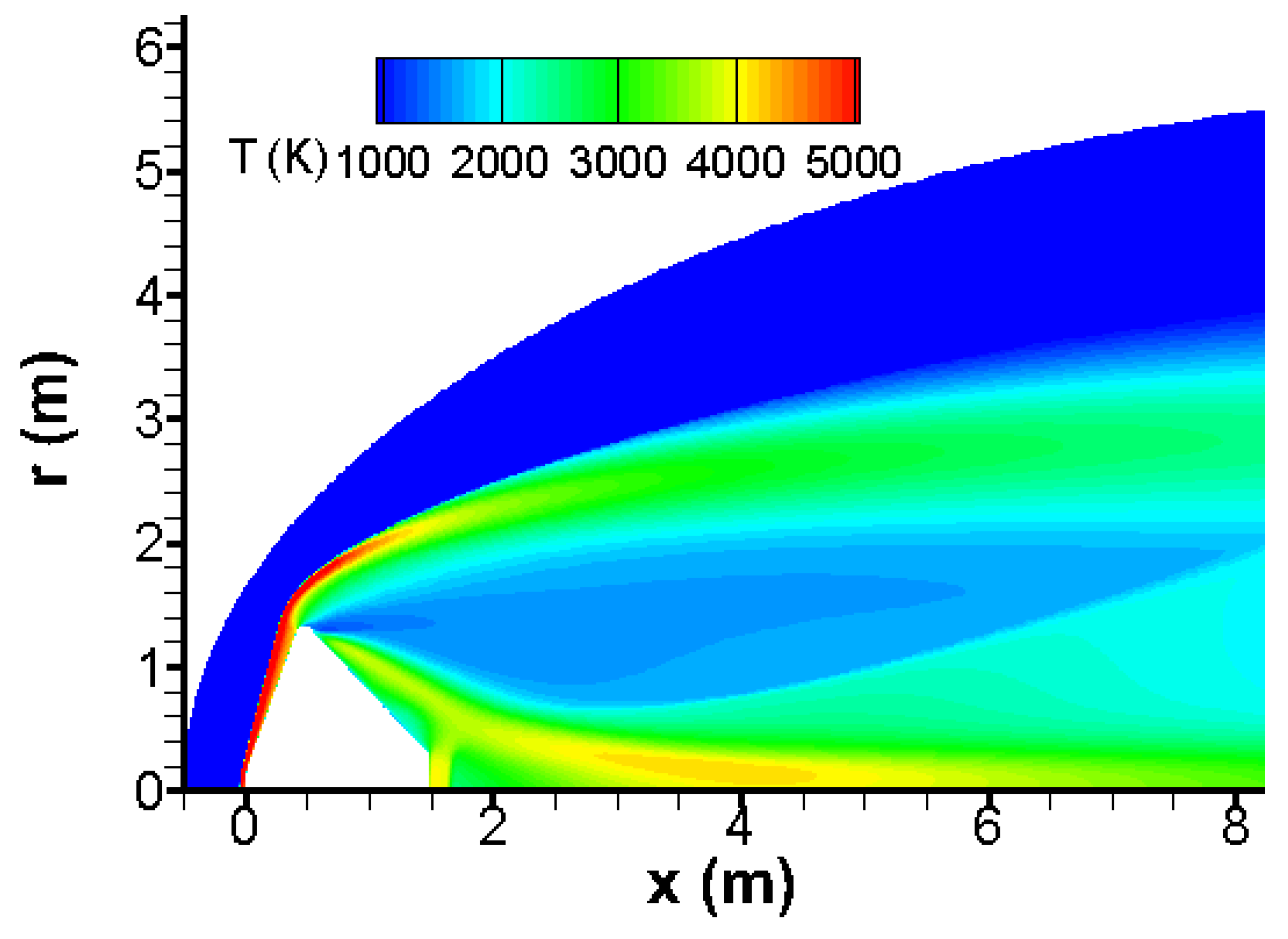
The temperature increases dramatically behind the bow wave and the conical shock waves as given in Figure 2. Moreover, the temperature field shows rarefaction and shock waves behind the Pathfinder vehicle. Remarkably, the temperature distribution of Figure 2 is in good agreement to that given in [14].

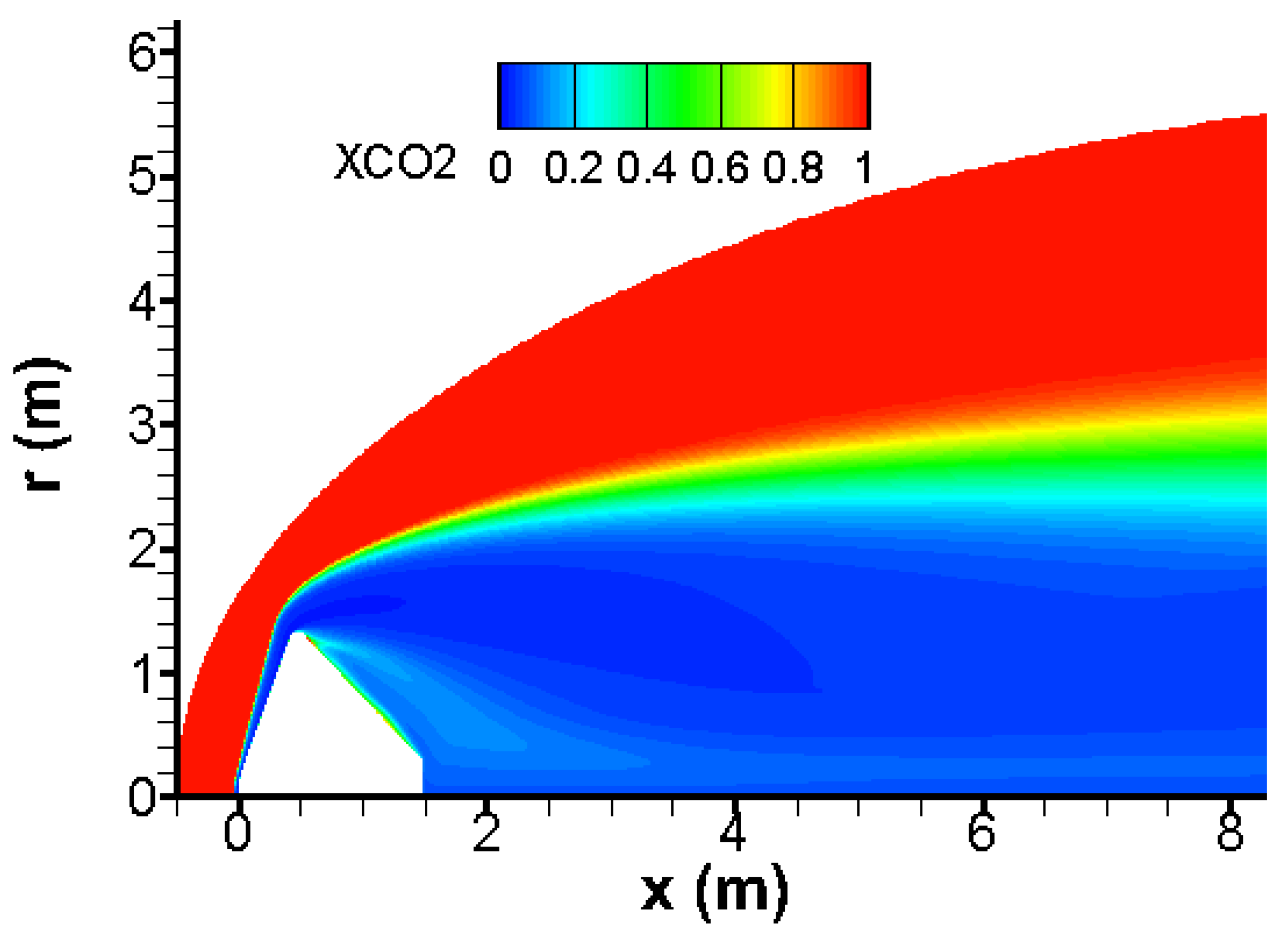
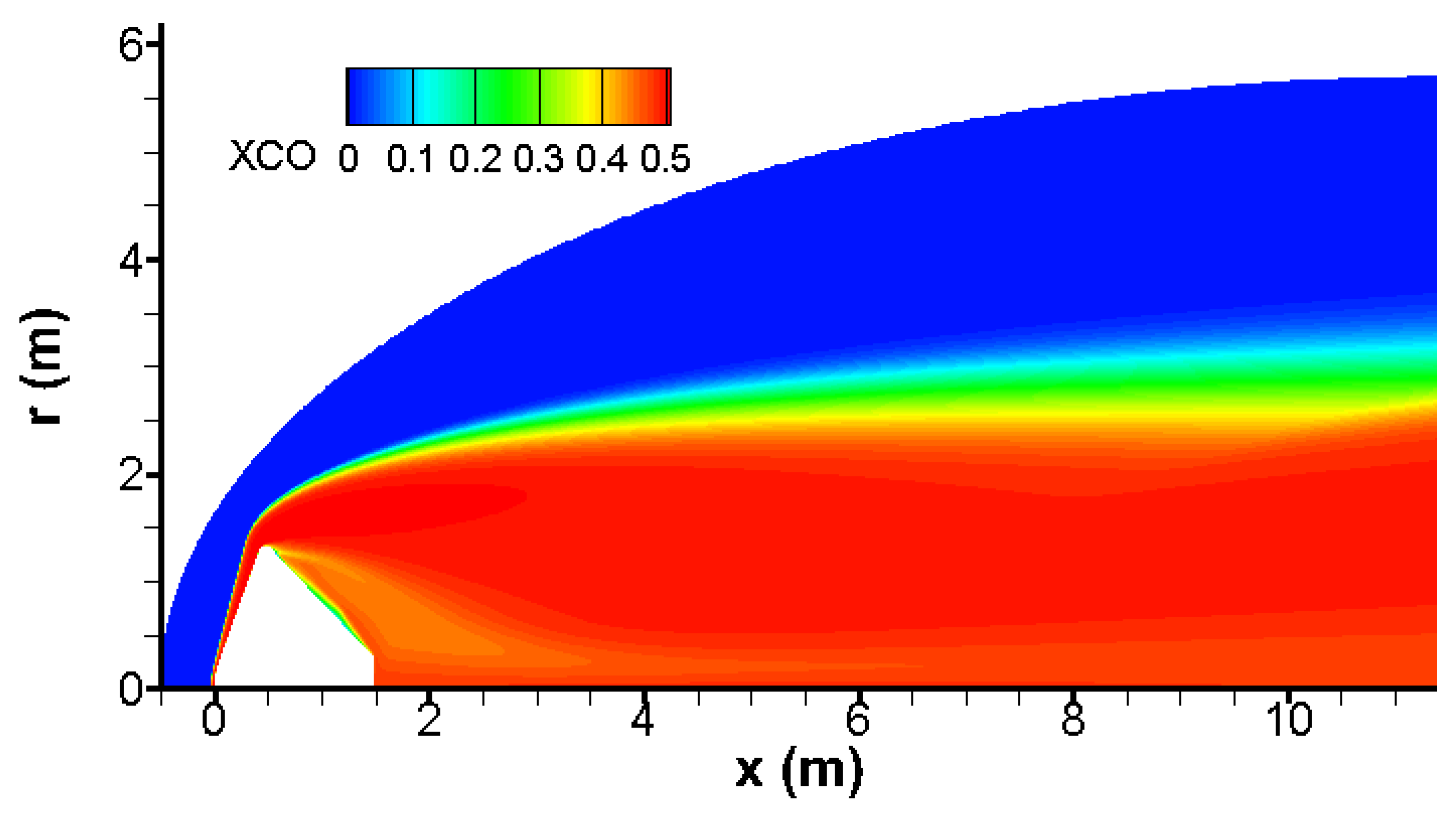
Almost all CO₂ is broken behind the bow wave as shown in Figure 3. Again, there is a good agreement with results published in [4,21].

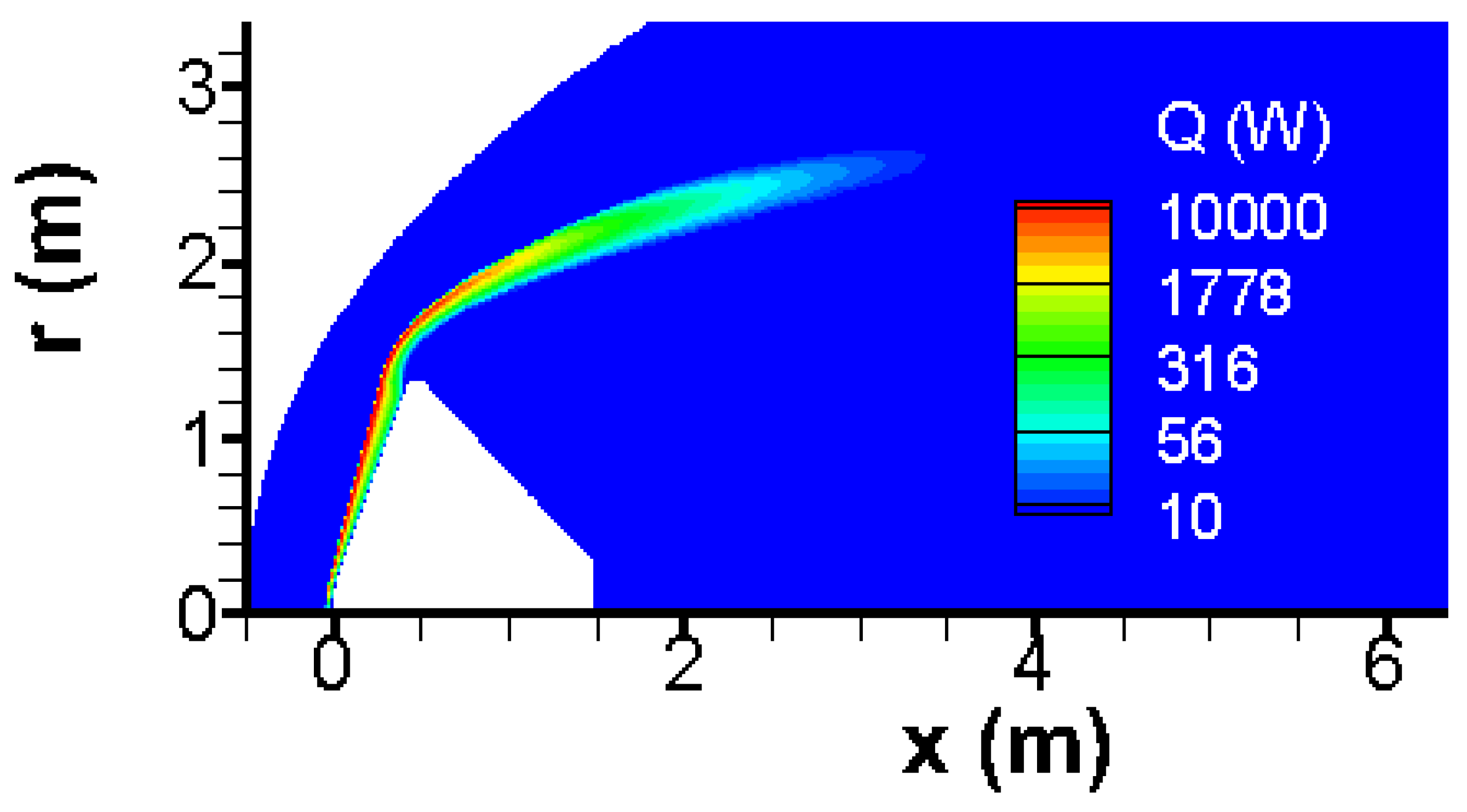
All chemical reactions of Table 1 are endothermal as shown in Figure 4; therefore, the task of thermal shield is alleviated impressively. One observes that the endothermal chemical reactions are concentrated in a narrow band behind the bow shock.

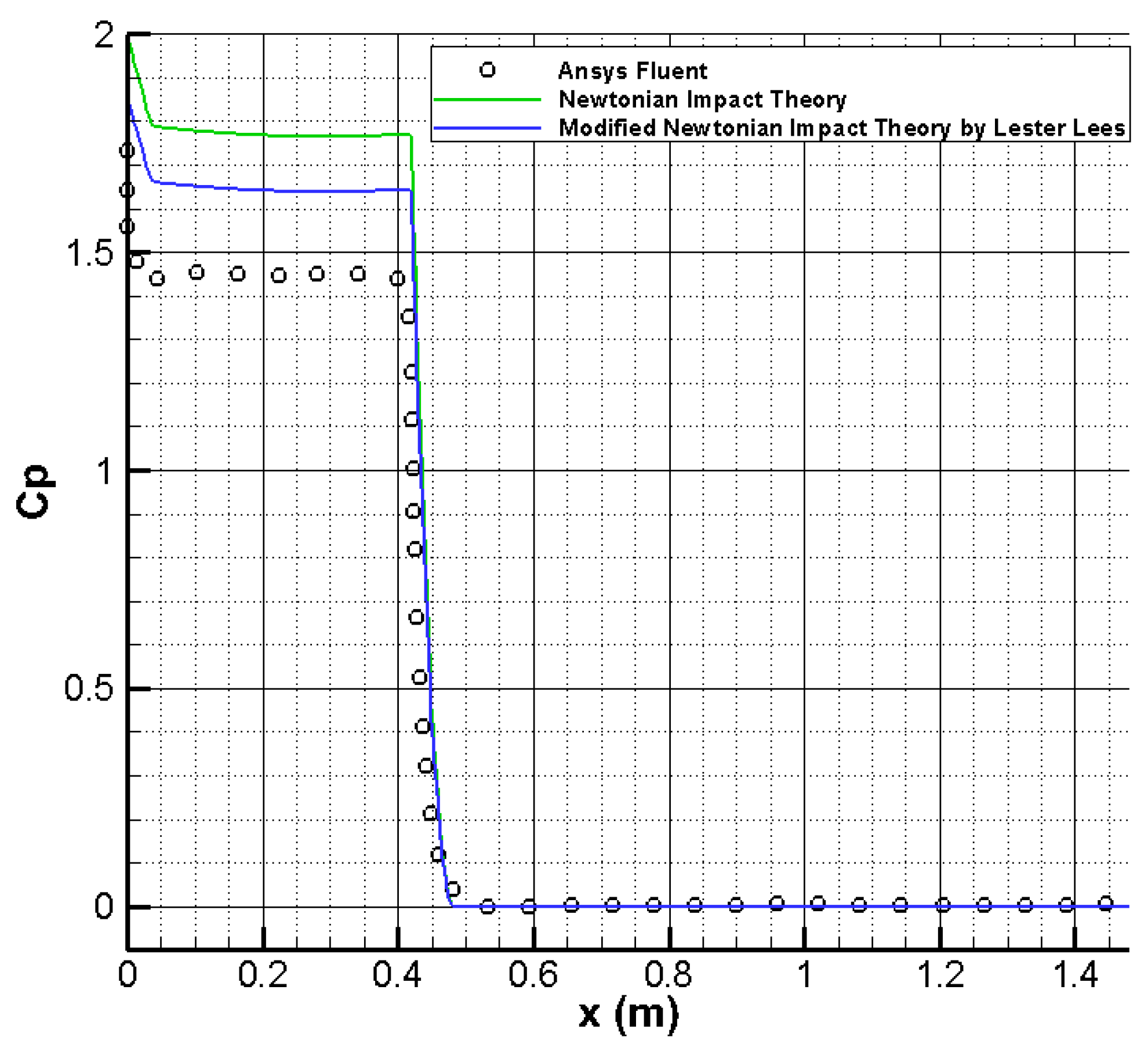
Pressure distribution on Pathfinder’s wall is given in Figure 5. One observes a good concordance among the pressure distribution on Pathfinder’s wall computed with Ansys Fluent and those predicted by Newtonian impact theory and modified Newtonian impact theory by Lester Lees [22,23]:

$${\mathrm{C}}_{\mathrm{p}}={\mathrm{C}}_{{\mathrm{p}}_{\mathrm{m}\mathrm{a}\mathrm{x}}}{\mathrm{s}\mathrm{i}\mathrm{n}}^2\mathrm{\theta }$$

(18)

where θ is the impact angle and

$${\mathrm{C}}_{{\mathrm{p}}_{\mathrm{m}\mathrm{a}\mathrm{x}}}={\displaystyle \frac{2}{{\mathrm{M}}_{\mathrm{\infty }}^2}}\left\{{\left[{\displaystyle \frac{{\left(\mathrm{\gamma }+1\right)}^2{\mathrm{M}}_{\mathrm{\infty }}^2}{4\mathrm{\gamma }{\mathrm{M}}_{\mathrm{\infty }}^2-2\left(\mathrm{\gamma }-1\right)}}\right]}^{{\displaystyle \frac{\mathrm{\gamma }}{\mathrm{\gamma }-1}}}\left({\displaystyle \frac{1-\mathrm{\gamma }+2\mathrm{\gamma }{\mathrm{M}}_{\mathrm{\infty }}^2}{\mathrm{\gamma }+1}}\right)-1\right\}$$

(19)

where γ is the specific heat ratio of gas mixture.

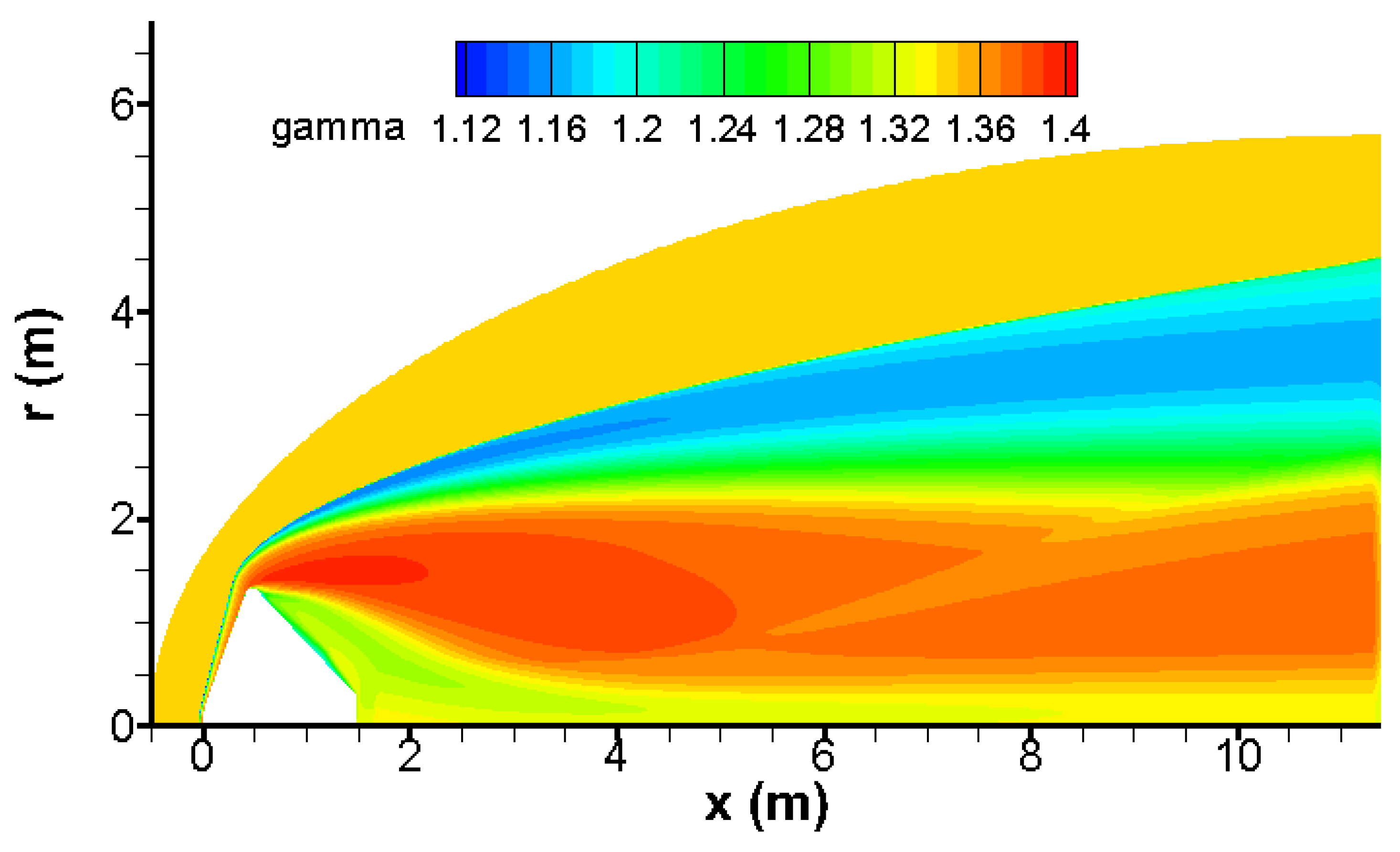
The contour of specific heat ratio of gas mixture γ is given in Figure 6 and clearly shows that the variation of this parameter must be considered.

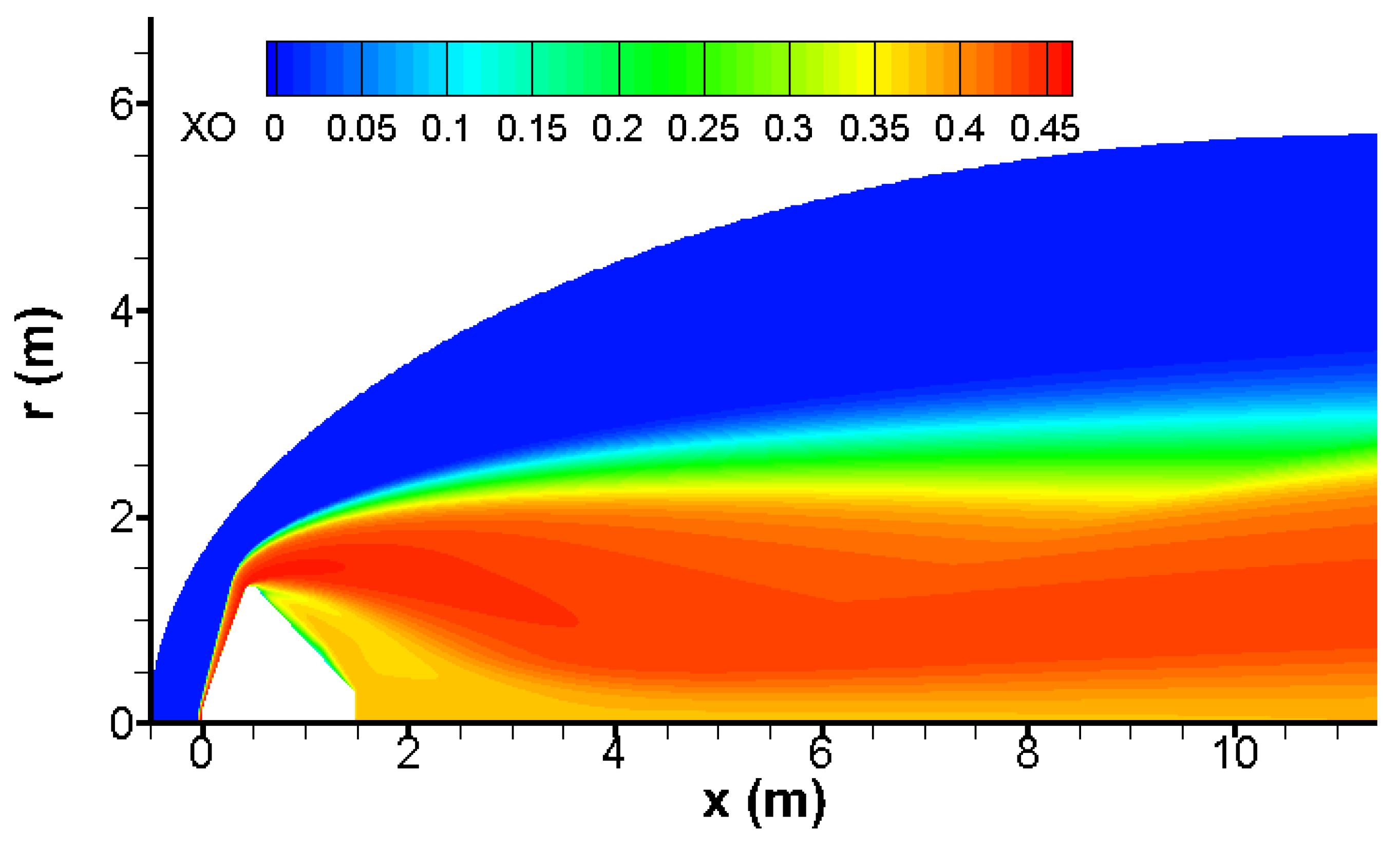
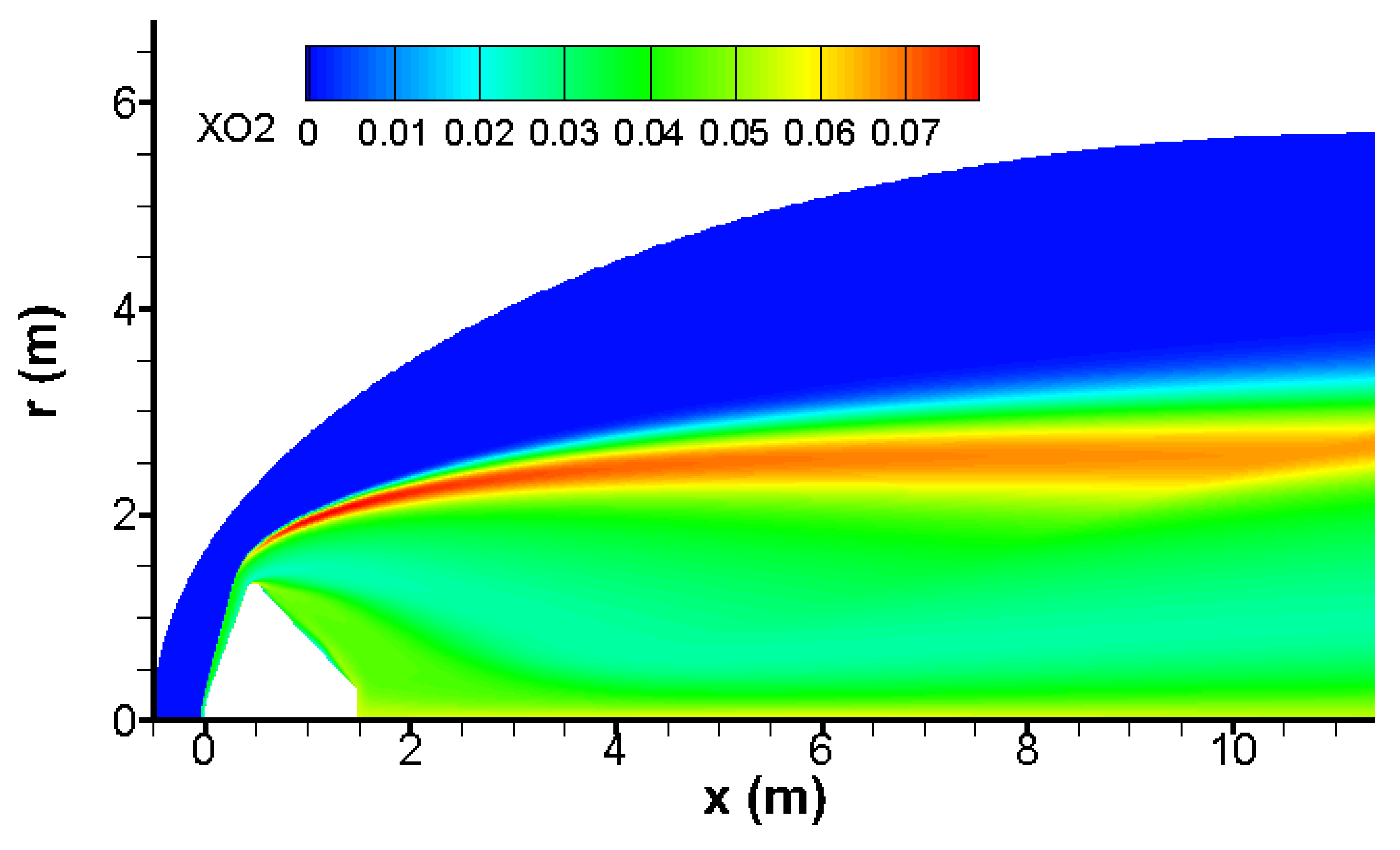
The bow wave induces an impressive temperature rise, which triggers strong endothermal chemical reactions given in Table 1. The outcome of these chemical reactions is a dramatic temperature decrease and a massive production of atomic and molecular oxygen as shown in Figure 7 and Figure 8.

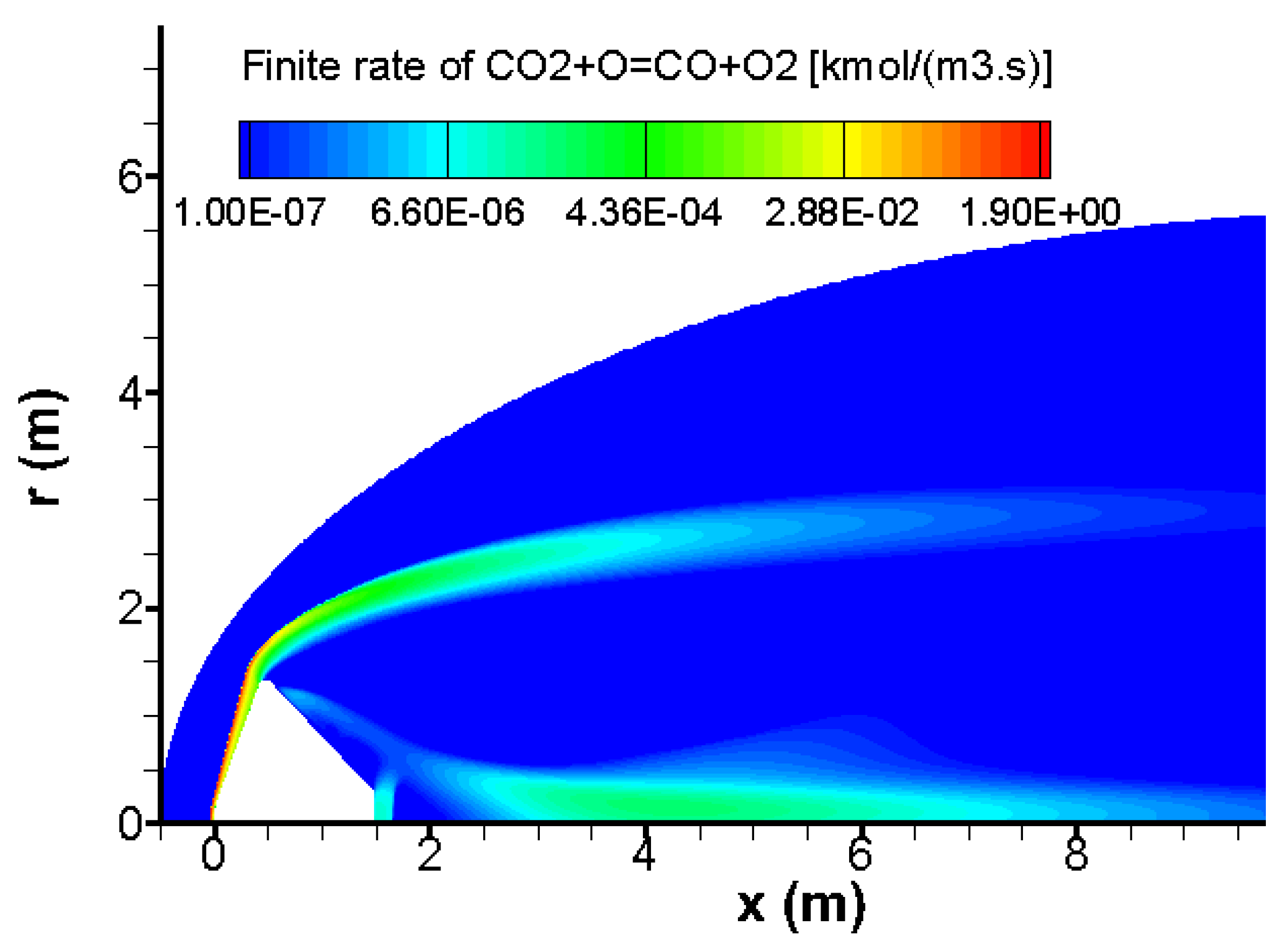
Behind the bow wave, almost half of carbon dioxide CO₂ is converted into carbon monoxide CO due to the chemical reactions CO₂ → CO + O and CO₂ + O → CO + O₂. This conversion and the kinetic rate of reaction CO₂ + O → CO + O₂ are given in Figure 9 and Figure 10 respectively. Practically, this reaction takes place in hot regions due to the bow wave and the conical shock waves.

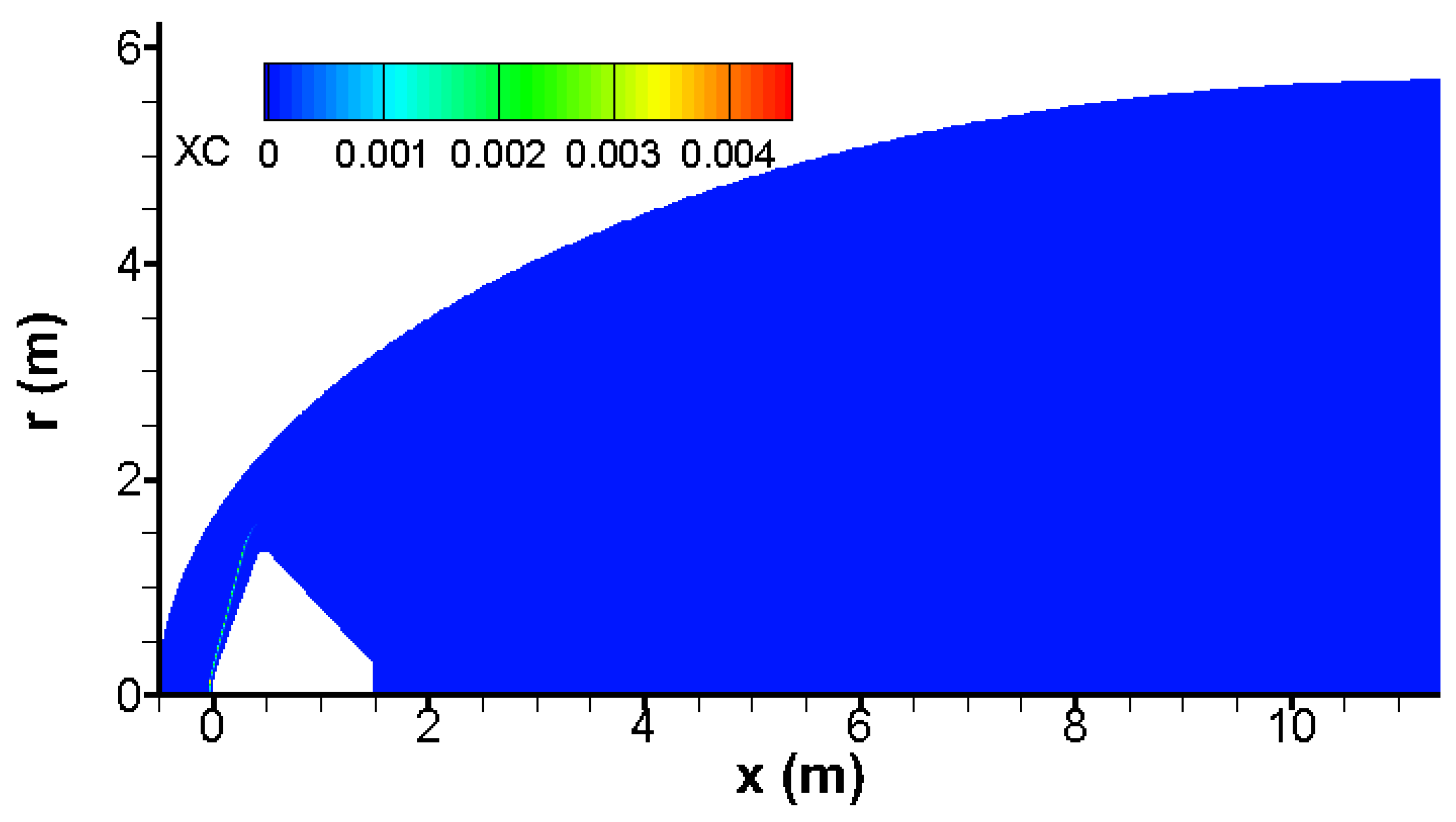
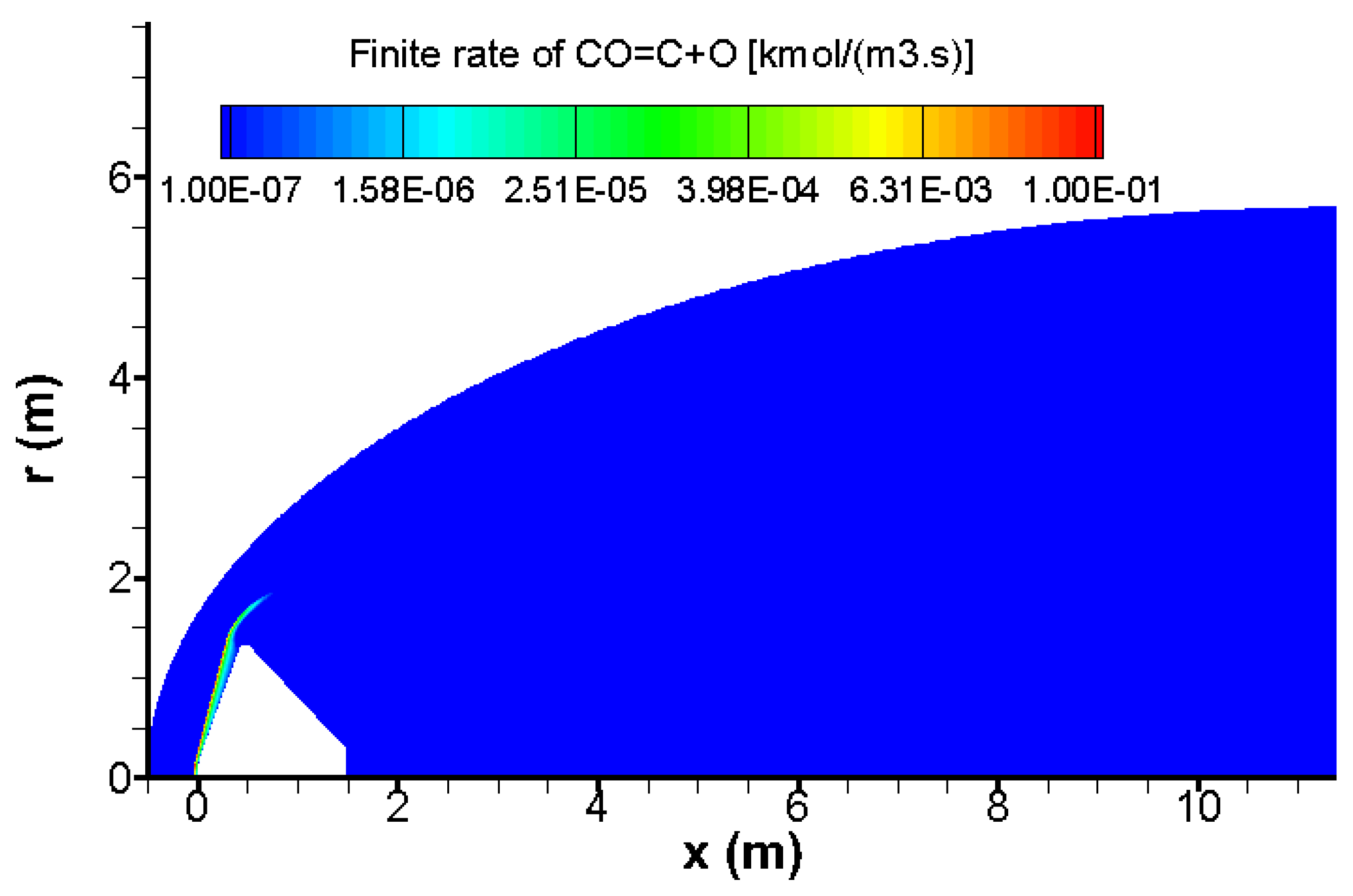
The quantity of carbon C generated by the chemical reactions CO → C + O, CO + O → C + O₂ and CO + CO → CO₂ + C is extremely small; its molar value does not exceed 0.0046 as shown in Figure 11. This suggests that the kinetic rates of reactions that create carbon is very low. Indeed, the speeds of reactions CO₂ → CO + O, CO₂ + O → CO + O₂ and O2 → 2O are close and bigger with at least an order of magnitude than those of reactions that produce carbon C (CO → C + O, CO + O → C + O₂ and CO + CO → CO₂ + C) as shown in Figure 10 and Figure 12. For this reason, these three chemical reactions with low kinetic rates could be neglected in preliminary design of Mars entry vehicles.

5. Conclusions

This paper shows that the commercial CFD code Ansys Fluent with Mars 5-species McKenzie model [13] is suitable to simulate Mars entry vehicles. Moreover, the modified Newtonian impact theory by Lester Lees provides very fast, useful information regarding the drag coefficient, which is the most important parameter to study the entry of Mars vehicles. Furthermore, the strong endothermal chemical reactions trigger by the bow wave and the conical shock waves, generate an impressive quantity of atomic and molecular oxygen.