Enhancing Fairness and Efficiency in PV Energy Curtailment: The Role of East-West Facing Bifacial Installations in Radial Distribution Networks

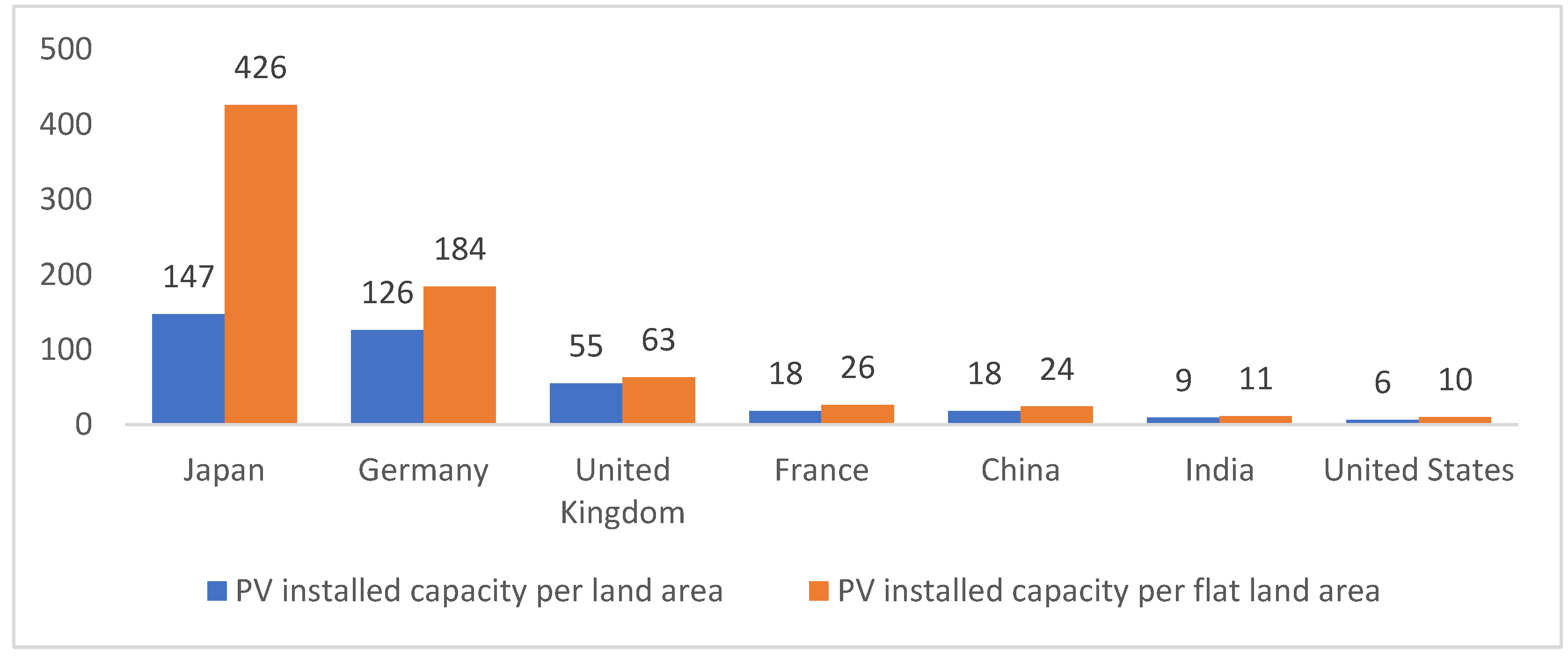
1. Introduction

The integration of solar-powered resources into power systems has increased worldwide in recent years. The cumulative solar capacity worldwide was approximately 1.2 TW (1185 GW) by 2022, up by 30% compared to 2021 levels, as the solar industry added 240 GW of new capacity, representing a 37% annual growth in PV installations [1]. Looking ahead, projections for 2027 forecast a solar market expansion to 3.5 TW of total operating capacity. This growth is attributed to several factors, with key drivers including the cost-competitiveness of solar-based sources, which facilitates both individual energy self-sufficiency and the comparatively quick deployment of utility-scale projects at low costs. Additionally, the continued restructuring of electricity markets, including feed-in tariffs (FIT) and feed-in premiums (FIP), has also promoted the effective selling of solar power. Hence, the business model of energy aggregation is gaining momentum where households can engage in contractual agreements with aggregators to trade surplus solar energy.

However, increased integration of photovoltaic systems in the distribution grids introduces operation and control challenges for power networks. Specifically, PV systems can generate reverse power flows and contribute to voltage rise resulting to overvoltage limit violations in distribution grids, especially during peak solar production hours around mid-day [2,3,4]. In response to this challenge, Distribution Network Operators (DNOs) curtail photovoltaic (PV) energy production to mitigate these violations, given the fact that networks are constrained by transmission line capacity and voltage limits. As such, aggregators encounter challenges in correctly determining bid volumes for energy markets, resulting in financial losses incurred due to penalties by market or grid operators due to supply-bid imbalances. Furthermore, households' potential earnings are reduced due to energy curtailment, which -prevents them from fully utilizing their excess PV energy [5,6,7]. Consequently, integrating PV systems into power grids requires suitable methods for balancing economic and operational demands on power networks.

To mitigate voltage violations, a number of strategies have been suggested by authors. Firstly, utilization of inverters with droop control (Volt/VAR and Volt/Watt) as presented in [8,9,10] lead to greater curtailment for downstream buses in radial distribution feeders [2,11,12]. This unfairly impact remote households necessitating a review of fairness in PV curtailment in distribution networks. To realize fairness, DNOs set static export limits during the initial connection of PV systems considering worst case scenarios [13,14,15,16]. However, these limits restrict the PV contribution from households in areas with either low PV penetration or in robust networks, especially during periods of minimal load. As a result, there is a growing advocacy for the implementation of flexible export limits based on network conditions [17,18,19].

Fairness in PV energy curtailment is critical to maintain equity among residential energy market participants. Unfair curtailment, particularly for houses at the end of distribution lines, not only lowers their economic return but also has the potential to undermine public support for solar energy adoption [20,21]. While minimizing total curtailment is often considered as the primary goal of distribution system operation, this approach may overlook fairness concerns and the significance of long-term public support. A fair distribution of curtailment guarantees that no single household is disproportionately affected, which is important in sustaining public trust and long-term adoption of PV systems. Various Optimal Power Flow (OPF) schemes have been developed to ensure fair curtailment. For example, authors in [2] created three Optimal Power Flow (OPF) schemes each with a distinct focus: PV harvesting, energy export, and financial benefits. Similarly, in [22], the authors suggested a distributed optimal power flow (DOPF) method for DER coordination that incorporates three equity principles: egalitarian, proportionate, and uniform dynamic PV curtailment redistribution. While these approaches can encourage fairness within their given frameworks, they may not fully resolve the trade-offs between fairness and system performance. As a result, the best appropriate fairness indicator is determined by the decision-makers' specific aims and constraints. Given the diversity of needs in modern distribution networks, it is necessary to develop multifaceted approaches that ensure both operational efficiency and fairness in curtailment.

In parallel with control-based strategies, recent studies have explored how physical system design (particularly PV orientation) affects not only generation performance but also curtailment dynamics. One of the greatest challenges in managing PV energy curtailment is the mismatch between peak solar power and network demand. Traditional mono-facial PV systems generate the most power at midday, which is generally the period when the grid is most constrained. As a consequence, energy curtailment is concentrated during these hours, resulting in significant PV energy loss. Vertically installed east-west facing bifacial PV systems have emerged as a promising architectural alternative.

Bifacial PV modules absorb sunlight from both the front and rear sides, shifting generation to morning and evening hours when demand is typically higher and grid constraints are less severe, thereby reducing the requirement for curtailment during midday peak hours. For instance, recent empirical studies have demonstrated that vertically mounted east–west bifacial installations can have installation efficiencies near those of conventional south-facing installations, due to their favorable angle-of-incidence characteristics that optimize solar irradiance collection in the morning and late afternoon [23]. This solves the issue of midday curtailment very effectively and offers a good way of reducing peak-time over voltages and energy losses. Figure 1 illustrates the differences in energy output between mono-facial and vertical sets of east-west facing bifacial PV panels, emphasizing the ability of bifacial systems to align generation with demand. Similarly, authors in [24] demonstrated that east-west vertically mounted bifacial PV systems had higher specific yields comparable to traditional south-facing systems but with the additional spatial and aesthetic benefits, which are especially valuable in urban green roofs. In addition, modelling results given in [25] suggested that vertical east-west oriented modules could outperform conventional setups, based on design specifications, curtailment strategies, and local electricity market prices.

This study proposes the installation of vertical east-west facing bifacial PV modules for residential systems as a novel approach to simultaneously minimize curtailment and enhance fairness in distribution networks While previous studies have established that vertically mounted east-west bifacial PV systems have the potential to increase energy yield distribution and spatial efficiency, they have largely overlooked the impact of such architectural configurations on fairness in curtailment distribution across network users. This work addresses that gap by examining the influence of vertical bifacial PV orientation on both operational performance and equitable curtailment allocation under radial distribution network conditions. Through the utilization of time-shifted generation characteristics as shown in Figure 1, this study incorporates fairness metrics into network models to provide new insights into the manner in which design choices can improve technical performance and fairness in distribution networks.

The installation of vertical sets of east-west facing bifacial PV modules is not only relevant in terms of improving distribution network operation performance and fairness in energy curtailment, but it will also improve economic returns for households, given that residential PV installations are likely to rise more in the future. Referring to Figure 2, Japan leads in solar PV installation capacity per land area among major countries, with a capacity twice that of Germany for flat land installations [26]. However, Japan’s capacity for further solar generation on flat land becomes increasingly difficult due to geographic and urban constraints [27,28]. Therefore, not only roof-top PV, but also innovative approaches such as wall-mounted PV systems on east-facing and west-facing walls, along with vertical bifacial installations are essential to maximize solar generation [29]. These systems are particularly promising for deployment on roof-top fences and ground installed fences around buildings, where space constraints can be mitigated by their vertical configuration. Additionally, they can also play a significant role in agrivoltaics, where they can coexist with agricultural activities such as pasturage to enhance land-use efficiency while generating PV energy [30,31,32].

To evaluate how the installation of vertical east-west bifacial PV affects curtailment dynamics in terms of fairness, three key metrics are used: Jain’s Fairness Index, Gini Index, and Curtailment Index. These metrics assess how equitably curtailment is distributed among households, offering a comprehensive understanding of the trade-offs between fairness and curtailment efficiency. To assess the effectiveness of these bifacial installations, this study compares energy output with mono-facial south-facing PV installations at various capacity levels (1 kW–20 kW). Fairness metrics are employed at a 10 kW PV capacity to quantify and evaluate curtailment distribution.

Figure 1. Comparison of solar output for (a) mono-facial, (b) vertical bifacial east-facing (BiE), and, (c) vertical bifacial west-facing (BiW) systems.

Figure 1. Comparison of solar output for (a) mono-facial, (b) vertical bifacial east-facing (BiE), and, (c) vertical bifacial west-facing (BiW) systems.

Figure 2. PV installed capacity per land area by country (kW/km²) [26].

Figure 2. PV installed capacity per land area by country (kW/km²) [26].

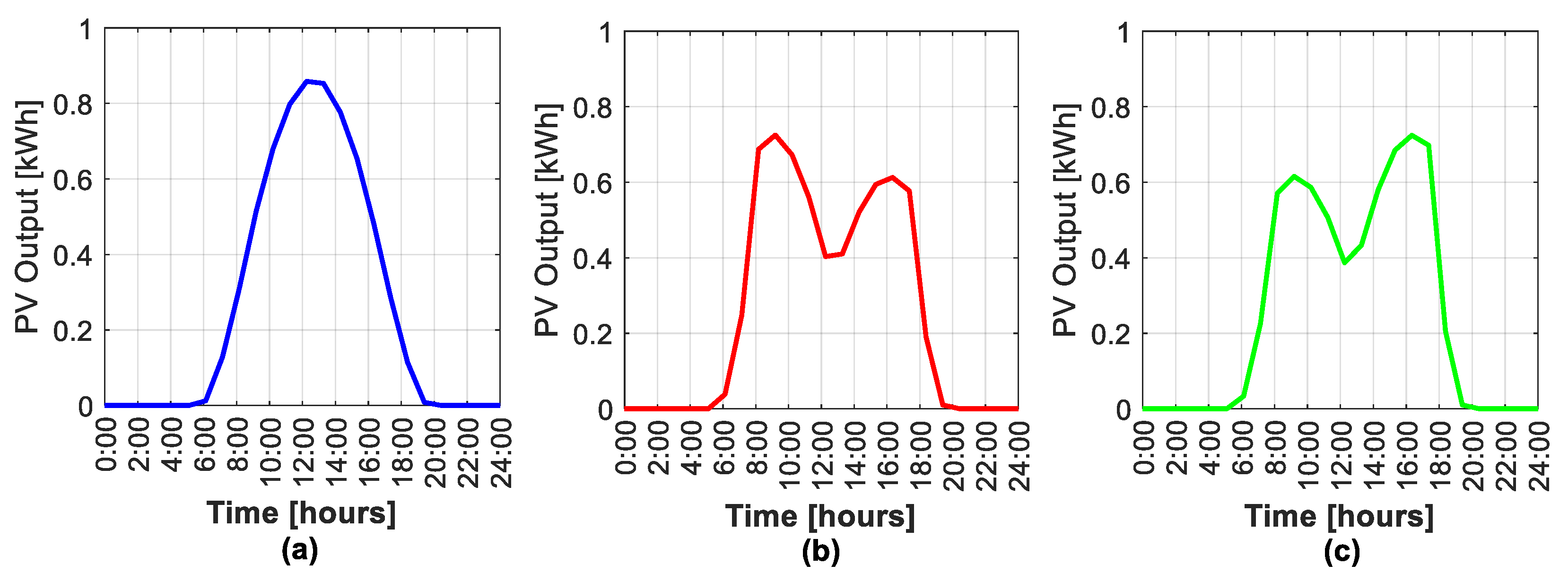
2. Vertical Bifacial Modules

Vertical bifacial PV modules offer versatility and adaptability in various installation scenarios making them particularly suitable for applications where space is limited or traditional horizontal installations are impractical. Their design flexibility enables integration in buildings expanding possibilities for solar energy deployment in urban environments.

2.1. Irradiance Calculation Model

This study considers east-west facing bifacial PV installations (BiE and BiW) characterized by two power peaks during morning and evening periods. According to [33,34] the global irradiance, $G_{Tf}$ on the frontside of a tilted surface is estimated from transposition models that assume the form

$$G_{Tf}=G_C+G_D+G_R,$$

(1)

where $G_c,G_D$ and $G_R$ represent direct, diffused and reflected irradiance. This study assumed isotropic sky model to estimate diffuse irradiance and the model developed by Liu and Jordan [35] was adopted. From Equation 1, the global irradiance was computed as follows

$$G_{Tf}=I_b{R}_b+I_d\left({\displaystyle \frac{1+cos\beta }{2}}\right)+I{\rho }_g\left({\displaystyle \frac{1-cos\beta }{2}}\right),$$

(2)

where $I_b$ is direct (beam) irradiance on horizontal surface, $I_d$ is the horizontal diffuse irradiance and $I$ is the total horizontal irradiance $(I=I_b+I_d$ ). $R_b$ represents geometric factor i.e., the ratio of beam radiation on a tilted surface to that of horizontal surface $(R_b={\displaystyle \frac{cos\theta }{cosZ}})$. $\theta ,Z$ and $\beta$ denote the incident angle, solar zenith angle, and surface tilt angle respectively. ${\rho }_g$ represents the ground surface albedo. Refer to [33] for the calculation method of radiation on tilted surfaces.

For bifacial PVs, the total irradiance is calculated by adding contributions from the front and rear sides. Following the IEC TS 60904-1-2 standard, which provides guidelines for evaluating bifacial PV performance under natural sunlight conditions, the total irradiance was calculated using

$$G_{total}=G_{Tf}+\phi G_{Tr,}$$

(3)

where $\phi$ and $G_{Tr}$ represents the bifaciality factor and rear irradiance respectively. Neglecting shadows and panel height, the rear irradiance was estimated using

$$G_{Tr}=I_b{R}_{b,rear}+I_d\left({\displaystyle \frac{1+\mathrm{c}\mathrm{o}\mathrm{s}(\pi -\beta )}{2}}\right)+I{\rho }_g\left({\displaystyle \frac{1-\mathrm{c}\mathrm{o}\mathrm{s}(\pi -\beta )}{2}}\right),$$

(4)

where $R_{b,rear}$ is the geometric factor for the rear side. Using Equation 3, PV output of bifacial PV model was given by

$$P_{PV}=G_{total}\times C_{PV}\times PR,$$

(5)

where $C_{PV}$ denotes installed panel capacity and $PR$ represents the PV system performance ratio. In this model, the performance ratio was assumed to be 0.8, and the bifaciality factor was set at 0.8. For the south-facing mono-facial panels, the bifaciality factor is zero; therefore, $G_{total}=G_{Tf}$, and Equation 5 is also applied to calculate their PV output. The tilt angle for the mono-facial south-facing installation was assumed to be 30 degrees.

3. Curtailment and Fairness Evaluation

3.1. Curtailment Energy Modelling

Distribution network operators usually curtail PV energy during periods of high generation to maintain grid stability and ensure a balance between supply and demand. This is necessary for preventing voltage rise, especially in distribution networks with high PV penetration, where reverse power flows can lead to overvoltage. In compliance with established grid codes and regulations, DNOs set upper voltage limits and actively monitor and manage the current flow and frequency stability across the network. For example, in Japan, voltage regulation standards specify that for low voltage customers voltages must be maintained within 101±6 V for a standard voltage of 100 V, and 202±20 V for a standard voltage of 200V [36,37]. Therefore, if reverse power flows cause voltage to deviate from these limitations, distributed generation installations, such as PV systems, should use reactive power control and output control functions to automatically control it. Therefore, while centralized generators are conventionally used to balance grids during periods with excess renewable generation, PV systems with advanced inverter control strategies (such as active power curtailment, Volt/VAR control, and Volt/Watt control) can play a vital role in locally addressing voltage rises where they occur, thereby providing a faster response. This reduces overreliance on centralized generation for voltage control and enhances the resilience of distribution grids, also considering that more renewable sources are being connected to grids. In addition to voltage management, network operators must maintain network frequency within permissible limits. The frequency must be kept within ±0.3 Hz of the standard frequency in Hokkaido/Okinawa and ±0.2 Hz in other locations. This comprehensive approach effectively facilitates the integration of distributed generation installations such as PV systems into the grid.

This study focuses on voltage curtailment as a mechanism to prevent voltage rise in distribution grids with high PV integration. The energy curtailment process is carried out at regular 5-minute intervals (288 timeframes per day) based on Newton-Raphson Power flow simulations. These simulations, combined with voltage profile analyses ensure that network operational limits are maintained at every timeframe by iteratively adjusting the power output at each bus as needed. Therefore, multiple iterations may be required for each timeframe as the bus voltage profiles are examined and curtailment applied until each bus’s voltage is within the acceptable limits.

Compared to other power flow models, such as the DistFlow model, the Newton-Raphson method was chosen for this study because of its robustness in solving non-linear power flow equations, making it ideal for dynamic voltage control in distribution grids with high PV integration where voltage conditions change rapidly. The iterative nature of the Newton-Raphson method ensures precise regulation of voltage levels across the network. In this model, the power output at each bus is adjusted based on the calculated voltage deviation at that bus. This localized decision-making allows for voltage regulation to be tailored to meet the specific needs of each bus, ensuring that curtailment is only applied when necessary.

Considering radial distribution networks, curtailment is not uniformly applied across all buses. Buses located farther from the substation are more prone to voltage rise and, as a result, experience more frequent and larger curtailment actions. Figure 3 illustrates the voltage profiles of the nearest and farthest buses in a 30-bus feeder system, highlighting how distant buses require more aggressive curtailment measures. The power curtailed at each bus $i$ during each simulation iteration, $P_{curtail}\left(i\right),$ is determined based on the excess voltage at the bus and is given by:

$$P_{curtail}\left(i\right)={\displaystyle \frac{V_{bus}\left(i\right)-V_{max}}{V_{bus}\left(i\right)}}\times P_{bus}\left(i\right),$$

(6)

where $V_{max}$ denotes the upper voltage limit, $V_{bus}\left(i\right)$ and $P_{bus}\left(i\right)$ represent the voltage and power output at bus $i$ respectively. This equation ensures that curtailment is applied precisely where voltage violations occur, enabling a dynamic, voltage-based curtailment strategy. The total energy curtailment at bus $i$, $E_{curtail}\left(i\right)$, for each 5-minute timeframe, $∆t$, is calculated by summing the power curtailed in all simulations within the interval, and is given by

$$E_{curtail}\left(i\right)=\left(\sum P_{curtail}\left(i\right)\right)\times ∆t.$$

(7)

Figure 3. Voltage profiles for (a) bus 1 and (b) bus 30.

Figure 3. Voltage profiles for (a) bus 1 and (b) bus 30.

3.2. Fairness Evaluation Metrics

Fairness in the context of residential PV energy curtailment refers to the equitable allocation of curtailment actions among the various households involved in energy markets [38]. In this study, three fairness indexes are utilized to assess the fairness of PV energy curtailment when vertical bifacial east-west facing PV installations are used in place of mono-facial south-facing PV systems. By providing a thorough examination of the distribution of curtailment among several buses, these indexes allow this paper to assess both the technical efficacy of the proposed curtailment approach and its effects on the social welfare of the various households.

3.2.1. Curtailed Energy Index (CEI)

The Curtailed Energy Index is specifically designed to assess the fairness of energy curtailment across the different buses in the distribution network. CEI evaluates curtailment fairness quantitatively by assessing the distribution of curtailed energy at 5-minute intervals following load flow simulations. CEI is computed using:

$$CEI=\sqrt{{\displaystyle \frac{{\sum }_{i=1}^n{\left(E_{curtail}\left(i\right)-E_{curtail}^{avg}\right)}^2}{2{·\left(E_{curtail}^{total}\right)}^2}}},$$

(8)

where $E_{curtail}\left(i\right)$ represents curtailed energy at the $i^{th}$ bus, and $E_{curtail}^{avg}$ represents the average curtailed energy in the network, while $E_{curtail}^{total}$ is the total amount of curtailed energy during the 5-minute timeframe. The factor of 2 normalizes the variation in curtailed energy among the different buses with respect to the total curtailed energy. The $CEI$ varies from 0 to 1, with a value of 0 denoting uniform distribution of curtailed energy, signifying that each bus experiences the same level of curtailment.

3.2.2. Jain Fairness Index (JFI)

Jain’s Fairness Index provides a measure of assessing fairness in resource allocation in various systems, including evaluating the level of equity in the distribution of curtailment impacts for residential PV in distribution networks [39]. In this study, it is used to evaluate the level of fairness in the distribution of energy sold relative to the surplus energy available at each bus, i.e., it measures how uniformly the available surplus energy is being converted into energy sold across the network at each 5-minute timeframe. $JFI$ is calculated using:

$$JFI\left(x_1,\dots ,x_n\right)={\displaystyle \frac{{\left({\sum }_{i=1}^n{x}_i\right)}^2}{n.{\sum }_{i=1}^n{x}_i^2}},$$

(9)

where $x_i={\displaystyle \frac{soldbusenergy}{surplusbusenergy}}$ represents the ratio of the energy that can be sold to the total surplus energy at the $i^{th}$ bus. $Surplusbusenergy$ refers to the energy which is generated by the PV systems connected at bus $i$ that exceeds load consumption at bus $i$and is available for sale to the grid. $Soldbusenergy$ is the actual amount of surplus bus energy that is sold after curtailment. The $JFI$ ranges between 0 and 1 where a value of 1 indicates perfect fairness meaning that all buses have an equal ratio of energy sold to surplus energy.

3.2.3. Gini Index (GI)

The Gini Index, a statistical measure frequently utilized to evaluate inequality in income distribution has been applied to analyse the fairness of energy curtailment in networks incorporating photovoltaic (PV) systems [40,41]. The Gini Index is adapted in this paper to evaluate how equitably $soldbusenergy$ is distributed across the different buses. Unlike the $JFI$ which measures fairness based on the $surplusbusenergy$ injection efficiency, the Gini Index assesses how evenly benefits of PV generation i.e., $soldbusenergy$ are distributed during each 5-minute timeframe. The Gini index is given by

$$GI={\displaystyle \frac{1}{2n^2\overline{y}}}{\sum }_{i=1}^n{\sum }_{j=1}^n\left|y_i-y_j\right|,$$

(10)

where $y_i$ and $y_j$ represent $soldbusenergy$ at the $i^{th}$ and $j^{th}$ buses respectively, and $\overline{y}$ is the average value of energy sold across all buses. The Gini Index ranges between 0 and 1 where a lower value reflects a fairer system in which all buses have an equal opportunity of selling energy generated. On the other hand, a higher value indicates that some buses benefit more than others from the energy sold due to their location or system configuration.

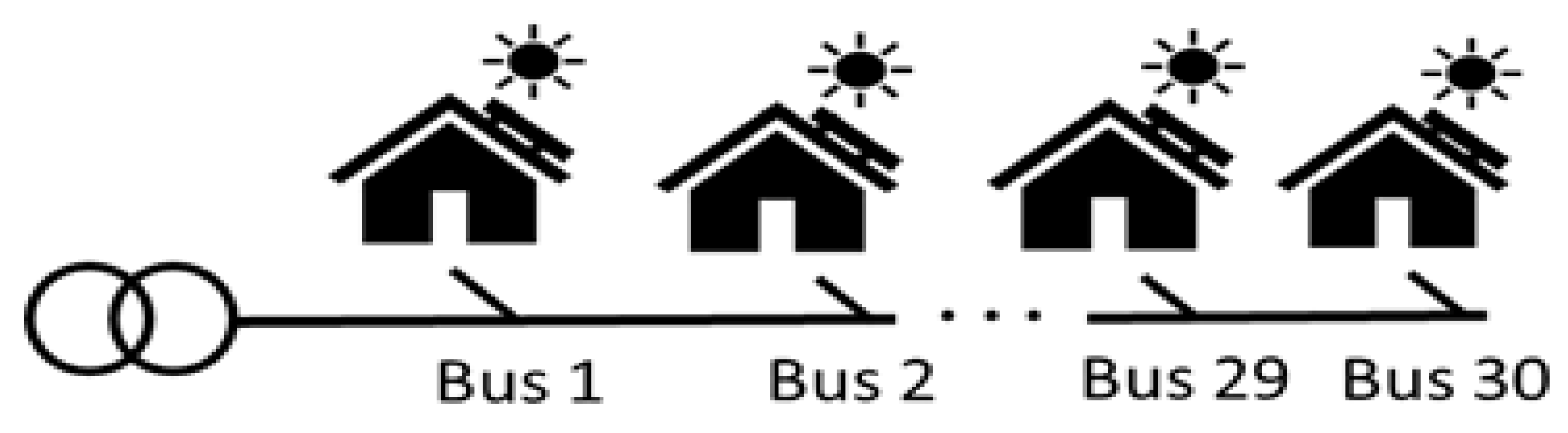
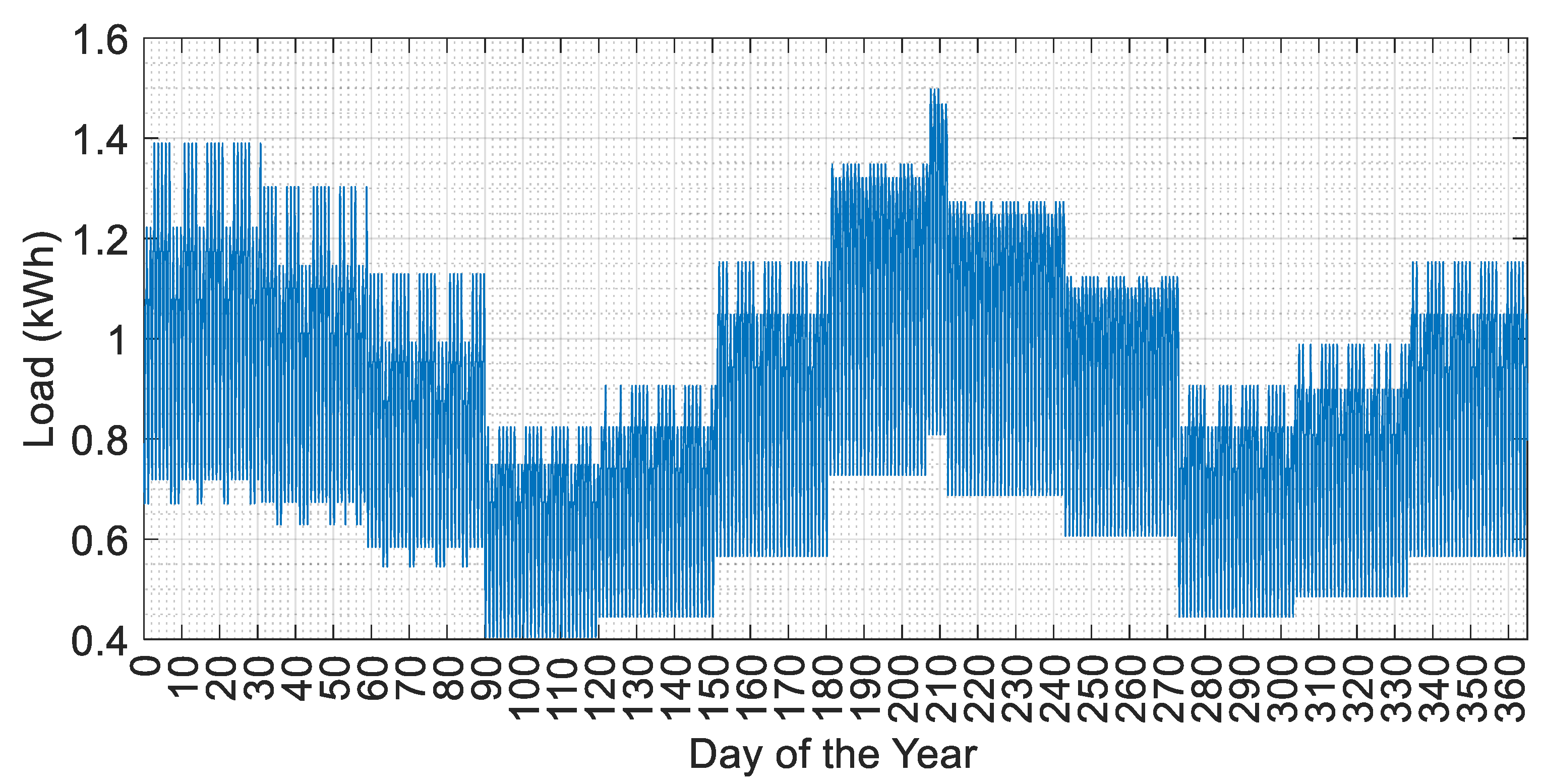
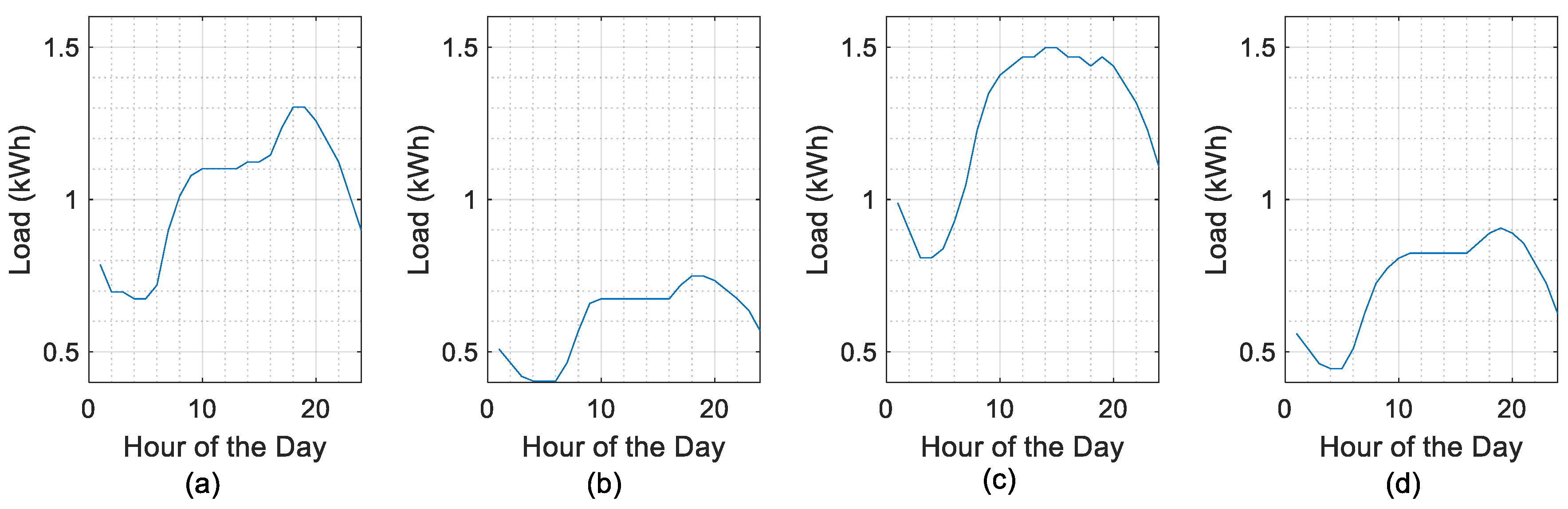
4. Simulation Conditions

In this study, a 30-bus distribution network shown in Figure 4, designed in a radial configuration, was constructed using MATLAB based on the JST-CREST 126 distribution feeder model data [42]. The separation between the buses was assumed to be 300m, and each bus was connected to 10 households, each equipped with its own photovoltaic (PV) system. The data used to construct the distribution network is presented in Table 1.

Figure 4. Model of the distribution network.

Figure 4. Model of the distribution network.

Table 1. Data for the distribution network.

Parameter	Value
LRT installed capacity	10 MVA
Reference Voltage	6.6 kV
Line type	ALOE32
Line impedance	0.928 +j 0.415 Ω/km
Susceptance	$2.844\times {10}^{-6}$S/km

Table 1. Data for the distribution network.

Parameter	Value
LRT installed capacity	10 MVA
Reference Voltage	6.6 kV
Line type	ALOE32
Line impedance	0.928 +j 0.415 Ω/km
Susceptance	$2.844\times {10}^{-6}$S/km

To simulate daily load data per household, this study employed the IEEJ residential load curve model [43]. This model encompasses load curves for both weekdays and holidays, structured around three seasonal profiles: winter, summer, and autumn/spring. To align the model with the consumption patterns of Fukui city, the model’s hourly load curves were normalized and adjusted to match the annual household electricity usage in Fukui city, which amounts to approximately 7,748 kWh per household per year [44]. Figure 5 shows the annual load curve adopted in this study. Figure 6 shows hourly load profiles at selected days of the annual load curve.

Figure 5. Annual load curve for a household.

Figure 5. Annual load curve for a household.

Figure 6. Hourly load profiles for selected days: (a) February 28th, (b) April 17th, (c) July 27th, and (d) October 18th.

Figure 6. Hourly load profiles for selected days: (a) February 28th, (b) April 17th, (c) July 27th, and (d) October 18th.

In this study, solar radiation data for Fukui city was sourced from AMeDAS system of Japan’s Meteorological Agency for the year 2022 [45]. Using this data, PV output curves for the various installation types on selected days of the year at 10 kW are illustrated in Figure 7. The transaction prices for daily PV energy sales across timeframes were determined based on the 2022 spot market prices for the Hokuriku region, as obtained from the Japan Electric Power Exchange [46].

Figure 7. PV output curves for selected days at 10-kW installation capacity: (a) February 28th, (b) April 17th, and (c) October 18th.

Figure 7. PV output curves for selected days at 10-kW installation capacity: (a) February 28th, (b) April 17th, and (c) October 18th.

For this study, three PV installation scenarios were considered for simulation to assess and compare the surplus and curtailed bus energies. The values for these energies were determined through load flow simulations conducted at 5-minute intervals. The scenarios considered were:

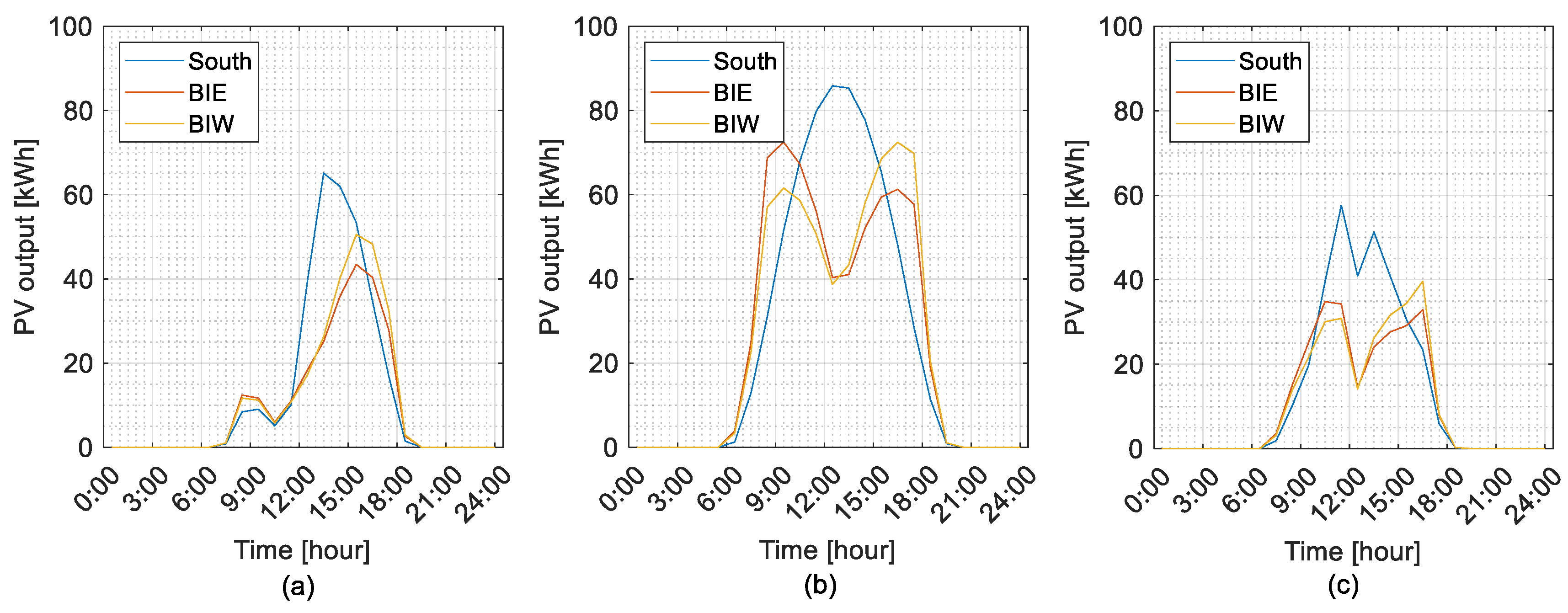
• All buses connected with mono-facial south-facing PV systems.
• All buses connected with bifacial PVs, with the front side facing east (BiE).
• All buses connected with bifacial PVs, with the front side facing west (BiW).

For each scenario, it was assumed that all households had uniform load and PV generation profiles. The upper limit for bus voltages was set at 1.05 per unit. Figure 8 illustrates the flowchart adopted for carrying out the simulations.

Figure 8. Flowchart of the simulation model.

Figure 8. Flowchart of the simulation model.

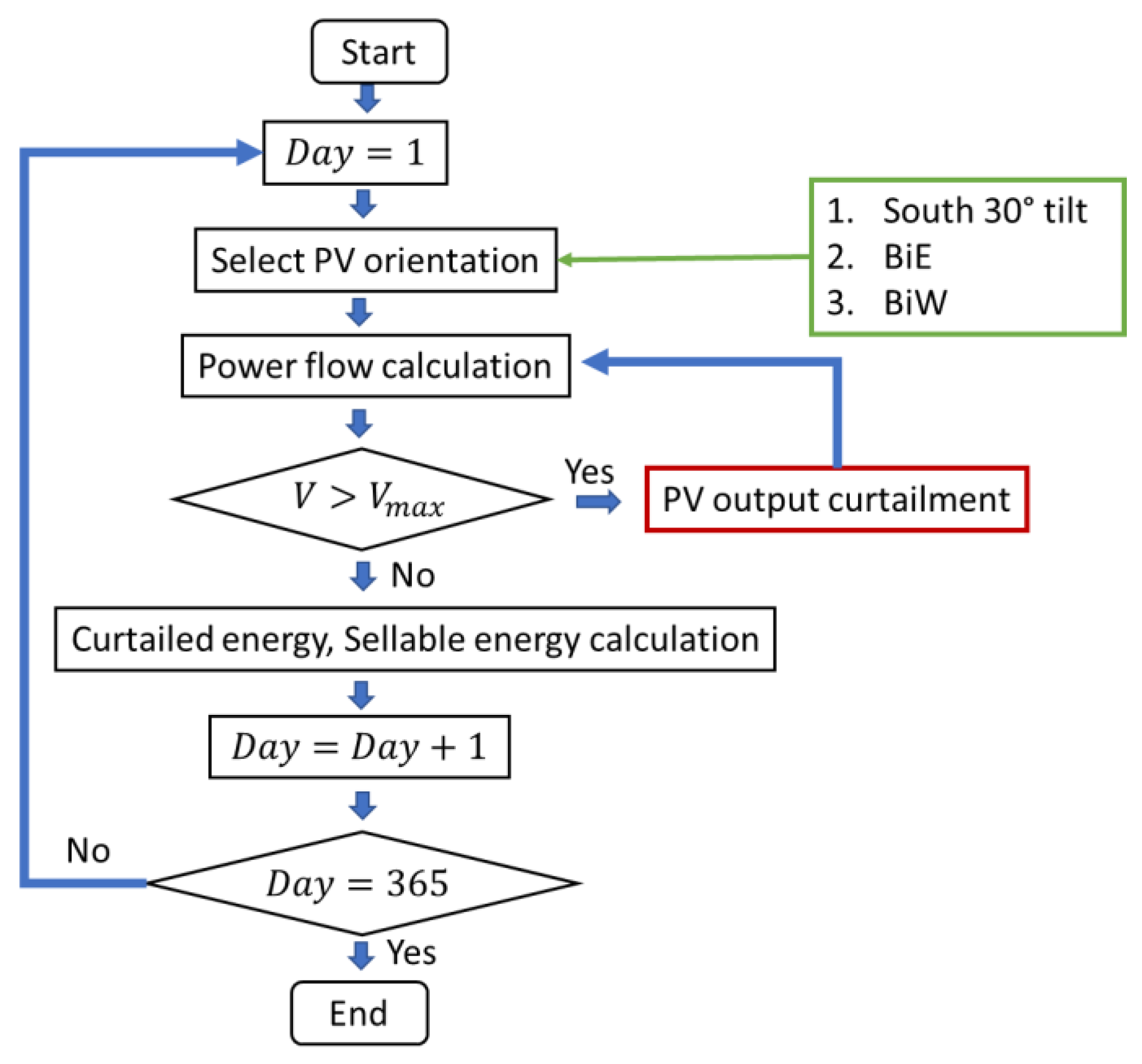
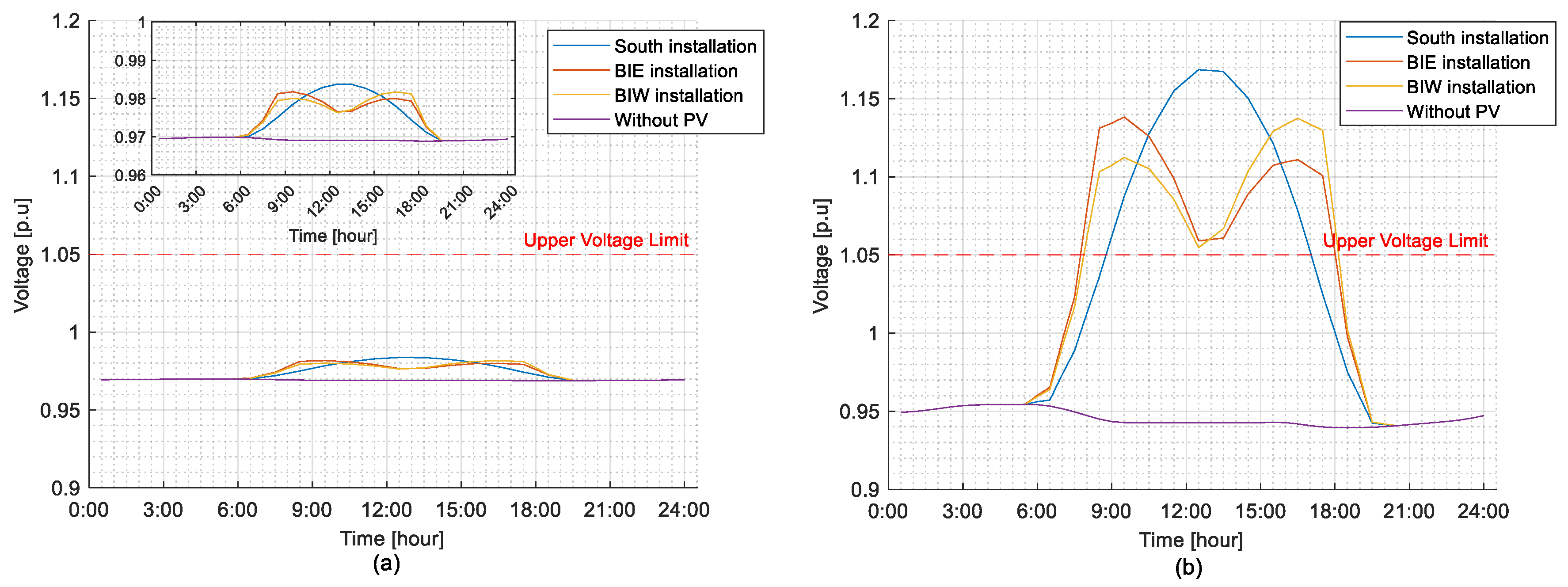
5. Simulation Results

5.1. Performance Analysis Across Different PV Capacities

The annual results for curtailed and bid energies as well as the revenue from bid energy at the different PV capacity levels are shown in Figure 9, Figure 11 and Figure 13 respectively. Additionally, Figure 10, Figure 12 and Figure 14 show incremental curtailed energy, incremental bid energy and incremental revenue respectively for each additional capacity increase. As illustrated in Figure 9 and Figure 10, curtailment begins at 5 kW for the mono-facial south-facing PV installation and 6 kW for both east-facing and west-facing bifacial installations. Curtailment significantly increases beyond these capacities for all the configurations with the south-facing installation curtailing more energy than the bifacials for each capacity increase. This can be attributed to the south-facing installations overproduction during peak sunlight hours leading to greater curtailment. On the other hand, BiE and BiW installations receive less intense sunlight during midday resulting to lower curtailment.

Figure 9. Curtailed energy versus system size for south-facing, BiE, and BiW PV configurations.

Figure 9. Curtailed energy versus system size for south-facing, BiE, and BiW PV configurations.

Figure 10. Incremental curtailed energy across system sizes.

Figure 10. Incremental curtailed energy across system sizes.

According to bid energy results shown in Figure 11, all the three installation types show consistent increase in bid energy as the installed capacity increases indicating that higher capacities will result to more energy sale. The south-facing installation shows higher initial bid energy amounts compared to the bifacial installation types with the bifacials catching up at higher capacities (the gap narrows towards 20 kW). This competitive performance demonstrated by bifacials indicates their efficiency in utilization of available solar irradiance. BiE and BiW installations exhibit similar patterns in the bid energy versus system size plots, as well as incremental bid energy versus system size plots with only slight variations beyond 12 kW in Figure 12. This consistency indicates that the performance for both BiE and BiW installations is nearly equally effective under similar conditions. Additionally, it is also noticeable from Figure 11 and Figure 12 that the rate of increase of bid energy seems to gradually plateau beyond 15 kW for all installation types signifying diminishing returns from sellable energy on additional capacity installations. The large increase in incremental bid energy at the initial capacities, from 1 kW to 5 kW for south-facing panels and up to 6 kW for bifacials, can be attributed to low base effect whereby slight increases in bid energies result to large percentage increases due to small initial values for bid energy.

Figure 11. Bid energy versus system size for south-facing, BiE and BiW PV configurations.

Figure 11. Bid energy versus system size for south-facing, BiE and BiW PV configurations.

Figure 12. Incremental bid energy across system sizes.

Figure 12. Incremental bid energy across system sizes.

Figure 13. Revenue versus system size for south-facing, BiE and BiW PV configurations.

Figure 13. Revenue versus system size for south-facing, BiE and BiW PV configurations.

Figure 14. Incremental revenue across system sizes.

Figure 14. Incremental revenue across system sizes.

Similar to bid energy, revenues from bid energy increased consistently with increase in installed capacity as shown in Figure 13 for all installation types. Initially, revenues from the south-facing installations are higher than for the bifacials. However, at installation capacities of around 10 kW and 12 kW, BiW and BiE configurations surpass that of the south-facing installation. This implies that BiE and BiW installations offer better financial returns from energy sold than south-facing installations in scenarios where higher capacities are feasible. Similar to incremental bid energy plot, the incremental revenue plot in Figure 14 shows diminishing marginal returns on capacities beyond 15kW as indicated by the plateau observed in revenue growth.

Furthermore, Figure 15 illustrates the sell-to-curtail energy ratio for all installation types at various capacities. From the figure, the ratio is initially high below 5 kW for south-facing and 6 kW for bifacial installations respectively due to zero curtailment. Beyond these capacities, the ratio decreases sharply as curtailment begins and then saturates at higher capacities. This indicates that curtailment becomes more significant as installed capacity increases, emphasizing the need for careful planning when selecting installation capacities to minimize curtailment while maximizing energy sales.

Figure 15. Sell-to-curtail energy ratio across all configuration types.

Figure 15. Sell-to-curtail energy ratio across all configuration types.

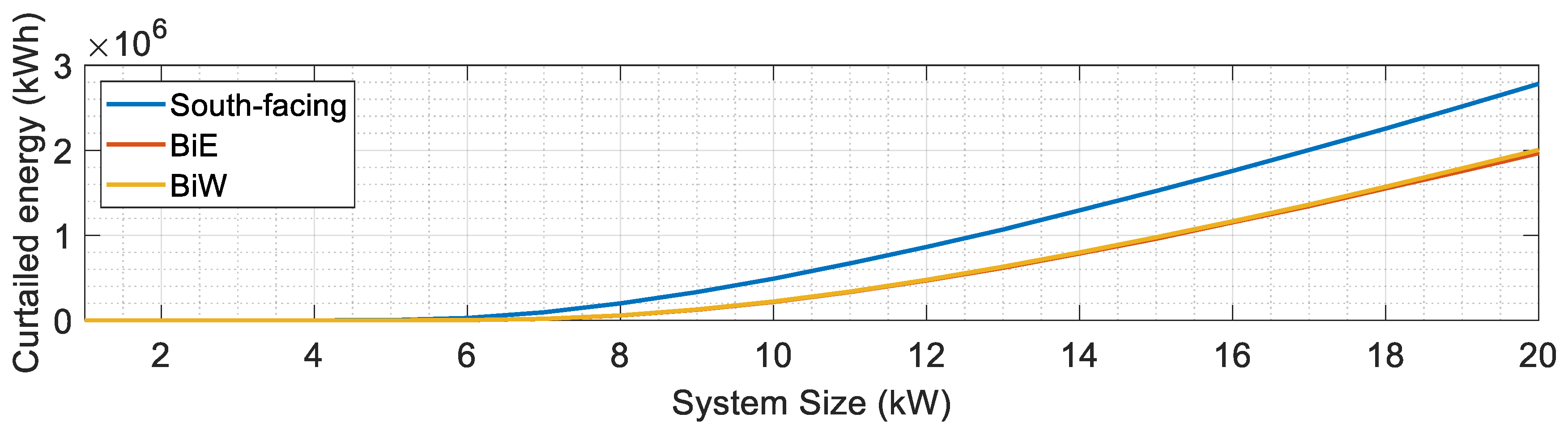
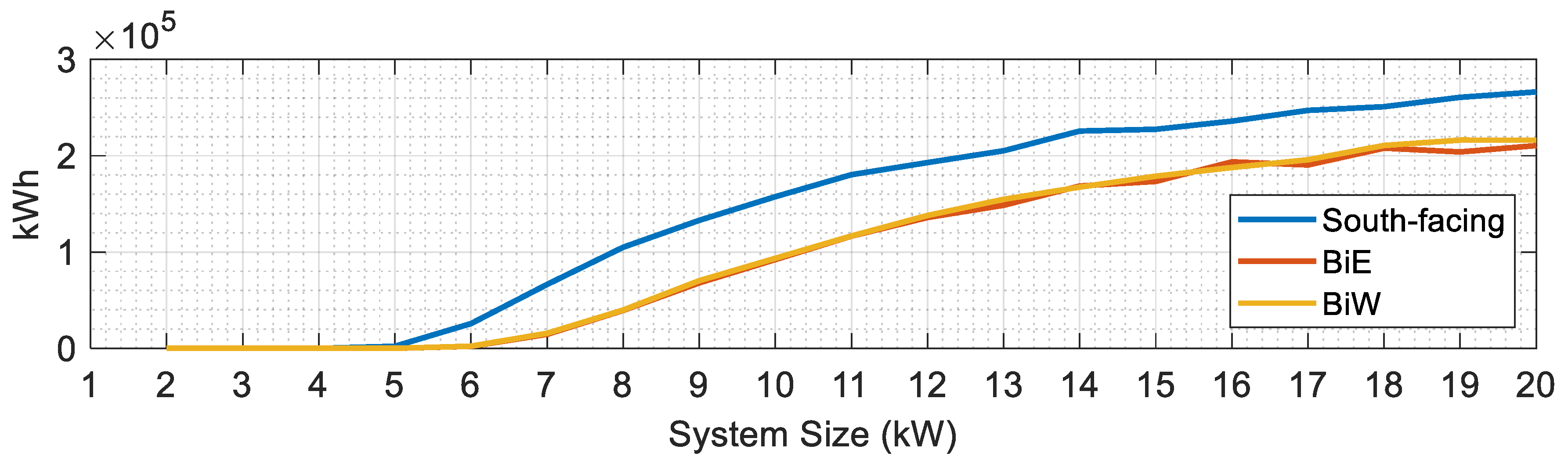
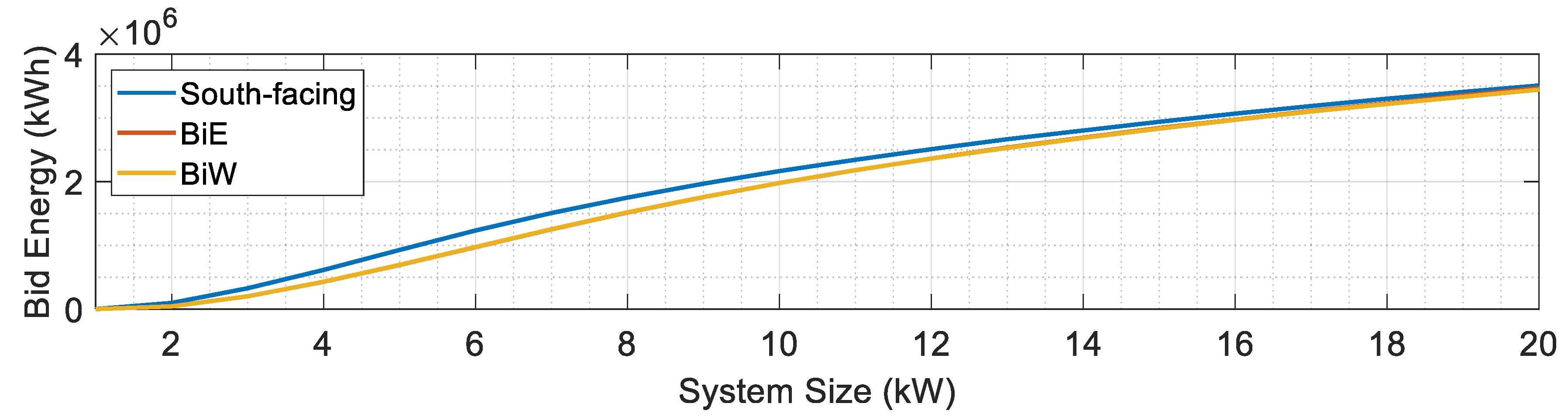
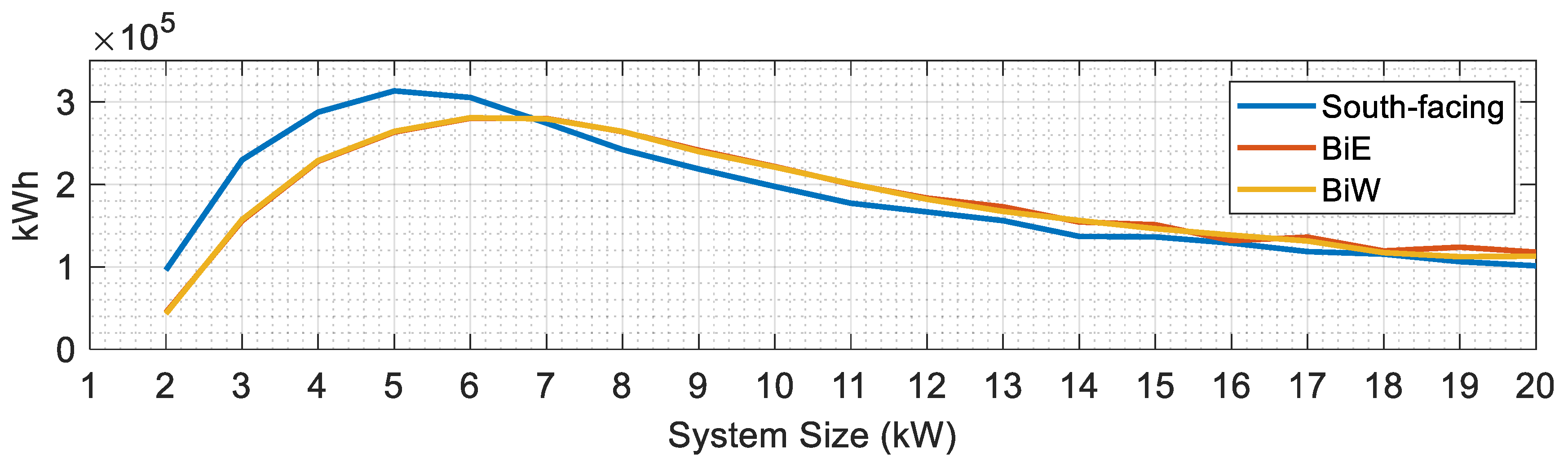
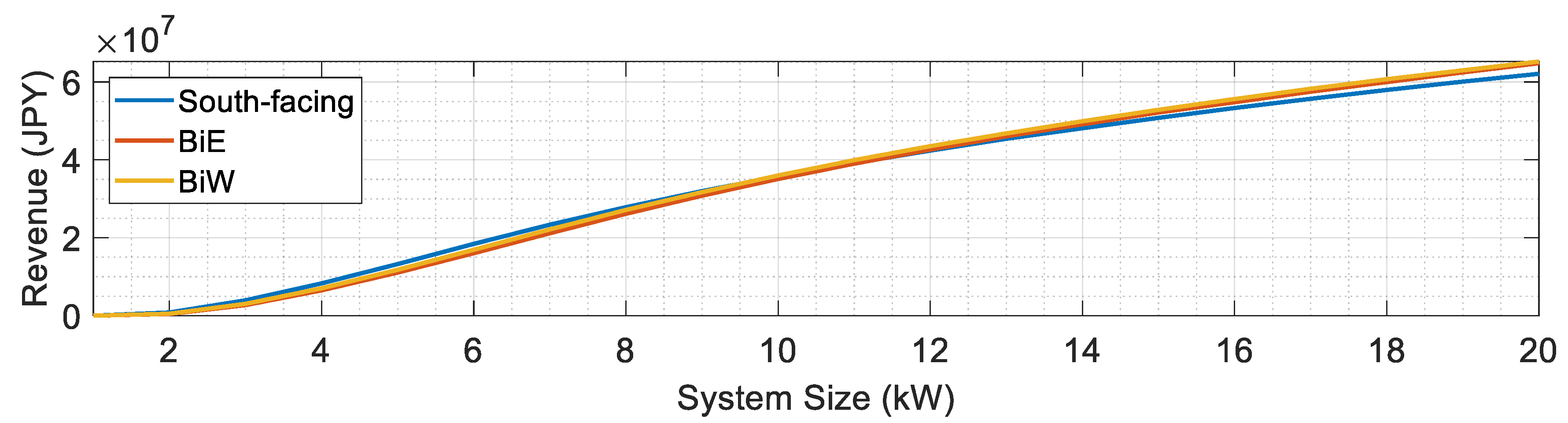
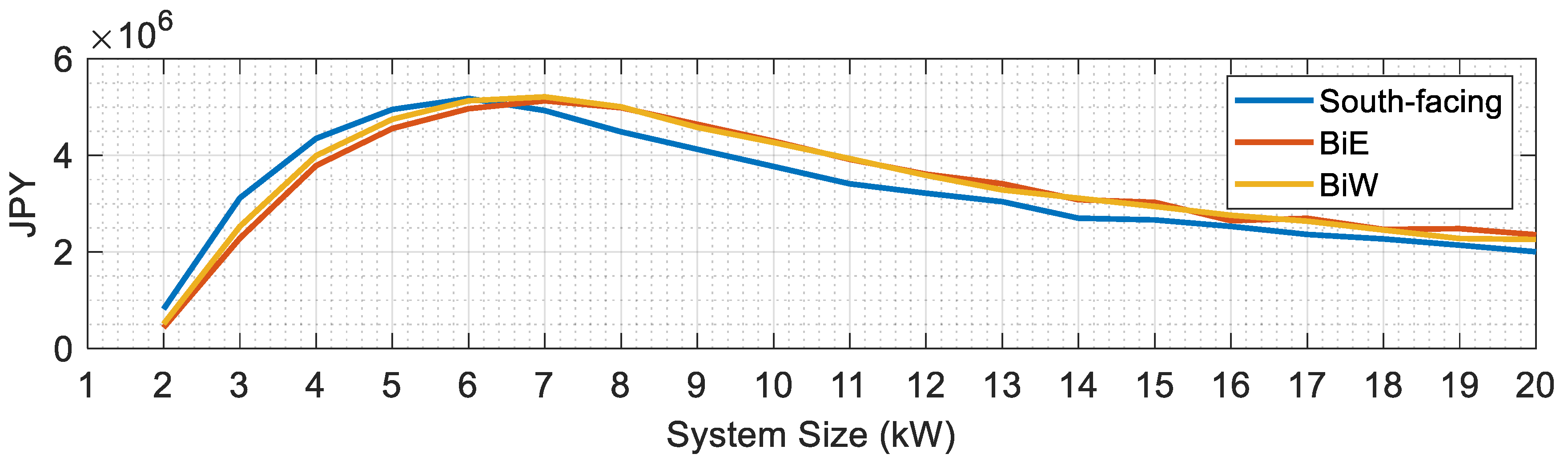
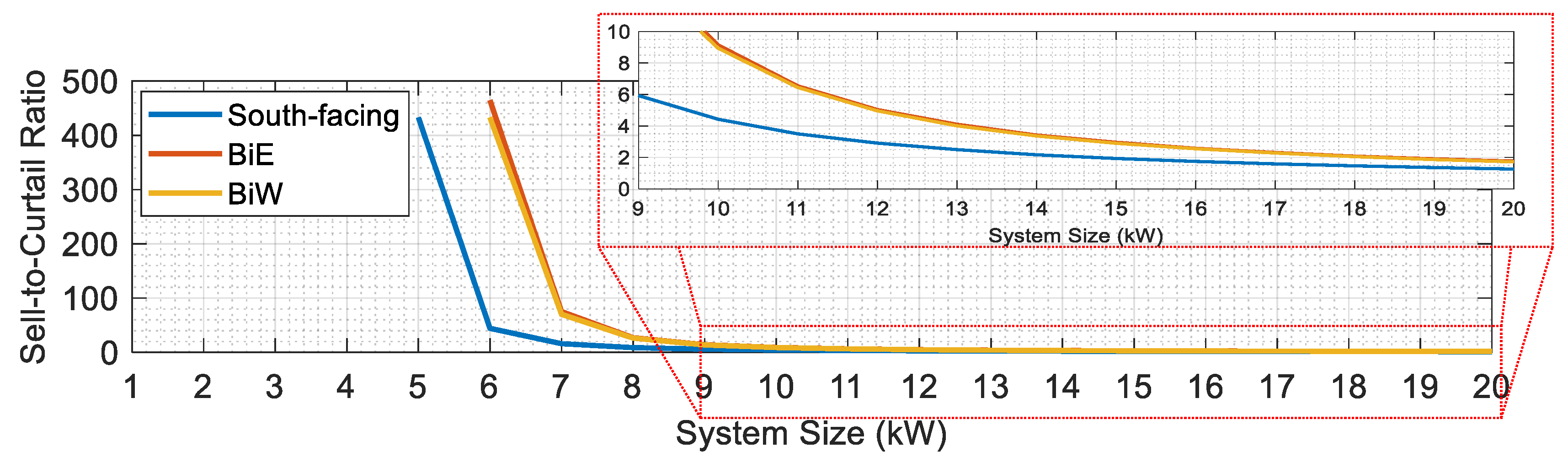
5.2. Fairness Evaluation at 10 kW Installation Capacity

Since implementing Japan’s Feed-in-Tariff scheme, the capacity for residential PV integration has expanded to 10 kW. Therefore, this study focused on a PV installation capacity of 10 kW and assessed fairness in energy curtailment across the different types of installation. The results include analyses of the day with the highest curtailed energy across all the installation types and the day with the lowest curtailed energy for each bifacial configuration.

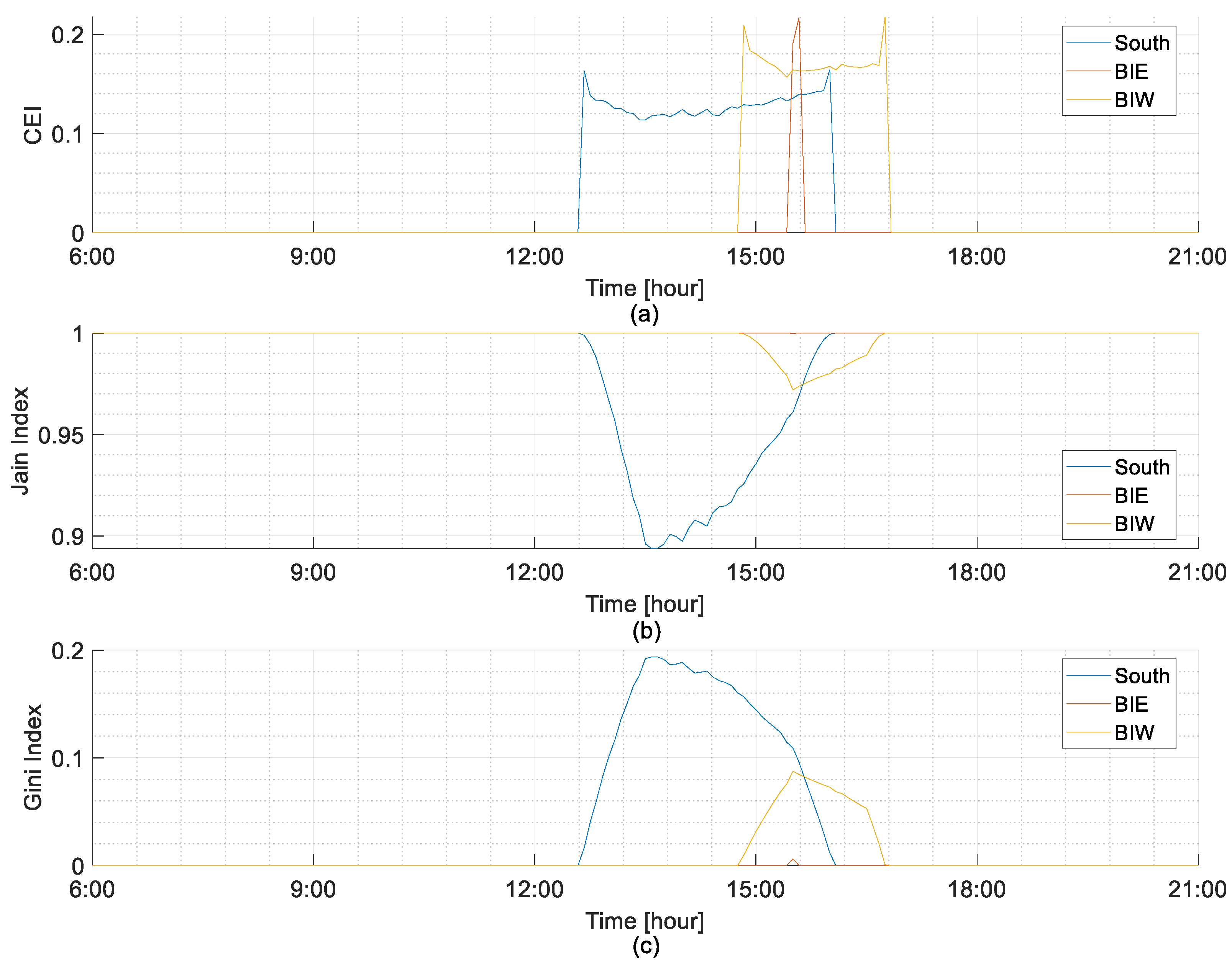
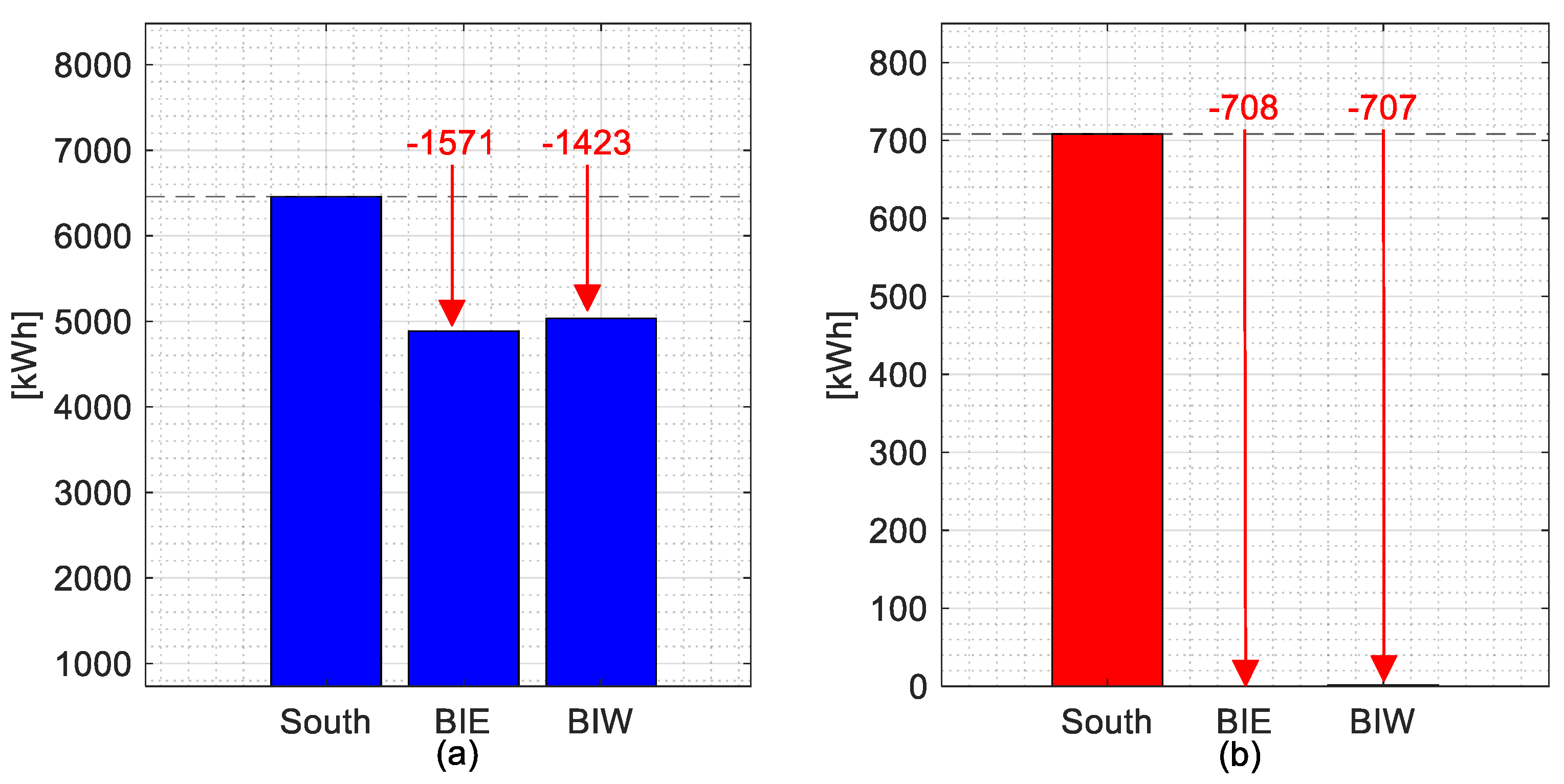
5.2.1. Highest Curtailed Energy Day

Figure 16 depicts the fairness index plots for April 17th, 2022, which was the day with the highest curtailed energy in all three installation types. The generated PV output plot for this day is shown in Figure 7. From the curtailment index plot, bifacial installations had a more spread-out curtailment pattern, and higher values than south-facing installations between 10:30 am and 3:30 pm. This implies that bifacials generated more energy compared to south-facing installation and as a result experience higher curtailment. From the Jain fairness index plot, it is observed that the south-facing installation had lower values than the bifacials between 10:30 am and 3:20 pm whose values were close to 1 between 12:30 pm to 1:30 pm. This indicates that the bifacials maintained fairness in the ratio of bus sellable to surplus PV energy even during midday. Furthermore, the Gini index plot which quantified fairness in terms of bus sellable energy also showed that bifacials effectively maintained fairness in sellable energy during this period compared to south-facing installation as indicated by the lower Gini values around midday. The bid and curtailed energies values for the day are shown in Figure 17. Compared to the bid and curtailed energy amounts of the mono-facial south-facing installation, the BiE and BiW installations increased bid energy by 815 kWh (7.2%) and 787 kWh (7.0%) respectively, while decreasing curtailed energy by 1566 kWh (27.9%) and 1499 kWh (26.7%) respectively.

Figure 16. Fairness metrics for April 17th: (a) Curtailment Index, (b) Jain Index, and (c) Gini Index.

Figure 16. Fairness metrics for April 17th: (a) Curtailment Index, (b) Jain Index, and (c) Gini Index.

Figure 17. (a) Bid energy and (b) curtailed energy for April 17th.

Figure 17. (a) Bid energy and (b) curtailed energy for April 17th.

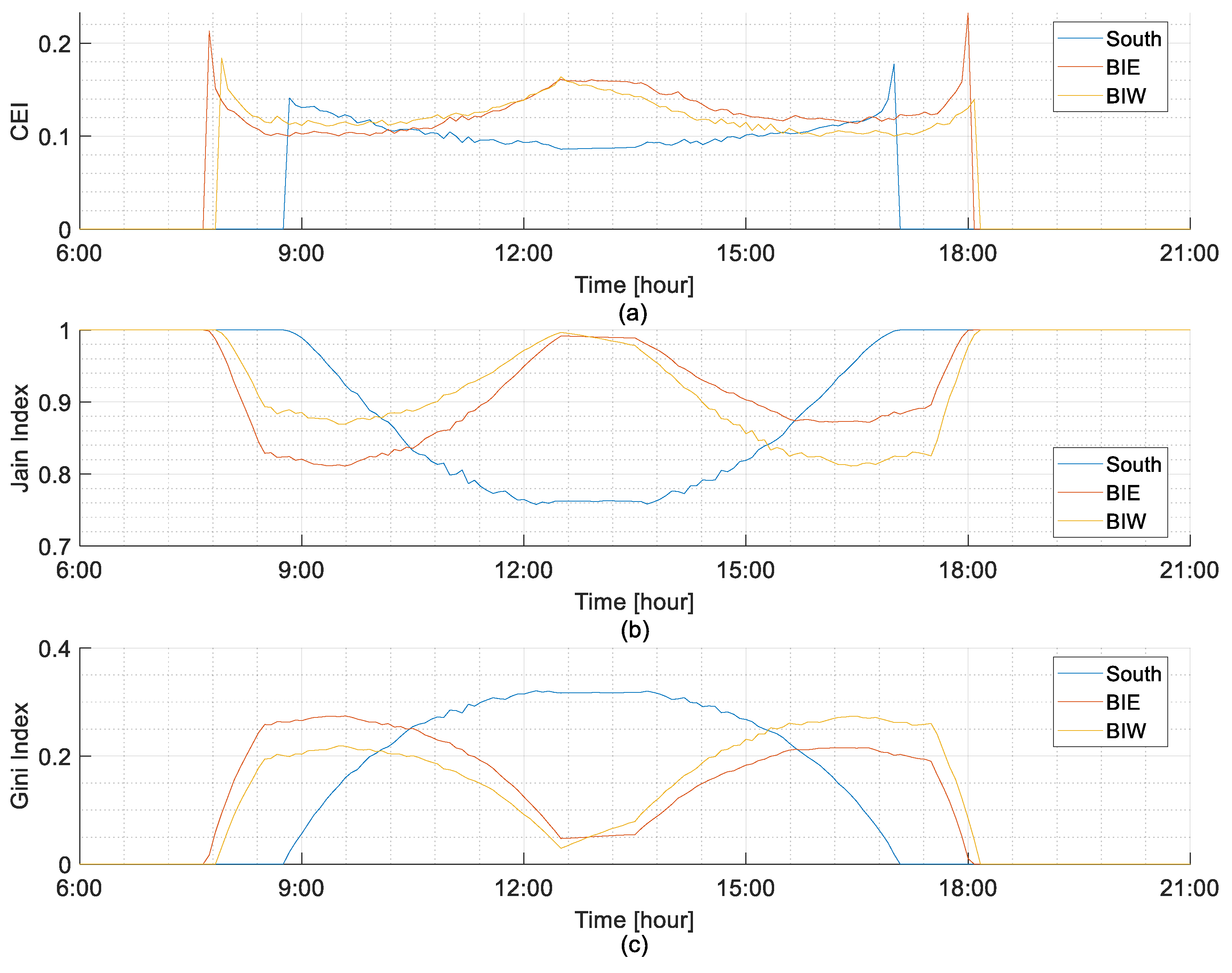
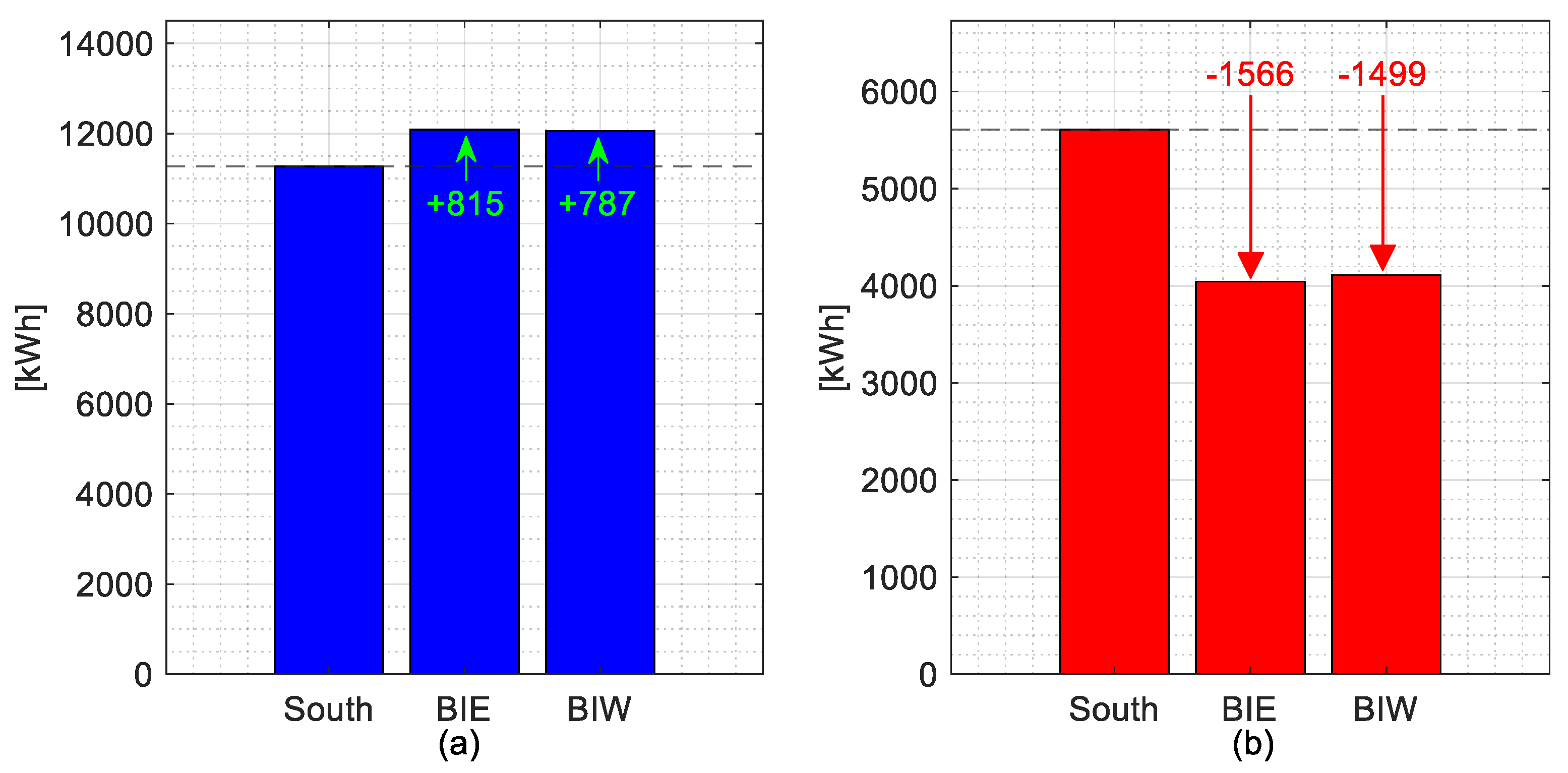
5.2.2. Lowest Curtailed Energy Days Considering BiE and BiW Installations

Figure 18 illustrates the fairness index plots for 28^th February 2022, the day with the lowest curtailed energy for the BiE configuration. As shown in the curtailment index plots, BiE and BiW installations achieved perfect fairness at all periods except from 3:25 pm to 3:40 pm and 2:45 pm to 4:50 pm, respectively. On the other hand, south-facing installation underwent curtailment between 12:35 pm to 4:05 pm. These observations imply that the bifacials are more effective in managing energy distribution without significant curtailment during periods with low solar intensity. Additionally, the BiE configuration achieved near perfect fairness in terms of the ratio of bus sellable to surplus energy and the equitable distribution of sellable energy as shown by the Jain and Gini index plots respectively. The bid and curtailed energy amounts for the day across the three installations are presented in Figure 19. The BiE and BiW installations reduced curtailed energy by 956 kWh (99.9%) and 783 kWh (81.9%) respectively, while their bid energy decreased by 1449 kWh (28.7%) and 935 kWh (18.5%) compared to the south-facing installation.

Similarly, Figure 20 presents the fairness index plots for 18^th October 2022, the day with the lowest curtailed energy for the BiW configuration. From the curtailment index both bifacial orientations achieved perfect fairness across the day except from 4:20 pm to 4:35 pm. In contrast, the south-facing installation underwent curtailment between 10:25 am and 2:45 pm which was unevenly distributed among the buses. Furthermore, as illustrated by the Jain and Gini index plots, bifacial installations exhibited a better performance in terms of both fairness and curtailment management compared to the south-facing installation. For the day’s bid and curtailed energies, as illustrated by Figure 21, the BiE and BiW configurations reduced curtailed energies by 708 kWh (100%) and 707 kWh (99.8%) respectively, while bid energies decreased by 1571 kWh (24.3%) and 1423 kWh (22.0%) compared to south-facing installation.

Figure 18. Fairness metrics for February 28th: (a) Curtailment index, (b) Jain index, and (c) Gini index.

Figure 18. Fairness metrics for February 28th: (a) Curtailment index, (b) Jain index, and (c) Gini index.

Figure 19. (a) Bid energy and (b) curtailed energy for February 28th.

Figure 19. (a) Bid energy and (b) curtailed energy for February 28th.

Figure 20. Fairness metrics for October 18^th: (a) Curtailment index, (b) Jain index, and (c) Gini index.

Figure 20. Fairness metrics for October 18^th: (a) Curtailment index, (b) Jain index, and (c) Gini index.

Figure 21. (a) Bid energy and (b) curtailed energy for October 18^th.

Figure 21. (a) Bid energy and (b) curtailed energy for October 18^th.

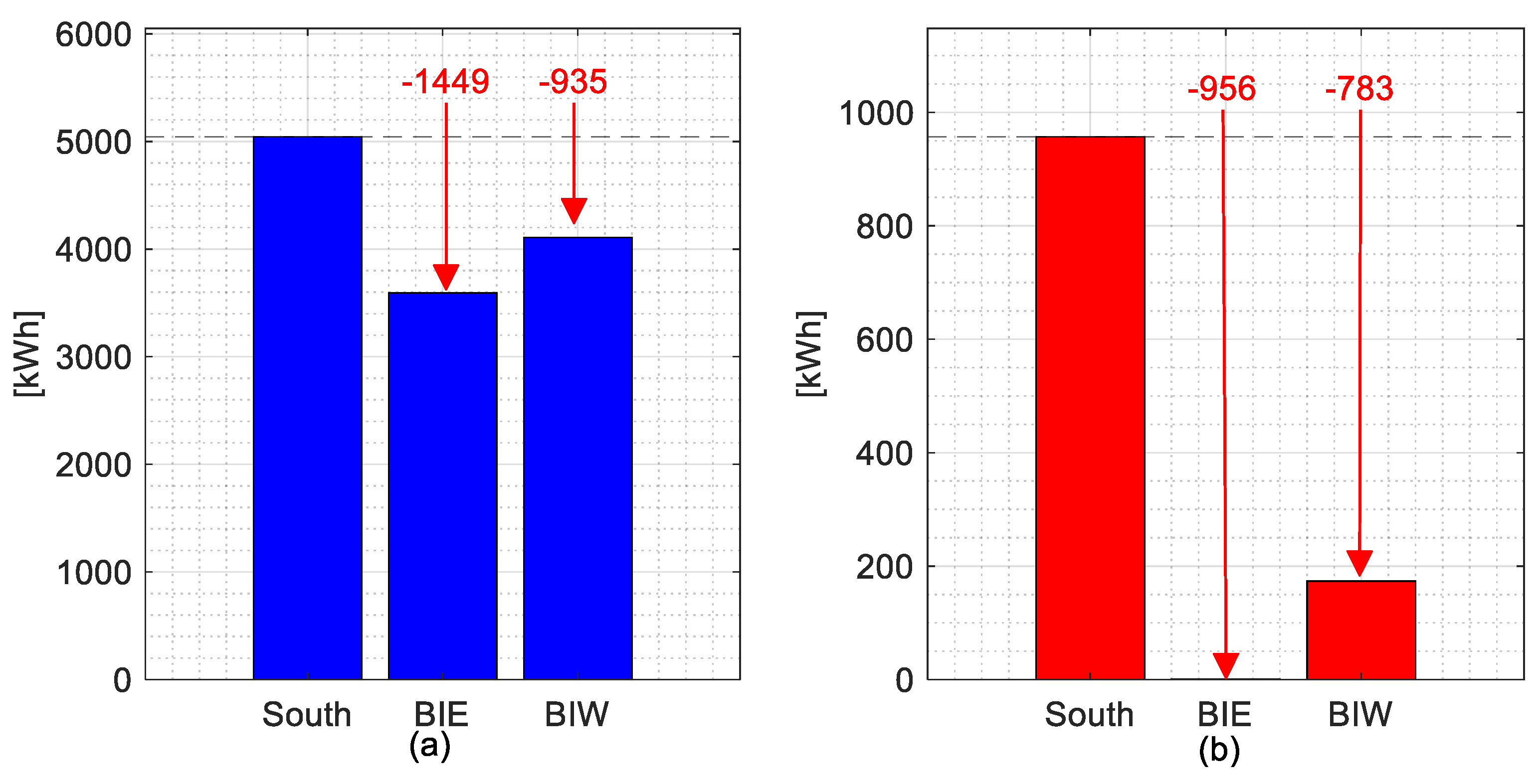
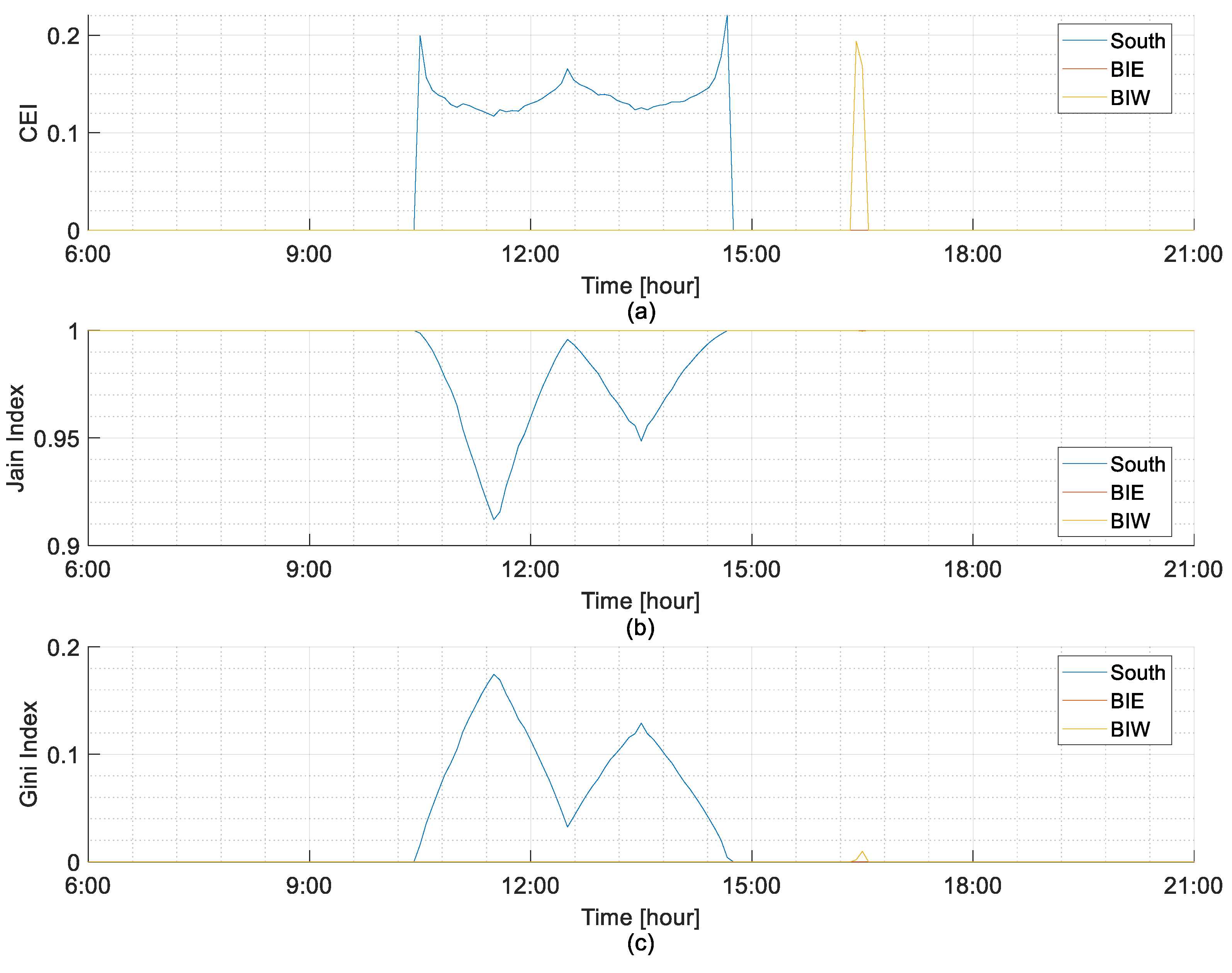
6. Conclusions

In this study, the installation of vertical set of east-west facing bifacial PV (BiE and BiW) for residential PV systems was proposed as a strategy to minimize curtailment and promote fairness in energy curtailment within distribution networks. Through analysis and comparison of the energy output of BiE and BiW installations and traditional mono-facial south-facing PV installations for various capacity sizes from 1 kW to 20 kW, this study demonstrates the effectiveness of bifacial installations in curtailment reduction in grids with highly integrated PV systems.

The results of simulations demonstrated that bifacial installations, especially at larger installation capacities, generate more energy and manage curtailment more efficiently than mono-facial south-facing installations. Their bid energy plots show similar trends, indicating that BiE and BiW configurations will perform nearly the same under similar situations. At higher capacity (more than 15 kW), the plots of incremental curtailed energy, bid energy, income from bid energy, and sell-to-curtail energy ratio show diminishing returns from sellable energy. This emphasizes the importance of optimizing system size in order to maximize energy sales revenue and operational efficiency.

Furthermore, fairness index plots evaluated at a 10-kW installation capacity demonstrate bifacial installations' superior performance in maintaining fairness in energy distribution without considerable curtailment during both low and high solar intensity periods highlighting their suitability for residential settings. On the day with highest curtailment, BiE and BiW installations increased bid energies by 815 kWh (7.2%) and 787 kWh (7.0%) respectively, while reducing curtailed energy by 1566 kWh (27.9%) and 1499 kWh (26.7%) respectively, compared to the mono-facial south-facing installation. During the day with lowest curtailed energy for BiE configuration, BiE and BiW installations reduced curtailed energy by 956 kWh (99.9%) and 783 kWh (81.9%) respectively although this was accompanied by a decrease in bid energy by 1449 kWh (28.7%) and 935 kWh (18.5%). Similarly, under the BiW configuration, BiE and BiW installations reduced curtailed energy by 708 kWh (100%) and 707 kWh (99.8%) respectively, with corresponding decreases in bid energy of 1571 kWh (24.3%) and 1423 kWh (22.0%).

While this study focused on a radial distribution network in Japan, the principles of dual-peak generation profiles and fairness-driven curtailment management could extend to other regions with similar grid constraints or high solar penetration. However, variations in grid topology, load profiles, and solar irradiance may affect performance, and broader validation across diverse systems is recommended. Future work will include cost-benefit analysis comparing bifacial and mono-facial installations over their lifecycle considering initial costs, maintenance and potential energy sale revenues. Additionally, an energy management system that predicts energy generation and demand will be developed to dynamically manage the distribution and curtailment of energy to improve fairness and efficiency. Future models will also explore the integration of Unit Commitment (UC), voltage control and fairness, as well as market factors like pricing and generation bids, to enhance the integration of PV systems into modern networks.