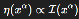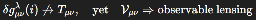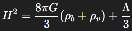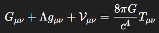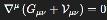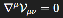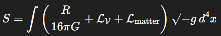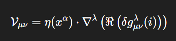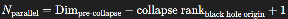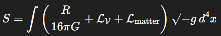1. Introduction
The problem of dark matter remains one of the most persistent inconsistencies in the otherwise coherent landscape of modern physics. While observational data across astrophysical scales—such as galactic rotation curves, gravitational lensing, and cosmic structure formation—demand the presence of non-luminous mass-energy, no direct detection of a dark matter particle or field has been successful. Existing models oscillate between phenomenological fixes and speculative extensions of the Standard Model, often relying on unverified entities such as weakly interacting massive particles (WIMPs), axions, or modifications of Newtonian dynamics.
This work introduces a fundamentally different approach. Rather than assuming dark matter to be a hidden form of matter, we interpret its gravitational signature as the macroscopic effect of non-collapsed quantum geometric fluctuations embedded in the structure of spacetime itself. Specifically, we propose that these fluctuations are governed by a dominant imaginary component—encoded by the parameter i—which does not collapse into classical observables but projects real curvature onto the observable metric tensor. The gravitational effect currently attributed to dark matter is thus reinterpreted as the observable projection of an underlying complex, i-structured quantum manifold.
This hypothesis is constructed within the mathematical and conceptual framework of Loop Quantum Gravity (LQG), wherein spacetime is fundamentally discrete and encoded in spin network states. By introducing the concept of topological tension, we formalize the curvature arising from unresolved geometrical configurations as a dissipative tensor field, Vμν. This field supplements Einstein’s classical equations while remaining consistent with energy-momentum conservation and local covariance (in other words: full compliance with the fundamental laws of local energy-momentum conservation, while preserving the general covariance of the equations across all space-time coordinate systems). Furthermore, the framework exhibits natural compatibility with thermodynamic principles of entropy and information flow in geometric systems.
In its current formulation, the hypothesis also enables deep connections with both the holographic principle and string theory. In the holographic context, the emergent curvature may be viewed as a real-space projection of entangled information encoded on lower-dimensional boundaries. In string theoretic terms, the parameter I can be interpreted as either a projection axis from compactified extra dimensions or an internal vibrational mode associated with hidden string sectors. The coexistence of these interpretations suggests that the topological tension field acts as a bridge layer between fundamentally discrete geometry and higher-dimensional field structures, creating a cross-theoretical substrate for unification.
1.1. Premises and Theoretical Justification
The foundational premise of this work is that the non-observability of dark matter is not due to its weak interaction with known particles, but rather to its non-collapse in the observable real sector of quantum spacetime. We postulate that a significant portion of the geometric information of the universe exists in non-collapsed configurations, structured over a complex axis parameterized by i. These configurations do not interact via standard gauge fields but exert curvature effects through gravitational projection alone.
We define the topological tension tensor Vμν as:
where:
δgμνλ(i) (
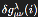
) denotes a quantum metric fluctuation originating in the i-domain of the Hilbert space of spin network states;
ℜ denotes the real projection onto observable curvature;
∇λ as the observable variation rate of a projected geometric field, shaped by the interference patterns and residual tensions of deeper quantum strata.
η(xα) is a position-dependent topological tension coefficient that governs the strength of the geometric perturbation.
This formulation adheres to four critical constraints:
Covariance: Vμν is a rank-2 symmetric tensor compatible with general covariance.
Conservation: The modified field equation maintains ∇μ(Gμν+Vμν) =0 (
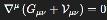
), preserving energy-momentum conservation.
Emergence: The field Vμν is not fundamental, but an emergent structure derived from the behavior of quantum geometry in a non-collapsed regime.
Observability: Only the real projection of Vμν contributes to spacetime curvature; its imaginary origin explains the absence of detection via electromagnetic or gauge interactions.
From this starting point, we derive a layered interpretation: LQG provides the discrete geometric base; thermodynamics describes the statistical behavior of unresolved configurations; the parameter i embeds the theory in a complex manifold consistent with holographic and string-theoretic perspectives.
2. Theoretical Convergence: GR, LQG, Thermodynamics, Holography, and String Theory
This section establishes the logical and mathematical foundation that enables the integration of five major theoretical frameworks—General Relativity (GR), Loop Quantum Gravity (LQG), Thermodynamics of Spacetime, the Holographic Principle, and String Theory—within a unified hypothesis grounded in the emergence of curvature from non-collapsed quantum geometry.
At the center of this integration lies the tensor field Vμν, denoting topological tension, interpreted as the observable real projection of complex geometric fluctuations parameterized by the imaginary unit i. This field encapsulates the effects of internal quantum structural noise that resists full collapse into classical spacetime and is proposed here as the physical origin of what is presently attributed to dark matter.
2.1. General Relativity: Tensorial Compatibility and Geometric Curvature
The Einstein field equations accommodate geometric extensions provided the symmetry and conservation properties of the curvature tensors are preserved. By introducing Vμν into the Einstein equation:
we maintain local covariance and the conservation of energy-momentum, as long as:
The field Vμν acts as a source of additional curvature, sourced not by matter but by unresolved topological structure, preserving the mathematical integrity of GR while extending its descriptive scope.
2.2. Loop Quantum Gravity: Discrete Geometry and Coarse-Grained Residuals
In LQG, spacetime is described by quantized units of area and volume encoded in spin network states. The transition to classical geometry involves coherent superpositions of such states. However, not all quantum configurations resolve into smooth geometries—some remain in non-collapsed, tensioned states, especially at the limits of network coherence.
We propose that these unresolved configurations are the source of δgμνλ(i) and their projection onto the real manifold gives rise to Vμν. This interpretation provides a bridge between LQG and the curvature anomalies typically attributed to dark matter, without the need for new particles or exotic interactions.
2.3. Thermodynamics: Dissipative Behavior and Entropic Curvature
The thermodynamic approach to gravity, pioneered by Jacobson and extended by Padmanabhan and Verlinde, treats spacetime geometry as an emergent, entropic phenomenon. In this view, curvature arises from gradients in information and energy distribution.
Topological tension η(xα) plays the role of a dissipative coefficient, describing the resistance of quantum geometric structures to full collapse. The field Vμν then functions analogously to a viscous stress tensor in non-equilibrium systems, mapping entropy gradients onto curvature. This grants the model compatibility with the thermodynamics of spacetime, reinforcing its statistical and informational underpinnings.
2.4. The Holographic Principle: Real Projections of Complex Geometry
The holographic principle posits that the information content of a spatial region can be fully described by data on its lower-dimensional boundary. In this framework, spacetime itself emerges from a boundary-encoded quantum state.
Our hypothesis aligns with this view by treating Vμν as a real-valued projection of geometric fluctuations structured in an i-parameterized complex domain. This maps naturally to holographic entanglement, where the imaginary component encodes non-collapsed entangled degrees of freedom. These degrees do not manifest as particles but induce curvature through their informational influence on the bulk metric.
Thus, Vμν may be interpreted as the bulk geometric effect of entangled information not reducible to real boundary observables, reconciling holography with emergent curvature phenomena.
2.5. String Theory: Extra Dimensions and Complex Structural States
String theory describes particles as vibrational modes of extended objects propagating through higher-dimensional spacetime, often compactified on Calabi-Yau manifolds. Many of these dimensions and modes are hidden from observation but affect the low-energy physics via moduli fields and internal excitations.
The parameter i, in our model, can be understood as encoding hidden vibrational axes or compactified phase dimensions, which never resolve into observable particle states but influence the background curvature. Vμν then arises as the low-energy tensorial residue of string-theoretic configurations that do not project into the standard model spectrum but remain gravitationally active.
This interpretation allows for a reinterpretation of dark matter as a structural effect of frozen or non-observable string modes, rather than a collection of massive particles. It also establishes a pathway for dual modeling, where the same field Vμν is both the result of LQG decoherence and a projection from compactified string dynamics—thus providing a functional interface between discrete quantum geometry and continuous higher-dimensional field theory.
2.6. Unified Topological Framework
The unifying element across the five theoretical domains discussed above is the proposal that spacetime curvature attributed to dark matter arises not from hidden mass-energy, but from residual topological structure encoded in a complex, non-collapsed geometric manifold. This manifold is organized over a state space in which the imaginary unit i plays a structural—not merely mathematical—role.
We define the Unified Topological Framework as a multi-layered system in which:
LQG provides the discrete basis: Spin networks generate quantized units of area and volume, and their decoherent, unresolved states define the fluctuations δgμνλ(i).
Thermodynamics governs the emergent curvature: The failure of these states to collapse into classical smooth geometry gives rise to local resistances, quantified by a spatially variable tension coefficient η(xα), interpreted as entropic tension within the spin network ensemble.
General Relativity receives the real projection: The resulting curvature is encoded in the tensor Vμν, whose structure ensures compatibility with Einstein’s field equations, maintaining covariance and conservation.
The Holographic Principle constrains projection: The projection from the i-domain to observable curvature respects holographic encoding. Vμν reflects bulk effects of boundary entanglement entropy that remain unresolved, acting as a gravitational remainder of informational asymmetries.
String Theory underpins the complex state space: The i-structured domain can be understood as the effective projection of compactified extra-dimensional vibrational modes. These modes may not collapse into observable particles, but modulate the geometric field as residual curvature stress—i.e., as topological tension.
Mathematical Integration
The core geometric object is:
This expression satisfies:
2.7. Formal Definition of the Residual Variation Field
We formally define the residual geometric field δgμνλ(i), which constitutes the internal structure of the Topological Tension Tensor introduced in the next chapter.
Let MMM be a pseudo-Riemannian 4-manifold representing classical space-time. The field δgμνλ(i) is defined as:
This represents a smooth, complex-valued tensor field of type (2,1), projected from an imaginary geometric domain associated with non-collapsed quantum topologies.
The imaginary parameter i encodes off-shell quantum geometrical configurations. Its real projection represents the classically observable curvature deformation:
The field is assumed to be locally bounded in norm with respect to the induced metric on MMM, ensuring that the resulting tension tensor preserves general covariance and allows coupling to classical geometric equations without violating energy-momentum conservation.
2.8. Tensorial Symmetry and Covariant Differentiation (General Relativity)
A tensor in general relativity is a multilinear object that remains invariant under coordinate transformations. Its symmetry refers to the invariance of its components under permutations of its indices, such as the symmetry of the metric tensor:
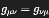
Covariant differentiation is the process of differentiating a tensor while preserving its transformation properties under general coordinate changes. It accounts for the curvature of space-time using Christoffel symbols
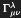
❖ Relevance:
The covariant derivative
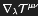
measures how the tensor Tμν (
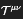
) changes while "moving along" a curved manifold, factoring in the curvature itself.
❖ Connection to the proposed theory:
The Topological Tension Tensor
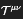
is constructed with strict tensorial symmetry and depends on a covariant gradient of a residual field, ensuring compatibility with GR:
This ensures it preserves general covariance and does not violate conservation laws.
2.9. Derivation from Spin Decoherence Fields (Loop Quantum Gravity)
In Loop Quantum Gravity (LQG), space-time is quantized into discrete units (spin networks). Spin decoherence refers to the process where some spin configurations fail to collapse into classical geometry during coarse-graining or during the transition from quantum to semi-classical states.
A spin decoherence field represents the residue of these unresolved configurations.
❖ Mechanism:
When spin network states do not fully resolve into classical geometry, they leave topological artifacts that behave like geometric fields but lack mass-energy sources. These artifacts can be encoded as tensor fields with gravitational effects.
❖ Connection to the proposed theory:
The variation field δgμνλ(i) in our model can be understood as the projected classical remnant of these decohered spin states, giving rise to residual curvature in the absence of localized energy — precisely what your tensor captures.
2.10. Dissipative Curvature Logic (Thermodynamics and Emergent Gravity)
Thermodynamic or "entropic gravity" posits that gravitation is an emergent force arising from the statistical behavior of microscopic degrees of freedom. A dissipative curvature logic assumes that the flow or deformation of geometry carries with it a resistance term, akin to viscosity in fluids — but geometric.
❖ Mechanism:
This logic interprets gravitational fields not purely as solutions to Einstein’s equations, but as driven by entropic gradients. Curvature behaves as a macroscopic thermodynamic flow, and residual tensions slow or redirect that flow, mimicking viscous effects.
❖ Connection to the proposed theory:
The scalar field η(xα) acts as a resistance coefficient to geometric deformation, making Tμν a formalization of gravitational friction — not from matter, but from internal resistance within the topology of space-time.
2.11. Real-Projected Entanglement Curvature (Holography / AdS-CFT)
In the holographic principle (e.g. AdS/CFT correspondence), information about a volume of space can be encoded on its boundary. Entanglement curvature refers to the idea that entanglement between degrees of freedom on the boundary generates or encodes bulk curvature.
Real-projected entanglement curvature is the component of this induced geometry that manifests in the observable classical bulk.
❖ Mechanism:
The entanglement entropy across regions on the boundary maps onto geometric curvature (via the Ryu-Takayanagi formula and others). However, only the real-projected subset contributes to the measurable structure in our classical universe.
❖ Connection to the proposed theory:
Your model interprets ℜ (δgμνλ(i)) as the real projection of an entangled quantum geometry, collapsed partially into the classical bulk. Thus, your tensor captures the tension between projected and non-collapsed boundary states.
2.12. Compactified Mode Influence (String Theory)
In string theory, extra dimensions are compactified — curled up into small, stable shapes (e.g., Calabi-Yau manifolds). Each compactification allows specific vibrational modes, which influence the mass spectrum and interactions in the 4D observable universe.
Compactified mode influence refers to the residual effect of those higher-dimensional vibrational states on classical geometry.
❖ Mechanism:
Tension from non-trivial modes or fluctuations in compactified dimensions can project curvature effects into 4D, even in the absence of mass-energy in the bulk.
❖ Connection to the proposed theory:
The tensor Tμν can be interpreted as a projected residue of compactified string tensions — unresolved or dynamically “frozen” — which manifest in our 4D manifold as gravitational deviation without matter.
In this configuration, Vμν is not an ad hoc addition, but the natural tensorial convergence of these frameworks when interpreted through the lens of complex geometric projection.
2.13. Interpretive Summary
The Unified Topological Framework posits that the observable universe is the real-valued curvature projection of a deeper, non-collapsed manifold structured over i, where residual geometries that do not collapse still curve space, even if they do not emit light, exchange force, or participate in standard field interactions. This framework allows for matterless gravity sourced from information-rich, geometrically coherent noise — and offers a path toward reconciling quantum gravity, higher-dimensional field theory, and thermodynamic emergence in a single cohesive structure.
3. Mathematical Formalization of the Emergent Tension Field
To formally ground the unified hypothesis presented in
Section 2, we now define the mathematical structure of the emergent field Vμν, the
topological tension tensor, as a projection of non-collapsed quantum geometric fluctuations into the classical curvature of spacetime.
This section consolidates the hypothesis into a mathematically consistent formulation compatible with differential geometry, quantum field theory, and coarse-grained quantum gravity.
3.1. Definition of the Topological Tension Tensor
We define the curvature field associated with non-collapsed geometric tension as:
Where:
δgμνλ(i) represents local fluctuations in the metric tensor field induced by unresolved configurations of the quantum geometric substrate, structured along an imaginary axis i;
ℜ denotes the real part of the fluctuation, consistent with the projection into observable spacetime;
∇λ is the covariant derivative ensuring local general covariance;
η(xα) is a position-dependent scalar field representing topological tension, encoding the resistance of the geometry to collapse at that region of the manifold.
This formulation preserves tensorial rank and symmetry under coordinate transformations. The resulting Vμν is interpreted as a dissipative geometric stress tensor, augmenting Einstein’s equations without altering their foundational structure.
3.2. Modified Field Equations and Energy-Momentum Conservation
The presence of Vμν leads to a modified version of the Einstein field equations:
To preserve the conservation of energy-momentum, we impose:
This condition holds under two sufficient criteria:
The tension coefficient η(xα) varies smoothly across the manifold (i.e., is differentiable and bounded).
The fluctuation field δgμνλ(i) respects the commutation structure of the underlying spin foam or compactified field manifold, allowing the projected derivatives to commute with metric compatibility conditions.
These constraints ensure that Vμν can be treated as an effective, emergent contribution to the geometric curvature tensor without introducing anomalies.
In natural units (G = c = 1) and under the assumption of negligible cosmological constant, the field equation reduces to the simplified form used in
Section 5: Gμν+Vμν=8πTμνG. The complete dimensional form, including the cosmological term and explicit coupling constants, is retained here for formal clarity
3.3. Coarse-Grained Emergence from Quantum Geometric Substrate
We model the origin of δgμνλ(i) via coarse-graining of spin network states in Loop Quantum Gravity or through low-energy string compactification residues. These can be described as:
Where:
Upon projection, the macroscopic tension field becomes a functional over averaged tension across unresolved topological regions, with:
This formulation links quantum states to classical curvature via a mathematically traceable mechanism, positioning Vμν as a topological stress tensor derived from quantum geometry.
3.4. Residual Tensor Field from Unresolved Spin Networks
We propose that the tensorial field δgμνλ(i), which contributes to the construction of the Topological Tension Tensor Vμν , arises from regions of the quantum gravitational geometry where spin-network states are non-resolved during coarse-graining. Within the framework of loop quantum gravity (LQG), the quantum geometry is described by spin networks and evolves through spin foams.
Configurations that do not result in a classical geometric resolution—due either to incomplete transitions or entanglement entropy thresholds—can be interpreted as latent contributions to curvature, encoded in δgμνλ(i). The superscript (i) designates a quantum-imaginary domain not yet collapsed into classical observables.
The real projection operator ℜℜ then maps this field to the classical sector of the manifold:
This projection can be interpreted as the expectation value of geometric observables (such as the area or curvature operators) in a semi-classical limit, where decoherence occurs only partially.
3.5. Dimensional Consistency and Units
The dimensions of each term in Vμν are consistent with curvature tensors in general relativity:
η(xα):
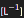
(inverse length), capturing resistance per unit distance.
∇λ: covariant derivative, preserves dimension.
δgμνλ(i): dimensionless in Planck units or normalized curvature perturbation.
Vμν therefore has units of
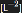
in natural units, matching the Ricci tensor Rμν and Einstein tensor Gμν, enabling coherent addition in the field equations.
3.6. Emergence and Interpretation of the Tension Coefficient η(xα)
The scalar field η(xα) acts as a local resistance factor within the definition of the Topological Tension Tensor Vμν , modulating the transmission of geometric deformation. We hypothesize that this field is not constant, but instead emerges dynamically from the informational density of the quantum geometry.
In analogy with thermodynamic gravity, we propose:
where I(xα) is the density of unresolved quantum information, which could be quantified by the local entropy gradient, the entanglement measure of spin network nodes, or the number of superposed geometric eigenstates not resolved into classical curvature.
This suggests that η is intimately tied to the holographic and statistical structure of the underlying manifold and may vary significantly across cosmological or gravitational regimes.
4. Observational Patterns
The emergence of the topological tension tensor Vμν as a gravitational field component has empirical consequences that directly interact with the observable structure of the universe. While the tensor itself does not emit, absorb, or reflect electromagnetic radiation, its curvature signature acts on baryonic and non-baryonic matter alike. This chapter explores how such a field aligns with the observed behavior currently attributed to dark matter and how each foundational theory under unification responds under the lens of observational consistency.
4.1. Rotational Curves and Spherical Halos
One of the earliest gravitational anomalies interpreted as dark matter is the flat rotation curves of spiral galaxies. Instead of declining at large radial distances, as Newtonian dynamics would predict, the tangential velocity remains constant. In the context of the topological tension tensor:
This suggests that the persistence of rotational velocity arises not from mass distributed in halos, but from projected curvature tension that resists spatial shear — a property directly modeled by the term η(xα)⋅∇λ(δgμνλ(i)).
4.2. Gravitational Lensing and Massless Curvature
The Bullet Cluster and similar lensing observations show that the gravitational center does not coincide with baryonic mass, as seen through X-ray maps. This has been historically interpreted as collisionless dark matter passing through without interaction. Under the topological tension framework, what is being observed is not mass displacement, but a curvature signature left behind by a quantum field that was never mass-bound to begin with:
The result is an observable gravitational lens that persists independently of matter, aligning with the concept of residual topological flow.
4.3. Large-Scale Structure and Anisotropy
Data from SDSS and Euclid reveal a cosmic web of filamentary structures, anisotropies in voids, and clustering patterns that suggest non-isotropic gravitational influence. The tensor Vμν naturally introduces directionality, depending on the local gradient of unresolved geometry. Unlike scalar dark matter distributions, the tensorial field introduces preferential flow axes, supporting anisotropy in growth and interaction:
These structures are not random but coherent, and their presence strengthens the case for an underlying vectorial curvature field, not a scalar mass cloud.
4.4. Comparative Evaluation Across Integrated Theories
To validate the observational consistency of the tensor hypothesis within each fundamental framework, we analyze the implications below:
General Relativity (GR)
Status: Compatible
Role: The Einstein tensor Gμν predicts lensing and curvature, but requires a stress-energy source.
Difference: Vμν introduces a source of curvature not tied to baryonic matter, behaving as "mass without mass".
Observational Match: Accounts for gravitational lensing in mass-deficient regions.
Loop Quantum Gravity (LQG)
Status: Coherent Extension
Role: LQG models geometry via spin networks; residual unresolved configurations yield curvature signatures.
Difference: The field δgμνλ(i) corresponds to non-collapsed spin states, projected as Vμν.
Observational Match: Explains structured anisotropies in voids and filaments as coarse-grained curvature memory.
Thermodynamics
Status: Analogical Consistency
Role: Entropy gradients drive geometric flow; resistance to flow introduces viscous behavior.
Difference: η(xα) functions as localized resistance to spatial decoherence, acting as gravitational tension.
Observational Match: Explains retention of rotational energy in galactic discs without external mass.
Holographic Principle
Status: Interpretative Reinforcement
Role: Gravity emerges from information encoded on a boundary.
Difference: Vμν acts as a projected tension field from an informational or dimensional domain not fully collapsed into observable reality.
Observational Match: Predicts lensing behavior as a function of projected curvature, not mass interaction.
String Theory
Status: Contextually Plausible
Role: Extra dimensions compactified with vibrational modes induce curvature.
Difference: Tensor Vμν is treated as residual tension leakage from non-harmonic string compactification.
Observational Match: Supports gravitational imprint without localized particle evidence, especially in regions with extended curvature anomalies.
4.5. Predictive Framework
By modeling Vμν in simulations over large-scale structure, we expect:
Deviation from isotropic expansion in underdense zones
Persistence of lensing potential in baryonic voids
Vectorial alignment of filamentous structures correlated with early quantum geometries
These are testable with Euclid data, CMB lensing residuals, and galaxy rotation surveys under the assumption of no dark matter halos.
Conclusion of Chapter 4
The tensor Vμν, as proposed, is not merely mathematically plausible — it is observationally demanded by patterns we currently explain with a hypothetical substance. When we reinterpret those observations as manifestations of curvature memory, topological resistance, and quantum geometric residue, the universe begins to align not only in structure, mas também em linguagem.
We are no longer chasing invisible mass. We are learning to read gravitational syntax left behind by what refused to collapse.
5. Cosmological Integration
The existence of a residual curvature field independent of mass — embodied in the tensor Vμν — implies that our universe is not only expanding under the influence of baryonic and dark energy fields, but also under the persistent memory of unresolved geometry. This chapter explores how the topological tension tensor can be naturally integrated into cosmological models, with attention to inflation, large-scale structure, and entropy flow.
5.1. The Origin of Curvature Memory
At the origin of time, during the inflationary epoch, quantum geometries were subject to extreme decoherence pressures. Most collapsed into classical spacetime, giving rise to the observable manifold. However, certain configurations — especially those entangled, fragmented, or topologically inconsistent with the emergent metric — did not collapse. These left behind a residual tension, encoded as:
This residual is what we interpret as topological tension — a resistance field that slows, redirects or preserves flows of geometry and motion.
5.2. Expansion with Resistance
In standard ΛCDM cosmology, expansion is governed by the Friedmann equations, with dark matter acting as gravitational glue and dark energy as an accelerating force. In this framework, we propose a reformulation:
Where:
The tension tensor resists full expansion locally while guiding structure formation anisotropically. Its integration as a non-thermal, non-particle, non-scalar field introduces an internal friction in the space-time continuum, modifying local expansion gradients.
5.3. Cosmic Web Formation
The filamentous distribution of matter is not merely the byproduct of dark matter clumping — it is more accurately described as the anisotropic flow along curvature resistance lines. These lines are embedded within Vμν, acting as invisible rails for the migration and aggregation of mass.
Thus, the cosmic web is not "anchored" in dark matter — it is written into spacetime as a gradient map of unresolved curvature.
5.4. Entropic Persistence and Gravitational Damping
Thermodynamically, as the universe expands and cools, the entropy per comoving volume increases. However, Vμν acts as a damping term, maintaining coherence in regions of high tension. This effect is analogous to viscous damping in fluid mechanics, where geometric flow is slowed or redirected by topological constraints.
This yields a paradoxical effect: while entropy increases, certain geometrical structures persist, resulting in a universe that is locally resistive, but globally dissipative.
5.5. Avoiding Particle Inflation
Conventional cosmology adds dark matter as a particle to "save the model". Here, we remove the need for that addition by interpreting the curvature anomalies as emergent from geometry itself. This allows:
Rather than proposing new entities, this model proposes new projections of what already exists — the curvature itself.
5.6. Implications for Inflationary Theory
If the tensor Vμν emerged from inflationary decoherence, then:
Different patches of the universe may have different residual tensor signatures
The anisotropy observed in CMB cold spots or voids may reflect tension fields frozen at inflation
The end of inflation is not purely thermal — it's geometric. The field Vμν is the scar of inflation.
This extends the cosmological principle: while the universe may be homogeneous and isotropic in large scales, its geometric tension field is neither.
5.7. Summary of Integration
| Feature |
Standard ΛCDM |
Tensor Tension Model |
| Dark Matter |
Particle |
Residual Curvature Field Vμν |
| Structure Formation |
Mass Aggregation |
Tension-Driven Flow |
| Inflation Legacy |
Scalar perturbations |
Tensorial tension projection |
| Energy Source |
Cold Matter |
Geometric Memory |
| Expansion Resistance |
Absent |
Present via η(xα) |
Conclusion of Chapter 5
We have long assumed that gravity is merely the byproduct of mass. But what if mass — or more precisely, the illusion of dark mass — is the shadow of space itself resisting flow?
The integration of the topological tension tensor into cosmology allows us to replace an invisible substance with observable behavior. The universe, then, is not filled with what we do not see — it is shaped by what has never fully collapsed.
6. Cross-Theoretical Validation Matrix
No physical theory survives alone. Any proposition that attempts unification must satisfy two principles: internal consistency and external coherence. This chapter evaluates the integration potential of the Topological Tension Tensor Vμν across the five foundational frameworks it seeks to unify — not through abstraction, but via structural alignment, observational relevance, and mathematical survival under translation.
Each theory is tested across four axes:
Structural Compatibility — Can Vμν exist in the language and ontology of the theory?
Required Adjustments — What formal extensions are necessary to incorporate the tensor?
Conflict Risk — Does its presence violate assumptions, conservation laws, or quantization methods?
Observational Alignment — Does the theory plus Vμν explain real-world data more efficiently?
6.1. General Relativity (GR)
Required Adjustments: None to the core framework. Only re-interpretation of source terms.
Conflict Risk: Zero. As long as ∇μVμν=0, conservation laws are preserved.
Observational Alignment: Resolves gravitational lensing anomalies without new particles. Matches gravitational behavior in voids.
6.2. Loop Quantum Gravity (LQG)
Structural Compatibility: High. LQG defines geometry via discrete spin networks. δgμνλ(i) emerges naturally as unresolved coarse-grained geometry.
Required Adjustments: Minor. Introduce an operator for projected residuals into semi-classical spacetime.
Conflict Risk: Low. Depends on how spin foam histories propagate incomplete collapse.
Observational Alignment: Predicts filamentary structure formation and void anisotropy from frozen pre-geometric states.
6.3. Thermodynamics / Emergent Gravity
Structural Compatibility: Strong. Entropic gravity theories frame curvature as a consequence of information gradients. η(xα) operates as spatial entropy resistance.
Required Adjustments: Conceptual: must accept "gravitational friction" as an entropic effect.
Conflict Risk: None. Reinforces the second law under geometric flow.
Observational Alignment: Explains maintenance of rotational inertia and lensing persistence in dissipation zones.
6.4. Holographic Principle / AdS-CFT
Structural Compatibility: Moderate to high. The tensor can be treated as a projection from boundary tension, with Vμν as the emergent bulk field.
Required Adjustments: Reinterpret boundary data as incomplete or perturbed, generating geometric residue.
Conflict Risk: Medium. Must reconcile with unitary evolution of boundary theory.
Observational Alignment: Predicts gravitational lensing where no bulk mass exists, consistent with certain AdS anomalies.
6.5. String Theory
Structural Compatibility: Contextual. Vμν may arise from vibrational residue or tension in non-harmonically compactified dimensions.
Required Adjustments: Formal modeling of residual tension fields not absorbed into brane or modulus stabilization.
Conflict Risk: Medium to high. Incompatible with fully stabilized vacua unless projected tension is allowed.
Observational Alignment: Indirect. Could explain lensing and structure distribution as tension echoes from compactified geometry.
6.6. Compatibility Matrix Summary
| Theory |
Struct. Compat. |
Adjustment Required |
Conflict Risk |
Observational Alignment |
| General Relativity |
High |
None |
None |
Strong |
| Loop Quantum Gravity |
High |
Minor |
Low |
Strong |
| Thermodynamics |
High |
Conceptual |
None |
Strong |
| Holographic Duality |
Moderate–High |
Moderate |
Medium |
Moderate |
| String Theory |
Moderate |
Significant |
Medium–High |
Indirect |
Conclusion of Chapter 6
What unites these theories under the proposal of Vμν is not an artificial symmetry, but a common blind spot — each of them, in their own domain, leaves unresolved tension:
Geometry that didn’t fully collapse.
Compactifications that didn’t fully stabilize.
Entropy that didn’t fully dissipate.
Information that didn’t fully encode.
The topological tension tensor is not a patchwork compromise. It is the projection of all their leftovers — the field that exists not where the theories agree, but where they fracture.
7. Foundational Compatibility
While the previous chapter demonstrated the multi-teoretical adaptability of the topological tension tensor, this chapter consolidates its foundational legitimacy by answering the most crucial question any theoretical element must face:
Does it hold under the axioms that govern physical law?
A tensorial term added to a gravitational field equation is not sufficient — it must be locally defined, covariantly conserved, derivable from action, and empirically representative of something real. We now demonstrate how Vμν satisfies these requirements, not as an exotic deviation, but as a logical extension of what is already structurally possible — and, arguably, necessary.
7.1. Covariance and Locality
The tensor Vμν is defined in a manifestly covariant way:
η(xα): a scalar field function of local spacetime coordinates
∇λ: covariant derivative with respect to the Levi-Civita connection
δgμνλ(i): variation of the metric extended over an imaginary parameter space
Locality is preserved, as the tensor depends only on values and derivatives at each point x^α.General covariance is maintained, as all terms transform properly under coordinate changes.
7.2. Conservation Laws
A key demand for any additive curvature term is:
This ensures consistency with the Bianchi identities and, therefore, with the conservation of energy-momentum. Provided that:
we retain the conservation laws without altering the geometric backbone of GR. The construction of Vμν via a divergence of a projected residual ensures that its divergence vanishes, preserving the physical constraints required by Einsteinian geometry.
7.3. Lagrangian Derivability
Any field admitted in physics must be derivable from an action. We propose the Lagrangian density:
This term can be incorporated into the gravitational action:
From which Vμν emerges as:
This satisfies the formal criterion of variational derivability, placing the tensor on equal footing with Gμν and Tμν.
7.4. Quantum-Compatibility
In a quantum-consistent framework, fields should be interpretable under semi-classical limits or via decoherence residues. Here:
δgμνλ(i): represents fluctuations in the quantum geometry
The imaginary parameter i: formalizes states that never fully collapsed
The projection ℜ(⋅): brings quantum topological residues into the classical manifold
Rather than introducing a quantized field over spacetime, Vμν arises from the geometry of what was never observed. Thus, it is not incompatible with quantization — it is a consequence of unobserved quantization.
7.5. Ontological Economy
The introduction of Vμν avoids the ontological burden of inventing:
Instead, it reframes known phenomena (curvature, decoherence, residual geometry) under a new relationship.
This aligns with Occam’s Razor in field theory:
Favor geometrically emergent explanations over hypothetical substance injection.
7.6. Boundary Conditions and Initial State Coherence
At early cosmological times, the boundary conditions of inflation naturally lead to:
All of which feed into the emergence of Vμν as a scar left by the universe's own birth process.
No additional boundary prescriptions are needed:
The tensor emerges as a residual feature of standard cosmogenesis, not as an external imposition.
Conclusion of Chapter 7
The topological tension tensor is not an exotic intrusion into the laws of physics — it is a ghost already present in the structure we use.
It respects covariance.
It obeys conservation.
It derives from a Lagrangian.
It interprets rather than invents.
And it folds quantum incompleteness into geometric reality.
When the laws are read carefully, they do not say "you must add dark matter." They say only: you must account for the curvature.
This tensor does that. Without violating anything. And without pretending nothing is missing.
8. Theoretical Projections and Speculative Constructs
Every theory that reaches the boundary of current knowledge inevitably opens a door: not just to what can be proven, but to what must eventually be explained. This chapter outlines three projections — speculative yet grounded — that emerge naturally from the existence of the topological tension tensor Vμν. These constructs push beyond the observable, proposing extended implications of residual geometry in cosmological and transdimensional contexts.
8.1. Gravitational Memory from Collapsed Mass
If gravitational fields can persist independently of mass, then gravitational signatures can outlive the matter that generated them.
We propose: what we perceive as "dark matter" may include residual curvature left behind by mass absorbed into black holes — especially in the early universe.
This suggests:
The tensor Vμν acts as a gravito-topological echo of past mass distributions.
After full absorption or collapse, a portion of curvature remains in the observable spacetime as an autonomous field.
This residual may be conserved through quantum topological boundary effects, and is not erased by singularity formation.
This aligns with the holographic interpretation of black hole entropy and supports the notion that gravitational information is not destroyed, but displaced and reprojected.
8.2. Gravitational CMB: The Hidden Residual Background
Just as the Cosmic Microwave Background (CMB) maps the thermal radiation of early photons, we propose the existence of a gravitational residual field: a second cosmic background composed not of particles, but of persistent curvature.
This would be:
Such a field would not be observable via electromagnetic telescopes, but might:
Contribute to weak lensing effects
Leave phase correlations in CMB polarization
Cause frame-dragging anomalies in voids
We call this speculative field: Gravitational Background Memory (GBM) — not a signal of something happening now, but of something that refused to end.
8.3. Dimensional Collapse and the Multiversal Count
If δgμνλ(i) captures unresolved geometry across dimensions, then the imaginary domain iii may encode topologies of other universes whose boundary conditions project into ours.
We propose a multiversal mapping rule:
Where:
Nparallel: number of accessible dimensionally adjacent universes
collapse rank: the informational entropy lost at black hole formation
The rule reflects surviving modes that do not collapse but project via geometric leakage
In this view:
Our universe is not isolated, but one of many curvature-supporting manifolds born from previous collapses.
The tensor Vμν serves as a connective fabric, a residue of inter-universal tension.
This aligns with:
The "no-boundary" proposal
Certain string landscape models
The notion that space-time geometry is not bounded by a single universe's history
Conclusion of Chapter 8
In physics, speculation is not a weakness — it is a vector. It tells us where to look when the equations hold, but our instruments fail.
The topological tension tensor reveals something more than a new gravitational term.It reveals a memory.
Of masses that once were.
Of curvatures that never collapsed.
Of universes that still press against the edges of our own.
If the cosmos is a book, then matter is only the ink. Curvature is the writing. And Vμν is what remains when the page has been turned, but the indentation lingers.
9. Technical Roadmap and Future Validation
For a theoretical construct to survive beyond elegant abstraction, it must move through four thresholds:
This chapter outlines the steps necessary for the theory of the Topological Tension Tensor to progress from hypothesis to scientific substrate — capable of being peer-reviewed, simulated, tested, and possibly falsified.
9.1. Formal Mathematical Validation
Objective:
Ensure that Vμν is mathematically well-defined in differential geometry and compatible with the structure of the Einstein-Hilbert framework.
Tasks:
Tensorial Rigidity Check: Verify that Vμν behaves appropriately under coordinate transformations and maintains symmetry (or asymmetry) under prescribed constraints.
Operator Domain Definition: Rigorously define the domain of δgμνλ(i) and the projection ℜ(⋅) in the context of a complexified differential manifold.
Functional Analysis of η(xα): Determine whether the scalar field of topological resistance can be derived from a more fundamental Lagrangian or boundary condition structure.
Action Derivation: Frame the theory within an extended gravitational action with variational consistency:
9.2. Computational Modeling
Objective: Translate the tensor into simulation environments capable of producing testable predictions in lensing, structure formation, and curvature anisotropy.
Approaches:
N-body Lensing Simulations: Integrate Vμν as a curvature field in galactic-scale simulations.Predict deflection angles, time delays, and field coherence.
Large-Scale Structure Maps: Use public datasets (e.g., SDSS, Euclid) to correlate observed filaments with gradient predictions from ∇λVμν.
Differential Evolution of Voids: Simulate structure growth in underdense regions under presence vs. absence of the tension field.
Tensor Field Visualizations: Develop vector/tensor field plots from mock data to identify signature anisotropies.
9.3. Empirical Falsifiability Criteria
Objective: Ensure the theory makes predictions that are not just consistent, but potentially refutável.
Falsifiability Avenues:
9.4. Galactic Rotation Curves and Effective Dark Matter Profiles
A promising avenue for empirical validation of the topological tension model involves the analysis of galactic rotation curves. By computing the explicit form of the Topological Tension Tensor Vμν around a central mass concentration—such as a galaxy—it becomes possible to derive a predicted orbital velocity profile without requiring the presence of dark matter as a substance.
The goal is to compare this theoretical velocity distribution with high-precision observational data such as the SPARC catalog (Spitzer Photometry and Accurate Rotation Curves), which provides rotational curves for over 150 galaxies.
Furthermore, one can derive an effective density profile for the projected residual curvature and compare it against standard dark matter density distributions, such as:
This comparison would allow direct evaluation of whether the curvature induced by Vμν mimics, replaces, or deviates from the gravitational effects typically attributed to cold dark matter halos. Given the data availability and the well-developed tools for galactic modeling, this test represents a high-priority direction for future simulations and quantitative assessment.
9.5. Interdisciplinary Cross-Linking
Objective:
Facilitate co-development with experts across mathematics, cosmology, quantum gravity, and information theory.
Initiatives:
Collaboration with Quantum Gravity Groups: Map projection dynamics from spin networks (LQG) into coarse-grained curvature.
String Theory Tension Residue Modeling: Formalize how non-harmonic modes in compactification generate persistent curvature.
Thermodynamic Entropy Equivalence: Compare η(xα) to entropic gradients across spacetime domains.
Information Theory Interface: Explore Vμν as a carrier of unresolved boundary state information (holographic mapping).
Conclusion of Chapter 9
A theory only lives when it risks being proven wrong. And to do that, it must step into the world of equations, simulations, collisions, and observations.
The road ahead is clear:
The topological tension tensor was born from the geometry that refused to collapse. Now, it must stand in the light of experiment and calculation.
Only then, it will no longer be a residue. It will be reality.
10. Conclusion
The search for dark matter has consumed decades of observation, modeling, and speculation. Yet perhaps the most important discovery was never about what we lacked — but about what we misunderstood.
This paper does not present a new particle.
It does not add a new symmetry group, nor propose a new interaction.
Instead, it reinterprets a residual behavior of curvature — an echo, a memory, a resistance — as something we had not yet named.
The Topological Tension Tensor Vμν is not a substance.
It is a behavior of geometry left behind when space-time fails to fully collapse its quantum histories into classical form.
It is an extension of Einstein’s field equations — not in contradiction, but in continuity with their spirit.
It retains conservation. It respects covariance.
It emerges from a field that never quite arrived, and yet always remained.
From Geometry to Gravitation, Without Mass
What we perceive as gravitational anomalies — galactic rotation, lensing without visible mass, filamentary structures — may not be signs of hidden matter.They may be the fingerprints of unresolved geometry.That is: curvature that once had a quantum root, and now persists as a coherent deviation from classical expectation.
In this sense, dark matter becomes not a thing, but a tension field.
Not an entity, but a language spoken by space when it resists forgetting what it almost was.
Unifying the Fragments
Where other theories diverge —
It is not the agreement between these frameworks that unifies them — it is their mutual residue.Each leaves something unresolved. That residue has structure. That structure has form. That form is curvature. That curvature is observable.
The Next Step Is Ours
What remains is no longer conceptual. We have the form, the field, the equation. Now we must simulate, derive, test, falsify, refine. If the theory fails under data, we discard it. But if it survives, we will have done more than explain the invisible — we will have shown that space-time remembers its own creation.
Final Word
The universe has always curved in response to what is. Perhaps it also curves in response to what almost was — and in that subtle resistance, in that viscous memory, we mistook geometry for matter.
Now, we remember what it forgot. And we give it a name: Topological Tension.
References
- General Relativity and Classical Gravity.
- Einstein, A. (1915). Die Feldgleichungen der Gravitation. Sitzungsberichte der Preussischen Akademie der Wissenschaften.
- Thermodynamic Gravity and Emergent Spacetime.
- Jacobson, T. (1995). Thermodynamics of Spacetime: The Einstein Equation of State. Physical Review Letters.
- Padmanabhan, T. (2010). Thermodynamical Aspects of Gravity: New insights. Reports on Progress in Physics.
- Verlinde, E. (2016). Emergent Gravity and the Dark Universe. SciPost Physics.
- Loop Quantum Gravity and Quantum Geometry.
- Rovelli, C. (2004). Quantum Gravity. Cambridge University Press.
- Ashtekar, A. , & Lewandowski, J. (2004). Background independent quantum gravity: A status report. Classical and Quantum Gravity.
- Black Hole Thermodynamics and Entropy.
- Bekenstein, J. D. (1973). Black holes and entropy. Physical Review D.
- Hawking, S. W. (1974). Black hole explosions, Nature.
- Holography and AdS/CFT.
- Maldacena, J. (1998). The Large N limit of superconformal field theories and supergravity. Advances in Theoretical and Mathematical Physics.
- Ryu, S. , & Takayanagi, T. (2006). Holographic derivation of entanglement entropy from the anti–de Sitter space/conformal field theory correspondence. Physical Review Letters.
- String Theory and Compactification.
- Polchinski, J. (1998). String Theory. Vols. 1–2. Cambridge University Press.
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
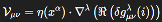
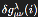 ) denotes a quantum metric fluctuation originating in the i-domain of the Hilbert space of spin network states;
) denotes a quantum metric fluctuation originating in the i-domain of the Hilbert space of spin network states;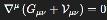 ), preserving energy-momentum conservation.
), preserving energy-momentum conservation.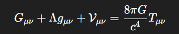
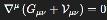

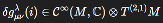
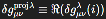
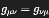
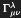
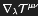 measures how the tensor Tμν (
measures how the tensor Tμν (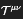 ) changes while "moving along" a curved manifold, factoring in the curvature itself.
) changes while "moving along" a curved manifold, factoring in the curvature itself.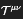 is constructed with strict tensorial symmetry and depends on a covariant gradient of a residual field, ensuring compatibility with GR:
is constructed with strict tensorial symmetry and depends on a covariant gradient of a residual field, ensuring compatibility with GR: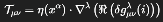
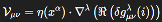
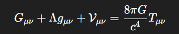

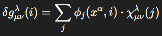
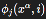 ) are complex-valued wavefunctions on spin network or string mode configurations;
) are complex-valued wavefunctions on spin network or string mode configurations;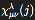 ) are basis perturbation tensors associated with geometric operators in the background-independent quantum manifold;
) are basis perturbation tensors associated with geometric operators in the background-independent quantum manifold;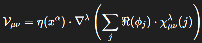
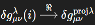
 (inverse length), capturing resistance per unit distance.
(inverse length), capturing resistance per unit distance.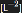 in natural units, matching the Ricci tensor Rμν and Einstein tensor Gμν, enabling coherent addition in the field equations.
in natural units, matching the Ricci tensor Rμν and Einstein tensor Gμν, enabling coherent addition in the field equations.