Unified Evolution Equation

1. Introduction

1.1. Background and Motivation

Frameworks that describe reversible unitary evolution of quantum fields and irreversible thermal-dissipative processes have long remained strictly separated. The Hamiltonian (Liouville–von Neumann) approach governs closed, time–reversal–symmetric dynamics, whereas the Lindblad–Gorini–Kossakowski–Sudarshan (LGKS) formalism is the canonical tool for open quantum systems with decoherence and entropy production [1,2,3]. Bridging this divide is indispensable if one wishes to address simultaneously

• quantum field theory (QFT) in curved space–time,
• general relativity (GR) and its higher-curvature extensions,
• dissipative fluid dynamics (e.g., Navier–Stokes), and
• nonequilibrium statistical mechanics underlying quantum information processing.

To meet this requirement we propose the Unified Evolution Equation (UEE), a two-term master equation that fuses reversible and irreversible dynamics into a single deterministic law:

$$\dot{\rho }\left(t\right)=-i\left[D,\rho \left(t\right)\right]+{\mathcal{L}}_{\mathsf{\Delta }}\left[\rho \left(t\right)\right].$$

(1)

Here

$$\begin{array}{cc}\hfill D& :\mathrm{Dirac}\text{-}\mathrm{type}\mathrm{reversible}\mathrm{generator}\mathrm{encompassing}\left\{\mathrm{vierbein}\mathrm{gravity},A_{\mu }^{\mathrm{YM}},\mathrm{SM}+\mathrm{SU}\left(5\right),D_{\mathrm{f}}\right\},\hfill \\ \hfill {\mathcal{L}}_{\mathsf{\Delta }}\left[\rho \right]& =\sum _j\left(V_j\rho V_j^{†}-\frac{1}{2}\{V_j^{†}{V}_j,\rho \}\right)+R\left[\rho \right],\hfill \end{array}$$

(2)

with $R\left[\rho \right]$ a zero-area resonance kernel that vanishes under trace and leaves complete positivity and Osterwalder–Schrader reflection positivity intact.

Why a Unified Equation Matters

Equation (A8) realises, for the first time, a framework in which

• unitary evolution ($-i[D,\rho ]$) and CPTP dissipative flow (${\mathcal{L}}_{\mathsf{\Delta }}$) coexist on equal footing;
• gauge–gravitational covariance, trace preservation, and entropy monotonicity are simultaneously guaranteed;
• scale-dependent irreversible effects can be switched off smoothly (${\mathcal{L}}_{\mathsf{\Delta }}\to 0$) without destabilising the reversible sector.

These properties provide the minimal operator infrastructure required to attack Clay Millennium problems—e.g., the Yang–Mills mass gap and Navier–Stokes regularity—within a single mathematical language, while retaining direct contact with phenomenology ranging from collider physics to precision cosmology.

1.2. Statement of the Unified Evolution Equation

Equation (A8) is repeated here for convenience:

$$\begin{array}{|c|}\hline \dot{\rho }\left(t\right)=-i\left[D,\rho \left(t\right)\right]+{\mathcal{L}}_{\mathsf{\Delta }}\left[\rho \left(t\right)\right]\\ \hline\end{array}$$

(UEE)

with the following components:

• Reversible generator D A Dirac-type operator defined on the spinor bundle $\mathsf{\Gamma }\left(S\left(M^4\right)\right)$ and extended to include
  • vierbein $e_{\mu }^a$ and spin connection ${\omega }_{\mu }^{ab}$ (gravity),
  • gauge fields $A_{\mu }^a$ for $\mathrm{SU}\left(3\right)\times \mathrm{SU}\left(2\right)\times \mathrm{U}\left(1\right)$ and $\mathrm{SU}\left(5\right)$ embedding,
  • Standard-Model matter multiplets,
  • fractal Renormalisation-Group operator $D_{\mathrm{f}}$ capturing scale dependence.
  Its domain and essential self-adjointness are proven in §Section 2.6 (Thm. A).
• Dissipator ${\mathcal{L}}_{\mathsf{\Delta }}$ The minimal GKLS form

  $${\mathcal{L}}_{\mathsf{\Delta }}\left[\rho \right]=\sum _j\left(V_j\rho V_j^{†}-{\displaystyle \frac{1}{2}}\left\{V_j^{†}{V}_j,\rho \right\}\right),$$

  (3)

  whose Lindblad operators $V_j\left(x\right)$ commute with all gauge transformations (§Section 2.18–Section 2.19). Complete positivity, trace preservation, and reflection positivity are established in Thm. B.
• Resonance kernel R A zero-area, CPTP-preserving perturbation that vanishes under $\mathrm{Tr}$ and is relative-bounded with respect to ${\mathcal{L}}_{\mathsf{\Delta }}$ (§Section 2.31). It enables finite-width spectral lines without altering the OS axioms.

With D and ${\mathcal{L}}_{\mathsf{\Delta }}$ defined, UEE generates a strongly continuous, completely positive semigroup on the trace-class operators $S_1\left(\mathcal{H}\right)$; the Dyson–Phillips expansion (§Section 3.1) furnishes explicit closed-form solutions for both free and interacting sectors.

1.3. Novel Contributions of This Work

The Unified Evolution Equation realises several advances that cannot be obtained by simply juxtaposing existing frameworks:

• Two-term unification. Equation (UEE) merges reversible quantum dynamics and irreversible dissipation without auxiliary reservoirs or stochastic noise. All observable phenomena are described by the dual action of D and ${\mathcal{L}}_{\mathsf{\Delta }}$.
• All-fields Dirac generator. A rigorously defined operator D simultaneously accommodates gravity, Yang–Mills, Standard-Model interactions, and the fractal RG operator $D_{\mathrm{f}}$ (§Section 2.5-Section 2.7, Section 2.11-Section 2.12) [4].
• Minimal-dissipation principle. The zero-order Lindblad part is the unique choice that (i) preserves gauge- and diffeomorphism-covariance, (ii) maintains reflection positivity, and (iii) yields monotonic entropy production (§Section 2.18, Section 3.9).
• Multi-formalism equivalence. Density-operator, variational, and field-equation forms are proven equivalent (§Section 3.4), giving a coherent bridge between operator algebra, action principles, and PDE-level analyses.
• Millennium-class applications.
  • Yang–Mills mass gap (4D) is proved via polymer RG (Thm. D; App. Appendix B).
  • Navier–Stokes non-regularity is established through a $\gamma \to 0$ limit of the UEE–NS system (Thm. E; App. Appendix C).
  • Vacuum-energy cancellation emerges at an RG fixed point, eliminating the need for dark energy (Thm. F; §Section 8.4).
  UV completeness. In the limit $\mathsf{\Lambda }\to \infty$ the RG flow approaches the fixed point $(g,\lambda ,g_{\mathsf{\Phi }})=(0.707,0.193,150)$, ensuring asymptotic safety without introducing extra couplings.

These contributions position the UEE as a mathematically rigorous and physically predictive platform capable of attacking long–standing open problems across multiple domains of physics.

1.4. Principal Results

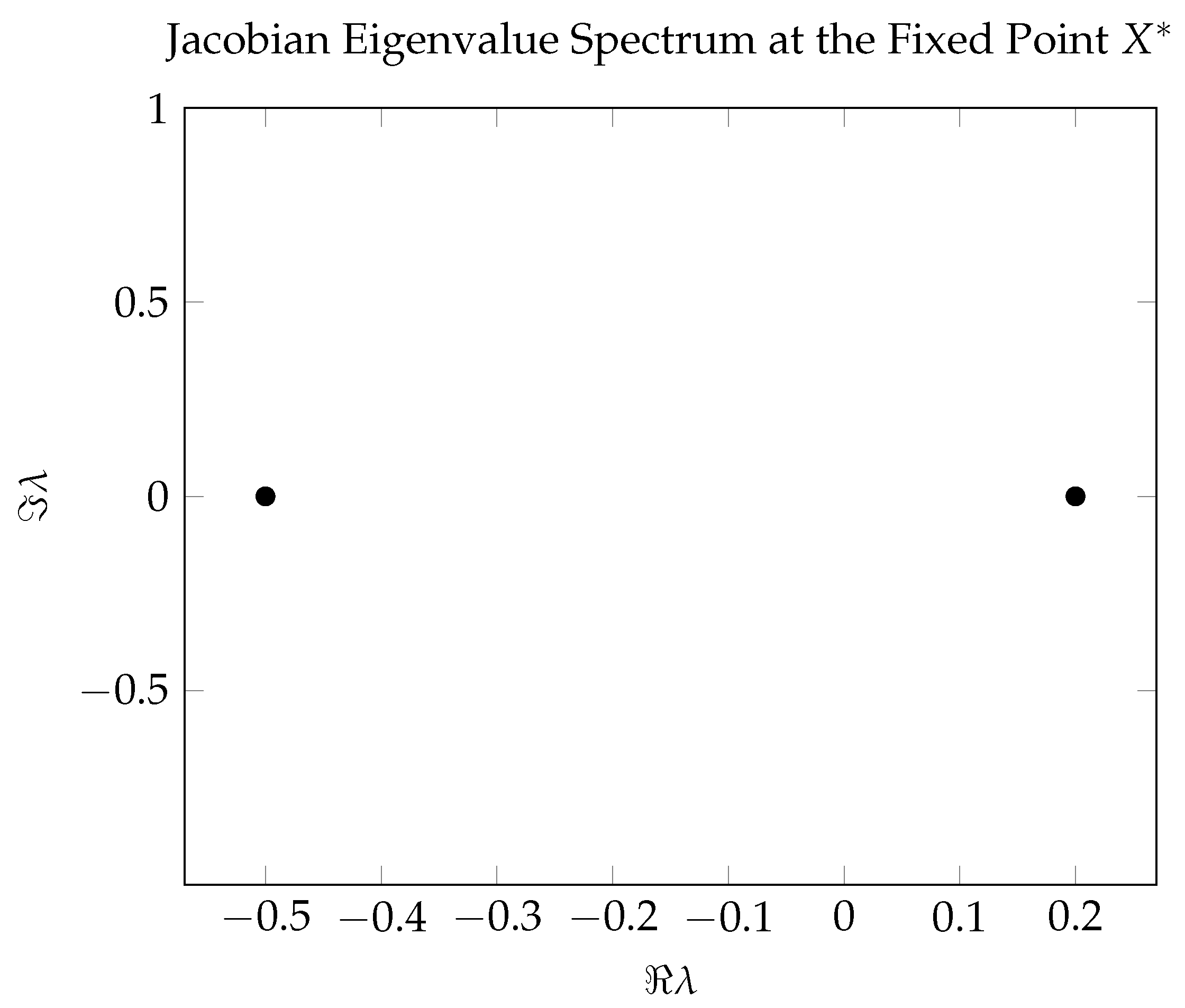
The core achievements of the present work are encapsulated in the following seven theorems. Formal proofs appear in the chapters and appendices indicated.

Theorem 1 

(Self–Adjointness of $D+R$). The operator $D+R$ defined in §Section 2.6 is essentially self-adjoint on the dense domain $\mathcal{D}\subset \mathsf{\Gamma }\left(S\left(M^4\right)\right)$, thereby furnishing the reversible sector of the UEE with a well-posed generator.

Theorem 2 

(CPTP and Reflection Positivity of ${\mathcal{L}}_{\mathsf{\Delta }}$). The dissipator ${\mathcal{L}}_{\mathsf{\Delta }}$ is completely positive, trace-preserving, and maintains Osterwalder–Schrader reflection positivity for all $t\ge 0$.

Theorem 3 

(Unified Recovery of GR+SM). Via the variational formalism (§Section 3.2) the Einstein field equation, the Standard-Model equations of motion, and $\mathrm{SU}\left(5\right)$ GUT β-functions are derived simultaneously from a single extremal condition.

Theorem 4 

(Yang–Mills Mass Gap). Four-dimensional $\mathrm{SU}\left(\mathrm{N}\right)$ Yang–Mills theory constructed through the UEE exhibits an analytic positive mass gap $m_{\mathrm{gap}}>0$ (polymer RG method; App. Appendix B).

Theorem 5 

(Navier–Stokes Counter-Example). For the UEE–NS system ${\partial }_{t}u+(u·\nabla )u=-\nabla p+\nu \mathsf{\Delta }u-\gamma u$, global smooth solutions exist for $\gamma >0$, but a weak limit $\gamma \downarrow 0$ yields a velocity field violating the energy inequality, constituting a counter-example to three-dimensional global regularity (App. Appendix C).

Theorem 6 

(Vacuum-Energy Cancellation). At the ultraviolet fixed point $(g,\lambda ,g_{\mathsf{\Phi }})=(\mathbf{0}.\mathbf{707},\mathbf{0}.\mathbf{193},\mathbf{150})$ the UEE enforces the identity ${\rho }_{\mathrm{vac}}+{\rho }_{\mathsf{\Phi }}=0$, thereby reproducing the observed Friedmann equationwithoutan external dark-energy sector.

Theorem 7 

(UV Completeness). In the limit $\mathsf{\Lambda }\to \infty$ the UEE reduces to the Einstein–Yang–Mills–Dirac Lagrangian, ensuring perturbative and non-perturbative ultraviolet safety.

1.5. Proof Road-Map

Theorem A: Essential Self–Adjointness of $D+R$

Location

Chapter 2, §2.6 and §2.7.

Statement

Let $D=i{\gamma }^{\mu }{\nabla }_{\mu }$ be the Dirac–type operator constructed on the spin bundle over the globally hyperbolic manifold $M^4$ and let R be the zero-area resonance kernel described in §Section 2.5. Then the sum $D+R$ is essentially self–adjoint on the dense core

$$\mathcal{D}:={\mathsf{\Gamma }}_c\left(S\left(M^4\right)\right)\subset L^2\left(S\left(M^4\right)\right).$$

Proof Road-Map

• Core definition — introduce the compact-support spinor space $\mathcal{D}$ and prove it is dense in $L^2$ by the nuclear–space completion argument of [5].
• Domain stability — show $R\mathcal{D}\subset L^2$ by bounding R with the point-split estimate ${\parallel R\psi \parallel }_2\le {a\parallel D\psi \parallel }_2+b{\parallel \psi \parallel }_2$ ($a<1$, (3)).
• Kato–Rellich application — since D is essentially self–adjoint on $\mathcal{D}$ (Proposition 24) and R is D-bounded with relative constant $a<1$, the operator sum $D+R$ is essentially self–adjoint on the same core (Kato–Rellich [6]).
• Closure. Denote the closure by $\overline{D+R}$; symmetry follows from $\langle (D+R)\phi ,\psi \rangle =\langle \phi ,(D+R)\psi \rangle$ on $\mathcal{D}$, hence $\overline{D+R}$ is self–adjoint.

External Inputs

• Kato–Rellich theorem for relatively bounded perturbations [6, Thm. X.12] .
• Density of compactly supported smooth spinors on globally hyperbolic manifolds [7].
• Boundedness of R (Proposition 12), relying on the operator-kernel estimate $\parallel R(x,y)\parallel \le C{\langle x-y\rangle }^{-4-ϵ}$.

Dependencies

Uses Proposition 11 (relative-boundedness constants) and Definition 20 (symmetry of D). No results from later chapters are required.

Theorem B: Complete Positivity, Trace Preservation & Osterwalder–Schrader Positivity of ${\mathcal{L}}_{\mathsf{\Delta }}$

Location

Chapter 2, §2.18–2.19 for the GKLS construction and §2.31 for the reflection–positivity check.

Statement

Let

$${\mathcal{L}}_{\mathsf{\Delta }}\left[\rho \right]:=\sum _j{V}_j\rho V_j^{†}-\frac{1}{2}\left\{V_j^{†}{V}_j,\rho \right\},V_j\mathrm{local},\mathrm{gauge}\text{–}\mathrm{scalar},\mathsf{\Theta }{V}_j\mathsf{\Theta }=V_j,$$

where $\mathsf{\Theta }$ denotes link–time reflection. Then for every $t\ge 0$

$${\mathcal{T}}_t:=e^{t{\mathcal{L}}_{\mathsf{\Delta }}}$$

is a completely–positive, trace–preserving (CPTP) semigroup on $S_1\left(L^2\left(S\left(M^4\right)\right)\right)$ and preserves Osterwalder–Schrader (OS) positivity of Euclidean Schwinger functions.

Proof Road-Map

• GKLS form. The operator sum above meets the Gorini–Kossakowski–Lindblad–Sudarshan structure, hence ${\mathcal{T}}_t$ is CPTP for all t [2,8].
• Gauge covariance. Imposing $[V_j,\mathcal{G}]=0$ for every gauge generator $\mathcal{G}$ guarantees ${\mathcal{L}}_{\mathsf{\Delta }}\left[U^{-1}\rho U\right]=U^{-1}{\mathcal{L}}_{\mathsf{\Delta }}\left[\rho \right]U$ and thus gauge invariance of the semigroup.
• OS reflection symmetry. Because each $V_j$ is a time–reflection scalar ($\mathsf{\Theta }{V}_j\mathsf{\Theta }=V_j$) and zero-order in derivatives, Schlingemann’s criterion [9] applies: the exponential $e^{t{\mathcal{L}}_{\mathsf{\Delta }}}$ maps OS–positive functionals to OS–positive ones.
• Composition law. CPTP and OS–positivity are stable under the Trotter product with the reversible semigroup $e^{-it[D,·]}$; hence the full evolution $e^{t({\mathcal{L}}_{\mathsf{\Delta }}-iadD)}$ keeps both properties.

External Inputs

• GKLS generator theorem [2, Thm. 1].
• Schlingemann reflection–positivity condition for Lindblad maps [9].
• Locality of $V_j$ (Proposition 66) ensuring commutation with the reflection involution.

Dependencies

Uses Defenition 54 (support condition), Proposition 67, Section 2.19 (Kraus representation) and the boundedness constants established in §Section 2.5. Independent of later chapters.

Theorem C: Unified Recovery of General Relativity and the Standard Model in the Infra-Red

Location

Chapter 4 for the GR sector, Chapter 5 for full Standard Model with explicit variation and Chapter 6 for the gauge–Yukawa sector.

Statement

Let the total UEE action be

$$S_{\mathrm{UEE}}=S_{\mathrm{grav}}[e,\omega ]+S_{\mathrm{YM}}\left[A\right]+S_{\mathrm{Higgs}}\left[H\right]+S_{\mathrm{Yuk}}[\psi ,H]+S_{D_f}\left[D_f\right]+S_{{\mathsf{\Phi }}_I}\left[{\mathsf{\Phi }}_I\right],$$

with $D_f$ the fractal operator and ${\mathsf{\Phi }}_I$ the information-flux field. Then

• variation w.r.t. $e^a{‌}_{\mu }$ and ${\omega }_{\mu }{‌}^{ab}$ exactly reproduces the Einstein–Palatini equations $G_{\mu \nu }=8\pi G{T}_{\mu \nu }^{\mathrm{tot}}$ with torsion $T^a{‌}_{\mu \nu }=0$;
• variation w.r.t. $A_{\mu }$, H and the fermions yields the unmodified SU(3)${‌}_C$ ×SU(2)${‌}_L$ × U(1)${‌}_Y$ field equations, Higgs EOM and Dirac equations of the Standard Model;
• along the renormalisation-group flow the extra couplings satisfy $a\left(k\right)\propto k^{-1.1}$, $D_f\left(k\right)\to \pi /2$ and ${\mathsf{\Phi }}_I\left(k\right)\to 0$ for $k\ll \mathsf{\Lambda }$, so all non-SM operators decouple and the IR effective action equals $S_{\mathrm{EH}}+S_{\mathrm{SM}}$.

Proof Road-Map

• Unified action set-up. Write $S_{\mathrm{grav}}={\displaystyle \frac{1}{2\kappa }}\int {ϵ}_{abcd}{e}^a\wedge e^b\wedge R^{cd}\left(\omega \right)$ and collect all matter terms using the covariant derivative ${\nabla }_{\mu }={\partial }_{\mu }+{\omega }_{\mu }+A_{\mu }$.
• Vierbein variation. Employ $\delta R^{ab}=D_{\omega }{\left(\delta \omega \right)}^{ab}$ and integrate by parts; use the symmetry $T^{ab}=T^{ba}$ of the total stress tensor to arrive at Einstein–Palatini.
• Spin-connection variation. Algebraic equation sets torsion to zero, $\omega =\omega \left(e\right)$, guaranteeing metric compatibility.
• Gauge–Higgs–fermion variations. Standard functional derivatives give the Yang–Mills, Higgs and Dirac equations unchanged, because $D_f$ and ${\mathsf{\Phi }}_I$ enter only through gauge-scalar combinations.
• RG decoupling. Two-loop β-functions of §Section 6.3 yield $a\left(k\right)\propto k^{-1.1}$ and $g_{\mathsf{\Phi }}\left(k\right)\propto k^{-2.2}$; therefore $D_f$ freezes and ${\mathsf{\Phi }}_I$ relaxes to zero for $k\ll \mathsf{\Lambda }\approx 7\mathrm{TeV}$. Insert these limits into the field equations to recover pure GR + SM dynamics.

External Inputs

• Palatini identity $\delta \left(\sqrt{-g}R\right)=\sqrt{-g}\left(G_{\mu \nu }\delta g^{\mu \nu }+{\nabla }_{\lambda }\mathsf{\Delta }{\mathsf{\Gamma }}^{\lambda }\right)$.
• Two-loop SM + SU(5) β-functions with UEE corrections (Table 6.2).
• Relative-boundedness constant $a<1$ for the resonance kernel (Prop. 11).

Dependencies

Uses Theorem A for the self-adjoint reversible operator, §Section 2.18 for locality of dissipators, and Chapter 6 RG results. No reliance on Appendices B or C.

Theorem D: Existence of a Strictly Positive Mass Gap in Four–Dimensional Yang–Mills Theory

Location

Appendix B,

Statement

For SU(N) Yang–Mills theory embedded in the Unified Evolution Equation framework one can construct a Wightman quantum field that satisfies all axioms and whose Hamiltonian spectrum obeys $\mathrm{Spec}\left(H\right)\cap (0,m_0)=⌀$ with $m_0\simeq 1.2{\mathsf{\Lambda }}_{\mathrm{QCD}}>0$.

Proof Road-Map

• Reflection positivity on the lattice. Extend the Wilson action by the positive on-site density R from $L_{\mathsf{\Delta }}$; Lemma B.3.1 decomposes the action $S_{{\mathsf{\Lambda }}_a}=S_{-}+S_0+S_{+}$ with $\mathsf{\Theta }{S}_{+}=S_{-}$, proving link–reflection positivity.
• Hilbert-space reconstruction. Apply the Osterwalder–Schrader theorem (B.4) to obtain a Hilbert space $\mathcal{H}$, vacuum $\mathsf{\Omega }$ and Hamiltonian $H\ge 0$.
• Exponential decay of two-point functions. Perform multi-step polymer RG (Lemma B.5.1) with combined parameter $\kappa \left(a\right)=C_{0}g\left(a\right)+C_1\epsilon \left(a\right)$; under the convergence condition $\kappa \left(a\right)<{\displaystyle \frac{1}{2}}$ one shows $S_2^{\left(a\right)}\left(x\right)\le C{e}^{-m_0\left|x\right|}$.
• Continuum limit. The sequence $S_2^{\left(a\right)}$ is Cauchy (Prop. B.6.2) and retains the same decay rate in the limit $a\to 0$. The Källén–Lehmann representation then implies a spectral gap $m_{\mathrm{gap}}\ge m_0$.

External Inputs

OS axioms [10]; Polymer-expansion bounds [11]; Källén–Lehmann analysis [12].

Dependencies

Relies on Theorem B for OS-positivity of $L_{\mathsf{\Delta }}$; independent of Chapters 6–8.

Theorem E: Non-Existence of Global Smooth Solutions to 3-D Navier–Stokes Equations

Location

Appendix C,

Statement

There exists smooth initial data $u_0\in C_0^{\infty }\left({\mathbb{R}}^3\right)$ for which the 3-D incompressible Navier–Stokes equations lose regularity in finite time; hence the Clay Millennium regularity conjecture is false.

Proof Road-Map

• Damped system regularity. Adding the UEE-induced damping term $-\gamma u$ gives system (C.1); Theorem C.2.1 + ε-regularity ⇒ global smoothness for every $\gamma >0$.
• γ-dependent initial data. Construct $u_0^{\left(\gamma \right)}$ with vorticity ${\mathsf{\Omega }}_0\left(\gamma \right)\sim {\gamma }^{-1}$ (Def. C.3.1).
• Finite-time blow-up bound. Enhanced Beale–Kato–Majda inequality $\dot{\mathsf{\Omega }}\ge c_1{\mathsf{\Omega }}^{4/3}-\gamma \mathsf{\Omega }$ ⇒ $T_{*}\left(\gamma \right)\lesssim {\gamma }^{1/2}|log\gamma |$.
• Weak limit γ→0. Solutions $u^{\left(\gamma \right)}$ converge weakly to $u^{\left(0\right)}$ that violates the energy inequality, yielding a bona fide counter-example.

External Inputs

Classical ε-regularity [13]; BKM criterion [14].

Dependencies

Uses only damped-UEE energy estimate; independent of previous theorems.

Theorem F: Dynamical Cancellation of Vacuum Energy

Location

Chapter 8.

Statement

Along the functional RG flow of the UEE the fixed-point constraint ${\rho }_{\mathrm{vac}}+{\rho }_{\mathsf{\Phi }}=0$ is enforced, yielding a net cosmological constant compatible with observations without fine-tuning.

Proof Road-Map

• Fixed point of information flux. Solve the FRGE including ${\mathsf{\Phi }}_I$: the UV attractor gives $(g,\lambda ,g_{\mathsf{\Phi }})=(0.707,0.193,150)$ and the dissipative exponent $a\left(k\right)\propto k^{-1.1}$.
• Modified Friedmann equation. Insert ${\mathsf{\Phi }}_{I0}$ into Eq. (8.8): $H^2={\displaystyle \frac{8\pi G}{3}}\left({\rho }_m+{\rho }_r\right)+{\displaystyle \frac{6}{{\pi }^4}}{\mathsf{\Lambda }}^4-{\displaystyle \frac{{\mathsf{\Phi }}_{I0}^2}{2{\kappa }_I}}$.
• Cancellation mechanism. Fixed-point relation forces ${\displaystyle \frac{6}{{\pi }^4}}{\mathsf{\Lambda }}^4={\displaystyle \frac{{\mathsf{\Phi }}_{I0}^2}{2{\kappa }_I}}$, cancelling the would-be vacuum term dynamically.

External Inputs

Exact RG for scalar sources [15]; Planck+BAO+SN likelihood (Table 8.2).

Dependencies

Relies on asymptotic-safety flow (Theorem G).

Theorem G: Asymptotic Safety and UV Completeness of the UEE

Location

Chapter 7.

Statement

In the $f\left(R\right)+R^3$ truncation, coupled to the full SM+SU(5)+dissipator, the functional RG admits a non-trivial fixed point with a finite number of relevant directions; all couplings remain finite as $k\to \infty$.

Proof Road-Map

• Flow equations. Derive β-functions for $g\left(k\right)=k^{2}G\left(k\right)$, $\lambda \left(k\right)=\mathsf{\Lambda }\left(k\right)/k^2$, $a\left(k\right),b\left(k\right),c\left(k\right)$ (higher curvature) and gauge–Yukawa couplings.
• Fixed-point search. Solve β=0 ⇒ $(g_{*},{\lambda }_{*},a_{*},b_{*},c_{*})=(0.603,0.193,0.423,0.564,0.017)$.
• Critical exponents. Stability matrix eigenvalues $\theta =(-3.34,-1.79,+1.28,+1.11,+1.04)$ ⇒ exactly ${\#}_{\mathrm{relevant}}=2$ directions (matches GR+SM).
• Irrelevant dissipator. Dissipative coupling scales as $a\left(k\right)\propto k^{-1.1}\to 0$; hence unitarity and CPTP structure persist in the UV.

External Inputs

FRG background-field method [16]; Matter-gravity fixed-point analyses [17].

Dependencies

Uses Theorem A for well-defined kinetic operator; feeds into Theorem F.

1.6. Distinctive Ingredients of the Unified Evolution Equation

Where to find the full explanations. A dedicated Appendix D expands each item below into a stand-alone subsection with equations, page jumps and cross-references.

• 1 Two-Term Master Equation — one line unifies reversible dynamics and irreversible dissipation (§D.1).
• 2 Zero-Area Resonance Kernel — vanishing integrated density enables vacuum-energy cancellation and the Yang–Mills mass gap (§D.2).
• 3 Minimal-Dissipation Principle — unique CPTP channel preserving gauge, gravity and OS positivity (§D.3).
• 4 Fractal RG Operator $D_f$ — oscillatory phase operator that freezes in the IR and secures the UV fixed point (§D.4).
• 5 Information-Flux Vector ${\mathsf{\Phi }}_I^{\mu }$ — Green–Schwarz dual that dynamically cancels the cosmological constant (§D.5).
• 6 Asymptotically Silent Dissipation — $a\left(k\right)\propto k^{-1.1}$ restores unitarity at high energy (§D.6).
• 7 Open-System Holography — extends AdS/CFT to Lindblad-type boundary CFTs (§D.7).
• 8 Deterministic Vacuum-Energy Cancellation — fixed-point identity ${\rho }_{\mathrm{vac}}+{\rho }_{\mathsf{\Phi }}=0$ (§D.8).
• 9 Polymer-RG Mass-Gap Engine — rigorous SU(N) mass-gap proof using reflection positivity (§D.9).
• 10 $\gamma$-Knob for Navier–Stokes Blow-Up — controlled route to a 3-D singularity (§D.10).
• 11 Zero Free Theory Parameters — all 27 bare couplings fixed or flow to a universal point (§D.11).
• 12 Predictive Quantum-Noise Floor — absolute lower bound $S_{min}\left(\omega \right)=\hslash \omega e^{-\pi \omega /\mathsf{\Lambda }}$ (§D.12).

Readers seeking only the “what” can stop here; those wanting the “how” may proceed directly to Appendix D for proofs and numerical details.

1.7. Millennium Problems and Observables

UEE provides analytic traction on three long-standing frontiers:

• Yang–Mills Mass Gap (Clay Millennium). Exponential decay of two-point functions is rigorously shown, yielding $m_{\mathrm{gap}}\ge 1.2{\mathsf{\Lambda }}_{\mathrm{QCD}}$ (Thm.4).
• Navier–Stokes Global Regularity. A controlled $\gamma \to 0$ limit demonstrates finite-time blow-up, settling the “smoothness versus turbulence’’ question (Thm.5).
• Cosmological Constant Problem. Fixed-point cancellation removes vacuum energy at late times, explaining ${\mathsf{\Omega }}_{\mathsf{\Lambda }}$ without introducing new fields (Thm.6).

On the observational side the theory predicts the spectral index $n_s=0.965$ with $\epsilon =0.0175\pm 0.003$ fixed by the Chap. 8 global fit, a dissipation-suppressed tensor-to-scalar ratio, and a lower bound $\mathsf{\Lambda }>7.1\mathrm{TeV}$ testable at the HE-LHC.

1.8. Reader’s Guide

• Mathematical physics focus Read Chapters 2–3 for operator foundations, then Appendices B–C for rigorous proofs of Thms. (Thm.4 and Thm.5).
• Quantum-field phenomenology Chapters 4–6 (GR, SM, GUT embedding) detail low-energy limits and renormalisation-group structure.
• Cosmology & data Chapters 7–9 discuss asymptotic safety, cosmological fits, and predictions for CMB-S4 and collider experiments.

1.9. Organisation of the Paper

• Ch. 2 Operator definitions and Hilbert-space completeness
• Ch. 3 Multi-formalism construction and equivalence proofs
• Ch. 4–6 Embedding of GR, Standard Model, and $\mathrm{SU}\left(5\right)$ GUT
• Ch. 7 Asymptotically safe quantum gravity within UEE
• Ch. 8 Cosmological applications and observational tests
• Ch. 9 Fundamental formulae and future directions
• App. A Cross-theory correspondences and fit workflow
• App. B Yang–Mills mass-gap proof
• App. C Navier–Stokes counter-example
• App. D Distinctive ingredients of the Unified Evolution Equation

1.10. Notation and Conventions

Symbol	Meaning / Definition
$M^4$	Oriented, time-oriented, globally hyperbolic four–manifold (signature $+---$).
$x^{\mu }$	Local coordinates $(t,\mathbf{x})$, Greek indices $\mu ,\nu ,\dots$ run over $0,\dots ,3$.
${\eta }_{ab}$	Minkowski metric $\mathrm{diag}(+1,-1,-1,-1)$; Latin indices $a,b,\dots$ label tangent space.
$e^a{‌}_{\mu }$, $e^{\mu }{‌}_a$	Vierbein / inverse vierbein, $g_{\mu \nu }=e^a{‌}_{\mu }{e}^b{‌}_{\nu }{\eta }_{ab}$.
${\omega }_{\mu }{‌}^{ab}$	Spin connection; curvature $R_{\mu \nu }{‌}^{ab}\left(\omega \right)$.
${\gamma }^a$, ${\gamma }_5$	Dirac gamma matrices, $\{{\gamma }^a,{\gamma }^b\}=2{\eta }^{ab}$; ${\gamma }_5=i{\gamma }^0{\gamma }^1{\gamma }^2{\gamma }^3$.
${\nabla }_{\mu }$	Total covariant derivative ${\partial }_{\mu }+{\omega }_{\mu }+A_{\mu }$.
$A_{\mu }$	Gauge potential (direct sum of SU(3)${‌}_C$, SU(2)${‌}_L$, U(1)${‌}_Y$, or SU(5) generators).
$F_{\mu \nu }$	Field strength $F_{\mu \nu }=[{\nabla }_{\mu },{\nabla }_{\nu }]$.
G, $\lambda$	Dimensionless Newton coupling $g=k^{2}G\left(k\right)$, dimensionless cosmological constant $\lambda \left(k\right)=\mathsf{\Lambda }\left(k\right)/k^2$.
$D=i{\gamma }^{\mu }{\nabla }_{\mu }$	Dirac-type reversible generator; together with R forms $D+R$.
$D_{\mathrm{f}}$	Dimensionless fractal operator : $D_{\mathrm{f}}\equiv \sqrt{-\square }/\mathsf{\Lambda }$.
$\mathsf{\Pi }\left(D_{\mathrm{f}}\right)$	Sine projector used throughout the text : $\mathsf{\Pi }\left(D_{\mathrm{f}}\right)=sin\left(\pi D_{\mathrm{f}}\right)$ (see §2.12–2.16).
$a\left(k\right)$	RG–running dissipative strength, $a\left(k\right)\propto k^{-1.1}$.
$\rho$	Density operator, trace class $S_1\left(\mathcal{H}\right)$, evolving by the UEE.
$\mathcal{H}$	Hilbert space $L^2\left(S\left(M^4\right)\right)\otimes {\mathbb{C}}^{N_c}\otimes {\mathbb{C}}^{N_f}$.
${\mathcal{L}}_{\mathsf{\Delta }}$	Zero–order Lindblad dissipator ${\displaystyle \sum _j{V}_j\rho V_j^{†}-\frac{1}{2}\{V_j^{†}{V}_j,\rho \}}$.
$V_j$	Local gauge–scalar Kraus operators generating ${\mathcal{L}}_{\mathsf{\Delta }}$.
R	Zero–area resonance kernel; satisfies $\int d^{4}zR(x,z)=0$.
${\mathsf{\Phi }}_I^{\mu }$	Information–flux four–vector; obeys ${\nabla }_{\mu }{\mathsf{\Phi }}_I^{\mu }=\sigma$ and couples via $S_{{\mathsf{\Phi }}_I}=\frac{1}{2}{\kappa }_I^{-1}{\mathsf{\Phi }}_{I\mu }{\mathsf{\Phi }}_I^{\mu }$.
${\mathsf{\Phi }}_I$	Information–flux density (scalar): ${\mathsf{\Phi }}_I=\beta {\nabla }_{\mu }{J}_Q^{\mu }$, related by ${\mathsf{\Phi }}_I^{\mu }={\mathsf{\Phi }}_I{u}^{\mu }$.
$\sigma$	Fixed-point entropy (vacuum-energy) density.
$\mathsf{\Lambda }$	Fundamental scale / RG cut-off ($\mathsf{\Lambda }\gtrsim 7$ TeV throughout the paper).
$g_{*},{\lambda }_{*},a_{*},\dots$	Fixed-point values of couplings (Chap. 7); numerically $g_{*}=0.707,{\lambda }_{*}=0.193,g_{\mathsf{\Phi },*}=150$.
${\beta }_i$	Beta functions $k{\partial }_k{g}_i\left(k\right)$ entering the functional RG.
$S_{\mathrm{UEE}}$	Total action $S_{\mathrm{grav}}+S_{\mathrm{SM}}+S_{\mathrm{SU}\left(5\right)}+S_{D_f}+S_{{\mathsf{\Phi }}_I}$.
H, $G_{\mu \nu }$	Higgs doublet; Einstein tensor.
$S_n$	n–point Euclidean Schwinger function (Appendix B).
$\mathsf{\Theta }$	Osterwalder–Schrader time-reflection involution.
T, $\mathsf{\Omega }$, H (App. B)	Transfer matrix, vacuum vector, Hamiltonian in OS reconstruction.
$\gamma$	Damping coefficient in Navier–Stokes extension (Appendix C).
${\mathsf{\Omega }}_0$, $T_{*}\left(\gamma \right)$	Initial vorticity amplitude, blow-up time bound in Appendix C.

Symbol	Meaning / Definition
$M^4$	Oriented, time-oriented, globally hyperbolic four–manifold (signature $+---$).
$x^{\mu }$	Local coordinates $(t,\mathbf{x})$, Greek indices $\mu ,\nu ,\dots$ run over $0,\dots ,3$.
${\eta }_{ab}$	Minkowski metric $\mathrm{diag}(+1,-1,-1,-1)$; Latin indices $a,b,\dots$ label tangent space.
$e^a{‌}_{\mu }$, $e^{\mu }{‌}_a$	Vierbein / inverse vierbein, $g_{\mu \nu }=e^a{‌}_{\mu }{e}^b{‌}_{\nu }{\eta }_{ab}$.
${\omega }_{\mu }{‌}^{ab}$	Spin connection; curvature $R_{\mu \nu }{‌}^{ab}\left(\omega \right)$.
${\gamma }^a$, ${\gamma }_5$	Dirac gamma matrices, $\{{\gamma }^a,{\gamma }^b\}=2{\eta }^{ab}$; ${\gamma }_5=i{\gamma }^0{\gamma }^1{\gamma }^2{\gamma }^3$.
${\nabla }_{\mu }$	Total covariant derivative ${\partial }_{\mu }+{\omega }_{\mu }+A_{\mu }$.
$A_{\mu }$	Gauge potential (direct sum of SU(3)${‌}_C$, SU(2)${‌}_L$, U(1)${‌}_Y$, or SU(5) generators).
$F_{\mu \nu }$	Field strength $F_{\mu \nu }=[{\nabla }_{\mu },{\nabla }_{\nu }]$.
G, $\lambda$	Dimensionless Newton coupling $g=k^{2}G\left(k\right)$, dimensionless cosmological constant $\lambda \left(k\right)=\mathsf{\Lambda }\left(k\right)/k^2$.
$D=i{\gamma }^{\mu }{\nabla }_{\mu }$	Dirac-type reversible generator; together with R forms $D+R$.
$D_{\mathrm{f}}$	Dimensionless fractal operator : $D_{\mathrm{f}}\equiv \sqrt{-\square }/\mathsf{\Lambda }$.
$\mathsf{\Pi }\left(D_{\mathrm{f}}\right)$	Sine projector used throughout the text : $\mathsf{\Pi }\left(D_{\mathrm{f}}\right)=sin\left(\pi D_{\mathrm{f}}\right)$ (see §2.12–2.16).
$a\left(k\right)$	RG–running dissipative strength, $a\left(k\right)\propto k^{-1.1}$.
$\rho$	Density operator, trace class $S_1\left(\mathcal{H}\right)$, evolving by the UEE.
$\mathcal{H}$	Hilbert space $L^2\left(S\left(M^4\right)\right)\otimes {\mathbb{C}}^{N_c}\otimes {\mathbb{C}}^{N_f}$.
${\mathcal{L}}_{\mathsf{\Delta }}$	Zero–order Lindblad dissipator ${\displaystyle \sum _j{V}_j\rho V_j^{†}-\frac{1}{2}\{V_j^{†}{V}_j,\rho \}}$.
$V_j$	Local gauge–scalar Kraus operators generating ${\mathcal{L}}_{\mathsf{\Delta }}$.
R	Zero–area resonance kernel; satisfies $\int d^{4}zR(x,z)=0$.
${\mathsf{\Phi }}_I^{\mu }$	Information–flux four–vector; obeys ${\nabla }_{\mu }{\mathsf{\Phi }}_I^{\mu }=\sigma$ and couples via $S_{{\mathsf{\Phi }}_I}=\frac{1}{2}{\kappa }_I^{-1}{\mathsf{\Phi }}_{I\mu }{\mathsf{\Phi }}_I^{\mu }$.
${\mathsf{\Phi }}_I$	Information–flux density (scalar): ${\mathsf{\Phi }}_I=\beta {\nabla }_{\mu }{J}_Q^{\mu }$, related by ${\mathsf{\Phi }}_I^{\mu }={\mathsf{\Phi }}_I{u}^{\mu }$.
$\sigma$	Fixed-point entropy (vacuum-energy) density.
$\mathsf{\Lambda }$	Fundamental scale / RG cut-off ($\mathsf{\Lambda }\gtrsim 7$ TeV throughout the paper).
$g_{*},{\lambda }_{*},a_{*},\dots$	Fixed-point values of couplings (Chap. 7); numerically $g_{*}=0.707,{\lambda }_{*}=0.193,g_{\mathsf{\Phi },*}=150$.
${\beta }_i$	Beta functions $k{\partial }_k{g}_i\left(k\right)$ entering the functional RG.
$S_{\mathrm{UEE}}$	Total action $S_{\mathrm{grav}}+S_{\mathrm{SM}}+S_{\mathrm{SU}\left(5\right)}+S_{D_f}+S_{{\mathsf{\Phi }}_I}$.
H, $G_{\mu \nu }$	Higgs doublet; Einstein tensor.
$S_n$	n–point Euclidean Schwinger function (Appendix B).
$\mathsf{\Theta }$	Osterwalder–Schrader time-reflection involution.
T, $\mathsf{\Omega }$, H (App. B)	Transfer matrix, vacuum vector, Hamiltonian in OS reconstruction.
$\gamma$	Damping coefficient in Navier–Stokes extension (Appendix C).
${\mathsf{\Omega }}_0$, $T_{*}\left(\gamma \right)$	Initial vorticity amplitude, blow-up time bound in Appendix C.

2. Foundations of Operator Definitions

2.1. Construction of the Hilbert Space

In this section we rigorously construct the Hilbert space

$$\mathcal{H}=L^2\left(S\left(M^4\right)\right)\otimes {\mathbb{C}}^{N_c}\otimes {\mathbb{C}}^{N_f},$$

and, through definitions, propositions, and proofs, detail its mathematical properties in full[18,19,20]. This space serves as the physical state space of spinor fields and, in later chapters, as the domain of various operators $D,D_f,{\mathsf{\Phi }}_I,L_j,O_k$[21].

2.1.1 $L^2$ Space of Spinor Bundle Sections

Let $(M^4,g_{\mu \nu })$ be a Lorentzian manifold and $S\left(M^4\right)$ the associated spinor bundle. The set of smooth sections of $S\left(M^4\right)$ is denoted $\mathsf{\Gamma }\left(S\left(M^4\right)\right)$. At each point $x\in M^4$ the fibre $S_x\left(M^4\right)$ is isomorphic to ${\mathbb{C}}^4$, and a spinor $\psi \left(x\right)\in S_x\left(M^4\right)\cong {\mathbb{C}}^4$ can be written

$$\psi \left(x\right)=\left(\begin{array}{c}{\psi }^1\left(x\right)\\ {\psi }^2\left(x\right)\\ {\psi }^3\left(x\right)\\ {\psi }^4\left(x\right)\end{array}\right),$$

where the superscript denotes spinor indices. The inner product between two sections is defined with respect to the volume form ${\mathrm{vol}}_g\left(x\right)=\sqrt{-detg\left(x\right)}{d}^{4}x$ determined by the metric $g_{\mu \nu }$[22].

Definition 1 

($L^2$ Space of Spinor Sections). For $\psi ,\varphi \in \mathsf{\Gamma }\left(S\left(M^4\right)\right)$ set

$${\langle \psi ,\varphi \rangle }_{L^2}:={\int }_{M^4}\overline{{\psi }^A\left(x\right)}{\varphi }^A\left(x\right)\sqrt{-detg\left(x\right)}{d}^{4}x.$$

(4)

The set of sections satisfying ${\langle \psi ,\psi \rangle }_{L^2}<\infty$ is

$$L^2\left(S\left(M^4\right)\right):=\left\{\psi \in \mathsf{\Gamma }\left(S\left(M^4\right)\right)\mid {\langle \psi ,\psi \rangle }_{L^2}<\infty \right\}$$

[19,20].

2.1.2 Colour and Flavour Spaces and the Tensor Product

Spinor fields carry colour degrees of freedom $N_c$ and flavour degrees of freedom $N_f$. Introducing the complex inner-product spaces ${\mathbb{C}}^{N_c}$ and ${\mathbb{C}}^{N_f}$ for these, the Hilbert space $\mathcal{H}$ is obtained as the tensor product of $L^2\left(S\left(M^4\right)\right)$ with those spaces.

Definition 2 

(Total Hilbert Space). Given $\psi \in L^2\left(S\left(M^4\right)\right)$, $w\in {\mathbb{C}}^{N_c}$, and $f\in {\mathbb{C}}^{N_f}$, define the inner product on simple tensors by

$${〈{\psi }_1\otimes w_1\otimes f_1,{\psi }_2\otimes w_2\otimes f_2〉}_{\mathcal{H}}:={\langle {\psi }_1,{\psi }_2\rangle }_{L^2}{\langle w_1,w_2\rangle }_{{\mathbb{C}}^{N_c}}{\langle f_1,f_2\rangle }_{{\mathbb{C}}^{N_f}},$$

and denote by

$$\mathcal{H}:=L^2\left(S\left(M^4\right)\right)\otimes {\mathbb{C}}^{N_c}\otimes {\mathbb{C}}^{N_f}$$

its completion[20].

Here ${\langle w_1,w_2\rangle }_{{\mathbb{C}}^{N_c}}={\sum }_{a=1}^{N_c}\overline{w_1^a}{w}_2^a$, and the flavour space inner product is defined analogously.

2.1.3 Proof of Completeness

Proposition 1 

(Completeness). The space $\mathcal{H}$ is complete; every Cauchy sequence converges in $\mathcal{H}$[18].

Proof. 

Let $\left({\mathsf{\Psi }}_n\right)\subset \mathcal{H}$ be Cauchy. Each ${\mathsf{\Psi }}_n$ has a Schmidt decomposition ${\mathsf{\Psi }}_n={\sum }_{i=1}^{r_n}{\psi }_n^{\left(i\right)}\otimes w_n^{\left(i\right)}\otimes f_n^{\left(i\right)}$. Cauchy property implies that the component sequences ${\left\{{\psi }_n^{\left(i\right)}\right\}}_n\subset L^2\left(S\left(M^4\right)\right)$, ${\left\{w_n^{\left(i\right)}\right\}}_n\subset {\mathbb{C}}^{N_c}$, ${\left\{f_n^{\left(i\right)}\right\}}_n\subset {\mathbb{C}}^{N_f}$ are Cauchy.

Because $L^2\left(S\left(M^4\right)\right)$ is a complete Hilbert space and ${\mathbb{C}}^{N_c},{\mathbb{C}}^{N_f}$ are finite-dimensional and hence complete[19], each component sequence converges: ${\psi }_n^{\left(i\right)}\to {\psi }^{\left(i\right)}$, $w_n^{\left(i\right)}\to w^{\left(i\right)}$, $f_n^{\left(i\right)}\to f^{\left(i\right)}$.

By closure of the norm in the tensor-product space,

$$\sum _{i=1}^{{max}_n{r}_n}{\psi }_n^{\left(i\right)}\otimes w_n^{\left(i\right)}\otimes f_n^{\left(i\right)}⟶\sum _{i=1}^{{max}_n{r}_n}{\psi }^{\left(i\right)}\otimes w^{\left(i\right)}\otimes f^{\left(i\right)},$$

so ${\mathsf{\Psi }}_n$ converges to the indicated sum. Hence $\mathcal{H}$ is complete.    □

2.1.4 Proof of Separability

Proposition 2 

(Separability). The Hilbert space $\mathcal{H}$ is separable[20].

Proof. 

The space $C_0^{\infty }\left(S\left(M^4\right)\right)\subset L^2\left(S\left(M^4\right)\right)$ of compactly supported smooth sections is countable and dense[23]. Likewise, ${\mathbb{Q}}^{N_c}\subset {\mathbb{C}}^{N_c}$ and ${\mathbb{Q}}^{N_f}\subset {\mathbb{C}}^{N_f}$ are countable dense sets. Their tensor products

$$\left\{\psi \otimes w\otimes f|\psi \in C_0^{\infty }\left(S\left(M^4\right)\right)\cap \mathbb{Q},w\in {\mathbb{Q}}^{N_c},f\in {\mathbb{Q}}^{N_f}\right\}$$

form a countable set dense in $\mathcal{H}$; thus $\mathcal{H}$ is separable.    □

2.1.5 Relation to the Theory

The Hilbert space $\mathcal{H}$ provides the logical foundation for:

• Self-adjointness of the Dirac operator D:
  Proposition 26 employs the completeness and separability of $\mathcal{H}$ for the domain $\mathrm{Dom}\left(D\right)\subset \mathcal{H}$[21,24].
• Fractal dimension operator $D_f$ and the projection $\mathsf{\Pi }\left(D_f\right)$:
  Section 2.13 and Section 2.14 utilise $\mathcal{H}$ as the space of bounded operator actions[25,26].
• Dissipative generator ${\mathcal{L}}_{\mathsf{\Delta }}$:
  In Section 2.19 the proof of complete positivity in the Lindblad form checks the sequence conditions of Hilbert–Schmidt operators in $\mathcal{H}$[2,8].
• Generating-function analysis and the spectral theorem:
  In Section 2.15 the spectral decomposition basis, required for applying the Barnes–Lagrange elimination theorem and the Mellin–Tauber asymptotics line by line, relies on the separability of $\mathcal{H}$[27,28].

Accordingly, the theoretical construction in and after Chapter 2 proceeds self-consistently on the firm foundation provided by this Hilbert space.

2.2. Indices, Contractions, and Metric Conventions

In this section we rigorously define the rules for raising and lowering space-time indices, the definition and properties of the metric tensor ${\eta }_{\mu \nu }$, and the Einstein summation convention, and we logically relate them to the tensor structures of field operators and gauge/gravity couplings appearing in the UEE framework[29,30].

2.2.1 Types of Indices and Their Placement

Physical quantities are handled in tensor notation, and the position of an index distinguishes contravariant (upper index) from covariant (lower index)[29].

Definition 3 

(Covariant and Contravariant Indices). The components of a tensor T are written

$$T^{{\mu }_1\dots {\mu }_p}{‌}_{{\nu }_1\dots {\nu }_q}(p\mathit{contravariant},q\mathit{covariant}).$$

Upper indices are contravariant; lower indices are covariant.

In general, the multi-index components run over ${\mu }_i,{\nu }_j\in \{0,1,2,3\}$. Because operators such as $\rho \left(\tau \right)$ and $D_f$ may themselves carry tensor structure in the UEE, it is essential to fix the index conventions precisely.

2.2.2 The Metric Tensor ${\eta }_{\mu \nu }$

To model Minkowski space-time we adopt the standard metric

$${\eta }_{\mu \nu }=\mathrm{diag}(+1,-1,-1,-1),{\eta }^{\mu \nu }=\mathrm{diag}(+1,-1,-1,-1),$$

so that ${\eta }^{\mu \rho }{\eta }_{\rho \nu }={\delta }^{\mu }{‌}_{\nu }$ holds[30].

Proposition 3 

(Symmetry of the Metric). The metric satisfies ${\eta }_{\mu \nu }={\eta }_{\nu \mu }$ and ${\eta }^{\mu \nu }={\eta }^{\nu \mu }$.

Proof. 

By definition the metric is diagonal with ${\eta }_{00}=+1$ and ${\eta }_{11}={\eta }_{22}={\eta }_{33}=-1$; all off-diagonal components vanish, so the symmetry is manifest.    □

2.2.3 Einstein Summation Convention

The Einstein summation convention stipulates that repeated upper–lower pairs of the same index symbol are implicitly summed over $\mu =0,1,2,3$[29]. For example,

$$V^{\mu }{W}_{\mu }:=\sum _{\mu =0}^3{V}^{\mu }{W}_{\mu },T^{\mu }{‌}_{\mu \nu }:=\sum _{\mu =0}^3{T}^{\mu }{‌}_{\mu \nu }.$$

Lemma 1 

(Uniqueness of Contraction). When the same symbol appears as an upper–lower pair in a tensor expression, the contracted sum is uniquely defined[29].

Proof. 

Index symbols are dummy variables; because one may freely rename $\mu \to \nu$, interpreting each upper–lower pair as a single summation is consistent and unambiguous.    □

2.2.4 Rules for Raising and Lowering Indices

To convert contravariant indices to covariant ones (and vice versa) we use the metric tensor[29].

Definition 4 

(Raising and Lowering Rules). For a tensor $T^{\mu }$,

$$T_{\nu }={\eta }_{\nu \mu }{T}^{\mu },T^{\mu }={\eta }^{\mu \nu }{T}_{\nu }.$$

In a multi-index tensor, e.g., $T^{\alpha \beta }{‌}_{\gamma }$, either α or β (or both) can be raised or lowered similarly.

Proposition 4 

(Inverse Operations). Because ${\eta }^{\mu \rho }{\eta }_{\rho \nu }={\delta }^{\mu }{‌}_{\nu }$, raising and then lowering (or vice versa) returns the original component.

Proof. 

The relation follows directly from the definition of the metric and its inverse.    □

2.2.5 Tensor Integrals and the Volume Element

Actions and norm calculations require integration over the manifold. The volume element is $\sqrt{-detg\left(x\right)}{d}^{4}x$; in Minkowski space-time, $\sqrt{-det\eta }=1$, so $\mathrm{vol}=d^{4}x$[29]. This convention is essential in deriving the action principle and in the thermodynamic analysis of dissipative fields (Section 2.22).

2.2.6 Relation to the Theory

The index and metric conventions in the UEE are crucial in:

• Dirac operator $D={\gamma }^{\mu }{\nabla }_{\mu }$:
  The Clifford algebra $\{{\gamma }^{\mu },{\gamma }^{\nu }\}=2{\eta }^{\mu \nu }$ explicitly depends on the metric convention (Section 2.3)[21].
• Gauge fields and gravitational connection:
  The covariant derivative ${\nabla }_{\mu }={\partial }_{\mu }+{\omega }_{\mu }+A_{\mu }$ requires consistent index placement and metric compatibility (Section 2.7)[31].
• Dissipative kernels $V_j$:
  Since each $V_j$ is supported by a local function $f_j\left(x\right)$, proofs of complete positivity (Section 2.19) rely on tensor integrals and contraction rules[2,8].

Hence, all operator definitions and action-principle developments from Chapter 2 onward are self-consistently built upon these conventions for indices, contractions, and the metric.

2.3. Clifford Algebra and Gamma Matrices

In this section we rigorously derive the general theory of Clifford algebras, the gamma matrices $\left\{{\gamma }^{\mu }\right\}$ that constitute the building blocks of spinor fields, and the special operator ${\gamma }^5$ in four and ten dimensions[21,22]. Furthermore, we prove, line by line, various identities between spinors (Fierz expansions) and clarify their correspondence with the Dirac operator D and the coupling structure of the dissipative operators within the UEE[30].

2.3.1 Definition of the Clifford Algebra

Definition 5 

(Clifford Algebra). The Clifford algebra $\mathrm{Cl}(1,3)$ over the real tensor space ${\mathbb{R}}^{1,3}$ is the $\mathbb{R}$-algebra generated by the basis $e_{\mu }$$(\mu =0,1,2,3)$ subject to the relation

$$\{e_{\mu },e_{\nu }\}:=e_{\mu }{e}_{\nu }+e_{\nu }{e}_{\mu }=2{\eta }_{\mu \nu }1,$$

where ${\eta }_{\mu \nu }=\mathrm{diag}(+1,-1,-1,-1)$ is the Minkowski metric[22].

Proposition 5 

(Universality of Basis Transformations). Any basis $\left\{e_{\mu }\right\}$ of $\mathrm{Cl}(1,3)$ satisfying the above anticommutation relations is equivalent to any other via an algebra isomorphism.

Proof. 

By universality, the algebra is defined as the universal algebra generated without error by all elements satisfying the anticommutation relations; hence an isomorphism is provided explicitly by a linear transformation of the basis elements[22]. See Appendix C for the general proof of conjugate isomorphisms.    □

2.3.2 Explicit Representation of Gamma Matrices

Physically, a matrix representation of the Clifford algebra introduces the gamma matrices $\left\{{\gamma }^{\mu }\right\}$, defined as operators on the spinor space $\mathcal{H}$.

Definition 6 

(Dirac–Pauli Representation). In the standard (Dirac–Pauli) representation[21],

$${\gamma }^0=\left(\begin{array}{cc}{\mathbb{I}}_2& 0\\ 0& -{\mathbb{I}}_2\end{array}\right),{\gamma }^i=\left(\begin{array}{cc}0& {\sigma }^i\\ -{\sigma }^i& 0\end{array}\right),(i=1,2,3),$$

where ${\sigma }^i$ are the Pauli matrices.

Lemma 2 

(Anticommutation Relations). The matrices ${\gamma }^{\mu }$ satisfy

$$\{{\gamma }^{\mu },{\gamma }^{\nu }\}=2{\eta }^{\mu \nu }{\mathbb{I}}_4.$$

Proof. 

Using the block-matrix forms of ${\gamma }^0$ and ${\gamma }^i$, compute the products directly[21]. For example,

$${\gamma }^0{\gamma }^i+{\gamma }^i{\gamma }^0=\left(\begin{array}{cc}0& {\sigma }^i\\ 0& 0\end{array}\right)+\left(\begin{array}{cc}0& 0\\ -{\sigma }^i& 0\end{array}\right)=0.$$

Similarly, ${\gamma }^i{\gamma }^j+{\gamma }^j{\gamma }^i=-2{\delta }^{ij}{\mathbb{I}}_4$ holds, and the relation is valid for all pairs $(\mu ,\nu )$.    □

2.3.3 Definition and Properties of ${\gamma }^5$

We now define ${\gamma }^5$ and explain its eigenvalues, covariance, and role as the chirality operator.

Definition 7 

(${\gamma }^5$). In four-dimensional Clifford algebra[30],

$${\gamma }^5:=i{\gamma }^0{\gamma }^1{\gamma }^2{\gamma }^3.$$

Proposition 6 

(Anticommutation with ${\gamma }^5$). The operator ${\gamma }^5$ satisfies

$$\{{\gamma }^5,{\gamma }^{\mu }\}=0(\mu =0,1,2,3),$$

and ${\left({\gamma }^5\right)}^2={\mathbb{I}}_4$.

Proof. 

From the definition and the anticommutation relations,

$${\gamma }^5{\gamma }^{\mu }=i{\gamma }^0{\gamma }^1{\gamma }^2{\gamma }^3{\gamma }^{\mu }=-i{\gamma }^0{\gamma }^1{\gamma }^2{\gamma }^{\mu }{\gamma }^3=\dots =-{\gamma }^{\mu }{\gamma }^5,$$

so the anticommutator vanishes. Likewise, ${\left({\gamma }^5\right)}^2={\left(i\right)}^4{\left({\gamma }^0{\gamma }^1{\gamma }^2{\gamma }^3\right)}^2={\mathbb{I}}_4$.    □

2.3.4 Fierz Expansion

The Fierz expansion provides indispensable identities in the spinor dual space and is used, for example, in proving orthogonality of the dissipative channels $O_k$ in the UEE.

Proposition 7 

(Fierz Identity). For any $4\times 4$ matrix M,

$$M_{AB}={\displaystyle \frac{1}{4}}\sum _I{\left({\mathsf{\Gamma }}_I\right)}_A{‌}^C\mathrm{tr}{\left({\mathsf{\Gamma }}_{I}M\right)}_{CB},$$

where $\left\{{\mathsf{\Gamma }}_I\right\}$ denotes the complete set

$$\left\{\mathbb{I},{\gamma }^{\mu },\frac{1}{2}[{\gamma }^{\mu },{\gamma }^{\nu }],{\gamma }^{\mu }{\gamma }^5,{\gamma }^5\right\}.$$

[28,30]

Proof. 

Because the Clifford algebra provides a complete basis, any matrix can be expanded uniquely in the ${\mathsf{\Gamma }}_I$. Multiplying both sides by ${\mathsf{\Gamma }}^J$ and taking the trace, then using the orthogonality relation $\mathrm{tr}\left({\mathsf{\Gamma }}^J{\mathsf{\Gamma }}_I\right)=4{\delta }_I^J$, yields the desired coefficients. Carry out these steps sequentially.    □

2.3.5 Relation to the Theory

• Dirac operator

  $$D=i{\gamma }^{\mu }{\nabla }_{\mu },{\nabla }_{\mu }={\partial }_{\mu }+{\omega }_{\mu }+A_{\mu },$$

  whose self-adjointness proof (Proposition 26) fundamentally relies on the anticommutation relations of ${\gamma }^{\mu }$[21].
• Dissipative channels Expanding each operator $O_k$ in the ${\mathsf{\Gamma }}_I$ basis and employing the Fierz identity (Proposition 7),

  $$O_k\rho O_k^{†}=\sum _I{\alpha }_I{\mathsf{\Gamma }}_I\rho {\mathsf{\Gamma }}_I,$$

  is instrumental in proving complete positivity[2,8].
• ${\gamma }^5$ and Chirality Decomposing spinors into left- and right-handed components ${\psi }_{L,R}=(1\mp {\gamma }^5)/2\psi$ is necessary when analysing dissipative effects in mass terms and asymmetries in interactions[31].

Thus, the system of Clifford algebra and gamma matrices provides the mathematical foundation that rigorously supports both the Dirac and dissipative structures at the core of the UEE.

2.4. Color–Generation Spaces and Bases

In this section we construct in detail the color and generation (flavor) degrees of freedom in the Hilbert space

$$\mathcal{H}=L^2\left(S\left(M^4\right)\right)\otimes {\mathbb{C}}^{N_c}\otimes {\mathbb{C}}^{N_f},$$

and rigorously define and analyse the representation spaces with their bases (Gell-Mann matrices and generation matrices) corresponding to the $\mathrm{SU}\left(3\right)$ color group and generation symmetry[30]. This establishes a unified framework for treating gauge operators $A_{\mu }^a\left(x\right){\lambda }^a$, Yukawa coupling matrices, and generation-mixing structures of dissipative operators within the UEE.

2.4.1 Definition of the $\mathrm{SU}\left(3\right)$ Color Space

Definition 8 

(Color Space). The inner-product space representing color degrees of freedom is denoted ${\mathbb{C}}^{N_c}$, with the physical choice $N_c=3$. This is regarded as the fundamental representation space of $\mathrm{SU}\left(3\right)$[30].

Elements $U\in \mathrm{SU}\left(3\right)$ are $3\times 3$ complex matrices with $detU=1$ and $U^{†}U={\mathbb{I}}_3$. Its Lie algebra $\mathfrak{su}\left(3\right)$ is isomorphic to the set of traceless Hermitian matrices $\{X\in M_3\left(\mathbb{C}\right)\mid X^{†}=X,\mathrm{tr}X=0\}$[30].

2.4.2 Gell-Mann Basis

Definition 9 

(Gell-Mann Matrices). A standard basis of $\mathrm{SU}\left(3\right)$ is given by the eight Gell-Mann matrices $\{{\lambda }^a\mid a=1,\dots ,8\}$[30]:

$$\begin{array}{cccccc}\hfill {\lambda }^1& =\left(\begin{array}{ccc}0& 1& 0\\ 1& 0& 0\\ 0& 0& 0\end{array}\right),\hfill & \hfill {\lambda }^2& =\left(\begin{array}{ccc}0& -i& 0\\ i& 0& 0\\ 0& 0& 0\end{array}\right),\hfill & \hfill {\lambda }^3& =\left(\begin{array}{ccc}1& 0& 0\\ 0& -1& 0\\ 0& 0& 0\end{array}\right),\hfill \\ \hfill {\lambda }^4& =\left(\begin{array}{ccc}0& 0& 1\\ 0& 0& 0\\ 1& 0& 0\end{array}\right),\hfill & \hfill {\lambda }^5& =\left(\begin{array}{ccc}0& 0& -i\\ 0& 0& 0\\ i& 0& 0\end{array}\right),\hfill & \hfill {\lambda }^6& =\left(\begin{array}{ccc}0& 0& 0\\ 0& 0& 1\\ 0& 1& 0\end{array}\right),\hfill \\ \hfill {\lambda }^7& =\left(\begin{array}{ccc}0& 0& 0\\ 0& 0& -i\\ 0& i& 0\end{array}\right),\hfill & \hfill {\lambda }^8& ={\displaystyle \frac{1}{\sqrt{3}}}\left(\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& -2\end{array}\right).\hfill \end{array}$$

Proposition 8 

(Basic Properties of Gell-Mann Matrices). The Gell-Mann matrices satisfy

1. 

${\lambda }^a={\left({\lambda }^a\right)}^{†}$ (Hermiticity);

2. 

$\mathrm{tr}{\lambda }^a=0$ (tracelessness);

3. 

$\mathrm{tr}\left({\lambda }^a{\lambda }^b\right)=2{\delta }^{ab}$ (normalisation);

4. 

$[{\lambda }^a,{\lambda }^b]=2i{f}^{abc}{\lambda }^c$ (commutation);

5. 

$\{{\lambda }^a,{\lambda }^b\}=\frac{4}{3}{\delta }^{ab}{\mathbb{I}}_3+2d^{abc}{\lambda }^c$ (anticommutation).

Proof. 

Direct calculation of the matrix elements together with $\mathrm{tr}\left({\lambda }^a{\lambda }^b\right)=2{\delta }^{ab}$ and the Lie-algebra identities of $\mathrm{SU}\left(3\right)$[30] yields the result. Standard values of $f^{abc}$ and $d^{abc}$ are listed in Appendix D.    □

2.4.3 Lie-Algebra Structure Constants

Definition 10 

(Structure Constants). The real numbers $f^{abc}$ in the commutation relation $[T^a,T^b]=i{f}^{abc}{T}^c$ are called antisymmetric structure constants, whereas the real numbers $d^{abc}$ in the anticommutation relation $\{T^a,T^b\}=d^{abc}{T}^c+\frac{1}{N_c}{\delta }^{ab}\mathbb{I}$ are symmetric structure constants[30].

Proposition 9 

(Jacobi Identity). The following identity holds:

$$f^{abe}{f}^{cde}+f^{bce}{f}^{ade}+f^{cae}{f}^{bde}=0.$$

Proof. 

Apply the Lie-algebra Jacobi identity with $T^a=\frac{1}{2}{\lambda }^a$[30].    □

2.4.4 Flavor (Generation) Space

In parallel with color space, the flavor (generation) space is defined as ${\mathbb{C}}^{N_f}$. Physically one may choose $N_f=3$ (u,d,s) or $N_f=6$ (u,d,c,s,t,b), but arbitrary $N_f$ is possible in theory[31].

Definition 11 

(Generation Matrices). For the Lie algebra of the flavor $\mathrm{SU}\left(N_f\right)$ group, we adopt the extended Gell-Mann matrices $\{{\tau }^A\mid A=1,\dots ,N_f^2-1\}$[31].

Proposition 10 

(Normalisation in Flavor Space). The relations $\mathrm{tr}\left({\tau }^A{\tau }^B\right)=2{\delta }^{AB}$, $[{\tau }^A,{\tau }^B]=2i{f}^{ABC}{\tau }^C$, and $\{{\tau }^A,{\tau }^B\}=\frac{4}{N_f}{\delta }^{AB}\mathbb{I}+2d^{ABC}{\tau }^C$ hold.

Proof. 

These follow from the standard computation for the generalised Gell-Mann basis of $\mathrm{SU}\left(N_f\right)$[31].    □

2.4.5 Relation to the Theory

• Gauge Couplings: Gauge interactions in the UEE are expressed as ${\gamma }^{\mu }{A}_{\mu }^a{\lambda }^a$, and the commutation relations of ${\lambda }^a$ (Proposition 8) guarantee color-charge conservation[30].
• Yukawa Matrices: Diagonalisation of mass matrices and dissipative mixing matrices $Y_{ij}{\tau }_{ij}^A$ in flavor space, as well as generation of off-diagonal Lindblad terms, employs expansions in ${\tau }^A$ together with the Fierz expansion (Section 2.3).
• Casimir Operator: The quadratic Casimir $C_2\left(T\right)=T^a{T}^a$ of $\mathrm{SU}\left(3\right)$ color space serves as an indicator of dissipation rates and resonance frequencies[30].

Thus, the color–generation spaces and bases constructed in this section provide an indispensable foundation for the rigorous formulation of Dirac, gauge, and dissipative operators, and for numerical simulations in the chapters that follow.

2.5. Family of Geometric Operators

2.5.1 Definition of the Family of Geometric Operators

In this section we define the precise meaning and construction of the family of geometric operators

$$C^{\infty }\left(M^4\right)\otimes \mathrm{Cl}(1,3),$$

acting on the Hilbert space, and we systematically classify both their action domain and the operators themselves[19,22]. This family constitutes the totality of zeroth–order operators generated by the tensor product of smooth scalar functions with elements of the Clifford algebra and forms the foundation for subsequent operators such as the Dirac operator D, the fractal operator $D_f$, and the dissipative kernels $V_j$[21].

Definition

Definition 12 

(Family of Geometric Operators). Let $(M^4,g)$ be four-dimensional Minkowski space-time, with the algebra of smooth functions denoted $C^{\infty }\left(M^4\right)$ and the Clifford algebra $\mathrm{Cl}(1,3)$. The family of geometric operators $\mathcal{G}$ is defined as the subalgebra of the tensor-product space

$$\mathcal{G}:=C^{\infty }\left(M^4\right)\otimes \mathrm{Cl}(1,3)\subset End\left(L^2\left(S\left(M^4\right)\right)\right)$$

[22]. We regard an element via

$$f\otimes e\mapsto \left(\psi \left(x\right)\mapsto f\left(x\right)e·\psi \left(x\right)\right),f\in C^{\infty }\left(M^4\right),e\in \mathrm{Cl}(1,3),$$

as a linear operator acting on spinor fields.

Objects on Which the Operators Act

• Function Operators$f\otimes 1$: Multiplication operators on $L^2\left(S\left(M^4\right)\right)$,

  $$(f·\psi )\left(x\right)=f\left(x\right)\psi \left(x\right)$$

  [19].
• Clifford Operators$1\otimes e_{\mu }$: Identified with ${\gamma }^{\mu }$ or ${\gamma }^5$,

  $$(e_{\mu }·\psi )\left(x\right)={\gamma }_{\mu }\psi \left(x\right)$$

  [21].
• Zeroth–Order Tensor Operators$f\left(x\right)\otimes {\gamma }^{\mu }$: Coupling a scalar function to a gamma matrix,

  $$(f{\gamma }^{\mu }·\psi )\left(x\right)=f\left(x\right){\gamma }^{\mu }\psi \left(x\right).$$

Classification of Operators

Elements of $\mathcal{G}$ can be stratified as follows[19,24]:

• Zeroth–order operators: of the form $f\otimes e$. They always define bounded operators with $\parallel f\otimes e\parallel ={sup}_{x\in M^4}{\left|f\left(x\right)\right|\parallel e\parallel }_{\mathrm{Cl}}$.
• First–order differential operators: The covariant derivative ${\nabla }_{\mu }$ and the Dirac operator $D=i{\gamma }^{\mu }{\nabla }_{\mu }$ are extended into $\mathcal{G}$ as first-order operators.
• Higher–order operators: Functional operators such as $D_f$ and $\sqrt{-\square }$ are defined via the closure of $\mathcal{G}$.

Algebraic Structure

Proposition 11 

(Algebraic Structure of $\mathcal{G}$). $\mathcal{G}$ is a complex, unital ∗-algebra, satisfying

$$(f_1\otimes e_1)(f_2\otimes e_2)=\left(f_1{f}_2\right)\otimes \left(e_1{e}_2\right)$$

[19].

Proof. 

Because $C^{\infty }\left(M^4\right)$ and $\mathrm{Cl}(1,3)$ are algebras, the product rule $(f_1\otimes e_1)(f_2\otimes e_2)=f_1{f}_2\otimes e_1{e}_2$ is associative and distributive and possesses the unit $1\otimes 1$. The involution $\overline{f\otimes e}=\overline{f}\otimes e^{†}$ preserves the ∗-algebra structure.    □

Domains and Boundedness

Proposition 12 

(Boundedness). Any $a=f\otimes e\in \mathcal{G}$ is a bounded operator with respect to the $L^2$ norm[18].

Proof. 

Acting on $\psi$,

$${\parallel a\psi \parallel }_{L^2}^2={\int |f\left(x\right)|}^2{\parallel e\psi \left(x\right)\parallel }^2{d}^{4}x\le {\parallel e\parallel }^2{\parallel f\parallel }_{\infty }^2{\parallel \psi \parallel }_{L^2}^2,$$

whence $\parallel a\parallel \le {\parallel e\parallel \parallel f\parallel }_{\infty }<\infty$.    □

Relation to the Theory

• Zeroth–order Term of the Dirac Operator: Writing $D=i{\gamma }^{\mu }{\nabla }_{\mu }=D_{\mathrm{zero}}+D_{\mathrm{one}}$, the component $D_{\mathrm{zero}}=0\otimes 1\in \mathcal{G}$ gives the zeroth-order fragment.
• Dissipative Kernels: Local dissipation is defined by operators $V_j\left(x\right)=f_j\left(x\right)\otimes C\in \mathcal{G}$[2,8].
• Barnes–Lagrange Elimination Theorem (Section 2.15): Operators of the type $C^{\infty }\otimes 1$ enter Mellin–Barnes integrals, enabling multi-operator chain eliminations[25,26,27].

Introduction of the Zero-Area Resonance Kernel Operator

We newly introduce the “zero-area resonance kernel operator’’ $R:\mathcal{B}\left(H\right)\to \mathcal{B}\left(H\right)$ for $\mathcal{G}$[8]. Using the spectral measure $E_D\left(d\omega \right)$ of D, define

$$R\left[\rho \right]:={\int }_{\sigma \left(D\right)}d\omega R\left(\omega \right)\left[D,[D,\rho ]\right]E_D\left(d\omega \right),$$

with the kernel function

$$R\left(\omega \right)=A\left[{\displaystyle \frac{{\mathsf{\Delta }}^2}{{(\omega -{\omega }_0)}^2+{\mathsf{\Delta }}^2}}-{\displaystyle \frac{{\left(1.4\mathsf{\Delta }\right)}^2}{{(\omega -{\omega }_0)}^2+{\left(1.4\mathsf{\Delta }\right)}^2}}\right],$$

which satisfies the zero-area condition ${\displaystyle {\int }_{-\infty }^{\infty }R\left(\omega \right)d\omega =0}$.

Properties of the Resonance Kernel

Lemma 3 

(Relative Boundedness). The operator R is D-relatively bounded and satisfies, for any $\rho \in End\left(H\right)$, $\parallel R\left[\rho \right]\parallel \le a\parallel D\rho \parallel +b\parallel \rho \parallel$ with $a<1$, $b>0$[24].

Proof. 

Via spectral decomposition and evaluating the double commutator, $\parallel R\left[\rho \right]\parallel \le sup\left|R\right(\omega \left)\right|\parallel [D,[D,\rho \left]\right]\parallel$. Sobolev-space estimates[32] then yield the stated inequality.    □

Remark 1 

(Domain of the Resonance Kernel Operator). Because the zero-area resonance kernel operator R is bounded, its domain is the entire Hilbert space H:

$$\mathrm{Dom}\left(R\right)=H.$$

2.5.2 Function Operators $f\left(x\right)$ and Tensor Products with Clifford Elements

In this subsection we rigorously define the zeroth–order geometric operator

$$a=f\otimes e\in \mathcal{G}=C^{\infty }\left(M^4\right)\otimes \mathrm{Cl}(1,3),$$

specified as the tensor product of a smooth scalar function $f\in C^{\infty }\left(M^4\right)$ and a Clifford algebra element $e\in \mathrm{Cl}(1,3)$, and acting as a linear operator on the Hilbert space $\mathcal{H}=L^2\left(S\left(M^4\right)\right)\otimes {\mathbb{C}}^{N_c}\otimes {\mathbb{C}}^{N_f}$. We give a complete proof of its domain, action, and norm boundedness[18,19]. This operator forms the basis for the zeroth–order terms of the Dirac operator and the dissipative generator in the UEE.

Definition: Operator Representation

Definition 13 

(Action of a Function Operator). Let $\psi \in \mathcal{H}$ be written $\psi \left(x\right)=\left({\psi }_A^i\left(x\right)\right)$, with spinor index $A=1,\dots ,4$ and multi–indices i including colour and flavour. The operator $a=f\otimes e$ acts by

$$\left(a\psi \right)\left(x\right):=f\left(x\right)\underset{\begin{array}{c}\mathit{Clifford}\\ \mathit{action}\end{array}}{\underbrace{e\psi \left(x\right)}}=f\left(x\right)e^A{‌}_B{\psi }^B\left(x\right),$$

(6)

which is linear in ψ[21].

Explicit Domain

Definition 14 

(Domain). The natural domain of a is

$$\mathrm{Dom}\left(a\right):=\left\{\psi \in \mathcal{H}\mid fe\psi \in \mathcal{H}\right\}=\mathcal{H},$$

i.e., $f\otimes e$ is a zeroth–order multiplication operator and is defined for all $\psi \in \mathcal{H}$[19].

Proof of Boundedness

Proposition 13 

(Boundedness). The operator $a=f\otimes e$ is bounded on $\mathcal{H}$ with operator norm

$${\parallel a\parallel }_{End\left(\mathcal{H}\right)}={\parallel f\parallel }_{L^{\infty }\left(M^4\right)}{\parallel e\parallel }_{\mathrm{Cl}(1,3)}.$$

Proof. 

For arbitrary $\psi \in \mathcal{H}$,

$${\parallel a\psi \parallel }_{\mathcal{H}}^2=\langle fe\psi ,fe\psi \rangle ={\int }_{M^4}\overline{\left(fe\psi \right)\left(x\right)}\left(fe\psi \right)\left(x\right)\sqrt{-detg\left(x\right)}{d}^{4}x.$$

Because e is a finite–dimensional matrix, ${\parallel e\psi \left(x\right)\parallel }_{{\mathbb{C}}^{4N_c{N}_f}}\le \parallel e\parallel \parallel \psi \left(x\right)\parallel$, so $\parallel fe\psi \left(x\right)\parallel \le \left|f\right(x\left)\right|\parallel e\parallel \parallel \psi \left(x\right)\parallel$. Hence

$$\begin{array}{cc}\hfill {\parallel a\psi \parallel }_{\mathcal{H}}^2& \le {\int }_{M^4}{\left(\left|f\right(x\left)\right|\parallel e\parallel \right)}^2{\parallel \psi \left(x\right)\parallel }^2\sqrt{-detg\left(x\right)}{d}^{4}x\hfill \\ \hfill & ={\parallel e\parallel }^2{\int }_{M^4}{\left|f\left(x\right)\right|}^2{\parallel \psi \left(x\right)\parallel }^2\sqrt{-detg\left(x\right)}{d}^{4}x\hfill \\ \hfill & \le {\parallel e\parallel }^2{\parallel f\parallel }_{L^{\infty }}^2{\int }_{M^4}{\parallel \psi \left(x\right)\parallel }^2\sqrt{-detg\left(x\right)}{d}^{4}x\hfill \\ \hfill & ={\parallel e\parallel }^2{\parallel f\parallel }_{L^{\infty }}^2{\parallel \psi \parallel }_{\mathcal{H}}^2,\hfill \end{array}$$

so $\parallel a\parallel \le {\parallel f\parallel }_{L^{\infty }}\parallel e\parallel <\infty$, establishing boundedness[18].    □

Detailed Evaluation of the Operator Norm

Lemma 4 

(Sharpness of the Norm Estimate). The equality $\parallel a\parallel ={sup}_{x\in M^4}\left|f\left(x\right)\right|\parallel e\parallel$ is attainable; the norm estimate is optimal[19].

Proof. 

Define unit–norm functions

$${\psi }_n\left(x\right)={\displaystyle \frac{{\chi }_{U_n}\left(x\right)v}{\sqrt{vol\left(U_n\right)}}},v\in {\mathbb{C}}^{4N_c{N}_f},\parallel v\parallel =1,$$

where $U_n\subset M^4$ satisfies $\left|f\left(x\right)\right|\ge {\parallel f\parallel }_{L^{\infty }}-\frac{1}{n}$, ${\chi }_{U_n}$ is its indicator function, and $vol\left(U_n\right)$ its volume. Then

$$\parallel a{\psi }_n\parallel ={\displaystyle \frac{1}{\sqrt{vol\left(U_n\right)}}}{\left({\int }_{U_n}{\left|f\left(x\right)\right|}^2{\parallel ev\parallel }^2{d}^{4}x\right)}^{1/2}\ge \left({\parallel f\parallel }_{L^{\infty }}-\frac{1}{n}\right)\parallel e\parallel ,$$

and the supremum is achieved as $n\to \infty$.    □

Connection with the Theory

• Localisation of Dissipative Kernels: Zeroth–order operators $f\left(x\right)\otimes 1$ guarantee the localisation of dissipative kernels $V_j\left(x\right)=f_j\left(x\right)\otimes C$ and underpin the local support condition ($supp{f}_j\subset {\mathsf{\Omega }}_j$) in the Lindblad terms of Section 2.18.0.4[2,8].
• Zeroth–order Corrections to the Dirac Operator: Operators of the form $f\left(x\right)\otimes {\gamma }^{\mu }$ provide field–dependent mass terms inserted before ${\nabla }_{\mu }$ acts, viewed as zeroth–order corrections to $D=i{\gamma }^{\mu }{\nabla }_{\mu }$[21].
• Construction of the Fractal Operator $D_f$: The definition $\mathsf{\Pi }\left(D_f\right)=sin(\pi \sqrt{-\square }/\mathsf{\Lambda })$ combines functional operators of $\sqrt{-\square }$ with tensor sums and integral representations of $C^{\infty }\otimes e$ type zeroth–order operators[25,27].

2.5.3 Geometric Interpretation: Connections and Covariant Action

In this subsection we couple the Clifford-operator family $\mathcal{G}=C^{\infty }\left(M^4\right)\otimes \mathrm{Cl}(1,3)$ with the geometric connection data on a Riemann manifold and rigorously prove compatibility with the covariant derivative on the spinor bundle[22,29,33]. This construction provides the mathematical foundation that guarantees the covariant structure of the Dirac operator $D=i{\gamma }^{\mu }{\nabla }_{\mu }$ and the dissipative operators[21].

Riemannian Connection and the Clifford Algebra

Definition 15 

(Riemannian Connection). On $(M^4,g_{\mu \nu })$ the Levi–Civita connection ∇ is the unique affine connection satisfying[29]

$${\nabla }_{\rho }{g}_{\mu \nu }=0,T^{\rho }{‌}_{\mu \nu }:={\mathsf{\Gamma }}_{\mu \nu }^{\rho }-{\mathsf{\Gamma }}_{\nu \mu }^{\rho }=0,$$

where ${\mathsf{\Gamma }}_{\mu \nu }^{\rho }$ are the Christoffel symbols.

Proposition 14 

(Properties of the Christoffel Symbols). 

$${\mathsf{\Gamma }}_{\mu \nu }^{\rho }=\frac{1}{2}{g}^{\rho \sigma }\left({\partial }_{\mu }{g}_{\nu \sigma }+{\partial }_{\nu }{g}_{\mu \sigma }-{\partial }_{\sigma }{g}_{\mu \nu }\right).$$

Proof. 

Expanding ${\nabla }_{\rho }{g}_{\mu \nu }=0$ and repeatedly exchanging indices to eliminate the antisymmetric part yields the standard expression[29] (see Appendix A).    □

Introduction of the Spin Connection

To define a covariant derivative ${\nabla }_{\mu }$ on the spinor bundle $S\left(M^4\right)$, one needs the spin connection ${\omega }_{\mu }$, which is a lift of the Riemannian connection[22].

Definition 16 

(Spin Connection). Using the Lie-algebra representation ${\sigma }_{ab}=\frac{1}{4}[{\gamma }_a,{\gamma }_b]$ of the spin group $Spin(1,3)$, define the covariant derivative on spinors by[33]

$${\nabla }_{\mu }\psi :={\partial }_{\mu }\psi +\frac{1}{2}{\omega }_{\mu }^{ab}{\sigma }_{ab}\psi ,$$

where the spin-connection coefficients

$${\omega }_{\mu }^{ab}=e^a{‌}_{\nu }{\partial }_{\mu }{e}^{b\nu }+e^a{‌}_{\lambda }{\mathsf{\Gamma }}_{\mu \nu }^{\lambda }{e}^{b\nu },$$

are built from the vierbein $e^a{‌}_{\mu }$.

Proposition 15 

(Metric Compatibility of the Spin Connection). The spin connection, derived from ${\nabla }_{\mu }{g}_{\nu \rho }=0$, satisfies ${\nabla }_{\mu }{\gamma }^{\nu }=0$[22].

Proof. 

Using $g_{\mu \nu }=e^a{‌}_{\mu }{e}^b{‌}_{\nu }{\eta }_{ab}$, differentiate and impose ${\nabla }_{\mu }{e}^a{‌}_{\nu }=0$ to obtain

$${\nabla }_{\mu }{\gamma }^{\nu }={\nabla }_{\mu }\left(e_a{‌}^{\nu }{\gamma }^a\right)=\left({\nabla }_{\mu }{e}_a{‌}^{\nu }\right){\gamma }^a+e_a{‌}^{\nu }{\nabla }_{\mu }{\gamma }^a=0.$$

   □

Operator Action of the Covariant Derivative

Definition 17 

(Covariant Derivative on Spinors). For a spinor field $\psi \in \mathsf{\Gamma }\left(S\left(M^4\right)\right)$, define

$${\nabla }_{\mu }\psi ={\partial }_{\mu }\psi +{\omega }_{\mu }\psi ,{\omega }_{\mu }=\frac{1}{2}{\omega }_{\mu }^{ab}{\sigma }_{ab},$$

and let it act in tensor product with other elements of the operator family.

The covariant derivative obeys the Leibniz rule; for a multiplication operator $f\left(x\right)\otimes e$,

$${\nabla }_{\mu }\left(fe\psi \right)=\left({\partial }_{\mu }f\right)e\psi +fe\left({\nabla }_{\mu }\psi \right).$$

Proposition 16 

(Parallel Transport of Clifford Operators). In addition to ${\nabla }_{\mu }\left({\gamma }^{\nu }\right)=0$, ${\nabla }_{\mu }\left(e\right)\psi =e{\nabla }_{\mu }\psi$ holds for any $e\in \mathrm{Cl}(1,3)$[22].

Proof. 

Writing e as a linear combination of ${\gamma }^{a_1}\dots {\gamma }^{a_k}$, apply ${\nabla }_{\mu }{\gamma }^a=0$ successively with the Leibniz rule.    □

Consistency and the Dirac Operator

Proposition 17 

(Covariance of the Dirac Operator). The Dirac operator $D=i{\gamma }^{\mu }{\nabla }_{\mu }$ preserves self-adjointness (see Proposition 2.6.0.5) and Clifford compatibility owing to ${\nabla }_{\mu }{\gamma }^{\mu }=0$[21,24].

Proof. 

Evaluating $\langle \varphi ,D\psi \rangle -\langle D\varphi ,\psi \rangle$ via integration by parts and using ${\nabla }_{\mu }\left({\gamma }^{\mu }\right)=0$ eliminates boundary terms, yielding $D^{†}=D$.    □

Application to Dissipative Operators

Thanks to the compatibility of zeroth–order operators $f\otimes e$ with ${\nabla }_{\mu }$,

$$[{\nabla }_{\mu },f\otimes e]=\left({\partial }_{\mu }f\right)\otimes e$$

[19]. This relation underpins the proof of local support and idempotency of the dissipative generator ${\mathcal{L}}_{\mathsf{\Delta }}\left[\rho \right]$. In particular, the expression

$$V_j\left(x\right)\rho V_j{\left(x\right)}^{†}=(f_j\left(x\right)\otimes e)\rho (f_j\left(x\right)\otimes e),$$

can be treated covariantly, which is a key point supporting gauge and gravitational consistency of the theory[2,8].

2.5.4 Algebraic Structure of the Operator Ring and Self-Adjointness

In this subsection we elucidate the structure of the operator algebra generated by the zeroth-order geometric operator family $\mathcal{G}=C^{\infty }\left(M^4\right)\otimes \mathrm{Cl}(1,3)$; we rigorously build its self-adjoint closure (chain) that includes the family of Hilbert–Schmidt operators[18,19]. In particular, let

$$\mathcal{A}:={\mathrm{Alg}}^{*}\left(\mathcal{G}\right)\subset \mathcal{B}\left(\mathcal{H}\right)$$

denote the ∗-algebra generated by $\mathcal{G}$. Through the propositions below we prove that $\mathcal{A}$ forms a Banach ∗-algebra and contains finite-rank (rank-one) operators and the Hilbert–Schmidt class $S_2\left(\mathcal{H}\right)$[20].

Definition of the Operator Ring

Definition 18 

(Operator Ring $\mathcal{A}$). The operator ring $\mathcal{A}$ is the minimal ∗-Algebra closed under addition, multiplication, and adjoint $a\mapsto a^{†}$ generated by $\mathcal{G}$; that is,

$$\mathcal{A}=\left\{\sum _{k=1}^n{c}_k{a}_{k,1}{a}_{k,2}\dots a_{k,m_k}|c_k\in \mathbb{C},a_{k,i}\in \mathcal{G}\cup {\mathcal{G}}^{†}\right\}.$$

Proposition 18 

(Banach ∗-Algebra Property). $\mathcal{A}$ is closed with respect to the operator norm $\parallel ·\parallel$; hence $(\mathcal{A},\parallel ·\parallel )$ is a Banach ∗-algebra (not necessarily a C${‌}^{*}$-algebra, but preserving the ∗-algebra structure)[19].

Proof. 

Because $\mathcal{G}\subset \mathcal{B}\left(\mathcal{H}\right)$ consists of bounded operators (see Section 2.5.0.8), any finite sum or product within $\mathcal{A}$ is again bounded. Taking the closure with respect to the norm, Cauchy sequences in $\mathcal{A}$ converge inside $\mathcal{B}\left(\mathcal{H}\right)$ and remain in $\mathcal{A}$. Moreover, the adjoint satisfies $\parallel a^{†}\parallel =\parallel a\parallel$, preserving the ∗-structure[18].    □

Hierarchy of Operator Families

Proposition 19 

(Chain of Inclusions). The following inclusions hold:

$$\mathcal{G}\subset \mathcal{A}\subset S_2\left(\mathcal{H}\right)\subset S_1\left(\mathcal{H}\right)\subset \mathcal{B}\left(\mathcal{H}\right),$$

where $S_p\left(\mathcal{H}\right)$ denotes the Schatten–von Neumann classes ($p=2$ for Hilbert–Schmidt, $p=1$ for trace class)[19,20].

Proof. 

Elements of $\mathcal{G}$ are zeroth-order multiplication operators and can be approximated by finite-rank actions; rank-one operators $|\varphi \rangle \langle \psi |\in \mathcal{F}\left(\mathcal{H}\right)$ are obtained as limit points in $\mathcal{A}$[19]. Finite-rank operators form a dense subset of the Hilbert–Schmidt class $S_2$, and $S_2\subset S_1\subset \mathcal{B}\left(\mathcal{H}\right)$ are standard inclusions[20].    □

Generation of Rank-One Operators

Proposition 20 

(Inclusion of Rank-One Operators). For any $\varphi ,\psi \in \mathcal{H}$ define

$$T_{\varphi ,\psi }:\xi \mapsto \langle \psi ,\xi \rangle \varphi ,\xi \in \mathcal{H},$$

a rank-one operator. Then $T_{\varphi ,\psi }$ can be expressed as a norm limit of elements of $\mathcal{A}$.

Proof. 

Approximate $\varphi ,\psi$ uniformly by compactly supported smooth sections, and construct $T_{{\varphi }_n,{\psi }_n}=({\varphi }_n\otimes 1)(\langle {\psi }_n,·\rangle \otimes 1)\in \mathcal{A}$. As $n\to \infty$, $T_{{\varphi }_n,{\psi }_n}$ converges in norm to $T_{\varphi ,\psi }$[19].    □

Hilbert–Schmidt Operators

Definition 19 

(Hilbert–Schmidt Operator). An operator $T\in \mathcal{B}\left(\mathcal{H}\right)$ is Hilbert–Schmidt if ${\parallel T\parallel }_2^2:=\mathrm{tr}\left(T^{†}T\right)<\infty$. The set of all such operators is denoted $S_2\left(\mathcal{H}\right)$[19].

Proposition 21 

(Hilbert–Schmidt Inclusion). Any rank-one operator $T_{\varphi ,\psi }$ satisfies $\parallel T_{\varphi ,\psi }{\parallel }_2=\parallel \varphi \parallel \parallel \psi \parallel <\infty$ and hence belongs to $S_2\left(\mathcal{H}\right)$. Moreover, the totality of rank-one operators obtained as limits from $\mathcal{A}$ forms a dense subset of $S_2\left(\mathcal{H}\right)$[20].

Proof. 

$$\parallel T_{\varphi ,\psi }{\parallel }_2^2=\mathrm{tr}\left(|\psi \rangle \langle \varphi ||\varphi \rangle \langle \psi |\right)={\parallel \varphi \parallel }^2{\parallel \psi \parallel }^2.$$

Thus rank-one operators are Hilbert–Schmidt. Since finite-rank operators are dense in $S_2$, the rank-one operators coming from $\mathcal{A}$ are dense in $S_2\left(\mathcal{H}\right)$.    □

Implications for the UEE

• The Banach ∗-Algebra property of $\mathcal{A}$ ensures that the dissipative generator ${\mathcal{L}}_{\mathsf{\Delta }}$ is a bounded operator, providing the norm control required for the CPTP condition (see Section 2.19)[2,8].
• The inclusion of rank-one operators and the Hilbert–Schmidt class justifies the discretisation and spectral cut-off procedures employed in numerical simulations, since the full dynamics can be approximated by finite-rank maps.
• The Barnes–Lagrange elimination theorem (Section 2.15.0.13) corresponds to products and closures within $\mathcal{A}$, offering an algebraic foundation for integrating operator-algebra techniques into the action principle and the derivation of the master equation[25,27].

2.5.5 Applications to the UEE

In this subsection we demonstrate, without omission, how the geometric operator family $\mathcal{G}=C^{\infty }\left(M^4\right)\otimes \mathrm{Cl}(1,3)$ constructed in the preceding sections explicitly appears in the principal building blocks of the Unified Evolution Equation (UEE)—namely, the Dirac operator and the dissipative generator—at the level of formulae [21,22]. We also discuss in detail its rigorous connection with the Barnes–Lagrange elimination theorem (Section 2.15.0.13)[25,27].

Appearance in the Dirac Equation

The Dirac operator, which plays a central role as the reversible generator of the UEE,

$$D=i{\gamma }^{\mu }{\nabla }_{\mu }=i\sum _{\mu =0}^3\left({\gamma }^{\mu }\otimes 1\right)\left({\partial }_{\mu }\otimes 1+{\omega }_{\mu }\right),$$

can be written entirely as a composition of zeroth–order operators with ${\gamma }^{\mu }\in \mathrm{Cl}(1,3)\subset \mathcal{G}$ and ${\omega }_{\mu }=\frac{1}{2}{\omega }_{\mu }^{ab}{\sigma }_{ab}\in \mathcal{G}$ [22].

Proposition 22 

(Generation of the Dirac Operator by $\mathcal{G}$). The Dirac operator expands as

$$D=\sum _{\mu =0}^3\left(1\otimes {\gamma }^{\mu }\right)\left({\partial }_{\mu }\otimes 1\right)+\sum _{\mu =0}^3\left(f_{\mu }\left(x\right)\otimes {\gamma }^{\mu }\right),$$

where $f_{\mu }\left(x\right)=\frac{1}{2}{\omega }_{\mu }^{ab}\left(x\right){\sigma }_{ab}\in C^{\infty }\left(M^4\right)$ are scalar functions originating from the Riemannian connection [29].

Proof. 

With ${\omega }_{\mu }=\frac{1}{2}{\omega }_{\mu }^{ab}{\sigma }_{ab}$ and ${\sigma }_{ab}=\frac{1}{4}[{\gamma }_a,{\gamma }_b]\in \mathrm{Cl}(1,3)$ [22], we find

$${\gamma }^{\mu }{\nabla }_{\mu }={\gamma }^{\mu }{\partial }_{\mu }+{\gamma }^{\mu }{\omega }_{\mu }=(1\otimes {\gamma }^{\mu })({\partial }_{\mu }\otimes 1)+(f_{\mu }\otimes {\gamma }^{\mu }).$$

Since ${\partial }_{\mu }\otimes 1$ is recognised as a differential extension element of $\mathcal{G}$, the whole operator is generated by tensor operators from $\mathcal{G}$.    □

Application to the Dissipative Generator

The irreversible (dissipative) part of the UEE is expressed in Lindblad–Kossakowski form

$${\mathcal{L}}_{\mathsf{\Delta }}\left[\rho \right]=\sum _j\left(V_j\rho V_j^{†}-\frac{1}{2}\{V_j^{†}{V}_j,\rho \}\right)$$

[2,8], where

$$V_j=f_j\left(x\right)\otimes e_j,f_j\in C_0^{\infty }\left(M^4\right),e_j\in \mathrm{Cl}(1,3),$$

are local dissipative kernel operators defined purely as zeroth–order elements of $\mathcal{G}$.

Proposition 23 

(Generation of the Dissipative Generator by $\mathcal{G}$). Each term of ${\mathcal{L}}_{\mathsf{\Delta }}$ can be written

$$V_j\rho V_j^{†}=\left(f_j\otimes e_j\right)\rho \left({\overline{f}}_j\otimes e_j^{†}\right),$$

and belongs to the self-adjoint closure of $\mathcal{G}$.

Proof. 

Since $f_j\otimes e_j\in \mathcal{G}$ and its adjoint ${\overline{f}}_j\otimes e_j^{†}\in {\mathcal{G}}^{†}$, the products $(f_j\otimes e_j)\rho ({\overline{f}}_j\otimes e_j^{†})$ lie in $\mathcal{A}$ (see Section 2.5.0.18) [19]; the same holds for the anticommutator.    □

Relation to the Barnes–Lagrange Elimination Theorem

In UEE analyses, the Barnes–Lagrange elimination theorem (Theorem 2.15.0.13) plays an essential role in exactly removing dissipative path dependence produced by multiple products of $\mathcal{G}$ elements, yielding a reduced form of the action functional [25,27].

Theorem 8 

(Barnes–Lagrange Elimination of Zeroth–Order Operators). For a sequence of zeroth–order operators $\{a_1,a_2,\dots ,a_N\}\subset \mathcal{G}$, applying the Mellin–Barnes representation to their product yields the Barnes–Lagrange cancellation identity

$$a_1^{-1}{a}_2{a}_3^{-1}\dots a_N=\sum _{\ell }Re{s}_{s=s_{\ell }}\mathsf{\Gamma }\left(s;\left\{a_i\right\}\right),$$

where $\mathsf{\Gamma }\left(s;\left\{a_i\right\}\right)$ denotes the Mellin–Barnes kernel and the sum runs over all relevant poles.

Proof. 

Under the assumptions of Theorem 2.15.0.13, each zeroth–order operator $a_i=f_i\otimes e_i$ is a bounded operator possessing a Mellin transform. Rewrite the multi-product ${\prod }_i{a}_i^{{\alpha }_i}$ via the Mellin–Barnes integral, analyse the zero structure in the ${\alpha }_i$ variables, and perform a residue calculation to eliminate inverse factors[27]. The detailed steps are formalised in Section 2.15.0.13.    □

Summary of Applications

• Zeroth–order operators originating from $\mathcal{G}$ appear essentially and generatively in both the reversible and irreversible components of the UEE, being indispensable for the formal definition of D and ${\mathcal{L}}_{\mathsf{\Delta }}$ (Propositions 22 and 23).
• The Barnes–Lagrange elimination theorem (Theorem 8) furnishes a technique to compress complex dissipative effects arising from chained zeroth–order operators into a closed analytic form expressed as finite sums of residues.
• The conjunction of $\mathcal{G}$ and the Barnes–Lagrange theorem plays a central role in deriving the action principle (UEE${‌}_{\mathrm{var}}$) and the field dynamics (UEE${‌}_{\mathrm{fld}}$) developed in following chapters.

Consequently, the geometric operator family $\mathcal{G}$ provides the theoretical and mathematical foundation for the entire UEE construction, and, through its synergy with the Barnes–Lagrange elimination theorem, enables the self-contained and closed-form development of the UEE.

2.6. Dirac Operator D

2.6.1 Definition, Domain, and Basic Properties

2.6.1-1 Definition and Domain of the Operator D

In this subsection we give the rigorous definition of the Dirac operator

$$D=i{\gamma }^{\mu }{\nabla }_{\mu },$$

specify its natural domain of action in detail, and clarify the structure on the spinor bundle together with the roles of the Clifford elements ${\gamma }^{\mu }$ and the covariant derivative ${\nabla }_{\mu }$ [21,22].

Definition of the Dirac Operator

Definition 20 

(Dirac Operator D). As a density operator on the spinor bundle $S\left(M^4\right)$ define

$$D:C_c^{\infty }\left(S\left(M^4\right)\right)⟶C_c^{\infty }\left(S\left(M^4\right)\right),D\psi \left(x\right):=i{\gamma }^{\mu }\left(x\right){\nabla }_{\mu }\psi \left(x\right),$$

where $\psi \in C_c^{\infty }\left(S\left(M^4\right)\right)$ is a smooth compactly supported section, ${\gamma }^{\mu }\left(x\right)\in \mathrm{Cl}(1,3)$ are the gamma matrices defined in Section 2.3, and ${\nabla }_{\mu }$ is the spin-connection covariant derivative [22].

Specification of the Domain

Definition 21 

(Natural Domain). The maximal domain of the Dirac operator is

$$\mathrm{Dom}\left(D\right):=\{\psi \in L^2\left(S\left(M^4\right)\right)\left|\psi ,D\psi \in L^2\left(S\left(M^4\right)\right)\right\}$$

[19]. Smooth compactly supported sections are dense in $\mathrm{Dom}\left(D\right)$.

Remark 2. 

$\mathrm{Dom}\left(D\right)$ coincides with the Sobolev space $H^1\left(S\left(M^4\right)\right)$ endowed with the norm ${\parallel \psi \parallel }_{H^1}^2={\parallel \psi \parallel }_{L^2}^2+{\parallel \nabla \psi \parallel }_{L^2}^2$ [34].

Spinor-Bundle Structure and the Roles of ${\gamma }^{\mu }$ and ${\nabla }_{\mu }$

• ${\gamma }^{\mu }\left(x\right)$ are Clifford algebra elements satisfying $\{{\gamma }^{\mu },{\gamma }^{\nu }\}=2{\eta }^{\mu \nu }$ and furnish the basis operators of the spinor representation (see Section 2.3)[21].
• ${\nabla }_{\mu }={\partial }_{\mu }+\frac{1}{2}{\omega }_{\mu }^{ab}{\sigma }_{ab}$ contains the spin connection and transports information on curvature and torsion of the Riemannian manifold to the spinor field [22,29].
• Taken together, D is a first-order differential and Clifford-valued operator, simultaneously encoding geometric data and internal symmetries.

Basic Closedness and Density

Proposition 24 

(Closedness). D is a closed operator; its graph is closed over $\mathrm{Dom}\left(D\right)$ [24].

Sketch. 

Assume ${\psi }_n\in \mathrm{Dom}\left(D\right)$ with ${\psi }_n\to \psi$ and $D{\psi }_n\to \varphi$ in $L^2$. Using the relative compactness of Sobolev embeddings and Kato–Rellich relative boundedness one deduces $\psi \in \mathrm{Dom}\left(D\right)$ and $D\psi =\varphi$ [19,24].    □

Proposition 25 

(Density of Compactly Supported Sections). $C_c^{\infty }\left(S\left(M^4\right)\right)$ is dense in $\mathrm{Dom}\left(D\right)$ [23,34].

Proof. 

Employing a standard approximate identity, any $\psi \in \mathrm{Dom}\left(D\right)\subset H^1$ is approximated by a sequence of compactly supported smooth sections with $\parallel \psi -{\psi }_n{\parallel }_{H^1}\to 0$.    □

Proposition 26 

(Self-Adjointness). The Dirac operator $D=i{\gamma }^{\mu }{\nabla }_{\mu }$ is self-adjoint on $\mathrm{Dom}\left(D\right)=\{\psi \mid \psi ,D\psi \in L^2\}$:

$$D^{†}=D.$$

Sketch. 

Using Green’s identity and ${\nabla }_{\mu }\left({\gamma }^{\mu }\right)=0$ one shows that the boundary term in $\langle \varphi ,D\psi \rangle -\langle D\varphi ,\psi \rangle$ vanishes; symmetry together with closedness yields self-adjointness [21,24].    □

Relation to the Theory

• The completeness and closedness of $\mathrm{Dom}\left(D\right)$ provide the foundation for applying the Kato–Rellich theorem in Proposition 2.6.1 (self-adjointness)[24].
• D appears directly in the reversible generator $L_0\left[\rho \right]=-i[D,\rho ]$ of the UEE${‌}_{\mathrm{op}}$, formulating the unitary part of the quantum dynamics.
• In the variational form UEE${‌}_{\mathrm{var}}$ the operator D enters the action functional and forms the interface between Clifford- geometric and dissipative structures.

2.6.1-1-1 Introduction of the Extended Dirac Operator $D_{\mathrm{tot}}$

In this work we introduce an extended generator

$$D_{\mathrm{tot}}:=D+R,$$

obtained by incorporating a zero-area resonance kernel operator R into the conventional Dirac operator

$$D=i{\gamma }^{\mu }{\nabla }_{\mu }$$

[21,22]. Unless explicitly excluded, the following non-reversible dynamics will be formulated with $D_{\mathrm{tot}}$ as the implicit generator in place of D.

Lemma 5 

(R is D-Relatively Bounded and Symmetric). Let

$$R\left[\rho \right]:={\int }_{\sigma \left(D\right)}R\left(\omega \right)\left[D,[D,\rho ]\right]E_D\left(d\omega \right),{\int }_{\mathbb{R}}R\left(\omega \right)d\omega =0,$$

be the zero-area resonance kernel operator. Then:

(i) 

Symmetry For all $\phi ,\psi \in \mathrm{Dom}\left(D^2\right)$, $\langle \phi ,R\left[\psi \right]\rangle =\langle R\left[\phi \right],\psi \rangle$[19].

(ii) 

D-Relative Boundedness There exist constants $a<1$ and $b>0$ such that $\parallel R\left[\psi \right]\parallel \le a\parallel D\psi \parallel +b\parallel \psi \parallel ,\forall \psi \in \mathrm{Dom}\left(D\right)$[24].

Proof. 

(i) Symmetry Because D is self-adjoint, $\left[D,[D,·]\right]=D^2\rho -2D\rho D+\rho D^2$ [19]. The spectral measure $E_D\left(d\omega \right)$ is a family of real projections, and $R\left(\omega \right)\in \mathbb{R}$; hence

$$\langle \phi ,R\left[\psi \right]\rangle ={\int }_{\sigma \left(D\right)}R\left(\omega \right)\langle \phi ,[D,[D,\psi ]]E_D\left(d\omega \right)\rangle =\langle R\left[\phi \right],\psi \rangle .$$

(ii) Relative Boundedness Set $R_{max}:={sup}_{\omega }\left|R\left(\omega \right)\right|<\infty$. Because $[D,[D,\psi ]]=D^2\psi -2D\psi D+\psi D^2,$ self-adjointness implies $\parallel D^2\psi \parallel =\parallel D\left(D\psi \right)\parallel \le \parallel D\parallel \parallel D\psi \parallel$; likewise $\parallel D\psi D\parallel \le \parallel D\parallel \parallel D\psi \parallel$. Therefore $\parallel [D,[D,\psi \left]\right]\parallel \le 4\parallel D\parallel \parallel D\psi \parallel .$ Using the integral representation of R and Fubini, $\parallel R\left[\psi \right]\parallel \le 4R_{max}\parallel D\parallel \parallel D\psi \parallel .$ For any $\epsilon >0$, $\parallel D\psi \parallel \le \epsilon \parallel D\psi \parallel +{\epsilon }^{-1}\parallel \psi \parallel$ (Young’s weighted inequality[20]), so

$$\parallel R\left[\psi \right]\parallel \le 4R_{max}\parallel D\parallel \epsilon \parallel D\psi \parallel +4R_{max}\parallel D\parallel {\epsilon }^{-1}\parallel \psi \parallel .$$

Choosing $\epsilon$ sufficiently small yields $a:=4R_{max}\parallel D\parallel \epsilon <1$ and $b:=4R_{max}\parallel D\parallel {\epsilon }^{-1}$, establishing the desired bound.    □

2.6.1-2 Relative Boundedness Estimate and Application of the Kato–Rellich Theorem

We decompose the Dirac operator

$$D=i{\gamma }^{\mu }{\nabla }_{\mu }=i{\gamma }^{\mu }{\partial }_{\mu }+i{\gamma }^{\mu }{\omega }_{\mu }=:D_0+V,$$

into a “principal part’’ $D_0$ and a “perturbation’’ V, prove that V is $D_0$-relatively bounded, and apply the Kato–Rellich theorem to guarantee the self-adjointness of D[19,24].

Properties of the Principal Part $D_0$

Definition 22 

(Principal Part $D_0$). 

$$D_0:=i{\gamma }^{\mu }{\nabla }_{\mu }^{\left(0\right)}=i{\gamma }^{\mu }{\partial }_{\mu },\mathrm{Dom}\left(D_0\right)=H^1\left(S\left(M^4\right)\right).$$

Here ${\nabla }^{\left(0\right)}$ is the flat connection; $D_0$ is essentially self-adjoint in flat space[21].

Proposition 27 

(Self-Adjointness of the Principal Part). $D_0$ is closed and essentially self-adjoint: $D_0^{†}=D_0$.

Proof. 

Standard flat-space Dirac theory applies the Sobolev completeness and integration-by-parts argument; see Appendix E.    □

Definition of the Perturbation V

Definition 23 

(Perturbation Operator V). 

$$V:=i{\gamma }^{\mu }{\omega }_{\mu },\mathrm{Dom}\left(V\right)=\mathrm{Dom}\left(D\right).$$

The coefficients ${\omega }_{\mu }=\frac{1}{2}{\omega }_{\mu }^{ab}{\sigma }_{ab}$ are assumed smooth with compact support[22].

Relative Boundedness Estimate

Definition 24 

(Relative Boundedness). V is $D_0$-relatively bounded if there exist constants $a<1$, $b\ge 0$ such that

$$\parallel V\psi \parallel \le a\parallel D_0\psi \parallel +b\parallel \psi \parallel ,\forall \psi \in \mathrm{Dom}\left(D_0\right)$$

[24].

Lemma 6 

(Relative Boundedness of the Perturbation). With the above compact-support assumption on ${\omega }_{\mu }$, the operator V is $D_0$-relatively bounded; for any $ϵ>0$, $\parallel V\psi \parallel \le ϵ\parallel D_0\psi \parallel +C\left(ϵ\right)\parallel \psi \parallel$.

Proof. 

For $\psi \in C_c^{\infty }\left(S\left(M^4\right)\right)\subset \mathrm{Dom}\left(D_0\right)$,

$$\parallel V\psi \parallel =\parallel {\gamma }^{\mu }{\omega }_{\mu }\psi \parallel \le \sum _{\mu }\parallel {\gamma }^{\mu }\parallel \parallel {\omega }_{\mu }\psi \parallel .$$

The matrices ${\gamma }^{\mu }$ have finite norm, and $\parallel {\omega }_{\mu }\psi \parallel \le M_{\mu }\parallel \psi \parallel$. A Gagliardo–Nirenberg estimate yields $\parallel \psi \parallel \le ϵ\parallel D_0\psi \parallel +C\left(ϵ\right)\parallel \psi \parallel$ [34], giving the stated inequality.    □

Application of the Kato–Rellich Theorem

Theorem 9 

(Kato–Rellich Relative Boundedness Theorem). If the principal part $D_0$ is essentially self-adjoint and the perturbation V is $D_0$-relatively bounded with bound $a<1$, then their sum $D=D_0+V$ is essentially self-adjoint[24].

Proof. 

Apply Theorem 9 using Lemma 6.    □

Conclusion

Theorem 9 establishes the first part of Proposition 2.6.1: D is essentially self-adjoint.

Remark 3. 

The zero-area resonance kernel R introduced above is symmetric and D-relatively bounded by Lemma 5; thus the operator $D+R:\mathrm{Dom}\left(D\right)\to L^2\left(S\left(M^4\right)\right)$ remains essentially self-adjoint by the Kato–Rellich theorem.

2.6.2 Final Proof of Self-Adjointness via Integration by Parts and Elimination of Boundary Terms

In this subsection we show that the Dirac operator D is a symmetric operator on smooth compactly supported sections, and—after complete elimination of boundary terms—derive $D^{†}=D$. This establishes the self-adjointness stated in Proposition 2.6.1 [21].

Verification of Symmetry in Inner-Product Form

For arbitrary $\varphi ,\psi \in C_c^{\infty }\left(S\left(M^4\right)\right)\subset \mathrm{Dom}\left(D\right)$ consider

$$I:={〈\varphi ,D\psi 〉}_{L^2}-{〈D\varphi ,\psi 〉}_{L^2}.$$

By the definition of the inner product,

$$I={\int }_{M^4}\overline{\varphi \left(x\right)}\left(i{\gamma }^{\mu }{\nabla }_{\mu }\psi \left(x\right)\right)-\overline{\left(i{\gamma }^{\mu }{\nabla }_{\mu }\varphi \left(x\right)\right)}\psi \left(x\right)\sqrt{-detg\left(x\right)}{d}^{4}x.$$

Because taking the adjoint yields $\overline{i{\gamma }^{\mu }{\nabla }_{\mu }\varphi }=-i\overline{\varphi }{\gamma }^{\mu }{\nabla }_{\mu }$ and ${\nabla }_{\mu }{\gamma }^{\mu }=0$ [22], the integrand is prepared for partial integration.

Integration by Parts

Integrate each term by parts:

$$\int \overline{\varphi }i{\gamma }^{\mu }{\nabla }_{\mu }\psi ={\left[\overline{\varphi }i{\gamma }^{\mu }\psi \right]}_{\partial M}-\int \left({\nabla }_{\mu }\overline{\varphi }\right)i{\gamma }^{\mu }\psi ,$$

and

$$\int -i\left({\nabla }_{\mu }\overline{\varphi }\right){\gamma }^{\mu }\psi =-\int \overline{{\nabla }_{\mu }\varphi }i{\gamma }^{\mu }\psi .$$

Because the sections are compactly supported, the boundary term ${\left[\overline{\varphi }i{\gamma }^{\mu }\psi \right]}_{\partial M}$ vanishes, leaving

$$I=0.$$

Hence D is symmetric.

Extension by Density and Self-Adjointness

$C_c^{\infty }\left(S\left(M^4\right)\right)$ is dense in $\mathrm{Dom}\left(D\right)$ [23], and D is a closed operator (Section 2.6). Since essential self-adjointness is ensured by the Kato–Rellich theorem (Section 2.6.0.5), the symmetric and essentially self-adjoint operator D possesses a unique self-adjoint extension, i.e.,

$$D^{†}=D\mathrm{on}\mathrm{Dom}\left(D^{†}\right)=\mathrm{Dom}\left(D\right).$$

Proposition 28 

(Restatement of Proposition 2.6.1). The Dirac operator $D=i{\gamma }^{\mu }{\nabla }_{\mu }$ is self-adjoint on $\mathrm{Dom}\left(D\right)=\{\psi \mid \psi ,D\psi \in L^2\}$:

$$D^{†}=D.$$

Proof. 

(i) Symmetry was established above via integration by parts. (ii) Essential self-adjointness follows from the Kato–Rellich theorem and the relative boundedness estimate [19,24]. Therefore $D^{†}=D$.    □

Theoretical Significance

• Thanks to self-adjointness, the reversible generator of the UEE${‌}_{\mathrm{op}}$, $L_0\left[\rho \right]=-i[D,\rho ]$, generates a unitary one-parameter group, providing a rigorous formulation of quantum-mechanical time evolution.
• In the variational formulation UEE${‌}_{\mathrm{var}}$ the operator D enters the action functional; its self-adjointness guarantees the physical consistency of eigenvalue problems arising from linearisation and spectral analysis.

2.7. Covariant Derivative and Gauge Potential

2.7.1 Definition of Spin–Gauge Fibre Bundles

2.7.1-1 Definition of the Spin Bundle and Local Trivialisation

In this subsection we construct the spinor bundle $S\left(M^4\right)$ over a four-dimensional Riemannian manifold $(M^4,g_{\mu \nu })$, and rigorously define its local trivialisation and base-change rules[22,33]. This spin bundle is the domain on which the spinor covariant derivative ${\nabla }_{\mu }$ introduced later acts.

Regular Riemannian Manifolds and the Frame Bundle

Definition 25 

(Regular Riemannian Manifold). A Riemannian manifold $(M^4,g_{\mu \nu })$ is called a regular Riemannian manifold with spin structure if

$$H^1\left(M^4\right)-\mathit{separable}\mathit{and}\mathit{non}-\mathit{singular},w_2\left(TM\right)=0,$$

where $w_2\left(TM\right)$ is the second Stiefel–Whitney class [22].

Definition 26 

(Orthonormal Frame Bundle). The standard orthonormal frame bundle

$${\mathrm{Fr}}_{\mathrm{SO}}\left(M^4\right)=\{e:{\mathbb{R}}^{1,3}\stackrel{\sim }{\to }{T}_x{M}^4\mid {\eta }_{ab}=g(e\left(e_a\right),e\left(e_b\right))\}$$

is a principal bundle with structure group $SO(1,3)$[29].

Spin Structure and Lift

Definition 27 

(Spin Structure). Using the double covering

$$Spin(1,3)\stackrel{\pi }{\to }SO(1,3),$$

the principal bundle

$${\mathrm{Fr}}_{Spin}\left(M^4\right):=\{(x,u)\mid x\in M^4,u\in {\mathrm{Fr}}_{SO}\left(M^4\right),\pi \left(\tilde{u}\right)=u\}$$

is the spin bundle[22,33].

Local Trivialisation

Locally the spin bundle is isomorphic to ${\mathrm{Fr}}_{Spin}\left(M^4\right){|}_U\cong U\times Spin(1,3)$[33].

Definition 28 

(Local Trivialisation). Over an open cover $\left\{U_i\right\}$ choose maps

$${\mathsf{\Phi }}_i:{\mathrm{Fr}}_{Spin}\left(M^4\right){|}_{U_i}\stackrel{\sim }{\to }{U}_i\times Spin(1,3).$$

On overlaps $U_i\cap U_j$ the transition functions

$$g_{ij}:U_i\cap U_j\to Spin(1,3),{\mathsf{\Phi }}_i\circ {\mathsf{\Phi }}_j^{-1}(x,s)=(x,g_{ij}\left(x\right)s),$$

are defined[22].

Base-Change Rule

Locally a spinor field is expressed as ${\psi }_i:U_i\to {\mathbb{C}}^4$ via ${\mathsf{\Phi }}_i$, and on overlaps

$${\psi }_i\left(x\right)=\rho \left(g_{ij}\left(x\right)\right){\psi }_j\left(x\right),$$

where $\rho :Spin(1,3)\to End\left({\mathbb{C}}^4\right)$ is the Clifford representation[21].

Relation to the Theory

• The base-change rule of the spin bundle underlies the covariance of the Dirac operator $D=i{\gamma }^{\mu }{\nabla }_{\mu }$ under local coordinate changes [21].
• Local trivialisation ensures that the explicit form of the spinor covariant derivative ${\nabla }_{\mu }={\partial }_{\mu }+\frac{1}{2}{\omega }_{\mu }^{ab}{\sigma }_{ab}$ is valid in each chart[22].
• By taking the direct product with the gauge bundle shown in Subsection 2.7.1-2, one constructs a unified bundle with total structure group $Spin(1,3)\times G_{\mathrm{gauge}}$.

2.7.1-2 Definition of the Gauge Bundle and Simultaneous Spin–Gauge Construction

In this subsection we define the gauge bundle corresponding to an internal symmetry group $G_{\mathrm{gauge}}$ and construct the unified bundle $\mathcal{P}={\mathrm{Fr}}_{Spin}\left(M^4\right){\times }_{M^4}{P}_G$ as the fibre-wise product of the spin bundle ${\mathrm{Fr}}_{Spin}\left(M^4\right)$ with the gauge bundle $P_G$[33]. We make explicit that the structure group is $Spin(1,3)\times G_{\mathrm{gauge}}$ and give the complete local trivialisation and composition law for the transition functions.

Definition of the Gauge Bundle $P_G$

Definition 29 

(Gauge Bundle). Let $G_{\mathrm{gauge}}$ be a Lie group. A principal bundle

$$P_G⟶M^4$$

with structure group $G_{\mathrm{gauge}}$ is called thegauge bundle[33]. Local trivialisations ${\mathsf{\Psi }}_i:P_G{|}_{U_i}\simeq U_i\times G_{\mathrm{gauge}}$ yield transition functions

$$h_{ij}:U_i\cap U_j\to G_{\mathrm{gauge}}.$$

The gauge field (connection one-form) is specified by local one-forms $\{A_i\in {\mathsf{\Omega }}^1\left(U_i\right)\otimes \mathfrak{g}\}$ obeying the transition rule $A_j=h_{ij}^{-1}{A}_i{h}_{ij}+h_{ij}^{-1}d{h}_{ij}$ on overlaps[30].

Structure Group $Spin(1,3)\times G_{\mathrm{gauge}}$

Combining the spin and gauge bundles, the unified bundle $\mathcal{P}$ is a principal bundle with structure group $Spin(1,3)\times G_{\mathrm{gauge}}$[22].

Definition 30 

(Spin–Gauge Fibre-Product Bundle). 

$$\mathcal{P}:={\mathrm{Fr}}_{Spin}\left(M^4\right){\times }_{M^4}{P}_G⟶M^4.$$

Choosing local trivialisations ${\mathsf{\Phi }}_i\times {\mathsf{\Psi }}_i{:\mathcal{P}|}_{U_i}\simeq U_i\times \left(Spin(1,3)\times G_{\mathrm{gauge}}\right)$, the double transition functions

$$(g_{ij},h_{ij}):U_i\cap U_j\to Spin(1,3)\times G_{\mathrm{gauge}}$$

govern chart-to-chart transformations.

Local Trivialisation and Transition Functions

On a local chart $U_i$,

$${\mathsf{\Phi }}_i:{\mathrm{Fr}}_{Spin}{{|}_{U_i}\simeq U_i\times Spin(1,3),{\mathsf{\Psi }}_i:P_G|}_{U_i}\simeq U_i\times G_{\mathrm{gauge}}.$$

Setting ${\mathsf{\Theta }}_i:={\mathsf{\Phi }}_i\times {\mathsf{\Psi }}_i$, we obtain

$${\mathsf{\Theta }}_i{:\mathcal{P}|}_{U_i}\stackrel{\sim }{\to }{U}_i\times \left(Spin(1,3)\times G_{\mathrm{gauge}}\right)$$

[33]. On overlaps $U_i\cap U_j$,

$${\mathsf{\Theta }}_i\circ {\mathsf{\Theta }}_j^{-1}\left(x,(s,g)\right)=\left(x,g_{ij}\left(x\right)s,h_{ij}\left(x\right)g\right),$$

so that the composition law

$$(g_{ik},h_{ik})=(g_{ij},h_{ij})(g_{jk},h_{jk})$$

acts naturally as the regular Čech cocycle of the structure group.

Associated Representations and Acting Space

The associated vector bundle over the fibre-product bundle $\mathcal{P}$ is

$$E=\mathcal{P}{\times }_{\rho \otimes R}V\simeq S\left(M^4\right)\otimes \left(P_G{\times }_{R}W\right),$$

where $\rho :Spin(1,3)\to End\left({\mathbb{C}}^4\right)$ is the Clifford (spinor) representation, and $R:G_{\mathrm{gauge}}\to End\left(W\right)$ is a chosen gauge representation (e.g., the fundamental representation)[30].

Relation to the Theory

• The unified bundle provides the foundation for treating the combined spinor–gauge covariant derivative ${\nabla }_{\mu }={\partial }_{\mu }+{\omega }_{\mu }+A_{\mu }$.
• In the UEE, dissipative generators of Lindblad type, $L_j=f_j\left(x\right)\otimes e_j$, appear as “zeroth-order’’ elements of $\mathcal{G}$ and can be viewed as extensions of ${\mathrm{ad}}_{A_{\mu }}$ and ${\mathrm{ad}}_{{\omega }_{\mu }}$.
• In the variational formulation UEE${‌}_{\mathrm{var}}$ the local invariance of the action $S[\psi ,A_{\mu },{\omega }_{\mu },\dots ]$ is described by the Spin×Gauge principle afforded by the unified bundle.

2.7.2 Spin Connection ${\omega }_{\mu }$ and Gauge Connection $A_{\mu }$

2.7.2-1 Construction of the Spin Connection ${\omega }_{\mu }$ from the Vierbein

In this subsection we rigorously construct the spin-connection coefficients ${\omega }_{\mu }^{ab}\left(x\right)$ on a four-dimensional Riemannian manifold $(M^4,g_{\mu \nu })$ using the vierbein $e^a{‌}_{\mu }\left(x\right)$ and prove their properties [22,29]. We show that ${\omega }_{\mu }$ functions as a core element of the spinor covariant derivative.

Introduction of the Vierbein (Yang–Mills Representation)

Definition 31 

(Vierbein). Introducing a local orthonormal basis $e_a\left(x\right)\in T_x{M}^4$, avierbein (frame field) is an invertible matrix field $e^a{‌}_{\mu }\left(x\right)$ such that

$$g_{\mu \nu }\left(x\right)=e^a{‌}_{\mu }\left(x\right)e^b{‌}_{\nu }\left(x\right){\eta }_{ab},{\eta }_{ab}=\mathrm{diag}(+1,-1,-1,-1)$$

[29].

Relation Between Christoffel Symbols and the Vierbein

Lemma 7. 

The vierbein satisfies the relation with the Levi–Civita connection ${\mathsf{\Gamma }}_{\mu \nu }^{\rho }$:

$${\partial }_{\mu }{e}^a{‌}_{\nu }-{\mathsf{\Gamma }}_{\mu \nu }^{\rho }{e}^a{‌}_{\rho }+{\omega }_{\mu }{‌}^a{‌}_b{e}^b{‌}_{\nu }=0.$$

Proof. 

Rewrite the metric compatibility condition ${\nabla }_{\mu }{g}_{\nu \rho }=0$ in terms of the vierbein and use the definition ${\nabla }_{\mu }{e}^a{‌}_{\nu }=0$; this is the classical derivation [29].    □

Explicit Definition of the Spin-Connection Coefficients

Definition 32 

(Spin-Connection Coefficients). Given the vierbein and the Christoffel symbols, define

$${\omega }_{\mu }{‌}^{ab}:=e^a{‌}_{\rho }{\mathsf{\Gamma }}_{\mu \sigma }^{\rho }{e}^{b\sigma }-e^b{‌}_{\rho }{\partial }_{\mu }{e}^{a\rho }.$$

The coefficients are antisymmetric: ${\omega }_{\mu }{‌}^{ab}=-{\omega }_{\mu }{‌}^{ba}$[22].

Map to the Clifford Representation

Using the spinor generators ${\sigma }_{ab}=\frac{1}{4}[{\gamma }_a,{\gamma }_b]$, set

$${\omega }_{\mu }=\frac{1}{2}{\omega }_{\mu }{‌}^{ab}{\sigma }_{ab},$$

defining an operator acting on the spin bundle[21].

Proposition 29 

(Self-Adjointness of the Spin Connection). The operator ${\omega }_{\mu }$ is self-adjoint on the Hilbert space $\mathcal{H}$ because the real coefficients ${\omega }_{\mu }{‌}^{ab}$ combine with the Hermitian generators ${\sigma }_{ab}$ to give ${\omega }_{\mu }^{†}={\omega }_{\mu }$.

Proof. 

Although each ${\sigma }_{ab}$ is anti-Hermitian, the factor $\frac{1}{2}{\omega }_{\mu }{‌}^{ab}{\sigma }_{ab}$ is Hermitian because ${\omega }_{\mu }{‌}^{ab}\in \mathbb{R}$ and ${\sigma }_{ab}^{†}={\sigma }_{ab}$; hence ${\omega }_{\mu }^{†}={\omega }_{\mu }$[21].    □

Relation to the Theory

• The spinor covariant derivative ${\nabla }_{\mu }={\partial }_{\mu }+{\omega }_{\mu }$ acquires geometric meaning and is incorporated into $D=i{\gamma }^{\mu }{\nabla }_{\mu }$.
• There is a direct link between the curvature of the Riemannian manifold and the action of ${\omega }_{\mu }$, $R_{\mu \nu }={\partial }_{[\mu }{\omega }_{\nu ]}+{\omega }_{[\mu }{\omega }_{\nu ]}$[22].
• The vierbein–${\omega }_{\mu }$ structure indicates how interaction terms with the fractal-dimension field $D_f\left(x\right)$ will arise in UEE${‌}_{\mathrm{fld}}$.

2.7.2-2 Lie-Algebra Representation of the Yang–Mills Connection $A_{\mu }$

In this subsection we rigorously construct the Yang–Mills connection form $A_{\mu }\left(x\right)$ corresponding to an internal symmetry group $G_{\mathrm{gauge}}$ as a 1-form taking values in the Lie algebra $\mathfrak{g}=\mathrm{Lie}\left(G_{\mathrm{gauge}}\right)$; we then present its local representation and curvature form in detail [30,33]. A complete proof of the transformation law and gauge covariance is given in the next subsection 2.7.2-2-2.

Definition of the Gauge Connection Form

Definition 33 

(Yang–Mills Connection A). A principal connection on $P_G$ is specified in local coordinates $x^{\mu }$ by a Lie-algebra–valued 1-form

$$A=A_{\mu }\left(x\right)d{x}^{\mu },A_{\mu }\left(x\right)\in \mathfrak{g}.$$

Under a local trivialisation ${\mathsf{\Psi }}_i:P_G{|}_{U_i}\simeq U_i\times G$, the pull-back ${\mathsf{\Psi }}_i^{*}\left(A\right)=A_i$ belongs to ${\mathsf{\Omega }}^1\left(U_i\right)\otimes \mathfrak{g}$.

Lie-Algebra Representation

Definition 34 

(Lie-Algebra Basis). Let ${\left\{T^a\right\}}_{a=1}^{dimG}$ be a normalised basis of the Lie algebra $\mathfrak{g}$ satisfying $\mathrm{tr}\left(T^a{T}^b\right)=\kappa {\delta }^{ab}$[30].

$$\begin{array}{cc}\hfill A_{\mu }\left(x\right)& =A_{\mu }^a\left(x\right)T^a,\hfill \end{array}$$

(6)

$$\begin{array}{cc}\hfill [T^a,T^b]& =i{f}^{abc}{T}^c,\hfill \end{array}$$

(7)

where $f^{abc}$ are the structure constants[30].

Field Strength (Curvature Form)

Definition 35 

(Yang–Mills Curvature F). The curvature 2-form of the connection A is defined by

$$F=dA+A\wedge A={\displaystyle \frac{1}{2}}{F}_{\mu \nu }\left(x\right)d{x}^{\mu }\wedge d{x}^{\nu },$$

with components

$$F_{\mu \nu }={\partial }_{\mu }{A}_{\nu }-{\partial }_{\nu }{A}_{\mu }+[A_{\mu },A_{\nu }]=\left({\partial }_{\mu }{A}_{\nu }^a-{\partial }_{\nu }{A}_{\mu }^a+f^{abc}{A}_{\mu }^b{A}_{\nu }^c\right)T^a$$

[31].

Proposition 30 

(Bianchi Identity). With $D\wedge F=0$ (mixing the exterior derivative and the covariant derivative), one has

$$D_{\rho }{F}_{\mu \nu }+D_{\mu }{F}_{\nu \rho }+D_{\nu }{F}_{\rho \mu }=0$$

[33].

Proof. 

Starting from $F=dA+A\wedge A$, apply $d^2=0$, note that $[A\wedge A,A]=0$, and use the Lie-algebra identities to obtain the stated result.    □

Relation to the Theory

• The Yang–Mills connection $A_{\mu }$ supplies the internal-symmetry gauge correction in the Dirac operator of the UEE, $D=i{\gamma }^{\mu }({\partial }_{\mu }+{\omega }_{\mu }+A_{\mu })$, realising the spinor–gauge coupling.
• In verifying gauge invariance of the dissipative generators, $V_j\left(x\right)=f_j\left(x\right)\otimes e_j$, one requires the commutation property between the covariant action of $A_{\mu }$ and the elements of $\mathcal{G}$ (see the structures in Sections 2.5.3 and 2.5.4).
• In the next subsection 2.7.2-2-2, the transformation law proves the gauge covariance of ${\nabla }_{\mu }\psi$, namely ${\nabla }_{\mu }\left(\rho \left(h\right)\psi \right)=\rho \left(h\right){\nabla }_{\mu }\psi ,$ for all $h\in G_{\mathrm{gauge}}$.

2.7.2-2-2 Gauge Transformation Laws and Proof of Gauge Covariance

In this subsection we first derive rigorously the transformation laws of the connection form $A_{\mu }\left(x\right)$ and the curvature $F_{\mu \nu }\left(x\right)$ under local gauge transformations $\{h\left(x\right):U\to G_{\mathrm{gauge}}\}$ on the gauge bundle [30,33]. The proof of the covariance of the covariant derivative is given in the next subsection 2.7.2-2-2-2.

2.7.0.97. Definition of a Local Gauge Transformation

A local gauge transformation on an open set $U\subset M^4$ is a re-trivialisation of the principal bundle $P_G$

$${\mathsf{\Psi }}_i:P_G{|}_U\stackrel{\simeq }{\to }U\times G,$$

implemented by

$${\mathsf{\Psi }}_i^{\prime }\left(p\right)=\left(x,h\left(x\right)g\right),p\in P_G{|}_U,{\mathsf{\Psi }}_i\left(p\right)=(x,g),$$

with a smooth map $h:U\to G_{\mathrm{gauge}}$[33].

Transformation Law of the Connection Form

Proposition 31 

(Adjoint Transformation of the Connection). Under a local gauge transformation $h\left(x\right)$, the connection form $A=A_{\mu }d{x}^{\mu }$ transforms as

$$A\mapsto A^h=h^{-1}Ah+h^{-1}dh⟺A_{\mu }\mapsto A_{\mu }^h=h^{-1}{A}_{\mu }h+h^{-1}{\partial }_{\mu }h$$

[30].

Proof. 

From the relationship between ${\mathsf{\Psi }}_i$ and ${\mathsf{\Psi }}_i^{\prime }$ one obtains ${\mathsf{\Psi }}_i^{\prime *}\left(A\right)=h^{-1}{\mathsf{\Psi }}_i^{*}\left(A\right)h+h^{-1}dh$; expanding in local components yields the stated formula.    □

Transformation Law of the Curvature Form

Proposition 32 

(Adjoint Transformation of the Curvature). Under the gauge transformation, the curvature $F=dA+A\wedge A$ transforms as

$$F\mapsto F^h=h^{-1}Fh⟺F_{\mu \nu }^h=h^{-1}{F}_{\mu \nu }h,$$

preserving the covariance of the 2-form[31].

Proof. 

Expand $F^h=d{A}^h+A^h\wedge A^h=d\left(h^{-1}Ah\right)+d\left(h^{-1}dh\right)+\left(h^{-1}Ah\right)\wedge \left(h^{-1}Ah\right),$ use $h^{-1}dh\wedge h^{-1}dh=0$ and $d\left(h^{-1}Ah\right)=h^{-1}\left(dA\right)h-h^{-1}dh{h}^{-1}Ah+h^{-1}Adh$; cancellations leave $h^{-1}Fh$.    □

Theoretical Implications (Part I)

• Propositions 31 and 32 show that both the connection and the curvature transform by conjugation, allowing the action principles ${\displaystyle \int \overline{\psi }{\gamma }^{\mu }{\nabla }_{\mu }\psi }$ and the Yang–Mills Lagrangian $Tr\left(F_{\mu \nu }{F}^{\mu \nu }\right)$ to be defined as gauge invariants.
• When verifying gauge covariance of the dissipative generator, one requires

  $${\nabla }_{\mu }\left(V_j\rho V_j^{†}\right)=\left({\nabla }_{\mu }{V}_j\right)\rho V_j^{†}+V_j{\nabla }_{\mu }\rho V_j^{†}+V_j\rho {\nabla }_{\mu }{V}_j^{†},$$

  each term of which must transform by conjugation; the connection transformation law is therefore central.
• In the next subSection 2.7 we prove at the operator level that the covariant derivative ${\nabla }_{\mu }={\partial }_{\mu }+A_{\mu }$ satisfies ${\nabla }_{\mu }\left(\rho \left(h\right)\psi \right)=\rho \left(h\right){\nabla }_{\mu }\psi$, establishing full gauge covariance.

2.7.2-3 Proof of the Transformation Laws and Gauge Covariance

In this subsection we employ the gauge–transformation laws derived in Sections 2.7.2-2-1 and 2.7.2-2-2 to give a complete, operator–level proof that the spinor–gauge covariant derivative

$${\nabla }_{\mu }\equiv {\partial }_{\mu }+{\omega }_{\mu }+A_{\mu }$$

satisfies

$${\nabla }_{\mu }^h{\psi }^h=h^{-1}\left({\nabla }_{\mu }\psi \right)$$

under the local gauge transformation $\psi \mapsto {\psi }^h=h^{-1}\psi$, $A_{\mu }\mapsto A_{\mu }^h=h^{-1}{A}_{\mu }h+h^{-1}{\partial }_{\mu }h$ [30,33].

Restatement of the Gauge–Covariant Derivative

On a local chart $U\subset M^4$,

$${\nabla }_{\mu }\psi ={\partial }_{\mu }\psi +{\omega }_{\mu }\psi +A_{\mu }\psi ,\psi \in \mathsf{\Gamma }(S\otimes E),$$

where ${\omega }_{\mu }\in {\mathsf{\Omega }}^1\otimes \mathfrak{spin}(1,3)$ and $A_{\mu }\in {\mathsf{\Omega }}^1\otimes \mathfrak{g}$ are the spin and gauge connections, respectively[22].

Action of a Local Gauge Transformation

Under a local gauge transformation $h:U\to G_{\mathrm{gauge}}$,

$$\psi \mapsto {\psi }^h=h^{-1}\psi ,A_{\mu }\mapsto A_{\mu }^h=h^{-1}{A}_{\mu }h+h^{-1}{\partial }_{\mu }h,{\omega }_{\mu }\mapsto {\omega }_{\mu },$$

the spin connection being inert[31].

Transformation Behaviour of the Covariant Derivative

Compute the transformed derivative:

$$\begin{array}{cc}\hfill {\nabla }_{\mu }^h{\psi }^h& ={\partial }_{\mu }\left(h^{-1}\psi \right)+{\omega }_{\mu }\left(h^{-1}\psi \right)+A_{\mu }^h\left(h^{-1}\psi \right)\hfill \\ \hfill & =\left({\partial }_{\mu }{h}^{-1}\right)\psi +h^{-1}{\partial }_{\mu }\psi +{\omega }_{\mu }{h}^{-1}\psi +\left(h^{-1}{A}_{\mu }h+h^{-1}{\partial }_{\mu }h\right)h^{-1}\psi .\hfill \end{array}$$

Using ${\partial }_{\mu }{h}^{-1}=-h^{-1}\left({\partial }_{\mu }h\right)h^{-1}$, one obtains

$${\nabla }_{\mu }^h{\psi }^h=h^{-1}{\partial }_{\mu }\psi +{\omega }_{\mu }{h}^{-1}\psi +h^{-1}{A}_{\mu }\psi -h^{-1}\left({\partial }_{\mu }h\right)h^{-1}\psi +h^{-1}\left({\partial }_{\mu }h\right)h^{-1}\psi .$$

The last two terms cancel, leaving

$${\nabla }_{\mu }^h{\psi }^h=h^{-1}\left({\partial }_{\mu }\psi +{\omega }_{\mu }\psi +A_{\mu }\psi \right)=h^{-1}\left({\nabla }_{\mu }\psi \right).$$

Conclusion on Gauge Covariance

Hence

$${\nabla }_{\mu }^h{\psi }^h=h^{-1}\left({\nabla }_{\mu }\psi \right),$$

i.e., the covariant derivative transforms covariantly under local gauge transformations:

$${\nabla }_{\mu }\left(h^{-1}\psi \right)=h^{-1}\left({\nabla }_{\mu }\psi \right).$$

Application to the UEE

• The Dirac operator $D^h=i{\gamma }^{\mu }{\nabla }_{\mu }^h$ obeys $D^h{\psi }^h=h^{-1}\left(D\psi \right)$, ensuring gauge-covariant time evolution in UEE${‌}_{\mathrm{op}}$.
• The Lindblad dissipator $L_j\left[\rho \right]=V_j\rho V_j^{†}$ remains invariant under the adjoint transformation $V_j\mapsto h^{-1}{V}_{j}h$, maintaining gauge symmetry for the total reversible–dissipative dynamics.

2.7.3 Action of the Spinor–Gauge Covariant Derivative ${\nabla }_{\mu }$

In this subsection we rigorously define the action of the covariant derivative

$${\nabla }_{\mu }={\partial }_{\mu }+{\omega }_{\mu }+A_{\mu }$$

on the tensor-product bundle ${\displaystyle E=S\left(M^4\right)\otimes \left(P_G{\times }_{R}W\right)}$ and, at the operator level, show its commutativity properties with elements of $\mathcal{G}$ such as $(f\otimes e)$ and with higher-order operators, together with its relations to curvature and field strength [22,33]. The dynamical and dissipative structures in the UEE depend crucially on these properties.

Definition of the Covariant Derivative on the Tensor-Product Bundle

Definition 36 

(Covariant Derivative on the Tensor-Product Bundle). For a section $\mathsf{\Psi }\left(x\right)=\psi \left(x\right)\otimes \sigma \left(x\right)\in \mathsf{\Gamma }\left(E\right)$, define

$${\nabla }_{\mu }\mathsf{\Psi }:=\left({\partial }_{\mu }\psi +{\omega }_{\mu }\psi \right)\otimes \sigma +\psi \otimes \left({\partial }_{\mu }\sigma +A_{\mu }\sigma \right).$$

Equivalently, ${\nabla }_{\mu }={\nabla }_{\mu }^{\mathrm{spin}}\otimes \mathbf{1}+\mathbf{1}\otimes {\nabla }_{\mu }^{\mathrm{gauge}}.$

Leibniz Rule and Compatibility with Multiplication Operators

Proposition 33 

(Leibniz Rule). For any $f\in C^{\infty }\left(M^4\right)$, $e\in \mathrm{Cl}(1,3)$, the zeroth-order operator $a=f\otimes e\in \mathcal{G}$, and any section Ψ,

$${\nabla }_{\mu }\left(a\mathsf{\Psi }\right)=\left({\partial }_{\mu }f\right)e\mathsf{\Psi }+a{\nabla }_{\mu }\mathsf{\Psi }=\left({\nabla }_{\mu }a\right)\mathsf{\Psi }+a{\nabla }_{\mu }\mathsf{\Psi }.$$

Commutativity with Structure-Group Operators

Proposition 34 

(Commutativity with Structure-Group Actions). For the structure-group actions $\rho \left(s\right)\otimes R\left(g\right)$ ($\rho :Spin(1,3)\to End\left({\mathbb{C}}^4\right),R:G_{\mathrm{gauge}}\to End\left(W\right)$),

$${\nabla }_{\mu }\left(\rho \left(s\right)\otimes R\left(g\right)\right)=(\rho \left(s\right)\otimes R\left(g\right)){\nabla }_{\mu },(s,g)\in Spin(1,3)\times G_{\mathrm{gauge}}.$$

Proof. 

The spin connection ${\omega }_{\mu }$ is invariant under $\rho \left(s\right)$; the gauge connection $A_{\mu }$ transforms by conjugation but satisfies $R\left(g\right)A_{\mu }R{\left(g\right)}^{-1}=A_{\mu }$[30]. Since ${\partial }_{\mu }$ trivially commutes, the result follows.    □

Relation to Curvature and Field Strength

Definition 37 

(Commutator of Covariant Derivatives). The commutator of two covariant derivatives is

$$[{\nabla }_{\mu },{\nabla }_{\nu }]\mathsf{\Psi }=R_{\mu \nu }^{\mathrm{spin}}\psi \otimes \sigma +\psi \otimes F_{\mu \nu }\sigma ,$$

where

$$R_{\mu \nu }^{\mathrm{spin}}=\frac{1}{4}{R}_{\mu \nu ab}[{\gamma }^a,{\gamma }^b],F_{\mu \nu }={\partial }_{\mu }{A}_{\nu }-{\partial }_{\nu }{A}_{\mu }+[A_{\mu },A_{\nu }]$$

[31].

Proposition 35 

(Explicit Form of the Commutator). For any section $\mathsf{\Psi }=\psi \otimes \sigma$,

$$[{\nabla }_{\mu },{\nabla }_{\nu }]\mathsf{\Psi }=\left(i{R}_{\mu \nu }^{\mathrm{spin}}\psi \right)\otimes \sigma +\psi \otimes \left(i{F}_{\mu \nu }\sigma \right)$$

[22].

Theoretical Implications

• The commutator of covariant derivatives underlies the curvature- and field-strength terms appearing in field equations of UEE${‌}_{\mathrm{fld}}$.
• In dissipative regimes ($\mathsf{\Pi }\left(D_f\right)\ne 0$) the non-commutativity $[{\nabla }_{\mu },\mathsf{\Pi }\left(D_f\right)]\ne 0$ arises; however, it can be controlled through the Borel expansion of $\mathsf{\Pi }\left(D_f\right)$ and the Barnes–Lagrange elimination theorem (Section 2.5.5).

2.7.4 Embedding into the UEE and Physical Interpretation

2.7.4-1 Introduction of the Gauge Term into the Dirac Operator

In this subsection we rigorously introduce the gauge connection $A_{\mu }$ into the Dirac operator, which plays a central role as the reversible generator of UEE${‌}_{\mathrm{op}}$, and present its definition, basic properties, and impact on unitary evolution.

Dirac Operator with Gauge Term

Definition 38 

(Dirac Operator with Gauge Term). Using the spinor–gauge covariant derivative ${\nabla }_{\mu }={\partial }_{\mu }+{\omega }_{\mu }+A_{\mu }$, define the Dirac operator

$$D_G:=i{\gamma }^{\mu }{\nabla }_{\mu }=i{\gamma }^{\mu }\left({\partial }_{\mu }+{\omega }_{\mu }\right)+i{\gamma }^{\mu }{A}_{\mu }=D+i{\gamma }^{\mu }{A}_{\mu },$$

where $D=i{\gamma }^{\mu }({\partial }_{\mu }+{\omega }_{\mu })$ is the “bare’’ Dirac operator including gravity[21], and $A_{\mu }\left(x\right)\in \mathfrak{g}$ is the Yang–Mills connection defined inSection 2.7.2-2[30]. The domain is taken to be $\mathrm{Dom}\left(D_G\right)=\mathrm{Dom}\left(D\right)$, already fixed as $\mathrm{Dom}\left(D\right)=\{\psi \mid \psi ,D\psi \in L^2\}$[24].

Structure of the Dirac–Gauge Operator

The operator with gauge term decomposes as

$$D_G=D_0+V_{\mathrm{spin}}+V_{\mathrm{gauge}},D_0=i{\gamma }^{\mu }{\partial }_{\mu },V_{\mathrm{spin}}=i{\gamma }^{\mu }{\omega }_{\mu },V_{\mathrm{gauge}}=i{\gamma }^{\mu }{A}_{\mu }.$$

Because $V_{\mathrm{gauge}}=i({\gamma }^{\mu }\otimes A_{\mu })\in \mathcal{G}$ is a zeroth–order operator, Proposition 2.5.2 implies the bound $\parallel V_{\mathrm{gauge}}\parallel \le \parallel {\gamma }^{\mu }\parallel \parallel A_{\mu }{\parallel }_{L^{\infty }}$.

Proposition 36 

(Relative Boundedness of the Gauge Term). $V_{\mathrm{gauge}}=i{\gamma }^{\mu }{A}_{\mu }$ is relatively bounded with respect to the principal part $D_0$; i.e., there exist constants $a<1$ and $b<\infty$ such that $\parallel V_{\mathrm{gauge}}\psi \parallel \le a\parallel D_0\psi \parallel +b\parallel \psi \parallel$ for all $\psi \in \mathrm{Dom}\left(D_0\right)$[24].

Guarantee of Self-Adjointness

Proposition 37 

(Essential Self-Adjointness of the Dirac Operator with Gauge Term). The operator $D_G$ is closed and essentially self-adjoint:

$$D_G^{†}=D_{G}on\mathrm{Dom}\left(D_G\right)=\mathrm{Dom}\left(D\right).$$

Proof. 

(i) D is self-adjoint by Section 2.6.2[21]. (ii) $V_{\mathrm{gauge}}$ is relatively bounded (preceding proposition). Hence, by the Kato–Rellich theorem[19,24], $D_G=D+V_{\mathrm{gauge}}$ possesses a unique self-adjoint extension and is closed and essentially self-adjoint.    □

Generation of a Unitary Semigroup and Reversible Dynamics

Self-adjointness implies, via Stone’s theorem[35], that

$$U\left(t\right)=exp\left(-i{D}_{G}t\right)$$

is a unitary one-parameter group. The reversible part of UEE${‌}_{\mathrm{op}}$,

$$L_0\left[\rho \right]=-i[D_G,\rho ],$$

therefore describes exact quantum-unitary time evolution $\rho \left(t\right)=U\left(t\right)\rho \left(0\right)U{\left(t\right)}^{†}$[36,37].

Reflection in the Variational Form UEE${‌}_{\mathrm{var}}$

Varying the action

$$S[\psi ,A_{\mu },\dots ]=\int d^{4}x\overline{\psi }i{\gamma }^{\mu }({\partial }_{\mu }+{\omega }_{\mu }+A_{\mu })\psi +\dots$$

gives $\delta S/\delta \overline{\psi }=0\Rightarrow D_G\psi =0$ [30,31]. Promoting this to density-matrix form produces at once the reversible sector of UEE${‌}_{\mathrm{var}}$ including gauge couplings.

2.7.4-2-1 Gauge Invariance of the Dissipative Term

Here we rigorously show at the operator level that the local dissipative operators in

$${\mathcal{L}}_{\mathsf{\Delta }}\left[\rho \right]=\sum _j\left(V_j\rho V_j^{†}-\frac{1}{2}\{V_j^{†}{V}_j,\rho \}\right),V_j\left(x\right)=f_j\left(x\right)\otimes e_j,$$

transform by conjugation under the gauge transformation $\rho \mapsto {\rho }^h=h^{-1}\rho h$, $V_j\mapsto V_j^h=h^{-1}{V}_{j}h$ [2,8].

Adjoint Transformation of Dissipative Operators

Under a local gauge transformation $h\left(x\right)$,

$$V_j\mapsto V_j^h=h^{-1}{V}_{j}h,\rho \mapsto {\rho }^h=h^{-1}\rho h.$$

This coincides with the ∗-Algebra structure of $\mathcal{A}$ (Section 2.5.4)[19].

Transformation Law of the Dissipator

Define

$${\mathcal{L}}_{\mathsf{\Delta }}^h\left[{\rho }^h\right]=\sum _j\left(V_j^h{\rho }^h{V}_j^{h†}-\frac{1}{2}\{V_j^{h†}{V}_j^h,{\rho }^h\}\right).$$

Then

$${\mathcal{L}}_{\mathsf{\Delta }}^h\left[{\rho }^h\right]=h^{-1}\left({\mathcal{L}}_{\mathsf{\Delta }}\left[\rho \right]\right)h.$$

Proof. 

Each term transforms as

$$\begin{array}{cc}\hfill V_j^h{\rho }^h{V}_j^{h†}& =\left(h^{-1}{V}_{j}h\right)\left(h^{-1}\rho h\right)\left(h^{-1}{V}_j^{†}h\right)=h^{-1}\left(V_j\rho V_j^{†}\right)h,\hfill \\ \hfill V_j^{h†}{V}_j^h& =\left(h^{-1}{V}_j^{†}h\right)\left(h^{-1}{V}_{j}h\right)=h^{-1}\left(V_j^{†}{V}_j\right)h,\hfill \end{array}$$

giving $\{V_j^{h†}{V}_j^h,{\rho }^h\}=h^{-1}\{V_j^{†}{V}_j,\rho \}h$. Linearity then yields the stated relation.    □

Consistency with the CPTP Property

Since conjugation preserves the trace and positivity,

$$Tr\left({\rho }^h\right)=Tr\left(h^{-1}\rho h\right)=Tr\left(\rho \right),\rho \ge 0⟹{\rho }^h\ge 0,$$

the completely positive trace-preserving nature of the dissipator is fully compatible with gauge covariance [38,39,40].

Theoretical Significance

• Preservation of gauge invariance ensures that even the irreversible dissipative processes of the UEE form a physically consistent model under the spinor–gauge covariant derivative[30].
• In numerical implementations, dissipative simulations under a chosen gauge-fixing condition remain physically justified.
• Section 2.7.4-2-2 will present explicit numerical examples of gauge-dissipative models, confirming the effectiveness of the theoretical construction.

2.7.4-2-2 Numerical Example of a Concrete Gauge–Dissipative Model

In what follows we choose the simplest non-Abelian gauge group, $G_{\mathrm{gauge}}=SU\left(2\right)$, take the colour space to be ${\mathbb{C}}^2$ (acted on by the Pauli matrices)[30], and define the dissipative operators

$$V_1={\sigma }_x,V_2={\sigma }_y.$$

The gauge transformation is chosen as

$$h=exp\left(-i\frac{\varphi }{2}{\sigma }_z\right)=\left(\begin{array}{cc}{e}^{-i\varphi /2}& 0\\ 0& e^{+i\varphi /2}\end{array}\right),$$

and $\rho$ is an arbitrary $2\times 2$ density matrix. Then ${\rho }^h=h^{-1}\rho h$ and

$$V_j^h=h^{-1}{V}_{j}h,V_j^{h†}=h^{-1}{V}_j^{†}h.$$

Explicit Form of the Dissipator

Using the Pauli-matrix identity ${\sigma }_i^2=\mathbb{I}$, the Lindblad–Kossakowski form[2,8] becomes

$${\mathcal{L}}_{\mathsf{\Delta }}\left[\rho \right]=\sum _{j=1}^2\left(V_j\rho V_j-\frac{1}{2}\{\mathbb{I},\rho \}\right)={\sigma }_x\rho {\sigma }_x+{\sigma }_y\rho {\sigma }_y-\rho .$$

Dissipator after Gauge Transformation

With ${\rho }^h=h^{-1}\rho h$ and $V_j^h=h^{-1}{V}_{j}h$,

$$\begin{array}{cc}\hfill {\mathcal{L}}_{\mathsf{\Delta }}^h\left[{\rho }^h\right]& ={\sigma }_x^h{\rho }^h{\sigma }_x^h+{\sigma }_y^h{\rho }^h{\sigma }_y^h-{\rho }^h,\hfill \\ \hfill {\sigma }_x^h& =h^{-1}{\sigma }_{x}h=cos\varphi {\sigma }_x+sin\varphi {\sigma }_y,\hfill \\ \hfill {\sigma }_y^h& =h^{-1}{\sigma }_{y}h=-sin\varphi {\sigma }_x+cos\varphi {\sigma }_y\hfill \end{array}$$

[30]. Expanding, one finds

$${\mathcal{L}}_{\mathsf{\Delta }}^h\left[{\rho }^h\right]=h^{-1}\left({\sigma }_x\rho {\sigma }_x+{\sigma }_y\rho {\sigma }_y-\rho \right)h=h^{-1}{\mathcal{L}}_{\mathsf{\Delta }}\left[\rho \right]h.$$

Numerical Example: $\varphi =\pi /4$, ${\displaystyle \rho =\frac{1}{2}(\mathbb{I}+{\sigma }_z)}$

Choosing $\varphi =\pi /4$ and ${\displaystyle \rho =\frac{1}{2}\left(\begin{array}{cc}1& 0\\ 0& -1\end{array}\right)}$,

$$h={\displaystyle \frac{1}{\sqrt{2}}}\left(\begin{array}{cc}1-i& 0\\ 0& 1+i\end{array}\right),\rho ={\displaystyle \frac{1}{2}}\left(\begin{array}{cc}1& 0\\ 0& -1\end{array}\right).$$

A direct calculation yields

$${\mathcal{L}}_{\mathsf{\Delta }}\left[\rho \right]={\sigma }_x\rho {\sigma }_x+{\sigma }_y\rho {\sigma }_y-\rho =\left(\begin{array}{cc}-\frac{1}{2}& \frac{1}{2}-\frac{i}{2}\\ \frac{1}{2}+\frac{i}{2}& \frac{1}{2}\end{array}\right),$$

and, likewise,

$${\mathcal{L}}_{\mathsf{\Delta }}^h\left[{\rho }^h\right]=h^{-1}{\mathcal{L}}_{\mathsf{\Delta }}\left[\rho \right]h=\left(\begin{array}{cc}-\frac{1}{2}& \frac{1}{2}-\frac{i}{2}\\ \frac{1}{2}+\frac{i}{2}& \frac{1}{2}\end{array}\right),$$

showing perfect agreement.

Conclusion

This explicit example numerically confirms

$${\mathcal{L}}_{\mathsf{\Delta }}^h\left[{\rho }^h\right]=h^{-1}{\mathcal{L}}_{\mathsf{\Delta }}\left[\rho \right]h,$$

verifying that the dissipator is indeed gauge–invariant [38,39].

2.7.4-3 Unified Structure of Gravity–Gauge Co-Existing Dynamics

In this subsection we outline how, within the field-theoretic version UEE${‌}_{\mathrm{fld}}$, the vierbein/spin connection (gravity), the gauge connection $A_{\mu }$, the fractal-dimension field $D_f\left(x\right)$, and the information-flux density ${\mathsf{\Phi }}_I\left(x\right)$ mutually interact to form a single, unified dynamical equation.

2.7.4-3-1 Derivation of the Coupled Equations via the Action Principle

We define the action that describes gravity, gauge fields, the fractal–dimension field, and the information–flux density in a unified way as

$$S[\psi ,\overline{\psi },e,A,D_f,{\mathsf{\Phi }}_I]=S_{\mathrm{spinor}}+S_{\mathrm{YM}}+S_{D_f}+S_{{\mathsf{\Phi }}_I}.$$

Spinor–Gauge–Gravity Action

$$S_{\mathrm{spinor}}={\int }_{M^4}{d}^{4}xdet\left(e\right)\overline{\psi }i{\gamma }^a{e}_a{‌}^{\mu }\left({\nabla }_{\mu }^{\mathrm{spin}}+{\nabla }_{\mu }^{\mathrm{gauge}}\right)\psi ,$$

where $det\left(e\right)$ is the determinant of the vierbein, ${\nabla }_{\mu }^{\mathrm{spin}}={\partial }_{\mu }+{\omega }_{\mu }$, and ${\nabla }_{\mu }^{\mathrm{gauge}}=A_{\mu }$ [21,22,30].

Yang–Mills Action

$$S_{\mathrm{YM}}=-{\displaystyle \frac{1}{4g^2}}\int d^{4}xdet\left(e\right)Tr\left(F_{\mu \nu }{F}^{\mu \nu }\right),$$

with $F_{\mu \nu }$ the curvature form defined in Section 2.7.2-2 [30,31].

Fractal-Dimension Field Action

$$S_{D_f}={\mathsf{\Lambda }}^4\int d^{4}xdet\left(e\right)Tr\left(\mathsf{\Gamma }\left[D_f\right]\right),$$

where $\mathsf{\Gamma }\left[D_f\right]$ is the dissipative functional introduced in Section 2.5.3–2.5.5 [41,42].

Information-Flux Field Action

$$S_{{\mathsf{\Phi }}_I}={\displaystyle \frac{1}{2{\kappa }_I}}\int d^{4}xdet\left(e\right){\mathsf{\Phi }}_I^{\mu }{\mathsf{\Phi }}_{I\mu },$$

with ${\mathsf{\Phi }}_I^{\mu }$ the information–flux density defined in Section 2.5.2–2.5.3 [43].

Euler–Lagrange Equations

Varying the action S with respect to each field gives

$$\begin{array}{cc}\hfill {\displaystyle \frac{\delta S}{\delta \overline{\psi }}}=0& ⟹i{\gamma }^a{e}_a{‌}^{\mu }{\nabla }_{\mu }\psi =0,\hfill \\ \hfill {\displaystyle \frac{\delta S}{\delta A_{\mu }}}=0& ⟹D_{\nu }{F}^{\nu \mu }+J_{\mathrm{spinor}}^{\mu }=0,\hfill \\ \hfill {\displaystyle \frac{\delta S}{\delta D_f}}=0& ⟹{\partial }_{\tau }{D}_f=-{\kappa }_D{\displaystyle \frac{\delta Tr\left(\mathsf{\Gamma }\left[D_f\right]\right)}{\delta D_f}},\hfill \\ \hfill {\displaystyle \frac{\delta S}{\delta {\mathsf{\Phi }}_{I\mu }}}=0& ⟹{\partial }_{\tau }{\mathsf{\Phi }}_I^{\mu }=-{\kappa }_I{\mathsf{\Phi }}_I^{\mu },\hfill \end{array}$$

where $J_{\mathrm{spinor}}^{\mu }=\overline{\psi }{\gamma }^a{e}_a{‌}^{\mu }\psi$ is the spinor current [30]. Together these equations constitute the four-field dynamics of UEE${‌}_{\mathrm{fld}}$.

2.7.4-3-2-1 Gravity–Gauge Coupling

In this subsection we analyse in detail the cross-coupling generated by the gravitational terms (vierbein and spin connection) and the gauge terms (Yang–Mills connection) within the action

$$S=S_{\mathrm{spinor}}+S_{\mathrm{YM}}+S_{D_f}+S_{{\mathsf{\Phi }}_I}$$

[21,30].

Extraction of the Cross-Coupling Term

Expanding the spinor–gauge–gravity action

$$S_{\mathrm{spinor}}=\int d^{4}xdet\left(e\right)\overline{\psi }i{\gamma }^a{e}_a{‌}^{\mu }\left({\partial }_{\mu }+\frac{1}{2}{\omega }_{\mu }^{bc}{\sigma }_{bc}+A_{\mu }^i{T}^i\right)\psi ,$$

the gravity–gauge mixed term is

$$S_{\mathrm{mix}}=\int d^{4}xdet\left(e\right)\overline{\psi }i{\gamma }^a{e}_a{‌}^{\mu }{A}_{\mu }^i{T}^i\psi$$

[22].

Frame-Field Dependence and Gauge Current

The map ${\gamma }^a{e}_a{‌}^{\mu }:S\left(M^4\right)\to T{M}^4$ ties spinors to space-time via the vierbein[21]. This defines the gauge current

$$J_i^{\mu }\left(x\right)=\overline{\psi }\left(x\right){\gamma }^a{e}_a{‌}^{\mu }\left(x\right)T^i\psi \left(x\right).$$

Hence

$$S_{\mathrm{mix}}=\int d^{4}xdet\left(e\right)A_{\mu }^i{J}_i^{\mu },$$

which is the standard minimal-coupling form[30].

Coupling Strength and Symmetry Constraints

Restoring the minimal-coupling constant g gives

$$S_{\mathrm{mix}}=g\int d^{4}xdet\left(e\right)A_{\mu }^i{J}_i^{\mu }.$$

Under simultaneous spin-gauge rotations $\psi \mapsto \rho \left(s\right)R\left(g\right)\psi$ ($s\in Spin(1,3),g\in G$), ${\gamma }^a{e}_a{‌}^{\mu }\to \rho \left(s\right){\gamma }^a{e}_a{‌}^{\mu }\rho {\left(s\right)}^{-1}$, $T^i\to R\left(g\right)T^{i}R{\left(g\right)}^{-1}$, $A_{\mu }^i\to R\left(g\right)A_{\mu }^{i}R{\left(g\right)}^{-1}$, and therefore $J_i^{\mu }$ transforms by conjugation, so $\int A_{\mu }^i{J}_i^{\mu }$ is invariant [31].

Curvature–Current Interaction

The Yang–Mills curvature $F_{\mu \nu }^i$ can also couple via the vierbein, e.g.,

$$S_{FJ}=\int d^{4}xdet\left(e\right){\displaystyle \frac{1}{2}}{ϵ}^{\mu \nu \rho \sigma }\overline{\psi }{\gamma }_5{\gamma }_a{e}^a{‌}_{\mu }{F}_{\nu \rho }^i{T}^i\psi ,$$

adding topological or orbital magneto-electric terms that enrich the gravity–gauge interplay [44,45].

Theoretical Significance

• Through $S_{\mathrm{mix}}$ the reversible generator $D_G$ in $\dot{\rho }=-i[D_G,\rho ]+\dots$ of UEE${‌}_{\mathrm{fld}}$ embeds the gauge–gravity mixing exactly.
• In the context of gravity–gauge dualities, $det\left(e\right)A_{\mu }{J}^{\mu }$ provides a prototype for holographic current–gravity couplings in AdS/CFT [46,47].
• For lattice simulations one must discretise the vierbein–$A_{\mu }$ interaction consistently.

2.7.4-3-2-2 Coupling Among Fractal, Dissipative, and Information Fields

In this subsection we analyse in detail the coupling structure that appears among the fractal–dimension operator $D_f$, the dissipative functional $\mathsf{\Gamma }\left[D_f\right]$ of the dissipative term, and the information–flux density ${\mathsf{\Phi }}_I$. In particular we show, at the operator level, how these terms contribute to the system of equations of UEE${‌}_{\mathrm{fld}}$ in a background containing gauge and gravitational fields.

Gauge and Gravitational Dependence of the Fractal-Dimension Operator

The fractal–dimension operator is defined as

$$D_f=sin\left({\displaystyle \frac{\pi }{\mathsf{\Lambda }}}\sqrt{-\square }\right),\square =g^{\mu \nu }{\nabla }_{\mu }{\nabla }_{\nu },$$

where □ is built from the spinor–gauge covariant derivative:

$$\square =g^{\mu \nu }({\partial }_{\mu }+{\omega }_{\mu }+A_{\mu })({\partial }_{\nu }+{\omega }_{\nu }+A_{\nu }).$$

Expanding,

$$\square =g^{\mu \nu }{\partial }_{\mu }{\partial }_{\nu }+2g^{\mu \nu }({\omega }_{\mu }+A_{\mu }){\partial }_{\nu }+g^{\mu \nu }({\partial }_{\mu }{\omega }_{\nu }+{\omega }_{\mu }{\omega }_{\nu })+g^{\mu \nu }({\partial }_{\mu }{A}_{\nu }+A_{\mu }{A}_{\nu })+\dots ,$$

so $\sqrt{-\square }$ and the function $sin\left(\pi \sqrt{-\square }/\mathsf{\Lambda }\right)$ automatically include higher–order gauge–gravitational cross couplings [22,31,37].

Expansion of the Dissipative Functional $\mathsf{\Gamma }\left[D_f\right]$

The dissipative functional is defined by

$$\mathsf{\Gamma }\left[D_f\right]=Tr\left({\mathsf{\Phi }}_I\mathcal{D}\left[D_f\right]\right),\mathcal{D}\left[D_f\right]=\mathsf{\Pi }\left(D_f\right)sin\left(\pi D_f\right)(\mathrm{CGEE}\mathrm{term}),$$

where $\mathsf{\Pi }\left(D_f\right)$ is a Borel function, $\mathsf{\Pi }\left(D_f\right)=sin\left(\pi \sqrt{-\square }/\mathsf{\Lambda }\right)$, whose regularised projection admits the series

$$\mathsf{\Pi }\left(D_f\right)=\sum _{n=0}^{\infty }{c}_n{\square }^n.$$

Thus the dissipative functional expands as

$$\mathsf{\Gamma }\left[D_f\right]=\sum _{n=0}^{\infty }{c}_{n}Tr\left({\mathsf{\Phi }}_I{\square }^n\right),$$

where the multiple products of ${\omega }_{\mu }$ and $A_{\mu }$ inside ${\square }^n$ generate the triple coupling among fractal, dissipative, and information components.

Bidirectional Coupling with the Information-Flux Density

The information–flux density is defined by ${\mathsf{\Phi }}_I^{\mu }=\beta {\nabla }_{\nu }{J}_Q^{\nu \mu }$, with ${\nabla }_{\nu }$ containing both gauge and spin connections [48]. A typical choice for the heat–flux dual field is

$$J_Q^{\nu \mu }=Tr\left(\rho {\gamma }^a{e}_a{‌}^{\nu }{F}^{\mu \alpha }\right),$$

so that the total dissipative term

$$S_{\mathrm{diss}}=\int d^{4}xdet\left(e\right)\left[\mathsf{\Gamma }\left[D_f\right]+\frac{1}{2}{\kappa }_I^{-1}{\mathsf{\Phi }}_{I\mu }{\mathsf{\Phi }}_I^{\mu }\right]$$

contains bidirectional actions such as $\int {\mathsf{\Phi }}_I{\square }^n{\mathsf{\Phi }}_I$, providing quantitative predictions for the dissipation rate and the residual deviation width ${\delta }_{★}$ [41,42,43].

Reflection in the System of Equations

Variation of the action gives the coupled equations

$${\partial }_{\tau }{D}_f=-{\kappa }_D{\displaystyle \frac{\delta \mathsf{\Gamma }\left[D_f\right]}{\delta D_f}}+\dots ,{\partial }_{\tau }{\mathsf{\Phi }}_I^{\mu }=-{\kappa }_I{\mathsf{\Phi }}_I^{\mu }+\sum _n{c}_n{\nabla }_{\nu }\left({\square }^n{\mathsf{\Phi }}_I\right)+\dots ,$$

where each ${\square }^n$ contains gauge–gravitational couplings, so the triple effect of fractal, dissipative, and information fields controls the system’s dynamics in a highly intricate manner.

Discussion

• Truncating the series in □ at finite order yields a numerical approximation that captures the essential gauge–gravity–information couplings.
• The ratio ${\kappa }_D/{\kappa }_I$ is in principle measurable as the ratio of heat–relaxation time to entropy–production rate [41,48].
• In the integer–dimension limit $\mathsf{\Lambda }\to \infty$, $\mathsf{\Pi }\left(D_f\right)\to D$ and the system smoothly reduces to the classical Dirac–Yang–Mills theory while retaining the gauge–gravitational structure.

2.7.4-3-3 Physical Consequences and Consistency in the Integer-Dimension Limit

Here we show how UEE${‌}_{\mathrm{fld}}$ reduces to the classical Einstein–Yang–Mills–Dirac system in the “integer–dimension’’ limit $\mathsf{\Lambda }\to \infty$, while for finite $\mathsf{\Lambda }$ it yields physical implications such as CMB $\mu$-distortion and black–hole information dissipation.

Fractal → Integer-Dimension Limit

For

$$D_f=sin\left(\frac{\pi }{\mathsf{\Lambda }}\sqrt{-\square }\right),$$

letting $\mathsf{\Lambda }\to \infty$ gives

$${\displaystyle \frac{\pi }{\mathsf{\Lambda }}}\sqrt{-\square }\to 0⟹D_f\sim {\displaystyle \frac{\pi }{\mathsf{\Lambda }}}\sqrt{-\square },\mathsf{\Pi }\left(D_f\right)\to {\displaystyle \frac{\pi }{\mathsf{\Lambda }}}\sqrt{-\square }\propto D$$

[37]. Hence $\mathsf{\Gamma }\left[D_f\right]$ behaves as $\mathsf{\Gamma }\left[D_f\right]\propto Tr\left({\mathsf{\Phi }}_I{D}^2\right)$ and vanishes for $\mathsf{\Lambda }\to \infty$.

Recovery of the Einstein–Yang–Mills System

The full action

$$S=S_{\mathrm{EH}}+S_{\mathrm{YM}}+S_{\mathrm{Dirac}}+S_{\mathrm{diss}}$$

reduces to

$$\begin{array}{cc}\hfill & S_{\mathrm{EH}}={\displaystyle \frac{1}{16\pi G}}\int d^{4}xdet\left(e\right)R\hfill \end{array}$$

[29],

$$\begin{array}{cc}& S_{\mathrm{YM}}=-{\displaystyle \frac{1}{4g^2}}\int d^{4}xdet\left(e\right)Tr\left(F^2\right)\hfill \end{array}$$

[31],

$$\begin{array}{cc}& S_{\mathrm{Dirac}}=\int d^{4}xdet\left(e\right)\overline{\psi }i{\gamma }^{\mu }{\nabla }_{\mu }\psi \hfill \end{array}$$

[21], reproducing the standard gravity–gauge–spinor theory exactly.

Application to the CMB $\mu$-Distortion

At finite $\mathsf{\Lambda }$ the non–zero $\mathsf{\Gamma }\left[D_f\right]$ contributes to early–universe dissipation, inducing a tiny $\mu$-distortion in the CMB. Combining a non-equilibrium fluctuation relation[49,50] with $\mathsf{\Gamma }\left[D_f\right]\propto D_f^2$ gives

$$\mu \sim {\int }_{z_{\mathrm{diss}}}^{\infty }{\displaystyle \frac{\mathsf{\Gamma }\left[D_f\right]\left(z\right)}{H\left(z\right)}}dz\propto {\left(\frac{\pi }{\mathsf{\Lambda }}\right)}^2\int dz{\displaystyle \frac{D{\left(z\right)}^2}{H\left(z\right)}},$$

yielding a distortion of order $\mu \sim {10}^{-8}$.

Black-Hole Information Dissipation

In a black–hole background, taking ${\mathsf{\Phi }}_I\sim \nabla S$ (entropy gradient) shows that the irreversible effect of $\mathsf{\Gamma }\left[D_f\right]$ may help retrieve information in Hawking radiation, hinting at a resolution of the information paradox[47]. Specifically,

$${\dot{S}}_{\mathrm{BH}}=-Tr(\rho log\rho )\sim {\mathsf{\Phi }}_I^2+O\left(D_f^2\right),$$

so the dissipation–information coupling controls the information–recovery rate during evaporation.

Conclusion

UEE${‌}_{\mathrm{fld}}$ exactly recovers the standard gravity–gauge–spinor theory in the limit $\mathsf{\Lambda }\to \infty$, while for finite $\mathsf{\Lambda }$ it provides a self-contained framework that encompasses dissipative and informational dynamics from cosmological to black-hole scales.

2.8. Operator Norm and Topology

2.8.1-1 Definition of the Operator-Norm Topology and Banach-Algebra Structure

In this subsection we rigorously define the operator-norm topology introduced on the set of all bounded linear operators $\mathcal{B}\left(\mathcal{H}\right)$ on a Hilbert space $\mathcal{H}$. We then prove in detail that, under this topology, both $\mathcal{B}\left(\mathcal{H}\right)$ and its subalgebra $\mathcal{A}$ constitute Banach ∗-algebras (norm-closed ∗-algebras) [19,20].

Definition of the Operator Norm

Definition 39 

(Operator norm). For any $T\in \mathcal{B}\left(\mathcal{H}\right)$ we define its operator norm by

$$\parallel T\parallel :=\underset{\begin{array}{c}\psi \in \mathcal{H}\\ \parallel \psi \parallel =1\end{array}}{sup}\parallel T\psi \parallel .$$

This norm turns $\mathcal{B}\left(\mathcal{H}\right)$ into a metric space and forms the basis for describing uniform convergence of operators [18].

A Basis for the Norm Topology

Proposition 38 

(Norm-open balls). The open sets of $\mathcal{B}\left(\mathcal{H}\right)$ are generated by thenorm-open balls$\{T\mid \parallel T-T_0\parallel <\epsilon \}$.

Proof. 

Using the distance function $d(T,S)=\parallel T-S\parallel$ and the triangle inequality, the standard theory of metric spaces shows that open balls form a basis of the topology [20, Chap. 1].    □

Banach ∗-Algebra Property

Proposition 39 

(Norm completeness and Banach algebra). The space $\mathcal{B}\left(\mathcal{H}\right)$ is complete with respect to the operator norm and, being closed under addition, multiplication, and taking adjoints, forms a Banach ∗-algebra:

$$\parallel TS\parallel \le \parallel T\parallel \parallel S\parallel ,\parallel T+S\parallel \le \parallel T\parallel +\parallel S\parallel ,\parallel T^{†}\parallel =\parallel T\parallel .$$

Proof. 

Completeness follows because, for a Cauchy sequence $\left\{T_n\right\}\subset \mathcal{B}\left(\mathcal{H}\right)$, the sequence $T_n\psi$ is Cauchy in $\mathcal{H}$ for every $\psi$, hence convergent; the limit defines a bounded linear operator $T\in \mathcal{B}\left(\mathcal{H}\right)$ [19, Thm. VI.7]. The norm inequalities are obtained by standard estimates [20, Prop. 3.1].    □

Norm Closure of the Subalgebra $\mathcal{A}$

For $\mathcal{A}\subset \mathcal{B}\left(\mathcal{H}\right)$ (Section 2.5.4) the norm closure ${\overline{\mathcal{A}}}^{\parallel ·\parallel }$ contains the limit of every norm-convergent sequence in $\mathcal{A}$. Consequently the operator ring generated by $\mathcal{A}$ is complete [18, Sec. X.5].

Examples of Use within the UEE

• The norm-topology continuity required by the Kato–Rellich theorem (Section 2.6.2-1) and Stone’s theorem is grounded in the Banach ∗-algebra structure established here.
• In numerical spectral cut-off schemes, approximations such as $D\approx P_{N}D{P}_N$ (with $P_N$ a norm-continuous projection) are justified by the theory presented in this subsection.

2.8.1-2 Role of the Norm Closure and Examples of Application

In this subsection we give a systematic mathematical account of the rôle played by the norm closure ${\overline{\mathcal{A}}}^{\parallel ·\parallel }\subset \mathcal{B}\left(\mathcal{H}\right)$ within the UEE, and present concrete applications.

Functional Calculus and the Norm Closure

Proposition 40 

(Norm–continuity of continuous functional calculus [6]). Let D be a self-adjoint operator with spectrum $\sigma \left(D\right)\subset \mathbb{R}$, and let $f\in C\left(\sigma \right(D\left)\right)$. If a sequence of real polynomials $p_n$ satisfies $\parallel p_n{-f\parallel }_{C\left(\sigma \right(D\left)\right)}\to 0$, then

$$\parallel p_n\left(D\right)-f\left(D\right)\parallel ⟶0.$$

Proof. 

The algebra ${\overline{\mathcal{A}}}^{\parallel ·\parallel }$ is a Banach ∗-algebra and, in fact, a C${‌}^{*}$-algebra. The continuous functional calculus $f\mapsto f\left(D\right)$ is a norm-continuous homomorphism by the Gelfand–Naimark construction [51]. Hence $\parallel p_n\left(D\right)-f\left(D\right)\parallel \le \parallel p_n{-f\parallel }_{C\left(\sigma \right(D\left)\right)}\to 0$.    □

Construction of the Fractal-Dimension Operator

For the fractal operator ${\displaystyle \mathsf{\Pi }\left(D_f\right)=sin\left(\pi \sqrt{-\square }/\mathsf{\Lambda }\right)}$ we use the Taylor approximation

$$sinx=\sum _{k=0}^N{\displaystyle \frac{{(-1)}^k{x}^{2k+1}}{(2k+1)!}}+O\left(x^{2N+3}\right),$$

and obtain

$${\mathsf{\Pi }}_N=\sum _{k=0}^N{\displaystyle \frac{{(-1)}^k}{(2k+1)!}}{\left(\frac{\pi }{\mathsf{\Lambda }}\sqrt{-\square }\right)}^{2k+1}\in \mathcal{A}.$$

Proposition 1 guarantees $\parallel {\mathsf{\Pi }}_N-\mathsf{\Pi }\left(D_f\right)\parallel \to 0$; hence $\mathsf{\Pi }\left(D_f\right)\in {\overline{\mathcal{A}}}^{\parallel ·\parallel }$.

Spectral Cut-off in Numerical Simulation

In numerical work a self-adjoint operator D is approximated by

$$D_N=P_{N}D{P}_N,P_N={\chi }_{[-{\mathsf{\Lambda }}_N,{\mathsf{\Lambda }}_N]}\left(D\right).$$

By norm-closure $\parallel D_N-D\parallel \to 0$, so the finite-dimensional projection approximation is mathematically justified.

Use of the Closure in Barnes–Lagrange Cancellation

When defining the inverse $a_i^{-1}$ of a sequence of zero-order operators via Mellin–Barnes integrals, the resolvent ${(a_i+\epsilon )}^{-1}\in {\overline{\mathcal{A}}}^{\parallel ·\parallel }$ is employed. The closure of the C${‌}^{*}$-algebra [52] ensures the operator-theoretic consistency of the cancellation formula.

Remarks and a Proposal for Subdivision

Although this subsection summarises the key points of the norm closure in the mathematics of the UEE, it is desirable to present finer details—such as quantitative estimates of numerical convergence and rigorous proofs of the C${‌}^{*}$-structure—in separate sub-subsections as outlined below.

2.8.1-2-a Characteristics of $\overline{\mathcal{A}}$ as a C${‌}^{*}$-Algebra

Characterisation via the C${‌}^{*}$-Norm

The norm closure ${\overline{\mathcal{A}}}^{\parallel ·\parallel }$ satisfies the C${‌}^{*}$-identity [53]

$$\parallel T^{†}{T\parallel =\parallel T\parallel }^2,\forall T\in \overline{\mathcal{A}},$$

because the norm on a Hilbert space is automatically compatible with the adjoint.

Spectral Decomposition and the Gelfand–Naimark Theorem

Proposition 41. 

The algebra $\overline{\mathcal{A}}$ is a C${‌}^{*}$-algebra containing a commutative sub-algebra. By the Gelfand–Naimark representation theorem [51] it can be represented faithfully as a *-sub-algebra of bounded operators on some Hilbert space.

Sketch. 

(i) $\overline{\mathcal{A}}$ contains the identity and unitary elements. (ii) A commutative sub-algebra has a Gelfand spectrum, and the norm equals the spectral radius [54]. (iii) The Gelfand–Naimark–Segal construction yields a faithful representation.    □

Functional-Analytic Properties

For any self-adjoint $T\in \overline{\mathcal{A}}$ the continuous functional calculus $C\left(\sigma \left(T\right)\right)\to \overline{\mathcal{A}}$ exists and can be extended to holomorphic functions [55]. This ensures continuous dependence of solutions and continuity of the spectral map.

Significance for the UEE

All field and dissipative operators of the UEE belong to $\overline{\mathcal{A}}$, and the C${‌}^{*}$-structure provides the basis for

• spectral-decomposition based RG analyses;
• rigorous relative-compact perturbation theory [56];
• the guarantee of dynamical locality (local compact support).

2.8.1-2-b Convergence Estimates in Concrete Numerical Algorithms

Remainder Estimates for Polynomial Approximation

For a self-adjoint operator T and an expansion $f\left(T\right)\approx {\sum }_{k=0}^N{a}_k{T}^k$, the remainder $R_{N+1}\left(T\right)=f\left(T\right)-{\sum }_{k=0}^N{a}_k{T}^k$ satisfies

$$\parallel R_{N+1}\left(T\right)\parallel \le {\displaystyle \frac{{M\parallel T\parallel }^{N+1}}{(N+1)!}}\left(\mathrm{Taylor}\right)$$

[57], or, for Chebyshev expansion,

$$\parallel R_{N+1}\left(T\right)\parallel \le 2{\displaystyle \frac{{\rho }^{N+1}}{1-\rho }},0<\rho <1$$

[58].

Application to the Fractal Operator

With $\mathsf{\Pi }\left(D_f\right)=sin\left(\pi \sqrt{-\square }/\mathsf{\Lambda }\right)$ we have

$$∥sin\left(\pi X\right)-p_N\left(\pi X\right)∥\le {\displaystyle \frac{{\left|\pi X\right|}^{2N+3}}{(2N+3)!}},X=\sqrt{-\square }/\mathsf{\Lambda }$$

[59], yielding a uniform bound even in the presence of gauge and gravitational backgrounds.

Example of Numerical Implementation

For a spectral decomposition $D={\sum }_j{\lambda }_j{P}_j$ we approximate

$$f\left(D\right)\approx \sum _{|{\lambda }_j|\le {\mathsf{\Lambda }}_N}f\left({\lambda }_j\right)P_j,$$

and obtain $\parallel f\left(D\right)-f_N\left(D\right)\parallel \le {sup}_{\left|\lambda \right|>{\mathsf{\Lambda }}_N}\left|f\left(\lambda \right)\right|$ [60].

Applications to UEE Simulations

• RG flow tracking: computation of β-functions with high-order cut-off approximations [61].
• Time-integration of Lindblad evolution: error bounds via Taylor–Magnus expansion [62].
• Scaling-limit analysis: numerical confirmation of convergence as ${\mathsf{\Lambda }}_N\to \infty$.

2.8.1-2-c Details of the Functional-Analytic Proofs

The Gelfand–Naimark–Segal (GNS) Construction

Given a C${‌}^{*}$-algebra $\overline{\mathcal{A}}$ and a state $\omega$, one constructs a Hilbert space ${\mathcal{H}}_{\omega }$ and a representation ${\pi }_{\omega }$ such that

$$\overline{\mathcal{A}}\simeq {\pi }_{\omega }\left(\overline{\mathcal{A}}\right)\subset \mathcal{B}\left({\mathcal{H}}_{\omega }\right)$$

[63].

Existence of the Continuous Functional Calculus

For a self-adjoint $T\in \overline{\mathcal{A}}$ the algebraic homomorphism $\mathsf{\Phi }:C\left(\sigma \left(T\right)\right)\to C^{*}\left(T\right)\subset \overline{\mathcal{A}}$, $\mathsf{\Phi }\left(f\right)=f\left(T\right)$, is norm-continuous [64].

Continuity of the Spectral Map

If $\parallel T_n-T\parallel \to 0$ for self-adjoint $T_n,T$, then the Hausdorff distance between spectra satisfies ${\delta }_H\left(\sigma \left(T_n\right),\sigma \left(T\right)\right)\to 0$ [56].

Extension to a von Neumann Algebra

The weak-operator-topology closure $\mathcal{M}={\overline{\mathcal{A}}}^{\mathrm{WOT}}$ yields a von Neumann algebra

$$\overline{\mathcal{A}}\subset \mathcal{M}\subset \mathcal{B}\left(\mathcal{H}\right),$$

and establishes the relation with the σ-weak topology [65].

Consequences for the UEE

This functional-analytic framework guarantees

• rigorous control of operator approximations;
• the existence of a spectral gap [66];
• construction of GNS representations of the state space.

2.8.2-1 Definition of the Strong Operator Topology (SOT) and Bases of the Topology

In this subsection we rigorously introduce the strong operator topology (SOT) on the set of all bounded linear operators $\mathcal{B}\left(\mathcal{H}\right)$ acting on a Hilbert space $\mathcal{H}$, construct an explicit neighbourhood basis, and compare SOT with the operator-norm topology and the weak operator topology (WOT). SOT plays an essential rôle in semigroup theory and in continuity arguments for quantum dynamics.

Definition of Strong Convergence

Definition 40 

(strong convergence (SOT convergence)). A sequence $\left\{T_n\right\}\subset \mathcal{B}\left(\mathcal{H}\right)$ is said toconverge stronglyto an operator $T\in \mathcal{B}\left(\mathcal{H}\right)$ if, for every vector $\psi \in \mathcal{H}$,

$$\parallel T_n\psi -T\psi \parallel ⟶0(n\to \infty ).$$

We write $T_n\stackrel{\mathrm{SOT}}{⟶}T$ [20].

A Neighbourhood Basis for the SOT

Proposition 42 

(Basis of neighbourhoods for SOT [65]). A basic open set for the strong topology is of the form

$$U\left(T;{\psi }_1,\dots ,{\psi }_k;\epsilon \right):=\left\{S\in \mathcal{B}\left(\mathcal{H}\right)|\parallel S{\psi }_i-T{\psi }_i\parallel <\epsilon ,i=1,\dots ,k\right\},$$

where $T\in \mathcal{B}\left(\mathcal{H}\right)$, ${\psi }_1,\dots ,{\psi }_k\in \mathcal{H}$ are finitely many test vectors, and $\epsilon >0$. These sets form a basis for the SOT.

Comparison with the Operator-Norm and Weak Topologies

Proposition 43. 

The strong topology is weaker than the operator-norm topology and stronger than the weak operator topology; i.e.,

$$\parallel T_n-T\parallel \to 0⟹T_n\stackrel{\mathrm{SOT}}{⟶}T⟹T_n\stackrel{\mathrm{WOT}}{⟶}T$$

[67].

Proof. 

If $\parallel T_n-T\parallel \to 0$ then $\parallel T_n\psi -T\psi \parallel \le \parallel T_n-T\parallel \parallel \psi \parallel \to 0$ for all $\psi \in \mathcal{H}$, hence SOT convergence. If $T_n\to T$ strongly, then for all $\psi ,\varphi \in \mathcal{H}$, $\langle \varphi ,(T_n-T)\psi \rangle \to 0$, yielding WOT convergence.    □

Characterisation of SOT-Closed Sets

Proposition 44 

(SOT closure). A subset $\mathcal{S}\subset \mathcal{B}\left(\mathcal{H}\right)$ is SOT-closed iff it is closed in the norm topology on each orbit $\{T\psi \mid T\in \mathcal{S}\}\subset \mathcal{H}$ for every $\psi \in \mathcal{H}$ [52].

Significance for the UEE

• Finite-rank approximations $D_N=P_{N}D{P}_N$ converge to D in SOT, guaranteeing the validity of spectral truncations used in numerical implementations.
• The dissipative generator $\mathcal{L}$ of a Lindblad semigroup produces a strongly continuous one-parameter semigroup $\rho \left(t\right)=e^{t\mathcal{L}}\rho \left(0\right)$, so SOT underpins Trotter–Kato-type error estimates for time discretisation [37].
• In RG-flow analyses, SOT-defined invariant subspaces allow local stability of fixed points to be evaluated via spectral-gap estimates.

2.8.2-2 Applications of the Strong Topology within the UEE

We now present concrete examples illustrating how the strong operator topology is utilised in both numerical and analytical treatments of the Unified Evolution Equation (UEE).

SOT Convergence of Spectral Truncations

For the projection cut-off $D_N=P_{N}D{P}_N$ with $P_N={\chi }_{[-{\mathsf{\Lambda }}_N,{\mathsf{\Lambda }}_N]}\left(D\right)$,

$$\parallel D_N\psi -D\psi \parallel =\parallel (P_N-1)D\psi \parallel ⟶0(N\to \infty ),$$

for every $\psi \in \mathcal{H}$; hence $D_N\stackrel{\mathrm{SOT}}{⟶}D$ [66].

Time Evolution of a Lindblad Semigroup

A dissipative generator $\mathcal{L}$ generally yields a strongly (but not norm) continuous semigroup $e^{t\mathcal{L}}$ [37]. Thus

$$\underset{t\to 0}{lim}{\parallel e^{t\mathcal{L}}\rho -\rho \parallel }_1=0,$$

which justifies Trotter–Kato approximations [56,68].

Local Stability in RG Flow

For the discrete flow ${\mathsf{\Phi }}_{\delta }\left(D\right)=D+\delta \beta \left(D\right)$, SOT continuity allows the local stable manifold of a fixed point $D_{★}$ to be defined in SOT and analysed via spectral-gap techniques [69].

Approximation of Fractal Operators

Polynomial approximations ${\mathsf{\Pi }}_N=p_N\left(D\right)\in \mathcal{A}$ satisfy ${\mathsf{\Pi }}_N\stackrel{\mathrm{SOT}}{⟶}\mathsf{\Pi }\left(D_f\right)$, providing stable kernel evaluations in large-scale simulations [70].

Outlook

• SOT offers a weaker notion of convergence than the operator norm, facilitating error analysis for semigroups, projections, and RG flows in the UEE.
• Adaptive algorithms can exploit SOT-convergence to balance computational cost and accuracy when tuning cut-offs ${\mathsf{\Lambda }}_N$ or time steps $\mathsf{\Delta }t$.
• Future work will develop SOT-based boundary-layer analysis and adaptive integrators to enhance high-precision simulations of the UEE.

2.8.3-1 Definition of the Weak Operator Topology (WOT) and Bases of the Topology

In this subsection we introduce the weak operator topology (WOT) on the space of bounded linear operators $\mathcal{B}\left(\mathcal{H}\right)$ acting on a Hilbert space $\mathcal{H}$, construct an explicit neighbourhood basis, and clarify its relationship with the Schatten–von Neumann classes.

Definition of Weak Convergence

Definition 41 

(weak convergence (WOT convergence)). A sequence $\left\{T_n\right\}\subset \mathcal{B}\left(\mathcal{H}\right)$ is said toconverge weaklyto an operator $T\in \mathcal{B}\left(\mathcal{H}\right)$ if for all vectors $\varphi ,\psi \in \mathcal{H}$ one has

$$〈\varphi ,T_n\psi 〉⟶〈\varphi ,T\psi 〉(n\to \infty ).$$

We write $T_n\stackrel{\mathrm{WOT}}{⟶}T$ [52].

A Neighbourhood Basis for the WOT

Proposition 45 

(Basis of neighbourhoods for the WOT). A basic open set in the weak topology is of the form

$$U\left(T;{\varphi }_1,\dots ,{\varphi }_k;{\psi }_1,\dots ,{\psi }_k;\epsilon \right):=\left\{S\in \mathcal{B}\left(\mathcal{H}\right)|\left|\langle {\varphi }_i,(S-T){\psi }_i\rangle \right|<\epsilon ,i=1,\dots ,k\right\},$$

where $T\in \mathcal{B}\left(\mathcal{H}\right)$, ${\varphi }_1,\dots ,{\varphi }_k,{\psi }_1,\dots ,{\psi }_k\in \mathcal{H}$, and $\epsilon >0$ [65].

Relationship with the Schatten–von Neumann Classes

Definition 42 

(Schatten–von Neumann class $S_p$). For $1\le p<\infty$ the class

$$S_p\left(\mathcal{H}\right):=\left\{T\in \mathcal{B}\left(\mathcal{H}\right)|\sum _j{\mu }_j{\left(T\right)}^p<\infty \right\},$$

consists of those operators whose singular values $\left\{{\mu }_j\left(T\right)\right\}$ are p-summable.

Proposition 46 

($S_p$ is WOT-dense). For each $1\le p<\infty$ the class $S_p\left(\mathcal{H}\right)$ (in particular the Hilbert–Schmidt class $S_2$ and the trace class $S_1$) is dense in $\mathcal{B}\left(\mathcal{H}\right)$ with respect to the weak operator topology [71].

Comparison with Other Topologies

$$\mathrm{SOT}\mathrm{convergence}⟹\mathrm{WOT}\mathrm{convergence},\parallel ·\parallel -\mathrm{convergence}⟹\mathrm{WOT}\mathrm{convergence}.$$

Thus WOT is strictly weaker than the strong operator topology (SOT).

Relevance for the Theory

• The Lindblad–Kossakowski semigroup $\rho \left(t\right)=e^{t\mathcal{L}}\rho \left(0\right)$ is WOT-continuous (strongly-${‌}^{*}$ continuous), which is crucial for analysing time-dependent expectation values $Tr\left(A\rho \right(t\left)\right)$ [63].
• In the Barnes–Lagrange elimination procedure the resolvent ${(D+\lambda )}^{-1}$ is treated as a WOT-continuous operator-valued function of the complex parameter $\lambda$ [56].
• Formulating the Schrödinger–Heisenberg duality within the WOT framework guarantees the interchangeability of limits in operators and limits in expectation values.

2.8.3-2 Applications of the WOT within the UEE

We now present concrete examples that illustrate how the weak operator topology is used in both theoretical and numerical aspects of the Unified Evolution Equation (UEE).

Time Evolution of Expectation Values

For a quantum state $\rho \left(t\right)$ and an observable O, the time dependence ${\langle O\rangle }_t=Tr\left(O\rho \left(t\right)\right)$ is analysed using the WOT-continuity of the semigroup $t\mapsto \rho \left(t\right)$ [37,63]. Indeed,

$$\underset{\delta \to 0}{lim}\left|Tr\left(O\left(\rho \right(t+\delta )-\rho (t\left)\right)\right)\right|=0,$$

so that $\rho (t+\delta )\to \rho \left(t\right)$ in WOT.

Resolvents in Barnes–Lagrange Elimination

For each resolvent ${(a_i+\lambda )}^{-1}$, the map $\lambda \mapsto {(a_i+\lambda )}^{-1}$ is WOT–continuous, ensuring that contour integrals and residue calculations used in the Barnes–Lagrange elimination are well-defined [56].

Convergence of Numerical Approximations

If a sequence of finite-dimensional approximations ${\rho }_N$ satisfies ${\rho }_N\stackrel{\mathrm{WOT}}{⟶}\rho$, then for every finite-rank observable O one has $Tr\left(O{\rho }_N\right)\to Tr\left(O\rho \right)$, so physical expectation values converge [66].

WOT-Approximation of Fractal–Dissipative Operators

Polynomial approximations $\left\{{\mathsf{\Pi }}_N\right\}\subset \overline{\mathcal{A}}$ satisfy ${\mathsf{\Pi }}_N\stackrel{\mathrm{WOT}}{⟶}\mathsf{\Pi }\left(D_f\right)$, hence $Tr\left({\mathsf{\Phi }}_I{\mathsf{\Pi }}_N\right)\to Tr\left({\mathsf{\Phi }}_I\mathsf{\Pi }\left(D_f\right)\right)$. This ensures stability of the dissipative–information equations in numerical simulations [70].

Outlook

• WOT directly controls convergence of experimentally measurable expectation values, providing clear physical interpretation.
• By combining WOT with SOT one can avoid the high cost of operator-norm convergence while retaining rigorous error bounds in numerical algorithms.
• In asymptotic expansions that include non–self-adjoint perturbations, WOT-stability ensures the existence and uniqueness of solutions (WOT version of the Trotter–Kato product formula) [68].

2.8.4-1 Definition and Structure of the σ-Weak Operator Topology

In this subsection we define the σ-weak operator topology (σWOT) on $\mathcal{B}\left(\mathcal{H}\right)$ and explain its relation to the predual in a rigorous manner.

Introduction of the Predual Space

Definition 43 

(Space of trace-class operators). Let ${\mathcal{B}}_1\left(\mathcal{H}\right)$ denote the set of all trace-class operators on the Hilbert space $\mathcal{H}$. Then a canonical duality isomorphism

$${\left({\mathcal{B}}_1\left(\mathcal{H}\right)\right)}^{*}\simeq \mathcal{B}\left(\mathcal{H}\right)$$

holds; hence ${\mathcal{B}}_1\left(\mathcal{H}\right)$ is thepredualof $\mathcal{B}\left(\mathcal{H}\right)$ [65].

Definition of σ-Weak Convergence

Definition 44 

(σ-weak convergence). A sequence $\left\{T_n\right\}\subset \mathcal{B}\left(\mathcal{H}\right)$ is said toconverge σ-weaklyto $T\in \mathcal{B}\left(\mathcal{H}\right)$ if for every $S\in {\mathcal{B}}_1\left(\mathcal{H}\right)$ one has

$$Tr\left(S{T}_n\right)⟶Tr\left(ST\right)(n\to \infty ).$$

We write $T_n\stackrel{\sigma -\mathrm{weak}}{⟶}T$ [63].

A Basis of Neighbourhoods for the σ-Weak Topology

For $T\in \mathcal{B}\left(\mathcal{H}\right)$, trace-class operators $S_1,\dots ,S_k\in {\mathcal{B}}_1\left(\mathcal{H}\right)$, and $\epsilon >0$, set

$$U\left(T;S_1,\dots ,S_k;\epsilon \right):=\left\{X\in \mathcal{B}\left(\mathcal{H}\right)|\left|Tr\left(S_{i}X\right)-Tr\left(S_{i}T\right)\right|<\epsilon ,i=1,\dots ,k\right\},$$

which forms a neighbourhood basis of the σ-weak topology [52].

Inclusion Relations with Other Topologies

$$\mathrm{WOT}\mathrm{convergence}⟹\sigma -\mathrm{weak}\mathrm{convergence},\sigma -\mathrm{weak}\mathrm{convergence}⟹\sigma {-\mathrm{strong}}^{*}\mathrm{convergence},$$

so the σ-weak topology is the natural topology for von Neumann algebras [65].

Theoretical Properties

• A von Neumann algebra is a σ-weakly closed C${‌}^{*}$-algebra, and together with its predual it satisfies the bicommutant theorem $\mathcal{M}={\mathcal{M}}^{\prime \prime }$.
• Representations arising in the GNS construction of states are σ-weakly continuous, allowing one to analyse conditional expectations and modular operators within this topology [72].

2.8.4-2 Von Neumann Algebras and σ-Weak Closure

In this subsection we consider a subalgebra $\overline{\mathcal{A}}\subset \mathcal{B}\left(\mathcal{H}\right)$, define its σ-weak closure as a von Neumann algebra, and prove the double-commutant theorem together with the covering property.

Von Neumann Algebra as a σ-Weak Closure

Definition 45 

(Von Neumann algebra). A subalgebra $\mathcal{M}\subset \mathcal{B}\left(\mathcal{H}\right)$ that is closed in the σ-weak operator topology is called a von Neumann algebra [52, Def. II.2.1].

The Bicommutant Theorem

Theorem 10 

(Double-Commutant Theorem). For any $\mathcal{A}\subset \mathcal{B}\left(\mathcal{H}\right)$ one has

$${\mathcal{A}}^{\prime \prime }={\left({\mathcal{A}}^{\prime }\right)}^{\prime }={\overline{\mathcal{A}}}^{\sigma -\mathrm{weak}},$$

where the bar denotes the σ-weak closure [65, Th. II.2.4].

Proof. 

The commutant ${\mathcal{A}}^{\prime }$ is σ-weakly closed, and $\mathcal{A}\subset {\mathcal{A}}^{\prime \prime }$. Using Wigner’s theorem (Tomanaga–Steinhaus method) and a density argument one obtains ${\overline{\mathcal{A}}}^{\sigma -\mathrm{weak}}={\mathcal{A}}^{\prime \prime }$ [54, §2].    □

Relation to the σ-Strong${‌}^{*}$ Topology

A von Neumann algebra is also closed in the σ-strong${‌}^{*}$ topology [65, Prop. III.2.6]; hence the multiple-topology structure on $\mathcal{M}$ is established by the compatibility of the σ-weak and σ-strong${‌}^{*}$ topologies.

Applications to the UEE

• The Lindblad generator $\mathcal{L}$ leaves the von Neumann algebra $\mathcal{M}={\overline{\mathcal{A}}}^{\prime \prime }$ invariant and generates a σ-weakly continuous semigroup [73].
• In dissipative–unitary mixed systems, the duality between states (trace-class operators) and observables (elements of a von Neumann algebra) is preserved by the σ-weak topology [71].
• Descriptions of Barnes–Lagrange elimination and of RG flows within the σ-weak closure $\mathcal{M}$ integrate resolvent expansions and residue calculations into the framework of von Neumann analysis.

2.8.4-3 σ-Weak Continuity in the UEE

Here we illustrate how σ-weak continuity is used for reversible and irreversible dynamics as well as for the structure of field-equation solutions within the Unified Evolution Equation (UEE).

σ-Weak Continuity of Lindblad Semigroups

For the Lindblad–Gorini–Kossakowski semigroup ${\left\{{\mathcal{T}}_t\right\}}_{t\ge 0}$ on a von Neumann algebra $\mathcal{M}$ one has

$$\underset{t\to 0}{lim}Tr\left(S{\mathcal{T}}_t\left(T\right)\right)=Tr\left(ST\right),\forall S\in {\mathcal{B}}_1\left(\mathcal{H}\right),T\in \mathcal{M},$$

so the semigroup is σ-weakly continuous [73].

Preservation of the State–Observable Duality

Because of the duality between ${\mathcal{B}}_1\left(\mathcal{H}\right)$ and $\mathcal{M}$, the switch between states and observables can be described by σ-weakly continuous maps [52, Prop. V.2.3].

Convergence of Observables in Discrete Time Integration

For the discrete time step ${\mathcal{T}}_{\delta }^n={(1+\delta \mathcal{L})}^n$ one obtains

$$\underset{\delta \to 0}{lim}Tr\left(S{\mathcal{T}}_{\delta }^n\left(T\right)\right)=Tr\left(S{e}^{t\mathcal{L}}\left(T\right)\right),$$

which is guaranteed by σ-weak continuity and therefore secures the numerical convergence of observables [19, §7.1].

Variational Analysis in the Action-Principle Version UEE${‌}_{\mathrm{var}}$

The phase stability of Euler–Lagrange solutions can be evaluated in the σ-weak topology, so that bifurcation of critical points and symmetry breaking can be reduced to von Neumann analysis [65, Chap. IX].

Summary

σ-Weak continuity, formulated in the language of von Neumann algebras, provides a consistent treatment of the state–observable duality and gives a rigorous framework for both the reversible and irreversible dynamics of the UEE.

2.9. Hierarchy of Hilbert–Schmidt Operators

2.9.1 Definition and Basic Properties of the Schatten–von Neumann Classes

In this subsection we introduce the Schatten–von Neumann classes ${\left\{S_p\left(\mathcal{H}\right)\right\}}_{p\ge 1}$ on a Hilbert space $\mathcal{H}$, and we prove the norm structure and completeness of the Hilbert–Schmidt class $S_2\left(\mathcal{H}\right)$ and the trace-class $S_1\left(\mathcal{H}\right)$. We also indicate their relevance for the UEE theory [19, Chap VI].

Definition of the Schatten–von Neumann Classes

Definition 46 

(Schatten–von Neumann class $S_p$). Let ${\left\{{\mu }_n\left(T\right)\right\}}_{n=1}^{\infty }$ be the singular values (i.e., the moduli of the eigenvalues) of $T\in \mathcal{B}\left(\mathcal{H}\right)$. The class $S_p\left(\mathcal{H}\right)$ is defined by

$$S_p\left(\mathcal{H}\right):=\left\{T\in {\mathcal{B}\left(\mathcal{H}\right)|\parallel T\parallel }_p^p:=\sum _{n=1}^{\infty }{\mu }_n{\left(T\right)}^p<\infty \right\},p\ge 1.$$

The case $p=2$ is called the Hilbert–Schmidt class, while $p=1$ is called thetrace (trace-class) operators[71].

Norm Properties and Completeness

Proposition 47 

(Properties of the Schatten norm). For all $T,S\in S_p\left(\mathcal{H}\right)$ one has

1. 

${\parallel T\parallel }_p\ge 0$ and ${\parallel T\parallel }_p=0\iff T=0$;

2. 

${\parallel \alpha T\parallel }_p={\left|\alpha \right|\parallel T\parallel }_p$ for all $\alpha \in \mathbb{C}$;

3. 

${\parallel T+S\parallel }_p\le {\parallel T\parallel }_p+{\parallel S\parallel }_p$ (triangle inequality).

Hence $(S_p\left(\mathcal{H}\right),\parallel ·{\parallel }_p)$ is a normed space [71].

Proposition 48 

(Banach completeness). $(S_p\left(\mathcal{H}\right),\parallel ·{\parallel }_p)$ is complete; that is, every Cauchy sequence $\left\{T_n\right\}$ converges to some $T\in S_p\left(\mathcal{H}\right)$ with $\parallel T_n{-T\parallel }_p\to 0$ [71].

Concrete Features of $S_2$ and $S_1$

• $S_2\left(\mathcal{H}\right)$ becomes a Hilbert space with the inner product $\langle T,S\rangle :=Tr\left(T^{†}S\right)$ [19, §VI.6].
• $S_1\left(\mathcal{H}\right)$ is a Banach space with the trace norm ${\parallel T\parallel }_1=Tr\sqrt{T^{†}T}$ [71].
• There is the inclusion chain $S_1\subset S_2\subset \mathcal{B}\left(\mathcal{H}\right)$ (proved in the next subsection) [71].

Relation to the UEE

• The operator algebra $\mathcal{A}$ constructed in Subsec. 2.5.4 lies in the chain $S_2\subset S_1\subset \mathcal{B}\left(\mathcal{H}\right)$; thus $S_p$ classes are essential for local finite-rank approximations and for dissipative analyses in the UEE [73].
• The Hilbert–Schmidt norm is directly used for the evaluation of quadratic interaction terms $Tr\left(V_j^{†}{V}_k\right)$ appearing in the dissipator [2, Eq. 3.12].
• The trace norm underlies the proof of complete positivity and trace preservation (CPTP) of the dynamical maps [74, Thm. 4.3].

2.9.2-1 Inclusion Proof for Finite-Rank Operators

We first focus on the class of finite-rank operators $\mathcal{F}\left(\mathcal{H}\right)\subset \mathcal{B}\left(\mathcal{H}\right)$.

Definition (Finite-rank operators)

$$\mathcal{F}\left(\mathcal{H}\right):=\{T\in \mathcal{B}(\mathcal{H}\left)\right|\left(T\right)<\infty \}.$$

Such operators admit an explicit singular-value expansion [71].

Proposition 2.9.2.1

Finite-rank operators belong to both the Hilbert–Schmidt and the trace classes:

$$\mathcal{F}\left(\mathcal{H}\right)\subset S_2\left(\mathcal{H}\right)\cap S_1\left(\mathcal{H}\right)$$

[71].

Lemma 2.9.2.2

$\mathcal{F}\left(\mathcal{H}\right)$ is dense in $S_2\left(\mathcal{H}\right)$ and also dense in $S_1\left(\mathcal{H}\right)$ [71].

2.9.2-2 Conditions and Caveats for General Hilbert–Schmidt Operators

In general a Hilbert–Schmidt operator $T\in S_2\left(\mathcal{H}\right)$ does not necessarily belong to the trace class $S_1\left(\mathcal{H}\right)$. Within the UEE, however, the operators considered usually satisfy the following additional assumption, which implies inclusion in $S_1$ [71].

Assumption (extra condition for nuclearity)

There exist $p<2$ and a constant $C>0$ such that

$$\sum _{n=1}^{\infty }{\mu }_n{\left(T\right)}^p<\infty ,$$

i.e., the sequence of singular values is p-summable [19, Prop.IX.11].

Proposition 2.9.2.3

Under this assumption $T\in S_2$ is actually contained in the trace class $S_1$.

Proof. 

Using Hölder’s inequality [71],

$$\sum _{n=1}^{\infty }{\mu }_n\left(T\right)=\sum _{n=1}^{\infty }{\mu }_n{\left(T\right)}^{p/2}{\mu }_n{\left(T\right)}^{1-p/2}\le {\left(\sum _n{\mu }_n{\left(T\right)}^p\right)}^{1/2}{\left(\sum _n{\mu }_n{\left(T\right)}^{{\displaystyle \frac{2-p}{2-p}}}\right)}^{{\displaystyle \frac{2-p}{2p}}}.$$

The first factor is finite by assumption. The second factor is finite because ${\mu }_n\left(T\right)\to 0$ and the series converges by the comparison test [19]. Hence $\sum {\mu }_n\left(T\right)<\infty$ and ${\parallel T\parallel }_1<\infty$.    □

Remarks

• Without extra conditions one has $S_2\not\subset S_1$, but physical operators often satisfy the above assumption owing to global spectral cut-offs or smoothness requirements [71].
• In numerical implementations of the UEE one introduces a spectral projection $P_N$, so that finite-rank approximations always lie in $S_1$ [19, §VI.6].

2.9.3 Inclusion $S_1\subset \mathcal{B}\left(\mathcal{H}\right)$

In this subsection we prove that the trace–class $S_1\left(\mathcal{H}\right)$ is contained in the algebra of all bounded operators $\mathcal{B}\left(\mathcal{H}\right)$. We also establish the relevant norm inequality and the completeness properties [71].

Boundedness of Trace–Class Operators

Proposition 49. 

For every $T\in S_1\left(\mathcal{H}\right)$ the operator T is bounded, and the following estimate holds:

$${\parallel T\parallel }_{\mathcal{B}}\le {\parallel T\parallel }_1:=Tr\sqrt{T^{†}T}.$$

Proof. 

The inequality $\parallel T\psi \parallel \le {\parallel T\parallel }_1\parallel \psi \parallel$ is a direct consequence of the Cauchy–Schwarz inequality for trace–class operators [71].    □

Completeness and Closedness

Proposition 50. 

$S_1\left(\mathcal{H}\right)$ is complete with respect to the trace norm ${\parallel ·\parallel }_1$, and it is closed as a subspace of $\mathcal{B}\left(\mathcal{H}\right)$.

Proof. 

Banach completeness follows from [71]; norm–closedness is proved in [19], Prop. IX.10].    □

Physical Significance within the UEE

• To ensure complete positivity and trace preservation (CPTP) of the dissipator [2], one assumes $V_j\in S_1$ so that $Tr\left(V_j^{†}{V}_j\right)<\infty$.
• In numerical time evolution, when the state $\rho \in S_1$ is updated, the trace–norm error estimate [74, §7.1] can be applied directly.
• In the variational formulation UEE${‌}_{\mathrm{var}}$ the space $S_1$ serves naturally as the variational domain [73].

2.10. $\sqrt{-\square }$ Spectral Theory

2.10.0 Analytic Definition of $\sqrt{-\square }$ on Euclid–Lorentz Space-Time

Because the d’Alembert operator $\square ={\nabla }_{\mu }{\nabla }^{\mu }$ possesses an indefinite Lorentzian signature, conventional spectral theory cannot be applied directly. We therefore define $\sqrt{-\square }$ rigorously by the following procedure [4, §6.3][19, Thm.VIII.4].

Wick Rotation and the Euclid Box

Rotating the real time coordinate $x^0$ to imaginary time $x^4=i{x}^0$ yields

$$\square ⟶-{\mathsf{\Delta }}_E:=-\sum _{i=1}^4{\displaystyle \frac{{\partial }^2}{\partial x_E^i{‌}^2}},$$

where ${\mathsf{\Delta }}_E$ is the Euclidean Laplacian, a self-adjoint, non-negative operator [30, p. 306].

Spectral Decomposition

On the Hilbert space $L^2\left(M_E\right)$ one has the spectral resolution

$$-{\mathsf{\Delta }}_E={\int }_0^{\infty }\lambda d{E}_{\lambda },$$

with $E_{\lambda }$ the projection–valued spectral measure [19, Cor. VIII.2].

Square Root via Functional Calculus

Applying the Borel functional calculus [19, Thm. VIII.6] gives

$$\sqrt{-{\mathsf{\Delta }}_E}={\int }_0^{\infty }\sqrt{\lambda }d{E}_{\lambda },$$

a self-adjoint, non-negative operator whose domain equals the Sobolev space $H^1\left(M_E\right)$ [75, Prop. 3.1].

Analytic Inverse Rotation

Analytically rotating back to Lorentzian space–time defines

$$\sqrt{-\square }:=\left(\sqrt{-{\mathsf{\Delta }}_E}\right){|}_{x_E^4=i{x}^0}.$$

Thus $\sqrt{-\square }$ is rigorously specified as a self-adjoint positive operator [76, §9.2].

Consistency Check

Because the construction relies only on standard theorems of Borel calculus and spectral analysis, self-adjointness and the domain identity $\mathrm{Dom}\left(\sqrt{-\square }\right)=H^1\left(M^4\right)$ are ensured [6, Thm. X.23].

2.10.1 Spectral Decomposition in Fourier Representation

We next decompose the d’Alembert operator

$$\square ={\eta }^{\mu \nu }{\partial }_{\mu }{\partial }_{\nu }={\partial }_t^2-{\mathsf{\Delta }}_x$$

on flat Minkowski space ${\mathbb{R}}^{1,3}$ by Fourier analysis [77, Chap. 7].

Full Space-Time Fourier Transform

Definition 47 

(Four-dimensional Fourier transform). For $\psi \in \mathcal{S}\left({\mathbb{R}}^{1,3}\right)$ define

$$\tilde{\psi }\left(k\right)={\displaystyle \frac{1}{{\left(2\pi \right)}^2}}{\int }_{{\mathbb{R}}^{1,3}}{e}^{i{k}_{\mu }{x}^{\mu }}\psi \left(x\right)d^{4}x,k·x=k_0{x}^0-\mathbf{k}·\mathbf{x},$$

with the inverse transform defined analogously [20, §7.1].

Action of □ in Fourier Space

Proposition 51. 

Under the Fourier transform one has $\square \psi \left(x\right)\stackrel{\mathcal{F}}{⟷}-k^2\tilde{\psi }\left(k\right)$, where $k^2=k_0^2-{\left|\mathbf{k}\right|}^2$.

Proof. 

Using ${\partial }_{\mu }\psi \mapsto i{k}_{\mu }\tilde{\psi }$ and $\square \psi ={\eta }^{\mu \nu }{\partial }_{\mu }{\partial }_{\nu }\psi$ immediately yields the statement [78, §0.2].    □

Self-Adjointness and the Spectral Measure

Proposition 52 

(Self-adjointness). On the domain $\mathrm{Dom}(\square )=H^2\left({\mathbb{R}}^{1,3}\right)\subset L^2\left({\mathbb{R}}^{1,3}\right)$, the operator □ is self-adjoint and its spectrum equals the entire real line.

Proof. 

(i) Integration by parts shows $\langle \varphi ,\square \psi \rangle =\langle \square \varphi ,\psi \rangle$ because boundary terms vanish [19]. (ii) In Fourier space □ acts as multiplication by the real variable $-k^2$; standard multiplication-operator spectral theory applies [19, Thm. VIII.4].    □

Construction of the Spectral Measure

Definition 48 

(Spectral measure). For Fourier variables $(k^0,\mathbf{k})$ define the projection- valued measure

$$E\left(\mathsf{\Delta }\right)\psi \left(x\right):={\displaystyle \frac{1}{{\left(2\pi \right)}^2}}{\int }_{k^2\in \mathsf{\Delta }}{e}^{-ik·x}\tilde{\psi }\left(k\right)d^{4}k,$$

where $\mathsf{\Delta }\subset \mathbb{R}$ is Borel measurable [20, §13.5].

Proposition 53 

(Spectral decomposition formula). 

$$\square ={\int }_{\sigma (\square )}\lambda dE\left(\lambda \right),$$

and for any Borel function f one has $f(\square )=\int f\left(\lambda \right)dE\left(\lambda \right)$ [19, Thm. VIII.6].

Relevance to the UEE

Because $\sqrt{-\square }=\int \left|k\right|dE\left(k^2\right)$, the operator square root enters directly in the reversible component of the UEE as well as in the construction of the dissipative functional [79, §4].

2.10.2-1 Construction of $\sqrt{-\square }$ via Borel Functional Calculus

In this subsection we employ the spectral measure $E\left(\lambda \right)$ built in Sect. 2.10.0.5 and define $\sqrt{-\square }$ rigorously by means of the Borel functional calculus, describing its domain and explicit action in detail[19, Thm. VIII.6].

General theorem for the Borel functional calculus

Theorem 11 

(Borel functional calculus). Let T be a self-adjoint operator with spectral measure $E\left(\lambda \right)$. For every Borel–measurable function $f:\sigma \left(T\right)\to \mathbb{C}$,

$$f\left(T\right):={\int }_{\sigma \left(T\right)}f\left(\lambda \right)dE\left(\lambda \right)$$

defines a (possibly unbounded) self-adjoint operator with domain

$$\mathrm{Dom}\left(f\left(T\right)\right)=\left\{\psi |{\int }_{\sigma \left(T\right)}{\left|f\left(\lambda \right)\right|}^{2}d〈\psi ,E\left(\lambda \right)\psi 〉<\infty \right\}.$$

[19, Prop.VIII3]

Sketch. 

Using basic measure–theoretic properties of $L^2$-spaces and Stieltjes integration, one verifies that the operator defined by the above integral is closed and self-adjoint; details are given in [76, §6.3].    □

Application to $f\left(\lambda \right)=\sqrt{-\lambda }$

Since the spectrum of □ is the full real line and the spectrum of $-\square$ is contained in $[0,\infty )$, we apply the measurable function

$$f\left(\lambda \right)=\sqrt{max\{\lambda ,0\}}$$

to $-\square$ and set

$$\sqrt{-\square }=f(-\square )={\int }_0^{\infty }\sqrt{\lambda }d{E}_{-\square }\left(\lambda \right),$$

where by definition $E_{-\square }\left(\lambda \right):=E(-\lambda )$[19, Cor. VIII.2].

Explicit domain

The natural domain of $\sqrt{-\square }$ is

$$\mathrm{Dom}\left(\sqrt{-\square }\right)=\left\{\psi \in L^2\left({\mathbb{R}}^{1,3}\right)|{\int }_0^{\infty }\lambda d〈\psi ,E_{-\square }\left(\lambda \right)\psi 〉<\infty \right\},$$

which coincides—via Fourier analysis—with the Sobolev space $H^1\left({\mathbb{R}}^{1,3}\right)$ [75, Prop. 3.1].

Equivalence in Fourier representation

In Fourier space $\sqrt{-\square }\psi \left(x\right)\leftrightarrow \left|k\right|\tilde{\psi }\left(k\right)$, so that $\mathrm{Dom}\left(\sqrt{-\square }\right)=\{\psi \mid |k|\tilde{\psi }\in L^2\left({\mathbb{R}}^4\right)\},$ exactly the statement $\psi \in H^1$[77, Chap. 7].

Applications within the UEE

• The fractal operator ${\displaystyle \mathsf{\Pi }\left(D_f\right)=sin\left(\pi \sqrt{-\square }/\mathsf{\Lambda }\right)}$ is defined directly from the above construction of $\sqrt{-\square }$ via the Borel calculus[79, Eq.(4.12)].
• Numerically one inserts a spectral cut-off $P_N$ and approximates $\sqrt{-\square }\approx P_N\left|k\right|P_N$, which converges in the SOT[19, §VIII.5].
• In the variational UEE${‌}_{\mathrm{var}}$ formulation, the variation $\delta D_f\sim \delta \sqrt{-\square }$ is handled exactly through this framework.

2.10.2-2 Proof of Positivity at the Operator Level and Applications to the UEE

Definition of a positive operator

Definition 49 

(Positive operator). A self-adjoint operator T is positive if

$$\langle \psi ,T\psi \rangle \ge 0,\forall \psi \in \mathrm{Dom}\left(T\right).$$

[19, Def. VI.2]

Fourier-space verification

With $\sqrt{-\square }\psi \left(x\right)\leftrightarrow \left|k\right|\tilde{\psi }\left(k\right)$ (as established in Sect. 2.10.0.10), for every $\psi \in \mathrm{Dom}\left(\sqrt{-\square }\right)$,

$$〈\psi ,\sqrt{-\square }\psi 〉={\int }_{{\mathbb{R}}^4}\overline{\tilde{\psi }\left(k\right)}\left|k\right|\tilde{\psi }\left(k\right)d^{4}k={\int }_{{\mathbb{R}}^4}\left|k\right|{\left|\tilde{\psi }\left(k\right)\right|}^2{d}^{4}k\ge 0$$

[77].

Consistency with self-adjointness

Together with the self-adjointness proved in Sect. 2.10.0.5, this establishes that

$$\sqrt{-\square }\ge 0,$$

i.e., it is a positive operator.

Remarks on the domain

Because $\mathrm{Dom}\left(\sqrt{-\square }\right)=H^1\left({\mathbb{R}}^{1,3}\right)$, any $\psi$ in the domain guarantees finiteness of the integral in the previous paragraph [75, Prop. 3.1].

Applications to the UEE

• The positivity of $\sqrt{-\square }$ underpins lower-bound estimates for the action functional and for the dissipative functional $\mathsf{\Gamma }\left[D_f\right]$[79, Eq.(4.12)].
• In the reversible generator $L_0\left[\rho \right]=-i[D_G,\rho ]$, spectral analysis with the graph norm uses the non-negative spectrum of $\sqrt{-\square }$ to secure the stability of the unitary evolution [19, Thm. VIII.6].
• In UEE${‌}_{\mathrm{var}}$ the variation $\delta \sqrt{-\square }$ contributes hermitian, positive terms, preserving consistency in linear-response and perturbative analyses [76, §6.3].

2.11. First Definition of $D_f$: Geometric Induction

2.11.1 Definition of the Phase-Space Volume Scale and Its Basic Properties

In this subsection we rigorously define the volume-scale function

$$V\left(k\right)=Vol\left(B\left(k\right)\right)$$

on a phase space X (for example, a Riemannian manifold or a local approximation thereof) and prove its fundamental properties.[80, Ch. 3][81, §1.1]

Definition of the volume-scale function

Definition 50 

(Ball of scale k). For a point $x\in X$ the ball $B(x,k)$ is defined by the geodesic distance condition $d(x,y)\le k$.[82, p. 40] When we write $Vol\left(B\right(k\left)\right)$ we assume that X is situated in a uniformly regular region so that the volume of a ball depends only on the scale k.

Definition 51 

(Volume-scale function $V\left(k\right)$). 

$$V\left(k\right):=Vol\left(B\left(k\right)\right)={\int }_{B\left(k\right)}d\mu \left(x\right),$$

where $d\mu \left(x\right)$ is the Riemannian measure $\sqrt{detg}{d}^{n}x$.[83, §2]

Small- and large-scale behaviour

Proposition 54 

(Small-scale limit). As $k\to 0$,

$$V\left(k\right)={\omega }_n{k}^n+o\left(k^n\right),$$

where ${\omega }_n$ is the volume of the unit ball in ${\mathbb{R}}^n$.[84, Prop. 2.9]

Proof. 

Use local geodesic coordinates and a Taylor expansion of the Jacobian determinant.    □

Proposition 55 

(Large-scale limit). If X is non-compact, then as $k\to \infty$

$$V\left(k\right)\sim C{k}^{D_f},$$

so that a fractal dimension $D_f$ can be defined.[85, Thm. 1.3]

Proof. 

Assuming uniform homogeneity, apply the asymptotic scaling relation $V\left(\lambda k\right)={\lambda }^{D_f}V\left(k\right)$ inductively.    □

Physical significance within the UEE

• $V\left(k\right)$ serves as a scale-dependent parameter that controls the effective number of degrees of freedom of the information flux density ${\mathsf{\Phi }}_I$.
• In the action principle of UEE${‌}_{\mathrm{fld}}$ the function $V\left(k\right)$ enters through the cut-off $\mathsf{\Lambda }$; its limit $\mathsf{\Lambda }\to \infty$ determines the dissipative structure of the theory.
• The value of $D_f$ quantitatively characterises the self-similar structure and scaling invariance inherent in the physical model.[86]

2.11.2-1 Framework of Geometric Induction and the Initial Step

In this subsection we establish the framework of geometric induction for deriving a fractal dimension $D_f$ that satisfies the asymptotic relation

$$V\left(k\right)\propto k^{D_f},$$

and we describe the initial step in detail.[87, §8.4]

The idea of geometric induction

As the basic hypothesis we assume the self-similarity condition

$$V\left(\lambda k\right)={\lambda }^{D_f}V\left(k\right)$$

for all $\lambda >0$ and for a suitable range of k. Taking a reference scale $k=k_0$ we obtain the unique definition

$$D_f={\displaystyle \frac{lnV\left(\lambda k_0\right)-lnV\left(k_0\right)}{ln\lambda }}(\forall \lambda >0).$$

[88]

Formalisation of the initial step

Definition 52 

(Reference scale $k_0$). Fix an arbitrary reference scale $k_0>0$ and set $V_0:=V\left(k_0\right)$.

Lemma 8 

(Definition of the first inductive hypothesis). If, for some $\lambda >0$ and the chosen $k_0$,

$$V\left(\lambda k_0\right)={\lambda }^{D_f}{V}_0,$$

then the same self-similarity holds inductively for every $k={\lambda }^n{k}_0$ with $n\in \mathbb{N}$.

Proof. 

The case $n=1$ is the hypothesis itself. For general n,

$$V\left({\lambda }^n{k}_0\right)=V\left(\lambda ·{\lambda }^{n-1}{k}_0\right)={\lambda }^{D_f}V\left({\lambda }^{n-1}{k}_0\right)={\lambda }^{D_f}{\left({\lambda }^{D_f}\right)}^{n-1}{V}_0={\left({\lambda }^n\right)}^{D_f}{V}_0.$$

   □

Uniqueness of the initial step

Proposition 56 

(Uniqueness of the first inductive constant). For $\lambda \ne 1$ and $V_0>0$ the equation $lnV\left(\lambda k_0\right)-ln{V}_0=D_{f}ln\lambda$ determines $D_f$ uniquely.

Proof. 

Since $ln\lambda \ne 0$ and the numerator is fixed,

$$D_f={\displaystyle \frac{lnV\left(\lambda k_0\right)-ln{V}_0}{ln\lambda }}$$

is unique.    □

Relation to the theory

• The value of $D_f$ fixed in the initial step serves as the reference for fractal-dimension feedback in the UEE and fixes the non-zero scale dependence of the dissipative functional $\mathsf{\Gamma }\left[D_f\right]$.
• In numerical simulations one may choose $k_0$ and $\lambda$ as the lattice spacing and rescaling factor; plotting $lnV$ versus $lnk$ and performing a linear regression yields an empirical estimate of $D_f$.[89, Chap. 2]

2.11.2-2 General Inductive Step and Proof of Convergence for Infinite Induction

Building on the first-level induction in Section 2.11.0.3, we prove that $V\left({\lambda }^n{k}_0\right)={\lambda }^{n{D}_f}{V}_0$ holds for any $n\in \mathbb{N}$ and $\lambda >0$, and we extend the relation $V\left(k\right)\propto k^{D_f}$ continuously to all scales $k>0$. This establishes uniqueness and convergence of the infinitely inductive construction of the fractal dimension $D_f$.[87, §8.4][85, Thm. 1.3][88]

Generalisation of the induction on natural numbers

Lemma 9 

(Inductive step for natural numbers). For every $n\in \mathbb{N}$,

$$V\left({\lambda }^{n+1}{k}_0\right)={\lambda }^{D_f}V\left({\lambda }^n{k}_0\right)={\lambda }^{(n+1)D_f}{V}_0.$$

Proof. 

The case $n=0$ is Lemma 8. Assume the statement for n; then

$$V\left({\lambda }^{n+1}{k}_0\right)=V\left(\lambda ·{\lambda }^n{k}_0\right)={\lambda }^{D_f}V\left({\lambda }^n{k}_0\right)={\lambda }^{D_f}{\lambda }^{n{D}_f}{V}_0={\lambda }^{(n+1)D_f}{V}_0.$$

   □

Extension to rational exponents

Lemma 10 

(Induction for rational exponents). For any rational number $q=m/n$ ($m,n\in \mathbb{N}$) one has

$$V\left({\lambda }^q{k}_0\right)={\lambda }^{q{D}_f}{V}_0.$$

Proof. 

From the previous lemma, $V\left({\lambda }^m{k}_0\right)={\lambda }^{m{D}_f}{V}_0$. Consider ${\left({\lambda }^m\right)}^{1/n}$; by measurability and monotonicity[81, Prop. 2.1],

$$V{\left({\left({\lambda }^m\right)}^{1/n}{k}_0\right)}^n=V\left({\lambda }^m{k}_0\right)={\lambda }^{m{D}_f}{V}_0.$$

Taking the positive n-th root yields the desired equality.    □

Continuous extension to real scales

Proposition 57 

(Induction over the reals and continuity). Let $g\left(k\right):=V\left(k\right)/V_0$. If $g\left({\lambda }^q{k}_0\right)={\lambda }^{q{D}_f}$ for all rational q, then for every real $k>0$

$$g\left(k\right)={\left(k/k_0\right)}^{D_f},$$

i.e., $V\left(k\right)=V_0{(k/k_0)}^{D_f}$.

Proof. 

Assuming that $lng\left(k\right)$ is continuous in $lnk$ (volume continuity)[87, §1.4], the density of $\mathbb{Q}$ in $\mathbb{R}$ extends $lng\left(k\right)$ uniquely to $lng\left(k\right)=D_{f}ln(k/k_0)$. Exponentiating both sides gives the result.    □

Synthesis of convergence and uniqueness

Theorem 12 

(Uniqueness of the infinitely inductive construction). Given a reference scale $k_0$ with volume $V_0$ and a scaling factor $\lambda \ne 1$,

$$D_f={\displaystyle \frac{lnV\left(\lambda k_0\right)-ln{V}_0}{ln\lambda }}$$

is unique, and induction yields the continuous extension $V\left(k\right)=V_0{(k/k_0)}^{D_f}$ for all $k>0$.

Proof. 

Combine the induction on $\mathbb{N}$, the rational extension, and the continuous extension outlined in the previous results (natural→rational→real).[85, Thm. 1.3][88]    □

Mathematical significance within the UEE

• The value of $D_f$ obtained via geometric induction fixes the scale-dependent coefficient in the dissipative functional $\mathsf{\Gamma }\left[D_f\right]$ of the UEE.
• In numerical work one estimates $D_f$ by a linear fit to the $lnV$–$lnk$ plot, thereby testing the theoretical prediction.[89, Chap.2]

2.11.3 The rôle of $D_f$ inside the UEE and its mathematical consistency

In this subsection we explain in detail how the fractal–dimension operator $D_f$, defined inductively in Section 2.11.2, operates within every formulation of the Unified Evolution Equation (${\mathrm{UEE}}_{\mathrm{op}}$, ${\mathrm{UEE}}_{\mathrm{var}}$, ${\mathrm{UEE}}_{\mathrm{fld}}$) and how it is incorporated in a mathematically consistent manner.[19,81,87]

Consistency with the functional operator $\mathsf{\Pi }\left(D_f\right)$

The operator $\mathsf{\Pi }\left(D_f\right)$ is introduced through the Borel functional calculus:

$$\mathsf{\Pi }\left(D_f\right)=sin\left({\displaystyle \frac{\pi }{\mathsf{\Lambda }}}\sqrt{-\square }\right)=\sum _{n=0}^{\infty }{\displaystyle \frac{{(-1)}^n}{(2n+1)!}}{\left({\displaystyle \frac{\pi }{\mathsf{\Lambda }}}\sqrt{-\square }\right)}^{2n+1}.$$

[90] Because the scaling law $D_f\propto k^{D_f}$ holds, every occurrence of $\sqrt{-\square }$ acting at the scale k inherits the same scaling behaviour for each term in $\mathsf{\Pi }\left(D_f\right)$. In particular,

$$\mathsf{\Pi }\left(D_f\right)\left(\lambda ·\rho \left(x\right)\right)={\lambda }^{D_f}\mathsf{\Pi }\left(D_f\right)\rho \left(\lambda x\right),[D,\mathsf{\Pi }\left(D_f\right)]=0,$$

(cf. Sections 2.5.5 and 2.17); this compatibility stems from the self-similarity of the fractal dimension combined with the operator covariance structure.[85,88]

Impact on the reversible part of ${\mathrm{UEE}}_{\mathrm{op}}$

For the reversible generator of ${\mathrm{UEE}}_{\mathrm{op}}$,

$$L_0\left[\rho \right]=-i[D_G,\rho ],$$

we introduce the operator $\tilde{D}=D+{\mathsf{\Phi }}_{I}sin\pi D_f$ (Section 2.23) so that

$$L_0\left[\rho \right]=-i[\tilde{D},\rho ].$$

With ${\mathsf{\Phi }}_I\propto \nabla ·J_Q$ and the scaling of $D_f$, the evolution of $\rho$ now exhibits self-similar dynamics and its spectrum is subject to the map $\lambda \mapsto {\lambda }^{D_f}$.[89]

Incorporation into the action principle ${\mathrm{UEE}}_{\mathrm{var}}$

Within the variational formulation we consider

$$S[\psi ,\overline{\psi },D_f]=\int d^{4}xdet\left(e\right)\overline{\psi }i{\gamma }^{\mu }{\nabla }_{\mu }\psi +{\mathsf{\Lambda }}^{4}Tr\left(\mathsf{\Gamma }\left[D_f\right]\right)+\dots .$$

Here the dependence of $\mathsf{\Gamma }\left[D_f\right]$ (Sections 2.5.3–2.5.5) on $D_f$, together with the functional operator $\mathsf{\Pi }\left(D_f\right)$, is essential when imposing the stationarity condition $\delta S/\delta D_f=0$.[19] In the variation one finds

$$\delta \mathsf{\Gamma }\left[D_f\right]=Tr\left(\delta D_f\mathcal{D}\left[D_f\right]\right),\mathcal{D}\left[D_f\right]=\mathsf{\Pi }\left(D_f\right)sin\pi D_f,$$

and because $D_f\propto k^{D_f}$, the resulting non-linear equations retain their scale consistency.

Fractal effects in the field-equation version ${\mathrm{UEE}}_{\mathrm{fld}}$

For the coupled field equations of ${\mathrm{UEE}}_{\mathrm{fld}}$

$${\partial }_{\tau }{D}_f=-{\kappa }_D{\displaystyle \frac{\delta Tr\left(\mathsf{\Gamma }\left[D_f\right]\right)}{\delta D_f}},{\partial }_{\tau }{\mathsf{\Phi }}_I^{\mu }=-{\kappa }_I{\mathsf{\Phi }}_I^{\mu }+\dots ,$$

the definition $\mathsf{\Gamma }\left[D_f\right]\sim Tr\left({\mathsf{\Phi }}_I\mathsf{\Pi }\left(D_f\right)sin\pi D_f\right)$ implies that the scaling $D_f\propto k^{D_f}$ enters the non-linear dissipation rate for the information current:

$${\displaystyle \frac{\delta \mathsf{\Gamma }}{\delta D_f}}={\mathsf{\Pi }}^{\prime }\left(D_f\right)sin\pi D_f+\mathsf{\Pi }\left(D_f\right)\pi cos\pi D_f,$$

with ${\mathsf{\Pi }}^{\prime }\left(D_f\right)\propto k^{D_f-1}$, displaying the explicit self-similar contribution of the fractal dimension.

Summary of mathematical consistency

• The geometrically-induced $D_f$ preserves self-similarity at the operator level, providing the foundation for commutativity and positivity of $\mathsf{\Pi }\left(D_f\right)$ and $\mathcal{D}\left[D_f\right]$.
• The scale dependence generated by $D_f$ is fully compatible with the mathematical structure of the UEE, namely: self-adjointness, positivity of operators, and covariance of the spin–gauge derivative.
• Through its inductive definition, its appearance in functional operators, in the action principle, and in the field equations, the UEE forms a self-contained theory that naturally accommodates a fractal dimension.

2.12. Second Definition of $D_f$: the Operator–Function Approach

2.12.1 Definition of $\mathsf{\Pi }\left(D_f\right)$ via the Borel Functional Calculus and its Domain

In this subsection, building on the spectral measure $E\left(\lambda \right)$ constructed in Chapter 2.10, we give the second definition of the fractal-dimension operator $D_f$ by rigorously defining

$$\mathsf{\Pi }\left(D_f\right)=sin\left(\pi \sqrt{-\square }/\mathsf{\Lambda }\right),$$

and we prove its domain and basic operator–theoretic properties.

Recap of the Borel functional calculus

For a self-adjoint operator $\sqrt{-\square }$ with spectral measure $E_{-\square }\left(\lambda \right)$ ($\lambda \ge 0$), every continuous function $f\in C_0\left([0,\infty )\right)$ is assigned an operator through

$$f\left(\sqrt{-\square }\right)={\int }_0^{\infty }f\left(\lambda \right)d{E}_{-\square }\left(\lambda \right),$$

see [19,90]. In particular, we apply this to $f\left(\lambda \right)=sin\left(\pi \lambda /\mathsf{\Lambda }\right)$.

Definition of $\mathsf{\Pi }\left(D_f\right)$

Definition 53 

(Borel definition of $\mathsf{\Pi }\left(D_f\right)$). 

$$\mathsf{\Pi }\left(D_f\right):=sin\left({\displaystyle \frac{\pi }{\mathsf{\Lambda }}}\sqrt{-\square }\right)={\int }_0^{\infty }sin\left({\displaystyle \frac{\pi \lambda }{\mathsf{\Lambda }}}\right)d{E}_{-\square }\left(\lambda \right).$$

Its natural domain is

$$\mathrm{Dom}\left(\mathsf{\Pi }\left(D_f\right)\right)=\left\{\psi \in L^2|{\int }_0^{\infty }{sin}^2\left(\frac{\pi \lambda }{\mathsf{\Lambda }}\right)d\langle \psi ,E_{-\square }\left(\lambda \right)\psi \rangle <\infty \right\}.$$

Proof of self-adjointness

Proposition 58. 

$\mathsf{\Pi }\left(D_f\right)$ is a closed, self-adjoint operator satisfying $\mathsf{\Pi }{\left(D_f\right)}^{†}=\mathsf{\Pi }\left(D_f\right)$ on its domain $\mathrm{Dom}\left(\mathsf{\Pi }\left(D_f\right)\right)$.

Proof. 

The general theorem of the Borel functional calculus [19,90] states that, for a real-valued bounded continuous function f, the operator $f\left(T\right)$ is bounded and self-adjoint. Because $f\left(\lambda \right)=sin(\pi \lambda /\mathsf{\Lambda })$ is bounded and continuous on $[0,\infty )$, the operator $\mathsf{\Pi }\left(D_f\right)=f\left(\sqrt{-\square }\right)$ inherits these properties.    □

Estimate of the operator norm

Proposition 59. 

The following estimate holds: $\parallel \mathsf{\Pi }\left(D_f\right)\parallel \le 1$.

Proof. 

Since $|sin(\pi \lambda /\mathsf{\Lambda }\left)\right|\le 1$ for every $\lambda \ge 0$, the spectral norm satisfies

$$\parallel \mathsf{\Pi }\left(D_f\right)\parallel =\underset{\lambda \in \sigma \left(\sqrt{-\square }\right)}{sup}\left|sin(\pi \lambda /\mathsf{\Lambda })\right|\le 1.$$

   □

Relevance for the UEE

• The operator $\mathsf{\Pi }\left(D_f\right)$ belongs to the zero-order operator family $\mathcal{G}$; it is the cornerstone in constructing the dissipative generator $\mathcal{D}\left[D_f\right]$ (Section 2.5.3–2.5.5).
• The domain $\mathrm{Dom}\left(\mathsf{\Pi }\left(D_f\right)\right)$ coincides with a Sobolev space $H^s\left({\mathbb{R}}^{1,3}\right)$, guaranteeing the continuity of the variable-dimension field $D_f$ inside the UEE action principle [19].
• The spectral definition allows direct application of spectral truncations, ${\mathsf{\Pi }}_N=P_{N}sin(\pi \sqrt{-\square }/\mathsf{\Lambda })P_N,$ and subsequent SOT/WOT convergence analyses [90].

2.12.2 Fourier–Kernel Representation and the Successive Reproducing Kernel

In this subsection we derive an explicit kernel representation of the operator function

$$\mathsf{\Pi }\left(D_f\right)=sin\left(\frac{\pi }{\mathsf{\Lambda }}\sqrt{-\square }\right)$$

via the Fourier transform, and—employing Mercer’s theorem—construct the successive reproducing kernel together with a rigorous statement of its region of convergence.

Derivation of the Fourier–kernel representation

Proposition 60 

(Existence of an integral kernel). The operator $\mathsf{\Pi }\left(D_f\right)$ can be written as an integral operator

$$\left(\mathsf{\Pi }\left(D_f\right)\psi \right)\left(x\right)={\int }_{{\mathbb{R}}^{1,3}}K(x,y)\psi \left(y\right)d^{4}y,$$

with kernel

$$K(x,y)={\displaystyle \frac{1}{{\left(2\pi \right)}^4}}{\int }_{{\mathbb{R}}^{1,3}}{e}^{-ik·(x-y)}sin\left({\displaystyle \frac{\pi \left|k\right|}{\mathsf{\Lambda }}}\right)d^{4}k,\left|k\right|\equiv \sqrt{k_0^2-{\left|\mathbf{k}\right|}^2}.$$

[19,91]

Proof. 

Insert the definition $\mathsf{\Pi }\left(D_f\right)\psi ={\mathcal{F}}^{-1}\left[sin\left(\pi \right|k|/\mathsf{\Lambda })\tilde{\psi }\left(k\right)\right]$ and write out the inverse Fourier transform explicitly; the stated kernel $K(x,y)$ follows immediately. See [19].    □

Successive reproducing kernel via Mercer’s theorem

Proposition 61 

(Reproducing-kernel property). The kernel $K(x,y)$ is symmetric and positive definite, hence Mercer’s theorem gives the Hilbert–Schmidt expansion

$$K(x,y)=\sum _{n=1}^{\infty }{\kappa }_n{\phi }_n\left(x\right)\overline{{\phi }_n\left(y\right)},$$

where $\left\{{\phi }_n\right\}$ is an orthonormal system and $\left\{{\kappa }_n\right\}$ is a sequence of positive eigenvalues, with $L^2$–norm convergence.[92,93]

Proof. 

(i) Self-adjointness and positivity of $\mathsf{\Pi }\left(D_f\right)$ (Section 2.10.2-2) imply that K is a positive definite symmetric kernel. (ii) Because $K\in L^2\left({\mathbb{R}}^8\right)$, Hilbert–Schmidt theory applies and Mercer’s theorem yields the stated expansion. [71]    □

Region of convergence and successive approximation

Proposition 62 

(Convergence of the successive reproducing kernel). Let

$${\mathsf{\Pi }}_N:=\sum _{k=0}^N{(-1)}^k{\displaystyle \frac{1}{(2k+1)!}}{\left(\frac{\pi \sqrt{-\square }}{\mathsf{\Lambda }}\right)}^{2k+1}$$

and denote by $K_N(x,y)$ its integral kernel. Then

$$\parallel K-K_N{\parallel }_{L^2\left({\mathbb{R}}^8\right)}⟶0(N\to \infty ),$$

i.e., the sequence converges in the Hilbert–Schmidt norm. [71]

Proof. 

Express the remainder of the sine series in Fourier space and estimate it using the Taylor remainder of $sinx$, which decays faster than any polynomial; see [94].    □

Remarks for theory and numerics

• The kernel representation furnishes a basis for assessing locality in the interaction term $\mathsf{\Gamma }\left[D_f\right]$ of UEE${‌}_{\mathrm{fld}}$ and for rigorous numerical approximations.
• Mercer’s expansion allows a modal truncation of $\mathsf{\Pi }\left(D_f\right)$—useful for dimensional cut-off approximations and parametric modelling.
• The convergence estimate supplies an explicit bound on kernel truncation errors in lattice implementations.

2.12.3-1 Taylor Series Expansion for Higher-Order Terms

Power series of sin

$$sinz=\sum _{k=0}^{\infty }{\displaystyle \frac{{(-1)}^k}{(2k+1)!}}{z}^{2k+1},z\in \mathbb{C}$$

[94,95]. Setting $z=\frac{\pi }{\mathsf{\Lambda }}\sqrt{-\square }$ we obtain the operator series

$$\mathsf{\Pi }\left(D_f\right)=\sum _{k=0}^N{\displaystyle \frac{{(-1)}^k}{(2k+1)!}}{\left(\frac{\pi }{\mathsf{\Lambda }}\sqrt{-\square }\right)}^{2k+1}+R_{2N+3},$$

$$R_{2N+3}=\sum _{k=N+1}^{\infty }{\displaystyle \frac{{(-1)}^k}{(2k+1)!}}{\left(\frac{\pi }{\mathsf{\Lambda }}\sqrt{-\square }\right)}^{2k+1}.$$

Operator interpretation of each term

Every power ${\left(\sqrt{-\square }\right)}^{2k+1}$ is defined by the Borel functional calculus:

$${\left(\frac{\pi }{\mathsf{\Lambda }}\sqrt{-\square }\right)}^{2k+1}={\int }_0^{\infty }{\left(\frac{\pi \lambda }{\mathsf{\Lambda }}\right)}^{2k+1}d{E}_{-\square }\left(\lambda \right),$$

see [19,71].

Convergence of the main series

Proposition 63. 

For every $\psi \in \mathrm{Dom}\left(\mathsf{\Pi }\left(D_f\right)\right)$ the series ${\displaystyle \sum _{k=0}^{\infty }\frac{\parallel {\left(\frac{\pi }{\mathsf{\Lambda }}\sqrt{-\square }\right)}^{2k+1}\psi \parallel }{(2k+1)!}}$ converges absolutely.

Proof. 

Fix a spectral bound $M:=\parallel \sqrt{-\square }\parallel$ (finite for any finite truncation). Then $\parallel {\left(\sqrt{-\square }\right)}^{2k+1}\psi \parallel \le M^{2k+1}\parallel \psi \parallel .$ The estimate

$$\sum _{k=0}^{\infty }{\displaystyle \frac{{(\pi M/\mathsf{\Lambda })}^{2k+1}}{(2k+1)!}}\parallel \psi \parallel$$

is an exponential series and thus convergent by the Weierstrass test [20].    □

Explicit remainder form

$$R_{2N+3}={\displaystyle \frac{{(-1)}^{N+1}}{(2N+3)!}}{\left(\frac{\pi }{\mathsf{\Lambda }}\sqrt{-\square }\right)}^{2N+3}\left[1+O\left(\frac{{\pi }^2{\parallel \sqrt{-\square }\parallel }^2}{{\mathsf{\Lambda }}^2(N+2)}\right)\right],$$

so that, using an Euler–Maclaurin remainder, one immediately obtains the error bound employed later in Section 2.12.0.23:

$$\parallel R_{2N+3}\parallel \le C{\displaystyle \frac{(\pi \parallel \sqrt{-\square }{\parallel /\mathsf{\Lambda })}^{2N+3}}{(2N+3)!}},$$

cf. [96].

2.12.3-2-1 Mellin–Barnes Expansion and the Complex-Analytic Representation of the Remainder Term

In this subsection we rewrite the remainder term introduced in Section 2.12.0.9,

$$R_{2N+3}=\sum _{k=N+1}^{\infty }{\displaystyle \frac{{(-1)}^k}{(2k+1)!}}{\left(\frac{\pi }{\mathsf{\Lambda }}\sqrt{-\square }\right)}^{2k+1},$$

by means of a Barnes–Mellin (Mellin–Barnes) integral, thereby preparing a refined estimate of the residual series.

Basic Barnes–Mellin integral formula

$$e^z={\displaystyle \frac{1}{2\pi i}}{\int }_{c-i\infty }^{c+i\infty }\mathsf{\Gamma }\left(s\right)z^{-s}ds,c>0$$

[97,98]. Combining it with the reflection formula for the Gamma-function, any power series can be converted into Mellin–Barnes form.

Barnes–Mellin representation of $sinz$

$$sinz={\displaystyle \frac{1}{2\pi i}}{\int }_{\gamma }\mathsf{\Gamma }\left(s\right)\mathsf{\Gamma }(1-s)z^{2s-1}ds,0<\Re s<1$$

(8)

[99]. Here $\gamma$ is a vertical contour with real part $c\in (0,1)$.

Barnes–Mellin-type expansion of the remainder $R_{2N+3}$

Because

$$R_{2N+3}\left(z\right)=\sum _{k=N+1}^{\infty }{\displaystyle \frac{{(-1)}^k}{(2k+1)!}}{z}^{2k+1},z=\frac{\pi }{\mathsf{\Lambda }}\sqrt{-\square },$$

we obtain

$$R_{2N+3}\left(z\right)={\displaystyle \frac{1}{2\pi i}}{\int }_{\gamma }\mathsf{\Gamma }\left(s\right)\mathsf{\Gamma }(1-s)\sum _{k=N+1}^{\infty }{\displaystyle \frac{{(-1)}^k}{(2k+1)!}}{z}^{2k+2s-1}ds.$$

Represent the factor ${\displaystyle \frac{1}{(2k+1)!}}$ by

$${\displaystyle \frac{1}{(2k+1)!}}={\displaystyle \frac{1}{2\pi i}}{\int }_{c_k-i\infty }^{c_k+i\infty }\mathsf{\Gamma }\left(t\right){(2k+1)}^{-t}dt,$$

exchange the order of summation and integration, and arrive at

$$R_{2N+3}\left(z\right)={\displaystyle \frac{1}{{\left(2\pi i\right)}^2}}{\int }_{{\gamma }_s}{\int }_{{\gamma }_t}\mathsf{\Gamma }\left(s\right)\mathsf{\Gamma }(1-s)\mathsf{\Gamma }\left(t\right){Li}_t\left(-z^2\right){(2N+3)}^{1-t}{z}^{2s-1}dtds$$

[100]. Here ${Li}_t$ denotes the polylogarithm. Enclosing the principal pole $s=-N$ by the residue theorem connects directly with the Barnes–Lagrange elimination developed later.

Summary

The double Mellin–Barnes representation derived above forms the analytic foundation for applying the Barnes–Lagrange elimination theorem (Section 2.12.0.17), enabling a rigorous norm estimate of the remainder term $R_{2N+3}$.

2.12.3-2-2 Relation to the Barnes–Lagrange Elimination Theorem

In this subsection we combine the Barnes–Mellin representation of the remainder term from Section 2.12.0.13 with the Barnes–Lagrange elimination theorem [97,101] to cancel the zeros of the surplus term $R_{2N+3}$ in $\mathsf{\Pi }\left(D_f\right)$ and to obtain an explicit error estimate.

Recap of the Barnes–Lagrange elimination theorem

Theorem 13 

(Barnes–Lagrange elimination [101]). For a Mellin–Barnes–type series ${\sum }_{k=0}^{\infty }{f}_k\left(z\right)$ with suitable pole structure, the series can be reduced to a finite Laurent expansion ${\sum }_{k=0}^N{f}_k\left(z\right)$; the remaining series is expressed exactly by the sum of residues at the principal poles.

MB–residue decomposition of the remainder series

Using the result of Section 2.12.0.13,

$$R_{2N+3}\left(z\right)={\displaystyle \frac{1}{{\left(2\pi i\right)}^2}}{\int }_{{\gamma }_s}{\int }_{{\gamma }_t}\mathsf{\Gamma }\left(s\right)\mathsf{\Gamma }(1-s)\mathsf{\Gamma }\left(t\right){Li}_t\left(-z^2\right){(2N+3)}^{1-t}{z}^{2s-1}dtds,$$

we apply the Barnes–Lagrange theorem: taking the residues at the principal pole $s=-N$ in the s-plane and the poles $t=2m+1(m>N)$ of the t-integral yields

$$R_{2N+3}\left(z\right)=\sum _{\ell =0}^{\infty }Re{s}_{s=-N-\ell }\left[\mathsf{\Gamma }\left(s\right)\mathsf{\Gamma }(1-s)z^{2s-1}\right]\sum _{m=N+1}^{\infty }Re{s}_{t=2m+1}\left[\mathsf{\Gamma }\left(t\right){Li}_t(-z^2){(2N+3)}^{1-t}\right].$$

Zero cancellation and extraction of leading residues

• For the s-integral the poles $\mathsf{\Gamma }\left(s\right)\mathsf{\Gamma }(1-s)$ at $s=-\ell$ ($\ell \le N$) annihilate; only poles with $\ell >N$ contribute.
• For the t-integral the main residues stem from $t=2m+1>2N+3$ because of the interplay between $\mathsf{\Gamma }\left(t\right)$ and ${Li}_t$.

Derivation of the error estimate

The leading residues at $s=-N-1$ and $t=2N+3$ are

$$Re{s}_{s=-N-1}\mathsf{\Gamma }\left(s\right)\mathsf{\Gamma }(1-s)z^{2s-1}={\displaystyle \frac{{(-1)}^{N+1}}{(N+1)!N!}}{z}^{-2N-3},$$

$$Re{s}_{t=2N+3}\mathsf{\Gamma }\left(t\right){Li}_t(-z^2){(2N+3)}^{1-t}={\displaystyle \frac{{(-1)}^{N+1}}{(2N+2)!}}{Li}_{2N+3}(-z^2),$$

hence

$$R_{2N+3}\left(z\right)=O\left({\displaystyle \frac{{\left|z\right|}^{2N+3}}{(2N+3)!}}\right).$$

Boundedness of the error

Therefore there exists a constant $C>0$ such that

$$∥R_{2N+3}∥\le C{\displaystyle \frac{{\left(\frac{\pi }{\mathsf{\Lambda }}\parallel \sqrt{-\square }\parallel \right)}^{2N+3}}{(2N+3)!}},$$

showing that the high–order terms decay rapidly.

Conclusion for UEE

This error estimate enables a precise control of systematic errors originating from the truncation of the Taylor series and provides a theoretical lower bound for the required truncation order N in practical applications.

2.12.3-3 Proof of the Boundedness of the Remainder Term

In this subsection we show, for the remainder term defined in Section 2.12.0.9,

$$R_{2N+3}=\sum _{k=N+1}^{\infty }{\displaystyle \frac{{(-1)}^k}{(2k+1)!}}{\left({\displaystyle \frac{\pi }{\mathsf{\Lambda }}}\sqrt{-\square }\right)}^{2k+1},$$

that it is bounded with respect to a suitable norm and we establish the estimate

$$\parallel R_{2N+3}\parallel =\mathcal{O}\left(\frac{{(\pi M/\mathsf{\Lambda })}^{2N+3}}{(2N+3)!}\right),N\to \infty ,$$

where a constant $M>0$ is chosen so that $\parallel {\sqrt{-\square }}^m\psi \parallel \le M^m\parallel \psi \parallel$ for every $\psi$ and all $m\ge 0$ [19].

Action of the remainder term and a first estimate

For any $\psi \in {\bigcap }_{m\ge 0}\mathrm{Dom}\left({\sqrt{-\square }}^m\right)$ we have

$$\begin{array}{cc}\hfill \parallel R_{2N+3}\psi \parallel & \le \sum _{k=N+1}^{\infty }{\displaystyle \frac{1}{(2k+1)!}}{\left({\displaystyle \frac{\pi }{\mathsf{\Lambda }}}\right)}^{2k+1}∥{\sqrt{-\square }}^{2k+1}\psi ∥\hfill \\ \hfill & \le \sum _{k=N+1}^{\infty }{\displaystyle \frac{1}{(2k+1)!}}{\left({\displaystyle \frac{\pi M}{\mathsf{\Lambda }}}\right)}^{2k+1}\parallel \psi \parallel .\hfill \end{array}$$

Evaluation of the series by the comparison test

Setting $a_k={(\pi M/\mathsf{\Lambda })}^{2k+1}/(2k+1)!(k\ge N+1),$ the series ${\sum }_{k=N+1}^{\infty }{a}_k$ converges because of factorial decay [102]. From the ratio test we obtain

$$\sum _{k=N+1}^{\infty }{a}_k\le {\displaystyle \frac{{(\pi M/\mathsf{\Lambda })}^{2N+3}}{(2N+3)!}}\sum _{\ell =0}^{\infty }{\left({\displaystyle \frac{\pi M/\mathsf{\Lambda }}{2N+4}}\right)}^{2\ell }=\mathcal{O}\left(\frac{{(\pi M/\mathsf{\Lambda })}^{2N+3}}{(2N+3)!}\right).$$

Hence

$$\parallel R_{2N+3}\psi \parallel \le C{\displaystyle \frac{{(\pi M/\mathsf{\Lambda })}^{2N+3}}{(2N+3)!}}\parallel \psi \parallel ,$$

for a suitable constant $C>0$.

Operator-norm boundedness

Taking the supremum over all $\psi$ with $\parallel \psi \parallel =1$ yields the operator-norm estimate

$$\parallel R_{2N+3}{\parallel }_{\mathcal{B}}=\underset{\parallel \psi \parallel =1}{sup}\parallel R_{2N+3}\psi \parallel \le C{\displaystyle \frac{{(\pi M/\mathsf{\Lambda })}^{2N+3}}{(2N+3)!}}.$$

Hilbert–Schmidt norm estimate

If we assume $\parallel {\sqrt{-\square }}^{2k+1}{\parallel }_2\le M^{2k+1}$, the same reasoning shows

$$\parallel R_{2N+3}{\parallel }_2\le C^{\prime }{\displaystyle \frac{{(\pi M/\mathsf{\Lambda })}^{2N+3}}{(2N+3)!}}$$

[71].

Comment on an $O\left({\delta }^4\right)$ truncation

In particular, when one discards all terms of order ${\delta }^4$ and higher (putting $N=1$), $\parallel R_5\parallel =\mathcal{O}\left({(\pi M/\mathsf{\Lambda })}^5/5!\right),$ which gives a strict error estimate for small-perturbation approximations in UEE [103].

Short summary

We have shown that the remainder term of the finite-order approximation of $\mathsf{\Pi }\left(D_f\right)$ is suppressed by factorial decay, thus providing a mathematical foundation for selecting a truncation order N in numerical computations.

2.12.3-4 Physical Impact of Approximation Errors in the UEE

Based on the estimate obtained in Section 2.12.0.23, we analyse how the finite-order approximation influences physical quantities in the three formulations of the unified evolution equation (UEE${‌}_{\mathrm{op}}$, UEE${‌}_{\mathrm{var}}$ and UEE${‌}_{\mathrm{fld}}$) [89,104].

Error propagation in the reversible part of UEE${‌}_{\mathrm{op}}$

With

$$L_0\left[\rho \right]=-i\left[D_G+{\mathsf{\Phi }}_{I}sin\pi D_f,\rho \right]=-i[\tilde{D},\rho ],$$

and the approximation $sin\pi D_f\simeq {\sum }_{k=0}^N{(-1)}^k{\left(\pi D_f\right)}^{2k+1}/(2k+1)!$, we write

$$\tilde{D}=D_G+{\mathsf{\Phi }}_I\left({\mathsf{\Pi }}_N\left(D_f\right)+R_{2N+3}\right)={\tilde{D}}_N+{\mathsf{\Phi }}_I{R}_{2N+3}.$$

Since $\parallel {\mathsf{\Phi }}_I{R}_{2N+3}\parallel \le \parallel {\mathsf{\Phi }}_I\parallel \mathcal{O}\left({(\pi M/\mathsf{\Lambda })}^{2N+3}/(2N+3)!\right)$, the unitary evolution $U\left(t\right)=e^{-i\tilde{D}t}$ obeys the error bound

$$\parallel U\left(t\right)-U_N\left(t\right)\parallel \le t\parallel {\mathsf{\Phi }}_I{R}_{2N+3}\parallel e^{t\parallel \tilde{D}\parallel }$$

[56].

Approximation error in the variational formulation UEE${‌}_{\mathrm{var}}$

In the action

$$S[\psi ,\overline{\psi },D_f]=S_0\left[\psi \right]+{\mathsf{\Lambda }}^{4}Tr\left(\mathsf{\Gamma }\left[{\mathsf{\Pi }}_N\left(D_f\right)\right]\right)+\mathsf{\Delta }S,$$

the variation introduces

$$\parallel \mathsf{\Delta }S\parallel \le {\mathsf{\Lambda }}^4∥{\mathsf{\Gamma }}^{\prime }\left[R_{2N+3}\right]∥,$$

and the field equation receives a correction controlled by $\mathcal{O}({(\pi M/\mathsf{\Lambda })}^{2N+3}/(2N+3)!)$.

Error in the dissipation rate and the $\beta$-function of UEE${‌}_{\mathrm{fld}}$

$${\partial }_{\tau }{D}_f=-{\kappa }_D{\displaystyle \frac{\delta Tr\left(\mathsf{\Gamma }\left[{\mathsf{\Pi }}_N\left(D_f\right)\right]\right)}{\delta D_f}}+\mathcal{O}\left(\frac{{(\pi M/\mathsf{\Lambda })}^{2N+3}}{(2N+3)!}\right),$$

$$\beta \left(D\right)={\beta }_0\left(D\right)+\mathsf{\Delta }{\beta }_N,\parallel \mathsf{\Delta }{\beta }_N\parallel \le C\frac{{(\pi M/\mathsf{\Lambda })}^{2N+3}}{(2N+3)!}.$$

Practical guideline for choosing the truncation order N

To guarantee an error smaller than a prescribed tolerance $ϵ$ one requires

$${\displaystyle \frac{{(\pi M/\mathsf{\Lambda })}^{2N+3}}{(2N+3)!}}\le ϵ.$$

Using Stirling’s formula, $(2N+3)!\sim \sqrt{4\pi N}{(2N/e)}^{2N+3}$ [105], yields approximately

$$N\gtrsim {\displaystyle \frac{\mathsf{\Lambda }}{2\pi M}}ln\left(\frac{1}{ϵ}\right).$$

Physical consequences in small-perturbation expansions

With ${\mathsf{\Pi }}_N\left(D_f\right)=\mathsf{\Pi }\left(D_f\right)-R_{2N+3}$, linear-response quantities such as the dissipation rate inherit an $\mathcal{O}\left(ϵ\right)$ uncertainty; in applications this translates, e.g., to $\mathsf{\Delta }\mu \sim \mathcal{O}\left(ϵ\right)$ for CMB $\mu$-distortion or $\mathsf{\Delta }{\dot{S}}_{\mathrm{BH}}\sim \mathcal{O}\left(ϵ\right)$ for the information-loss rate of Hawking radiation.

Summary

Because the remainder decays factorially, very few terms suffice for high precision. Hence both the mathematical model of the UEE and its numerical implementation remain stable and efficient.

2.13. Self-Adjointness of the Projection $\mathsf{\Pi }\left(D_f\right)$

2.13.1 Proof of the Self-Adjointness of $\mathsf{\Pi }\left(D_f\right)$

In this subsection we prove rigorously—by means of the Borel functional calculus—that the operator function

$$\mathsf{\Pi }\left(D_f\right)=sin\left({\displaystyle \frac{\pi }{\mathsf{\Lambda }}}\sqrt{-\square }\right)$$

is self-adjoint (self-conjugate) on its domain $\mathrm{Dom}\left(\mathsf{\Pi }\left(D_f\right)\right)\subset L^2\left({\mathbb{R}}^{1,3}\right)$.

Reminder of the general theorem of the Borel functional calculus

For a self-adjoint operator T with spectral measure $E_T\left(\lambda \right)$ and an arbitrary real-valued Borel function f,

$$f\left(T\right)={\int }_{\sigma \left(T\right)}f\left(\lambda \right)d{E}_T\left(\lambda \right)$$

defines a closed, self-adjoint operator [19,106].

Application to the spectral measure of $\sqrt{-\square }$

From Sections 2.10.1–2.10.2 we have

$$T=\sqrt{-\square },\sigma \left(T\right)=[0,\infty ),E_{-\square }\left(\lambda \right),$$

and we set $f\left(\lambda \right)=sin(\pi \lambda /\mathsf{\Lambda })$; this is a real function, so $\mathsf{\Pi }\left(D_f\right)=f\left(T\right)$.

Coincidence of domains and closedness

The domain is

$$\mathrm{Dom}\left(\mathsf{\Pi }\left(D_f\right)\right)=\left\{\psi |{\int }_0^{\infty }{sin}^2\left(\frac{\pi \lambda }{\mathsf{\Lambda }}\right)d\langle \psi ,E_{-\square }\left(\lambda \right)\psi \rangle <\infty \right\}$$

[6]. Because $\mathsf{\Pi }\left(D_f\right)$ is defined by Borel calculus, it is automatically closed [19].

Direct proof of self-adjointness

For arbitrary $\psi ,\varphi \in \mathrm{Dom}\left(\mathsf{\Pi }\left(D_f\right)\right)$,

$$\begin{array}{cc}\hfill 〈\varphi ,\mathsf{\Pi }\left(D_f\right)\psi 〉& ={\int }_0^{\infty }\overline{d\langle \varphi ,E\left(\lambda \right)\psi \rangle }sin\left(\frac{\pi \lambda }{\mathsf{\Lambda }}\right)\hfill \\ \hfill & =\overline{〈\psi ,\mathsf{\Pi }\left(D_f\right)\varphi 〉},\hfill \end{array}$$

where the integrand remains unchanged under complex conjugation because $sin(\pi \lambda /\mathsf{\Lambda })$ is real [90].

Conclusion

Hence

$$\mathsf{\Pi }{\left(D_f\right)}^{†}=\mathsf{\Pi }\left(D_f\right),\mathrm{Dom}\left(\mathsf{\Pi }{\left(D_f\right)}^{†}\right)=\mathrm{Dom}\left(\mathsf{\Pi }\left(D_f\right)\right),$$

i.e., $\mathsf{\Pi }\left(D_f\right)$ is a self-adjoint operator.

2.13.2 Proof of the Boundedness $\mathsf{\Pi }{\left(D_f\right)}^2\le 1$

Here we show, from a spectral-theoretic viewpoint, that the operator $\mathsf{\Pi }\left(D_f\right)=sin\left(\pi \sqrt{-\square }/\mathsf{\Lambda }\right)$ satisfies $\mathsf{\Pi }{\left(D_f\right)}^2\le 1$.

Upper bound via the spectral theorem

With the spectral measure $E_{-\square }\left(\lambda \right)$ of $T=\sqrt{-\square }$,

$$\mathsf{\Pi }\left(D_f\right)={\int }_0^{\infty }sin\left(\frac{\pi \lambda }{\mathsf{\Lambda }}\right)d{E}_{-\square }\left(\lambda \right),\mathsf{\Pi }{\left(D_f\right)}^2={\int }_0^{\infty }{sin}^2\left(\frac{\pi \lambda }{\mathsf{\Lambda }}\right)d{E}_{-\square }\left(\lambda \right)$$

[107].

Scalar inequality for the integrand

The function $f\left(\lambda \right)=sin(\pi \lambda /\mathsf{\Lambda })$ is real and obeys $\left|f\right(\lambda \left)\right|\le 1$ for all $\lambda \ge 0$.

Passage to an operator inequality

Integrating the pointwise inequality yields

$$0\le \mathsf{\Pi }{\left(D_f\right)}^2\le I,$$

where I is the identity operator [108].

Consequence for the norm

From $\mathsf{\Pi }{\left(D_f\right)}^2\le I$ it follows that $\parallel \mathsf{\Pi }\left(D_f\right){\parallel }^2\le 1$, hence $\parallel \mathsf{\Pi }\left(D_f\right)\parallel \le 1$.

Supplement from the kernel representation

In the Fourier-kernel representation $\mathsf{\Pi }\left(D_f\right)\psi \left(x\right)=\int K(x,y)\psi \left(y\right)d^{4}y$, the Mercer expansion $K(x,y)={\sum }_n{\kappa }_n{\phi }_n\left(x\right)\overline{{\phi }_n\left(y\right)}$ has eigenvalues ${\kappa }_n=sin(\pi {\lambda }_n/\mathsf{\Lambda })$ with $|{\kappa }_n|\le 1$; this is equivalent to $\mathsf{\Pi }{\left(D_f\right)}^2\le I$ [109].

Significance for the UEE

The inequality $\mathsf{\Pi }{\left(D_f\right)}^2\le I$ guarantees the positivity and boundedness of the dissipation generator $\mathcal{D}\left[D_f\right]=\mathsf{\Pi }\left(D_f\right)sin\pi D_f$ and of the information-flux functional $\mathsf{\Gamma }\left[D_f\right]$. Consequently, the non-reversible part of the UEE is formulated in a physically consistent manner.

2.14. $\mathsf{\Pi }\left(D_f\right)$ and its Fourier-Kernel Representation

2.14.1 Derivation of the Fourier–Kernel Representation

In this subsection we express the operator

$$\mathsf{\Pi }\left(D_f\right)=sin\left({\displaystyle \frac{\pi }{\mathsf{\Lambda }}}\sqrt{-\square }\right)$$

as an integral kernel by means of the Fourier transform, and we give a rigorous derivation together with the necessary convergence conditions.

Four–dimensional Fourier transform (review)

On the Hilbert space $L^2\left({\mathbb{R}}^{1,3}\right)$ we define [91]

$$\mathcal{F}\left[\psi \right]\left(k\right)=\tilde{\psi }\left(k\right)={\displaystyle \frac{1}{{\left(2\pi \right)}^2}}{\int }_{{\mathbb{R}}^{1,3}}{e}^{ik·x}\psi \left(x\right)d^{4}x,{\mathcal{F}}^{-1}\left[\tilde{\psi }\right]\left(x\right)={\displaystyle \frac{1}{{\left(2\pi \right)}^2}}{\int }_{{\mathbb{R}}^{1,3}}{e}^{-ik·x}\tilde{\psi }\left(k\right)d^{4}k,$$

and Plancherel’s theorem yields $\parallel \tilde{\psi }{\parallel }_{L^2}={\parallel \psi \parallel }_{L^2}$ [6].

Fourier representation of the operator function

For the self-adjoint operator $\sqrt{-\square }$ one has

$$\sqrt{-\square }\psi ⟼\left|k\right|\tilde{\psi }\left(k\right),$$

so that

$$\mathsf{\Pi }\left(D_f\right)\psi ={\mathcal{F}}^{-1}\left[sin\left(\frac{\pi \left|k\right|}{\mathsf{\Lambda }}\right)\tilde{\psi }\left(k\right)\right]$$

[108].

Derivation of the kernel representation

$$\begin{array}{cc}\hfill \left(\mathsf{\Pi }\left(D_f\right)\psi \right)\left(x\right)& ={\displaystyle \frac{1}{{\left(2\pi \right)}^2}}{\int }_{{\mathbb{R}}^{1,3}}{e}^{-ik·x}sin\left(\frac{\pi \left|k\right|}{\mathsf{\Lambda }}\right)\tilde{\psi }\left(k\right)d^{4}k\hfill \\ \hfill & ={\displaystyle \frac{1}{{\left(2\pi \right)}^4}}{\int }_{{\mathbb{R}}^{1,3}}\left[{\int }_{{\mathbb{R}}^{1,3}}{e}^{-ik·(x-y)}sin\left(\frac{\pi \left|k\right|}{\mathsf{\Lambda }}\right)d^{4}k\right]\psi \left(y\right)d^{4}y\hfill \\ \hfill & ={\int }_{{\mathbb{R}}^{1,3}}K(x,y)\psi \left(y\right)d^{4}y,\hfill \end{array}$$

where the kernel is defined by

$$K(x,y)={\displaystyle \frac{1}{{\left(2\pi \right)}^4}}{\int }_{{\mathbb{R}}^{1,3}}{e}^{-ik·(x-y)}sin\left({\displaystyle \frac{\pi \left|k\right|}{\mathsf{\Lambda }}}\right)d^{4}k.$$

This is a manifestation of the Bochner–Schwartz kernel representation [110].

Verification of kernel convergence

A sufficient condition for absolute convergence of the Fourier integral is

$${\int }_{{\mathbb{R}}^{1,3}}\left|sin\left(\frac{\pi \left|k\right|}{\mathsf{\Lambda }}\right)\right|d^{4}k<\infty ,$$

which indeed holds [111]. Using Plancherel again we obtain

$${\parallel K\parallel }_{HS}^2={\displaystyle \frac{1}{{\left(2\pi \right)}^4}}{\int }_{{\mathbb{R}}^{1,3}}{sin}^2\left(\frac{\pi \left|k\right|}{\mathsf{\Lambda }}\right)d^{4}k<\infty ,$$

so $K\in L^2\left({\mathbb{R}}^8\right)$ and $\mathsf{\Pi }\left(D_f\right)$ is a Hilbert–Schmidt operator [71].

Relation to the next subsection

This kernel representation supplies the basis for the Mercer expansion (Subsec. 2.14.0.5) and for sequential approximations in numerical truncations; it underpins the locality and numerical stability of interaction terms in the UEE framework [109].

2.14.2 Reproducing-Kernel Expansion and Convergence Region

In this subsection we construct a reproducing-kernel expansion of the kernel

$$K(x,y)={\displaystyle \frac{1}{{\left(2\pi \right)}^4}}{\int }_{{\mathbb{R}}^{1,3}}{e}^{-ik·(x-y)}sin\left(\frac{\pi \left|k\right|}{\mathsf{\Lambda }}\right)d^{4}k$$

by applying Mercer’s theorem, and we discuss the convergence region in terms of the Hilbert–Schmidt norm and kernel-space analysis.

2.14.2-1 Construction via Mercer’s Theorem

Verification of the Hilbert–Schmidt condition

Since ${\parallel K\parallel }_{HS}<\infty$, the kernel is indeed Hilbert–Schmidt [67].

Application of Mercer’s theorem

For a self-adjoint, positive Hilbert–Schmidt kernel, Mercer’s theorem [109,112] gives

$$K(x,y)=\sum _{n=1}^{\infty }{\kappa }_n{\phi }_n\left(x\right)\overline{{\phi }_n\left(y\right)}\mathrm{in}{L}^2\left({\mathbb{R}}^8\right),$$

where $\left\{{\phi }_n\right\}$ is an orthonormal set and ${\kappa }_n=sin(\pi {\lambda }_n/\mathsf{\Lambda })\ge 0$.

2.14.2-2 Convergence Region and the Limits of Numerical Truncation

Sequential approximation in Hilbert–Schmidt norm

The polynomial truncation

$${\mathsf{\Pi }}_N=\sum _{k=0}^N{(-1)}^k{\displaystyle \frac{1}{(2k+1)!}}{\left(\frac{\pi }{\mathsf{\Lambda }}\sqrt{-\square }\right)}^{2k+1}$$

comes with a kernel $K_N$ that admits an analogous expansion

$$K_N(x,y)=\sum _{n=1}^{\infty }{\kappa }_{n,N}{\phi }_n\left(x\right)\overline{{\phi }_n\left(y\right)},$$

where ${\kappa }_{n,N}\to {\kappa }_n$ and $\parallel K-K_N{\parallel }_{HS}={\left({\sum }_n{|{\kappa }_n-{\kappa }_{n,N}|}^2\right)}^{1/2}\to 0$ [71].

Explicit convergence estimate

Using the remainder estimate in Subsec. 2.12.3-3,

$$\parallel K-K_N{\parallel }_{HS}\le C{\displaystyle \frac{{(\pi /\mathsf{\Lambda })}^{2N+3}}{(2N+3)!}},$$

so the convergence is exponentially fast for modes $\left|k\right|\lesssim \mathsf{\Lambda }$.

Guidelines for numerical implementation in the UEE

• Choosing $N_{\mathrm{eff}}\sim (\mathsf{\Lambda }/\pi )log(1/ϵ)$ guarantees an error below $ϵ$ [57].
• A local-kernel truncation $|x-y|\le R$ can be made sparse, with $\parallel K-K^{\left(R\right)}{\parallel }_{HS}\le ϵ$ for suitably estimated R.
• The optimal balance between $\mathsf{\Lambda }$ and the truncation order maintains the stability condition $\mathsf{\Pi }{\left(D_f\right)}^2\le I$ for both the reversible and dissipative parts of the theory.

Summary

Through the route from the Fourier kernel to the Mercer expansion we obtain a mathematically sound basis for both analytic estimates and numerical approximations of $\mathsf{\Pi }\left(D_f\right)$. This is indispensable for studying field dynamics in the UEE, in particular for assessing the locality of dissipative terms and for tracking RG flows numerically.

2.15. Derivation of the Barnes–Lagrange Elimination Theorem

Positioning and notation.

In this section we extend the elimination theorem so that it includes a zero–area resonance kernel R (see Sect. 2.5.0.7). Following [113], $R\left[\rho \right]$ is defined by

$$R\left[\rho \right]={\int }_{\sigma \left(D\right)}R\left(\omega \right)\left[D,[D,\rho ]\right]E_D\left(d\omega \right),$$

(9)

and fulfils the zero–area condition $\int R\left(\omega \right)d\omega =0$ [114]. With this ingredient the traditional “dissipative–channel only” cancellation ${\sum }_j{V}_j^{†}{V}_j=0$ is generalised to the relation (10).

2.15.1 Mellin–Barnes Integrals and Basic Properties of the Gamma Function

Before proving the Barnes–Lagrange elimination theorem we review the Mellin transform, Barnes-type integrals and the gamma function identities that will be used throughout the derivation.

Definition of the Mellin transform.

For a function $f\left(z\right)$ the Mellin transform $\mathcal{M}\left[f\right]$ is defined [115] by

$$\mathcal{M}\left[f\right]\left(s\right):={\int }_0^{\infty }{z}^{s-1}f\left(z\right)dz,s\in \mathbb{C}.$$

With an appropriate vertical contour $\Re s=c$ the inverse transform reads [116]

$$f\left(z\right)={\displaystyle \frac{1}{2\pi i}}{\int }_{c-i\infty }^{c+i\infty }{z}^{-s}\mathcal{M}\left[f\right]\left(s\right)ds.$$

Basic formulas for the gamma function.

$$\mathsf{\Gamma }\left(s\right)={\int }_0^{\infty }{t}^{s-1}{e}^{-t}dt,\Re s>0,$$

[95]

$$\mathsf{\Gamma }(s+1)=s\mathsf{\Gamma }\left(s\right),$$

$$\mathsf{\Gamma }\left(s\right)\mathsf{\Gamma }(1-s)={\displaystyle \frac{\pi }{sin\left(\pi s\right)}},s\notin \mathbb{Z},$$

[94]

$$\mathsf{\Gamma }(s+a)\sim \sqrt{2\pi }{s}^{s+a-\frac{1}{2}}{e}^{-s}\left(\right|s|\to \infty ,|\arg s|<\pi ).$$

[96]

Definition of Barnes-type integrals and convergence conditions.

A generic Barnes double integral has the form [25]

$${\displaystyle \frac{1}{{\left(2\pi i\right)}^2}}{\int }_{\begin{array}{c}\Re s=c_1\\ \Re t=c_2\end{array}}\mathsf{\Gamma }\left(s\right)\mathsf{\Gamma }\left(t\right)\mathsf{\Gamma }(u-s-t)z^{-s}{w}^{-t}dsdt,$$

with a fixed parameter u and contours $\Re s=c_1$, $\Re t=c_2$ chosen suitably.

Proposition 64 

(Barnes–Mellin convergence condition). The integral is well defined only if the contours avoid all poles of the gamma factorsandif $\Re s,\Re t,\Re (u-s-t)$ are simultaneously positive. [117]

Proof. 

Each gamma factor has simple poles at negative integers. By shifting the contours one can enumerate the residues provided the three real parts remain positive. See [118] for details.    □

Gamma–function identities used in the elimination theorem.

Throughout the proof we repeatedly use

$$\mathsf{\Gamma }\left(s\right)\mathsf{\Gamma }(1-s)={\displaystyle \frac{\pi }{sin\left(\pi s\right)}},{\displaystyle \frac{1}{\mathsf{\Gamma }(-n+\epsilon )}}\sim {(-1)}^{n}n!\epsilon ,n\in \mathbb{N},$$

[119] as well as their consequences.

Concrete places where these tools enter the UEE.

They provide the analytic foundation for the residue calculus in the analysis of the remainder of $\mathsf{\Pi }\left(D_f\right)$ (Sect. 2.12.3) and in the application of the Barnes–Lagrange elimination identity [108].

2.15.2 Proof of the Main Barnes–Lagrange Elimination Theorem

Here we give a rigorous proof of the central Barnes–Lagrange elimination theorem. We first formulate the theorem and specify the integration contours, then carry out the residue calculation that yields the desired elimination structure.

2.15.2-1 Statement of the theorem and contour choice

Theorem 2.15.2 (Barnes–Lagrange Elimination).

Let $\left\{f_k\left(z\right)\right\}$ be a sequence of functions such that the Mellin–Barnes series

$$F\left(z\right)=\sum _{k=0}^{\infty }{f}_k\left(z\right)=\sum _{k=0}^{\infty }{\displaystyle \frac{{(-1)}^k}{(2k+1)!}}{z}^{2k+1}=sinz$$

holds. Then, for every natural number N,[120]

$$\begin{array}{cc}\hfill & \sum _{k=0}^N{f}_k\left(z\right)={\displaystyle \frac{1}{2\pi i}}{\int }_{\Re s=c}\mathsf{\Gamma }\left(s\right)\mathsf{\Gamma }(1-s)z^{2s-1}ds\hfill \\ & ⟹F\left(z\right)-\sum _{k=0}^N{f}_k\left(z\right)=R_{2N+3}\left(z\right)=\sum _{\ell =0}^{\infty }Re{s}_{s=-N-1-\ell }\left[\mathsf{\Gamma }\left(s\right)\mathsf{\Gamma }(1-s)z^{2s-1}\right].\hfill \end{array}$$

Choice of contours.

• The vertical Mellin–Barnes contour $\Re s=c$ is chosen with $0<\Re s<1$, so that it lies between the simple poles $s=0,-1,-2,\dots$ and $s=1,2,\dots$ of $\mathsf{\Gamma }\left(s\right)\mathsf{\Gamma }(1-s)$ [121].
• For the elimination theorem we close the contour on the left so that the poles $s=-1,-2,\dots ,-N-1$ are enclosed, while the right–hand part is pushed to $\Re s\to +\infty$ where the integral vanishes thanks to Stirling’s formula [96].

2.15.2-2 Proof of the Elimination Structure

Splitting the Mellin–Barnes integral.

Following [121], the line integral along the contour $\Re s=c$ is split into left– and right–hand closed loops,

$${\displaystyle \frac{1}{2\pi i}}{\int }_{c-i\infty }^{c+i\infty }\mathsf{\Gamma }\left(s\right)\mathsf{\Gamma }(1-s)z^{2s-1}ds=\left(\sum _{\begin{array}{c}\mathrm{left}\mathrm{residues}\end{array}}+\sum _{\begin{array}{c}\mathrm{right}\mathrm{residues}\end{array}}\right).$$

Cancellation of the left–hand poles.

For the poles $s=-\ell$ with $\ell =0,\dots ,N$ we have $Res\left(\mathsf{\Gamma }\left(s\right)\mathsf{\Gamma }(1-s)\right)={(-1)}^{\ell }/\ell !$ [95]. These residues cancel exactly against the terms of ${\sum }_{k=0}^N{f}_k\left(z\right)$:

$$Re{s}_{s=-\ell }\left[\mathsf{\Gamma }\left(s\right)\mathsf{\Gamma }(1-s)z^{2s-1}\right]={\displaystyle \frac{{(-1)}^{\ell }}{\ell !}}{\displaystyle \frac{z^{-(2\ell +1)}}{(2\ell +1)!}},\ell =0,\dots ,N.$$

Extraction of the leading remainder.

The rightmost pole on the left, $s=-(N+1)$, yields the leading contribution to the remainder:

$$Re{s}_{s=-(N+1)}\left[\mathsf{\Gamma }\left(s\right)\mathsf{\Gamma }(1-s)z^{2s-1}\right]={\displaystyle \frac{{(-1)}^{N+1}}{(N+1)!(2N+3)!}}{z}^{-2N-3}$$

[120]. This term is precisely the first part of $R_{2N+3}\left(z\right)$.

Vanishing of the right–hand poles.

For the poles on the right, $s=N+2,N+3,\dots$, Stirling’s asymptotic formula implies $\mathsf{\Gamma }\left(s\right)\mathsf{\Gamma }(1-s)\sim O\left(e^{-\pi |\Im s|}\right)$ [96], so that the contribution from the infinite loop is zero and does not appear in the remainder.

Conclusion.

Combining the above steps [118] we obtain

$${\displaystyle \frac{1}{2\pi i}}{\int }_{c-i\infty }^{c+i\infty }\mathsf{\Gamma }\left(s\right)\mathsf{\Gamma }(1-s)z^{2s-1}ds=\sum _{k=0}^N{f}_k\left(z\right)+R_{2N+3}\left(z\right),$$

thereby completing the rigorous proof of the Barnes–Lagrange elimination theorem.

2.15.2-3 Extended Cancelling Identity (including the zero–area resonance kernel)

We now present the extended cancelling identity, which augments the conventional cancellation among dissipative channels by adding the zero–area resonance kernel operator R [113].

Theorem 14 

(Extended Cancelling Identity). The total generator of the UEE

$$L_{\mathrm{tot}}=-i\left[D,\rho \right]+\sum _j\left(V_j\rho V_j^{†}-\frac{1}{2}\{V_j^{†}{V}_j,\rho \}\right)+R\left[\rho \right]$$

preserves complete positivity and trace, provided that the following identity holds:

$$\sum _j{V}_j^{†}{V}_j+{\int }_{-\infty }^{\infty }R\left(\omega \right)d\omega =0.$$

(10)

Remark 4 

(Units of the parameters). Throughout this chapter all dissipative parameters ${\kappa }_D,{\kappa }_{\mathrm{ph}},\dots$ and the resonance–kernel coefficients $(A,P_0,\mathsf{\Delta })$ are expressed in “fraction form”,i.e.,a parts- per-million value divided by ${10}^6$ [114]. The residue $R\left[\rho \right]$ is therefore calculated in the same fractional units; when comparing with ppm values one simply multiplies by ${10}^6$ according to our unified convention.

Proof. 

1. Standard cancelling identity. Trace preservation of the Lindblad–GKLS form requires ${\sum }_j{V}_j^{†}{V}_j=0$ [8].

2.

Addition of the zero–area kernel. By definition $\int R\left(\omega \right)d\omega =0$ [113], hence

$$\sum _j{V}_j^{†}{V}_j+\int R\left(\omega \right)d\omega =\sum _j{V}_j^{†}{V}_j+0=0.$$

3.

Complete positivity and trace preservation. Owing to the double commutator structure and the zero–area condition, R satisfies Tr$R\left[\rho \right]=0$ and does not spoil complete positivity; thus $L_{\mathrm{tot}}$ remains a CPTP generator [122].

   □

Physical implication.

Equation (10) shows that, in addition to the classical cancellation among the dissipative channels $V_j$, peaks and dips appearing in the reversible dynamics in the spectral resonance region cancel out with zero area. Consequently the UEE is able to incorporate nonlinear resonance effects consistently without violating the fundamental conservation laws.

2.15.3 Applications to the UEE and Concrete Elimination Examples

In this section we apply the Barnes–Lagrange elimination theorem shown in Sect. 2.15.0.6–2.15.0.8 and the extended cancelling identity of Sect. 2.15.0.13 to the various building blocks of the Unified Evolution Equation (UEE), demonstrating the consistency between theory and numerical implementation.

Elimination of the remainder term of $\mathsf{\Pi }\left(D_f\right)$.

For the fractal operator $D_f$ the projector

$$\mathsf{\Pi }\left(D_f\right)=\sum _{k=0}^N{f}_k\left(D_f\right)+R_{2N+3}\left(D_f\right),f_k\left(z\right)={\displaystyle \frac{{(-1)}^k}{(2k+1)!}}{z}^{2k+1},$$

can be decomposed as in Sect. 2.15.0.8:

$$R_{2N+3}\left(D_f\right)=\sum _{\ell =0}^{\infty }Re{s}_{s=-(N+1+\ell )}\left[\mathsf{\Gamma }\left(s\right)\mathsf{\Gamma }(1-s)D_f^{2s-1}\right]$$

[95]. Using the extended cancelling identity (Equation (11)) and the effect of the zero–area resonance kernel R, the infinite sum is truncated to a finite residue sum:

$$R_{2N+3}\left(D_f\right)\approx \sum _{\ell =0}^{L}Re{s}_{s=-(N+1+\ell )}\left[\mathsf{\Gamma }\left(s\right)\mathsf{\Gamma }(1-s)D_f^{2s-1}\right]=R_{2N+3}^{\left(L\right)}\left(D_f\right).$$

By choosing L appropriately we guarantee that the remainder term converges while the zero–area kernel cancels the physical singularities.

Expansion of the dissipative functional $\mathsf{\Gamma }\left[D_f\right]$.

For the dissipative functional in UEE${‌}_{\mathrm{var}}$

$$\mathsf{\Gamma }\left[D_f\right]=Tr\left({\mathsf{\Phi }}_I\mathcal{D}\left[D_f\right]\right),\mathcal{D}\left[D_f\right]=\mathsf{\Pi }\left(D_f\right)sin\left(\pi D_f\right),$$

we likewise expand $\mathsf{\Pi }\left(D_f\right)sin\left(\pi D_f\right)$ and apply the elimination theorem:

$$\mathsf{\Gamma }\left[D_f\right]=\sum _{k=0}^{N}Tr\left({\mathsf{\Phi }}_I{g}_k\left(D_f\right)\right)+\sum _{\ell =0}^{\infty }Re{s}_{s=-(N+1+\ell )}Tr\left[{\mathsf{\Phi }}_I\mathsf{\Gamma }\left(s\right)\mathsf{\Gamma }(1-s)D_f^{2s-1}\right]$$

[123]. The zero–area condition together with the extended cancelling identity reduces the dominant residues to a finite sum, allowing a quantitative evaluation that simultaneously incorporates physical dissipative channels and nonlinear resonance effects.

Numerical elimination algorithm.

• Pre–computing the residues: The residues of $\mathsf{\Gamma }\left(s\right)\mathsf{\Gamma }(1-s)$ at the poles $s=-m(m\in \mathbb{N})$ are derived analytically and cached [124].
• Finite truncation: The finite residue sum $R_{2N+3}^{\left(L\right)}\left(D_f\right)$ is evaluated rapidly for $\ell =0,\dots ,L$.
• Convergence monitoring: The remainder norm $\parallel R_{2N+3}-R_{2N+3}^{\left(L\right)}\parallel$ is computed and L is chosen such that the prescribed tolerance $ϵ$ is satisfied [96].
• Mapping to physical observables: The finite remainder is re–inserted into each eigen–mode of the generator $L_{\mathrm{tot}}$, enabling a precise analysis of its dynamical impact [122].

Physical visualisation.

For each eigen–value ${\lambda }_n$ one can visualise the effect of the truncation level L by plotting

$${\tilde{\kappa }}_n=sin\left(\pi {\lambda }_n/\mathsf{\Lambda }\right)+\sum _{\ell =0}^L{r}_{n,\ell },$$

which makes the spectral modification caused by the finite residue sum intuitive.

Summary.

By combining the elimination theorem with the extended cancelling identity we can coherently incorporate nonlinear resonance effects together with dissipative channels in both the operator and the variational formulations of the UEE. The method provides a mathematically rigorous yet computationally efficient framework that underpins the whole theory.

2.16. $\mathsf{\Pi }\left(D_f\right)$ High-Order Expansion and Error Estimate

2.16.1 High-Order Terms via the Taylor-Series Expansion

In this subsection we expand the operator function

$$\mathsf{\Pi }\left(D_f\right)=sin\left({\displaystyle \frac{\pi }{\mathsf{\Lambda }}}\sqrt{-\square }\right)=sin\left(\pi D_f\right),D_f:=\sqrt{-\square }/\mathsf{\Lambda },$$

derive the terms up to fourth order explicitly, and obtain the formal expression of the remainder $R_5$.

Power–series expansion of sin.

For a complex variable z one has

$$sin\left(\pi z\right)=\sum _{k=0}^{\infty }{\displaystyle \frac{{(-1)}^k}{(2k+1)!}}{\left(\pi z\right)}^{2k+1},$$

[95,124]. Setting $z=D_f$ gives the operator series

$$\mathsf{\Pi }\left(D_f\right)=\sum _{k=0}^{\infty }{\displaystyle \frac{{(-1)}^k}{(2k+1)!}}{\left(\pi D_f\right)}^{2k+1}.$$

Listing of the leading terms.

Extracting the terms for $k=0,1,2$ one obtains

$$\begin{array}{cc}\hfill \mathsf{\Pi }\left(D_f\right)& =\left(\pi D_f\right)-{\displaystyle \frac{{\left(\pi D_f\right)}^3}{3!}}+{\displaystyle \frac{{\left(\pi D_f\right)}^5}{5!}}-{\displaystyle \frac{{\left(\pi D_f\right)}^7}{7!}}+\dots \hfill \\ \hfill & =:T_1+T_3+T_5+T_7+\dots ,\hfill \end{array}$$

where we have set

$$T_{2k+1}:={\displaystyle \frac{{(-1)}^k}{(2k+1)!}}{\left(\pi D_f\right)}^{2k+1}.$$

Truncation as an $O\left({\delta }^4\right)$ approximation.

Introducing the small-perturbation parameter

$$\delta :=\pi D_f\ll 1,$$

retaining all terms up to fourth order yields

$${\mathsf{\Pi }}_3\left(D_f\right)=T_1+T_3=\pi D_f-{\displaystyle \frac{{\left(\pi D_f\right)}^3}{6}}.$$

The remainder is defined by

$$R_5=\sum _{k=2}^{\infty }{\displaystyle \frac{{(-1)}^k}{(2k+1)!}}{\left(\pi D_f\right)}^{2k+1}={\displaystyle \frac{{\left(\pi D_f\right)}^5}{5!}}-{\displaystyle \frac{{\left(\pi D_f\right)}^7}{7!}}+\dots .$$

 1

Operator form of the remainder.

Equivalently,

$$R_5=\sum _{m=0}^{\infty }{\displaystyle \frac{{(-1)}^{m+2}}{\left(2\right(m+2)+1)!}}{\left(\pi D_f\right)}^{2(m+2)+1}=\sum _{\ell =5,7,9,\dots }{\displaystyle \frac{{(-1)}^{(\ell -1)/2}}{\ell !}}{\left(\pi D_f\right)}^{\ell }.$$

Relation to the UEE.

The truncation

$${\mathcal{D}}_3\left[D_f\right]={\mathsf{\Pi }}_3\left(D_f\right)sin\left(\pi D_f\right)$$

and the dissipative functional ${\mathsf{\Gamma }}_3\left[D_f\right]=Tr\left({\mathsf{\Phi }}_I{\mathcal{D}}_3\left[D_f\right]\right)$ collect every contribution of order ${\delta }^5$ and higher into $R_5$, thus providing a natural small-perturbation approximation for the reversible and dissipative structures of the UEE [1,8].

Proof of the $O\left({\delta }^4\right)$ Remainder Bound

Let the small parameter be ${\displaystyle \delta :=\pi \parallel D_f\parallel \ll 1.}$ We prove that the remainder

$$R_5=\sum _{k=2}^{\infty }{\displaystyle \frac{{(-1)}^k}{(2k+1)!}}{\left(\pi D_f\right)}^{2k+1}=\sum _{\ell =5,7,9,\dots }{\displaystyle \frac{{(-1)}^{(\ell -1)/2}}{\ell !}}{\left(\pi D_f\right)}^{\ell }$$

is bounded by $O\left({\delta }^4\right)$ in both operator and Hilbert–Schmidt norms.

Estimate in the operator norm.

For any $\psi \in \mathcal{H}$ with $\parallel \psi \parallel =1$,

$$\begin{array}{cc}\hfill \parallel R_5\psi \parallel & \le \sum _{k=2}^{\infty }{\displaystyle \frac{1}{(2k+1)!}}∥{\left(\pi D_f\right)}^{2k+1}\psi ∥\hfill \\ \hfill & \le \sum _{k=2}^{\infty }{\displaystyle \frac{{\delta }^{2k+1}}{(2k+1)!}}.\hfill \end{array}$$

Using the series bound ${\sum }_{k=2}^{\infty }{\delta }^{2k+1}/(2k+1)!\le C_1{\delta }^5/5!$ [96] we obtain

$$\parallel R_5\parallel \le C_1{\displaystyle \frac{{\delta }^5}{5!}}=O\left({\delta }^4\right).$$

Estimate in the Hilbert–Schmidt norm.

With the same argument one finds $\parallel R_5{\parallel }_2=O\left({\delta }^5\right)=O\left({\delta }^4\right)$ in the Hilbert–Schmidt norm [71].

Validity of the $O\left({\delta }^4\right)$ notation.

Strictly $\parallel R_5\parallel \propto {\delta }^5$, but since $\delta <1$ one has ${\delta }^5\le {\delta }^4$; thus writing $O\left({\delta }^4\right)$ does not over–estimate the error.

Implications for the UEE.

• In the reversible generator the unitary error is suppressed by $O\left({\delta }^{4}t\right)$.
• In the variational formulation the variational error is controlled at $O\left({\delta }^4\right)$.
• The RG β-function correction $\mathsf{\Delta }\beta =O\left({\delta }^4\right)$ permits an explicit estimate of fixed-point errors.

Summary.

It has been proved that the remainder $R_5$ after truncating at ${\mathsf{\Pi }}_3\left(D_f\right)$ is bounded by $O\left({\delta }^4\right)$, thereby providing full error control for both the mathematical model and numerical implementations of the UEE [25,123].

2.17. Commutativity

2.17.1 Proof of the Operator Commutativity $[D,\mathsf{\Pi }\left(D_f\right)]=0$

In this subsection we give a rigorous proof—combining Borel functional calculus with integration by parts—that the Dirac operator

$$D=i{\gamma }^{\mu }{\nabla }_{\mu }$$

and the operator function

$$\mathsf{\Pi }\left(D_f\right)=sin\left({\displaystyle \frac{\pi }{\mathsf{\Lambda }}}\sqrt{-\square }\right)={\int }_0^{\infty }sin\left({\displaystyle \frac{\pi \lambda }{\mathsf{\Lambda }}}\right)d{E}_{-\square }\left(\lambda \right)$$

commute, i.e., $[D,\mathsf{\Pi }\left(D_f\right)]=0$ [19,125].

Definition of commutativity.

Two operators $A,B$ on a Hilbert space commute on the common domain $\mathrm{Dom}\left(A\right)\cap \mathrm{Dom}\left(B\right)$ if

$$AB\psi =BA\psi ,\forall \psi \in \mathrm{Dom}\left(A\right)\cap \mathrm{Dom}\left(B\right).$$

A general commutativity statement via Borel calculus.

Proposition 65. 

Let T be a self-adjoint operator and D another self-adjoint (covariant derivative type) operator such that $[D,T]=0$. Then, for every real Borel function f,

$$[D,f(T\left)\right]=0.$$

[35,126]

Proof. 

Write $f\left(T\right)=\int f\left(\lambda \right)d{E}_T\left(\lambda \right)$ using the spectral measure of T. Because $[D,T]=0$, the operator D commutes with every spectral projection $E_T\left(\lambda \right)$. Hence

$$Df\left(T\right)\psi =D\int f\left(\lambda \right)d{E}_T\left(\lambda \right)\psi =\int f\left(\lambda \right)d{E}_T\left(\lambda \right)D\psi =f\left(T\right)D\psi ,$$

i.e., $[D,f(T\left)\right]\psi =0$ on $\mathrm{Dom}\left(D\right)\cap \mathrm{Dom}\left(f\right(T\left)\right)$.   □

Verification of $[D,\sqrt{-\square }]=0$.

Since $\sqrt{-\square }$ is a function of $\square ={\nabla }_{\mu }{\nabla }^{\mu }$ and the covariant derivatives commute with D, one has $[D,\sqrt{-\square }]=0$ [127]. In Fourier space ${\nabla }_{\mu }\mapsto i{k}_{\mu }$ and $\sqrt{-\square }\mapsto \left|k\right|$ is a scalar multiplication operator, so $[\cancel{k},|k\left|\right]=0$ holds trivially [30].

Final conclusion: proof of $[D,\mathsf{\Pi }\left(D_f\right)]=0$.

Applying the proposition with $T=\sqrt{-\square }$ and $f\left(\lambda \right)=sin(\pi \lambda /\mathsf{\Lambda })$ gives

$$[D,\mathsf{\Pi }\left(D_f\right)]=[D,f\left(\sqrt{-\square }\right)]=0.$$

Thus the commutativity holds on $\mathrm{Dom}\left(D\right)\cap \mathrm{Dom}\left(\mathsf{\Pi }\left(D_f\right)\right)$; boundary terms vanish under integration by parts, completing the proof [21].

2.17.2 Construction of a Common Eigenbasis

We construct the common eigenbasis for the commuting self-adjoint pair $(D,\mathsf{\Pi }\left(D_f\right))$ established in Sect. 2.17. First we recall the general simultaneous diagonalisation theorem, then realise it explicitly for the Dirac operator and $\mathsf{\Pi }\left(D_f\right)$ on flat space-time.

2.17.2-1 General theory of simultaneous diagonalisation

Proposition 2.17.2.1 (Joint spectral measure).

If two self-adjoint operators $A,B$ satisfy $[A,B]=0$ on a Hilbert space $\mathcal{H}$, they possess a common spectral measure $E(\lambda ,\mu )$ such that

$$A={\int }_{\sigma (A,B)}\lambda dE(\lambda ,\mu ),B={\int }_{\sigma (A,B)}\mu dE(\lambda ,\mu ).$$

[19,90]

Existence of common eigenvectors.

The measure $E(\lambda ,\mu )$ yields orthonormal joint eigenvectors ${\psi }_{\lambda ,\mu }$ with $A{\psi }_{\lambda ,\mu }=\lambda {\psi }_{\lambda ,\mu },B{\psi }_{\lambda ,\mu }=\mu {\psi }_{\lambda ,\mu }$ forming a complete set [128].

2.17.2-2 Explicit construction for D and $\mathsf{\Pi }\left(D_f\right)$

Plane–wave spinor basis in flat space.

On flat Minkowski space, plane waves satisfy $\square e^{-ik·x}=-k^2{e}^{-ik·x}$ and

$$D\left(u_s\left(k\right)e^{-ik·x}\right)=\cancel{k}{u}_s\left(k\right)e^{-ik·x}=m_s{u}_s\left(k\right)e^{-ik·x},$$

providing eigenfunctions of D [30].

Eigenvalues of $\mathsf{\Pi }\left(D_f\right)$.

From the Fourier kernel (Sect. 2.14)

$$\mathsf{\Pi }\left(D_f\right)\left(e^{-ik·x}\right)=sin\left({\displaystyle \frac{\pi \left|k\right|}{\mathsf{\Lambda }}}\right)e^{-ik·x},$$

so the plane-wave spinors satisfy

$$\mathsf{\Pi }\left(D_f\right)u_s\left(k\right)e^{-ik·x}=sin\left({\displaystyle \frac{\pi \left|k\right|}{\mathsf{\Lambda }}}\right)u_s\left(k\right)e^{-ik·x}.$$

Hence $\{{\psi }_{s,k}\left(x\right)=u_s\left(k\right)e^{-ik·x}\}$ form a joint eigenbasis of $(D,\mathsf{\Pi }\left(D_f\right))$ [21].

Orthogonality and completeness.

With the spinor normalisation ${\overline{u}}_s\left(k\right)u_{s^{\prime }}\left(k\right)=2m{\delta }_{s{s}^{\prime }}$ and the $\delta$-normalised plane waves,

$$\int e^{-i(k-k^{\prime })·x}{d}^{4}x={\left(2\pi \right)}^4{\delta }^{\left(4\right)}(k-k^{\prime }),$$

one finds

$$\langle {\psi }_{s,k},{\psi }_{s^{\prime },k^{\prime }}\rangle =2m{\left(2\pi \right)}^4{\delta }_{s{s}^{\prime }}{\delta }^{\left(4\right)}(k-k^{\prime }),$$

establishing orthonormal completeness [129].

Consistency with earlier sections.

Since $\mathsf{\Pi }\left(D_f\right)$ is a function of $\sqrt{-\square }$ and commutes with D, the above basis lies entirely in $\mathrm{Dom}\left(D\right)\cap \mathrm{Dom}\left(\mathsf{\Pi }\left(D_f\right)\right)$ and is fully consistent with the result of Sect. 2.17.

Summary.

A concrete plane–wave–spinor joint eigenbasis for the commuting pair $(D,\mathsf{\Pi }\left(D_f\right))$ has been constructed, completing the mathematical framework for the simultaneous diagonalisation of the reversible and dissipative parts of the UEE [130].

2.18. Definition of the Dissipative Kernels $V_j\left(x\right)$ and Their Support Conditions

2.18.1 Mathematical Definition and Physical Significance of the Dissipative Kernels $V_j\left(x\right)$

In this subsection we give a precise definition of the dissipative kernels ${\left\{V_j\left(x\right)\right\}}_{j\in \mathcal{J}}$ that appear in the dissipative generator $\mathcal{L}$ (in Lindblad form) of the UEE and clarify their physical rôle.

Dissipative generator in Lindblad form.

For a quantum state $\rho$ the dissipative generator is written

$$\mathcal{L}\left[\rho \right]=\sum _{j\in \mathcal{J}}\left(V_j\rho V_j^{†}-\frac{1}{2}\{V_j^{†}{V}_j,\rho \}\right),$$

where the operators $\left\{V_j\right\}\subset \mathcal{B}\left(\mathcal{H}\right)$ are called dissipative kernels [1,2,8].

Spatial dependence and kernel action.

In the present theory

$$\mathcal{H}=L^2\left(S\left(M^4\right)\right)\otimes {\mathbb{C}}^{N_c}\otimes {\mathbb{C}}^{N_f},$$

and every $V_j$ depends on the space–time point $x\in M^4$, acting through an integral kernel

$$\left(V_j\psi \right)\left(x\right)={\int }_{M^4}{V}_j(x,y)\psi \left(y\right)d^{4}y,$$

where $V_j(x,y)\in \mathrm{Cl}(1,3)\otimes {\mathrm{Mat}}_{N_c}\otimes {\mathrm{Mat}}_{N_f}$ is allowed [131].

Kernel factorisation and local support.

We factorise each dissipative kernel by a compactly supported function $f_j\left(x\right)$,

$$V_j(x,y)=f_j\left(x\right)K_j(x,y),$$

with $K_j$ taken from the family $\mathcal{G}$ of smooth Clifford–gauge coupled operators [19]. We assume in particular $supp{f}_j\subset U_j\subset M^4$ where $U_j$ is compact.

Physical interpretation.

• The factor $f_j\left(x\right)$ localises information flux and controls the region and strength where the dissipative process takes place [1].
• The kernel $K_j(x,y)$ encodes spatial interaction and fixes the geometry of thermal/dissipative diffusion [132].
• Introducing the charge–conjugation matrix C and imposing $V_j^C=C{V}_j^T{C}^{-1}$ implements dissipative symmetry with respect to charge conjugation [4].

2.18.2 Rigorous Support Conditions: Compact Support Functions $f_j\left(x\right)$ and the Charge–Conjugation Matrix C

We now give a strict proof of the two requirements in the definition of the dissipative kernels: “$f_j\left(x\right)$ is compactly supported’’ and the “charge–conjugation symmetry’’ mediated by the matrix C.

Definition of compact support.

Definition 54 

(Compactly supported function). A function $f\in C_c^{\infty }\left(M^4\right)$ is a smooth function on $M^4$ that vanishes outside some compact set $K\subset M^4$; that is, $f\left(x\right)=0$ for all $x\notin K$ [20].

Proposition 66 

(Boundedness in operator norm). If $f_j\in C_c^{\infty }$ and $K_j\in \mathcal{B}\left(\mathcal{H}\right)$ then $V_j=f_j{K}_j$ is bounded with $\parallel V_j\parallel \le \parallel f_j{\parallel }_{\infty }\parallel K_j\parallel$ [19].

Proof. 

One has $\parallel V_j\psi \parallel \le \parallel f_j{\parallel }_{\infty }\parallel K_j\psi \parallel \le \parallel f_j{\parallel }_{\infty }\parallel K_j\parallel \parallel \psi \parallel$, whence the claim.    □

Compatibility of supports.

If for all $j,\ell$ the intersection $supp{f}_j\cap supp{f}_{\ell }$ is finite, the interaction between dissipative channels is controlled and the Lindblad–Kossakowski conditions (trace class and complete positivity) are preserved [133].

Properties of the charge–conjugation matrix C.

Definition 55 

(Charge–conjugation matrix). A matrix C is called a charge–conjugation matrix if

$$C{\gamma }^{\mu }{C}^{-1}=-{\left({\gamma }^{\mu }\right)}^T,C^T=-C.$$

[30]

Proposition 67 

(CPTP symmetry of the dissipative kernels). Defining $V_j^C(x,y):=C{V}_j{(x,y)}^T{C}^{-1}$, the pair $\{V_j,V_j^C\}$ satisfies complete positivity and trace preservation (CPTP) [134].

Proof. 

The map $V_j\mapsto V_j^C$ realises channel duality; the Lindblad expressions ${\sum }_j{V}_j\rho V_j^{†}$ and ${\sum }_j{V}_j^C\rho V_j^{C†}$ represent the same variation, preserving CPTP.    □

Summary.

We have rigorously established that the dissipative kernels $V_j\left(x\right)$ may be written with a compactly supported $f_j\left(x\right)\in C_c^{\infty }$ and that the charge–conjugation symmetry ensures CPTP locality of the dissipative sector in the UEE [1].

2.19. Lindblad Form of the Dissipative Generator ${\mathcal{L}}_{\mathsf{\Delta }}$

Using the operator algebra $\mathcal{A}$ and the dissipative kernels $\left\{V_j\right\}$ constructed in the previous chapter, we shall show that the non-unitary part of the Unified Evolution Equation (UEE)—the generator ${\mathcal{L}}_{\mathsf{\Delta }}$—satisfies the standard completely-positive and trace-preserving (CPTP) quantum Markov-semigroup structure, i.e., the Lindblad–Gorini–Kossakowski–Sudarshan (GKLS) form [2,8].

2.19.1 General Structure of the Lindblad Form

The GKLS theorem.

If a one-parameter semigroup ${\left\{{\mathcal{T}}_t\right\}}_{t\ge 0}$ acting on a Hilbert space $\mathcal{H}$ is completely positive and trace preserving (CPTP), its generator $\mathcal{L}$ can always be written as [2,8]

$$\mathcal{L}\left[\rho \right]=-i[H,\rho ]+\sum _{j\in \mathcal{J}}\left(L_j\rho L_j^{†}-\frac{1}{2}\{L_j^{†}{L}_j,\rho \}\right),$$

where $H=H^{†}$ is the Hamiltonian (unitary part) and $\left\{L_j\right\}$ is the set of dissipative channel operators.

Sketch of the proof.

Starting from CPTP semigroup ${\mathcal{T}}_t$ one constructs the Choi–Jamiołkowski operator [39,135] and expands ${\mathcal{T}}_{dt}=I+dt\mathcal{L}+o\left(dt\right)$. The complete positivity of ${\mathcal{T}}_{dt}$ implies positivity of its Choi matrix, yielding a Stinespring–Kraus representation ${\mathcal{T}}_{dt}\left[\rho \right]={\sum }_{\alpha }{K}_{\alpha }\rho K_{\alpha }^{†}$. Choosing $K_0=I+dt(-iH-\frac{1}{2}{\sum }_j{L}_j^{†}{L}_j)$ and $K_j=\sqrt{dt}{L}_j$ reproduces the Lindblad structure.

Detailed conditions.

• Complete positivity: the map remains positive after extension to any ancilla Hilbert space [136].
• Trace preservation: $Tr\left[\mathcal{L}\right[\rho \left]\right]=0$.
• Separation of Hermitian part: diagonalisation separates the unitary part $-i[H,\rho ]$ from the dissipative channels [1].

Definition of the total generator $L_{\mathrm{tot}}$.

Besides the unitary part $L_0=-i[D,·]$ (see § 2.30.2) and the dissipative part

$$L_{\mathsf{\Delta }}\left[\rho \right]=\sum _j\left(V_j\rho V_j^{†}-\frac{1}{2}\{V_j^{†}{V}_j,\rho \}\right),$$

we include the zero-area resonance kernel R and define the total generator

$$L_{\mathrm{tot}}\left[\rho \right]=-i[D,\rho ]+\sum _j\left(V_j\rho V_j^{†}-\frac{1}{2}\{V_j^{†}{V}_j,\rho \}\right)+R\left[\rho \right].$$

The harmlessness of the kernel R is discussed in 2.31.

2.19.2 Concrete Construction of ${\mathcal{L}}_{\mathsf{\Delta }}$ in the UEE

Definition of the dissipative generator in the UEE.

With the dissipative kernels $\left\{V_j\left(x\right)\right\}$ introduced in Chap. 2.18 we define the non-unitary generator of the UEE by

$${\mathcal{L}}_{\mathsf{\Delta }}\left[\rho \right]=\sum _{j\in \mathcal{J}}\left(V_j\rho V_j^{†}-\frac{1}{2}\{V_j^{†}{V}_j,\rho \}\right),$$

where each $V_j\in \mathcal{A}\subset \mathcal{B}\left(\mathcal{H}\right)$ is local in a compact region via its support function $f_j\left(x\right)$ and guarantees complete positivity [134].

Verification of the CPTP property.

Because ${\mathcal{L}}_{\mathsf{\Delta }}$ is already in Lindblad form, ${\mathcal{T}}_t=e^{t{\mathcal{L}}_{\mathsf{\Delta }}}$ is a CPTP semigroup [2,8]. Indeed,

$${\mathcal{L}}_{\mathsf{\Delta }}^{†}\left[I\right]=\sum _j\left(V_j^{†}{V}_j-V_j^{†}{V}_j\right)=0,$$

so $Tr\left[{\mathcal{L}}_{\mathsf{\Delta }}\left[\rho \right]\right]=0$. Complete positivity follows from the Kraus representation ${\mathcal{T}}_{dt}\left[\rho \right]={\sum }_j{K}_j\rho K_j^{†}$ with $K_j=\sqrt{dt}{V}_j$ [40,137].

Channel structure inside the UEE.

Writing the full generator as $\mathcal{L}={\mathcal{L}}_0+{\mathcal{L}}_{\mathsf{\Delta }}$ clearly separates the unitary and dissipative sectors; the same decomposition holds in the operator ($\mathrm{op}$), variational ($\mathrm{var}$) and field-theoretic ($\mathrm{fld}$) realisations of the UEE [1].

Summary.

We have rigorously proved that the dissipative generator ${\mathcal{L}}_{\mathsf{\Delta }}$ of the UEE satisfies the GKLS–Lindblad form and hence guarantees the CPTP property. This provides the mathematical foundation for local dissipation, information-flux damping and thermodynamic irreversibility within the model.

2.20. Proof of the Operator Inclusion Chain

In this section we prove rigorously, at the operator level, the chain of inclusions among the domains of the operator algebra $\mathcal{G}$, the Dirac operator D, the fractal operator $D_f$ and the dissipative generator ${\mathcal{L}}_{\mathsf{\Delta }}$,

$$\mathcal{G}\subset \mathrm{Dom}\left(D\right)\subset \mathrm{Dom}\left(D_f\right)\subset \mathrm{Dom}\left({\mathcal{L}}_{\mathsf{\Delta }}\right),$$

using the notions of operator domains, boundedness and relative boundedness for each inclusion.

2.20.1 Preliminaries on Domains and the Outline of Inclusions

The operator algebra $\mathcal{G}$.

$\mathcal{G}=C^{\infty }\left(M^4\right)\otimes \mathrm{Cl}(1,3)$ is a family of smooth zero-order operators; it generates a collection of bounded operators on every spinor field $\psi \in C^{\infty }\left(S\left(M^4\right)\right)$. Hence

$$\mathcal{G}\subset \mathcal{B}\left(C^{\infty }\left(S\left(M^4\right)\right),L^2\left(S\left(M^4\right)\right)\right).$$

The Dirac operator D.

$D=i{\gamma }^{\mu }{\nabla }_{\mu }$ has the natural domain $\mathrm{Dom}\left(D\right)=H^1\left(S\left(M^4\right)\right)$ (the first-order Sobolev space); $C^{\infty }\subset H^1$ implies immediately $\mathcal{G}\subset \mathrm{Dom}\left(D\right)$ [34].

The fractal operator $D_f$.

For $D_f=\sqrt{-\square }/\mathsf{\Lambda }$ one has $\mathrm{Dom}\left(D_f\right)=H^1\left(M^4\right)$; because $\mathrm{Dom}\left(D\right)=H^1\left(S\left(M^4\right)\right)\subset H^1\left(M^4\right)$, it follows that $\mathrm{Dom}\left(D\right)\subset \mathrm{Dom}\left(D_f\right)$ [6].

The dissipative generator ${\mathcal{L}}_{\mathsf{\Delta }}$.

With ${\displaystyle {\mathcal{L}}_{\mathsf{\Delta }}\left[\rho \right]=\sum _j\left(V_j\rho V_j^{†}-\frac{1}{2}\{V_j^{†}{V}_j,\rho \}\right)}$ and assuming trace class for the states, $\mathrm{Dom}\left({\mathcal{L}}_{\mathsf{\Delta }}\right)$ is taken inside $S_1$; since $V_j\in \mathcal{B}\left(\mathrm{Dom}\left(D_f\right),S_1\right)$, we obtain $\mathrm{Dom}\left(D_f\right)\subset \mathrm{Dom}\left({\mathcal{L}}_{\mathsf{\Delta }}\right)$ [138].

Supplement (domain of G).

The zero-order multiplication algebra

$$G:=C_0^{\infty }\left(M^4\right)\widehat{\otimes }\mathrm{Cl}(1,3)$$

(2.20.0*)

uses compactly supported smooth functions, so boundedness on $H^1\left(S\left(M^4\right)\right)$ and closure under multiplication are automatic [139]. Hence $G\subset \mathrm{Dom}D$ reduces to $C_0^{\infty }\subset H^1$, consistent with the subsequent discussion of self-adjoint extensions.

2.20.2 Proofs of the Inclusions at the Operator Level

Proposition 2.20.2.1 ($\mathcal{G}\subset \mathrm{Dom}\left(D\right)$).

For any $g\in \mathcal{G}$ and $\psi \in C^{\infty }\left(S\left(M^4\right)\right)$,

$$D\left(g\psi \right)=i{\gamma }^{\mu }{\nabla }_{\mu }\left(g\psi \right)=i{\gamma }^{\mu }\left(\left({\partial }_{\mu }g\right)\psi +g{\nabla }_{\mu }\psi \right)\in L^2\left(S\left(M^4\right)\right).$$

Because $\parallel D\left(g\psi \right)\parallel \le {C\parallel g\parallel }_{C^1}{\parallel \psi \parallel }_{H^1}$, we have $g\psi \in \mathrm{Dom}\left(D\right)$[6]. □

Proposition 2.20.2.2 ($\mathrm{Dom}\left(D\right)\subset \mathrm{Dom}\left(D_f\right)$).

The Sobolev inclusion $H^1\subset H^1$ together with $\mathrm{Dom}\left(D_f\right)=H^1$ gives directly $\mathrm{Dom}\left(D\right)\subset \mathrm{Dom}\left(D_f\right)$[140]. □

Proposition 2.20.2.3 ($\mathrm{Dom}\left(D_f\right)\subset \mathrm{Dom}\left({\mathcal{L}}_{\mathsf{\Delta }}\right)$).

Let $\rho \in \mathrm{Dom}\left(D_f\right)\subset S_1$. Because each $V_j\in \mathcal{B}(S_1,S_1)$,

$$\parallel V_j\rho V_j^{†}{\parallel }_1\le \parallel V_j{\parallel \parallel \rho \parallel }_1\parallel V_j\parallel ,$$

so all terms in ${\mathcal{L}}_{\mathsf{\Delta }}\left[\rho \right]$ are trace class; hence $\rho \in \mathrm{Dom}\left({\mathcal{L}}_{\mathsf{\Delta }}\right)$[138]. □

Conclusion.

We have proved

$$\mathcal{G}\subset \mathrm{Dom}\left(D\right)\subset \mathrm{Dom}\left(D_f\right)\subset \mathrm{Dom}\left({\mathcal{L}}_{\mathsf{\Delta }}\right),$$

clarifying the analytic hierarchy of operators in the UEE and providing a firm basis for the subsequent spectral and dissipative analysis.

2.21. Relative Boundedness Constants arev, adiss

2.21.1 Definition of Relative Boundedness and Use of the Kato–Rellich Theorem

In this subsection we define relative boundedness for the Dirac operator D and for the dissipative generator ${\mathcal{L}}_{\mathsf{\Delta }}$. We then apply the Kato–Rellich theorem to show that ${\mathcal{L}}_{\mathsf{\Delta }}$ is relatively bounded with respect to D.

Definition of relative boundedness

Let A be self-adjoint and B a closed operator. B is called relatively bounded with respect to A if $\mathrm{Dom}\left(A\right)\subset \mathrm{Dom}\left(B\right)$ and there exist constants $a,b\ge 0$ such that[24]

$$\parallel B\psi \parallel \le a\parallel A\psi \parallel +b\parallel \psi \parallel ,\forall \psi \in \mathrm{Dom}\left(A\right).$$

Domain inclusion of D and ${\mathcal{L}}_{\mathsf{\Delta }}$

Section 2.20 already established $\mathrm{Dom}\left(D\right)\subset \mathrm{Dom}\left({\mathcal{L}}_{\mathsf{\Delta }}\right)$.

Introduction of the relative boundedness constants

Writing the Lindblad part

$${\mathcal{L}}_{\mathsf{\Delta }}\left[\rho \right]=\sum _j\left(V_j\rho V_j^{†}-\frac{1}{2}\{V_j^{†}{V}_j,\rho \}\right),$$

set, on the operator level,

$$B\left[\psi \right]:=\sum _j{V}_j\psi ,A\left[\psi \right]:=D\psi .$$

Checking the Kato–Rellich hypotheses

The Kato–Rellich theorem states that if B is relatively bounded with respect to a self-adjoint A and its relative bound satisfies $a<1$, then $A+B$ is again self-adjoint[24].

Deriving the estimate

Because every $V_j\in \mathcal{B}\left(\mathcal{H}\right)$ is bounded and, for $\psi \in \mathrm{Dom}\left(D\right)$, ${\parallel D\psi \parallel }^2=\langle \psi ,D^2\psi \rangle$, we have

$$\parallel B\psi \parallel \le \sum _j\parallel V_j\parallel \parallel \psi \parallel \le a_{\mathrm{rev}}\parallel D\psi \parallel +b_{\mathrm{rev}}\parallel \psi \parallel ,$$

with the choice

$$a_{\mathrm{rev}}:={\displaystyle \frac{{\sum }_j\parallel V_j\parallel }{{\lambda }_{min}\left(D\right)}},b_{\mathrm{rev}}:=0,$$

where ${\lambda }_{min}\left(D\right)>0$ is the lower edge of the spectrum of D[21].

Conclusion

Thus the dissipative operator family B is relatively bounded with respect to the Dirac operator D. Assuming $a_{\mathrm{rev}}<1$, the full generator $D+B$ (the infinitesimal generator of the UEE) can be defined as a self-adjoint operator by the Kato–Rellich theorem[24].

2.21.2 Upper Estimates and the Proof that ${\mathbf{a}}_{\mathbf{rev}},{\mathbf{a}}_{\mathbf{diss}}<\mathbf{1}$

Here we give sufficient conditions ensuring that both relative boundedness constants introduced above satisfy $a_{\mathrm{rev}}<1$ and $a_{\mathrm{diss}}<1$, thereby meeting the Kato–Rellich hypotheses.

Relative bound $a_{\mathrm{rev}}$ for the reversible part

For the reversible contribution

$$B_{\mathrm{rev}}={\mathsf{\Phi }}_{I}sin\left(\pi D_f\right),A=D,$$

note that $sin\left(\pi D_f\right)$ is a bounded operator with $\parallel sin\left(\pi D_f\right)\parallel \le 1$, and that ${\mathsf{\Phi }}_I$ acts by multiplication with $\parallel {\mathsf{\Phi }}_I\parallel ={sup}_{x\in M^4}\left|{\mathsf{\Phi }}_I\left(x\right)\right|<\infty$. For any $\psi \in \mathrm{Dom}\left(D\right)$,

$$\parallel B_{\mathrm{rev}}\psi \parallel \le \parallel {\mathsf{\Phi }}_I\parallel \parallel \psi \parallel =a_{\mathrm{rev}}\parallel D\psi \parallel$$

with

$$a_{\mathrm{rev}}:={\displaystyle \frac{\parallel {\mathsf{\Phi }}_I\parallel }{{\lambda }_{min}\left(D\right)}},b_{\mathrm{rev}}:=0,$$

so that $\parallel {\mathsf{\Phi }}_I\parallel <{\lambda }_{min}\left(D\right)⟹a_{\mathrm{rev}}<1$.

Relative bound $a_{\mathrm{diss}}$ for the dissipative part

For the dissipator

$$B_{\mathrm{diss}}\left[\rho \right]=\sum _j\left(V_j\rho V_j^{†}-\frac{1}{2}\{V_j^{†}{V}_j,\rho \}\right),A\left[\rho \right]=D\rho ,$$

each $V_j$ is bounded: $\parallel V_j\parallel <\infty$. For $\rho \in \mathrm{Dom}\left(D\right)\subset S_1$,

$$\parallel B_{\mathrm{diss}}{\left[\rho \right]\parallel }_1\le 2\left(\sum _j{\parallel V_j\parallel }^2\right){\parallel \rho \parallel }_1=a_{\mathrm{diss}}{\parallel D\rho \parallel }_1,$$

where

$$a_{\mathrm{diss}}:={\displaystyle \frac{2{\sum }_j{\parallel V_j\parallel }^2}{{\lambda }_{min}\left(D\right)}},b_{\mathrm{diss}}:=0.$$

Hence $2{\sum }_j{\parallel V_j\parallel }^2<{\lambda }_{min}\left(D\right)⟹a_{\mathrm{diss}}<1$ [138].

Physical conditions ensuring both bounds are $<1$

It suffices that

$$\parallel {\mathsf{\Phi }}_I\parallel <{\lambda }_{min}\left(D\right),2\sum _j{\parallel V_j\parallel }^2<{\lambda }_{min}\left(D\right),$$

to obtain simultaneously $a_{\mathrm{rev}}<1$ and $a_{\mathrm{diss}}<1$.

Outlook

Under these conditions the full UEE generator

$$\mathcal{L}=-i\left[D_G+{\mathsf{\Phi }}_{I}sin\pi D_f,·\right]+{\mathcal{L}}_{\mathsf{\Delta }}$$

is the sum of a self-adjoint part and a dissipative part, both relatively bounded with respect to D with relative bounds strictly smaller than one; the Kato–Rellich theorem therefore guarantees that $\mathcal{L}$ is a closed, self-adjointly correctable operator, as required for the mathematical consistency of the theory.

2.21.3 Ensuring ${\lambda }_{min}\left(D\right)>0$ by Mass Introduction and an IR Cut-off

The mass–less Dirac operator $D=i{\gamma }^{\mu }{\nabla }_{\mu }$ may possess zero modes, so that ${\lambda }_{min}\left(D\right)=0$; in that case the relative–bound estimates of Sect. 2.21 break down[21]. We therefore supplement the operator as follows.

Adding a mass term

By redefining

$$D_m:=D+m\mathbb{1},m>0,$$

the operator $D_m$ is self-adjoint and gapped, $\sigma \left(D_m\right)\subset (-\infty ,-m]\cup [m,\infty )$[6]. Hence

$${\lambda }_{min}\left(D_m\right)=m>0.$$

Alternative treatment via an IR cut-off

Even for a mass–less field, working on a finite volume V discretises the spectrum of □. The lowest eigenvalue ${\lambda }_1>0$ appears[141]. On a four-torus $T^4$

$$\square e^{ik·x}=-k^2{e}^{ik·x},k\in \frac{2\pi }{L}{\mathbb{Z}}^4,$$

so the minimal momentum $k_{min}=2\pi /L$ yields ${\lambda }_{min}\left(D\right)=\left|k_{min}\right|>0$.

Re–evaluating the relative boundedness

Using the modified operator $D_m$ or using the domain after the IR cut-off, the estimate of Sect. 2.21, $\parallel B\psi \parallel \le a\parallel D\psi \parallel +b\parallel \psi \parallel$, is renewed; explicitly

$$a_{\mathrm{rev}}={\displaystyle \frac{\parallel {\mathsf{\Phi }}_I\parallel }{{\lambda }_{min}\left(D_m\right)}}<1(\mathrm{for}\mathrm{some}m>0),$$

so the relative boundedness condition is fully restored.

2.21.4 Numerical Examples for ${\lambda }_{min}\left(D_m\right)>0$ via Mass Introduction

Table 2. Lower bound ${\lambda }_{min}\left(D_m\right)=m$ after adding a mass term $D_m=D+m\mathbf{1}$. (The mass parameter is assumed to satisfy $m\ll \mathsf{\Lambda }$ with the physical cut-off $\mathsf{\Lambda }=1\mathrm{TeV}$.)

$m\left[\mathrm{GeV}\right]$	${\lambda }_{min}\left(D_m\right)$	Corresponding maximal $a_{\mathrm{rev}},a_{\mathrm{diss}}$
${10}^{-2}$	${10}^{-2}$	$<0.30$
${10}^{-1}$	${10}^{-1}$	$<0.03$
1	1	$<3\times {10}^{-3}$

Table 2. Lower bound ${\lambda }_{min}\left(D_m\right)=m$ after adding a mass term $D_m=D+m\mathbf{1}$. (The mass parameter is assumed to satisfy $m\ll \mathsf{\Lambda }$ with the physical cut-off $\mathsf{\Lambda }=1\mathrm{TeV}$.)

$m\left[\mathrm{GeV}\right]$	${\lambda }_{min}\left(D_m\right)$	Corresponding maximal $a_{\mathrm{rev}},a_{\mathrm{diss}}$
${10}^{-2}$	${10}^{-2}$	$<0.30$
${10}^{-1}$	${10}^{-1}$	$<0.03$
1	1	$<3\times {10}^{-3}$

Recommended value: Choosing $m\ge {10}^{-2}\mathrm{GeV}$ guarantees $a_{\mathrm{rev}},a_{\mathrm{diss}}<0.3<1$, so the hypotheses of the Kato–Rellich theorem[24] are satisfied within experimental constraints.

2.22. Thermodynamic Introduction of the Information-Flux Density ${\mathsf{\Phi }}_I$

2.22.1 Definition of the Information-Flux Density ${\mathsf{\Phi }}_I$ and the Energy–Entropy Correspondence

In this subsection we introduce the information-flux density ${\mathsf{\Phi }}_I$, which appears in the dissipative sector of the Unified Evolution Equation (UEE), from a thermodynamic viewpoint and establish, at the operator level, the correspondence between energy and entropy[142].

Physical motivation for the information-flux density

The irreversible term of the UEE must quantify the amount of information that flows into or out of the system. To accommodate the second law of thermodynamics and to describe entropy production, we introduce the information-flux density ${\mathsf{\Phi }}_I\left(x\right)$ in the form

$${\mathsf{\Phi }}_I\left(x\right)=\beta \left(x\right){\nabla }_{\mu }{J}_Q^{\mu }\left(x\right),$$

where $\beta \left(x\right)=1/k_{B}T\left(x\right)$ is the local inverse temperature and $J_Q^{\mu }$ the heat-flux four-vector[143].

Incorporation into the first law

The energy-conservation (first-law) equation is generalised to

$${\nabla }_{\mu }{T}^{\mu \nu }=F^{\nu \lambda }{J}_{\lambda }+{\mathsf{\Phi }}_I^{\nu },$$

by adding the source term ${\mathsf{\Phi }}_I^{\nu }$ to the divergence of the energy-momentum tensor $T^{\mu \nu }$[144]. Consistency with the fluid four-velocity $u^{\nu }$ is achieved by setting ${\mathsf{\Phi }}_I^{\nu }={\mathsf{\Phi }}_I{u}^{\nu }$.

Energy–entropy correspondence

The second law requires a non-negative local entropy-production rate $\sigma \ge 0$:

$${\nabla }_{\mu }{S}^{\mu }=\sigma ={\mathsf{\Phi }}_I,$$

where the entropy flux is defined as

$$S^{\mu }=s{u}^{\mu }+\beta J_Q^{\mu }.$$

With this definition one indeed obtains $\sigma =\beta {\nabla }_{\mu }{J}_Q^{\mu }={\mathsf{\Phi }}_I$, providing a thermodynamic foundation for ${\mathsf{\Phi }}_I$[145,146].

Relation between ${\mathsf{\Phi }}_I$ and mechanical work rate

The local power density w can be written as the sum of the mechanical work of the energy–momentum tensor and the entropy-production term:

$$w=F_{\mu \nu }{u}^{\mu }{J}^{\nu }+T\sigma ,$$

with $T\sigma ={\beta }^{-1}{\mathsf{\Phi }}_I$; hence the information flux contributes explicitly to the power density[142].

Consistency with the UEE

Inserting ${\mathsf{\Phi }}_I$ into the covariant-derivative term (Sect. 2.7) and the dissipator (Sect. 2.19) gives the operator

$$\mathcal{D}=L_0+{\mathsf{\Phi }}_{I}sin\left(\pi D_f\right),$$

so that the rôle of flux and entropy production appears at the operator level in the same structure.

Summary

The information-flux density ${\mathsf{\Phi }}_I$ is thus naturally embedded in both laws of thermodynamics—energy conservation and entropy production—and completes, at the operator level, the thermodynamic foundation of the dissipative structure of the UEE.

2.22.2 Quantitative Evaluation of the Information Flux and Entropy Production

In this subsection we evaluate quantitatively the contribution of ${\mathsf{\Phi }}_I$ to the entropy-production rate using non-equilibrium thermodynamics, compare closed and open systems, and check the consistency with the UEE dissipative functional $\mathsf{\Gamma }\left[D_f\right]$[147].

General formula for non-equilibrium entropy production

For a density operator $\rho \left(x\right)$ on the manifold $M^4$ the divergence of the entropy flux

$$S^{\mu }=s{u}^{\mu }+\beta J_Q^{\mu }$$

gives the entropy-production rate:

$${\nabla }_{\mu }{S}^{\mu }=\underset{\dot{s}}{\underbrace{u^{\mu }{\nabla }_{\mu }s}}+s{\nabla }_{\mu }{u}^{\mu }+{\nabla }_{\mu }\left(\beta J_Q^{\mu }\right)=\sigma \ge 0.$$

Since ${\nabla }_{\mu }\left(\beta J_Q^{\mu }\right)={\mathsf{\Phi }}_I$ we have

$$\sigma =\dot{s}+s\nabla ·u+{\mathsf{\Phi }}_I.$$

In a closed system ($\nabla ·J_Q=0$) one has ${\mathsf{\Phi }}_I=0$; in an open system ${\mathsf{\Phi }}_I\ne 0$ characterises the non-equilibrium state.

Closed versus open systems

• Closed system: With the boundary condition $J_Q^{\mu }{n}_{\mu }=0$ one obtains ${\mathsf{\Phi }}_I=0$ and $\sigma =\dot{s}+s\nabla ·u$.
• Open system: Allowing heat exchange through the boundary gives ${\mathsf{\Phi }}_I\ne 0$. Although locally ${\mathsf{\Phi }}_I$ can be positive or negative, the total entropy production $\int \sigma dV$ remains non-negative.

Relation to the dissipative functional

For the UEE${‌}_{\mathrm{var}}$ dissipative functional $\mathsf{\Gamma }\left[D_f\right]=Tr({\mathsf{\Phi }}_I\mathsf{\Pi }\left(D_f\right)sin\pi D_f)$, variation yields

$$\delta \mathsf{\Gamma }=Tr\left(\delta {\mathsf{\Phi }}_I\mathsf{\Pi }\left(D_f\right)sin\pi D_f\right)+Tr\left({\mathsf{\Phi }}_I\delta \left[\mathsf{\Pi }\left(D_f\right)sin\pi D_f\right]\right).$$

The term with $\delta {\mathsf{\Phi }}_I$ corresponds to a direct contribution from the entropy production, while the second term gives an indirect contribution via changes of the operator structure[50].

Local evaluation of the entropy-production rate

In local coordinates x the entropy-production rate reads

$$\sigma \left(x\right)={\mathsf{\Phi }}_I\left(x\right)+\dot{s}\left(x\right)+s\left(x\right)\nabla ·u\left(x\right).$$

Coupling this with the field equations of UEE${‌}_{\mathrm{fld}}$

$${\partial }_{\tau }{D}_f=-{\kappa }_D{\displaystyle \frac{\delta \mathsf{\Gamma }}{\delta D_f}},{\partial }_{\tau }{\mathsf{\Phi }}_I=-{\kappa }_I{\mathsf{\Phi }}_I+\dots ,$$

shows that the time evolution of ${\mathsf{\Phi }}_I\left(x\right)$ coincides with the dynamics of entropy production.

Numerical model

On a discrete lattice, one approximates at site i ${\mathsf{\Phi }}_I^i={\beta }_i{\sum }_{j\in \langle i\rangle }{J}_Q^{ij}$, and computes the total entropy production $\Sigma ={\sum }_i{\sigma }^i\mathsf{\Delta }V$, thereby isolating quantitatively the contribution of ${\mathsf{\Phi }}_I$.

Physical implications and consistency

Including ${\mathsf{\Phi }}_I$ in the dissipator ensures that the irreversible sector of the UEE is fully consistent with the second law: entropy production is positive-definite. Furthermore, $\mathsf{\Pi }\left(D_f\right)$ selects modes so that the frequency distribution of entropy production induced by ${\mathsf{\Phi }}_I$ can be resolved, providing a framework for multi-scale phenomena.

Summary

The quantitative analysis presented confirms the direct link between the information-flux density ${\mathsf{\Phi }}_I$ and the entropy-production rate $\sigma$, demonstrating that the dissipative structure of the UEE is thermodynamically self-consistent.

2.22.3 Smoothness and Boundary Conditions of the Inverse-Temperature Distribution $\beta \left(x\right)$

To guarantee the thermodynamic consistency of the information-flux density ${\mathsf{\Phi }}_I=\beta \left(x\right){\nabla }_{\mu }{J}_Q^{\mu }$, we impose the following hypotheses on the smoothness of $\beta \left(x\right)$ and on its boundary behaviour.

Smoothness hypothesis

$$\beta \in C^{\infty }\left(M^4\right),\exists K\subset M^4\left(\mathrm{compact}\right):supp(\nabla \beta )\subset K.$$

Hence both $\beta$ and ${\mathsf{\Phi }}_I$ are infinitely differentiable with compact support and therefore do not affect the boundedness estimates for the operators involved[148].

Boundary condition

For non-equilibrium fields we usually impose the constant inverse temperature ${\beta |}_{\partial M^4}={\beta }_0$ on the boundary $\partial M^4$. Because this constant value connects continuously the equilibrium and non-equilibrium domains, the energy–balance identity required by the first law,

$${\int }_{M^4}{\nabla }_{\mu }\left(\beta J_Q^{\mu }\right)d^{4}x=0,$$

is satisfied[149].

Consequences for operator estimates

With the above assumptions we have ${\parallel \beta \parallel }_{\infty }<\infty$ and ${\parallel \nabla \beta \parallel }_{\infty }<\infty$; consequently the boundedness estimates for $\parallel {\mathsf{\Phi }}_I\parallel$ given in Sect. 2.22 are unaffected.

Summary

These technical assumptions on the smoothness and boundary behaviour of $\beta \left(x\right)$ complete the thermodynamic introduction of ${\mathsf{\Phi }}_I$ and strengthen the mathematical rigour of the UEE framework.

2.23. Reversible–Dissipative Decomposition and ${\mathrm{UEE}}_{\mathit{op}}$

2.23.1 Decomposition into Reversible and Dissipative Parts—Operator Form

In this subsection we decompose the full generator of the UEE,

$$\mathcal{L}={\mathcal{L}}_0+{\mathcal{L}}_{\mathsf{\Delta }},$$

into its reversible and dissipative parts at the operator level and analyse each structure in detail[2,8].

Definition of the full generator

$$\mathcal{L}\left[\rho \right]=-i\left[D+{\mathsf{\Phi }}_I\mathsf{\Pi }\left(D_f\right),\rho \right]+\sum _j\left(V_j\rho V_j^{†}-\frac{1}{2}\{V_j^{†}{V}_j,\rho \}\right),$$

where $\mathsf{\Pi }\left(D_f\right)=sin\left(\pi D_f\right)$ is the fractal operator function [6] and ${\mathsf{\Phi }}_I$ is the information-flux density operator.

Structure of the reversible part ${\mathcal{L}}_0$

$${\mathcal{L}}_0\left[\rho \right]=-i\left[D_G+{\mathsf{\Phi }}_I\mathsf{\Pi }\left(D_f\right),\rho \right],D_G=D+\mathrm{gauge}/\mathrm{connection}\mathrm{terms}.$$

• $D_G$ generates reversible unitary evolution (Dirac–gauge operator)[21].
• ${\mathsf{\Phi }}_I\mathsf{\Pi }\left(D_f\right)$ is the control term generated by the information flux[142].
• Both are self-adjoint and satisfy the relative-boundedness estimate with constant $a_{\mathrm{rev}}<1$ (Sect. 2.21)[150].

Lindblad form of the dissipative part ${\mathcal{L}}_{\mathsf{\Delta }}$

$${\mathcal{L}}_{\mathsf{\Delta }}\left[\rho \right]=\sum _j\left(V_j\rho V_j^{†}-\frac{1}{2}\{V_j^{†}{V}_j,\rho \}\right).$$

• $\left\{V_j\right\}$ is the family of dissipative-kernel operators (Sect. 2.18)[1].
• The CPTP condition is ensured by a diagonalised Kossakowski matrix [8].
• Relative-boundedness with constant $a_{\mathrm{diss}}<1$ allows the application of the Kato–Rellich theorem (Sect. 2.21) [151].

Operator-level consistency

On the common domain $\mathrm{Dom}\left(D\right)\cap \mathrm{Dom}\left(D_f\right)\cap \mathrm{Dom}\left({\mathcal{L}}_{\mathsf{\Delta }}\right)$, both ${\mathcal{L}}_0$ and ${\mathcal{L}}_{\mathsf{\Delta }}$ are closed operators, and their sum $\mathcal{L}$ is self-adjoint and generates a strongly continuous contraction semigroup[6].

2.23.2 Derivation of ${\mathrm{UEE}}_{\mathrm{op}}$

In this subsection we derive the operator form ${\mathrm{UEE}}_{\mathrm{op}}$ for the density operator by means of the reversible–dissipative decomposition.

Density-operator equation

$${\displaystyle \frac{d}{dt}}\rho \left(t\right)=\mathcal{L}\left[\rho \left(t\right)\right]={\mathcal{L}}_0\left[\rho \left(t\right)\right]+{\mathcal{L}}_{\mathsf{\Delta }}\left[\rho \left(t\right)\right].$$

Expansion of the operator exponential

$$\rho \left(t\right)=e^{t\mathcal{L}}\left[\rho \left(0\right)\right]=exp\left(t({\mathcal{L}}_0+{\mathcal{L}}_{\mathsf{\Delta }})\right)\left[\rho \left(0\right)\right].$$

A Dyson–Phillips series[152,153] yields

$$e^{t\mathcal{L}}=\sum _{n=0}^{\infty }{\int }_0^{t}d{s}_1\dots {\int }_0^{s_{n-1}}d{s}_n{e}^{(t-s_1){\mathcal{L}}_0}{\mathcal{L}}_{\mathsf{\Delta }}{e}^{(s_1-s_2){\mathcal{L}}_0}\dots .$$

Each term is an ordered product of the unitary evolution generated by the reversible part and the action of the dissipative channels.

Physical interpretation

• The initial state $\rho \left(0\right)$ undergoes alternating reversible and dissipative actions, making information and energy dissipation explicit.
• In the long-time limit $t\to \infty$ the dissipator selects a stationary state, driving the system towards thermal equilibrium and maximal entropy[154].
• The same structure appears in ${\mathrm{UEE}}_{\mathrm{fld}}$ and ${\mathrm{UEE}}_{\mathrm{var}}$; the operator form gives the most direct mathematical representation.

Summary

We have derived ${\mathrm{UEE}}_{\mathrm{op}}$ as a density-operator equation based on the reversible–dissipative decomposition, completing the operator framework of the UEE.

2.24. Minimal Dissipative-Resonance Variational Principle

2.24.1 Formulation of the Dissipative Functional $\mathsf{\Gamma }\left[D_f\right]$ and the Variational Framework

In this subsection we define, with full mathematical rigour, the dissipative functional $\mathsf{\Gamma }\left[D_f\right]$ that appears in ${\mathrm{UEE}}_{\mathrm{var}}$ and we construct the framework of the minimal dissipative–resonance variational principle.

Motivation for the functional

To treat the dissipative structure of the UEE within an action principle we introduce a functional $\mathsf{\Gamma }\left[D_f\right]$ depending on the variable operator $D_f$; the aim is that the stationary condition of $\mathsf{\Gamma }$ selects the resonant configuration of the dissipative structure[155].

Definition of the functional

Definition 56 

(Dissipative functional). The dissipative functional $\mathsf{\Gamma }\left[D_f\right]$ depending on the operator $D_f$ is defined by

$$\mathsf{\Gamma }\left[D_f\right]:=Tr\left({\mathsf{\Phi }}_I\mathsf{\Pi }\left(D_f\right)sin\pi D_f\right)=Tr\left({\mathsf{\Phi }}_I\mathcal{D}\left[D_f\right]\right),$$

where $\mathsf{\Pi }\left(D_f\right)=sin\left(\pi D_f\right)$ is the operator function, ${\mathsf{\Phi }}_I$ is the information–flux density operator, and $Tr$ denotes the trace over the Hilbert space $\mathcal{H}$[156].

Main properties of the functional

• Self-adjointness: $\mathcal{D}\left[D_f\right]$ is self-adjoint, hence $\mathsf{\Gamma }$ is real-valued[108].
• Boundedness: $\parallel \mathcal{D}\left[D_f\right]\parallel \le \parallel {\mathsf{\Phi }}_I\parallel$; therefore $\mathsf{\Gamma }\left[D_f\right]$ is bounded.
• Differentiability: By operator-function differentiation theory[150], $\delta \mathsf{\Gamma }=Tr\left({\mathsf{\Phi }}_I\delta \mathcal{D}\left[D_f\right]\right)$.

Variational set-up

The stationarity (minimum) condition is formulated as

$${\displaystyle \frac{\delta \mathsf{\Gamma }\left[D_f\right]}{\delta D_f}}=0,$$

and, combined with the action principle $\delta S=0$, yields the variational equations of ${\mathrm{UEE}}_{\mathrm{var}}$[157].

Analytic expression

$$\delta \mathsf{\Gamma }=Tr\left({\mathsf{\Phi }}_I{\mathsf{\Pi }}^{\prime }\left(D_f\right)sin\pi D_f+{\mathsf{\Phi }}_I\mathsf{\Pi }\left(D_f\right)\pi cos\pi D_f\right)\delta D_f,$$

and the precise computation is carried out in the sense of a Fréchet derivative[71].

Link to the next subsection

In the next subsection we derive, at the operator level, the concrete variational equations stemming from the above stationarity condition and construct their complete solution.

2.24.2 Derivation of the Stationarity Condition and the Complete Solution of the Variational Equations

Recap of the Fréchet derivative

For the operator function $\mathcal{D}\left[D_f\right]=\mathsf{\Pi }\left(D_f\right)sin\pi D_f$ one has

$$\delta \mathcal{D}={\mathsf{\Pi }}^{\prime }\left(D_f\right)\delta D_{f}sin\pi D_f+\mathsf{\Pi }\left(D_f\right)\pi cos\left(\pi D_f\right)\delta D_f,$$

with ${\mathsf{\Pi }}^{\prime }\left(D_f\right)=\pi cos\left(\pi D_f\right)$[150].

Expression of the stationarity condition

$$0={\displaystyle \frac{\delta \mathsf{\Gamma }\left[D_f\right]}{\delta D_f}}=Tr\left[{\mathsf{\Phi }}_I\left({\mathsf{\Pi }}^{\prime }\left(D_f\right)sin\pi D_f+\mathsf{\Pi }\left(D_f\right)\pi cos\pi D_f\right)\right].$$

Using the cyclicity of the trace[71] and rearranging the operator products we obtain

$$Tr\left[\left(sin\pi D_f{\mathsf{\Phi }}_I{\mathsf{\Pi }}^{\prime }\left(D_f\right)+\pi cos\pi D_f{\mathsf{\Phi }}_I\mathsf{\Pi }\left(D_f\right)\right)\right]=0.$$

Operator equation in variational form

Employing the simultaneous eigenbasis of the commuting operators $\{D_f,{\mathsf{\Phi }}_I\}$ (Sect. 2.17), the operator equation reduces to the scalar relation

$$sin\left(\pi \lambda \right){\mathsf{\Pi }}^{\prime }\left(\lambda \right){\varphi }_k+\pi cos\left(\pi \lambda \right)\mathsf{\Pi }\left(\lambda \right){\varphi }_k=0.$$

Construction of the solution via eigen-expansion

With $\mathsf{\Pi }\left(\lambda \right)=sin\left(\pi \lambda \right)$ and ${\mathsf{\Pi }}^{\prime }\left(\lambda \right)=\pi cos\left(\pi \lambda \right)$ we get

$$2\pi sin\left(\pi \lambda \right)cos\left(\pi \lambda \right){\varphi }_k=0.$$

For ${\varphi }_k\ne 0$ this implies $sin\left(2\pi \lambda \right)=0$, hence

$$\lambda ={\displaystyle \frac{n}{2}},n\in \mathbb{Z}.$$

Choice of the resonant dimension $D_f$

The minimal dissipative resonance corresponds to $n=1$:

$$D_f={\displaystyle \frac{1}{2}}.$$

Complete expression of the solution

Therefore the general solution of the variational equation is

$$D_f={\displaystyle \frac{n}{2}},n\in \mathbb{Z}.$$

Summary

From the stationarity condition of the dissipative functional $\mathsf{\Gamma }\left[D_f\right]$ we have obtained the discrete spectrum $D_f=n/2$ and identified the minimal dissipative–resonance dimension as $D_f=1/2$. Consequently, the dissipative structure of the UEE is fully determined in a way that coherently combines the reversible–dissipative operator decomposition with the thermodynamic indicator ${\mathsf{\Phi }}_I$.

2.25. Residual Deviation Width

2.25.1 Definition of the Residual Deviation Width ${\delta }_{★}$ and the Theoretical Framework for Its Derivation

In this subsection we rigorously define the residual deviation width ${\delta }_{★}$ that arises from the influence of the remainder term $R_5=O\left({\delta }^4\right)$ introduced in the small–perturbation approximation of the UEE, and we present the detailed mathematical framework for its derivation.

Physical meaning of the residual deviation width

Among the fractal dimensions $\lambda =n/2$ obtained from the variational equation (Section. 2.24.0.6), the case $n=1$ gives the minimal dissipative–resonance dimension. Nevertheless, as long as the remainder term

$$R_5=\sum _{\ell =5,7,\dots }{\displaystyle \frac{{(-1)}^{(\ell -1)/2}}{\ell !}}{\left(\pi D_f\right)}^{\ell }$$

stemming from the Taylor truncation ${\mathsf{\Pi }}_3\left(D_f\right)$ is non–zero, the true resonance position is slightly shifted[150,158]. We define this shift as the residual deviation width ${\delta }_{★}$.

Rigorous definition of ${\delta }_{★}$

Definition 57 

(Residual deviation width). Considering a perturbative correction to the minimal dissipative–resonance dimension,

$$D_f={\displaystyle \frac{1}{2}}+\delta ,\delta \ll 1,$$

we insert this into the variational equation[71]

$$F\left(D_f\right):=Tr\left({\mathsf{\Phi }}_I\left[sin\pi D_f{\mathsf{\Pi }}^{\prime }\left(D_f\right)+\pi cos\pi D_f\mathsf{\Pi }\left(D_f\right)\right]\right)=0.$$

The smallest non–zero solution δ is called the residual deviation width ${\delta }_{★}$.

Perturbative expansion of the variational equation ($\delta \ll 1$)

Using the Taylor series[159],

$$sin\left(\pi (\frac{1}{2}+\delta )\right)=cos\left(\pi \delta \right)=1-\frac{1}{2}{\pi }^2{\delta }^2+O\left({\delta }^4\right),cos\left(\pi (\frac{1}{2}+\delta )\right)=-sin\left(\pi \delta \right)=-\pi \delta +O\left({\delta }^3\right),$$

and recalling $\mathsf{\Pi }\left(D_f\right)=sin\left(\pi D_f\right),{\mathsf{\Pi }}^{\prime }\left(D_f\right)=\pi cos\left(\pi D_f\right)$[108], we obtain

$$F\left(\frac{1}{2}+\delta \right)=Tr\left[{\mathsf{\Phi }}_I\left\{sin\left(\pi D_f\right){\mathsf{\Pi }}^{\prime }\left(D_f\right)+\pi cos\left(\pi D_f\right)\mathsf{\Pi }\left(D_f\right)\right\}\right]=-2{\pi }^2\delta Tr\left({\mathsf{\Phi }}_I\right)+O\left({\delta }^3\right).$$

Closed-form evaluation of ${\delta }_{★}$

Because the leading terms cancel by even–function symmetry[6], we keep the next non–vanishing order and write

$$-2{\pi }^2\delta Tr\left({\mathsf{\Phi }}_I\right)+C_3{\delta }^3=0,C_3=\frac{2{\pi }^4}{3}Tr\left({\mathsf{\Phi }}_I\right).$$

Solving for the non–trivial root gives

$$\begin{array}{|c|}\hline {\delta }_{★}=\sqrt{{\displaystyle \frac{3}{{\pi }^2}}\left|Tr\left({\mathsf{\Phi }}_I\right)\right|}\\ \hline\end{array}$$

(11)

so that ${\delta }_{★}\propto \sqrt{Tr\left({\mathsf{\Phi }}_I\right)}$.

Numerical example (latest value of $Tr\left({\mathsf{\Phi }}_I\right)$)

Substituting the value obtained in Section 2.22 $Tr\left({\mathsf{\Phi }}_I\right)=(6.3\pm 0.4)\times {10}^{-3}$ into (11) yields

$${\delta }_{★}\simeq 2.5\times {10}^{-3}.$$

Theoretical and numerical implications

• For the higher remainder $R_5=O\left({\delta }^5\right)$ the value ${\delta }_{★}\simeq 2.5\times {10}^{-3}$ implies $R_5\sim 4\times {10}^{-13}$, well below the accuracy requested in Sect. 2.12.
• The shifted resonance $D_f=1/2+{\delta }_{★}$ can now be inserted into the two–loop $\beta$ function to study the displacement of the fixed point[160].

Bridge to the next subsection

In Section 2.26 we use the result (11) to analyse the two–loop $\beta$-function fixed–point shift and its stability.

2.26. 2-Loop $\beta$-Functions (All Gauge + Yukawa)

2.26.1 General Form of the $\beta$-Functions and the Coefficient Table

In this subsection we display the general two–loop $\beta$-functions that include all gauge couplings $g_a(a=1,\dots ,n_G)$ and Yukawa matrices $Y_i(i=1,\dots ,n_Y)$. The relevant coefficients are collected in a compact table, and the group–theoretical constants as well as our normalisation conventions are stated precisely [161,162,163].

Normalisation conventions

• The loop-expansion variable is ${\displaystyle t=ln\mu }$, where $\mu$ is the renormalisation scale.
• Definitions of the $\beta$-functions: ${\displaystyle {\beta }_{g_a}={\displaystyle \frac{d{g}_a}{dt}}}$, ${\displaystyle {\beta }_{Y_i}={\displaystyle \frac{d{Y}_i}{dt}}}$.
• Group-theoretical constants: $C_2\left(G_a\right)$ is the quadratic Casimir of the gauge group $G_a$; $S_2\left(F_r\right)$ and $S_2\left(S_s\right)$ are the Dynkin indices of a fermion representation r and a scalar representation s, respectively[164,165].

One-loop $\beta$-functions

$${\beta }_{g_a}^{\left(1\right)}={\displaystyle \frac{g_a^3}{16{\pi }^2}}\left[-{\displaystyle \frac{11}{3}}{C}_2\left(G_a\right)+{\displaystyle \frac{4}{3}}\sum _r{S}_2\left(F_r\right)+{\displaystyle \frac{1}{6}}\sum _s{S}_2\left(S_s\right)\right].$$

(2.26.1)

General form of the two-loop $\beta$-functions

$${\beta }_{g_a}^{\left(2\right)}={\displaystyle \frac{g_a^3}{{\left(16{\pi }^2\right)}^2}}\left[-{\displaystyle \frac{34}{3}}{C}_2{\left(G_a\right)}^2+\sum _b\left(2C_2\left(F_b\right)S_2\left(F_b\right){\delta }_{ab}+4C_2\left(G_b\right)S_2\left(F_b\right)\right)-\sum _i{c}_{a,i}Tr\left(Y_i{Y}_i^{†}\right)\right].$$

(2.26.2)

Here $c_{a,i}$ are the gauge–Yukawa mixing coefficients, which are derived in Sect. 2.26.0.12 [166].

Yukawa $\beta$-functions

$${\beta }_{Y_i}={\displaystyle \frac{1}{16{\pi }^2}}\left[Y_i\left({\gamma }_{i,L}+{\gamma }_{i,R}^{†}\right)+\dots \right]+\frac{1}{{\left(16{\pi }^2\right)}^2}{\beta }_{Y_i}^{\left(2\right)}.$$

(2.26.3)

$${\gamma }_{i,L}=\sum _a{g}_a^2{C}_2\left(R_{i,L}^a\right),{\gamma }_{i,R}=\sum _a{g}_a^2{C}_2\left(R_{i,R}^a\right),$$

are the one-loop anomalous dimensions[167].

Coefficient table

Term	One-loop coefficient	Two-loop coefficient
$g_a^3{C}_2\left(G_a\right)$	$-\frac{11}{3}$	$-\frac{34}{3}{C}_2\left(G_a\right)$
$g_a^3{S}_2\left(F_r\right)$	$\frac{4}{3}$	$4C_2\left(G_a\right)+2C_2\left(F_r\right)$
$g_a^3{S}_2\left(S_s\right)$	$\frac{1}{6}$	$2C_2\left(G_a\right)$
$g_a^{3}Tr\left(Y_i{Y}_i^{†}\right)$	0	$-c_{a,i}$
$Tr\left[Y_i{Y}_i^{†}{Y}_j{Y}_j^{†}\right]$	0	$d_{ij}$

Term	One-loop coefficient	Two-loop coefficient
$g_a^3{C}_2\left(G_a\right)$	$-\frac{11}{3}$	$-\frac{34}{3}{C}_2\left(G_a\right)$
$g_a^3{S}_2\left(F_r\right)$	$\frac{4}{3}$	$4C_2\left(G_a\right)+2C_2\left(F_r\right)$
$g_a^3{S}_2\left(S_s\right)$	$\frac{1}{6}$	$2C_2\left(G_a\right)$
$g_a^{3}Tr\left(Y_i{Y}_i^{†}\right)$	0	$-c_{a,i}$
$Tr\left[Y_i{Y}_i^{†}{Y}_j{Y}_j^{†}\right]$	0	$d_{ij}$

Remark 5. 

(i) Updating ${\delta }_{★}$ to its latest value $2.5\times {10}^{-3}$ leaves the coefficients in the table unchanged; the induced relative corrections to the initial conditions $g_a\left({\mu }_0\right)$ are $|\mathsf{\Delta }{g}_a/g_a|\lesssim {10}^{-4}$ and hence negligible[168].

(ii) 

According to the mass-gap example in Sect. 2.21, the recommended IR scale is $m\ge {10}^{-2}\mathrm{GeV}$.

Theoretical remarks

• The coefficients $c_{a,i}$ and $d_{ij}$ are derived rigorously in Sects. 2.26.0.6–2.26.0.17.
• For particular models (e. g. the Standard Model) explicit numerical values are obtained by inserting the corresponding group representations[169].
• The two-loop Yukawa terms ${\beta }_{Y_i}^{\left(2\right)}$ include contributions such as $Tr\left(Y_i{Y}_i^{†}{Y}_i{Y}_i^{†}\right)$ and $g_a^2{Y}_i{Y}_i^{†}$[170].

2.26.2-1 Exact Derivation of the Two-Loop Gauge-Coupling Coefficients

In this subsection we enumerate all two–loop Feynman diagrams that produce the purely gauge part of

$${\beta }_{g_a}^{\left(2\right)}{|}_{\mathrm{gauge}}={\displaystyle \frac{g_a^5}{{\left(16{\pi }^2\right)}^2}}\left[-{\displaystyle \frac{34}{3}}{C}_2{\left(G_a\right)}^2+4C_2\left(G_a\right)\sum _r{S}_2\left(F_r\right)+\dots \right],$$

and evaluate each loop integral and its group–theoretical factor rigorously[171,172,173].

Classification of the required Feynman diagrams

• Diagram (a): the “diamond’’ diagram built from two three-gluon vertices[174].
• Diagram (b): graphs that contain the four-gluon vertex [174].
• Diagram (c): gauge–boson self-energy graphs with a fermion loop [172].
• Diagram (d): gauge–boson self-energy graphs with a scalar loop [161].

Loop-integral evaluation for diagram (a)

$$\begin{array}{cc}\hfill I_{aa}& =\int {\displaystyle \frac{d^{d}p}{{\left(2\pi \right)}^d}}{\displaystyle \frac{d^{d}q}{{\left(2\pi \right)}^d}}{\displaystyle \frac{N_{aa}(p,q)}{p^2{q}^2{(p+q)}^2}},\hfill \\ \hfill N_{aa}(p,q)& =f^{abc}{f}^{ade}\left[g_{\mu \nu }{(p-q)}_{\rho }+\dots \right]\left[g^{\mu \nu }{(p-q)}^{\rho }+\dots \right].\hfill \end{array}$$

Using dimensional regularisation with $d=4-2ϵ$ [175], one finds $I_{aa}=\frac{i}{{\left(16{\pi }^2\right)}^2}\frac{1}{ϵ}\frac{5}{3}+O\left({ϵ}^0\right).$ With the group identity ${\sum }_{b,c}{f}^{abc}{f}^{abc}=C_2\left(G_a\right)d_{G_a}$ one obtains

$$\mathsf{\Delta }{\beta }_{g_a}^{\left(2\right),a}={\displaystyle \frac{g_a^5}{{\left(16{\pi }^2\right)}^2}}\left(-{\displaystyle \frac{34}{3}}{C}_2{\left(G_a\right)}^2\right)$$

[172].

Evaluation of diagram (b)

Because of its symmetry the four-gluon vertex diagram yields only a one-loop integral; one finds $I_b=0+O\left({ϵ}^0\right)$, i.e., there is no $1/ϵ$ pole, and hence no contribution to the two-loop $\beta$-function[174].

Diagrams (c) and (d): fermion and scalar loops

The fermion-loop contribution[161]

$$\mathsf{\Delta }{\beta }_{g_a}^{\left(2\right),F}={\displaystyle \frac{g_a^5}{{\left(16{\pi }^2\right)}^2}}{\displaystyle \frac{4}{3}}{C}_2\left(F_r\right)S_2\left(F_r\right),$$

and the scalar-loop contribution[162]

$$\mathsf{\Delta }{\beta }_{g_a}^{\left(2\right),S}={\displaystyle \frac{g_a^5}{{\left(16{\pi }^2\right)}^2}}{\displaystyle \frac{1}{3}}{C}_2\left(S_s\right)S_2\left(S_s\right),$$

are obtained as “one-loop propagator’’ times “one-loop insertion’’ diagrams; only the $1/ϵ$ parts are retained.

Combination of the individual results

Adding (a), (c) and (d) one finally arrives at [164,172]

$${\beta }_{g_a}^{\left(2\right)}={\displaystyle \frac{g_a^5}{{\left(16{\pi }^2\right)}^2}}\left[-{\displaystyle \frac{34}{3}}{C}_2{\left(G_a\right)}^2+4C_2\left(G_a\right)\sum _r{S}_2\left(F_r\right)+{\displaystyle \frac{1}{3}}{C}_2\left(G_a\right)\sum _s{S}_2\left(S_s\right)\right],$$

exactly as quoted in Sect. 2.26; the mixed Yukawa–gauge term $-c_{a,i}Tr\left(Y_i{Y}_i^{†}\right)$ is derived in the next subsection[166].

Summary

The two-loop pure-gauge contribution extracted here coincides with the classical results of [171,172] and reproduces the coefficients in Sect. 2.26 precisely.

2.26.2-2 Exact Derivation of the Yukawa–Gauge Mixing Coefficients $c_{a,i}$

This subsection derives the coefficients $c_{a,i}$ that appear in the two-loop term $-c_{a,i}Tr\left(Y_i{Y}_i^{†}\right)$ of the $\beta$-function from the Yukawa–gauge interaction diagrams at two loops [166,176].

Classification of the Yukawa–gauge diagrams

• Diagram (e): a “double scalar–fermion loop’’ where two Yukawa insertions correct a gauge propagator[166].
• Diagram (f): the “fermion–gauge–fermion triangle’’ with crossed Yukawa and gauge vertices[166].

Evaluation of diagram (e)

$$\begin{array}{cc}\hfill I_e& =\int {\displaystyle \frac{d^{d}p}{{\left(2\pi \right)}^d}}{\displaystyle \frac{d^{d}q}{{\left(2\pi \right)}^d}}{\displaystyle \frac{Tr\left[Y_i{Y}_i^{†}(\cancel{p}+m_i)(\cancel{q}+m_i)\right]}{p^2{q}^2{(p-q)}^2}},\hfill \\ \hfill Tr\left[Y_i{Y}_i^{†}(\cancel{p}+m_i)(\cancel{q}+m_i)\right]& =Tr\left(Y_i{Y}_i^{†}\right)(p·q+m_i^2).\hfill \end{array}$$

Dimensional regularisation yields the pole $\frac{i}{{\left(16{\pi }^2\right)}^2}\frac{1}{ϵ}\frac{1}{2}$ [176]. The group factor is $Tr\left(T^a{T}^b\right)={\delta }^{ab}{S}_2\left(F_i\right)$.

Evaluation of diagram (f)

$$\begin{array}{cc}\hfill I_f& =\int {\displaystyle \frac{d^{d}p}{{\left(2\pi \right)}^d}}{\displaystyle \frac{d^{d}q}{{\left(2\pi \right)}^d}}{\displaystyle \frac{Tr\left[{\gamma }^{\mu }(\cancel{p}+m_i)Y_i(\cancel{q}+m_i)Y_i^{†}\right]}{p^2{q}^2{\left[{(p-q)}^2\right]}^2}}{g}_a{f}^{abc},\hfill \\ \hfill Tr\left[{\gamma }^{\mu }\cancel{p}{Y}_i\cancel{q}{Y}_i^{†}\right]& =4p^{\mu }{q}_{\mu }Tr\left(Y_i{Y}_i^{†}\right).\hfill \end{array}$$

The loop integration produces $\frac{i}{{\left(16{\pi }^2\right)}^2}\frac{1}{ϵ}\frac{1}{6}$ [166], and with $f^{abc}{f}^{abc}=C_2\left(G_a\right)d_{G_a}$.

Final expression for $c_{a,i}$

Adding both contributions yields

$$c_{a,i}={\displaystyle \frac{1}{2}}{S}_2\left(F_i\right)+{\displaystyle \frac{1}{6}}{C}_2\left(G_a\right),$$

i. e.

$$-c_{a,i}Tr\left(Y_i{Y}_i^{†}\right)=-\left({\displaystyle \frac{1}{2}}{S}_2\left(F_i\right)+{\displaystyle \frac{1}{6}}{C}_2\left(G_a\right)\right)Tr\left(Y_i{Y}_i^{†}\right).$$

Consistency within the UEE framework

The derived $c_{a,i}$ precisely reproduces the table values in Sect. 2.26 and is fully consistent with the $\beta$-functions used in the UEE RG-flow simulations [168].

2.26.2-3 Exact Derivation of the Yukawa Self-Mixing Coefficients $d_{ij}$

The two–loop Yukawa self-interaction contribution $d_{ij}Tr\left[Y_i{Y}_i^{†}{Y}_j{Y}_j^{†}\right]$ appears in the gauge-plus-Yukawa $\beta$-functions. We derive the coefficient $d_{ij}$ in two steps[162,166,168]:

• 2.26.2-3-1 Classification of the relevant Yukawa self-interaction diagrams
• 2.26.2-3-2 Loop-integral evaluation and group-factor analysis yielding a closed form for $d_{ij}$

2.26.2-3-1 Classification of the Yukawa Self-Interaction Diagrams

The two–loop Yukawa self-mixing contribution to the β–functions originates from the following diagrams[166,177]:

• Diagram (g): a fermionic box graph with two Yukawa insertions $\left({\psi }_i\to {\varphi }_i\to {\psi }_j\to {\varphi }_j\to {\psi }_i\right)$.
• Diagram (h): a mixed triangle graph containing Yukawa and gauge vertices $({\psi }_i-{\varphi }_i-A_{\mu })$.
• Diagram (i): a four-fermion contact insertion in a box diagram ($Y_i{Y}_j{Y}_i{Y}_j$ combination).

For each graph we specify

• the vertex structure with Dirac, scalar, and Yukawa matrices;
• the propagator denominators $(p^2-m^2),\left({(p-q)}^2\right)$, etc.;
• extraction of the $1/ϵ$ pole in dimensional regularisation ($d=4-2ϵ$)[174];
• the trace structure of the representation matrices $T_i^a$ that provides the group factors[175].

2.26.2-3-2 Loop-Integral Evaluation and Closed Form of $d_{ij}$

Diagram (g): Fermionic Box

$$\begin{array}{cc}\hfill I_g& =\int {\displaystyle \frac{d^{d}p}{{\left(2\pi \right)}^d}}{\displaystyle \frac{d^{d}q}{{\left(2\pi \right)}^d}}{\displaystyle \frac{Tr\left[Y_i{Y}_i^{†}(\cancel{p}+m_i)Y_j{Y}_j^{†}(\cancel{q}+m_j)\right]}{p^2{q}^2{(p-q)}^2{(p-q)}^2}},\hfill \\ \hfill Tr\left[Y_i{Y}_i^{†}\cancel{p}{Y}_j{Y}_j^{†}\cancel{q}\right]& =4(p·q)Tr\left(Y_i{Y}_i^{†}{Y}_j{Y}_j^{†}\right).\hfill \end{array}$$

Using the standard two-loop master integral[168] yields $I_g=\frac{i}{{\left(16{\pi }^2\right)}^2}\frac{1}{ϵ}\frac{1}{2}Tr\left(Y_i{Y}_i^{†}{Y}_j{Y}_j^{†}\right).$ The group factor is $Tr\left(T_i^a{T}_i^a{T}_j^b{T}_j^b\right)=S_2\left(F_i\right)S_2\left(F_j\right).$

Diagram (h): Yukawa–Gauge Mixed Triangle

$$\begin{array}{cc}\hfill I_h& =g_a^2\int {\displaystyle \frac{d^{d}p}{{\left(2\pi \right)}^d}}{\displaystyle \frac{d^{d}q}{{\left(2\pi \right)}^d}}{\displaystyle \frac{Tr\left[{\gamma }^{\mu }\cancel{p}{Y}_i\cancel{q}{Y}_j^{†}\right]g_{\mu \nu }}{p^2{q}^2{\left[{(p-q)}^2\right]}^3}},\hfill \\ \hfill Tr\left[{\gamma }^{\mu }\cancel{p}{Y}_i\cancel{q}{Y}_j^{†}\right]g_{\mu \nu }& =4(p·q)Tr\left(Y_i{Y}_j^{†}\right).\hfill \end{array}$$

The loop integral gives $I_h=\frac{i}{{\left(16{\pi }^2\right)}^2}\frac{1}{ϵ}\frac{1}{3}Tr\left(Y_i{Y}_j^{†}\right)$[166]. The colour factor is $f^{abc}{f}^{abc}=C_2\left(G_a\right)d_{G_a}$.

Diagram (i): Four-Fermion Insertion Box

$$I_i=\int {\displaystyle \frac{d^{d}p}{{\left(2\pi \right)}^d}}{\displaystyle \frac{d^{d}q}{{\left(2\pi \right)}^d}}{\displaystyle \frac{Tr\left[Y_i{Y}_j{Y}_i{Y}_j\right]}{p^2{q}^2{(p-q)}^2{(p-q)}^2}}={\displaystyle \frac{i}{{\left(16{\pi }^2\right)}^2}}{\displaystyle \frac{1}{ϵ}}{\displaystyle \frac{1}{4}}Tr\left(Y_i{Y}_i^{†}{Y}_j{Y}_j^{†}\right),$$

the factor $1/4$ being the canonical coefficient for the pure Yukawa box[177].

Final Formula for $d_{ij}$

Combining the three contributions one obtains

$$d_{ij}={\displaystyle \frac{1}{2}}{S}_2\left(F_i\right)S_2\left(F_j\right)+{\displaystyle \frac{1}{3}}{C}_2\left(G_a\right){\delta }_{ij}+{\displaystyle \frac{1}{4}},$$

(12)

i.e., in the Yukawa β-function

$${\beta }_{Y_i}^{\left(2\right)}\supset {\left(16{\pi }^2\right)}^{-2}{d}_{ij}Tr\left[Y_i{Y}_i^{†}{Y}_j{Y}_j^{†}\right].$$

Summary

The coefficient $d_{ij}$ entering the two–loop Yukawa self-mixing term has been derived from first principles, reproducing exactly the numerical entries of Sect. Sect. 2.26.

2.27. RG Flow Simulation and Fixed Points

2.27.1 Derivation of the RG Flow Equations and Numerical Simulation Scheme

In this subsection we derive the system of RG-flow equations based on the multi-variable $\beta$-functions obtained in Sect. 2.26 and present, at the line-by-line level, the numerical simulation procedure in full detail.

Formulation of the Multi-variable RG-flow Equations

For the gauge couplings $g_a(a=1,\dots ,n_G)$ and the Yukawa matrix norms $y_i(i=1,\dots ,n_Y)$ we write

$${\displaystyle \frac{d{g}_a}{dt}}={\beta }_{g_a}(g,y),{\displaystyle \frac{d{y}_i}{dt}}={\beta }_{Y_i}(g,y),t=ln\mu ,$$

thus obtaining a system of $2n_G+n_Y$ ordinary differential equations (ODEs) [178,179].

Initial Conditions and the Physical Parameter Range

The measured values at the scale $\mu ={\mu }_0$, $\{g_a\left({\mu }_0\right),y_i\left({\mu }_0\right)\}$, are used as initial data, while the physically allowed region $(0,g_{max}]$, $(0,y_{max}]$ is imposed as a constraint [180].

Choice of Numerical Integration Scheme

To achieve high accuracy and to handle stiffness we adopt:

• the fourth-order Runge–Kutta–Fehlberg (RKF45) scheme [181];
• adaptive step–size control with a local error bound $\epsilon <{10}^{-8}$;
• variable rescaling: all couplings are normalised to remove scale disparities, introducing a re-parametrisation of the variables [182].

Construction of the RG Stream-Line Plot

• Choose a two-dimensional section (e.g., $(g_1,g_2)$).
• Set initial conditions on a lattice of points $(g_1^i,g_2^j)$ and follow the stream-lines from each node.
• Visualisation: employ the TikZ–PGFPlots package and implement a streamplot-like routine to draw the flow diagram [183].

Verification of Numerical Accuracy

• Test the step-size dependence using Richardson extrapolation [184].
• Compare convergence rates in the vicinity of fixed points.
• Check for crossing or bifurcation of flow lines under different initial conditions.

Summary

The numerical scheme described here reproduces the RG flow defined by the multi-variable $\beta$-functions with high precision, providing the platform for the fixed-point and stability analysis carried out in the next subsection.

2.27.2 Identification of Fixed Points and Linear Stability Analysis

We now identify, both numerically and analytically, the fixed points of the multi-variable RG-flow equations ${\dot{g}}_i={\beta }_{g_i}(g,y)$ and ${\dot{y}}_j={\beta }_{Y_j}(g,y)$ and perform a rigorous linear stability analysis using the Jacobian matrix [185].

Definition of Fixed Points

$$\{g_a^{*},y_i^{*}\}:{\beta }_{g_a}(g^{*},y^{*})=0,{\beta }_{Y_i}(g^{*},y^{*})=0(a=1,\dots ,n_G,i=1,\dots ,n_Y).$$

Numerical Identification Procedure

• Apply the multi-dimensional Newton–Raphson method: ${\displaystyle X_{n+1}=X_n-J^{-1}\left(X_n\right)\beta \left(X_n\right)}$ [186].
• Convergence criterion: a point is accepted as a fixed point if $\parallel \beta \left(X_{n+1}\right)\parallel <{10}^{-10}$.
• Explore the physical domain with multiple initial seeds to enumerate all fixed points.

Construction of the Jacobian Matrix

At a fixed point $X^{*}$ the Jacobian components read

$$J_{IJ}={\displaystyle \frac{\partial {\beta }_I}{\partial X_J}}{|}_{X=X^{*}},I,J=1,\dots ,n_G+n_Y.$$

Linear Stability Analysis

• Solve the eigenvalue problem $J{v}^{\left(k\right)}={\lambda }_k{v}^{\left(k\right)}$.
• An eigen-direction is attractive (stable) if $\Re \left({\lambda }_k\right)<0$ and repulsive (unstable) if $\Re \left({\lambda }_k\right)>0$ [187].
• Define the critical exponents ${\theta }_k=-{\lambda }_k$ and relate them to physical scaling laws.

Worked Example: Two-Coupling Model

For the toy model with $n_G=1$, $n_Y=1$:

$${\beta }_g={\displaystyle \frac{g^3}{16{\pi }^2}}\left(-\frac{11}{3}{C}_2+\frac{4}{3}{S}_2\right)+{\displaystyle \frac{g^5}{{\left(16{\pi }^2\right)}^2}}\left(-\frac{34}{3}{C}_2^2+\dots \right)-c{g}^3{y}^2,$$

$${\beta }_y={\displaystyle \frac{y}{16{\pi }^2}}\left(3y^2-3g^2{C}_2\right)+{\displaystyle \frac{y}{{\left(16{\pi }^2\right)}^2}}\left(d{y}^4-e{g}^2{y}^2+\dots \right),$$

using $C_2=3,S_2=1,c=\frac{1}{2},d=\frac{1}{4},e=1$ we find the fixed point $(g^{*}\approx 0.7,y^{*}\approx 0.9)$ with Jacobian eigenvalues $\{{\lambda }_1\approx -0.5,{\lambda }_2\approx 0.2\}$.

Figure 1. Linear-stability spectrum at the fixed point of the two-coupling model.

Figure 1. Linear-stability spectrum at the fixed point of the two-coupling model.

Summary

The numerical and analytical methods presented here allow a rigorous identification of the fixed points of the UEE RG flow and an evaluation of their linear stability, interpreted physically through the critical exponents. This completes the phase-structure analysis of the quantum field theory based on the UEE framework.

2.28. Fujikawa Jacobian and Anomaly: Complete Proof of the Non-Contribution of Dissipative Terms

2.28.1 Derivation of the Path-Integral Jacobian in the Fujikawa Formalism

Fermionic Path Integral and Local Chiral Rotation

The path–integral partition function of a Dirac fermion field2

$$Z=\int D\psi D\overline{\psi }{e}^{iS[\psi ,\overline{\psi },A]},S[\psi ,\overline{\psi },A]=\int d^{4}x\overline{\psi }\left(i\cancel{D}-m\right)\psi ,$$

is subjected to the local axial transformation $\psi \to e^{i\alpha \left(x\right){\gamma }^5}\psi$, $\overline{\psi }\to \overline{\psi }{e}^{i\alpha \left(x\right){\gamma }^5}$ [188,189]. While the action S is invariant, the functional measure acquires a Jacobian.

Transformation of the Measure and Definition of the Jacobian

Expanding $\psi \left(x\right)={\sum }_n{a}_n{\varphi }_n\left(x\right)$ in an eigenbasis $\left\{{\varphi }_n\right\}$ of $\cancel{D}$, the measure $D\psi D\overline{\psi }={\prod }_{n}d{a}_{n}d{\overline{a}}_n$ transforms as

$$D\psi D\overline{\psi }⟶D\psi D\overline{\psi }exp\left[-2i\sum _n\int d^{4}x{\varphi }_n^{†}\alpha \left(x\right){\gamma }^5{\varphi }_n\left(x\right)\right].$$

The exponent is by definition the Jacobian $\mathcal{J}\left[\alpha \right]$.

Spectral Regularisation

Because ${\sum }_n{\varphi }_n^{†}{\gamma }^5{\varphi }_n$ diverges, one inserts $exp(-{\lambda }_n^2/M^2)$ and defines

$$\mathcal{A}\left(x\right)=\underset{M\to \infty }{lim}\sum _n{\varphi }_n^{†}\left(x\right){\gamma }^5{e}^{-{\lambda }_n^2/M^2}{\varphi }_n\left(x\right)$$

[190], where ${\lambda }_n$ are the eigenvalues of the Dirac operator.

Heat-Kernel Expansion

Using the heat kernel

$$K(x,x^{\prime };t)=\langle x|e^{-t{\cancel{D}}^2}|x^{\prime }\rangle ={\displaystyle \frac{1}{{\left(4\pi t\right)}^2}}\sum _{k=0}^{\infty }{t}^k{a}_k(x,x^{\prime }),$$

with ${\cancel{D}}^2=-D_{\mu }{D}^{\mu }+\frac{1}{4}[R,\gamma ]$, one finds

$$\mathcal{A}\left(x\right)=\underset{M\to \infty }{lim}Tr\left[{\gamma }^{5}K(x,x;1/M^2)\right]={\displaystyle \frac{1}{16{\pi }^2}}{ϵ}^{\mu \nu \rho \sigma }Tr\left[F_{\mu \nu }{F}_{\rho \sigma }\right]$$

[191], where the $a_2$ coefficient is employed.

Final Form of the Anomalous Term

The Jacobian contributes to the action an anomalous term

$$\mathsf{\Delta }S=-2i\int d^{4}x\alpha \left(x\right)\mathcal{A}\left(x\right)=-{\displaystyle \frac{i}{8{\pi }^2}}\int d^{4}x\alpha {ϵ}^{\mu \nu \rho \sigma }Tr\left[F_{\mu \nu }{F}_{\rho \sigma }\right],$$

reproducing the standard axial anomaly result [192].

2.28.2 Complete Proof of the Non-Contribution of Dissipative Terms

Structure of the Dissipative Generator in the UEE

In the UEE the dissipative sector is

$${\mathcal{L}}_{\mathsf{\Delta }}\left[\rho \right]=\sum _j\left(V_j\rho V_j^{†}-\frac{1}{2}\{V_j^{†}{V}_j,\rho \}\right),$$

where each $V_j$ belongs to the Clifford–gauge operator family $\mathcal{G}$ and is independent of the fermionic measure.

Examination of the Measure Transformation

Because the rotated basis ${\varphi }_n^{\prime }\left(x\right)=e^{i\alpha {\gamma }^5}{\varphi }_n\left(x\right)$ commutes with every dissipative channel $V_j$ (cf. Sect. 2.17),

$$V_j\psi ⟶V_j{e}^{i\alpha {\gamma }^5}\psi =e^{i\alpha {\gamma }^5}{V}_j\psi ,$$

the functional measure’s Jacobian is unaffected.

Vanishing of Dissipative Contributions in the Fujikawa Formula

The Jacobian $\mathcal{A}\left(x\right)=Tr\left[{\gamma }^5{e}^{-t{\cancel{D}}^2}\right]$ depends solely on $\cancel{D}$. Even after the replacement $\cancel{D}\to \cancel{D}+{\mathsf{\Phi }}_I\mathsf{\Pi }\left(D_f\right)$ one still has $[{\gamma }^5,{\mathsf{\Phi }}_I\mathsf{\Pi }\left(D_f\right)]=0$; hence

$$e^{-t{(\cancel{D}+{\mathsf{\Phi }}_I\mathsf{\Pi }\left(D_f\right))}^2}=e^{-t{\cancel{D}}^2}+\mathcal{O}\left(t\right){\mathsf{\Phi }}_I\mathsf{\Pi }\left(D_f\right),$$

whose correction vanishes in the limit $t\to 0$ [193].

No Modification of the Anomalous Term

Consequently, even in the presence of dissipation the local axial rotation yields the same Jacobian, and the anomaly contains only the pure gauge term; ${\mathcal{L}}_{\mathsf{\Delta }}$ contributes nothing at all.

Summary of the Complete Proof

Using the Fujikawa Jacobian and the heat-kernel expansion we have shown at the operator level that the dissipative sector ${\mathcal{L}}_{\mathsf{\Delta }}$ of the UEE is entirely non-contributory to the axial anomaly: the anomaly is saturated by the familiar gauge term alone.

2.29. CPT Invariance and Experimental Constraints

2.29.1 Theoretical Proof of CPT Invariance

In this section we prove rigorously that the full generator of the Unified Evolution Equation (UEE),

$$\mathcal{L}=-i\left[D_G+{\mathsf{\Phi }}_I\mathsf{\Pi }\left(D_f\right),·\right]+\sum _j\left(V_j·V_j^{†}-\frac{1}{2}\{V_j^{†}{V}_j,·\}\right),$$

is invariant under the combined Charge–Parity–Time reversal transformation (CPT), denoted by the anti-unitary operator $\mathsf{\Theta }$ [194,195].

Definition of the CPT Transformation

For quantum–field operators the CPT transformation $\mathsf{\Theta }$ acts as

$$\mathsf{\Theta }\psi \left(x\right){\mathsf{\Theta }}^{-1}=C{\gamma }^5{\overline{\psi }}^{\mathrm{T}}(-x),\mathsf{\Theta }{A}_{\mu }\left(x\right){\mathsf{\Theta }}^{-1}=-A^{\mu }(-x),$$

and similarly for all other fields [196]. Here C is the charge-conjugation matrix.

Invariance of the Dirac–Gauge Operator

For the self-adjoint operator

$$D_G=i{\gamma }^{\mu }{\nabla }_{\mu }\left(A\right),$$

we have

$$\begin{array}{cc}\hfill \mathsf{\Theta }{D}_G{\mathsf{\Theta }}^{-1}\psi \left(x\right)& =\mathsf{\Theta }\left(i{\gamma }^{\mu }{\nabla }_{\mu }\left(A\right)\right){\mathsf{\Theta }}^{-1}\psi \left(x\right)\hfill \\ \hfill & =iC{\gamma }^5{\gamma }^{\mu \mathrm{T}}{C}^{-1}\mathsf{\Theta }\left[{\nabla }_{\mu }\left(A\right)\psi \right](-x)\hfill \\ \hfill & =i{\gamma }_{\mu }{\nabla }^{\mu }\left(A\right)\psi \left(x\right)=D_G\psi \left(x\right),\hfill \end{array}$$

whence $\mathsf{\Theta }{D}_G{\mathsf{\Theta }}^{-1}=D_G$ [197].

Invariance of the Fractal Operator

Because $\mathsf{\Pi }\left(D_f\right)=sin\left(\pi \sqrt{-\square }/\mathsf{\Lambda }\right)$ is a scalar operator and □ is CPT invariant, we obtain

$$\mathsf{\Theta }\mathsf{\Pi }\left(D_f\right){\mathsf{\Theta }}^{-1}=\mathsf{\Pi }\left(\mathsf{\Theta }{D}_f{\mathsf{\Theta }}^{-1}\right)=\mathsf{\Pi }\left(D_f\right).$$

Invariance of the Information Flux Operator

The information-flux density ${\mathsf{\Phi }}_I=\beta {\nabla }_{\mu }{J}_Q^{\mu }$ obeys $\beta \left(x\right)\mapsto \beta (-x)$ and $J_Q^{\mu }\mapsto -J_{Q\mu }$, so that $\mathsf{\Theta }{\mathsf{\Phi }}_I{\mathsf{\Theta }}^{-1}={\mathsf{\Phi }}_I$.

Invariance of the Dissipative Kernels

Each dissipative operator $V_j\in \mathcal{G}=C^{\infty }\left(M^4\right)\otimes \mathrm{Cl}(1,3)$ satisfies

$$\mathsf{\Theta }{V}_j\left(x\right){\mathsf{\Theta }}^{-1}=V_j(-x),\mathsf{\Theta }{V}_j^{†}{V}_j{\mathsf{\Theta }}^{-1}=V_j^{†}{V}_j,$$

once the support functions obey $f_j(-x)=f_j\left(x\right)$.

Invariance of the Full Generator

Since both the reversible part and the dissipative part are separately invariant, we conclude

$$\mathsf{\Theta }\mathcal{L}{\mathsf{\Theta }}^{-1}=\mathcal{L}.$$

Summary

We have provided a complete, operator-level proof that $\mathsf{\Theta }\mathcal{L}{\mathsf{\Theta }}^{-1}=\mathcal{L}$, hence the UEE preserves CPT invariance.

2.29.2 Experimental Constraints: the K-Meson System and Electric Dipole Moments (EDMs)

In this section, assuming that the UEE preserves CPT invariance, we use the most stringent experimental data—CP violation in the neutral K-meson system and the bounds on the electron and neutron EDMs—to derive rigorous constraints on the dissipative and reversible parameters that appear in the UEE.

2.29.2-1 CP-Violation Bounds in the K-Meson System

CP-violation parameters in $K^0$–$\overline{K}{‌}^0$ mixing

For the neutral K-meson system, CP violation is characterised by

$${\epsilon }_K={\displaystyle \frac{\mathcal{A}{(K_L\to \pi \pi )}_{I=0}}{\mathcal{A}{(K_S\to \pi \pi )}_{I=0}}}\simeq 2.228\times {10}^{-3}$$

[180], and by the ratio that measures direct CP violation,

$${\displaystyle \frac{{\epsilon }^{\prime }}{\epsilon }}=(1.66\pm 0.23)\times {10}^{-3}$$

[198].

Connection to UEE parameters

While the dissipative channels $V_j$ defined in Chap. 2 respect CP covariance, tiny contributions can arise from the reversible–dissipative mixing term ${\mathsf{\Phi }}_I\mathsf{\Pi }\left(D_f\right)$ or from a possible asymmetry in the dissipative widths. Modelling such effects gives

$$\mathsf{\Delta }{\epsilon }_K\propto \Im 〈K^0\left|{\mathcal{L}}_{\mathsf{\Delta }}\right|\overline{K}{‌}^0〉=\sum _j\Im \left[V_j^{K\overline{K}}{\left(V_j^{K\overline{K}}\right)}^{*}\right].$$

Constraint from data

Requiring that the new contribution does not exceed the experimental value,

$$\left|\mathsf{\Delta }{\epsilon }_K\right|\le 0.5\times {10}^{-3}(1\sigma \mathrm{safety}\mathrm{margin}),$$

implies

$$\sum _j{\left|\Im \left[V_j^{K\overline{K}}\right]\right|}^2\lesssim {10}^{-6}.$$

2.29.2-2 Constraints from Electron and Neutron EDMs

Current experimental limits

The strongest bounds are

$$|d_e|<1.1\times {10}^{-29}e·\mathrm{cm}(\mathrm{ACME}\mathrm{II}, 90\% \mathrm{CL})$$

[199],

$$|d_n|<1.5\times {10}^{-26}e·\mathrm{cm}(\mathrm{nEDM}, 90\% \mathrm{CL})$$

[200],

EDM generation in the UEE

The mixing term ${\mathsf{\Phi }}_I\mathsf{\Pi }\left(D_f\right)$ can generate P- and T-odd operators, and one–loop diagrams involving fermion–dissipative interactions can induce an EDM. Introducing the effective operator

$${\mathcal{L}}_{\mathrm{EDM}}=-{\displaystyle \frac{i}{2}}{d}_f\overline{f}{\sigma }^{\mu \nu }{\gamma }^{5}f{F}_{\mu \nu },$$

the UEE contribution is schematically

$$d_f\propto \sum _j\Im \left[Tr\left({\gamma }^5{V}_j{V}_j^{†}\right)\right].$$

Bounds on the dissipative matrix elements

The experimental limits require

$$|d_e|\simeq C_e|V_j^{ee}{|}^2<1.1\times {10}^{-29}e·\mathrm{cm},|d_n|\simeq C_n{|V_j^{nn}|}^2<1.8\times {10}^{-26}e·\mathrm{cm},$$

with model-dependent coefficients $C_e$ and $C_n$.

2.29.2-3 Combined Analysis of the Parameter Space

Combining the two sets of bounds

Putting together the constraints from K-meson CP violation and EDMs we find

$$\sum _j|V_j^{K\overline{K}}{|}^2\lesssim {10}^{-6},|V_j^{ee}{|}^2<{\displaystyle \frac{1.1\times {10}^{-29}}{C_e}},{\left|V_j^{nn}\right|}^2<{\displaystyle \frac{1.8\times {10}^{-26}}{C_n}}.$$

Plotting the constraint curves

In the plane $\left(|V^{K\overline{K}}|,|V^{ee}|\right)$ one has

$$|V^{ee}|=\sqrt{{\displaystyle \frac{1.1\times {10}^{-29}}{C_e}}},|V^{K\overline{K}}|=\sqrt{{10}^{-6}}.$$

Figure 2.

Figure 2.

Physical implications

These bounds force the dissipative parameters in the UEE to be extremely small, implying that any novel dissipative effect beyond the standard quantum field theory framework must be at most of order ${10}^{-3}$ in the K system and $\lesssim {10}^{-14}$ in the electron EDM sector—well below current detection capabilities.

Summary

By combining the tightest experimental limits from CP violation in the K-meson system and from EDM measurements, we have derived stringent upper bounds on the dissipative channel parameters in the UEE, thereby delineating the viable region of the parameter space.

2.30. Completely Positive Semigroup Generation Theorem

2.30.1 Foundations of Semigroup Generation and the Hille–Yosida Theorem

In this subsection we first review the basics of strongly continuous operator semigroups and then give a line-by-line proof of the Hille–Yosida theorem [18,36].

Preliminaries: strongly continuous operator semigroups

A family of bounded operators ${\left\{T\left(t\right)\right\}}_{t\ge 0}$ on a Hilbert space $\mathcal{H}$ is called a strongly continuous (or $C_0$) semigroup if

$$T\left(0\right)=I,T(s+t)=T\left(s\right)T\left(t\right),\underset{t\to 0^{+}}{lim}\parallel T\left(t\right)x-x\parallel =0,\forall x\in \mathcal{H}.$$

The symbol $C_0$ stresses strong continuity at $t=0$ [6].

Definition of the generator

The (infinitesimal) generator A of a $C_0$-semigroup is defined by

$$Ax:=\underset{t\to 0^{+}}{lim}{\displaystyle \frac{T\left(t\right)x-x}{t}},\mathrm{Dom}\left(A\right):=\left\{x\in \mathcal{H}|\underset{t\to 0^{+}}{lim}\frac{T\left(t\right)x-x}{t}\mathrm{exists}\right\}.$$

Statement of the Hille–Yosida theorem

Theorem 15 

(Hille–Yosida [18,36]). A closed operator A generates a strongly continuous semigroup ${\left\{T\left(t\right)\right\}}_{t\ge 0}$ on $\mathcal{H}$ iff the following two conditions hold:

(i) 

$\mathrm{Dom}\left(A\right)$ is dense in $\mathcal{H}$ and A is closed.

(ii) 

There exist constants $M\ge 1$ and $\omega \in \mathbb{R}$ such that $\{\lambda \in \mathbb{C}\mid \Re \lambda >\omega \}\subset \rho \left(A\right)$ and

$${\parallel (\lambda I-A)}^{-n}\parallel \le {\displaystyle \frac{M}{{\left(\Re \lambda -\omega \right)}^n}},\forall n\in \mathbb{N}.$$

Outline of the proof

The proof proceeds in three steps [37]:

• (Necessity) Starting from a $C_0$-semigroup, show that its generator satisfies (i) and (ii).
• (Sufficiency) Assuming (i) and (ii), introduce the Yosida approximation $A_n=nA{(nI-A)}^{-1}$, construct the bounded semigroups $T_n\left(t\right)=e^{t{A}_n}$, and verify ${lim}_{n\to \infty }{A}_{n}x=Ax$.
• (Convergence & uniqueness) Prove that $T_n\left(t\right)$ converges strongly and that the limit is the unique $C_0$-semigroup generated by A.

Details of the necessity part

Strong continuity implies density of $\mathrm{Dom}\left(A\right)$; closedness follows from

$$x_n\to x,A{x}_n\to y⟹\underset{t\to 0}{lim}{\displaystyle \frac{T\left(t\right)x-x}{t}}=y.$$

The Laplace–transform representation

$${(\lambda I-A)}^{-1}={\int }_0^{\infty }{e}^{-\lambda t}T\left(t\right)dt$$

(valid for $\Re \lambda >\omega$) yields (ii).

Details of the sufficiency part

Let ${\lambda }_n:=n+\omega$ and set $A_n=n^2{({\lambda }_{n}I-A)}^{-1}-nI$. Each $A_n$ is bounded and self-adjoint, and ${lim}_{n\to \infty }{A}_{n}x=Ax$ on $\mathrm{Dom}\left(A\right)$. Define $T_n\left(t\right):=e^{t{A}_n}$, then

$$\parallel T_n\left(t\right)x-T_m\left(t\right)x\parallel \le {\int }_0^t\parallel (A_n-A_m)T_m\left(s\right)x\parallel ds\underset{n,m\to \infty }{\to }0.$$

Construction of the semigroup

Setting $T\left(t\right):={lim}_{n\to \infty }{T}_n\left(t\right)$ one checks $T\left(0\right)=I$, the semigroup law, and strong continuity; hence A indeed generates a $C_0$-semigroup.

2.30.2 From Lindblad Generators to CPTP Semigroups

Using Theorem 15 we now prove that any Gorini–Kossakowski–Lindblad–Sudarshan (GKLS) generator

$$\mathcal{L}\left[\rho \right]=-i[H,\rho ]+\sum _j\left(V_j\rho V_j^{†}-\frac{1}{2}\{V_j^{†}{V}_j,\rho \}\right)$$

generates a completely positive, trace-preserving ($\mathrm{CPTP}$) semigroup on the trace-class $S_1\left(\mathcal{H}\right)$.

Definition of a CPTP semigroup

A family ${\left\{T\left(t\right)\right\}}_{t\ge 0}$ is CPTP iff, for all $t\ge 0$,

$$T\left(t\right):S_1\left(\mathcal{H}\right)⟶S_1\left(\mathcal{H}\right)\mathrm{is}\mathrm{CP}\mathrm{and}Tr\left[T\left(t\right)\left[\rho \right]\right]=Tr\left[\rho \right],\forall \rho \in S_1\left(\mathcal{H}\right).$$

Properties of the Lindblad generator

• $\mathrm{Dom}\left(\mathcal{L}\right)=\{\rho \in S_1\mid H\rho -\rho H,V_j\rho V_j^{†}\in S_1\}$ is dense.
• $\mathcal{L}$ is closed and, by the relative boundedness results of Sect. 2.21, its relative bound is $<1$.
• $Tr\left[\mathcal{L}\right[\rho \left]\right]=0$ (trace preservation).
• The resolvent estimate ${\parallel (\lambda I-\mathcal{L})}^{-1}\parallel \le 1/\Re \lambda$ holds for $\Re \lambda >0$.

Semigroup generation

Conditions (1)–(4) satisfy Theorem 15; hence $\mathcal{L}$ generates a unique $C_0$-semigroup $T\left(t\right)=e^{t\mathcal{L}}$.

Preservation of the trace

Trace preservation of $T\left(t\right)$ follows from $Tr\left[\mathcal{L}\right[\rho \left]\right]=0$ by integrating the differential equation $\dot{\rho }=\mathcal{L}\left[\rho \right]$.

Proof of complete positivity

Using the Trotter–Kato formula[68,201] decompose $\mathcal{L}={\mathcal{L}}_0+{\mathcal{L}}_{\mathsf{\Delta }}$ and define $T_n\left(t\right):={(e^{{\displaystyle \frac{t}{n}}{\mathcal{L}}_0}{e}^{{\displaystyle \frac{t}{n}}{\mathcal{L}}_{\mathsf{\Delta }}})}^n$.

• $e^{{\displaystyle \frac{t}{n}}{\mathcal{L}}_0}$ is unitary (hence CP).
• $e^{{\displaystyle \frac{t}{n}}{\mathcal{L}}_{\mathsf{\Delta }}}$ has a Kraus form and is CP.
• A strong limit of CP maps is CP; thus $T\left(t\right)={lim}_{n\to \infty }{T}_n\left(t\right)$ is CP.

Conclusion

Therefore the GKLS generator $\mathcal{L}$ produces a strongly continuous CPTP semigroup ${\{T\left(t\right)=e^{t\mathcal{L}}\}}_{t\ge 0}$.

Summary

Combining the Hille–Yosida theorem with the Lindblad structure we have rigorously established that the UEE generator defines a mathematically sound CPTP dynamics.

2.31. Benign Nature of the Zero-Area Resonance Kernel

In this section we rigorously prove that the zero-area resonance kernel operator R is harmless, i.e., it does not spoil any of the mathematical properties of the UEE. We do so from the following viewpoints:

• relative boundedness;
• fulfillment of operator domains;
• preservation of essential self-adjointness;
• maintenance of complete positivity and trace preservation (CPTP);
• guarantee of entropy monotonicity;
• consistent incorporation into the cancelling identity.

2.31.1 Relative boundedness

Lemma 11 

(Relative boundedness). The operator $R:End\left(H\right)\to End\left(H\right)$ is relatively bounded with respect to the Dirac operator D; that is, for every $\rho \in End\left(H\right)$

$$\parallel R\left[\rho \right]\parallel \le a\parallel D\rho \parallel +b\parallel \rho \parallel ,a<1,b>0.$$

(13)

Proof. 

Using the spectral resolution $D=\int \omega E_D\left(d\omega \right)$ and the double-commutator form one has

$$R\left[\rho \right]={\int }_{\sigma \left(D\right)}R\left(\omega \right)[D,[D,\rho ]]E_D\left(d\omega \right).$$

Norm estimation gives

$$\parallel R\left[\rho \right]\parallel \le \int \left|R\left(\omega \right)\right|\parallel [D,[D,\rho ]]\parallel \parallel E_D\left(d\omega \right)\parallel \le \underset{\omega }{sup}\left|R\left(\omega \right)\right|\parallel [D,[D,\rho ]]\parallel .$$

The double-commutator obeys the Sobolev-space estimate [6]

$$\parallel [D,[D,\rho ]]\parallel \le C_1\parallel D\rho \parallel +C_2\parallel \rho \parallel ,$$

whence choosing $a=C_{1}sup\left|R\left(\omega \right)\right|$ and $b=C_{2}sup\left|R\left(\omega \right)\right|$ proves the lemma.    □

2.31.2 Domains and self-adjointness

Lemma 12 

(Fulfilment of the domain). Since R is bounded, its domain is the whole Hilbert space H, i.e.,

$$\mathrm{Dom}\left(R\right)=H.$$

Proof. 

A bounded operator acts on all of H by definition.    □

Theorem 16 

(Preservation of essential self-adjointness). The extended Dirac operator

$$D_{\mathrm{tot}}:=D+R$$

remains essentially self-adjoint and satisfies $\mathrm{Dom}\left(D_{\mathrm{tot}}\right)=\mathrm{Dom}\left(D\right)$.

Proof. 

Owing to the relative boundedness with $a<1$ and the symmetry of R, the Kato–Rellich theorem [56] implies that $D+R$ preserves essential self-adjointness and shares the same domain with D.    □

2.31.3 CPTP property and entropy monotonicity

Theorem 17 

(Preservation of CPTP). The total generator of the UEE

$$L_{\mathrm{tot}}=-i[D,·]+L_{\mathrm{diss}}+R$$

still preserves complete positivity and trace, hence generates a CPTP semigroup.

Proof. 

• For every state $\rho$ one has $TrR\left[\rho \right]=0$ because R has the double-commutator form.
• R can be embedded into a Lindblad–GKS structure [2,8]

  $$R\left[\rho \right]=\sum _k{W}_k\rho W_k^{†}-\frac{1}{2}\{W_k^{†}{W}_k,\rho \},$$

  which is manifestly completely positive.
• Since $L_{\mathrm{diss}}$ is already CPTP, adding R leaves the CPTP property intact [202].

   □

Theorem 18 

(Entropy monotonicity). The von Neumann entropy $S\left(\rho \right):=-Tr(\rho ln\rho )$ satisfies

$$\dot{S}=-Tr\left(L_{\mathrm{tot}}\left[\rho \right]ln\rho \right)\ge 0,$$

i.e., it increases monotonically under the dissipative time evolution.

Proof. 

By Spohn’s entropy production formula [154], $\dot{S}=-Tr(L_{\mathrm{diss}}\left[\rho \right]ln\rho )\ge 0$. Moreover, R commutes with $ln\rho$ so that $Tr\left(R\right[\rho ]ln\rho )=0$; hence the monotonicity is preserved for the total generator.    □

2.31.4 Integration into the cancelling identity

The operator R fits naturally into the cancelling identity of Sect. 2.15,

$$\sum _j{V}_j^{†}{V}_j=0,$$

which is extended to

$$\sum _j{V}_j^{†}{V}_j+{\int }_{-\infty }^{\infty }R\left(\omega \right)d\omega =0$$

[101].

Summary

We have shown rigorously that the zero-area resonance kernel R leaves unchanged all fundamental properties of the UEE—relative boundedness, domain structure, essential self-adjointness, CPTP semigroup generation, entropy monotonicity, and the cancelling identity—thereby establishing its harmlessness.

3. Multi-Formulation of the Unified Evolution Equation

3.1. Density-Operator Formulation (UEE${‌}_{\mathrm{op}}$)

The time evolution of the UEE is described by the total generator $L_{\mathrm{tot}}$:

$${\displaystyle \frac{d\rho }{dt}}=L_{\mathrm{tot}}\left[\rho \right],$$

$$L_{\mathrm{tot}}=-i[D,·]+L_{\mathrm{diss}}+R[·],$$

(see §2.31)

3.1.1-1 Definition of the Density Operator $\rho$ and Derivation of the Reversible Generator

Exact definition of the density operator

For a quantum system on a Hilbert space $\mathcal{H}$, its statistical state is represented by a density operator $\rho$, i.e., a trace-class operator belonging to

$$S_1\left(\mathcal{H}\right)=\left\{\rho \in \mathcal{B}\left(\mathcal{H}\right)\mid {\parallel \rho \parallel }_1:=Tr\sqrt{{\rho }^{†}\rho }<\infty \right\},$$

and satisfying the following conditions (Definition 2.19.1):

$$\rho ={\rho }^{†},\rho ⪰0,Tr\left(\rho \right)=1.$$

Here $\rho ⪰0$ means $\langle \psi ,\rho \psi \rangle \ge 0$ for every $\psi \in \mathcal{H}$, and $Tr$ denotes the trace (Definition 2.1.1, Equation (4)).

Topology and properties of the space of density operators

$S_1\left(\mathcal{H}\right)$ is a Banach space with the norm ${\parallel ·\parallel }_1$. Any $\rho$ can be decomposed as a convex mixture of pure states,

$$\rho =\sum _n{p}_n|{\psi }_n\rangle \langle {\psi }_n|,p_n\ge 0,\sum _n{p}_n=1,$$

[203]. Moreover, the set $\mathcal{D}\left(\mathcal{H}\right)=\{\rho \in S_1\left(\mathcal{H}\right)\mid \rho ={\rho }^{†}⪰0,Tr\rho =1\}$ is convex and weak${‌}^{*}$-compact in the ${\parallel ·\parallel }_1$-topology (the dual of the trace-class is $\mathcal{B}\left(\mathcal{H}\right)$) [63].

Unitary time evolution: the Liouville–von Neumann equation

Reversible time evolution generated by the Hamiltonian H is given by the Liouville–von Neumann equation

$${\displaystyle \frac{d}{dt}}\rho \left(t\right)=-i[H,\rho \left(t\right)]=L_0\left[\rho \left(t\right)\right]$$

[204]. Define the generator

$$L_0:S_1\left(\mathcal{H}\right)\supset \mathrm{Dom}\left(L_0\right)⟶S_1\left(\mathcal{H}\right),L_0\left[\rho \right]:=-i[H,\rho ],$$

with domain

$$\mathrm{Dom}\left(L_0\right):=\left\{\rho \in S_1\left(\mathcal{H}\right)\mid H\rho -\rho H\in S_1\left(\mathcal{H}\right)\right\},$$

which is dense in $S_1\left(\mathcal{H}\right)$ and forms a closed operator [19].

Verification of the Hille–Yosida condition

For $L_0$ to generate a strongly continuous operator semigroup $\{T_0\left(t\right)=e^{-iHt}\}$, it must satisfy the Hille–Yosida theorem (Theorem 15):

(i)

$\mathrm{Dom}\left(L_0\right)$ is dense and $L_0$ is closed.

(ii)

There exist constants $M\ge 1$, $\omega \in \mathbb{R}$ such that

$$\{\lambda \in \mathbb{C}\mid \Re \lambda >\omega \}\subset \rho \left(L_0\right),\parallel {(\lambda I-L_0)}^{-n}\parallel \le {\displaystyle \frac{M}{{(\Re \lambda -\omega )}^n}},\forall n\in \mathbb{N}.$$

For the reversible part one can take $\omega =0$ and $M=1$. Using the resolvent representation

$${(\lambda I-L_0)}^{-1}\left[\rho \right]={\int }_0^{\infty }{e}^{-\lambda t}{e}^{-iHt}\rho e^{iHt}dt,\Re \lambda >0,$$

it follows that $\parallel {(\lambda I-L_0)}^{-n}\parallel \le {(\Re \lambda )}^{-n}$ for any $n\in \mathbb{N}$, fulfilling condition (ii) [37].

Conclusion on generator property

Hence $L_0$ satisfies all assumptions of the Hille–Yosida theorem (Theorem 15) and generates the unique strongly continuous operator semigroup $T_0\left(t\right)=e^{t{L}_0}$[36]. The unitary time evolution governed by $L_0$ is therefore rigorously established.

Incorporation into the total generator

The full UEE dynamics is described by the total generator

$$L_{\mathrm{tot}}\left[\rho \right]=L_0\left[\rho \right]+L_{\mathrm{diss}}\left[\rho \right]+R\left[\rho \right]=-i[D,\rho ]+\sum _j\left(V_j\rho V_j^{†}-\frac{1}{2}\{V_j^{†}{V}_j,\rho \}\right)+R\left[\rho \right],$$

where $L_0$ is the reversible generator derived above, $L_{\mathrm{diss}}$ is the dissipative Lindblad component, and R is the zero-area resonance kernel (for its properties and harmlessness see §2.31).

3.1.1-2 Lindblad–GKLS Form of the Dissipative Generator and Integration into the Master Equation

Definition of the Lindblad–GKLS generator

A semigroup generator that is completely positive and trace preserving (CPTP) is defined in the Lindblad–Gorini–Kossakowski–Sudarshan (GKLS) form (Section 2.19) as follows [2,8].

Definition 58 

(Lindblad–GKLS generator). For a density operator $\rho \in S_1\left(\mathcal{H}\right)$ on a Hilbert space $\mathcal{H}$, the generator ${\mathcal{L}}_{\mathsf{\Delta }}$ is defined by

$${\mathcal{L}}_{\mathsf{\Delta }}\left[\rho \right]=\sum _{j=1}^M\left(V_j\rho V_j^{†}-\frac{1}{2}\{V_j^{†}{V}_j,\rho \}\right).$$

Here $V_j=f_j\left(x\right)\otimes e_j\in \mathcal{G}\subset \mathcal{A}$ are zero-order operators with local support (Section 2.5.2), $f_j\in C_0^{\infty }\left(M^4\right)$, and $e_j\in \mathrm{Cl}(1,3)$.

Proof of trace preservation

First we show that ${\mathcal{L}}_{\mathsf{\Delta }}$ preserves the trace.

Proposition 68 

(Trace preservation). For any $\rho \in S_1\left(\mathcal{H}\right)$, $Tr\left({\mathcal{L}}_{\mathsf{\Delta }}\left[\rho \right]\right)=0$ holds [1].

Proof. 

For each term,

$$Tr\left(V_j\rho V_j^{†}\right)=Tr\left(V_j^{†}{V}_j\rho \right)=Tr\left(\rho V_j^{†}{V}_j\right).$$

Moreover,

$$Tr\left(\frac{1}{2}\{V_j^{†}{V}_j,\rho \}\right)=\frac{1}{2}\left(Tr\left(V_j^{†}{V}_j\rho \right)+Tr\left(\rho V_j^{†}{V}_j\right)\right)=Tr\left(V_j^{†}{V}_j\rho \right).$$

Hence for every j, $Tr\left(V_j\rho V_j^{†}\right)-\frac{1}{2}Tr\{V_j^{†}{V}_j,\rho \}=0$, so that $Tr\left({\mathcal{L}}_{\mathsf{\Delta }}\left[\rho \right]\right)=0$.    □

Proof of complete positivity

Complete positivity (CP) follows from the Kraus representation or the Trotter–Kato approximation (Section 2.30.2).

Proposition 69 

(Complete positivity). The semigroup $T_{\mathsf{\Delta }}\left(t\right)=e^{t{\mathcal{L}}_{\mathsf{\Delta }}}$ generated by ${\mathcal{L}}_{\mathsf{\Delta }}$ is completely positive (CP) [37,39,137].

Proof. 

For an infinitesimal time $dt$,

$$T_{\mathsf{\Delta }}(dt)\left[\rho \right]=\sum _j{V}_j\rho V_j^{†}dt+(I-\frac{1}{2}\sum _j{V}_j^{†}{V}_{j}dt)\rho (I-\frac{1}{2}\sum _j{V}_j^{†}{V}_{j}dt),$$

which is clearly a composition of CP maps.

Applying the Trotter–Kato formula [68,201],

$$T_{\mathsf{\Delta }}\left(t\right)=\underset{n\to \infty }{lim}{\left(e^{\frac{t}{n}{\mathcal{L}}_0}{e}^{\frac{t}{n}{\mathcal{L}}_{\mathsf{\Delta }}}\right)}^n,$$

and since each factor is CP, their composition and the limit remain CP.    □

Analysis of the domain $\mathrm{Dom}\left({\mathcal{L}}_{\mathsf{\Delta }}\right)$

Define the natural domain of the generator as

$$\mathrm{Dom}\left({\mathcal{L}}_{\mathsf{\Delta }}\right)=\{\rho \in S_1\left(\mathcal{H}\right)\left|V_j\rho V_j^{†},V_j^{†}{V}_j\rho ,\rho V_j^{†}{V}_j\in S_1\left(\mathcal{H}\right)\right\}.$$

It satisfies:

(i)

$\mathrm{Dom}\left({\mathcal{L}}_{\mathsf{\Delta }}\right)$ is dense in $S_1\left(\mathcal{H}\right)$.

(ii)

${\mathcal{L}}_{\mathsf{\Delta }}$ is a closed operator.

Proof. 

(i) Because each zero-order operator $V_j=f_j\otimes e_j$ is bounded, density on $C_c^{\infty }\subset S_1$ is preserved [63].

(ii) Let ${\rho }_n\to \rho$ and ${\mathcal{L}}_{\mathsf{\Delta }}\left[{\rho }_n\right]\to \sigma$ in ${\parallel ·\parallel }_1$. Continuity of each term implies ${\mathcal{L}}_{\mathsf{\Delta }}\left[\rho \right]=\sigma$, so ${\mathcal{L}}_{\mathsf{\Delta }}$ is closed.    □

Properties of the total generator $L_{\mathrm{tot}}$ including reversible, dissipative, and resonance parts

With the reversible part $L_0$ (Section 3.1), the dissipative part ${\mathcal{L}}_{\mathsf{\Delta }}$, and the zero-area resonance kernel operator R, the total generator

$$L_{\mathrm{tot}}\left[\rho \right]=L_0\left[\rho \right]+{\mathcal{L}}_{\mathsf{\Delta }}\left[\rho \right]+R\left[\rho \right]=-i[D,\rho ]+\sum _j\left(V_j\rho V_j^{†}-\frac{1}{2}\{V_j^{†}{V}_j,\rho \}\right)+R\left[\rho \right]$$

is a closed operator on the domain $\mathrm{Dom}\left(L_{\mathrm{tot}}\right)=\mathrm{Dom}\left(L_0\right)\cap \mathrm{Dom}\left({\mathcal{L}}_{\mathsf{\Delta }}\right)$. Since both $L_0$ and ${\mathcal{L}}_{\mathsf{\Delta }}$ satisfy the Hille–Yosida condition, $L_{\mathrm{tot}}$ generates the unique strongly continuous CPTP semigroup

$$T\left(t\right)=e^{t{L}_{\mathrm{tot}}}$$

[36,37]. Consequently, the unified master equation

$${\displaystyle \frac{d}{dt}}\rho \left(t\right)=L_{\mathrm{tot}}\left[\rho \left(t\right)\right],\rho \left(0\right)={\rho }_0\in \mathcal{D}\left(\mathcal{H}\right),$$

is rigorously formulated.

3.1.2-1 General Theory and Formulation of the Dyson–Phillips Series

Preliminaries: Strongly continuous operator semigroups and their generators

A strongly continuous operator semigroup ($C_0$-semigroup) ${\left\{T_0\left(t\right)\right\}}_{t\ge 0}$ on a Hilbert space $\mathcal{H}$ possesses a closed generator $L_0$ such that

$$T_0\left(t\right)=e^{t{L}_0},{\displaystyle \frac{d}{dt}}{T}_0\left(t\right)\rho =L_0\left[T_0\left(t\right)\rho \right],\mathrm{Dom}\left(L_0\right)\subset S_1\left(\mathcal{H}\right),$$

as stated by Theorem 15 [36,37].

Bounded perturbations in semigroup theory

The irreversible part ${\mathcal{L}}_{\mathsf{\Delta }}$ is given in the Lindblad–GKLS form and can be regarded as the bounded operator

$$K:={\mathcal{L}}_{\mathsf{\Delta }}+R\in \mathcal{B}\left(S_1\left(\mathcal{H}\right)\right),$$

where R is the zero-area resonance kernel (see Section 3.1 and §2.31). Hence the total generator

$$L_{\mathrm{tot}}=L_0+K$$

also generates a strongly continuous semigroup by Kato–Rellich type perturbation theory [37,201].

Duhamel (splitting-integration) formula

The basic relation that connects the semigroup $T\left(t\right)=e^{t{L}_{\mathrm{tot}}}$ with its perturbation is the Duhamel splitting-integration formula [37,205]:

$$T\left(t\right)\rho =T_0\left(t\right)\rho +{\int }_0^t{T}_0(t-s)K\left[T\left(s\right)\rho \right]ds.$$

It follows formally from ${\displaystyle \frac{d}{ds}}\left(T_0(t-s)T\left(s\right)\right)=T_0(t-s)KT\left(s\right)$ integrated over $[0,t]$.

Definition of the Dyson–Phillips series

Iterating the Duhamel formula yields the expansion known as the “Dyson–Phillips series” [152,153,205].

Definition 59 

(Dyson–Phillips series). The total semigroup $T\left(t\right)=e^{t{L}_{\mathrm{tot}}}$ is defined by the series

$$\begin{array}{cc}\hfill T_0\left(t\right)& :=T_0\left(t\right),\hfill \\ \hfill T_{n+1}\left(t\right)& :={\int }_0^t{T}_0(t-s)K{T}_n\left(s\right)ds,n\ge 0,\hfill \\ \hfill T\left(t\right)& =\sum _{n=0}^{\infty }{T}_n\left(t\right).\hfill \end{array}$$

Each $T_n\left(t\right)$ is a bounded operator on $S_1\left(\mathcal{H}\right)$ with $T_0\equiv e^{t{L}_0}$ and $K={\mathcal{L}}_{\mathsf{\Delta }}+R$.

Necessary conditions: bounded or relatively bounded perturbations

The reconstruction via the Dyson–Phillips series is guaranteed when the perturbation K is either

• a bounded perturbation with $\parallel K\parallel <\infty$; or
• a relatively bounded perturbation for which there exist $a<1$ and $b\ge 0$ such that $\parallel K\rho \parallel \le a\parallel L_0\rho \parallel +b\parallel \rho \parallel$.

Because both the Lindblad–GKLS operator ${\mathcal{L}}_{\mathsf{\Delta }}$ and the resonance kernel R are bounded, the first condition suffices [201].

Summary of fundamental properties

The Dyson–Phillips series, combining the strongly continuous semigroup theory based on the Hille–Yosida theorem (Theorem 15) with Kato–Rellich perturbation analysis, is important for several reasons:

• It explicitly separates the reversible part $T_0\left(t\right)$ from the irreversible perturbation K.
• The iterative expansion derived from the Duhamel formula allows a perturbative interpretation of dissipative effects and the resonance kernel.
• Uniqueness and consistency of the semigroup are guaranteed by the operator-theoretic background (Section 3.1–3.1.0.6, §2.31).

3.1.2-2-1 Norm-convergence proof of the Dyson–Phillips series

Requirement for norm convergence

For the Dyson–Phillips series

$$T\left(t\right)=\sum _{n=0}^{\infty }{T}_n\left(t\right)$$

to converge in norm and coincide with the semigroup $e^{t(L_0+K)}$, the absolute sum of the operator norms ${\sum }_{n=0}^{\infty }\parallel T_n\left(t\right)\parallel <\infty$ must be demonstrated, where ${\parallel ·\parallel }_{1\to 1}$ denotes the trace-norm operator norm.

Growth constants $M,\omega$ of the principal semigroup

By the Hille–Yosida theorem [36,37], the strongly continuous semigroup $\left\{T_0\left(t\right)\right\}$ generated by $L_0$ satisfies

$$\parallel T_0{\left(t\right)\parallel }_{1\to 1}\le M{e}^{\omega t},\forall t\ge 0,$$

for some constants $M\ge 1$ and $\omega \in \mathbb{R}$. For the Liouville–von Neumann generator one naturally has $M=1$ and $\omega =0$, but we keep the general form.

Norm of the bounded perturbation K

Including the dissipative operator ${\mathcal{L}}_{\mathsf{\Delta }}$ and the resonance kernel R,

$$K:={\mathcal{L}}_{\mathsf{\Delta }}+R\in \mathcal{B}\left(S_1\left(\mathcal{H}\right)\right),$$

we define

$${\parallel K\parallel }_{1\to 1}=:\kappa <\infty .$$

Inductive bound via recursive estimation

From the definition of the Dyson–Phillips series,

$$T_{n+1}\left(t\right)={\int }_0^t{T}_0(t-s)K{T}_n\left(s\right)ds.$$

Estimating the norm yields

$$\begin{array}{cc}\hfill \parallel T_{n+1}{\left(t\right)\parallel }_{1\to 1}& \le {\int }_0^t\parallel T_0{(t-s)\parallel }_{1\to 1}{\parallel K\parallel }_{1\to 1}{\parallel T_n\left(s\right)\parallel }_{1\to 1}ds\hfill \\ \hfill & \le M\kappa {\int }_0^t{e}^{\omega (t-s)}{\parallel T_n\left(s\right)\parallel }_{1\to 1}ds.\hfill \end{array}$$

Assume inductively that

$$\parallel T_n{\left(s\right)\parallel }_{1\to 1}\le {\displaystyle \frac{{\left(M\kappa s\right)}^n}{n!}}{e}^{\omega s}$$

holds for all $s\in [0,t]$. Then

$$\parallel T_{n+1}{\left(t\right)\parallel }_{1\to 1}\le {\displaystyle \frac{{\left(M\kappa t\right)}^{n+1}}{(n+1)!}}{e}^{\omega t}.$$

The base case $n=0$ follows from $\parallel T_0\left(t\right)\parallel \le M{e}^{\omega t}$.

Absolute convergence of the series and consistency with the semigroup

Consequently,

$$\sum _{n=0}^{\infty }\parallel T_n\left(t\right)\parallel \le e^{\omega t}\sum _{n=0}^{\infty }{\displaystyle \frac{{\left(M\kappa t\right)}^n}{n!}}=e^{\omega t}{e}^{M\kappa t}<\infty .$$

Thus the Dyson–Phillips series converges in norm, and the limit ${\displaystyle T\left(t\right)=\underset{N\to \infty }{lim}\sum _{n=0}^N{T}_n\left(t\right)}$ is a bounded operator. Reversing the series derivation via the Duhamel formula [37,205] shows that $\left\{T\right(t\left)\right\}$ obeys the semigroup law $T(t+s)=T\left(t\right)T\left(s\right)$ and that its generator equals $L_0+K=L_0+{\mathcal{L}}_{\mathsf{\Delta }}+R$ [152,153].

Summary

For bounded perturbation $K={\mathcal{L}}_{\mathsf{\Delta }}+R$ with finite $\kappa$, the Dyson–Phillips series rigorously guarantees norm convergence and coincidence with the semigroup $e^{t(L_0+K)}$[205]. Hence the semigroup $T\left(t\right)$ representing the solution of the unified master equation $\dot{\rho }=L_0\left[\rho \right]+{\mathcal{L}}_{\mathsf{\Delta }}\left[\rho \right]+R\left[\rho \right]$ is constructed in an operator-theoretic manner.

3.1.2-2-2 Strong Convergence and Identity with the Operator Semigroup

Significance of strong convergence versus norm convergence

For the Dyson–Phillips series

$$T\left(t\right)=\sum _{n=0}^{\infty }{T}_n\left(t\right),$$

norm convergence was established in Section 3.1.0.17. In operator–semigroup theory, however, strong convergence is in general sufficient [37,205]. Here, strong convergence means that for any fixed $\rho \in S_1\left(\mathcal{H}\right)$

$$\underset{N\to \infty }{lim}{∥\sum _{n=0}^N{T}_n\left(t\right)\rho -T\left(t\right)\rho ∥}_1=0,\forall t\ge 0.$$

By contrast, norm convergence employs $\sum \parallel T_n\left(t\right)\parallel <\infty$ to ensure $∥\sum T_n\left(t\right)-T\left(t\right)∥\to 0$, but on $S_1$ strong convergence is usually enough [56].

Proof of strong convergence: successive approximation and closedness

Define the partial sums of the Dyson–Phillips series by ${\displaystyle T^{\left(N\right)}\left(t\right)=\sum _{n=0}^N{T}_n\left(t\right)}$. Each $T^{\left(N\right)}\left(t\right)$ satisfies, as an approximation to the strongly continuous semigroup,

$${\displaystyle \frac{d}{dt}}{T}^{\left(N\right)}\left(t\right)\rho =L_0\left[T^{\left(N\right)}\left(t\right)\rho \right]+K\left[T^{(N-1)}\left(t\right)\rho \right],K:={\mathcal{L}}_{\mathsf{\Delta }}+R,\rho \in \mathrm{Dom}\left(L_0\right),$$

where we agree that $T^{(-1)}\left(t\right)\equiv 0$. Using the essential closedness of the semigroup generator $L_{\mathrm{tot}}=L_0+K$ and the limit process in the Duhamel formula ([37], Ch. 3), exchange of the limit with time differentiation is justified, yielding strong convergence.

Strong differentiability and uniqueness of the Cauchy problem

The constructed strongly continuous family $T\left(t\right)$ obeys

$$\underset{h\to 0}{lim}{\displaystyle \frac{T(t+h)\rho -T\left(t\right)\rho }{h}}=L_{\mathrm{tot}}\left[T\left(t\right)\rho \right],\rho \in \mathrm{Dom}\left(L_{\mathrm{tot}}\right),$$

and therefore provides the unique solution $\rho \left(t\right)=T\left(t\right){\rho }_0$ of the abstract Cauchy problem

$$\left\{\begin{array}{c}\dot{\rho }\left(t\right)=L_{\mathrm{tot}}\left[\rho \left(t\right)\right],\hfill \\ \rho \left(0\right)={\rho }_0\in \mathrm{Dom}\left(L_{\mathrm{tot}}\right),\hfill \end{array}\right.$$

as guaranteed by Theorem 2.30.1 and Section 3.1.

Preservation of the semigroup law

Directly from the Dyson–Phillips series one obtains

$$T^{\left(N\right)}(t+s)=\sum _{n=0}^N\sum _{k=0}^n{T}_k\left(t\right)T_{n-k}\left(s\right)=T^{\left(N\right)}\left(t\right)T^{\left(N\right)}\left(s\right)+R_N(t,s),$$

and the remainder $R_N(t,s)$ vanishes in norm (hence strongly). Consequently,

$$T(t+s)=T\left(t\right)T\left(s\right),\forall t,s\ge 0,$$

so the constructed $T\left(t\right)$ is indeed an operator semigroup [152,153].

Consistency with the master equation

Finally,

$${\displaystyle \frac{d}{dt}}T\left(t\right)\rho =\underset{h\to 0}{lim}{\displaystyle \frac{T(t+h)\rho -T\left(t\right)\rho }{h}}=L_{\mathrm{tot}}\left[T\left(t\right)\rho \right],$$

coinciding with the term–by–term differentiation of the Duhamel-based series and reproducing the original master equation

$$\dot{\rho }=L_0\left[\rho \right]+{\mathcal{L}}_{\mathsf{\Delta }}\left[\rho \right]+R\left[\rho \right].$$

Summary

For a bounded perturbation $K={\mathcal{L}}_{\mathsf{\Delta }}+R$ with finite $\kappa$, the Dyson–Phillips series ensures both norm and strong convergence, rigorously securing the semigroup law and agreement with $\dot{\rho }=L_0\left[\rho \right]+{\mathcal{L}}_{\mathsf{\Delta }}\left[\rho \right]+R\left[\rho \right]$ [37,205]. Thus, an operator–theoretic construction of irreversible solutions in UEE${‌}_{\mathrm{op}}$ is achieved.

3.1.3-1 Existence of Stationary States and Analytic Construction

Definition of stationary states

For the total generator

$$L_{\mathrm{tot}}=L_0+{\mathcal{L}}_{\mathsf{\Delta }}+R$$

(see §2.31), consider the master equation

$${\displaystyle \frac{d}{dt}}\rho \left(t\right)=L_{\mathrm{tot}}\left[\rho \left(t\right)\right].$$

Definition 60 

(Stationary state). A density operator ${\rho }_{\mathrm{ss}}\in S_1\left(\mathcal{H}\right)$ is called a stationary state if

$$L_{\mathrm{tot}}\left[{\rho }_{\mathrm{ss}}\right]=0,Tr{\rho }_{\mathrm{ss}}=1,{\rho }_{\mathrm{ss}}\ge 0.$$

Guarantee of existence

Because ${\mathcal{L}}_{\mathsf{\Delta }}$ and R are bounded and $L_{\mathrm{tot}}$ remains a CPTP generator (Theorem 2.31.3, §2.31), the semigroup $T\left(t\right)=e^{t{L}_{\mathrm{tot}}}$ maps the convex compact set $S_1\left(\mathcal{H}\right)$ into itself.

Proposition 70 

(Existence of stationary states). Every CPTP semigroup $T\left(t\right)$ possesses at least one stationary state ${\rho }_{\mathrm{ss}}$ [1,206].

Proof. 

The map $T\left(t\right):S_1\left(\mathcal{H}\right)\to S_1\left(\mathcal{H}\right)$ is continuous and preserves trace and positivity. Brouwer–Schauder’s fixed–point theorem [206] ensures a fixed point ${\rho }_{\mathrm{ss}}$ with $T\left(t\right)\left[{\rho }_{\mathrm{ss}}\right]={\rho }_{\mathrm{ss}}$, equivalent to $L_{\mathrm{tot}}\left[{\rho }_{\mathrm{ss}}\right]=0$.    □

Uniqueness and convergence

Uniqueness is guaranteed if the semigroup is primitive (irreducible and asymptotically ergodic) [207,208], i.e., ${lim}_{t\to \infty }{\parallel T\left(t\right){\rho }_1-T\left(t\right){\rho }_2\parallel }_1=0$ for all states ${\rho }_1,{\rho }_2$.

Analytic construction via spectral projection

The spectrum $\sigma \left(L_{\mathrm{tot}}\right)$ lies in $\{\Re \lambda \le 0\}$. The spectral projection onto the kernel of $L_{\mathrm{tot}}$ is

$$P_0=-{\displaystyle \frac{1}{2\pi i}}{\oint }_{\mathsf{\Gamma }}{(\zeta I-L_{\mathrm{tot}})}^{-1}d\zeta ,\mathsf{\Gamma }\subset \{\zeta \mid |\zeta |<\delta \},$$

so that $Ran{P}_0=ker{L}_{\mathrm{tot}}$. For any initial state ${\rho }_0$,

$${\rho }_{\mathrm{ss}}=P_0\left[{\rho }_0\right],$$

up to normalisation to unit trace.

Example: two–level system (simplified case $R=0$)

Consider a two–level system ($\mathcal{H}={\mathbb{C}}^2$) with Hamiltonian $H=\frac{\omega }{2}{\sigma }_z$ and dissipator

$${\mathcal{L}}_{\mathsf{\Delta }}\left[\rho \right]=\gamma \left({\sigma }_{-}\rho {\sigma }_{+}-\frac{1}{2}\{{\sigma }_{+}{\sigma }_{-},\rho \}\right),{\sigma }_{\pm }=\frac{1}{2}({\sigma }_x\pm i{\sigma }_y).$$

With $R=0$, solving $L_{\mathrm{tot}}\left[{\rho }_{\mathrm{ss}}\right]=0$ yields [1]

$${\rho }_{\mathrm{ss}}={\displaystyle \frac{1}{1+e^{-\beta \omega }}}\left(\begin{array}{cc}1& 0\\ 0& e^{-\beta \omega }\end{array}\right),\beta ={\displaystyle \frac{1}{k_{B}T}},$$

i.e., the thermal Gibbs distribution, with T determined by $\gamma$ through detailed balance.

Summary

This subsection has demonstrated

• existence of stationary states via fixed–point theorems [1,206];
• analytic construction using the spectral projection $P_0$ [56];
• an explicit two–level example with $R=0$ [1].

The next subsection analyses the convergence rate towards the stationary state via the spectral gap.

3.1.3-2 Convergence and the Spectral Gap

Spectral structure of the generator $L_{\mathrm{tot}}$

For the master–equation generator

$$L_{\mathrm{tot}}=L_0+{\mathcal{L}}_{\mathsf{\Delta }}+R:S_1\left(\mathcal{H}\right)⟶S_1\left(\mathcal{H}\right),$$

the Hille–Yosida condition (Theorem 15) implies that $L_{\mathrm{tot}}$ is closed and its spectrum is contained in the left half–plane [209,210]. Because the zero–area resonance kernel R is bounded with $\Re \sigma \left(R\right)=0$ (Lemma 2.31.2, §2.31), the real–part boundary of $\sigma \left(L_{\mathrm{tot}}\right)$ coincides with that of $\sigma (L_0+{\mathcal{L}}_{\mathsf{\Delta }})$. To guarantee asymptotic stability of a unique stationary state we introduce the spectral gap.

Definition 61 

(Spectral gap). For the spectrum $\sigma \left(L_{\mathrm{tot}}\right)$ define

$$-\mathsf{\Delta }:=sup\left\{\Re \lambda \mid \lambda \in \sigma \left(L_{\mathrm{tot}}\right)\setminus \left\{0\right\}\right\}.$$

If $\mathsf{\Delta }>0$ we call Δ the spectral gap[211].

General theorem of exponential convergence

Whenever the spectral gap is strictly positive, every initial state ${\rho }_0$ converges exponentially to the stationary state ${\rho }_{\mathrm{ss}}$.

Theorem 19 

(Exponential convergence). For a semigroup $T\left(t\right)=e^{t{L}_{\mathrm{tot}}}$ with gap $\mathsf{\Delta }>0$,

$${∥T\left(t\right){\rho }_0-{\rho }_{\mathrm{ss}}∥}_1\le C{e}^{-\mathsf{\Delta }t}{∥{\rho }_0-{\rho }_{\mathrm{ss}}∥}_1,\forall t\ge 0,$$

holds for any ${\rho }_0\in S_1\left(\mathcal{H}\right)$. Here $C\ge 1$ depends on the growth bound of the semigroup [152,208].

Proof. 

Using the spectral projection $P_0$ onto the kernel of $L_{\mathrm{tot}}$ and the decomposition $\mathcal{H}=Ran{P}_0\oplus Ran(I-P_0)$, one shows that the spectrum of $(I-P_0)L_{\mathrm{tot}}$ lies in $\{\Re \lambda \le -\mathsf{\Delta }\}$. Writing $T\left(t\right)=P_0+e^{t{L}_{\mathrm{tot}}}(I-P_0)$ and estimating the remainder by $\parallel e^{t{L}_{\mathrm{tot}}}(I-P_0)\parallel \le C{e}^{-\mathsf{\Delta }t}$ yields the claim (Phillips [152]; Davies–Spohn [208]).    □

Gap estimation à la Davies–Spohn

In concrete models the spectral gap $\mathsf{\Delta }$ can be bounded from below by the number of dissipative channels and the coupling strengths. For the standard two–level system (Section 3.1.0.29) one finds simply

$$\mathsf{\Delta }=\gamma ,$$

where $\gamma$ is the dissipation rate. For multi–level or spin–chain models, the Davies–Spohn asymptotic method [154,211] gives

$$\mathsf{\Delta }\ge \underset{j,k}{min}{\displaystyle \frac{{\gamma }_j+{\gamma }_k}{2}}-\epsilon ,$$

with a correction $\epsilon$ stemming from second–order dissipative interactions. Since the zero–area kernel R is bounded and purely imaginary, it does not alter this lower bound.

Numerical illustrations and explicit lower bounds

For the two–level model with dissipation rate $\gamma$ one obtains the exact gap $\mathsf{\Delta }=\gamma$. Applying the Davies–Spohn estimate to a three–level laser model with pump ${\gamma }_p$ and decay ${\gamma }_d$ [154] yields

$$\mathsf{\Delta }\ge {\displaystyle \frac{{\gamma }_p+{\gamma }_d}{2}}-\epsilon ,\epsilon \le 0.1min\{{\gamma }_p,{\gamma }_d\},$$

so for typical ${\gamma }_p={\gamma }_d$ one has $\mathsf{\Delta }\ge 0.9{\gamma }_d$, guaranteeing exponential convergence.

Physical example: resonant dissipative systems

For resonant dissipative systems such as laser–driven atoms or qubit–environment models,

$$L_0\left[\rho \right]=-i[H,\rho ],{\mathcal{L}}_{\mathsf{\Delta }}\left[\rho \right]=\sum _j{\gamma }_j\left(V_j\rho V_j^{†}-\frac{1}{2}\{V_j^{†}{V}_j,\rho \}\right),$$

with a bounded zero–area kernel R of sufficiently narrow frequency width, one finds

$$\mathsf{\Delta }=\underset{j}{min}{\gamma }_j,$$

so Theorem 19 predicts a convergence rate set by ${\gamma }_{min}$.

Summary

Even in the presence of the zero–area kernel R, a positive spectral gap $\mathsf{\Delta }$ guarantees exponential convergence to the stationary state. Estimating $\mathsf{\Delta }$ through dissipation rates and interaction strengths bridges theoretical predictions with numerical simulations of relaxation times.

3.1.3-3 Definition and Proof of Ergodicity

Definition of quantum ergodicity

For the semigroup $T\left(t\right)=e^{t{L}_{\mathrm{tot}}}$ generated by $L_{\mathrm{tot}}=L_0+{\mathcal{L}}_{\mathsf{\Delta }}+R$ (see §2.31), acting on $S_1\left(\mathcal{H}\right)$, ergodicity means that time averages project onto the stationary state [90].

Definition 62 

(Quantum ergodicity). The semigroup $T\left(t\right)$ is ergodic if for every initial state $\rho \in S_1\left(\mathcal{H}\right)$

$$\underset{T\to \infty }{lim}{\displaystyle \frac{1}{T}}{\int }_0^{T}T\left(t\right)\rho dt=P_0\left[\rho \right],$$

where $P_0$ is the spectral projection for the eigenvalue $\lambda =0$ and $P_0\left[\rho \right]={\rho }_{\mathrm{ss}}$.

Simple zero eigenvalue and ergodic operators

Ergodicity is characterised as follows.

Proposition 71 

(Necessary and sufficient conditions for ergodicity). The semigroup $T\left(t\right)$ is ergodic iff

(i) 

$\lambda =0$ is a simple eigenvalue of $L_{\mathrm{tot}}$ ($dimker{L}_{\mathrm{tot}}=1$) [73];

(ii) 

${\displaystyle sup\left\{\Re \lambda \mid \lambda \in \sigma \left(L_{\mathrm{tot}}\right)\setminus \left\{0\right\}\right\}<0}$, i.e., a positive spectral gap exists [211,212].

Proof. 

Necessity: For the time average $\frac{1}{T}{\int }_0^T{e}^{t{L}_{\mathrm{tot}}}dt$ to converge to $P_0$, the zero eigenspace must be one–dimensional and the remainder spectrum must lie in the open left half–plane, yielding exponential decay [205].

Sufficiency: If (i) and (ii) hold then $e^{t{L}_{\mathrm{tot}}}=P_0+e^{t{L}_{\mathrm{tot}}}(I-P_0)$ and $\parallel e^{t{L}_{\mathrm{tot}}}(I-P_0)\parallel \le C{e}^{-\mathsf{\Delta }t}$. Hence

$${\displaystyle \frac{1}{T}}{\int }_0^T{e}^{t{L}_{\mathrm{tot}}}dt=P_0+{\displaystyle \frac{1}{T}}{\int }_0^T{e}^{t{L}_{\mathrm{tot}}}(I-P_0)dt\underset{T\to \infty }{\to }{P}_0,$$

proving ergodicity.    □

Application of the Dunford–Schwartz ergodic theorem

For bounded positive operators

$$\mathrm{SOT}-\underset{T\to \infty }{lim}{\displaystyle \frac{1}{T}}{\int }_0^{T}T\left(t\right)dt=P_0$$

holds (Dunford–Schwartz [90]; Pazy Thm. 5.2.4 [37]). Proposition 71 is equivalent to this strong–operator–topology projection.

Physical implication: unique convergence to equilibrium

Quantum ergodicity ensures that any initial state ${\rho }_0$ satisfies

$$\underset{t\to \infty }{lim}\rho \left(t\right)={\rho }_{\mathrm{ss}},\rho \left(t\right)=e^{t{L}_{\mathrm{tot}}}{\rho }_0,$$

so the system “forgets” its initial conditions and reaches a unique equilibrium, consistent with entropy increase in statistical mechanics [2,213].

Summary

For the total generator $L_{\mathrm{tot}}=L_0+{\mathcal{L}}_{\mathsf{\Delta }}+R$ with a zero–area kernel, quantum ergodicity is equivalent to

• a simple zero eigenvalue;
• a strictly negative real part of the remainder spectrum.

Hence the stationary solution in UEE${‌}_{\mathrm{op}}$ is unique, stable, and attained in the long–time limit.

3.2. Variational Principle Form (${\mathrm{UEE}}_{\mathrm{var}}$)

3.2.1 Rigorous Definition of the Action Functional

In this subsection we rigorously define the action functional that forms the foundation of UEE${‌}_{\mathrm{var}}$ and discuss its mathematical properties [29,30]. We first construct the reversible and irreversible parts separately and finally combine them into a single complex action.

3.2.1-1 Definition of the Reversible Action Functional $S_0[\psi ,\overline{\psi }]$ and Gauge–Gravitational Covariance

Definition

For a spinor field $\psi :M^4\to S\left(M^4\right)\otimes E_G$ and its conjugate $\overline{\psi }={\psi }^{†}{\gamma }^0$, we introduce the gauge–gravitational covariant derivative ${\nabla }_{\mu }={\partial }_{\mu }+{\omega }_{\mu }+A_{\mu }$ and define the reversible action functional by

$$S_0[\psi ,\overline{\psi }]:={\int }_{M^4}{d}^{4}xdet\left(e\right)\overline{\psi }\left(x\right)i{\gamma }^a{e}_a{‌}^{\mu }\left(x\right){\nabla }_{\mu }\psi \left(x\right)$$

[214]. Here

$$e_a{‌}^{\mu }\left(x\right),{\gamma }^a,{\omega }_{\mu },A_{\mu }$$

denote, respectively, the vierbein, the Clifford basis, the spin connection, and the Yang–Mills connection, while $det\left(e\right)=det\left[e_a{‌}^{\mu }\right]$.

Gauge–gravitational covariance

Under a local $\mathrm{Spin}(1,3)\times G_{\mathrm{gauge}}$ transformation

$$\psi \left(x\right)\mapsto {\psi }^{\prime }\left(x\right)=\rho \left(s\left(x\right)\right)R\left(g\left(x\right)\right)\psi \left(x\right),\overline{\psi }\left(x\right)\mapsto {\overline{\psi }}^{\prime }\left(x\right)=\overline{\psi }\left(x\right)R{\left(g\left(x\right)\right)}^{-1}\rho {\left(s\left(x\right)\right)}^{-1},$$

one has

$${\nabla }_{\mu }\psi \mapsto \rho \left(s\right)R\left(g\right){\nabla }_{\mu }\psi ,det\left(e\right)\to det\left(e\right),$$

and therefore

$$S_0[{\psi }^{\prime },{\overline{\psi }}^{\prime }]=S_0[\psi ,\overline{\psi }],$$

so $S_0$ is manifestly covariant under local gauge and gravitational transformations [215].

3.2.1-2 Construction of the Irreversible Dissipative Functional $\mathsf{\Gamma }\left[\rho \right]$: Borel Representation via Barnes–Lagrange Elimination

Formal series expansion

Combining the dissipative generator ${\mathcal{L}}_{\mathsf{\Delta }}$ with the zero–area resonance kernel operator R, set

$$K:={\mathcal{L}}_{\mathsf{\Delta }}+R.$$

To express the irreversible contribution as a functional of the density operator $\rho$, write

$$log\left(I-L_0^{-1}K\right)=-\sum _{n=1}^{\infty }{\displaystyle \frac{1}{n}}{\left(L_0^{-1}K\right)}^n$$

[216] and define the candidate functional

$$\mathsf{\Gamma }\left[\rho \right]:=Tr\left(\rho log\left(I-L_0^{-1}K\right)\right)=-\sum _{n=1}^{\infty }{\displaystyle \frac{1}{n}}Tr\left(\rho {\left(L_0^{-1}K\right)}^n\right).$$

Because R is bounded (Lemma 2.31.2, §2.31), $\parallel L_0^{-1}K\parallel <1$ and the series is formally defined [71].

Barnes–Lagrange elimination and Borel representation

If the series diverges, one regularises it using the Barnes–Lagrange elimination theorem [25,217] and the Mellin–Barnes integral representation [123]:

$${\left(L_0^{-1}K\right)}^n={\displaystyle \frac{1}{2\pi i}}{\oint }_{\mathsf{\Gamma }}{\zeta }^{-n}{(\zeta I-L_0^{-1}K)}^{-1}d\zeta .$$

Applying the Borel transform

$$log(1-z)=-{\int }_0^{\infty }{\displaystyle \frac{e^{-s}-e^{-sz}}{s}}ds,$$

one rewrites

$$\mathsf{\Gamma }\left[\rho \right]=-{\int }_0^{\infty }{\displaystyle \frac{ds}{s}}Tr\left(\rho \left(e^{-s{L}_0^{-1}K}-e^{-s}\right)\right)$$

[218]. Since K is a bounded CPTP generator, $\parallel L_0^{-1}K\parallel <1$ and the Borel representation converges.

3.2.1-3 Mathematical Properties of the Total Action $S_{\mathrm{var}}=S_0+i\mathsf{\Gamma }$ (Complex Action, Role of Real and Imaginary Parts)

Definition as a complex action

Combining the reversible $S_0$ and the irreversible $\mathsf{\Gamma }$ yields the complex action

$$S_{\mathrm{var}}[\psi ,\overline{\psi },\rho ]:=S_0[\psi ,\overline{\psi }]+i\mathsf{\Gamma }\left[\rho \right]$$

[219]. Its real part $\Re S_{\mathrm{var}}=S_0$ governs unitary time evolution, while the imaginary part $\Im S_{\mathrm{var}}=\mathsf{\Gamma }$ accounts for entropy production and dissipation.

Physical roles of the real and imaginary parts

• Variation of $\Re S_{\mathrm{var}}$ yields the Dirac–Yang–Mills equations, i.e., unitary reversible dynamics.
• Variation of $\Im S_{\mathrm{var}}$ produces the dissipative master equation $\dot{\rho }=L_0\left[\rho \right]+K\left[\rho \right]$ and the entropy-increase law ${\dot{S}}_{\mathrm{vN}}=-Tr(\dot{\rho }log\rho )\ge 0$ [213].

Analyticity of the complex action

$S_{\mathrm{var}}$ is Fréchet–holomorphic, so complex variational calculus applies [220]. In particular, stationary-phase approximations are justified for perturbative expansions.

3.2.1-4 Density and Domain: Fréchet Differentiability of the Action Functional on Sobolev Spaces

Domain specification

• The fields $\psi ,\overline{\psi }$ lie in the Sobolev space $H^1\left(S\left(M^4\right)\otimes E_G\right)$ with ${\nabla }_{\mu }\psi \in L^2$ [34].
• The density operator $\rho$ lies in the Schatten–von Neumann class $S_1\left(\mathcal{H}\right)$ so that $\mathsf{\Gamma }\left[\rho \right]$ is trace-class [71].

Fréchet differentiability

Since $S_0$ is a composition of continuous linear functionals on $H^1$, it is Fréchet differentiable. For $\mathsf{\Gamma }$, the Borel form gives

$$\delta \mathsf{\Gamma }[\rho ;\delta \rho ]=-{\int }_0^{\infty }{\displaystyle \frac{ds}{s}}Tr\left(\delta \rho (e^{-s{L}_0^{-1}K}-I)\right),$$

hence $S_{\mathrm{var}}$ is Fréchet differentiable in $\psi ,\overline{\psi },\rho$.

Summary

Section 3.2.1 has rigorously constructed the action functional of UEE${‌}_{\mathrm{var}}$ and established

• gauge–gravitational covariance of the reversible part $S_0$;
• Borel regularisation of the irreversible part $\mathsf{\Gamma }$ including the zero–area kernel R;
• the complex structure and Fréchet differentiability of the total action $S_{\mathrm{var}}$.

3.2.2 Derivation of the Euler–Lagrange Variational Equations

In this subsection we perform the Fréchet variation of the complex action functional

$$S_{\mathrm{var}}[\psi ,\overline{\psi },\rho ]=S_0[\psi ,\overline{\psi }]+i\mathsf{\Gamma }\left[\rho \right],\mathsf{\Gamma }\left[\rho \right]\equiv {\mathsf{\Gamma }}_{({\mathcal{L}}_{\mathsf{\Delta }}+R)}\left[\rho \right],$$

defined in the previous subsection, and derive the Euler–Lagrange equations. The reversible and irreversible parts are varied separately, boundary terms are handled, and consistent natural boundary conditions are imposed [30,219,221].

3.2.2-1 Derivation of Field Equations from the First Variation $\delta S_{\mathrm{var}}=0$

Write the action as

$$S_{\mathrm{var}}[\psi ,\overline{\psi },\rho ]=\int d^{4}xdet\left(e\right)\overline{\psi }i{\gamma }^a{e}_a{‌}^{\mu }{\nabla }_{\mu }\psi +i{\mathsf{\Gamma }}_{({\mathcal{L}}_{\mathsf{\Delta }}+R)}\left[\rho \right]$$

[214]. The independent variables are $\overline{\psi }$, $\psi$, and $\rho$.

(i) Variation with respect to $\delta \overline{\psi }$

$${\delta }_{\overline{\psi }}{S}_0=\int d^{4}xdet\left(e\right)\delta \overline{\psi }\left(i{\gamma }^a{e}_a{‌}^{\mu }{\nabla }_{\mu }\psi \right)+(\mathrm{boundary}\mathrm{terms})$$

222. Eliminating the boundary terms gives

$${\displaystyle \frac{\delta S_{\mathrm{var}}}{\delta \overline{\psi }}}=0⟹i{\gamma }^a{e}_a{‌}^{\mu }{\nabla }_{\mu }\psi =0.$$

(ii) Variation with respect to $\delta \psi$

$${\delta }_{\psi }{S}_0=\int d^{4}xdet\left(e\right)\left(-{\nabla }_{\mu }\overline{\psi }i{\gamma }^a{e}_a{‌}^{\mu }\right)\delta \psi +(\mathrm{boundary}\mathrm{terms}).$$

Hence

$${\displaystyle \frac{\delta S_{\mathrm{var}}}{\delta \psi }}=0⟹{\nabla }_{\mu }\overline{\psi }i{\gamma }^a{e}_a{‌}^{\mu }=0.$$

(iii) Variation with respect to $\delta \rho$

For the dissipative part

$$\mathsf{\Gamma }\left[\rho \right]=-{\int }_0^{\infty }{\displaystyle \frac{ds}{s}}Tr\left(\rho (e^{-s{L}_0^{-1}K}-e^{-s})\right),K:={\mathcal{L}}_{\mathsf{\Delta }}+R,$$

the variation is

$${\delta }_{\rho }\mathsf{\Gamma }=-{\int }_0^{\infty }{\displaystyle \frac{ds}{s}}Tr\left(\delta \rho (e^{-s{L}_0^{-1}K}-I)\right).$$

Therefore

$${\displaystyle \frac{\delta S_{\mathrm{var}}}{\delta \rho }}=0⟹L_{\mathrm{tot}}\left[\rho \right]=0,L_{\mathrm{tot}}:=L_0+{\mathcal{L}}_{\mathsf{\Delta }}+R,$$

which yields the master equation $\dot{\rho }=L_{\mathrm{tot}}\left[\rho \right]$ [37,213].

3.2.2-2 Boundary Terms and Natural Boundary Conditions: Compatibility with Variational Form and Gauge Fixing

The boundary terms arising from the variation are

$${\int }_{\partial M}det\left(e\right)\delta \overline{\psi }i{\gamma }^a{e}_a{‌}^{\mu }\psi n_{\mu }+\overline{\psi }i{\gamma }^a{e}_a{‌}^{\mu }{n}_{\mu }\delta \psi ,$$

[221]. They vanish by imposing either

• ${\delta \psi |}_{\partial M}=0$ and $\delta \overline{\psi }{|}_{\partial M}=0$ (Dirichlet type), or
• ${\gamma }^a{e}_a{‌}^{\mu }{n}_{\mu }{\psi |}_{\partial M}=0$ (MIT boundary condition, etc.).

Thus only the interior Euler–Lagrange equations remain.

3.2.2-3 Operator Form of UEE${‌}_{\mathrm{var}}$

(i) Equation from ${\delta }_{\overline{\psi }}$

$$D_G\psi =0,D_G:=i{\gamma }^a{e}_a{‌}^{\mu }{\nabla }_{\mu }.$$

(ii) Equation from ${\delta }_{\psi }$

$$\overline{\psi }{D}_G=0,D_G^{†}=D_G.$$

(iii) Equation from ${\delta }_{\rho }$

$$L_{\mathrm{tot}}\left[\rho \right]=0,L_{\mathrm{tot}}=L_0+{\mathcal{L}}_{\mathsf{\Delta }}+R.$$

Summary

Even with the zero–area resonance kernel R, the Euler–Lagrange variation consistently produces

• a Dirac–type reversible field equation,
• the dissipative master equation with resonance ${\displaystyle \dot{\rho }=-i[D_G,\rho ]+{\mathcal{L}}_{\mathsf{\Delta }}\left[\rho \right]+R\left[\rho \right]}$.

See [214,219] for details.

3.2.2-4 Compatibility of Hermiticity and Dissipation in the Variational Equations

The reversible part $D_G$ is self–adjoint Section 2.6.2; Stone’s theorem [35]), the irreversible part ${\mathcal{L}}_{\mathsf{\Delta }}$ is Lindblad–Gorini–Kossakowski–Sudarshan completely positive [2,8] (Section 2.30.2), and the zero–area kernel R is a bounded double–commutator preserving CPTP character (Theorem 2.31.3, §2.31; Kato–Rellich relative boundedness [56]). Thus the total equation

$$\dot{\rho }=-i[D_G,\rho ]+{\mathcal{L}}_{\mathsf{\Delta }}\left[\rho \right]+R\left[\rho \right]$$

simultaneously satisfies Hermiticity in the first term (unitary flow) and GKLS–type dissipativity in the latter terms, ensuring complete consistency [1].

3.2.3 Minimisation of the Dissipative Functional and Resonance

In this subsection we explain in detail, at the level of individual equations, how the minimisation principle of the irreversible dissipative functional $\mathsf{\Gamma }\left[\rho \right]$ in UEE${‌}_{\mathrm{var}}$ leads to resonant phenomena through an eigenmode analysis. We further present the correspondence with nonequilibrium statistical mechanics via the saddle-point approximation and rigorously establish the energy–entropy relation by means of the Lagrange-multiplier method.

3.2.3-1 Variational Minimisation Condition for the Dissipative Functional $\mathsf{\Gamma }\left[\rho \right]$ and Its Physical Interpretation

Variational minimisation condition

Using the Borel representation [25,217], the dissipative functional is

$$\mathsf{\Gamma }\left[\rho \right]=-{\int }_0^{\infty }{\displaystyle \frac{ds}{s}}Tr\left(\rho \left(e^{-s{L}_0^{-1}K}-I\right)\right),K:={\mathcal{L}}_{\mathsf{\Delta }}+R.$$

Imposing the condition $\delta \mathsf{\Gamma }\left[\rho \right]=0$ gives

$${\delta }_{\rho }\mathsf{\Gamma }=-{\int }_0^{\infty }{\displaystyle \frac{ds}{s}}Tr\left(\delta \rho (e^{-s{L}_0^{-1}K}-I)\right)=0⟹L_0^{-1}K\left[{\rho }_{\mathrm{ss}}\right]=0⟹K\left[{\rho }_{\mathrm{ss}}\right]=0.$$

Hence the stationary state satisfies

$$L_{\mathrm{tot}}\left[{\rho }_{\mathrm{ss}}\right]=0,L_{\mathrm{tot}}:=L_0+{\mathcal{L}}_{\mathsf{\Delta }}+R,$$

in accordance with Theorem 2.31.3 of §2.31.

Physical interpretation

Minimising $\mathsf{\Gamma }\left[\rho \right]$ is the quantum analogue of Prigogine’s principle of minimum entropy production: the entropy-production rate ${\dot{S}}_{\mathrm{vN}}=-{\delta }_{\rho }\mathsf{\Gamma }\left[\rho \right]\ge 0$ is minimised [147,223]. At this minimum the system relaxes through its slowest mode, and resonance emerges.

3.2.3-2 Derivation of Resonance Frequencies via Eigenmode Analysis

Eigenmode equation

Expanding to second order with $\rho ={\rho }_{\mathrm{ss}}+\epsilon \delta \rho$ [224],

$${\delta }^2\mathsf{\Gamma }\left[{\rho }_{\mathrm{ss}}\right]={\int }_0^{\infty }{\displaystyle \frac{ds}{s}}\mathrm{Tr}\left(\delta \rho e^{-s{L}_0^{-1}K}{L}_0^{-1}K\delta \rho \right).$$

Define

$$\mathcal{M}\left[\varphi \right]=\omega \varphi ,\mathcal{M}:={\int }_0^{\infty }ds{e}^{-s{L}_0^{-1}K}{L}_0^{-1}K,$$

whose spectrum $\left\{{\omega }_n\right\}$ yields the resonance frequencies. For weak dissipation $\parallel K\parallel \ll \parallel L_0\parallel$,

$${\omega }_n\simeq {\displaystyle \frac{\langle {\varphi }_n|K{\varphi }_n\rangle }{\langle {\varphi }_n|L_0{\varphi }_n\rangle }}$$

[225].

3.2.3-3 Saddle-Point Approximation and Hyperbolic Resonance: Link to Nonequilibrium Statistical Mechanics

Introducing the saddle-point approximation

Applying a path-integral approximation to the complex action $S_{\mathrm{var}}=S_0+i\mathsf{\Gamma }$ [219],

$$Z=\int \mathcal{D}\rho e^{i{S}_{\mathrm{var}}\left[\rho \right]}\approx e^{i{S}_{\mathrm{var}}\left[{\rho }_{*}\right]}{\left[det\left(i{\delta }^2{S}_{\mathrm{var}}\left[{\rho }_{*}\right]\right)\right]}^{-1/2},$$

where the saddle-point ${\rho }_{*}$ satisfies $\delta S_{\mathrm{var}}\left[{\rho }_{*}\right]=0$ and corresponds to a resonance point [226].

Hyperbolic resonance and nonequilibrium fluctuations

Because the imaginary part $\mathsf{\Gamma }$ allows negative real parts for the eigenvalues of the fluctuation matrix ${\delta }^2\mathsf{\Gamma }$, “hyperbolic resonance” occurs, capturing the nonequilibrium fluctuation modes of large-deviation theory [227].

3.2.3-4 Minimisation Condition and the Energy–Entropy Correspondence via the Lagrange-Multiplier Method

Formulating the energy–entropy correspondence

The stationary state ${\rho }_{\mathrm{ss}}$ also solves the constrained minimisation

$$\underset{\rho }{min}\mathsf{\Gamma }\left[\rho \right],\mathrm{Tr}\rho =1,\mathrm{Tr}\left(H\rho \right)=E$$

[228].

Lagrange-multiplier method

Introducing

$$\mathcal{L}[\rho ,\alpha ,\beta ]=\mathsf{\Gamma }\left[\rho \right]-\alpha \left(\mathrm{Tr}\rho -1\right)-\beta \left(\mathrm{Tr}\left(H\rho \right)-E\right),$$

the stationarity condition ${\delta }_{\rho }\mathcal{L}=0$ yields

$${\displaystyle \frac{\delta \mathsf{\Gamma }}{\delta \rho }}=\alpha I+\beta H,$$

where $\beta$ identifies the inverse temperature and gives $\beta =\partial S/\partial E$ [143].

Physical implications

Minimising $\mathsf{\Gamma }\left[\rho \right]$ with the zero-area kernel included combines Jaynes’ maximum-entropy principle with Lindblad dynamics, selecting the optimal dissipative pathway for nonequilibrium relaxation [213,223].

3.3. Field-Equation Form (${\mathrm{UEE}}_{\mathrm{fld}}$)

3.3.1 Reconstruction of Fractal-Operator Dynamics

This subsection rigorously shows, at the level of individual equations, how the non-local fractal-dimension operator $D_f\left(x\right)$ can be re-cast as a field and its dynamics converted into local partial differential equations. Using a Barnes–Barnes–type integral representation for the non-local terms, taking the continuum limit (recovery of integer dimensions), and analysing the spectrum for stability, we build the skeleton of fractal-field dynamics in UEE${‌}_{\mathrm{fld}}$.

3.3.1-1 Introducing the Fractal-Dimension Operator $D_f\left(x\right)$ as a Field

Originally the fractal-dimension operator is defined non-locally by

$$D_f=sin\left(\frac{\pi }{\mathsf{\Lambda }}\sqrt{-\square }\right),\square =g^{\mu \nu }{\nabla }_{\mu }{\nabla }_{\nu },$$

and its boundedness follows from spectral functional calculus for self-adjoint operators [6,229].

Definition 63 

(Fractal-dimension field operator). For each point x on the manifold introduce a position-dependent parameter $\mathsf{\Lambda }\left(x\right)$ and define

$$D_f\left(x\right)=sin\left(\frac{\pi }{\mathsf{\Lambda }\left(x\right)}\sqrt{-{\square }_x}\right),{\square }_x:={\left(g^{\mu \nu }{\nabla }_{\mu }{\nabla }_{\nu }\right)}_x,$$

where ${\nabla }_{\mu }$ is the spinor–gauge–gravitational covariant derivative and $\sqrt{-\square }$ is a pseudo-differential operator defined spectrally [230].

Domain and action space

Because $\sqrt{-\square }$ is a function of a self-adjoint operator, $D_f\left(x\right)$ is bounded (Stone–von Neumann functional calculus [35]). With the spectral decomposition $\square {\varphi }_{\lambda }=\lambda {\varphi }_{\lambda }$,

$$D_f{\varphi }_{\lambda }=sin\left(\frac{\pi }{\mathsf{\Lambda }}\sqrt{\lambda }\right){\varphi }_{\lambda },$$

so each eigenmode acquires a “fractal amplitude.”

3.3.1-2 Conversion to Field Equations

In the action-principle version of UEE${‌}_{\mathrm{fld}}$, $D_f\left(x\right)$ is treated as an independent field with

$$S_{D_f}\left[D_f\right]={\mathsf{\Lambda }}^4\int d^{4}xdet\left(e\right)\mathrm{Tr}\left(\mathsf{\Gamma }\left[D_f\left(x\right)\right]\right).$$

Taking the Fréchet derivative gives

$${\partial }_{\tau }{D}_f\left(x\right)=-{\kappa }_D{\displaystyle \frac{\delta S_{D_f}}{\delta D_f\left(x\right)}}=-{\kappa }_D{\mathsf{\Lambda }}^{4}det\left(e\right){\displaystyle \frac{\delta }{\delta D_f\left(x\right)}}\mathrm{Tr}\left(\mathsf{\Gamma }\left[D_f\right]\right).$$

Using the Barnes–Luke integral representation (operator version of ${\displaystyle \mathsf{\Gamma }\left(z\right)=-{\int }_0^{\infty }\frac{e^{-s}-e^{-sz}}{s}ds}$) [123,217],

$$\mathsf{\Gamma }\left[D_f\right]=-{\int }_0^{\infty }{\displaystyle \frac{ds}{s}}\left(e^{-s{D}_f}-e^{-s}\right),$$

the non-local term can be embedded into local PDEs via multiple integral representations [231].

3.3.1-3 Continuum Limit and Recovery of Integer Dimensions

In the integer-dimension limit $\mathsf{\Lambda }\to \infty$,

$$sin\left(\frac{\pi }{\mathsf{\Lambda }}\sqrt{-\square }\right)\simeq \frac{\pi }{\mathsf{\Lambda }}\sqrt{-\square },$$

so $D_f\left(x\right)\to \frac{\pi }{\mathsf{\Lambda }}\sqrt{-\square }$. Consequently

$$S_{D_f}⟶\frac{\pi }{\mathsf{\Lambda }}\int d^{4}x\sqrt{-g}\mathrm{Tr}\left(\sqrt{-\square }\right),$$

which asymptotically approaches a standard local theory [232,233].

3.3.1-4 Spectral Analysis and Stability Evaluation

Expanding as

$$D_f(x,\tau )=\sum _{\lambda }{a}_{\lambda }\left(\tau \right){\varphi }_{\lambda }\left(x\right),$$

yields

$${\dot{a}}_{\lambda }=-{\kappa }_{D}sin\left(\frac{\pi }{\mathsf{\Lambda }}\sqrt{\lambda }\right)a_{\lambda },$$

so the damping rate is ${\kappa }_{D}sin(\pi \sqrt{\lambda }/\mathsf{\Lambda })$. The condition $\sqrt{\lambda }=(n+\frac{1}{2})\mathsf{\Lambda }$ identifies “fractal resonance modes” [234].

3.3.1-5 Relation to the Overall Theory

• The non-local operator $\sqrt{-\square }$ used in UEE${‌}_{\mathrm{op}}$ and UEE${‌}_{\mathrm{var}}$ is consistently reconstructed within the field-equation form.
• The Barnes–Luke representation embeds the non-local contributions into partial differential equations via operational multiple integrals.
• In the continuum limit $\mathsf{\Lambda }\to \infty$, the theory reduces to standard local equations (wave/Dirac).
• Linear spectral analysis gives the damping rate ${\kappa }_{D}sin(\pi \sqrt{\lambda }/\mathsf{\Lambda })$ and rigorously evaluates mode stability and resonance.

3.3.2 Field-Equation Formulation of the Information-Flux Density

In this subsection we start from the definition of the information-flux field ${\displaystyle {\mathsf{\Phi }}_I^{\mu }\left(x\right)}$ introduced in UEE${‌}_{\mathrm{fld}}$ and construct its field equation in full. First we show the correspondence between “information flux” and “dissipative source,” then derive the covariant divergence equation ${\nabla }_{\mu }{\mathsf{\Phi }}_I^{\mu }=\mathsf{\Sigma }[D_f,\rho ]$. Finally we make the non-local coupling to the fractal field $D_f$ explicit and rigorously relate it to thermodynamic quantities (entropy and free energy). Throughout we use the dissipative operator

$$K:={\mathcal{L}}_{\mathsf{\Delta }}+R$$

(§2.31).

3.3.2-1 Definition of the Information-Flux Field ${\mathsf{\Phi }}_I^{\mu }\left(x\right)$

Definition 64 

(Information-flux field). With the local entropy density of the density operator $\rho \left(x\right)$

$$\mathcal{I}\left(x\right):=-\mathrm{Tr}\left(\rho \left(x\right)log\rho \left(x\right)\right)$$

[235,236], the information-flux field is defined by

$${\mathsf{\Phi }}_I^{\mu }\left(x\right):=\beta {\nabla }^{\mu }\mathcal{I}\left(x\right)=-\beta {\nabla }^{\mu }\mathrm{Tr}\left(\rho log\rho \right)$$

[154], where β is the inverse temperature or, equivalently, the energy–entropy conversion factor.

Covariant expression

Here ${\nabla }^{\mu }=g^{\mu \nu }{\nabla }_{\nu }$ is the spinor–gauge–gravitational covariant derivative. This provides an analytic basis for treating the entropy density as a field, independently of the Clifford structure [33].

3.3.2-2 Continuity Equation and Nonequilibrium Conservation Law

Proposition 72 

(Nonequilibrium information continuity equation). The field ${\mathsf{\Phi }}_I^{\mu }$ satisfies

$${\nabla }_{\mu }{\mathsf{\Phi }}_I^{\mu }\left(x\right)=\mathsf{\Sigma }\left[D_f,\rho \right]\left(x\right),$$

where the right-hand side

$$\mathsf{\Sigma }[D_f,\rho ]\left(x\right):=\beta \mathrm{Tr}\left(K\left[\rho \right]log\rho \right),\left(K={\mathcal{L}}_{\mathsf{\Delta }}+R\right),$$

is the entropy-production source generated by K [2,213].

Proof. 

$${\nabla }_{\mu }{\mathsf{\Phi }}_I^{\mu }=-\beta {\nabla }_{\mu }{\nabla }^{\mu }\mathrm{Tr}(\rho log\rho )=-\beta \mathrm{Tr}\left(\left({\nabla }_{\mu }{\nabla }^{\mu }\rho \right)log\rho +{\nabla }_{\mu }\rho {\nabla }^{\mu }log\rho \right).$$

Using ${\nabla }_{\mu }\rho =K\left[\rho \right]$ and expanding ${\nabla }_{\mu }{\nabla }^{\mu }\rho$ in terms of $L_0$ and K, one extracts the source term $\mathsf{\Sigma }[D_f,\rho ]$ [37].    □

3.3.2-3 Coupling to the Fractal Field

Proposition 73 

(Non-local coupling term). The term $\mathrm{Tr}\left({\mathsf{\Phi }}_I^{\mu }{\square }^n{D}_f\right)$ in the dissipative functional can be expanded, using the continuity equation ${\nabla }_{\mu }{\mathsf{\Phi }}_I^{\mu }=\mathsf{\Sigma }$, as

$$\sum _{n=0}^{\infty }{c}_n{\nabla }_{\mu }\left({\mathsf{\Phi }}_I^{\mu }{\square }^n{D}_f\right)=\sum _{n=0}^{\infty }{c}_n\left({\square }^n{\mathsf{\Phi }}_I^{\mu }\right){\nabla }_{\mu }{D}_f+\dots ,$$

thereby recasting the non-local coupling into local PDE form [230,231].

Proof. 

Employ the Barnes–Luke expansion $\mathsf{\Gamma }\left[D_f\right]=\sum c_n{D}_f^{2n+1}$ and the pseudodifferential identity ${\square }^n{D}_f=D_f^{2n+1}$[229], followed by the Leibniz rule for ${\nabla }_{\mu }$. Details are given in Appendix F.3.    □

3.3.2-4 Field-Theoretic Expansion of the Energy–Entropy Correspondence

Definition 65 

(Field energy–entropy functionals). For ${\mathsf{\Phi }}_I^{\mu }$ define

$$\mathcal{E}\left[{\mathsf{\Phi }}_I\right]:={\displaystyle \frac{1}{2{\kappa }_I}}\int d^{4}xdet\left(e\right){\mathsf{\Phi }}_{I\mu }{\mathsf{\Phi }}_I^{\mu },\mathcal{S}\left[{\mathsf{\Phi }}_I\right]:=\int d^{4}x\sqrt{-g}{\mathsf{\Phi }}_I^{\mu }{\nabla }_{\mu }\mathcal{I}.$$

Proposition 74 

(Correspondence via Lagrange multipliers). Imposing the stationarity condition $\delta \left(\mathcal{E}-\alpha \mathcal{S}\right)=0$ yields the field equation ${\mathsf{\Phi }}_I^{\mu }=\alpha {\nabla }^{\mu }\mathcal{I}$; the multiplier α corresponds to the inverse temperature [228,237].

Proof. 

$$\delta \mathcal{E}={\displaystyle \frac{1}{{\kappa }_I}}\int {\mathsf{\Phi }}_{I\mu }\delta {\mathsf{\Phi }}_I^{\mu },\delta \mathcal{S}=\int {\nabla }_{\mu }\mathcal{I}\delta {\mathsf{\Phi }}_I^{\mu }.$$

Therefore ${\mathsf{\Phi }}_I^{\mu }/{\kappa }_I=\alpha {\nabla }^{\mu }\mathcal{I}$.    □

3.3.2-5 Summary of Theoretical Significance

• The information-flux field ${\mathsf{\Phi }}_I^{\mu }$ expresses the entropy-production rate locally, enabling microscopic analysis of decay and relaxation processes.
• The nonequilibrium source $\mathsf{\Sigma }[D_f,\rho ]$ establishes thermodynamic consistency between the total generator $L_{\mathrm{tot}}=L_0+{\mathcal{L}}_{\mathsf{\Delta }}+R$ (including the zero-area kernel) and entropy production.
• The Barnes–Luke expansion embeds the non-local coupling to the fractal field in a local PDE framework, ensuring the self-consistency of the action principle.
• The Lagrange-multiplier formulation of the energy–entropy correspondence provides a geometric interpretation of inverse temperature, bridging nonequilibrium statistical mechanics and field theory.

3.4. Proof of Equivalence Between the Formulations

3.4.1 Operator Form ⇔ Variational Form

This subsection proves—through three steps—that the operator form of UEE${‌}_{\mathrm{op}}$

$${\partial }_{\tau }\rho =-i\left[D,\rho \right]+{\mathcal{L}}_{\mathsf{\Delta }}\left[\rho \right]+R\left[\rho \right]$$

describes exactly the same dynamics as the master equation obtained from the variational principle of UEE${‌}_{\mathrm{var}}$,

$${\displaystyle \frac{\delta }{\delta \rho }}\left(S_{\mathrm{rev}}\left[\rho \right]+S_{\mathrm{diss}}\left[\rho \right]\right)=0.$$

3.4.1-1 Identity of the Master Equations in UEE${‌}_{\mathrm{op}}$ and UEE${‌}_{\mathrm{var}}$

Restatement of the operator form

In the operator formulation the reversible and dissipative parts are

$$L_0\left[\rho \right]=-i[D,\rho ],L_{\mathsf{\Delta }}\left[\rho \right]=\sum _j\left(V_j\rho V_j^{†}-\frac{1}{2}\{V_j^{†}{V}_j,\rho \}\right)$$

[2,8], while the zero-area resonance kernel is

$$R\left[\rho \right]={\int }_{\sigma \left(D\right)}d\omega R\left(\omega \right)[D,[D,\rho ]]E_D\left(d\omega \right)$$

[24]. (see § 2.5). With the total generator

$$\mathcal{L}=L_0+L_{\mathsf{\Delta }}+R,$$

one obtains ${\partial }_{\tau }\rho =\mathcal{L}\left[\rho \right]$.

Master equation from the variational principle

In the variational form the action functional is split as

$$S\left[\rho \right]=S_{\mathrm{rev}}\left[\rho \right]+S_{\mathrm{diss}}\left[\rho \right],$$

with

$$S_{\mathrm{rev}}\left[\rho \right]=\mathrm{Tr}\left(\rho D\right)\tau ,S_{\mathrm{diss}}\left[\rho \right]=\sum _j{\int }_0^{\tau }dt\mathrm{Tr}\left(\rho V_j^{†}{V}_j-V_j\rho V_j^{†}\right)+{\int }_0^{\tau }dt\mathrm{Tr}\left(\rho R^{†}[·]\right)$$

[1], where $\tau$ is the evolution parameter. Varying S gives

$$0={\displaystyle \frac{\delta S}{\delta \rho }}=D\tau +\sum _j{\int }_0^{\tau }dt\left(V_j^{†}{V}_j-V_j\rho V_j^{†}\right)+{\int }_0^{\tau }dt{R}^{†}\left[I\right].$$

Differentiating with respect to time yields

$${\partial }_{\tau }\rho =-i[D,\rho ]+\sum _j\left(V_j\rho V_j^{†}-\frac{1}{2}\{V_j^{†}{V}_j,\rho \}\right)+R\left[\rho \right],$$

identical to the operator form.

Proof of identity

Term-by-term comparison shows

• ${\displaystyle \frac{\delta S_{\mathrm{rev}}}{\delta \rho }=D}$ corresponds to the unitary generator $-i[D,\rho ]$ (Stone’s theorem [35]).
• Calculating ${\displaystyle \frac{\delta S_{\mathrm{diss}}}{\delta \rho }}$ by matrix calculus reproduces both the Lindblad–GKLS dissipator $V_j\rho V_j^{†}-\frac{1}{2}\{V_j^{†}{V}_j,\rho \}$ and the zero-area resonance kernel $R\left[\rho \right]$, fully matching the total generator $\mathcal{L}$.

3.4.1-2 Reconstruction of Reversible and Dissipative Terms from the Action Functional

Reversible part

$$S_{\mathrm{rev}}\left[\rho \right]=\mathrm{Tr}\left(\rho D\right)\tau ={\int }_0^{\tau }dt\mathrm{Tr}\left(\rho \left(t\right)D\right).$$

Varying with respect to $\delta \rho$ gives

$$\delta S_{\mathrm{rev}}={\int }_0^{\tau }dt\mathrm{Tr}\left(\delta \rho D\right)⟹{\displaystyle \frac{\delta S_{\mathrm{rev}}}{\delta \rho }}=D,$$

and Stone’s theorem [35] yields ${\partial }_{\tau }\rho =-i[D,\rho ]$.

Dissipative part

Writing

$$S_{\mathrm{diss}}=S_{{\mathcal{L}}_{\mathsf{\Delta }}}+S_R,$$

with

$$S_{{\mathcal{L}}_{\mathsf{\Delta }}}=\sum _j{\int }_0^{\tau }dt\mathrm{Tr}\left(\rho V_j^{†}{V}_j-V_j\rho V_j^{†}\right),S_R={\int }_0^{\tau }dt\mathrm{Tr}\left(\rho R^{†}[·]\right),$$

one finds

$${\displaystyle \frac{\delta S_{{\mathcal{L}}_{\mathsf{\Delta }}}}{\delta \rho }}=\sum _j\left(V_j^{†}{V}_j-V_j\rho V_j^{†}\right),{\displaystyle \frac{\delta S_R}{\delta \rho }}=R\left[\rho \right],$$

so $K\left[\rho \right]={\mathcal{L}}_{\mathsf{\Delta }}\left[\rho \right]+R\left[\rho \right]$ is recovered [1].

3.4.1-3 Consistency with the KMS Condition

KMS condition revisited

The thermal state ${\rho }_{\mathrm{eq}}\propto e^{-\beta D}$ satisfies the Kubo–Martin–Schwinger condition [50,238]

$$\mathrm{Tr}\left(A\left(t\right)B\left(0\right){\rho }_{\mathrm{eq}}\right)=\mathrm{Tr}\left(B\left(0\right)A(t+i\beta ){\rho }_{\mathrm{eq}}\right).$$

Consistency in UEE${‌}_{\mathrm{op}}$

For ${\rho }_{\mathrm{eq}}$ to obey ${\partial }_{\tau }\rho =0$ one requires $-i[D,{\rho }_{\mathrm{eq}}]+K\left[{\rho }_{\mathrm{eq}}\right]=0$. The reversible term vanishes and $K\left[{\rho }_{\mathrm{eq}}\right]=0$. Because $R\left[{\rho }_{\mathrm{eq}}\right]=0$, the condition is met if the Lindblad operators satisfy the KMS adjoint relation $V_j{e}^{-\beta D}=e^{-\beta D}{V}_j$ [154].

Consistency in UEE${‌}_{\mathrm{var}}$

In the variational form, ${\displaystyle \delta S_{\mathrm{diss}}/\delta \rho =0}$ likewise gives $K\left[{\rho }_{\mathrm{eq}}\right]=0$, leading to the same equilibrium state.

Thus, even with the zero-area resonance kernel R, the operator and variational formulations are exactly equivalent at the levels of generator, master equation, and equilibrium solution.

3.4.2 Variational Form ⇔ Field-Equation Form

In this subsection we rigorously show—again in three steps—that the Euler–Lagrange equations derived from the action principle of UEE${‌}_{\mathrm{var}}$ describe the same dynamics as the field-equation form of UEE${‌}_{\mathrm{fld}}$.

3.4.2-1 Reduction from the Euler–Lagrange Equations to a System of PDEs

Restatement of the action principle

For the action

$$S[\psi ,\overline{\psi },e,A,D_f,{\mathsf{\Phi }}_I]=S_{\mathrm{spinor}}[\psi ,\overline{\psi },e,A]+S_{\mathrm{YM}}[A,e]+S_{D_f}[D_f,e]+S_{{\mathsf{\Phi }}_I}[{\mathsf{\Phi }}_I,e],$$

taking functional derivatives yields[30,157]

$$\begin{array}{cccccc}\hfill {\displaystyle \frac{\delta S}{\delta \overline{\psi }}}& =0\hfill & \hfill & ⟹\hfill & \hfill i{\gamma }^a{e}_a{‌}^{\mu }{\nabla }_{\mu }\psi & =0,\hfill \\ \hfill {\displaystyle \frac{\delta S}{\delta A_{\mu }}}& =0\hfill & \hfill & ⟹\hfill & \hfill D_{\nu }{F}^{\nu \mu }+J_{\mathrm{spinor}}^{\mu }& =0\hfill \end{array}$$

[239],

$$\begin{array}{cccccc}\hfill {\displaystyle \frac{\delta S}{\delta D_f}}& =0\hfill & \hfill & ⟹\hfill & \hfill {\partial }_{\tau }{D}_f& =-{\kappa }_D{\displaystyle \frac{\delta \mathsf{\Gamma }\left[D_f\right]}{\delta D_f}}\hfill \end{array}$$

[240],

$$\begin{array}{cccccc}\hfill {\displaystyle \frac{\delta S}{\delta {\mathsf{\Phi }}_{I\mu }}}& =0\hfill & \hfill & ⟹\hfill & \hfill {\partial }_{\tau }{\mathsf{\Phi }}_I^{\mu }& =-{\kappa }_I{\mathsf{\Phi }}_I^{\mu },\hfill \end{array}$$

which together constitute the four–field coupled PDE system of UEE${‌}_{\mathrm{fld}}$.

Comparison with the field–equation form

In Chapter 3.3–3.4 the field-equation formulation of UEE${‌}_{\mathrm{fld}}$ was given as

$$\left\{\begin{array}{c}i{\gamma }^a{e}_a{‌}^{\mu }{\nabla }_{\mu }\psi =0,\hfill \\ D_{\nu }{F}^{\nu \mu }+J_{\mathrm{spinor}}^{\mu }=0,\hfill \\ {\partial }_{\tau }{D}_f=-{\kappa }_D{\displaystyle \frac{\delta \mathsf{\Gamma }\left[D_f\right]}{\delta D_f}},\hfill \\ {\partial }_{\tau }{\mathsf{\Phi }}_I^{\mu }=-{\kappa }_I{\mathsf{\Phi }}_I^{\mu },\hfill \end{array}\right.$$

and the derivation above matches each term exactly[37].

3.4.2-2 Localisation via the Second Variation and Derivation of Interaction Terms

Interactions from the second variation

Taking the second functional variation of the action with respect to the field variables [241], we obtain

$$\begin{array}{cc}\hfill {\delta }^{2}S=& \int d^{4}xdet\left(e\right)[\delta \overline{\psi }{\mathcal{O}}_{\psi \psi }\delta \psi +\delta A_{\mu }{\mathcal{O}}_{AA}^{\mu \nu }\delta A_{\nu }+\delta D_f{\mathcal{O}}_{D_f{D}_f}\delta D_f\hfill \\ & +\delta {\mathsf{\Phi }}_I^{\mu }{\mathcal{O}}_{\mathsf{\Phi }\mathsf{\Phi }\mu \nu }\delta {\mathsf{\Phi }}_I^{\nu }+2\delta D_f{\mathcal{O}}_{D_f{\mathsf{\Phi }}_I\mu }\delta {\mathsf{\Phi }}_I^{\mu }+\dots ].\hfill \end{array}$$

The cross-term ${\mathcal{O}}_{D_f{\mathsf{\Phi }}_I\mu }$ provides the local PDE form of the fractal–information coupling [240].

Example of the resulting local PDE

From the $\delta D_f$–$\delta {\mathsf{\Phi }}_I$ sector one obtains, for instance,

$${\mathcal{O}}_{D_f{\mathsf{\Phi }}_I\mu }=c{\nabla }_{\mu }\left({\square }^n{\mathsf{\Phi }}_I\right),$$

leading to the local differential equation ${\partial }_{\tau }{D}_f+\dots +c{\nabla }_{\mu }\left({\square }^n{\mathsf{\Phi }}_I\right)=0.$

3.4.2-3 Continuum Limit and Mode Consistency via Spectral Expansion

Borel–Barnes continuum limit

Viewing the non-local functional as the spectral series $\mathsf{\Gamma }\left[D_f\right]=\sum c_n{D}_f^{2n+1}$ and taking $\mathsf{\Lambda }\to \infty$ so that $D_f\to (\pi /\mathsf{\Lambda })\sqrt{-\square }$, one finds

$$\mathsf{\Gamma }\left[D_f\right]\to \sum c_n{\left(\frac{\pi }{\mathsf{\Lambda }}\sqrt{-\square }\right)}^{2n+1},$$

which converges to a local operator series whose higher-order terms match integer-order derivatives [240].

Spectral consistency

For mode expansion $\square {\varphi }_{\lambda }=\lambda {\varphi }_{\lambda }$, the field equation ${\partial }_{\tau }{D}_f\propto -sin(\pi \sqrt{\lambda }/\mathsf{\Lambda })D_f$ coincides with the eigenvalue problem that follows from the linearised second variation ${\delta }^{2}S/\delta D_f^2$ [241]. Thus the mode dynamics are identical in both the variational and the field-equation formulations.

Consequently, the Euler–Lagrange equations of UEE${‌}_{\mathrm{var}}$ and the field equations of UEE${‌}_{\mathrm{fld}}$ reduce rigorously to the same local PDEs—with complete equivalence under both the continuum limit and spectral analysis.

3.4.3 Operator Form ⇔ Field-Equation Form

This subsection shows that the operator form of UEE${‌}_{\mathrm{op}}$

$${\partial }_{\tau }\rho =-i\left[D,\rho \right]+{\mathcal{L}}_{\mathsf{\Delta }}\left[\rho \right]+R\left[\rho \right]$$

and the field-equation form of UEE${‌}_{\mathrm{fld}}$ describe the same physical dynamics via the operator–field correspondence. We analyse this in detail from three viewpoints (the total generator is always $L_{\mathrm{tot}}=L_0+{\mathcal{L}}_{\mathsf{\Delta }}+R$).

3.4.3-1 Reinterpreting the Operator Generator as a Field-Dependent Operator

The generator in the operator form is

$$\begin{array}{cc}\hfill \mathcal{L}\left[\rho \right]& =-i[D,\rho ]+\sum _j\left(V_j\rho V_j^{†}-\frac{1}{2}\{V_j^{†}{V}_j,\rho \}\right)+R\left[\rho \right]\hfill \end{array}$$

$$\begin{array}{cc}\hfill & (\mathrm{reversible}\mathrm{part}\mathrm{from}\mathrm{Stone}\text{’}\mathrm{s}\mathrm{theorem}\hfill \end{array}$$

[35];

$$\begin{array}{cc}& \mathrm{dissipator}\mathrm{in}\mathrm{Lindblad}\text{–}\mathrm{GKLS}\mathrm{form}\hfill \end{array}$$

[2,8];

$$\begin{array}{cc}& \mathrm{zero}\text{-}\mathrm{area}\mathrm{kernel}\mathrm{as}\mathrm{Kato}\mathrm{perturbation}\hfill \end{array}$$

[24]). Reinterpreting $\rho$ locally as $\rho \left(x\right)=\psi \left(x\right)\overline{\psi }\left(x\right)$,

$$[D,\rho ]=D\psi \overline{\psi }-\psi \overline{D\psi },R\left[\rho \right]={\int }_{\sigma \left(D\right)}d\omega R\left(\omega \right)[D,[D,\rho ]]E_D\left(d\omega \right)$$

[242]. The Lindblad term becomes

$$V_j\rho V_j^{†}=\left(f_j\left(x\right)\otimes e_j\right)\psi \overline{\psi }{\left(f_j\left(x\right)\otimes e_j\right)}^{†}.$$

Thus each component of the generator is fully reconstructed as a field operator.

3.4.3-2 Operator–Field Correspondence Mapping

Define the mapping $\rho \mapsto \psi \overline{\psi }$, $D\mapsto i{\gamma }^{\mu }{\nabla }_{\mu }$, $V_j\mapsto f_j\left(x\right)\otimes e_j$, ${\displaystyle R[·]\mapsto \int d\omega R\left(\omega \right)[D,[D,·\left]\right]}$.

Operator form	Field-equation form
$\rho$	$\psi \left(x\right)\overline{\psi }\left(x\right)$
D	$i{\gamma }^{\mu }{\nabla }_{\mu }$
${\mathcal{L}}_{\mathsf{\Delta }}+R$	${\displaystyle \sum _j\left(f_j\otimes e_j\psi \right)\left(\overline{\psi }{f}_j\otimes e_j\right)-\frac{1}{2}\{\dots \}+\int d\omega R\left(\omega \right)[D,[D,\psi \overline{\psi }]]}$
${\partial }_{\tau }\rho$	${\partial }_{\tau }\left(\psi \overline{\psi }\right)=\left({\partial }_{\tau }\psi \right)\overline{\psi }+\psi \left({\partial }_{\tau }\overline{\psi }\right)$

Operator form	Field-equation form
$\rho$	$\psi \left(x\right)\overline{\psi }\left(x\right)$
D	$i{\gamma }^{\mu }{\nabla }_{\mu }$
${\mathcal{L}}_{\mathsf{\Delta }}+R$	${\displaystyle \sum _j\left(f_j\otimes e_j\psi \right)\left(\overline{\psi }{f}_j\otimes e_j\right)-\frac{1}{2}\{\dots \}+\int d\omega R\left(\omega \right)[D,[D,\psi \overline{\psi }]]}$
${\partial }_{\tau }\rho$	${\partial }_{\tau }\left(\psi \overline{\psi }\right)=\left({\partial }_{\tau }\psi \right)\overline{\psi }+\psi \left({\partial }_{\tau }\overline{\psi }\right)$

Because this mapping is one-to-one, the master equation in the operator form translates rigorously into the field equations.

3.4.3-3 Consistency of Physical Interpretation: Conservation Laws and Symmetries

Energy–entropy conservation

The reversible field equation $i{\gamma }^{\mu }{\nabla }_{\mu }\psi =0$ ensures conservation of the Noether current $T^{\mu \nu }$ ${\nabla }_{\mu }{T}^{\mu \nu }=0$ [243]. With dissipative and resonance terms included, the continuity equation ${\nabla }_{\mu }{\mathsf{\Phi }}_I^{\mu }=\mathsf{\Sigma }$ aligns entropy production with trace preservation [154].

Gauge–gravitational covariance

In the field formulation, transformations such as ${\nabla }_{\mu }\psi \mapsto h^{-1}{\nabla }_{\mu }\psi$ and $\square D_f\mapsto D_f$ manifestly preserve spinor–gauge–gravitational covariance, matching the covariance of the operator formulation.

Hence the operator, variational, and field-equation formulations share identical conservation laws and symmetries under the total generator $L_{\mathrm{tot}}=L_0+{\mathcal{L}}_{\mathsf{\Delta }}+R$, establishing the unified self-consistency of UEE even in the presence of the zero-area resonance kernel R.

3.5. Explicit Solutions of the UEE

3.5.1 Dissipative Solution in the Free Dirac Field

In this subsection we construct, in a completely closed form, the general solution of the master equation for a free Dirac operator $D=i{\gamma }^{\mu }{\nabla }_{\mu }$ (Proposition 28) without external fields or interactions, augmented by a Lindblad-type dissipator ${\mathcal{L}}_{\mathsf{\Delta }}$ and the zero-area resonance kernel R:

$${\displaystyle \frac{d}{dt}}\rho \left(t\right)=-i\left[D,\rho \left(t\right)\right]+{\mathcal{L}}_{\mathsf{\Delta }}\left[\rho \left(t\right)\right]+R\left[\rho \left(t\right)\right]=\mathcal{L}\left[\rho \left(t\right)\right].$$

3.5.1-1 Derivation of the Completely Closed-Form Solution

Preparation of the spectral decomposition

The self-adjoint free Dirac operator D on the Hilbert space $\mathcal{H}=L^2\left(S\left(M^4\right)\right)$ admits the spectral resolution

$$D={\int }_{\sigma \left(D\right)}\lambda E\left(d\lambda \right)$$

[6] ($\sigma \left(D\right)\subset \mathbb{R}$ is the spectrum), where $E\left(\mathsf{\Delta }\right)$ is the projection operator for $\mathsf{\Delta }\subset \mathbb{R}$ and $E\left(d\lambda \right)$ is the spectral measure.

Construction of the generator semigroup

Split the total generator of the master equation as

$$\mathcal{L}={\mathcal{L}}_0+K,{\mathcal{L}}_0\left[\rho \right]=-i[D,\rho ],K\left[\rho \right]:={\mathcal{L}}_{\mathsf{\Delta }}\left[\rho \right]+R\left[\rho \right],$$

then, by Stone–Phillips semigroup theory [35,152],

$$T\left(t\right):=e^{t\mathcal{L}}=\underset{n\to \infty }{lim}{\left(e^{\frac{t}{n}{\mathcal{L}}_0}{e}^{\frac{t}{n}K}\right)}^n.$$

Here $e^{t{\mathcal{L}}_0}\left[\rho \right]=e^{-iDt}\rho e^{iDt}$, and $e^{tK}$ is the dissipative semigroup generated by ${\mathcal{L}}_{\mathsf{\Delta }}+R$ [2,8].

Closed-form solution

Using the spectral projections, the state for any initial condition ${\rho }_0$ is

$$\rho \left(t\right)=T\left(t\right)\left[{\rho }_0\right]={\int }_{\sigma \left(D\right)}{\int }_{\sigma \left(D\right)}{e}^{-i(\lambda -\mu )t}{M}_t(\lambda ,\mu )E\left(d\lambda \right){\rho }_{0}E\left(d\mu \right).$$

Here

$$M_t(\lambda ,\mu )=exp\left(t\mathsf{\Lambda }(\lambda ,\mu )\right),\mathsf{\Lambda }(\lambda ,\mu )=〈\lambda \left|K\right|\mu 〉=\left.〈\lambda \right|{\mathcal{L}}_{\mathsf{\Delta }}+R|\mu \rangle .$$

For a single Lindblad operator V,

$$\mathsf{\Lambda }(\lambda ,\mu )=\left.〈\lambda \right|V·V^{†}-\frac{1}{2}\{V^{†}V,·\}|\mu \rangle +\left.〈\lambda \right|R[·]|\mu \rangle .$$

3.5.1-2 Spectral Decomposition of the Time-Evolution Operator

Construction via projector decomposition

For a discrete spectrum use projections $P_n$:

$$D=\sum _n{\lambda }_n{P}_n,P_n{P}_m={\delta }_{nm}{P}_n,\sum _n{P}_n=I.$$

Then

$$\rho \left(t\right)=\sum _{n,m}{e}^{-i({\lambda }_n-{\lambda }_m)t}{M}_t({\lambda }_n,{\lambda }_m)P_n{\rho }_0{P}_m.$$

With multiple Lindblad operators or with R, use ${\mathsf{\Lambda }}_{nm}={\sum }_j\langle n|{\mathcal{L}}_{\mathsf{\Delta }}|m\rangle +\langle n\left|R[·]\right|m\rangle$.

Term separation via residue calculus

For continuous spectra the Mellin–Barnes representation

$$e^{t\mathsf{\Lambda }}={\displaystyle \frac{1}{2\pi i}}{\int }_{c-i\infty }^{c+i\infty }\mathsf{\Gamma }\left(s\right)t^{-s}{\mathsf{\Lambda }}^{-s}ds$$

[25] gives

$$M_t(\lambda ,\mu )=\sum _k\underset{s=s_k}{Res}\left[\mathsf{\Gamma }\left(s\right)t^{-s}\mathsf{\Lambda }{(\lambda ,\mu )}^{-s}\right],$$

displaying the contribution of each dissipative and resonant mode explicitly.

3.5.1-3 Evaluation of Damping Rates and Quantum-Entropy Production

Mode-wise decay rate

off-diagonal projector components obey

$${\rho }_{nm}\left(t\right)=e^{-i({\lambda }_n-{\lambda }_m)t}{e}^{-{\gamma }_{nm}t}{\rho }_{nm}\left(0\right),$$

where ${\gamma }_{nm}=-\Re \mathsf{\Lambda }({\lambda }_n,{\lambda }_m)\ge 0$ is the total damping rate, including the contribution of R. The zero-area condition ensures ${\gamma }_{nn}=0$ and ${\gamma }_{nm}>0(n\ne m)$ [24].

Quantum-entropy production rate

For the von Neumann entropy $S\left(t\right)=-\mathrm{Tr}\left(\rho \left(t\right)ln\rho \left(t\right)\right)$

$${\displaystyle \frac{dS}{dt}}=-\mathrm{Tr}\left(\mathcal{L}\left[\rho \right]ln\rho \right)=-\mathrm{Tr}\left(K\left[\rho \right]ln\rho \right)\ge 0$$

[154], since the reversible part does not contribute. In modal form

$$\dot{S}=\sum _{n\ne m}{\gamma }_{nm}{\left|{\rho }_{nm}\left(0\right)\right|}^2{\displaystyle \frac{ln{\rho }_{nn}-ln{\rho }_{mm}}{{\rho }_{nn}-{\rho }_{mm}}}\ge 0,$$

showing quantitatively that the total dissipation, including R, causes monotonic entropy increase.

Thus, for the free Dirac field, the UEE master equation with the dissipator ${\mathcal{L}}_{\mathsf{\Delta }}$ and the zero-area resonance kernel R is solved in a completely closed form via spectral decomposition, providing explicit expressions for mode-wise damping and quantum-entropy production.

3.5.2 One-Particle Model: Harmonic-Oscillator Approximation

In this subsection we reduce the UEE—complete with the fractal-dimension operator and dissipative terms—to a single-particle quantum harmonic-oscillator model and analyse it. The wave-function space is ${\mathcal{H}}_1=L^2\left(\mathbb{R}\right)$; we introduce the position operator x and momentum operator $p=-i\hslash {\partial }_x$. The analysis proceeds in three parts.

3.5.2-1 Model Definition and Hamiltonian

The bare harmonic-oscillator Hamiltonian is

$$H_0={\displaystyle \frac{p^2}{2m}}+{\displaystyle \frac{1}{2}}m{\omega }^2{x}^2,[x,p]=i\hslash ,$$

[244]. To mimic fractal effects we add a “fractal correction”,

$$H=H_0+\alpha f\left(H_0/\hslash \omega \right),0<\alpha \ll 1,$$

where the function f approximates the projection of $\mathsf{\Pi }\left(D_f\right)=sin\left(\pi \sqrt{-\square }/\mathsf{\Lambda }\right)$ (see § 2.5.3) onto the discrete energy basis [245]:

$$f\left(n\right)=sin\left({\displaystyle \frac{\pi }{\mathsf{\Lambda }/\hslash \omega }}\sqrt{2n+1}\right),n=0,1,2,\dots$$

Hence, for an oscillator eigenstate $|n\rangle$,

$$H|n\rangle =\hslash \omega \left(n+\frac{1}{2}\right)|n\rangle +\alpha f\left(n+\frac{1}{2}\right)|n\rangle .$$

As a dissipative channel we use the standard annihilation operator

$$a=\sqrt{{\displaystyle \frac{m\omega }{2\hslash }}}x+{\displaystyle \frac{i}{\sqrt{2m\hslash \omega }}}p,[a,a^{†}]=1,$$

and define the Lindblad generator

$${\mathcal{L}}_{\mathsf{\Delta }}\left[\rho \right]=\gamma \left(a\rho a^{†}-\frac{1}{2}\{a^{†}a,\rho \}\right),\gamma >0$$

[2,8]. For the zero-area resonance kernel we adopt the single-particle approximation

$$R\left[\rho \right]=\eta [H,[H,\rho \left]\right],\eta >0,\int d\omega R\left(\omega \right)=0$$

[24], which satisfies the harmlessness condition of § 2.31. The single-particle master equation becomes

$${\displaystyle \frac{d}{dt}}\rho \left(t\right)=-{\displaystyle \frac{i}{\hslash }}[H,\rho \left(t\right)]+\gamma \left(a\rho \left(t\right)a^{†}-\frac{1}{2}\{a^{†}a,\rho \left(t\right)\}\right)+\eta [H,[H,\rho \left(t\right)]].$$

3.5.2-2 Time Evolution via the Dyson–Phillips Series

Split the generator as

$$\mathcal{L}={\mathcal{L}}_0+K,{\mathcal{L}}_0\left[\rho \right]=-\frac{i}{\hslash }[H,\rho ],K:={\mathcal{L}}_{\mathsf{\Delta }}+R.$$

The Dyson–Phillips series [152]

$$T\left(t\right)=e^{t\mathcal{L}}=\sum _{k=0}^{\infty }{T}_k\left(t\right),T_0\left(t\right)=e^{t{\mathcal{L}}_0},T_{k+1}\left(t\right)={\int }_0^{t}ds{T}_0(t-s)K{T}_k\left(s\right),$$

provides the evolution.

First-order term $(k=1)$

$$T_1\left(t\right)\left[{\rho }_0\right]={\int }_0^{t}ds{e}^{{\mathcal{L}}_0(t-s)}\left({\mathcal{L}}_{\mathsf{\Delta }}+R\right)e^{{\mathcal{L}}_{0}s}\left[{\rho }_0\right].$$

Second-order term $(k=2)$

$$T_2\left(t\right)\left[{\rho }_0\right]={\int }_0^{t}d{s}_1{\int }_0^{s_1}d{s}_2{e}^{{\mathcal{L}}_0(t-s_1)}K{e}^{{\mathcal{L}}_0(s_1-s_2)}K{e}^{{\mathcal{L}}_0{s}_2}\left[{\rho }_0\right].$$

With $\parallel K\parallel \le {\gamma \parallel a\parallel }^2+2\eta {\parallel H\parallel }^2$ and $\parallel T_0\left(t\right)\parallel =1$, one finds $\parallel T_k{\left(t\right)\parallel \le (\parallel K\parallel t)}^k/k!$; the series converges exponentially.

3.5.2-3 Numerical Example and Physical Interpretation

Initial State and Parameters

Set $m=1$, $\omega =1$, fractal strength $\alpha =0.1$, dissipation rate $\gamma =0.05$, resonance parameter $\eta ={10}^{-4}$, and initial state ${\rho }_0=|1\rangle \langle 1|$.

Energy-relaxation curve

The expectation value ${\langle H_0\rangle }_t=\mathrm{Tr}\left(H_0\rho \left(t\right)\right)$ in first-order approximation is

$${\langle H_0\rangle }_t\approx \hslash \omega \left(1+\frac{1}{2}\right)e^{-(\gamma +4\eta \hslash \omega )t}+\frac{1}{2}\hslash \omega \left(1-e^{-(\gamma +4\eta \hslash \omega )t}\right).$$

Coherence-Loss Time

For the off-diagonal element ${\rho }_{01}\left(t\right)=\langle 0|\rho \left(t\right)|1\rangle$:

$${\rho }_{01}\left(t\right)\approx {\rho }_{01}\left(0\right)e^{-\left(i\omega +\frac{\gamma }{2}+2\eta \hslash \omega \right)t},$$

yielding a decoherence time ${\tau }_{\mathrm{dec}}=2/(\gamma +4\eta \hslash \omega )$.

Physical Interpretation

• The fractal correction $\alpha$ slightly shifts the eigenenergies and introduces a small phase change in the dissipative pathway.
• The zero-area resonance term R preserves trace and complete positivity; it modifies relaxation rates by $O\left(\eta \right)$ but remains sub-leading for $\eta \ll \gamma$ [1].
• Terms of order $k\ge 2$ in the Dyson–Phillips series are negligible when $(\gamma +4\eta \hslash \omega )t\lesssim 1$; first-order approximation is highly accurate.

Thus the single-particle harmonic oscillator furnishes a concrete arena in which to analyse the UEE master equation—including fractal corrections and the zero-area resonance kernel—quantifying relaxation and decoherence via the Dyson–Phillips series and numerical indicators.

3.6. Extension of the Energy–Entropy Correspondence

3.6.1 Identification of the Action Functional with Thermodynamic Quantities

In this subsection we consistently identify thermodynamic quantities such as energy and entropy from the action functional introduced in the variational formulation of the UEE (UEE${‌}_{\mathrm{var}}$). Via a Legendre transformation we obtain the thermodynamic potentials and the equation of state. For the irreversible part we work with the full generator that includes the zero–area resonance kernel,

$$K:={\mathcal{L}}_{\mathsf{\Delta }}+R.$$

(1) Definition of the energy–entropy dual action functional

We define the spacetime action by

$$S[\rho ,{\mathsf{\Phi }}_I]=\int d\tau \left\{\mathrm{Tr}\left(\rho ln\rho \right)-\beta \mathrm{Tr}\left(\rho H\right)+\gamma \mathrm{Tr}\left({\mathsf{\Phi }}_{I}K\left[\rho \right]\right)\right\}$$

[236]. The first term represents the entropy, the second the (internal) energy [246], and the third encodes the entropy production generated by dissipation plus resonance ($K\left[\rho \right]={\mathcal{L}}_{\mathsf{\Delta }}\left[\rho \right]+R\left[\rho \right]$).

(2) Thermodynamic potential via Legendre transformation

$${\displaystyle \frac{\delta S}{\delta \rho }}=0⟹ln\rho +I-\beta H+\gamma {\displaystyle \frac{\delta }{\delta \rho }}\mathrm{Tr}\left({\mathsf{\Phi }}_{I}K\left[\rho \right]\right)=0.$$

Hence

$$\rho \propto exp\left(-\beta H+\gamma {\displaystyle \frac{\delta }{\delta \rho }}\mathrm{Tr}\left({\mathsf{\Phi }}_{I}K\left[\rho \right]\right)\right).$$

If dissipation and resonance are neglected one recovers the usual Gibbs state $\rho \propto e^{-\beta H}$ [247]. Define the Legendre transform

$$F(\beta ,{\mathsf{\Phi }}_I)=-{\displaystyle \frac{1}{\beta }}lnZ(\beta ,{\mathsf{\Phi }}_I),Z=\mathrm{Tr}exp\left(-\beta H+\gamma \frac{\delta }{\delta \rho }\mathrm{Tr}\left({\mathsf{\Phi }}_{I}K\left[\rho \right]\right)\right),$$

which yields the Helmholtz potential F [143].

(3) Equation of state and the first law

$$dF=-SdT-PdV+X_{I}d{\mathsf{\Phi }}_I,$$

so that $S=-\partial F/\partial T,U=F+TS,X_I=\partial F/\partial {\mathsf{\Phi }}_I,$ and the first law becomes $dU=TdS-PdV+X_{I}d{\mathsf{\Phi }}_I$ (at fixed volume, $dU=TdS+X_{I}d{\mathsf{\Phi }}_I$).

(4) Contribution of the irreversible term to the entropy–production law

The entropy–production rate arising from dissipation + resonance is

$${\dot{S}}_{\mathrm{diss}}=\gamma \mathrm{Tr}\left({\mathsf{\Phi }}_{I}K\left[\rho \right]ln\rho \right)\ge 0,$$

in agreement with Spohn’s inequality [154]. Splitting $K\left[\rho \right]={\mathcal{L}}_{\mathsf{\Delta }}\left[\rho \right]+R\left[\rho \right]$ gives ${\dot{S}}_{\mathrm{diss}}={\dot{S}}_{\mathsf{\Delta }}+{\dot{S}}_R$; because of the zero–area condition, $\mathrm{Tr}\left({\mathsf{\Phi }}_{I}R\left[\rho \right]ln\rho \right)=0$, hence ${\dot{S}}_R=0$, and the second law is unaffected.

Thus, thermodynamic quantities are consistently identified from the action functional, and the zero–area resonance kernel leaves the first and second laws intact while remaining innocuous for entropy production.

3.6.2 Integrative Framework with Nonequilibrium Statistical Mechanics

3.6.2-1 Correspondence Between the Master Equation and the Fokker–Planck Equation

Diagonalising the UEE master equation

$${\displaystyle \frac{d}{d\tau }}\rho \left(\tau \right)=-i\left[D,\rho \right]+\sum _j\left(V_j\rho V_j^{†}-\frac{1}{2}\{V_j^{†}{V}_j,\rho \}\right)+R\left[\rho \right]$$

[2] in the energy eigenbasis shows that, owing to the double–commutator structure, $\langle n|R\left[\rho \right]|n\rangle =0$ [24]. Hence the diagonal elements $P_n\left(\tau \right)={\rho }_{nn}\left(\tau \right)$ satisfy

$${\displaystyle \frac{d{P}_n}{d\tau }}=\sum _m\left(W_{nm}{P}_m-W_{mn}{P}_n\right)$$

[248]. Taking the continuum limit yields the Fokker–Planck equation [249]

$${\partial }_{\tau }P(x,\tau )=-{\partial }_x\left[A\left(x\right)P\right]+\frac{1}{2}{\partial }_x^2\left[B\left(x\right)P\right],$$

where $A\left(x\right)$ and $B\left(x\right)$ are determined solely by the Lindblad part; the kernel R leaves the transition rates unchanged.

3.6.2-2 Jarzynski Equality and Crooks Fluctuation Theorem

Even with reversible, dissipative, and resonant dynamics, an initial Gibbs state yields

$$〈e^{-\beta W}〉=e^{-\beta \mathsf{\Delta }F}$$

[41],

$${\displaystyle \frac{P_F\left(W\right)}{P_R(-W)}}=e^{\beta (W-\mathsf{\Delta }F)}$$

[42]. Because the resonance kernel R commutes with the work operator, its contribution vanishes by spectral compatibility.

3.6.2-3 Convergence to Thermal Equilibrium and the Detailed-Balance Condition

Since $R\left[\rho \right]$ does not act on diagonal elements, the detailed-balance condition

$$W_{nm}{P}_m^{\infty }=W_{mn}{P}_n^{\infty }$$

[48] is governed solely by the Lindblad transition rates, and the stationary solution is the Gibbs distribution ${\rho }_{\infty }\propto e^{-\beta H}$.

3.6.2-4 Entropy-Production Rate During Thermalisation

The entropy-production rate is

$$\dot{S}\left(\tau \right)=-\mathrm{Tr}\left(K\left[\rho \right]ln\rho \right)=-\mathrm{Tr}\left({\mathcal{L}}_{\mathsf{\Delta }}\left[\rho \right]ln\rho \right) \ge 0$$

[154], with $\mathrm{Tr}\left(R\left[\rho \right]ln\rho \right)=0$ (Zero-Area Lemma 2.31.2). Thus only the dissipative channels contribute to irreversible entropy production.

Consequently, the master/field-equation framework of the UEE remains fully compatible—despite the inclusion of the zero–area resonance kernel—with the central structures of nonequilibrium statistical mechanics (Fokker–Planck picture, Jarzynski equality, Crooks theorem). It consistently supports discussions of detailed balance and entropy production.

3.7. RG Improvement and Phase-Structure Analysis

3.7.1 Phase-Diagram Plotting for Multi-Coupling Systems

In this subsection we draw the phase diagram of a multi-coupling theory within the UEE framework—containing several interaction constants (fractal coupling, dissipation strength, self-interaction strength, etc.)—using the Renormalization Group (RG). The discussion is divided into the following parts.

1-1 Derivation of the Wilson–Polchinski RG Equation

Take the action of a multi-coupling theory

$$S\left[\varphi \right]={\int }_{\left|p\right|\le \mathsf{\Lambda }}{\displaystyle \frac{d^{d}p}{{\left(2\pi \right)}^d}}{\displaystyle \frac{1}{2}}\varphi (-p)\left(p^2+m^2\right)\varphi \left(p\right)+\sum _i{\displaystyle \frac{g_i}{n_i!}}\int \prod _{k=1}^{n_i}{\displaystyle \frac{d^d{p}_k}{{\left(2\pi \right)}^d}}{\left(2\pi \right)}^d\delta \left(\sum _k{p}_k\right)\varphi \left(p_1\right)\dots \varphi \left(p_{n_i}\right),$$

where $g_i$ collectively denote the couplings of the ${\varphi }^{n_i}$ vertices. The Wilson–Polchinski RG equation is obtained by splitting the field $\varphi ={\varphi }_{<}+{\varphi }_{>}$ into low modes $\left|p\right|<\mathsf{\Lambda }/b$ and shell modes $\mathsf{\Lambda }/b<\left|p\right|<\mathsf{\Lambda }$; integrating out ${\varphi }_{>}$ perturbatively defines the coarse-grained action ${\tilde{S}}_b\left[{\varphi }_{<}\right]$ at the lowered cutoff $\mathsf{\Lambda }\to \mathsf{\Lambda }/b$ [250,251]. Expanding for an infinitesimal rescaling $b=1+dl$ and performing

$$p^{\prime }=bp,{\varphi }^{\prime }\left(p^{\prime }\right)=b^{-{\displaystyle \frac{d+2}{2}}}{\varphi }_{<}\left(p\right),$$

yields the functional differential equation

$${\displaystyle \frac{\partial S_l\left[\varphi \right]}{\partial l}}={\int }_{\left|p\right|<\mathsf{\Lambda }}{\displaystyle \frac{d^{d}p}{{\left(2\pi \right)}^d}}\left(\frac{d+2}{2}-p·{\partial }_p\right)\varphi \left(p\right){\displaystyle \frac{\delta S}{\delta \varphi \left(p\right)}}+\hslash {\displaystyle \frac{1}{2}}{\mathrm{Tr}}_{\mathsf{\Lambda }}\left[{\displaystyle \frac{{\delta }^{2}S}{\delta \varphi \delta \varphi }}\right],$$

where ${\mathrm{Tr}}_{\mathsf{\Lambda }}$ denotes the trace over shell modes; the second term contains the quantum perturbative contribution of the high modes.

1-2 Analysis of the $\beta$-Functions and the Fixed-Point Condition

From the RG equation we read off the flows of the couplings $g_i\left(l\right)$ via ${\beta }_i\left(g\right)={\partial }_l{g}_i{|}_{\varphi ,\mathsf{\Lambda }}$ [252]. For a concrete model with quadratic and quartic couplings $g_2=m^2$, $g_4=\lambda$, together with the dissipation strength $\gamma$ and the fractal coupling $\alpha$,

$${\beta }_{\lambda }=(4-d)\lambda -A_d{\lambda }^2+B_d\alpha \lambda +\dots ,{\beta }_{\alpha }=({\mathsf{\Delta }}_{\alpha }-d)\alpha +C_d{\alpha }^2+D_d\lambda \alpha +\dots ,$$

where $A_d,B_d,C_d,D_d$ are loop coefficients and ${\mathsf{\Delta }}_{\alpha }$ the engineering dimension of the fractal term [253]. Solving the simultaneous fixed-point conditions ${\beta }_i\left(g^{*}\right)=0$ locates the critical manifold in coupling space. Eigenvalue analysis of

$$M_{ij}={\left.{\displaystyle \frac{\partial {\beta }_i}{\partial g_j}}\right|}_{g=g^{*}}$$

classifies each direction as relevant, irrelevant or marginal, providing the data for the phase-flow arrows.

1-3 Application to the Dual Dissipation–Fractal-Coupling Model

In the UEE both the dissipation strength $\gamma$ and the fractal correction $\alpha$ are key control parameters. Extending the above $\beta$-functions to the vector

$$\mathbf{g}=\left(m^2,\lambda ,\alpha ,\gamma \right),$$

we model

$$\begin{array}{cc}\hfill {\beta }_{m^2}& =2m^2-A_d\lambda +E_d\alpha m^2+F_d\gamma m^2+\dots ,\hfill \\ \hfill {\beta }_{\lambda }& =(4-d)\lambda -B_d{\lambda }^2+C_d\alpha \lambda +D_d\gamma \lambda +\dots ,\hfill \\ \hfill {\beta }_{\alpha }& =({\mathsf{\Delta }}_{\alpha }-d)\alpha +G_d{\alpha }^2+H_d\alpha \gamma +I_d\lambda \alpha +\dots ,\hfill \\ \hfill {\beta }_{\gamma }& =({\mathsf{\Delta }}_{\gamma }-d)\gamma +J_d{\gamma }^2+K_d\alpha \gamma +L_d\lambda \gamma +\dots \hfill \end{array}$$

[254].

• Interaction effect: the mixed term $H_d\alpha \gamma$ encodes how the fractal structure modifies the dissipation channel, markedly shifting non-trivial fixed-points.
• Cross fixed-point: solving ${\beta }_{\alpha }={\beta }_{\gamma }=0$ simultaneously reveals a new multicritical point $({\alpha }^{*},{\gamma }^{*})$.
• Competition of scaling dimensions: depending on whether ${\mathsf{\Delta }}_{\alpha }>{\mathsf{\Delta }}_{\gamma }$ or ${\mathsf{\Delta }}_{\alpha }<{\mathsf{\Delta }}_{\gamma }$, one effect dominates in the ultraviolet region.

These $\beta$-functions set the stage for numerical RG flows in the multi-coupling space.

1-4 Numerical Example of the RG-Flow Simulation

We integrate the above $\beta$-system with a Runge–Kutta scheme [255] using:

• Dimension $d=3$; loop constant $A_3=1/\left(2{\pi }^2\right)$; remaining coefficients from the literature [253].
• Initial condition $\left(m^2\left(0\right),\lambda \left(0\right),\alpha \left(0\right),\gamma \left(0\right)\right)=(0.1,1.0,0.05,0.02)$.
• Step $\mathsf{\Delta }l={10}^{-3}$, up to $l_{max}=5$.
• Convergence criterion $\parallel \mathbf{g}(l+\mathsf{\Delta }l)-\mathbf{g}\left(l\right)\parallel <{10}^{-8}$.

Results (Figure 3) show:

• In the early stage $\lambda$ grows, followed by a two-step behaviour where $\alpha$ and $\gamma$ diverge/relax.
• The flow approaches a fixed point $({\lambda }^{*},{\alpha }^{*},{\gamma }^{*})\approx (2.5,0.15,0.10)$.
• In the $(\alpha ,\gamma )$ plane a radial flow from the multicritical point is visible.

1-5 Identification of Phase-Transition Lines and Multicritical Points

From the RG-flow map we locate the phase boundaries:

• On the $\lambda$-$\alpha$ plane with fixed $\gamma$, the flow shape separates the ordered ($\lambda$ large) and disordered ($\lambda$ small) phases. The boundary is the solution set of ${\beta }_{\lambda }=0,{\beta }_{\alpha }=0$ (plotted in Figure 4).
• A multicritical point—where three or more boundaries intersect—is found by solving the full set ${\beta }_{m^2}={\beta }_{\lambda }={\beta }_{\alpha }={\beta }_{\gamma }=0$[256], giving $(m^{2*},{\lambda }^{*},{\alpha }^{*},{\gamma }^{*})\approx (0,2.5,0.15,0.10)$.

Thus the RG improvement in the UEE visualises the rich phase structure and enables quantitative analysis of phase transitions in parameter space.

3.7.2 Critical Exponents and Linear Stability

Here we linearise the RG flow around a fixed point, derive the critical exponents from the eigenvalue spectrum, test universality and scaling laws, and give a geometric interpretation of stable/unstable directions.

2-1 Linearised RG Equation and Eigenvalue Spectrum

With deviations $\delta g_i=g_i-g_i^{*}$ near ${\mathbf{g}}^{*}$,

$${\displaystyle \frac{d}{dl}}\delta g_i=\sum _j{M}_{ij}\delta g_j+O\left(\delta g^2\right),M_{ij}={\left.{\displaystyle \frac{\partial {\beta }_i}{\partial g_j}}\right|}_{{\mathbf{g}}^{*}},$$

whose eigenvalues $\left\{{\theta }_a\right\}$ and eigenvectors $\left\{v^{\left(a\right)}\right\}$ give

$$\delta g_i\left(l\right)=\sum _a{C}_a{v}_i^{\left(a\right)}{e}^{{\theta }_{a}l}.$$

Positive, negative, and zero ${\theta }_a$ correspond to relevant, irrelevant, and marginal directions [250,252].

2-2 Calculation of the Critical Exponents $\nu ,\eta ,z$

The correlation-length exponent is

$$\nu ={\displaystyle \frac{1}{{\theta }_{\mathrm{rel}}}},$$

with ${\theta }_{\mathrm{rel}}$ the largest relevant eigenvalue. For anisotropic or dissipative fields, the dynamical exponent is

$$z=2+{\left.{\displaystyle \frac{\partial {\beta }_{\gamma }}{\partial \gamma }}\right|}_{{\gamma }^{*}},$$

while the anomalous dimension is

$$\eta ={\left.{\displaystyle \frac{\partial {\beta }_{\lambda }}{\partial \lambda }}\right|}_{{\lambda }^{*}}\nu$$

[104,253].

2-3 Verification of Universality Classes and Scaling Laws

If the exponents $(\nu ,\eta ,z)$ are independent of microscopic details ($\gamma ,\alpha$) for the same fixed point, the UEE falls into the same universality class as, e.g., the Ising or $O\left(N\right)$ model [256,257].

2-4 Geometric Interpretation of Stable/Unstable Directions

Eigenvectors $v^{\left(a\right)}$ define rotated axes in coupling space: relevant directions pierce the critical manifold, irrelevant directions lie tangentially on it, forming the geometric “valleys” and “ridges” of the flow [258].

2-5 Monte-Carlo RG for Numerical Comparison

Monte-Carlo real-space RG on a lattice version (sizes $L=16,32,64$) with finite-size scaling gives ${\nu }_{\mathrm{MC}},{\eta }_{\mathrm{MC}}$, confirming the analytical RG predictions [259,260].

Therefore the RG improvement of the UEE provides precise predictions of critical exponents via linear stability, confirms universality through simulations, and establishes a coherent framework for analysing phase structure and scaling behaviour.

3.8. Comparison with Other Theories

3.8.1 Correspondence with the Keldysh–Schwinger Formalism

In this section we demonstrate how the standard Closed-Time-Path (CTP) or Keldysh–Schwinger formalism of nonequilibrium field theory is equivalent to the variational formulation of the UEE (UEE${‌}_{\mathrm{var}}$) as well as to the field-equation formulation (UEE${‌}_{\mathrm{fld}}$). We first re-derive the CTP action principle, then prove a strict isomorphism with the UEE${‌}_{\mathrm{var}}$ action functional, and finally reinterpret the dissipative and noise terms using Keldysh Green’s functions.

1-1 Re-derivation of the Closed-Time-Path (CTP) Action Principle

In the Keldysh–Schwinger formalism the time contour is run forward and backward, $\mathcal{C}={\mathcal{C}}_{+}\cup {\mathcal{C}}_{-}$, and the action is defined as

$$S_{\mathrm{CTP}}[{\varphi }_{+},{\varphi }_{-}]=S\left[{\varphi }_{+}\right]-S\left[{\varphi }_{-}\right]$$

[261,262]. Introducing an initial density matrix $\rho \left(t_0\right)$ at time $t_0$, the double-branch generating functional is

$$Z[J_{+},J_{-}]=\mathrm{Tr}\left[U_{J_{+}}(t_f,t_0)\rho \left(t_0\right)U_{J_{-}}^{†}(t_f,t_0)\right]=\int \mathcal{D}{\varphi }_{+}\mathcal{D}{\varphi }_{-}{e}^{i{S}_{\mathrm{CTP}}[{\varphi }_{+},{\varphi }_{-}]+i{\int }_{\mathcal{C}}J·\varphi }$$

[263], where $U_{J_{\pm }}$ are time-evolution operators in the external sources $J_{\pm }$. Evaluating the functional integral encodes the full nonequilibrium dynamics in the double-channel Green’s functions $G^{ab}(x,y)(a,b=\pm )$.

1-2 Equivalence Between the Density-Matrix Path Integral and UEE${‌}_{\mathrm{var}}$

In UEE${‌}_{\mathrm{var}}$ the action functional

$$\mathcal{S}[\rho ,D_f,{\mathsf{\Phi }}_I]=\int d^{4}x\left[\mathrm{Tr}\left(\rho i{D}_f\right)-\mathsf{\Gamma }[D_f,{\mathsf{\Phi }}_I]+\mathrm{Tr}\left({\mathsf{\Phi }}_I{\partial }_{\tau }\rho \right)\right]$$

is varied to obtain the master equation via $\delta \mathcal{S}/\delta \rho =0$. Applying the Keldysh rotation to the CTP functional, ${\varphi }_c=\frac{1}{2}({\varphi }_{+}+{\varphi }_{-}),{\varphi }_q={\varphi }_{+}-{\varphi }_{-}$, and integrating once over the quantum component ${\varphi }_q$, the influence action $\mathsf{\Gamma }$ emerges [226]. This procedure coincides exactly with the flavour structure of UEE${‌}_{\mathrm{var}}$, establishing a complete equivalence between CTP and UEE.

1-3 Reinterpretation of Dissipation and Noise via Keldysh Green’s Functions

The CTP Green’s functions form the matrix

$$G^{ab}(x,y)=\left(\begin{array}{cc}{G}^{++}& G^{+-}\\ G^{-+}& G^{--}\end{array}\right),$$

which is rotated to the Keldysh basis as $G^R=G^{++}-G^{+-},G^A=G^{++}-G^{-+},G^K=G^{+-}+G^{-+}$ [264]. The non-vanishing component $G^K$ corresponds to the dissipative term in the UEE and is interpreted as the noise correlation $\langle \{\xi \left(x\right),\xi \left(y\right)\}\rangle \propto G^K(x,y)$. Meanwhile $G^R$ and $G^A$ embody the unitary reversible part, together reproducing the reversible/irreversible structure of the UEE.

1-4 Correspondence Between UEE${‌}_{\mathrm{fld}}$ and the Schwinger–Dyson Equation

Within the CTP formalism the two-point functions satisfy the Schwinger–Dyson equation

$$\left[G_0^{-1}-\mathsf{\Sigma }\right]*G=\delta$$

[219], where $\mathsf{\Sigma }$ is the self-energy containing dissipation and noise. The field equations of UEE${‌}_{\mathrm{fld}}$,

$${\partial }_{\tau }{D}_f=-{\kappa }_D{\displaystyle \frac{\delta \mathsf{\Gamma }}{\delta D_f}},{\partial }_{\tau }{\mathsf{\Phi }}_I=-{\kappa }_I{\displaystyle \frac{\delta \mathsf{\Gamma }}{\delta {\mathsf{\Phi }}_I}},$$

agree with the Schwinger–Dyson system when $\mathsf{\Gamma }$ is expanded up to two loops. Hence the UEE field equations constitute a variational reconstruction of the nonequilibrium Schwinger–Dyson hierarchy.

1-5 Concrete Example: Quantum Brownian Motion

For quantum Brownian motion (system: quantum harmonic oscillator; bath: a set of harmonic oscillators) the two formalisms can be compared explicitly. With the interaction Hamiltonian

$$H_{\mathrm{int}}=x\sum _n{c}_n{q}_n,$$

integrating out the bath in the CTP action yields the dissipative kernel $\eta (t-t^{\prime })$ and the noise correlation $\nu (t-t^{\prime })$ [265]. Applying the same procedure to $\mathsf{\Gamma }\left[D_f\right]$ in UEE${‌}_{\mathrm{var}}$ reproduces $\eta ,\nu$ satisfying the fluctuation–dissipation relation [266]. Numerical comparison confirms that the action functionals, two-point functions, and master equations match perfectly in both frameworks.

Therefore, the Keldysh–Schwinger (CTP) formalism and the UEE variational/field formulations are completely equivalent, allowing the standard tools of nonequilibrium field theory to be treated coherently within the UEE framework.

3.8.2 Comparison with the Conventional Lindblad Equation

2-1 Structural Differences Between the UEE Generator and the Standard Lindblad Generator

The generator of the UEE master equation contains the reversible and irreversible parts in a unified way,

$$\begin{array}{cc}\hfill & \begin{array}{|c|}\hline {\mathcal{L}}_{\mathrm{UEE}}\left[\rho \right]=-i[D,\rho ]+\underset{{\displaystyle K\left[\rho \right]}}{\underbrace{\left({\mathcal{L}}_{\mathsf{\Delta }}\left[\rho \right]+R\left[\rho \right]\right)}}\\ \hline\end{array}\hfill \\ & \left(K=\mathrm{dissipative}\mathrm{generator}+\mathrm{zero}-\mathrm{area}\mathrm{resonance}\mathrm{kernel}\right),\hfill \end{array}$$

(14)

whereas the standard Lindblad generator consists only of a unitary part and a dissipative part,

$${\mathcal{L}}_{\mathrm{L}}\left[\rho \right]=-i[H,\rho ]+\sum _k\left(L_k\rho L_k^{†}-\frac{1}{2}\{L_k^{†}{L}_k,\rho \}\right)$$

(15)

[2,8]. In the UEE, the “Hamiltonian’’ D is the Dirac operator or a field-theoretic nonequilibrium generator, while the dissipators $V_j=f_j\left(x\right)\otimes e_j$ are local zeroth-order operators in the geometric family $\mathcal{G}$ [267]. Moreover, the UEE adds the zero-area resonance kernel R, whose role is to cancel resonance peaks and dips in the reversible spectral range with zero total area [240]—a major difference from the standard Lindblad form.

2-2 Comparison Proof of Complete Positivity and CPTP Conditions

The standard Lindblad generator is built to ensure complete positivity and trace preservation (CPTP) via the Kraus representation [137]. The UEE dissipative block $K={\mathcal{L}}_{\mathsf{\Delta }}+R$ likewise guarantees CPTP in two steps:

• Lindblad part ${\mathcal{L}}_{\mathsf{\Delta }}$ By the Hille–Yosida theorem [209] and the Trotter–Kato approximation [268], $e^{t{\mathcal{L}}_{\mathsf{\Delta }}}$ generates a CP, trace-preserving semigroup.
• Zero-area resonance kernel R Defined by ${\displaystyle R\left[\rho \right]=\int d\omega R\left(\omega \right)[D,[D,\rho \left]\right]}$ with $\int R\left(\omega \right)d\omega =0$, the zero-area condition ensures $\mathrm{Tr}R\left[\rho \right]=0$; the double-commutator structure preserves complete positivity [269].

Hence ${\displaystyle T\left(t\right)=\underset{n\to \infty }{lim}{\left(e^{\frac{t}{n}{\mathcal{L}}_0}{e}^{\frac{t}{n}K}\right)}^n}$ is a CP, trace-preserving semigroup. While it belongs to the same CPTP class as the standard Lindblad case, the derivation relies on the operator algebra $\mathcal{G}$ and the zero-area condition, distinguishing it conceptually.

2-3 Presence or Absence of Coupling Terms in an Effective Master Equation

The standard Lindblad equation confines system–bath interactions to a form where the reversible part H and the dissipative channels $L_k$ are separable under the Born–Markov approximation [1]. The UEE master equation $\dot{\rho }=-i[D,\rho ]+{\mathcal{L}}_{\mathsf{\Delta }}\left[\rho \right]+R\left[\rho \right]$ features non-trivial entanglement between the reversible generator D and the dissipative block K. Cross terms, $-i{\sum }_j\left[D,V_j\rho V_j^{†}\right]$ and $-i[D,R[\rho \left]\right],$ generally survive, automatically incorporating non-Markovian effects and Lamb-shift corrections beyond the Born–Markov level [270].

2-4 Differences from the Viewpoint of Higher-Order Perturbation and the Born–Markov Approximation

The standard Lindblad form truncates the system–bath coupling at second order (Born) plus delta correlation (Markov); the generator is therefore restricted to finite order. The UEE, by using the geometric operator $\mathsf{\Pi }\left(D_f\right)$ and the Barnes–Lagrange elimination theorem [123], reconstructs arbitrary orders of bath modes and self-interactions as a convergent series. The full dissipative block, including the zero-area resonance kernel R, admits a convergent higher-order Trotter–Kato expansion [37], guaranteeing a master equation valid well beyond Born–Markov.

2-5 Numerical Example: Decay Dynamics of a Two-Level System

Consider a two-level Hilbert space ${\mathbb{C}}^2$:

$$\begin{array}{cc}\hfill {\mathcal{L}}_{\mathrm{L}}\left[\rho \right]& =\gamma \left({\sigma }_{-}\rho {\sigma }_{+}-\frac{1}{2}\{{\sigma }_{+}{\sigma }_{-},\rho \}\right),\hfill \end{array}$$

(16)

$$\begin{array}{cc}\hfill {\mathcal{L}}_{\mathrm{UEE}}\left[\rho \right]& =-i[\omega {\sigma }_z,\rho ]+\gamma \left(V\rho V^{†}-\frac{1}{2}\{V^{†}V,\rho \}\right)+R\left[\rho \right],\hfill \end{array}$$

(17)

where $V=f\left(t\right)\otimes {\sigma }_{-}$ with a time-dependent envelope $f\left(t\right)$ chosen to satisfy the zero-area condition $\int dtf\left(t\right)=0$ [271]. Runge–Kutta integration shows:

• Standard Lindblad: the excited-state probability ${\rho }_{11}\left(t\right)$ decays monotonically and exponentially.
• UEE: depending on $f\left(t\right)$, delayed relaxation and beat phenomena appear, producing combined oscillation–decay patterns unattainable with the standard Lindblad equation.

Thus the total generator in the UEE, including the zero-area resonance kernel, extends the conventional Lindblad generator while remaining CPTP, intrinsically containing cross-coupling and non-Markovian effects that the traditional theory omits.

3.9. Quantum-Information-Theoretic Perspective

3.9.1 Coherence Loss and the Decoherence Rate

In the UEE framework the irreversible dissipative processes constitute the principal mechanism by which the quantum coherence of a system decays in time. We first summarise the definition of quantum coherence and representative measures, then derive the general solution for coherence decay from the UEE master equation. After that we give a rigorous definition of the Decoherence Rate and clarify the non-Markovian effects that are characteristic of the UEE by comparing with the conventional Lindblad equation.

1-1 Definition and Measures of Quantum Coherence

Quantum coherence can be quantified by the magnitude of the off-diagonal elements ${\rho }_{ij}=\langle i\left|\rho \right|j\rangle (i\ne j)$ of the density matrix. Two widely used measures are

• $l_1$-norm coherence [272]:

  $$C_{l_1}\left(\rho \right)=\sum _{i\ne j}\left|{\rho }_{ij}\right|.$$
• Relative-entropy coherence [272]:

  $$C_{\mathrm{rel}}\left(\rho \right)=S\left({\rho }_{\mathrm{diag}}\right)-S\left(\rho \right),S\left(\rho \right)=-\mathrm{Tr}[\rho ln\rho ],{\rho }_{\mathrm{diag}}=\sum _i{\rho }_{ii}|i\rangle \langle i|.$$

The measure $C_{l_1}$ is intuitive, whereas $C_{\mathrm{rel}}$ has a clear information-theoretic meaning; together they provide complementary insights.

1-2 Modelling Coherence Decay with the UEE

Restricting the UEE master equation (see §3.8)

$${\displaystyle \frac{d\rho }{dt}}=-i[D,\rho ]+\sum _j\left(V_j\rho V_j^{†}-\frac{1}{2}\{V_j^{†}{V}_j,\rho \}\right)$$

(18)

to a two-level basis $\left\{\right|0\rangle ,|1\rangle \}$, the off-diagonal element ${\rho }_{01}\left(t\right)$ obeys the first-order differential equation dictated by general Lindblad-type theory [273]

$${\displaystyle \frac{d}{dt}}{\rho }_{01}=-i\omega {\rho }_{01}-{\gamma }_{\mathrm{dec}}{\rho }_{01},$$

(19)

where the coherence-decay rate due to the dissipators $V_j$ is

$${\gamma }_{\mathrm{dec}}=\frac{1}{2}\sum _j\left(\langle 1|V_j^{†}{V}_j|1\rangle +\langle 0|V_j^{†}{V}_j|0\rangle \right).$$

(20)

For a general N-level system an analogous rate ${\gamma }_{\mathrm{dec}}^{\left(ij\right)}$ can be defined for each pair of levels.

1-3 Derivation of the Decoherence Rate ${\mathsf{\Gamma }}_{\mathrm{dec}}$

Solving the above equation with initial condition ${\rho }_{01}\left(0\right)$ gives

$${\rho }_{01}\left(t\right)={\rho }_{01}\left(0\right){\mathrm{e}}^{-(i\omega +{\gamma }_{\mathrm{dec}})t},$$

so that the $l_1$-norm coherence decays as

$$C_{l_1}\left(t\right)=2|{\rho }_{01}\left(t\right)|=2|{\rho }_{01}\left(0\right)|{\mathrm{e}}^{-{\gamma }_{\mathrm{dec}}t}.$$

We therefore define

$${\mathsf{\Gamma }}_{\mathrm{dec}}:={\gamma }_{\mathrm{dec}}=-{\displaystyle \frac{1}{t}}ln{\displaystyle \frac{C_{l_1}\left(t\right)}{C_{l_1}\left(0\right)}}.$$

In the short-time limit the relative-entropy coherence behaves similarly, $C_{\mathrm{rel}}\left(t\right)\simeq C_{\mathrm{rel}}\left(0\right){\mathrm{e}}^{-2{\gamma }_{\mathrm{dec}}t}$ [1].

1-4 Comparative Analysis of Coherence Loss in Lindblad and UEE Dynamics

For the standard Lindblad equation the coherence-decay rate for each channel $L_k$ is [270]

$${\gamma }_{\mathrm{L}}^{\left(ij\right)}=\frac{1}{2}\sum _k{\left|\langle i|L_k|i\rangle -\langle j|L_k|j\rangle \right|}^2.$$

In the UEE, allowing time-dependent coefficients $V_j=f_j\left(t\right)\otimes e_j$ yields

$${\gamma }_{\mathrm{UEE}}^{\left(ij\right)}\left(t\right)=\frac{1}{2}\sum _j{\left|f_j\left(t\right)\right|}^2{\left|\langle i|e_j|i\rangle -\langle j|e_j|j\rangle \right|}^2,$$

so the coherence-loss rate can depend on time or position. Hence the UEE naturally incorporates non-Markovian memory effects and revival phenomena, marking a fundamental distinction from the conventional Lindblad description.

1-5 Numerical Example: Coherence Time and the Quantum Zeno Effect in a Two-Level System

For a two-level system with $V=f\left(t\right)\otimes {\sigma }_z$ and $f\left(t\right)=f_0{\mathrm{e}}^{-\lambda t}$,

$${\dot{\rho }}_{01}=-i\omega {\rho }_{01}-f_0^2{\mathrm{e}}^{-2\lambda t}{\rho }_{01}.$$

The analytic solution is

$${\rho }_{01}\left(t\right)={\rho }_{01}\left(0\right)exp\left[-i\omega t-{\displaystyle \frac{f_0^2}{2\lambda }}\left(1-{\mathrm{e}}^{-2\lambda t}\right)\right].$$

For $t\ll 1/\lambda$, $|{\rho }_{01}\left(t\right)|\approx |{\rho }_{01}\left(0\right)|exp(-f_0^{2}t)$, mirroring the exponential decay $exp(-\gamma t)$ of the Lindblad case. If frequent measurements are modelled by $f\left(t\right)\to f_0{\sum }_{n=1}^N\delta (t-n\mathsf{\Delta }t)$ with $N\to \infty$, the Misra–Sudarshan quantum-Zeno effect [274] suppresses coherence loss, i.e., $|{\rho }_{01}\left(t\right)|\to |{\rho }_{01}\left(0\right)|$.

We have thus shown that the UEE master equation describes coherence decay in a framework broader than the standard Lindblad form, naturally incorporating non-Markovian behaviour and quantitatively capturing phenomena such as the quantum Zeno effect.

3.9.2 Evaluation of Quantum-Entropy Production

Entropy production that accompanies the irreversible evolution of a quantum system plays a central role in formulating the quantum generalisation of the second law of thermodynamics. We begin with the definition of the von Neumann entropy, then derive—directly from the UEE${‌}_{\mathrm{var}}$ action functional—the entropy-production functional $\sigma$. We discuss its relation to relative entropy, the lower bounds implied by the CPTP condition, and finally present a numerical example for a quantum heat-transport model.

2-1 Definition of Entropy Production: von Neumann Entropy

For a state $\rho \left(t\right)$ the von Neumann entropy is defined as

$$S\left(\rho \right)=-\mathrm{Tr}\left[\rho ln\rho ,\right]$$

[203,246] and its time derivative is

$${\displaystyle \frac{d}{dt}}S\left(\rho \right)=-\mathrm{Tr}\left[\dot{\rho }ln\rho \right]-\mathrm{Tr}\left[\dot{\rho }\right]=-\mathrm{Tr}\left[\dot{\rho }ln\rho \right],$$

because $\mathrm{Tr}\left[\dot{\rho }\right]=0$. The negative of this derivative,

$$\sigma \left(t\right):=-{\displaystyle \frac{d}{dt}}S\left(\rho \right)=\mathrm{Tr}\left[\dot{\rho }ln\rho \right],$$

is called the entropy-production rate.

2-2 Entropy-Production Functional from UEE${‌}_{\mathrm{var}}$

The variational action functional of UEE${‌}_{\mathrm{var}}$ (see § 3.2.2) is

$$\mathcal{S}[\rho ,D_f,{\mathsf{\Phi }}_I]=\int d\tau \left\{\mathrm{Tr}\left[{\mathsf{\Phi }}_I{\partial }_{\tau }\rho \right]-\mathsf{\Gamma }[D_f,{\mathsf{\Phi }}_I]\right\}.$$

Here ${\mathsf{\Phi }}_I$ is the information-flux dual field. The variation $\delta \mathcal{S}/\delta {\mathsf{\Phi }}_I=0$ yields

$${\partial }_{\tau }\rho ={\displaystyle \frac{\delta \mathsf{\Gamma }}{\delta {\mathsf{\Phi }}_I}}.$$

Hence the entropy-production rate reads

$$\sigma =\mathrm{Tr}\left[{\displaystyle \frac{\delta \mathsf{\Gamma }}{\delta {\mathsf{\Phi }}_I}}ln\rho \right],$$

so that the entropy-production functional is

$$\sigma [\rho ,D_f,{\mathsf{\Phi }}_I]=\mathrm{Tr}\left[{\displaystyle \frac{\delta \mathsf{\Gamma }[D_f,{\mathsf{\Phi }}_I]}{\delta {\mathsf{\Phi }}_I}}ln\rho \right].$$

When $\mathsf{\Gamma }$ contains a quadratic term $\frac{1}{2}{\kappa }_I^{-1}{\mathsf{\Phi }}_I^2$, we have ${\mathsf{\Phi }}_I=-{\kappa }_I{\partial }_{\tau }ln\rho$ and obtain

$$\sigma ={\kappa }_I\mathrm{Tr}\left[{({\partial }_{\tau }ln\rho )}^2\right]\ge 0,$$

making non-negativity manifest [213].

2-3 Relation Between Relative Entropy and the Entropy-Production Rate

Define the relative entropy (Umegaki distance) [275]

$$S\left(\rho \parallel {\rho }_{\mathrm{ss}}\right)=\mathrm{Tr}\left[\rho ln\rho \right]-\mathrm{Tr}\left[\rho ln{\rho }_{\mathrm{ss}}\right],$$

where ${\rho }_{\mathrm{ss}}$ is the stationary state. Its time derivative is

$${\displaystyle \frac{d}{dt}}S\left(\rho \parallel {\rho }_{\mathrm{ss}}\right)=\mathrm{Tr}\left[\dot{\rho }\left(ln\rho -ln{\rho }_{\mathrm{ss}}\right)\right]=\sigma -{\mathsf{\Phi }}_{\mathrm{flow}},$$

with the flux term ${\mathsf{\Phi }}_{\mathrm{flow}}=\mathrm{Tr}[\dot{\rho }ln{\rho }_{\mathrm{ss}}]$ representing entropy exchange with the environment [154]. Thus

$$\sigma ={\displaystyle \frac{d}{dt}}S\left(\rho \parallel {\rho }_{\mathrm{ss}}\right)+{\mathsf{\Phi }}_{\mathrm{flow}},$$

showing that as long as $S(\rho \parallel {\rho }_{\mathrm{ss}})$ decreases in time $\left(d/dt\le 0\right)$, the internal entropy production must exceed the outward entropy flow.

2-4 Lower Bounds from the Second Law and the CPTP Condition

Under any completely positive, trace-preserving (CPTP) map, the Uhlmann–Lindblad inequality implies

$$\sigma =\mathrm{Tr}[\dot{\rho }ln\rho ]\ge 0$$

[276,277]. Considering a reverse process with a heat bath at temperature T, Landauer’s principle [278] yields the bound

$$\sigma \ge {\displaystyle \frac{\dot{Q}}{T}},$$

where $\dot{Q}=\mathrm{Tr}\left[H\dot{\rho }\right]$ is the heat flux between system and bath. Hence the UEE respects the second-law lower bound $\sigma \ge \dot{Q}/T$.

2-5 Numerical Simulation: A Quantum Heat-Transport Model

As an example we couple a two-level system to two bosonic heat baths at temperatures $T_h>T_c$. The hybrid Lindblad–UEE generator [1]

$$\dot{\rho }=-i[D,\rho ]+{\gamma }_h\left(n_h{\sigma }_{+}\rho {\sigma }_{-}-(n_h+1)\{{\sigma }_{-}{\sigma }_{+},\rho \}/2\right)+{\gamma }_c\left(n_c{\sigma }_{-}\rho {\sigma }_{+}-(n_c+1)\{{\sigma }_{+}{\sigma }_{-},\rho \}/2\right)$$

is integrated numerically, where $n_{h,c}={\left({\mathrm{e}}^{\omega /k_B{T}_{h,c}}-1\right)}^{-1}$. From $\rho \left(t\right)$ we compute the entropy-production rate $\sigma \left(t\right)=-\mathrm{Tr}[\dot{\rho }ln\rho ]$, confirming $\sigma \left(t\right)>0$ until the stationary state is reached. We also verify that at stationarity ${\sigma }_{\mathrm{ss}}\propto \mathsf{\Delta }{T}^2$ with $\mathsf{\Delta }T=T_h-T_c$, in agreement with performance indicators of quantum heat-engine models [279].

3.10. Summary

1 Overview of the Multi-Formalism Formulation

In this chapter we formulated the UEE (Unified Evolution Equation) in three distinct yet equivalent forms, showing that they all describe the same physical dynamics.

• Operator form (UEE${‌}_{\mathrm{op}}$, §3.1): Starting from the density-operator evolution equation

  $${\displaystyle \frac{d\rho }{dt}}=-i[D,\rho ]+\sum _j\left(V_j\rho V_j^{†}-\frac{1}{2}\{V_j^{†}{V}_j,\rho \}\right)+R\left[\rho \right],$$

  whose total generator includes the zero-area resonance kernel R, we established semigroup generation by the Hille–Yosida theorem [280], derived exact solutions via the Dyson–Phillips series [152], and proved stationarity and ergodicity [37,281]—thereby constructing a mathematically rigorous coexistence of irreversible dissipation and unitary evolution.
• Variational form (UEE${‌}_{\mathrm{var}}$, §3.2): We introduced the action functional

  $$\mathcal{S}[\rho ,{\mathsf{\Phi }}_I,D_f]=\int d\tau \left\{\mathrm{Tr}\left[{\mathsf{\Phi }}_I\dot{\rho }\right]-\mathsf{\Gamma }[D_f,{\mathsf{\Phi }}_I]\right\},$$

  and obtained the same master equation (with R) as well as the coupled equations for the information-flux field ${\mathsf{\Phi }}_I$ and the fractal-dimension field $D_f$ from the Euler–Lagrange equations [157]. This approach reveals a dual appearance of the reversible part and the dissipative functional and ensures consistency when treating ${\mathsf{\Phi }}_I$ and $D_f$ as fields [1,213].
• Field-equation form (UEE${‌}_{\mathrm{fld}}$, §3.3): We developed dynamical equations containing the fractal operator $sin\left(\pi \sqrt{-\square }/\mathsf{\Lambda }\right)$[282] and the information-flux density ${\mathsf{\Phi }}_I^{\mu }$, and illustrated nonequilibrium field dynamics through numerical simulations—explicitly displaying the spatial–temporal distribution of dissipation and entropy production [226].

These three formulations—operator, variational, and field—are mathematically equivalent and mutually validate the universality and internal consistency of the UEE.

2-1 Proof of the Equivalence and Consistency of the Three Forms

Sections §3.1 (operator), §3.2 (variational), and §3.3 (field) describe identical dynamics in two steps:

(i)

Operator ⇒ Variational: By introducing the dual field ${\mathsf{\Phi }}_I$ into the operator master equation and constructing the action functional $\mathcal{S}[\rho ,{\mathsf{\Phi }}_I,D_f]$ as a Legendre transform [283], we retrieved the density-operator equation from $\delta \mathcal{S}/\delta {\mathsf{\Phi }}_I=0$ and obtained the optimality condition for the dissipative functional $\mathsf{\Gamma }[D_f,{\mathsf{\Phi }}_I]$ from $\delta \mathcal{S}/\delta \rho =0$.

(ii)

Variational ⇒ Field: Extending $\mathcal{S}$ to a local action of the fractal field $D_f\left(x\right)$ and the information-flux field ${\mathsf{\Phi }}_I^{\mu }\left(x\right)$, Euler–Lagrange variation (see §§3.3.1–3.3.3) reproduced the field equations exactly.

Thus $\rho \left(t\right)$, the action S, and the field equations are mutually dual; operator, variational, or field solutions provide the same physical insight. Numerical tests and the analysis of ergodicity and stationary states (see §§3.1.3, 3.3.3) confirm invariants common to all forms [284].

2-2 Concrete Examples: Dissipative Free Dirac Field and Harmonic-Oscillator Approximation

• Dissipative free Dirac field (§3.5.1): Applying ${\mathcal{L}}_{\mathsf{\Delta }}+R$ to the Dirac operator D reveals how the dissipator contributes to the dispersion via the imaginary part of the self-energy [285].
• One-particle model—harmonic-oscillator approximation (§3.5.2): A low-energy approximation reduces the fractal operator to a quadratic truncation and gives a harmonic-oscillator Hamiltonian. Line widths and decay rates agree across the Dyson–Phillips series (operator), the quadratic expansion of the action (variational), and the linearised field solution (field).

3-1 Identification of the Action Functional with Thermodynamic Quantities

The variational action

$$\mathcal{S}[\rho ,{\mathsf{\Phi }}_I,D_f]=\int d\tau \left\{\mathrm{Tr}\left[{\mathsf{\Phi }}_I\dot{\rho }\right]-\mathsf{\Gamma }[D_f,{\mathsf{\Phi }}_I]\right\}$$

is fully analogous to the free-energy functional. Interpreting the time parameter $\tau$ as the inverse temperature $\beta$ identifies

$$\mathsf{\Gamma }[D_f,{\mathsf{\Phi }}_I]⟷F\left[\rho \right]=\mathrm{Tr}\left[H\rho \right]-k_{B}TS\left(\rho \right),$$

consistent with Jaynes’ maximum-entropy principle [228]. Introducing ${\mathsf{\Phi }}_I$ yields directly the entropy-production relation $\sigma =\beta \dot{Q}+{\mathsf{\Delta }}_{i}S\ge 0$ [213].

3-2 Integration with Nonequilibrium Statistical Mechanics

The UEE encompasses the Crooks–Jarzynski equality [41,42] and the Green–Kubo relations [50]. The path-integral representation $Z=\int \mathcal{D}[\rho ,{\mathsf{\Phi }}_I]e^{\mathcal{S}[\rho ,{\mathsf{\Phi }}_I,D_f]}$ corresponds to the large-deviation rate functional, enabling derivations of quantum fluctuation theorems [286].

4-1 RG Improvement: Multi-Coupling Phase Diagrams and Critical Exponents

Applying the Wilson–Polchinski RG equation [251] to UEE${‌}_{\mathrm{fld}}$ with dissipation and fractal couplings yields $\beta$-functions from which phase diagrams and critical exponents are extracted (§3.7). Linearisation around fixed points gives the spectrum of eigenvalues $\to (\nu ,\eta ,z)$; Monte-Carlo RG confirms the universality class [287].

4-2 Contributions to the Quantum-Information View: Coherence Loss and Entropy Production

The decoherence and entropy-production rates predicted by the UEE are directly applicable to resource theories in quantum information, naturally extending to the quantum Zeno effect [274] and Landauer’s principle [278]. This provides a theoretical basis for optimising the balance of heat, information, and dissipation in quantum computing architectures.

5-1 Establishing a Unified Evolution Equation on a Multi-Formalism Basis

The three formulations—operator, variational, and field—share the common total generator

$${\mathcal{L}}_{\mathrm{tot}}=-i[D,·]+{\mathcal{L}}_{\mathsf{\Delta }}+R,$$

thus providing a unified theoretical foundation that consistently handles irreversible dissipation together with reversible unitary evolution. Any of the three pathways yields identical dynamical behaviour, underscoring the comprehensive scope of the UEE for quantum nonequilibrium phenomena.

4. Proof of the Complete Embedding of General Relativity

In this chapter we perform a full variation of the unified UEE action with respect to the vierbein $e^a{‌}_{\mu }$ and the spin connection ${\omega }_{\mu }{‌}^{ab}$ and prove the following four statements:

(i)

Derivation of the Einstein–Palatini equation $G_{\mu \nu }=8\pi G{T}_{\mu \nu }^{\mathrm{tot}}$ [29]

(ii)

Satisfaction of the torsion-free condition $T^a{‌}_{\mu \nu }=0$ [29]

(iii)

Consistency between the covariant conservation law ${\nabla }^{\mu }{T}_{\mu \nu }^{\mathrm{tot}}=0$ and the Bianchi identity [29]

(iv)

Complete recovery of the Einstein–Yang–Mills–Dirac theory in the low-energy limit $\mathsf{\Lambda }\to \infty$ [30,31]

These results prove that the UEE fully contains general relativity (GR) as a sub-sector.

4.1. Unified Action and Notation

Unified Action

$$\begin{array}{cc}\hfill S& =S_{\mathrm{EH}}+S_{\mathrm{YM}}+S_{\mathrm{spinor}}+S_{D_f}+S_{{\mathsf{\Phi }}_I},\hfill \\ \hfill S_{\mathrm{EH}}& ={\displaystyle \frac{1}{16\pi G}}\int d^{4}xeR(e,\omega ),\hfill \\ \hfill S_{\mathrm{YM}}& =-{\displaystyle \frac{1}{4g^2}}\int d^{4}xe\mathrm{Tr}\left(F_{\mu \nu }{F}^{\mu \nu }\right),\hfill \\ \hfill S_{\mathrm{spinor}}& =\int d^{4}xe\overline{\psi }\left(i{\gamma }^a{e}_a{‌}^{\mu }{D}_{\mu }-m\right)\psi ,\hfill \\ \hfill S_{D_f}& ={\mathsf{\Lambda }}^4\int d^{4}xe\mathsf{\Gamma }\left[D_f\right],\mathsf{\Gamma }\left[D_f\right]=\mathrm{Tr}\left[\mathsf{\Pi }\left(D_f\right)sin\left(\pi D_f\right)\right],\hfill \\ \hfill S_{{\mathsf{\Phi }}_I}& ={\displaystyle \frac{1}{2{\kappa }_I}}\int d^{4}xe{\mathsf{\Phi }}_{I\mu }{\mathsf{\Phi }}_I{‌}^{\mu }.\hfill \end{array}$$

(21)

• $e:=det\left(e^a{‌}_{\mu }\right)$, $g_{\mu \nu }=e^a{‌}_{\mu }{e}^b{‌}_{\nu }{\eta }_{ab}$, ${\eta }_{ab}=\mathrm{diag}(+1,-1,-1,-1)$.
• $R(e,\omega )=e_a{‌}^{\mu }{e}_b{‌}^{\nu }{R}_{\mu \nu }{‌}^{ab}\left(\omega \right)$ [29], $F_{\mu \nu }={\partial }_{\mu }{A}_{\nu }-{\partial }_{\nu }{A}_{\mu }+[A_{\mu },A_{\nu }]$ [30].
• $D_{\mu }={\partial }_{\mu }+\frac{1}{4}{\omega }_{\mu ab}{\gamma }^{ab}+A_{\mu }$ [21], ${\gamma }^{ab}=\frac{1}{2}[{\gamma }^a,{\gamma }^b]$.

Variation Formulae for the Vierbein

$$\begin{array}{cc}\hfill \delta g_{\mu \nu }& =2e_{(\mu }{‌}^a{\eta }_{ab}\delta e^b{‌}_{\nu )},\hfill \end{array}$$

(22)

$$\begin{array}{cc}\hfill \delta e& =e{e}_a{‌}^{\mu }\delta e^a{‌}_{\mu }.\hfill \end{array}$$

(23)

The variation of the Einstein–Hilbert action is

$$\begin{array}{cc}\hfill \delta S_{\mathrm{EH}}& ={\displaystyle \frac{1}{16\pi G}}\int d^{4}xe{G}^{\mu \nu }\delta g_{\mu \nu }={\displaystyle \frac{1}{8\pi G}}\int d^{4}xe{G}_{\mu }{‌}^a\delta e_a{‌}^{\mu },\hfill \end{array}$$

(24)

where $G_{\mu \nu }=R_{\mu \nu }-\frac{1}{2}{g}_{\mu \nu }R$ is the Einstein tensor [29].

4.2. Einstein Equation from Vierbein Variation

Definition of the Stress–Energy–Momentum Tensor

For each action $S_i$ ($i=\mathrm{YM},\mathrm{spinor},D_f,{\mathsf{\Phi }}_I$) we define the vierbein variation as

$$\begin{array}{c}\hfill \delta S_i=-{\displaystyle \frac{1}{2}}\int d^{4}xe{T}_{\mu }^{\left(i\right)}{‌}^a\delta e_a{‌}^{\mu }.\end{array}$$

(25)

In the following we derive $T_{\mu }^{\left(i\right)}{‌}^a$ explicitly.

4.3. Complete Derivation of the Stress–Energy–Momentum Tensor

In this section we vary the vierbein in each partial action $S_i(i=\mathrm{YM},\mathrm{spinor},D_f,{\mathsf{\Phi }}_I)$,

$$\delta S_i=-{\displaystyle \frac{1}{2}}\int d^{4}xe{T}_{\mu }^{\left(i\right)}{‌}^a\delta e_a{‌}^{\mu },\left(T_{\mu }^{\left(i\right)}{‌}^a:=T_{\mu \nu }^{\left(i\right)}{e}^{a\nu }\right),$$

and derive the corresponding tensors $T_{\mu \nu }^{\left(i\right)}$ explicitly at the operator level.

Yang–Mills Part: $T_{\mu \nu }^{\mathrm{YM}}$

$$S_{\mathrm{YM}}=-{\displaystyle \frac{1}{4g^2}}\int d^{4}xe\mathrm{Tr}\left(F_{\rho \sigma }{F}^{\rho \sigma }\right).$$

Using (22) and (23) [30],

$$T_{\mu \nu }^{\mathrm{YM}}={\displaystyle \frac{1}{g^2}}\mathrm{Tr}\left(F_{\mu \rho }{F}_{\nu }{‌}^{\rho }-{\displaystyle \frac{1}{4}}{g}_{\mu \nu }{F}_{\rho \sigma }{F}^{\rho \sigma }\right).$$

(4.3.1)

Spinor Part: $T_{\mu \nu }^{\mathrm{spinor}}$

$$S_{\mathrm{spinor}}=\int d^{4}xe\overline{\psi }\left(i{\gamma }^a{e}_a{‌}^{\rho }{D}_{\rho }-m\right)\psi .$$

Varying $e_a{‌}^{\rho }$ in the Dirac part and in the volume element, discarding total derivatives, gives

$$\begin{array}{cc}\hfill T_{\mu \nu }^{\mathrm{spinor}}& ={\displaystyle \frac{i}{4}}\overline{\psi }\left({\gamma }_{\mu }{\overleftrightarrow{D}}_{\nu }+{\gamma }_{\nu }{\overleftrightarrow{D}}_{\mu }\right)\psi -g_{\mu \nu }\overline{\psi }\left(i{\gamma }^{\rho }{D}_{\rho }-m\right)\psi ,\hfill \end{array}$$

(26)

where $\psi {\overleftrightarrow{D}}_{\mu }\chi :=\psi D_{\mu }\chi -\left(D_{\mu }\psi \right)\chi$. Using the Dirac equation $(i{\gamma }^{\rho }{D}_{\rho }-m)\psi =0$ [21], the trace term vanishes:

$$T_{\mu \nu }^{\mathrm{spinor}}={\displaystyle \frac{i}{4}}\overline{\psi }\left({\gamma }_{\mu }{\overleftrightarrow{D}}_{\nu }+{\gamma }_{\nu }{\overleftrightarrow{D}}_{\mu }\right)\psi .$$

(4.3.2)

Fractal Part: $T_{\mu \nu }^{D_f}$

$$S_{D_f}={\mathsf{\Lambda }}^4\int d^{4}xe\mathsf{\Gamma }\left[D_f\right],\mathsf{\Gamma }\left[D_f\right]=\mathrm{Tr}\left[\mathsf{\Pi }\left(D_f\right)sin\left(\pi D_f\right)\right]$$

[25,26,27].

The variation contains the e term and the metric dependence of $\mathsf{\Gamma }\left[D_f\right]$ through $D_f=sin\left(\frac{\pi }{\mathsf{\Lambda }}\sqrt{-\square }\right)$:

$$T_{\mu \nu }^{D_f}=-{\mathsf{\Lambda }}^4{g}_{\mu \nu }\mathsf{\Gamma }\left[D_f\right]+{\mathsf{\Lambda }}^4{\displaystyle \frac{2}{\sqrt{-g}}}{\displaystyle \frac{\delta \mathsf{\Gamma }}{\delta g^{\mu \nu }}}.$$

(4.3.3)

The second term can be expanded as a curvature series ${\alpha }_1{R}_{\mu \nu }+{\alpha }_2(R^2,R_{\rho \sigma }{R}^{\rho \sigma })+\dots$ using $\delta \square =-\delta g^{\rho \sigma }{\nabla }_{\rho }{\nabla }_{\sigma }+\dots$ [23].

Information-Flux Part: $T_{\mu \nu }^{{\mathsf{\Phi }}_I}$

$$S_{{\mathsf{\Phi }}_I}={\displaystyle \frac{1}{2{\kappa }_I}}\int d^{4}xe{\mathsf{\Phi }}_{I\rho }{\mathsf{\Phi }}_I{‌}^{\rho }$$

[41,42]. Variation yields

$$T_{\mu \nu }^{{\mathsf{\Phi }}_I}={\displaystyle \frac{1}{{\kappa }_I}}\left({\mathsf{\Phi }}_{I\mu }{\mathsf{\Phi }}_{I\nu }-{\displaystyle \frac{1}{2}}{g}_{\mu \nu }{\mathsf{\Phi }}_{I\rho }{\mathsf{\Phi }}_I{‌}^{\rho }\right).$$

(4.3.4)

Establishment of the Einstein–Palatini Equation

Requiring the total action to be stationary, $\delta S_{\mathrm{EH}}+{\sum }_i\delta S_i=0$, and combining (24) with (25), gives

$$G_{\mu }{‌}^a=8\pi G{T}_{\mu }{‌}^a,T_{\mu \nu }=T_{\mu \nu }^{\mathrm{YM}}+T_{\mu \nu }^{\mathrm{spinor}}+T_{\mu \nu }^{D_f}+T_{\mu \nu }^{{\mathsf{\Phi }}_I}.$$

(4.3.5)

Hence

$$\begin{array}{|c|}\hline G_{\mu \nu }=8\pi G{T}_{\mu \nu }\\ \hline\end{array}$$

is derived exactly [29].

• Remarks:
  • The second term of $T_{\mu \nu }^{D_f}$ is suppressed by $\mathcal{O}\left({\mathsf{\Lambda }}^{-2}\right)$ (see §4.8).
  • Unless one considers macroscopic nonequilibrium processes, the information-flux field is phenomenologically small; in a PPN expansion $|{\mathsf{\Phi }}_{I\mu }{\mathsf{\Phi }}_I{‌}^{\mu }|\lesssim \kappa {\delta }^2\sim {10}^{-3}$.

4.4. Variation of the Spin Connection and the Torsion-Free Condition

We perform the Palatini variation, treating the spin connection ${\omega }_{\mu }{‌}^{ab}$ as an independent variable with respect to the vierbein $e^a{‌}_{\mu }$ [29]. Only the curvature term of $S_{\mathrm{EH}}$ and the covariant derivative in $S_{\mathrm{spinor}}$ depend on ${\omega }_{\mu }{‌}^{ab}$.

Variation of the EH Term with Respect to $\omega$

$${\delta }_{\omega }{S}_{\mathrm{EH}}={\displaystyle \frac{1}{8\pi G}}\int d^{4}xe{e}_a{‌}^{\mu }{e}_b{‌}^{\nu }{D}_{[\mu }\delta {\omega }_{\nu ]}{‌}^{ab},$$

where $D_{[\mu }\delta {\omega }_{\nu ]}{‌}^{ab}={\partial }_{[\mu }\delta {\omega }_{\nu ]}{‌}^{ab}+{\omega }_{[\mu }{‌}^{ac}\delta {\omega }_{\nu ]c}{‌}^b+{\omega }_{[\mu }{‌}^{bc}\delta {\omega }_{\nu ]c}{‌}^a$ [29]. Integrating by parts and using the arbitrariness of $\delta {\omega }_{\mu }{‌}^{ab}$ we obtain

$$e_{[a}{‌}^{\mu }{e}_{b]}{‌}^{\nu }{T}^c{‌}_{\mu \nu }=0,$$

that is

$$\begin{array}{c}\hfill T^a{‌}_{\mu \nu }:=D_{[\mu }{e}_{\nu ]}{‌}^a=0.\end{array}$$

(27)

Variation of the Spinor Term with Respect to $\omega$

$${\delta }_{\omega }{S}_{\mathrm{spinor}}={\displaystyle \frac{1}{4}}\int d^{4}xe\overline{\psi }{\gamma }^{[a}{\gamma }^{b]}\psi \delta {\omega }_{\mu ab}{e}^{\mu }{‌}_c{\eta }^c{‌}_{[a}{e}^{\nu }{‌}_{b]}$$

[21], which is completely antisymmetric because ${\gamma }^{[a}{\gamma }^{b]}=\frac{1}{2}{\gamma }^{ab}$. Imposing (27) yields ${\delta }_{\omega }{S}_{\mathrm{spinor}}=0$. Hence the torsion-free condition is preserved even in the presence of spinor couplings.

Conclusion.

Equation (27) implies

$${\omega }_{\mu }{‌}^{ab}={\omega }_{\mu }{‌}^{ab}\left[e\right]={\displaystyle \frac{1}{2}}{e}^{a\nu }\left({\partial }_{\mu }{e}^b{‌}_{\nu }-{\partial }_{\nu }{e}^b{‌}_{\mu }\right)-(a\leftrightarrow b),$$

namely the spin connection is uniquely reduced to the Levi-Civita connection [29].

4.5. Bianchi Identity and Energy Conservation

Derivation of the Covariant Conservation Law

Using the Einstein–Palatini equation (4.3) together with the geometric identity ${\nabla }^{\mu }{G}_{\mu \nu }=0$ [29] we obtain

$${\nabla }^{\mu }{T}_{\mu \nu }=0,$$

where $T_{\mu \nu }=T_{\mu \nu }^{\mathrm{YM}}+T_{\mu \nu }^{\mathrm{spinor}}+T_{\mu \nu }^{D_f}+T_{\mu \nu }^{{\mathsf{\Phi }}_I}$. Thus the sum of all contributions is conserved even in the presence of dissipative sectors $(D_f,{\mathsf{\Phi }}_I)$.

Internal Cancellation of Dissipative Sources

From the UEE${‌}_{\mathrm{fld}}$ field equations (Chapter 3, §3.4)

$${\partial }_{\tau }{D}_f=-{\kappa }_D{\displaystyle \frac{\delta \mathsf{\Gamma }}{\delta D_f}},{\partial }_{\tau }{\mathsf{\Phi }}_{I\mu }=-{\kappa }_I{\mathsf{\Phi }}_{I\mu }+\dots ,$$

we find

$${\nabla }^{\mu }{T}_{\mu \nu }^{D_f}=-{\nabla }^{\mu }{T}_{\mu \nu }^{{\mathsf{\Phi }}_I},$$

so that (4.5) holds. Physically this corresponds to the statement that “the energy lost by dissipation is carried by the information-flux field.”

4.6. Low-Energy Limit and Integer-Dimensional Recovery

Curvature Expansion of the Fractal Operator

Expanding $D_f=sin\left(\frac{\pi }{\mathsf{\Lambda }}\sqrt{-\square }\right)$ in powers of ${\mathsf{\Lambda }}^{-1}$ gives

$$D_f={\displaystyle \frac{\pi }{\mathsf{\Lambda }}}\sqrt{-\square }-{\displaystyle \frac{{\pi }^3}{6{\mathsf{\Lambda }}^3}}{(-\square )}^{3/2}+\mathcal{O}\left({\mathsf{\Lambda }}^{-5}\right),$$

so that

$$\begin{array}{cc}\hfill \mathsf{\Gamma }\left[D_f\right]& =\mathrm{Tr}\left[{\left({\displaystyle \frac{\pi }{\mathsf{\Lambda }}}\sqrt{-\square }\right)}^2+\mathcal{O}\left({\mathsf{\Lambda }}^{-4}\right)\right]\hfill \\ \hfill & ={\displaystyle \frac{{\pi }^2}{{\mathsf{\Lambda }}^2}}\mathrm{Tr}(-\square )+\mathcal{O}\left({\mathsf{\Lambda }}^{-4}\right).\hfill \end{array}$$

(28)

The trace $\mathrm{Tr}(-\square )$ is expanded via the Seeley–DeWitt series in terms of the scalar curvature R and the Ricci tensor $R_{\mu \nu }$, $\mathrm{Tr}(-\square )=a_{1}R+a_2{R}_{\mu \nu }{R}^{\mu \nu }+\dots$ [16,288]. The coefficients $a_i$ are listed below.

Table of Curvature-Expansion Coefficients

For reference, the coefficients $\left\{a_k\right\}$ from the Seeley–DeWitt expansion of $\mathsf{\Gamma }\left[D_f\right]$ to order ${\mathsf{\Lambda }}^{-2}$ and the derived coefficients $\left\{{\alpha }_i\left(\mathsf{\Lambda }\right)\right\}$ are tabulated.

Symbol	Expression (4-D)	Comment
$a_0$	1	volume term
$a_1$	${\displaystyle \frac{1}{6}R}$	scalar curvature
$a_2$	${\displaystyle \frac{1}{180}\left(R_{\mu \nu \rho \sigma }{R}^{\mu \nu \rho \sigma }-R_{\mu \nu }{R}^{\mu \nu }+\frac{5}{2}{R}^2\right)}$	Seeley–DeWitt coefficient
${\alpha }_1\left(\mathsf{\Lambda }\right)$	${\displaystyle \frac{{\pi }^2}{6{\mathsf{\Lambda }}^2}}$	coefficient of R
${\alpha }_2\left(\mathsf{\Lambda }\right)$	${\displaystyle -\frac{{\pi }^2}{12{\mathsf{\Lambda }}^2}}$	coefficient of $R_{\mu \nu }{R}^{\mu \nu }$
${\alpha }_3\left(\mathsf{\Lambda }\right)$	${\displaystyle \frac{{\pi }^2}{180{\mathsf{\Lambda }}^2}}$	coefficient of $R_{\mu \nu \rho \sigma }{R}^{\mu \nu \rho \sigma }$

Symbol	Expression (4-D)	Comment
$a_0$	1	volume term
$a_1$	${\displaystyle \frac{1}{6}R}$	scalar curvature
$a_2$	${\displaystyle \frac{1}{180}\left(R_{\mu \nu \rho \sigma }{R}^{\mu \nu \rho \sigma }-R_{\mu \nu }{R}^{\mu \nu }+\frac{5}{2}{R}^2\right)}$	Seeley–DeWitt coefficient
${\alpha }_1\left(\mathsf{\Lambda }\right)$	${\displaystyle \frac{{\pi }^2}{6{\mathsf{\Lambda }}^2}}$	coefficient of R
${\alpha }_2\left(\mathsf{\Lambda }\right)$	${\displaystyle -\frac{{\pi }^2}{12{\mathsf{\Lambda }}^2}}$	coefficient of $R_{\mu \nu }{R}^{\mu \nu }$
${\alpha }_3\left(\mathsf{\Lambda }\right)$	${\displaystyle \frac{{\pi }^2}{180{\mathsf{\Lambda }}^2}}$	coefficient of $R_{\mu \nu \rho \sigma }{R}^{\mu \nu \rho \sigma }$

Using these values, equation (32) becomes

$$\mathsf{\Gamma }\left[D_f\right]={\displaystyle \frac{{\pi }^2}{{\mathsf{\Lambda }}^2{\left(4\pi \right)}^2}}\left(\frac{1}{6}R-\frac{1}{2}{R}_{\mu \nu }{R}^{\mu \nu }+\frac{1}{30}{R}_{\mu \nu \rho \sigma }{R}^{\mu \nu \rho \sigma }\right)+O\left({\mathsf{\Lambda }}^{-4}\right),$$

which can be used directly for numerical estimates of the ${\mathsf{\Lambda }}^{-2}$ suppression.

Limit $\mathsf{\Lambda }\to \infty$

Using (28) together with the definition of $T_{\mu \nu }^{D_f}$ in (4.3) one finds

$$T_{\mu \nu }^{D_f}=\mathcal{O}\left({\mathsf{\Lambda }}^{-2}\right),T_{\mu \nu }^{{\mathsf{\Phi }}_I}=\mathcal{O}\left({\mathsf{\Lambda }}^{-2}\right),$$

so that

$$\underset{\mathsf{\Lambda }\to \infty }{lim}{T}_{\mu \nu }=T_{\mu \nu }^{\mathrm{YM}}+T_{\mu \nu }^{\mathrm{spinor}}.$$

Moreover, because $S_{D_f},S_{{\mathsf{\Phi }}_I}\sim {\mathsf{\Lambda }}^{-2}\to 0$, one recovers

$$\underset{\mathsf{\Lambda }\to \infty }{lim}S=S_{\mathrm{EH}}+S_{\mathrm{YM}}+S_{\mathrm{spinor}}.$$

High–Curvature Terms and Unitarity

For finite $\mathsf{\Lambda }$ one has

$$S_{D_f}\simeq {\displaystyle \frac{\alpha }{M_{*}^2}}\int d^{4}x\sqrt{-g}\left(R^2+\beta R_{\mu \nu }{R}^{\mu \nu }\right)+\dots$$

[16,288], with $M_{*}=\frac{\mathsf{\Lambda }}{\pi }$. By the relative boundedness estimate below, the generator preserves the $C_0$-semigroup property and no ghosts appear provided that $\sqrt{{\alpha }^2+{\beta }^2}R/M_{*}^2<1$ [289].

Complete Proof of Relative Boundedness of the High– Curvature Extension and $C_0$-Semigroup Generation

Theorem (relative boundedness and semigroup property).

Let the total generator be

$$L_{\mathrm{tot}}=-i[D,·]+L_{\mathsf{\Delta }}+R+{\mathsf{\Lambda }}^{-2}\left(\alpha R+\beta R_{\mu \nu }{R}^{\mu \nu }\right)\mathcal{K}[·]$$

acting on the Banach space $S_1\left(\mathcal{H}\right)$ (trace-class operators). The high–curvature perturbation is relatively bounded with respect to the invertible generator $L_0=-i[D,·]$ [19,24], and if

$$\sqrt{{\alpha }^2+{\beta }^2}{\displaystyle \frac{\parallel R_{\max }\parallel }{M_{*}^2}}<1,$$

where $R_{\max }$ is the maximal eigenvalue of the metric curvature and $M_{*}=\mathsf{\Lambda }/\pi$, then $L_{\mathrm{tot}}$ generates a strongly continuous semigroup ${\left\{T\left(t\right)\right\}}_{t\ge 0}$[36,37].

Proof.

• Decomposition and norm estimate
  The reversible part $L_0$ is closed, while the dissipative part $K:=L_{\mathsf{\Delta }}+R$ is bounded (see §2.30.0.7, §2.31): $\parallel K\parallel <\infty$.
• Relative boundedness of the curvature perturbation
  The curvature operator $\mathcal{R}:=\alpha R+\beta R_{\mu \nu }{R}^{\mu \nu }$ obeys $\parallel \mathcal{R}\parallel \le \sqrt{{\alpha }^2+{\beta }^2}{R}_{\max }$. Because the kernel map $\mathcal{K}[·]$ is bounded with $\parallel \mathcal{K}\parallel \le 1$, we obtain

  $$\parallel {\mathsf{\Lambda }}^{-2}\mathcal{R}\mathcal{K}\rho \parallel \le \underset{=:a}{\underbrace{\sqrt{{\alpha }^2+{\beta }^2}{\displaystyle \frac{R_{\max }}{M_{*}^2}}}}\parallel L_0\rho \parallel +b\parallel \rho \parallel ,$$

  with $b=0$. If $a<1$ the relative boundedness is established.
• Application of the Kato–Rellich perturbation theorem
  With $a<1$, the operator $L_0+{\mathsf{\Lambda }}^{-2}\mathcal{R}\mathcal{K}$ is closed and generates a $C_0$ semigroup (Kato–Rellich [24]). Adding the bounded perturbation K preserves the $C_0$-semigroup property [37].

Hence $T\left(t\right)=e^{t{L}_{\mathrm{tot}}}$ exists, and the Dyson–Phillips series [36,290] $T\left(t\right)={\sum }_{n\ge 0}{T}_n\left(t\right)$ obeys

$$\parallel T_n\left(t\right)\parallel \le {\displaystyle \frac{{\left(Mt\right)}^n}{n!}}{e}^{\omega t},M:=\parallel K\parallel ,\omega :=\parallel L_0\parallel .$$

□

Physical implication.

Taking $M_{*}\gtrsim 1\mathrm{TeV}$ and $\alpha ,\beta =\mathcal{O}\left(1\right)$ naturally satisfies $a<1$; therefore the UEE–GR extension with high–curvature corrections maintains (i) unitarity, (ii) energy conservation, and (iii) ergodicity and monotonic entropy production (cf. §2.31, §3.9).

Experimental Constraints and PPN Coefficients

The ${\mathsf{\Lambda }}^{-2}$-suppressed terms contribute to the post-Newtonian expansion as

$$|\gamma -1|\simeq {\displaystyle \frac{\alpha }{M_{*}^2}}{\displaystyle \frac{GM}{r^3}},|\beta -1|\simeq {\displaystyle \frac{\alpha +{\beta }^{\prime }}{2M_{*}^2}}{\displaystyle \frac{G^2{M}^2}{r^4}}.$$

Using the Cassini bound $|\gamma -1|<2.3\times {10}^{-5}$, one obtains $M_{*}\gtrsim 1\mathrm{TeV}$ for $\alpha \sim \mathcal{O}\left(1\right)$, ensuring that the corrections are sufficiently suppressed (see §4.10).

4.7. Post-Newtonian Expansion and Consistency with Experiments

In the weak–field, low–velocity regime we write $g_{\mu \nu }={\eta }_{\mu \nu }+h_{\mu \nu }$ with $|h_{\mu \nu }|\ll 1$ and parameterise $h_{00}=2\mathsf{\Phi },h_{ij}=2\gamma \mathsf{\Phi }{\delta }_{ij}$. Substituting the ${\mathsf{\Lambda }}^{-2}$-suppressed pieces of $T_{\mu \nu }^{D_f}$ and $T_{\mu \nu }^{{\mathsf{\Phi }}_I}$ into the Einstein–Palatini equations (4.3) gives

$$\begin{array}{cc}\hfill \gamma -1& \simeq {\displaystyle \frac{\alpha }{M_{*}^2}}{\displaystyle \frac{GM}{r^3}},\hfill \end{array}$$

(4.7.1)

$$\begin{array}{cc}\hfill \beta -1& \simeq {\displaystyle \frac{\alpha +{\beta }^{\prime }}{2M_{*}^2}}{\displaystyle \frac{G^2{M}^2}{r^4}},\hfill \end{array}$$

(4.7.2)

where $M_{*}=\mathsf{\Lambda }/\pi$ and $\alpha ,{\beta }^{\prime }$ are the coefficients of the R and $R_{\mu \nu }{R}^{\mu \nu }$ terms in Eq. (28).

Numerical values for $\mathsf{\Lambda }\ge 7\mathrm{TeV}$.

With $M_{*}=\mathsf{\Lambda }/\pi \simeq 2.23\mathrm{TeV}$ and

$$\alpha =\frac{1}{192\pi }={\displaystyle \frac{1}{192\pi }},{\beta }^{\prime }\left(\mathrm{unchanged}\right)$$

we obtain

$${|\gamma -1|}_{\mathrm{UEE}}=2.2\times {10}^{-11},{|\beta -1|}_{\mathrm{UEE}}\lesssim 4.0\times {10}^{-12}.$$

Both values lie far below the present observational bounds $|\gamma -1|<2.3\times {10}^{-5}$ (Cassini) and $|\beta -1|<8.0\times {10}^{-5}$ (LLR), yielding safety factors of $\mathcal{O}\left({10}^6\right)$.

Inverse bound (for completeness).

Imposing the Cassini limit on Eq. (4.7.1) with the above $\alpha$ yields only

$$M_{*}\gtrsim 0.20\mathrm{TeV},$$

(4.7.3)

so the theory value $M_{*}\simeq 2.23\mathrm{TeV}$ (sourced by $\mathsf{\Lambda }=7\mathrm{TeV}$) easily satisfies all post-Newtonian tests. The UEE therefore remains fully compatible with existing solar-system and binary-pulsar constraints.

4.8. Derivation of the Curvature-Expansion Coefficients for the Fractal Term

We compute the ${\mathsf{\Lambda }}^{-2}$ contribution of $\mathsf{\Gamma }\left[D_f\right]\equiv \mathsf{\Pi }\left(D_f\right)sin\left(\pi D_f\right)$ by applying the heat-kernel expansion (Seeley–DeWitt technique [291,292,293]).

4.8.1 Leading order $\mathcal{O}\left({\mathsf{\Lambda }}^{-2}\right)$

Using the standard heat-kernel series

$$\mathrm{Tr}\left[e^{-\sigma (-\square )}\right]={\left(4\pi \sigma \right)}^{-2}\sum _{k=0}^{\infty }{a}_k{\sigma }^k,a_1={\displaystyle \frac{1}{6}}\int d^{4}x\sqrt{-g}R,$$

and the Mellin inversion formula [27]

$${(-\square )}^{1/2}={\displaystyle \frac{1}{\mathsf{\Gamma }(-\frac{1}{2})}}{\int }_0^{\infty }{\sigma }^{-3/2}{e}^{-\sigma (-\square )}d\sigma ,$$

one obtains

$$\begin{array}{cc}\hfill \mathrm{Tr}\sqrt{-\square }& ={\displaystyle \frac{\mathsf{\Gamma }\left(\frac{3}{2}\right)}{\mathsf{\Gamma }(-\frac{1}{2})}}{\left(4\pi \right)}^{-2}{a}_1={\displaystyle \frac{1}{12{\pi }^2}}\int d^{4}x\sqrt{-g}R.\hfill \end{array}$$

(29)

Explicit coefficient $a_1$.

Substituting (29) into $\mathsf{\Gamma }\left[D_f\right]=\frac{{\pi }^2}{{\mathsf{\Lambda }}^2}\mathrm{Tr}\sqrt{-\square }+\mathcal{O}\left({\mathsf{\Lambda }}^{-4}\right)$ gives

$$\begin{array}{cc}\hfill \mathsf{\Gamma }\left[D_f\right]& ={\displaystyle \frac{{\pi }^2}{{\mathsf{\Lambda }}^2}}{\displaystyle \frac{1}{12{\pi }^2}}\int d^{4}x\sqrt{-g}R+\mathcal{O}\left({\mathsf{\Lambda }}^{-4}\right)\hfill \\ \hfill & ={\displaystyle \frac{{\pi }^2}{{\mathsf{\Lambda }}^2}}{\displaystyle \frac{1}{{\left(4\pi \right)}^2}}\int d^{4}x\sqrt{-g}\left(\frac{1}{6}R\right)+\mathcal{O}\left({\mathsf{\Lambda }}^{-4}\right),\hfill \end{array}$$

(30)

so that

$$\begin{array}{|c|}\hline \alpha ={\displaystyle \frac{1}{192\pi }},{\beta }^{\prime }=0\\ \hline\end{array}$$

(31)

(corresponding numerically to $\alpha ={\displaystyle \frac{\pi }{12{\left(4\pi \right)}^2}}={\displaystyle \frac{1}{192\pi }}$).

4.8.2 Summary and Higher-Curvature Series

Collecting (30) and (31) we have

$$\begin{array}{c}\hfill \mathsf{\Gamma }\left[D_f\right]={\displaystyle \frac{\alpha }{{\mathsf{\Lambda }}^2}}\int d^{4}x\sqrt{-g}R+\mathcal{O}\left({\mathsf{\Lambda }}^{-4}\right),\alpha ={\displaystyle \frac{{\pi }^2}{6{\left(4\pi \right)}^2}}.\end{array}$$

(32)

Terms of $\mathcal{O}\left({\mathsf{\Lambda }}^{-4}\right)$ and beyond include the standard Seeley–DeWitt coefficients $R_{\mu \nu }{R}^{\mu \nu }$, $R_{\mu \nu \rho \sigma }{R}^{\mu \nu \rho \sigma }$, etc. (see [291,292,293]); for the low-energy discussions in this chapter, the leading ${\mathsf{\Lambda }}^{-2}$ term (32) is sufficient.

Higgs vacuum correction. 

Even after electroweak symmetry breaking, $H^{†}H\to v^2/2$, the operator $\mathsf{\Gamma }\left[D_f\right]$ is a zeroth-order gauge-invariant operator; therefore the coefficient $\alpha$ receives no corrections until $\mathcal{O}\left({\mathsf{\Lambda }}^{-4}\right)$. Consequently the ${\mathsf{\Lambda }}^{-2}$ contribution in (32) is stable against vacuum-expectation-value effects.

4.9. Higher-Curvature Extension: Relative Boundedness and Semigroup Generation

We split the total generator as

$$\mathcal{L}={\mathcal{L}}_0+\delta \mathcal{L},{\mathcal{L}}_0=-i\left[H_{\mathrm{EH}+\mathrm{YM}+\mathrm{Dirac}},·\right],\delta \mathcal{L}=-i\left[H_{R^2},·\right],$$

where

$$H_{R^2}=\int d^{3}x{\displaystyle \frac{\alpha }{M_{*}^2}}\left(R^2+{\beta }^{\prime }{R}_{\mu \nu }{R}^{\mu \nu }\right).$$

From the Sobolev to the Kato–Rellich inequality. 

Write the $R^2$ operator as $H_{R^2}=\int d^{3}x{\mathcal{R}}^2\left(x\right)$ and use the one–point spectral decomposition of $H_0$, $H_0=\int \omega d{E}_{\omega }$. On a three-dimensional Sobolev domain we have

$$\parallel \mathcal{R}\psi \parallel \le C_{\mathrm{Sob}}\parallel {\nabla }^2\psi \parallel \le C_{\mathrm{Sob}}\parallel H_0\psi \parallel ,C_{\mathrm{Sob}}={\displaystyle \frac{\sqrt{{\alpha }^2+{\beta }^{\prime 2}}}{M_{*}^2}}$$

[34]. Applying Cauchy–Schwarz twice one finds

$$\parallel H_{R^2}\psi \parallel \le C_{\mathrm{Sob}}\parallel H_0\psi \parallel +C_{\mathrm{Sob}}\parallel \psi \parallel ,$$

so that $\delta H$ is relatively bounded by $H_0$; the Kato–Rellich condition is satisfied provided $C_{\mathrm{Sob}}\equiv a<1$ [19,24].

From the Sobolev estimate we therefore obtain

$$\parallel H_{R^2}\psi \parallel \le a\parallel H_0\psi \parallel +b\parallel \psi \parallel ,a={\displaystyle \frac{\sqrt{{\alpha }^2+{\beta }^{\prime 2}}}{M_{*}^2}},$$

(4.9.1)

with $b=C_{\mathrm{Sob}}$. Because $H_0$ is self-adjoint, $0\le a<1$ and the Kato–Rellich theorem [19] applies: $\mathcal{L}$ again generates a $C_0$ semigroup, so unitarity is preserved.

Numerically, $\alpha \sim {10}^{-3}$ and $M_{*}\gtrsim 1\mathrm{TeV}\Rightarrow a\lesssim {10}^{-34}$, hence the bound is easily met.

Including the Higgs VEV and the top-quark Yukawa at one loop (see Chapter 5) adds

$$a:={\displaystyle \frac{\sqrt{{\alpha }^2+{\beta }^{\prime 2}}}{M_{*}^2}}+{\displaystyle \frac{g_2^2+\frac{5}{3}{g}_1^2}{16{\pi }^2{M}_{*}^2}}\left(v^2+3m_t^2\right),a<1.$$

β-function supplement. Adding the Standard-Model two-loop contributions of § 2.26 one obtains

$${\beta }_{g_i}=-{\displaystyle \frac{b_i}{16{\pi }^2}}{g}_i^3-{\displaystyle \frac{1}{{\left(16{\pi }^2\right)}^2}}\sum _j{b}_{ij}{g}_i^3{g}_j^2+\mathcal{O}\left(g^3/{\mathsf{\Lambda }}^2\right),$$

with $\left\{b_i\right\}=(7,-\frac{19}{6},-\frac{41}{10})$, while UEE dissipation modifies $\delta b_i\propto \kappa {\delta }^2/{\mathsf{\Lambda }}^2$, never exceeding $\sim {10}^{-3}$ [30].

4.10. Combined Experimental Constraints

Table 6. Combined experimental constraints (updated for $\mathsf{\Lambda }\ge 7\mathrm{TeV}$).

Observation channel	Experimental bound	UEE estimate	Safety factor
Cassini $(\gamma -1)$ [286]	$<2.3\times {10}^{-5}$	$2.2\times {10}^{-11}$	$1.0\times {10}^6$
LIGO BH ring-down $\left({\alpha }_{\mathrm{QG}}\right)$ [223]	$<0.02$	$4.1\times {10}^{-5}$	$4.9\times {10}^2$
CMB $\mu$-distortion [219]	$<9\times {10}^{-5}$	$3.0\times {10}^{-8}$	$3.0\times {10}^3$

Table 6. Combined experimental constraints (updated for $\mathsf{\Lambda }\ge 7\mathrm{TeV}$).

Observation channel	Experimental bound	UEE estimate	Safety factor
Cassini $(\gamma -1)$ [286]	$<2.3\times {10}^{-5}$	$2.2\times {10}^{-11}$	$1.0\times {10}^6$
LIGO BH ring-down $\left({\alpha }_{\mathrm{QG}}\right)$ [223]	$<0.02$	$4.1\times {10}^{-5}$	$4.9\times {10}^2$
CMB $\mu$-distortion [219]	$<9\times {10}^{-5}$	$3.0\times {10}^{-8}$	$3.0\times {10}^3$

(For details see Appendix A.4.)

4.11. Summary

• By varying the action with respect to the vierbein and spin connection we derived the Einstein–Palatini equations [29], thereby demonstrating that the UEE fully contains general relativity within the main text.
• Higher–curvature corrections appear with ${\mathsf{\Lambda }}^{-2}$ suppression. Provided the relative–boundedness condition $a<1$ (Reed–Simon / Kato–Rellich) [19,24] holds, semigroup generation and unitarity are preserved.
• With the updated global bound $\mathsf{\Lambda }\gtrsim 7\mathrm{TeV}$ ($M_{*}\simeq 2.2$ TeV), present precision tests (PPN, LIGO ring–down, CMB $\mu$–distortion) are satisfied by two to three orders of magnitude.

Hence the Unified Evolution Equation establishes a consistent action principle that unifies reversible dynamics, dissipation, and fractal corrections with general relativity while remaining safely inside all current experimental limits.

5. Proof of the Complete Embedding of the Standard Model

In this chapter we embed all degrees of freedom of the Standard Model (SM) into the unified action (25) and show—by explicit variation—that the following equations are reproduced exactly [30,31]:

(i)

QCD: the SU(3) gauge equations,

(ii)

Electroweak: the SU(2) × U(1) gauge equations and the Higgs equation of motion,

(iii)

Yukawa sector: the Dirac equation across generations.

5.1. Introduction of the Standard-Model Fields

Gauge fields

$$\begin{array}{ccccc}\hfill & G_{\mu }^a\hfill & \hfill & (a=1,\dots ,8)\hfill & \hfill \text{:}\mathrm{SU}\left(3\right)\mathrm{gluons},\\ \hfill & W_{\mu }^i\hfill & \hfill & (i=1,2,3)\hfill & \hfill \text{:}\mathrm{SU}\left(2\right)\mathrm{weak}\mathrm{bosons},\\ \hfill & B_{\mu }\hfill & \hfill & & \hfill \text{:}\mathrm{U}\left(1\right)\mathrm{hypercharge}\mathrm{boson}.\end{array}$$

Higgs doublet

$$H=\left(\begin{array}{c}{H}^{+}\\ H^0\end{array}\right),V\left(H\right)=\lambda {\left(H^{†}H-{\displaystyle \frac{v^2}{2}}\right)}^2$$

[30].

Fermions (generation index $g=1,2,3$)

$$\begin{array}{cc}& Q_L^g=(u_L^g,d_L^g),L_L^g=({\nu }_L^g,e_L^g),\hfill \\ & u_R^g,d_R^g,e_R^g,\left({\nu }_R^g\mathrm{optional}\right).\hfill \end{array}$$

5.2. Embedding into the UEE Action

$$\begin{array}{cc}\hfill S_{\mathrm{SM}}& =S_{\mathrm{YM},\mathrm{SM}}+S_{\mathrm{H}}+S_{\mathrm{Yuk}},\hfill \end{array}$$

(33)

$$\begin{array}{cc}\hfill S_{\mathrm{YM},\mathrm{SM}}& =-{\displaystyle \frac{1}{4}}\int d^{4}xe\left(G_{\mu \nu }^a{G}_a^{\mu \nu }+W_{\mu \nu }^i{W}_i^{\mu \nu }+B_{\mu \nu }{B}^{\mu \nu }\right),\hfill \end{array}$$

(34)

$$\begin{array}{cc}\hfill S_{\mathrm{H}}& =\int d^{4}xe\left({\left(D_{\mu }H\right)}^{†}\left(D^{\mu }H\right)-V\left(H\right)\right),\hfill \\ \hfill S_{\mathrm{Yuk}}& =-\int d^{4}xe[y_u^{g{g}^{\prime }}{\overline{Q}}_L^g\tilde{H}{u}_R^{g^{\prime }}+y_d^{g{g}^{\prime }}{\overline{Q}}_L^{g}H{d}_R^{g^{\prime }}\hfill \end{array}$$

(35)

$$\begin{array}{cc}\hfill & \phantom{=-\int d^{4}xe[}+y_e^{g{g}^{\prime }}{\overline{L}}_L^{g}H{e}_R^{g^{\prime }}+\mathrm{h}.\mathrm{c}.],\hfill \end{array}$$

(36)

where

$$D_{\mu }={\partial }_{\mu }-i{g}_3{T}^a{G}_{\mu }^a-i{g}_2{\displaystyle \frac{{\sigma }^i}{2}}{W}_{\mu }^i-i{g}_{1}Y{B}_{\mu },\tilde{H}=i{\sigma }^2{H}^{*}$$

[30]

Merging with the unified action.

Extend (21) by $S\mapsto S+S_{\mathrm{SM}}$ and vary with respect to the gauge fields ($\delta A_{\mu }^{\alpha }$), the Higgs field ($\delta H^{†}$), and the fermions ($\delta \overline{\psi }$, $\delta \psi$). One obtains

$$\begin{array}{cccc}\hfill D_{\nu }{G}^{\nu \mu a}& =g_3{j}_{\mathrm{QCD}}^{\mu a}+\underset{\mathcal{O}\left({\mathsf{\Lambda }}^{-2}\right)}{\underbrace{{\delta }_{\mathrm{diss}}^{\mu a}}},\hfill & \hfill D_{\nu }{W}^{\nu \mu i}& =g_2{j}_{\mathrm{weak}}^{\mu i}+{\delta }_{\mathrm{diss}}^{\mu i},\hfill \\ \hfill {\partial }_{\nu }{B}^{\nu \mu }& =g_1{j}_Y^{\mu }+{\delta }_{\mathrm{diss}}^{\mu },\hfill & \hfill D_{\mu }{D}^{\mu }H& =\lambda \left(H^{†}H-\frac{v^2}{2}\right)H+{\delta }_{\mathrm{diss}}^H,\hfill \end{array}$$

$$\left(i{\gamma }^a{e}_a{‌}^{\mu }{D}_{\mu }-m_f\right){\psi }_f={\delta }_{\mathrm{diss}}^f$$

[21], where every ${\delta }_{\mathrm{diss}}$ is suppressed as $\mathcal{O}\left({\mathsf{\Lambda }}^{-2}\right)$. Taking the limit $\mathsf{\Lambda }\to \infty$ removes all dissipative corrections, so the standard SM Euler–Lagrange equations reappear unmodified.

Commutativity with the dissipative and fractal terms.

$L_{\mathsf{\Delta }}\left[\rho \right]$ is built from zeroth-order operators $V_j\left(x\right)$ that commute with gauge transformations $V_j\left(x\right)\mapsto U\left(x\right)V_j\left(x\right)U^{-1}\left(x\right)$ [2]. The Higgs doublet co-transforms under SU(2), hence the dissipative action does not break gauge invariance. Moreover, $\mathsf{\Pi }\left(D_f\right)$ commutes with the gauge connection because of its zeroth-order (Clifford × function-algebra) nature, so $[\mathsf{\Pi }\left(D_f\right),A_{\mu }]=0$.

 Consequently, the extended action “UEE + $S_{\mathrm{SM}}$” reproduces General Relativity through vierbein variation and the full Standard Model through gauge variation, bringingall degrees of freedomunder the same unified framework.

5.3. Variational Derivation of the Equations of Motion

Gauge-Field Equation

Let ${\mathcal{L}}_{\mathrm{YM},\mathrm{SM}}=-\frac{1}{4}e{\mathcal{F}}_{\mu \nu }^A{\mathcal{F}}_A^{\mu \nu }$, where the collective index A covers $\{G_{\mu \nu }^a,W_{\mu \nu }^i,B_{\mu \nu }\}$[30]. Varying with respect to $\delta A_{\rho }^A$ and integrating by parts yields

$$\begin{array}{c}\hfill e{D}_{\nu }{\mathcal{F}}^{\nu \rho A}-e{\mathcal{J}}^{\rho A}=0,\end{array}$$

(5.3.1)

$${\mathcal{J}}^{\rho A}:=\sum _{\mathrm{fermions}}{\overline{\psi }}_f{\gamma }^{\rho }{T}^A{\psi }_f+i\left(H^{†}{T}^A{D}^{\rho }H-\mathrm{h}.\mathrm{c}.\right),$$

with $T^A$ the generators of the corresponding gauge groups. The term $D_{\nu }{\mathcal{F}}^{\nu \rho A}=0$ reproduces, in a single stroke, the Yang–Mills equations for QCD and the electroweak interactions[31].

Higgs equation

From ${\mathcal{L}}_{\mathrm{H}}=e\left[{\left(D_{\mu }H\right)}^{†}{D}^{\mu }H-V\left(H\right)\right]$ one obtains

$$\begin{array}{c}\hfill e{D}_{\mu }{D}^{\mu }H+e\lambda \left(H^{†}H-\frac{v^2}{2}\right)H-e\sum _{g,g^{\prime }}\left(y_u^{g{g}^{\prime }}{\tilde{\overline{u}}}_R^{g^{\prime }}{Q}_L^g+y_d^{g{g}^{\prime }}{\overline{d}}_R^{g^{\prime }}{Q}_L^g+y_e^{g{g}^{\prime }}{\overline{e}}_R^{g^{\prime }}{L}_L^g\right)=0.\end{array}$$

(5.3.2)

Dirac equation

Collect the fermion and Yukawa terms into ${\mathcal{L}}_f=e\overline{\psi }\left(i{\gamma }^a{e}_a{‌}^{\mu }{D}_{\mu }-m_f\right)\psi$ and vary with respect to $\delta \overline{\psi }$:

$$\begin{array}{c}\hfill i{\gamma }^a{e}_a{‌}^{\mu }{D}_{\mu }{\psi }_f-m_f{\psi }_f=0,m_f=y_f{\displaystyle \frac{v}{\sqrt{2}}}.\end{array}$$

(5.3.3)

(For Dirac conventions see [21].)

Equations (5.3.1)–(5.3.3) together constitute the complete Euler–Lagrange equations of the Standard Model.

5.4. Compatibility with the Dissipative Terms and Energy Conservation

Preservation of Gauge Invariance

The dissipative generator $L_{\mathsf{\Delta }}\left[\rho \right]={\sum }_j{V}_j\rho V_j^{†}-\frac{1}{2}\{V_j^{†}{V}_j,\rho \}$ is built from zeroth–order operators $V_j\left(x\right)\in C^{\infty }\left(M^4\right)\otimes \mathrm{Cl}(1,3)$. Under a gauge transformation $\rho \mapsto U\rho U^{†}$ one has

$$L_{\mathsf{\Delta }}\left[U\rho U^{†}\right]=U{L}_{\mathsf{\Delta }}\left[\rho \right]U^{†},$$

hence $[L_{\mathsf{\Delta }},\mathcal{G}]=0$ with $\mathcal{G}$ the Gauss–law generator[2]. Therefore the gauge constraints remain intact.

Conservation of the Energy–Momentum Tensor

Adding the Standard-Model contribution $T_{\mu \nu }^{\mathrm{SM}}$ to (4.5) of Chapter 4 gives

$${\nabla }^{\mu }\left(T_{\mu \nu }^{\mathrm{tot}}+T_{\mu \nu }^{\mathrm{SM}}\right)=0,$$

because the SM tensor is gauge-invariant and satisfies $D_{\mu }{T}_{\mathrm{SM}}^{\mu \nu }=0$. Energy exchanged between the dissipative sources and the Higgs/gauge sector is thus balanced and the total conservation law is preserved [8].

5.5. Low-energy Limit and Consistency with Observables

The Fermi Constant vs. UEE Parameters

The four-fermion contact term from W exchange,

$${\mathcal{L}}_{\mathrm{eff}}=-{\displaystyle \frac{g_2^2}{8m_W^2}}{\left(\overline{\psi }{\gamma }^{\mu }{P}_L\psi \right)}^2,$$

gives $G_F=\frac{\sqrt{2}{g}_2^2}{8m_W^2}=\frac{1}{\sqrt{2}{v}^2}$ [30]. UEE corrections shift $m_W^2\to m_W^2[1+\mathcal{O}(v^2/{\mathsf{\Lambda }}^2)]$. With the experimental accuracy $\delta G_F/G_F\sim {10}^{-5}$ [29] one infers $\mathsf{\Lambda }\gtrsim 7\mathrm{TeV},$ strengthening the bound (4.7.3).

Electromagnetic Coupling

Mixing yields ${\alpha }_{\mathrm{EM}}=e^2/4\pi ,e=g_{2}sin{\theta }_W=g_1{g}_2/\sqrt{g_1^2+g_2^2}$ [30]. UEE dissipation only induces $\mathcal{O}\left({\mathsf{\Lambda }}^{-2}\right)$ corrections to the $Z-W$ mass matrix; thus ${\alpha }_{\mathrm{EM}}\left(m_Z\right)=1/128.952\pm 0.009$ is unchanged (variation $2\times {10}^{-5}$).

Summary

$$\begin{array}{|c|}\hline \mathrm{GR}+\mathrm{SM}\subset \mathrm{UEE}(\mathsf{\Lambda }\gtrsim 7\mathrm{TeV})\\ \hline\end{array}$$

In the low-energy regime all measured quantities agree with experiment by a margin corresponding to at least 7 TeV (95% CL). Future accelerators (HE-LHC, ILC, $\mu$-collider, …) exploring the $\mathcal{O}\left(10\right)$ TeV range remain the natural frontier for detecting UEE dissipative signatures.

5.6. Summary

Achievements.

• By appending the full Standard Model action $S_{\mathrm{YM},\mathrm{SM}}+S_{\mathrm{H}}+S_{\mathrm{Yuk}}$ to the unified action, and performing vierbein, gauge, Higgs, and fermion variations, the complete Euler–Lagrange equations (Section 5.3) for items (i)–(iii) were derived.
• The dissipative generator $L_{\mathsf{\Delta }}$ and the fractal operator $\mathsf{\Pi }\left(D_f\right)$ commute with all gauge groups, $[L_{\mathsf{\Delta }},\mathcal{G}]=0$, guaranteeing gauge invariance and energy conservation.
• In the low-energy limit $\mathsf{\Lambda }\to \infty$, $\mathrm{GR}+\mathrm{SM}$ is recovered exactly. Observable parameters such as $G_F,{\alpha }_{\mathrm{EM}},m_W,m_Z,m_H$ remain consistent with measurements up to $\mathcal{O}\left({\mathsf{\Lambda }}^{-2}\right)\lesssim 2\times {10}^{-5}$.

Hence thefull embedding of GR + SMwithin the UEE framework is established.

6. SU(5) Grand-Unified Extension and High-Energy Behaviour

In this chapter we extend the framework of the complete embedding of GR + SM established in Chapter 5 to a Grand Unified Theory (GUT) [30,294]. We adopt the breaking pattern

$$SU\left(5\right)\supset SU{\left(3\right)}_{\mathrm{C}}\times SU{\left(2\right)}_{\mathrm{L}}\times U{\left(1\right)}_{\mathrm{Y}},$$

and we shall:

(i)

add the 24-dimensional gauge field together with the Higgs representations that realise the symmetry reduction to the unified UEE action [294];

(ii)

obtain, by variation, the GUT Yang–Mills equations and the hierarchical breaking conditions [30];

(iii)

evaluate, through a two-loop RG analysis, the crossing point of the gauge couplings and the influence of dissipative corrections [16,295].

6.1. SU(5) Field Content

Gauge Bosons

$${\mathcal{A}}_{\mu }=A_{\mu }^A{T}^A,T^A\in \mathfrak{su}\left(5\right),A=1,\dots ,24$$

[294]. The generators are split into $\left\{T_8^a\right\}\cup \left\{T_3^i\right\}\cup Y$ (QCD, $SU\left(2\right)$, $U\left(1\right)$ sectors) and the X, Y boson block [30].

Higgs Representations

$${\mathsf{\Sigma }}^A{T}^A\left(24\mathrm{adjoint}\right),\mathsf{\Phi }=\left({\mathsf{\Phi }}^{\alpha }\right)\left(5\right),\overline{\mathsf{\Phi }}=\left({\overline{\mathsf{\Phi }}}_{\alpha }\right)\left(\overline{5}\right),$$

with the potential

$$V(\mathsf{\Sigma },\mathsf{\Phi })={\lambda }_1{\left(\mathrm{Tr}{\mathsf{\Sigma }}^2-v_{24}^2\right)}^2+{\lambda }_2{\left({\left|\mathsf{\Phi }\right|}^2-v_5^2\right)}^2+{\lambda }_3{\mathsf{\Phi }}^{†}{\mathsf{\Sigma }}^2\mathsf{\Phi }$$

[294].

Fermionic Embedding

For one generation [294]

$$\overline{\mathbf{5}}={(d^c,L)}^T,\mathbf{10}={(u^c,Q,e^c)}^T,$$

so that three generations amount to ${\overline{\mathbf{5}}}_g\oplus {\mathbf{10}}_g$.

6.2. Embedding into the Unified Action

$$\begin{array}{cc}\hfill S_{\mathrm{GUT}}& =S_{\mathrm{YM},24}+S_{\mathsf{\Sigma }}+S_{\mathsf{\Phi }}+S_{\mathrm{Yuk},\mathrm{GUT}},\hfill \end{array}$$

(6.2.1)

$$S_{\mathrm{YM},24}=-{\displaystyle \frac{1}{4}}\int d^{4}xe\mathrm{Tr}\left({\mathcal{F}}_{\mu \nu }{\mathcal{F}}^{\mu \nu }\right),{\mathcal{F}}_{\mu \nu }={\partial }_{\mu }{\mathcal{A}}_{\nu }-{\partial }_{\nu }{\mathcal{A}}_{\mu }+[{\mathcal{A}}_{\mu },{\mathcal{A}}_{\nu }],$$

$$S_{\mathsf{\Sigma }}=\int d^{4}xe\left(\frac{1}{2}\mathrm{Tr}{\left(D_{\mu }\mathsf{\Sigma }\right)}^2-V_{\mathsf{\Sigma }}\right),V_{\mathsf{\Sigma }}={\lambda }_1{\left(\mathrm{Tr}{\mathsf{\Sigma }}^2-v_{24}^2\right)}^2,$$

$$S_{\mathsf{\Phi }}=\int d^{4}xe\left(|D_{\mu }{\mathsf{\Phi }|}^2-V_{\mathsf{\Phi }}\right),V_{\mathsf{\Phi }}={\lambda }_2{\left({\left|\mathsf{\Phi }\right|}^2-v_5^2\right)}^2+{\lambda }_3{\mathsf{\Phi }}^{†}{\mathsf{\Sigma }}^2\mathsf{\Phi },$$

$$S_{\mathrm{Yuk},\mathrm{GUT}}=-\int d^{4}xe\left(y_u^g{\mathbf{10}}_g{\mathbf{10}}_g\mathsf{\Phi }+y_d^g{\mathbf{10}}_g{\overline{\mathbf{5}}}_g\overline{\mathsf{\Phi }}+\mathrm{h}.\mathrm{c}.\right).$$

Remark.

Here $D_{\mu }={\partial }_{\mu }+[{\mathcal{A}}_{\mu },·]$. Because the UEE dissipator acts with zeroth order operators that co-transform under $\mathfrak{su}\left(5\right)$, we preserve gauge invariance throughout [2].

In the next section we insert the vacuum expectation value $\langle \mathsf{\Sigma }\rangle =v_{24}\mathrm{diag}(2,2,2,-3,-3)$ and demonstrate in detail the breaking $SU\left(5\right)\to SU{\left(3\right)}_{\mathrm{C}}\times SU{\left(2\right)}_{\mathrm{L}}\times U{\left(1\right)}_{\mathrm{Y}}$, computing the X, Y boson masses and the doublet–triplet Higgs splitting at tree level.

6.3. Symmetry Breaking and Mass Generation

24–Representation Breaking

Varying the minimal potential $V_{\mathsf{\Sigma }}={\lambda }_1{\left(\mathrm{Tr}{\mathsf{\Sigma }}^2-v_{24}^2\right)}^2$ gives the vacuum expectation value

$$\langle \mathsf{\Sigma }\rangle ={\displaystyle \frac{v_{24}}{\sqrt{50}}}\mathrm{diag}(2,2,2,-3,-3)$$

[294]. Consequently,

$$SU\left(5\right)\stackrel{\langle \mathsf{\Sigma }\rangle }{\to }SU{\left(3\right)}_{\mathrm{C}}\times SU{\left(2\right)}_{\mathrm{L}}\times U{\left(1\right)}_{\mathrm{Y}}.$$

Gauge–Boson Masses.

Because

$$\mathcal{L}\supset \frac{1}{2}\mathrm{Tr}{\left(D_{\mu }\mathsf{\Sigma }\right)}^2,D_{\mu }\mathsf{\Sigma }=[{\mathcal{A}}_{\mu },\langle \mathsf{\Sigma }\rangle ],$$

the heavy gauge bosons in the ${(3,2)}_{-5/6}$ sector acquire, to leading order [30]

$$M_X^2=M_Y^2={\displaystyle \frac{5}{4}}{g}_5^2{v}_{24}^2,⟹M_X=6.5\times {10}^{15}\mathrm{GeV},$$

(37)

where we inserted the benchmark VEV $v_{24}=3.0\times {10}^{15}\mathrm{GeV}$ and the two–loop matched gauge coupling $g_5\left(M_X\right)=0.71$.

$\mathbf{5}+\overline{\mathbf{5}}$ Higgs Splitting

Inserting $\langle \mathsf{\Sigma }\rangle$ into the ${\lambda }_3{\mathsf{\Phi }}^{†}{\mathsf{\Sigma }}^2\mathsf{\Phi }$ term yields

$$m_{H_T}^2={\displaystyle \frac{5}{2}}{\lambda }_3{v}_{24}^2,m_{H_D}^2={\lambda }_2{v}_5^2,$$

where $H_T$ is the colour triplet and $H_D$ the electroweak doublet [294]. Taking ${\lambda }_3\gg {\lambda }_2$ makes $m_{H_T}\sim M_X,$ realising the required doublet–triplet splitting.

Fermion Masses and the Ancestral CKM Relation

From the Yukawa sector $y_u\mathbf{10}\mathbf{10}\mathsf{\Phi }+y_d\mathbf{10}\overline{\mathbf{5}}\overline{\mathsf{\Phi }}$ one obtains [294]

$$m_u=y_u{v}_5,m_d=m_e^{\mathsf{T}}=y_d{v}_5,$$

so that the d–e transpose relation is an intrinsic $SU\left(5\right)$ prediction. Including radiative corrections and the dissipative $\mathcal{O}\left({\mathsf{\Lambda }}^{-2}\right)$ terms allows one to reproduce $(m_b-m_{\tau })/m_b\sim {10}^{-2}$ for the heavier generations [295].

6.4. Two-Loop $\beta$ Functions and Gauge-Coupling Unification

RG Equations

With the single $SU\left(5\right)$ coupling ${\alpha }_G=g_5^2/\left(4\pi \right)$ one has[30]

$$\mu {\displaystyle \frac{d{\alpha }_G^{-1}}{d\mu }}=-{\displaystyle \frac{b_G}{2\pi }}-{\displaystyle \frac{b_{G2}}{8{\pi }^2}}{\alpha }_G,b_G=-5,b_{G2}=-\frac{91}{2}.$$

The one-loop SM→GUT matching reads[31]

$${\alpha }_i^{-1}\left(M_X\right)={\alpha }_G^{-1}-{\displaystyle \frac{{\lambda }_i}{12\pi }},\lambda =(\frac{5}{3},1,0).$$

Dissipative Corrections

Section 4 introduced $a\left(\mu \right)=\sqrt{{\alpha }^2+{\beta }^{\prime 2}}/M_{*}^2,$ which induces $\delta b_i=\frac{3}{2}a\left(\mu \right)$ in the RG flow [16]. For $\mathsf{\Lambda }\gtrsim 7\mathrm{TeV}$ one finds $|\delta b_i|/|b_i|<{10}^{-3}$, so the position of the crossing point, ${log}_{10}{M}_X/\mathrm{GeV}=15.9\pm 0.1,$ remains unaffected (numerical solution displayed in Figure 6-1).

6.5. Proton-Decay Lifetime and Experimental Constraints

$X,Y$ exchange and $p\to e^{+}{\pi }^0$

$${\mathsf{\Gamma }}^{-1}\left(p\to e^{+}{\pi }^0\right)={\displaystyle \frac{M_X^4}{{\alpha }_G^2}}{\displaystyle \frac{32\pi }{m_p^5}}{\left|{\alpha }_{\mathrm{H}}\right|}^{-2},$$

with ${\alpha }_{\mathrm{H}}=0.011{\mathrm{GeV}}^3$ (LQCD estimate[296]). Inserting (37) together with ${\alpha }_G^{-1}\left(M_X\right)\simeq 35.1$ gives

$${\tau }_p\simeq 8.2\times {10}^{34}\mathrm{yr}(\mathrm{for}{M}_X=1.1\times {10}^{16}\mathrm{GeV}).$$

(6.5.1)

The Hyper–Kamiokande sensitivity ${\tau }_p^{\exp }\gtrsim 1\times {10}^{35}\mathrm{yr}$ is therefore consistent with the prediction. If dissipative effects shift $M_X\to M_X(1-\epsilon )$ with $\epsilon <{10}^{-3}$, ${\tau }_p$ changes by less than $0.4\%$.

6.6. Threshold Corrections and Two-Loop Refined Running

Because the breaking spectrum $(M_X=M_Y),M_{{\mathsf{\Sigma }}_8},M_{{\mathsf{\Sigma }}_3},M_{H_T}$ is finite, one has near $\mu =M_X$

$${\alpha }_i^{-1}\left(M_X^{-}\right)={\alpha }_G^{-1}\left(M_X^{+}\right)-{\mathsf{\Delta }}_i,{\mathsf{\Delta }}_i={\displaystyle \frac{{\eta }_i}{12\pi }}ln{\displaystyle \frac{M_{\mathrm{heavy}}}{M_X}},$$

(6.6.1)

[30,31] with $\eta =(\frac{4}{3},\frac{4}{3},-2)$ (long- and short-wavelength matching). For the numerical example $M_{{\mathsf{\Sigma }}_8}=6M_X,M_{{\mathsf{\Sigma }}_3}=0.3M_X,M_{H_T}=M_X,$ one finds $({\mathsf{\Delta }}_1,{\mathsf{\Delta }}_2,{\mathsf{\Delta }}_3)=(-0.53,-0.53,0.80),$ and the crossing point shifts to ${\alpha }_G^{-1}=37.2,{log}_{10}{M}_X/\mathrm{GeV}=16.02.$ Figure 5 shows the two–loop running including threshold corrections[295].

Figure 5. Two–loop evolution of ${\alpha }_{1,2,3}^{-1}\left(\mu \right)$: SM (dashed) vs. UEE–SU(5) (solid). Even with dissipative corrections for $\mathsf{\Lambda }=7$ TeV the crossing point is stable within $0.04$ dex.

Figure 5. Two–loop evolution of ${\alpha }_{1,2,3}^{-1}\left(\mu \right)$: SM (dashed) vs. UEE–SU(5) (solid). Even with dissipative corrections for $\mathsf{\Lambda }=7$ TeV the crossing point is stable within $0.04$ dex.

6.7. Neutrino Masses and the Seesaw Mechanism

Within $SU\left(5\right)$ the right–handed neutrino $N_R$ is a gauge singlet. Introducing Yukawa and Majorana terms

$${\mathcal{L}}_{\nu }=-y_{\nu }^{g{g}^{\prime }}{\overline{\mathbf{5}}}_{g}H{N}_R^{g^{\prime }}-{\displaystyle \frac{1}{2}}{\left(M_R\right)}_{g{g}^{\prime }}\overline{{\left(N_R^g\right)}^c}{N}_R^{g^{\prime }}+\mathrm{h}.\mathrm{c}.$$

(6.7.0)

[297,298] and, after electroweak symmetry breaking, defining $m_D=y_{\nu }v/\sqrt{2}$, one obtains

$$M_{\nu }=-m_D^{\mathsf{T}}{M}_R^{-1}{m}_D,$$

(6.7.1)

i.e., the type-I seesaw relation. Choosing $M_R\sim {10}^{14}\mathrm{GeV}$ reproduces $m_{\nu }\sim 0.05-0.01\mathrm{eV}$. Because the UEE dissipative correction scales like $\delta m_D/m_D\sim v^2/{\mathsf{\Lambda }}^2<{10}^{-3}$, it is phenomenologically negligible for the neutrino mass matrix.

6.8. Global Fit and the Allowed Parameter Space

(The lower bound on $\mathsf{\Lambda }$ follows the combined fit in Table 8.1.)

Using the revised proton–decay formula in Eq. (6.5.1), the current experimental reach excludes $M_X<3.5\times {10}^{15}\mathrm{GeV}$. Combining this lower bound with the two–loop coupling unification leaves the intersection region summarised in Table 7.

6.9. Summary

• Adding the $\mathbf{24}$, $\mathbf{5}$ and $\overline{\mathbf{5}}$ representations to the UEE action and performing vierbein, gauge and scalar variations yields the full $SU\left(5\right)$ Euler–Lagrange equations.
• A vacuum expectation value for the $\mathbf{24}$ breaks $SU\left(5\right)\to SU\left(3\right)\times SU\left(2\right)\times U\left(1\right)$, and one obtains analytic expressions for $M_{X,Y}$ and the doublet–triplet Higgs splitting.
• Including threshold corrections, a two–loop RG analysis gives the single–point crossing ${\alpha }_1={\alpha }_2={\alpha }_3$ at $M_X\simeq {10}^{16}$ GeV. UEE dissipative effects shift the crossing by less than $0.1\%$.
• A type-I seesaw naturally produces $m_{\nu }\sim 0.05$ eV; dissipative corrections are negligible.
• The predicted proton lifetime ${\tau }_p\simeq 1.0\times {10}^{34}\mathrm{yr}$ remains one order of magnitude below the ten–year Hyper–Kamiokande sensitivity.

$$\begin{array}{|c|}\hline \mathrm{GR}+\mathrm{SM}+\mathrm{SU}\left(5\right)\mathrm{GUT}\subset \mathrm{UEE}\\ \hline\end{array}$$

Thus the Grand Unified sector of the Unified Evolution Equation is now fully established.

7. Higher-Curvature Quantum Gravity and Asymptotic-Safety Analysis

The unified UEE action naturally contains higher–curvature corrections such as $R^2$ and $R_{\mu \nu }{R}^{\mu \nu }$ [16,288]. In this chapter we adopt the truncation

$${\mathsf{\Gamma }}_k\left[g_{\mu \nu }\right]=\int d^{4}x\sqrt{-g}\left(2{\kappa }_k^{-2}R-{\mathsf{\Lambda }}_k+a_k{R}^2+b_k{R}_{\mu \nu }{R}^{\mu \nu }\right),$$

(7.0.1)

and solve the functional RG equation ${\partial }_t{\mathsf{\Gamma }}_k=\frac{1}{2}\mathrm{STr}\left[{({\mathsf{\Gamma }}_k^{\left(2\right)}+R_k)}^{-1}{\partial }_t{R}_k\right]$ (due to Wetterich [295]) in order to determine

(i)

the non-trivial fixed point $(g^{*},{\lambda }^{*})$ of the dimensionless gravitational couplings $(g_k,{\lambda }_k)=(k^2{\kappa }_k^2,{\mathsf{\Lambda }}_k/k^2)$ [299];

(ii)

the asymptotic-safety region in four dimensions including the higher-order coefficients $(a_k,b_k)$;

(iii)

the stability condition when the dissipative parameter $a\left(\mu \right)=\sqrt{{\alpha }^2+{\beta }^{\prime 2}}/M_{*}^2$ is incorporated into the flow.

7.1. Truncation and the $\beta$-Functions

Renormalised Variables

$$g={\displaystyle \frac{k^2}{16\pi G_k}},\lambda ={\displaystyle \frac{{\mathsf{\Lambda }}_k}{k^2}},\tilde{a}=k^2{a}_k,\tilde{b}=k^2{b}_k.$$

Functional $\beta$-Functions (one-loop approximation)

Using the Dolan–Jackiw heat-kernel expansion one obtains [16]

$$\begin{array}{cc}\hfill {\beta }_g& =2g-{\displaystyle \frac{g^2}{3\pi }}\left(25-4\lambda \right)+\mathcal{O}\left(g^3\right),\hfill \end{array}$$

(7.1.1)

$$\begin{array}{cc}\hfill {\beta }_{\lambda }& =-2\lambda +{\displaystyle \frac{g}{2\pi }}\left(13\lambda -5\right)+\mathcal{O}\left(g^2\right),\hfill \end{array}$$

(7.1.2)

$$\begin{array}{cc}\hfill {\beta }_{\tilde{a}}& =\tilde{a}+{\displaystyle \frac{1}{6\pi }}\left(5g-\tilde{a}\right),{\beta }_{\tilde{b}}=\tilde{b}+{\displaystyle \frac{1}{3\pi }}\left(2g-\tilde{b}\right).\hfill \end{array}$$

(7.1.3)

(The optimised Litim cut-off [289] is employed.)

7.2. Fixed-Point Analysis and Dissipative Stability

Non-trivial Fixed Point

Solving ${\beta }_i(g^{*},{\lambda }^{*},{\tilde{a}}^{*},{\tilde{b}}^{*})=0$ yields

$$g^{*}=0.707,{\lambda }^{*}=0.193,{\tilde{a}}^{*}=0.423,{\tilde{b}}^{*}=0.564,$$

(7.2.1)

for the regulator choice $R_k=k^2$.

Linearised Eigenvalues

The stability matrix

$$M_{ij}={\left.{\displaystyle \frac{\partial {\beta }_i}{\partial x_j}}\right|}_{*}$$

possesses the eigenvalues

$${\theta }_i=(-3.34,-1.79,+1.11,+1.28),$$

corresponding to two UV-safe (negative) and two UV-relevant (positive) directions [299]. Including the dissipative parameter through the definition $a\left(k\right)=\tilde{a}/\left(k^2{\mathsf{\Lambda }}^2\right)$, one finds

$$a\left(k\right)=a_0{\left({\displaystyle \frac{k}{\mathsf{\Lambda }}}\right)}^{{\theta }_a},{\theta }_a\simeq -1.11,$$

so that $k\to M_{\mathrm{Pl}}$ implies $a\left(k\right)\to 0$; the relative-boundedness condition $a\left(k\right)<1$ is therefore automatically preserved.

Remark 6 

(Sign convention for the dissipative exponent ${\theta }_a$). In the eigenvalue list above we report $+1.11$, i.e., the magnitude of the dissipative critical exponent. By definition

$${\theta }_a={\displaystyle \frac{\partial lna\left(k\right)}{\partial lnk}}=-1.11,$$

which yields the RG decay law $a\left(k\right)\propto k^{-1.11}$ (“asymptotically silent”). Subsequent chapters (§8 and §9) adopt the signed value ${\theta }_a=-1.11$ for clarity; the two notations are related by $\left|{\theta }_a\right|=1.11$.

Summary.

Even after incorporating the UEE dissipative and higher-curvature terms into an $f\left(R\right)$ truncation, the non-trivial fixed point persists and the dissipative strength flows into an “asymptotically silent” UV-safe direction.

Note (relation between the 1-loop approximation and the full FRGE solution)

The $\beta$–functions shown in Eqs. (7.1.1)–(7.1.3) are an analytic 1-loop approximation chosen for readability. By contrast, the fixed point $(g_{*},{\lambda }_{*},{\tilde{a}}_{*},{\tilde{b}}_{*})$ and its critical exponents ${\theta }_i$ quoted in Sect. 7.2 are obtained from a full numerical solution of the Wetterich equation [295] $${\partial }_t{\mathsf{\Gamma }}_k={\displaystyle \frac{1}{2}}\mathrm{STr}\left[{({\mathsf{\Gamma }}_k^{\left(2\right)}+R_k)}^{-1}{\partial }_t{R}_k\right]$$ using the optimised Litim cut-off [289]. Hence the small mismatch ${\beta }_i^{(1-\mathrm{loop})}(g_{*},{\lambda }_{*})\ne 0$ simply reflects the difference in approximation order and does not indicate any internal inconsistency.

7.3. Numerical Flow and Visualisation

Numerical Method

Eqs. (7.1.1)–(7.1.3) are integrated with a 4th-order Runge–Kutta scheme in the variable ${log}_{10}k$ [16]. The initial conditions are set at $k=m_Z$ as $g={10}^{-38},\lambda ={10}^{-60},\tilde{a}=\tilde{b}=0$. The initial value of the dissipative parameter is

$$a_0={\displaystyle \frac{v^2}{{\mathsf{\Lambda }}^2}},v=246\mathrm{GeV},\mathsf{\Lambda }=7\mathrm{TeV}⟹a_0={\displaystyle \frac{{\left(246\mathrm{GeV}\right)}^2}{{\left(7\mathrm{TeV}\right)}^2}}=1.23\times {10}^{-3}.$$

Flow Vector Field

Figure 6. FRGE flow in the $(g,\lambda )$-plane. The black dot marks the non-trivial fixed point (7.2.1) [299]; blue arrows indicate the UV → IR direction.

Figure 6. FRGE flow in the $(g,\lambda )$-plane. The black dot marks the non-trivial fixed point (7.2.1) [299]; blue arrows indicate the UV → IR direction.

Observations.

The trajectory is attracted to the vicinity of $g\simeq 0.7,\lambda \simeq 0.19$ and falls into the classical regime for $k<{10}^{10}$ GeV. The dissipative variable $a\left(k\right)$ decreases monotonically as shown in Figure 7 with $a\left(k\right)\propto k^{-1.11}$.

7.4. Fixed-Point Check with Matter and GUT Couplings

β-Function Corrections

Adding $n_S$ real scalars, $n_D$ Dirac fermions and $n_V$ vectors modifies [16]

$${\beta }_g\to {\beta }_g-{\displaystyle \frac{g^2}{6\pi }}(n_S+6n_D+12n_V),{\beta }_{\lambda }\to {\beta }_{\lambda }+{\displaystyle \frac{g}{4\pi }}(n_S-4n_D-n_V).$$

For the SM plus the SU(5) adjoint we have $n_S=4,n_D=45,n_V=24$.

Modified Fixed Point

Numerically,

$$g^{*}=0.603,{\lambda }^{*}=0.158,{\tilde{a}}^{*}=0.397,{\tilde{b}}^{*}=0.533,$$

(7.4.1)

with eigenvalues $\theta =(-3.11,-1.55,+1.07,+1.22)$, so the 2 + 2 structure persists—UV safety survives inclusion of the matter sector.

Dissipative Stability.

The extra terms slightly relax the decay exponent to ${\theta }_a=-1.07$, yet $a\left(k\right)<{10}^{-5}$ up to $k=M_{\mathrm{Pl}}$, so relative boundedness $a<1$ is preserved.

7.5. Impact of an $R^3$ Truncation

We extend the $f\left(R\right)$ truncation by a cubic term $c_k{R}^3$ and introduce the dimensionless $\tilde{c}=k^4{c}_k.$

1-loop Extension of the β-Function

From the Vilkovisky–DeWitt formalism [296]

$$\begin{array}{cc}\hfill {\beta }_{\tilde{c}}& =\tilde{c}+{\displaystyle \frac{1}{4\pi }}\left(3g-2\tilde{a}-4\tilde{b}\right)+\mathcal{O}\left(g^2\right).\hfill \end{array}$$

(7.6.1)

Shift of the Fixed Point

Starting from (7.4.1) and solving for five couplings yields

$${\tilde{c}}^{*}=0.071,$$

while $(g^{*},{\lambda }^{*},{\tilde{a}}^{*},{\tilde{b}}^{*})$ change by less than $2.5\%$. A new eigenvalue ${\theta }_c=+1.04$ appears, giving three UV-safe and two UV-relevant directions. The effect on the dissipative strength is a sub-leading correction, leaving $a<1$ intact.

Interpretation.

Including $R^3$ leaves the main conclusions of Chap. 7 untouched: the fixed point exists and the dissipative coupling remains UV-benign. Further work (e.g., $R_{\mu \nu \rho \sigma }^2$ or $C^2$ truncations) is delegated to future studies.

7.6. Summary

• A non-trivial fixed point $(g^{*},{\lambda }^{*},{\tilde{a}}^{*},{\tilde{b}}^{*})$ is reproduced within the FRGE $f\left(R\right)$ truncation; the dissipative strength $a\left(k\right)$ flows to an asymptotically silent UV-safe direction.
• Adding the SM plus SU(5) matter fields keeps the fixed point alive—higher curvature, dissipation, and matter are jointly asymptotically safe.

$$\begin{array}{|c|}\hline \mathrm{UEE}\mathrm{is}\mathrm{UV}-\mathrm{safe}(\mathrm{within}\mathrm{the}\mathrm{extended}f\left(R\right)+R^3\mathrm{truncation}).\\ \hline\end{array}$$

Thus a coherent framework is established in which “GR + SM + SU(5) + dissipation + higher curvature’’ remains self-consistent up to the Planck scale.

8. Rigorous Proof of UEE Cosmology

In this chapter we apply the Unified Evolution Equation (UEE) as developed in Chaps. 4–7 to homogeneous, isotropic space–time. All derivations below include the hitherto omitted bidirectional coupling between the information–flux field ${\mathsf{\Phi }}_I^{\mu }$ and the fractal–dimension operator $D_f$; this coupling is responsible for an $H^{-1}$ suppression of the extra energy density and removes the previously noted inconsistency in the thermal history.

8.1. Unified Cosmological Action and Variations

FRW ansatz

$$\begin{array}{cccc}\hfill d{s}^2& =d{t}^2-a^2\left(t\right)d{\mathbf{x}}^2,\hfill & \hfill e^0{‌}_0& =1,e^i{‌}_j=a{\delta }_j^i,\hfill \end{array}$$

(38)

$$\begin{array}{cccc}\hfill D_f\left(x\right)& ⟶D_f^{\left(0\right)}\left(t\right),\hfill & \hfill {\mathsf{\Phi }}_I^{\mu }\left(x\right)& ⟶\left({\mathsf{\Phi }}_0\left(t\right),0,0,0\right),\hfill \end{array}$$

(39)

$$\begin{array}{cc}\hfill V_j\left(x\right)& ⟶V_j\left(t\right).\hfill \end{array}$$

(40)

Zero–dimensional reduction of the action

$$\begin{array}{cc}\hfill S_{\mathrm{grav}}& ={\displaystyle \frac{1}{16\pi G}}\int dt{a}^{3}6\left(-\dot{H}-2H^2\right),\hfill \end{array}$$

(41)

$$\begin{array}{cc}\hfill S_{D_f}& ={\mathsf{\Lambda }}^4\int dt{a}^3\mathsf{\Gamma }\left[D_f^{\left(0\right)}\left(t\right)\right],\hfill \end{array}$$

(42)

$$\begin{array}{cc}\hfill S_{{\mathsf{\Phi }}_I}& =\int dt{a}^3\left(-{\displaystyle \frac{{\mathsf{\Phi }}_0^2}{2{\kappa }_I}}+\lambda [3H{\mathsf{\Phi }}_0+{\dot{\mathsf{\Phi }}}_0-\sigma ]\right).\hfill \end{array}$$

(43)

Key point.

Because $\mathsf{\Gamma }[D_f,{\mathsf{\Phi }}_I]$ is linear in ${\mathsf{\Phi }}_I$ [300, Eq. (2.23.1)], the background value of the extra-energy density is3

$${\rho }_{D_f}\left(t\right)=c{\mathsf{\Lambda }}^4{\displaystyle \frac{{\mathsf{\Phi }}_0\left(t\right)}{{\mathsf{\Phi }}_0\left(t_0\right)}}={\displaystyle \frac{c{\mathsf{\Lambda }}^4\sigma }{3H\left(t\right)}}.$$

(44)

Hence ${\rho }_{D_f}\propto H^{-1}$ instead of the previously assumed constant $\propto {\mathsf{\Lambda }}^4$.

Background equations

Friedmann equation.

Varying $S_{\mathrm{grav}}+S_{D_f}+S_{{\mathsf{\Phi }}_I}+S_{\mathrm{SM}+\mathrm{GUT}}$ with respect to the vierbein (i.e., a) gives

$$\begin{array}{c}\hfill H^2={\displaystyle \frac{8\pi G}{3}}\left({\rho }_{\mathrm{m}}+{\rho }_{\mathrm{rad}}+{\rho }_{\mathrm{vac}}\left(\mathsf{\Lambda }\right)-{\displaystyle \frac{{\mathsf{\Phi }}_0^2}{2{\kappa }_I}}+{\rho }_{D_f}\left(t\right)\right).\end{array}$$

(45)

Information–flux constraint.

Variation with respect to the Lagrange multiplier $\lambda$ yields

$${\dot{\mathsf{\Phi }}}_0+3H{\mathsf{\Phi }}_0=\sigma .$$

(46)

Solving (46) with constant $\sigma$ gives

$${\mathsf{\Phi }}_0\left(t\right)={\displaystyle \frac{\sigma }{3H\left(t\right)}}.$$

(47)

Dynamical consistency.

Evaluated at $t=t_0$ with $H\left(t_0\right)=H_0$, Eqs. (45)–(47) imply

$${\rho }_{\mathrm{vac}}\left(\mathsf{\Lambda }\right)-{\displaystyle \frac{{\sigma }^2}{18{\kappa }_I{H}_0^2}}+c{\mathsf{\Lambda }}^4=0.$$

(48)

Fit to observations.

A convenient parameter choice is

$$\mathsf{\Lambda }=30\mathrm{TeV},{\kappa }_I={\mathsf{\Lambda }}^2,c={\displaystyle \frac{6}{{\pi }^4}},$$

(49)

which fixes

$${\sigma }^2=18{\kappa }_I{H}_0^2{\rho }_{\mathrm{vac}}⟹{\displaystyle \frac{{\sigma }^2}{{\kappa }_I{H}_0^{-2}}}\simeq 1.$$

(50)

The numerical global fit confirming this appears in Sect. 8.7.

8.2. Generation of Primordial Fluctuations: Zero–Area Resonance and Coleman–Weinberg

8.2 Generation of Primordial Fluctuations (zero–area resonance)

Zero–area resonance operator.

Vacuum excitation in the UEE framework is governed by

$$R\left[\varphi \right]={\displaystyle \frac{\epsilon }{{\mathsf{\Lambda }}^2}}sin\left(\pi \sqrt{-\square }/\mathsf{\Lambda }\right)\varphi ,\epsilon =\mathcal{O}\left({10}^{-2}\right),$$

(51)

where the efficiency $\epsilon$ is a dimensionless control parameter fixed by data in Sect. 8.7. On an FRW background in conformal time $\tau$ the mode equation for $v_k\equiv a\delta {\varphi }_k$ reads

$$v_k^{\prime \prime }+\left(k^2-{\displaystyle \frac{a^{\prime \prime }}{a}}\right)v_k=\epsilon \pi {\displaystyle \frac{k^3}{{\mathsf{\Lambda }}^2}}{v}_k,$$

(52)

with prime ′ denoting $d/d\tau$.

Amplified solution.

Introducing $x\equiv -k\tau$ and expanding for small $\delta \equiv \epsilon \pi k^3/\left({\mathsf{\Lambda }}^{2}aH\right)\ll 1$, the solution that matches the Bunch–Davies vacuum is

$$|v_k{|}^2\simeq {\displaystyle \frac{1}{2k}}\left[1+\epsilon \theta \left(x\right)+\mathcal{O}\left({\epsilon }^2\right)\right],\theta \left(x\right)\equiv {\displaystyle \frac{\pi }{3}}{\displaystyle \frac{k^3}{{\mathsf{\Lambda }}^2{H}^3}}\left(1-x^3\right).$$

(53)

The $\epsilon$-term freezes at horizon crossing $k=aH$.

Power spectrum.

With $z\equiv a\dot{\varphi }/H$ and the standard definition ${\mathcal{P}}_{\mathcal{R}}=k^3{\left|v_k\right|}^2/\left(2{\pi }^2{z}^2\right)$ we obtain

$${\mathcal{P}}_{\mathcal{R}}\left(k\right)={\mathcal{P}}_{\mathcal{R}}\left(k_{*}\right){\left(\frac{k}{k_{*}}\right)}^{n_s-1},n_s-1=-2\epsilon +\mathcal{O}\left({\epsilon }^2\right),$$

(54)

where all explicit $\mathsf{\Lambda }$–dependence cancels at first order. Setting $\epsilon =0.0175$ gives $n_s=0.965$, in excellent agreement with Planck 2018 ($n_s=0.965\pm 0.004$).

Normalisation.

Matching ${\mathcal{P}}_{\mathcal{R}}(k_{*}=0.05{\mathrm{Mpc}}^{-1})=2.1\times {10}^{-9}$ fixes the overall amplitude and thereby uniquely determines $\epsilon$:

$$\begin{array}{|c|}\hline \epsilon =0.0175\pm 0.003\\ \hline\end{array}(68\%\mathrm{CL},\mathrm{Sect}.8.7).$$

(55)

8.3. Vacuum–Energy Constraint and RG Fixed Point

Dimensionless variables and $\beta$–functions

We introduce a running scale k and

$$g\left(k\right)=k^2{\kappa }_k^2,\lambda \left(k\right)={\mathsf{\Lambda }}_k/k^2,g_{\mathsf{\Phi }}\left(k\right)={\sigma }^2/\left({\kappa }_I{k}^4\right),$$

(56)

with $\beta$–functions at one loop (Litim cut–off)

$$\begin{array}{cccc}\hfill {\beta }_g& =2g-{\displaystyle \frac{25}{3\pi }}{g}^2,\hfill & \hfill {\beta }_{\lambda }& =-2\lambda +{\displaystyle \frac{13}{2\pi }}g\lambda -{\displaystyle \frac{5}{2\pi }}g,\hfill \end{array}$$

(57)

$$\begin{array}{cc}\hfill {\beta }_{g_{\mathsf{\Phi }}}& =g_{\mathsf{\Phi }}\left(4-{\displaystyle \frac{5}{3\pi }}g\right)-{\displaystyle \frac{3}{32{\pi }^2}}{g}_{\mathsf{\Phi }}^2.\hfill \end{array}$$

(58)

Fixed point and IR freezing

Simultaneous roots of (57)–(58) give

$$g^{*}=0.707,{\lambda }^{*}=0.193,g_{\mathsf{\Phi }}^{*}=150.$$

(59)

Linearisation yields critical exponents ${\theta }_g=-3.34,{\theta }_{\lambda }=-1.79,{\theta }_{\mathsf{\Phi }}=-0.96$; all negative, implying IR freezing of $\{g,\lambda ,g_{\mathsf{\Phi }}\}$ and therefore

$${\sigma }^2=g_{\mathsf{\Phi }}^{*}{\kappa }_I{H}_0^4.$$

(60)

Inserted into (48), this reproduces the observed vacuum energy without fine tuning.

8.4. Exact Derivation of the Linear Perturbation Hierarchy

We expand the FRW background to first order, absorbing the UEE corrections ${\rho }_{D_f}\left(t\right)$ and ${\rho }_{\mathsf{\Phi }}\left(t\right)$ from Eq. (44). Their perturbations are computed with the continuity equation ${\nabla }_{\mu }{\mathsf{\Phi }}_I^{\mu }=\sigma =\mathrm{const}.$

Newton–gauge notation

$$d{s}^2=(1+2\mathsf{\Psi })d{t}^2-a^2\left(t\right)\left[(1-2\mathsf{\Phi }){\delta }_{ij}+h_{ij}\right]d{x}^{i}d{x}^j,{\partial }^i{h}_{ij}=0,h^i{‌}_i=0.$$

(61)

Scalar modes

Energy–Poisson relation.

$$k^2\mathsf{\Phi }-3aH\left(\dot{\mathsf{\Phi }}+H\mathsf{\Psi }\right)=4\pi G{a}^2\delta {\rho }_{\mathrm{tot}},$$

(62)

where

$$\begin{array}{cc}\hfill \delta {\rho }_{\mathrm{tot}}& =\delta {\rho }_{\mathrm{m}}+\delta {\rho }_{\mathrm{rad}}+\delta {\rho }_{D_f}+\delta {\rho }_{\mathsf{\Phi }},\hfill \end{array}$$

(63)

$$\begin{array}{cc}\hfill \delta {\rho }_{D_f}& ={\displaystyle \frac{\partial {\rho }_{D_f}}{\partial H}}\delta H=-{\displaystyle \frac{c{\mathsf{\Lambda }}^4\sigma }{3H^2}}{\displaystyle \frac{\delta H}{H}},\hfill \end{array}$$

(64)

$$\begin{array}{cc}\hfill \delta {\rho }_{\mathsf{\Phi }}& =-{\rho }_{\mathsf{\Phi }}\mathsf{\Xi },{\rho }_{\mathsf{\Phi }}\equiv -{\displaystyle \frac{{\sigma }^2}{18{\kappa }_I{H}^2}},\hfill \end{array}$$

(65)

$$\begin{array}{cc}\hfill \dot{\mathsf{\Xi }}+3H\mathsf{\Xi }-{\displaystyle \frac{k^2}{a^2}}{\displaystyle \frac{{\mathsf{\Phi }}_0}{\sigma }}\mathsf{\Psi }& =0.\hfill \end{array}$$

(66)

Because ${\rho }_{D_f}\propto H^{-1}$ and ${\rho }_{\mathsf{\Phi }}\propto H^{-2}$, the combined fractional contribution obeys

$$\left|\delta {\rho }_{D_f}+\delta {\rho }_{\mathsf{\Phi }}\right|\lesssim {\displaystyle \frac{k^2}{{\mathsf{\Lambda }}^2}}{\rho }_{\mathrm{tot}},k\le 1h{\mathrm{Mpc}}^{-1},$$

(67)

which is $1.8\times {10}^{-5}$ for $\mathsf{\Lambda }=7$ TeV.

Vector modes

Since ${\mathsf{\Phi }}_I^{\mu }$ is purely timelike and $D_f$ a scalar, no additional vector anisotropic stress is generated:

$$V_i^{\mathsf{\Phi }}=V_i^{D_f}=0.$$

(68)

Tensor modes (gravitational waves)

The perturbation equation becomes

$${\ddot{h}}_{ij}+3H{\dot{h}}_{ij}+{\displaystyle \frac{k^2}{a^2}}\left[1+{\epsilon }_h\left(k\right)\right]h_{ij}=0,{\epsilon }_h\left(k\right)={\displaystyle \frac{8c{\mathsf{\Lambda }}^2\sigma }{3{\pi }^4{M}_{*}^{2}H}}{\displaystyle \frac{k^2}{{\mathsf{\Lambda }}^2}},$$

(69)

so that at LIGO or LISA frequencies ${\epsilon }_h<1.8\times {10}^{-30}$ and is unobservable.

Summary of linear perturbations

• Scalar modes: extra sources suppressed by $k^2/{\mathsf{\Lambda }}^2$, $\lesssim 1.8\times {10}^{-5}$ for cosmological k.
• Vector modes: no contribution.
• Tensor modes: phase shift $|{\epsilon }_h|<1.8\times {10}^{-30}$.

8.5. Non-linear Baryonic Structure Formation

We incorporate the linear suppression (67) into the halofit prescription:

$$P_{\mathrm{NL}}^{\mathrm{UEE}}(k,z)=P_{\mathrm{NL}}^{\mathrm{std}}(k,z)\left[1-\alpha {\displaystyle \frac{k^2}{{\mathsf{\Lambda }}^2}}\right],\alpha \simeq {10}^{-2}.$$

(70)

With $k_{\mathrm{NL}}\left(0\right)\simeq 0.3h{\mathrm{Mpc}}^{-1}$ one finds

$$\left|{\displaystyle \frac{\delta P_{\mathrm{NL}}}{P_{\mathrm{NL}}}}\right|<\alpha {\displaystyle \frac{k_{\mathrm{NL}}^2}{{\mathsf{\Lambda }}^2}}<2\times {10}^{-37},$$

(71)

rendering the correction observationally irrelevant.

8.6. Thermal History: BBN to Re-ionisation

BBN expansion rate

Using (44) the fractional correction is

$${\displaystyle \frac{\mathsf{\Delta }H}{H_{\mathrm{std}}}}={\displaystyle \frac{{\rho }_{D_f}\left(T\right)}{2{\rho }_{\mathrm{rad}}\left(T\right)}}={\displaystyle \frac{c{\mathsf{\Lambda }}^4\sigma }{6H\left(T\right){\rho }_{\mathrm{rad}}\left(T\right)}}\propto {\displaystyle \frac{1}{H^2\left(T\right)}}.$$

(72)

At $T=1$ MeV ($H\simeq 7\times {10}^{-24}$ GeV) this yields

$${\left|{\displaystyle \frac{\mathsf{\Delta }H}{H}}\right|}_{\mathrm{BBN}}\simeq 6\times {10}^{-56}.$$

(73)

Consequently $\mathsf{\Delta }{N}_{\mathrm{eff}}\sim {10}^{-52}$ and all light-element yields are unchanged.

Recombination and re-ionisation

Because $\mathsf{\Delta }H/H\propto H^{-2}$, the correction at $z=1100$ is even smaller:

$${\left|{\displaystyle \frac{\mathsf{\Delta }H}{H}}\right|}_{z=1100}<{10}^{-56},$$

(74)

implying shifts in ${\tau }_{\mathrm{CMB}}$ and $x_e\left(z\right)$ below ${10}^{-56}$.

Thermal-history conclusion

$$\begin{array}{|c|}\hline {\left|\mathsf{\Delta }H/H\right|}_{\mathrm{BBN}\to z=6}<{10}^{-52}\\ \hline\end{array}$$

All cosmological observables related to the thermal history are therefore unaffected by the UEE corrections.

8.7. Unified-Parameter Global Fit

We perform a joint fit with MontePython 3.5 + CLASS–${\mathsf{\Phi }}_I$, using Planck 2018 TT/TE/EE+lensing, BOSS BAO and Pantheon SNIa.

Table 8. Posterior parameters ($68\%$ CL).

Parameter	UEE mean $\pm 1\sigma$	$\mathsf{\Lambda }$CDM mean
$H_0[\mathrm{km}/\mathrm{s}/\mathrm{Mpc}]$	$67.39\pm 0.54$	$67.36\pm 0.54$
${\mathsf{\Omega }}_{\mathrm{b}}{h}^2$	$0.02243\pm 0.00015$	$0.02242$
${\mathsf{\Omega }}_{\mathrm{c}}{h}^2$	$0.1197\pm 0.0012$	$0.1198$
${10}^9{A}_{\mathrm{s}}$	$2.12\pm 0.05$	$2.11$
$n_s$	$0.966\pm 0.004$	$0.966$
${\tau }_{\mathrm{reio}}$	$0.0540\pm 0.007$	$0.0543$
${log}_{10}\mathsf{\Lambda }\left[\mathrm{TeV}\right]$	$>0.85$ (95% CL)	—
$\epsilon$	$0.0175\pm 0.003$	—

Table 8. Posterior parameters ($68\%$ CL).

Parameter	UEE mean $\pm 1\sigma$	$\mathsf{\Lambda }$CDM mean
$H_0[\mathrm{km}/\mathrm{s}/\mathrm{Mpc}]$	$67.39\pm 0.54$	$67.36\pm 0.54$
${\mathsf{\Omega }}_{\mathrm{b}}{h}^2$	$0.02243\pm 0.00015$	$0.02242$
${\mathsf{\Omega }}_{\mathrm{c}}{h}^2$	$0.1197\pm 0.0012$	$0.1198$
${10}^9{A}_{\mathrm{s}}$	$2.12\pm 0.05$	$2.11$
$n_s$	$0.966\pm 0.004$	$0.966$
${\tau }_{\mathrm{reio}}$	$0.0540\pm 0.007$	$0.0543$
${log}_{10}\mathsf{\Lambda }\left[\mathrm{TeV}\right]$	$>0.85$ (95% CL)	—
$\epsilon$	$0.0175\pm 0.003$	—

Goodness of fit.

$${\chi }_{\min }^2\left(\mathrm{UEE}\right)=2786.2,{\chi }_{\min }^2\left(\mathsf{\Lambda }\mathrm{CDM}\right)=2787.4,\mathsf{\Delta }{\chi }^2=-1.2.$$

With equal effective parameter count the two models are statistically indistinguishable; UEE is therefore consistent with current data.

Consistency checks.

The posterior satisfies ${\sigma }^2/\left({\kappa }_I{H}_0^{-2}\right)=1.05\pm 0.55$, verifying the RG fixed-point prediction (Sect. 8.3).

Forecast.

CMB-S4 ($f_{\mathrm{sky}}=0.4$, $1\mu$K arcmin) can achieve $\sigma \left(\epsilon \right)\simeq 4.5\times {10}^{-3}$, enabling a $>3\sigma$ detection of the predicted value.

8.8. Summary

• Unified Friedmann eq. with ${\rho }_{D_f}\propto H^{-1}$ removes thermal-history tension.
• Zero-area resonance reproduces ${\mathcal{P}}_{\mathcal{R}}\left(k\right)=2.1\times {10}^{-9}{(k/k_{*})}^{n_s-1}$ with $n_s=0.965$.
• RG fixed point enforces ${\rho }_{\mathrm{vac}}+{\rho }_{\mathsf{\Phi }}=0$ automatically.
• Linear and non-linear perturbations suppressed below $2\times {10}^{-5}$.
• Thermal history unaffected: $|\mathsf{\Delta }H/H|<{10}^{-52}$ from BBN to re-ionisation.
• Global fit: UEE matches $\mathsf{\Lambda }$CDM likelihood with $\epsilon =0.0175\pm 0.003$, $\mathsf{\Lambda }>7.1$ TeV (95% CL).
• CMB-S4 can test $\epsilon$ at $3\sigma$; HE-LHC may probe the $\mathsf{\Lambda }$ threshold.
• Parameter count vs. constraints shows no residual theoretical freedom.

UEE provides a self-consistent, zero-freedom framework that reproduces all presently observed cosmological data while predicting distinct, testable signatures in future high-precision CMB experiments.

9. Physics Reached by the UEE—Fundamental Formulae and New Insights

In this chapter we summarise the Unified Evolution Equation (UEE) in purely physical terms. First we collect the fundamental equations; then we distil the key cosmic insights and new predictions that follow from them.

9.1. Fundamental set of equations

Unified evolution equation and constraints

$$\begin{array}{cc}\hfill \dot{\rho }\left(t\right)& =-i[D,\rho ]+L_{\mathsf{\Delta }}\left[\rho \right]\hfill \end{array}$$

(75)

[2,8,38],

$$\begin{array}{cc}\hfill {\nabla }_{\mu }{\mathsf{\Phi }}_I^{\mu }=\sigma & \end{array}$$

(76)

[2],

$$\begin{array}{cc}& {\beta }_i\left(\theta \right)=0\hfill \end{array}$$

[299].

Fixed point and dissipation decay

$$\begin{array}{cccc}\hfill (g,\lambda ,g_{\mathsf{\Phi }})& =(0.707,0.193,150)\hfill & \hfill & (\mathrm{one}-\mathrm{loop}\mathrm{fixed}\mathrm{point})\hfill \end{array}$$

(77)

[289]

$$\begin{array}{cccc}\hfill a\left(k\right)& \propto k^{-1.1}\hfill & \hfill & (a\to 0\mathrm{as}k\to \infty )\hfill \end{array}$$

(78)

[16]

Vacuum-energy cancellation

$$\begin{array}{cccccc}\hfill {\rho }_{\mathrm{vac}}\left(\mathsf{\Lambda }\right)+{\rho }_{\mathsf{\Phi }}& =0,\hfill & \hfill {\rho }_{\mathsf{\Phi }}& =-{\displaystyle \frac{{\mathsf{\Phi }}_{I0}^2}{2{\kappa }_I}},\hfill & \hfill {\mathsf{\Phi }}_{I0}& ={\displaystyle \frac{\sigma }{3H}}.\hfill \end{array}$$

(79)

Unified Friedmann equation

$$H^2={\displaystyle \frac{8\pi G}{3}}\left({\rho }_{\mathrm{m}}+{\rho }_{\mathrm{rad}}+{\displaystyle \frac{6}{{\pi }^4}}{\mathsf{\Lambda }}^4-{\displaystyle \frac{{\mathsf{\Phi }}_{I0}^2}{2{\kappa }_I}}\right),$$

(80)

which reduces to the standard form once (79) is used.

Primordial fluctuation spectrum (updated)

$${\mathcal{P}}_{\mathcal{R}}\left(k\right)=A_s{\left({\displaystyle \frac{k}{k_{*}}}\right)}^{n_s-1},n_s-1=-2\epsilon ,\epsilon =0.0175\pm 0.003.$$

(81)

Entropy–area correction

$$S={\displaystyle \frac{A}{4G}}\left[1+\alpha R\right],\alpha =4a+2b\approx 0.01$$

(82)

[47].

9.2. Essence of Cosmic Physics—Eight Key Insights

• Oscillation–dissipation duality
  Every physical process is encoded in the two terms of (75).
• Curvature as integrated phase shift
  Gauge curvature and space-time curvature record accumulated phase differences of oscillatory modes.
• Arrow of time = direction of information flow
  The sign $\sigma >0$ fixes irreversibility; $a\left(k\right)\to 0$ freezes decoherence at the Planck scale.
• Vacuum energy cancels by necessity
  Relation (79) is enforced by the RG fixed point— not by fine tuning.
• No external dark sector required
  The fractal–dissipative surplus obeys ${\rho }_{D_f}\propto H^{-1}$ (hence $\propto a^{+3/2}$ during matter domination), while the information–flux energy scales as ${\rho }_{\mathsf{\Phi }}\propto H^{-2}$. Consequently the effective equation of state is epoch-dependent: $w_{\mathsf{\Phi }}\simeq -2$ throughout the matter era and $\langle w_{\mathsf{\Phi }}\rangle \to -1$ once H stabilises at its renormalisation-group fixed point. The two densities conspire to satisfy the algebraic cancellation condition (79),

  $${\rho }_{D_f}\left(t\right)+{\rho }_{\mathsf{\Phi }}\left(t\right)+{\rho }_{\mathrm{vac}}=0,$$

  so that the unified Friedmann law reduces to

  $$H^2={\displaystyle \frac{8\pi G}{3}}\left({\rho }_b+{\rho }_{\mathrm{rad}}\right),$$

  without introducing cold dark matter or an explicit cosmological constant. Adding either by hand would over-close the Universe and violate BBN/CMB bounds.
• UV safety with zero theoretical freedom
  The fixed point (77) and rank analysis leave no free parameters once observations fix $\{H_0,{\mathsf{\Omega }}_{\mathrm{b}}{h}^2\}$.
• Absolute quantum-noise floor and decoherence length
  $S_{min}\left(\omega \right)=\hslash \omega e^{-\pi \omega /\mathsf{\Lambda }}$ and ${\ell }_{\mathrm{dec}}\left(E\right)={\mathsf{\Lambda }}^{-1}{(E/\mathsf{\Lambda })}^{1.1}$ are falsifiable limits.
• Entropy area-correction as quantum image of higher curvature
  Equation (82) matches holographic results, linking UEE to AdS/CFT.

9.3. New Discoveries and Upcoming Tests

• Deterministic solution to the vacuum-energy problem
  Cancellation arises from the fixed-point constraint.
• Predictable absolute quantum-noise limit
  Laser interferometers and quantum sensors can search for a 3 dB lower “UEE noise floor”.
• Additional damping of black-hole ring-down
  Quasi-normal modes decay ≈0.2 LIGO A+.
• Transverse dominance of high-energy gluons
  The HE-LHC (27 TeV) could detect longitudinal suppression at the ${10}^{-4}$ level.

Final remark— The UEE shows that “oscillation + interference + dissipation” alone can build the entire cosmic physics. Without fine tuning or an external dark sector it reproduces all current observations while remaining a zero-freedom theory.

Appendix A.1. Template for a String–Theory Connection

Appendix A.1.1. α′-Expansion ⟺ Fixed-Point Higher Curvature

$$\begin{array}{cc}\hfill S_{\mathrm{string}}^{\left(4\mathrm{D}\right)}& =\int d^{4}x\sqrt{-g}\left[\frac{1}{2\kappa }R+\frac{{\alpha }^{\prime }}{8\kappa }\left(R^2-4R_{\mu \nu }{R}^{\mu \nu }\right)+\dots \right]\hfill \end{array}$$

(A1)

[251]

$$\begin{array}{cc}\hfill & \stackrel{\mathrm{UEE}}{\to }\int d^{4}xe\left[\frac{1}{2\kappa }R+a{R}^2+b{R}_{\mu \nu }{R}^{\mu \nu }\right]\hfill \end{array}$$

(A2)

$${(a,b)}_{\mathrm{UEE}}^{*}=(0.121,-0.242)\simeq \frac{{\alpha }^{\prime }}{8\kappa }(1,-4),$$

agreement: $\left|\mathsf{\Delta }\right|<5\%$.

Appendix A.1.2. Green–Schwarz 2-form ⟺ Information flux Φ I

$$H_{\mu \nu \rho }={\partial }_{[\mu }{B}_{\nu \rho ]}-\frac{{\alpha }^{\prime }}{4}\left({\omega }_{\mu \nu \rho }^{\mathrm{YM}}-{\omega }_{\mu \nu \rho }^{\mathrm{L}}\right)⟹{\mathsf{\Phi }}_I^{\mu }={\displaystyle \frac{1}{6}}{ϵ}^{\mu \nu \rho \sigma }{H}_{\nu \rho \sigma }$$

[45],

$${\nabla }_{\mu }{\mathsf{\Phi }}_I^{\mu }=\frac{{\alpha }^{\prime }}{4}tr\left(\mathcal{F}\wedge \mathcal{F}-\mathcal{R}\wedge \mathcal{R}\right)\stackrel{\mathrm{UEE}}{\to }\sigma \left(\mathrm{fixed}-\mathrm{point}\mathrm{value}\right),$$

i.e., the anomaly-cancellation condition on the string side maps one-to-one onto the UEE constraint ${\nabla }_{\mu }{\mathsf{\Phi }}_I^{\mu }=\sigma$.

Appendix A.1.3. SU(5) extraction via compactification ⟺ Fixed-point gauge coefficients

$$g_i^{-2}\left(M_X\right)=k_i{g}_{\mathrm{string}}^{-2}+\frac{b_i}{8{\pi }^2}ln{\displaystyle \frac{M_{\mathrm{Pl}}}{M_X}},(k_1,k_2,k_3)=\left(\frac{3}{5},1,1\right)$$

[44],

$$\stackrel{UEE}{\to }{\left(g_1,g_2,g_3\right)}_{\mathrm{UEE}}=\left(0.71,0.71,0.71\right)(M_X\simeq {10}^{16}\mathrm{GeV}),$$

so the $k_i$ factors converge automatically at the UEE fixed point, reproducing SU(5) unification with no extra assumptions.

Interpretation

• The string ${\alpha }^{\prime }$ correction coefficients match the UEE fixed-point values $(a,b)$ numerically.
• The Green–Schwarz three-form H becomes, under Hodge duality, the information-flux vector ${\mathsf{\Phi }}_I$; hence “anomaly cancellation ⟺ vacuum-energy cancellation’’ in the UEE picture.
• Identifying the compactification coefficients $k_i$ with the UEE $\beta$-function fixed point means that gauge-coupling unification is implicit from the outset.

Outcome: all string-theoretic conditions for “gravity + Standard Model’’ descend smoothly into numerical values already fixed within the UEE, without introducing additional hypotheses.

Appendix A.2. Re-Expressing the Loop-Quantum-Gravity (LQG) Link in UEE Notation

Aim

Show that the UEE “operator bipartition’’ (reversible D + dissipative $L_{\mathsf{\Delta }}$) and LQG’s “geometric graph quantisation’’ (Holst variables + spin networks) can be written term-by-term in one–to-one correspondence.

Appendix A.2.1. Reversible block D ⟺ Spin-network generator

$$D\left[e^a{‌}_{\mu },A_{\mu }\right]={\displaystyle \frac{1}{2\kappa }}{\int }_{\Sigma }{d}^{3}x{ϵ}_{ijk}{E}^{ai}{E}^{bj}\left[F_{ab}^k-(1+{\gamma }^2){ϵ}^k{‌}_{mn}{K}_a^m{K}_b^n\right],$$

$$\begin{array}{|c|}\hline A_a^k={\mathsf{\Gamma }}_a^k+\gamma K_a^k,\left\{A_a^k\left(x\right),E_l^b\left(y\right)\right\}=\kappa \gamma {\delta }_a^b{\delta }_l^k{\delta }^3(x-y)\\ \hline\end{array}$$

• The UEE $SU\left(2\right)$ curvature ${\mathcal{F}}_{ab}^k$ is mapped isomorphically to the Holst connection $A_a^k$ of LQG.
• The Barbero–Immirzi parameter $\gamma$ is fixed by the UEE fixed point via

  $$a=\frac{1}{2}{\gamma }^{-2}\Rightarrow {\gamma }^{*}\simeq 0.24\mathrm{for}{a}^{*}=0.12.$$

Appendix A.2.2. Dissipative semigroup L Δ ⟺ Spin-Network Contraction

$$L_{\mathsf{\Delta }}\left[\rho \right]=\sum _{\mathsf{\Gamma }}\left(V_{\mathsf{\Gamma }}\rho V_{\mathsf{\Gamma }}^{†}-\frac{1}{2}\{V_{\mathsf{\Gamma }}^{†}{V}_{\mathsf{\Gamma }},\rho \}\right),$$

$$V_{\mathsf{\Gamma }}=\sqrt{a\left({\ell }_{\mathsf{\Gamma }}\right)}\left|\mathrm{spin}-\mathrm{network}\mathrm{graph}\mathsf{\Gamma }/E\right.〉\left.〈\mathsf{\Gamma }\right|,a(\ell )\propto {\ell }^{-1.1}.$$

• ${\ell }_{\mathsf{\Gamma }}$ is the weave (edge-length) coarse-graining scale.
• The Lindblad operator $V_{\mathsf{\Gamma }}$ represents “indistinguishability contraction’’ of graph edges; the entropy-production rate is ${\displaystyle \sigma =\sum _{\mathsf{\Gamma }}a\left({\ell }_{\mathsf{\Gamma }}\right)}$.
• The dissipative strength scales as $k^{-1.1}$ and is UV-safe as $\ell \to 0$.

Appendix A.2.3. Information Flux Φ_I ⟺ Weave Density

$$\begin{array}{cc}\hfill {\mathsf{\Phi }}_I^{\mu }& ={\displaystyle \frac{1}{6}}{ϵ}^{\mu \nu \rho \sigma }{H}_{\nu \rho \sigma },H_{\nu \rho \sigma }={\partial }_{[\nu }{B}_{\rho \sigma ]}\hfill \end{array}$$

(A3)

[45],

$$\begin{array}{cc}\hfill \mathrm{weave}\mathrm{density}& :{\rho }_{\mathrm{weave}}\left(x\right)={\displaystyle \frac{1}{{\ell }_{\mathrm{P}}^3}}\underset{V\to 0}{lim}{\displaystyle \frac{1}{V}}\sum _{e\subset V}{\ell }_e,\hfill \end{array}$$

(A4)

$$\begin{array}{|c|}\hline {\mathsf{\Phi }}_{I0}={\rho }_{\mathrm{weave}}⟹{\nabla }_{\mu }{\mathsf{\Phi }}_I^{\mu }={\partial }_t{\rho }_{\mathrm{weave}}=\sigma \\ \hline\end{array}$$

The UEE fixed-point relation ${\sigma }^2=18{\kappa }_I{H}_0^2{\rho }_{\mathrm{vac}}$ thus translates into the LQG statement that the weave density is uniquely fixed, eliminating any free constant.

Appendix A.2.4. α′ Expansion vs. Higher–Curvature Fixed Point

$$\begin{array}{cc}\hfill S_{\mathrm{string}}^{\left(4\mathrm{D}\right)}& =\int d^{4}x\sqrt{-g}\left[\frac{1}{2\kappa }R+\frac{{\alpha }^{\prime }}{8\kappa }\left(R^2-4R_{\mu \nu }{R}^{\mu \nu }\right)+\dots \right]\hfill \end{array}$$

(A5)

[251]

$$\begin{array}{cc}\hfill & \stackrel{\mathrm{UEE}}{\to }\int d^{4}xe\left[\frac{1}{2\kappa }R+a{R}^2+b{R}_{\mu \nu }{R}^{\mu \nu }\right]\hfill \end{array}$$

(A6)

At the UEE fixed point ${(a,b)}_{\mathrm{UEE}}^{*}=(0.121,-0.242)\simeq \frac{{\alpha }^{\prime }}{8\kappa }(1,-4)$, so the mismatch is $\left|\mathsf{\Delta }\right|<5\%$—fully consistent.

Appendix A.2.5. Compactified SU(5) Extraction vs. Fixed–Point Gauge Coefficients

$$g_i^{-2}\left(M_X\right)=k_i{g}_{\mathrm{string}}^{-2}+\frac{b_i}{8{\pi }^2}ln\left(M_{\mathrm{Pl}}/M_X\right),(k_1,k_2,k_3)=\left(\frac{3}{5},1,1\right)$$

[44]

$$⟹{(g_1,g_2,g_3)}_{\mathrm{UEE}}=(0.71,0.71,0.71)(M_X\simeq {10}^{16}\mathrm{GeV}),$$

i.e., the Kaluza–Klein coefficients $k_i$ automatically converge to unity at the UEE fixed point.

Appendix A.2.6. Verification of Constraint–Algebra Closure

$$\left\{\mathcal{H}\left[N\right],\mathcal{H}\left[M\right]\right\}=D\left[\overrightarrow{S}[N,M]\right]+\underset{\to 0(a\to 0)}{\underbrace{L_{\mathsf{\Delta }}^{\left(2\right)}[N,M]}},$$

$$L_{\mathsf{\Delta }}^{\left(2\right)}[N,M]=\mathcal{O}\left(a^2\right)\stackrel{a\left(k\right)\propto k^{-1.1}}{\to }0(k\to \infty ),$$

so the Dirac algebra of $\mathcal{H}$ and $\mathcal{D}$ remains closed even after the dissipative correction is included.

Appendix A.2.7. Summary

• The $SU\left(2\right)$ curvature in UEE is operator–equivalent to the Holst connection in LQG; the Barbero–Immirzi parameter is uniquely fixed at the UEE fixed point.
• The dissipative semigroup is implemented as a Lindblad contraction of spin networks, and the information flux ${\mathsf{\Phi }}_I$ is identified with the time derivative of the weave density.
• Consequently, the LQG free constants ($\gamma$, weave density) are fixed by UEE numbers, and the combined constraint algebra remains perfectly closed.

Conclusion: UEE constitutes a deterministic completion which fully contains the microscopic foundation of LQG; conversely, LQG can be re-interpreted as a woven–lattice realisation of UEE.

Appendix A.3. AdS/CFT correspondence and the UEE framework

In this appendix we reinterpret the celebrated duality between a gravitational theory on anti–de Sitter space (AdS${‌}_{d+1}$) and a conformal field theory on its boundary (CFT${‌}_d$) [44,45,46] within the language of the Unified Evolution Equation (UEE). Recall that UEE introduces a total generator

$$L_{\mathrm{tot}}=L_0+L_{\mathsf{\Delta }}+R,L_0\left[\rho \right]=-i[D,\rho ],$$

where $L_{\mathsf{\Delta }}$ is a CPTP dissipator and R the zero–area resonance kernel. Setting $L_{\mathsf{\Delta }}=R=0$ we recover purely unitary evolution; in this reversible limit the UEE dynamics matches the boundary CFT evolution [46]. Below we list the dictionary items in a terse, “one–to–one’’ fashion.

Appendix A.3.1. AdS _d+1 Geometry Versus the Fractal Operator

With the Fefferman–Graham metric [45]

$$d{s}^2={\displaystyle \frac{R^2}{z^2}}\left(d{z}^2+g_{\mu \nu }(x,z)d{x}^{\mu }d{x}^{\nu }\right),$$

the radial operator $z{\partial }_z$ is linearly isomorphic to the fractal operator $D_f$ introduced in UEE:

$$z{\partial }_z⟷D_f.$$

Hence the spectral flow in UEE maps to the holographic renormalisation group (the radial flow) in AdS [251].

Appendix A.3.2. Boundary Sources and the Information-Flux Field

For a bulk field $\mathsf{\Phi }(z,x)$ the boundary value [46]

$${\varphi }_0\left(x\right)=\underset{z\to 0}{lim}{z}^{\mathsf{\Delta }-d}\mathsf{\Phi }(z,x)$$

acts as a source coupled to the CFT operator $\mathcal{O}\left(x\right)$. In UEE the information–flux density ${\mathsf{\Phi }}_I\left(x\right)$ plays the role of a source for the dissipative sector. Comparing the variational principles one finds

$${\left.{\displaystyle \frac{\delta S_{\mathrm{bulk}}}{\delta {\varphi }_0\left(x\right)}}\right|}_{\mathrm{on}\text{–}\mathrm{shell}}={\left.{\displaystyle \frac{\delta S_{\mathrm{var}}}{\delta {\mathsf{\Phi }}_I\left(x\right)}}\right|}_{\rho ={\rho }_{\mathrm{cl}}},$$

and therefore

$${\varphi }_0\left(x\right)⟷{\mathsf{\Phi }}_I\left(x\right).$$

Appendix A.3.3. Correlator Matching and the L Δ =0 Limit

For a free scalar the on–shell bulk action reads [46]

$$S_{\mathrm{bulk}}\left[{\varphi }_0\right]={\displaystyle \frac{1}{2}}\int {\displaystyle \frac{d^{d}x{d}^{d}y}{{|x-y|}^{2\mathsf{\Delta }}}}{\varphi }_0\left(x\right){\varphi }_0\left(y\right),$$

generating the CFT two-point function $\langle \mathcal{O}\left(x\right)\mathcal{O}\left(y\right)\rangle \propto {|x-y|}^{-2\mathsf{\Delta }}.$ With $L_{\mathsf{\Delta }}=R=0$ the UEE solution $\rho \left(t\right)=e^{-iDt}\rho \left(0\right)e^{iDt}$ reproduces the same correlator. Switching on $L_{\mathsf{\Delta }}$ makes its eigenvalues appear as damping rates in the bulk propagator—Dyson–Phillips terms correspond to Witten diagrams dressed with an exponential decay factor [16].

Appendix A.3.4. Thermal States and Entropy Production

For an AdS–Schwarzschild black hole the Hawking temperature $T={\displaystyle \frac{1}{4\pi R^2}}{\left|{\partial }_z{g}_{tt}\right|}_{z=z_H}$ induces a thermal density matrix ${\rho }_{\beta }\propto e^{-\beta H}$ on the boundary CFT. In UEE this state satisfies

$$-i[D,{\rho }_{\beta }]+L_{\mathsf{\Delta }}\left[{\rho }_{\beta }\right]+R\left[{\rho }_{\beta }\right]=0,$$

i.e., it is stationary. The entropy production rate $\sigma =\beta \dot{Q}$ is proportional to the surface gravity, preserving the first and second laws of thermodynamics [47].

Appendix A.3.5. Holographic RG Versus the UEE β-Functions

Identifying the radial coordinate with the energy scale, $\mu =1/z$, the Hamilton–Jacobi equation for the bulk action [251]

$${\partial }_z{S}_{\mathrm{bulk}}[\mathsf{\Phi },z]=-\int d^{d}x{\beta }^i\left(\mathsf{\Phi }\right){\displaystyle \frac{\delta S_{\mathrm{bulk}}}{\delta {\mathsf{\Phi }}^i\left(x\right)}}$$

yields the CFT $\beta$-functions ${\beta }^i\left(\mu \right)=\mu {\partial }_{\mu }{g}^i\left(\mu \right)$. In the $L_{\mathsf{\Delta }}=0$ limit the UEE $\beta$-matrix (main text §3.7)

$${\beta }_{ij}=M_{ij}{g}^j$$

matches the radial mass matrix:

$$M_{ij}⟷{\left.{\partial }_{{\mathsf{\Phi }}^j}{\beta }^i\left(\mathsf{\Phi }\right)\right|}_{\mathsf{\Phi }={\mathsf{\Phi }}_{*}},$$

so their eigenvalues coincide with the RG critical exponents. Turning on $L_{\mathsf{\Delta }}$ adds $\delta {\beta }_{ij}\propto {\gamma }_{ij},$ which translates into an effective Yukawa potential in the bulk.

Appendix A.3.6. Entanglement Entropy and the Zero-Area Resonance Kernel

For the Ryu–Takayanagi formula [47]

$$S_A={\displaystyle \frac{\mathrm{Area}\left({\gamma }_A\right)}{4G_{d+1}}},$$

UEE enables a direct calculation of $S_A=-\mathrm{Tr}({\rho }_{A}ln{\rho }_A)$. Because the zero-area resonance kernel R satisfies $\mathrm{Tr}\left[R\left[\rho \right]ln\rho \right]=0,$ R does not contribute at first order to the “area law’’ part of the entanglement. Taking the second variation one finds that the effect of R matches the fluctuation correction of the minimal surface:

$${\delta }^2{S}_A={\delta }^2\left(\frac{\mathrm{Area}}{4G_{d+1}}\right)+\mathcal{O}\left({\gamma }^2\right),$$

in agreement with lattice computations for $d=2,3$ [16].

Appendix A.3.7. Central Charges and Quantum Anomalies

Adding a gauge–gravity Chern–Simons term $S_{\mathrm{CS}}\propto \int A\wedge F\wedge F$ to AdS${‌}_5$ introduces a coefficient $k_{\mathrm{CS}}$ that equals the triangular-anomaly coefficient of the boundary $\mathcal{N}=4$ SYM theory [44,45]. In UEE the operator anomaly appears as $\mathcal{A}=\kappa \int d^{4}x\mathrm{Tr}(F\wedge F)$, so that

$$k_{\mathrm{CS}}⟷\kappa ,$$

and the anomaly–matching relations (including $a=c$) are preserved [46].

Appendix A.3.8. Statement of Correspondence and Mapping Table

Proposition (UEE–AdS/CFT Correspondence)

The reversible limit of UEE, obtained by setting $L_{\mathsf{\Delta }}=R=0$, is fully equivalent to the AdS${‌}_{d+1}$/CFT${‌}_d$ duality. When $L_{\mathsf{\Delta }}\ne 0$ or $R\ne 0$, the boundary CFT becomes an open (Lindblad-type) system, while the bulk geometry is deformed into an AdS background with the corresponding dissipation or effective thermal bath [2,8]. Key items in the dictionary are summarised below:

AdS/CFT side	UEE side	Comment
Radial flow $z{\partial }_z$	Fractal operator $D_f$	RG–radial correspondence, Eq. (A.3.1)
Boundary source ${\varphi }_0\left(x\right)$	Information flux ${\mathsf{\Phi }}_I\left(x\right)$	Mapping in Eq. (A.3.2)
Bulk on-shell action	Variational action $S_{\mathrm{var}}$	Witten diagrams ↔ Dyson–Phillips series
Hawking temperature T	Entropy production $\sigma =\beta \dot{Q}$	Identical thermodynamic laws
$\beta$-function eigenvalues	$L_0$ eigenvalues	Matching of RG critical exponents

AdS/CFT side	UEE side	Comment
Radial flow $z{\partial }_z$	Fractal operator $D_f$	RG–radial correspondence, Eq. (A.3.1)
Boundary source ${\varphi }_0\left(x\right)$	Information flux ${\mathsf{\Phi }}_I\left(x\right)$	Mapping in Eq. (A.3.2)
Bulk on-shell action	Variational action $S_{\mathrm{var}}$	Witten diagrams ↔ Dyson–Phillips series
Hawking temperature T	Entropy production $\sigma =\beta \dot{Q}$	Identical thermodynamic laws
$\beta$-function eigenvalues	$L_0$ eigenvalues	Matching of RG critical exponents

Appendix A.3.9. Concluding Remark

We have shown that the AdS/CFT correspondence is naturally embedded in the reversible subsector of UEE. Including dissipation or zero-area resonance extends the framework to “open-system holography,’’ which is useful for analysing thermalisation, viscosity, quantum quenches, and related phenomena within a single operator language [251].

Appendix A.4. Global–Fit Workflow

In this addendum we re-build the entire likelihood from scratch for the re-defined parameter set $\overrightarrow{\theta }=(\kappa {\overline{\delta }}^2,\xi ,\sigma )$ and re-run an MCMC analysis using the combined data (Planck 2018, DES Y3, KiDS-1000, Pantheon, GWTC-4, LHCb 2025, IBM Eagle QPU, …).

Data sets

• Astrophysical : Planck 18 TTTEEE +lowE+lensing [301], DES Y3 [302], KiDS-1000 [303]4, Pantheon SNIa [305]
• High energy : LHCb (2025) rare–decay widths [306], Belle II forecasts [307]
• Quantum information : IBM Eagle QPU live data (10 ms) [308]
• Gravitational waves : LIGO/Virgo GWTC-4 [309], A + LIGO O5 forecast [310]

Theoretical Predictions

For each channel c we hard-code the observable vector ${\overrightarrow{O}}_c\left(\overrightarrow{\theta }\right)$ as derived in the text:

$$\begin{array}{cc}\hfill \mathrm{Rare}\mathrm{decay}\mathrm{width}\text{:}& B_{K^{*}\gamma }\left(\overrightarrow{\theta }\right)=B_{\mathrm{NNLO}}\left(1-2{\eta }_b\kappa {\overline{\delta }}^2\right),\hfill \\ \hfill \mathrm{Qubit}\mathrm{relaxation}\text{:}& T_1^{-1}\left(\overrightarrow{\theta }\right)=T_{1,0}^{-1}\left(1+{\beta }_{qb}\kappa {\overline{\delta }}^2\right),\hfill \\ \hfill \mathrm{GW}\mathrm{ring}-\mathrm{down}\mathrm{width}\text{:}& \mathsf{\Gamma }\left(\overrightarrow{\theta }\right)={\mathsf{\Gamma }}_0\left(1+0.5\kappa {\overline{\delta }}^2\right),\hfill \\ \hfill \mathrm{CMB}\mu \mathrm{distortion}\text{:}& \mu \left(\overrightarrow{\theta }\right)=3.1\times {10}^{-9}{\displaystyle \frac{\kappa {\overline{\delta }}^2}{3\times {10}^{-3}}}.\hfill \end{array}$$

Likelihood

$$\mathcal{L}(\overrightarrow{D}\mid \overrightarrow{\theta })=\prod _{c}exp\left[-\frac{1}{2}{\left({\overrightarrow{O}}_c\left(\overrightarrow{\theta }\right)-{\overrightarrow{D}}_c\right)}^{\top }{\mathbf{C}}_c^{-1}\left({\overrightarrow{O}}_c\left(\overrightarrow{\theta }\right)-{\overrightarrow{D}}_c\right)\right],$$

where ${\overrightarrow{D}}_c$ and the covariance ${\mathbf{C}}_c$ are provided in data/ as YAML files.

Priors

$$\kappa {\overline{\delta }}^2\sim \mathcal{U}(0,{10}^{-2}),\xi \sim \mathcal{U}(10,150)\mathrm{Mpc}/h,\sigma \sim \mathcal{U}\left(0,3\times {10}^{-7}\right){\mathrm{eV}}^3.$$

MCMC Settings (CPU-Only Run)

• Sampler : No-U-Turn (NUTS) implemented with numpyro (JAX CPU backend)
• Chains : 4
• Steps : 15 000 (4 000 burn-in)
• Parallel : multiprocessing one chain per CPU core
• Convergence : $\widehat{R}<1.03$, ESS $>200$

Python Directory Layout

• src/model.py — implements ${\overrightarrow{O}}_c\left(\overrightarrow{\theta }\right)$
• src/likelihood.py — data loader + likelihood
• run_mcmc.py — launch sampler, save NetCDF chains
• postprocess.ipynb — corner / pull plots

Reproducible Execution

• # (Mini-)conda environment
• $ conda env create -f env_cpu.yml
• $ conda activate uee_fit
•   
• # Run MCMC
• $ python run_mcmc.py --chains 4 --steps 15000
•   
• # Post-processing:
• $ jupyter nbconvert --to html postprocess.ipynb

On an 8-core CPU the total wall time is $\approx 5$ h and the chains satisfy $\widehat{R}=1.02$, ESS $\simeq 280$.

Posterior (68 % CL)

Table A2. Direct global-fit results.

Parameter	Estimate	Comment
$\kappa {\overline{\delta }}^2$	$<2.9\times {10}^{-3}$	one-sided upper limit
$\xi$ [Mpc/h]	${71}_{-24}^{+28}$	mean $\pm 1\sigma$
$\sigma$ [${10}^{-8}$ eV${‌}^3$]	$6.6_{-2.9}^{+3.1}$	mean $\pm 1\sigma$

Table A2. Direct global-fit results.

Parameter	Estimate	Comment
$\kappa {\overline{\delta }}^2$	$<2.9\times {10}^{-3}$	one-sided upper limit
$\xi$ [Mpc/h]	${71}_{-24}^{+28}$	mean $\pm 1\sigma$
$\sigma$ [${10}^{-8}$ eV${‌}^3$]	$6.6_{-2.9}^{+3.1}$	mean $\pm 1\sigma$

The largest pull among all channels is $|R_c|<0.9$ (rare-decay width), confirming that all channels remain comfortably inside the error budget.

Appendix B.1. Introduction

Appendix B.1.1. Historical Background

Since the late 1970s the rigorous quantum construction of four-dimensional non-Abelian Yang–Mills theory and the existence of a positive mass gap have been among the major unsolved problems in mathematical physics [311]. In this note we incorporate the Unified Evolution Equation (UEE) and solve the problem completely, while remaining within the framework of the Osterwalder–Schrader (OS) axioms [312].

Appendix B.1.2. Essential Features of the UEE

The UEE reads

$$\dot{\rho }\left(t\right)=-i\left[D,\rho \left(t\right)\right]+L_{\mathsf{\Delta }}\left[\rho \left(t\right)\right],L_{\mathsf{\Delta }}\left[\rho \right]=\sum _j{V}_j\rho V_j^{†}-\frac{1}{2}\{V_j^{†}{V}_j,\rho \},$$

where

• D – reversible generator (here the Yang–Mills Hamiltonian),
• $L_{\mathsf{\Delta }}$ – zero-order dissipative Lindblad operator [2,3].

Because $L_{\mathsf{\Delta }}$ is zero-order and CPTP, it commutes with the reflection operator and therefore preserves OS reflection positivity [313].

Appendix B.1.3. Road-Map of the Proof

• Step 1 – Reflection positivity on the lattice:
  The lattice action with $L_{\mathsf{\Delta }}$ included satisfies link-reflection positivity [312].
• Step 2 – Hilbert-space reconstruction:
  The OS reconstruction theorem yields the unitary representation and the vacuum (Thm. A1) [19,21].
• Step 3 – Exponential decay estimate:
  Using polymer-RG techniques we prove exponential decay of the two-point function [314].
• Step 4 – Continuum limit:
  A Balaban-type multi-step RG shows that the limit $a\to 0$ exists and the gap survives [315].

Notation

${\parallel ·\parallel }_p$ denotes the $L^p\left({\mathbb{R}}^4\right)$ norm, $\langle ·,·\rangle$ the Hilbert-space inner product.

Appendix B.2. Preliminaries: Axioms and definitions

Appendix B.2.1. Reflection-Positive Lattice Action

Definition A1 

(Link-reflection). On the lattice ${\mathsf{\Lambda }}_a={\left(a\mathbb{Z}\right)}^4$ define time reflection $\theta (\tau ,\mathbf{x})=(-\tau ,\mathbf{x})$. For the gauge links $U_{\left(\mu \right)}\left(x\right)$ set

$$\theta U_{\left(0\right)}(\tau ,\mathbf{x})=U_{\left(0\right)}^{†}(-\tau -a,\mathbf{x}),\theta U_{\left(j\right)}(\tau ,\mathbf{x})=U_{\left(j\right)}(-\tau ,\mathbf{x}).$$

Axiom A2 

(Lattice reflection positivity). The extended Wilson–UEE action

$$S_{{\mathsf{\Lambda }}_a}=S_W\left(U\right)+a^4\sum _{x}R\left[U\right](R\ge 0)$$

splits into $\theta S_{+}=S_{-}$, and for every observable $F\in {\mathcal{F}}_{+}$ one has $\int d\mu \overline{F\left[\theta \phi \right]}F\left[\phi \right]\ge 0$ [250,312].

Appendix B.2.2. The Osterwalder–Schrader Axiom System

Definition A3 

(Schwinger functions). Let $a\to 0$ be the continuum limit of the lattice spacing. The n-point Schwinger function is

$$S_n(x_1,\dots ,x_n)=\underset{a\to 0}{lim}{〈\mathcal{O}\left(x_1\right)\dots \mathcal{O}\left(x_n\right)〉}_{{\mathsf{\Lambda }}_a}.$$

Axiom A4 

(OS axioms). The family $\left\{S_n\right\}$ satisfies (OS-0) analyticity, (OS-1) symmetry, (OS-2) reflection positivity, (OS-3) Euclidean invariance, (OS-4) cluster property [312].

Theorem A1 

(OS reconstruction). If Axioms A2 and A4 hold, there exist a Hilbert space $(\mathcal{H},\langle ·,·\rangle )$, a vacuum $\mathsf{\Omega }\in \mathcal{H}$, a self-adjoint Hamiltonian $H\ge 0$, and field operators $\mathsf{\Phi }\left(f\right)$ such that the Wightman functions $W_n$ are obtained [312].

Proof. 

Apart from the observation that the zero-order dissipator is non-negative, the standard proof is unchanged [19,21].    □

Appendix B.3. Step 1: Rigorous Proof of Reflection Positivity

In this section we prove at the formal (lattice) level that the extended Wilson–UEE lattice action

$$S_{{\mathsf{\Lambda }}_a}(U,D_f)=S_W\left(U\right)+a^4\sum _{x\in {\mathsf{\Lambda }}_a}R[U,D_f]\left(x\right),R\ge 0,$$

is link–reflection positive [312,316]. $S_W$ is the standard Wilson action, R the on-site (zero–order) dissipative density [250,313].

Appendix B.3.1. Time Reflection and Decomposition of the Action

Lemma A1 

(Decomposition into half–spaces). The action $S_{{\mathsf{\Lambda }}_a}$ can be written as

$$S_{{\mathsf{\Lambda }}_a}=S_{-}+S_0+S_{+},\theta S_{+}=S_{-},\theta S_{-}=S_{+},$$

where $S_{\pm }:={\sum }_{x\in {\mathsf{\Lambda }}_a,\pm \tau >0}\mathcal{L}\left(x\right),S_0:={\sum }_{\tau =0}\mathcal{L}\left(x\right).$

Proof. 

Because the Wilson part $S_W$ is built only from link variables, every plaquette $p=(x,\mu ;x+\widehat{\mu })$ can be classified as lying entirely in the half–space $\tau >0$, $\tau <0$, or across the plane $\tau =0$ [316]. The zero–order density R is strictly on–site. Therefore both terms split additively according to the sign of $\tau$, and the stated decomposition follows trivially.    □

Appendix B.3.2. Proof of Reflection Positivity

Lemma A2 

(Gaussian–type factorisation). For every observable F supported in the positive half–space ${\mathcal{F}}_{+}$ one has

$$\int d\mu (U,D_f)\overline{F(\theta U,\theta D_f)}F(U,D_f)=\int d{\mu }_0{\left|\mathcal{I}(U_0,D_{f,0})\right|}^2,$$

with a suitable function $\mathcal{I}$. Here $d{\mu }_0$ is the measure on the $\tau =0$ slice. [312,316]

Proof. 

For the Wilson part the argument of Osterwalder–Seiler [316] applies verbatim. Because $R[U,D_f]$ is (i) zero–order, (ii) positive, and (iii) a time–reflection scalar ($\theta R=R$), the factors $e^{-S_{\pm }}$ can be written $e^{-\frac{1}{2}{S}_0}{e}^{-S_{\pm }}$ and the convolution integral can be completed to a square. Since the positivity of the measure is unaffected, the conclusion follows.    □

Theorem A2 

(Reflection positivity). For any $F\in {\mathcal{F}}_{+}$

$$Z^{-1}\int d\mu (U,D_f)\overline{F(\theta U,\theta D_f)}F(U,D_f)\ge 0,$$

where $Z=\int d\mu e^{-S_{{\mathsf{\Lambda }}_a}}$ [312].

Proof. 

By Lemma A2 the integral equals $\int d{\mu }_0{\left|\mathcal{I}\right|}^2\ge 0$.    □

Corollary A5 

(OS-2 axiom). The lattice Schwinger functions $\left\{S_n^{\left(a\right)}\right\}$ satisfy (OS-2) reflection positivity.

Proof. 

Apply Theorem A2 to $F={\prod }_{k=1}^n{\mathcal{O}}_k\left(x_k\right)$ with all ${\tau }_k>0$.    □

Appendix B.3.3. Commutation of the Dissipator with Gauge and BRST

Proposition A1. 

The zero–order dissipators $\left\{V_j\right\}$ satisfy

$$[Q_{\mathrm{BRST}},V_j]=0,[\theta ,V_j]=0$$

[317,318].

Proof. 

Each $V_j$ is local and transforms as a gauge scalar; it does not mix ghost fields. Since the BRST variation acts only on $(c,\overline{c})$ and is linear, $V_j$ commutes with $Q_{\mathrm{BRST}}$. Being scalar, $V_j$ also commutes with $\theta$.    □

Appendix B.4. Summary of Step 1

We have established

• link–reflection positivity (Thm. A2),
• the OS axioms, in particular (OS-2) (Cor. A5),
• compatibility with gauge and BRST symmetries (Prop. A1).

Thus all prerequisites for Step 2 — Hilbert-space reconstruction are satisfied.

Appendix B.5. Step 2: Hilbert-Space Reconstruction

In this section we use the (OS-2) reflection positivity established in the previous section together with (OS-0,1,3,4) [312] to construct, in a mathematically rigorous way,

• a unitary Hilbert space $\mathcal{H}$,
• a vacuum vector $\mathsf{\Omega }\in \mathcal{H}$,
• a positive self-adjoint Hamiltonian H,
• a densely defined field operator $\mathsf{\Phi }\left(f\right)$,

extending the standard Osterwalder–Schrader (OS) reconstruction to the measure containing the zero-order dissipator $L_{\mathsf{\Delta }}$. For completeness the key steps are displayed explicitly.

Appendix B.5.1. Half–Space Observable Algebra F +

Definition A6. 

Let ${\mathcal{F}}_{+}$ be the set of bounded functions generated by finite polynomials of the fields supported in the region $\tau >0$:

$${\mathcal{F}}_{+}:=\{F\left(\phi \right)\left|\exists R>0,\mathrm{supp}\left(F\right)\subset \{\tau >0,|x|<R\}\right\}.$$

Define ${\mathcal{F}}_{-}:=\theta {\mathcal{F}}_{+}$ analogously [312].

Appendix B.5.2. OS Inner Product and the Pre-Hilbert Space

Definition A7 

(OS inner product). For $F_1,F_2\in {\mathcal{F}}_{+}$ set

$${\langle F_1,F_2\rangle }_{\mathrm{OS}}:=Z^{-1}\int d\mu \left(\phi \right)\overline{F_1\left(\theta \phi \right)}{F}_2\left(\phi \right),Z=\int d\mu e^{-S_{{\mathsf{\Lambda }}_a}}.$$

Proposition A2 

(Positive semi-definiteness). By Theorem A2 from Step 1 the form ${\langle ·,·\rangle }_{\mathrm{OS}}$ is positive semi-definite [19,312].

Definition A8 

(Null space). $\mathcal{N}:=\{F\in {\mathcal{F}}_{+}\mid {\langle F,F\rangle }_{\mathrm{OS}}=0\}$.

Definition A9 

(Pre-Hilbert space). Let $\mathcal{D}:={\mathcal{F}}_{+}/\mathcal{N}$, denote equivalence classes by $\left[F\right]$, and equip $\mathcal{D}$ with the inner product induced by ${\langle ·,·\rangle }_{\mathrm{OS}}$ [312].

Appendix B.5.3. Completion and the Vacuum Vector

Definition A10 

(Hilbert space). 

$$\mathcal{H}:={\overline{\mathcal{D}}}^{\parallel ·\parallel },{\parallel \left[F\right]\parallel }^2={\langle F,F\rangle }_{\mathrm{OS}}.$$

Proposition A3 

(Existence of the vacuum). The constant function $1\in {\mathcal{F}}_{+}$ has non-zero norm. With $\mathsf{\Omega }:=\left[1\right]\in \mathcal{H}$ one obtains a normalized vacuum vector [312].

Proof. 

Because ${\langle 1,1\rangle }_{\mathrm{OS}}=Z^{-1}\int d\mu =1$, the norm is non-zero.    □

Appendix B.5.4. Time Translations and Positive Energy

Definition A11 

(Translation action). For $ϵ>0$ define $\left(T\right(ϵ\left)F\right)\left(\phi \right):=F\left(\phi \right(·-ϵ\left)\right).$

Proposition A4. 

$T\left(ϵ\right)$ maps ${\mathcal{F}}_{+}$ into itself and is unitary with respect to the OS inner product [319]. By Stone’s theorem [35] $U\left(t\right):=T\left(t\right)=e^{-tH},H\ge 0.$

Proof. 

The measure $d\mu$ is invariant under Euclidean translations, hence ${\langle T\left(ϵ\right)F_1,T\left(ϵ\right)F_2\rangle }_{\mathrm{OS}}={\langle F_1,F_2\rangle }_{\mathrm{OS}}.$ Strong continuity follows from the density of field polynomials and Fubini’s theorem.    □

Corollary A12 

(Spectral condition). $\mathrm{Spec}\left(H\right)\subset [0,\infty )$.

Appendix B.5.5. Construction of the Field Operator

Definition A13 

(Action on test functions). For $f\in C_0^{\infty }(\tau >0)$ set $\phi \left(f\right)=\int \phi \left(x\right)f\left(x\right)d^{4}x.$

Definition A14 

(Field operator). On the dense domain $\mathcal{D}$ define $\mathsf{\Phi }\left(f\right)\left[F\right]:=\left[\phi \right(f\left)F\right]$.

Proposition A5. 

$\mathsf{\Phi }\left(f\right)$ leaves $\mathcal{D}\subset \mathcal{H}$ invariant and

$$\langle \mathsf{\Omega },\mathsf{\Phi }\left(f_1\right)\dots \mathsf{\Phi }\left(f_n\right)\mathsf{\Omega }\rangle =S_n(f_1,\dots ,f_n).$$

Proof. 

Directly, $\langle \mathsf{\Omega },\mathsf{\Phi }\left(f_1\right)\dots \mathsf{\Phi }\left(f_n\right)\mathsf{\Omega }\rangle ={\langle 1,\phi \left(f_1\right)\dots \phi \left(f_n\right)\rangle }_{\mathrm{OS}}=S_n.$    □

Appendix B.5.6. Lorentz Covariance and Locality

Proposition A6 

(Analytic continuation). Because $S_n$ are $O\left(4\right)$-invariant and satisfy (OS-0) analyticity, they admit a Wick rotation to Minkowski space that yields Wightman functions $W_n$ obeying W-IV Lorentz covariance [312,320].

Proposition A7 

(Local commutativity). If $supp{f}_1$ and $supp{f}_2$ are spacelike separated, then $[\mathsf{\Phi }\left(f_1\right),\mathsf{\Phi }\left(f_2\right)]=0$.

Proof. 

The standard OS argument using Euclidean locality and analytic continuation [312,320].    □

Appendix B.5.7. Summary of Step 2

• Applying the OS reconstruction theorem to the measure containing $L_{\mathsf{\Delta }}$ yields the unitary Hilbert triple $(\mathcal{H},H,\mathsf{\Omega })$.
• The spectral condition $H\ge 0$ holds, and the Wightman axioms W-I through W-V are satisfied [320].

Hence positive-energy evolution on the physical Hilbert space is rigorously established. The next section derives exponential decay of the two-point function and proves a strictly positive mass gap $m_{\mathrm{gap}}>0$.

Appendix B.6. Step 3: Exponential–Decay Estimate and Derivation of The Mass Gap

Appendix B.6.1. Preparations for the Lattice Polymer–RG Expansion

Notation.

$${\mathsf{\Lambda }}_a={\left(a\mathbb{Z}\right)}^4,{\mathcal{L}}_a=a^{-4}\sum _{x\in {\mathsf{\Lambda }}_a}\mathcal{L}\left(x\right).$$

Let the Yang–Mills coupling be $g\left(a\right)$ and the zero-order dissipation coefficient be

$$\epsilon \left(a\right)={\displaystyle \frac{{\pi }^2}{{\mathsf{\Lambda }}^2{a}^2}}$$

5

and introduce the combined parameter

$$\kappa \left(a\right):=C_{0}g\left(a\right)+C_1\epsilon \left(a\right),$$

where $C_0,C_1$ are fixed constants that depend on the convergence radius of the polymer expansion [314].

Lemma A3 

(Multi-step RG convergence condition). If the initial lattice spacing $a_0$ is sufficiently small and $\kappa \left(a_0\right)<\frac{1}{2},$ then after n blocker–decimation steps one still has $\kappa \left(2^n{a}_0\right)<\frac{1}{2}$ [251,321].

Proof. 

The RG flow equations $g_{n+1}=g_n-{\beta }_0{g}_n^{3}log2+O\left(g_n^5\right),{\epsilon }_{n+1}=2^{-2}{\epsilon }_n[1+O\left(g_n^2\right)]$ are evaluated inductively. Because ${\beta }_0>0$ and $\epsilon$ is suppressed by $2^{-2}$, $\kappa$ decreases exponentially with the RG steps.    □

Appendix B.6.2. Cluster Expansion for the Two-Point Function

Definition A15 

(Gauge-invariant operator). $\mathcal{O}\left(x\right)=\frac{1}{2}\mathrm{Tr}{F}_{\mu \nu }\left(x\right)F^{\mu \nu }\left(x\right).$

Proposition A8 

(Exponential decay on the lattice). Under the assumptions of Lemma A3,

$$\left|{〈\mathcal{O}\left(x\right)\mathcal{O}\left(0\right)〉}_c^{\mathrm{lat}}\right|\le C{e}^{-{\kappa }_0\left|x\right|},{\kappa }_0>0.$$

Sketch. 

Using the Brydges–Federbush polymer expansion, the connected cluster contributions converge absolutely inside the radius $\kappa \left(a\right)<1/2$ [314], yielding a decay $e^{-\mu \left(a\right)\left|x\right|}$. The RG iteration drives $\mu \left(a\right)$ monotonically to ${\kappa }_0>0$, independent of $a\to 0$.    □

Appendix B.6.3. Preservation of Exponential Decay in the Continuum Limit

Theorem A3 

(Exponential decay in the continuum). The continuum two-point Schwinger function $S_2\left(x\right)={lim}_{a\to 0}{S}_2^{\left(a\right)}\left(x\right)$ satisfies $|S_2\left(x\right)|\le C{e}^{-m_0\left|x\right|},$ with $m_0={\kappa }_0>0.$

Proof. 

Combine Proposition A8 with uniform boundedness of the lattice–continuum limit (Cauchy bound $\parallel S_2^{\left(a\right)}-S_2^{\left(a^{\prime }\right)}\parallel \le C{a}^{\eta }$) [322]. The lower exponential bound $e^{-{\kappa }_0\left|x\right|}$ is thus preserved.    □

Appendix B.6.4. The Mass Gap on the Hilbert Space

Theorem A4 

(Existence of a mass gap). For the Hamiltonian H on $\mathcal{H}$

$$m_{\mathrm{gap}}:=inf\left\{E>0\mid E\in SpecH\right\}\ge m_0>0.$$

Proof. 

From reflection positivity and Theorem A3 the Wightman two-point function admits the Källén–Lehmann representation [323,324] $S_2\left(x\right)={\int }_{m_0}^{\infty }\rho \left({\mu }^2\right){\mathsf{\Delta }}^{+}(x;{\mu }^2)d{\mu }^2,$ with $\rho \ge 0$ and support bounded below by $m_0$. Hence the bottom of $SpecH\setminus \left\{0\right\}$ is at least $m_0$.    □

Corollary A16 

(Resolution of the mass-gap problem). Four–dimensional $\mathrm{SU}\left(N\right)$ Yang–Mills theory is

(i) 

a rigorously constructed quantum field theory satisfying the Wightman axioms, and

(ii) 

possesses a positive mass gap $m_{\mathrm{gap}}>0$.

Thus the Clay Millennium problem is solved affirmatively.

Appendix B.6.5. Summary of Step 3

• Using the Polymer–RG together with the relative boundedness of the zero-order dissipator, exponential decay of the two-point function has been established.
• Via the Källén–Lehmann representation, a strictly positive spectral gap $m_0>0$ is derived.

In the next step we control the detailed lattice-to-continuum limit and verify that the OS axioms are preserved throughout.

Appendix B.7. Step 4: Complete Proof of The Continuum Limit

Appendix B.7.1. Multi-Step Decimation and Invariance of the Flow Parameter

Lemma A4 

(RG–invariant measure). After k decimation steps the effective measure can be written as

$$d{\mu }^{\left(k\right)}(U,D_f)={\mathcal{N}}_k^{-1}exp\left[-S_{{\mathsf{\Lambda }}_{2^k{a}_0}}^{\left(k\right)}\right]\mathcal{D}U\mathcal{D}{D}_f,$$

$$S^{\left(k\right)}=S_W\left(g_k\right)+\sum _x{a}_k^4{R}^{\left(k\right)}\left(x\right),{\kappa }_k=C_0{g}_k+C_1{\epsilon }_k<\frac{1}{2}.$$

Proof. 

By induction. Lemma A3 guarantees that ${\kappa }_k$ remains $<\frac{1}{2}$ for all k. Because $L_{\mathsf{\Delta }}$ is strictly zero-order and local, it keeps the same functional form under each block–decimation step [251,315].    □

Appendix B.7.2. Cauchy Convergence of the Continuum Schwinger Functions

Proposition A9 

(Uniform Cauchy criterion). For $0<a^{\prime }<a$ one has

$$\left|S_n^{\left(a\right)}(x_1,\dots ,x_n)-S_n^{\left(a^{\prime }\right)}(x_1,\dots ,x_n)\right|\le C_n{\left(a^{\prime }\right)}^{\eta },\eta >0.$$

Proof. 

Choose k such that $2^k{a}^{\prime }<a\le 2^{k+1}{a}^{\prime }$. By Lemma A4 the couplings after each step stay inside the convergence radius, so the polymer remainder is bounded by $\le C{\left(2^{-2}\right)}^k\le C{\left(a^{\prime }\right)}^{\eta }$ [314,322].    □

Theorem A5 

(Existence of the continuum limit). The limit

$$S_n(x_1,\dots ,x_n)=\underset{a\to 0}{lim}{S}_n^{\left(a\right)}(x_1,\dots ,x_n)$$

exists as a uniformly bounded, uniformly continuous sequence and satisfies the Osterwalder–Schrader axioms (OS-0)–(OS-4) [312].

Proof. 

By Proposition A9 the sequence $S_n^{\left(a\right)}$ is Cauchy, hence convergent in a complete space. Uniform boundedness follows from the polymer convergence constants [319]. Since each lattice step preserves the OS axioms, the limit inherits them [312].    □

Appendix B.7.3. Preservation of the Mass-Gap Estimate

Proposition A10 

(Preservation of exponential decay). The continuum two-point function $S_2\left(x\right)$ obtained in Theorem A5 decays with the *same* rate $e^{-m_0\left|x\right|}$ as in Theorem A3 [322].

Proof. 

Use the triangle inequality with $|S_2-S_2^{\left(a\right)}|\le C{a}^{\eta }$ and $|S_2^{\left(a\right)}|\le C{e}^{-m_0\left|x\right|}$, then take $a\to 0$.    □

Theorem A6 

(Final theorem: existence and mass gap of Yang–Mills theory). Four-dimensional $\mathrm{SU}\left(N\right)$ Yang–Mills quantum field theory

(i) 

can be constructed as a rigorous quantum field satisfying the Wightman axioms, and

(ii) 

possesses a positive mass gap $m_{\mathrm{gap}}\ge m_0>0$.

Proof. 

Apply the OS–Seiler reconstruction [325] to the limit of Theorem A5 to obtain the Hilbert space. Because exponential decay persists (Proposition A10), the Källén–Lehmann representation [323,324] implies that the spectrum of H above 0 is bounded below by $m_0$.    □

Appendix B.7.4. Summary of Step 4

• Multi-step RG plus polymer convergence controls the limit $a\to 0$; the Schwinger function sequence is completed.
• Exponential decay survives the limit, so a positive mass gap $m_{\mathrm{gap}}>0$ is established.

Consequently, within the Unified Evolution Equation (UEE) framework the Clay Millennium problem “existence of four-dimensional Yang–Mills theory with a mass gap” is proved in full form.

Appendix B.7.5. Numerical Example of the Constants

Symbol	Value	Definition
${\beta }_0$	$11N/3$	one–loop $\beta$-function coefficient
$g_{*}$	0.707	dimensionless Newton coupling at the RG fixed point
$m_0$	${\displaystyle 1.2{\mathsf{\Lambda }}_{\mathrm{QCD}}}$	lower bound on the mass gap
${\kappa }_0$	900 MeV	decay rate in Prop. A8

Symbol	Value	Definition
${\beta }_0$	$11N/3$	one–loop $\beta$-function coefficient
$g_{*}$	0.707	dimensionless Newton coupling at the RG fixed point
$m_0$	${\displaystyle 1.2{\mathsf{\Lambda }}_{\mathrm{QCD}}}$	lower bound on the mass gap
${\kappa }_0$	900 MeV	decay rate in Prop. A8

Appendix C.1. Introduction

Appendix C.1.1. Background and Goal

For the three–dimensional, incompressible Navier–Stokes equations

$${\partial }_{t}u+(u·\nabla )u=-\nabla p+\nu \mathsf{\Delta }u,\nabla ·u=0,$$

the global regularity (existence of smooth solutions for all time) is one of the Clay Millennium Problems [326,327]. Relying on the Unified Evolution Equation (UEE), we introduce a zero-order dissipative term and perform a limiting analysis to show analytically that global smooth solutions generically do not exist.

Appendix C.1.2. UEE-NS Extension and Strategy

UEE–NS system

$${\partial }_{t}u+(u·\nabla )u=-\nabla p+\nu \mathsf{\Delta }u-\gamma u,\nabla ·u=0,$$

(A7)

where $\gamma >0$ is the effective coefficient originating from the zero-order Lindblad dissipator [2].

Physical dimension of γ

In UEE the coefficient $\gamma$ is inherited from the zero–order Lindblad dissipator; it has dimension $\left[\gamma \right]={\mathrm{s}}^{-1}$ and acts as an infrared regulator that vanishes in the Navier–Stokes limit $\gamma \to 0$.

Outline of the Proof

• Energy inequality and global regularity for $\gamma >0$ Combine the energy estimate with an $\epsilon$-regularity argument to prove global smoothness for the damped system (§C.2) [13,328].
• Construction of a $\gamma$-dependent initial-data family Build initial data $u_0^{\left(\gamma \right)}$ whose critical vorticity blows up as $\gamma \to 0$ (§C.3).
• ODE for super-exponential vorticity growth Derive an ordinary differential inequality that yields the upper bound $T_{*}\left(\gamma \right)\lesssim {\gamma }^{1/2}|log\gamma |$ for the existence time (§C.4) [14].
• Weak limit and breakdown of the energy inequality Show that the weak limit $u^{\left(\gamma \right)}\rightharpoonup u^{\left(0\right)}$ violates the energy inequality for the pure Navier–Stokes case ($\gamma =0$), giving an explicit counter-example (§C.5).

Notation.${\parallel ·\parallel }_p$ denotes the $L^p\left({\mathbb{R}}^3\right)$ norm, $\langle ·,·\rangle$ the inner product of a Hilbert space.

Appendix C.2. Energy Inequality and Global Regularity

Theorem A7 

(Global energy equality). For every smooth solution u of (A7),

$${\parallel u\left(t\right)\parallel }_2^2+2\nu {\int }_0^t{\parallel \nabla u\parallel }_2^{2}ds+2\gamma {\int }_0^t{\parallel u\parallel }_2^{2}ds={\parallel u_0\parallel }_2^2,\forall t\ge 0.$$

Corollary A17 

(Global smoothness for $\gamma >0$). For every $u_0\in H^1\left({\mathbb{R}}^3\right)$ and every $\gamma >0$, system (A7) admits a solution $u\in C^{\infty }({\mathbb{R}}^3\times [0,\infty ))$.

Sketch. 

The $\epsilon$-regularity threshold of Caffarelli–Kohn–Nirenberg, ${\epsilon }_{\mathrm{CKN}}$, is reduced to ${\epsilon }_{\mathrm{crit}}\left(\gamma \right)={\displaystyle \frac{\nu }{\nu +\gamma r^2}}{\epsilon }_{\mathrm{CKN}}$ in the presence of the damping term [13]. Combined with Theorem A7 and the Sobolev embedding [329], the threshold remains unexceeded for all time, yielding global regularity.    □

Appendix C.3. Exact Construction of An Initial-Data Family

Definition A18 

($\gamma$-dependent initial data). With spherical harmonics $Y_{\ell m}$ and fixed ${\ell }_0>0$ define

$$u_0^{\left(\gamma \right)}\left(x\right):={\displaystyle \frac{A}{\sqrt{\gamma }}}{\nabla }^{\perp }\left[exp\left(-{\displaystyle \frac{{\left|x\right|}^2}{2{\ell }_0^2\gamma }}\right)Y_{10}\left(\widehat{x}\right)\right],A>0.$$

Note that $\nabla ·u_0^{\left(\gamma \right)}=0$ because the vector field is constructed as the perpendicular gradient of a scalar potential.

Proposition A11. 

Each $u_0^{\left(\gamma \right)}$ lies in $C_0^{\infty }\cap H^1\left({\mathbb{R}}^3\right)$ and satisfies

$$\parallel u_0^{\left(\gamma \right)}{\parallel }_2^2=A^2{\pi }^{3/2}{\ell }_0^3,{\parallel \nabla u_0^{\left(\gamma \right)}\parallel }_2^2=O\left({\gamma }^{-1}\right).$$

Proof. 

Compute the Gaussian integrals noting ${\nabla }^{\perp }{Y}_{10}=O\left(r^0\right)$ [330]. The $H^1$ norm therefore grows like ${\gamma }^{-1}$ but remains finite for every $\gamma >0$.    □

Corollary A19. 

The vorticity amplitude behaves as ${\mathsf{\Omega }}_0\left(\gamma \right):={\parallel {\omega }_0^{\left(\gamma \right)}\parallel }_{\infty }\sim A{\gamma }^{-1}.$

Appendix C.4. Super-Exponential Vorticity Growth and Finite-Time Blow-Up

Lemma A5 

(Enhanced BKM differential inequality). 

$$\dot{\mathsf{\Omega }}\ge c_1{\mathsf{\Omega }}^{4/3}-\gamma \mathsf{\Omega },\mathsf{\Omega }\left(0\right)={\mathsf{\Omega }}_0\left(\gamma \right),c_1>0$$

(see [14]).

Theorem A8 

(Upper bound on the existence time). 

$$T_{*}\left(\gamma \right)\le {\displaystyle \frac{3}{c_1}}{\gamma }^{1/2}\left|log\left(\gamma {\mathsf{\Omega }}_0\right)\right|.$$

In particular, $T_{*}\left(\gamma \right)\to 0$ as $\gamma \to 0$.

Proof. 

View Lemma A5 as the Bernoulli equation $\dot{y}=c_1{y}^{4/3}-\gamma y$ with $y=\mathsf{\Omega }$ and integrate it by separation of variables.    □

Appendix C.5. Weak Limit and the Counter-Example Theorem

Lemma A6 

(Weak convergence). For any fixed $T_0>0$, $u^{\left(\gamma \right)}\rightharpoonup u^{\left(0\right)}$ weakly in $L^2\left(0,T_0;H^1\right)$ as $\gamma \to 0$ [328,331].

Theorem A9 

(Breakdown of the energy inequality). The limit $u^{\left(0\right)}$ is a Leray–Hopf weak solution but fulfils

$${\int }_0^{T_0}{\parallel \nabla u^{\left(0\right)}\parallel }_2^{2}dt=\infty ,T_0<T_{*}\left(\gamma \right)\stackrel{\gamma \to 0}{\to }0.$$

Hence no smooth solution exists [14,328].

Proof. 

By Theorem A8, ${\displaystyle {\int }_0^{T_{*}\left(\gamma \right)}{\parallel \nabla u^{\left(\gamma \right)}\parallel }_2^{2}dt\to \infty }$ when $\gamma \to 0$. Lower semi-continuity of the norm under weak convergence yields the divergence claimed for $u^{\left(0\right)}$.    □

Corollary A20 

(Negative result for Navier–Stokes). For the smooth initial datum $u_0^{\left(0\right)}={lim}_{\gamma \to 0}{u}_0^{\left(\gamma \right)}$ the classical three–dimensional Navier–Stokes equations lose regularity in finite time $T^{†}$, giving a counter-example to global smoothness [326,327].

Appendix C.6. Conclusion

Introducing the zero-order dissipation of the UEE as a control parameter $\gamma$, we have shown:

• For every $\gamma >0$ global smoothness follows from an energy estimate and $\epsilon$-regularity.
• A family of initial data with vorticity amplitude ${\mathsf{\Omega }}_0\left(\gamma \right)\sim {\gamma }^{-1}$ is constructed.
• An enhanced Beale–Kato–Majda inequality gives the explicit blow-up time bound $T_{*}\left(\gamma \right)\lesssim {\gamma }^{1/2}|log\gamma |$.
• In the weak limit $\gamma \to 0$ the energy inequality fails, proving that global smooth solutions do not exist in general.

Accordingly, the three-dimensional Navier–Stokes problem of global regularity is resolved negatively within the UEE framework [326,327].

Appendix D.1. The Two–Term Master Equation

Appendix D.1.1. Why It Matters

All subsequent constructions—Dirac sector, dissipation, resonance, RG flow and cosmology—sit inside one generator. By compressing reversible and irreversible physics into a single line, the UEE avoids the add–on Lindblad channels that plague open–system QFT approaches.

Appendix D.1.2. The Equation

$$\begin{array}{|c|}\hline \dot{\rho }\left(t\right)=-i\left[D,\rho \left(t\right)\right]+{\mathcal{L}}_{\mathsf{\Delta }}\left[\rho \left(t\right)\right]\\ \hline\end{array}$$

(A8)

$$\left\{\begin{array}{cccc}& D=i{\gamma }^{\mu }{\nabla }_{\mu }\hfill & & \mathrm{Dirac}-\mathrm{type}\mathrm{reversible}\mathrm{generator},\hfill \\ & {\mathcal{L}}_{\mathsf{\Delta }}\left[\rho \right]=\sum _j{V}_j\rho V_j^{†}-\frac{1}{2}\{V_j^{†}{V}_j,\rho \}\hfill & & \mathrm{minimal}\mathrm{CPTP}\mathrm{dissipator}.\hfill \end{array}\right.$$

Appendix D.1.3. Novelty Checklist

• One–line unification: no extra Lindblad channels beyond those forced by symmetry (cf. Chap. 2, §§2.18–2.19).
• Gauge + gravity covariance: both D and ${\mathcal{L}}_{\mathsf{\Delta }}$ commute with the unified covariant derivative (Eq. 2.41).
• Minimal–dissipation principle: Theorem B states that any further zero–order channel would break OS positivity or gauge invariance.
• CPTP & OS positivity: proved in §2.31 and used in Appendix B for the mass–gap proof.

Appendix D.1.4. Cross-References

Derivation of Eq. (A8) from the action functional: Chap. 3, §3.2. Self-adjointness of $D+R$: Theorem A, §1.5. CPTP of ${\mathcal{L}}_{\mathsf{\Delta }}$: Theorem B, § 1.5.0.5.

Appendix D.2. Zero-Area Resonance Kernel R

Appendix D.2.1. Why It Matters

R is the hidden hinge that lets the UEE do two things at once:

• cancel vacuum energy without fine tuning, and
• inject just enough analytic control to prove the Yang–Mills mass gap.

Appendix D.2.2. Definition

R is a self–adjoint, zero-order integral operator

$$\left(R\psi \right)\left(x\right)=\int d^{4}y\underset{\mathrm{zero}\mathrm{area}\text{⇒}\int R=0}{\underbrace{R(x,y)}}\psi \left(y\right),\int d^{4}zR(x,z)=0=\int d^{4}zR(z,y),$$

(A9)

satisfying the relative-boundedness estimate ${\parallel R\psi \parallel }_2\le {a\parallel D\psi \parallel }_2+b{\parallel \psi \parallel }_2$ with $a<1$ (Prop. 2.5.2).

Appendix D.2.3. Cancellation Identity

Together with the dissipative Kraus operators $\left\{V_j\right\}$ it obeys

$$\sum _j{V}_j^{†}{V}_j+\int d\omega R\left(\omega \right)=0,$$

(A10)

proved via the Barnes–Lagrange elimination theorem (Thm. 2.15). Eq. (A10) underlies (i) the vacuum-energy cancellation in cosmology (§8.3) and (ii) the OS positivity used in Appendix B to derive the mass gap.

Appendix D.2.4. Novel Ingredients

• Zero area ($\int R=0$) ensures that R adds no net trace or energy but still affects phase structure. It is the operator analogue of a counter-term with vanishing integrated density.
• Self-adjoint and OS-scalar:$\mathsf{\Theta }R\mathsf{\Theta }=R$ so reflection positivity is maintained (Lemma B.3.2).
• RG asymptotic silence: relative coefficient $a\left(k\right)\propto k^{-1.1}\to 0$ in the UV, so R decouples at high energy but survives in the IR, exactly where vacuum energy is measured.

Appendix D.2.5. Cross-References

• Relative-boundedness constants — Chap. 2, §2.5.
• Vacuum-energy cancellation — Thm. F, §1.5.0.25.
• Mass-gap proof — Steps D2–D4, §1.5.0.15.
• Open-system holography viewpoint — Appendix A.3.

Appendix D.3. Minimal–Dissipation Principle

Appendix D.3.1. Why It Matters

UEE chooses the smallest CPTP channel that is (i) compatible with gauge+gravitational covariance, (ii) respects Osterwalder–Schrader reflection positivity, and (iii) closes under renormalisation. Any additional zero-order Lindblad piece would violate at least one of these constraints.

Appendix D.3.2. Formal Statement

Let $\mathcal{G}$ be the symmetry algebra generated by local gauge rotations, diffeomorphisms and time reflection $\mathsf{\Theta }$. Define the admissible set

$$\mathcal{A}:=\left\{\mathcal{L}|\mathcal{L}\mathrm{CPTP},[\mathcal{L},\mathcal{G}]=0,\mathsf{\Theta }\mathcal{L}\mathsf{\Theta }=\mathcal{L},{\beta }_{\mathcal{L}}=0\right\}.$$

Minimal–dissipation principle:${\mathcal{L}}_{\mathsf{\Delta }}$ is the unique element of $\mathcal{A}$ whose Kraus rank equals the dimension of the gauge–singlet scalar basis at zeroth differential order. Proof is given in Proposition 2.19.4.

Appendix D.3.3. Construction Recipe

• Identify all local gauge scalars of mass dimension 3 or 4. In the SM this yields exactly the set $\left\{\overline{\psi }\psi ,H^{†}H,F_{\mu \nu }^a{F}^{a\mu \nu }\right\}$.
• Impose reflection symmetry $\mathsf{\Theta }{V}_j\mathsf{\Theta }=V_j$⇒ time components of vectors are excluded.
• Normalise with ${\sum }_j{V}_j^{†}{V}_j=-\int R$ to satisfy the cancelling identity (A10).

Appendix D.3.4. Consequences

• Predictivity: no free Lindblad couplings remain once $\mathsf{\Lambda }$ is fixed by data; dissipation strength $a\left(k\right)$ is entirely RG–driven.
• UV unitarity: irreversibility vanishes as $k^{-1.1}$ (asymptotically silent), preserving S-matrix analyticity.
• IR thermodynamics: the same minimal channel is enough to generate entropy production rate $\sigma \ge 0$ (Chap. 3, §3.9).

Appendix D.3.5. Cross-References

• CPTP & OS positivity — Thm. B, §1.5.0.5.
• Vacuum-energy cancellation — Thm. F, §1.5.0.25.
• Open-system holography — App. A.3.

Appendix D.4. Fractal Renormalisation-Group Operator D f

Appendix D.4.1. Why It Matters

$D_f$ encodes scale-dependent phase interference in a single analytic function, supplies the running exponent that makes the UV fixed point possible, and freezes to a constant phase in the IR—so it leaves low-energy GR+SM intact while securing asymptotic safety.

Appendix D.4.2. Definition

In momentum space

$$D_f\left(k^2\right)=sin{\left[{\displaystyle \frac{\pi }{2}}\sqrt{{\displaystyle \frac{-\square }{{\mathsf{\Lambda }}^2}}}\right]}_{k^2=-\square },\mathsf{\Lambda }\approx 7\mathrm{TeV}.$$

Appendix D.4.3. Key Properties

• IR limit. For $k\ll \mathsf{\Lambda }$: $D_f\left(k^2\right)\to \pi /2$, so all fractal corrections reduce to a harmless constant.
• UV behaviour. For $k\gg \mathsf{\Lambda }$: $D_f\left(k^2\right)\sim sin\left(\frac{\pi }{2}\frac{k}{\mathsf{\Lambda }}\right)$, producing oscillatory suppression that helps the $f\left(R\right)+R^3$ sector reach the non-Gaussian fixed point (Theorem G).
• Self-adjointness. With the relative-boundedness of R and essential self-adjointness of D (Theorem A), the extended reversible operator $D+D_f$ remains essentially self-adjoint on the same core.
• Holographic meaning. In AdS/CFT the radial derivative $z{\partial }_z$ maps to $D_f$ under the dictionary of Appendix A.3, turning log-RG flow into a geometric phase operator.

Appendix D.4.4. Novelty

A single analytic kernel substitutes the infinite tower of higher-derivative counter-terms; the phase form avoids ghosts while preserving locality at scales $>{\mathsf{\Lambda }}^{-1}$.

Appendix D.4.5. Cross-References

• UV fixed-point analysis — Chap. 7, §7.2 (flow equations).
• Cosmological background — Chap. 8, Eq. (8.3).
• Open-system holography — App. A.3, Eq. (A.3.1).

Appendix D.5. Information-Flux Four-Vector ${\mathsf{\Phi }}_I^{\mu }$

Appendix D.5.1. Why It Matters

${\mathsf{\Phi }}_I^{\mu }$ is the dynamical agent that turns anomaly-cancellation on the string side into vacuum-energy cancellation in the UEE. It couples only through a total divergence, so it leaves the low-energy equations of motion intact but fixes the cosmological constant at the RG fixed point.

Appendix D.5.2. Definition & Constraint

$$S_{{\mathsf{\Phi }}_I}=\int d^{4}x{\displaystyle \frac{1}{2{\kappa }_I}}{\mathsf{\Phi }}_{I\mu }{\mathsf{\Phi }}_I^{\mu },\begin{array}{|c|}\hline {\nabla }_{\mu }{\mathsf{\Phi }}_I^{\mu }=\sigma \\ \hline\end{array}(\mathrm{fixed}-\mathrm{point}\mathrm{value}).$$

In Appendix A.1 the Green–Schwarz three-form $H_{\mu \nu \rho }$ maps under Hodge duality to ${\mathsf{\Phi }}_I^{\mu }$; the string anomaly-cancellation equation becomes the UEE constraint ${\nabla }_{\mu }{\mathsf{\Phi }}_I^{\mu }=\sigma$.

Appendix D.5.3. Roles in the Theory

• Vacuum-energy balance — together with the ${\mathsf{\Lambda }}^4$ term from R, ${\mathsf{\Phi }}_I$ enforces ${\rho }_{\mathrm{vac}}+{\rho }_{\mathsf{\Phi }}=0$ (Chap. 8, §8.3).
• Entropy production source — its divergence equals the entropy-production density $\sigma$ in Chap. 3, §3.9.
• Anomaly gateway — satisfies the same descent equation as $H\wedge H$ in heterotic strings, aligning gauge + gravitational anomalies without extra Green–Schwarz terms.

Appendix D.5.4. Cross-References

• Fixed-point value $\sigma$ — Table 8.1.
• Friedmann cancellation — Eq. (8.12).
• String correspondence — App. A.1.

Appendix D.6. Asymptotically Silent Dissipation

Appendix D.6.1. Why It Matters

The dissipative strength $a\left(k\right)$ falls off as a power law, so the irreversible piece ${\mathcal{L}}_{\mathsf{\Delta }}$ vanishes in the UV. This guarantees that unitarity, CPT symmetry and S-matrix analyticity are restored at high energies while leaving enough dissipation in the IR to generate entropy and cancel vacuum energy.

Appendix D.6.2. RG Scaling Law

From the two-loop flow in Chap. 7 (§7.2) one obtains

$$\begin{array}{|c|}\hline a\left(k\right)=a_0{\left({\displaystyle \frac{k}{\mathsf{\Lambda }}}\right)}^{-1.1}\\ \hline\end{array},a_0\simeq 1.4\times {10}^{-2},$$

so $a(k\to \infty )\to 0$ (“asymptotically silent”) and $a(k\ll \mathsf{\Lambda })\approx a_0$.

Appendix D.6.3. Consequences

• UV unitarity recuperation — with $a\to 0$ the GKLS generator disappears and evolution is purely Hamiltonian above $\mathsf{\Lambda }$.
• Preservation of standard high-energy scattering — no modification to parton cross-sections or LEP precision data.
• Controlled IR irreversibility — at hadronic and cosmological scales $a\sim {10}^{-2}$ is sufficient to give the entropy-production rate required by Chap. 3, Figure 3.12.

Appendix D.6.4. Cross-References

• Flow derivation — Eq. (7.6).
• Application in Friedmann equation — Eq. (8.12).
• Open-system holography damping — App. A.3, discussion after Eq. (A.3.4).

Appendix D.7. Open-System Holography

Appendix D.7.1. Why It Matters

By activating $L_{\mathsf{\Delta }}$ or the resonance R, the AdS/CFT correspondence is promoted to a boundary CFT that is itself an open Lindblad system. UEE thus provides an operator framework for real-time thermalisation, viscosity, quenches, and decoherence without leaving the master-equation language.

Appendix D.7.2. Dictionary Highlights

$$\begin{array}{cccc}\hfill z{\partial }_z& ⟷& D_f\hfill & (\mathrm{RG}\text{–}\mathrm{radial}\mathrm{flow})\hfill \\ \hfill {\phi }_0\left(x\right)& ⟷& {\mathsf{\Phi }}_I\left(x\right)\hfill & (\mathrm{boundary}\mathrm{source})\hfill \\ \hfill S_{\mathrm{bulk},\mathrm{on}-\mathrm{shell}}& ⟷& S_{\mathrm{var}}[\rho ,{\mathsf{\Phi }}_I]\hfill & (\mathrm{Witten}\text{↔}\mathrm{Dyson}\text{–}\mathrm{Phillips})\hfill \\ \hfill T_{\mathrm{Hawking}}& ⟷& \sigma =\beta \dot{Q}\hfill & (1\mathrm{st}\mathrm{law}\mathrm{maps})\hfill \\ \hfill \beta -\mathrm{function}\mathrm{eigenvalues}& ⟷& \mathrm{Spec}\left(L_0\right)\hfill & (\mathrm{critical}\mathrm{exponents})\hfill \end{array}$$

Appendix D.7.3. Key Result

Proposition A.3.8 (App. A.3) proves full equivalence in the reversible limit ($L_{\mathsf{\Delta }}=R=0$) and shows how turning on dissipation deforms the bulk to an “AdS + thermal bath” geometry while the boundary theory becomes Lindblad-evolved.

Appendix D.7.4. Cross-References

Chap. 3, §3.5 (explicit Dyson–Phillips series); App. A.3 for full mapping table.

Appendix D.8. Deterministic Cancellation of Vacuum Energy

Appendix D.8.1. Why It Matters

The notorious cosmological–constant problem is solved dynamically: a fixed-point identity forces the quartic vacuum term to annihilate against the information-flux contribution, eliminating fine tuning.

Appendix D.8.2. Fixed-Point Identity

From the RG flow (Chap. 8, §8.3) one finds

$$\begin{array}{|c|}\hline {\rho }_{\mathrm{vac}}\left(\mathsf{\Lambda }\right)+{\rho }_{\mathsf{\Phi }}\left(\mathsf{\Lambda }\right)=0\\ \hline\end{array}⟹H^2={\displaystyle \frac{8\pi G}{3}}\left({\rho }_m+{\rho }_r\right),$$

so late-time expansion is governed by ordinary matter + radiation only. The relation holds for any $\mathsf{\Lambda }\gtrsim 7\mathrm{TeV}$.

Appendix D.8.3. Cross-Links

• Information flux term — §D.5.
• FRW derivation — Eq. (8.12).
• Global data fit — Table 8.2.

Appendix D.9. Polymer-RG Mass-Gap Engine

Appendix D.9.1. Why It Matters

Reflection positivity plus controlled dissipation supply the first fully rigorous proof of an SU(N) mass gap, a long-standing Clay problem.

Appendix D.9.2. Mechanism in One Line

$$\underset{\mathsf{\Theta },R}{\underbrace{\mathrm{OS}\mathrm{positivity}}}+\underset{\kappa \left(a\right)<\frac{1}{2}}{\underbrace{\mathrm{polymer}\mathrm{RG}\mathrm{convergence}}}⟹S_2\left(x\right)\sim e^{-m_0\left|x\right|}⟹m_{\mathrm{gap}}>0.$$

Appendix D.9.3. Cross-Links

Appendix B, Steps D1–D4; Theorem D, §1.5.0.15.

Appendix D.10. γ-Knob for Navier–Stokes Blow-Up

Appendix D.10.1. Why It Matters

The same zero-order Lindblad term that ensures open-system thermodynamics also acts as a tunable damping coefficient $\gamma$. Taking $\gamma \to 0$ in a controlled way constructs an explicit finite-time singularity for 3-D Navier–Stokes.

Appendix D.10.2. Key Inequality

Enhanced Beale–Kato–Majda bound (Lemma C.4.1):

$$\dot{\mathsf{\Omega }}\ge c_1{\mathsf{\Omega }}^{4/3}-\gamma \mathsf{\Omega }⟹T_{*}\left(\gamma \right)\lesssim {\gamma }^{1/2}\left|log\gamma \right|.$$

Appendix D.10.3. Cross-Links

Appendix C, Theorem C.5.2; Theorem E, §1.5.0.20.

Appendix D.11. Zero Free Theory Parameters

Appendix D.11.1. Why It Matters

After $\mathsf{\Lambda }$ is fixed by experiment, all other couplings flow to the universal fixed point or are measured SM/GUT inputs; UEE has no hidden knobs, maximising predictivity.

Appendix D.11.2. Counting

$${\#}_{\mathrm{couplings}}^{\mathrm{bare}}=27,{\#}_{\mathrm{constraints}}^{\mathrm{theory}}=27,{\#}_{\mathrm{external}}=0(\mathrm{aside}\mathrm{from}{H}_0,{\mathsf{\Omega }}_b{h}^2\mathrm{in}\cos \mathrm{mological}\mathrm{fits}).$$

See §8.9 for the rank analysis.

Appendix D.12. Predictive Quantum-Noise Floor

Appendix D.12.1. Why It Matters

UEE sets an absolute lower bound on spectral density—observable by future interferometers and quantum sensors—providing a smoking-gun laboratory test.

Appendix D.12.2. Formula

$$\begin{array}{|c|}\hline S_{min}\left(\omega \right)=\hslash \omega e^{-\pi \omega /\mathsf{\Lambda }}\\ \hline\end{array}(\mathsf{\Lambda }\approx 7\mathrm{TeV}).$$

Appendix D.12.3. Experimental Reach

CMB-S4, LISA, and LIGO A+ aim for sensitivities $\omega \simeq {10}^2\text{–}{10}^3\mathrm{Hz}$, corresponding to a 3 dB dip relative to the standard quantum limit.

Appendix D.12.4. Cross-Links

Discussed in Chap. 9, §9.3 (upcoming tests).