A New Frailty Model Based Archimedean Bivariate Copula That Models Only Positive Dependency

1. Introduction

A copula is a function mapping ${\left[\mathrm{0,1}\right]}^2\to \left[\mathrm{0,1}\right]$  and satisfying the boundary condition in the form of  $C\left(u,0\right)=C\left(0,v\right)=0\forall u\&v\in \left[\mathrm{0,1}\right]$ , the unit marginal conditions in the form of $C\left(1,v\right)=v\&C\left(u,1\right)=u\forall u\&v\in \left[\mathrm{0,1}\right]$ , and 2-increasing property that states,

$\forall u\mathrm{ },\mathrm{ }{u}^{\mathrm{\text{'}}},\mathrm{ }v\mathrm{ },\mathrm{ }{v}^{\mathrm{\text{'}}}\in \mathrm{ }\left[\mathrm{0,1}\right]andu\le u^{\mathrm{\text{'}}\mathrm{ }}andv\mathrm{ }\le \mathrm{ }{v}^{\mathrm{\text{'}}}$  then,

$C\left(\left[u,u^{\mathrm{\text{'}}}\right]\times \left[v,v^{\mathrm{\text{'}}}\right]\right)=C\left(u^{\mathrm{\text{'}}},v^{\mathrm{\text{'}}}\right)-C\left(u,v^{\mathrm{\text{'}}}\right)-C\left(u^{\mathrm{\text{'}}},v\right)+C\left(u^{\mathrm{\text{'}}},v^{\mathrm{\text{'}}}\right)\ge 0$ .

$C\left(u,v\right)\le C\left(u^{\mathrm{\text{'}}},v\right)\mathrm{ }\mathrm{ }$ and   $C\left(u,v\right)\le C\left(u,v^{\mathrm{\text{'}}}\right)$ for   $\forall u\le u^{\mathrm{\text{'}}}\mathrm{ }\mathrm{ }and\mathrm{ }\mathrm{ }v\le v^{\mathrm{\text{'}}}$ , hence satisfying Lipschitz condition that is   $\left|C\left(u,v\right)-\mathrm{ }C\left(u^{\mathrm{\text{'}}},v^{\mathrm{\text{'}}}\right)\right|\le \mathrm{ }\left|u-u^{\mathrm{\text{'}}}\right|+\left|v-v^{\mathrm{\text{'}}}\right|\forall u\mathrm{ },\mathrm{ }{u}^{\mathrm{\text{'}}},\mathrm{ }v\mathrm{ },\mathrm{ }{v}^{\mathrm{\text{'}}}\in \mathrm{ }\left[\mathrm{0,1}\right]\mathrm{ }$.

Sklar (Sklar, 1973) showed that a copula exists for any multivariate distribution, such that the joint distribution equals the copula applied to the marginal. In other words, Let  X and Y be random variables with joint distribution $H$ and marginal distribution functions $F$and $G$ , respectively. Then there is a uniquely determined copula, C, on the  $RangeF\times RangeG$ , such that  $H\left(x,y\right)=C\left(F\left(x\right),G\left(y\right)\right)$ for  $\forall x,y\in \left[-\infty ,\infty \right]$ So copulas connect joint distributions functions to their margins. They are crucial for constructing bivariate and multivariate distributions because they are a statistical method for studying scale-free measures of dependence.

Definition1 (Sklar’s theorem 1): For any bivariate distribution function H with marginal $F$ and $G$ , there exists a copula such that

$H\left(x,y\right)=C\left(F\left(x\right),G\left(y\right)\mathrm{ }\right),\mathrm{ }\mathrm{ }x,y\in \left[-\mathrm{\infty },\mathrm{\infty }\right]$

If H is continuous, then the copula C is unique. Otherwise, it is uniquely determined on the $F\left(R\right)\times G\left(R\right)$  . The converse is also true, for any copula and univariate distribution functions $F$ and $G$ , the function $C\left(F\left(x\right),G\left(y\right)\right)$  is a bivariate distribution function with margins $F$ and $G$ .

Definition 2 : A  bivariate Archimedean copula $C(u,v)$ can be written in the form of  $C\left(u,v\right)={\phi }^{-1}\left(\phi \left(u\right)+\phi \left(v\right)\right)$ with marginal $u=F_X\left(x\right)$ and  $v=F_Y\left(y\right)$, where $\phi \left(u\right)$ is the generator function being continuous, strictly decreasing and convex function mapping $\left[\mathrm{0,1}\right]$ onto $[0,\infty )$ , in other words ,  ${\phi }^{\text{'}}\left(u\right)<0$( decreasing) and ${\phi }^{\text{'}\text{'}}\left(u\right)>0$ ( convex)  , $\phi \left(0\right)=\infty$ , and $\phi \left(1\right)=0$

Definition 3: a bivariate copula has   ${\displaystyle \frac{\partial C\left(u,v\right)}{\partial u\partial v}}=c(u,v)$  which is the joint PDF of the copula.

So the copula links the marginal distributions through the dependency parameter.

The singular part of the copula is defined by (Genest & Mackay, 1986) in the following Theorem, the ratio between the generator and the first derivative of the generator evaluated at zero does not equal zero.

Theorem: the distribution $C(u,v)$ generated by $\phi$  has a singular component iff  ${\displaystyle \frac{\phi \left(0\right)}{{\phi }^{\text{'}}\left(0\right)}}\ne 0$     in that case, $\phi \left(u\right)+\phi \left(v\right)=\phi \left(0\right)$    with probability = $-{\displaystyle \frac{\phi \left(0\right)}{{\phi }^{\text{'}}\left(0\right)}}$In the last few years many models have been proposed for copulas. The applications of copulas are too plentiful to list so further improvements of copulas are encouraged to be further advanced. The applied applications rely mainly on the parametric models for copulas in comparison to the semi-parametric and non-parametric model for copulas which have limited applied implementations in real life.

Many eminent scientists and authors had in depth papers discussing the estimation methods, simulation, probabilistic interpretations, and analytical properties. Many problems face the statistical scientific community and in need for solutions. (Nadarajah et al., 2018) mentioned some of these problems like estimation of copula under misspecification, copula density estimation , Bayesian copula, change point estimation of copulas, efficient estimation and simulation algorithms, characterization of copulas, selection criteria between two or more copulas, time series models constructed on copulas, bounds for copulas, copula calibration, transformations to enhance fits of copulas, extreme value manners of bivariate and multivariate copulas, compatibility of copulas, additional measures of asymmetry for bivariate and multivariate copulas, extra tests for symmetry for bivariate and multivariate copulas, , time varying copulas, space changing copulas and copulas fluctuating with sense of  both time and space.

Many books had been written by pioneer and innovator scientists in the field of copulas like books written by  (Drouet-Mari & Kotz, 2001), (Cuadras et al., 2002), (Cherubini et al., 2004), (Genest, 2005a), (Genest, 2005b), (Nelson, 2006), (McNeil et al., 2005), (Alsina et al., 2006), (Mai & Scherer, 2014), (Durante & Sempi, 2015), (Salvadori et al., 2007), (Malevergne & Sornette, 2006), (Schweizer & Sklar, 2005), (Jaworski et al., 2010),(Jaworski et al., 2013), (Jaworski et al., 2010; Joe, 2014), (Joe, 1997)and many others.  Numerous papers had been published by many prominent scientists like (Nelsen, 2002), (Embrechts et al., 2003), (Manner & Reznikova, 2012), (Patton, 2012),(Genest et al., 2009),(Schweizer, 1991), (Kolev et al., 2006), (Kolev & Paiva, 2009), and (Frees & Valdez, 1998).

The copula can be grouped into five subgroups which are the Archimedean copulas, the elliptical copulas, the Eyraud-Farlie-Gumbel-Morgenstern (EFGM) copula, extreme value copulas, and other copulas. Each of these subgroups includes more copulas.  For more details, the reader can be referred to the paper of  (Nadarajah et al., 2018) and references therein.

The simplest copula is the product copula or the independence copula $C\left(u,v\right)=uv$ .It is for two independent random variables with  $H\left(x,y\right)=F\left(x\right)G\left(y\right)$ .The other two very essential dependencies between two variables are the perfect positive and the perfect negative dependencies. These can be expressed by copulas. For the positive state, this yields $M\left(u,v\right)=min\left(u,v\right)$. Hence, for random variables X and Y with distributions $F$, $G$ and the joint distribution $M\left(F\left(x\right),G\left(y\right)\right)$ ,and because the copula is symmetric, the random variable X is an increasing function of Y and vice versa. The converse, with decreasing instead of increasing holds true for the joint distribution function $W\left(F,G\right)$ with $W\left(u,v\right)=max\left(u+v-1\right)$. This one is also a copula. These boundaries are themselves copulas and they are called Frechet-Hoeffding upper and lower bound respectively. As long as both $M$ and $W$ are not differentiable in u and v, they have no density functions. Joe (Joe, 1990), (Joe & Hu, 1996), (Joe, 1993) developed copulas that allow for positive dependency only. These copulas are recently used in portfolio risk analysis with Asian equity markets (Ozun & Cifter, 2007).

This paper is structured in 9 sections. Section 1 discusses the methodology of derivation. section 2 illustrates the generator and its properties.  Section 3 explores the inverse generator and its properties. Section 4 explains the Kendal Tau measure of dependency. Section 5 enlightens how the copula can model both lower and upper tail dependencies. Section 6 elucidates methods of estimation. Section 7 demonstrates real data analysis. Section 8 comprehends the conclusion. Section 9 states future works.

2. Methodology of Derivation

This copula depends on the frailty method for generating the copula. Assuming two individuals have survival time distributed as exponential $T_1$ and $T_2$ .They have exponential baseline hazard function with  ${\lambda }_1={\lambda }_2=1$ . The survival function is shown in equation (1) and the hazard function in equation (2)

$S\left(t\right)=Prob\left(T>t\right)=1-F\left(t\right)(1)$

$h\left(t\right)=-{\displaystyle \frac{\partial \ln S\left(t\right)}{\partial \mathrm{ }t}}=\mathrm{ }{\displaystyle \frac{f\left(t\right)}{S\left(t\right)}}(2)$

The Cox proportional hazard model uses the hazard function as shown in equation (3)

$h\left(t,Z\right)=e^{\beta Z}\mathrm{ }b\left(t\right)\mathrm{ }(3)$

where the Z are the explanatory variables in survival analysis and b(t) is the baseline hazard function. And B is the vector of regression coefficients. It is proportional because all information is contained in the multiplicative factor  $\gamma =e^{BZ}$ , this is called the frailty model when some explanatory variables (Z) and hence the factor  $\gamma$ are unobserved. And the factor $\gamma$ is called the frailty parameter.$S\left(t|\gamma \right)$ is the result of integration and exponentiation of the negative hazard  $h\left(t\right)$ in equation (2) or hazard $h\left(t,Z\right)$ in equation(3). For exponential random variable the hazard is expressed in terms of explanatory variables, for example 2 variables as  $\lambda =e^{{\beta }_0+{\beta }_1{Z}_1+{\beta }_2{Z}_2}=e^{{\beta }_0}{e}^{{\beta }_1{Z}_1+{\beta }_2{Z}_2}={\lambda }_0{e}^{{\beta }_1{Z}_1+{\beta }_2{Z}_2}={\lambda }_0\gamma$where  $e^{{\beta }_0}={\lambda }_0$ and assume${\lambda }_0=1$.

$S\left(t|\gamma \right)=exp\left(-{\int }_0^t-{\displaystyle \frac{\partial \ln S\left(t\right)}{\partial \mathrm{ }t}}\right)dt=exp\left(-{\int }_0^{t}h\left(t\right)\right)dt=exp\left(-{\int }_0^t\lambda \right)dt=exp\left(-{\int }_0^t{e}^{{\beta }_0+{\beta }_1{Z}_1+{\beta }_2{Z}_2}\right)dt$

$=\mathrm{ }exp\left(-{\int }_0^t{\lambda }_0\mathrm{ }\gamma \mathrm{ }\mathrm{ }\mathrm{ }\right)dt=\mathrm{ }exp\left(-\gamma {\int }_0^t{\lambda }_0\right)dt=\mathrm{ }{e}^{\left(-\gamma {\int }_0^t{\lambda }_0\mathrm{ }dt\right)}={\left[e^{\left(-{\int }_0^t{\lambda }_0\mathrm{ }dt\right)}\right]}^{\gamma }={\left[e^{-t{\lambda }_0}\right]}^{\gamma }=\mathrm{ }{\left[B\left(t\right)\right]}^{\gamma }$

where $B\left(t\right)$ is the baseline hazard, to sum up ${\left[e^{-t{\lambda }_0}\right]}^{\gamma }=\mathrm{ }{\left[e^{-S_{0\left(t\right)}}\right]}^{\gamma }=\mathrm{ }{e}^{-t\gamma }=S\left(t|\gamma \right)$ assuming ${\lambda }_0=1$ .

The marginal distribution for a single life time T is obtained by taking expectation over the potential values of $\gamma$ that is  $E\left(e^{-t\gamma }\right)$ , assuming the $f\left(\gamma \right)$ is the PDF of the frailty variable so

$E\left(e^{-t\gamma }\right)=\mathrm{ }{\int }_0^{\mathrm{\infty }}{e}^{-t\gamma }\mathrm{ }f\left(\gamma \right)d\gamma \mathrm{ }$Let y be a random variable distributed as Median Based Unit Rayleigh (MBUR) (Attia, M.I., 2024), transform this variable to be defined on the interval from zero to infinity as shown below. The PDF of the Median Based Unit Rayleigh (MBUR) is shown in equation (4)

${\displaystyle \frac{6}{{\alpha }^2}}\mathrm{ }\left[1-y^{{\displaystyle \frac{1}{{\alpha }^2}}}\right]y^{\left({\displaystyle \frac{2}{{\alpha }^2}}-1\right)}\mathrm{ },0<y<1\mathrm{ },\alpha >0\mathrm{ }(4)$

The transformation in equation (5.A) and the Jacobian in equation (5.B) will be applied to the above PDF:

  $w=-\ln {\left(y\right)}^{{\displaystyle \frac{1}{{\alpha }^2}}}\to w={\displaystyle \frac{-\ln y}{{\alpha }^2}}\to -w{\alpha }^2=\ln y\mathrm{ }\to y=\mathrm{ }{e}^{-{\alpha }^{2}w}\mathrm{ }(5.A)$

$dy=e^{-{\alpha }^{2}w}\left(-{\alpha }^2\right)\mathrm{ }dw(5.B)$

Replace equation (5) into equation (4) as shown in equation (6):

${\int }_0^{\mathrm{\infty }}{\displaystyle \frac{6}{{\alpha }^2}}\mathrm{ }\left[1-{\left(e^{-{\alpha }^2\mathrm{ }w\mathrm{ }}\right)}^{{\displaystyle \frac{1}{{\alpha }^2}}}\right]{\left(e^{-{\alpha }^{2}w\mathrm{ }\mathrm{ }}\right)}^{\left({\displaystyle \frac{2}{{\alpha }^2}}\right)}{\left(e^{-{\alpha }^{2}w\mathrm{ }\mathrm{ }}\right)}^{-1}\left({\alpha }^2\right)e^{-{\alpha }^{2}w}\mathrm{ }dw={\int }_0^{\mathrm{\infty }}6\mathrm{ }\left[1-e^{-{\displaystyle \frac{{\alpha }^2\mathrm{ }w}{{\alpha }^2}}\mathrm{ }\mathrm{ }}\right]e^{-{\displaystyle \frac{2{\alpha }^2\mathrm{ }w}{{\alpha }^2}}\mathrm{ }\mathrm{ }}\mathrm{ }dw$$f_W\left(w\right)=\mathrm{ }\mathrm{ }6\mathrm{ }\left[1-e^{-w\mathrm{ }\mathrm{ }}\right]e^{-2w\mathrm{ }\mathrm{ }\mathrm{ }}\mathrm{ }(6)$

Now this w is the frailty variable$\gamma$ which is distributed as unbounded MBUR defined on the interval $\left(0,\infty \right)$. Now take the conditional expectation of the survival function of the time distributed as exponential random variable with hazard rate equal one (scale parameter or lambda=1) given the frailty variable as shown in equation (7)

$E\left(e^{-t\gamma }\right)=\mathrm{ }{\int }_0^{\mathrm{\infty }}{e}^{-t\gamma }\mathrm{ }f\left(\gamma \right)d\gamma \mathrm{ }=\mathrm{ }{\int }_0^{\mathrm{\infty }}\left(e^{-t\gamma }\right)\mathrm{ }\mathrm{ }6\mathrm{ }\left[1-e^{-\gamma \mathrm{ }\mathrm{ }}\right]e^{-2\gamma \mathrm{ }\mathrm{ }}\mathrm{ }d\gamma =6{\int }_0^{\mathrm{\infty }}{e}^{-\gamma \left(t+2\right)}\mathrm{ }\mathrm{ }\mathrm{ }d\gamma -6\mathrm{ }{\int }_0^{\mathrm{\infty }}{e}^{-\gamma \left(t+3\right)}\mathrm{ }\mathrm{ }\mathrm{ }d\gamma \mathrm{ }\mathrm{ }$

$E\left(e^{-t\gamma }\right)=E\left(S\left(t\right|\gamma \right))=6\mathrm{ }{\left.\left[\mathrm{ }{\displaystyle \frac{e^{-\gamma \left(t+2\right)}}{-\left(t+2\right)}}\right]\right|}_0^{\mathrm{\infty }}-6\mathrm{ }{\left.\left[\mathrm{ }{\displaystyle \frac{e^{-\gamma \left(t+3\right)}}{-\left(t+3\right)}}\right]\right|}_0^{\mathrm{\infty }}=6\left[\left({\displaystyle \frac{1}{t+2}}\right)-\left({\displaystyle \frac{1}{t+3}}\right)\right]\mathrm{ }=\mathrm{ }{\displaystyle \frac{6}{t^2+5t+6}}\mathrm{ }(7)$

We can think of this expectation as a function of the frailty variable, it is averaging the probability to survive beyond specific time given that frailty. It is the expectation of a function of the frailty not the variable frailty itself so this function which is the baseline survival function should be multiplied by the PDF of the frailty variable. This way the frailty variable is integrated out.  So this expectation is considered as the joint CDF of the two random variables T1 and T2. How to get this time?  By inverting this expectation as shown in equation (8). Let us call this expectation u then solving second degree polynomial to get its root.

$\left(u=\mathrm{ }{\displaystyle \frac{6}{t^2+5t+6}}\right)\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\to \mathrm{ }\mathrm{ }\left({\displaystyle \frac{6}{u}}=\mathrm{ }{t}^2+5t+6\right)\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\to \mathrm{ }\left(t^2+5t+6-{\displaystyle \frac{6}{u}}=0\right)$$t={\displaystyle \frac{-5+\sqrt{25-4\left(1\right)\left(6\right)\left(1-\frac{1}{u}\right)}}{2}}\mathrm{ }={\displaystyle \frac{-5+\sqrt{25-24\left(1-\frac{1}{u}\right)}}{2}}={\displaystyle \frac{\left(-5+\sqrt{\mathrm{ }\mathrm{ }\left(25-24+\frac{24}{u}\right)}\right)}{2}}=\mathrm{ }\mathrm{ }{\displaystyle \frac{\left(-5+\sqrt{\mathrm{ }\mathrm{ }\left(1+\frac{24}{u}\right)}\right)}{2}}\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }(8)$

3. The Generator

In equation (8); the generator is not defined in term of the dependency parameter so re-parameterization of the generator yielded a generator with a dependency parameter. The author added dependency parameter and remove the denominator as shown in equation (9),  $u$ is the marginal CDF.

$t\mathrm{ }=\mathrm{ }\theta {\left(-5+\mathrm{ }{\left(1+{\displaystyle \frac{24}{u}}\right)}^{{\displaystyle \frac{1}{2}}}\right)}^{{\displaystyle \frac{1}{\theta }}},\mathrm{ }\mathrm{ }0<u<1\mathrm{ }(9)$

This (t) is the generator and (u) is the inverse generator. So the time (t) is a function of (u)

Preposition 1: the generator shown in equation (9) ,  $t=\theta {\left(-5+{\left(1+{\displaystyle \frac{24}{u}}\right)}^{{\displaystyle \frac{1}{2}}}\right)}^{{\displaystyle \frac{1}{\theta }}}$can be considered as a generator for this new  Archimedean copula.

Proof : The generator in equation (9) fulfills  the sufficient conditions of a generator.

(1)$\phi \left(0\right)=\theta {\left(-5+\mathrm{ }{\left(1+{\displaystyle \frac{24}{\left(0\right)}}\right)}^{{\displaystyle \frac{1}{2}}}\right)}^{{\displaystyle \frac{1}{\theta }}}=\mathrm{\infty }$

(2)$\phi \left(1\right)=\theta {\left(-5+\mathrm{ }{\left(1+{\displaystyle \frac{24}{\left(1\right)}}\right)}^{{\displaystyle \frac{1}{2}}}\right)}^{{\displaystyle \frac{1}{\theta }}}=0$

(3)${\phi }^{\mathrm{\text{'}}}\left(u\right)=\mathrm{ }{\left(-5+\mathrm{ }{\left(1+{\displaystyle \frac{24}{u}}\right)}^{{\displaystyle \frac{1}{2}}}\right)}^{{\displaystyle \frac{1}{\theta }}-1}\mathrm{ }\mathrm{ }{\left(1+{\displaystyle \frac{24}{u}}\right)}^{-0.5}\mathrm{ }\left({\displaystyle \frac{-12}{u^2}}\right)\mathrm{ }<0$

This ensures that the generator is a decreasing function in u .

(4)${\phi }^{\mathrm{\text{'}}\mathrm{\text{'}}}\left(u\right)=\mathrm{ }\left({\displaystyle \frac{1}{\theta }}-1\right){\left(-5+\mathrm{ }{\left(1+{\displaystyle \frac{24}{u}}\right)}^{{\displaystyle \frac{1}{2}}}\right)}^{{\displaystyle \frac{1}{\theta }}-2}\mathrm{ }{\left(1+{\displaystyle \frac{24}{u}}\right)}^{-1}\mathrm{ }{\left({\displaystyle \frac{-12}{u^2}}\right)}^2+{\left(-5+\mathrm{ }{\left(1+{\displaystyle \frac{24}{u}}\right)}^{{\displaystyle \frac{1}{2}}}\right)}^{{\displaystyle \frac{1}{\theta }}-1}\left({\displaystyle \frac{-1}{2}}\right){\left(1+{\displaystyle \frac{24}{u}}\right)}^{-1.5}\mathrm{ }{\left({\displaystyle \frac{-12}{u^2}}\right)}^2\mathrm{ }$$+{\left(-5+{\left(1+{\displaystyle \frac{24}{u}}\right)}^{{\displaystyle \frac{1}{2}}}\right)}^{{\displaystyle \frac{1}{\theta }}-1}{\left(1+{\displaystyle \frac{24}{u}}\right)}^{-0.5}\left({\displaystyle \frac{24}{u^3}}\right)>0$

This ensures that the generator is a convex function  at  $0<\theta \le 1$For bivariate distribution with uniform marginal CDF (u) and (v), the generators are shown in equations (10-12)

$\phi \left(u\right)=\mathrm{ }\theta {\left(-5+\mathrm{ }{\left(1+{\displaystyle \frac{24}{u}}\right)}^{{\displaystyle \frac{1}{2}}}\right)}^{{\displaystyle \frac{1}{\theta }}}(10)$         &&              $\phi \left(v\right)=\mathrm{ }\theta {\left(-5+\mathrm{ }{\left(1+{\displaystyle \frac{24}{v}}\right)}^{{\displaystyle \frac{1}{2}}}\right)}^{{\displaystyle \frac{1}{\theta }}}(11)$$\phi \left(w\right)\mathrm{ }=\phi \left(u\right)+\phi \left(v\right)=\left\{{\left(-5+\mathrm{ }{\left(1+{\displaystyle \frac{24}{u}}\right)}^{{\displaystyle \frac{1}{2}}}\right)}^{{\displaystyle \frac{1}{\theta }}}+\mathrm{ }{\left(-5+\mathrm{ }{\left(1+{\displaystyle \frac{24}{v}}\right)}^{{\displaystyle \frac{1}{2}}}\right)}^{{\displaystyle \frac{1}{\theta }}}\right\}(12)$

4. The Inverse Generator

To get the inverse generator of this modified generator, the author inverts this (t) as shown in equation (13), as long as t equals:

$\mathrm{ }t=\mathrm{ }\phi \left(u\right)=\mathrm{ }\theta {\left(-5+\mathrm{ }{\left(1+{\displaystyle \frac{24}{u}}\right)}^{{\displaystyle \frac{1}{2}}}\right)}^{{\displaystyle \frac{1}{\theta }}}\mathrm{ }\mathrm{ },0<\theta \le 1\mathrm{ }sou=\mathrm{ }{\phi }^{-1}\left(t\right)=\mathrm{ }{\displaystyle \frac{24}{{\left[{\left(\frac{t}{\theta }\right)}^{\theta }+5\right]}^2-1}}\mathrm{ }=\mathrm{ }\mathrm{ }24\mathrm{ }{\left({\left[{\left({\displaystyle \frac{t}{\theta }}\right)}^{\theta }+5\right]}^2-1\right)}^{-1}(13)\mathrm{ }$

Recall that   $C\left(\phi \left(u\right)+\phi \left(v\right)\right)={\phi }^{-1}\left(\phi \left(u\right)+\phi \left(v\right)\right)$  and  a valid bivariate Archimedean copula can be expressed as  $\mathrm{C}\left(u,v\right)=C\left(F_X\left(x\right),F_Y\left(y\right)\right)$

Proposition 2: The copula expressed in equation (13) can be assumed to be a valid copula if it fulfills the boundary conditions, the marginal uniformity and 2- increasing conditions. And these are the necessary conditions that should be fulfilled by the inverse generator.

Proof:

 $\mathrm{C}\left(0,v\right)=\mathrm{C}\left(u,0\right)=0$, boundary conditions are fulfilled

$\mathrm{C}\left(0,v\right)=\mathrm{ }\mathrm{ }24\mathrm{ }{\left({\left[{\left({\displaystyle \frac{\theta \left\{{\left(-5+\mathrm{ }{\left(1+\frac{24}{0}\right)}^{\frac{1}{2}}\right)}^{\frac{1}{\theta }}+\mathrm{ }{\left(-5+\mathrm{ }{\left(1+\frac{24}{v}\right)}^{\frac{1}{2}}\right)}^{\frac{1}{\theta }}\right\}}{\theta }}\right)}^{\theta }+5\right]}^2-1\right)}^{-1}=0$

$\mathrm{C}\left(1,v\right)=vand\mathrm{C}\left(u,1\right)=u$ , the marginal uniformity, when u=1

$\mathrm{C}\left(1,v\right)=\mathrm{ }\mathrm{ }24\mathrm{ }{\left({\left[{\left({\displaystyle \frac{\theta \left\{{\left(-5+\mathrm{ }{\left(1+\frac{24}{1}\right)}^{\frac{1}{2}}\right)}^{\frac{1}{\theta }}+\mathrm{ }{\left(-5+\mathrm{ }{\left(1+\frac{24}{v}\right)}^{\frac{1}{2}}\right)}^{\frac{1}{\theta }}\right\}}{\theta }}\right)}^{\theta }+5\right]}^2-1\right)}^{-1}=v$

$\mathrm{C}\left(1,v\right)=\mathrm{ }\mathrm{ }24\mathrm{ }{\left({\left[{\left(\left\{{\left(-5+\mathrm{ }{\left(1+{\displaystyle \frac{24}{1}}\right)}^{{\displaystyle \frac{1}{2}}}\right)}^{{\displaystyle \frac{1}{\theta }}}+\mathrm{ }{\left(-5+\mathrm{ }{\left(1+{\displaystyle \frac{24}{v}}\right)}^{{\displaystyle \frac{1}{2}}}\right)}^{{\displaystyle \frac{1}{\theta }}}\right\}\right)}^{\theta }+5\right]}^2-1\right)}^{-1}$

$\mathrm{C}\left(1,v\right)=\mathrm{ }\mathrm{ }24\mathrm{ }{\left({\left[{\left({\left(-5+\mathrm{ }{\left(1+{\displaystyle \frac{24}{v}}\right)}^{{\displaystyle \frac{1}{2}}}\right)}^{{\displaystyle \frac{1}{\theta }}}\right)}^{\theta }+5\right]}^2-1\right)}^{-1}=\mathrm{ }24\mathrm{ }{\left({\left[-5+\mathrm{ }{\left(1+{\displaystyle \frac{24}{v}}\right)}^{{\displaystyle \frac{1}{2}}}+5\right]}^2-1\right)}^{-1}$

$\mathrm{C}\left(1,v\right)=24\mathrm{ }{\left({\left[\mathrm{ }{\left(1+{\displaystyle \frac{24}{v}}\right)}^{{\displaystyle \frac{1}{2}}}\right]}^2-1\right)}^{-1}=\mathrm{ }\mathrm{ }24\mathrm{ }{\left(\left(1+{\displaystyle \frac{24}{v}}\right)-1\right)}^{-1}=\mathrm{ }\mathrm{ }24\mathrm{ }{\left({\displaystyle \frac{24}{v}}\right)}^{-1}=v$

$C\left(1,v\right)\mathrm{ }$ The same is true for v , if v=1 so $C\left(u,1\right)\mathrm{ }\mathrm{ }=24\mathrm{ }{\left({\displaystyle \frac{24}{u}}\right)}^{-1}=u\mathrm{ }$

Proposition 3:  This is a valid copula as it is 2-increasing, i.e.    ${\displaystyle \frac{{\partial }^2\mathrm{C}\left(u,v\right)}{\partial u\partial v}}\ge 0$ ,  as shown in equation (14)

Proof:

Let  $p=-5+\mathrm{ }{\left(1+{\displaystyle \frac{24}{u}}\right)}^{{\displaystyle \frac{1}{2}}}\mathrm{ }\mathrm{ }and\mathrm{ }\mathrm{ }q=\mathrm{ }-5+\mathrm{ }{\left(1+{\displaystyle \frac{24}{v}}\right)}^{{\displaystyle \frac{1}{2}}}$

${\displaystyle \frac{\partial C\left(u,v\right)}{\partial u}}=$

$-48{\left[{\left({\left(p^{{\displaystyle \frac{1}{\theta }}}+q^{{\displaystyle \frac{1}{\theta }}}\right)}^{\theta }+5\right)}^2-1\right]}^{-2}\left[{\left(p^{{\displaystyle \frac{1}{\theta }}}+q^{{\displaystyle \frac{1}{\theta }}}\right)}^{\theta }+5\right]{\left[p^{{\displaystyle \frac{1}{\theta }}}+q^{{\displaystyle \frac{1}{\theta }}}\right]}^{\theta -1}\left[p^{{\displaystyle \frac{1}{\theta }}-1}\right]{\left(1+{\displaystyle \frac{24}{u}}\right)}^{{\displaystyle \frac{-1}{2}}}\left({\displaystyle \frac{-12}{u^2}}\right)$

${\displaystyle \frac{\partial }{\partial v}}\left({\displaystyle \frac{\partial C\left(u,v\right)}{\partial u}}\right)={\displaystyle \frac{{\partial }^2\mathrm{C}\left(u,v\right)}{\partial u\partial v}}=\mathrm{ }$

$=\left(-48\right)\left({\displaystyle \frac{144}{u^2{v}^2}}\right){\left[\left(1+{\displaystyle \frac{24}{u}}\right)\left(1+{\displaystyle \frac{24}{v}}\right)\right]}^{{\displaystyle \frac{-1}{2}}}\left[{\left(pq\right)}^{{\displaystyle \frac{1}{\theta }}-1}\right]{\left[{\left({\left(p^{{\displaystyle \frac{1}{\theta }}}+q^{{\displaystyle \frac{1}{\theta }}}\right)}^{\theta }+5\right)}^2-1\right]}^{-2}{\left[p^{{\displaystyle \frac{1}{\theta }}}+q^{{\displaystyle \frac{1}{\theta }}}\right]}^{\theta -2}\mathrm{ }$

$\times \left\{\left(-4\right)\mathbf{ }{\left[{\left({\left(p^{{\displaystyle \frac{1}{\theta }}}+q^{{\displaystyle \frac{1}{\theta }}}\right)}^{\theta }+5\right)}^2-1\right]}^{-1}\mathbf{ }{\left[{\left(p^{{\displaystyle \frac{1}{\theta }}}+q^{{\displaystyle \frac{1}{\theta }}}\right)}^{\theta }+5\right]}^2{\left[p^{{\displaystyle \frac{1}{\theta }}}+q^{{\displaystyle \frac{1}{\theta }}}\right]}^{\theta }\mathrm{ }\mathrm{ }+{\left[p^{{\displaystyle \frac{1}{\theta }}}+q^{{\displaystyle \frac{1}{\theta }}}\right]}^{\theta }+\left[{\left(p^{{\displaystyle \frac{1}{\theta }}}+q^{{\displaystyle \frac{1}{\theta }}}\right)}^{\theta }+5\right]\left[{\displaystyle \frac{\theta -1}{\theta }}\right]\right\}(14)$

${\displaystyle \frac{{\partial }^2\mathrm{C}\left(u,v\right)}{\partial u\partial v}}\ge 0,\forall \theta \in \left(0\right.,\left.1\right]$   satisfying the 2-increasing condition.

This density function in equation 14 integrates to one using MCMC simulation from zero to one.

Proposition 4:  This copula is absolutely continuous copula and it has no singular part.

Proof: to test for singularity:  $\underset{u\to 0}{\lim }{\displaystyle \frac{\phi \left(0\right)}{{\phi }^{\text{'}}\left(0\right)}}=0$  as shown in equation (15). If this limit is zero so the copula has no singular part.

${\displaystyle \frac{\phi \left(u\right)}{{\phi }^{\mathrm{\text{'}}}\left(u\right)}}\mathrm{ }=\mathrm{ }\mathrm{ }{\displaystyle \frac{\mathrm{ }\theta {\left(-5+\mathrm{ }{\left(1+\frac{24}{u}\right)}^{\frac{1}{2}}\right)}^{\frac{1}{\theta }}}{\mathrm{ }\theta \left(\frac{1}{\theta }\right){\left(-5+\mathrm{ }{\left(1+\frac{24}{u}\right)}^{\frac{1}{2}}\right)}^{\frac{1}{\theta }-1}\left(\frac{1}{2}\right){\left(1+\frac{24}{u}\right)}^{-0.5}\left(\frac{-24}{u^2}\right)}}=\mathrm{ }\left({\displaystyle \frac{-\theta }{12}}\right)\left(-5+\mathrm{ }{\left(1+{\displaystyle \frac{24}{u}}\right)}^{{\displaystyle \frac{1}{2}}}\right){\left(1+{\displaystyle \frac{24}{u}}\right)}^{0.5}{u}^2$$\underset{u\to 0}{\mathrm{l}\mathrm{i}\mathrm{m}}\mathrm{ }{\displaystyle \frac{5\theta \mathrm{ }{\left(\frac{24+u}{u}\right)}^{0.5}{u}^2}{12}}+\mathrm{ }\underset{u\to 0}{\mathrm{l}\mathrm{i}\mathrm{m}}\mathrm{ }{\displaystyle \frac{\theta \left(\frac{24+u}{u}\right)u^2}{-12}}=\mathrm{ }\underset{u\to 0}{\mathrm{l}\mathrm{i}\mathrm{m}}\mathrm{ }{\displaystyle \frac{5\theta {\left(u+24\right)}^{0.5}{u}^{1.5}}{12\mathrm{ }}}+\mathrm{ }\underset{u\to 0}{\mathrm{l}\mathrm{i}\mathrm{m}}\mathrm{ }\mathrm{ }{\displaystyle \frac{\theta u\left(24+u\right)}{-12}}=0-0=0(15)$

As long as this limit is zero at u=0 so the copula has no singular part and it is absolutely continuous copula.

5. Kendall Tau Measure of Dependency

Proposition 5: Kendall tau for this copula is $\tau =1-0.797\theta$ in equation (16)

Proof:        $\tau =4\mathrm{ }{\int }_0^1{\displaystyle \frac{\phi \left(u\right)}{{\phi }^{\mathrm{\text{'}}}\left(u\right)}}du\mathrm{ }\mathrm{ }+1$

${\int }_0^1{\displaystyle \frac{\phi \left(u\right)}{{\phi }^{\mathrm{\text{'}}}\left(u\right)}}\mathrm{ }du=\mathrm{ }{\int }_0^1\left({\displaystyle \frac{5\theta {\left(u+24\right)}^{0.5}{u}^{1.5}}{12\mathrm{ }}}+\mathrm{ }\mathrm{ }\mathrm{ }{\displaystyle \frac{\theta u\left(24+u\right)}{-12}}\right)\mathrm{ }du\mathrm{ }=\mathrm{ }\mathrm{ }=\theta {\int }_0^1{\displaystyle \frac{5}{12}}{\left(u+24\right)}^{0.5}{u}^{1.5}\mathrm{ }du+{\displaystyle \frac{-\theta }{12}}{\int }_0^1\mathrm{ }\mathrm{ }24\mathrm{ }u+u^2\mathrm{ }du\mathrm{ }\mathrm{ }$

$=\theta {\int }_0^1{\displaystyle \frac{5}{12}}{\left(u+24\right)}^{0.5}{u}^{1.5}\mathrm{ }du+{\displaystyle \frac{-\theta }{12}}{\int }_0^1\mathrm{ }\mathrm{ }24\mathrm{ }u+u^2\mathrm{ }du\mathrm{ }=\mathrm{ }\theta \left(0.8286\right)-{\displaystyle \frac{\theta }{12}}\left(12+{\displaystyle \frac{1}{3}}\right)=-0.1992\theta$

$\mathrm{ }=\theta \left(0.8286\right)-{\displaystyle \frac{\theta }{12}}\left(12+{\displaystyle \frac{1}{3}}\right)=-0.1992\theta$

$\tau =4\mathrm{ }{\int }_0^1{\displaystyle \frac{\phi \left(u\right)}{{\phi }^{\mathrm{\text{'}}}\left(u\right)}}du\mathrm{ }\mathrm{ }+1=\mathrm{ }4\mathrm{ }\left(-0.1992\mathrm{ }\theta \right)\mathrm{ }\mathrm{ }+1=1-0.797\left(\theta \right)\approx 1-0.8\left(\theta \right)\mathrm{ }(16)$

Figures (1-30) illustrate the joint PDF, the joint CDF and the related generator for the copula with different values of dependency parameter.

6. Tail Dependency

Preposition 6: The upper and lower tail dependency for this copula exist as shown in equation (17-18).

Proof:   for the upper tail dependency    ${\lambda }_U=\underset{u\to 1}{\lim }{\displaystyle \frac{1-2u+C\left(u,u\right)}{1-u}}$

${\displaystyle \frac{1-2u+C\left(u,u\right)}{1-u}}={\displaystyle \frac{1-2u+24{\left[{\left({\left(p^{\frac{1}{\theta }}+p^{\frac{1}{\theta }}\right)}^{\theta }+5\right)}^2-1\right]}^{-1}}{1-u}}={\displaystyle \frac{1-2u+24{\left[{\left({\left(2p^{\frac{1}{\theta }}\right)}^{\theta }+5\right)}^2-1\right]}^{-1}}{1-u}}$

$={\displaystyle \frac{1-2u+24{\left[{\left(2^{\theta }p+5\right)}^2-1\right]}^{-1}}{1-u}}\mathrm{ }use\mathrm{L}\mathrm{’}\mathrm{H}\mathrm{o}\mathrm{p}\mathrm{i}\mathrm{t}\mathrm{a}\mathrm{l}\mathrm{ }\mathrm{r}\mathrm{u}\mathrm{l}\mathrm{e}\mathbf{ }{\lambda }_U=\underset{u\to 1}{\lim }{\displaystyle \frac{-2-24{\left[{\left(2^{\theta }p+5\right)}^2-1\right]}^{-2}\mathrm{ }\left(2\right)\mathrm{ }\left(2^{\theta }p+5\right)\mathrm{ }\left(2^{\theta }{p}^{\mathrm{\text{'}}}\right)}{-1}}\mathrm{ }$

where $p^{\mathrm{\text{'}}}=\mathrm{ }{\displaystyle \frac{1}{2}}{\left(1+{\displaystyle \frac{24}{u}}\right)}^{-{\displaystyle \frac{1}{2}}}\left({\displaystyle \frac{-24}{u^2}}\right)\mathrm{ }and\mathrm{ }p=-5+\mathrm{ }{\left(1+{\displaystyle \frac{24}{u}}\right)}^{{\displaystyle \frac{1}{2}}}$

$Whenu\to 1then\mathrm{ }{p}^{\mathrm{\text{'}}}=\mathrm{ }{\displaystyle \frac{1}{2}}{\left(1+{\displaystyle \frac{24}{1}}\right)}^{-{\displaystyle \frac{1}{2}}}\left({\displaystyle \frac{-24}{1}}\right)\mathrm{ }=\mathrm{ }{\displaystyle \frac{-12}{5}}\mathrm{ }and\mathrm{ }p=0$

${\lambda }_U={\displaystyle \frac{-2-24{\left[{\left(2^{\theta }\left(0\right)+5\right)}^2-1\right]}^{-2}\mathrm{ }\left(2\right)\mathrm{ }\left(2^{\theta }\left(0\right)+5\right)\mathrm{ }\left(2^{\theta }\left[\frac{-12}{5}\right]\right)}{-1}}=\mathrm{ }{\displaystyle \frac{-2-24{\left[{\left(5\right)}^2-1\right]}^{-2}\mathrm{ }\left(2\right)\mathrm{ }\left(5\right)\mathrm{ }\left(2^{\theta }\left[\frac{-12}{5}\right]\right)}{-1}}$

${\lambda }_U=2-24{\left[24\right]}^{-2}\mathrm{ }\left(2\right)\mathrm{ }\mathrm{ }\left(2^{\theta }\left[12\right]\right)=2-\mathrm{ }{2}^{\theta }\in \left(\mathrm{0,1}\right)for\mathrm{ }\forall \alpha \mathrm{ }\in \left(\mathrm{0,1}\right)\mathrm{ }(17)\mathrm{ }$

For lower tail dependency:         ${\lambda }_L=\underset{u\to 0}{\lim }{\displaystyle \frac{C\left(u,u\right)}{u}}=\underset{u\to 0}{\lim }{\displaystyle \frac{24{\left[{\left({\left(2p^{\frac{1}{\theta }}\right)}^{\theta }+5\right)}^2-1\right]}^{-1}}{u}}\mathrm{ }\mathrm{ }using\mathrm{ }\mathrm{L}\mathrm{’}\mathrm{H}\mathrm{o}\mathrm{p}\mathrm{i}\mathrm{t}\mathrm{a}\mathrm{l}\mathrm{ }\mathrm{r}\mathrm{u}\mathrm{l}\mathrm{e}\mathrm{ }\mathrm{ }$

${\lambda }_L=\underset{u\to 0}{\lim }{\displaystyle \frac{-24{\left[{\left(2^{\theta }p+5\right)}^2-1\right]}^{-2}\mathrm{ }\left(2\right)\mathrm{ }\left(2^{\theta }p+5\right)\mathrm{ }\left(2^{\theta }{p}^{\mathrm{\text{'}}}\right)}{1}}\mathrm{ }\mathrm{ }=\mathrm{ }\underset{u\to 0}{\lim }-24{\left[{\left(2^{\theta }p+5\right)}^2-1\right]}^{-2}\mathrm{ }\left(2\right)\mathrm{ }\left(2^{\theta }p+5\right)\mathrm{ }\left(2^{\theta }{p}^{\mathrm{\text{'}}}\right)\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }$

$Whenu\to 0then\mathrm{ }{p}^{\mathrm{\text{'}}}=\mathrm{ }{\displaystyle \frac{1}{2}}{\left(1+{\displaystyle \frac{24}{0}}\right)}^{-{\displaystyle \frac{1}{2}}}\left({\displaystyle \frac{-24}{0}}\right)\mathrm{ }=-\mathrm{ }\mathrm{\infty }\mathrm{ }and\mathrm{ }p=\mathrm{\infty }$

$\underset{u\to 0}{\lim }-24{\left[{\left(2^{\theta }p+5\right)}^2-1\right]}^{-2}\mathrm{ }\left(2\right)\mathrm{ }\left(2^{\theta }p+5\right)\mathrm{ }\left(2^{\theta }{p}^{\mathrm{\text{'}}}\right)\mathrm{ }\mathrm{ }=\underset{u\to 0}{\lim }-24{\left[\mathrm{\infty }\right]}^{-2}\mathrm{ }\left(2\right)\mathrm{ }\left(\mathrm{\infty }\right)\mathrm{ }\left(-\mathrm{\infty }\right)\mathrm{ }=\mathrm{ }\underset{u\to 0}{\lim }48{\left[\mathrm{\infty }\right]}^{-2}\mathrm{ }\mathrm{ }{\left(\mathrm{\infty }\right)}^2\mathrm{ }\mathrm{ }=48$

But the lower tail dependency coefficient is between 0 and 1 and it cannot exceed the 1, so$for\forall \alpha \in \left(\mathrm{0,1}\right)$ it is calculated as   

${\lambda }_L=\underset{u\to 0}{\lim }{\displaystyle \frac{C\left(u,u\right)}{u}}=-24{\left[{\left(2^{\theta }p+5\right)}^2-1\right]}^{-2}\mathrm{ }\left(2\right)\mathrm{ }\left(2^{\theta }p+5\right)\mathrm{ }\left(2^{\theta }{p}^{\mathrm{\text{'}}}\right)\mathrm{ }\mathrm{ }\in \left(0\right.,\left.1\right)it\mathrm{ }cannot\mathrm{ }exceed\mathrm{ }1\mathrm{ }\mathrm{ }\forall \alpha \mathrm{ }\in \mathrm{ }\left(0,\right.\left.1\right](18)\mathrm{ }\mathrm{ }$

So the upper tail dependence coefficient for   $\forall \alpha \in \left(0,\right.\left.1\right]$ of this copula is $2-2^{\theta }$, also the copula has a lower tail dependency not exceeding the one  for$\forall \alpha \in \left(0,\right.\left.1\right]$ . The ${\lambda }_U=1$ , when dependency parameter approaches 0. While  ${\lambda }_U=0$ , when this parameter is 1. The ${\lambda }_L\in \left(\mathrm{0,1}\right)$ exists as shown in equation (18) and cannot exceed one.   Also the following equations (19-20) support these findings.

Upper tail dependency          ${\lambda }_U=2-2.\underset{u\to 0}{\lim }\mathrm{ }{\displaystyle \frac{{\phi }^{\mathrm{\text{'}}}\left(2u\right)}{{\phi }^{\mathrm{\text{'}}}\left(u\right)}}=2-{\left(\sqrt{2}\right)}^{{\displaystyle \frac{-1}{\theta }}+2}(19)$

$\underset{u\to 0}{\lim }\mathrm{ }{\displaystyle \frac{{\phi }^{\mathrm{\text{'}}}\left(2u\right)}{{\phi }^{\mathrm{\text{'}}}\left(u\right)}}=\mathrm{ }\underset{u\to 0}{\mathrm{l}\mathrm{i}\mathrm{m}}{\displaystyle \frac{{\left(-5+\mathrm{ }{\left(1+\frac{24}{2u}\right)}^{\frac{1}{2}}\right)}^{\frac{1}{\theta }-1}\mathrm{ }\frac{1}{2}\mathrm{ }{\left(1+\frac{24}{2u}\right)}^{-0.5}\mathrm{ }\left(\frac{-24}{2u^2}\right)}{{\left(-5+\mathrm{ }{\left(1+\frac{24}{u}\right)}^{\frac{1}{2}}\right)}^{\frac{1}{\theta }-1}\mathrm{ }\mathrm{ }\left(\frac{1}{2}\right){\left(1+\frac{24}{u}\right)}^{-0.5}\mathrm{ }\left(\frac{-24}{u^2}\right)}}$

$\underset{u\to 0}{\lim }\mathrm{ }{\displaystyle \frac{{\phi }^{\mathrm{\text{'}}}\left(2u\right)}{{\phi }^{\mathrm{\text{'}}}\left(u\right)}}=\mathrm{ }\underset{u\to 0}{\mathrm{l}\mathrm{i}\mathrm{m}}{\displaystyle \frac{{\left(-5+\mathrm{ }{\left(1+\frac{24}{2u}\right)}^{\frac{1}{2}}\right)}^{\frac{1}{\theta }-1}\mathrm{ }\mathrm{ }{\left(1+\frac{12}{u}\right)}^{-0.5}\mathrm{ }\left(\frac{-12}{u^2}\right)}{{\left(-5+\mathrm{ }{\left(1+\frac{24}{u}\right)}^{\frac{1}{2}}\right)}^{\frac{1}{\theta }-1}\mathrm{ }\mathrm{ }{\left(1+\frac{24}{u}\right)}^{-0.5}\mathrm{ }\left(\frac{-24}{u^2}\right)}}$

As long as u is small       ${\left(1+{\displaystyle \frac{24}{u}}\right)}^{{\displaystyle \frac{1}{2}}}\cong {\left({\displaystyle \frac{24}{u}}\right)}^{{\displaystyle \frac{1}{2}}}\mathrm{ }for\mathrm{ }\mathrm{ }u\in \left(\mathrm{0,1}\right)$

$\underset{u\to 0}{\mathrm{l}\mathrm{i}\mathrm{m}}{\displaystyle \frac{{\left(-5+\mathrm{ }{\left(\frac{24}{2u}\right)}^{\frac{1}{2}}\right)}^{\frac{1}{\theta }-1}\mathrm{ }\mathrm{ }{\left(\frac{12}{u}\right)}^{-0.5}\left(\mathrm{ }12\right)}{{\left(-5+\mathrm{ }{\left(\frac{24}{u}\right)}^{\frac{1}{2}}\right)}^{\frac{1}{\theta }-1}\mathrm{ }\mathrm{ }{\left(\frac{24}{u}\right)}^{-0.5}\mathrm{ }\left(24\right)}}=\mathrm{ }\underset{u\to 0}{\mathrm{l}\mathrm{i}\mathrm{m}}{\displaystyle \frac{{\left(-5+\mathrm{ }\frac{\sqrt{12}}{\sqrt{u}}\right)}^{\frac{1}{\theta }-1}\mathrm{ }\mathrm{ }\frac{\sqrt{u}}{\sqrt{12}}\mathrm{ }\left(12\right)}{{\left(-5+\mathrm{ }\frac{\sqrt{24}}{\sqrt{u}}\right)}^{\frac{1}{\theta }-1}\mathrm{ }\mathrm{ }\frac{\sqrt{u}}{\sqrt{24}}\mathrm{ }\left(24\right)}}=\underset{u\to 0}{\mathrm{l}\mathrm{i}\mathrm{m}}\mathrm{ }\mathrm{ }{\left({\displaystyle \frac{\frac{-5\sqrt{u}+\mathrm{ }\sqrt{12}}{\sqrt{u}}}{\frac{-5\sqrt{u}+\mathrm{ }\sqrt{24}}{\sqrt{u}}}}\right)}^{{\displaystyle \frac{1}{\theta }}-1}\left(\sqrt{2}\right)\mathrm{ }\left({\displaystyle \frac{1}{2}}\right)$

$=\underset{u\to 0}{\mathrm{l}\mathrm{i}\mathrm{m}}\mathrm{ }{\left({\displaystyle \frac{-5\sqrt{0}+\mathrm{ }\sqrt{12}}{-5\sqrt{0}+\mathrm{ }\sqrt{24}}}\right)}^{{\displaystyle \frac{1}{\theta }}-1}\mathrm{ }\left({\displaystyle \frac{\sqrt{2}}{2}}\right)=\mathrm{ }{\left({\displaystyle \frac{\mathrm{ }\sqrt{12}}{\mathrm{ }\sqrt{24}}}\right)}^{{\displaystyle \frac{1}{\theta }}-1}\left({\displaystyle \frac{\sqrt{2}}{2}}\right)={\displaystyle \frac{\sqrt{2}}{2}}\mathrm{ }\mathrm{ }{\left(\sqrt{{\displaystyle \frac{12}{24}}}\right)}^{{\displaystyle \frac{1}{\theta }}-1}\mathrm{ }=\mathrm{ }{\displaystyle \frac{\sqrt{2}}{2}}\mathrm{ }\mathrm{ }{\left(\sqrt{{\displaystyle \frac{1}{2}}}\right)}^{{\displaystyle \frac{1}{\theta }}-1}=\mathrm{ }{\displaystyle \frac{\sqrt{2}}{2}}\mathrm{ }\mathrm{ }{\left(\sqrt{2}\right)}^{{\displaystyle \frac{-1}{\theta }}+1}=\mathrm{ }{\displaystyle \frac{{\left(\sqrt{2}\right)}^{\frac{-1}{\theta }+2}}{2}}$

${\lambda }_U=2-2.\underset{u\to 0}{\lim }\mathrm{ }{\displaystyle \frac{{\phi }^{\mathrm{\text{'}}}\left(2u\right)}{{\phi }^{\mathrm{\text{'}}}\left(u\right)}}=\mathrm{ }2-2\left({\displaystyle \frac{{\left(\sqrt{2}\right)}^{\frac{-1}{\theta }+2}}{2}}\right)=\mathrm{ }2-{\left(\sqrt{2}\right)}^{{\displaystyle \frac{-1}{\theta }}+2}\mathrm{ }$

This upper tail dependency cannot exceed one especially at very small values of the dependency parameter.

Lower tail dependency:        ${\lambda }_L=2-2.\underset{u\to 0}{\lim }\mathrm{ }{\displaystyle \frac{{\phi }^{\mathrm{\text{'}}}\left(u\right)}{{\phi }^{\mathrm{\text{'}}}\left(2u\right)}}=2\left[1-2\mathrm{ }{\left(\sqrt{2}\right)}^{{\displaystyle \frac{1}{\theta }}-2}\right]\mathrm{ }(20)$

$\underset{u\to 0}{\lim }\mathrm{ }{\displaystyle \frac{{\phi }^{\mathrm{\text{'}}}\left(u\right)}{{\phi }^{\mathrm{\text{'}}}\left(2u\right)}}=\mathrm{ }\underset{u\to 0}{\mathrm{l}\mathrm{i}\mathrm{m}}{\displaystyle \frac{{\left(-5+\mathrm{ }{\left(1+\frac{24}{u}\right)}^{\frac{1}{2}}\right)}^{\frac{1}{\theta }-1}\mathrm{ }\mathrm{ }\left(\frac{1}{2}\right){\left(1+\frac{24}{u}\right)}^{-0.5}\mathrm{ }\left(\frac{-24}{u^2}\right)}{{\left(-5+\mathrm{ }{\left(1+\frac{24}{2u}\right)}^{\frac{1}{2}}\right)}^{\frac{1}{\theta }-1}\mathrm{ }\frac{1}{2}\mathrm{ }{\left(1+\frac{24}{2u}\right)}^{-0.5}\mathrm{ }\left(\frac{-24}{2u^2}\right)}}\mathrm{ }$

$\underset{u\to 0}{\lim }\mathrm{ }{\displaystyle \frac{{\phi }^{\mathrm{\text{'}}}\left(u\right)}{{\phi }^{\mathrm{\text{'}}}\left(2u\right)}}={\displaystyle \frac{{\left(-5+\mathrm{ }{\left(1+\frac{24}{u}\right)}^{\frac{1}{2}}\right)}^{\frac{1}{\theta }-1}\mathrm{ }\mathrm{ }{\left(1+\frac{24}{u}\right)}^{-0.5}\mathrm{ }\left(\frac{-24}{u^2}\right)}{{\left(-5+\mathrm{ }{\left(1+\frac{12}{u}\right)}^{\frac{1}{2}}\right)}^{\frac{1}{\theta }-1}\mathrm{ }\mathrm{ }{\left(1+\frac{12}{u}\right)}^{-0.5}\mathrm{ }\left(\frac{-12}{u^2}\right)}}$

$\mathrm{ }\mathrm{ }{\left(1+{\displaystyle \frac{24}{u}}\right)}^{{\displaystyle \frac{1}{2}}}\cong {\left({\displaystyle \frac{24}{u}}\right)}^{{\displaystyle \frac{1}{2}}}\mathrm{ }for\mathrm{ }\mathrm{ }u\in \left(\mathrm{0,1}\right)$

$\underset{u\to 0}{\lim }\mathrm{ }{\displaystyle \frac{{\phi }^{\mathrm{\text{'}}}\left(u\right)}{{\phi }^{\mathrm{\text{'}}}\left(2u\right)}}={\displaystyle \frac{{\left(-5+\mathrm{ }{\left(\frac{24}{u}\right)}^{\frac{1}{2}}\right)}^{\frac{1}{\theta }-1}\mathrm{ }\mathrm{ }\frac{\sqrt{u}}{\sqrt{24}}\mathrm{ }\left(2\right)}{{\left(-5+\mathrm{ }{\left(\frac{12}{u}\right)}^{\frac{1}{2}}\right)}^{\frac{1}{\theta }-1}\mathrm{ }\mathrm{ }\frac{\sqrt{u}}{\sqrt{12}}\mathrm{ }}}=\mathrm{ }\underset{u\to 0}{\lim }2\mathrm{ }\sqrt{{\displaystyle \frac{12}{24}}}\mathrm{ }{\left({\displaystyle \frac{\frac{-5\sqrt{u}+\mathrm{ }\sqrt{24}}{\sqrt{u}}}{\frac{-5\sqrt{u}+\mathrm{ }\sqrt{12}}{\sqrt{u}}}}\right)}^{{\displaystyle \frac{1}{\theta }}-1}$

$=\mathrm{ }\underset{u\to 0}{\lim }\mathrm{ }2\sqrt{{\displaystyle \frac{12}{24}}}\mathrm{ }{\left({\displaystyle \frac{-5\sqrt{0}+\mathrm{ }\sqrt{24}}{-5\sqrt{0}+\mathrm{ }\sqrt{12}}}\right)}^{{\displaystyle \frac{1}{\theta }}-1}=2\mathrm{ }\mathrm{ }\sqrt{{\displaystyle \frac{1}{2}}}\mathrm{ }{\left(\sqrt{2}\right)}^{{\displaystyle \frac{1}{\theta }}-1}=\mathrm{ }\mathrm{ }{\displaystyle \frac{2}{\sqrt{2}}}{\left(\sqrt{2}\right)}^{{\displaystyle \frac{1}{\theta }}-1}\mathrm{ }\mathrm{ }=\mathrm{ }2\mathrm{ }{\left(\sqrt{2}\right)}^{{\displaystyle \frac{1}{\theta }}-2}$

${\lambda }_L=2-2.\underset{u\to 0}{\lim }\mathrm{ }{\displaystyle \frac{{\phi }^{\mathrm{\text{'}}}\left(u\right)}{{\phi }^{\mathrm{\text{'}}}\left(2u\right)}}=\mathrm{ }\mathrm{ }2-2\left(2\mathrm{ }{\left(\sqrt{2}\right)}^{{\displaystyle \frac{1}{\theta }}-2}\right)=2\left[1-2\mathrm{ }{\left(\sqrt{2}\right)}^{{\displaystyle \frac{1}{\theta }}-2}\right]$

This lower tail dependency cannot exceed one especially at very small values of the dependency parameter.

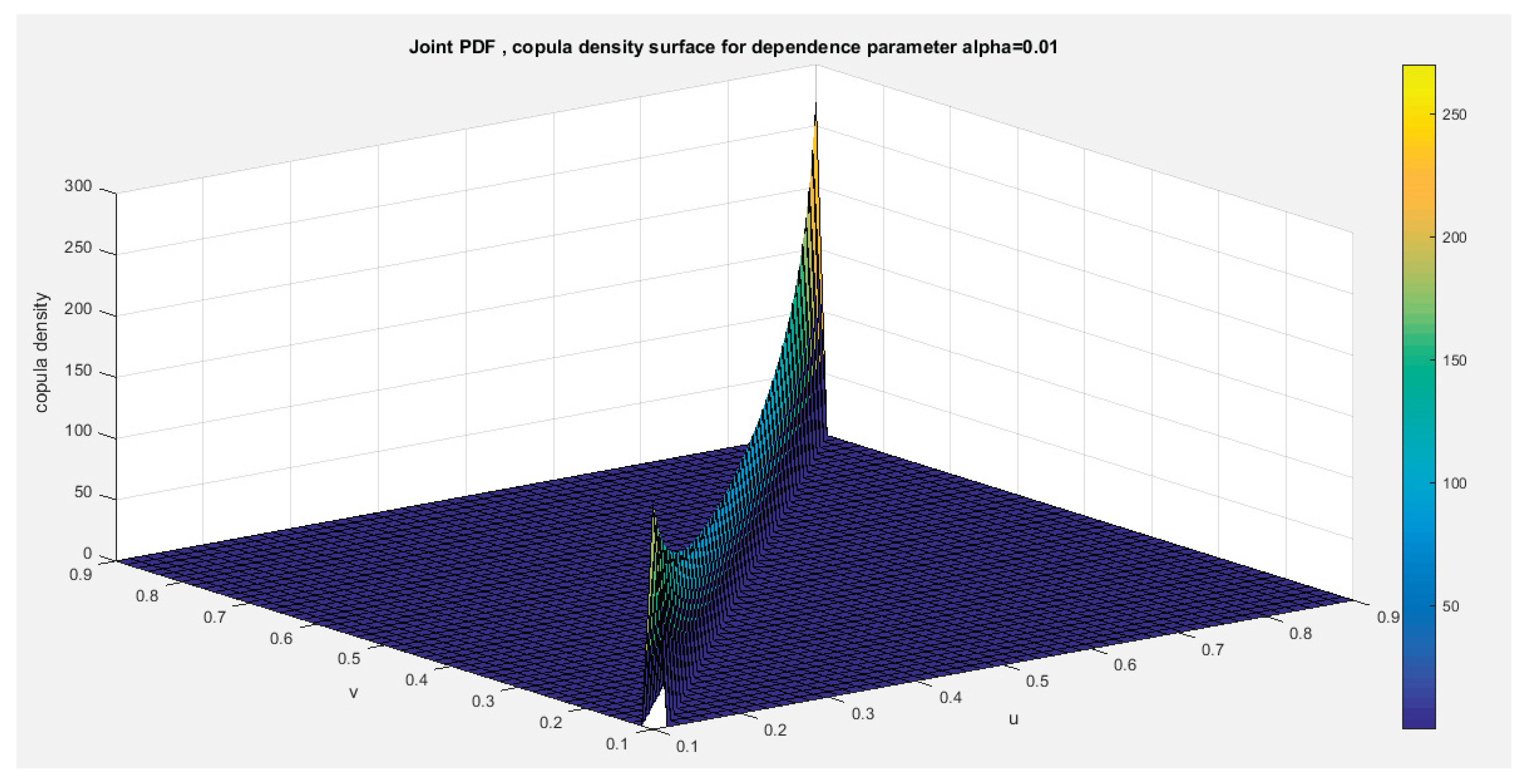
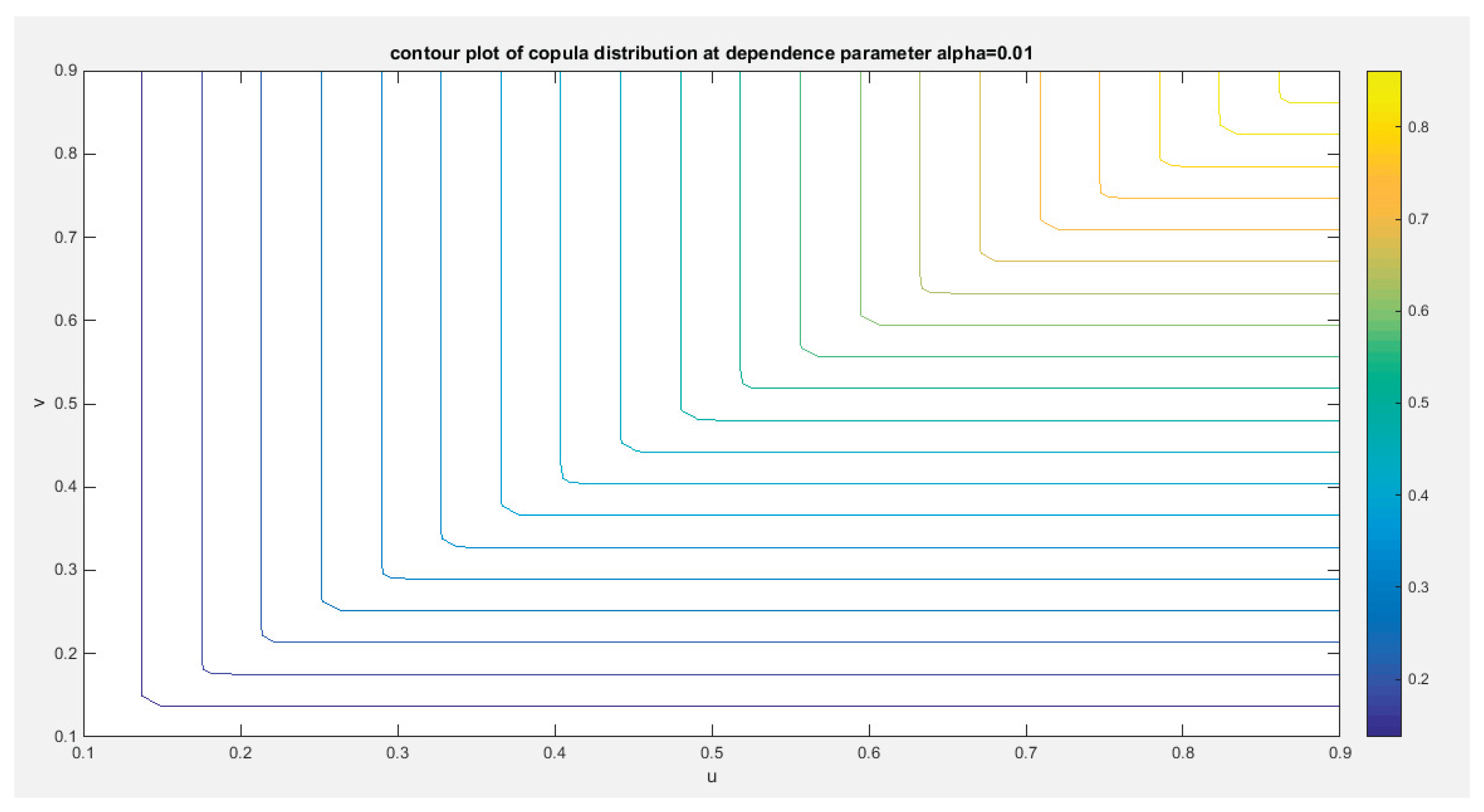
Figures (1-2) illustrate the contour plot and the surface of the copula density and distribution with different values of the dependency parameter.

Figure 1. shows copula density surface with dependency parameter 0.1.

Figure 1. shows copula density surface with dependency parameter 0.1.

Figure 2. shows the contour plot of the copula distribution with dependency parameter 0.01.

Figure 2. shows the contour plot of the copula distribution with dependency parameter 0.01.

7. Methods of Estimation

(Weiß, 2011), (Chen, 2007), and (Tsukahara, 2005) provided a comprehensive overview of various estimation methods, including the following:

7.1. Maximum Likelihood Estimation (MLE)

The process involves a single step in which all parameters—both marginal and copula—are estimated for the complete joint density function. This is accomplished by taking the log-likelihood of the full joint function, differentiating it with respect to each of the marginal parameters and the copula parameter, then setting the resulting equations equal to zero. Finally, the system of equations is solved numerically.

7.2. Inference Function of Margins (IFM)

In the context of bivariate copula-based models, estimating all model parameters simultaneously using maximum likelihood can be computationally challenging (Al Turk et al., 2017). To address this issue, a two-stage estimation procedure has been suggested by researchers such as  (Joe, 2005) and (Xu, 2009). n the first stage of this approach, the marginal parameters are estimated independently using maximum likelihood, as detailed in equation (21). Here, "s" represents the score function or gradient, which plays a crucial role in the estimation process.

$s_i^{\left(1\right)}=\mathrm{ }{\displaystyle \frac{\partial }{\partial {\theta }_1}}\ln f_X\left(x_i;{\theta }_{marginal\mathrm{ }1}\right)\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }and\mathrm{ }\mathrm{ }\mathrm{ }{s}_i^{\left(2\right)}=\mathrm{ }{\displaystyle \frac{\partial }{\partial {\theta }_2}}\ln f_Y\left(y_i;{\theta }_{marginal\mathrm{ }2}\right)\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }(21)$

By accurately estimating the marginal parameter, you unlock the potential to derive the marginal cumulative distribution function (CDF) for each variable, as demonstrated in equation (22). This pivotal step not only deepens your understanding of each variable's behavior but also equips you with powerful insights that can significantly enhance your analysis. Embrace this method to elevate the sophistication of your findings!

$u_i=\mathrm{ }{\widehat{F}}_1\left(x_i;{\widehat{\theta }}_1\mathrm{ }\right)\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }and\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }{v}_i=\mathrm{ }{\widehat{F}}_2\left(y_i;{\widehat{\theta }}_2\mathrm{ }\right)\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }(22)\mathrm{ }$

In the second stage of the analysis, we focus on maximizing the likelihood of the dependence parameters while keeping the marginal parameters fixed, as determined in the first stage. This process involves calculating the log-likelihood of the copula density, which is represented in equation (23). To further this analysis, we then differentiate the log-likelihood with respect to the copula dependency parameter, as outlined in equation (24).

$\ln L_{\left(IFM\right)}=\sum _{i=1}^n\ln c\mathrm{ }\left(\mathrm{ }\mathrm{ }{\widehat{F}}_1\left(x_i;{\widehat{\theta }}_1\mathrm{ }\right),\mathrm{ }{\widehat{F}}_2\left(y_i;{\widehat{\theta }}_2\mathrm{ }\right)\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ };{\theta }_{copula}\mathrm{ }\right)\mathrm{ }=\sum _{i=1}^n\ln c\mathrm{ }\left(\mathrm{ }{u}_i,\mathrm{ }{v}_i\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ };{\theta }_{copula}\mathrm{ }\right)\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }(23)$

${\displaystyle \frac{\partial \ln L_{\left(IFM\right)}}{\partial {\theta }_{copula}}}=\mathrm{ }{\displaystyle \frac{\partial }{\partial {\theta }_{copula}}}\left[\sum _{i=1}^n\ln c\mathrm{ }\left(\mathrm{ }\mathrm{ }{\widehat{F}}_1\left(x_i;{\widehat{\theta }}_1\mathrm{ }\right),\mathrm{ }{\widehat{F}}_2\left(y_i;{\widehat{\theta }}_2\mathrm{ }\right)\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ };{\theta }_{copula}\mathrm{ }\right)\right]\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }(24)$

In this paper, the author used IFM.

Taking the first derivative of the log-likelihood of equation (14) with respect to copula parameter as described below:  the copula density can be written as  $c\left(u,v\right)=constant*t_1*t_2*t_3*t_4$ so

${\displaystyle \frac{\partial \ln L_{\left(IFM\right)}}{\partial {\theta }_{copula}}}=\sum _{i=1}^n\left({\displaystyle \frac{t_1^{\mathrm{\text{'}}}}{t_1}}+{\displaystyle \frac{t_2^{\mathrm{\text{'}}}}{t_2}}+{\displaystyle \frac{t_3^{\mathrm{\text{'}}}}{t_3}}+{\displaystyle \frac{t_4^{\mathrm{\text{'}}}}{t_4}}\right)$

$t_1={\left(pq\right)}^{{\displaystyle \frac{1}{\theta }}-1}\to t_1^{\mathrm{\text{'}}}={\left(pq\right)}^{{\displaystyle \frac{1}{\theta }}-1}\left({\displaystyle \frac{-1}{{\theta }^2}}\right)\ln \left(pq\right)$

$t_2={\left[{\left({\left(p^{{\displaystyle \frac{1}{\theta }}}+q^{{\displaystyle \frac{1}{\theta }}}\right)}^{\theta }+5\right)}^2-1\right]}^{-2}\to$

$t_2^{\mathrm{\text{'}}}=-2{\left[{\left({\left(p^{{\displaystyle \frac{1}{\theta }}}+q^{{\displaystyle \frac{1}{\theta }}}\right)}^{\theta }+5\right)}^2-1\right]}^{-3}2\left[{\left(p^{{\displaystyle \frac{1}{\theta }}}+q^{{\displaystyle \frac{1}{\theta }}}\right)}^{\theta }+5\right]\left[\theta {\left(p^{{\displaystyle \frac{1}{\theta }}}+q^{{\displaystyle \frac{1}{\theta }}}\right)}^{\theta -1}\left(p^{{\displaystyle \frac{1}{\theta }}}\left({\displaystyle \frac{-1}{{\theta }^2}}\right)\ln \left(p\right)+q^{{\displaystyle \frac{1}{\theta }}}\left({\displaystyle \frac{-1}{{\theta }^2}}\right)\ln \left(q\right)\right)+{\left(p^{{\displaystyle \frac{1}{\theta }}}+q^{{\displaystyle \frac{1}{\theta }}}\right)}^{\theta }\ln \left(p^{{\displaystyle \frac{1}{\theta }}}+q^{{\displaystyle \frac{1}{\theta }}}\right)\right]$

$t_3={\left(p^{{\displaystyle \frac{1}{\theta }}}+q^{{\displaystyle \frac{1}{\theta }}}\right)}^{\theta -2}\to$

$t_3^{\mathrm{\text{'}}}=\left(\theta -2\right){\left(p^{{\displaystyle \frac{1}{\theta }}}+q^{{\displaystyle \frac{1}{\theta }}}\right)}^{\theta -3}\left(p^{{\displaystyle \frac{1}{\theta }}}\left({\displaystyle \frac{-1}{{\theta }^2}}\right)\ln \left(p\right)+q^{{\displaystyle \frac{1}{\theta }}}\left({\displaystyle \frac{-1}{{\theta }^2}}\right)\ln \left(q\right)\right)+{\left(p^{{\displaystyle \frac{1}{\theta }}}+q^{{\displaystyle \frac{1}{\theta }}}\right)}^{\theta -2}\ln \left(p^{{\displaystyle \frac{1}{\theta }}}+q^{{\displaystyle \frac{1}{\theta }}}\right)$

$t_4=\left\{\left(-4\right){\left[{\left({\left(p^{{\displaystyle \frac{1}{\theta }}}+q^{{\displaystyle \frac{1}{\theta }}}\right)}^{\theta }+5\right)}^2-1\right]}^{-1}{\left[{\left(p^{{\displaystyle \frac{1}{\theta }}}+q^{{\displaystyle \frac{1}{\theta }}}\right)}^{\theta }+5\right]}^2{\left[p^{{\displaystyle \frac{1}{\theta }}}+q^{{\displaystyle \frac{1}{\theta }}}\right]}^{\theta }+{\left[p^{{\displaystyle \frac{1}{\theta }}}+q^{{\displaystyle \frac{1}{\theta }}}\right]}^{\theta }+\left[{\left(p^{{\displaystyle \frac{1}{\theta }}}+q^{{\displaystyle \frac{1}{\theta }}}\right)}^{\theta }+5\right]\left[{\displaystyle \frac{\theta -1}{\theta }}\right]\right\}$

This t₄ can be written as $t_4=\left(-4\mathrm{*}{f}_1\mathrm{*}{f}_2\mathrm{*}{f}_3+f_3+\left[{\left(p^{{\displaystyle \frac{1}{\theta }}}+q^{{\displaystyle \frac{1}{\theta }}}\right)}^{\theta }+5\right]\left[{\displaystyle \frac{\theta -1}{\theta }}\right]\right)$ and

let’s call $h=\left[{\left(p^{{\displaystyle \frac{1}{\theta }}}+q^{{\displaystyle \frac{1}{\theta }}}\right)}^{\theta }+5\right]andk=\left[{\displaystyle \frac{\theta -1}{\theta }}\right]$

$t_4^{\mathrm{\text{'}}}=-4\mathrm{*}{f}_1^{\mathrm{\text{'}}}\mathrm{*}{f}_2\mathrm{*}{f}_3-4\mathrm{*}{f}_1\mathrm{*}{f}_2^{\mathrm{\text{'}}}\mathrm{*}{f}_3-4\mathrm{*}{f}_1\mathrm{*}{f}_2\mathrm{*}{f}_3^{\mathrm{\text{'}}}+f_3^{\mathrm{\text{'}}}+h^{\mathrm{\text{'}}}k+h{k}^{\mathrm{\text{'}}}$

${f_1=\left[{\left({\left(p^{{\displaystyle \frac{1}{\theta }}}+q^{{\displaystyle \frac{1}{\theta }}}\right)}^{\theta }+5\right)}^2-1\right]}^{-1}$

$f_1^{\mathrm{\text{'}}}=-{\left[{\left({\left(p^{{\displaystyle \frac{1}{\theta }}}+q^{{\displaystyle \frac{1}{\theta }}}\right)}^{\theta }+5\right)}^2-1\right]}^{-2}2\left[{\left(p^{{\displaystyle \frac{1}{\theta }}}+q^{{\displaystyle \frac{1}{\theta }}}\right)}^{\theta }+5\right]\left[\theta {\left(p^{{\displaystyle \frac{1}{\theta }}}+q^{{\displaystyle \frac{1}{\theta }}}\right)}^{\theta -1}\left(p^{{\displaystyle \frac{1}{\theta }}}\left({\displaystyle \frac{-1}{{\theta }^2}}\right)\ln \left(p\right)+q^{{\displaystyle \frac{1}{\theta }}}\left({\displaystyle \frac{-1}{{\theta }^2}}\right)\ln \left(q\right)\right)+{\left(p^{{\displaystyle \frac{1}{\theta }}}+q^{{\displaystyle \frac{1}{\theta }}}\right)}^{\theta }\ln \left(p^{{\displaystyle \frac{1}{\theta }}}+q^{{\displaystyle \frac{1}{\theta }}}\right)\right]$

$f_2={\left[{\left(p^{{\displaystyle \frac{1}{\theta }}}+q^{{\displaystyle \frac{1}{\theta }}}\right)}^{\theta }+5\right]}^2$

$f_2^{\mathrm{\text{'}}}=2\left[{\left(p^{{\displaystyle \frac{1}{\theta }}}+q^{{\displaystyle \frac{1}{\theta }}}\right)}^{\theta }+5\right]\left[\theta {\left(p^{{\displaystyle \frac{1}{\theta }}}+q^{{\displaystyle \frac{1}{\theta }}}\right)}^{\theta -1}\left(p^{{\displaystyle \frac{1}{\theta }}}\left({\displaystyle \frac{-1}{{\theta }^2}}\right)\ln \left(p\right)+q^{{\displaystyle \frac{1}{\theta }}}\left({\displaystyle \frac{-1}{{\theta }^2}}\right)\ln \left(q\right)\right)+{\left(p^{{\displaystyle \frac{1}{\theta }}}+q^{{\displaystyle \frac{1}{\theta }}}\right)}^{\theta }\ln \left(p^{{\displaystyle \frac{1}{\theta }}}+q^{{\displaystyle \frac{1}{\theta }}}\right)\right]$

$f_3={\left(p^{{\displaystyle \frac{1}{\theta }}}+q^{{\displaystyle \frac{1}{\theta }}}\right)}^{\theta }\to f_3^{\mathrm{\text{'}}}=\theta {\left(p^{{\displaystyle \frac{1}{\theta }}}+q^{{\displaystyle \frac{1}{\theta }}}\right)}^{\theta -1}\left(p^{{\displaystyle \frac{1}{\theta }}}\left({\displaystyle \frac{-1}{{\theta }^2}}\right)\ln \left(p\right)+q^{{\displaystyle \frac{1}{\theta }}}\left({\displaystyle \frac{-1}{{\theta }^2}}\right)\ln \left(q\right)\right)+{\left(p^{{\displaystyle \frac{1}{\theta }}}+q^{{\displaystyle \frac{1}{\theta }}}\right)}^{\theta }\ln \left(p^{{\displaystyle \frac{1}{\theta }}}+q^{{\displaystyle \frac{1}{\theta }}}\right)$

$h=\left[{\left(p^{{\displaystyle \frac{1}{\theta }}}+q^{{\displaystyle \frac{1}{\theta }}}\right)}^{\theta }+5\right]\to h^{\mathrm{\text{'}}}=\theta {\left(p^{{\displaystyle \frac{1}{\theta }}}+q^{{\displaystyle \frac{1}{\theta }}}\right)}^{\theta -1}\left(p^{{\displaystyle \frac{1}{\theta }}}\left({\displaystyle \frac{-1}{{\theta }^2}}\right)\ln \left(p\right)+q^{{\displaystyle \frac{1}{\theta }}}\left({\displaystyle \frac{-1}{{\theta }^2}}\right)\ln \left(q\right)\right)+{\left(p^{{\displaystyle \frac{1}{\theta }}}+q^{{\displaystyle \frac{1}{\theta }}}\right)}^{\theta }\ln \left(p^{{\displaystyle \frac{1}{\theta }}}+q^{{\displaystyle \frac{1}{\theta }}}\right)$

$k=\left[{\displaystyle \frac{\theta -1}{\theta }}\right]\to k^{\mathrm{\text{'}}}={\displaystyle \frac{1}{{\theta }^2}}$

Applying Quasi-Newton method

${\alpha }^{\left(a+1\right)}={\alpha }^{\left(a\right)}+M^{-1}\left({\alpha }^{\left(a\right)}\right)S\left({\alpha }^a\right)$ where $S\left(\alpha \right)={\displaystyle \frac{\partial \ln L_{\left(IFM\right)}}{\partial {\theta }_{copula}}}$ , $M=S^{T}S$ and $M^{-1}\left(\alpha \right)$ can approximate the variance of the dependency parameter estimator.

Each marginal parameter possesses its own variance, which is determined in the first stage of the (IFM) approach. In the second stage, these parameters are treated as fixed, which means they do not directly influence the variance of the estimated dependency parameter. While the variance of the copula parameter derived from the second stage remains valid under the IFM approach, it consistently underestimates the total uncertainty by neglecting the variability associated with the estimation of marginal parameters. To effectively propagate uncertainty from the first stage to the second stage, it is imperative to employ the Godambe information matrix (commonly referred to as the sandwich estimator), as articulated (Godambe, 1991). This rigorous approach facilitates the calculation of the joint variance-covariance matrix for all parameters, encompassing both marginal and copula parameters. The sandwich estimator is a robust variance estimator, crucial for obtaining the asymptotic variance of parameter estimates, particularly when the likelihood function is estimated in multiple stages or is mis-specified due to failure to utilize the full joint likelihood. The variance is defined by the following equation (25):

${\tilde{F}}_i\left(x_i\right)={\displaystyle \frac{\sum _{i=1}^{n}I\left(X_i\le x_i\right)}{n+1}}and{\tilde{F}}_i\left(y_i\right)={\displaystyle \frac{\sum _{i=1}^{n}I\left(Y_i\le y_i\right)}{n+1}}(25)$

The second stage involves estimating the copula dependency parameter using the pseudo likelihood function as shown in equation (26-28) and maximizing this function.

$\ln L_{\left(SP\right)}=\sum _{i=1}^n\ln c\left({\tilde{F}}_i\left(x_i\right),{\tilde{F}}_i\left(y_i\right);{\theta }_{copula}\right)(26)$

${\displaystyle \frac{\partial \ln L_{\left(SP\right)}}{\partial {\theta }_{copula}}}={\displaystyle \frac{\partial }{\partial {\theta }_{copula}}}\left[\sum _{i=1}^n\ln c\left({\tilde{F}}_i\left(x_i\right),{\tilde{F}}_i\left(y_i\right);{\theta }_{copula}\right)\right](27)$

$var\left(\widehat{\alpha }\right)=H^{-1}S{H}^{-1}(28)$

where S is the outer product of the gradient of parameter estimator (marginal and copula) or the score function as shown in equation (29).

$S={\displaystyle \frac{1}{n}}\left[\begin{array}{c}{\displaystyle \frac{\partial \ln f_X\left(x_i;{\theta }_{marginal}\right)}{\partial {\theta }_{marginal}}}\\ {\displaystyle \frac{\partial \ln f_Y\left(y_i;{\theta }_{marginal}\right)}{\partial {\theta }_{marginal}}}\\ {\displaystyle \frac{\partial \ln L_{\left(IFM\right)}}{\partial {\theta }_{copula}}}\end{array}\right]\left[\begin{array}{ccc}{\displaystyle \frac{\partial \ln f_X\left(x_i;{\theta }_{1marginal}\right)}{\partial {\theta }_{1marginal}}}& {\displaystyle \frac{\partial \ln f_Y\left(y_i;{\theta }_{2marginal}\right)}{\partial {\theta }_{2marginal}}}& {\displaystyle \frac{\partial \ln L_{\left(IFM\right)}}{\partial {\theta }_{copula}}}\end{array}\right](29)$

$H^{-1}$ is the inverse of the negative of the expectation of the information matrix, in other words, the variance of the parameter estimator (marginal and copula). It is a diagonal matrix. $H=-E\left({\displaystyle \frac{{\partial }^{2}l}{\partial {\alpha }^2}}\right)=I$ , the inverse of this H or inverse of this I is the variance of marginal parameter estimators in the first stage and the variance of the copula estimator in the second stage. So let’s call this inverse the A matrix, so the sandwich estimator can be expressed as shown in equations (30-31)

$var\left(\widehat{\theta }\right)=H^{-1}S{H}^{-1}=ASA(30)$

$var-cov\left(\widehat{\theta }\right)=\left[\begin{array}{ccc}var\left({\theta }_1\right)& 0& 0\\ 0& var\left({\theta }_2\right)& 0\\ 0& 0& var\left({\alpha }_{copula}\right)\end{array}\right]\left[\begin{array}{ccc}{s}_{11}& s_{12}& s_{13}\\ s_{21}& s_{22}& s_{23}\\ s_{31}& s_{32}& s_{33}\end{array}\right]\left[\begin{array}{ccc}var\left({\theta }_1\right)& 0& 0\\ 0& var\left({\theta }_2\right)& 0\\ 0& 0& var\left({\alpha }_{copula}\right)\end{array}\right]$

$var-cov\left(\widehat{\theta }\right)=\left[\begin{array}{ccc}{v_1^{2}s}_{11}& v_1{v}_2{s}_{12}& v_1{v}_3{s}_{13}\\ v_1{v}_2{s}_{21}& {v_2^{2}s}_{22}& {v_2{v}_{3}s}_{23}\\ {v_1{v}_{3}s}_{31}& {v_2{v}_{3}s}_{32}& {v_3^{2}s}_{33}\end{array}\right](31)$

This variance covariance matrix captures the covariance between the marginal and the copula parameter estimators which are not captured in the naive block-separated IFM variances.

7.3. Semiparametric Method (SP)

The third method introduced by (Kim et al., 2007) is the estimation by semiparametric method (SP This process is divided into two stages, similar to (IFM). In the first stage, the variables are transformed into their marginal empirical cumulative distribution functions (eCDF). Essentially, this involves converting the observations into pseudo-observations by applying the empirical distribution function to each marginal distribution, as demonstrated in equation (32).

${\tilde{F}}_i\left(x_i\right)={\displaystyle \frac{\sum _{i=1}^{n}I\left(X_i\le x_i\right)}{n+1}}and{\tilde{F}}_i\left(y_i\right)={\displaystyle \frac{\sum _{i=1}^{n}I\left(Y_i\le y_i\right)}{n+1}}(32)$

The second stage involves estimating the copula dependency parameter using the pseudo likelihood function as shown in equation (33-34) and maximizing this function.

$\ln L_{\left(SP\right)}=\sum _{i=1}^n\ln c\left({\tilde{F}}_i\left(x_i\right),{\tilde{F}}_i\left(y_i\right);{\theta }_{copula}\right)(33)$

${\displaystyle \frac{\partial \ln L_{\left(SP\right)}}{\partial {\theta }_{copula}}}={\displaystyle \frac{\partial }{\partial {\theta }_{copula}}}\left[\sum _{i=1}^n\ln c\left({\tilde{F}}_i\left(x_i\right),{\tilde{F}}_i\left(y_i\right);{\theta }_{copula}\right)\right](34)$

8. Real Data Analysis

8.1. Data Description

The OECD data platform, offered by the Organization for Economic Cooperation and Development (OECD), serves as a valuable resource by collecting comprehensive data across diverse economic, social, and environmental sectors, including the economy, health, trade, education, labor, innovation, and development. This platform presents a wide array of indicators that effectively describe these aspects. In this analysis, the focus will be on two key indicators to examine their interrelationships and explore how new copulas can be utilized to model these dependencies. The selected indicators include: ‘feeling safe walking alone at night’ and ‘the quality of support networks’ coded (1) & (2) respectively in Table (1). The data collection encompasses 41 countries, providing a robust foundation for our insights and conclusions. The data can be found on the following site: https://stats.oecd.org/index.aspx?DataSetCode=BLI .

The indicators ( let’s call it the y variable) in Table (1) are distributed as Median Based Unit Rayleigh (MBUR) previously discussed by Iman Attia (Attia, 2024) with the following PDF in equation (35), CDF in equation (36), and, quantile function in equation (37):

$f\left(y\right)={\displaystyle \frac{6}{{\alpha }^2}}\left[1-y^{{\displaystyle \frac{1}{{\theta }^2}}}\right]y^{\left({\displaystyle \frac{2}{{\theta }^2}}-1\right)},0<y<1,\theta >0(35)$

$F\left(y\right)={3y}^{{\displaystyle \frac{2}{{\theta }^2}}}-{2y}^{{\displaystyle \frac{3}{{\theta }^2}}},0<y<1,\theta >0(36)$

$y={\left\{-.5\left(cos\left[{\displaystyle \frac{{cos}^{-1}\left(1-2u\right)}{3}}\right]-\sqrt{3}sin\left[{\displaystyle \frac{{cos}^{-1}\left(1-2u\right)}{3}}\right]\right)+.5\right\}}^{{\theta }^2},0<u<1,\theta >0(37)$

Table 1. the 2 indicators in OECD data and the 2 indicators. 1 for ‘feeling safe walking alone’ and 2 for ‘Quality of support network’.

	Australia	Austria	Belgium	Canada	Chile	Colombia	Costa Rica	Czechia
1	0.67	0.86	0.56	0.78	0.41	0.50	0.47	0.77
2	0.93	0.92	0.90	0.93	0.88	0.80	0.92	0.96
	Denmark	Estonia	Finland	France	Germany	Greece	Hungary	Iceland
1	0.85	0.79	0.88	0.74	0.76	0.69	0.74	0.85
2	0.95	0.95	0.96	0.94	0.90	0.78	0.94	0.98
	Ireland	Israel	Italy	Japan	Korea	Latvia	Lithuania	Luxembourg
1	0.76	0.80	0.73	0.77	0.82	0.72	0.62	0.87
2	0.96	0.95	0.89	0.89	0.80	0.92	0.89	0.91
	Mexico	Netherlands	New Zealand	Norway	Poland	Portugal	Slovak Republic	Slovenia
1	0.42	0.83	0.66	0.93	0.71	0.83	0.76	0.91
2	0.77	0.94	0.95	0.96	0.94	0.87	0.95	0.95
	Spain	Sweden	Switzerland	Turkey	United Kingdom	United States	Brazil	Russia
1	0.80	0.79	0.86	0.59	0.78	0.78	0.45	0.64
2	0.93	0.94	0.94	0.85	0.93	0.94	0.83	0.89
	South Africa
1	0.40
2	0.89

Table 1. the 2 indicators in OECD data and the 2 indicators. 1 for ‘feeling safe walking alone’ and 2 for ‘Quality of support network’.

	Australia	Austria	Belgium	Canada	Chile	Colombia	Costa Rica	Czechia
1	0.67	0.86	0.56	0.78	0.41	0.50	0.47	0.77
2	0.93	0.92	0.90	0.93	0.88	0.80	0.92	0.96
	Denmark	Estonia	Finland	France	Germany	Greece	Hungary	Iceland
1	0.85	0.79	0.88	0.74	0.76	0.69	0.74	0.85
2	0.95	0.95	0.96	0.94	0.90	0.78	0.94	0.98
	Ireland	Israel	Italy	Japan	Korea	Latvia	Lithuania	Luxembourg
1	0.76	0.80	0.73	0.77	0.82	0.72	0.62	0.87
2	0.96	0.95	0.89	0.89	0.80	0.92	0.89	0.91
	Mexico	Netherlands	New Zealand	Norway	Poland	Portugal	Slovak Republic	Slovenia
1	0.42	0.83	0.66	0.93	0.71	0.83	0.76	0.91
2	0.77	0.94	0.95	0.96	0.94	0.87	0.95	0.95
	Spain	Sweden	Switzerland	Turkey	United Kingdom	United States	Brazil	Russia
1	0.80	0.79	0.86	0.59	0.78	0.78	0.45	0.64
2	0.93	0.94	0.94	0.85	0.93	0.94	0.83	0.89
	South Africa
1	0.40
2	0.89

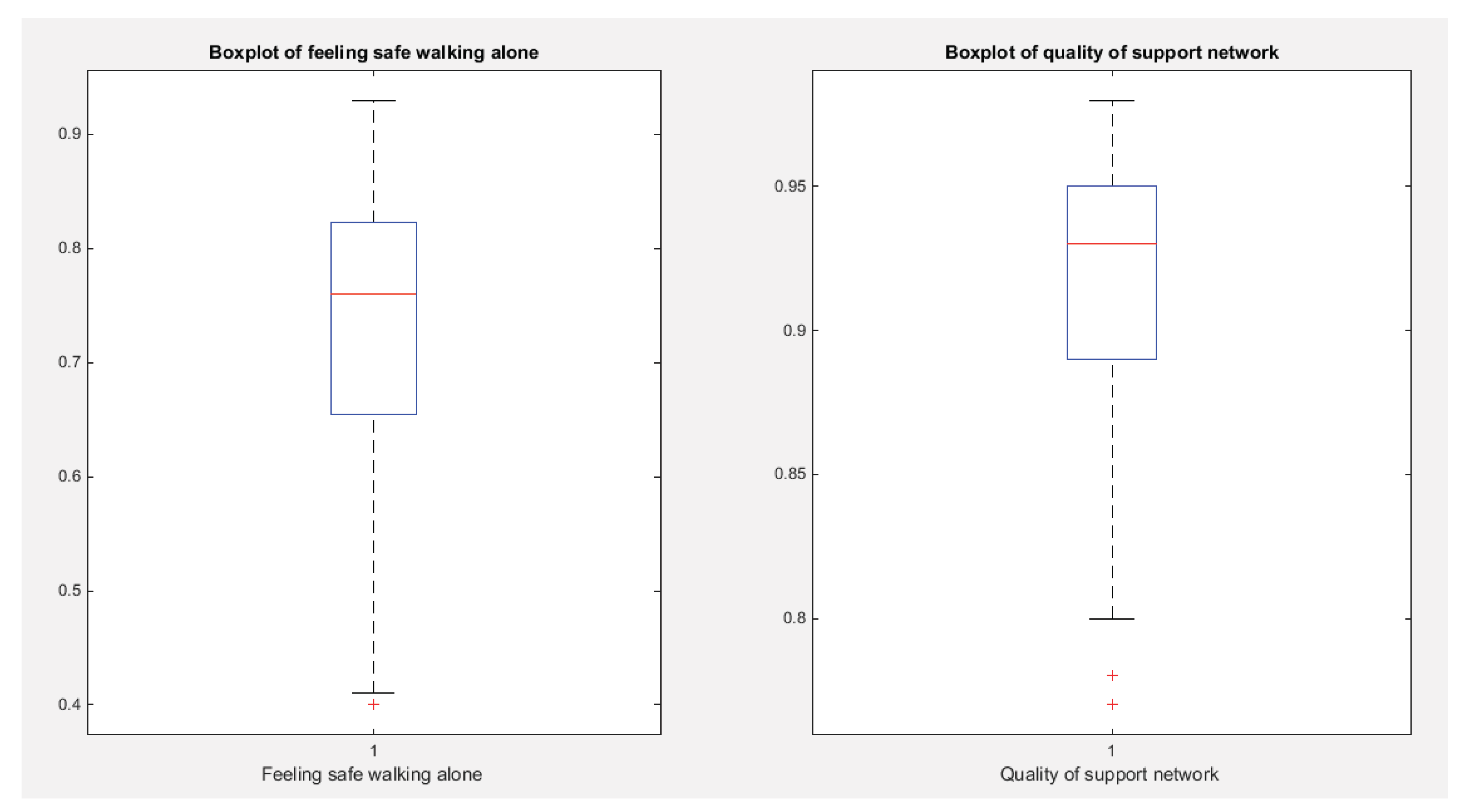
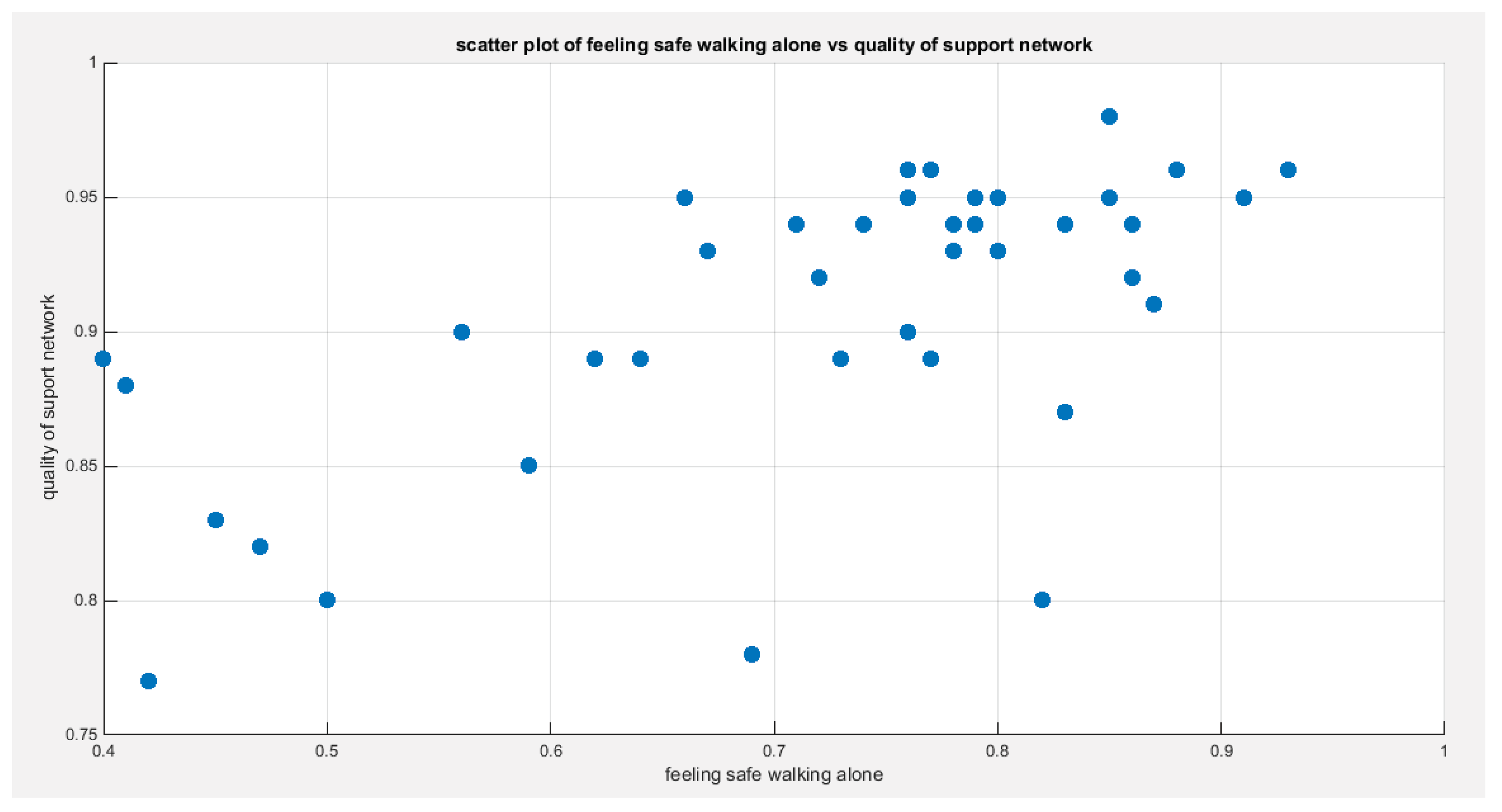
The indicator of ‘feeling safe walking alone’ measures the percentage of people who report feeling safe when walking alone in their local area after dark. The ‘quality of support network’ indicator measures the accessibility and trustworthiness of social support for individuals and it is explicated as the percentage of population with social support who described having someone they can depend on for support when they need it. Table (2) shows the descriptive statistics of the 2 indicators. Table (3) shows the empirical Kendall tau coefficient and its associated p-value. Figure (3) shows the boxplot for each indicator. Figure (4) show the scatter plot of the dependent indicators. Each indicator fits the Median Based Unit Rayleigh Distribution (MBUR). Table (4) shows the statistical validity indices for each indicator. Figure (5) shows the histogram and the fitted MBUR curve for each indicator.

Table 2. descriptive statistics for the 2 indicators:.

Indicator	Min	Mean	Standard Deviation	Skewness	Kurtosis	25percentile	50percentile	75percentile	Max
Feeling safe walking alone	0.4	0.7207	0.143	-0.9486	3.0353	0.655	0.76	0.8225	0.93
Quality of support network	0.77	0.9078	0.0538	-1.176	3.5406	0.89	0.93	0.95	0.98

Table 2. descriptive statistics for the 2 indicators:.

Indicator	Min	Mean	Standard Deviation	Skewness	Kurtosis	25percentile	50percentile	75percentile	Max
Feeling safe walking alone	0.4	0.7207	0.143	-0.9486	3.0353	0.655	0.76	0.8225	0.93
Quality of support network	0.77	0.9078	0.0538	-1.176	3.5406	0.89	0.93	0.95	0.98

Table 3. empirical Kendall tau coefficient of the 2 indicators:.

	Feeling Safe Walking Alone	Quality of Support Network
Feeling safe walking alone	1	0.4344 (0.0001)
Quality of support network	0.4344 (0.0001)	1

Table 3. empirical Kendall tau coefficient of the 2 indicators:.

	Feeling Safe Walking Alone	Quality of Support Network
Feeling safe walking alone	1	0.4344 (0.0001)
Quality of support network	0.4344 (0.0001)	1

Table 4. statistical validity indices of the distributional fit (MBUR) of the 2 indicators:.

Indicator	Estimated Theta	variance	AIC	CAIC	BIC	HQIC	KS-test	Ho	p-Value of KS-test
Feeling safe walking alone	0.6494	0.0013	-47.1347	-47.0321	-45.4211	-46.5107	0.1206	Fail to reject	0.5492
Quality pf support network	0.3444	0.00037494	-131.6505	-131.6505	-131.5479	-131.0265	0.1806	Fail to reject	0.1217

Table 4. statistical validity indices of the distributional fit (MBUR) of the 2 indicators:.

Indicator	Estimated Theta	variance	AIC	CAIC	BIC	HQIC	KS-test	Ho	p-Value of KS-test
Feeling safe walking alone	0.6494	0.0013	-47.1347	-47.0321	-45.4211	-46.5107	0.1206	Fail to reject	0.5492
Quality pf support network	0.3444	0.00037494	-131.6505	-131.6505	-131.5479	-131.0265	0.1806	Fail to reject	0.1217

Figure 3. shows the Boxplot for each indicator. They show similar pattern of skewness (left sides skewness). The quality of support network variable exhibits more skewness than the feeling safe walking alone variable.

Figure 3. shows the Boxplot for each indicator. They show similar pattern of skewness (left sides skewness). The quality of support network variable exhibits more skewness than the feeling safe walking alone variable.

Figure 4. shows the scatter plot of the variable feeling safe walking alone vs the variable of the quality of support network. The data are concentrated on the right upper corner of the graph.

Figure 4. shows the scatter plot of the variable feeling safe walking alone vs the variable of the quality of support network. The data are concentrated on the right upper corner of the graph.

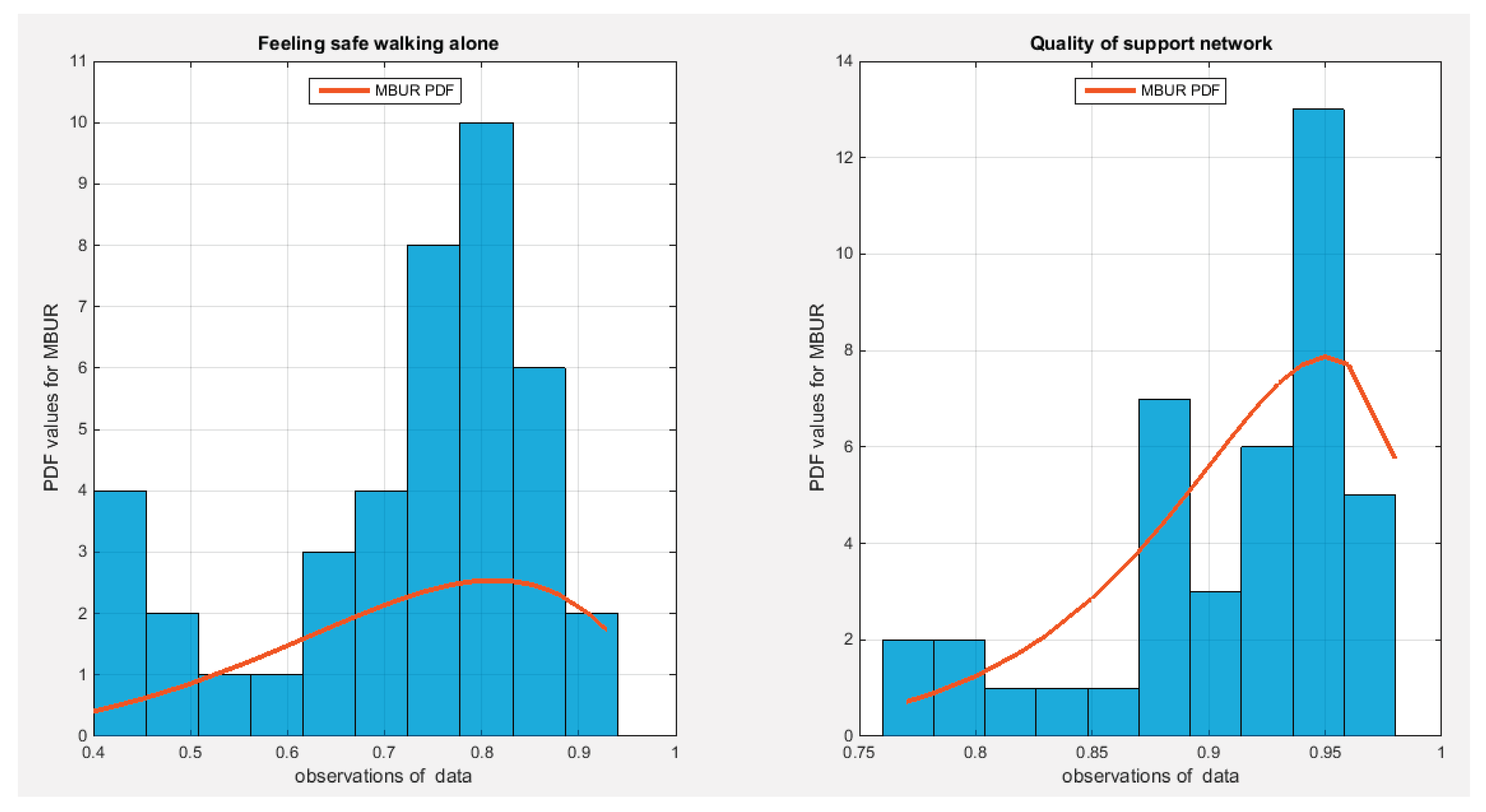
Figure 5. shows the histogram of the two indicators which exhibit left sided skewness. The graph also shows the fitted MBUR curve for each indicator. The two indicators more or less have near similar kurtosis but the second one is more left skewed than the first. Copula that can fit symmetrical dependency can model dependency between such variables.

Figure 5. shows the histogram of the two indicators which exhibit left sided skewness. The graph also shows the fitted MBUR curve for each indicator. The two indicators more or less have near similar kurtosis but the second one is more left skewed than the first. Copula that can fit symmetrical dependency can model dependency between such variables.

8.2. Procedure of Analysis (IFM)

After running the inference function for margins (IFM) and estimating the marginal parameter for each pair of variables then fitting each copula to estimate its parameter. Goodness of Fit tests are conducted to assess the dependence relationship for each pair of the variables.

The steps of analysis are as follows:

• Estimate the marginal parameters for each variable.
• Use the IFM procedure to estimate the dependency parameter of the proposed copula model.
• Obtain the theoretical tau from the specific relation between dependency parameter and the Kendall tau for the copula.
• Obtain the Cramer Von Mises test from this estimation process and call it CVM_data that will be compared to CVM_samples
• Run sampling technique like Metropolis Hasting (MH) procedure to test the null hypothesis using the estimated dependency parameter and both the estimated marginal parameters.
• Construct sampling distribution for the estimated-theta_samples , theoretical-tau_samples , and CVM_samples .

For each of the sample generated by MH using the estimated dependency parameter and the estimated marginal parameters, they will be transformed back into variables using the specific quantiles. These variables will be subjected to the IFM procedure; first estimate the marginal parameters then using the estimated marginal CDF for each variable to estimate the dependency parameter, in other words, repeat steps (1 to 4) for each sample so you can be able to construct the sampling distribution, hence, constructing the confidence interval for each of the statistical indices. ${theta}_{data}$ denotes theta estimated from the data.

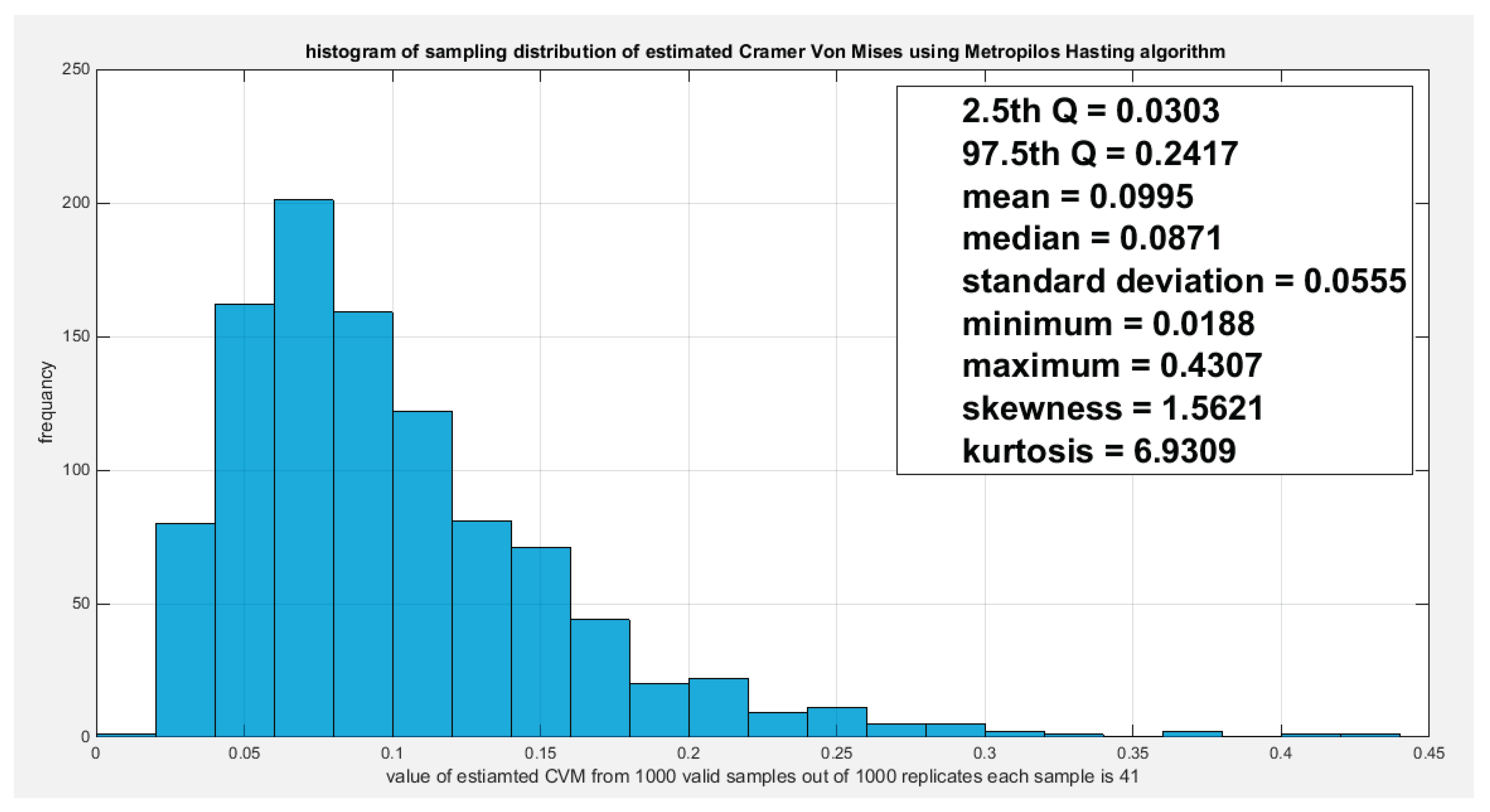
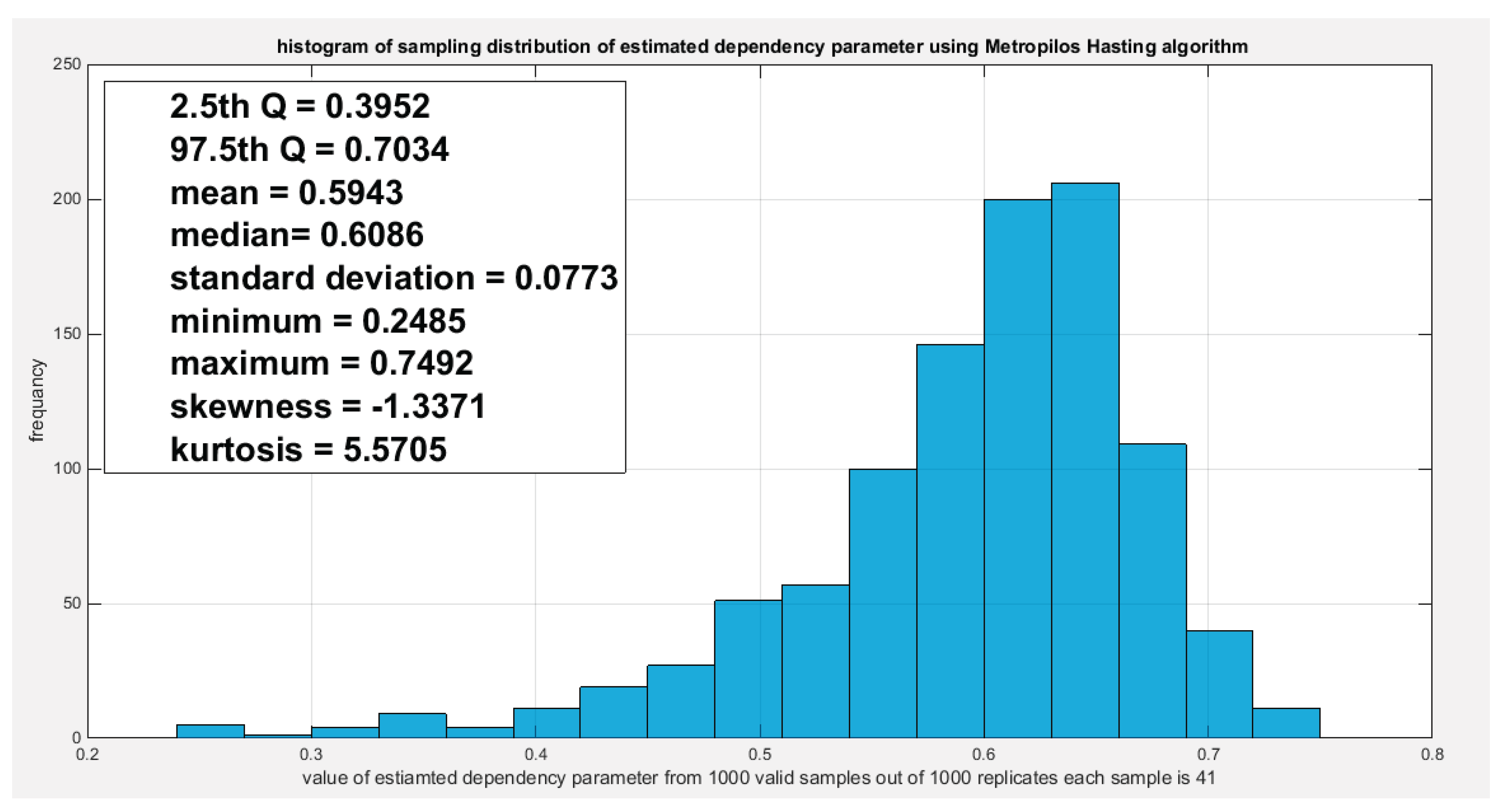
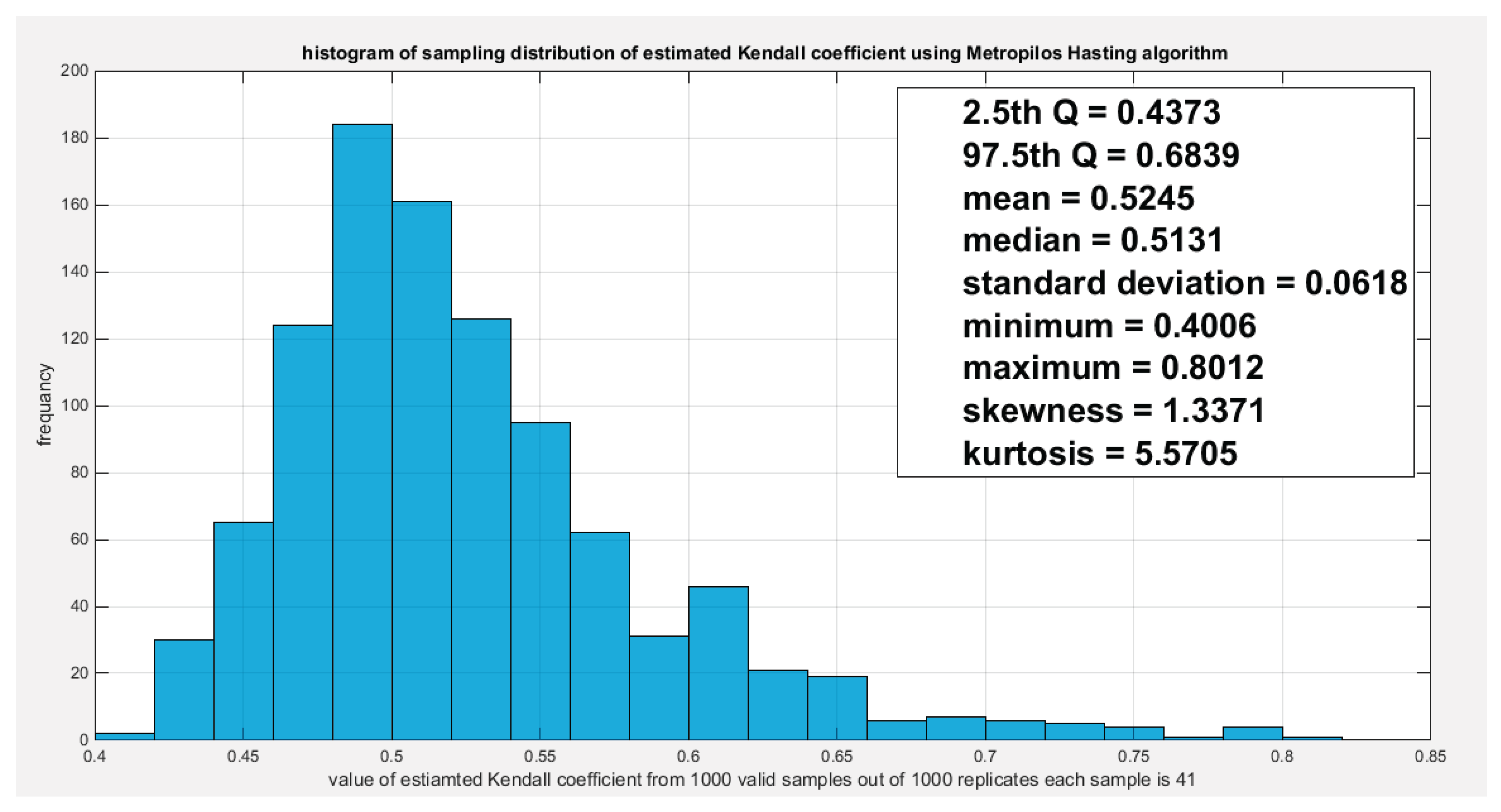
The null hypothesis for the dependency parameter is: $H_0:{theta}_{samples}={theta}_{data}$The alternative hypothesis for the dependency parameter is: $H_1:{theta}_{samples}\ne {theta}_{data}$The null hypothesis for the Kendall tau coefficient is: $H_0:{tau}_{samples}={tau}_{data}$The alternative hypothesis for the Kendall tau coefficient is: $H_1:{tau}_{samples}\ne {tau}_{data}$The null hypothesis for the CVM is: $H_0:{CVM}_{samples}={CVM}_{data}$The alternative hypothesis for the CVM is: $H_1:{CVM}_{samples}\ne {CVM}_{data}$Model the dependency between the ‘feeling safe walking alone’ and ‘Quality support network’: The empirical tau equals 0.4344 while the theoretical tau is 0.5428 with difference value of 0.1084. The estimated dependency parameter, theta $\widehat{\theta }$ , is 0.5714 with estimated variance of 0.0066. The Cramer Von Mises test (CVM) is 0.1948. The null hypothesis for dependency was tested by conducting resampling using the Metropolis Hasting algorithm of MCMC procedure. The proposed null hypothesis was that the dependency parameter equals the estimated theta against the alternative hypothesis that the population dependency parameter does not equal the estimated theta. Also the null hypothesis for the population Kendall tau coefficient being equal to the theoretical tau against the alternative hypothesis of not being equal to it was tested. The null hypothesis for the CVM proposing that the sampling CVM equals observed CVM obtained from the estimation procedure was investigated. The sampling distribution of each of the previously mentioned indices, thetas, tau and CVM is shown in Figures (6-8). For each figure, the descriptive statistics indices are shown. From the figures the indices are placed within the acceptance zone between the 2.5^th and 97.5^th quantiles. So the null hypotheses fail to be rejected. The copula fits the data well. And the dependence parameter models, within the context of the copula, the relation between the two variables. The confidence interval (CI) for the estimated dependence parameter is (0.3952, 0.7034), for the theoretical tau; it is (0.4373, 0.6839), and for CVM; it is (0.0303, 0.2417).

According to the sandwich variance the variance covariance matrix for this model is:

$var-cov=\left[\begin{array}{ccc}0.081& 0.0247& 0.00001\\ 0.0247& 0.0076& 0.00001\\ 0.00001& 0.00001& 0.00016\end{array}\right]$

The validity indices for the second stage are:

$AIC=-21.9209,CAIC=-21.8183BIC=-20.2073HQIC=-21.2969$The validity indices for the whole model is the summation of these indices for marginal (first stage) and copula (second stage):

$AIC=-200.7060,CAIC=-20.3983BIC=-195.5653HQIC=-198.8341$Theoretical upper tail coefficient is 0.514. At quantile 0.7; the empirical upper tail coefficient in the direction of the ‘feeling safe walking alone’ variable is 0.5 (5 points showing joint match out of 10 points in the upper tail at this threshold, 0.7) and in the direction of the ‘Quality support network’ variable is 0.4545 (5 points showing joint match out of 11 points in the upper tail at this threshold, 0.7) while the confidence interval of the empirical distribution obtained from bootstrap sampling under the null hypothesis in both directions is [0.3 ,0.8889]. This is expected because of the small sample size and left skewness of data.

Theoretical lower tail coefficient is 0.4529. At quantile 0.1; the empirical lower tail coefficient in the direction of the ‘feeling safe walking alone’ variable is 0.5 (3 points showing joint match out of 6 points in the lower tail at this threshold, 0.1) and in the direction of the ‘Quality support network’ variable is 0.6 (3 points showing joint match out of 5 points in the lower tail at this threshold, 0.1) while the confidence interval of the empirical distribution obtained from bootstrap sampling under the null hypothesis in both directions is [0 ,1]. This is expected because of the small sample size and left skewness of data.

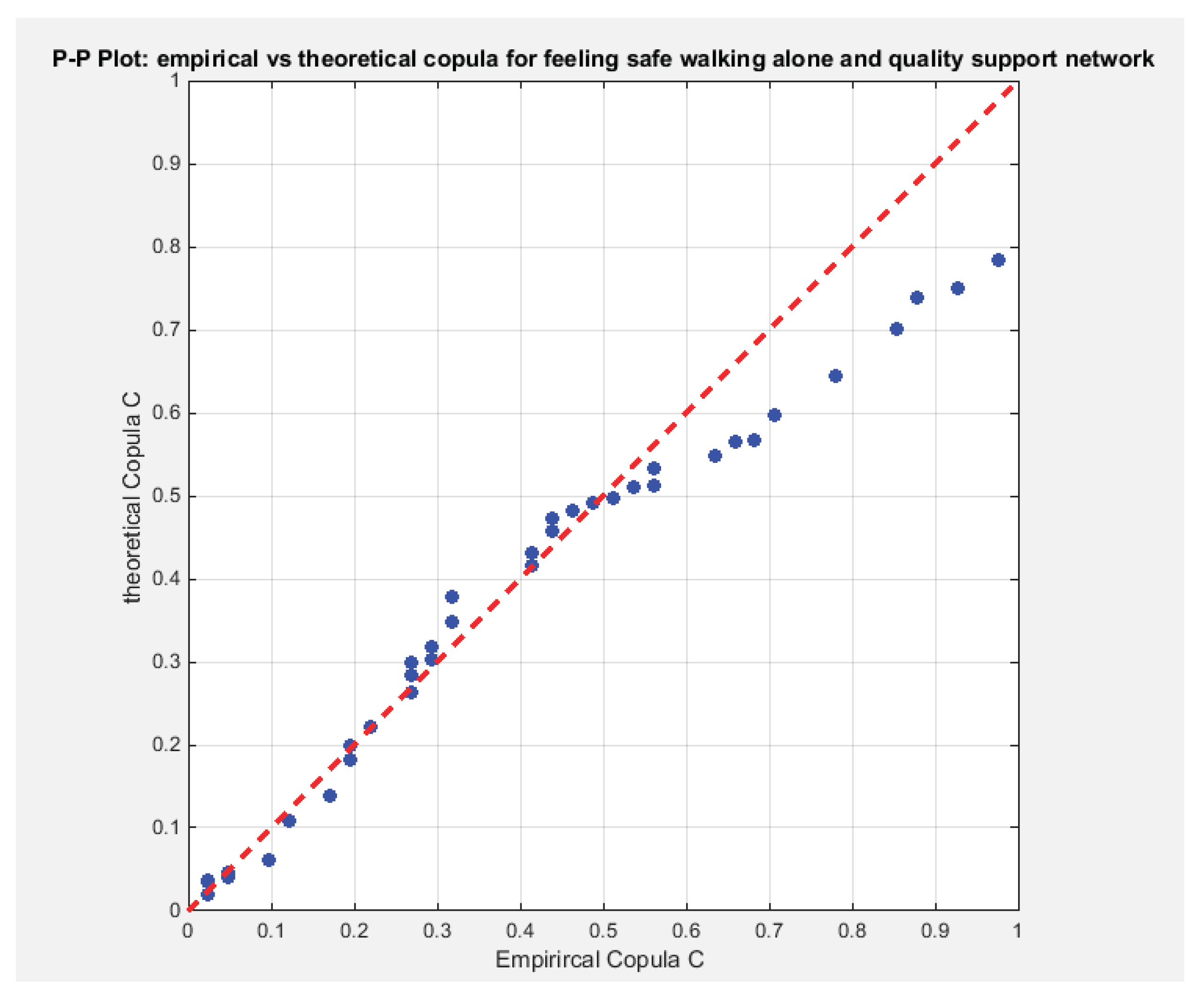
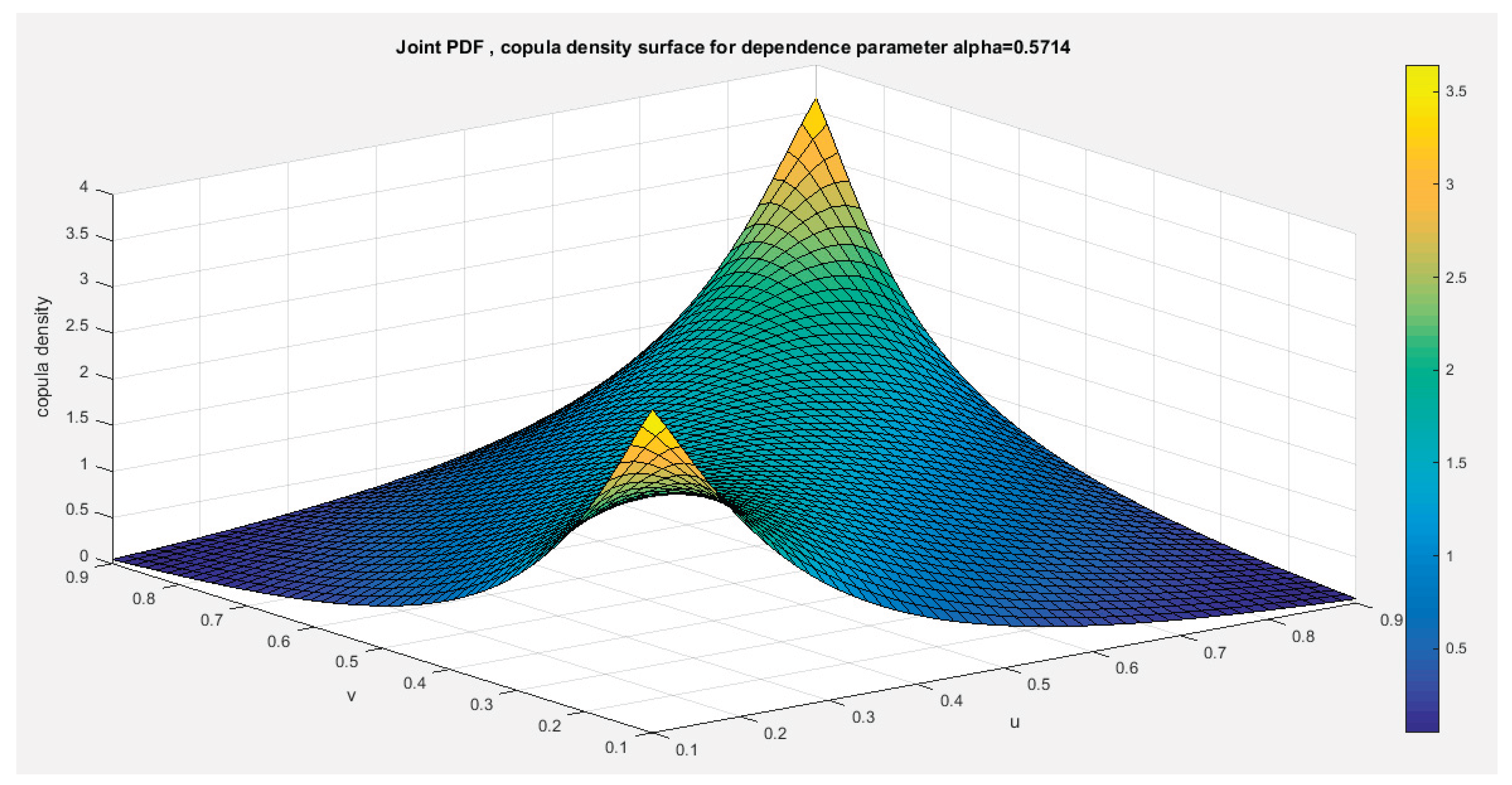
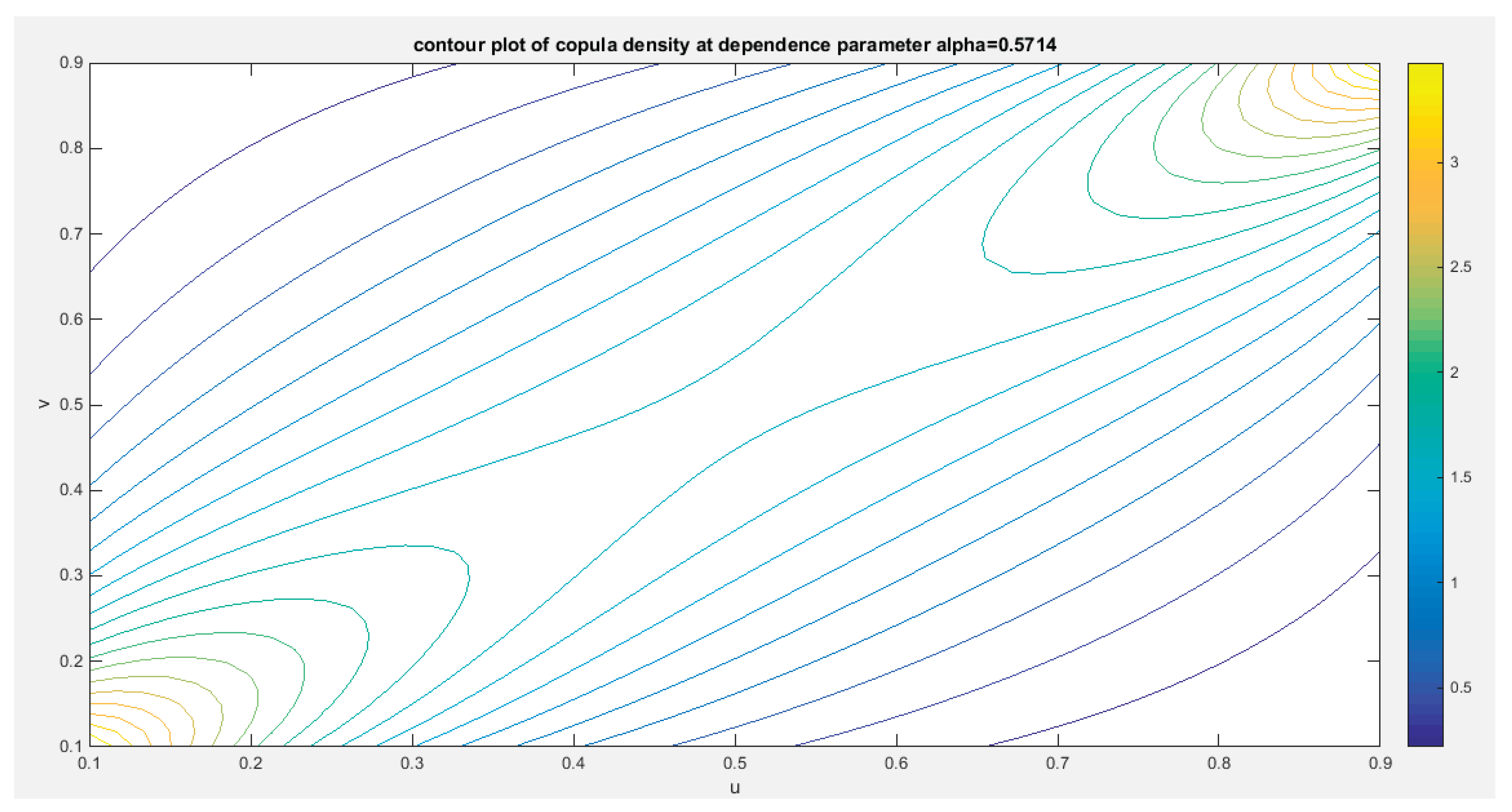
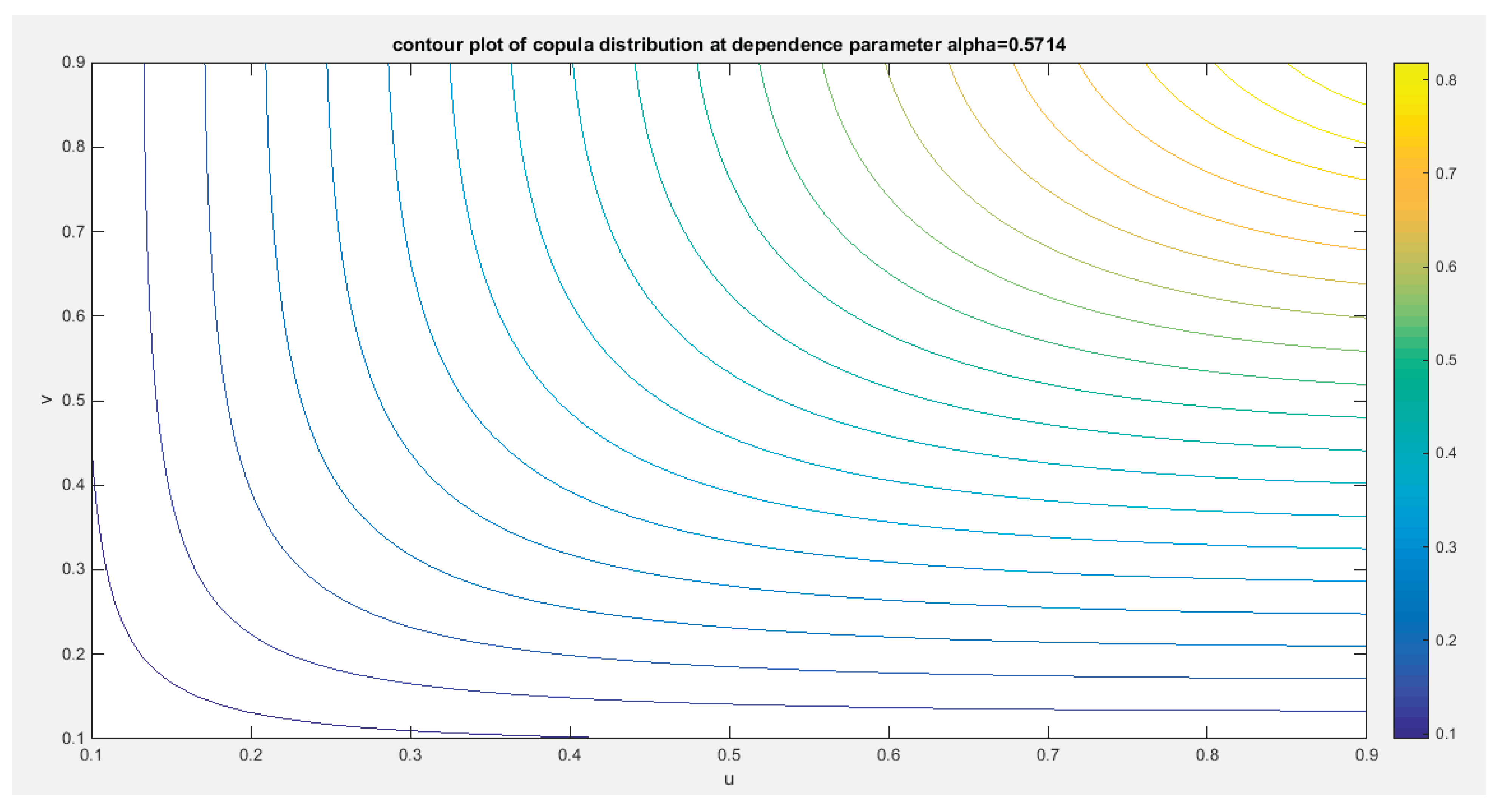
Figure 9 shows the P-P plot of the empirical vs the theoretical copula. Figure 10-12 show the surface of the copula density, the contour plot of the copula density, and the contour plot of the copula distribution at the estimated dependency parameter.

Figure 6. shows the sampling distribution of the CVM. The CVM_data is 0.1948 and it lies between the 2.5^th and the 97.5^th quantiles so null hypothesis is failed to be rejected and the copula fits the data well. The p-value (probability of values less than or equal to 0.1948) is 0.938, in other words, this 0.1948 does not lay in either of the tail region of rejection. .

Figure 6. shows the sampling distribution of the CVM. The CVM_data is 0.1948 and it lies between the 2.5^th and the 97.5^th quantiles so null hypothesis is failed to be rejected and the copula fits the data well. The p-value (probability of values less than or equal to 0.1948) is 0.938, in other words, this 0.1948 does not lay in either of the tail region of rejection. .

Figure 7. shows the sampling distribution of the dependency parameter. The 0.5714 lies in the acceptance region between the two quantiles, the 2.5^th and the 97.5^th quantiles. So the null hypothesis fails to reject its assumption. The p-value (probability of the values being less than or equal to this 0.5714) is 0.2950 which indicates that this 0.5714 is not placed in either zones of rejection.

Figure 7. shows the sampling distribution of the dependency parameter. The 0.5714 lies in the acceptance region between the two quantiles, the 2.5^th and the 97.5^th quantiles. So the null hypothesis fails to reject its assumption. The p-value (probability of the values being less than or equal to this 0.5714) is 0.2950 which indicates that this 0.5714 is not placed in either zones of rejection.

Figure 8. shows the sampling distribution of the Kendal tau coefficient. Its value 0.5428 is between the two quantiles 2.5^th and 97.5^th which is the acceptance zones. So the null hypothesis fails to reject its assumption. The p-values (probability of the values less than or equal to 0.5428) is 0.7050 which denotes that this value is far away from both rejection zones.

Figure 8. shows the sampling distribution of the Kendal tau coefficient. Its value 0.5428 is between the two quantiles 2.5^th and 97.5^th which is the acceptance zones. So the null hypothesis fails to reject its assumption. The p-values (probability of the values less than or equal to 0.5428) is 0.7050 which denotes that this value is far away from both rejection zones.

Figure 9. shows the P-P plot of the empirical vs the theoretical copula. The theoretical copula shows near perfect alignment of its lower and central part with the diagonal line than its upper part.

Figure 9. shows the P-P plot of the empirical vs the theoretical copula. The theoretical copula shows near perfect alignment of its lower and central part with the diagonal line than its upper part.

Figure 10. shows the PDF surface of copula density with parameter 0.5714.

Figure 10. shows the PDF surface of copula density with parameter 0.5714.

Figure 11. shows the contour plot of the copula density with parameter 0.5714.

Figure 11. shows the contour plot of the copula density with parameter 0.5714.

Figure 12. shows the contour plot of the copula distribution with dependency parameter 0.5714.

Figure 12. shows the contour plot of the copula distribution with dependency parameter 0.5714.

9. Conclusions

This copula which is based on frailty model and cox proportional hazard model can only model positive dependency. It can model upper and lower tail dependency. The author discussed one dataset exhibiting left skewness. the copula fit the data well. The complexity of the copula density function dictates uses of IFM method of estimation. This method is favored over the MLE for its simplicity and straightforwardness. The robust variance or sandwich variance captures the covariance between the marginal and the copula parameter estimators which are not captured by separately estimating the variances in each stage. The variance of the estimators of marginal parameters increases while the variance of the estimator of copula parameter decreases. Although the sample size used in the analysis were moderate(n=41), the copula models the upper and lower tail dependency well and this was supported by the sampling distribution of both the empirical upper and lower tail dependency coefficients. These copulas can be used to construct bivariate distributions other than bivariate MBUR as discussed in this paper. While the joint distribution function, $H\left(x,y\right)=C\left(F\left(x\right),G\left(y\right)\right)$ for two random variables X and Y, the bivariate density function of these 2 variables is shown in equation (38)

$h_{X,Y}\left(x,y\right)={\displaystyle \frac{\partial H\left(x,y\right)}{\partial x\partial y}}=f_X\left(x\right)f_Y\left(y\right)\mathrm{c}\left(F_X\left(x\right),F_Y\left(y\right)\right)=f_X\left(x\right)f_Y\left(y\right){\displaystyle \frac{{\partial }^2\mathrm{C}\left(u,v\right)}{\partial u\partial v}}(38)$

10. Future Work

This copula can be mixed with other copulas to better model data with asymmetric dependency. Also other methods of estimation can be attempted like the semiparametric estimation and MLE. Bayesian inference can also be considered.