4.1. data description
The OECD data platform delivered by the OECD (organization for economic Cooperation and development) collects data on a wide range of economic, social, and environmental sectors including data about economy, health, trade, education, labor, innovation, and development. It contains many indicators describing these data. The data can be found on the following site: In this analysis, 3 indicators are used to find the dependency between and how the previously new copulas can model this dependency. The indicators are the quality of support network, water quality, and feeling safe walking alone at night. The data are collected from 41 countries as shown in
Table 1.
https://stats.oecd.org/index.aspx?DataSetCode=BLI.
The indicators (let’s call it the y variable) in
Table 1 and in
Table 5 are distributed as Median Based Unit Rayleigh (MBUR) previously discussed by Iman Attia (Attia, 2024) with the following PDF in equation (21), CDF in equation (22), and, quantile function in equation (23):
Table 1.
The three indicators of the OECD data.
Table 1.
The three indicators of the OECD data.
| Country |
Water quality |
Feeling safe walking alone |
Quality of support network |
| Australia |
0.92 |
0.67 |
0.93 |
| Austria |
0.92 |
0.86 |
0.92 |
| Belgium |
0.79 |
0.56 |
0.90 |
| Canada |
0.90 |
0.78 |
0.93 |
| Chile |
0.62 |
0.41 |
0.88 |
| Colombia |
0.82 |
0.50 |
0.80 |
| Costa Rica |
0.87 |
0.47 |
0.82 |
| Czechia |
0.89 |
0.77 |
0.96 |
| Denmark |
0.93 |
0.85 |
0.95 |
| Estonia |
0.86 |
0.79 |
0.95 |
| Finland |
0.97 |
0.88 |
0.96 |
| France |
0.78 |
0.74 |
0.94 |
| Germany |
0.91 |
0.76 |
0.90 |
| Greece |
0.67 |
0.69 |
0.78 |
| Hungary |
0.81 |
0.74 |
0.94 |
| Iceland |
0.97 |
0.85 |
0.98 |
| Ireland |
0.80 |
0.76 |
0.96 |
| Israel |
0.77 |
0.80 |
0.95 |
| Italy |
0.77 |
0.73 |
0.89 |
| Japan |
0.87 |
0.77 |
0.89 |
| Korea |
0.82 |
0.82 |
0.80 |
| Latvia |
0.83 |
0.72 |
0.92 |
| Lithuania |
0.83 |
0.62 |
0.89 |
| Luxembourg |
0.85 |
0.87 |
0.91 |
| Mexico |
0.75 |
0.42 |
0.77 |
| Netherlands |
0.91 |
0.83 |
0.94 |
| New Zealand |
0.85 |
0.66 |
0.95 |
| Norway |
0.98 |
0.93 |
0.96 |
| Poland |
0.82 |
0.71 |
0.94 |
| Portugal |
0.89 |
0.83 |
0.87 |
| Slovak Republic |
0.81 |
0.76 |
0.95 |
| Slovenia |
0.93 |
0.91 |
0.95 |
| Spain |
0.76 |
0.80 |
0.93 |
| Sweden |
0.97 |
0.79 |
0.94 |
| Switzerland |
0.96 |
0.86 |
0.94 |
| Turkey |
0.62 |
0.59 |
0.85 |
| United kingdom |
0.82 |
0.78 |
0.93 |
| United states |
0.88 |
0.78 |
0.94 |
| Brazil |
0.70 |
0.45 |
0.83 |
| Russia |
0.62 |
0.64 |
0.89 |
| South Africa |
0.72 |
0.40 |
0.89 |
The ‘water quality’ indicator measures the self-reported satisfaction with water quality as regard drinking clean water and extent of water pollution. It is expressed as the percentage of people who report satisfaction. The indicator of ‘feeling safe walking alone’ measures the percentage of people who report feeling safe when walking alone in their local area after dark. The ‘quality of support network’ indicator measures the accessibility and trustworthiness of social support for individuals and it is explicated as the percentage of population with social support who described having someone they can depend on for support when they need it.
Table 2 shows the descriptive statistics of the 3 indicators.
Table 3 shows the empirical Kendall tau coefficient and its associated p-value.
Figure 7 shows the boxplot for each indicator.
Figure 8,
Figure 9 and
Figure 10 show the scatter plot of the dependent indicators. Each indicator fits the Median Based Unit Rayleigh Distribution (MBUR).
Table 4 shows the statistical validity indices for each indicator.
Figure 11 shows the histogram and the fitted MBUR curve for each indicator.
Table 2.
descriptive statistics for the 3 indicators.
Table 2.
descriptive statistics for the 3 indicators.
| indicator |
min |
mean |
Standard deviation |
skewness |
kurtosis |
25percentile
|
50percentile
|
75percentile
|
max |
| Water quality |
0.62 |
0.8332 |
0.0972 |
-0.6059 |
2.9144 |
0.7775 |
0.83 |
0.91 |
0.98 |
| Feeling safe walking alone |
0.4 |
0.7207 |
0.143 |
-0.9486 |
3.0353 |
0.655 |
0.76 |
0.8225 |
0.93 |
| Quality of support network |
0.77 |
0.9078 |
0.0538 |
-1.176 |
3.5406 |
0.89 |
0.93 |
0.95 |
0.98 |
Table 3.
empirical Kendall tau coefficient of the three indicators.
Table 3.
empirical Kendall tau coefficient of the three indicators.
| |
Water quality |
Feeling safe walking alone |
Quality of support network |
| Water quality |
1 |
0.5206
(0.000)
|
0.3929
(0.0006)
|
| Feeling safe walking alone |
0.5206
(0.000)
|
1 |
0.4344
(0.0001)
|
| Quality of support network |
0.3929
(0.0006)
|
0.4344
(0.0001)
|
1 |
Table 4.
statistical validity indices of the distributional fit (MBUR) of the three indicators.
Table 4.
statistical validity indices of the distributional fit (MBUR) of the three indicators.
| indicator |
Estimated theta |
variance |
AIC |
CAIC |
BIC |
HQIC |
KS-test |
Ho |
p-value of KS-test |
| Water quality |
0.4776 |
0.00072157 |
-78.9952 |
-78.8926 |
-77.2817 |
-78.3712 |
0.0991 |
Fail to reject |
0.7789 |
| Feeling safe walking alone |
0.6494 |
0.0013 |
-47.1347 |
-47.0321 |
-45.4211 |
-46.5107 |
0.1206 |
Fail to reject |
0.5492 |
| Quality pf support network |
0.3444 |
0.00037494 |
-131.6505 |
-131.6505 |
-131.5479 |
-131.0265 |
0.1806 |
Fail to reject |
0.1217 |
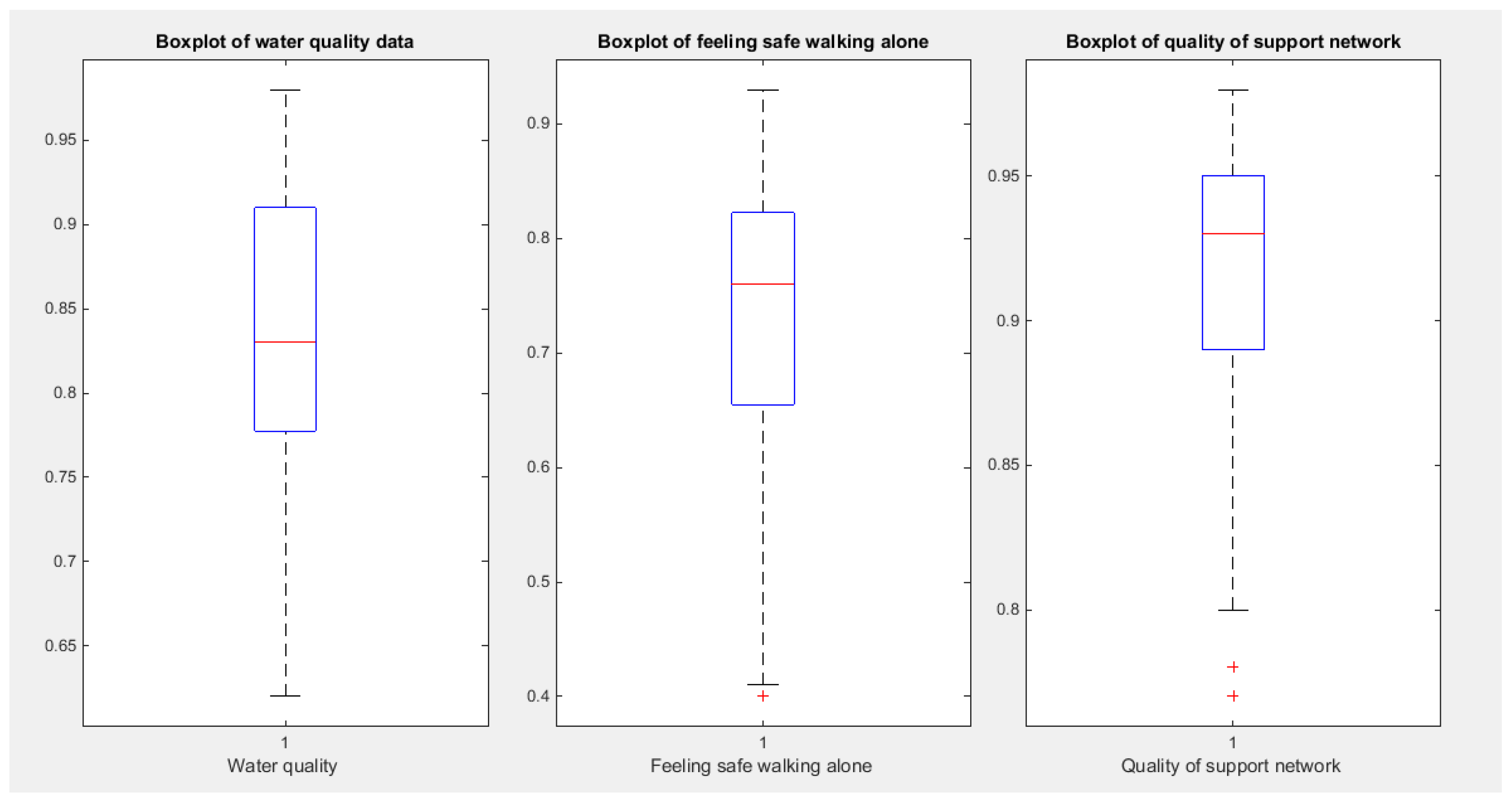
Figure 7.
shows the Boxplot for each indicator. The first two indicators show similar pattern of skewness (left sides skewness) while the third indicator exhibits more left sided skewness than the previous two indicators.
Figure 7.
shows the Boxplot for each indicator. The first two indicators show similar pattern of skewness (left sides skewness) while the third indicator exhibits more left sided skewness than the previous two indicators.
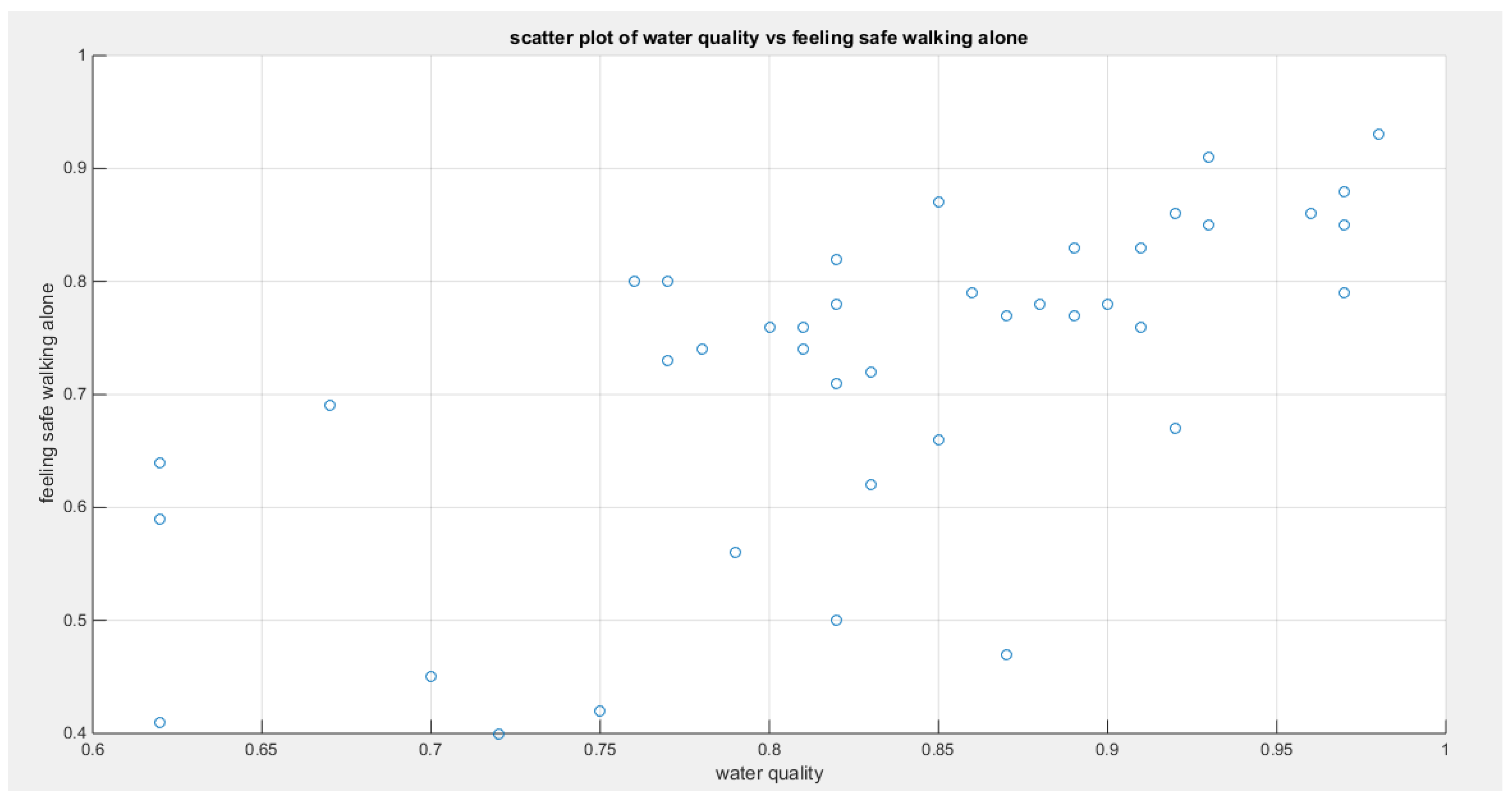
Figure 8.
shows the scatter plot of the water quality variable vs the variable describing feeling safe walking alone. The data are mainly concentrated on the upper left side of the graph most probably reflecting upper tail dependency.
Figure 8.
shows the scatter plot of the water quality variable vs the variable describing feeling safe walking alone. The data are mainly concentrated on the upper left side of the graph most probably reflecting upper tail dependency.
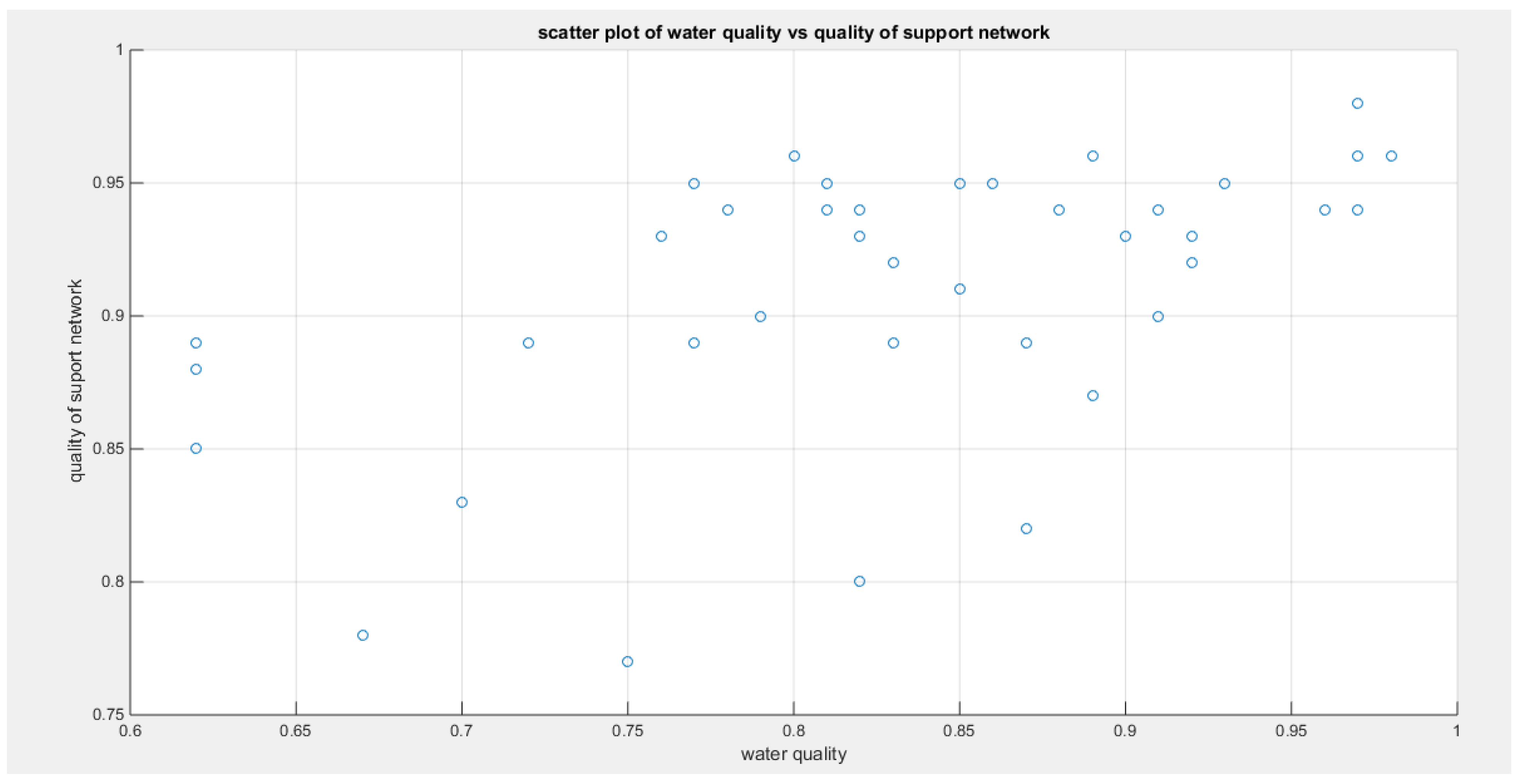
Figure 9.
shows the scatter plot of the variable water quality vs the variable quality of support network, also the data are mainly concentrated in the upper left corner of the scatter presumably reflecting upper tail dependency.
Figure 9.
shows the scatter plot of the variable water quality vs the variable quality of support network, also the data are mainly concentrated in the upper left corner of the scatter presumably reflecting upper tail dependency.
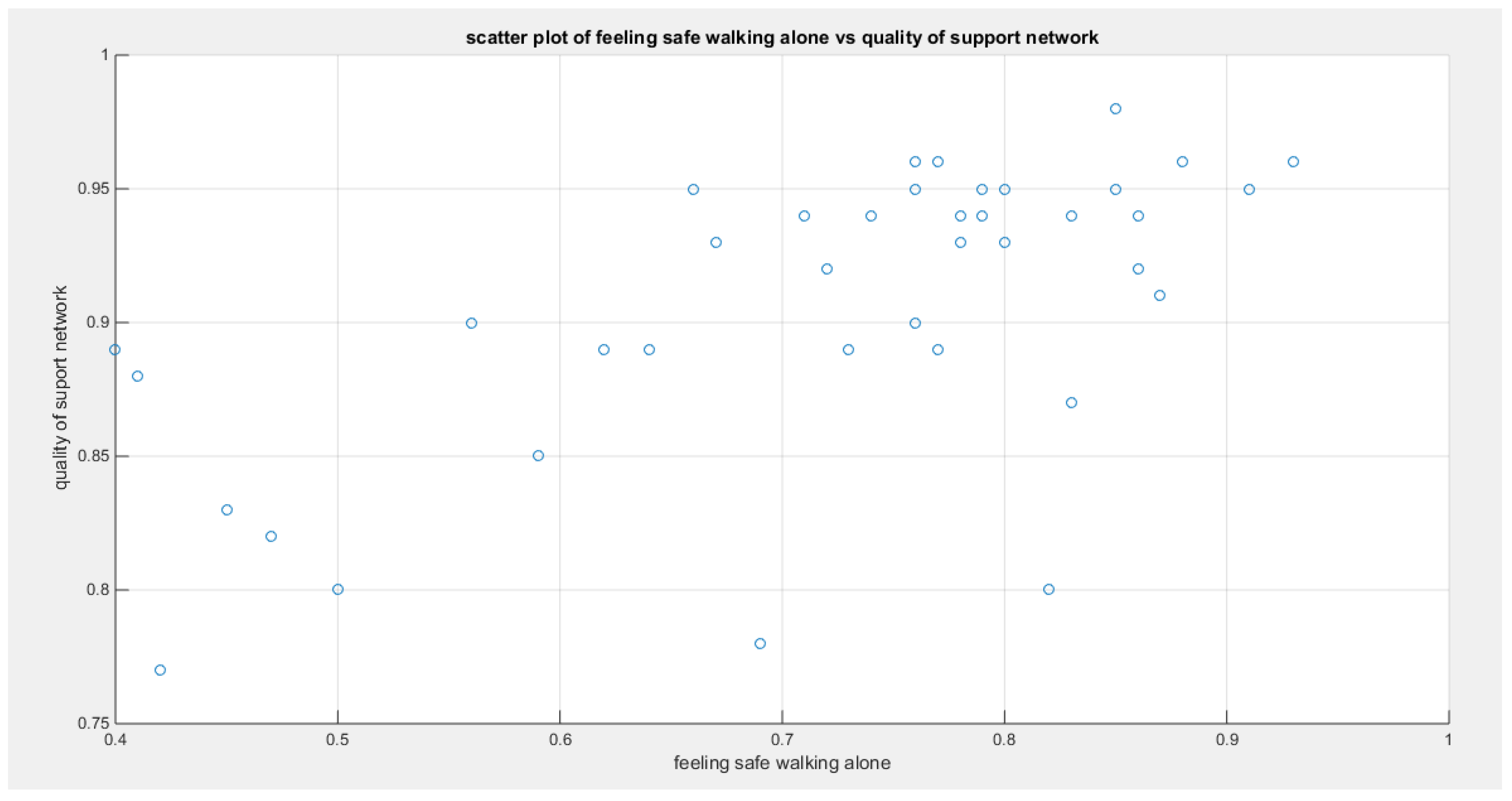
Figure 10.
shows the scatter plot of the variable feeling safe walking alone vs the variable of the quality of support network. The data are also concentrated on the right upper corner of the graph likely denoting the presence of upper tail dependency.
Figure 10.
shows the scatter plot of the variable feeling safe walking alone vs the variable of the quality of support network. The data are also concentrated on the right upper corner of the graph likely denoting the presence of upper tail dependency.
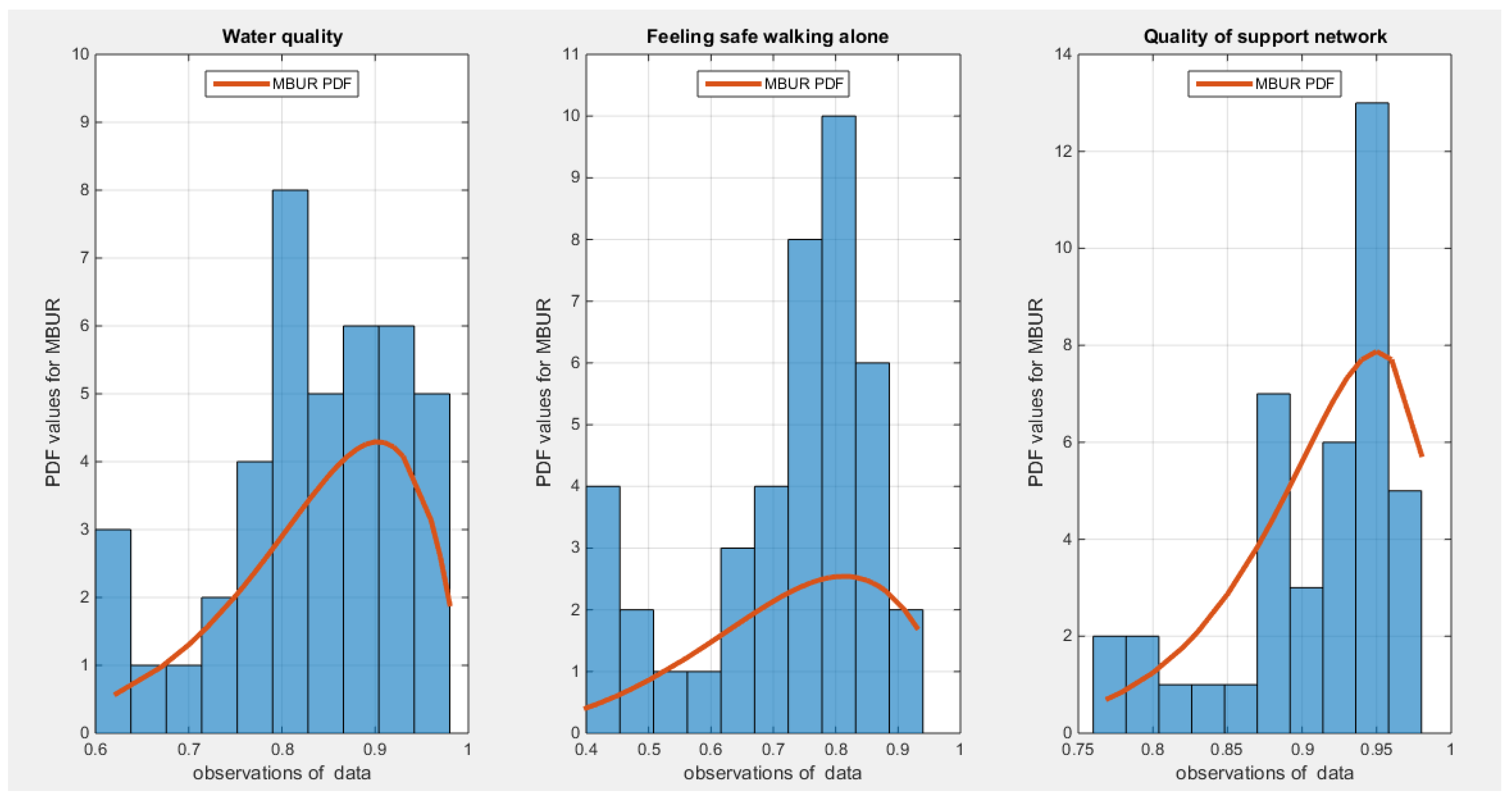
Figure 11.
shows the histogram of the three indicators which exhibit left sided skewness. The graph also shows the fitted MBUR curve for each indicator. The three indicators more or less have near similar kurtosis and skewness. Copula that can fit symmetrical dependency can model dependency between such variables.
Figure 11.
shows the histogram of the three indicators which exhibit left sided skewness. The graph also shows the fitted MBUR curve for each indicator. The three indicators more or less have near similar kurtosis and skewness. Copula that can fit symmetrical dependency can model dependency between such variables.
4.2. procedure of analysis (IFM)
After running the inference function for margins (IFM) and estimating the marginal parameter for each pair of variables then fitting each copula to estimate its parameter. Goodness of Fit tests are conducted to assess the dependence relationship for each pair of the variables.
The steps of analysis are as follows:
Estimate the marginal parameters for each variable.
Use the IFM procedure to estimate the dependency parameter of the proposed copula model.
Obtain the theoretical tau from the specific relation between dependency parameter and the Kendall tau dor each copula.
Obtain the Cramer Von Mises test from this estimation process and call it CVMdata that will be compared to CVMsamples
Run sampling technique like Metropolis Hasting (MH) procedure to test the null hypothesis using the estimated dependency parameter and both the estimated marginal parameters.
Construct sampling distribution for the estimated-thetasamples, theoretical-tausamples, and CVMsamples.
For each of the sample generated by MH using the estimated dependency parameter and the estimated marginal parameters, they will be transformed back into variables using the specific quantiles. These variables will be subjected to the IFM procedure; first estimate the marginal parameters then using the estimated marginal CDF for each variable to estimate the dependency parameter, in other words, repeat steps (1 to 4) for each sample so you can be able to construct the sampling distribution, hence, constructing the confidence interval for each of the statistical indices. denotes theta estimated from the data.
The null hypothesis for the dependency parameter is:
The alternative hypothesis for the dependency parameter is:
The null hypothesis for the Kendall tau coefficient is:
The alternative hypothesis for the Kendall tau coefficient is:
The null hypothesis for the CVM is:
The alternative hypothesis for the CVM is:
First Copula:
Model the dependency between the ‘water quality’ and ‘feeling safe walking alone’: The empirical tau equals 0.5206 while the theoretical tau is 0.5202 with difference value of 3.6968e-04. The estimated dependency parameter, theta
, is 0.4798 with estimated variance of 8.3533e-06. The Cramer Von Mises test (CVM) is 0.1388. The null hypothesis for dependency was tested by conducting resampling using the Metropolis Hasting algorithm of MCMC procedure. The proposed null hypothesis was that the dependency parameter equals the estimated theta against the alternative hypothesis that the population dependency parameter does not equal the estimated theta. Also the null hypothesis for the population Kendall tau coefficient being equal to the theoretical tau against the alternative hypothesis of not being equal to it was tested. The null hypothesis for the CVM proposing that the sampling CVM equals observed CVM obtained from the estimation procedure was investigated. The sampling distribution of each of the previously mentioned indices, thetas, tau and CVM is shown in
Figure 12,
Figure 13 and
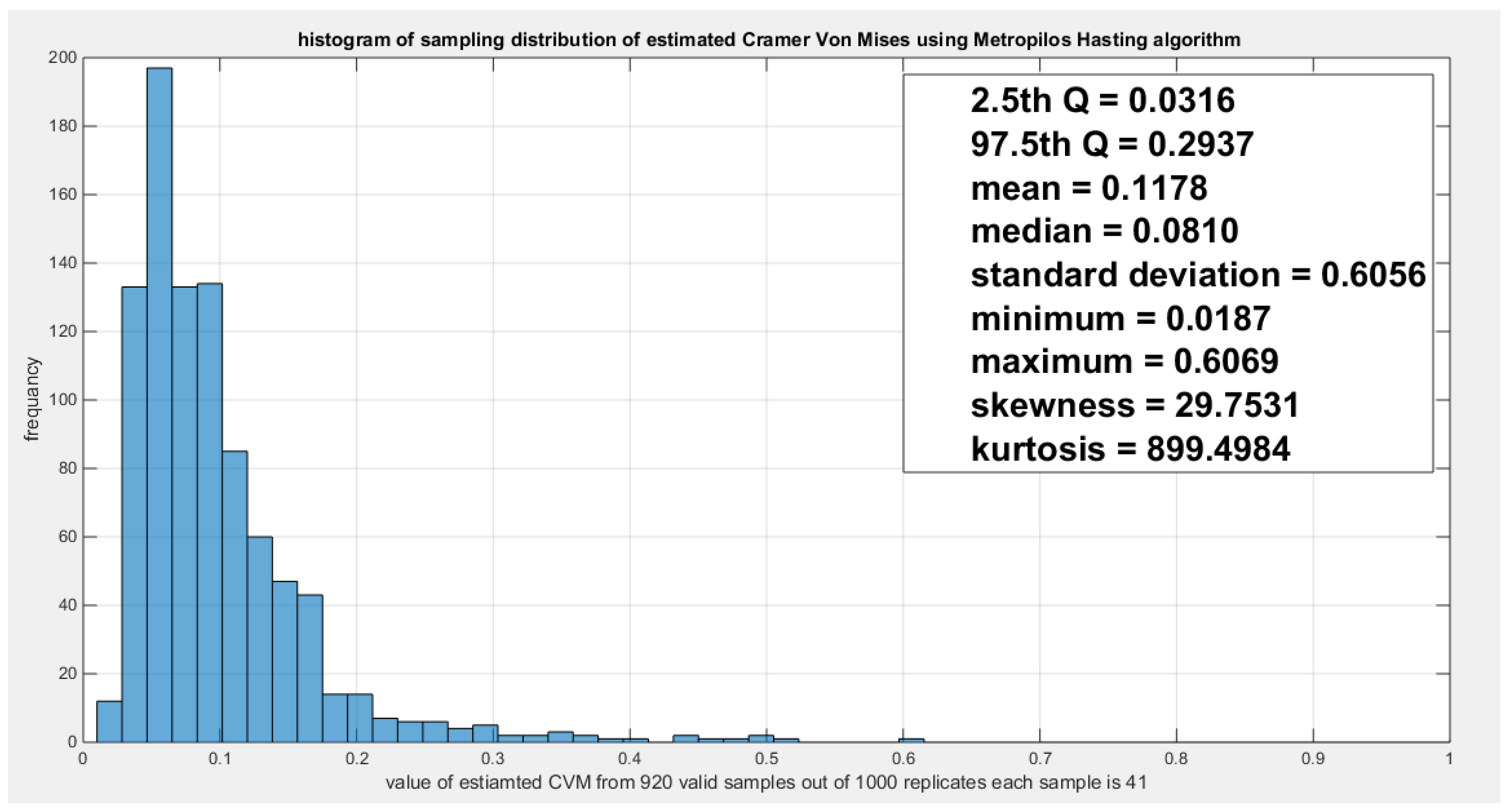
Figure 14. For each figure, the descriptive statistics indices are shown. From the figures the indices are placed within the acceptance zone between the 2.5th and 97.5th quantiles. So the null hypotheses fail to be rejected. The copula fits the data well. And the dependence parameter models, within the context of the copula, the relation between the two variables. The confidence interval (CI) for the estimated dependence parameter is (0.1822, 0.8084), for the theoretical tau; it is (0.1916, 0.8178), and for CVM; it is (0.0316, 0.2937).
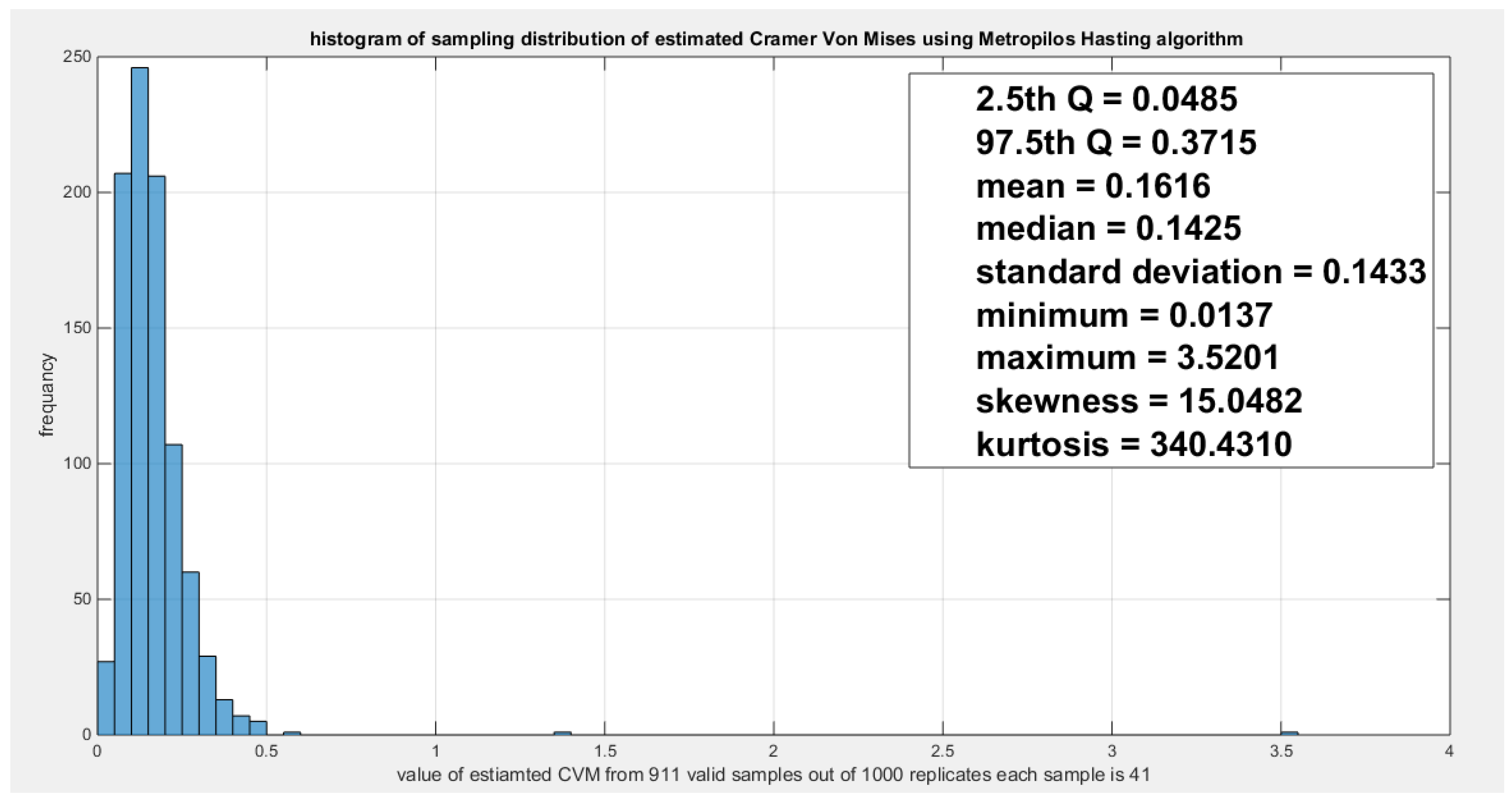
Figure 12.
shows the sampling distribution of the CVM. The CVM data is 0.1388 and it lays between the 2.5th and the 97.5th quantiles so null hypothesis is failed to be rejected and the copula fits the data well. The p-value (probability of values less than or equal to 0.1388) is 0.8207, in other words, this 0.1388 does not lay in either of the tail region of rejection.
Figure 12.
shows the sampling distribution of the CVM. The CVM data is 0.1388 and it lays between the 2.5th and the 97.5th quantiles so null hypothesis is failed to be rejected and the copula fits the data well. The p-value (probability of values less than or equal to 0.1388) is 0.8207, in other words, this 0.1388 does not lay in either of the tail region of rejection.
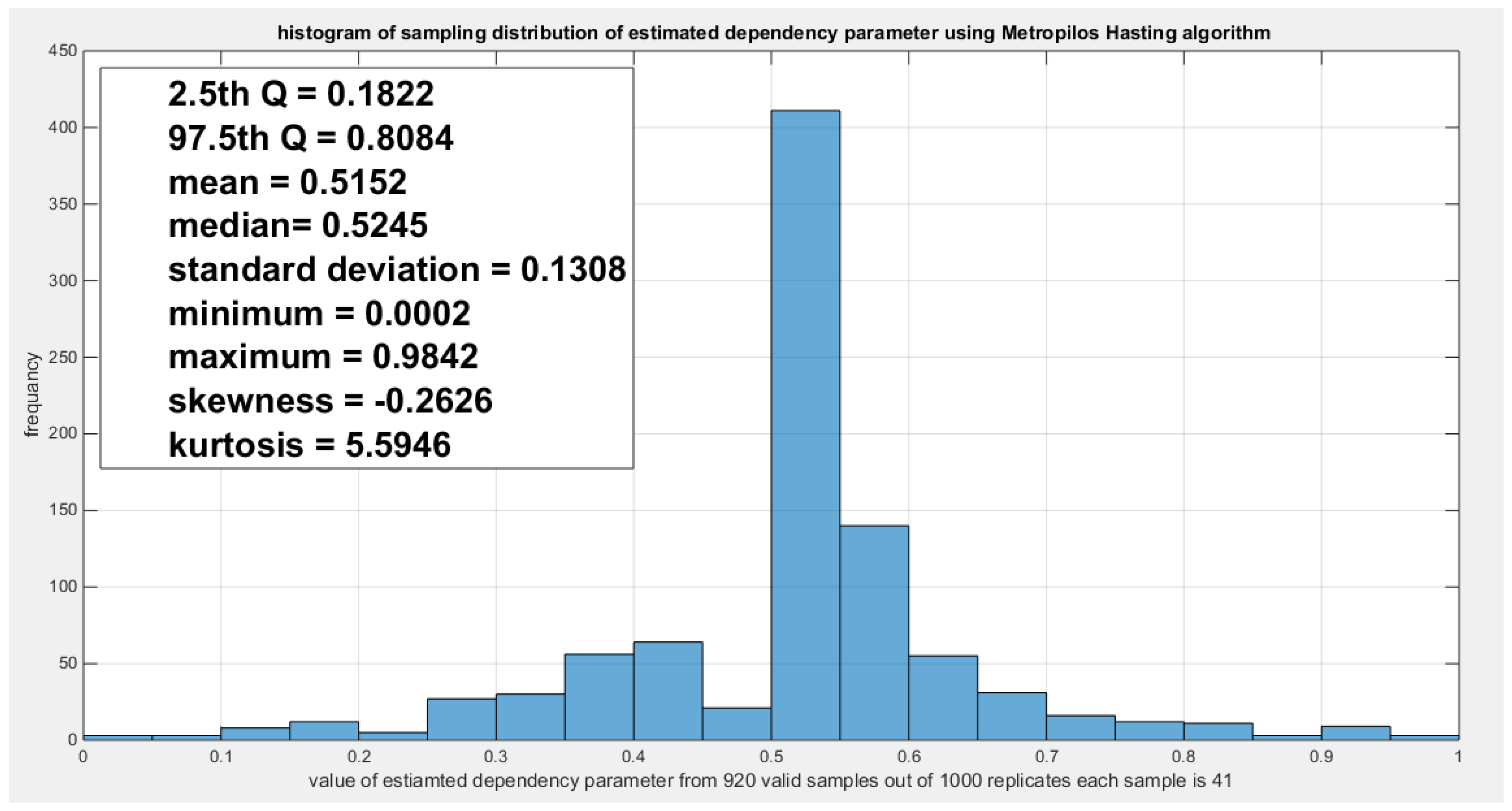
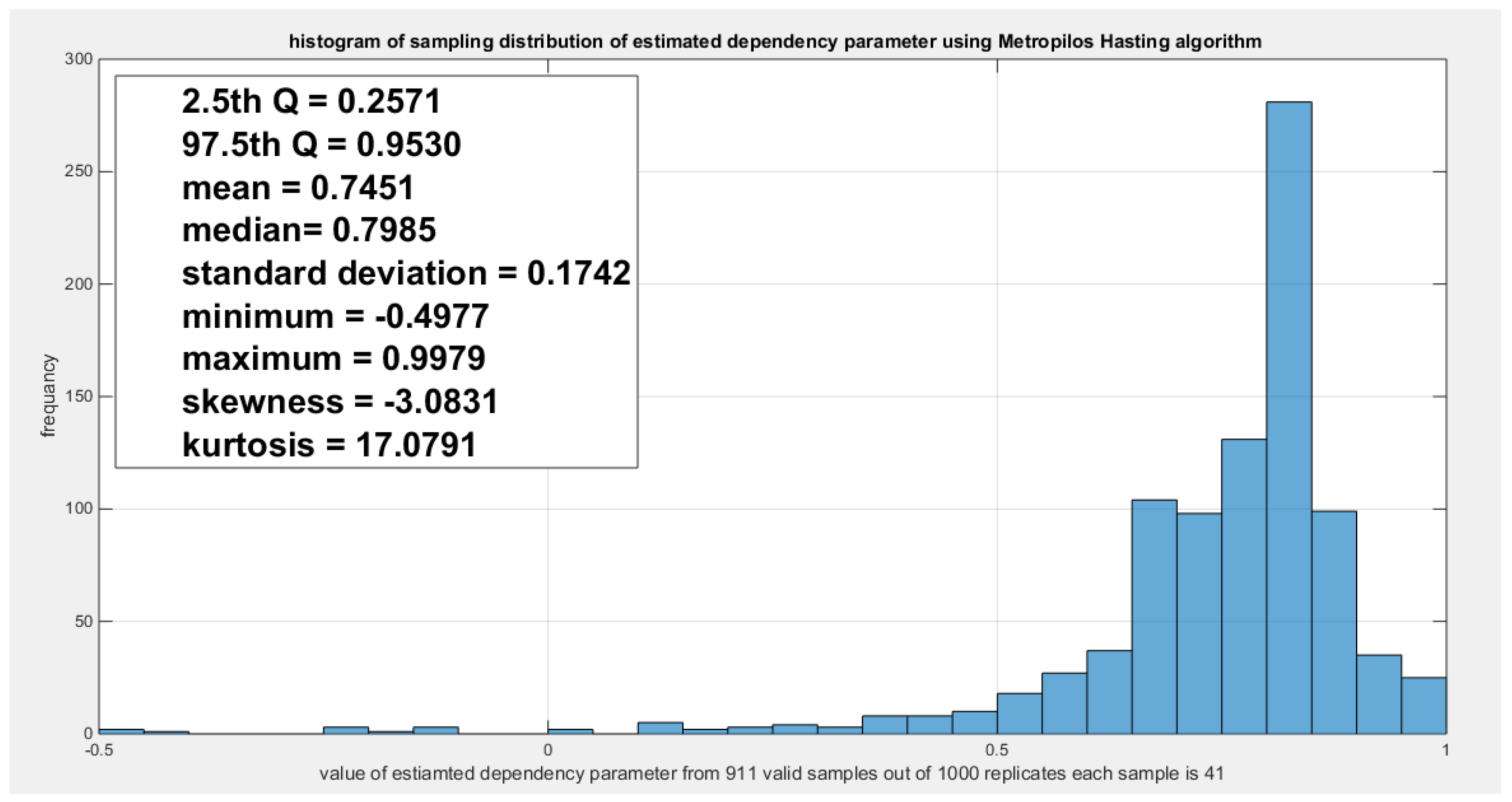
Figure 13.
shows the sampling distribution of the dependency parameter. The 0.4798 lays in the acceptance region between the two quantiles, the 2.5th and the 97.5th quantiles. So the null hypothesis fails to reject its assumption. The p-value (probability of the values being less than or equal to this 0.4798) is 0.2304 which indicates that 0.4798 is not placed in either zones of rejection.
Figure 13.
shows the sampling distribution of the dependency parameter. The 0.4798 lays in the acceptance region between the two quantiles, the 2.5th and the 97.5th quantiles. So the null hypothesis fails to reject its assumption. The p-value (probability of the values being less than or equal to this 0.4798) is 0.2304 which indicates that 0.4798 is not placed in either zones of rejection.
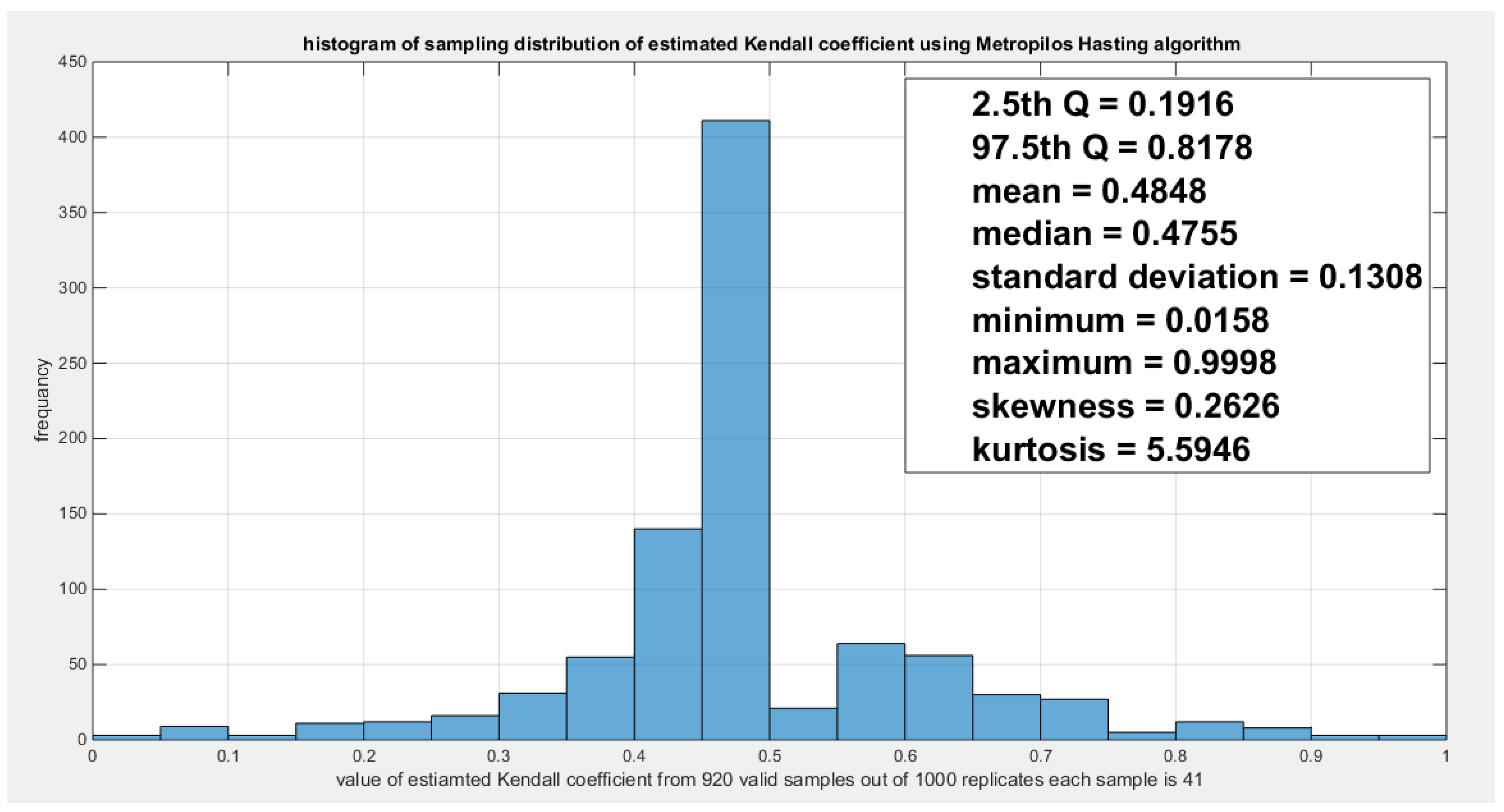
Figure 14.
shows the sampling distribution of the Kendal tau coefficient. Its value 0.5202 is between the two quantiles 2.5th and 97.5th which is the acceptance zones. So the null hypothesis fails to reject its assumption. The p-values (probability of the values less than or equal to 0.5202) is 0.7696 which denotes that this value is far away from both rejection zones.
Figure 14.
shows the sampling distribution of the Kendal tau coefficient. Its value 0.5202 is between the two quantiles 2.5th and 97.5th which is the acceptance zones. So the null hypothesis fails to reject its assumption. The p-values (probability of the values less than or equal to 0.5202) is 0.7696 which denotes that this value is far away from both rejection zones.
According to the sandwich variance the variance covariance matrix for this model is:
The validity indices for the second stage are:
The validity indices for the whole model is the summation of these indices for marginal (first stage) and copula (second stage):
Theoretical upper tail coefficient is 0.6054. At quantile 0.85; the empirical upper tail coefficient in the direction of the ‘water quality’ variable is 0.2 (one point showing joint match out of 5 points in the upper tail at this threshold, 0.85) and in the direction of the ‘feeling safe walk at night’ variable is 0.5 (one point showing joint match out of 2 points in the upper tail at this threshold, 0.85) while the confidence interval of the empirical distribution obtained from bootstrap sampling under the null hypothesis is [0,1]. This is expected because of the small sample size and left skewness of data.
Figure 15 shows the P-P plot of the empirical vs the theoretical copula.
Figure 16,
Figure 17 and
Figure 18 show the surface of the copula density, the contour plot of the copula density, and the contour plot of the copula distribution at the estimated parameter.
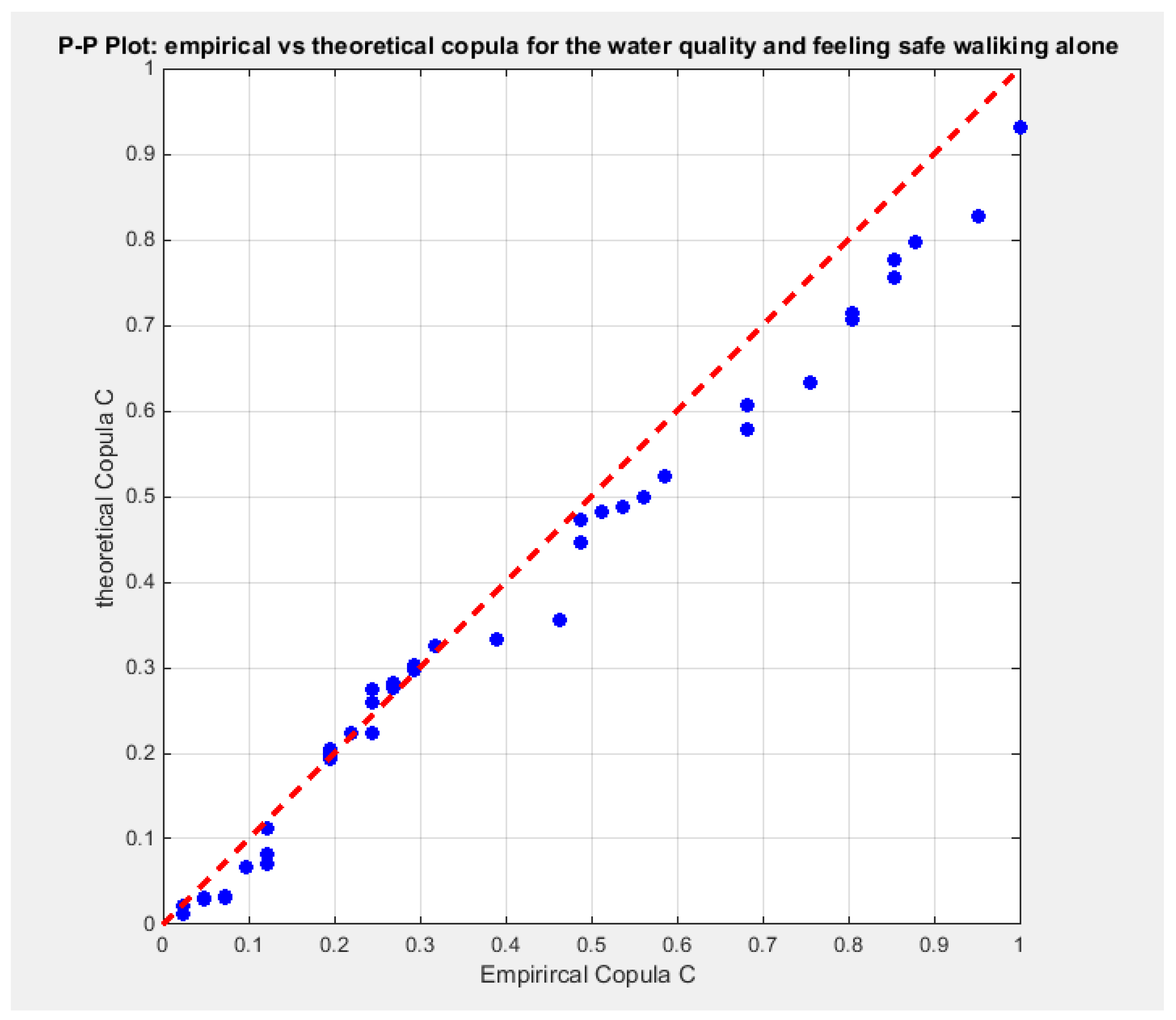
Figure 15.
shows the P-P plot of the empirical vs the theoretical copula. The theoretical copula shows near perfect alignment of its lower part with the diagonal line than its upper part.
Figure 15.
shows the P-P plot of the empirical vs the theoretical copula. The theoretical copula shows near perfect alignment of its lower part with the diagonal line than its upper part.
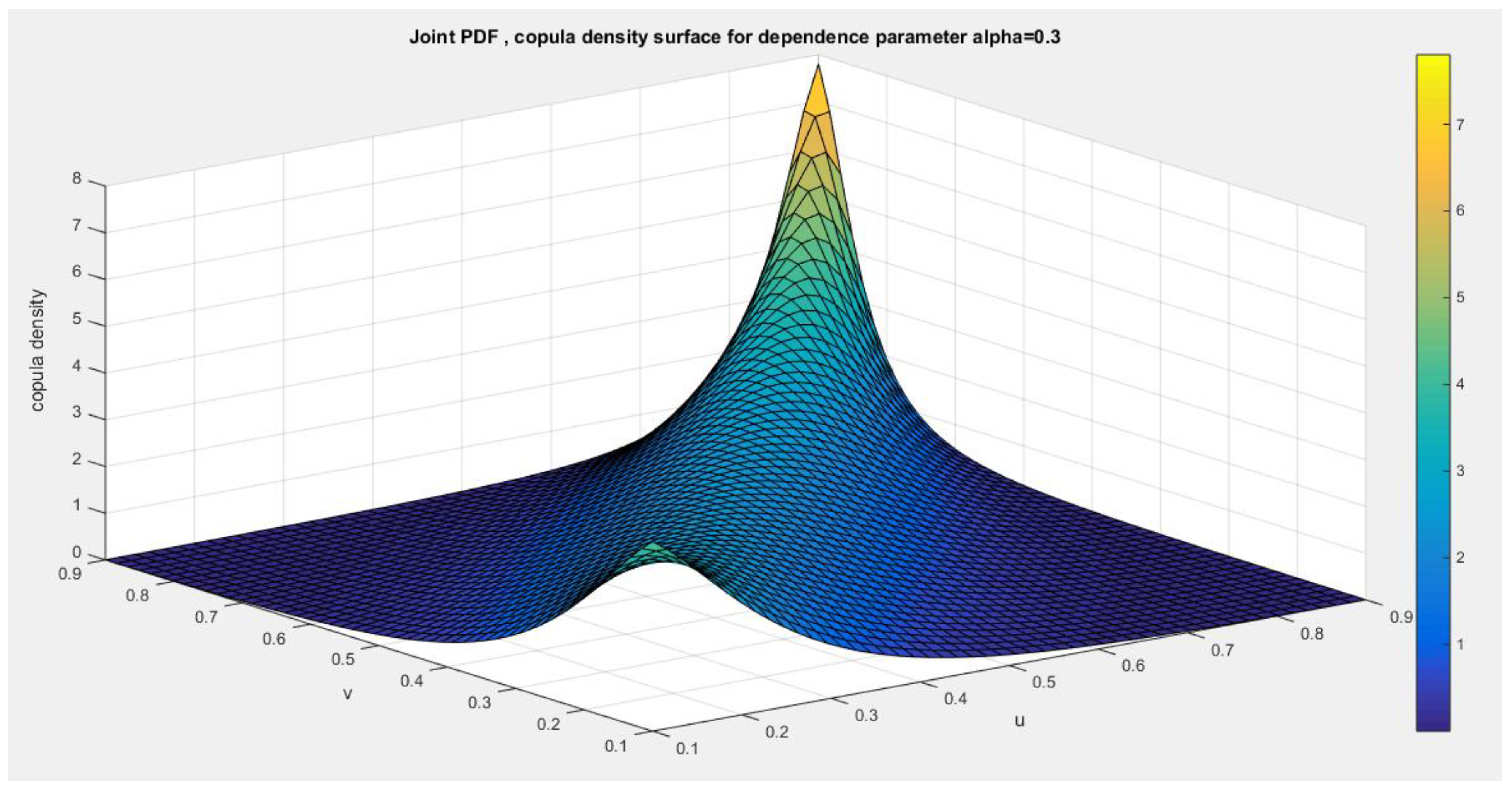
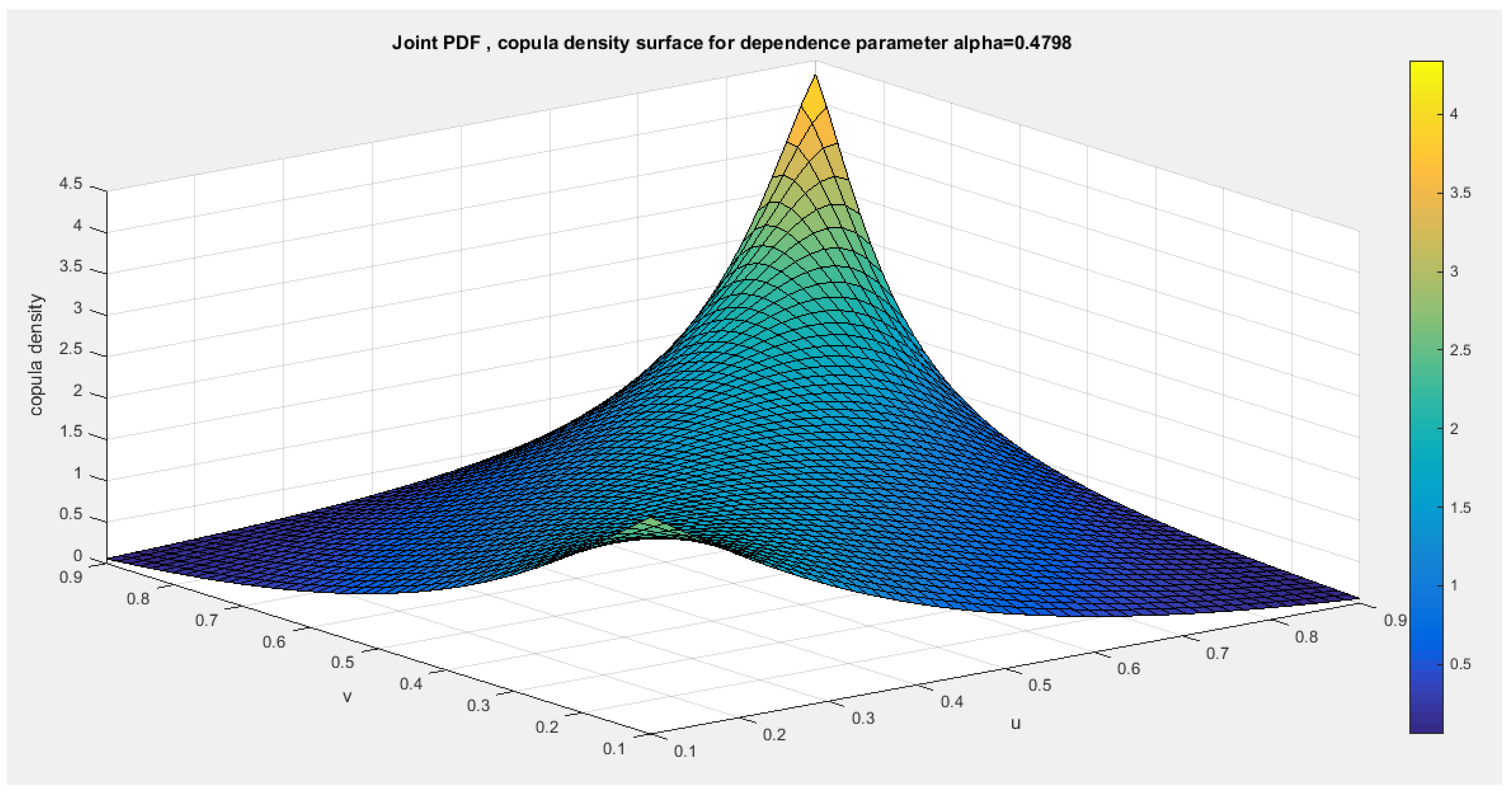
Figure 16.
shows the PDF surface of copula density with parameter 0.4798.
Figure 16.
shows the PDF surface of copula density with parameter 0.4798.
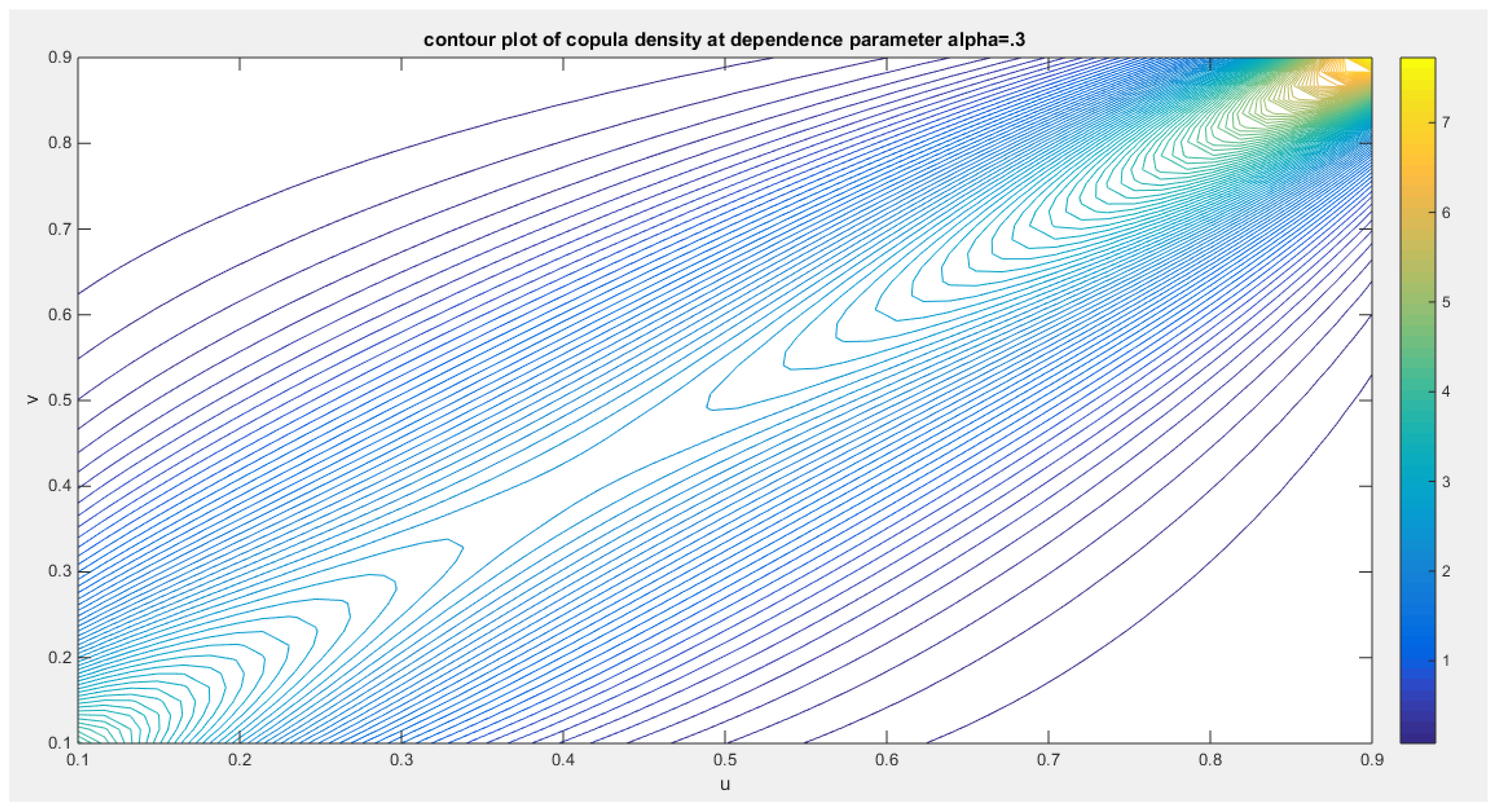
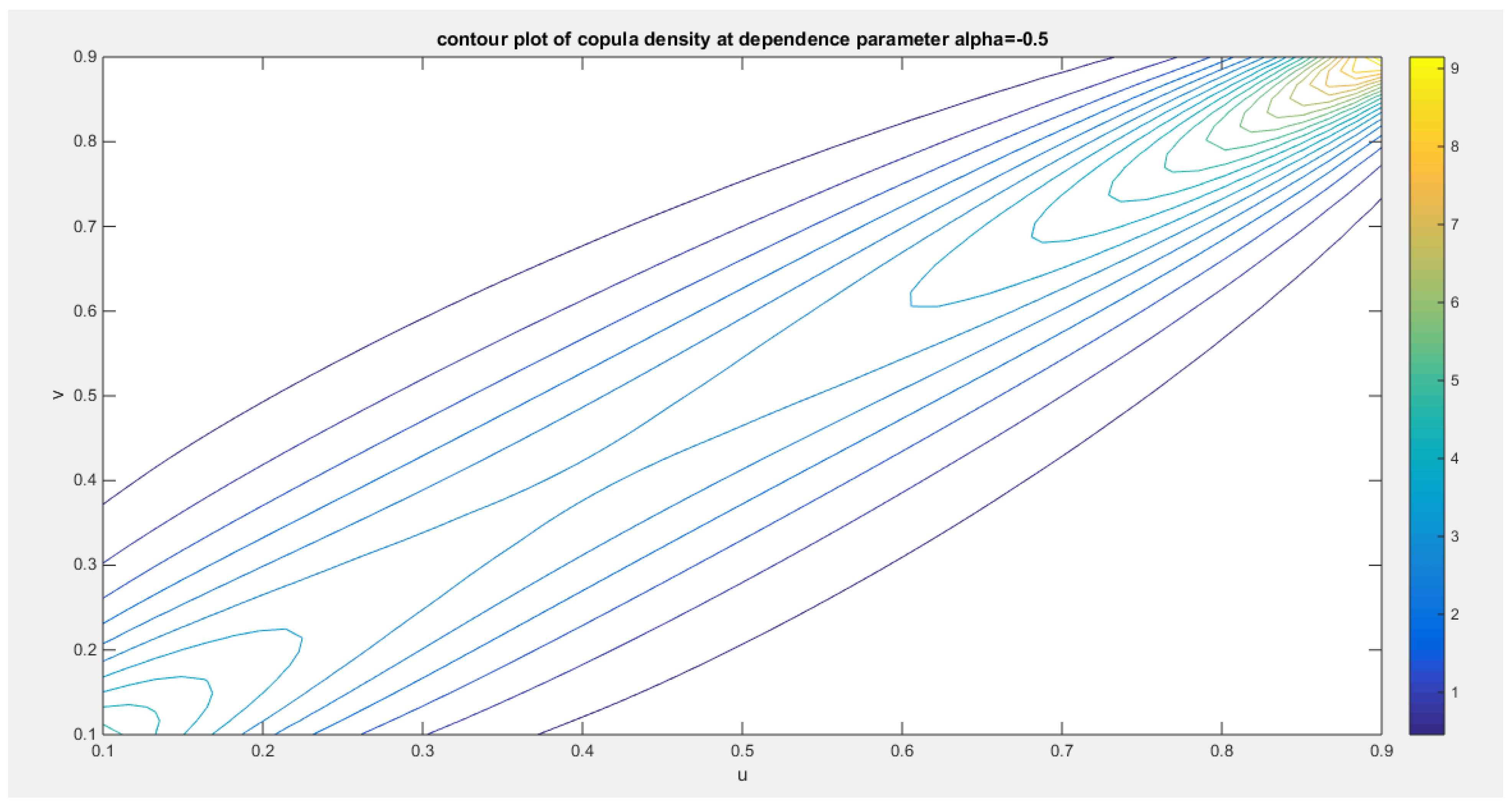
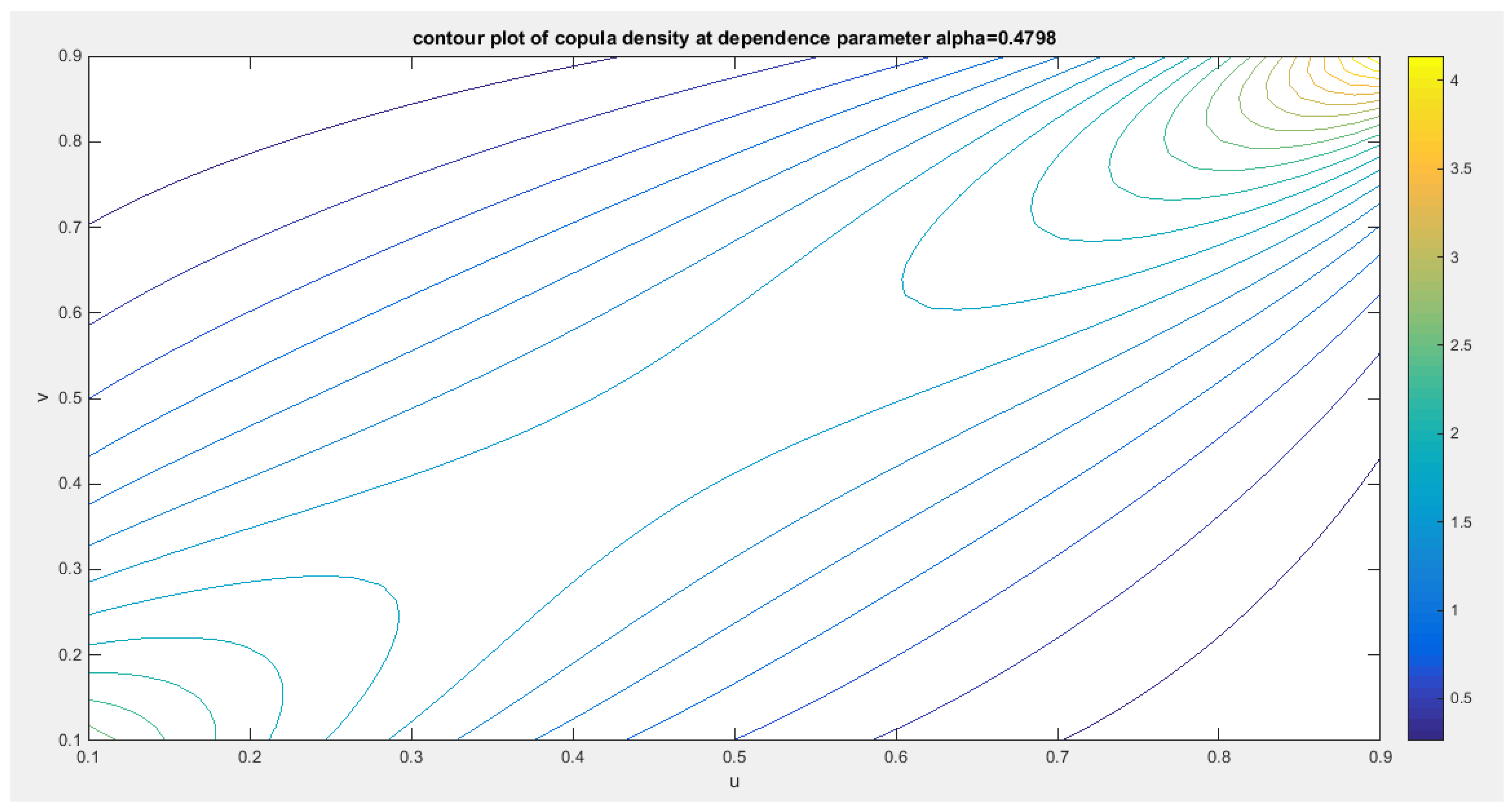
Figure 17.
shows the contour plot of the copula density with parameter 0.4798.
Figure 17.
shows the contour plot of the copula density with parameter 0.4798.
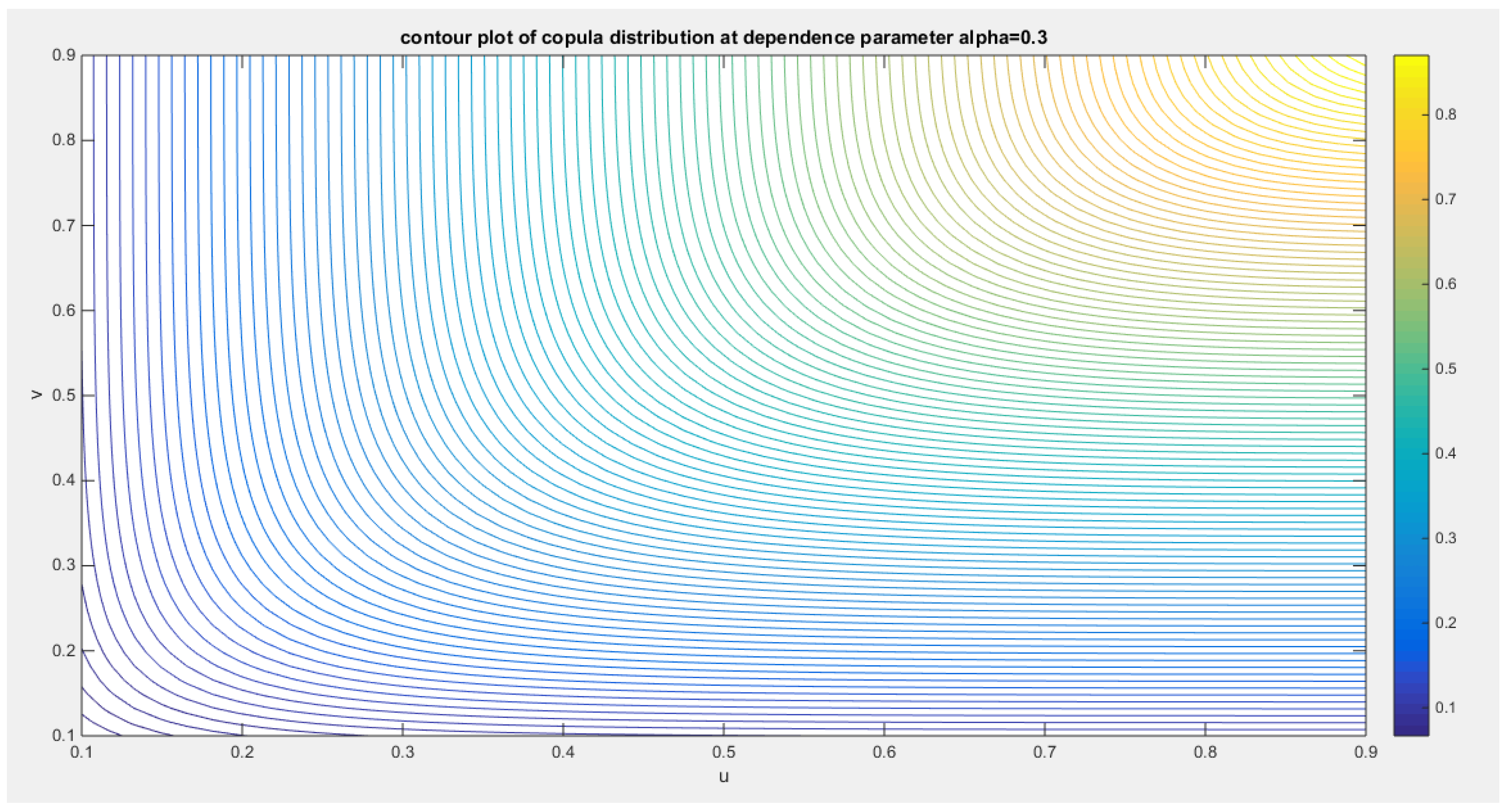
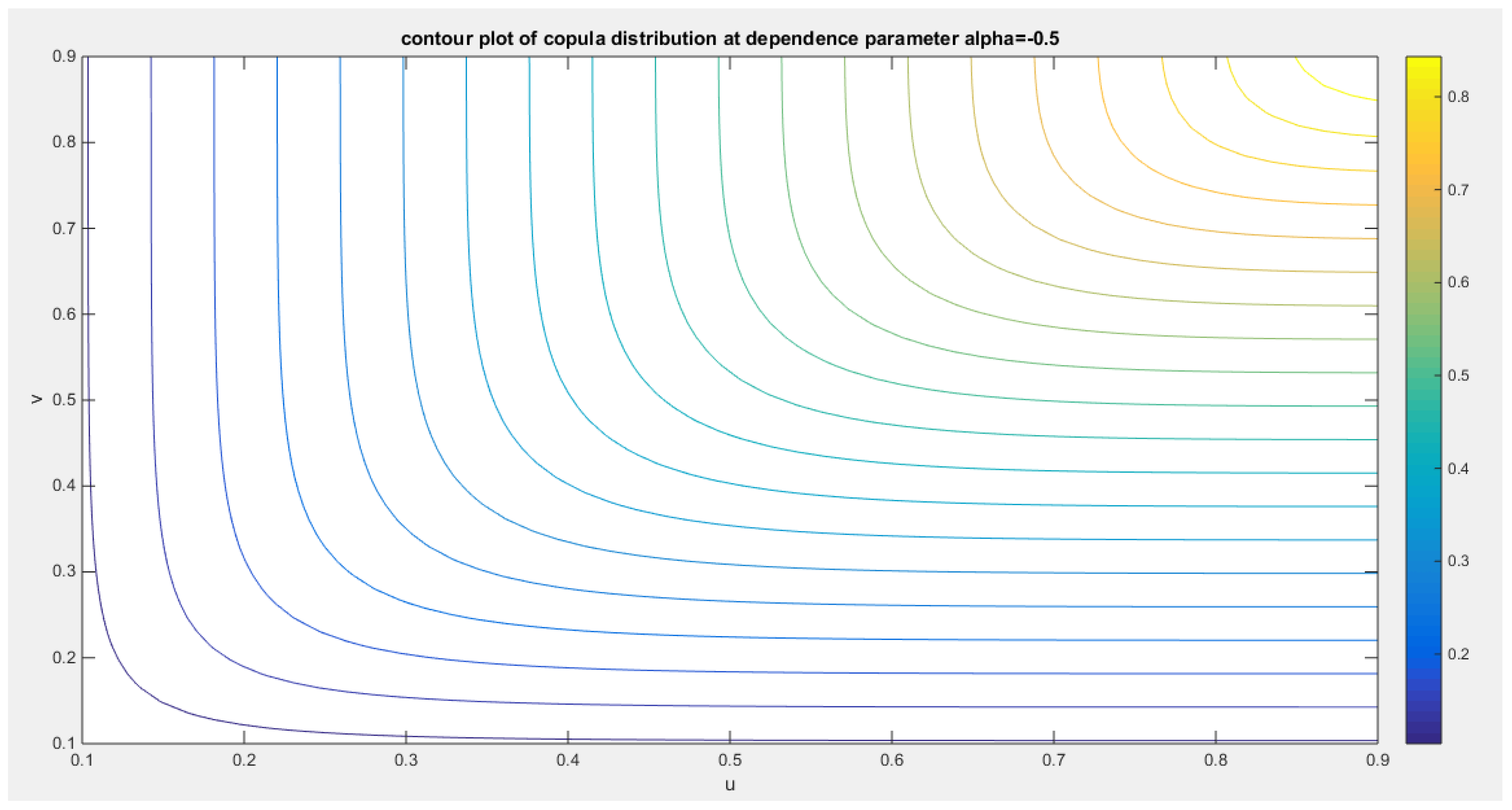
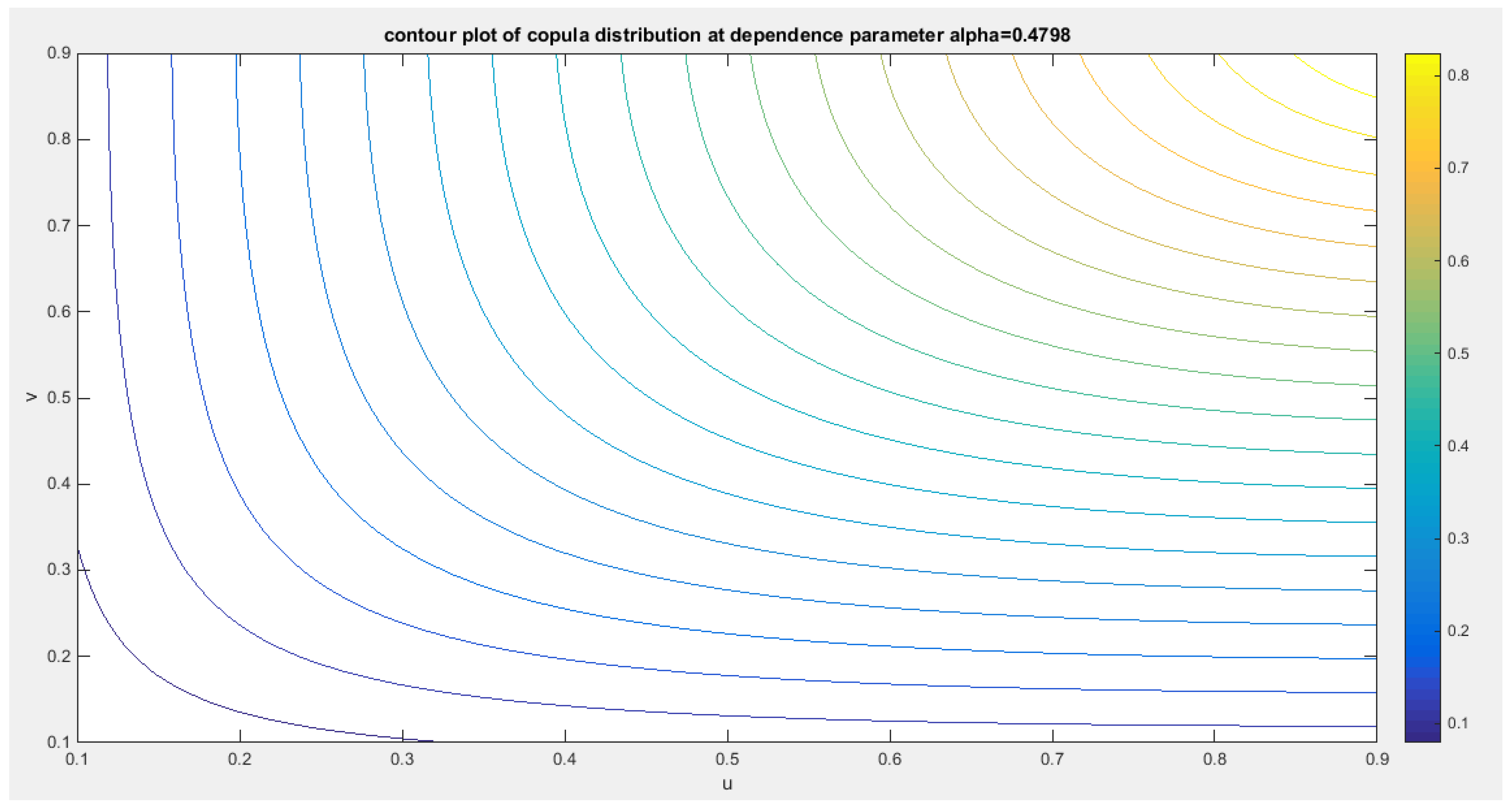
Figure 18.
shows the contour plot of the copula distribution with dependency parameter 0.4798.
Figure 18.
shows the contour plot of the copula distribution with dependency parameter 0.4798.
Second copula
Model the dependency between the ‘water quality’ and ‘quality of support network’: The empirical tau is 0.3929 and the theoretical tau is 0.3926 with dissimilarity value of 3.8927e-04 The estimated dependency parameter, theta
, is 0.7794 and estimated variance of 0.0018. The Cramer Von Mises test (CVM) is 0.2142. to test the null hypothesis for dependency, resampling using the Metropolis Hasting algorithm of MCMC procedure was performed. The propositional null hypothesis was stated that the population dependency parameter equals the estimated theta against the alternative hypothesis that the population dependency parameter does not equal the estimated theta. Moreover, the null hypothesis for the equality of the population Kendall tau with the theoretical tau is tested against the alternative hypothesis of not being equal to each other. The null hypothesis for the CVM suggesting that the sampling CVM equals the observed CVM attained from the estimation procedure was also investigated. These are all two sided tests. The sampling distribution of each of the previously mentioned indices, thetas, tau and CVM is shown in
Figure 19,
Figure 20 and
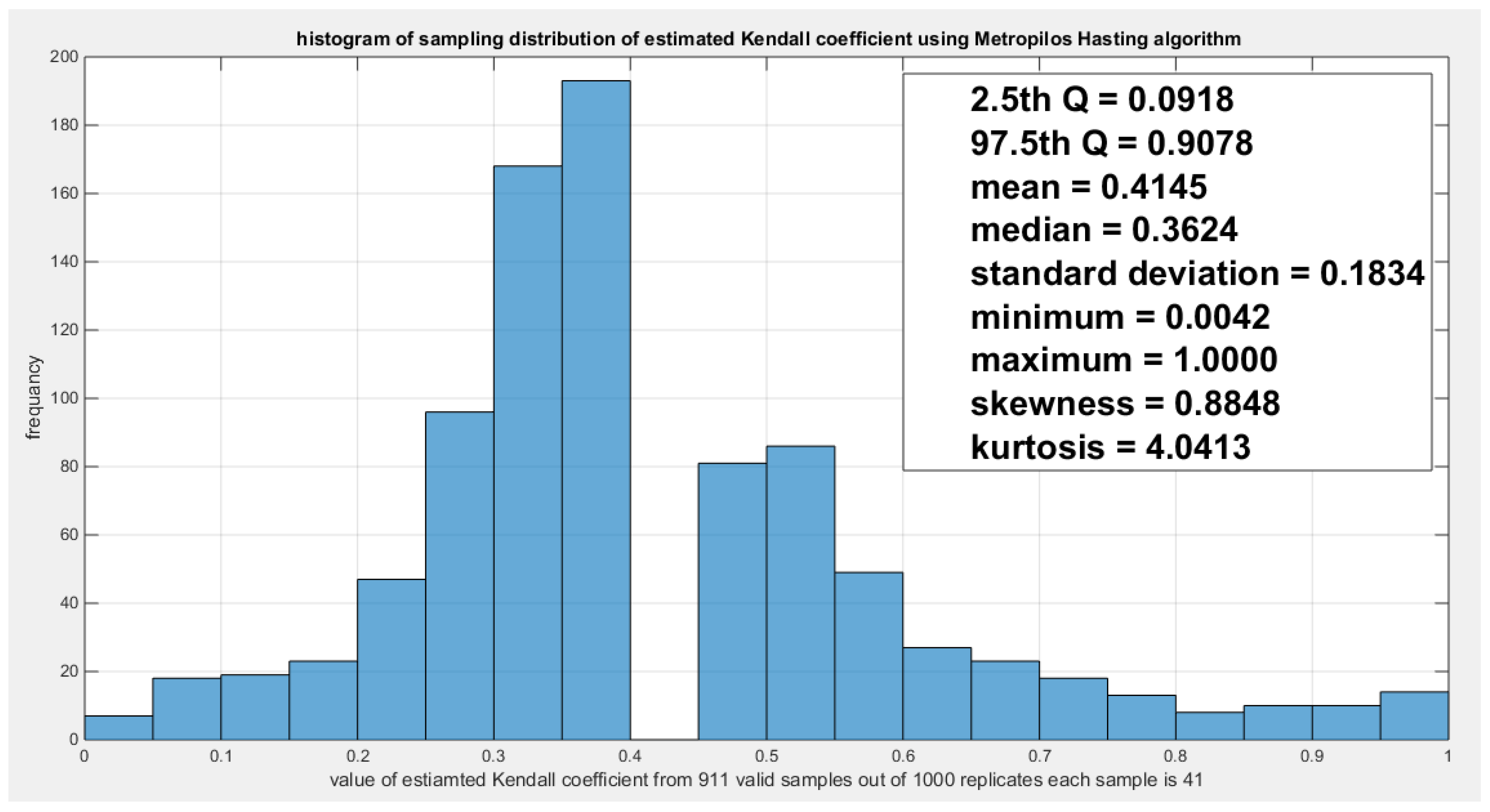
Figure 21. The descriptive statistical indices are shown in each figure. Analysis of the figures denoted that the indices are located within the acceptance region between the 2.5th and 97.5th quantiles. So the null hypotheses fail to be rejected. The copula can be said to pass some of the goodness of fit (GOF) tests for this data. And the dependence parameter mockups, within the milieu of this copula, the connection between the two variables. The confidence interval (CI) for the estimated dependence parameter is (0.2571, 0.9530), for the theoretical tau; it is (0.0918, 0.9078), and for CVM; it is (0.0485, 0.3715).
Figure 19.
shows the sampling distribution of the CVM. The data obtained CVM is 0.2142 and it lies between the 2.5th and the 97.5th quantiles so the null hypothesis is failed to be rejected and the copula fits the data well. The p-value (probability of values less than or equal to 0.2142) is 0.7846, in other words, this 0.2142 does not lay in either of the tail region of rejection.
Figure 19.
shows the sampling distribution of the CVM. The data obtained CVM is 0.2142 and it lies between the 2.5th and the 97.5th quantiles so the null hypothesis is failed to be rejected and the copula fits the data well. The p-value (probability of values less than or equal to 0.2142) is 0.7846, in other words, this 0.2142 does not lay in either of the tail region of rejection.
Figure 20.
shows the sampling distribution of the dependency parameter. The 0.7794 lies in the acceptance region between the two quantiles, the 2.5th and the 97.5th quantiles. So the null hypothesis fails to reject its assumption. The p-value (probability of the values being less than or equal to this 0.7794) is 0.3725which indicates that 0.7794 is not placed in either zones of rejection.
Figure 20.
shows the sampling distribution of the dependency parameter. The 0.7794 lies in the acceptance region between the two quantiles, the 2.5th and the 97.5th quantiles. So the null hypothesis fails to reject its assumption. The p-value (probability of the values being less than or equal to this 0.7794) is 0.3725which indicates that 0.7794 is not placed in either zones of rejection.
Figure 21.
shows the sampling distribution of the Kendal tau coefficient. Its value 0.3926 is between the two quantiles 2.5th and 97.5th which is the acceptance zones. So the null hypothesis fails to reject its assumption. The p-values (probability of the values less than or equal to 0.3926) is 0.6275 which denotes that this value 0.3926 is far away from both rejection zones on the right and the left.
Figure 21.
shows the sampling distribution of the Kendal tau coefficient. Its value 0.3926 is between the two quantiles 2.5th and 97.5th which is the acceptance zones. So the null hypothesis fails to reject its assumption. The p-values (probability of the values less than or equal to 0.3926) is 0.6275 which denotes that this value 0.3926 is far away from both rejection zones on the right and the left.
According to the sandwich variance the variance covariance matrix for this model is:
The validity indices for the second stage are:
The validity indices for the whole model is the summation of these indices for marginal (first stage) and copula (second stage):
Theoretical upper tail coefficient is 0.4764. At quantile 0.85; the empirical upper tail coefficient in the direction of the ‘water quality’ variable is 0.2 (one point showing joint match out of 5 points in the upper tail at this threshold, 0.85) and in the direction of the ‘Quality of support network’ variable is 1 (one point showing joint match out of 1 point in the upper tail at this threshold, 0.85) while the confidence interval of the empirical distribution obtained from bootstrap sampling under the null hypothesis is [0,1]. This is expected because of the small sample size and left skewness of data.
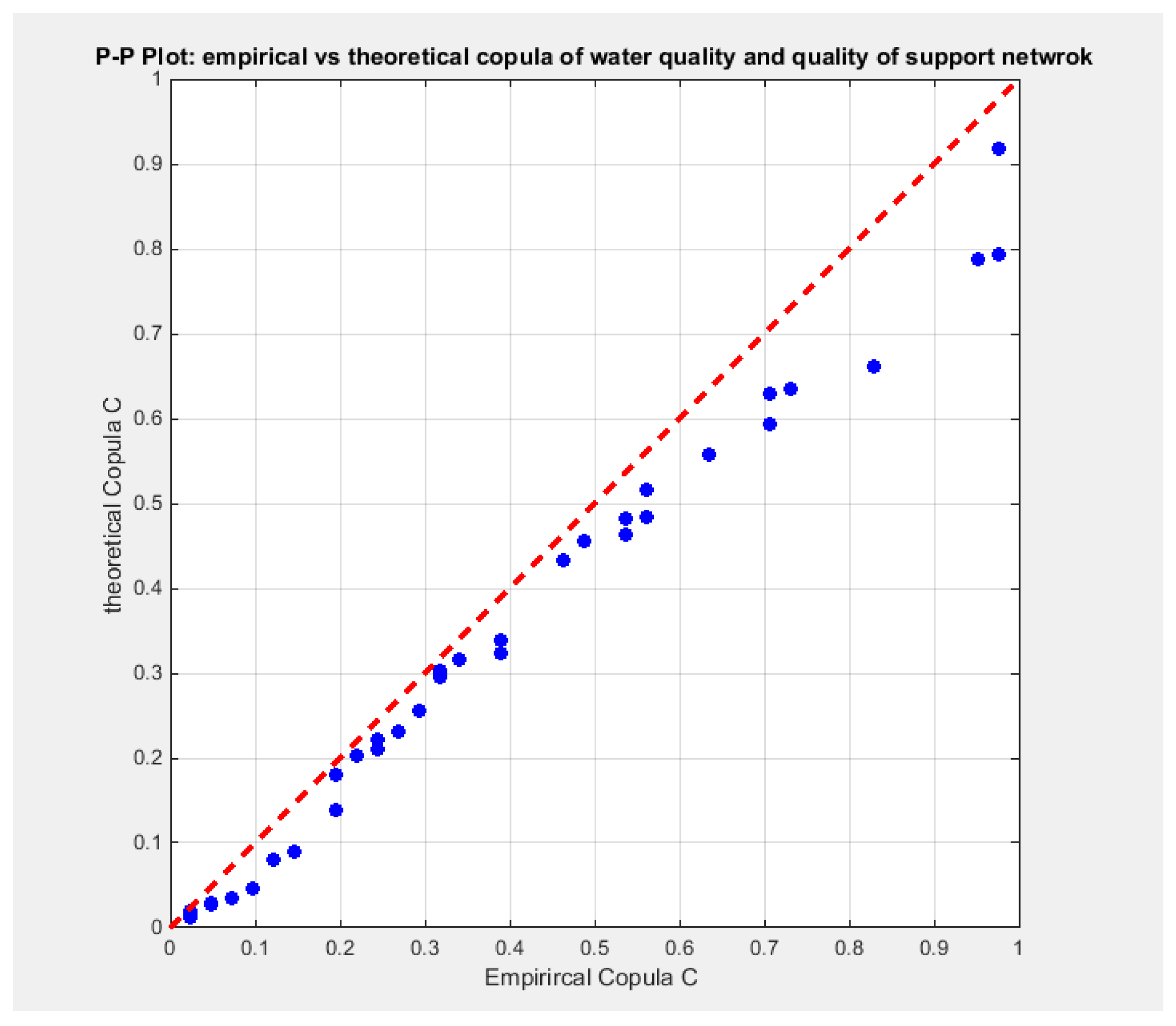
Figure 22 shows the P-P plot of the empirical vs the theoretical copula.
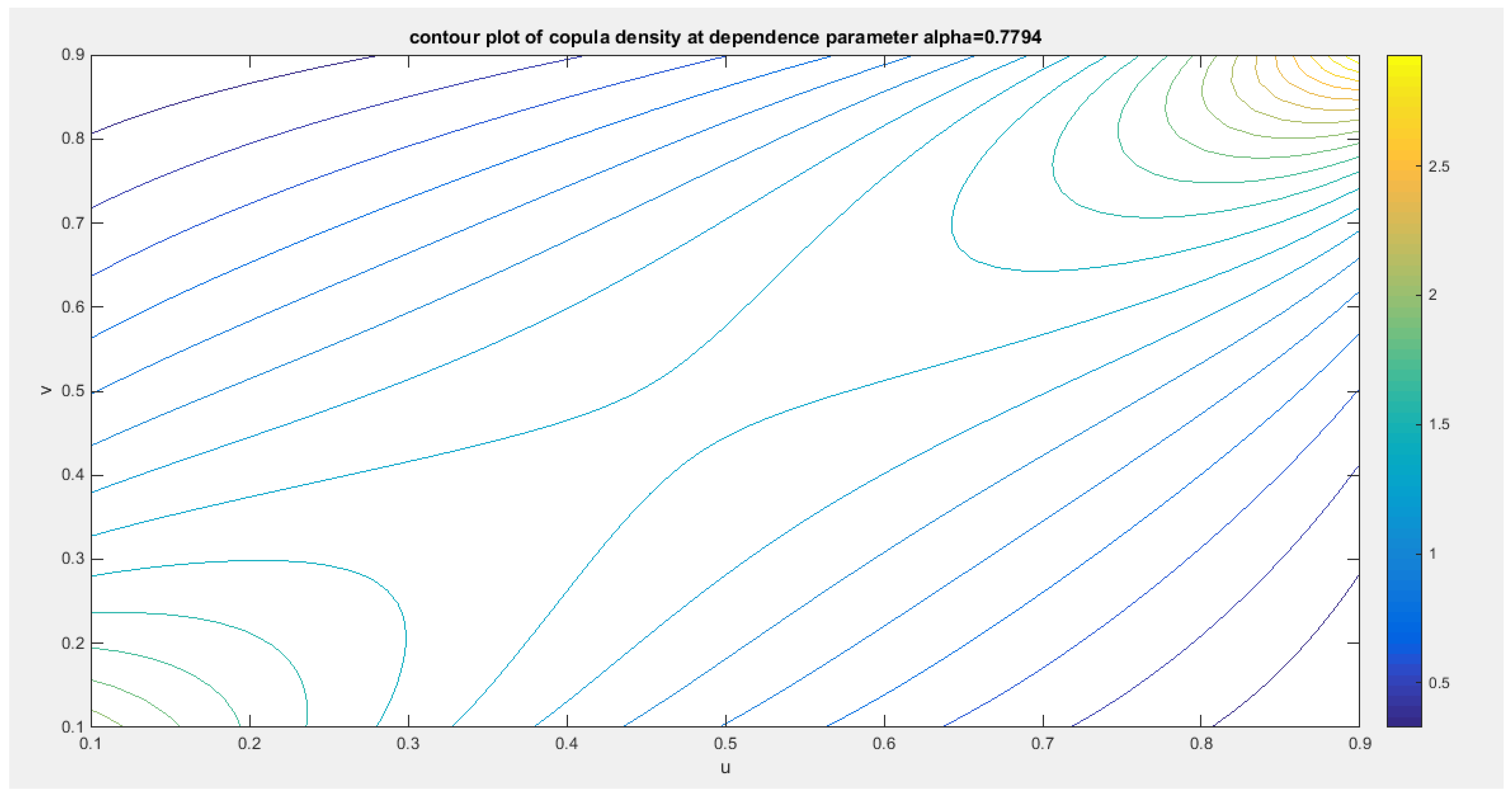
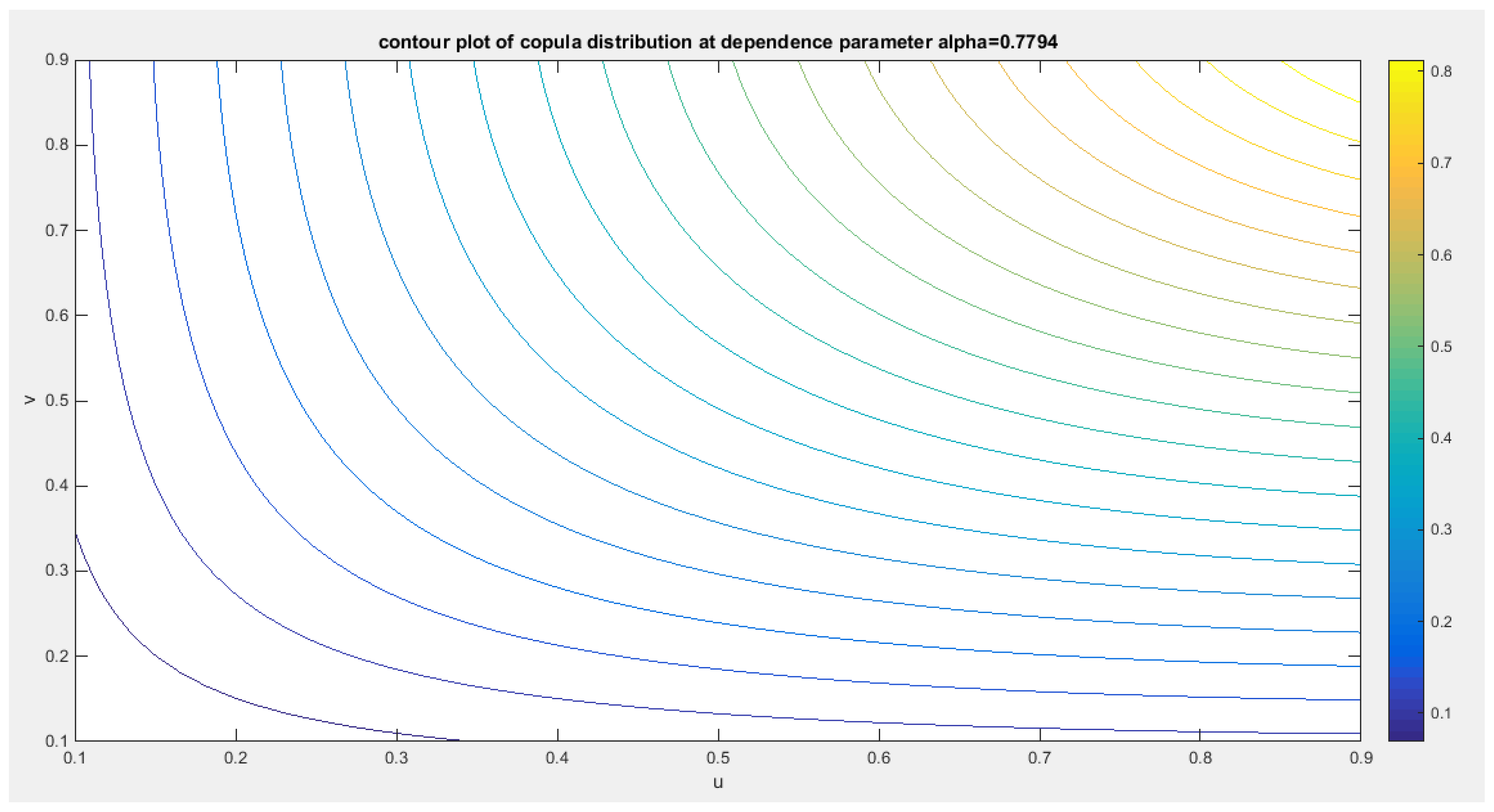
Figure 23,
Figure 24 and
Figure 25 show the contour plot of the copula density, the contour plot of the copula distribution, and the surface of the copula density at the estimated parameter.
Figure 22.
shows the P-P plot of the empirical vs the theoretical copula. The theoretical copula shows near perfect alignment of its lower part and its center with the diagonal line than its upper part.
Figure 22.
shows the P-P plot of the empirical vs the theoretical copula. The theoretical copula shows near perfect alignment of its lower part and its center with the diagonal line than its upper part.
Figure 23.
shows the contour plot of the copula density with parameter 0.7794.
Figure 23.
shows the contour plot of the copula density with parameter 0.7794.
Figure 24.
shows the contour plot of the copula distribution with parameter 0.7794.
Figure 24.
shows the contour plot of the copula distribution with parameter 0.7794.
Figure 25.
shows the surface of the copula density with dependency parameter 0.7794.
Figure 25.
shows the surface of the copula density with dependency parameter 0.7794.
Another 2 pair of variables for the second copula:
For the OECD data, another two pair of variables are analyzed the household net wealth and the personal earnings. The household net wealth measures the total value of assets possessed by the household minus their obligations like debts, loans, and mortgages. These data are available in USD, and converted to unit interval through division by 1000000. The personal earnings measure the average income earned by persons, typically on an annual or monthly basis, reflecting the income levels and earning potential of the workforce. These data are also expressed in USD and converted to belong to unit interval through division by 100000. These data are available for 24 countries in this same data platform as shown in
Table 5.
Table 5.
Household net wealth indicator versus personal earnings indicator in the OECD countries.
Table 5.
Household net wealth indicator versus personal earnings indicator in the OECD countries.
| |
Austria |
Belgium |
Canada |
Chile |
Denmark |
Estonia |
Finland |
| Household net wealth |
309637 |
447607 |
478240 |
135787 |
149864 |
188627 |
230032 |
| Personal earnings |
53132 |
54327 |
55342 |
26729 |
58430 |
30720 |
46230 |
| |
France |
Germany |
Greece |
Hungary |
Ireland |
Italy |
Latvia |
| Household net wealth |
298639 |
304317 |
148323 |
150296 |
370341 |
295020 |
79245 |
| Personal earnings |
45581 |
53745 |
27207 |
25409 |
49474 |
37769 |
29876 |
| |
Lithuania |
Luxembourg |
Netherlands |
Poland |
Portugal |
Slovak
Republic
|
Slovenia |
| Household net wealth |
182039 |
941162 |
248599 |
233221 |
255303 |
171425 |
233286 |
| Personal earnings |
31811 |
65854 |
58828 |
32527 |
28410 |
23619 |
41445 |
| |
Spain |
United Kingdom |
United states |
|
|
|
|
| Household net wealth |
366534 |
524422 |
684500 |
|
|
|
|
| Personal earnings |
37922 |
47147 |
69392 |
|
|
|
|
Table 6.
descriptive statistics of the indicators (household net wealth and personal earnings).
Table 6.
descriptive statistics of the indicators (household net wealth and personal earnings).
| indicator |
min |
mean |
Standard deviation |
skewness |
kurtosis |
25percentile
|
50percentile
|
75percentile
|
max |
| Household net wealth |
0.0792 |
0.3094 |
0.1951 |
1.8194 |
6.9370 |
0.1767 |
0.252 |
0.3684 |
0.9412 |
| Personal earnings |
0.2362 |
0.4296 |
0.1369 |
0.2503 |
1.8851 |
0.3030 |
0.4351 |
0.5404 |
0.6939 |
Table 7.
Kendall tau coefficient of the indicators.
Table 7.
Kendall tau coefficient of the indicators.
| |
Household net wealth |
Personal earnings |
| Household net wealth |
1 |
0.5507
(0.0001)
|
| Personal earnings |
0.5507
(0.0001)
|
1 |
Table 8.
statistical validity indices of the two indicators.
Table 8.
statistical validity indices of the two indicators.
| indicator |
Estimated theta |
variance |
AIC |
CAIC |
BIC |
HQIC |
KS-test |
Ho |
p-value of KS-test |
| Household net wealth |
1.2689 |
0.0087 |
-10.423 |
-10.2411 |
-9.2449 |
-10.1104 |
0.2341 |
Fail to reject |
0.1219 |
| Personal earnings |
1.0418 |
0.0058 |
-12.9361 |
-12.7543 |
-11.758 |
-12.6236 |
0.2496 |
Fail to reject |
0.0837 |
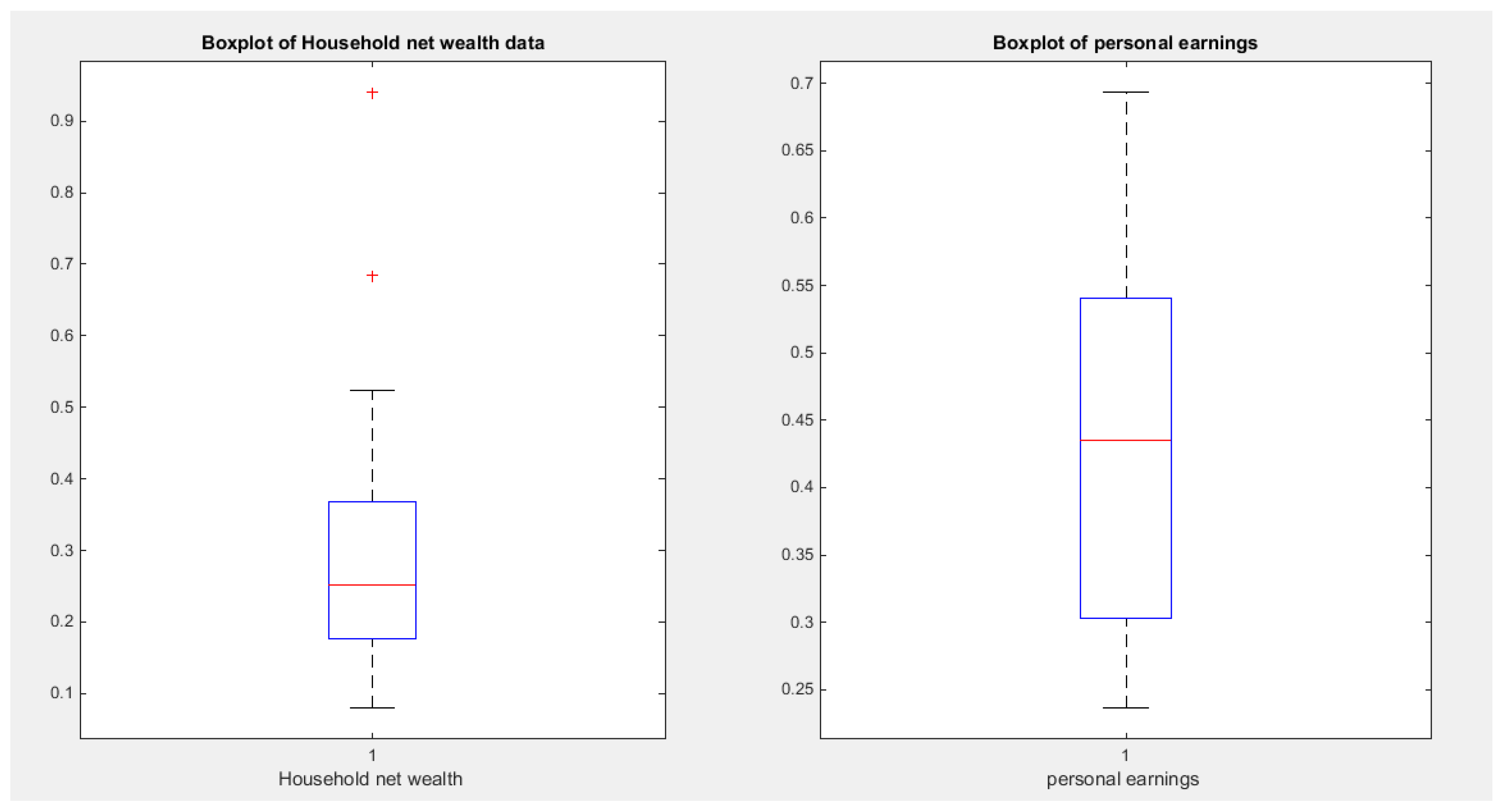
Figure 26.
shows Boxplot of household net wealth and the personal earnings denoting right side skewness.
Figure 26.
shows Boxplot of household net wealth and the personal earnings denoting right side skewness.
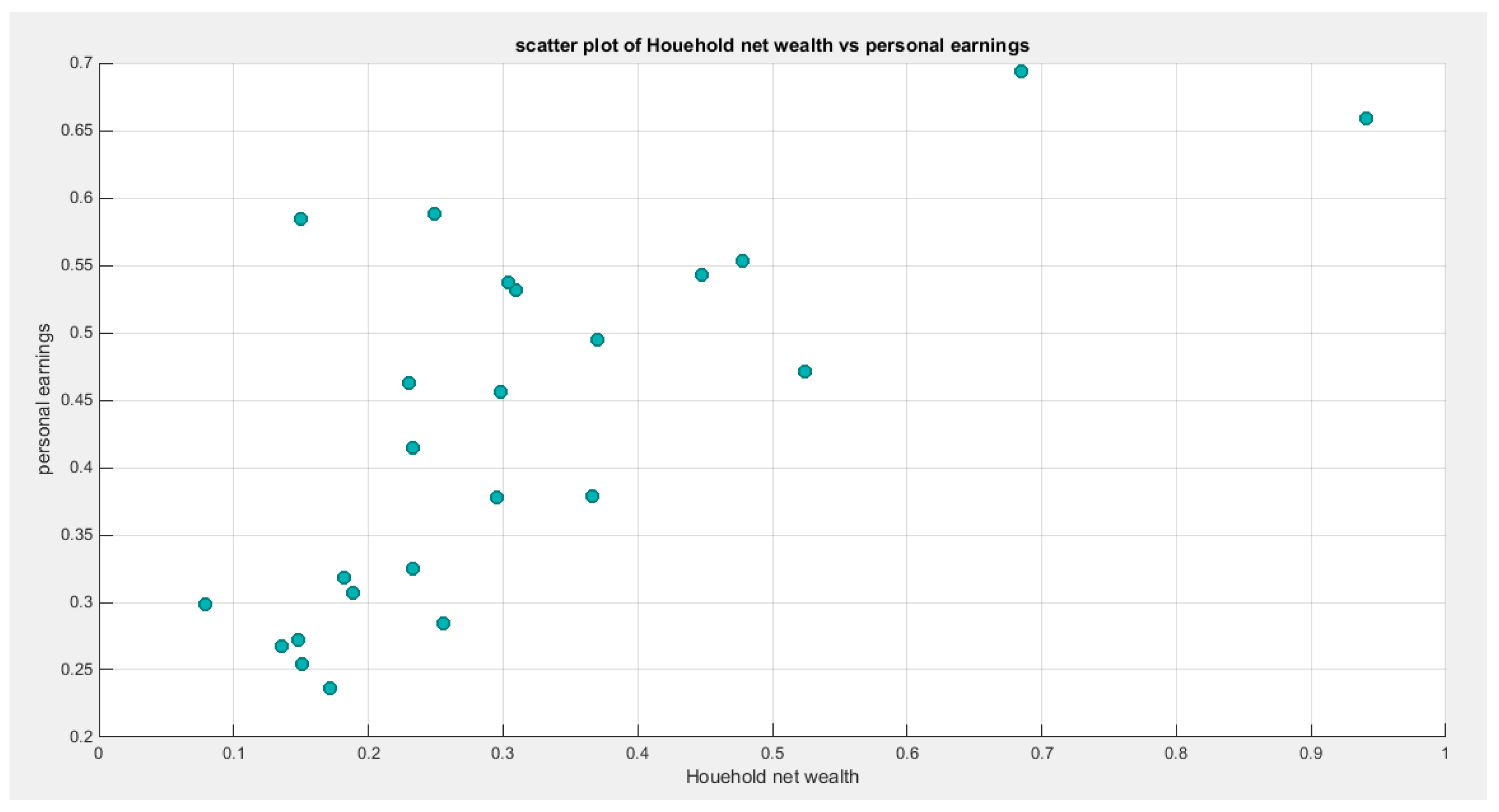
Figure 27.
shows scatter plot of the household net wealth vs personal earnings and the data are mainly concentrated on the left lower corner and the center pointing to the presence of lower tail dependency.
Figure 27.
shows scatter plot of the household net wealth vs personal earnings and the data are mainly concentrated on the left lower corner and the center pointing to the presence of lower tail dependency.
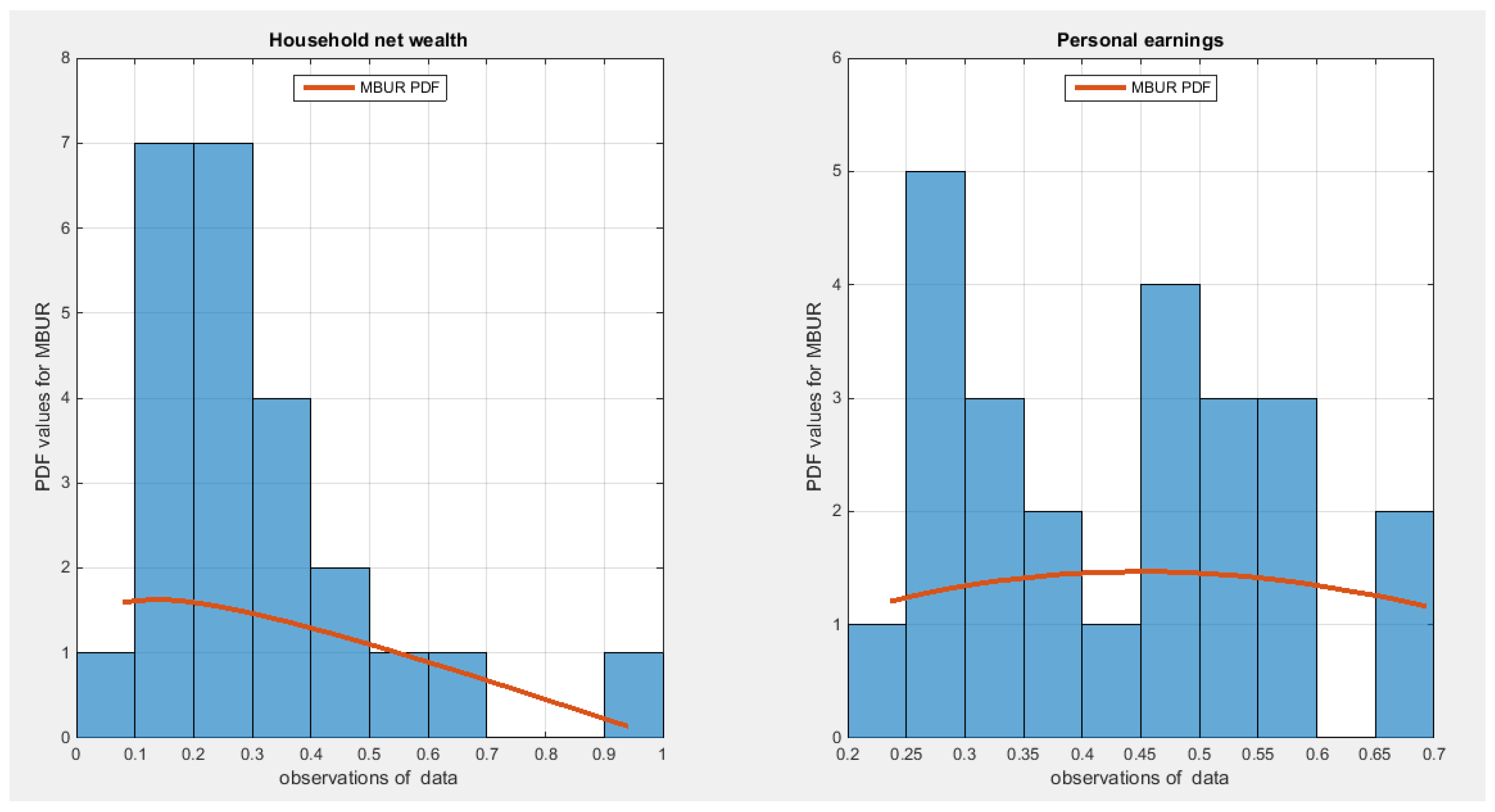
Figure 28.
shows the histogram of the two indicators which exhibit right sided skewness. The graph also shows the fitted MBUR curve for each indicator. The household net wealth indicator exhibits more kurtosis and skewness than the personal earnings indicator.
Figure 28.
shows the histogram of the two indicators which exhibit right sided skewness. The graph also shows the fitted MBUR curve for each indicator. The household net wealth indicator exhibits more kurtosis and skewness than the personal earnings indicator.
Second copula Model the dependency between the ‘household net wealth’ and ‘personal earnings’: The empirical tau is 0.5507 and the theoretical tau is 0.5507 with dissimilarity value of 7.1985e-05. The estimated dependency parameter, theta
, is 0.6703 and estimated variance of 0.0018. The Cramer Von Mises test (CVM) is 0.4281. to test the null hypothesis for dependency, resampling using the Metropolis Hasting algorithm of MCMC procedure was performed. The propositional null hypothesis was stated that the population dependency parameter equals the estimated theta against the alternative hypothesis that the population dependency parameter does not equal the estimated theta. Moreover, the null hypothesis for the equality of the population Kendall tau with the theoretical tau is tested against the alternative hypothesis of not being equal to each other. The null hypothesis for the CVM suggesting that the sampling CVM equals the observed CVM attained from the estimation procedure was also investigated. These are all two sided tests. The sampling distribution of each of the previously mentioned indices, thetas, tau and CVM is shown in
Figure 29,
Figure 30 and
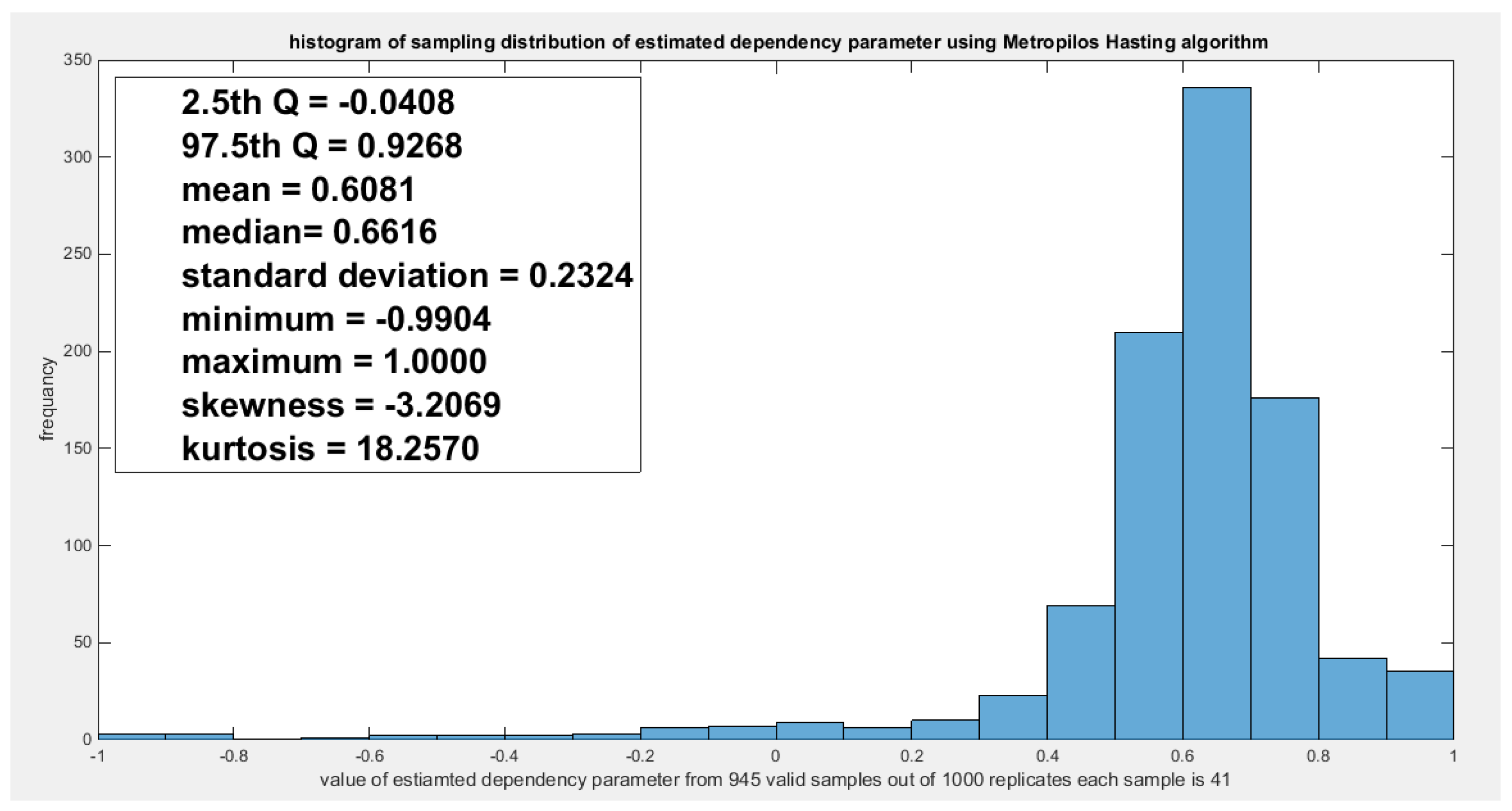
Figure 31. The descriptive statistical indices are shown in each figure. Analysis of the figures denoted that the indices are located within the acceptance region between the 2.5th and 97.5th quantiles. So the null hypotheses fail to be rejected. The copula can be said to pass some of the goodness of fit (GOF) tests for this data. And the dependence parameter mockups, within the milieu of this copula, the connection between the two variables. The confidence interval (CI) for the estimated dependence parameter is (-0.0408, 0.9268), for the theoretical tau; it is (0.1314, 0.9756), and for CVM; it is (0.0368, 0.4871).
Figure 29.
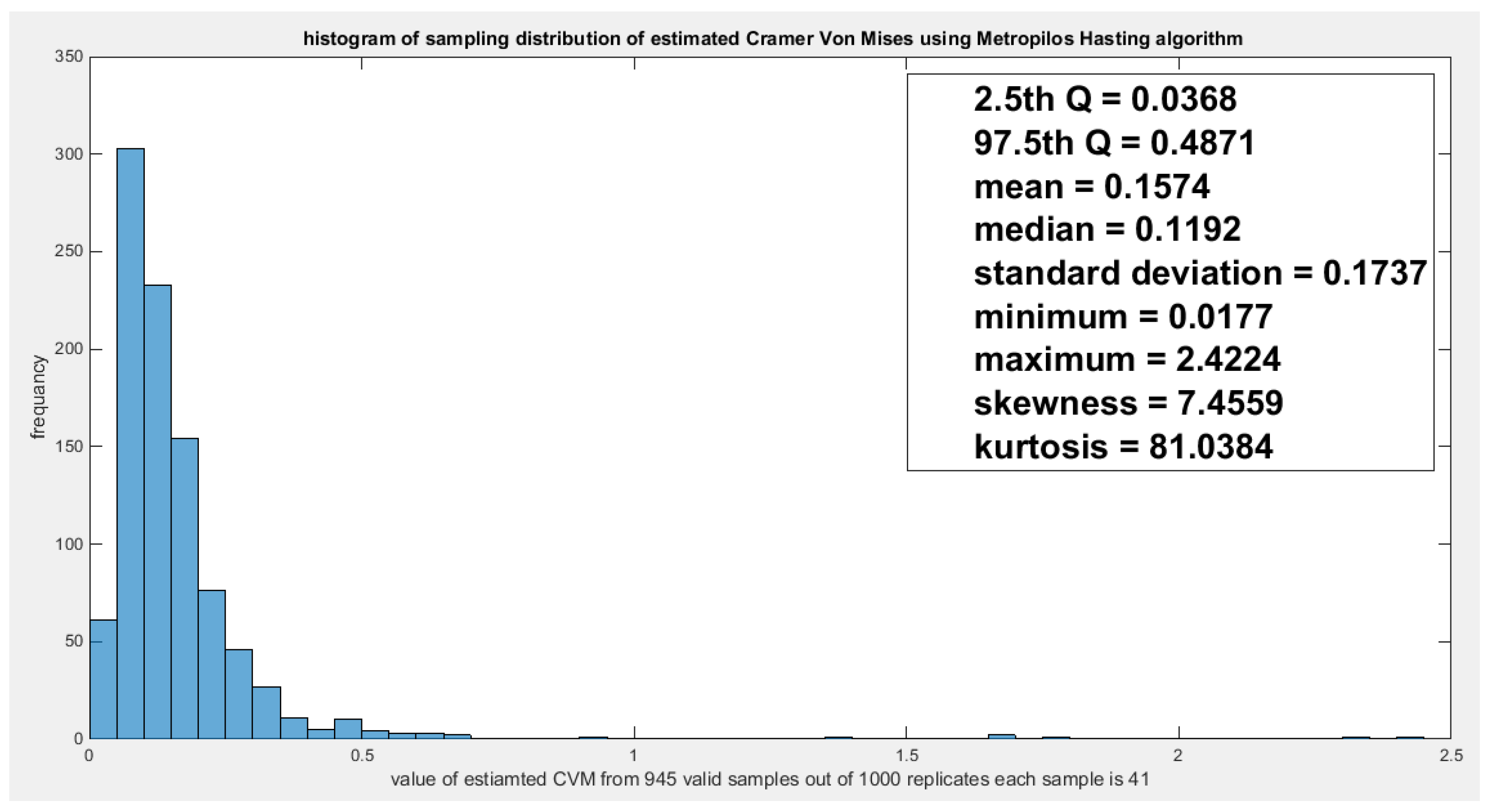
shows the sampling distribution of the CVM. The data obtained CVM is 0.4281 and it lays between the 2.5th and the 97.5th quantiles so the null hypothesis is failed to be rejected and the copula fits the data well. The p-value (probability of values less than or equal to 0.4281) is 0.9683, in other words, this 0.4281 does not lay in either of the tail regions of rejection.
Figure 29.
shows the sampling distribution of the CVM. The data obtained CVM is 0.4281 and it lays between the 2.5th and the 97.5th quantiles so the null hypothesis is failed to be rejected and the copula fits the data well. The p-value (probability of values less than or equal to 0.4281) is 0.9683, in other words, this 0.4281 does not lay in either of the tail regions of rejection.
Figure 30.
shows the sampling distribution of the dependency parameter. The 0.6703 lays in the acceptance region between the two quantiles, the 2.5th and the 97.5th quantiles. So the null hypothesis fails to reject its assumption. The p-value (probability of the values being less than or equal to this 0.6703) is 0.5651, which indicates that 0.6703 is not placed in either zones of rejection.
Figure 30.
shows the sampling distribution of the dependency parameter. The 0.6703 lays in the acceptance region between the two quantiles, the 2.5th and the 97.5th quantiles. So the null hypothesis fails to reject its assumption. The p-value (probability of the values being less than or equal to this 0.6703) is 0.5651, which indicates that 0.6703 is not placed in either zones of rejection.
Figure 31.
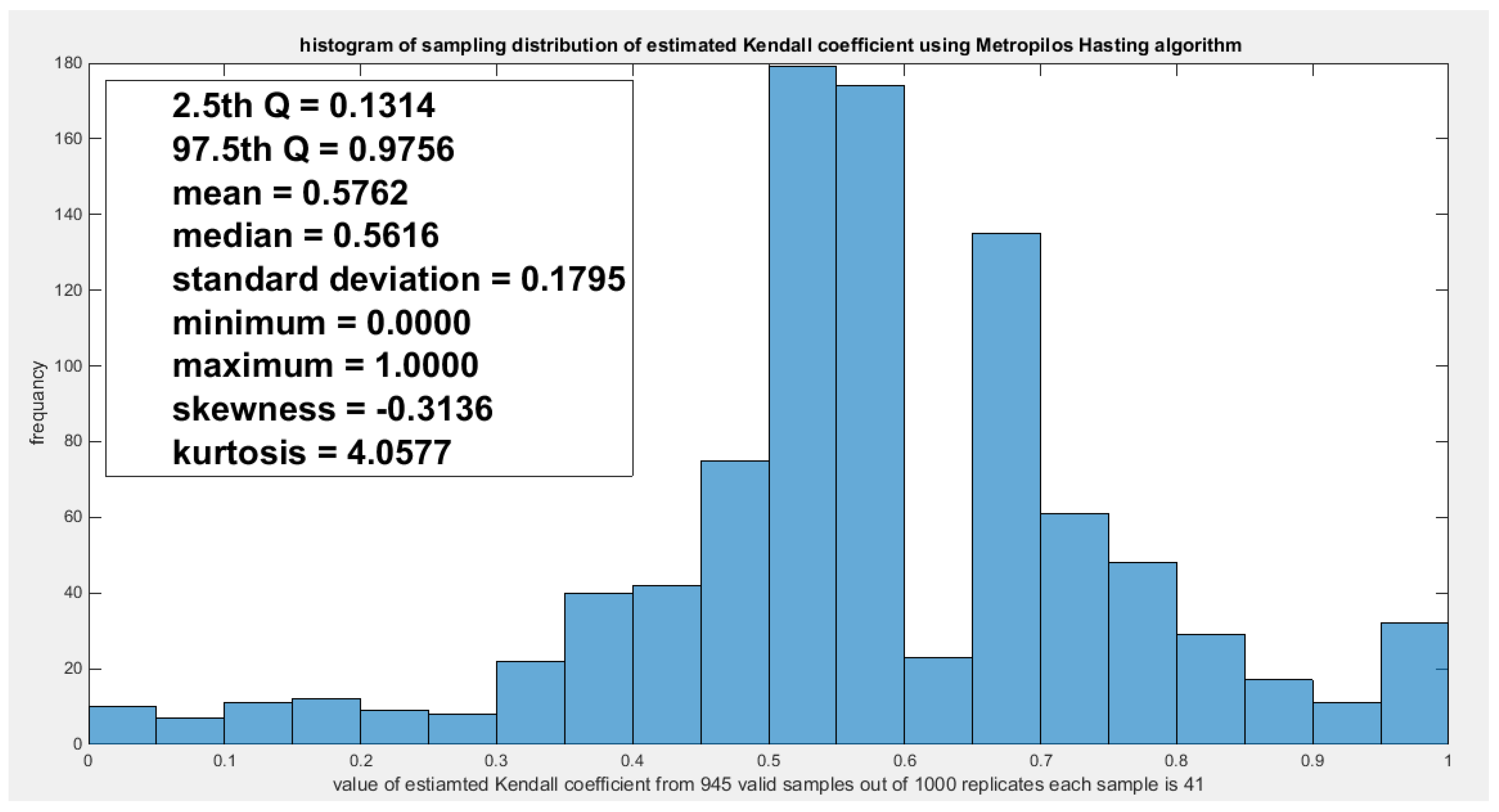
shows the sampling distribution of the Kendal tau coefficient. Its value 0.5507 is between the two quantiles 2.5th and 97.5th which is the acceptance zone. So the null hypothesis fails to reject its assumption. The p-values (probability of the values less than or equal to 0.5507) is 0.4423 which denotes that this value 0.5507 is far away from both rejection zones on the right and the left.
Figure 31.
shows the sampling distribution of the Kendal tau coefficient. Its value 0.5507 is between the two quantiles 2.5th and 97.5th which is the acceptance zone. So the null hypothesis fails to reject its assumption. The p-values (probability of the values less than or equal to 0.5507) is 0.4423 which denotes that this value 0.5507 is far away from both rejection zones on the right and the left.
According to the sandwich variance the variance covariance matrix for this model is:
The validity indices for the second stage are:
The validity indices for the whole model is the summation of these indices for marginal (first stage) and copula (second stage):
Theoretical upper tail coefficient is 0.6346. At quantile 0.7; the empirical upper tail coefficient in the direction of the ‘households net wealth’ variable is 0.6667 (2 points showing joint match out of 3 points in the upper tail at this threshold, 0.7) and in the direction of the ‘personal earnings’ variable is 1 (2 points showing joint match out of 2 points in the upper tail at this threshold, 0.7) while the confidence interval of the empirical distribution obtained from bootstrap sampling under the null hypothesis is [333,1] in the ‘ households net wealth’ and [0.2857,1] in the direction of ‘personal earnings’. This is expected because of the small sample size and left skewness of data.
Figure 32 shows the P-P plot of the empirical and theoretical copula.
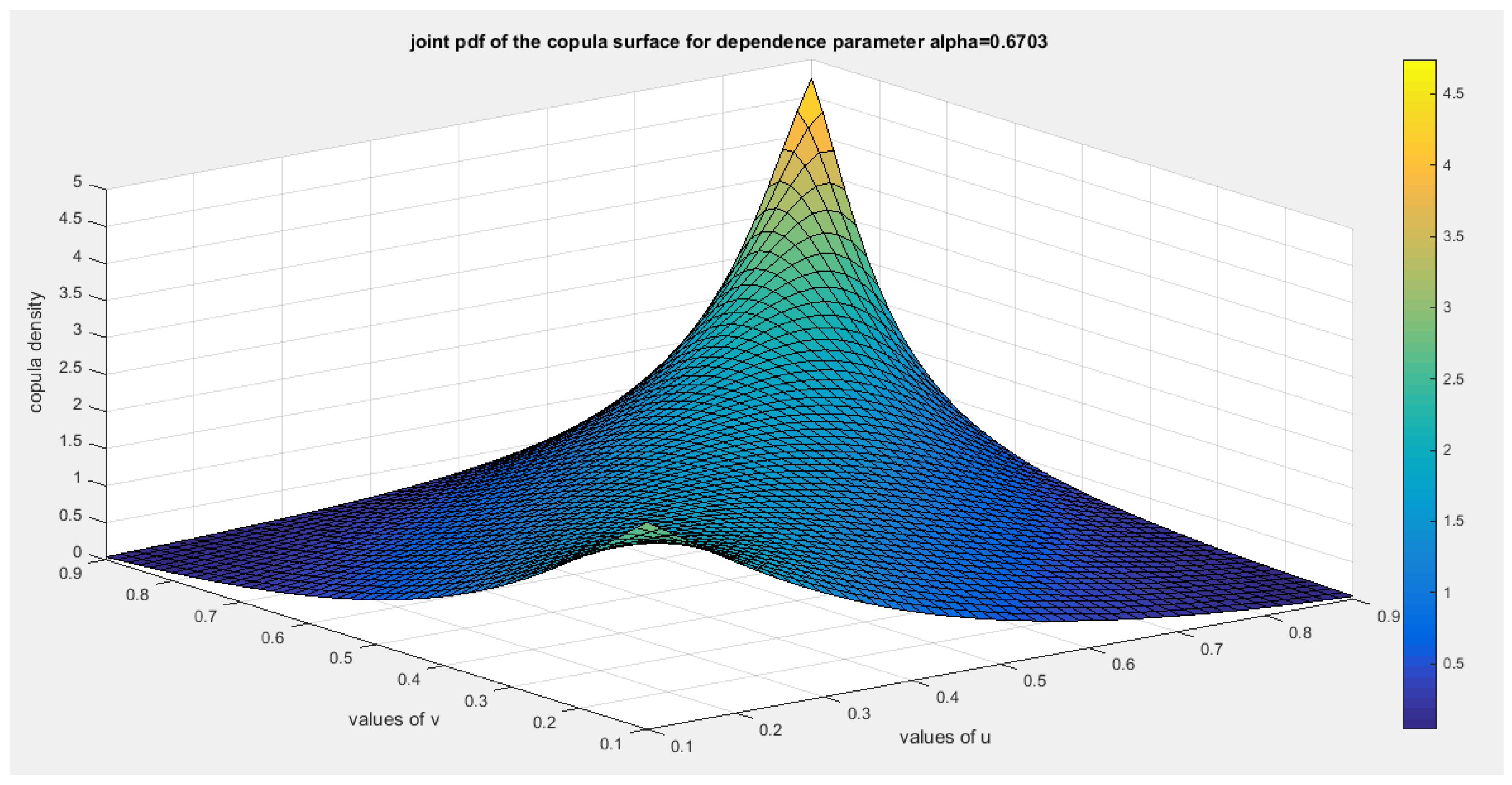
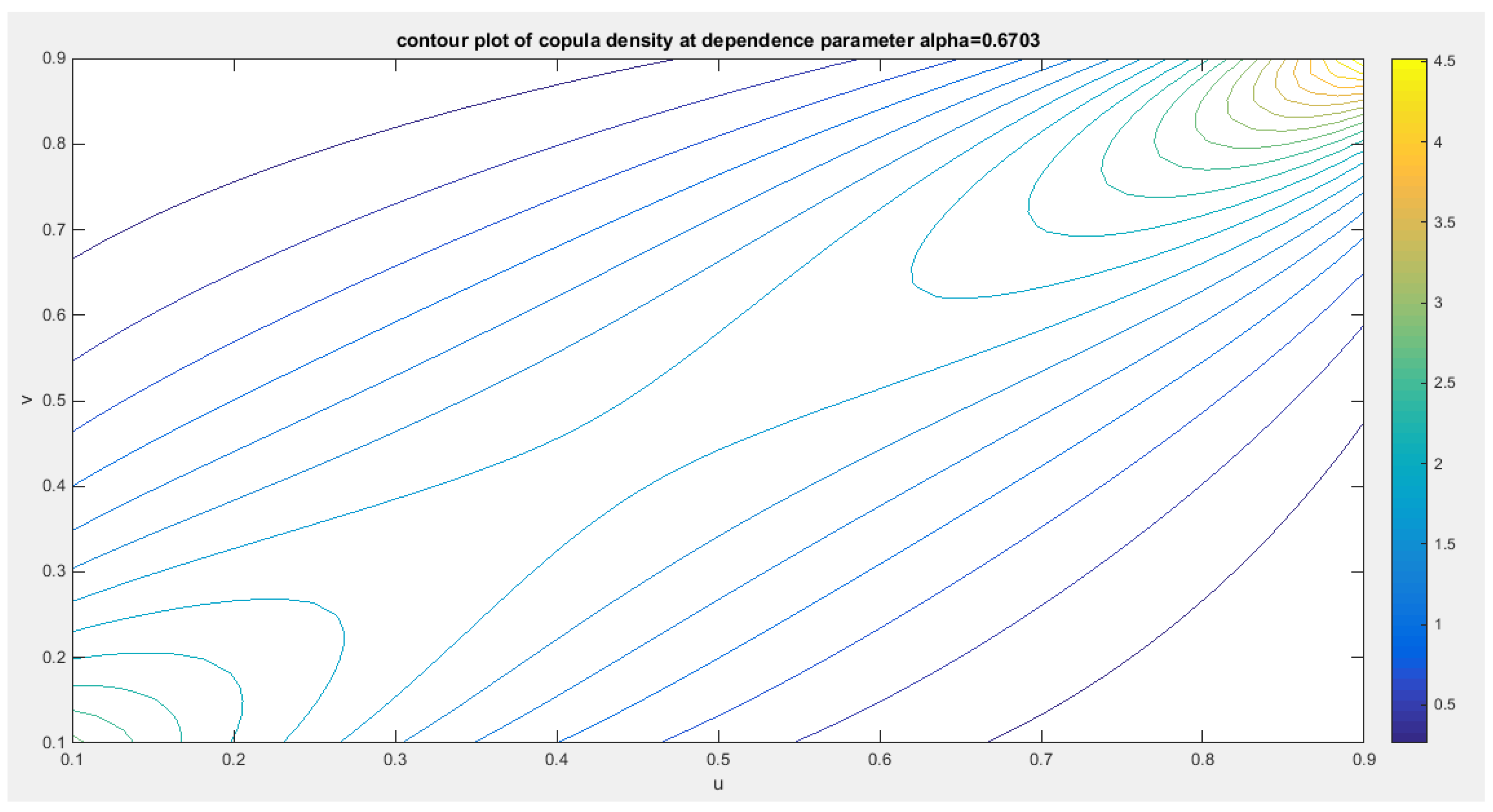
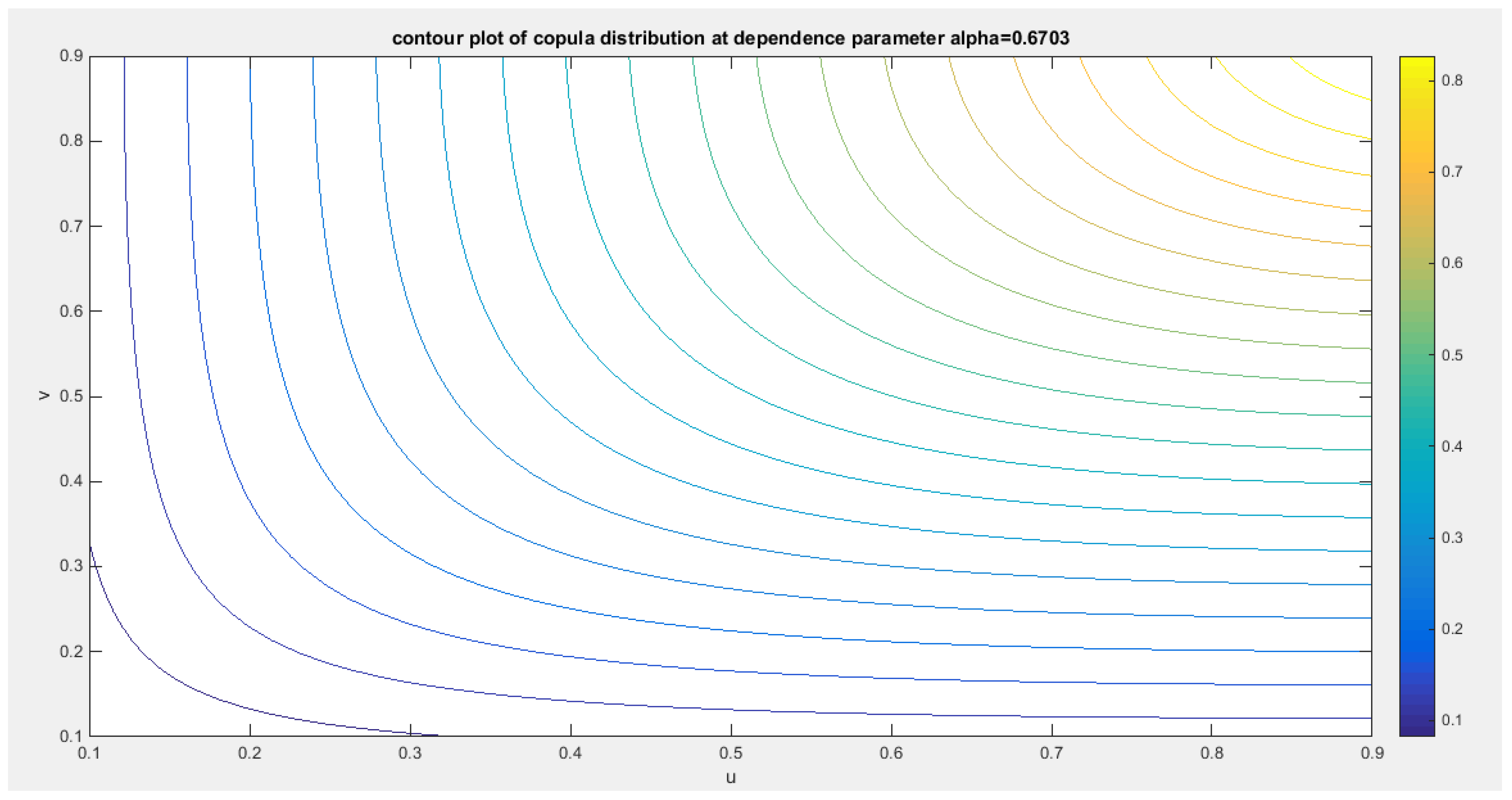
Figure 33,
Figure 34 and
Figure 35 show the surface of the density copula, the contour plot of the density copula and the contour plot of the distribution copula at the estimated dependency parameter.
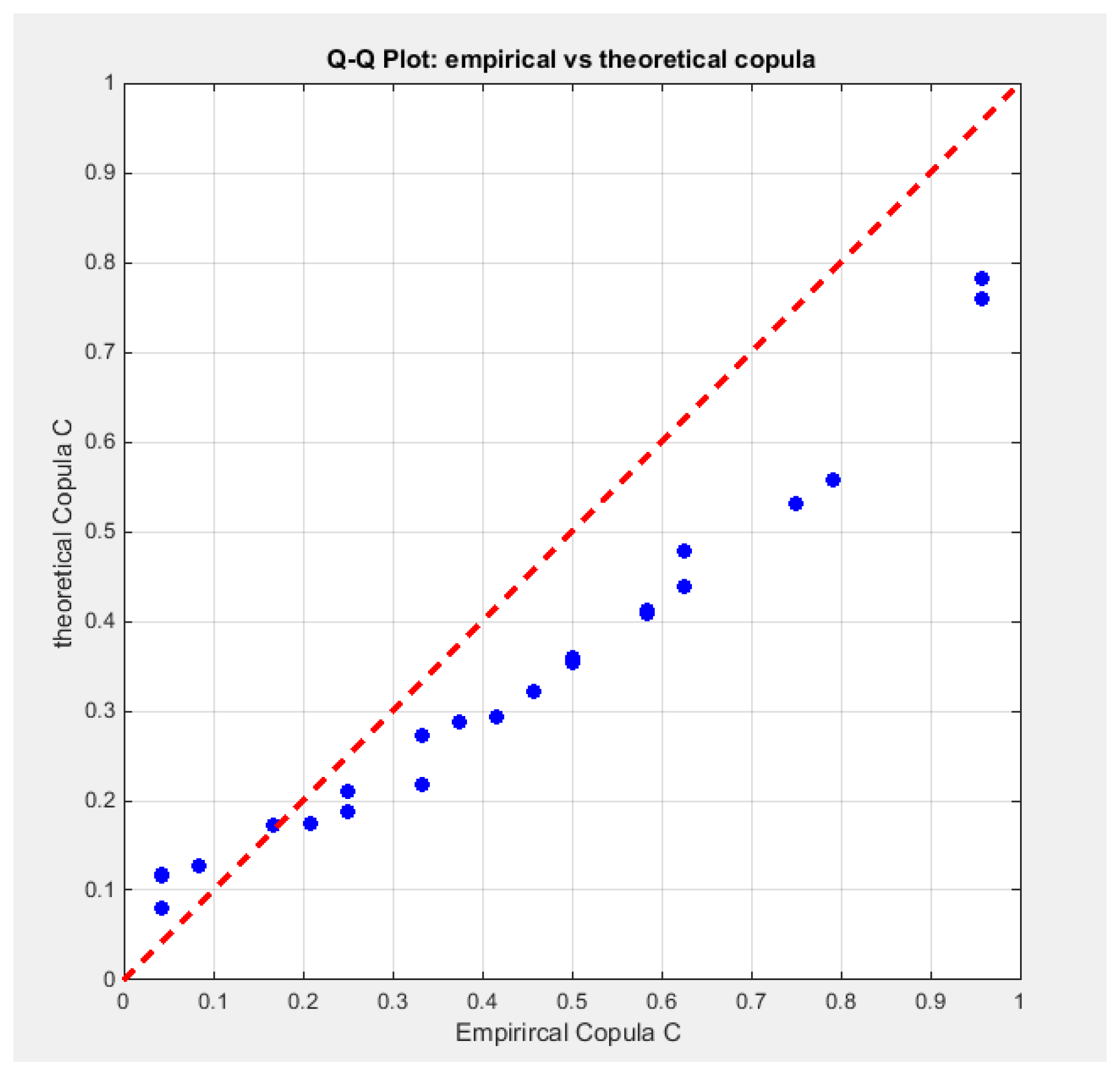
Figure 32.
shows the P-P plot of the empirical vs the theoretical copula. The theoretical copula shows near perfect alignment of its lower part with the diagonal line than its upper part.
Figure 32.
shows the P-P plot of the empirical vs the theoretical copula. The theoretical copula shows near perfect alignment of its lower part with the diagonal line than its upper part.
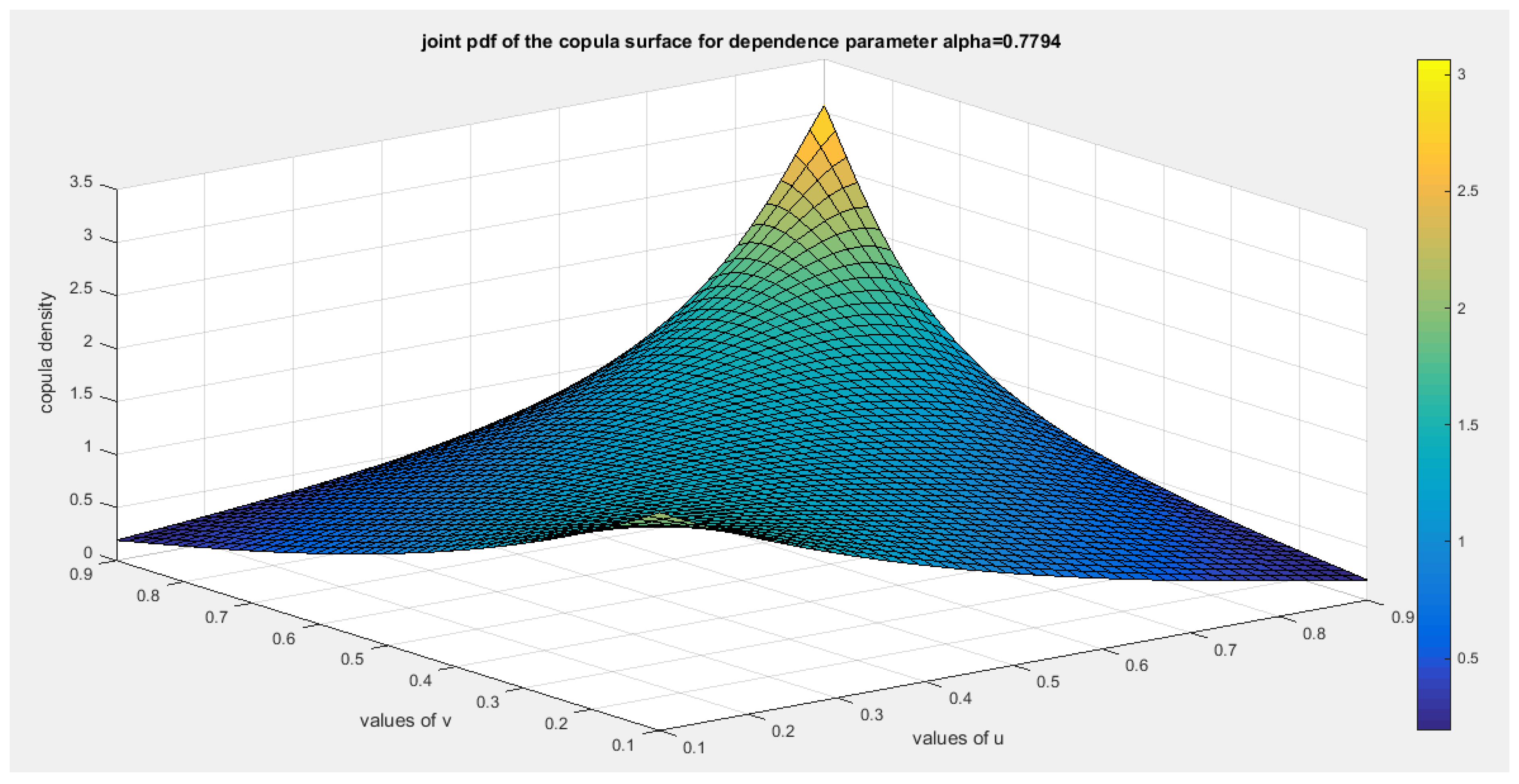
Figure 33.
shows the surface of the copula density with dependency parameter 0.6703.
Figure 33.
shows the surface of the copula density with dependency parameter 0.6703.
Figure 34.
shows the contour plot of the copula density with dependency parameter 0.6703.
Figure 34.
shows the contour plot of the copula density with dependency parameter 0.6703.
Figure 35.
shows the contour plot of the copula distribution with dependency parameter 0.6703.
Figure 35.
shows the contour plot of the copula distribution with dependency parameter 0.6703.