Investigating Thermal Conductivity in Graphene Moiré Superlattices Through Approach-to-Equilibrium Molecular Dynamics

1. Introduction

Thermal management is a fundamental challenge in the electronics industry, especially in the design of next-generation integrated circuits. Efficient heat dissipation is crucial for the performance and reliability of ultra-large-scale integrated circuits, where excess heat can degrade functionality and lifespan [1]. Graphene, with its extraordinarily high intrinsic thermal conductivity, offers a promising solution for thermal management applications, ranging from heat spreaders to thermoelectric energy conversion and advanced cooling systems [2,3].

Despite its high thermal conductivity, several factors influence heat transport in graphene, including defects, grain boundaries, isotopic composition, strain, and substrate interactions [1,2,3,4,5,6,7,8,9]. In particular, nanostructuration techniques, such as nanopatterning and chemical functionalization (e.g., hydrogenation, fluorination), have been explored to modulate graphene phonon transport properties [10,11,12,13,14]. These methods introduce phonon scattering sites that can either suppress or enhance heat conduction depending on the specific engineering approach. A recent and highly effective method for tuning graphene thermal conductivity is the creation of Moiré superlattices: these are formed when two graphene layers are stacked with a twisting angle, creating periodic interference patterns that significantly alter electronic and phononic properties [15]. In 2011, theoretical studies identified that specific twisting angles, known as "magic angles," result in flat electronic bands in twisted bilayer graphene (TBG), with the first magic angle commonly reported around ${1.1}^{°}$ [16]. This discovery led to the observation of exotic phenomena such as correlated insulating states, unconventional superconductivity, and magnetic ordering in TBG and other 2D material heterostructures [17,18].

Beyond electronic properties, recent studies have shown that Moiré superlattices also impact phonon transport and thermal conductivity in TBG. Similarly to other nanostructures, where thermal conductivity can be tweaked by imposing a superperiodicity [19,20], the realization of Moiré pattern can enhance or suppress thermal transport properties. Molecular dynamics simulations indicate that the thermal conductivity of TBG varies non-monotonically with twisting angle [21]. Specifically, the conductivity decreases as the twisting angle increases, reaching a local minimum at approximately $1.{08}^{°}$, followed by an increase up to $\sim 3^{°}$, after which it stabilizes. This non-trivial dependence is attributed to the emergence of Moiré phonons—phonon modes induced by interlayer twisting—that modify phonon dispersion and introduce additional scattering mechanisms [22]. Theoretical studies on phonons in twisted bilayer graphene reveal that the stacking order plays a critical role in phonon transport. Phonon dispersion in AA-stacked, AB-stacked, and twisted bilayer graphene with various rotation angles shows that the stacking configuration predominantly affects the out-of-plane acoustic phonon modes [23]. The introduction of Moiré superlattices leads to new phonon branches—entangled phonons—that originate from the mixing of phonon modes from different high-symmetry directions in the Brillouin zone. The frequencies of these entangled phonons depend strongly on the twisting angle and can serve as a mean for non-contact identification of twisting angles in graphene samples. Furthermore, the emergence of these Moiré phonons significantly influences the thermal conductivity of twisted bilayer graphene, modifying phonon scattering mechanisms and transport properties [23]. Additionally, twisted multilayer SnSe₂ Moiré superlattices have been experimentally synthesized and demonstrate a substantial reduction in thermal conductivity compared to their untwisted counterparts [15]. This is primarily due to enhanced phonon scattering, increased lattice mismatch, and the emergence of localized phonon modes. These findings highlight the potential of superperiodic structures and Moiré engineering for precise control over heat transport in 2D materials.

Despite these advancements, research on the thermal properties of Moiré superlattices remains in its early stages, with a limited number of studies focusing on small twisting angles and their phonon interactions. In this work, we explore the twisting angle dependence of thermal transport in TBG, with an emphasis on the first magic angle, $1.1^{°}$. Furthermore, we aim to establish a connection between the variations in thermal conductivity and the underlying phonon characteristics of Moiré superlattices. By investigating the role of Moiré phonons and their influence on heat transport, this study provides new insights into the fundamental mechanisms governing thermal conductivity in twisted 2D materials.

2. Methods

In this study, we employed classical molecular dynamics (MD) simulations to calculate the thermal conductivity of TBG at various twisting angles using the approach-to-equilibrium molecular dynamics (AEMD) method [24,25,26]. TBG samples were prepared by first initializing the atomic coordinates of monolayer graphene sheets with an interatomic spacing of $0.142$ nm [27,28]. The sheets were then duplicated and separated along the z-axis by $0.335$ nm [29] to form bilayers. We then rotated one layer by a precise twisting angle $\theta$ around a common center, forming a Moiré superlattice. The lattice parameters of the resulting structure were determined using the relation [30]:

$$a_{\mathrm{moire}}={\displaystyle \frac{\sqrt{3}a}{2sin(\theta /2)}}$$

(1)

where a is the lattice constant of graphene ($\approx 0.246$ nm). The number of atoms per Moiré unit cell was calculated as:

$$N_{\mathrm{moire}}={\displaystyle \frac{1}{{sin}^2(\theta /2)}}$$

(2)

We considered nine twisting angles $\theta$: $0.91$°, $1.02$°, $1.05$°, $1.08$°, $1.12$°, $1.20$°, $1.35$°, and $1.54$°, corresponding to Moiré unit cells with longitudinal dimensions L ranging from 15.9 to 26.9 nm and lateral dimensions d from 9.2 to 15.5 nm. The number of atoms in these unit cells varied between 11096 and 30248 (see Table 1). To construct the simulation supercells, the Moiré unit cells were replicated along their longest edge, forming samples with lengths L and widths d, containing between one and seven Moiré unit cells. To avoid artificial strains or stresses, an energy minimization step (box relaxation) was performed before each simulation.

To implement AEMD approach we defined separated regions within our simulation cell, as illustrated in Figure 1b. A step-like temperature profile is initially realized by thermalizing the top and bottom halves at temperatures $T_1=350$ K and $T_2=250$ K, respectively. The system is then evolved in the NVE ensemble while monitoring the temperature difference $\Delta T\left(t\right)$ between the average temperatures of the two halves of the supercell. The temperature difference follows an exponential decay, given by [24,26]

$$\Delta T\left(t\right)={\displaystyle \frac{8\left(T_1-T_2\right)}{{\pi }^2}}\sum _{m=0}^{\infty }{\displaystyle \frac{1}{{\left(2m+1\right)}^2}}{e}^{-{\left(2m+1\right)}^{2}t/\tau }$$

(3)

where $\tau$ was used as fitting parameter. The thermal conductivity $\kappa$ is finally calculated according to

$$\kappa ={\displaystyle \frac{3N{k}_B}{4{\pi }^2\tau }}{\displaystyle \frac{L}{S}}$$

(4)

where N is the number of atoms in the system, and $k_B=1.380·{10}^{-23}$ J K⁻¹ is the Boltzmann constant. The simulation cell section S is estimated as the width d of the sample multiplied by the interlayer distance and the number of layers. The length, width, and interlayer distance, are obtained from a fully relaxed box.

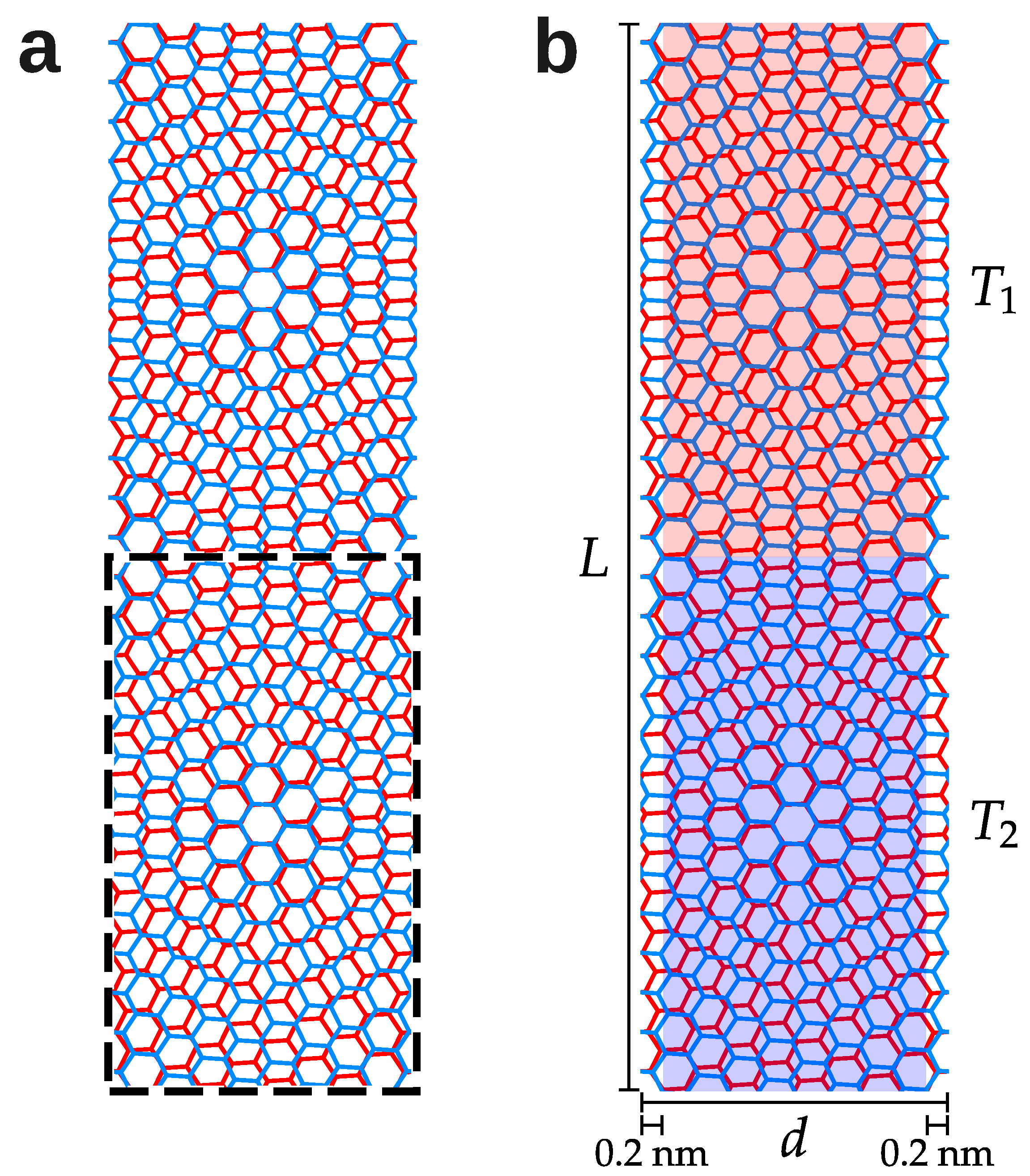
In order to assess the convergence of our results, we adopted the approach proposed by in Ref. [24]:

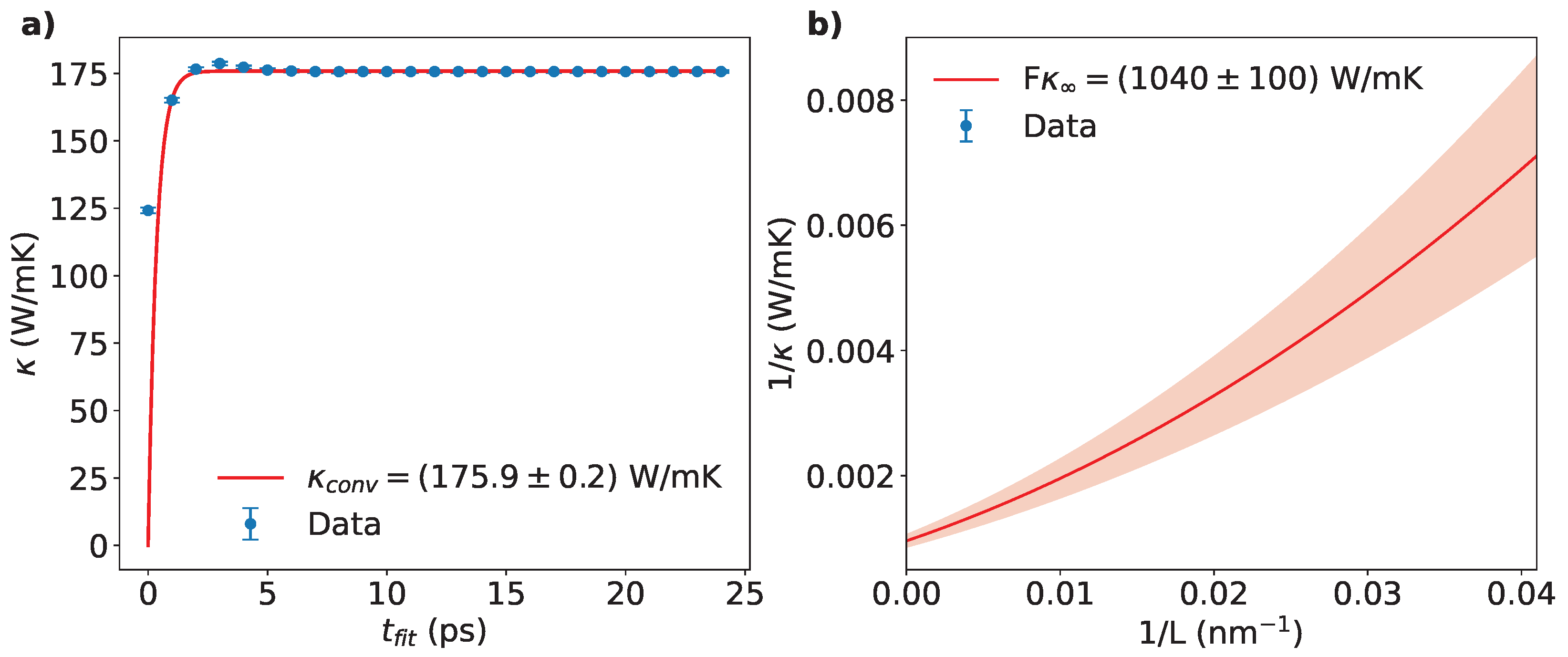
• the converged thermal conductivity ${\kappa }_{conv}$ is estimated for an infinitely long NVE simulation, according to

  $$\kappa \left(t_{run}\right)={\kappa }_{conv}\left(1-\beta e^{-t_{run}/\gamma }\right)$$

  (5)
• the thermal conductivity ${\kappa }_{\infty }$ for an infinitely long sample is obtained by a finite-size extrapolation, a commonly used approach in non-equilibrium simulations [31]

  $${\displaystyle \frac{1}{{\kappa }_{conv}}}={\displaystyle \frac{1}{{\kappa }_{\infty }}}\left(1+{\displaystyle \frac{{\lambda }_1}{L}}+{\displaystyle \frac{{\lambda }_2}{L^2}}+\cdots \right)$$

  (6)

MD simulations were performed using LAMMPS [31], employing the AIREBO potential [32,33] with a time step of 1 fs. The cutoff radius for the Lennard-Jones term was set to 1.02 nm1. NVE runs lasted between 25 to 35 ps, depending of the simulation cell size. To showcase the adopted protocol in detail, we consider here the smallest sample of AA-stacked bilayer graphene as a case study. We remark that the same procedure was applied to all the samples investigated in this work. First, $\Delta T\left(t\right)$ was fitted using Eq. (3) for different fitting times, $t_{fit}$, ranging from 1 ps (the first 1000 time-steps of the NVE run) to 25 ps, effectively covering the entire NVE run.

The obtained values of $\tau$ along with their corresponding uncertainties, $\delta \tau$, are used to obtain $\kappa$ and an associated error using Eq. (4), as shown in Figure 2a. We found our simulation results to be converged using a number $N_{exp}=5$ of terms in the sum of Eq. (3), although even a lower $N_{exp}$ yielded nearly identical: for example, the results for $N_{exp}=5$ and $N_{exp}=50$ differ by less than 0.1%, within the uncertainty margin. This is in line with the findings of Melis et al. [34], who also observed rapid convergence with increasing $N_{exp}$. The calculated $\kappa$ for each sample were determined by performing a weighted average on 4 statistically independent run with different initial velocities. The averaged values were reported as a function of L on a $1/\kappa$ vs. $1/L$ plot: Figure 2b shows the case of the AA-stacked graphene sample. A final extrapolation via Eq. (6) up to the second order of the Taylor expansion, was then used to produce the final value of $\kappa$ for that specific configuration. In what follows, we will refer to the extrapolated thermal conductivity ${\kappa }_{\infty }$ and its uncertainty simply as $\kappa$ and $\delta \kappa$.

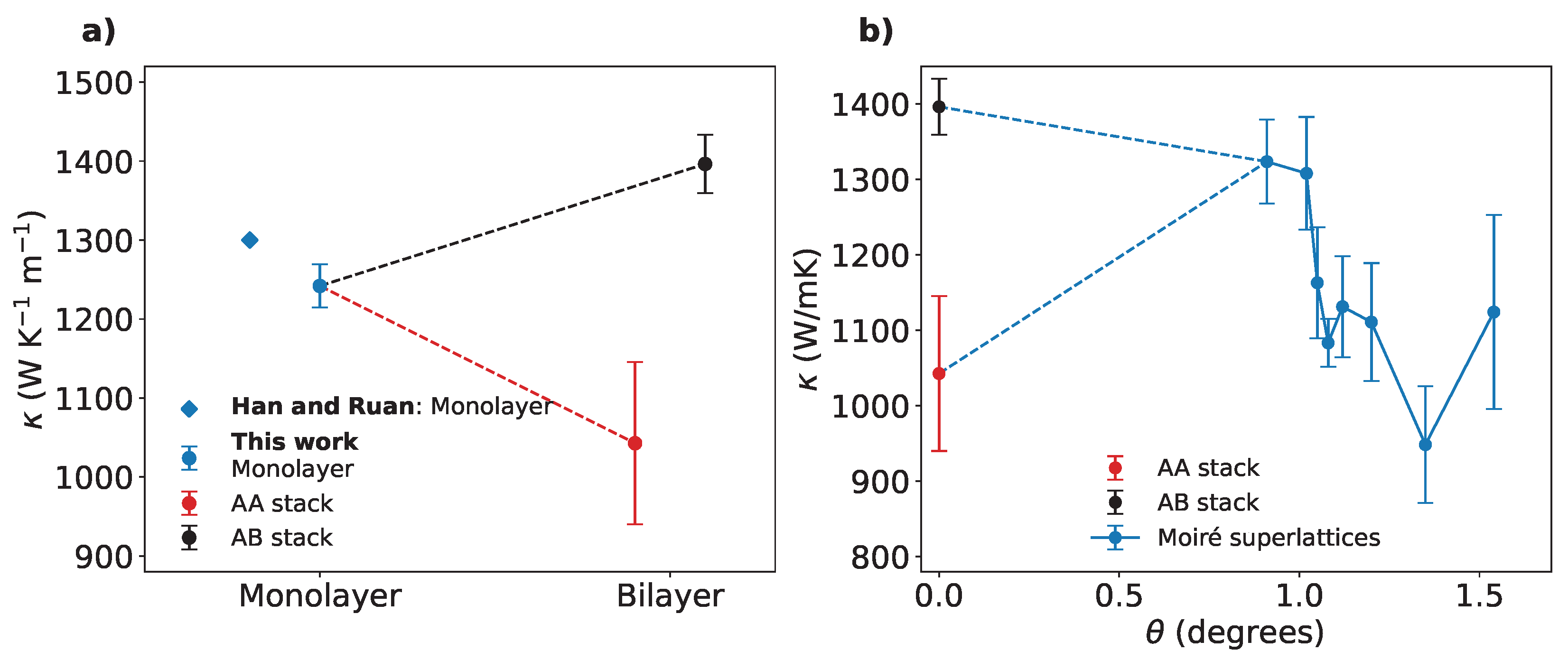
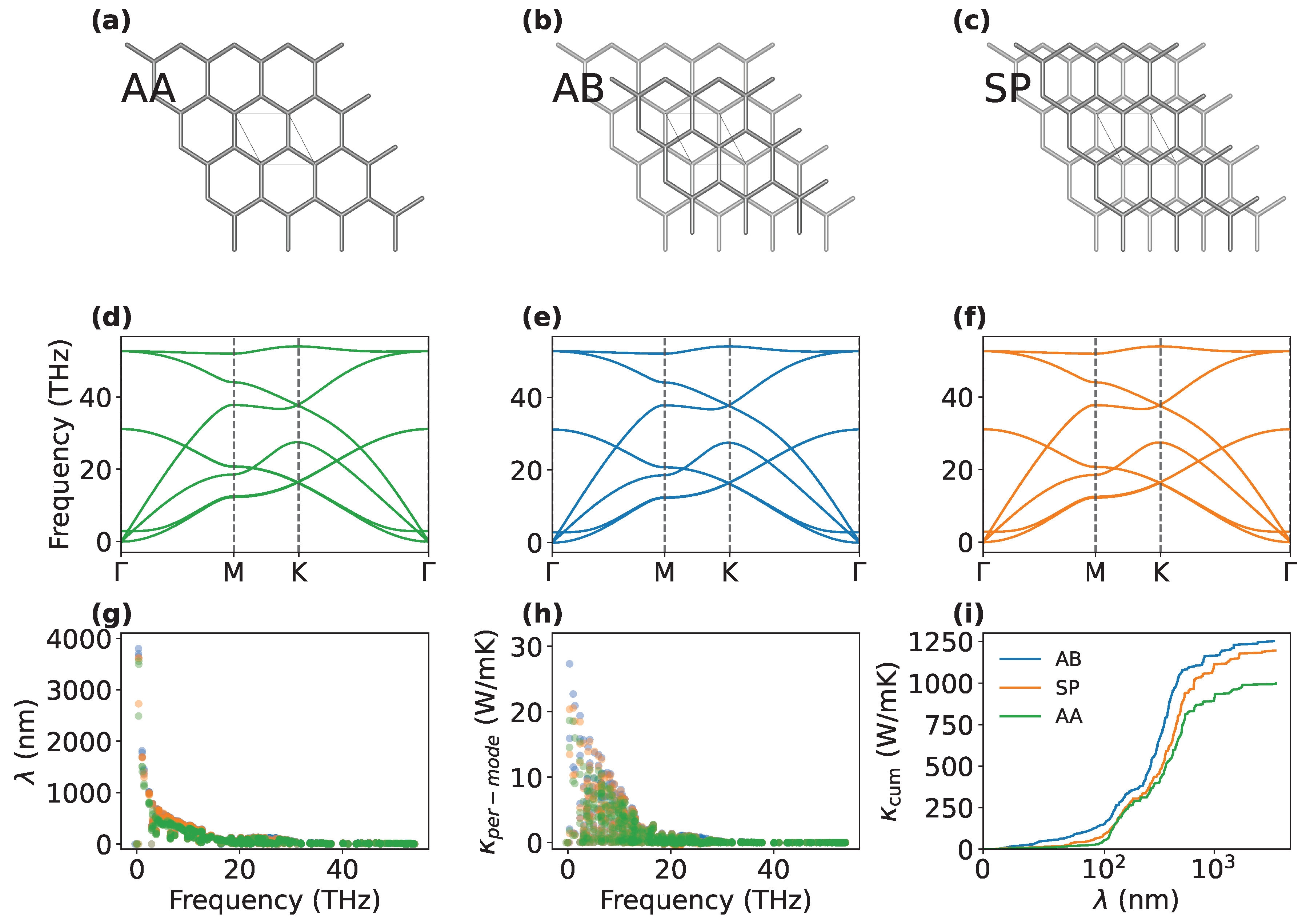
3. Results and Discussion

Using this procedure, we initially estimated the thermal conductivities of the graphene monolayer and bilayers in both the AA and AB stacking configurations, as reported in Table 2:

As stated in the introduction, the thermal conductivity of monolayer graphene remains an area of active research, with reported values ranging from 600 to 5000 W·${\text{m}}^{-1}·$K⁻¹ [28,35,36,37,38]. However, our prediction of $\kappa =(1240\pm 30)$ W/mK can be limited by size effects, as phonon mean free paths (MFP) in monolayer graphene can extend up to 10 $\mu$m [39]. However, the study of these size effects is beyond the scope of the present work. Our result is in good agreement with Han and Ruan [40], in which the thermal conductivity at room temperatures converges to 1300 W/mK for macroscopic sizes. Interestingly, the stacking of the layers appears to significantly influence the thermal conductivity of bilayer graphene: in Figure Table 2 we compare our data with those in Han and Ruan [40]. Although there is no general consensus about thermal conductivity in AA and AB stack [41,42], we remark that the value reported here are influenced by the adopted interatomic potential. According to the AIREBO potential, the AA stacking configuration results in an energy of $E_{AA}=-7.8489$ eV per atom, while for the AB stacking, $E_{AB}=-7.84936$ eV per atom, confirming the AB-stacked bilayer as the most stable configuration, as also reported by other studies [43]. However, the energy difference is less than 0.4 meV per atom—well below the thermal energy at ambient temperature (approximately 25 meV at 300 K). Given this small difference, we exclude the large variation in $\kappa$ to depend exclusively on the relative stability of the two configurations (equivalent calculations performed on ab initio system using PBE exchange-correlation functional confirmed AB as the most stable structure with an energy difference of $\sim 1.5$ meV). Furthermore, the interlayer distances between the two configuration differ by only $\sim 0.03$Å ($d_{\mathrm{AB}}=3.39$Å and $d_{\mathrm{AA}}=3.42$Å). Therefore, we cannot attribute the observed differences in thermal conductivity solely to variations in interlayer distance. We conclude that the significant difference in thermal conductivity is primarily driven by the stacking of the layers, rather than indirect factors such as equilibrium energy, interlayer distance, or size. The different stacking configurations likely modulate phonon transport through the bilayer, potentially suppressing or promoting it.

We report the thermal conductivity values for the TBG as a function of the twisting angle $\theta$ in Figure 3b. While the AB stacking configuration remains the most conductive, the conductivity values show a considerable variability with respect to the twisting angle. When comparing our results with those of [44] for the same temperature of 300 K, we observe a significant discrepancy, with their values being approximately twice as large as ours. As already pointed out, differences can be attributed by the choice of different force fields, which can have a substantial impact on the computed thermal transport properties of graphene [45,46,47]. While a non-monotonic trend with respect to $\theta$ can be identified, we also observe that a minimum in $\kappa$ occurs at $1.{35}^{°}$. Our results suggest a more irregular trend in the thermal conductivity of TBG for small twisting angles than initially anticipated, with very small angle variation resulting in large fluctuation in thermal conductivity. We cannot rule out the possibility that a more detailed study might reveal additional maxima and minima in this trend. Thermal conductivity of Moiré superlattices of graphene appears to be a highly-tunable property: in particular, variations of $\sim 33$% from the AB stack are observed within less than $2^{°}$. We attempt a qualitative explanation from our estimations for the thermal conductivity of the AA and AB stacks. In fact, Moiré superlattices in graphene are characterized by the presence of both the stacking types: the great difference in thermal conductivity manifested by AA and AB stacks can then have a major role in such tunability. The observed variation in thermal conductivity in TBG can be understood by considering the local stacking configurations that emerge within the Moiré superstructure. Due to the periodicity of the Moiré pattern, different stacking regions coexist, each exhibiting distinct phonon transport properties. We quantified the contribution of different configurations, by estimating the thermal conductivity for three notable stacking configurations in bilayer graphene—AA, AB, and SP (saddle-point) stacking (shown in Figure 4a,b,c)—by solving the Boltzmann Transport Equation (BTE) using the $\kappa$ALDo code [48,49]. $\kappa$ALDo computes phonon transport properties using the finite displacement method, which estimates interatomic force constants (IFCs) by considering harmonic and anharmonic lattice vibrations, to diagonalize the dynamical matric and solve the BTE.

The analysis of phonon dispersion curves reported in Figure 4d, e, and g for the AA, AB, and SP configurations respectively, does not reveal any significant variation in the phonon frequencies across the different stackings. However, more subtle features exhibit marked differences that critically impact the thermal transport. In particular, the analysis of the MFP distribution (Fig. Figure 4g) and the mode-resolved conductivity for the three stacking configurations (Fig. Figure 4h) results in some dependence especially in the low frequency region. The MFP spectral distribution reveals that the AA stacking has lower values than those of AB and SP, mainly occurring at low frequencies corresponding to acoustic phonon modes. While the phonon dispersion curves show negligible changes in phonon dispersion and group velocities, the observed differences in the acoustic regime are reflected in the mode-resolved conductivity: in agreement with the MFP analysis, AB and SP $\kappa$ distribution is highly peaked around 3-4 THz, where low-frequency modes (known as quasi-acoustic, low-frequency modes often fundamental for the propagation of sound-like waves at long wavelengths [50]) contribute with higher values of thermal conductivity compared to AA. This enhancement is due to their larger MFP and more efficient phonon transport in the acoustic range. The cumulative conductivity as a function of the MFP, shown in the right panel of Figure 4h, provides an additional point of view of the phenomenon: while phonons in the whole MFP range transport heat more effectively than the SP configuration, AA $\kappa$ saturates at lower values for phonons with a reduced extension.

The calculated values for total thermal conductivity from the BTE calculations are:

• AA: 1027.406 W·${\text{m}}^{-1}·$K⁻¹
• AB: 1274.969 W·m⁻¹·K⁻¹
• SP: 1217.723 W·m⁻¹·K⁻¹

The results indicate that the SP configuration closely resembles the AB stacking in terms of thermal transport properties, even when considering the offset between the two atomic planes. These results confirm the findings obtained through the AEMD simulations, both in terms of absolute thermal conductivity values and the overall trend. From this comparison, it emerges that the SP configuration is closer to the AB than to the AA stacking. AA stacking has the highest symmetry among the three, which could lead to fewer restrictions on phonon-phonon scattering processes (like Umklapp scattering). The lower symmetry of AB and SP configurations imposes stricter selection rules on which phonon interactions are allowed and this can suppress certain scattering channels that limit thermal conductivity, effectively increasing the phonon lifetime and thus $\kappa$ compared to AA [51]. This reflection symmetry is usually altered by interlayer interactions, which allows more scattering processes. These data suggest that the overall thermal conductivity for intermediate twisting angles is strongly influenced by the percentage of atoms that are in an intermediate configuration between the two stacking limits. In fact, although these stacking modes where previously considered as scattering sites that reduce thermal conductivity in the non-uniform structure [21], we infer from our observations that the thermal conductivity of TBG samples is intimately related to the composition in intermediate stacking configurations. In fact, since AB and SP represent structures where the perfect atom-on-atom stacking of AA is broken by a shift, the thermal conductivity of all the possible stacking configurations occurring between the AA and AB should be lower than in the extreme cases. The primary hypothesis to explain this behavior is based on an analogy with silicon/germanium alloys, where thermal conductivity varies according to the stoichiometry of the mixture [52]. The direct calculation via BTE cannot be performed, since these intermediate configurations are found to be metastable with respect to AA, AB, and SP (which we remark to be almost degenerate with respect to AB, as also found in [53]). Hence, to verify our hypothesis, we quantified for each twisting angle configuration the percentage of atoms that are exactly in one of the three notable stacking phases. This estimate was obtained by evaluating the x and y distances of corresponding atoms in the two layers and adopting a tolerance of 0.05Å. The result of this analysis (Fig. Figure 5) shows a trend similar to that of thermal conductivity, with a minimum that closely reproduces the minimum observed in the angular dependence of $\kappa$.

It is worth noting that, although there is a clear correlation between the percentage of atoms in defined stacking configurations and thermal conductivity, the two curves do not perfectly overlap. This discrepancy can be attributed to several factors: limited statistics, as the error bars in the simulations remain relatively large and may require more samples to improve precision; non-linear phonon effects, since the phononic states in intermediate configurations may not follow a simple interpolating trend between the two extreme stackings; complex atomic dynamics, as the assumption of stacking configuration stability, particularly for the AA phase at finite temperature, may not be entirely valid. Furthermore, as already mentioned, a treatment based on the BTE would be impractical for the intermediate stacking configurations and even less feasible for the TBG, due to the very large number of IFCs required to solve the equations.

4. Conclusions

In this work, we investigated the thermal conductivity of twisted bilayer graphene (TBG) as a function of the twisting angle using both classical molecular dynamics simulations and lattice dynamics calculations via the Boltzmann Transport Equation. Our results confirm that the thermal transport properties of TBG are highly sensitive to the twisting angle, with variations up to 30% observed over a range of less than 2°. The thermal conductivity reaches a minimum near the first magic angle and displays a non-monotonic dependence that correlates with the evolution of local stacking configurations.

By analyzing ideal AA, AB, and SP stacking arrangements, we showed that the reduced conductivity of AA stacking is primarily due to reduced mean free paths for low-frequency acoustic modes. In contrast, both AB and SP stackings are characterized by extended vibrational modes, particularly in the acoustic regime, which enhances their ability to conduct heat. These observations were corroborated by mode-resolved and cumulative thermal conductivity analyses. In addition, we showed that the thermal conductivity of TBG can be qualitatively explained by the different distribution of stacking configurations within the Moiré supercell. In particular, we found that the local proportion of AA, AB, and SP stacking regions plays a critical role in determining the effective thermal transport. Regions with higher AA, AB and SP content contribute more efficiently to heat conduction, while areas characterized by intermediate stacking arrangement can act as bottlenecks due to suppressed acoustic phonon transport. The correlation between the relative abundance of these stacking configurations and the total thermal conductivity underscores the highly tunable nature of heat transport in TBG, strongly affected by the microscopic structural composition of the Moiré pattern.