1. Introduction
Twisted Bilayer Graphene (TBLG) exposed to a constant electric field undergoes a zero-resistance state at a temperature below 1.7K [
1]. The TBLG has remarkable properties; superconductivity [
1], Mott insulator behavior [
2], suppressing group velocity at certain angles and its relationship with electronic correlation [
3,
4,
5,
6]. The relative twisted angle between layers, in 2D materials such as TBLG [
7,
8], has become an undeniable phenomenon and a new field. In this way, magic angle value provided a novel knob for tuning superconducting properties [
1] and many-body effects [
2,
9,
10]. By contrast, recently superconductivity was reported in non-twisted rhombohedral trilayer graphene, a system without moiré patterns [
11]. This could lead one to think that a specific piece of a TBLG could originate the superconductor state. Nevertheless, to achieve this specific piece, from a technical point of view, it is easier to twist a set of layers than to achieve very tiny displacements between them.
These quite specific structures drive towards providing needed characteristics to the superconductivity become possible. In the end, all of them could have in common a fundamental characteristic: the Cooper pairs. To set superconductivity up, the electrons belonging to a Cooper pair and their interaction by phonon must keep up energy and momentum conservation laws. Also, this kind of interaction must have enough energy to overcome repulsive Coulomb interaction so that the superconductor phase becomes feasible. Each of these conditions is corresponded with a probability. If then a sum of overall electronic energies are performed over the product of these probabilities, it turns to end a simultaneous probability to get a Cooper pair as a function of lattice vibrational energy and
, namely
function [
12]. This function is built from the well-established Eliashberg spectral function and phonon density of states, calculated by first principles (for more details see reference [
12]). Cooper-pairs distribution function
promises to provide information about the superconductor state through the determination of the spectral regions of Cooper-pairs formation. In addition, from
function is possible to obtain the N
parameter, which is proportional to the total number of Cooper-Pairs formed at temperature
[
13,
14].
function has been used to evaluate some superconductor systems [
12,
13,
14,
15].
In this paper, we aim to contribute to the understanding of superconducting fundamentals of challenging structures such as TBLG. We study an untwisted-misaligned bilayer graphene (UMBLG) structure, which mimics a specific region of a TBLG lattice, using Cooper-pairs distribution function . Here, we report and analyze function of UMBLG structures in the presence of a perpendicular external electric field, at temperature K. The findings show that superconductivity in these structures responds to slight relative displacement between graphene sheets and to external electric fields, as in magic angle TBLG.
2. Materials and Methods
In order to build the
function, calculations of electronic density states, vibrational density states, and the Eliashberg function of the concerned structure are required. To perform these ab initio calculations, we first relaxed the internal degrees of freedom and the lattice vectors of the crystal structure using the Broyden–Fletcher–Goldfarb–Shanno (BFGS) quasi-Newton algorithm [
16,
17]. From these relaxed structure configurations, electronic and phonon band structures, electron (DOS) and phonon (PhDOS) densities of states, and the Eliashberg function
are calculated, for this study, in the presence of perpendicular electric fields;
, 3
, and 5
, with
mV/
Å. We used a kinetic energy cut-off of 70 Ry for the expansion of the wave function into plane waves and 280 Ry for the density. To integrate over the Brillouin zone, we used for the electronic integration a k-grid of 32 × 32 × 1 and the phononic integration a q-grid of
, according to the Monkhorst–Pack scheme [
18]. We performed the calculations using the pseudopotential plane-wave (PW) method of Perdew
et al. [
19], the generalized gradient approximation (GGA), and a Troullier and Martins [
20] norm-conserving pseudopotential. The cut-off and grids were chosen big enough to obtain a good precision in
calculated within the density-functional perturbation theory (DFPT) frame [
21,
22]. We used the Quantum Espresso code [
23] for all these calculations.
2.1. Cooper-Pairs Distribution Function
Conventional superconductivity can be explained by an attractive electron-electron interaction (Cooper pair) mediated by the lattice phonons. Cooper-pairs formation is induced by the simultaneous occurrence of specific physical conditions, which can be described as a product of probabilities in terms of electronic and vibrational states, and electron-phonon interaction of a system, that summed over all electronic states defines Cooper-pair distribution function
, given by
where
and
are the simultaneous probability at
T related with the presence of electronic states occupied and available (near to the Fermi level), as well as optimal vibrational frequencies, which are candidates for the consolidation of a attractive interaction potential, that drives Cooper pair formation. Further,
establishes the electron-phonon coupling probability [
24,
25], through the well-known Eliashberg spectral function and phonon density of states. In this sense,
function provides the spectral range where Cooper pairs could be formed.
Furthermore, from
function it is possible to estimate the total number of Cooper pairs formed at the temperature through a quantity proportional to it, the parameter
, given by
Where is phonon energy and is a cutoff energy, so that to is negligible.
2.2. Structure
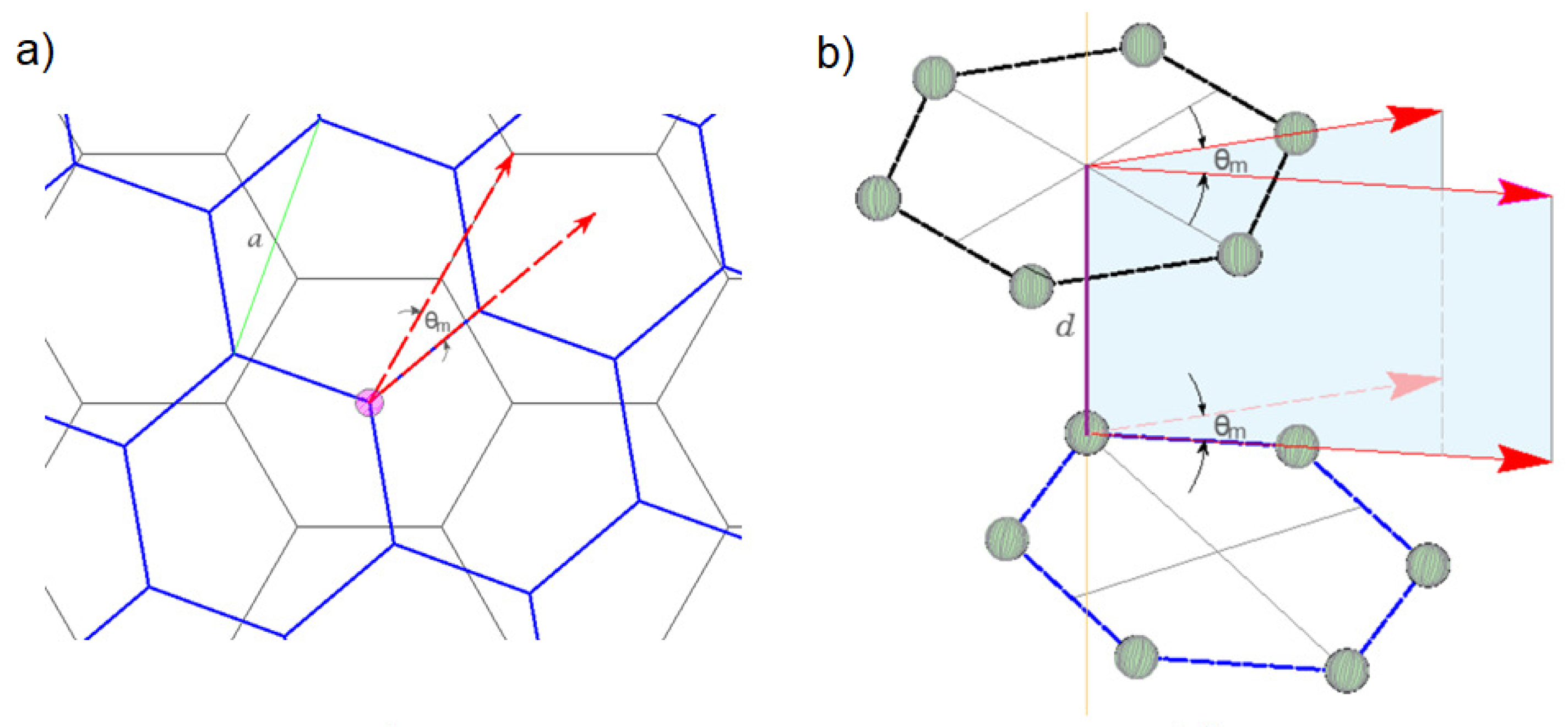
Figure 1 illustrates the AB-staked TBLG structure. The top view, in
Figure 1a, shows two hexagonal layers, where one is rotated with respect to the other at a small angle
, and
Figure 1b illustrated the side view showing the corresponding interlayer distance
d.
Figure 2 summarizes the geometric concepts used to determine the structural, electronic and vibrational properties of the AB-stacked TBLG structure. The rotation angle
in a commensurate rotation condition (
) [
26] is determined as following:
with
, allows long-wave-length Moiré pattern with
[
27].
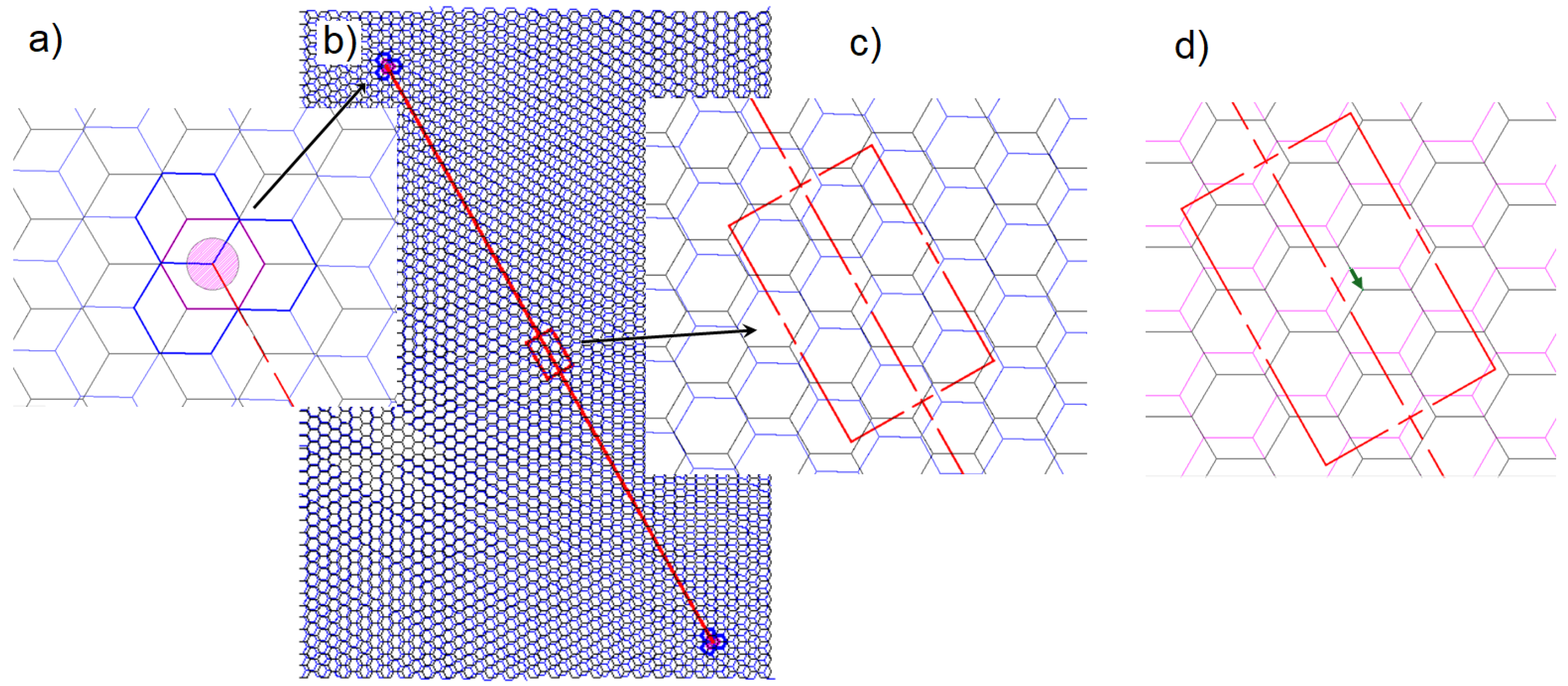
With the purpose of establishing a possible UMBLG structure associated with a TBLG structure, we initially consider a supercell of an AB-stacked BLG rotated at a specific small angle
(
Figure 2b), in which were identified two equivalent regions where AB-staked TBLG configuration are situated particularly around a rotation axis (see
Figure 2a). In the midpoint of these regions, corresponding to
, we encounter a lattice arrangement akin to Misaligned Bilayer Graphene, which is observed as two AB-stacked layers with a parallel displacement between them, as illustrated in
Figure 2c. We established that the value of this displacement
is linked to the twisted angle
of the TBLG structure associated. Moreover, this displaced structure can be easily built from an untwisted bilayer graphene (
Figure 2d).
Table 1 shows the geometrical characteristics of three configurations, and the respective displacement values
associated to each twisted angle
.
The structure proposed in this study consists of four carbon atoms (two per-layer) whose positions and internal parameters generate two displaced-layers graphene layers, which reproduce the AB-stakes BLG structure in the zone . In this cell unit, a of 12 Å vacuum gap was used to eliminate interactions between periodic images perpendicular to the slab surface.
3. Results and Discussion
Relaxation procedure leads to a lattice constant of
Å, which is in good agreement with other theoretical reports [
22,
28]. On the other hand, we find out the inter-layer distance
Å,
Figure 1b. By contrast, experimental and theoretical reports are 3.35
Å and 3.31
Å [
28,
29] to AB-stake BLG. The discrepancy is due to the bilayer has been put isolated. To do so, we set the AB-stakes bilayer up into a cell with a vertical length of more than eleven times the lattice constant to dismiss the inter-bilayer interaction. We used the Quantum Espresso code [
23] for all these calculations.
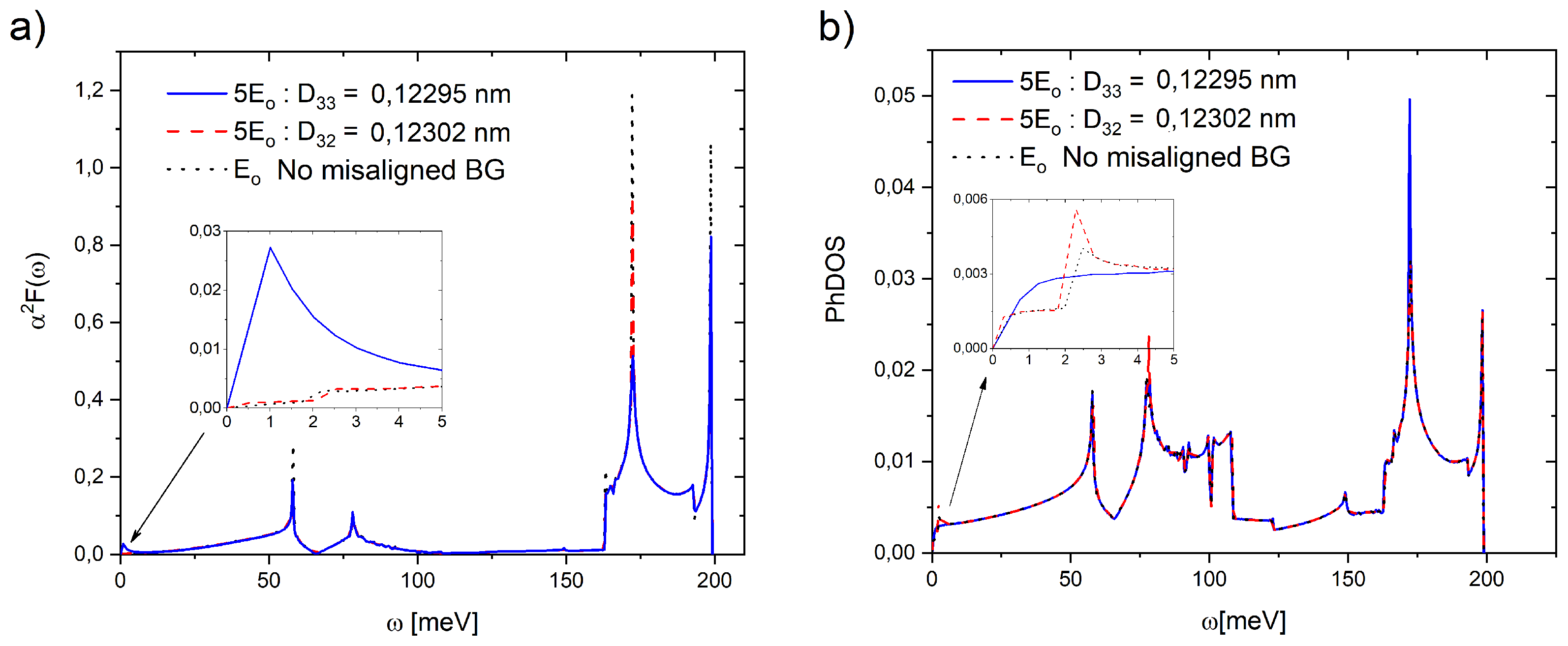
Figure 3 shows the Eliashberg function
and Phonon density of states (PhDOS) calculated for AB-stacked Bilayer Graphene proposed in presence of a perpendicular electric field proportional to
mV/
Å, and AB-stacked Untwisted-Misaligned Bilayer Graphene (associated with
and
angles of a TBLG) in presence of a perpendicular electric field of
. These spectra show four characteristic peaks located approximately at 60, 80, 170 and 200 meV, which are consistent with the theoretical calculations of AB-stacked Bilayer Graphene (with 10 000 atoms) reported by Choi
et al. [
30,
31] using
, and PhDOS of TBLG at
and
(with 28 and 76 atoms, respectively) reported by Cocemasov
et al. [
32].
It is observed from
Figure 3 that the
and PhDOS are nearly insensitive to the small displacements associated with twist-angle (
) as well as to the presence of an electrical field. Besides, the insensitive of PhDOS (TBLG) to the twist-angle was observed by Cocemasov
et al. [
32]. Therefore, it is almost not possible to establish significant differences induced by displacements (associated with
) or
, more than those observed below 5 meV (see inset of
Figure 3). At first sight, these slight differences do not seem to offer significant information about variations in the MUBLG properties. However, with these spectra, it is possible to obtain the Cooper-pairs distribution function
, which allows evaluating the system in the superconducting state [
12,
14].
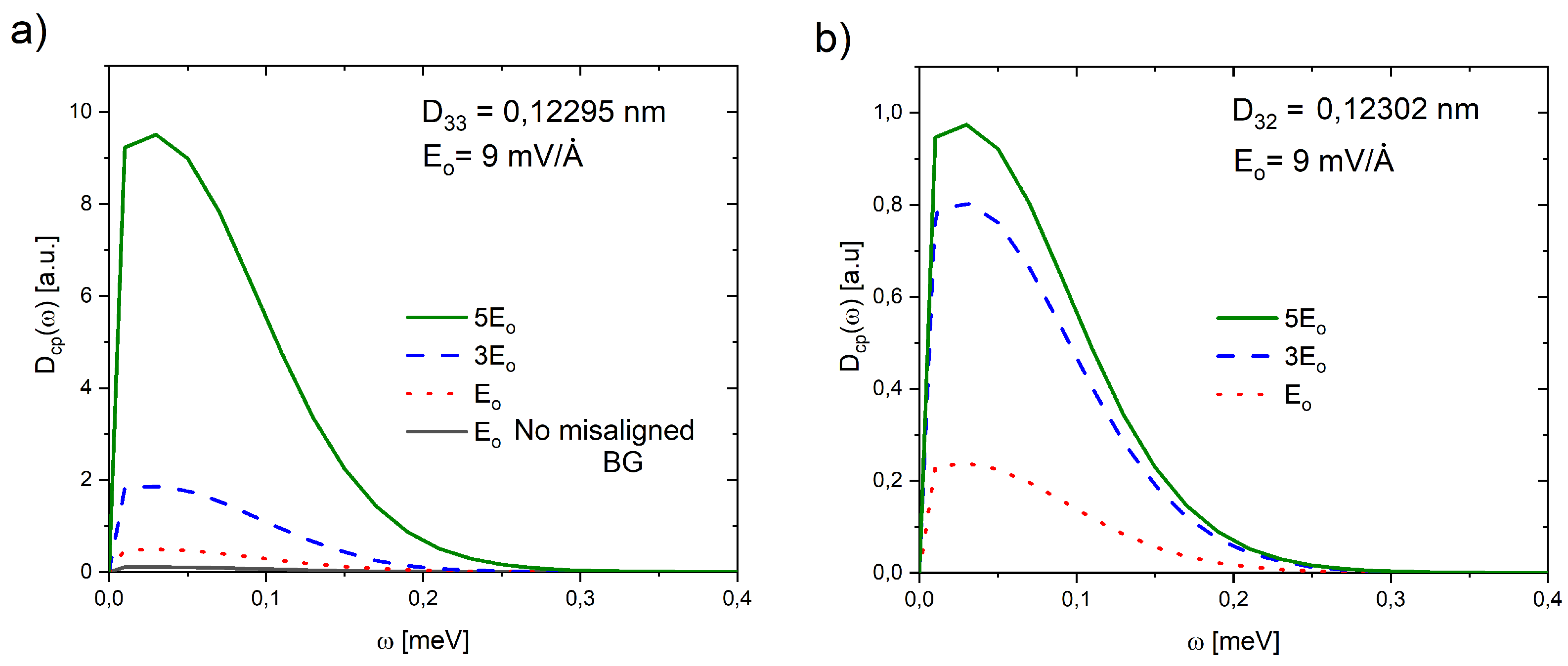
Figure 4 shows the
function of AB-stacked Untwisted-Misaligned Bilayer Graphene (associated with angles
and
) in presence of an electrical field.
function of MUBLG suggests that Cooper-pairs are possible in the low-frequency vibration region. By contrast, BLG with a perpendicular electric field of magnitude
(
Figure 4a), it is in the normal state (non-superconducting). It is inferred because it reports a
. Namely, the superconducting phase is theoretically observing if
function is not zero, which, in this case, is achieved when Bilayer Graphene is displaced (associated with a rotation small angle) in the presence of the electric field. This condition matches the experimental reports (superconductivity in magic-angle graphene superlattices [
1]). It suggests the origin of superconductivity in this kind of structure could be a little misaligned piece. It is also evident from
Figure 4 that the
function reveals a significant sensitivity to displacements associated with small variations of
as well as to the presence of an electric field (note the scale differences between
Figure 4 a) and b). This is possibly due to the correlational analysis of the electronic and phononic properties of the system that the
function achieves, which cannot be determined from an individual evaluation of such properties, as was evidenced with the results presented in
Figure 3. However, the sensitivity of the
function is a criterion that requires more calculations to be validated, in addition to those already carried out (H
S [
12], Nb [
13] and D
S [
14]).
function of MUBLG shows a quasi-gaussian form, which is appreciably affected by
and the presence of an electric field. It is observed that an increase in the intensity of the electric field leads to an increase in the area under the spectral line and moves it slightly towards higher values of frequencies, for both angles. However, the effect was more marked for
(note the difference in the scale of the vertical axes in
Figure 4.
is only observed at frequencies below
meV (centered around
meV), which seems consistent with the low critical temperature of TBLG (
K [
1]).
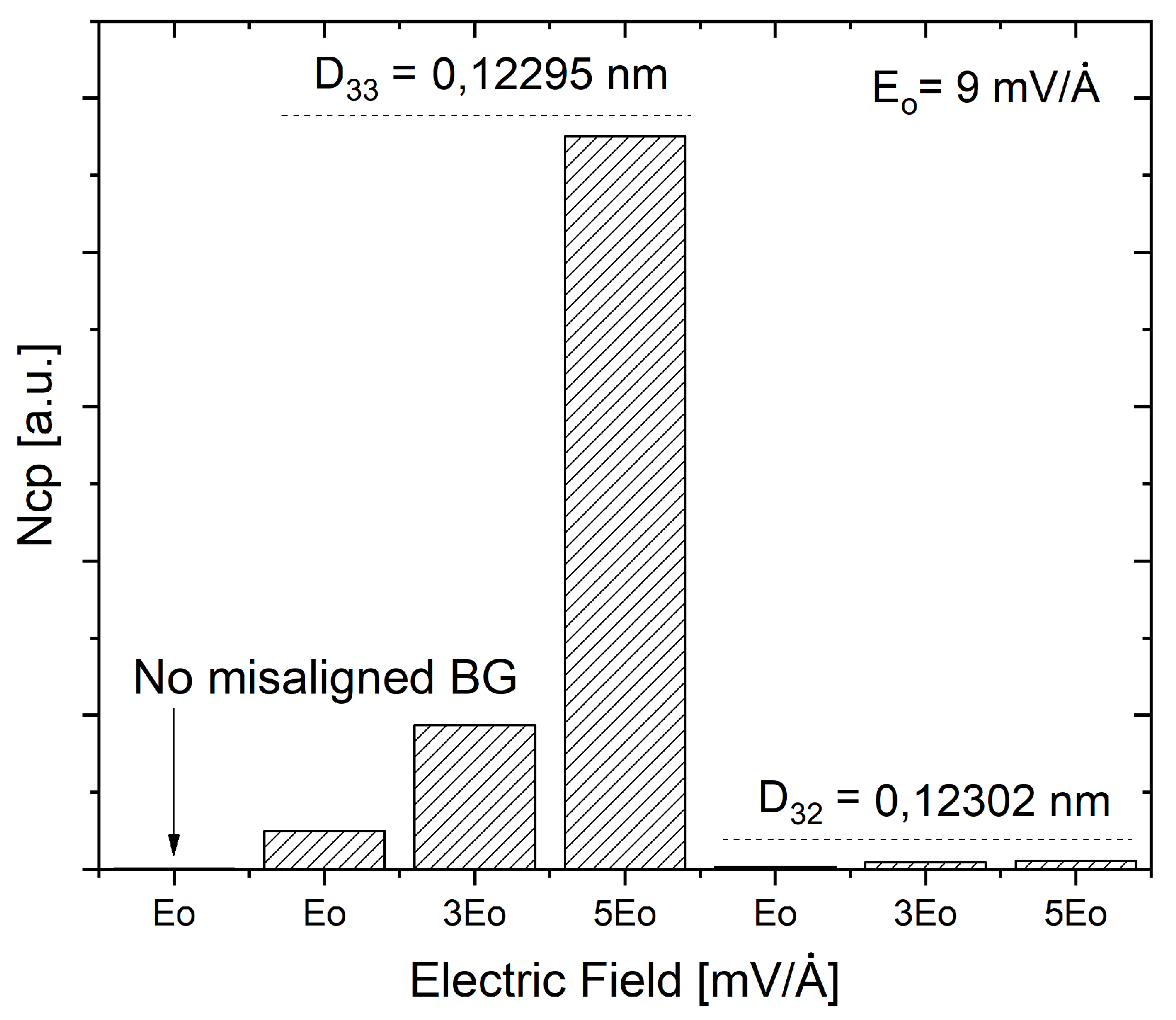
Furthermore, from
function it is possible to get an estimate of the total number of Cooper pairs formed at temperature T
through a quantity proportional to it,
parameter [
13,
14]. The comparison of
parameters obtained from each
as a function of an electrical field, for both misaligned structures which are associated with two angles, is shown in
Figure 5.
It is observed in
Figure 5 that an electric field has a greater effect on
parameters obtained of UMTBLG associate with the angle
, compared to
. This could be because the electric field affects the flat band physics (dispersion and topological properties) [
33,
34], which are associated with the superconducting phase. Since a high
value implies a high
[
13,
14], hence it can be suggested from
Figure 4 that an increase in the intensity of the electric field could lead to an increase in
in TBLG, for a specific angle of rotation. Besides, calculations to
nm (
) were performed also. Outcomes showed the regarding
function much less than
nm (
) in case, so it was not included in
Figure 4 and
Figure 5.
Finally, despite the consistent results shown up to now, some expression of the characteristics flat bands of TBLG [
33] are not observed directly in the version of
used in this study. This requires further analysis.
4. Conclusions
In this study, we reported for the first time, to the best of our knowledge, the Cooper-pairs distribution function of Untwisted-Misaligned Bilayer Graphene (UMBLG), under the influence of external electric fields. The UMBLG structure was proposed as a structural geometric approximation that mimics a characteristic region of a Twisted Bilayer Graphene (TBLG) structure. This UMBLG structure was modeled as two AB-stacked layers with a parallel displacement between them. We consider three displacements nm, nm, and nm, which are linked with the rotation angles (near to magic-angle) , , and , respectively, associated to Twisted Bilayer Graphene (TBG). function of Bilayer Graphene in the presence of an electric field was also calculated, as a reference. As it was expected, the reference structure showed a negligible function due to it is not a superconductor one. However, function of UMBLG structures with and displacements showed characteristics indicative of superconducting behavior, which became more noticeable with the increase of the electric field. This behavior was greater for () than for (). Furthermore, function of these structures suggests that Cooper-pairs are possible in the low-frequency vibration region. In addition, the calculation of the parameters allowed us to suggest that for specific displacements, an increase in could be induced by applying and increasing the external perpendicular electric field. This implies an increase in the number of Cooper-pairs and therefore an increase in the superconducting critical temperature. The displacement in the UMBLG structure indicated that it does not exhibit superconductivity under this particular configuration.All these results demonstrated that the structural geometric approximation appears to be consistent with the presence of the superconducting state observed in TBLG at small angles, which allowed evaluation of the possible effect of the electric field.