A Comprehensive Analysis Perspective on Path Optimization of Multimodal Electric Transportation Vehicles: Problems, Models, Methods, and Future Research Directions

1. Introduction

1.1. Background

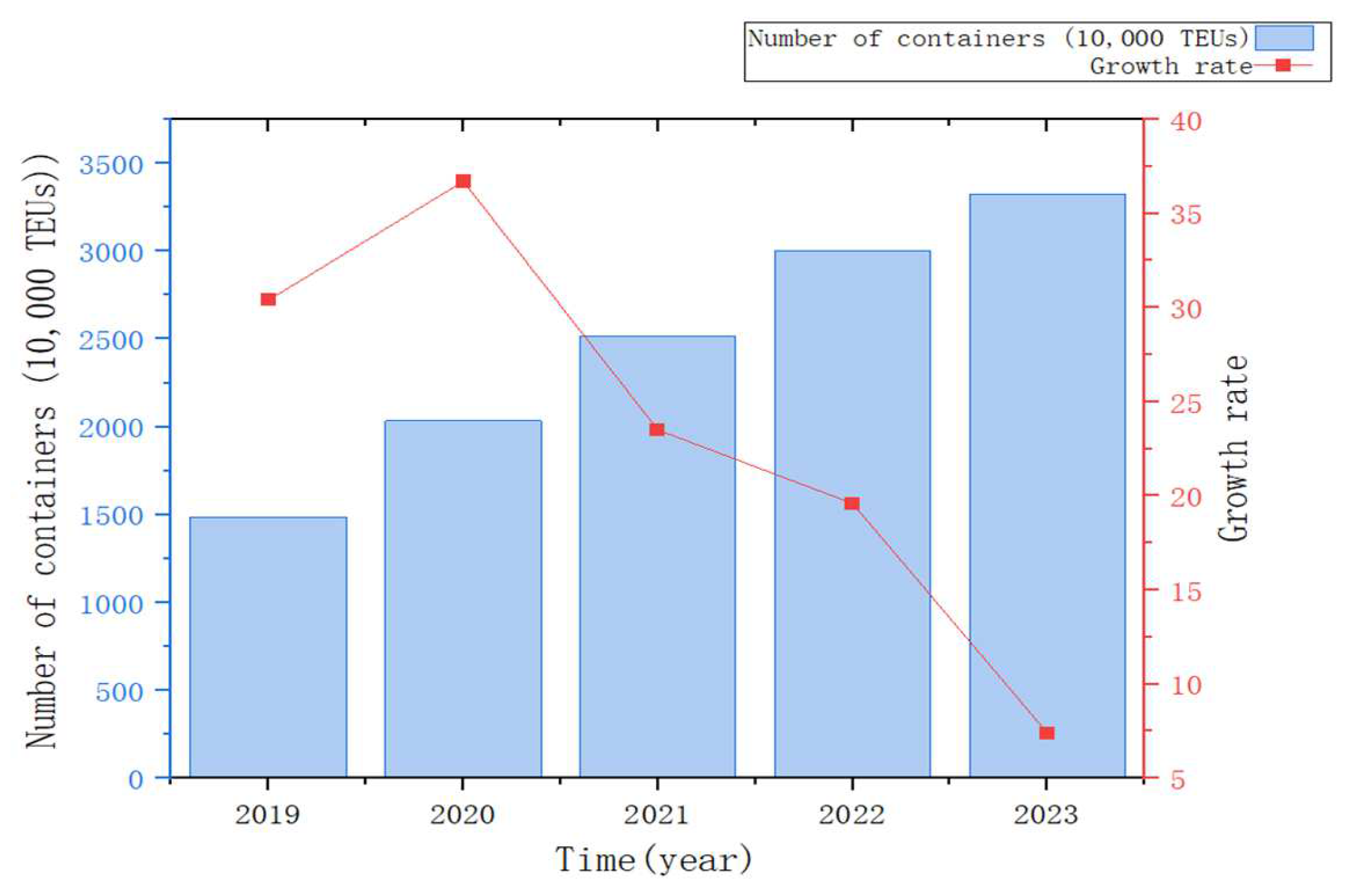
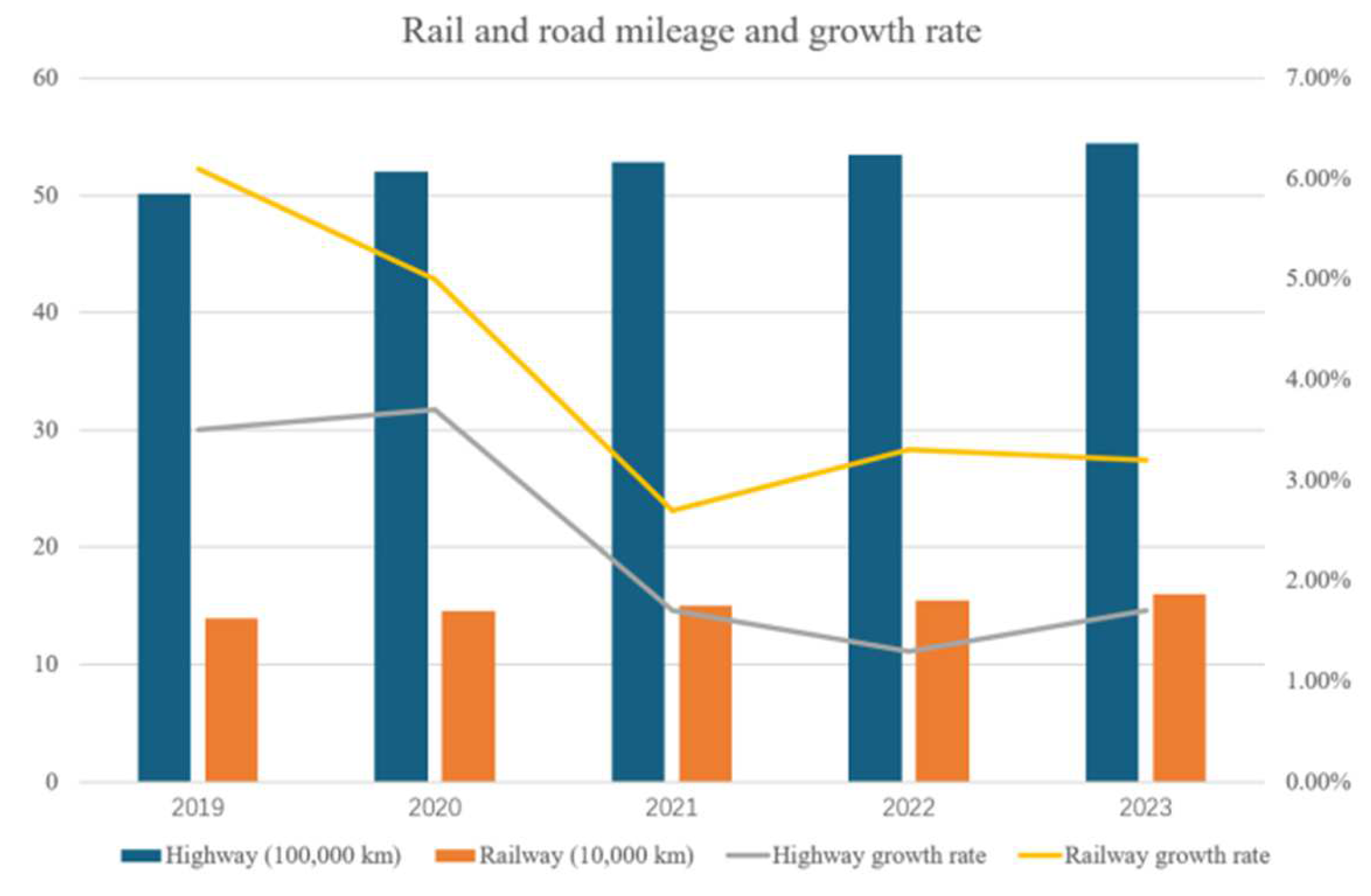
Multimodal transport through various transportation mode service connections, and unified standards, to achieve the goal of cost reduction and efficiency. In recent years, the traffic and transportation network has been improving day by day, the mileage of highways and railroads is increasing, the container throughput of railroads and waterways is also showing an upward trend, the market scale of China’s smart port industry is developing rapidly, and the volume of multimodal transportation is proliferating [1]. The multimodal transport path optimization problem has become a research hotspot nowadays, which is a comprehensive decision-making problem involving various factors such as economy, environment, and service. Various uncertainties in the transportation process and multiple optimization objectives are considered under the national dual-carbon policy. How to solve these complex problems is the core challenge of multimodal transport path optimization. Therefore, it is particularly important to deal with the uncertainties in the transportation process. 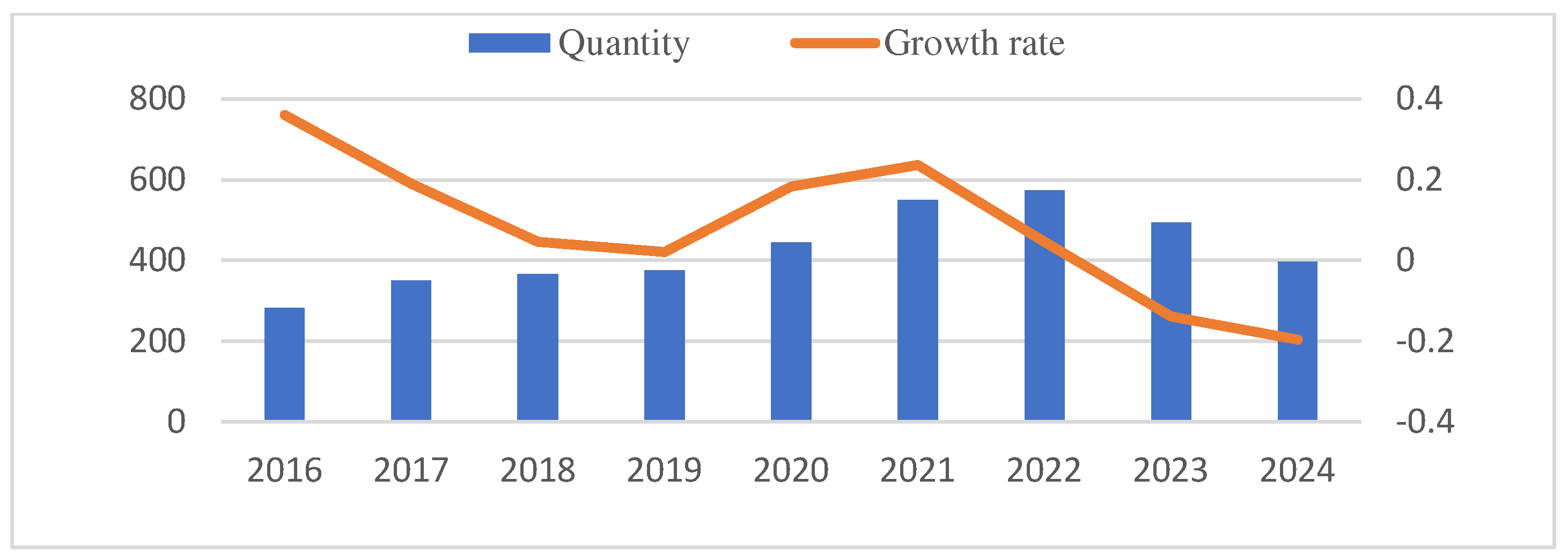The container throughput and infrastructure construction are shown in Figure 1 and Figure 2.

China’s multimodal transportation is in a rapid development stage. Although there is a large increase in the number of public rail lines every year, it is relatively small compared to the whole intermodal network, resulting in an imperfect basic intermodal network, Ye et al. [2] consider the development of multimodal transportation at the same time, there is a growing need for the construction of new infrastructures. Moreover, as intermodal transportation moves towards intelligence and efficiency, integrating advanced digital technologies and ensuring environmental sustainability in logistics is becoming a necessity for the new intermodal transportation concept of the times. In this digital era, advanced digital technologies are not fully utilized in multimodal transportation [3]. And Komashinskiy et al. [4], regarding this issue, explored the intelligent basis of multimodal transportation systems and their further development strategies.

1.2. Review of Multimodal Transports

To ensure the continuous development of multimodal transport path optimization, it is necessary to focus on the problem of cooperative scheduling in the transport process. Zhang et al. [5] proposed that the key to the high-quality development of multimodal transport is the efficient connection of various modes of transportation, to achieve collaborative scheduling. Shen et al. [6] conducted a review based on domestic and international literature, analyzed and explored the operation mechanism, development mode, and evolution trend of multimodal transport, and mentioned that the suitable multimodal transport development mode in China is to focus on coordinating modes of transport to create an integrated scheduling-type multimodal transport system.

Claudia et al. [7] reviewed the literature on multimodal transportation up to 2020. It was found that the phenomenon of single transportation is still prominent. And the current research hotspot is the research considering carbon emission and transshipment cost, and many scholars are indeed doing related work at present. In the multimodal transport path optimization literature from 2016 to the present, more scholars have begun to consider more complex situations, and they will use low carbon as the background to consider the multi-objective problem and multiple uncertainty problems in transport, which undoubtedly makes the problem more and more complicated.

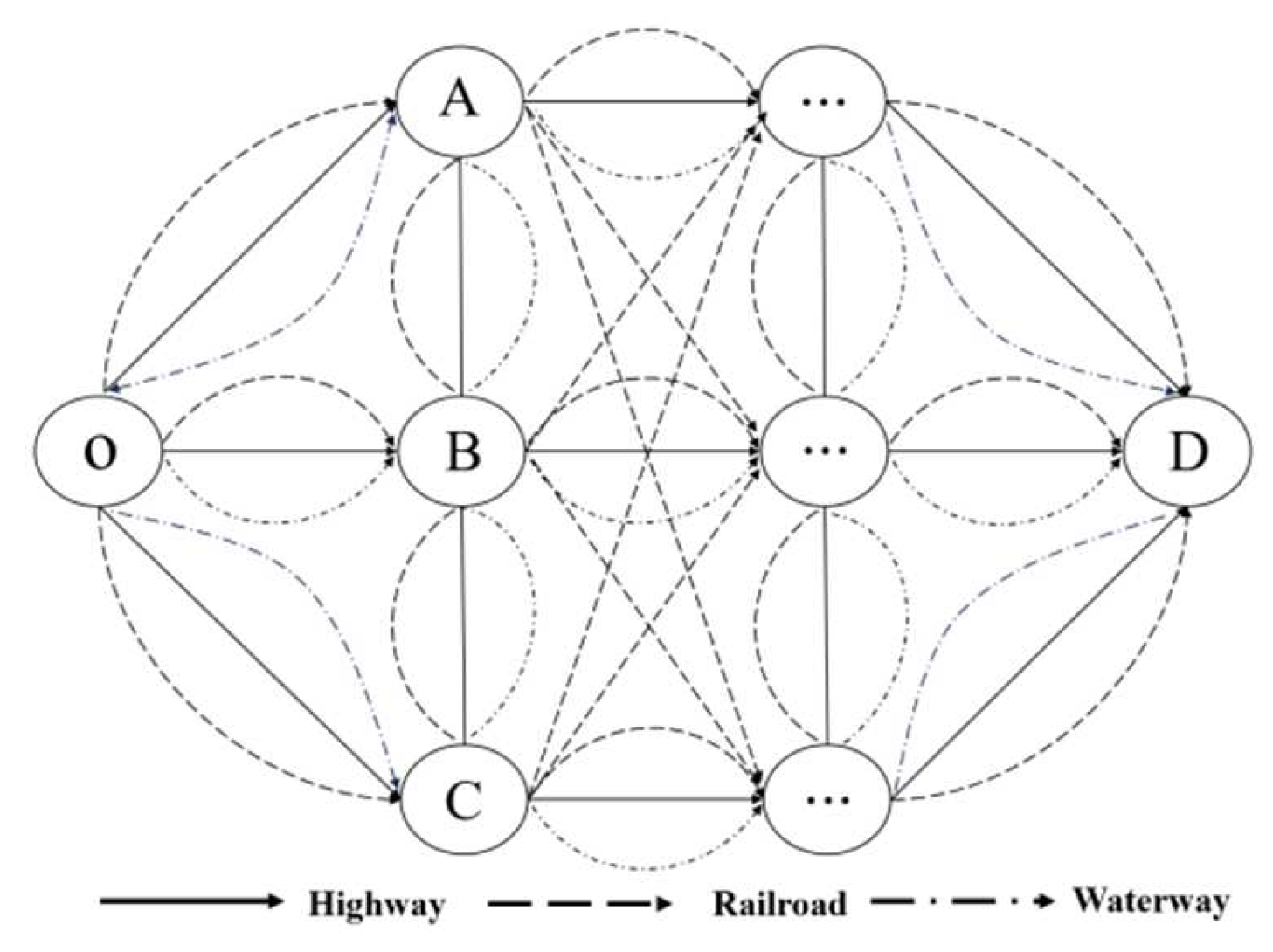
Through analysis and summarization, the following problems in the existing research have been identified:(1) The multimodal path optimization problem encompasses a variety of types of problems, and the current research lacks a persuasive and clear classification framework; (2) The path optimization problem has been proved to be a typical NP-hard problem, which has been studied by a large number of scholars. However, for this kind of problem, most scholars analyze the specific problem and model the solution and lack of statistics and comparisons of existing models and algorithms. The multimodal transportation path optimization network is shown in Figure 3. (3) Despite the numerous academic research results on path optimization problems, their practical applications still lag. Existing studies rarely summarize and analyze the potential future research directions and possible challenges in development. To comprehensively solve the multimodal transportation path optimization problem, the following work will be carried out:

(1) Existing research articles on multimodal path optimization will be collected and classified according to the research object. Based on this classification, a structured classification framework that distinguishes it from other studies will be proposed to analyze the focus areas and applicable scenarios of various types of models.

(2) Also consider the mathematical modeling approaches adopted for different path optimization problems. Moreover, the problem is essentially an NP-hard problem, and it is more complicated to obtain the optimal solution directly, and the common solution algorithms for solving this problem will be summarized.

(3) Summarize the current research status of the multimodal transportation path optimization problem and discuss the potential future research directions.

The structure of the subsequent part of this paper is as follows: Section 2 analyzes in detail the current research status of domestic and foreign scholars on multimodal transportation path optimization problems according to different research objectives and other factors; Section 3 summarizes the mathematical modeling methods according to the characteristics of various types of models and summarizes and analyzes the solution algorithms; Section 4 summarizes and puts forward two potential future directions according to the current research status; Section 5 gives the main conclusions of the research. The section gives the main conclusions of the study. The structural framework diagram of this paper is shown in Figure 4.

2. Overview of Research Status

The multimodal transportation path optimization problem has been a hot research topic in recent years. Searching with ’multimodal transportation’ as the keyword, we can see the number of articles published by CSDN and WOS in recent years and the growth rate. Specifically, as shown in Figure 5 and Figure 6.

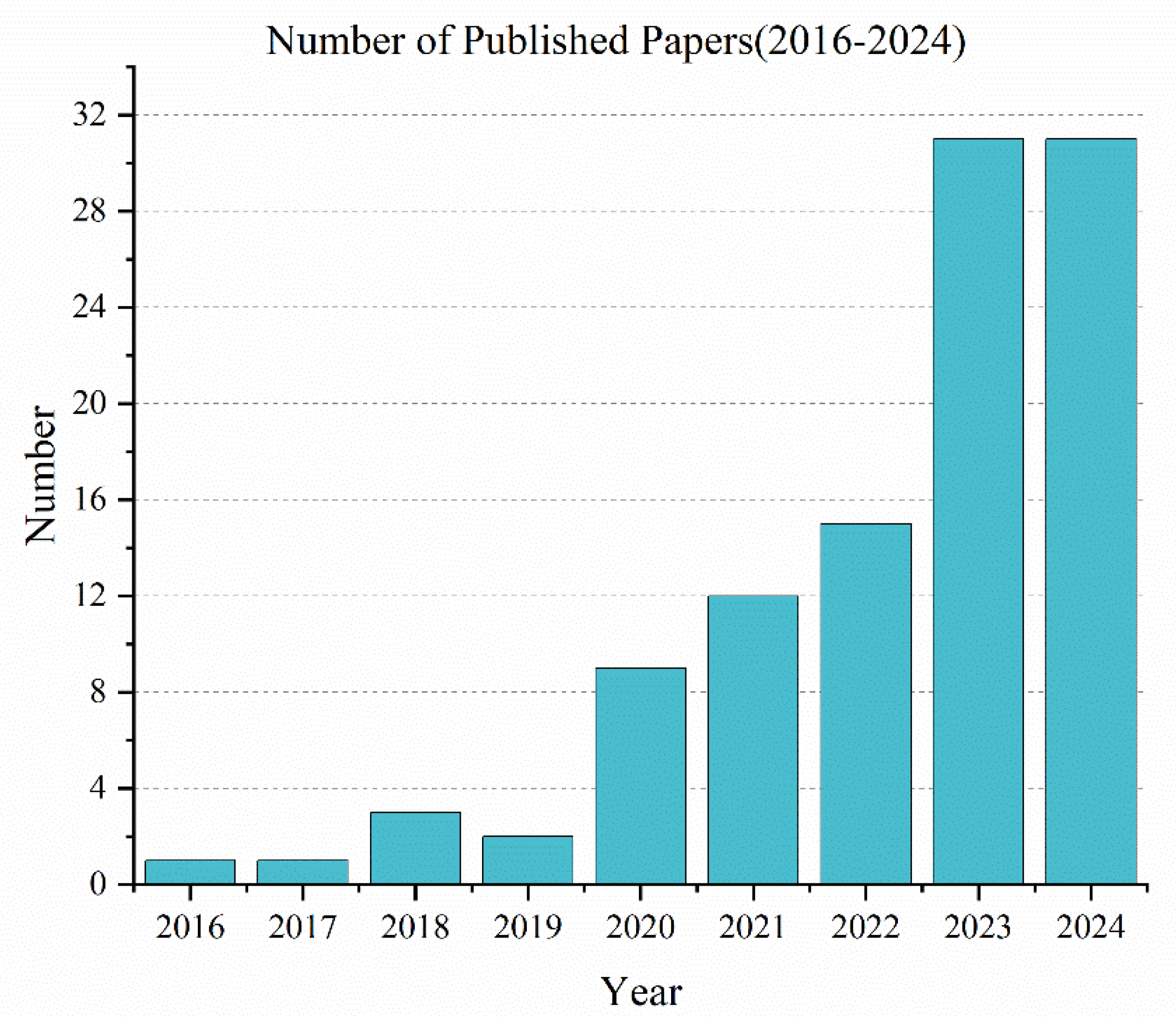
A comprehensive review of the literature on multimodal path optimization from 2016-2024 was conducted by searching for relevant keywords: ’multimodal transportation’, ’path optimization’, and ’vehicle scheduling’ on CNKI and WOS, respectively ‘, the literature related to the study was selected. Then, the references as well as the keywords of these literatures were searched and studied again to broaden the search scope. 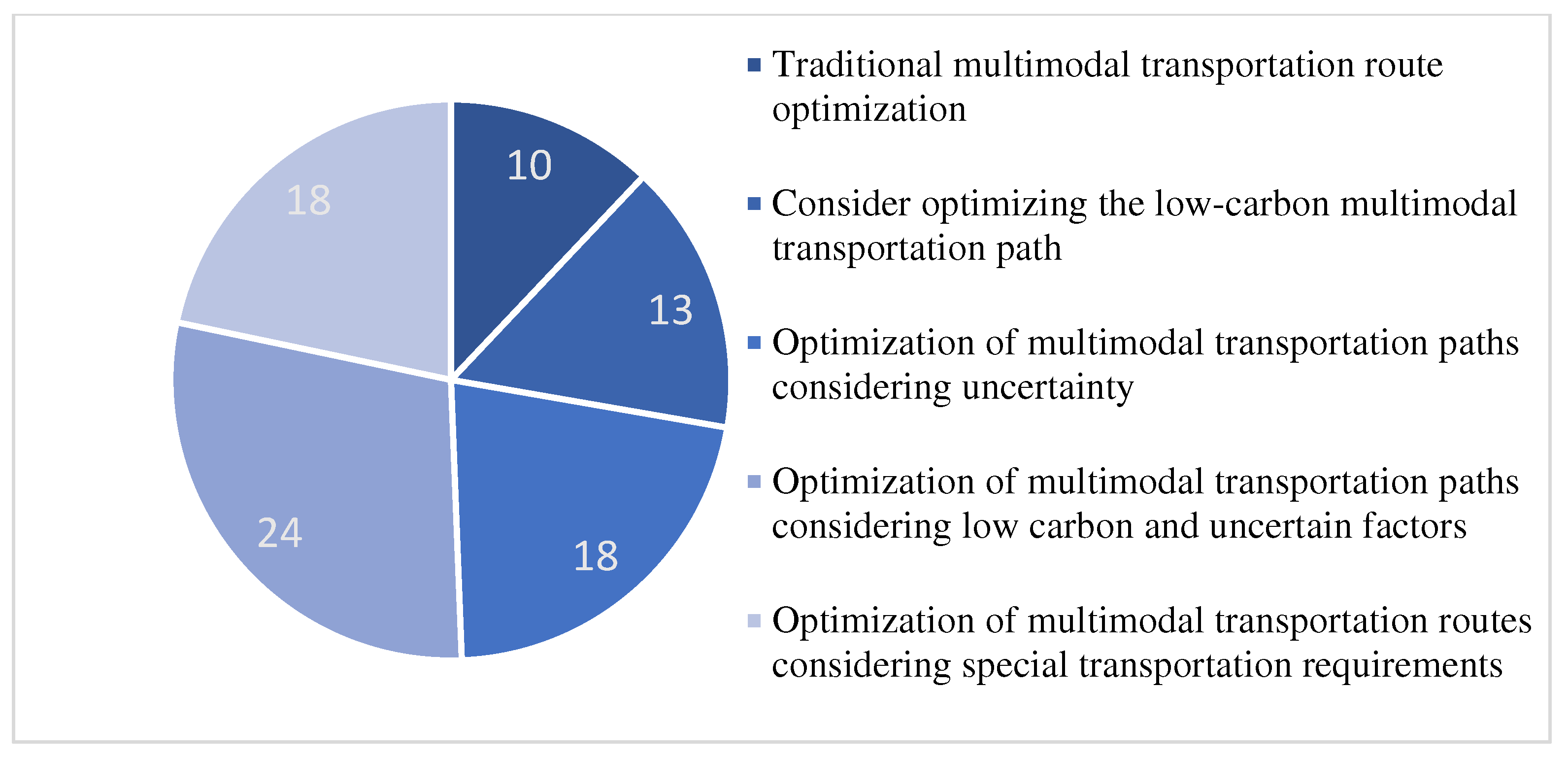Finally, after a rigorous screening process to exclude some lower relevance as well as lower value literatures, 104 literatures were selected to be analyzed and categorized with respect to the date of the literatures, as shown in Figure 7. According to the research hotspots and directions in recent years, the multimodal transport path optimization problems are classified into five categories here: traditional multimodal transport path optimization, multimodal transport path optimization considering carbon emission, multimodal transport path optimization considering uncertainties, multimodal transport path optimization considering uncertainties under low carbon, and multimodal transport path optimization considering special needs. As shown in Figure 8.

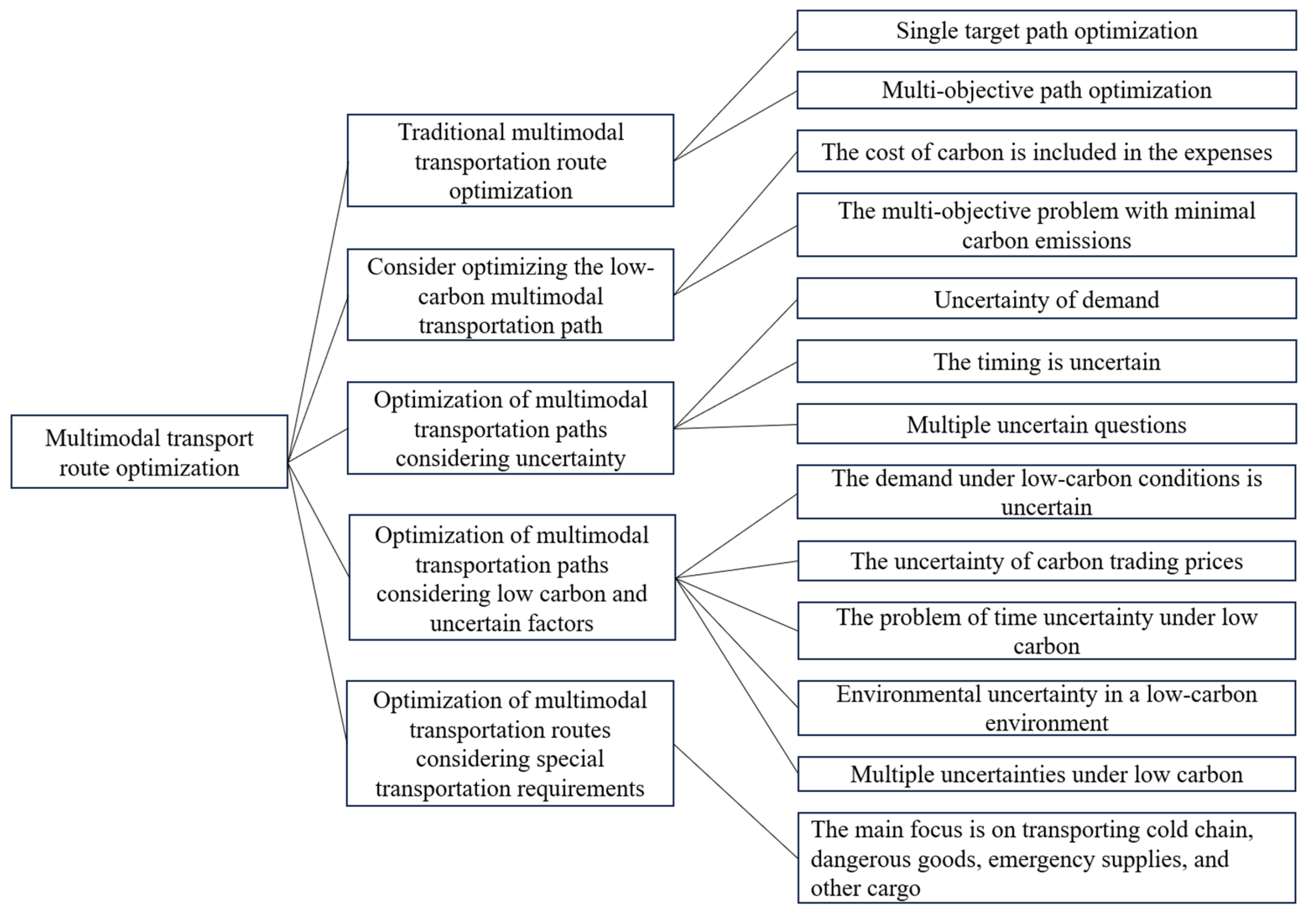
The multimodal transportation path optimization problem involves a variety of transportation modes as well as transit scheduling. Meanwhile, different transportation objectives, different transportation modes, and different model algorithms lead to a path optimization process full of complexity, dynamics, and other characteristics. Here, under the five general directions, the literature is further subdivided according to the different research objectives. The overall literature category framework is shown in Figure 9.

The rest of this chapter will review the literature by breaking it down into five major directions as well as a number of minor directions, following the framework shown above.

2.1. Traditional Multimodal Transportation Path Optimization

Before the promulgation of the national low-carbon policy, few scholars have considered low-carbon issues and various uncertainty factors when studying multimodal transportation path planning. Therefore, the research that has not yet considered the low-carbon environment and uncertainty factors is categorized as the traditional multimodal transportation path planning problem. Domestic and international research on the optimization of traditional multimodal transport routes mainly focuses on single-objective optimization or multi-objective optimization with cost optimization and time optimization.

2.1.1. Single-Objective Multimodal Transportation Path Optimization

As for cost objective optimization, some scholars focus on cost calculation and pricing problems. Kovalenko A. et al. [8] extended a theoretical framework for evaluating the generalized transportation cost of multimodal transport solutions in the maritime sector. Pian et al. [9] address the problem of equilibrium pricing of direct container road transport versus intermodal transport via dry ports taking into account scale discounts for rail transportation.

Cargo transportation is required to be completed within a certain timeframe, which requires comprehensive consideration of constraints such as the node operation time window, mode of transportation, fixed departure moments, and collection time window at the endpoint in the freight transportation process [10]. Peng et al. [11] established a 0-1 integer planning model with cost minimization for the dual constraint problem of intermodal path optimization with time windows and schedules. Liang [12] quantified multimodal transportation satisfaction by using the affiliation function of trapezoidal fuzzy numbers and obtained a soft time window for the cargo arrival time frame. Farahani et al. [13] used an advanced multimodal transportation service network model (AI-SNM). A mixed integer planning model is constructed with the objective of cost minimization by considering multiple modes of transportation, resource constraints, and time window constraints in the intermodal transportation process.

Most of the scholars only consider the transportation of single commodity flow, and some scholars also address the problem of multi-commodity flow. Qi et al. [14] constructed a container multimodal transport path optimization model with the minimum total cost including transportation, transshipment, waiting, and penalty for multi-tasks with different receiving and dispatching places and different time windows, while considering the shift restrictions and the influence of capacity of water and railway transportation. Multi-commodity transportation is more complex than single-commodity flows because it involves multiple origins and multiple points of shipment.

2.1.2. Multi-Objective Intermodal Transportation Path Optimization

The establishment and solution of the multi-objective model is much more complicated than when the objective model. In the research of multi-objective, some scholars study with the objective of minimizing cost and time. Wu et al. [15] studied the container intermodal transportation problem under the condition of considering the time value of goods, container box type, and other factors, established a dual-objective optimization model, and then discussed how to balance these two conflicting objectives so that they can apply linear weighting method to transform the dual-objective problem into a single-objective problem. And Wang et al. [16] established a bi-objective optimization model with the objectives of minimizing cost and maximizing customer satisfaction considering inventory and road disruption. Seo et al. [17] explored various alternative routes for exporting laptop computers from Chongqing, China to Rotterdam, the Netherlands, considering multiple objectives such as transportation cost, transit time, and other objectives for the path selection.

In summary, multi-objective optimization compared to single-objective problems, the model will be more complex, because often there is a phenomenon of benefit backwardness between various factors, for some relatively simple single-objective models, you can also use the exact algorithm to solve, but for multi-objective problems, how to deal with the weight relationship between each objective, how to choose the appropriate algorithm for solving the problem is a problem that requires extra attention. The summary table of traditional multimodal transportation path optimization research is shown in Table 1.

2.2. Optimization of Intermodal Transport Routes with Low Carbon Considerations

Multimodal transportation is a mode of transportation that consists of multiple modes of transportation collaborating with each other, and different modes of transportation have large differences in carbon emissions, with railroad transportation being the mode of transportation with the lowest carbon emissions, followed by waterways, and roads with the highest. Under the national dual-carbon policy, transportation as the second largest carbon emission field, and intermodal transportation is an effective solution to reduce carbon emissions. In long-distance transportation, multimodal transportation has low cost and low carbon emission compared to single road transportation [18]. Low-carbon subsidies will have an impact on the cost, so Zhang et al. [19] conducted a study on low-carbon subsidies, which constructed a two-layer planning model to compare and discuss four subsidy schemes, taking the logistics network of land and water intermodal transportation in the middle reaches of the Yangtze River Economic Belt as an example.

Compared with the traditional multimodal transport path optimization problem, considering low carbon undoubtedly makes the model more complicated. Scholars have made various attempts on how to deal with the carbon emission problem, which are mainly divided into two kinds, one is to count the carbon emission cost into the total cost and establish a multi-objective model with the lowest total cost or including the total cost, and the other is that some scholars directly establish the model with the minimum carbon emission as an optimization objective.

2.2.1. Problems of Including Carbon Price in Costs

Aiming at the different impacts of different policies on the carbon price, Zhang et al. [20] constructed a minimum cost multimodal transport path optimization model including carbon emission cost according to carbon emission, carbon tax, carbon trading, and carbon compensation policies, and analyzed and compared the path optimization problems under different carbon emission policies through different examples. Guo [1] constructed a minimum-cost multimodal transport path optimization model with the total cost including carbon emission cost by taking into account the factor of railroad skylight. Wu et al. [21] and Chen et al. [22] internalized carbon emission into carbon tax cost to solve the problem.

2.2.2. Multi-Objective Problem with Carbon Emission Minimization

In the context of the carbon neutral strategy, the carbon emissions generated when goods switch modes of transportation in the intermodal transport process and transit nodes should be taken as an important influencing factor, and the impacts such as transportation costs and transportation time generated in the intermodal transport process and transit should be taken into account [23]. At the same time, carbon emission is taken as an optimization objective for multi-objective optimization research. Therefore, more scholars construct the multi-objective model by minimizing cost, time, and carbon emissions.

Liu et al. [24], Wan et al. [25], Yin et al. [26], and Hou et al. [27] all considered the factor of carbon emission in the optimization of multimodal transport paths and established a multi-objective optimization model with the minimum of carbon emission, cost and time [28]. Wu et al. [29,30] have repeatedly studied the multimodal transport path optimization problem in a low-carbon environment and constructed a multi-objective green multimodal transport optimization model by considering the cost and carbon emission minimization at the same time. Wang [31] solved the problems of carbon emission, average customer satisfaction, and area utilization of ro-ro ships for the transit link of public-water intermodal transport.

In summary, the introduction of the carbon cost problem in the calculation of cost, if the establishment of a single-objective problem with the goal of cost minimization, is less difficult both in the establishment of the model and the difficulty of the solution if it is a multi-objective problem established directly with the minimization of carbon emissions, many scholars are also attempting to weight multi-objective processing into single-objective. Considering the summary table of multimodal transportation path optimization research in a low-carbon environment is shown in Table 2.

2.3. Multimodal Transportation Path Optimization Considering Uncertainties

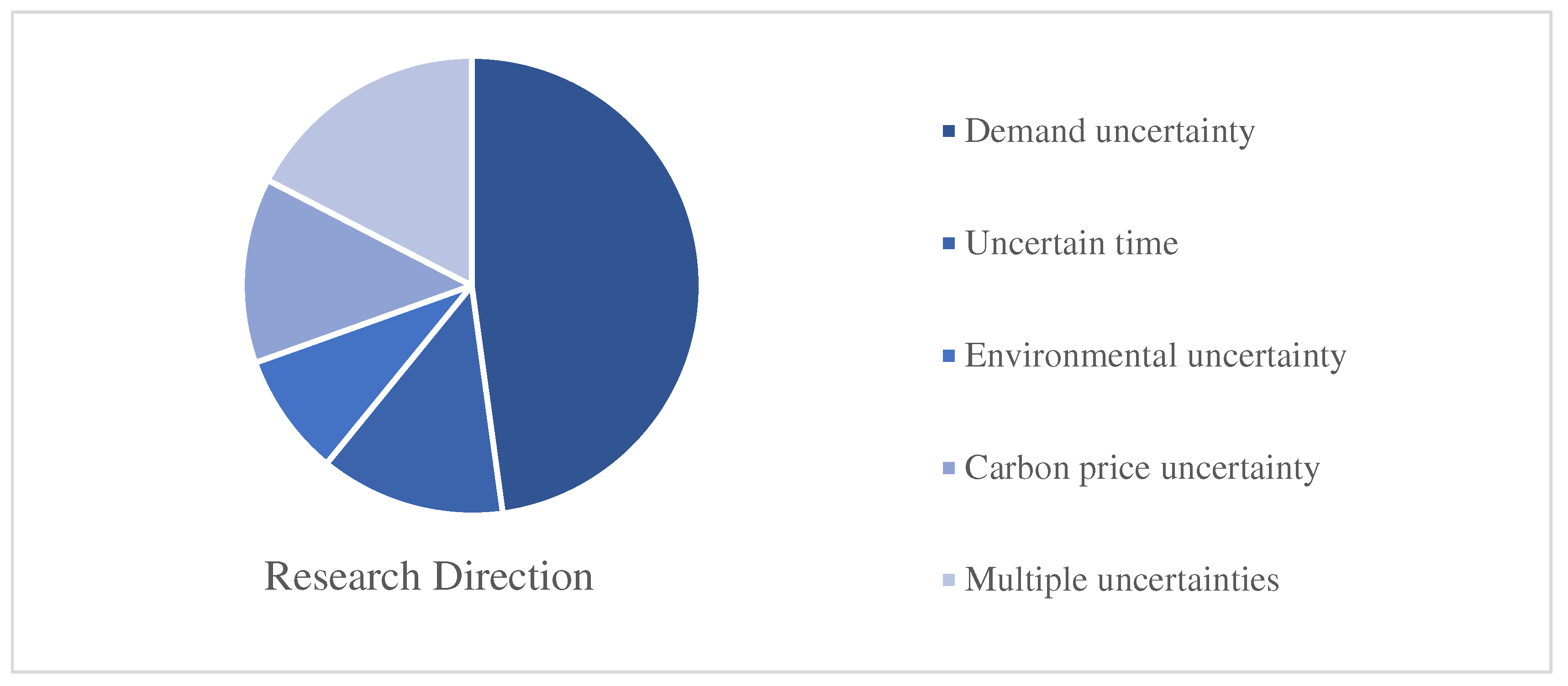
Multimodal transportation projects are affected by a variety of factors, including credit surveys, multimodal operator preferences, policy introduction, and extreme weather [32]. In recent years, more and more scholars have begun to consider the uncertainty problems in the multimodal transportation process, such as demand uncertainty, time uncertainty, and environmental uncertainty. Most scholars consider individual uncertainties, among which the uncertainty of demand is considered the most. Various types of uncertainty account for as shown in Figure 10.

2.3.1. Consideration of Demand Uncertainties

The demand uncertainty factor refers to the fact that in the process of multimodal transportation, the demand for cargo transportation has a large change or is difficult to accurately predict and grasp due to a variety of reasons, such as market environment, seasonal changes, and unexpected events. This uncertainty may lead to changes in cargo transport volume, transport time, transport mode, etc., thus affecting the optimization decision of multimodal transport path. The focus of the research should be on multimodal transportation demand [33].

Uncertainty in demand increases transportation costs and time. Therefore, many scholars try to use various methods to solve this problem. Li [34] designed a two-stage stochastic planning-based transit point location and sequential decision-making path planning for uncertain demand, thus realizing the design of cost-effective multimodal transportation network. Qiu et al. [35] introduced the theory of time value of goods to measure the loss of time value of goods in the transportation process and used the scenario method in robust optimization to establish a robust optimization model of multimodal transportation paths with the lowest cost synthesis. Sun et al. [36] and Yu et al. [37] constructed a fuzzy multi-objective model by using the triangular fuzzy number and the fuzzy ranking method of Žimmerne for the clear treatment of the uncertain demand.

Regarding the multimodal transportation path optimization problem under sourcing uncertainty. Chen et al. [38] by building an uncertainty model and using an improved genetic algorithm to solve the uncertainty of the type of goods and demand. Guo et al. [39] studied the joint decision-making problem of multi-temporal sourcing and intermodal transportation under an uncertain environment and its robust optimization method.

2.3.2. Considering Problems with Time Uncertainty

Regarding the multimodal transportation path optimization problem under time uncertainty. In the multimodal transportation process, multiple shipments need to be transported from the starting point to the endpoint within a specified time through a combined transportation network that includes three modes of transportation, road, rail, and waterway. Due to the limited capacity of transshipment nodes and transportation routes, transportation delays or congestion may occur, which leads to the loss of time value of goods and the increase of transportation cost [40]. Tong [41] used triangular fuzzy numbers and opportunity-constrained planning theory to solve the multimodal transportation path optimization problem under the condition of transportation time uncertainty. Zhang et al. [42] proposed a multiorganization weighting and Q-weighting method based on a positively skewed distribution to depict the uncertainty of time. An optimization framework based on multi-objective weighting and Q-learning to deal with time uncertainty.

During the implementation of multimodal transportation, the intervention of natural and human factors can lead to uncertainty in the values of cargo transportation speed, on-time delivery probability thresholds, and transit time values [43]. Guo et al. [44] considered this problem and incorporated practical constraints in the parameter uncertainty to develop and solve a robust shortest-circuit mixed integer programming model based on multimodal transportation networks under transportation time uncertainty.

2.3.3. The Problem of Considering Multiple Uncertainties

Considering multiple uncertainties simultaneously in multimodal path optimization is a complex but crucial task. In the multimodal transportation path optimization problem considering multiple uncertainties. Zhang et al. [45] investigated for the multimodal transportation path optimization problem with time and demand uncertainty, using trapezoidal fuzzy numbers to deal with time and demand uncertainty. Tang et al. [46] considers the dynamic correlation between transit time and transportation demand, constructs a multi-objective model with the lowest total transportation cost and total transportation time, and uses opportunity constrained planning theory to clarify the model. Li et al. [47] study the uncertainty problem of different cargo transportation as well as time in Yangtze River container intermodal path optimization and design a dynamic planning algorithm based on depth-first traversal for intermodal path optimization to achieve the solution. Lu et al. [48] study the fuzzy intercontinental intermodal path problem with the uncertainty of time and train capacity and establish an uncertainty model to solve it.

Unforeseen events during transportation may lead to disruptions or delays. He et al. [49] proposed a network modeling and robustness assessment method for intermodal freight networks with respect to unforeseen events. Xu et al. [50] considered the use of collaborative multimodal transportation with its flexible and sustainable features to solve the problem of uncertainty considering the unforeseen situations and uncertainty in the demand during transportation. Guo et al. [51] used a storage service strategy to investigate the multicycle intermodal transportation path problem with time and train capacity uncertainty. Investigated the multi-period intermodal routing and transportation planning problem using a stored service strategy to build a robust mixed-integer planning model with the objective of time minimization, and solved it using an improved Dijkstra algorithm.

Based on the above several literatures considering uncertainties, it can be seen that most of the uncertainties such as demand and time are handled using triangular fuzzy numbers and opportunity constrained planning theory. A summary of multimodal route optimization studies considering uncertainties is shown in Table 3.

2.4. Optimization of Multimodal Transportation Paths Considering Low Carbon and Uncertain Factors

With the increasing heat of intermodal transport, scholars’ research on intermodal transport path optimization has become more and more in-depth. From the very beginning of modeling and solving the problem purely for containerized freight transport, later began to consider the carbon price and various uncertainties in the cost calculation. Zhang studies various uncertainty problems under low carbon based on the uncertainty of demand under low carbon [52], the uncertainty of demand and carbon trading price [53], and the uncertainty of demand and time under low carbon [54]. Currently, multimodal transportation path optimization under low carbon considering multiple uncertainties such as demand, time, and environment has become the most popular problem.

2.4.1. Demand Uncertainty Problem Under Low Carbon

Research on multimodal transportation uncertainty mainly focuses on demand, and fluctuations in freight demand can lead to a chain effect of transportation cost and time consumption, which in turn affects the selection of transportation options [55]. There are various ways to deal with demand uncertainty in the problem of low-carbon intermodal transport path optimization under consideration of demand uncertainty.

When dealing with the problem of demand uncertainty, a model of demand certainty can be established, and then uncertainty factors are added, to construct the formation of a low-carbon multimodal transportation path optimization model under uncertain demand [56,57,58].

As an effective method for solving uncertain optimization problems, the application of the interval robust optimization method to multimodal transportation path optimization under uncertain demand kind also has wide applications [59]. Wang [60] established a single-objective model to minimize the total cost and then followed the transformation steps of Bertsima robust optimization method to solve the problem by using dyadic theory. Qiu [35] and others introduced the theory of the time value of goods to measure the loss of time value of goods during transportation under demand uncertainty and modeled the solution using the scenario method in robust optimization.

The fuzzy opportunity constraint theory is also an effective method to deal with uncertainty, which can use either triangular fuzzy numbers or trapezoidal fuzzy numbers according to the specific demand, and use opportunity constraint planning to deal with the uncertain demand expressed by trapezoidal fuzzy numbers according to the specific problem [61,62,63,64]. Deng et al. [65] dealt with the uncertainty problem by first transforming the multi-objective problem into a single-objective problem using the linear weighting method, and then making the model clear through the trapezoidal fuzzy number as well as the opportunity-constrained planning theory.

2.4.2. Uncertainty Problem of Carbon Trading Price

Under the low-carbon environment, carbon emission becomes an important index to measure the environmental friendliness of transportation modes. Path optimization requires the selection of transportation modes and paths with low carbon emissions. The change in carbon trading price has a large impact on the total cost.

In considering the low-carbon multimodal transport path optimization problem under the uncertainty of carbon trading price. Cheng et al. [66] considered the uncertainty of carbon trading policy and studied it by robust optimization. Yang et al. [67] in order to solve the cold chain multimodal transportation path optimization problem under the uncertainty of carbon trading price, use the triangular fuzzy number to describe the carbon trading price based on the existing characteristics of carbon trading price changes in the market.

2.4.3. Problem Considering Time Uncertainty

In the low-carbon multimodal transport path optimization problem under the consideration of time uncertainty, the research on multimodal transport timeliness mainly focuses on the receiving time window [11]. Ai et al. [68] comprehensively considered the effects of transportation cost, time, and carbon emission, paid attention to the uncertainty of node operation time, generated random numbers to enrich the data through Box-Muller transformation, and used Monte Carlo simulation to statistically characterize the statistical characteristics of the total transportation time under the uncertainty of transportation time. Chen et al. [69] considered the low-carbon problem of receiving time window in multimodal transportation path optimization designed a soft time window for receiving goods based on shipper’s satisfaction, and used the Z fuzzy affiliation function to describe the functional relationship between transportation time and consignee’s satisfaction. Zhou et al. [70], on the other hand, used trapezoidal fuzzy numbers to portray the uncertainty characteristics of transportation time and transit time in multimodal transportation.

2.4.4. Consideration of Environmental Uncertainty

In the low-carbon multimodal transport path optimization problem under consideration of environmental uncertainty, Li et al. [71], for the multimodal transport path planning problem under uncertain environment, built a model with cost, time, and carbon emission as the optimization objectives, and used a combination of game theory and weighted summation to obtain the optimal multimodal transport path. Yang et al. [72] established a low-carbon and low-cost multimodal transport path optimization model under fuzzy demand and fuzzy transport time, considering that enterprises must ensure the robustness and risk-resistance of the plan when making plans.

2.4.5. Considering Multiple Uncertainties Under Low Carbon

Combining the uncertainty factors mentioned above, the main ones are demand uncertainty, time uncertainty, carbon price uncertainty, and environmental uncertainty. In the low-carbon multimodal transport path optimization problem multiple uncertainties are considered. Zhang et al. [73] considered the uncertainties of demand and time as well as mandatory carbon emission, carbon tax, carbon trading, and carbon offset policies in the multimodal transport process. A fuzzy demand opportunity constraint planning model and a fuzzy time interval planning model were developed. Dai [74] considered the multimodal transportation path optimization problem under various uncertainties including carbon price in the multimodal transportation process, and built a path optimization model considering different carbon policies. Sun et al. [75] took into account the various uncertainties of cost and time in multimodal transportation, introduced the road congestion index and the hybrid embedded time window, and constructed the cost of transportation, carbon emission, and time penalties included in the Model. Li et al. [76] analyze the transportation cost, carbon emission cost and time penalty cost when it obeys the stochastic distribution for the problem of time, demand and capacity uncertainty, so as to get the more ideal scheme under different weights.

Table 4. Summary of multimodal transport route optimization studies considering low carbon and uncertainty factors.

Literature	Objective	function	Modeling/Solving	Examples
Zhang et al. [45]	Route optimization of low carbon multimodal transport with uncertain demand and time	Min cost, max customer satisfaction	Multi-objective fuzzy chance constrained planning model + NSGA-II	Simulation case
Tang et al. [46]	Intermodal transportation path selection considering dynamic transit time	Min cost/time	Multi-objective-MIP + Linear weighting method + Fuzzy chance constrained planning + GA-SA	Simulation case
Li et al. [47]	Container routing optimization with uncertain demand and time	Min cost	IP + Dynamic planning algorithm	Simulation case
Lu et al. [48]	Intercontinental multimodal transport with uncertain time and capacity	Min cost	MILP+ CPLEX 12.8	China-Europe freight transport
Xu et al. [50]	Path optimization with uncertain demand and environment	Min cost	MIP + GA	Simulation case
Zhang et al. [52]	Low carbon path optimization under uncertain demand	Min cost	Integer programming model + robust optimization + Monte Carlo catastrophe adaptive GA	Simulation case
Yuan et al. [59]	Low carbon path optimization under uncertain demand	Min cost	Fuzzy robust optimization model + Catastrophe adaptive GA	Simulation case
Huang et al. [62]	Low carbon path optimization under uncertain demand	Min cost/carbon emissions	MIP + Fuzzy chance constraint programming + Harris Eagle algorithm	Nanning-Harbin freight transport
Wang [63]	Low carbon path optimization under uncertain demand	Min cost	MIP + Fuzzy chance constraint theory + Heuristic algorithm	Shanghai-Chengdu freight
Deng et al. [65]	Low carbon path optimization under uncertain demand	Min cost/carbon emissions	MIP + SA-PSO	Simulation case
Chen et al. [69]	Low carbon multimodal transport under uncertainty of time and satisfaction	Min cost	IP + ACO	Simulation case
Zhou et al. [70]	Optimization of low-carbon multimodal transport routes under time uncertainty	Min cost/time/carbon emissions	MIP + Evolutionary algorithm	Simulation case
Li et al. [71]	Low-carbon multimodal transport route planning under demand uncertainty	Min cost/time/carbon emissions	MINLP + Fuzzy chance constraint + Cooperative game + Particle swarm algorithm	Guangdong-Beijing freight transport
Yang et al. [72]	Optimization of low-carbon multimodal transport routes with uncertain demand and time	Min cost/carbon emissions	Uncertainty model + Fuzzy chance constraint model + Adaptive differential evolution algorithm	Simulation case
Sun et al. [75]	Low-carbon multimodal transport path planning considering multiple cost factors	Min cost	MINLP + Logistic-Tent + Adaptive lens reverse learning strategy + Hybrid sand cat swarm optimization algorithm	Simulation case
Literature	Objective	function	Modeling/Solving	Examples
Zhang et al. [45]	Route optimization of low carbon multimodal transport with uncertain demand and time	Min cost, max customer satisfaction	Multi-objective fuzzy chance constrained planning model + NSGA-II	Simulation case
Tang et al. [46]	Intermodal transportation path selection considering dynamic transit time	Min cost/time	Multi-objective-MIP + Linear weighting method + Fuzzy chance constrained planning + GA-SA	Simulation case
Li et al. [47]	Container routing optimization with uncertain demand and time	Min cost	IP + Dynamic planning algorithm	Simulation case
Lu et al. [48]	Intercontinental multimodal transport with uncertain time and capacity	Min cost	MILP+ CPLEX 12.8	China-Europe freight transport
Xu et al. [50]	Path optimization with uncertain demand and environment	Min cost	MIP + GA	Simulation case
Zhang et al. [52]	Low carbon path optimization under uncertain demand	Min cost	Integer programming model + robust optimization + Monte Carlo catastrophe adaptive GA	Simulation case
Yuan et al. [59]	Low carbon path optimization under uncertain demand	Min cost	Fuzzy robust optimization model + Catastrophe adaptive GA	Simulation case
Huang et al. [62]	Low carbon path optimization under uncertain demand	Min cost/carbon emissions	MIP + Fuzzy chance constraint programming + Harris Eagle algorithm	Nanning-Harbin freight transport
Wang [63]	Low carbon path optimization under uncertain demand	Min cost	MIP + Fuzzy chance constraint theory + Heuristic algorithm	Shanghai-Chengdu freight
Deng et al. [65]	Low carbon path optimization under uncertain demand	Min cost/carbon emissions	MIP + SA-PSO	Simulation case
Chen et al. [69]	Low carbon multimodal transport under uncertainty of time and satisfaction	Min cost	IP + ACO	Simulation case
Zhou et al. [70]	Optimization of low-carbon multimodal transport routes under time uncertainty	Min cost/time/carbon emissions	MIP + Evolutionary algorithm	Simulation case
Li et al. [71]	Low-carbon multimodal transport route planning under demand uncertainty	Min cost/time/carbon emissions	MINLP + Fuzzy chance constraint + Cooperative game + Particle swarm algorithm	Guangdong-Beijing freight transport
Yang et al. [72]	Optimization of low-carbon multimodal transport routes with uncertain demand and time	Min cost/carbon emissions	Uncertainty model + Fuzzy chance constraint model + Adaptive differential evolution algorithm	Simulation case
Sun et al. [75]	Low-carbon multimodal transport path planning considering multiple cost factors	Min cost	MINLP + Logistic-Tent + Adaptive lens reverse learning strategy + Hybrid sand cat swarm optimization algorithm	Simulation case

IP: Integer Planning Model; MIP: Mixed Integer Planning Model; MILP: Mixed Integer Linear Programming; MINLP: Mixed Integer Nonlinear Programming; GA: Genetic Algorithm; NSGA- II: Non-dominated Sorting Genetic Algorithm-II; ACO: Ant Colony Optimization; PSO: Particle Swarm Optimization; SA: Simulated Annealing.

Table 4. Summary of multimodal transport route optimization studies considering low carbon and uncertainty factors.

Literature	Objective	function	Modeling/Solving	Examples
Zhang et al. [45]	Route optimization of low carbon multimodal transport with uncertain demand and time	Min cost, max customer satisfaction	Multi-objective fuzzy chance constrained planning model + NSGA-II	Simulation case
Tang et al. [46]	Intermodal transportation path selection considering dynamic transit time	Min cost/time	Multi-objective-MIP + Linear weighting method + Fuzzy chance constrained planning + GA-SA	Simulation case
Li et al. [47]	Container routing optimization with uncertain demand and time	Min cost	IP + Dynamic planning algorithm	Simulation case
Lu et al. [48]	Intercontinental multimodal transport with uncertain time and capacity	Min cost	MILP+ CPLEX 12.8	China-Europe freight transport
Xu et al. [50]	Path optimization with uncertain demand and environment	Min cost	MIP + GA	Simulation case
Zhang et al. [52]	Low carbon path optimization under uncertain demand	Min cost	Integer programming model + robust optimization + Monte Carlo catastrophe adaptive GA	Simulation case
Yuan et al. [59]	Low carbon path optimization under uncertain demand	Min cost	Fuzzy robust optimization model + Catastrophe adaptive GA	Simulation case
Huang et al. [62]	Low carbon path optimization under uncertain demand	Min cost/carbon emissions	MIP + Fuzzy chance constraint programming + Harris Eagle algorithm	Nanning-Harbin freight transport
Wang [63]	Low carbon path optimization under uncertain demand	Min cost	MIP + Fuzzy chance constraint theory + Heuristic algorithm	Shanghai-Chengdu freight
Deng et al. [65]	Low carbon path optimization under uncertain demand	Min cost/carbon emissions	MIP + SA-PSO	Simulation case
Chen et al. [69]	Low carbon multimodal transport under uncertainty of time and satisfaction	Min cost	IP + ACO	Simulation case
Zhou et al. [70]	Optimization of low-carbon multimodal transport routes under time uncertainty	Min cost/time/carbon emissions	MIP + Evolutionary algorithm	Simulation case
Li et al. [71]	Low-carbon multimodal transport route planning under demand uncertainty	Min cost/time/carbon emissions	MINLP + Fuzzy chance constraint + Cooperative game + Particle swarm algorithm	Guangdong-Beijing freight transport
Yang et al. [72]	Optimization of low-carbon multimodal transport routes with uncertain demand and time	Min cost/carbon emissions	Uncertainty model + Fuzzy chance constraint model + Adaptive differential evolution algorithm	Simulation case
Sun et al. [75]	Low-carbon multimodal transport path planning considering multiple cost factors	Min cost	MINLP + Logistic-Tent + Adaptive lens reverse learning strategy + Hybrid sand cat swarm optimization algorithm	Simulation case
Literature	Objective	function	Modeling/Solving	Examples
Zhang et al. [45]	Route optimization of low carbon multimodal transport with uncertain demand and time	Min cost, max customer satisfaction	Multi-objective fuzzy chance constrained planning model + NSGA-II	Simulation case
Tang et al. [46]	Intermodal transportation path selection considering dynamic transit time	Min cost/time	Multi-objective-MIP + Linear weighting method + Fuzzy chance constrained planning + GA-SA	Simulation case
Li et al. [47]	Container routing optimization with uncertain demand and time	Min cost	IP + Dynamic planning algorithm	Simulation case
Lu et al. [48]	Intercontinental multimodal transport with uncertain time and capacity	Min cost	MILP+ CPLEX 12.8	China-Europe freight transport
Xu et al. [50]	Path optimization with uncertain demand and environment	Min cost	MIP + GA	Simulation case
Zhang et al. [52]	Low carbon path optimization under uncertain demand	Min cost	Integer programming model + robust optimization + Monte Carlo catastrophe adaptive GA	Simulation case
Yuan et al. [59]	Low carbon path optimization under uncertain demand	Min cost	Fuzzy robust optimization model + Catastrophe adaptive GA	Simulation case
Huang et al. [62]	Low carbon path optimization under uncertain demand	Min cost/carbon emissions	MIP + Fuzzy chance constraint programming + Harris Eagle algorithm	Nanning-Harbin freight transport
Wang [63]	Low carbon path optimization under uncertain demand	Min cost	MIP + Fuzzy chance constraint theory + Heuristic algorithm	Shanghai-Chengdu freight
Deng et al. [65]	Low carbon path optimization under uncertain demand	Min cost/carbon emissions	MIP + SA-PSO	Simulation case
Chen et al. [69]	Low carbon multimodal transport under uncertainty of time and satisfaction	Min cost	IP + ACO	Simulation case
Zhou et al. [70]	Optimization of low-carbon multimodal transport routes under time uncertainty	Min cost/time/carbon emissions	MIP + Evolutionary algorithm	Simulation case
Li et al. [71]	Low-carbon multimodal transport route planning under demand uncertainty	Min cost/time/carbon emissions	MINLP + Fuzzy chance constraint + Cooperative game + Particle swarm algorithm	Guangdong-Beijing freight transport
Yang et al. [72]	Optimization of low-carbon multimodal transport routes with uncertain demand and time	Min cost/carbon emissions	Uncertainty model + Fuzzy chance constraint model + Adaptive differential evolution algorithm	Simulation case
Sun et al. [75]	Low-carbon multimodal transport path planning considering multiple cost factors	Min cost	MINLP + Logistic-Tent + Adaptive lens reverse learning strategy + Hybrid sand cat swarm optimization algorithm	Simulation case

IP: Integer Planning Model; MIP: Mixed Integer Planning Model; MILP: Mixed Integer Linear Programming; MINLP: Mixed Integer Nonlinear Programming; GA: Genetic Algorithm; NSGA- II: Non-dominated Sorting Genetic Algorithm-II; ACO: Ant Colony Optimization; PSO: Particle Swarm Optimization; SA: Simulated Annealing.

2.5. Multimodal Transport Route Optimization Considering Special Transport Needs

Research on the optimization of multimodal transport routes for special transport needs mainly focuses on the transport of cold chains, dangerous goods, emergency supplies and other goods. Multimodal transportation for special transportation needs needs to take more factors into consideration, and, at present, the transportation of special cargoes often takes into account the low carbon and uncertainty factors.

2.5.1. Cold Chain Multimodal Transportation Path Planning

Cold chain is often used in the transportation of fresh products or some medicines, the common point of these items is that they need to keep the goods in a specific temperature range to ensure their freshness and quality, and the excessive use of refrigeration will lead to an increase in carbon emissions. Timeliness is very important in cold chain transportation, which requires the vehicle to be very fast. Li [77] considered adding high-speed rail transportation to multimodal transportation for the small-volume and time-sensitive transportation needs of fresh products. Cui [78] established a refrigerated container multimodal transport path optimization model with the minimum total transport time, the minimum total transport cost, and the maximum satisfaction of the cargo owner as the multi-objectives based on constructing a time-varying network during the actual operation of refrigerated container multimodal transport. Meng et al. [79] simultaneously considered the characteristics of cold chain transportation and intermodal transportation, combined customer satisfaction with the quality and time of fresh products, introduced customer satisfaction parameters, and considered low-carbon strategies.

Most of the cold chain multimodal transportation studies consider the transportation demand as a fixed value, and the carbon emission of refrigerated container refrigeration is considered to be related to the transportation distance. However, in the actual transportation process, the goods transported in the cold chain are affected by natural conditions and market factors, and there is uncertainty in the transportation demand, refrigerated containers still need refrigeration and generate carbon emissions when they are transiting at the nodes or stopping and waiting on the way, and the correlation between carbon emissions from refrigeration of reefer containers and the transportation time is stronger [80,81]. Liu et al. [82] considered the carbon emission limitation and solved the problem that rail-water transportation in the process of multimodal transportation has a time limit for sending classes as well as the refrigeration cost and cargo difference in the transportation of reefer containers.

2.5.2. Multimodal Transportation Path Planning for Emergency Supplies

The transportation of emergency supplies has time urgency and importance, and needs to be delivered to the disaster area in the shortest time. A combination of multiple modes of transportation, such as highway, railroad, and aviation, is chosen to cope with different traffic conditions. Zhang et al. [83] used the joint transportation method for the urgency of emergency material transportation after a disaster and the realistic mode of level-by-level deployment.

The objectives are different at different times after an emergency. Yuan et al. [84] proposed a multi-stage emergency material multimodal transportation scheduling framework based on the characteristics of different phases of emergency relief, considering uncertainty factors and material dispatching needs. The three phases respectively aim at minimizing material dispatch time, material satisfaction, and dispatch cost. Maghfiroh et al. [85] proposed a multimodal distribution model for multimodal transportation with a three-level chain, with supply chain nodes at the first level, logistic operation areas at the second level, and disaster-stricken areas at the third level.

The transportation process of emergency supplies is full of uncertainties, for example, it may face challenges such as traffic congestion and road disruption, etc. Meng et al. [86] proposed a hierarchical assignment-based multimodal transportation strategy link to deal with disruption risk and network uncertainty in response to the dynamic uncertainty of natural disasters. Liu et al. [87] establish a reliable path optimization model for multimodal transportation of emergency supplies under double uncertainty by considering shift limitations, time-variation, uncertainty of transportation demand, cost constraints, the risk of nodes infected with epidemics, and node transshipment capacity constraints.

When an emergency event occurs, rescue needs to be mobilized from the surrounding areas first, Li et al. [88] took this into account and used multimodal transportation to deal with the emergency transportation problem, and in this way established an emergency rescue and multimodal transportation optimization model that considered multiple types. Guo et al. [89] also brought the multimodal transportation idea into the emergency transportation problem and established a multi-objective mixed integer planning model to deal with the problem. Wang Zhe [90] realized the decision-making of emergency logistics transportation vehicle paths by determining the feasibility of intermodal solutions with the help of the results of calculating the space-cum-capacity with the help of a perfect intermodal transportation network.

2.5.3. Multimodal Transportation Path Planning for Dangerous Goods and Bulk Cargoes

Dangerous goods transportation is high-risk and requires special transportation and security measures. Moreover, dangerous goods may leak, explode, and other dangerous situations during transportation, posing a threat to people and the environment.

In the study of multimodal transportation path optimization problems for dangerous goods. Zhang et al. [91] considered the increasing use of intermodal transport of dangerous goods in recent years and the clustering of transshipment volume at network transfer points, which led to higher safety risks, and therefore proposed a site selection based on the risk classification of transfer points as well as a charging strategy. Zhang [92], Zhou et al. [93] and others found that the demand for liquefied natural gas (LNG), a clean energy source, is increasing, and the former aimed to minimize the total intermodal transport cost minus the establishment provided by the port as the goal to optimize LGN carrier allocation, storage planning, and transportation planning. The latter constructs a two-stage integer planning optimization model with minimum cost to optimize the routes.

Other related scholars have considered the research problem of carbon emission in hazardous materials transportation. Zahra et al. [94] considered the factors of accident probability, emission factor, and storage cost uncertainty, and built a mixed integer model with multi-objective uncertainty in terms of carbon emission, risk, and cost minimization, using robust pairwise to deal with uncertainty, and a bounded-objective approach to deal with three conflicting objectives.

Large cargoes are characterized by a long form factor, large height, irregular shape, large mass, and non-disintegrable. When considering intermodal path planning for large cargo transportation, it is necessary to comprehensively consider several aspects, including cargo attributes, transportation mode selection, and transportation route optimization. Wang et al. [95] considered the use of multimodal transportation methods to transport large cargoes, introduced the energy consumption factor, designed the formula for calculating the carbon emissions of the multimodal transportation of large cargoes during in-transit transportation, transformation and reloading, and considered constraints such as post-loading contour dimensions of large cargoes, limit boundaries, the load-bearing capacity of bridges, and node reloading capacity in an integrated manner, taking into account the transformation of transportation road sections.

Table 5. Summary of research on multimodal transport route optimization considering special transport needs.

Literature	Objective	function	Modeling/Solving	Examples
Sun et al. [36]	Multimodal transport of dangerous goods under uncertain demand	Min cost	MIP + Fuzzy chance constraint programming + Rimer fuzzy sorting method + $\mathsf{\epsilon }$-constraint method	Simulation case
Guo et al. [51]	Multi-objective multimodal transport path optimization for emergency transportation	Min cost/path/time	MIP + Dijkstra algorithm + Ideal point + Multi-objective k-short path algorithm + CPLEX12.6.3	Simulation case
Yang et al. [67]	Optimization of cold chain multimodal transport routes under carbon trading uncertainty	Min cost, max satisfaction	Dual-objective mixed integer programming model + Fuzzy adaptive non-dominated sorting GA	Simulation case
Li et al. [77]	Route optimization of highspeed railway fresh products considering time window	Min cost	MIP + Hybrid Taguchi GA	Taking the fresh products from Harbin to Kunming
Cui [78]	Reefer container multimodal transport	Min time/cost, max cargo owner satisfaction	MIP + Linear weighting method + GA	Transportation of three types of refrigerated cargo
Meng et al. [79]	Optimization of low-carbon cold chain multimodal transport routes	Min cost, max customer satisfaction	MIP + Emperor penguin optimization algorithm	Simulation case
Su et al. [80]	Refrigerated container multimodal transport route optimization	Min cost	MIP + Fuzzy chance constraint theory + COPT7.0	Guangzhou-Dalian freight transportation
Sun et al. [81]	Reefer container multimodal transport	Min cost/carbon emissions	MIP + genetic algorithm based on simulated annealing	Simulation case
Yuan et al. [84]	Multi-stage multimodal transport dispatch of emergency materials	Min time/cost, max satisfaction	Multi-stage model + Linear weighting method + GA-SA	Emergency supplies distribution in Yaan earthquake
Maghfiroh et al. [85]	Multimodal transport route planning for post-disaster emergency supplies	Min cost/time	MIP + CPLEX 12.8	Taking Java Island and Yogyakarta Province in Indonesia
Meng et al. [86]	Multimodal transport path planning for post-disaster emergency supplies	Min cost/time	Two-stage chance-constrained random programming model + CPLEX+ Evolutionary algorithm	Emergency supplies distribution in Yaan earthquake
Liu et al. [87]	Multimodal transport under uncertain demand and environment	Max reliability	MIP + Monte Carlo GA	Simulation case
Li et al. [89]	Multimodal transport path optimization under emergency events	Min cost/time	MINLP + Gray wolf optimization algorithm	Emergency rescue transportation under the epidemic in Hubei Province
Zhang et al. [92]	Optimization of multimodal transportation and storage of energy	Min cost	MINLP + GUROBI 10.0.0	Simulation case
Zhou et al. [93]	LNG tank container multimodal transport considering cross terminal	Min cost	Two-stage MIP + CEPLEX + DICOPT	Simulation case
Zahra et al. [94]	Multi-objective low-carbon multimodal transport path planning under accident, emission and storage uncertainty	Min cost/carbon emissions/risk	MIP + Robust duality + Bounded objectives	Simulation case
Wang et al. [95]	Optimization of multimodal transport routes for large cargo under low carbon conditions	Min cost/carbon emissions	MIP + Adaptive elite GA	Simulation case

IP: Integer Planning Model; MIP: Mixed Integer Planning Model; MILP: Mixed Integer Linear Programming; MINLP: Mixed Integer Nonlinear Programming; NSGA-2: Non-dominated Sorting Genetic Algorithm-II; ACO: Ant Colony Optimization; PSO: Particle Swarm Optimization; SA: Simulated Annealing.

Table 5. Summary of research on multimodal transport route optimization considering special transport needs.

Literature	Objective	function	Modeling/Solving	Examples
Sun et al. [36]	Multimodal transport of dangerous goods under uncertain demand	Min cost	MIP + Fuzzy chance constraint programming + Rimer fuzzy sorting method + $\mathsf{\epsilon }$-constraint method	Simulation case
Guo et al. [51]	Multi-objective multimodal transport path optimization for emergency transportation	Min cost/path/time	MIP + Dijkstra algorithm + Ideal point + Multi-objective k-short path algorithm + CPLEX12.6.3	Simulation case
Yang et al. [67]	Optimization of cold chain multimodal transport routes under carbon trading uncertainty	Min cost, max satisfaction	Dual-objective mixed integer programming model + Fuzzy adaptive non-dominated sorting GA	Simulation case
Li et al. [77]	Route optimization of highspeed railway fresh products considering time window	Min cost	MIP + Hybrid Taguchi GA	Taking the fresh products from Harbin to Kunming
Cui [78]	Reefer container multimodal transport	Min time/cost, max cargo owner satisfaction	MIP + Linear weighting method + GA	Transportation of three types of refrigerated cargo
Meng et al. [79]	Optimization of low-carbon cold chain multimodal transport routes	Min cost, max customer satisfaction	MIP + Emperor penguin optimization algorithm	Simulation case
Su et al. [80]	Refrigerated container multimodal transport route optimization	Min cost	MIP + Fuzzy chance constraint theory + COPT7.0	Guangzhou-Dalian freight transportation
Sun et al. [81]	Reefer container multimodal transport	Min cost/carbon emissions	MIP + genetic algorithm based on simulated annealing	Simulation case
Yuan et al. [84]	Multi-stage multimodal transport dispatch of emergency materials	Min time/cost, max satisfaction	Multi-stage model + Linear weighting method + GA-SA	Emergency supplies distribution in Yaan earthquake
Maghfiroh et al. [85]	Multimodal transport route planning for post-disaster emergency supplies	Min cost/time	MIP + CPLEX 12.8	Taking Java Island and Yogyakarta Province in Indonesia
Meng et al. [86]	Multimodal transport path planning for post-disaster emergency supplies	Min cost/time	Two-stage chance-constrained random programming model + CPLEX+ Evolutionary algorithm	Emergency supplies distribution in Yaan earthquake
Liu et al. [87]	Multimodal transport under uncertain demand and environment	Max reliability	MIP + Monte Carlo GA	Simulation case
Li et al. [89]	Multimodal transport path optimization under emergency events	Min cost/time	MINLP + Gray wolf optimization algorithm	Emergency rescue transportation under the epidemic in Hubei Province
Zhang et al. [92]	Optimization of multimodal transportation and storage of energy	Min cost	MINLP + GUROBI 10.0.0	Simulation case
Zhou et al. [93]	LNG tank container multimodal transport considering cross terminal	Min cost	Two-stage MIP + CEPLEX + DICOPT	Simulation case
Zahra et al. [94]	Multi-objective low-carbon multimodal transport path planning under accident, emission and storage uncertainty	Min cost/carbon emissions/risk	MIP + Robust duality + Bounded objectives	Simulation case
Wang et al. [95]	Optimization of multimodal transport routes for large cargo under low carbon conditions	Min cost/carbon emissions	MIP + Adaptive elite GA	Simulation case

IP: Integer Planning Model; MIP: Mixed Integer Planning Model; MILP: Mixed Integer Linear Programming; MINLP: Mixed Integer Nonlinear Programming; NSGA-2: Non-dominated Sorting Genetic Algorithm-II; ACO: Ant Colony Optimization; PSO: Particle Swarm Optimization; SA: Simulated Annealing.

3. Model and Algorithm Analysis

Through the above grasp of the current status and trend of research on multimodal transport path optimization problems, it can be found that more and more scholars focus on multimodal transport with the combination of low carbon and uncertainty conditions. Most authors consider the uncertainty of demand and carbon trading price, and less consideration is given to the uncertainty of node operation time and unexpected situations in the multimodal transportation process.

3.1. Model Analysis

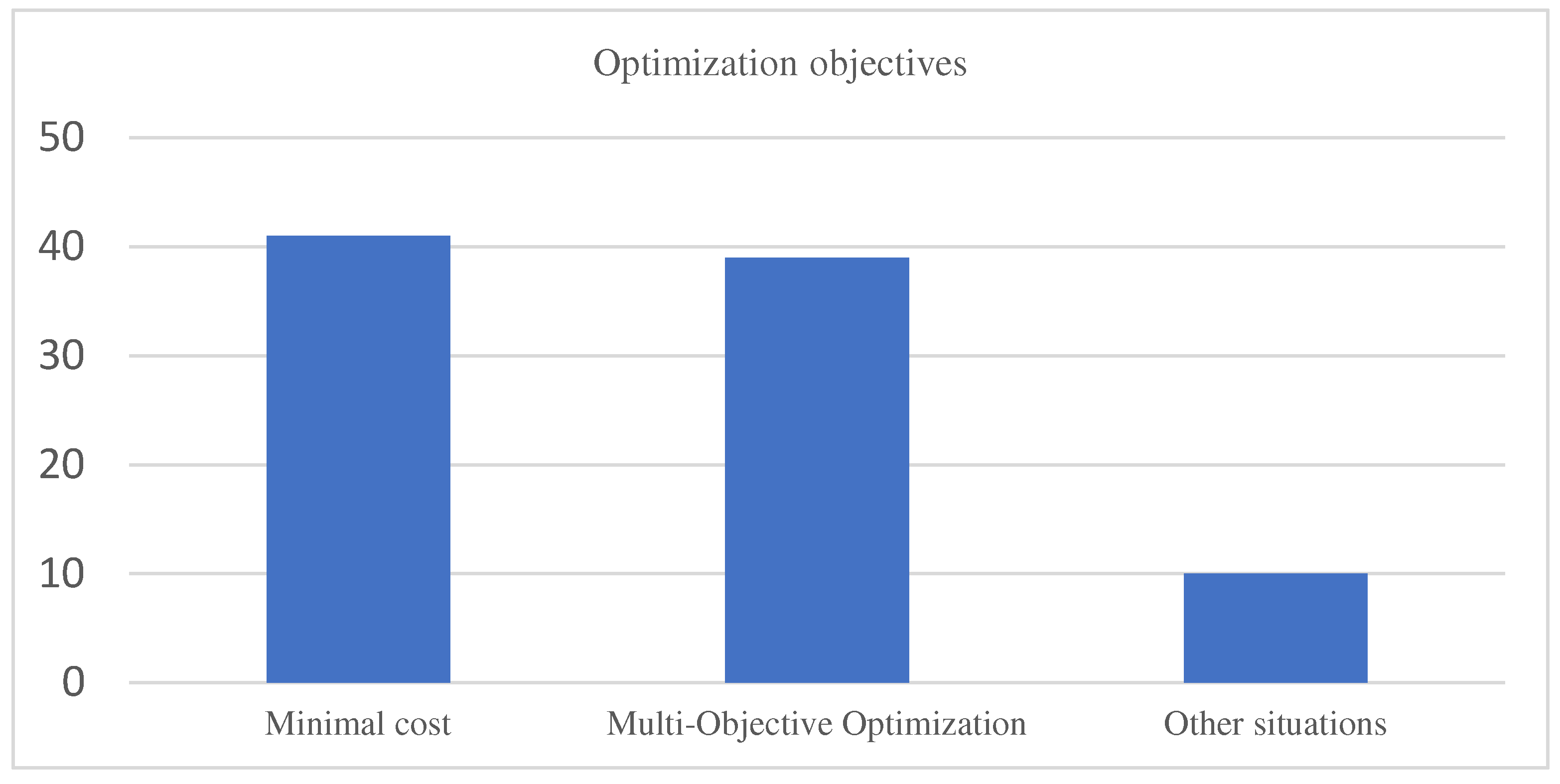
In terms of model building, according to the analysis of the current state of research, it is found that the optimization that only considers a single objective is beginning to become less, and more scholars are beginning to consider multi-objective optimization problems. In the single-objective optimization problems, most of them take cost and time minimization as the objective, and there are many scholars who also use carbon price to calculate carbon emission, and then calculate it into the cost, so that the model construction and algorithm will be simpler compared to the multi-objective optimization problems that consider cost and carbon emission minimization at the same time.

In multi-objective optimization problems, the main objective is to minimize the cost and time, or to minimize the cost, time and carbon emissions as the optimization objective. The treatment for multi-objective optimization can also be mainly divided into the following two kinds. One is to weight each objective according to the corresponding weights, transformed into a single-objective optimization problem, although the transformation process is more cumbersome, need to consider more factors, but the victory is that the solution is simple. There is also a choice of heuristic or meta-heuristic algorithms, according to the specific problem for the corresponding improvement, but can not get the optimal solution, can only get the corresponding pareto solution set, and then select the appropriate solution according to the specific situation. The model objectives are summarized in Table 6 and Figure 11.

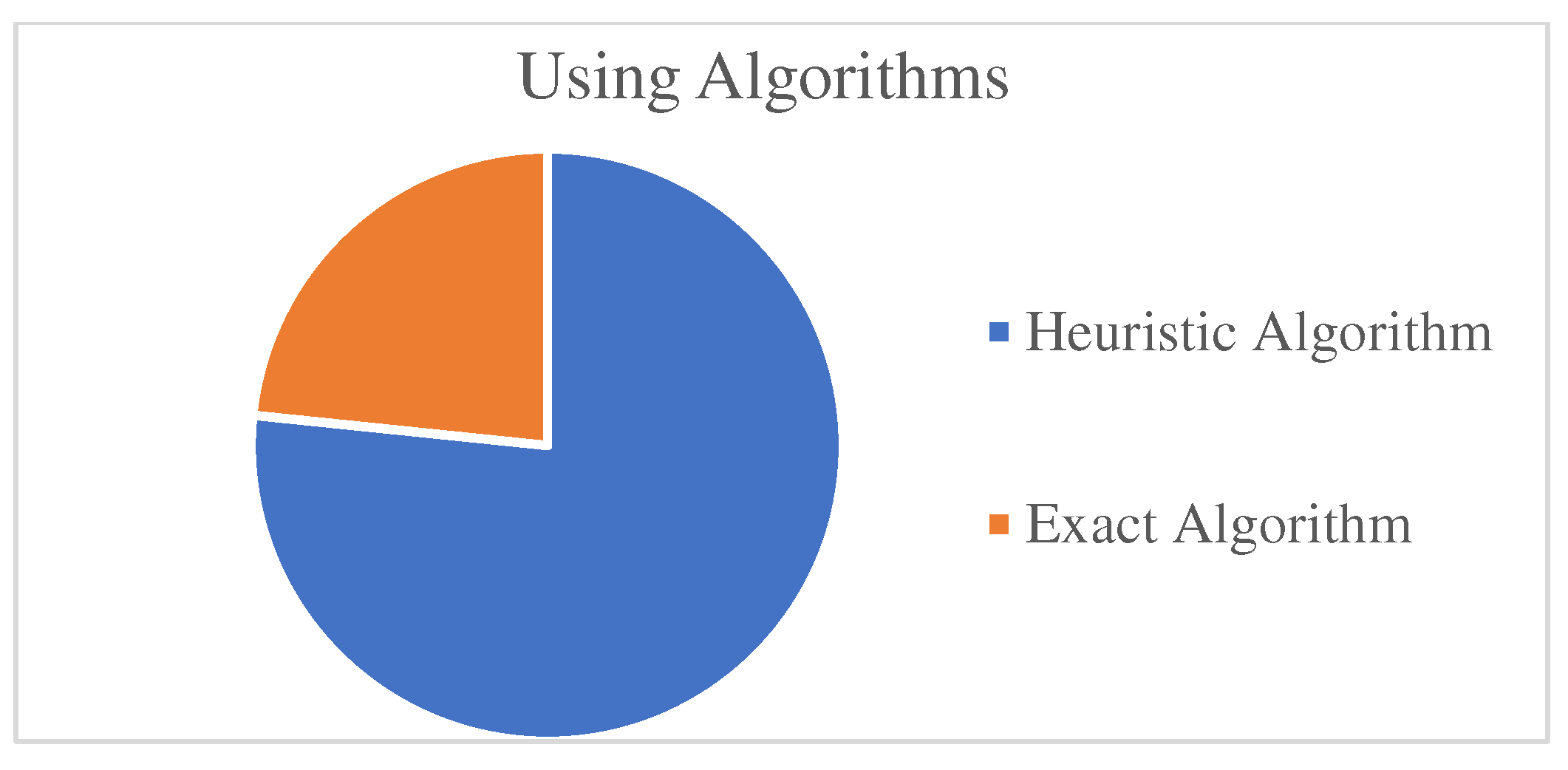
3.2. Algorithm Analysis

For algorithms, the main ones are exact algorithms, heuristic algorithms. The most used heuristic algorithm is genetic algorithm, and there are many other bionic intelligence algorithms, such as whale optimization algorithm [21], Harris hawk algorithm [62], and hybrid sand cat swarm optimization algorithm [75]. Although heuristic algorithms are flexible and efficient, and can deal with large-scale data, nonlinear constraints, and multi-objective functions, the solution results change with the change of parameters set by their own experience, with a high degree of dependence on the parameters set by the autonomy, and there is a certain probability that they will fall into the local optimal solution. Therefore, the vast majority of authors improve the genetic algorithm according to the specific analysis of specific problems, which in turn derives the improved genetic algorithm of elite strategy [14], the fuzzy adaptive non-dominated sorting genetic algorithm [67], the Monte Carlo genetic algorithm [87], and so on.

Some other scholars try to combine multiple heuristic algorithms based on different advantages, both hybrid optimization algorithms, such as genetic algorithm based on simulated annealing [46], particle swarm algorithm based on simulated annealing [65]. Accurate algorithms, on the other hand, are solved using mathematical optimization software, such as CPLEX, LINGO, etc., and the algorithms they use are mainly K-short-circuit algorithm and Dijkstra’s algorithm. The summary table of algorithms is shown in Table 7 and Figure 12.

4. Future Directions

Based on the above grasp of the research status and trend of the container intermodal transportation path optimization problem, the following 2 potential research directions are proposed.

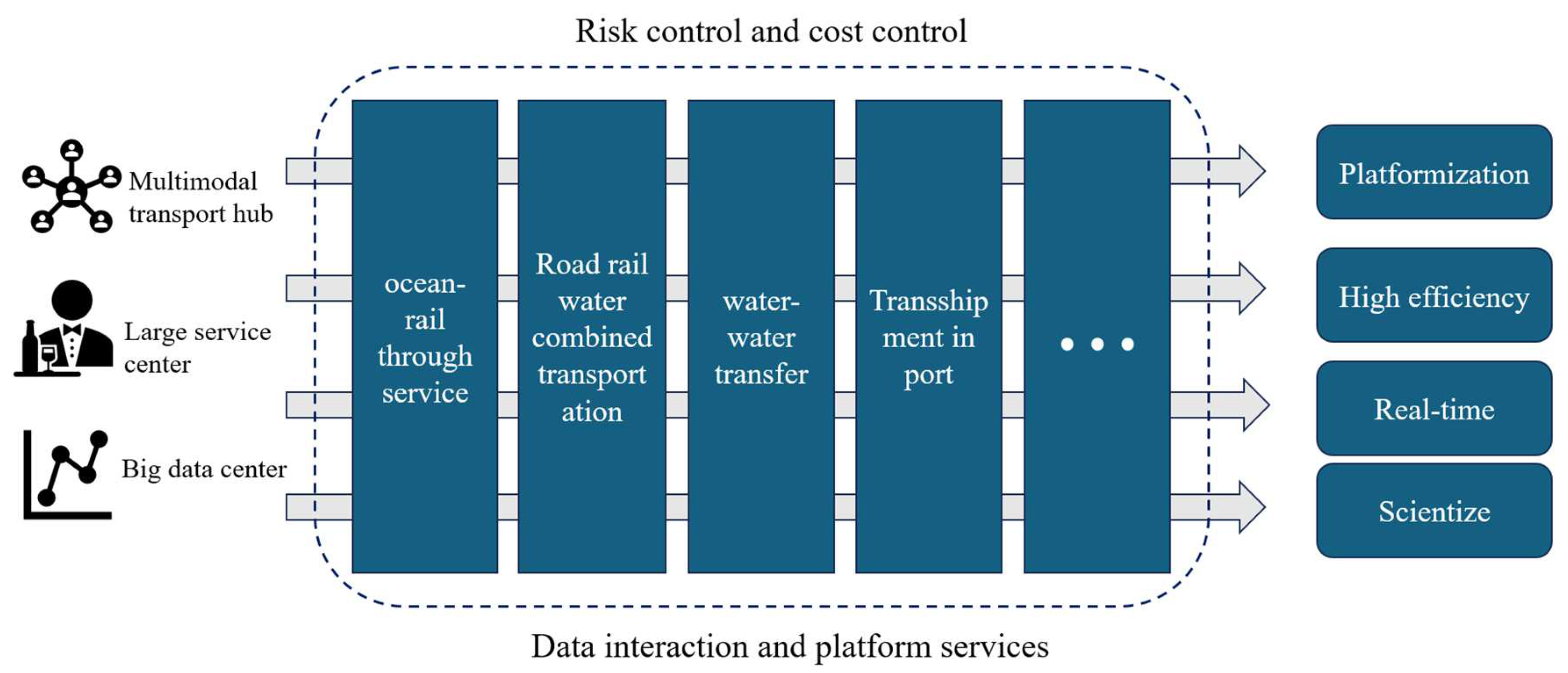
4.1. Collaborative Scheduling Problem of Intermodal Transportation Path Planning

Regarding the multimodal transportation path optimization scheduling problem, some scholars consider automated, unmanned scenarios. Zhao [96] takes the three directions of automated terminal public-water intermodal transportation, automated terminal public-rail-water intermodal transportation, and port-public hybrid collector truck fleet scheduling as backgrounds, respectively, and establishes an unmanned collector truck scheduling model to reduce transportation costs. Li [97], for the NVOCC multimodal transportation scheduling and organization optimization problem, divided the transportation organization optimization problem with multiple transportation origins and multiple transportation destinations into three phases of initial consolidation, trunk transportation, and end distribution, and decomposed it into two major types of transportation scheduling problems.

The key to promoting the high-quality development of China’s multimodal transportation is to clarify the key technologies applicable to China’s multimodal transportation linkage, build a multimodal transportation linkage key technology system, and synergistically develop and apply them in the production practice [5,6]. Compared with the previous multimodal transport path optimization problem, the high flexibility and real-time information of collaborative transport can further improve transport efficiency [98], and the flexible and sustainable characteristics of collaborative multimodal transport can solve the problem of uncertainty [47,89]. Therefore, the issues of how to realize the flexible selection of three modes of transfer, namely, public, railway, and water, how to make transfer decisions based on real-time information of vehicle operation, and how to make full use of the flexibility provided by coordinated transport through real-time mode changes in path optimization problems to reduce the total cost of transfer will be the focus of future research. The collaborative transportation architecture is shown in Figure 13.

4.2. Demand Forecasting Problem in Multimodal Transportation Path Planning

Currently, most scholars use methods such as fuzzy number and opportunity constrained planning theory to solve the uncertainty of demand and time in the multimodal transportation process. However, with the rapid development of computer hardware capability, deep learning models rely on their strong learning ability and will have good prediction effect in the face of various uncertainties in the process of multimodal transportation path optimization.

Deep learning, as a powerful machine learning technology, has significant advantages in dealing with complex and nonlinear problems. By constructing time series prediction models or regression models, deep learning can capture seasonal, cyclical, and trend changes in transportation demand, thus improving the accuracy of prediction. Using historical transportation data, deep learning models can learn and predict future transportation demand. This helps companies plan transportation resources and routes to cope with demand uncertainty.

Already scholars have started to use deep learning to address demand uncertainty in multimodal transportation. Both, the dynamic prediction of intermodal freight transportation volume. Peng [99] used the Pearson correlation coefficient method for feature extraction of influencing factors, and then built a combined prediction model based on seasonal autoregressive moving average model as well as long and short-term memory neural networks based on the characteristics of sea-rail intermodal transport volume data. Wang et al. [100] developed a framework for OD traffic prediction in intelligent and multi-modal urban transportation systems FusionTransNet.

The emergence of deep learning techniques has profoundly changed various application domains, including path prediction in transportation networks [101]. Deineko et al. [102] found that path optimization problems can be solved using deep learning methods, and neural combinatorial optimization can achieve real-time decision-making under uncertainty by considering the current overall state after learning. Ferjani et al. [103] proposed a decision support system coupled with simulation and optimization models. The system helps in evaluating various routes and generating optimal solutions based on user preferences and considering environmental considerations.

Other scholars have considered the privacy issues in performing demand forecasting, resulting in the fact that existing multimodal demand forecasting methods are often unable to use shared raw data to improve demand forecasting performance. Attentional federated learning programs were designed. The research gap in enhancing multimodal demand forecasting without relying on direct data sharing was addressed [104].

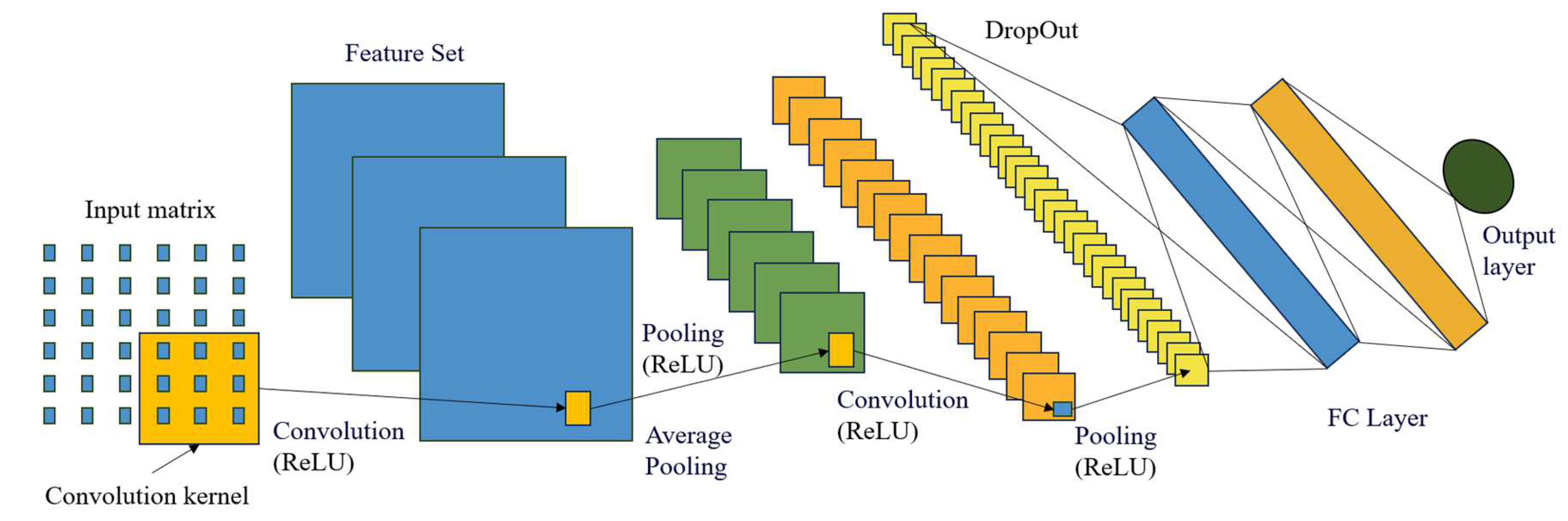
With the development of multimodal transportation, scholars are beginning to use more innovative and effective model architectures and solution algorithms to solve more practical multimodal transportation path optimization problems. For uncertainties such as demand, deep learning methods can be used for regression prediction to help enterprises more flexibly choose the three modes of transportation: public, railway and water, in order to help enterprises realize cost reduction and efficiency, of course, not only for the uncertainty of demand, but also for other uncertainties such as time, environment, and other uncertainties, the deep learning model will also have a very good performance. The framework for regression prediction using CNN (Convolutional Neural Network) is shown in the Figure 14.

5. Summary and Prospects

In recent years, many scholars have conducted research on the path planning problem for various modes of transportation such as sea-rail intermodal transportation, public-rail intermodal transportation, public-rail-water intermodal transportation, etc., and have considered low-carbon policies and various uncertainties, as well as researched on the solution to the transportation of special items through intermodal transportation. According to the research directions and objectives of the existing literature, this paper is divided into: traditional intermodal transport path optimization, intermodal transport path optimization considering carbon emission, intermodal transport path optimization considering uncertainties, intermodal transport path optimization considering uncertainties under low carbon, intermodal transport path optimization considering special needs, and is subdivided again for a review.

Meanwhile, the model building and model solving for different research directions and objectives are summarized and analyzed, and the methods commonly used by scholars to solve various problems are summarized.

Finally, considering the current rapid development of cooperative transportation and the wide application of deep learning in various fields. Based on this review, two future research directions are proposed: the cooperative scheduling problem in multimodal transportation path planning and the demand forecasting problem in multimodal transportation path planning.

The problem of regression prediction of uncertain demand using deep learning methods in a low-carbon context is a potential future research focus. Predicting future transportation demand through deep learning regression helps enterprises plan transportation resources and paths in advance to reduce costs and unnecessary losses. Therefore, when developing the path planning scheme, it is necessary to comprehensively consider multiple objectives, such as carbon emission situation, transportation time, cost, etc., and find the balance point between multiple objectives to achieve the overall scheme optimization. At the same time, deep learning models are used to make reasonable predictions of demand and other dynamic information, and real-time adjustments are made to the operation path to ensure that transportation efficiency is maximized.