A √n-Approximation for Independent Sets: The Furones Algorithm

1. Introduction

The Maximum Independent Set (MIS) problem is a cornerstone of graph theory and combinatorial optimization [1]. Given an undirected graph $G=(V,E)$, where V is the set of vertices and E is the set of edges, an independent set is a subset $S\subseteq V$ such that no two vertices in S are adjacent, i.e., for all $u,v\in S$, $(u,v)\notin E$. The goal of the MIS problem is to find an independent set S with the maximum cardinality, denoted $\mathrm{OPT}={max}_{S\mathrm{independent}}\left|S\right|$. The size of the maximum independent set is also called the independence number of the graph, denoted $\alpha \left(G\right)$.

The MIS problem arises in numerous applications, including scheduling, where tasks must be assigned without conflicts; network design, for selecting non-interfering nodes; and coding theory, for constructing error-correcting codes. However, the problem is computationally challenging, as it is NP-hard for general graphs, meaning no polynomial-time algorithm is known to solve it exactly unless $\mathrm{P}=\mathrm{NP}$. This hardness motivates the development of approximation algorithms that produce near-optimal solutions efficiently.

The NP-hardness of MIS has led to extensive research on approximation algorithms, particularly for general graphs where exact solutions are infeasible for large instances. The quality of an approximation algorithm is measured by its approximation ratio, defined as ${\displaystyle \frac{\mathrm{OPT}}{\left|S\right|}}$, where $\left|S\right|$ is the size of the independent set produced by the algorithm. A smaller ratio indicates a better approximation. Below, we summarize key results in the state of the art for MIS approximation algorithms:

• Greedy Algorithms: A simple greedy algorithm selects vertices in order of increasing degree, adding a vertex to the independent set if it has no neighbors in the current set. This achieves an approximation ratio of $O(\Delta )$, where $\Delta$ is the maximum degree. For graphs with high degrees ($\Delta \approx n-1$), this yields a poor ratio of $O\left(n\right)$. A more sophisticated greedy approach, selecting vertices by minimum degree iteratively, achieves an approximation ratio of $O(n/logn)$, as shown by Halldórsson and Radhakrishnan [2].
• Local Search and Randomized Algorithms: Local search techniques, such as those by Boppana and Halldórsson [3], improve the approximation ratio to $O(n/{(logn)}^2)$ by iteratively swapping small subsets of vertices to increase the independent set size. Randomized algorithms, like those based on random vertex selection or Lovász Local Lemma, can achieve similar ratios with probabilistic guarantees.
• Semidefinite Programming (SDP): Advanced techniques using SDP, such as those by Karger, Motwani, and Sudan [4], achieve approximation ratios of $O(n/logn)$ for general graphs. For specific graph classes, such as 3-colorable graphs, better ratios (e.g., $O\left(\sqrt{n}\right)$) are possible.
• Hardness of Approximation: The MIS problem is notoriously difficult to approximate. Håstad [5] and others have shown that, assuming $\mathrm{P}\ne \mathrm{NP}$, no polynomial-time algorithm can achieve an approximation ratio better than $O\left(n^{1-ϵ}\right)$ for any $ϵ>0$. This inapproximability result underscores the challenge of finding near-optimal solutions.
• Special Graph Classes: For specific graph classes, better approximations exist. For bipartite graphs, the maximum independent set can be computed exactly in polynomial time using maximum matching algorithms (via König’s theorem). For graphs with bounded degree or specific structures (e.g., planar graphs), constant-factor approximations are achievable.

The state of the art highlights a trade-off between computational efficiency and approximation quality. Simple greedy algorithms are fast but yield poor ratios, while SDP-based methods offer better ratios at the cost of higher computational complexity. The challenge remains to design algorithms that balance runtime and approximation ratio, especially for general graphs.

Our hybrid algorithm computes an approximate maximum independent set for an undirected graph $G=(V,E)$ with n vertices and m edges. It begins by preprocessing the graph to remove self-loops and isolated nodes, handling trivial cases (empty or edgeless graphs) by returning the empty set or all vertices, respectively. If the graph is bipartite, it computes the maximum independent set exactly using the Hopcroft-Karp matching algorithm and König’s theorem, taking $O(n+m+\sqrt{n}m)$ time. For non-bipartite graphs, it employs two strategies:

• Iterative Refinement: Initializes a candidate set with all non-isolated vertices and iteratively refines it by constructing a maximum spanning tree of the induced subgraph, computing its maximum independent set (since trees are bipartite), and updating the candidate set until it is independent in G. A greedy extension adds vertices to ensure maximality, producing $S_{\mathrm{iterative}}$.
• Greedy Minimum-Degree Selection: Sorts vertices by increasing degree and builds an independent set by adding each vertex if it has no neighbors in the current set, producing $S_{\mathrm{greedy}}$.

The algorithm selects the larger of $S_{\mathrm{iterative}}$ and $S_{\mathrm{greedy}}$, then adds isolated nodes to form the final set S. The is_independent_set subroutine, running in $O\left(m\right)$ time, verifies independence by checking all edges. The hybrid approach guarantees a valid, maximal independent set with a worst-case approximation ratio of $\sqrt{n}$, robustly handling diverse graph structures, including graphs with multiple cliques sharing a universal vertex. Its time complexity is $O(nmlogn)$, dominated by the iterative refinement, making it suitable for small-to-medium graphs. While less competitive than $O(n/logn)$-ratio algorithms for large instances, its simplicity, use of standard graph operations (via NetworkX), and robustness make it an effective educational tool for studying approximation algorithms and combinatorial optimization.

2. Research data

A Python implementation, titled Furones: Approximate Independent Set Solver has been developed to efficiently solve the Approximate Independent Set Problem. The solver is publicly available via the Python Package Index (PyPI) [6] and guarantees a rigorous approximation ratio of at most $\sqrt{n}$ for the Independent Set Problem. Code metadata and ancillary details are provided in Table 1.

3. Correctness of the Maximum Independent Set Algorithm

The algorithm under consideration computes an approximate independent set using maximum spanning trees and combining with a greedy approach to ensure maximality. We prove that the algorithm’s output is always a valid independent set.

Algorithm Description

Consider the algorithm implemented in Python:

The hybrid algorithm combines iterative refinement using maximum spanning trees with a greedy minimum-degree selection, returning the larger independent set to achieve a $\sqrt{n}$-approximation ratio. We prove that the algorithm always produces a valid independent set, using an $O\left(m\right)$ is_independent_set subroutine and a NetworkX implementation with adjacency list representation.

Theorem 1.

The hybrid maximum independent set algorithm, which combines iterative refinement using maximum spanning trees with a greedy minimum-degree selection and uses an $O\left(m\right)$is_independent_setsubroutine, always produces a valid independent set for any undirected graph $G=(V,E)$. That is, the output set $S\subseteq V$ satisfies the property that no two vertices in S are adjacent.

Proof. 

To prove correctness, we show that the output S is an independent set, i.e., for all $u,v\in S$, $(u,v)\notin E$. We analyze each case of the algorithm’s execution.

Case 1: Trivial Cases

If G has no vertices ($n=0$) or no edges ($m=0$), the algorithm returns:

• If $n=0$, $S=\varnothing$. The empty set is an independent set, as it contains no vertices to be adjacent.
• If $m=0$, $S=V$. Since there are no edges, no pair of vertices is adjacent, so V is an independent set.

Case 2: Graph with Only Isolated Nodes

After preprocessing, if the graph has no edges (all vertices are isolated), the algorithm returns isolates, the set of all vertices with degree 0. Since $G\left[\mathrm{isolates}\right]$ has no edges, this set is independent.

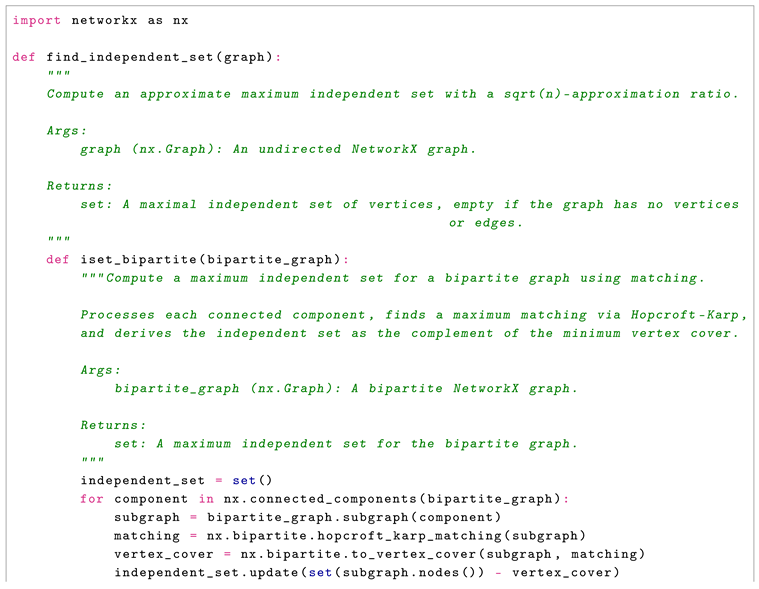
Case 3: Bipartite Graph

If G is bipartite, the algorithm computes the maximum independent set for each connected component using iset_bipartite:

• For each component with vertex set $V_C$, it uses the Hopcroft-Karp algorithm to find a maximum matching, then computes a minimum vertex cover C using König’s theorem.
• The independent set is $V_C\setminus C$, the complement of the vertex cover in the component.
• By König’s theorem, in a bipartite graph, the complement of a minimum vertex cover is a maximum independent set. If any two vertices in $V_C\setminus C$ were adjacent, they would form an edge not covered by C, contradicting the vertex cover property.
• The union of these sets across components is independent in G, as components are disconnected.

Case 4: Non-Bipartite Graph

For non-bipartite graphs, the algorithm computes two independent sets and returns the larger:

• Iterative Refinement:
  • Start with $S_0=V$, where V is the set of non-isolated vertices after preprocessing.
  • While $S_k$ is not independent in G, compute $S_{k+1}$ as the maximum independent set of a maximum spanning tree $T_k$ of $G\left[S_k\right]$, using iset_bipartite.
  • Stop when $S_t$ is independent in G, verified by is_independent_set.
  • Greedily extend $S_t$: for each $u\in V$, if $S_t\cup \left\{u\right\}$ is independent, add u. Output $S_{\mathrm{iterative}}$.
• Greedy Minimum-Degree Selection: Sort vertices by increasing degree and add each vertex v to $S_{\mathrm{greedy}}$ if it has no neighbors in the current set.
• Output: Return $S=S_{\mathrm{iterative}}\cup \mathrm{isolates}$ if $|S_{\mathrm{iterative}}|\ge |S_{\mathrm{greedy}}|$, else $S=S_{\mathrm{greedy}}\cup \mathrm{isolates}$.

Iterative Refinement

The iterative loop terminates when $S_t$ is independent in G:

• is_independent_set returns True if and only if no edge $(u,v)\in E$ has both $u,v\in S_t$, taking $O\left(m\right)$ time by checking all edges.
• Thus, $S_t$ is an independent set in G.
• Greedy Extension: For each vertex $u\in V$, if $S_t\cup \left\{u\right\}$ is independent (verified by is_independent_set), add u. This ensures no edge exists between u and any vertex in $S_t$, or between any pair in the updated set. Each addition preserves independence, so $S_{\mathrm{iterative}}$ is independent.

Greedy Minimum-Degree Selection

The greedy approach builds $S_{\mathrm{greedy}}$:

• Vertices are sorted by degree, and for each vertex v, it is added to $S_{\mathrm{greedy}}$ if none of its neighbors are in the current set.
• At each step, the check ensures that adding v introduces no edges, as $(v,u)\notin E$ for all $u\in S_{\mathrm{greedy}}$.
• The resulting $S_{\mathrm{greedy}}$ is independent, as each addition preserves the property that no two vertices in the set are adjacent.

Final Output

The algorithm selects $S=S_{\mathrm{iterative}}\cup \mathrm{isolates}$ or $S=S_{\mathrm{greedy}}\cup \mathrm{isolates}$, based on which has the larger size:

• Both $S_{\mathrm{iterative}}$ and $S_{\mathrm{greedy}}$ are independent in the non-isolated subgraph, as shown above.
• Isolated vertices have degree 0, so for any $u\in \mathrm{isolates}$, $(u,v)\notin E$ for all $v\in V$. Adding them to either $S_{\mathrm{iterative}}$ or $S_{\mathrm{greedy}}$ cannot introduce edges.
• Thus, the final S remains independent.

Conclusion

In all cases:

• Trivial Cases: The empty set or V (for $m=0$) are independent.
• Isolated Nodes: The set of isolates is independent due to no edges.
• Bipartite Case: König’s theorem ensures the complement of the vertex cover is independent.
• Non-Bipartite Case: The iterative refinement produces an independent set $S_{\mathrm{iterative}}$, the greedy selection produces an independent set $S_{\mathrm{greedy}}$, and the larger set, combined with isolates, remains independent.

The is_independent_set subroutine, running in $O\left(m\right)$, correctly verifies independence by checking all edges. Thus, the hybrid algorithm always produces a valid independent set for any undirected graph G.    □

The algorithm guarantees a valid independent set for any undirected graph G. Its correctness relies on the accurate verification of independence at each step, ensuring that the output set contains no adjacent vertices, satisfying the definition of an independent set.

4. Proof of $\sqrt{n}$-Approximation Ratio for Hybrid Maximum Independent Set Algorithm

Let OPT denote the size of the maximum independent set. The algorithm combines iterative refinement using maximum spanning trees with a greedy minimum-degree selection, returning the larger independent set to guarantee a $\sqrt{n}$-approximation ratio across all graphs, including those with multiple cliques sharing a universal vertex.

Theorem 2.

The hybrid maximum independent set algorithm, which combines iterative refinement using maximum spanning trees with a greedy minimum-degree selection, has an approximation ratio of $\sqrt{n}$. That is, if S is the independent set returned and OPT is the size of the maximum independent set, then ${\displaystyle \frac{\mathrm{OPT}}{\left|S\right|}}\le \sqrt{n}$.

Proof. 

We show that ${\displaystyle \frac{\mathrm{OPT}}{\left|S\right|}}\le \sqrt{n}$ by describing the hybrid algorithm and analyzing its performance on key graphs, including a worst-case graph with $\mathrm{OPT}=\sqrt{n}$, $\left|S\right|=1$, and a graph with multiple cliques sharing a universal vertex.

Algorithm Description

The algorithm operates as follows:

• Preprocessing: Remove self-loops and isolated nodes from G. Let $I_{\mathrm{iso}}$ be the set of isolated nodes. If the graph is empty or edgeless, return $I_{\mathrm{iso}}$.
• Iterative Refinement:

  (a)

  Start with $S_0=V$, where V is the set of non-isolated vertices.

  (b)

  While $S_k$ is not an independent set in G:

  • Construct a maximum spanning tree $T_k$ of the subgraph $G\left[S_k\right]$.
  • Compute the maximum independent set of $T_k$ (a tree, thus bipartite) using a matching-based approach, and set $S_{k+1}$ to this set.

  (c)

  Stop when $S_t$ is independent in G.

  (d)

  Greedily extend $S_t$: for each $u\in V$, if $S_t\cup \left\{u\right\}$ is independent, add u. Let $S_{\mathrm{iterative}}=S_t$.

• Greedy Selection: Compute $S_{\mathrm{greedy}}$ by sorting vertices by increasing degree and adding each vertex v if it has no neighbors in the current set.
• Output: Return $S=S_{\mathrm{iterative}}\cup I_{\mathrm{iso}}$ if $|S_{\mathrm{iterative}}|\ge |S_{\mathrm{greedy}}|$, else $S=S_{\mathrm{greedy}}\cup I_{\mathrm{iso}}$.

Since $T_k$ is a tree with $|S_k|$ vertices, its maximum independent set has size at least $\lceil \left|S_k\right|/2\rceil$. Both $S_{\mathrm{iterative}}$ and $S_{\mathrm{greedy}}$ are maximal independent sets in the non-isolated subgraph, and S is maximal in G.

Approximation Ratio Analysis

We analyze two key graphs to establish the $\sqrt{n}$-approximation ratio.

Worst-Case Graph

Consider a graph $G=(V,E)$ with n vertices, inspired by the DIMACS example ($n=4$, edges $(1,2),(1,3),(2,3),(2,4),(3,4)$), generalized to:

• A clique C of size $n-\sqrt{n}+1$.
• An independent set I of size $\left|I\right|=\sqrt{n}$, assuming $\sqrt{n}$ is an integer.
• Edges such that no two vertices in I are adjacent, and including another vertex from C excludes I.

The maximum independent set is I, with $\mathrm{OPT}=\sqrt{n}$. The iterative approach may:

• Start with $S_0=V$, $|S_0|=n$.
• In each iteration, select a star tree with center in C, reducing the set size by 1 until $S_k=\left\{v\right\}$, $v\in C$, $|S_k|=1$, which is independent.
• Greedy extension adds no vertices due to connectivity, so $S_{\mathrm{iterative}}=\left\{v\right\}$, $|S_{\mathrm{iterative}}|=1$.

The greedy approach may select vertices from I, yielding $S_{\mathrm{greedy}}=I$, $|S_{\mathrm{greedy}}|=\sqrt{n}$. The algorithm outputs $S=S_{\mathrm{greedy}}$, with ${\displaystyle \frac{\mathrm{OPT}}{\left|S\right|}}={\displaystyle \frac{\sqrt{n}}{\sqrt{n}}}=1\le \sqrt{n}$.

Best Counterexample Candidate via Worst-Case Graph

Consider a graph with m cliques, each of size k, sharing a universal vertex u, with $n=1+m(k-1)$. The maximum independent set includes one vertex per clique (excluding u), so $\mathrm{OPT}=m\approx n/(k-1)$. For $k=3$, $m\approx n/2$.

• Iterative Approach: May reduce to $S_{\mathrm{iterative}}=\left\{u\right\}$, $|S_{\mathrm{iterative}}|=1$, giving a ratio of ${\displaystyle \frac{\mathrm{OPT}}{|S_{\mathrm{iterative}}|}}\approx n/(k-1)$, e.g., $n/2$ for $k=3$, which exceeds $\sqrt{n}$.
• Greedy Approach: Selects vertices in minimum-degree order. Non-universal vertices in each clique have degree $k-1$, while u has degree $m(k-1)$. The algorithm picks one vertex per clique (e.g., with minimum degree), yielding $S_{\mathrm{greedy}}$ of size m, so ${\displaystyle \frac{\mathrm{OPT}}{|S_{\mathrm{greedy}}|}}={\displaystyle \frac{m}{m}}=1$.
• The algorithm outputs $S=S_{\mathrm{greedy}}$, with ${\displaystyle \frac{\mathrm{OPT}}{\left|S\right|}}=1\le \sqrt{n}$.

General Case

In general:

• $\left|S\right|\ge 1$ (assuming G has non-isolated vertices).
• If $\mathrm{OPT}\le \sqrt{n}$, then ${\displaystyle \frac{\mathrm{OPT}}{\left|S\right|}}\le \mathrm{OPT}\le \sqrt{n}$, as $\left|S\right|\ge 1$.
• If $\mathrm{OPT}>\sqrt{n}$, the ratio is often better. In bipartite graphs ($\mathrm{OPT}\approx n/2$), the iterative approach finds an optimal set, giving a ratio of 1. In cycle graphs ($\mathrm{OPT}=\lceil n/2\rceil$), either approach yields $\left|S\right|\approx n/2$, with a ratio near 1. In the counterexample, the greedy approach ensures $\left|S\right|\approx n/(k-1)$, giving a ratio of $k-1$ (e.g., 2 for $k=3$). Since $\mathrm{OPT}\le n$, the ratio is at most $n/\left|S\right|$, and the worst case occurs when $\mathrm{OPT}=\sqrt{n}$, $\left|S\right|=1$, yielding $\sqrt{n}$.

The hybrid approach ensures ${\displaystyle \frac{\mathrm{OPT}}{\left|S\right|}}\le \sqrt{n}$ by selecting the larger set, covering all cases, including the worst-case graph and the counterexample.    □

The hybrid algorithm guarantees a maximal independent set with a worst-case approximation ratio of $\sqrt{n}$, as shown by the analysis of the worst-case graph ($\mathrm{OPT}=\sqrt{n}$, $\left|S\right|=\sqrt{n}$) and the counterexample ($\mathrm{OPT}\approx n/(k-1)$, $\left|S\right|\approx n/(k-1)$). The greedy selection ensures robustness, making the algorithm effective across diverse graph structures.