New Upper Bounds on the Number of Maximum Independent Sets of a Graph

1. Introduction

Throughout this research, let G be a simple graph, i.e., a finite, undirected, loopless, and without multiple edges. The vertex set is denoted $V\left(G\right)=V$ and the edge set is denoted $E\left(G\right)=E$.

For the graph G, we denote: $n=n\left(G\right)=\left|V\right|$ - the number of vertices in G, $m=m\left(G\right)=\left|E\right|$ - the number of edges in G, $N\left(v\right)$ - the set of neighbors of vertex $v\in V$, $N\left(A\right)$ - the set of neighbors of $A\subset V$, $N\left[A\right]=N\left(A\right)\cup A$ - the closed neighborhood of A, $\alpha =\alpha \left(G\right)$ - the independence number of G, $\omega =\omega \left(G\right)$ - the clique number of G, $\mathrm{core}\left(G\right)$ - the intersection of all maximum independent sets in G, $\xi =\xi \left(G\right)=\left|\mathrm{core}\right(G\left)\right|$ - the cardinality of the intersection of all maximum independent sets, $\Omega =\Omega \left(G\right)$ - the set of all maximum independent sets, $\mathsf{\Psi }=\mathsf{\Psi }\left(G\right)$ - the set of all maximum cliques.

If $U\subset V$ is any set of vertices in G, then $G\left[U\right]$ denotes the subgraph of G spanned by U. The notation $G-U$ refers to the subgraph $G[V-U]$. If $U=\left\{v\right\}$ is a singleton, we write $G-v$ instead of $G-\left\{v\right\}$.

Here, $K_n$ denotes a complete graph with n vertices, $C_n$ denotes a cycle with n vertices, and the union of two disjoint graphs G and H is denoted $G\cup H$, where $V(G\cup H)=V\left(G\right)\cup V\left(H\right)$ and $E(G\cup H)=E\left(G\right)\cup E\left(H\right)$. The notation $kG$ represents the union of k copies of disjoint graphs isomorphic to G.

The corona of two graphs $G_1$ and $G_2$, denoted $G_1\circ G_2$ [4], is defined as the graph obtained by taking one copy of $G_1$ and $\left|V\right(G_1\left)\right|$ copies of $G_2$, with an edge connecting each vertex $v_i\in V\left(G_1\right)$ to every vertex in the i-th copy of $G_2$.

A permutation graph is defined as a graph whose vertices represent the elements of a permutation, with edges representing pairs of elements that are reversed by the permutation. If $\sigma =({\sigma }_1,{\sigma }_2,\dots ,{\sigma }_n)$ is a permutation of the numbers from 1 to n, the corresponding permutation graph has n vertices $v_1,v_2,\dots ,v_n$. An edge $v_i{v}_j$ exists between two vertices for any indices i and j such that $i<j$ and ${\sigma }_i>{\sigma }_j$. Thus, two indices i and j define an edge in the permutation graph precisely when they form an inversion in the permutation. Consequently, the longest increasing subsequence in the sequence of numbers represented by the permutation corresponds to a maximum independent set in G, while then longest decreasing subsequence corresponds to a maximum clique in G.

A comparability graph is an undirected graph that connects pairs of elements that are comparable in a partial order. For any strict partially ordered set $(S,<)$, the comparability graph of $(S,<)$ is defined such that the vertices are the elements of S, and an edge exists between a pair of elements $\{u,v\}$ if $u<v$.

A matching in a graph is a set of edges such that no two edges share a common vertex. A maximum matching is a matching that contains the largest possible number of edges. The size, of the maximum matching in a graph is called the matching number.

Erdős and Moser raised the problem of determining the maximum number of cliques in a graph G of order n and identifying those graphs that achieve this maximum [3]. Moon and Moser established an upper bound for maximum number of cliques [20]. Recall that an independent set in a graph corresponds to a clique in its complement graph and vice versa.

The problem of finding the number of maximum independent sets $s_{\alpha }$ of various types of graphs has been extensively studied in [2,6,8,9,10,11,14,16,18,19,21,22,23,24,25,26].

The main finding of the article is the upper bound on the number of maximum independent sets $s_{\alpha }$ using various graph invariants, including the number of vertices n, the independence number $\alpha$, the clique number $\omega$ and $\xi$, which denotes the cardinality of the intersection of all maximum independent sets. It reads as follows:

$$s_{\alpha }\le \sum _{k=0}^{\alpha -\xi }\left({\displaystyle \genfrac{}{}{0pt}{}{n-\alpha -\omega +1}{k}}\right)+(\omega -1)·\sum _{k=0}^{\alpha -\xi -1}\left({\displaystyle \genfrac{}{}{0pt}{}{n-\alpha -\omega +1}{k}}\right)$$

$$\le \omega ·2^{min(\alpha -\xi ,n-\alpha -\omega -\xi +1)}.$$

If G is a triangle-free graph, i.e., $\omega \left(G\right)=2$ the above inequality is specializing as $s_{\alpha }\le 2^{min(\alpha -\xi +1,n-\alpha -\xi )}$. Moreover, if T is a tree, then $s_{\alpha }\le 2^{n-\alpha -\xi }$, because $\alpha \left(T\right)\ge {\displaystyle \frac{n}{2}}$ for every T.

We are now in a position to compare our results with the corresponding inequalities from [26] claiming that $s_{\alpha }\le 2^{\alpha -1}+1$ for trees. Clearly, if $\alpha >{\displaystyle \frac{n}{2}}$, then $2^{n-\alpha -\xi }<2^{\alpha -1}+1$. Additionally, if $\alpha ={\displaystyle \frac{n}{2}}$, then $2^{n-\alpha -\xi }<2^{\alpha -1}+1$, whenever $\xi \ge 1$.

2. The Upper Bound of Maximum Independent Sets of a Graph

In the sequel, we need the following characterization of a maximum independent set of a graph, due to Berge.

Theorem 1. 

[1]. An independent set S belongs to Ω if and only if every independent set A of G, disjoint from S, can be matched into S.

2.1. The Main Lemma

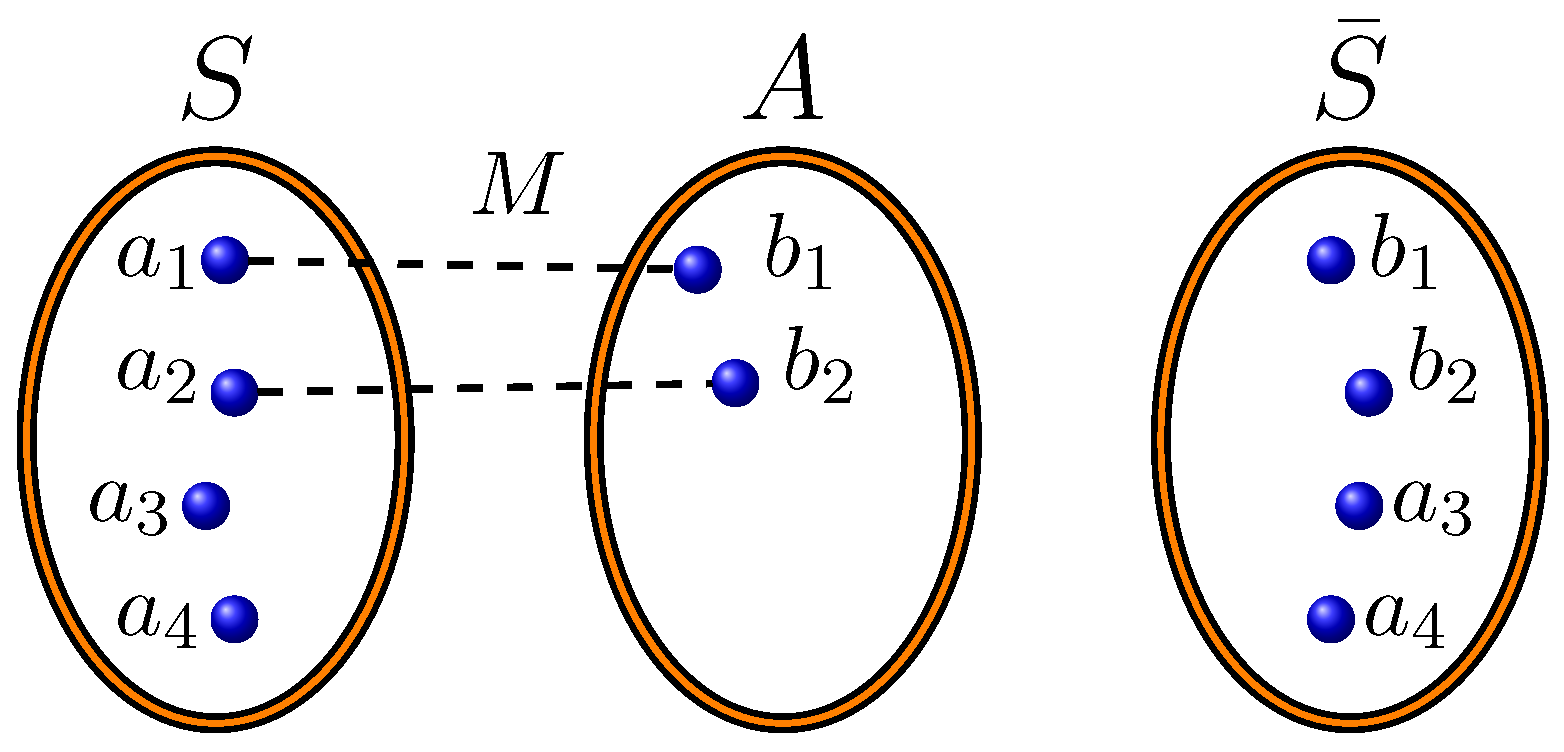
Let G be a graph. Suppose $S=\{a_1,a_2,\dots ,a_{\alpha }\}\in \Omega$ is a maximum independent set in G, and let $A=\{b_1,b_2,\dots ,b_k\}$ be an independent set in G ($k\le \alpha$) disjoint from S, i.e., $A\cap S=\varnothing$. By Theorem 1, there exists a matching M from A to S:

$$M(A,S)=\{(b_1,a_{i_1}),\dots ,(b_k,a_{i_k})\}.$$

We can generate a new set $\overline{S}$ of cardinality $\alpha$ by replacing k vertices in S with vertices from A, i.e.,

$$\overline{S}=A\cup (S\setminus M\left(A\right)),$$

and we have $|\overline{S}|=\alpha$.

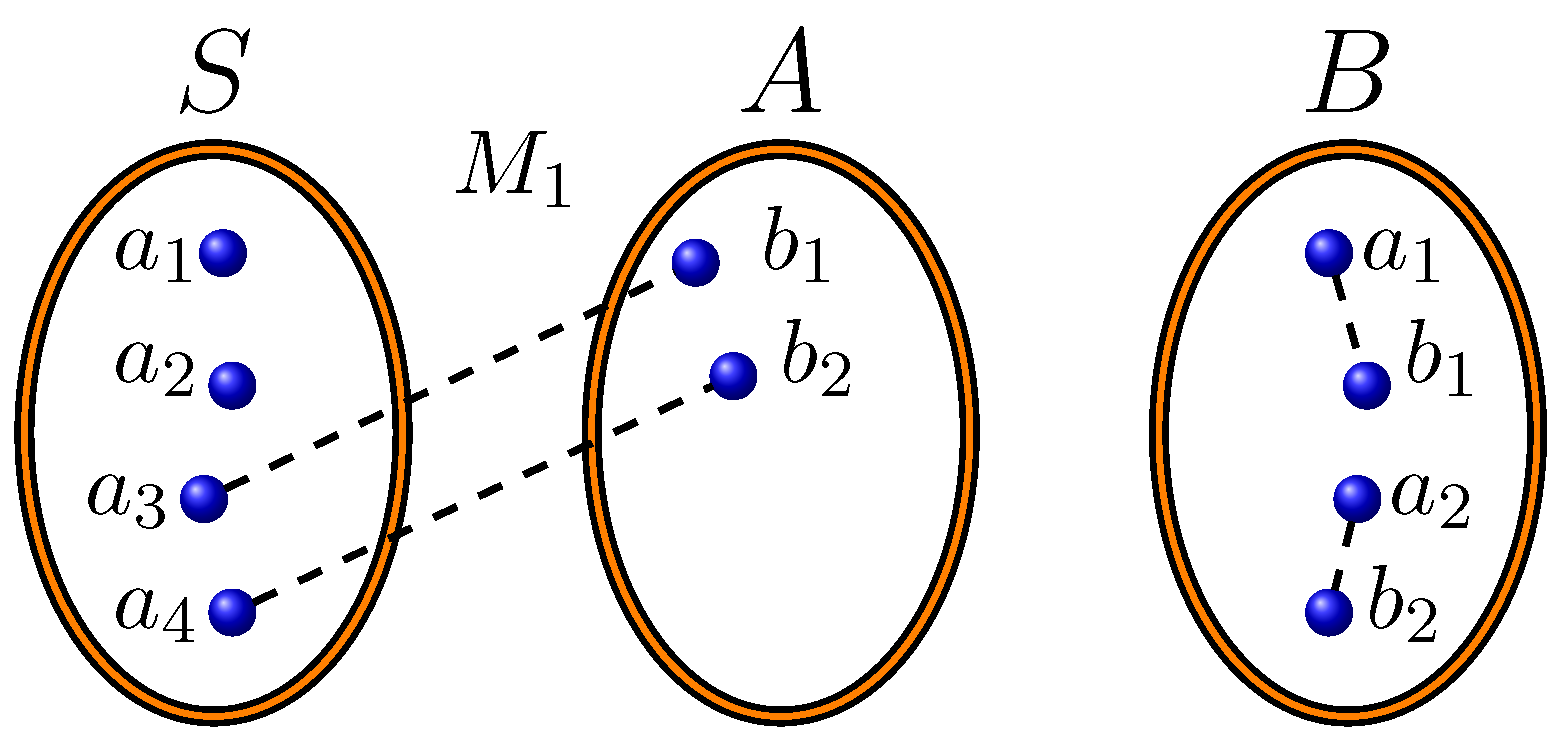
Lemma 1. 

Let G be a graph. Suppose $S\in \Omega$. Then we can generate all maximum independent sets with the help of the independent sets disjoint from S. Moreover, we cannot generate more than one maximum independent set using an independent set disjoint from S.

Proof. 

Let A be an independent set disjoint from S.

• First, we will prove that we can generate every maximum independent set using an independent set A. There are two options:

  (a)

  If the graph contains at least two maximum independent sets $S_1$ and $S_2$, let $A=S_2\setminus (S_1\cap S_2)$. Then, A is independent and $A\cap S_1=\varnothing$. By Berge’s Theorem [1], there exists a matching $M(A,S_1$) and $S_2=A\cup (S_1\setminus M(A,S_1))$.

  (b)

  If the graph contains only one maximum independent set S, we can generate S with the help of the empty set.

• Now, let us prove that we cannot generate more than one maximum independent set using an independent set A. Let

  $$\overline{S}=A\cup (S\setminus M\left(A\right))=\{b_1,\dots ,b_k,a_{k+1},\dots ,a_{\alpha }\}$$

  be an independent set, which implies $\overline{S}\in \Omega$ (see Figure 1). Let

  $$M_1(A,S)=\{(b_1,a_{i_1}),\dots ,(b_k,a_{i_k})\}$$

  be a matching different from M, such that for some j, we have

  $$(b_j,a_{i_j})\ne (b_j,a_j).$$
  Thus, a new set

  $$B=A\cup (S\setminus M_1\left(A\right))$$

  is not independent since there exists an edge $(a_j,b_j)\in B$
  (see Figure 2).

This completes the proof. □

2.2. Upper Bounds for $s_{\alpha }$

2.2.1. Upper Bound for $s_{\alpha }$ if Every Maximum Independent Set Has a Nonempty Intersection with every Maximum Clique

Theorem 2. 

Let G be a graph such that for every $S\in \Omega$ and every $Q\in \mathsf{\Psi }$, we have $S\cap Q\ne \varnothing .$ Then,

$$s_{\alpha }\le \sum _{k=0}^{\alpha }\left({\displaystyle \genfrac{}{}{0pt}{}{n-\alpha -\omega +1}{k}}\right)+(\omega -1)·\sum _{k=0}^{\alpha -1}\left({\displaystyle \genfrac{}{}{0pt}{}{n-\alpha -\omega +1}{k}}\right)={\Sigma }_1.$$

(1)

Proof. 

Note that the set $S\cap Q$ consists of a single element, which we denote by $q_0$, thus $S\cap Q=\left\{q_0\right\}$.

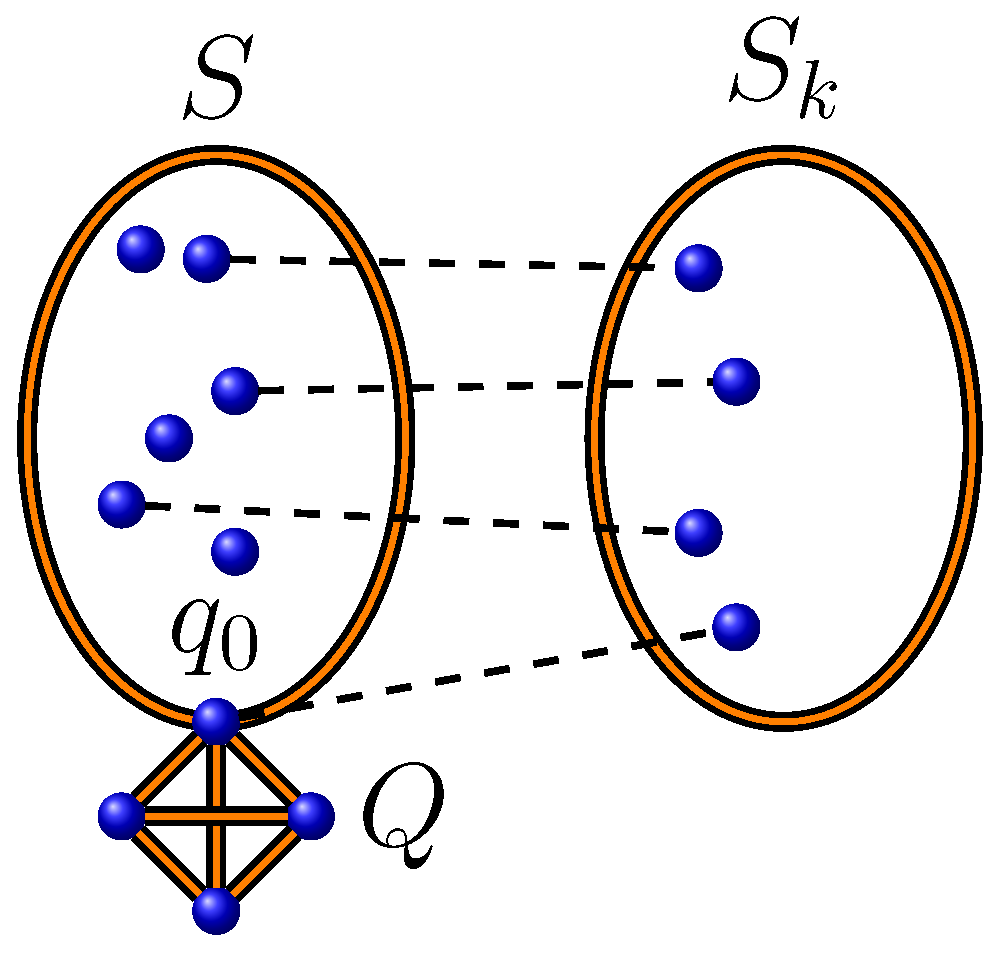
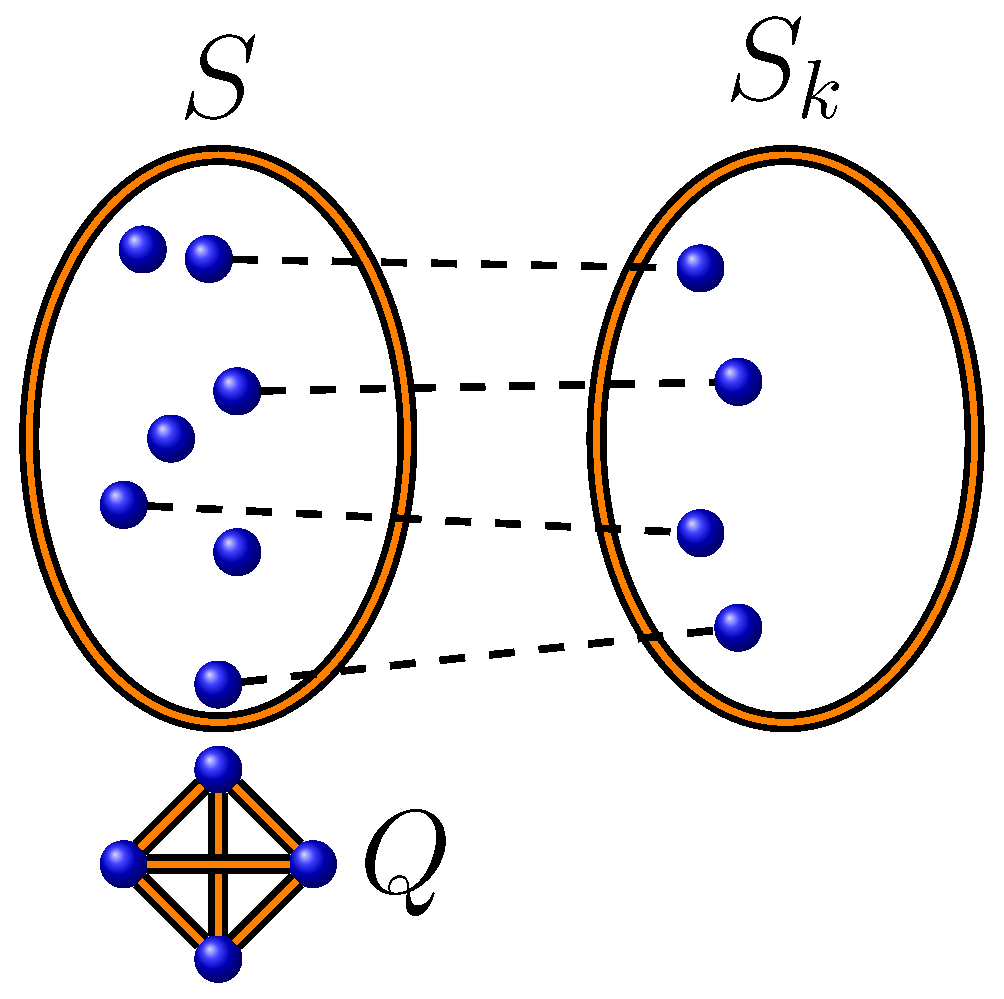
By Lemma 1, we can construct a new maximum independent set using any independent set $S_k$ that satisfies the conditions of Lemma 1. The number of suitable vertices to generate different independent sets is less than or equal to $n-\alpha -\omega +1$ (since we can use only one vertex from the maximum clique), resulting in no more than $\left({\displaystyle \genfrac{}{}{0pt}{}{n-\alpha -\omega +1}{k}}\right)$ maximum independent sets. There are two cases to form the set $S_k$:

• $S_k\cap Q=\varnothing$ (see Figure 3). In this case, $k\le \alpha$, and we have at most

  $$\sum _{k=0}^{\alpha }\left({\displaystyle \genfrac{}{}{0pt}{}{n-\alpha -\omega +1}{k}}\right)$$

  maximum independent sets. Note that if $\alpha \ge n-\alpha -\omega +1$, the upper limit of the summation must be $n-\alpha -\omega +1$.
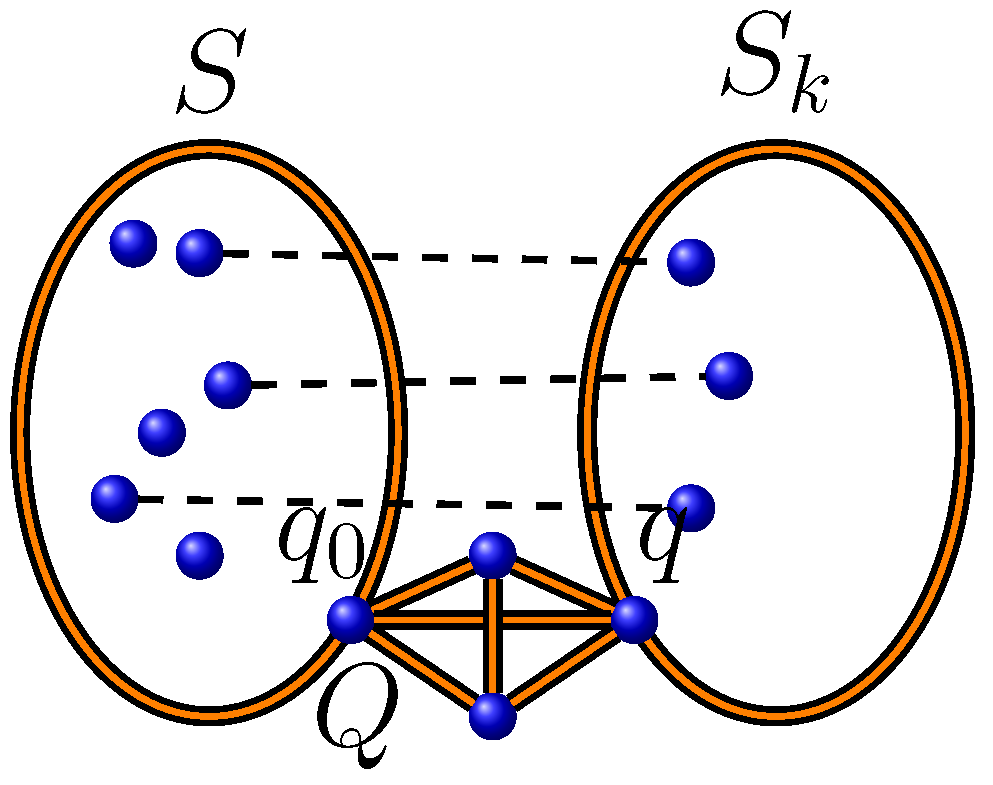
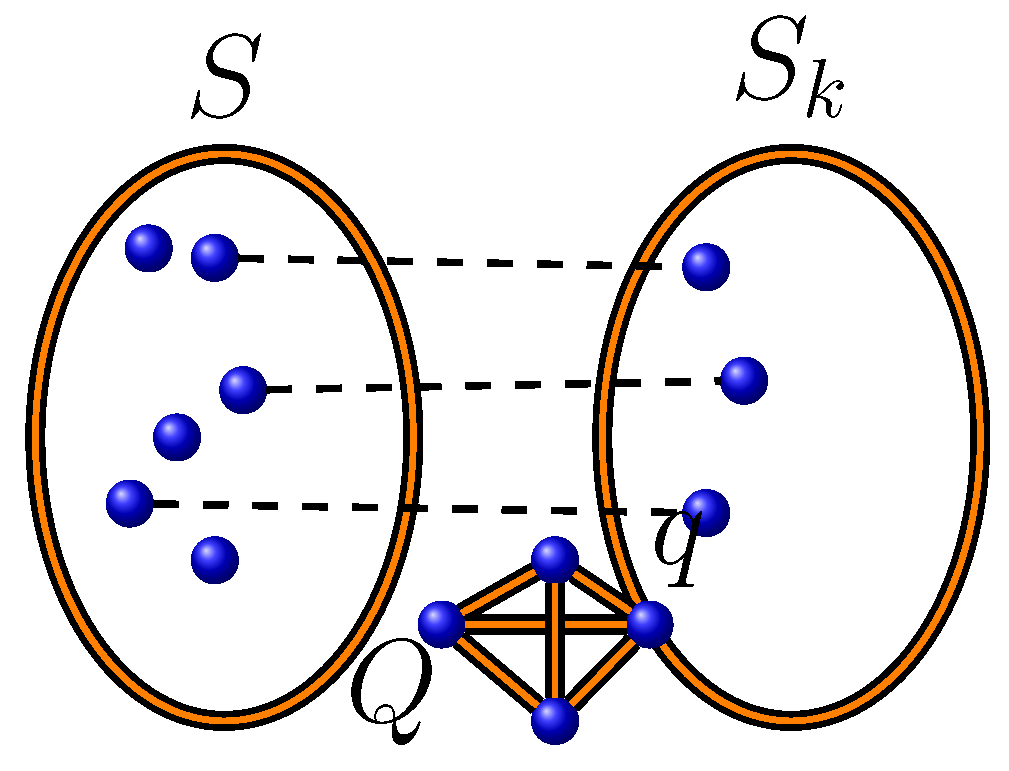
• $S_k\cap Q=\left\{q\right\}$ (see Figure 4). In this case, $k\le \alpha -1$, and we can use $\omega -1$ vertices (except $q_0$) instead of q from the maximum clique Q. Thus, we have at most

  $$(\omega -1)·\sum _{k=0}^{\alpha -1}\left({\displaystyle \genfrac{}{}{0pt}{}{n-\alpha -\omega +1}{k}}\right)$$

  maximum independent sets. If $\alpha -1\ge n-\alpha -\omega +1$, then the upper limit of the summation is equal to $n-\alpha -\omega$.

Hence, the inequality (1) is valid. □

Example 1. 

In the case when $\alpha =1$, we have the complete graph with $\omega =n$. The number of maximum independent sets is equal to the number of vertices, $s_{\alpha }=n$: $n-\alpha -\omega +1=0$ and ${\Sigma }_1=1+(\omega -1)=n$.

Example 2. 

In the case when G is a graph with the number of edges $\left|m\right|=0$, we have the independence number $\alpha =n$, the clique number $\omega =1$, and the number of maximum independent sets $s_{\alpha }=1$. Moreover,

$${\Sigma }_1=\sum _{k=0}^{\alpha }\left({\displaystyle \genfrac{}{}{0pt}{}{n-n-1+1}{k}}\right)+0=1.$$

Example 3. 

A CIS graph is a graph in which every maximal independent set and every maximal clique intersect [7] (CIS stands for"Clique Intersect Stable Set"). Note that the CIS graph satisfies the conditions of Theorem 2.

2.2.2. Upper Bound for $s_{\alpha }$ when There Exists Maximum Independent Set and Maximum Clique Which Have an Empty Intersection

Theorem 3. 

Let G be a graph in which there exists a maximum independent set $S\in \Omega$ and a maximum clique $Q\in \mathsf{\Psi }$ such that $S\cap Q=\varnothing .$ Then

$$s_{\alpha }\le {\Sigma }_2,$$

(2)

where

$${\Sigma }_2=\sum _{k=0}^{\alpha }\left({\displaystyle \genfrac{}{}{0pt}{}{n-\alpha -\omega }{k}}\right)+\omega ·\sum _{k=0}^{\alpha -1}\left({\displaystyle \genfrac{}{}{0pt}{}{n-\alpha -\omega }{k}}\right).$$

Proof. 

Note that in this case, G cannot be a complete graph, which implies that $\alpha \ge 2$. By Lemma 1, we can construct a new maximum independent set based on any independent set $S_k$ that satisfies the conditions of Lemma 1. The number of suitable vertices available for generating different independent sets is at most $n-\alpha -\omega$, and there are at most $\left({\displaystyle \genfrac{}{}{0pt}{}{n-\alpha -\omega }{k}}\right)$ maximum independent sets. Two cases arise for forming the set $S_k$:

• $S_k\cap Q=\varnothing$. In this case (see Figure 5), there are at most

  $$\sum _{k=0}^{\alpha }\left({\displaystyle \genfrac{}{}{0pt}{}{n-\alpha -\omega }{k}}\right)$$

  maximum independent sets that do not intersect with Q.
• $S_k\cap Q\ne \varnothing$. In this situation (see Figure 6), it is possible to generate independent set $S_k$ using all $\omega$ vertices from Q. Thus, we have at most

  $$\omega ·\sum _{k=0}^{\alpha -1}\left({\displaystyle \genfrac{}{}{0pt}{}{n-\alpha -\omega }{k}}\right)$$

  maximum independent sets.

Hence, the inequality (2) is established. □

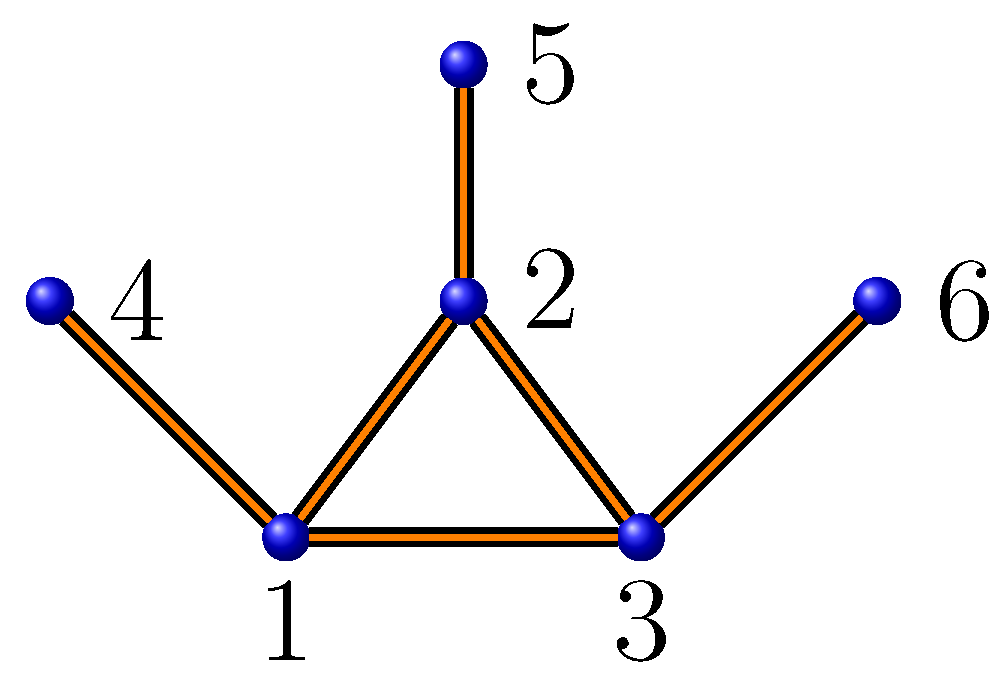
Example 4. 

Consider the graph $K_p\circ K_1$ (see Figure 7). Here, we have $n=2p$, $\omega =p$, $\alpha =p$, and $s_{\alpha }=p+1$, with $n-\alpha -\omega =0$.

$${\Sigma }_2=\sum _{i=0}^p\left({\displaystyle \genfrac{}{}{0pt}{}{0}{i}}\right)+p·\sum _{i=0}^{p-1}\left({\displaystyle \genfrac{}{}{0pt}{}{0}{i}}\right)=\left({\displaystyle \genfrac{}{}{0pt}{}{0}{0}}\right)+p·\left({\displaystyle \genfrac{}{}{0pt}{}{0}{0}}\right)=p+1.$$

Thus, we conclude that $s_{\alpha }={\Sigma }_2$.

2.2.3. Comparison of the Two Upper Bounds

Theorem 4. 

$${\Sigma }_1>{\Sigma }_2.$$

(3)

Proof.

• Let $\alpha >2$ and $\omega \ge 2$ (note that when $\omega =1$, the graph consists of isolated vertices, as detailed in Example 2). Denote $c=n-\alpha -\omega$ and simplify the inequality (1). We get:

  $${\Sigma }_1=\sum _{k=0}^{\alpha }\left({\displaystyle \genfrac{}{}{0pt}{}{n-\alpha -\omega +1}{k}}\right)+(\omega -1)·\sum _{k=0}^{\alpha -1}\left({\displaystyle \genfrac{}{}{0pt}{}{n-\alpha -\omega +1}{k}}\right)$$

  $$=\sum _{k=0}^{\alpha }\left({\displaystyle \genfrac{}{}{0pt}{}{c+1}{k}}\right)+(\omega -1)·\sum _{k=0}^{\alpha -1}\left({\displaystyle \genfrac{}{}{0pt}{}{c+1}{k}}\right)$$

  $$=\left({\displaystyle \genfrac{}{}{0pt}{}{c+1}{\alpha }}\right)+\sum _{k=0}^{\alpha -1}\left({\displaystyle \genfrac{}{}{0pt}{}{c+1}{k}}\right)+\omega ·\sum _{k=0}^{\alpha -1}\left({\displaystyle \genfrac{}{}{0pt}{}{c+1}{k}}\right)-\sum _{k=0}^{\alpha -1}\left({\displaystyle \genfrac{}{}{0pt}{}{c+1}{k}}\right)$$

  $$=\left({\displaystyle \genfrac{}{}{0pt}{}{c+1}{\alpha }}\right)+\omega ·\sum _{k=0}^{\alpha -1}\left({\displaystyle \genfrac{}{}{0pt}{}{c+1}{k}}\right).$$
  Now, for ${\Sigma }_2$:

  $${\Sigma }_2=\sum _{k=0}^{\alpha }\left({\displaystyle \genfrac{}{}{0pt}{}{c}{k}}\right)+\omega ·\sum _{k=0}^{\alpha -1}\left({\displaystyle \genfrac{}{}{0pt}{}{c}{k}}\right).$$
  Thus, calculating ${\Sigma }_1-{\Sigma }_2$:

  $${\Sigma }_1-{\Sigma }_2=\left({\displaystyle \genfrac{}{}{0pt}{}{c+1}{\alpha }}\right)+\omega ·\sum _{k=0}^{\alpha -1}\left({\displaystyle \genfrac{}{}{0pt}{}{c+1}{k}}\right)-\sum _{k=0}^{\alpha }\left({\displaystyle \genfrac{}{}{0pt}{}{c}{k}}\right)-\omega ·\sum _{k=0}^{\alpha -1}\left({\displaystyle \genfrac{}{}{0pt}{}{c}{k}}\right)$$

  $$=\left({\displaystyle \genfrac{}{}{0pt}{}{c+1}{\alpha }}\right)+\omega ·\sum _{k=0}^{\alpha -1}\left({\displaystyle \genfrac{}{}{0pt}{}{c}{k-1}}\right)-\sum _{k=0}^{\alpha }\left({\displaystyle \genfrac{}{}{0pt}{}{c}{k}}\right)$$

  $$=\left({\displaystyle \genfrac{}{}{0pt}{}{c+1}{\alpha }}\right)+\omega ·\sum _{k=0}^{\alpha -2}\left({\displaystyle \genfrac{}{}{0pt}{}{c}{k}}\right)-\left({\displaystyle \genfrac{}{}{0pt}{}{c}{\alpha }}\right)-\left({\displaystyle \genfrac{}{}{0pt}{}{c}{\alpha -1}}\right)-\sum _{k=0}^{\alpha -2}\left({\displaystyle \genfrac{}{}{0pt}{}{c}{k}}\right)$$

  $$=(\omega -1)·\sum _{k=0}^{\alpha -2}\left({\displaystyle \genfrac{}{}{0pt}{}{c}{k}}\right)>0.$$
  The last inequality follows from the facts that $\omega \ge 2$ and $\alpha >2$.
• If $\alpha =2$ and $\omega \le n-2$, then $c=n-\alpha -\omega \ge n-2-n+2=0$. Thus,

  $${\Sigma }_1-{\Sigma }_2=(\omega -1)·\sum _{k=0}^0\left({\displaystyle \genfrac{}{}{0pt}{}{c}{k}}\right)=\omega -1>0.$$
• If $\alpha =2$ and $\omega =n-1$, then G consists of a clique and a single vertex. Consequently, $s_{\alpha }=n-1$, and G satisfies the conditions of Theorem 2.

This completes the proof. □

Corollary 1. 

$$s_{\alpha }\le {\Sigma }_2<{\Sigma }_1\le \omega ·2^{min(\alpha ,n-\alpha -\omega +1)}.$$

(4)

Proof. 

In the expression for ${\Sigma }_1$, we can increase the upper limit of the second sum to $\alpha$ instead of $\alpha -1$:

$${\Sigma }_1=\sum _{k=0}^{\alpha }\left({\displaystyle \genfrac{}{}{0pt}{}{n-\alpha -\omega +1}{k}}\right)+(\omega -1)·\sum _{k=0}^{\alpha -1}\left({\displaystyle \genfrac{}{}{0pt}{}{n-\alpha -\omega +1}{k}}\right)$$

$$\le \sum _{k=0}^{\alpha }\left({\displaystyle \genfrac{}{}{0pt}{}{n-\alpha -\omega +1}{k}}\right)+(\omega -1)·\sum _{k=0}^{\alpha }\left({\displaystyle \genfrac{}{}{0pt}{}{n-\alpha -\omega +1}{k}}\right)$$

$$=\omega ·\sum _{k=0}^{\alpha }\left({\displaystyle \genfrac{}{}{0pt}{}{n-\alpha -\omega +1}{k}}\right)\le \omega ·2^{min(\alpha ,n-\alpha -\omega +1)}.$$

Indeed, if $n-\alpha -\omega +1\ge \alpha$, then $\alpha$ is the upper limit of summation, if $n-\alpha -\omega +1<\alpha$, we set $n-\alpha -\omega +1$ as the upper limit of summation. Thus, $s_{\alpha }\le {\Sigma }_1\le \omega ·2^{min(\alpha ,n-\alpha -\omega +1)}.$ □

Corollary 2. 

If G is a triangle-free graph, then

$$s_{\alpha }\le 2^{min(\alpha +1,n-\alpha )}.$$

(5)

Proof. 

In fact, by the definition of a triangle-free graph, $\omega =2$. Then, substituting 2 for $\omega$ in (4), we obtain:

$$s_{\alpha }\le 2·2^{min(\alpha ,n-\alpha -2+1)}=2^{min(\alpha +1,n-\alpha )}.$$

□

2.3. Upper Bounds for $s_{\alpha }$ Using the $core\left(G\right)$

Recall that by $core\left(G\right)$ we denote the intersection of all maximum independent sets, and let $\xi =\xi \left(G\right)=\left|core\right(G\left)\right|$ be the cardinality of $core\left(G\right)$. The set $N\left[core\right(G\left)\right]$ is defined as the union of $core\left(G\right)$ and the set $N\left(core\right(G\left)\right)$ of all the neighbors of $core\left(G\right)$. Let G be a graph in which $core\left(G\right)$ is not empty. We ask whether it is possible to use this additional information to improve the accuracy of the upper bound of $s_{\alpha }$. To address this we define a new graph $\overline{G}=G\setminus N\left[core\left(G\right)\right]$ and investigate the relationships between $\overline{\alpha }\left(\overline{G}\right),\overline{\omega }\left(\overline{G}\right),\overline{n}\left(\overline{G}\right)$ and $\alpha \left(G\right),\omega \left(G\right),n$, respectively.

Theorem 5. 

The cardinality of an independent set A in G such that

$A\cap N\left[core\right]=\varnothing$ is less than or equal to $\alpha -\xi$; that is, $\left|A\right|\le \alpha -\xi .$

Proof. 

If $A\cap N\left[core\right]=\varnothing$, then $A\cap core=\varnothing$. As a result, $A\cup core$ is also an independent set in G with $|A\cup core|=\left|A\right|+\xi .$ Since $\alpha$ defines the size of a maximum independent set in G, it follows that $\left|A\right|+\xi \le \alpha \mathrm{or}\left|A\right|\le \alpha -\xi .$ □

Corollary 3. 

$\overline{\alpha }=\alpha -\xi$.

Proof. 

By Theorem 5, we have $\overline{\alpha }\le \alpha -\xi$. The equality is achieved for all $S\in \Omega$, since for every $S\in \Omega$ we have $S\cap N\left(core\right)=\varnothing$. Thus, $\overline{S}=S\setminus core$ and $\overline{\alpha }=\left|\overline{S}\right|=\alpha -\xi$. Consequently, $\overline{S}\in \overline{\Omega }\left(\overline{G}\right)$ is the maximum independent set in $\overline{G}$. □

Corollary 4. 

${\overline{s}}_{\alpha }=s_{\alpha }$.

Proof. 

The set $\overline{\Omega }$ of all maximum independent sets in $\overline{G}$ is formed by removing the core from each set in $\Omega$. Any independent set $A\in G$ such that $\left|A\right|<\alpha$ and A does not intersect with $N\left[core\right]$ converts to $\overline{A}$ with $|\overline{A}|<\alpha -\xi$. Therefore, $\overline{A}$ cannot be a maximum independent set. □

From this, we obtain: $\left|N\left[core\right(G\left)\right]\right|=n-\xi -\left|N\left(core\right(G\left)\right)\right|,\overline{\alpha }=\alpha -\xi ,$ ${\overline{s}}_{\alpha }=s_{\alpha }.$ Now, concerning $\overline{\omega }$, the number of vertices in the maximum clique $\overline{Q}\in \overline{\mathsf{\Psi }}$ is at least $\overline{\omega }\ge \omega -\left|N\left(core\left(G\right)\right)\right|-1,$ since Q may share only one vertex with $core\left(G\right)$ and may contain vertices from $N\left(core\right)$. Thus, we have:

Corollary 5. 

$\overline{n}-\overline{\alpha }-\overline{\omega }\le n-\alpha -\omega +1.$

Proof. 

We can show that

$$\overline{n}-\overline{\alpha }-\overline{\omega }\le n-\xi -\left|N\left(core\left(G\right)\right)\right|-(\alpha -\xi )-\left(\omega -\left|N\right(core\left(G\right)\left)\right|-1\right)=n-\alpha -\omega +1.$$

□

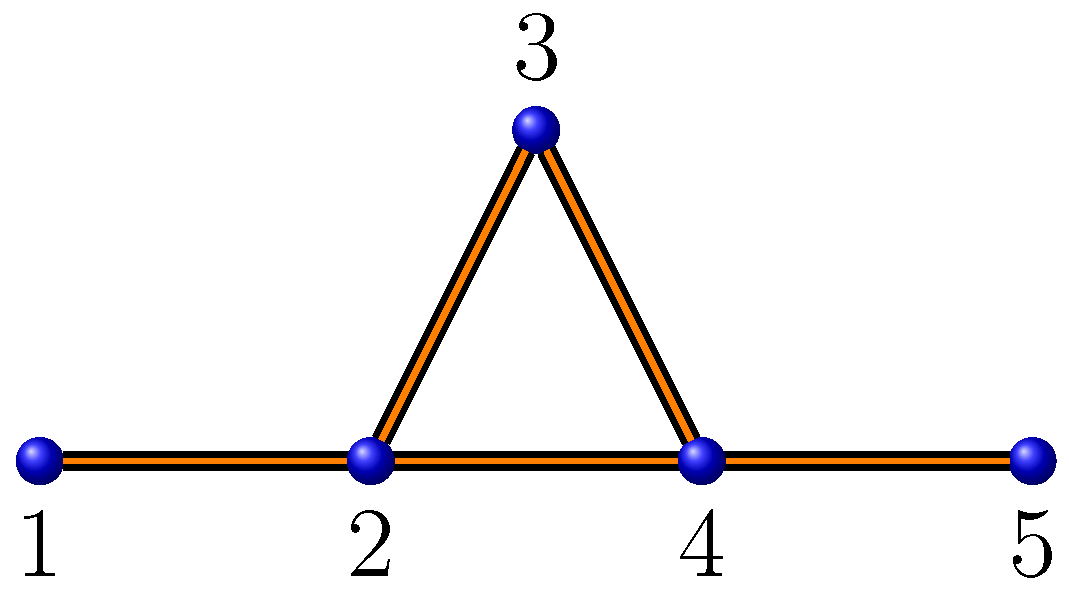
Example 5. 

Consider a graph where $\overline{\omega }=\omega -\left|N\left(core\left(G\right)\right)\right|-1$ (see Figure 8). Here, we have $n=5,\omega =3,\Omega =\left\{\right(1,3,5\left)\right\},\alpha =3,\xi =3$, $core\left(G\right)=(1,3,5),\mathsf{\Psi }=\left\{\right(2,3,4\left)\right\},N\left(core\right(G\left)\right)=(2,4),N\left[core\right(G\left)\right]=(1,2,3,4,5)$. Thus, $G\setminus N\left[core\right(G\left)\right]=\varnothing ,$ leading to $\overline{\omega }=0$ and $\omega -\left|N\right(core\left(G\right)\left)\right|-1=3-2-1=0$.

The results from Corollaries 3 and 4 enable an estimation of the total number of maximum independent sets $s_{\alpha }$ using ${\overline{s}}_{\overline{\alpha }}$ and allow for a more accurate estimation of $s_{\alpha }$. Theorems 2 and 3 provide two bounds on the number of maximum independent sets of a graph. Notably, the set H of all simple graphs can be decomposed into two disjoint subsets $H_1$ and $H_2$, where $H_1$ satisfies the conditions of Theorem 2, and $H_2$ satisfies the conditions of Theorem 3: $H_1\cup H_2=H,$ and $H_1\cap H_2=\varnothing$. Thus, we can estimate $\overline{s_{\alpha }}$ based on the inequality (1), resulting in a weaker bound (Theorem 4) compared to the inequality (2). Therefore, we conclude with the following.

Theorem 6. 

Let G be a graph. Then

$$s_{\alpha }\le \sum _{k=0}^{\alpha -\xi }\left({\displaystyle \genfrac{}{}{0pt}{}{n-\alpha -\omega +1}{k}}\right)+(\omega -1)·\sum _{k=0}^{\alpha -\xi -1}\left({\displaystyle \genfrac{}{}{0pt}{}{n-\alpha -\omega +1}{k}}\right)$$

(6)

$$\le \omega ·2^{min(\alpha -\xi ,n-\alpha -\omega -\xi +1)}.$$

Proof. 

First,

$$s_{\alpha }\le \sum _{k=0}^{\alpha -\xi }\left({\displaystyle \genfrac{}{}{0pt}{}{n-\alpha -\omega +1}{k}}\right)+(\omega -1)·\sum _{k=0}^{\alpha -\xi -1}\left({\displaystyle \genfrac{}{}{0pt}{}{n-\alpha -\omega +1}{k}}\right)$$

by Theorem 2, Theorem 4, Corollary 3, and Corollary 4.

Further, we proceed to prove the second inequality as follows:

$$\sum _{k=0}^{\alpha -\xi }\left({\displaystyle \genfrac{}{}{0pt}{}{n-\alpha -\omega +1}{k}}\right)+(\omega -1)·\sum _{k=0}^{\alpha -\xi -1}\left({\displaystyle \genfrac{}{}{0pt}{}{n-\alpha -\omega +1}{k}}\right)$$

$$\le \sum _{k=0}^{\alpha -\xi }\left({\displaystyle \genfrac{}{}{0pt}{}{n-\alpha -\omega +1}{k}}\right)+(\omega -1)·\sum _{k=0}^{\alpha -\xi }\left({\displaystyle \genfrac{}{}{0pt}{}{n-\alpha -\omega +1}{k}}\right)$$

$$\le \omega ·\sum _{k=0}^{\alpha -\xi }\left({\displaystyle \genfrac{}{}{0pt}{}{n-\alpha -\omega +1}{k}}\right)\le \omega ·2^{min(\alpha -\xi ,n-\alpha -\omega -\xi +1)}.$$

□

Corollary 6. 

If G is a triangle-free graph, then

$$s_{\alpha }\le 2^{min(\alpha -\xi +1,n-\alpha -\xi )}.$$

(7)

Proof. 

In fact, by the definition of a triangle-free graph, $\omega =2$. Then, substituting 2 for $\omega$ in (6), we obtain:

$$s_{\alpha }\le 2·2^{min(\alpha -\xi ,n-\alpha -2-\xi +1)}=2^{min(\alpha -\xi +1,n-\alpha -\xi )}.$$

□

Example 6. 

Let G be a graph with a non-empty $core\left(G\right)$ such that for all $S\in \Omega$ and $Q\in \mathsf{\Psi }$, $S\cap Q\ne \varnothing$ (see Figure 9). Here, we have $n=11,$

$\Omega =\left\{\right(2,5,8,9,11),(3,6,8,9,11),(2,6,8,9,11),(3,5,8,9,11\left)\right\},$ and $\alpha =5,s_{\alpha }=4,\xi =3,$ with $core\left(G\right)=(8,9,11),\alpha -\xi =2,Q=\left\{\right(1,2,3\left)\right\},\omega =3.$ According to Theorem 2, we have $n-\alpha -\omega +1=4$, leading to:

$$\begin{array}{c}{s}_{\alpha }\le {\Sigma }_1=\sum _{k=0}^5\left({\displaystyle \genfrac{}{}{0pt}{}{4}{k}}\right)+2·\sum _{k=0}^4\left({\displaystyle \genfrac{}{}{0pt}{}{4}{k}}\right)=\left({\displaystyle \genfrac{}{}{0pt}{}{4}{0}}\right)+\left({\displaystyle \genfrac{}{}{0pt}{}{4}{1}}\right)+\\ \left({\displaystyle \genfrac{}{}{0pt}{}{4}{2}}\right)+\left({\displaystyle \genfrac{}{}{0pt}{}{4}{3}}\right)+\left({\displaystyle \genfrac{}{}{0pt}{}{4}{4}}\right)+2·\left[\left({\displaystyle \genfrac{}{}{0pt}{}{4}{0}}\right)+\left({\displaystyle \genfrac{}{}{0pt}{}{4}{1}}\right)+\left({\displaystyle \genfrac{}{}{0pt}{}{4}{2}}\right)+\left({\displaystyle \genfrac{}{}{0pt}{}{4}{3}}\right)+\left({\displaystyle \genfrac{}{}{0pt}{}{4}{4}}\right)\right]=48.\end{array}$$

Now, let us evaluate $s_{\alpha }$ using the core. According to Theorem 6, we obtain:

$$s_{\alpha }\le \sum _{k=0}^2\left({\displaystyle \genfrac{}{}{0pt}{}{4}{k}}\right)+2·\sum _{k=0}^1\left({\displaystyle \genfrac{}{}{0pt}{}{4}{k}}\right)=\left({\displaystyle \genfrac{}{}{0pt}{}{4}{0}}\right)+\left({\displaystyle \genfrac{}{}{0pt}{}{4}{1}}\right)+\left({\displaystyle \genfrac{}{}{0pt}{}{4}{2}}\right)+2·\left[\left({\displaystyle \genfrac{}{}{0pt}{}{4}{0}}\right)+\left({\displaystyle \genfrac{}{}{0pt}{}{4}{1}}\right)\right]=21.$$

Thus, utilizing the core of the graph provides a better estimate for $s_{\alpha }$.

3. An Application: New Upper Bounds on the Numbers of Longest Increasing Subsequences and Longest Decreasing Subsequences

Consider the sequence $\left\{a_i\right\}$ of different real numbers, and define the partial order on the pairs $(i,a_i)$ as follows: $(i,a_i)<(j,a_j)$ if $i<j$ and $a_i<a_j$. This partial order induces a comparability graph G. The complement graph $\overline{G}$ is defined by the reverse order: $(i,a_i)<(j,a_j)$ if $i<j$ and $a_i>a_j$. Consequently, both G and its complement $\overline{G}$ are comparability graphs, indicating that G is a permutation graph. Thus, we can view a sequence of different real numbers as a permutation graph, where its longest increasing subsequence corresponds to a maximum independent set in G, and its longest decreasing subsequence corresponds to a maximum clique in G. Notably, an increasing subsequence can share at most one element with a decreasing subsequence.

For a sequence of different real numbers $A=\{a_1,a_2,\dots ,a_n\}$, we denote: S - the longest increasing subsequence, Q - the longest decreasing subsequence, $lis=lis\left(S\right)$ - the length of the longest increasing subsequence, $\#lis=\#lis\left(S\right)$ - the number of all longest increasing subsequences, $lds=lds\left(Q\right)$ the length of the longest decreasing subsequence, $\#lds=\#lds\left(Q\right)$ - the number of all longest decreasing subsequences.

Corollary 7. 

Let $A=\{a_1,a_2,\dots ,a_n\}$ be a sequence of different real numbers Then, we have:

$$\#lis\le lds·2^{n-lis-lds+1}.$$

(8)

Proof. 

From 4, it immediately follows that:

$$\begin{array}{c}\#lis\le \sum _{i=0}^{lis}\left({\displaystyle \genfrac{}{}{0pt}{}{n-lis-lds+1}{i}}\right)+(lds-1)·\sum _{i=0}^{lis-1}\left({\displaystyle \genfrac{}{}{0pt}{}{n-lis-lds+1}{i}}\right)\\ \le lds·2^{n-lis-lds+1}.\end{array}$$

Thus, inequality (8) holds. □

Corollary 8. 

Let $A=\{a_1,a_2,\dots ,a_n\}$ be a sequence of different real numbers.Then:

$$\#lis·\#lds\le {\left({\displaystyle \frac{n+1}{2}}\right)}^2·4^{n-lis-lds+1}.$$

(9)

Proof. 

From Corollary 7, we also have:

$$\#lds\le lis·2^{n-lis-lds+1}.$$

(10)

Now, let us multiply (8) and (10):

$$\#lis·\#lds\le lis·lds·4^{n-lis-lds+1}.$$

According to [12], the necessary and sufficient conditions for the existence of a sequence of length $n\ge 1$ containing a longest increasing subsequence of length $lis\ge 1$ and a longest decreasing subsequence of length $lds\ge 1$ are given by:

$$lis·lds\ge nandlis+lds\le n+1.$$

(11)

Therefore, we have:

$$lis·lds\le {\left({\displaystyle \frac{lis+lds}{2}}\right)}^2\le {\left({\displaystyle \frac{n+1}{2}}\right)}^2.$$

(12)

Thus, inequality (9) holds. □

Corollary 9. 

Let $A=\{a_1,a_2,\dots ,a_n\}$ be a sequence of different real numbers. Then:

$$\#lis+\#lds\le (n+1)·4^{n-lis-lds+1}.$$

(13)

Proof. 

By combining 7 and 10, we see that:

$$\#lis+\#lds\le lds·4^{n-lis-lds+1}+lis·4^{n-lis-lds+1}=$$

$$\left(lis+lds\right)·4^{n-lis-lds+1}\le (n+1)·4^{n-lis-lds+1}.$$

Thus, inequality (13) holds. □

Conjecture 1. 

Let $A=\{a_1,a_2,\dots ,a_n\}$ be a sequence of different real numbers. Then:

$$\#lis·\#lds\le n·4^{n-lis-lds+1}.$$

Example 7. 

Consider a sequence where for all $lis$ and $lds$, the following inequality holds: $lis\cap lds\ne \varnothing$. Let

$$\begin{array}{c}A=\{5,6,7,2,3,4\},\Omega =\left\{\right\{5,6,7\},\{2,3,4\left\}\right\},\\ \mathsf{\Psi }=\left\{\right\{5,2\},\{5,3\},\{5,4\},\{6,2\},\{6,3\},\{6,4\},\{7,2\},\{7,3\},\{7,4\left\}\right\}.\end{array}$$

(14)

Example 8. 

Consider a sequence where there exist $lis$ and $lds$ such that the following equality holds: $lis\cap lds=\varnothing$. Let

$$A=\{3,6,9,2,5,8,1,4,7\},lis=\{3,6,7\},lds=\{9,5,4\}.$$

When considering estimates of the products $\#lis·\#lds$ and $lis·lds$, several questions immediately arise regarding how to improve the estimates given by (9) and (12).

4. Conclusions

In the future,

• We aim to strengthen our upper bounds by incorporating additional graph invariants, such as the matching number, among others.
• We plan to compare our upper bounds with the corresponding ones developed in [19].