1. Introduction
Currently, the most prominent example of a fluctuation-induced force is the force due to quantum or thermal fluctuations of the electromagnetic field, leading to the so-called QED Casimir effect, named after the Dutch physicist H.B. Casimir who first realized that in the case of two perfectly-conducting, uncharged, and smooth plates parallel to each other in vacuum, at
these fluctuations lead to an
attractive force between them [
1]. Thirty years after Casimir, Fisher and De Gennes [
2] showed that a very similar effect exists in critical fluids, today known as critical Casimir effect. A summary of the results available for this effect can be found in the recent reviews [
3,
4,
5,
6]. The description of the critical Casimir effect is based on finite-size scaling theory [
7,
8,
9]. Let us envisage a system with a film geometry
,
, and with boundary conditions
imposed along the spatial direction of finite extent
L. Take
to be the total free energy of such a system within the grand canonical ensemble (GCE). Then, if
is the free energy per area
A of the system, one can define the Casimir force for critical systems in the grand-canonical
-ensemble, see, e.g. Refs. [
4,
9,
10,
11]::
where
is the so-called excess (over the bulk) free energy per area and per
. Here we suppose a system at temperature
T is exposed to an external ordering field
h, which couples linearly to its order parameter
—such as the number density, the concentration difference, the magnetization etc. Actually, the thermodynamic Casimir force
per area is the excess pressure over the bulk one due to the finite size
of that system:
Here
is the pressure in the finite system under boundary conditions
, while
is the one in the infinite, i.e., macroscopically large, system. The above definition is actually equivalent to Eq. (1.1). Note that
is the excess grand potential per area,
is the grand canonical potential per area of the finite system, while
has the meaning of the grand potential per volume
V for the macroscopically large system. The equivalence between the definitions in Eqs. (1.1) and (1.3) stems from the observation that for the finite system one has
, while for the bulk one and
.
When the excess pressure is inward towards the system, i.e., there is an attraction of the surfaces of the system towards each other and a repulsion if .
2. The Casimir Force Within the Continuum Gaussian Model
The continuum version of the Gaussian model with a scalar order parameter consists of the linear and bilinear terms in the Ginzburg-Landau-Wilson formulation of a system in
d dimensions that undergoes a continuous symmetry-breaking phase transition at low temperatures. The partition function of this system is the functional integral
where
In (2.2)
t is the reduced temperature, proportional to
, and
h is the spatially constant ordering field. Because of the Gaussian nature of the free energy functional
the partition function resolves into the product
where
is the partition function of the system with
. The geometry of the system under consideration is a slab of large—ultimately infinite—cross section and finite thickness
L.
With regard to scaling considerations, there are two combinations of parameters that reflect the predictions of finite size scaling. They are
where
, the correlation length exponent, is equal to 1/2 in the Gaussian model, and as noted above
d is the dimensionality of the system. Our end results for the Casimir forces acting upon the systems will depend on the boundary conditions imposed. In all cases, the form of the Casimir force is
All results reported in this portion of the article rely on two results, which can be obtained with the use of contour integration techniques; see also [
12]. The two results are
In order to carry out the evaluation of the free energy of the Gaussian model we turn to the basis set of functions that will be used to construct the free energy with and without an ordering field. These functions allow us to evaluate the partition function by integrating over the amplitudes of the contributions of each member of the set to the order parameter. Here, we focus on the case of periodic boundary conditions. Ignoring the dependence on position in the “plane” of the slab, the functions are the orthonormal set
with
n a positive integer. It is straightforward to show that this set is orthonormal as a function of
z in that
The three function types are all mutually orthogonal. In the case of higher dimensions, we construct a new basis set by multiplying the functions (2.9)–(2.11) by suitable functions of the orthogonal position variables. Those functions can be taken to be of the form
, where
is a
-dimensional position vector in the plane of the slab and
is in its reciprocal space.
We then express the order parameter as follows
The free energy for a given configuration of the Gaussian order parameter, in terms of the amplitudes in the expansion of the order parameter in the basis set (2.12)–(2.14), is
The last term in brackets above reflects the fact that the only basis function that the constant external field couples to is the constant function in (2.11)
The next step is to exponentiate the expression in (2.16), multiply by either
, or setting
, by -1, and, after that, to perform the Gaussian integrals over the
’s, the
’s, and
. The resulting partition function is given by
The coefficient
A in (2.17) is the
dimensional area of the slab.
As our next step we evaluate the sum over
n on the right hand side of the expression for the partition function. To achieve this, we take the
t-derivative of the logarithm of the summand, perform the sum over
n and then integrate the resulting expression with respect to
t. Taking the derivative of the summand in (2.17) with respect to
t leaves us with the sum
which follows from (2.7). This integrates up to
The large-
L limit of (2.19) is
To find the contribution to the Casimir force per unit area, we take the
L-derivative of the difference between (2.20) and (2.19) and then integrate over
. The derivative yields
The sum over values of
is expressible as an integral, which takes the form
where, to get to the last line of (2.22) we defined a new integration variable
and then made use of the definition (2.4) of
. The implication of (2.22) is that we can express the
contribution to the Casimir force as
times a function of the scaling temperature variable
. The coefficient
in the equations above is the geometric factor
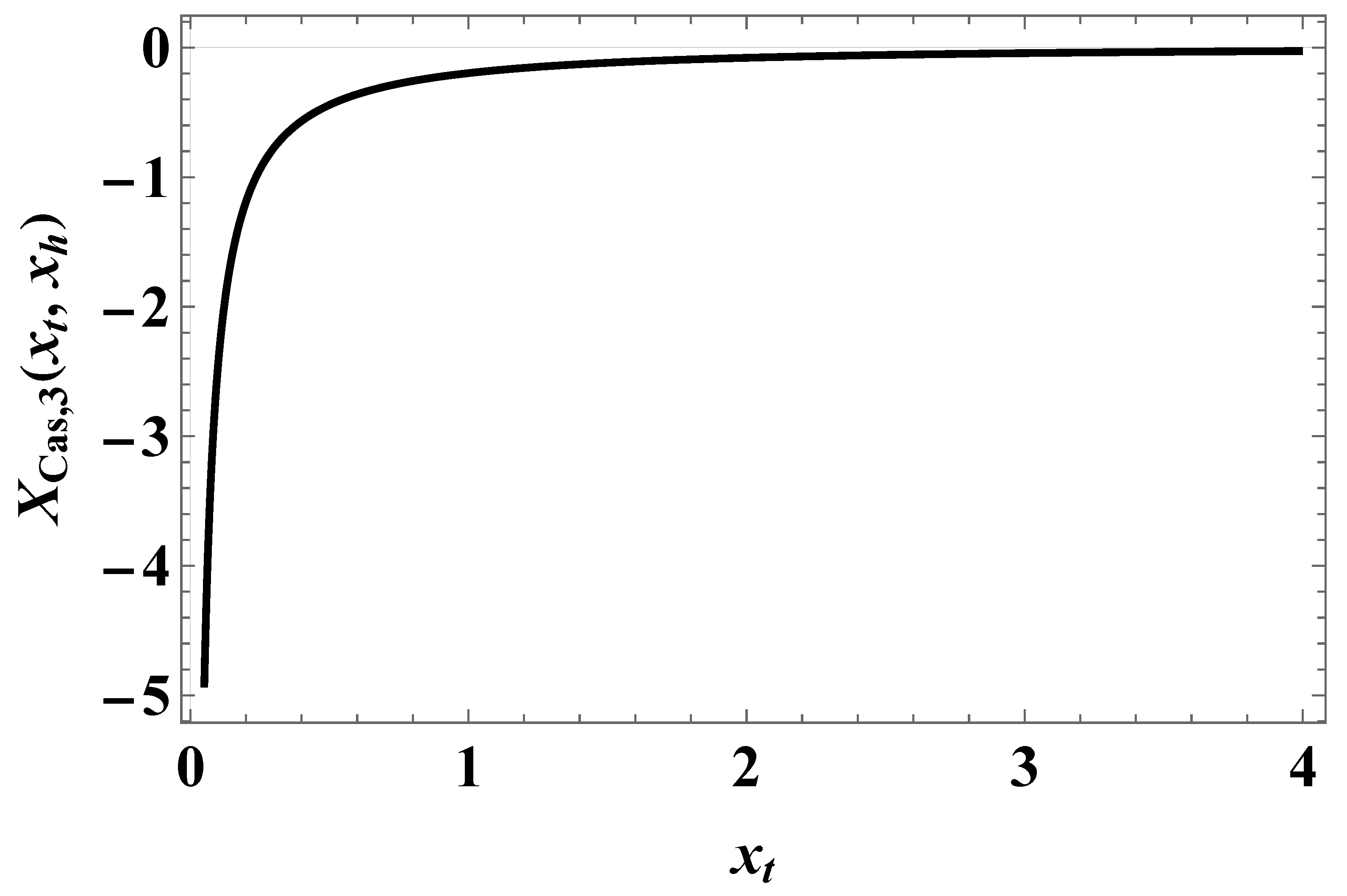
In the case of three dimensions, further processing of the result (2.22) is possible. We find
where
is the polylogarithm function; see [
13]. A plot of the function
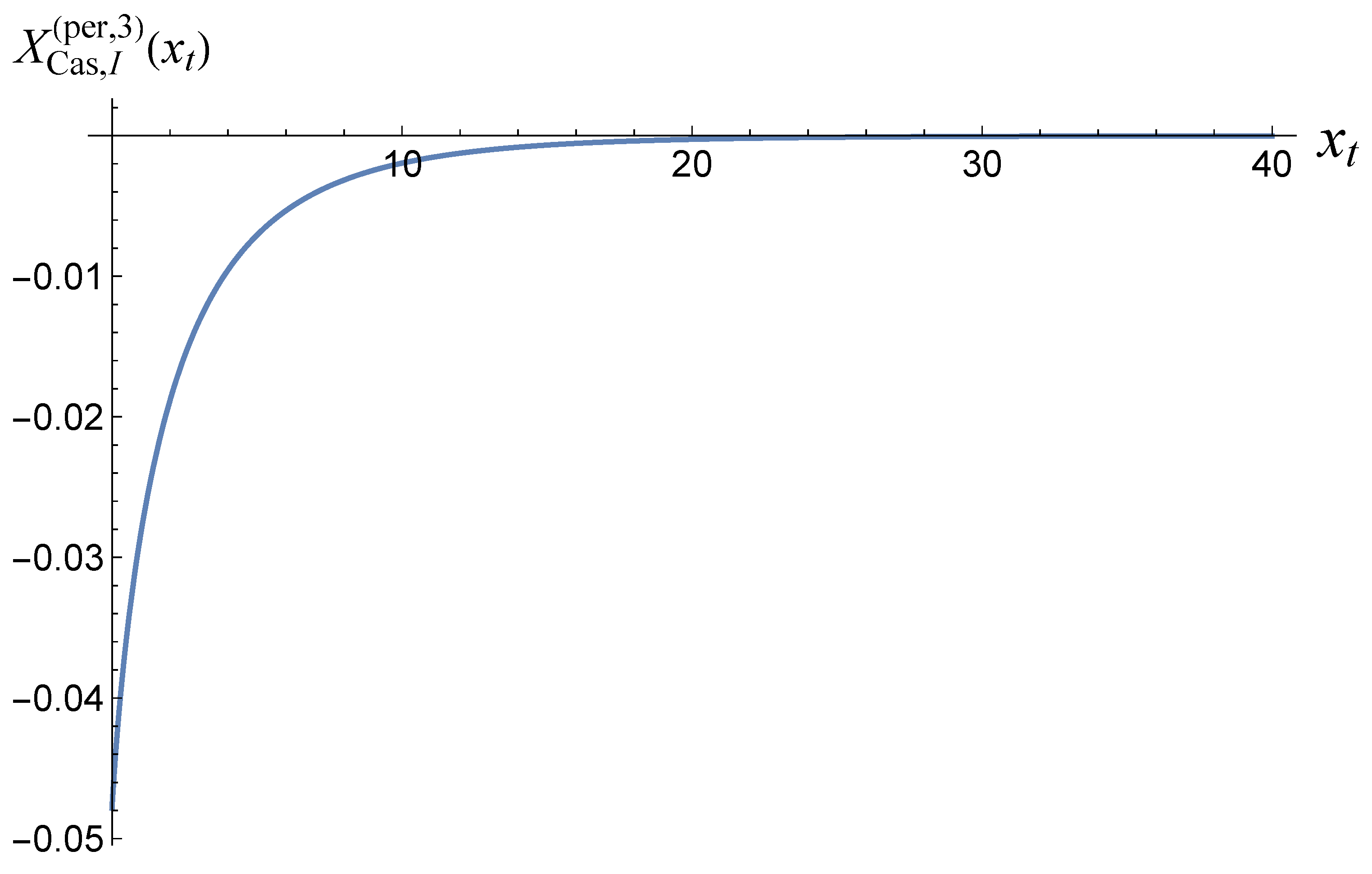
is shown in
Figure 1.
The first term in parentheses in Eq. (2.17) gives us the h-dependent contribution to the free energy: . This is to be compared to the corresponding free energy of a neighboring bulk phase, which goes as , where is an extent that will ultimately be taken to go to infinity. If you add the two free energies, the dependence on L, the thickness of the slab, disappears. This means that there is no h-dependent free energy when slab boundary conditions are periodic, and hence no h-dependent contribution to the Casimir force.
The calculations in the case of periodic boundary conditions point the way to evaluating the partition function and the Casimir force of the case of Dirichlet-Neumann boundary conditions.
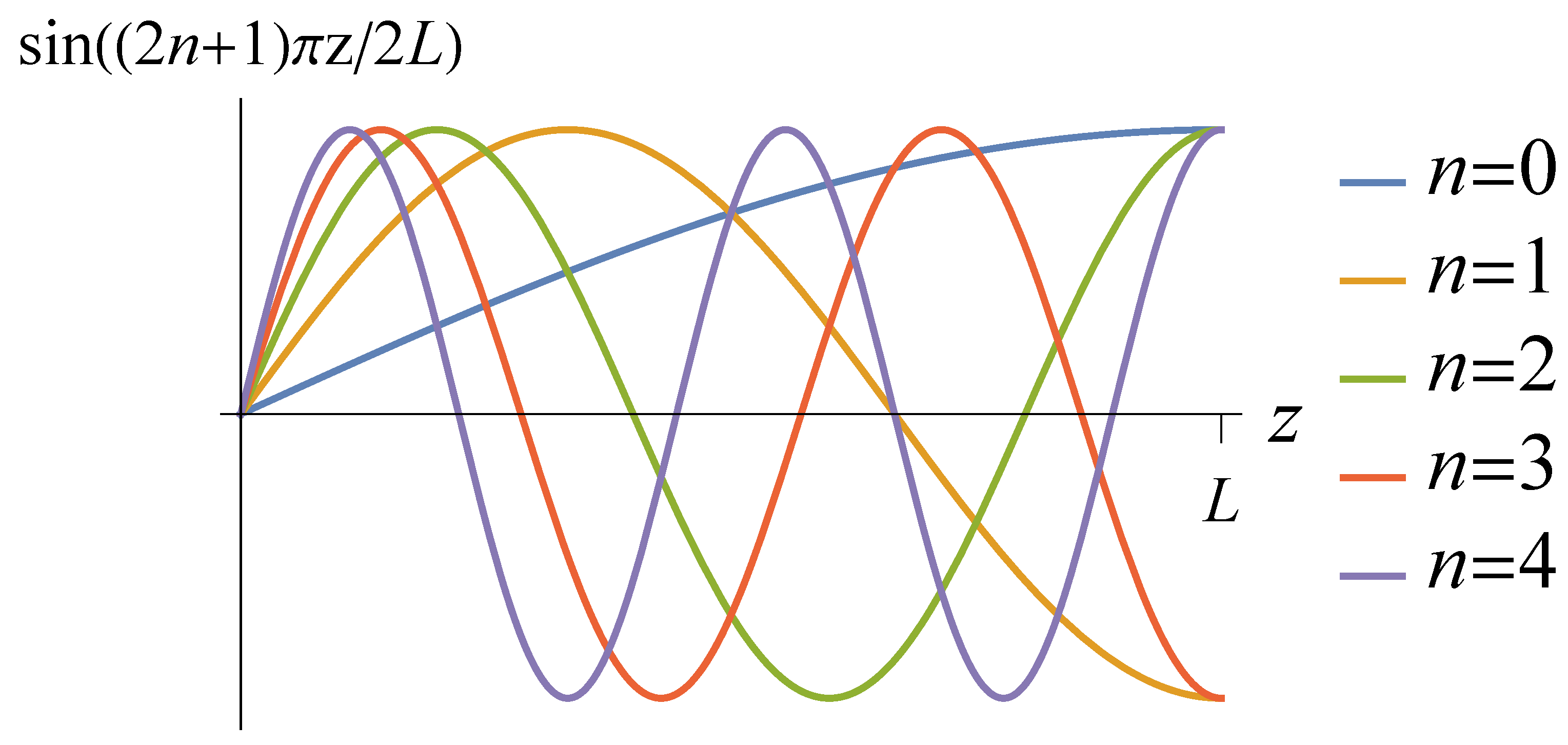
In this case the (unnormalized) basis functions are, exclusive of their dependence on the in-plane coordinates,
Examples of these functions are shown in
Figure 2. Focusing on the
h-independent contribution to the partition function, the sum to perform in this case is (see (2.28))
Note that in the limit of large
L the right hand side goes to the expected asymptotic form. If we subtract that limiting form, and integrate with respect to
t, we are left with
Finally, we take minus the derivative of this with respect to
L, leaving us with
Making use of the analysis of previous sections, this leaves us with the following result for the Casimir force in the case of the
d-dimensional Gaussian model with Dirichlet-Neumann boundary conditions
When
, we have
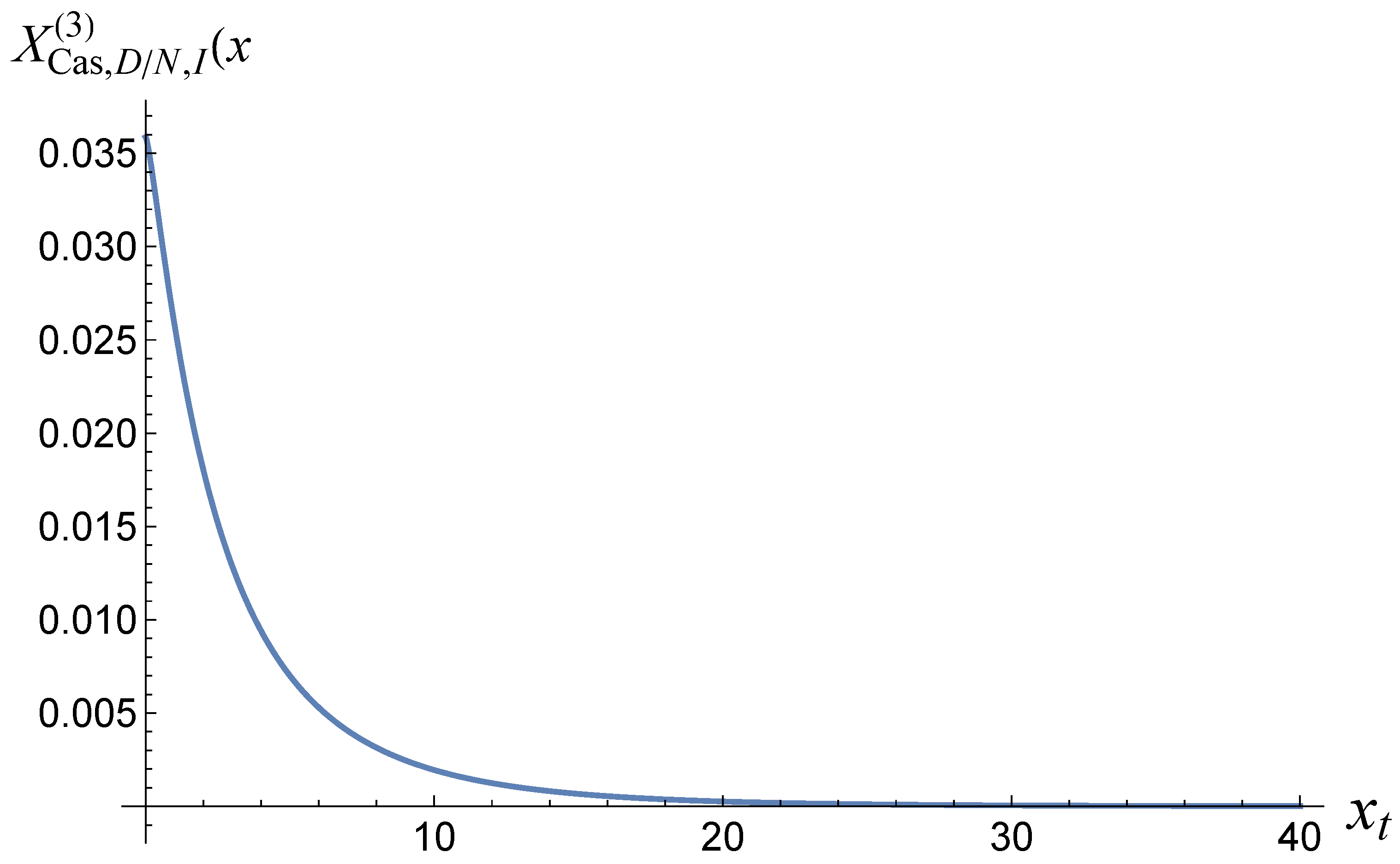
Figure 3 shows what the function
looks like when
.
In order to find the
h-dependent contribution to the Casimir force we turn to the normalized the basis set in the case of Dirichlet-Neumann boundary conditions. Assuming that the boundary conditions are Dirichlet at
and Neumann at
, this basis set is
with
n an integer and
It is straightforward to establish that
while
As it turns out there is no need to take into account any dependence of the basis set on coordinates in the plane of the slab. This is because a constant ordering field couples only to order parameter configurations that are independent of those coordinates.
With this in mind, we expand the order parameter as follows
The Gaussian integrations over the
’s leaves us with the summation over
n for the
h-dependent contribution to the partition function
where the evaluation of the sum over
n in (2.36) is accomplished with the use of (2.8) and a partial fraction decomposition of the summand. The first term in parentheses on the last line of (2.36) gives us exactly the same expression as the
h-dependent contribution to the partition function of the slab with periodic boundary conditions. Its influence on the Casimir force is exactly canceled by the influence of the bulk. What remains is
where we have made use of the definition of the scaling combination
in (2.5). The scaling form of the contribution to the Casimir force is, then
This function is shown in
Figure 4. Note that this function is
aways attractive.
The total scaling function
is given by
Figure 5 shows what this function looks like.
Another depiction of the scaling contribution to the Casimir force for Dirichlet-Neumann boundary conditions in the three dimensional Gaussian model with a scalar order paremeter,
,
Figure 6, highlights the regions in which the function is attractive and repulsive.
3. The Casimir Force Within the Lattice Gaussian Model
We consider a ferromagnetic model with nearest-neighbor interactions on a fully finite d-dimensional hypercubic lattice of sites. Let us take to be the parallelepiped , where × denotes the direct (Cartesian) product of the finite sets .
It is convenient to consider the configuration space
as an Euclidean vector space in which each configuration is represented by a column-vector
with components labeled according to the lexicographic order of the set
. Let
be the corresponding transposed row-vector and let the dot (·) denote matrix multiplication. Then, for given boundary conditions
, specified for each pair of opposite faces of
by some
takes the form
Here
, where
J is the interaction constant (to be set to
in the remainder), and the
interaction matrix
can be written as
where
is the one-dimentional discrete Laplacian defined on the finite chain
under boundary conditions
, and
is the
unit matrix.
By using the results of [
9], we can write down the eigenfunctions of the interaction matrix (3.2) in the form
and obtain the corresponding eigenvalues of it
Obviously,
. Note that the interaction Hamiltonian (3.1) has negative eigenvalues, which makes necessary the inclusion of a positive-definite quadratic form in the Gibbs exponent, to ensure the existence of the corresponding partition function. Thus, we consider the Hamiltonian
Here
is a column-vector representing (in units of
) the inhomogeneous magnetic field configuration acting upon the system, and let
be the transposed row-vector.
In order to ensure the existence of the partition function, all the eigenvalues
,
, of the quadratic form in
, ought to be positive. Hence, the field
must satisfy the inequality
with
defining the critical temperature of the
finite system. Since, as stated above
, it is clear that for the infinite system
The free energy density of a
finite system in a region
is
In Eq. (3.9) the first two terms do not depend on the size of the system, i.e., they are the same in both finite and infinite systems. The other two terms do depend, however on the size of the system. The function
is due to the spin-spin interaction (and will be called "interaction term"); it depends on
s, but does not depend on
h. It is equal to
and is obtained after performing the corresponding Gaussian integrals in the free energy of the finite system. The dependence of the free energy on the field variables
h is given by the "field term"
Here
denotes the projection of the magnetic field configuration
on the eigenfunction
( by
we denote the complex conjugate of
):
Defining
so, that
the above expressions can be rewritten in the form
and
Using the notations of [
9], below we give a list of the complete sets of orthonormal eigenfunctions,
,
, of the one-dimensional discrete Laplacian under the Neumann - Dirichlet (ND) boundary conditions:
periodic (p) boundary conditions
Neumann - Dirichlet (ND) boundary conditions
The quantities
,
, are defined as follows
Now we are ready to find the finite-size behavior of the Gaussian model under the Dirichlet-Neumann boundary conditions. According to Eq. (3.17), , i.e., one has there realization of Neumann boundary conditions, while , which corresponds to Dirichlet boundary conditions. Thus, in the envisaged one-dimensional chain one has L independent spin variables .
We start with the consideration of dimensional system. Note that:
under fully periodic (p) boundary conditions, , one has , hence .
under Neumann-Dirichlet boundary conditions along z direction, i.e., , one has , hence .
3.1. The Gaussian Model on a Lattice for the Case
We recall that for this model
and
[
9,
14].
The behavior of the interaction term
We set
and use the short-hand notation
for these boundary conditions. Then, we perform in Eq. (3.10) the limits
, keeping
fixed. For the interaction term one then obtains
where
The behavior of the interaction term in the bulk system
In accord with Eq. (3.20), one has
The behavior of the interaction term in the film system with Neumann-Dirichlet boundary conditions
Explicitly, from Eq. (3.19) one obtains
with
This sum is of the form
where
is defined as
The summations in Eq. (3.24) can be performed using [
12] the identity
With the help of the identity one derives
Obviously
. Thus, the part of the excess free energy under Neumann – Dirichlet boundary conditions that depends only on the interaction term is
Thus,
can be decomposed in the sum of
and
where
and
Let us consider the behavior of
and
in the scaling regime
Let us first start with the function
. Obviously, if
then
will be exponentially small. Thus, we need to consider the regime
. It follows that
. From Eq. (3.25) we obtain
It follows that
where we have introduced polar coordinates. In terms of them
becomes
where
R can be defined from the constraint
, i.e.,
.
Next, we deal with
. Taking into account that
is small we derive
Note that for
one has that for the
L-dependent part
of
one has
, i.e.,
is one order of magnitude
smaller that
. Because of that,
contributes only sub-leading contributions to
L-dependent part of the excess free energy and, therefore, to the Casimir force. Based on the above, we will no longer be interested in the function
.
Summarizing the above, we conclude that the excess free energy can be written in a scaling form
where
is a non-universal constants, and
is an universal scaling function,
, where
T has the meaning of the temperature of the system, and
is its bulk temperature. From Eq. (3.34), taking into account that with
one has
, we identify that
The behavior of the field term
The dependence of the free energy on the field variable is given by the "field term", given by Eq. (3.15). For a homogeneous filed h and for and boundary conditions, it is easy to obtain that
-
for
boundary conditions
and
for
boundary conditions
Thus, setting
and
, for a film geometry we arrive at
It is easy to show that
Thus, one has
Let us consider the small
k behavior of the above sum. One derives
In the limits
and
for the behavior of the field term one obtains
When
, then
, we obtain that
which indeed equals the bulk expression - see Eq. (3.40).
From Eq. (3.45) for the behavior of the susceptibility in the finite system we derive
According to the finite-size scaling theory [
9,
15]
where
and
are non-universal constants, and
is an universal scaling function,
, where
T has the meaning of the temperature of the system, and
is its bulk temperature. From Eq. (3.48), taking into account that
, we identify that
It is clear that the field term in the free energy of the finite system will be of the same order as the field term, i.e.,
if
. In order to achieve that, we define a field dependent scaling variable
In terms of it, Eq. (3.45) becomes
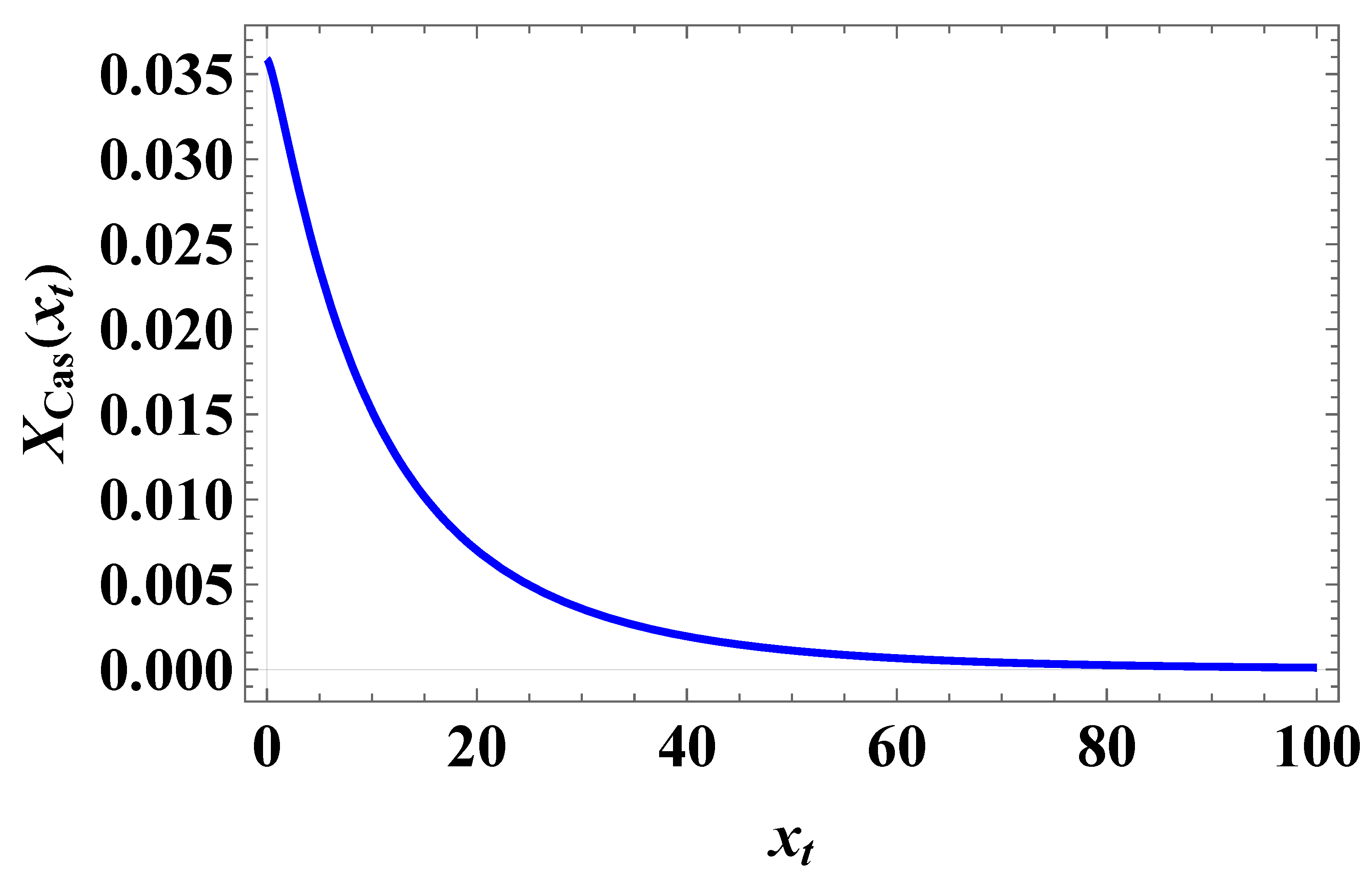
The behavior of the scaling function
is given in
Figure 7.
Then for the excess free energy related to the field term, see Eq. (3.9), one derives
3.2. The Behavior of the Casimir Force
Let us determine the contributions of the interaction term
and of the field term
. Obviously, one has
We start with determining the behavior of
. By definition, it is equal to
From Eq. (3.28) we derive the
exact expression
Here we did not make any assumption bout
L. Naturally, we will obtain a scaling form of
only for
. Then Eq. (3.32) is valid and, after performing the integration, we arrive at
where
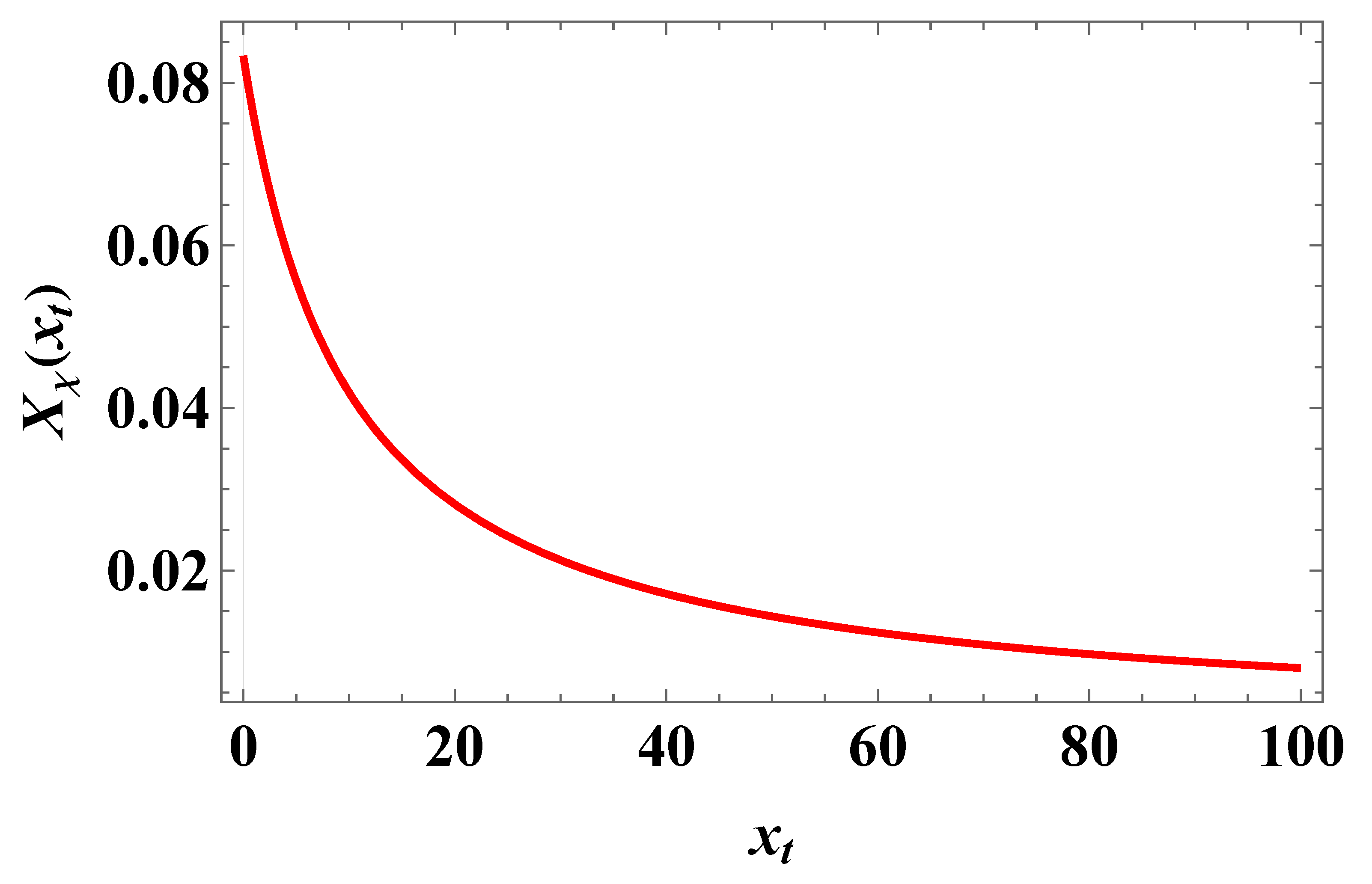
The behavior of the scaling function
is given in
Figure 8. Obviously, the function is positive, which means that the Casimir force is repulsive when the external field is zero. For the Casimir amplitude we obtain
Obviously, Eq. (3.59) coincides with the corresponding result for the Gaussian model obtained via studying the
,
model — see [
4, Eq.(6.99)]. Analogically, after proper renaming of the scaling variable the expression Eq. (3.58) of the scaling function of the force coinsides with the corresponding one for the
,
model — see [
4, Eq.(6.104)].
Let us now determine the
h-dependent part of the Casimir force. By definition, one has
Then, from Eq. (3.53) one obtains
where
A visualization of
as a function of
y for
is shown in
Figure 9.
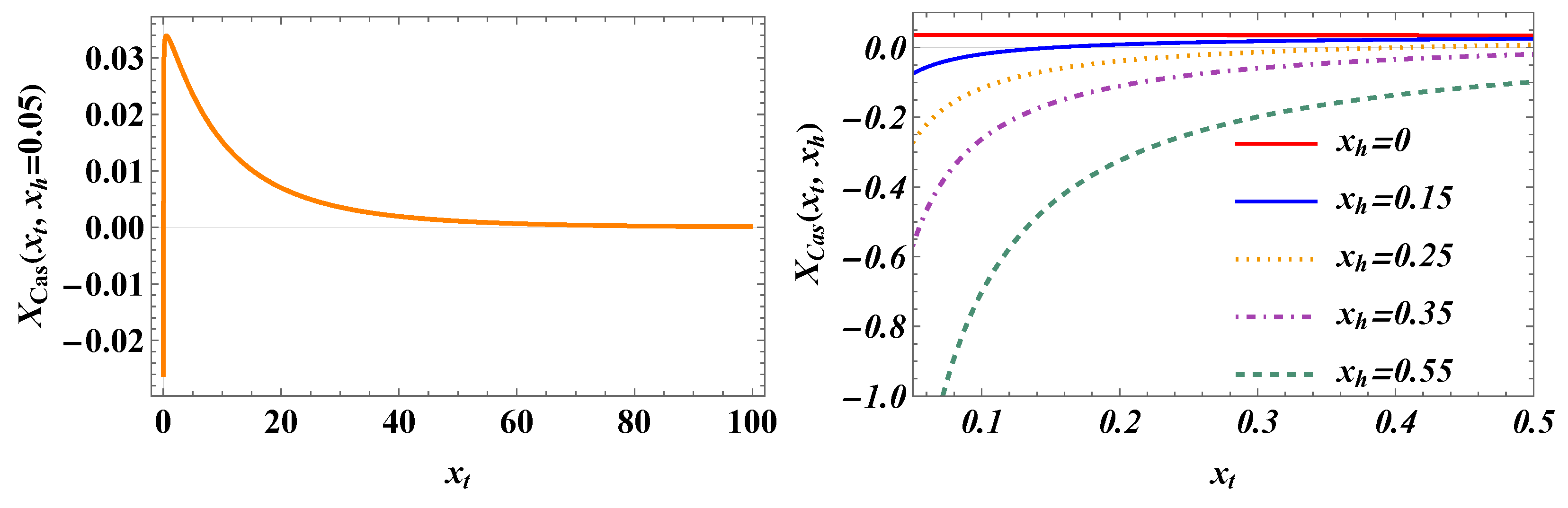
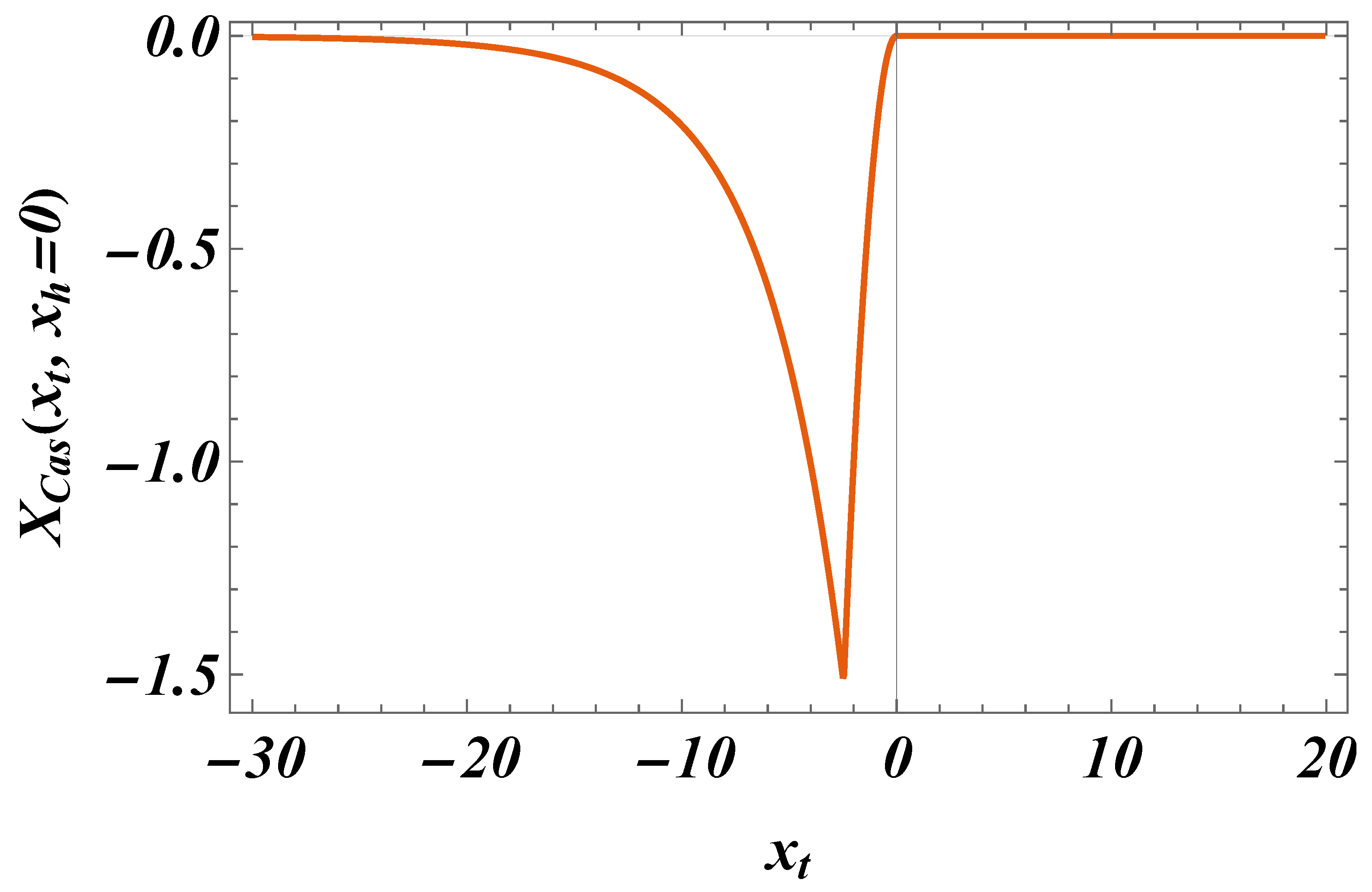
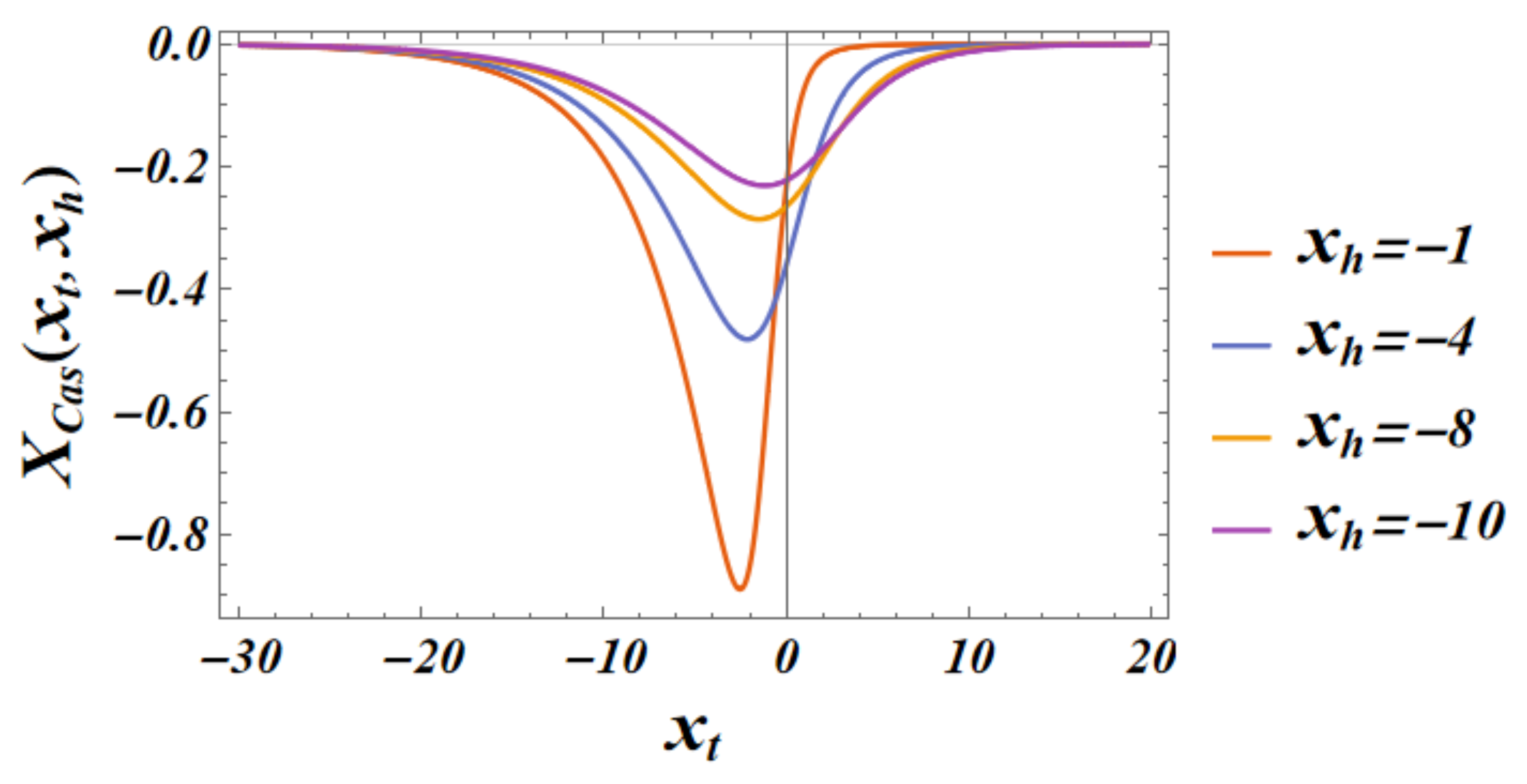
The total Casimir force is a sum of
, see Eq. (3.58), and
given by Eq. (3.63). The plot of the result as a function of
for
is shown in
Figure 10. As we see, the force can be both positive and negative, i.e.,
repulsive and
attractive.
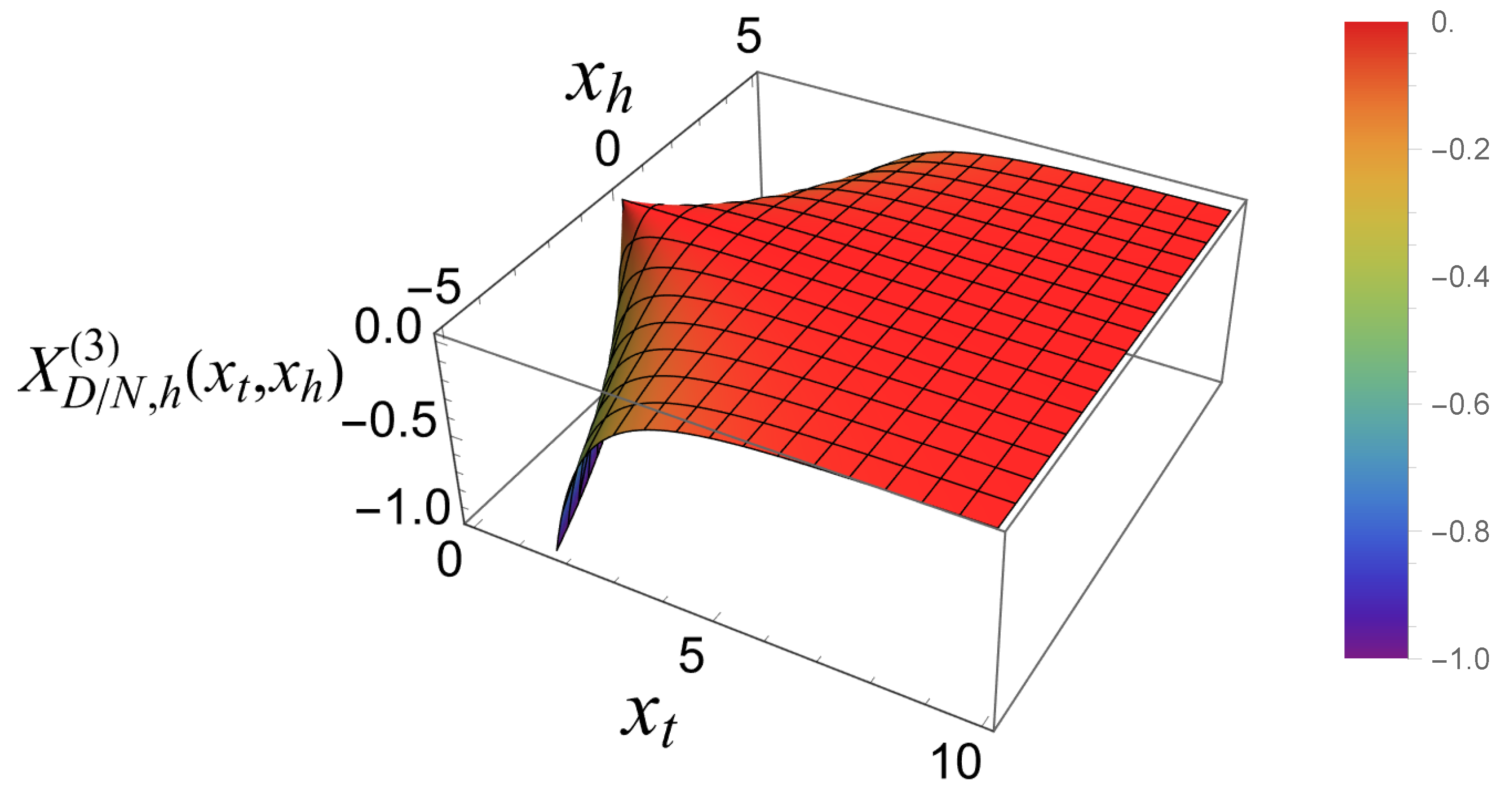
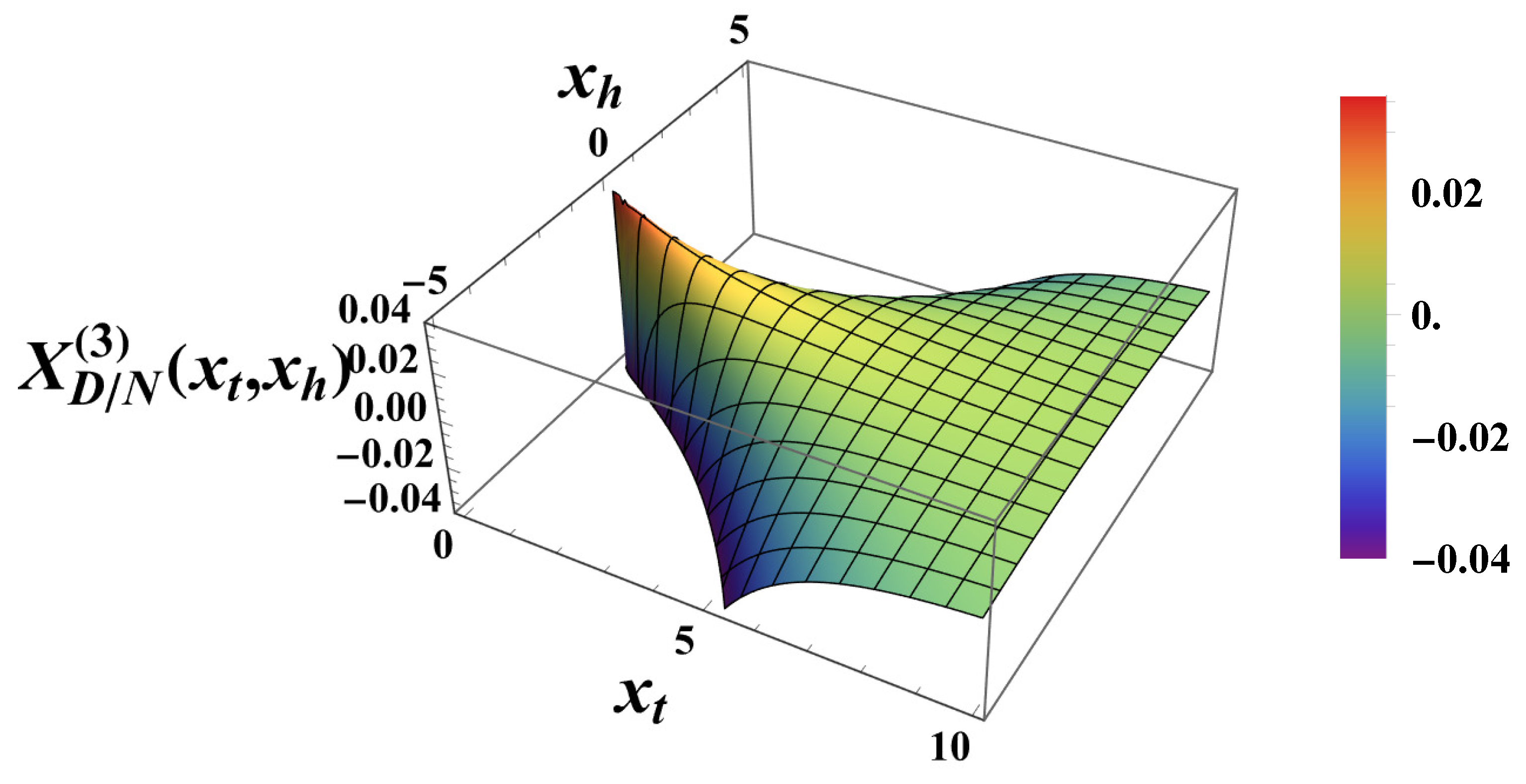
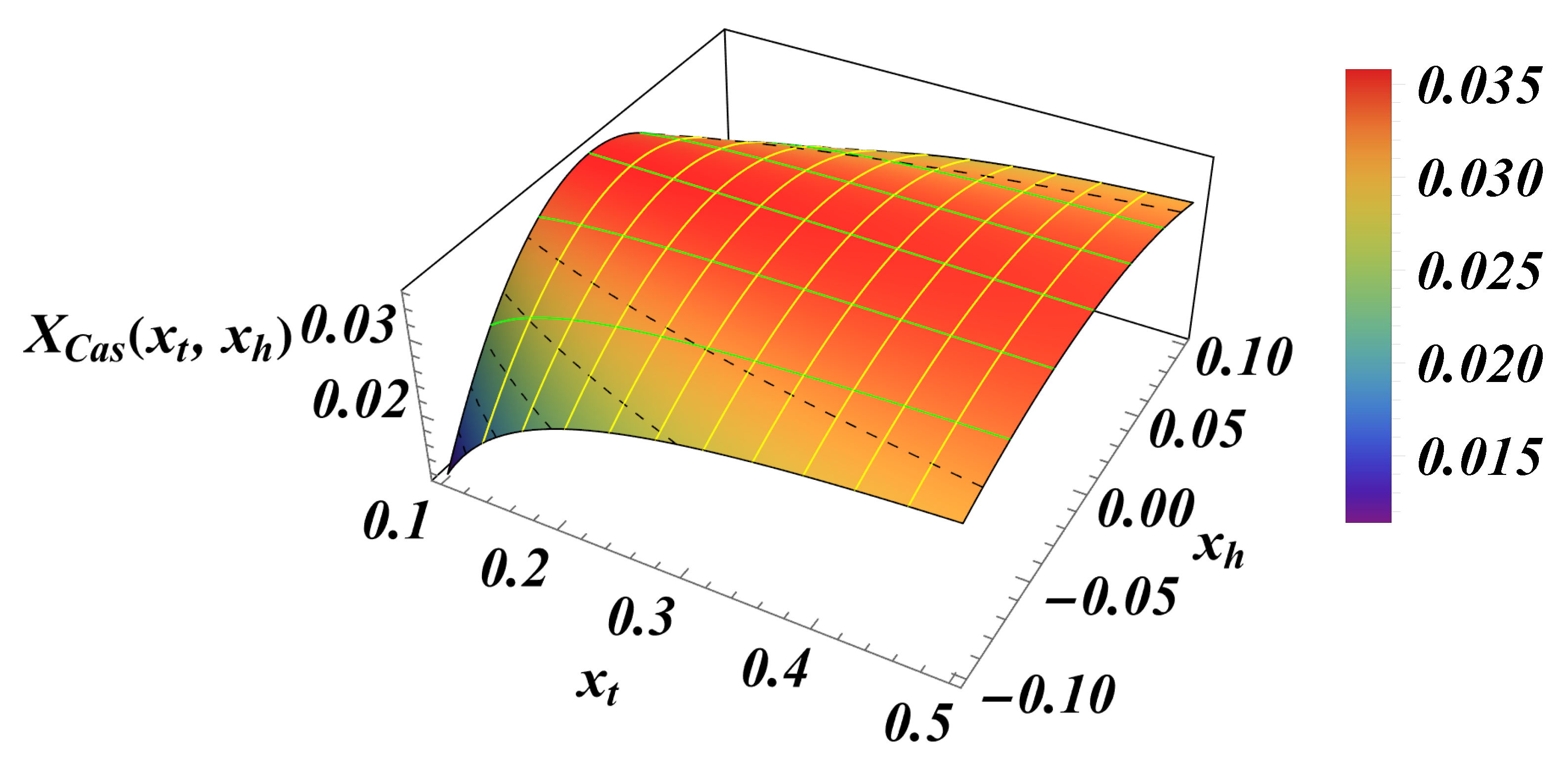
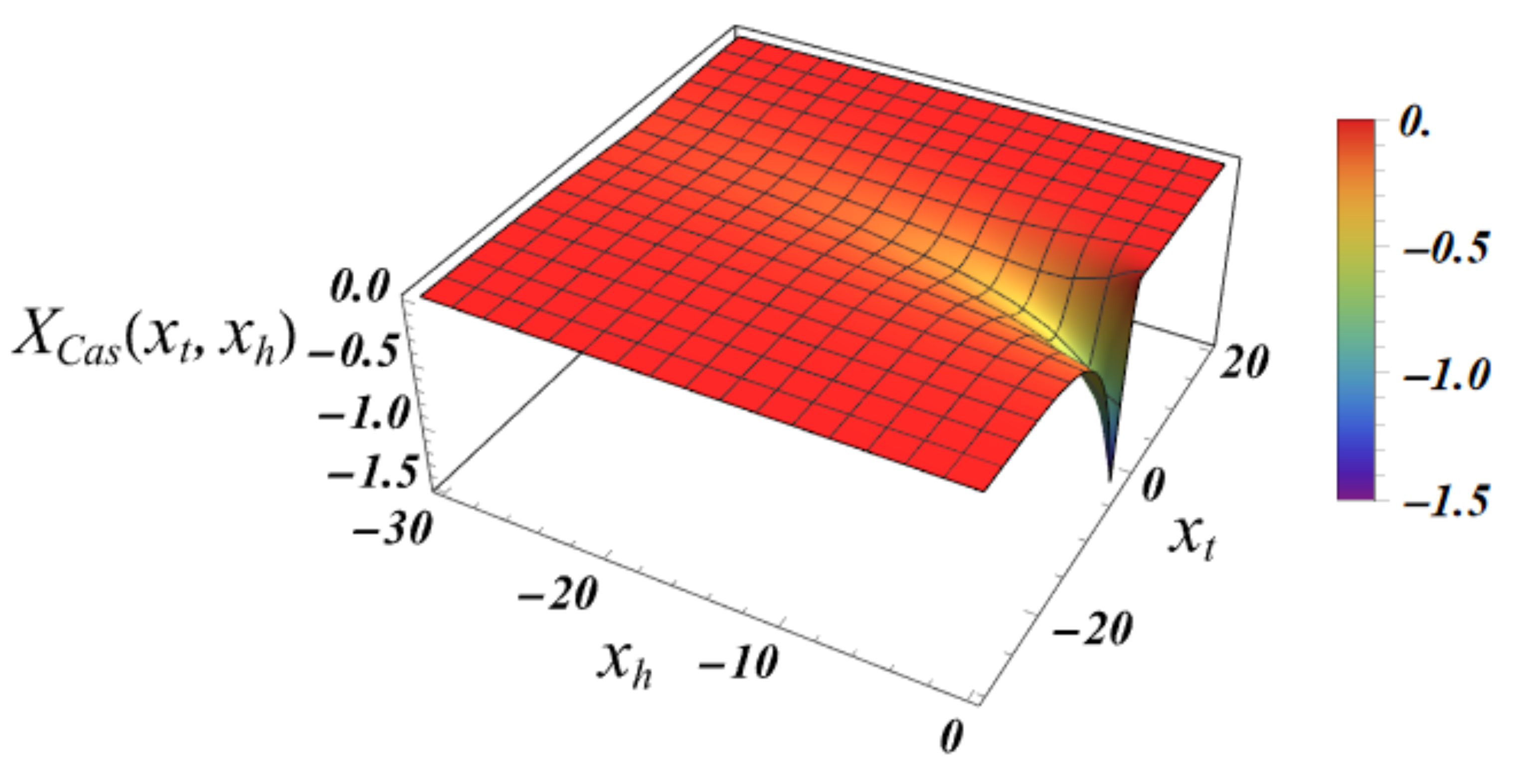
The overall
behavior of the force as a function both on
and
is given in
Figure 11.
Figure 1.
The function , plotted versus
Figure 1.
The function , plotted versus
Figure 2.
The functions in (2.25)
Figure 2.
The functions in (2.25)
Figure 3.
The function , as given in (2.30).
Figure 3.
The function , as given in (2.30).
Figure 4.
The function , as given by (2.38).
Figure 4.
The function , as given by (2.38).
Figure 5.
The total scaling contribution to the Casimir force for Dirichlet-Neumann boundary conditions in the three dimensional Gaussian model with a scalar order parameter,. Note that this function can be both positive (repulsive) and negative (attractive).
Figure 5.
The total scaling contribution to the Casimir force for Dirichlet-Neumann boundary conditions in the three dimensional Gaussian model with a scalar order parameter,. Note that this function can be both positive (repulsive) and negative (attractive).
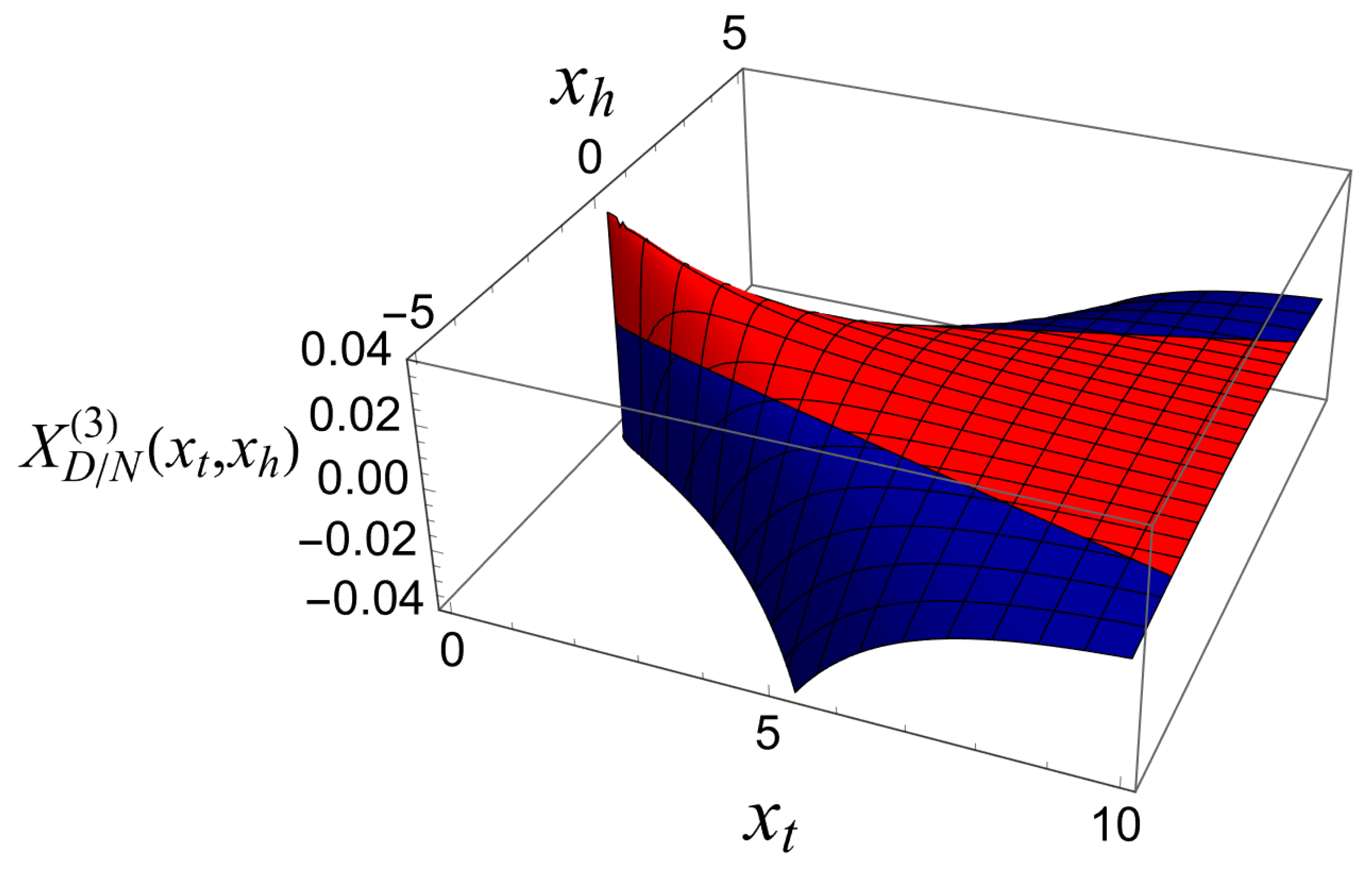
Figure 6.
The total scaling contribution to the Casimir force for Dirichlet-Neumann boundary conditions in the three dimensional Gaussian model with a scalar order parameter,. The red region in the figure corresponds to a repulsive force, and the blue region corresponds to an attractive force.
Figure 6.
The total scaling contribution to the Casimir force for Dirichlet-Neumann boundary conditions in the three dimensional Gaussian model with a scalar order parameter,. The red region in the figure corresponds to a repulsive force, and the blue region corresponds to an attractive force.
Figure 7.
The behavior of the scaling function .
Figure 7.
The behavior of the scaling function .
Figure 8.
The behavior of the scaling function when .
Figure 8.
The behavior of the scaling function when .
Figure 9.
The behavior of the scaling function . We observe that the force is attractive.
Figure 9.
The behavior of the scaling function . We observe that the force is attractive.
Figure 10.
The behavior of the scaling function of the total Casimir force as a function of y for several values of . Left panel: We see that for the force is attractive very near the critical temperature, then becomes repulsive with increase of (i.e., of T). Right panel: It is clear, that for zero field the force is repulsive, then — for small values of — the force changes sign from attractive to repulsive with the increase of (i.e., of the temperature), while for large values of the force becomes attractive for all values of T (i.e., ).
Figure 10.
The behavior of the scaling function of the total Casimir force as a function of y for several values of . Left panel: We see that for the force is attractive very near the critical temperature, then becomes repulsive with increase of (i.e., of T). Right panel: It is clear, that for zero field the force is repulsive, then — for small values of — the force changes sign from attractive to repulsive with the increase of (i.e., of the temperature), while for large values of the force becomes attractive for all values of T (i.e., ).
Figure 11.
The behavior of the scaling function . Here and .
Figure 11.
The behavior of the scaling function . Here and .
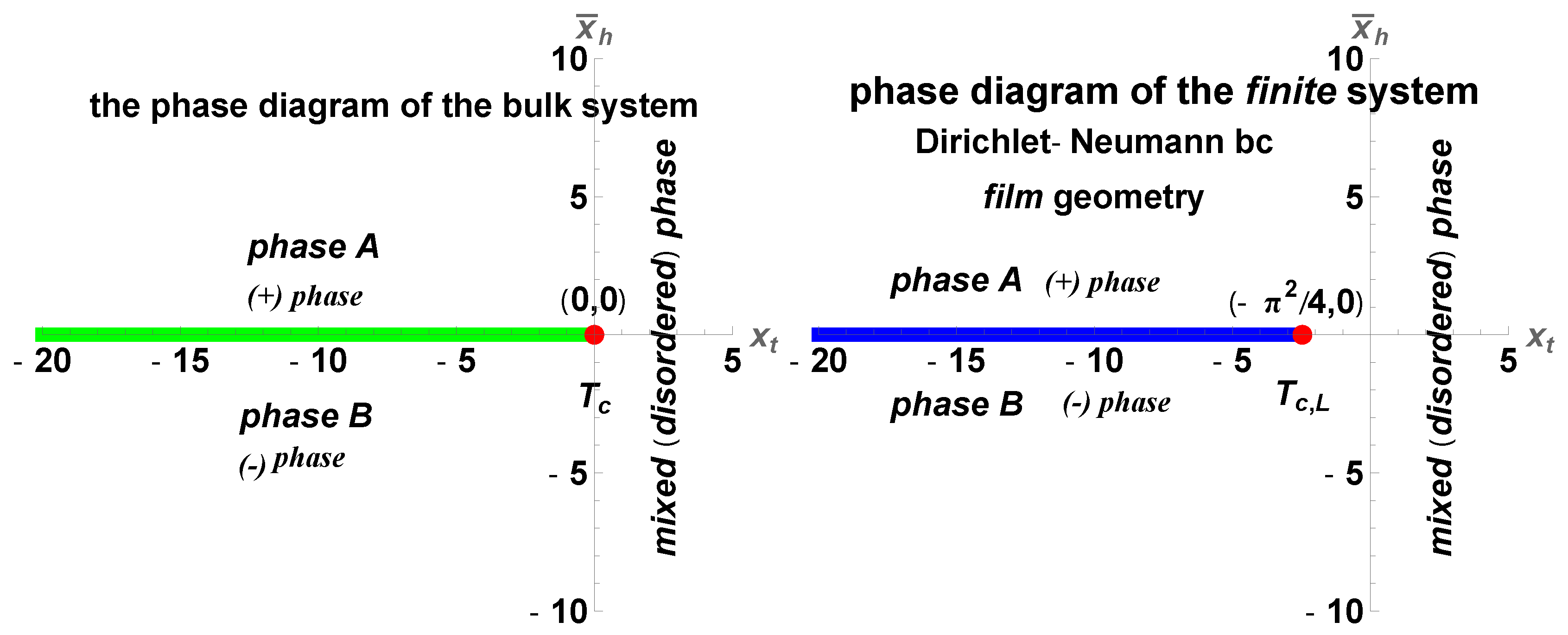
Figure 12.
Phase diagrams. Left panel: The phase diagram of the bulk system. Right panel: The phase diagram of the finite system with Dirichlet-Neumann boundary conditions. In the bulk system a phase transition of first order happens when crossing the phase coexistence line that is at and spans for . At the system exhibits a second order phase transition. In the finite system the coexistence line is at and spans for . The second order phase transition happens at . Note the change with Dirichlet-Dirichlet boundary conditions where the critical point is at .
Figure 12.
Phase diagrams. Left panel: The phase diagram of the bulk system. Right panel: The phase diagram of the finite system with Dirichlet-Neumann boundary conditions. In the bulk system a phase transition of first order happens when crossing the phase coexistence line that is at and spans for . At the system exhibits a second order phase transition. In the finite system the coexistence line is at and spans for . The second order phase transition happens at . Note the change with Dirichlet-Dirichlet boundary conditions where the critical point is at .
Figure 13.
The behavior of the scaling function for . We observe that the force is attractive, contrary to the corresponding result for the Gaussian model.
Figure 13.
The behavior of the scaling function for . We observe that the force is attractive, contrary to the corresponding result for the Gaussian model.
Figure 14.
The behavior of the scaling function , for several values of . We observe that the force is attractive.
Figure 14.
The behavior of the scaling function , for several values of . We observe that the force is attractive.
Figure 15.
The behavior of the scaling function , , . We observe that the force is attractive.
Figure 15.
The behavior of the scaling function , , . We observe that the force is attractive.