Submitted:
09 December 2024
Posted:
11 December 2024
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. The Model in Canonical Ensemble
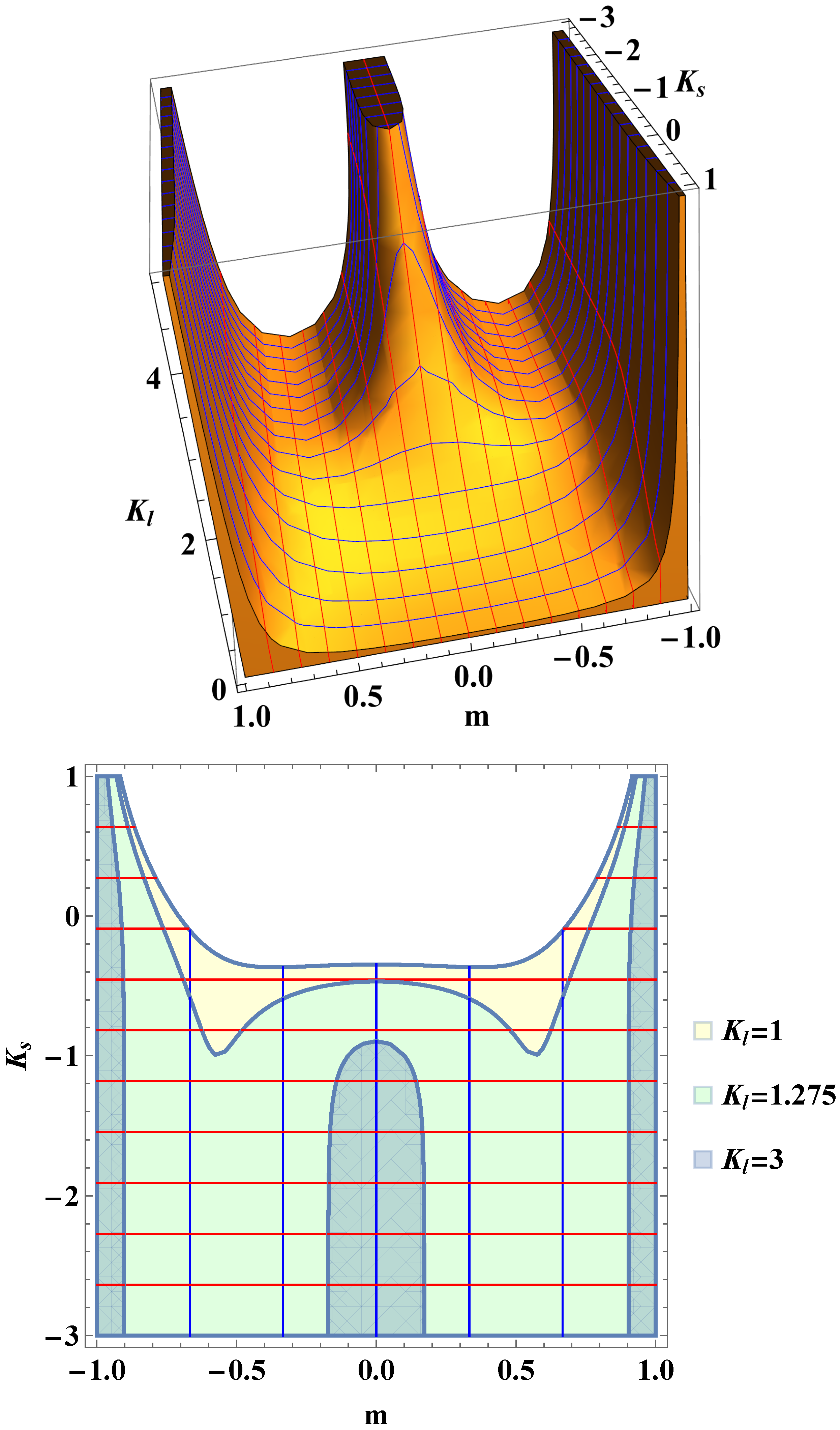
3. On the Phase Diagram in Canonical Ensemble
- the second order phase transition exists when , with ;
- there is a tricritical point in the system at , i.e., , and .
- The overall phase diagram in the plane is shown in Figure 6. There the position at which three phase coexist having the same energy as the one with is determined by solving numerically the system of equations
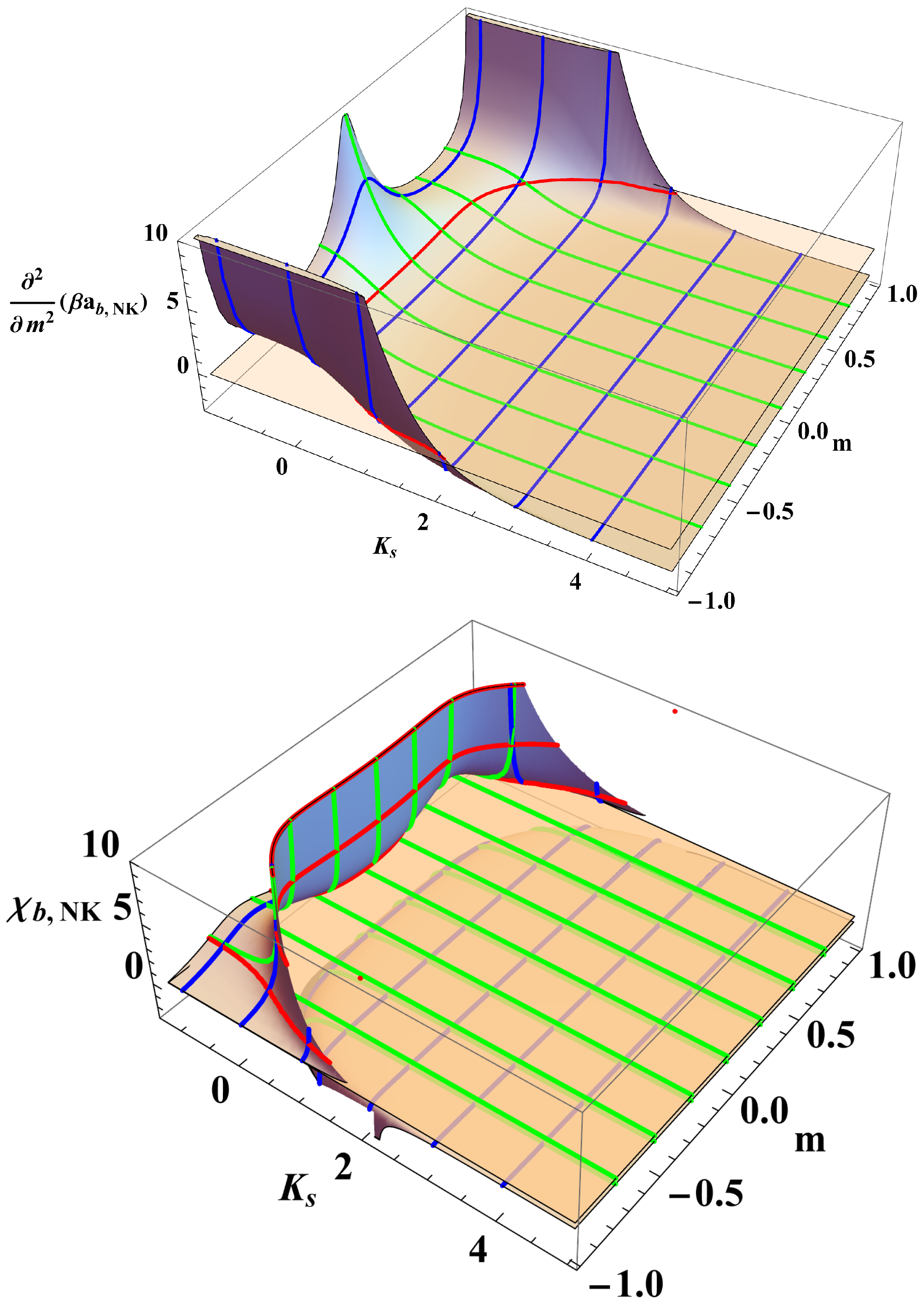
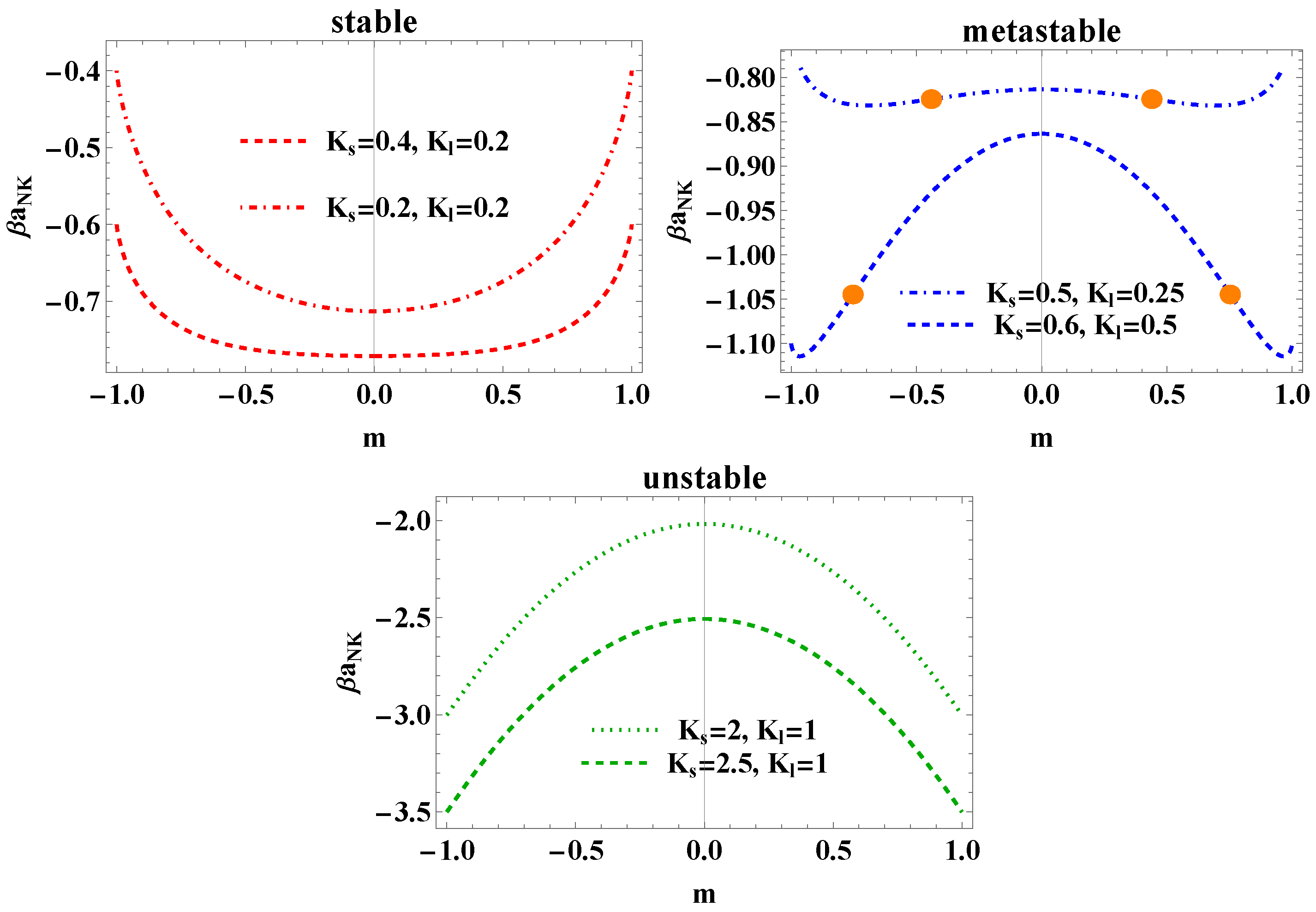
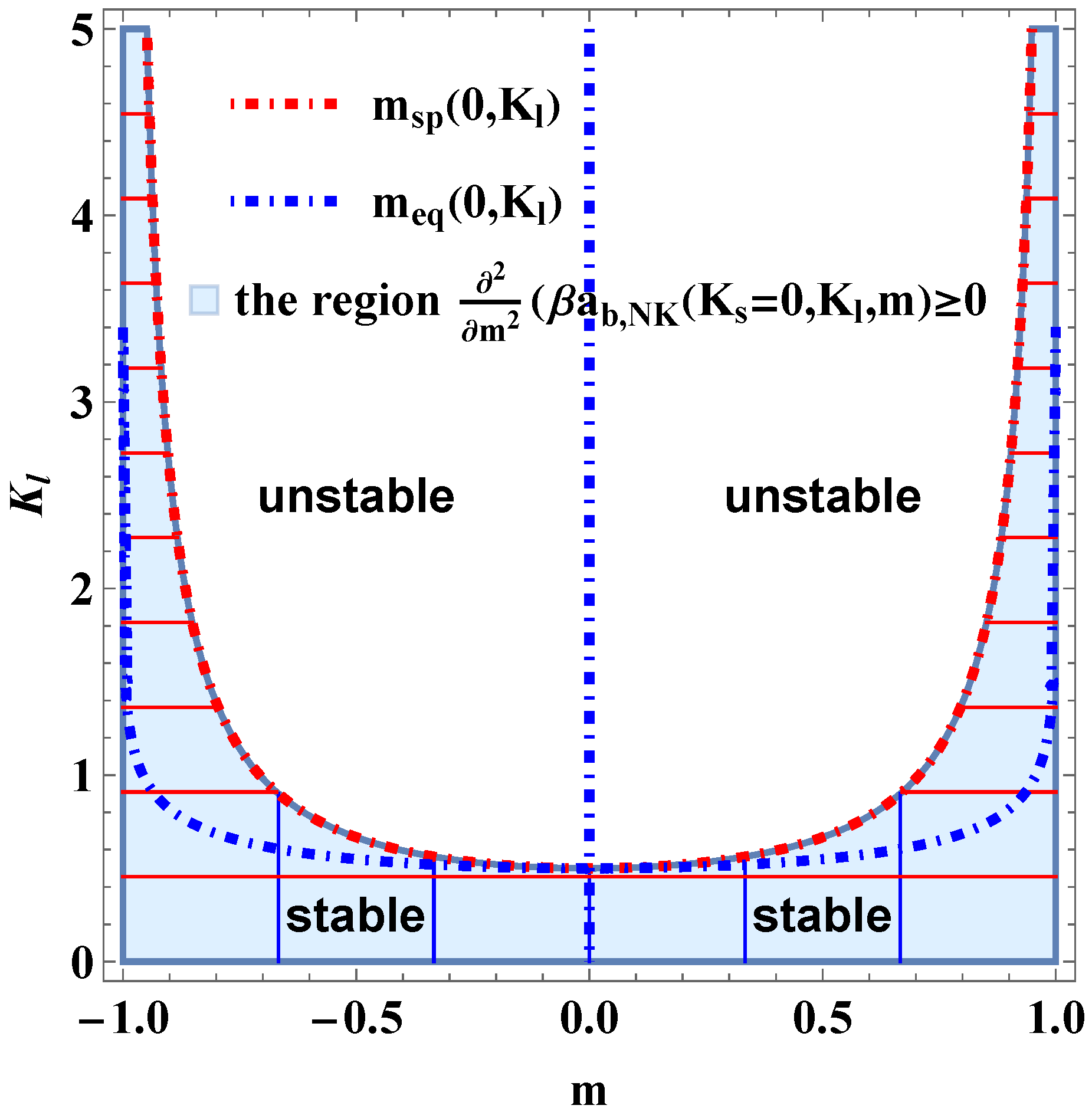
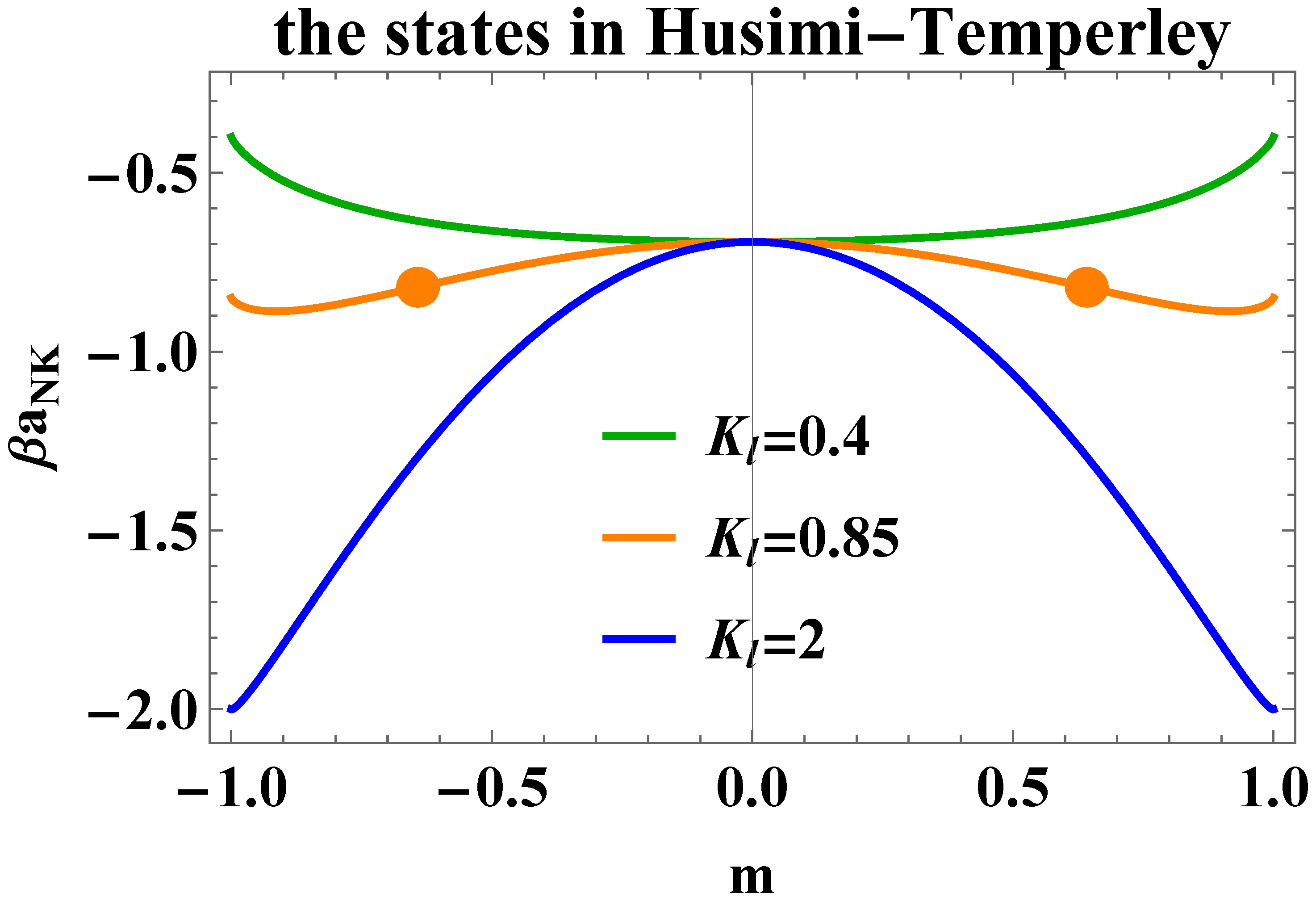
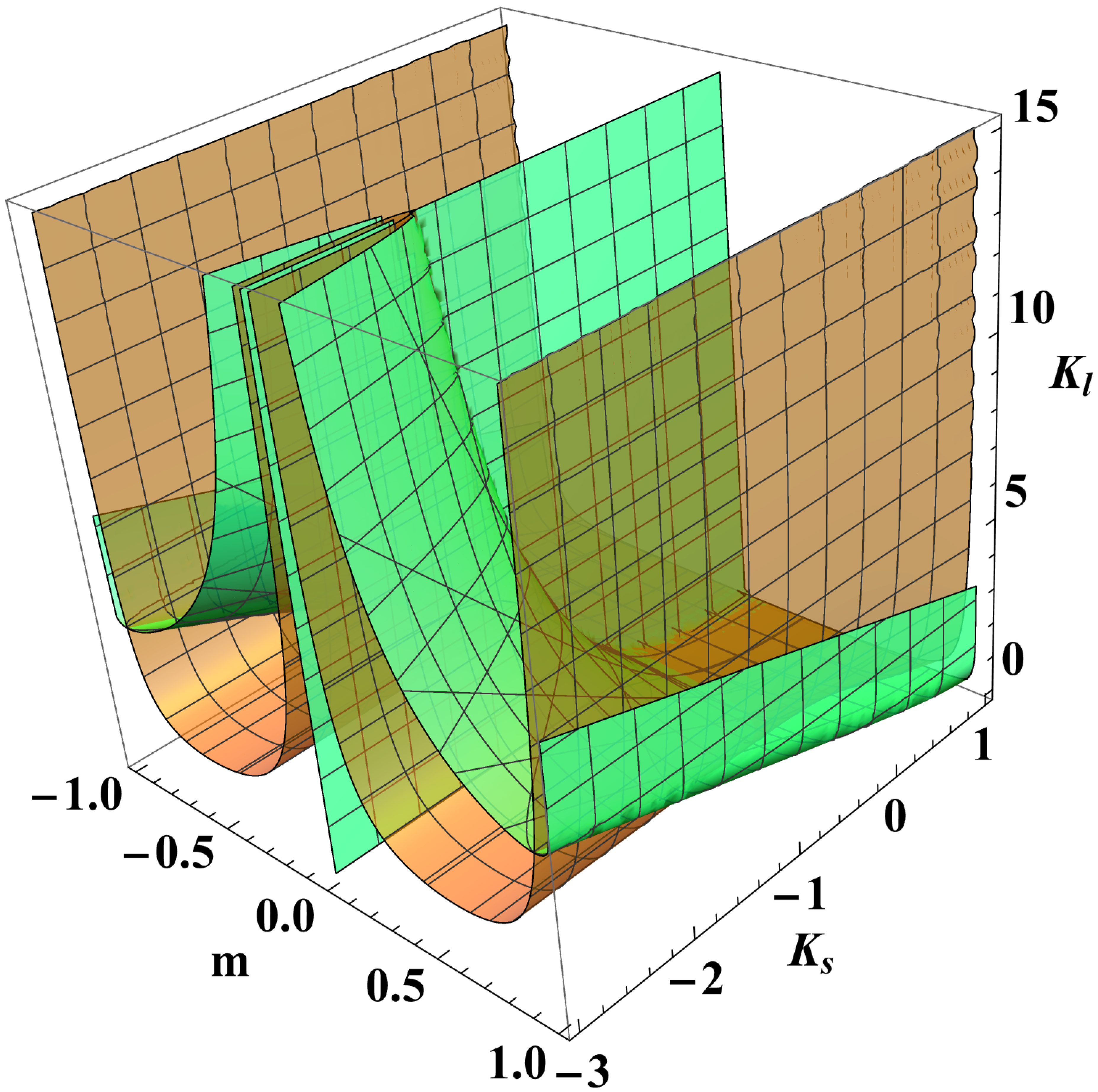
4. On the Stability of the System
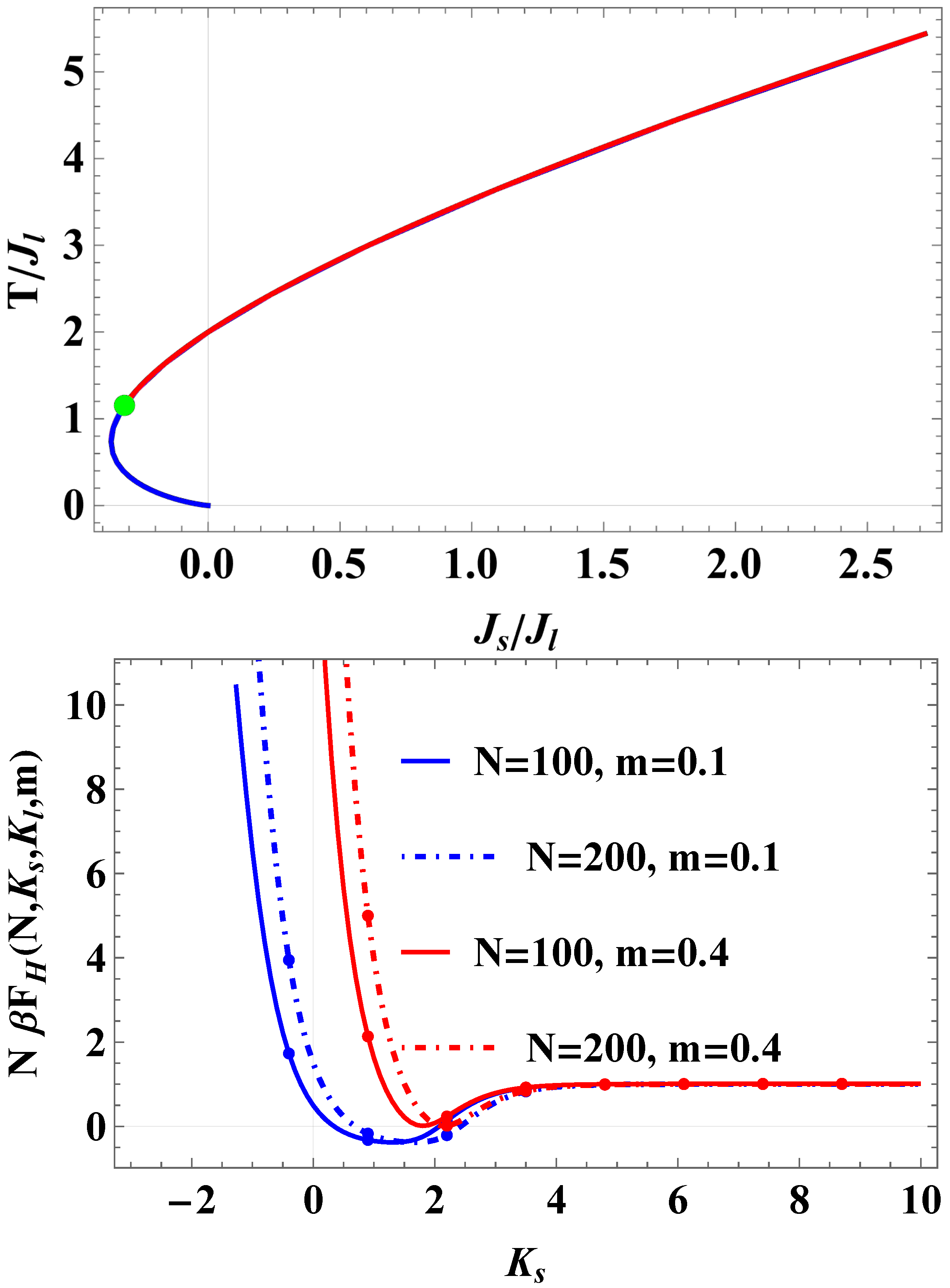
5. On the Behavior of the Helmholtz Force
6. Discussion and Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CE | canonical ensemble |
| GCE | grand canonical ensemble |
| CCF | critical Casimir force |
| PBC’s | periodic boundary conditions |
References
- Dantchev, D.; Tonchev, N.; Rudnick, J. Finite-size Nagle-Kardar model: Casimir force 2024. arXiv:cond-mat.stat-mech/2404.18324. [CrossRef]
- Casimir, H.B. On the Attraction Between Two Perfectly Conducting Plates. Proc. K. Ned. Akad. Wet. 1948, 51, 793–796. [Google Scholar]
- Fisher, M.E.; de Gennes, P.G. Phénomènes aux parois dans un mélange binaire critique. C. R. Seances Acad. Sci. Paris Ser. B 1978, 287, 207–209. [Google Scholar]
- Maciołek, A.; Dietrich, S. Collective behavior of colloids due to critical Casimir interactions. Rev. Mod. Phys. 2018, 90, 045001. [Google Scholar] [CrossRef]
- Dantchev, D.; Dietrich, S. Critical Casimir effect: Exact results. Phys. Rep. 2023, 1005, 1–130. [Google Scholar] [CrossRef]
- Gambassi, A.; Dietrich, S. Critical Casimir forces in soft matter. Soft Matter 2024. [Google Scholar] [CrossRef]
- Dantchev, D. On Casimir and Helmholtz Fluctuation-Induced Forces in Micro- and Nano-Systems: Survey of Some Basic Results. Entropy 2024, 26, 499. [Google Scholar] [CrossRef] [PubMed]
- Barber, M.N. Finite-size Scaling. In Phase Transitions and Critical Phenomena; Domb, C.; Lebowitz, J.L., Eds.; Academic, London, 1983; Vol. 8, chapter 2, pp. 146–266.
- Privman, V. Finite-size scaling theory. In Finite Size Scaling and Numerical Simulations of Statistical Systems; Privman, V., Ed.; World Scientific, Singapore, 1990; pp. 1–98.
- Brankov, J.G.; Dantchev, D.M.; Tonchev, N.S. The Theory of Critical Phenomena in Finite-Size Systems - Scaling and Quantum Effects; World Scientific, Singapore, 2000. [CrossRef]
- Garcia, R.; Chan, M.H.W. Critical Fluctuation-Induced Thinning of 4He Films near the Superfluid Transition. Phys. Rev. Lett. 1999, 83, 1187–1190. [Google Scholar] [CrossRef]
- Garcia, R.; Chan, M.H.W. Critical Casimir Effect near the 3He-4He Tricritical Point. Phys. Rev. Lett. 2002, 88, 086101. [Google Scholar] [CrossRef]
- Ganshin, A.; Scheidemantel, S.; Garcia, R.; Chan, M.H.W. Critical Casimir Force in 4He Films: Confirmation of Finite-Size Scaling. Phys. Rev. Lett. 2006, 97, 075301. [Google Scholar] [CrossRef]
- Hertlein, C.; Helden, L.; Gambassi, A.; Dietrich, S.; Bechinger, C. Direct measurement of critical Casimir forces. Nature 2008, 451, 172–175. [Google Scholar] [CrossRef] [PubMed]
- Schmidt, F.; Callegari, A.; Daddi-Moussa-Ider, A.; Munkhbat, B.; Verre, R.; Shegai, T.; Käll, M.; Löwen, H.; Gambassi, A.; Volpe, G. Tunable critical Casimir forces counteract Casimir–Lifshitz attraction. Nat. Phys. 2022. [Google Scholar] [CrossRef]
- Dantchev, D.; Rudnick, J. Exact expressions for the partition function of the one-dimensional Ising model in the fixed-M ensemble. Phys. Rev. E 2022, 106. [Google Scholar] [CrossRef] [PubMed]
- Dantchev, D.M.; Tonchev, N.S.; Rudnick, J. Casimir versus Helmholtz forces: Exact results. Ann. Phys-New. York. 2023, 459. [Google Scholar] [CrossRef]
- Dantchev, D.; Tonchev, N. A Brief Survey of Fluctuation-induced Interactions in Micro- and Nano-systems and One Exactly Solvable Model as Example. arXiv:2403.17109 [cond-mat.stat-mech], arXiv:2403.17109 [cond-mat.stat-mech] 2024, [arXiv:cond-mat.stat-mech/2403.17109]. [CrossRef]
- Dantchev, D.; Tonchev, N.; Rudnick, J. Casimir and Helmholtz forces in one-dimensional Ising model with Dirichlet (free) boundary conditions. Ann. Phys-new. York. 2024, 464, 169647. [Google Scholar] [CrossRef]
- Baker, G.A. Ising model with a long-range interaction in presence of residual short-range interactions. Phys. Rev. 1963, 130, 1406–1411. [Google Scholar] [CrossRef]
- Nagle, J.F. Ising chain with competing interactions. Phys. Rev. A 1970, 2, 2124. [Google Scholar] [CrossRef]
- Kardar, M. Crossover to equivalent-neighbor multicritical behavior in arbitrary dimensions. Phys. Rev. B 1983, 28, 244–246. [Google Scholar] [CrossRef]
- Patelli, A.; Ruffo, S. Statistical mechanics and dynamics of long-range interacting systems. Rivista Di Matematica Della Universita Di Parma 2013, 4, 345–396. [Google Scholar]
- Campa, A.; Dauxois, T.; Fanelli, D.; Ruffo, S. Physics of long-range interacting systems, first edition. ed.; Oxford University Press: Oxford, 2014; pp. 410p. [Google Scholar]
- Gupta, S.; Ruffo, S. The world of long-range interactions: A bird’s eye view. Int. J. Mod. Phys. A 2017, 32. [Google Scholar] [CrossRef]
- K.Husimi. Statistical mechanics of condensation. In Proceedings of the Proc. Intern. Conf. Theor. Phys. Kyoto and Tokyo, 1953, p. 531.
- Temperley, H.N.V. The Mayer theory of condensation tested against a simple model of imperfect gas. Proc. Phys. Soc. London 1954, A 67, 233. [Google Scholar] [CrossRef]
- Hoye, J.S. Spin model with antiferromagnetic and ferromagnetic interactions. Physical Review B 1972, 6, 4261. [Google Scholar] [CrossRef]
- Kaufman, M.; Kahana, M. Cayley-tree Ising-model with antiferromagnetic nearest-neighbor and ferromagnetic equivalent-neighbor interactions. Phys. Rev. B 1988, 37, 7638–7642. [Google Scholar] [CrossRef]
- Vieira, A.; Goncalves, L. One-dimensional lattice gas. Condens. Matter Phys. 1995, 5, 210–225. [Google Scholar] [CrossRef]
- Paladin, G.; Pasquini, M.; Serva, M. Ferrimagnetism in a disordered Ising-model. Journal De Physique I 1994, 4, 1597–1617. [Google Scholar] [CrossRef]
- Vieira, A.P.; Goncalves, L.L. One-dimensional Ising model with long-range and random short-range interactions. J. Magn. Magn. Mater. 1999, 192, 177–190. [Google Scholar] [CrossRef]
- Boukheddaden, K.; Linares, J.; Spiering, H.; Varret, F. One-dimensional Ising-like systems: an analytical investigation of the static and dynamic properties, applied to spin-crossover relaxation. Eur. Phys. J. B 2000, 15, 317–326. [Google Scholar] [CrossRef]
- Mukamel, D.; Ruffo, S.; Schreiber, N. Breaking of ergodicity and long relaxation times in systems with long-range interactions. Phys. Rev. Lett. 2005, 95. [Google Scholar] [CrossRef] [PubMed]
- Mukamel, D. Notes on the Statistical Mechanics of Systems with Long-Range Interactions. arXiv:0905.1457 [cond-mat.stat-mech], arXiv:0905.1457 [cond-mat.stat-mech] 2009. [CrossRef]
- Campa, A.; Dauxois, T.; Ruffo, S. Statistical mechanics and dynamics of solvable models with long-range interactions. Phys. Rep. 2009, 480, 57–159. [Google Scholar] [CrossRef]
- Bouchet, F.; Gupta, S.; Mukamel, D. Thermodynamics and dynamics of systems with long-range interactions. Physica A 2010, 389, 4389–4405. [Google Scholar] [CrossRef]
- Ostilli, M. Mean-field models with short-range correlations. Epl 2012, 97. [Google Scholar] [CrossRef]
- Salmon, O.D.R.; de Sousa, J.R.; Neto, M.A. Phase diagrams of a spin-1 Ising system with competing short- and long-range interactions. Phys. Rev. E 2015, 92. [Google Scholar] [CrossRef] [PubMed]
- Kardar, M.; Kaufman, M. Competing Criticality of Short- and Infinite-Range Interactions on the Cayley Tree. Phys. Rev. Lett. 1983, 51, 1210–1213. [Google Scholar] [CrossRef]
- Kaufman, M.; Kahana, M. Cayley-tree Ising model with antiferromagnetic nearest-neighbor and ferromagnetic equivalent-neighbor interactions. Phys. Rev. B 1988, 37, 7638. [Google Scholar] [CrossRef]
- Cohen, O.; Rittenberg, V.; Sadhu, T. Shared information in classical mean-field models. J. Phys. A 2015, 48. [Google Scholar] [CrossRef]
- Li, Z.X.; Hou, J.X. Cooling a long-range interacting system faster via applying an external magnetic field. Mod. Phys. Lett. B 2022, 36. [Google Scholar] [CrossRef]
- Campa, A.; Gori, G.; Hovhannisyan, V.; Ruffo, S.; Trombettoni, A. Ising chains with competing interactions in the presence of long-range couplings. J. Phys. A 2019, 52. [Google Scholar] [CrossRef]
- Yang, J.T.; Hou, J.X. Effect of the nearest-neighbor biquadratic interactions on the spin-1 Nagle-Kardar model. Eur. Phys. J. B 2022, 95. [Google Scholar] [CrossRef]
- Salmon, O.D.R.; de Sousa, J.R.; Neto, M.A.; Padilha, I.T.; Azevedo, J.R.V.; Neto, F.D. The spin-3/2 Blume-Capel model with competing short- and long-range interactions. Physica a-Statistical Mechanics and Its Applications 2016, 464, 103–114. [Google Scholar] [CrossRef]
- Yao, Y.C.; Hou, J.X. Phase Diagram of the Nagel-Kardar Model in the Microcanonical-Canonical Crossover. Int. J. Theor. Phys. 2021, 60, 968–975. [Google Scholar] [CrossRef]
- Campa, A.; Gori, G.; Hovhannisyan, V.; Ruffo, S.; Trombettoni, A. Computation of Microcanonical Entropy at Fixed Magnetization Without Direct Counting. J. Stat. Phys. 2021, 184. [Google Scholar] [CrossRef]
- Yang, J.T.; Tang, Q.Y.; Hou, J.X. Ensemble inequivalence in an extended spin-1 Nagle-Kardar model. Chinese Journal of Physics 2024, 89, 1325–1332. [Google Scholar] [CrossRef]
- Li, Z.X.; Hou, J.X. Cooling a long-range interacting system faster via applying an external magnetic field. Mod. Phys. Lett. B 2022, 36. [Google Scholar] [CrossRef]
- Kislinsky, V.B.; Yukalov, V.I. Crossover between short-term and long-range interactions in the one-dimensional Ising-model. J. Phys. A 1988, 21, 227–232. [Google Scholar] [CrossRef]
- Mori, T. Instability of the mean-field states and generalization of phase separation in long-range interacting systems. Phys. Rev. E 2011, 84, 031128. [Google Scholar] [CrossRef] [PubMed]
- Mori, T. Phase transitions in systems with non-additive long-range interactions. J. Stat. Mech: Theory Exp. 2013, 2013, P10003. [Google Scholar] [CrossRef]
- Abramowitz, M.; Stegun, I.A. Handbook of mathematical functions with formulas, graphs, and mathematical tables; Dover, New York, 1970.
- Kardar, M. Statistical Physics of Fields; Cambridge University Press, Cambridge, 2007. [CrossRef]
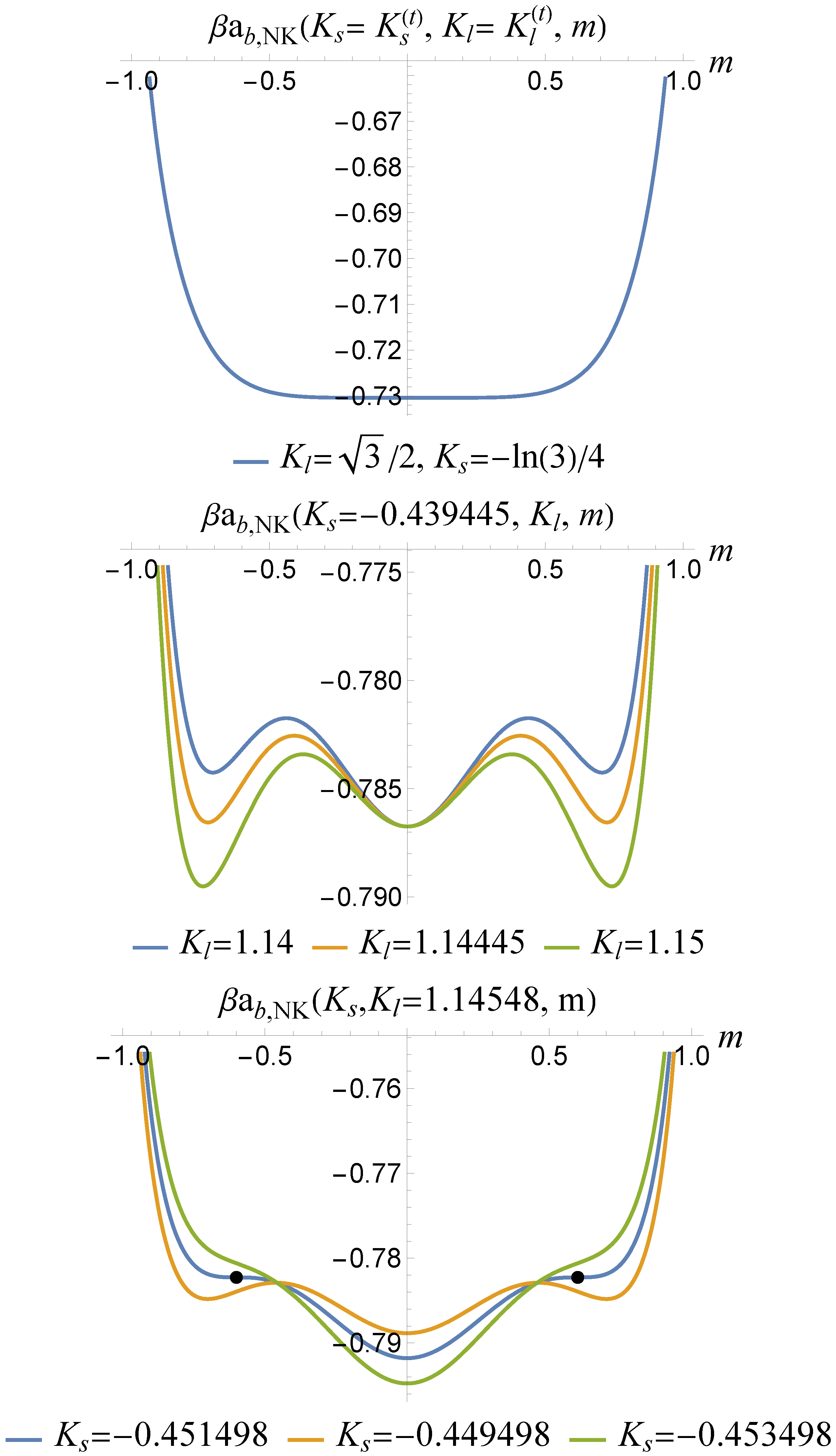
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).



