Gaussian Versus Mean-Field Model: Contradictory Predictions for the Casimir Force Under Dirichlet–Neumann Boundary Conditions

1. Introduction

Currently, the most prominent example of a fluctuation-induced force is the force due to quantum or thermal fluctuations of the electromagnetic field, leading to the so-called QED Casimir effect [1,2,3,4,5], named after the Dutch physicist H. B. Casimir who first realized that in the case of two perfectly-conducting, uncharged, and smooth plates parallel to each other in vacuum, at $T=0$ these fluctuations lead to an attractive force between them [1]. Nowadays, investigations devoted to that effect are performed on many fronts of research ranging from attempts to unify the four fundamental forces of nature [2,4,6] to rather practical issues such as the design and the performance of MEMS and NEMS [7,8,9,10,11].

Thirty years after Casimir, Fisher and De Gennes [12] showed that a very similar effect exists in critical fluids, today known as critical Casimir effect. A summary of the results available for this effect can be found in the recent reviews [13,14,15,16]. We note that the critical Casimir effect has been observed experimentally [17,18,19,20,21,22,23,24,25,26,27,28,29,30].

The description of the critical Casimir effect is based on finite-size scaling theory [31,32,33,34]. Let us envisage a system with a film geometry ${\infty }^{d-1}\times L$, $L\equiv L_{\perp }$, and with boundary conditions $\zeta$ imposed along the spatial direction of finite extent L. Take ${\mathcal{F}}_{\mathrm{tot}}^{\left(\zeta \right)}$ to be the total free energy of such a system within the grand canonical ensemble (GCE). Then, if $f^{\left(\zeta \right)}(T,h,L)\equiv {lim}_{A\to \infty }{\mathcal{F}}_{\mathrm{tot}}^{\left(\zeta \right)}/A$ is the free energy per area A of the system, one can define the Casimir force for critical systems in the grand-canonical $(T-h)$-ensemble, see, e.g., Refs. [14,34,35,36]::

$$\beta F_{\mathrm{Cas}}^{\left(\zeta \right)}(L,T,h)\equiv -{\displaystyle \frac{\partial }{\partial L}}{f}_{\mathrm{ex}}^{\left(\zeta \right)}(L,T,h)$$

(1)

where

$$f_{\mathrm{ex}}^{\left(\zeta \right)}(L,T,h)\equiv f^{\left(\zeta \right)}(L,T,h)-L{f}_b(T,h)$$

(2)

is the so-called excess (over the bulk) free energy per area and per ${\beta }^{-1}=k_{B}T$. Here we suppose a system at temperature T is exposed to an external ordering field h, which couples linearly to its order parameter—such as the number density, the concentration difference, the magnetization, etc. Actually, the thermodynamic Casimir force $F_{\mathrm{Cas}}^{\left(\zeta \right)}(T,h,L)$ per area is the excess pressure over the bulk one due to the finite size $(L<\infty )$ of that system:

$$F_{\mathrm{Cas}}^{\left(\zeta \right)}(T,h,L)=P_L^{\left(\zeta \right)}(T,h)-P_b(T,h).$$

(3)

Here $P_L^{\left(\zeta \right)}$ is the pressure in the finite system under boundary conditions $\zeta$, while $P_b$ is the pressure in the infinite, i.e., macroscopically large, system. The above definition is actually equivalent to Equation (1). Note that $f_{\mathrm{ex}}^{\left(\zeta \right)}(L,T,h)$ is the excess grand potential per area, $f^{\left(\zeta \right)}(L,T,h)$ is the grand canonical potential per area of the finite system, while $f_b(T,h)$ has the meaning of the grand potential per volume V for the macroscopically large system. The equivalence between the definitions in Equations (1) and (3) stems from the observation that for the finite system one has $P_L=-\partial f^{\left(\zeta \right)}(L,T,h)/\partial L$, while for the bulk one and $f_b=-P_b$.

When $F_{\mathrm{Cas}}^{\left(\zeta \right)}(L,t,h)<0$ the excess pressure is inward towards the system, i.e., there is an attraction of the surfaces of the system towards each other and a repulsion if $F_{\mathrm{Cas}}^{\left(\zeta \right)}(L,t,h)>0$.

In the remainder we will consider the behavior of the Casimir force under periodic and Neumann-Dirichlet boundary conditions within the Gaussian and mean-field models. These are two of the principal models of the statistical physics. We will show, however, that they might produce contradictory predictions for the behavior of the Casimir force, including even if the force for given T and h is attractive, or repulsive. Before passing to the specific calculations, let us mention the Gaussian model has been intensively used to study the behavior of the critical Casimir effect [34,37,38,39,40,41,42,43], as well as the Ising mean-field model [41,44,45,46,47,48,49,50,51,52]; for a review — see Refs. [14].

We start by considering the behavior of the Casimir force within the Gaussian model - both for its continuum, as well as lattice versions.

2. The Casimir Force Within the Continuum Gaussian Model

The continuum version of the Gaussian model with a scalar order parameter consists of the linear and bilinear terms in the Ginzburg-Landau-Wilson formulation of a system in d dimensions that undergoes a continuous symmetry-breaking phase transition at low temperatures. The partition function of this system is the functional integral

$${\mathcal{Z}}_G(t,h)=\int exp[-\mathcal{F}\left(\psi \left(\overrightarrow{r}\right)\right)]\mathcal{D}\left\{\psi \left(\overrightarrow{r}\right)\right\}$$

(4)

where

$$\mathcal{F}\left(\psi \left(\overrightarrow{r}\right)\right)=\int \left[t\psi {\left(\overrightarrow{r}\right)}^2+{\left|\overrightarrow{\nabla }\psi \left(\overrightarrow{r}\right)\right|}^2-h\psi \left(\overrightarrow{r}\right)\right]d^{d}r$$

(5)

In (5) t is the reduced temperature, proportional to $T-T_c$, and h is the spatially constant ordering field. Because of the Gaussian nature of the free energy functional $\mathcal{F}\left(\psi \left(\overrightarrow{r}\right)\right)$ the partition function resolves into the product

$${\mathcal{Z}}_G(t,h)={\mathcal{Z}}_{G,I}\left(t\right)\times {\mathcal{Z}}_{G,h}(t,h)$$

(6)

where ${\mathcal{Z}}_{G,I}\left(t\right)$ is the partition function of the system with $h=0$. The geometry of the system under consideration is a slab of large—ultimately infinite—cross section and finite thickness L.

With regard to scaling considerations, there are two combinations of parameters that reflect the predictions of finite size scaling. They are

$$\begin{array}{ccc}\hfill x_t& =& t{L}^{1/\nu }=t{L}^2,\hfill \end{array}$$

(7)

$$\begin{array}{ccc}\hfill x_h& =& h{L}^{(d+2-\eta )/2}=h{L}^{(d+2)/2},\hfill \end{array}$$

(8)

where $\nu$, the correlation length exponent, is equal to 1/2 in the Gaussian model, and as noted above d is the dimensionality of the system. Our end results for the Casimir forces acting upon the systems will depend on the boundary conditions imposed. In all cases, the form of the Casimir force is

$$\begin{array}{ccc}\hfill f_{\mathrm{Cas}}(t,h,L)& =& L^{-d}\left(w_{\mathrm{Cas},\mathrm{I}}\left(x_t\right)+x_h^2{w}_{\mathrm{Cas},\mathrm{h}}\left(x_t\right)\right)\hfill \end{array}$$

(9)

All results reported in this portion of the article rely on two results, which can be obtained with the use of contour integration techniques; see also [53]. The two results are

$$\begin{array}{ccc}\hfill \sum _{n=-\infty }^{\infty }{\displaystyle \frac{1}{a{n}^2+b}}& =& {\displaystyle \frac{\pi coth\left(\pi \sqrt{b/a}\right)}{\sqrt{ab}}},\hfill \end{array}$$

(10)

$$\begin{array}{ccc}\hfill \sum _{n=0}^{\infty }{\displaystyle \frac{1}{c{(2n+1)}^2+d}}& =& {\displaystyle \frac{\pi tanh(\pi /2\sqrt{d/c})}{4\sqrt{cd}}}.\hfill \end{array}$$

(11)

In order to carry out the evaluation of the free energy of the Gaussian model we turn to the basis set of functions that will be used to construct the free energy with and without an ordering field. These functions allow us to evaluate the partition function by integrating over the amplitudes of the contributions of each member of the set to the order parameter. Here, we focus on the case of periodic boundary conditions. Ignoring the dependence on position in the “plane” of the slab, the functions are the orthonormal set

$$\begin{array}{ccc}\hfill {\psi }_c^{\left(n\right)}\left(z\right)& =& \sqrt{2/L}cos(2\pi nz/L)\hfill \end{array}$$

(12)

$$\begin{array}{ccc}\hfill {\psi }_s^{\left(n\right)}\left(z\right)& =& \sqrt{2/L}sin(2\pi nz/L)\hfill \end{array}$$

(13)

$$\begin{array}{ccc}\hfill {\psi }_0\left(z\right)& =& \sqrt{1/L}\hfill \end{array}$$

(14)

with n a positive integer. It is straightforward to show that this set is orthonormal as a function of z in that

$$\begin{array}{ccc}\hfill {\int }_0^L{\psi }_c^{\left(n\right)}\left(z\right){\psi }_c^{\left(m\right)}\left(z\right)dz& =& {\delta }_{m,n}\hfill \end{array}$$

(15)

$$\begin{array}{ccc}\hfill {\int }_0^L{\psi }_s^{\left(n\right)}\left(z\right){\psi }_s^{\left(m\right)}\left(z\right)dz& =& {\delta }_{m,n}\hfill \end{array}$$

(16)

$$\begin{array}{ccc}\hfill {\int }_0^L{\psi }_0{\left(z\right)}^{2}dz& =& 1\hfill \end{array}$$

(17)

The three function types are all mutually orthogonal. In the case of higher dimensions, we construct a new basis set by multiplying the functions (12)–() by suitable functions of the orthogonal position variables. Those functions can be taken to be of the form $e^{i\overrightarrow{Q}·\overrightarrow{R}}$, where $\overrightarrow{R}$ is a $d-1$-dimensional position vector in the plane of the slab and $\overrightarrow{Q}$ is in its reciprocal space.

We then express the order parameter as follows

$$\psi (z,\overrightarrow{R})=\sum _{\overrightarrow{Q}}{e}^{i\overrightarrow{Q}·\overrightarrow{R}}\left(\sum _{n=1}^{\infty }{a}_n^{\left(c\right)}{\psi }_c^{\left(n\right)}\left(z\right)+\sum _{n=1}^{\infty }{a}_n^{\left(s\right)}{\psi }_c^{\left(n\right)}\left(z\right)+a_0{\psi }_0\left(z\right)\right)$$

(18)

The free energy for a given configuration of the Gaussian order parameter, in terms of the amplitudes in the expansion of the order parameter in the basis set (15)–(), is

$$\sum _{\overrightarrow{Q}}\left[\sum _{n=1}^{\infty }(a_n^{\left(c\right)2}+a_n^{\left(s\right)2})\left(t+Q^2+{(2\pi n/L)}^2\right)+a_0^{2}t-h{a}_0\sqrt{L}\right]$$

(19)

The last term in brackets above reflects the fact that the only basis function that the constant external field couples to is the constant function in ()

The next step is to exponentiate the expression in (19), multiply by either $-1/\beta$, or setting $\beta =1$, by -1, and, after that, to perform the Gaussian integrals over the $a_n^{\left(c\right)}$’s, the $a_n^{\left(s\right)}$’s, and $a_0$. The resulting partition function is given by

$$\begin{array}{c}\hfill {\displaystyle \mathcal{Z}}\\ & =& exp\left[{\displaystyle \frac{1}{\beta }}\left({\displaystyle \frac{h^{2}LA}{4t}}+{\displaystyle \frac{A}{{\left(2\pi \right)}^{d-1}}}\int d^{d-1}Q\sum _{n=-\infty }^{\infty }{\displaystyle \frac{1}{2}}ln\left({\displaystyle \frac{t+Q^2+{(2\pi n/L)}^2}{\pi }}\right)\right)\right]\hfill \\ \hfill \end{array}$$

(20)

The coefficient A in (20) is the $d-1$ dimensional area of the slab.

As our next step we evaluate the sum over n on the right hand side of the expression for the partition function. To achieve this, we take the t-derivative of the logarithm of the summand, perform the sum over n and then integrate the resulting expression with respect to t. Taking the derivative of the summand in (20) with respect to t leaves us with the sum

$$\begin{array}{c}\hfill {\displaystyle \frac{1}{2}}\sum _{n=-\infty }^{\infty }{\displaystyle \frac{1}{t+Q^2+{(2\pi n/L)}^2}}={\displaystyle \frac{Lcoth\left(\frac{1}{2}L\sqrt{Q^2+t}\right)}{2\sqrt{Q^2+t}}}\end{array}$$

(21)

which follows from (10). This integrates up to

$$\begin{array}{c}\hfill 2\ln \left(sinh\left(L\sqrt{Q^2+t}/2\right)\right)\end{array}$$

(22)

The large-L limit of (22) is

$$L\sqrt{t+Q^2}$$

(23)

To find the contribution to the Casimir force per unit area, we take the L-derivative of the difference between (23) and (22) and then integrate over $\overrightarrow{Q}$. The derivative yields

$${\displaystyle \frac{1}{2}}\sqrt{Q^2+t}\left(1-coth\left(L\sqrt{Q^2+t}\right)\right)=-\sqrt{Q^2+t}{\displaystyle \frac{e^{-L\sqrt{Q^2+t}}}{e^{L\sqrt{Q^2+t}}-e^{-L\sqrt{Q^2+t}}}}$$

(24)

The sum over values of $\overrightarrow{Q}$ is expressible as an integral, which takes the form

$$\begin{array}{c}{\displaystyle -\frac{K_{d-1}}{{\left(2\pi \right)}^{d-1}}{\int }_0^{\infty }{Q}^{d-2}\sqrt{Q^2+t}\frac{e^{-L\sqrt{Q^2+t}}}{e^{L\sqrt{Q^2+t}}-e^{-L\sqrt{Q^2+t}}}dQ}\hfill \\ ={\displaystyle \frac{1}{L^d}}\left(-{\displaystyle \frac{K_{d-1}}{{\left(2\pi \right)}^{d-1}}}{x}_t^{d/2}{\int }_0^{\infty }{w}^{d-2}\sqrt{1+w^2}{\displaystyle \frac{e^{-\sqrt{x_t(1+w^2)}}}{e^{\sqrt{x_t(1+w^2)}}-e^{-\sqrt{x_t(1+w^2)}}}}dw\right)\hfill \\ ={\displaystyle \frac{1}{L^d}}{X}_I^{(\mathrm{per},3)}\left(x_t\right)\hfill \end{array}$$

(25)

where, to get to the last line of (25) we defined a new integration variable $w=Q/\sqrt{t}$ and then made use of the definition (7) of $x_t$. The implication of (25) is that we can express the $h=0$ contribution to the Casimir force as $L^{-d}$ times a function of the scaling temperature variable $x_t$. The coefficient $K_d$ in the equations above is the geometric factor

$$K_d={\displaystyle \frac{2{\pi }^{d/2}}{\Gamma \left(\frac{d}{2}\right)}}$$

(26)

In the case of three dimensions, further processing of the result (25) is possible. We find

$$X_{\mathrm{Cas},\mathrm{I}}^{\mathrm{per},3}\left(x_t\right)=-{\displaystyle \frac{2\sqrt{x_t}{\mathrm{Li}}_2\left(e^{-2\sqrt{x_t}}\right)+{\mathrm{Li}}_3\left(e^{-2\sqrt{x_t}}\right)-2x_{t}log\left(1-e^{-2\sqrt{x_t}}\right)}{8\pi }}$$

(27)

where ${\mathrm{Li}}_j\left(x\right)$ is the polylogarithm function; see [54]. A plot of the function $X_{\mathrm{Cas},\mathrm{I}}^{\mathrm{per},3}\left(x_t\right)$ is shown in Figure 1.

The first term in parentheses in Equation (20) gives us the h-dependent contribution to the free energy: $-h^{2}LA/4t$. This is to be compared to the corresponding free energy of a neighboring bulk phase, which goes as $-h^2(L_0-L)A/4t$, where $L_0$ is an extent that will ultimately be taken to go to infinity. If you add the two free energies, the dependence on L, the thickness of the slab, disappears. This means that there is no h-dependent free energy when slab boundary conditions are periodic, and hence no h-dependent contribution to the Casimir force.

The calculations in the case of periodic boundary conditions point the way to evaluating the partition function and the Casimir force of the case of Dirichlet-Neumann boundary conditions.

In this case the (unnormalized) basis functions are, exclusive of their dependence on the in-plane coordinates,

$$sin\left(\right(2n+1)\pi z/2L)$$

(28)

Examples of these functions are shown in Figure 2.

Focusing on the h-independent contribution to the partition function, the sum to perform in this case is (see ())

$${\displaystyle \frac{1}{2}}\sum _{n=0}^{\infty }{\displaystyle \frac{1}{t+Q^2+{((2n+1)\pi /2L)}^2}}={\displaystyle \frac{Ltanh\left(L\sqrt{t+Q^2}\right)}{4\sqrt{t+Q^2}}}$$

(29)

Note that in the limit of large L the right hand side goes to the expected asymptotic form. If we subtract that limiting form, and integrate with respect to t, we are left with

$${\displaystyle \frac{1}{2}}\left(log\left(cosh\left(L\sqrt{t+Q^2}\right)\right)-L\sqrt{t+Q^2}\right)$$

(30)

Finally, we take minus the derivative of this with respect to L, leaving us with

$${\displaystyle \frac{1}{2}}\left(-\sqrt{r+Q^2}tanh\left(L\sqrt{t+Q^2}\right)+\sqrt{t+Q^2}\right)=\sqrt{t+Q^2}{\displaystyle \frac{e^{-L\sqrt{t+Q^2}}}{e^{L\sqrt{t+Q^2}}+e^{-L\sqrt{t+Q^2}}}}$$

(31)

Making use of the analysis of previous sections, this leaves us with the following result for the Casimir force in the case of the d-dimensional Gaussian model with Dirichlet-Neumann boundary conditions

$$\begin{array}{c}{\displaystyle \frac{K_{d-1}}{{\left(2\pi \right)}^{d-1}}{\int }_0^{\infty }{Q}^{d-2}\sqrt{t+Q^2}\frac{e^{-L\sqrt{t+Q^2}}}{e^{L\sqrt{t+Q^2}}+e^{-L\sqrt{t+Q^2}}}dQ}\hfill \\ ={\displaystyle \frac{K_{d-1}}{{\left(2\pi \right)}^{d-1}}}{\displaystyle \frac{1}{L^d}}{\left(x_t\right)}^{d/2}{\int }_0^{\infty }{w}^{d-2}\sqrt{1+w^2}{\displaystyle \frac{e^{-\sqrt{x_t}\sqrt{1+w^2}}}{e^{\sqrt{x_t}\sqrt{1+w^2}}+e^{-\sqrt{x_t}\sqrt{1+w^2}}}}dw\hfill \\ ={\displaystyle \frac{1}{L^d}}{X}_{\mathrm{Cas},\mathrm{D}/\mathrm{N}}^{\left(d\right)}\left(x_t\right)\hfill \end{array}$$

(32)

When $d=3$, we have

$$X_{\mathrm{Cas},\mathrm{D}/\mathrm{N},\mathrm{I}}^{\left(3\right)}\left(x_t\right)=-{\displaystyle \frac{2\sqrt{x_t}{\mathrm{Li}}_2\left(-e^{-2\sqrt{x_t}}\right)+{\mathrm{Li}}_3\left(-e^{-2\sqrt{x_t}}\right)-2x_{t}log\left(e^{-2\sqrt{x_t}}+1\right)}{8\pi }}$$

(33)

Figure 3 shows what the function $X_{\mathrm{Cas},\mathrm{D}/\mathrm{N},\mathrm{I}}^{\left(d\right)}\left(x_t\right)$ looks like when $d=3$.

In order to find the h-dependent contribution to the Casimir force we turn to the normalized the basis set in the case of Dirichlet-Neumann boundary conditions. Assuming that the boundary conditions are Dirichlet at $z=0$ and Neumann at $z=L$, this basis set is

$${\psi }_{DN}^{\left(n\right)}\left(z\right)=\sqrt{2/L}sin\left((n+1/2)\pi z/L\right)$$

(34)

with n an integer and

$$0\le n<\infty$$

(35)

It is straightforward to establish that

$${\int }_0^L{\psi }_{DN}^{\left(n\right)}{\left(z\right)}^{2}dL=1$$

(36)

while

$${\int }_0^L{\psi }_{DN}^{\left(n\right)}\left(z\right)dL={\displaystyle \frac{2\sqrt{2L}}{(2n+1)\pi }}$$

(37)

As it turns out there is no need to take into account any dependence of the basis set on coordinates in the plane of the slab. This is because a constant ordering field couples only to order parameter configurations that are independent of those coordinates.

With this in mind, we expand the order parameter as follows

$$\mathrm{\Psi }\left(z\right)=\sum _{n=0}^{\infty }{a}_n^{\left(DN\right)}{\psi }_{DN}^{\left(n\right)}\left(z\right)$$

(38)

The Gaussian integrations over the $a_n^{\left(DN\right)}$’s leaves us with the summation over n for the h-dependent contribution to the partition function

$$\begin{array}{c}{\displaystyle exp\left[h^2\sum _{n=0}^{\infty }{\left(\frac{2\sqrt{2L}}{(2n+1)\pi }\right)}^2\frac{1}{4({(\pi (n+1/2)/L)}^2+t)}\right]}\hfill \\ =exp\left[h^2\left({\displaystyle \frac{L}{4t}}-{\displaystyle \frac{tanh\left(L\sqrt{t}\right)}{4t^{3/2}}}\right)\right]\hfill \\ =exp\left[{\displaystyle \frac{h^2}{4t^{3/2}}}\left(L\sqrt{t}-tanh\left(L\sqrt{t}\right)\right)\right]\hfill \end{array}$$

(39)

where the evaluation of the sum over n in (39) is accomplished with the use of () and a partial fraction decomposition of the summand. The first term in parentheses on the last line of (39) gives us exactly the same expression as the h-dependent contribution to the partition function of the slab with periodic boundary conditions. Its influence on the Casimir force is exactly canceled by the influence of the bulk. What remains is

$$\begin{array}{ccc}\hfill -h^2{\displaystyle \frac{\partial }{\partial L}}tanh\left(L\sqrt{t}\right)/4t^{3/2}& =& -{\displaystyle \frac{h^2}{4t}}{\mathrm{sech}}^2\left(L\sqrt{t}\right)\hfill \\ & =& -{\displaystyle \frac{h^2{L}^2}{4x_t}}{\mathrm{sech}}^2\left(\sqrt{x_t}\right)\hfill \\ & =& -{\displaystyle \frac{1}{L^d}}{\displaystyle \frac{x_h^2}{4x_t}}{\mathrm{sech}}^2\left(\sqrt{x_t}\right)\hfill \end{array}$$

(40)

where we have made use of the definition of the scaling combination $x_h$ in (). The scaling form of the contribution to the Casimir force is, then

$$X_{D/N}^{\left(3\right)}(x_t,x_h)={\displaystyle \frac{-x_h^2}{4x_t}}\stackrel{2}{\mathrm{sech}}\left(\sqrt{x_t}\right)$$

(41)

This function is shown in Figure 4. Note that this function is aways attractive.

The total scaling function $X_{D/N}^{\left(3\right)}(x_t,x_h)$ is given by

$$X_{D/N,h}^{\left(3\right)}(x_t,x_h)=-{\displaystyle \frac{2\sqrt{x_t}{\mathrm{Li}}_2\left(-e^{-2\sqrt{x_t}}\right)+{\mathrm{Li}}_3\left(-e^{-2\sqrt{x_t}}\right)-2x_{t}log\left(e^{-2\sqrt{x_t}}+1\right)}{8\pi }}-{\displaystyle \frac{x_h^2}{4x_t}}{\mathrm{sech}}^2\left(\sqrt{x_t}\right).$$

(42)

Figure 5 shows what this function looks like.

Another depiction of the scaling contribution to the Casimir force for Dirichlet-Neumann boundary conditions in the three dimensional Gaussian model with a scalar order paremeter, $X_{D/N}^{\left(3\right)}(x_t,x_h)$, Figure 6, highlights the regions in which the function is attractive and repulsive.

3. The Casimir Force Within the Lattice Gaussian Model

We consider a ferromagnetic model with nearest-neighbor interactions on a fully finite d-dimensional hypercubic lattice $\mathrm{\Lambda }\in Z^d$ of $\left|\mathrm{\Lambda }\right|$ sites. Let us take $\mathrm{\Lambda }\in Z^d$ to be the parallelepiped $\mathrm{\Lambda }={\mathcal{L}}_1\times \cdots \times {\mathcal{L}}_d$, where × denotes the direct (Cartesian) product of the finite sets ${\mathcal{L}}_{\nu }=\{1,\cdots ,L_{\nu }\}$.

It is convenient to consider the configuration space ${\Omega }_{\mathrm{\Lambda }}=R^{\left|\mathrm{\Lambda }\right|}$ as an Euclidean vector space in which each configuration is represented by a column-vector $S_{\mathrm{\Lambda }}$ with components labeled according to the lexicographic order of the set $\{\mathbf{r}=(r_1,\cdots ,r_d)\in \mathrm{\Lambda }\}$. Let $S_{\mathrm{\Lambda }}^{†}$ be the corresponding transposed row-vector and let the dot (·) denote matrix multiplication. Then, for given boundary conditions $\tau =({\tau }_1,\cdots ,{\tau }_d)$, specified for each pair of opposite faces of $\mathrm{\Lambda }$ by some ${\tau }_{\nu }$ takes the form

$$\beta {\mathcal{H}}_{\mathrm{\Lambda }}^{\left(\tau \right)}\left(S_{\mathrm{\Lambda }}\right|K)=-{\displaystyle \frac{1}{2}}K{S}_{\mathrm{\Lambda }}^{†}·Q_{\mathrm{\Lambda }}^{\left(\tau \right)}·S_{\mathrm{\Lambda }}.$$

(43)

Here $K=\beta J$, where J is the interaction constant (to be set to $J=1$ in the remainder), and the $\left|\mathrm{\Lambda }\right|\times \left|\mathrm{\Lambda }\right|$ interaction matrix $Q_{\mathrm{\Lambda }}^{\left(\tau \right)}$ can be written as

$$Q_{\mathrm{\Lambda }}^{\left(\tau \right)}=({\mathrm{\Delta }}_1^{\left({\tau }_1\right)}+2E_1)\times \cdots \times ({\mathrm{\Delta }}_d^{\left({\tau }_d\right)}+2E_d),$$

(44)

where ${\mathrm{\Delta }}_{\nu }^{\left({\tau }_{\nu }\right)}$ is the one-dimentional discrete Laplacian defined on the finite chain ${\mathcal{L}}_{\nu }$ under boundary conditions ${\tau }_{\nu }$, and $E_{\nu }$ is the $L_{\nu }\times L_{\nu }$ unit matrix.

By using the results of [34] (Chapter 7), we can write down the eigenfunctions of the interaction matrix (44) in the form

$$u_{\mathrm{\Lambda }}^{\left(\tau \right)}(\mathbf{r},\mathbf{k})=u_{L_1}^{\left({\tau }_1\right)}(r_1,k_1)\cdots u_{L_d}^{\left({\tau }_d\right)}(r_d,k_d),\mathbf{k}=(k_1,\cdots ,k_d)\in \mathrm{\Lambda },$$

(45)

and obtain the corresponding eigenvalues of it

$${\mu }_{\mathrm{\Lambda }}^{\left(\tau \right)}\left(\mathbf{k}\right)=2\sum _{\nu =1}^{d}cos{\phi }_{L_{\nu }}^{\left({\tau }_{\nu }\right)}\left(k_{\nu }\right),\mathbf{k}\in \mathrm{\Lambda }.$$

(46)

Obviously, ${max}_{\mathbf{k}\in \mathrm{\Lambda }}{\mu }_{\mathrm{\Lambda }}^{\left(\tau \right)}\left(\mathbf{k}\right)=2d$. Note that the interaction Hamiltonian (43) has negative eigenvalues, which makes necessary the inclusion of a positive-definite quadratic form in the Gibbs exponent, to ensure the existence of the corresponding partition function. Thus, we consider the Hamiltonian

$$\beta {\mathcal{H}}_{\mathrm{\Lambda }}^{\left(\tau \right)}\left(S_{\mathrm{\Lambda }}\right|\beta ,h_{\mathrm{\Lambda }};s)=-{\displaystyle \frac{1}{2}}\beta S_{\mathrm{\Lambda }}^{†}·Q_{\mathrm{\Lambda }}^{\left(\tau \right)}·S_{\mathrm{\Lambda }}+s{S}_{\mathrm{\Lambda }}^{†}·S_{\mathrm{\Lambda }}-h_{\mathrm{\Lambda }}^{†}·S_{\mathrm{\Lambda }}.$$

(47)

Here $h_{\mathrm{\Lambda }}=\{h\left(\mathbf{r}\right),\mathbf{r}\in \mathrm{\Lambda }\}$ is a column-vector representing (in units of $k_{B}T$) the inhomogeneous magnetic field configuration acting upon the system, and let $h_{\mathrm{\Lambda }}^{†}$ be the transposed row-vector.

In order to ensure the existence of the partition function, all the eigenvalues $-{\displaystyle \frac{1}{2}}\beta {\mu }_{\mathrm{\Lambda }}^{\left(\tau \right)}\left(\mathbf{k}\right)+s$, $\mathbf{k}\in \mathrm{\Lambda }$, of the quadratic form in $\beta {\mathcal{H}}_{\mathrm{\Lambda }}^{\left(\tau \right)}\left(S_{\mathrm{\Lambda }}\right|\beta ,h_{\mathrm{\Lambda }};s)$, ought to be positive. Hence, the field $s^{\left(\tau \right)}$ must satisfy the inequality

$$s>{\displaystyle \frac{1}{2}}\beta \underset{\mathbf{k}\in \mathrm{\Lambda }}{max}{\mu }_{\mathrm{\Lambda }}^{\left(\tau \right)}\left(\mathbf{k}\right)\equiv {\displaystyle \frac{1}{2}}\beta {\mu }_{\mathrm{\Lambda }}^{\left(\tau \right)}\left({\mathbf{k}}_0\right),$$

(48)

with

$${\beta }_{c,L}={\displaystyle \frac{1}{2}}{\mu }_{\mathrm{\Lambda }}^{\left(\tau \right)}\left({\mathbf{k}}_0\right)$$

(49)

defining the critical temperature of the finite system. Since, as stated above ${max}_{\mathbf{k}\in \mathrm{\Lambda }}{\mu }_{\mathrm{\Lambda }}^{\left(\tau \right)}\left(\mathbf{k}\right)=2d$, it is clear that for the infinite system

$${\beta }_c=d.$$

(50)

The free energy density of a finite system in a region $\mathrm{\Lambda }$ is

$$\begin{array}{c}\hfill \beta f_{\mathrm{\Lambda }}^{\left(\tau \right)}(\beta ,h_{\mathrm{\Lambda }})={\displaystyle \frac{1}{2}}\left\{ln(\beta /2\pi )-2s+{\mathcal{U}}_{\mathrm{\Lambda }}^{\left(\tau \right)}(\beta ,s)-P_{\mathrm{\Lambda }}^{\left(\tau \right)}(\beta ,h_{\mathrm{\Lambda }},s)\right\}.\end{array}$$

(51)

In Equation (51) the first two terms do not depend on the size of the system, i.e., they are the same in both finite and infinite systems. The other two terms do depend, however on the size of the system. The function ${\mathcal{U}}_{\mathrm{\Lambda }}^{\left(\tau \right)}(\beta ,s)$ is due to the spin-spin interaction (and will be called "interaction term"); it depends on s, but does not depend on h. It is equal to

$${\mathcal{U}}_{\mathrm{\Lambda }}^{\left(\tau \right)}(\beta ,s)={\left|\mathrm{\Lambda }\right|}^{-1}\sum _{\mathbf{k}\in \mathrm{\Lambda }}ln\left[{\displaystyle \frac{2s}{\beta }}-{\mu }_{\mathrm{\Lambda }}^{\left(\tau \right)}\left(\mathbf{k}\right)\right],$$

(52)

and is obtained after performing the corresponding Gaussian integrals in the free energy of the finite system. The dependence of the free energy on the field variables h is given by the "field term"

$$P_{\mathrm{\Lambda }}^{\left(\tau \right)}(\beta ,h_{\mathrm{\Lambda }};s)={\displaystyle \frac{1}{\beta \left|\mathrm{\Lambda }\right|}}\sum _{\mathbf{k}\in \mathrm{\Lambda }}{\displaystyle \frac{|{\widehat{h}}_{\mathrm{\Lambda }}^{\left(\tau \right)}{\left(\mathbf{k}\right)|}^2}{2s/\beta -{\mu }_{\mathrm{\Lambda }}^{\left(\tau \right)}\left(\mathbf{k}\right)}}.$$

(53)

Here ${\widehat{h}}_{\mathrm{\Lambda }}^{\left(\tau \right)}\left(\mathbf{k}\right)$ denotes the projection of the magnetic field configuration $h_{\mathrm{\Lambda }}$ on the eigenfunction $\{{\overline{u}}_{\mathrm{\Lambda }}^{\left(\tau \right)}(\mathbf{r},\mathbf{k}),$$\mathbf{k}\in \mathrm{\Lambda }\}$ ( by $\overline{u}$ we denote the complex conjugate of $u\in \mathbf{C}$):

$${\widehat{h}}_{\mathrm{\Lambda }}^{\left(\tau \right)}\left(\mathbf{k}\right)=\sum _{\mathbf{r}\in \mathrm{\Lambda }}h\left(\mathbf{r}\right){\overline{u}}_{\mathrm{\Lambda }}^{\left(\tau \right)}(\mathbf{r},\mathbf{k}).$$

(54)

Defining ${\beta }_c$ so, that

$${\displaystyle \frac{2s}{\beta }}=2d{\displaystyle \frac{{\beta }_c}{\beta }},$$

(55)

the above expressions can be rewritten in the form

$${\mathcal{U}}_{\mathrm{\Lambda }}^{\left(\tau \right)}\left(\beta \right)={\left|\mathrm{\Lambda }\right|}^{-1}\sum _{\mathbf{k}\in \mathrm{\Lambda }}ln\left[2d({\beta }_c/\beta -1)+2d-{\mu }_{\mathrm{\Lambda }}^{\left(\tau \right)}\left(\mathbf{k}\right)\right],$$

(56)

and

$$P_{\mathrm{\Lambda }}^{\left(\tau \right)}(\beta ,h_{\mathrm{\Lambda }})={\displaystyle \frac{1}{\beta \left|\mathrm{\Lambda }\right|}}\sum _{\mathbf{k}\in \mathrm{\Lambda }}{\displaystyle \frac{|{\widehat{h}}_{\mathrm{\Lambda }}^{\left(\tau \right)}{\left(\mathbf{k}\right)|}^2}{2d({\beta }_c/\beta -1)+2d-{\mu }_{\mathrm{\Lambda }}^{\left(\tau \right)}\left(\mathbf{k}\right)}}.$$

(57)

Using the notations of [34] (Chapter 7), below we give a list of the complete sets of orthonormal eigenfunctions, $\{u_L^{\left(\tau \right)}(r,k)$, $k=1,\cdots ,L\}$, of the one-dimensional discrete Laplacian under the Neumann - Dirichlet (ND) boundary conditions:

• periodic (p) boundary conditions

  $$u_L^{\left(p\right)}(r,k)=L^{-1/2}exp[-\mathrm{i}r{\phi }_L^{\left(p\right)}\left(k\right)];$$

  (58)
• Neumann - Dirichlet (ND) boundary conditions

  $$u_L^{\left(\mathrm{ND}\right)}(r,k)=2{(2L+1)}^{-1/2}cos(r-1/2){\phi }_L^{\left(\mathrm{ND}\right)}\left(k\right).$$

  (59)

The quantities ${\phi }_L^{\left(\tau \right)}$, $k=1,\cdots ,L$, are defined as follows

$$\begin{array}{cc}{\phi }_L^{\left(p\right)}\left(k\right)=2\pi k/L,\hfill & {\phi }_L^{\left(\mathrm{ND}\right)}\left(k\right)=\pi (2k-1)/(2L+1).\hfill \end{array}$$

(60)

Now we are ready to find the finite-size behavior of the Gaussian model under the Dirichlet-Neumann boundary conditions. According to Equation (59), $S\left(0\right)=S\left(1\right)$, i.e., one has there realization of Neumann boundary conditions, while $L+1=0$, which corresponds to Dirichlet boundary conditions. Thus, in the envisaged one-dimensional chain one has L independent spin variables $\left\{S\left(1\right),S\left(2\right),\cdots ,S\left(L\right)\right\}$.

We start with the consideration of $d=3$ dimensional system. Note that:

• under fully periodic (p) boundary conditions, $\tau =(p,p,p)$, one has ${\mathbf{k}}_0=(L_1,L_2,L_3)$, hence ${\mu }_{\mathrm{\Lambda }}^{(p,p,p)}\left({\mathbf{k}}_0\right)=6$.
• under Neumann-Dirichlet boundary conditions along z direction, i.e., $\tau =(p,p,\mathrm{ND})$, one has ${\mathbf{k}}_0=(L_1,L_2,1)$, hence ${\mu }_{\mathrm{\Lambda }}^{(p,p,\mathrm{ND})}\left({\mathbf{k}}_0\right)=4+2cos[\pi /(2L+1)]$.

3.1. The Gaussian Model on a Lattice for the Case $d=3$

We recall that for this model $\alpha =1/2,\gamma =1$ and $\nu =1/2$ [34,55].

The Behavior of the Interaction Term ${\mathcal{U}}_{\mathrm{\Lambda }}^{\left(\tau \right)}\left(\beta \right)$

We set $\tau =(p,p,\mathrm{ND})$ and use the short-hand notation $\tau =\mathrm{ND}$ for these boundary conditions. Then, we perform in Equation (52) the limits $L_1,L_2\to \infty$, keeping $L_3=L$ fixed. For the interaction term one then obtains

$${\mathcal{U}}_{L,3}^{\left(\mathrm{ND}\right)}\left(\beta \right)=\underset{L_1,L_2\to \infty }{lim}{\mathcal{U}}_{\mathrm{\Lambda }}^{(p,p,\mathrm{ND})}\left(\beta \right)={\displaystyle \frac{1}{L}}\sum _{k=1}^L{\mathcal{V}}_2\left[6({\beta }_c/\beta -1)+2\left(1-cos\pi {\displaystyle \frac{2k-1}{2L+1}}\right)\right],$$

(61)

where

$${\mathcal{V}}_d\left(z\right):={\displaystyle \frac{1}{{\left(2\pi \right)}^d}}{\int }_{-\pi }^{\pi }\mathrm{d}{\theta }_1\cdots {\int }_{-\pi }^{\pi }\mathrm{d}{\theta }_{d}ln\left[z+2\sum _{\nu =1}^d(1-cos{\theta }_{\nu })\right].$$

(62)

The Behavior of the Interaction Term in the Bulk System

In accord with Equation (62), one has

$${\mathcal{U}}_{\infty ,3}\left(\beta \right)={\mathcal{V}}_3\left[6({\beta }_c/\beta -1)\right].$$

(63)

The Behavior of the Interaction Term in the Film System with Neumann-Dirichlet Boundary Conditions

Explicitly, from Equation (61) one obtains

$${\mathcal{U}}_{L,3}^{\left(\mathrm{ND}\right)}\left(\beta \right)={\displaystyle \frac{1}{L}}\sum _{k=1}^L{\mathcal{V}}_2\left[6({\beta }_c/\beta -1)+2\left(1-cos\pi {\displaystyle \frac{2k-1}{2L+1}}\right)\right]={\displaystyle \frac{1}{{\left(2\pi \right)}^2}}{\int }_{-\pi }^{\pi }\mathrm{d}{\theta }_1{\int }_{-\pi }^{\pi }\mathrm{d}{\theta }_2{S}^{\left(\mathrm{ND}\right)}(\beta ,L|{\theta }_1,{\theta }_2),$$

(64)

with

$$S^{\left(\mathrm{ND}\right)}(\beta ,L|{\theta }_1,{\theta }_2)={\displaystyle \frac{1}{L}}\sum _{k=1}^{L}ln\left[6({\beta }_c/\beta -1)+2\sum _{\nu =1}^2(1-cos{\theta }_{\nu })+2\left(1-cos\pi {\displaystyle \frac{2k-1}{2L+1}}\right)\right].$$

(65)

This sum is of the form

$$S^{\left(\mathrm{ND}\right)}(x,L)={\displaystyle \frac{1}{L}}ln\prod _{k=0}^{L-1}2\left[cosh\left(x\right)-cos\pi {\displaystyle \frac{2k+1}{2L+1}}\right],$$

(66)

where $x=x\left(\beta \right|{\theta }_1,{\theta }_2)$ is defined as

$$coshx=1+3({\beta }_c/\beta -1)+\sum _{\nu =1}^2(1-cos{\theta }_{\nu }).$$

(67)

The summations in Equation (66) can be performed using [53] the identity

$${\displaystyle \frac{cosh\left[(L+1/2)x\right]}{cosh(x/2)}}=\prod _{k=0}^{L-1}2\left[coshx-cos\pi {\displaystyle \frac{2k+1}{2L+1}}\right].$$

(68)

With the help of the identity one derives

$$S^{\left(\mathrm{ND}\right)}(x,L)={\displaystyle \frac{1}{L}}ln{\displaystyle \frac{cosh\left[(L+1/2)x\right]}{cosh(x/2)}}.$$

(69)

Obviously ${lim}_{L\to \infty }{S}^{\left(\mathrm{ND}\right)}(x,L)=x$. Thus, the part of the excess free energy under Neumann – Dirichlet boundary conditions that depends only on the interaction term is

$$\begin{array}{ccc}\hfill \beta \mathrm{\Delta }{f}_{\mathrm{ex},3}^{\left(\mathrm{ND}\right)}(\beta ,h=0)& =& {\displaystyle \frac{1}{2}}L\left[{\mathcal{U}}_{L,3}^{\left(\mathrm{ND}\right)}\left(\beta \right)-{\mathcal{U}}_{\infty ,3}\left(\beta \right)\right]\hfill \\ & =& {\displaystyle \frac{L}{8{\pi }^2}}{\int }_{-\pi }^{\pi }\mathrm{d}{\theta }_1{\int }_{-\pi }^{\pi }\mathrm{d}{\theta }_2\left[{\displaystyle \frac{1}{L}}ln{\displaystyle \frac{cosh\left[(L+1/2)x\right]}{cosh(x/2)}}-x\right]\hfill \\ & =& {\displaystyle \frac{1}{8{\pi }^2}}{\int }_{-\pi }^{\pi }\mathrm{d}{\theta }_1{\int }_{-\pi }^{\pi }\mathrm{d}{\theta }_2\left[ln\left({\displaystyle \frac{e^{-(2L+1)x}+1}{e^{-x}+1}}\right)\right].\hfill \end{array}$$

(70)

Thus, $\beta \mathrm{\Delta }{f}_{\mathrm{ex},3}^{\left(\mathrm{ND}\right)}(\beta ,h=0)$ can be decomposed in the sum of $g_1(L,\varphi )$ and $g_2(L,\varphi )$ where

$$g_1(L,\beta )={\displaystyle \frac{1}{8{\pi }^2}}{\int }_{-\pi }^{\pi }\mathrm{d}{\theta }_1{\int }_{-\pi }^{\pi }\mathrm{d}{\theta }_{2}ln\left(e^{-(2L+1)x}+1\right),$$

(71)

and

$$g_2(L,\beta )=-{\displaystyle \frac{1}{8{\pi }^2}}{\int }_{-\pi }^{\pi }\mathrm{d}{\theta }_1{\int }_{-\pi }^{\pi }\mathrm{d}{\theta }_{2}ln\left(e^{-x}+1\right).$$

(72)

Let us consider the behavior of $g_1$ and $g_2$ in the scaling regime

$$x_t=6({\beta }_c/\beta -1){(2L+1)}^2=\mathcal{O}\left(1\right).$$

(73)

Let us first start with the function $g_1(L,\varphi )$. Obviously, if $x=\mathcal{O}\left(1\right)$ then $g_1$ will be exponentially small. Thus, we need to consider the regime $(2L+1)x=\mathcal{O}\left(1\right)$. It follows that $x\ll 1$. From Equation (67) we obtain

$$1+{\displaystyle \frac{1}{2}}{x}^2=3({\beta }_c/\beta -1)+{\displaystyle \frac{1}{2}}\left({\theta }_1^2+{\theta }_2^2\right).$$

(74)

It follows that

$$x^2=6({\beta }_c/\beta -1)+\left({\theta }_1^2+{\theta }_2^2\right)=6({\beta }_c/\beta -1)+r^2,$$

(75)

where we have introduced polar coordinates. In terms of them $g_1(L,\beta )$ becomes

$$\begin{array}{ccc}\hfill g_1(L,\beta )& \simeq & {\displaystyle \frac{1}{4\pi }}{\int }_0^{R}ln\left(e^{-(2L+1)x}+1\right)d{r}^2\simeq {\displaystyle \frac{1}{4\pi }}{\int }_{\sqrt{6({\beta }_c/\beta -1)}}^{\infty }ln\left(e^{-(2L+1)x}+1\right)d{x}^2\hfill \\ & =& -{\displaystyle \frac{1}{4\pi }}{\displaystyle \frac{\sqrt{x_t}{\mathrm{Li}}_2\left(-e^{-\sqrt{x_t}}\right)+{\mathrm{Li}}_3\left(-e^{-\sqrt{x_t}}\right)}{{(2L+1)}^2}},\hfill \end{array}$$

(76)

where R can be defined from the constraint $\left(2\pi \right)\times \left(2\pi \right)=4{\pi }^2=\pi R^2$, i.e., $R=2\sqrt{\pi }$.

Next, we deal with $g_2(L,\varphi )$. Taking into account that $x_L$ is small we derive

$$\begin{array}{ccc}\hfill g_2(L,\beta )& =& -{\displaystyle \frac{1}{8{\pi }^2}}{\int }_{-\pi }^{\pi }\mathrm{d}{\theta }_1{\int }_{-\pi }^{\pi }\mathrm{d}{\theta }_{2}ln\left(e^{-x}+1\right)\simeq -{\displaystyle \frac{1}{8{\pi }^2}}{\int }_{-\pi }^{\pi }\mathrm{d}{\theta }_1{\int }_{-\pi }^{\pi }\mathrm{d}{\theta }_2\left[ln2-{\displaystyle \frac{1}{2}}x\right]\hfill \\ & =& -{\displaystyle \frac{1}{2}}ln2+{\displaystyle \frac{1}{16{\pi }^2}}{\int }_{-\pi }^{\pi }\mathrm{d}{\theta }_1{\int }_{-\pi }^{\pi }\mathrm{d}{\theta }_{2}x\simeq -{\displaystyle \frac{1}{2}}ln2+{\displaystyle \frac{1}{8\pi }}{\int }_{\sqrt{6({\beta }_c/\beta -1)}}^{R}xd{x}^2\hfill \\ & =& -{\displaystyle \frac{1}{2}}ln2+{\displaystyle \frac{1}{12\pi }}\left\{R^3-{\left({\displaystyle \frac{\sqrt{x_t}}{2L+1}}\right)}^3\right\}.\hfill \end{array}$$

(77)

Note that for $x_t=\mathcal{O}\left(1\right)$ one has that for the L-dependent part $\mathrm{\Delta }{g}_2(L,\beta )$ of $g_2$ one has $\mathrm{\Delta }{g}_2(L,\varphi )\propto L^{-3}$, i.e., $\mathrm{\Delta }{g}_2$ is one order of magnitude smaller that $g_1$. Because of that, $g_2$ contributes only sub-leading contributions to L-dependent part of the excess free energy and, therefore, to the Casimir force. Based on the above, we will no longer be interested in the function $g_2$.

Summarizing the above, we conclude that the excess free energy can be written in a scaling form

$$\beta \mathrm{\Delta }{f}_{\mathrm{ex},3}^{\left(\mathrm{ND}\right)}(\beta ,h=0)=-{\displaystyle \frac{1}{L^2}}{X}_{\mathrm{ex}}\left(a_{\beta }t{L}^{1/\nu }\right)$$

(78)

where $a_{\beta }$ is a non-universal constants, and $X_{\mathrm{ex}}$ is an universal scaling function, $t=(T-T_c)/T_c$, where T has the meaning of the temperature of the system, and $T_c$ is its bulk temperature. From Equation (76), taking into account that with $\nu =1/2$ one has ${(2L+1)}^2\simeq 4L^2\simeq L^{1/\nu }$, we identify that

$$X_{\mathrm{ex}}\left(x_t\right)={\displaystyle \frac{1}{16\pi }}\left[\sqrt{x_t}{\mathrm{Li}}_2\left(-e^{-\sqrt{x_t}}\right)+{\mathrm{Li}}_3\left(-e^{-\sqrt{x_t}}\right)\right].$$

(79)

The behavior of the field term $P_{\mathrm{\Lambda }}^{\left(\tau \right)}(\beta ,h_{\mathrm{\Lambda }})$

The dependence of the free energy on the field variable is given by the "field term", given by Equation (53). For a homogeneous filed h and for $\left(\mathrm{per}\right)\equiv (p,p,p)$ and $\mathrm{ND}\equiv (p,p,\mathrm{ND})$ boundary conditions, it is easy to obtain that

• for $(p,p,p)$ boundary conditions

  $${\widehat{h}}_{\mathrm{\Lambda }}^{\left(\mathrm{per}\right)}\left(\mathbf{k}\right)=\sum _{\mathbf{r}\in \mathrm{\Lambda }}h\left(\mathbf{r}\right){\overline{u}}_{\mathrm{\Lambda }}^{\left(\left(\mathrm{per}\right)\right)}(\mathbf{r},\mathbf{k})=\sqrt{L_1{L}_2{L}_3}{\delta }_{k_1,0}{\delta }_{k_2,0}{\delta }_{k_3,0}h,$$

  (80)

  and

  $$P_L^{\left(\mathrm{per}\right)}(K,h;\varphi )={\displaystyle \frac{h^2}{6\beta ({\beta }_c/\beta -1)}}.$$

  (81)
  Obviously

  $$P_{\infty }(\beta ,h)=\underset{L\to \infty }{lim}{P}_L^{\left(\mathrm{per}\right)}(K,h;\varphi )={\displaystyle \frac{h^2}{6\beta ({\beta }_c/\beta -1)}}.$$

  (82)
• for $(p,p,\mathrm{ND})$ boundary conditions

  $${\widehat{h}}_{\mathrm{\Lambda }}^{\left(\mathrm{ND}\right)}\left(\mathbf{k}\right)=\sum _{\mathbf{r}\in \mathrm{\Lambda }}h\left(\mathbf{r}\right){\overline{u}}_{\mathrm{\Lambda }}^{\left(\mathrm{ND}\right)}(\mathbf{r},\mathbf{k})=2\sqrt{{\displaystyle \frac{L_1{L}_2}{2L_3+1}}}{\delta }_{k_1,0}{\delta }_{k_2,0}h\sum _{r=1}^{L_3}cos\left[(r-1/2){\phi }_{L_3}^{\left(\mathrm{ND}\right)}\left(k_3\right)\right],{\phi }_{L_3}^{\left(\mathrm{ND}\right)}\left(k_3\right)=\pi {\displaystyle \frac{2k_3-1}{2L_3+1}}.$$

  (83)
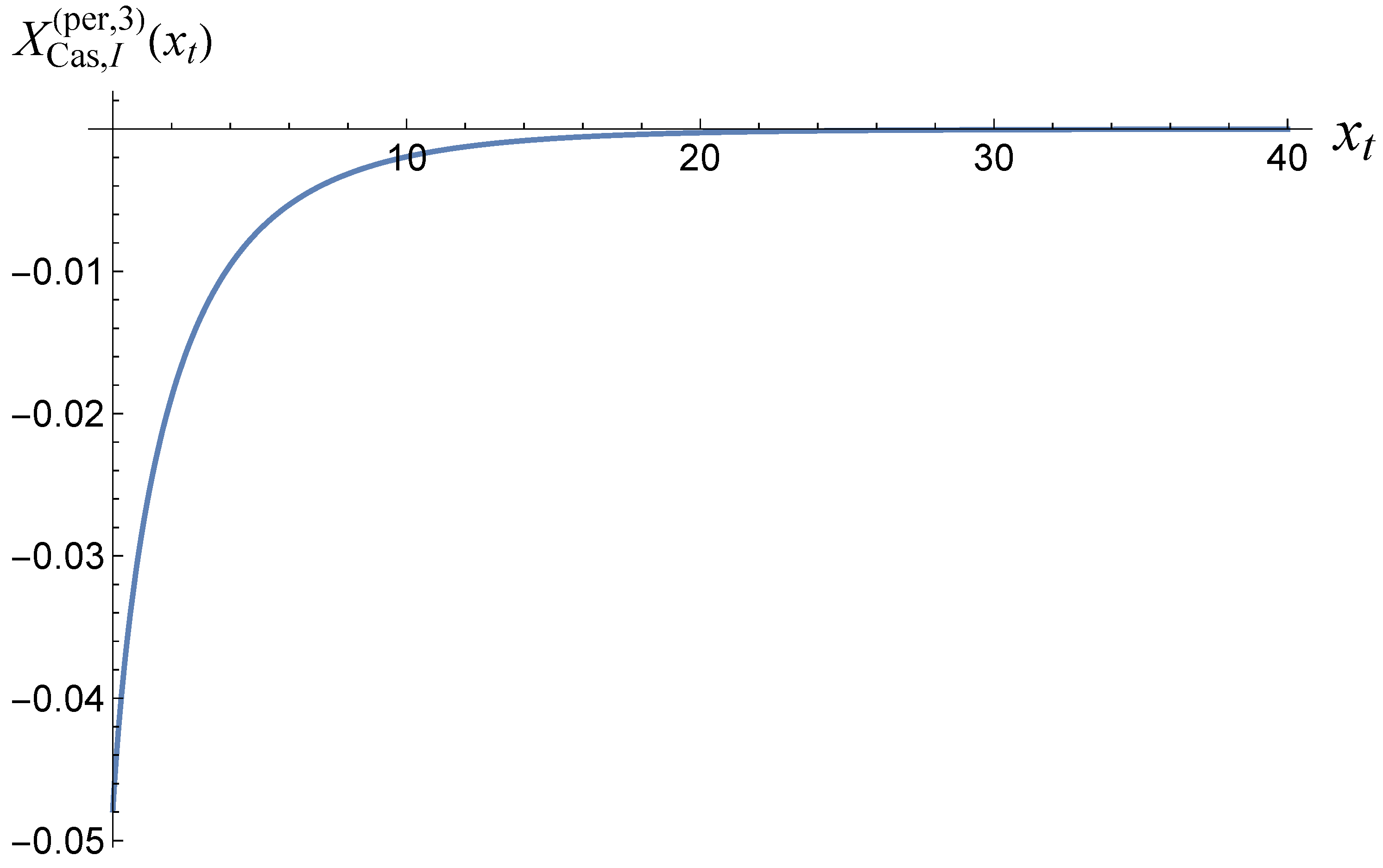
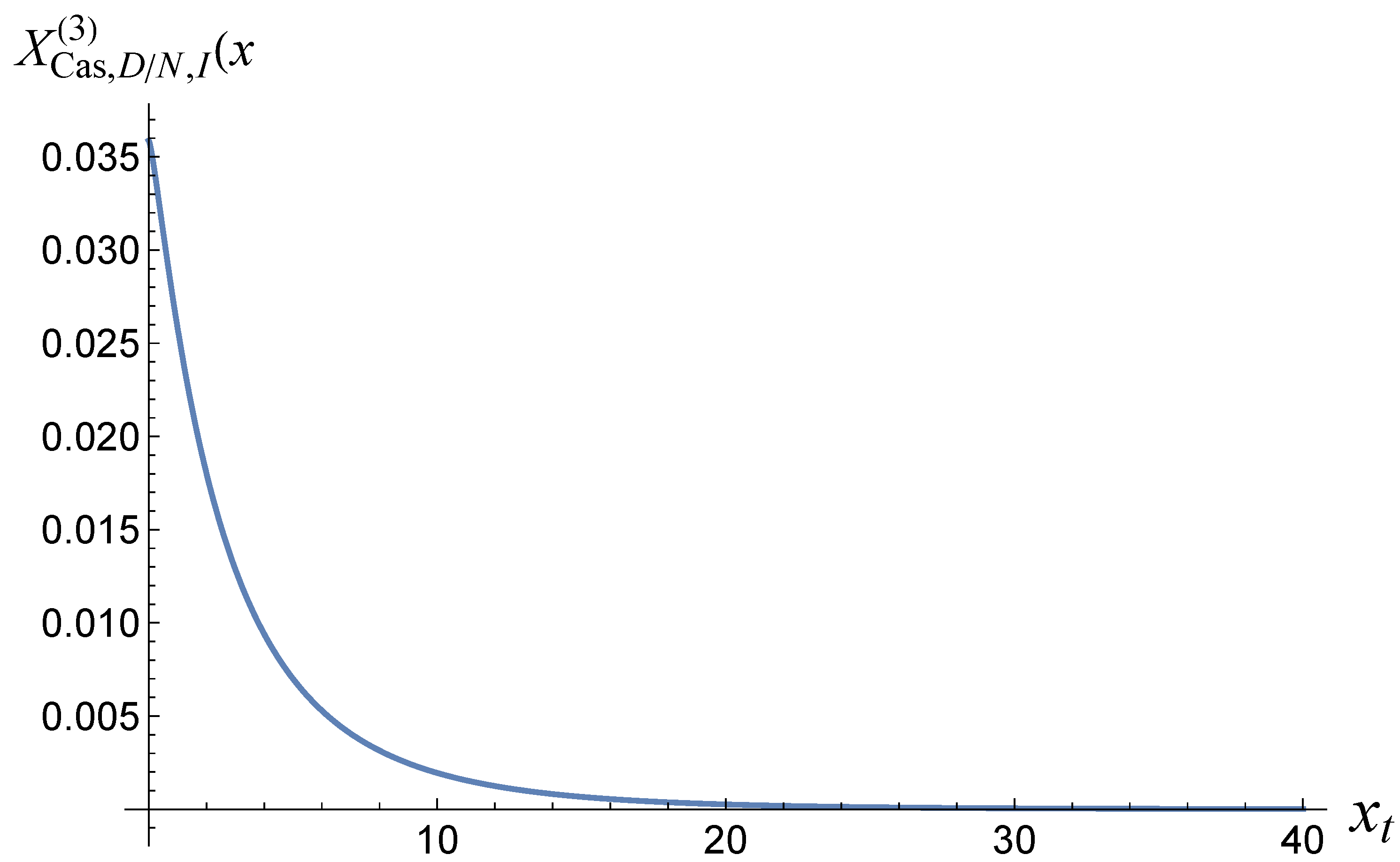
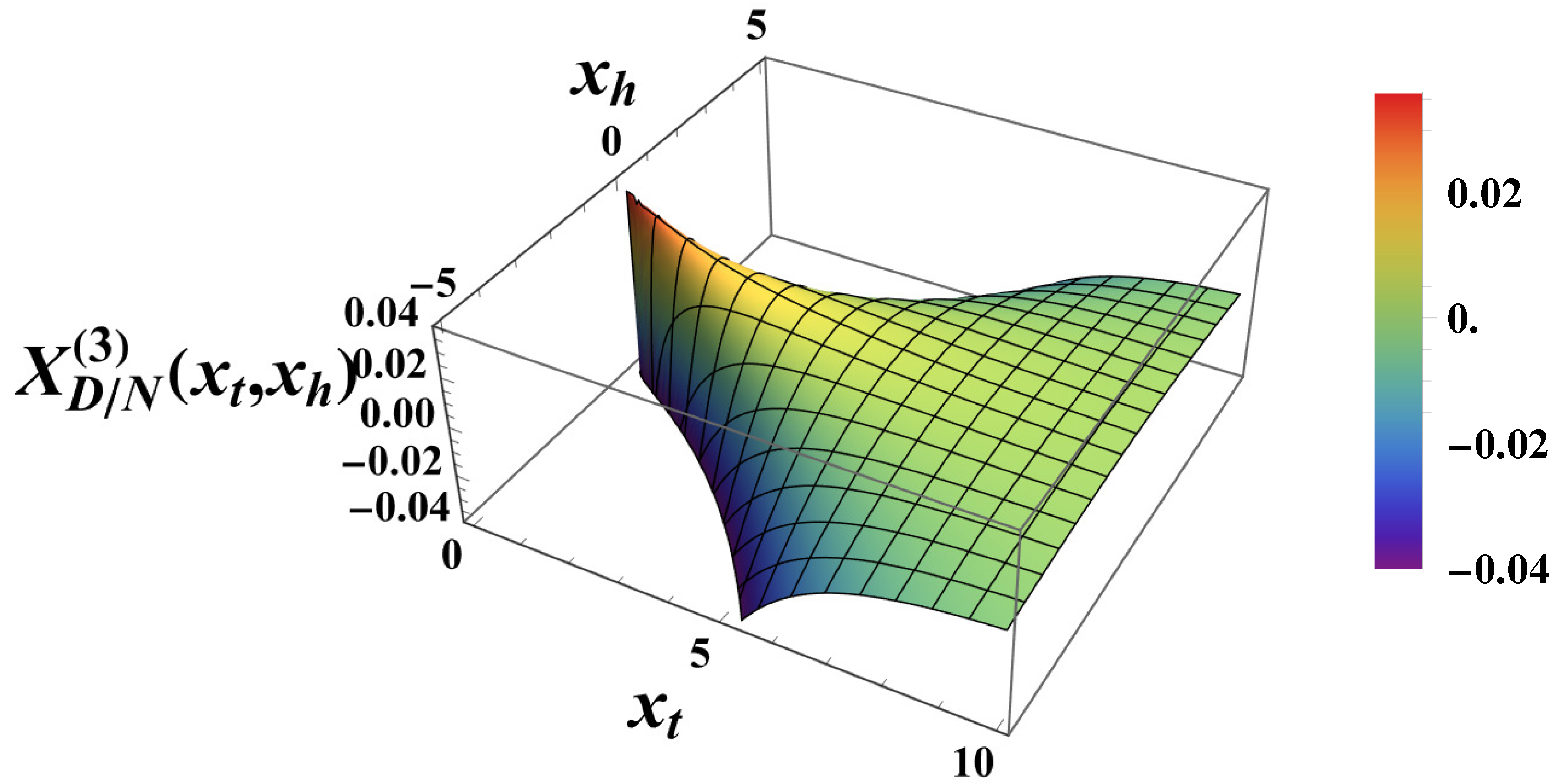
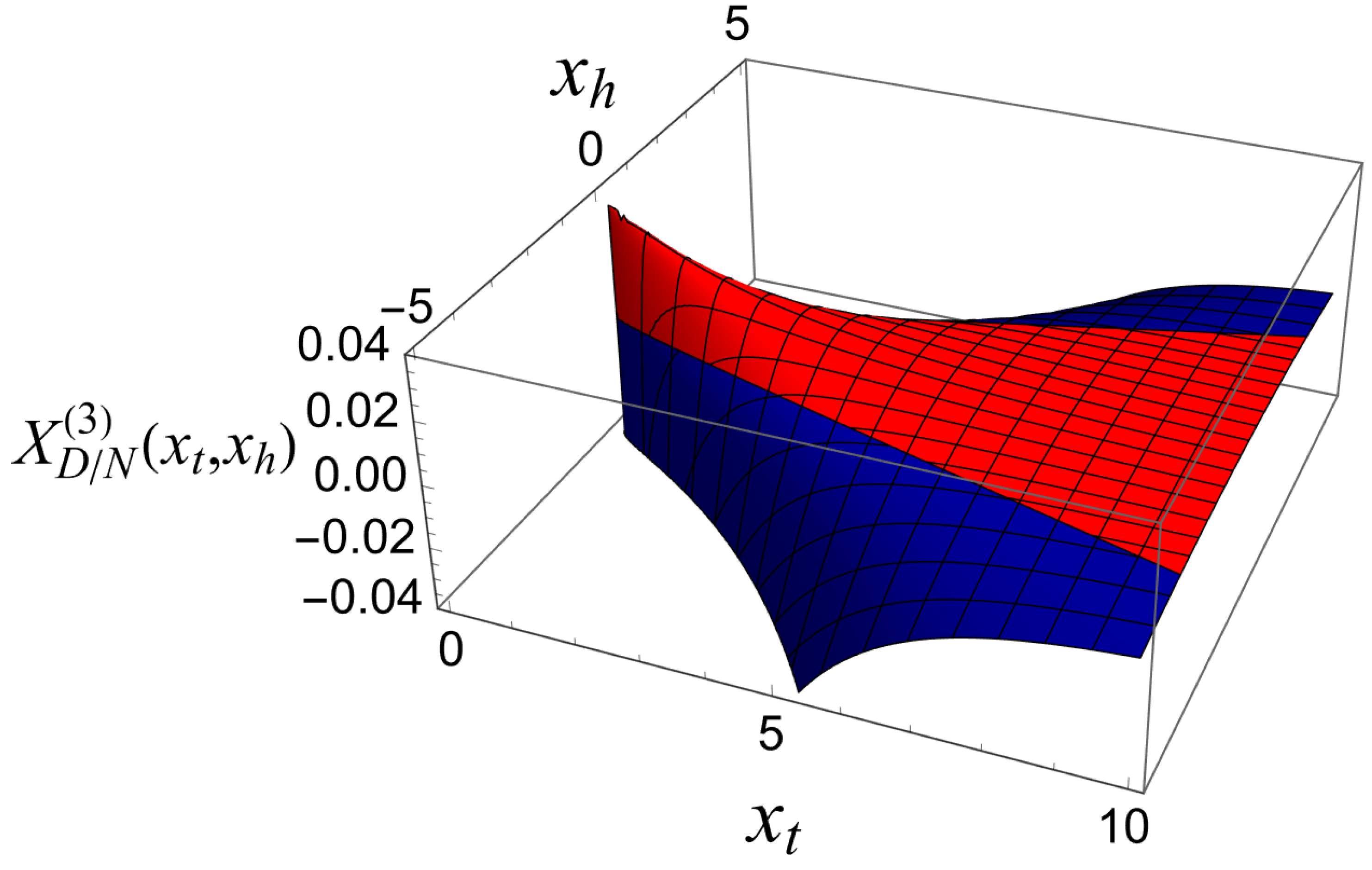
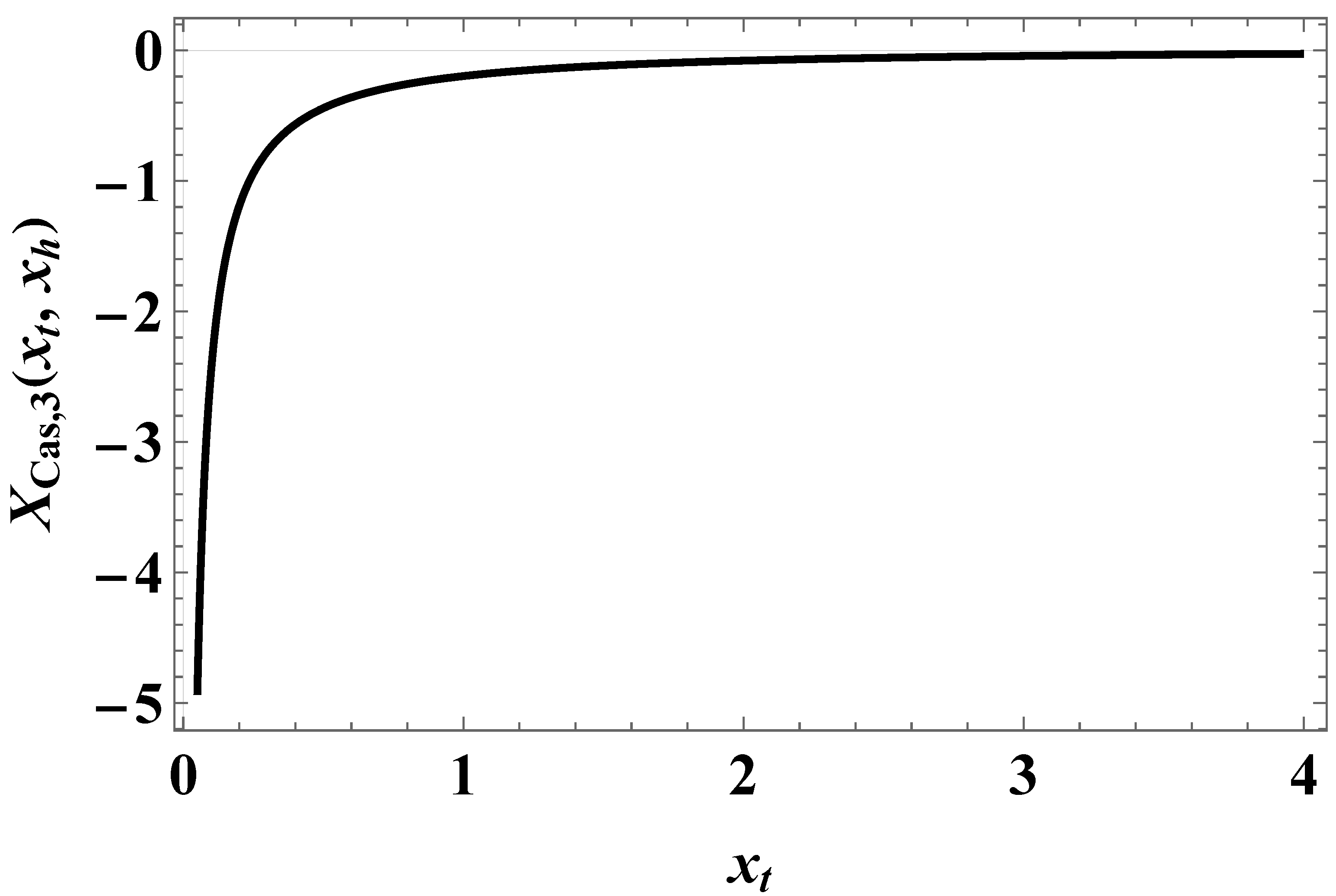
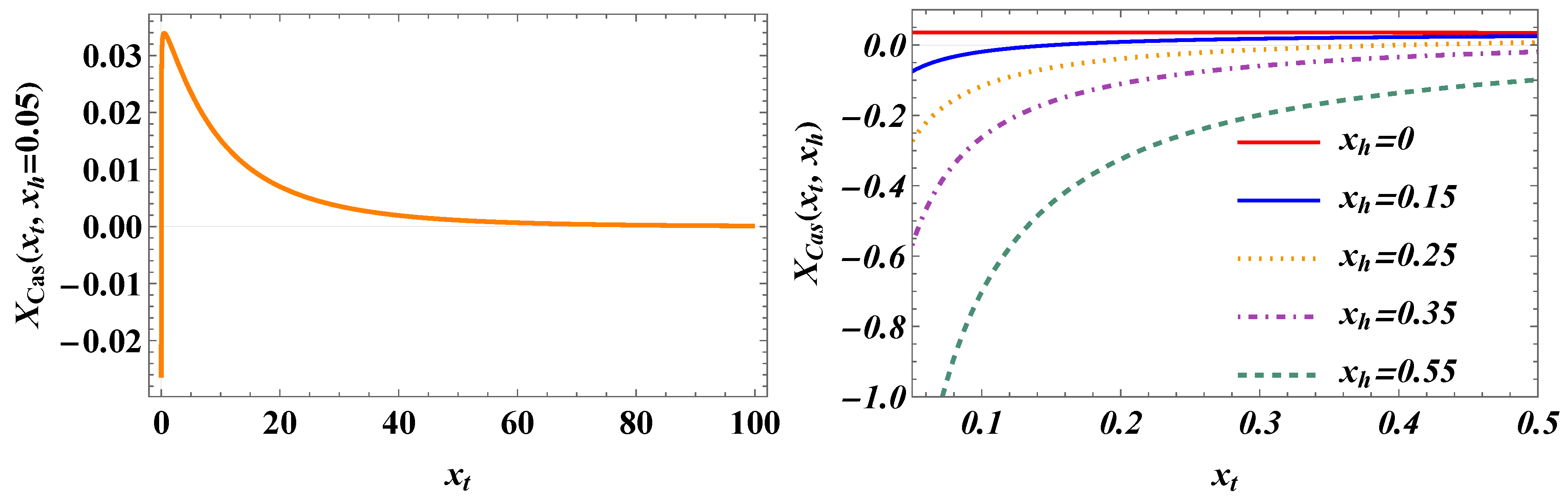
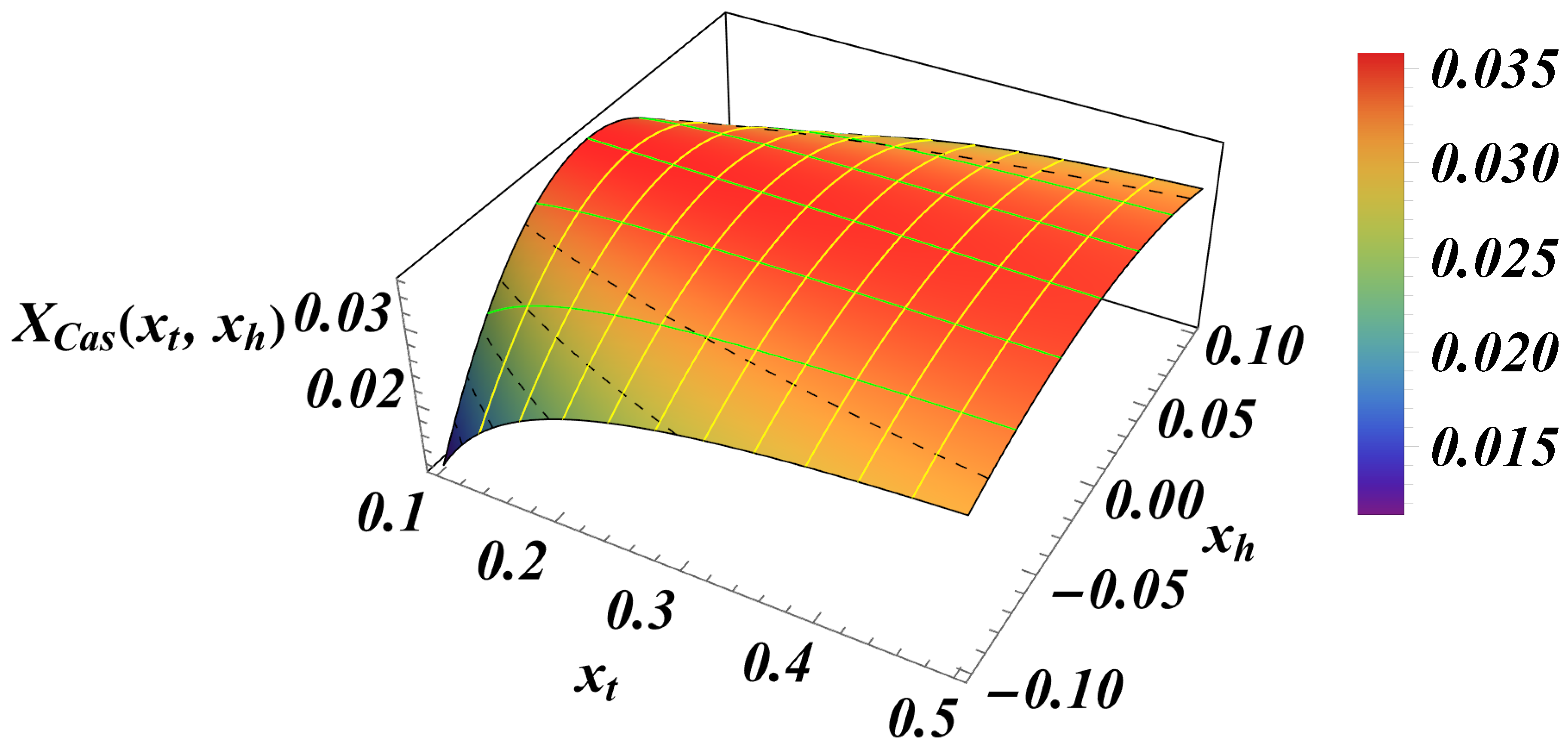
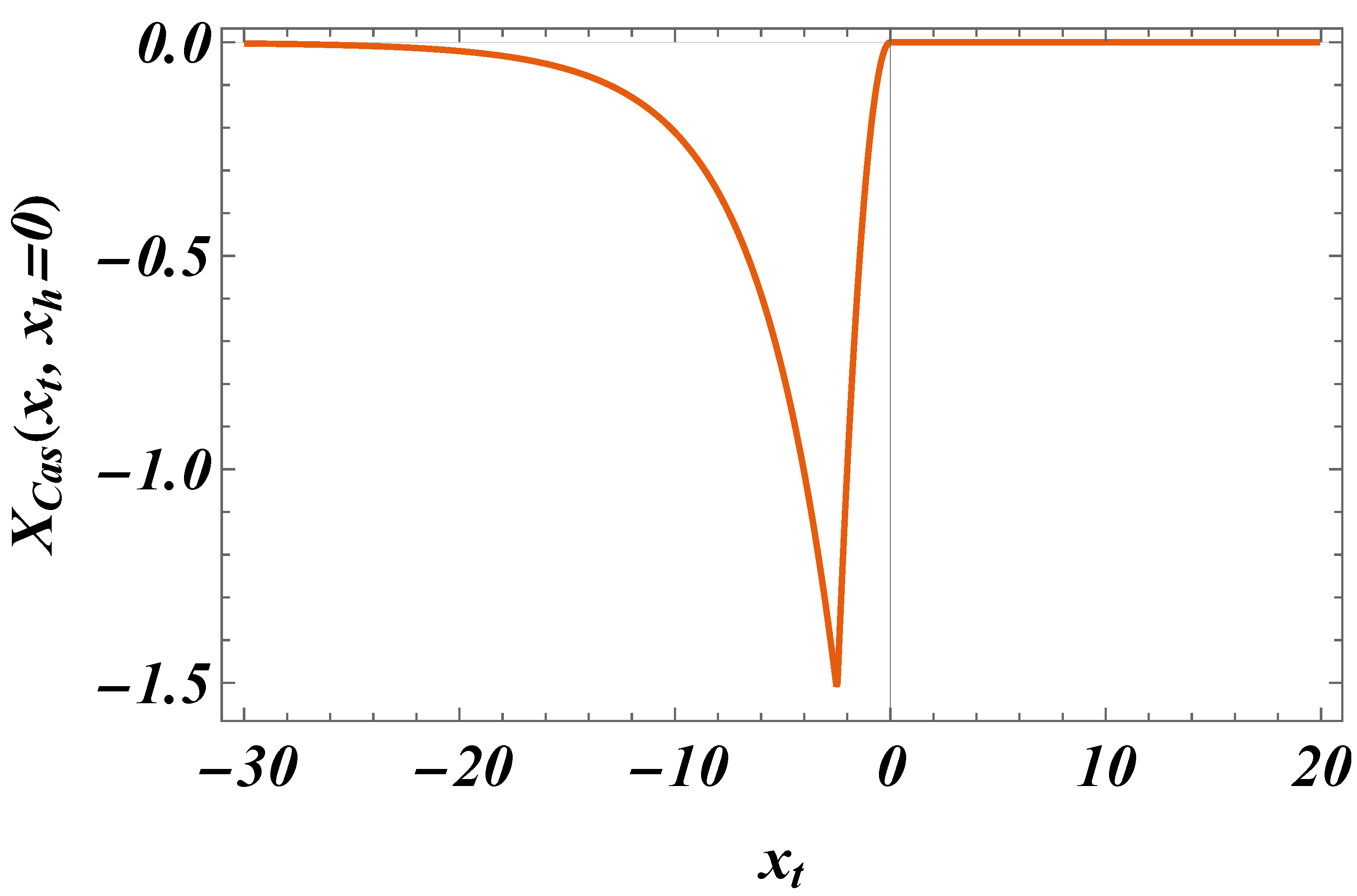
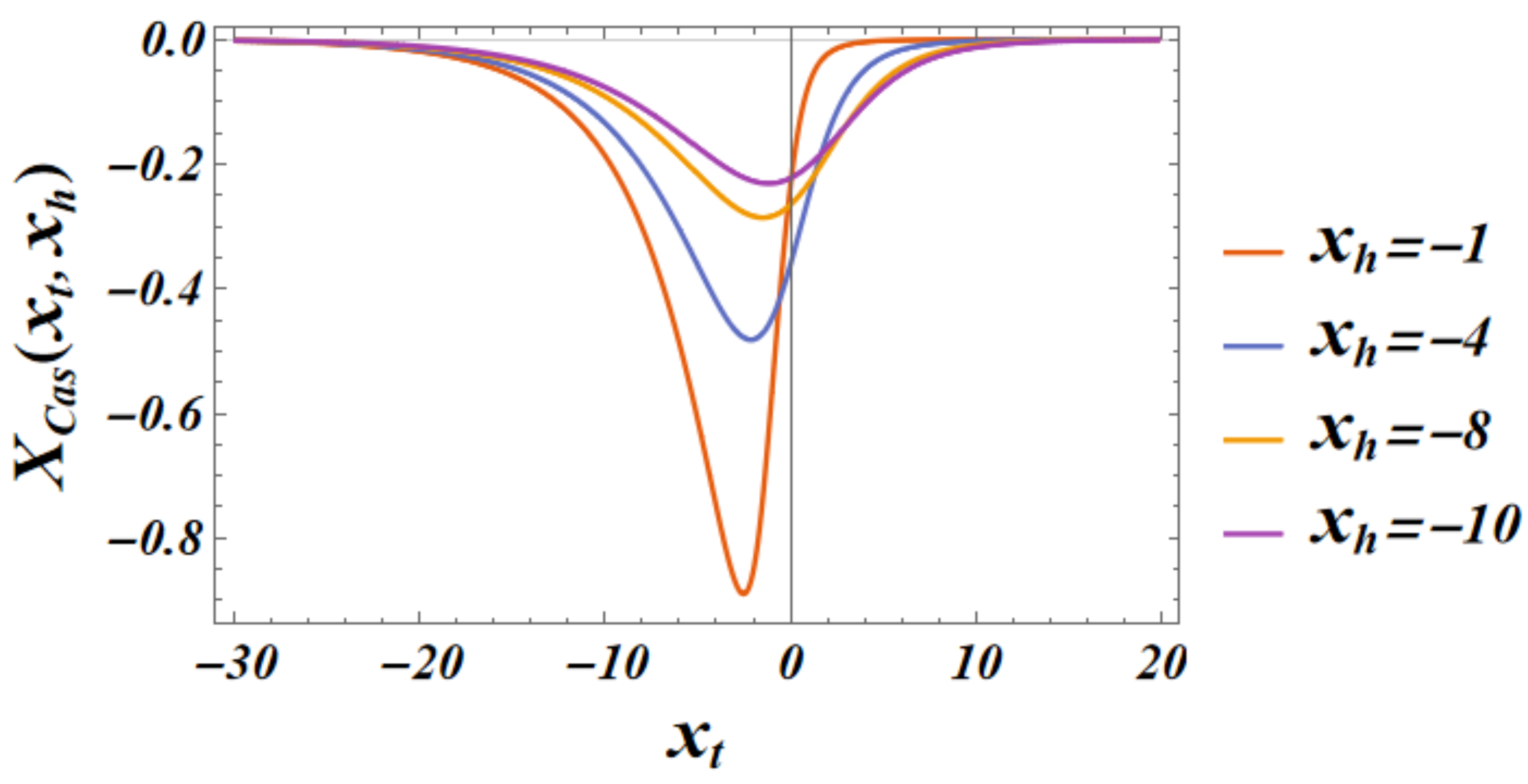
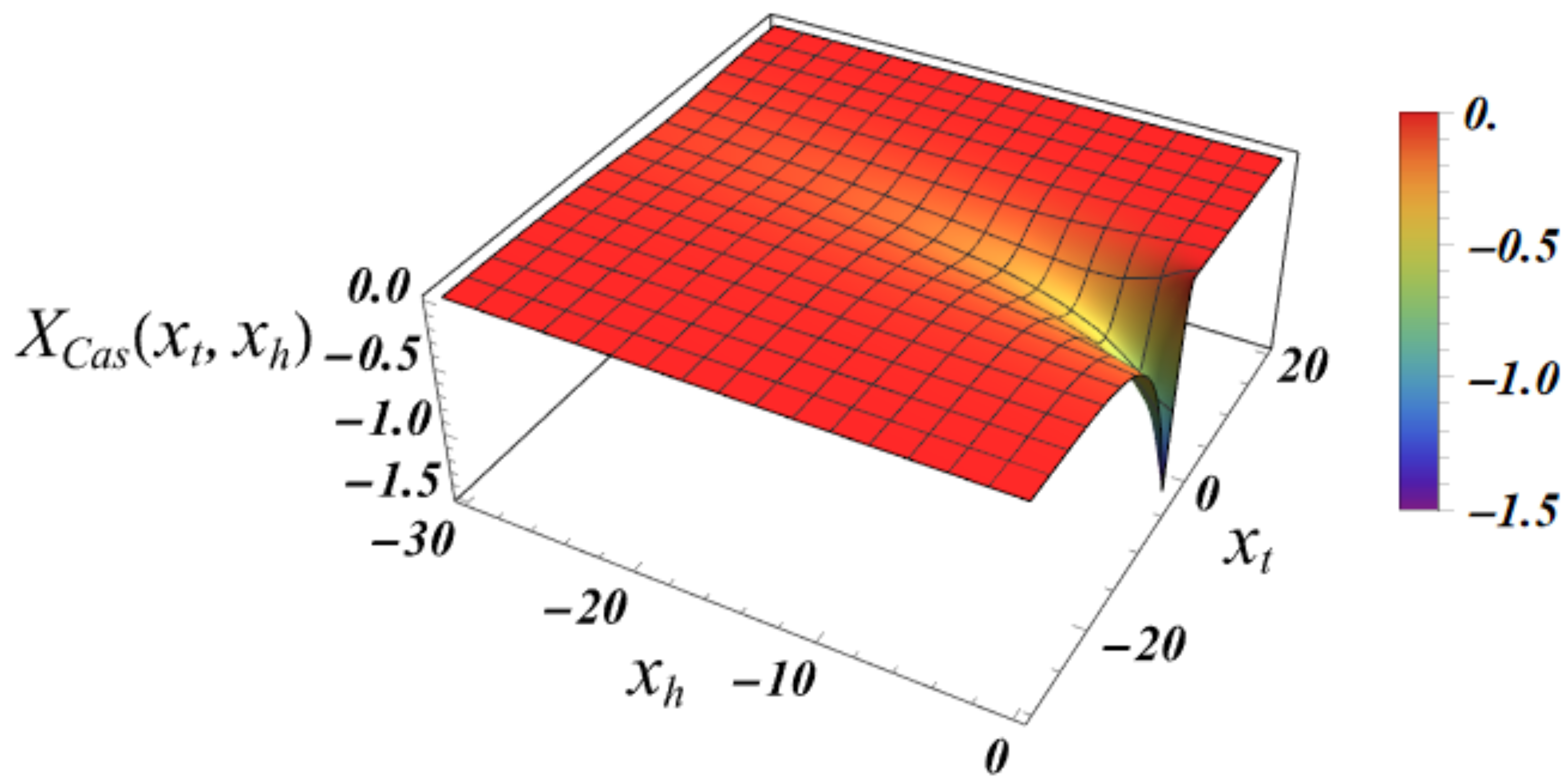
  Thus, setting $k_3=k,r_3=r$ and $L_3=L$, for a film geometry we arrive at

  $$P_L^{\left(\mathrm{ND}\right)}(\beta ,h)={\displaystyle \frac{4h^2}{\beta L(2L+1)}}\sum _{k=1}^L{\displaystyle \frac{{\left|{\sum }_{r=1}^{L}cos\left[(r-1/2)\pi \frac{2k-1}{2L+1}\right]\right|}^2}{6({\beta }_c/\beta -1)+2\left(1-cos\pi \frac{2k-1}{2L+1}\right)}}.$$

  (84)
  It is easy to show that

  $$2\sum _{r=1}^{L}cos\left(\pi (r-1/2){\displaystyle \frac{(2k-1)}{(2L+1)}}\right)={\displaystyle \frac{sin\left(\pi \frac{2k-1}{2L+1}L\right)}{sin\left(\frac{\pi }{2}\frac{2k-1}{2L+1}\right)}}.$$

  (85)
  Thus, one has

  $$P_L^{\left(\mathrm{ND}\right)}(\beta ,h)={\displaystyle \frac{h^2}{\beta L(2L+1)}}\sum _{k=1}^L{\displaystyle \frac{{cot}^2\left(\frac{\pi }{2}\frac{2k-1}{2L+1}\right)}{6({\beta }_c/\beta -1)+2\left(1-cos\pi \frac{2k-1}{2L+1}\right)}}.$$

  (86)
  Let us consider the small k behavior of the above sum. One derives

  $$\begin{array}{ccc}\hfill P_L^{\left(\mathrm{ND}\right)}(\beta ,h)& \simeq & {\displaystyle \frac{h^2}{\beta }}{\displaystyle \frac{1}{L(2L+1)}}\sum _{k=1}^L{\displaystyle \frac{1}{{\left[\frac{\pi (2k-1)}{2(2L+1)}\right]}^2\left\{6({\beta }_c/\beta -1)+{\left[\frac{\pi (2k-1)}{2L+1}\right]}^2\right\}}}\hfill \\ & \simeq & {\displaystyle \frac{4}{{\pi }^2}}{\displaystyle \frac{h^2}{\beta }}{\displaystyle \frac{{(2L+1)}^3}{L}}\sum _{k=1}^L{\displaystyle \frac{1}{{(2k-1)}^2\left[x_t+{\pi }^2{(2k-1)}^2\right]}}\hfill \\ & =& {\displaystyle \frac{h^2}{\beta }}{\displaystyle \frac{{(2L+1)}^3}{L}}\left\{{\displaystyle \frac{1}{2x_t}}\left[1-{\displaystyle \frac{tanh\left(\sqrt{x_t}/2\right)}{\sqrt{x_t}/2}}\right]+\mathcal{O}\left(L^{-3}\right)\right\}.\hfill \end{array}$$

  (87)
  In the limits $x_t\to 0$ and $x_t\to \infty$ for the behavior of the field term one obtains

  $$P_L^{\left(\mathrm{ND}\right)}(\beta ,h)\simeq {\displaystyle \frac{h^2}{\beta }}{\displaystyle \frac{{(2L+1)}^3}{L}}\left\{\begin{array}{cc}1/24+\mathcal{O}\left(x_t\right),& x_t\to 0;\\ & \\ 1/\left(2x_t\right)+\mathcal{O}\left[exp(-\sqrt{x_t})\right],& x_t\gg 1.\end{array}\right.$$

  (88)
  When $L\to \infty$, then $x_t\to \infty$, we obtain that

  $$\underset{L\to \infty }{lim}{P}_L^{\left(\mathrm{ND}\right)}(\beta ,h)={\displaystyle \frac{h^2}{6\beta ({\beta }_c/\beta -1)}},$$

  (89)

  which indeed equals the bulk expression - see Equation (82).
  From Equation (87) for the behavior of the susceptibility in the finite system we derive

  $${\chi }_L^{\left(\mathrm{ND}\right)}(\beta ,h)={\displaystyle \frac{1}{\beta }}{\displaystyle \frac{{(2L+1)}^3}{L}}{\displaystyle \frac{1}{x_t}}\left[1-{\displaystyle \frac{tanh\left(\sqrt{x_t}/2\right)}{\sqrt{x_t}/2}}\right].$$

  (90)
  According to the finite-size scaling theory [34,56]

  $${\chi }_L^{\left(\zeta \right)}\left(t\right)=a_h{L}^{\gamma }{X}_{\chi }\left(a_{\beta }t{L}^{1/\nu }\right),$$

  (91)

  where $a_h$ and $a_{\beta }$ are non-universal constants, and $X_{\chi }$ is an universal scaling function, $t=(T-T_c)/T_c$, where T has the meaning of the temperature of the system, and $T_c$ is its bulk temperature. From Equation (90), taking into account that ${(2L+1)}^3/L\simeq 8L^2$, we identify that

  $$\gamma =2,\nu =1/2,andt{L}^2=x_t.$$

  (92)
  It is clear that the field term in the free energy of the finite system will be of the same order as the field term, i.e., $\propto L^{-3}$ if $h\propto L^{-5/2}$. In order to achieve that, we define a field dependent scaling variable

  $$x_h={\beta }^{-1/2}{(2L+1)}^{3/2}Lh.$$

  (93)
  In terms of it, Equation (87) becomes

  $$P_L^{\left(\mathrm{ND}\right)}(x_h,x_t)={\displaystyle \frac{x_h^2}{L^3}}{X}_{\chi }\left(x_t\right),\mathrm{where}{X}_{\chi }\left(x_t\right)={\displaystyle \frac{1}{2x_t}}\left[1-{\displaystyle \frac{tanh\left(\sqrt{x_t}/2\right)}{\sqrt{x_t}/2}}\right].$$

  (94)
  The behavior of the scaling function $X\chi \left(x_t\right)$ is given in Figure 7.
  Then for the excess free energy related to the field term, see Equation (51), one derives

  $$\beta \mathrm{\Delta }{f}_{\mathrm{ex},3}^{\left(\mathrm{ND}\right)}(\beta ,h)=-{\displaystyle \frac{1}{2}}L\left[P_L^{\left(\mathrm{ND}\right)}(h;\beta )-P_{\infty }(h;\beta )\right]={\displaystyle \frac{x_h^2}{L^2}}{\displaystyle \frac{tanh\left(\sqrt{x_t}/2\right)}{2x_t^{3/2}}}.$$

  (95)

3.2. The Behavior of the Casimir Force

Let us determine the contributions of the interaction term $\mathrm{\Delta }{F}_{\mathrm{Cas}}^{\left(\mathrm{ND}\right)}(\beta ,h=0)$ and of the field term $\mathrm{\Delta }{F}_{\mathrm{Cas}}^{\left(\mathrm{ND}\right)}(\beta ,h\ne 0)$. Obviously, one has

$$\mathrm{\Delta }{F}_{\mathrm{Cas},3}^{\left(\mathrm{ND}\right)}(\beta ,h)=\mathrm{\Delta }{F}_{\mathrm{Cas},3}^{\left(\mathrm{ND}\right)}(\beta ,h=0)+\mathrm{\Delta }{F}_{\mathrm{Cas},3}^{\left(\mathrm{ND}\right)}(\beta ,h\ne 0).$$

(96)

We start with determining the behavior of $\mathrm{\Delta }{F}_{\mathrm{Cas}}^{\left(\mathrm{ND}\right)}(\beta ,h=0)$. By definition, it is equal to

$$\mathrm{\Delta }{F}_{\mathrm{Cas},3}^{\left(\mathrm{ND}\right)}(\beta ,h=0)\equiv -{\displaystyle \frac{\partial }{\partial L}}\beta \mathrm{\Delta }{f}_{\mathrm{ex},3}^{\left(\mathrm{ND}\right)}(\beta ,h=0).$$

(97)

From Equation (70) we derive the exact expression

$$\beta \mathrm{\Delta }{F}_{\mathrm{Cas},3}^{\left(\mathrm{ND}\right)}(\beta ,h=0)={\displaystyle \frac{1}{4{\pi }^2}}{\int }_{-\pi }^{\pi }\mathrm{d}{\theta }_1{\int }_{-\pi }^{\pi }\mathrm{d}{\theta }_2{\displaystyle \frac{x}{e^{(2L+1)x}+1}}.$$

(98)

Here we did not make any assumption bout L. Naturally, we will obtain a scaling form of $\beta \mathrm{\Delta }{F}_{\mathrm{Cas},3}^{\left(\mathrm{ND}\right)}(\beta ,h=0)$ only for $L\gg 1$. Then Equation (74) is valid and, after performing the integration, we arrive at

$$\begin{array}{ccc}\hfill \beta \mathrm{\Delta }{F}_{\mathrm{Cas},3}^{\left(\mathrm{ND}\right)}(\beta ,h=0)& =& -{\displaystyle \frac{1}{(2{(L+1)}^3}}{\displaystyle \frac{1}{\pi }}\left\{{\mathrm{Li}}_3\left(-e^{-\sqrt{x_t}}\right)+\sqrt{x_t}{\mathrm{Li}}_2\left(-e^{-\sqrt{x_t}}\right)-{\displaystyle \frac{1}{2}}{x}_{t}log\left(e^{-\sqrt{x_t}}+1\right)\right\}\hfill \\ & =& {\displaystyle \frac{1}{{(L+1/2)}^3}}{X}_{\mathrm{Cas},3}\left(x_t\right),\hfill \end{array}$$

(99)

where

$$X_{\mathrm{Cas},3}\left(y\right)=-{\displaystyle \frac{1}{8\pi }}\left\{{\mathrm{Li}}_3\left(-e^{-\sqrt{x_t}}\right)+\sqrt{x_t}{\mathrm{Li}}_2\left(-e^{-\sqrt{x_t}}\right)-{\displaystyle \frac{1}{2}}{x}_{t}log\left(e^{-\sqrt{x_t}}+1\right)\right\}.$$

(100)

The behavior of the scaling function $X_{Cas}(x_t,h=0)$ is given in Figure 8. Obviously, the function is positive, which means that the Casimir force is repulsive when the external field is zero. For the Casimir amplitude we obtain

$${\mathrm{\Delta }}_{\mathrm{Cas},3}^{\left(\mathrm{ND}\right)}\equiv X_{\mathrm{Cas},3}(x_t=0,h=0)/2={\displaystyle \frac{3}{64\pi }}\zeta \left(3\right).$$

(101)

Obviously, Equation (101) coincides with the corresponding result for the Gaussian model obtained via studying the $O\left(n\right)$, $n=1,d=3$${\mathrm{\Phi }}^4$ model — see [14] (Equation (6.99)). Analogically, after proper renaming of the scaling variable the expression Equation (100) of the scaling function of the force coinsides with the corresponding one for the $O\left(n\right)$, $n=1,d=3$${\mathrm{\Phi }}^4$ model — see [14] (Equation (6.104)).

Let us now determine the h-dependent part of the Casimir force. By definition, one has

$$\mathrm{\Delta }{F}_{\mathrm{Cas},3}^{\left(\mathrm{ND}\right)}(\beta ,h)\equiv -{\displaystyle \frac{\partial }{\partial L}}\beta \mathrm{\Delta }{f}_{\mathrm{ex},3}^{\left(\mathrm{ND}\right)}(\beta ,h).$$

(102)

Then, from Equation (95) one obtains

$$\begin{array}{ccc}\hfill \mathrm{\Delta }{F}_{\mathrm{Cas},3}^{\left(\mathrm{ND}\right)}(\beta ,h)& =& -{\displaystyle \frac{\partial }{\partial L}}\left[{\displaystyle \frac{x_h^2}{L^2}}{\displaystyle \frac{tanh\left(\sqrt{x_t}/2\right)}{2x_t^{3/2}}}\right]\simeq -{\displaystyle \frac{x_h^2}{2L^2(1+2L)}}\left[{\displaystyle \frac{{\sec \mathrm{h}}^2\left(\sqrt{x_t}/2\right)}{x_t}})\right]\hfill \end{array}$$

(103)

$$\begin{array}{ccc}& =& {\displaystyle \frac{1}{L^2(L+1/2)}}{X}_{\mathrm{Cas},3}(x_t,x_h),\hfill \end{array}$$

(104)

where

$$X_{\mathrm{Cas},3}(x_t,x_h)=-{\displaystyle \frac{x_h^2}{4}}\left[{\displaystyle \frac{{\sec \mathrm{h}}^2\left(\sqrt{x_t}/2\right)}{x_t}}\right]<0.$$

(105)

A visualization of $X_{\mathrm{Cas},3}(y,x_h)$ as a function of y for $x_h=1$ is shown in Figure 9.

The total Casimir force is a sum of $X_{\mathrm{Cas},3}\left(x_t\right)$, see Equation (100), and $X_{\mathrm{Cas},3}(x_t,x_h)$ given by Equation (105). The plot of the result as a function of $x_t$ for $x_h=0.05$ is shown in Figure 10. As we see, the force can be both positive and negative, i.e., repulsive and attractive.

The overall $3D$ behavior of the force as a function both on $x_t$ and $x_h$ is given in Figure 11.

4. The Casimir Force Within the Mean-Field Model

We start by defining the mean-field model used in the current study.

4.1. The Ginzburg-Landau Functional

In the present work we consider the standard ${\varphi }^4$ Ginzburg–Landau functional

$$\mathcal{F}\left[\varphi \right|\tau ,h,L]={\int }_0^L\mathcal{L}(\varphi ,{\varphi }^{\prime }|\tau ,h)\mathrm{d}z$$

(106)

with

$$\mathcal{L}(\varphi ,{\varphi }^{\prime }|\tau ,h)={\displaystyle \frac{1}{2}}{\varphi }^{\prime 2}+{\displaystyle \frac{1}{2}}\tau {\varphi }^2+{\displaystyle \frac{1}{4}}g{\varphi }^4-h\varphi .$$

(107)

Here $L,g\in {\mathbb{R}}^{+}$, while $\tau ,h\in \mathbb{R}$, $z\in (0,L)$ and $\varphi =\varphi \left(z\right)$ are the independent and dependent variables, respectively, and the prime indicates differentiation with respect to the variable z.

The functional (106) describes a critical system of Ising type in a film geometry ${\infty }^2\times L$, where the film thickness L is supposed to be along the z axis. In Equation (106), $\varphi \left(z\right|\tau ,h,L)$ is the order parameter of the system, which is assumed to depend on the perpendicular position $z\in (0,L)$ only, g is the bare coupling constant, and $\tau =(T-T_c)/T_c$ is the bare reduced temperature, and h is the external ordering field. Given $\tau$, h and L, the physical state of the regarded system is described by the minimizer of the respective Ginzburg–Landau functional $\mathcal{F}[\varphi ;\tau ,h,L]$ given above whose extremals are determined by the solutions of the corresponding Euler-Lagrange equation

$${\displaystyle \frac{d}{dz}}{\displaystyle \frac{\partial \mathcal{L}}{\partial {\varphi }^{\prime }}}-{\displaystyle \frac{\partial \mathcal{L}}{\partial \varphi }}=0.$$

(108)

In case the Lagrangian density $\mathcal{L}$ is defined by Equation (107), Equation (108) reads

$${\varphi }^{\prime \prime }-\varphi \left[\tau +g{\varphi }^2\right]+h=0.$$

(109)

Multiplying Equation (109) by ${\varphi }^{\prime }$ and integrating once over z one obtains that

$$P\left[\varphi \right]\equiv {\displaystyle \frac{1}{2}}{{\varphi }^{\prime }}^2-{\displaystyle \frac{1}{2}}\tau {\varphi }^2-{\displaystyle \frac{1}{4}}g{\varphi }^4+h\varphi$$

(110)

is a first integral of Equation (109), cf., e.g., [14]. This means that P is a constant on any smooth solution $\varphi \left(z\right|\tau ,h,L)$ of the Euler-Lagrange Equation (109).

In general, the thermodynamic Casimir force $F_{\mathrm{Cas}}(\tau ,h,L)$ in such a system is the excess pressure, over the bulk one, acting on the boundaries of the finite system, which is due to the finite size of that system, i.e.,

$$F_{\mathrm{Cas}}(\tau ,h,L)=P_L(\tau ,h)-P_b(\tau ,h).$$

(111)

Here $P_L$ is the pressure in the finite system, while $P_b$ is that one in the infinite system.

Now, assuming that the thickness L of the film is free to move, the variation $\delta \mathcal{F}$ of the free energy $\mathcal{F}\left[\varphi \right|\tau ,h,L]$ of the finite system is given as follows

$$\delta \mathcal{F}={\int }_0^L\left({\displaystyle \frac{\partial \mathcal{L}}{\partial \varphi }}-{\displaystyle \frac{d}{dz}}{\displaystyle \frac{\partial \mathcal{L}}{\partial {\varphi }^{\prime }}}\right)\delta \varphi dz+{\left.{\mathcal{L}}_{{\varphi }^{\prime }}\delta \varphi \right|}_0^L-{\left.\left({\varphi }^{\prime }{\mathcal{L}}_{{\varphi }^{\prime }}-\mathcal{L}\right)\delta z\right|}_0^L$$

(112)

(see, e.g., [57] (p. 54), [58] (p. 260) and [59]), where $\delta z$ and $\delta \varphi$ are the variations of the independent and dependent variables, while

$$T_{zz}={\varphi }^{\prime }{\mathcal{L}}_{{\varphi }^{\prime }}-\mathcal{L}$$

(113)

is the one-dimensional counterpart of the stress tensor (see, e.g., [60,61]). Relation (112) estimates the change of the finite-size contribution to the free energy of the system corresponding to a small variation of the variables including the variation of the film thickness L. In this sense, ${\left.T_{zz}\right|}_L$ can be interpreted (see, e.g., [51,62]) as the pressure in the finite system, that is

$$P_L={\left.T_{zz}\right|}_L.$$

(114)

On the other hand, taking into account Equations (107) and (113), one can see that

$$T_{zz}=P\left[\varphi \right]$$

(115)

and hence $T_{zz}$ is a constant on any smooth solution $\varphi \left(z\right|\tau ,h,L)$ of the Euler-Lagrange Equation (109) including the minimizer of the Ginzburg–Landau functional (106). Thus, the pressure in the finite system is

$$P_L(\tau ,h)={\displaystyle \frac{1}{2}}{{\varphi }_{min}^{\prime }}^2-{\displaystyle \frac{1}{4}}g{\varphi }_{min}^4-{\displaystyle \frac{1}{2}}\tau {\varphi }_{min}^2+h{\varphi }_{min}$$

(116)

where ${\varphi }_{min}$ is the foregoing minimizer.

As for the bulk system, it is easy to see following the same way of reasoning that the corresponding pressure is

$$P_b(\tau ,h)=-{\displaystyle \frac{1}{4}}g{\varphi }_b^4-{\displaystyle \frac{1}{2}}\tau {\varphi }_b^2+h{\varphi }_b.$$

(117)

Here, the value ${\varphi }_b$ of the order parameter of the bulk system is determined as the constant solution of Equation (109), i.e., as the root of the cubic equation

$$-{\varphi }_b\left[\tau +g{\varphi }_b^2\right]+h=0,$$

(118)

that minimizes

$${\mathcal{L}}_b={\displaystyle \frac{1}{2}}\tau {\varphi }_b^2+{\displaystyle \frac{1}{4}}g{\varphi }_b^4-h{\varphi }_b.$$

(119)

Of course, ${\varphi }_b$ does not depend on the boundary conditions at all. Let us note that $P_b=-{\mathcal{L}}_b$, i.e., $P_b$ has its maximum over the solution ${\varphi }_b$ of the cubic equation for (118).

Obviously, the relation (116) does not depend on the boundary conditions applied on the finite system too. This dependence arises solely from the dependency of the order parameter profile that minimizes the particular boundary value problem considered.

In the light of the above it is evident that once the order parameter profile ${\varphi }_{min}$ and its bulk value ${\varphi }_b$ are known in analytic form for given values of the parameters $\tau$ and h, then the respective Casimir force is determined in an exact manner by Equation (111).

In the current article we consider the Dirichlet-Neumann boundary conditions meaning that

$$\varphi (z=0|\tau ,h,L)=0and{\displaystyle \frac{\partial }{\partial z}}\varphi {\left(z\right|\tau ,h,L)}_{{|}_{z=1}}=0.$$

(120)

In addition, $\nu$ is a critical exponent characterizing the behavior of the correlation length, while $\mathrm{\Delta }$ is another exponent related to the behavior of, say, order parameter as a function of the external field h.

It is convenient to introduce new parameters

$$x_t={\displaystyle \frac{\tau L^{1/\nu }}{{\left[{\xi }_0^{+}\right]}^{1/\nu }}},x_h={\displaystyle \frac{\sqrt{2g}h{L}^{\mathrm{\Delta }/\nu }}{{\left[{\xi }_{0,h}\right]}^{\mathrm{\Delta }/\nu }}}$$

(121)

and variables

$$\zeta =z/L,\varphi \left(z\right)=\sqrt{{\displaystyle \frac{2}{g}}}{L}^{-\beta /\nu }{X}_m\left(\zeta \right|x_t,x_h),$$

(122)

where $\beta =\nu =1/2$ and $\mathrm{\Delta }=3/2$, while ${\xi }_0^{+}$ and ${\xi }_{0,h}$ are the respective amplitudes of the correlation length along the $\tau$ and h axes (see, e.g., [14]). In terms of these new parameters and variables, Equations (106), (107), (109) and (110) becomes

$$\mathcal{F}\left[X_m\right|x_t,x_h]={\displaystyle \frac{1}{g{L}^4}}{\int }_0^1\mathcal{L}[X_m,X_m^{\prime }|x_t,x_h]d\zeta ,$$

(123)

$$\mathcal{L}[X_m,X_m^{\prime }|x_t,x_h]=X_m^{\prime 2}\left(\zeta \right)+X_m^4\left(\zeta \right)+x_t{X}_m^2\left(\zeta \right)-x_h{X}_m\left(\zeta \right),$$

(124)

$$X_m^{\prime \prime }\left(\zeta \right)=X_m\left(\zeta \right)\left[x_t+2X_m^2\left(\zeta \right)\right]-{\displaystyle \frac{x_h}{2}},$$

(125)

and

$$P\left[X_m\left(\zeta \right)\right]=X_m^{\prime 2}\left(\zeta \right)-X_m^4\left(\zeta \right)-x_t{X}_m^2\left(\zeta \right)+x_h{X}_m\left(\zeta \right),$$

(126)

respectively. The primes here and hereafter indicate differentiation with respect to the variable $\zeta \in [0,1]$. Then, according to Equations (111), (116) and (117), the expression for the Casimir force $X_{\mathrm{Cas}}(x_t,x_h)$ written by means of the new parameters (121) and variables (122) reads

$$X_{\mathrm{Cas}}(x_t,x_h)={\widehat{X}}_m^{\prime 2}-\left({\widehat{X}}_m^4-X_b^4\right)-x_t\left({\widehat{X}}_m^2-X_b^2\right)+x_h\left({\widehat{X}}_m-X_b\right),$$

(127)

where ${\widehat{X}}_m$ and $X_b$ are the minimizers of the functional (123) and its “bulk counterpart” corresponding to $x_t$ and $x_h$.

As mentioned above, in the present article we assume that the system is subject to Dirichlet-Neumann boundary conditions, that is

$$X_m(\zeta =0|x_t,x_h)=0and{X}_m^{\prime }(\zeta =1|x_t,x_h)=0.$$

(128)

In other words, we are interested in the solution of Equation (125) that meet the conditions (128). It should be remarked that exact results associated with the Casimir effect have been derived in the cases of $(+,+)$, $(+,-)$ and Dirichlet-Dirichlet boundary conditions - see Ref. [14] for a review.

4.2. The Casimir Force for Zero External Field

In Ref. [63] it has been shown that for $x_t\in \left(-\infty ,-{\pi }^2/4\right]$ there are tow order parameter profiles that minimize the functional (123) in the case of Dirichlet-Neumann boundary conditions and zero external field. They can be expressed using an auxiliary parameter $k\in [0,1]$ as follows

$${\widehat{X}}_m\left(\zeta \right)=\pm kK\left(k\right)\mathrm{sn}\left(\zeta K\left(k\right)|k\right)$$

(129)

at

$$x_t=-\left(k^2+1\right)K{\left(k\right)}^2,$$

(130)

where $K(·)$ is the complete elliptic integral of the first kind and $\mathrm{sn}\left(·|·\right)$ is the sine Jacobi elliptic function. Simultaneously, it is easy to see that in this case

$$X_b={\displaystyle \frac{1}{\sqrt{2}}}\sqrt{\left(k^2+1\right)K{\left(k\right)}^2}.$$

(131)

Now, substituting Equations (129) and (131) into Equation (127) one obtains

$$X_{\mathrm{Cas}}(x_t,x_h=0)=-{\displaystyle \frac{1}{4}}{\left(k^2-1\right)}^{2}K{\left(k\right)}^4,$$

(132)

for the Casimir force at $x_t\in \left(-\infty ,-{\pi }^2/4\right]$ given by Equation (130).

If $x_t\in \left(-{\pi }^2/4,0\right]$, then ${\widehat{X}}_m=0$, $X_b=-\sqrt{-x_t/2}$ and hence, according to Equation (127), the expression for the Casimir force reads

$$X_{\mathrm{Cas}}(x_t,x_h=0)=-{\displaystyle \frac{x_t^2}{4}}.$$

(133)

Finally, if $x_t\in \left(0,\infty \right)$, then $X_{\mathrm{Cas}}(x_t,x_h=0)=0$. Combining these results one can write down

$$\begin{array}{c}\hfill X_{\mathrm{Cas}}(x_t,x_h=0)=\left\{\begin{array}{cc}-{\displaystyle \frac{1}{4}}{\left(k^2-1\right)}^{2}K{\left(k\right)}^4,& x_t\in \left(-\infty ,-{\displaystyle \frac{{\pi }^2}{4}}\right],\\ -x_t^2/4,& x_t\in \left(-{\displaystyle \frac{{\pi }^2}{4}},0\right],\\ 0,& x_t\in \left(0,\infty \right).\end{array}\right.\end{array}$$

(134)

The behavior of the scaling function $X_{\mathrm{Cas}}(x_t,x_h=0)$ for $x_t\in [-30,30]$ is depicted in Figure 13.

4.3. The Casimir Force for Nonzero External Field

In Ref. [63] it has been shown, following [64] (p. 454), that each solution of Equation (125) that meets Dirichlet-Neumann boundary conditions can be written in the form

$$X_m\left(\zeta |x_t,x_h,X_{m,r}\right)=X_{m,r}+{\displaystyle \frac{6X_{m,r}\left(x_t+2X_{m,r}^2\right)-3x_h}{12\wp \left(\zeta -1;g_2,g_3\right)-\left(x_t+6X_{m,r}^2\right)}},$$

(135)

where $X_{m,r}=X_{m,r}(x_t,x_h)$ is a real number that depends only on the values of the parameters $x_t$ and $x_t$. Here $\wp \left(\nu ;g_2,g_3\right)$ is the Weierstrass elliptic function corresponding to the invariants $g_2$ and $g_3$ given as follows

$$\begin{array}{ccc}\hfill & & g_2={\displaystyle \frac{1}{12}}{x}_t^2-X_{m,r}\left(X_{m,r}^3+x_t{X}_{m,r}-x_h\right),\hfill \\ & & g_3=-{\displaystyle \frac{1}{432}}\left[27x_h^2+2x_t^3+72x_t{X}_{m,r}\left(X_{m,r}^3+x_t{X}_{m,r}-x_h\right)\right].\hfill \end{array}$$

(136)

It is easy to see that $X_{m,r}$ is the value of the order parameter at the right end of the system since $\wp \left(\nu ;g_2,g_3\right)$ tents to infinity when $\nu$ tends to zero. It is also easy to see that $X_m^{\prime }\left(\zeta \to 1|x_t,{\overline{x}}_h,X_{m,r}\right)=0$, i.e., each function of the form (135) meets the boundary condition imposed on the right end of the system. The only remaining requirement that $X_m\left(\zeta \to 0|x_t,x_h,X_{m,r}\right)=0$ leads to an transcendental equation from where we have to determine $X_{m,r}$. Usually, one obtains several solution of this equation. However, the one that corresponds to the physical reality is the one that minimizes the energy given by Equations (123) and (124). In this way we find the order parameter profile ${\widehat{X}}_m$ as a function of the parameters $x_t$ and $x_h$. We also obtain $X_b$ as a function of $x_t$ and $x_h$.

Finally, using Equation (127) we obtain the Casimir force $X_{\mathrm{Cas}}(x_t,x_h)$.

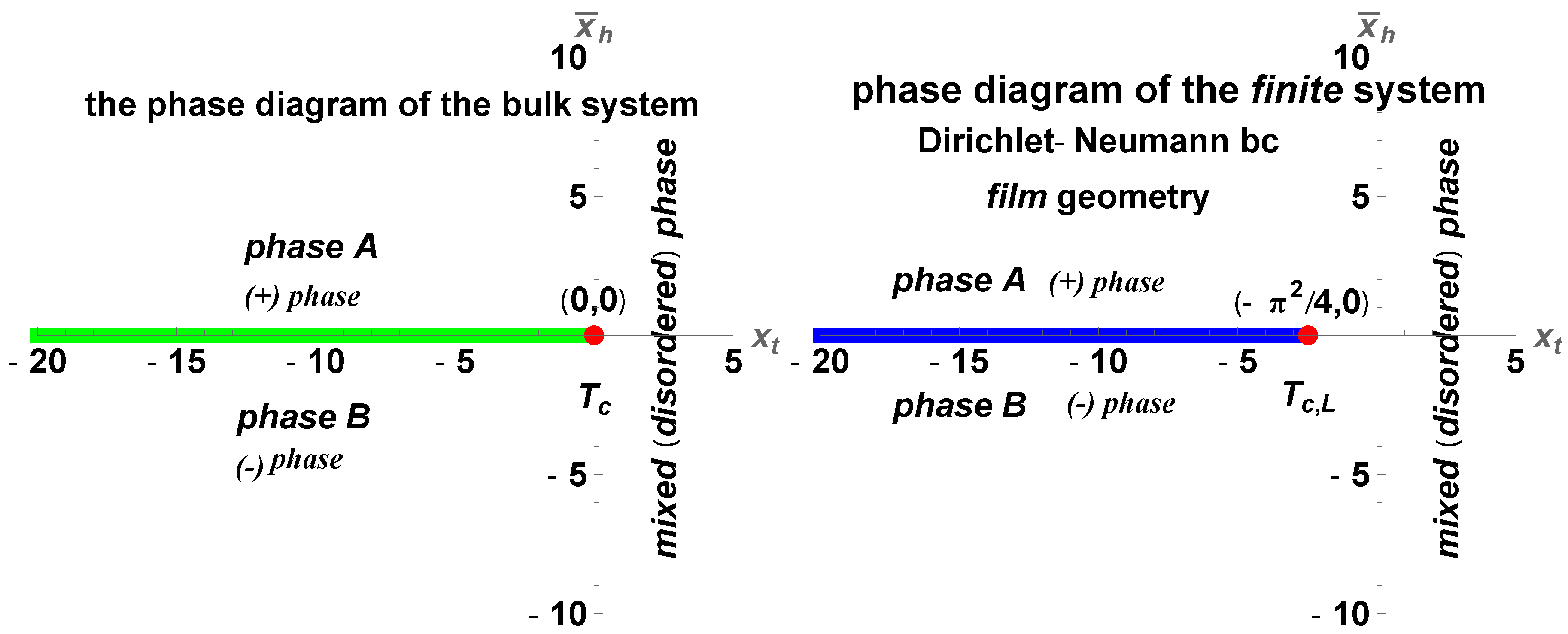
5. Conclusions

As reported above, we have obtained exact results for the Casimir force in two basic statistical mechanical models: the Gaussian and the mean field model. In the case of the Gaussian model we performed the calculations for two realizations: a continuum version, see Section 2, and a lattice version — see Section 3 realizations. The mean-field model is considered in Section 4. The models are considered under Neumann-Dirichlet boundary conditions in the presence of an external magnetic field h.

We summarize our main results as follows:

I

We derived exact closed form expression for the free energy of the Gaussian model in both the continuum version (CGM) and the lattice formulation of the model (LGM). The results for the Casimir force can be written as a sum of

i)

expressions pertinent to the $h=0$ case - see Equation (33) for CGM and Equation (100) for the LGM.

ii)

equations for the field-dependent parts of the force — see Equation (41) for the CGM, and Equation (105) for the LGM.

We observe that these expression are identical, as is to be expected on the ground of the universality hypothesis, provided proper definitions of the scaling variables are used.

II

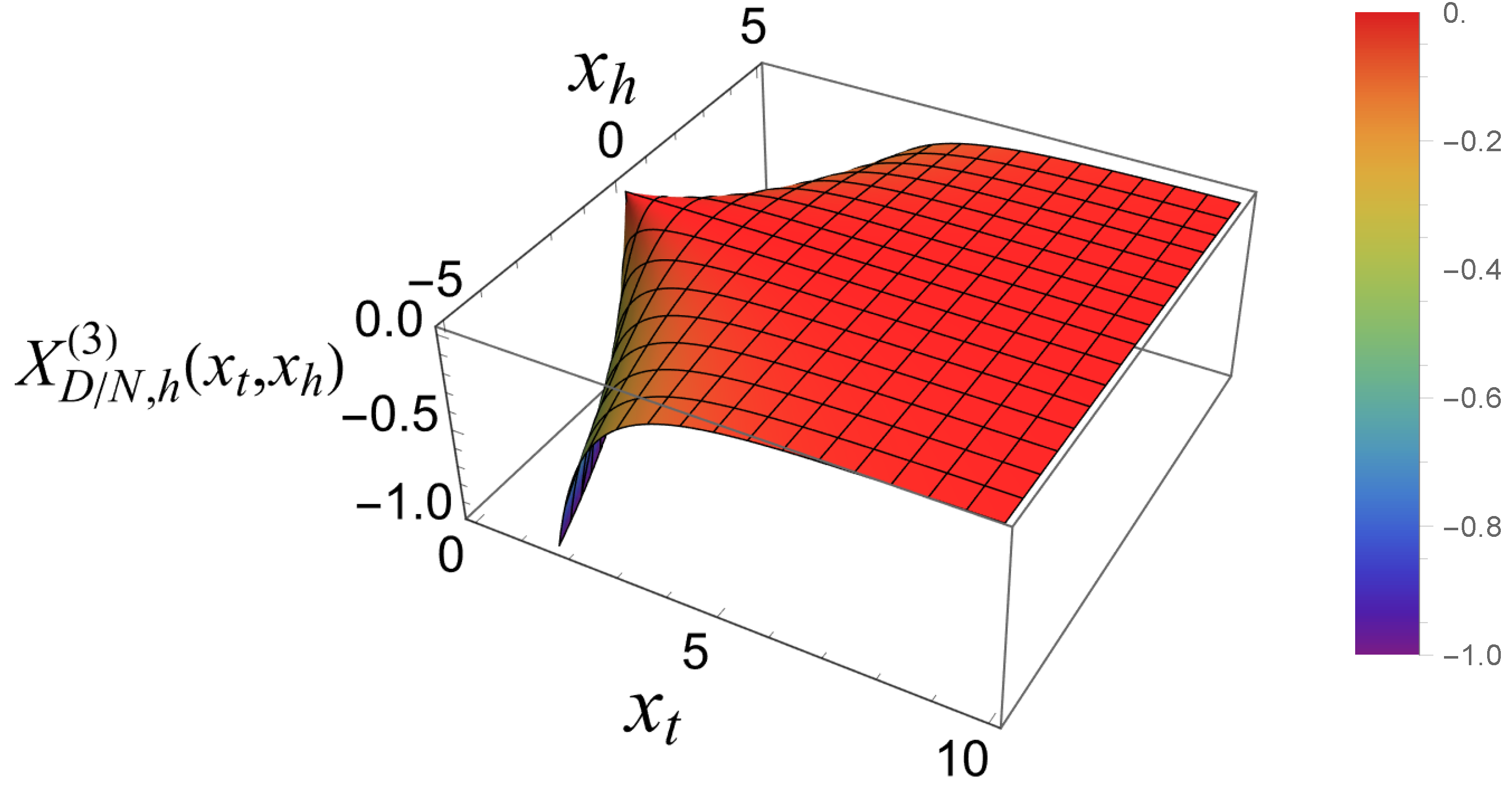
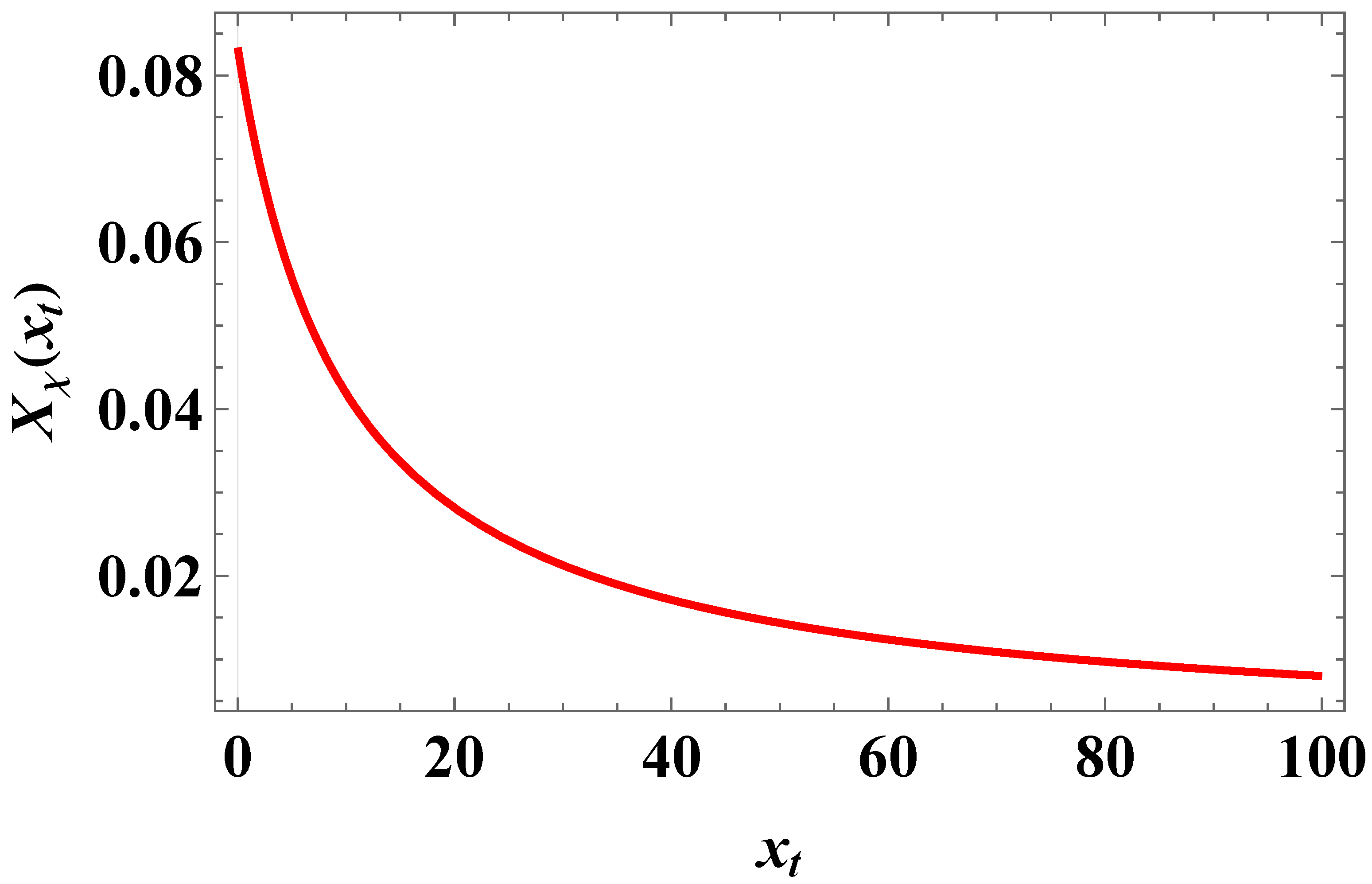
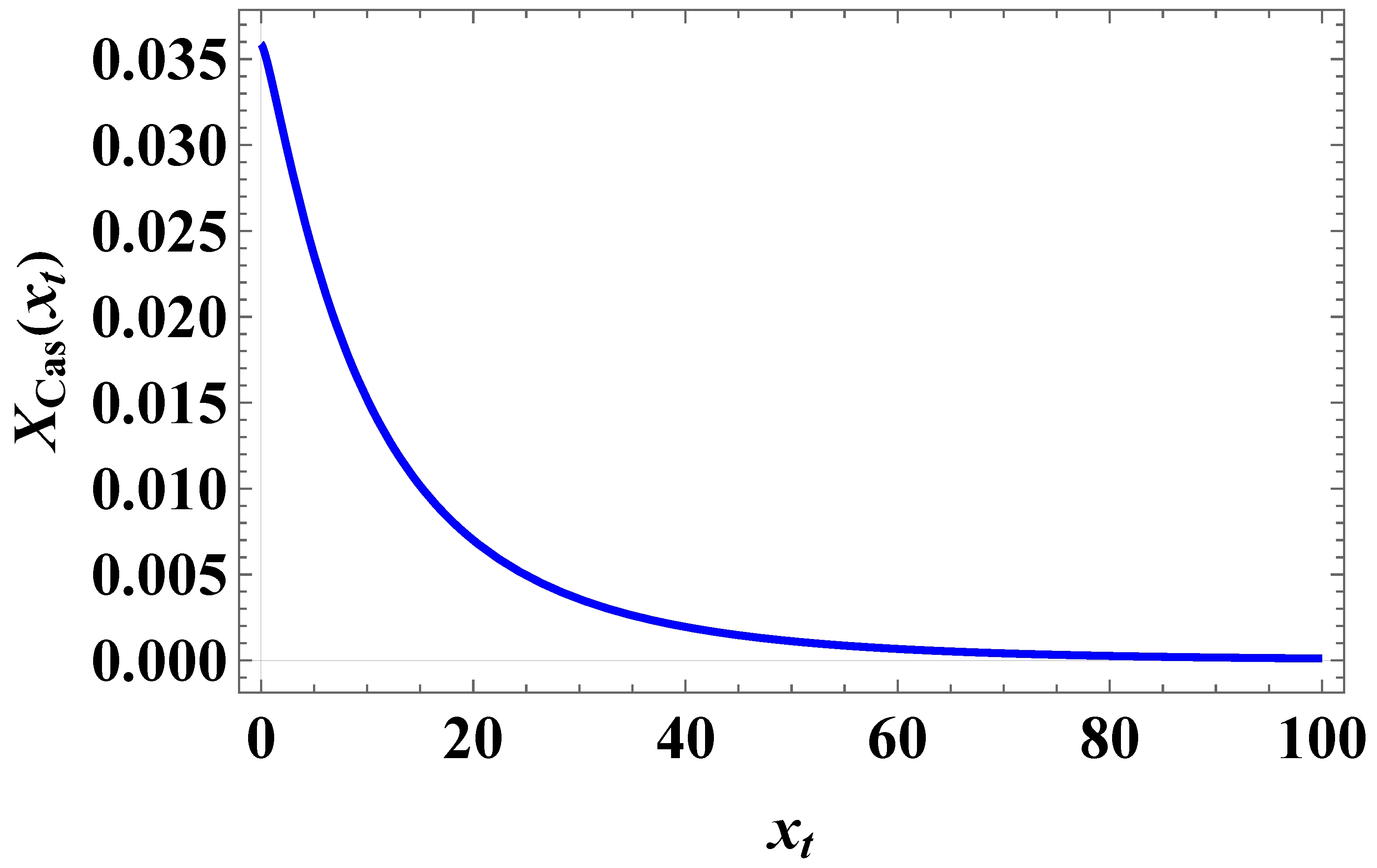
The behavior of the Casimir force in the CGM is shown in Figure 3 and Figure 5, and the behavior for the LGM - in Figure 8, Figure 9, Figure 10 and Figure 11. We observe that for $h=0$ the force is repulsive and, depending on magnitude of h, it can be both repulsive or attractive for $h\ne 0$. Contrary to this behavior, we observe that the force in the MFM is always attractive - both for $h=0$, see Figure 13, as well as for $h\ne 0$ – see Figure 14 and Figure 15.

From all of the above one can, at the very least, conclude the following:

(*)

The sign of the Casimir force for the GM is not necessarily the same for $h=0$, for which case they are very well known - see, e.g., [14,34,37,65], as it is for $h\ne 0$.

(**)

The predictions of the “workhorse" of statistical mechanics — the mean-field approach sometimes—in particular in the studies of the Casimir force—can be wrong even with respect to the predicted sign of the force.

The results presented in the current article are based on exact analytical expressions for both the Gaussian and mean-field model.