1. Introduction and Related Work
In Internet of Things (IoT) application, both reducing a transmission bandwidth and removing noise are necessary. The image compression can involve algorithm such, MPEG, but this algorithm is not able to remove the noise in the signal. Removing noise from images is quite a difficult task considering the content of the images and the possible types of noise.
An image is created by reflected light into the camera lens and captures by the sensor, that convert the variable levels of the light into digital signals for each image element (pixel). In the most common sensor, an amplifier is attached to each pixel and adjusts the output making the image darker or brighter, respectively. The output voltage is converted using an analog-to-digital converter where the variance in voltage to each pixel gets a binary value.
Noise represents unwanted content in an image caused by the condition existing when the image is captured: low light, slow shutter, sensor issues [
1]. Sharp and sudden disturbances could be appeared in the image, as well as uniform or constant disturbances. There are several noise sources. Most of the noise comes from the sensor or analog-to-digital conversion. For example, gaussian noise is a type of sensor noise as an effect of sensor heat. Another example, the salt and pepper noise manifests as pixels erroneously bright values in dark parts of the image or dark values in bright parts. It is similar with dead pixels, except salt and pepper noise will produce this effect randomly. Usually, analog-to-digital conversion cause this kind of noise or in transmitting images over noisy digital links. One class of denoising methods are based on filtering. Various filters are used to remove the noise in image. However, that filters produce approximations, and the noise characteristics and the unknown positions of noised pixels may cause errors in reconstructed image. This aspect represents motivation to develop non-filtering denoising techniques, based on detection and reconstruction of affected pixels [
1]. There are many methods to remove noise (median filtering, discrete cosine transform, wavelet transform, etc.) but each method can lead to blurring of the image or the removal of fine details from the image. On the other hand, the implementation of the noise elimination algorithm on microcontrollers with relatively limited resources and lower precision are aspects that must be studied.
This paper considers an image processing algorithm that involve compressive sensing and random sample consensus. It involves the discrete cosine transform (DCT) and can be used both to compress the image and to denoise it. This approach could remove efficiently different types of noise combined. The algorithm intensively uses the matrix multiplications.
In the literature is shown that sparse signals can be reconstructed from a reduced number of measurements. Digital images can be represented (for example in a discrete cosine transform – DCT) by a small number of coefficients with significant values and can be considered as sparse or approximately sparse in this domain. Other methods have been developed in the noise elimination from images which employ sparsity [
2,
3,
4,
5,
6]:
- -
weighted encoding with sparse nonlocal regularization (WESNR) based on soft impulse pixel detection, weighted encoding, and an integration of the sparsity and non-local self-similarity
- -
block-matching 3D (BM3D) algorithm based on the grouping of similar blocks, a collaborative filtering (an adaptive filter and a two-stage average adaptive filter) by shrinkage in the transform domain, and then combine back the blocks into a two-dimensional signal
- -
total-variation (TV) L1 methodology based on solving a minimization problem, considering that the image has a high total variation
- -
hyperspectral denoising, using the spatio-spectral total variation
- -
denoising algorithms based on deep learning and convolutional neural networks
- -
variants of the traditional mean and median filters
The compressive sensing idea is based on the sparsity of the sampled signal. Sparsity means that a discrete-time signal depends on several degrees of freedom much smaller than its finite length [
7,
8]. Many natural signals are sparse or compressible in the sense that they have concise representations when expressed in the proper basis or transformation
. There is a duality between time and transformation domain (frequency) that expresses the idea that samples having a sparse representation in transformation domain (frequency) must be spread out in the domain in which they are acquired (time). We consider
where
is an image with size
pixels represented as a vector, with
,
is a matrix of size
and
is a vector of size
. The small coefficients
may be discard in the representation of
without much loss. The right choice of coefficients can lead both to the elimination of noise and to the compression of the image. Let
be a vector of size
with
random chosen elements of
in the set
and the rest zero elements and
a matrix of size
with rows of the inverse of matrix
selected by elements in set
. The coefficients can be chosen using the compressive sensing principle. The coefficients are computing as
and then the signal is reconstructed as
. The vector
will be selected so that
to be minimum. The vector
can be chosen using random sampling consensus (CS-RANSAC) algorithm that works well in presence of relatively large number of disrupted pixels that will be considered as outliers. The other pixels, undisturbed or disturbed by weak noise will be considered as inliers and will be selected by CS-RANSAC algorithm as consensus set. The consensus set is the vector
and will be used in compressive sensing reconstruction as explain above.
The paper analyzes a noise elimination algorithm (CS-RANSAC) based on compressing sense and RANSAC combined with the DCT transform [
8,
9,
10]. It is focused on the implementation on microcontrollers (for the IoT applications) and performance analysis (execution time and precision) to reduce the calculation time. The following sections will describe the algorithm in detail, its performance with infinite precision, the implementation of proposed algorithm using microcontrollers and the performances obtained using finite precision. To improve the execution time, a modified algorithm that involve DCT denoising for image’s regions less affected by noise and CS-RANSAC algorithm for the image’s regions more affected by noise can be used. To do this, a simplified algorithm to estimate the noise power can be used [
18]. Finally, the results are shown and commented. The conclusion is that such non-filtering denoising techniques can be applied with good performance to eliminate or reduce the noise in images, and to compress the image, and suitable for IoT applications.
2. The Algorithm Description
The above-mentioned algorithm is based on sparsity of discrete cosine transform.
The CS-RANSAC algorithm is used to choose the non-noisy pixels. The DCT coefficients are determined using the compressive sensing method. The image to be processed is divided into blocks of smaller size (chosen according to the size of the two-dimensional DCT transform) and each block is processed separately. The two-dimensional DCT transforms (direct and inverse) will be calculated as matrix multiplications, considering that the block to be processed is transformed into a column vector, of dimensions with which will be multiplied by a matrix of dimensions determined by the DCT transformation matrix with where is the Kronecker product. The DCT transform will be and the inverse DCT transform is determined as . For each of the blocks, a subset of the set with pixels is randomly chosen. A matrix is then determined which contains the lines of transpose of corresponding to the indices of the elements chosen from the . Using the matrix, and the vector , the first coefficients of the two-dimensional DCT transform are determined. Using these coefficients, the vector is reconstructed and the error between nd is determined. These steps are repeated until the error is small enough or the number of iterations exceeds a maximum imposed number. The last determined DCT coefficients will be the coefficients used to restore the pixels from the processed block.
The algorithm uses two functions:
- -
the
CSrec function which receives as parameters the set of randomly chosen elements for determining non-noisy pixels, the modified transformation matrix and the number of DCT coefficients (sparsity factor) and returns the DCT coefficients that will be used to reconstruct the elements in the block [
9].
- -
the
pseudoinv function, which calculates the inverse of a matrix using an iterative method [
17].
The algorithm is designed so that it can be implemented as efficiently as possible (both on a computer with infinite precision and on a microcontroller with fewer resources and lower precision). The critical elements for a microcontroller implementation are matrix multiplication and calculation precision, especially when implementing the inverse matrix function. These aspects will be discussed in the microcontrollers’ implementation section. The algorithm is illustrated in
Figure 1. It was implemented in MATLAB (on a computer with an Intel I5-10210U processor at 1.60GHz, 4 cores, 6MB cache memory, 16 GB memory RAM and operating system Windows 10 Pro 64-bit) in order to validate the its functionality and to evaluate the performances obtained with infinite precision. Two implementations in C language were made using the Visual DSP++ development environment for Blackfin microcontrollers and a Maxim Eclipse SDK for MAX78000 microcontroller, including ARM, RISC V and CNN cores, with 32 bits finite precision fixed point.
The following sections describe the performance obtained for the MATLAB implementation, the specific implementation for microcontrollers and compare the performance obtained in the two implementations.
3. The Algorithm Performance Evaluation
This section describes the performance of above described algorithm in terms of quality of the reconstructed image. Selected parameters of the algorithm are:
The image size is set to 512 pixels in height and 512 pixels in width [
16] (for both type of implementations – MATLAB and microcontrollers). Gaussian noise, salt, and pepper noise (impulsive) and multiplicative noise (speckle) were successively added to the test images. Also, the image was blurred.
The performance of the algorithm was evaluated using peak signal to noise ratio
with
the noisy image, and
the reconstructed image, both of dimensions
, and structural similarity index measure
with
,
,
,
, and
are the mean, the variance and the covariance of pixels in windows
and
The constant coefficients
and
are used to stabilize the division with weak denominator. The
quantifies image quality degradation caused by data compression or by losses in data transmission. Unlike PSNR, SSIM is based on visible structures in the image and perhaps represents a more reliable indicator of image quality degradation. PSNR is an alternative measurement of quality of reconstructed image [
15]. The
Figure 2,
Figure 3 and
Figure 4 illustrate the performance of denoising algorithm with infinite precision (MATLAB implementation – 64 bits floating point). The noise is mixed noise. The results show an image quality improvement in both PSNR (up to 6 dB) and SSIM (up to 3 times) when using the CS-RANSAC algorithm.
The
Table 1 summarizes the performance of CS-RANSAC algorithm comparing with DCT denoising at the same level of sparsity. One can observe that the performance is netter for CS-RANSAC algorithm both for PSNR and SSIM criteria.
A more detailed performance evaluation is given in [
9]. In this paper, we evaluate the algorithm performance, in various implementation, to give a performance comparison between these implementations and to prove the possibility to implement, with good performance, relative complex image processing algorithms using microcontrollers in IoT applications.
4. The Microcontrollers’ Implementations
Two 32 bits fixed point microcontroller (e.g. Blackfin BF5xx, and MAX7800x, Analog Device) implementations are proposed in this section.
The Blackfin architecture is designed for multimedia applications, the accessible memory is up to hundreds of Mbytes and the processor clock frequency is up to 750 MHz The instruction set is powerful (arithmetic instructions, multiplications with accumulation, dual and quad instructions, hardware loops, multifunction instructions) [
13,
14].
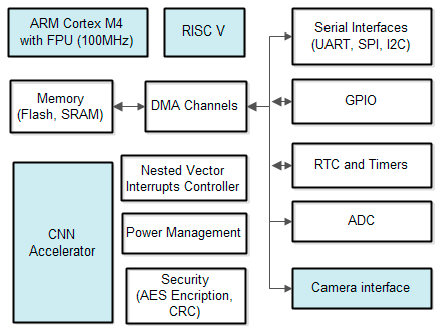
The MAX7800x chip is a dual core ultra-low power microcontroller with an ARM Cortex M4 processor with FPU up to 100 MHz with 16KB instruction cache, 512KB flash memory and 128KB SRAM, and a RISC-V Coprocessor up to 60MHz for digital signal processing instructions. There are many interfaces (general purpose IO pins – GPIO, serial ports, analog to digital convertor (10 bit, 8 channels), neural network accelerator optimized for deep convolutional neural networks (442k 8-bit weight capacity, network depth up to 64 layers with up to 1024 channels per layer), power management for battery operations, real time clock, timers, AES 128/192/256 and CRC hardware acceleration engine. The ARM Cortex-M4 with FPU processor CM4 is well suited for the neural networks system control and combines high-efficiency signal processing functionality with low energy consumption. The 32-bit RISC-V coprocessor is dedicated for ultra-low power consumption signal processing. The instructions set include: four parallel 8-bit additions/subtractions, floating point single precision operations, two parallel 16-bit additions/subtractions, two parallel MACs, 32- or 64-bit accumulate, signed, unsigned, data with or without saturation. A Convolutional Neural Network (CNN) unit is included in MAX7800x chip.
A more detailed architecture description of MAX 7800x and how the proposed implementation uses the CNN accelerator, and ARM and RISC V cores is shown in a next section.
The above presented algorithm was written in C programming language, using as integrated development environment Visual DSP ++ 5.1 and Maxim Eclipse SDK. The code was automatically optimized for speed (hardware loops, interprocedural analysis) [
12]. Some adaptations of the algorithm were made to reduce the execution time: for S = 15, the method of determining the set S has been changed (considering that the number of possible combinations is 16, a combination will be chosen randomly and the number of iterations in the CS-RANSAC algorithm is limited to a maximum of 16 iterations) and VSDP++ library functions were used for all matrix and vector operations [
11,
12]: matrix multiplication -
matmmltf, matrix addition and subtraction -
matsadd,
matssub, matrix transpose -
transpm, maximum and minimum element in a vector -
vecmax ,
vecmin, location of maximum and minimum element in a vector,
vecmaxloc,
vecminloc. The code uses a 32 bits representation for floating point algorithm variables and computations (multiplications and additions) [
11]. This approach will cause a slight decrease in precision and therefore the quality of the reconstructed image, but the use of a 32-bits fixed-point representation would excessively increase the execution time. The use of fixed-point representation keeps the processing time at reasonable values with an acceptable decrease in performance. The execution time was measured, in processor cycles, using the IDEs’ code profiler.
5. The Performance Using 32-Bits Fixed Point Microcontrollers
This section describes the results obtained using the 32 bits processor. The execution time and the effect of finite precision is shown in the
Figure 5,
Figure 6 and
Figure 7. One can observe, in these figures, that the performance is good. For low and medium levels of mixed noise, the CS-RANSAC algorithm has a PSNR greater with up to 4 dB and a SSIM greater up to 80%. The SSIM obtained with CS-RANSAC is better than that of DCT even the differences in PSNR are not so high for high level of mixed noise. The CS-RANSAC algorithm responds better for impulsive noise, as is shown in
Figure 7.
Table 2 summarizes the performances and
Table 3 compares the implementation in MATLAB with Blackfin implementation.
Table 4 illustrated the execution time considering a Blackfin processor at 750 MHz. An improved implementation using MAX7800x (with ARM core at 100 MHz, RISC V core at 60 MHz and CNN accelerator with 64 cores at 50 MHz) will be described in next sections.
Table 2.
Performance comparison (32-bits fixed point implementation).
Table 2.
Performance comparison (32-bits fixed point implementation).
| Noised Image |
DCT Reconstructed Image |
CS-RANSAC Reconstructed Image |
Execution Time CS-RANSAC Blackfin |
| PSNR |
SSIM |
PSNR |
SSIM |
PSNR |
SSIM |
Cycles |
Time |
| 20.48 |
0.36 |
23.92 |
0.46 |
26.04 |
0.59 |
4,675,862,063 |
6.23 |
| 17.14 |
0.21 |
20.8 |
0.29 |
24.18 |
0.54 |
5,662,802,735 |
7.55 |
| 14.29 |
0.15 |
17.87 |
0.21 |
22.21 |
0.62 |
8,728,624,005 |
11.64 |
| 15.04 |
0.18 |
18.04 |
0.25 |
19.47 |
0.42 |
7,584,207,993 |
10.11 |
| 19.6 |
0.38 |
22.45 |
0.46 |
23.45 |
0.57 |
4,520,337,537 |
6.03 |
Table 3.
Performance comparison (32-bits fixed point vs MATLAB implementation).
Table 3.
Performance comparison (32-bits fixed point vs MATLAB implementation).
| Noised Image |
DCT Reconstructed Image (Fixed Point 32 Bits) |
CS-RANSAC Reconstructed Image (Fixed Point 32 Bits ) |
DCT Reconstructed Image (MATLAB) |
CS-RANSAC Reconstructed Image (MATLAB) |
| PSNR |
SSIM |
PSNR |
SSIM |
PSNR |
SSIM |
PSNR |
SSIM |
PSNR |
SSIM |
| 20.48 |
0.36 |
23.92 |
0.46 |
26.04 |
0.59 |
24.04 |
0.46 |
28.14 |
0.63 |
| 17.14 |
0.21 |
20.8 |
0.29 |
24.18 |
0.54 |
20.91 |
0.29 |
26.92 |
0.58 |
| 14.29 |
0.15 |
17.87 |
0.21 |
22.21 |
0.62 |
18.03 |
0.21 |
25.41 |
0.71 |
Table 4.
Execution time – seconds (32 bits fixed point vs MATLAB implementation).
Table 4.
Execution time – seconds (32 bits fixed point vs MATLAB implementation).
| Noised Image |
Execution Time CS-RANSAC 32 Bits Fixed Point |
Execution Time CS-RANSAC MATLAB |
| PSNR |
SSIM |
Cycles |
Time |
Time |
| 20.48 |
0.36 |
4,675,862,063 |
6.23 |
2.49 |
| 17.14 |
0.21 |
5,662,802,735 |
7.55 |
4.79 |
One can observe, for medium to high noise, that the execution time is reasonable (about seconds). The execution time can be decrease by using a dual-core Blackfin processor. An implementation based on an accelerator for convolutional neural networks (CNN) is possible by implementing matrix multiplication using a 1x1 convolution performed with CNN.
6. The Improving of Processing Time Using CNN Accelerator
The multiplication of two matrices
and
with the result
and
can be performed using a fully interconnected layer as in
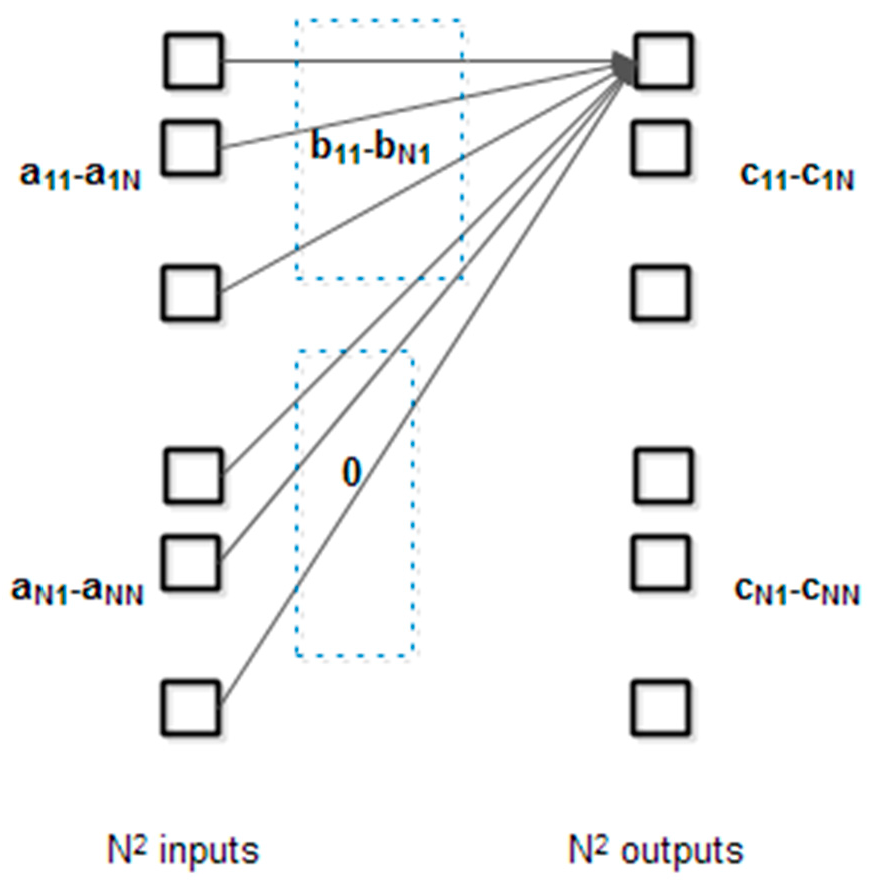
Figure 8:
The input layer consists of each row in matrix and the output layer contains the elements of product matrix. For each input elements, the weights are the corresponding elements of columns in matrix or zero elements. For clarity, only the weights for one output elements are shown.
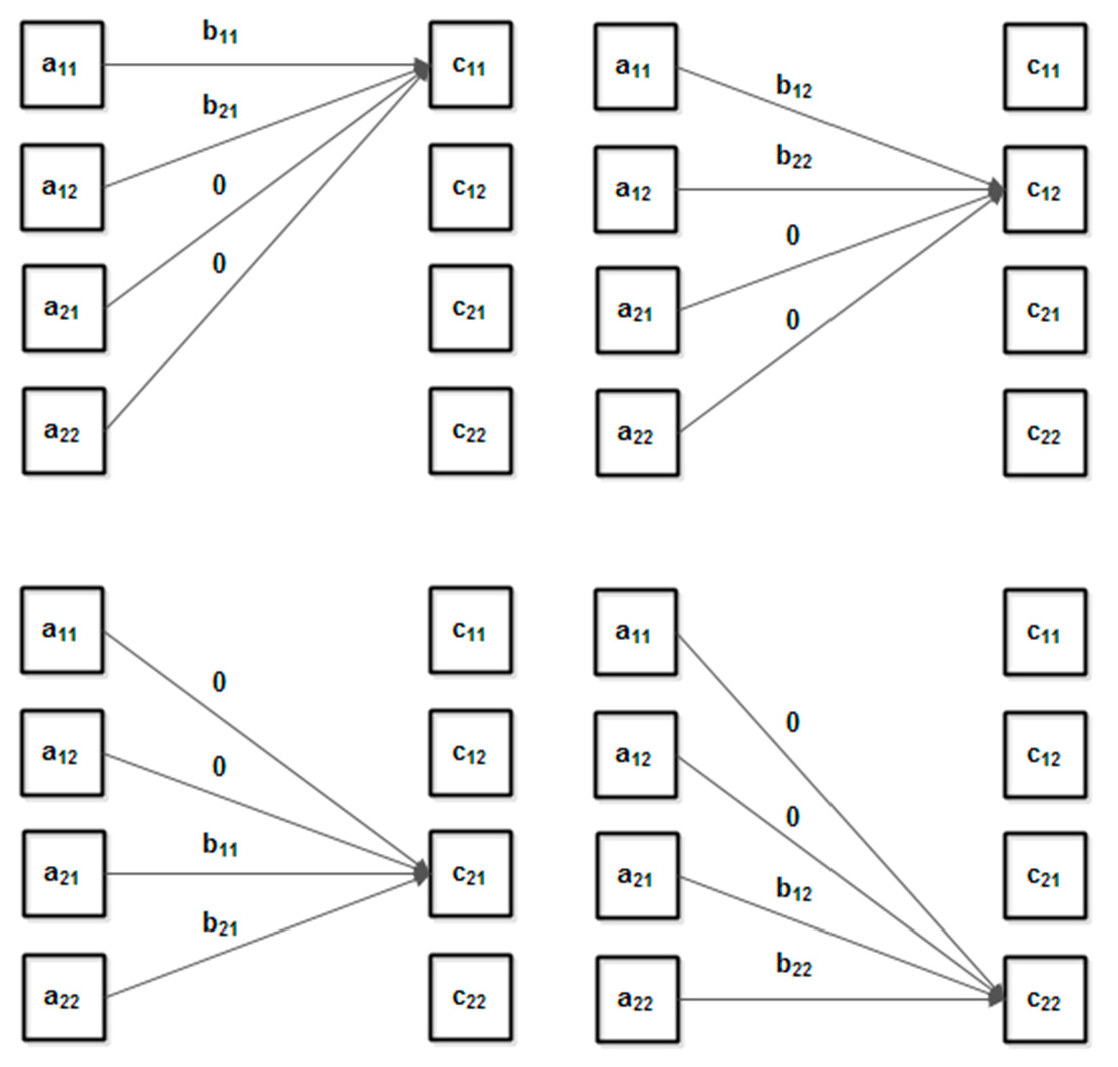
Figure 9 details the weights for a simple example (
):
For more clarity, the weights have shown individually for each output element.
The implementation of fully interconnected layer can be done in CNN by enabling the flatten mode (this mode supports a series of 1×1 convolution emulating a fully interconnected network with up to 1024 inputs).
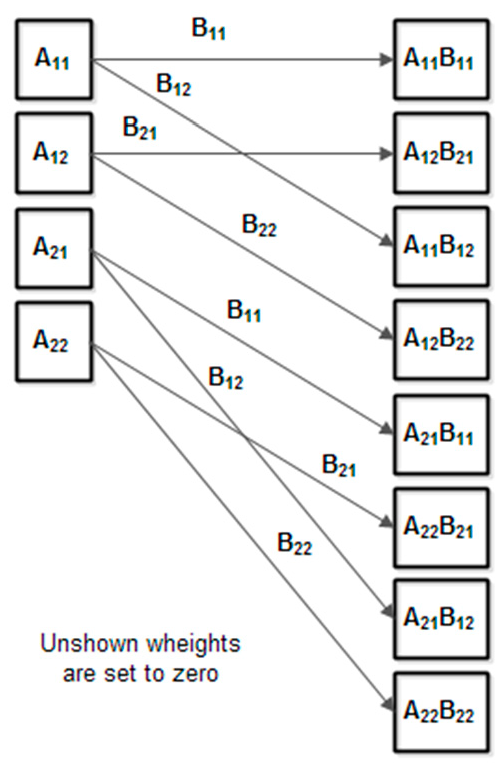
The matrix multiplication (fixed point) is shown in
Figure 10.
Using the above algorithm, a speedup about 30 times can be achieved for integer matrix multiplication, comparing with the implementation on a 32 bits fixed-point microcontroller. This can be useful for algorithms based on matrix computation that does not require large dynamic range.
In common CNNs the values of neural network layers and weights are represented in fixed point with 8 bits. There are certain applications that require more precision. For example, CS-RANSAC algorithm, presented in previous sections, requires higher precision due the DCT coefficients of lower order.
We proposed an approach that make possible the matrix multiplication with increased precision, considering a floating-point representation of matrix elements.
We assume that the values of matrix elements are
,
and
with
- mantises and
- exponents represented as fixed point integers with 8 bits. The output elements are
. The term
will be computed using a full interconnected layer as it has shown previously (with a slight modification of weights – see
Figure 11.) and the term
will be computed using the element-wise function (the element-wise function must be enabled in CNN and the addition function must be selected).
Then the maximum exponent is calculated as
and all the terms
will multiplied with
in a second full interconnected layer. The results
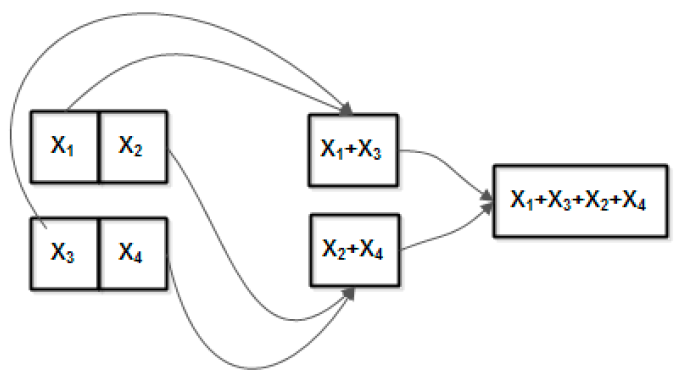
are summed using the element wise CNN features. The sum is calculated iteratively using the element wise addition in
steps as in
Figure 12.
Finally, in a third full interconnected layer the elements of matrix products
are calculated. We assume that in an image processing one matrix (image to process) has sub-unitary mantises and
The other matrix’s exponents and mantises are constant, therefore
and
can be passed as parameters in the matrix multiplication function. The complete algorithm is illustrated in
Figure 13:
The algorithm illustrated in
Figure 13 can be efficiently implemented using the MAX78000 chip [
19,
20]. The block diagram of MAX7800 is illustrated in
Figure 14. The CNN accelerator consists of 64 parallel processors with 512KB of SRAM-based storage. Each processor includes a pooling unit and a convolutional engine with dedicated weight memory. Four processors share one data memory. These are further organized into groups of 16 processors that share common controls. A group of 16 processors operates as a slave to another group or independently. Data is read from SRAM associated with each processor and written to any data memory located within the accelerator. Any given processor has visibility of its dedicated weight memory and to the data memory instance it shares with the three others.
In general, an algorithm (or working task) with instructions with average execution time per instruction can be divided in two parts: - running using one processor with average execution time per instruction and - running using processors with average execution time per instruction, with . The speedup is calculated as . Considering and with the speedup becomes
All the computations involved in matrix processing (multiplication, addition) can be implemented using the CNN block in flattened or element wise modes. The above presented CS-RANSAC algorithm illustrated above was implemented using MAX78000 and its CNN accelerator. The numerical precision is similar with numerical precision obtained with previous implementation on Blackfin (the ARM and RISC cores in MAX78000 also use 32 bits fixed point representation).
In the speedup relation we set (the number of cores in CNN), the ratio between ARM microcontroller speed and Blackfin microcontroller), the ratio between CNN cores speed and Blackfin microcontroller), and the algorithm code that not contain matrix operations that can be performed in CNN). With this value the theoretical speedup (between Blackfin implementation and MAX7800 implementation) is The effective speedup (obtained by counting processor cycles by the IDE code profiler) is lower due the data transfers performed using RISC V.
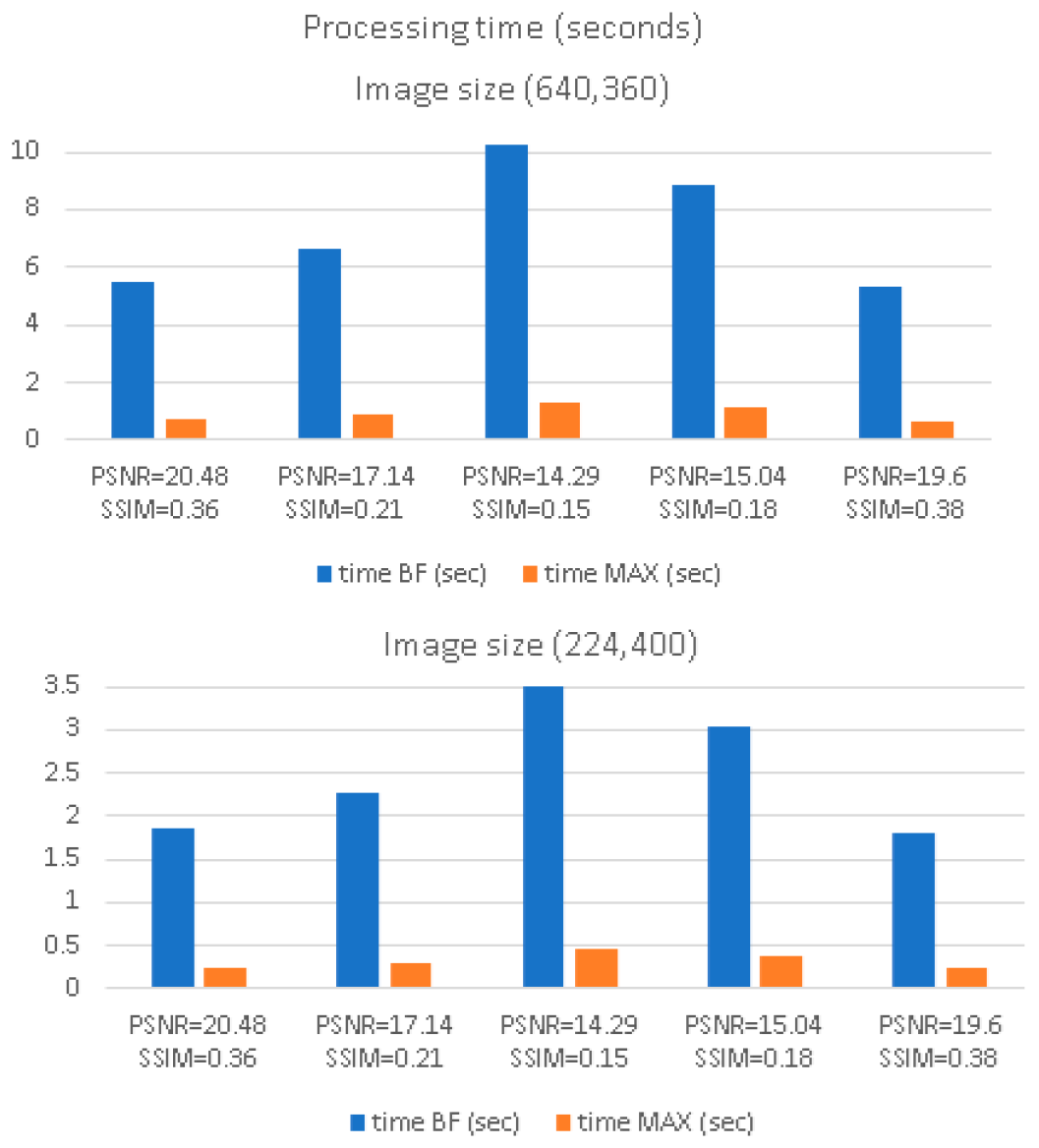
Figure 15 illustrated the execution time obtained with CNN implementation. In this case (software floating point implementation) the speedup obtained is about 7 times for the CS-RANSAC algorithm.
The computing time of the algorithm can be improved modifying the way to calculate DCT coefficients using original DCT or CS-RANSAC depends if the block is noisy or not, and using in parallel the ARM and CNN
For the first improving method, the original CS-RANSAC algorithm was combined with a noise estimator [
21]. Each block is marked as light noised or heavy noised and is processed using simple DCT or CS-RANSAC, respectively. The noise estimator can be implemented in fixed point using in parallel the ARM and RISC-V microcontrollers in MC78000 chip.
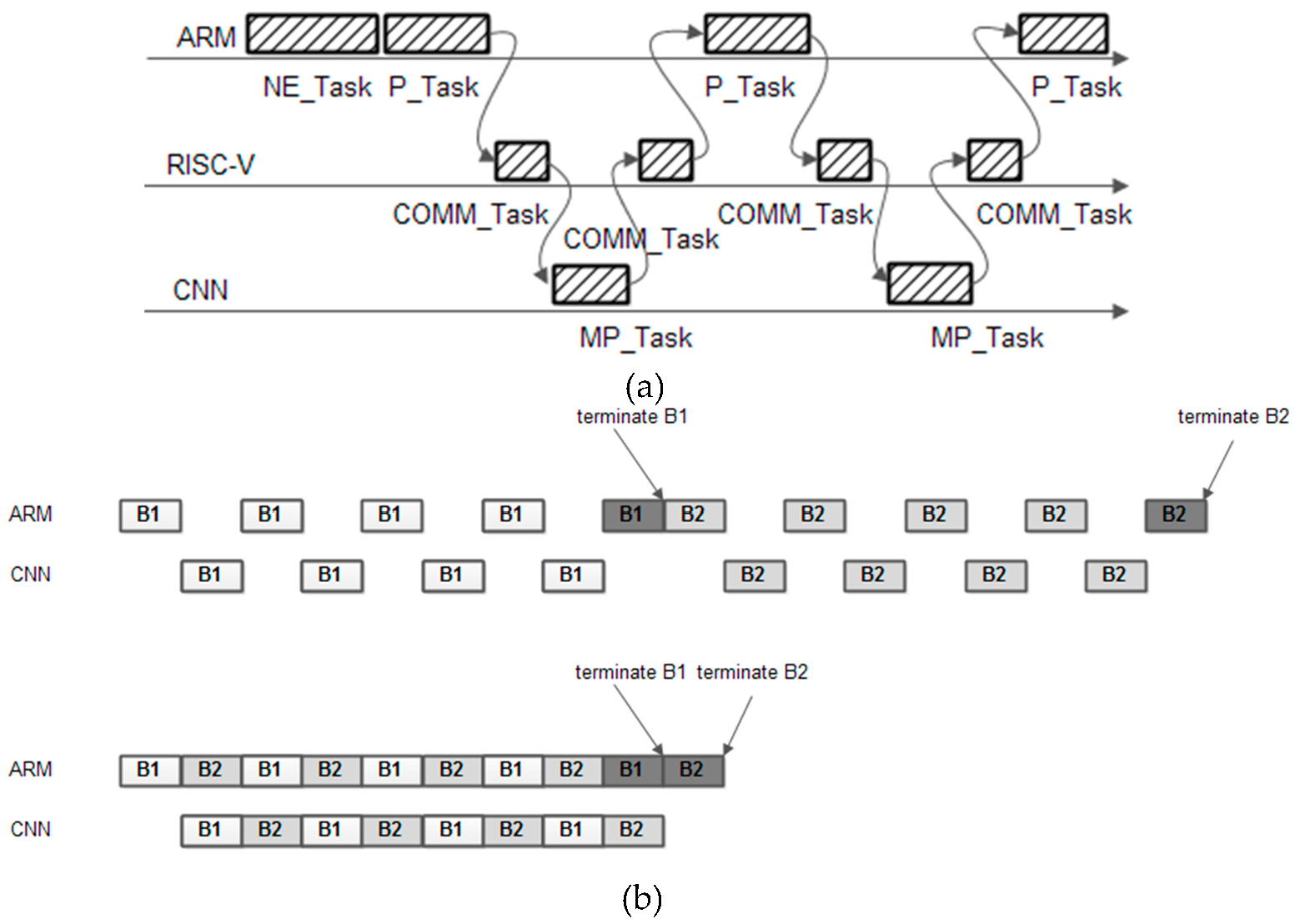
Figure 16(a) shows how the tasks for such implementation can be scheduled.
The following tasks is defined: NE_Task - for noise estimate, P_Task - the processing task that implement all the processing for DCT and CS-RANSAC noise removal and compression algorithms excepts the matrix multiplications and matrix additions which are computed by the a matrix processing task - MP_Task and COMM_task - a communication task that transfer using DMA channels the information (matrix values) between CNN and ARM. The tasks: NE_Task and P_Task are running in ARM core, the task COMM_task is running in ARM coprocessor (that acts as a direct memory access - DMA controller). All the matrix manipulations are passed to CNN accelerator (programmed in flatten mode for matrix multiplications or element wise mode for matrix additions or subtractions) and are computed by MP_Task. All tasks are synchronized using global semaphores.
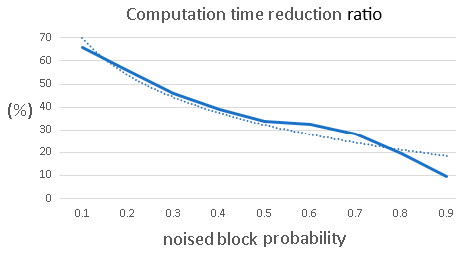
Depend on noise level, the execution time can be reduced as is illustrated in
Figure 17 [
22].
For an average noise probability of 50% one can observe that the computation time reduction ratio is about 35%. If the noise estimator is not used, the task
NE_Task in the scheduling tasks from
Figure 16 is removed.
The second method ensures halving of computation time. This goal is achieved by partitioning the computation in matrix operations (multiplications, addition)- performed in CNN and non-matrix operations (all the remaining computations) - performed in ARM. Two blocks are processing in parallel in ARM and CNN, alternatively, as it is shown in
Figure 16(b).
7. Conclusion
This paper focuses on the analysis of the possibility of accelerating the necessary processing in algorithms based on matrix operations. Accelerating these operations can be achieved using neural network processing units (NPUs) integrated into the architecture of today’s high-performance microcontrollers. As an example, the paper presents implementations and performance analysis of an image compression and noise removal algorithm based on compressive sensing and CS-RANSAC.
This algorithm was validated as good algorithm in terms of noise removal and image compression using infinite precision implementation (e.g. MATLAB simulations). The main goal of this work is to evaluate if a microcontroller implementation is feasible in terms of processing accuracy and computation time to be used in IoT applications that involve hardware nodes with resources constrains.
The obtained results show that a good quality of the reconstructed image can be obtained for medium to high noise levels in a calculation time of the order of seconds or tenth of seconds.
Also, the paper proposes methods to improve the algorithm: (1) by selectively applying DCT or the CS-RANSAC to each block in the image (without degrading the quality of the image), and (2) be using in parallel the ARM microcontroller and CNN cores or using a dual core Blackfin microcontroller.
Author Contributions
Conceptualization, S.Z.; methodology, R.Z.; software, S.Z.; validation. R.Z.; formal analysis, R.Z.; investigation, S.Z.; resources, S.Z.; data curation, R.Z.; writing—original draft preparation, S.Z.; writing—review and editing, R.Z., S.Z.; visualization, R.Z.; funding acquisition, S.Z. All authors have read and agreed to the published version of the manuscript.
Funding
The research leading to these results received funding from the Research Centre on Systems Software and Networks in Telecommunication (CCSRST).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bartyzel, K. Adaptive Kuwahara filter. Signal Imag Video Process 2016, 10, 663–670. [Google Scholar] [CrossRef]
- Jiang, J.; Zhang, L.; Yang, J. Mixed Noise removal by weighted encoding with sparse nonlocal regularization. IEEE Trans Image Process 2014, 23, 2651–2662. [Google Scholar] [CrossRef] [PubMed]
- Strong, D.; Chan, T. Edge-preserving and scale-dependent properties of total variation regularization. 2003. [Google Scholar] [CrossRef]
- Dabov, K.; Foi, A.; Katkovnik, V.; Egiazarian, K. Image denoising by sparse 3D transform-domain collaborative filtering. IEEE Transactions on Image Processing 2017, 16, 2080–2095. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Sun, J.; Li, H.; Xu, Z. ADMM-CSNEt: a deep learning approach for image compressive sensing. IEEE Trans Pattern Anal Mach Intell 2020, 42, 521–538. [Google Scholar] [CrossRef] [PubMed]
- Yu, G.; Sapiro, G. DCT Image Denoising: A Simple and Effective Image Denoising Algorithm. Image Processing Online 2011, 1, 292–296. [Google Scholar] [CrossRef]
- Strutz, T. Data Fitting and Uncertainty (A practical introduction to weighted least squares and beyond), 2nd editionSpringer Vieweg, 2016; ISBN 978-3-658-11455-8. [Google Scholar]
- Raguram, R.; Frahm, J.M.; Pollefeys, M. A Comparative Analysis of RANSAC Techniques Leading to Adaptive Real-Time Random Sample Consensus. In Proceedings of the 10th European Conference on Computer Vision Part II; 2008; pp. 500–513. [Google Scholar] [CrossRef]
- Stanković, I.; Brajović, M.; Lerga, J.; et al. Image denoising using RANSAC and compressive sensing. Multimedia Tools Appl 2022, 81, 44311–44333. [Google Scholar] [CrossRef]
- Candes, E.J.; Wakin, M.B. An Introduction to Compressive Sampling. IEEE Signal Processing Magazine 2008, 25, 21–30. [Google Scholar] [CrossRef]
- Fast Floating-Point Arithmetic Emulation on Blackfin Processors. Retrieved May 2024. https://www.analog.com/media/en/technical-documentation/application-notes/ee.185.rev.4.08.07.pdf.
- VisualDSP++ 5.0 C/C++ Compiler and Library Manual for Blackfin Processors. Retrieved May 2024. https://www.analog.com/media/en/dsp-documentation/software-manuals/50_bf_cc_rtl_mn_rev_5.4.pdf.
- ADSP-BF533 Blackfin Processor Hardware Reference. Retrieved May 2024. https://www.analog.com/media/en/dsp-documentation/processor-manuals/ADSP-BF533_hwr_rev3.6.pdf.
- ADSP-BF533 EZ-KIT Lite® Evaluation System Manual. https://www.analog.com/media/en/technical-documentation/user-guides/ADSP-BF533_ezkit_man_rev.3.2.pdf.
- Horé, A.; Ziou, D. Image Quality Metrics: PSNR vs. SSIM. In Proceedings of the 2010 20th International Conference on Pattern Recognition, Istanbul, Turkey; 2010; pp. 2366–2369. [Google Scholar] [CrossRef]
- Retrieved May 2024. https://webpages.tuni.fi/imaging/tampere17/tampere17_grayscale.zip.
- Retrieved May 2024. https://aalexan3.math.ncsu.edu/articles/mat-inv-rep.pdf.
- Ponomarenko, M.; Gapon, N.; Voronin, V.; Egiazarian, K. Blind estimation of white Gaussian noise variance in highly textured images. In Proceedings of the Image Processing: Algorithms and Systems XVI; 2018. [Google Scholar] [CrossRef]
-
https://www.analog.com/media/en/technical-documentation/data-sheets/MAX78000.pdf.
-
https://www.analog.com/media/en/technical-documentation/user-guides/max78000-user-guide.pdf.
- Ponomarenko, M.; Gapon, N.; Voronin, V.; Egiazarian, K. Blind estimation of white Gaussian noise variance in highly textured images. In Proceedings of the Image Processing: Algorithms and Systems XVI; 2018. [Google Scholar] [CrossRef]
- Zoican, S.; Zoican, R.; Galatchi, D. Image denoising algorithm for IoT based on compressive sensing principle and Blackfin microcontrollers. In Proceedings of the 2024 15th International Conference on Communications (COMM), Bucharest, Romania; 2024; pp. 1–4. [Google Scholar] [CrossRef]
Figure 1.
The CS-RANSAC algorithm.
Figure 1.
The CS-RANSAC algorithm.
Figure 2.
Performance evaluation for low noise (noised image PSNR 20 dB, SSIM 0.36). Mixed noise: gaussian variance = 0.001; salt and pepper density 2%; blur kernel window length = 3; speckle variance = 0.001.
Figure 2.
Performance evaluation for low noise (noised image PSNR 20 dB, SSIM 0.36). Mixed noise: gaussian variance = 0.001; salt and pepper density 2%; blur kernel window length = 3; speckle variance = 0.001.
Figure 3.
Performance evaluation for large noise (noised image PSNR 17 dB, SSIM 0.22). Mixed noise: gaussian variance = 0.001; salt and pepper density 5%; blur kernel window length = 3; speckle variance = 0.001.
Figure 3.
Performance evaluation for large noise (noised image PSNR 17 dB, SSIM 0.22). Mixed noise: gaussian variance = 0.001; salt and pepper density 5%; blur kernel window length = 3; speckle variance = 0.001.
Figure 4.
Performance evaluation for impulsive noise. Noise density 10% (noised image PSNR 14 dB, SSIM 0.15).
Figure 4.
Performance evaluation for impulsive noise. Noise density 10% (noised image PSNR 14 dB, SSIM 0.15).
Figure 5.
Performance evaluation for low noise (noised image PSNR 20 dB, SSIM 0.36). Mixed noise: gaussian variance = 0.001; salt and pepper density 2%; blur kernel window length = 3; speckle variance = 0.001.
Figure 5.
Performance evaluation for low noise (noised image PSNR 20 dB, SSIM 0.36). Mixed noise: gaussian variance = 0.001; salt and pepper density 2%; blur kernel window length = 3; speckle variance = 0.001.
Figure 6.
Performance evaluation for large noise (noised image PSNR 17 dB, SSIM 0.22). Mixed noise: gaussian variance = 0.001; salt and pepper density 5%; blur kernel window length = 3; speckle variance = 0.001.
Figure 6.
Performance evaluation for large noise (noised image PSNR 17 dB, SSIM 0.22). Mixed noise: gaussian variance = 0.001; salt and pepper density 5%; blur kernel window length = 3; speckle variance = 0.001.
Figure 7.
Performance evaluation for impulsive noise (noised image PSNR 14 dB, SSIM 0.15). Noise density 10%.
Figure 7.
Performance evaluation for impulsive noise (noised image PSNR 14 dB, SSIM 0.15). Noise density 10%.
Figure 8.
Neural network fully interconnected layer used for matrix multiplication.
Figure 8.
Neural network fully interconnected layer used for matrix multiplication.
Figure 9.
Neural network fully interconnected layer used for matrix multiplication (detailed example for ).
Figure 9.
Neural network fully interconnected layer used for matrix multiplication (detailed example for ).
Figure 10.
Matrix multiplication CNN-based algorithm (fixed point).
Figure 10.
Matrix multiplication CNN-based algorithm (fixed point).
Figure 11.
The full interconnected layer for floating point implementation ().
Figure 11.
The full interconnected layer for floating point implementation ().
Figure 12.
Element wise addition (example for ).
Figure 12.
Element wise addition (example for ).
Figure 13.
Matrix multiplication CNN-based algorithm (floating point).
Figure 13.
Matrix multiplication CNN-based algorithm (floating point).
Figure 14.
The MAX7800x general architecture.
Figure 14.
The MAX7800x general architecture.
Figure 15.
Processing time (various noised image sizes) for two 32-bits fixed point implementations (Blackfin and Max78000 CNN).
Figure 15.
Processing time (various noised image sizes) for two 32-bits fixed point implementations (Blackfin and Max78000 CNN).
Figure 16.
(a) Tasks scheduling for the algorithm (b) algorithm improving using parallel processing (RISC V is not shown, for clarity).
Figure 16.
(a) Tasks scheduling for the algorithm (b) algorithm improving using parallel processing (RISC V is not shown, for clarity).
Figure 17.
Computing time reduction (in dot line – trendline of ratio).
Figure 17.
Computing time reduction (in dot line – trendline of ratio).
Table 1.
DCT denoising vs CS-RANSAC denoising.
Table 1.
DCT denoising vs CS-RANSAC denoising.
| Noised Image |
DCT Reconstructed Image |
CS-RANSAC Reconstructed Image |
| PSNR |
SSIM |
PSNR |
SSIM |
PSNR |
SSIM |
| 20.48 |
0.36 |
24.04 |
0.46 |
28.14 |
0.63 |
| 17.14 |
0.21 |
20.91 |
0.29 |
26.92 |
0.58 |
| 14.29 |
0.15 |
18.03 |
0.21 |
25.41 |
0.71 |
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).