Gravitational Waves as a Probe to the Early Universe

1. Introduction

The stochastic background of the primordial gravitational wave (GW) was predicted in inflationary cosmology [1,2,3,4]. These stochastic GWs are a source of CMB anisotropies and polarizations [5]. In particular, the “B-mode” pattern in the polarization of the Cosmic Microwave Background (CMB) is due to these stochastic GWs [6]. Detecting these characteristic modes will show the existence of primordial GWs whose spectrums can provide more information about the early universe before the last scattering surface. In general, the spectrum of GWs depends on several processes in cosmic history. They are sensitive to inflationary models [1,4], especially during the late stage of the inflationary epoch or the early stage of the radiation era. After the transition phase, these GWs were red-shifted in subsequent eras, while their amplitude kept decaying, modifying the amplitude of the GW spectrum. The free streaming of neutrinos that took place during the radiation-dominant era, as analyzed by Weinberg [7] along with other relevant research [8,9,10], is a well-known process for altering the spectrum of primordial GWs. In addition, the late-time acceleration of the universe can also adjust the spectrum. [11].

In the early universe, it is essential for primordial inflation to conclude with a transition to the radiation-dominant phase in the standard Big Bang model [12]. This transition opens up a variety of possibilities, as numerous post-inflation models exist, including a large-scale reheating period [13,14,15]. A compelling issue then arises: how can we effectively differentiate between these models by theoretical arguments and observational data?

A promising approach is to analyze the amplitude spectrum of primordial GWs. Each unique scenario of early cosmic history imprints distinct signatures on this spectrum, providing crucial insights. Regardless of the specific route a model may assume, all of them illustrate the transformation of spacetime from a de Sitter phase to a radiation-dominant state. By examining the gravitational wave equation, which incorporates a scale factor and its derivative, one can unfold the post-inflationary expansion toward the radiation-dominant epoch followed by the typical hot Big Bang trajectory.

We are particularly concerned with how the transition from the exponential expansion in de Sitter space to the power-law expansion at the radiation-dominant stage may have significant implications. Whether this transition occurs smoothly or abruptly can lead to distinctly different contributions to the higher-order derivatives of scale factors, ultimately shaping the nuances of the gravitational wave spectrum. Among viable scenarios, the Running Vacuum Model (RVM) [16,17,18], which introduces an evolving vacuum energy density and is expressed as a function of the Hubble parameter H, provides a seamless bridge from inflation to the radiation-dominant epoch. The evolution of spacetime within the RVM framework suggests that particle creation plays a pivotal role in altering the equation of state. We can interpret this phenomenon as a back-reaction process, where the accumulation of perturbations influences the fabric of de Sitter space, gradually transforming it into a radiation-dominant universe.

In this paper, we aim to investigate the gravitational waves generated during the inflationary period and how they evolve through a smooth transition phase. Our objective is to examine the modifications to the gravitational wave spectrum. We will consider the effects of back-reaction, reformulating the gravitational wave equation into an inhomogeneous equation, which we will solve using the retarded Green’s function. In addition, we plan to identify key parameters that can be adjusted to model the transition time scale and to observe the resulting changes in the spectrum. Specifically, we are interested in how the spectrum is modified when de Sitter spacetime transitions to radiation-dominant spacetime, whether this change occurs slowly or quickly.

2. Methodology

We revisit the generation of primordial gravitational waves within the framework of the running vacuum model, as studied in [19], but with a novel approach. The RVM posits that vacuum energy is dynamic and can be expressed in relation to the Hubble parameter that governs cosmic expansion. At an early epoch, this dynamic vacuum energy coexists with radiation, facilitating a smooth transition from the primordial inflationary phase to the radiation-dominant era of the universe, which is rooted in the standard Hot Big Bang theory. We interpret this evolution as a consequence of the increasing radiation component, which transforms the initial de Sitter spacetime into a radiation-dominated state. To explore this further, we reformulate the gravitational wave equation of motion as an inhomogeneous equation. The left-hand side of this equation encapsulates the inflationary expansion of the cosmic background, while the terms on the right-hand side are responsible for accounting for the effects of backreaction. We then go on to calculate the gravitational wave spectrum and analyze its dynamic behavior within the continuously expanding background.

2.1. The Background Model

The primeval evolution of the Universe can be described using a spatially flat Friedmann–Lemaître– Robertson–Walker (FLRW) metric, characterized by a scale factor $a\left(t\right)$, as

$$d{s}^2=d{t}^2-a^2\left(t\right)d{x}^{i}d{x}^j,$$

(1)

where the cosmic background expands in conjunction with the Hubble parameter $H=\dot{a}/a$. In this framework, the dynamics of the decaying vacuum is governed by $\Lambda \left(H\right)$ [20,21]. To define the vacuum energy density, we adopt the functional form for $\Lambda \left(H\right)$ as proposed in [19]:

$$8\pi G{\rho }_{\mathrm{vac}}\left(H\right)=\Lambda \left(H\right)={\Lambda }_b+3{\displaystyle \frac{H^3}{H_I}},$$

(2)

where ${\Lambda }_b$ represents the bare cosmological constant and $H_I$ is the initial Hubble parameter that defines the early de Sitter phase. If we express the equation of state of the Universe as $p=w\rho$, the Hubble parameter must satisfy the equation of motion,

$$2{\displaystyle \frac{H^{\prime }}{a}}+3\left(1+w\right)H^2\left[1-{\displaystyle \frac{H}{H_I}}\right]-\left(1+w\right){\Lambda }_b=0,$$

(3)

where primes indicate derivatives with respect to the conformal time $\eta$ such that $dt=a\left(\eta \right)d\eta$. Assuming the vacuum decays predominantly into ultra-relativistic particles with $w=1/3$, radiation naturally emerges and coexists with the dynamical vacuum at times when the bare term can be neglected, i.e., ${\Lambda }_b\ll H^3/H_I$. This leads us to a non-linear equation for the scale factor:

$$a^{\prime \prime }-{\displaystyle \frac{2}{H_I}}{\left({\displaystyle \frac{a^{\prime }}{a}}\right)}^3=0.$$

(4)

Integrating the equation above yields

$$\begin{array}{c}\hfill a\left(\eta \right)={\displaystyle \frac{1}{2C_1}}\left[\eta +C_2+\sqrt{{\left(\eta +C_2\right)}^2+{\displaystyle \frac{4C_1}{H_I}}}\right],\end{array}$$

(5)

where $C_1$ and $C_2$ are determined by the continuity of $a\left(\eta \right)$ and $a^{\prime }\left(\eta \right)$. It is essential for the scale factor to reduce to the form characteristic of de Sitter spacetime, such that $a\left(\eta \right)\propto {\left|\eta \right|}^{-1}$ in the distant past, and $a\left(\eta \right)\propto \eta$ during the radiation-dominant phase. Consequently, the comparison of these two trends will enable us to pinpoint the moment when radiation energy becomes significant, thereby allowing us to estimate the duration of the post-inflationary reheating stages.

The reduced Hubble parameter during the post-inflationary transition, denoted as ${\mathcal{H}}_{\mathrm{T}}$, is an important measure for characterizing cosmic expansion that takes place before the onset of the radiation-dominant epoch. It can be easily determined using Equation (5) such that

$$\begin{array}{c}\hfill {\mathcal{H}}_{\mathrm{T}}\left(\eta \right)={\displaystyle \frac{a^{\prime }}{a}}={\displaystyle \frac{1}{\sqrt{{\left(\eta +C_2\right)}^2+\frac{4C_1}{H_I}}}}.\end{array}$$

(6)

This function reaches its maximum value at ${\eta }_{\max }=-C_2$, leading to

$${\mathcal{H}}_{\mathrm{T}}\left(-C_2\right)={\mathcal{H}}_{\mathrm{T}}\left({\eta }_{\max }\right)\equiv {\mathcal{H}}_{\max }=\sqrt{{\displaystyle \frac{H_I}{4C_1}}}.$$

(7)

Under the circumstances, the Hubble function can then be expressed in terms of ${\eta }_{\max }$ and ${\mathcal{H}}_{\max }$ as follows:

$$\begin{array}{c}\hfill {\mathcal{H}}_{\mathrm{T}}\left(\eta \right)={\displaystyle \frac{1}{\sqrt{{\left(\eta -{\eta }_{\max }\right)}^2+\frac{1}{{\mathcal{H}}_{\max }^2}}}}.\end{array}$$

(8)

2.2. Cosmological Tensor Perturbations

In the conformally flat FLRW geometry, gravitational waves can be induced by a small tensor perturbation $h_{ij}$ defined in

$$\begin{array}{c}\hfill d{s}^2=a^2\left(\eta \right)\left[d{\eta }^2-\left({\delta }_{ij}+h_{ij}\right)d{x}^{i}d{x}^j\right],\end{array}$$

(9)

where $\left|h_{ij}\right|\ll 1$, and is transverse-traceless satisfying the gauge conditions: $h_{0\mu }=0$, $h_i^i=0$, and ${\nabla }^j{h}_{ij}=0$. Accordingly, the wave equation for GWs in this framework is expressed as ${\partial }_{\mu }\left(\sqrt{-g}{\partial }^{\mu }{h}_{ij}\left(\eta ,\mathbf{x}\right)\right)=0$. The general solution to this equation can be expanded in Fourier space as usual and is given by

$$\begin{array}{c}\hfill h_{ij}\left(\eta ,\mathbf{x}\right)=\int {\displaystyle \frac{d^3\mathbf{n}}{{\left(2\pi \right)}^3}}\sum _{\gamma =+,\times }{ϵ}_{ij}^{\gamma }\left(\mathbf{n}\right)\left[h_n^{\gamma }\left(\eta \right)e^{i\mathbf{n}·\mathbf{x}}+\mathrm{h}.\mathrm{c}.\right],\end{array}$$

(10)

where the mode function $h_n^{\gamma }\left(\eta \right)$ adheres to the symmetry condition $h_{-k}^{\gamma *}\left(\eta \right)=h_k^{\gamma }\left(\eta \right)$. Here, $\mathbf{n}$ denotes the comoving wave vector and ${ϵ}_{ij}^{\gamma }\left(\mathbf{n}\right)$ represents the transverse-traceless polarization tensor. The relationship between the comoving wave number n associated with the wave length $\lambda$ and the scale factor $a\left(\eta \right)$ is expressed as

$$\begin{array}{c}\hfill n=\left|\mathbf{n}\right|={\displaystyle \frac{2\pi a\left(\eta \right)}{\lambda }}=ka\left(\eta \right).\end{array}$$

(11)

Consequently, the evolution of the mode function, with the polarization index $\gamma$ omitted for simplicity, is governed by the following mode equation:

$$\begin{array}{c}\hfill h_n^{\prime \prime }\left(\eta \right)+2\mathcal{H}\left(\eta \right)h_n^{\prime }\left(\eta \right)+n^2{h}_n\left(\eta \right)=0.\end{array}$$

(12)

By introducing the substitution ${\mu }_n\left(\eta \right)=a\left(\eta \right)h_n\left(\eta \right)$, the mode equation can be recast into a more manageable form,

$$\begin{array}{c}\hfill {\mu }_n^{\prime \prime }+\left(n^2-{\displaystyle \frac{a^{\prime \prime }}{a}}\right){\mu }_n=0.\end{array}$$

(13)

It is noteworthy that the term $a^{\prime \prime }/a$ can be interpreted as an effective potential, which exhibits a bell-shaped barrier. This term becomes negligible when $n^2$ is sufficiently large relative to the height of the barrier, indicating that the mode is situated well outside the potential region. Under such conditions, ${\mu }_n$ behaves as a simple harmonic oscillator with a stationary amplitude, resulting in the decay of $h_n\left(\eta \right)$ as the universe expands. Conversely, when the condition $n^2$ is smaller than the height of the potential barrier, the amplitudes of the low-frequency modes remain approximately constant during periods of effective potential domination [2]. It is only after these modes exit the potential region that their amplitudes begin to decrease due to the expansion of space. If we analyze the dynamics more closely during the transient period between the inflationary phase and the radiation-dominant era, the behavior of the scale factor becomes significantly more intricate. Consequently, the resulting solutions to the GW equation yield corrections to the gravitational wave power spectrum [10].

2.3. Gravitational Waves Solutions in Transition

The significance of the gravitational potential barrier prompts us to rewrite (13) as

$$\begin{array}{c}\hfill {\mu }_n^{\prime \prime }+\left(n^2-V_{\mathrm{T}}\left(\eta \right)\right){\mu }_n=0,\end{array}$$

(14)

where the effective potential during the transition between the inflation phase and the radiation-dominant era is defined as

$$\begin{array}{c}\hfill V_{\mathrm{T}}\left(\eta \right)={\displaystyle \frac{a^{\prime \prime }}{a}}={\mathcal{H}}_{\mathrm{T}}^2+{\mathcal{H}}_{\mathrm{T}}^{\prime }={\mathcal{H}}_{\mathrm{T}}^2\left[1-{\mathcal{H}}_{\mathrm{T}}\left(\eta -{\eta }_{\max }\right)\right].\end{array}$$

(15)

The expression for $V_{\mathrm{T}}\left(\eta \right)$ is derived from ${\mathcal{H}}_{\mathrm{T}}^{\prime }=-{\mathcal{H}}_{\mathrm{T}}^3\left(\eta -{\eta }_{\max }\right)$ as seen in Equation (8). Moreover, by setting $\tau =\eta -{\eta }_{\max }$ the reduced Hubble parameter during the transition period (8) can be further simplified as

$${\mathcal{H}}_{\mathrm{T}}\left(\eta \right)={\displaystyle \frac{1}{\sqrt{{\tau }^2+\frac{1}{{\mathcal{H}}_{\max }^2}}}}\approx {\displaystyle \frac{1}{\tau }}\left(1-{\displaystyle \frac{1}{2{\tau }^2{\mathcal{H}}_{\max }^2}}\right),$$

(16)

where the approximation utilizes the binomial expansion, valid under the assumption that $\left|{\tau }^2{\mathcal{H}}_{\max }^2\right|\gg 1$ in the context of the early universe. Subsequently, we can approximate the effective potential as

$$\begin{array}{c}\hfill V_{\mathrm{T}}\left(\eta \right)\approx {\displaystyle \frac{1}{{\tau }^2}}{\left(1-{\displaystyle \frac{1}{2{\tau }^2{\mathcal{H}}_{\max }^2}}\right)}^2{\displaystyle \frac{1}{2{\tau }^2{\mathcal{H}}_{\max }^2}},\end{array}$$

(17)

This modification allows us to reformulate Equation (14) into the following expression:

$$\begin{array}{c}\hfill {\mu }_n^{\prime \prime }+\left[n^2-{\displaystyle \frac{1}{{\tau }^2}}{\left(1-{\displaystyle \frac{1}{2{\tau }^2{\mathcal{H}}_{\max }^2}}\right)}^2{\displaystyle \frac{1}{2{\tau }^2{\mathcal{H}}_{\max }^2}}\right]{\mu }_n=0,\end{array}$$

(18)

which encapsulates the dynamics of the system under the stated approximations and provides a foundation for further analysis. By changing the variable to ${\mu }_n={\tau }^{1/2}S$, Equation (18) transforms into

$$\begin{array}{c}\hfill S^{\prime \prime }+{\tau }^{-1}{S}^{\prime }+\left\{n^2-{\displaystyle \frac{1}{{\tau }^2}}\left[{\left(1-{\displaystyle \frac{1}{2{\tau }^2{\mathcal{H}}_{\max }^2}}\right)}^2{\displaystyle \frac{1}{2{\tau }^2{\mathcal{H}}_{\max }^2}}+{\displaystyle \frac{1}{4}}\right]\right\}S=0.\end{array}$$

(19)

In practice, one can recast this equation as an inhomogeneous equation such that

$$\begin{array}{c}\hfill {\tau }^2{S}^{\prime \prime }+\tau S^{\prime }+\left(n^2{\tau }^2-{\displaystyle \frac{9}{4}}\right)S=\left[{\left(1-{\displaystyle \frac{1}{2{\tau }^2{\mathcal{H}}_{\max }^2}}\right)}^2{\displaystyle \frac{1}{2{\tau }^2{\mathcal{H}}_{\max }^2}}-2\right]S.\end{array}$$

(20)

Moreover, by setting $x=n\tau$ and relabeling $y\left(x\right)=S\left(n\tau \right)$, the above equation becomes

$$\begin{array}{c}\hfill x^2{y}^{\prime \prime }+x{y}^{\prime }+\left(x^2-{\displaystyle \frac{9}{4}}\right)y=\left[{\left(1-{\displaystyle \frac{n^2}{2x^2{\mathcal{H}}_{\max }^2}}\right)}^2{\displaystyle \frac{n^2}{2x^2{\mathcal{H}}_{\max }^2}}-2\right]y.\end{array}$$

(21)

Here, the Bessel functions $Y_{3/2}\left(x\right)$ and $J_{3/2}\left(x\right)$ serve as two independent solutions to the homogeneous equation. Thus, the general solution of Equation (21) can be constructed as

$$\begin{array}{c}\hfill y\left(x\right)=b_1{Y}_{3/2}\left(x\right)+b_2{J}_{3/2}\left(x\right)+{\int }_{-\infty }^{x}G\left(x,t\right)\left[{\left(1-{\displaystyle \frac{n^2}{2t^2{\mathcal{H}}_{\max }^2}}\right)}^2{\displaystyle \frac{n^2}{2t^2{\mathcal{H}}_{\max }^2}}-2\right]y\left(t\right)dt.\end{array}$$

(22)

where $b_1$ and $b_2$ are constants to be determined by initial conditions, while $G\left(x,t\right)$ is a retarded Green’s function,

$$\begin{array}{c}\hfill G\left(x,t\right)={\displaystyle \frac{1}{t^{2}W\left(y_1,y_2\right)\left(t\right)}}\left[J_{3/2}\left(x\right)Y_{3/2}\left(t\right)-Y_{3/2}\left(x\right)J_{3/2}\left(t\right)\right],\end{array}$$

(23)

with a Wronskian $W(y_1,y_2)\left(t\right)=-{\displaystyle \frac{2}{\pi t}}$. The integral term involving $G(x,t)$ in Equation (22) accounts for the contribution from the backreaction source, which is expected to be negligible during the very early stages of cosmic evolution. Consequently, the general solution simplifies to the homogeneous solutions in the remote past, a period characterized by primordial inflation.

2.4. Parametrizing the Expansion History

In order to accurately acquire the spectrum of primordial gravitational waves with the appropriate amplitudes, it is imperative to meticulously parametrize the expansion history of the Universe. Given the continuous evolution of spacetime, it is essential to apply specific junction conditions to the scale factor a and its derivative $a^{\prime }$ to facilitate a smooth transition between distinct cosmic eras. Notably, the value of $C_1$ in Equation (5), as determined by these junction conditions, will significantly influence the details of the evolutionary process preceding the onset of the radiation-dominant phase. This raises pertinent inquiries regarding the temporal dynamics of how early and how long spacetime may deviate from the initial de Sitter state before ultimately settling into the radiation-dominant phase. For instance, substituting $C_1=H_I/4{\mathcal{H}}_{\max }^2$ while setting $C_2=0$ in Equation (5), one derives a valid scale factor as

$$\begin{array}{c}\hfill a_{\mathrm{PR}}\left(\eta \right)={\displaystyle \frac{2{\mathcal{H}}_{\max }^2}{H_I}}\left[\eta +\sqrt{{\eta }^2+{\displaystyle \frac{1}{{\mathcal{H}}_{\max }^2}}}\right]\mathrm{for}-\infty \le \eta \le {\eta }_r,\end{array}$$

(24)

which describes the pre-radiation (PR) stage that encompasses all phases of cosmic evolution preceding the equality time ${\eta }_r$ when the vacuum energy density equals the radiation energy density.

We parameterize the subsequent expansionary process in accordance with [2]. In the radiation stage, the scale factor is given by

$$\begin{array}{c}\hfill a\left(\eta \right)=a_e\left(\eta -{\eta }_e\right)\mathrm{for}{\eta }_r\le \eta \le {\eta }_2,\end{array}$$

(25)

where ${\eta }_2$ denotes the equality time between the radiation and matter eras, and ${\eta }_e$ is a constant determined by the junction condition. In the matter stage, the scale factor is defined as

$$\begin{array}{c}\hfill a\left(\eta \right)=a_m{\left(\eta -{\eta }_m\right)}^2\mathrm{for}{\eta }_2\le \eta \le {\eta }_H,\end{array}$$

(26)

where $a_m$ and ${\eta }_m$ represent constants to be established. We subsequently define the ratios

$$\begin{array}{c}\hfill {\zeta }_2\equiv {\displaystyle \frac{a\left({\eta }_H\right)}{a\left({\eta }_2\right)}},{\zeta }_r\equiv {\displaystyle \frac{a\left({\eta }_2\right)}{a\left({\eta }_r\right)}}\end{array}$$

(27)

and utilize the approximations ${\zeta }_2\approx {10}^4$ and ${\zeta }_r\approx {10}^{24}$ as noted in [2].

To achieve overall normalization, we define ${\eta }_H-{\eta }_m=1$ for the current time ${\eta }_H$. We can express this relationship as

$$\begin{array}{c}\hfill H\left({\eta }_H\right)={\left({\displaystyle \frac{a^{\prime }}{a^2}}\right)}_{{\eta }_H}={\displaystyle \frac{2}{a_m}}={\displaystyle \frac{1}{{\ell }_H}},\end{array}$$

(28)

where ${\ell }_H$ denotes the Hubble radius for the present universe. From the above equation, we conclude that $a_m=2{\ell }_H$.

The continuity of the scale factor $a\left(\eta \right)$ and its derivative $a’\left(\eta \right)$ at the points ${\eta }_2$ and ${\eta }_r$ necessitates the following conditions:

$$\begin{array}{ccc}\hfill {\eta }_2-{\eta }_m& =& {\zeta }_2^{-1/2}\hfill \end{array}$$

(29)

$$\begin{array}{ccc}\hfill {\eta }_2-{\eta }_e& =& {\displaystyle \frac{1}{2}}{\zeta }_2^{-1/2}\hfill \end{array}$$

(30)

$$\begin{array}{ccc}\hfill {\eta }_r-{\eta }_e& =& {\displaystyle \frac{1}{2}}{\zeta }_2^{-1/2}{\zeta }_r^{-1}\hfill \end{array}$$

(31)

$$\begin{array}{ccc}\hfill {\eta }_r& =& \sqrt{{\left({\displaystyle \frac{1}{2}}{\zeta }_2^{-1/2}{\zeta }_r^{-1}\right)}^2-{\displaystyle \frac{1}{{\mathcal{H}}_{\max }^2}}}.\hfill \end{array}$$

(32)

These conditions yield the following final relations:

$$\begin{array}{ccc}\hfill a_e& =& 4{\ell }_H{\zeta }_2^{-1/2}\hfill \end{array}$$

(33)

$$\begin{array}{ccc}\hfill {\displaystyle \frac{1}{{\mathcal{H}}_{\max }^2}}& =& {\displaystyle \frac{\sqrt{{\left(\frac{1}{2}{\zeta }_2^{-1/2}{\zeta }_r^{-1}\right)}^2-\frac{1}{{\mathcal{H}}_{\max }^2}}+\frac{1}{2}{\zeta }_2^{-1/2}{\zeta }_r^{-1}}{H_I{\ell }_H{\zeta }_2^{-1}{\zeta }_r^{-1}}}.\hfill \end{array}$$

(34)

By inputting the values of ${\zeta }_2$ and ${\zeta }_r$, one can ascertain the values of ${\mathcal{H}}_{\max }^2$, which is essential for analyzing the deviations between the inflationary phase and the radiation stage. This analysis is critical for advancing our understanding of cosmological dynamics.

2.5. Gravitational Wave Spectrum

The spectrum is delineated through the variance of the field amplitude, represented as

$$\begin{array}{c}\hfill \langle 0|h_{ij}\left(\eta ,\mathbf{x}\right)h^{ij}\left(\eta ,\mathbf{x}\right)|0\rangle \equiv {\int }_0^{\infty }{h}^2\left(n,\eta \right){\displaystyle \frac{dn}{n}},\end{array}$$

(35)

where $h\left(n,\eta \right)$ denotes a dimensionless quantity, commonly referred to as the root-mean-square (rms) amplitude. Utilizing Equation (10), we are enabled to derive the spectrum

$$\begin{array}{c}\hfill h\left(n,\eta \right)={\displaystyle \frac{2}{\pi }}{n}^{3/2}\left|h_n\left(\eta \right)\right|.\end{array}$$

(36)

This formulation elucidates the relationship between the spectrum and the corresponding amplitudes, facilitating a comprehensive understanding of the underlying physics.

In the pre-radiation stage, characterized by the interval where $-\infty \le \eta \le {\eta }_r$, the mode function $h_n\left(\eta \right)$ exhibits a direct relationship with the function $y\left(x\right)$ as articulated in Equation (22) as

$$\begin{array}{c}\hfill h_n\left(\eta \right)={\displaystyle \frac{A_0}{a\left(\eta \right)}}{\mu }_n\left(\eta \right)={\displaystyle \frac{A_0}{a\left(\eta \right)}}{\eta }^{1/2}y\left(x\right)\end{array}$$

(37)

Here, $A_0$ represents a constant determined by the initial spectral amplitude. With the integration of Equations (22) and (37), the expression for $h_n$ during the PR stage is derived as

$$\begin{array}{c}\hfill h_n\left(\eta \right)={\displaystyle \frac{A_0}{a\left(\eta \right)}}{\eta }^{{\displaystyle \frac{1}{2}}}\left\{b_1{Y}_{{\displaystyle \frac{3}{2}}}\left(x\right)+b_2{J}_{{\displaystyle \frac{3}{2}}}\left(x\right)+{\int }_{-\infty }^{x}G\left(x,t\right)\left[{\left(1-{\displaystyle \frac{n^2}{2t^2{\mathcal{H}}_{\max }^2}}\right)}^2{\displaystyle \frac{n^2}{2t^2{\mathcal{H}}_{\max }^2}}-2\right]y\left(t\right)dt\right\}\end{array}$$

(38)

with

$$\begin{array}{c}\hfill b_1=i\sqrt{{\displaystyle \frac{\pi }{2}}},b_2=-\sqrt{{\displaystyle \frac{\pi }{2}}}.\end{array}$$

(39)

This is because the mode function in the remote past must be regarded as the adiabatic vacuum in de Sitter spacetime.

In the radiation-dominated stage, the mode function is expressed as

$$\begin{array}{c}\hfill h_n\left(\eta \right)=y^{-1/2}\left[c_1{J}_{1/2}\left(ny\right)+c_2{Y}_{1/2}\left(ny\right)\right],\end{array}$$

(40)

where $y=\eta -{\eta }_e$. The constants $c_1$ and $c_2$ are determined by the continuity conditions of both $h_n\left(\eta \right)$ and its first derivative $h{’}_n\left(\eta \right)$ at the point ${\eta }_r$. On the other hand, during the matter-dominated stage, the mode function can be represented as

$$\begin{array}{c}\hfill h_n\left(\eta \right)=z^{-3/2}\left[d_1{J}_{3/2}\left(nz\right)+d_2{Y}_{3/2}\left(nz\right)\right],\end{array}$$

(41)

where $z=\eta -{\eta }_m$. The coefficients $d_1$ and $d_2$ are similarly established through continuity at ${\eta }_2$. Consequently, we derive the mode function at ${\eta }_H$, leading to the spectrum represented by

$$\begin{array}{c}\hfill h\left(n,{\eta }_H\right)={\displaystyle \frac{2}{\pi }}{n}^{3/2}\left|h_n\left({\eta }_H\right)\right|.\end{array}$$

(42)

As it is well established, the initial spectrum of relic gravitational waves at the horizon crossing time ${\eta }_{*}$ exhibits a nearly scale-invariant characteristic, articulated as

$$\begin{array}{c}\hfill h_i\left(n,{\eta }_{*}\right)=A{\left({\displaystyle \frac{n}{n_H}}\right)}^{2+\beta }.\end{array}$$

(43)

In this context, $\beta =-2$ pertains to de Sitter expansion [2]. The constant A can be determined through the CMB anisotropy $\Delta T/T\simeq 0.37\times {10}^{-5}$ at the quadrupole moment $l\sim 2$, correlating with the scale of the Hubble radius ${\ell }_H$. the ratio of tensor to scalar perturbations is described by $r=0.22$. Consequently, the value for $h_n$ becomes

$$\begin{array}{c}\hfill h\left(n_H,{\eta }_H\right)=0.37\times {10}^{-5}\times 0.{22}^{1/2},\end{array}$$

(44)

which facilitates the derivation of the constant A. Ultimately, it is possible to ascertain $A_0$, which is proportional to A as indicated in (36) via (38).

3. Result and Discussion

Our investigation into the power spectrum of primordial gravitational waves aligns with established methodologies found in the literature. We concentrate on the dynamics occurring during the transition from the inflationary epoch to the radiation-dominated era, employing the Running Vacuum Model with a specific formulation of vacuum energy characterized in terms of the Hubble parameter [See (2)]. However, we reformulated the GW mode equation within the context of RVM into an inhomogeneous equation (21), thereby addressing it as a back-reaction problem. This analytical perspective enables us to discern the corresponding behavior of the GW power spectrum in relation to spacetime evolution, which is evidenced by the deviations observed in the pre-radiation scale factor from the inflationary trajectory. The scale factor () during the pre-radiation stage, in the limit of the far past, where $\left|\eta \right|=-\eta$ and ${\eta }^2\gg {\mathcal{H}}_{\max }^{-2}$, is

$$\begin{array}{c}\hfill a_{\mathrm{PR}}\left(\eta \right)\approx {\displaystyle \frac{2{\mathcal{H}}_{\max }^2}{H_I}}\left[\eta -\eta \left(1+{\displaystyle \frac{1}{2{\mathcal{H}}_{\max }^2{\eta }^2}}\right)\right]=-{\displaystyle \frac{1}{H_I\eta }},\end{array}$$

(45)

which precisely represents the scale factor of inflation in conformal time.

From Equation (45), it becomes evident that the parameter ${\mathcal{H}}_{\max }$ fundamentally alters the shape of the scale factor, thereby providing critical insights into the temporal transition when de Sitter spacetime underwent significant alteration and exited the inflationary phase. The determination of ${\mathcal{H}}_{\max }$ is rooted in the cosmic history spanning from the radiation-dominated era to the present epoch [See (7)]. Furthermore, this parameter plays a pivotal role in modifying the transient period preceding the radiation stage [See (45)]. Consequently, variations in ${\mathcal{H}}_{\max }$ correspond to distinct cosmic histories. By slightly manipulating this parameter, one may elucidate the intricate relationship between cosmic history and the gravitational wave spectrum, particularly during the transient period, which bears a resemblance to the reheating phase in generic cosmological models.

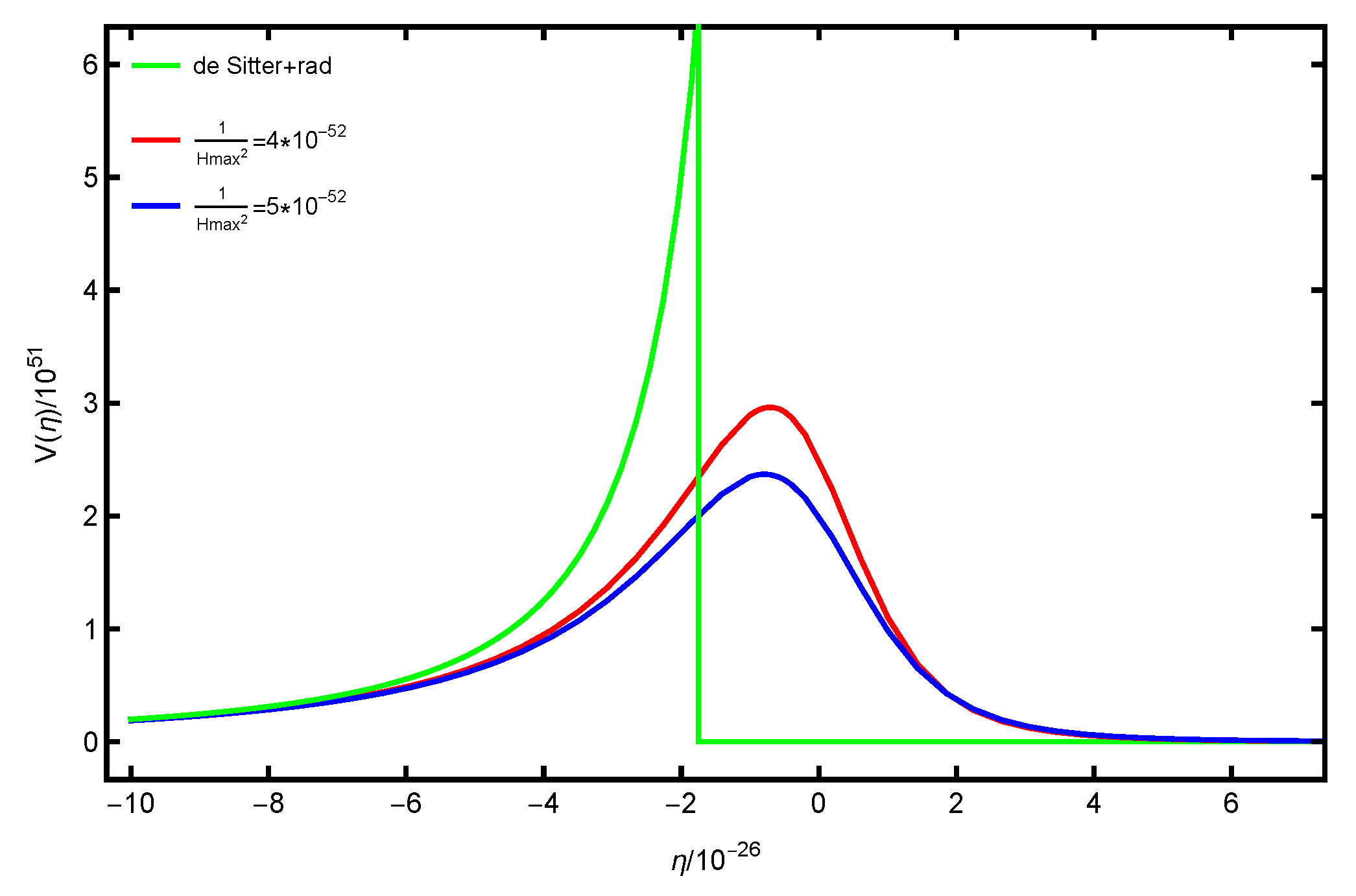
Figure 1 elucidates the point at which spacetime begins to diverge from de Sitter spacetime, as delineated by Equations (45), utilizing two distinct values of ${\mathcal{H}}_{\max }^{-2}$: $5\times {10}^{-52}$ and $4\times {10}^{-52}$. The curves depicted herein correspond to instances wherein $a_{\mathrm{PR}}\left(\eta \right)$ starts to deviate from $a_I\left(\eta \right)$ at approximately $\eta =-2\times {10}^{-24}$ and $\eta =-1.8\times {10}^{-24}$, which correlate to e-folding numbers $N=26.02$ and $N=25.91$, respectively. It is imperative to note that the temporal values presented are estimations. This investigation aims to discern the implications of early and significant deviations from inflation on the spectrum of gravitational waves. Furthermore, the figure illustrates that $a_{\mathrm{PR}}\left(\eta \right)$ transitions smoothly to the radiation stage, in contrast to the abrupt transition characteristic of inflation. 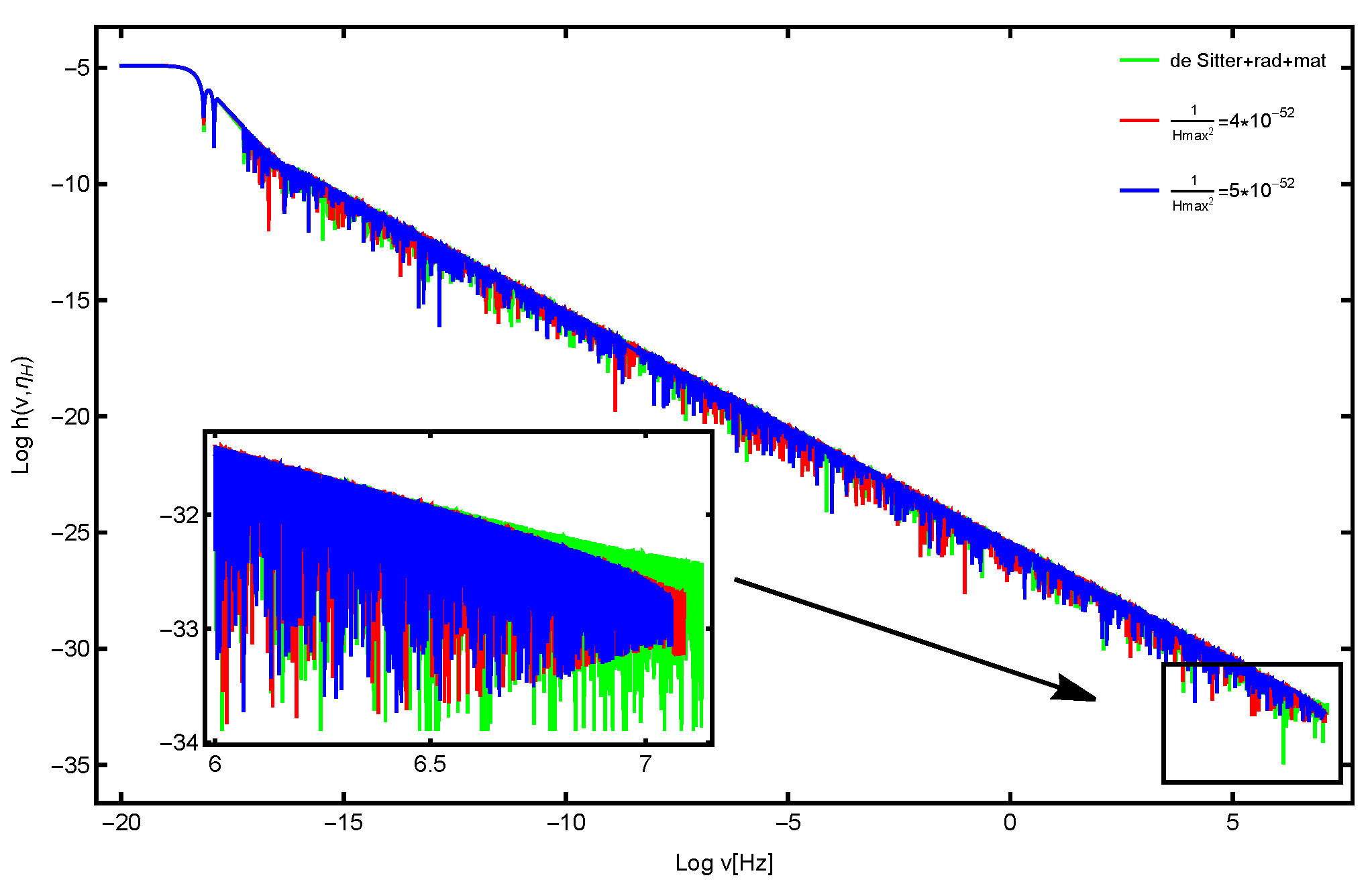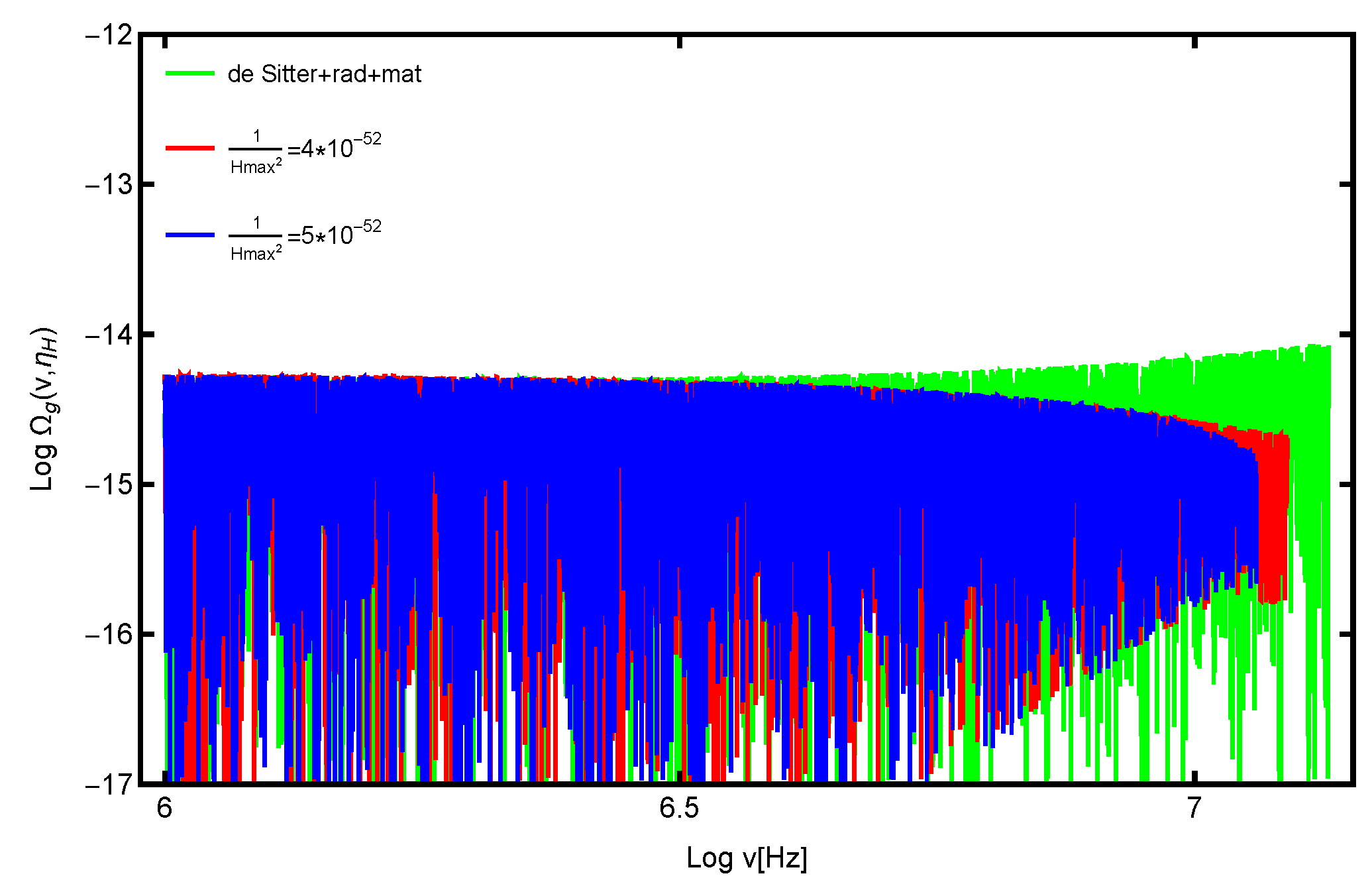Analysis of Figure 1 and Figure 2 reveals that earlier deviations in the inflationary scale factor yield a diminished maximum value of effective potential, thereby culminating in reduced high-frequency gravitational wave production, as depicted in Figure 3. This phenomenon can be interpreted as an earlier onset of particle creation, which induces a more gradual alteration of spacetime, resulting in a reduced rate of change of the scale factor. Consequently, this leads to a lesser maximum value of effective potential, which is integral in distinguishing extended wavelength modes as presented in Equation (13).

Our findings indicate that the power spectrum increasingly resembles a sudden transition from an inflationary phase to a radiation-dominated era, particularly as the transient period within the Running Vacuum Model (RVM) is shortened. This observation, illustrated in Figure 1, Figure 2 and Figure 3 suggests that while the RVM serves as a framework for understanding this transient period, analogous alterations in spacetime dynamics may emerge from various physical processes, such as reheating. Should this transient interval indeed correlate with reheating, our analysis reveals that a reduced duration of reheating is associated with enhanced amplitude damping at lower frequencies, as evidenced by the slope variations depicted in Figure 3.

4. Conclusions

The spectrum of gravitational waves manifests variations commensurate with the alterations in spacetime across diverse epochs of cosmic history. These spacetime alterations serve as reflections of the universe’s evolving constituents or fluctuations in the equation of state. In this context, it is essential to note that Robertson-Walker spacetimes exhibit conformal flatness, thereby designating the scale factor as the singular parameter that encapsulates spacetime evolution.

Instead of developing discrete reheating models and subsequently deriving their associated gravitational wave spectra, this analysis employs the Running Vacuum Model as a continuous transient model. By varying its parameters, we investigate the interplay between the gravitational wave spectrum and pivotal factors such as the deviation timescale, equality time, and the initial Hubble parameter. These variables yield invaluable insights into the transient timescale and the duration of the radiation-dominated era. Conversely, observational constraints on these factors derived from the gravitational wave spectrum facilitate a more profound comprehension of cosmic history.

To elucidate the physics underlying the graceful exit through gravitational waves, we reformulate the gravitational wave equation within the RVM framework into an inhomogeneous equation. The homogeneous solution aligns with that of de Sitter space, whereas the particular solution is expressed as the integral of a kernel that incorporates the scale factor and the retarded Green function. This particular solution represents the cumulative back-reaction to gravitational waves in de Sitter space, contingent upon the processes governing the transition from inflation to the radiation-dominated era.

While the RVM is utilized to characterize the transient period, analogous spacetime alterations may emerge from alternative physical processes, including reheating. Our investigation emphasizes the correlation between spacetime evolution during this transient phase and its distinctive signature within the gravitational wave spectrum. Notably, our findings indicate that a protracted transient process results in greater amplitude damping at lower frequencies, contrasting with the scenario of an abrupt transition from inflation to the radiation-dominated era.