Submitted:
27 March 2025
Posted:
31 March 2025
You are already at the latest version
Abstract
Keywords:
MSC: 65L60; 65N30; 74S05
1. Introduction
2. Tensor Product Elements
2.1. General Expressions
2.2. Quadratic Interpolation
3. Traditional Transfinite Elements
4. T-Meshed Patch Elements: Constraints and Elimination
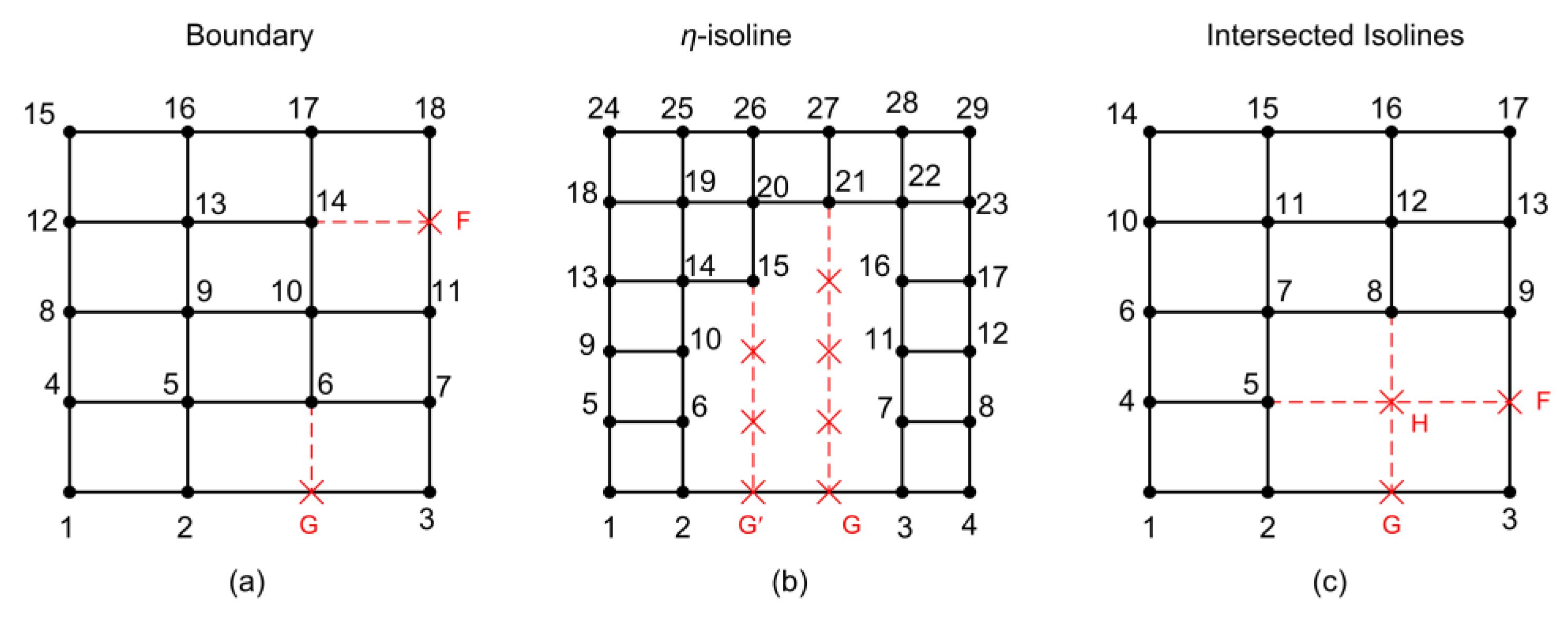
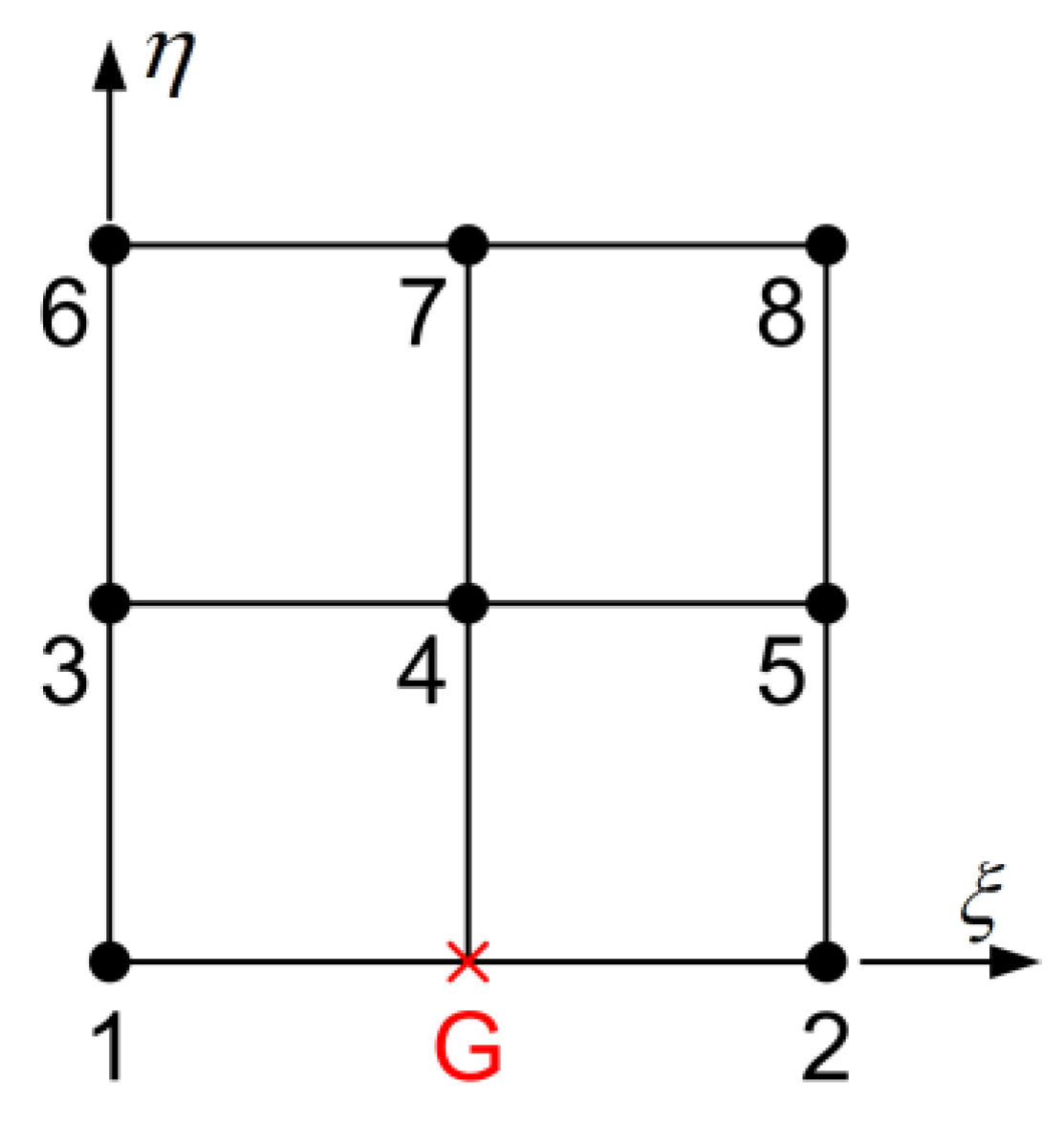
- Elements where the missing nodes belong to the boundary of the patch (e.g., nodes G and F as illustrated in Figure 4a).
- Elements with hanging internal nodes (denoted by a red cross ) that belong to the extension of isolines in only one direction (e.g., in Figure 4b these isolines are directed toward the -direction).
- Elements with hanging internal nodes that belong to the intersection of two isolines (e.g., node H as illustrated in Figure 4c).
- Technique 1: Eliminate H by considering it within the projector but ignoring it within the projector , i.e., considering the trial function along the horizontal isoline to be defined by the nodes (4, 5, and F). However, this trick cannot be applied to complicated T-meshes.
- Technique 2: Interpolate the nodal value at H once along a horizontal and another time along the vertical isoline passing through H and then consider the mean average value of these interpolations. Therefore, it is possible to eliminate the auxiliary node H, as later shown in Subsection 5.5.
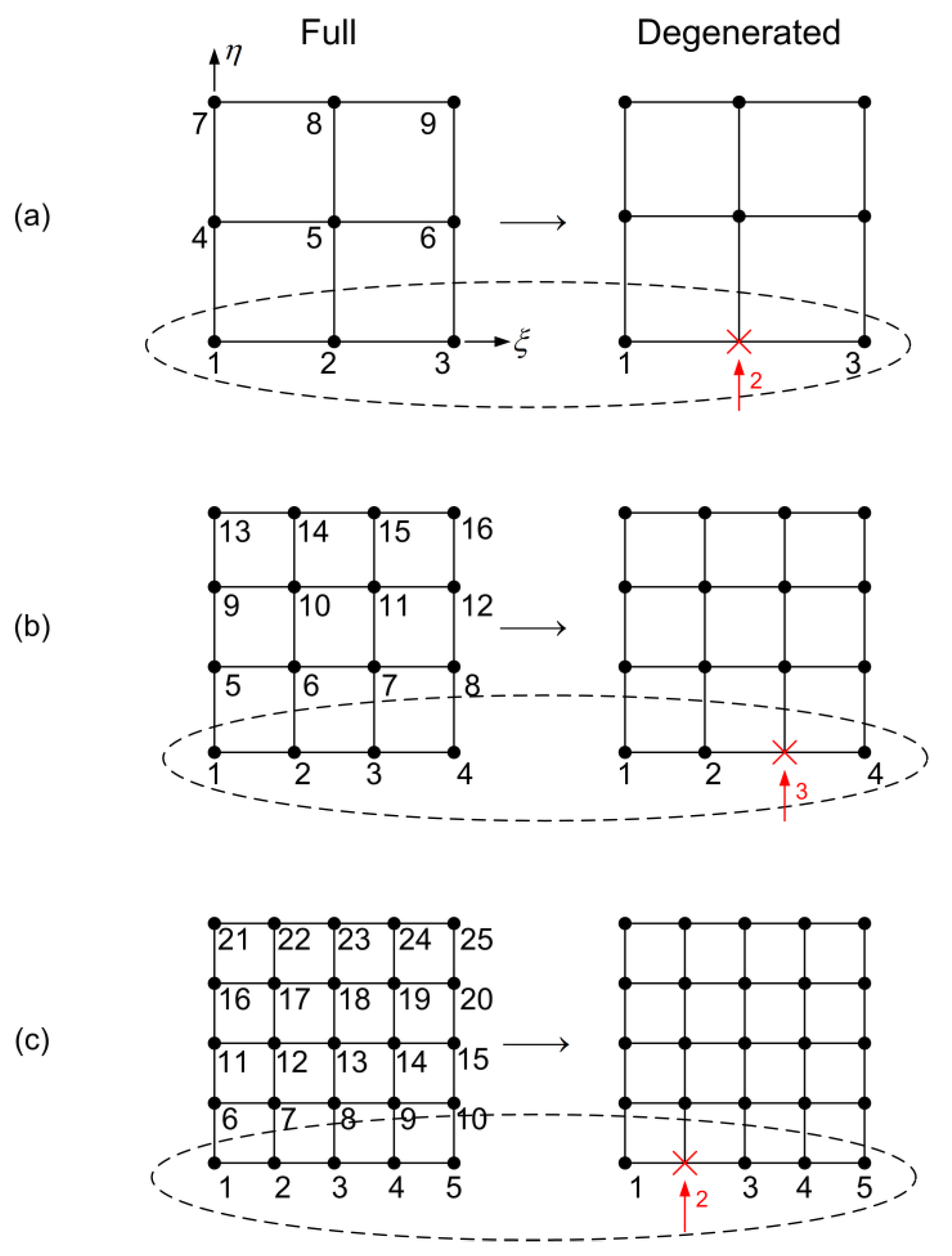
5. Constraints
5.1. Quadratic Polynomials and Linear Constraints
5.2. Cubic Polynomials and Quadratic Constraints
5.3. Quartic Polynomials and Cubic Constraints
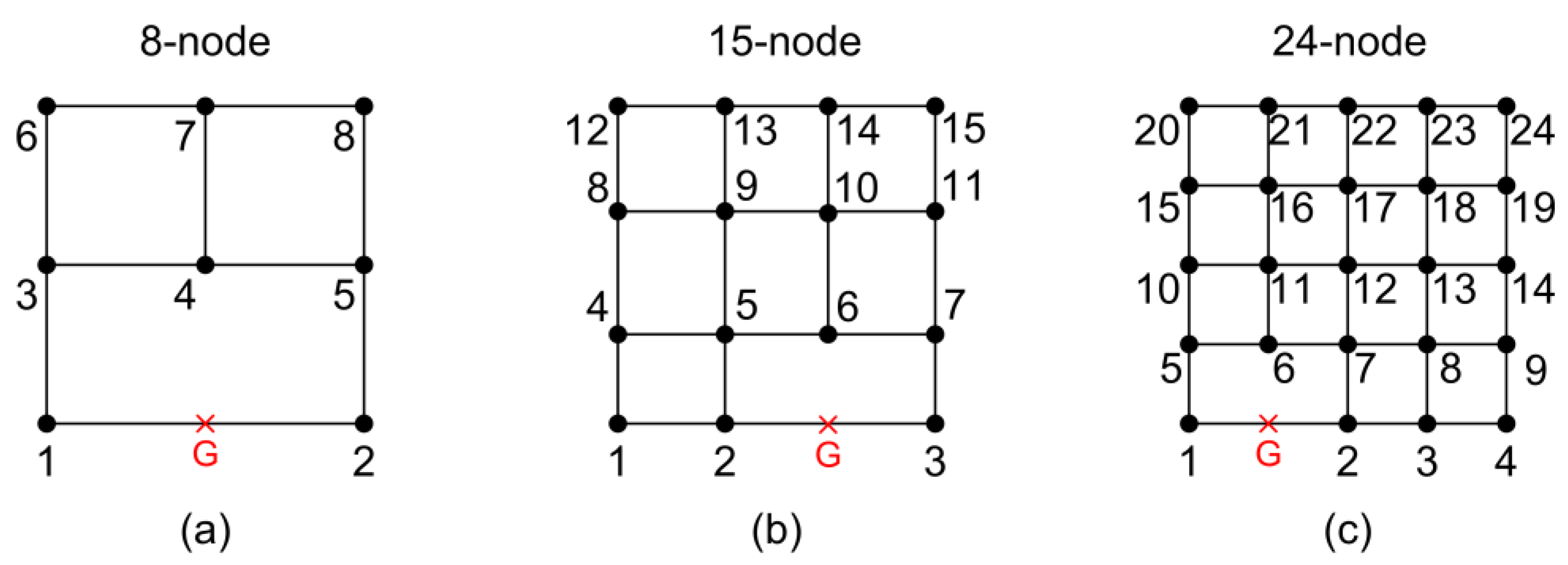
5.4. Implementation of an Eight-Node Transfinite Element
5.4.1. Approach 1: Transfinite Interpolation
5.4.2. Approach 2: Successive Node Elimination from an Initial Tensor Product
5.5. Elimination of Internal Nodes
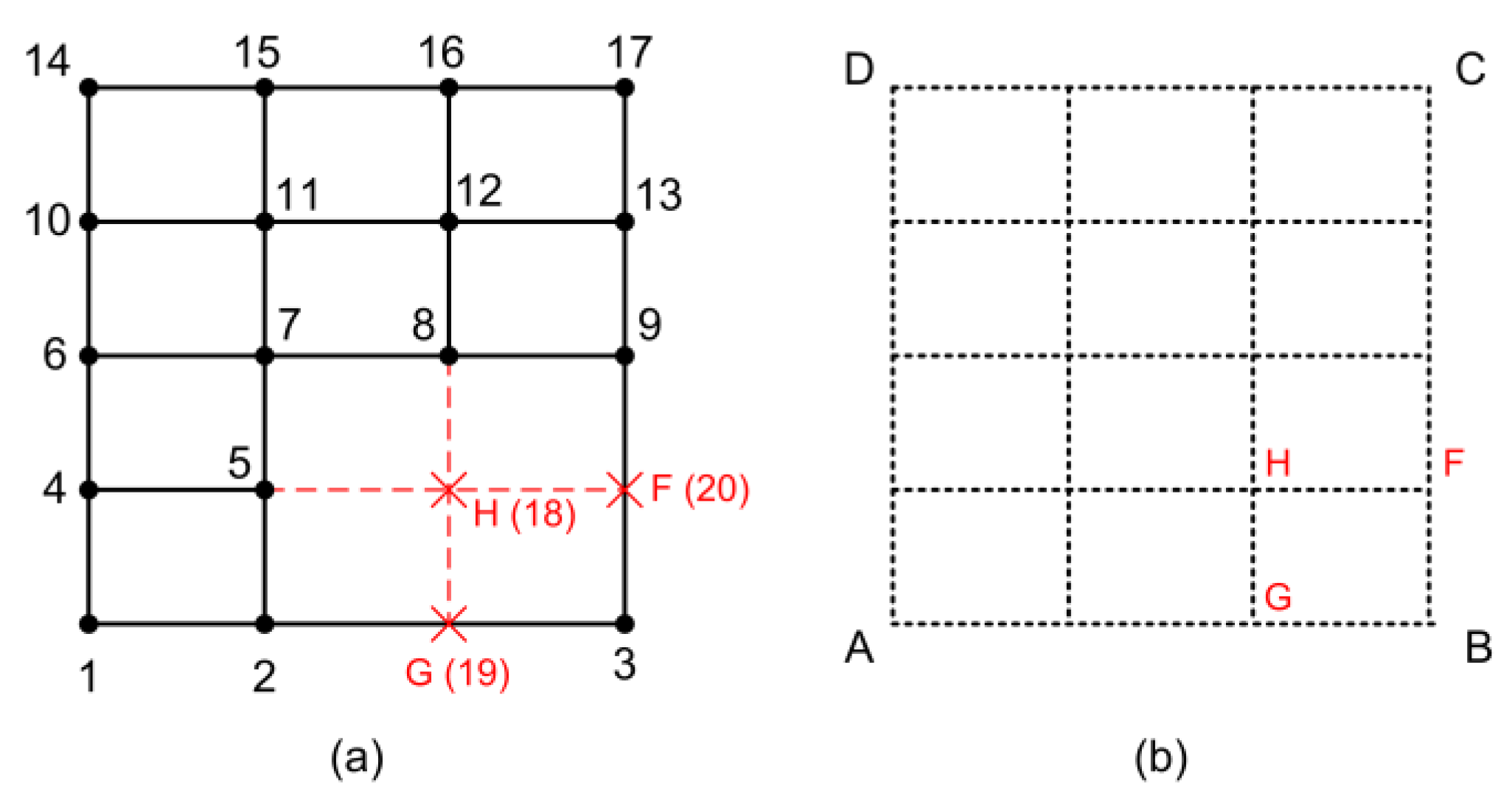
6. Construction of the 17-Node and 18-Node T-Mesh Elements
6.1. Approach 1 to Derive T-Mesh Elements
6.1.1. General Remarks
- the two artificial values on the boundary () are eliminated,
- the one in the interior () remains.
6.2. Approach 2 to Derive the 17-Node and 18-Node T-Mesh Elements
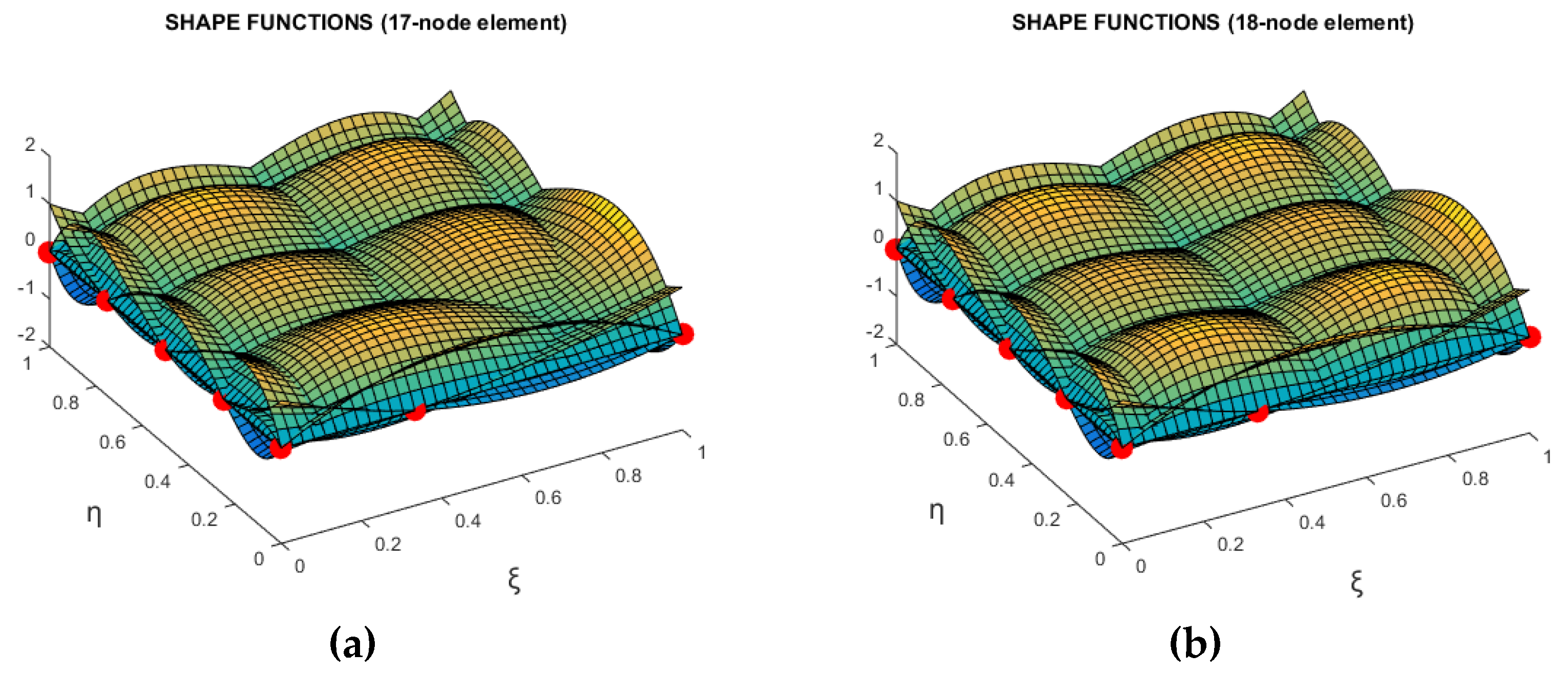
6.2.1. The 18-Node Element
6.2.2. The 17-Node Element
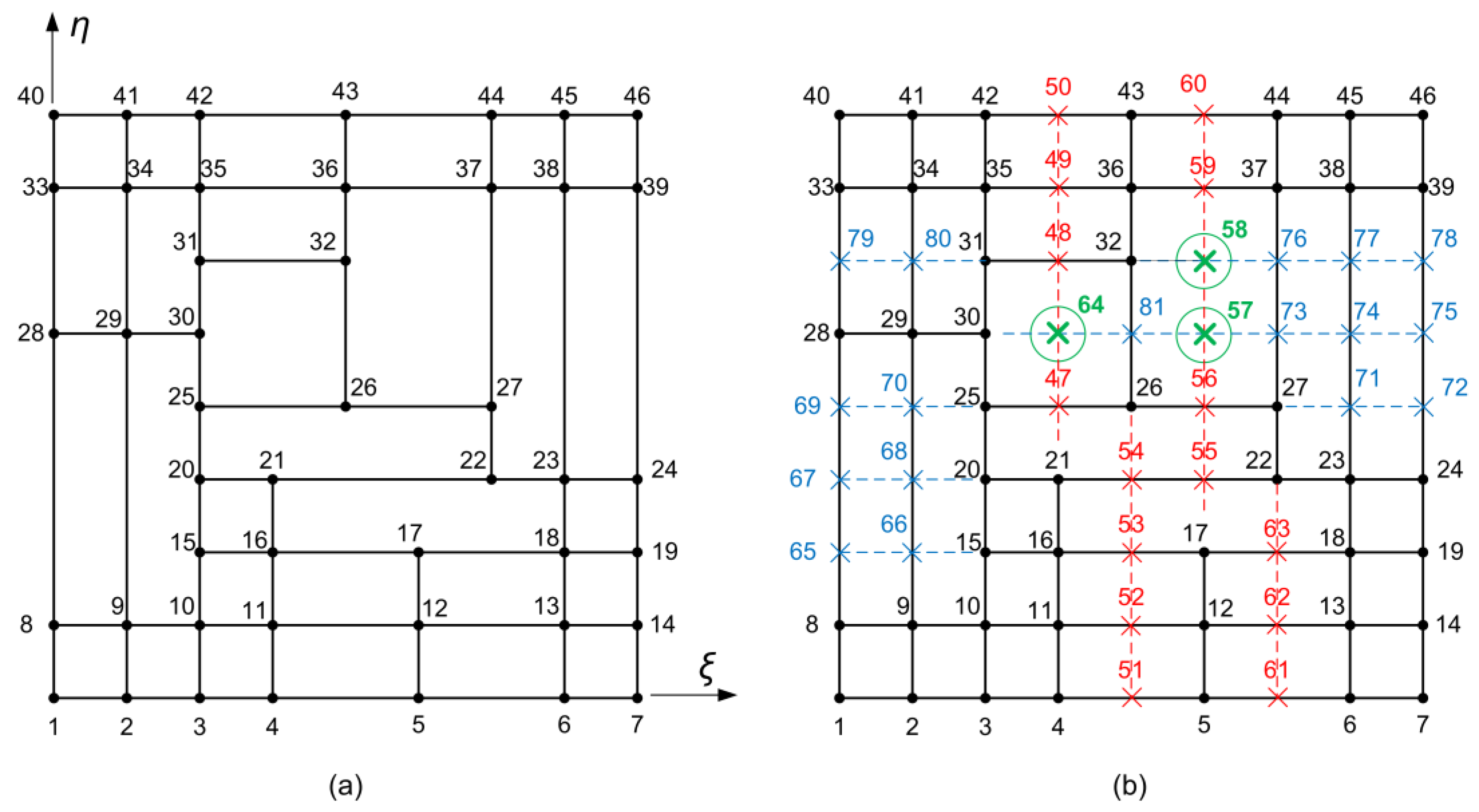
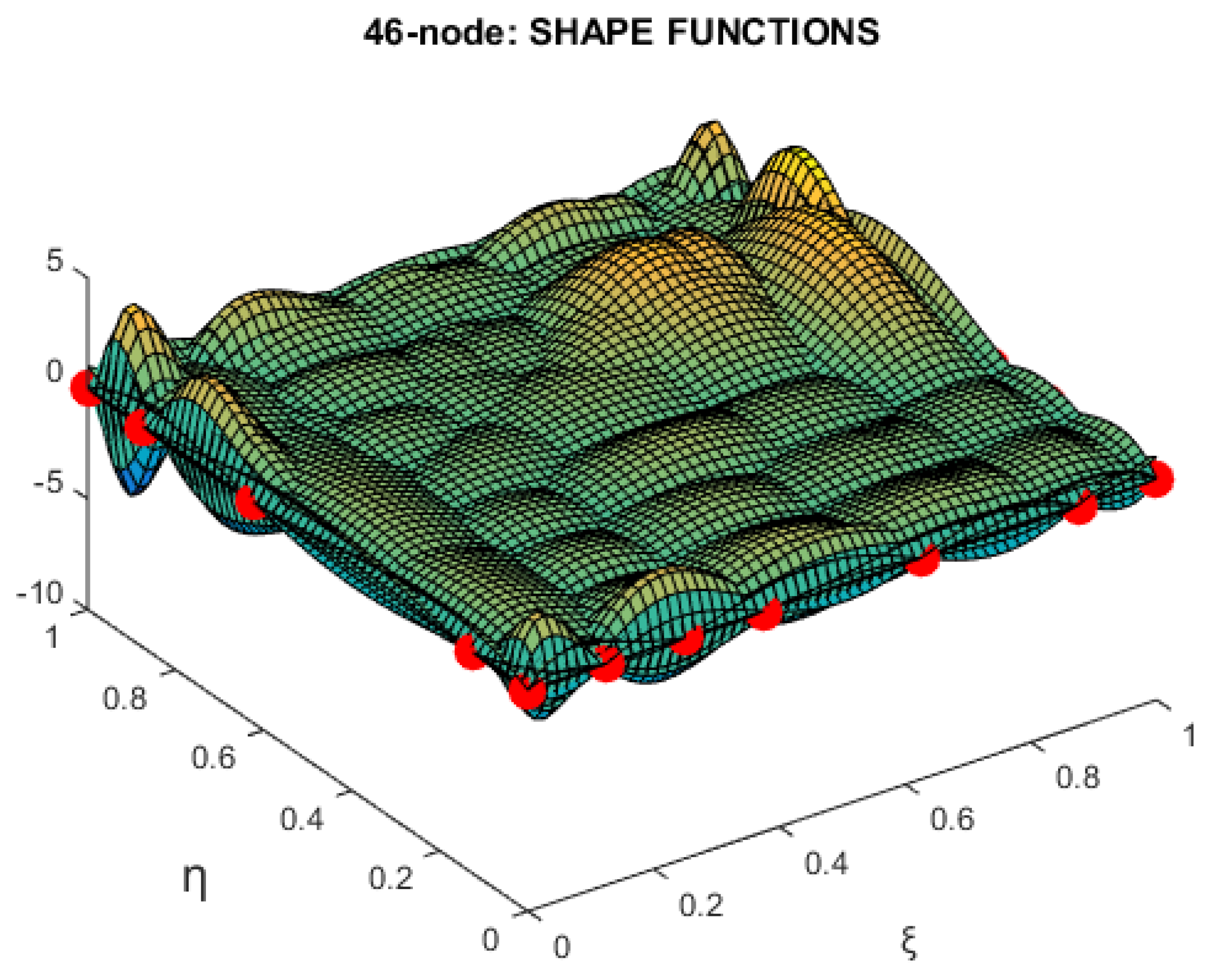
7. 46-Node T-Element
7.1. Description of the Stations
- Station H1 at , which is defined by the seven nodes , is described by a set of 7 nonuniform Lagrange polynomials. All the involved nodes are primary.
- Station H2 at , which is defined by the seven nodes (), is again described by a set of 7 nonuniform Lagrange polynomials. All the involved nodes are primary.
- Station H3 at , which is defined by the seven nodes , is described by a set of 7 nonuniform Lagrange polynomials. Note that the first two nodes are secondary and are required to complete the support on the left part of station H3, whereas the auxiliary (background) nodes 53 and 63 are not required because they are between existing supports.
- Station H4 at , which is defined by the seven nodes, is described by a set of 7 nonuniform Lagrange polynomials. Note that the first two nodes are secondary.
- Station H5 at , which is defined by the seven nodes , is described by a set of 7 nonuniform Lagrange polynomials. Note that here, in addition to the first secondary nodes , additional auxiliary nodes are used to complete the support on the right side of the station.
- Station H6 at , which is defined by the seven nodes of which the last four are secondary, is described by a set of 7 nonuniform Lagrange polynomials.
- Station H7 at , which is defined by the nodes , of which five are secondary, is described by a set of 7 nonuniform Lagrange polynomials.
- Station H8 at , which is defined by the nodes , is described by a set of 7 nonuniform Lagrange polynomials. All the involved nodes are primary.
- Station H9 at , which is defined by the seven nodes , is described by a set of 7 nonuniform Lagrange polynomials. All the involved nodes are primary.
- One may observe that all the above trial functions are nonuniform polynomials of the same degree 7, but this is an accidental event (which does not occur for the vertical stations).
- Regarding the vertical stations we have the following trial functions
- Station V1 at , which is defined by the five nodes , is described by a set of 5 nonuniform Lagrange polynomials. All the involved nodes are primary.
- Station V2 at , which is defined by the five nodes , is described by a set of 5 nonuniform Lagrange polynomials. All the involved nodes are primary.
- Station V3 at , which is defined by the nine nodes , is described by a set of 9 uniform Lagrange polynomials. All the involved nodes are primary, and it is the only station which involves the maximum allowable number of nine primary nodes.
- Station V4 at , which is defined by the eight nodes of which the last four are secondary, is described by a set of 8 nonuniform Lagrange polynomials.
- Station V5 at , which is defined by the eight nodes of which the first four are secondary, is described by a set of 8 nonuniform Lagrange polynomials.
- Station V6 at , which is defined by the seven nodes of which the last four are secondary, is described by a set of 7 nonuniform Lagrange polynomials. Note the big gap between the secondary nodes and .
- Station V7 at , which is defined by the seven nodes of which the first three are secondary, is described by a set of 7 nonuniform Lagrange polynomials. Note the big gap between and .
- Station V8 at , which is defined by the six nodes , is described by a set of 6 nonuniform Lagrange polynomials. Note that all the involved nodes are primary, while there is a big gap between and .
- Station V9 at , which is defined by the six nodes , is described by a set of 6 nonuniform Lagrange polynomials. Note that all the involved nodes are primary, while there is a big gap between and .
7.2. Imposition of Linear Constraints at Secondary Nodes
7.2.1. Approach 1:
7.2.2. Approach 2
- If the auxiliary DOF clearly belongs to a single station ( or ), then we interpolate in terms of the nodal values associated with this specific station. All the auxiliary nodes except of three ones belong to this category (see below).
- If the auxiliary DOF does not clearly belong to a single station but to the intersection of two sections, then we interpolate , in both directions, using the mean average of the two values (one for the horizontal and the other for the vertical section). For the configuration of Figure 10, the relevant nodes (for averaging like Equation (36)) are 57, 58 and 64.
- Therefore, for the 46node T-element of this section, we impose 32 simple interpolations along either horizontal or vertical isolines and 3 averaging procedures using both mutually perpendicular isolines passing through the intersected nodes (57, 58 and 64).
- For example, considering the nonuniform Lagrange polynomials based on the nodal points (1,2,3,4,5,6,7) on the bottom edge AB of the quadrilateral patch, the nodal values at the points 51 and 61 are eliminated in terms of the primary nodal values of the same edge by the linear relationships:
- Similar constraints such as those of Equation (57) are obtained for the 17 (i.e., not all the 18) iso-lines and for all the secondary nodes except for (57, 58, and 64) which belong to two isolines simultaneously. As already mentioned, for the latter three secondary nodes, we take the mean average of the two constraints as previously shown in Equation (36).
- Since the secondary nodes are a linear combination of the primary ones (a portion given by Equation (57)), we can eventually find a numerical matrix (of size 35 × 46), according to Equation (54). Obviously, when Equation (54) is considered in the tensor product of the 81 terms, this will be eventually expressed in terms of the 46 primary variables only (i.e., the vector ). The procedure is very similar to that for a smaller mesh (see Subsection 6.2.2), which was described in detail through a MATLAB® computer program in Appendix A.
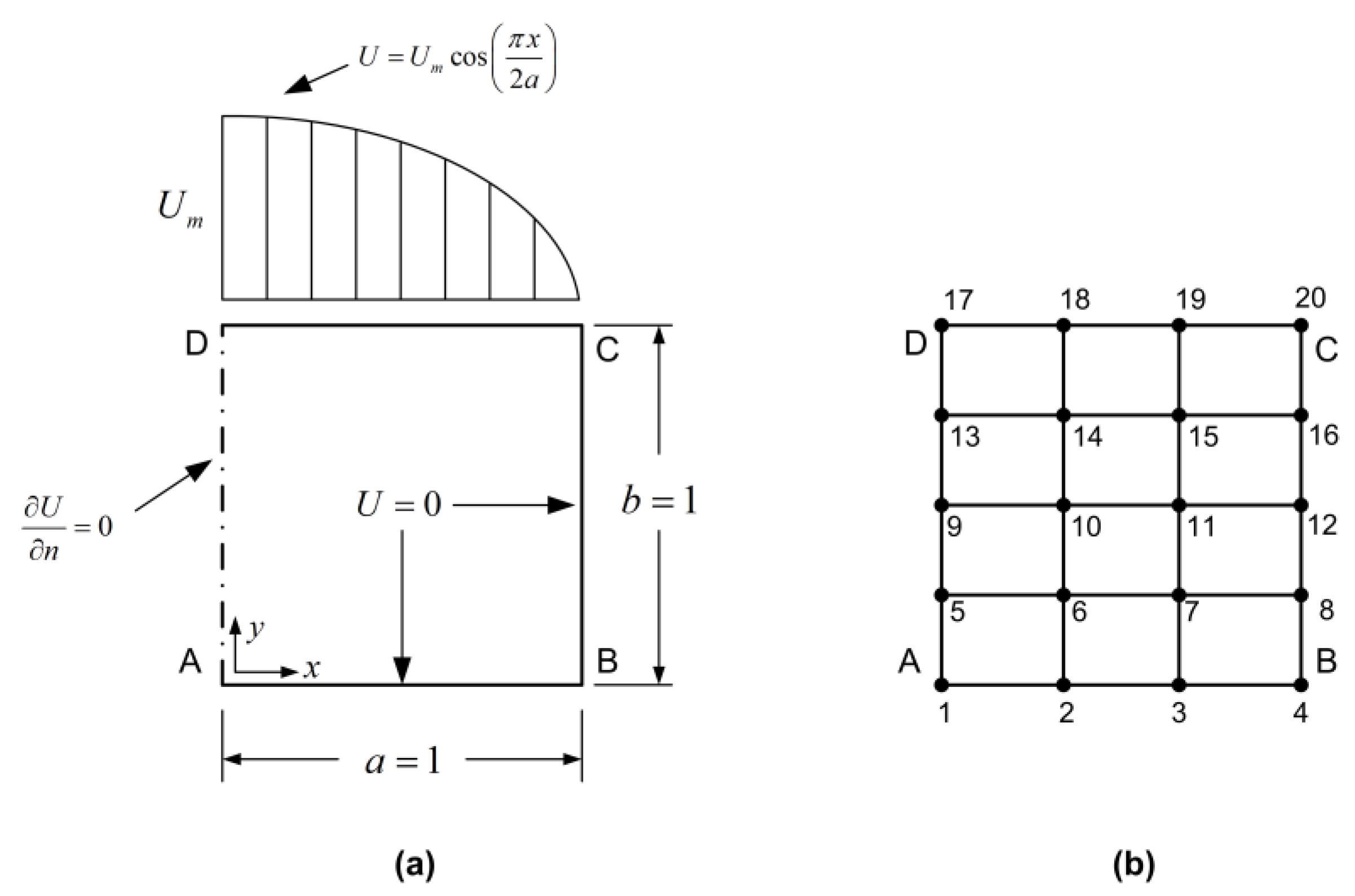
8. Numerical Verification
- The accuracy of the 8-node transfinite element is acceptable.
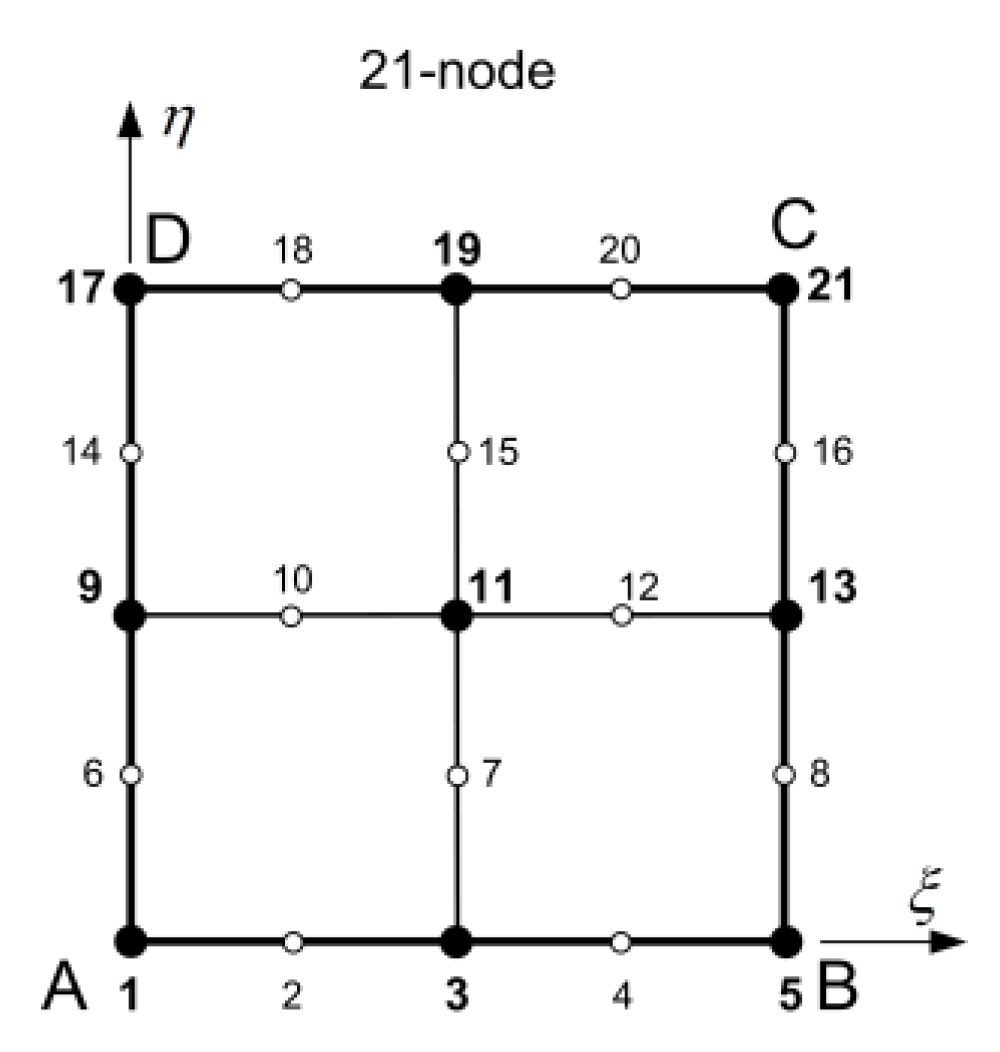
- The accuracy of the traditional 21-node transfinite element is excellent.
- The accuracy in the 17-, 18-, and 20-node transfinite elements is acceptable and very similar.
- The additional constraints to come from a 20 to an 18 and 17 node element decrease the accuracy
- The constraints on internal secondary nodes are worse for the accuracy.
- The accuracy of the complicated 46-node T-element is the best of all.
9. Discussion
10. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
Appendix A: Shape functions of 17-, 18-, and 19-node T-Mesh Elements

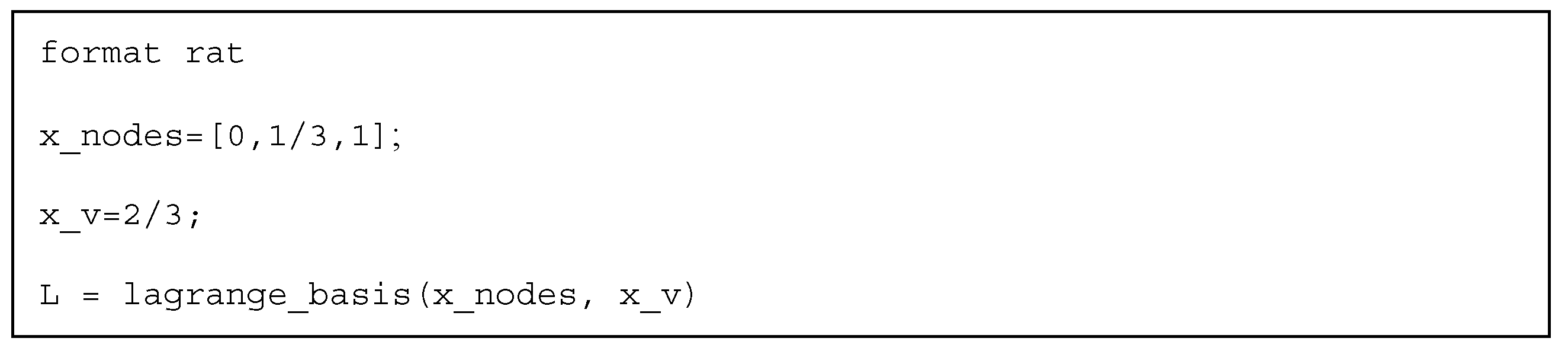

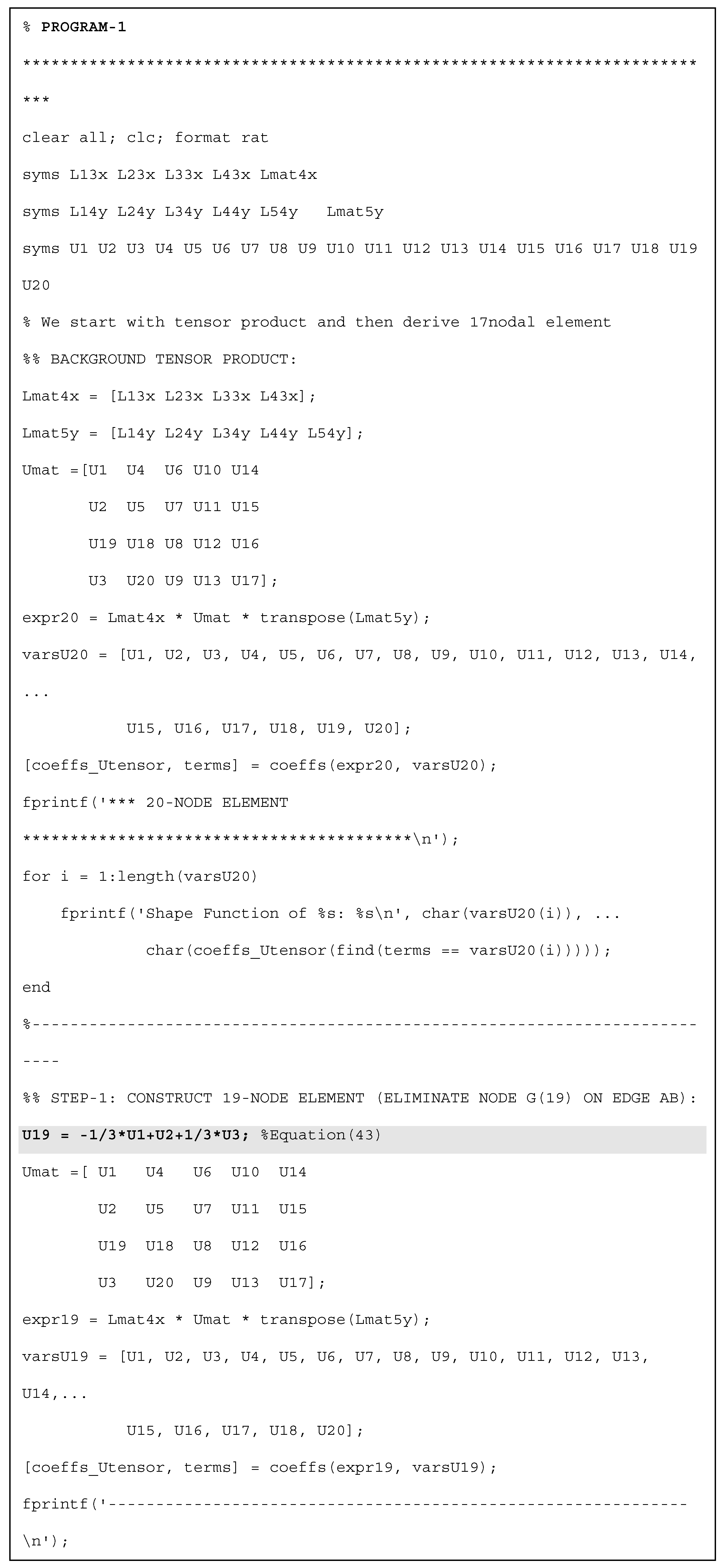


Appendix B: Global Shape Functions of the 46node T-like Element
References
- Zienkiewicz, O.C.; Taylor, R.L.; Zhu, J.Z. The Finite Element Method, 7th ed. Butterworth-Heinemann, Oxford, 2013.
- Bathe, K.-J. Finite Element Procedures, 2nd edition ed. Bathe, K.-J., Watertown, MA, 2014.
- Hughes, T.J.R. The Finite Element Method. Dover Publications, Mineola, NY, 2000.
- Taig, I.C. Structural analysis by the matrix displacement method. Tech. rep., British Aircraft Corporation, Warton Aerodrome: English Electric Aviation Limited, Report Number SO 17 based on work performed ca. 1957, 1962.
- Brebbia, C.A.; Ferrante, A.J. Computational Methods for the Solution of Engineering Problems, 3rd rev ed. Pentech Pr., London, 1986.
- Szabó, B.; Babuška, I. Finite Element Analysis. Wiley, New York, 1991.
- Rønquist, E.M.; Patera, A.T. A Legendre spectral element method for the Stefan problem. International Journal for Numerical Methods in Engineering 1987, 24, 2273–2299. [Google Scholar] [CrossRef]
- I. Babuska, B. A. Szabo, and I. N. Katz. The p-Version of the Finite Element Method. SIAM Journal on Numerical Analysis 1981, 18, 515–545. [CrossRef]
- Szabó, B.; Düster, A.; Rank, E. The p-Version of the Finite Element Method. In: Encyclopedia of Computational Mechanics (eds E. Stein, R. Borst and T.J.R. Hughes), 2004. [CrossRef]
- El-Zafrany, A.; Cookson, R.A. Derivation of Lagrangian and Hermitian shape functions for quadrilateral elements. International Journal for Numerical Methods in Engineering 1986, 23(10), 1939–1958. [Google Scholar] [CrossRef]
- Pozrikidis, C. Introduction to Finite and Spectral Element Methods Using MATLAB, 2nd ed. CRC Press, New Yrk, 2014. [CrossRef]
- de Boor, C. A Practical Guide to Splines, rev ed. Springer, New York, 2001.
- Eisenträger, S.; Kapuria, S.; Jain, M.; Zhang, J. On the Numerical Properties of High-Order Spectral (Euler-Bernoulli) Beam Elements, Z Angew Math Mech. 2023, 103(9), e202200422 (2023). [CrossRef]
- Patera, A.T. A spectral element method for fluid dynamics: Laminar flow in a channel expansion. Journal of Computational Physics 1984, 54(3), 468–488. [Google Scholar] [CrossRef]
- Eisenträger, S.; Eisenträger, J.; Gravenkamp, H.; Provatidis, C.G. High order transition elements: The xNy-element concept, Part II: Dynamics. Comput. Methods Appl. Mech. Eng. 2021, 387, 114145. [Google Scholar] [CrossRef]
- Gordon, W.J.; Hall, C.A. Transfinite element methods: Blending-function interpolation over arbitrary curved element domains. Numerische Mathematik 1973, 21, 109–129. [Google Scholar] [CrossRef]
- Cavendish, J.C.; Gordon, W.J.; Hall, C.A. Ritz-Galerkin approximations in blending function spaces. Numerische Mathematik 1976, 26, 155–178. [Google Scholar] [CrossRef]
- Cavendish, J.C.; Gordon, W.J.; Hall, C.A. Substructured macro elements based on locally blended interpolation. International Journal for Numerical Methods in Engineering 1977, 11, 1405–1421. [Google Scholar] [CrossRef]
- Coons, S.A. Surfaces for computer-aided design of space forms. Tech. rep., Massachusetts Institute of Technology, 1967.
- Provatidis, C.G. Coons-patch macroelements in two-dimensional parabolic problems. Applied Mathematical Modelling 2006, 30, 319–351. [Google Scholar] [CrossRef]
- Provatidis, C.G. Two-dimensional elastostatic analysis using Coons-Gordon interpolation. Meccanica 2011, 47, 951–967. [Google Scholar] [CrossRef]
- Provatidis, C.G. Precursors of isogeometric analysis: Finite elements, Boundary elements, and Collocation methods. Springer, Cham, 2019.
- Provatidis, C. G. Free vibration analysis of two-dimensional structures using Coons-patch macroelements. Finite Elements in Analysis and Design 2006, 42, 518–531. [Google Scholar] [CrossRef]
- Duczek, S.; Saputra, A.A.; Gravenkamp, H. High Order Transition Elements: The xNy-Element Concept—Part I: Statics, Computer Methods in Applied Mechanics and Engineering 2020, 362, 112833. [CrossRef]
- Provatidis, C.G. Solution of two-dimensional Poisson problems in quadrilateral domains using transfinite Coons interpolation. Communications in Numerical Methods in Engineering 2004, 20(7), 521–533. [Google Scholar] [CrossRef]
- Provatidis, C.G. Eigenanalysis of Two-Dimensional Acoustic Cavities Using Transfinite Interpolation. Journal of Algorithms & Computational Technology 2009, 3, 477–502. [Google Scholar] [CrossRef]
- Birkhoff, G; Cavendish, J.C.; Gordon, W.J. Multivariate Approximation by Locally Blended Univariate Interpolants. Proc. Nat. Acad. Sci. USA 1974, 71, 3423–3425. [CrossRef]
- Sederberg, T.W.; Zheng, J.; Bakenov, A.; Nasri, A. T-splines and T-NURCCs. ACM transactions on graphics (TOG) 2003, 22, 477–484. [Google Scholar] [CrossRef]
- Bazilevs, Y.; Calo, V.M.; Cottrell, J.A.; Evans, J.A.; Hughes, T.J.R.; Lipton, S.; Scott, M.A.; Sederberg, T.W. Isogeometric analysis using T-splines. Computer Methods in Applied Mechanics and Engineering 2010, 199, 229–263. [Google Scholar] [CrossRef]
- Dörfel, M.R.; Jüttler, B.; Simeon, B. Adaptive isogeometric analysis by local h-refinement with T-splines. Computer Methods in Applied Mechanics and Engineering 2010, 199, 264–275. [Google Scholar] [CrossRef]
- Wang, A.; Li, L.; Wang, W.; Du, X.; Xiao, F.; Cai, Z.; Zhao, G. Linear Independence of T-Spline Blending Functions of Degree One for Isogeometric Analysis. Mathematics 2021, 9. [Google Scholar] [CrossRef]
- EL-Fakkoussi, S.; Gouzi, M.B.; Elkhalfi, A.; Vlase, S.; Scutaru, M.L. Integrate the Isogeometric Analysis Approach Based on the T-Splines Function for the Numerical Study of a Liquefied Petroleum Gas (LPG) Cylinder Subjected to a Static Load. Applied Sciences 2025, 15. [Google Scholar] [CrossRef]
- Guo, M.; Wang, W.; Zhao, G.; Du, X.; Zhang, R.; Yang, J. T-splines for isogeometric analysis of the large deformation of elastoplastic Kirchhoff–Love shells. Applied Sciences 2023, 13. [Google Scholar] [CrossRef]
- Provatidis, C.G. Transfinite patches for isogeometric analysis. Mathematics 2025, 13. [Google Scholar] [CrossRef]
- Provatidis, C.G. Non-rational and rational transfinite interpolation using Bernstein polynomials. International Journal of Computational Geometry and Applications 2022, 32(1-2), 55–89. [CrossRef]
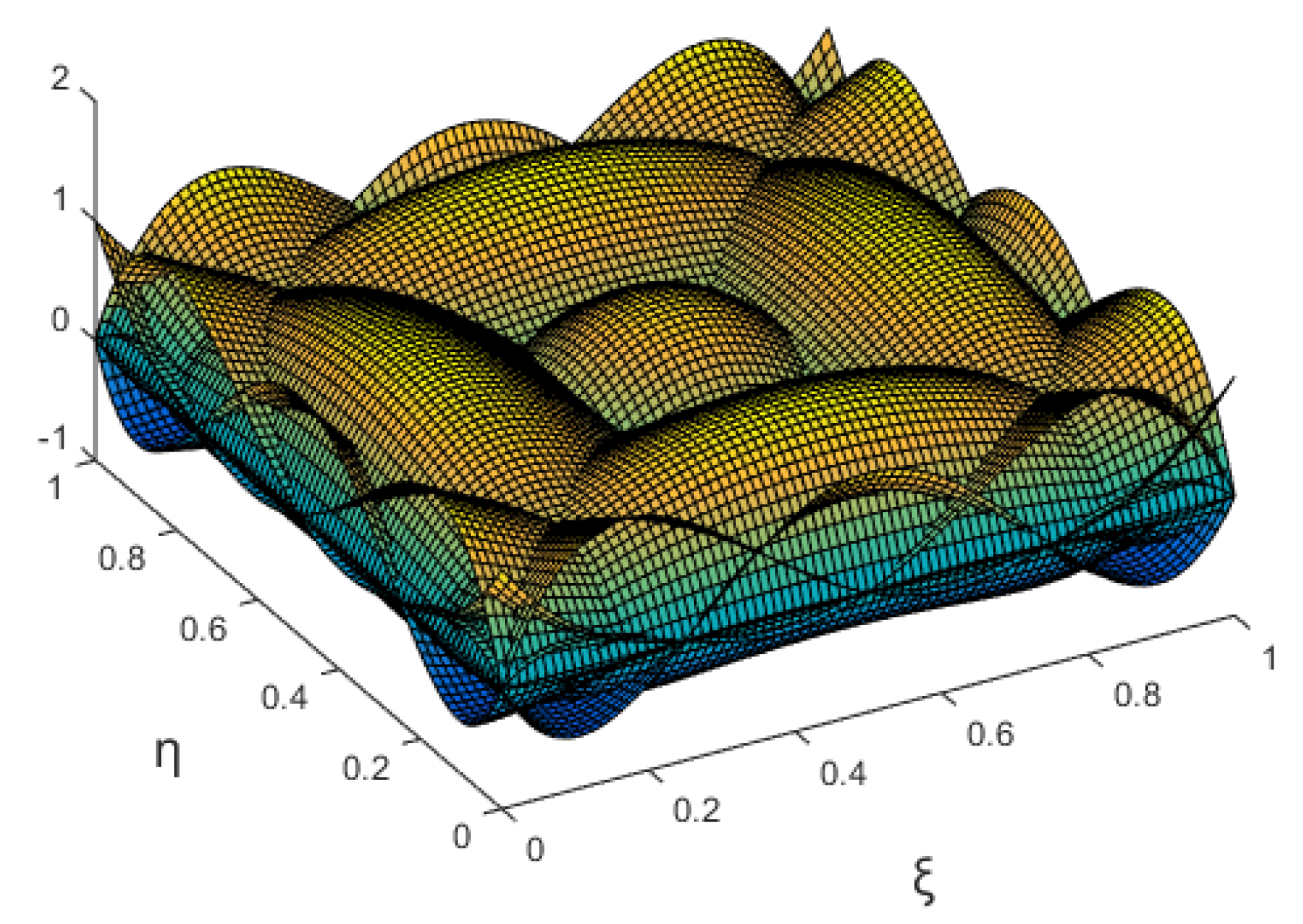
| Element type | Figure | L2 error norm (in %) |
| 8node | 4a | 3.2184 |
| Transfinite element (21 DOF) | 2 | 0.0526 |
| Tensor-product (20 DOF) | 6a (and 10b) | 0.2025 |
| 18 nodes | 6a | 0.2035 |
| 17 nodes | 6a | 0.3275 |
| 46 nodes | 8 | 0.0115 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





