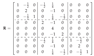Transfinite Elements Using Bernstein Polynomials

1. Introduction

Engineering analysis of two- and three-dimensional boundary-value (including eigenvalue) problems is usually performed using tensor product expansion of the problem variable, applying either local or global interpolation. In chronological sequence, from older to the most recent, the mostly used univariate functions were Lagrange polynomials, Bernstein polynomials, B-splines and NURBS ([1,2,3], among others). And, since these univariate functions are constituent elements of usual tensor products, they have successively passed from tensor product Lagrange polynomials to tensor product NURBS.

In the advent of isogeometric analysis (IGA), Lagrange polynomials have been progressively substituted by Bernstein polynomials as well as B-splines and NURBS [3]. In some simple cases such as ideal tensor products implemented with Lagrange polynomials, the nodal values $U_i$’s can be blindly replaced by the generalized coefficients ${\alpha }_i$’s and the Lagrange by Bernstein polynomials [4,5], but the range of applicability of this method is still unknown. Regarding two-dimensional problems, it has been shown that Lagrange and non-rational Bernstein polynomials are equivalent, and thus lead to the same numerical results [6]. However, as we will discuss in the paper at hand, this blind replacement is not generally applicable. Note that one practical reason for replacing Lagrange by Bernstein polynomials is because the latter allow for the introduction of weights that may ensure the accurate representation of conics and surfaces such as cylindrical and spherical parts. However, this can be achieved not only for IGA-tensor-products but for transfinite patches as well [4]. Regarding the analysis module, which refers to the numerical solution to a partial differential equation (PDE) with given boundary conditions, the isoparametric concept has been adopted in all cases, which uses the same set of basis functions for the approximation of the geometry $x(\xi ,\eta )$ and the primary variable of the problem $U(\xi ,\eta )$.

For the sake of clarity and focus, this paper restricts itself to the use of Bernstein polynomials only, excluding discussions of B-splines and NURBS. Overall, five categories of transfinite elements are investigated, as follows:

• Tensor product elements.
• Traditional transfinite elements (fully structured).
• Distorted tensor products.
• Elements with different degrees on opposite edges (partially unstructured).
• Coons elements.

The study opens with a review of the tensor product formulation, leading to the derivation of a general transformation matrix that maps Lagrange polynomials to their Bernstein counterparts. This matrix is subsequently employed to establish the relationship between the nodal values $U_i$’s and the generalized coefficients $a_i$’s.

Next, the paper examines classical transfinite elements in a structured setting, where it uncovers the implicit transformation matrix governing the interpolation. It then extends the analysis to tensor product elements with distorted boundaries, identifying the relationship between nodal points and control points for both Lagrange and Bernstein representations.

The fourth part investigates non-tensor-product elements, characterized by variable polynomial interpolation orders along their four edges. For these cases, a robust Bernstein-based basis is proposed, and avenues for future research are discussed. Finally, the paper presents a variation of the transfinite element inspired by the Coons patch, wherein nodal or control points are defined solely along the boundary.

The proposed methodology is validated through two benchmark problems: a boundary-value problem governed by the Laplace equation, and an acoustic eigenvalue problem. Both cases possess known closed-form solutions, allowing for rigorous accuracy assessment.

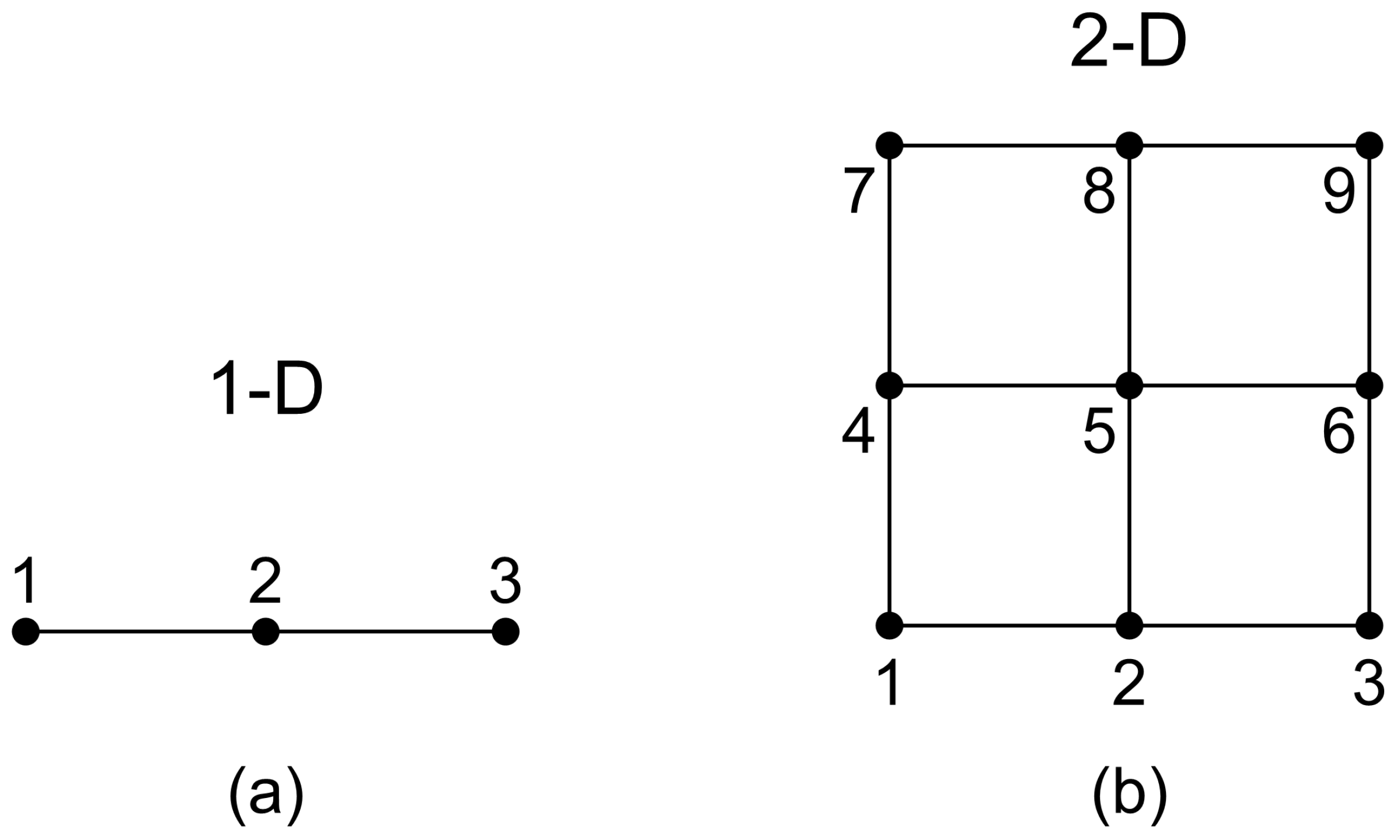
2. Basic Theory

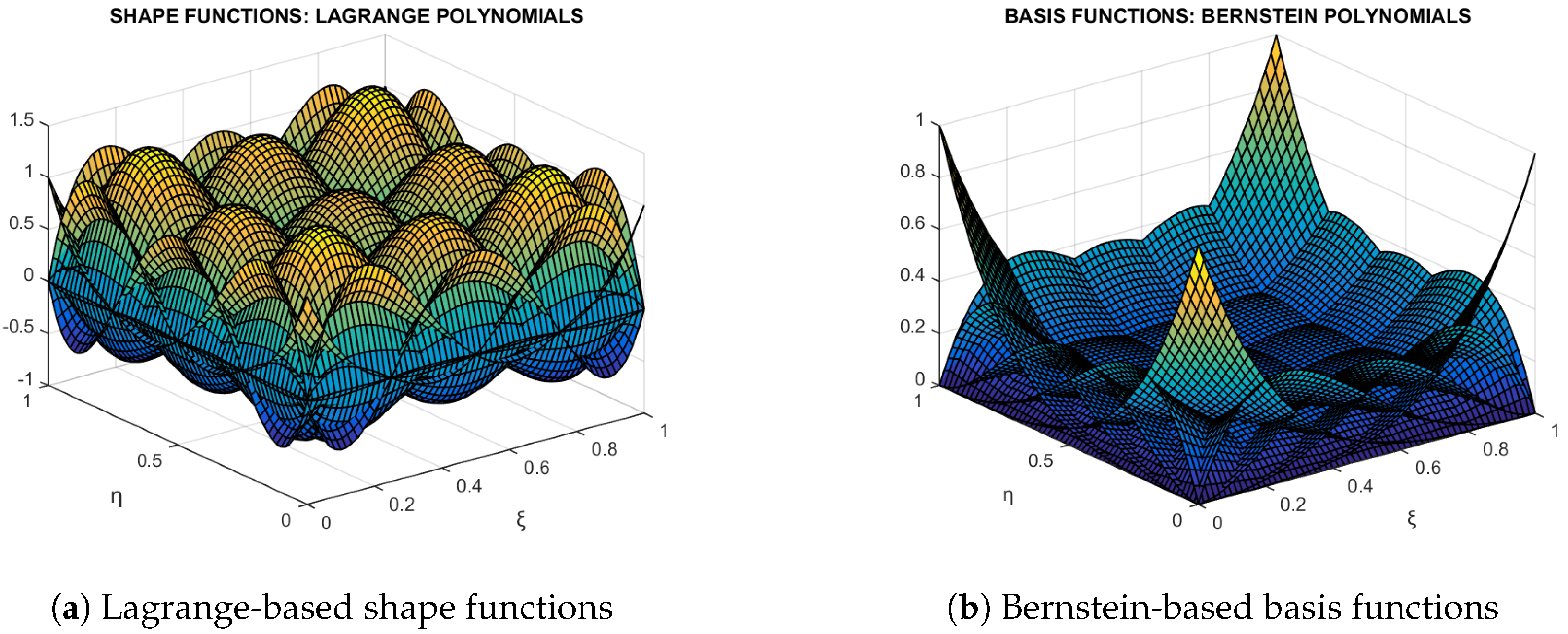
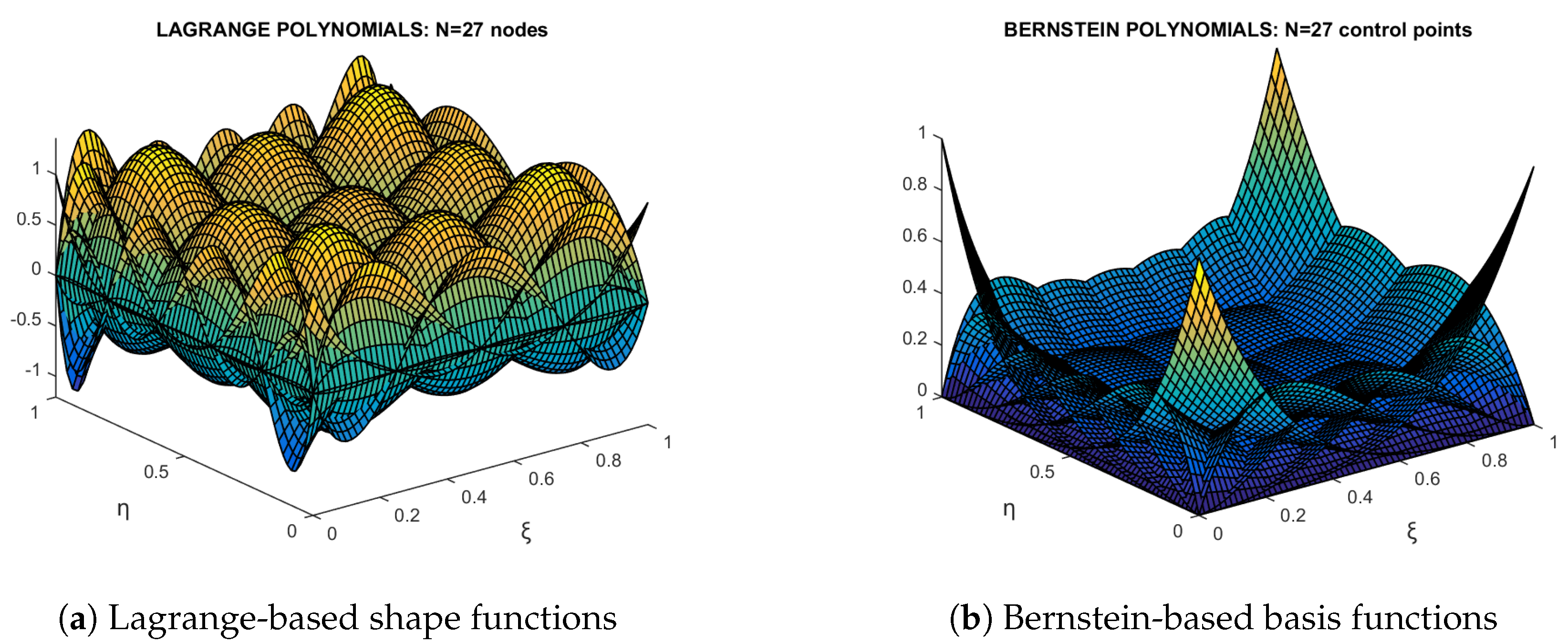
2.1. Bernstein Polynomials

It is well known that Bézier interpolation of a curve of degree n, or a univariate function has the following form

$$\mathbf{C}\left(\xi \right)=\sum _{i=1}^{n+1}{B}_{i,n}\left(\xi \right){\mathbf{P}}_i,0\le \xi \le 1,$$

(1)

with the Bernstein polynomials given by

$$B_{i,n}\left(\xi \right)={\displaystyle \frac{n!}{(i-1)!(n-i+1)!}}{\xi }^{i-1}{(1-\xi )}^{n-i+1},i=1,\dots ,n+1.$$

(2)

whereas ${\mathbf{P}}_i$ are the $(n+1)$ control points. In case of a univariate function $U\left(\xi \right)$, the control points are substituted by the generalized coefficients ${\alpha }_i$.

Since Bernstein and Lagrange polynomials share the same monomials ${\xi }^i$, it is concluded that these two sets are equivalent [6]. Therefore, bivariate and trivariate tensor product Lagrange polynomials are equivalent to those of Bernstein polynomials. Nevertheless, Bernstein polynomials are preferable because they can easily be combined with weight factors and thus accurately represent conics and quadric surfaces.

2.2. Relationship Between Bernstein and Lagrange Polynomials

2.2.1. Univariate Approximation

Previously in References [4,5,6], we have shown that univariate uniform Lagrange polynomials and Bernstein polynomials of the same degree are merely interrelated through a transformation matrix. In more detail, if the x-axis $(0\le x\le a)$ is uniformly subdivided into m segments, the $(m+1)$ associated Lagrange polynomials (of degree m) form a column vector ${\mathbf{L}}_x$, whereas the $(m+1)$ associated Bernstein polynomials form another column vector ${\mathbf{B}}_x$. These two sets of polynomials of the same degree m, are interrelated by

$${\mathbf{L}}_x={\mathbf{T}}_x{\mathbf{B}}_x,\mathrm{and}{\mathbf{B}}_x={\mathbf{T}}_x^{-1}{\mathbf{L}}_x,$$

(3)

where ${\mathbf{T}}_x$ is a transformation matrix of size $(m+1)\times (m+1)$. Typical values for $m=1,\dots ,4$ may be found in Refs. [4,5,6].

2.2.2. Tensor Products

Similar expressions may be written also for the y-direction, where the corresponding column vectors $({\mathbf{L}}_y,{\mathbf{B}}_y$) and the associated transformation matrix ${\mathbf{T}}_y$ appear:

$${\mathbf{L}}_y={\mathbf{T}}_y{\mathbf{B}}_y,\mathrm{and}{\mathbf{B}}_y={\mathbf{T}}_y^{-1}{\mathbf{L}}_y.$$

(4)

In case of a tensor product of degree $(m,n)$, using $(m+1)$ and $(n+1)$ nodal points along the axes x and y, respectively (i.e., totally $(m+1)\times (n+1)$ nodal points), we can write (see [5]):

$$U(\xi ,\eta )={\mathbf{L}}_x^T\mathbf{U}{\mathbf{L}}_y={\mathbf{B}}_x^T\mathbf{A}{\mathbf{B}}_y,$$

(5)

where the matrix $\mathbf{A}$ of generalized coefficients (in tensor product Bernstein polynomials) is related to the matrix $\mathbf{U}$ (including all the nodal values) through the two univariate transformation matrices, as follows:

$$\mathbf{A}={\mathbf{T}}_x^T\mathbf{U}{\mathbf{T}}_y,$$

(6)

and

$$\mathbf{U}={\left({\mathbf{T}}_x^{-1}\right)}^T\mathbf{A}\left({\mathbf{T}}_y^{-1}\right).$$

(7)

Implementation to a 9-node tensor product element is demonstrated in Section 3.5.

2.3. Non-Uniform Lagrange Polynomials

The standard expressions for the transformation matrices $\mathbf{T}$, which have been reported in previous papers [5,6], have been derived for uniform (equally spaced) Lagrange polynomials. However, when the intermediate nodes on a line segment (in the parametrc interval $[0,1]$) are moved from their initial uniform position, the set of nodal points on which Lagrange polynomials are based changes, merely because the nodal values $U_i$ change. In contrast, Bernstein polynomials are of standard form according to Equation 1, and thus they do not depend on the position of the associated control points. In conclusion, the change of nodal points along a segment $[0,L]$ implies a change of the transformation matrix $\mathbf{T}$ (i.e., ${\mathbf{T}}_x$ or ${\mathbf{T}}_y$), and change of the generalized coefficients. The numerical estimation of each one-dimensional transformation matrix (for example, ${\mathbf{T}}_x$), can be done by collocating Equation 5 at all the nodal points of $[0,L]$, which gives ${\mathbf{U}}_{nodal}=\left[\mathbf{C}\right]\mathbf{a}$. For each position of internal nodes with value ${\mathbf{U}}_{nodal}$ (of size $(m+1)\times 1$), the matrix $\left[\mathbf{C}\right]$ (of size $(m+1)\times (m+1)$) takes a diffenent value, the vector of coefficients becomes $\mathbf{a}={\mathbf{C}}^{-1}{\mathbf{U}}_{nodal}$, and thus ${\mathbf{T}}_x={\left({\mathbf{C}}^{-1}\right)}^T$.

3. Transformation Matrices Between Tensor Product Bernstein and Lagrange Functional Sets

In this section we shall derive the general expression for the transformation matrix $\mathbf{R}$ which correlates the tensor product Bernstein and Lagrange polynomial sets. To this purpose, as an example, first we start with the quadratic interpolation, and then present the general expression.

3.1. Quadratic Interpolation

Let us consider a quadratic element (1-2-3) shown in Figure 1a. As has been proven previously in Refs. [5,6], the relationship between the three quadratic Lagrange polynomials $({\mathbf{L}}_x={[L_{1,2}\left(x\right),L_{2,2}\left(x\right),L_{3,2}\left(x\right)]}^T)$ associated with the nodes (1,2,3) and the corresponding Bernstein polynomials $({\mathbf{B}}_x={[B_{1,2}\left(x\right),B_{2,2}\left(x\right),B_{3,2}\left(x\right)]}^T)$, is as follows:

$$\left[\begin{array}{c}{L}_{1,2}\left(\xi \right)\\ L_{2,2}\left(\xi \right)\\ L_{3,2}\left(\xi \right)\end{array}\right]=\left[\begin{array}{ccc}1& -{\displaystyle \frac{1}{2}}& 0\\ 0& 2& 0\\ 0& -{\displaystyle \frac{1}{2}}& 1\end{array}\right]\left[\begin{array}{c}{B}_{1,3}\left(\xi \right)\\ B_{2,3}\left(\xi \right)\\ B_{3,3}\left(\xi \right)\end{array}\right].$$

(8)

Note that regarding the subscripts in both polynomials of Equation 8, i.e., $L_{i,j}$ and $B_{i,j}$, the first index ‘$\mathit{i}$’ refers to the serial number of the node (measured from the left end) whereas the second index ‘$\mathit{j}$’ (after comma) refers to the polynomial degree (here, $j=p=2$).

Obviously, since each boundary edge of the bi-quadratic quadrilateral element shown in Figure 1b is entirely self-contained, the relationship by Equation 8 is useful for interpolation along the horizontal edges toward $\xi$-direction (1-2-3 and 7-8-9). Moreover, regarding the vertical $\eta$-direction, the independent variable $\xi$ in both parts of Equation 8 must be substituted by the independent variable $\eta$.

To derive the bivariate shape functions of the element in Figure 1b, both parts of Equation 8 are multiplied by $L_{1,2}\left(\eta \right)$, which in turn is further replaced by the same transformation in $\eta$, and thus we receive:

$$\begin{array}{cc}\hfill & \left[\begin{array}{c}{L}_{1,2}\left(\xi \right)\\ L_{2,2}\left(\xi \right)\\ L_{3,2}\left(\xi \right)\end{array}\right]L_{1,2}\left(\eta \right)=\left[\begin{array}{ccc}1& -\frac{1}{2}& 0\\ 0& 2& 0\\ 0& -\frac{1}{2}& 1\end{array}\right]\left[\begin{array}{c}{B}_{1,2}\left(\xi \right)\\ B_{2,2}\left(\xi \right)\\ B_{3,2}\left(\xi \right)\end{array}\right]L_{1,2}\left(\eta \right)\hfill \\ \hfill & =\left(\left[\begin{array}{ccc}1& -\frac{1}{2}& 0\\ 0& 2& 0\\ 0& -\frac{1}{2}& 1\end{array}\right]\left[\begin{array}{c}{B}_{1,2}\left(\xi \right)\\ B_{2,2}\left(\xi \right)\\ B_{3,2}\left(\xi \right)\end{array}\right]\right)·\left(\left[\begin{array}{ccc}0& -\frac{1}{2}& 0\end{array}\right]\left[\begin{array}{c}{B}_{1,2}\left(\eta \right)\\ B_{2,2}\left(\eta \right)\\ B_{3,2}\left(\eta \right)\end{array}\right]\right).\hfill \end{array}$$

(9)

whence we have:

$$\left[\begin{array}{c}{L}_{1,2}\left(\xi \right)L_{1,2}\left(\eta \right)\\ L_{2,2}\left(\xi \right)L_{1,2}\left(\eta \right)\\ L_{3,2}\left(\xi \right)L_{1,2}\left(\eta \right)\end{array}\right]=\left[\begin{array}{cccccc}1& -{\displaystyle \frac{1}{2}}& 0& -{\displaystyle \frac{1}{2}}& {\displaystyle \frac{1}{4}}& 0\\ 0& 2& 0& 0& -1& 0\\ 0& -{\displaystyle \frac{1}{2}}& 1& 0& {\displaystyle \frac{1}{4}}& -{\displaystyle \frac{1}{2}}\end{array}\right]\left[\begin{array}{c}{B}_{1,2}\left(\xi \right)B_{1,2}\left(\eta \right)\\ B_{2,2}\left(\xi \right)B_{1,2}\left(\eta \right)\\ B_{3,2}\left(\xi \right)B_{1,2}\left(\eta \right)\\ B_{1,2}\left(\xi \right)B_{2,2}\left(\eta \right)\\ B_{2,2}\left(\xi \right)B_{2,2}\left(\eta \right)\\ B_{3,2}\left(\xi \right)B_{2,2}\left(\eta \right)\end{array}\right].$$

(10)

In a similar way, multiplying Equation 8 by $L_{2,2}\left(\eta \right)$, we receive a shorter expression:

$$\left[\begin{array}{c}{L}_{1,2}\left(\xi \right)L_{2,2}\left(\eta \right)\\ L_{2,2}\left(\xi \right)L_{2,2}\left(\eta \right)\\ L_{3,2}\left(\xi \right)L_{2,2}\left(\eta \right)\end{array}\right]=\left[\begin{array}{ccc}2& -1& 0\\ 0& 4& 0\\ 0& -1& 2\end{array}\right]\left[\begin{array}{c}{B}_{1,2}\left(\xi \right)B_{2,2}\left(\eta \right)\\ B_{2,2}\left(\xi \right)B_{2,2}\left(\eta \right)\\ B_{3,2}\left(\xi \right)B_{2,2}\left(\eta \right)\end{array}\right].$$

(11)

Also, multiplying Equation 8 by $L_{3,2}\left(\eta \right)$, we receive:

$$\left[\begin{array}{c}{L}_{1,2}\left(\xi \right)L_{3,2}\left(\eta \right)\\ L_{2,2}\left(\xi \right)L_{3,2}\left(\eta \right)\\ L_{3,2}\left(\xi \right)L_{3,2}\left(\eta \right)\end{array}\right]=\left[\begin{array}{cccccc}-{\displaystyle \frac{1}{2}}& {\displaystyle \frac{1}{4}}& 0& 1& -{\displaystyle \frac{1}{2}}& 0\\ 0& -1& 0& 0& 2& 0\\ 0& {\displaystyle \frac{1}{4}}& -{\displaystyle \frac{1}{2}}& 0& -{\displaystyle \frac{1}{2}}& 1\end{array}\right]\left[\begin{array}{c}{B}_{1,2}\left(\xi \right)B_{2,2}\left(\eta \right)\\ B_{2,2}\left(\xi \right)B_{2,2}\left(\eta \right)\\ B_{3,2}\left(\xi \right)B_{2,2}\left(\eta \right)\\ B_{1,2}\left(\xi \right)B_{3,2}\left(\eta \right)\\ B_{2,2}\left(\xi \right)B_{3,2}\left(\eta \right)\\ B_{3,2}\left(\xi \right)B_{3,2}\left(\eta \right)\end{array}\right].$$

(12)

If all the nine shape functions of each functional set are packed into two column vectors as follows:

(13)

the combination of Equation 10 to Equation 13 determines a linear relationship between them, i.e.:

$${\mathbf{n}}_L=\mathbf{R}{\mathbf{n}}_B,$$

(14)

with

(15)

3.2. Generalization

It is worth mentioning that in the general case of a ‘square’ tensor product $p\times p$ associated with a univariate transformation matrix $\mathbf{T}={\mathbf{T}}_x={\mathbf{T}}_y$:

$$\mathbf{T}=\left[\begin{array}{ccc}{t}_{1,1}& \dots & t_{1,p+1}\\ ⋮& \ddots & ⋮\\ t_{p+1,1}& \dots & t_{p+1,p+1}\end{array}\right],$$

(16)

the transformation matrix $\mathbf{R}$ may be written as follows:

(17)

Moreover, in the most general case of a ‘rectangular’ tensor product of degree $(p,q)$ associated with univariate transformation matrices ${\mathbf{T}}_x(p\times p)$ and ${\mathbf{T}}_y(q\times q)$, the transformation matrix $\mathbf{R}$ may be written as follows:

(18)

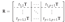
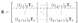
3.3. Transformation of Structural Engineering Matrices (K, M)

When the stiffness (and mass) matrix is known in the functional system of Lagrange polynomials, it is also known in terms Bernstein polynomials. In this context, omitting the corresponding factor (e.g., the density $\rho$ in elastodynamics, or the inverse of speed squared $1/c^2$ in acoustics), the mass matrix (${\mathbf{M}}_L$ in the Lagrangian basis and ${\mathbf{M}}_B$ in the Bézierian one) will be interrelated through the abovementioned transformation matrix $\mathbf{R}$, one being a quadratic form of the other, as follows:

$$\begin{array}{cc}\hfill {\mathbf{M}}_L& =\underset{\Omega }{\int \int }{\mathbf{n}}_L{\mathbf{n}}_L^{T}d\Omega \hfill \\ \hfill & =\underset{\Omega }{\int \int }\left(\mathbf{R}{\mathbf{n}}_B\right){\left(\mathbf{R}{\mathbf{n}}_B\right)}^{T}d\Omega =\underset{\Omega }{\int \int }\left(\mathbf{R}{\mathbf{n}}_B\right){\mathbf{n}}_B^T{\mathbf{R}}^{T}d\Omega \hfill \\ \hfill & =\mathbf{R}\left[\underset{\Omega }{\int \int }{\mathbf{n}}_B{\mathbf{n}}_B^{T}d\Omega \right]{\mathbf{R}}^T\hfill \\ \hfill & =\mathbf{R}{\mathbf{M}}_B{\mathbf{R}}^T.\hfill \end{array}$$

(19)

In a similar way, the stiffness matrices in the two systems will be interrelated by:

$${\mathbf{K}}_L=\mathbf{R}{\mathbf{K}}_B{\mathbf{R}}^T,$$

(20)

whereas, by virtue of Equation 14, the force vectors will be interrelated by:

$${\mathbf{f}}_L=\oint {\mathbf{n}}_L\left({\displaystyle \frac{\partial U}{\partial n}}\right)d\Gamma =\oint \mathbf{R}{\mathbf{n}}_B\left({\displaystyle \frac{\partial U}{\partial n}}\right)d\Gamma =\mathbf{R}\oint {\mathbf{n}}_B\left({\displaystyle \frac{\partial U}{\partial n}}\right)d\Gamma =\mathbf{R}{\mathbf{f}}_B.$$

(21)

Considering a static problem, for the functional set including Lagrange polynomials, the equilibrium equation becomes:

$${\mathbf{K}}_L{\mathbf{u}}_L={\mathbf{f}}_L,$$

(22)

and by virtue of Equation 20 and Equation 21 becomes:

$$\left(\mathbf{R}{\mathbf{K}}_B{\mathbf{R}}^T\right){\mathbf{u}}_L=\mathbf{R}{\mathbf{f}}_B.$$

(23)

After simplification of matrix $\mathbf{R}$ in both parts of Equation 23, we receive:

$${\mathbf{K}}_B\left({\mathbf{R}}^T{\mathbf{u}}_L\right)={\mathbf{f}}_B.$$

(24)

Moreover, since the displacement field does not depend on the functional basis but is the same in both of them, we have:

$$\begin{array}{cc}\hfill U(\xi ,\eta )& ={\mathbf{n}}_L^T{\mathbf{u}}_L={\mathbf{n}}_B^T{\mathbf{a}}_B.\hfill \end{array}$$

(25)

Substitution of Equation 14 into Equation 25 gives:

$$\begin{array}{cc}\hfill & {\left(\mathbf{R}{\mathbf{n}}_B\right)}^T{\mathbf{u}}_L={\mathbf{n}}_B^T{\mathbf{a}}_B\hfill \\ \hfill & \Rightarrow {\mathbf{n}}_B^T{\mathbf{R}}^T{\mathbf{u}}_L={\mathbf{n}}_B^T{\mathbf{a}}_B\hfill \\ \hfill & \Rightarrow \begin{array}{|c|}\hline {\mathbf{R}}^T{\mathbf{u}}_L={\mathbf{a}}_B\\ \hline\end{array}.\hfill \end{array}$$

(26)

Substituting Equation 26 into Equation 24, we receive:

$${\mathbf{K}}_B{\mathbf{a}}_B={\mathbf{f}}_B,\mathrm{Q}.\mathrm{E}.\mathrm{D}..$$

(27)

3.4. Numerical Verification

In addition to the above theoretical presentation, we also demonstrate the numerical coincidence (and a small difference regarding the condition number) in the following BVP (Example 1) that is characterized by different polynomial degrees in each direction and a non-polynomial exact solution.

$\mathbf{Example}\mathbf{1}$: Heat-flow in rectangular sheet

Let us consider a square sheet of dimensions $(a=b=1)$ in which Laplace equation dominates $({\nabla }^{2}U=0)$. The boundary conditions are partially Dirichlet and Neumann type, as shown in Figure 2a. The temperature along the top edge is given as

$$U(x,y=b)=U_{m}cos\left({\displaystyle \frac{\pi x}{2a}}\right),0\le x\le a.$$

(28)

The exact solution is given as:

$$U(x,y)=U_m{\displaystyle \frac{sinh\left(\frac{\pi y}{2a}\right)}{sinh\left(\frac{\pi b}{2a}\right)}}cos\left({\displaystyle \frac{\pi x}{2a}}\right),0\le x\le a,0\le y\le b;$$

(29)

whereas the error norm $L_2$, is defined (in percent %) as:

$$L_2={\left[{\displaystyle \frac{{\int \int }_{\Omega }{(u_{calculated}-u_{exact})}^{2}d\Omega }{{\int \int }_{\Omega }{\left(u_{exact}\right)}^{2}d\Omega }}\right]}^{1/2}\times 100(\%).$$

(30)

Solution: The entire patch $ABCD$ was discretized as a single tensor product element of 20 degrees of freedom (DOFs) shown in Figure 2b (with polynomial degrees $p_x=3$ and $p_y=4$), of which only nine DOFs are unrestrained. Using either Lagrange or Bernstein polynomials, the calculated error was found to be the same, equal to $L_2=0.2035\%$ (coincidence until the 14th decimal point). The only difference in the two numerical solutions was the condition number of the equations’ matrix (of size $9\times 9$), which was found equal to 41.8 and 55.3 for Lagrange and Bernstein polynomials, respectively. To further investigate the relationship between equivalent Lagrange and Bernstein polynomials, in the tensor product we used non-uniform Lagrange polynomials toward the y-direction, with nodal points at $y=0.0,0.3,0.6,0.8$ (or $0.85),1.0$ (i.e., slightly refined close to the top edge DC). It was found that, in the formulation using nonuniform Lagrange polynomials, the $L_2$-norm was insensitive (it changed with respect to the above uniform solution only after the 13rd decimal point). In contrast, the condition number was sensitive, since it varied between 37.7 and 53.2 for the ordinate of the nodal point 13 below the corner D shown in Figure 2b, with $y_{13}=0.85$ and $y_{13}=0.80$, respectively. Despite the non-uniform location of nodal points in the y-direction, the linear mapping was preserved (i.e., $y(\xi ,\eta )=\eta$) and (closely related) the determinant of the Jacobian was always constant, equal to unity. Moreover, in the formulation using Bernstein polynomials, it is critical to preserve the control points at their initial uniform positions to ensure this linear mapping (and not to move them at the nonuniform nodal points of the Lagrange-based model), and then (obviously) the $L_2$-norm is preserved the same as in Lagrange polynomials formulation (since nothing changes), otherwise the Jacobian becomes variable and the $L_2$ error norm substantially increases.

Comparing the two column-vectrs in Equation 13, one may observe that in tensor products Bernstein polynomials, it is merely necessary to substitute Lagrange polynomials with Bernstein polynomials of the same degree. Nevertheless, it is still unknown whether this receipe can be extended to other classes of non-tensor product macroelements. One of this class refers to the traditional transfinite elements which are similar to the tensor product, thus of structured form, but many nodes of the ideal tensor-prduct are missing. This case is fully studied in Section 4.

3.5. Cross-Check

The same result with Equation 15 can be obtained performing the operations in Equation 6. For the 9-node element with node numbering according to Figure 1b, each of the transformation matrices ${\mathbf{T}}_x={\mathbf{T}}_y$ is equal to the $3\times 3$ matrix shown in the right-hand side of Equation 8. The matrices $\mathbf{A}$ and $\mathbf{U}$ include the following entries:

$$\mathbf{A}=\left[\begin{array}{ccc}{a}_1& a_4& a_7\\ a_2& a_5& a_8\\ a_3& a_6& a_9\end{array}\right]\mathrm{and}\mathbf{U}=\left[\begin{array}{ccc}{U}_1& U_4& U_7\\ U_2& U_5& U_8\\ U_3& U_6& U_9\end{array}\right].$$

(31)

The interested reader may also consult a MATLAB script given in Appendix A, which performs the comparison between the matrix $\mathbf{A}$ (of size $3\times 3$) with the column-vector $\tilde{\mathbf{A}}$ (of size $9\times 1$), which is calculated through Equation 15 and is defined as

$$\tilde{\mathbf{A}}={\left[\begin{array}{ccccccccc}{a}_1& a_2& a_3& a_4& a_5& a_6& a_7& a_8& a_9\end{array}\right]}^T.$$

(32)

4. Traditional Transfinite Elements

Traditional transfinite elements cover the entire or a large portion of a parametric quadrilateral patch $ABCD$. They consist of nodes ordered along horizontal and vertical stations (cuts) which are perpendicular to the $\xi$ and $\eta$ parametric axes, and are very similar to the 21-node element shown in Figure 3. Traditionlly, the transfinite elements are characterized by the following two functional sets:

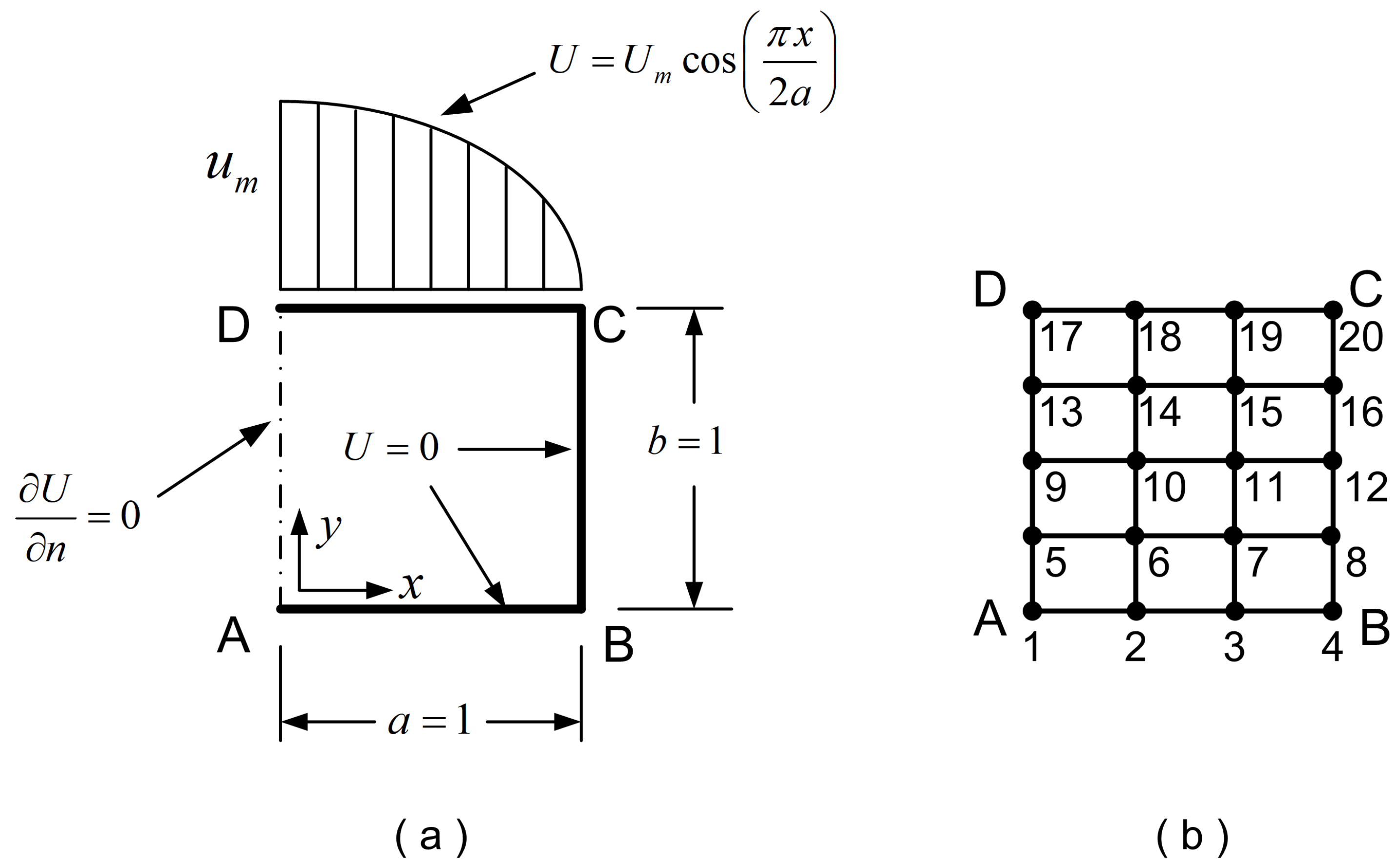
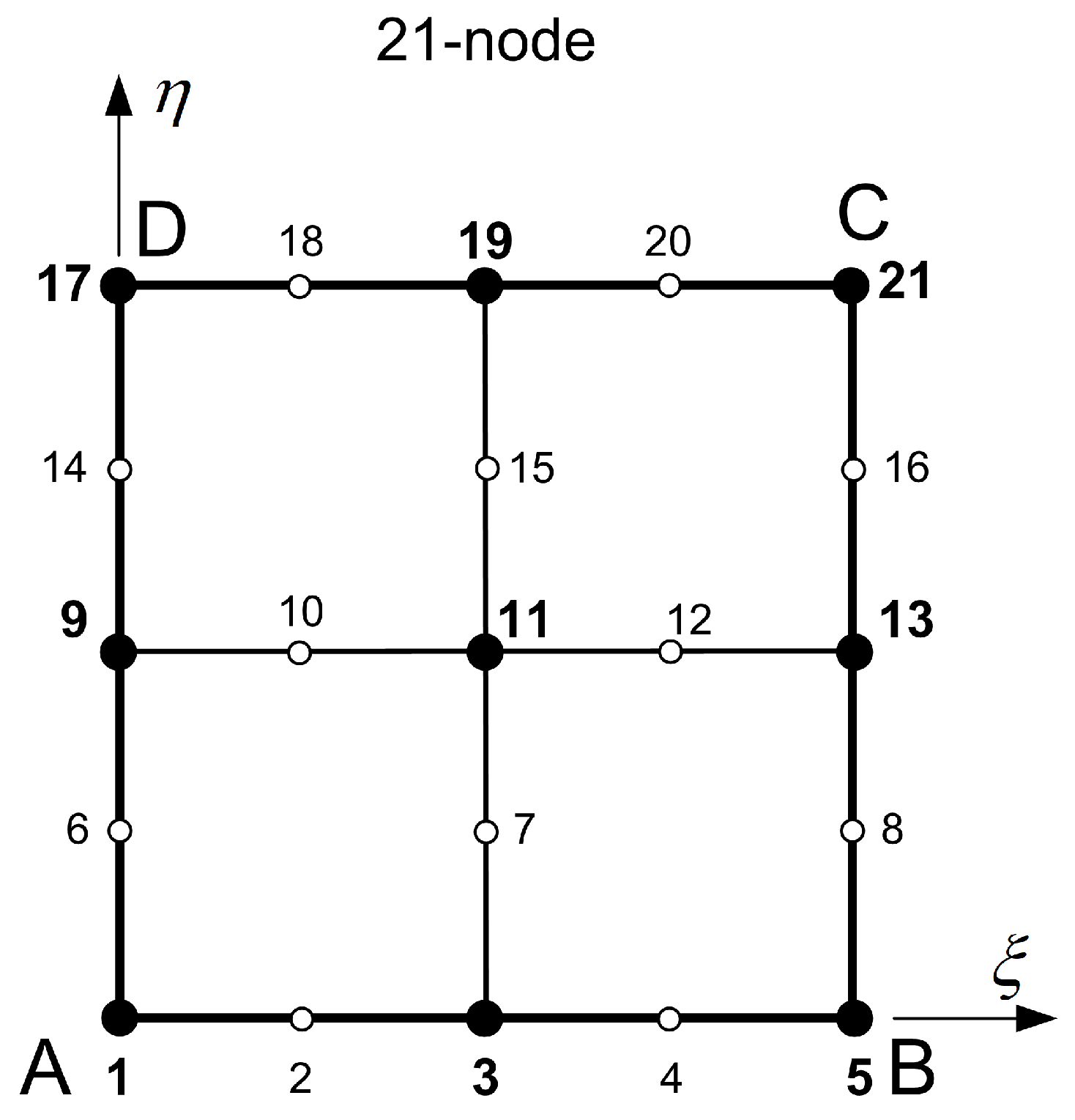
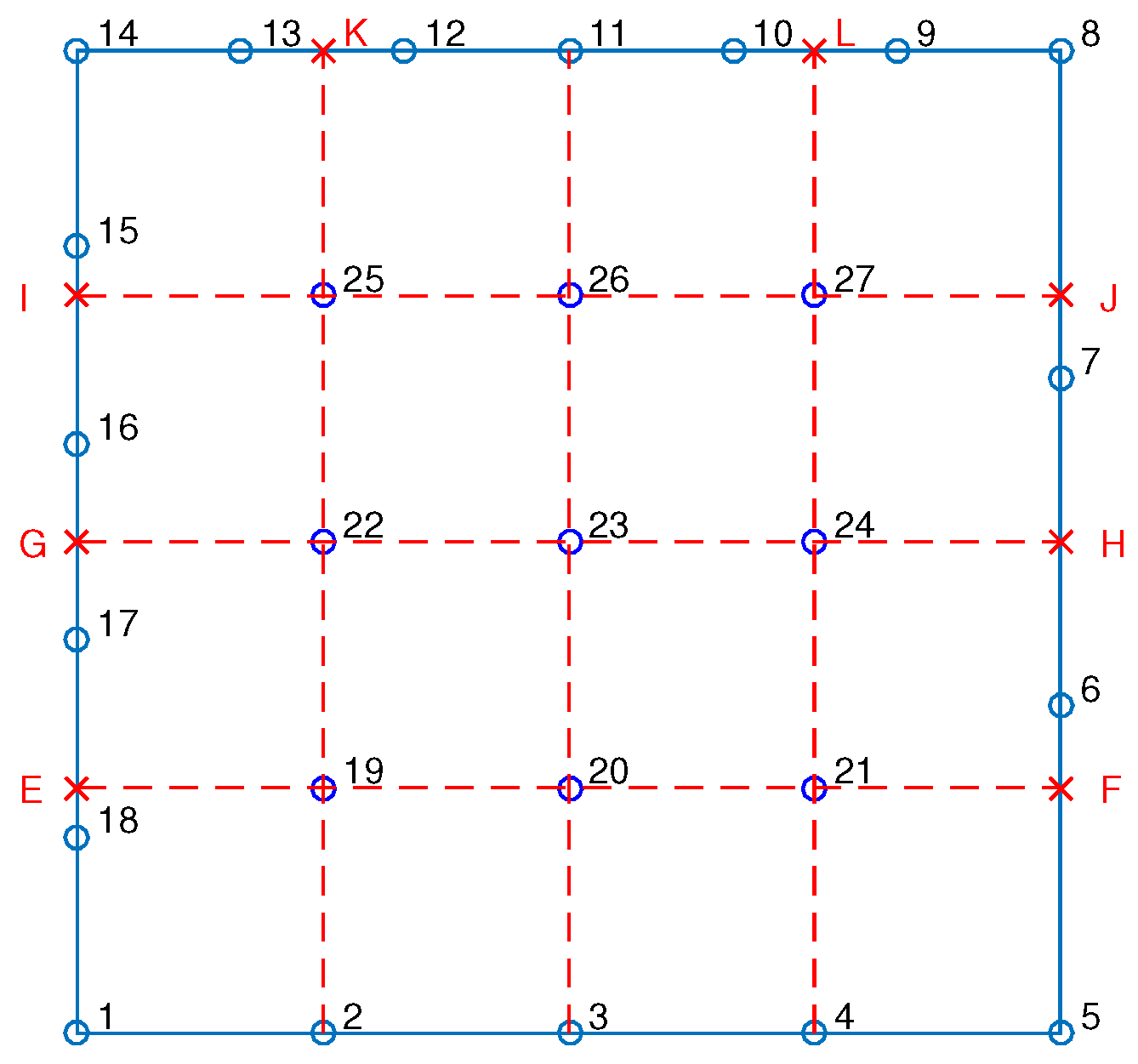
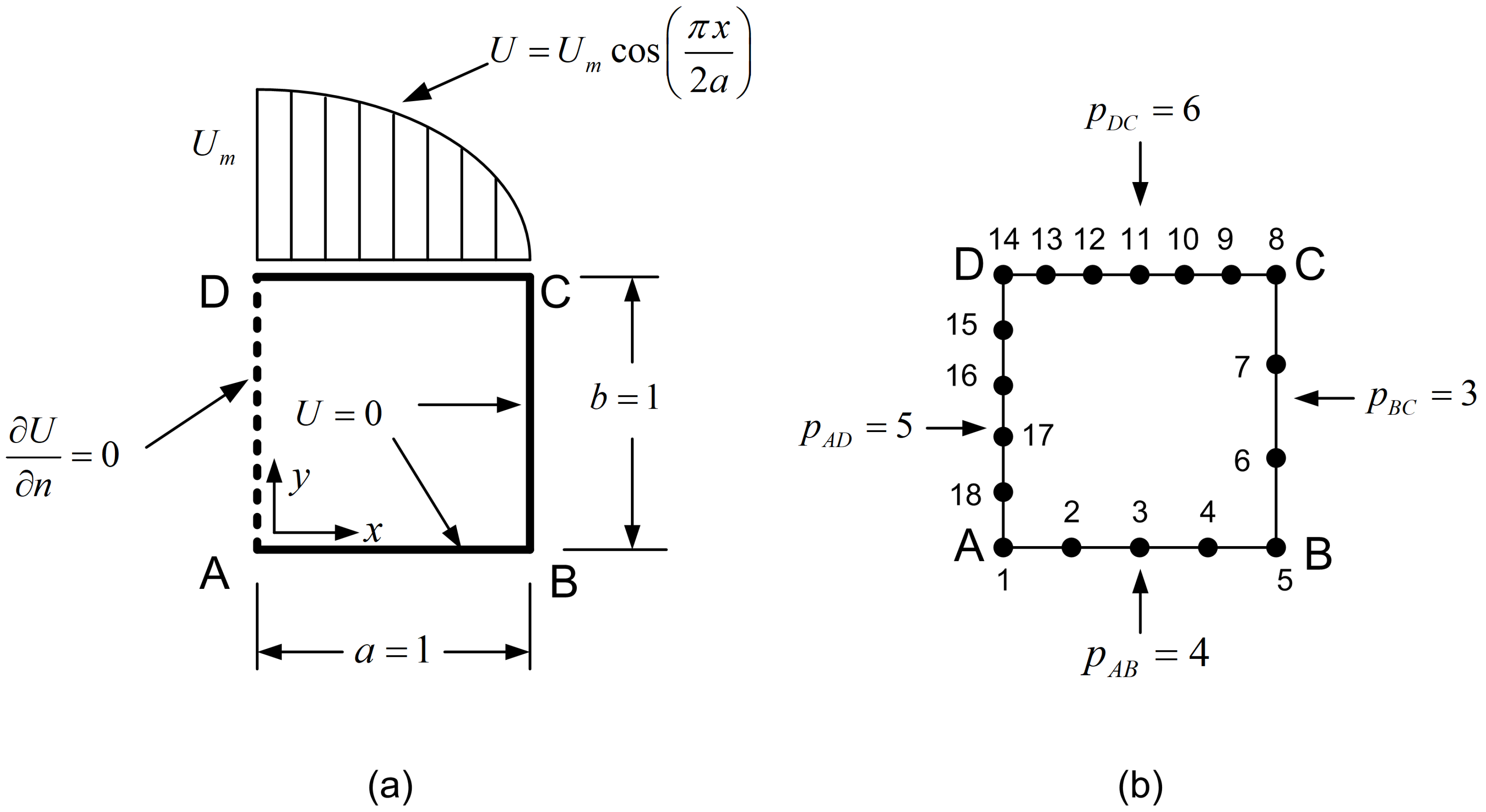
• Blending functions. For each direction ($\xi$ or $\eta$), the number of blending functions equals to the number $n_{st}$ of corresponding sections, and thus their polynomial degree ($p_{\xi }$ or $p_{\eta }$, accordingly) equals to $(n_{st}-1)$. For example, in the 21-node element shown in Figure 3, there are three stations per direction and thus $p_{\xi }=p_{\eta }=2$. Perpendicularly to the $\xi$-direction (toward $\eta$-axis), the first vertical station is the edge AD (with nodes 1-6-9-14-17), the second vertical station consists of the nodes (3-7-11-15-19) and the third one includes the nodes along edge BC (with nodes 5-8-13-16-21). Similarly, perpendicularly to $\eta$-direction (toward $\xi$-axis), there are also three horizontal stations, i.e., the edge AB (with nodes 1-to-5), the isoline made of nodes (9-10-11-12-13), and eventually the edge DC (with nodes 17-to-21).
• Trial functions. These refer to the interpolation along the stations. In this example, each station consists of 5 nodes (4 node spans), and thus the polynomial degree will be $p_{\xi }^{\prime }=4$ (e.g. along the horizontal edge $AB$), and similarly $p_{\eta }^{\prime }=4$ (e.g. along the vertical edge $AD$). In general (for other discretizations), we may have $p_{\xi }^{\prime }\ne p_{\eta }^{\prime }$.

One may observe that this specific 21-node element may be produced from a tensor product of size $5\times 5$ (25 nodes), from which 4 nodes (i.e., the centers of the four cells: 1-3-11-9, 3-5-13-11, etc.) are missing. Elements of this type have been extensively studied by their originators [7] as well as by later researchers (the reader is addressed to a specific monograph [8] and a later paper [9]). At this point, we must point out that the utilization of Lagrange polynomials in transfinite formulation is very clear and reasonable (however heuristic), as follows. The blending functions interpolate the quantity $U(\xi ,\eta )$ along the horizontal and vertical stations independently (thus forming the projectors $P_{\xi }$ and $P_{\eta }$ ), and then perform a bivariate correction by subtracting the projector $P_{\xi \eta }$.

While the utilization of Lagrange polynomials in traditional transfinite elements is very clear, the same is not the case for the Bernstein ones. It has been previously discussed that Bernstein and Lagrange polynomials are mathematically equivalent for the same degree, in the sense that the first set is a linear transformation of the second, and vice versa [4,5]. While this fact holds for a tensor product, it is not yet clear whether it is also valid in other situations. For example, a previous intuitive study has shown that non-tensor-product traditional transfinite elements based on Lagrange polynomials may be easily treated by Bernstein polynomials, merely substituting the former by the latter polynomials of the same degree in the final expression of shape functions, for both the blending and trial functions [4]. Nevertheless, not a rigorous explanation has been provided so far.

In the paper at hand, we shall investigate in detail the deeper reasons for the numerical coincidence in the reported accuracy between Lagrange and Bernstein polynomials, and whether it is only a matter of substituting polynomials of the same degree.

4.1. General Relationships Between Initial and Transformed Bases

Before going on, it is worth mentioning that on any change of basis there are some standard relationships between the quantities of the two sets. A special discussion on the symmetric eigenvalue problem may be found in Ref. [2](pp. 51-60). In more detail, let $\left\{\varphi \right\}$ be the column-vector of all the shape functions, $\left\{\mathbf{x}\right\}$ the vector of the Cartesian coordinates of nodal points, and $\left\{\mathbf{U}\right\}$ the nodal displacements (potentials) in the system of Lagrange polynomials. Moreover, in the Bernstein set the corresponding shape functions are $\left\{\psi \right\}$, the control points are $\left\{{\mathbf{x}}^c\right\}$, and the coefficients (generalized coordinates) are $\left\{\mathbf{a}\right\}$. Between Lagrange and Bernstein-based systems, we have the following linear relationships:

For the shape functions we have:

$$\left\{\varphi (\xi ,\eta )\right\}=\left[\mathbf{R}\right]\left\{\psi (\xi ,\eta )\right\}.$$

(33)

For the degrees of freedom (DOF) we have:

$$\left\{\mathbf{a}\right\}={\left[\mathbf{R}\right]}^T\left\{\mathbf{U}\right\}.$$

(34)

One may observe that the above matrix formulations are consistent to the expressions of the dependent variable $U(\xi ,\eta )$ in the two systems, as follows:

$$U(\xi ,\eta )={\left\{\varphi \right\}}^T\left\{\mathbf{U}\right\}={\left\{\psi \right\}}^T\left\{\mathbf{a}\right\}.$$

(35)

To determine the control points which define the same parameterization in both systems, we adopt the isoparametric concept (very similar to Equation 35):

$$\mathbf{x}(\xi ,\eta )={\left\{\varphi \right\}}^T\left\{{\mathbf{x}}_{nodal}\right\}={\left\{\psi \right\}}^T\left\{{\mathbf{x}}^c\right\},$$

(36)

and thus, the analogous expression with Equation 34 for the control points is:

$$\left\{{\mathbf{x}}^c\right\}={\left[\mathbf{R}\right]}^T\left\{\mathbf{x}\right\}.$$

(37)

4.2. Structured Transfinite Elements

In this subsection we focus on the traditional structured transfinite elements, which are characterized by some horizontal and vertical stations that are subdivided by several nodes as the 21-node element shown in Figure 3. The characteristic of this element, and similar ones, is the same number and the same location of nodal points along all parallel stations to one direction, separately. It has been discussed in [4] that, taking into consideration that the blending functions are quadratic Lagrange polynomials (because there are three parallel stations per direction) whereas the trial functions are quintic Lagrange polynomials (because there are five nodes per station), the three projectors $(P_{\xi },P_{\eta },P_{\xi \eta })$ of the Boolean sum can be constructed. To shorten their presentation, here we prefer an alternative, that is the following robust matrix formulation:

$$P_{\xi }=\underset{{\mathbf{L}}_{5,y}^T}{\underbrace{\left[\begin{array}{ccccc}{L}_{1,4}\left(\eta \right)& L_{2,4}\left(\eta \right)& L_{3,4}\left(\eta \right)& L_{4,4}\left(\eta \right)& L_{5,4}\left(\eta \right)\end{array}\right]}}\underset{{\mathbf{U}}_{\xi }}{\underbrace{\left[\begin{array}{ccc}{U}_1& U_3& U_5\\ U_6& U_7& U_8\\ U_9& U_{11}& U_{13}\\ U_{14}& U_{15}& U_{16}\\ U_{17}& U_{19}& U_{21}\end{array}\right]}}\underset{{\mathbf{L}}_{3,x}}{\underbrace{\left[\begin{array}{c}{L}_{1,2}\left(\xi \right)\\ L_{2,2}\left(\xi \right)\\ L_{3,2}\left(\xi \right)\end{array}\right]}}$$

(38)

$$P_{\eta }=\underset{{\mathbf{L}}_{5,x}^T}{\underbrace{\left[\begin{array}{ccccc}{L}_{1,4}\left(\xi \right)& L_{2,4}\left(\xi \right)& L_{3,4}\left(\xi \right)& L_{4,4}\left(\xi \right)& L_{5,4}\left(\xi \right)\end{array}\right]}}\underset{{\mathbf{U}}_{\eta }}{\underbrace{\left[\begin{array}{ccc}{U}_1& U_9& U_{17}\\ U_2& U_{10}& U_{18}\\ U_3& U_{11}& U_{19}\\ U_4& U_{12}& U_{20}\\ U_5& U_{13}& U_{21}\end{array}\right]}}\underset{{\mathbf{L}}_{3,y}}{\underbrace{\left[\begin{array}{c}{L}_{1,2}\left(\eta \right)\\ L_{2,2}\left(\eta \right)\\ L_{3,2}\left(\eta \right)\end{array}\right]}}$$

(39)

and

$$P_{\xi \eta }=\underset{{\mathbf{L}}_{3,x}^T}{\underbrace{\left[\begin{array}{ccc}{L}_{1,2}\left(\xi \right)& L_{2,2}\left(\xi \right)& L_{3,2}\left(\xi \right)\end{array}\right]}}\underset{{\mathbf{U}}_{\xi \eta }}{\underbrace{\left[\begin{array}{ccc}{U}_1& U_9& U_{17}\\ U_3& U_{11}& U_{19}\\ U_5& U_{13}& U_{21}\end{array}\right]}}\underset{{\mathbf{L}}_{3,y}}{\underbrace{\left[\begin{array}{c}{L}_{1,2}\left(\eta \right)\\ L_{2,2}\left(\eta \right)\\ L_{3,2}\left(\eta \right)\end{array}\right]}}$$

(40)

According to the standard theory [9], the transfinite interpolation of the bivariate dependent variable $U(\xi ,\eta )$ is given, in terms of three projectors, as:

$$U(\xi ,\eta )=P_{\xi }+P_{\eta }-P_{\xi \eta }.$$

(41)

Substituting the three projectors, i.e., Equations 38 to 40 into Equation 41, extraction of coefficients gives the expression:

$$U(\xi ,\eta )=\sum _{j=1}^{21}{\varphi }_j(\xi ,\eta )U_j,$$

(42)

where the global bivariate shape functions ${\varphi }_j$ are given in terms of Lagrange polynomials by:

$$\begin{array}{cc}\hfill & {\varphi }_1(\xi ,\eta )=L_{1,2}\left(\xi \right)L_{1,4}\left(\eta \right)+L_{1,4}\left(\xi \right)L_{1,2}\left(\eta \right)-L_{1,2}\left(\xi \right)L_{1,2}\left(\eta \right),\hfill \\ \hfill & {\varphi }_2(\xi ,\eta )=L_{2,4}\left(\xi \right)L_{1,2}\left(\eta \right),\hfill \\ \hfill & {\varphi }_3(\xi ,\eta )=L_{2,2}\left(\xi \right)L_{1,4}\left(\eta \right)+L_{3,4}\left(\xi \right)L_{1,2}\left(\eta \right)-L_{2,2}\xi )L_{1,2}\left(\eta \right),\hfill \\ \hfill & {\varphi }_4(\xi ,\eta )=L_{4,4}\left(\xi \right)L_{1,2}\left(\eta \right),\hfill \\ \hfill & {\varphi }_5(\xi ,\eta )=L_{3,2}\left(\xi \right)L_{1,4}\left(\eta \right)+L_{5,4}\left(\xi \right)L_{1,2}\left(\eta \right)-L_{3,2}\left(\xi \right)L_{1,2}\left(\eta \right),\hfill \\ \hfill & {\varphi }_6(\xi ,\eta )=L_{1,2}\left(\xi \right)L_{2,4}\left(\eta \right),\hfill \\ \hfill & {\varphi }_7(\xi ,\eta )=L_{2,2}\left(\xi \right)L_{2,4}\left(\eta \right),\hfill \\ \hfill & {\varphi }_8(\xi ,\eta )=L_{3,2}\left(\xi \right)L_{2,4}\left(\eta \right),\hfill \\ \hfill & {\varphi }_9(\xi ,\eta )=L_{1,2}\left(\xi \right)L_{3,4}\left(\eta \right)+L_{1,4}\left(\xi \right)L_{2,2}\left(\eta \right)-L_{1,2}\left(\xi \right)L_{2,2}\left(\eta \right),\hfill \\ \hfill & {\varphi }_{10}(\xi ,\eta )=L_{2,4}\left(\xi \right)L_{2,2}\left(\eta \right),\hfill \\ \hfill & {\varphi }_{11}(\xi ,\eta )=L_{2,2}\left(\xi \right)L_{3,4}\left(\eta \right)+L_{3,4}\left(\xi \right)L_{2,2}\left(\eta \right)-L_{2,2}\left(\xi \right)L_{2,2}\left(\eta \right),\hfill \\ \hfill & {\varphi }_{12}(\xi ,\eta )=L_{4,4}\left(\xi \right)L_{2,2}\left(\eta \right),\hfill \\ \hfill & {\varphi }_{13}(\xi ,\eta )=L_{3,2}\left(\xi \right)L_{3,4}\left(\eta \right)+L_{5,4}\left(\xi \right)L_{2,2}\left(\eta \right)-L_{3,2}\left(\xi \right)L_{2,2}\left(\eta \right),\hfill \\ \hfill & {\varphi }_{14}(\xi ,\eta )=L_{1,2}\left(\xi \right)L_{4,4}\left(\eta \right),\hfill \\ \hfill & {\varphi }_{15}(\xi ,\eta )=L_{2,2}\left(\xi \right)L_{4,4}\left(\eta \right),\hfill \\ \hfill & {\varphi }_{16}(\xi ,\eta )=L_{3,2}\left(\xi \right)L_{4,4}\left(\eta \right),\hfill \\ \hfill & {\varphi }_{17}(\xi ,\eta )=L_{1,2}\left(\xi \right)L_{5,4}\left(\eta \right)+L_{1,4}\left(\xi \right)L_{3,2}\left(\eta \right)-L_{1,2}\left(\xi \right)L_{3,2}\left(\eta \right),\hfill \\ \hfill & {\varphi }_{18}(\xi ,\eta )=L_{2,4}\left(\xi \right)L_{3,2}\left(\eta \right),\hfill \\ \hfill & {\varphi }_{19}(\xi ,\eta )=L_{2,2}\left(\xi \right)L_{5,4}\left(\eta \right)+L_{3,4}\left(\xi \right)L_{3,2}\left(\eta \right)-L_{2,2}\left(\xi \right)L_{3,2}\left(\eta \right),\hfill \\ \hfill & {\varphi }_{20}(\xi ,\eta )=L_{4,4}\left(\xi \right)L_{3,2}\left(\eta \right),\hfill \\ \hfill & {\varphi }_{21}(\xi ,\eta )=L_{3,2}\left(\xi \right)L_{5,4}\left(\eta \right)+L_{5,4}\left(\xi \right)L_{3,2}\left(\eta \right)-L_{3,2}\left(\xi \right)L_{3,2}\left(\eta \right).\hfill \end{array}$$

(43)

If we return to Equations 38 to 40, we can easily replace the univariate row and column vectors of the Lagrange polynomials (${\mathbf{L}}_x$ or ${\mathbf{L}}_y$) by the equal products of the transformation matrices (${\mathbf{T}}_x$ or ${\mathbf{T}}_y$) times the corresponding vector of Bernstein polynomials (${\mathbf{B}}_x$ or ${\mathbf{B}}_y$) according to Equations 3 and 4. Then, in short notation, Equation 41 becomes:

$$\begin{array}{cc}\hfill U(\xi ,\eta )& =\left({\mathbf{L}}_{5,y}^T\right)\left[{\mathbf{U}}_{\xi }\right]\left({\mathbf{L}}_{3,x}\right)+\left({\mathbf{L}}_{5,x}^T\right)\left[{\mathbf{U}}_{\eta }\right]\left({\mathbf{L}}_{3,y}\right)-\left({\mathbf{L}}_{3,x}^T\right)\left[{\mathbf{U}}_{\xi \eta }\right]\left({\mathbf{L}}_{3,y}\right)\hfill \\ \hfill & =\left({\mathbf{B}}_{5,y}^T\right)\underset{\left[{\mathbf{A}}_{\xi }\right]}{\underbrace{\left\{\left({\mathbf{T}}_{5,y}^T\right)\left[{\mathbf{U}}_{\xi }\right]\left({\tilde{\mathbf{T}}}_{3,x}\right)\right\}}}\left({\mathbf{B}}_{3,x}\right)\hfill \\ \hfill & +\left({\mathbf{B}}_{5,x}^T\right)\underset{\left[{\mathbf{A}}_{\eta }\right]}{\underbrace{\left\{\left({\mathbf{T}}_{5,x}^T\right)\left[{\mathbf{U}}_{\eta }\right]\left({\tilde{\mathbf{T}}}_{3,y}\right)\right\}}}\left({\mathbf{B}}_{3,y}\right)\hfill \\ \hfill & -\left({\mathbf{B}}_{3,x}^T\right)\underset{\left[{\mathbf{A}}_{\xi \eta }\right]}{\underbrace{\left\{\left({\mathbf{T}}_{3,x}^T\right)\left[{\mathbf{U}}_{\xi \eta }\right]\left({\tilde{\mathbf{T}}}_{3,y}\right)\right\}}}\left({\mathbf{B}}_{3,y}\right).\hfill \end{array}$$

(44)

One may observe that the right-hand side of Equation 44 includes three matrices, of which the entries are linear combinations of the $U_i$’s (obviously, they represent generalized coefficients), i.e.:

$$\begin{array}{cc}\hfill \left[{\mathbf{A}}_{\xi }\right]& =\left({\mathbf{T}}_{5,y}^T\right)\left[{\mathbf{U}}_{\xi }\right]\left({\tilde{\mathbf{T}}}_{3,x}\right)\hfill \end{array}$$

(45)

$$\begin{array}{cc}\hfill {\mathbf{A}}_{\eta }]& =\left({\mathbf{T}}_{5,x}^T\right)\left[{\mathbf{U}}_{\eta }\right]\left({\tilde{\mathbf{T}}}_{3,y}\right)\hfill \end{array}$$

(46)

$$\begin{array}{cc}\hfill {\mathbf{A}}_{\xi \eta }]& =\left({\mathbf{T}}_{3,x}^T\right)\left[{\mathbf{U}}_{\xi \eta }\right]\left({\tilde{\mathbf{T}}}_{3,y}\right),\hfill \end{array}$$

(47)

and thus Equation 44 can be written as:

$$U(\xi ,\eta )=\left({\mathbf{B}}_{5,y}^T\right)\left[{\mathbf{A}}_{\xi }\right]\left({\mathbf{B}}_{3,x}\right)+\left({\mathbf{B}}_{5,x}^T\right)\left[{\mathbf{A}}_{\eta }\right]\left({\mathbf{B}}_{3,y}\right)-\left({\mathbf{B}}_{3,x}^T\right)\left[{\mathbf{A}}_{\xi \eta }\right]\left({\mathbf{B}}_{3,y}\right).$$

(48)

From the two equalities of Equation 44, which are very similar, the first in terms of Lagrange and the second in terms of Bernstein polynomials, one may easily understand that the two sets of Lagrange polynomials in Equation 43, i.e., those of degree $p_x=p_y=2$ and $p_x=p_y=4$, are replaced by Bernstein polynomials of the same degree, one-by-one. Therefore, the second equality of Equation 44 eventually leads to the expression:

$$U(\xi ,\eta )=\sum _{j=1}^{21}{\psi }_j(\xi ,\eta )a_j,$$

(49)

where $a_j$ are the generalized coordinates (DOF in Bernstein system). Moreover, the produced functional set is quite equivalent, given by:

$$\begin{array}{cc}\hfill & {\psi }_1(\xi ,\eta )=B_{1,2}\left(\xi \right)B_{1,4}\left(\eta \right)+B_{1,4}\left(\xi \right)B_{1,2}\left(\eta \right)-B_{1,2}\left(\xi \right)B_{1,2}\left(\eta \right),\hfill \\ \hfill & {\psi }_2(\xi ,\eta )=B_{2,4}\left(\xi \right)B_{1,2}\left(\eta \right),\hfill \\ \hfill & {\psi }_3(\xi ,\eta )=B_{2,2}\left(\xi \right)B_{1,4}\left(\eta \right)+B_{3,4}\left(\xi \right)B_{1,2}\left(\eta \right)-B_{2,2}\xi )B_{1,2}\left(\eta \right),\hfill \\ \hfill & {\psi }_4(\xi ,\eta )=B_{4,4}\left(\xi \right)B_{1,2}\left(\eta \right),\hfill \\ \hfill & {\psi }_5(\xi ,\eta )=B_{3,2}\left(\xi \right)B_{1,4}\left(\eta \right)+B_{5,4}\left(\xi \right)B_{1,2}\left(\eta \right)-B_{3,2}\left(\xi \right)B_{1,2}\left(\eta \right),\hfill \\ \hfill & {\psi }_6(\xi ,\eta )=B_{1,2}\left(\xi \right)B_{2,4}\left(\eta \right),\hfill \\ \hfill & {\psi }_7(\xi ,\eta )=B_{2,2}\left(\xi \right)B_{2,4}\left(\eta \right),\hfill \\ \hfill & {\psi }_8(\xi ,\eta )=B_{3,2}\left(\xi \right)B_{2,4}\left(\eta \right),\hfill \\ \hfill & {\psi }_9(\xi ,\eta )=B_{1,2}\left(\xi \right)B_{3,4}\left(\eta \right)+B_{1,4}\left(\xi \right)B_{2,2}\left(\eta \right)-B_{1,2}\left(\xi \right)B_{2,2}\left(\eta \right),\hfill \\ \hfill & {\psi }_{10}(\xi ,\eta )=B_{2,4}\left(\xi \right)B_{2,2}\left(\eta \right),\hfill \\ \hfill & {\psi }_{11}(\xi ,\eta )=B_{2,2}\left(\xi \right)B_{3,4}\left(\eta \right)+B_{3,4}\left(\xi \right)B_{2,2}\left(\eta \right)-B_{2,2}\left(\xi \right)B_{2,2}\left(\eta \right),\hfill \\ \hfill & {\psi }_{12}(\xi ,\eta )=B_{4,4}\left(\xi \right)B_{2,2}\left(\eta \right),\hfill \\ \hfill & {\psi }_{13}(\xi ,\eta )=B_{3,2}\left(\xi \right)B_{3,4}\left(\eta \right)+B_{5,4}\left(\xi \right)B_{2,2}\left(\eta \right)-B_{3,2}\left(\xi \right)B_{2,2}\left(\eta \right),\hfill \\ \hfill & {\psi }_{14}(\xi ,\eta )=B_{1,2}\left(\xi \right)B_{4,4}\left(\eta \right),\hfill \\ \hfill & {\psi }_{15}(\xi ,\eta )=B_{2,2}\left(\xi \right)B_{4,4}\left(\eta \right),\hfill \\ \hfill & {\psi }_{16}(\xi ,\eta )=B_{3,2}\left(\xi \right)B_{4,4}\left(\eta \right),\hfill \\ \hfill & {\psi }_{17}(\xi ,\eta )=B_{1,2}\left(\xi \right)B_{5,4}\left(\eta \right)+B_{1,4}\left(\xi \right)B_{3,2}\left(\eta \right)-B_{1,2}\left(\xi \right)B_{3,2}\left(\eta \right),\hfill \\ \hfill & {\psi }_{18}(\xi ,\eta )=B_{2,4}\left(\xi \right)B_{3,2}\left(\eta \right),\hfill \\ \hfill & {\psi }_{19}(\xi ,\eta )=B_{2,2}\left(\xi \right)B_{5,4}\left(\eta \right)+B_{3,4}\left(\xi \right)B_{3,2}\left(\eta \right)-B_{2,2}\left(\xi \right)B_{3,2}\left(\eta \right),\hfill \\ \hfill & {\psi }_{20}(\xi ,\eta )=B_{4,4}\left(\xi \right)B_{3,2}\left(\eta \right),\hfill \\ \hfill & {\psi }_{21}(\xi ,\eta )=B_{3,2}\left(\xi \right)B_{5,4}\left(\eta \right)+B_{5,4}\left(\xi \right)B_{3,2}\left(\eta \right)-B_{3,2}\left(\xi \right)B_{3,2}\left(\eta \right).\hfill \end{array}$$

(50)

Interestingly, the three matrices, i.e., ($\left[{\mathbf{A}}_{\xi }\right],\left[{\mathbf{A}}_{\eta }\right]$ and $\left[{\mathbf{A}}_{\xi \eta }\right]$), do not have the structured form of ($\left[{\mathbf{U}}_{\xi }\right],\left[{\mathbf{U}}_{\eta }\right]$ and $\left[{\mathbf{U}}_{\xi \eta }\right]$) shown in Equation 38 to 40, but are influenced by all the coefficients $a_i$’s $(i=1,\dots ,21)$ in a rather complicated way. This in turn means that the three projectors do not preserve their form in the two functional systems separately, but the totality in their Boolean sum (Equation 41) does so.

Furthermore, using their actual binomial forms and equating the coefficients of the same monomials in both systems (Lagrange, Bernstein), it can be shown (and is easily validated) that the two functional sets, i.e., $\left\{\varphi \right\}={[{\varphi }_1,\dots ,{\varphi }_{21}]}^T$ and $\left\{\psi \right\}={[{\psi }_1,\dots ,{\psi }_{21}]}^T$ are linearly interrelated according to Equation 33, where the transformation matrix is given as:

$$\mathbf{R}=\left[\begin{array}{ccccccccccccccccccccc}\hfill 1& -13/12& 13/18& -1/4& 0& -13/12& 1& 0& 13/18& 1& -13/36& -1/36& 0& -1/4& -1/36& 0& 0& 0& 0& 0& 0\\ \hfill 0& 4& -32/9& 4/3& 0& 0& -2/3& 0& 0& -8/3& 8/9& -4/3& 0& 0& 10/9& 0& 0& 0& 0& 0& 0\\ \hfill 0& -3& 20/3& -3& 0& 0& -7/4& 0& 0& 15/4& -1/3& 15/4& 0& 0& -29/12& 0& 0& 0& 0& 0& 0\\ \hfill 0& -1/4& 13/18& -13/12& 1& 0& 1& -13/12& 0& -1/36& -13/36& 1& 13/18& 0& -1/36& -1/4& 0& 0& 0& 0& 0\\ \hfill 0& 0& 0& 0& 0& 4& -8/3& 0& 0& -32/9& -2/3& 8/9& 10/9& 0& 4/3& -4/3& 0& 0& 0& 0& 0\\ \hfill 0& 0& 0& 0& 0& 0& 28/3& 0& 0& -4& -16/3& -4& 0& 0& 4& 0& 0& 0& 0& 0& 0\\ \hfill 0& 0& 0& 0& 0& 0& -8/3& 4& 0& 10/9& 8/9& -2/3& -32/9& 0& -4/3& 4/3& 0& 0& 0& 0& 0\\ \hfill 0& 0& 0& 0& 0& -3& 15/4& 0& 20/3& -7/4& -1/3& -29/12& 0& -3& 15/4& 0& 0& 0& 0& 0& 0\\ \hfill 0& 0& 0& 0& 0& 0& -4& 0& 0& 28/3& -16/3& 4& 0& 0& -4& 0& 0& 0& 0& 0& 0\\ \hfill 0& 0& 0& 0& 0& 0& -5/2& 0& 0& -5/2& 18& -5/2& 0& 0& -5/2& 0& 0& 0& 0& 0& 0\\ \hfill 0& 0& 0& 0& 0& 0& -4& 0& 0& 4& -16/3& 28/3& 0& 0& -4& 0& 0& 0& 0& 0& 0\\ \hfill 0& 0& 0& 0& 0& 0& 15/4& -3& 0& -29/12& -1/3& -7/4& 20/3& 0& 15/4& -3& 0& 0& 0& 0& 0\\ \hfill 0& 0& 0& 0& 0& 4/3& -4/3& 0& -32/9& -2/3& 8/9& 10/9& 0& 4& -8/3& 0& 0& 0& 0& 0& 0\\ \hfill 0& 0& 0& 0& 0& 0& 4& 0& 0& -4& -16/3& -4& 0& 0& 28/3& 0& 0& 0& 0& 0& 0\\ \hfill 0& 0& 0& 0& 0& 0& -4/3& 4/3& 0& 10/9& 8/9& -2/3& -32/9& 0& -8/3& 0& 0& 0& 0& 0& 0\\ \hfill 0& 0& 0& 0& 0& -1/4& -1/36& 0& 13/18& 1& -13/36& -1/36& 0& -13/12& 1& 0& 1& -13/12& 13/18& -1/4& 0\\ \hfill 0& 0& 0& 0& 0& 0& 10/9& 0& 0& -8/3& 8/9& -4/3& 0& 0& -2/3& 0& 0& 4& -32/9& 4/3& 0\\ \hfill 0& 0& 0& 0& 0& 0& -29/12& 0& 0& 15/4& -1/3& 15/4& 0& 0& -7/4& 0& 0& -3& 20/3& -3& 0\\ \hfill 0& 0& 0& 0& 0& 0& 10/9& 0& 0& -4/3& 8/9& -8/3& 0& 0& -2/3& 0& 0& 4/3& -32/9& 4& 0\\ \hfill 0& 0& 0& 0& 0& 0& -1/36& -1/4& 0& -1/36& -13/36& 1& 13/18& 0& 1& -13/12& 0& -1/4& 13/18& -13/12& 1\end{array}\right].$$

(51)

4.3. Numerical Verification of 21-Node Traditional Transfinite Element

The 21-node transfinite element is one of the elements studied by the GMRL team in mid-1970s [9]. The nodal points are arranged along three stations per direction, in such a way that one node is missing for each of the four cells of this patch, to form the associated ideal tensor product.

We solved again the same problem (Laplace equation) with the same boundary conditions as in Example 1, but now using a single 21-node macroelement (Figure 3). In both formulations (Lagrange, Bernstein), the error norm was found to be $L_2=0.0526\%$. Obviously, this finding is consistent to the existence of the transformation matrix $\mathbf{R}$ (given by Equation 51) between these two functional sets, as discussed in Section 4.2.

Important remark: From the above discussion, it becomes obvious that, in tensor products and for traditional (structured) transfinite elements, the expressions of the basis functions using Bernstein polynomials are the same with those of shape functions using Lagrange polynomials, where the same degree is considered.

5. Distorted Tensor Products of Partially Unstructured Transfinite Elements

The meaning of this section is to investigate whether the same expression between Lagrange polynomials and Bernstein polynomials remains, for other transfinite configurations as well. So far, in addition to the tensor product (Figure 4a) and the structured transfinite elements (Figure 4b), partially unstructured elements like those illustrated in Figure 4c have been studied. The characteristic issues of these elements is that (i) the internal nodes form a tensor product (uniform or not) and (ii) the normal projection of the nodal points on all the four edges of the quadrilateral patch do not necessarily match with the nodal points on the boundary. In this class of elements, not only a deviation may occur in the position of the internal nodes compared to the boundary nodes, but also a different number may exist between the nodes of an edge and the internal ones parallel to it (for example, Figure 4d shows a standard of 3 nodes per direction whereas the intermidiate ones are 2 for edge $BC$, 5 for edge $DC$ and 4 for edge $AD$).

An older study [6] which dealt with six boundary-value problems, but also a recent one [5] concerning the approximation quality of a given function using its nodal values, have shown that:

• Tensor product Lagrange and tensor product non-rational Bernstein polynomials lead to the same error norm, although the condition number of equationes system is generally different [6].
• Traditional (structured) transfinite elements lead to the same error norm, either Lagrange or Bernstein polynomials are used [4,5].

We recall that in the first two categories regarding tensor product and traditional structured transfinite elements (Figure 4a,b), the paper at hand has theoretically shown (see, in Section 3 and Section 4, respectively), that Lagrange polynomials may merely be substituted by Bernstein polynomials of the same degree, and then the numerical resuts remain unchanged except of the condition number of equations system.

Regarding distorted tensor products of 25-node elements (Figure 4c), a very recent paper [5](p.22) has reported coincidence of the results, while a minor difference between Lagrange and Bernstein polynomials was reported for a 27-node element (Figure 4d). However, but the latter report is not reasonable, and therefore, the same example was studied again and the reason for the supposed difference is clarified below.

5.1. Simple Distortion

This section refers to elements of which the internal nodes are uniformly arranged, for example in the form of a tensor product, but the position of boundary nodes does not fully match to them (see, Figure 4c). In this case, Lagrange polynomials are used as uniform blending functions ($E_i\left(\xi \right)$ and $E_j\left(\eta \right)$, here of degree 4), whereas the trial functions ($L_i\left(\xi \right)$ and $L_j\left(\eta \right)$)) are uniform or non-uniform polynomials of also fourth degree. Clearly, the difference between blending and trial functions, both of degree $p=4$, is that the former are uniform whereas the latter are based on generally non-uniform node sequence along the four edges.

5.1.1. Closed-Form Expressions

It has been shown elsewhere (one of the most recent is [10] and papers therein), that despite the geometric distortion of the element, transfinite interpolation is applicable although it requires the use of auxiliary (artificial) nodes, which eventually are eliminated (the procedure is also shown in Sect.Section 5.2.1). Therefore, the analogue of Equation 43, based on the implementation of transfinite interpolation in conjunction with Lagrange polynomials only, is the following set of basis functions (we restrict the presentation to those associated with the bottom edge $AB$):

$$\begin{array}{cc}\hfill & {\varphi }_1(\xi ,\eta )=E_{1,4}\left(\xi \right)L_{1,4}^{AD}\left(\eta \right)+L_{1,4}^{AB}\left(\xi \right)E_{1,4}\left(\eta \right)-E_{1,4}\left(\xi \right)E_{1,4}\left(\eta \right),\hfill \\ \hfill & {\varphi }_2(\xi ,\eta )=L_{2,4}^{AB}\left(\xi \right)E_{1,4}\left(\eta \right),\hfill \\ \hfill & {\varphi }_3(\xi ,\eta )=L_{3,4}^{AB}\left(\xi \right)E_{1,4}\left(\eta \right),\hfill \\ \hfill & {\varphi }_4(\xi ,\eta )=L_{4,4}^{AB}\left(\xi \right)E_{1,4}\left(\eta \right),\hfill \\ \hfill & {\varphi }_5(\xi ,\eta )=E_{5,4}\left(\xi \right)L_{1,4}^{BC}\left(\eta \right)+L_{5,4}^{AB}\left(\xi \right)E_{1,4}\left(\eta \right)-E_{5,4}\left(\xi \right)L_{1,4}\left(\eta \right),\hfill \\ \hfill & \dots .\hfill \end{array}$$

(52)

In Equation 52, the superscripts (${\square }^{AB}$) and (${\square }^{AD}$) were set to denote the edges along which the non-uniform Lagrange polynomials operate. Clearly, Lagrange polynomials require uniform (evenly) and non-uniform (non equally spaced) sets of nodal points.

The utilization of Bernstein polynomials for the same element (Figure 4c) is not very obvious at a first glance. For example, with the exception of the four edges of the patch, interpolation along any isoline depends on all the coefficients a, thus not only on the degrees of freedom (or the coordinates) of the isoline under consideration. In contrast, the cardinality of Lagrange polynomials allows us for the abovementioned treatment through artifical nodes. In any case, in [5] it has been conjectured that Bernstein polynomals may operate for both the blending and trial functions, and thus the (uniform and non-uniform) Lagrange polynomials involved in Equation 50 are replaced by Bernstein polynomials of the same degree. Then, the analogue of Equation 50 will be:

$$\begin{array}{cc}\hfill & {\psi }_1(\xi ,\eta )=B_{1,4}\left(\xi \right)B_{1,4}\left(\eta \right)+\cancel{B_{1,4}\left(\xi \right)B_{1,4}\left(\eta \right)}-\cancel{B_{1,4}\left(\xi \right)B_{1,4}\left(\eta \right)},\hfill \\ \hfill & {\psi }_2(\xi ,\eta )=B_{2,4}\left(\xi \right)B_{1,4}\left(\eta \right),\hfill \\ \hfill & {\psi }_3(\xi ,\eta )=B_{3,4}\left(\xi \right)B_{1,4}\left(\eta \right),\hfill \\ \hfill & {\psi }_4(\xi ,\eta )=B_{4,4}\left(\xi \right)B_{1,4}\left(\eta \right),\hfill \\ \hfill & {\psi }_5(\xi ,\eta )=B_{5,4}\left(\xi \right)B_{1,4}\left(\eta \right)+\cancel{B_{5,4}\left(\xi \right)B_{1,4}\left(\eta \right)}-\cancel{B_{5,4}\left(\xi \right)B_{1,4}\left(\eta \right)},\hfill \\ \hfill & \dots .\hfill \end{array}$$

(53)

A careful inspection on Equation 53 reveals that the bivariate basis functions associated to the element shown in Figure 4c are merely the tensor products of Bernstein polynomials. In other words, and regarding distrorted tensor products, while the shape functions (associated with Lagrange polynomials) depend on the position of nodal points, the basis functions (associated with Bernstein polynomials) are constant (see Figure 5). Therefore, in case of Bernstein polynomials the distortion (symmetry break) is ‘absorbed’ by the generalized coefficients $a_i,i=1,\dots ,25$. Not only that, but to derive the same results with those using Lagrange polynomials, it is necessary to put the control points ${\mathbf{x}}_{ij}^c$ at specific positions which are not the same with the Cartesian coordinates of the nodal points, but are interreleted with them through the well known expression:

$$\mathbf{x}(\xi ,\eta )=\sum _{i=1}^5\sum _{j=1}^5{B}_i\left(\xi \right)B_j\left(\eta \right){\mathbf{x}}_{ij}^c.$$

(54)

Collocating Equation 54 at the 25 nodal points involved in the Lagrange set, their coordinates $\mathbf{x}$ are included in the left-hand side, whereas the right-hand side includes the unknown control points for which we solve a system of 25 equations with 25 unknowns.

5.1.2. Numerical Verification

It is worth mentioning that, when Example 1 was solved using the two functional sets for the 25-node element, the error-norm was found to be identically equal to $L_2=0.0232\%$. The same error was found when we varied the position of the nodes along the three edges ($AB$,$BC$, and $AD$). A minor change was observed when we varied the position of three intermediate nodes along the top edge $DC$ on which the non-homogeneous boundary conditions of Dirichlet type are imposed (e.g., for Cartesian coordinates $x_{22}=0.2,x_{23}=0.60,x_{24}=0.8$ in Lagrange model, and associated change in Bernstein model, in both formulations the error became $L_2=0.0238\%$). Again, these findings were anticipated because the two functional systems are interrelated through an inherent transformation matrix $\mathbf{R}$, according to Equation 14.

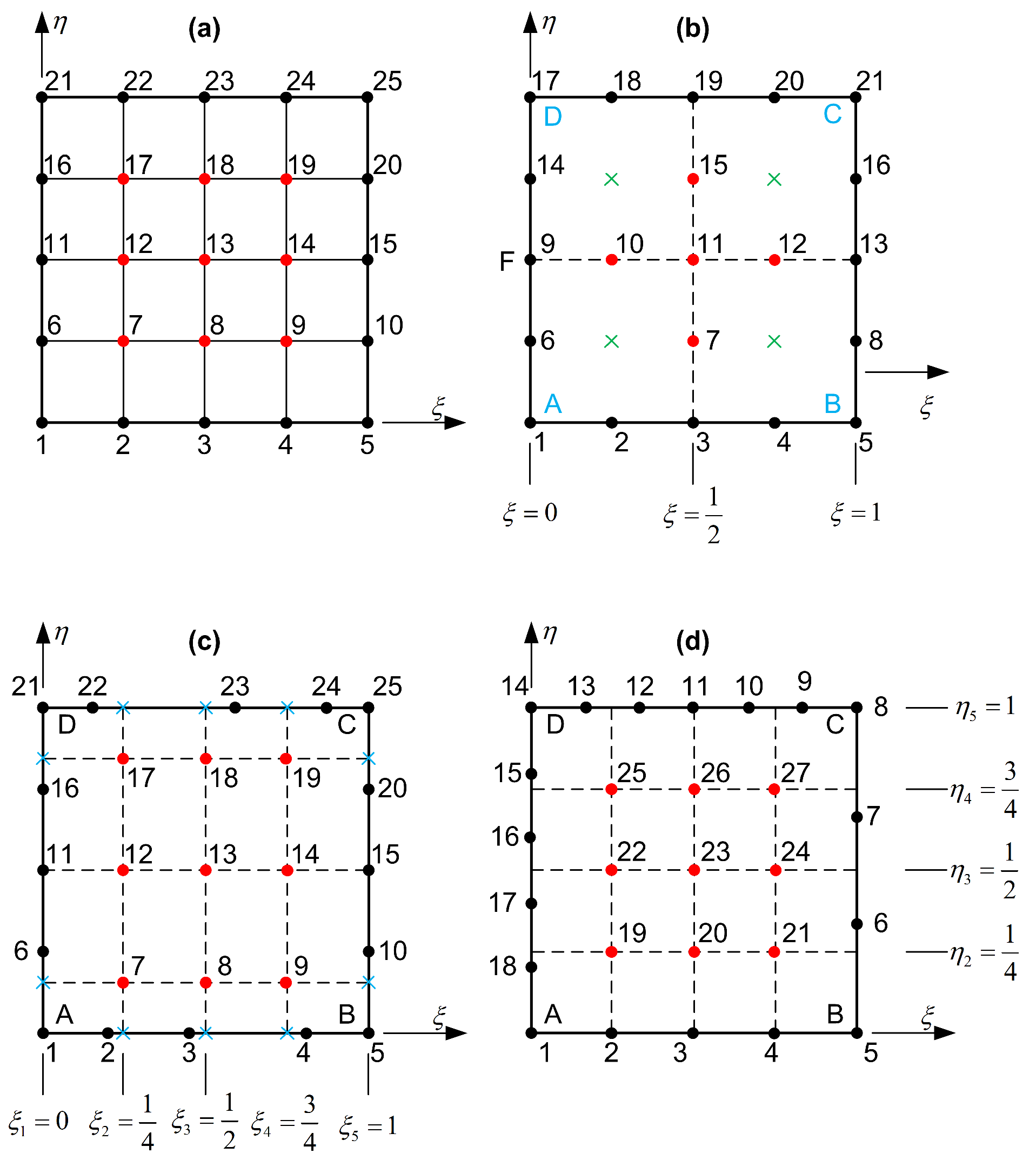
5.2. Distortion Combined with Node Refinement or Removal on Edges

In the previous section we discussed simple distortion of the patch $ABCD$, in which the boundary nodes had been moved from their initial position associated with the ideal tensor product. In this section we consider the same distortion, and in addition we modify the number of nodes on one or more edges. For example, in Figure 4d one may see that the edge $AB$ is intact, one node has been subtracted from edge $BC$, two nodes have been added to edge $DC$, and one node has been added to edge $AD$. As a result, the ideal 25-node of Section 5.1 has been transformed to a 27-node transfinite element having 18 boundary and 9 internal nodes.

In the set of Lagrange polynomials, the shape functions have the form of those involved in Equation 43, which means that:

• Shape functions associated with corner nodes, consist of three terms (influenced by all the three projectors $P_{\xi },P_{\eta },P_{\xi \eta }$).
• Shape functions associated with intermediate nodes on the edges, consist of one term, which is related to the projector having as subscript the axis perpendicular to the current edge. For example, the shape functions of nodes along edge $AB$ are influenced by only the projector $P_{\eta }$.
• Shape functions associated with internal nodes equal to the tensor product of the blending functions only.

Typical expressions, one for each category are given in Equation 55 below:

$$\begin{array}{cc}\hfill \mathrm{Corner}\mathrm{node}\text{:}{\varphi }_1(\xi ,\eta )& =E_1\left(\xi \right)L_1\left(\eta \right)+E_1\left(\eta \right)L_1\left(\xi \right)-E_1\left(\xi \right)E_1\left(\eta \right)\hfill \\ \hfill \mathrm{Intermediate}\mathrm{to}AB:{\varphi }_2(\xi ,\eta )& =E_1\left(\eta \right)L_2\left(\xi \right)\hfill \\ \hfill \mathrm{Internal}\mathrm{node}\text{:}{\varphi }_{19}(\xi ,\eta )& =E_1\left(\xi \right)E_1\left(\eta \right).\hfill \end{array}$$

(55)

Not still having a rigorous mathematical foundation but only the previous numerical experience, a reasonable choice is to replace the blending functions, from Lagrange polynomials of fourth degree by Bernstein polynomials of the same degree, i.e.:

$$E_1={(1-s)}^4,E_2=4{(1-s)}^{3}s,E_3=6{(1-s)}^2{s}^2,E_4=4(1-s)s^3,E_5=s^4,$$

(56)

where s represents either of the parameters $\xi$ or $\eta$. Similarly, the trial functions along the edges $AB$ to $DA$ which are Lagrange polynomials of degree 4,3,6, and 5, respectively, are substituted by Bernstein polynomials of the same degree, as shown in Equation 57 below:

$$\begin{array}{cc}\hfill \mathrm{Corner}\mathrm{DOF}\text{:}{\psi }_1(\xi ,\eta )& =B_{1,4}\left(\xi \right)B_{1,5}\left(\eta \right)+B_{1,4}\left(\eta \right)B_{1,4}\left(\xi \right)-B_{1,4}\left(\xi \right)B_{1,4}\left(\eta \right)\hfill \\ \hfill \mathrm{Intermediate}\mathrm{to}AB:{\psi }_2(\xi ,\eta )& =B_{1,4}\left(\eta \right)B_{2,4}\left(\xi \right)\hfill \\ \hfill \mathrm{Internal}\mathrm{DOF}\text{:}{\psi }_{19}(\xi ,\eta )& =B_{1,4}\left(\xi \right)B_{1,4}\left(\eta \right).\hfill \end{array}$$

(57)

In both cases, the shape (bivariate Lagrange) and basis (bivariate Bernstein) functions fulfil the partition of unity (rigid-body) and the constant strain property, as shown in Equation 58 below:

$$\begin{array}{cccc}\hfill \sum _{i=1}^{27}{\varphi }_i(\xi ,\eta )& =1,\hfill & \hfill \sum _{i=1}^{27}{\psi }_i(\xi ,\eta )& =1,\hfill \\ \hfill \sum _{i=1}^{27}{\displaystyle \frac{\partial {\varphi }_i(\xi ,\eta )}{\partial \xi }}& =0,\hfill & \hfill \sum _{i=1}^{27}{\displaystyle \frac{\partial {\psi }_i(\xi ,\eta )}{\partial \xi }}& =0,\hfill \\ \hfill \sum _{i=1}^{27}{\displaystyle \frac{\partial {\varphi }_i(\xi ,\eta )}{\partial \eta }}& =0,\hfill & \hfill \sum _{i=1}^{27}{\displaystyle \frac{\partial {\psi }_i(\xi ,\eta )}{\partial \eta }}& =0.\hfill \end{array}$$

(58)

Moreover, in bot cases the determinant of the Jacobian equals to unity (det$\left(J\right)=0$), which implies that the mapping from the parametric space to the physical space is affine (or identity-like in behavior) over a square.

5.2.1. Justification

An explanation for the above discrepancy is provided below. When working in conjunction with Lagrange polynomials (which directly refer to the nodal values $U_i$), the mechanism to derive the bivariate interpolation is the transfinite interpolation [9]. In this context, the blending functions $E_i\left(\xi \right)$ interpolate functions $U(\overline{\xi },\eta )$ along isolines which are perpendicular to $\xi$-axis at positions $\overline{\xi }$, and this interpolation is the projector $P_{\xi }$. Similarly, the blending functions $E_j\left(\eta \right)$ interpolate functions $U(\xi ,\overline{\eta })$ along isolines which are perpendicular to $\eta$-axis at positions $\overline{\eta }$, and this interpolation is the projector $P_{\eta }$. Moreover, to avoid repetion of values when the sum $P_{\xi }+P_{\eta }$ is performed, a corrective term $P_{\xi \eta }$ is considered as well. The final interpolation follows the Boolean sum shown in Equation 41 (i.e., $P_{\xi }\oplus P_{\eta }=P_{\xi }+P_{\eta }-P_{\xi \eta }$).

In the example of the 27-node transfinite element shown again in Figure 6, a characteristic is that the orthogonal projections of some internal nodes onto the edges do not coincide with existing nodes (here all internal nodes suffer at least in one direction). Thus, ‘artificial nodes’ ($E,F,G,H,I,J,K,L$) are introduced to make up the missing starting or/and ending nodal points of relevant sequence of Lagrange polynomials, so that the expression of the abovementioned functions $U(\overline{\xi },\eta )$ and $U(\xi ,\overline{\eta })$ becomes possible.

We recall that the corrective projector $P_{\xi \eta }$ includes all the ($5\times 5$) intersections between five stations per direction, and thus may be written in terms of primary and artificial (red-colored) nodes as

$$P_{\xi \eta }=\underset{{\mathbf{E}}_5^T\left(\xi \right)}{\underbrace{\left[\begin{array}{ccccc}{E}_{1,4}\left(\xi \right)& E_{2,4}\left(\xi \right)& E_{3,4}\left(\xi \right)& E_{4,4}\left(\xi \right)& E_{5,4}\left(\xi \right)\end{array}\right]}}\underset{{\mathbf{U}}_{int}}{\underbrace{\left[\begin{array}{ccccc}{U}_1& \begin{array}{c}{U}_E\end{array}& \begin{array}{c}{U}_G\end{array}& \begin{array}{c}{U}_I\end{array}& U_{14}\\ U_2& U_{19}& U_{22}& U_{25}& \begin{array}{c}{U}_K\end{array}\\ U_3& U_{20}& U_{23}& U_{26}& U_{11}\\ U_4& U_{21}& U_{24}& U_{27}& \begin{array}{c}{U}_L\end{array}\\ U_5& \begin{array}{c}{U}_F\end{array}& \begin{array}{c}{U}_H\end{array}& \begin{array}{c}{U}_J\end{array}& U_8\end{array}\right]}}\underset{{\mathbf{E}}_5\left(\eta \right)}{\underbrace{\left[\begin{array}{c}{E}_{1,4}\left(\eta \right)\\ E_{2,4}\left(\eta \right)\\ E_{3,4}\left(\eta \right)\\ E_{4,4}\left(\eta \right)\\ E_{5,4}\left(\eta \right)\end{array}\right]}}$$

(59)

Obviously, each vector including blending functions (Lagrange polynomials of degree 5) can be substituted by Bernstein polynomials of degree 5 as well, where

$${\mathbf{E}}_5={\mathbf{T}}_5{\mathbf{B}}_5,.$$

(60)

with

$${\mathbf{T}}_5=\left[\begin{array}{cccccc}1& -77/60& 269/240& -77/120& 1/5& 0\\ 0& 5& -145/24& 185/48& -5/4& 0\\ 0& -5& 295/24& -115/12& 10/3& 0\\ 0& 10/3& -115/12& 295/24& -5& 0\\ 0& -5/4& 185/48& -145/24& 5& 0\\ 0& 1/5& -77/120& 269/240& -77/60& 1\end{array}\right]$$

(61)

This in turn means that the projector $P_{\xi \eta }$ preserves its form after transformation, of Lagrange by Bernstein polynomials, which then becomes:

$$P_{\xi \eta }={\mathbf{B}}_5^T\left(\xi \right)\left({\mathbf{T}}_5^T{\mathbf{U}}_{int}{\mathbf{T}}_5\right){\mathbf{B}}_5\left(\eta \right).$$

(62)

On the other hand, the projector $P_{\xi }$ includes some of the primary nodes (1 to 27) and some of the artificial nodes. In more detail:

• The function $U(0,\eta )$ consists of six nodal values $(U_1,U_{18},U_{17},U_{16},U_{15},U_{14})$, which define 5 node spans and fully define a polynomial of degree 5. Note that the artificial nodes $(E,J,I)$ are not included because they are not needed.
• The function $U({\displaystyle \frac{1}{4}},\eta )$ consists of 5 nodal values $(U_2,U_{19},U_{22},U_{25},U_K)$ (4 node spans), and thus fully define a polynomial of degree 4. Note that the artificial node K, on the boundary, is required to determine the missing end of nodal sequence.
• The function $U({\displaystyle \frac{1}{2}},\eta )$ consists of 5 nodal values $(U_3,U_{20},U_{23},U_{26},U_{11})$ (4 node spans), and thus fully define a polynomial of degree 4. All entries of nodal sequance are primary nodes which belong to the 27-node element.
• The function $U({\displaystyle \frac{3}{4}},\eta )$ consists of 5 nodal values $(U_4,U_{21},U_{24},U_{27},U_L)$ (4 node spans), and thus fully define a polynomial of degree 4. Note that the artificial node L is required to determine the missing end of nodal sequence.
• The function $U(1,\eta )$ consists of four nodal values $(U_5,U_6,U_7,U_8)$, which define 3 node spans and fully define a polynomial of degree 3. Note that the artificial nodes $(F,H,J)$, on the boundary, are not included because they are not needed.

The abovementioned different number of nodes along the isolines at $(\xi =0,{\displaystyle \frac{1}{4}},{\displaystyle \frac{1}{2}},{\displaystyle \frac{3}{4}},1)$, does not allow for an elegant mathematical form as that in Equation 59. This means that neither a row vector of the Lagrange polynomials in $\eta$ can be extracted as a common factor, nor the next matrix of the nodal values is fully populated. Therefore, we write $P_{\xi }$ in a conventional manner as follows:

$$\begin{array}{cc}\hfill P_{\xi }& =\underset{{\mathbf{E}}_5^T\left(\eta \right)}{\underbrace{\left[\begin{array}{cccccc}{L}_{1,5}\left(\eta \right)& L_{2,5}\left(\eta \right)& L_{3,5}\left(\eta \right)& L_{4,5}\left(\eta \right)& L_{5,5}\left(\eta \right)& L_{6,5}\left(\eta \right)\end{array}\right]}}\left[\begin{array}{c}{U}_1\\ U_{18}\\ U_{17}\\ U_{16}\\ U_{15}\\ U_{14}\end{array}\right]E_{1,4}\left(\xi \right)\hfill \\ \hfill & +\underset{{\mathbf{E}}_4^T\left(\eta \right)}{\underbrace{\left[\begin{array}{ccccc}{L}_{1,4}\left(\eta \right)& L_{2,4}\left(\eta \right)& L_{3,4}\left(\eta \right)& L_{4,4}\left(\eta \right)& L_{5,4}\left(\eta \right)\end{array}\right]}}\left[\begin{array}{c}{U}_2\\ U_{19}\\ U_{22}\\ U_{25}\\ \begin{array}{c}{U}_K\end{array}\end{array}\right]E_{2,4}\left(\xi \right)\hfill \\ \hfill & +\underset{{\mathbf{E}}_4^T\left(\eta \right)}{\underbrace{\left[\begin{array}{ccccc}{L}_{1,4}\left(\eta \right)& L_{2,4}\left(\eta \right)& L_{3,4}\left(\eta \right)& L_{4,4}\left(\eta \right)& L_{5,4}\left(\eta \right)\end{array}\right]}}\left[\begin{array}{c}{U}_3\\ U_{20}\\ U_{23}\\ U_{26}\\ U_{11}\end{array}\right]E_{3,4}\left(\xi \right)\hfill \\ \hfill & +\underset{{\mathbf{E}}_4^T\left(\eta \right)}{\underbrace{\left[\begin{array}{ccccc}{L}_{1,4}\left(\eta \right)& L_{2,4}\left(\eta \right)& L_{3,4}\left(\eta \right)& L_{4,4}\left(\eta \right)& L_{5,4}\left(\eta \right)\end{array}\right]}}\left[\begin{array}{c}{U}_4\\ U_{21}\\ U_{24}\\ U_{27}\\ \begin{array}{c}{U}_K\end{array}\end{array}\right]E_{4,4}\left(\xi \right)\hfill \\ \hfill & +\underset{{\mathbf{E}}_3^T\left(\eta \right)}{\underbrace{\left[\begin{array}{cccc}{L}_{1,3}\left(\eta \right)& L_{2,3}\left(\eta \right)& L_{3,3}\left(\eta \right)& L_{4,3}\left(\eta \right)\end{array}\right]}}\left[\begin{array}{c}{U}_5\\ U_6\\ U_7\\ U_8\end{array}\right]E_{5,4}\left(\xi \right).\hfill \end{array}$$

(63)

One may observe in Equation 63 that only two out of the eight artificial nodes ($U_K,U_L$) are included in $P_{\xi }$.

Similar observations may be made for projector $P_{\eta }$, which can be written as follows:

$$\begin{array}{cc}\hfill P_{\eta }& =\underset{{\mathbf{E}}_4^T\left(\xi \right)}{\underbrace{\left[\begin{array}{ccccc}{L}_{1,4}\left(\xi \right)& L_{2,4}\left(\xi \right)& L_{3,4}\left(\xi \right)& L_{4,4}\left(\xi \right)& L_{5,4}\left(\xi \right)\end{array}\right]}}\left[\begin{array}{c}{U}_1\\ U_2\\ U_3\\ U_4\\ U_5\end{array}\right]E_{1,4}\left(\eta \right)\hfill \\ \hfill & +\underset{{\mathbf{E}}_4^T\left(\xi \right)}{\underbrace{\left[\begin{array}{ccccc}{L}_{1,4}\left(\xi \right)& L_{2,4}\left(\xi \right)& L_{3,4}\left(\xi \right)& L_{4,4}\left(\xi \right)& L_{5,4}\left(\xi \right)\end{array}\right]}}\left[\begin{array}{c}\begin{array}{c}{U}_E\end{array}\\ U_{19}\\ U_{20}\\ U_{21}\\ \begin{array}{c}{U}_F\end{array}\end{array}\right]E_{2,4}\left(\eta \right)\hfill \\ \hfill & +\underset{{\mathbf{E}}_4^T\left(\xi \right)}{\underbrace{\left[\begin{array}{ccccc}{U}_G& L_{2,4}\left(\xi \right)& L_{3,4}\left(\xi \right)& L_{4,4}\left(\xi \right)& L_{5,4}\left(\xi \right)\end{array}\right]}}\left[\begin{array}{c}\begin{array}{c}{U}_G\end{array}\\ U_{22}\\ U_{23}\\ U_{24}\\ \begin{array}{c}{U}_H\end{array}\end{array}\right]E_{3,4}\left(\eta \right)\hfill \\ \hfill & +\underset{{\mathbf{E}}_4^T\left(\xi \right)}{\underbrace{\left[\begin{array}{ccccc}{L}_{1,4}\left(\xi \right)& L_{2,4}\left(\xi \right)& L_{3,4}\left(\xi \right)& L_{4,4}\left(\xi \right)& L_{5,4}\left(\xi \right)\end{array}\right]}}\left[\begin{array}{c}\begin{array}{c}{U}_I\end{array}\\ U_{25}\\ U_{26}\\ U_{27}\\ \begin{array}{c}{U}_J\end{array}\end{array}\right]E_{4,4}\left(\eta \right)\hfill \\ \hfill & +\underset{{\mathbf{E}}_6^T\left(\xi \right)}{\underbrace{\left[\begin{array}{ccccccc}{L}_{1,6}\left(\xi \right)& L_{2,6}\left(\xi \right)& L_{3,6}\left(\xi \right)& L_{4,6}\left(\xi \right)& L_{5,6}\left(\xi \right)& L_{6,6}\left(\xi \right)& L_{7,6}\left(\xi \right)\end{array}\right]}}\left[\begin{array}{c}{U}_{14}\\ U_{13}\\ U_{12}\\ U_{11}\\ U_{10}\\ U_9\\ U_8\end{array}\right]E_{5,4}\left(\eta \right).\hfill \end{array}$$

(64)

One may observe in Equation 64 that six out of the eight artificial nodes ($U_E,U_F,U_G,U_H,U_I,U_J$) are included in $P_{\eta }$.

In summary:

• The projector $P_{\xi }$ includes 2 out of the 8 artificial nodal values.
• The projector $P_{\eta }$ includes the rest 6 out of the 8 artificial nodal values.
• The subtractive corrective projector $P_{\xi \eta }$ includes all the 8 artificial nodes.

Interestingly, for every chosen artificial nodal value, for example for $U_E$, the unique associated term $E_{1,4}\left(\xi \right)U_E{E}_{2,4}\left(\eta \right)$ in $P_{\eta }$ is cancelled by the corresponding opposite term cited in $P_{\xi \eta }$. Totally, one may verify that two terms of $P_{\xi }$ and six terms of $P_{\eta }$, which include artficial DOFs, are cancelled by the corresponding eight terms in $P_{\xi \eta }$, and thus are eventually eliminated. As a result, the Boolean sum $P_{\xi }\oplus P_{\eta }=P_{\xi }+P_{\eta }-P_{\xi \eta }$ will contain only the 27 primary DOFs which define the 27-node transfinite element. In more details, the terms related to the eight auxiliary (artificial) points vanish, as follows:

• We notice the terms: $U_E\left[\cancel{E_{1,4}\left(\xi \right)E_{2,4}\left(\eta \right)}-\cancel{E_{1,4}\left(\xi \right)E_{2,4}\left(\eta \right)}\right]$, coming from $P_{\eta }$ and $P_{\xi \eta }$.
• We notice the terms: $U_F[\cancel{E_{5,4}\left(\xi \right)E_{2,4}\left(\eta \right)}-\cancel{E_{5,4}\left(\xi \right)E_{2,4}\left(\eta \right)}]$, coming from $P_{\eta }$ and $P_{\xi \eta }$.
• We notice the terms: $U_G\left[\cancel{E_{1,4}\left(\xi \right)E_{3,4}\left(\eta \right)}-\cancel{E_{1,4}\left(\xi \right)E_{3,4}\left(\eta \right)}\right]$, coming from $P_{\eta }$ and $P_{\xi \eta }$.
• We notice the terms: $U_H[\cancel{E_{5,4}\left(\xi \right)E_{3,4}\left(\eta \right)}-\cancel{E_{5,4}\left(\xi \right)E_{3,4}\left(\eta \right)}]$, coming from $P_{\eta }$ and $P_{\xi \eta }$.
• We notice the terms: $U_I\left[\cancel{E_{1,4}\left(\xi \right)E_{4,4}\left(\eta \right)}-\cancel{E_{1,4}\left(\xi \right)E_{4,4}\left(\eta \right)}\right]$, coming from $P_{\eta }$ and $P_{\xi \eta }$.
• We notice the terms: $U_J[\cancel{E_{5,4}\left(\xi \right)E_{4,4}\left(\eta \right)}-\cancel{E_{5,4}\left(\xi \right)E_{4,4}\left(\eta \right)}]$, coming from $P_{\eta }$ and $P_{\xi \eta }$.
• We notice the terms: $U_K[\cancel{E_{2,4}\left(\xi \right)E_{5,4}\left(\eta \right)}-\cancel{E_{2,4}\left(\xi \right)E_{5,4}\left(\eta \right)}]$, coming from $P_{\xi }$ and $P_{\xi \eta }$.
• We notice the terms: $U_L[\cancel{E_{4,4}\left(\xi \right)E_{5,4}\left(\eta \right)}-\cancel{E_{4,4}\left(\xi \right)E_{5,4}\left(\eta \right)}]$, coming from $P_{\xi }$ and $P_{\xi \eta }$.

Substituting Equations 59, 63 and 64 into the Boolean sum $U=P_{\xi }+P_{\eta }+P_{\xi \eta }$, for the Lagrange based system, the latter gives the following shape functions (see also in Figure 7a):

$$\begin{array}{cc}\hfill & {\varphi }_1(\xi ,\eta )=L_{1,4}\left(\xi \right)L_{1,5}\left(\eta \right),\hfill \\ \hfill & {\varphi }_2(\xi ,\eta )=L_{2,4}\left(\xi \right)L_{1,4}\left(\eta \right),\hfill \\ \hfill & {\varphi }_3(\xi ,\eta )=L_{3,4}\left(\xi \right)L_{1,4}\left(\eta \right),\hfill \\ \hfill & {\varphi }_4(\xi ,\eta )=L_{4,4}\left(\xi \right)L_{1,4}\left(\eta \right),\hfill \\ \hfill & {\varphi }_5(\xi ,\eta )=L_{5,4}\left(\xi \right)L_{1,3}\left(\eta \right),\hfill \\ \hfill & {\varphi }_6(\xi ,\eta )=L_{5,4}\left(\xi \right)L_{2,3}\left(\eta \right),\hfill \\ \hfill & {\varphi }_7(\xi ,\eta )=L_{5,4}\left(\xi \right)L_{3,3}\left(\eta \right),\hfill \\ \hfill & {\varphi }_8(\xi ,\eta )=L_{4,3}\left(\eta \right)L_{5,4}\left(\xi \right)-L_{5,4}\left(\xi \right)L_{5,4}\left(\eta \right)+L_{5,4}\left(\eta \right)L_{7,6}\left(\xi \right),\hfill \\ \hfill & {\varphi }_9(\xi ,\eta )=L_{5_4}\left(\eta \right)L_{6,6}\left(\xi \right),\hfill \\ \hfill & {\varphi }_{10}(\xi ,\eta )=L_{5_4}\left(\eta \right)L_{5,6}\left(\xi \right),\hfill \\ \hfill & {\varphi }_{11}(\xi ,\eta )=L_{4_6}\left(\xi \right)L_{5,4}\left(\eta \right),\hfill \\ \hfill & {\varphi }_{12}(\xi ,\eta )=L_{3_6}\left(\xi \right)L_{5,4}\left(\eta \right),\hfill \\ \hfill & {\varphi }_{13}(\xi ,\eta )=L_{2,6}\left(\xi \right)L_{5,4}\left(\eta \right),\hfill \\ \hfill & {\varphi }_{14}(\xi ,\eta )=L_{1,6}\left(\xi \right)L_{5,4}\left(\eta \right)-L_{1,4}\left(\xi \right)L_{5,4}\left(\eta \right)+L_{1,4}\left(\xi \right)L_{6,5}\left(\eta \right),\hfill \\ \hfill & {\varphi }_{15}(\xi ,\eta )=L_{1,4}\left(\xi \right)L_{5,5}\left(\eta \right),\hfill \\ \hfill & {\varphi }_{16}(\xi ,\eta )=L_{1,4}\left(\xi \right)L_{4,5}\left(\eta \right),\hfill \\ \hfill & {\varphi }_{17}(\xi ,\eta )=L_{1,4}\left(\xi \right)L_{3,5}\left(\eta \right),\hfill \\ \hfill & {\varphi }_{18}(\xi ,\eta )=L_{1,4}\left(\xi \right)L_{2,5}\left(\eta \right),\hfill \\ \hfill & {\varphi }_{19}(\xi ,\eta )=L_{2,4}\left(\xi \right)L_{2,4}\left(\eta \right),\hfill \\ \hfill & {\varphi }_{20}(\xi ,\eta )=L_{2,4}\left(\eta \right)L_{3,4}\left(\xi \right),\hfill \\ \hfill & {\varphi }_{21}(\xi ,\eta )=L_{2,4}\left(\eta \right)L_{4,4}\left(\xi \right),\hfill \\ \hfill & {\varphi }_{22}(\xi ,\eta )=L_{2,4}\left(\xi \right)L_{3,4}\left(\eta \right),\hfill \\ \hfill & {\varphi }_{23}(\xi ,\eta )=L_{3,4}\left(\xi \right)L_{3,4}\left(\eta \right),\hfill \\ \hfill & {\varphi }_{24}(\xi ,\eta )=L_{3,4}\left(\eta \right)L_{4,4}\left(\xi \right),\hfill \\ \hfill & {\varphi }_{25}(\xi ,\eta )=L_{2,4}\left(\xi \right)L_{4,4}\left(\eta \right),\hfill \\ \hfill & {\varphi }_{26}(\xi ,\eta )=L_{3,4}\left(\xi \right)L_{4,4}\left(\eta \right),\hfill \\ \hfill & {\varphi }_{27}(\xi ,\eta )=L_{4,4}\left(\xi \right)L_{4,4}\left(\eta \right).\hfill \end{array}$$

(65)

Interestingly, the shape functions ${\varphi }_1(\xi ,\eta )$ and ${\varphi }_2(\xi ,\eta )$, although are associated with corner nodes, they consist of only one term (i.e., eventually influenced by only the projector $P_{\xi }$), because the trial functions along their common edge $AB$ are exactly equal to the corresponding blending functions (uniform of degree 4).

We recall that the origin of transfinite interpolation is heuristic, and thus any extension of that will be heuristic as well. In this context, by intuition, one could conjecture that transfinite interpolation is also applicable using Bernstein polynomials in the position of blending and trial functions as well. Then, Equation 65 would take the form (see, Figure 7):

$$\begin{array}{cc}\hfill & {\psi }_1(\xi ,\eta )=B_{1,4}\left(\xi \right)B_{1,5}\left(\eta \right),\hfill \\ \hfill & {\psi }_2(\xi ,\eta )=B_{2,4}\left(\xi \right)B_{1,4}\left(\eta \right),\hfill \\ \hfill & {\psi }_3(\xi ,\eta )=B_{3,4}\left(\xi \right)B_{1,4}\left(\eta \right),\hfill \\ \hfill & {\psi }_4(\xi ,\eta )=B_{4,4}\left(\xi \right)B_{1,4}\left(\eta \right),\hfill \\ \hfill & {\psi }_5(\xi ,\eta )=B_{5,4}\left(\xi \right)B_{1,3}\left(\eta \right),\hfill \\ \hfill & {\psi }_6(\xi ,\eta )=B_{5,4}\left(\xi \right)B_{2,3}\left(\eta \right),\hfill \\ \hfill & {\psi }_7(\xi ,\eta )=B_{5,4}\left(\xi \right)B_{3,3}\left(\eta \right),\hfill \\ \hfill & {\psi }_8(\xi ,\eta )=B_{4,3}\left(\eta \right)B_{5,4}\left(\xi \right)-B_{5,4}\left(\xi \right)B_{5,4}\left(\eta \right)+B_{5,4}\left(\eta \right)B_{7,6}\left(\xi \right),\hfill \\ \hfill & {\psi }_9(\xi ,\eta )=B_{5_4}\left(\eta \right)B_{6,6}\left(\xi \right),\hfill \\ \hfill & {\psi }_{10}(\xi ,\eta )=B_{5_4}\left(\eta \right)B_{5,6}\left(\xi \right),\hfill \\ \hfill & {\psi }_{11}(\xi ,\eta )=B_{4_6}\left(\xi \right)B_{5,4}\left(\eta \right),\hfill \\ \hfill & {\psi }_{12}(\xi ,\eta )=B_{3_6}\left(\xi \right)B_{5,4}\left(\eta \right),\hfill \\ \hfill & {\psi }_{13}(\xi ,\eta )=B_{2,6}\left(\xi \right)B_{5,4}\left(\eta \right),\hfill \\ \hfill & {\psi }_{14}(\xi ,\eta )=B_{1,6}\left(\xi \right)B_{5,4}\left(\eta \right)-B_{1,4}\left(\xi \right)B_{5,4}\left(\eta \right)+B_{1,4}\left(\xi \right)B_{6,5}\left(\eta \right),\hfill \\ \hfill & {\psi }_{15}(\xi ,\eta )=B_{1,4}\left(\xi \right)B_{5,5}\left(\eta \right),\hfill \\ \hfill & {\psi }_{16}(\xi ,\eta )=B_{1,4}\left(\xi \right)B_{4,5}\left(\eta \right),\hfill \\ \hfill & {\psi }_{17}(\xi ,\eta )=B_{1,4}\left(\xi \right)B_{3,5}\left(\eta \right),\hfill \\ \hfill & {\psi }_{18}(\xi ,\eta )=B_{1,4}\left(\xi \right)B_{2,5}\left(\eta \right),\hfill \\ \hfill & {\psi }_{19}(\xi ,\eta )=B_{2,4}\left(\xi \right)B_{2,4}\left(\eta \right),\hfill \\ \hfill & {\psi }_{20}(\xi ,\eta )=B_{2,4}\left(\eta \right)B_{3,4}\left(\xi \right),\hfill \\ \hfill & {\psi }_{21}(\xi ,\eta )=B_{2,4}\left(\eta \right)B_{4,4}\left(\xi \right),\hfill \\ \hfill & {\psi }_{22}(\xi ,\eta )=B_{2,4}\left(\xi \right)B_{3,4}\left(\eta \right),\hfill \\ \hfill & {\psi }_{23}(\xi ,\eta )=B_{3,4}\left(\xi \right)B_{3,4}\left(\eta \right),\hfill \\ \hfill & {\psi }_{24}(\xi ,\eta )=B_{3,4}\left(\eta \right)B_{4,4}\left(\xi \right),\hfill \\ \hfill & {\psi }_{25}(\xi ,\eta )=B_{2,4}\left(\xi \right)B_{4,4}\left(\eta \right),\hfill \\ \hfill & {\psi }_{26}(\xi ,\eta )=B_{3,4}\left(\xi \right)B_{4,4}\left(\eta \right),\hfill \\ \hfill & {\psi }_{27}(\xi ,\eta )=B_{4,4}\left(\xi \right)B_{4,4}\left(\eta \right).\hfill \end{array}$$

(66)

It can be verified that both sets of shape and basis functions, respectively, fulfil the partition of unity property:

$$\sum _{i=1}^{27}{\varphi }_i(\xi ,\eta )=1,\mathrm{and}\sum _{i=1}^{27}{\psi }_i(\xi ,\eta )=1,.$$

(67)

Nevertheless, there is no guarantee that these two bases are completely equivalent (see Section 5.2.2). One may observe that due to the non-symmetric form of the terms involved in Equation 63 and Equation 64, the direct substitution of Lagrange by Bernstein polynomials does not achieve the same expression exactly. In more detail, each of the row vectors in Equation 63 can be replaced by a matrix equation like that of Equation 60. For degree $p=5$ we have the transformation matrix given by Equation 61, whereas for degrees 3, 4 and 6, we have:

$$\begin{array}{cc}\hfill {\mathbf{T}}_3& =\left[\begin{array}{cccc}1& -5/6& 1/3& 0\\ 0& 3& -3/2& 0\\ 0& -3/2& 3& 0\\ 0& 1/3& -5/6& 1\end{array}\right]\hfill \end{array}$$

(68)

$$\begin{array}{cc}\hfill {\mathbf{T}}_4& =\left[\begin{array}{ccccc}1& -13/12& 13/18& -1/4& 0\\ 0& 4& -32/9& 4/3& 0\\ 0& -3& 20/3& -3& 0\\ 0& 4/3& -32/9& 4& 0\\ 0& -1/4& 13/18& -13/12& 1\end{array}\right]\hfill \end{array}$$

(69)

$$\begin{array}{cc}\hfill {\mathbf{T}}_6& =\left[\begin{array}{ccccccc}1& -29/20& 227/150& -227/200& 29/50& -1/6& 0\\ 0& 6& -222/25& 189/25& -102/25& 6/5& 0\\ 0& -15/2& 201/10& -837/40& 123/10& -15/4& 0\\ 0& 20/3& -308/15& 30& -308/15& 20/3& 0\\ 0& -15/4& 123/10& -837/40& 201/10& -15/2& 0\\ 0& 6/5& -102/25& 189/25& -222/25& 6& 0\\ 0& -1/6& 29/50& -227/200& 227/150& -29/20& 1\end{array}\right]\hfill \end{array}$$

(70)

Applying the transformation matrix ${\mathbf{T}}_4$ (see Equation ) to the Bernstein-based basis functions ${\psi }_1(\xi ,0)$ through ${\psi }_5(\xi ,0)$ along edge $AB$ yields an accurate reconstruction of the corresponding Lagrange-based shape functions ${\varphi }_1(\xi ,0)$ through ${\varphi }_5(\xi ,0)$. Similar results are observed for the remaining three edges as well.

One would anticipate that replacing all Lagrange polynomials involved in the three projectors (Equation 59, Equation 63 and Equation 64), through transformation matrices, would lead to an expression of the bivariate function $U(\xi ,\eta )$ in terms of Berntein polynomials. Nevertheless, such an approach would lead to a high number of products in the form $B_i\left(\xi \right)B_j\left(\eta \right)$. A rough estimation gives 180 terms while we need only 27, plus a few more for the basis functions ${\psi }_1,{\psi }_5,{\psi }_8,{\psi }_{14}$ associated with the corners. Theoretically, such a functional set probably exists, but the paper at hand has not achieved to tackle this topic, which still remains open. Some initial observations may be useful for future research:

• It the transformation matrix $\mathbf{R}$ which fulfils the relationship $\mathbf{a}={\mathbf{R}}^T\mathbf{U}$ is determined by applying it to all the 27 nodal points of the element, we receive that det$\left(\mathbf{R}\right)\ne 0$.
• The recalculation of the Lagrange based bivariate shape functions ${\varphi }_i(\xi ,\eta )$ in terms of the Bernstein based ones ${\psi }_i(\xi ,\eta )$, using the relation ${\varphi }_i=\mathbf{R}{\psi }_i$, shows a large error (about $\pm 0.67$) in the interior of the element, whereas on the boundary and at the nodal points it vanishes.
• A similar discrepancy was obseved when the relationship $\mathbf{a}={\mathbf{R}}^T\mathbf{U}$ was applied to more points, and this least-squares scheme led again to a similar deviation between the initial and the recalculted ${\varphi }_i$’s.

5.2.2. Numerical Verification

The same BVP was solved using the 27-node transfinite element, with uniform discretization per edge, in conjunction with both formulations. The results are as follows:

• The requirement to use the parameters $(\xi ,\eta )$ defined by the nodal points of the Lagrange model, and then map the control points to the nodal points $(x(\xi ,\eta )={\sum }_{i=1}^{27}{\psi }_i(\xi ,\eta )x_i^c)$, leads to coincidence between them.
• In both systems the determinant of the Jacobian all over the rectangular domain equals to unity.
• The $L_2$ error norm was found to be slightly different in each system: $0.0191\%$ for the Lagrange polynomials and $0.0126\%$ for the Bernstein ones.

Although the Bernstein basis is robust, the discrepancy between the two polynomial systems (Lagrange and Bernstein) depicts that the simple replacement of Lagrange by Bernstein polynomials is not the best case for this kind of transfinite elements. Further theoretical analysis is required to provide full explanations, similar to those provided in Section 4.2.

6. Coons Interpolation

Coons interpolation [11] is probably the oldest interpolaton formula in computer-aided geometric design (CAGD) [12], which later inspired the transfinite interpolation [9]. It refers to a quadrilateral patch $ABCD$, of which the four edges are of given geometry x or of given function U. Given the linear blending functions, and the four univariate functions associated with the four edges, at each pair $(\xi ,\eta )$ the variable U is interpolated by:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill U(\xi ,\eta )=& E_0\left(\xi \right)U(0,\eta )+E_1\left(\xi \right)U(1,\eta )+E_0\left(\eta \right)U(\xi ,0)+E_1\left(\eta \right)U(\xi ,1)\hfill \\ \hfill & -E_0\left(\xi \right)E_0\left(\eta \right)-E_1\left(\xi \right)E_0\left(\eta \right)-E_1\left(\xi \right)E_1\left(\eta \right)-E_0\left(\xi \right)E_1\left(\eta \right).\hfill \end{array}\end{array}$$

(71)

Now, we test whether Lagrange polynomials in Equation 71 may be substituted by Bernstein ones while the result remains the same. It is trivial to notice that linear Bernstein polynomials are identical with linear Lagrange polynomials, and therefore no question about the replacement of $E_0$ and $E_1$ by $B_{1,1}$ and $B_{1,2}$, respectively. Moreover, since each edge is equivalently described by either a set of Lagrange or a set of (non-rational) Bernstein polynomials, because both sets are unitary (take unit value) at the corners, it is obvious that the four univariate functions $U(0,\eta ),U(1,\eta ),U(\xi ,0)$ and $U(\xi ,1)$ may be equivalently represented in these two ways. Consequently, we have proven that all terms in Coons interpolation formula described by Equation 71 can be represented either in terms of Lagrange or in terms of Bernstein polynomials. In other words, every expression -such as the set of shape functions- has been derived from Coons’ interpolation and has been expressed by Lagrange polynomials, can be also expressed in terms of Bernstein polynomials, merely replacing the Lagrange polynomials, one-by-one, with a Berstein polynomial of the same degree.

Typical shape functions in terms of Lagrange polynomials are given below:

$$\begin{array}{cc}\hfill \mathrm{Corner}\mathrm{node}\text{:}{\varphi }_1(\xi ,\eta )& =(1-\xi )L_{1,p_{AD}}\left(\eta \right)+(1-\eta )L_{1,p_{AB}}\left(\xi \right)-(1-\xi )(1-\eta )\hfill \\ \hfill \mathrm{Intermediate}\mathrm{to}AB:{\varphi }_2(\xi ,\eta )& =(1-\eta )L_{2,p}\left(\xi \right),\hfill \end{array}$$

(72)

where $p_{AD}$ and $p_{AB}$ are the polynomial degrees along the edges $AD$ and $AB$, respectively.

Moreover, typical basis functions in terms of Bernstein polynomials are given below:

$$\begin{array}{cc}\hfill \mathrm{Corner}\mathrm{node}\text{:}{\psi }_1(\xi ,\eta )& =(1-\xi )B_{1,p_{AD}}\left(\eta \right)+(1-\eta )B_{1,p_{AB}}\left(\xi \right)-(1-\xi )(1-\eta )\hfill \\ \hfill \mathrm{Intermediate}\mathrm{to}AB:{\psi }_2(\xi ,\eta )& =(1-\eta )B_{2,p_{AB}}\left(\xi \right).\hfill \end{array}$$

(73)

6.1. Numerical Verification

The same BVP (Laplace equation in square domain) was solved for a single Coons element made of 18 DOFs, as shown in Figure 8b (note that this Coons element is the same as the 27-node element shown in Figure 4d, without the 9 internal nodes). This was chosen to cover one of the most general cases, because the polynomial degrees in the trial functions along the four edges equal to 4, 3, 6, and 5, respectively. Using either of the polynomial sets, i.e., Lagrange or Bernstein, the error norm $L_2$ was found equal to 2.3013%.

Working in a similar way as in Section 4.2, the transformation matrix ($\mathbf{R}$) between the Lagrange and Bernstein basis (see Equation 33), for the 18-node Coons element, is:

$$\mathbf{R}=\left[\begin{array}{cccccccccccccccccc}\hfill 1& -13/12& 13/18& -1/4& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 1/5& -77/120& 269/240& -77/60\\ \hfill 0& 4& -32/9& 4/3& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ \hfill 0& -3& 20/3& -3& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ \hfill 0& 4/3& -32/9& 4& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ \hfill 0& -1/4& 13/18& -13/12& 1& -5/6& 1/3& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ \hfill 0& 0& 0& 0& 0& 3& -3/2& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ \hfill 0& 0& 0& 0& 0& -3/2& 3& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ \hfill 0& 0& 0& 0& 0& 1/3& -5/6& 1& -29/20& 227/150& -227/200& 29/50& -1/6& 0& 0& 0& 0& 0\\ \hfill 0& 0& 0& 0& 0& 0& 0& 0& 6& -222/25& 189/25& -102/25& 6/5& 0& 0& 0& 0& 0\\ \hfill 0& 0& 0& 0& 0& 0& 0& 0& -15/2& 201/10& -837/40& 123/10& -15/4& 0& 0& 0& 0& 0\\ \hfill 0& 0& 0& 0& 0& 0& 0& 0& 20/3& -308/15& 30& -308/15& 20/3& 0& 0& 0& 0& 0\\ \hfill 0& 0& 0& 0& 0& 0& 0& 0& -15/4& 123/10& -837/40& 201/10& -15/2& 0& 0& 0& 0& 0\\ \hfill 0& 0& 0& 0& 0& 0& 0& 0& 6/5& -102/25& 189/25& -222/25& 6& 0& 0& 0& 0& 0\\ \hfill 0& 0& 0& 0& 0& 0& 0& 0& -1/6& 29/50& -227/200& 227/150& -29/20& 1& -77/60& 269/240& -77/120& 1/5\\ \hfill 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 5& -145/24& 185/48& -5/4\\ \hfill 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& -5& 295/24& -115/12& 10/3\\ \hfill 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 10/3& -115/12& 295/24& -5\\ \hfill 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& -5/4& 185/48& -145/24& 5\end{array}\right].$$

(74)

7. Numerical Solution of an Eigenvalue Problem

In addition to Laplace equation which was the first example in the previous sections of the paper at hand, in this section we deal with a second problem, as follows.

Example-2: Eigenvalue analysis of rectangle acoustic cavity:

A rectangular acoustic cavity of dimensions $a\times b=2.5\times 1.1$ and normalized wave velocity $c=1m/s$, is under Neumann boundary conditions (${\displaystyle \frac{\partial U}{\partial n}}=0$) which represent hard walls (i.e., full reflection). The exact solution is given as (see Ref. [13]):

$${\omega }_{mn}^2={\pi }^2{c}^2\left({\displaystyle \frac{m^2}{a^2}}+{\displaystyle \frac{n^2}{b^2}}\right),m,n=0,1,\dots ,\infty .$$

(75)

For each eigenvalue, the error (in %) is calculated by the formula:

$$E_{mn}={\displaystyle \frac{{\left({\omega }_{mn}\right)}_{calculated}^2-{\left({\omega }_{mn}\right)}_{exact}^2}{{\left({\omega }_{mn}\right)}_{exact}^2}}\times 100(\%).$$

(76)

This problem was solved using the following four models:

• Coons interpolation (18 DOFs).
• Tensor product uniform (25 DOFs).
• Tensor product distorted (25 DOFs).
• Transfinite non-uniform (27 DOFs, as shown in Figure 2a).

Using either Lagrange polynomials or Bernstein polynomials, for the above first three models (18-node and 25-node elements), for all natural modes the results are the same, as selectively shown in Table 1.

Moreover, for the 27-node element the results differ, as shown in Table 2. One may observe that now the two models (Lagrange and Bernstein) do not coincide, but the quality of the results is similar, if not slightly better for the Bézier-based element.

8. Discussion

In this paper five classes of transfinite elements were investigated, as described in Introduction section (Section 1). Below, we summarize our findings for each of them.

Coons Element. The simplest transfinite element is Coons element, which consists of boundary nodes only. It was theoretically explained and numerically verified that, if either Lagrange or Bernstein polynomials are implemented to Coons interpolation formula, the result in the numerical solution of a PDE is the same (see Section 6.1). Moreover, for a 18-node Coons element, the transformation matrix between the Lagrange-based and Bernstein-based bivariate shape functions was determined.

Tensor Product Element. It was well known that tensor product Lagrange polynomials is equivalent to non-rational tensor product Bernstein polynomials (see [6], among others). In the paper at hand, it was demonstrated that there is an inherent transformation matrix between these two bivariate functional sets, which can be systematically determined in terms of two one-dimensional matrices, i.e., one per direction.

Traditional Transfinite Element (Structured). It was also known, by numerical experience, that traditional transfinite elements with structured horizontal and vertical stations (such that of 21-node shown in Figure 3) can be equally treated substituting both the blending and trial functions one-by-one, from Lagrange polynomials to Bernstein polynomials of the same degree [4]. The paper at hand shows that when mathematically replacing univariate Lagrange polynomials by univariate Bernstein polynomials within the transfinite interpolation formula, we receive the same expression in which the Lagrange-based bivariate shape functions have been merely substituted by Bernstein-based bivariate basis functions. Moreover, the nature of associated generalized coefficients (in terms of nodal values $U_i$) has been revealed. Eventually, the inherent transformation matrix between the two bivariate sets of shape and basis functions was explicitely determined (see Equation 51).

Distorted Tensor Product Element. It was also known that, even elements in which the boundary nodes do not match to the orthogonal projections of internal nodes onto the edges, can be treated using the transfinite interpolation formula [9]. This issue has been reported at least since 1995 (see details in [2]) by introducing ‘artificial’ nodes which eventually disappear, while a recent survey on this issue may be found in [10]. In brief, the shape functions associated with the interior of edges and the interior of the domain are local tensor products of blending and trial functions, whereas those associated with the four corners of the patch are influenced by all the three projectors $(P_{\xi },P_{\eta },P_{\xi \eta })$. The paper at hand shows that, the same numerical result with the aforementined ‘distorted’ transfinite element based on Lagrange polynomials is also obtained when using tensor product Bernstein polynomials with properly chosen control points. The required condition is that the ‘images’ of the control points (see Equation 37) must be exactly that of the distrorted element nodes in the Lagrange based formulation.

Partially Unstructured Element. Beyond the aforementioned simple distortion of tensor-product elements with respect to node placement, there exists a case where a given edge of the patch $ABCD$ contains a different number of nodal points than its opposite (and parallel, in the parametric $\xi \eta$ space) edge. For instance, the 27-node element depicted in Fig.Figure 4d (as well as in Fig.Figure 6) can be treated as a transfinite element, similarly to the previously discussed 25-node distorted configuration. However, when Bernstein polynomials are directly substituted for Lagrange polynomials of the same degree, a prior study reported only a slight difference in average interpolation error—specifically, 0.6408% for the Lagrange system versus 0.6154% for the Bernstein system—when interpolating the bivariate function $U(x,y)=e^{x}cos\left(\pi y\right)$ [2]. To further investigate this discrepancy, the present work revisits the topic within the framework of a boundary value problem (BVP), where a similar trend was observed: the $L_2$ error norm of the numerical solution differed only slightly (0.0191% for Lagrange vs. 0.0126% for Bernstein), as shown in Sect.Section 5.2.1. It was also found that a standard transformation matrix $\mathbf{R}$ between Lagrange and Bernstein basis functions does not exist in a general sense, as it depends on the specific test points at which the two bases are related. A second example, presented in Section 7, confirmed a comparable behavior. Interestingly, in all three test cases, the Bézier-based model marginally outperformed the corresponding Lagrange-based formulation.

In summary, the findings of this study indicate that:

(1)

For four broad classes—namely, (i) Coons elements, (ii) tensor-product elements, (iii) traditional transfinite elements with a structured pattern of internal nodes, and (iv) distorted tensor-product elements—Bernstein polynomials can serve as a direct replacement for Lagrange polynomials of the same degree, with identical accuracy.

(2)

In a fifth class, involving transfinite elements with arbitrary boundary nodes combined with a tensor-product distribution of internal nodes, Bernstein polynomials may also replace Lagrange polynomials of the same degree. However, this substitution does not guarantee identical results. While the overall performance of such arbitrarily-noded transfinite elements remains sufficient for practical use, further investigation is warranted, particularly in cases involving non-uniform polynomial degrees.

9. Conclusions

This study demonstrates that transfinite finite elements can be effectively combined with Bernstein–Bézier polynomials by replacing Lagrange polynomials with their Bernstein counterparts. This substitution is mathematically valid and computationally robust across four major classes of elements: Coons-based, tensor-product, structured-node transfinite elements, and distorted tensor-product elements. In all these cases, the method preserves essential properties such as the partition of unity. However, when applied to a fifth category—elements with arbitrarily placed nodes and differing polynomial degrees along opposite edges—minor discrepancies were observed. While the substitution remains practically successful, the question of full mathematical equivalence in this general case remains open and warrants further investigation.