Impact of Monthly Load Variability on the Energy Consumption of Twin Belt Conveyors in a Lignite Mine

1. Introduction–Collected Data

Belt conveyors are not only a more cost-effective alternative to wheeled transport [1,2,3,4,5,6,7], but they are also more environmentally friendly due to their use of electric motors for propulsion and bulk material handling [8,9,10]. Additionally, when operating on downhill slopes, they can serve as energy generators [11,12], contributing to energy recovery and efficiency improvements.

Beyond their primary function in material transport, belt conveyors present innovative opportunities for energy management. They can serve as a form of dry energy storage, similar to pumped-storage power plants [13], by utilizing gravitational energy. Additionally, they can help mitigate renewable energy curtailment by enabling the seasonal transfer of surplus energy from summer to winter. This can be achieved by integrating conveyors with bucket-wheel excavators that remove overburden and expose lignite seams near power plants, effectively creating coal storage reserves [14]. In some cases, conveyors can be powered directly by solar panels, providing both a renewable energy source and protection for transported materials against adverse weather conditions [15].

This study explores the impact of varying conveyor loads on energy consumption, analyzing extensive operational data collected from a Polish lignite mine over four years. The findings aim to enhance the efficiency of belt conveyor systems and identify potential strategies for reducing energy consumption in large-scale mining operations.

Energy and Economic Efficiency of Belt Conveyors

The energy and economic efficiency of belt conveyors, both in standard applications and specialized scenarios like those mentioned earlier, depend largely on the energy required to transport a unit of mass over a distance of 1 km. A unit energy consumption indicator (ZE) was introduced in previous studies [16,17,18,19,20,21] to facilitate accurate comparisons between different conveyor systems, providing a standardized metric for evaluating conveyor performance. This indicator also enables the optimal selection of conveyors for specific transport tasks, including open pit optimization [22,23,24,25] and the selection of belt conveyors for underground operations [26].

Extensive research, including both laboratory and industrial studies, has been conducted to analyze the primary sources of conveyor motion resistance. Findings indicate that indentation rolling resistance [27,28,29,30,31] contributes to over 60% of total motion resistance (Figure 1). Researchers have also sought to systematically assess the energy efficiency of belt conveyors [21, 2024] and explore methods for reducing energy consumption.

Key areas of investigation include:

-

Reduction of idler resistance [32,33,34,35],

-

The development of energy-saving belt conveyors and conveyor belts [36,37,38,39],

-

Adjustments of belt speed to improve trough loading efficiency [8,40,41,42,43],

-

Optimization of chute design to minimize energy losses [44,45,46,47,48].

A methodology for comparing the energy consumption of belt conveyors was presented in previous studies [16]. These studies demonstrated that variations in monthly energy consumption are statistically significant, making direct comparisons between different conveyors challenging. Even when operating under nearly identical conditions, fluctuations in transported mass and monthly energy usage resulted in considerable differences.

This study focuses on two twin conveyors operating in parallel coal transport lines. Despite their nearly identical construction and function—both transferring coal from the same pit to the same power plant during similar periods—they exhibited negligible small differences in length (Table 1) and, more importantly, in the total mass of coal transported and the total time of their operation (Table 2). This difference directly influenced their average capacity and, consequently, the degree to which their theoretical capacity was utilized (Table 3).

The width and speed of the belts were identical for both conveyors, ensuring that variations in energy consumption were not due to structural differences or external weather conditions. Instead, discrepancies in energy use were solely attributed to differences in transferred coal mass and achieved monthly performance levels.

Because these conveyors operated in parallel, direct comparison was complicated by significant monthly and overall differences in transported coal mass and operating time. Consequently, their actual average efficiency—measured as the ratio of transported mass to operating time—varied monthly. Additionally, Conveyor A’s data was incomplete, missing 12 months of measurements.

Direct energy consumption values were not used to ensure a fair and reliable comparison. Instead, the unit energy consumption indicators (ZE) were analyzed, allowing for a standardized evaluation of conveyor efficiency across varying operational conditions.

2. Results and Discussion

2.1. Comparison of the Average Monthly Capacities of the Tested Conveyors

During the analyzed period, the average capacity of Conveyor A was 2,381.99 Mg/h, with an energy consumption index (ZEA) of 286.45 Wh/Mg/km. Conveyor B had an average capacity of 2,309.47 Mg/h, with a slightly higher energy consumption index (ZEB) of 300.69 Wh/Mg/km (Table 3). This means Conveyor B consumed 14.24 Wh/Mg/km more energy per transported unit than Conveyor A. Although the relative difference of 4.97% was not substantial, it was statistically significant and caused by a 1.13% increase in average conveyor capacity.

Interestingly, an inverse relationship was observed between capacity and energy efficiency. Despite being less loaded, Conveyor B had a lower average monthly capacity (72.51 Mg/h, or 3.04%, compared to Conveyor A). This suggests that higher unit energy consumption was associated with lower capacity utilization. A strong negative correlation was identified between ZE and conveyor capacity (R² = -0.84 and -0.85 for conveyors A and B, respectively). A 35% relative increase in capacity (from 2000 up to 2700 Mg/h) led to a 26% reduction in ZE (from 340 down to 250 Wh/Mg/km), equating to a 90 Wh/Mg/km decrease. Proper load distribution could reduce unit energy consumption by up to 30%.

Research manuscripts reporting large datasets deposited in a publicly available database should specify where the data have been deposited and provide the relevant accession numbers. If the accession numbers have not yet been obtained at the time of submission, please state that they will be provided during review. They must be provided before publication.

A statistical comparison of two independent sample distributions was conducted to verify the significance of these differences. The results, illustrated in Figure 1, show the histograms of monthly average capacities for both conveyors. The modal value for Conveyor A (~2400 Mg/h) is slightly higher than that for Conveyor B (~2300 Mg/h), indicating a small but measurable shift in performance.

Figure 2. Comparison of the histograms of monthly average capacities (Q) for Conveyors A and B.

Figure 2. Comparison of the histograms of monthly average capacities (Q) for Conveyors A and B.

A more detailed view of the density distributions (Figure 3) confirms this shift. The peak value for Conveyor A is approximately 135 Mg/h higher than that for Conveyor B, which is almost twice the difference observed in the mean values (72.51 Mg/h). Additionally, the efficiency distribution of Conveyor A shows slight left-hand asymmetry, while Conveyor B exhibits a right-hand asymmetry, suggesting different operational characteristics.

Figure 3. Density traces of monthly average capacities (Q) for Conveyors A and B.

Figure 3. Density traces of monthly average capacities (Q) for Conveyors A and B.

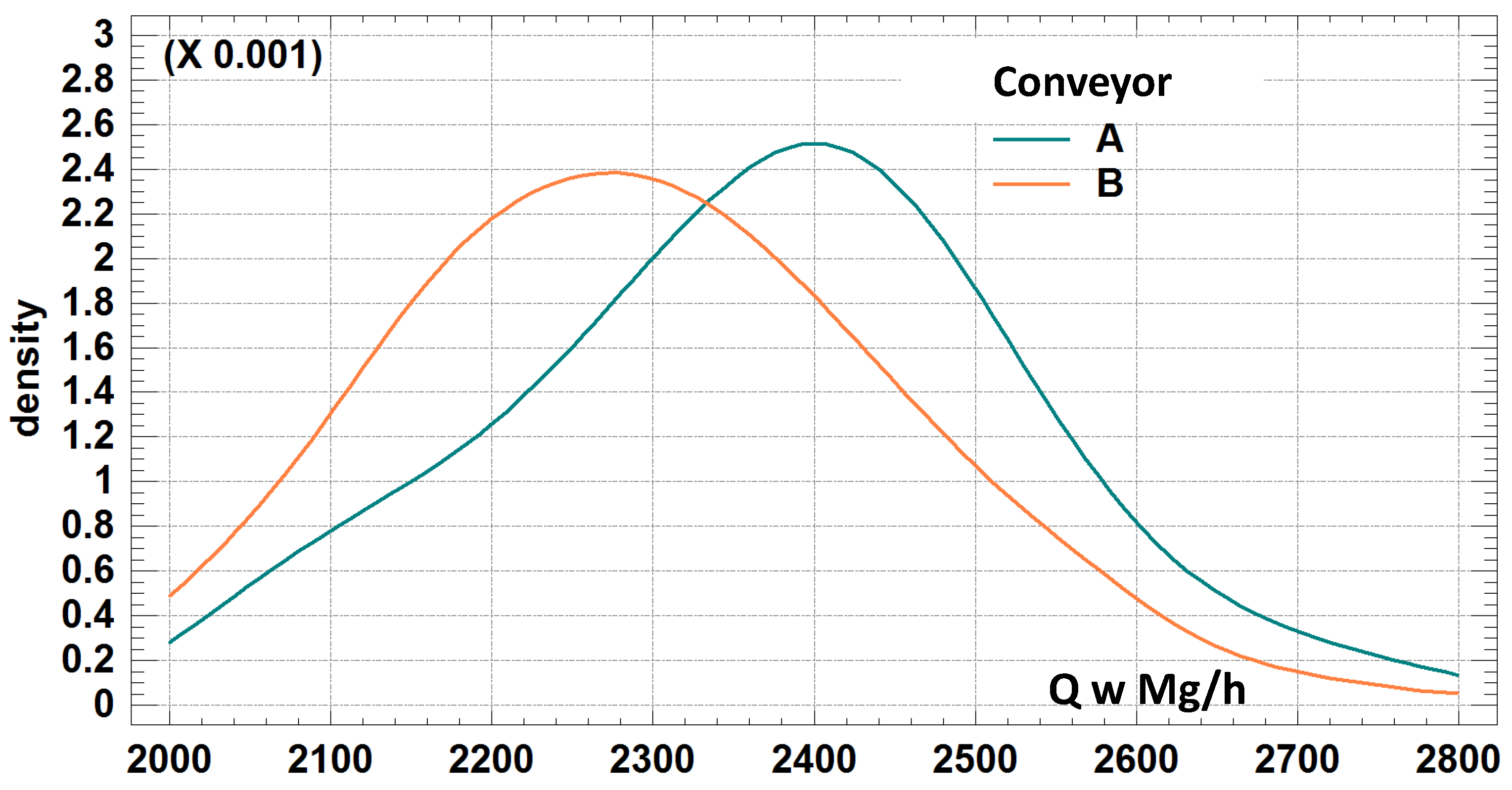
2.2. Statistical Analysis of Conveyor Capacities

Table 1 presents key descriptive statistics for the analyzed datasets of monthly capacities. Notably, Conveyor A consistently exhibited higher values across various measures of central tendency (mean, median), with differences ranging from 3% to 4%. The median showed the most significant difference (-4.36%), while the harmonic mean differed the least (-3.1%).

In terms of dispersion, Conveyor A displayed more significant variability, with a higher standard deviation (146.62 Mg/h vs. 142.20 Mg/h) and variance. Conveyor B’s variance was 5.94% lower, and its standard error was 16.01% lower, indicating slightly more consistent performance.

Table 4. Basic statistics for monthly average capacities (Q) of Conveyors A and B.

Descriptive Statistics	Conveyor A	Conveyor B	Absolute Difference	Relative Difference (%)
No. of Measurements	36	48	12	33.33
Mean in Mg/h	2,370.56	2,296.89	-73.67	-3.11
Median in Mg/h	2390.60	2,286.37	-104.23	-4.36
Geometric Mean in Mg/h	2,366.14	2,292.63	-73.51	-3.11
Harmonic Mean in Mg/h	2,361.69	2,288.42	-73.27	-3.10
Standard Deviation in Mg/h	146.62	142.20	-4.42	-3.02
Coefficient of Variation	6.19%	6.19%	0.10	0.10
Standard Error in Mg/h	24.437	20.525	-3.912	-16.01
Variance in Mg2/h2	21,498.1	20,221.2	-1276.9	-5.94
Minimum Capacity in Mg/h	2119.17	2045.89	-73.28	-3.46
Maximum Capacity in Mg/h	2693.29	2692.01	-1.28	-0.05
Range in Mg/h	574.12	646.12	72.00	12.54
Lower Quartile (Q1) in Mg/h	2307.98	2200.30	-107.68	-4.67
Upper Quartile (Q3) in Mg/h	2445.07	2409.83	-35.24	-1.44
Interquartile Range in Mg/h	137.10	209.53	72.44	52.84
Skewness	0.0178	0.4232	0.4053	2273.16
Kurtosis	-0.0170	0.0559	0.0729	-427.76

Table 4. Basic statistics for monthly average capacities (Q) of Conveyors A and B.

Descriptive Statistics	Conveyor A	Conveyor B	Absolute Difference	Relative Difference (%)
No. of Measurements	36	48	12	33.33
Mean in Mg/h	2,370.56	2,296.89	-73.67	-3.11
Median in Mg/h	2390.60	2,286.37	-104.23	-4.36
Geometric Mean in Mg/h	2,366.14	2,292.63	-73.51	-3.11
Harmonic Mean in Mg/h	2,361.69	2,288.42	-73.27	-3.10
Standard Deviation in Mg/h	146.62	142.20	-4.42	-3.02
Coefficient of Variation	6.19%	6.19%	0.10	0.10
Standard Error in Mg/h	24.437	20.525	-3.912	-16.01
Variance in Mg2/h2	21,498.1	20,221.2	-1276.9	-5.94
Minimum Capacity in Mg/h	2119.17	2045.89	-73.28	-3.46
Maximum Capacity in Mg/h	2693.29	2692.01	-1.28	-0.05
Range in Mg/h	574.12	646.12	72.00	12.54
Lower Quartile (Q1) in Mg/h	2307.98	2200.30	-107.68	-4.67
Upper Quartile (Q3) in Mg/h	2445.07	2409.83	-35.24	-1.44
Interquartile Range in Mg/h	137.10	209.53	72.44	52.84
Skewness	0.0178	0.4232	0.4053	2273.16
Kurtosis	-0.0170	0.0559	0.0729	-427.76

Key Observations:

• Consistent Variation:

  -

  The coefficient of variation was nearly identical (6.19%) for both conveyors despite differences in mean values.

  -

  The maximum capacities were almost the same (~2,693 Mg/h), while the minimum capacity was lower for Conveyor B.

• Higher Dispersion in Conveyor B:

  -

  The range of fluctuations in Conveyor B’s capacity was 72 Mg/h higher than in Conveyor A (646.12 Mg/h vs. 574.12 Mg/h).

  -

  This wider range may be due to seasonal and operational factors, requiring further investigation.

• Efficiency Distribution Differences:

  -

  Interquartile and intersextile ranges suggest a more concentrated distribution in Conveyor A, while Conveyor B exhibited greater dispersion at the extremes.

  -

  The kurtosis values suggest that both datasets approximate a normal distribution, though Conveyor A’s slight negative kurtosis (-0.017) contrasts with Conveyor B’s positive kurtosis (0.056).

  -

  Conveyor B exhibited stronger right-side skewness (0.42), indicating higher occurrences of lower-than-average capacities than Conveyor A (skewness = 0.017).

While statistically significant, the observed differences in capacities between the two conveyors do not appear to be solely due to construction differences. Instead, variations in load distribution, seasonal effects, and potential external factors likely contributed to the discrepancies. These factors warrant further exploration, particularly concerning their impact on energy consumption trends.

A separate study is needed to investigate atmospheric and seasonal influences on belt conveyor efficiency, as these may also explain the observed variability in capacity utilization.

2.1.1. Statistical Significance of Differences in Monthly Average Capacities

The differences observed visually (Figure 1 and Figure 2) and identified through various descriptive statistics (Table 1) may appear significant but could still be coincidental. A series of tests was conducted to formally verify their statistical significance. Given that the differences affect not only central tendency measures but also positional statistics and density distribution traces (Figure 2), they are unlikely to occur by chance. However, a rigorous statistical approach is required.

• Confidence Intervals for Monthly Average Capacities

To compare the means of the two conveyors, 95% confidence intervals were determined:

• Conveyor A: 2,370.56 ± 49.61 [2,320.95; 2420.17]
• Conveyor B: 2,296.89 ± 41.29 [2,255.59; 2338.18]

Additionally, a 95% confidence interval was calculated for the differences in the unit energy consumption index (ZE), assuming equal variances:

• ZE Difference: 73.67 ± 63.21 [10.47; 136.88]

Since this interval does not contain zero, we conclude that the difference in means is statistically significant at the 95% confidence level.

• Student’s t-Test for Mean Comparison

A Student’s t-test was performed to compare the means of the two samples. The null hypothesis (H0) assumed equal means, while the alternative hypothesis (H1) suggested a difference. Assuming equal variances:

• t-statistic: 2.31884
• P-value: 0.02289

Since the P-value is less than 0.05, we reject the null hypothesis, confirming a statistically significant difference between the mean capacities of Conveyors A and B.

• F-Test for Variance Comparison

Before performing the t-test, an F-test was conducted to check whether the two samples had equal variances. The standard deviations were:

• Conveyor A: 146.622 [118.92; 191.26]
• Conveyor B: 142.201 [118.38; 178.18]
• Variance Ratio: 1.0632
• 95% Confidence Interval for Variance Ratio: [0.57575; 2.0211]

The F statistic was 1.06315 with a P-value of 0.83486. Since the P-value exceeds 0.05, we do not reject the null hypothesis, confirming no statistically significant difference in standard deviations.

• Mann-Whitney (Wilcoxon) Test for Median Comparison

A Mann-Whitney test was conducted to compare the medians:

• Median Capacities:

  -

  Conveyor A: 2,390.6

  -

  Conveyor B: 2,286.37

• Mean Ranks:

  -

  Conveyor A: 49.6111

  -

  Conveyor B: 37.1667

• W-statistic: 608
• P-value: 0.02092

Since the P-value is less than 0.05, we reject the null hypothesis and confirm a statistically significant difference between the medians at the 95% confidence level.

• Kolmogorov-Smirnov Test for Distribution Compatibility

The Kolmogorov-Smirnov (K-S) test was used to compare the distributions of both samples:

• DN Statistic: 0.3819
• K-S Statistic: 1.7323
• P-value: 0.00049

Since the P-value is below 0.05, we conclude that there is a statistically significant difference between the two distributions at a 95% confidence level.

Figure 4 compares Box-and-Whisker plots, scatter plots, and confidence intervals for the mean and median monthly capacities of both conveyors. The intervals do not overlap, reinforcing the statistical significance of the differences.

Figure 4. Graphical Analysis of Confidence Intervals.

Figure 4. Graphical Analysis of Confidence Intervals.

Figure 5 displays cumulative empirical distribution functions, showing that the distribution shift is most pronounced in the central region, with smaller variations at the tails.

Figure 5. Chart of two cumulative empirical distributions for the monthly averages of capacity Q for conveyors A and B.

Figure 5. Chart of two cumulative empirical distributions for the monthly averages of capacity Q for conveyors A and B.

Conclusion

The statistical tests confirm that Conveyors A and B’s observed differences in monthly average capacities are significant. These differences primarily impact the variation of the unit energy consumption index (ZE). The next chapter will explore the relationship between capacity and energy efficiency in greater detail through regression analysis.

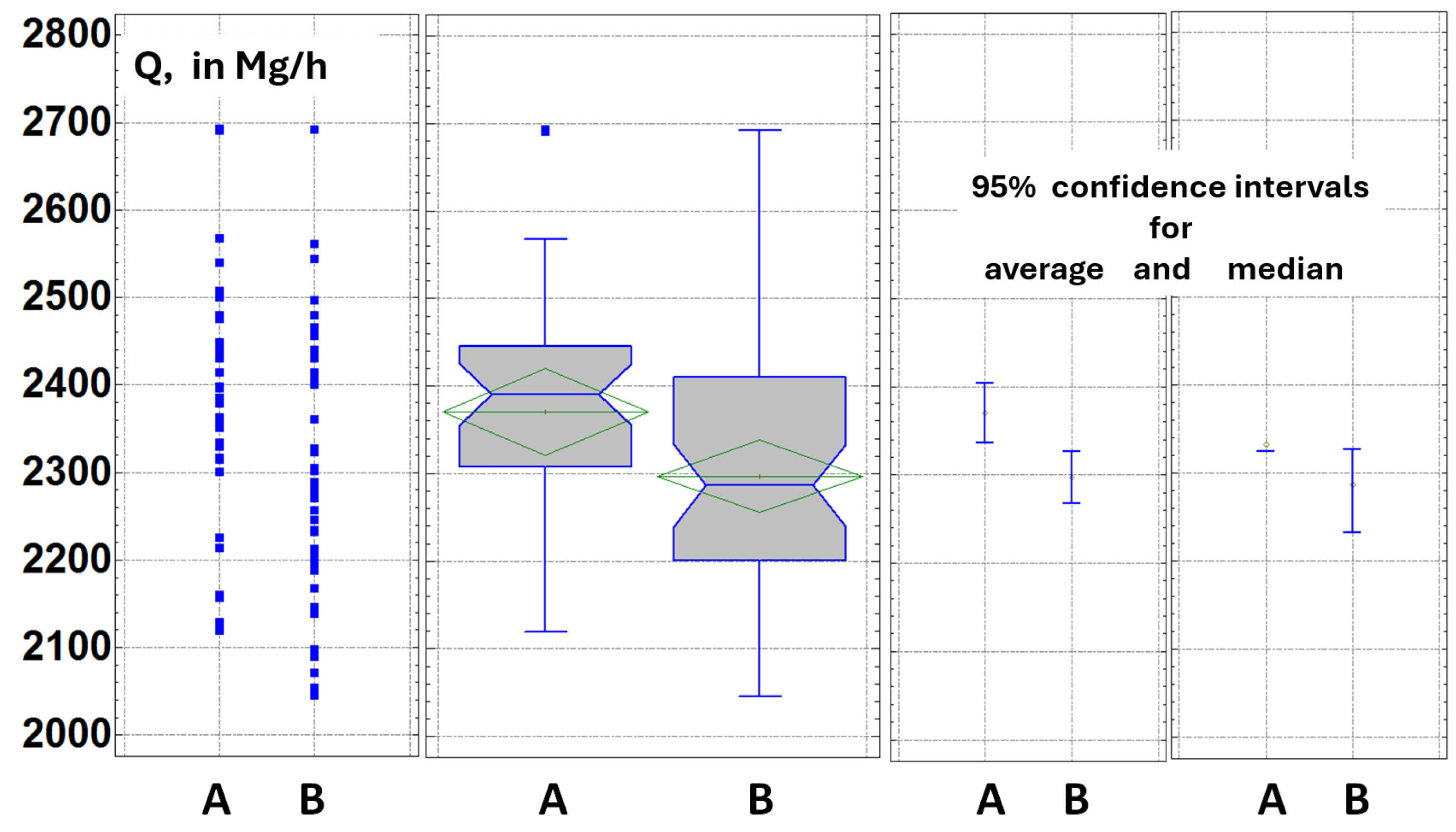
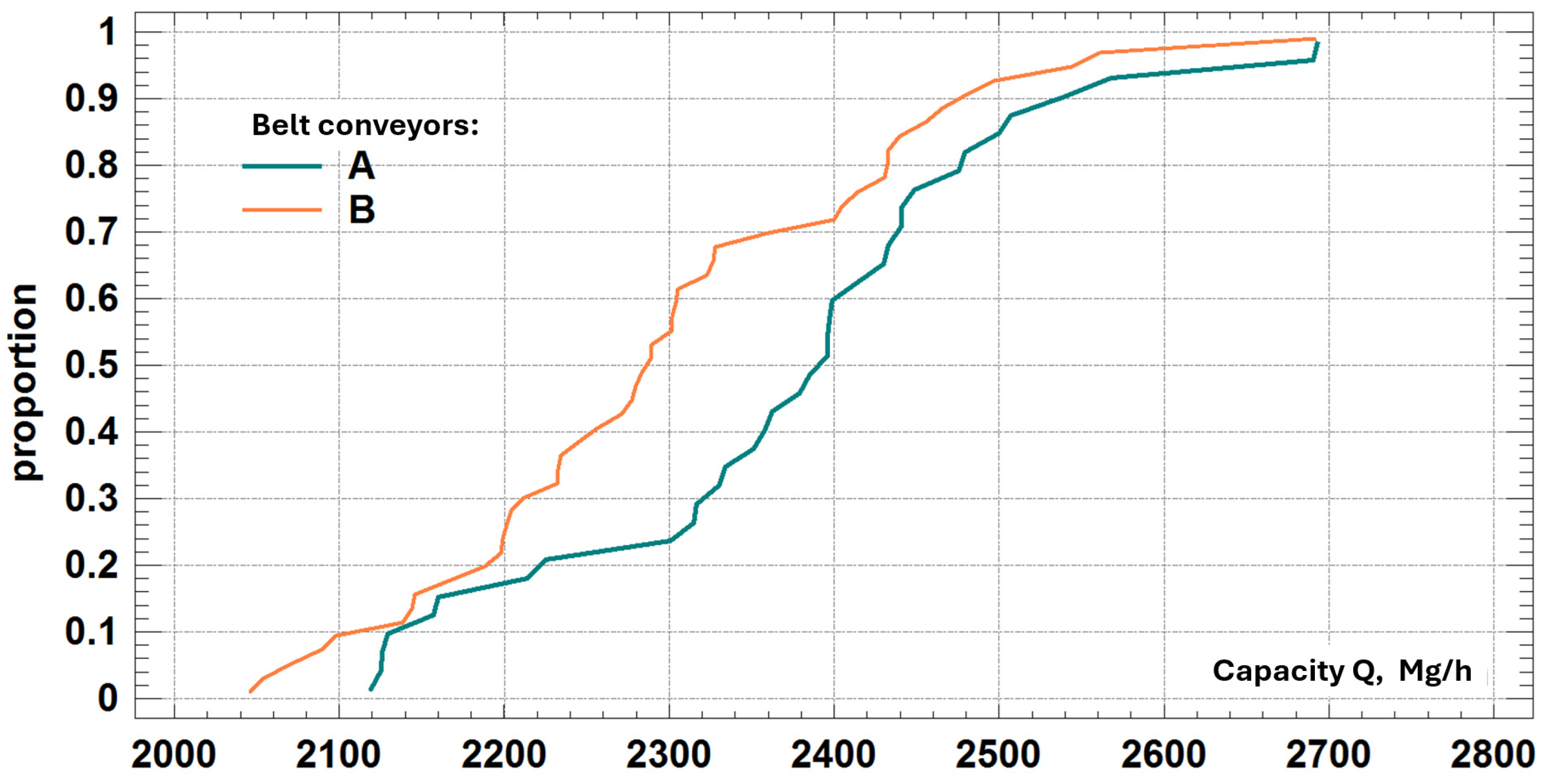
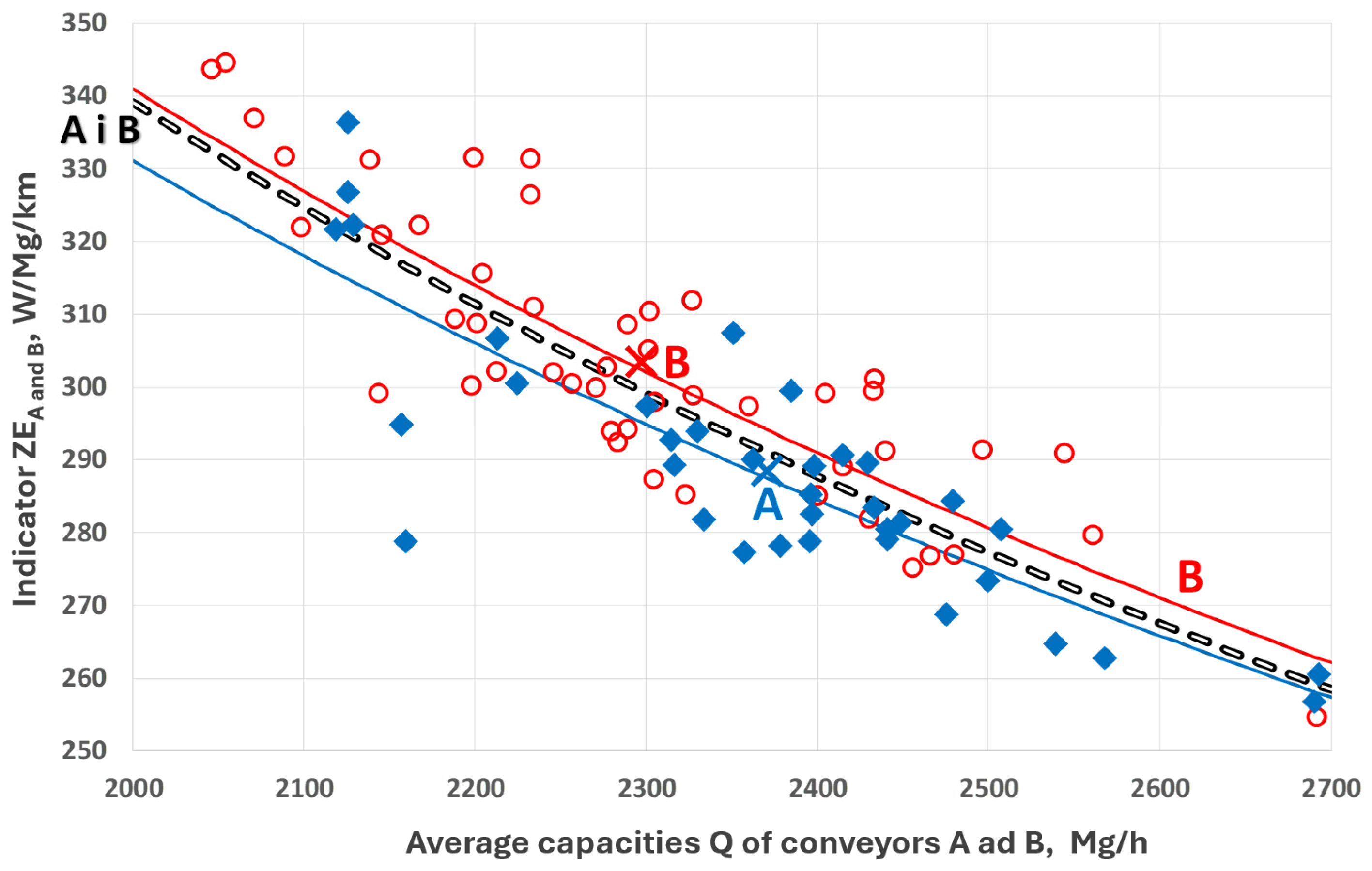
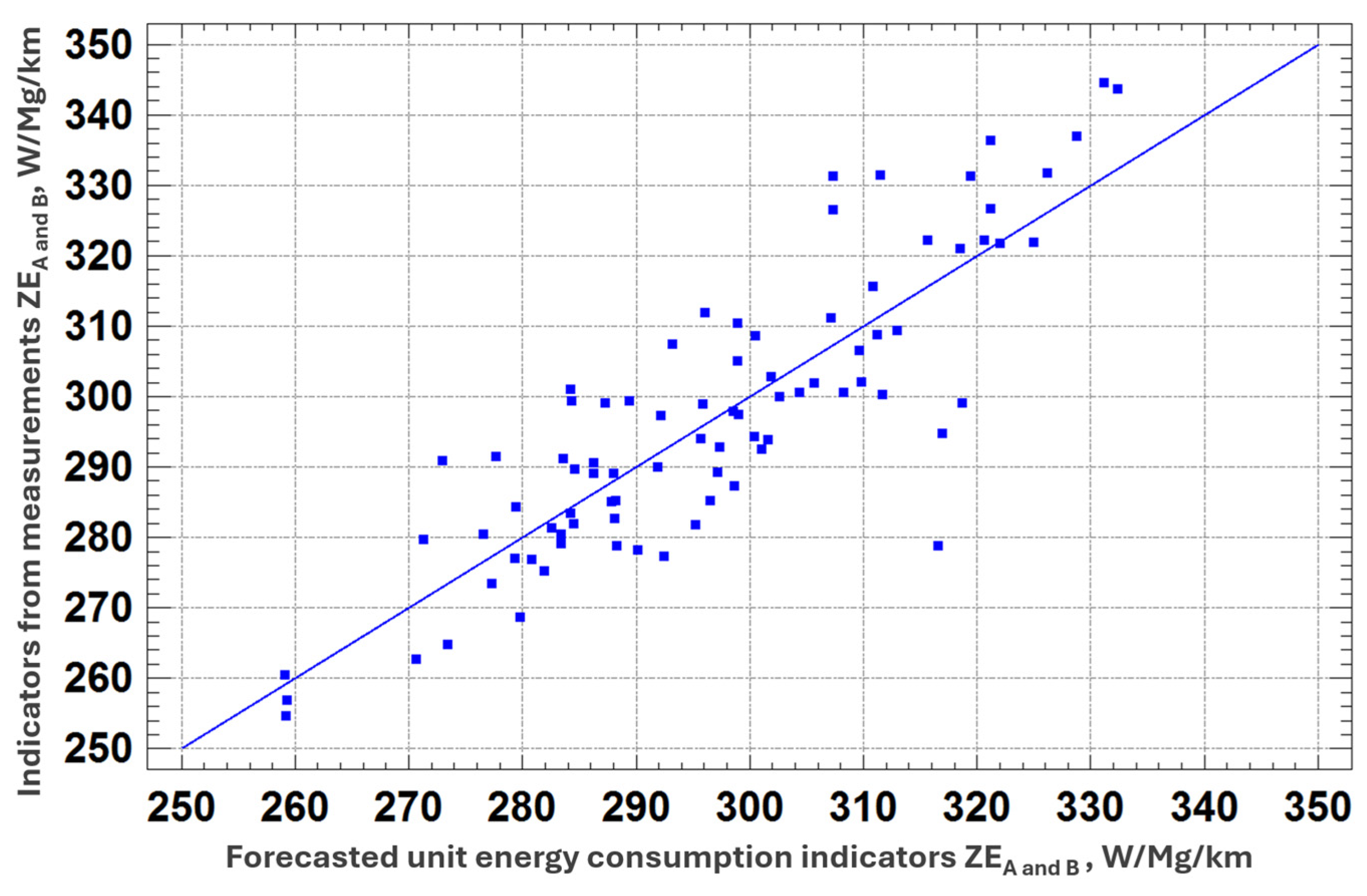
2.3. Regression of the Unit Energy Consumption Indicator ZE Against the Average Capacity of the Conveyor

The impact of the monthly average capacity on the specific energy consumption index of the conveyor can be observed in the matrix graph (Figure 5), where all data points are plotted, differentiating between conveyors A and B. The points are mixed and aligned along a negatively inclined diagonal, confirming a strong negative correlation (-0.84 and -0.85 for conveyors A and B, respectively).

The graph (Figure 6) presents 84 complete data pairs (36 for conveyor A and 48 for conveyor B). More blue points (conveyor A) are located in the lower part of the graph, while red points (conveyor B) dominate the upper part. This indicates differences in the average specific energy consumption for conveyor A (288.6 Wh/Mg/km) and conveyor B (303.6 Wh/Mg/km), primarily due to differences in their monthly average capacities: 2370.6 Mg/h for A and 2296.9 Mg/h for B.

Figure 6. Matrix diagram showing the impact of monthly average capacity Q on the specific unit energy consumption indicator ZE for conveyors A and B.

Figure 6. Matrix diagram showing the impact of monthly average capacity Q on the specific unit energy consumption indicator ZE for conveyors A and B.

Figure 7. Scatter plot of average capacities Q and energy consumption indicators ZE for each month, with calculated averages (denoted by “X”) for conveyors A and B.

Figure 7. Scatter plot of average capacities Q and energy consumption indicators ZE for each month, with calculated averages (denoted by “X”) for conveyors A and B.

A simple regression test was performed to analyze the relationship between the dependent variable (unit energy consumption indicator ZE) and the independent variable (average efficiency Q) for conveyors A and B separately and together.

For conveyor A, the best-fit model was a hyperbolic function (inverse linear for Y), expressed as Equation (1):

ZE_A = 1 / (0.0005512 + 0.000001235 Q_A)

(1)

The estimation analysis, including ANOVA, yielded the following results:

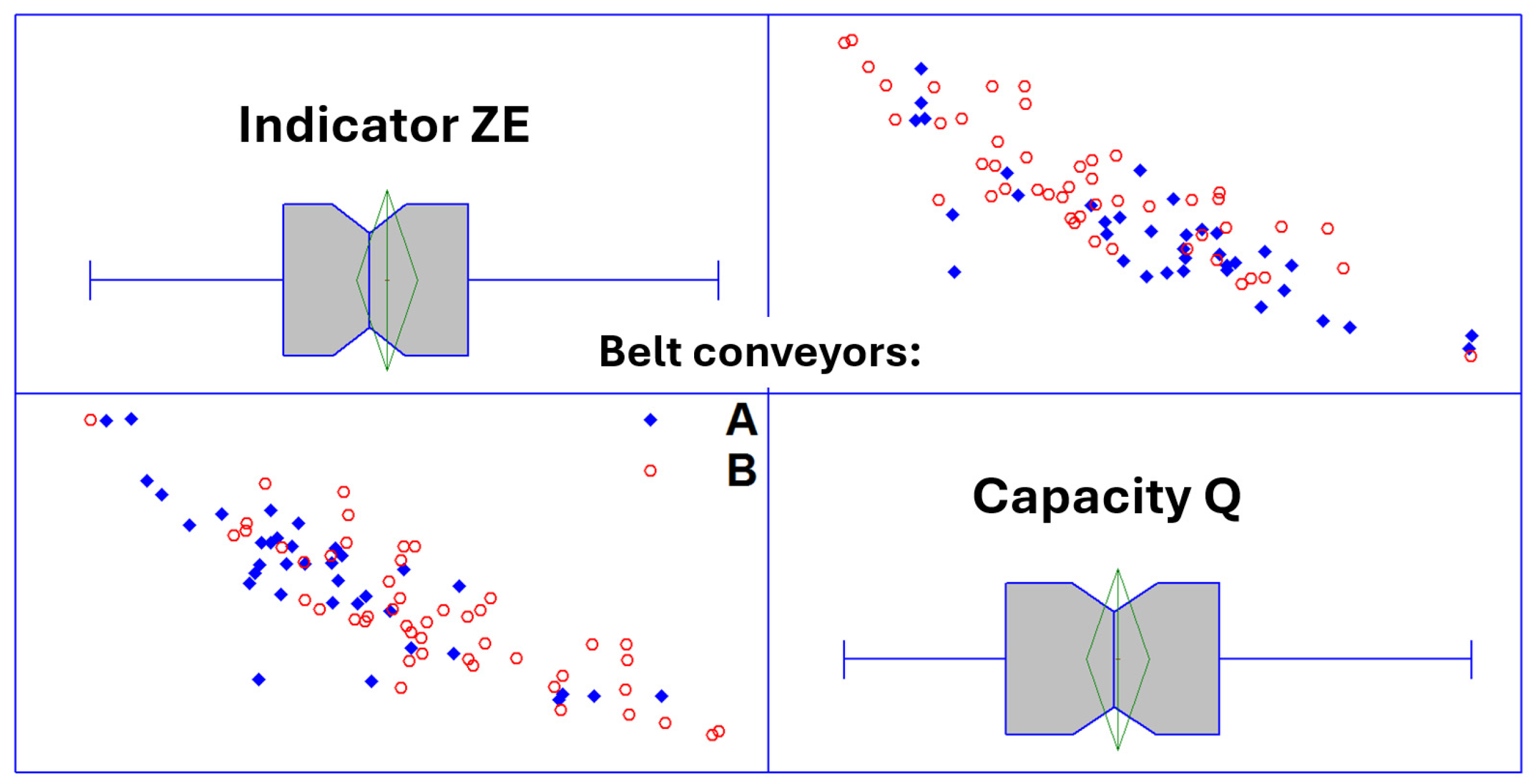
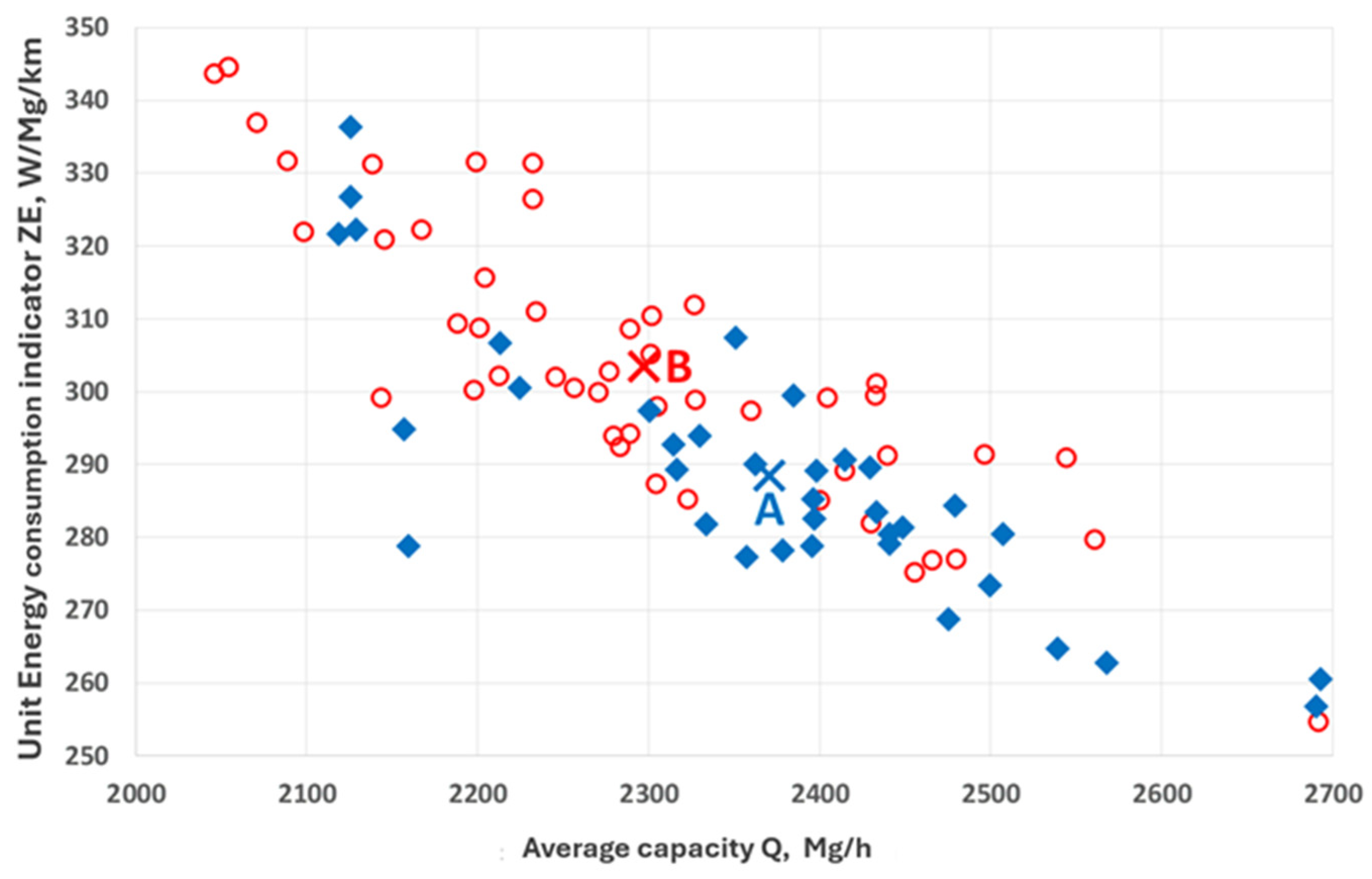
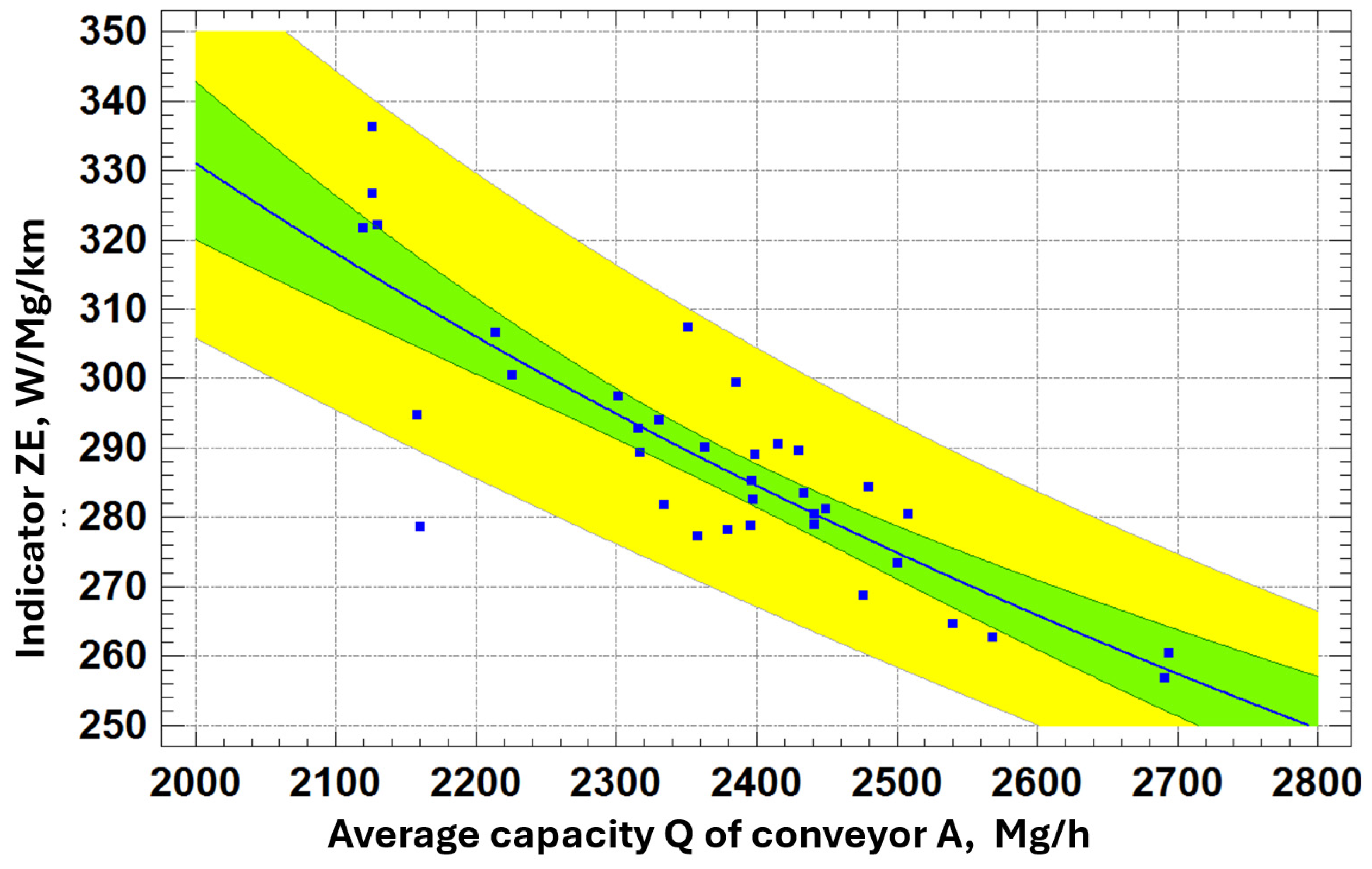
• Correlation coefficient: 0.854862
• R-squared: 73.0789%
• R-squared (df corrected): 72.2871%
• Standard error of estimation: 0.0000796077
• Mean absolute error: 0.0000882741
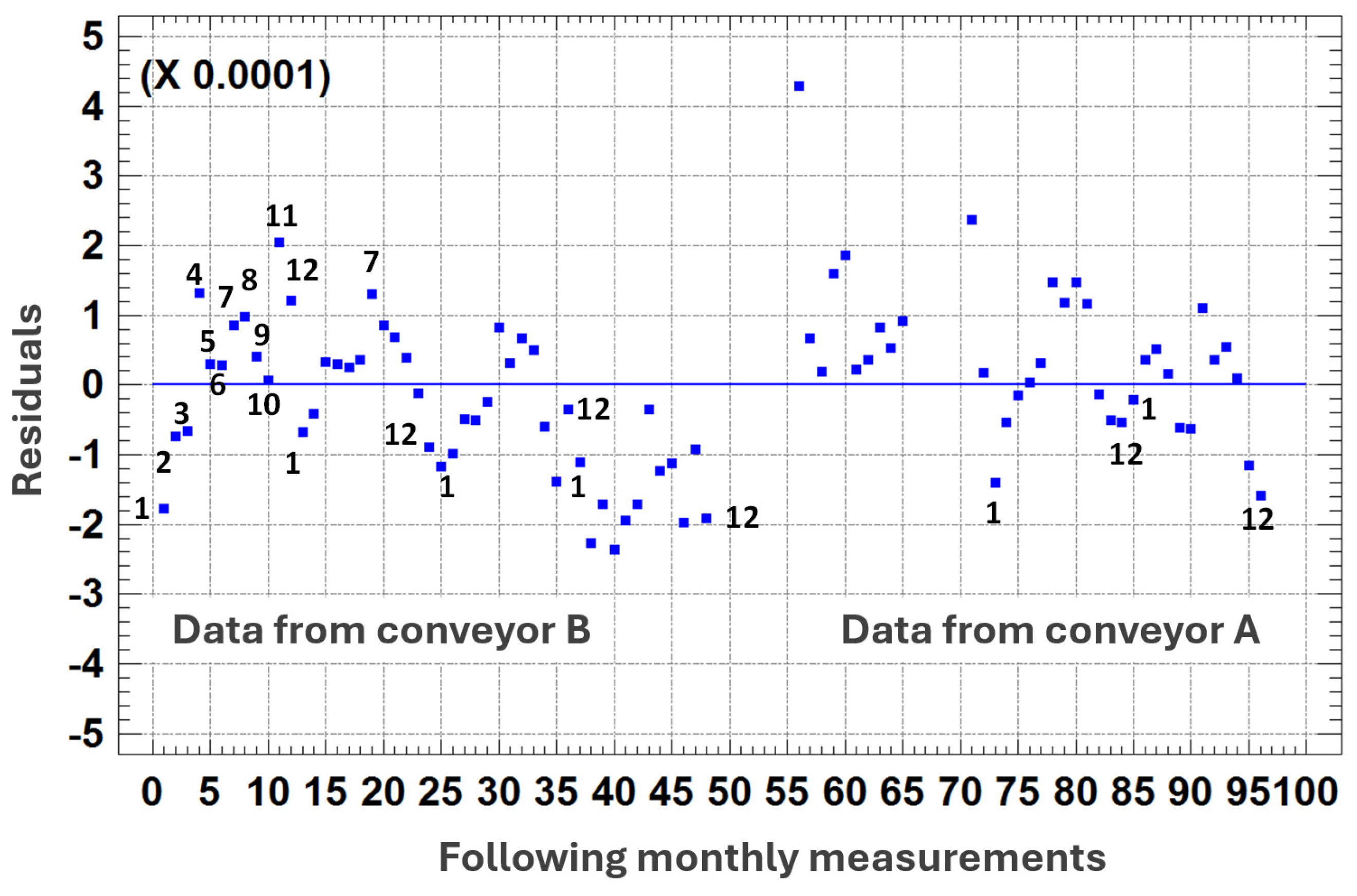
• Durbin-Watson statistic: 0.909369 (P = 0.00001)
• Residual autocorrelation Lag 1: 0.335697

Since the P-value in the ANOVA table (Table 5) is below 0.05, a statistically significant relationship exists between the indicator ZEA and capacity QA at a 95% confidence level.

Table 5. Coefficients and variance analysis (D_f – degrees of freedom).

	Least squares method	Standard	Statistics	Value
Parameter	Estimate	Error	T	P
Offset	0.0005512	0.00030525	1.8057	0.0798
Slope	0.000001235	1.2853 E-7	9.6070	0.0000
Variance Analysis
Source	Sum of squares	Df	Medium squares	F-statyst.	Value P
Model	0.0000011472	1	0.0000011472	92.30	0.0000
The Rest	4.22607 E-7	34	1.24296 E-8
Together (Corr.)	0.00000157	35

Table 5. Coefficients and variance analysis (D_f – degrees of freedom).

	Least squares method	Standard	Statistics	Value
Parameter	Estimate	Error	T	P
Offset	0.0005512	0.00030525	1.8057	0.0798
Slope	0.000001235	1.2853 E-7	9.6070	0.0000
Variance Analysis
Source	Sum of squares	Df	Medium squares	F-statyst.	Value P
Model	0.0000011472	1	0.0000011472	92.30	0.0000
The Rest	4.22607 E-7	34	1.24296 E-8
Together (Corr.)	0.00000157	35

The R² statistic shows that the model explains 73.1% of the variability in the energy consumption index of conveyor A. The correlation coefficient (0.854862) indicates a moderately strong relationship between the variables. The residuals’ standard deviation is 0.0001115. The mean absolute error (MAE) is 0.000079608, and the Durbin-Watson statistic suggests some serial correlation due to potential seasonal variations in the data.

Figure 8. A simple regression of ZE for conveyor A against average capacity Q over the analyzed months.

Figure 8. A simple regression of ZE for conveyor A against average capacity Q over the analyzed months.

For conveyor B, multiple models were tested (logistic S curve, double hyperbolic, hyperbolic for the logarithm), but differences in correlation coefficients and R² values were minimal. The best correlation coefficient was 0.8616, while the hyperbolic model’s correlation was slightly lower at 0.8603, making it the most comparable model. The Equation (2) is:

ZE_B = 1 / (0.0004123 + 0.00000126 Q_B)

(2)

The estimation analysis, including ANOVA, yielded:

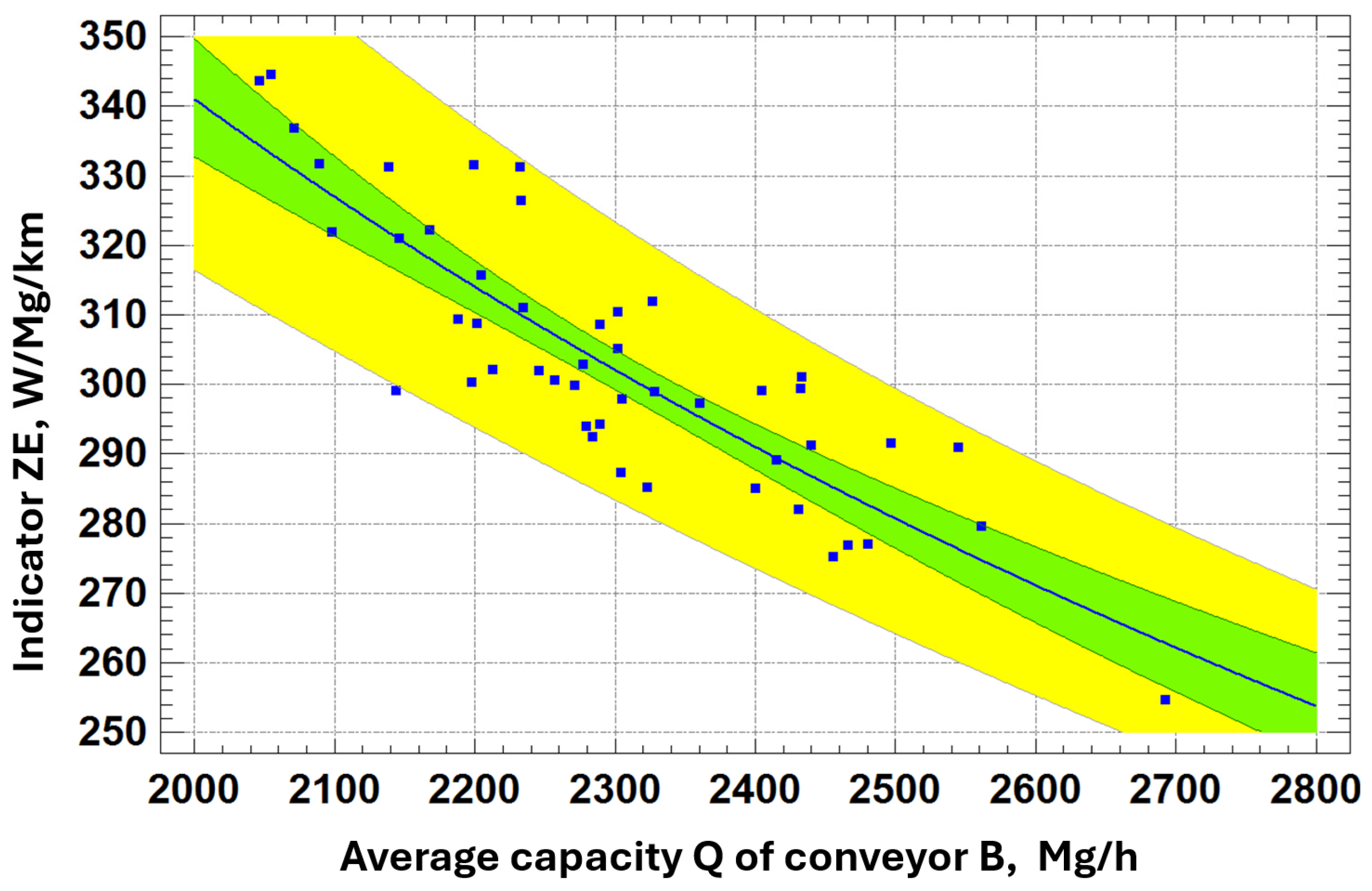
• Correlation coefficient: 0.86031
• R-squared: 74.012%
• Standard error of estimation: 0.00010734
• Mean absolute error: 0.000089
• Durbin-Watson statistic: 0.58731 (P = 0.0000)
• Residual autocorrelation Lag 1: 0.66312

Since the P-value in ANOVA (Table 6) is below 0.05, a statistically significant relationship exists between indicator ZE_B and Q_B at a 95% confidence level.

Table 6. Coefficients and variance analysis (D_f – degrees of freedom).

	Least squares method	Standard	Statistics	Value
Parameter	Estimate	Error	T	P
Offset	0.00041227	0.00025337	1.6277	0.1105
Slope	0.0000012602	1.10102 E-7	11.446	0.0000
Variance Analysis
Source	Sum of squares	Df	Medium squares	F-statyst.	Value P
Model	0.0000015094	1	0.0000015094	131.01	0.0000
The Rest	5.29975 E-7	46	1.15212 E-8
Together (Corr.)	0.000002039	47

Table 6. Coefficients and variance analysis (D_f – degrees of freedom).

	Least squares method	Standard	Statistics	Value
Parameter	Estimate	Error	T	P
Offset	0.00041227	0.00025337	1.6277	0.1105
Slope	0.0000012602	1.10102 E-7	11.446	0.0000
Variance Analysis
Source	Sum of squares	Df	Medium squares	F-statyst.	Value P
Model	0.0000015094	1	0.0000015094	131.01	0.0000
The Rest	5.29975 E-7	46	1.15212 E-8
Together (Corr.)	0.000002039	47

Figure 9. A simple regression of ZE for conveyor B against average capacity Q.

Figure 9. A simple regression of ZE for conveyor B against average capacity Q.

When analyzing data from both conveyors together, the hyperbolic model ranked third after logarithmic and square root hyperbolic models. The minor differences in correlation coefficient (0.0001 lower) and R² index (0.07 lower) made the hyperbolic model suitable for comparative purposes. The Equation (3) is:

ZE_{A and B} = 1 / (0.00031769 + 0.0000013153 Q_{A and B})

(3)

The combined regression analysis resulted in:

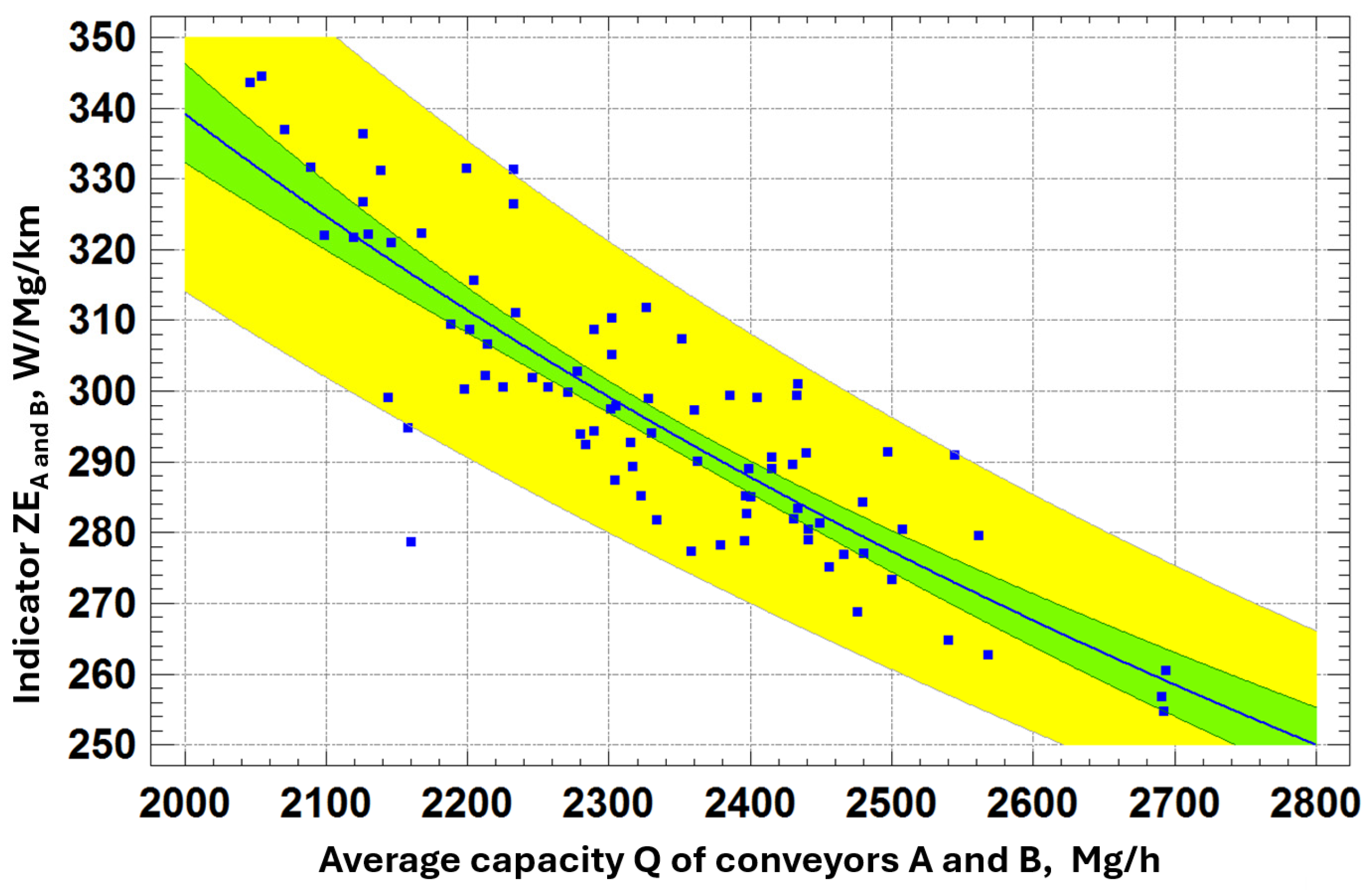
• Correlation coefficient: 0.86312
• R-squared: 74.498%
• Standard error of estimation: 0.00011448
• Mean absolute error: 0.000088274
• Durbin-Watson statistic: 1.0102 (P = 0.0000)
• Residual autocorrelation Lag 1: 0.46853

The model explains 74.498% of the unit energy consumption indicators variability for both conveyors.

The selected regression curves for conveyors A, B, and combined data were plotted on a standard graph (Figure 10). The regression curves run almost parallel, with minor differences in energy consumption indices. The difference for 2,000 Mg/h is 9.9 Wh/Mg/km, reducing to 4.3 Wh/Mg/km at 2700 Mg/h, a decrease from 3% to 1.7%.

Figure 10. A simple regression of ZE for conveyors A and B against average capacity Q.

Figure 10. A simple regression of ZE for conveyors A and B against average capacity Q.

The hyperbolic model fits well, with point dispersion (forecast vs. observed) being mostly uniform, except for a few outliers (Figure 11). However, a variance of up to 30 Wh/Mg/km suggests that factors other than capacity influence energy consumption.

Figure 11. Comparison of regression models for conveyors A, B, and combined data.

Figure 11. Comparison of regression models for conveyors A, B, and combined data.

Seasonal temperature variations appear to contribute significantly, with negative residuals in winter-spring and positive ones in summer-autumn (Figure 12). Future analysis will explore the influence of atmospheric conditions.

Figure 12. Comparison of predicted and observed values.

Figure 12. Comparison of predicted and observed values.

Figure 13. Distribution of residuals over analyzed months for conveyors A and B.

Figure 13. Distribution of residuals over analyzed months for conveyors A and B.

3. Conclusions

This study demonstrates that variations in conveyor energy consumption primarily result from differences in load distribution. A statistically significant disparity was observed between the average capacities of conveyors A and B, with A operating at 2,381.99 Mg/h and B at 2,309.47 Mg/h—an absolute difference of 72.51 Mg/h (3.04%).

A strong negative correlation was identified between ZE and conveyor capacity (R² = -0.84 and -0.85 for conveyors A and B, respectively). A 35% relative increase in capacity (from 2000 up to 2700 Mg/h) led to a 26% reduction in ZE (from 340 down to 250 Wh/Mg/km), equating to a 90 Wh/Mg/km decrease. Proper load distribution could potentially reduce unit energy consumption by up to 30%.

Optimizing conveyor utilization—such as alternating higher load levels between conveyor lines—can yield substantial energy savings. For instance, instead of running both lines at 30% capacity daily, increasing one line’s load to 60% while idling the other could further reduce energy consumption by as much as 150 Wh/Mg/km. These optimizations require no additional infrastructure investment, making them a cost-effective strategy for improving efficiency.

The Bełchatów power plant receives 30-40 million Mg of coal annually, transported over conveyor lines spanning several dozen kilometers. For 10 million Mg/year over 10 km, this equates to potential energy savings of 9 GWh (or 15 GWh at 60%). Scaling up to actual conditions—four times the coal volume and double the conveyor length—yields estimated savings of 72 GWh (or 120 GWh). Including overburden removal, these estimates could increase further (by multiplication by overburden to coal ratio + 1), emphasizing the potential of improved load management through centralized control in surface mines.

An additional opportunity lies in synchronizing conveyor operations with the daily solar cycle for overburden removal and coal extraction. Excess renewable energy, particularly from PV sources, often results in low or negative electricity prices and RES curtailments. Dynamic load control allows conveyor utilization to maximize this opportunity during peak solar production. A recent study in Energies explored this approach, demonstrating its feasibility in developing the Złoczew lignite deposit [RES].

Future research will investigate additional energy-saving measures, such as energy-saving conveyor belts, and evaluate the benefits of load optimization and technological improvements. Further studies will also assess the impact of environmental factors, particularly temperature, on energy consumption variability, as preliminary findings suggest that up to 75% of ZE fluctuations stem from load variations.

Identifying the primary drivers of conveyor energy consumption under long-term industrial conditions enhances predictive accuracy and highlights significant opportunities for efficiency improvements. These findings provide practical guidelines for reducing operational costs and improving the sustainability of belt conveyor systems in lignite mining operations.