The Origin of the Universe

Introduction

Theory and Calculation

Theory and Calculation

If one is willing to study mass, and inherently gravity, one is appealingly tempted to start with string theory and QM, since it is a successful theory, and one is also tempted to study GR, yet liable to omit and neglect QM. However, if one is dealing with the fundamental question of the very origin of the beginning (or vice versa, depending on who one asked to) it is clear that one can neither dismiss nor leave aside QM. One (QM) offers an interpretation of the physical universe in terms of probabilistic and pure indeterminate behavior, yet, perhaps it closes the experimental value if one decided to assess the wave-particle duality [8–10,20,21,24,27,133,134] , perhaps becoming superdeterministic in the end [135] , and the other (GR) proposes (and repeatedly proves) a deterministic universe and a physical view of the physical universe that can be predicted, thus open to be experimentally proven beyond any doubt, a view that seems wrong or incomplete though [16,17,20,32,79] .

So, either one (QM) or the other (GR) has to be wrong, or else, it is the interpretation what may need a correction. In this last sense, it was proposed the principle of fundamental interaction [50] , instead of the action [4,136,137] , as the most fundamental way to approach both theories at the same time, and, possibly, to target any unification if “any one” could exist . Firstly, if Planck [14,15] proposed the quanta to fix the untraviolet catastrophe in the blackbody radiation, one ought not to forget that very radiation, and the quanta’s carrier: if one considers the quanta and carrier as a duality, then, perhaps one is open to a shallower interpretation. Since the problem in quantum-gravity is that once in the QM framework it is hard to recover gravity as quanta from that fundamental level, we hereby will try to keep it in the other way around.

Secondly, the previously (former) mentioned, meaning that one ought to take into account whether rotation, spin or radiation is happening in the in-flight, travelling, or quantized particle to consider both, the curved spacetime approach and the probabilistic particle-wave quantum-field behavior for the Lagrangian, or (for the Hamiltonian [137] ):

${\left(\delta S\right)}_{\mathrm{T}}=0+{\left(\delta S\right)}_{{\mathrm{T}}_0}$ or ${\left(\delta S\right)}_{\mathrm{T}}=0\pm {\left(\delta S\right)}_{{\mathrm{T}}_0}$ if one considers that at T₀, both can be changing or adding at a quantum level, i.e. principle of fundamental interaction.                                               □

Figure 1. Principle of Least Action (a), and Principle of Interaction (b), where arrows might get cancelled. Once considered, if that is the case, the background field (BF) is and keeps integrated (c). ± signals the direction [50,93,138,139].

Figure 1. Principle of Least Action (a), and Principle of Interaction (b), where arrows might get cancelled. Once considered, if that is the case, the background field (BF) is and keeps integrated (c). ± signals the direction [50,93,138,139].

So, one is keeping the background field (BF) as part of the theory, and of the system. In the end, as John Wheeler summed up: “spacetime tells matter how to move; matter tells spacetime how to curve...”.

Then, the Least-Interaction, in which gravity could be minimally coupled to mass (see Quintessence [60–63] ), taking into consideration verbatim the caveat of Dirac [93,139] , it would not be in disagreement with regarding the entire field as a Universe or, by the by, the entire Universe as a self-interacting field [50,67,68] .

So, the very baryonic mass, even though making only the ≈ 4,6% of the universe, it may play a role regarding the behavior of the Universe (and also in any possible role herewith attributed in the CCP), especially if the very fabric of spacetime is considered as a whole system interacting with itself [50,67–69] .

After giving some background of the topic, trying to not extend it too much, and to avoiding mess with the many interpretations, one may proceed to offer some foundation, and it seems more profitable, “beable” (one means viable in GR terms), and quite uniform, to use GR, and even more fundamental to make it feasible, one may start making a regression to the very origin, wherein we, in some sense, may be able to theoretically ”decouple” gravity (as an innate gravity proposed in Bentley §2.(2) [140] , and further discussed between Bentley and Newton himself [140,141] , which, to some extent, may be considered as a gravitization of the quantum (the whole Universe as a “packet”), keeping into consideration the minimally coupled gravity to mass, and the principle of fundamental interaction, presented in Figure 1 , it would allow to breach the gap adding MONDian for the small distances. It requires accepting the Big Bang, and rejecting the logical atomism (see Democritus, and Russell [142] ) for the beginning [50] , once considered, and, if one considers, CCC.

First, one may start with special relativity, which is well known for: $\mathrm{E}=\mathsf{\mu }{\mathrm{c}}^2$ . However, as it is clear, it lacks something, or it seems so (otherwise, not even GR would have been required).

One, then, may proceed with Klein-Gordon proposal [143,144] , as it even included light’s momentum.

${\mathrm{E}}^2={\mathrm{p}}^2·{\mathrm{c}}^2+{\mathsf{\mu }}^2·{\mathrm{c}}^4$ ∴ $\mathrm{E}=\mathrm{p}·\mathrm{c}+\mathsf{\mu }·{\mathrm{c}}^2$ [143,144]

where E=Energy, p=momentum, c=speed of light, and μ or M is the mass.

Then one may proceed with a dimensional analysis, in order to check for fundamental equivalences (it will be introduced the principle of fundamental interaction [50] in following steps).

$\mathrm{E}=\mathrm{p}·(\mathrm{m}/\mathrm{s})+\mathsf{\mu }·{(\mathrm{m}/\mathrm{s})}^2$ As one approaches the origin, it is expected that it becomes plasma, so one may expect light and mass to be in the same footing, so momentum (p) becomes:

$\mathrm{E}=\mathsf{\mu }·\mathrm{v}·\mathrm{c}+\mathsf{\mu }·{(\mathrm{m}/\mathrm{s})}^2$$\mathrm{E}=\mathsf{\mu }·(\mathrm{m}/\mathrm{s})·(\mathrm{m}/\mathrm{s})+\mathsf{\mu }·{(\mathrm{m}/\mathrm{s})}^2$ we arrange it:

$\mathrm{E}=\mathsf{\mu }·{(\mathrm{m}/\mathrm{s})}^2+\mathsf{\mu }·{(\mathrm{m}/\mathrm{s})}^2$ and, before rearranging it for mass:

$\mathrm{E}=2(\mathsf{\mu }·{\left({\displaystyle \frac{\mathrm{m}}{\mathrm{s}}}\right)}^2)$ Then, one may rearrange it for mass (we kept the non-linear fraction, for the sake of clarity and it will be interesting as well as important in the end):

${\displaystyle \frac{\mathrm{E}}{2}}=\mathsf{\mu }·{\left({\displaystyle \frac{\mathrm{m}}{\mathrm{s}}}\right)}^2$${\displaystyle \frac{\mathrm{E}}{2{\left(\frac{\mathrm{m}}{\mathrm{s}}\right)}^2}}=\mathsf{\mu }$ Thus, it presents the opportunity to rearrange it (we will change mass to M):

${\displaystyle \frac{\mathrm{E}}{2\frac{{\mathrm{m}}^2}{{\mathrm{s}}^2}}}=\mathrm{M}$${\displaystyle \frac{\mathrm{E}·{\mathrm{s}}^2}{2{\mathrm{m}}^2}}=\mathrm{M}$ Now, as the equivalence is done, one may perceive that mass is obtained, and it is done. However, applying Dirac’s observation regarding the physical meaning of +/- [50,68,138,139] , and his advice to the next generations regarding that and other intuitions in science [139] and, specifically, what he and Anderson had found 40 years previously [145,146] , we proceed to define mass (M) as if, it was energy,

Since one has both units in different sides or directions (and if they are equalled they are supposed to be the same, yet one the inverse of the other),

so, as they (mass and energy) are the inverse (side) one of the other, to place as if mass was the same than energy, ${\displaystyle \frac{1}{\mathrm{M}}}={\displaystyle \frac{2{\mathrm{m}}^2}{\mathrm{E}·{\mathrm{s}}^2}}$ following that:

${\displaystyle \frac{1}{\mathrm{M}}}={\displaystyle \frac{2{\mathrm{m}}^2}{\mathrm{E}·{\mathrm{s}}^2}}$${\mathrm{M}}_{{\mathrm{T}}_0}\triangleq {\displaystyle \frac{2{\mathrm{m}}^2}{\mathrm{E}·{\mathrm{s}}^2}}$*mass in terms of energy (defined as energy) in the very origin, is equal to 2 times a squared length (a surface) distributed in or along, Energy and time squared (acceleration). (One may consider as a hint that at time set as 0...)

we now proceed to check mass units at that very origin:

${\mathrm{M}}_{{\mathrm{T}}_0}\triangleq {\displaystyle \frac{2{\mathrm{m}}^2}{\mathsf{\mu }·{\left(\frac{\mathrm{m}}{\mathrm{s}}\right)}^2·{\mathrm{s}}^2}}$${\mathrm{M}}_{{\mathrm{T}}_0}\triangleq {\displaystyle \frac{2{\mathrm{m}}^2}{\mathsf{\mu }·\left(\frac{{\mathrm{m}}^2}{{\mathrm{s}}^2}\right)·{\mathrm{s}}^2}}$${\mathrm{M}}_{{\mathrm{T}}_0}·\mathsf{\mu }\triangleq 2$which gave us that 2 masses in interaction is completely equal or defined to be (in the very origin) 2 something (or anything) adimensional, or if the masses are crossed as an “X” it would tend to 1... which is, possibly, a hint [50,68,69].

At least, that Mass in the mass-energy side or energy version, in the very beginning, it would be adimensional [147,148,149,150,151], which can be related to phase transition [150,152,153,154] through Coulomb interaction [154,155].

So it is expected that, without length, it would interact with itself, so, as a fundamental mechanism, it, perhaps, would become kinetic energy. From a dimensional analysis and a physics perspective,

when one has something in a higher dimension, and it is interacting with the item in lower dimension, the former tends to bend and fold to cover the latter under gravitational effects, within a gravitational field...

Now, if it was checked, we obtained that mass (as energy) is 2 interacting entities, and (in the same footing) 2, which has no physical meaning, but, perhaps, it may have geometrical meaning, as, if we take the Universe as a whole as a geometrical entity:

the universe as a graph, can be considered as a collection of faces connected by points (vertices) and lines (edges) where each edge connects exactly two vertices. Euler characteristic proposes that V+F-E=2 where V= vertices, F=faces and E=edges. Let the universe be a graph, and if it is closed, assumed to be a sphere, no matter how many faces, vertices and edges, the outcome will be:

$\mathrm{V}+\mathrm{F}-\mathrm{E}=2$assumed to be an inverted sphere in accelerated expansion [68], the outcome would be the inverted of their signs:

$-V-F+E=-2$where the sign is a change in the direction of time,

and assumed to be flat (k set as 0):

$4+2-4=2$which may offer some insights to the theoretical meaning of one of the proposals in [68], and the main proposal in [50], at a fundamental level.

It also tends towards the shell proposal [145] for the electron, and also for the universe [156], as well as the theory in [70]. The results in Euler characteristic has no physical meaning but the representation of the Weyl Curvature Hypothesis [157] as a paradox and as the connection between geometry and physical meaning for the Universe [46,51] in the beginning, or either in the transition from the nothingness towards a Universe [50], or from one universe to the next within the CCC [43,46,47,51]. As a reference from [157] and in [51] regarding the connection and interaction between m¹ and m¹ the formation of a surface (m²), and m⁰, i.e. either as plasma or a Bose-Einstein condensate: “while the space–time Ricci curvature is singular, the Weyl curvature is not: he (Penrose) conjectures that it must be finite or zero” [51, p. 6], and “the metric and Ricci tensor are singular but the Weyl tensor is not” [51, p. 6].

If we assume a gravitational field in the origin, and once in the very origin, considered [128,129,130,131,132], mass could become kinetic energy. So,

$\mathrm{M}={\displaystyle \frac{\mathrm{E}·{\mathrm{s}}^2}{2{\mathrm{m}}^2}}$${\displaystyle \frac{1}{2}}\mathrm{M}·{\mathrm{v}}^2={\displaystyle \frac{\mathrm{E}·{\mathrm{s}}^2}{2{\mathrm{m}}^2}}$${\displaystyle \frac{1}{2}}\mathrm{M}·{(\mathrm{m}/\mathrm{s})}^2={\displaystyle \frac{\mathrm{E}·{\mathrm{s}}^2}{2{\mathrm{m}}^2}}$$\mathrm{M}={\displaystyle \frac{\mathrm{E}·{\mathrm{s}}^2}{{\mathrm{m}}^2{(\mathrm{m}/\mathrm{s})}^2}}$$\mathrm{M}={\displaystyle \frac{\mathrm{E}·{\mathrm{s}}^2}{\frac{{\mathrm{m}}^4}{s^2}}}={\displaystyle \frac{\mathrm{E}·{\mathrm{s}}^4}{{\mathrm{m}}^4}}$$\mathrm{M}={\displaystyle \frac{\mathrm{E}·{\mathrm{s}}^4}{{\mathrm{m}}^4}}={\displaystyle \frac{\mathrm{E}}{{\mathrm{m}}^2}}·{\displaystyle \frac{{\mathrm{s}}^4}{{\mathrm{m}}^2}}$$\mathrm{M}={\displaystyle \frac{\mathsf{\mu }·\frac{{\mathrm{m}}^2}{{\mathrm{s}}^2}}{{\mathrm{m}}^2}}·{\displaystyle \frac{{\mathrm{s}}^4}{{\mathrm{m}}^2}}$$\mathrm{M}={\displaystyle \frac{\mathsf{\mu }·\frac{{\mathrm{m}}^4}{{\mathrm{s}}^2}}{{\mathrm{m}}^2}}·{\displaystyle \frac{{\mathrm{s}}^4}{{\mathrm{m}}^2}}$$\mathrm{M}=\mathsf{\mu }·{\displaystyle \frac{{\mathrm{m}}^4}{{\mathrm{s}}^2}}·{\displaystyle \frac{{\mathrm{s}}^4}{{\mathrm{m}}^2}}=\mathsf{\mu }·{\displaystyle \frac{{\mathrm{m}}^4·{\mathrm{s}}^4}{{\mathrm{s}}^2{·\mathrm{m}}^2}}$$\mathrm{M}=\mathsf{\mu }·{\displaystyle \frac{{\mathrm{m}}^2·{\mathrm{s}}^2}{{\mathrm{s}}^2·{\mathrm{m}}^2}}$∴

${\displaystyle \frac{{\mathrm{M}}_k}{{\mathsf{\mu }}_k}}={\mathrm{m}}^2·{\mathrm{s}}^2$Let the mass be fundamental, one may say that, in the origin:

${\mathrm{M}}_k·{\mathsf{\mu }}_k\triangleq {\mathrm{m}}^2·{\mathrm{s}}^2$ ; ${\displaystyle \frac{{\mathrm{M}}_k}{{\mathsf{\mu }}_k}}={\mathrm{m}}^2·{\mathrm{s}}^2$which coincides with two entities, a M — μ ratio, and can be interpreted as a transference between two masses, generating one (massive) universe, and another (anti - massive) mirror universe, and means that one may consider Mass equals Energy in the beginning as space and time are considered the same in GR, or increasing at an accelerated pace along a flat space, and the mass having 4 dimensions of length as Energy distributed along 4 dimensions-length in GR,

${\displaystyle \frac{1}{2}}\mathrm{M}·{(\mathrm{m}/\mathrm{s})}^2={\displaystyle \frac{\mathrm{E}·{\mathrm{s}}^2}{2{\mathrm{m}}^2}}$${\mathrm{M}}_{\mathrm{k}}={\displaystyle \frac{\mathrm{E}·{\mathrm{s}}^2}{{\mathrm{m}}^2·{(\mathrm{m}/\mathrm{s})}^2}}$${\mathrm{M}}_0={\displaystyle \frac{\mathrm{E}·{\mathrm{s}}^2}{{\mathrm{m}}^2·{\left(\frac{\mathrm{m}}{\mathrm{s}}\right)}^2}}={\displaystyle \frac{\mathrm{E}·{\mathrm{s}}^2}{\frac{{\mathrm{m}}^4}{{\mathrm{s}}^2}}}$${\mathrm{M}}_0={\displaystyle \frac{\mathrm{E}·{\mathrm{s}}^4}{{\mathrm{m}}^4}}$Another way is to consider in the relativistic Klein-Gordon equation, that even before the Big Bang, Mass (M) would become a wave or quantum field (as photons), let light be kept as mass-momentum (μ) and let Mass become mass-momentum:

$\mathrm{E}=\mathrm{p}·\mathrm{c}+{(\mathrm{M}·{\mathrm{c}}^2)}^2$ , $\mathrm{E}=\mathsf{\mu }·{\mathrm{m}}^2/{\mathrm{s}}^2+{\mathsf{\mu }}^2·{{\mathrm{m}}^4/\mathrm{s}}^4$ , $1\mathrm{E}=\mathsf{\mu }·{\mathrm{m}}^2/{\mathrm{s}}^2+{\mathsf{\mu }}^2·{{\mathrm{m}}^4/\mathrm{s}}^4$${\displaystyle \frac{1}{{{(\mathrm{m}}^4/\mathrm{s}}^4)}}={\mathsf{\mu }}^2$mass-momentum as a 4-dimensions space accelerated (a²) [50,68].

Now, to recover the physical meaning, one may return to the previous. And unified all the mass as the same M:

$\mathrm{M}={\displaystyle \frac{\mathrm{E}}{2({\mathrm{m}}^2/{\mathrm{s}}^2)}}$And, rearranging it a bit,

$\mathrm{M}={\displaystyle \frac{\mathrm{E}·{\mathrm{s}}^2}{2{\mathrm{m}}^2}}$However, if one considers now mass in the usual equivalence to energy, as one goes to the origin, considered entropy and its true (probabilistic re-organization) meaning, mass becomes a kinetic entity.

Let mass be a kinetic entity in the origin:

${\displaystyle \frac{1}{2}}\mathrm{M}·\left({\mathrm{m}}^2/{\mathrm{s}}^2\right)={\displaystyle \frac{\mathrm{E}·{\mathrm{s}}^2}{2{\mathrm{m}}^2}}$Now, we arranged it:

${\mathrm{M}}_{\mathrm{k}}=\left({\displaystyle \frac{\mathrm{E}·{\mathrm{s}}^2}{2{\mathrm{m}}^2}}\right)/\left({\displaystyle \frac{{\mathrm{m}}^2}{{\mathrm{s}}^2}}\right)$If we arrange it now to check it,

${\mathrm{M}}_{\mathrm{k}}={\displaystyle \frac{2\mathrm{E}·{\mathrm{s}}^2}{\frac{2\left({\mathrm{m}}^2\right)}{\frac{{\mathrm{m}}^2}{{\mathrm{s}}^2}}}}$${\mathrm{M}}_{\mathrm{k}}={\displaystyle \frac{2\mathrm{E}·{\mathrm{s}}^4}{2\left({\mathrm{m}}^4\right)}}$${\mathrm{M}}_{\mathrm{k}}={\displaystyle \frac{\mathrm{E}}{\left({\mathrm{m}}^2\right)}}·{\displaystyle \frac{{\mathrm{s}}^4}{\left({\mathrm{m}}^2\right)}}$${\mathrm{M}}_{\mathrm{k}}={\displaystyle \frac{{\mathsf{\mu }}_{\mathrm{k}}·\left(\frac{{\mathrm{m}}^2}{{\mathrm{s}}^2}\right)}{\left({\mathrm{m}}^2\right)}}·{\displaystyle \frac{{\mathrm{s}}^4}{\left({\mathrm{m}}^2\right)}}$${\displaystyle \frac{{\mathrm{M}}_{\mathrm{k}}}{{\mathsf{\mu }}_{\mathrm{k}}}}\to {\mathrm{M}}_{\mathrm{k}0}$${\mathrm{M}}_{\mathrm{k}0}={\displaystyle \frac{\left(\frac{{\mathrm{m}}^2}{{\mathrm{s}}^2}\right)}{\left({\mathrm{m}}^2\right)}}·{\displaystyle \frac{{\mathrm{s}}^4}{\left({\mathrm{m}}^2\right)}}$${\mathrm{M}}_{\mathrm{k}0}={\displaystyle \frac{\left(\frac{{\mathrm{m}}^2}{{\mathrm{s}}^2}\right)·{\mathrm{s}}^4}{\left({\mathrm{m}}^2\right)}}=\left({\displaystyle \frac{{\mathrm{m}}^4}{{\mathrm{s}}^2}}\right)·{\displaystyle \frac{{\mathrm{s}}^4}{\left({\mathrm{m}}^2\right)}}={\displaystyle \frac{{(\mathrm{m}}^4·{\mathrm{s}}^4)}{({\mathrm{m}}^2·{\mathrm{s}}^2)}}$${\mathrm{M}}_{\mathrm{k}0}={\displaystyle \frac{{(\mathrm{m}}^2·{\mathrm{s}}^2)}{({\mathrm{m}}^2·{\mathrm{s}}^2)}}$${\mathrm{M}}_{\mathrm{k}0}={\displaystyle \frac{{(\mathrm{m}}^2·{\mathrm{s}}^2)}{1}}$${\mathrm{M}}_{\mathrm{k}0}={(\mathrm{m}}^2·{\mathrm{s}}^2)$Thus, the ${\displaystyle \frac{{\mathrm{M}}_{\mathrm{k}}}{{\mathsf{\mu }}_{\mathrm{k}}}}$ (kinetic mass) for the origin of the universe (${\mathrm{M}}_{\mathrm{k}0}$), it yields ${(\mathrm{m}}^2·{\mathrm{s}}^2)$ .

With that, one may propose the following:

In Figure 2, it was assumed the current value for the CC to be greater than 0, with a constant value Λ=1,1056 · 10^–52 at least locally, yet after a considerable (perhaps exponential) reduction [111] before the Big Bang (or the very beginning, for the very first Big Bang, considered CCC [43,45,46,47], and [50,67,68]).

In the following figures (Figs. 3 and 4), other possibilities are considered which makes no difference at greater scales, so LCDM could be considered successful [100], but that may be interesting for the sake of the small distances, the understanding of local systems, and that may have an impact regarding the behavior (and the understanding of such behavior/s) of clusters and galaxies [129,131,158,159,160,161].

Figure 3. It was considered the CCP within the Figure 2 approach, but if assumed changes in cosmological constants (varying cosmological and/or others) [63,66,93,94,96,115,138,139] whether locally or within the great scale of the cosmos (at a very local, zoomed-time, moments, and not necessary very large changes, or not for a long period to even be considered important, at great scale, and at first glance), it may lead to emergent epochs [93], and emergent properties, such as local gravities, to be studied with a brief departure of newtonian dynamics [81,82,83,84].

Figure 3. It was considered the CCP within the Figure 2 approach, but if assumed changes in cosmological constants (varying cosmological and/or others) [63,66,93,94,96,115,138,139] whether locally or within the great scale of the cosmos (at a very local, zoomed-time, moments, and not necessary very large changes, or not for a long period to even be considered important, at great scale, and at first glance), it may lead to emergent epochs [93], and emergent properties, such as local gravities, to be studied with a brief departure of newtonian dynamics [81,82,83,84].

Figure 4. Space-time and mass within the Universe as a self-interacting field, is represented expanding at a frequency (either constant or flickering), promoting emergence of properties due to the interaction with the very environment [162]. The frequency was set, fixed at value offered in [163, p. 211] with the electron (e^–) reduced Compton frequency (ƛe^–) per Planck space, or the actual value used, i.e., per Planck time (5.391247 · 10^-44). Whether the progression were constant, or flickering (steady-state), it was shown as a constant progression for spacetime, at a constant reduced Compton frequency for the electron.

Figure 4. Space-time and mass within the Universe as a self-interacting field, is represented expanding at a frequency (either constant or flickering), promoting emergence of properties due to the interaction with the very environment [162]. The frequency was set, fixed at value offered in [163, p. 211] with the electron (e^–) reduced Compton frequency (ƛe^–) per Planck space, or the actual value used, i.e., per Planck time (5.391247 · 10^-44). Whether the progression were constant, or flickering (steady-state), it was shown as a constant progression for spacetime, at a constant reduced Compton frequency for the electron.

As for the Universe in the very beginning, even though (and precisely because) that Mass in the mass-energy side or energy version, in the very beginning, it would be adimensional, that 2 still keeps its definition as ${\mathrm{M}}_{{\mathrm{T}}_0}·\mathsf{\mu }\triangleq 2{\mathrm{m}}^0$, and from a dimensional point of view ${\mathrm{M}}_{{\mathrm{T}}_0}·\mathsf{\mu }\triangleq {\displaystyle \frac{2{\mathrm{m}}^0}{{\mathrm{s}}^0}}$ , especially from a T₀ or a time (s) set as 0 for the linear or GR perspective. From the geometric point of view, Euler characteristic may be interpreted for a Planck string showing up before the Big Bang, which would be not planar, as 2V+0F-1E=1; while Euler characteristic shows that, to be planar, it requires an outcome of 2, leading to [50,67,68,70], since not only do 2 Planck strings showing up before the Big Bang would include and allow interaction [50] and emergence [158,159,160,161,162,164], but it also would include Euler characteristic from a geometric point of view, since 4V+0F-2E=2, both for the emergence of, at least, one Universe that includes emergence as a property itself [158,159,161], and not only the anthropic principle [165]. In respect of that last one, it has been proposed a more relaxed interpretation of the anthropic principle [166]. Regarding the multiverse, assumed it to be the correct, one may also consider that it integrates a universe within which the multiverse is possible (can exist), yet one may well consider that there is a universe in which the multiverse (whether as improbable or not allowed by that very universe features and physical laws) cannot exist. In that case, one may apply the Ockham razor, so it reduces the paradox between two possibilities: either there is a multiverse that includes its own contradiction, or there is a unique universe that excludes any possibility of multiverse by definition. The multiverse approach is the widest, so wide that in so doing, it includes itself a paradox and existential contradiction. On the other hand, the second (unique universe) is even included in the widest, discarded approach of the multiverse. So one may turn to the simplest one.

Again, it reduces the paradox between two possibilities: either there is a multiverse that includes its own contradiction, or there is a unique universe that excludes any possibility of multiverse by definition. Or else, one may consider a shared coordinate [50,67,68], as an exception to GR, harboring a sea-quark and quark-soup [128,129,130,131,132] within the very nothingness, that may enable the primordial quantum fluctuations [127], and may contain either a probabilistic multiverse, or an entropic multiverse in the sense of quantum darwinism [167], otherwise the simplistic approach would leave out the possibility of intersection, pure probabilistic pre-ordering, and observed quantum phenomena, neglecting QM. Perhaps, it is gravity and/or GG which adds up order in the end [162,168,169,170].

In the present paper, from an outlook aiming the unification, one may tend to the paradoxical existence of both. To solve the paradox and taking into account that, while the wider approach of accepting the multiverse as a scientific fact, that very approach includes its own contradiction, the existence of an unique universe does not (and there are proposals that can be compatible with that, in an unified framework, such as CCC), and regarding approaches in the latter way [43,46,50,70], which for instance may include the shell [156] or mirrored-universe like the one by Boyle, Finn, & Turok [70], it could integrate a kind of multiverse in the origin forming the quantum foam within a very small self-interacting length or two Planck strings, yielding a transplanckian [171] surface of 2,612280225025 · 10^–70, fulfilling the physical meaning of the Weyl curvature hypothesis [51,157].

Now, applying the Ockham’s razor between the completely assumed Multiverse of the Everett’s interpretation [172,173], and the unique Universe open to harboring a special field with either probabilistic or quantum darwinist behavior regarding a multiverse in the origin, one may make the “cut” towards the approach that does not contain itself a contradiction or that too wide an approach that even yields to the secondary proposal. I.e., the unique Universe open to quantum foam within the entropic determinism, before the current epoch, including strict or quantum darwinist behavior regarding a multiverse in the origin [127,131,132,160,161,162,167,172,174,175,176,177].

Whether a cross-interaction between two Planck strings, or two massive points with dimension m⁰ (length L⁰), it may lead to a driving force [56,60,63], and it has been studied as the geometry and physical meaning of the Weyl curvature hypothesis [46,51,157].

We have obtained a formulation for a quintessence or driving force with physical meaning (Figure 2) according to the (contradictory) observations in cosmology, i.e. CCP. However, thereafter it would take out all the units in the real energy side, so:$\mathrm{M}=\mathrm{E}·{\mathrm{s}}^2·{\displaystyle \frac{1}{2{\mathrm{m}}^2}}$if one considers 1 to be everything, one may interpret it as all the Energy, shell and surface in the Universe and all the time considered, before the beginning if regarded as a physical magnitude, contained, distributed, or at the point to be distributed along a squared length (surface) increasing by two. Let 1 be considered everything, in the beginning it may be at the point to be distributed or refrained (before the Big Bang), within a surface that could match the Weyl curvature hypothesis (and paradox, of how can a, whether 3D or 4D, universe, become and come from a surface). That question will be tackled in the last section, but before, one may offer,

$\mathrm{M}=\mathrm{E}·{\mathrm{s}}^2·{\displaystyle \frac{1}{2{\mathrm{m}}^2}}$$\mathrm{M}=\mathsf{\mu }·\left({\displaystyle \frac{{\mathrm{m}}^2}{{\mathrm{s}}^2}}\right)·{\mathrm{s}}^2·{\displaystyle \frac{1}{2{\mathrm{m}}^2}}$${\displaystyle \frac{\mathrm{M}}{\mathsf{\mu }}}=\left({\displaystyle \frac{{\mathrm{m}}^2}{{\mathrm{s}}^2}}\right)·{\mathrm{s}}^2·{\displaystyle \frac{1}{2{\mathrm{m}}^2}}$${\displaystyle \frac{\mathrm{M}}{\mathsf{\mu }}}={\displaystyle \frac{1}{2\left({\mathrm{m}}^0\right)}}$where (each) m⁰ represent a point.

yet, let both masses be at the very beginning:

Figure 5. A string at t > 0 (a), becoming a string at time (t) = 0 (b), so m¹ can be interpreted as m⁰.

Figure 5. A string at t > 0 (a), becoming a string at time (t) = 0 (b), so m¹ can be interpreted as m⁰.

If a string is assumed to be dimension m¹, one can show a Planck string (or two) in the beginning, becoming the behavior of two point-like masses, toward m⁰, when time (t) was set at 0.

Figure 6. After b) in Figure 5, it could go either following a)’ or b)’. It represents a configuration space: a)’ represents an expansion of the Weyl curvature hypothesis to a 2 dimensions configuration space while b)’ represents a one dimension configuration space. An electron-pair phase shift ${\mathsf{\psi }}^{\mathrm{\text{'}}}=e^{i\pi \mathsf{\eta }}\mathsf{\psi }$

Figure 6. After b) in Figure 5, it could go either following a)’ or b)’. It represents a configuration space: a)’ represents an expansion of the Weyl curvature hypothesis to a 2 dimensions configuration space while b)’ represents a one dimension configuration space. An electron-pair phase shift ${\mathsf{\psi }}^{\mathrm{\text{'}}}=e^{i\pi \mathsf{\eta }}\mathsf{\psi }$

; ${\mathsf{\psi }}^{\mathrm{\text{'}}}=-\mathsf{\psi }$ which leads to antisymmetric quantum wavefunction.

In the equation ${\displaystyle \frac{{\mathrm{M}}_k}{{\mathsf{\mu }}_k}}={\mathrm{m}}^2·{\mathrm{s}}^2$ one has two kinetic masses, that, while conserved from the QM framework, at T₀, it would become a Bose-Condensate [147,149,150,152,159,161] at t = 0. Considered the very beginning both sharing a spatial coordinate [50,67,68] or m⁰, yielding a flat connection known as the Weyl curvature hypothesis [51,157], it would yield

${\mathrm{M}}_{k0}={\mathrm{m}}^2·{\mathrm{s}}^2$in that special state or phase-state of matter, interaction or weak interaction [149,150,159,161] that has also been named as Minkowski fluctuation [159], yet both entities are conserved and remain in both frameworks GR and QM, therefore, being kept in the argument.

Now, one may proceed from that. Since we obtained the geometry of mass (kinetic mass) for the origin, and we know (or assumed) that our gravity (g) in our gravitational field, before interacting with mass, is an acceleration (m/s²).

Let G be $\mathrm{G}=\mathrm{N}·{\mathrm{m}}^2/{\mathrm{M}}^2$, and let G be Grand Gravity (GG) in the origin, as it was proposed [50, 69, 140, §2.(3), §2.(4.)(1)] as universal gravity in the origin (as “innate gravity” [140, §2.(2)]), and as opposed to mundane gravity (g) [140, §2.(4.)(2)]

$\mathrm{G}\mathrm{G}={\displaystyle \frac{\mathrm{M}·\mathrm{g}·{\mathrm{m}}^2}{{\mathrm{M}}^2}}$$\mathrm{G}\mathrm{G}={\displaystyle \frac{{(\mathrm{m}}^2·{\mathrm{s}}^2)·\left(\mathrm{m}/{\mathrm{s}}^2\right)·{\mathrm{m}}^2}{{{(\mathrm{m}}^2·{\mathrm{s}}^2)}^2}}$$\mathrm{G}\mathrm{G}={\displaystyle \frac{{\mathrm{m}}^5}{{\mathrm{m}}^4·{\mathrm{s}}^4}}$$\mathrm{G}\mathrm{G}={\displaystyle \frac{{\mathrm{m}}^1}{{\mathrm{s}}^4}}$or else, it may be recovered from:

$\mathrm{G}={\displaystyle \frac{\mathrm{M}·\mathrm{g}·{\mathrm{m}}^2}{{\mathrm{M}}^2}}$$\mathrm{G}={\displaystyle \frac{\mathrm{g}·{\mathrm{m}}^2}{{\mathrm{m}}^2·{\mathrm{s}}^2}}={\displaystyle \frac{\left(\frac{\mathrm{m}}{{\mathrm{s}}^2}\right)·{\mathrm{m}}^2}{{\mathrm{m}}^2·{\mathrm{s}}^2}}={\displaystyle \frac{{\mathrm{m}}^3}{{\mathrm{m}}^2·{\mathrm{s}}^4}}$$\mathrm{G}={\displaystyle \frac{\mathrm{m}}{{\mathrm{s}}^4}}$while, returning to the very beginning, and retrieving Figure 6, time (s) set as 0, as nature is neither constricted to mathematics nor necessarily to logical arguments, physics is not necessarily restricted to mathematics constraints either,

so, let time (s) be 0 in the very beginning,

$\mathrm{G}=\mathrm{m}$in the very beginning.

As we shall see, this extra m might represent the quantum pressure.

Then, GG, which physical meaning may be that emerges as an emergent property of the interaction of two Planck strings of length dimension (m) as well, in or giving birth to the quantum foam, may be interpreted as a Planck string in the very origin, yet traversing the ‘Universe as a whole-system field’ at m/s⁴ thus, possibly being a (machian) grand gravitational field.

One can also retrieve GG from universal G, as follows,

$\mathrm{G}\approx {\displaystyle \frac{{\mathrm{c}}^2·{\mathrm{R}}_{\mathrm{u}}}{{\mathrm{M}}_u}}$thus,

$\mathrm{G}\mathrm{G}=\mathrm{G}\approx {\displaystyle \frac{{\mathrm{c}}^2·{\mathrm{R}}_{\mathrm{u}}}{{\mathrm{M}}_u}}\approx {\displaystyle \frac{{(\mathrm{m}}^2/{\mathrm{s}}^2)·\mathrm{m}}{{(\mathrm{m}}^2·{\mathrm{s}}^2)}}$$\mathrm{G}\mathrm{G}=\mathrm{G}\approx {\displaystyle \frac{{(\mathrm{m}}^2/{\mathrm{s}}^2)·\mathrm{m}}{{(\mathrm{m}}^2·{\mathrm{s}}^2)}}$∴

$\mathrm{G}\mathrm{G}=\mathrm{G}\approx \mathrm{m}$ □

And, if one is up to retry gravity from E = Mc²

substituting gravity (g) as if it were potential energy (in the beginning, time (s) set as 0, so GG=g₀),: g₀≟Mc²/m E/(M·m)=m/s²

$g\stackrel{?}{=}\mathrm{M}{\mathrm{c}}^2$it requires to divide by M and m for that equivalence to hold,

${\displaystyle \frac{g}{\mathrm{M}·\mathrm{m}}}=\mathrm{M}·\left({\mathrm{m}}^2/{\mathrm{s}}^2\right)$so placing Energy (E) and GG or g₀ as m,

${\displaystyle \frac{\mathrm{E}}{\mathrm{M}·\mathrm{m}}}=\left(\mathrm{m}/{\mathrm{s}}^2\right)$so,

$g={\displaystyle \frac{\mathrm{E}}{\mathrm{M}·\mathrm{m}}}$∴

$\mathrm{E}=\mathrm{M}·g·{\mathrm{m}}^1$where m¹ is the correspondent unit for G at the very origin, before the Big Bang, i.e. for GG.[1]

from potential energy (U) as the distance would be 0 and the analogy then may hold:

$\mathrm{U}=\mathrm{M}·g·\mathrm{h}$$g={\displaystyle \frac{\mathrm{U}}{\mathrm{M}·\mathrm{h}}}$so, known (or assumed) the units of local gravity (acceleration=m/s²), we can recover the units of mass (and its meaning as well)[2]

$g={\displaystyle \frac{\mathrm{U}}{{\mathrm{m}}^2·{\mathrm{s}}^2·\mathrm{m}}}$$g={\displaystyle \frac{\mathrm{U}}{{\mathrm{m}}^3·{\mathrm{s}}^2}}$thus, mass is a physical magnitude or property, which energy is distributed along 3 lengths (volume) and accelerated along two dimensions of time.

Recovering gravity (g):

$g={\displaystyle \frac{{\mathrm{m}}^2·{\mathrm{s}}^2·{\mathrm{m}}^2/{\mathrm{s}}^2}{{\mathrm{m}}^2·{\mathrm{s}}^2·\mathrm{m}}}$$g=\mathrm{m}/{\mathrm{s}}^2$One may recover the dimensions of mass from $\mathrm{G}={\displaystyle \frac{\mathrm{m}}{{\mathrm{s}}^4}}$ :

$\mathrm{G}={\displaystyle \frac{\mathrm{m}}{{\mathrm{s}}^4}}$since [178] “The physical quantity responsible for the gravitational attraction between bodies is GM, which has units of m³ · s⁻² , being measured, hence, with clocks and rulers”, and it seems that this common knowledge faded out at some in point between the XVIII and the XIX century:

“... the unit of mass is deduced from the units of time and length, combined with the fact of universal gravitation. The astronomical unit of mass is that mass which attracts another body placed at the unit of distance so as to produce in that body the unit of acceleration... If, as in the astronomical system the unit of mass is defined with respect to its attractive power, the dimensions of M are L³T⁻².” Maxwell [179, in: 178, p. 6].

one may recover gravity from density in classical terms ($M=m^3/s^2$; density: $D={\displaystyle \frac{M}{m^3}}$ ) by adding what it lacks (G in meters) and what is going to be checked:

$D={\displaystyle \frac{GM}{m^3}}$For the same argument of nature under the study of physics, which may not be under the full constraints of mathematics [180,181,182],

$g=G{\displaystyle \frac{M_{\oplus }}{r^2}}$where $M_{\oplus }$ is the mass of the planet, Earth for instance, if one is locally situated in the center of the planet, gravity would become G$M_{\oplus }$, or applying the full meaning of mathematics, gravity could be considered infinity, just not necessarily in quantity, but its physical meaning being to be conservative.

So, let gravity (g) of a planet which mass is estimated as $M_{\oplus }$ and which distance to its center for the measurement (regarding $g=G{\displaystyle \frac{M·\mu }{r^2}}$ ) is set to 0,

$g=G{\displaystyle \frac{M_{\oplus }}{0}}=G{M}_{\oplus }$or $g=G{\displaystyle \frac{M·\mu }{0}}=G·M·\mu$but the physical meaning (not the mathematical one) added as being conservative.

For the relativistic equation of Klein-Gordon [140,141],

$\mathrm{E}=\mathrm{p}·\mathrm{c}+\mathrm{M}·{\mathrm{c}}^2$looking for gravity (g)

$g\stackrel{?}{=}\mathrm{M}·\mathrm{m}/\mathrm{s}·\mathrm{m}/\mathrm{s}+\mathrm{M}·{\mathrm{m}}^2/{\mathrm{s}}^2$$g\stackrel{?}{=}\mathrm{M}·{\mathrm{m}}^2/{\mathrm{s}}^2+\mathrm{M}·{\mathrm{m}}^2/{\mathrm{s}}^2$$g\stackrel{?}{=}{\displaystyle \frac{\mathrm{M}·{\mathrm{m}}^2/{\mathrm{s}}^2+\mathrm{M}·{\mathrm{m}}^2/{\mathrm{s}}^2}{2\mathrm{M}·\mathrm{m}}}$thus,

${\displaystyle \frac{\mathrm{E}}{2\mathrm{M}·\mathrm{m}}}=\mathrm{m}/{\mathrm{s}}^2$$g={\displaystyle \frac{\mathrm{E}}{2\mathrm{M}·\mathrm{m}}}$Where M is mass but m is length of one dimension (m¹).

One now can infer a value of energy for gravity, as

$g={\displaystyle \frac{\mathrm{6,62607015}·{10}^{-34}}{2·(\mathrm{2,176434}·{10}^{-8})·(\mathrm{1,616255}·{10}^{-35})}}=\mathrm{9,41825946}·{10}^8{\displaystyle \frac{m/s^2}{hertz}}$$g={\displaystyle \frac{\mathrm{6,62607015}·{10}^{-34}}{2·(\mathrm{2,176434}·{10}^{-8})}}=\mathrm{1,52223089466531031954104741977}·{10}^{-26}{\displaystyle \frac{\mathrm{J}}{hertz}}$Should one assume that energy in nature comes in quanta, as usually is assumed length too, with the exception of the Weyl curvature hypothesis for a piece of work for nature which might be creating a universe and a whole system to harbor it and for it to emerge,

$g={\displaystyle \frac{\mathrm{6,62607015}·{10}^{-34}}{2}}=\mathrm{3,313035075}·{10}^{-34}\mathrm{J}$One prediction is that in idealistic conditions, a square will require the squared energy to move (e.g. a rotation around it) with respect to the same to pull a sphere, since the upper “contact” between gravity and the square would be a unidimensional length, while the contact between the square and the surface would be length squared; on the other hand, while the sphere’s upper contact would also be a unidimensional length, and the contact with the surface over it as it moves would tend to a unidimensional length as well. __ _If the surface (m²) under the object within a gravitational field, disappears,then the object would fall, as $p={\displaystyle \frac{F}{m^2}}$ where p is pressure, F is a force, and m² a surface in contact.

$p=(\mu ·a)/m^2$ , $p=(\mu ·g)/m^2$, $p={\displaystyle \frac{\mathrm{P}}{{\mathrm{m}}^2}}$ ,

where p is pressure, μ a mass, a an acceleration, g gravity in m/s², m² a surface or a length squared, and P stands for weight (μ · g), so, if m² disappears it means (physical meaning) that $p={\displaystyle \frac{\mathrm{P}}{0}}$ without the constraints of mathematics and regarding only the physical meaning:

$p=\mathrm{P}$where p is pressure, and P stands for weight (μ · g), then, if one makes the mass disappear and sets time as 0 as a time-reversal from a gravitational potential,

$p=\mu ·g$ , $p=m/s^2$ , $p=\left({\displaystyle \frac{m}{0}}\right)$ , $p=m/s^2$ , $p=m$one may clear μ and time (s) up, or make it zero, restraining its effect to the physical meaning, with no constraints from mathematics, or keep it acquiring the physical meaning of being conservative.

So, let a gravitational potential be acting on no mass (before acting on any mass), no surface of contact (gravitational potential, indeed), and setting the time at zero, then

$p=m$which implies that gravity is a unidimensional pressure.Thus, gravity can be regarded as an acceleration that when interacting with mass becomes weight, when interacting with a surface becomes pressure, and when the surface disappears can be fundamentally regarded as a pressure of unidimensional length.

In physical terms, it may be interpreted as gravity adding a length dimension (m¹) to a mass-surface, i.e., mass in a flat (m²) space would be becoming a volume (a body confining mass, or a mass-volume) as it is interacting with gravity that adds an extra space-dimension to the mass-surface within the gravitational field. To be expanded in following works.

Another prediction, for the Zeno’s paradox, a lynx moving at 17 m/s will get a snail at 22m that were able to escape at 1,55 m/s (same direction), in

$(\mathrm{23,55}/17)=\mathrm{1,3852941}$; $(\mathrm{1,3852941}-1)/17=0.02266436$;

$\mathrm{1,3852941}+0.02266436=\mathrm{1,4667819892}\mathrm{s}$ even faster than the standard solution and Cauchy’s infinitesimals, since their relative motion within the gravitational field, taking into account the principle of fundamental interaction, it integrates gravity (acceleration) even at linear displacement at constant speed, wherein that gravitational field, both animals exploit gravity at T₀ due to their elastic elements, yet the one that exploit it better not only would reach the higher speed, but also would exploit it better for their relative motion. Indeed, it is due to gravity that the cheetah catches that speeding snail, and probably Zeno’s paradox the reason why animals like these also developed limbs.

Final proposed prediction, particles with undefined spin (undefined η in Figure 6 before interacting with gravity whether a η=0 boson or a geometric property adding direction) will be found in pure surfaces (m²) once we are able to reach the sophisticated level of artificial human-made pure surfaces, as the Weyl curvature hypothesis posited, being the natural analogy the only exception to the 3rd postulate in [68] for the very beginning, as in the possibility for the proposal in CCC, if any of the previous were considered. Thus, whether a darkon or anyon, one will not name that particle, only relating them as undefined-spin particles in pure 2D confined surfaces or spaces, which could be interpreted as in a state of gravitational confinement, or a sort of gravitational shielding, which will allow them to acquire spin-3 from gravity (scalar) to, probably, obtaining the inverted (opposite) direction, therefore, perhaps showing $spin–{\displaystyle \frac{1}{3}}$ .

Finally, regarding the why (why the Universe started or originated), or questions such as who created the nothingness, even though it might be a question beyond science, and even beyond philosophy of science, a complete nothingness would mean a unique microstate (individual). The concept of entropy not only refers to the classes of states, but also to the individual states (see [157, p. 8]). A unique microstate, thus, can be regarded as a superorganized state, one microstate among an infinite other probabilistic (higher entropy) states, within and/or leading to the opposite extreme (as in Everett interpretation [173] at that local level). No gain of information, so the entropy would be 0 [183,184].

$S=k_B\ln \mathsf{\Omega }$let Ω be 1, (both, the microstate and the macrostate are one and the same), then,

$S=k_B\ln 1=0$Entropy is a physical property which is described as the physical magnitude that describes and is described by the measure of the energy dispersal for a system, by the number of currently accessible microstates related to all the possible (probabilistic) accessible microstates for the system, and, also, by the spreading of information [183,184,185,186,187]. The main contributions to entropy are characterized by the physical meaning of distribution of heat (kinetic energy), distribution in space (purely probabilistic spatial distribution of atoms and/or molecules, i.e. energy-information distribution related to Brownian motion), and radiation [183,187,188]. Even though entropy is usually only equated to randomness and disorder, it is a wider concept regarding spreading of energy or information, current microscopic state in relation to all possible microstates, configurations or distributions within the system or macrostate [185,186,188], and its emergent physical property, usually referred as the “arrow of time” [189,190,191]. Hereby we associated to the system the three contributions and/or widest (inclusive) possible concept of entropy, within a process-processes perspective, and the emergent behavior [131,160,164] as an inherent property.

Once the uncertainty is set as zero, in the local spacetime referred as “the beginning”, the flickering state and color confinement at small or zero spatial volume and weak coupling [149,192], is expected, increasing entropy and generating quantum fluctuations [127,131,164,192], within the quantum foam [193,194], allowing a microstate randomly organizing as one unique universe (in which a multiverse might or might not be allowed) at least one time [50,165,166,167,169]. It accounts for varying entropy [195,196,197], symmetry-breaking [158,198] and the emergence of matter [128,129,131,132,158,160,164], yielding one universe within which galaxies (especially early formations) could be seeded by primordial black holes [50,67,68,69,98,118,119,196].

Even though the whole system may be considered and regarded as a mixed-system, one universe reinstates one-state (inverted spatial-distribution or concentration) within its “grid” or local spacetime, i.e., low entropy. The spreading perspective of entropy as a physical attribute [185,197], predicts spreading and dispersal, setting multiple microstates (probabilistic, phase space configuration, or fields) such as these proposed by QM. The outcome: a (probably variable/flickering) cosmological constant Λ (+/–) with an initial drop (‒) led by dispersion or spreading [185,197], e.g. mass filling empty space and coupled possibly non-linear gravity [66,152,198,199]. ____ ___ From a low entropy state, it increases at a cosmological level, but once mass is far enough, it starts a freeze-out [97,98,99,100,101] applying MONDian dynamics [81,82,83,84,104]. It is a decrease in local entropy that is compensated by anticlockwise dispersion in local empty space, where mass and G are equivalent.

This, whether related or inherently added to radiation property of entropy [188], has been explored as regular electrically charged black holes and electromagnetic solitons, predicted by analysis of regular solutions to dynamical equations of non-linear electrodynamics, that, whether minimally coupled to gravity [152,198] or mediated by the interaction with its environment [152,162], may serve as non-dissipative source of the electromagnetic and gravitational fields [198,199,200,201]. The minimally coupled to gravity proposal needs no other assumption to be added [198]. __ _ It may lead to a mirror-like behavior [187], probably the emergence of galaxy black holes or spacetime singularities [47,202] setting the arrow of time (an inversion to the cosmological setting’s “logical”, entropy-wise, dynamics), in such a way that it increases local entropy and local gravity emerges, especially when equilibrium is reached (local gravities are set, such as g in Earth). That will apply again regarding M — μ relation, yet when upper-bottom distances approach 0, that local gravity effects might be nullified, and, after all, transplanckian dynamics might apply again [171]. A fourth quark might be travelling faster than light, in the inner core, or it just might be annihilating in pair-annihilation processes channelling with momentum the lowest (and purest) level of mass-dynamics and “stabilization”, at its very core [128,129,130,131,132,145,149,203], and at its very fundamental energy-mass level as herein proposed; as in the very beginning.

The universe may well have started from a nothingness, which only state makes sound that its probabilistic state, to remain completely empty, is a microstate over all the other possible states (including the appearance of a multiverse), according to the law of entropy [183,184,185,186,187,197]. _ _ This last one leading to the opposite state, it may have led to eigenselection: a quantum-darwinism regarding the fluctuations within the quantum foam, in which the emergence of a sea-quark or quark-soup [131,132] could have, can, and will, happen(ed), in an indeterminate state, probably leading to the emergence of celestial bodies, including planets, in such an amount to integrate Carter’s anthropic principle [165,166], promoting a (also indeterminate, in time-wise fashion) unique universe [50 p. 145, p. 159, p. 160, 68 p. 278, p. 296, 166]. Symmetry-breaking, at this point, might just be and be regarded as a spandrel, and, perhaps, an entropic by-product, superdeterministic and fine-tuned, but as a consequence, instead of a cause.

Indeed, gravitational constant (G) it seems, in our view, it is a composite constant [163, p. 202], which can be reduced to L¹ (or m), in the very origin, as and at, a fundamental level.

If one reflects about angular momentum and the principle of fundamental interaction, in regard to gravity, it is not easy to understand that as the bodies confining mass (μ) within a gravitational field, e.g. Earth’s gravitational field, are travelling along Earth (M) rotation, μ is seemingly not escaping or “falling” towards the center of Earth. That is, obviously, due to g. So, either μ is falling down, or something is required to keep μ travelling along M’s rotation. What is not so obvious is that μ has and keeps its own newtonian mass inertia, that is being modified (travelling) with M’s rotation, yet it would but will not, also travel with Earth (M) orbit, being contradictious the one to the other at T₀, in an Ehrenfest paradox-like way [204,205,206]. Thereby, it is not that masses μ are falling to Earth’s center, but Earth (M) is going against masses’ μ inertia and acquired angular momentum, due to Earth’s (M) centrifugal force, generating that paradoxical g or local gravity, which we propose as quantic and relativity counter-action in K-space, or harmonization).

Cautious caveat. This work is highly speculative, based on data and published research though. It was conducted following data-driven discovery and symbolic regression [207,208] arising the abovementioned conclusions offered for the years to come.

If one is required, if any, to proceed to the GR-QM unification, one would do it at a fundamental level, as it might be sage to follow the sage, and the wisdom, which proposes to gravitize the quantum [65,209].

It is not a surprise that, if one was required to pick up one of these theories, they would be the last three in the beginning.

Conclusions

• After the review of topical, broad physics and philosophical bibliography, three main theories were proposed due to their completeness, matching some other theories that were tackling more specific particular problems between theories and observations, converging in mirror-like universe, conformal and/or cyclic, cosmology (CCC), and either steady-state and/or flickering Λ, matching other proposals such as freeze-out, and whether multiple Big Bangs [43,47,50,68] or microcyclic “universes” [50,166,195], they would fit well with the observations, and tackle properly the CCP. One might highlight some interesting words by Wang & Unruh [195]: “The spacetime dynamics sourced by this large negative λ_eff would be similar to the cyclic model of the universe in the sense that at small scales every point in space is a “micro-cyclic universe” which is following an eternal series of oscillations between expansions and contractions” [195, p. 1]; “Moreover, if the bare cosmological constant λ_B is dominant, the size of each “micro-universe” would increase a tiny bit at a slowly accelerating rate during each micro-cycle of the oscillation due to the weak parametric resonance effect produced by the fluctuations of the quantum vacuum stress energy tensor.” [195, p. 1]. It can be inferred substantiated by other proposals, that not a driving-force, but a “driving-force” or some kind of quintessence spacetime energy is either driving the expansion, being driven with the expansion of spacetime, or both, as hereby proposed (it was set as m⁴ in GR framework, or m² · s² where mass M₀ is set as a kinetic mass M—μ ratio integrating that dimension in the driving energy, for a QM-GR unified framework). However, it was noticed that, if the previous can be matched with dark energy, gravitational constant G can also be related or equated with that particular energy in the beginning (GG), and with mass locally (G), pertaining, perhaps, to different minute-layouts or stages for entropy-spacetime relationship.
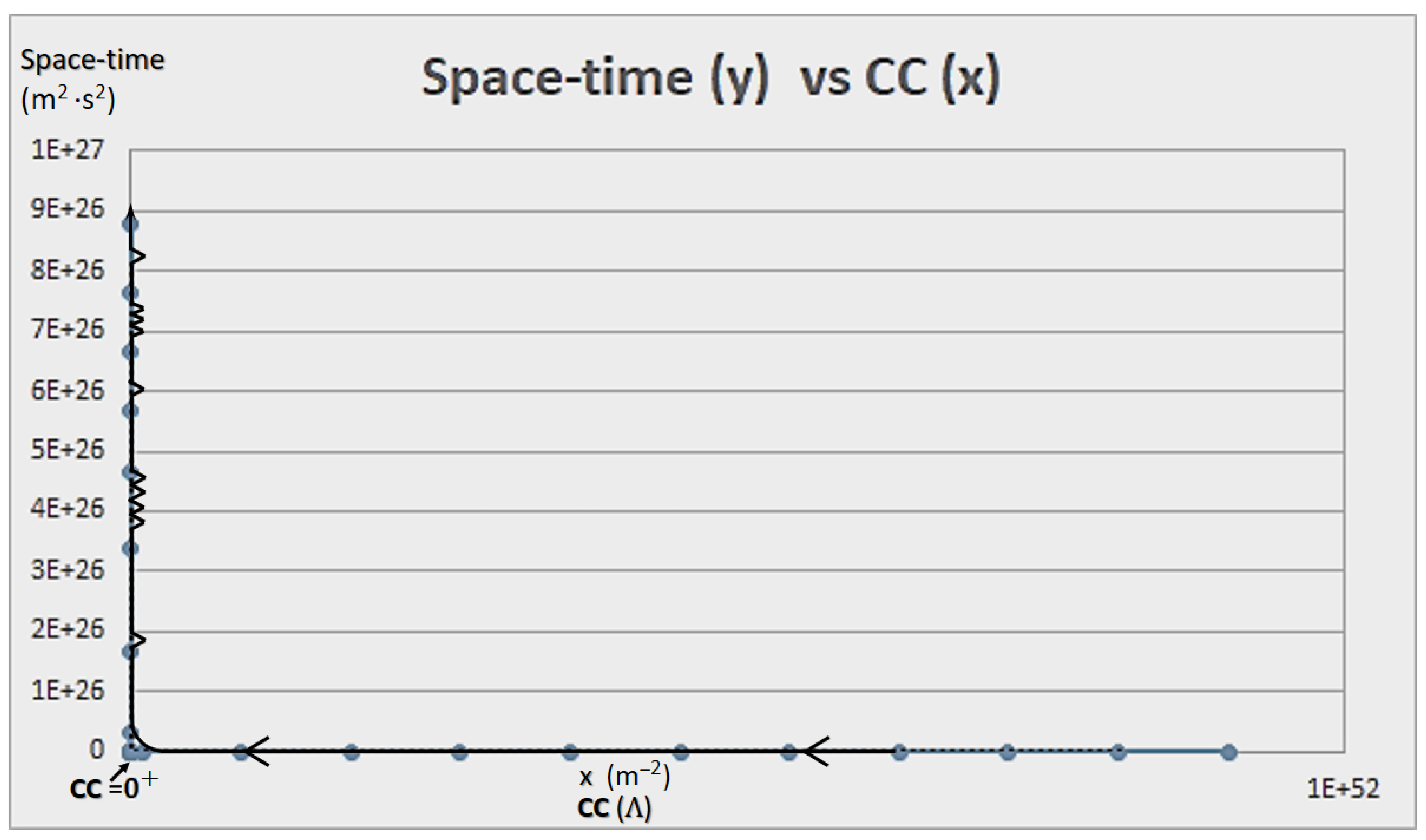
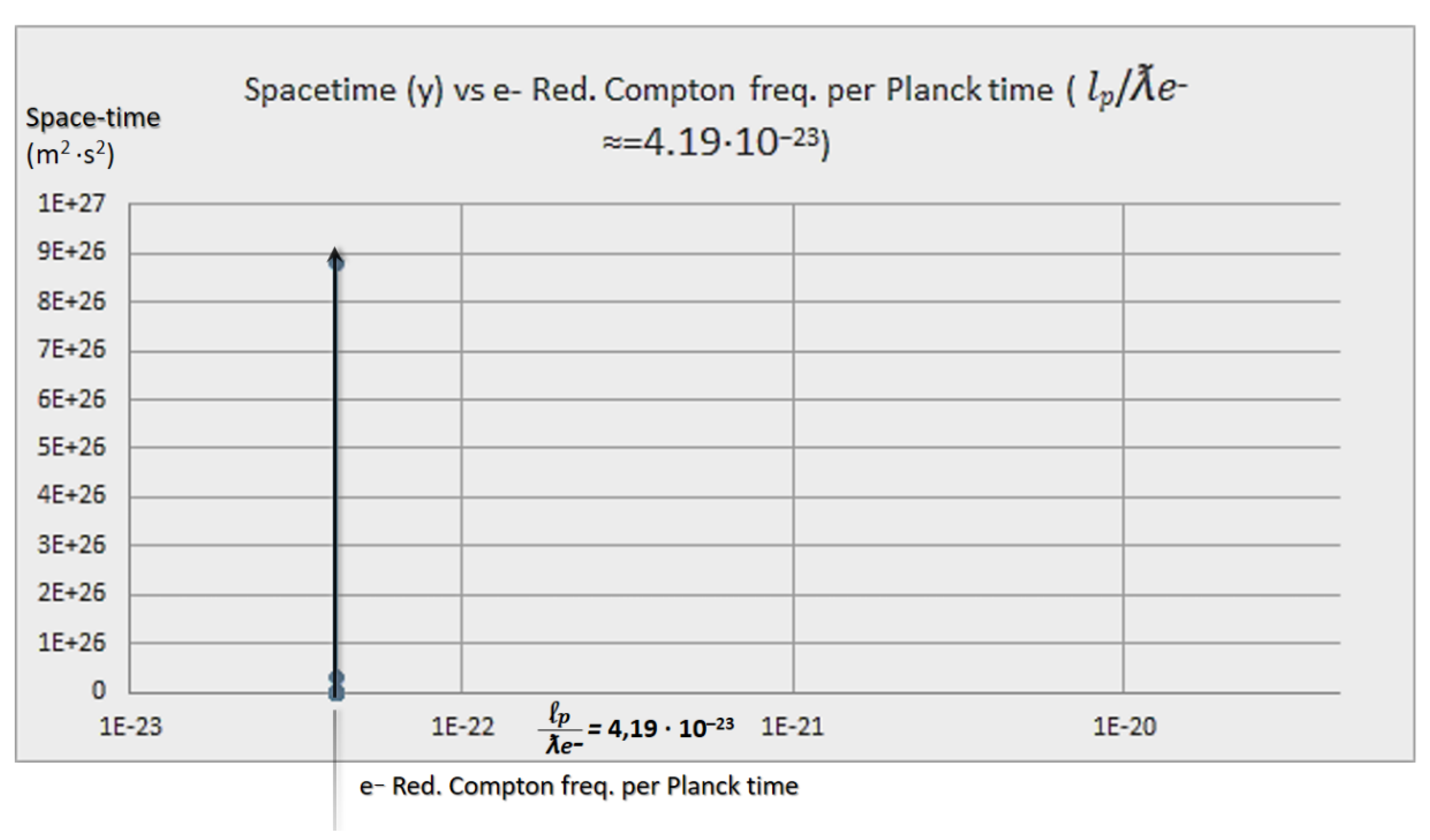
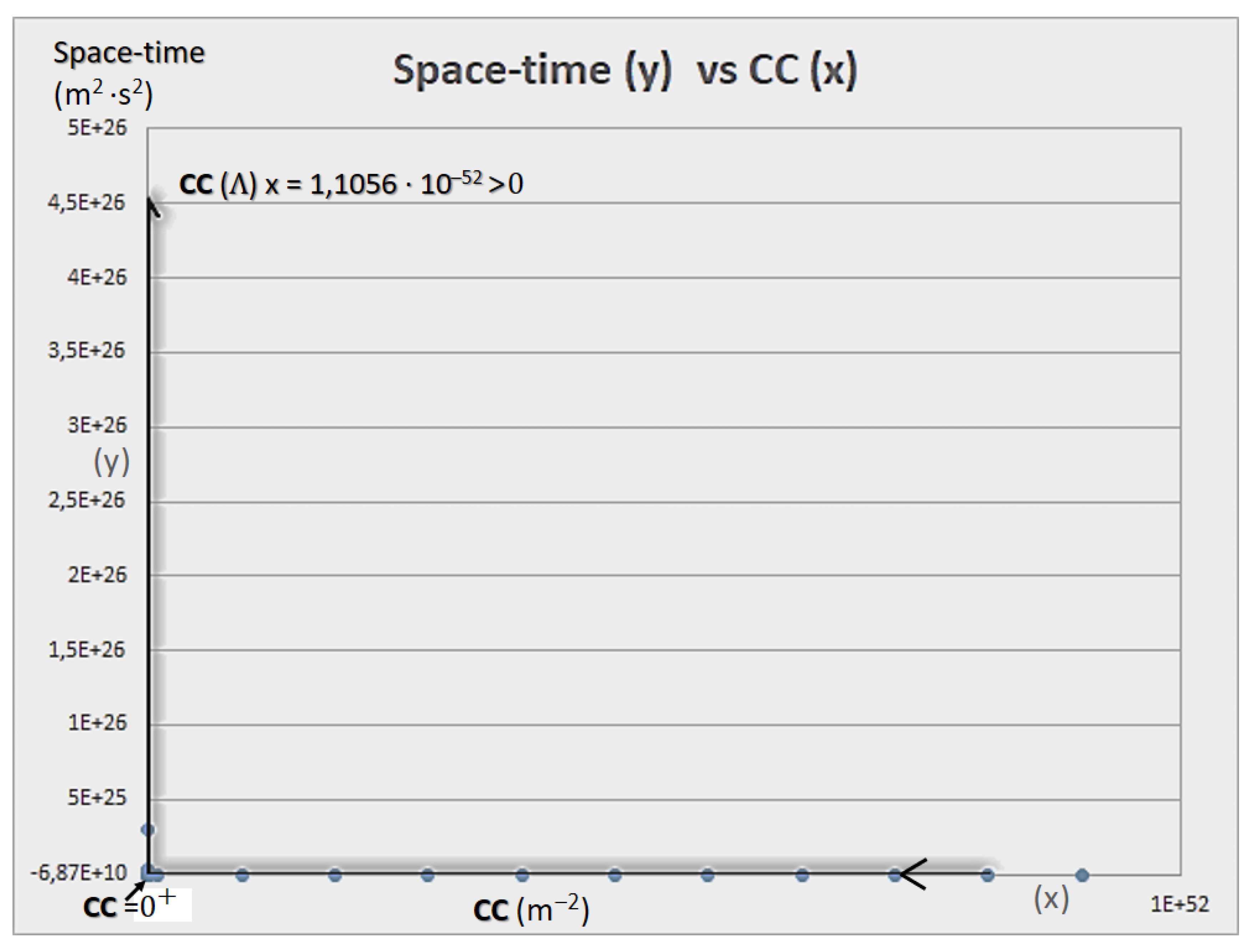
• Indeed, the CC (Λ) has units of m². Therefore, as it can be regarded in Figs. 2, 3, and 4, as space increases, Λ decreases, which does not necessarily implies that time does as well, even though we use it to measure changes (whether +/- or null), and to relate distance to our framework, or if the rate of change (expansion), is stable, null, or steadily (or unsteadily) increasing, which perhaps to our understanding and at a cosmological scale has meaning, but at universal scale is a claim that, again, tends to the anthropomorphization of the universe and nature. As it was pointed out in an interestingly work [178]: “Newton did not express his law of gravitation in a way that explicitly included a constant G, its presence was implied as if it had a value equal to 1. It was not until 1873 that Cornu and Bailey explicitly introduced a symbol for the coupling constant in Newton’s law of gravity, in fact, they called it f. (The current designation G for the gravitational constant was only introduced sometime in the 1890s.)” in [178, p. 6, cfr. 210, p. 2].
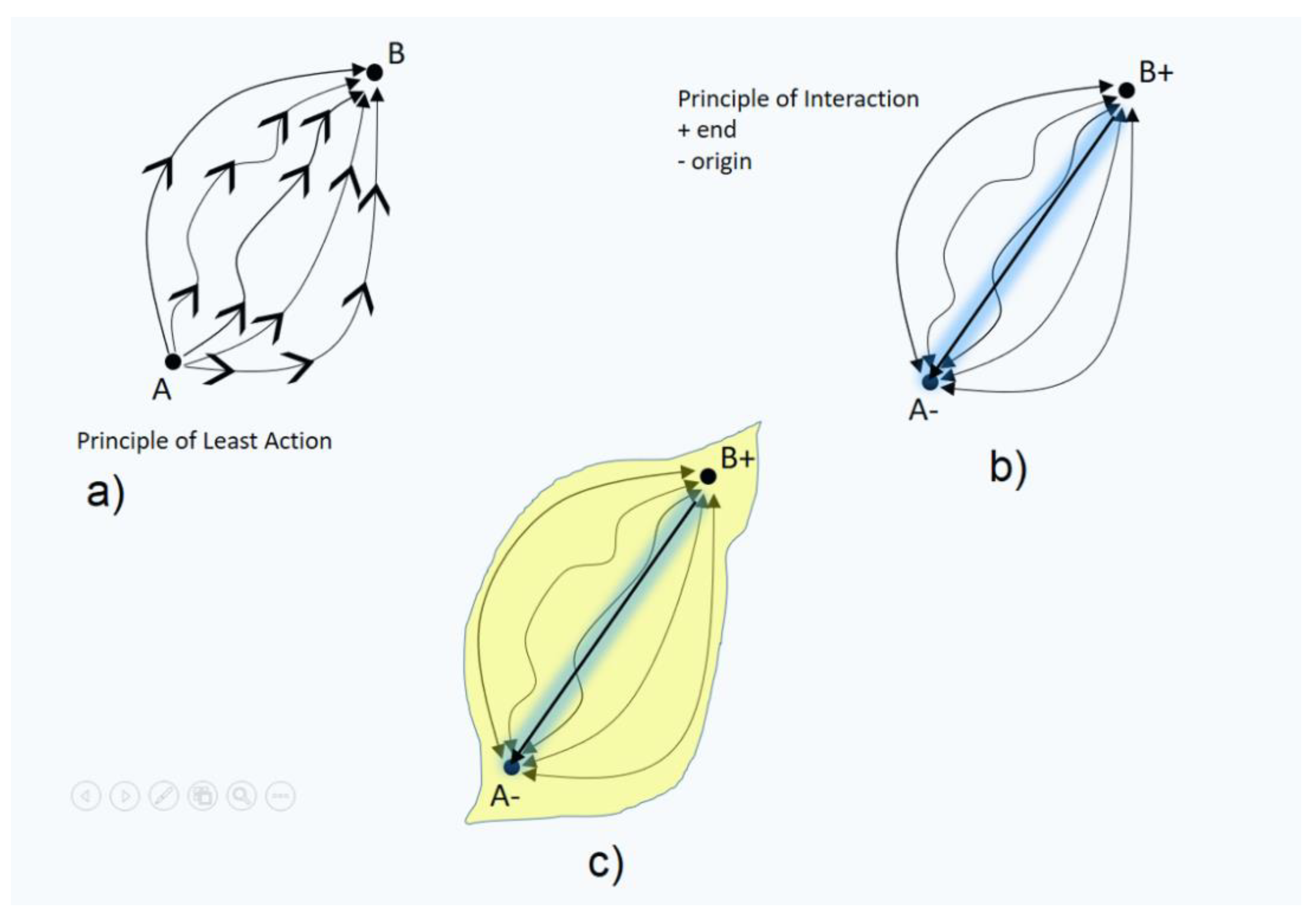
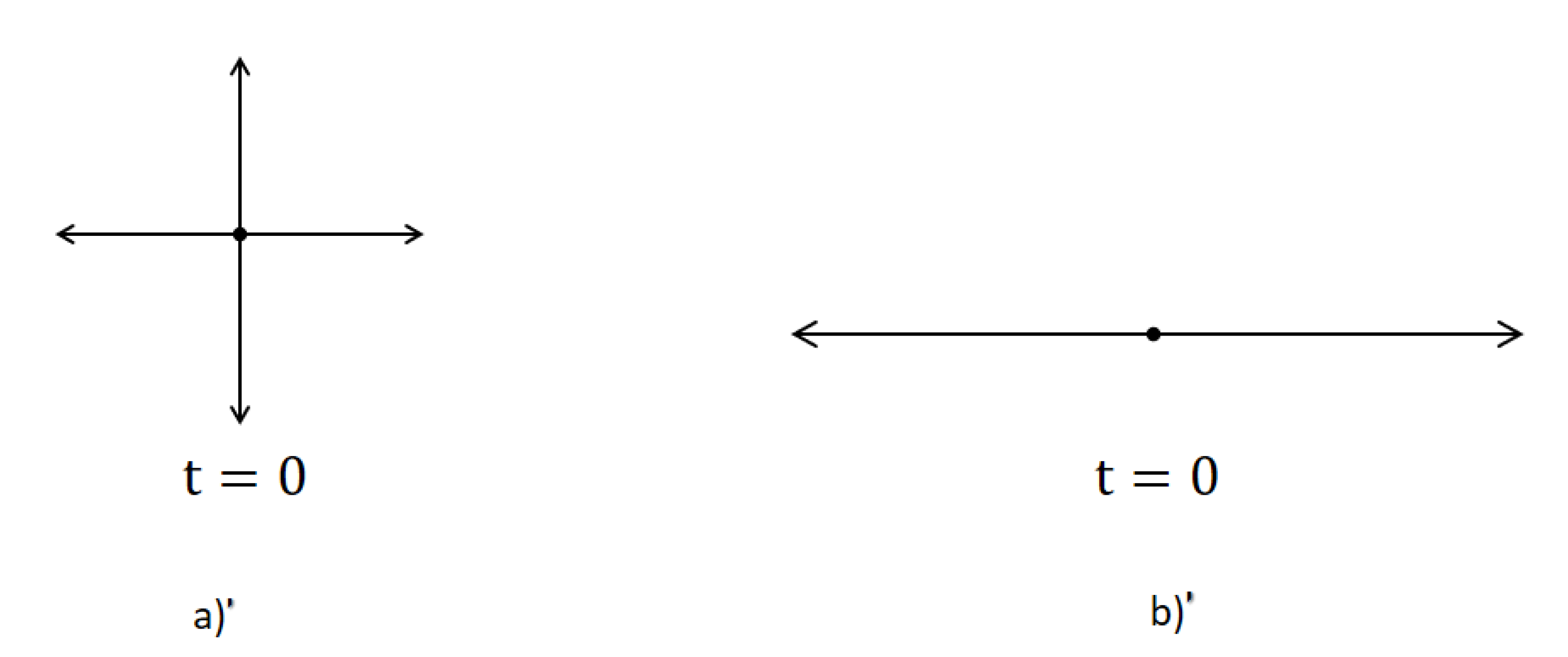
• Therefore, gravity might be setting the direction, and with the other fundamental variables (such as mass, entropy, and space) interaction, the “arrow of time” and our universe, as emergent properties.So, spacetime tells matter how to move, matter tells spacetime how to curve [194], and gravity tells the direction.
• A more inclusive approach was taken in regard the multiverse and the anthropic principle requirement. Applying Ockham’s razor one can ponder that it leads to a CCC—mirror-like—located sea-quark approach that allows one-universe—multiverse convergence (divergence actually). Anthropomorphization was rejected. For instance, Wang & Unruh [195] concluded “in this way, the large cosmological constant generated at small scales is hidden at observable scale and no fine-tuning of λ_B to the accuracy of 10⁻¹²² is needed”. Cosmological constant, fine-tuning, superdeterminism and symmetry-breaking may just be a spandrel, an outcome, instead of a cause or causes. Inflationary and Big Bang were assumed. Logical atomism was also rejected.
• Torsion was not treated but it seems both, plausible, and an increasingly wide approach that seems to properly solve the problem regarding “before the beginning”, boundary, or also called or related to Weyl Curvature Hypothesis [50,66,67,68,196,211], for instance to obtain renormalized energy–momentum tensors and thermodynamics of 2d black holes [211]. Time seems to lose meaning within a scale unified cosmos, cogitations such as a universe (with us within it) living in its very first second [69] or indeterminate time [50 p. 145, p. 159, p. 160, 68 p. 278, p. 296, 166] arisen. Anthropomorphization of time was also pointed and rejected. _ Entropy (space distribution, heat distribution, and radiation) and stochastic-like G‒mass‒energy equivalences seem to have more appropriated meaning and accuracy in scientific and physical terms.
• More research is required within this topic.

Data References

Data statement

References

1. Feynman, R. P. (1985). QED. The Strange Theory of Light and Matter. (Alix G. Mautner Memorial Lectures). Princeton University Press.
2. Weinberg, S. (2021). Foundations of modern physics.
3. Lagrange, J. L. (1772). Essai d’une nouvelle méthode pour résoudre le problême des trois corps. Académie Royale des Sciences.
4. Lagrange, J. L. (1788). Mécanique analytique.
5. Du Châtelet, G. E. (1740). Institutions physiques de Madame la marquise du Châstellet. Ed. Prault fils.
6. Du Châtelet, G. E. (1759). Principes mathématiques de la philosophie naturelle, par feue Madame la Marquise du Chastellet. Addendum, Tr. de Principia de Isaac Newton (1686). Ed. Desaint et Saillant, & Lambert.
7. Newton, I. (1687). Philosophiæ naturalis principia mathematica.
8. Newton, I. (1704). Opticks, or, a Treatise of the Reflections, Refractions, Inflections, and Colours of Light. Ed. Sam Smith & Benj Walford. Royal Society.
9. Huygens, Ch. (1690). Traité de la Lumière: Où sont expliquées les causes de ce qui luy arrive dans la reflexion & dans la refraction. Ed. Pierre van der Aa.
10. Leibniz, G. W. (1720). Lehr-Sätze über die Monadologie.
11. Einstein, A. (1931). Cosmic religion: with other opinions and aphorism. Covici-Friede Inc.
12. Einstein, A. (1915). Zür allgemeinen Relativitätstheorie. Preuss. Akad. Wiss. Berlin, Sitzber, 47.
13. Einstein, A. (1916). Die Grundlage der allgemeinen Relativitätstheorie. Ann. der Phys., 49. [CrossRef]
14. Planck, M. (1901a). Ueber das Gesetz der Energieverteilung im Normalspectrum. Ann. der Physik., 309. [CrossRef]
15. Planck, M. (1901b). Ueber die Elementarquanta der Materie und der Elektricität. Ann. der Physik, 309. [CrossRef]
16. Aspect, A. , Clauser, J. F., & Zeilinger, A. (2022). Entangled states – from theory to technology. In: The Nobel Prize in Physics 2022. Royal Swedish Academy of Science. https://www.nobelprize. 2022. [Google Scholar]
17. Aspect, A. , Dalibard, J., & Roger, G. (1982). Experimental test of Bell’s inequalities using time-varying analyzers. Phys. Rev. Lett., 49, 1807. [Google Scholar] [CrossRef]
18. Bell, J. S. (1975). The theory of local beables. In: Contribution to 6th Gift Seminar on Theoretical Physics: Quantum Field Theory; Dialectica, 39(1985), 86-96. [CrossRef]
19. Bell, J. S. (1981). Bertlmann‟s socks and the nature of reality. Journal de Physique Colloques, 42. [CrossRef]
20. Bell, J. S, Clauser, J. F, Horne, M. A., & Shimony, A. (1985). An exchange on local beables. ( 39, 85–96. [CrossRef]
21. Davisson, C. & Germer, L. H. (1927). The scattering of electrons by a single crystal of nickel. H. ( 119(2998), 558–560. [CrossRef]
22. Schrödinger, E. (1926). An Undulatory Theory of the Mechanics of Atoms and Molecules. Phys. Rev., 28, 1070. [Google Scholar] [CrossRef]
23. Schrödinger, E. (1935a). Die gegenwärtige Situation in der Quantenmechanik. Die Naturwissen-schaften, 23. [CrossRef]
24. Schrödinger, E. (1935b). Discussion of Probability Relations between Separated Systems. Math. Proc. Cambridge Philos. Soc., 31. [CrossRef]
25. Heisenberg, W. (1927). Über den anschaulichen Inhalt der quantentheoretischen Kinematik und Mechanik. Zeitschrift fur Physik, 43. [CrossRef]
26. Einstein, A. (1905a). Zür elektrodynamik bewegter körper. Ann. der Physik, 322. [CrossRef]
27. Einstein, A. , Podolsky, B., & Rosen, N. (1935). Can quantum-mechanical description of physical reality be considered complete? Phys. Rev., 47. [CrossRef]
28. de Broglie, L. (1923). Waves and quanta. Nature, 112. [CrossRef]
29. de Broglie, L. (1924) Recherches sur la théorie des quanta. (Tesis Doctoral), Masson, Paris. [CrossRef]
30. Bohm, D. (1952). A Suggested Interpretation of the Quantum Theory in Terms of ’Hidden Variables’ I. Physical Review, 85. [CrossRef]
31. Young, T. (1804). The Bakerian Lecture. Experiments and calculations relative to physical optics. Philos. Trans. R. Soc. London, 94, /: https, 1095. [Google Scholar]
32. Zeilinger, A. (1986). Testing Bell‟s inequalities with periodic switching. Phys. Lett. A, 118. [CrossRef]
33. Friedmann, A. (1924). Über die Möglichkeit einer Welt mit konstanter negativer Krümmung des Raumes. Zeitschrift für Physik, 21. [CrossRef]
34. Hubble, E. (1929). A relation between distance and radial velocity among extra-galactic nebulae. P.N.A.S., 15. [CrossRef]
35. Lemaître, G. (1927). Un Univers homogène de masse constante et de rayon croissant rendant compte de la vitesse radiale des nébuleuses extra-galactiques. Annales de la Societe Scietifique de Bruxelles, 47, /: https, 1927. [Google Scholar]
36. Robertson, H. P. (1936). Kinematics and world structure III. Astrophysical Journal, 83. [CrossRef]
37. Vittorio, N. & Silk, J. (1984). Fine-scale anisotropy of the cosmic microwave background in a universe dominated by cold dark matter. Astrophysical Journal, Part 2 - Letters to the Editor, 285. [CrossRef]
38. Walker, A. G. (1937). On Milne’s theory of world-structure. Proc. of the London Math. Soc., S2-42. [CrossRef]
39. Zwicky, F. (1933). Die Rotverschiebung von extragalaktischen Nebeln. Helvetica Physica Acta, 6. [CrossRef]
40. Banks, T. , Fischler, W., Shenker, S. H., & Susskind, L. (1997). M theory as a matrix model: A conjecture. Phys. Rev. D, 55. [CrossRef]
41. Kaku, M. & Kikkawa, K. (1974). Field theory of relativistic strings. II. Loops and Pomerons. ( 10(6), 1823–1843. [CrossRef]
42. Susskind, L. (1970). Structure of hadrons implied by duality. Phys. Rev. D, 1, 1186. [Google Scholar]
43. Penrose, R. (2010). Cycles of Time: An Extraordinary New View of the Universe. The Bodley Head.
44. Gurzadyan, V. G. & Penrose, R. (2013). On CCC-predicted concentric low-variance circles in the CMB sky. Eur. Phys. J. Plus, 128. [CrossRef]
45. Meissner, K. A. & Nurowski, P. (2017). Conformal transformations and the beginning of the Universe. ( 95(8), 084016. [CrossRef]
46. An, D. , Meissner, K. ( 495(3), 3403–3408. [CrossRef]
47. Penrose, R. (2020). Nobel Prize lecture on physics and chemistry. In: R. Penrose, R., Genzel, & A. Ghez, Black holes and the Milky Way’s darkest secret. The Nobel Prize in Physics 2020. Royal Swedish Academy of Sciences. [https://www.nobelprize. 2020. [Google Scholar]
48. Nurowski, P. (2021). Poincaré–Einstein approach to Penrose’s conformal cyclic cosmology. Class. Quantum Gravity 38, 4500. [Google Scholar] [CrossRef]
49. Bodnia, E. , Isenbaev, V., Colburn, K., Swearngin, J., & Bouwmeester, D. (2024). Conformal cyclic cosmology signatures and anomalies of the CMB sky. ( 2024(9), 1–25. [CrossRef]
50. Bache, M. A. B. (2024a). Teoría X. Hacia la congruencia interdisciplinar entre universo y realidad(es). In: M. A. B. Bache & J. C. Rodríguez-Rodríguez (Eds.), Psicología, Complejidad y Sistemas (pp. 106-191). Dykinson.
51. Tod, P. (2024). Conformal methods in mathematical cosmology. Phil. Trans. R. Soc. A, 382. [CrossRef]
52. Rovelli, C. & Smolin, L. (1988). Knot theory and quantum gravity. ( 61(10), 1155–1158. [CrossRef] [PubMed]
53. Rovelli, C. & Smolin, L. (1995). Discreteness of area and volume in quantum gravity. ( 442(3), 593–619.
54. Thiemann, T. (1996). Anomaly-free formulation of non-perturbative, four-dimensional Lorentzian quantum gravity. Physics Letters B, 380.
55. Rovelli, C. (1996). Black hole entropy from loop quantum gravity. Physical Review Letters, 77, 3291. [Google Scholar] [CrossRef]
56. Rovelli, C. & Vidotto, F. (2014). Planck stars. ( 23(12), 1442026.
57. Alexander, S. , Marcianò, A., & Tacchi, R. A. (2012). Towards a Loop Quantum Gravity and Yang–Mills unification. Physics Letters B, 716.
58. Freidel, L. & Krasnov, K. (2008). A new spin foam model for 4d gravity. ( 25(12), 125018.
59. Rovelli, C. (2004). Quantum Gravity.
60. Caldwell, R. R. , Dave, R., & Steinhardt, P. J. (1998). Cosmological imprint of an energy component with general equation of state. J. ( 80(8), 1582–1585.
61. Steinhardt, P. J. , Wang, L., & Zlatev, I. (1999). Cosmological tracking solutions. ( 59(12), 123504.
62. Dave, R. , Caldwell, R. R., & Steinhardt, P. J. (2002). Sensitivity of the cosmic microwave background anisotropy to initial conditions in quintessence cosmology. J. ( 66(2), 023516.
63. Bhandari, G. , Pathak, S. D., Sharma, M., & Wang, A. (2024). Distortion of quintessence dynamics by the Generalized Uncertainty Principle. ( 473, 169895. [CrossRef]
64. Arkani-Hamed, N. , & Trnka, J. (2014). The amplituhedron. ( 2014(10), 1–33. [CrossRef]
65. Penrose, R. (2015). Palatial twistor theory and the twistor googly problem. Philos. Trans. Roy. Soc. A: Math., Phys. and Eng. Sci., 373, 2014. [Google Scholar] [CrossRef]
66. Waeber, S. & Yarom, A. (2021). Stochastic gravity and turbulence. ( 2021(12), 1–24. [CrossRef]
67. Bache, M. A. B. (2021). On the very origins of the Universe. An exacting mathematical verification. Spanish Government Intellectual Property Registry, Scientific Works. 2021. [Google Scholar]
68. Bache, M. A. B. (2023a). Sobre los orígenes del universo: una comprobación meticulosa desde el punto de vista matemático en la 5ª dimensión. In: J. C. Rodríguez Rodríguez (Ed.), Psicología siglo XXI: una mirada amplia e integradora. Vol. 3 (pp. 252-308). Dykinson.
69. Bache, M. A. B. (2023b). Grand Gravity and X-Theory. On the Unification of Relativity and Quantum Mechanics. US-China Education Review, 13. [CrossRef]
70. Boyle, L. , Finn, K., & Turok, N. (2018). CPT-symmetric universe. Phys. Rev. Lett., 121. [CrossRef]
71. Einstein, A. (1905b). Ist die Tragheit eines Korpers von sienem Energiegehalt Abhangig? Ann. Phys, 323. [CrossRef]
72. Einstein, A. (1912). Einstein’s manuscript on the special theory of relativity. In: M. Klein, A. J. Kox., J. Renn, & R. Schulmann (Eds.), The collected papers of Albert Einstein Princeton, The Swiss years: writings 1912-1914, 1995 [1912] (pp. 9-108). Princeton University Press. https://einsteinpapers.press.princeton.edu/vol4-trans/61?
73. ‘t Hooft, G. & Veltman, M. (1972). Regularization and renormalization of gauge fields. ( 44(1), 189–213. [CrossRef]
74. ‘t Hooft, G. & Veltman, M. (1974). One-loop divergencies in the theory of gravitation. Annales de l’institut Henri Poincaré. Section A, Physique Théorique, 20, /: http, 7579. [Google Scholar]
75. Deser, S. , Tsao, H. S., & Van Nieuwenhuizen, P. (1974). One-loop divergences of the Einstein-Yang-Mills system. Physical Review D. [CrossRef]
76. Weinberg, S. (1972). Gravitation and cosmology.
77. ‘t Hooft, G. (2005). The conceptual basis of Quantum Field Theory. Utrecht University Open. https://dspace.library.uu. 1874. [Google Scholar]
78. Einstein, A. (1927). Einstein contributions to the 5th Solvay Conference. In: H. Lorentz (Ed.), Electrons et Photons, 5th Solvay Conference, 24 to. 29 October.
79. Böhr, N. (1949). Discussion with Einstein on epistemological problems in atomic physics. In: P. A. Schilpp. (Ed.), Albert Einstein: philosopher-scientist (pp. 200-241). The Library of Living Philosophers.
80. L’Huillier, A. , Agostini, P., & Krausz, F. (2023). Electrons as pulses of light. In: The Nobel Prize in Physics 2023. Royal Swedish Academy of Science.
81. Bekenstein, J. & Milgrom, M. (1984). Does the missing mass problem signal the breakdown of Newtonian gravity? Astr. J., 286. [CrossRef]
82. Milgrom, M. & Bekenstein, J. (1987). The modified Newtonian dynamics as an alternative to hidden matter. In: Symposium-International astronomical union, 117, 319-333. Cambridge University Press.
83. Milgrom, M. (2023). Generalizations of quasilinear MOND. Phys. Rev. D, 108, 4005. [Google Scholar] [CrossRef]
84. Chae, K. H. & Milgrom, M. (2022). Numerical Solutions of the External Field Effect on the Radial Acceleration in Disk Galaxies. ( 928(1), 24. [CrossRef]
85. Robertson, B. , Johnson, B. D., Tacchella, S., Eisenstein, D. J., Hainline, K., Arribas, S.,... & Witstok, J. (2024). Earliest Galaxies in the JADES Origins Field: Luminosity Function and Cosmic Star Formation Rate Density 300 Myr after the Big Bang. Astr. J., 970. [CrossRef]
86. Lovell, C. C. , Harrison, I., Harikane, Y., Tacchella, S., & Wilkins, S. M. (2023). Extreme value statistics of the halo and stellar mass distributions at high redshift: are JWST results in tension with ΛCDM? M.N.R.A.S., 518. [CrossRef]
87. Xiao, M. , Oesch, P. A., Elbaz, D., Bing, L., Nelson, E. J., Weibel, A.,... & Wyithe, J. S. B. (2024). Accelerated formation of ultra-massive galaxies in the first billion years. Nature, 635. [CrossRef]
88. Carniani, S. , Hainline, K., D’Eugenio, F., Eisenstein, D. J., Jakobsen, P., Witstok, J.,... & Willmer, C. N. (2024). Spectroscopic confirmation of two luminous galaxies at a redshift of 14. Nature, 633. [CrossRef]
89. Primack, J. R. (2024). Galaxy Formation in ΛCDM Cosmology. Annual Review of Nuclear and Particle Science, 74. [CrossRef]
90. Arrabal Haro, P. , Dickinson, M., Finkelstein, S. L., Kartaltepe, J. S., Donnan, C. T., Burgarella, D.,... & Zavala, J. A. (2023). Confirmation and refutation of very luminous galaxies in the early Universe. Nature, 622. [CrossRef]
91. [91] Carniani, S. & Hainline, K. (2024). NASA’s James Webb Space Telescope finds most distant known galaxy. https://blogs.nasa.gov/webb/2024/05/30/nasas-james-webb-space-telescope-finds-most-distant-known-galaxy/ [Accessed 16/01/2025].
92. Gupta, R. P. (2023). JWST early Universe observations and ΛCDM cosmology. M.N.R.A.S., 524, 3395. [Google Scholar] [CrossRef]
93. Dirac, P. A. M. (1938). A new basis for cosmology. Proceedings of the Royal Society of London. Series A. Mathematical and Physical Sciences, 165. [CrossRef]
94. Gupta, R. P. (2022). Effect of evolving physical constants on type Ia supernova luminosity. M.N.R.A.S., 511, 4250. [Google Scholar] [CrossRef]
95. Melnikov, V. N. (1994). Fundamental physical constants and their stability: A review. International Journal of Theoretical Physics, 33, 1579. [Google Scholar] [CrossRef]
96. Gupta, R. P. (2023a). Constraining Co-Varying Coupling Constants from Globular Cluster Age. Universe, 9. [CrossRef]
97. McQuinn, K. B. , Newman, M. J., Skillman, E. D., Telford, O. G., Brooks, A., Adams, E. A.,... & Goldman, S. R. (2024). The Ancient Star Formation History of the Extremely Low-mass Galaxy Leo P: An Emerging Trend of a Post-reionization Pause in Star Formation. Astr. J., 976. [CrossRef]
98. Slob, M. , Kriek, M., Beverage, A. G., Suess, K. A., Barro, G., Bezanson, R.,... & Weisz, D. R. (2024). The JWST-SUSPENSE Ultradeep Spectroscopic Program: Survey Overview and Star-Formation Histories of Quiescent Galaxies at 1< z< 3. Astr. J., 973. [CrossRef]
99. Birrell, J. , Yang, C. T., Chen, P., & Rafelski, J. (2014). Relic neutrinos: Physically consistent treatment of effective number of neutrinos and neutrino mass. Physical Review D, 89. [CrossRef]
100. Rafelski, J. , Birrell, J., Steinmetz, A., & Yang, C. T. (2023). A short survey of matter-antimatter evolution in the primordial universe. Universe, 9. [CrossRef]
101. Rafelski, J. , Birrell, J., Grayson, Ch., Steinmetz, A., Yang, Ch. T. (2024). Quarks to Cosmos: Particles and Plasma in Cosmological evolution. In: XVI Quark Confinement and the Hadron Spectrum Conference, 19 to. 24 August.
102. Yung, L. A. , Somerville, R. S., Finkelstein, S. L., Wilkins, S. M., & Gardner, J. P. (2024). Are the ultra-high-redshift galaxies at z> 10 surprising in the context of standard galaxy formation models? M.N.R.A.S., 527. [CrossRef]
103. Menci, N. , Castellano, M., Santini, P., Merlin, E., Fontana, A., & Shankar, F. (2022). High-redshift galaxies from early JWST observations: constraints on dark energy models. Astr. J. Lett., 938. [CrossRef]
104. Mayer, A. C. , Teklu, A. F., Dolag, K., & Remus, R. S. (2023). ΛCDM with baryons versus MOND: The time evolution of the universal acceleration scale in the Magneticum simulations. M.R.N.A.S. 518. [CrossRef]
105. Scarpa, R. , Falomo, R., & Treves, A. (2022). On the orbital velocity of isolated galaxy pairs: II accurate MOND predictions. M.N.R.A.S., 512. [CrossRef]
106. Schmidt, B. P. , Suntzeff, N. B., Phillips, M. M., Schommer, R. A., Clocchiatti, A., Kirshner, R. P., … & Riess, A. G. (1998). The high-Z supernova search: Measuring cosmic deceleration and global curvature of the universe using type Ia supernovae. Astr. J., 507. [CrossRef]
107. Perlmutter, S. , Aldering, G., Goldhaber, G., Knop, R. A., Nugent, P., Castro, P. G.,... & Supernova Cosmology Project. (1999). Measurements of Ω and Λ from 42 high-redshift supernovae. Astr. J., 517. [CrossRef]
108. Riess, A. G. , Schmidt, B. P., & Perlmutter, S. (2011). The accelerating universe. Nobel Prize in Physics “for the discovery of the accelerating expansion of the Universe through observations of distant supernovae”. In: The Nobel Prize in Physics 2011. Royal Swedish Academy of Sciences.
109. https://www.nobelprize. 2011.
110. [https://www.nobelprize.org/uploads/2018/06/advanced-physicsprize2011.
111. Carroll, S. M. (2001). The cosmological constant. Living Reviews in Relativity, 4. [CrossRef]
112. Hoavo, H. O. V. A. (2020). Accelerating universe with decreasing gravitational constant. Journal of King Saud University-Science, 32, 1463. [Google Scholar] [CrossRef]
113. Babourova, O. V. & Frolov, B. N. (2020). On the exponential decrease of the “cosmological constant” in the super-early Universe. Journal of Physics: Conference Series, 1557. [CrossRef]
114. Foundational Aspects of Dark Energy (FADE) Collaboration, Bernardo, H., Bose, B., Franzmann, G., Hagstotz, S., He, Y., Litsa, A., & Niedermann, F. (2023). Modified Gravity Approaches to the Cosmological Constant Problem. Universe, 9. [CrossRef]
115. Weinberg, S. (1989). The cosmological constant problem. Reviews of Modern Physics, 61. [CrossRef]
116. Zel’Dovich, Y. B. (1968). The cosmological constant and the theory of elementary particles. Soviet Physics Uspekhi, 11(3), 381. [Zel’dovich, Y. B. (1967). JETP Lett. 6. [CrossRef]
117. Kaloper, N. & Westphal, A. (2022). Quantum-mechanical mechanism for reducing the cosmological constant. Physical Review D, 106. [CrossRef]
118. Bousso, R. (2007). The cosmological constant. General Relativity and Gravitation. 40. [CrossRef]
119. Preskill, J. , Wise, M., Wilczek, F. (1983). Cosmology of the invisible axion. Physics Letters B, 120.
120. Zhang, S. , Ilie, C., & Freese, K. (2024). Detectability of Supermassive Dark Stars with the Roman Space Telescope. ( 965(2), 121. [CrossRef]
121. Yuan, G. W. , Lei, L., Wang, Y. Z., Wang, B., Wang, Y. Y., Chen, C.,... & Fan, Y. Z. (2024). Rapidly growing primordial black holes as seeds of the massive high-redshift JWST Galaxies. Science China Physics, Mechanics & Astronomy, 67. [CrossRef]
122. Griest, K. (1993). The search for the dark matter: WIMPs and MACHOs. Annals of the New York Academy of Sciences. 688. [CrossRef]
123. Meng, Y. , Wang, Z., Tao, Y., Abdukerim, A., Bo, Z., Chen, W.,... & (PandaX-4T Collaboration). (2021). Dark matter search results from the PandaX-4T commissioning run. Physical Review Letters, 127. [CrossRef]
124. Kaplan, D. E. , Krnjaic, G. Z., Rehermann, K. R., & Wells, C. M. (2010). Atomic dark matter. M. ( 2010(05), 021. [CrossRef]
125. Bansal, S. , Barron, J., Curtin, D., & Tsai, Y. (2023). Precision cosmological constraints on atomic dark matter. ( 2023(10), 1–37. [CrossRef]
126. Fermi, E. (1934). Versuch einer Theorie der β-Strahlen. I. Zeitschrift für Physik A, 88.
127. Cowan Jr, C. L. , Reines, F., Harrison, F. B., Kruse, H. W., & McGuire, A. D. (1956). Detection of the free neutrino: a confirmation. Science, 124. [CrossRef]
128. Boyarsky, A. , Drewes, M., Lasserre, T., Mertens, S., & Ruchayskiy, O. (2019). Sterile neutrino dark matter. ( 104, 1–45. [CrossRef]
129. Krauss, L. M. (2012). A universe from nothing: Why there is something rather than nothing. Simon and Schuster.
130. Gell-Mann, M. (1964). A Schematic Model of Baryons and Mesons. Physics Letters, 8.
131. Zweig, G. (1964). An SU3 model for strong interaction symmetry and its breaking. In: D. Lichtenberg & S. Rosen. (Eds.), Developments in the Quark Theory of Hadrons. Vol. 1 (pp. 22-101). Nonantum, Mass., Hadronic Press. [CrossRef]
132. Bjørken, B. J. & Glashow, S. L. (1964). Elementary particles and SU (4). L. ( 11(3), 255–257. [CrossRef]
133. van Hove, L. (1987). Theoretical prediction of a new state of matter, the “Quark-Gluon plasma” (also called “Quark Matter”). In: Proceedings of the XVII international symposium on multiparticle dynamics, 20(10), 20030911. https://cds.cern.ch/record/183417?
134. Brodsky, S. J. , Hoyer, P., Peterson, C., & Sakai, N. (1980). The intrinsic charm of the proton. ( 93(4), 451–455. [CrossRef]
135. Wheeler, J. A. (1978). The “past” and the “delayed-choice” double-slit experiment. In: A. R. Marlow (Ed.), Mathematical foundations of quantum theory (pp. 9-48). Academic Press.
136. Vedovato, F. , Agnesi, C., Schiavon, M., Dequal, D., Calderaro, L., Tomasin, M., … & Villoresi, P. (2017). Extending Wheeler’s delayed-choice experiment to space. Science Advances, 3. [CrossRef]
137. Hossenfelder, S. , & Palmer, T. (2020). Rethinking superdeterminism. ( 8, 139. [CrossRef]
138. Feynman, R. P. (1948). Space-Time approach to non-relativistic Quantum Mechanics. Reviews of Modern Physics, 20.
139. Hamilton, W. R. (1834). On a general method in dynamics. Phil. Trans. R. Soc.,. [CrossRef]
140. Dirac, P. A. M. (1933). Theory of electrons and positrons. In: The Nobel Prize in Physics 1933. Royal Swedish Academy of Science. https://www.nobelprize. 1933. [Google Scholar]
141. Dirac, P. A. M. (1975). The story of the positron. In: The Development of Quantum Mechanics, Accademia dei Lincei, Roma (pp. 11). www.lincei. 1504. [Google Scholar]
142. https://youtu. 2025.
143. Bentley, R. (1693). Original letter from Richard Bentley to Newton, Feb. 18. 1693. In: The Newton Project, 189.R.4.47, ff. 3-4, 2007. Trinity College Library, Cambridge, UK. https://www.newtonproject.ox.ac. 0025. [Google Scholar]
144. Newton, I. (1693). Original letter from Isaac Newton to Richard Bentley, Feb. 25. 1693. In: The Newton Project 189.R.4.47, ff. 7-8, 2007. Trinity College Library, Cambridge, UK https://www.newtonproject.ox.ac. 0025. [Google Scholar]
145. Russell, B. (1924). Logical Atomism. In: The Philosophy of Logical Atomism (2009). Routledge.
146. Klein, O. (1927). Elektrodynamik und wellenmechanik vom standpunkt des korrespondenzprinzips. Zeitschrift für Physik A, Hadrons and nuclei, 41. [CrossRef]
147. Gordon, W. (1926). Der comptoneffekt nach der schrödingerschen theorie. Zeitschrift für Physik, 40. [CrossRef]
148. Dirac, P. A. M. (1931). Quantised singularities in the electromagnetic field. Proc. of the Roy. Soc. Lond. Ser. A, Cont. Pap. Math. and Phys. Char., 133. [CrossRef]
149. Anderson, C. D. (1933). The Positive Electron. Phys. Rev. 43. [CrossRef]
150. Bose. (1924). Plancks gesetz und lichtquantenhypothese. Zeitschrift für Physik, 26. [CrossRef]
151. Einstein, A. (1924). Quantentheorie des einatomigen idealen Gases II, Sitz. K. Preuss. Akad. Wiss., 1, 3-14.
152. Hanada, M. , Shimada, H., & Wintergerst, N. (2021). Color confinement and Bose-Einstein condensation. JHEP, 2021. [CrossRef]
153. Shieh, T. T. (2015). From gradient theory of phase transition to a generalized minimal interface problem with a contact energy. Discrete and Continuous Dynamical Systems, 36, 2755. [Google Scholar] [CrossRef]
154. Wieman, C. , Ketterle, W., & Cornell, E. (2001). New state of matter revealed: Bose-Einstein Condensate. In: The Nobel Prize in Physics 2001. Royal Swedish Academy of Science. https://www.nobelprize. 2001. [Google Scholar]
155. Sen, S. & Gangopadhyay, S. (2024). Probing the quantum nature of gravity using a Bose-Einstein condensate. Physical Review D, 110. [CrossRef]
156. McDonald, K. T. (2024). Bose and the angular momentum of the photon. American Journal of Physics, 92. [CrossRef]
157. Vlasov, A. A. (1968). The Vibrational Properties of an Electron Gas. Soviet Physics Uspekhi. 10. [CrossRef]
158. Merrill, H. J. & Webb, H. W. (1939). Electron scattering and plasma oscillations. W. ( 55(12), 1191–1198.
159. Lossev, A. & Novikov, I. D. (1992). The Jinn of the time machine: non-trivial selfconsistent solutions. Class. Quantum Grav., 9, 2321. [Google Scholar] [CrossRef]
160. Penrose, R. (1979). Singularities and time-asymmetry. In: S. Hawking & W. Israel (Eds.), General Relativity : An Einstein Centenary Survey (pp. 581-638). Cambridge University Press.
161. Prigogine, I. , & Nicolis, G. (1967). On symmetry-breaking instabilities in dissipative systems. The Journal of Chemical Physics, 46.
162. Prigogine, I. (1989). Thermodynamics and cosmology. International Journal of Theoretical Physics, 28.
163. Prigogine, I. & Stengers, I. (1984). Order out of chaos: The evolutionary paradigm and the physical sciences. Bantam Books.
164. Kosterlitz, J. M. , Haldane, F. D. M., & Thouless, D. J. (2016). Nobel Prize “for theoretical discoveries of topological phase transitions and topological phases of matter”. In: The Nobel Prize in Physics 2016. Royal Swedish Academy of Science. https://www.nobelprize. 2016. [Google Scholar]
165. Joos, E. & Zeh, H. D. (1985). The emergence of classical properties through interaction with the environment. Zeitschrift für Physik B Condensed Matter, 59. [CrossRef]
166. Haug, E. G. (2023). Different mass definitions and their pluses and minuses related to gravity. Foundations, 3. [CrossRef]
167. Prigogine, I. (1977). Time, Structure and Fluctuations. Nobel Lecture. In: The Nobel Prize in Chemistry 1977. Royal Swedish Academy of Science. https://www.nobelprize. 1977. [Google Scholar]
168. Carter, B. (1974). Large number coincidences and the anthropic principle in cosmology. In: M. S. Longair (Ed.), Confrontation of Cosmological Theories with Observational Data (pp. 291–298). International Astronomical Union.
169. Bache, M. A. B. (2024b). Universo frente a realidad. Revisión de la aplicación del principio antrópico-Del nonsequitur de Copenhague a la selección natural. In: IV CIISEP, 25 to (AIISEP). https://youtu. 27 September.
170. Zurek, W. H. (2009). Quantum darwinism. Nature Physics, 5. [CrossRef]
171. Penrose, R. (2007). The Road to Reality.
172. Zurek, W. H. (2003). Decoherence, einselection, and the quantum origins of the classical. Reviews of Modern Physics. 75. [CrossRef]
173. Penrose, R. (1996). On Gravity’s role in Quantum State Reduction. Gen. Rel. and Grav., 28. [CrossRef]
174. Hamada, K. J. (2022). Revealing a trans-Planckian world solves the cosmological constant problem. Progress of Theoretical and Experimental Physics, 2022. [CrossRef]
175. Everett III, H. (1957). Relative state formulation of quantum mechanics. Reviews of Modern Physics, 29.
176. Everett III, H. , Wheeler, J. A., DeWitt, B. S., Cooper, L. N., Van Vechten, D., & Graham, N. (1973). The Many-Worlds Interpretation of Quantum Mechanics. In: B. S. DeWitt & G. R. Neill (Eds.), Princeton Series in Physics. Princeton University Press.
177. Blume-Kohout, R. & Zurek, W. H. (2006). Quantum Darwinism: Entanglement, branches, and the emergent classicality of redundantly stored quantum information. Physical Review A—Atomic, Molecular, and Optical Physics, 73. [CrossRef]
178. Blume-Kohout, R. , & Zurek, W. H. (2008). Quantum Darwinism in quantum Brownian motion. H. ( 101(24), 240405. [CrossRef]
179. Unden, T. K. , Louzon, D., Zwolak, M., Zurek, W. H., & Jelezko, F. (2019). Revealing the emergence of classicality using nitrogen-vacancy centers. Physical Review Letters, 123. [CrossRef]
180. Schmitt, M. , Rams, M. M., Dziarmaga, J., Heyl, M., & Zurek, W. H. (2022). Quantum phase transition dynamics in the two-dimensional transverse-field Ising model. Science Advances, 8. [CrossRef]
181. Matsas, G. E. , Pleitez, V., Saa, A., & Vanzella, D. A. (2024). The number of fundamental constants from a spacetime-based perspective. Scientific Reports, 14. [CrossRef]
182. Maxwell, J. C. (1878). A Treatise on Electricity and Magnetism, (Clarendon, 1878), 1954. [Google Scholar]
183. Gödel, K. (1931). Über formal unentschedibare Sätze der Principia Mathematica und verwandter Systeme, I. Monatsh. Math. Phys., 38. [CrossRef]
184. Wigner, E. P. (1960). The unreasonable effectiveness of mathematics in the natural sciences. Richard courant lecture in mathematical sciences delivered at New York University, May 11, 1959. Communications on Pure and Applied Science, 13, 11 May. [CrossRef]
185. Cohen, P. J. (1963). The independence of the continuum hypothesis. P.N.A.S., 50, 1148. [Google Scholar] [CrossRef]
186. Shannon, C. E. (1948). A mathematical theory of communication. The Bell System Technical Journal, 27. [CrossRef]
187. Boltzmann, L. (1877). Über die Beziehung zwischen dem zweiten Hauptsatze der mechanischen Wärmetheorie und der Wahrscheinlichkeitsrechnung, respektive den Sätzen über das Wärmegleichgewicht. Sitzungsber. Kais. Akad. Wiss. Wien Math. Naturwiss. Class., 76.
188. Leff, H. S. (1996). Thermodynamic entropy: The spreading and sharing of energy. American Journal of Physics, 64, 1271. [Google Scholar] [CrossRef]
189. von Neumann, (1927). Thermodynamik quantummechanischer gesamheiten. Gott. Nach., 1, /: 273-291. http, 5923.
190. Sharp, K. & Matschinsky, F. (2015). Translation of Ludwig Boltzmann’s paper “On the Relationship between the Second Fundamental Theorem of the Mechanical Theory of Heat and Probability Calculations Regarding the Conditions for Thermal Equilibrium” Sitzung. Kaiser. Akad. Wissensch. Mathem.-Natur. Class., Abt. II, LXXVI 1877, pp 373-435 (Wien. Ber. 1877, 76, 373-435). Reprinted in Wiss. Abhandlungen, Vol. II, reprint 42, p. 164-223, Barth, Leipzig, 1909. Entropy, 17. [CrossRef]
191. Boltzmann, L. (1884). Ableitung des Stefanschen Gesetzes, betreffend die Abhängigkeit der Wärmestrahlung von der Temperatur aus der elektromagnetischen Lichttheorie. Annalen der Physik, 258. [CrossRef]
192. Carathéodory, C. (1909). Untersuchungen über die Grundlagen der Thermodynamik. Math. Ann., 67. [CrossRef]
193. Clausius, R. (1854). Über eine veränderte Form des zweiten Hauptsatzes der mechanischen Wärmetheorie. Annalen der Physik, 169. [CrossRef]
194. Zeh, H. D. (1989). The direction of time.
195. Leinweber, D. B. (2000). Visualizations of the QCD vacuum. arXiv preprint. [CrossRef]
196. Wheeler, J. A. (1955). Geons. Physical Review, 97. [CrossRef]
197. Wheeler, J. A. & Ford, K. (2000). Geons, black holes, and quantum foam: A life in physics.
198. Wang, Q. & Unruh, W. G. (2020). Vacuum fluctuation, microcyclic universes, and the cosmological constant problem. G. ( 102(2), 023537. [CrossRef]
199. Ng, Y. J. (2019). Entropy and Gravitation—From Black Hole Computers to Dark Energy and Dark Matter. Entropy, 21. [CrossRef]
200. Styer, D. F. (2000). Insight into entropy. American Journal of Physics, 68, 1096. [Google Scholar] [CrossRef]
201. Dymnikova, I. & Galaktionov, E. (2021). Regular electrically charged objects in Nonlinear Electrodynamics coupled to Gravity. Journal of Physics: Conference Series, 2103. [CrossRef]
202. Agazie, G. , Anumarlapudi, A., Archibald, A. M., Arzoumanian, Z., Baker, P. T., Bécsy, B.,... & NANOGrav Collaboration. (2023). The NANOGrav 15 yr data set: Evidence for a gravitational-wave background. Astroph. J. Lett., 951. [CrossRef]
203. Dymnikova, I. (2015). Electromagnetic source for the Kerr–Newman geometry. Int. J. Mod. Phys. D, 24, 5500. [Google Scholar] [CrossRef]
204. Dymnikova, I. (2015). Elementary Superconductivity in Nonlinear Electrodynamics Coupled to Gravity. Journal of Gravity, 2015, 4171. [Google Scholar] [CrossRef]
205. Penrose, R. (1965). Gravitational collapse and space-time singularities. Phys. Rev. Lett., 14. [CrossRef]
206. Andersson, B. , Gustafson, G., & Peterson, C. (1977). The relationship between the meson, baryon, photon and quark fragmentation distributions. ( 69(2), 221–224. [CrossRef]
207. Ehrenfest, P. (1909). Gleichförmige rotation starrer körper und relativitätstheorie. Physikalische Zeitschrift, 10, 2025. [Google Scholar]
208. Grøn, Ø. (1979). Relativistic description of a rotating disk with angular acceleration. Foundations of Physics, 9. [CrossRef]
209. Kumar, J. (2024). Ehrenfest paradox: A careful examination. American Journal of Physics, 92(2), 140–145. [CrossRef]
210. North, J. S. , Wikle, C. K., & Schliep, E. M. (2023). A Review of Data-Driven Discovery for Dynamic Systems. Int. Stat. Rev., 91. [CrossRef]
211. Wang, Y. , Wagner, N., & Rondinelli, J. M. (2019). Symbolic regression in materials science. M. ( 9(3), 793–805. [CrossRef]
212. Penrose, R. (1968). Twistor quantisation and curved space-time. International Journal of Theoretical Physics, 1(1), 61-99. [CrossRef]
213. Quinn, T. & Speake, C. (2014). The Newtonian constant of gravitation - a constant too difficult to measure? An introduction. Philos. Trans. R. Soc. A, 372, 4025. [Google Scholar] [CrossRef]
214. Paci, G. & Zanusso, O. (2025). Weyl cohomology and the conformal anomaly in the presence of torsion. ( 473, 169877. [CrossRef]