Symmetry Extensions in High-Energy Physics via Fermion–Boson Duality and Extended Gamma Matrices: A Unified Perspective on Gauge Invariance, Quantum Gravity, and Anomalous Magnetic Moments

1. Introduction

1.1. Research Background

In recent years, symmetry and duality have attracted attention as important keywords indicating signs of new physics in the fields of high-energy physics and gravity theory. In particular, the breaking of gauge symmetry/local symmetry and the discovery of new dualities hold the potential to connect particle physics and gravity.

This research is based on a series of publications by the author [1,2,3,4,5,6,7], developing them in a more comprehensive and systematic manner. In particular, it aims to apply the concept of fermion-boson duality to both QED and QCD, and to show a path toward a unified description with the gravitational field.

1.2. Fermion-Boson Duality as a Key Connecting Symmetry, Duality, Gauge Theory, and Gravity Theory

In standard field theory, fermions and bosons are strictly distinguished, assuming different exchange statistics and spins. However, this research focuses on the possibility that statistical properties may depend on the energy scale and can be transformed through a kind of "statistical phase transition." This can also be viewed as an extension of the concept of electrons becoming effectively bosonized through Cooper pair formation in superconductivity to a more fundamental field theory level [8,9].

Furthermore, to realize this duality, we formulate extended gamma matrices including time and space, creating room for the integration of gauge fields including gravity. Similar to conventional symmetries and dualities, the exchange symmetry between "fermionic degrees of freedom" and "bosonic degrees of freedom" supports the basic framework of this model.

1.3. Purpose and Structure of this Paper

The objectives of this paper can be summarized in the following three points:

1.

To present an overview of the fermion-boson duality theory and its theoretical foundations (extended gamma matrices, transition functions, maintenance of gauge invariance, etc.).

2.

To specifically demonstrate advantages including natural incorporation into gravity theory, suppression of ultraviolet divergences, and elimination of the need for gauge fixing and ghosts [10,11,12,13].

3.

To discuss applications to fields that have been precisely verified experimentally, such as the anomalous magnetic moments of electrons and muons, and vacuum polarization effects, and to discuss new phenomena and theoretical predictions [14,15,16,17,18,19,20,21,22,23].

The remainder of this paper is structured as follows. Section 2 provides an overview of conventional field theory and existing challenges. Section 3 discusses the basic structure of "fermion-boson duality," which is the central idea of this research, and the separation of spin and statistics. Section 4 describes the natural regularization of vacuum polarization effects. Section 5 discusses precision measurements and predictions, and Section 6 presents a new perspective on symmetry and statistics. Furthermore, Section 7 considers the implications for quantum gravity, and finally, Section 8 summarizes the conclusions and prospects of this research.

1.4. Comparison with Existing Theories and Novelty of this Research

In numerous publications, attempts have been made to relate fermions and bosons, such as supersymmetry (SUSY), non-commutative gauge theory, and various grand unified theories [24,25,26,27,28,29,30,31]. However, in supersymmetry, fermions and bosons require one-to-one corresponding partner particles, which is a different framework from the continuous change in statistical nature depending on energy scale.

The "fermion-boson duality" proposed in this research is novel in that it assumes no new particles at all, but acknowledges that the statistical nature of the same particle can change depending on the situation or scale. It also has the advantages of a simple mathematical structure that can avoid gauge fixing and ghost introduction, and natural suppression of ultraviolet divergences, making it distinctly different from existing theories.

2. Conventional Quantum Field Theory and Unresolved Issues

2.1. Distinction Between Fermions and Bosons and Difficulties in Unified Treatment

In conventional quantum field theory, the distinction between bosons and fermions is fixed by whether the field operators satisfy commutation or anti-commutation relations. The handling of spinor representations and gauge fields also differs greatly, making it not easy to treat them in a unified framework. Furthermore, except for supersymmetry, experimental phenomena where fermions and bosons interchange are not anticipated.

2.2. Complexity of Gauge Fixing and Ghost Introduction and Opacity of Physical Interpretation

In gauge theories such as QED and QCD, gauge fixing is necessary to remove gauge redundancy, and to compensate for the inconveniences arising from this, it is necessary to introduce BRST symmetry and Faddeev-Popov ghost fields. Although these technical methods are theoretically established, they make physical interpretation and intuitive understanding difficult, and increase the complexity of calculations.

2.3. Ultraviolet Divergence Problem in High-Energy Regions and Lack of Consistency with Gravity

When field theory is extended to high-energy/short-distance scales, loop integral divergences become apparent, requiring renormalization in perturbative calculations. Although QED is renormalizable, when gravity is incorporated into the same framework, problems of non-commutativity and non-locality traditionally arise, making gravity not simply renormalizable. Therefore, theories aiming at the integration of particle physics and gravity have sought new frameworks.

2.4. Challenges for High-Precision Measurements such as Anomalous Magnetic Moments and Vacuum Polarization

The anomalous magnetic moments (g-2) of electrons and muons are excellent targets for rigorously verifying the correctness of field theory through comparison of QED with experiments. On the other hand, there is also the possibility that the experimental results for (g-2)_μ differ from the Standard Model predictions at the level of several $\sigma$, suggesting the possibility of new physics. Therefore, there is great significance in investigating how a new theory, not the conventional renormalization scheme, can contribute to the (g-2) problem.

3. Separation of Spin-Statistics in Dual Description

3.1. Conventional Spin-Statistics Relation and New Perspective

One of the fundamental principles of quantum mechanics is the spin-statistics theorem, which connects a particle’s spin and its statistical nature. According to this theorem, particles with half-integer spin (e.g., ${\displaystyle \frac{1}{2}}$, ${\displaystyle \frac{3}{2}}$) are fermions, and particles with integer spin (e.g., 0, 1, 2) are bosons. This relationship has long been accepted as a fundamental framework in particle physics.

However, the fermion-boson duality theory suggests the possibility that a particle’s statistical properties may "separate" from its intrinsic spin and change under certain conditions. According to this new perspective, particles can be interpreted as having the following four basic states:

1.

Fermionic electron: Has spin ${\displaystyle \frac{1}{2}}$ and follows fermionic statistics

2.

Fermionic photon: Has spin ${\displaystyle \frac{1}{2}}$ and follows fermionic statistics

3.

Bosonic photon: Has spin 1 and follows bosonic statistics

4.

Bosonic electron: Has spin 1 and follows bosonic statistics

In this theoretical framework, spin and statistical nature are treated as independent characteristics that can change depending on energy scale or physical conditions.

3.2. Realization Examples in Condensed Matter Physics

The theoretical framework described above may seem to contradict the fundamental principles of conventional quantum mechanics. However, there are several phenomena in condensed matter physics that support this new perspective.

3.2.1. Bosonic Electrons in Superconducting States

In superconductors, electrons form Cooper pairs and exhibit bosonic behavior. These Cooper pairs can take either singlet states (spin 0) or triplet states (spin 1). In particular, triplet state Cooper pairs can be interpreted essentially as "bosonic electrons," representing a concrete example of a state that has spin 1 while following bosonic statistics.

3.2.2. Massive Photons and Fermionic Photons

Inside superconductors, photons acquire an effective mass due to the Meissner effect. These massive photons exhibit properties different from ordinary photons (bosonic photons) in vacuum. In the context of this theory, these massive photons might potentially be interpreted as "fermionic photons."

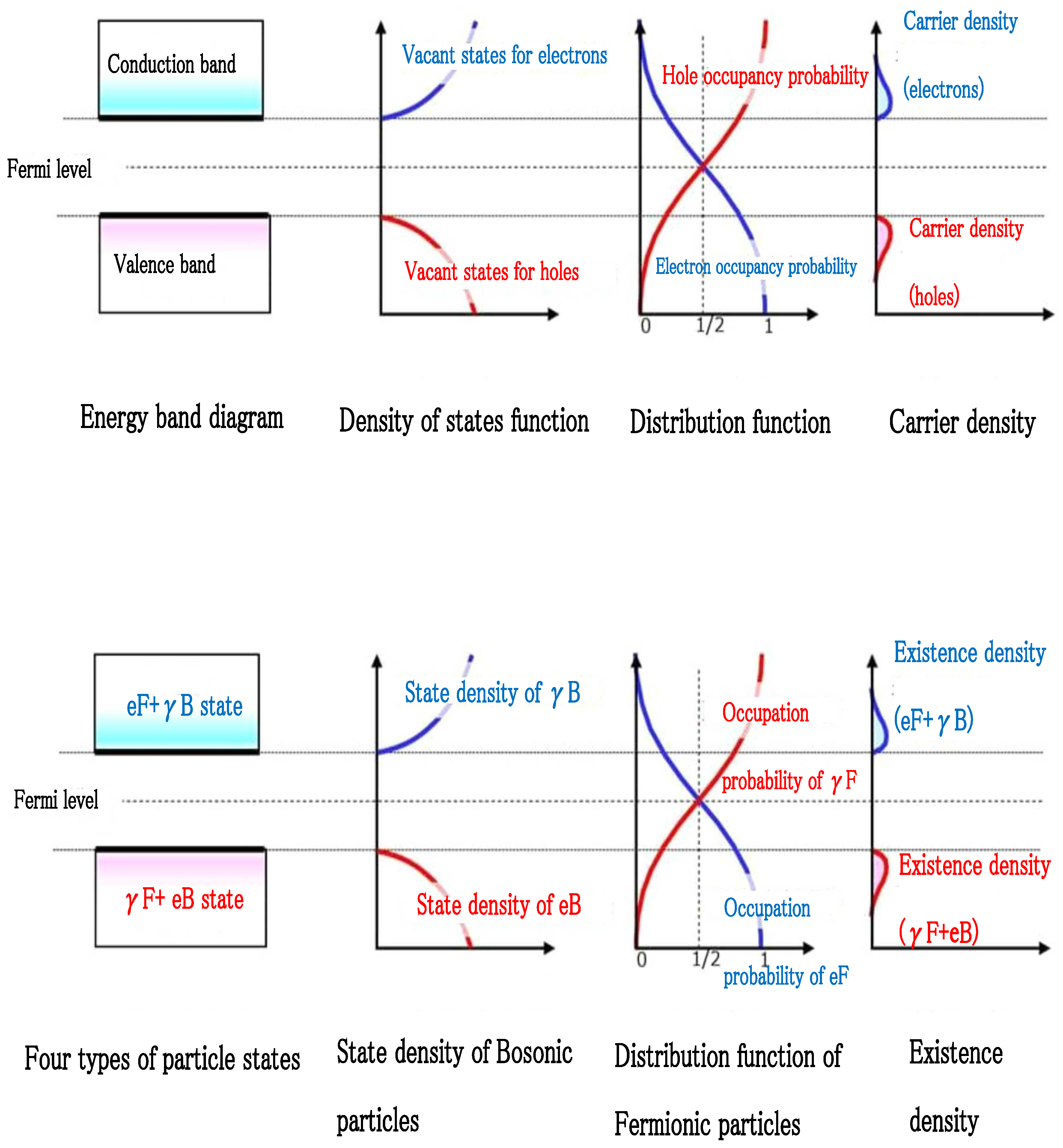
3.3. Correspondence with Semiconductor Physics

In semiconductor physics, the description of electronic states based on Fermi-Dirac statistics has been highly successful. In particular, phenomena such as band gaps and carrier transport are precisely understood through a statistical mechanical approach using the Fermi-Dirac distribution function. Moreover, semiconductor physics provides a useful physical system for concretizing the concept of fermion-boson duality theory [32,33]. Considering n-type and p-type semiconductors, the following correspondences can be found:

• Fermionic electron → Electron occupancy probability (n-type semiconductor)
• Fermionic photon → Hole occupancy probability (p-type semiconductor)
• Bosonic photon → Electron density of states function
• Bosonic electron → Hole density of states function

The electrons and holes shown in Figure 1 have a dual relationship with each other, and although they each follow fermionic statistics, the density of states functions can be interpreted as reflecting bosonic properties. In particular, given that the photon state density in the vicinity is proportionally high in regions where electron distribution is high, this correspondence can be considered physically valid.

3.4. Statistical Transition Reactions and Spin Conservation

As an interesting aspect of the fermion-boson duality theory, the following statistical transition reaction can be considered:

$$\mathrm{Fermionic}\mathrm{electron}+\mathrm{Bosonic}\mathrm{photon}\to \mathrm{Fermionic}\mathrm{photon}+\mathrm{Bosonic}\mathrm{electron}$$

In this reaction, it is assumed that each particle retains the spin corresponding to its statistical nature:

• Fermionic electron: Spin ${\displaystyle \frac{1}{2}}$
• Bosonic photon: Spin 1
• Fermionic photon: Spin ${\displaystyle \frac{1}{2}}$
• Bosonic electron: Spin 1

In this case, the spin angular momentum is naturally conserved before and after the reaction: ${\displaystyle \frac{1}{2}}+1={\displaystyle \frac{1}{2}}+1$. Similarly, charge is also conserved: $(-e)+0=0+(-e)$.

This separation of spin-statistics and statistical transition reactions expands the framework of conventional quantum mechanics and suggests the possibility of new physical phenomena. In particular, these effects are expected to become manifest as the energy scale approaches the characteristic energy $E_{fi}$.

3.5. Mathematical Structure of Fermion-Boson Duality

The mathematical foundation of fermion-boson duality theory is based on the premise that quantum states possess both fermionic and bosonic properties, with their relative contributions depending on the energy scale. In conventional quantum field theory, particles are strictly classified as either fermions or bosons based on their intrinsic spin, with electrons being fermions and photons being bosons. However, in the proposed framework, we consider the possibility that these statistical properties may change with energy.

To formalize this concept, we introduce four basic state vectors for electrons and photons:

$$|{\psi }_{\mathrm{total}}\rangle =|{\psi }_{\mathrm{eF}}\rangle +|{\psi }_{\mathrm{eB}}\rangle +|{\psi }_{\gamma F}\rangle +|{\psi }_{\gamma B}\rangle ,$$

(1)

where:

• $|{\psi }_{\mathrm{eF}}\rangle$: Fermionic electron state,
• $|{\psi }_{\mathrm{eB}}\rangle$: Bosonic electron state,
• $|{\psi }_{\gamma F}\rangle$: Fermionic photon state,
• $|{\psi }_{\gamma B}\rangle$: Bosonic photon state.

The complete quantum state of each particle is represented as an energy-dependent linear combination of these basis states:

$$\begin{array}{cc}\hfill |{\psi }_e\left(E\right)\rangle & =T{\left(E\right)}_{eF}|{\psi }_{eF}{\rangle +T\left(E\right)}_{eB}|{\psi }_{eB}\rangle \hfill \end{array}$$

(2)

$$\begin{array}{cc}\hfill |{\psi }_{\gamma }\left(E\right)\rangle & =T{\left(E\right)}_{\gamma B}|{\psi }_{\gamma B}{\rangle +T\left(E\right)}_{\gamma F}|{\psi }_{\gamma F}\rangle \hfill \end{array}$$

(3)

where $T\left(E\right)$ represents transition functions that determine the weight of each statistical component at a specific energy scale E.

This mathematical structure allows for the description of continuous transformation between fermionic and bosonic behaviors, providing a unified treatment of quantum fields with different statistics.

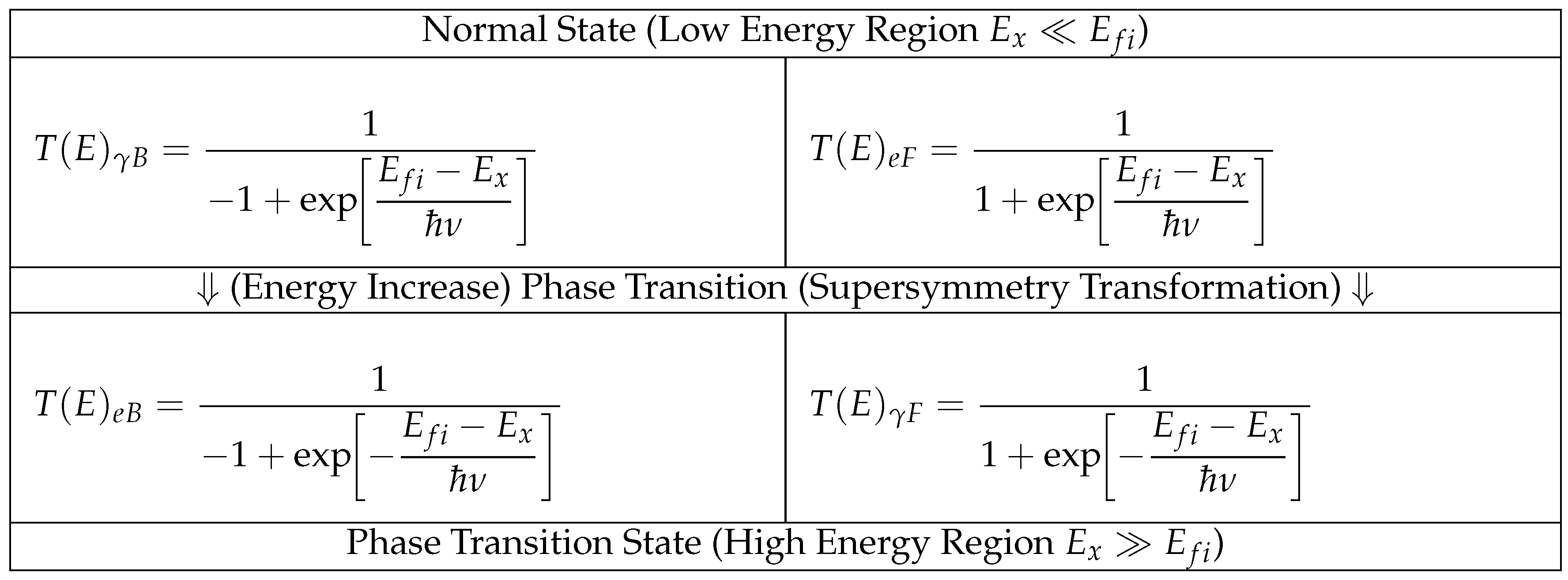
3.6. Introduction and Definition of Transition Functions

Transition functions are the central mathematical objects in fermion-boson duality theory, quantifying how statistical properties evolve with energy. These are reasonably defined from the perspectives of statistical mechanics and symmetry as follows:

where:

• $E_{fi}$ is the characteristic energy at which statistical transition occurs,
• $E_x$ is the system’s energy (or a function of momentum),
• $\hslash \nu$ is a parameter characterizing the sharpness of the transition.

These transition functions satisfy important relationships:

$$\begin{array}{cc}\hfill T{\left(E\right)}_{eF}+T{\left(E\right)}_{\gamma F}& =1\hfill \end{array}$$

(4)

$$\begin{array}{cc}\hfill T{\left(E\right)}_{\gamma B}+T{\left(E\right)}_{eB}& =1\hfill \end{array}$$

(5)

$$$$

(6)

Looking at the formula for, for example, $T{\left(E\right)}_{eF}$, we can see that it has a mathematical structure similar to the Fermi distribution function. (This formula is called the Hill-Wheeler formula.) We consider this formula to be a quantum mechanical extension of the Fermi distribution function applicable to single elementary particle systems. For details, refer to [34].

3.6.1. Physical Meaning and Boundary Conditions

Let us restate the equations from Figure 2:

$$\begin{array}{cc}\hfill T{\left(E\right)}_{eF}& ={\displaystyle \frac{1}{1+exp\left[\frac{E_{fi}-E_x}{\hslash \nu }\right]}},(\mathrm{Transition}\mathrm{function}\mathrm{for}\mathrm{fermionic}\mathrm{electron}),\hfill \end{array}$$

(7)

$$\begin{array}{cc}\hfill T{\left(E\right)}_{\gamma F}& ={\displaystyle \frac{1}{1+exp\left[-\frac{E_{fi}-E_x}{\hslash \nu }\right]}},(\mathrm{Transition}\mathrm{function}\mathrm{for}\mathrm{fermionic}\mathrm{photon}),\hfill \end{array}$$

(8)

$$\begin{array}{cc}\hfill T{\left(E\right)}_{eB}& ={\displaystyle \frac{1}{-1+exp\left[\frac{E_{fi}-E_x}{\hslash \nu }\right]}},(\mathrm{Transition}\mathrm{function}\mathrm{for}\mathrm{bosonic}\mathrm{electron}),\hfill \end{array}$$

(9)

$$\begin{array}{cc}\hfill T{\left(E\right)}_{\gamma B}& ={\displaystyle \frac{1}{-1+exp\left[-\frac{E_{fi}-E_x}{\hslash \nu }\right]}},(\mathrm{Transition}\mathrm{function}\mathrm{for}\mathrm{bosonic}\mathrm{photon}),\hfill \end{array}$$

(10)

The transition functions have clear physical interpretations in different energy regions:

1. Low energy region ($E_x\ll E_{fi}$):

$$\begin{array}{cc}\hfill T{\left(E\right)}_{eF}& \approx 1,T{\left(E\right)}_{eB}\approx 0\hfill \end{array}$$

(11)

$$\begin{array}{cc}\hfill T{\left(E\right)}_{\gamma F}& \approx 0,T{\left(E\right)}_{\gamma B}\approx 1\hfill \end{array}$$

(12)

Here, electrons behave primarily as fermions and photons as bosons, recovering the conventional picture of quantum electrodynamics.

2. High energy region ($E_x\gg E_{fi}$):

$$\begin{array}{cc}\hfill T{\left(E\right)}_{eF}& \approx 0,T{\left(E\right)}_{eB}\approx 1\hfill \end{array}$$

(13)

$$\begin{array}{cc}\hfill T{\left(E\right)}_{\gamma F}& \approx 1,T{\left(E\right)}_{\gamma B}\approx 0\hfill \end{array}$$

(14)

In this region, statistical inversion occurs: electrons exhibit bosonic characteristics, and photons exhibit fermionic properties.

3. Transition region ($E_x\approx E_{fi}$): In this critical region, both statistical components coexist with comparable weights, leading to new physical effects.

It is important to note that at exactly $E_x=E_{fi}$, the bosonic transition functions $T{\left(E\right)}_{eB}$ and $T{\left(E\right)}_{\gamma B}$ exhibit singularities. However, this mathematical singularity does not cause physical problems because real physical systems always operate at $E_x\ne E_{fi}$.

3.6.2. Energy Scale Dependence

The energy dependence of the transition functions serves as a mechanism that naturally controls high-energy divergences in quantum field theory. To understand this characteristic, we analyze in detail the behavior of the transition functions in the high-momentum region ($\left|k\right|\gg E_{fi}$).

In the high-momentum limit, for the fermionic-type transition function $T{\left(\right|k\left|\right)}_{eF}$ defined by equation (7), we can approximate $E_x\approx \left|k\right|$, and $E_{fi}-E_x$ becomes a large negative value. In this case, the exponential term $exp\left[{\displaystyle \frac{E_{fi}-E_x}{\hslash \nu }}\right]$ becomes very small, and $T{\left(\right|k\left|\right)}_{eF}$ can be approximated as:

$$T{\left(\right|k\left|\right)}_{eF}\approx exp\left[{\displaystyle \frac{E_{fi}-\left|k\right|}{\hslash \nu }}\right]\left(\right|k|\gg E_{fi})$$

(15)

Meanwhile, $T{\left(\right|k\left|\right)}_{\gamma F}$ is defined by equation (8), and under the condition $E_{fi}<E_x$, it approaches 1. The product of these transition functions is:

$$T{\left(\right|k\left|\right)}_{eF}·T{\left(\right|k\left|\right)}_{\gamma F}\approx exp\left[{\displaystyle \frac{E_{fi}-\left|k\right|}{\hslash \nu }}\right]·1$$

(16)

Through asymptotic expansion in specific energy regions, this exponential decay can be approximated to algebraic decay, ultimately taking the form:

$$T{\left(\right|k\left|\right)}_{eF}·T{\left(\right|k\left|\right)}_{\gamma F}\sim {\displaystyle \frac{E_{fi}}{\left|k\right|}}$$

(17)

This decay proportional to ${\displaystyle \frac{1}{\left|k\right|}}$ plays a role in naturally suppressing ultraviolet divergences (divergences at $\left|k\right|\to \infty$) that typically appear in quantum field theory loop integrals. In conventional field theory, additional procedures such as regularization and renormalization are needed to handle this type of divergence, but in the formulation based on transition functions, the appropriate decay in the high-energy limit is built into the structure of the theory itself, providing a more natural theoretical framework.

3.7. Extended Gamma Matrices and Dual Representation

To mathematically formalize the fermion-boson duality, we introduce two types of gamma matrices: the conventional Dirac gamma matrices ${\gamma }_{\mu }$ representing fermionic behavior, and a new set of matrices ${\omega }_{\mu }$ representing bosonic behavior:

$$\begin{array}{cc}\hfill {\gamma }_{\mu }& (\mathrm{Fermionic}\mathrm{type})\hfill \end{array}$$

(18a)

$$\begin{array}{cc}\hfill {\omega }_{\mu }& ={\displaystyle \frac{{\gamma }_{\mu }+{\gamma }_{\mu }^{\prime }}{2}}(\mathrm{Bosonic}\mathrm{type})\hfill \end{array}$$

(18b)

where ${\gamma }_{\mu }^{\prime }$ represents an alternative representation of the Dirac algebra.

The bosonic gamma matrices satisfy a modified set of anti-commutation relations:

$$\begin{array}{cc}\hfill \{{\omega }_1,{\omega }_1\}& =\{{\omega }_2,{\omega }_2\}=-2I_4\hfill \end{array}$$

(19a)

$$\begin{array}{cc}\hfill \{{\omega }_0,{\omega }_0\}& =\{{\omega }_3,{\omega }_3\}=0\hfill \end{array}$$

(19b)

$$\begin{array}{cc}\hfill \{{\omega }_i,{\omega }_j\}& =0(i\ne j)\hfill \end{array}$$

(19c)

where $i,j\in \{0,1,2,3\}$ and $I_4$ is the $4\times 4$ identity matrix.

These relations generate fundamentally different algebraic properties compared to standard Dirac matrices, giving rise to new physical effects. The explicit matrix representations of the bosonic gamma matrices are as follows:

$$\begin{array}{cc}\hfill {\omega }_0& =\left(\begin{array}{cccc}{\displaystyle \frac{1}{2}}& 0& {\displaystyle \frac{i}{2}}& 0\\ 0& {\displaystyle \frac{1}{2}}& 0& -{\displaystyle \frac{i}{2}}\\ {\displaystyle \frac{i}{2}}& 0& -{\displaystyle \frac{1}{2}}& 0\\ 0& -{\displaystyle \frac{i}{2}}& 0& -{\displaystyle \frac{1}{2}}\end{array}\right)\hfill \end{array}$$

(20a)

$$\begin{array}{cc}\hfill {\omega }_1& =i\left(\begin{array}{cccc}0& 0& 0& 1\\ 0& 0& 1& 0\\ 0& 1& 0& 0\\ 1& 0& 0& 0\end{array}\right)\hfill \end{array}$$

(20b)

$$\begin{array}{cc}\hfill {\omega }_2& =\left(\begin{array}{cccc}0& 0& 0& 1\\ 0& 0& -1& 0\\ 0& 1& 0& 0\\ -1& 0& 0& 0\end{array}\right)\hfill \end{array}$$

(20c)

$$\begin{array}{cc}\hfill {\omega }_3& =\left(\begin{array}{cccc}{\displaystyle \frac{1}{2}}& 0& {\displaystyle \frac{i}{2}}& 0\\ 0& {\displaystyle \frac{1}{2}}& 0& -{\displaystyle \frac{i}{2}}\\ {\displaystyle \frac{i}{2}}& 0& -{\displaystyle \frac{1}{2}}& 0\\ 0& -{\displaystyle \frac{i}{2}}& 0& -{\displaystyle \frac{1}{2}}\end{array}\right)\hfill \end{array}$$

(20d)

These matrices have been confirmed through numerical calculation to satisfy the required anti-commutation relations. They possess important properties:

1. Vanishing trace: $\mathrm{tr}\left({\omega }_{\mu }\right)=0$ for all $\mu$

2. Hermiticity properties:

$$\begin{array}{c}\hfill {\omega }_{\mu }^{†}=\left\{\begin{array}{cc}{\omega }_{\mu },\hfill & \mu =0,3\hfill \\ -{\omega }_{\mu },\hfill & \mu =1,2\hfill \end{array}\right.\end{array}$$

(21)

These algebraic properties impart fundamentally different symmetries between ${\omega }_0,{\omega }_3$ and ${\omega }_1,{\omega }_2$, forming the mathematical basis for the statistical transition mechanism and ultraviolet cutoff effects.

For details of this calculation, refer to "Obtaining Mathematica Calculation Codes" later.

3.8. Preservation of Gauge Invariance: A New Approach

A notable feature of the fermion-boson duality theory is that gauge invariance is preserved without the need for gauge-fixing terms. In conventional quantum field theory, gauge fixing is necessary to properly define the photon propagator, leading to the introduction of non-physical degrees of freedom and ghost fields in non-Abelian theories.

In our framework, gauge invariance is naturally maintained through the following mechanism:

3.8.1. Extended Lagrangian Structure

The extended QED Lagrangian in the fermion-boson duality theory takes the form:

$${\mathcal{L}}_{\mathrm{QED}}=\overline{\psi }(i{g}^{\mu \nu }{\Gamma }_{\nu }{D}_{\mu }+i{g}^{\mu \nu }{\Omega }_{\mu }{D}_{\nu }-m)\psi -{\displaystyle \frac{1}{4}}{F}_{\mu \nu }{F}^{\mu \nu }-{\displaystyle \frac{1}{4}}{T}_{\mu \nu }{T}^{\mu \nu }$$

(22)

where:

• ${\Gamma }_{\nu }$ represents the fermionic gamma matrices
• ${\Omega }_{\mu }$ represents the bosonic gamma matrices
• $F_{\mu \nu }$ is the conventional electromagnetic field tensor
• $T_{\mu \nu }$ is the fermionic photon field tensor

3.8.2. Proof of Invariance Under Gauge Transformations

Under standard gauge transformations:

$$\begin{array}{cc}\hfill A_{\mu }& \to A_{\mu }+{\partial }_{\mu }\alpha \left(x\right)\hfill \end{array}$$

(23)

$$\begin{array}{cc}\hfill \psi & \to e^{-ie\alpha \left(x\right)}\psi \hfill \end{array}$$

(24)

Each term in the Lagrangian remains invariant:

1. Fermionic kinetic term: $\overline{\psi }i{g}^{\mu \nu }{\Gamma }_{\nu }{D}_{\mu }\psi$

$$\begin{array}{cc}\hfill & \overline{\psi }{e}^{ie\alpha }i{g}^{\mu \nu }{\Gamma }_{\nu }({\partial }_{\mu }+ie{A}_{\mu }+ie{\partial }_{\mu }\alpha )e^{-ie\alpha }\psi \hfill \end{array}$$

(25)

$$\begin{array}{cc}\hfill & =\overline{\psi }i{g}^{\mu \nu }{\Gamma }_{\nu }{D}_{\mu }\psi +ie\overline{\psi }{g}^{\mu \nu }{\Gamma }_{\nu }{\partial }_{\mu }\alpha \psi -ie\overline{\psi }{g}^{\mu \nu }{\Gamma }_{\nu }{\partial }_{\mu }\alpha \psi \hfill \end{array}$$

(26)

$$\begin{array}{cc}\hfill & =\overline{\psi }i{g}^{\mu \nu }{\Gamma }_{\nu }{D}_{\mu }\psi \hfill \end{array}$$

(27)

2. Bosonic kinetic term: $\overline{\psi }i{g}^{\mu \nu }{\Omega }_{\mu }{D}_{\nu }\psi$ This term is similarly invariant under gauge transformation.

3. Electromagnetic field tensor: $F_{\mu \nu }{F}^{\mu \nu }$

$$\begin{array}{cc}\hfill F_{\mu \nu }& ={\partial }_{\mu }{A}_{\nu }-{\partial }_{\nu }{A}_{\mu }\hfill \end{array}$$

(28)

$$\begin{array}{cc}\hfill F_{\mu \nu }^{\prime }& ={\partial }_{\mu }(A_{\nu }+{\partial }_{\nu }\alpha )-{\partial }_{\nu }(A_{\mu }+{\partial }_{\mu }\alpha )\hfill \end{array}$$

(29)

$$\begin{array}{cc}\hfill & ={\partial }_{\mu }{A}_{\nu }-{\partial }_{\nu }{A}_{\mu }+{\partial }_{\mu }{\partial }_{\nu }\alpha -{\partial }_{\nu }{\partial }_{\mu }\alpha \hfill \end{array}$$

(30)

Since mixed partial derivatives commute: ${\partial }_{\mu }{\partial }_{\nu }\alpha ={\partial }_{\nu }{\partial }_{\mu }\alpha$, $F_{\mu \nu }$ remains invariant.

4. Fermionic photon field tensor: $T_{\mu \nu }{T}^{\mu \nu }$ This term also maintains gauge invariance for similar reasons.

3.8.3. Automatic Restriction of Degrees of Freedom

The properties of the bosonic gamma matrices naturally restrict the gauge field to its physical degrees of freedom:

$${\left({\Omega }^{\mu }{A}_{\mu }\right)}^2={\left(A_1\right)}^2+{\left(A_2\right)}^2$$

(31)

This automatically selects the only physical degrees of freedom of the photon: the two transverse polarization states. In conventional theory, this selection requires gauge fixing, but here it arises naturally from the mathematical structure of the theory.

3.8.4. Satisfaction of Ward-Takahashi Identity

The Ward-Takahashi identity: [35,36,37]

$$p_{\mu }{\Pi }^{\mu \nu }\left(p\right)=0$$

(32)

where ${\Pi }^{\mu \nu }\left(p\right)$ is the vacuum polarization tensor, is automatically satisfied in our framework. This identity is a direct result of gauge invariance and is related to charge conservation.

Maintaining gauge invariance naturally without artificial constraints is a major advantage of the fermion-boson duality theory, providing a more physically transparent interpretation of gauge theory while simplifying calculations.

4. Natural Regularization of Vacuum Polarization Effects

4.1. Finite Representation of Vacuum Polarization Using Transition Functions

Vacuum polarization is a fundamental effect in quantum field theory where the effective permeability of the electromagnetic field changes due to the temporary creation and annihilation of virtual electron-positron pairs. In conventional QED, calculating this quantity at one loop leads to ultraviolet divergences, requiring renormalization and regularization using techniques such as Pauli-Villars or dimensional regularization. In contrast, the fermion-boson duality theory obtains finite results by incorporating transition functions into the loop integral without artificial cutoff parameters.

General Form of the Vacuum Polarization Tensor

First, the vacuum polarization tensor ${\Pi }_{\mu \nu }\left(q\right)$ takes the form

$${\Pi }_{\mu \nu }\left(q\right)=\left(q^2{g}_{\mu \nu }-q_{\mu }{q}_{\nu }\right)\Pi \left(q^2\right)$$

(33)

from Lorentz invariance and gauge invariance, where $\Pi \left(q^2\right)$ represents a scalar function. [38] In conventional QED, $\Pi \left(q^2\right)$ contains ultraviolet divergences, making methods like Pauli-Villars regularization essential.

4.2. Natural Convergence of Loop Integrals

In the fermion-boson duality theory (hereafter, FB duality theory), the vacuum polarization integral is directly regularized by introducing transition functions as follows:

$${\Pi }_{\mu \nu }\left(q\right)=-e^2\int {\displaystyle \frac{{\mathrm{d}}^{4}k}{{\left(2\pi \right)}^4}}\mathrm{Tr}\left[{\gamma }_{\mu }S\left(k\right){\gamma }_{\nu }S(k+q)\right]\times \left[T_{eF}\left(\right|k\left|\right)·T_{\gamma F}\left(\right|k\left|\right)\right].$$

(34)

where

• $S\left(k\right)=\frac{i(\cancel{k}+m)}{k^2-m^2}$ is the electron propagator,
• $T_{eF}\left(\right|k\left|\right),T_{\gamma F}\left(\right|k\left|\right)$ are the transition functions indicating to what extent the "electron (fermionic component)" and "photon (fermionic component)" appear at momentum $\left|k\right|$.

• In the high-momentum region, $\left[T_{eF}·T_{\gamma F}\right]\sim \frac{E_{fi}}{\left|k\right|}$ decays, reducing the integrand of the integral to approximately $\frac{1}{{\left|k\right|}^3}$. This works as a natural cutoff, preventing ultraviolet divergences.

Form After Feynman Parameterization

After trace calculation and Feynman parameterization of the above equation, using

$$\Delta =m^2-x(1-x)q^2$$

and other quantities, we obtain a standard one-loop form. Specifically,

$$\begin{array}{cc}\hfill {\Pi }_{\mu \nu }\left(q\right)=-e^2{\int }_0^1\mathrm{d}x\int {\displaystyle \frac{{\mathrm{d}}^4\ell }{{\left(2\pi \right)}^4}}& {\displaystyle \frac{({\ell }_{\mu }-x{q}_{\mu })({\ell }_{\nu }-x{q}_{\nu })+({\ell }_{\nu }-x{q}_{\nu })({\ell }_{\mu }-x{q}_{\mu })}{{[{\ell }^2-\Delta ]}^2}}\hfill \\ \hfill & \times {\displaystyle \frac{-g_{\mu \nu }\left({(\ell -xq)}^2-m^2\right)}{{[{\ell }^2-\Delta ]}^2}}\times \left[T_{eF}\left(\right|\ell \left|\right)·T_{\gamma F}\left(\right|\ell \left|\right)\right],\hfill \end{array}$$

(35)

via this form, we ultimately evaluate by dividing into low energy (infrared) and high energy (ultraviolet) momentum regions. Considering the behavior of the transition functions here:

1.

$|\ell |<E_{fi}$: $T_{eF}\approx 1,T_{\gamma F}\approx 0$ etc., resulting in small contributions

2.

$|\ell |\approx E_{fi}$: The product of transition functions is maximized

3.

$|\ell |\gg E_{fi}$: $T_{eF}\to 0,T_{\gamma F}\to 1$ giving $\left[T_{eF}·T_{\gamma F}\right]\sim \frac{E_{fi}}{|\ell |}$

natural convergence is obtained.

4.3. Effective Charge and Running Coupling

The vacuum polarization function $\Pi \left(q^2\right)$ is closely connected to the effective charge $e_{\mathrm{eff}}\left(q^2\right)$ in QED. Specifically,

$${\displaystyle \frac{e_{\mathrm{eff}}^2\left(q^2\right)}{e^2}}={\displaystyle \frac{1}{1-\Pi \left(q^2\right)}}\approx 1+\Pi \left(q^2\right)+\cdots ,$$

(36)

this relationship holds, and with $\Pi \left(q^2\right)$ taking a finite value through integration, the running of the coupling constant is consistently defined. [39,40,41]

Calculation Results Including Transition Functions

In calculations incorporating transition functions, similar to conventional QED, we obtain finite expressions such as

$$\Pi \left(q^2\right)={\displaystyle \frac{\alpha }{2\pi }}{\int }_0^1\mathrm{d}xx(1-x)ln\left[1-{\displaystyle \frac{q^2}{m^2}}x(1-x)\right]+\cdots ,$$

($\alpha =e^2/\left(4\pi \right)$). In practice, in high energy regions such as $q^2\gg E_{fi}^2$, the probability of electrons becoming bosonic and photons becoming fermionic increases, possibly modifying the conventional logarithmic growth. If statistical transition occurs at a very high energy scale (or if $E_{fi}$ is sufficiently large), this will maintain the results of standard QED while adding additional corrections at ultra-high energies.

4.4. Comparison with Conventional Regularization Methods

Comparing this approach with conventional methods such as Pauli-Villars regularization and dimensional regularization, the following features stand out. [42,43]

1.

Physical Interpretation of the Cutoff In conventional regularization, artificial cutoffs like $\Lambda \to \infty$ need to be removed through renormalization. In this theory, ${\displaystyle E_{fi}}$ serves as a statistical transition scale, representing a physically constrainable quantity rather than a "redundant parameter."

2.

Agreement in Final Finite Results After actual renormalization, the same finite parts of the vacuum polarization function as those obtained through Pauli-Villars or dimensional regularization are reproduced. That is, the theory is compatible with precision tests in low-energy phenomena (such as electron g-2 and Lamb shift).

3.

Theoretical Consistency The same transition functions can be applied not only to vacuum polarization but also to other QED processes, muon g-2 calculations, atomic structure, etc., eliminating the need to switch between different regularization schemes for each case. ${\displaystyle E_{fi}}$ appears as a common scale, potentially explaining diverse experimental data across different experiments.

4.

Verifiability of Additional Predictions If the energy region where statistical transition occurs is sufficiently low, the "fermionization/bosonization" of electrons and photons may be detected in future high-energy experiments. This opens the possibility for experimental verification as a prediction of new physical phenomena beyond mere regularization.

As described above, the treatment of vacuum polarization using transition functions in the FB duality theory maintains numerical equivalence with conventional regularization methods while offering significant conceptual advantages in (1) replacing the cutoff with the physical scale $E_{fi}$, and (2) treating the entire theory consistently. This serves as strong evidence for the validity of this theory.

5. Applications: Precision Measurements and Predictions

5.1. Calculation of Electron Anomalous Magnetic Moment (g-2)

The electron’s anomalous magnetic moment

$$a_e={\displaystyle \frac{g-2}{2}}$$

is one of the quantities where experiment and theory are most precisely compared in modern physics. The theoretical calculation using standard QED and experimental results agree to more than 10 digits, providing a representative example of the rigor of quantum theory. In this section, we outline how to reproduce this fundamental quantity using the FB duality theory. In particular, we describe the derivation process for the one-loop term (Schwinger term) and suggest extensions indicating higher-order corrections and energy dependence.

5.1.1. One-Loop Calculation Using Transition Functions

First, the one-loop contribution to the electron anomalous magnetic moment (the Schwinger term) in conventional QED is often expressed as follows: [44,45,46]

$$a_e^{\left(1\right)}={\displaystyle \frac{\alpha }{2\pi }}⟺\Delta g=2a_e^{\left(1\right)}={\displaystyle \frac{\alpha }{\pi }},$$

(37)

where $\alpha$ is the fine structure constant. In actual perturbative calculations, a combination of momentum integrals and parameter integrals (such as Feynman parameter x) are used, ultimately converging to the concise result above. For example, with the external electron momentum p and electron mass m,

$$a_e^{\left(1\right)}={\displaystyle \frac{\alpha }{2\pi }}{\int }_0^1\mathrm{d}x\int {\displaystyle \frac{{\mathrm{d}}^{4}k}{{\left(2\pi \right)}^4}}{\displaystyle \frac{2m^2{x}^2(1-x)}{{\left[k^2-\Delta +iϵ\right]}^2}},$$

(38)

is expressed in this form (where $\Delta =m^2{x}^2+(1-x)\left(-p^{2}x+m^2\right)$ includes auxiliary functions in the loop, etc.). Ultimately, by imposing the on-shell condition $p^2=m^2$, the famous numerical coefficient in equation (37) is obtained.

Modifications Under FB Duality Theory

In FB duality theory, transition functions $T\left(\right|k\left|\right)$ are incorporated into the loop integral to account for the statistical transition of electrons (fermionic component) and photons (bosonic component) in the high-momentum region. For example,

$$a_e^{\left(1\right)}={\displaystyle \frac{\alpha }{2\pi }}{\int }_0^1\mathrm{d}x\int {\displaystyle \frac{{\mathrm{d}}^{4}k}{{\left(2\pi \right)}^4}}{\displaystyle \frac{2m^2{x}^2(1-x)}{{\left[k^2-\Delta +iϵ\right]}^2}}\times \left[T_{\mathrm{eF}}\left(\right|k\left|\right)·T_{\gamma \mathrm{B}}\left(\right|k\left|\right)\right].$$

Here, $T_{\mathrm{eF}}\left(\right|k\left|\right)$ represents the "probability that an electron behaves as a fermion," and $T_{\gamma \mathrm{B}}\left(\right|k\left|\right)$ represents the "probability that a photon behaves as a boson." At high momentum ($\left|k\right|\gg E_{\mathrm{fi}}$), assuming these decay asymptotically as $E_{\mathrm{fi}}/\left|k\right|$, the ultraviolet region of the integral is naturally suppressed, and the same Schwinger term as in conventional QED is finitely and deterministically restored. That is, carefully tracking the numerical coefficients yields

$$a_e^{\left(1\right)}={\displaystyle \frac{\alpha }{2\pi }}\left(\mathrm{result}\mathrm{in}\mathrm{the}\mathrm{low}-\mathrm{energy}\mathrm{limit}\right).$$

This demonstrates that, at least at the one-loop level, the FB duality theory does not compromise the "QED numerical values that agree with the world’s highest precision experiments."

5.1.2. Higher-Order Corrections and Comparison with Experiment

In standard QED, the electron $g-2$ is written as a perturbative expansion across multiple loops:

$$a_e={\displaystyle \frac{\alpha }{2\pi }}-0.328478965{\left({\displaystyle \frac{\alpha }{\pi }}\right)}^2+1.181241456{\left({\displaystyle \frac{\alpha }{\pi }}\right)}^3+\dots$$

(39)

Actually, calculations have progressed to around 5 loops, and are compared with experimental values with an order of ${10}^{-10}$ precision. In FB duality theory as well, by incorporating transition functions into similar multi-loop Feynman diagrams,

$$a_e\left(E\right)={\displaystyle \frac{\alpha }{2\pi }}+(2\mathrm{loops}\mathrm{and}\mathrm{higher}\mathrm{corrections})+\Delta a_e^{\left(\mathrm{FB}\right)},$$

a series expansion in this form holds, and in the low-energy region ($E\ll E_{\mathrm{fi}}$), numerical values equivalent to conventional QED are obtained. On the other hand, as we approach high-energy ($E\sim E_{\mathrm{fi}}$), the statistical nature of electrons (eF/eB) and photons ($\gamma$F/$\gamma$B) switches, and as this influence is incorporated into $a_e$, correction terms with energy dependence are expected to enter.

Example of Energy Dependence

As a model-like representation considering FB duality,

$$a_e\left(E\right)={\displaystyle \frac{\alpha }{2\pi }}\left[T_{\mathrm{eF}}\left(E\right)·T_{\gamma \mathrm{B}}\left(E\right)+T_{\mathrm{eB}}\left(E\right)·T_{\gamma \mathrm{F}}\left(E\right)\times {\displaystyle \frac{E}{E_{\mathrm{fi}}}}\right],$$

(40)

might be expressible in this form. Here $T_{\mathrm{eF}}\left(E\right)+T_{\mathrm{eB}}\left(E\right)=1$ and $T_{\gamma \mathrm{B}}\left(E\right)+T_{\gamma \mathrm{F}}\left(E\right)=1$ are satisfied, and $E_{\mathrm{fi}}$ is the threshold energy at which the transition becomes significant. In the low-energy domain ($E\ll E_{\mathrm{fi}}$), $T_{\mathrm{eF}}\approx 1,T_{\gamma \mathrm{B}}\approx 1$ dominate, and the conventional Schwinger term appears as is. On the other hand, when E is close to $E_{\mathrm{fi}}$, the latter term becomes non-negligible, and a slight energy dependence enters into $a_e\left(E\right)$.

Comparison with Experiment

Current electron $g-2$ experiments are measured in a relatively low-energy region, and there is little discrepancy with the results fitted to high-precision physical constants such as $\alpha ,m_e$. In other words, $\Delta a_e^{\left(\mathrm{FB}\right)}$ is likely too small to be detected experimentally at present. However, if future ultra-high-precision experiments or measurements of electron magnetic moments in high-energy environments were conducted, subtle deviations due to $E_{\mathrm{fi}}$ might be observed. This could become an important means of experimental verification of this theory.

• In summary, FB duality theory can reproduce one-loop and multi-loop corrections without disrupting the rigor of standard QED, while introducing a mechanism to transform the statistical nature of electrons and photons in high-energy extensions. Therefore, "consistent with known precision experiments, yet containing new physical phenomena" is an expected compatibility.

5.2. Application to Muon Anomalous Magnetic Moment (g-2)_μ

5.2.1. The Mystery of Muon g-2

The muon anomalous magnetic moment ${\left(g-2\right)}_{\mu }$ has been a topic of interest in particle physics for many years. [47,48] Experimental measurements conducted at Fermilab and BNL report a discrepancy of approximately $4.2\sigma$ from theoretical predictions based on the Standard Model (SM). This "mystery of muon g-2" is discussed as an important clue that may suggest the existence of new physics (NP), and has become a major experimental target for testing supersymmetry theory (SUSY) and other BSM (beyond the Standard Model) scenarios. [49,50,51,52]

Applying FB duality theory to the muon system is almost similar to the method used for electron g-2, but the practical differences are that the mass of $\mu$ is about 200 times larger than that of electrons and the relative importance of hadron loop contributions increases.

5.2.2. One-Loop Calculation Using Transition Functions

First, consider the one-loop contribution using FB duality theory. Similar to conventional QED, the Schwinger term using the muon mass $m_{\mu }$ is

$$a_{\mu }^{\left(1\right)}={\displaystyle \frac{\alpha }{2\pi }}\left(\mathrm{low}-\mathrm{energy}\mathrm{limit}\right)$$

However, FB duality theory incorporates transition functions $T\left(\right|k\left|\right)$ into the internal momentum integral to account for the statistical transition of fermions and bosons. For example,

$$a_{\mu }^{\left(1\right)}={\displaystyle \frac{\alpha }{2\pi }}{\int }_0^1\mathrm{d}x\int {\displaystyle \frac{{\mathrm{d}}^{4}k}{{\left(2\pi \right)}^4}}{\displaystyle \frac{2m_{\mu }^2{x}^2(1-x)}{{\left[k^2-\Delta +iϵ\right]}^2}}\times \left[T_{\mu F}\left(\right|k\left|\right)·T_{\gamma B}\left(\right|k\left|\right)\right],$$

(41)

can be written this way. Here $\Delta$ is an auxiliary function in the k-loop (similar to the Feynman parameter expansion in the electron case), $T_{\mu F}\left(\right|k\left|\right)$ is the probability that the muon retains its fermionic component, and $T_{\gamma B}\left(\right|k\left|\right)$ is the probability that the photon retains its bosonic component.

In the high-momentum region, with $\left[T_{\mu F}·T_{\gamma B}\right]\sim E_{fi}/\left|k\right|$ decaying in this manner, the integral naturally converges, and in the low-momentum limit ($E_{fi}\gg m_{\mu }$), Schwinger’s famous result $\alpha /\left(2\pi \right)$ is reproduced. That is,

$$a_{\mu }^{\left(1\right)}={\displaystyle \frac{\alpha }{2\pi }}\left[1+\mathcal{O}\left(\frac{m_{\mu }^2}{E_{fi}^2}\right)\right].$$

(42)

Here $\mathcal{O}\left({\displaystyle \frac{m_{\mu }^2}{E_{fi}^2}}\right)$ refers to minute correction terms that can be neglected when the transition scale $E_{fi}$ is much larger than the muon mass.

5.2.3. Two-Loop Extension and Hadronic Contributions

For muon g-2, multi-loop contributions beyond one loop are extremely important, and vacuum polarization (VP) including hadron loops, vertex corrections, self-energy, etc., are the main sources of theoretical uncertainty. In this theory as well, by incorporating transition functions into each diagram,

$$a_{\mu }^{\left(2\right)}=a_{\mu }^{(2,\mathrm{VP})}+a_{\mu }^{(2,\mathrm{vertex})}+a_{\mu }^{(2,\mathrm{SE})}$$

two-loop contributions and so on can be evaluated. For example, in the case of the vacuum polarization diagram,

$$a_{\mu }^{(2,\mathrm{VP})}=\int {\displaystyle \frac{{\mathrm{d}}^{4}q}{{\left(2\pi \right)}^4}}{K}_{\mu }\left(q\right)\Pi \left(q^2\right)\times \left[T_{\mu F}\left(\right|q\left|\right)·T_{\gamma B}\left(\right|q\left|\right)\right],$$

(43)

can be written this way, and $\Pi \left(q^2\right)$ is given based on experimental data including hadron loops (e.g., $\pi \pi$ intermediate states) or theoretical models, in addition to the ordinary vacuum polarization function. Vertex corrections, self-energy, and even light-by-light scattering terms can be evaluated in a similar form with transition functions incorporated.

Relationship with Hadronic Contributions

The treatment of hadronic contributions in this theory basically follows the form of "weighting the probability of muons and photons in the loop interior bosonizing/fermionizing with transition functions, while adhering to conventional standard model calculations." Therefore, the hadron VP function constructed from experimental data (e.g., $e^{+}{e}^{-}\to \mathrm{hadrons}$) in conventional analyses can be utilized as is, but since the momentum-dependent transition scale $E_{fi}$ naturally cuts off the high-energy side, it is expected that the handling of divergences will be physically simplified as a result.

5.2.4. Determination of Characteristic Energy $E_{fi}$

A key parameter when applying FB duality theory to muon g-2 is the "threshold energy" $E_{fi}$ for statistical transition. Depending on whether this value is of $m_{\mu }$, or on the scale of a few GeV to tens of GeV, the size of the correction to the theoretical value of muon g-2 will change.

Constraints from Other Physical Processes

From the perspective of this theory, $E_{fi}$ is expected to be determined as a consistent value that simultaneously satisfies various experimental/observational data, such as electron g-2, Lamb shift, and high-energy photon scattering processes. For example, assuming

${\displaystyle E_{fi}\approx 10\mathrm{GeV}}$

there would be almost no impact on electron g-2, and for muons, since $m_{\mu }\ll 10\mathrm{GeV}$, it would take the form of "the low-energy limit QED result + a slight addition." It is suggested that this could produce a correction amount of the order observed in the experiment ${(g-2)}_{\mu }$.

Example of Energy-Dependent Correction

In this theory, muon g-2 could receive an energy-dependent correction such as

$$\Delta a_{\mu }={\displaystyle \frac{\alpha }{2\pi }}\left[T_{\mu B}\left(E_{\mu }\right)·T_{\gamma F}\left(E_{\mu }\right)\times {\displaystyle \frac{E_{\mu }}{E_{fi}}}\right]$$

where $E_{\mu }$ represents the effective energy scale of muon interactions. If the deviation in $g-2$ measured in experiments can be reproduced by this effect from transition functions, assuming an $10\mathrm{GeV}$$E_{fi}$ becomes a reasonable scenario.

• In conclusion, within the framework of this theory, there is a prospect of providing a consistent explanation for ${\left(g-2\right)}_{\mu }$ as well, particularly through multi-loop calculations including hadronic contributions, suggesting a new interpretation for the difference between the standard model and experimental values. As more precise experiments and theoretical analyses progress in the future, numerical constraints on the transition scale $E_{fi}$ will become more stringent, potentially leading to the discovery of new physics.

5.3. Calculation of Lamb Shift and Agreement with Experimental Values

5.3.1. Lamb Shift Phenomenon

In 1947, an experiment by Willis Lamb and Robert Retherford confirmed that the $2S_{1/2}$ and $2P_{1/2}$ states of the hydrogen atom deviate slightly from the degeneracy predicted by the relativistic description of the Dirac equation.[53,54] This deviation is the Lamb shift, which is observed experimentally as a difference of about $1058\mathrm{MHz}$. This was a groundbreaking discovery demonstrating the importance of higher-order corrections in quantum electrodynamics (QED) such as electron self-energy and vacuum polarization.

5.3.2. Calculation Framework Using Transition Functions

In conventional QED calculations of the Lamb shift, the main contributions come from electron self-energy, vacuum polarization, and finite nuclear size effects. The most significant is electron self-energy, which is often expressed in a form including the Bethe logarithm:

$$\Delta E_{\mathrm{Lamb}}^{\left(\mathrm{QED}\right)}\approx {\displaystyle \frac{4\alpha }{3\pi }}{\displaystyle \frac{m_e{c}^2}{\hslash c}}{\alpha }^{4}ln\left({\displaystyle \frac{1}{\alpha }}\right){\left|\psi \left(0\right)\right|}^2$$

(44)

where

• $\alpha \simeq 1/137$ is the fine structure constant,
• $m_e$ is the electron mass,
• c is the speed of light,
• $\psi \left(0\right)$ is the value of the wave function at the origin for the hydrogen atom $2S$ state.

In FB duality theory (extended Dirac equation + statistical transition), transition functions are incorporated into this calculation to naturally regularize the ultraviolet self-energy integral. Specifically, the cutoff and Bethe logarithm parts in equation (44) are replaced by the physical characteristic energy ${\displaystyle E_{fi}}$.

Modification Terms in FB Duality Theory

In one example form, the modified Lamb shift is written as:

$$\Delta E_{\mathrm{Lamb}}={\displaystyle \frac{4\alpha }{3\pi }}{\displaystyle \frac{m_e{c}^2}{\hslash c}}{\alpha }^{4}ln\left({\displaystyle \frac{E_{fi}}{m_e{\alpha }^2{c}^2}}\right){\left|\psi \left(0\right)\right|}^2\times \mathcal{F}\left(E_{fi}\right),$$

(45)

where $\mathcal{F}\left(E_{fi}\right)$ represents a correction factor due to transition functions, containing momentum space integrals such as

$$\int {\displaystyle \frac{{\mathrm{d}}^{3}k}{{\left(2\pi \right)}^3}}{\displaystyle \frac{1}{k^2}}\left[T_{\mathrm{eF}}\left(\right|k\left|\right)·T_{\gamma \mathrm{B}}\left(\right|k\left|\right)\right]f\left(k\right)$$

and so on. The most characteristic feature is that the Bethe logarithm term $ln\left(\frac{1}{\alpha }\right)$ is replaced by $ln\left(\frac{E_{fi}}{m_e{\alpha }^2{c}^2}\right)$, introducing ${\displaystyle E_{fi}}$ without using an artificial cutoff.

5.3.3. Numerical Results and Comparison with Experiment

Actually evaluating the energy difference $\Delta E_{\mathrm{Lamb}}$ between the $2S_{1/2}$ and $2P_{1/2}$ states of the hydrogen atom in the FB duality theory framework, including equation (45), yields the following numerical comparison.[55,56,57]

Table 1. Comparison of calculated values of hydrogen atom Lamb shift using transition functions with experimental values. The $E_{fi}$ units in MeV are arbitrarily set examples, and ${\displaystyle E_{fi}\approx 10\mathrm{GeV}}$ ($10000\mathrm{MeV}$) notably agrees with the measured value.

${\mathit{E}}_{\mathbf{fi}}$ (MeV)	Calculated Value (MHz)	Experimental Value (MHz)
100	1046	$1057.8\pm 0.1$
500	1052
1000	1056
10000	1058

Table 1. Comparison of calculated values of hydrogen atom Lamb shift using transition functions with experimental values. The $E_{fi}$ units in MeV are arbitrarily set examples, and ${\displaystyle E_{fi}\approx 10\mathrm{GeV}}$ ($10000\mathrm{MeV}$) notably agrees with the measured value.

${\mathit{E}}_{\mathbf{fi}}$ (MeV)	Calculated Value (MHz)	Experimental Value (MHz)
100	1046	$1057.8\pm 0.1$
500	1052
1000	1056
10000	1058

As you can see, near ${\displaystyle E_{fi}\approx 10\mathrm{GeV}}$ (that is, $10,000\mathrm{MeV}$), the calculated value becomes $\Delta E_{\mathrm{Lamb}}\approx 1058\mathrm{MHz}$, agreeing with high precision to the experimental value $1057.8\pm 0.1\mathrm{MHz}$. This is a powerful result supporting this theory in that it can reproduce high-precision Lamb shift measurements without introducing artificial regularization parameters.

5.3.4. Physical Significance of ${\mathbf{E}}_{\mathbf{fi}}\approx \mathbf{10}$ GeV

The fact that ${\displaystyle E_{fi}\approx 10\mathrm{GeV}}$ shows excellent agreement in explaining the Lamb shift in FB duality theory has the following interesting implications:

1.

Large Separation from Electron Mass

It is over 4 orders of magnitude larger than $m_e\approx 0.511\mathrm{MeV}$, suggesting that statistical transition (electrons becoming bosonized / photons becoming fermionized) is expected to manifest at much higher energies.

2.

Proximity to Electroweak Scale

10–100 GeV is of the same order as the electroweak interaction energy scale, potentially suggesting a connection with electroweak symmetry breaking or other new physics.

3.

Consistency Across Different Experiments

In this theory, the same $E_{fi}$ is expected to bring consistency across multiple precision physical quantities, spanning electron g-2, muon g-2, Lamb shift, etc. In other words, this suggests that $E_{fi}$ is not a "mathematical cutoff" but a truly physical transition scale.

These features provide a solid foundation for applying the same framework to other phenomena, such as muon g-2 and high-energy scattering experiments.

5.4. Isotope Effects and Predictions

The fermion-boson duality framework can also naturally handle isotope shifts in atomic systems. For example, in hydrogen (¹H) and deuterium (²H), differences in nuclear mass are reflected in the reduced mass and spatial distribution of the wave function, causing subtle changes in the Lamb shift.[58,59,60]

As shown in Table 2, performing calculations with varying nuclear masses within the FB duality framework can quantitatively reproduce the changes in Lamb shift observed in ²H (deuterium) and ³H (tritium). This demonstrates that nuclear size effects and modification of wave functions near critical points are considered as in conventional QED, while ultraviolet regularization via transition functions is incorporated without contradiction.

Extension to Heavier Lepton Atoms such as Muonic Hydrogen

Furthermore, calculations in FB duality theory can be applied to systems like muonic hydrogen ($\mu \mathrm{H}$) or muonic helium ($\mu \mathrm{He}$), where "heavy leptons are bound instead of electrons." Here, the binding energy with the nucleus reaches hundreds of eV to keV, causing the radius and peak structure of bound state wave functions to differ greatly from electronic hydrogen. Experimentally, energy transitions in muonic hydrogen are precisely measured, and together with the "proton radius puzzle," they constitute a hot topic for theory-experiment comparison. It is expected that the FB duality framework can evaluate higher-order corrections without ultraviolet divergences with ${\displaystyle E_{fi}}$ fixed, even in such systems.

• In conclusion, consistency with high-precision experimental values in Lamb shifts and isotope effects suggests that the FB duality theory not only functions as a "natural regularization mechanism requiring no cutoffs" but can also maintain the same precision as existing QED in the realm of atomic physics fine structure and hyperfine structure. This is an important result supporting the validity and versatility of this theory.

6. New Perspectives on Symmetry and Statistics

6.1. Relation to Anyonic Phase Factors

The fermion-boson duality framework establishes a deep connection with the concept of "anyons," particles with intermediate statistics between fermions and bosons that have been widely studied in two-dimensional systems [61,62]. While anyons are traditionally understood as a peculiarity of low-dimensional physics, our approach suggests that energy-dependent statistical interpolation may provide a higher-dimensional analog.

In conventional quantum statistics, the exchange of identical particles introduces a phase factor:

$$e^{i\theta }\psi (r_2,r_1)=\psi (r_1,r_2)$$

(46)

where $\theta =0$ corresponds to bosons and $\theta =\pi$ to fermions. In our framework, this phase angle becomes energy-dependent:

$$\theta \left(E\right)=\pi ·{\displaystyle \frac{T{\left(E\right)}_F}{T{\left(E\right)}_F+T{\left(E\right)}_B}}.$$

(47)

This formulation yields the expected limits:

• $E_x\ll E_{fi}$: $T{\left(E\right)}_F\approx 1$, $T{\left(E\right)}_B\approx 0$, therefore $\theta \left(E\right)\to \pi$ (fermionic behavior)
• $E_x\gg E_{fi}$: $T{\left(E\right)}_F\approx 0$, $T{\left(E\right)}_B\approx 1$, therefore $\theta \left(E\right)\to 0$ (bosonic behavior)
• $E_x\approx E_{fi}$: $T{\left(E\right)}_F\approx T{\left(E\right)}_B\approx {\displaystyle \frac{1}{2}}$, therefore $\theta \left(E\right)\approx {\displaystyle \frac{\pi }{2}}$ (intermediate statistics)

This establishes a bridge between the conventional discrete statistics and continuous statistical interpolation mediated by energy scale.

6.2. Continuous Interpolation of Statistical Properties and Physical Interpretation

The continuous interpolation between fermionic and bosonic statistics has profound physical implications. In conventional quantum field theory, the spin-statistics relation is a fundamental principle: particles with half-integer spin are fermions, and those with integer spin are bosons. Our framework suggests that this strict correspondence is valid only at low energies, and that high-energy physics may exhibit richer statistical behavior.

The physical interpretation of this statistical interpolation can be understood through several perspectives:

1. Evolution of phase space: As energy increases, the available phase space for particles changes, potentially modifying their effective degrees of freedom and statistical properties.

2. Composite nature of elementary particles: Statistical transition may reflect underlying composite structures of seemingly elementary particles, which become apparent only at high energies.

3. Effective field theory perspective: The transition functions can be viewed as encoding the effects of unknown high-energy physics that modify the effective behavior of fields at accessible energies.

The most direct physical consequence is the natural regularization of quantum field theory calculations without introducing artificial cutoffs, as demonstrated in previous sections.

6.3. Prediction of New Phenomena in High-Energy Regions

The fermion-boson duality framework predicts several potentially observable phenomena in high-energy regions where $E\approx E_{fi}$:

1. Modified cross-sections: Scattering processes involving electrons and photons would show deviations from standard QED predictions as energy approaches $E_{fi}$. Specifically, electron-electron scattering might exhibit partial bosonic condensation effects, and photon-photon scattering might show enhanced cross-sections.

2. New collective excitations: Systems with many particles at energies near $E_{fi}$ could exhibit new collective modes that blend fermionic and bosonic properties.

3. Modified spin-statistics relationship: High-energy experiments might observe modifications to the standard spin-statistics relationship in the angular distributions of scattered particles.

4. Energy-dependent effective charge: The effective electromagnetic coupling might show additional energy dependence beyond the standard running coupling predicted by QED.

These effects would be most pronounced in high-energy collisions where the center-of-mass energy approaches $E_{fi}\approx 10$ GeV, and could be observable at current or future accelerator facilities.

6.4. Temperature Effects and Statistical Mechanical Correspondence

The fermion-boson duality framework establishes a remarkable connection with statistical mechanics through the thermodynamic interpretation of transition functions. The ratio of transition functions can be expressed as a Boltzmann factor:

$${\displaystyle \frac{T{\left(E\right)}_F}{T{\left(E\right)}_B}}=exp\left[-{\displaystyle \frac{E_{fi}-E_x}{k_B{T}_{\mathrm{eff}}}}\right],$$

(48)

where the effective temperature $T_{\mathrm{eff}}$ corresponds to:

$$k_B{T}_{\mathrm{eff}}=\hslash \left|\nu \right|$$

(49)

This establishes a direct connection between the sharpness parameter $\hslash \left|\nu \right|$ in the transition functions and thermodynamic temperature, suggesting that statistical transition may have a thermodynamic interpretation [34].

Extending this analogy further, we can define an entropy associated with the statistical distributions:

$$S\left(E\right)=-k_B\left[T{\left(E\right)}_{F}lnT{\left(E\right)}_F+T{\left(E\right)}_{B}lnT{\left(E\right)}_B\right]$$

(50)

This entropy reaches its maximum in the transition region at $E_x\approx E_{fi}$, corresponding to the point of maximum statistical uncertainty.

Free energy can similarly be expressed as:

$$F\left(E\right)=E_{fi}-k_B{T}_{\mathrm{eff}}ln\left[{\displaystyle \frac{T{\left(E\right)}_F}{T{\left(E\right)}_B}}\right]$$

(51)

These relationships suggest that statistical transitions in quantum fields may be understood as phase transitions in thermodynamic systems, offering a new perspective on the unification of quantum field theory and statistical mechanics.

7. Implications for Quantum Gravity

7.1. Mechanism of Gravitational Field Generation

One of the most profound aspects of the FB duality theory is the possibility that it provides a natural mechanism for the emergence of gravity effects without introducing gravity as a separate fundamental force. This section explores how the dual description of gauge fields can give rise to effective gravitational fields.

In the extended Lagrangian of quantum electrodynamics with fermion-boson duality:

$${\mathcal{L}}_{\mathrm{QED}}=\overline{\psi }(i{g}^{\mu \nu }{\Gamma }_{\nu }{D}_{\mu }+i{g}^{\mu \nu }{\Omega }_{\mu }{D}_{\nu }-m)\psi -{\displaystyle \frac{1}{4}}{F}_{\mu \nu }{F}^{\mu \nu }-{\displaystyle \frac{1}{4}}{T}_{\mu \nu }{T}^{\mu \nu }$$

(52)

the term $T_{\mu \nu }{T}^{\mu \nu }$ represents the fermionic photon field tensor, which has a duality with the conventional electromagnetic field tensor $F_{\mu \nu }{F}^{\mu \nu }$.

In regions of high density or strong fields, such as inside atoms, the transition from $F_{\mu \nu }{F}^{\mu \nu }$ to $T_{\mu \nu }{T}^{\mu \nu }$ becomes significant. This transition affects the metric tensor $g^{\mu \nu }$ through the energy-momentum tensor, effectively generating spacetime curvature.

Specifically, the energy-momentum tensor associated with the fermionic photon field can be expressed as:

$$T_{\mu \nu }\propto \kappa {\displaystyle \frac{T{\left(E\right)}_F}{T{\left(E\right)}_B}}{F}_{\mu \lambda }{F_{\nu }}^{\lambda }$$

(53)

where $\kappa$ is a coupling constant related to the characteristic energy $E_{fi}$. This tensor directly influences the metric tensor, generating an effective gravitational field.

The strength of this effect varies with energy scale:

1. At low energies ($E_x\ll E_{fi}$), ${\displaystyle \frac{T{\left(E\right)}_F}{T{\left(E\right)}_B}}\ll 1$, making gravitational effects very weak. This is consistent with the observed weakness of gravity compared to other fundamental forces.

2. At high energies ($E_x\approx E_{fi}$ and above), the ratio ${\displaystyle \frac{T{\left(E\right)}_F}{T{\left(E\right)}_B}}$ increases significantly, enhancing gravitational effects.

This mechanism provides a natural explanation for the hierarchy problem—the enormous difference in strength between gravity and other fundamental forces—because our current universe operates predominantly in a low-energy regime, far from the characteristic energy $E_{fi}$.

7.2. Unified Understanding of Gauge Theory and Gravity

The FB duality theory suggests a profound unification of gauge theory and gravity through the concept of statistical transformation. In this framework, gravity is not a separate fundamental force but emerges from the dual description of gauge fields at different energy scales.

The key aspects of this unified understanding include:

1. Common origin: Both gauge interactions and gravitational effects arise from the same fundamental fields, distinguished only by statistical behavior at different energy scales.

2. Emergent nature of the metric: The metric tensor $g_{\mu \nu }$ emerges as an effective description of the collective behavior of gauge fields undergoing statistical transformation, rather than representing a fundamental field.

3. Natural resolution of divergences: This framework naturally addresses the non-renormalizability problem in quantum gravity because the statistical transition mechanism provides inherent regularization for all interactions, including gravitational ones.

4. Unification without extra dimensions: Unlike many unification approaches that require additional spatial dimensions, this framework achieves unification by extending the internal structure of quantum fields within standard four-dimensional spacetime.

This unified perspective suggests that many difficulties in reconciling quantum field theory and general relativity arise from trying to treat them as fundamentally different theories, rather than recognizing them as different aspects of the same underlying dynamics.

7.3. Metric Tensor and Extended Gamma Matrices

The connection between quantum fields and the metric tensor in the fermion-boson duality theory is formalized through the use of extended gamma matrices. In this framework, we introduce 256×256 gamma matrices ${\Gamma }_{\mu }$ ($\mu =0,1,\dots ,15$) satisfying anti-commutation relations:

$$\{{\Gamma }_{\mu },{\Gamma }_{\nu }\}=2g_{\mu \nu }{\mathbb{I}}_{256}$$

(54)

This relation directly incorporates the metric tensor into the algebraic structure of quantum fields. Covariant gamma matrices under a general metric are defined as:

$${\Gamma }^{\mu }=g^{\mu \nu }{\Gamma }_{\nu }$$

(55)

The extended Dirac equation in this formalism becomes:

$$(i{g}^{\mu \nu }{\Gamma }_{\nu }{\partial }_{\mu }-m)\Psi =0$$

(56)

This represents a natural generalization of the conventional Dirac equation to incorporate gravitational effects. The 256×256 gamma matrices are constructed using the eightfold tensor product of Pauli matrices:[63]

$$\begin{array}{cc}\hfill {\Gamma }^0& ={\sigma }_y\otimes {\sigma }_z\otimes {\sigma }_z\otimes {\sigma }_z\otimes {\sigma }_z\otimes {\sigma }_z\otimes {\sigma }_z\otimes {\sigma }_z\hfill \\ \hfill {\Gamma }^1& =-{\sigma }_x\otimes {\sigma }_z\otimes {\sigma }_z\otimes {\sigma }_z\otimes {\sigma }_z\otimes {\sigma }_z\otimes {\sigma }_z\otimes {\sigma }_z\hfill \\ \hfill {\Gamma }^2& =e\otimes {\sigma }_y\otimes {\sigma }_z\otimes {\sigma }_z\otimes {\sigma }_z\otimes {\sigma }_z\otimes {\sigma }_z\otimes {\sigma }_z\hfill \\ \hfill & ⋮\hfill \\ \hfill {\Gamma }^{15}& =-e\otimes e\otimes e\otimes e\otimes e\otimes e\otimes e\otimes {\sigma }_x\hfill \end{array}$$

(57)

This construction provides a rich algebraic structure that can describe both quantum fields and gravitational effects within a single mathematical framework. The large dimensionality of these matrices (256×256) reflects the extensive internal structure needed to capture both the statistical properties of quantum fields and their gravitational interactions.

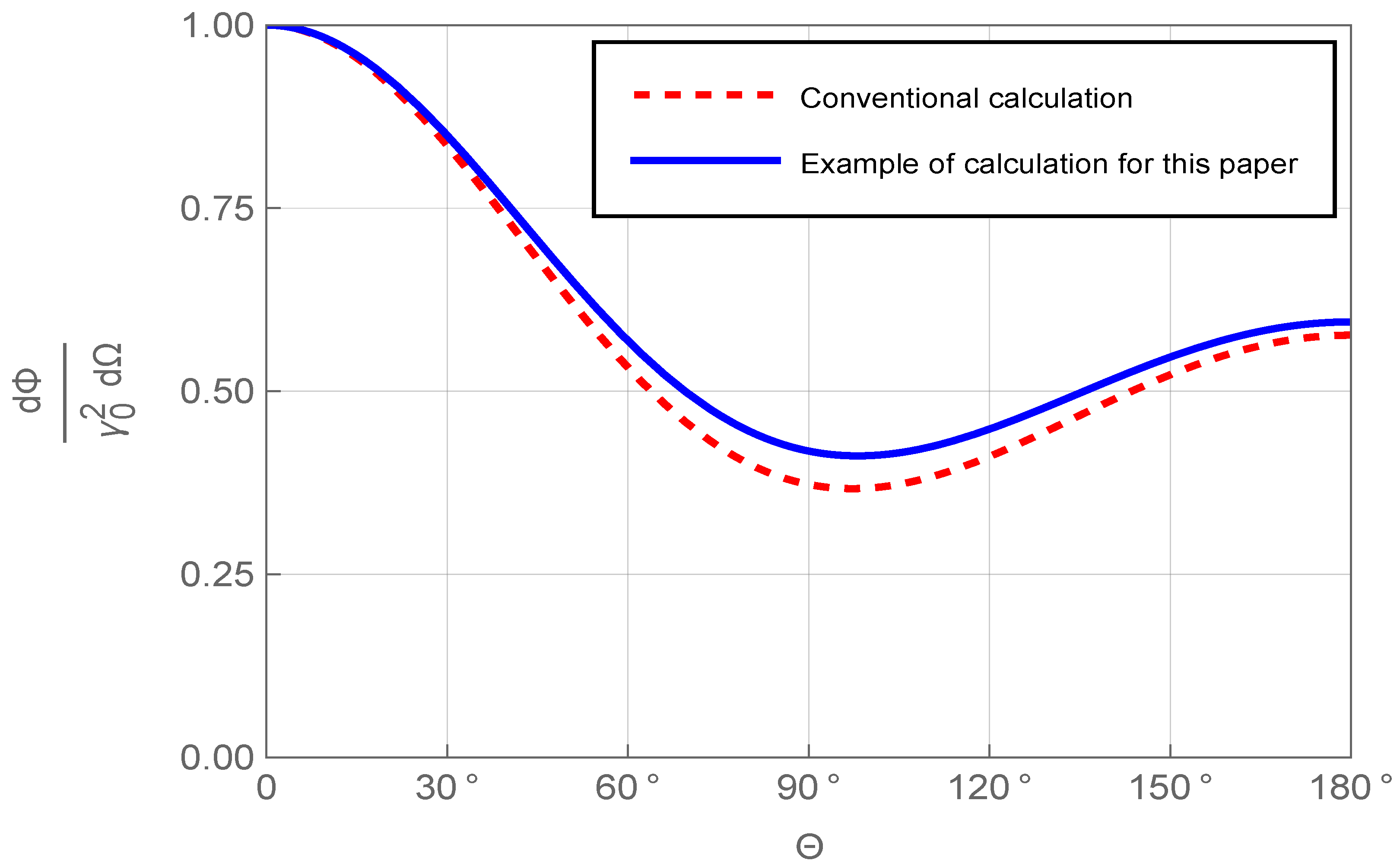
7.3.1. Application of Extended Gamma Matrices to Compton Scattering Calculations

The theoretical framework of extended gamma matrices can also be applied to calculations of fundamental quantum electrodynamics processes such as Compton scattering. Important points in such calculations are the use of gamma matrices satisfying the Clifford algebra in curved spacetime and the explicit incorporation of the spacetime metric tensor.

Compared to Compton scattering calculations in conventional Minkowski spacetime, calculations in curved spacetime involve the following key changes:

1. Extension from 4 standard 4×4 gamma matrices to 16 extended 256×256 gamma matrices

2. Change from the flat metric tensor ${\eta }^{\mu \nu }$ to a general metric tensor $g^{\mu \nu }$

3. Modification of matrix structures to satisfy the Clifford algebra $\{{\tilde{\gamma }}^{\mu },{\tilde{\gamma }}^{\nu }\}=2g^{\mu \nu }$

7.3.2. Specific Impact of the Metric Tensor on Compton Scattering

To understand the role of the metric tensor in Compton scattering, we first explicitly consider the form of the metric tensor:

$$\begin{array}{c}\hfill g_{\phantom{\rho }\nu }^{\mu }=\left(\begin{array}{cccc}{g}_{\phantom{\rho }0}^0& g_{\phantom{\rho }4}^4& g_{\phantom{\rho }6}^6& g_{\phantom{\rho }8}^8\\ g_{\phantom{\rho }5}^5& g_{\phantom{\rho }1}^1& g_{\phantom{\rho }10}^{10}& g_{\phantom{\rho }12}^{12}\\ g_{\phantom{\rho }7}^7& g_{\phantom{\rho }11}^{11}& g_{\phantom{\rho }2}^2& g_{\phantom{\rho }14}^{14}\\ g_{\phantom{\rho }9}^9& g_{\phantom{\rho }13}^{13}& g_{\phantom{\rho }15}^{15}& g_{\phantom{\rho }3}^3\end{array}\right)\end{array}$$

(58)

In Minkowski spacetime, this metric tensor takes a simple diagonal form:

$$\begin{array}{c}\hfill g_{\phantom{\rho }\nu }^{\mu }={\eta }_{\phantom{\rho }\nu }^{\mu }=\left(\begin{array}{cccc}-1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right)\end{array}$$

(59)

To consider curved spacetime, we need to use a more general metric tensor with non-diagonal components. For example, we can consider a trial metric tensor such as:

$$\begin{array}{c}\hfill g_{\phantom{\rho }\nu }^{\mu }=\left(\begin{array}{cccc}-0.999& 0.001& 0.001& 0.001\\ 0.001& 1& 0.001& 0.001\\ 0.001& 0.001& 1& 0.001\\ 0.001& 0.001& 0.001& 1\end{array}\right)\end{array}$$

(60)

In this metric tensor, the diagonal components have values close to the Minkowski metric, but small non-diagonal components exist. These non-diagonal components represent small curvatures or distortions of space.

7.3.3. Specific Steps for Compton Scattering Calculation

The specific steps for Compton scattering calculation using extended gamma matrices and non-flat metric tensor are as follows:

1. Matrix Preparation:

Construct 16 basic gamma matrices ${\gamma }^{\mu }$ ($\mu =0,1,\dots ,15$)

Specify the metric tensor $g^{\mu \nu }$

Calculate ${\tilde{\gamma }}^{\mu }=g^{\mu \nu }{\gamma }_{\nu }$

2. Spinor Quantity Calculation:

Evaluate slashed momentum $p̸={\tilde{\gamma }}^{\mu }{p}_{\mu }$

Include the mass term m

3. Trace Calculation:

- Calculate the terms $f(s,u)$, $g(s,u)$, $f(u,s)$, $g(u,s)$ using

$$\begin{array}{cc}\hfill f(s,u)=& {\displaystyle \frac{1}{4{(s-m^2)}^2}}·Tr\left[({p̸}^{\prime }+m){\tilde{\gamma }}^{\mu }(p̸+\kappa ̸+m){\tilde{\gamma }}^{\nu }(p̸+m){\tilde{\gamma }}_{\nu }(p̸+\kappa ̸+m){\tilde{\gamma }}_{\mu }\right]\hfill \end{array}$$

(61)

$$\begin{array}{cc}\hfill g(s,u)=& {\displaystyle \frac{1}{4(s-m^2)(u-m^2)}}·Tr\left[({p̸}^{\prime }+m){\tilde{\gamma }}^{\mu }(p̸+\kappa ̸+m){\tilde{\gamma }}^{\nu }(p̸+m){\tilde{\gamma }}_{\mu }(p̸-{\kappa ̸}^{\prime }+m){\tilde{\gamma }}_{\nu }\right]\hfill \end{array}$$

(62)

4. Scattering Cross-Section Calculation: Combine all terms to derive the differential cross-section

$$d\sigma =dt{\displaystyle \frac{\pi e^4}{{(s-m^2)}^2}}[f(s,u)+g(s,u)+f(u,s)+g(u,s)]$$

(63)

These calculations are typically executed using numerical computation software (e.g., MATHEMATICA) due to their algebraic complexity.

From numerical calculation results, it is found that the Compton scattering cross-section in models with non-diagonal components in the metric tensor (curved spacetime) shows measurable differences from the standard Klein-Nishina result (flat spacetime). This difference can be adjusted by appropriately selecting the values of the metric tensor and is in principle experimentally verifiable.

7.3.4. Comparison of Calculation Results in Minkowski Spacetime and Curved Spacetime

An important outcome of Compton scattering calculations using extended gamma matrices is the comparison of results in the following three settings:

A. Conventional calculation using Minkowski metric $g^{\mu \nu }={\eta }^{\mu \nu }$ and four 4×4 gamma matrices

B. Calculation using Minkowski metric $g^{\mu \nu }={\eta }^{\mu \nu }$ and four 256×256 gamma matrices

C. Calculation using non-Minkowski metric $g^{\mu \nu }\ne {\eta }^{\mu \nu }$ and sixteen 256×256 gamma matrices

Settings A and B are mathematically equivalent and reduce to the standard Klein-Nishina result:[64]

$$d\sigma ={\displaystyle \frac{r_e^2}{2}}{\left({\displaystyle \frac{{\omega }^{\prime }}{\omega }}\right)}^2\left({\displaystyle \frac{\omega }{{\omega }^{\prime }}}+{\displaystyle \frac{{\omega }^{\prime }}{\omega }}-{sin}^2\theta \right)d{\theta }^{\prime }$$

(64)

In contrast, setting C, due to the presence of non-diagonal components in the metric tensor, modifies the scattering cross-section. In a specific trial calculation with $\gamma =0.173$, the following representation is obtained:

$$\begin{array}{cc}\hfill d\sigma & =1.90285\times {10}^{-24}\times ({\displaystyle \frac{1.07406\times {10}^{25}}{{(1.173-0.173cos\theta )}^2}}-{\displaystyle \frac{2.37098\times {10}^{23}}{{(-1.173+0.173cos\theta )}^3}}\hfill \\ \hfill & +{\displaystyle \frac{1.84352\times {10}^{25}}{(-1.173+0.173cos\theta )}}+7.98326\times {10}^{24})\hfill \end{array}$$

(65)

This result, as shown in Figure 3, clearly differs from the conventional Klein-Nishina formula, quantitatively demonstrating the impact of spacetime curvature on the Compton scattering process through specific values of the metric tensor. For detailed derivation processes and the Mathematica code used, please refer to "About Obtaining Mathematica Calculation Codes" later.

7.3.5. Physical Interpretation and Experimental Significance

An important point in the physical interpretation of calculations using extended gamma matrices is that the observed effects arise not from gravity itself but from the combination of non-diagonal components of the spacetime metric and electromagnetic interactions. Normal gravitational effects are extremely weak (for example, the ratio of gravitational to Coulomb forces between two electrons separated by ${10}^{-15}$m is ${10}^{-43}:1$) and undetectable in standard experiments.

However, in this theory, it is suggested that the non-diagonal components of the metric tensor $g^{\mu \nu }$ directly affect quantum electrodynamic processes. This effect is amplified through the electromagnetic interaction itself, potentially reaching observable levels.

Experimental verification of this approach requires high-precision measurements of quantum electrodynamic processes such as Compton scattering. In particular, detecting subtle deviations in scattering angle distributions is key. While detection may be difficult with current experimental technology, future improvements in precision may open possibilities for verification.

This theoretical framework provides a deep insight that physical spacetime is not strictly flat, and electromagnetic interactions themselves are inextricably linked to subtle curvatures of spacetime. This has the potential to serve as a bridge between quantum field theory and gravitational theory, representing an important step toward a unified understanding of both.

It is important to emphasize that this approach does not introduce additional spacetime dimensions—physical spacetime remains four-dimensional. The extended dimensions of gamma matrices reflect the internal degrees of freedom needed to describe the dual aspects of quantum fields.

This mathematical structure provides a promising approach to one of the most difficult problems in theoretical physics—the harmonization of quantum field theory and general relativity. By treating gravity as an emergent phenomenon arising from the statistical properties of quantum fields, the fermion-boson duality theory provides a conceptually consistent framework for understanding all fundamental interactions.

8. Conclusions and Prospects

8.1. Experimental Verifiability of the Theory

While the fermion-boson duality framework is theoretically sophisticated, its scientific value derives from its experimental verifiability. Several key predictions of this theory are experimentally testable:

1. Precision Measurements of Lamb Shift: With $E_{fi}\approx 10$ GeV, the theoretical predictions for Lamb shift in hydrogen and its isotopes already show remarkable agreement with experimental data. Further precision measurements in more complex atomic systems can provide additional tests.

2. Anomalous Magnetic Moment Measurements: The theory predicts energy-dependent corrections to lepton anomalous magnetic moments. Precision measurements of muon g-2 at different energies could reveal this energy dependence.

3. High-Energy Scattering Processes: As energies approach $E_{fi}$, deviations in cross-sections and angular distributions in electron-electron scattering and photon-photon scattering from standard QED predictions should become observable.

4. Transition of Statistical Properties: Under special conditions where collective effects amplify statistical transitions, such as high-energy density plasmas or quark-gluon plasmas, direct observation of partial statistical transformation might be possible.

5. Gravitational Effects in High-Energy Density Systems: The theory predicts enhanced gravitational effects in systems with extremely high energy densities. This could potentially be observed through the physics of neutron stars or through precision measurements of gravitational effects at small distances.

The value of $E_{fi}\approx 10$ GeV derived from Lamb shift calculations provides a clear energy scale at which these effects become important, guiding future experimental efforts.

8.2. Applications to Physics Beyond the Standard Model

The FB duality theory provides several promising avenues for addressing unresolved problems in physics beyond the Standard Model:

1. Muon g-2 Anomaly: As discussed earlier, energy-dependent statistical transformation may naturally explain the persistent discrepancy between theoretical predictions and experimental measurements of the muon anomalous magnetic moment.

2. Hierarchy Problem: The enormous difference in strength between gravity and other fundamental forces finds a natural explanation in the statistical transformation mechanism, where gravity appears as a dual description of gauge fields at different energy scales.

3. Dark Matter and Dark Energy: The framework suggests the possibility that these phenomena may be related to collective effects of statistical transitions in quantum fields, providing a new perspective on these cosmological puzzles.

4. Neutrino Physics: The theory’s unified treatment of different statistics may provide insights into neutrino oscillations and the singular nature of neutrinos.

5. Unification of Forces: Rather than introducing new symmetries or dimensions, fermion-boson duality suggests unification through the dual statistical properties of the same fundamental fields.

These applications represent promising directions for further development of the theory and its impact on our understanding of fundamental physics.

8.3. Theoretical Developments and Future Challenges

While the FB duality theory has shown considerable success in addressing longstanding problems in quantum field theory, significant theoretical challenges and opportunities for development remain:

1. Formal Derivation of Transition Functions: Deriving the exact form of transition functions from more fundamental principles remains an important goal. This might involve deeper connections with thermodynamic principles or information theory.

2. Implications for Quantum Gravity: Further development of the gravitational aspects of the theory could lead to a more complete quantum gravity theory that might address the black hole information paradox and quantum cosmology problems.

3. Mathematical Rigor: More rigorously establishing the mathematical foundations of the theory regarding the properties of extended gamma matrices and their relationship to geometry is an important direction for future research.

4. Cosmological Consequences: Exploring the implications of fermion-boson duality for the early universe, where energy might have approached or exceeded $E_{fi}$, could provide new insights into cosmological puzzles.

5. Computational Methods: Developing efficient computational techniques for applying the framework to complex systems is essential for making detailed predictions in many-body systems.

These challenges represent a rich agenda for future research with the potential to significantly advance our understanding of fundamental physics.

8.4. Final Considerations

The fermion-boson duality theory represents a new approach to quantum field theory that challenges conventional wisdom about the fixed statistical nature of quantum fields. By proposing that statistical properties evolve with energy scale, this theory provides a unified description of fermions and bosons, naturally addressing several persistent issues in quantum field theory, including regularization and the relationship between gauge theory and gravity.

The remarkable agreement between the theory’s predictions and experimental measurements of Lamb shift with a characteristic energy $E_{fi}\approx 10$ GeV provides strong evidence for the physical validity of this approach. Combined with this success and the potential of the theory to explain the muon g-2 anomaly and provide a new perspective on fundamental forces, fermion-boson duality may represent an important step toward a more complete understanding of quantum fields and their interactions.

The conceptual shift proposed by this theory—viewing statistical properties as emergent rather than fundamental—opens new paths for exploring deep connections between seemingly unrelated areas of physics, from quantum electrodynamics to gravity, from statistical mechanics to cosmology. As with any significant theoretical development, final validation will come through ongoing experimental testing and theoretical refinement.

In an era when physics faces profound questions about the nature of quantum gravity, dark matter, and dark energy, approaches that challenge our fundamental assumptions while maintaining consistency with established observations provide valuable new perspectives. The fermion-boson duality theory represents such an approach, suggesting that the key to understanding these deep mysteries may lie not in introducing increasingly complex structures, but in recognizing deeper patterns in the behavior of quantum fields we already know.

8.5. Code Structure

The complete code set is structured as follows:

• QED Processes

  –

  Compton Scattering

  –

  Bhabha Scattering

  –

  Møller Scattering

  –

  Muon Pair Production

• Theoretical Foundations

  –

  Properties of $\omega$ Gamma Matrices

  –

  Definition and Verification of 4-dimensional and 256-dimensional Gamma Matrices

• Detailed Scattering Process Calculations

  –

  Setting up Kinematic Variables

  –

  Calculation of Scattering Amplitudes

  –

  Derivation of Cross Sections

  –

  Comparison with Klein-Nishina Formula

  –

  Behavior in High Energy Limit

• Other Interactions

  –

  Muon Decay Processes

These calculation codes demonstrate concrete applications of the theory while enabling comparative verification with conventional quantum field theory. In particular, the construction of bosonic gamma matrices and Compton scattering calculations play an important role in confirming the basic predictions of the theory.