Introduction
It has now been established that a quasi-periodic effect on a dynamic system located near the self-excitation boundary of its own self-oscillations can lead to the emergence of complex oscillatory processes. The mechanism of this phenomenon, as indicated in [
1], is based on the chaotization of the underexcited mode of the system under the influence of an external quasi-periodic effect. The results of an experimental study of the dynamics of an amplifying cascade activated by a bipolar transistor during amplification of a quasi-periodic signal are published in [
2]. The transition to chaos in such a system is caused either by the periodic excitation of the system’s own self-oscillatory process associated with the development of oscillations at combination and difference frequencies, or by the mechanism of chaotization of the system’s own mode described in [
1]. In addition, it was noted that the mechanisms of oscillation chaotization investigated in [
2] were not observed simultaneously in systems known in the scientific literature when modeling the processes occurring in them, which indicates the absence of models that adequately describe microwave systems.
The issues of development of dynamic processes in oscillatory systems have been widely studied within the framework of the general theory of stability of circuits containing active elements [
3,
4,
5]. Phenomena associated with changes in stability are also observed in a number of cases in multimode active systems [
6,
7], as well as when exposed to complex signals, such as biharmonic signals [
8,
9], both with greatly differing frequencies and with close frequencies. When interacting with the natural modes of the system, the output signal becomes chaotic for certain parameter values. It is shown that the interaction of high-frequency and low-frequency oscillations leads to the emergence of additional synchronization regions as a result of three-frequency interaction between the frequencies of such an impact and the natural frequency of the generator, which leads to the emergence of additional bistable states. Using the example of the destruction of a series of pulses in a nonlinear generator and a harmonic oscillation in a two-mode system, the effects caused by the interaction of high-frequency and low-frequency oscillations are considered. The most important manifestations of such interaction are the formation of chaotic instabilities
On the other hand, scientific works lack models that adequately describe the processes in real systems during the amplification of complex oscillations, such as those studied in [
2].
The purpose of this work is to show that the phenomena discovered during the amplification of quasi-periodic signals presented in [
2] can take place in a generator with isolated inertia [
10,
11].
The Results and Its Discussion
Let us consider the dynamics of a generator with selected inertia in an underexcited mode under the action of a quasi-harmonic signal. The equations describing such a system, taking into account the works [
10,
11], have the form:
where
A1, A2, are the amplitudes and frequencies of the acting oscillations,
x,
y,
z,
– are the dimensionless voltage at the input of the nonlinear amplifier, the current in the feedback circuit, the voltage at the output of the half-wave inertial converter, the current in the input circuit, respectively,
m1,
m2,
q,
g are the parameters of excitation, dissipation, limitation and inertia,
I(
a) is the unit Heaviside function,
m1 = - 0,1,
m2 = 0,2,
q =1,
A1 =
A2 = 1,2.
As in [
2], in the present work two different cases were identified: the first corresponded to the condition |
f1 —
f2| <<
, the second — |
f1 —
f2| ~
, where = 1/Q, Q is the generator quality factor,
f1 =
1/2
,
f2 =
2/2
.
Let us consider the first case, when the frequency distance between the components of the quasi-harmonic signal is much less than 0,01. When the frequency difference of the quasi-harmonic signal is much less than , two effects are observed:
in the generator, the excitation of combination components occurs based on the frequencies of the quasi-harmonic oscillatory process with the frequency arrangement ,
at a certain difference in the frequencies of the acting quasi-harmonic signal, chaotic instability of the oscillatory process occurs in the generator.
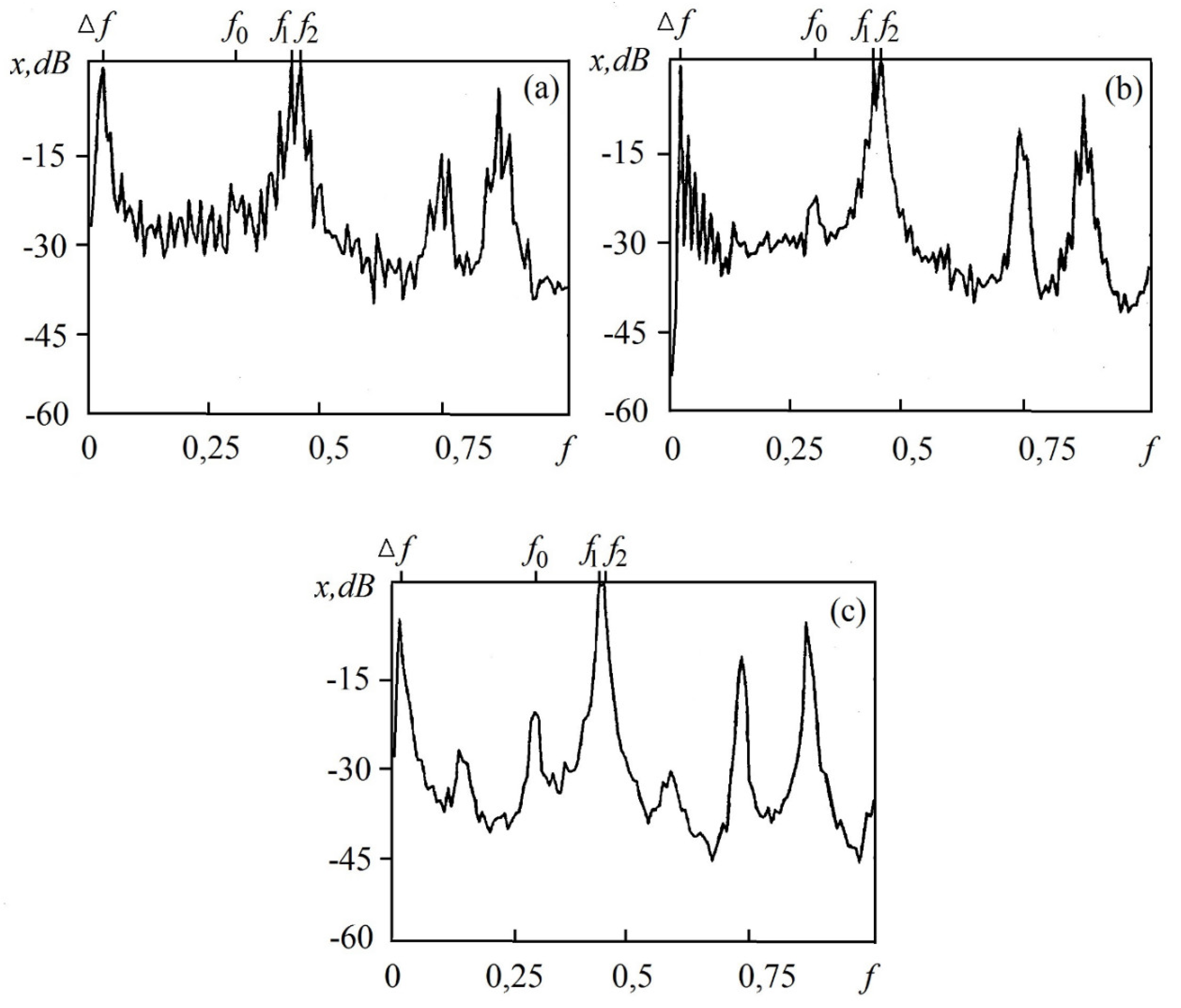
The characteristic power spectra of oscillations of the variable
x at |
f1 —
f2| <<
shown in
Figure 1. Initially (
Figure 1, a), the power spectrum of oscillations is equidistant with the arrangement of combination components through the frequency interval
. With a decrease in
, provided that ,
< 1.004, chaotic instability arises in the system based on three-frequency dynamics, which is manifested in the power spectrum as a chaotic component of system oscillations (
Figure 1, b). A further decrease in the interval leads to an increase in chaotic instability, which is manifested in the spectral representation as smoothing of the spectral envelope.
= 1.002, the system motion becomes chaotic (
Figure 1, c), while the frequency peak of the chaotic component is at the frequency of the system’s natural mode
. An interesting fact is the presence of a low-frequency component of large-amplitude system oscillations, the important role of which will be shown below. The considered mechanism of transition to chaotic dynamics is characterized by a regime of irregular intermittency between trains of oscillations of different durations and a random initial phase with a preliminary additive increase in the number of spectral components.
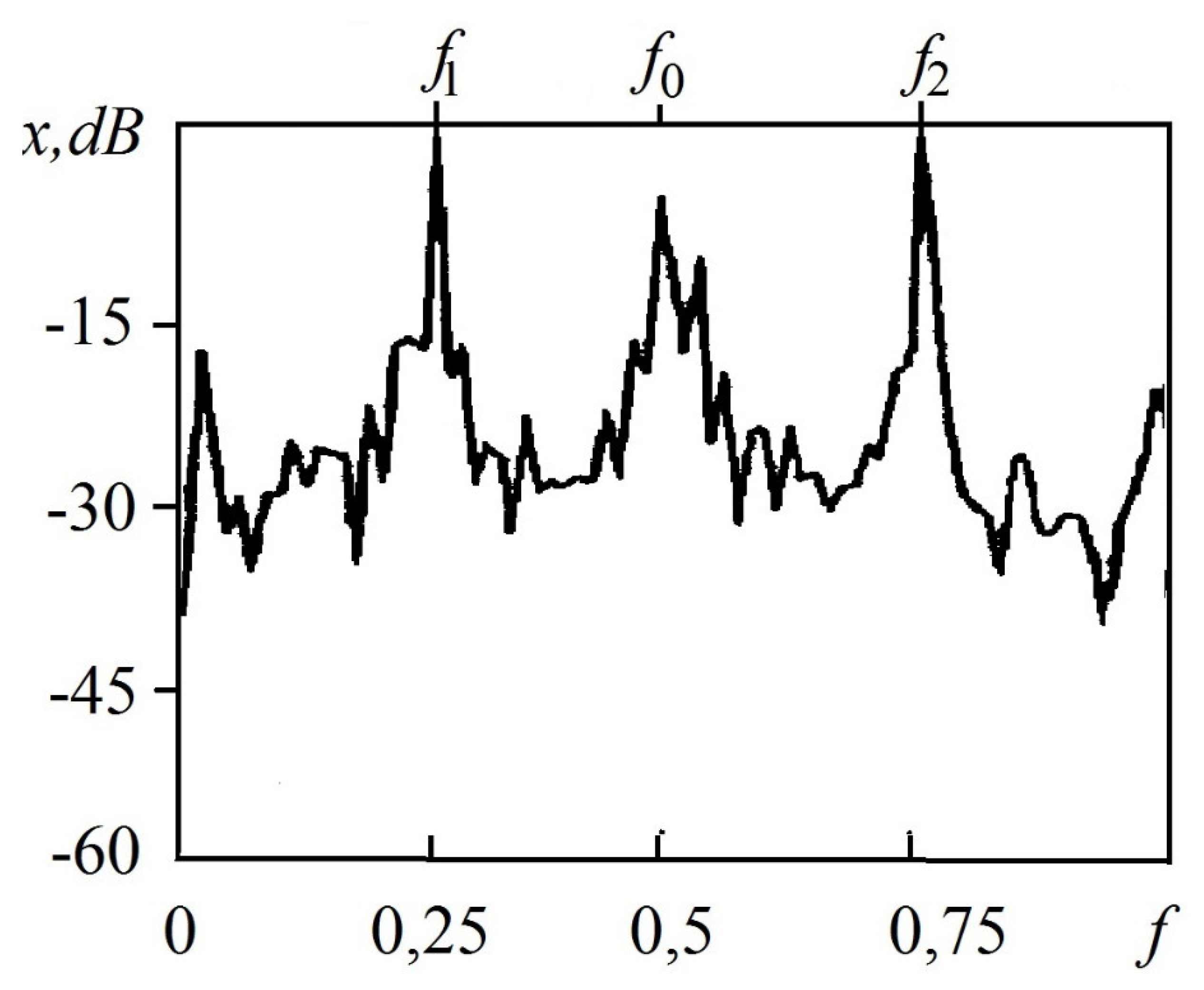
In the second case |
f1 —
f2| ~
, the power spectrum of the oscillations of the variable x contains the frequency components of the quasi-periodic signal
f1,
f2 and a chaotic component, the maximum level of which corresponds to the frequency of the fundamental mode of the system (1) in the autonomous mode (
Figure 2). Changing the frequencies and amplitudes of the components of the external acting signal over a wide range does not lead to a qualitative change in the nature of the oscillatory process of the system. In the case under consideration, there is no competition between the frequency components of the quasi-periodic signal and the system’s own mode. An additional synchronization region is realized in the system, which manifests itself as a chaotic component.
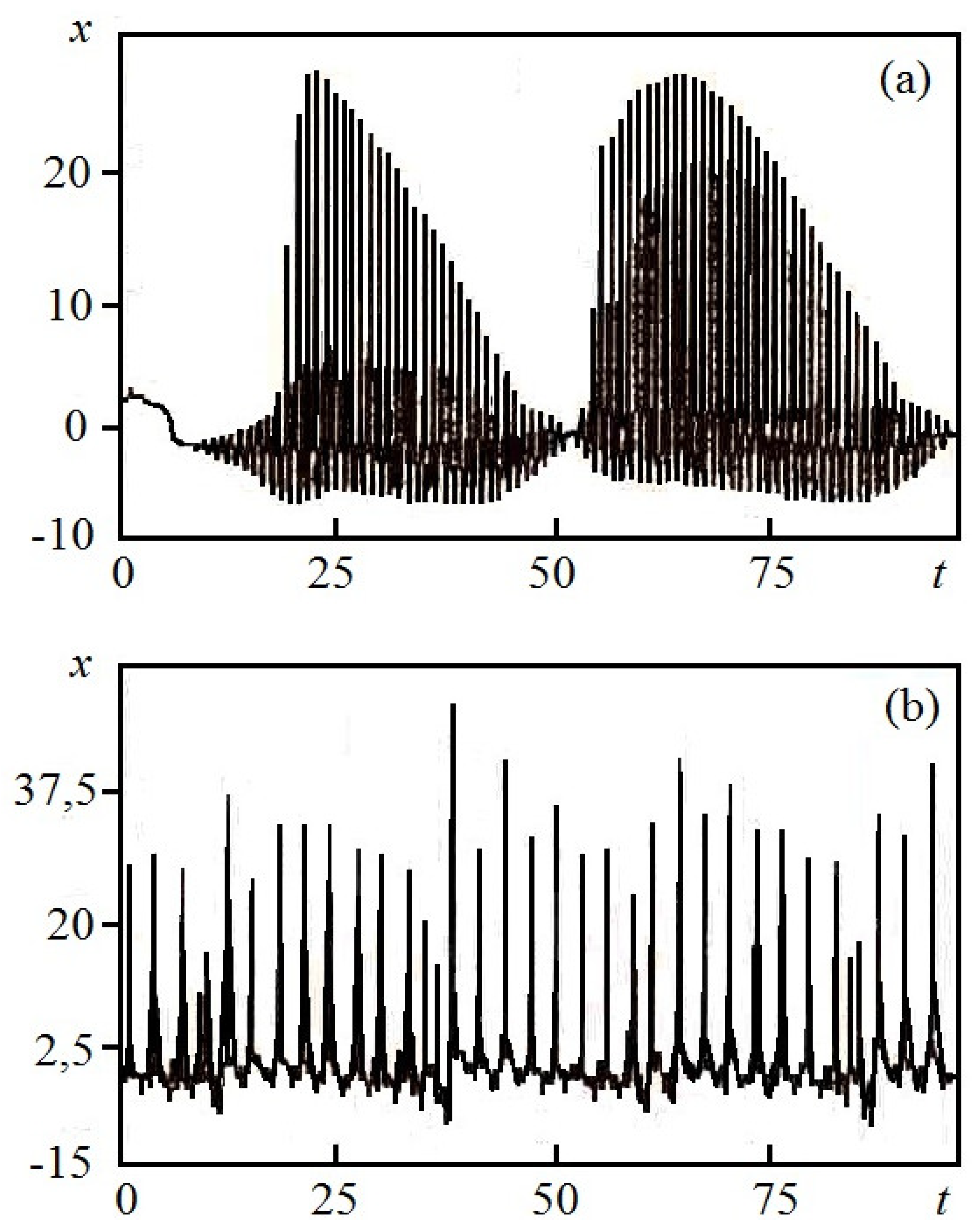
To demonstrate the mechanisms of oscillation chaotization in both cases, we will turn to the implementations of the oscillatory process of the variable x. Let us consider the case of a close frequency distribution |
f1 —
f2| <<
of a quasiperiodic signal corresponding to the power spectrum shown in
Figure 1, c. The implementation of the oscillatory process shown in Figure 3, a demonstrates a sequence of trains of system oscillations, the average duration of which is determined by time
. The dynamics of the system is characterized by the fact that at the moment of time corresponding to the end of the next oscillation train, the first derivative of the variable
x becomes positive due to the large amplitude of the low-frequency component, the conditions for self-excitation of natural oscillations are met and the system goes into the mode of generating a new train. Time
determines additional inertia and, at small
, characterizes the chaotic component of the system dynamics.
Under the condition |
f1 —
f2|~
the nature of the oscillatory process is different. The implementation of the variable x, corresponding to the power spectrum in
Figure 2, is shown in Figure 3, b. It is evident that the oscillatory process is determined to the greatest extent by the external signal, and the oscillations based on the frequency
f0 are determined by the intrinsic inertia of the system; the conditions for self-excitation in the system are not met in this case.
Figure 2.
Time realizations of the oscillatory process: = 1,001, (a); |f1 — f2|~, (b).
Figure 2.
Time realizations of the oscillatory process: = 1,001, (a); |f1 — f2|~, (b).
Conclusions
Thus, a presented numerical studies have demonstrated that in a system with a selected inertia near the self-excitation boundary with quasi-harmonic pumping, two different mechanisms of oscillation chaotization are characteristic, depending on the mutual ratio of the frequencies of the external quasi-periodic signal. The first case, corresponding to the condition , is characterized by the generation of combination components based on the modes of the external quasi-periodic signal, which precede the chaotization of oscillations with a decrease in the frequency interval between the components of the quasi-periodic signal . The mechanism of chaotization in this case is based on the sequential generation of oscillation trains of different durations with an arbitrary initial phase, and the frequency of the generated oscillations is generally uncorrelated with the frequencies of the input bi-harmonic signal.
In the second case, when the condition is satisfied for the components of the external quasiperiodic signal , the system experiences the formation of chaotic instability on the fundamental mode of the system, which, as shown in the work, manifests itself in the spectral representation as a noise pedestal; moreover, the amplitude of this noise pedestal is an order of magnitude smaller than the amplitudes of the components of the quasiperiodic signal. That is, in this case, the conditions for the chaotization of the system’s eigenmode are realized in the system.
The complete qualitative correspondence between the dynamics of the system with the allocated inertia with quasi-harmonic action and the experimental results obtained in [
2] allows us to use system (1) as a model for describing real microwave range systems.