Secrets of Kleiber’s and Maximum Metabolic Rate Allometries Revealed with a Link to Oxygen-Deficient -Combustion -Engineering

1. Introduction, Literature Review and Objectives

Recent efforts aim to connect thermodynamics and combustion with biology to better understand the virus evolution, develop empirical formulae for viruses, and analyze biological processes through Gibbs function and energy release within biological systems (BS) [1,2,3]. This study extends previous work linking the field of oxygen-deficient combustion (ODC) with oxygen-deficient metabolism (ODM) [3] to predict the specific organ metabolic rates (SorMR_k) of vital organ k of mass m_k (W/kg of k, k= Kidneys (Kids), Heart, Brain and Liver) of 114 BS ranging in mass from 10 g to 6,650 kg by using i) data on SorMR_k of two BS named as reference species (Shrew, 0.0076 kg: RS-1; Rat, 0.390 kg: RS-2), ii) data on organ masses of 116 species (114 +2 RS), and iii) established metabolic energy release relationships from ODC/porous char combustion literature. By summing the organ metabolic rates {MR} of individual organs (OrMR_k=SorMR_k x m_k) across all organs, the whole-body metabolic rate (BMR) as a function of body mass (M_B) is obtained. The ODM approach is validated by demonstrating Kleiber’s law and comparing the predicted allometric constants with literature data. The study provides a brief overview of Kleiber’s law, followed by i) a review of current theories explaining the ¾-power law, ii) an introduction to ODC, the dimensionless group number G , ODM and corresponding G_OD # for organs, iv) the methodology adopted for the prediction of SOrMR_k of 114 species using only two RS, and v) validation and extension to allometry for maximal metabolic rate (MMR). A higher G_OD # indicates a higher degree of oxygen deficiency.

1.1. Kleiber’s Law and Organ Metabolic Rates

Allometry refers to how the characteristics of biological species (BS), including morphological traits (e.g., brain size) and physiological traits (e.g., metabolic rate (MR), life span), change with body mass. The allometric relation for MR in BS is given as:

$${\dot{q}}_B = a M_B^b$$

(1)

where M_B is body mass (kg) and (${\dot{q}}_B$), MR is in watts. In 1932, Kleiber obtained a = 3.4, b = 0.74 for M_B ranging from 0.15 to 679 kg, known as Kleiber’s law [4,5], which persisted for over 70 years [6]. The specific basal metabolic rate (SBMR, W/kg of body mass) is written as

$${\dot{q}}_{B,M} = a M_B b\text{'}$$

(2)

Where b’ = b - 1 = -0.26

Nutrients consumed through the mouth are essential for energy release ${\dot{q}}_B$ through oxidation. The review in Ref. [[8] suggests that O₂, which enters through nasal intake, must also be considered a “nutrient” since it is essential for energy release. The energy release rate (ERR) is related to the oxygen consumption rate $\left\{{\dot{m}}_{O2,B} \right\}$ within whole body since ERR_B = $\left\{{\dot{m}}_{O2,B} \right\}HH{V}_{O2}$, where HHV_O2 t is the energy release per unit mass of oxygen consumed and it is almost constant at about 14335 J/g of O2 for most fuels and nutrients [1]. If O₂ supply falls below a critical level $\left\{{\dot{m}}_{O2,crit} \right\}$ then its uptake $\left\{{\dot{m}}_{O2} \right\}$ is limited by the supply from blood vessels, which is a common assumption used in the classical WBE {West, Brown and Enquist} hypothesis for demonstrating Kleiber’s law.

The scaling function for metabolic rate with body size M_B is explained with two existing theories:

I). West et al. [7] proposed a fractal or “nutrient (including oxygen) distribution network” hypothesis (also referred to as the “upstream” or supply side [8] or “outward-directed vascular network” [9]) and illustrated Kleiber’s law by minimizing the heart’s work required to pump the unit amount of blood, i.e., a network which minimizes the pressure difference (P_aorta-P_cap). The scaling function is explained with O₂ delivery to cells as the limiting factor.

II). Bejan [10,11] proposed that architectures and organs must develop in such a way that resistance to flow current (e.g., water flow in trees) must be minimized, or equivalently, that entropy generation is minimized, resulting in lower energy consumption and food requirements.

The Biologists have raised the following issues as unknown: “The allometric size relationship is somehow ‘programmed’ into cells, although the factors that let them know whether they are in a small or large organism are still unknown” [12]. That is, existing biological data indicates that organs increase their metabolic rates per unit mass when within a smaller body and vice versa. In earlier work, the author proposed the “Oxygen-Deficient Metabolism (ODM)“ hypothesis to explain these unknowns [3]. In the current work the same ODM hypothesis is extended to predict the specific organ metabolic rate of organ k {SOrMR_k , k= k= kidneys (kids), heart, brain and liver} of 114 BS ranging in mass from 10 g to 6,650 kg using data on SOrMR_k of two reference BS { RS-1 of lowest M_B , Shrew, 7.5 g; RS-2 elected with M_B much higher than that of RS-1: Rat, 380 g }. With known vital organ masses m_k , the OrMR_k {= SOrMR_k · m_k} are estimated and summed up to yield the whole-body basal metabolic rate ${\dot{q}}_B$ as a function of body mass (M_B) for 116 BS ranging in mass from 0.0076 kg to 650 kg, The log-log plot yields Kleiber’s law for 116 species ranging in mass from 0.007 kg to 650 kg, with an allometric exponent of b= 0.747. More importantly, the ODM presents a dimensionless group (G_OD)_k for biology literature to indicate the extent of OD within an organ.

1.2. Literature Review

While combustion is a rapid oxidation process that typically occurs at high oxygen mass fraction, Y_O2,air = 0.23 (mole fraction =0.21 or 23% or 210,000 ppm), resulting in a significant temperature rise, the metabolism is a slow oxidation process that typically occurs at a low oxygen mass fraction, Y_O2 ($Y_{O_2} = 0.0415 x p_{O_2}$ [13]), where p_O2 is the partial pressure of O₂ in mm of Hg. While the pO2 in alveolar is 106 mm of Hg , the p_O2 in tissues is about 40-50 mm Hg and dissolved O₂ is on the order of 1-6 ppm, thus resulting in a lower temperature rise. Sometimes, the biology literature calls ${\dot{q}}_B$as “heat produced” or “power produced“ [51], while the engineering literature defines${\dot{q}}_B$ as the energy release rate (ERR) by all the cells within the body. The ${\dot{q}}_B$ is a sum of the work delivery rate, ${\dot{W}}_B$, (i.e., ATP delivery rate, approximately 25% of ${\dot{q}}_B$) and the heat transfer rate (${\dot{Q}}_B$, approximately 75 % of ${\dot{q}}_B$, [52]) due to the temperature difference (ΔT) across the cells and the rest of the body.

The required O₂ uptake $\left\{{\dot{m}}_{O2} \right\}$ (biology uses volume units ${\dot{V}}_{O2}$ in mL/min, ${\dot{m}}_{O2}$in mg/min=1.42 x ${\dot{V}}_{O2}$ ) by mitochondria in the cells is supplied by blood vessels via capillaries, followed by diffusion from capillaries to cells and then from cells to mitochondria.

The hypotheses used for demonstrating Kleiber’s law {${\dot{q}}_B$ vs M_B } fall under two broad groups: I) Homogeneous and II) Heterogeneous.

I). Homogeneous hypothesis:

This hypothesis considers the whole body as a system; the hypotheses include: i) the law of surface area to volume ratio of the whole body, yielding b=2/3, b’=-1/3, as described by Rubner’s law in 1883, ii) WBE’s fractal geometry [14] (geometry of circulatory system: macro and microcirculation), which relies on minimization of dissipative energy in the vascular system supplying oxygen and nutrients. Savage et al. showed that the WBE model is applicable only for BS of infinite body size (or network) [15], and when finite size is included, it yields scaling exponents as a function of body size. Further, Weibel and [16] question the universal models based on “the fractal design of the vasculature and the fractal nature of the total effective surface of mitochondria and capillaries” since they predict b= ¾ for both basal and maximal metabolic rates. Silva et al. [17] suggest that there are mathematical and conceptual errors in network models, weakening the proposed theoretical arguments. The same review suggests that the power law exponent b should vary between 2/3 and 1 based on ‘metabolic level’ (activity level of the organism or metabolic intensity). Painter et al. [18] agreed with the assumption of blood volume ∝ M_B but questioned the assumptions of uptake nutrient consumption rate (called total current in the network) proportional to blood volume, iii) network structures [9], iv) quantum mechanics [19], and v) topology [10].

II). Heterogeneous Hypothesis:

The heterogeneous hypothesis considers the whole-body metabolic rate ${\dot{q}}_B$ as a sum of the OrMR_k with k= kids, H,Br,L and RM where RM represents all the remaining weakly metabolizing tissues. The mass of RM is given as

$$m_{RM}= M_B-m_{vit}, m_{vit}= {\displaystyle \sum m_k}, k=Kids,H,Br,L$$

a) Body Mass Based Allometry Wang et al. used a heterogeneous or reductionist approach for estimating the whole-body metabolic rate { ${\dot{q}}_B$} [20,21,22]:

$${\dot{q}}_B=a {M_B}^b={\displaystyle \sum _k {\dot{q}}_{k,m} m_k} , M_B= {\displaystyle \sum _k m_k}, k= Kids,H,Br,L,RM$$

(3)

where ${\dot{q}}_{k,m}$ is the SOrMR_k of k^th organ { W/kg of k}given by the body mass based allometry (BMA) given by

$${\dot{q}}_{k,m}=e_{k,6}{M_B}^{f_{k,6}}, f_{k,6} < 0 , k= Kids,H,Br,L,RM$$

(4)

Here afterwards, this method of computing SOrMR_k using the empirical allometric relations ( EAR) will be termed as EAR method. Wang et al. presented allometric relations for organ masses [21]:

$$m_k=c_{k,6}{M_B}^{d_{k,6}}, d_{k,6}>0, k= Kids,H,Br,L,RM$$

(5)

Using Equation 4 and Equation 5 , the ${\dot{q}}_B$ is obtained as

$${\dot{q}}_B={\displaystyle \sum _k {\dot{q}}_{k,m} m_k}= \left({\displaystyle \sum _k c_{k,6} e_{k,6} {M_B}^{d_{k,6}+f_{k,6}}}\right) , k= Kids,H,Br,L,RM,$$

(6)

Based on data on the organ mass and ${\dot{q}}_{k,m}$of six species (ranging from 0.48 kg of rat to 70 kg of human), Ref. [21] tabulates the constants c_k,6, d_k,6, e_k,6 and f_k,6. Table 1 tabulates the allometric constants c_k,6, d_k,6, e_k,6 and f_k,6. Since d_{k,6 6} > 0, organ sizes are positively related to M_B, while the SOrMR_k, Equation 4) are negatively correlated with body mass (f_k,6<0). The additional subscript “6” indicates that the empirical constants are based on six species. As opposed to a majority of BS, , human brain masses are relatively larger, and the allometric relation underpredicts m_Br for humans. Thus, human brain mass is estimated using the encephalization quotient (EQ), which is the ratio of measured brain mass to the mass predicted with allometry. Gallagher et al. report that for a reference human of 70 kg [23], the RM for the 5-organ model is 66.2 kg, while the masses of Kids, H, Br, and L are 0.31, 0.33, 1.4 and 1.8 kg, respectively; this results in 94.5% of body mass being RM, while vital organs account for 5.5%. Each of these vital organs contribute 8.7% (Kids), 8.2% (Heart), 21.6% (Brain) and 20.2% (Liver) of the total BMR [24]. However, if one uses the data on c_k,6 and d_k,6 tabulated in Table 1, the resulting mass percentages are 0.37% (Kids), 0.58% (Heart), 0.40% (Brains) and 1.90% (Liver), with vital organ mass percentage at 3.25%. The corresponding energy percentages are 7.36% (Kids), 12.81% (Heart), 3.97% (Brain), and 17.10% (Liver), with vital organ energy percentage at 41%. While the brain mass for 70 kg human is predicted as 0.28 kg from allometry, Gallagher’s data brain mass is 1.4 kg indicating high EQ. The underprediction of human brain mass and energy percentage is due to the EQ factor, as humans have the highest EQ (i.e., a larger brain size compared to animals of similar mass). This additional brain mass enhances cognitive abilities beyond general brain mass versus body mass scaling laws. See Section 3.4 for further discussion on brain mass and its effects on human results.

b) Organ Mass Based Allometry (OMA) Exponents for SOrMR_k or ${\dot{q}}_{k,m}$: It is noted that “f_k,6” in BMA for the vital organs of the six species selected in EAR by Wang et al. [21] are all negative. To explain the negative values of f_k,6 in BMA for organs, the BMA is replaced by organ mass-based allometry [3], using the relation between organ mass and body mass. Thus,

$${\dot{q}}_{k,m}=e_{k,6}{M_B}^{f_{k,6}}=E_{k,6}{m_k}^{F_{k,6}}, f_{k,6} < 0, F_{k,6} < 0, k=Br,H,K,L,R$$

(7)

where $F_{k,6}=\left({\displaystyle \frac{f_{k,6}}{d_{k,6}}}\right), E_{k,6}=\left({\displaystyle \frac{e_{k,6}}{{c_{k,6}}^{(f_{k,6}/d_{k,6})}}}\right)$

See Table 1 for the listing of E_k,6 and F_k,6. The F_k,6 becomes more and more negative for increasing organ masses. Ref. [3] explains the rationale for F_k,6 vs m_k using the ODM hypothesis. It is apparent from the constant e_k,6 and f _k,6, or E_k,6 and F_k,6 (Table 1) that different organs consume oxygen at different rates, thus indicating different O₂ profiles. Since the ODM hypothesis is used to predict SOrMR_k and demonstrate Kleiber’s law in the current work, a brief outline of Ref. [3] on ODC and ODM is presented below for the convenience of readers.

B) Group or Oxygen-Deficient Combustion (GC or ODC) in Engineering: The engineering literature models the combustion of dense fuel particle suspension (e.g., coal suspensions fired into a boiler) using a spherical fuel-particle cloud of radius R_,FC , mass m_FC and number density of fuel articles n_FC, with its surface exposed to a known oxygen mass fraction at the surface Y_O2,FC,s (Figure 1) where FC stands for fuel cloud. Thus, the oxygen concentration, Y_O2(r), within the FC is a function of r, and consequently, the energy release rate (ERR) varies as a function of r, with the highest value near aerobic cloud surface and lowest value at the core of the suspension. This model is referred to as a group combustion or oxygen-deficient combustion (GC or ODC) in engineering literature, implying that particles at the core may not receive enough oxygen to burn. Detailed literature on ODC in engineering is provided in a three-part series of articles [25,26,27]. The local O₂ consumption rate by each particle located at r { ${\dot{w}}_{O2,p}(r)$}, is given as (Figure 1d)

$${\dot{w}}_{O2,p}(r) =C_{ch,p}{Y}_{O2}(r),$$

(8)

where the characteristic oxygen consumption rate, C_ch,p, for each particle changes depending on kinetics control (C_Ch,p = C_Ch,p,kin) with a first-order reaction or diffusion control (C_Ch,p = C_Ch,p,dif ). The basic relations for C_ch,p are given in Ref. [3]. The engineering literature presents the solutions for the i) Y_O2(r) profiles within the fuel cloud (FC) and ii) the consumption rate of O₂ by all the particles within the cloud ${\dot{w}}_{O2,FC}$. The energy release rate (ERR) of FC is given in terms of oxygen consumption by FC {$ERR= {\dot{w}}_{O2,FC} HH{V}_{O2}$, See Table 1 for HHV_O2 }. Then, the specific energy release rate of whole cloud , SERRm, is given as ERR/m_FC. The SERRm decreases with an increase in R_,FC or m_,FC – that is, the increase in ERR is less than proportional to the increase in m_,FC due to core particles contributing negligible energy release due to OD. The solutions for ${\dot{w}}_{O2,FC}$, or ERR of FC, are presented in terms of the effectiveness factor (η_eff,,FC) of the FC. The η_eff,,FC is defined as a ratio of the O₂ consumption rate by all particles within the cloud to the rate of consumption of O₂ in the case that each particle within the FC is subjected to Y_O2,FC,s.

$${\eta }_{eff,FC} ={\displaystyle \frac{{\dot{w}}_{O2,FC}}{{\dot{w}}_{O2,FC}\left(Y_{O2,FC,s}\right)}} or {\displaystyle \frac{{\dot{w}}_{O2,FC,m}}{{\dot{w}}_{O2,FC,m}\left(Y_{O2,FC,s}\right)}} ={\displaystyle \frac{ERR}{ERR with Y_{O2,FC,s}}} or {\displaystyle \frac{SERR}{SERR with Y_{O2,FC,s}}}$$

(9)

The solution for η_eff,FC for a spherical FC is obtained with known YO₂(r) profiles:

$${\eta }_{eff,FC} = 3 {\displaystyle \underset{0}{\overset{1}{\int }}} \left\{{\displaystyle \frac{Y_{O2}(r)}{Y_{O2,FC,s}}}\right\} {\displaystyle \frac{r}{R}} d\left({\displaystyle \frac{r}{R}}\right) = {\displaystyle \frac{3}{\sqrt{G}}} \left\{ {\displaystyle \frac{1}{\tanh \left(\sqrt{G}\right)}}-{\displaystyle \frac{1}{\sqrt{G}}}\right\} , Sphere, Carbon Cloud$$

(10)

where the dimensionless group G for FC is defined as:

$$G={\displaystyle \frac{C_{ch,p} n_{FC} R_{FC}^2}{\rho D}}={\Psi }_T^2 ,$$

(11)

and the G number for FC is shown to be related to Thiele Modulus, Ψ_T (G= Ψ_T ²) in porous char combustion literature [26,27,28]: Using Equation 10, the effectiveness factor can be plotted against G as shown in Figure 2. It is noted that G ∝ R_FC ², and since the mass of the fuel cloud, m_FC ∝ R_FC ³ and hence G ∝ m_FC (2/3), assuming a constant number density of fuel particles (n_FC).

Figure 2 shows the results for η_eff vs. G for a spherical FC. There are three regimes of FC oxidation: Zone I – Dilute Cloud {G<1} where a low number density “n_FC” for given FC size R_FC or smaller cloud size for given number density “n_FC” i.e. “m_FC” low) a) indicates high SERR (W/kg). It is constant throughout the cloud since Y_O2 = Y_{O2,FC, s} and η_eff,FC ≈ 1. The particles in Zone I burn almost uniformly with an O₂ concentration at Y_{O2,FC, s} for all particles as though each particle is isolated. Zone II – Dense Cloud {1 < G < 100} , where the cloud size R_FC is large, “m_FC” is higher, and SERR is a function of r since Y_O2 (r) < Y_{O2,FC, s}. This is the ODC mode or “crowd” effect as called in biology [12], where oxygen concentration decreases with decreasing r, forming an anaerobic core of radius R_an where the O₂ concentration is almost zero. For this zone, η_eff,FC < 1 (Figure 1b). Zone III – Very Dense Cloud {G > 100}, where particles at the core experience severe ODC, with G > 100. (Figure 1c). Except for a thin aerobic film near the surface of FC, the anaerobic core radius is almost the same as R_FC. For this zone, η_eff,FC << 1.

C) Oxygen-Deficient Metabolism (ODM) in Biology:

The oxygen diffuses from capillaries towards the metabolic cells contained within interstitial fluid (IF). Even though the biology literature suggests a radial diffusion distance of the order of 100 μm (where pO₂ ≈ 0) from the capillaries, the actual path may be longer, leading to a decreased O₂ transport rate (or decreased effective diffusivity) to the mitochondria. The diffusive O₂ transport rate is affected due to the following:

$${\dot{q}}_{k,m }\left({\displaystyle \frac{W}{kg of organ k}}\right)=e_{k,6}{M}_B^{f_{k,6}}= E_{k,6} {m_k}^{F_{k,6} }, m_k = c_{k,6} {M_B}^{d_{k,6} }; F_{k,6}= \left({\displaystyle \frac{f_{k,6}}{d_{k,6}}}\right), E_{k,6}=\left\{{\displaystyle \frac{e_{k,6}}{ c_{k,6} \frac{f_{k,6}}{d_{k,6}}}}\right\}; m_k,M_B in kg$$

If the mass of each kidney (k= Skid, single kidney) is used, m_Skid = m_Kid/2, ${\dot{q}}_{Kid,m }\left({\displaystyle \frac{W}{kg of organ Kid}}\right)=e_{k,6}{M}_B^{f_{k,6}}= E_{k,6} {m_{Kids}}^{F_{k,6} }= E_{Skid,6} {m_{Skid}}^{F_{k,6} }, E_{Skid,6}= 2^{F_{k,6} }{E}_{k,6}, k=Kid$HHV_O2= 14,335 kJ/kg of O₂ or 18.7 kJ/SATP L of O₂ or 20.5 J/CST mL of O₂ or 18.1 J/mL of O₂ at 36.2 °C

HHVO₂, kJ/L O₂ 71 to 92 kg = 15.818 + 5.17* RQ [30,31,32]: i) closely packed cells (number density of cells, n, or crowding effect) [33], ii) tortuous oxygen path, iii) amount of aqueous fluid, iv) extracellular structures or cell barriers, and v) presence of cytoplasm (which alone reduces D by 30 times the normal level). As a result, cells cannot maintain the required O₂ flow for ATP production [34], leading to oxygen deficiency (OD).

ODM in Organs: Hypoxic conditions (low pO₂ in cells) decrease the oxygen consumption rate ${\left\{{\dot{w}}_{O2} \right\}}_{cell}$ by cells, while anemic conditions or a reduction in blood flow [35] or reduced Hb contents cause a decrease in O₂ supply to the cells from capillaries. Hypoxic conditions cause in reduction of ATP production rate leading to “bioenergetic collapse” [36]. Furthermore, Y_O2 within cells may fall below the “extinction” level, causing cells to cease oxidation and become sleeper cells. OD in cells under hypoxic conditions prevent oxidation of pyruvate and hence it converts to lactate, increasing acidity which then results in the production of protein called HIF (hypoxia-induced factor). HIF enables the activity of genes to switch from oxidative phosphorylation to glycolytic pathways [37] for energy and ATP release, altering the apparent “software” for energy release from oxidation to glycolysis. ODM promotes a switch to glycolysis, where only two ATP are obtained per CH compared to 32 ATP via oxidative phosphorylation, resulting in the decrease of overall energy release [38] via glycolysis path. Increased ATP requirements cause consumption of more nutrients to adopt an altered metabolic path for energy release, i.e., glycolysis under low-oxygen environments, which supports rapid cell division and serves as a source of energy for cancer cells [39,40]. Rats are known to sustain anoxia for extended periods by using fructose as a nutrient for glycolysis [13,41]. It is well known that oxygen deficiency (OD) or hypoxia contributes to several diseases, including cancer, stroke, anemia and heart disease. There appears to be a positive correlation between the mass of an organ and the number of cancer cases [42], which is attributed to the link between excess fat in organs and obesity.

ODM in Cell Clouds:

Singer’s Phenomenological type of ODM Model: Singer et al. studied the role of OD or the “crowding effect” on the metabolic rates of in-vitro organ samples and developed a phenomenological type of model. Just like particles in FC, the cells near the aerobic surface undergo high SOrMR_k while those cells near the anerobic core may undergo only glycolysis.

Detailed ODM Model following ODC Literature in Engineering: More detailed ODM models were developed by Annamalai by adapting the ODC literature from engineering to biology [3]. Unlike the Krogh cylinder model, where the capillary is placed on the axis (COA) of a cylinder containing metabolic cells , the ODM model uses a spherical cloud of cells (CC) of radius R_CC having n_CC, cells per unit volume with capillaries on the surface (COS) of CC with mass of CC, m_cc {Figure 3a}. The COS model is also known as the “solid cylinder” model in biology [43]. A detailed comparison between ODC and ODM models, and relations for several variables of interest, are presented in Ref. [3]. In ODM, the carbon cloud is replaced by a cell cloud (CC), particles are replaced by cells of the BS, and Y_O2,FC,s becomes Y_O2,CC,s. The radius R_FC is replaced by R_CC, the ERR is replaced by the organ metabolic rate (OrMR) and ERR_m is replaced by SOrMR in cell clouds, defined as SOrMR = OrMR / m_CC. The G number in engineering ( [27]) is also replaced by G_OD,k for organ k. The oxidation rate for each particle is replaced by the cell metabolic rate (Figure 3d). These relations will be summarized in the methodology section.

Just like FC, there exists three zones of operation of CC: Dilute, Dense and very dense CC. More details for CC are provided in the caption of Figure 2. Those cells near the surface are aerobic with higher rate of oxidation of nutrients while those cells near the core of the cloud are anaerobic with very little oxygen. Cells near core may undergo only glycolysis {Figure 3b}.

While resting, limited capillaries are perfused with blood (Figure 3b, surface at Y_O22,cc,s), whereas under exercise, all the capillaries are perfused (Figure 3c} increasing Y_O22,CC,s at the surface of CC { e.g., Maximum Metabolic Rate (MMR) when there is increased blood flow through selected organs during exercise}.

The literature review suggests that despite several hypotheses outlined in Section 1.2 for the 3/4 law, “the hunt for an explanation of the 3/4 law continues” [44]. The current ODM hypothesis focusses on the metabolic rate he controlled by “downstream demand-side” oxygen consumption of all the cells within an organ and provides another “hunt” for an explanation of the 3/4 law. Attempts have also the been made to extend ODM hypothesis predict the allometric constants of maximal metabolic rate (MMR) vs. body mass using known data on the percentage of blood perfused under rest and during exercise, attributing the increase in MR to enhanced oxygen concentration under the redistribution of perfusion percentage of capillaries.

1.3. Objectives

The overall objectives of the current work are to i) link the field of group or oxygen-deficient combustion (ODC) in engineering with the field of oxygen-deficient metabolism (ODM) in biology, ii) adopt the relations developed for energy release rate per unit mass (ERR_m, W/kg cloud) to predict SOrMRk (W/kg of k) of 116 BS ranging in mass from 0.0075 to 6,650 kg using known data from two BS, referred to as Reference Species (RS), where RS-1 has the lowest body mass, M_B,RS-1 (Shrew, 0.0075 kg), and RS-2 has m_RS-2 body mass much higher than m_RS-1 (Rat Wistar of 0.390 kg, η_eff,k < 1), and iii) estimate the whole-body metabolic rate versus M_B using a heterogeneous approach and known organ masses, demonstrating Kleiber’s law with an exponent close to 0.75. In addition, predict a) a hypothetical upper metabolic rate (UMR) for organs, and, consequently, the whole body in the case all the cells within the organ metabolize without the presence of oxygen concentration gradients, b) the maximal metabolic rate (MMR) under exercise, when all the capillaries at the cell cloud surface are perfused, with increased average oxygen concentration at the cell cloud surface (CC,s) and show that whole-body allometric law yields an exponent close to 0.87, as quoted in the literature, and c) provide a method for detecting the degree of oxygen deficiency within organs for medical personnel.

2. Materials and Methods

2.1. ODM Hypothesis

The ODM hypothesis assumes that each organ k consists of multiple cell clouds (CC), with each cell cloud having a mass mass m_cc,k with radius R_CC,k, which is related to the organ mass m_k by R_CC,k α m_k ^1/3. It is also possible that capillaries do not fully cover the entire spherical surface enclosing the cells (Figure 3). Typically, 25-35 % of an organ’s capillaries are perfused at rest, with perfusion increasing during exercise since there is increased metabolic demand and a higher perfusion percentage results in a higher Y_O2,cc,s. Using the Krogh-Erlang equation, Ostergaad demonstrated that only 10% of SM capillaries are perfused at rest, but more capillaries are recruited during exercise [46]. Further details can be found in Section 2.2 and Section 3.4.

Smaller species have smaller organs (e.g., shrew of mass 0.0075 kg), while larger species have larger organs, as indicated by d_k > 0 in the allometric exponents for organ sizes. Thus, the smaller organs of smaller species may have shorter distances for O₂ diffusion from capillaries to cells, allowing metabolism to occur as if each cell within the CC is exposed to the same O₂ concentration as Y_O2,CC,s (η_eff ≈1), resulting in SOrMR_k ≈ SOrMR_k,iso,. However, isolated cell metabolic rates can still vary from organ to organ, even in smaller species, due to differences in functional requirements, cell reactivity, and O₂ transport rate (e.g., heart tissues containing M_b can deliver O₂ at faster rate resulting in increased effective transport coefficients for O₂ from capillaries to mitochondria). As organ mass increases (e.g., in the liver), η_eff,k < 1, and SOrMR_k ≈ η_eff,k x SOrMR_k,iso, where it is assumed that for any given organ k, SOrMR_k,iso remains constant for all BS regardless of body size, but becomes extremely low for larger organs in larger species, leading to lower values of η_eff,k.

2.2. Methodology

Detailed comparisons of the governing conservation equations and several relations in the fields of ODC in engineering and ODM in biology literatures are presented in Ref. [3]. These include: i) conservation equations for both fields, ii) the ERR of a single particle in a FC and a single cell in a CC in terms of Y_O2, iii) oxygen profiles in FC versus CC, iv) the dimensionless G number for FC {Equation 118 } and corresponding G_OD,k for the CC of organ k in biology { Equation 14} and v) the specific ERR (SERR) of FC (W/kg of cloud) in terms of the effectiveness factor and G, and specific organ metabolic rate (SOrMR_k) of CC (W/kg of cell cloud of organ k) in terms of the effectiveness factor and G_{OD, k}. The relevant relations for the current work are briefly summarized below.

i) 

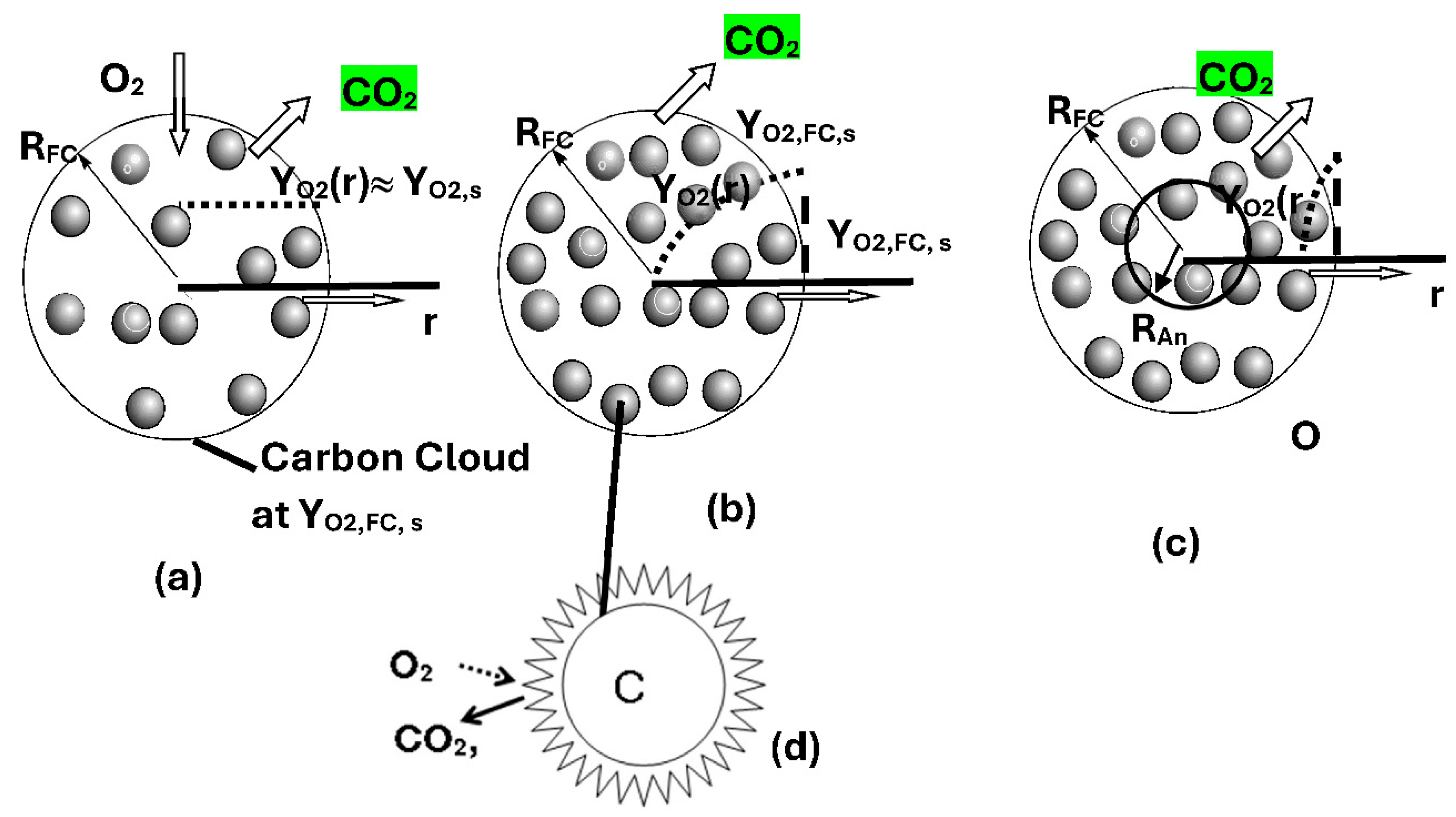
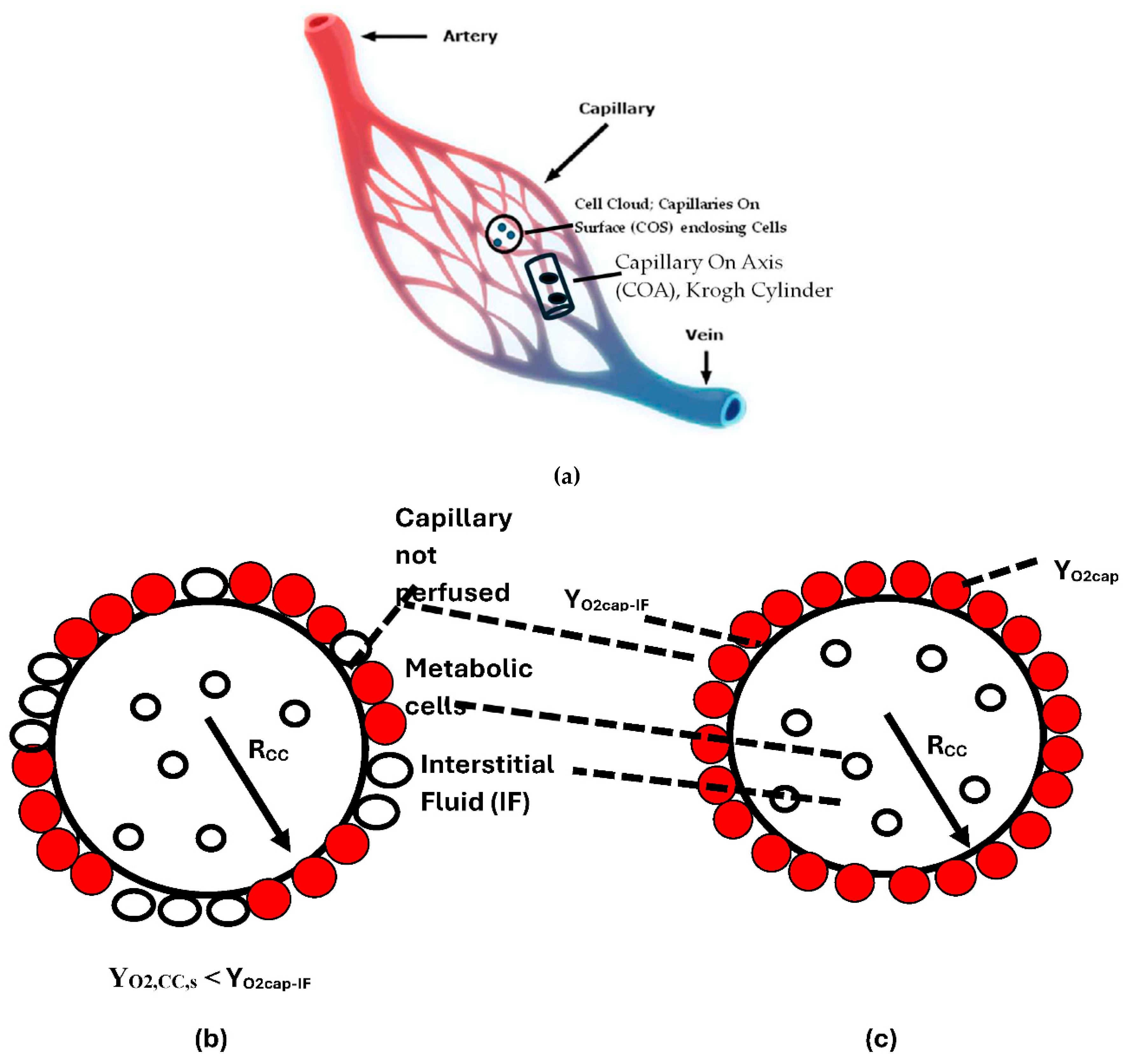
Metabolic Rate of single cell located at r in CC {Figure 3}

$${\dot{w}}_{O2,cell,k}(r) ={\left(C_{ch,cell}\right)}_k Y_{O2}(r),$$

(12)

where C_Ch,cell, characteristic cell O₂ consumption rate when Y_O2 = 1; the relations for C_Ch,cell under kinetic control or diffusion controlled O₂ consumption rates are given in Ref. [3].

ii) 

Oxygen Profiles within CC

For the cell cloud within organ k, Ref. [3] presents

$${\displaystyle \frac{Y_{O2,k}(\xi )}{{\left(Y_{O2,k}\right)}_{\xi =1}}} = {\displaystyle \frac{Y_{O2,k}(\xi )}{\left(Y_{O2,CC,s}\right)}} = \left({\displaystyle \frac{1}{\xi }}\right){\displaystyle \frac{\mathrm{Sinh} \left(G_{OD,k}^{1/2}\xi \right)}{\mathrm{Sinh} \left(G_{OD,k}^{1/2}\right)}}, \xi = \left({\displaystyle \frac{r}{R_{CC,k}}}\right)$$

(13)

where for organ k

$$G_{OD,k}={\displaystyle \frac{{\left(C_{ch,cell}\right)}_k n_k R_{CC,k}^2}{\rho D}} = {\displaystyle \frac{Charactristic O_{2}consumption rate by cell cloud}{Charactristic O_{2}transport rate to cells from cell cloud surface }}$$

(14)

where k= Kid, H, Br, L and R_CC,k α m_k^1/3, C_Ch,cell, characteristic O2 consumption rate by cell

iii) 

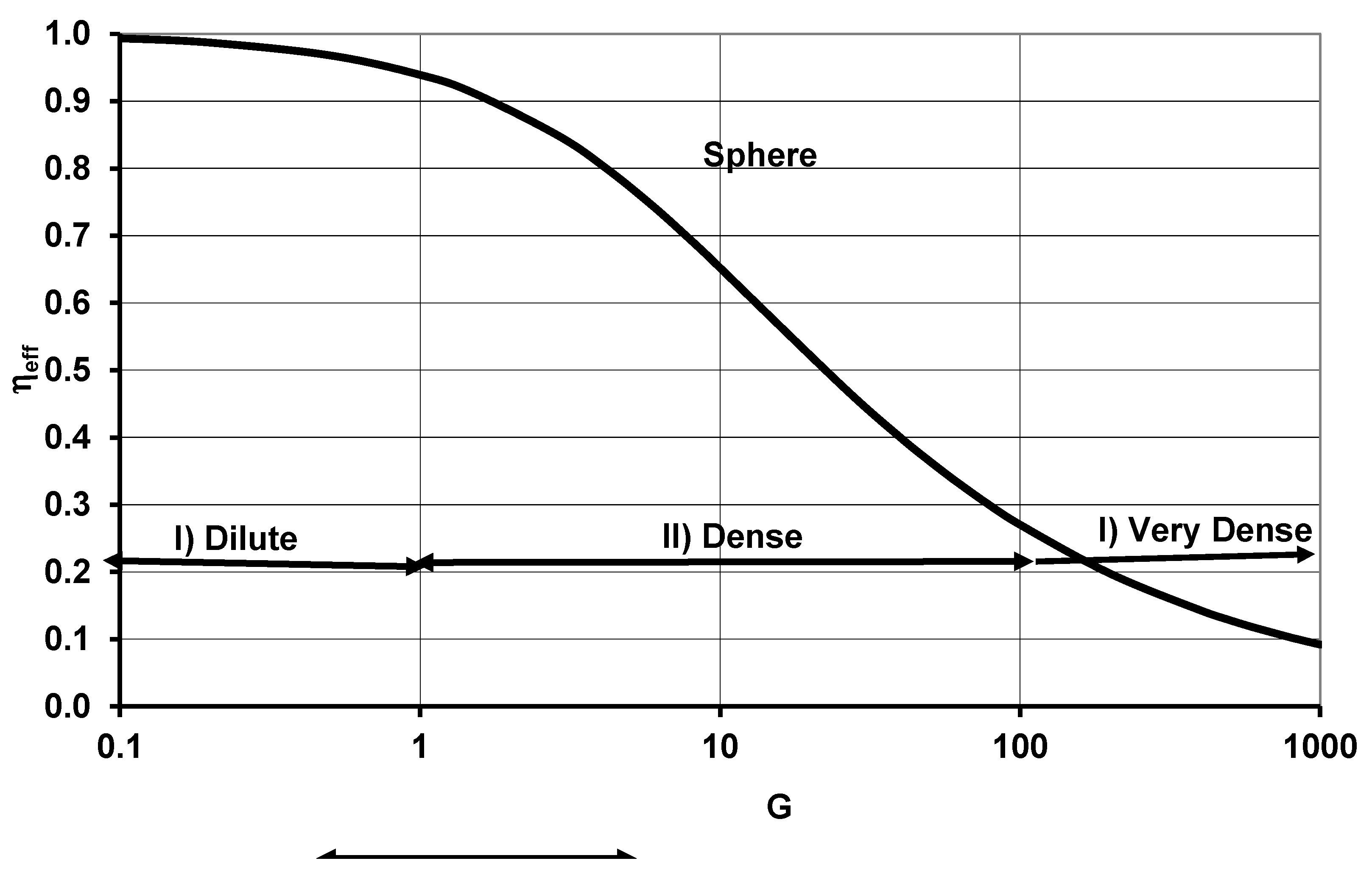
Effectiveness Factor of Spherical CC and Specific Organ Metabolic Rate {SOrMR_k}

Adopting the same procedure as in engineering,

$${\eta }_{eff,k} ={\displaystyle \frac{{\dot{w}}_{O2,m,k}}{{\dot{w}}_{O2,m,k}\left(Y_{O2,CC,s}\right)}}={\displaystyle \frac{{\left\{SOrMR\right\}}_k}{{\left\{SOrMR\left(Y_{O2,CC,s}\right)\right\}}_k }}= 3 {\displaystyle \underset{0}{\overset{1}{\int }}} \left\{{\displaystyle \frac{Y_{O2,k}(r)}{{\left(Y_{O2,CC,s}\right)}_k}}\right\} {\displaystyle \frac{r}{R_{CC,k}}} d\left({\displaystyle \frac{r}{R_{CC,k}}}\right), Spherical CC$$

(15)

With Y_O2 profile from Equation 13, the η_eff,k is derived as:

$${\eta }_{eff,k} ={\displaystyle \frac{{\left\{SOrMR\right\}}_k}{{\left\{SOrMR\left(Y_{O2,CC,s}\right)\right\}}_k }}= {\displaystyle \frac{3}{\sqrt{G_{OD,k}}}} \left\{ {\displaystyle \frac{1}{\tanh \left(\sqrt{G_{OD,k}}\right)}}-{\displaystyle \frac{1}{\sqrt{G_{OD,k}}}}\right\}, Spherical CC$$

(16)

where k = Kids, H, Br, and L Using the definition of η_eff,k , the SOrMR_k is given as

$${\left\{SOrMR\right\}}_k = {\eta }_{eff,k} {\left\{SOrMR\left(Y_{O2,CC,s}\right)\right\}}_k = {\eta }_{eff,k} {\dot{q}}_{\mathrm{k},\mathrm{m},\mathrm{iso} }$$

(17)

where ${\dot{q}}_{\mathrm{k},\mathrm{m},\mathrm{iso} } ={\left\{SOrMR\left(Y_{O2,CC,s}\right)\right\}}_k$ . Equation 17 reveals that SOrMR_k is a function of G_OD,k in biology due to dependence of η_eff,k on G_OD,k . I) When G_OD,k << 1 (dilute cloud), then, η_eff,k→1 (Equation 1613, Figure 2 with η_{eff =} η_eff,k, G = G_OD,k). II) As the organ size increases, G_OD,k also increases, and the effectiveness factor decreases (dense cloud, 1 < G_OD,k < 100). III) When G_OD,k > 100, the cell cloud is very dense. All three regimes of η_eff,k of CC within an organ are shown in Figure 2.

iv) 

Metabolic Rate of Vital Organs {${\dot{q}}_{vit }$}: Using Equation 17 for the vital organs, the metabolic rates of vital organs of any BS:

$$\begin{array}{l}{\dot{q}}_{vit } = {\eta }_{eff,Kid} {\dot{q}}_{Kid,m,iso} m_{Kids}+ {\eta }_{eff,H} {\dot{q}}_{H,m,iso} m_H + \\ {\eta }_{eff,Br} {\dot{q}}_{Br,m,,iso}{m}_{Br} +{\eta }_{eff,L }{\dot{q}}_{L,m,,iso} m_L \end{array}$$

(18)

v) 

Metabolic Rate of Remaining Mass (RM) of Tissues {${\dot{q}}_{RM}$} for any BS

The remaining mass of organs (RM) represents a sum of all “minor” organs (e.g., SM, skin, etc.) within the body, and the specific metabolic rate of RM (W/kg of RM) is needed. There are several possible approaches: a) Select data for each of minor organ if available, estimate the effectiveness factor for all minor organs, and adopt a similar procedure outlined for vital organs , b) Use the EAR for RM: ${\dot{q}}_{RM,m}= e_{RM,6} {M_B}^{f_{RM,6}}$ , e_RM,6 =1.45, f_{RM,6 =} -0.17, ${\dot{q}}_{RM,m}$ in W/kg, c) Assume Elia’s constant values for ${\dot{q}}_{RM,m}$ as 0.581 W/kg for all BS. In the current work, methods (b) and (c) are adopted for estimating ${\dot{q}}_{RM,m}$.

$${\dot{q}}_{RM} = {\dot{q}}_{RM,m} m_{RM} , m_{RM} = M_B -m_{vit}$$

(19)

vi) 

Whole Body Metabolic Rate (${\dot{q}}_B$) under Rest

The effective area for O₂ exchange.is limited, as only 25% to 35% of available capillaries are perfused under BMR conditions [45], which affects O₂ diffusion distance and hence the metabolic rate within the organ. Adopting the heterogeneous method, whole body metabolic rate under rest, {${\dot{q}}_B$} is given as

$$\begin{array}{l}{\dot{q}}_B = {\dot{q}}_{vit} + {\dot{q}}_{RM} ={\eta }_{eff,Kids} {\dot{q}}_{Kid,m,iso} m_{Kids}+ {\eta }_{eff,H} {\dot{q}}_{H,m,iso} m_H + \\ {\eta }_{eff,H} {\dot{q}}_{Br,m,,iso}{m}_{Br} +{\eta }_{eff,L }{\dot{q}}_{L,m,,iso} m_L+ {\dot{q}}_{RM,m} m_{RM} \end{array}$$

(20)

vii) 

Metabolic Rate of RM {${\dot{q}}_{RM,Ex}$} and Whole Body Metabolic Rate {${\dot{q}}_{B,Ex}$} under Exercise

During exercise, blood flow to the skeletal muscle (SM) is increased to supply the required oxygen and nutrients. Thus, SM becomes metabolically more active compared to other tissues within the RM due to increased capillary perfusion, increasing from approximately 25% at rest to nearly 90 % during exercise.

$${\dot{q}}_{SM} = {\dot{q}}_{SM,m} m_{SM}$$

(21)

Relations for ${\dot{q}}_{SM,m}$ depends upon the Y_{O2, CC,s} and hence the percentage of capillaries perfused. The remaining mass of tissues under exercise is given as $m_{RM,Ex} =M_B -m_{vit}-m_{SM}$

$${\dot{q}}_{B,Ex} = {\dot{q}}_{vit,Ex} + {\dot{q}}_{SM}+{\dot{q}}_{RM-Ex}$$

(22)

Where ${\dot{q}}_{vit,Ex}$is different from ${\dot{q}}_{vit}$ under rest due to the percentage of capillaries perfused under exercise are different from those at rest. The ${\dot{q}}_{RM,Ex}$ during exercise is given as,

$${\dot{q}}_{RM,Ex} = {\dot{q}}_{RM,Ex,m} m_{RM,Ex} , m_{RM,Ex} =M_B -m_{vit}-m_{SM}$$

(23)

viii) 

Upper Metabolic Rate (UPR,${\dot{q}}_{B,UPR}$) and Maximum Metabolic Rate (MMR,${\dot{q}}_{B,MMR}$) of Whole Body

A hypothetical upper MR of organ k (not the maximum MR) and, hence, the whole-body MR can be estimated by setting η_eff,k = 1 for all organs {i.e. no oxygen gradients within CC}, including RM from Equation 1613 to Equation 2016.

When the CC surface is covered with more perfused capillaries, the Y_O2,CC,s increases and most of the cells are aerobic resulting in the maximum metabolic rate, MMR and leading to a whole-body allometric law with an exponent higher than 0.75. The MMR, such as during exercise, is obtained by setting η_eff,k = 1 for all organs, including SM, and RM-Ex during exercise, while adjusting the percentage of capillaries perfused. Further blood flow to organs other than SM are also altered. This adjustment affects Y_O2,CC,s for all organs due to change in blood flow rates . The percentage of perfusion affects Y_O2,CC,s (Figure 3b and Figure 3c). The change in Y_O2,CC,s is given by the following relation:

$${\displaystyle \frac{{\left(Y_{O2,CC,s}\right)}_{\mathrm{k},\mathrm{MMR}}}{{\left(Y_{O2,CC,s}\right)}_{\mathrm{k},\mathrm{rest}}}} = {\displaystyle \frac{Blood flow rate to organ k under MMR}{Blood flow rate to organ k under \mathrm{Re}st}}$$

(24)

The increased Y_O2,CC,s causes isolated rates to increase, thereby increasing the whole-body metabolic rate. The percentage of capillaries perfused under rest and exercise conditions is shown in . Note that blood flow rate to organ k is given by the product of blood flow fraction to organ k and the pumping rate of blood by the heart and pumping rate changes depending upon the rest or exercise conditions.

2.3. Estimation of OD Number (G_OD,k) and Effectiveness Factor (η_eff,k) of Organ k any BS

The estimation of η_eff,k requires knowledge of the dimensionless number G_OD,k (Equation 14), which depends on i) the reactivity of cells within organ k undergoing metabolism (C_Ch,cell) either under diffusion or kinetic control { Michaelis Menten (MM) constant for first order reaction under adsorption control} ii) the overall transport coefficient D of oxygen from capillaries to mitochondria, and iii) a knowledge of (Y_O2,CC,s)_k dictated by capillary number density and percentage of capillaries perfused. There are two methods for estimating SOrMR_k of organs:

A) Basic Method: This approach requires basic data for C_Ch,cell, D, (Y_O2,CC,s)_k, MM constant and the percentage of capillaries perfused for each organ k. Consequently, greater uncertainty exists in the estimation of G_OD,k and SOrMR_k due to variations in these parameters across the organs of 116 species.

B) Ratio Method or Reference Species (RS) Method:

The current work uses the references species (RS) method, also known as the ratio method, and assumes that the SOrMR_k of two references species, RS-1 and RS-2, are known. This approach reduces uncertainty in the results by relying on ratios. This method is based on the premise thats${\dot{q}}_{\mathrm{k},\mathrm{m},\mathrm{iso} }$ of any BS is same as ${\dot{q}}_{\mathrm{k},\mathrm{m} }$of RS-1 having lowest body mass and hence lowest organ mass. In RS-1, all cells within the vital organ k operate under an isolated mode (i.e., all cells at Y_O2,CC,s, η_eff,k ≈ 1). The RS-1 is selected as the BS with the lowest body mass (e.g., RS-1: Shrew, 7.6 g). Justification is as follows. Makarieva et al. [47] demonstrated that SBMR varied from 0.3 W/kg to 9 W/kg (a 25-fold variation), despite a 10²⁰-fold difference in body mass for “bacteria to elephants and algae to trees.” This suggests that SBMR is relatively consistent among mammalian species [48]. Since the number of cells per unit mass is similar across BS, then cell metabolic rate (CMR) does not vary significantly. This view is confirmed by Lindstedt and Schafeer [49], who stated that the “150-ton blue whale,” which is 75 million times the mass of the 2g Etruscan shrew, “shares the same architecture… organ systems, biochemical pathways.” Therefore, the isolated metabolic rate of cells in a vital organ k of any BS is assumed to be same as that of organ k of RS-1.

The RS-2 is selected as a BS with a significantly higher body mass (e.g., Rat Wistar, 390 g) than RS-1. In RS-2, the G_OD,k falls within the dense zone (i.e., the steeper part of η_eff,k vs. G_OD,k, Zone II in Figure 2), and hence (η_eff,k)_RS-2 < 1. With the known SOrM_k data for RS-1 and RS-2, (η_eff,k) _RS-2 is estimated as

$${\left\{{\eta }_{eff,k}\right\}}_{RS-2} ={\displaystyle \frac{\left(SOrM{R}_{k,RS-2}\right)}{\left(SOrM{R}_{k,iso,RS-2}\right)}} \approx {\displaystyle \frac{\left(SOrM{R}_{k,RS-2}\right)}{\left(SOrM{R}_{k,RS-1}\right)}}$$

(25)

and the corresponding (G_OD,k)_RS-2 is evaluated using Equation 1613. With the assumption of a constant cell diameter (2a) for a given organ k across BS (Schmidt-Nielsen [58], Savage et al. [49]) and the number density of cells, and using the definition of G_OD,k (Equation 14), G_OD,k ∝ R_CC,k ² and since the mass of the cell cloud, m_CC,k ∝ R_CC,k ^1/3, G_OD,k ∝ m_CC,k ^2/3, the G_OD,k for 116 other BS (other than RS-1 and RS-2) with body masses ranging from 0.010 kg to 6,650 kg are estimated using the following relation:

$${\displaystyle \frac{{\left(G_{OD,k}\right)}_{BS}}{{\left(G_{OD,k}\right)}_{RS-2}}}= {\left({\displaystyle \frac{m_{k,BS}}{m_{k,RS-2}}}\right)}^{(2/3)}$$

(26)

and the corresponding η_eff,k is estimated using Equation 1613. Thus, the SOrMR_k for k = Kids, H, Br and L, ${\dot{q}}_{vit}$ is determined from Equation 1814, ${\dot{q}}_{RM,m}$, using Equation 1915, where SOrMR_RM ( ${\dot{q}}_{RM.m}$) of the RM, which consists of several organs with metabolically weak cells, is estimated by following EAR (Table 1, [21]) since organ masses are not known with remainder tissue mass or using Elia’s constant for SOrMR_RM (Table 1), and finally, ${\dot{q}}_B$can be estimated from Equation 2016, based on the organ masses of 116 species. Results are presented in the next section. A step-by-step procedure is presented in Appendix B and is briefly described here.

3. Results and Discussion

3.1. Whole Body Metabolic Rate using EAR for All Organs and the Effect of Elia’s Constant for ${\dot{q}}_{RM,m}$on Whole-Body Allometry

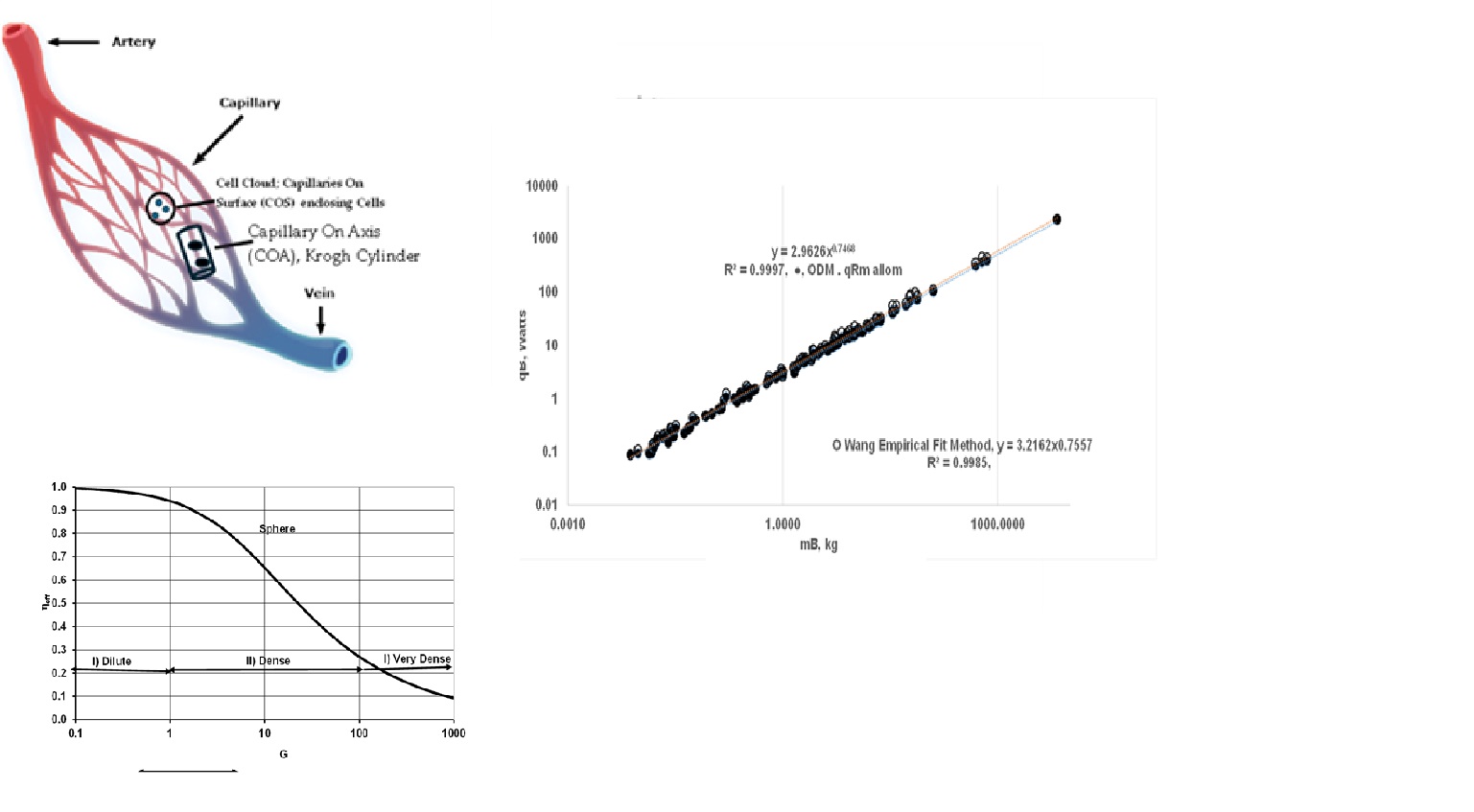
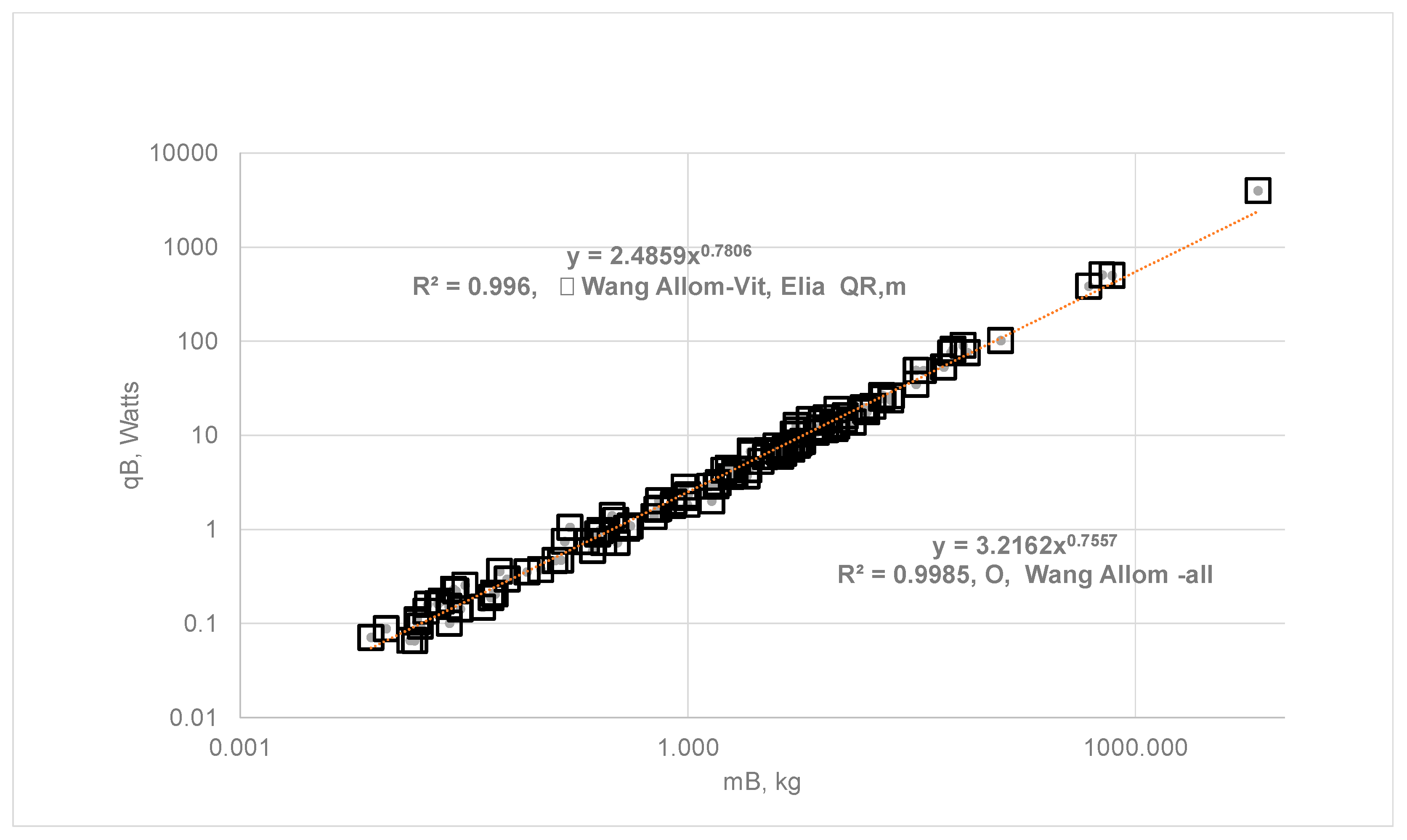
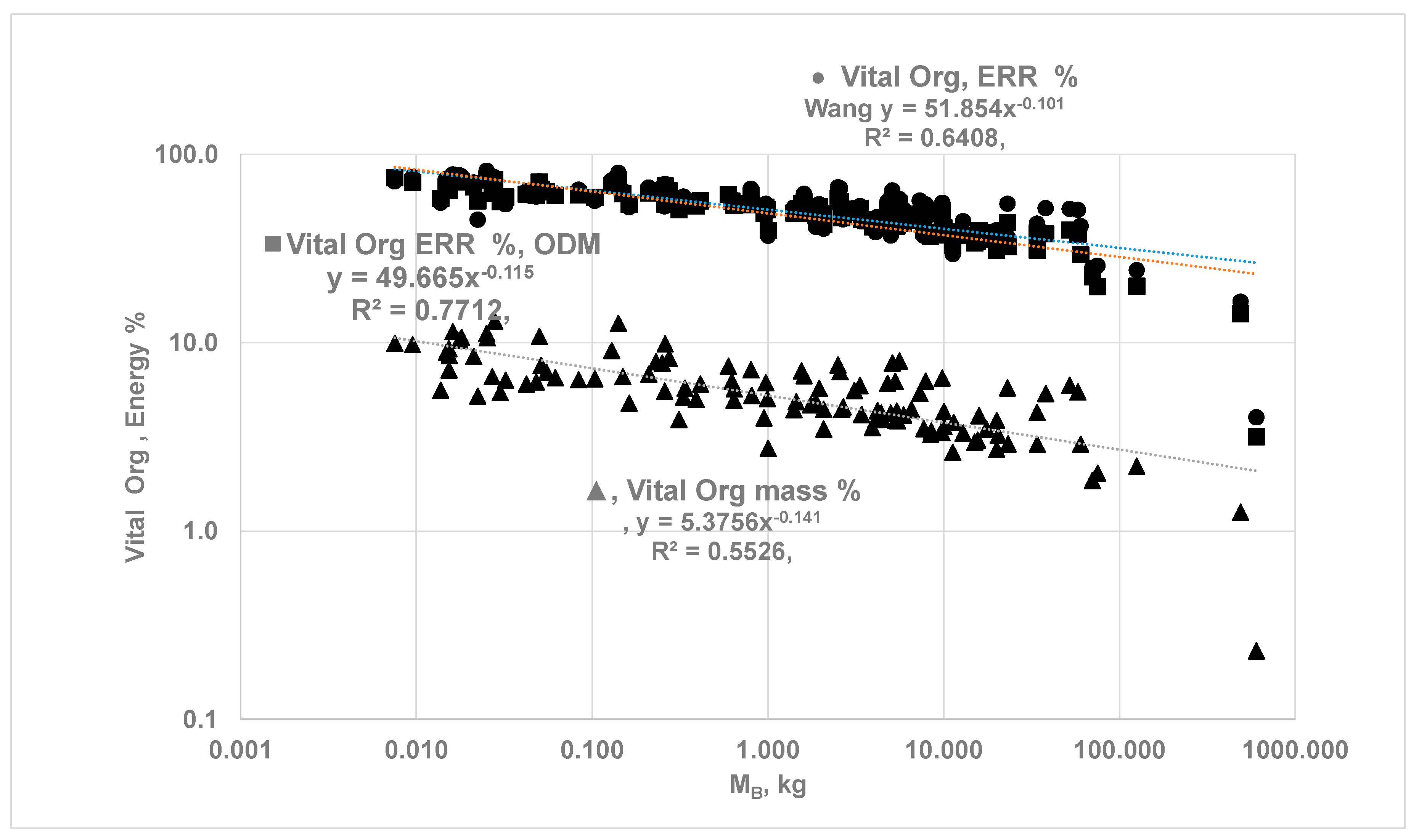
• Empirical Allometric Relations (EAR) for all Organs: Hereafter, Wang’s allometric relations will be referred to as EAR (Equation 4) or, ${\dot{q}}_{k,m} = e_k {M_B}^{f_k}$, which are obtained with data on SOrMR_k ( ${\dot{q}}_{k,m}$, W/kg of k, k=Kids, H, Br, L and RM) vers us the body mass for six species. The same allometric constants were then extended to estimate SOrMRk of 116 species, summing up OrMR_k to obtain the whole-body metabolic rate and validating Wang’s approach by demonstrating Kleiber’s law with a = 3.22 and b = 0.76. Note that EAR is used only for ${\dot{q}}_{k,m}$ and ${\dot{q}}_k$ is estimated using organ masses listed in Table 3 {Appendix A} which tabulates the BS, body mass, organ masses for 116 species, and${\dot{q}}_B$ using EAR.
• EAR for Vital Organs and Elia Constant for RM: The author used the same allometric constants for vital organs but assumed Elia’s constant q_RM of 0.581 W/kg and computed the whole-body metabolic rate. With Elia’s constant, ${\dot{q}}_{RM,m}$, the Kleiber’s law exponents become a = 2.49, and b = 0.78. It is seen from Figure 4 that the slope b increased from 0.76 to 0.78, representing a 3.3 % increase in the exponent b when Elis’s constant is used for RM.

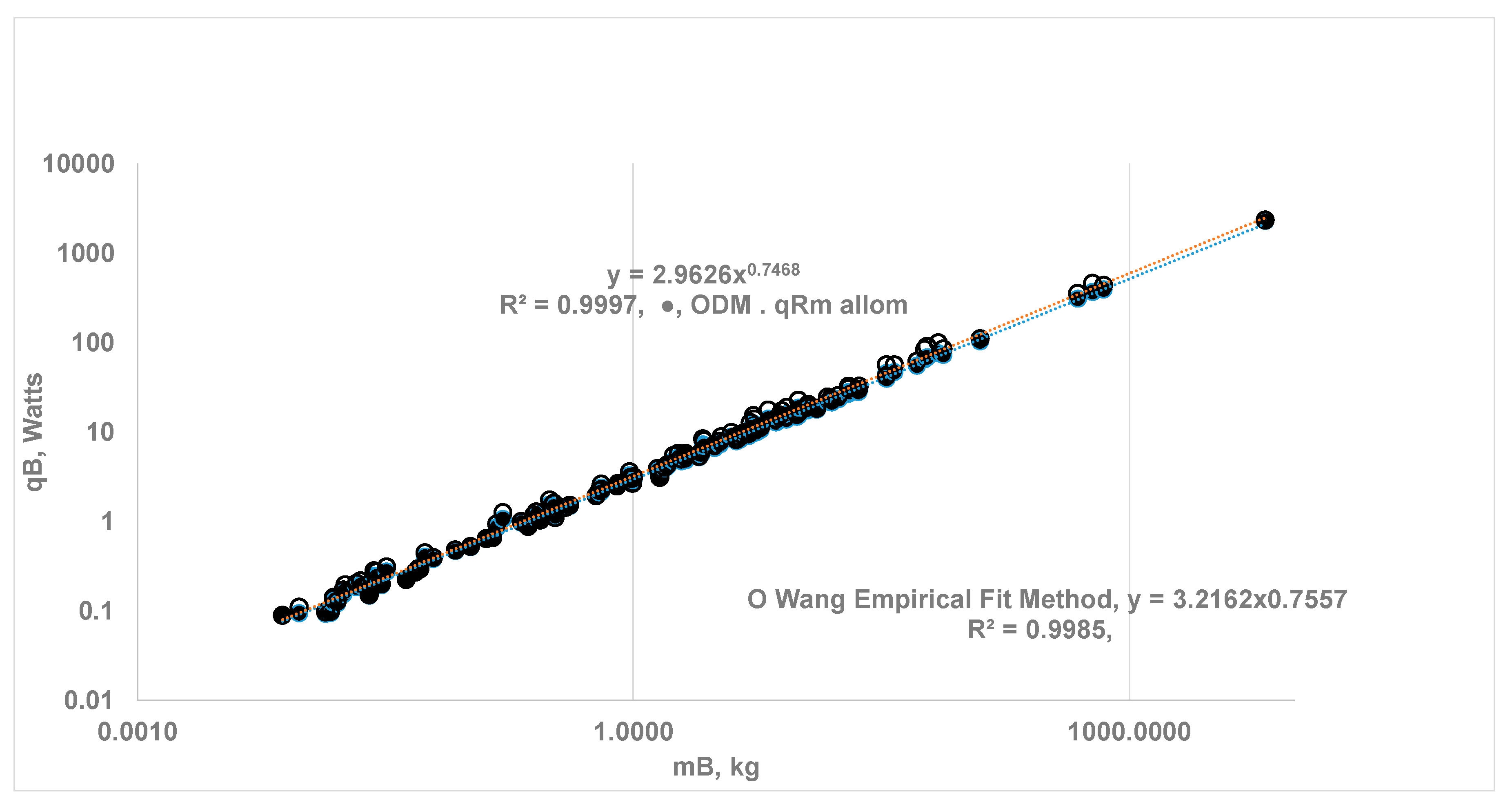
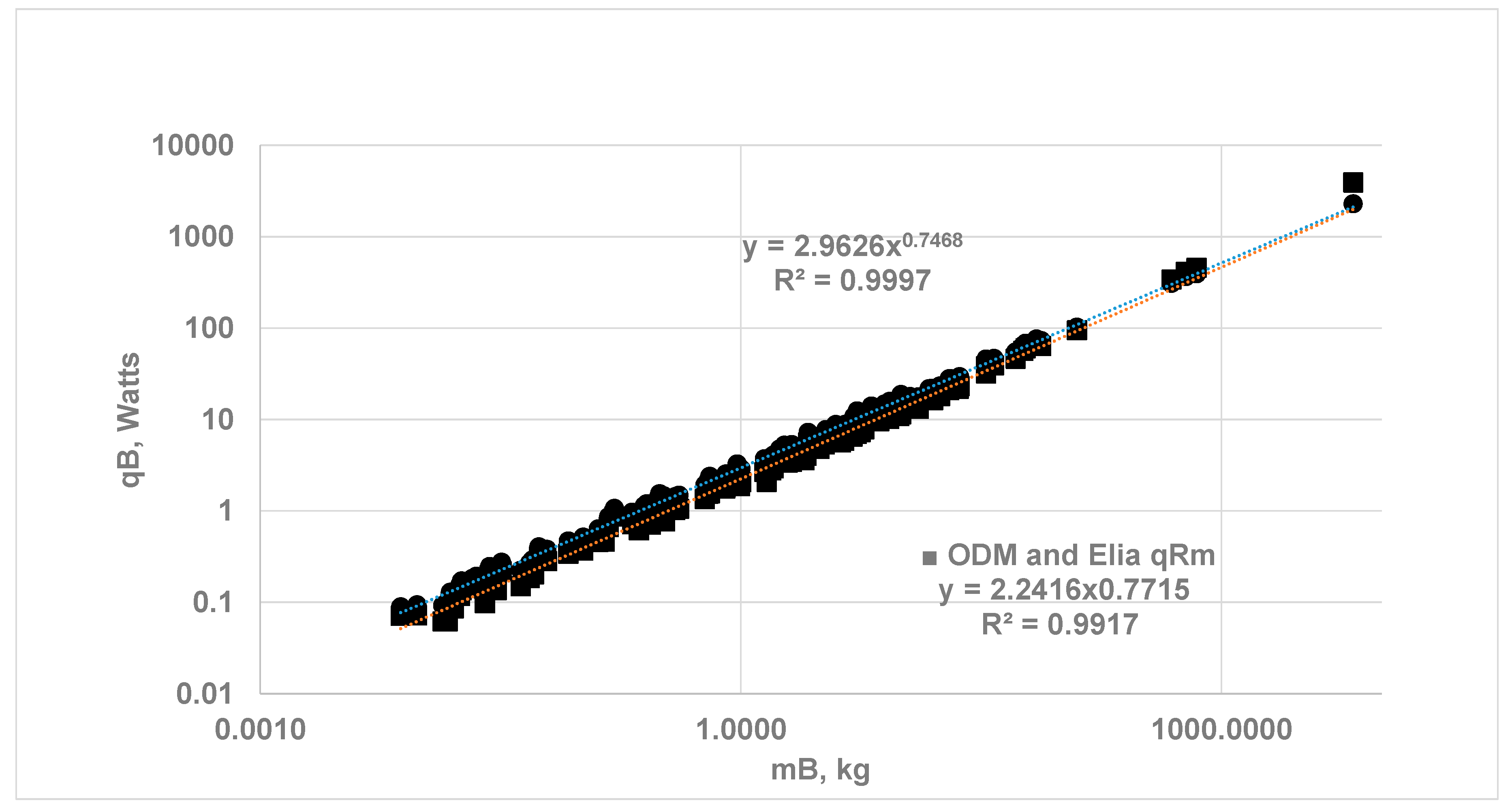
3.2. Whole Body Metabolic Rate Using ODM Hypothesis and Comparison with Results from EAR Method

A). ODM and EAR for SOrMR_k of RM: The ODM model uses the relation for effectiveness factor of four vital organs to predict SOrMR_k and then whole body metabolic rate using summation over all organs. Figure 5 shows the results for the metabolic rate vs. body mass obtained using ODM hypothesis and using allometric law for ${\dot{q}}_{RM,m}$ since RM consists we did not carry this fir RM since it has multiple organs of widely varying organ masses with wide variation in allometric exponent “f_k” . Thus Used EAR for “ RM” of several metabolically weaker organs .

$${\dot{q}}_B \left(W\right)= a {M_B}^b, a=3.04, b=0.75, M_B = 0.0075 kg to 6650$$

(27)

The same figure provides a comparison with Wang’s results using EAR. Note that the ODM method relies only on data from two reference species, RS-1 and RS-2, to predict SOrMR_k and whole-body metabolic rates for the remaining 114 species. Table 3 compares ODM based metabolic rate ${\dot{q}}_B$for 116 species with those ${\dot{q}}_B$ using EAR (last 2 columns).

If the error percentage is defined as {MR with ODM - MR with EAR ) * 100 } / {MR with EAR } , then the highest error occurs for a 60 kg human at 24.07%. The average error across 116 species is 8.14%.

B). ODM and Elia’s Constant SOrMR_k for RM: Instead of using the allometric relation for SOrMR_k of RM, if Elia’s consonant value for RM (${\dot{q}}_{RM,m} = 0.581$W/kg) is applied, the allometric constant b increases from 0.75 to 0.77 (Figure 6). When Elia’s constant value for is used instead of EAR for RM, lower values re obtained for smaller species but, while higher ${\dot{q}}_B$values are observed for larger species, resulting in a 3.3% increase in the slope of b.

i) If MR of residual mass (RM), ${\dot{q}}_{RM,m}= a_{RM } {M_B}^{b_{RM }}, a_{RM } = 1.45, b_{RM } = -0.17$, then for the whole body, a = 3.2162, b = 0.756,

ii) If ${\dot{q}}_{RM,m} = 0.581$ W/kg {Elia’s constant value} of then a = 2.486, b = 0.781.

This increase in b is nearly the same as in the EAR method. The residual mass (non-vital mass) seems to play a minor role in determining the exponent b, since the vital organs are more metabolically [40] active. The current ODM method for SOrMR_k is validated, as it supports Kleiber’s law using data from only two BS (Figure 5).

When the EAR method for SOrMR is used [21], the whole-body specific metabolic rate for a 60 kg human is 1.51 W/kg and 1.41 W/kg for a 70 kg human. In contrast, the current ODM estimates 1.144 W/kg for a 60 kg human and 1.108 W/kg for a 70 kg human. Holliday et al. (1967) reported an observed value of 1.21 W/kg [50]. Thus, the results from the ODM method align more closely with the literature data on humans.

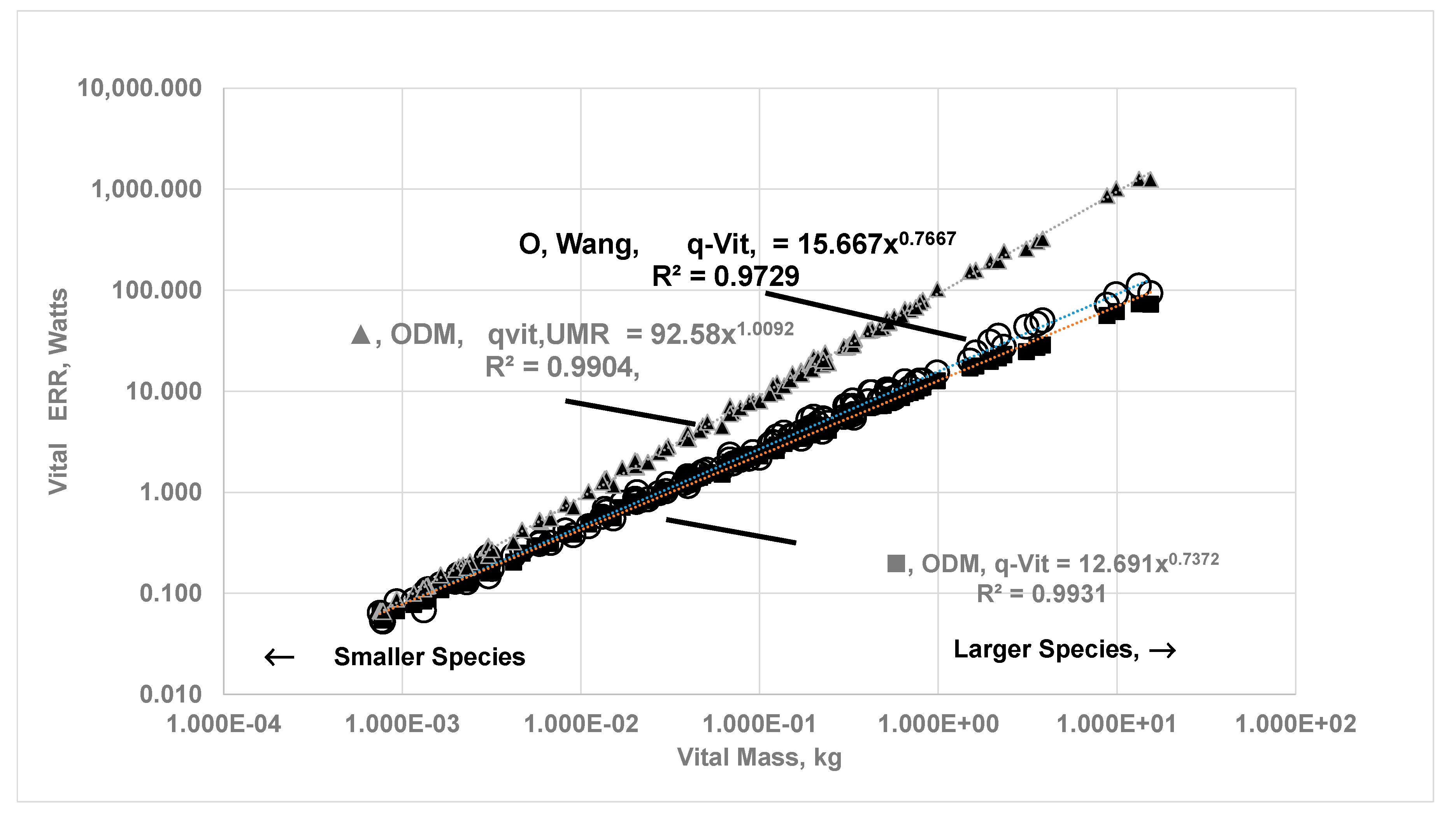
3.3. Vital Organ Contribution Percentage via ODM and Comparison of results with Empirical Allometric Laws

As a further validation of the ODM method, the predicted percentage contribution of vital organs is compared with literature data. Figure 7 shows the computed ERR from the four vital organs versus m_vit, while Figure 8 compares the percentage energy contribution of vital organs estimated using ODM with those obtained using EAR. If the allometric fit for ${\dot{q}}_{vit}$ is expressed as ${\dot{q}}_{vit} = {\alpha }_{vit} {m_{vit}}^{\beta vit}$ with ${\dot{q}}_{vital}$ in watts, m_vit in kg and vital energy contribution as $\% vit = {\gamma }_{vit} {M_B}^{{\nu }_{vit}}$, the fits yield α _vital = 12.69, β _vital = 0.74, γ_vit = 51.85, ν _vil = -0.115, while previous literature with EAR method for all vital organs suggests α _vit = 15.67, β _vit = 0.77. γ_vit = 49.67 and ν_vil = -0.101 [21]. The energy contribution estimated from ODM appears to agree with data from the EAR method for M_B up to 500 kg. The OD in organs results in a slope of ${\dot{q}}_{vit}$vs. m_vit that is less than 1.

3.4. The Upper Metabolic Rate of Organ {UMR_B }, Maximum Metabolic Rate of Organ (MMR_k) and MMR_B of Whole-Body

Equation 2016 states that whole-body metabolic rate {${\dot{q}}_B$} increases with the increase of η_eff,k, ${\dot{q}}_{k,m,iso}$for metabolically dominant vital organs and the remaining tissue masses. The η_eff,k is a function of O2 gradients within cell clouds; steeper the gradients lower is η_eff,k. Furthermore, ${\dot{q}}_B$of aby BS is a strong function of SOrMR_k {= η_eff,k ${\dot{q}}_{k,m,iso}$}, and ${\dot{q}}_{k,m,iso}$ is affected by Y_O2,CC,s which depends on the percentage of capillaries perfused at the CC surface. .

A). Hypothetical Upper Metabolic Rates of Organs and whole body

The resting or basal metabolic rate (BMR) is based on oxygen consumption, typically with partial perfusion from capillaries. What if there is no oxygen concentration gradient? what is the effect of O2 gradients on “ b”? Would this result in an isometric scaling law (b = 1 or b’ = 0), despite differences in organ masses? Mathematically, it can be shown that b ≠ 1 or b’ ≠ 0 due to differing SOrMR_k of organs, rather than differences in organ masses. By setting η_eff,k = 1 for all organs, a hypothetical upper metabolic rate (UMR) for the whole body can be obtained. By setting η_eff,k = 1 for all vital organs, two cases were studied; using EAR for RM, the whole-body allometric relation is given as ${\dot{q}}_{B,UMR} = a_{UMR} {M_B}^{ b_{UMR}}=6.282 {M_B}^{ 0.864}$ where a_UMR = 6.28, b_UMR = 0.864 {Figure 9}; it is apparent that “b” increases from 0.747 to 0.864 in absence of O₂ gradients. As such , the difference between ${\dot{q}}_{B,UMR}$ and${\dot{q}}_B$ is due to the effects of O₂ gradients within vital organs.

B). Maximum Metabolic Rates of Organs:

For maximal O₂ consumption (VO₂max), increased blood flow rates lead to higher capillary perfusion percentage, thereby increasing Y_O2,CC,s. Since ${\dot{q}}_B= \left|{\dot{Q}}_B\right|+{\dot{W}}_B$ increases during exercise, both ${\dot{W}}_B$ { ATP work} and |${\dot{Q}}_B$ | { heat loss from skin } must also increase, leading to a rise in internal temperature due to an increased |${\dot{Q}}_B$ | nd ATP, or “work.” This rise |${\dot{Q}}_B$ | is accompanied by increased blood flow through the outer skin to enhance heat dissipation. The primary organs contributing to MMR are the heart and SM.

The cardiac output is approximately 5–6 LPM, with capillaries partially perfused on CC surface { about 25-30% of capillaries in vital organs and 15-25% in SM} . At rest, about 80% of the blood pumped by the heart flows through the four vital organs [54]. The b for BMR ranges from 0.66-0.75. Ref. [45] reports the percentage of capillaries perfused for organs falls within the 25-25% range.

Under exercise, cardiac output increases to approximately 25-35 LPM. During exercise, kidney perfusion accounts for 20-25% of resting blood flow [53,54] i.e. the flow though kidneys decrease under exercise {see Table 2} . The increased ERR (${\dot{q}}_{B,MMR}$) is driven by a higher percentage of perfused capillaries (almost 100% exercise [55]) and decreased vascular resistance due to an increased diameter of small arteries (100–300 μm) [56], which increases blood supply rates, thus affecting the scaling law for ${\dot{q}}_{B,MMR}$. Further blood flow is diverted from various organs (e.g., stomach, kidneys). SM, which comprises about 40 % of the body mass, is almost 100% perfused during exercise. The increased O₂ delivery during exercise is also due to a lower pH (due to increased CO₂, or increased acidity), reduced oxy-Hb affinity, and hence, an increased release of O₂ from Hb which promotes higher Y_O2,CC,s . The OEF increases from 0.25-0.33 [54,61] at rest to almost 0.75 [54] for MMR.

Since SM plays a major role in metabolism during exercise, allometric laws for mass of SM vs. M_B and increased blood flow are used in the ODM model: i) Prange’s SM mass in kg: m_SM = 0.061 M_B ^1.09 [62] (M_B from 0.01 to 10,000 kg); ii) Kayser: m_SM = 0.093 M_B ^1.142 [63]; iii) Painter: m_SM = 0.0961 M_B ^1.06 [15]; iv) White: m_SM = 0.0645 M_B ^1.02 [64]; hence, 5.1 kg for a 58 kg person according to the Prange law but 9.6 kg according to the Kayser law, but the literature suggest SM is 24.4 kg for a 58 kg person [65].

For the ODM model during exercise, m_RM,ex = M_B – m_vit - m_SM. According to the ODM hypothesis, the increase in MMR is due to an increased O₂ supply to organs {particularly to SM and Heart} , with a higher perfusion percentage on the CC surface, thus increasing Y_O2,CC,s and possibly due to an increased η_eff,CC (See Section 4.8 in Ref. [66]} originating from an increased pO₂. With the following relations,

$${\left({\displaystyle \frac{Y_{O2,cc,s,Ex}}{Y_{O2,cc,s,\mathrm{Re}st}}}\right)}_k= \left\{{\displaystyle \frac{Blood Flow to organ k Exercise}{Blood Flow to k under Rest}}\right\} , k= Kids, H, Br,L, SM$$

$${\dot{q}}_{k,m,Ex} = \left\{{\dot{q}}_{k,m,\mathrm{Re}st} {\left( {\displaystyle \frac{Y_{O2,cc,s,Ex}}{Y_{O2,cc,s,\mathrm{Re}st}}}\right)}_k\right\}, {\dot{q}}_{SM,Ex} = \left\{{\dot{q}}_{SM,\mathrm{Re}st} {\displaystyle \frac{Y_{O2,cc,s,Ex}}{Y_{O2,cc,s,\mathrm{Re}st}}}\right\},\left\{{\dot{q}}_{RM,Ex,m}\right\} = \left\{{\dot{q}}_{RM,m} \right\}$$

$${\dot{q}}_{SM,m,\mathrm{Re}st} = {\dot{q}}_{RM,m,} = a_{RM} {M_B}^{b_{RM}}=e_{RM,6} {M_B}^{f_{RM,6}}{a}_{RM\hspace{0.17em}}\hspace{0.17em}=\hspace{0.17em}{e}_{k,6}=1.45,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{b}_{RM\hspace{0.17em}}\hspace{0.17em}\hspace{0.17em}=\hspace{0.17em}{f}_{k,6}=\hspace{0.17em}-0.17,$$

For predicting MMR using the ODM model, perfusion ratios are used {Table 2} . The myoglobin( Mb) which aids in transport of O2 in H and SM increases during exercise indicating an increase of diffusivity “D”{i.e lower G_OD,k, k=H, SM} and the core cells may also get O2 decreasing OD and increasing {η_eff,CC}_k . Highest possible value {η_eff,CC}_k is 1 for SM and H. Thus. the following parametric studies have been conducted:

a)

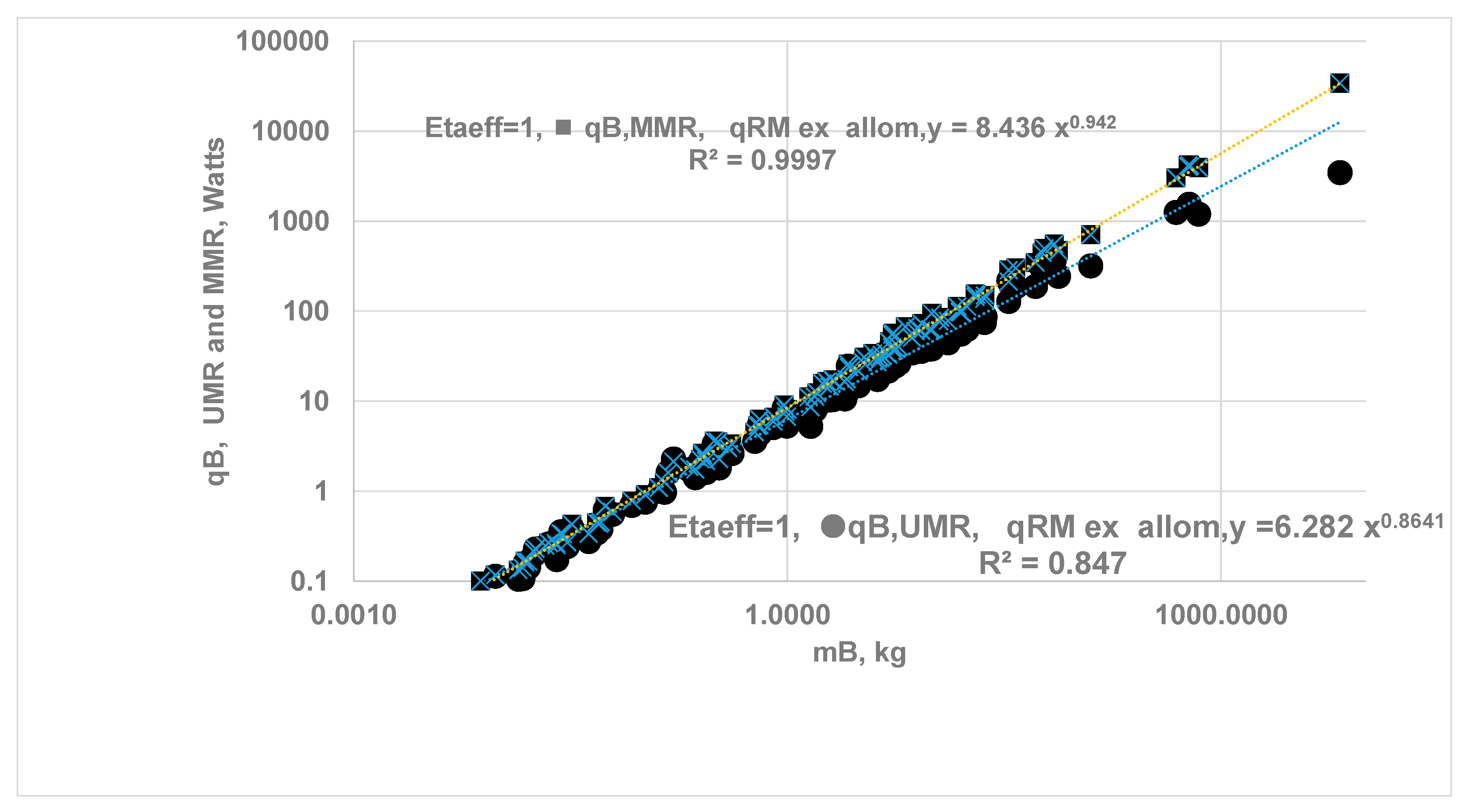
The {η_eff,CC}_k is finite for vital organs but isolated metabolic rate is altered due to change in capillary perfusion ratio (Equation 2420, Table 2 }: reduced for kidneys (0.55) and liver (0.67) but increased for H (3) , SM (10.4) and RM-ex (1.16). For SM and RM-ex, the SOrMRk are given by the product of allometric laws of RM as at rest and perfusion ratio. Figure 9 compares the results for ${\dot{q}}_{B,MMR}$ under ODM with the literature data for ${\dot{q}}_{B,MMR}$ . If ${\dot{q}}_{B,MMR} = a_{MMR} {M_B}^{ b_{MMR}}$ , a _MMR= 4.015 and b_MMR = 0.798. The slope under exercise is steeper than the slope under rest.

b)

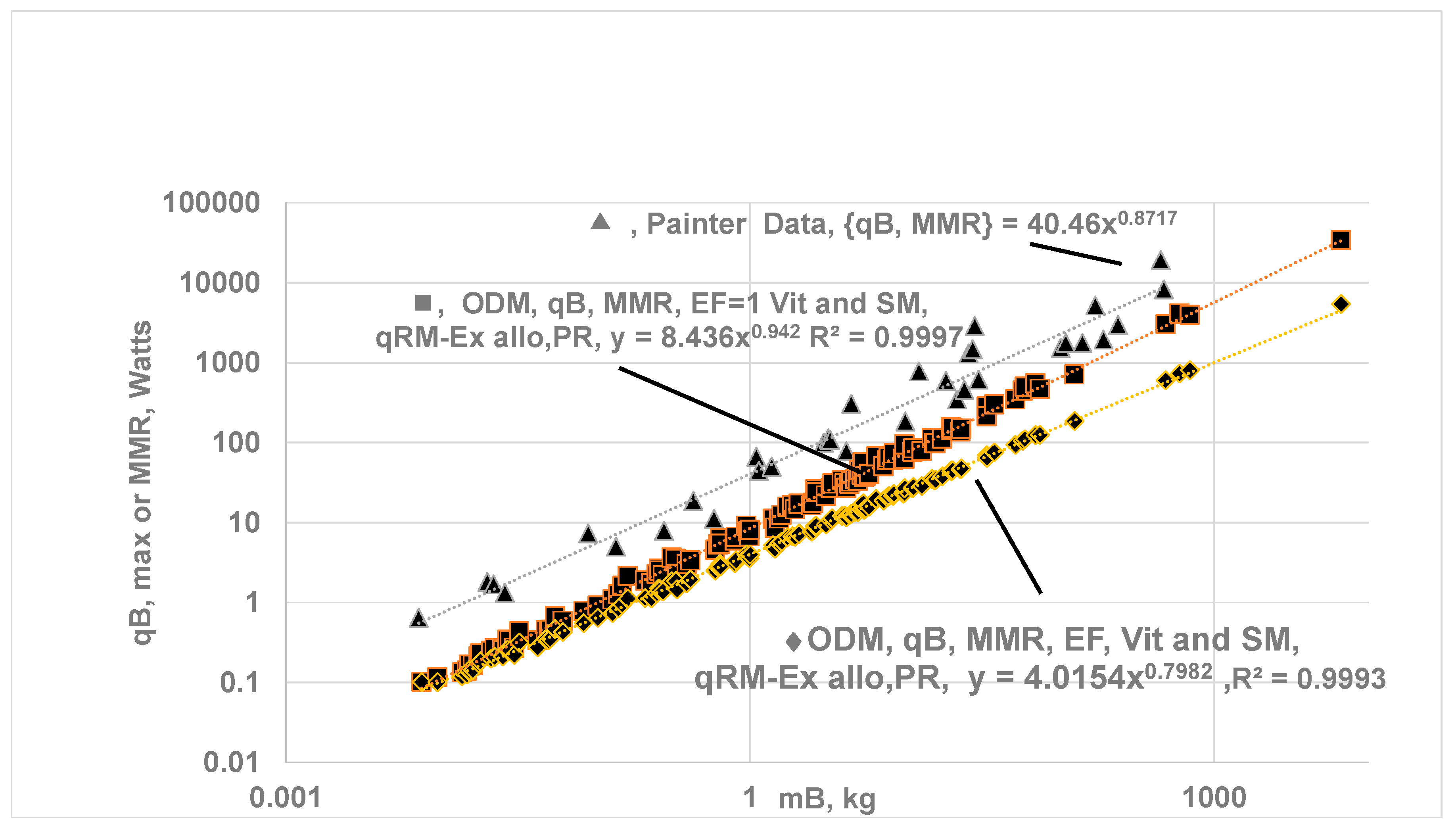
The η_eff,CC is set to 1 for all vital organs and SM {i.e no O2 gradient during exercise} but RM-ex given by allometric law with correction for perfusion ratio of 1.16. Even if O2 gradients are present for organs other than H and SM, results may not change since metabolic rate from SM dominates. a _MMR= 8.436 and b_MMR = 0.942, η_eff,k=1.

Validation of ODM Based MMR Allometry:

i)

The predicted values for b_MMR range from 0.798 to 0.942 with an average of 0.87. The upper value of b_MMR indicates almost isometric law. It is believed that MMR must follow an isometric law since the “cost” of transportation (e.g., tread mill, jogging) must be proportional to body mass, meaning SMMR {specific maximum metabolic rate, W/kg} must not differ between smaller and larger species during exercise. Ref. [8] states that when a 20 g mouse and 500 kg racehorse run at their maximum capacity, their specific maximal metabolic rate (W/g) is nearly the same. This finding agrees with the ODM model, indicating all cells within an organ are subjected to oxygen concentrations close to their highest possible values.

ii)

The literature data mostly reports ${\dot{V}}_{O2max}$ {mL of O2 per min} vs M_B under exercise. It is converted into watts using HHV_O2 of 20.5 J/mL of O2. ${\dot{q}}_{B,MMR} = 0.342 {\dot{V}}_{O2max}$ where ${\dot{q}}_{B,MMR}$ in Watts and ${\dot{V}}_{O2max}$in mL/min . Painter collected data on MMR for 32 mammalian BS ranging from 0.007 kg (pygmy mice) to 575 kg (cattle), found that b_MMR = 0.872 (95% CI : b_MMR = 0.812-0.931) found and attributes the increase from 0.75 at rest to 0.872 under exercise to the increased O₂ transport to cells with the heart as the limiting step [15]. Based on VO₂max [67] in mL/min, a_MMR = 40.46 b_MMR = 0.872 .Weibel et al. [16] conducted treadmill experiments in animals to measure VO₂ max (highest rate for 5 min) and reported a_MMR = 118 mL/min or 40.4 W, with b_MMR = 0.872 for 34 mammalian species, including both athletic and non-athletic groups (0.007 to 500 kg). They further reported b_MMR =0.942 for the athletic group {predicted upper value for bMMR when ηeff=1 for vital organs and SM} and 0.849 for non-athletic group [16]. Data from Talyor et al. [67] and Ref. [8] report b_mMR = 0.87 - 0.88 for homeotherm.

iii)

Ref. [6], b_MMR = 0.872 or 7/8 (see Fig. 6 in Ref. [6]), [15] ; Agutter b_MMR = 0.86 [72]. Ref [68]: b_MMR = 0. for M_B =0.3 to 300 kg, but increases to 0.86 for M_B = 0.3 to 500 kg. Single Flow Network model b_MMR = 6/7 [58] . However the predicted aMMR is low compared to literature data. MMR is largely driven by the high MR of SM, and the predicted low values of a_MMR orignate from the allometric relation of SM and body mass used in the current ODM model. This model assumes a similar SM mass percentage relative to body mass across species, yielding low SM values for humans. According to Weibel and Hoppeler [16], SM is about 42% of body mass in the athletic wood mouse (small animal), 45% in the pronghorn and 25% in the goat, with an average of 36% of body mass. Further, skeleton mass varies significantly, with the shrew at 5% and the elephant at 25% [71]. These findings indicate a wide variation in SM mass across body sizes.

iv)

The current results for MMR are validated further with the data reported by Midorikawa et al [65]. The VO₂max (during maximal exercise) of sumo wrestlers is about 30 mL/min/kg or 10.25 W/kg, attributed to SM, liver and kidneys [65]. For a 58 kg individual, reported data show ${\dot{q}}_{B,MMR}$ =1320 W, while the predicted value is ${\dot{q}}_{B,MMR}$ 446 W . Why do measured values exceed predictions from the ODM model ? The allometry for SM predicts a mass of 5.1 kg for 58 kg human, whereas the measured value is 24 kg for a 58 kg person! When the author used the actual SM mass of 24 kg (without using allometric SM mass) and m_RM-EX = M_B - m_SM - m_vit = 58 - 24 - 5.4 = 28.6 kg, the predicted ${\dot{q}}_{B,MMR}$ increased to 1045 W (${\dot{q}}_{RM,ex}$ =296 W, EAR) with reported data at ${\dot{q}}_{B,MMR}$ =1320 W.

3.4. A Method of Tracking G_{ODk Number} for Organs During Growth of Humans or any other BS by Medical Personnel

If O₂ diffusion follows an increasingly tortuous path for certain populations as humans grow, the effective diffusion coefficient decreases, causing G_OD,k variation to become much steeper than normal. This indicates higher ODM and a greater likelihood of energy release adaptation by the body via glycolysis at a specific (G_OD,k)_gly. Thus, estimating (G_OD,k) as M_B(t) during the growth is of interest. How can medical personnel determine G_OD,k?

I)

Direct Method: Measure Organ Masses and known SOrMR_k of RS-1: Measure blood flow rate and the change in O₂ concentration between the arterial and venous ends of the organ to estimate OrMR_k. Directly measure organ masses using CT scan or MRI, then estimate SOrMR_k (=OrMR_k / m_k) and compare with SOrMR_k of the shrew (i.e., isolated). Estimate η_eff,k and determine G_{OD, k} of organ k using Equation 1613.

II)

Ratio method for Same BS: Assume that (G_{OD k} at any age / G_{OD k} at birth) = ( m_k / m_k,birth)^lk if G_OD,k at birth and m_k,birth are known.Typically l_k =2/3.

III)

G_OD,k for normal growth in terms of Body Mass data M_B(t): The ODM method presents SOrMRk in terms of a powerful dimensionless parameter G_{OD k}, which is proportional to m_k^l. Using the allometric law for organ masses (Equation 5) , $G_{OD k} \propto M_B{\left(t\right)}^{{\mathcal{l}}_k d_k}, t in years$ where l_k =2/3 and d_k values are tabulated in Table 1.

IV)

Ratio Method, G_OD,k in terms of measured Organ Masses and Reference Species RS-2: Assuming Rat Wistar as RS-2 and knowing G_{OD ,k} of RS-2, one can determine G_{OD ,k} if organ mass data is available.

$${\displaystyle \frac{ G_{OD,k}\left(t\right)}{G_{OD,k,RS-2}}} = {\left\{ {\displaystyle \frac{ m_k\left(t\right)}{m_{k,RS-2}}}\right\}}^{{\mathcal{l}}_k}, {\mathcal{l}}_k = {\displaystyle \frac{2}{3}}, t in years$$

(28)

For example, selecting organ masses for a 10 kg (or 1 year old) infant from Ref. [73], the estimated G_{OD ,k} values and corresponding η_eff,k (in parentheses) are : 65 (0.33) for the kidneys, 148 (0.23) for the heart, 1,007 (0.092) for the brain, and 522 (0.13) for the liver. For a dog of similar 10 kg body mass, the brain is much smaller, resulting in a significantly lower G_OD,Br (179) and a higher η_eff,Br (0.21), leading to a higher metabolic rate per unit mass of the dog’s brain compared to a human’s. As a human grows to 70 kg, the G_{OD ,k} increases while η_eff,k decreases. Using the same reference, the values become: 160 (0.22) for the kidneys, 520 (0.13) for the heart, 1,260 (0.082) for the brain, and 1,422 (0.077) for the liver. Note the rapid growth of the liver and slow growth of the brain for a healthy human. If organ mass m_k(t) is measured as a function of age in years, then Equation 2824 can be used to estimate G_{OD ,k} .

Organ G_OD,k# and Cancer: Since ODM promotes hypoxic conditions, with increased HIF activity and, consequently, decreased mitochondrial mass and oxygen consumption, the author speculates that ODM promotes a shift toward the glycolysis pathway for energy release, which may contribute to the onset of cancer. While literature data indicates a positive correlation between organ mass and the number of cancer cases [42], which is attributed to the link between excess fat in organs and obesity, the author speculates that an increasing G_OD,k# is an indication of increased oxygen deficiency, an increased HIF1α factor and a possible shift to the glycolysis pathway, similar to how elevated Prostate-Specific Antigen (PSA) levels are used as an indicator of prostate cancer (see Section on Future Work).

4. Summary and Conclusions

The earlier literature: i) adopted empirical allometric laws of organs and a heterogenous approach and EAR for allometry of all organs for estimating BMR of the whole body, yielding Kleiber’s aM_B^b with a = 3.216, b = 0.756, [21]; ii) raised several puzzles in biology, such as a) why F_k values are negative [3] in OMA for k = Kids, H, Br and L; and b) how organs “know” they are in a smaller or large body mass and adjust their metabolic rates accordingly. The author’s previous work answered these puzzles by linking the field of ODC literature in engineering to ODM in biology [3]. The current ODM method applies the effectiveness factor relation from engineering literature in terms of G (or Ψ_T ²,Thiele Modulus²), and modifies G as G_OD (G-oxygen-deficiency) for biological applications. It demonstrates that G_{OD, k} ∝ R_CC,k² (∝ m_CC,k^2/3 ∝ m_k^2/3). The ODM hypothesis is extended for: i) predicting the specific SOrMR_k of organ _k for 114 BS using only the SOrMRk of two reference species (Shrew of 0.0076 kg: RS-1, Rat of 0.380 kg: RS-2) and organ and body masses of 116 species, ii) demonstration of Kleiber’s power law (${\dot{q}}_B = a {M_B}^b$) with a = 2.962, b = 0.747 for M_B = 0.0075 kg to 6,650, iii) illustration of the link between morphological traits and physiological traits in metabolic rates, iv) extension of the method to deduce the allometric law for maximal metabolic rate (MMR under exercise) and validation with literature data. Even if all cells are irrigated with the same O₂ concentration, the exponent b is not equal to 1 due to varying organ masses, but b = 1 if all organ masses are equal. Thus, ODM hypothesis aligns with Silva’s [17] review, which suggests that the power law exponent b should vary between 2/3 and 1 based on ‘metabolic level’ (i.e., the organism’s activity level or metabolic intensity). Allometric laws on maximum metabolic rate (MMR) vs. body mass M_B are also validated using the ODM approach, yielding an exponent of 0.87-0.92, as reported in biology literature. That is, MMR per kg body mass ∝ M_B (-0.13) to M_B (-0.08) {i.e. weak function of body mass }, appearing consistent (e.g., VO₂max/M_B in Ref. [8]), even though the SBMR (W/g body mass) of a 20 g mice is five times that of a 500 kg horse. A method for estimating the dimensionless (G_OD)_k for organs is “suggested” for use by medical personnel whether the increasing (G_OD)_k of organs indicate a progression toward oxygen deficiency. Note that glycolysis generates only 2 ATP per CH molecule and as such generation of 32 ATP ( as in case of oxidation) requires 16 times more consumption of O2 and hence fall in CH level is an indication of likelihood of occurrence of cancer.

5. Future Work

• Whether the secrets of Kleiber’s law and maximal metabolic rate allometries in biology can be revealed from oxygen-deficient combustion engineering remains an open question. Additional supporting data are needed either to confirm or question the ODM hypothesis.
• While the present study focuses on interspecific relations across 116 species, the approach may also apply to intraspecific relations, such as human growth from 2 kg to 70 kg. As organs grow, G_{OD, k} can be monitored throughout the development process. Notably, human brain growth appears to deviate from the allometric laws for organ masses based on Wang’s six-species data.
• Collect statistical data to determine whether cancer development correlates with abnormal increases in G_OD,k and assess its relationship with cancer occurrence.
• Conduct future studies on the impact of RS-2 selection on Kleiber’s law.
• A more precise allometric relationship is needed for SM mass relative to body mass M_B since it directly affects the predicted MMR in the ODM model.
• Develop a Krogh-type COA model incorporating the ODM method, define G_OD,k for COA and evaluate whether Kleiber’s law holds.
• Gather data on cell reactivity, cell size, cell density and organ mass to estimate G_OD,k using fundamental biological parameters.
• While the current work follows a “downstream” hypothesis based on cell kinetics, the WBE employs an “upstream” flow network (or supply-side) hypothesis and optimization. Future work should aim to integrate these two hypotheses to understand their combined effects on mass fraction of O2 at the cell cloud surface {Y_O2,cc,s }.