Submitted:
01 April 2025
Posted:
02 April 2025
Read the latest preprint version here
Abstract
Keywords:
1. Introduction
2. Discussions Based on Transmission Line Theory
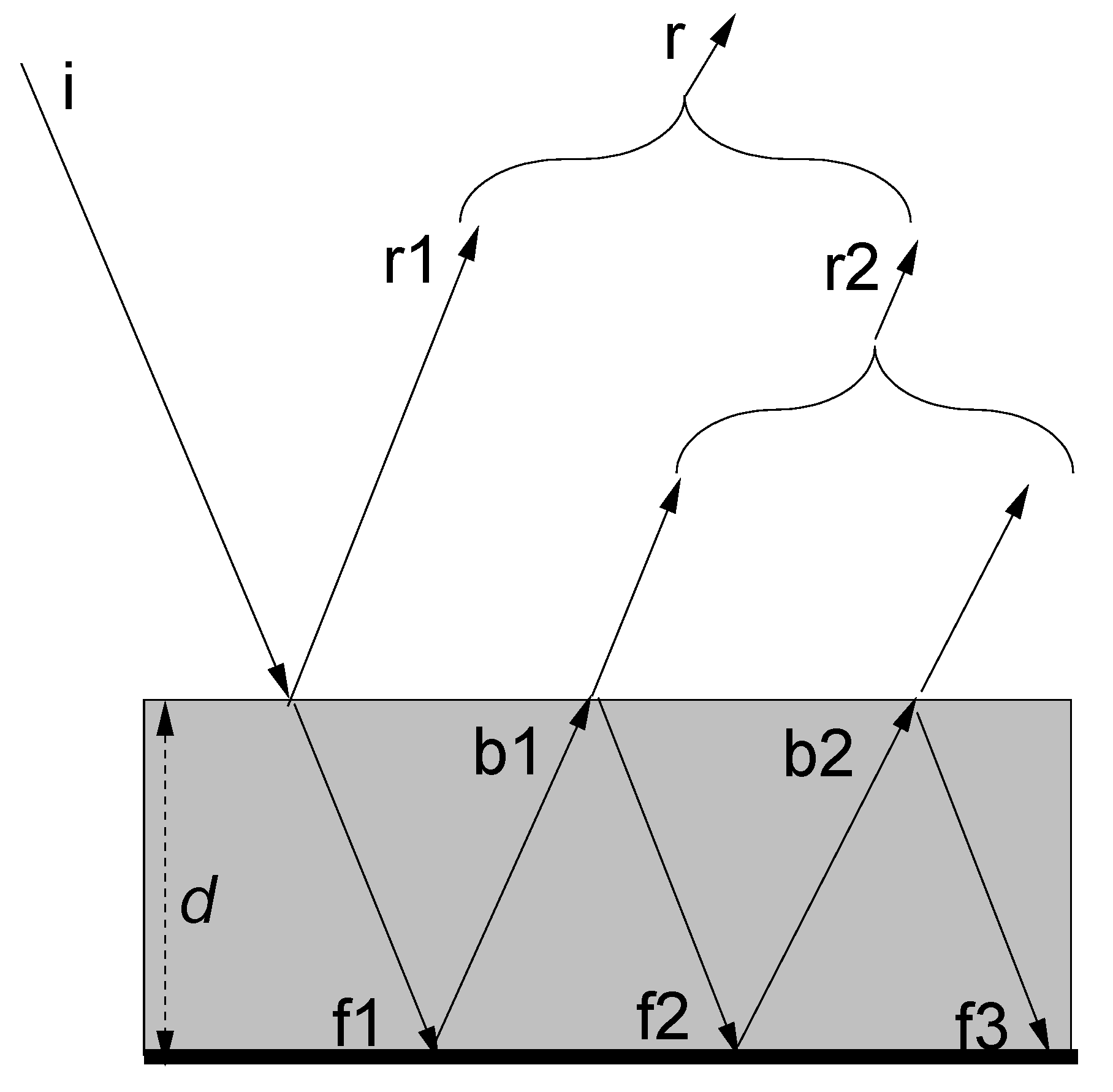
2.1. The Transmission Line Theory-Based Wave Mechanics Theory of Microwave Absorption
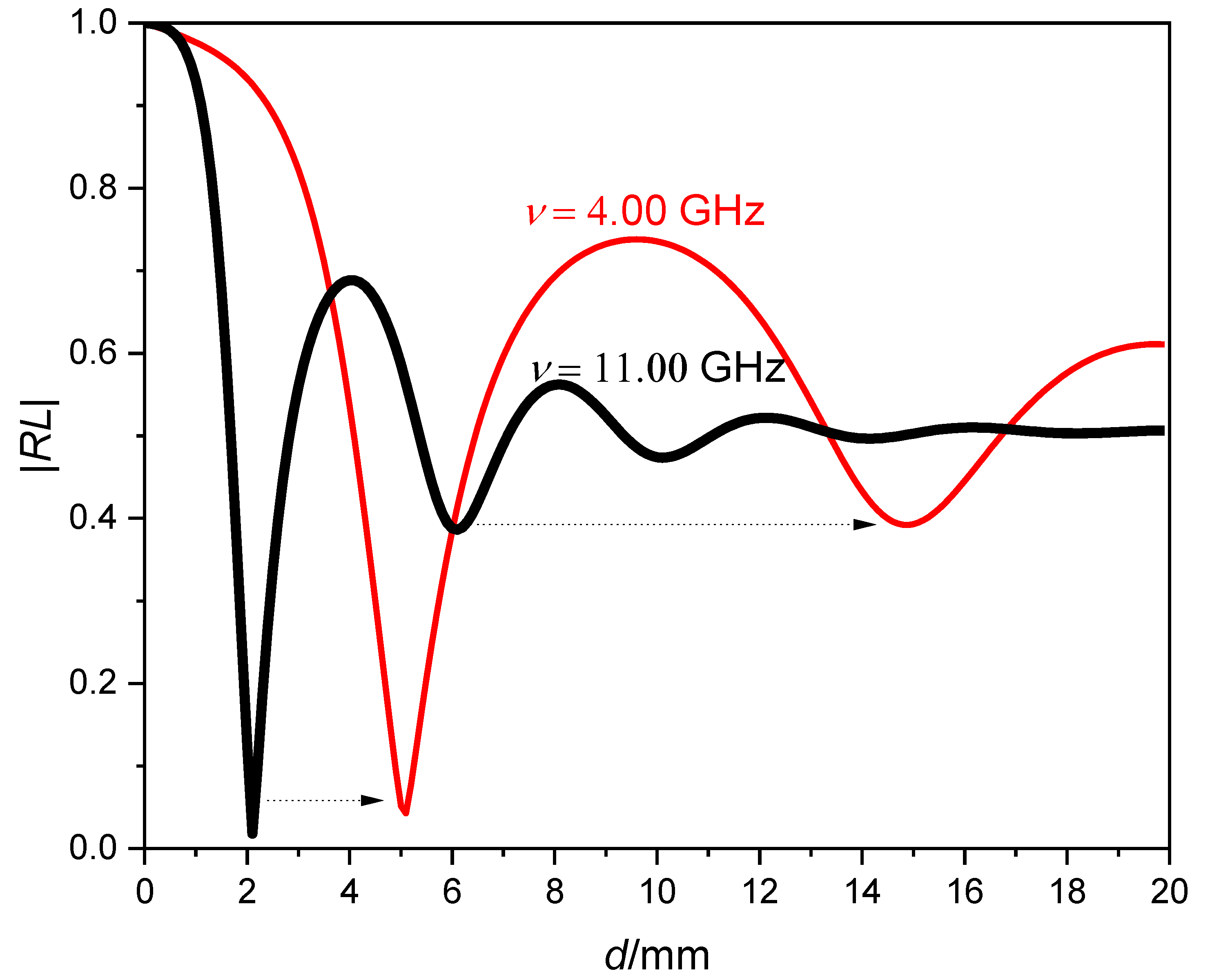
2.2. The Misunderstanding of Transmission Line Theory
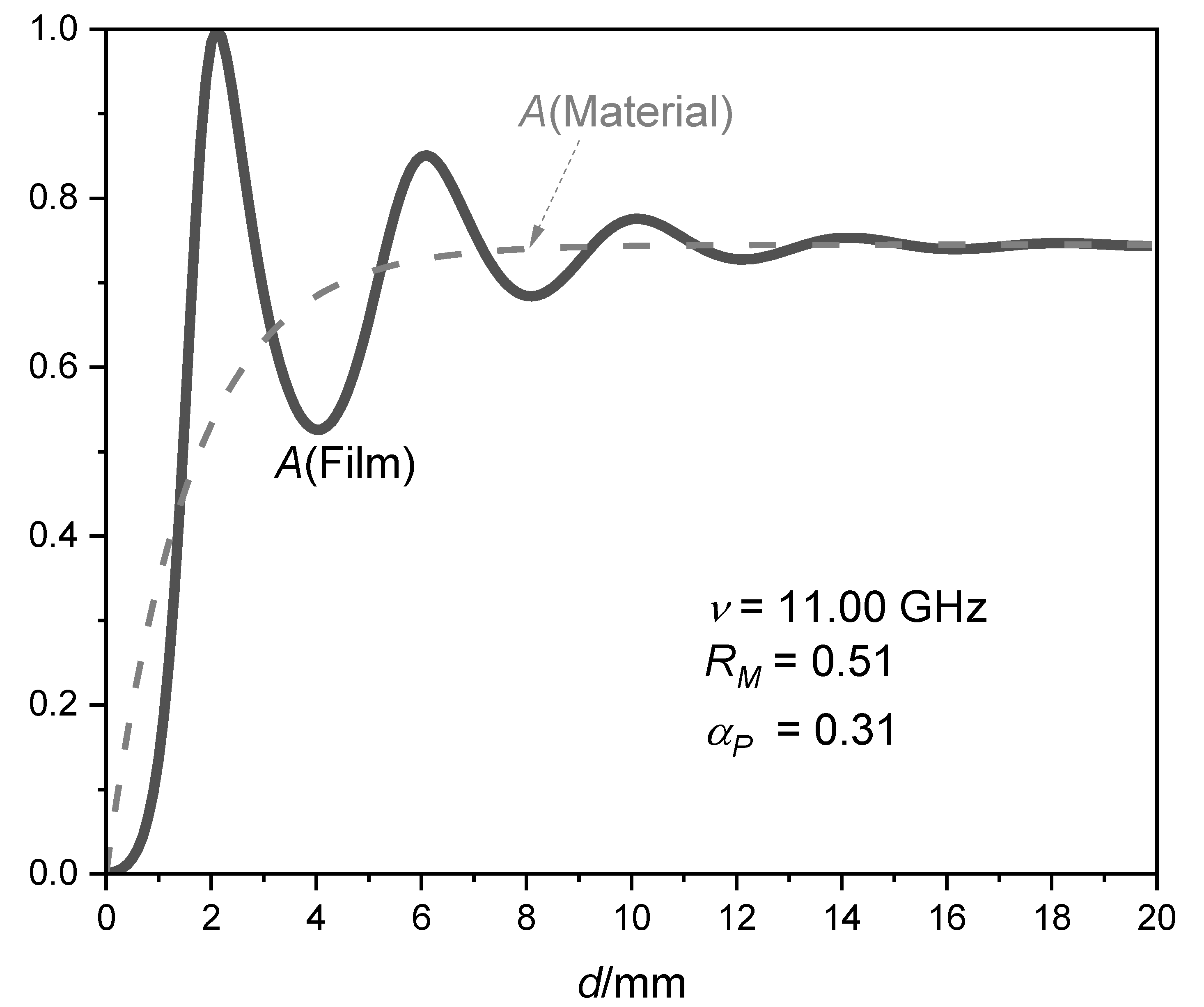
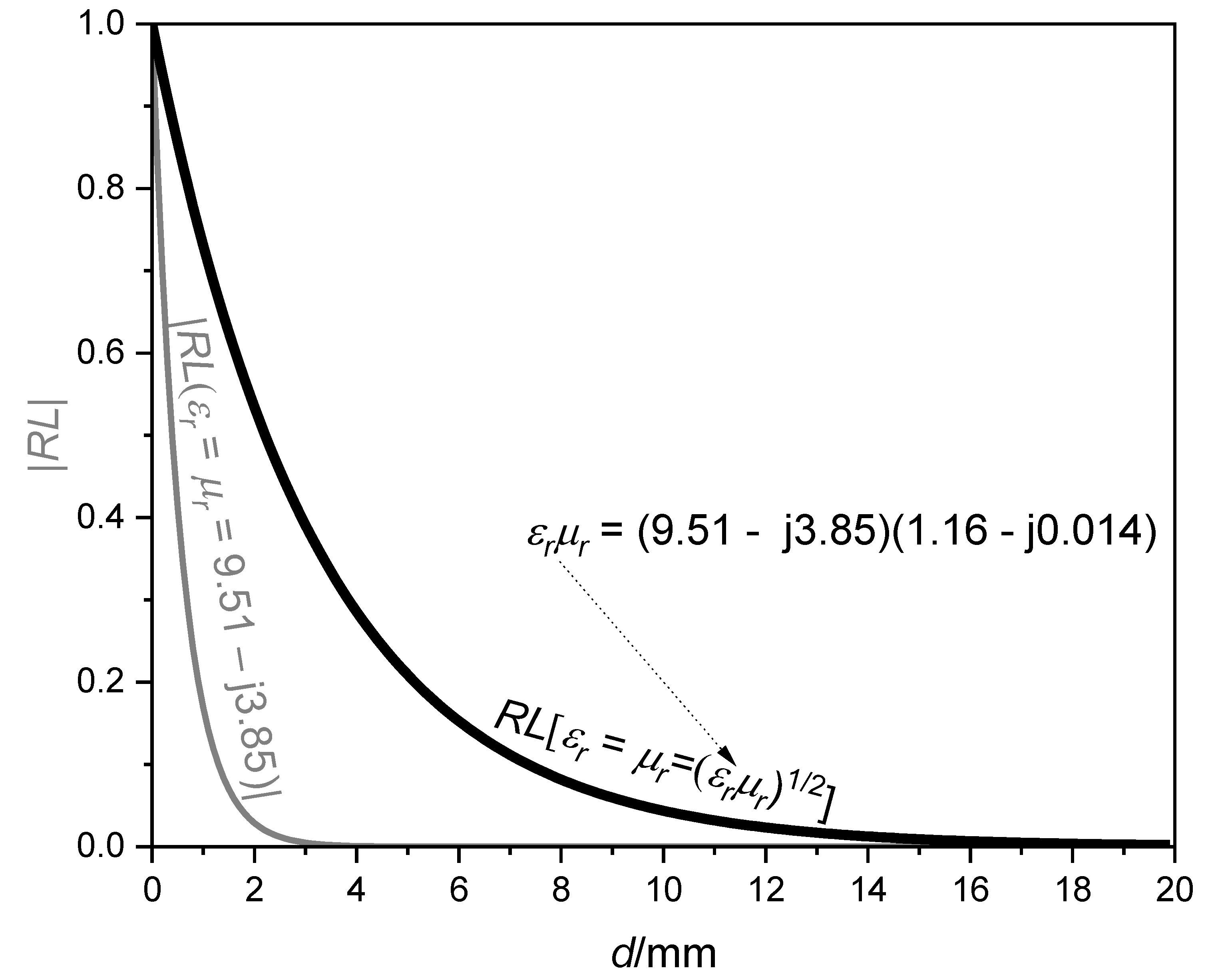
2.3. The Flaws in Impedance Matching Theory Revealed from the Mechanics Theory
2.4. The Roles Played by Theoretical Research
3. Conclusions
Data Availability Statement
References
- Nayani, P. S.; Moradi, M.; Salami, P.; Ra’di, Y. Passive highly dispersive matching network enabling broadband electromagnetic absorption. Nat Commun 2025, 16, 905. [Google Scholar] [CrossRef] [PubMed]
- Qu, N.; Sun, H.; Sun, Y.; He, M.; Xing, R.; Gu, J.; Kong, J. 2D/2D coupled MOF/Fe composite metamaterials enable robust ultra-broadband microwave absorption. Nat Commun 2024, 15, 5642. [Google Scholar] [CrossRef] [PubMed]
- Jin, H.; Liu, M.; Wang, L.; You, W.; Pei, K.; Cheng, H. W.; Che, R. Design and fabrication of 1D nanomaterials for electromagnetic wave absorption. Natl Sci Rev 2025, 12, nwae420. [Google Scholar] [CrossRef] [PubMed]
- Zuo, D.; Jia, Y.; Xu, J.; Fu, J. High-Performance Microwave Absorption Materials: Theory, Fabrication, and Functionalization. Industrial & Engineering Chemistry Research 2023, 62, 14791–14817. [Google Scholar] [CrossRef]
- Wang, B.; Huang, J.; Liu, G.; Ge, C.; Wang, L.; Xu, K.; Liu, T.; Wang, W.; Wang, L. Design and optimization oriented composition and morphology engineering for MOF derived microwave absorbents. Nano Materials Science 2025. [Google Scholar] [CrossRef]
- Chen, Y.; Quan, B.; Liu, J.; Lu, X.; Lin, L.; Shao, G.; Wen, Y.; Jin, R.; Shen, X.; Huang, X. High-Performance Flexible Microwave Absorption Films with Dynamic Adjustable Macrostructures and Alterable Electromagnetic Field Polarizations. ACS Appl Mater Interfaces 2025, 17, 9748–9759. [Google Scholar] [CrossRef]
- Xing, L.; Cheng, H.; Li, Y.; Chen, Q.; Liu, C.; Shen, C.; Liu, X. MoS(2) Decorated on 1D MoS(2)@Co/NC@CF Hierarchical Fibrous Membranes for Enhanced Microwave Absorption. Small 2025, 21, e2407337. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, Y.; Drew, M. G. B. Recognizing Problems in Publications Concerned with Microwave Absorption Film and Providing Corrections: A Focused Review. Industrial & Engineering Chemistry Research 2025, 64, 3635–3650. [Google Scholar] [CrossRef]
- Liu, Y.; Drew, M. G. B.; Li, H.; Liu, Y. An experimental and theoretical investigation into methods concerned with “reflection loss” for microwave absorbing materials. Materials Chemistry and Physics 2020, 243, 122624. [Google Scholar] [CrossRef]
- Liu, Y.; Drew, M. G. B.; Liu, Y. A physics investigation of impedance matching theory in microwave absorption film— Part 2: Problem analyses. Journal of Applied Physics 2023, 134, 045304. [Google Scholar] [CrossRef]
- Liu, Y.; Zhao, K.; Drew, M. G. B.; Liu, Y. A theoretical and practical clarification on the calculation of reflection loss for microwave absorbing materials. AIP Advances 2018, 8, e015223. [Google Scholar] [CrossRef]
- Elmahaishi, M. F.; Azis, R. a. S.; Ismail, I.; Muhammad, F. D. A review on electromagnetic microwave absorption properties: their materials and performance. Journal of Materials Research and Technology 2022, 20, 2188–2220. [Google Scholar] [CrossRef]
- Andriyanti, W.; Choir Hidayati Nur, M. A.; Puspitarum, D. L.; Sujitno, T.; Suprihatin, H.; Purwanto, S.; Suharyadi, E. Microstructures, magnetic properties and microwave absorption of ion-implanted bismuth ferrite thin films. Physica B: Condensed Matter 2024, 676, 415690. [Google Scholar] [CrossRef]
- Abu Sanad, A. A.; Mahmud, M. N.; Ain, M. F.; Ahmad, M. A. B.; Yahaya, N. Z. B.; Mohamad Ariff, Z. Theory, Modeling, Measurement, and Testing of Electromagnetic Absorbers: A Review. physica status solidi (a) 2024, 221, 2300828. [Google Scholar] [CrossRef]
- Cao, M.; Han, C.; Wang, X.; Zhang, M.; Zhang, Y.; Shu, J.; Yang, H.; Fang, X.; Yuan, J. Graphene nanohybrids: excellent electromagnetic properties for the absorbing and shielding of electromagnetic waves. Journal of Materials Chemistry C 2018, 6, 4586–4602. [Google Scholar] [CrossRef]
- Liu, Y.; Drew, M. G. B.; Liu, Y. A physics investigation of impedance matching theory in microwave absorption film—Part 1: Theory. Journal of Applied Physics 2023, 134, 045303. [Google Scholar] [CrossRef]
- Liu, Y.; Drew, M. G. B.; Liu, Y. A theoretical exploration of impedance matching coefficients for interfaces and films. Applied Physics A 2024, 130, 212. [Google Scholar] [CrossRef]
- Liu, Y.; Ding, Y.; Liu, Y.; Drew, M. G. B. Unexpected Results in Microwave Absorption -- Part 1: Different absorption mechanisms for metal-backed film and for material. Surfaces and Interfaces 2023, 40, 103022. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, Y.; Drew, M. G. B. A theoretical investigation on the quarter-wavelength model — Part 1:Analysis. Physica Scripta 2021, 96, 125003. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, Y.; Drew, M. G. B. A theoretical investigation of the quarter-wavelength model-part 2: verification and extension. Physica Scripta 2022, 97, 015806. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, Y.; Drew, M. G. B. A re-evaluation of the mechanism of microwave absorption in film – Part 3: Inverse relationship. Materials Chemistry and Physics 2022, 290, 126521. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, Y.; Drew, M. G. B. Wave Mechanics of Microwave Absorption in Films: Multilayered Films. Journal of Electronic Materials 2024, 53, 8154–8170. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, Y.; Drew, M. G. B. A Re-evaluation of the mechanism of microwave absorption in film – Part 2: The real mechanism. Materials Chemistry and Physics 2022, 291, 126601. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, Y.; Drew, M. G. B. Wave mechanics of microwave absorption in films: A short review. Optics and Laser Technology 2024, 178, 111211. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, Y.; Drew, M. G. B. Review of Wave Mechanics Theory for Microwave Absorption by Film. Journal of Molecular Science 2024, 40, 300–305. [Google Scholar] [CrossRef]
- Lim, D. D.; Ibarra, A.; Lee, J.; Jung, J.; Choi, W.; Gu, G. X. A tunable metamaterial microwave absorber inspired by chameleon’s color-changing mechanism. Sci Adv 2025, 11, eads3499. [Google Scholar] [CrossRef]
- Sharma, S.; Parne, S. R.; Panda, S. S. S.; Gandi, S. Progress in microwave absorbing materials: A critical review. Adv Colloid Interface Sci 2024, 327, 103143. [Google Scholar] [CrossRef]
- Li, M.; Li, W.; Wang, Y.; Sun, F.; Wang, Q.; Tan, D.; Zhang, R.; Wang, H.; Shao, G.; Liu, Y.; et al. Entropy-driven microwave absorption enhancement in hexagonal (Ba1/3Sr1/3Ca1/3)FeO3 perovskite. Journal of Advanced Ceramics 2025. [Google Scholar] [CrossRef]
- Zhuang, X.; Ning, M.; Pan, L.; Gao, Y.; Zhang, Q.; Mu, C.; Ma, H.; Li, J.; Tan, G.; Man, Q.; et al. Optimized Microwave Absorption and Structural Compression Sensing via Magnetic Fiber-Infused Aerogels with Reduced Graphene Oxide and Carbon Frameworks. ACS Applied Electronic Materials 2025, 7, 601–611. [Google Scholar] [CrossRef]
- Xu, J.; Gao, T.; Liu, S.; Jiao, Y. Enhanced microwave absorption and thermal conductivity of biomass-derived BCNO materials. Journal of Materials Science: Materials in Electronics 2025, 36. [Google Scholar] [CrossRef]
- Wu, D.; Fan, C.; Luo, W.; Jin, Y.; He, Q.; Wang, Y. Enhanced interfacial polarization loss induced by hollow engineering of hollow alloyed CoFe-ZIF nanocages/carbon nanofibers for efficient microwave absorption. Inorganic Chemistry Frontiers 2025. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, Y.; Drew, M. G. B. Wave mechanics of microwave absorption in films - Distinguishing film from material. Journal of Magnetism and Magnetic Materials 2024, 593, 171850. [Google Scholar] [CrossRef]
- Ray, S.; Panwar, R. Advances in Polymer-Based Microwave Absorbers—From Design Principles to Technological Breakthroughs: A Review. IEEE Journal on Flexible Electronics 2024, 3, 401–417. [Google Scholar] [CrossRef]
- Zhou, Y.; He, P.; Ma, W.; Zuo, P.; Xu, J.; Tang, C.; Zhuang, Q. The Developed Wave Cancellation Theory Contributing to Understand Wave Absorption Mechanism of ZIF Derivatives with Controllable Electromagnetic Parameters. Small 2023, 2305277. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, Y. Microwave absorption mechanism for film. Journal of Molecular Science 2023, 39, 521–527. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, Y.; Drew, M. G. B. A Re-evaluation of the mechanism of microwave absorption in film – Part 1: Energy conservation. Materials Chemistry and Physics 2022, 290, 126576. [Google Scholar] [CrossRef]
- Liu, Y.; Drew, M. G. B.; Liu, Y. Chapter 4: Fundamental Theory of Microwave Absorption for Films of Porous Nanocomposites: Role of Interfaces in Composite-Fillers. In Porous Nanocomposites for Electromagnetic Interference Shielding, Thomas, S., Paoloni, C., Pai, A. R. Eds.; Elsevier, 2024; pp 59 - 90.
- Liu, Y.; Ding, Y.; Liu, Y.; Drew, M. G. B. Unexpected results in Microwave absorption -- Part 2:Angular effects and the wave cancellation theory. Surfaces and Interfaces 2023, 40, 103024. [Google Scholar] [CrossRef]
- Liu, Y.; Ding, Y.; Chen, Q.; Liu, Y. Preparation of NiFe2-xMxO4(M=Ce,Sm,Gd) and microwave absorption properties of its films. Journal of Shenyang Normal University (Natural Science Edition) 2023, 41, 98–103. [Google Scholar] [CrossRef]
- Liu, Y.; Yin, X.; Drew, M. G. B.; Liu, Y. Microwave absorption of film explained accurately by wave cancellation theory. Physica B: Condensed Matter 2023, 666, 415108. [Google Scholar] [CrossRef]
- Liu, Y.; Yin, X.; Drew, M. G. B.; Liu, Y. Reflection Loss is a Parameter for Film, not Material. Non-Metallic Material Science 2023, 5, 38–48. [Google Scholar] [CrossRef]
- Planck, M. Scientific Autobiography and Other Paper; William & Norgate, 1950.
- Honjo, T. https://dataverse.harvard.edu/file.xhtml?fileId=5112613&version=1.1, English translation of the views of Nobel laureate Tasuku Honjo from a Chinese website: “first-class work often overturns the established conclusion, so it is unpopular. The reviewers cannot fully understand your work and will give you many negative comments, …. Articles catering to the trend of the times are easy to be accepted, otherwise, it will take a long time to get recognized” (2000) “If your research can’t overturn the established conclusion, science can’t progress. Of course, your research will be not recorded in history. The academic world is conservative. If you don’t write your paper according to the existing conclusion, it will be very difficult for your paper to be accepted, and you will suffer a lot, but the research that can survive in history is exactly this kind of research.“ (2013) 02 “Kyoto University has a tradition that ‘it is better to be unique than to be the foremost among others.’ …. If you continue to study your findings and expand from there, the world will become very broad. This is my pleasure in doing research. Don’t be in such a practice that when seeing someone else is digging a gold mine, you immediately follow in to join in the fun and become one of the many gold miners. Instead, continue to dig deep along with your own discoveries. In this way, other researchers will come to study your project” (2000). https://www.sohu.com/a/423577113_788170 (accessed 2025 1, Apr).
- Li, B. “Academic garbage is harmful and public hazard (95% of scientific research papers are garbage). It can be translated into English easily by machine translation. Available online: https://www.sohu.com/a/400765429_665896 (accessed on 1 April 2025).
- Judo, P. The scientist who faked over 50 studies. YouTube, 2023. Available online: https://www.youtube.com/watch?v=z_lB9-4R40o (accessed on 1 April 2025).
- Judo, P. Academia is BROKEN! - Harvard Fake Data Scandal Explained. YouTube, 2023. Available online: https://www.youtube.com/watch?v=d2Tm3Yx4HWI (accessed on 1 April 2025).
- Young, N. S.; Ioannidis, J. P.; Al-Ubaydli, O. Why current publication practices may distort science. PLoS Med 2008, 5, e201. [Google Scholar] [CrossRef] [PubMed]
- Harvard calls for retraction of dozens of studies by noted cardiologist, “some scientists wondered how a questionable line of research persisted for so long … experts were just too timid to take a stand”. https://www.staradvertiser.com/2018/10/16/news/harvard-calls-for-retraction-of-dozens-of-studies-by-noted-cardiologist/. New York Times, 2018, 16 Oct 2018. Available online: http://www.staradvertiser.com/2018/10/16/news/harvard-calls-for-retraction-of-dozens-of-studies-by-noted-cardiologist/.
- Ziliak, S. T.; McCloskey, D. N. The cult of statistical significance: how the standard error costs us jobs, justice, and lives; The University of Michigan Press, 2008.
- Weinstein, E. The Problem With Peer Review. YouTube, 2020. Available online: https://www.youtube.com/watch?v=U5sRYsMjiAQ (accessed on 1 April 2025).
- Murphy, B. D. Is Science Broken? The Failure of Peer Review. YouTube, 2021. Available online: https://www.youtube.com/watch?v=M2ZvEEvTuP8 (accessed on 1 April 2025).
- Deciderata. Is peer review broken? YouYube, 2016. Available online: https://www.youtube.com/watch?v=EZa0Xihih9w (accessed on 1 April 2025).
- Judo, P. The BROKEN system at the heart of Academia. YouTube, 2023. Available online: https://www.youtube.com/watch?v=JxB3yy2H7j4 (accessed on 1 April 2025).
- Liu, Y.; Drew, M. G. B.; Li, H.; Liu, Y. A theoretical analysis of the relationships shown from the general experimental results of scattering parameters s11 and s21 -- Exemplified by the film of BaFe12-iCeiO19/polypyrene with i = 0.2, 0.4, 0.6. Journal of Microwave Power and Electromagnetic Energy 2021, 55, 197–218. [Google Scholar] [CrossRef]
- Wang, T.; Chen, G.; Zhu, J.; Gong, H.; Zhang, L.; Wu, H. Deep understanding of impedance matching and quarter wavelength theory in electromagnetic wave absorption. J Colloid Interface Sci 2021, 595, 1–5. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Yu, H.; Drew, M. G. B.; Liu, Y. A systemized parameter set applicable to microwave absorption for ferrite based materials. Journal of Materials Science: Materials in Electronics 2018, 29, 1562–1575. [Google Scholar] [CrossRef]
- Hou, Z.-L.; Gao, X.; Zhang, J.; Wang, G. A perspective on impedance matching and resonance absorption mechanism for electromagnetic wave absorbing. Carbon 2024, 222, 118935. [Google Scholar] [CrossRef]
- Cheng, J.; Zhang, H.; Ning, M.; Raza, H.; Zhang, D.; Zheng, G.; Zheng, Q.; Che, R. Emerging Materials and Designs for Low- and Multi-Band Electromagnetic Wave Absorbers: The Search for Dielectric and Magnetic Synergy? Advanced Functional Materials 2022, 32, 2200123. [Google Scholar] [CrossRef]
- Wang, T.; Han, R.; Tan, G.; Wei, J.; Qiao, L.; Li, F. Reflection loss mechanism of single layer absorber for flake-shaped carbonyl-iron particle composite. Journal of Applied Physics 2012, 112, 104903. [Google Scholar] [CrossRef]
- Chen, X.; Zhou, M.; Zhao, Y.; Gu, W.; Wu, Y.; Tang, S.; Ji, G. Morphology control of eco-friendly chitosan-derived carbon aerogels for efficient microwave absorption at thin thickness and thermal stealth. Green Chemistry 2022, 24, 5280–5290. [Google Scholar] [CrossRef]
- Liu, Y.; Tian, C.; Wang, F.; Hu, B.; Xu, P.; Han, X.; Du, Y. Dual-pathway optimization on microwave absorption characteristics of core–shell Fe3O4@C microcapsules: Composition regulation on magnetic core and MoS2 nanosheets growth on carbon shell. Chemical Engineering Journal 2023, 461, 141867. [Google Scholar] [CrossRef]
- Akinay, Y.; Gunes, U.; Çolak, B.; Cetin, T. Recent progress of electromagnetic wave absorbers: A systematic review and bibliometric approach. ChemPhysMater 2023, 2, 197–206. [Google Scholar] [CrossRef]
- Editorial Policies. Available online: https://www.researchsquare.com/legal/editorial.
- Warburton, N. Must science be testable? 2016. Available online: https://aeon.co/essays/the-string-theory-wars-show-us-how-science-needs-philosophy.
- Cao, Z. Is physics an experimental science? This is a big misunderstanding. 2016. Available online: https://www.sohu.com/a/114689319_373567.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).



