Submitted:
03 March 2025
Posted:
05 March 2025
You are already at the latest version
Abstract
In this study, we analyze the long-term climate dynamics in Poland (1901–2010), using Shannon entropy as a measure of uncertainty and complexity in the atmospheric system. We focus on the monthly distributions of precipitation and temperature, modeled using a bivariate Clayton copula with a normal marginal distribution for temperature and a gamma distribution for precipitation. The correctness of the selected distributions was confirmed by the Anderson-Darling test. The conducted analysis reveals distinct trends in entropy values, indicating an increase in climate instability, which may lead to a higher frequency of extreme weather events. Nonparametric tests enabled the identification of key patterns and potential critical points in the evolution of climate variables. The structure of entropy variability was described in phase space using an attractor, revealing both periodic and chaotic components in climate dynamics. The obtained results highlight the increasing complexity of the climate system and suggest that Shannon entropy can be an effective tool not only for analyzing historical trends but also for forecasting future climate variability. This study confirms that climate is a nonlinear, dynamic system susceptible to chaotic fluctuations, which has crucial implications for modeling and predicting extreme weather conditions.

Keywords:
1. Introduction
- Agriculture – for predicting droughts, optimizing irrigation systems, and managing agricultural production [12],
- Water management – for forecasting water resources and managing retention and flood protection [13],
- Energy sector – for assessing water availability for power plant cooling and forecasting energy demand [14],
- Urban planning – for reducing flood risk and protecting infrastructure [12],
- Medicine and public health – for predicting the impacts of heatwaves and humidity changes on human health [15].
2. Data Preparation for Analysis
2. Methodology
- Firstly, analyses based on monthly values provide greater statistical stability, an appropriate frequency for assessing periodicity, and better detection of seasonal cycles. Statistical stability is particularly important in long-term studies, as excessive data variability could lead to misinterpretations and incorrect decisions [42],
- Secondly, using mean values allows for the analysis of a larger number of observations, making the results more representative of long-term trends [43],
- Additionally, this approach better reflects reality, as it focuses on typical values rather than isolated extremes, which could distort the overall picture of climate change. A methodology based on average values not only offers greater statistical stability but also incorporates a larger dataset, leading to more precise assessments of long-term climate changes. This approach is crucial for informed decision-making and effective adaptation planning in response to climate change [34,41].
3. Bootstrap Resampling Technique
4. Fitting the Normal and Gamma Distribution
5. Fitting the Copula Clayton Function
6. Shannon Entropy
- Sensitivity to measurement scale: Entropy calculations are sensitive to the measurement scale. The chosen units can significantly affect the computed entropy, requiring precise definitions and appropriate scaling.
- Assumption of uniform distribution: In meteorological data, assuming a uniform distribution of all outcomes may be inaccurate, particularly since variables such as precipitation have natural constraints. This can lead to underestimation of entropy values.
- Ignoring correlations: Neglecting correlations between variables, such as temperature and precipitation, may result in overly simplified models that fail to capture the full complexity of the data.
- Data discretization: The process of categorizing data affects entropy calculations. The chosen discretization method should align with the nature of the data to ensure accurate entropy measurement.
7. Statistical Tests Used
8. Analysis of Shannon's Entropy Trend Variation
9. Results of the Analyses and Discussion
9.1. Analysis of Shannon Entropy Values in Second-Order River Basins
9.2. Analysis of Shannon Entropy Values in the Context of Public Administration Activities
9.3. Recommendations for Public Administration in the Context of Drought and Flood Protection and Climate Change Adaptation
10. Trend and Seasonal Variability of Shannon Entropy in the Context of Climate Change
10.1. Attractor of the Mean Shannon Entropy
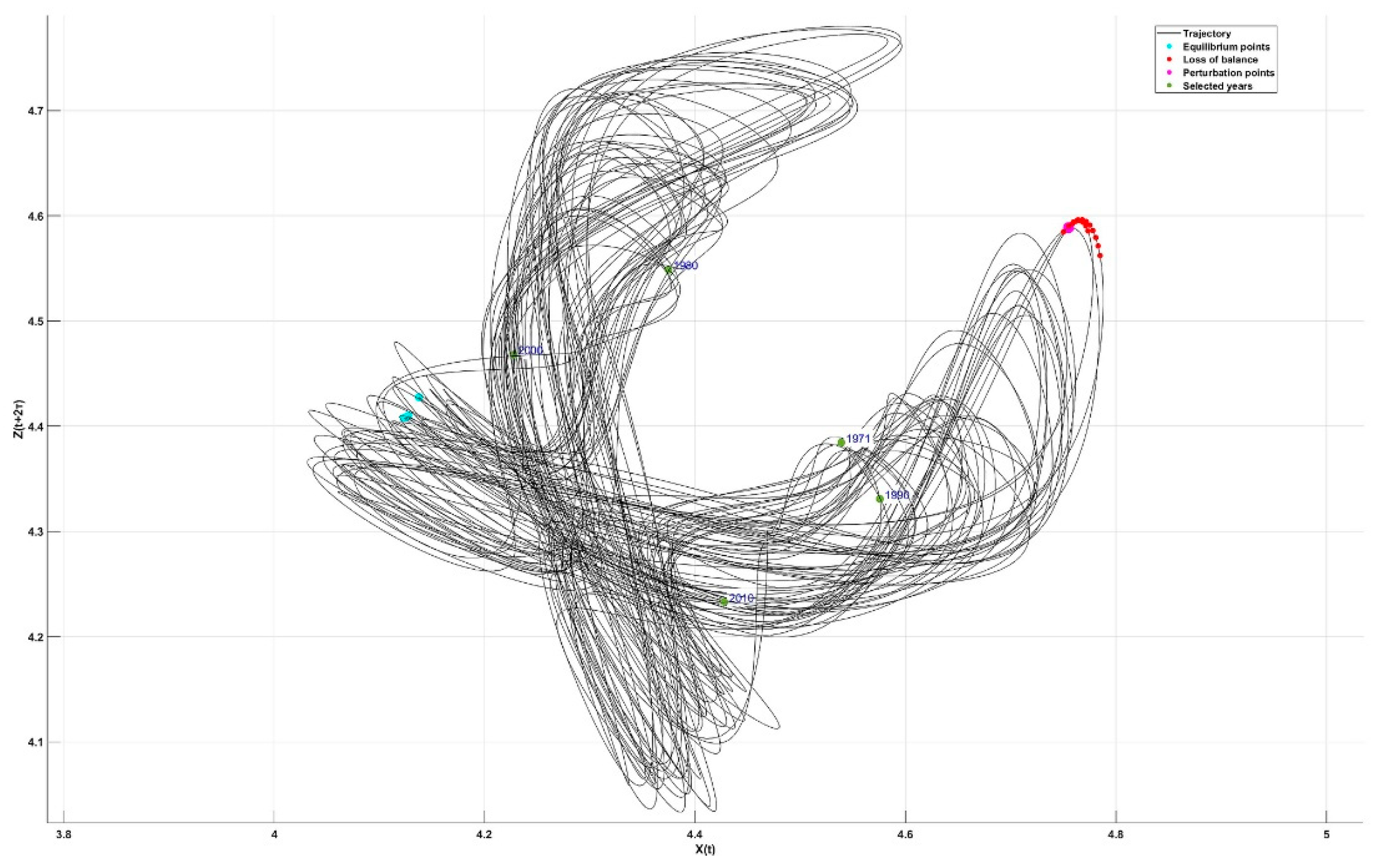
| No. | Continent | X(t) | Y(t+τ) | Z(t+2τ) |
| 1 | Equilibrium Points | 4.124 4.127 4.138 |
4.387 4.413 4.431 |
4.408 4.410 4.428 |
| 3 | Unstable Points | 4.768 | 4.053 | 4.588 |
| 4 | Perturbation Points | 4.755 | 4.056 | 4.589 |
| Selected Years | ||||
| 5 | 1971 | 4.539 | 4.099 | 4.3845 |
| 6 | 1980 | 4.598 | 4.127 | 4.412 |
| 7 | 1990 | 4.667 | 4.113 | 4.408 |
| 8 | 2000 | 4.707 | 4.049 | 4.515 |
| 9 | 2010 | 4.760 | 4.076 | 4.588 |
11. Summary
References
- Lucarini, V.; Fraedrich, K.; Lunkeit, F. ‘Thermodynamics of climate change: Generalized sensitivities’, Atmos. Chem. Phys., vol. 10, no. 20, pp. 9729–9737, 2010. [CrossRef]
- Bannon, P.R. ‘Entropy production and climate efficiency’, J. Atmos. Sci., vol. 72, no. 8, pp. 3268–3280, 2015. [CrossRef]
- Pitt, M.A. ‘Increased Temperature and Entropy Production in the Earth’s Atmosphere: Effect on Wind, Precipitation, Chemical Reactions, Freezing and Melting of Ice and Electrical Activity’, J. Mod. Phys., vol. 10, no. 08, pp. 966–973, 2019. [CrossRef]
- Gibbins, G.; Haigh, J.D. ‘Entropy production rates of the climate’, J. Atmos. Sci., vol. 77, no. 10, pp. 3551–3566, 2020. [CrossRef]
- Ghanghermeh, A.; Roshan, G.; Orosa, J.A.; Costa, Á.M. ‘Analysis and comparison of spatial-temporal entropy variability of tehran city microclimate based on climate change scenarios’, Entropy, vol. 21, no. 1, 2019. [CrossRef]
- Atieh, M.; Rudra, R.; Gharabaghi, B. ‘Investigation of spatial and temporal variability of precipitation using an entropy theory’, ASABE 1st Clim. Chang. Symp. Adapt. Mitig., pp. 191–194, 2015. [CrossRef]
- Organization, W.M. Guide to Climatological Practices 2018 edition, no. WMO-No. 100. 2018.
- de P, V.; Filho, A.F.B.; Almeida, R.S.R.; de Holanda, R.M.; da Cunha Campos, J.H.B. ‘Shannon information entropy for assessing space-time variability of rainfall and streamflow in semiarid region’, Sci. Total Environ., vol. 544, pp. 330–338, 2016. [CrossRef]
- Lewis, S.C.; King, A.D. ; Evolution of mean, variance and extremes in 21st century temperatures’, Weather Clim. Extrem., vol. 15, no. 16, pp. 1–10, 2017. 20 November. [CrossRef]
- Pfleiderer, P.; Schleussner, C.F.; Mengel, M.; Rogelj, J. ‘Global mean temperature indicators linked to warming levels avoiding climate risks’, Environ. Res. Lett., vol. 13, no. 6, 2018. [CrossRef]
- Miętus, M. ‘Climate of Poland 2022’, 2023, [Online]. Available: www.imgw.pl.
- Mesbahzadeh, T.; Miglietta, M.M.; Mirakbari, M.; Sardoo, F.S.; Abdolhoseini, M. ‘Joint Modeling of Precipitation and Temperature Using Copula Theory for Current and Future Prediction under Climate Change Scenarios in Arid Lands (Case Study, Kerman Province, Iran)’, Adv. Meteorol., vol. 2019, 2019. [CrossRef]
- Chen, L.; Guo, S. Copulas and its application in hydrology and water resources. 2019.
- Tu, Y.X.; Kubatko, O.; Piven, V.; Sotnyk, I.; Kurbatova, T. ‘Determinants of Renewable Energy Development: Evidence from the EU Countries’, Energies, vol. 15, no. 19, pp. 1–14, 2022. [CrossRef]
- Dankers, R.; Hiederer, R. ‘Extreme Temperatures and Precipitation in Europe: Analysis of a High-Resolution Climate Change Scenario’, JRC Sci. Tech. Reports, p. 82, 2008.
- Rawat, A.; Kumar, D.; Khati, B.S. ‘A review on climate change impacts, models, and its consequences on different sectors: a systematic approach’, J. Water Clim. Chang., vol. 15, no. 1, pp. 104–126, 2024. [CrossRef]
- Vinod, H.D.; López-de-Lacalle, J. ‘Maximum entropy bootstrap for time series: The meboot R package’, J. Stat. Softw., vol. 29, no. 5, pp. 1–19, 2009. [CrossRef]
- Singh, P.; Gupta, A.; Singh, M. ‘Hydrological inferences from watershed analysis for water resource management using remote sensing and GIS techniques’, Egypt. J. Remote Sens. Sp. Sci., vol. 17, no. 2, pp. 111–121, 2014. [CrossRef]
- Lal, P.N. et al., National systems for managing the risks from climate extremes and disasters, vol. 9781107025. 2012.
- Guntu, R.K.; Agarwal, A. ‘Investigation of Precipitation Variability and Extremes Using Information Theory’, p. 14, 2021. [CrossRef]
- Varbanov, P.S.; et al. ‘Efficiency measures for energy supply and use aiming for a clean circular economy’, Energy, vol. 283, p. 129035, Nov. 2023. [CrossRef]
- Staffas, L.; Gustavsson, M.; McCormick, K. ‘Strategies and policies for the bioeconomy and bio-based economy: An analysis of official national approaches’, Sustain., vol. 5, no. 6, pp. 2751–2769, 2013. [CrossRef]
- Marosz, M.; Miętus, M.; Biernacik, D. ‘Features of Multiannual Air Temperature Variability in Poland (1951–2021)’, Atmosphere (Basel)., vol. 14, no. 2, 2023. [CrossRef]
- Cebulska, M.; Szczepanek, R.; Twardosz, R. Rozkład przestrzenny opadów atmosferycznych w dorzeczu górnej Wisły. 2013.
- Cebulska, M.; Twardosz, R. ‘the Distribution of Extreme Monthly Precipitation Totals in the Polish Western Carpathians and Their Foreland Over the Year’, Prz. Geofiz., vol. 65, no. 1–2, pp. 55–68, 2020. [CrossRef]
- Młyński, D.; Cebulska, M.; Wałȩga, A. ; Trends; variability, and seasonality of maximum annual daily precipitation in the Upper Vistula Basin, Poland’, Atmosphere (Basel)., vol. 9, no. 8, pp. 1–14, 2018. [CrossRef]
- Ziernicka-Wojtaszek, A.; Zawora, T. ‘Thermal regions in light of contemporary climate change in Poland’, Polish J. Environ. Stud., vol. 20, no. 6, pp. 1627–1632, 2011.
- Struzewska, J.; Kaminski, J.W.; Jefimow, M. ‘Changes in Temperature and Precipitation Trends in Selected Polish Cities Based on the Results of Regional EURO-CORDEX Climate Models in the 2030–2050 Horizon’, Appl. Sci., vol. 14, no. 1, 2024. [CrossRef]
- Venegas-Cordero, N.; Kundzewicz, Z.W.; Jamro, S.; Piniewski, M. ‘Detection of trends in observed river floods in Poland’, J. Hydrol. Reg. Stud., vol. 41, no. 21, 2022. 20 December. [CrossRef]
- Christensen, J.H.; et al. ‘Climate phenomena and their relevance for future regional climate change’, Clim. Chang. 2013 Phys. Sci. Basis Work. Gr. I Contrib. to Fifth Assess. Rep. Intergov. Panel Clim. Chang., vol. 9781107057, pp. 1217–1308, 2013. [CrossRef]
- Easterling, D.R.; Kunkel, K.E.; Wehner, M.F.; Sun, L. ‘Detection and attribution of climate extremes in the observed record’, Weather Clim. Extrem., vol. 11, pp. 17–27, 2016. [CrossRef]
- Zhang, Y.; Zhao, Y.; Shen, X.; Zhang, J., ‘A comprehensive wind speed prediction system based on Monte Carlo and artificial intelligence algorithms’. Appl. Energy 2021, 305, 117815. [CrossRef]
- Młyński, D.; Wałȩga, A.; Petroselli, A.; Tauro, F.; Cebulska, M. ‘Estimating maximum daily precipitation in the Upper Vistula Basin, Poland’, Atmosphere (Basel)., vol. 10, no. 2, 2019. [CrossRef]
- Stocker, T.F.; et al. ‘Physical Climate Processes and Feedbacks’, Clim. Chang. 2001 Sci. Bases. Contrib. Work. Gr. I to Third Assess. Rep. Intergov. Panel Clim. Chang., p. 881, 2001.
- Beillouin, D.; Schauberger, B.; Bastos, A.; Ciais, P.; Makowski, D. ‘Impact of extreme weather conditions on European crop production in 2018: Random forest - Yield anomalies’, Philos. Trans. R. Soc. B Biol. Sci., vol. 375, no. 1810, 2020. [CrossRef]
- Twaróg, B. ‘Application of Shannon Entropy in Assessing Changes in Precipitation Conditions and Temperature Based on Long-Term Sequences Using the Bootstrap Method’, Atmosphere (Basel)., vol. 15, no. 8, 2024. [CrossRef]
- Menne, M.J.; Durre, I.; Vose, R.S.; Gleason, B.E.; Houston, T.G. ‘An overview of the global historical climatology network-daily database’, J. Atmos. Ocean. Technol., vol. 29, no. 7, pp. 897–910, 2012. [CrossRef]
- Donat, M.G.; et al. ‘Updated analyses of temperature and precipitation extreme indices since the beginning of the twentieth century : The HadEX2 dataset’, vol. 118, pp. 2098–2118, 2013. [CrossRef]
- Becker, A.; et al. ‘A description of the global land-surface precipitation data products of the Global Precipitation Climatology Centre with sample applications including centennial (trend) analysis from 1901-present’, Earth Syst. Sci. Data, vol. 5, no. 1, pp. 71–99, 2013. [CrossRef]
- B. Twaróg, ‘Assessing the Polarization of Climate Phenomena Based on Long-Term Precipitation and Temperature Sequences’, 2023. doi: 2023040380. [CrossRef]
- Allan, R.P.; Soden, B.J. ‘Atmospheric warming and the amplification of precipitation extremes’, Science (80-. )., vol. 321, no. 5895, pp. 1481–1484, 2008. [CrossRef]
- Labriet, M.; Espegren, K.; Giannakidis, G.; Gallachóir, B.Ó., Aligning the Energy Transition with the Sustainable Development Goals: Key Insights from Energy System Modelling, vol. 101. 2024.
- Asadieh, B.; Krakauer, N.Y. ‘Global trends in extreme precipitation: Climate models versus observations’, Hydrol. Earth Syst. Sci., vol. 19, no. 2, pp. 877–891, 2015. [CrossRef]
- Hao, Z. ‘Application of Entropy Theory In Hydrologic Analysis And Simulation’, PENGARUH Pengguna. PASTA LABU KUNING (Cucurbita Moschata) UNTUK SUBSTITUSI TEPUNG TERIGU DENGAN PENAMBAHAN TEPUNG ANGKAK DALAM PEMBUATAN MIE KERING, vol. 15, no. 1, pp. 165–175, 2016, [Online]. Available: https://core.ac.uk/download/pdf/196255896.pdf.
- Hou, W.; Yan, P.; Feng, G.; Zuo, D. ‘A 3D Copula Method for the Impact and Risk Assessment of Drought Disaster and an Example Application’, Front. Phys., vol. 9, no. April, pp. 1–14, 2021. [CrossRef]
- DeDeo, S.; Hawkins, R.X.D.; Klingenstein, S.; Hitchcock, T. ‘Bootstrap methods for the empirical study of decision-making and information flows in social systems’, Entropy, vol. 15, no. 6, pp. 2246–2276, 2013. [CrossRef]
- Ng, J.L.; Aziz, S.A.; Huang, Y.F.; Mirzaei, M.; Wayayok, A.; Rowshon, M.K. ‘Uncertainty analysis of rainfall depth duration frequency curves using the bootstrap resampling technique’, J. Earth Syst. Sci., vol. 128, no. 5, pp. 1–15, 2019. [CrossRef]
- C. De Michele and F. Avanzi, ‘Superstatistical distribution of daily precipitation extremes: A worldwide assessment’, Sci. Rep., vol. 8, no. 1, pp. 1–11, 2018. [CrossRef]
- Huser, R.; Davison, A.C. ‘Space-time modelling of extreme events’, J. R. Stat. Soc. Ser. B Stat. Methodol., vol. 76, no. 2, pp. 439–461, 2014. [CrossRef]
- Gurmu, S.; Dagne, G.A. ‘Bayesian approach to zero-inflated bivariate ordered probit regression model, with an application to tobacco use’, J. Probab. Stat., 2012. [CrossRef]
- Ross, S.M. Introduction to Probability and Statistics for Engineers and Scientists, Fifth Edition. 2014.
- Ogwang, T. ‘Calculating a standard error for the Gini coefficient: Some further results: Reply’, Oxf. Bull. Econ. Stat., vol. 66, no. 3, pp. 435–437, 2004. [CrossRef]
- Samson, P.; Carlen, E. Concentration of measure principle and entropy-inequalities. 2017.
- Zhang, L.; Singh, V.P. ‘Bivariate rainfall frequency distributions using Archimedean copulas’, J. Hydrol., vol. 332, no. 1–2, pp. 93–109, 2007. [CrossRef]
- Najjari, V.; Unsal, M.G. ‘An Application of Archimedean Copulas for Meteorological Data’, Gazi Univ. J. Sci., vol. 25, no. 2, pp. 417–424, 2012.
- Frees, E.W.; Valdez, E.A. ‘Understanding Relationships Using Copulas’, no. 1996, pp. 1–25, 1997.
- Management, F.R. ‘Copulas in Financial Risk Management’, Math. Financ., no. August, 2000.
- Cherubini, U.; Luciano, E. Copula methods in finance. 2004.
- Panchenko, V. ‘Goodness-of-fit test for copulas’, Phys. A Stat. Mech. its Appl., vol. 355, no. 1, pp. 176–182, 2005. [CrossRef]
- Fermanian, J.D. ‘Goodness-of-fit tests for copulas’, J. Multivar. Anal., vol. 95, no. 1, pp. 119–152, 2005. [CrossRef]
- Christianto, V.; Smarandache, F. ‘A Thousand Words: How Shannon Entropy Perspective Provides Link between Exponential Data Growth, Average Temperature of the Earth and Declining Earth Magnetic Field’, Bull. Pure Appl. Sci. Geol., vol. 38f, no. 2, p. 225, 2019. [CrossRef]
- Chakrabarti, C.G.; Chakrabarty, I. ‘Shannon entropy: Axiomatic characterization and application’, Int. J. Math. Math. Sci., vol. 2005, no. 17, pp. 2847–2854, 2005. [CrossRef]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory. John Wiley & Sons, Inc, 1991.
- Silini, R.; Masoller, C. ‘Fast and effective pseudo transfer entropy for bivariate data-driven causal inference’, Sci. Rep., vol. 11, no. 1, pp. 1–13, 2021. [CrossRef]
- Zhang, L.; Singh, V.P. ‘Bivariate rainfall and runoff analysis using entropy and copula theories’, Entropy, vol. 14, no. 9, pp. 1784–1812, 2012. [CrossRef]
- N. N. Karmeshu Supervisor Frederick Scatena, ‘Trend Detection in Annual Temperature & Precipitation using the Mann Kendall Test – A Case Study to Assess Climate Change on Select States in the Northeastern United States’, Mausam, vol. 66, no. 1, pp. 1–6, 2015, [Online]. Available: http://repository.upenn.edu/mes_capstones/47.
- Wibig, J.; Glowicki, B. ‘Trends of minimum and maximum temperature in Poland’, Clim. Res., vol. 20, no. 2, pp. 123–133, 2002. [CrossRef]
- Conte, L.C.; Bayer, D.M.; Bayer, F.M. ‘Bootstrap Pettitt test for detecting change points in hydroclimatological data: case study of Itaipu Hydroelectric Plant, Brazil’, Hydrol. Sci. J., vol. 64, no. 11, pp. 1312–1326, 2019. [CrossRef]
- Pettitt, A.N. ‘A Non-Parametric Approach to the Change-Point Problem’, J. R. Stat. Soc. Ser. C (Applied Stat., vol. 28, no. 2, pp. 126–135, Apr. 1979. [CrossRef]
- Jaiswal, R.K.; Lohani, A.K.; Tiwari, H.L. ‘Statistical Analysis for Change Detection and Trend Assessment in Climatological Parameters’, Environ. Process., vol. 2, no. 4, pp. 729–749, 2015. [CrossRef]
- Hirsch, R.M.; Slack, J.R.; Smith, R.A. ‘Techniques of trend analysis for monthly water quality data’, Water Resour. Res., vol. 18, no. 1, pp. 107–121, Feb. 1982. [CrossRef]
- Froyland, G.; Giannakis, D.; Lintner, B.R.; Pike, M.; Slawinska, J. ‘Spectral analysis of climate dynamics with operator-theoretic approaches’, Nat. Commun., vol. 12, no. 1, pp. 1–21, 2021. [CrossRef]
- Essex, C.; Lookman, T.; Nerenberg, M.A.H. ‘The climate attractor over short timescales’, Nature, vol. 326, no. 6108, pp. 64–66, 1987. [CrossRef]
- Kovács, T. ‘How can contemporary climate research help understand epidemic dynamics? Ensemble approach and snapshot attractors’, J. R. Soc. Interface, vol. 17, no. 173, 2020. [CrossRef]
- Bhattacharya, K. ; The climate attractor’; Sci, P.I.A.S.-E.P.; vol.; no.; pp., 1993. [CrossRef]
- Brunetti, M.; Ragon, C. ‘Attractors and bifurcation diagrams in complex climate models’, Phys. Rev. E, vol. 107, no. 5, 2023. [CrossRef]



| Bivariate copula function | |
| , where: | (4) |
| Kendall’s τ | |
| (5) | |
| Month | JAN | FEB | MAR | APR | MAY | JUN | JUL | AUG | SEP | OCT | NOV | DEC |
| 0.361 | 0.180 | 0.091 | 0.045 | 0.041 | 0.033 | 0.025 | 0.037 | 0.016 | 0.066 | 0.295 | 0.293 |
| CODE | NAME | JAN | FEB | MAR | APR | MAY | JUN | JUL | AUG | SEP | OCT | NOV | DEC |
| 24 | Nysa Kłodzka | 4.620 | 4.663 | 4.389 | 3.996 | 4.334 | 4.286 | 4.730 | 4.498 | 4.463 | 4.384 | 4.183 | 4.249 |
| 28 | Barycz | 4.664 | 4.641 | 4.368 | 3.726 | 4.043 | 3.986 | 4.628 | 4.107 | 4.054 | 4.179 | 4.039 | 4.461 |
| 35 | Cieśnina Dziwna | 4.812 | 4.785 | 4.319 | 3.925 | 3.956 | 3.822 | 4.395 | 4.045 | 4.083 | 4.144 | 4.078 | 4.370 |
| 44 | Parsęta | 4.970 | 4.916 | 4.590 | 4.077 | 4.033 | 4.031 | 4.643 | 4.285 | 4.550 | 4.411 | 4.347 | 4.745 |
| 45 | Odra od Baryczy do Bobru (l) | 4.769 | 4.780 | 4.395 | 3.898 | 4.130 | 4.008 | 4.722 | 4.199 | 4.166 | 4.166 | 4.095 | 4.485 |
| 45 | Przymorze od Parsęty do Wieprzy | 4.900 | 4.859 | 4.434 | 4.069 | 4.488 | 4.277 | 4.729 | 4.543 | 4.466 | 4.564 | 4.405 | 4.607 |
| 46 | Wieprza | 4.879 | 4.823 | 4.450 | 3.979 | 4.140 | 4.052 | 4.562 | 4.332 | 4.437 | 4.468 | 4.359 | 4.690 |
| 51 | Odra od Bobru do Warty (p) | 4.817 | 4.813 | 4.375 | 4.059 | 4.181 | 4.061 | 4.674 | 4.208 | 4.122 | 4.176 | 4.084 | 4.472 |
| 51 | Zalew Wiślany do Nogatu | 4.787 | 4.917 | 4.296 | 3.886 | 4.171 | 4.128 | 4.464 | 4.357 | 4.421 | 4.411 | 4.319 | 4.881 |
| 52 | Nogat | 4.911 | 4.769 | 4.247 | 3.809 | 4.078 | 4.094 | 4.392 | 4.191 | 4.417 | 4.132 | 4.175 | 4.687 |
| 55 | Zalew Wiślany od Elbląga do Pasłęki | 4.903 | 4.959 | 4.369 | 3.851 | 4.155 | 4.102 | 4.455 | 4.336 | 4.467 | 4.480 | 4.392 | 4.949 |
| 62 | Świsłocz (l) | 4.681 | 4.613 | 4.357 | 4.018 | 4.130 | 4.159 | 4.634 | 4.304 | 4.137 | 4.237 | 4.118 | 4.355 |
| 64 | Bóbr | 5.103 | 5.012 | 4.620 | 4.293 | 4.397 | 4.205 | 4.853 | 4.443 | 4.461 | 4.533 | 4.365 | 4.682 |
| 64 | Czarna Hańcza (l) | 4.711 | 4.638 | 4.373 | 3.980 | 4.076 | 4.188 | 4.733 | 4.425 | 4.178 | 4.351 | 4.230 | 4.345 |
| 72 | Lechnawa | 4.551 | 4.643 | 4.606 | 4.189 | 4.286 | 4.290 | 4.442 | 4.243 | 4.479 | 4.534 | 4.404 | 4.756 |
| 77 | Odra do Nysy Kłodzkiej (l) | 4.504 | 4.624 | 4.307 | 4.013 | 4.285 | 4.193 | 4.619 | 4.204 | 4.328 | 4.343 | 4.189 | 4.340 |
| 84 | Rega | 5.070 | 4.962 | 4.606 | 4.137 | 4.112 | 3.962 | 4.567 | 4.331 | 4.386 | 4.433 | 4.364 | 4.667 |
| 91 | Odra od Nysy Kłodzkiej do Baryczy (p) | 4.602 | 4.642 | 4.280 | 3.899 | 4.227 | 4.130 | 4.704 | 4.272 | 4.196 | 4.260 | 4.092 | 4.340 |
| 92 | Wisła od Sanu do Wieprza (p) | 4.666 | 4.731 | 4.544 | 4.152 | 4.099 | 4.323 | 4.588 | 4.298 | 4.220 | 4.278 | 4.335 | 4.466 |
| 96 | Orlica (Dzika Orlica) | 4.605 | 4.600 | 4.257 | 4.173 | 4.330 | 4.159 | 4.702 | 4.447 | 4.311 | 4.302 | 4.089 | 4.362 |
| 96 | Martwa Wisła | 4.683 | 4.608 | 4.046 | 3.925 | 4.121 | 3.984 | 4.433 | 4.401 | 4.333 | 4.340 | 4.176 | 4.592 |
| 112 | Drwęca | 4.780 | 4.876 | 4.311 | 3.831 | 4.108 | 4.228 | 4.579 | 4.176 | 4.401 | 4.243 | 4.188 | 4.760 |
| 112 | Pasłęka | 5.015 | 5.019 | 4.546 | 3.944 | 4.175 | 4.256 | 4.493 | 4.388 | 4.549 | 4.491 | 4.387 | 5.022 |
| 114 | Odra od Warty do ujścia | 4.842 | 4.837 | 4.254 | 3.963 | 4.017 | 4.031 | 4.460 | 4.032 | 4.035 | 4.142 | 4.011 | 4.337 |
| 144 | Wieprz | 4.657 | 4.669 | 4.560 | 4.027 | 4.021 | 4.187 | 4.427 | 4.175 | 4.135 | 4.236 | 4.265 | 4.460 |
| 174 | Wisła od Drwęcy do ujścia | 4.850 | 4.773 | 4.356 | 3.895 | 4.085 | 4.125 | 4.609 | 4.157 | 4.341 | 4.250 | 4.226 | 4.698 |
| 175 | Wisła od Wieprza do Narwi (p) | 4.686 | 4.655 | 4.482 | 3.942 | 4.127 | 4.192 | 4.566 | 4.097 | 4.117 | 4.127 | 4.260 | 4.461 |
| 188 | Przymorze od Wieprzy do Martwej Wisły | 4.865 | 4.815 | 4.344 | 3.976 | 4.162 | 3.995 | 4.576 | 4.400 | 4.398 | 4.454 | 4.382 | 4.692 |
| 198 | San | 4.552 | 4.649 | 4.619 | 4.173 | 4.270 | 4.284 | 4.468 | 4.156 | 4.354 | 4.387 | 4.317 | 4.578 |
| 243 | Wisła od Narwi do Drwęcy ( l ) | 4.641 | 4.694 | 4.224 | 3.890 | 4.160 | 4.247 | 4.641 | 4.116 | 4.174 | 4.145 | 4.259 | 4.593 |
| 348 | Pregoła | 4.900 | 4.845 | 4.521 | 3.907 | 4.057 | 4.214 | 4.576 | 4.418 | 4.429 | 4.388 | 4.365 | 4.711 |
| 357 | Wisła do Sanu | 4.776 | 4.841 | 4.731 | 4.281 | 4.363 | 4.389 | 4.682 | 4.274 | 4.491 | 4.460 | 4.467 | 4.524 |
| 486 | Warta | 4.687 | 4.743 | 4.374 | 3.849 | 4.142 | 4.172 | 4.665 | 4.127 | 4.207 | 4.237 | 4.171 | 4.527 |
| 1014 | Narew | 4.705 | 4.707 | 4.389 | 3.925 | 4.088 | 4.196 | 4.498 | 4.229 | 4.186 | 4.232 | 4.194 | 4.462 |
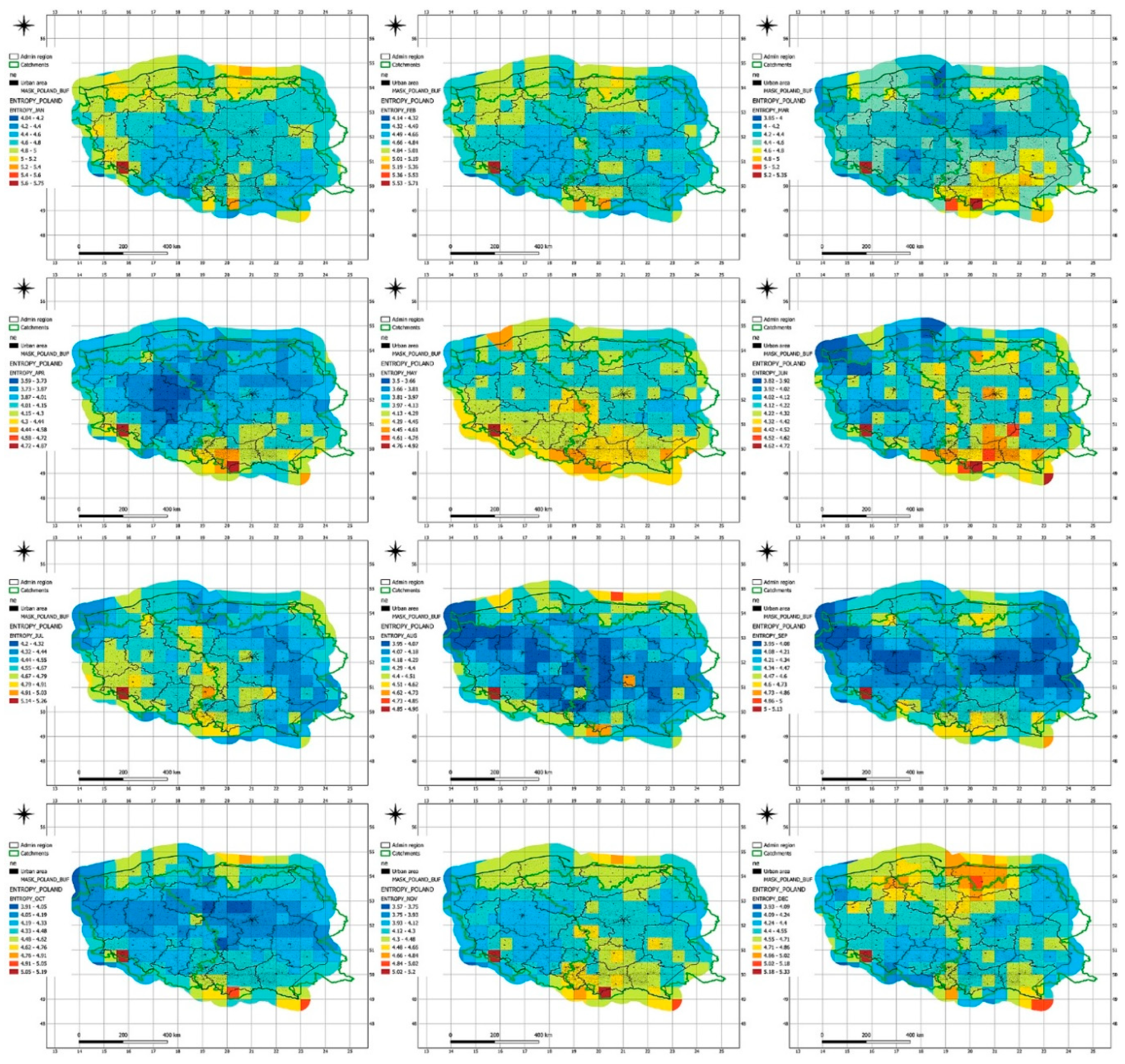
| CODE | NAME_ | JAN | FEB | MAR | APR | MAY | JUN | JUL | AUG | SEP | OCT | NOV | DEC |
| 2 | dolnośląskie | 4.781 | 4.782 | 4.418 | 4.073 | 4.317 | 4.192 | 4.769 | 4.372 | 4.318 | 4.373 | 4.213 | 4.461 |
| 4 | kujawsko-pomorskie | 4.683 | 4.746 | 4.231 | 3.786 | 4.079 | 4.228 | 4.680 | 4.168 | 4.237 | 4.130 | 4.147 | 4.618 |
| 6 | lubelskie | 4.660 | 4.669 | 4.576 | 4.040 | 4.026 | 4.197 | 4.441 | 4.160 | 4.147 | 4.242 | 4.271 | 4.471 |
| 8 | lubuskie | 4.816 | 4.825 | 4.404 | 3.976 | 4.155 | 4.065 | 4.694 | 4.182 | 4.151 | 4.180 | 4.113 | 4.512 |
| 10 | łódzkie | 4.609 | 4.680 | 4.350 | 3.904 | 4.252 | 4.225 | 4.670 | 4.086 | 4.162 | 4.216 | 4.310 | 4.484 |
| 12 | małopolskie | 4.733 | 4.808 | 4.692 | 4.286 | 4.366 | 4.383 | 4.647 | 4.277 | 4.492 | 4.428 | 4.400 | 4.510 |
| 14 | mazowieckie | 4.689 | 4.671 | 4.325 | 3.921 | 4.066 | 4.205 | 4.503 | 4.190 | 4.136 | 4.150 | 4.227 | 4.510 |
| 16 | opolskie | 4.499 | 4.609 | 4.257 | 3.896 | 4.213 | 4.120 | 4.593 | 4.117 | 4.293 | 4.297 | 4.071 | 4.365 |
| 18 | podkarpackie | 4.605 | 4.672 | 4.669 | 4.172 | 4.292 | 4.314 | 4.494 | 4.191 | 4.383 | 4.391 | 4.334 | 4.612 |
| 20 | podlaskie | 4.685 | 4.674 | 4.374 | 3.910 | 4.081 | 4.168 | 4.579 | 4.305 | 4.167 | 4.284 | 4.173 | 4.359 |
| 22 | pomorskie | 4.840 | 4.774 | 4.293 | 3.926 | 4.127 | 4.039 | 4.524 | 4.301 | 4.384 | 4.356 | 4.276 | 4.695 |
| 24 | śląskie | 4.689 | 4.807 | 4.561 | 4.185 | 4.360 | 4.324 | 4.780 | 4.226 | 4.386 | 4.450 | 4.449 | 4.484 |
| 26 | świętokrzyskie | 4.745 | 4.780 | 4.610 | 4.106 | 4.231 | 4.321 | 4.711 | 4.128 | 4.366 | 4.304 | 4.344 | 4.449 |
| 28 | warmińsko-mazurskie | 4.880 | 4.895 | 4.503 | 3.896 | 4.095 | 4.218 | 4.504 | 4.338 | 4.469 | 4.386 | 4.333 | 4.834 |
| 30 | wielkopolskie | 4.660 | 4.697 | 4.333 | 3.753 | 4.111 | 4.135 | 4.633 | 4.116 | 4.175 | 4.217 | 4.098 | 4.524 |
| 32 | zachodniopomorskie | 4.919 | 4.878 | 4.456 | 4.022 | 4.073 | 4.014 | 4.571 | 4.186 | 4.294 | 4.316 | 4.234 | 4.568 |
| Regional Water Management Strategies | |
| Provinces with High Winter Entropy (e.g., West Pomeranian, Warmian-Masurian): | Expansion of retention systems and flood reservoirs to counteract sudden thaws and heavy rainfall. Modernization of flood embankments and drainage systems in areas most at risk of flooding. Implementation of smart water management systems to monitor river levels and predict flood risks |
| Provinces with High Summer Entropy (e.g., Lower Silesian, Silesian, Świętokrzyskie, Lublin): | Small retention programs – construction of ponds and reservoirs to store water for drought periods. Grants for rainwater harvesting and reuse systems for households and businesses. Support for agriculture through drip irrigation and water-saving technologies. |
| Provinces with Low Spring Entropy (e.g., Kuyavian-Pomeranian, Greater Poland): | Monitoring of prolonged dry periods and implementation of irrigation systems for farmland. Development of localized water management plans tailored to soil and climate conditions. Prevention of soil degradation by increasing green areas and protecting forests. |
| Development of Monitoring and Forecasting Systems | |
| Modern Early Warning Systems for Extreme Weather Events: | Installation of water level and precipitation sensors in areas with high climatic variability. Implementation of AI-based forecasting systems to predict extreme rainfall and drought periods. Improvement of hydrological models incorporating Shannon entropy data to plan crisis response actions. |
| Spatial and Urban Adaptation | |
| Climate-Resilient Urban Planning: | Reduction of urban surface sealing and introduction of green roofs and permeable pavements. Expansion of urban green spaces to mitigate the urban heat island effect and improve rainwater infiltration. Development of flood risk maps based on entropy analysis for better infrastructure planning. |
| Education and Public Engagement | |
| Raising Public Awareness of Climate Change Impacts: | Educational campaigns on water conservation and efficient usage. Subsidy programs for residents to install retention tanks and rainwater management systems. Promotion of sustainable agricultural practices in drought-prone areas. |
| Interregional Cooperation and Administrative Integration | |
| Coordination Between National and Local Authorities: | Establishment of regional crisis management centers to analyze entropy and climate variability data. Cooperation between provinces with similar climatic conditions, e.g., joint investments in water systems. Integration of water policy with regional development strategies to align investments with projected climate changes. |
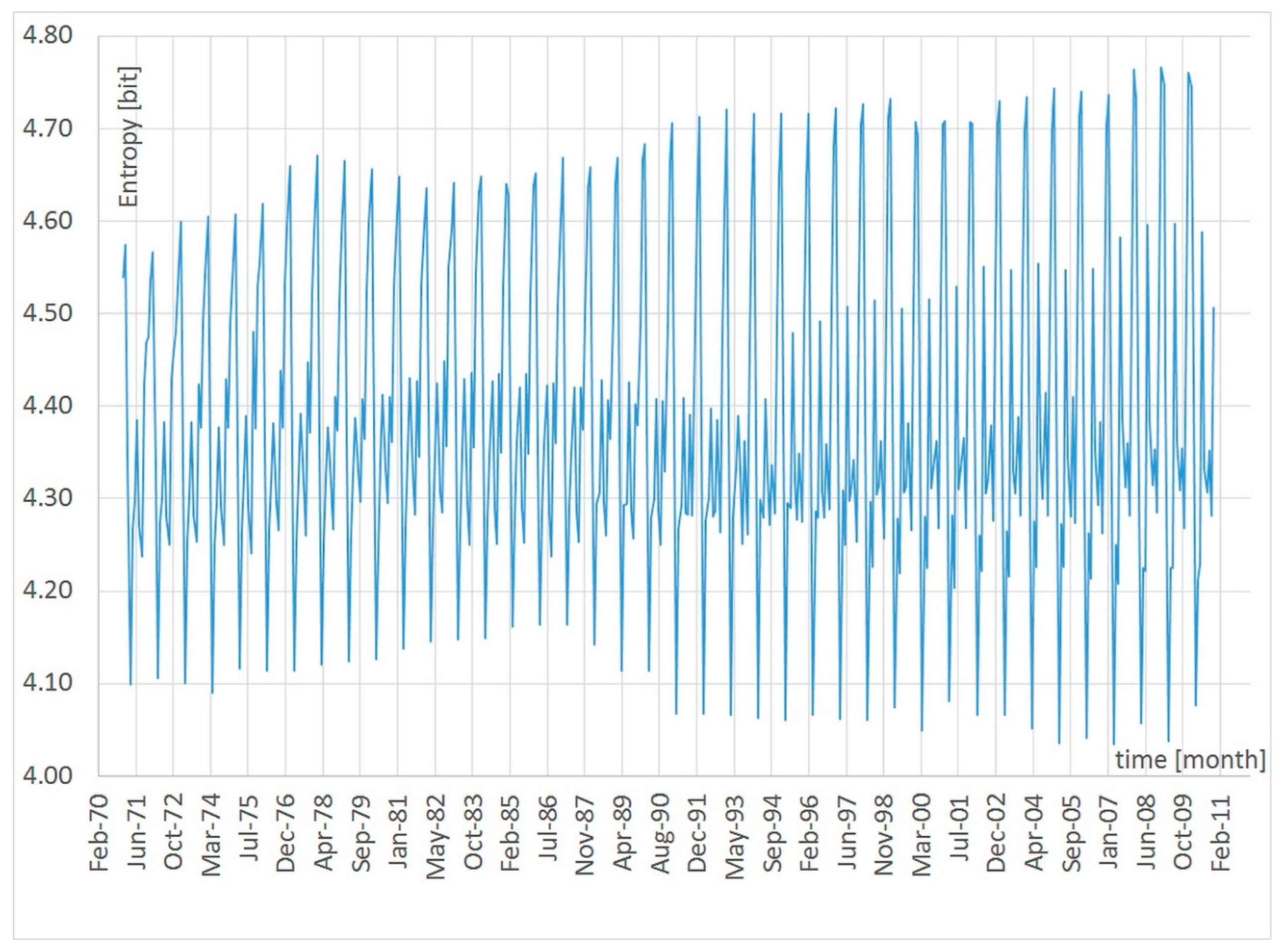
| Period | JAN | FEB | MAR | APR | MAY | JUN | JUL | AUG | SEP | OCT | NOV | DEC |
| 1901-1971 | 4.539 | 4.574 | 4.342 | 4.099 | 4.267 | 4.297 | 4.385 | 4.272 | 4.237 | 4.425 | 4.469 | 4.474 |
| 1902-1972 | 4.537 | 4.566 | 4.335 | 4.106 | 4.274 | 4.301 | 4.382 | 4.280 | 4.249 | 4.430 | 4.459 | 4.480 |
| 1903-1973 | 4.528 | 4.599 | 4.333 | 4.100 | 4.253 | 4.303 | 4.383 | 4.282 | 4.254 | 4.423 | 4.377 | 4.489 |
| 1904-1974 | 4.543 | 4.605 | 4.326 | 4.090 | 4.250 | 4.294 | 4.377 | 4.292 | 4.250 | 4.429 | 4.377 | 4.490 |
| 1905-1975 | 4.536 | 4.607 | 4.353 | 4.116 | 4.264 | 4.324 | 4.389 | 4.293 | 4.241 | 4.480 | 4.376 | 4.529 |
| 1906-1976 | 4.555 | 4.619 | 4.354 | 4.114 | 4.267 | 4.319 | 4.382 | 4.294 | 4.266 | 4.438 | 4.377 | 4.532 |
| 1907-1977 | 4.594 | 4.659 | 4.346 | 4.114 | 4.253 | 4.320 | 4.392 | 4.316 | 4.260 | 4.447 | 4.371 | 4.523 |
| 1908-1978 | 4.590 | 4.671 | 4.359 | 4.120 | 4.250 | 4.322 | 4.376 | 4.317 | 4.267 | 4.410 | 4.373 | 4.514 |
| 1909-1979 | 4.583 | 4.665 | 4.359 | 4.125 | 4.258 | 4.327 | 4.387 | 4.329 | 4.296 | 4.408 | 4.365 | 4.524 |
| 1910-1980 | 4.598 | 4.656 | 4.369 | 4.127 | 4.244 | 4.340 | 4.412 | 4.331 | 4.295 | 4.410 | 4.361 | 4.530 |
| 1911-1981 | 4.607 | 4.648 | 4.372 | 4.137 | 4.269 | 4.348 | 4.430 | 4.327 | 4.283 | 4.427 | 4.346 | 4.530 |
| 1912-1982 | 4.598 | 4.636 | 4.395 | 4.145 | 4.266 | 4.347 | 4.425 | 4.307 | 4.285 | 4.448 | 4.357 | 4.550 |
| 1913-1983 | 4.592 | 4.642 | 4.389 | 4.148 | 4.263 | 4.350 | 4.429 | 4.293 | 4.250 | 4.436 | 4.355 | 4.544 |
| 1914-1984 | 4.633 | 4.648 | 4.388 | 4.149 | 4.276 | 4.348 | 4.427 | 4.289 | 4.252 | 4.435 | 4.350 | 4.529 |
| 1915-1985 | 4.640 | 4.629 | 4.368 | 4.161 | 4.278 | 4.361 | 4.420 | 4.290 | 4.252 | 4.435 | 4.349 | 4.521 |
| 1916-1986 | 4.639 | 4.652 | 4.346 | 4.164 | 4.283 | 4.358 | 4.422 | 4.283 | 4.238 | 4.425 | 4.360 | 4.509 |
| 1917-1987 | 4.603 | 4.668 | 4.347 | 4.164 | 4.292 | 4.349 | 4.420 | 4.285 | 4.254 | 4.421 | 4.375 | 4.498 |
| 1918-1988 | 4.637 | 4.658 | 4.353 | 4.142 | 4.295 | 4.307 | 4.428 | 4.295 | 4.260 | 4.406 | 4.364 | 4.502 |
| 1919-1989 | 4.642 | 4.669 | 4.357 | 4.114 | 4.293 | 4.295 | 4.426 | 4.289 | 4.257 | 4.402 | 4.379 | 4.489 |
| 1920-1990 | 4.667 | 4.683 | 4.368 | 4.113 | 4.280 | 4.299 | 4.408 | 4.285 | 4.250 | 4.406 | 4.329 | 4.490 |
| 1921-1991 | 4.665 | 4.706 | 4.381 | 4.067 | 4.267 | 4.293 | 4.409 | 4.283 | 4.283 | 4.391 | 4.282 | 4.485 |
| 1922-1992 | 4.621 | 4.713 | 4.366 | 4.067 | 4.277 | 4.301 | 4.397 | 4.281 | 4.286 | 4.385 | 4.263 | 4.479 |
| 1923-1993 | 4.614 | 4.720 | 4.377 | 4.066 | 4.281 | 4.333 | 4.389 | 4.330 | 4.252 | 4.362 | 4.261 | 4.469 |
| 1924-1994 | 4.625 | 4.717 | 4.363 | 4.063 | 4.299 | 4.279 | 4.408 | 4.325 | 4.271 | 4.336 | 4.284 | 4.489 |
| 1925-1995 | 4.649 | 4.716 | 4.391 | 4.061 | 4.295 | 4.290 | 4.479 | 4.319 | 4.277 | 4.349 | 4.275 | 4.500 |
| 1926-1996 | 4.646 | 4.717 | 4.393 | 4.066 | 4.286 | 4.279 | 4.491 | 4.308 | 4.279 | 4.359 | 4.289 | 4.508 |
| 1927-1997 | 4.682 | 4.722 | 4.402 | 4.062 | 4.308 | 4.250 | 4.507 | 4.298 | 4.315 | 4.341 | 4.253 | 4.521 |
| 1928-1998 | 4.705 | 4.726 | 4.389 | 4.061 | 4.297 | 4.226 | 4.514 | 4.305 | 4.314 | 4.363 | 4.257 | 4.500 |
| 1929-1999 | 4.713 | 4.732 | 4.402 | 4.074 | 4.278 | 4.220 | 4.506 | 4.307 | 4.313 | 4.382 | 4.266 | 4.505 |
| 1930-2000 | 4.707 | 4.692 | 4.398 | 4.049 | 4.281 | 4.225 | 4.515 | 4.312 | 4.334 | 4.362 | 4.268 | 4.508 |
| 1931-2001 | 4.704 | 4.709 | 4.427 | 4.081 | 4.282 | 4.203 | 4.529 | 4.310 | 4.333 | 4.366 | 4.268 | 4.515 |
| 1932-2002 | 4.708 | 4.705 | 4.422 | 4.066 | 4.260 | 4.222 | 4.550 | 4.305 | 4.320 | 4.380 | 4.276 | 4.525 |
| 1933-2003 | 4.706 | 4.729 | 4.414 | 4.067 | 4.265 | 4.216 | 4.547 | 4.330 | 4.306 | 4.388 | 4.282 | 4.529 |
| 1934-2004 | 4.699 | 4.735 | 4.413 | 4.052 | 4.275 | 4.226 | 4.554 | 4.347 | 4.300 | 4.414 | 4.281 | 4.506 |
| 1935-2005 | 4.698 | 4.744 | 4.414 | 4.036 | 4.273 | 4.226 | 4.547 | 4.344 | 4.280 | 4.410 | 4.274 | 4.482 |
| 1936-2006 | 4.714 | 4.741 | 4.413 | 4.041 | 4.262 | 4.213 | 4.548 | 4.352 | 4.293 | 4.382 | 4.262 | 4.498 |
| 1937-2007 | 4.705 | 4.737 | 4.425 | 4.034 | 4.250 | 4.208 | 4.583 | 4.386 | 4.312 | 4.361 | 4.281 | 4.522 |
| 1938-2008 | 4.764 | 4.733 | 4.421 | 4.057 | 4.225 | 4.222 | 4.596 | 4.383 | 4.314 | 4.353 | 4.286 | 4.515 |
| 1939-2009 | 4.767 | 4.747 | 4.430 | 4.038 | 4.225 | 4.225 | 4.597 | 4.362 | 4.309 | 4.355 | 4.269 | 4.512 |
| 1940-2010 | 4.760 | 4.744 | 4.425 | 4.076 | 4.211 | 4.229 | 4.588 | 4.331 | 4.307 | 4.352 | 4.281 | 4.506 |
| Month | Entropy Change (1940–2010) – (1901–1971) |
Average Growth Rate (per Decade) |
| [bits] | [bits/10 years] | |
| JAN | +0.221 (4.760 - 4.539) | 0.055 |
| FEB | +0.170 (4.744 - 4.574) | 0.043 |
| MAR | +0.083 (4.425 - 4.342) | 0.021 |
| APR | -0.023 (4.076 - 4.099) | -0.006 |
| MAY | -0.056 (4.211 - 4.267) | -0.014 |
| JUN | -0.068 (4.229 - 4.297) | -0.017 |
| JUL | +0.203 (4.588 - 4.385) | 0.051 |
| AUG | +0.059 (4.331 - 4.272) | 0.015 |
| SEP | +0.070 (4.307 - 4.237) | 0.018 |
| OCT | -0.073 (4.352 - 4.425) | -0.018 |
| NOV | -0.188 (4.281 - 4.469) | -0.047 |
| DEC | +0.032 (4.506 - 4.474) | 0.008 |
| CODE | Name_ | JAN | FEB | MAR | APR | MAY | JUN | JUL | AUG | SEP | OCT | NOV | DEC |
| 2 | dolnośląskie | 1988 | 1987 | 1991 | 1990 | 1990 | 1989 | 1992 | 1994 | 1991 | 1989 | 1989 | 1989 |
| 4 | kujawsko-pomorskie | 1994 | 1989 | 1990 | 1990 | 1993 | 1996 | 1994 | 1988 | 1992 | 1984 | 1990 | 1996 |
| 6 | lubelskie | 1992 | 1989 | 1991 | 1989 | 1990 | 1994 | 1996 | 1991 | 1988 | 1989 | 1989 | 1994 |
| 8 | lubuskie | 1995 | 1990 | 1993 | 1992 | 1990 | 1992 | 1993 | 1994 | 1991 | 1990 | 1991 | 1990 |
| 10 | łódzkie | 1989 | 1991 | 1991 | 1988 | 1997 | 1993 | 1996 | 1989 | 1993 | 1988 | 1988 | 1994 |
| 12 | małopolskie | 1992 | 1989 | 1985 | 1989 | 1991 | 1991 | 1992 | 1990 | 1984 | 1988 | 1987 | 1989 |
| 14 | mazowieckie | 1995 | 1989 | 1988 | 1990 | 1995 | 1993 | 1994 | 1992 | 1994 | 1987 | 1990 | 1996 |
| 16 | opolskie | 1992 | 1987 | 1990 | 1988 | 1990 | 1989 | 1993 | 1992 | 1989 | 1990 | 1989 | 1985 |
| 18 | podkarpackie | 1991 | 1987 | 1990 | 1992 | 1991 | 1991 | 1994 | 1992 | 1985 | 1990 | 1991 | 1995 |
| 20 | podlaskie | 1984 | 1991 | 1986 | 1989 | 1994 | 1992 | 1994 | 1994 | 1990 | 1988 | 1990 | 1989 |
| 22 | pomorskie | 1991 | 1990 | 1996 | 1991 | 1991 | 1992 | 1995 | 1992 | 1990 | 1987 | 1990 | 1993 |
| 24 | śląskie | 1983 | 1989 | 1991 | 1990 | 1988 | 1995 | 1994 | 1991 | 1991 | 1990 | 1989 | 1991 |
| 26 | świętokrzyskie | 1990 | 1991 | 1987 | 1987 | 1996 | 1987 | 1996 | 1994 | 1982 | 1988 | 1983 | 1989 |
| 28 | warmińsko-mazurskie | 1988 | 1991 | 1992 | 1989 | 1995 | 1994 | 1994 | 1989 | 1992 | 1985 | 1990 | 1996 |
| 30 | wielkopolskie | 1992 | 1990 | 1993 | 1990 | 1992 | 1992 | 1994 | 1991 | 1992 | 1989 | 1990 | 1991 |
| 32 | zachodniopomorskie | 1995 | 1990 | 1993 | 1990 | 1995 | 1989 | 1994 | 1989 | 1987 | 1988 | 1989 | 1986 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).




