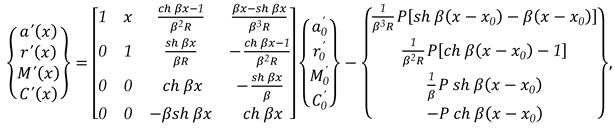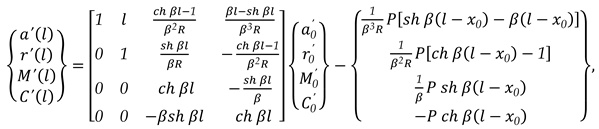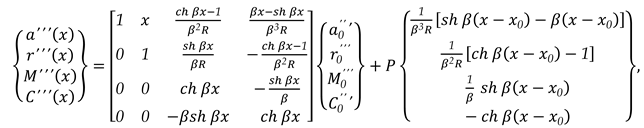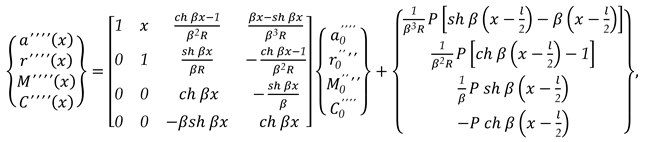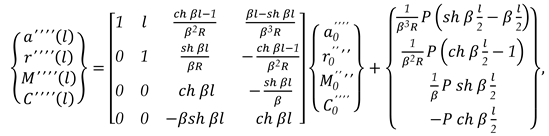Calculus of Long Rectangular Plates Embedded of The Long Borders with Uniform Vertical Load on a Line Parallel to The Long Borders through Transfer-Matrix Method for Applications in Vehicle Industry

1. Introduction

This study was done due to the need to calculate the resistance of plates for the vehicle industry. Vehicles are complex assemblies that have several components like plates. Not only is it important in the automobile industry, plate calculus is important, but also in construction, in medicine, in orthodontics and in many other fields. This work is original and new. The Transfer-Matrix Method (TMM) is a mathematical approach for the calculus of different structures that can be discretized into elements, using an iterative calculation as in [1]. Classical calculus of Material Resistance is presented in [2] and [3]. [4] gives the calculus of long cylinder tube for industrial applications by TMM. An approach with TMM for mandible body bone calculus shows in [5]. [6] presents the calculus through the TMM of a beam with intermediate support with applications in dental restorations. Another approach by the Finite Elements Method (FEM) applied for calculus of rectangular plates is presented in [7] and [8]. Study of bending for a rectangular plate with each edges arbitrary point supported under a concentrated load is given in [9]. [10] presents an analysis of folded plate structures by a combined Boundary Element-TMM and [11] gives a FEM-TMM for dynamic analysis of frame structures. Elastic analysis and application tables of rectangular plates with unilateral contact support conditions is given in [12]. [13] presents theoretical aspects for time-harmonic analysis of acoustic pulsation in gas pipeline systems using the FEM and TMM. [14] gives an integrated TMM for multiply connected mufflers and [15] presents the determination of the stress-strain state in thin orthotropic plates on Winkler’s elastic foundations. Evaluation of a hybrid underwater sound-absorbing meta-structure by using the TMM is given in [16]. Some theoretical and experimental extensions based on the properties of the Intrinsic Transfer Matrix are presented in [17]. The TMM is applied to the parallel assembly of sound absorbing materials in [18]. [19] and [20] gives the TMM for multibody in the past, the present, and the future and its applications. [21] presents the muffler modeling by TMM and experimental verification. [22] gives a development of two-dimensional theory of thick plates bending based on general solution of Lamé equations. A study of coupling TMM to FEM for analyzing the acoustics of complex hollow body networks is presented in [23]. Equivalent systems for the analysis of rectangular plates of varying thickness is shown in [24]. About the classical theory of plates is presented in [25]. Study about the bending of clamped rectangular plates is given in [26]. Determination of plane stress and strain of plates on basis of three-dimensional theory of elasticity is shown in [27]. Analysis of hypotheses used when constructing the theory of beams and plates is presented in [28]. About the calculus of plates by the series representation of the deflection function is given in [29]. [30] presents a solution of non-rectangular plates with macro element method. The stress state of compound polygonal plate is shown in [31]. [32] gives a solution of thin rectangular plates with various boundary conditions and [33] gives an exact solution for the deflection of a clamped rectangular plate under uniform load. Stress-strain state in the corner points of a clamped plate under uniformly distributed normal load is given in [34] and a static analysis of an orthotropic plate is presented in [35]. The theory of plates and shells is given in [36]. Study about stress–strain analysis of rectangular plates with a variable thickness and constant weight is presented in [37] and an analysis of homogeneous and non-homogeneous plates is shown in [38]. A theoretical and comparative study regarding the mechanical response under the static loading for different rectangular plates is given in [39]. Approximate analytical solutions in the analysis of thin elastic plates are given in [40]. Some aspects of implementation of boundary elements method in plate theory are presented in [41]. A convergence analysis of finite element approach to classical approach for analysis of plates in bending is given in [42]. Another study by a method of matched sections as a beam-like approach for plate analysis is presented in [43]. Application of numerical methods in solving a phenomenon of the theory for thin plates is shown in [44]. A review of a few selected theories of plates in bending is given in [45]. [46] presents the calculus of plate-beam systems by method of boundary elements. Analytical solutions of the mechanical answer of thin orthotropic plates are shown in [47]. Optimized Transfer Matrix approach for global buckling analysis with bypassing zero matrix inversion is given in [48]. [49] is the American Standard Test Method for Measurement of Normal Incidence Sound Transmission of Acoustical Materials Based on the TMM from American Society for Testing and Materials.

2. CalculusPremises through The Transfer-Matrix Method for The Long Rectangular Plates

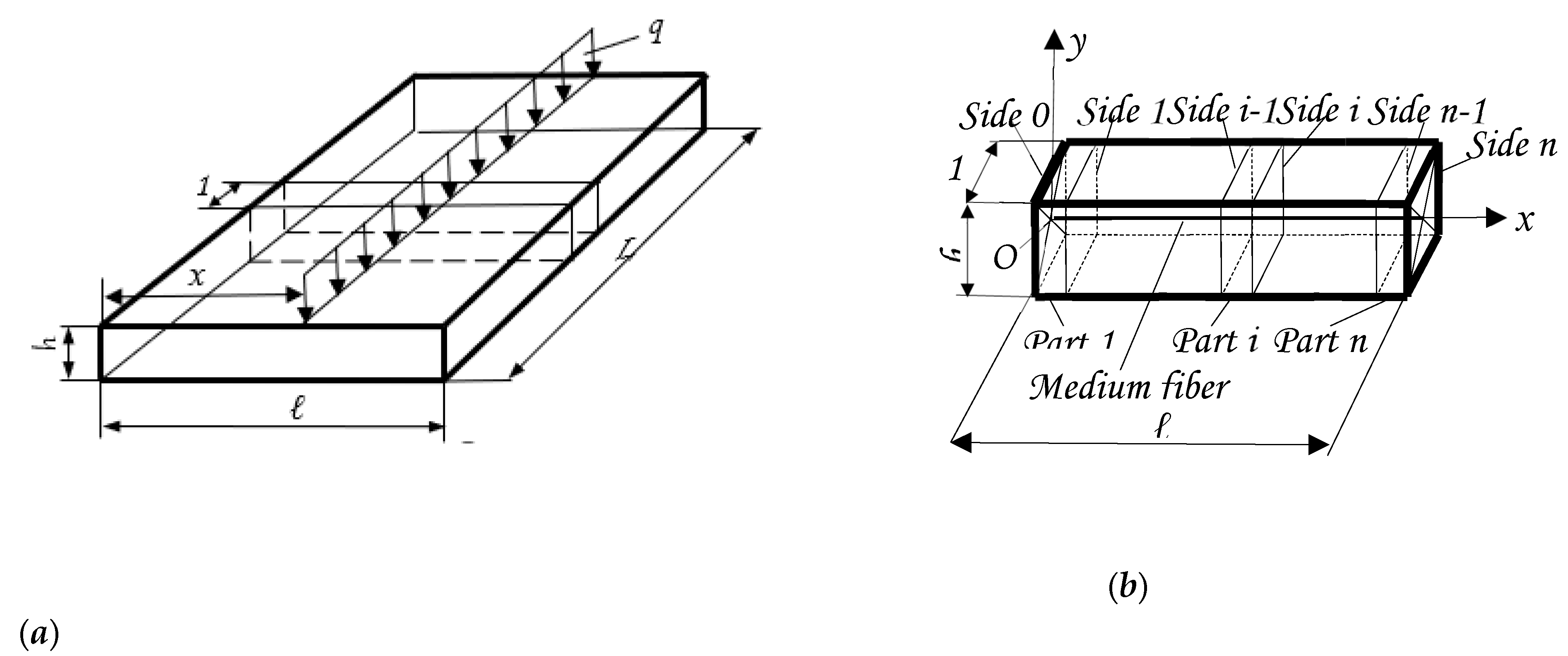
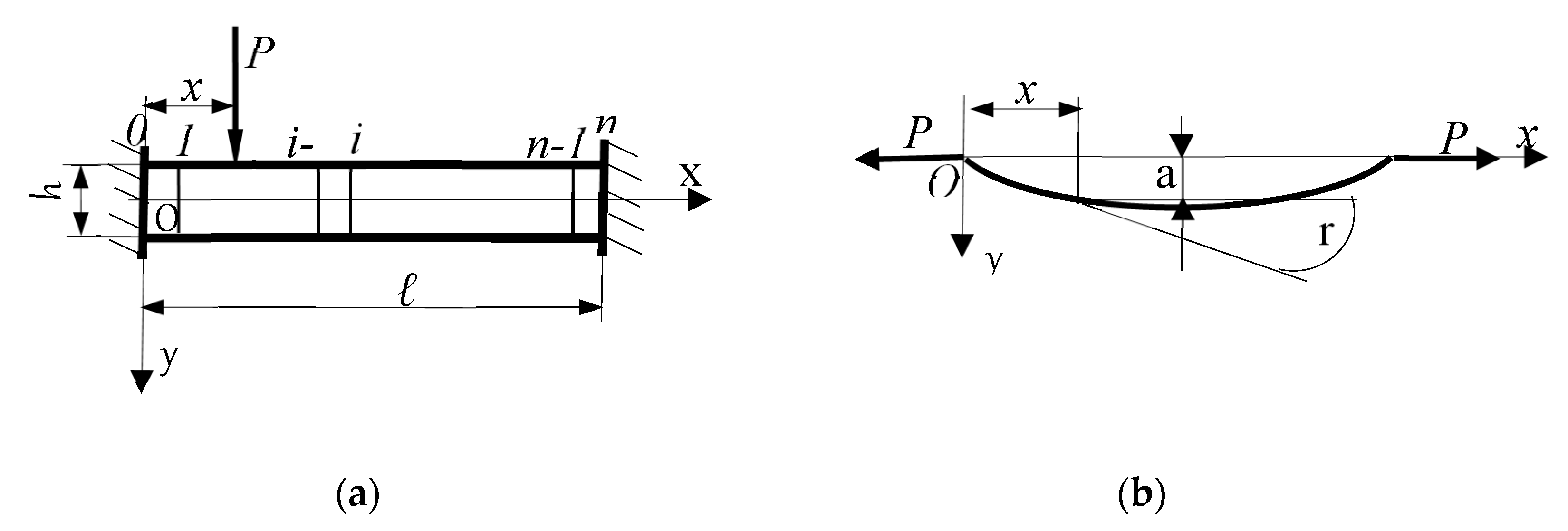
A rectangular plate with long lengths can be calculated through the TMM. The plate is discretized, of its lengths, into pieces, as in Figure 1., (a) and (b).

A piece (a beam) has the width equal to unity.

2.1. The State Vectors and The Transfer-Matrix for A Long Rectangular Plate

2.1.1. State Vectors

For the unitary beam, with the width equal to unity, as in Figure 2., (a), it can be associated a Transfer-Matrix. It is deformed, as in Figure 2., (b).

Along its length, which is the width of the rectangular plate, the unitary beam can also be discretized into n parts (Figure 1., (b), Figure 2., (a)). The sectioning of the beam is done perpendicularly to the Ox axis. For each part has it can be defined as the left side and a right side. For the first left part, it is defined as the left side noted 0 and the right side is noted 1 and for the last right side of the last part n (on the right of the beam), is noted by n. So, the beam has n parts and n+1 sides.

It is associated for each side a state vector, for some side x, it is associated a state vector {V(x)} = {V}_x with four elements (a(x), r(x), M(x), C(x)). The state vector and its elements have always the index of the side it is on, (Figure 2., (b)), as in (1):

$$\left\{V\left(x\right)\right\}={\left\{V\right\}}_x={\left\{a\left(x\right), r\left(x\right), M\left(x\right),C\left(x\right)\right\}}^{-1}={\left\{a_x,r_x,M_x,C_x\right\}}^{-1},$$

(1)

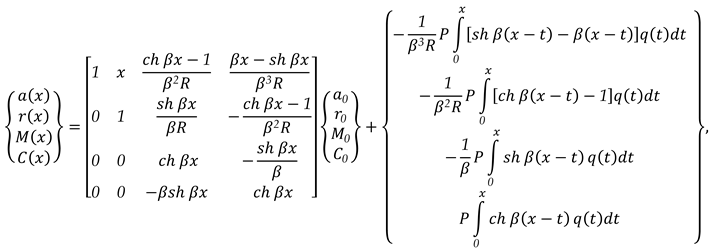
when:

-

{V(x)} = {V}_x is state vector corresponding at the side x;

-

a(x ) = a_x is the arrow;

-

r(x) = r_x is the rotation of the average fiber in the x section;

-

M(x) = M_x is the bending moment;

-

C(x) = C_x is the cutting force at the x-axis point.

For x = 0, it can be written for the side 0 as (2):

$$\left\{V\left(0\right)\right\}={\left\{V\right\}}_0={\left\{a\left(0\right), r\left(0\right), M\left(0\right),C\left(0\right)\right\}}^{-1}={\left\{a_0,r_0,M_0,C_0\right\}}^{-1},$$

(2)

For the last side n, for which x = l, (for the last part n, the right part, that is the right end of the beam, the state vector can be written as (3):

$$\left\{V\left(l\right)\right\}={\left\{V\right\}}_l={\left\{a\left(l\right), r\left(l\right), M\left(l\right),C\left(l\right)\right\}}^{-1}={\left\{a_l,r_l,M_l,C_l\right\}}^{-1},$$

(3)

2.1.2. Transfer-Matrix

For some part x of the beam, a Transfer-Matrix [M]_x is associated. The Transfer-Matrix connects two consecutive sides of a part of beam after the following matrix relation for the part 1, as (4):

$${\left\{V\right\}}_1={\left[M\right]}_1{\left\{V\right\}}_0+{\left\{V_e\right\}}_1,$$

(4)

when:

-

{V_e}₁ is the state vector corresponding to the external forces acting on part 1.

The matrix relation (3) can be written as (5) for some part x:

$${\left\{V\right\}}_x={\left[M\right]}_x{\left\{V\right\}}_0+{\left\{V_e\right\}}_x,$$

(5)

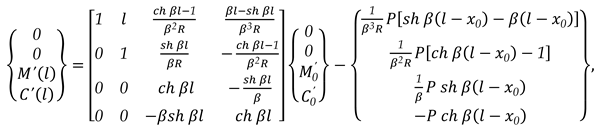
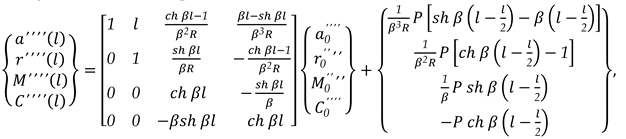
For the last side, the side n, for x = l, the matrix relation (5) can be written as (6):

$${\left\{V\right\}}_l={\left[M\right]}_l{\left\{V\right\}}_0+{\left\{V_e\right\}}_l,$$

(6)

In (6), the conditions of the ends can be put, and the elements of the state vector at the origin can be calculated and, also, the elements for the state vector associated at the last side can be calculated too. Now, matrix relation (5) can be used in which different values can be given for x and the state vectors can be calculated for all sections of the unit beam.

2.2. Approach for Analytical Calculus of A Long Rectangular Plate

The rectangle plate is considered embedded at both ends, charged to bending along a line parallel to the long borders with an uniform constant vertical load q, with a charge density q(x) acting along of a generator, as in Figure 1., (a).

2.2.1. Study Hypotheses

For this work, there are considered some hypotheses:

-

the plate is subjected to an axial force along the long sides, per unit side being P (as in Figure 2., (b));

-

the charge density q(x) is expressed per unit of length;

-

the bending moment due to a single external load is denoted by m(x).

2.2.2. The Arrow Calculus for The Unit Beam

The expression of the total moment M(x) is as (7):

$$M\left(x\right)=m\left(x\right)+Pa\left(x\right),$$

(7)

when a(x) is the arrow corresponding to the section x. For the bending moment m(x) it can be written (8):

$${\displaystyle \frac{d^{2}m}{d{x}^2}}=q\left(x\right),$$

(8)

The average deformed fiber has the differential equation as (9):

$${\displaystyle \frac{d^{4}m}{d{x}^4}}-{\displaystyle \frac{12\left(1-{\nu }^2\right)}{E{h}^3}}·{\displaystyle \frac{d^{2}a\left(x\right)}{d{x}^2}}P={\displaystyle \frac{12\left(1-{\nu }^2\right)}{E{h}^3}}q\left(x\right),$$

(9)

with R as the bending stiffness of a plate with the thickness h, as (10):

$$R={\displaystyle \frac{E{h}^3}{12\left(1-{\nu }^2\right)}},$$

(10)

when:

-

E is the Young’s modulus;

-

h is the thickness of the plate;

-

ν is the Poisson’s coefficient.

It is replaced (10) in expression (9) and it can be written (9) as (11):

$${\displaystyle \frac{d^{4}m}{d{x}^4}}-{\displaystyle \frac{1}{R}}{\displaystyle \frac{d^{2}a\left(x\right)}{d{x}^2}}P={\displaystyle \frac{1}{R}}q\left(x\right),$$

(11)

It is noted by (12):

$${\beta }^2={\displaystyle \frac{1}{R}}P,$$

(12)

The differential equation (11) with (12) becomes as (13):

$${\displaystyle \frac{d^{4}m}{d{x}^4}}-{\beta }^2{\displaystyle \frac{d^{2}a\left(x\right)}{d{x}^2}}={\displaystyle \frac{1}{R}}q\left(x\right),$$

(13)

The differential equation (13) without the second term has the solution as (14):

$$a_1\left(x\right)=A_1 ch \beta x+A_2 sh \beta x+A_{3}x+A_4,$$

(14)

(15) is the particular solution:

$$a^{*}\left(x\right)={\displaystyle \frac{1}{R{\beta }^3}}\underset{0}{\overset{x}{{\displaystyle \int }}}\left[sh \beta \left(x-t\right)-\beta \left(x-t\right)\right]q\left(t\right)dt,$$

(15)

The conditions (16) can be verified:

$$a^{*}\left(0\right)=a^{*}\text{'}\left(0\right)=a^{*\text{'}\text{'}}\left(0\right)=a^{*\text{'}\text{'}\text{'}}\left(0\right),$$

(16)

when, (17):

$$\{\begin{array}{c}{a}^{*}\text{'}\left(0\right)={\displaystyle \frac{d{a}^{*}}{dx}}\left(0\right)\\ a^{*\text{'}\text{'}}\left(0\right)={\displaystyle \frac{d{a}^{*\text{'}}}{dx}}\left(0\right)\\ a^{*\text{'}\text{'}\text{'}}\left(0\right)={\displaystyle \frac{d{a}^{*\text{'}\text{'}}}{dx}}\left(0\right)\end{array},$$

(17)

For x = 0, in the origin, it can be written the conditions as (18):

$$\{\begin{array}{c}a\left(0\right)=a_0\\ r\left(0\right)=r_0\\ M\left(0\right)=M_0 \\ C\left(0\right)=C_0\end{array},$$

(18)

With the integration constants A_i, i = 1,.4 , it can be written (19):

$$\{\begin{array}{c}{a}_0=A_1+A_4\\ r_0=\beta A_2+A_3\\ M_0={\beta }^2{A}_1{A}_4\\ C_0=-{\beta }^3{A}_2{A}_4\end{array},$$

(19)

The four integration constants A_i, i = 1,4, depending on the efforts and deformations from the origin, are as (20):

$$\{\begin{array}{c}{A}_1={\displaystyle \frac{1}{{\beta }^{2}R}}{M}_0\\ A_2=-{\displaystyle \frac{1}{{\beta }^{3}R}}{C}_0\\ A_3=r_0+{\displaystyle \frac{1}{{\beta }^{3}R}}{C}_0\\ A_4=a_0-{\displaystyle \frac{1}{{\beta }^{2}R}}{M}_0\end{array},$$

(20)

The deformation has the mathematical expression as (21):

$$a\left(x\right)=a_0+r_{0}x+{\displaystyle \frac{ch \beta x-1}{{\beta }^{2}R}}{M}_0+{\displaystyle \frac{\beta x-sh \beta x}{{\beta }^{3}R}}{C}_0+{\displaystyle \frac{1}{{\beta }^{3}R}}\underset{0}{\overset{x}{{\displaystyle \int }}}\left[sh \beta \left(x-t\right)-\beta \left(x-t\right)\right]q\left(t\right)dt,$$

(21)

2.3. Transfer-Matrix for A Long Rectangular Plate

With mathematical formalism given by Dirac’s and Heaviside’s Functions and operators, [1], the matrix relation (5), for a long rectangular plate, can be written as (22):

(22)

Simplified, the matrix relation (22) can be written as (23):

$$\left\{V\left(x\right)\right\}={\left[M\right]}_x{\left\{V\right\}}_0+{\left\{V_e\right\}}_x ,$$

(23)

matrix relation identical to (5), when the Transfer-Matrix [M]_x is as (24), [1]:

$${\left[M\right]}_x=\left[\begin{array}{cccc}1& x& {\displaystyle \frac{ch \beta x-1}{{\beta }^{2}R}}& {\displaystyle \frac{\beta x-sh \beta x}{{\beta }^{3}R}}\\ 0& 1& {\displaystyle \frac{sh \beta x}{\beta R}}& -{\displaystyle \frac{ch \beta x-1}{{\beta }^{2}R}}\\ 0& 0& ch \beta x& -{\displaystyle \frac{sh \beta x}{\beta }}\\ 0& 0& -\beta sh \beta x& ch \beta x\end{array}\right],$$

(24)

3. Applications and Results for The Calculus of a Long Rectangular Plate Embedded at The Two Long Borders Charged with Vertical Uniform Loads That Act on A Line Parallel Along of The Long Borders

As applications, they are studied long rectangular plates, embedded on the two long borders. The plate is discretized in beams with width equal to unity, as in Figure 1., (a)) with the length equal to the width l of the plate and with the thickness h, equal to the thickness of the long rectangular plate. To simplify the writing, the same notations will be kept in all cases, even if it is obvious that the elements of the state vectors, of the transfer matrices and of the vectors corresponding to the external forces are different.

In the matrix relation (23), the conditions of the ends can be put, and the elements of the state vector at the origin can be calculated and, also, the elements for the state vector associated at the last side can be calculated too. (23) serves to calculate the elements for the state vectors for all sections of the unity beam and after, the efforts and deformations in the origin section, and then, the efforts, deformations and stresses can be calculated in any section of the beam, respectively for the long rectangular plate.

In the following, four cases of loading with a concentrated vertical force will be studied for the plate embedded on the two long borders.

3.1. Unit Width Beam Embedded at The Two Edges Charged with A Concentrated Load (Figure 3., (a), (b), (c) and (d))

A unit beam embedded at the two edges, charged with a concentrated load P in different situations is considered, as in Figure 3., (a), (b), (c) and (d).

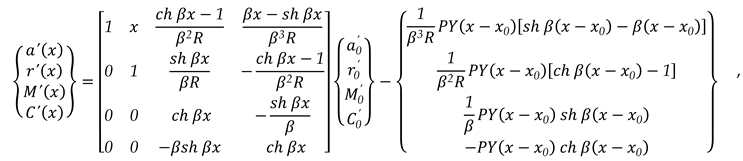
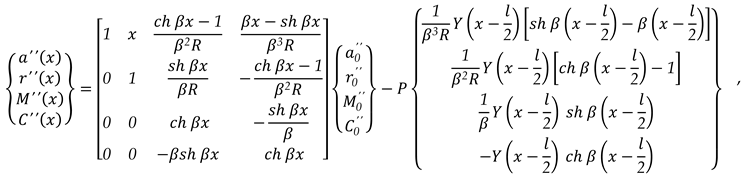
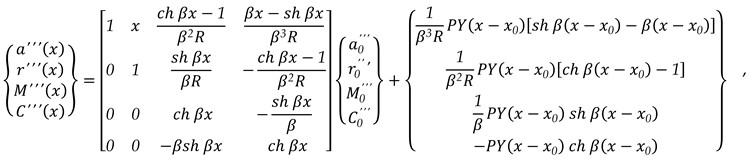
3.1.1. Unit Width Beam Embedded at The Two Edges Charged with A Concentrated Load (-P) Which Acts in a Certain Section x₀ (as in Figure 3., (a))

It can be written the charge density, as (25):

$$q\text{'}\left(x\right)=-P\left(x-x_0\right),$$

(25)

The state vector {$V_e^{\text{'}}$}_x corresponding at exterior load is, With Dirac’s and Heaviside’s functions and operators, as (26):

$${\left\{V_e^{\text{'}}\right\}}_x=\left\{\begin{array}{c}-{\displaystyle \frac{1}{{\beta }^{3}R}}PY\left(x-x_0\right)\left[sh \beta \left(x-x_0\right)-\beta \left(x-x_0\right)\right]\\ -{\displaystyle \frac{1}{{\beta }^{2}R}}PY\left(x-x_0\right)\left[ch \beta \left(x-x_0\right)-1\right]\\ -{\displaystyle \frac{1}{\beta }}PY\left(x-x_0\right) sh \beta \left(x-x_0\right)\\ PY\left(x-x_0\right) ch \beta \left(x-x_0\right)\end{array}\right\},$$

(26)

In this case, the matrix relation is as (27):

(27)

Or, it can be written (27) as (28):

(28)

Expression (28) becomes (29) for the right end, for x = l:

(29)

For the two embedded ends of the beam, the conditions are (30):

$$\{\begin{array}{c}{a}_0^{\text{'}}=0\\ r_0^{\text{'}}=0\\ a\text{'}\left(l\right)=0 \\ r\text{'}\left(l\right)=0\end{array},$$

(30)

The matrix relation (29), with (30), becomes (31):

(31)

It can be written (31) more simply as (32):

$$\left\{\begin{array}{c}0\\ 0\\ M\text{'}\left(l\right)\\ C\text{'}\left(l\right)\end{array}\right\}=\left[\begin{array}{cccc}{m}_{11}^{\text{'}}& m_{12}^{\text{'}}& m_{13}^{\text{'}}& m_{14}^{\text{'}}\\ m_{21}^{\text{'}}& m_{22}^{\text{'}}& m_{23}^{\text{'}}& m_{24}^{\text{'}}\\ m_{31}^{\text{'}}& m_{32}^{\text{'}}& m_{33}^{\text{'}}& m_{34}^{\text{'}}\\ m_{41}^{\text{'}}& m_{42}^{\text{'}}& m_{43}^{\text{'}}& m_{44}^{\text{'}}\end{array}\right]\left\{\begin{array}{c}0\\ 0\\ M_0^{\text{'}}\\ C_0^{\text{'}}\end{array}\right\}-P\left\{\begin{array}{c}{v}_{e{l}_1}^{\text{'}}\\ v_{e{l}_2}^{\text{'}}\\ v_{e{l}_3}^{\text{'}}\\ v_{e{l}_4}^{\text{'}}\end{array}\right\},$$

(32)

or, (33):

$$\left\{\begin{array}{c}0\\ 0\\ M\text{'}\left(l\right)\\ C\text{'}\left(l\right)\end{array}\right\}=\left[\begin{array}{cccc}1& l& m_{13}^{\text{'}}& m_{14}^{\text{'}}\\ 0& 1& m_{23}^{\text{'}}& m_{24}^{\text{'}}\\ 0& 0& m_{33}^{\text{'}}& m_{34}^{\text{'}}\\ 0& 0& m_{43}^{\text{'}}& m_{44}^{\text{'}}\end{array}\right]\left\{\begin{array}{c}0\\ 0\\ M_0^{\text{'}}\\ C_0^{\text{'}}\end{array}\right\}-P\left\{\begin{array}{c}{v}_{e{l}_1}^{\text{'}}\\ v_{e{l}_2}^{\text{'}}\\ v_{e{l}_3}^{\text{'}}\\ v_{e{l}_4}^{\text{'}}\end{array}\right\},$$

(33)

From the matrix relation (33), it can be written the first two lines and a linear system of two equations with two unknowns is obtained as (34), the unknowns being the two elements of the state vector of side 0, $M_0^{\text{'}}$and $C_0^{\text{'}}$:

$$\{\begin{array}{c}{m}_{13}^{\text{'}}{M}_0^{\text{'}}+m_{14}^{\text{'}}{C}_0^{\text{'}}=v_{e{l}_1}^{\text{'}}P\\ m_{23}^{\text{'}}{M}_0^{\text{'}}+m_{24}^{\text{'}}{C}_0^{\text{'}}=v_{e{l}_2}^{\text{'}}P \end{array}$$

(34)

with solution (35):

$$\{\begin{array}{c}{M}_0^{\text{'}}={\displaystyle \frac{v_{e{l}_1}^{\text{'}}{m}_{24}^{\text{'}}-v_{e{l}_2}^{\text{'}}{m}_{14}^{\text{'}}}{m_{13}^{\text{'}}{m}_{24}^{\text{'}}-m_{14}^{\text{'}}{m}_{23}^{\text{'}}}}P=b_1^{\text{'}}P\\ C_0^{\text{'}}={\displaystyle \frac{v_{e{l}_1}^{\text{'}}{m}_{23}^{\text{'}}+v_{e{l}_2}^{\text{'}}{m}_{13}^{\text{'}}}{m_{14}^{\text{'}}{m}_{23}^{\text{'}}-m_{13}^{\text{'}}{m}_{24}^{\text{'}}}}P=b_1^{\text{'}}P\end{array},$$

(35)

The other two elements of the state vector for the last side on the right end, the side n, for x = l, with (35), will be like as (36):

$$\{\begin{array}{c}M\text{'}\left(l\right)=m_{33}^{\text{'}}{M}_0^{\text{'}}+m_{34}^{\text{'}}{C}_0^{\text{'}}-v_{e{l}_3}^{\text{'}}P\\ C\text{'}\left(l\right)=m_{43}^{\text{'}}{M}_0^{\text{'}}+m_{44}^{\text{'}}{C}_0^{\text{'}}-v_{e{l}_4}^{\text{'}}P\end{array} ,$$

(36)

with solution, as (37):

$$\{\begin{array}{c}M\text{'}\left(l\right)=\left(m_{33}^{\text{'}}{b}_1^{\text{'}}+m_{34}^{\text{'}}{b}_2^{\text{'}}-v_{e{l}_3}^{\text{'}}\right)P\\ C\text{'}\left(l\right)=\left(m_{43}^{\text{'}}{b}_1^{\text{'}}+m_{44}^{\text{'}}{b}_2^{\text{'}}-v_{e{l}_4}^{\text{'}}\right)P\end{array} ,$$

(37)

In this moment, all elements of any state vector of any side can be calculated for all parts in which the unit beam has been discretized.

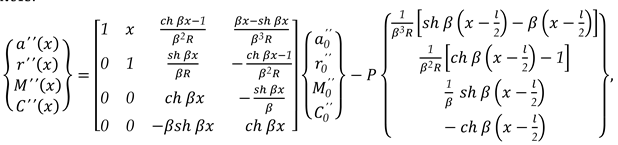
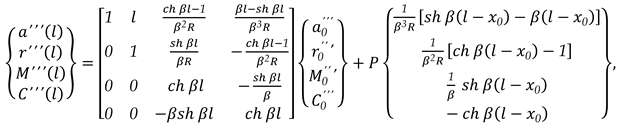
3.1.2. Unit Width Beam Embedded at The Two Edges Charged with A Concentrated Load (-P) which Acts in A Section x₀ = l/2, (as in Figure 3., (b))

The charge density for a vertical concentrated load (-P) at the middle, for x₀ = l/2, (Figure 3., (b)), is as (38):

$$q\text{'}\text{'}\left(x\right)=-P\left(x-{\displaystyle \frac{l}{2}}\right),$$

(38)

The state vector {$V_e^{\text{'}\text{'}}$}_x corresponding at exterior load is as (39):

$${\left\{V_e^{\text{'}\text{'}}\right\}}_x=\left\{\begin{array}{c}-{\displaystyle \frac{1}{{\beta }^{3}R}}PY\left(x-{\displaystyle \frac{l}{2}}\right)\left[sh \beta \left(x-{\displaystyle \frac{l}{2}}\right)-\beta \left(x-{\displaystyle \frac{l}{2}}\right)\right]\\ -{\displaystyle \frac{1}{{\beta }^{2}R}}PY\left(x-{\displaystyle \frac{l}{2}}\right)\left[ch \beta \left(x-{\displaystyle \frac{l}{2}}\right)-1\right]\\ -{\displaystyle \frac{1}{\beta }}PY\left(x-{\displaystyle \frac{l}{2}}\right) sh \beta \left(x-{\displaystyle \frac{l}{2}}\right)\\ PY\left(x-{\displaystyle \frac{l}{2}}\right) ch \beta \left(x-{\displaystyle \frac{l}{2}}\right)\end{array}\right\} ,$$

(39)

In this case, the matrix relation is as (40):

(40)

The matrix relation (40) can be written as (41), with Dirac’s and Heaviside’s functions and operators:

(41)

Expression (41) becomes (42) for the right end, for x = l:

(42)

or, (43):

$$\left\{\begin{array}{c}a\text{'}\text{'}\left(l\right)\\ r\text{'}\text{'}\left(l\right)\\ M\text{'}\text{'}\left(l\right)\\ C\text{'}\text{'}\left(l\right)\end{array}\right\}=\left[\begin{array}{cccc}1& l& {\displaystyle \frac{ch \beta l-1}{{\beta }^{2}R}}& {\displaystyle \frac{\beta l-sh \beta l}{{\beta }^{3}R}}\\ 0& 1& {\displaystyle \frac{sh \beta l}{\beta R}}& -{\displaystyle \frac{ch \beta l-1}{{\beta }^{2}R}}\\ 0& 0& ch \beta l& -{\displaystyle \frac{sh \beta l}{\beta }}\\ 0& 0& -\beta sh \beta l& ch \beta l\end{array}\right]\left\{\begin{array}{c}{a}_0^{\text{'}\text{'}}\\ r_0^{\text{'}\text{'}}\\ M_0^{\text{'}\text{'}}\\ C_0^{\text{'}\text{'}}\end{array}\right\}-P\left\{\begin{array}{c}{\displaystyle \frac{1}{{\beta }^{3}R}}\left(sh \beta {\displaystyle \frac{l}{2}}-\beta {\displaystyle \frac{l}{2}}\right)\\ {\displaystyle \frac{1}{{\beta }^{2}R}}\left(ch \beta {\displaystyle \frac{l}{2}}-1\right)\\ {\displaystyle \frac{1}{\beta }} sh \beta {\displaystyle \frac{l}{2}}\\ -ch \beta {\displaystyle \frac{l}{2}}\end{array}\right\},$$

(43)

For the two embedded ends of the beam, the conditions are (44):

$$\{\begin{array}{c}{a}_0^{\text{'}\text{'}}=0\\ r_0^{\text{'}\text{'}}=0\\ a\text{'}\text{'}\left(l\right)=0 \\ r\text{'}\text{'}\left(l\right)=0\end{array},$$

(44)

The matrix relation (43) becomes (45) with (44):

$$\left\{\begin{array}{c}0\\ 0\\ M\text{'}\text{'}\left(l\right)\\ C\text{'}\text{'}\left(l\right)\end{array}\right\}=\left[\begin{array}{cccc}1& l& {\displaystyle \frac{ch \beta l-1}{{\beta }^{2}R}}& {\displaystyle \frac{\beta l-sh \beta l}{{\beta }^{3}R}}\\ 0& 1& {\displaystyle \frac{sh \beta l}{\beta R}}& -{\displaystyle \frac{ch \beta l-1}{{\beta }^{2}R}}\\ 0& 0& ch \beta l& -{\displaystyle \frac{sh \beta l}{\beta }}\\ 0& 0& -\beta sh \beta l& ch \beta l\end{array}\right]\left\{\begin{array}{c}0\\ 0\\ M_0^{\text{'}\text{'}}\\ C_0^{\text{'}\text{'}}\end{array}\right\}-P\left\{\begin{array}{c}{\displaystyle \frac{1}{{\beta }^{3}R}}\left(sh \beta {\displaystyle \frac{l}{2}}-\beta {\displaystyle \frac{l}{2}}\right)\\ {\displaystyle \frac{1}{{\beta }^{2}R}}\left(ch \beta {\displaystyle \frac{l}{2}}-1\right)\\ {\displaystyle \frac{1}{\beta }}sh \beta {\displaystyle \frac{l}{2}}\\ -ch \beta {\displaystyle \frac{l}{2}}\end{array}\right\},$$

(45)

It can be written more simply (45) as (46):

$$\left\{\begin{array}{c}0\\ 0\\ M\text{'}\text{'}\left(l\right)\\ C\text{'}\text{'}\left(l\right)\end{array}\right\}=\left[\begin{array}{cccc}{m}_{11}^{\text{'}\text{'}}& m_{12}^{\text{'}\text{'}}& m_{13}^{\text{'}\text{'}}& m_{14}^{\text{'}\text{'}}\\ m_{21}^{\text{'}\text{'}}& m_{22}^{\text{'}\text{'}}& m_{23}^{\text{'}\text{'}}& m_{24}^{\text{'}\text{'}}\\ m_{31}^{\text{'}\text{'}}& m_{32}^{\text{'}\text{'}}& m_{33}^{\text{'}\text{'}}& m_{34}^{\text{'}\text{'}}\\ m_{41}^{\text{'}\text{'}}& m_{42}^{\text{'}\text{'}}& m_{43}^{\text{'}\text{'}}& m_{44}^{\text{'}\text{'}}\end{array}\right]\left\{\begin{array}{c}0\\ 0\\ M_0^{\text{'}\text{'}}\\ C_0^{\text{'}\text{'}}\end{array}\right\}-P\left\{\begin{array}{c}{v}_{e{l}_1}^{\text{'}\text{'}}\\ v_{e{l}_2}^{\text{'}\text{'}}\\ v_{e{l}_3}^{\text{'}\text{'}}\\ v_{e{l}_4}^{\text{'}\text{'}}\end{array}\right\},$$

(46)

or, (47):

$$\left\{\begin{array}{c}0\\ 0\\ M\text{'}\text{'}\left(l\right)\\ C\text{'}\text{'}\left(l\right)\end{array}\right\}=\left[\begin{array}{cccc}1& l& m_{13}^{\text{'}\text{'}}& m_{14}^{\text{'}\text{'}}\\ 0& 1& m_{23}^{\text{'}\text{'}}& m_{24}^{\text{'}\text{'}}\\ 0& 0& m_{33}^{\text{'}\text{'}}& m_{34}^{\text{'}\text{'}}\\ 0& 0& m_{43}^{\text{'}\text{'}}& m_{44}^{\text{'}\text{'}}\end{array}\right]\left\{\begin{array}{c}0\\ 0\\ M_0^{\text{'}\text{'}}\\ C_0^{\text{'}\text{'}}\end{array}\right\}-P\left\{\begin{array}{c}{v}_{e{l}_1}^{\text{'}\text{'}}\\ v_{e{l}_2}^{\text{'}\text{'}}\\ v_{e{l}_3}^{\text{'}\text{'}}\\ v_{e{l}_4}^{\text{'}\text{'}}\end{array}\right\},$$

(47)

From the matrix relation (47), a linear system of two equations with two unknowns is obtained as (48), the unknowns being the two elements of the state vector of side 0, $M_0^{\text{'}\text{'}}$and $C_0^{\text{'}\text{'}}$:

$$\{\begin{array}{c}{m}_{13}^{\text{'}\text{'}}{M}_0^{\text{'}\text{'}}+m_{14}^{\text{'}\text{'}}{C}_0^{\text{'}\text{'}}=v_{e{l}_1}^{\text{'}\text{'}}P\\ m_{23}^{\text{'}\text{'}}{M}_0^{\text{'}\text{'}}+m_{24}^{\text{'}\text{'}}{C}_0^{\text{'}\text{'}}=v_{e{l}_2}^{\text{'}\text{'}}P \end{array}$$

(48)

with solution (49):

$$\{\begin{array}{c}{M}_0^{\text{'}\text{'}}={\displaystyle \frac{v_{e{l}_1}^{\text{'}\text{'}}{m}_{24}^{\text{'}\text{'}}-v_{e{l}_2}^{\text{'}\text{'}}{m}_{14}^{\text{'}\text{'}}}{m_{13}^{\text{'}\text{'}}{m}_{24}^{\text{'}\text{'}}-m_{14}^{\text{'}\text{'}}{m}_{23}^{\text{'}\text{'}}}}P=b_1^{\text{'}\text{'}}P\\ C_0^{\text{'}\text{'}}={\displaystyle \frac{v_{e{l}_1}^{\text{'}\text{'}}{m}_{23}^{\text{'}\text{'}}+v_{e{l}_2}^{\text{'}\text{'}}{m}_{13}^{\text{'}\text{'}}}{m_{14}^{\text{'}\text{'}}{m}_{23}^{\text{'}\text{'}}-m_{13}^{\text{'}\text{'}}{m}_{24}^{\text{'}\text{'}}}}P=b_1^{\text{'}\text{'}}P\end{array},$$

(49)

The other two elements of the state vector for the last side on the right end, the side n, for x = l, with (49), will be like as (50):

$$\{\begin{array}{c}M\text{'}\text{'}\left(l\right)=m_{33}^{\text{'}\text{'}}{M}_0^{\text{'}\text{'}}+m_{34}^{\text{'}\text{'}}{C}_0^{\text{'}\text{'}}-v_{e{l}_3}^{\text{'}\text{'}}P\\ C\text{'}\text{'}\left(l\right)=m_{43}^{\text{'}\text{'}}{M}_0^{\text{'}\text{'}}+m_{44}^{\text{'}\text{'}}{C}_0^{\text{'}\text{'}}-v_{e{l}_4}^{\text{'}\text{'}}P\end{array} ,$$

(50)

with solution, as (51):

$$\{\begin{array}{c}M\text{'}\text{'}\left(l\right)=\left(m_{33}^{\text{'}\text{'}}{b}_1^{\text{'}\text{'}}+m_{34}^{\text{'}\text{'}}{b}_2^{\text{'}\text{'}}-v_{e{l}_3}^{\text{'}\text{'}}\right)P\\ C\text{'}\text{'}\left(l\right)=\left(m_{43}^{\text{'}\text{'}}{b}_1^{\text{'}\text{'}}+m_{44}^{\text{'}\text{'}}{b}_2^{\text{'}\text{'}}-v_{e{l}_4}^{\text{'}\text{'}}\right)P\end{array} ,$$

(51)

In this moment, all elements of any state vector of any side can be calculated for all parts in which the unit beam has been discretized.

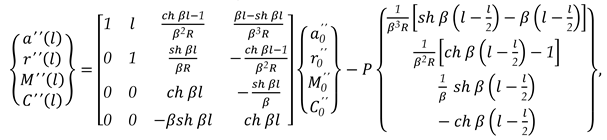
3.1.3. Unit Width Beam Embedded at The Two Edges Charged with A Concentrated Load P Which Acts in a Certain Section x₀ (as in Figure 3., (c))

In this case, the charge density can be written as (52):

$$q\text{'}\text{'}\text{'}\left(x\right)=P\left(x-x_0\right),$$

(52)

The state vector {$V_e^{\text{'}\text{'}}\text{'}$}_x corresponding at exterior load is as (53):

$${\left\{V_e^{\text{'}\text{'}\text{'}}\right\}}_x=\left\{\begin{array}{c}{\displaystyle \frac{1}{{\beta }^{3}R}}PY\left(x-x_0\right)\left[sh \beta \left(x-x_0\right)-\beta \left(x-x_0\right)\right]\\ {\displaystyle \frac{1}{{\beta }^{2}R}}PY\left(x-x_0\right)\left[ch \beta \left(x-x_0\right)-1\right]\\ {\displaystyle \frac{1}{\beta }}PY\left(x-x_0\right) sh \beta \left(x-x_0\right)\\ -PY\left(x-x_0\right) ch \beta \left(x-x_0\right)\end{array}\right\},$$

(53)

In this case, the matrix relation is as (54):

(54)

Or, (54) can be written as (55):

(55)

Expression (55) becomes as (56) for the right end, for x = l:

(56)

The conditions for the two embedded ends of the beam are (57):

$$\{\begin{array}{c}{a}_0^{\text{'}\text{'}\text{'}}=0\\ r_0^{\text{'}\text{'}}\text{'}=0\\ a\text{'}\text{'}\text{'}\left(l\right)=0 \\ r\text{'}\text{'}\text{'}\left(l\right)=0\end{array},$$

(57)

With (57), the matrix relation (56) becomes as (58):

$$\left\{\begin{array}{c}0\\ 0\\ M\text{'}\text{'}\text{'}\left(l\right)\\ C\text{'}\text{'}\text{'}\left(l\right)\end{array}\right\}=\left[\begin{array}{cccc}1& l& {\displaystyle \frac{ch \beta l-1}{{\beta }^{2}R}}& {\displaystyle \frac{\beta l-sh \beta l}{{\beta }^{3}R}}\\ 0& 1& {\displaystyle \frac{sh \beta l}{\beta R}}& -{\displaystyle \frac{ch \beta l-1}{{\beta }^{2}R}}\\ 0& 0& ch \beta l& -{\displaystyle \frac{sh \beta l}{\beta }}\\ 0& 0& -\beta sh \beta l& ch \beta l\end{array}\right]\left\{\begin{array}{c}0\\ 0\\ M_0^{\text{'}\text{'}}\text{'}\\ C_0^{\text{'}\text{'}\text{'}}\end{array}\right\}+P\left\{\begin{array}{c}{\displaystyle \frac{1}{{\beta }^{3}R}}\left[sh \beta \left(l-x_0\right)-\beta \left(l-x_0\right)\right]\\ {\displaystyle \frac{1}{{\beta }^{2}R}}\left[ch \beta \left(l-x_0\right)-1\right]\\ {\displaystyle \frac{1}{\beta }} sh \beta \left(l-x_0\right)\\ - ch \beta \left(l-x_0\right)\end{array}\right\},$$

(58)

or, more simply is as (59):

$$\left\{\begin{array}{c}0\\ 0\\ M\text{'}\text{'}\text{'}\left(l\right)\\ C\text{'}\text{'}\text{'}\left(l\right)\end{array}\right\}=\left[\begin{array}{cccc}{m}_{11}^{\text{'}\text{'}\text{'}}& m_{12}^{\text{'}\text{'}\text{'}}& m_{13}^{\text{'}\text{'}\text{'}}& m_{14}^{\text{'}\text{'}\text{'}}\\ m_{21}^{\text{'}\text{'}\text{'}}& m_{22}^{\text{'}\text{'}\text{'}}& m_{23}^{\text{'}\text{'}\text{'}}& m_{24}^{\text{'}\text{'}\text{'}}\\ m_{31}^{\text{'}\text{'}\text{'}}& m_{32}^{\text{'}\text{'}\text{'}}& m_{33}^{\text{'}\text{'}\text{'}}& m_{34}^{\text{'}\text{'}\text{'}}\\ m_{41}^{\text{'}\text{'}\text{'}}& m_{42}^{\text{'}\text{'}\text{'}}& m_{43}^{\text{'}\text{'}\text{'}}& m_{44}^{\text{'}\text{'}\text{'}}\end{array}\right]\left\{\begin{array}{c}0\\ 0\\ M_0^{\text{'}\text{'}}\text{'}\\ C_0^{\text{'}\text{'}\text{'}}\end{array}\right\}+P\left\{\begin{array}{c}{v}_{e{l}_1}^{\text{'}\text{'}\text{'}}\\ v_{e{l}_2}^{\text{'}\text{'}\text{'}}\\ v_{e{l}_3}^{\text{'}\text{'}\text{'}}\\ v_{e{l}_4}^{\text{'}\text{'}\text{'}}\end{array}\right\},.$$

(59)

or, (60):

$$\left\{\begin{array}{c}0\\ 0\\ M\text{'}\text{'}\text{'}\left(l\right)\\ C\text{'}\text{'}\text{'}\left(l\right)\end{array}\right\}=\left[\begin{array}{cccc}1& l& m_{13}^{\text{'}\text{'}\text{'}}& m_{14}^{\text{'}\text{'}\text{'}}\\ 0& 1& m_{23}^{\text{'}\text{'}\text{'}}& m_{24}^{\text{'}\text{'}\text{'}}\\ 0& 0& m_{33}^{\text{'}\text{'}\text{'}}& m_{34}^{\text{'}\text{'}\text{'}}\\ 0& 0& m_{43}^{\text{'}\text{'}\text{'}}& m_{44}^{\text{'}\text{'}\text{'}}\end{array}\right]\left\{\begin{array}{c}0\\ 0\\ M_0^{\text{'}\text{'}\text{'}}\\ C_0^{\text{'}\text{'}\text{'}}\end{array}\right\}+P\left\{\begin{array}{c}{v}_{e{l}_1}^{\text{'}\text{'}\text{'}}\\ v_{e{l}_2}^{\text{'}\text{'}\text{'}}\\ v_{e{l}_3}^{\text{'}\text{'}\text{'}}\\ v_{e{l}_4}^{\text{'}\text{'}\text{'}}\end{array}\right\},$$

(60)

A linear system of two equations with two unknowns is obtained as (61), the unknowns being the two elements of the state vector of side 0, $M_0^{\text{'}\text{'}\text{'}}$and $C_0^{\text{'}\text{'}\text{'}}$:

$$\{\begin{array}{c}{m}_{13}^{\text{'}\text{'}\text{'}}{M}_0^{\text{'}\text{'}\text{'}}+m_{14}^{\text{'}\text{'}\text{'}}{C}_0^{\text{'}\text{'}\text{'}}=-v_{e{l}_1}^{\text{'}\text{'}\text{'}}P\\ m_{23}^{\text{'}\text{'}\text{'}}{M}_0^{\text{'}\text{'}\text{'}}+m_{24}^{\text{'}\text{'}\text{'}}{C}_0^{\text{'}\text{'}\text{'}}=-v_{e{l}_2}^{\text{'}\text{'}\text{'}}P \end{array}$$

(61)

with solution (62):

$$\{\begin{array}{c}{M}_0^{\text{'}\text{'}\text{'}}={\displaystyle \frac{v_{e{l}_2}^{\text{'}\text{'}\text{'}}{m}_{14}^{\text{'}\text{'}\text{'}}-v_{e{l}_1}^{\text{'}\text{'}\text{'}}{m}_{24}^{\text{'}\text{'}\text{'}}}{m_{13}^{\text{'}\text{'}\text{'}}{m}_{24}^{\text{'}\text{'}\text{'}}-m_{14}^{\text{'}\text{'}\text{'}}{m}_{23}^{\text{'}\text{'}\text{'}}}}P=b_1^{\text{'}\text{'}\text{'}}P\\ C_0^{\text{'}\text{'}\text{'}}={\displaystyle \frac{v_{e{l}_2}^{\text{'}\text{'}\text{'}}{m}_{13}^{\text{'}\text{'}\text{'}}-v_{e{l}_1}^{\text{'}\text{'}\text{'}}{m}_{23}^{\text{'}\text{'}\text{'}}}{m_{14}^{\text{'}\text{'}\text{'}}{m}_{23}^{\text{'}\text{'}\text{'}}-m_{13}^{\text{'}\text{'}\text{'}}{m}_{24}^{\text{'}\text{'}\text{'}}}}P=b_1^{\text{'}\text{'}\text{'}}P\end{array},$$

(62)

With (62), the other two elements of the state vector for the last side on the right end, the side n, for x = l, will be like as (63):

$$\{\begin{array}{c}{M}^{\text{'}\text{'}\text{'}\left(l\right)}=m_{33}^{\text{'}\text{'}\text{'}}{M}_0^{\text{'}\text{'}\text{'}}+m_{34}^{\text{'}\text{'}\text{'}}{C}_0^{\text{'}\text{'}\text{'}}+v_{e{l}_3}^{\text{'}\text{'}\text{'}}P\\ C^{\text{'}\text{'}\text{'}\left(l\right)}=m_{43}^{\text{'}\text{'}\text{'}}{M}_0^{\text{'}\text{'}\text{'}}+m_{44}^{\text{'}\text{'}\text{'}}{C}_0^{\text{'}\text{'}\text{'}}+v_{e{l}_4}^{\text{'}\text{'}\text{'}}P\end{array} ,$$

(63)

with solution, as (64):

$$\{\begin{array}{c}M\text{'}\text{'}\text{'}\left(l\right)=\left(m_{33}^{\text{'}\text{'}\text{'}}{b}_1^{\text{'}\text{'}\text{'}}+m_{34}^{\text{'}\text{'}\text{'}}{b}_2^{\text{'}\text{'}\text{'}}+v_{e{l}_3}^{\text{'}\text{'}\text{'}}\right)P\\ C\text{'}\text{'}\text{'}\left(l\right)=\left(m_{43}^{\text{'}\text{'}\text{'}}{b}_1^{\text{'}\text{'}\text{'}}+m_{44}^{\text{'}\text{'}\text{'}}{b}_2^{\text{'}}+v_{e{l}_4}^{\text{'}\text{'}\text{'}}\right)P\end{array} ,$$

(64)

In this moment, all elements of any state vector of any side can be calculated for all parts in which the unit beam has been discretized.

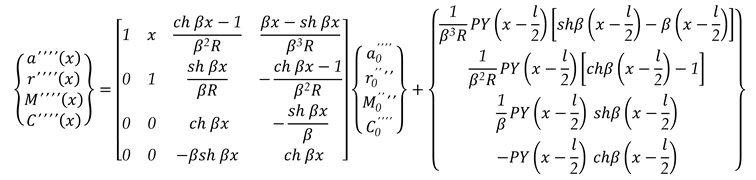
3.1.4. Unit Width Beam Embedded at The Two Edges Charged with A Concentrated Load P Which Acts in the Section x₀ = l/2, (Figure 3., (d))

For the vertical concentrated load at the middle, for x₀ = l/2, (Figure 3., (d)), the charge density is as (65):

$$q\text{'}\text{'}\text{'}\text{'}\left(x\right)=P\left(x-{\displaystyle \frac{l}{2}}\right),$$

(65)

With Dirac’s and Heaviside’s functions and operators, the state vector {$V_e^{\text{'}\text{'}}\text{'}\text{'}$}_x corresponding at exterior load is as (66):

$${\left\{V_e^{\text{'}\text{'}\text{'}\text{'}}\right\}}_x=\left\{\begin{array}{c}{\displaystyle \frac{1}{{\beta }^{3}R}}PY\left(x-{\displaystyle \frac{l}{2}}\right)\left[sh \beta \left(x-{\displaystyle \frac{l}{2}}\right)-\beta \left(x-{\displaystyle \frac{l}{2}}\right)\right]\\ {\displaystyle \frac{1}{{\beta }^{2}R}}PY\left(x-{\displaystyle \frac{l}{2}}\right)\left[ch \beta \left(x-{\displaystyle \frac{l}{2}}\right)-1\right]\\ {\displaystyle \frac{1}{\beta }}PY\left(x-{\displaystyle \frac{l}{2}}\right) sh \beta \left(x-{\displaystyle \frac{l}{2}}\right)\\ -PY\left(x-{\displaystyle \frac{l}{2}}\right) ch \beta \left(x-{\displaystyle \frac{l}{2}}\right)\end{array}\right\},$$

(66)

(67)

With Dirac’s and Heaviside’s functions and operators the matrix relation (67) can be written as (68):

(68)

For the right end, for x = l, expression (68) becomes (69):

(69)

or, (70):

(70)

The conditions for the two embedded ends of the beam are (71):

$$\{\begin{array}{c}{a}_0^{\text{'}\text{'}\text{'}\text{'}}=0\\ r_0^{\text{'}\text{'}}\text{'}\text{'}=0\\ a\text{'}\text{'}\text{'}\text{'}\left(l\right)=0 \\ r\text{'}\text{'}\text{'}\text{'}\left(l\right)=0\end{array},$$

(71)

With (71), the matrix relation (70) becomes as (72):

$$\left\{\begin{array}{c}0\\ 0\\ M\text{'}\text{'}\text{'}\text{'}\left(l\right)\\ C\text{'}\text{'}\text{'}\text{'}\left(l\right)\end{array}\right\}=\left[\begin{array}{cccc}1& l& {\displaystyle \frac{ch \beta l-1}{{\beta }^{2}R}}& {\displaystyle \frac{\beta l-sh \beta l}{{\beta }^{3}R}}\\ 0& 1& {\displaystyle \frac{sh \beta l}{\beta R}}& -{\displaystyle \frac{ch \beta l-1}{{\beta }^{2}R}}\\ 0& 0& ch \beta l& -{\displaystyle \frac{sh \beta l}{\beta }}\\ 0& 0& -\beta sh \beta l& ch \beta l\end{array}\right]\left\{\begin{array}{c}0\\ 0\\ M_0^{\text{'}\text{'}}\text{'}\text{'}\\ C_0^{\text{'}\text{'}\text{'}\text{'}}\end{array}\right\}+P\left\{\begin{array}{c}{\displaystyle \frac{1}{{\beta }^{3}R}}\left[sh \beta \left(l-x_0\right)-\beta \left(l-x_0\right)\right]\\ {\displaystyle \frac{1}{{\beta }^{2}R}}\left[ch \beta \left(l-x_0\right)-1\right]\\ {\displaystyle \frac{1}{\beta }} sh \beta \left(l-x_0\right)\\ - ch \beta \left(l-x_0\right)\end{array}\right\},$$

(72)

or, it can be written more simply as (73):

$$\left\{\begin{array}{c}0\\ 0\\ M\text{'}\text{'}\text{'}\text{'}\left(l\right)\\ C\text{'}\text{'}\text{'}\text{'}\left(l\right)\end{array}\right\}=\left[\begin{array}{cccc}{m}_{11}^{\text{'}\text{'}\text{'}\text{'}}& m_{12}^{\text{'}\text{'}\text{'}\text{'}}& m_{13}^{\text{'}\text{'}\text{'}}\text{'}& m_{14}^{\text{'}\text{'}\text{'}\text{'}}\\ m_{21}^{\text{'}\text{'}\text{'}\text{'}}& m_{22}^{\text{'}\text{'}\text{'}\text{'}}& m_{23}^{\text{'}\text{'}\text{'}\text{'}}& m_{24}^{\text{'}\text{'}\text{'}\text{'}}\\ m_{31}^{\text{'}\text{'}\text{'}}\text{'}& m_{32}^{\text{'}\text{'}\text{'}\text{'}}& m_{33}^{\text{'}\text{'}\text{'}\text{'}}& m_{34}^{\text{'}\text{'}\text{'}}\text{'}\\ m_{41}^{\text{'}\text{'}\text{'}\text{'}}& m_{42}^{\text{'}\text{'}\text{'}\text{'}}& m_{43}^{\text{'}\text{'}\text{'}\text{'}}& m_{44}^{\text{'}\text{'}\text{'}\text{'}}\end{array}\right]\left\{\begin{array}{c}0\\ 0\\ M_0^{\text{'}\text{'}}\text{'}\text{'}\\ C_0^{\text{'}\text{'}\text{'}\text{'}}\end{array}\right\}+P\left\{\begin{array}{c}{v}_{e{l}_1}^{\text{'}\text{'}\text{'}\text{'}}\\ v_{e{l}_2}^{\text{'}\text{'}\text{'}\text{'}}\\ v_{e{l}_3}^{\text{'}\text{'}\text{'}\text{'}}\\ v_{e{l}_4}^{\text{'}\text{'}\text{'}\text{'}}\end{array}\right\},$$

(73)

or, (74):

$$\left\{\begin{array}{c}0\\ 0\\ M\text{'}\text{'}\text{'}\text{'}\left(l\right)\\ C\text{'}\text{'}\text{'}\text{'}\left(l\right)\end{array}\right\}=\left[\begin{array}{cccc}1& l& m_{13}^{\text{'}\text{'}\text{'}\text{'}}& m_{14}^{\text{'}\text{'}\text{'}\text{'}}\\ 0& 1& m_{23}^{\text{'}\text{'}\text{'}\text{'}}& m_{24}^{\text{'}\text{'}\text{'}\text{'}}\\ 0& 0& m_{33}^{\text{'}\text{'}\text{'}\text{'}}& m_{34}^{\text{'}\text{'}\text{'}\text{'}}\\ 0& 0& m_{43}^{\text{'}\text{'}\text{'}\text{'}}& m_{44}^{\text{'}\text{'}\text{'}\text{'}}\end{array}\right]\left\{\begin{array}{c}0\\ 0\\ M_0^{\text{'}\text{'}\text{'}\text{'}}\\ C_0^{\text{'}\text{'}\text{'}\text{'}}\end{array}\right\}+P\left\{\begin{array}{c}{v}_{e{l}_1}^{\text{'}\text{'}\text{'}\text{'}}\\ v_{e{l}_2}^{\text{'}\text{'}\text{'}\text{'}}\\ v_{e{l}_3}^{\text{'}\text{'}\text{'}\text{'}}\\ v_{e{l}_4}^{\text{'}\text{'}\text{'}\text{'}}\end{array}\right\},$$

(74)

By writing the first two lines from the matrix relation (74), a linear system of two equations with two unknowns is obtained as (75), the unknowns being the two elements of the state vector of side 0, $M_0^{\text{'}\text{'}\text{'}\text{'}}$and $C_0^{\text{'}\text{'}\text{'}\text{'}}$:

$$\{\begin{array}{c}{m}_{13}^{\text{'}\text{'}\text{'}\text{'}}{M}_0^{\text{'}\text{'}\text{'}\text{'}}+m_{14}^{\text{'}\text{'}\text{'}\text{'}}{C}_0^{\text{'}\text{'}\text{'}\text{'}}=v_{e{l}_1}^{\text{'}\text{'}\text{'}\text{'}}P\\ m_{23}^{\text{'}\text{'}\text{'}\text{'}}{M}_0^{\text{'}\text{'}\text{'}\text{'}}+m_{24}^{\text{'}\text{'}\text{'}\text{'}}{C}_0^{\text{'}\text{'}\text{'}\text{'}}=v_{e{l}_2}^{\text{'}\text{'}\text{'}\text{'}}P \end{array}$$

(75)

with solution (76):

$$\{\begin{array}{c}{M}_0^{\text{'}\text{'}\text{'}\text{'}}={\displaystyle \frac{v_{e{l}_2}^{\text{'}\text{'}\text{'}\text{'}}{m}_{14}^{\text{'}\text{'}\text{'}\text{'}}-v_{e{l}_1}^{\text{'}\text{'}\text{'}\text{'}}{m}_{24}^{\text{'}\text{'}\text{'}\text{'}}}{m_{13}^{\text{'}\text{'}\text{'}\text{'}}{m}_{24}^{\text{'}\text{'}\text{'}\text{'}}-m_{14}^{\text{'}\text{'}\text{'}\text{'}}{m}_{23}^{\text{'}\text{'}\text{'}\text{'}}}}P=b_1^{\text{'}\text{'}\text{'}\text{'}}P\\ C_0^{\text{'}\text{'}\text{'}\text{'}}={\displaystyle \frac{v_{e{l}_2}^{\text{'}\text{'}\text{'}\text{'}}{m}_{13}^{\text{'}\text{'}\text{'}\text{'}}-v_{e{l}_1}^{\text{'}\text{'}\text{'}\text{'}}{m}_{23}^{\text{'}\text{'}\text{'}\text{'}}}{m_{14}^{\text{'}\text{'}\text{'}\text{'}}{m}_{23}^{\text{'}\text{'}\text{'}\text{'}}-m_{13}^{\text{'}\text{'}\text{'}\text{'}}{m}_{24}^{\text{'}\text{'}\text{'}\text{'}}}}P=b_1^{\text{'}\text{'}\text{'}\text{'}}P\end{array},$$

(76)

With (75), the other two elements of the state vector for the last side on the right end, the side n, for x = l, will be like as (77):

$$\{\begin{array}{c}{M}^{\text{'}\text{'}\text{'}\text{'}\left(l\right)}=m_{33}^{\text{'}\text{'}\text{'}\text{'}}{M}_0^{\text{'}\text{'}\text{'}\text{'}}+m_{34}^{\text{'}\text{'}\text{'}\text{'}}{C}_0^{\text{'}\text{'}\text{'}\text{'}}+v_{e{l}_3}^{\text{'}\text{'}\text{'}\text{'}}P\\ C^{\text{'}\text{'}\text{'}\text{'}\left(l\right)}=m_{43}^{\text{'}\text{'}\text{'}\text{'}}{M}_0^{\text{'}\text{'}\text{'}\text{'}}+m_{44}^{\text{'}\text{'}\text{'}\text{'}}{C}_0^{\text{'}\text{'}\text{'}\text{'}}+v_{e{l}_4}^{\text{'}\text{'}\text{'}\text{'}}P\end{array} ,$$

(77)

with solution, as (78):

$$\{\begin{array}{c}M\text{'}\text{'}\text{'}\text{'}\left(l\right)=\left(m_{33}^{\text{'}\text{'}\text{'}\text{'}}{b}_1^{\text{'}\text{'}\text{'}\text{'}}+m_{34}^{\text{'}\text{'}\text{'}\text{'}}{b}_2^{\text{'}\text{'}\text{'}\text{'}}+v_{e{l}_3}^{\text{'}\text{'}\text{'}\text{'}}\right)P\\ C\text{'}\text{'}\text{'}\text{'}\left(l\right)=\left(m_{43}^{\text{'}\text{'}\text{'}\text{'}}{b}_1^{\text{'}\text{'}\text{'}\text{'}}+m_{44}^{\text{'}\text{'}\text{'}\text{'}}{b}_2^{\text{'}\text{'}}+v_{e{l}_4}^{\text{'}\text{'}\text{'}\text{'}}\right)P\end{array} ,$$

(78)

In this moment, all elements of any state vector of any side can be calculated for all parts in which the unit beam has been discretized.

4. Discussion

This work is an original and new approach to calculate the long rectangle plates for applications in the vehicle industry. They are studied long rectangular plates, embedded on the two long borders, as applications. The plate was discretized in unity beams with width equal to unity, with the length equal to the width of the plate and the thickness equal to the thickness of the long rectangular plate. The unit beam is discretized into parts, each part having two sides with state vectors associated. For each of the four cases, a matrix relationship was written for side x, based on a transfer matrix of part x, the state vector corresponding to face 0 and the vector due to the action of external forces acting on part x. In the next step, it can be written the state vector for the last right section, for x = l. In this matrix relation, conditions of two ends can be placed, on the two embedded supports of the unitary beam. After, it can be calculated, the unknown elements of the state vector of face 0, and then the unknown elements of the state vector of the last face on the right end can also be calculated. In this moment, it is possible to calculate all the state vectors for all sides of the unity beam. Now, the efforts, deformations and stress can be calculated in any section of the beam, respectively for the long rectangular plate. This calculus will serve as calculus of resistance for different pieces of components of vehicles.

5. Conclusions

Besides the FEM, widely used today for resistance calculus of various structures, the TMM is a method that can be used especially where repetitive, iterative calculus are required. TMM can be programmed very easily, and the software can be attached to a code to optimize the constructive form of the structure, in this case - the constructive form of a rectangular plate, to have fast and reliable results. In the future, it is intended to study parts that will assimilate with the long rectangular plates of the vehicle. This work presents one of the multiple applications of TMM, in the calculus of long rectangular plates, loaded with a linear load uniformly distributed on a line parallel to the long sides for plates, embedded at the long two borders. The stresses and strains are calculated too.