New Algorithm for Entanglement Swapping

1. Introduction

Quantum superposition, or superposition for short, is a peculiar quantum mechanics phenomenon, which indicates that a quantum system can be in multiple different states simultaneously [1]. The most common case is the superposition of two opposing states, and one of the most famous examples is “Schr$\ddot{\mathrm{o}}$dinger’s cat”, which can be vividly expressed as “a cat can be both alive and dead at the same time” [2].

Quantum entanglement, abbreviated as entanglement, is a quantum mechanics phenomenon built on superposition. In other words, the primary premise for the existence of entanglement is superposition. An entangled system is a composite of two or more subsystems, and if one of the subsystems is observed, the state of the other subsystems will change immediately without any time delay [1]. In a entangled state, the properties of each particle have been integrated into a whole property, and it is impossible to describe the properties of each particle separately, only the properties of the whole system can be described [1,3].

Entanglement swapping is another quantum mechanics phenomenon, which builds on entanglement. Entanglement swapping has attracted extensive attention in the academic community since its discovery, mainly because it is one of the core resources for preparing quantum repeaters, which makes long-distance quantum communication and and large-scale quantum networks possible [3,4,5]. In addition, entanglement swapping provides a new approach for the preparation of entangled states and is also an important resource for designing quantum cryptography protocols and quantum algorithms [5,6].

The original idea of entanglement swapping was included in the quantum teleportation scheme proposed by Bennett et al. in 1992 [7]. Subsequently, Zeilinger et al. experimentally realised entanglement swapping for the first time in 1993, and formally proposed the concept of entanglement swapping [4]. Bose et al. described the entanglement swapping of 2-level cat states [8]. Hardy and Song considered the entanglement swapping of general pure states [9]. Bouda and Bu$\check{\mathrm{z}}$ek generalized the entanglement swapping scheme originally proposed for two pairs of qubits to multi-qudit systems [10]. Karimipour et al. introduced generalized cat states for d-level systems and obtain the formulas for their entanglement swapping with generalized Bell states [11]. Sen et al. investigated various entanglement swapping schemes for Werner states [12]. Roa et al. studied the entanglement swapping of X states [13]. Kirby et al. proposed a general analytical solution for entanglement swapping of arbitrary two-qubit states, which provides a comprehensive method for analyzing entanglement swapping in quantum networks [14]. Recently, Bergou et al. investigated the connection between entanglement swapping and concurrence [15].

The theory of quantum mechanics has developed rapidly over the past century and has been widely applied in quantum information processing in the last three decades. However, the fundamental principles behind quantum mechanical phenomena have always been unknown, and no one has been able to provide a widely convincing explanation for a century, which means that relying solely on scientific exploration does not seem to be effective. In this case, we turn our attention to ancient Chinese philosophy and attempt to seek the answers we desire. Inspired by some basic theories in the I Ching and the Tao Te Ching, we combine the law of conservation of energy in classical physics with the principles of quantum mechanics in this paper, put forward a theoretical framework and design a novel algorithm for entanglement swapping based on it. We then demonstrate the algorithm through the entanglement swapping between two entangled states with two particles each, and verify the correctness of the algorithm through the entanglement swapping between two Bell states (also commonly referred to as Einstein-Podolsky-Rosen pairs, abbreviated as EPR pairs [16]), which is achieved by performing a Bell measurement on the first particle in each Bell state. As is well-known, the establishment of the principles of quantum mechanics stems from the observation of natural phenomena. It is precisely from this perspective that we derive the quantum states after entangled swapping from all possible observation results.

In the following text, we will introduce the algebraic algorithm for entanglement swapping between two Bell states in Sec. 2, then present our proposed algorithm in Sec. 3. In Sec. 4, we give some views on the fundamental laws of nature, which may help to better understand the proposed algorithm. The last section is the summary of our work.

2. Entanglement Swapping Between Two Bell States

Suppose that there are two or more independent entangled states, and select some particles from each state and then perform joint quantum measurements on them. At this point, the measured particles collapse into a new entangled state, while all unmeasured particles collapse into another new entangled state. This phenomenon is called entanglement swapping [5]. The algebraic calculation process of entanglement swapping can be simply described as the expansion of a polynomial composed of vectors, combining like terms, permutation, followed by the re-expansion of the polynomial, and then combining like terms [17].

In what follows, we will introduce the entanglement swapping between two Bell states. Bell states contains four different states, which can be denoted as [17]

$$\begin{array}{c}\left|\phi \left({\lambda }_1,{\lambda }_2\right)\right.〉={\displaystyle \frac{1}{\sqrt{2}}}{\left[\left|0{\lambda }_2\right.〉+{(-1)}^{{\lambda }_1}\left|1{\overline{\lambda }}_2\right.〉\right]}_{1,2},\\ {\lambda }_1,{\lambda }_2\in \{0,1\},\end{array}$$

(1)

where the subscripts 1,2 denote the two particles in each state (similarly hereinafter). It is known that four Bell states form a complete orthogonal basis, i.e., the Bell basis [5], which are therefore widely used as measurement operators to extract information carried on entangled states or to implement entanglement swapping.

Let us suppose that there are two Bell states, denoted as ${\left|\phi \left({\lambda }_1^1,{\lambda }_2^1\right)\right.〉}_{1,2},{\left|\phi \left({\lambda }_1^2,{\lambda }_2^2\right)\right.〉}_{3,4}$, where the subscripts 1,2 and 3,4 denote the particles in the two Bell states, respectively, and suppose that a Bell measurement is performed on the first particle in each state, such that the entanglement swapping between two Bell states can be expressed as [17]

$$\begin{array}{cc}\hfill & {\left|\phi \left({\lambda }_1^1,{\lambda }_2^1\right)\right.〉}_{1,2}\otimes {\left|\phi \left({\lambda }_1^2,{\lambda }_2^2\right)\right.〉}_{3,4}\hfill \\ \hfill =& {\displaystyle \frac{1}{2}}{\left[\left|0{\lambda }_2^{1}0{\lambda }_2^2\right.〉+{(-1)}^{{\lambda }_1^2}\left|0{\lambda }_2^{1}1{\overline{\lambda }}_2^2\right.〉+{(-1)}^{{\lambda }_1^1}\left|1{\overline{\lambda }}_2^{1}0{\lambda }_2^2\right.〉+{(-1)}^{{\lambda }_1^1+{\lambda }_1^2}\left|1{\overline{\lambda }}_2^{1}1{\overline{\lambda }}_2^2\right.〉\right]}_{1234}\hfill \end{array}$$

(2a)

$$\begin{array}{c}\hfill \Rightarrow {\displaystyle \frac{1}{2}}{\left[\left|00{\lambda }_2^1{\lambda }_2^2\right.〉+{(-1)}^{{\lambda }_1^2}\left|01{\lambda }_2^1{\overline{\lambda }}_2^2\right.〉+{(-1)}^{{\lambda }_1^1}\left|10{\overline{\lambda }}_2^1{u}_2^2\right.〉+{(-1)}^{{\lambda }_1^1+u_1^2}\left|11{\overline{\lambda }}_2^1{\overline{\lambda }}_2^2\right.〉\right]}_{1324}\end{array}$$

(2b)

$$\begin{array}{cc}\hfill =& {\displaystyle \frac{1}{4}}\left[1+{(-1)}^{{\lambda }_1^1+{\lambda }_1^2}\right]\left(\left|\phi \left(0,0\right)\right.〉\left|\phi \left(0,{\lambda }_1^2\right)\right.〉\pm \left|\phi \left(1,0\right)\right.〉\left|\phi \left(1,{\overline{\lambda }}_1^2\right)\right.〉\right)\hfill \\ \hfill +& {\displaystyle \frac{1}{4}}\left[1-{(-1)}^{{\lambda }_1^1+{\lambda }_1^2}\right]\left(\left|\phi \left(1,0\right)\right.〉\left|\phi \left(0,{\lambda }_1^2\right)\right.〉\pm \left|\phi \left(0,0\right)\right.〉\left|\phi \left(1,{\overline{\lambda }}_1^2\right)\right.〉\right)\hfill \\ \hfill +& {\displaystyle \frac{1}{4}}\left[{(-1)}^{{\lambda }_1^2}+{(-1)}^{{\lambda }_1^1}\right]\left(\left|\phi \left(0,1\right)\right.〉\left|\phi \left(0,{\lambda }_2^2\right)\right.〉\pm \left|\phi \left(1,1\right)\right.〉\left|\phi \left(1,{\overline{\lambda }}_2^2\right)\right.〉\right)\hfill \\ \hfill +& {\displaystyle \frac{1}{4}}\left[{(-1)}^{{\lambda }_1^2}-{(-1)}^{{\lambda }_1^1}\right]\left(\left|\phi \left(1,1\right)\right.〉\left|\phi \left(0,{\lambda }_2^2\right)\right.〉\pm \left|\phi \left(0,1\right)\right.〉\left|\phi \left(1,{\overline{\lambda }}_2^2\right)\right.〉\right).\hfill \end{array}$$

(2c)

This formula demonstrates a detailed algebraic calculation process for deriving entanglement swapping results. Eq. 2a shows the result after the expansion of polynomials and the merging of similar terms; Eq. 2b shows the result after permutation; Eq. 2c shows the result after the re-expansion of the polynomial and the combining of like terms.

Ref. [5] provides another expression for entanglement swapping between two Bell states, which are given by

$$\begin{array}{cc}\hfill & {\left(\left|0i\right.〉\pm \left|1\overline{i}\right.〉\right)}_{12}\otimes {\left(\left|0i\right.〉\pm \left|1\overline{i}\right.〉\right)}_{34}\hfill \\ \hfill \Rightarrow & \left\{\begin{array}{cc}\hfill & {\left|{\varphi }^{+}\right.〉}_{13}{\left|{\varphi }^{+}\right.〉}_{24}+{\left|{\varphi }^{-}\right.〉}_{13}{\left|{\varphi }^{-}\right.〉}_{24}\pm {\left|{\psi }^{+}\right.〉}_{13}{\left|{\psi }^{+}\right.〉}_{24}\pm {\left|{\psi }^{-}\right.〉}_{13}{\left|{\psi }^{-}\right.〉}_{24}\mathrm{if}\phantom{i}i=0;\hfill \\ \hfill & {\left|{\varphi }^{+}\right.〉}_{13}{\left|{\varphi }^{+}\right.〉}_{24}-{\left|{\varphi }^{-}\right.〉}_{13}{\left|{\varphi }^{-}\right.〉}_{24}\pm {\left|{\psi }^{+}\right.〉}_{13}{\left|{\psi }^{+}\right.〉}_{24}\mp {\left|{\psi }^{-}\right.〉}_{13}{\left|{\psi }^{-}\right.〉}_{24}\mathrm{if}\phantom{i}i=1,\hfill \end{array}\right.\hfill \end{array}$$

(3a)

$$\begin{array}{cc}\hfill & {\left(\left|0i\right.〉\pm \left|1\overline{i}\right.〉\right)}_{12}\otimes {\left(\left|0i\right.〉\mp \left|1\overline{i}\right.〉\right)}_{34}\hfill \\ \hfill \Rightarrow & \left\{\begin{array}{c}\phantom{-}{\left|{\varphi }^{+}\right.〉}_{13}{\left|{\varphi }^{-}\right.〉}_{24}+{\left|{\varphi }^{-}\right.〉}_{13}{\left|{\varphi }^{+}\right.〉}_{24}\mp {\left|{\psi }^{+}\right.〉}_{13}{\left|{\psi }^{-}\right.〉}_{24}\mp {\left|{\psi }^{-}\right.〉}_{13}{\left|{\psi }^{+}\right.〉}_{24}\mathrm{if}\phantom{i}i=0;\hfill \\ -{\left|{\varphi }^{+}\right.〉}_{13}{\left|{\varphi }^{-}\right.〉}_{24}+{\left|{\varphi }^{-}\right.〉}_{13}{\left|{\varphi }^{+}\right.〉}_{24}\pm {\left|{\psi }^{+}\right.〉}_{13}{\left|{\psi }^{-}\right.〉}_{24}\mp {\left|{\psi }^{-}\right.〉}_{13}{\left|{\psi }^{+}\right.〉}_{24}\mathrm{if}\phantom{i}i=1,\hfill \end{array}\right.\hfill \end{array}$$

(3b)

$$\begin{array}{cc}\hfill & {\left(\left|0i\right.〉\pm \left|1\overline{i}\right.〉\right)}_{12}\otimes {\left(\left|0\overline{i}\right.〉\pm \left|1i\right.〉\right)}_{34}\hfill \\ \hfill \Rightarrow & \left\{\begin{array}{cc}\hfill & {\left|{\varphi }^{+}\right.〉}_{13}{\left|{\psi }^{+}\right.〉}_{24}+{\left|{\varphi }^{-}\right.〉}_{13}{\left|{\psi }^{-}\right.〉}_{24}\pm {\left|{\psi }^{+}\right.〉}_{13}{\left|{\varphi }^{+}\right.〉}_{24}\pm {\left|{\psi }^{-}\right.〉}_{13}{\left|{\varphi }^{-}\right.〉}_{24}\mathrm{if}\phantom{i}i=0;\hfill \\ \hfill & {\left|{\varphi }^{+}\right.〉}_{13}{\left|{\psi }^{+}\right.〉}_{24}-{\left|{\varphi }^{-}\right.〉}_{13}{\left|{\psi }^{-}\right.〉}_{24}\pm {\left|{\psi }^{+}\right.〉}_{13}{\left|{\varphi }^{+}\right.〉}_{24}\mp {\left|{\psi }^{-}\right.〉}_{13}{\left|{\varphi }^{-}\right.〉}_{24}\mathrm{if}\phantom{i}i=1,\hfill \end{array}\right.\hfill \end{array}$$

(3c)

$$\begin{array}{cc}\hfill & {\left(\left|0i\right.〉\pm \left|1\overline{i}\right.〉\right)}_{12}\otimes {\left(\left|0\overline{i}\right.〉\mp \left|1i\right.〉\right)}_{34}\hfill \\ \hfill \Rightarrow & \left\{\begin{array}{c}\phantom{-}{\left|{\varphi }^{+}\right.〉}_{13}{\left|{\psi }^{-}\right.〉}_{24}+{\left|{\varphi }^{-}\right.〉}_{13}{\left|{\psi }^{+}\right.〉}_{24}\mp {\left|{\psi }^{+}\right.〉}_{13}{\left|{\varphi }^{-}\right.〉}_{24}\mp {\left|{\psi }^{-}\right.〉}_{13}{\left|{\varphi }^{+}\right.〉}_{24}\mathrm{if}\phantom{i}i=0;\hfill \\ -{\left|{\varphi }^{+}\right.〉}_{13}{\left|{\psi }^{-}\right.〉}_{24}+{\left|{\varphi }^{-}\right.〉}_{13}{\left|{\psi }^{+}\right.〉}_{24}\pm {\left|{\psi }^{+}\right.〉}_{13}{\left|{\varphi }^{-}\right.〉}_{24}\mp {\left|{\psi }^{-}\right.〉}_{13}{\left|{\varphi }^{+}\right.〉}_{24}\mathrm{if}\phantom{i}i=1,\hfill \end{array}\right.\hfill \end{array}$$

(3d)

in which the inessential coefficients are ignored, and $\left|{\varphi }^{+}\right.〉,\left|{\varphi }^{-}\right.〉,\left|{\psi }^{+}\right.〉,\left|{\psi }^{-}\right.〉$ represent four Bell states, respectively,

$$\begin{array}{c}\left|{\varphi }^{+}\right.〉={\displaystyle \frac{1}{\sqrt{2}}}\left(\left|00\right.〉+\left|11\right.〉\right),\left|{\varphi }^{-}\right.〉={\displaystyle \frac{1}{\sqrt{2}}}\left(\left|00\right.〉-\left|11\right.〉\right),\\ \left|{\psi }^{+}\right.〉={\displaystyle \frac{1}{\sqrt{2}}}\left(\left|01\right.〉+\left|10\right.〉\right),\left|{\psi }^{-}\right.〉={\displaystyle \frac{1}{\sqrt{2}}}\left(\left|01\right.〉-\left|10\right.〉\right).\end{array}$$

(4)

Eq. 4 is another way to characterize four Bell states besides Eq. 1, and this characterization is widely adopted in various quantum information processing schemes.

3. The New Algorithm for Entanglement Swapping

In this section, we will provide a detailed description of the proposed algorithm. Before that, let us first establish a theoretical framework, which serves as the foundation for designing this algorithm.

3.1. The Theoretical Framework

From classical physics theory, it is known that energy cannot appear out of thin air, and matter is no exception. Therefore, at the beginning of the birth of the universe, there must have been nothing at all, that is, the origin of the universe was empty; In other words, the emptiness state is the starting state of the universe. However, the birth of infinite energy and countless kinds of substances in the universe indicates that the origin of the universe is all-encompassing, that is to say, the all-encompassing state is the beginning state of the universe. By the way, as for why the primitive energy appeared, it seems to me that this question may never be answered.

To sum up, the origin of the universe is both “empty” and “all-embracing”, which can be said to be the superposition or mixture of the two opposing states. Using mathematical representations in quantum mechanics, we would like to represent the “empty state” and “all-embracing state” separately as $\left|\mathcal{N}\right.〉$ and $\left|\mathcal{Y}\right.〉$, and use $\left|\mathcal{O}\right.〉$ to represent the origin of the universe, then one can get $\left|\mathcal{O}\right.〉=\left|\mathcal{Y}\right.〉+\left|\mathcal{N}\right.〉$. When we discuss or make a judgment about the existence of everything in the universe, it is actually because we have made local observations of $\left|\mathcal{O}\right.〉$, which causes $\left|\mathcal{O}\right.〉$ to collapse, and thus obtains the observation result $\left|\mathcal{Y}\right.〉$ or $\left|\mathcal{N}\right.〉$.

It is widely accepted that there is energy in the universe first, and then energy is transformed into various substances. However, the premise of accepting this viewpoint is that energy exists, that is, $\left|\mathcal{O}\right.〉$ is observed to collapse into the state $\left|\mathcal{Y}\right.〉$. As mentioned above, according to the law of conservation of energy, energy cannot be generated out of thin air, hence the total energy in the universe must be zero. This means that energy must be divided into two types: positive energy and negative energy, and both are equal in quantity (i.e., they are balanced), making the total amount zero. Let us take the number axis as an example. The positive and negative energies correspond to the positive and negative half axes of the number axis, respectively, and the number 0 in the center of the number axis corresponds to the state after adding the two energies, as shown in Figure 1.

Figure 1.

Figure 1.

To further explore the state of the origin of the universe, let us assume that there is a quantum system that is always isolated from the outside world, which means that there has never been any energy exchange between the system and the external environment. As above, the energy possessed by the system must be divided into positive energy and negative energy, and they are balanced. Here, we might as well use $\left|\phi \right.〉$ to represent the states of the quantum system, and $\left|\alpha \right.〉$ and $\left|\beta \right.〉$ to represent the state of the positive and negative energy of the system, respectively, where $\left|\phi \right.〉$ can be assumed to be of any dimension. Without loss of generality, we would like to assume that $\left|\phi \right.〉$ is a d-dimensional quantum system ( also known as a d-level quantum system). Due to the energy of the system is zero, we can write it as

$$\begin{array}{c}\hfill \left|\phi \right.〉={\left(0,0,\dots ,0\right)}^{\mathrm{T}},\end{array}$$

(5)

that is, $\left|\phi \right.〉$ is a vector containing d 0 elements. Furthermore, let us represent $\left|\alpha \right.〉$ as

$$\begin{array}{c}\hfill \left|\alpha \right.〉={\left({\gamma }_1,{\gamma }_2,\dots ,{\gamma }_d\right)}^{\mathrm{T}}.\end{array}$$

(6)

Since the balance between the positive energy and negative energy, we have

$$\begin{array}{c}\hfill \left|\beta \right.〉={\left(-{\gamma }_1,-{\gamma }_2,\dots ,-{\gamma }_d\right)}^{\mathrm{T}}=-\left|\alpha \right.〉={\mathrm{e}}^{i\pi }\left|\alpha \right.〉.\end{array}$$

(7)

It is clear that

$$\begin{array}{c}\hfill \left|\alpha \right.〉+\left|\beta \right.〉\equiv \left|\phi \right.〉.\end{array}$$

(8)

When conducting local observations on the system (i.e., performing quantum measurements on $\left|\alpha \right.〉$ or $\left|\beta \right.〉$), based on the theory of quantum measurements, only the state $\left|\alpha \right.〉$ can be obtained, attributed to

$$\begin{array}{c}\hfill \left.〈\beta \right|M_m^{+}{M}_m\left|\beta \right.〉=\left.〈\alpha \right|{\mathrm{e}}^{-i\pi }{M}_m^{+}{M}_m{\mathrm{e}}^{i\pi }\left|\alpha \right.〉=\left.〈\alpha \right|M_m^{+}{M}_m\left|\alpha \right.〉,\end{array}$$

(9)

where $M_m$ represents a measurement operator and the subscript m represents a possible measurement result [1]. Obviously, when the observation result is $\left|\alpha \right.〉$, the original state of the system is the superposition of $\left|\alpha \right.〉$ and $\left|\beta \right.〉$ (i.e., $-\left|\alpha \right.〉$), which is an interesting and shocking phenomenon. More precisely, since the probability of the observation result being either $\left|\alpha \right.〉$ or $\left|\beta \right.〉$ is 50%, we can denote the system $\left|\phi \right.〉$ as

$$\begin{array}{c}\hfill \left|\phi \right.〉={\displaystyle \frac{1}{\sqrt{2}}}\left(\left|\alpha \right.〉+\left|\beta \right.〉\right).\end{array}$$

(10)

Let us now assume that someone observes a certain state of the system $\left|\alpha \right.〉$ and the possible observation results are $\left|\xi \right.〉$ and $\left|\overline{\xi }\right.〉$, then we can denote $\left|\alpha \right.〉$ as

$$\begin{array}{c}\left|\alpha \right.〉={\eta }_1\left|\xi \right.〉+{\eta }_2\left|\overline{\xi }\right.〉,\\ \mathrm{s}.\mathrm{t}.{∥{\eta }_1∥}^2+{∥{\eta }_2∥}^2=1.\end{array}$$

(11)

Here we only need to focus on the observation results, without paying attention to the coefficients; Therefore, to simplify the expression, we would like to set ${\lambda }_1={\lambda }_2={\displaystyle \frac{1}{\sqrt{2}}}$, such that $\left|\alpha \right.〉={\displaystyle \frac{1}{\sqrt{2}}}\left(\left|\xi \right.〉+\left|\overline{\xi }\right.〉\right)$. Then we have

$$\begin{array}{cc}\hfill \left|\phi \right.〉=& {\displaystyle \frac{1}{\sqrt{2}}}\left(\left|\alpha \right.〉+\left|\beta \right.〉\right)\hfill \\ \hfill =& {\displaystyle \frac{1}{\sqrt{2}}}\left\{{\displaystyle \frac{1}{\sqrt{2}}}\left(\left|\xi \right.〉+\left|\overline{\xi }\right.〉\right)+\left[-{\displaystyle \frac{1}{\sqrt{2}}}\left(\left|\xi \right.〉+\left|\overline{\xi }\right.〉\right)\right]\right\}\hfill \\ \hfill =& {\displaystyle \frac{1}{\sqrt{2}}}\left\{{\displaystyle \frac{1}{\sqrt{2}}}\left(\left|\xi \right.〉-\left|\overline{\xi }\right.〉\right)+\left[-{\displaystyle \frac{1}{\sqrt{2}}}\left(\left|\xi \right.〉-\left|\overline{\xi }\right.〉\right)\right]\right\}\hfill \\ \hfill =& {\displaystyle \frac{1}{2}}\left[\left|\xi \right.〉+\left(-\left|\xi \right.〉\right)\right]+{\displaystyle \frac{1}{2}}\left[\left|\overline{\xi }\right.〉+\left(-\left|\overline{\xi }\right.〉\right)\right].\hfill \end{array}$$

(12)

As can be seen from Eq. 12, in addition to $\left|\xi \right.〉$, $\left|\overline{\xi }\right.〉$ and ${\displaystyle \frac{1}{\sqrt{2}}}\left(\left|\xi \right.〉+\left|\overline{\xi }\right.〉\right)$, ${\displaystyle \frac{1}{\sqrt{2}}}\left(\left|\xi \right.〉-\left|\overline{\xi }\right.〉\right)$ can be observed from the system $\left|\phi \right.〉$, which is undoubtedly an interesting and shocking phenomenon. Furthermore, to be precise, countless states can be observed from $\left|\phi \right.〉$, and the observed states are entirely determined by measurement operators. Let us give a few familiar examples, let $\left|\alpha \right.〉$ be $\left|+\right.〉={\displaystyle \frac{1}{\sqrt{2}}}\left(\left|0\right.〉+\left|1\right.〉\right)$, then one can get

$$\begin{array}{cc}\hfill \left|\phi \right.〉=& {\displaystyle \frac{1}{\sqrt{2}}}\left\{{\displaystyle \frac{1}{\sqrt{2}}}\left(\left|0\right.〉+\left|1\right.〉\right)+\left[-{\displaystyle \frac{1}{\sqrt{2}}}\left(\left|0\right.〉+\left|1\right.〉\right)\right]\right\}\hfill \\ \hfill =& {\displaystyle \frac{1}{\sqrt{2}}}\left\{{\displaystyle \frac{1}{\sqrt{2}}}\left(\left|0\right.〉-\left|1\right.〉\right)+\left[-{\displaystyle \frac{1}{\sqrt{2}}}\left(\left|0\right.〉-\left|1\right.〉\right)\right]\right\}\hfill \\ \hfill =& {\displaystyle \frac{1}{2}}\left[\left|0\right.〉+\left(-\left|0\right.〉\right)\right]+{\displaystyle \frac{1}{2}}\left[\left|1\right.〉+\left(-\left|1\right.〉\right)\right].\hfill \end{array}$$

(13)

It can be seen that there are four states that can be observed from the system $\left|\phi \right.〉$, as follows:

$$\begin{array}{c}\hfill \left|0\right.〉,\left|1\right.〉,\left|+\right.〉,\left|-\right.〉,\end{array}$$

(14)

where $\left|-\right.〉={\displaystyle \frac{1}{\sqrt{2}}}\left(\left|0\right.〉-\left|1\right.〉\right)$. In other words, if the system is observed locally, the four states shown in Eq. 14 can be observed. Treating $\left|0\right.〉$ and $\left|1\right.〉$ as vectors, we can establish a coordinate system as shown in Figure 2.

Figure 2.

Figure 2.

Next, let us consider the case of conducting local observations on two quantum systems. To study this problem, let us assume that there are two independent quantum systems, $\left|{\mathbf{\Psi }}_1\right.〉$ and $\left|{\mathbf{\Psi }}_2\right.〉$, in the states of

$$\begin{array}{cc}\hfill & \left|{\mathbf{\Psi }}_1\right.〉={\displaystyle \frac{1}{\sqrt{2}}}\left\{{\displaystyle \frac{1}{\sqrt{2}}}\left(\left|u_1\right.〉+\left|{\overline{u}}_1\right.〉\right)+\left[-{\displaystyle \frac{1}{\sqrt{2}}}\left(\left|u_1\right.〉+\left|{\overline{u}}_1\right.〉\right)\right]\right\},\hfill \\ \hfill & \left|{\mathbf{\Psi }}_2\right.〉={\displaystyle \frac{1}{\sqrt{2}}}\left\{{\displaystyle \frac{1}{\sqrt{2}}}\left(\left|u_2\right.〉+\left|{\overline{u}}_2\right.〉\right)+\left[-{\displaystyle \frac{1}{\sqrt{2}}}\left(\left|u_2\right.〉+\left|{\overline{u}}_2\right.〉\right)\right]\right\},\hfill \end{array}$$

(15)

where $\left\{u_1,{\overline{u}}_1\right\}$ and $\left\{u_2,{\overline{u}}_2\right\}$ are the observation results of $\left|{\mathbf{\Psi }}_1\right.〉$ and $\left|{\mathbf{\Psi }}_2\right.〉$, respectively. Then we can arrive at

$$\begin{array}{cc}\hfill & \left|{\mathbf{\Psi }}_1\right.〉\otimes \left|{\mathbf{\Psi }}_2\right.〉\hfill \\ \hfill =& {\displaystyle \frac{1}{\sqrt{2}}}\left\{{\displaystyle \frac{1}{\sqrt{2}}}\left(\left|u_1\right.〉+\left|{\overline{u}}_1\right.〉\right)+\left[-{\displaystyle \frac{1}{\sqrt{2}}}\left(\left|u_1\right.〉+\left|{\overline{u}}_1\right.〉\right)\right]\right\}\otimes {\displaystyle \frac{1}{\sqrt{2}}}\left\{{\displaystyle \frac{1}{\sqrt{2}}}\left(\left|u_2\right.〉+\left|{\overline{u}}_2\right.〉\right)+\left[-{\displaystyle \frac{1}{\sqrt{2}}}\left(\left|u_2\right.〉+\left|{\overline{u}}_2\right.〉\right)\right]\right\}\hfill \end{array}$$

$$\begin{array}{cc}\hfill \Rightarrow & {\displaystyle \frac{1}{2\sqrt{2}}}\left\{\left(\left|u_1{u}_2\right.〉+\left|u_1{\overline{u}}_2\right.〉+\left|{\overline{u}}_1{u}_2\right.〉+\left|{\overline{u}}_1{\overline{u}}_2\right.〉\right)+\left[-\left(\left|u_1{u}_2\right.〉+\left|u_1{\overline{u}}_2\right.〉+\left|{\overline{u}}_1{u}_2\right.〉+\left|{\overline{u}}_1{\overline{u}}_2\right.〉\right)\right]\right\}\hfill \\ \hfill =& {\displaystyle \frac{1}{2}}\left\{{\displaystyle \frac{1}{\sqrt{2}}}\left(\left|u_1{u}_2\right.〉+\left|{\overline{u}}_1{\overline{u}}_2\right.〉\right)+\left[-{\displaystyle \frac{1}{\sqrt{2}}}\left(\left|u_1{u}_2\right.〉+\left|{\overline{u}}_1{\overline{u}}_2\right.〉\right)\right]\right\}\hfill \end{array}$$

(16a)

$$\begin{array}{cc}\hfill & +{\displaystyle \frac{1}{2}}\left\{{\displaystyle \frac{1}{\sqrt{2}}}\left(\left|u_1{\overline{u}}_2\right.〉+\left|{\overline{u}}_1{u}_2\right.〉\right)+\left[-{\displaystyle \frac{1}{\sqrt{2}}}\left(\left|u_1{\overline{u}}_2\right.〉+\left|{\overline{u}}_1{u}_2\right.〉\right)\right]\right\}\hfill \\ \hfill =& {\displaystyle \frac{1}{2}}\left\{{\displaystyle \frac{1}{\sqrt{2}}}\left(\left|u_1{u}_2\right.〉-\left|{\overline{u}}_1{\overline{u}}_2\right.〉\right)+\left[-{\displaystyle \frac{1}{\sqrt{2}}}\left(\left|u_1{u}_2\right.〉-\left|{\overline{u}}_1{\overline{u}}_2\right.〉\right)\right]\right\}\hfill \end{array}$$

(16b)

$$\begin{array}{cc}\hfill & +{\displaystyle \frac{1}{2}}\left\{{\displaystyle \frac{1}{\sqrt{2}}}\left(\left|u_1{\overline{u}}_2\right.〉-\left|{\overline{u}}_1{u}_2\right.〉\right)+\left[-{\displaystyle \frac{1}{\sqrt{2}}}\left(\left|u_1{\overline{u}}_2\right.〉-\left|{\overline{u}}_1{u}_2\right.〉\right)\right]\right\}.\hfill \end{array}$$

(16c

Note here that the second step in the above equation has undergone probability normalization. From Eqs. 16a, 16b and 16c, it can be seen that the following states can be observed from the composite system $\left|{\mathbf{\Psi }}_1\right.〉\otimes \left|{\mathbf{\Psi }}_2\right.〉$:

$$\begin{array}{c}\left\{\left|u_1{u}_2\right.〉,\left|u_1{\overline{u}}_2\right.〉,\left|{\overline{u}}_1{u}_2\right.〉,\left|{\overline{u}}_1{\overline{u}}_2\right.〉\right\},\\ \left\{\left|{\chi }_1\right.〉,\left|{\chi }_2\right.〉,\left|{\chi }_3\right.〉,\left|{\chi }_4\right.〉\right\},\\ \mathrm{where}\left|{\chi }_1\right.〉={\displaystyle \frac{1}{\sqrt{2}}}\left(\left|u_1{u}_2\right.〉+\left|{\overline{u}}_1{\overline{u}}_2\right.〉\right),\left|{\chi }_2\right.〉={\displaystyle \frac{1}{\sqrt{2}}}\left(\left|u_1{u}_2\right.〉-\left|{\overline{u}}_1{\overline{u}}_2\right.〉\right),\\ \left|{\chi }_3\right.〉={\displaystyle \frac{1}{\sqrt{2}}}\left(\left|u_1{\overline{u}}_2\right.〉+\left|{\overline{u}}_1{u}_2\right.〉\right),\left|{\chi }_4\right.〉={\displaystyle \frac{1}{\sqrt{2}}}\left(\left|u_1{\overline{u}}_2\right.〉-\left|{\overline{u}}_1{u}_2\right.〉\right).\end{array}$$

(17)

A familiar example is when $u_1\in \{0,1\},{\overline{u}}_1\in \{0,1\}\setminus \left\{u_1\right\}$ and $u_2\in \{0,1\},{\overline{u}}_2\in \{0,1\}\setminus \left\{u_2\right\}$, one can observe the following states:

$$\begin{array}{c}\left\{\left|00\right.〉,\left|01\right.〉,\left|10\right.〉,\left|11\right.〉\right\},\\ \left\{\left|{\varphi }^{+}\right.〉,\left|{\varphi }^{-}\right.〉,\left|{\psi }^{+}\right.〉,\left|{\psi }^{-}\right.〉\right\},\end{array}$$

(18)

where $\left|{\varphi }^{+}\right.〉,\left|{\varphi }^{-}\right.〉,\left|{\psi }^{+}\right.〉,\left|{\psi }^{-}\right.〉$ are Bell states (see Eq. 4). This example shows a surprising result, which may explain why Bell states exist in nature. Of course, as before, countless types of quantum states can be observed from $\left|{\mathbf{\Psi }}_1\right.〉\otimes \left|{\mathbf{\Psi }}_2\right.〉$, which will not be elaborated here. By the way, two coordinate systems shown in Figure 3 can be established.

Figure 3.

Figure 3.

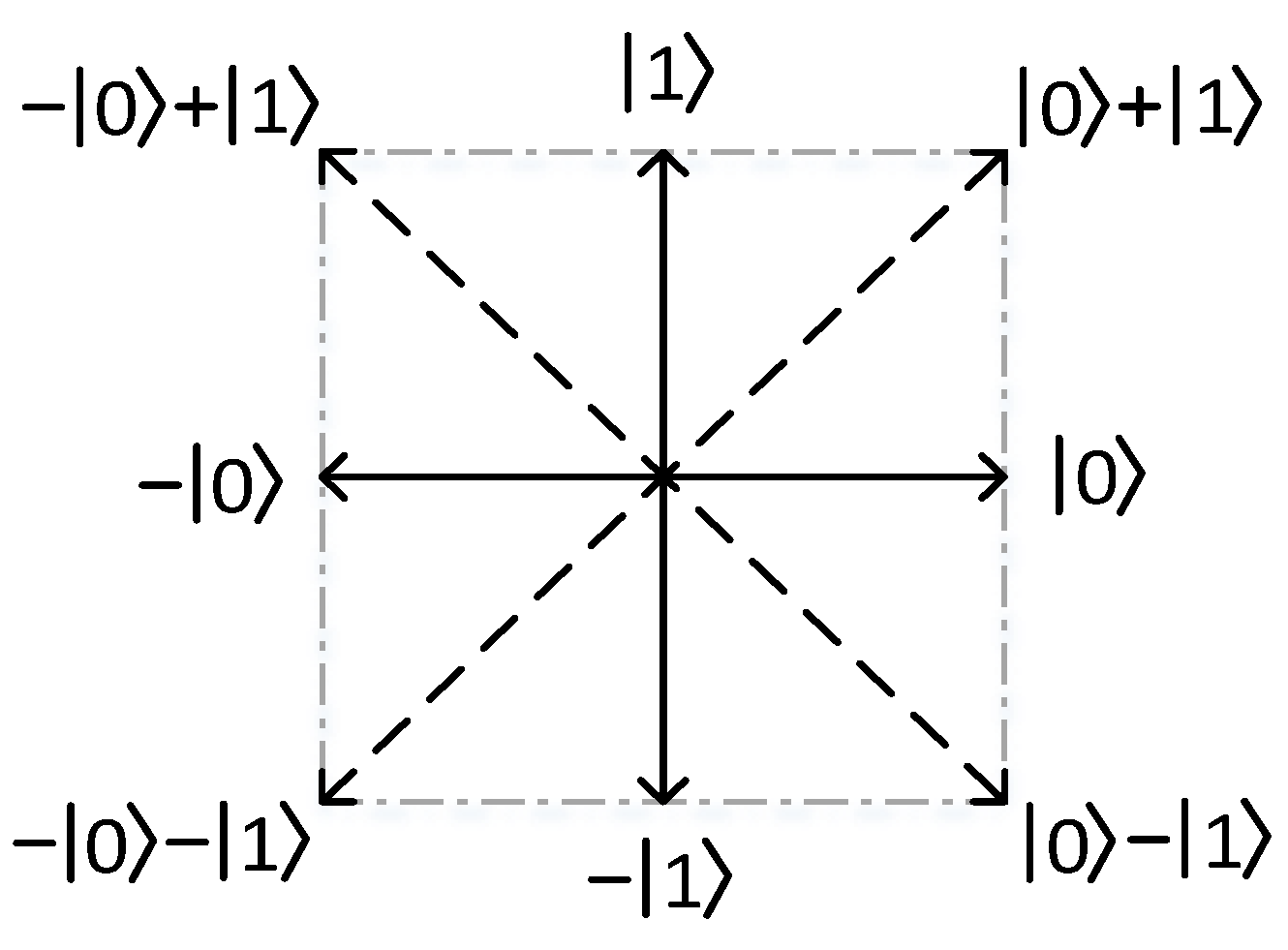
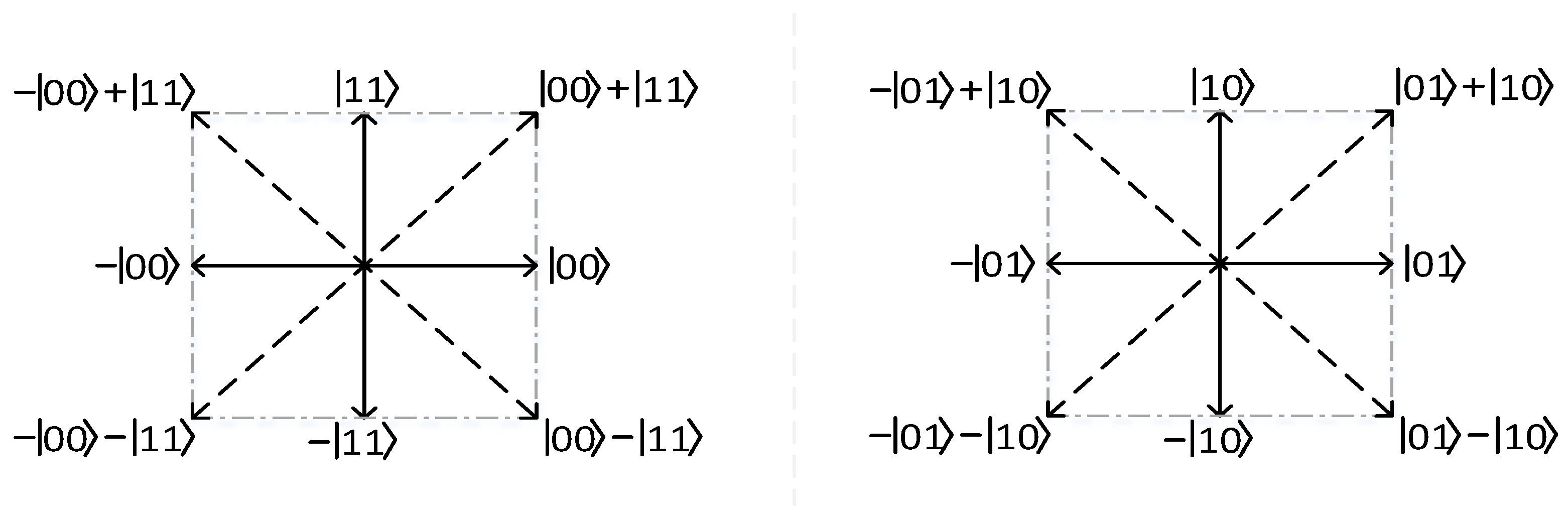
3.2. The Proposed Algorithm

From Eq. 16a, it can be seen that when $\left|u_1{u}_2\right.〉$ is obtained, the combination of the states of the two systems is $\left\{\left|u_1\right.〉,\left|u_2\right.〉\right\}$ or $\left\{-\left|u_1\right.〉,-\left|u_2\right.〉\right\}$. Furthermore, to obtain state $\left|{\chi }_1\right.〉$, the state combinations of the two systems are the four combinations shown in Table 1, numbered 1, 2, 3 and 4. Similarly, the state combinations of the two systems can be derived when the states $\left|{\chi }_2\right.〉$, $\left|{\chi }_3\right.〉$ and $\left|{\chi }_4\right.〉$ are obtained, respectively, which will not be repeated here.

Joint state	Combinations of the states of two subsystems
$\left|{\chi }_1\right.〉$	1       $\left\{\left|u_1\right.〉,\left|u_2\right.〉\right\}$ or $\left\{\left|{\overline{u}}_1\right.〉,\left|{\overline{u}}_2\right.〉\right)$
	2       $\left\{\left|u_1\right.〉,\left|u_2\right.〉\right\}$ or $\left\{-\left|{\overline{u}}_1\right.〉,-\left|{\overline{u}}_2\right.〉\right\}$
	3       $\left\{-\left|u_1\right.〉,-\left|u_2\right.〉\right\}$ or $\left\{-\left|{\overline{u}}_1\right.〉,-\left|{\overline{u}}_2\right.〉\right\}$
	4       $\left\{-\left|u_1\right.〉,-\left|u_2\right.〉\right\}$ or $\left\{\left|{\overline{u}}_1\right.〉,\left|{\overline{u}}_2\right.〉\right\}$

Joint state	Combinations of the states of two subsystems
$\left|{\chi }_1\right.〉$	1       $\left\{\left|u_1\right.〉,\left|u_2\right.〉\right\}$ or $\left\{\left|{\overline{u}}_1\right.〉,\left|{\overline{u}}_2\right.〉\right)$
	2       $\left\{\left|u_1\right.〉,\left|u_2\right.〉\right\}$ or $\left\{-\left|{\overline{u}}_1\right.〉,-\left|{\overline{u}}_2\right.〉\right\}$
	3       $\left\{-\left|u_1\right.〉,-\left|u_2\right.〉\right\}$ or $\left\{-\left|{\overline{u}}_1\right.〉,-\left|{\overline{u}}_2\right.〉\right\}$
	4       $\left\{-\left|u_1\right.〉,-\left|u_2\right.〉\right\}$ or $\left\{\left|{\overline{u}}_1\right.〉,\left|{\overline{u}}_2\right.〉\right\}$

In what follows, let us introduce the new algorithm for deriving entanglement swapping results. For simplicity, we would only like to consider the entanglement swapping between two composite system each containing two systems. Of course, the algorithm is also applicable to multi-particle systems, since multi-particle systems are just the generalization of two-particle systems. Let us assume there are two two-particle systems that are independent of the external environment and each other. Without loss of generality, let us represent the two systems as ${\left|{\mathcal{A}}^{\pm }\right.〉}_{1,2}$ and ${\left|{\mathcal{B}}^{\pm }\right.〉}_{3,4}$, respectively, which are given by

$$\begin{array}{c}\hfill {\left|{\mathcal{A}}^{\pm }\right.〉}_{1,2}={\displaystyle \frac{1}{\sqrt{2}}}\left|a_1{a}_2\right.〉\pm {\displaystyle \frac{1}{\sqrt{2}}}\left|{\overline{a}}_1{\overline{a}}_2\right.〉,\\ \hfill {\left|{\mathcal{B}}^{\pm }\right.〉}_{3,4}={\displaystyle \frac{1}{\sqrt{2}}}\left|b_1{b}_2\right.〉\pm {\displaystyle \frac{1}{\sqrt{2}}}\left|{\overline{b}}_1{\overline{b}}_2\right.〉.\end{array}$$

(19)

Note here that we only care about the results of entanglement swapping, thus we ignore $-{\left|{\mathcal{A}}^{\pm }\right.〉}_{1,2}$ and $-{\left|{\mathcal{B}}^{\pm }\right.〉}_{3,4}$. Let us further assume that the first particle in both ${\left|{\mathcal{A}}^{\pm }\right.〉}_{3,4}$ and ${\left|{\mathcal{B}}^{\pm }\right.〉}_{1,2}$ is observed simultaneously, and the observation result is denoted as ${\mathcal{M}}_1$, while the state that the remaining subsystems collapse onto is denoted as ${\mathcal{M}}_2$. In addition, we use the symbol $\mathcal{S}$ to represent the combinations of the states of the two particles. Indeed, the entanglement swapping between ${\left|{\mathcal{A}}^{\pm }\right.〉}_{1,2}$ and ${\left|{\mathcal{B}}^{\pm }\right.〉}_{3,4}$ include four cases: $\left\{{\left|{\mathcal{A}}^{+}\right.〉}_{1,2},{\left|{\mathcal{B}}^{+}\right.〉}_{3,4}\right\}$, $\left\{{\left|{\mathcal{A}}^{+}\right.〉}_{1,2},{\left|{\mathcal{B}}^{-}\right.〉}_{3,4}\right\}$, $\left\{{\left|{\mathcal{A}}^{-}\right.〉}_{1,2},{\left|{\mathcal{B}}^{+}\right.〉}_{3,4}\right\}$, and $\left\{{\left|{\mathcal{A}}^{-}\right.〉}_{1,2},{\left|{\mathcal{B}}^{-}\right.〉}_{3,4}\right\}$. For the first case, all the possible states of the particles and the corresponding observation results are listed in the four sub-tables in Table 2 (Note that for the sake of simplicity, unnecessary coefficients are ignored in the table.)

Table 2. States of particles and observation results

(a)			(b)
$\mathcal{S}$	${\mathcal{M}}_1$	${\mathcal{M}}_2$	$\mathcal{S}$	${\mathcal{M}}_1$	${\mathcal{M}}_2$
$\left\{\left|a_1\right.〉,\left|a_2\right.〉\right\}$	$\left|a_1\right.〉\left|b_1\right.〉$	$\left|a_2\right.〉\left|b_2\right.〉$	$\left\{\left|a_1\right.〉,\left|a_2\right.〉\right\}$	$\left|a_1\right.〉\left|b_1\right.〉$	$\left|a_2\right.〉\left|b_2\right.〉$
$\left\{\left|{\overline{a}}_1\right.〉,\left|{\overline{a}}_2\right.〉\right\}$	$\left|a_1\right.〉\left|{\overline{b}}_1\right.〉$	$\left|a_2\right.〉\left|{\overline{b}}_2\right.〉$	$\left\{\left|{\overline{a}}_1\right.〉,\left|{\overline{a}}_2\right.〉\right\}$	$-\left|a_1\right.〉\left|{\overline{b}}_1\right.〉$	$-\left|a_2\right.〉\left|{\overline{b}}_2\right.〉$
$\left\{\left|b_1\right.〉,\left|b_2\right.〉\right\}$	$\left|{\overline{a}}_1\right.〉\left|b_1\right.〉$	$\left|{\overline{a}}_2\right.〉\left|b_2\right.〉$	$\left\{\left|b_1\right.〉,\left|b_2\right.〉\right\}$	$\left|{\overline{a}}_1\right.〉\left|b_1\right.〉$	$\left|{\overline{a}}_2\right.〉\left|b_2\right.〉$
$\left\{\left|{\overline{b}}_1\right.〉,\left|{\overline{b}}_2\right.〉\right\}$	$\left|{\overline{a}}_1\right.〉\left|{\overline{b}}_1\right.〉$	$\left|{\overline{a}}_2\right.〉\left|{\overline{b}}_2\right.〉$	$\left\{-\left|{\overline{b}}_1\right.〉,-\left|{\overline{b}}_2\right.〉\right\}$	$-\left|{\overline{a}}_1\right.〉\left|{\overline{b}}_1\right.〉$	$-\left|{\overline{a}}_2\right.〉\left|{\overline{b}}_2\right.〉$
(c)			(d)
$\mathcal{S}$	${\mathcal{M}}_1$	${\mathcal{M}}_2$	$\mathcal{S}$	${\mathcal{M}}_1$	${\mathcal{M}}_2$
$\left\{\left|a_1\right.〉,\left|a_2\right.〉\right\}$	$\left|a_1\right.〉\left|b_1\right.〉$	$\left|a_2\right.〉\left|b_2\right.〉$	$\left\{\left|a_1\right.〉,\left|a_2\right.〉\right\}$	$\left|a_1\right.〉\left|b_1\right.〉$	$\left|a_2\right.〉\left|b_2\right.〉$
$\left\{-\left|{\overline{a}}_1\right.〉,-\left|{\overline{a}}_2\right.〉\right\}$	$\left|a_1\right.〉\left|{\overline{b}}_1\right.〉$	$\left|a_2\right.〉\left|{\overline{b}}_2\right.〉$	$\left\{-\left|{\overline{a}}_1\right.〉,-\left|{\overline{a}}_2\right.〉\right\}$	$-\left|a_1\right.〉\left|{\overline{b}}_1\right.〉$	$-\left|a_2\right.〉\left|{\overline{b}}_2\right.〉$
$\left\{\left|b_1\right.〉,\left|b_2\right.〉\right\}$	$-\left|{\overline{a}}_1\right.〉\left|b_1\right.〉$	$-\left|{\overline{a}}_2\right.〉\left|b_2\right.〉$	$\left\{\left|b_1\right.〉,\left|b_2\right.〉\right\}$	$-\left|{\overline{a}}_1\right.〉\left|b_1\right.〉$	$-\left|{\overline{a}}_2\right.〉\left|b_2\right.〉$
$\left\{\left|{\overline{b}}_1\right.〉,\left|{\overline{b}}_2\right.〉\right\}$	$-\left|{\overline{a}}_1\right.〉\left|{\overline{b}}_1\right.〉$	$-\left|{\overline{a}}_2\right.〉\left|{\overline{b}}_2\right.〉$	$\left\{-\left|{\overline{b}}_1\right.〉,-\left|{\overline{b}}_2\right.〉\right\}$	$\left|{\overline{a}}_1\right.〉\left|{\overline{b}}_1\right.〉$	$\left|{\overline{a}}_2\right.〉\left|{\overline{b}}_2\right.〉$

Table 2. States of particles and observation results

(a)			(b)
$\mathcal{S}$	${\mathcal{M}}_1$	${\mathcal{M}}_2$	$\mathcal{S}$	${\mathcal{M}}_1$	${\mathcal{M}}_2$
$\left\{\left|a_1\right.〉,\left|a_2\right.〉\right\}$	$\left|a_1\right.〉\left|b_1\right.〉$	$\left|a_2\right.〉\left|b_2\right.〉$	$\left\{\left|a_1\right.〉,\left|a_2\right.〉\right\}$	$\left|a_1\right.〉\left|b_1\right.〉$	$\left|a_2\right.〉\left|b_2\right.〉$
$\left\{\left|{\overline{a}}_1\right.〉,\left|{\overline{a}}_2\right.〉\right\}$	$\left|a_1\right.〉\left|{\overline{b}}_1\right.〉$	$\left|a_2\right.〉\left|{\overline{b}}_2\right.〉$	$\left\{\left|{\overline{a}}_1\right.〉,\left|{\overline{a}}_2\right.〉\right\}$	$-\left|a_1\right.〉\left|{\overline{b}}_1\right.〉$	$-\left|a_2\right.〉\left|{\overline{b}}_2\right.〉$
$\left\{\left|b_1\right.〉,\left|b_2\right.〉\right\}$	$\left|{\overline{a}}_1\right.〉\left|b_1\right.〉$	$\left|{\overline{a}}_2\right.〉\left|b_2\right.〉$	$\left\{\left|b_1\right.〉,\left|b_2\right.〉\right\}$	$\left|{\overline{a}}_1\right.〉\left|b_1\right.〉$	$\left|{\overline{a}}_2\right.〉\left|b_2\right.〉$
$\left\{\left|{\overline{b}}_1\right.〉,\left|{\overline{b}}_2\right.〉\right\}$	$\left|{\overline{a}}_1\right.〉\left|{\overline{b}}_1\right.〉$	$\left|{\overline{a}}_2\right.〉\left|{\overline{b}}_2\right.〉$	$\left\{-\left|{\overline{b}}_1\right.〉,-\left|{\overline{b}}_2\right.〉\right\}$	$-\left|{\overline{a}}_1\right.〉\left|{\overline{b}}_1\right.〉$	$-\left|{\overline{a}}_2\right.〉\left|{\overline{b}}_2\right.〉$
(c)			(d)
$\mathcal{S}$	${\mathcal{M}}_1$	${\mathcal{M}}_2$	$\mathcal{S}$	${\mathcal{M}}_1$	${\mathcal{M}}_2$
$\left\{\left|a_1\right.〉,\left|a_2\right.〉\right\}$	$\left|a_1\right.〉\left|b_1\right.〉$	$\left|a_2\right.〉\left|b_2\right.〉$	$\left\{\left|a_1\right.〉,\left|a_2\right.〉\right\}$	$\left|a_1\right.〉\left|b_1\right.〉$	$\left|a_2\right.〉\left|b_2\right.〉$
$\left\{-\left|{\overline{a}}_1\right.〉,-\left|{\overline{a}}_2\right.〉\right\}$	$\left|a_1\right.〉\left|{\overline{b}}_1\right.〉$	$\left|a_2\right.〉\left|{\overline{b}}_2\right.〉$	$\left\{-\left|{\overline{a}}_1\right.〉,-\left|{\overline{a}}_2\right.〉\right\}$	$-\left|a_1\right.〉\left|{\overline{b}}_1\right.〉$	$-\left|a_2\right.〉\left|{\overline{b}}_2\right.〉$
$\left\{\left|b_1\right.〉,\left|b_2\right.〉\right\}$	$-\left|{\overline{a}}_1\right.〉\left|b_1\right.〉$	$-\left|{\overline{a}}_2\right.〉\left|b_2\right.〉$	$\left\{\left|b_1\right.〉,\left|b_2\right.〉\right\}$	$-\left|{\overline{a}}_1\right.〉\left|b_1\right.〉$	$-\left|{\overline{a}}_2\right.〉\left|b_2\right.〉$
$\left\{\left|{\overline{b}}_1\right.〉,\left|{\overline{b}}_2\right.〉\right\}$	$-\left|{\overline{a}}_1\right.〉\left|{\overline{b}}_1\right.〉$	$-\left|{\overline{a}}_2\right.〉\left|{\overline{b}}_2\right.〉$	$\left\{-\left|{\overline{b}}_1\right.〉,-\left|{\overline{b}}_2\right.〉\right\}$	$\left|{\overline{a}}_1\right.〉\left|{\overline{b}}_1\right.〉$	$\left|{\overline{a}}_2\right.〉\left|{\overline{b}}_2\right.〉$

From the four sub-tables, we can summarize the following corresponding relationships:

$$\begin{array}{ccc}\hfill \left(a\right)& \left\{\begin{array}{c}\left(\left|a_1{b}_1\right.〉+\left|{\overline{a}}_1{\overline{b}}_1\right.〉,\left|a_2{b}_2\right.〉+\left|{\overline{a}}_2{\overline{b}}_2\right.〉\right),\hfill \\ \left(\left|a_1{\overline{b}}_1\right.〉+\left|{\overline{a}}_1{b}_1\right.〉,\left|a_2{\overline{b}}_2\right.〉+\left|{\overline{a}}_2{b}_2\right.〉\right),\hfill \end{array}\right.\left(b\right)\hfill & \hfill \left\{\begin{array}{c}\left(\left|a_1{b}_1\right.〉-\left|{\overline{a}}_1{\overline{b}}_1\right.〉,\left|a_2{b}_2\right.〉-\left|{\overline{a}}_2{\overline{b}}_2\right.〉\right),\hfill \\ \left(-\left|a_1{\overline{b}}_1\right.〉+\left|{\overline{a}}_1{b}_1\right.〉,-\left|a_2{\overline{b}}_2\right.〉+\left|{\overline{a}}_2{b}_2\right.〉\right),\hfill \end{array}\right.\\ \hfill \left(c\right)& \left\{\begin{array}{c}\left(\left|a_1{b}_1\right.〉-\left|{\overline{a}}_1{\overline{b}}_1\right.〉,\left|a_2{b}_2\right.〉-\left|{\overline{a}}_2{\overline{b}}_2\right.〉\right),\hfill \\ \left(\left|a_1{\overline{b}}_1\right.〉-\left|{\overline{a}}_1{b}_1\right.〉,\left|a_2{\overline{b}}_2\right.〉-\left|{\overline{a}}_2{b}_2\right.〉\right),\hfill \end{array}\right.\left(d\right)\hfill & \hfill \left\{\begin{array}{c}\left(\left|a_1{b}_1\right.〉+\left|{\overline{a}}_1{\overline{b}}_1\right.〉,\left|a_2{b}_2\right.〉+\left|{\overline{a}}_2{\overline{b}}_2\right.〉\right),\hfill \\ \left(-\left|a_1{\overline{b}}_1\right.〉-\left|{\overline{a}}_1{b}_1\right.〉,-\left|a_2{\overline{b}}_2\right.〉-\left|{\overline{a}}_2{b}_2\right.〉\right),\hfill \end{array}\right.\end{array}$$

(20)

then we can get the result of the entanglement swapping between ${\left|{\mathcal{A}}^{+}\right.〉}_{1,2}$ and ${\left|{\mathcal{B}}^{+}\right.〉}_{3,4}$,

$$\begin{array}{cc}\hfill {\left|{\mathcal{A}}^{+}\right.〉}_{1,2}\otimes {\left|{\mathcal{B}}^{+}\right.〉}_{3,4}⟶& \left(\left|a_1{b}_1\right.〉+\left|{\overline{a}}_1{\overline{b}}_1\right.〉\right)\otimes \left(\left|a_2{b}_2\right.〉+\left|{\overline{a}}_2{\overline{b}}_2\right.〉\right)\hfill \\ \hfill +& \left(\left|a_1{\overline{b}}_1\right.〉+\left|{\overline{a}}_1{b}_1\right.〉\right)\otimes \left(\left|a_2{\overline{b}}_2\right.〉+\left|{\overline{a}}_2{b}_2\right.〉\right)\hfill \\ \hfill +& \left(\left|a_1{b}_1\right.〉-\left|{\overline{a}}_1{\overline{b}}_1\right.〉\right)\otimes \left(\left|a_2{b}_2\right.〉-\left|{\overline{a}}_2{\overline{b}}_2\right.〉\right)\hfill \\ \hfill +& \left(\left|a_1{\overline{b}}_1\right.〉-\left|{\overline{a}}_1{b}_1\right.〉\right)\otimes \left(\left|a_2{\overline{b}}_2\right.〉-\left|{\overline{a}}_2{b}_2\right.〉\right).\hfill \end{array}$$

(21)

In a similar way, we can further obtain the results for other entangled swapping cases, which are given by

$$\begin{array}{cc}\hfill {\left|{\mathcal{A}}^{+}\right.〉}_{1,2}\otimes {\left|{\mathcal{B}}^{-}\right.〉}_{3,4}⟶& \left(\left|a_1{b}_1\right.〉+\left|{\overline{a}}_1{\overline{b}}_1\right.〉\right)\otimes \left(\left|a_2{b}_2\right.〉-\left|{\overline{a}}_2{\overline{b}}_2\right.〉\right)\hfill \\ \hfill -& \left(\left|a_1{\overline{b}}_1\right.〉+\left|{\overline{a}}_1{b}_1\right.〉\right)\otimes \left(\left|a_2{\overline{b}}_2\right.〉-\left|{\overline{a}}_2{b}_2\right.〉\right)\hfill \\ \hfill +& \left(\left|a_1{b}_1\right.〉-\left|{\overline{a}}_1{\overline{b}}_1\right.〉\right)\otimes \left(\left|a_2{b}_2\right.〉+\left|{\overline{a}}_2{\overline{b}}_2\right.〉\right)\hfill \\ \hfill -& \left(\left|a_1{\overline{b}}_1\right.〉-\left|{\overline{a}}_1{b}_1\right.〉\right)\otimes \left(\left|a_2{\overline{b}}_2\right.〉+\left|{\overline{a}}_2{b}_2\right.〉\right),\hfill \end{array}$$

(22)

$$\begin{array}{cc}\hfill {\left|{\mathcal{A}}^{-}\right.〉}_{1,2}\otimes {\left|{\mathcal{B}}^{+}\right.〉}_{3,4}⟶& \left(\left|a_1{b}_1\right.〉+\left|{\overline{a}}_1{\overline{b}}_1\right.〉\right)\otimes \left(\left|a_2{b}_2\right.〉-\left|{\overline{a}}_2{\overline{b}}_2\right.〉\right)\hfill \\ \hfill +& \left(\left|a_1{\overline{b}}_1\right.〉+\left|{\overline{a}}_1{b}_1\right.〉\right)\otimes \left(\left|a_2{\overline{b}}_2\right.〉-\left|{\overline{a}}_2{b}_2\right.〉\right)\hfill \\ \hfill +& \left(\left|a_1{b}_1\right.〉-\left|{\overline{a}}_1{\overline{b}}_1\right.〉\right)\otimes \left(\left|a_2{b}_2\right.〉+\left|{\overline{a}}_2{\overline{b}}_2\right.〉\right)\hfill \\ \hfill +& \left(\left|a_1{\overline{b}}_1\right.〉-\left|{\overline{a}}_1{b}_1\right.〉\right)\otimes \left(\left|a_2{\overline{b}}_2\right.〉+\left|{\overline{a}}_2{b}_2\right.〉\right),\hfill \end{array}$$

(23)

$$\begin{array}{cc}\hfill {\left|{\mathcal{A}}^{-}\right.〉}_{1,2}\otimes {\left|{\mathcal{B}}^{-}\right.〉}_{3,4}⟶& \left(\left|a_1{b}_1\right.〉+\left|{\overline{a}}_1{\overline{b}}_1\right.〉\right)\otimes \left(\left|a_2{b}_2\right.〉+\left|{\overline{a}}_2{\overline{b}}_2\right.〉\right)\hfill \\ \hfill -& \left(\left|a_1{\overline{b}}_1\right.〉+\left|{\overline{a}}_1{b}_1\right.〉\right)\otimes \left(\left|a_2{\overline{b}}_2\right.〉+\left|{\overline{a}}_2{b}_2\right.〉\right)\hfill \\ \hfill +& \left(\left|a_1{b}_1\right.〉-\left|{\overline{a}}_1{\overline{b}}_1\right.〉\right)\otimes \left(\left|a_2{b}_2\right.〉-\left|{\overline{a}}_2{\overline{b}}_2\right.〉\right)\hfill \\ \hfill -& \left(\left|a_1{\overline{b}}_1\right.〉-\left|{\overline{a}}_1{b}_1\right.〉\right)\otimes \left(\left|a_2{\overline{b}}_2\right.〉-\left|{\overline{a}}_2{b}_2\right.〉\right),\hfill \end{array}$$

(24)

Let $a_1,{\overline{a}}_1,a_2,{\overline{a}}_2,b_1,{\overline{b}}_1,b_2,{\overline{b}}_2\in \left\{0,1\right\}$, one can get the entanglement swapping between the Bell states, given by

$$\begin{array}{c}{\left|{\varphi }^{+}\right.〉}_{1,2}\otimes {\left|{\varphi }^{+}\right.〉}_{3,4}\to {\left|{\varphi }^{+}\right.〉}_{1,3}\otimes {\left|{\varphi }^{+}\right.〉}_{2,4}+{\left|{\varphi }^{-}\right.〉}_{1,3}\otimes {\left|{\varphi }^{-}\right.〉}_{2,4}+{\left|{\psi }^{+}\right.〉}_{1,3}\otimes {\left|{\psi }^{+}\right.〉}_{2,4}+{\left|{\psi }^{-}\right.〉}_{1,3}\otimes {\left|{\psi }^{-}\right.〉}_{2,4},\end{array}$$

(25a)

$$\begin{array}{c}{\left|{\varphi }^{+}\right.〉}_{1,2}\otimes {\left|{\psi }^{+}\right.〉}_{3,4}\to {\left|{\varphi }^{+}\right.〉}_{1,3}\otimes {\left|{\psi }^{+}\right.〉}_{2,4}+{\left|{\psi }^{+}\right.〉}_{1,3}\otimes {\left|{\varphi }^{+}\right.〉}_{2,4}+{\left|{\varphi }^{-}\right.〉}_{1,3}\otimes {\left|{\psi }^{-}\right.〉}_{2,4}+{\left|{\psi }^{-}\right.〉}_{1,3}\otimes {\left|{\varphi }^{-}\right.〉}_{2,4},\end{array}$$

(25b)

$$\begin{array}{c}{\left|{\psi }^{+}\right.〉}_{1,2}\otimes {\left|{\varphi }^{+}\right.〉}_{3,4}\to {\left|{\varphi }^{+}\right.〉}_{1,3}\otimes {\left|{\psi }^{+}\right.〉}_{2,4}+{\left|{\psi }^{+}\right.〉}_{1,3}\otimes {\left|{\varphi }^{+}\right.〉}_{2,4}-{\left|{\varphi }^{-}\right.〉}_{1,3}\otimes {\left|{\psi }^{-}\right.〉}_{2,4}-{\left|{\psi }^{-}\right.〉}_{1,3}\otimes {\left|{\varphi }^{-}\right.〉}_{2,4},\end{array}$$

(25c)

$$\begin{array}{c}{\left|{\psi }^{+}\right.〉}_{1,2}\otimes {\left|{\psi }^{+}\right.〉}_{3,4}\to {\left|{\varphi }^{+}\right.〉}_{1,3}\otimes {\left|{\varphi }^{+}\right.〉}_{2,4}+{\left|{\psi }^{+}\right.〉}_{1,3}\otimes {\left|{\psi }^{+}\right.〉}_{2,4}-{\left|{\varphi }^{-}\right.〉}_{1,3}\otimes {\left|{\varphi }^{-}\right.〉}_{2,4}-{\left|{\psi }^{-}\right.〉}_{1,3}\otimes {\left|{\psi }^{-}\right.〉}_{2,4},\end{array}$$

(25d)

$$\begin{array}{cc}\hfill & {\left|{\varphi }^{+}\right.〉}_{1,2}\otimes {\left|{\varphi }^{-}\right.〉}_{3,4}\to {\left|{\varphi }^{+}\right.〉}_{1,3}\otimes {\left|{\varphi }^{-}\right.〉}_{2,4}+{\left|{\varphi }^{-}\right.〉}_{1,3}\otimes {\left|{\varphi }^{+}\right.〉}_{2,4}-{\left|{\psi }^{+}\right.〉}_{1,3}\otimes {\left|{\psi }^{-}\right.〉}_{2,4}-{\left|{\psi }^{-}\right.〉}_{1,3}\otimes {\left|{\psi }^{+}\right.〉}_{2,4},\hfill \end{array}$$

(26a)

$$\begin{array}{cc}\hfill & {\left|{\varphi }^{+}\right.〉}_{1,2}\otimes {\left|{\psi }^{-}\right.〉}_{3,4}\to {\left|{\varphi }^{+}\right.〉}_{1,3}\otimes {\left|{\psi }^{-}\right.〉}_{2,4}-{\left|{\psi }^{+}\right.〉}_{1,3}\otimes {\left|{\varphi }^{-}\right.〉}_{2,4}+{\left|{\varphi }^{-}\right.〉}_{1,3}\otimes {\left|{\psi }^{+}\right.〉}_{2,4}-{\left|{\psi }^{-}\right.〉}_{1,3}\otimes {\left|{\varphi }^{+}\right.〉}_{2,4},\hfill \end{array}$$

(26b)

$$\begin{array}{cc}\hfill & {\left|{\psi }^{+}\right.〉}_{1,2}\otimes {\left|{\varphi }^{-}\right.〉}_{3,4}\to -{\left|{\varphi }^{+}\right.〉}_{1,3}\otimes {\left|{\varphi }^{-}\right.〉}_{2,4}+{\left|{\psi }^{+}\right.〉}_{1,3}\otimes {\left|{\varphi }^{-}\right.〉}_{2,4}+{\left|{\varphi }^{-}\right.〉}_{1,3}\otimes {\left|{\psi }^{+}\right.〉}_{2,4}-{\left|{\psi }^{-}\right.〉}_{1,3}\otimes {\left|{\varphi }^{+}\right.〉}_{2,4},\hfill \end{array}$$

(26c)

$$\begin{array}{cc}\hfill & {\left|{\psi }^{+}\right.〉}_{1,2}\otimes {\left|{\psi }^{-}\right.〉}_{3,4}\to -{\left|{\varphi }^{+}\right.〉}_{1,3}\otimes {\left|{\varphi }^{-}\right.〉}_{2,4}+{\left|{\psi }^{+}\right.〉}_{1,3}\otimes {\left|{\psi }^{-}\right.〉}_{2,4}+{\left|{\varphi }^{-}\right.〉}_{1,3}\otimes {\left|{\varphi }^{+}\right.〉}_{2,4}-{\left|{\psi }^{-}\right.〉}_{1,3}\otimes {\left|{\psi }^{+}\right.〉}_{2,4},\hfill \end{array}$$

(26d)

$$\begin{array}{cc}\hfill & {\left|{\varphi }^{-}\right.〉}_{1,2}\otimes {\left|{\varphi }^{+}\right.〉}_{3,4}\to {\left|{\varphi }^{+}\right.〉}_{1,3}\otimes {\left|{\varphi }^{-}\right.〉}_{2,4}+{\left|{\psi }^{+}\right.〉}_{1,3}\otimes {\left|{\psi }^{-}\right.〉}_{2,4}+{\left|{\varphi }^{-}\right.〉}_{1,3}\otimes {\left|{\varphi }^{+}\right.〉}_{2,4}+{\left|{\psi }^{-}\right.〉}_{1,3}\otimes {\left|{\psi }^{+}\right.〉}_{2,4},\hfill \end{array}$$

(27a)

$$\begin{array}{cc}\hfill & {\left|{\varphi }^{-}\right.〉}_{1,2}\otimes {\left|{\psi }^{+}\right.〉}_{3,4}\to {\left|{\varphi }^{+}\right.〉}_{1,3}\otimes {\left|{\psi }^{-}\right.〉}_{2,4}+{\left|{\psi }^{+}\right.〉}_{1,3}\otimes {\left|{\varphi }^{-}\right.〉}_{2,4}+{\left|{\varphi }^{-}\right.〉}_{1,3}\otimes {\left|{\psi }^{+}\right.〉}_{2,4}+{\left|{\psi }^{-}\right.〉}_{1,3}\otimes {\left|{\varphi }^{+}\right.〉}_{2,4},\hfill \end{array}$$

(27b)

$$\begin{array}{cc}\hfill & {\left|{\psi }^{-}\right.〉}_{1,2}\otimes {\left|{\varphi }^{+}\right.〉}_{3,4}\to -{\left|{\varphi }^{+}\right.〉}_{1,3}\otimes {\left|{\psi }^{-}\right.〉}_{2,4}-{\left|{\psi }^{+}\right.〉}_{1,3}\otimes {\left|{\varphi }^{-}\right.〉}_{2,4}+{\left|{\varphi }^{-}\right.〉}_{1,3}\otimes {\left|{\psi }^{+}\right.〉}_{2,4}+{\left|{\psi }^{-}\right.〉}_{1,3}\otimes {\left|{\varphi }^{+}\right.〉}_{2,4},\hfill \end{array}$$

(27c)

$$\begin{array}{cc}\hfill & {\left|{\psi }^{-}\right.〉}_{1,2}\otimes {\left|{\psi }^{+}\right.〉}_{3,4}\to -{\left|{\varphi }^{+}\right.〉}_{1,3}\otimes {\left|{\varphi }^{-}\right.〉}_{2,4}-{\left|{\psi }^{+}\right.〉}_{1,3}\otimes {\left|{\psi }^{-}\right.〉}_{2,4}+{\left|{\varphi }^{-}\right.〉}_{1,3}\otimes {\left|{\varphi }^{+}\right.〉}_{2,4}+{\left|{\psi }^{-}\right.〉}_{1,3}\otimes {\left|{\psi }^{+}\right.〉}_{2,4},\hfill \end{array}$$

(27d)

$$\begin{array}{cc}\hfill & {\left|{\varphi }^{-}\right.〉}_{1,2}\otimes {\left|{\varphi }^{-}\right.〉}_{3,4}\to {\left|{\varphi }^{+}\right.〉}_{1,3}\otimes {\left|{\varphi }^{+}\right.〉}_{2,4}-{\left|{\psi }^{+}\right.〉}_{1,3}\otimes {\left|{\psi }^{+}\right.〉}_{2,4}+{\left|{\varphi }^{-}\right.〉}_{1,3}\otimes {\left|{\varphi }^{-}\right.〉}_{2,4}-{\left|{\psi }^{-}\right.〉}_{1,3}\otimes {\left|{\psi }^{-}\right.〉}_{2,4},\hfill \end{array}$$

(28a)

$$\begin{array}{cc}\hfill & {\left|{\varphi }^{-}\right.〉}_{1,2}\otimes {\left|{\psi }^{-}\right.〉}_{3,4}\to {\left|{\varphi }^{+}\right.〉}_{1,3}\otimes {\left|{\psi }^{+}\right.〉}_{2,4}-{\left|{\psi }^{+}\right.〉}_{1,3}\otimes {\left|{\varphi }^{+}\right.〉}_{2,4}+{\left|{\varphi }^{-}\right.〉}_{1,3}\otimes {\left|{\psi }^{-}\right.〉}_{2,4}-{\left|{\psi }^{-}\right.〉}_{1,3}\otimes {\left|{\varphi }^{-}\right.〉}_{2,4},\hfill \end{array}$$

(28b)

$$\begin{array}{cc}\hfill & {\left|{\psi }^{-}\right.〉}_{1,2}\otimes {\left|{\varphi }^{-}\right.〉}_{3,4}\to {\left|{\varphi }^{+}\right.〉}_{1,3}\otimes {\left|{\psi }^{+}\right.〉}_{2,4}-{\left|{\psi }^{+}\right.〉}_{1,3}\otimes {\left|{\varphi }^{+}\right.〉}_{2,4}-{\left|{\varphi }^{-}\right.〉}_{1,3}\otimes {\left|{\psi }^{-}\right.〉}_{2,4}+{\left|{\psi }^{-}\right.〉}_{1,3}\otimes {\left|{\varphi }^{-}\right.〉}_{2,4},\hfill \end{array}$$

(28c)

$$\begin{array}{cc}\hfill & {\left|{\psi }^{-}\right.〉}_{1,2}\otimes {\left|{\psi }^{-}\right.〉}_{3,4}\to {\left|{\varphi }^{+}\right.〉}_{1,3}\otimes {\left|{\varphi }^{+}\right.〉}_{2,4}-{\left|{\psi }^{+}\right.〉}_{1,3}\otimes {\left|{\psi }^{+}\right.〉}_{2,4}-{\left|{\varphi }^{-}\right.〉}_{1,3}\otimes {\left|{\varphi }^{-}\right.〉}_{2,4}+{\left|{\psi }^{-}\right.〉}_{1,3}\otimes {\left|{\psi }^{-}\right.〉}_{2,4},\hfill \end{array}$$

(28d)

The cases shown in Eqs. (25a, 25d, 28a, 28d) are included in Eq. 3a. Furthermore, Eqs. (26a, 26d, 27a, 27d) are included in Eq. 3b. Eqs. (25b, 25c, 28b, 28c) are included in Eq. 3c. and Eqs. (26b, 26c, 27b, 27c) are included in Eq. 3d. It can be seen that the correctness of the proposed algorithm has been verified by comparing the calculation results.

4. Discussion

From the law of conservation of energy, one can know that energy is constantly transforming, which means that the positive and negative energy in the universe are constantly transforming into each other. Since the total energy is always zero, when a certain amount of positive energy is converted into negative energy, there will be an equal amount of negative energy converted into positive energy. In short, the two are opposites, coexisting, balanced, and constantly transform each other, which is completely consistent with the yin-yang theory in the I Ching (also called the “Book of Changes”): Yin and Yang are opposing, coexisting, balanced and mutually transforming, where Yin and Yang refer to two opposing things, respectively, including positive energy and negative energy, the wave and particle nature of light, good and bad, right and wrong, etc.

As mentioned above, the existence of Yin and Yang is due to local observations, that is, the existence of any two opposing matter is the result of local observations. If a holistic observation can be made, the result would be ’emptiness’ (’void’ or ’nothingness’). Due to the quantization of energy, we hold the opinion that the sense organs on human bodies are essentially quantum measuring instruments, while human beings are actually programmed, emotional, and self-aware “intelligent robots”, and our observations and judgments are based on the databases in the brain. Specifically, we measure the received energy through our physical senses (quantum measuring instruments), analyze and process the measurement results based on the data in our own database, and then make actions such as judgments or feedback.

In summary, through local observation of “emptiness”, the existence of infinite positive and negative energy can be observed, and it is believed that energy is transformed into countless and diverse substances, which is consistent with the statement of Tao Te Ching: all things in the world are born of existence, and existence is born of nothingness. People may ask: What is the state of “emptiness" and what force created it? In Tao Te Ching, it is stated that “Tao gives birth to one, one gives birth to two, two gives birth to three, and three gives birth to everything”. Therefore, the answer we find is that the “Tao” gives birth to “emptiness”. Here, “one” is “emptiness”, corresponding to the state $\left|\phi \right.〉$ in Eq. 10, while “two” refers to the positive and negative energy, plus the state after the fusion of positive and negative energy, there is “three”. Of course, the core theory in the Tao Te Ching is not limited to this, and here is just one of the explanations.

The Tao Te Ching states that the “Tao” is unknowable and unspeakable, and one possible important reason, we believe, is that humans are unable to observe the universe as a whole, that is, humans can only observe local parts of the universe and cannot see the whole picture. For example, if we live in a virtual world created for us by an infinitely large quantum computer with infinite computing power, we will never know what this computer looks like. In other words, the fundamental and eternal rules followed by the evolution of all things in the universe are unknowable and indescribable. On the contrary, the truth that can be explained clearly is definitely not eternal, as stated in Tao Te Ching: The principle that can be told is not the eternal principle. Of course, the portrayal of the fundamental laws of nature in this article is also ambiguous, which can be considered as the ignorance and arrogance of the authors.

5. Conclusion

We have proposed a new algorithm for obtaining entanglement swapping results and verified its correctness through entanglement swapping of two Bell states. In fact, the discovery and establishment of entangled states are derived from all possible observational results, which is the basic idea of our proposed algorithm. Our work provides new ideas and perspectives for studying the principles of quantum mechanics and exploring the mysteries of nature. Unfortunately, if the universe is seen as an entangled state containing countless subsystems, then one can only observe a small subset of all the subsystems but not the entire system, thus cannot know the truth. A very unsettling question is: Who formulated the fundamental rules that govern the operation of all things in the universe?