EEG Channel Selection Based on Time–Frequency Hellinger Distance

1. Introduction

Electroencephalography (EEG) has gained increasing attention in brain-computer interface (BCI) applications and clinical diagnostics due to its non-invasive nature and ability to capture real-time neural activity [1,2]. Despite these benefits, EEG signals are characteristically non-stationary and prone to various sources of noise, such as physiological artifacts and external electromagnetic interference. These challenges often lead to substantial variability in the recorded data, complicating the extraction of reliable features for classification or clinical interpretation.

Channel selection, a process of identifying the most informative subset of electrodes, has emerged as a key strategy for managing this complexity. By reducing the dimensionality of the data, channel selection not only streamlines computational overhead but can also enhance classification accuracy by excluding channels with predominantly noisy or irrelevant signals. Traditional approaches to channel selection rely on criteria such as mutual information or variance-based metrics; however, they may not be robust in capturing subtle changes in EEG signals’ spectral content or in handling highly non-stationary properties [3].

To address these gaps, this study proposes a novel pipeline centered on the Hellinger Distance computed over time-frequency representations (TFRs) of EEG. In abstract, we first transform raw EEG signals into the time-frequency domain utilizing Short-Time Fourier Transform (STFT) and Continuous Wavelet Transform (CWT). Then, we employ Hellinger Distance to perform two critical steps: automatic detection and removal of outlier epochs, and ranking and selection of the most informative channels based on their ability to discriminate between different classes or conditions. By leveraging Hellinger Distance for both noise mitigation and feature selection, our framework provides a unified approach to boosting classification performance.

2. Analysis

The overall goal is in two phase: first, to establish a procedure for detecting and eliminating noisy epochs that may adversely affect classification performance; and second, to identify a minimal, yet informative set of channels that maximizes discriminative power.

We begin by revisiting the core principles of time-frequency representations (Section 2.1), emphasizing the importance of capturing transient spectral fluctuations in EEG signals. Next, we introduce Hellinger Distance as a measure of distributional divergence (Section 2.2), illustrating its dual role in noise detection (Section 2.3) and channel selection (Section 2.4).

2.1. Time-Frequency Representation of EEG Signals

Let EEG signal be $x\in {\mathbb{R}}^{N\times C\times T}$, where N is the number of samples, C is the number of channels, and T is the number of timepoints, and $x\left(t\right)\in {\mathbb{R}}^{N\times C}$ be the signal where $time=t$.

As EEG signals are non-stationary, meaning its distribution varies over time, we analyze it by transforming it into a time-frequency domain to transient spectral features. By utilizing Short-Time Fourier Transform(STFT), Time-Frequency Representation(TFR) of a signal $X(t,f)$ can be calculated as

$$X(t,f)={\int }_{-\infty }^{\infty }x\left(\tau \right)w(\tau -t)e^{-j2\pi f\tau }d\tau$$

(1)

where $w(·)$ is the window function centered at time $\tau$ [2]. Analogous to STFT, Continuous Wavelet Transform(CWT) can be utilized by calculating

$$W(s,t)={\int }_{-\infty }^{\infty }x\left(u\right){\psi }_{s,t}\left(u\right)du,$$

(2)

where the wavelet function ${\psi }_{s,t}\left(x\right)\equiv {\displaystyle \frac{1}{\sqrt{s}}}{\psi }^{*}\left({\displaystyle \frac{x-t}{s}}\right)$. In this study, Morlet wavelet function was used, which is defined as

$$\psi \left(t\right)={\pi }^{-{\displaystyle \frac{1}{4}}}{e}^{-{\displaystyle \frac{1}{2}}{t}^2}{e}^{-j{\omega }_{0}t},$$

(3)

where ${\omega }_0$ is the central frequency and $\sigma$ controls the time spread. [4].

Continuous Wavelet Transform(CWT) can be utilized using $\psi \left(t\right)$ as

$$W(a,b)\equiv {\displaystyle \frac{1}{\sqrt{a}}}{\int }_{-\infty }^{\infty }x\left(t\right){\psi }^{*}\left({\displaystyle \frac{t-b}{a}}\right)dt,$$

(4)

where a is the inverse frequency and b is the time shift. [5]

2.2. Utilization of Hellinger Distance for Z-Score Calculation

Hellinger Distance is a measure of difference between two probability distributions. For two discrete distributions: $P=\left\{p_i\right\}$ and $Q=\left\{q_i\right\}$, Hellinger distance $H(P,Q)$ is defined as

$$H(P,Q)={\displaystyle \frac{1}{\sqrt{2}}}\sqrt{\sum _i{(\sqrt{p_i}-\sqrt{q_i})}^2}$$

(5)

In this study, Hellinger distance is utilized in two different ways: noise removal and channel selection.

2.3. Noise Removal

For calculating the z-score for each epoch, we calculate $H_i$. where $H_i=H(W_i,\overline{W_i})$ for each epoch i, where $\overline{W_i}$ represents overall average of $W_i$. This $H_i$ serves as a measure of how discriminative epoch i’s features are between conditions. By subtracting ${\mu }_H$, which is the average of $H_i$, and dividing with ${\sigma }_H$, which is the standard deviation of $H_i$, we get each epoch i’s Z-score:

$$Z_i={\displaystyle \frac{H_i-{\mu }_H}{{\sigma }_H}}$$

(6)

Epochs having large Z-score indicate how extreme the signal of each trial is compared to other epochs. Therefore, we assume epochs having high Z-score as outliers(in this case noise), and remove it.

Therefore, we can define $X^{*}$, which indicates non-noisy trials, as

$$X^{*}=\left\{X_i\right|Z_i<\alpha \},$$

(7)

where $X_i$ indicates the raw time-domain EEG data corresponding to the ith epoch.

2.4. Channel Selection

After removing noisy epochs, the most informative EEG channels classification is identified. The goal of this process is to retain channels that maximize class separability while discarding those that contribute redundant or noisy information. This is achieved by computing the Hellinger Distance between class-specific time-frequency representations (TFRs) of each EEG channel.

The TFR features extracted from each channel serve as probability distributions of spectral power. Let the normalized power spectrum of a channel c for class 1 and class 2 be represented as $P_c\left(f\right)$ and $Q_c\left(f\right)$, respectively. The Hellinger Distance for a given channel c is computed as:

$$H_c={\displaystyle \frac{1}{\sqrt{2}}}\sqrt{\sum _f{\left(\sqrt{P_c\left(f\right)}-\sqrt{Q_c\left(f\right)}\right)}^2}.$$

(8)

The computed Hellinger Distance $H_c$ for each channel provides a measure of how well the channel distinguishes between the two classes. A higher $H_c$ value indicates greater separability. To rank channels, we define the effect size $E_c$ as:

$$E_c=\underset{k\in class}{max}{H}_c(P_c^k,\overline{P_c}),$$

(9)

where $\overline{P_c}$ is the overall mean spectral distribution across all epochs. The channels are then sorted in descending order based on $E_c$.

3. Results

By [3], CSP based motor imagery classification algorithms can be enumerated as CSP, L1 Norm of CSP, SCSP, FBCSP, and E-CSP. The accuracy of each algorithm, including HD-CSP(Hellinger Distance CSP), is computed using the BCI competition IVa dataset, which is a publicly available dataset consisting of imagery of four classes: left hand movement, right hand movement, leg movement, and tongue movement [1], to evaluate HD-CSP’s performance. Each subject’s dataset is divided in 5-fold cross manner for evaluation and training. CSP filter is applied to transform the signal, and train an Support Vector Machine (SVM) classifier.

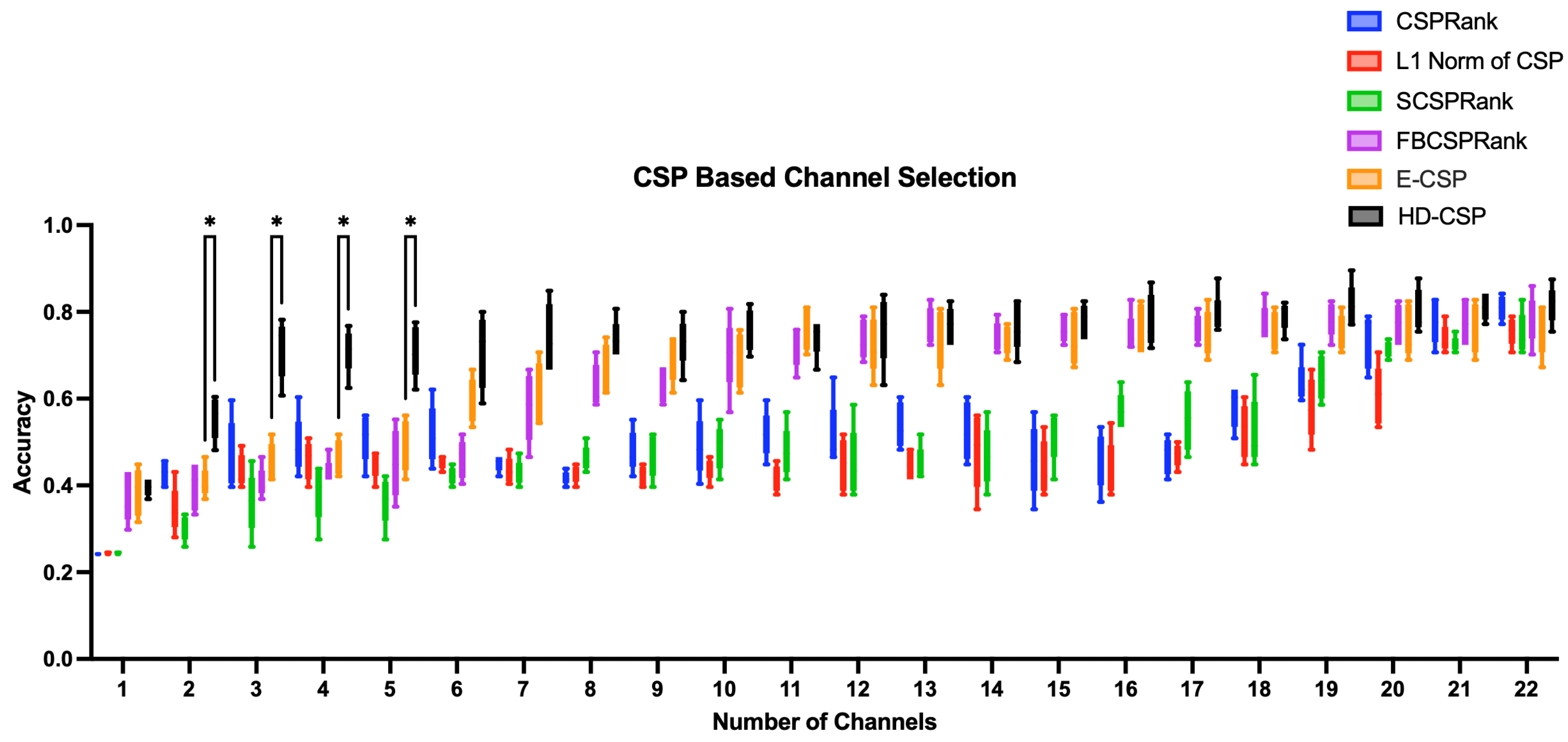
In our comparative evaluation of multiple variants of CSP (standard CSP, $L_1$ Norm CSP, SCSP, FBCSP, E-CSP, and HD-CSP) under different number of EEG channels (Table 1), HD-CSP consistently outperformed competing approaches in all tested conditions, except one case in 11 channel configuration. The results show that HD-CSP not only yields superior classification accuracy overall but also maintains a stable advantage across different channel counts (Figure 1).

Notably, in the most restrictive scenario of only three channels, HD-CSP still manages to reach around 70% classification accuracy. This outcome is particularly compelling because many methods suffer a significant drop in performance when the dimensionality of the EEG data is limited. Except for this model, the rest of the models show an accuracy of 36% - 46%. The robust performance of HD-CSP in this low-channel regime illustrates its suitability for practical applications where hardware or time constraints require the use of fewer electrodes.

Moreover, even as the number of channels increases, HD-CSP remains consistently superior. Its classification accuracy continues to surpass that of standard CSP, $L_1$ Norm CSP, SCSP, FBCSP, and E-CSP for all tested configurations, reaching accuracy of 80% in 19 channel configuration, which none of other models have reached. These findings highlight HD-CSP’s efficacy in balancing feature extraction quality and noise handling, suggesting it can serve as a strong default method for both minimal-channel and full-cap montage scenarios.