Biswas-Chatterjee-Sen model on Solomon Networks in (1 ≤ D ≤ 6)-Dimensional Lattices

1. Introduction

The critical properties of a system undergoing a second-order phase transition is strongly dependent on the dimension of the underlying lattice. In fact, the lattice dimension is one of the crucial factors to determine the universality class of a particular second-order phase transition (the other factors consist of the dimension of the order parameter and symmetry and range of the particle interactions). The renormalization group theory turned out to be a successful framework to understand the universal aspects of the critical phenomena from the knowledge of the basic microscopic interactions (see, for instance, Ref. [1] and references therein).

It is also well established in the literature that each system has its proper lower critical dimension $D_{\ell }$, below which there is no phase transition, and also an upper critical dimension $D_u$, above which the transition is governed by the mean-field exponents [2]. Of course, the upper critical dimension has only a theoretical interest, because $D_u$ is usually above the three-dimensional space of the physical sample realizations [3]. Just to cite some examples, we have $D_{\ell }=1$ and $D_u=4$ for the Ising model [1], $D_{\ell }=2$ and $D_u=4$ for the isotropic Heisenberg model [1], $D_{\ell }=2$[4] and $D_u=6$[5] for the Ising spin-glass system. More recently, it has been reported that $D_{\ell }=1$ and $D_u=6$ for the majority vote model on regular lattices [6].

The magnetic models cited above, defined on regular Bravais lattices, are well studied in the literature because they are in some sense easier to define, suitable to being simulated using different sort of computer algorithms, and with plenty physical realizations to be compared to. Nevertheless, magnetic models can as well be defined on scaling free lattices, like networks and specific graphs. In this case, however, it is not possible to assert, a priori, whether the system will or will not have a phase transition. Moreover, when a phase transition is present, one has to carefully investigate whether the transition is of first or second order. Some magnetic systems, like Ising, Potts and Blume-Capel models, have already been studied on some complex lattices comprising Appolonian, Barabási-Albert, Voronoi-Delauny and small-world networks [7].

There are also different sort of dynamical systems, not along the line of the magnetic ones, that are studied on regular lattices. In this case, the determination of the lower and upper dimensions turns to be a point of theoretical interest. For instance, an interesting result has been obtained for the majority vote model [8] through Monte Carlo simulations in several D-dimensional lattices [6]. It has been reported that the model do present an upper critical dimension $D_u=6$, despite for $D=2$ the majority vote model being in the same universality class as the Ising model (recall that $D_u=4$ of the Ising class).

In this work, we will address to the question of the upper critical dimension of the Biswas-Chatterjee-Sen (BChS) model, in its discrete version, and defined on Solomon networks (SNs). The BChS model is a complex system that takes into account the dynamics of opinions of its individual constituents [9,10,11]. Intrinsic in the system is the fact that the individuals in a community can not only influence their neighbors but be influenced by them as well. Accordingly, the individual opinion variables evolve according to pair interactions that are allowed to be positive or negative. The interaction signs are then modeled by a single noise probability q that represents the fraction of negative interactions. This noise probability plays a crucial role in the dynamics of this system. In fact, q is the temperature equivalent in magnetic models.

On regular lattices, and also in some special networks, the BChS model has a second-order phase transition at a critical value $q_c$, with critical exponents different from the usual magnetic models and dependent on the particular chosen lattice [12]. For a recent review on the progress already made in this model see Ref. [13].

With respect to scaling free lattices, in the direction of treating opinion dynamics, a more realistic environment has been proposed by Sorin Solomon [14,15], who considers two different lattices. One lattice reflects one kind of environment, for instance the home place, and the other lattice a different situation, for instance the workplace. In practice, labeling i the sites in the workplace lattice, a random permutation $P\left(i\right)$ of the order already established in this lattice provides the sites in the home place lattice. The actuality in this process resides in the fact that the neighbors at home differ from the neighbors at the workplace. Thus, like in the King Solomon biblical story, in such construction each individual is equally shared by two lattices. So, the net interaction of the relevant variables defined at site i turns out to be a sum of the corresponding interactions of the site i with its neighboring sites on the workplace lattice, plus the interactions with the neighbor sites of $P\left(i\right)$ on the home place lattice. It should be stressed that the increase in the connectivity of each site i makes the SNs close to small-world networks [16,17].

The BChS model has been previously studied in $D=1$, $D=2$, and $D=3$ SNs [12,18,19]. The critical exponents of the second-order phase transition depend on the dimension of the lattices D, as expected from general renormalization group arguments. Since the majority vote model present an upper critical dimension, it would be worthwhile to see whether the BChS model in higher dimension SNs will have critical exponents in the direction of the mean-field ones.

Thus, in the present work, the BChS dynamical system on SNs has been studied through extensive Monte Carlo simulations by considering lattices in $D=4-6$ dimensions. In the next section we have: the definition of the BChS model in the discrete opinion dynamics; the themodynamic-like variables that are used in describing the phase transition; and the corresponding finite-size-scaling relations together with some details of the Monte Carlo simulations. The results are discussed in Section 3 and some concluding remarks are summarized in the last section.

2. Model, Thermodynamic-like Variables and Simulations

The BChS model, in its discrete form, and the corresponding thermodynamic-like variables have already been extensively described in previous papers. However, for completeness, we will give below a brief description of the model and the used quantities from which the phase transition properties can be obtained. It is also discussed some details of the employed Monte Carlo simulations, together with the finite-size-scaling relations of the relevant quantities to treat the model on lattices of linear size L in several dimensions namely $D=4$, 5 and 6.

2.1. Biswas-Chatterjee-Sen Model

The BChS model has been previously described in some detail and studied in different regular lattices and networks (see, for instance Refs. [9,10,18,19,20]). Below, we have just the main ingredients of the dynamical system, directed specifically to the SNs. We will keep here the same notation, for the relevant variables, that has been used in the previous studies of this model in other contexts.

Agents, or individuals, are set on each i node of a SN with $N=L^D$ sites. At time step t, the agents have opinion variables defined by $o_i\left(t\right)$. These opinion variables can assume three different values namely $-1$, 0, or $+1$ . The BChS rules, adopted here for updating $o_i\left(t\right)$, are as follows.

(i)

An initial configuration at time $t=0$ is set on the network by randomly assigning, to each site i, one of the three opinion states. This initial configuration of the opinion variables can be labeled as $\left\{o_i(t=0)\right\}=\left\{o_i\right\}$.

(ii)

The workplace lattice is sequentially swept and every site i is updated according to the rule (iv) below. One eventually has $\left\{o_i\left(t\right)\right\}=\left\{o_i\right\}$, where all $\left\{o_i\right\}$ are the corresponding opinion variables that have been updated at time $t-1$.

(iii)

For a given site i, one of its nearest neighbors j is randomly selected and an affinity ${\mu }_{ij}$ is ascribed for this pair bond. This affinity parameter is another discrete variable that assumes a value $+1$, but can be turned negative with a probability q. It is this probability q that acts as an external noise, modeling the local discordances.

(iv)

The opinion variable of both sites i and j are then assigned new values according to

$$\begin{array}{ccc}\hfill o_i+{\mu }_{ij}{o}_j& \to & o_i,\hfill \end{array}$$

(1)

$$\begin{array}{ccc}\hfill o_j+{\mu }_{ij}{o}_i& \to & o_j,\hfill \end{array}$$

(2)

where in the right hand side $o_i$ and $o_j$ are the updated opinion states.

(v)

Another site ℓ, randomly distant $|\overrightarrow{R}|$ from the site i, is additionally selected and an affinity ${\mu }_{i\ell }$ is ascribed for this bond in the same way as before.

(vi)

The opinion variable of these sites are now updated as

$$\begin{array}{ccc}\hfill o_i+{\mu }_{i\ell }{o}_{\ell }& \to & o_i,\hfill \end{array}$$

(3)

$$\begin{array}{ccc}\hfill o_{\ell }+{\mu }_{i\ell }{o}_i& \to & o_{\ell }.\hfill \end{array}$$

(4)

(vii)

If the opinion state turns out to be out of the interval $[-1,+1]$, it is automatically made $o_i=+1$ if $o_i>+1$, or $o_i=-1$ if $o_i<-1$.

(viii)

One sweep through the network constitutes one Monte Carlo step per site (MCS) from time t to $t+1$. Thus, one has $\left\{o_i(t+1)\right\}=\left\{o_i\right\}$, with $o_i$ the updated set of opinion variables from itens (iii)-(vii).

Note that the above procedure uses only the workplace lattice and makes use of a two-step selection comprising a nearest neighbor j and an additional distant site ℓ. This results in a simplified, and less computer time consuming, version of the original two lattices SN [11].

2.2. Thermodynamic-like Variables

The convenient order parameter O that has been usually defined for this model consists of averaging the opinion variables $o_i\left(t\right)$ over all individuals, i.e.,

$$O=\left|\sum _{i=1}^N{o}_i\left(t\right)\right|/N,$$

(5)

where N is the total number of sites of the SN. In the above equation, the time t is chosen to be large enough for the system having reached its stationary state. In contrast to ordinary magnetic systems, where one has a thermal driven phase transition, in the present model one has a kind of a random configuration driven phase transition. The phase transition here means that for $q<q_c$, $O\ne 0$ and an ordered phase is established, while for $q>q_c$, $O=0$ and the system is in a disordered phase. Exactly at $q=q_c$, a second-order phase transition takes place.

From the order parameter defined in (5), it is possible to construct its magnetic-like variables, such as the order parameter fluctuation $O_f\left(q\right)$ or susceptibility (being the analogous to the magnetic susceptibility), its reduced fourth-order Binder cumulant $O_4\left(q\right)$, the derivative of the cumulant with respect to the noise probability q, and so on. These observables, from which it is possible to fully categorize the possible phase transition, can be formally expressed as

$$\begin{array}{ccc}\hfill O\left(q\right)& =& [{\langle O\rangle }_t{]}_{av},\hfill \end{array}$$

(6)

$$\begin{array}{ccc}\hfill O_f\left(q\right)& =& N[{\langle O^2\rangle }_t-{\langle O\rangle }_t^2{]}_{av},\hfill \end{array}$$

(7)

$$\begin{array}{ccc}\hfill O_4\left(q\right)& =& 1-[{\displaystyle \frac{{\langle O^4\rangle }_t}{3{\langle O^2\rangle }_t^2}}{]}_{av},\hfill \end{array}$$

(8)

where ${\langle \cdots \rangle }_t$ stands for different time averages (which are computed after the system has reached the stationary state), and ${[\cdots ]}_{av}$ means the averages taken over different initial configurations.

2.3. Finite-Size Scaling Relations and Monte Carlo Simulations

All the variables above can be obtained as a function of q, for several SN network sizes L, in a particular spatial dimension D. The criticality or any possible phase transition exhibited by the model can thus be inferred by analyzing the behavior of Eqs. (6)-(8) close to the transition point $q_c$ as a function of L. This analysis is done by using the finite-size scaling hypothesis. This hypothesis states that, for large system sizes L, the relevant variables above should follow a power-law behavior of the form (for further details see, for instance, Refs. [21,22,23])

$$\begin{array}{ccc}\hfill O\left(q\right)& =& L^{-\beta /\nu }{f}_O\left(x\right),\hfill \end{array}$$

(9)

$$\begin{array}{ccc}\hfill O_f\left(q\right)& =& L^{\gamma /\nu }{f}_{O_f}\left(x\right),\hfill \end{array}$$

(10)

$$\begin{array}{ccc}\hfill O_4\left(q\right)& =& f_{O_4}\left(x\right),\hfill \end{array}$$

(11)

$$\begin{array}{ccc}\hfill {\displaystyle \frac{d{O}_4}{dq}}& =& L^{1/\nu }{f}_d\left(x\right),\hfill \end{array}$$

(12)

$$\begin{array}{ccc}\hfill q_c\left(L\right)& =& q_c+q_0{L}^{-1/\nu },\hfill \end{array}$$

(13)

where $\beta$, $\nu$, and $\gamma$ are the critical exponents of the order parameter, correlation length, and fluctuation of the order parameter, respectively. $f_k\left(x\right)$ are the respective scaling functions, with the scaling variable $x=L^{1/\nu }(q-q_c)$ and $k=\{O,O_f,O_4,d\}$. ${\displaystyle \frac{d{O}_4}{dq}}$ is the derivative of the fourth-order Binder cumulant with respect to q. In Eq. (13), the critical noise probability $q_c\left(L\right)$, for a given lattice size L, can be chosen, for example, the estimate of the position of the peak of the fluctuation $O_f$ or the position of the maximum value of the magnitude of the derivative ${\displaystyle \frac{d{O}_4}{dq}}$. In this equation, $q_c$ is the critical noise probability in the thermodynamic limit with $q_0$ a non-universal constant. When the large lattice regime has not been reached, corrections to the finite-size scaling can be implemented in the above equations with additional exponents and fitting parameters.

The regular procedure to determine the transition point and the corresponding exponents are now as follows. A ln-ln plot of the maximum value of the magnitude of the derivative ${\displaystyle \frac{d{O}_4}{dq}}$, as a function of L, allows one to extract the critical exponent $1/\nu$. From the position $q_c\left(L\right)$ of these maxima, as well as from the position of the peaks of the order parameter fluctuation $O_f$, and using Eq. (13) with $1/\nu$ in hands, one obtains the critical noise probability $q_c$ in the thermodynamic limit. Back to Eqs. (9) and (10), ln-ln plots of $O\left(q_c\right)$ and $O_f\left(q_c\right)$ furnish the exponent rations $\beta /\nu$ and $\gamma /\nu$, respectively. The peak values $O_f\left(q_{max}\right)$ of the fluctuation $O_f$ gives also an additional estimate of $\gamma /\nu$.

The Monte Carlo simulations have been performed according to the algorithm above described in itens (i)-(viii) on several SNs of finite sizes L. Since the number of sites exponentially increases with the dimension, smaller sizes have been simulated as D increases. In this way, for $D=4$ we have $L=4$, $5$, $6$, $7$, $8$, 9 up to 10; for $D=5$ we have $L=3$, $4$, $5$, $6$; and for $D=6$ we have $L=2$, $3$, $4$, $5$, and $6$. All relevant quantities in Eqs. (6)-(8) have been computed as a function of the noise probability q and, close to the transition region, the noise probability steps have been chosen as $\Delta q=0.001$.

In all simulations, in order to compute the desired observables, several MCS have been performed on the SNs. In general, 120 different SNs realizations for each network size have been simulated to make the quench averages. For each network replica, ${10}^5$ MCS have been done to let the system evolve to a stationary state and then another ${10}^5$ MCS have been done to collect the ${10}^5$ values of the opinion variables used to measure the desired observables. Error bars have been estimated by using the jackknife resampling technique [22,24].

3. Results and Discussion

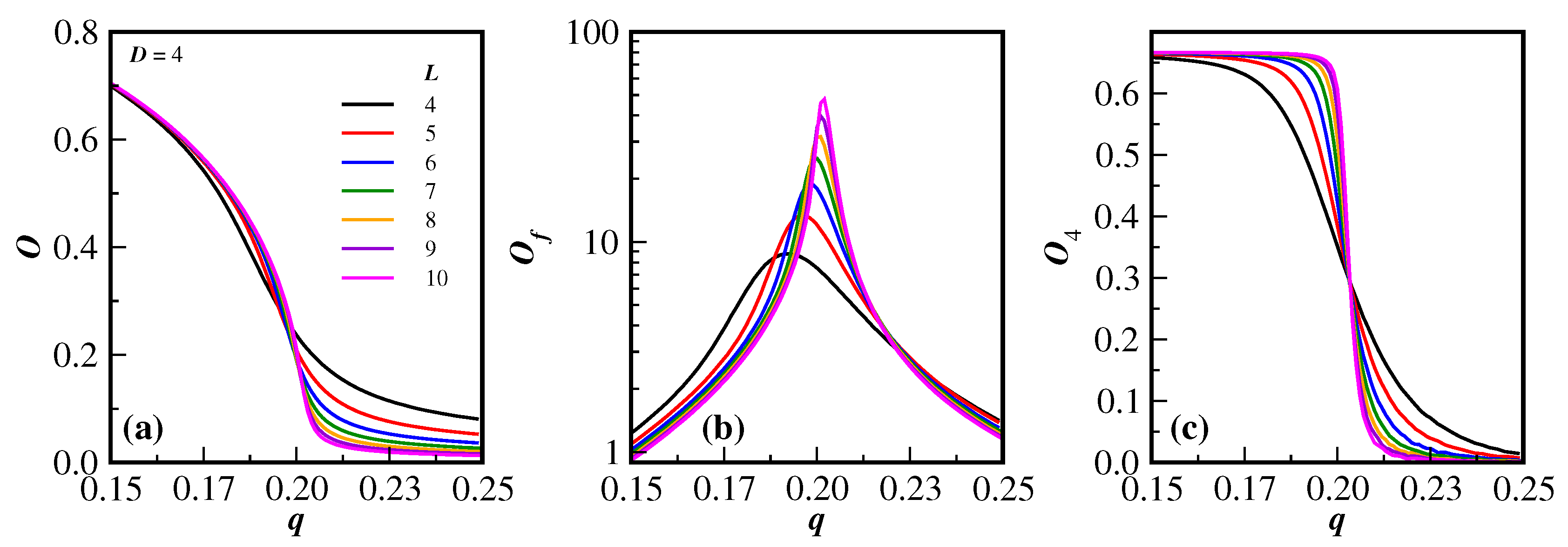
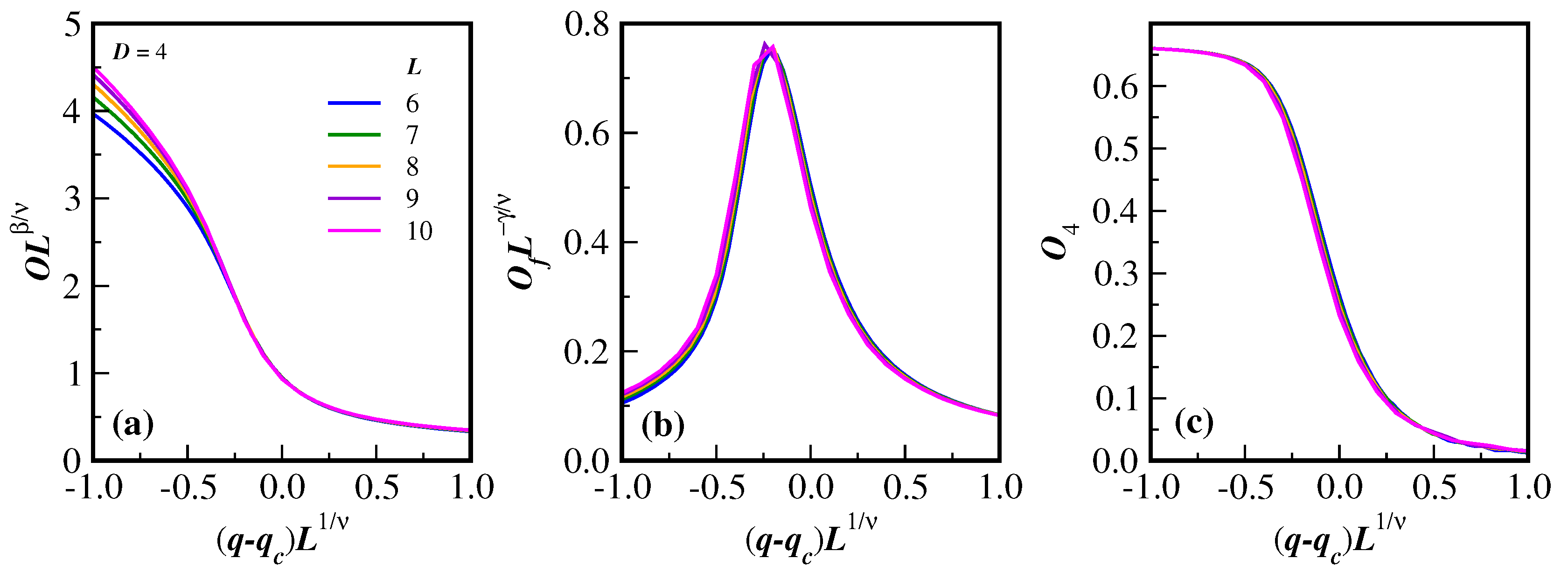
As a matter of example, the general behavior of the relevant quantities for this model in $D=4$ namely O, $O_f$ and $O_4$, given by Eqs. (6)-(8), are respectively displayed in the three panels (a), (b) and (c) of Figure 1. The different lattice sizes are listed in the legend of Figure 1(a). In all these panels, only the lines of the data are shown for a clearer visualization of the dependence of the respective quantities as a function of the noise probability q. From the behavior of O, $O_f$ and $O_4$ close to the transition region, it is clear that the system undergoes a phase transition, since the derivatives of O and $O_4$ with respect to q increase in magnitude as the lattice size increases, so does the peak of $O_f$ (note that, for a better view of the peaks, the vertical axis of Figure 1(b) gives $O_f$ in a logarithm scale). In addition, the fourth order Binder cumulants $O_4$ cross at the same region, which is equivalent to the critical noise transition. Similar patterns, as highlighted in this figure, have been previously obtained for $D\le 3$ and are also obtained for $D=5$ and 6. However, as it will be seen below, the cumulant crossing for higher dimensions $D\ge 5$ are not so well defined as for the case $D\le 4$. Some details of extracting the critical properties of the model from these kind of data are discussed below.

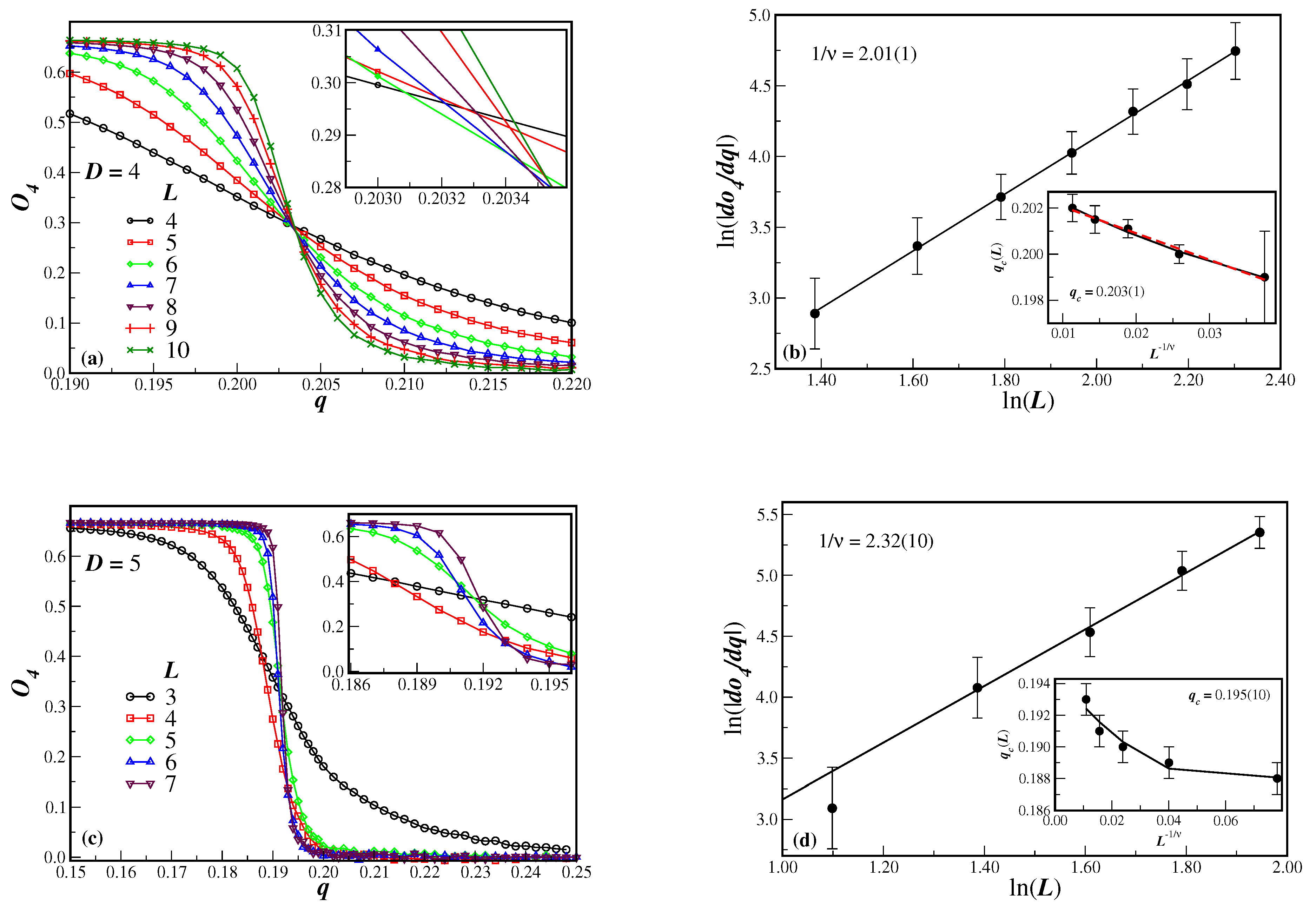
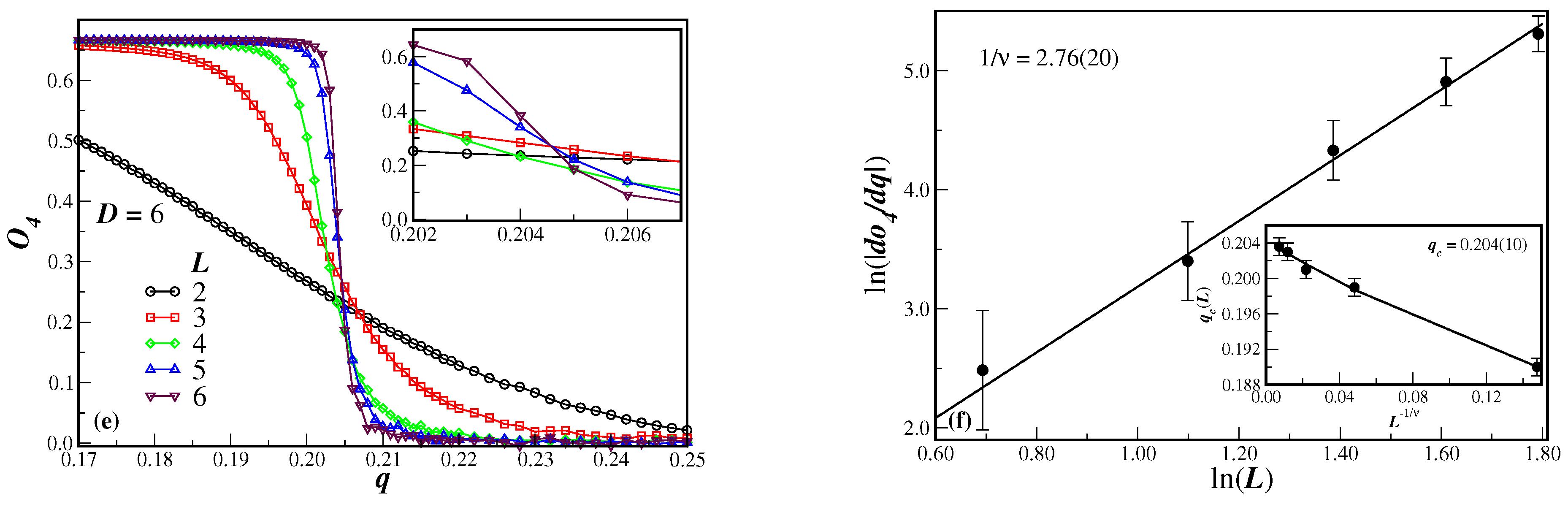
Let us first consider the fourth-order Binder cumulant of the order parameter $O_4$, as a function of the disorder parameter q, which is depicted in the left panels of Figure 2 for several lattice sizes L and dimension D. In panels Figure 2(a), Figure 2(c) and Figure 2(e), we have $D=4$, $D=5$ and $D=6$, respectively. One can clearly see from panel Figure 2(a) for $D=4$ that the system undergoes a second-order phase transition, since the cumulants tend to cross at the same value q, which corresponds to the critical disorder parameter $q_c$[21]. In the axes scales used in Figure 2(a) one can make a rough estimate of the critical noise and the universal value of the Binder cumulant $q_c=0.204\left(5\right)$ and $O_4^{*}=0.291\left(2\right)$, respectively. It can also be noticed that from Figure 2(c) and Figure 2(e) ($D=5$, $D=6)$ we do not have a clear estimate either of $q_c$ or $O_4^{*}$. This is a result of the smaller lattices that have been used because the number of sites to be simulated exponentially increases with D. Nevertheless, from the inset of the left panels it is seen that the slope of $O_4$ systematically increases with the lattice size. From the maximum value of the slope of $O_4$ with respect to q one is able to obtain the correlation length exponent $1/\nu$. The magnitude of the derivative $d{O}_4/dq$ has been numerically computed from the original simulated data. The ln-ln plot of this derivative, as function of the lattice size L, is illustrated in the main graphs of the right panels of Figure 2 for each considered dimension D. The slope of the linear fit of the data, according to Eq. (12), corresponds to the exponent ratio $1/\nu$. The values of $1/\nu$ are given in the proper figures. In dimensions $D=5$ and $D=6$ the smaller lattices have not been taken in the linear fit.

The position $q_c\left(L\right)$ of the peak of the derivative $d{O}_4/dq$ can also be used to estimate the critical value $q_c$ in the thermodynamic limit. The behavior of $q_c\left(L\right)$ as a function of $L^{-1/\nu }$ is shown in the inset of Figure 2(b), Figure 2(d) and Figure 2(f). It is quite apparent the non linearity of the data due to the finite-size effects, mainly for $D>4$. Thus, rather than using Eq. (13), the data should be fitted by resorting to finite-size-scaling corrections. In this case, usual power law corrections, which are quite common in several models, do not produce a reasonable fit to the $q_c\left(L\right)$. Instead, the data could be well fitted with logarithm corrections of the form

$$q_c\left(L\right)=q_c+q_0{L}^{-1/\nu }[1+q_1/ln\left(L\right)],$$

(14)

where $q_c$ is the critical noise of the infinite system and $q_0$ and $q_1$ are non-universal constants. The corresponding critical noise are given in the insets for each value of the lattice dimension D. The value of the critical noise probability seems not to change with the lattice dimension, whereas the exponents do significantly change with D.

Although for $D=5$ and $D=6$ the value of extrapolated $q_c$ is not clearly seen in the cumulants crossings, for $D=4$ the exrapolated $q_c=0.203\left(1\right)$ value is, within the error bars, comparable to crossings in Figure 2(a), namely $q_c=0.204\left(1\right)$. Even a linear fit to data in the inset of Figure 2(b) gives a comparable value $q_c=0.203\left(2\right)$. However, good estimates of the universal value $O_4^{*}$ are still quite unprecise from Figure 2(c) and (e). This means that for the lattice sizes used in the present model, finite-size-effects turn out to become actually important for dimensions $D>4$.

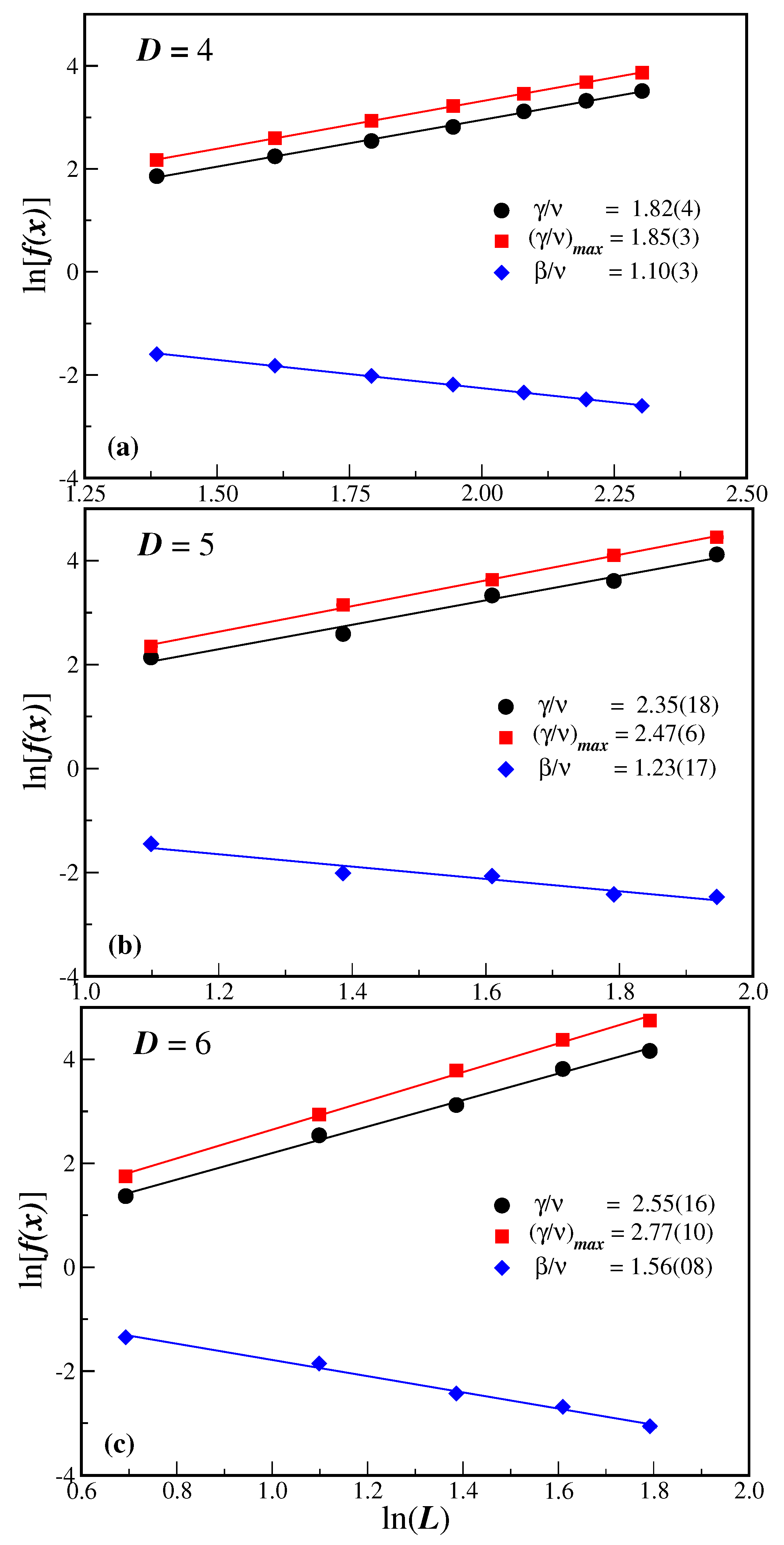
The estimate of the critical noise probability $q_c$ allows us now, through Eqs. (9) and (10), to evaluate the critical exponent ratio $\beta /\nu$ and $\gamma /\nu$ by just computing the order parameter $O\left(q_c\right)$ and its fluctuation $O_f\left(q_c\right)$ at $q_c$ for different lattice sizes L and spatial dimensions D. In the case of $O_f$, we also have its maximum value $O_f\left(q_{max}\right)$ at the noise probability $q_{max}$. Figure 3 depicts the ln-ln plot of these quantities as a function of the system size L. The corresponding slopes of the linear fit give the respective critical exponent ratios and are written in the legends of Figure 3(a), (b) and (c) for $D=4$, $D=5$ and $D=6$, respectively. Although $O_f\left(q_c\right)$ and $O_f\left(q_{max}\right)$ have different values for each lattice size, the $\gamma /\nu$ exponent estimate agree well within the error bars.

The noise probability $q_{max}$, at which the fluctuation variable $O_f$ exhibits a maximum, can be interpreted as another $q_c\left(L\right)$. Accordingly, new estimates of the critical value $q_c$ can be done using Eq. (14). Figure 4 displays the values of $q_c\left(L\right)$ so obtained as a function of $L^{-1/\nu }$ for the different lattice dimension D. As in the inset of the panels in Figure 2, the non-alignment of the data is apparent, and needs the consideration of finite-size-scaling corrections to estimate the critical noise probability. The full line in Figure 4 give indeed the best fit according to Eq. (14). The results of $q_c$ for each dimension is given in the legend of the figure. The error in $q_{max}$ has been adopted as $0.001$, the interval used to increase the noise probability in the simulations.

Finally, Figure 5 also shows, in $D=4$ dimension, the data collapse obtained for the rescaled order parameter $O{L}^{\beta /\nu }$ in panel (a), for the rescaled fluctuation of the order parameter $O_f{L}^{-\gamma /\nu }$ in panel (b), and for the rescaled reduced Binder cumulant $O_4$ in panel (c). All quantities are given as a function of the rescaled probability displacement $(q-q_c)L^{1/\nu }$. As in the panels of Figure 1, just the lines of the actual Monte Carlo data have been plotted for a better evaluation of the collapse and the accuracy of the critical quantities. The corresponding lattice sizes L are listed in the legend of Figure 5(a), where the two smaller lattice sizes have been omitted in the data collapse. Apart from the order parameter for small values of the noise probability, it is apparent the excellent agreement with the scaling relations given in Eqs. (9), (10), and (13). This is a clear indication that the evaluation of the critical exponents ratio $\beta /\nu$, $\gamma /\nu$, and $1/\nu$ are reasonably accurate.

Despite the finite-size effects being more pronounced as the lattice dimension increases, similar results, as those illustrated in Figure 1 and Figure 5, are also obtained for higher dimensions D using the corresponding critical values of the noise probability and exponent ratios.

4. Concluding Remarks

The discrete version of the Biswas-Chatterjee-Sen model, defined on $4-$, 5- and 6-dimensional Solomon networks, has been studied through extensive Monte Carlo simulations as a function of the local consensus controlling probability. From the computer simulation data and from the scaling behavior of the used thermodynamical-like quantities, it has been seen that the model really undergoes a well defined second-order phase transition for all treated dimensions.

Table 1 summarizes the numerical results of the criticality observed for the present values of lattice dimension D namely $D=4$, 5, and 6, together with the results previously obtained for $D=1$, 2 and 3 from Refs. [18,19]. An inspection of this table readily says: (i) the critical noise probability seems not to strongly depend on the lattice dimension, as is usual in spin systems, where in the latter case the increase of the number of nearest-neighbors effectively increases the transition temperature; (ii) the critical exponents, on the other hand, do depend on the lattice dimension, as is expected from universality arguments. In this case, the exponent ratios systematically increase as D increases; (iii) the hyperscaling relation $D=2\beta /\nu +\gamma /\nu$ is, within the error bars, not violated and it is actually satisfied in all of the studied dimensions. The same holds for the equivalent relation $D\nu =2$ using the correlation length exponent, although in the latter case one observes a larger error; (iv) the lower critical dimension for this model is 0, but from the present simulations there is no indication of an upper critical dimensional from where the mean-field exponents are valid. We can note from Table 1 that the closest mean-field exponents one obtains is for dimension $D=2$.

As a result, contrary to the majority vote model [6], the BChS model on SNs seems not to present an upper critical dimension. In addition, the model has logarithm finite-size corrections, as evidenced in the behavior of critical noise probability as a function of the lattice size.

The crossings of the cumulants, which in general give further estimates of $q_c\left(L\right)$, could not be considered in this dynamical system for $D\ge 4$, although for $D=3$ it was possible to obtain good estimates of $q_c$ and $O_4^{*}$ from them [12] (also using logarithm-like corrections). In the present dimensions, even and odd lattice sizes follow different uniform trends to reach the thermodynamic limit value. However, since larger lattices could not be simulated, estimates for the critical quantities turned out to be very poor due to few data available for the proper fits.

As a final remark, it can be noticed that for $D\le 6$ the exponent ratios $\gamma /\nu$ and $\gamma /{\nu }_{q_{max}}$ are, within the error bars, almost identical to each other. This is in agreement of what happens for equilibrium Ising-like models [22]. However, such equality does not happen for BChS model on directed Barabási-Albert Networks [25].