Transverse Wave Equation from Weber’s Electrodynamics

Qingsong Li

doi:10.20944/preprints202502.0649.v1

Submitted:

08 February 2025

Posted:

10 February 2025

You are already at the latest version

Abstract

It has been a common view that electromagnetic wave equation in vacuum cannot be obtained with Weber’s electrodynamics. With a polarizable vacuum postulate, an electric wave equation was recently derived from Weber’s electrodynamics. However, this wave equation only applies to longitudinal wave propagation. It does not work for transverse wave since it requires non-zero divergence of electric field. In this paper, we try to derive a wave equation for transverse wave propagation using the curl component of electric field with zero divergence.

Keywords:

transverse wave

;

Weber’s Electrodynamics

;

vacuum polarization

;

wave equation

;

Ampere’s circuital law

;

Faraday’s induction law

Subject:

Physical Sciences - Theoretical Physics

Introduction

In the past century, Maxwell equations and Lorentz force (Maxwell-Lorentz electrodynamics) have been generally accepted as the dominant theory for studying classical electromagnetic phenomena. On the other hand, its alternative, Weber’s electrodynamics, has been barely used or noticed [1]. There are some similarities and differences between Maxwell-Lorentz electrodynamics and Weber’s electrodynamics [2,3,4]. The difference mainly sits in cases when dealing with interaction of individual charges. On the other hand, they give identical solutions in cases involving current loops [5].

There have been historical critiques to Weber’s electrodynamics. Many pioneer studies have been trying to address these critiques [6]. However, some major critiques still remain, which include: 1. The action at a distance nature of Weber’s force seems contradict with locality principle. 2. The current form of Weber’s electrodynamics may lead to negative mass and infinite acceleration. 3. Weber’s electrodynamics does not apply to electromagnetic wave in vacuum.

There are some recent studies addressing these remaining critiques. For example, ideas have been proposed to reconcile the locality principle and action at a distance force [7,8]. New potential and kinetic energy forms were introduced to avoid the infinite acceleration problem [9,10]. And polarizable vacuum was postulated for deriving a wave equation from Weber’s electrodynamics [11]. However, this derived wave equation only works for longitudinal wave since it uses non-zero divergence of electric field. In this paper, we try to derive a wave equation for transverse wave from Weber’s electrodynamics, while keeping the divergence of electric field equal zero.

Weber’s Force

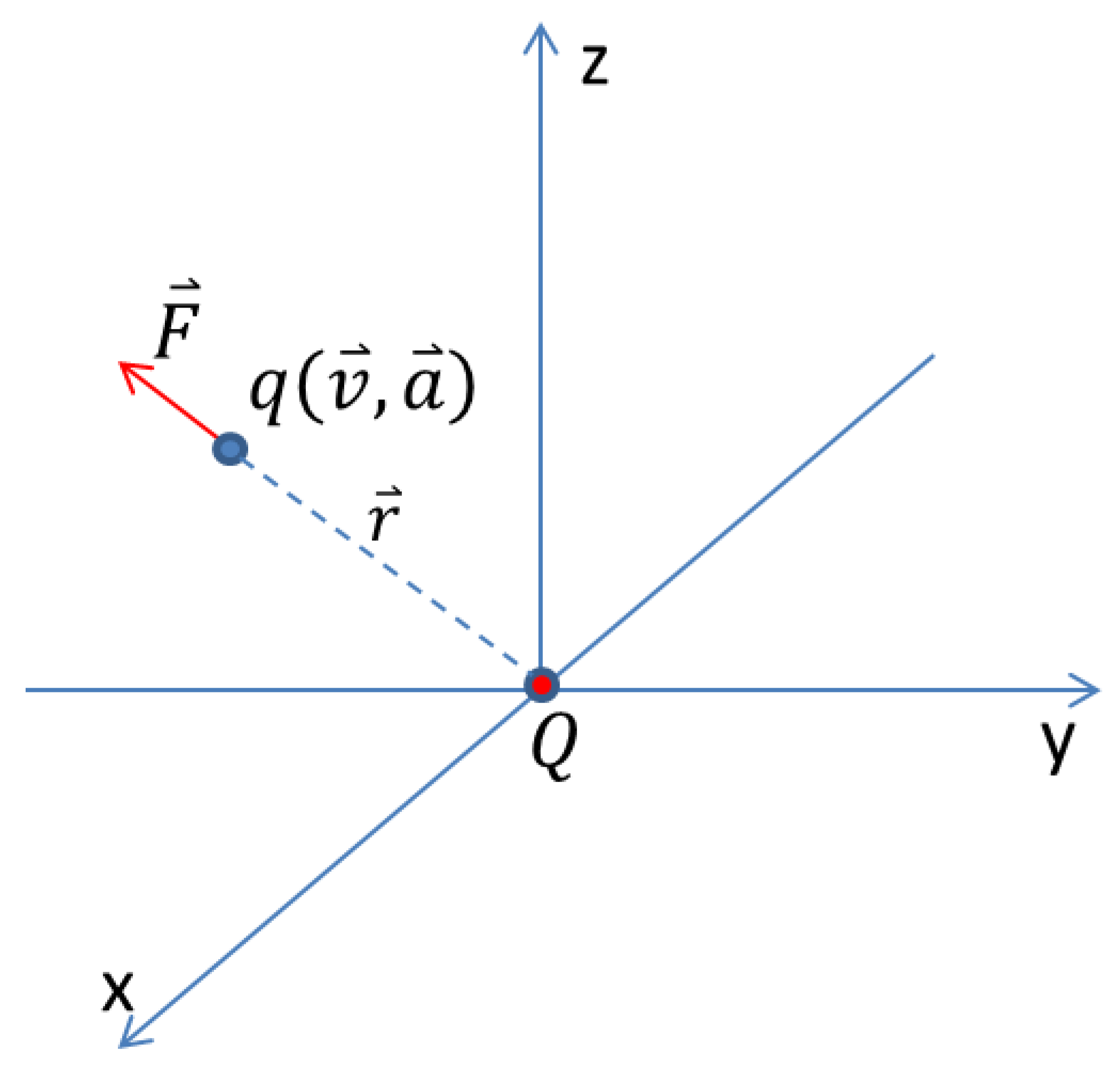
Weber’s force describes the interaction between two charges (Figure 1). It is an action at a distance force. It can be given by [12]:

\overset{⃑}{F} = \frac{Q q \hat{r}}{4 π ε_{0} r^{2}} [1 + \frac{1}{c^{2}} (\overset{⃑}{v} \cdot \overset{⃑}{v} - \frac{3}{2} {(\hat{r} \cdot \overset{⃑}{v})}^{2} + r \hat{r} \cdot \overset{⃑}{a})]

(1)

Where

Q

and

q

are two electrical charges,

\overset{⃑}{F}

is the force that charge

Q

exerts on charge

q

,

r

is the distance between the two charges,

\hat{r}

is the unit vector pointing from charge

Q

to charge

q

,

\overset{⃑}{v}

and

\overset{⃑}{a}

are velocity and acceleration of charge

q

relative to charge

Q

,

ε_{0}

is the dielectric constant and

c

is the speed of light.

Vacuum Polarization

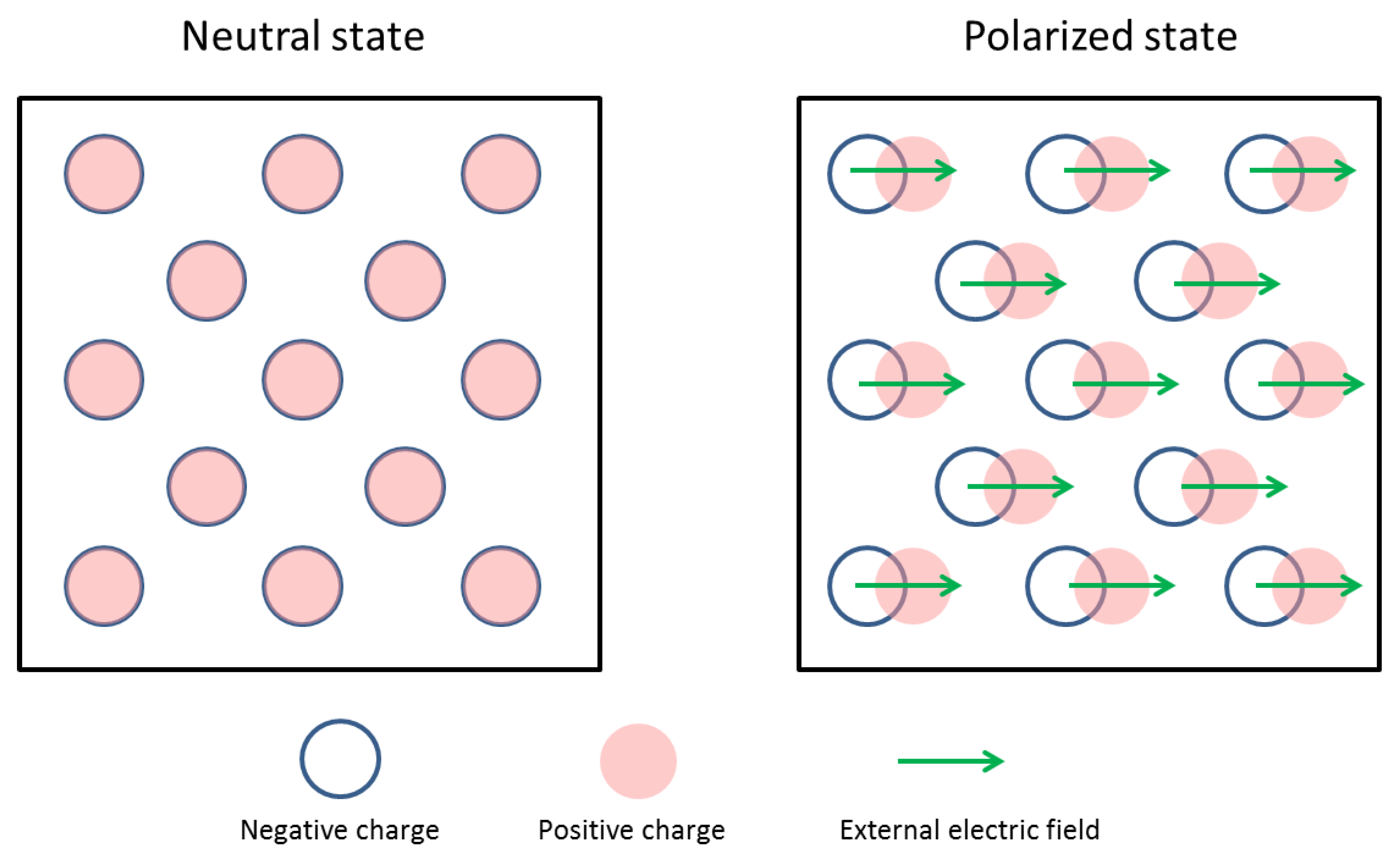
It was postulated that the vacuum is filled with positive-negative charge pairs, and stays neutral [11]. Under external electric field, the positive charge and negative charge have a displacement relative to each other (Figure 2). The positive charge has a displacement

{\overset{⃑}{D}}_{+}

, and negative charge has a displacement

{\overset{⃑}{D}}_{-}

. The displacement is linearly proportional to the external electric field.

{\overset{⃑}{D}}_{+} = - {\overset{⃑}{D}}_{-} = ε_{0} \overset{⃑}{E} / (2 ρ)

.

ρ

is the density of positive charge and/or negative charge. It is assumed that the external electric field and displacement fields are continuous both temporally and spatially.

The displacement vector field can be decomposed into a gradient component and a curl component:

{\overset{⃑}{D}}_{+} = \nabla φ + \nabla \times \overset{⃑}{A}

, where

φ

is a scalar potential field, and

\overset{⃑}{A}

is a vector potential field. In this paper, we only consider the second component and let

φ

equal zero. The first component was used in the previous paper [11] to derive the longitudinal wave equation. Then the displacement here got a property,

{\nabla \cdot \overset{⃑}{D}}_{+} = 0

.

The time derivative of displacement field becomes velocity field, and the time derivative of velocity field becomes acceleration field.

{\overset{⃑}{v}}_{+} = \frac{d {\overset{⃑}{D}}_{+}}{d t}

and

{\overset{⃑}{a}}_{+} = \frac{d {\overset{⃑}{v}}_{+}}{d t}

. Here we only consider a situation of low velocity in a laboratory rest frame. Thus the Lagrangian derivative can be approximated as a Eulerian derivative:

{\overset{⃑}{v}}_{+} = \frac{\partial {\overset{⃑}{D}}_{+}}{\partial t}

and

{\overset{⃑}{a}}_{+} = \frac{\partial {\overset{⃑}{v}}_{+}}{\partial t}

.

Deriving Magnetic Circuital Law (Ampere’s Circuital Law)

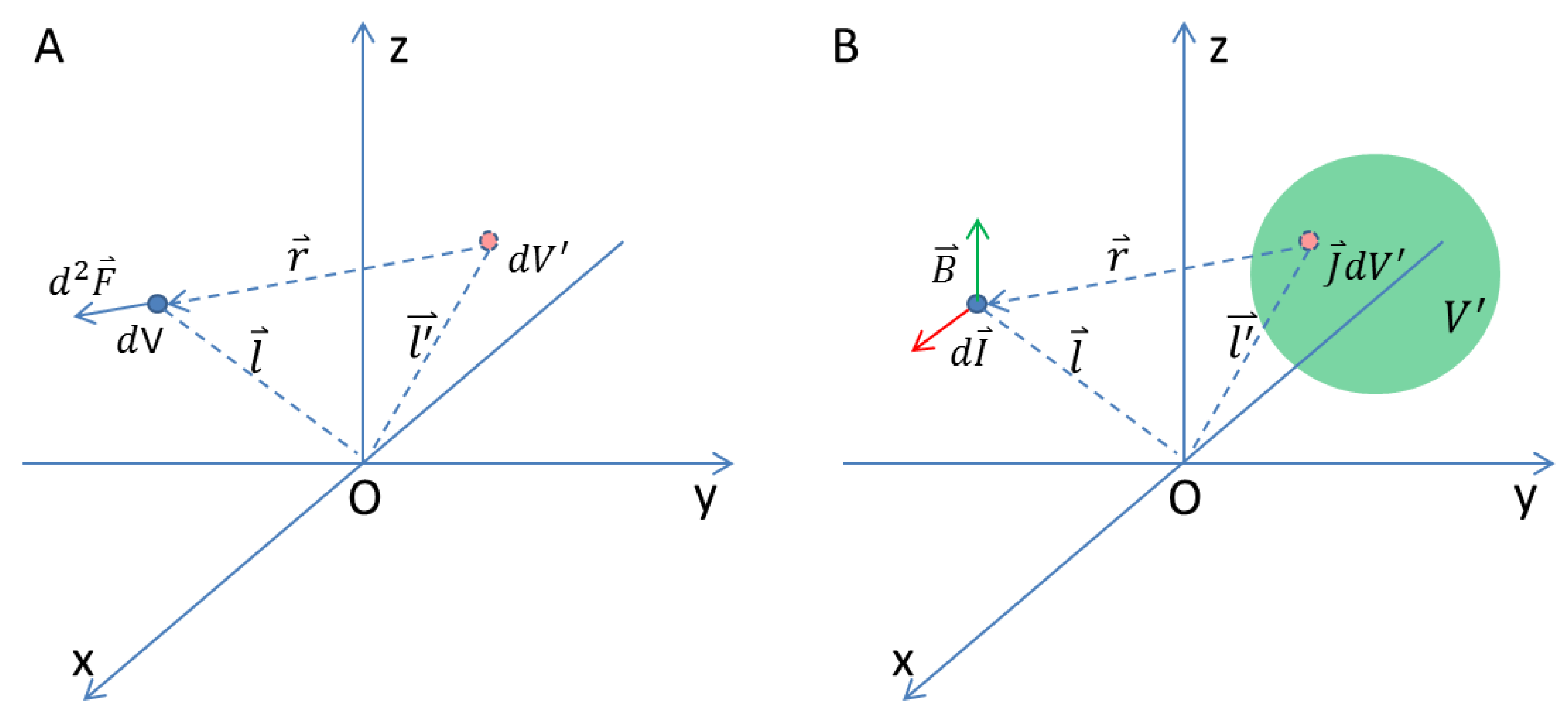
Let’s consider two tiny parcels

d V

and

d V^{'}

, which contain positive-negative charge pairs (Figure 3A). The positive charge and negative charge each has a density

ρ

. The interaction between the two parcels is the force among positive-negative charge pairs. The force

d^{2} \overset{⃑}{F}

exerted to

d V

by

d V^{'}

can be described with Weber’s force. It has four components, representing the force between positive and positive charge, the force between negative and negative charge, the force between positive and negative charge, and the force between negative and positive charge.

\begin{matrix} d^{2} \overset{⃑}{F} = \frac{(ρ d V) (ρ d V^{'}) \hat{r}}{4 π ε_{0} r^{2}} [1 \\ + \frac{1}{c^{2}} (({\overset{⃑}{v}}_{+} - {\overset{⃑}{v}}_{+}^{'}) \cdot ({\overset{⃑}{v}}_{+} - {\overset{⃑}{v}}_{+}^{'}) - \frac{3}{2} {(\hat{r} \cdot ({\overset{⃑}{v}}_{+} - {\overset{⃑}{v}}_{+}^{'}))}^{2} + r \hat{r} \cdot ({\overset{⃑}{a}}_{+} - {\overset{⃑}{a}}_{+}^{'}))] \\ + \frac{(- ρ d V) (- ρ d V^{'}) \hat{r}}{4 π ε_{0} r^{2}} [1 \\ + \frac{1}{c^{2}} (({\overset{⃑}{v}}_{-} - {\overset{⃑}{v}}_{-}^{'}) \cdot ({\overset{⃑}{v}}_{-} - {\overset{⃑}{v}}_{-}^{'}) - \frac{3}{2} {(\hat{r} \cdot ({\overset{⃑}{v}}_{-} - {\overset{⃑}{v}}_{-}^{'}))}^{2} + r \hat{r} \cdot ({\overset{⃑}{a}}_{-} - {\overset{⃑}{a}}_{-}^{'}))] \\ + \frac{(ρ d V) (- ρ d V^{'}) \hat{r}}{4 π ε_{0} r^{2}} [1 \\ + \frac{1}{c^{2}} (({\overset{⃑}{v}}_{+} - {\overset{⃑}{v}}_{-}^{'}) \cdot ({\overset{⃑}{v}}_{+} - {\overset{⃑}{v}}_{-}^{'}) - \frac{3}{2} {(\hat{r} \cdot ({\overset{⃑}{v}}_{+} - {\overset{⃑}{v}}_{-}^{'}))}^{2} + r \hat{r} \cdot ({\overset{⃑}{a}}_{+} - {\overset{⃑}{a}}_{-}^{'}))] \\ + \frac{(- ρ d V) (ρ d V^{'}) \hat{r}}{4 π ε_{0} r^{2}} [1 \\ + \frac{1}{c^{2}} (({\overset{⃑}{v}}_{+} - {\overset{⃑}{v}}_{+}^{'}) \cdot ({\overset{⃑}{v}}_{+} - {\overset{⃑}{v}}_{+}^{'}) - \frac{3}{2} {(\hat{r} \cdot ({\overset{⃑}{v}}_{-} - {\overset{⃑}{v}}_{+}^{'}))}^{2} + r \hat{r} \cdot ({\overset{⃑}{a}}_{-} - {\overset{⃑}{a}}_{+}^{'}))] \end{matrix}

(2)

where

\hat{r}

is a unit vector pointing from

d V^{'}

to

d V

,

r

is the distance between two parcels,

{\overset{⃑}{v}}_{+}

,

{\overset{⃑}{v}}_{-}

,

{\overset{⃑}{v}}_{+}^{'}

,

{\overset{⃑}{v}}_{-}^{'}

,

{\overset{⃑}{a}}_{+}

,

{\overset{⃑}{a}}_{-}

,

{\overset{⃑}{a}}_{+}^{'}

,

{\overset{⃑}{a}}_{-}^{'}

are velocity and acceleration of positive charge and negative charge in each parcel respectively.

The parcel

d V

can be seen as containing a small current element

d \overset{⃑}{I} = ρ d V ({\overset{⃑}{v}}_{+} - {\overset{⃑}{v}}_{-})

. The current density

\overset{⃑}{J} = d \overset{⃑}{I} / d V = ρ ({\overset{⃑}{v}}_{+} - {\overset{⃑}{v}}_{-})

. The same applies to parcel

d V^{'}

. As shown in section 4.2 of Assis’s “Weber’s Electrodynamics” [5], the force in equation (2) can lead to Ampere’s force between current elements (force that current element

d {\overset{⃑}{I}}^{'} = \overset{⃑}{J} d V^{'}

exerted to current element

d \overset{⃑}{I}

).

d^{2} \overset{⃑}{F} = - \frac{\hat{r}}{4 π ε_{0} c^{2} r^{2}} [2 (d \overset{⃑}{I} \cdot d {\overset{⃑}{I}}^{'}) - 3 (\hat{r} \cdot d \overset{⃑}{I}) (\hat{r} \cdot d {\overset{⃑}{I}}^{'})]

(3)

Since we only consider the curl portion of displacement field, we have

{\nabla \cdot \overset{⃑}{D}}_{+} = 0

and

\nabla \cdot \overset{⃑}{J} = 0

. Thus the current always form loops. If we integrate for current in a volume, it has the same property as integration along loops. As shown in section 4.5 of Assis’s “Weber’s Electrodynamics” [5], the integrated force of a volumetric current acting on a small current element is identical between Ampere’s force and Grassman’s force. Thus, the force

d \overset{⃑}{F}

acting on current element

d \overset{⃑}{I}

by current volume

V^{'}

(Figure 3B) can be written as

d \overset{⃑}{F} = d \overset{⃑}{I} \times \overset{⃑}{B}

(4)

Where

\overset{⃑}{B} = \frac{1}{4 π ε_{0} c^{2}} ∭_{V^{'}}^{‌} \frac{\overset{⃑}{J} d V^{'} \times \hat{r}}{r^{2}}

(5)

Equation (5) has the same form as the well-known Biot-Savart law. The major difference is that the current here is not the current of ordinary charges (e.g., electron, positron etc.). Instead, it is the displacement current in vacuum.

Let

\overset{⃑}{r} = \overset{⃑}{l} - {\overset{⃑}{l}}^{'}

, where

\overset{⃑}{l}

is the position vector of

d V

, and

{\overset{⃑}{l}}^{'}

is the position vector of

d V^{'}

(Figure 3B).

\nabla

is the gradient operator with respect to

\overset{⃑}{l}

, and

\nabla^{'}

is the gradient operator with respect to

{\overset{⃑}{l}}^{'}

. Then there exist the relations below:

\frac{\hat{r}}{r^{2}} = \frac{\overset{⃑}{l} - {\overset{⃑}{l}}^{'}}{{|\overset{⃑}{l} - {\overset{⃑}{l}}^{'}|}^{3}} = - \nabla \frac{1}{|\overset{⃑}{l} - {\overset{⃑}{l}}^{'}|} = \nabla^{'} \frac{1}{|\overset{⃑}{l} - {\overset{⃑}{l}}^{'}|}

(6)

\nabla \times \frac{\overset{⃑}{J} ({\overset{⃑}{l}}^{'})}{|\overset{⃑}{l} - {\overset{⃑}{l}}^{'}|} = \frac{1}{|\overset{⃑}{l} - {\overset{⃑}{l}}^{'}|} \nabla \times \overset{⃑}{J} ({\overset{⃑}{l}}^{'}) - \overset{⃑}{J} ({\overset{⃑}{l}}^{'}) \times \nabla \frac{1}{|\overset{⃑}{l} - {\overset{⃑}{l}}^{'}|}

(7)

With above relations, equation (5) can become

\overset{⃑}{B} = \frac{1}{4 π ε_{0} c^{2}} \nabla \times ∭_{V^{'}}^{‌} \frac{\overset{⃑}{J} ({\overset{⃑}{l}}^{'}) d V^{'}}{|\overset{⃑}{l} - {\overset{⃑}{l}}^{'}|}

(8)

Next, applying curl to both sides of equation (8), and using relations below

\nabla \times \nabla \times \frac{\overset{⃑}{J} ({\overset{⃑}{l}}^{'})}{|\overset{⃑}{l} - {\overset{⃑}{l}}^{'}|} = \nabla (\nabla \cdot \frac{\overset{⃑}{J} ({\overset{⃑}{l}}^{'})}{|\overset{⃑}{l} - {\overset{⃑}{l}}^{'}|}) - \nabla^{2} \frac{\overset{⃑}{J} ({\overset{⃑}{l}}^{'})}{|\overset{⃑}{l} - {\overset{⃑}{l}}^{'}|}

(9)

\nabla \cdot \frac{\overset{⃑}{J} ({\overset{⃑}{l}}^{'})}{|\overset{⃑}{l} - {\overset{⃑}{l}}^{'}|} = \frac{1}{|\overset{⃑}{l} - {\overset{⃑}{l}}^{'}|} \nabla \cdot \overset{⃑}{J} ({\overset{⃑}{l}}^{'}) + \overset{⃑}{J} ({\overset{⃑}{l}}^{'}) \cdot \nabla \frac{1}{|\overset{⃑}{l} - {\overset{⃑}{l}}^{'}|}

(10)

we can get

\nabla \times \overset{⃑}{B} = \frac{1}{4 π ε_{0} c^{2}} \nabla ∭_{V^{'}}^{‌} \overset{⃑}{J} ({\overset{⃑}{l}}^{'}) \cdot \nabla \frac{1}{|\overset{⃑}{l} - {\overset{⃑}{l}}^{'}|} d V^{'} - \frac{1}{4 π ε_{0} c^{2}} ∭_{V^{'}}^{‌} \overset{⃑}{J} ({\overset{⃑}{l}}^{'}) \nabla^{2} (\frac{1}{|\overset{⃑}{l} - {\overset{⃑}{l}}^{'}|}) d V^{'}

(11)

With relations in equation (7, 10) and Gauss’s theorem, we can get

\begin{matrix} ∭_{V^{'}}^{‌} \overset{⃑}{J} ({\overset{⃑}{l}}^{'}) \cdot \nabla \frac{1}{|\overset{⃑}{l} - {\overset{⃑}{l}}^{'}|} d V^{'} = - ∭_{V^{'}}^{‌} \overset{⃑}{J} ({\overset{⃑}{l}}^{'}) \cdot \nabla^{'} \frac{1}{|\overset{⃑}{l} - {\overset{⃑}{l}}^{'}|} d V^{'} \\ = - ∭_{V^{'}}^{‌} \nabla^{'} \cdot \frac{\overset{⃑}{J} ({\overset{⃑}{l}}^{'})}{|\overset{⃑}{l} - {\overset{⃑}{l}}^{'}|} d V^{'} + ∭_{V^{'}}^{‌} \frac{1}{|\overset{⃑}{l} - {\overset{⃑}{l}}^{'}|} \nabla^{'} \cdot \overset{⃑}{J} ({\overset{⃑}{l}}^{'}) d V^{'} \\ = - \iint_{S^{'}}^{‌} \frac{\overset{⃑}{J} ({\overset{⃑}{l}}^{'})}{|\overset{⃑}{l} - {\overset{⃑}{l}}^{'}|} \cdot d S^{'} + ∭_{V^{'}}^{‌} \frac{1}{|\overset{⃑}{l} - {\overset{⃑}{l}}^{'}|} \nabla^{'} \cdot \overset{⃑}{J} ({\overset{⃑}{l}}^{'}) d V^{'} \end{matrix}

(12)

Supposing that the current has a finite spatial extent and that the volumetric integration fully cover the current extent, we can get that the surface integration in

S^{'}

equals to zero. Thus equation (11) becomes

\nabla \times \overset{⃑}{B} = \frac{1}{4 π ε_{0} c^{2}} \nabla ∭_{V^{'}}^{‌} \frac{1}{|\overset{⃑}{l} - {\overset{⃑}{l}}^{'}|} \nabla^{'} \cdot \overset{⃑}{J} ({\overset{⃑}{l}}^{'}) d V^{'} - \frac{1}{4 π ε_{0} c^{2}} ∭_{V^{'}}^{‌} \overset{⃑}{J} ({\overset{⃑}{l}}^{'}) \nabla^{2} (\frac{1}{|\overset{⃑}{l} - {\overset{⃑}{l}}^{'}|}) d V^{'}

(13)

Using

\nabla^{'} \cdot \overset{⃑}{J} ({\overset{⃑}{l}}^{'}) = 0

, and the relation below

\nabla^{2} (\frac{1}{|\overset{⃑}{l} - {\overset{⃑}{l}}^{'}|}) = - 4 π δ (\overset{⃑}{l} - {\overset{⃑}{l}}^{'})

(14)

we can get

\nabla \times \overset{⃑}{B} = μ_{0} \overset{⃑}{J}

(15)

Equation (15) is the well-known Ampere’s circuital law (magnetic circuital law). A detail derivation of magnetic circuital law from Ampere’s force law can be found in section 4.7 of Assis’s Weber’s Electrodynamics [5].

Deriving Faraday’s Induction Law

That Faraday’s law can be derived from Weber’s Electrodynamics has been shown previously by Maxwell, O'Rahilly, Whittaker, and Wesley for cases of current loops [5]. A detailed proof can be found in section 5.2 and 5.3 of Assis’s book “Weber’s Electrodynamics” [5]. In this paper, we only consider displacement current instead of currents of ordinary charges. Even so, the displacement current acts the same as current of ordinary charges under Weber’s force (and Ampere’s force) because the displacement current is due to the movement of positive-negative charge pairs in vacuum.

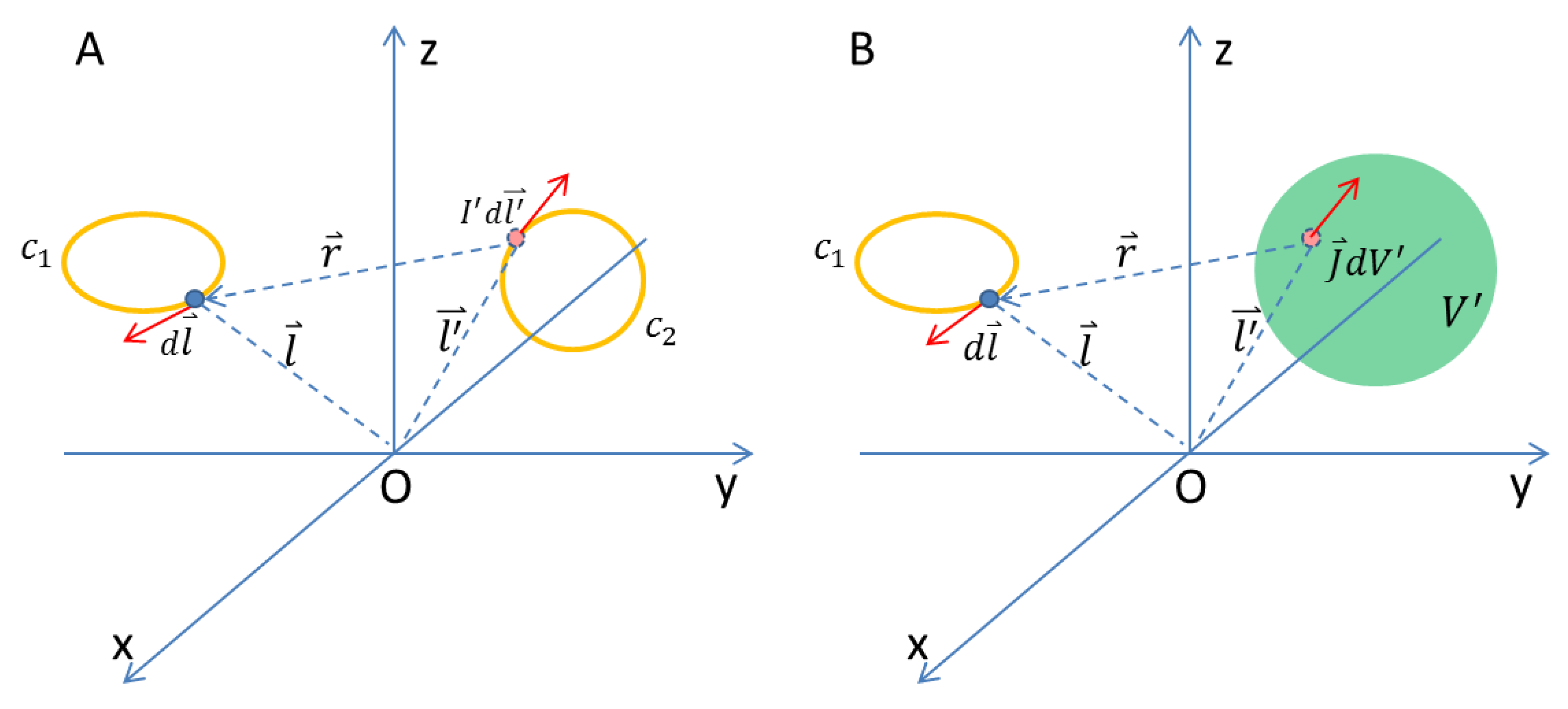
In the case of two current loops (Figure 4A), the electromotive force in the loop

c 1

caused by current

I^{'}

in loop

c 2

equals [5]:

{e m f}_{c 1} = \int_{c 1}^{‌} \overset{⃑}{E} \cdot d \overset{⃑}{l} = - \frac{d}{d t} (I^{'} M)

(16)

Where

M

is the mutual inductance of the two current loops.

M = \frac{1}{4 π ε_{0} c^{2}} \int_{c 1}^{‌} \int_{c 2}^{‌} \frac{d \overset{⃑}{l} \cdot d {\overset{⃑}{l}}^{'}}{r}

(17)

Where

d \overset{⃑}{l}

is a differential element of loop

c 1

in the direction of conventional current,

d {\overset{⃑}{l}}^{'}

is a differential element of loop

c 2

. It was mathematically proved that this is an equivalent form of Faraday’s law [5]. And this form of Faraday’s law can lead to its differentiation form (section 5.2 of Assis’s Weber’s electrodynamics [5]):

\nabla \times \overset{⃑}{E} = - \frac{\partial \overset{⃑}{B}}{\partial t}

(18)

Where

\overset{⃑}{B} = \frac{1}{4 π ε_{0} c^{2}} \int_{c 2}^{‌} \frac{I^{'} d {\overset{⃑}{l}}^{'} \times \hat{r}}{r^{2}}

(19)

In this paper, the current is volumetric instead of a thin loop (Figure 4B). We can change the loop integration to a volumetric integration, and the above approval process shall still hold. Similarly, we can get the electromotive force in loop

c 1

caused by currents in volume

V^{'}

:

{e m f}_{c 1} = \int_{c 1}^{‌} \overset{⃑}{E} \cdot d \overset{⃑}{l} = - \frac{d}{d t} (Φ)

(20)

Where

Φ = \frac{1}{4 π ε_{0} c^{2}} \int_{c 1}^{‌} ∭_{V^{'}}^{‌} \frac{d \overset{⃑}{l} \cdot \overset{⃑}{J} d V^{'}}{r}

(21)

Similarly, this form of Faraday’s law can lead to its differentiation form

\nabla \times \overset{⃑}{E} = - \frac{\partial \overset{⃑}{B}}{\partial t}

(22)

Where

\overset{⃑}{B} = \frac{1}{4 π ε_{0} c^{2}} ∭_{V^{'}}^{‌} \frac{\overset{⃑}{J} d V^{'} \times \hat{r}}{r^{2}}

(23)

Deriving Transverse Wave Equation

Applying curl to equation (22) and using equation (15), we can get

\begin{matrix} \nabla \times \nabla \times \overset{⃑}{E} = - \frac{\partial (\nabla \times \overset{⃑}{B})}{\partial t} = - \frac{\partial (μ_{0} \overset{⃑}{J})}{\partial t} = - μ_{0} ρ \frac{\partial ({\overset{⃑}{v}}_{+} - {\overset{⃑}{v}}_{-})}{\partial t} = - μ_{0} ρ \frac{\partial^{2} ({\overset{⃑}{D}}_{+} - {\overset{⃑}{D}}_{-})}{\partial t^{2}} \\ = - μ_{0} ε_{0} \frac{\partial^{2} \overset{⃑}{E}}{\partial t^{2}} = - \frac{1}{c^{2}} \frac{\partial^{2} \overset{⃑}{E}}{\partial t^{2}} \end{matrix}

(24)

With the curl rule similar to equation (9), we can get

\nabla (\nabla \cdot \overset{⃑}{E}) - \nabla^{2} \overset{⃑}{E} = - \frac{1}{c^{2}} \frac{\partial^{2} \overset{⃑}{E}}{\partial t^{2}}

(25)

Because

{\nabla \cdot \overset{⃑}{D}}_{+} = 0

and displacement field is linearly proportional to electric field, we get

\nabla \cdot \overset{⃑}{E} = 0

. Finally, we arrive at the wave equation

\nabla^{2} \overset{⃑}{E} = \frac{1}{c^{2}} \frac{\partial^{2} \overset{⃑}{E}}{\partial t^{2}}

(26)

Equation (26) is the well-known wave equation of electric field

\overset{⃑}{E}

, which has only transverse component.

Discussion

This paper derives a transverse electric wave equation in a similar way as that derived from Maxwell equations. In this derivation, we drop the gradient term of displacement field (and electric field). The gradient term was used previously in deriving wave equation for longitudinal wave. Moreover, in this derivation we only consider a slow velocity situation, and approximate Lagrangian derivatives to Eulerian derivatives. Thus, we may suspect that Maxwell’s equations and its derived wave equation represent only a special case with limitations (slow velocity, no longitudinal wave).

In modern opinion of Maxwell equations and its derived wave equation, the vacuum is seen as empty. Electric and magnetic fields travel by themselves through the vacuum. In this paper, the wave propagation is through perturbation of polarizable vacuum, i.e., the displacement current (or displacement field). Since the electric field is linearly proportional to displacement field, the wave propagation is also through the perturbation of electric field. We should point it out that Maxwell equations also have the concept of displacement current. However, its physical meaning was not as clear as what we give here: the relative movement of positive-negative charge pairs.

In this paper’s theory, the medium is a requirement for electric wave propagation. Historically, Luminiferous aether has been proposed to explain electric wave propagation. However, the property of aether varies in different theories. One type of theory assumes a sound-wave like mechanical analogue [13]. It requires the vacuum to be both extremely stiff and extremely non-viscous. Stiffness is for it to propagate high frequency electric wave without energy loss. The non-viscous requirement is for objects to freely move in vacuum. In this paper’s theory, there is no need to require stiffness of the vacuum. The Weber’s force and the positive-negative charge pairs allow the transverse wave to propagate. Other medium theories assume a vacuum filled with molecular vortices [14], or circuits of inductance-capacitance [15], etc.

The historical medium theories of electric waves were largely abandoned after a number of experiments looking for luminiferous aether. E.g., the Michelson–Morley experiment has null result [16], which indicate the medium (aether), if exists, has to travel together with the earth. And the Michelson–Gale–Pearson experiment has positive result [17], which indicates that the medium (aether) does not rotate together with the earth. The observation of stellar aberration of light may mean that medium (aether) is not fully dragged by the earth according to Fresnel’s aether drag theory [18]. The Lorentz theory of contraction aether can explain the above experiments [19]. However, it falls into the Occam's Razor as an unnecessary concept after the introducing of Einstein’s special relativity which does not need an aether at all [18].

In this paper, we did consider a wave source for keeping the paper simple and concise. To derive a wave equation with a source term is left for future studies.

Conclusions

We successfully derived a transverse wave equation from Weber’s electrodynamics. In the derivation, we used the Weber’s force, the polarizable vacuum postulate, and the great work done by pioneers in deriving Ampere’s force, magnetic circuital law, and Faraday’s induction law from Weber’s electrodynamics. This work hopefully can soften the historic critiques that Weber’s electrodynamics does not apply to electromagnetic wave in vacuum.

Acknowledgements

Q.L. thanks Steffen Kühn, and Andre Koch Torres Assis for their constructive suggestions and feedback.

References

Tran, M. Evidence for Maxwell’s equations, fields, force laws and alternative theories of classical electrodynamics. Eur. J. Phys. 2018, 39, 063001. [Google Scholar] [CrossRef]
Assis, Andre & Torres, Hector. (2012). Comparison between Weber’s electrodynamics and classical electrodynamics. Pramana Journal of Physics. 55. 393-404. [CrossRef]
Li Q (2021) Electric Field Theory Based on Weber’s Electrodynamics. Int J Magnetics Electromagnetism 7:039.
S. Kühn (2024): Weber–Maxwell electrodynamics: classical electromagnetism in its most compact and pure form, Electromagnetics. [CrossRef]
Assis, A.K.T. Weber’s Electrodynamics; Springer: Dordrecht, The Netherlands, 1994. [Google Scholar]
Baumgärtel, C.; Maher, S. Foundations of Electromagnetism: A Review of Wilhelm Weber’s Electrodynamic Force Law. Foundations 2022, 2, 949–980. [Google Scholar] [CrossRef]
Li, Q.; Smith, R.T.; Maher, S. Instantaneous Action at a Distance and the Principle of Locality, a new Proposal about their Possible Connection. Preprints 2024, 2024041741. [Google Scholar]
Montes Martos, J.M. Pseudo-Instantaneous Action-at-a-Distance with Weberian Potentials. Preprints 2024, 2024020881. [Google Scholar]
Li, Q. Extending Weber’s Electrodynamics to High Velocity Particles. Int. J. Magn. Electromagn. 2022, 8, 1–9. [Google Scholar]
Montes, J.M. On the Modernisation of Weber’s Electrodynamics. Magnetism 2023, 3, 102–120. [Google Scholar] [CrossRef]
Li, Q., & Maher, S. (2023). Deriving an Electric Wave Equation from Weber’s Electrodynamics. Foundations, 3(2), 323-334.
A. K. T. Assis and M. Tajmar, Rotation of a superconductor due to electromagnetic induction using Weber's electrodynamics, Annales de la Fondation Louis de Broglie, Vol. 44, pp. 111-123 (2019).
Haj Yousef, Mohamed. (2018). DUALITY OF TIME: Complex-Time Geometry and Perpetual Creation of Space. ISBN 978-1-5395-7920-5.
Maxwell, J.C. (1861). On Physical Lines of Force. Philosophical Magazine. 90. 11-23. [CrossRef]
Fukai, J. A Promenade Along Electrodynamics; Vales Lake Publishing: Pueblo West, CO, USA, 2003.
Michelson, Albert A.; Morley, Edward W. (1887). "On the Relative Motion of the Earth and the Luminiferous Ether". American Journal of Science. 34 (203): 333–345.
Michelson, A.A.; Gale, Henry G. (1925). "The Effect of the Earth's Rotation on the Velocity of Light, II". Astrophysical Journal. 61: 140.
K.F. Schaffner, Nineteenth-Century Aether Theories, Pergamon, 1972, pp. 125–35. [CrossRef]
Lorentz, Hendrik Antoon (1904), "Electromagnetic phenomena in a system moving with any velocity smaller than that of light" , Proceedings of the Royal Netherlands Academy of Arts and Sciences, 6: 809–831.

Figure 1. Sketch illustrating the force that charge

Q

exerts on charge

q

.

Figure 1. Sketch illustrating the force that charge

Q

exerts on charge

q

.

Figure 2. Sketch illustrating the polarizable vacuum in neutral state (left) and polarized state (right).

Figure 3. (A) Sketch illustrating the action upon parcel

d V

from parcel

d V^{'}

. (B) Sketch illustrating the action upon current element

d \overset{⃑}{I}

by volumetric current in

V^{'}

.

Figure 3. (A) Sketch illustrating the action upon parcel

d V

from parcel

d V^{'}

. (B) Sketch illustrating the action upon current element

d \overset{⃑}{I}

by volumetric current in

V^{'}

.

Figure 4. (A) Sketch illustrating the induction exerted to circuit

c 1

by circuit

c 2

. (B) Sketch illustrating the induction exerted to circuit

c 1

by volumetric current in

V^{'}

.

Figure 4. (A) Sketch illustrating the induction exerted to circuit

c 1

by circuit

c 2

. (B) Sketch illustrating the induction exerted to circuit

c 1

by volumetric current in

V^{'}

.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

Transverse Wave Equation from Weber’s Electrodynamics

Abstract

Keywords:

Subject:

Introduction

Weber’s Force

Vacuum Polarization

Deriving Magnetic Circuital Law (Ampere’s Circuital Law)

Deriving Faraday’s Induction Law

Deriving Transverse Wave Equation

Discussion

Conclusions

Acknowledgements

References

MDPI Initiatives

Important Links

Subscribe