FLPSHARD: A Flexible and Efficient Blockchain Sharding Solution for IIoT

1. Introduction

The Industrial Internet of Things(IIoT), which is considered a subset of the Internet of Things (IoT), pertains to the application of the Internet of Things in the industrial realm. It constitutes a system wherein industrial applications of interconnected sensors, instruments, other apparatuses, and computers in multiple sectors such as manufacturing and energy management are networked [1]. The IIoT is capable of integrating the data generated by diverse departments, thereby facilitating the accomplishment of production tasks in a more efficacious manner. The decentralized structure and data traceability of blockchain technology have conspicuously augmented the security and integrity of data [2]. Consequently, in recent years, it has been extensively adopted and applied within the domain of the IIoT. However, the traditional blockchain architecture is circumscribed in terms of scalability, processing capacity, and customization. This gives rise to the consumption of substantial storage and communication resources during the process of attaining consensus and synchronizing data, thereby posing numerous challenges to the application of blockchain technology in the IIoT field. In response to these conundrums, sharding technology, as an innovative solution, is progressively emerging as a focal point of research and has garnered extensive attention from both the academic and industrial arenas.  [2] Sharding technology partitions blockchain nodes into multiple independent units, with each unit being denominated as a shard, and each shard can be construed as an independent blockchain. Within the same blockchain network, individual shards are capable of generating blocks in parallel, thereby surmounting the limitations of performance and scalability from an architectural perspective and augmenting the throughput of the entire blockchain system. In the context of sharding technology, owing to the presence of cross-shard transactions, the overall throughput is not a direct summation of the throughputs of each shard. The performance of nodes within each shard, network latency, and the network magnitude not only dictate the processing capacity of the shard per se but also exert an influence on the throughput of the entire system. Consequently, the allocation of nodes has become a pivotal issue in sharding technology. The amelioration objectives of the majority of sharding strategies are centered around augmenting the overall processing efficacy of the system. This is typically accomplished through strategies such as curtailing the occurrence rate of cross-shard transactions and alleviating the workload of each individual shard. These improvement measures predominantly concentrate on the optimization of shard dimensions and node configuration. However, within the application backdrop of the IIoT, several distinctive requisites surface: Primarily, in light of the intricate nature of the organizational structure, it is imperative to guarantee that nodes affiliated with the same department or specific production unit can be centrally arranged within the same shard. Secondly, due to operational interdependencies, nodes in close geographical proximity ought to be allotted to the same shard. Thirdly, for nodes with stable network connections and frequent data exchanges, it should be ensured that they are situated within the same shard to address the high demand for data exchanges. Ultimately, since the quantity of industrial nodes fluctuates with the construction of new sites and the obsolescence of old ones, the sharding strategy must possess sufficient flexibility to accommodate alterations in the number of nodes. In modern sharding consensus protocols including POS [3], POA [4], and PBFT [5], the leader node occupies a predominant role in information dissemination among nodes.Consequently, an optimal blockchain sharding design should factor in other pertinent elements such as the distance between nodes and the leader node, network propagation velocity, transaction frequency, and network communication milieu, so as to effectively conglomerate the nodes around the leader node. This bears resemblance to the production - sales network of factories/customers. If the leader node of the shard is analogized to the factory and the remaining ordinary nodes of the shard are likened to the customers, then the sharding quandary of the blockchain can be approximately formulated as a problem of how to strategize the factory location such that the aggregate of the communication costs from the customers to the factory is minimized. In the present research, we put forward a novel blockchain dynamic sharding strategy termed FLPShard, which is predicated on the SSCFLP. The objective of FLPShard is to take into account multiple crucial factors comprehensively, with the aim of realizing an efficient dynamic sharding mechanism. This scheme endeavors to optimize the performance of the blockchain network and ensure that the system can maintain high efficiency and stability when dealing with a large volume of transactions and data. Additionally, the goal of FLPShard extends beyond merely providing a dynamic sharding solution; it is also committed to enhancing the overall performance of the system holistically, encompassing increasing the transaction processing speed, bolstering the network’s scalability, and diminishing the communication latency between nodes.

Our contributions are enumerated as follows:

(1)

We have contrived an innovative sharding architecture that can function in parallel and handle transactions within and across shards effectively.

(2)

We have, for the first time, proposed a sharding method based on the SSCFLP model. In contrast to the currently prevalent random sharding techniques, our FLPShard method is capable of rationally assigning nodes to each shard in accordance with multiple informational dimensions, including but not limited to node distance, latency between nodes, and node bandwidth. This not only heightens the consensus efficiency within the shard but also markedly augments the overall throughput of the system.

(3)

We have actualized the prototype algorithm of this sharding scheme and examined its feasibility via a simulator. Through in-depth analysis and experimental corroboration, we have ascertained that the FLPShard scheme exhibits significant advantages over the random sharding scheme with regard to transaction confirmation latency and system throughput.

The remainder of this paper is organized as follows: The second section elaborates on related work, the third section delineates the overall architecture of FLPShard, the fourth section expounds on the algorithm design and verification of FLPShard, and the fifth section proffers a summary.

2. Related Work

Blockchain, fundamentally, represents a decentralized distributed ledger. It establishes a peer-to-peer network regime independent of any single reliable third-party entity by leveraging cryptographic principles and consensus algorithms. In 2014, the advent of Ethereum [6] introduced the notion of smart contracts, which further elevated the blockchain into a decentralized computing platform [7].

Internet of Things (IoT) applications permit direct data interchange and interaction amongst devices via the network [8]. Distinct from conventional Internet applications, the operations of IoT devices can exert an influence on the physical world. The distributed characteristic of blockchain technology furnishes the Internet of Things with a secure and traceable means of data management. It does not hinge on any centralized server. When combined with smart contracts, it can substantially augment the integrity and trustworthiness of data [9].

Sharding: Sharding technology stemmed from the management and optimization of large databases. It partitions massive databases into multiple data shards that are more manageable, facilitating parallel processing of data and significantly enhancing the overall performance of the system. In recent years, sharding technology has been introduced into the blockchain domain, with the aim of bolstering the scalability of the blockchain while retaining its core characteristic of decentralization [10].

Presently, numerous sharding schemes have been put forward, such as Elastic [11], Omiledger [12], and RapidChain [13]. These schemes are mainly designed for public chains. When initializing the blockchain system, these schemes determine the total number of shards and utilize randomized algorithms to assign shard identifiers to participating nodes, so as to ensure that the number of nodes in each shard is approximately balanced. However, as the number of nodes in the system increases, the total number of shards remains unchanged, which restricts the capacity and throughput of the system to a certain extent and endows them with a theoretical upper limit. In the Industrial Internet, the majority of transactions on the blockchain are initiated by various devices, and there often exists a geographical correlation among these devices. Given that transactions are more likely to occur between devices in close geographical proximity, adopting a geographical location-based sharding strategy can effectively curtail the demand for cross-shard transactions.

The efficient strategy of partitioning shards according to the geographical distribution of nodes constitutes a method for optimizing the performance of the blockchain network [14]. The SensorChain [15] scheme devised a geographical location-based sharding approach predicated on the Voronoi Diagram, which is capable of partitioning shards in accordance with the actual locations of nodes. Building on this foundation, FISSION [16] introduced an improvement by proposing a dynamic sharding method grounded in the Voronoi Diagram and furnished specific sharding algorithms. FISSION permits nodes to dynamically join the blockchain network and dynamically modifies the size and number of shards based on the geographical positions of nodes and the count of nodes within each shard.

Facility Location Problem: The Facility Location Problem (FLP) pertains to the quest for optimal facility locations and finds extensive application in arenas such as factory site selection [17], Transportation planning [17], wireless hotspot placement  [18]and humanitarian efforts [19]. FLP done in applying FLPs to humanitarian efforts [19]. FLP is further subdivided into diverse sub-problems contingent upon varying conditions, such as whether locations are continuous and whether facility capacities are constrained. SSCFLP represents a particular instance of FLP. Its hallmark is that each demand point can be serviced by only one service point, constituting a discrete location problem with capacity constraints. SSCFLP is an NP-hard problem [20]. Currently, there exist two modalities for solving SSCFLP [21,22]. One involves seeking exact solutions, exemplified by the branch-and-bound algorithms [23] and column generation methods [24]. The other entails employing heuristic algorithms to derive approximate solutions, as typified by the Lagrange relaxation [25,26,27] , Very large-scale neighborhood search [28], tabu search [29] and Kernel Search [30]. While greedy algorithms generally do not perform well on FLPs, the primal-dual greedy algorithm presented by Jain and Vazirani tends to be faster in solving the uncapacitated FLP than LP-rounding algorithms, which solve the LP relaxation of the integer formulation and round the fractional results [31].

In this paper, the blockchain sharding problem is approximated to an SSCFLP. Consequently, the SSCFLP model can be marshaled to furnish a valuable theoretical underpinning for the development of blockchain sharding.

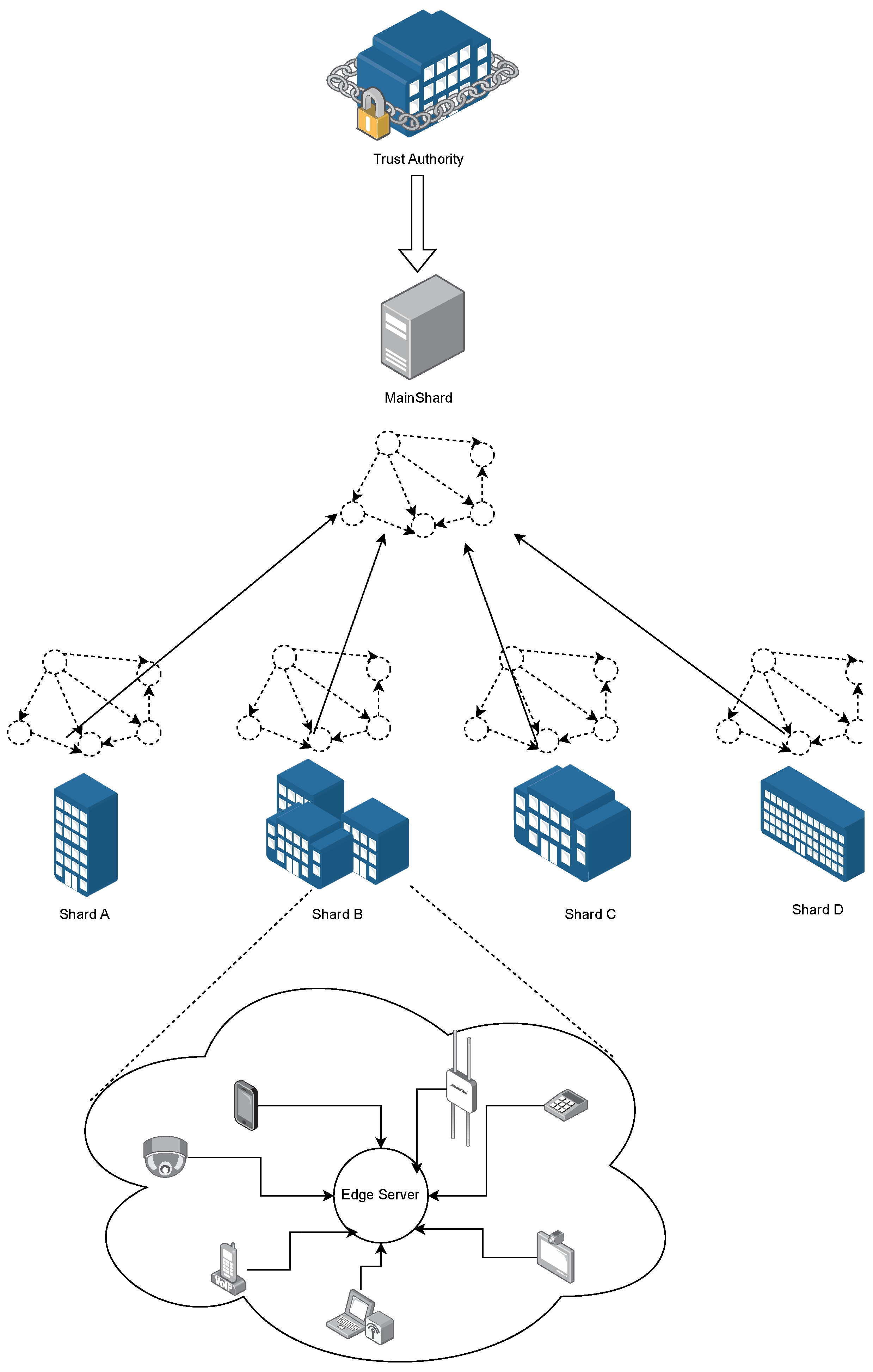
3. Overview of System Model

In this section, we will introduce FLPShard, a flexible sharding scheme that allocates shards to nodes based on various conditions such as node geographical location and inter-node latency, and adjusts the size and number of shards. FLPShard can adopt appropriate access methods based on different device characteristics and can apply more conditions for sharding according to the application scenarios. In response to the dynamic changes in the number of blockchain nodes, FLPShard also offers a dynamic adjustment scheme.

Figure 1 depicts an overview of the principal constituents of the FLPShard system model. In order to actualize sharding, FLPShard necessitates possessing the information of each individual node. Consequently, the overall system is generally partitioned into two tiers. FLPShard endeavors to place disparate transaction information within distinct physical networks so as to optimize the system’s throughput, privacy, and security to the greatest extent. FLPShard is comprised of several pivotal entity groups: trusted institutions, edge servers, main chains, business chains, and industrial nodes. Each entity group within the system is constituted by devices fulfilling the same function, possessing analogous hardware resources and trust levels. FLPShard is capable of devising sharding strategies either independently or in combination, predicated on factors such as the bandwidth between nodes, transaction frequency, network latency, bandwidth, and geographical location. It also furnishes a dynamic mechanism for nodes to join and exit, enabling adaptation to a multiplicity of scenarios. The detailed particulars of the entity groups are as follows:

(1)

Industrial devices: The Industrial Internet encompasses a multitude of devices, including cameras, sensors, and computers. These devices typically exhibit limited storage capacity and relatively feeble computing power, rendering them incapable of undertaking the responsibilities of blockchain nodes. In our design, the primary function of industrial devices is to supply data to edge servers.

(2)

Edge servers: In the context of FLPSHARD, there exist multiple edge servers, each denoted as $S_n,n\in (1,2,...)$. Edge servers are tasked with gathering data from industrial devices and collating it.

(3)

Main chain nodes: In FLPSHARD, the nodes of the main blockchain, known as main chain nodes, are assembled from the most potent servers. Their role is to maintain the global ledger as full nodes and store information such as the geographical location, network connectivity, number of shards, and shard number of each node. They also perform sharding on the business chain network and oversee cross-shard transactions and final consensus.

(4)

Business chain nodes: These nodes handle intra-shard transactions. The business blockchain is segmented into several shards by the main chain and dynamically adjusts the shard size and number when requisite.

Given that the sharding is based on units rather than actual nodes, a particular unit within the shard corresponds to a conglomeration of multiple nodes of the business chain. We have opted for the PBFT (Practical Byzantine Fault Tolerance) consensus mechanism to be implemented in FLPShard. In fact, both the Proof of Work (POW) and Proof of Authority (POA) consensus mechanisms could potentially serve as the consensus algorithm within the shard. However, in comparison to POW, the PBFT consensus mechanism alleviates the burden of requisite mathematical proofs, and the validity of transactions does not mandate multiple confirmations. This renders PBFT more amenable to handling the dynamic ingress and egress of nodes, and it also facilitates the replacement of shard leader nodes and the adjustment of shard scale. To streamline the calculations, we have adopted two-dimensional coordinates and have neglected the scenario where nodes are situated at different heights.

4. Blockchain Sharding Scheme Based on the Improved SSCFLP Model

In this section, we will expound on the design specifics of FLPShard, encompassing the optimization and adjustment of the SSCFLP model, the initial construction algorithm of shards, and the dynamic adjustment strategy for shards when the number of nodes varies.

4.1. Modification of SSCFLP

As has been stated previously, the FLPSHARD adopts a dual-layer blockchain architecture. It stores crucial information such as the locations of business chain nodes, the latency among nodes, and the bandwidth of nodes on the main chain, and then conducts sharding on business chain nodes and dynamically adjusts the shards based on this information. For the sake of facilitating reading, the symbols employed and their corresponding meanings are listed as follows:

Table 1. Symbols and notations.

No	Symbols	Notations
1	S	All nodes set
2	$S^F$	Leader node candidates
3	$S^C$	Set of ordinary node candidates
4	c	Communication cost between nodes
5	d	Unit or node occupancy capacity
6	f	Cost for a new shard
7	s	Capacity of shard
8	H	Values exceeding the shard capacity limit
9	L	Value below the lower limit of shard capacity
10	Q	Number of shards affected in each iteration

Table 1. Symbols and notations.

No	Symbols	Notations
1	S	All nodes set
2	$S^F$	Leader node candidates
3	$S^C$	Set of ordinary node candidates
4	c	Communication cost between nodes
5	d	Unit or node occupancy capacity
6	f	Cost for a new shard
7	s	Capacity of shard
8	H	Values exceeding the shard capacity limit
9	L	Value below the lower limit of shard capacity
10	Q	Number of shards affected in each iteration

Consequently, the problem can be depicted in the following manner: Given a set of nodes denoted as S, a portion of the nodes within it constitutes a set of units U, which is referred to as the unit set. These units are composed of several nodes, and these nodes cannot be partitioned into different shards. Units themselves are not befitting to act as leader nodes.Units only exist during the sharding process. In the business chain, units will be transformed into a node set $S^u$, and engage in the consensus process. Our objective is to select a set of leader nodes. With these nodes as the core, shards will be constructed. Each shard encompasses only one leader node. The tenet of shard construction lies in minimizing the overall communication cost within the shard while ensuring the least number of shards. To align with SSCFLP, the relevant parameter definitions are presented as follows: Definition 1: Factory Set (Leader Node Set) and Customer Set (Non-central Leader Node Set): We equate the leader nodes of shards to factories in SSCFLP and non-leader nodes to customers. In FLPShard, two sets are defined: the leader node set (factory set) $S^F$, and the ordinary node set (customer set) $S^C$, There might be some nodes in the set $S^C$, During the sharding process, these nodes are bundled into several units, and these units are regarded as nodes with a demand greater than 1.These two sets can be equal, that is, $S^F=S^C$, or a part of the ordinary node set can be chosen as facility nodes as per requirements, that is , $S^F\in S^C$, Nodes that form units cannot serve as central nodes. When the two sets are equal, the scope of application is broader and the sharding results may be more favorable. When facility nodes are selected in advance, the time needed for the initial sharding and subsequent dynamic adjustment of shards is shorter. In this paper, we focus on the first approach, namely, that the two sets are equal.

Definition 2: Factory Capacity and Customer Demand: Herein, we stipulate that the shard centered around any candidate central node $i(i\in S^F)$ has a maximum number of nodes $s_i$, which corresponds to the concept of factory capacity in SSCFLP. The number of nodes included in unit $j(j\in S^c)$ is $d_j$, which corresponds to customer demand. For ordinary nodes that are not units, $d_j=1$. Definition 3: Transportation Cost: Here, we set the communication cost between nodes to correspond to the transportation cost in SSCFLP. Suppose the communication cost between any two nodes $m,n$ in S is $c_{mn}$. The variable $c_{mn}$ is formed by the comprehensive integration of multiple factors.

In this paper, with the aim of evaluating the communication cost more precisely, we have employed the Euclidean distance and network latency as the metrics for gauging the communication cost. In the actual blockchain network milieu, if the Euclidean distance between two nodes is relatively short, there is a high likelihood that they are situated within the coverage area of the same network server. Conversely, if the network latency between two nodes is relatively high, it is rather probable that these two nodes do not fall under the purview of the same network server. The Euclidean distance is defined in the following manner:

$$di{s}_{ij}=\sqrt{{(la{t}_i-la{t}_j)}^2+{(lo{n}_i-lo{n}_j)}^2}$$

(1)

We make use of the $Rtt$ value $la{g}_{ij}$ to measure the network latency between two nodes. Given that the $Rtt$ varies with different network conditions, we have adopted the $SimleRtt$ algorithm in $TCP/IP$to compute the average value.

For the convenience of data processing, we prescribe that the upper limit of the latency between two points is $Rt{t}_{max}$, The algorithm is detailed as follows:

$$la{g}_{ij}=\left\{\begin{array}{cc}la{g}_{ij},\hfill & la{g}_{ij}<=Rt{t}_{max}\hfill \\ Rt{t}_{max},\hfill & la{g}_{ij}>Rt{t}_{max}\hfill \end{array}\right.$$

(2)

To better accommodate the influence of distance and latency, we have normalized these two data and subsequently aggregated them. The communication cost can thus be expressed as follows: where $\upsilon$ is a constant, which facilitates the adjustment of relevant parameters.

$$c_{ij}=(Kdi{s}_{ij}+Nla{g}_{ij})*\upsilon$$

(3)

Among them, $K,N$ are parameters utilized to modulate the influence weights of the two values. In this paper, $K=1,N=1$.

Definition 4: Cost of Initiating a New Factory: For node$S_i$, the cost entailed in designating this node as the leader node is $f_i$.

Based on the above definitions, the sharding problem can be formulated using the classic SSCFLP model as follows:

$$miniF=min\sum _{i\in I}{f}_i{y}_i+\sum _{i\in I}\sum _{j\in J}{c}_{ij}{x}_{ij}$$

(4)

s.t.

$$x_{ij}=\left\{\begin{array}{cc}1,\hfill & \mathrm{if} \mathrm{client} \mathrm{is} \mathrm{assigined} \mathrm{to} \mathrm{facility} i\hfill \\ 0,\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

(5)

$$y_i=\left\{\begin{array}{cc}1,\hfill & \mathrm{if} \mathrm{facility} i \mathrm{is} \mathrm{open}\hfill \\ 0,\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

(6)

$$\begin{array}{c}\sum _{i\in I}{x}_{ij}=1,\forall j\in J\end{array}$$

(7)

$$\begin{array}{c}\sum _{j\in J}{d}_j{x}_{ij}\le s_i{y}_i,\forall i\in I\end{array}$$

(8)

$$\begin{array}{c}{x}_{ij}\in \{0,1\},\forall i\in I,\forall j\in J\end{array}$$

(9)

$$\begin{array}{c}{y}_i\in \{0,1\},\forall i\in I\end{array}$$

(10)

Among them, $x_{ij}$ indicates whether the j-th node is affiliated with the i-th central node, and $y_j$ indicates whether the j-th node is operative. Expression 4 minimizes the initiation cost and the communication cost between nodes and the central node. Expression 7 guarantees that each node is affiliated with only one central node. Expression 8 ascertains that all nodes are affiliated with the central node and that there is no capacity overrun. Generally, it is rather challenging to quantify the initiation cost $f_i$ of the central node. Therefore, a fixed value M can be assigned to $f_i$ according to specific circumstances. If the value of Mis relatively large, the sharding strategy leans towards filling the shards first and then contemplating the reduction of the overall communication cost. If the value of M is relatively small, priority will be accorded to the communication cost and then sharding is performed. In practical applications, the following scenarios might be encountered: (1) In a particular shard, any two or more ordinary nodes are connected to the central node, but these nodes are not connected to each other. In this case, it could lead to a decelerated speed of reaching consensus, thereby impeding the throughput of the shard. (2) There might be a situation where the number of nodes within a shard is insufficient, which could undermine data security. Although it can be rectified by adjusting the value of M, extreme situations cannot be entirely precluded. To tackle the above issues, we have appended two special constraints: (1) The nodes within a shard are interconnected, that is, we establish an upper limit for the network latency between a node within a shard and the other nodes. If it exceeds this upper limit, this solution will be deemed infeasible. Let the upper limit of this latency be $ShardRt{t}_{max}$.

$$la{g}_{jmn}<ShardRt{t}_{max}$$

(11)

(2) We establish the lower limit of the number of nodes within a shard as a constant $\alpha$. This measure is implemented to avert the circumstance where an insufficient number of nodes leads to inadequate data backup.

$$\sum _{i\in I}{y}_i\ge \alpha$$

(12)

4.2. Sharding Construction

To actualize sharding, we are required to address the variant of the SSCFLP problem. In relation to SSCFLP, two principal solution strategies exist: exact solution methods and Heuristic Algorithms. Exact solution methods, such as the Branch-and-Bound Approach, albeit capable of furnishing elaborate solutions, entail high computational costs and cannot assure the discovery of the optimal solution at all times. By contrast, Heuristic Algorithms, including the LH Algorithm, Tabu Search Algorithm, and Greedy Algorithm, offer rapid problem-solving capabilities but may not culminate in the most favorable solution. In practical applications, the attainment of the optimal solution is not invariably indispensable. To expeditiously construct shards, we have opted to employ Heuristic Algorithms for procuring approximate solutions. In the practical context of the IIoT, the presence of a copious number of nodes renders the execution of SSCFLP calculations on all nodes extremely time-consuming. To augment computational efficiency, certain candidate central nodes can be predetermined. Nevertheless, in the present study, we have still elected to conduct computations on all nodes. To hasten the calculation process, we have adopted the relatively swift yet potentially suboptimal greedy algorithm to initialize the shards and thereby obtain an initial solution. Subsequently, through an iterative progression, we randomly select a neighborhood from the current solution, formulate new sub-problems, and resolve them to procure new solutions. If the new solution surpasses the initial solution in quality, the initial solution is updated. This iterative process persists until the new solution ceases to outperform the previous one or the preset number of iterations is attained.

In heuristic algorithms, an excessive number of constraint conditions might preclude the acquisition of an effective initial solution. To surmount this issue, it is commonplace to obtain the initial solution by relaxing specific constraints (for instance, via the application of Lagrange relaxation). In this study, we contemplated the feasibility of solutions in the following sequence: assignment constraints, factory quantity constraints, upper limit constraints on internal communication latency of nodes, and factory capacity constraints. Given that the factory capacity constraints in FLPSHARD are comparatively intricate and arduous to fulfill when upper and lower limits are in place, we relaxed the limitations pertaining to factory capacity, that is, the restrictions on the number of nodes, and transmuted them into soft constraints. We introduced two auxiliary variables, $H_i$ and $L_i$, which respectively signify the magnitudes by which the number of nodes within a shard exceeds the upper capacity limit and falls below the lower capacity limit. When a node represents a single entity and a unit represents multiple entities in accordance with the number of internal nodes, these variables respectively denote the numbers of nodes that overstep the upper shard capacity limit and dip below the lower shard capacity limit. Herein, $\beta$ is a relatively large number, which serves to facilitate the attainment of a feasible initial solution and further optimize the solution during subsequent iterations and splitting procedures. Moreover, this adjustment also paves the way for the implementation of the subsequent dynamic shard adjustment algorithm.

$$min:\sum _{i\in S_F}{f}_i+\sum _{j\in S_C}{c}_{ij}{x}_{ij}+\beta \sum _{i\in S_F}\left(H_i+L_i\right)$$

(13)

$$H_i=\{0,1,2...\},\forall i\in S_F$$

(14)

$$\alpha -L_i\le \sum _{j\in S_C}{d}_i{x}_{ij}\le s_i{y}_i+H_i,\forall i\in S_F$$

(15)

Based on this line of thought, the heuristic algorithm is elucidated as Algorithm 1.

Algorithm 1: Shards construction.

Require: member nodes $S_{start}^F$ and $S_{start}^C$, nodes set S , max loop number:$maxloops$

Ensure: shards set D

1: $D=GreedSolution(S_{start}^F,S_{start}^C)$

2: for 0 < l < $maxloops$ do

3:    $(S^F*,S^C*)\leftarrow SelectNeighBorHood(S,D)$ Take a neighborhood from the current set of nodes and construct a new set of nodes.

4:    $D*=SolveSubProblemWithGreed(S_F*,S_C*);$ Obtain the corresponding sharding scheme for the current set of nodes.

5:    if $f(D*)<f\left(D\right)$ then

6:       $D\leftarrow D*$

7:    end if

8: end for

9. return D

During this process, the number of iterations of the loop can be preset. If the number of iterations is zero, the standard GREED algorithm is executed; if the number of iterations is non-zero, the GREED algorithm combined with neighborhood search is executed. The specific steps are as follows: (1) Relax the constraint conditions and apply the GREED algorithm to construct an initial solution. (2) Randomly select an element based on the current solution, determine the demand points in the neighborhood, the current facilities, and the candidate facility set. (3) Construct a sub-problem model in the neighborhood and solve it to update the current solution. (4) Repeatedly execute steps 2 and 3 until the number of iterations is satisfied. (5) If no better solution is found after a certain number of iterations, the algorithm will stop executing.The algorithm for dynamically expanding the network is illustrated in Algorithm 2.

4.3. Dynamic Expansion of the Network

When a new node joins the blockchain network, it will be added to the shard where the leader node with the minimum communication cost with it is located. To find this shard, we adopt the simplest traversal method, calculate the communication costs between all shard leader nodes and the newly added node, and then select the shard with the minimum communication cost.

Algorithm 2: Dynamic Expansion of the Network.

Require:  facility nodes set $S^F$, new node ${S^C}_n$ Ensure:  $S_j^F$  1: $i\leftarrow length\left(S^F\right)-1$  2: $j\leftarrow i$  3: $c_{ni}=costOfCF(S_i^F,S_n^C)$  4: $c_{nj}=c_{ni}$  5: while$i\ge 0$do  6:    if $c_{ni}<c_{nj}$ then  7:      $j\leftarrow i$  8:      $c_{nj}=c_{ni}$  9:    end if  10:    $i\leftarrow i-1$  11:    if $i\ge 0$ then  12:      $c_{ni}=costOfCF(S_i^F,S_n^C)$  13:    end if  14: end while  15: return   $S_j^F$

4.4. Dynamic Allocation Method

When nodes join or leave a shard, it may cause the size of the shard to exceed the preset maximum capacity or fall below the minimum capacity, thus triggering the dynamic redistribution of nodes. During this process, the greatest challenge lies in how to effectively adjust the shards. The strategy we adopt is to construct a large neighborhood and transform the problem into finding a solution within this neighborhood.

When the size of a shard exceeds its upper limit, the shard will be split into two or more new shards. Taking the newly added node as the center, a neighborhood is constructed, and central nodes, ordinary nodes, and unit sets are selected within this neighborhood to form an SSCLP problem and solve it. The specific operation steps are as follows: In the shard with overcapacity, identify the last added node. According to the principle of ascending communication cost with this node, select Q central nodes of the shards. Then, the set of ordinary nodes in the shards where these Q central nodes are located and the current shard form a subset of ordinary nodes $S^{\prime }$, and convert the dynamic adjustment into an SSCFLP on this set. It should be particularly noted that if $Q=1$, only the current shard will be independently adjusted, and there will be no impact on neighboring shards. If the number of nodes in a certain current shard is below the lower limit of nodes, a neighborhood will be constructed with the leader node of this shard as the center for the re-sharding operation.

During this process, the value of Q is crucial. If Qis too small, a single redistribution will only affect a few neighboring shards. From the perspective of the entire blockchain network, the result of shard adjustment may not be optimal, and after dynamic adjustment, these shards may still be in a critical state of dynamic allocation. The addition of new nodes may trigger dynamic allocation again. Conversely, if Qis too large, the neighborhood scale will be too large, resulting in low computational efficiency and requiring a long time for calculation. In practical operations, we usually consider the number of candidate central nodes. In this paper, the upper limit value of Q is set to 6. If the number of shards in the blockchain network is small, the value of Q is set to half of the current number of shards, that is, $Q=min({\displaystyle \frac{L}{2}},6)$.

Even so, in actual operation, we may still encounter situations where we need to solve the dynamic allocation problem in a set containing 360 or even more nodes. If we solve it in a node set of this size as in the initial sharding, it may cause a certain delay in the operation of the blockchain. To ensure the processing speed and minimize the problem of leader node conversion caused by shard splitting, we set the candidate central nodes in the current subset as the central nodes of the original Q shards and a set of Q ordinary nodes randomly selected from the current subset of ordinary nodes. If the involved node set is very large, we continue to use the heuristic method of the greedy algorithm; when the total number of nodes is small, we can directly use the branch-and-bound method to obtain the exact solution. The dynamic allocation method is presented in Algorithm 3.

Algorithm 3: Dynamic Allocation Method.

Require:  member nodes $S^F$ and $S^C$, max loop number:$maxloops$, shards set D Ensure:  shards set D 1: SELECT shard set Q from D sort by c from $S^F$ and $S^C$ 2: from Q shards construct a sub set $S^{\prime }$, $S^{F^{\prime }}$ and $S^{C^{\prime }}$ 3: $D^{\prime }=GreedSolution(S^{F^{\prime }},S^{C^{\prime }})$ 4: for 0 < l < $maxloops$ do 5:    $(S^{F^{\prime }}*,S^{C^{\prime }}*)\leftarrow SelectNeighBorHood(S^{\prime },D^{\prime })$ Take a neighborhood from the current set of nodes and construct a new set of nodes. 6:    $D*=SolveSubProblemWithGreed(S_{F^{\prime }}*,S_{C^{\prime }}*);$ Obtain the corresponding sharding scheme for the current set of nodes. 7:    if $f(D*)<f\left(D^{\prime }\right)$ then 8:      $D^{\prime }\leftarrow D*$ 9:    end if 10: end for 11: UPDATE D by $D^{\prime }$  12:  return D

5. Performance Evaluation

In this chapter, we employed a simulator to conduct an assessment of FLPShard.

5.1. Theoretical Analysis

SSCFLP is an NP-hard problem, signifying that its computational time escalates rapidly with the augmentation of scale. To tackle this predicament, we have implemented the following strategies: (1) 1. We opted for the relatively expeditious greedy algorithm for problem-solving. This choice, however, may lead to the initial sharding outcomes not attaining optimality. Given that whenever a new node is incorporated, the system will effectuate adjustments predicated on the extant shards. Since the initial solution is not exact, the shard adjustment procedure is fundamentally an iterative optimization process, and the solving process will progressively optimize the overall sharding results. In other words, the addition or deletion of nodes will instigate local allocation optimization, and the longer the blockchain system operates, the closer the throughput of the blockchain network will approach the ideal value. (2) The initial sharding is executed on the entire dataset, which might consume a considerable amount of time. When subsequent nodes are appended, each round will only modulate the shards wherein the number of nodes surpasses the upper limit or falls below the lower limit. In accordance with the above theoretical design, as shows in Table 2, a shard adjustment pertains, at most, to 6 surrounding shards. Since each shard has an upper bound on the number of nodes, this culminates in the number of affected nodes being a constant within a specific range. In other words, each shard adjustment operation is essentially an O(c) problem. If the number of nodes within a shard is relatively scant (less than 10), it is even feasible to endeavor to obtain the exact solution in each round.

5.2. Experimental Environment Design

(1) Experimental Model Construction: We devised a suite of code based on the greedy algorithm, with the aim of resolving the SSCFLP variant problem and actualizing the initial configuration of shards as well as their dynamic adjustment. For the facilitation of testing, we further developed a simulator using Python 3.12 to fabricate a simulator prototype capable of executing sharding and its dynamic adjustment functions. The experiment was carried out on a computer furnished with an Intel Xeon 5-2640v4 processor and 16GB RAM, operating under the Windows 11 system and utilizing Python 3.12 as the programming language. To streamline the experiment, we set all shard capacities to be uniform, and each unit occupied solely one capacity unit. Within the shards, we implemented the PBFT consensus mechanism and permitted ordinary nodes to be candidates for central nodes. For the sake of equitable comparison, we set the factory capacity to be exceedingly large, compelling the algorithm to prioritize filling the existing shards. Although this might result in the FLPSHARD outcome not being optimal, it could ensure that the number of shards corresponded to that of the random algorithm. It is noteworthy that the employment of neighborhood optimization might cause the number of shards to deviate from that of the random algorithm. For example, in the case of 200 nodes and a maximum shard capacity of 10, the random algorithm might evenly apportion them into 20 shards, while the FLPSHARD scheme might generate 22 or 25 shards. To nullify the numerical discrepancies induced by the different numbers of shards, we assigned an extremely large initial value to the cost function $f_i$ in the FLPShard, coercing the algorithm to initiate a new shard after filling one shard, so as to maintain the number of shards in the FLPSHARD scheme congruent with that of the random algorithm. Meanwhile, we annulled the optimization process, that is, we contrasted the initial solution with the maximum deviation from the optimal solution with the random algorithm. The results manifested that even with such an initial solution, its efficiency markedly surpassed that of the random algorithm.

(2) Dataset: We randomly engendered several sets of nodes dispersed across three central cities. The communication delays between nodes within each city and across cities were disparate, and the delays between nodes were randomly assigned. We contrived different numbers of node sets and diverse upper and lower limits of shard capacities to corroborate the advantages of the FLPSHARD scheme.

(3) Testing: We contrasted the consistent hashing algorithm sharding scheme applied in blockchains such as Ethereum2.0 with the FLPSHARD scheme in terms of their operational outcomes, centering on the impact of the number of nodes and node capacities on the throughput of shards and the consensus time within shards. (4) Evaluation: We probed into the influence of different numbers of nodes and different shard sizes on throughput, as well as the effect of cross-shard transactions on network throughput. Additionally, we also verified the alterations in throughput after dynamically adding nodes and triggering re-sharding.

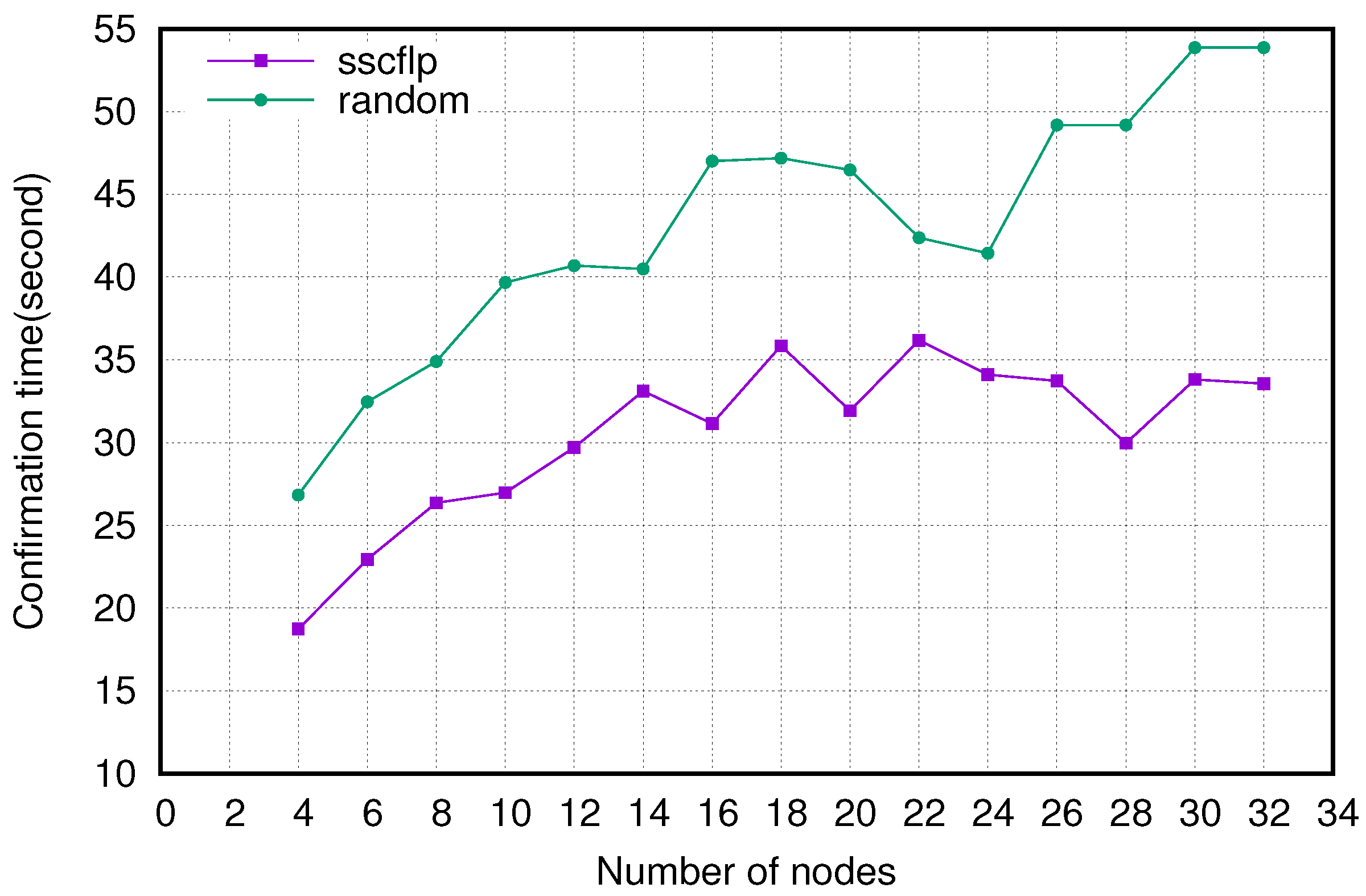
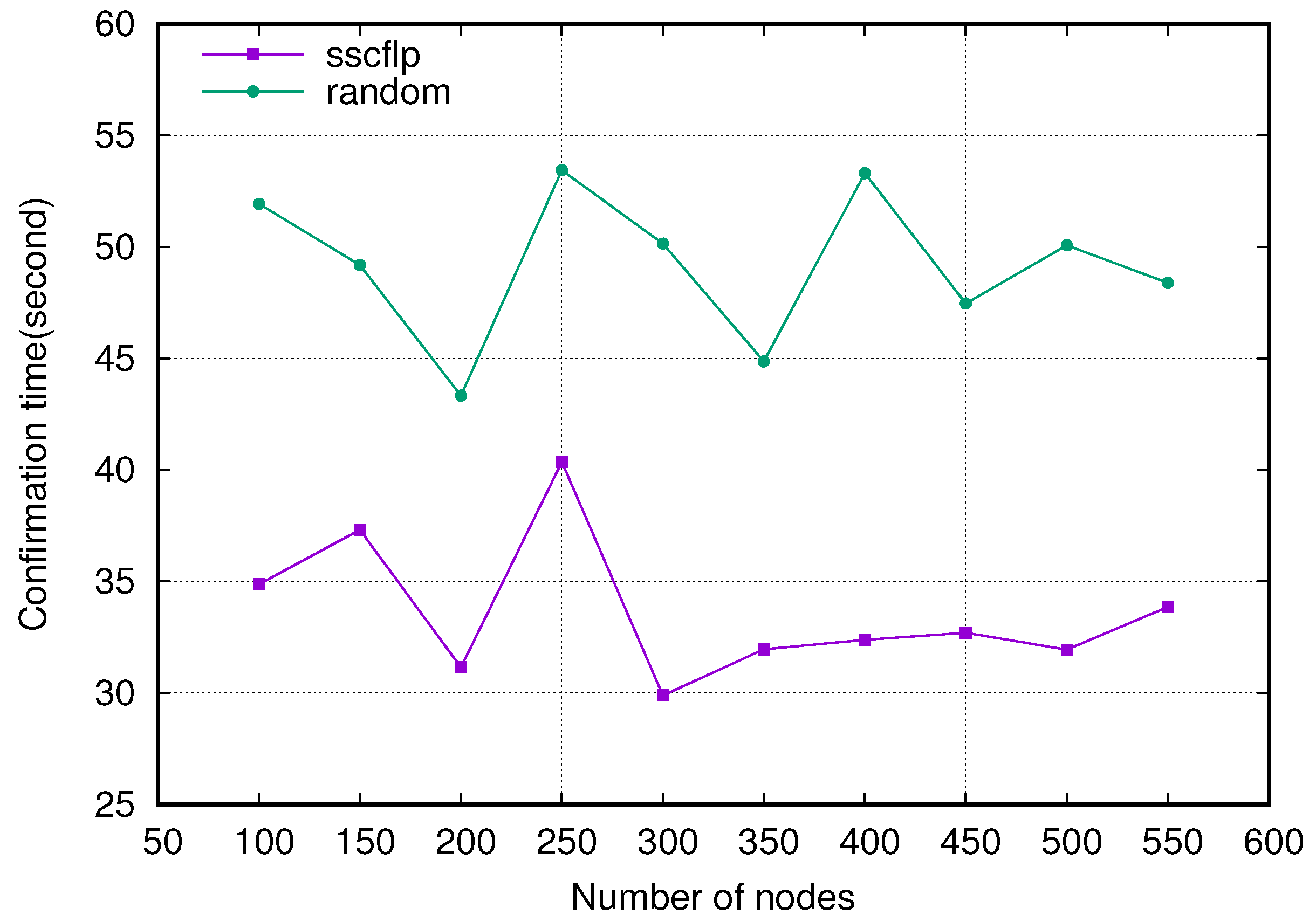
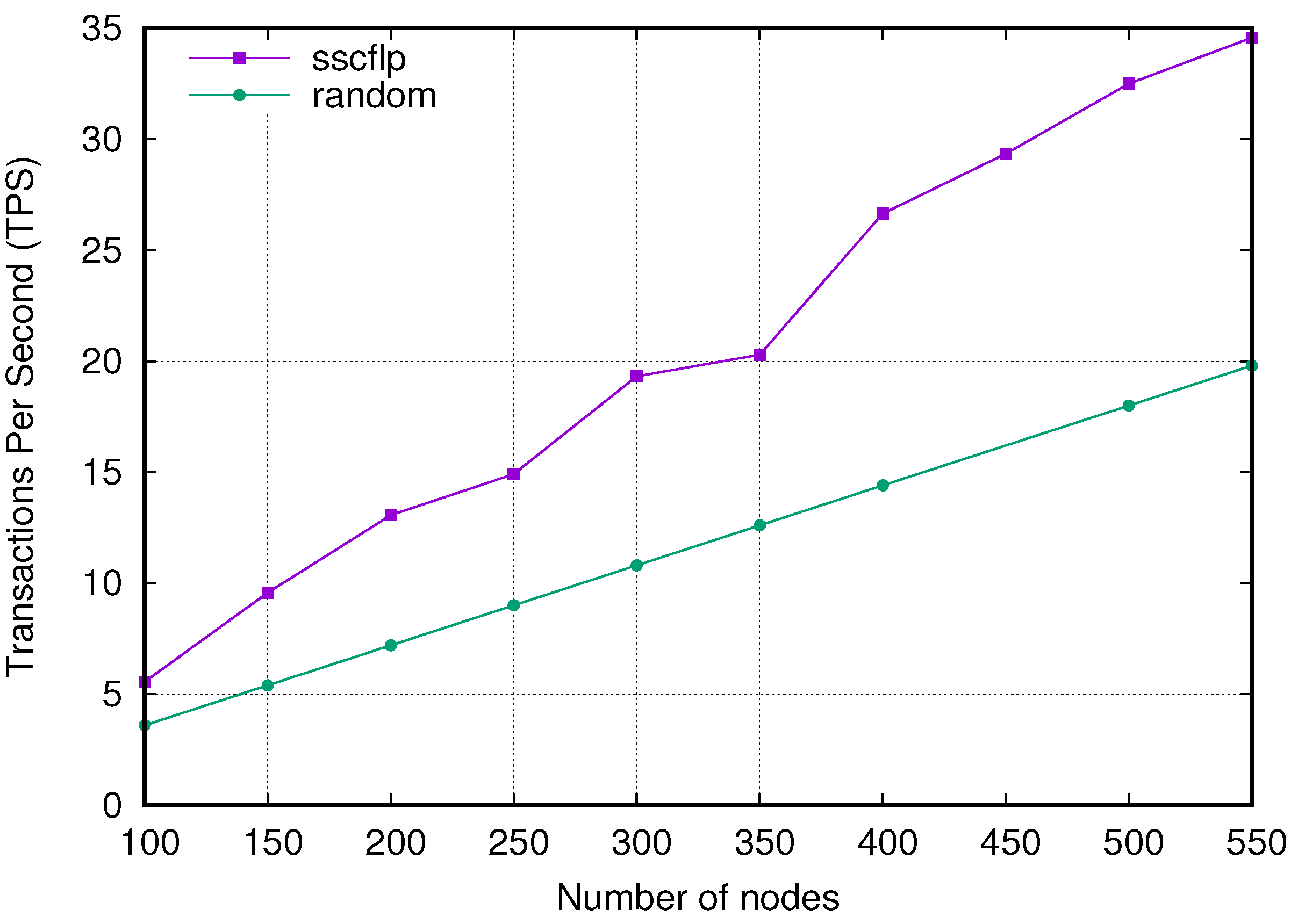
5.3. Experimental Results and Analysis

Table 3 exhibits the correlative relationship between the quantity of diverse nodes and the time requisite for the accomplishment of sharding during the initial sharding phase. Although the refined greedy algorithm does not attain the optimal solution, it has achieved a computational speed that satisfies the requisites of practical applications, while guaranteeing the high caliber of the sharding outcomes.

Figure 2 showcases the impact of different shard sizes on the time for consummating transactions within shards under the random allocation scheme and the FLPShard scheme. Within the shards, we implemented the PBFT consensus mechanism. From Figure 2, it can be discerned that as the shard size augments, the time required for finalizing transactions within the shard also ascends. In contrast to the random sharding scheme, the FLPSHARD scheme markedly curtails the time for effectuating transactions within the shard by apportioning nodes with lower network latency to the same shard, and this time differential continuously widens with the alteration in the number of nodes within the shard.

Figure 3 illustrates the influence of the increment in the total number of nodes on the time for consummating transactions within the shard when the shard size is fixed. It can be perceived that the transaction time within the shard tends to vacillate within a certain range. When the number of nodes surpasses 300, the FLPShard scheme demonstrates a propensity to stabilize. This is because as the number of nodes proliferates, the FLPShard scheme has more opportunities to allocate nodes with lower network latency to the same shard, thus causing the transaction time within the shard to gravitate towards a stable median value.

It can be observed from Figure 4 that, with the shard size remaining invariable, the network throughput escalates as the number of nodes mounts. In the simulator settings, the throughput growth of the random sharding scheme exhibits a linear tendency, while the FLPShard scheme occasionally manifests a throughput leap phenomenon when the number of nodes augments.

In summary, the FLPShard scheme is indubitably an efficacious sharding method applicable to the Industrial Internet milieu. Firstly, FLPShard is capable of dynamically adjusting shards in accordance with the ingress and egress of nodes, and during the adjustment process, it only impacts a few adjacent shards (up to 6 shards according to the current configurations). Secondly, the throughput of the FLPShard scheme can achieve linear growth as the number of nodes amplifies. It should be accentuated that the above tests were conducted without predetermining the set of leader nodes in advance. If an independent set of candidate leader nodes can be established, the efficiency of sharding will be conspicuously enhanced. Moreover, under ordinary circumstances, administrators will optimize the computing power and network environment of fixed candidate leader nodes, so the overall sharding effect is anticipated to be further ameliorated.

6. Conclusions

This paper introduces FLPShard, which innovatively applies the operations research concept of SSCFLP (Single-Source Capacitated Facility Location Problem) to address the multi-constraint issues faced in blockchain sharding. Within FLPShard, we have refined the greedy algorithm to facilitate both the initial sharding and dynamic adjustment of the blockchain, ensuring that nodes are allocated to shards with the optimal network and communication environments as much as possible. Our experimental results demonstrate that FLPShard holds a significant advantage over random sharding schemes in terms of system throughput and transaction confirmation latency. In our future work, we plan to investigate consensus mechanisms that complement FLPShard, aiming to further enhance the security and performance within IIoT (Industrial Internet of Things).