Submitted:
19 March 2024
Posted:
19 March 2024
You are already at the latest version
Abstract
Keywords:
1. Introduction
1.1. Research Background
1.2. Related Works
1.3. Motivation and Challenge
2. Materials and Methods
2.1. Why PFQN?
2.2. Blockchain Setting
2.3. Model Assumption
2.4. Model and Derivation
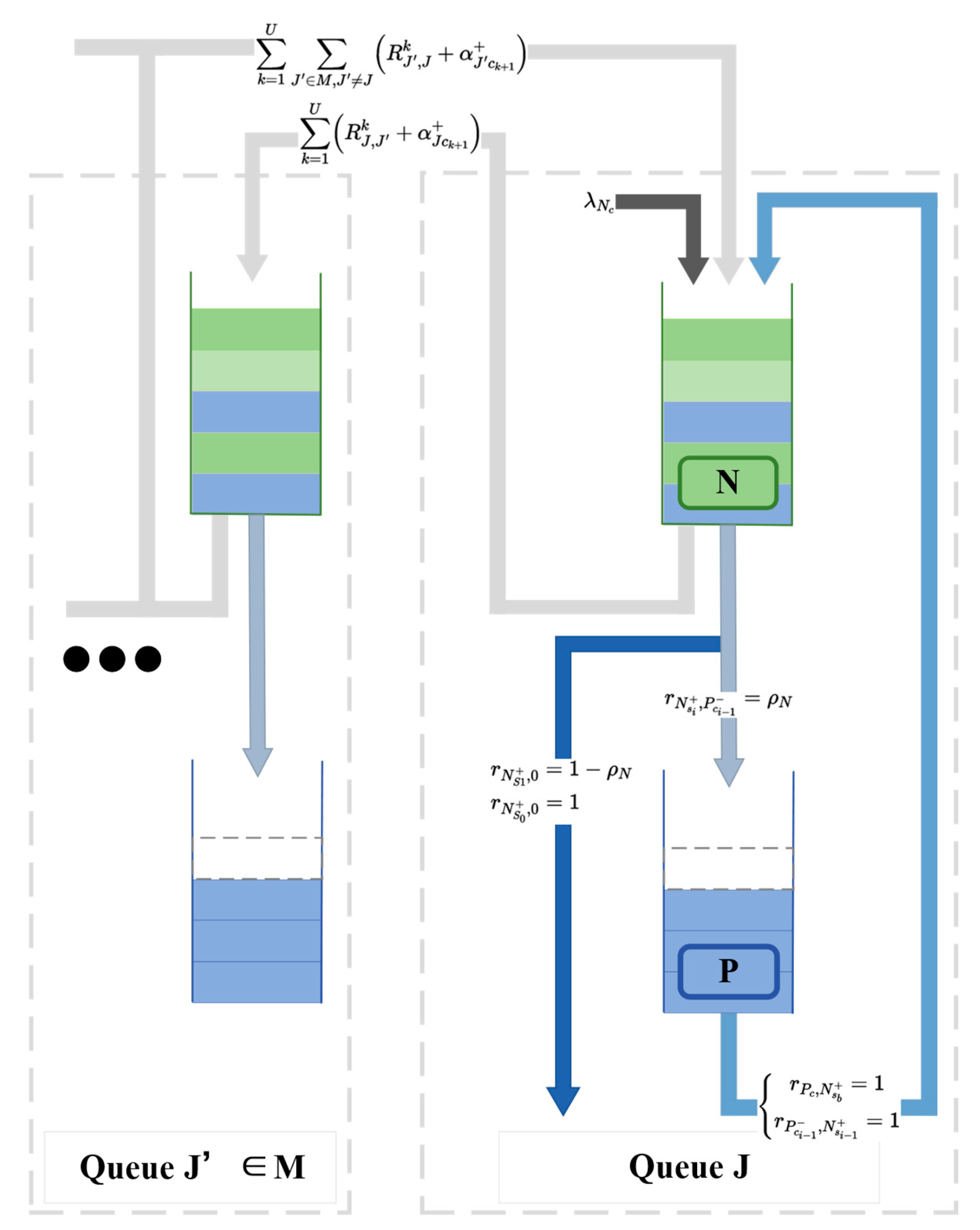
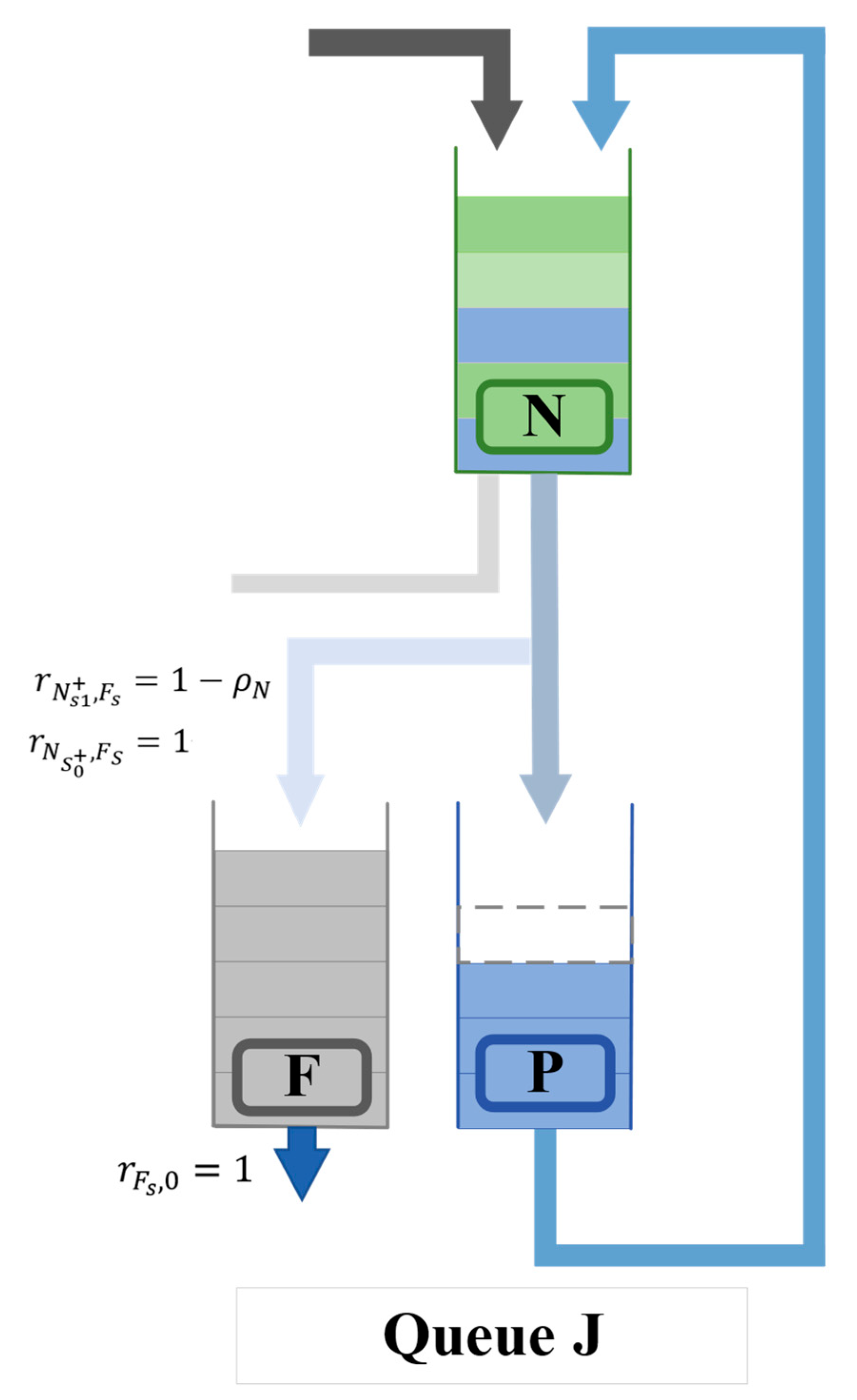
2.4.1. PFQN Model
2.4.2. Derivation of Transaction Confirmation Delay
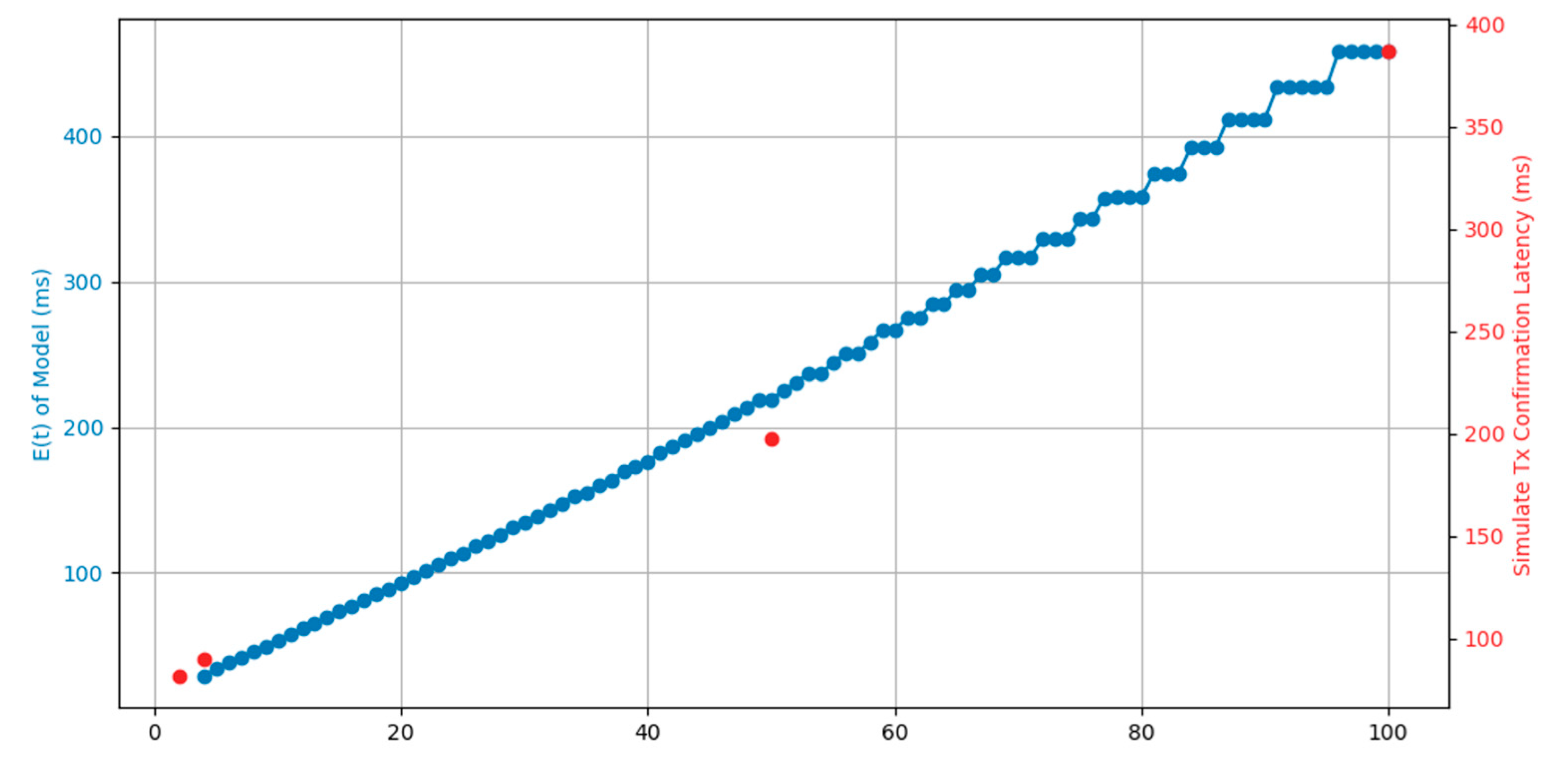
3. Results
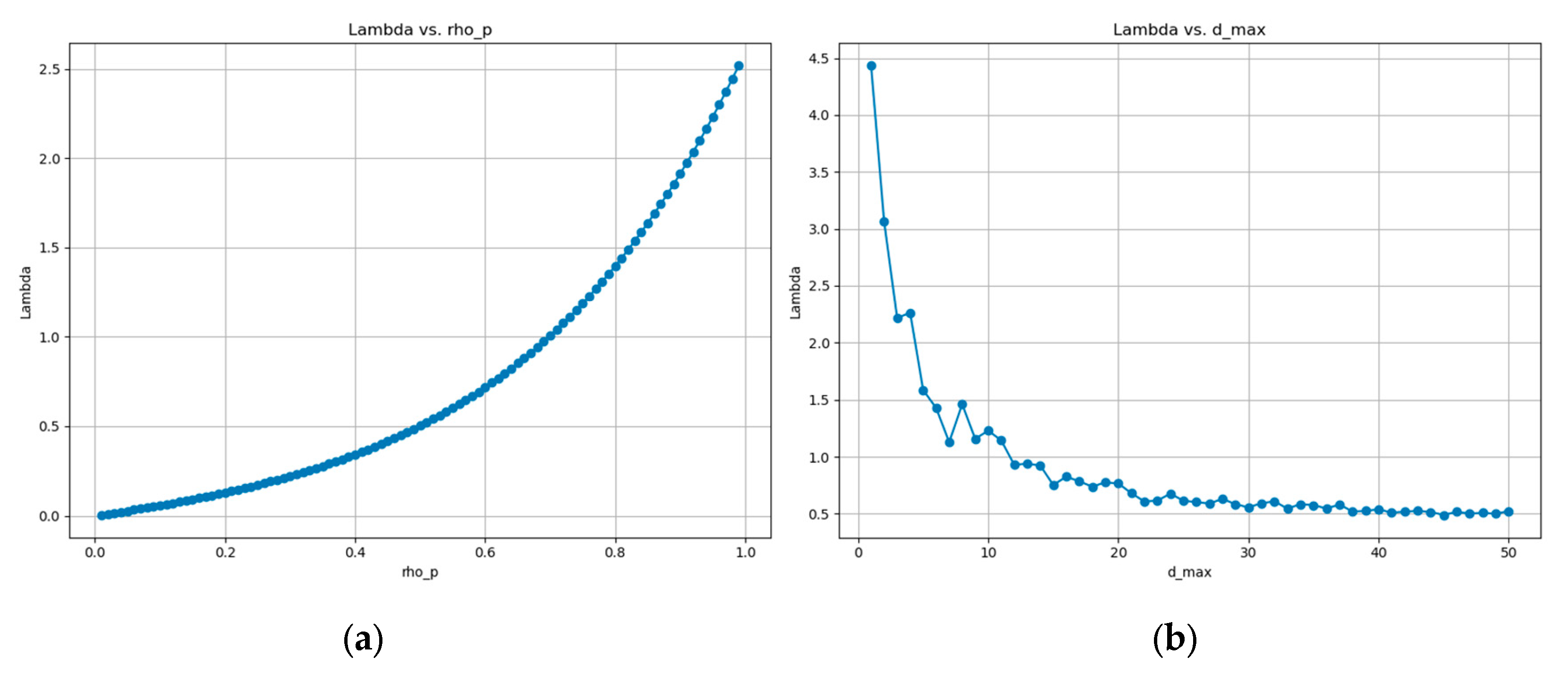
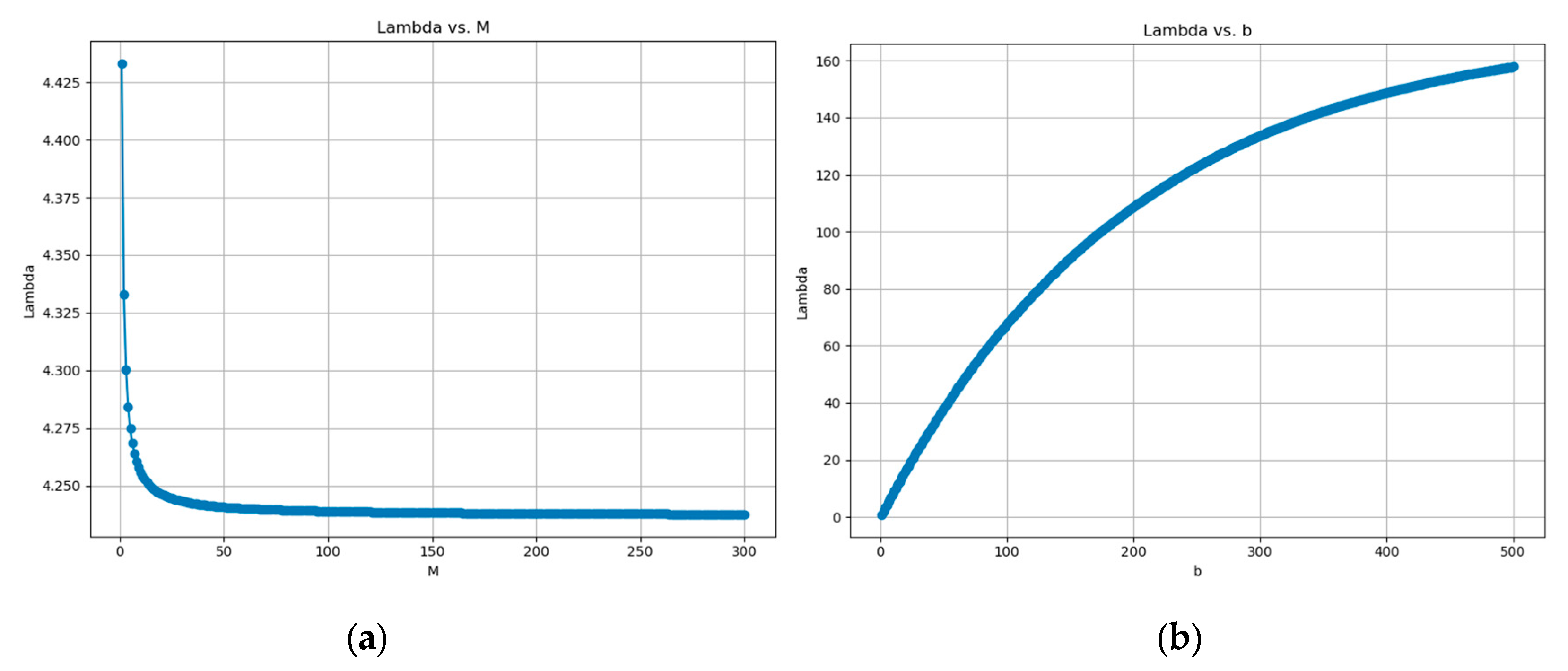
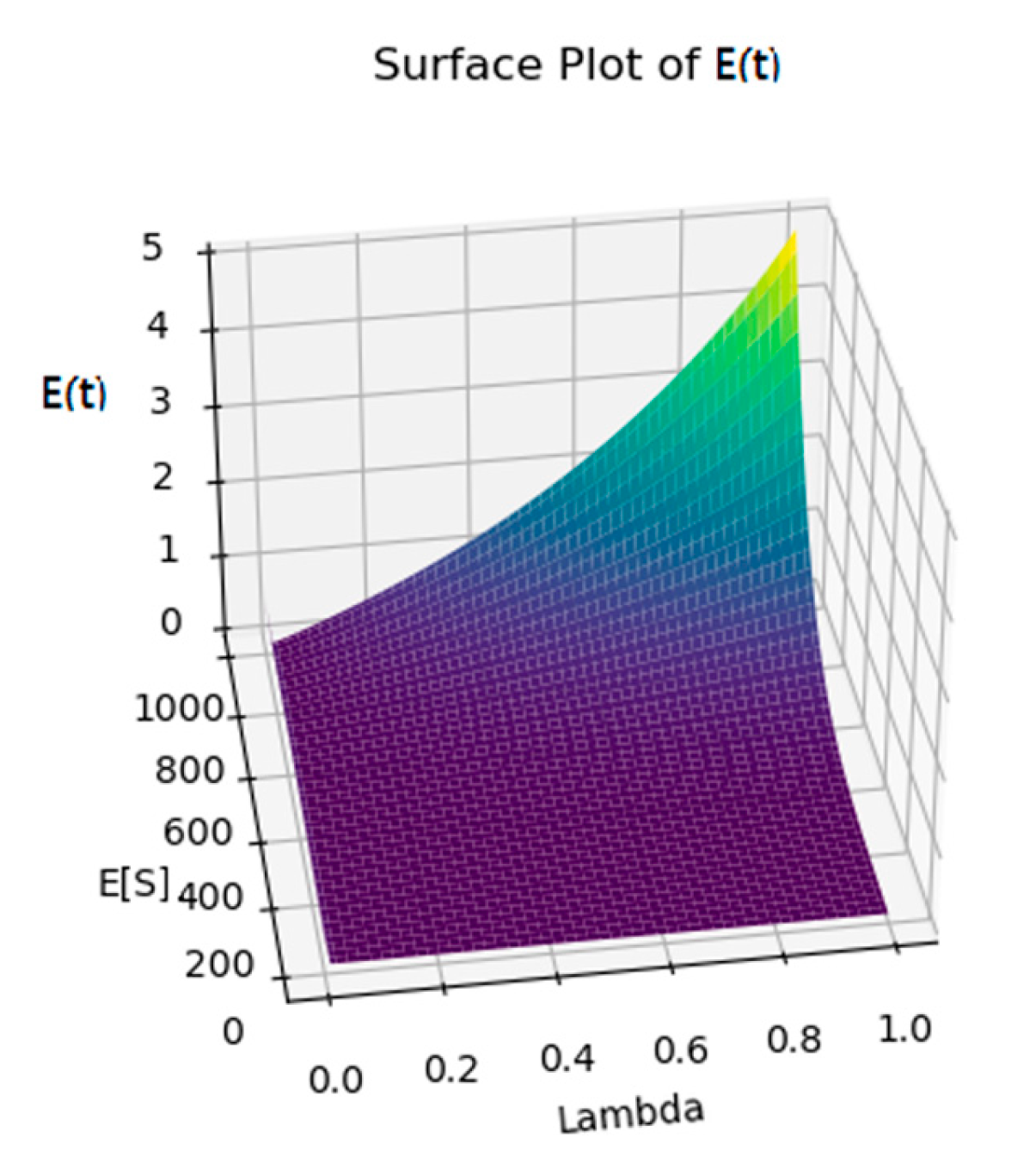
4. Discussion
4.1. PFQN and Sharded Blockchain Simulation
4.2. Security Analysis
4.2.1. Prior Research on Quantum-Safe Blockchain
4.2.2. Attack Models and Assumptions
| NIST level | Encryption Standard |
|---|---|
| 1 | AES 128 |
| 2 | SHA3-256 |
| 3 | AES192 |
| 4 | SHA3-384 |
| 5 | AES256 |
| Algorithm Category | Cryptographic Algorithm | Private Key Length (bytes) |
Public Key Length (bytes) |
NIST Level | Approximate Probability of Compromise |
|---|---|---|---|---|---|
| Post-quantum encryption algorithm | CYSTAL-Dilithium3 | 1952 | 4000 | 3 | |
| FALCON | 1793 | 2305 | 5 | ||
| Classic | RSA | 3072 | 3072 | 1 | |
| ECDSA | 256 | 512 | 1 |
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Description of parameters | |
| Parameter | Description |
| M | Set of queues |
| λ | Customer input rate per shard |
| d | Total number of destination fields in a TX |
| D[d] | The probability distribution for 'd' |
| b | Maximum number of TXs allowed in a block |
| c | Regular customer |
| K stages cross-shard signal | |
| s | Block components |
| The arrival rate of customer type e to queue J | |
| to queue J | |
| to queue J | |
| U | |
| for network queue J | |
| Service rate for customer type e in a standard queue J | |
| The utilization factor incurred by customer type e on a typical queue J | |
Appendix A
References
- Zheng, P.; Xu, Q.; Zheng, Z.; Zhou, Z.; Yan, Y.; Zhang, H. "Meepo: Sharded Consortium Blockchain." In Proceedings of the 2021 IEEE 37th International Conference on Data Engineering (ICDE), 2021; IEEE: pp. 1847–1852. [CrossRef]
- Luu, L.; Narayanan, V.; Zheng, C.; Baweja, K.; Gilbert, S.; Saxena, P. "A Secure Sharding Protocol For Open Blockchains." In Proceedings of the 2016 ACM SIGSAC Conference on Computer and Communications Security (CCS '16), New York, NY, USA, 2016; ACM: New York, NY, USA, pp. 17–30. [CrossRef]
- Kokoris-Kogias, E.; Jovanovic, P.; Gasser, L.; Gailly, N.; Syta, E.; Ford, B. "OmniLedger: A Secure, Scale-Out, Decentralized Ledger via Sharding." In Proceedings of the 2018 IEEE Symposium on Security and Privacy (SP), 2018, pp. 583–598.
- Zamani, M.; Movahedi, M.; Raykova, M. "RapidChain: Scaling Blockchain via Full Sharding." In Proceedings of the 2018 ACM SIGSAC Conference on Computer and Communications Security (CCS '18), New York, NY, USA, 2018; ACM: New York, NY, USA, pp. 931–948. [CrossRef]
- Wang, J.; Wang, H. "Monoxide: Scale out blockchains with asynchronous consensus zones." In Proceedings of the 16th USENIX Symposium on Networked Systems Design and Implementation (NSDI 19), 2019, pp. 95-112.
- Okanami, N.; Nakamura, R.; Nishide, T. “Load balancing for sharded blockchains.” In Financial Cryptography and Data Security, Springer International Publishing, 2020, pp. 512-524. [CrossRef]
- Zhang, Y.; Pan, S.; Yu, J. "TxAllo: Dynamic Transaction Allocation in Sharded Blockchain Systems." CoRR, abs/2212.11584, 2022. [CrossRef]
- Ricci, S; Ferreira, E; Menasche, DS; Ziviani, A; Souza, JE; Vieira, AB. Learning blockchain delays: A queueing theory approach. ACM SIGMETRICS Performance Evaluation Review. 2019 Jan 25;46(3):122-5.
- Li, QL; Ma, JY; Chang; YX. Blockchain queue theory. InComputational Data and Social Networks: 7th International Conference, CSoNet 2018, Shanghai, China, December 18–20, 2018, Proceedings 7 2018 (pp. 25–40). Springer International Publishing.
- Soltani, P.; Ashtiani, F. “Technical Report: Analytical Modeling and Throughput Computation of Blockchain Sharding.” ArXiv abs/2210.04599 (2022): n. pag. [Online]. Available: https://arxiv.org/abs/2210.04599.
- Kawase, Y.; Kasahara, S. "Transaction-Confirmation Time for Bitcoin: A Queueing Analytical Approach to Blockchain Mechanism." In Yue, W.; Li, Q.L.; Jin, S.; Ma, Z., Eds., Queueing Theory and Network Applications, QTNA 2017, Lecture Notes in Computer Science, vol. 10591, Cham: Springer, 2017. [CrossRef]
- Kasahara, S.; Kawahara, J. "Effect of Bitcoin fee on transaction-confirmation process.". arXiv:1604.00103[cs.CR].
- Huang, H.; Peng, X.; Zhan, J.; Zhang, S.; Lin, Y.; Zheng, Z.; Guo, S. “BrokerChain: A cross-shard blockchain protocol for account/balance-based state sharding.” In IEEE INFOCOM, 2022.
- Bano, S.; et al. “SoK: Consensus in the age of blockchains.” In Proceedings of the 1st ACM Conference on Advances in Financial Technologies, October 2019; ACM: New York, NY, USA, pp. 183–198.
- Liu, Y.; Liu, J.; Salles, M. A. V.; Zhang, Z.; Li, T.; Hu, B.; Henglein, F.; Lu, R. "Building blocks of sharding blockchain systems: Concepts, approaches, and open problems." Computer Science Review, vol. 46, 2022, 100513. ISSN 1574-0137. [CrossRef]
- "Segregated Witness (Consensus Layer)." Accessed on 2022. [Online]. Available: https://github.com/bitcoin/bips/blob/master/bip-0141.mediawiki.
- QuarkChain Development Team. "Address, Shard Key, Chain Id, Shard Id." In QuarkChain pyquarkchain Documentation, GitHub, 2024. [Online]. Available: https://github.com/QuarkChain/pyquarkchain/wiki/Address%2C-Shard-Key%2C-Chain-Id%2C-Shard-Id.
- Kawase, Y.; Kasahara, S. "A batch-service queueing system with general input and its application to analysis of mining process for bitcoin blockchain." In Proceedings of the IEEE International Conference on Internet of Things (iThings), IEEE Green Computing and Communications (GreenCom), IEEE Cyber, Physical and Social Computing (CPSCom), IEEE Smart Data (SmartData), 2018, pp. 1440–1447.
- Li, Q.-L.; Ma, J.-Y.; Chang, Y.-X. “Blockchain queue theory.” In Proceedings of the International Conference on Computing and Social Networks, 2018, pp. 25–40.
- Narayanan, A.; Bonneau, J.; Felten, E. Bitcoin and Cryptocurrency Technologies: A Comprehensive Introduction. Princeton University Press: Princeton, NJ, USA, July 2016.
- Elrond, A. "Highly scalable public blockchain via adaptive state sharding and secure proof of stake." Whitepaper, 2019. [Online]. Available: https://www.chainwhy.com/upload/default/20190705/75d146eec7c85680f34461a0fe8a621b.pdf.
- Delgado-Segura, S.; Pérez-Solà, C.; Navarro-Arribas, G.; Herrera-Joancomartí, J. "Analysis of the Bitcoin UTXO Set." In Finan-cial Cryptography and Data Security, FC 2018, Lecture Notes in Computer Science, vol. 10958, Zohar, A., et al., Eds.; Springer: Berlin, Heidelberg, 2019; pp. [CrossRef]
- Huang, H.; Ye, G.; Chen, Q.; Yin, Z.; Luo, X.; Lin, J.; Li, T.; Yang, Q.; Zheng, Z. "BlockEmulator: An Emulator Enabling to Test Blockchain Sharding Protocols." In arXiv preprint, arXiv:2311.03612, 2023.
- Avarikioti, Z.; Desjardins, A.; Kokoris-Kogias, L.; Wattenhofer, R. "Divide & Scale: Formalization and Roadmap to Robust Sharding." In Structural Information and Communication Complexity: 30th International Colloquium, SIROCCO 2023, Proceedings, pp. 199–245, Springer-Verlag, Alcalá de Henares, Spain, 2023. [CrossRef]
- Ikeda, K. (2019). qBitcoin: A Peer-to-Peer Quantum Cash System. In: Arai, K., Kapoor, S., Bhatia, R. (Eds.), Intelligent Computing. Advances in Intelligent Systems and Computing, Vol. 858. Cham: Springer.
- Wang, W., Yu, Y., & Du, L. (2022). Quantum blockchain based on asymmetric quantum encryption and a stake vote consensus algorithm. Scientific Reports, 12, Article 8606.
- Thanalakshmi, P.; Rishikhesh, A.; Marion Marceline, J.; Joshi, G.P.; Cho, W. (2023). A Quantum-Resistant Blockchain System: A Comparative Analysis. Mathematics, 11, Article 3947.
- Quantum Blockchain. (2020). Quantum Cryptography vs Post-Quantum Cryptography. FedTech Magazine.
- Ikeda, K. (2018). Security and Privacy of Blockchain and Quantum Computation. In: Raj, P., Deka, G.C. (Eds.), Advances in Computers, Vol. 111. Elsevier. Pages 199-228. ISSN 0065-2458, ISBN 9780128138526.
- Grover, L.K. (1996). A fast quantum mechanical algorithm for database search. In: Proceedings of the Twenty-Eighth Annual ACM Symposium on Theory of Computing (pp. 212-219).
- Shor, P.W. (1999). Polynomial-time algorithms for prime factorization and discrete logarithms on a quantum computer. SIAM Review, 41(2), pp. 303-332.
- Post-Quantum Cryptography Standardization. (n.d.). Security (Evaluation Criteria). Available online: https://csrc.nist.gov/projects/post-quantum-cryptography/post-quantum-cryptography-standardization/evaluation-criteria/security-(evaluation-criteria) (accessed on 19 3 2024).
- Kumar, M. (2022). Post-quantum cryptography Algorithm's standardization and performance analysis. Array, Volume 15, Article 100242. ISSN 2590-0056.
| Reference | Methodology | Focus Area | Key Findings | Contributions to the Field |
|---|---|---|---|---|
| [8] | GI/M/1 queue with batch-service | Transaction confirmation in Single-chain systems | Developed a queueing theory model for blockchain systems, identifying average transaction numbers and confirmation times | Introduced an analytical approach for blockchain queueing systems |
| [9] | M/G/1 for delay characterization, Machine learning for transaction classification | Transaction confirmation in Single-chain systems | Proposed a machine learning framework for transaction classification and queueing theory for delays | Enhanced understanding of blockchain delays and transaction confirmation dynamics |
| [10] | PFQN | Sharded blockchain efficiency | Established a model for sharded blockchain and derived maximum throughput | Introduced a new model for analyzing sharded blockchain performance |
| [11,12] | M/G/1 queue with batch service | Transaction confirmation time in Bitcoin | Analyzed transaction confirmation time in Bitcoin using queue theory | Applied queue theory to understand Bitcoin's transaction dynamics |
| Attack Type | Affected Blockchain Component | Attack Purpose | Means of Attack |
|---|---|---|---|
| Block Replacement Attack | Blockchain Historical Records | To replace the existing blockchain rewrite historical records. | Using Grover's algorithm to calculate nonces |
| Signature Forgery Attack | Transaction and Message Signatures | To tamper with or forge transactions | Using Shor's algorithm to break public key encryption systems |
| Signatures/s | Verifications/s | Max Safe Transactions | Expected Encryption Time Per Transaction | |
|---|---|---|---|---|
| CYSTAL-Dilithium3 | 6,506.33 | 17,561.33 | 0.000154 | |
| FALCON | 1,446.52 | 9,782.67 | 0.000691 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).




