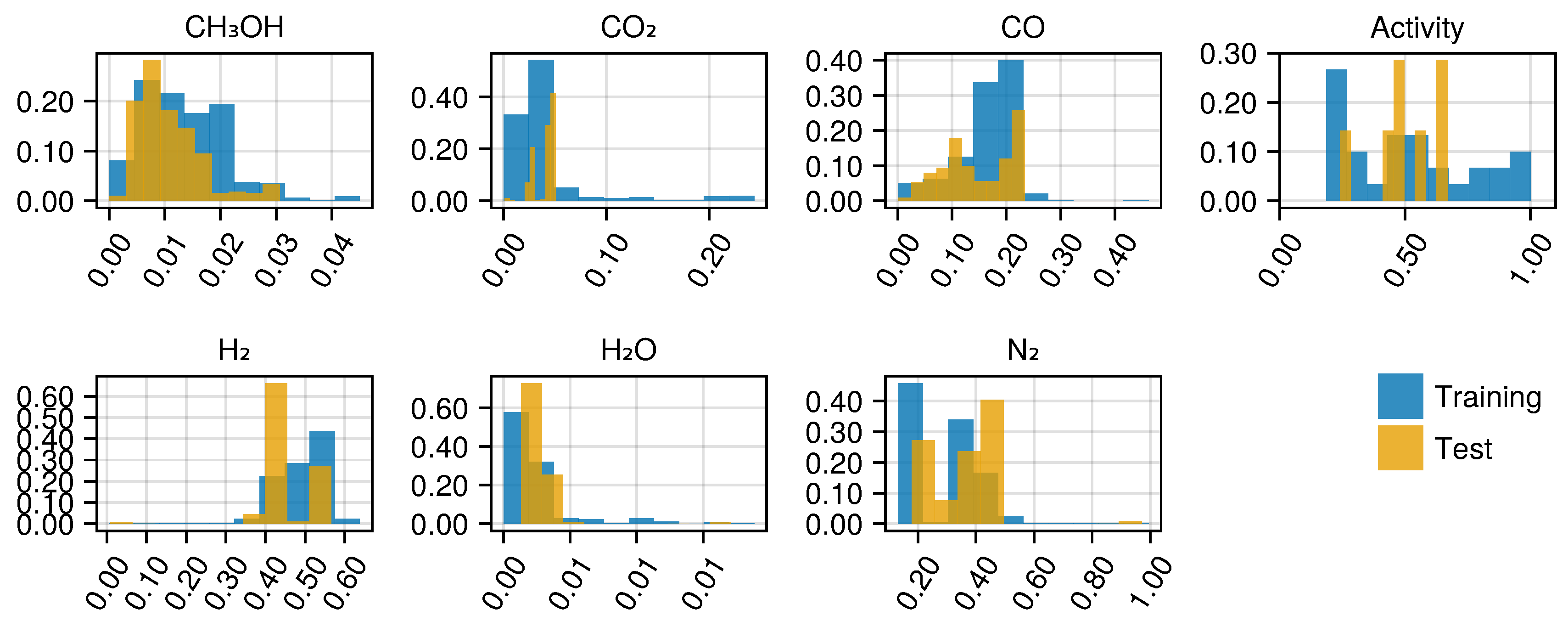Optimal Experiments for Hybrid Modeling of Methanol Synthesis Kinetics

1. Introduction

Methanol is an essential chemical with various applications. Next to its use as an intermediary product in synthesizing complex chemicals, it can be used to store electrical excess energy from renewable sources ([1]). As such, power-2-methanol processes are practical options for both synthesizing methanol from and storing said energies. Typically, green hydrogen produced via the electrolysis of water using electrical energy from renewable resources serves as the basis for this process. Hence, it is subject to inherent fluctuation of the energy source and, in turn, to comparable highly dynamic operating conditions. Advanced control schemes are needed to maximize the throughput of the process and allow the maximization of the process conversion rate under these non-stationary environmental conditions. Model-based (optimal) control is often at the heart of such strategies, see e.g. [2]. Although methanol synthesis is an established process, the development and research on the mechanism has been and still is an active field of research ([3,4]). To this end, hybrid models often serve as a valid alternative to classical, entirely mechanistic approaches. Here, machine learning models, such as neural networks, replace partially unknown or uncertain parts to account for the lack of prior scientific knowledge. Especially in the context of (industrial) chemical process engineering, training these models poses a non-trivial issue: How can hybrid models be trained reliably with minimum amount of data? This work shows how optimal experimental design can help to improve parameter estimation in the physics based model for the reaction kinetics developed by [5,6,7], which will act as a baseline for our evaluation, and fitting of hybrid models. 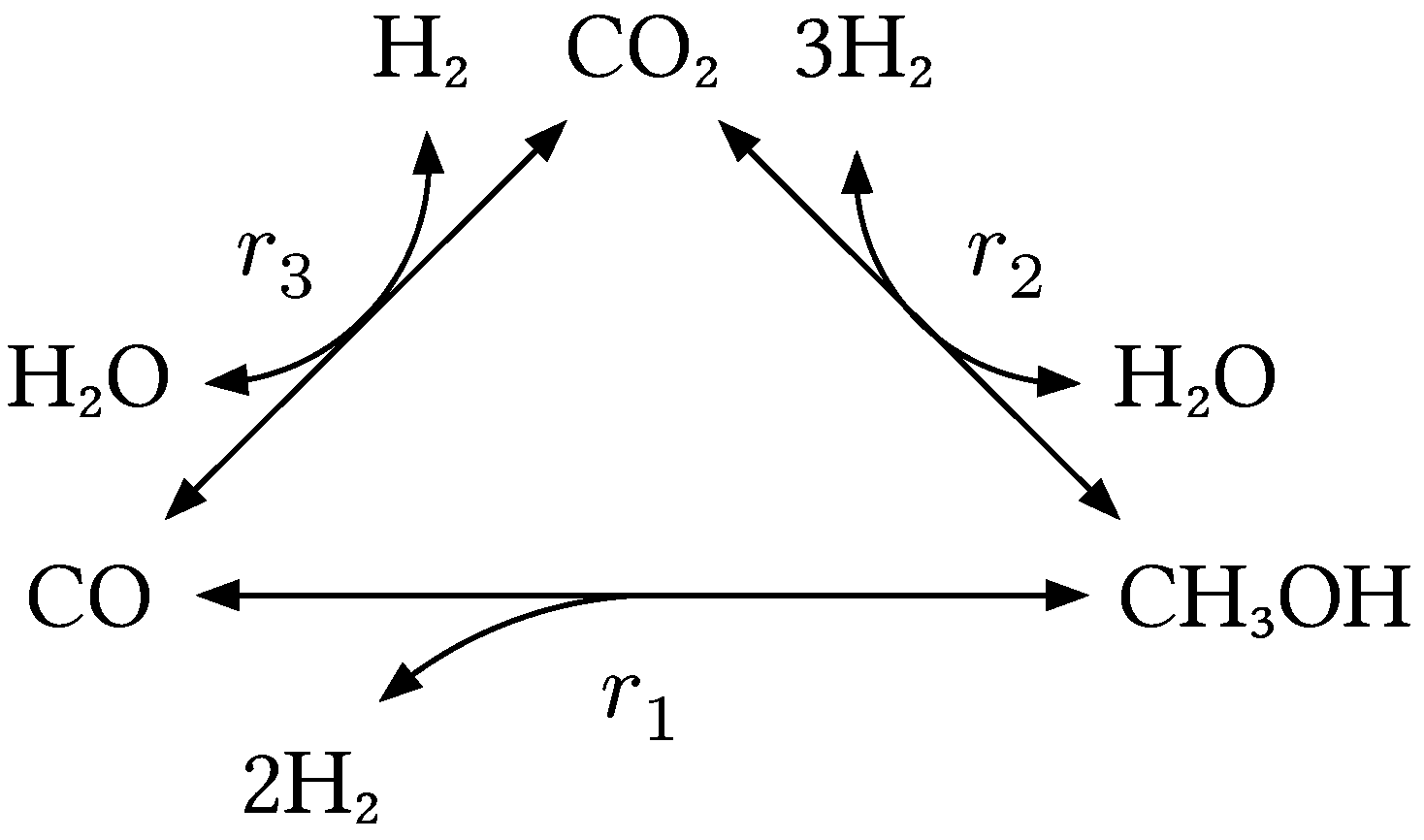The model quantifies the heterogeneously catalyzed synthesis of methanol using hydrogenation of CO and CO₂ over a CuO/ZnO/Al₂O₃ catalyst. The underlying reaction network is shown in Figure 1 network MeOH and hints at the complexity of the chemistry. The overall reaction can be broken down to three main equilibrium-limited reactions: the hydrogenation of carbon monoxide (1), the hydrogenation of carbon dioxide (1) and the reverse water-gas shift reaction (1).

$$\begin{array}{cc}\hfill \begin{array}{c}\hfill CO+2H_2\end{array}& <=>\left[r_1\right]C{H}_{3}OH\hfill \end{array}$$

(1)

$$\begin{array}{cc}\hfill \begin{array}{c}\hfill C{O}_2+3H_2\end{array}& <=>\left[r_2\right]C{H}_{3}OH+H_{2}O\hfill \end{array}$$

(1)

$$\begin{array}{cc}\hfill \begin{array}{c}\hfill C{O}_2+H_2\end{array}& <=>\left[r_1\right]CO+H_{2}O\hfill \end{array}$$

(3)

To mathematically describe the chemical relationship, we start from the mechanistic model derived and parameterized in [5,6,7] with experimental data acquired by [8]. In earlier work the deactivation of the catalyst was not taken into account for the parameter identification, but will be considered within this contribution. Due to that reason and additional aging effects of the catalyst stored over several years, the mechanistic model was recalibrated first in this project. Subsequently, optimal experiments were designed and realized to improve the mechanistic model further.

Next, we move on replacing a part of the differential algebraic equation model with a neural network, following [9], which was trained on experimental data generated thus far. Using the approaches proposed in [10], we compute an additional experimental design aimed at generating further insightful data for the training of this hybrid model.

The rest of the paper is structured as follows: In sec:methods, we introduce the used methods and materials. We start by describing a newly built experimental set-up containing a well-mixed Berty type reactor as the data-generating unit. In the following, we introduce the mechanistic model, motivate the use of its hybrid counterpart, and provide a brief introduction to optimal experimental design from the perspective of optimal control. sec:results evaluates the results of the derived models, focusing on the difference in predictive performance when including or excluding optimal experimental design. sec:discussion concludes this paper by discussing the results and outlining further research directions.

Figure 1. Reaction network of methanol synthesis showing the different pathways and their respective reaction rates, which depend on the current state of the catalyst.

Figure 1. Reaction network of methanol synthesis showing the different pathways and their respective reaction rates, which depend on the current state of the catalyst.

2. Materials and Methods

2.1. Experimental Set-Up

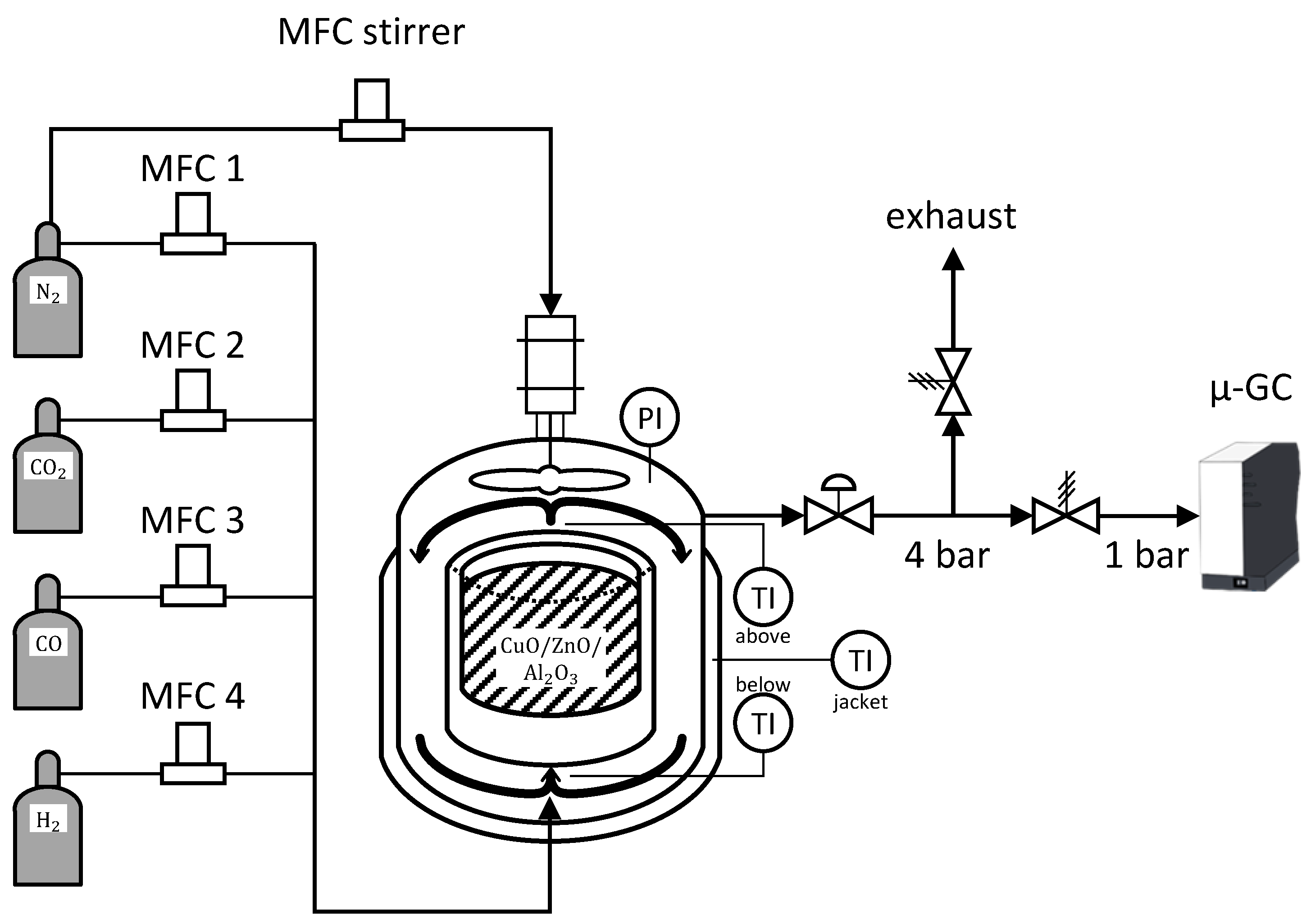
Experimental data is acquired by a self developed set-up depicted in Figure 2 of experimental set up. The reaction is carried out in a gradient-less Berty-type reactor built by the FAU Erlangen Nuremberg according to [11], containing a fixed bed of 4.3g commercial CuO/ZnO/Al₂O₃ catalyst (CZA) from BASF. The catalyst had been ground to 0.315-0.5mm particles to avoid intraparticular transport limitations. The used catalyst was acquired in a former PhD project ([8]) and was stored at ambient conditions since then. The remaining gas volume of the reactor is approximately 280mL including inert filling material as spherical $\gamma$-Al₂O₃ (charge no. 5) or 286mL without additional filling (charge no. 6). To verify the assumption of an ideal CSTR behaviour, the rotation speed of the stirrer had been varied during preliminary tests. Above 3000rpm no changes were observed. Thus, the value was set to 4000rpm with additional safety. The stirrer is driven by an electric engine, equipped with permanent magnets that disintegrate when getting in contact with hydrogen or hydrocarbons. Due to constructional reasons, the engine is connected to the reaction chamber. Furthermore, permanent magnets lose their field strength when heated, so the stirrer performance would be permanently negatively affected. For these reasons, it is particular important to cool and flush the engine of the stirrer with nitrogen. This constrains the concentration of the educts, but since nitrogen is an inert for the reaction, it can be used as an indicator for the occurring volume contraction. The experimental set-up is designed for reaction conditions up to 260°C and 60bar.

The utilized gases are supplied from gas bottles with a high purity of 99.999vol.-% for N₂, H₂ and CO₂ and 99.97vol.-% for CO. Bronkhorst mass flow controllers (MFC) are used to dose the educt gases (further information in E.2). Additional piping length is given to mix the gases at the inlet in order to precondition for the reaction. The entire piping periphery around the reactor is heated to avoid condensation.

The experimental set-up is designed to perform steady state and dynamic experiments under isothermal and isobaric conditions. Changes in temperature and pressure during operation are recorded and can be evaluated posterior. However, due to the sheer caloric mass of the reactor, intentional alterations in temperature within an experiment are unfavourable. They greatly increase the required time for an experimental investigation. Therefore experiments are mostly designed to stay at one temperature.

Several temperature probes are located in the reactor. One sensor is situated above and one beneath the catalyst bed. Two further sensors are measuring the heating jacket. Hence, only a small amount of enthalpy is released from the reaction and the great thermal mass of the reactor itself is acting as a dampener, one of the jacket sensors is used to control the reactor temperature. This has proven to be the most stable operation to keep a constant reaction temperature.

A dome pressure regulator (Equilibar) was used to keep a constant pressure in the reactor allowing a discharge during continuous experiments. Hence analytic devices are usually particularly sensitive regarding their inlet pressure, the outlet stream after the dome pressure regulator is first depressurized via a relief valve to 4bar and afterwards further reduced to 1bar using a Swagelok downstream pressure regulator. This method ensures constant pressure at the analytics while inlet conditions to the reactor can be dynamically modified. The total flowrate at the reactor outlet is not measured. If the reactor pressure is increased during an experiment the dome pressure regulator reduces the outlet flow until the pressure level is reached. In this case the analytic flow could be inappropriate.

One part of the automation is managed by Siemens’ PCS7. This ensures the acquisition of plant related data and the operation of actuators. The other part of automation is realized via MATLAB in the interest of applying complex mathematical inlet perturbations, precise timing of new conditions, creating a flexible, user friendly interface and recording data during the time of an experiment for simpler analysis. PCS7 and MATLAB where connected through OPC DA, a proven industrial communication standard.

This allows imposing classical step changes between different constant input values with varying time intervals, as well as periodical perturbation of inlet conditions (e.g. simultaneous modulation of inlet concentration and total flow rate as phase shifted sinusoidal wave form) as shown in Figure 3, making this plant an unique experimental set up. Besides that, another degree of freedom is the use of different fillings of the reactor with fresh catalyst. We refer to this by a catalyst charge number.

Outlet concentrations are quantified in terms of molar fractions of the components CH₃OH, CO₂, CO, H₂, H₂O and N₂ using a µ-GC from Agilent (model 490). Samples are measured by a method that takes approximately 90s, which had been optimized to execute with precise component determination and fast sampling. This allows an almost continuous collection of data points. Further details about the analytics are summarized in the E.1.

Figure 2. Scheme of experimental set-up: gas supply from gas bottles via mass flow controllers (MFC’s), Berty type reactor filled with CuO/ZnO/Al₂O₃ catalyst and analytics (µ-gas chromatography from Agilent). The reactor is monitored and controlled for temperature and pressure. The latter is regulated via a membrane back pressure regulator. Further on the downstream side the pressure is released through a relief valve to 4bar, ensuring a continuous effluent flow. In order to protect the electric engine of the stirrer from the reaction media and heat, N₂ is flushed through from the top into the reaction chamber. N₂ is used also as an indicator component to quantify the volume contraction caused by the reactions.

Figure 2. Scheme of experimental set-up: gas supply from gas bottles via mass flow controllers (MFC’s), Berty type reactor filled with CuO/ZnO/Al₂O₃ catalyst and analytics (µ-gas chromatography from Agilent). The reactor is monitored and controlled for temperature and pressure. The latter is regulated via a membrane back pressure regulator. Further on the downstream side the pressure is released through a relief valve to 4bar, ensuring a continuous effluent flow. In order to protect the electric engine of the stirrer from the reaction media and heat, N₂ is flushed through from the top into the reaction chamber. N₂ is used also as an indicator component to quantify the volume contraction caused by the reactions.

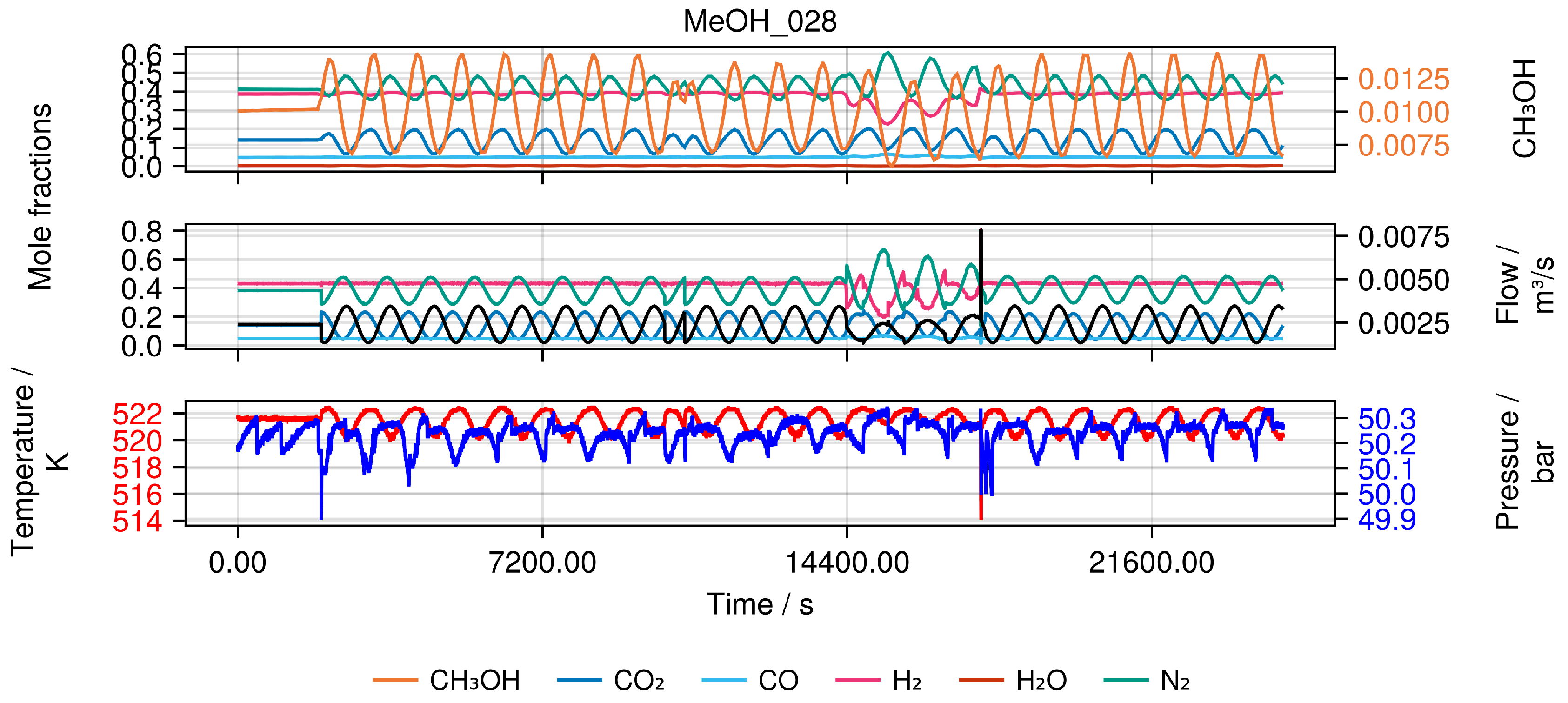
Figure 3. Example of a single experiment (MeOH_028). Top Measured output of the reactor as mole fractions. Middle Incoming feed of the reactor as mole fractions and volume flow. Bottom Temperature and pressure of the reactor.

Figure 3. Example of a single experiment (MeOH_028). Top Measured output of the reactor as mole fractions. Middle Incoming feed of the reactor as mole fractions and volume flow. Bottom Temperature and pressure of the reactor.

2.2. Experimental Procedure

When fresh catalyst was filled into the reactor, it was reduced using 2vol.-% of H₂ in N₂ with a total volumetric flowrate of 500NmL/min at ambient pressure starting from room temperature heating up to 180°C within 2h and keeping this temperature for another 12h according to [8]. This procedure was repeated after every shutdown of the plant and sometimes additionally to check for the effect on the catalytic performance. Otherwise the catalyst was flushed with nitrogen between methanol synthesis experiments.

To start a methanol synthesis experiment with already preconditioned catalyst the flow of the inert flushing of the stirrer is increased depending on the aimed pressure and the stirrer speed is set to 4000rpm. Afterwards, the inertized reactor is heated up at ambient pressure to the desired temperature. Meanwhile the pressure of the gas supply is adjusted. While N₂, H₂ and CO are fed directly from gas bottles, CO₂ is pressurized with a compressor from Maximator to reach up to 65bar. The CO₂ piping is heated to avoid condensation. After the temperature is reached, the pressure is built up with the dome pressure regulator feeding only N₂. At the same time, the heating of the whole piping periphery, the analytics, the process control system and the data acquisition must be prepared. Then an experiment can be started by dosing the reactants with the MFC. When the experiment is finished, the reactor is depressurized, inertized and most of the time cooled down to 180°C.

Catalysts are known to deactivate during operation ([12]). The deactivation of the CZA methanol synthesis catalyst is addressed in several studies, e.g., [13,14,15]. Catalyst deactivation is not the focus of this contribution, but must be taken into account. To quantify irreversible deactivation effects, a daily updated catalyst activity was measured prior to a new experimental run. This is done by applying a reference condition summarized in Table A5. The condition is kept until steady state is reached. Applying this procedure, a deactivation independent evaluation of the generated kinetic data is attempted. Additionally, due to the initial exposure to the same feed and thus the same reduction potential the catalyst is preconditioned with regard to reversible dynamic changes of the active sites. After that, the desired experiments were started.

The hydrogenation reactions (namely reaction 1 and 2) cause a reduction in gas volume, thus a volume contraction is defined as the ratio of inlet to outlet molar fraction of the inert nitrogen. Multiplying this ratio to the inlet volumetric flow rate ${\dot{V}}_{total}^{in,n}$ under norm conditions (273.15K and 1.01325bar) results in the norm outlet flow rate ${\dot{V}}_{total}^{out,n}$:

$${\dot{V}}_{total}^{out,n}={\displaystyle \frac{x_{N_2}^{in}}{x_{N_2}^{out}}}·{\dot{V}}_{total}^{in,n}$$

(4)

Given the experimentally recorded molar fractions $x_i$ of each component i, the above calculated total outlet volumetric flow rate ${\dot{V}}_{total}^{out,n}$ and the ideal gas law concludes to the corresponding outlet molar flow rate ${\dot{n}}_i^{out}$:

$${\dot{n}}_i^{out}=x_i·{\displaystyle \frac{p^n}{R·T^n}}·{\dot{V}}_{total}^{out,n}$$

(5)

Engineering metrics as the carbon based yield of methanol can be calculated as shown in eq:yield MeOH C-based. This value results from the ratio of calculated outlet molar flow rate of methanol to the sum of input molar flow rates of all carbon species (i.e. CO and CO₂).

$$Y_{C{H}_{3}OH}={\displaystyle \frac{{\dot{n}}_{C{H}_{3}OH}^{out}}{{\dot{n}}_{CO}^{in}+{\dot{n}}_{C{O}_2}^{in}}}$$

(6)

The value of the catalytic activity a is determined via calculating the current methanol yield $Y_{C{H}_{3}OH,ref}^{cur}$ with eq:yield MeOH C-based divided by the initial methanol yield $Y_{C{H}_{3}OH,ref}^0$ determined with the fresh catalyst of the corresponding charge, i.e. the stationary outlet result under reference condition after 1st reduction (Equation (7)).

$$a={\displaystyle \frac{Y_{C{H}_{3}OH,ref}^{cur}}{Y_{C{H}_{3}OH,ref}^0}}$$

(7)

The catalytic activity a is used as an identical pre-factor for all three reaction rates as shown in Equation (8).

$$r_j=a·r_j^{\prime },j=1,2,3$$

(8)

Thus, the assumption was made that the deactivation influences all three reactions Equations (1)–(3). in the same way and does not change drastically over the course of one specific experiment. Thus, a is one fixed value for every experiment, ranging from 0.14 to 1 for the entire data used in this work and from 0.14 to 0.33 for the optimally designed experiments.

The whole set of experimental data used in this contribution is available under Kaps et al. (2025).

2.3. Mechanistic and Hybrid Modeling of the Methanol Synthesis

We base our approach upon the established kinetic model, capable to quantify the rates of the three key reactions proceeding during methanol synthesis, derived in [5,6,7] (see F). This kinetic model is connected to the mass balances valid for an ideally mixed, isothermal, isobaric and continuously operated reactor model. The whole model consists of a set of differential-algebraic equations (DAE) of the form

$$\begin{array}{c}\hfill J(x,q,t,u)\dot{x}-\left[\begin{array}{c}A(x,q,t,u)·a·\gamma (x,q,t,u)\odot r(x,q,t,u)+b(x,q,t,u)\\ f_{\varphi }(x,q,t,u)\end{array}\right]=0\end{array}$$

(9)

Here $t\in \left[t_0,t_f\right]$ denotes the time and $x\in \mathcal{X}$ denotes the state which consists of the mole fractions of the six chemical species $x_i,i\in \{{\mathrm{CH}}_3\mathrm{OH}$, CO, ${\mathrm{CO}}_2$, ${\mathrm{H}}_2$, ${\mathrm{H}}_2\mathrm{O}$, ${\mathrm{N}}_2\}$ and an additional state $\varphi$ which represents the distribution of the active centers of the catalyst. $q\in \mathcal{Q}$ denotes a set of parameters (see G.1) and $u\in \mathcal{U}$ the inputs of the system, which consist of temperature, pressure, feed and flow. The matrix valued functions $J\in {\mathbb{R}}^{6\times 6}$ account for the gradient of the surface coverage of the individual species and $A\in {\mathbb{R}}^{6\times 3}$ combines the stoichiometric coefficients with the catalyst mass (constant for every experiment) in dependence of the states. $a\in \{0,1\}$ denotes the activity level of the catalyst as described in Section 2.2.

An important feature of the kinetic model is the incorporation of dynamic changes of the catalyst. $\gamma$ captures the influence of the degree of reduction of the catalyst $\varphi$ on each of the reaction rates. Of special interest are the three scaling pre-factors $\gamma :\mathcal{X}\times \mathbb{R}\times \mathcal{Q}\times \mathcal{U}\mapsto {\mathbb{R}}_{+}^3$, which were previously modeled based on a heuristic

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\gamma }_{\mathrm{CO}}& =1-\varphi \hfill \\ \hfill {\gamma }_{{\mathrm{CO}}_2}& ={\varphi }^2\hfill \\ \hfill {\gamma }_{\mathrm{RWGS}}& ={\displaystyle \frac{\varphi }{1-\varphi }}\hfill \end{array}\end{array}$$

(10)

which only depends on the catalyst state $\varphi$ ([5,6]). In this work, we propose to replace this heuristic with a fully connected feed-forward neural network to describe $\gamma$, resulting in a hybrid model. Hybrid modeling aims at combining the advantages of two different modeling paradigms. First, the interpretability and data-efficiency of rigorous modeling based on first principles and specific domain knowledge, and second the flexibility of data-driven models such as neural networks, which are able to learn unknown functional relationships from data. In the context of differential equations, such models are commonly called universal differential equations ([9]).

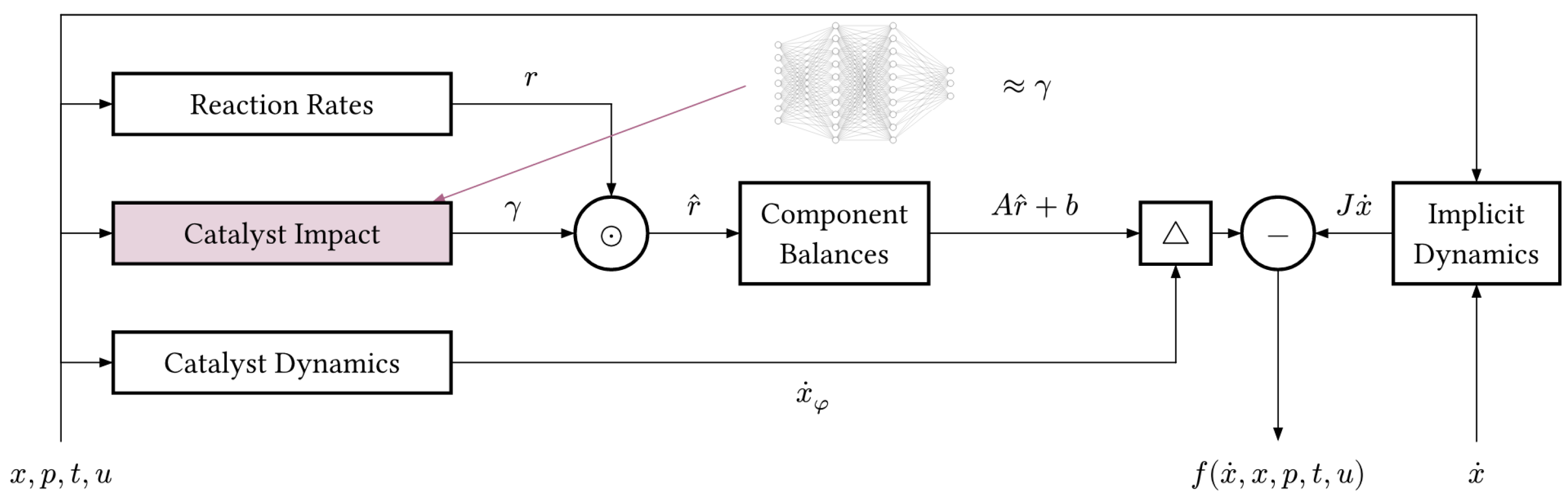
The hybrid DAE model can be written in its implicit form as

$$\begin{array}{c}\hfill f(\dot{x},x,q,t,u)=f_{\Sigma }\left(\widehat{f}(\dot{x},x,t,\widehat{q},u),U(x,\theta )\right)=0\end{array}$$

(11)

where $\widehat{f}:{\mathcal{X}}_t\times \mathcal{X}\times \mathcal{U}\times {\mathcal{Q}}_P\mapsto {\mathcal{Z}}_P$ describes the parts of the model which are known from first principles and which may depend on physical parameters $\widehat{q}\in {\mathcal{Q}}_P$. Second, a universal approximator, e.g., a feed-forward neural network, $U:\mathcal{X}\times {\mathcal{Q}}_U\mapsto {\mathcal{Z}}_U$ with weights and biases $\theta \in {\mathcal{Q}}_U$ is used to model the unknown parts of the dynamics. The function $f_{\Sigma }$ encodes the overall structure of the hybrid model, i.e., how known and unknown parts of the dynamics interact. Figure 4 shows the mechanistic model in the form of a block diagram, highlighting the catalyst impact $\gamma$ which we are replacing.

Figure 4. Block diagram of the mechanistic model in the form of a DAE system. Our goal is to learn the impact $\gamma$ of the catalyst state $\varphi$ on the reaction rates r directly from the data. The triangle ▵ represents concatenation.

Figure 4. Block diagram of the mechanistic model in the form of a DAE system. Our goal is to learn the impact $\gamma$ of the catalyst state $\varphi$ on the reaction rates r directly from the data. The triangle ▵ represents concatenation.

The feasibility of this approach applied already to methanol synthesis was shown in [16], however based on synthetic data obtained via simulating the mechanistic model of [5,6,7]. In this study, we focus on the training of hybrid models on experimental data.

2.4. Data Preparation

The collected experimental data $\mathcal{D}=\{{\mathcal{D}}_1,\cdots ,{\mathcal{D}}_{44}\},{\mathcal{D}}_i=\{X,U,\tau \}$ was divided into a training ${\mathcal{D}}_{TR}\subset \mathcal{D}$ and test ${\mathcal{D}}_{TT}\subset \mathcal{D}$ data set using a stratified 80-20 train-test split, see G.3. Here $X=\left\{x_i\right|x_i\in {\mathcal{X}}^{\prime }\subset \mathcal{X}\}$ denotes the set of state measurements of the reactor output and $U=\left\{u_i\right|u_i\in \mathcal{U}\}$ the set of inputs consisting of feed, flow, pressure and temperature. Finally, $\tau =\{t_i|t_i\in \mathbb{R}\}$ denote the time points of the measurements.

2.5. Parameter Estimation

The parameter estimation was performed by solving the following optimization problem:

$$\underset{q}{\min } \frac{\left|{\mathcal{D}}_{TR}\right|}{1}\sum _{{\mathcal{D}}_i\in {\mathcal{D}}_{TR}}\frac{\left|{\mathcal{D}}_i\right|}{1}\sum _{tj\in \mathcal{D}i}\mathcal{L}\left({\widehat{x}}_{i,j},x_{i,j}\right)$$

(12a)

$$\text{s.t.} 0=f\left(\stackrel{·}{x},x,q,t,u\right)$$

(12b)

$$q\in Q$$

(12c)

We used an average sample-wise (12a) $\mathcal{L}:\mathcal{X}\times \mathcal{X}\mapsto \mathbb{R}$ between the measurements $\widehat{x}$ (outlet molar fractions) and predictions x given by the weighted sum-of-squares error

$$\mathcal{L}\left({\widehat{x}}_{i,j},x_{i,j}\right)={\displaystyle \frac{1}{\left|{\mathcal{S}}^{\prime }\right|}}\sum _{k\in {\mathcal{S}}^{\prime }}{w}_{i,j,k}{\left({\widehat{x}}_{i,j,k}-x_{i,j,k}\right)}^2,{\mathcal{S}}^{\prime }=\{{\mathrm{CH}}_3\mathrm{OH},\mathrm{CO},{\mathrm{CO}}_2,{\mathrm{H}}_2\mathrm{O}\}$$

We included only a subset of species, namely the carbon-based species with a high accuracy in the analytics and water as co-product, present often only in small amounts but very important for the kinetic model. The weights have been chosen to be $w_{i,j,k}={\left({\widehat{x}}_{i,j,k}+ϵ\right)}^2$, $ϵ\ge 0$, to adjust the contribution of each species relative to its magnitude. () describes the dynamics of the system. Instead of modeling the domain (), we used the exponential transformation to ensure that a subset of parameters is positive to account for its physical meaning. The initial conditions and domains of the parameters have been set according to [7], and can be seen in G.1. To solve (), we used Optimization.jl ([17]), a solver agnostic interface to several optimization routines. To fit the mechanistic model, we used the implementation of L-BFGS ([18]) of Optim.jl ([19]). To investigate the impact of the experimental designs, once the parameter estimation problem is solved on the full training data with all experimental designs and once on the training data excluding the optimal experimental designs.

2.6. Hybrid Model Fitting

To find a suitable candidate for the hybrid model, we performed a simple hyperparameter search over different architectures by employing a full factorial design over the number and size of the hidden layers as well as their activation function in Lux.jl (Pal (2023)). We adapted (12) by adding a L₁ norm regularization with regularization parameter $\lambda =1e-5$ on the weights of the network to counteract overfitting. The options of this hyperparameter search are given in Table 1. The neural networks are modeled to take the full state x as an input. Moreover, the output layer uses the softplus function ${\sigma }_{+}:\mathbb{R}\mapsto {\mathbb{R}}^{+}$, ${\sigma }_{+}\left(x\right)=log\left(exp\left(x\right)+1\right)$ to ensure a positive output. Each candidate architecture has been trained five times with different random seeds used for initialization of the weights $\theta$ for a total number of 500 iterations using Adam ([20]) from Optimisers.jl and mini-batching of the data set. Next, a suitable candidate has been selected by accounting for both complexity of the network and conformity with the data. We selected the top-k candidates using the coefficient of determination on the training set and subsequently retrained these models using L-BFGS.

Table 1. Hyperparameters for initial training of hybrid model. The function swish is given by $\mathrm{swish}\left(x\right)={\displaystyle \frac{x}{1+exp(-x)}}$, $\sigma$ denotes the typical sigmoid function $\sigma \left(x\right)={\displaystyle \frac{1}{1+exp(-x)}}$.

Hyperparameter	Hidden Layers	Layer Width	Activation
Options	2, 3, 4	5, 10, 15	$\mathrm{swish},\sigma$

Table 1. Hyperparameters for initial training of hybrid model. The function swish is given by $\mathrm{swish}\left(x\right)={\displaystyle \frac{x}{1+exp(-x)}}$, $\sigma$ denotes the typical sigmoid function $\sigma \left(x\right)={\displaystyle \frac{1}{1+exp(-x)}}$.

Hyperparameter	Hidden Layers	Layer Width	Activation
Options	2, 3, 4	5, 10, 15	$\mathrm{swish},\sigma$

2.7. Optimal Experimental Design

To minimize the effort of experimental data collection, we want to collect as much information about the uncertain parameters as possible from each experimental run. Optimal experimental design (OED) is a well-established concept in Chemical Engineering ([21,22]) and a natural approach to come up with informative experiments for subsequent parameter estimation problems or model identification. See [23,24,25,26] for a general introduction into the topic. In [27,28] the concept was applied to dynamical systems given by parameterized ODE or DAE models. In this context, degrees of freedom are the decisions when to measure each observed variable $y\in \mathcal{Y}$ and how to stimulate the system in an optimal way. The problem of computing an optimal experimental design can thus be cast as an optimal control (OC) problem, see I.1 for detailed explanation. The goal is to optimize the time-dependent inputs $u\in \mathcal{U}$ and the initial conditions $x\left(t_0\right)\in \mathcal{X}$ such that a suitable objective function of the variance-covariance matrix is minimized. This requires to augment the system using the forward sensitivity equations and the differential equation of the Fisher information matrix, adding states in the order of $\mathcal{O}\left(\right|Q{|}^2)$.

In this work, we use OED in two ways. First, we use it to compute four informative experiments for estimating the physical parameters of the heuristic model. More specifically, these experiments each aim at the identification of different subsets of parameters, namely the parameters in the Arrhenius equations of the three elementary reactions and two rate constants in the kinetic equation for the state $\varphi$. Second, in the case of a hybrid model, i.e., the parameters q of the underlying model include both physical parameters $\widehat{q}$ and weights and biases of a neural network $\theta$. In this context, the OED problem may also be solved aimed at generating data to train the embedded neural network on. However, problems may arise due to the usually large parameter space of the neural network. The quadratic dependence of the size of the augmented system of differential equations on the number of parameters as explained above leads to a high computational effort even for integration of the augmented system. Moreover, setting up the variational differential equations analytically may be prohibitively expensive. Another difficulty arises from the observation that weights of neural networks are not uniquely identifiable. Therefore, resulting Fisher information matrices in the underlying optimization problem are usually ill-conditioned and not amenable to optimization. However, as argued in [10], one can often circumvent these problems by identifying a suitable subset of parameters $\tilde{q}\subset q,\left|\tilde{q}\right|\ll \left|q\right|$ via a singular value decomposition of the Fisher information matrix. This way, the size of the system of differential equations is reduced and positive definiteness of the Fisher information matrix assured.

All OED problems were solved in a first-discretize-then-optimize single shooting approach on a time horizon $\mathcal{T}=[t_0,t_f]=[0,7200]$s with the A-Criterion as the objective function. The control functions u include the inlet composition, i.e., $x_{C{O}_2}^{in}\left(t\right),x_{CO}^{in}\left(t\right),x_{H_2}^{in}\left(t\right)$ and $x_{N_2}^{in}\left(t\right)$ as well as the inlet volumetric flow rate ${\dot{V}}_N^{in}\left(t\right)$ and are discretized as piecewise constant values on an equidistant timegrid. For the experimental designs for the mechanistic model we chose a discretization parameter of $\Delta t=900$s, whereas for the hybrid model it was chosen as $\Delta t=600$s. The temperature T is included as a control value, constant over time. The problems are further simplified by assuming that measurements are taken continuously, as explained in 2.1. Hence, we do not need to determine optimal measurement times. Furthermore, we need to include simple upper and lower bounds on the control functions and values, these are stated in Table 2. Also, general constraints on the inlet composition need to be fulfilled, requiring that the molar fractions of the incoming species add up to 100 percent at each point in time. Also, a minimum level of nitrogen needs to be present in the inlet due to required flushing of the stirrer magnet. The amount depends on the current volumetric flow rate and the pressure p. Formally, these constraints read

$$\begin{array}{cc}\hfill x_{C{O}_2}^{in}\left(t\right)+x_{CO}^{in}\left(t\right)+x_{H_2}^{in}\left(t\right)+x_{N_2}^{in}\left(t\right)& =1,\hfill \end{array}$$

(13)

$$\begin{array}{cc}\hfill x_{N_2}^{in}\left(t\right)·{\dot{V}}_N^{in}\left(t\right)& \ge 8·p.\hfill \end{array}$$

(14)

Table 2. Lower and upper bounds on control functions and control values for the optimal experimental design.

Variable	Lower Bound	Upper Bound	Unit
T	500.0	530.0	K
${\dot{V}}_N^{in}\left(t\right)$	0.5	4.0	NL / min
$x_{C{O}_2}^{in}\left(t\right)$	0.0	40.0	%
$x_{CO}^{in}\left(t\right)$	0.0	40.0	%
$x_{H_2}^{in}\left(t\right)$	0.0	75.0	%
$x_{N_2}^{in}\left(t\right)$	0.0	100.0	%

Table 2. Lower and upper bounds on control functions and control values for the optimal experimental design.

Variable	Lower Bound	Upper Bound	Unit
T	500.0	530.0	K
${\dot{V}}_N^{in}\left(t\right)$	0.5	4.0	NL / min
$x_{C{O}_2}^{in}\left(t\right)$	0.0	40.0	%
$x_{CO}^{in}\left(t\right)$	0.0	40.0	%
$x_{H_2}^{in}\left(t\right)$	0.0	75.0	%
$x_{N_2}^{in}\left(t\right)$	0.0	100.0	%

The initial conditions of the molar fractions of the species and the initial distribution of active centers on the catalyst are given in Table 3. The pressure is fixed at $p=50$ bar for all designs to simplify the optimization problem. Low reactant molar fractions in the feed are realized by compensation with nitrogen. This method also simplifies the experimental procedure and is in accordance to the assumed ideal gas behaviour. The problems are then solved via Ipopt ([29]). More information on the parameters considered in the designs and the obtained solutions are given in I.

Table 3. Initial conditions $x(t_0$ assumed in all OED problems.

State	Initial value
$x_{{\mathrm{CH}}_3\mathrm{OH}}$	0.00854
$x_{{\mathrm{CO}}_2}$	0.02494
$x_{\mathrm{CO}}$	0.22906
$x_{{\mathrm{H}}_2}$	0.55062
$x_{{\mathrm{H}}_2\mathrm{O}}$	0.00184
$x_{{\mathrm{N}}_2}$	0.18499
$\varphi$	0.7

Table 3. Initial conditions $x(t_0$ assumed in all OED problems.

State	Initial value
$x_{{\mathrm{CH}}_3\mathrm{OH}}$	0.00854
$x_{{\mathrm{CO}}_2}$	0.02494
$x_{\mathrm{CO}}$	0.22906
$x_{{\mathrm{H}}_2}$	0.55062
$x_{{\mathrm{H}}_2\mathrm{O}}$	0.00184
$x_{{\mathrm{N}}_2}$	0.18499
$\varphi$	0.7

3. Results

This section discusses the results of the parameter identification for the deterministic and hybrid model architectures as described in sec:methods. In detail, the performance of the model is evaluated and compared for each of the conducted studies. Furthermore, we investigate the final hybrid model in detail. As an illustrative example for all models we choose an experiment which was not part of the initial training or testing set, namely experiment MeOH_079. It has been carried out using a set of heuristically informed inputs, which closely resemble industrial conditions. An overview of the results is given in Table 4.

Table 4. Results of the different model architectures and fitting procedure. We report the mean absolute percentage error MAPE ${\displaystyle \frac{100}{N}}{\sum }_{i=1}^N\left|{\displaystyle \frac{{\widehat{x}}_i-x_i}{{\widehat{x}}_i}}\right|$ for the respective dataset and species ($x_i$ denotes the states). (OED) indiciates the use of the full training data including the data from the optimal experimental designs, (NOED) the use of the dataset without optimal designs. The hybrid model (INIT) denotes the best architecture after hyperoptimization and subsequent fit using L-BFGS. The best value of each column is bold.

	MAPE
State	$x_{{\mathrm{CH}}_3\mathrm{OH}}$	$x_{\mathrm{CO}}$	$x_{{\mathrm{CO}}_2}$	$x_{{\mathrm{H}}_2}$	$x_{{\mathrm{H}}_2\mathrm{O}}$	$x_{{\mathrm{N}}_2}$	Total
Train
Mechanistic (OED)	13.60	6.89	6.41	6.42	6.89	7.15	7.90
Mechanistic (NOED)	25.20	6.69	5.79	6.57	16.10	7.27	11.30
Hybrid Model (INIT)	14.80	7.22	6.72	6.46	9.25	7.19	8.61
Hybrid Model (NOED)	32.90	5.96	7.19	7.01	16.40	7.70	12.90
Hybrid Model (OED)	14.10	6.34	6.41	6.36	6.85	7.10	7.86
Test
Mechanistic (OED)	22.80	50.30	27.70	39.50	11.30	8.68	26.70
Mechanistic (NOED)	44.80	51.30	27.40	39.40	14.30	8.79	31.00
Hybrid Model (INIT)	25.00	50.70	27.90	39.70	13.10	8.75	27.50
Hybrid Model (NOED)	30.90	50.70	27.90	40.00	13.90	8.94	28.70
Hybrid Model (OED)	21.70	50.50	27.60	39.30	10.70	8.58	26.40

Table 4. Results of the different model architectures and fitting procedure. We report the mean absolute percentage error MAPE ${\displaystyle \frac{100}{N}}{\sum }_{i=1}^N\left|{\displaystyle \frac{{\widehat{x}}_i-x_i}{{\widehat{x}}_i}}\right|$ for the respective dataset and species ($x_i$ denotes the states). (OED) indiciates the use of the full training data including the data from the optimal experimental designs, (NOED) the use of the dataset without optimal designs. The hybrid model (INIT) denotes the best architecture after hyperoptimization and subsequent fit using L-BFGS. The best value of each column is bold.

	MAPE
State	$x_{{\mathrm{CH}}_3\mathrm{OH}}$	$x_{\mathrm{CO}}$	$x_{{\mathrm{CO}}_2}$	$x_{{\mathrm{H}}_2}$	$x_{{\mathrm{H}}_2\mathrm{O}}$	$x_{{\mathrm{N}}_2}$	Total
Train
Mechanistic (OED)	13.60	6.89	6.41	6.42	6.89	7.15	7.90
Mechanistic (NOED)	25.20	6.69	5.79	6.57	16.10	7.27	11.30
Hybrid Model (INIT)	14.80	7.22	6.72	6.46	9.25	7.19	8.61
Hybrid Model (NOED)	32.90	5.96	7.19	7.01	16.40	7.70	12.90
Hybrid Model (OED)	14.10	6.34	6.41	6.36	6.85	7.10	7.86
Test
Mechanistic (OED)	22.80	50.30	27.70	39.50	11.30	8.68	26.70
Mechanistic (NOED)	44.80	51.30	27.40	39.40	14.30	8.79	31.00
Hybrid Model (INIT)	25.00	50.70	27.90	39.70	13.10	8.75	27.50
Hybrid Model (NOED)	30.90	50.70	27.90	40.00	13.90	8.94	28.70
Hybrid Model (OED)	21.70	50.50	27.60	39.30	10.70	8.58	26.40

3.1. Fit of Mechanistic Model

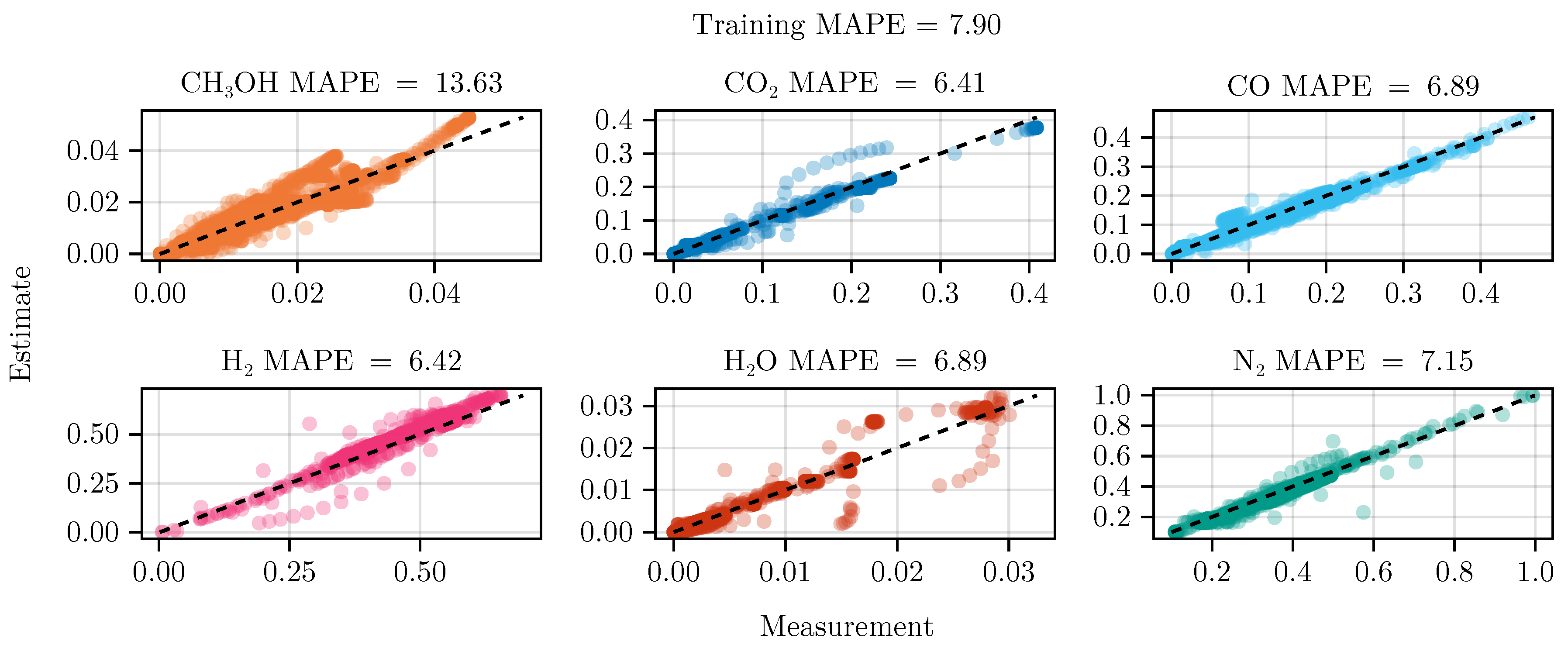
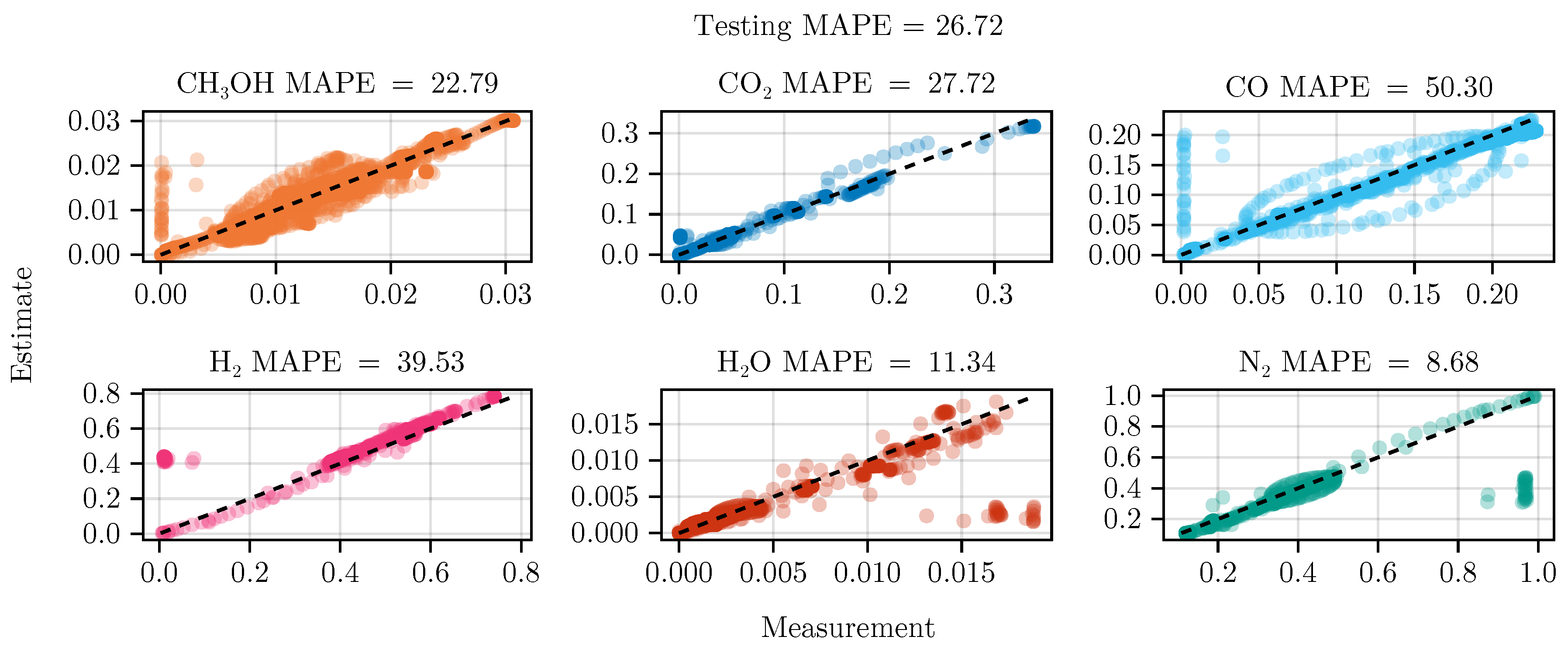
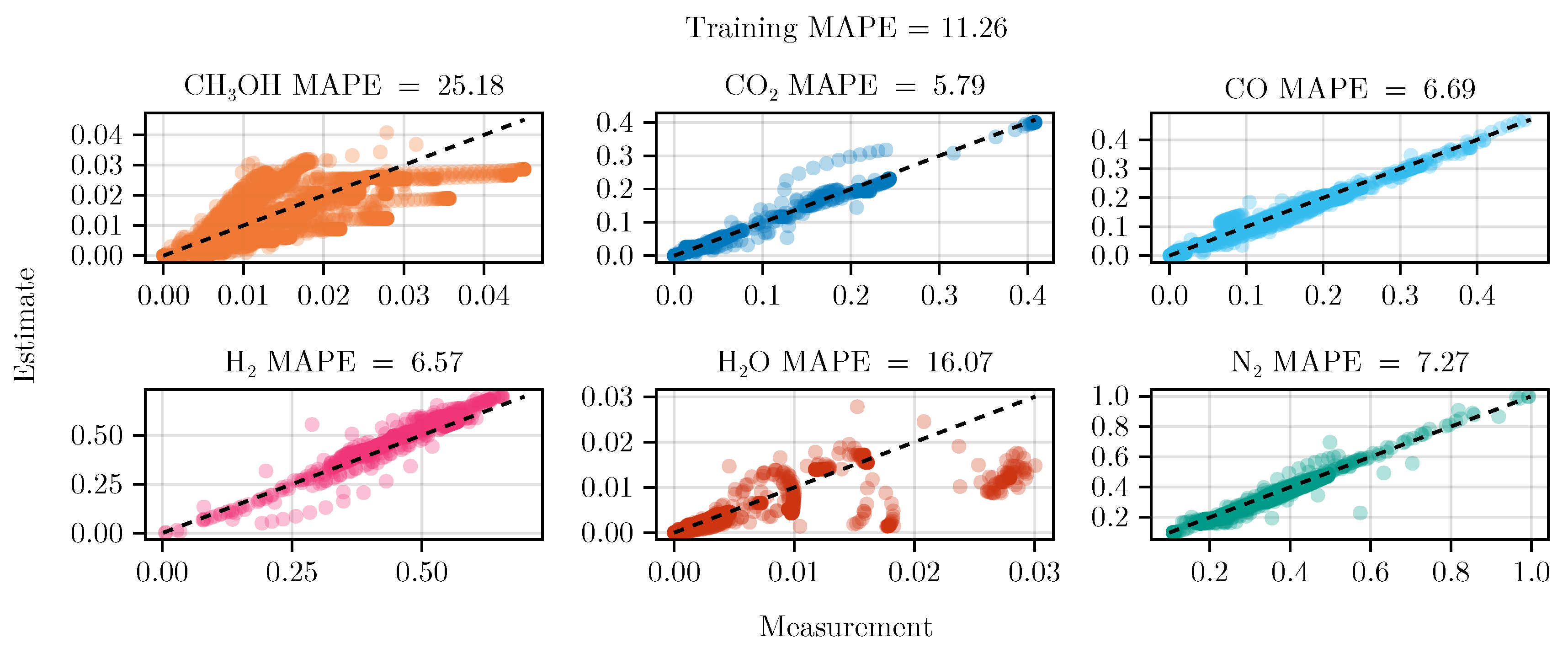
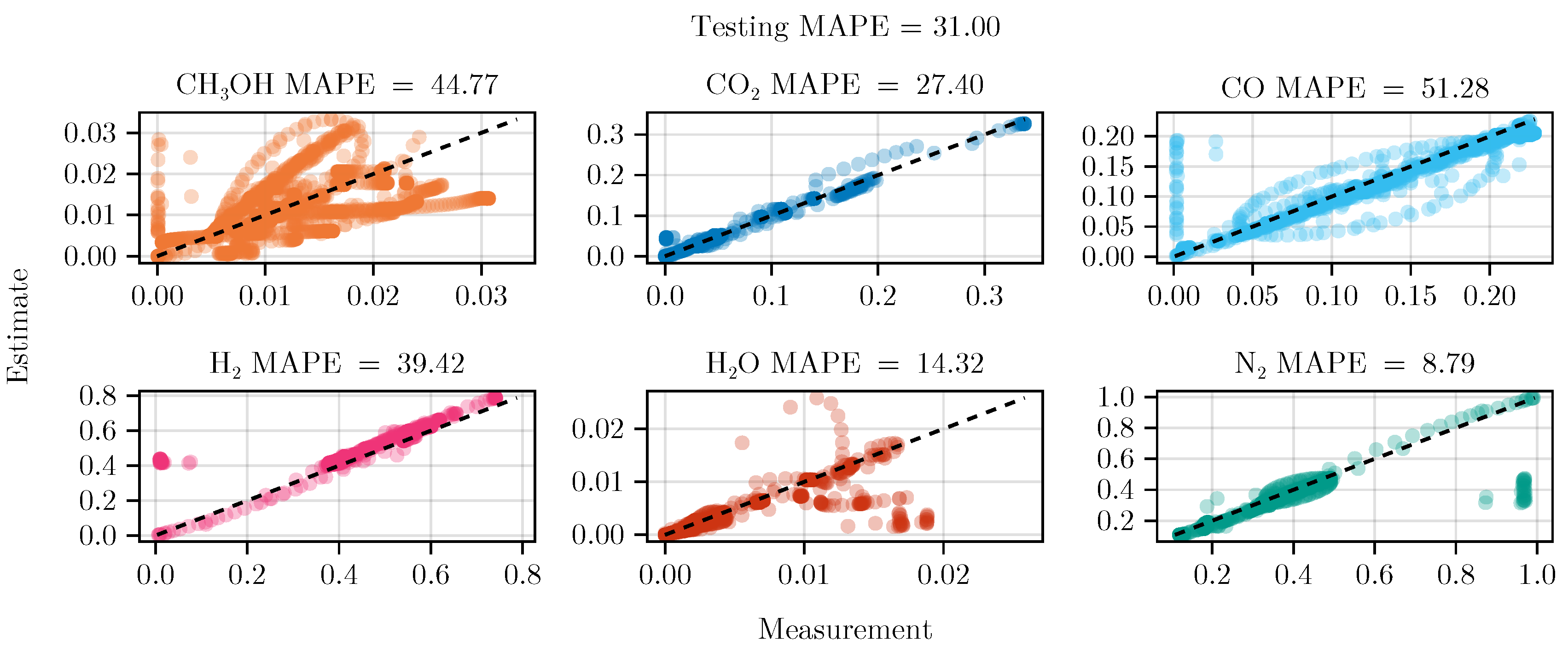
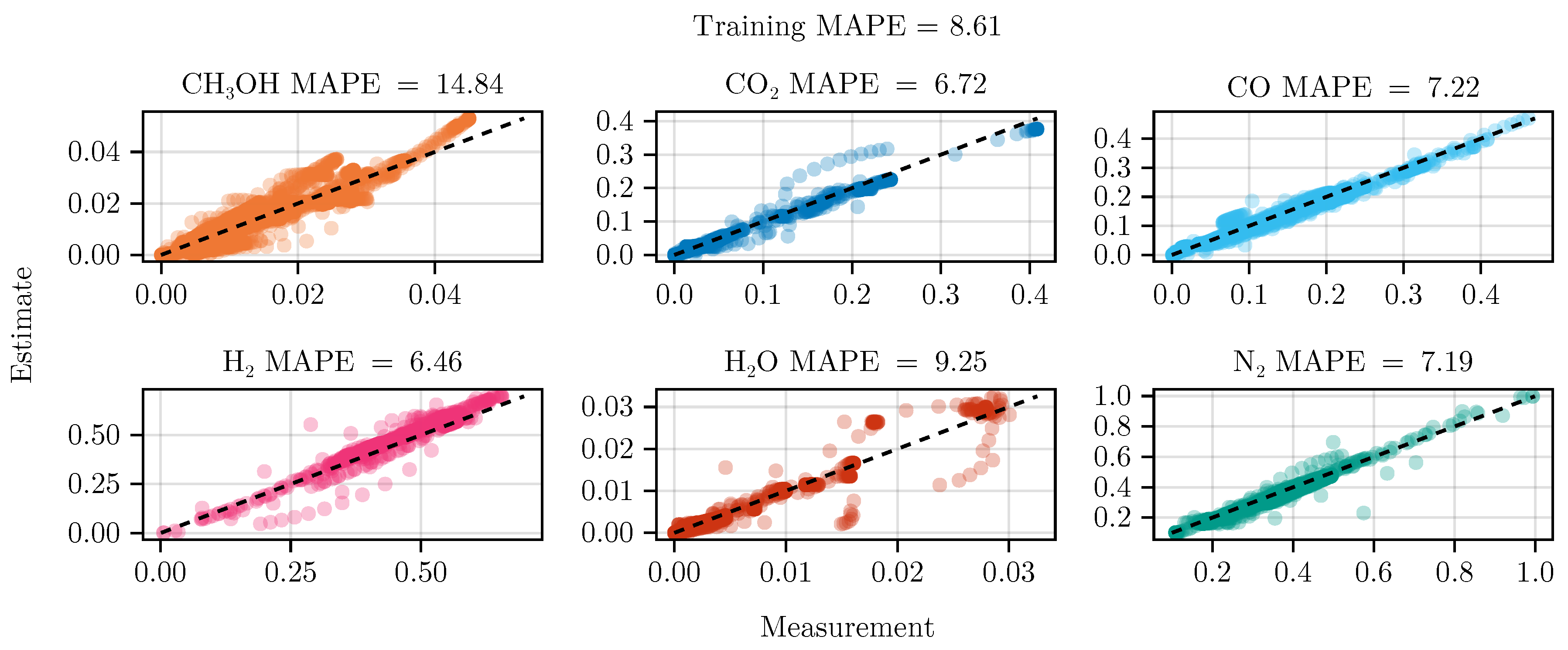
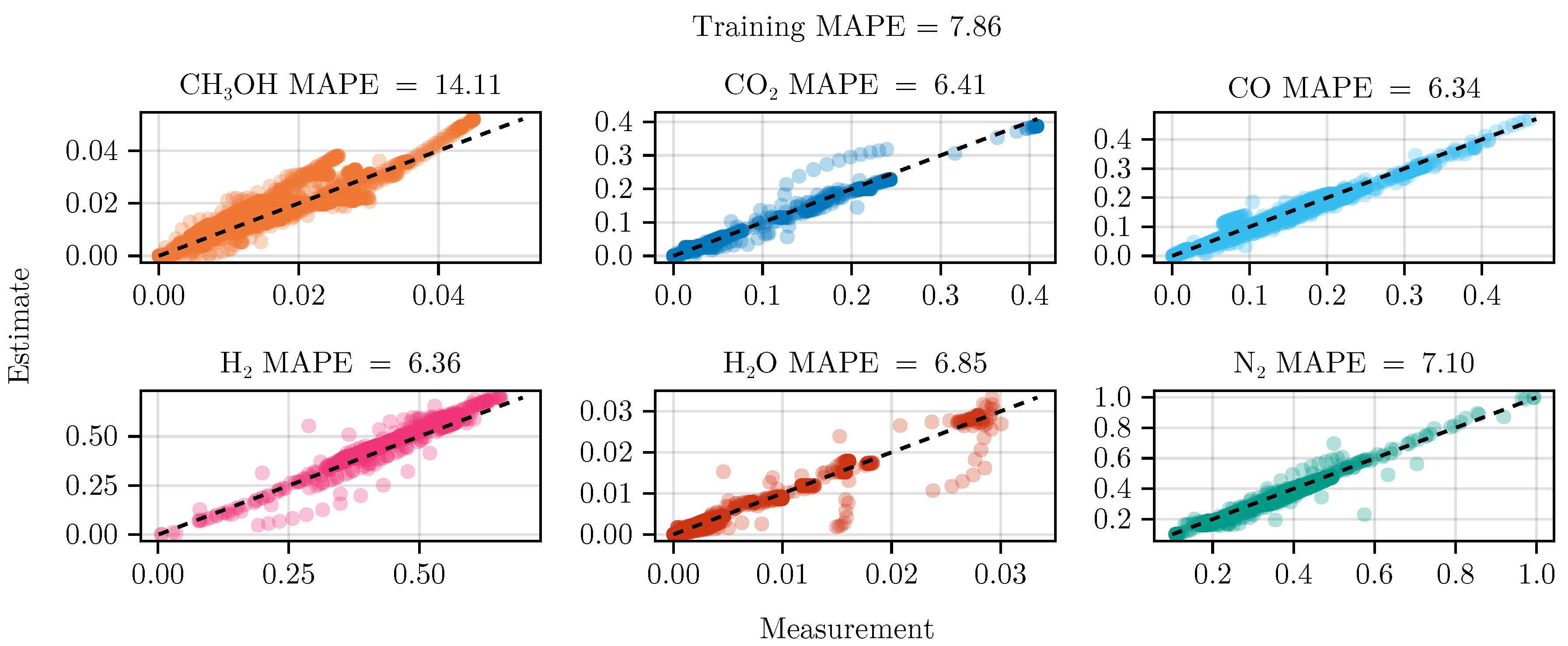
The fit of the mechanistic model has been conducted as described in sec:parameterestimation. The resulting set of parameters, fitted using the training set, including the collected data from the experimental designs, shows good parity with the data, as shown in Figure 5. The performance on the test set is equally good, depicted in Figure 6. Figure 7 shows the model’s prediction on the validation experiment MeOH_079.

Figure 5. Parity plot of the fitted mechanistic model over the training data set.

Figure 5. Parity plot of the fitted mechanistic model over the training data set.

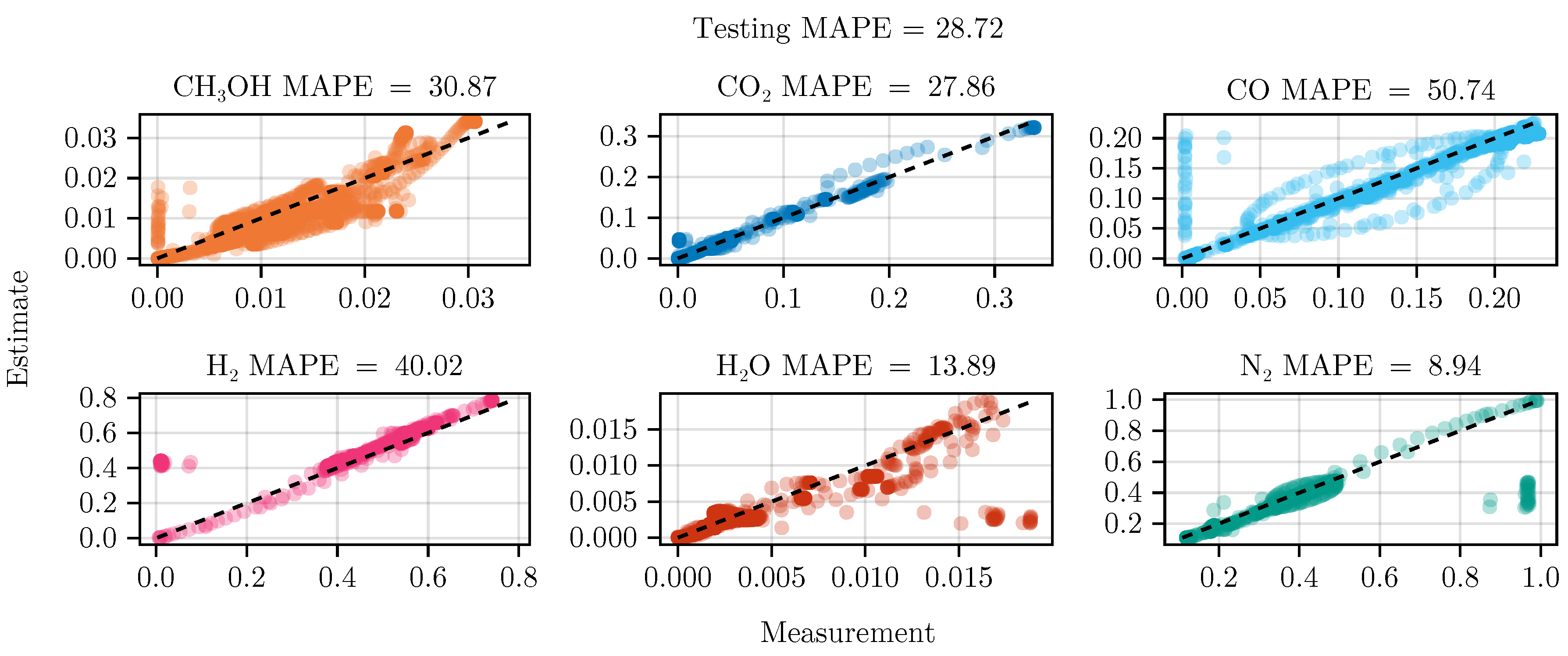
Figure 6. Parity plot of the fitted mechanistic model over the test data set.

Figure 6. Parity plot of the fitted mechanistic model over the test data set.

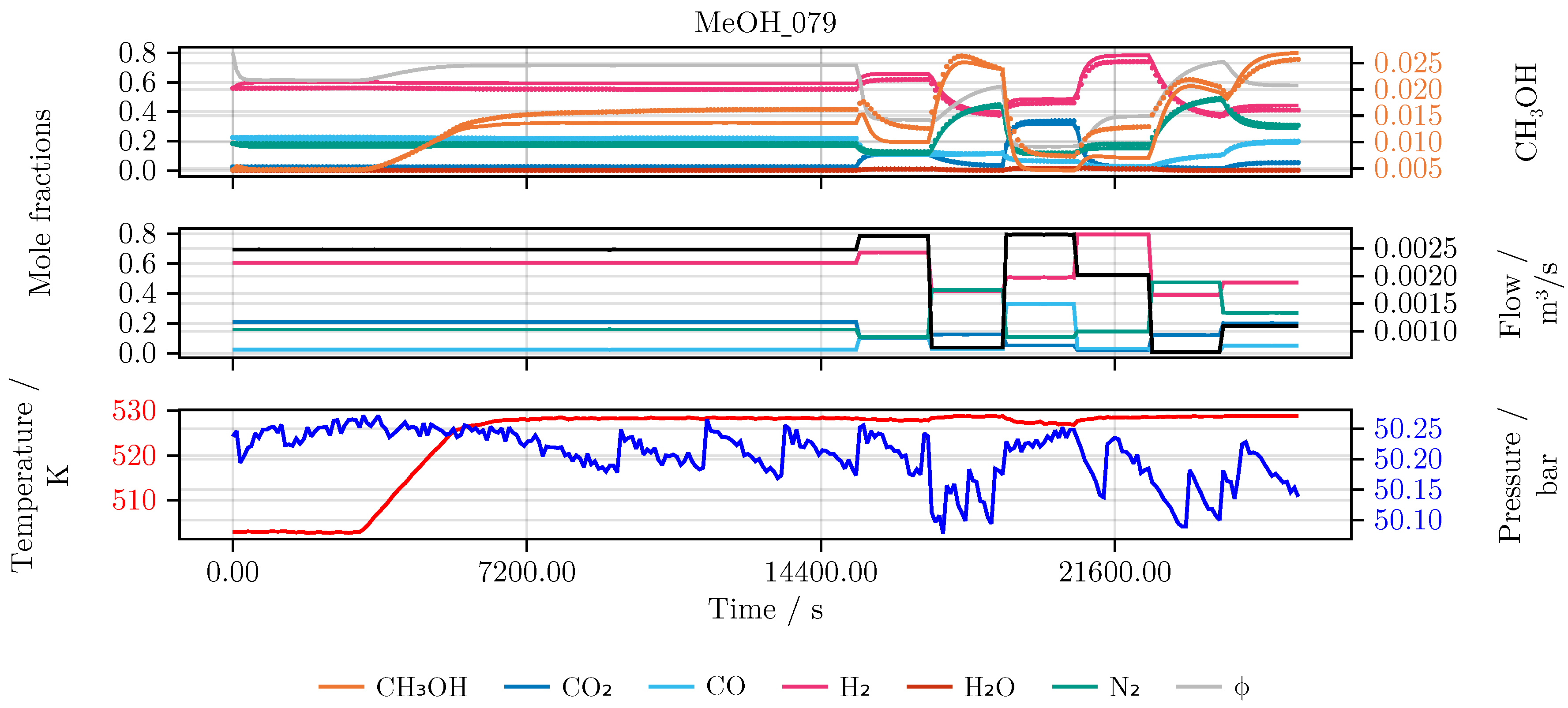
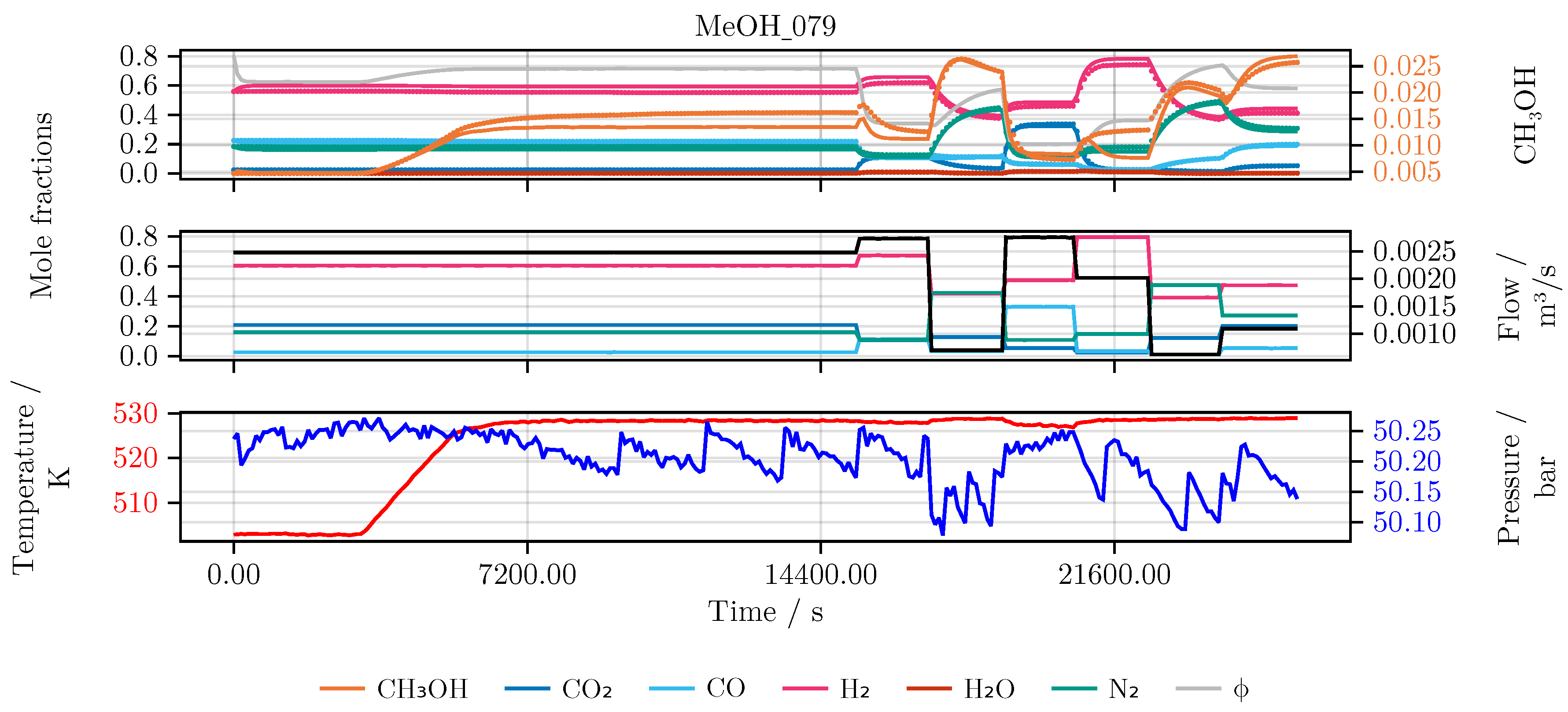
Figure 7. Model prediction on the experiment MeOH_079. After the initial catalyst activity was determined at the reference condition the reactor was heated up. The temperature and the following six feed compositions and flow rates, each applied for 20 min, were chosen randomly within relevant process boundaries. Top The state trajectory. Colored scatter denotes the data, full lines the prediction. Middle The feed of the reactor in mole fractions using the respective color for each species. The black line denotes the incoming volume flow. Bottom The temperature (red) and pressure (blue) over the time course of the experiment.

Figure 7. Model prediction on the experiment MeOH_079. After the initial catalyst activity was determined at the reference condition the reactor was heated up. The temperature and the following six feed compositions and flow rates, each applied for 20 min, were chosen randomly within relevant process boundaries. Top The state trajectory. Colored scatter denotes the data, full lines the prediction. Middle The feed of the reactor in mole fractions using the respective color for each species. The black line denotes the incoming volume flow. Bottom The temperature (red) and pressure (blue) over the time course of the experiment.

The exclusion of the optimal experimental designs from the training data set significantly impacts the fitting outcome, see Table 4. While the overall coefficient of determination, dominated by abundant species such as ${\mathrm{CO}}_2$, CO, ${\mathrm{H}}_2$, and ${\mathrm{N}}_2$, is still comparable to the previous model, less abundant species, ${\mathrm{CH}}_3\mathrm{OH}$ and ${\mathrm{H}}_2\mathrm{O}$, show a degradation in predictive power. This effect is even more visible on the test set, where the MAPE of ${\mathrm{CH}}_3\mathrm{OH}$ increases from $22.80$ to $44.80$. The parameter values and additional results for each of the fits are listed in G.1.

3.2. Fit of Hybrid Model

To conduct the hyperparameter search for a suitable neural network architecture and initial parameter values, a total of ninety hybrid models have been trained, resulting from a full factorial design of the search parameters given in Table 1. The top five models and their respective performance on the training set are shown in Table 5. We choose two models as the foundation for further training marked as A and B in Table 5. Model A was chosen due to its simple architecture and overall coefficient of determination, model B due to its balanced performance over all individual species. Both models have 88 trainable parameters in total, and are trained further, using L-BFGS based optimization similar to the mechanistic model. 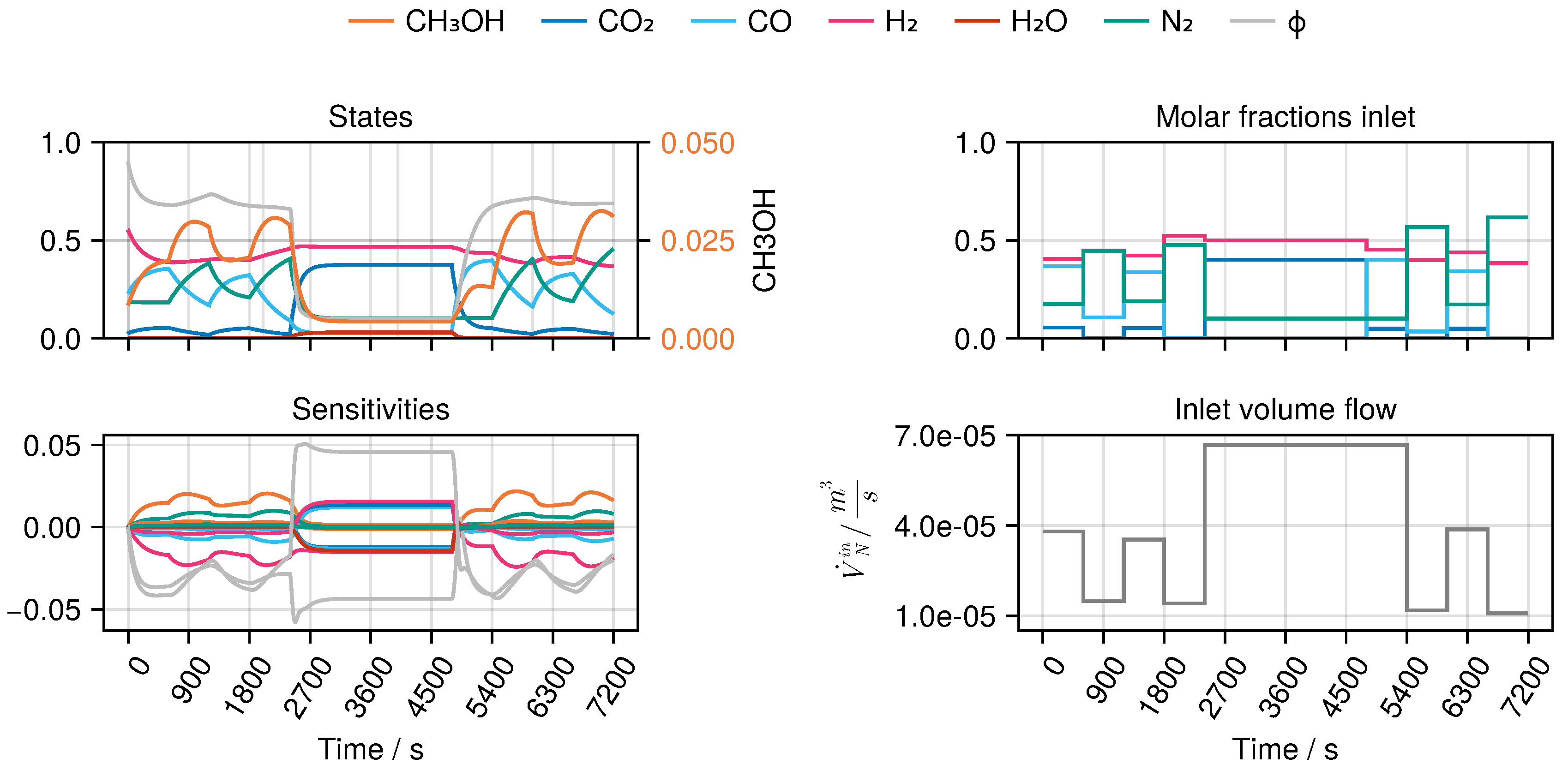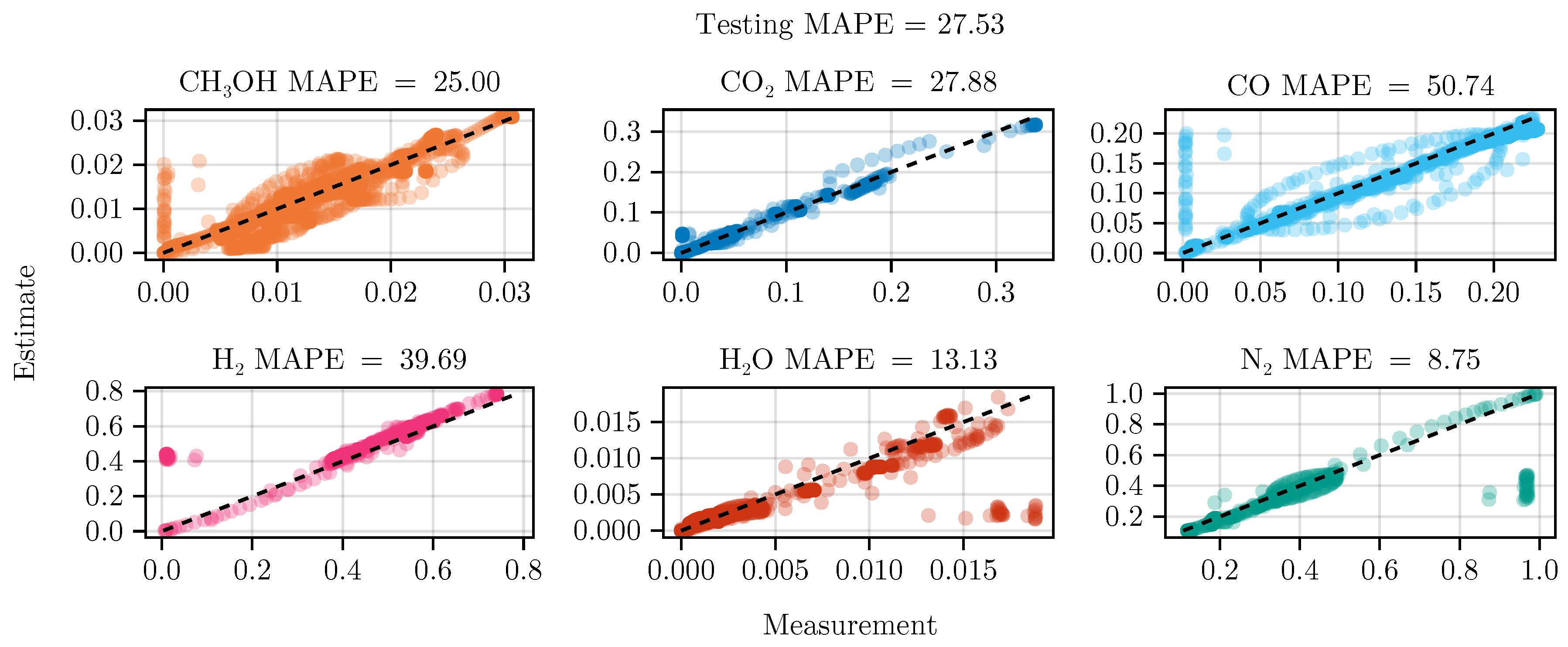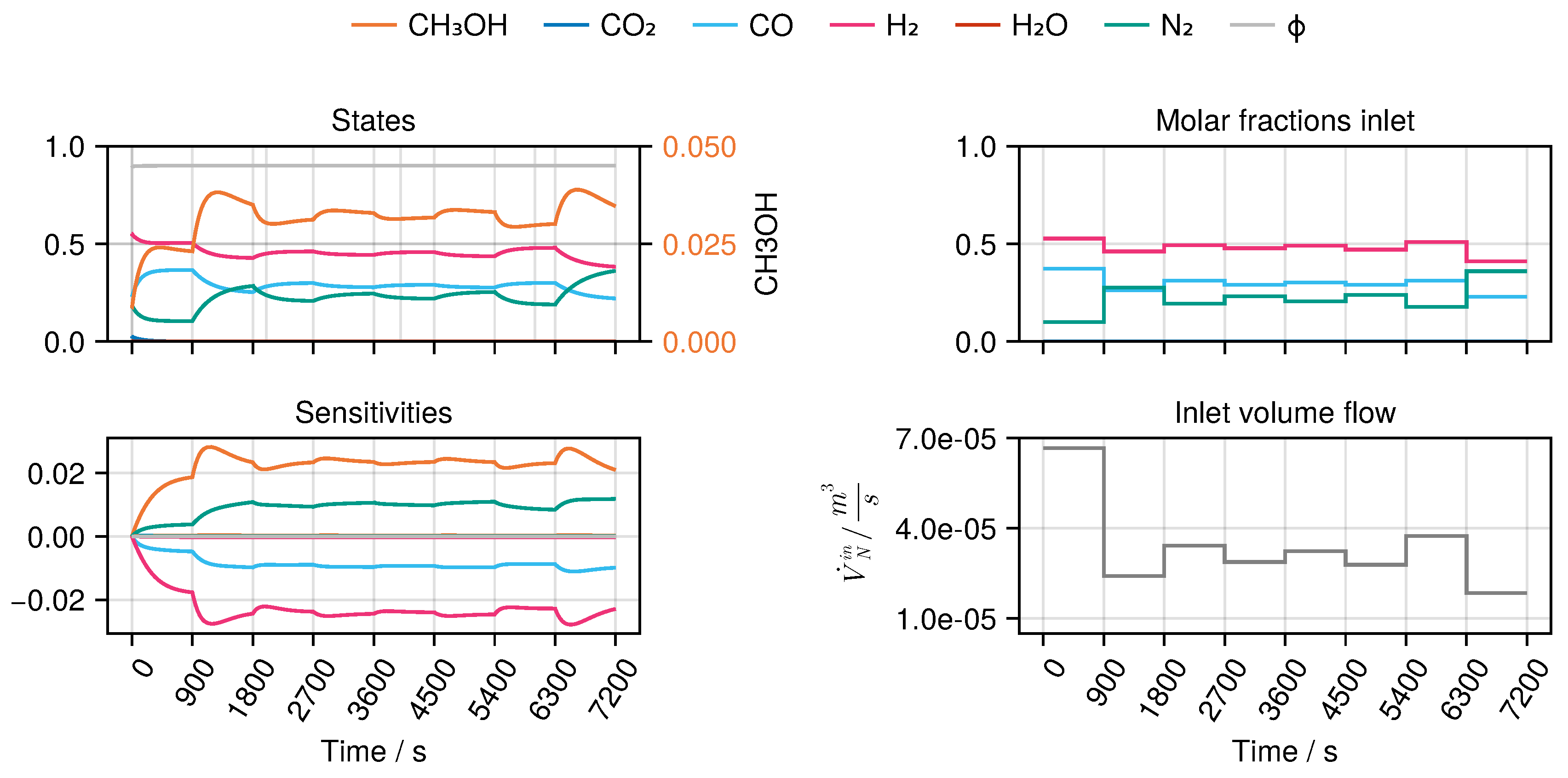Afterwards, we used model B to derive an optimal experimental design, MeOH_083, see Figure 8. The design calculated in this way only takes into account the weights of the trained network in the singular value decomposition, ignoring any physical parameters.

Figure 8. Optimal experimental design MeOH_083 of the selected architecture B. The temperature was determined as $T=530.0$ K.

Figure 8. Optimal experimental design MeOH_083 of the selected architecture B. The temperature was determined as $T=530.0$ K.

Finally, we refitted both models again with the collected experimental data. While model B became numerically instable after a few iterations of optimization, model A was successfully fitted, resulting in increased predictive performance. As a comparison we refitted the model starting from the same initial conditions without including the experimental plan, see Table 4.

3.2.1. Neural Network Analysis

In this subsection, we investigate the final, fully trained neural network A. In detail, we are comparing the surrogate model with the heuristic by a) performing sensitivity analysis and b) examining the outputs.

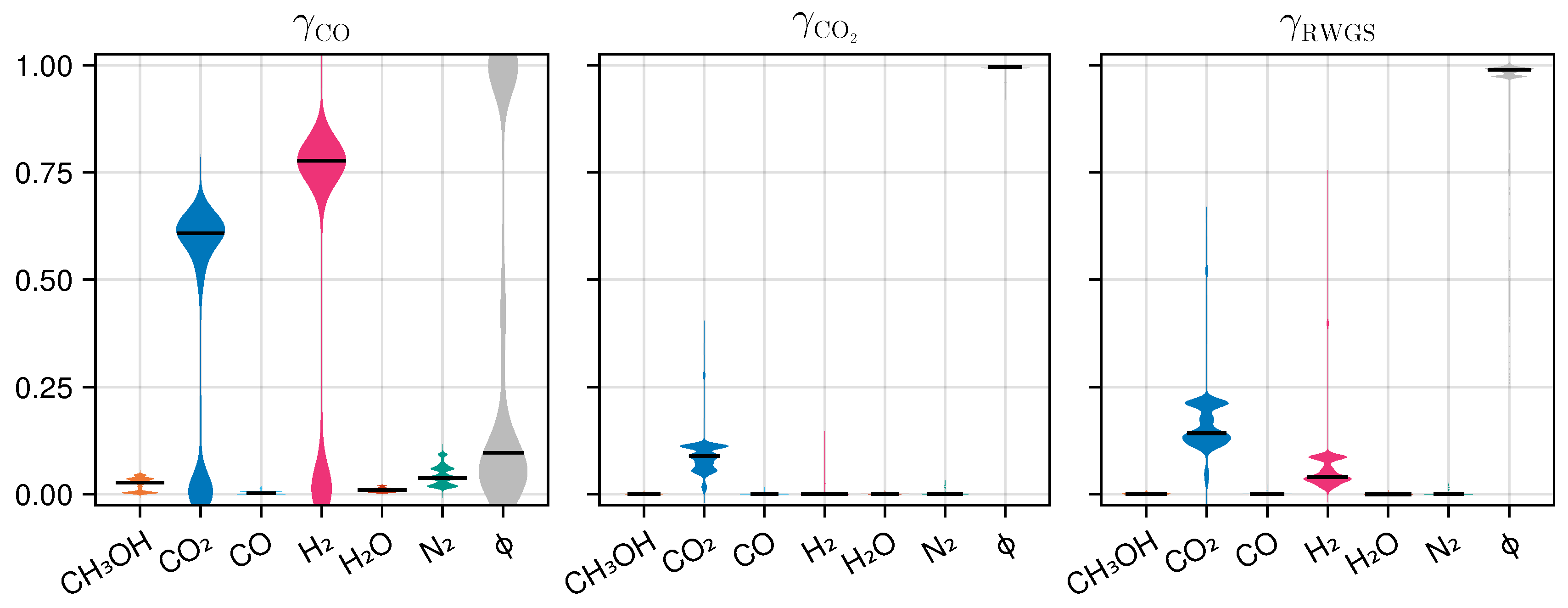
The sensitivity analysis is used to determine which input features are dominating the learned impact $\gamma$ on the three reaction rates. To this end, we compute the squared gradient of the output of the trained neural network $U(x;\theta )\in {\mathbb{R}}^3$ with respect to the input $x\in {\mathbb{R}}^7$${\left({\partial }_{x}U(x,\theta )\right)}^2\in {\mathbb{R}}^{3\times 7}$ for each measurement in the training set and perform a row-wise normalization using L₂-Norm. This results in a simple relevance score from the interval $[0,1]$ for each training sample and each predicted quantity, indicating the importance of each input quantity. Figure 9 illustrates the distributions of these relevance scores for the surrogate model.

Figure 9. Distribution of relevance scores of the input features of the neural network A with respect to the output ${\gamma }_{\mathrm{CO}}$, ${\gamma }_{{\mathrm{CO}}_2}$ and ${\gamma }_{\mathrm{RWGS}}$ on the training set. A higher value indicates a stronger influence.

Figure 9. Distribution of relevance scores of the input features of the neural network A with respect to the output ${\gamma }_{\mathrm{CO}}$, ${\gamma }_{{\mathrm{CO}}_2}$ and ${\gamma }_{\mathrm{RWGS}}$ on the training set. A higher value indicates a stronger influence.

The results reveal several instructive trends. First, for ${\gamma }_{{\mathrm{CO}}_2}$ and ${\gamma }_{\mathrm{RWGS}}$, the neural network bases is primarily depending on the state $\varphi$. Other states are being ignored for the most part, similar to the heuristic eq:gammaheuristic used in the mechanistic model. For the ${\gamma }_{\mathrm{CO}}$ predictions, however, the molar fractions of CO₂ and H₂ play a major role.

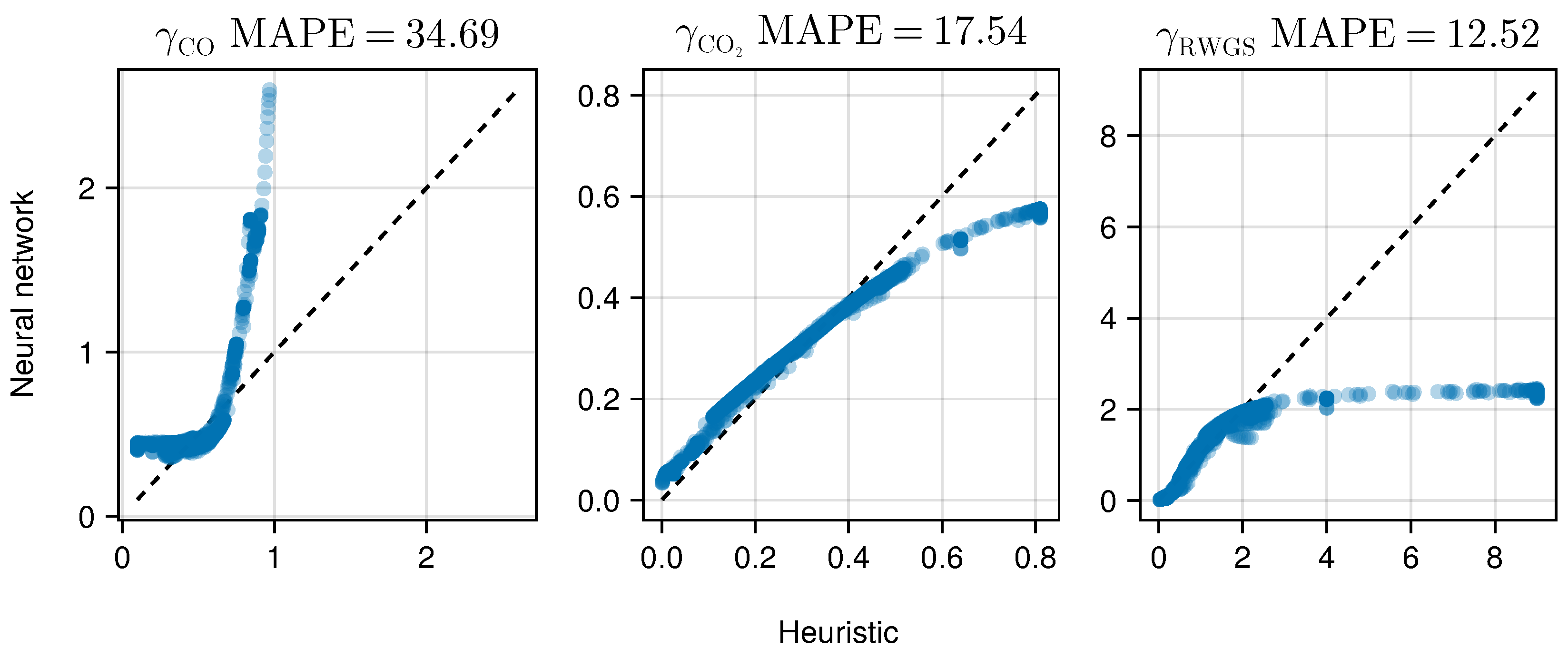
Comparing the functional relationship encoded in the trained neural network with the heuristic shown in Figure 10, both ${\gamma }_{{\mathrm{CO}}_2}$ and ${\gamma }_{\mathrm{RWGS}}$ show a high agreement with the heuristic with MAPE scores of $17.54$ and $12.52$ respectively. Only ${\gamma }_{\mathrm{CO}}$ shows a higher deviation from the heuristic, resulting in a MAPE of $34.69$. For ${\gamma }_{\mathrm{RWGS}}$ there is a high level of agreement especially for small predicted values with ${\gamma }_{\mathrm{RWGS}}\le 3$, which account for $97\%$ of the shown samples. Restricted to this domain, we observe a MAPE of $10.78$. For larger values of the heuristic ${\gamma }_{\mathrm{RWGS}}$, the deviation increases as the output of the neural network stays constant.

Figure 10. Parity plot comparing the functional relationship of the trained neural network and the previous heuristic for the impacts $\gamma$eq:gammaheuristic evaluated on the train dataset. While the neural network and the heuristic deviate for ${\gamma }_{\mathrm{CO}}$, there is a high level of agreement for both ${\gamma }_{{\mathrm{CO}}_2}$ and ${\gamma }_{\mathrm{RWGS}}$. The visible mismatch for RWGS stems from only the top 3% of data. Note The mean absolute percentage error does not indicate a goodness-of-fit in this case, but rather the divergence between the heuristic and the ML model.

Figure 10. Parity plot comparing the functional relationship of the trained neural network and the previous heuristic for the impacts $\gamma$eq:gammaheuristic evaluated on the train dataset. While the neural network and the heuristic deviate for ${\gamma }_{\mathrm{CO}}$, there is a high level of agreement for both ${\gamma }_{{\mathrm{CO}}_2}$ and ${\gamma }_{\mathrm{RWGS}}$. The visible mismatch for RWGS stems from only the top 3% of data. Note The mean absolute percentage error does not indicate a goodness-of-fit in this case, but rather the divergence between the heuristic and the ML model.

4. Discussion and Conclusion

In this contribution, an existing heuristic kinetic model for the heterogeneously catalyzed methanol synthesis from [5,6,7] was first recalibrated utilizing new experimental data generated in a recently built experimental setup. From this starting point, optimal experimental designs were computed to collect dedicated data to increase the model performance, while reducing further experimental effort. The experiments were realized and the subsequent parameter identification led to a further improved heuristic model. In the next step, the important but not fully understood part of the model describing the complex influence of reversible changes of the active catalytic sites on each reaction was substituted with neural networks. Several varieties were tested and compared with respect to their goodness-of-fit. To further improve the data basis for the training, an additional experimental design based on a selected hybrid model was computed and carried out experimentally. The built experimental setup is able to deliver time-resolved data (approx. every 90s) for the analysis of perturbations of the reactor inlet which is of major importance for more flexible power-2-X processes. The reversible catalyst dynamics can not be understood based on only steady state experiments. The possibility of fast and automated adaptions of both feed composition and total flowrate allows for the realization of optimal designs with a high degree of freedom. Additionally, the new experimental setup offers the option to test forced periodic feed changes with the goal to increase the time-averaged process performance which is part of ongoing work.

In general, we see that the hybrid model is on par with the mechanistic model. No great improvements in terms of predictive performance have been achieved, which at first glance suggests that the effort of using data-driven models is not justified. We suspect that this is a result of our decision to a) only learn a small submodel and b) fix the mechanistic parameters. This could constrain the functional relationship too tightly, introduce a strong bias, and hinder a sufficient exploration of alternatives. Therefore, future research should investigate relaxing the use of prior knowledge, allowing the neural network to explore different possible functional relationships. This remains a challenging task, given that the gained flexibility often results in the need for more data and comes at the cost of interpretability.

Despite the aforementioned analysis, the results of the trained hybrid model contribute to the understanding of the kinetic model. The results suggest that both heuristics for ${\gamma }_{{\mathrm{CO}}_2}$ and ${\gamma }_{\mathrm{RWGS}}$ are capable of modeling the impact of the distribution of active centers over the catalyst. Hence, we were able to validate two heuristics over a broad range of the data purely based on training the hybrid model. Figure 9 and Figure 10 ncourage that other formulations of ${\gamma }_{\mathrm{CO}}$ might be possible without losing predictive performance. All pathways show influences of the species ${\mathrm{CO}}_2$ and ${\mathrm{H}}_2$, indicating the possibility of reformulating the impacts $\gamma$ in terms of the respective states. In addition to the reaction mechanism used in the model, there are other potential reaction pathways, which could explain the observed behavior.

We found that optimal experimental design is helpful for both mechanistic and hybrid models. Especially in the case of hybrid models, we suspect that considering experimental designs leads to an increase in robustness of training, even if the experimental designs were derived from a structurally different hybrid model. Confirmation of this claim requires further investigation from theoretical and practical point of view. Moreover, we believe that the methodology presented in this paper is not only useful for methanol synthesis but can also be transferred to other synthesis reactions.

Appendix E.1. Analytics - Gas Chromatography

The reactor outlet stream is measured with an Agilent 490 $\mu$ GC with a thermal conductivity detector. Hydrogen, nitrogen and carbon monoxide are separated in a 10m long column containing a mole sieve (MSA5) as stationary phase using argon as mobile phase (130°C column temperature, 250 $\mathrm{k}$$\mathrm{Pa}$ initial pressure, 120ms injection time, 60s run time). The other reactants are discarded with a back flush after an initial separation (8s) via a pre-column for this channel. Carbon dioxide, methanol and water were analyzed using a 10m long PPU column with helium as mobile phase (145°C column temperature, 120kPa initial pressure, 120ms injection time, 60s run time). The injector and sample line temperature were 100°C. With this method approximately every 90s a measurement is conducted during experiments. The gaseous components at ambient conditions were calibrated with calibration gas bottles. For the calibration of methanol and water a defined nitrogen stream was saturated in a tempered steel vessel filled with glass rings and the the respective component. The saturation was checked with a condensation trap. After a measurement series is finished, the detector signal of the gas chromatograph is imported into Matlab and processed there. This allows a fast and flexible handling of a large number of single measurements.

Appendix E.2. Mass Flow Controller

The mass flow controllers (Bronkhorst) were calibrated with the help of a Coriolis mass flow meter from Bronkhorst and a pressure regulator from Swagelok to adjust the pressure in the calibration bypass according to the aimed process conditions. The calibration factors of the MFC are interpolated values between the calibrated points. If the flowrate, the feed pressure or the reactor pressure change, the calibration factors are adjusted automatically while the MFC are used.

Appendix E.3. Catalyst Activity

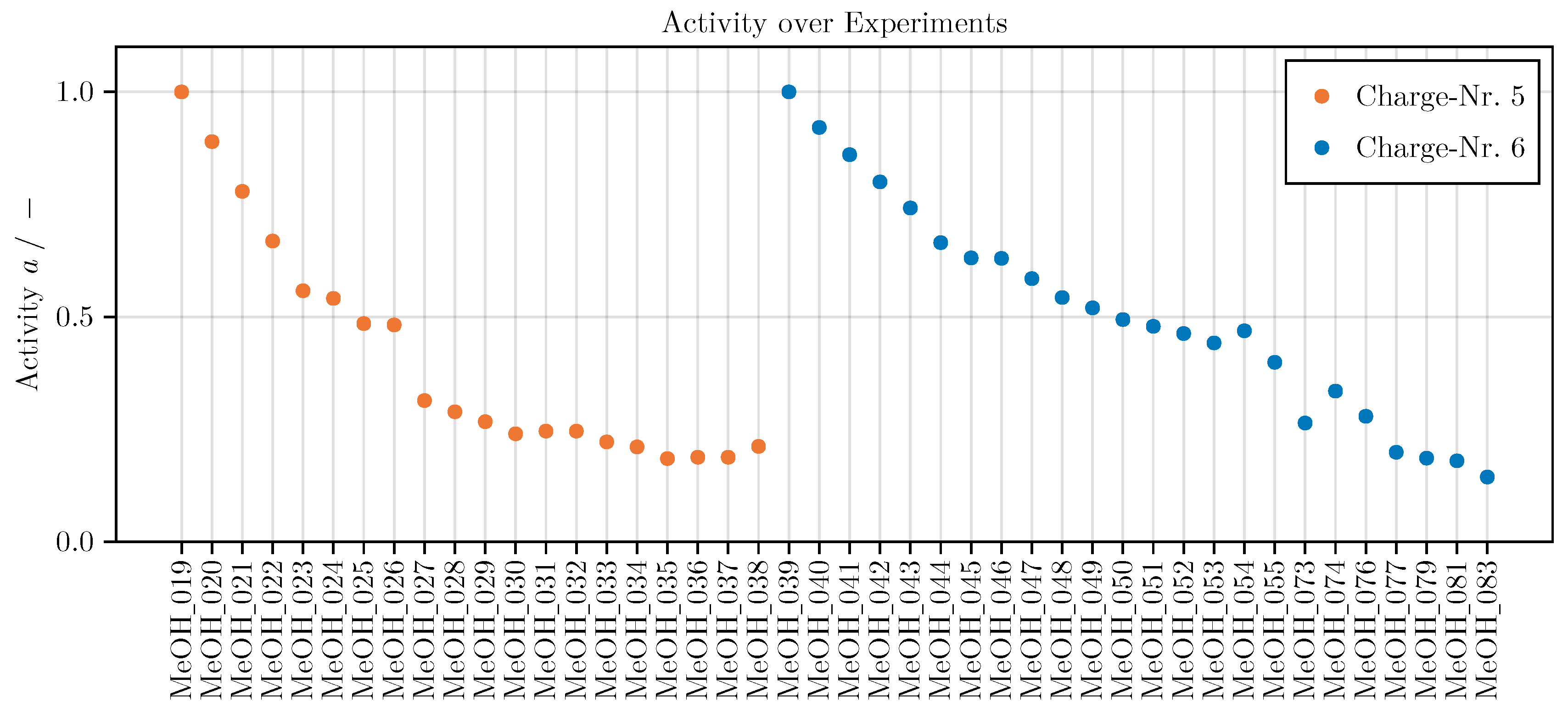
The steady inlet conditions applied for the determination of a reference yield of methanol for the approximation of an catalytic activity are listed in Table A5 conditions. Figure A11 depicts the decrease in activity of each catalyst charge over the experiments using it. The data is published in Kaps et al. (2025).

Table A5. Reference reaction and inlet conditions for activity measurements.

Charge-Nr.	T	p	${\dot{\mathit{V}}}_{\mathit{t}\mathit{o}\mathit{t}\mathit{a}\mathit{l}}^{\mathit{i}\mathit{n},\mathit{n}}$	${\mathit{x}}_{\mathit{C}{\mathit{O}}_2}^{\mathit{i}\mathit{n}}$	${\mathit{x}}_{\mathit{C}\mathit{O}}^{\mathit{i}\mathit{n}}$	${\mathit{x}}_{{\mathit{H}}_2}^{\mathit{i}\mathit{n}}$	${\mathit{x}}_{{\mathit{N}}_2}^{\mathit{i}\mathit{n}}$
-	°C	bar	NL/min	%	%	%	%
5	230	30	2	2.56	20.82	60.59	16.03
6	230	50	3.3333	2.56	20.82	60.59	16.03

Table A5. Reference reaction and inlet conditions for activity measurements.

Charge-Nr.	T	p	${\dot{\mathit{V}}}_{\mathit{t}\mathit{o}\mathit{t}\mathit{a}\mathit{l}}^{\mathit{i}\mathit{n},\mathit{n}}$	${\mathit{x}}_{\mathit{C}{\mathit{O}}_2}^{\mathit{i}\mathit{n}}$	${\mathit{x}}_{\mathit{C}\mathit{O}}^{\mathit{i}\mathit{n}}$	${\mathit{x}}_{{\mathit{H}}_2}^{\mathit{i}\mathit{n}}$	${\mathit{x}}_{{\mathit{N}}_2}^{\mathit{i}\mathit{n}}$
-	°C	bar	NL/min	%	%	%	%
5	230	30	2	2.56	20.82	60.59	16.03
6	230	50	3.3333	2.56	20.82	60.59	16.03

Figure A11. Catalytic activity (see eq:defact) of all 44 experiments.

Figure A11. Catalytic activity (see eq:defact) of all 44 experiments.

Appendix C.1. Fitting Results

This section shows the results of the parameter fitting of the mechanistic model in tab:parameterfitresults and a subset of trajectories. The parameters equal to zero in the initial parameter set are still zero after the refit with the new experimental data set with and without using the optimal experimental designs in the parameter estimation. This strengthens the assumption that those are not sensitive. ${\beta }_2$, ${\beta }_4$ and ${\beta }_6$ are directly related to the activation energies of the three reactions rates and their temperature dependence respectively. These differ significantly between the three parameter sets, indicating that these parameters are hard to identify. This may be due to the fact that the three reactions in reaction network according to fig:reaction network MeOH are not linear independent of each other. Whether starting from CO or CO₂ as reactant, as long as H₂ and H₂O are present in the reaction mixture, there are always two pathways to methanol (direct hydrogenation and (R)WGS + hydrogenation). Thus, also the temperature dependency of the methanol synthesis in terms of ${\beta }_2$, ${\beta }_4$ and ${\beta }_6$ might be shiftable between these three parameters. Changes of the kinetic parameters determined within this study compared to the initial values from [7] may also simply result from the fact that the set of experiments used in this study contains time-resolved data while the previously utilized data set ([8]) consisted almost exclusively of steady state data.

Table A7. Result of the parameter fitting for the mechanistic model. Transformed values of the parameters are in brackets. Initial values are taken from [7]. The different data settings are similar to Table 4, e.g. OED includes the full training set and NOED the dataset excluding the experimental designs. Values $\le -36.00$ of exponentially transformed variables equate to zero. The parameter set OED was used for the hybrid model.

${\mathit{q}}_{\mathit{i}}$	Transform	Initial Value	OED	NOED
$G_1$		0.34	0.26	-0.73
$G_2$		21.84	21.38	21.92
$k_1$	exp	-4.84	-8.25	-3.11
$k_2$	exp	-10.88	-4.19	-8.90
${\beta }_1$		-5.01	-5.68	-4.65
${\beta }_2$	exp	3.64 (26.46)	6.91 (38.18)	4.40 (81.45)
${\beta }_3$		-3.15	-3.86	-4.00
${\beta }_4$	exp	0.42 (1.53)	2.63 (13.90)	1.21 (3.35)
${\beta }_5$		-4.46	-1.78	-2.46
${\beta }_6$	exp	2.74 (15.62)	4.08 (59.42)	1.66 (5.26)
${\beta }_7$	exp	0.10 (1.11)	-0.54 (0.58)	-0.26 (0.77)
${\beta }_8$	exp	-36.05 (0.00)	-36.04 (0.00)	-36.04 (0.00)
${\beta }_9$	exp	-36.05 (0.00)	-36.04 (0.00)	-36.04 (0.00)
${\beta }_{10}$	exp	-36.05 (0.00)	-36.04 (0.00)	-36.04 (0.00)
${\beta }_{11}$	exp	1.90 (0.15)	-0.61 (0.54)	1.02 (2.77)
${\beta }_{12}$	exp	-36.05 (0.00)	-36.04 (0.00)	-36.04 (0.00)
${\beta }_{13}$	exp	-2.77 (0.06)	-2.43 (0.09)	-3.39 (0.03)
${\beta }_{14}$	exp	-36.05 (0.00)	-36.04 (0.00)	-36.04 (0.00)

Table A7. Result of the parameter fitting for the mechanistic model. Transformed values of the parameters are in brackets. Initial values are taken from [7]. The different data settings are similar to Table 4, e.g. OED includes the full training set and NOED the dataset excluding the experimental designs. Values $\le -36.00$ of exponentially transformed variables equate to zero. The parameter set OED was used for the hybrid model.

${\mathit{q}}_{\mathit{i}}$	Transform	Initial Value	OED	NOED
$G_1$		0.34	0.26	-0.73
$G_2$		21.84	21.38	21.92
$k_1$	exp	-4.84	-8.25	-3.11
$k_2$	exp	-10.88	-4.19	-8.90
${\beta }_1$		-5.01	-5.68	-4.65
${\beta }_2$	exp	3.64 (26.46)	6.91 (38.18)	4.40 (81.45)
${\beta }_3$		-3.15	-3.86	-4.00
${\beta }_4$	exp	0.42 (1.53)	2.63 (13.90)	1.21 (3.35)
${\beta }_5$		-4.46	-1.78	-2.46
${\beta }_6$	exp	2.74 (15.62)	4.08 (59.42)	1.66 (5.26)
${\beta }_7$	exp	0.10 (1.11)	-0.54 (0.58)	-0.26 (0.77)
${\beta }_8$	exp	-36.05 (0.00)	-36.04 (0.00)	-36.04 (0.00)
${\beta }_9$	exp	-36.05 (0.00)	-36.04 (0.00)	-36.04 (0.00)
${\beta }_{10}$	exp	-36.05 (0.00)	-36.04 (0.00)	-36.04 (0.00)
${\beta }_{11}$	exp	1.90 (0.15)	-0.61 (0.54)	1.02 (2.77)
${\beta }_{12}$	exp	-36.05 (0.00)	-36.04 (0.00)	-36.04 (0.00)
${\beta }_{13}$	exp	-2.77 (0.06)	-2.43 (0.09)	-3.39 (0.03)
${\beta }_{14}$	exp	-36.05 (0.00)	-36.04 (0.00)	-36.04 (0.00)

Table A8. Result of the parameter fitting for the mechanistic model. Transformed values of the parameters are in brackets. Initial values are taken from [7]. The different data settings are similar to Table 4, e.g. OED includes the full training set and NOED the dataset excluding the experimental designs. Values $\le -36.00$ of exponentially transformed variables equate to zero. The parameter set OED was used for the hybrid model.

${\mathit{q}}_{\mathit{i}}$	Transform	Initial Value	OED	NOED
$G_1$		0.34	0.26	-0.73
$G_2$		21.84	21.38	21.92
$k_1$	exp	-4.84	-8.25	-3.11
$k_2$	exp	-10.88	-4.19	-8.90
${\beta }_1$		-5.01	-5.68	-4.65
${\beta }_2$	exp	3.64 (26.46)	6.91 (38.18)	4.40 (81.45)
${\beta }_3$		-3.15	-3.86	-4.00
${\beta }_4$	exp	0.42 (1.53)	2.63 (13.90)	1.21 (3.35)
${\beta }_5$		-4.46	-1.78	-2.46
${\beta }_6$	exp	2.74 (15.62)	4.08 (59.42)	1.66 (5.26)
${\beta }_7$	exp	0.10 (1.11)	-0.54 (0.58)	-0.26 (0.77)
${\beta }_8$	exp	-36.05 (0.00)	-36.04 (0.00)	-36.04 (0.00)
${\beta }_9$	exp	-36.05 (0.00)	-36.04 (0.00)	-36.04 (0.00)
${\beta }_{10}$	exp	-36.05 (0.00)	-36.04 (0.00)	-36.04 (0.00)
${\beta }_{11}$	exp	1.90 (0.15)	-0.61 (0.54)	1.02 (2.77)
${\beta }_{12}$	exp	-36.05 (0.00)	-36.04 (0.00)	-36.04 (0.00)
${\beta }_{13}$	exp	-2.77 (0.06)	-2.43 (0.09)	-3.39 (0.03)
${\beta }_{14}$	exp	-36.05 (0.00)	-36.04 (0.00)	-36.04 (0.00)

Table A8. Result of the parameter fitting for the mechanistic model. Transformed values of the parameters are in brackets. Initial values are taken from [7]. The different data settings are similar to Table 4, e.g. OED includes the full training set and NOED the dataset excluding the experimental designs. Values $\le -36.00$ of exponentially transformed variables equate to zero. The parameter set OED was used for the hybrid model.

${\mathit{q}}_{\mathit{i}}$	Transform	Initial Value	OED	NOED
$G_1$		0.34	0.26	-0.73
$G_2$		21.84	21.38	21.92
$k_1$	exp	-4.84	-8.25	-3.11
$k_2$	exp	-10.88	-4.19	-8.90
${\beta }_1$		-5.01	-5.68	-4.65
${\beta }_2$	exp	3.64 (26.46)	6.91 (38.18)	4.40 (81.45)
${\beta }_3$		-3.15	-3.86	-4.00
${\beta }_4$	exp	0.42 (1.53)	2.63 (13.90)	1.21 (3.35)
${\beta }_5$		-4.46	-1.78	-2.46
${\beta }_6$	exp	2.74 (15.62)	4.08 (59.42)	1.66 (5.26)
${\beta }_7$	exp	0.10 (1.11)	-0.54 (0.58)	-0.26 (0.77)
${\beta }_8$	exp	-36.05 (0.00)	-36.04 (0.00)	-36.04 (0.00)
${\beta }_9$	exp	-36.05 (0.00)	-36.04 (0.00)	-36.04 (0.00)
${\beta }_{10}$	exp	-36.05 (0.00)	-36.04 (0.00)	-36.04 (0.00)
${\beta }_{11}$	exp	1.90 (0.15)	-0.61 (0.54)	1.02 (2.77)
${\beta }_{12}$	exp	-36.05 (0.00)	-36.04 (0.00)	-36.04 (0.00)
${\beta }_{13}$	exp	-2.77 (0.06)	-2.43 (0.09)	-3.39 (0.03)
${\beta }_{14}$	exp	-36.05 (0.00)	-36.04 (0.00)	-36.04 (0.00)

Figure A12. Parity plot of the fitted mechanistic baseline model over the training data set excluding optimal experimental designs.

Figure A12. Parity plot of the fitted mechanistic baseline model over the training data set excluding optimal experimental designs.

Figure A13. Parity plot of the fitted mechanistic baseline model over the test data set excluding optimal experimental designs.

Figure A13. Parity plot of the fitted mechanistic baseline model over the test data set excluding optimal experimental designs.

Appendix C.2. Initial Fit

Given that we fitting the model while additional experiments where still conducted, we started with a set of 37 dynamic experiments (MeOH_018 - MeOH_054).

Instead of optimization problem (), we initially considered the following optimization problem

$$\underset{q}{\min } \frac{\left|{\mathcal{D}}_{TR}\right|}{1}\sum _{{\mathcal{D}}_i\in {\mathcal{D}}_{TR}}\frac{\left|{\mathcal{D}}_i\right|}{1}\sum _{t_j\in {\mathcal{D}}_i}\frac{\left|{\mathcal{S}}_i\right|}{1}\sum _{tk\in \mathcal{S}i}\left(\frac{{\widehat{x}}_{i,j,k}-x_{i,j,k}}{{\widehat{x}}_{i,j,k}}\right)$$

(A31a)

$$\text{s.t.} 0=f\left(\stackrel{·}{x},x,q,t,u\right)$$

(A31b)

$$q\in Q$$

(A31c)

with

$$\begin{array}{c}\hfill {\mathcal{S}}^{\prime }=\{{\mathrm{CH}}_3\mathrm{OH},\mathrm{CO},{\mathrm{CO}}_2\}\end{array}$$

(A32)

However, we found that including the species ${\mathrm{H}}_2$ improved the models performance. Prior to the parameter transformation, the positivity of a subset of the parameters was enforced via a penalty approach.

In addition, we used a sequential optimization procedure starting with 1000 iterations Nelder-Mead, to find a better starting position followed with a mesh adaptive direct search via NOMAD to find a set of parameters. Choosing these (gradient-free) optimization algorithms was mainly due to an earlier implementation of the model and objective, which did not allow numerical differentiation. The final version of the model allowed the use of numerical differentiation, hence a more sophisticated method was selected.

Note that we are not particularly interested in an exact estimate at this early stage. The initial estimation is only about finding a sufficient starting point for the optimal experimental design.

Appendix G.3. Data Preparation

For each experiment, the mean value of observed mole fractions, the measured catalyst activity, the mole fraction of the feed, the nominal volume flow at the inlet, temperature and pressure were used to stratify the data accordingly. A more detailed assignment of each experiment can be seen in the detailed result tables of G.4.

Figure A14 shows the histogram of the observed mole fractions at the reactor outlet and the catalyst’s activity level.

Figure A14. Histogram of the mole fractions of the output species and the estimated activity levels for the training and testing data sets. The occurrence is normalized by the probability weight of each bin.

Figure A14. Histogram of the mole fractions of the output species and the estimated activity levels for the training and testing data sets. The occurrence is normalized by the probability weight of each bin.

Appendix G.4. Model Evaluation

Table A9. Detailed MAPE values of the mechanistic model (OED) corresponding to Table 4.

Dataset	Experiment	${\mathit{x}}_{{\mathbf{CH}}_3\mathbf{OH}}$	${\mathit{x}}_{\mathbf{CO}}$	${\mathit{x}}_{{\mathbf{CO}}_2}$	${\mathit{x}}_{{\mathbf{H}}_2}$	${\mathit{x}}_{{\mathbf{H}}_2\mathbf{O}}$	${\mathit{x}}_{{\mathbf{N}}_2}$	Total
Testing	MeOH_025	8.27	6.33	3.41	5.59	11.5	8.96	7.35
	MeOH_027	52.5	130	68.6	98.9	12.4	7.09	61.7
	MeOH_033	12.3	6.55	4.07	5.5	21.5	9.04	9.84
	MeOH_041	12.4	6.35	13.6	5.69	10.9	9.92	9.8
	MeOH_042	13.6	15.9	8.03	6.46	7.2	6.71	9.66
	MeOH_044	41.4	157	82.8	131	8.45	7.33	71.3
	MeOH_053	7.46	6.85	14.2	6.85	13.8	9.31	9.75
	MeOH_054	14.8	8.82	6.79	5.12	7.28	11.1	9
	MeOH_076	22.1	14.7	4.66	7.37	8.94	9.73	11.2
	MeOH_079	12.8	7.51	3.11	6.49	16.5	9.73	9.34
Training	MeOH_019	18.1	7.45	23.9	5.52	13.8	8.76	12.9
	MeOH_020	15.6	6.78	10.9	4.55	4.54	7.88	8.37
	MeOH_021	17.7	5.9	3.32	5.52	9.81	8.09	8.39
	MeOH_022	30.6	8.07	1.16	4.04	8.76	3.24	9.32
	MeOH_023	5.1	6.09	1.42	5.23	2.34	8.76	4.82
	MeOH_024	16.4	5.92	4.79	5.35	2.78	8.56	7.31
	MeOH_026	10.8	2.84	1.47	5.66	2.97	6.1	4.97
	MeOH_028	23.7	6.66	5.26	6.84	12.2	4.38	9.84
	MeOH_029	19.9	6.29	4.96	6.3	13.3	4.03	9.13
	MeOH_030	3.59	7.08	3.43	5.89	1.79	9.12	5.15
	MeOH_031	2.7	6.85	2.67	5.72	0.976	9.08	4.67
	MeOH_032	4.05	6.03	2.56	5.23	1.23	8.53	4.6
	MeOH_034	9	27.6	12.4	18.9	3.88	9.24	13.5
	MeOH_035	2.55	5.71	2.2	5.16	0.947	8.98	4.26
	MeOH_036	12.4	11.4	4.12	5.5	1.31	8.92	7.27
	MeOH_037	23.1	6.14	7.07	5.55	6.66	8.93	9.57
	MeOH_038	35.9	18.5	13	5.6	8.07	8.92	15
	MeOH_039	19.7	7.63	16	8.24	9.99	10.9	12.1
	MeOH_040	15.9	7.65	16.4	7.75	14.2	10.2	12
	MeOH_043	8.79	4.9	7.61	6.44	6.05	4.75	6.42
	MeOH_045	12.7	7.49	17.1	7.69	13.4	9.88	11.4
	MeOH_046	9.43	6.42	10.3	7.98	5.95	6.58	7.78
	MeOH_047	6.41	6.6	9.98	7.85	2.69	5.92	6.57
	MeOH_048	15.8	9.66	8.74	6.96	5.31	6.13	8.77
	MeOH_049	8.5	6.23	8.85	7.59	4.81	5.55	6.92
	MeOH_050	4.55	5.81	9.35	7.33	3.76	5.84	6.11
	MeOH_051	7.86	5.24	8.32	6.45	5.95	5.83	6.61
	MeOH_052	8.95	5.62	8.39	6.4	4.98	5.16	6.58
	MeOH_055	13.1	8.1	15.5	8.18	18.6	10.3	12.3
	MeOH_073	21.6	6.81	10.7	6.97	16.4	8.93	11.9
	MeOH_074	8.9	16.6	4.18	7.37	10.1	9.18	9.4
	MeOH_077	4.43	8.19	1.11	6.56	12.4	10.1	7.13
	MeOH_081	16.8	17.6	6.65	9.51	18.7	11.3	13.4
	MeOH_083	16.5	14.8	3.54	7.14	19.8	9.21	11.8

Table A9. Detailed MAPE values of the mechanistic model (OED) corresponding to Table 4.

Dataset	Experiment	${\mathit{x}}_{{\mathbf{CH}}_3\mathbf{OH}}$	${\mathit{x}}_{\mathbf{CO}}$	${\mathit{x}}_{{\mathbf{CO}}_2}$	${\mathit{x}}_{{\mathbf{H}}_2}$	${\mathit{x}}_{{\mathbf{H}}_2\mathbf{O}}$	${\mathit{x}}_{{\mathbf{N}}_2}$	Total
Testing	MeOH_025	8.27	6.33	3.41	5.59	11.5	8.96	7.35
	MeOH_027	52.5	130	68.6	98.9	12.4	7.09	61.7
	MeOH_033	12.3	6.55	4.07	5.5	21.5	9.04	9.84
	MeOH_041	12.4	6.35	13.6	5.69	10.9	9.92	9.8
	MeOH_042	13.6	15.9	8.03	6.46	7.2	6.71	9.66
	MeOH_044	41.4	157	82.8	131	8.45	7.33	71.3
	MeOH_053	7.46	6.85	14.2	6.85	13.8	9.31	9.75
	MeOH_054	14.8	8.82	6.79	5.12	7.28	11.1	9
	MeOH_076	22.1	14.7	4.66	7.37	8.94	9.73	11.2
	MeOH_079	12.8	7.51	3.11	6.49	16.5	9.73	9.34
Training	MeOH_019	18.1	7.45	23.9	5.52	13.8	8.76	12.9
	MeOH_020	15.6	6.78	10.9	4.55	4.54	7.88	8.37
	MeOH_021	17.7	5.9	3.32	5.52	9.81	8.09	8.39
	MeOH_022	30.6	8.07	1.16	4.04	8.76	3.24	9.32
	MeOH_023	5.1	6.09	1.42	5.23	2.34	8.76	4.82
	MeOH_024	16.4	5.92	4.79	5.35	2.78	8.56	7.31
	MeOH_026	10.8	2.84	1.47	5.66	2.97	6.1	4.97
	MeOH_028	23.7	6.66	5.26	6.84	12.2	4.38	9.84
	MeOH_029	19.9	6.29	4.96	6.3	13.3	4.03	9.13
	MeOH_030	3.59	7.08	3.43	5.89	1.79	9.12	5.15
	MeOH_031	2.7	6.85	2.67	5.72	0.976	9.08	4.67
	MeOH_032	4.05	6.03	2.56	5.23	1.23	8.53	4.6
	MeOH_034	9	27.6	12.4	18.9	3.88	9.24	13.5
	MeOH_035	2.55	5.71	2.2	5.16	0.947	8.98	4.26
	MeOH_036	12.4	11.4	4.12	5.5	1.31	8.92	7.27
	MeOH_037	23.1	6.14	7.07	5.55	6.66	8.93	9.57
	MeOH_038	35.9	18.5	13	5.6	8.07	8.92	15
	MeOH_039	19.7	7.63	16	8.24	9.99	10.9	12.1
	MeOH_040	15.9	7.65	16.4	7.75	14.2	10.2	12
	MeOH_043	8.79	4.9	7.61	6.44	6.05	4.75	6.42
	MeOH_045	12.7	7.49	17.1	7.69	13.4	9.88	11.4
	MeOH_046	9.43	6.42	10.3	7.98	5.95	6.58	7.78
	MeOH_047	6.41	6.6	9.98	7.85	2.69	5.92	6.57
	MeOH_048	15.8	9.66	8.74	6.96	5.31	6.13	8.77
	MeOH_049	8.5	6.23	8.85	7.59	4.81	5.55	6.92
	MeOH_050	4.55	5.81	9.35	7.33	3.76	5.84	6.11
	MeOH_051	7.86	5.24	8.32	6.45	5.95	5.83	6.61
	MeOH_052	8.95	5.62	8.39	6.4	4.98	5.16	6.58
	MeOH_055	13.1	8.1	15.5	8.18	18.6	10.3	12.3
	MeOH_073	21.6	6.81	10.7	6.97	16.4	8.93	11.9
	MeOH_074	8.9	16.6	4.18	7.37	10.1	9.18	9.4
	MeOH_077	4.43	8.19	1.11	6.56	12.4	10.1	7.13
	MeOH_081	16.8	17.6	6.65	9.51	18.7	11.3	13.4
	MeOH_083	16.5	14.8	3.54	7.14	19.8	9.21	11.8

Table A10. Detailed MAPE values of the mechanistic model (NOED) corresponding to Table 4.

Dataset	Experiment	${\mathit{x}}_{{\mathbf{CH}}_3\mathbf{OH}}$	${\mathit{x}}_{\mathbf{CO}}$	${\mathit{x}}_{{\mathbf{CO}}_2}$	${\mathit{x}}_{{\mathbf{H}}_2}$	${\mathit{x}}_{{\mathbf{H}}_2\mathbf{O}}$	${\mathit{x}}_{{\mathbf{N}}_2}$	Total
Testing	MeOH_025	27.8	4.97	3.63	6.37	13.6	9.87	11
	MeOH_027	34.2	132	68.7	100	8.41	7.62	58.5
	MeOH_033	89.8	7.23	1.32	5.42	15.7	8.78	21.4
	MeOH_041	16.7	7.95	13.6	5.4	18.6	9.53	11.9
	MeOH_042	42.8	17.8	6.17	5.3	16.3	6.17	15.8
	MeOH_044	91	155	82.4	128	15.6	6.45	79.8
	MeOH_053	25.2	5.39	14.3	7.68	21.1	10.3	14
	MeOH_054	16	8.37	6.21	4.93	9.2	11	9.27
	MeOH_076	37.2	33.4	5.87	7.35	17.5	9.79	18.5
	MeOH_079	43.2	7.31	3.6	7.58	15	10.7	14.6
Training	MeOH_019	35.7	9.77	24.8	5.18	12.4	8.42	16.1
	MeOH_020	16.7	6.15	10.4	5.25	7.65	8.68	9.13
	MeOH_021	23.9	6.42	1.26	5.59	20.7	7.93	11
	MeOH_022	4.58	3.81	1.6	5.72	3.69	4.45	3.97
	MeOH_023	6.2	6.33	2.37	5.32	20.1	8.76	8.18
	MeOH_024	27.6	6.73	4.33	5.41	16.6	8.74	11.6
	MeOH_026	17	2.56	0.581	5.97	16.8	6.31	8.21
	MeOH_028	8.56	4.88	6.72	7.75	3.46	5.02	6.06
	MeOH_029	11.1	4.68	6.4	7.17	3.23	4.67	6.21
	MeOH_030	7.24	7.2	1.85	6.01	20.5	9.17	8.67
	MeOH_031	6.36	6.97	1.08	5.84	18.4	9.13	7.96
	MeOH_032	8.43	6.12	1.1	5.35	19	8.59	8.1
	MeOH_034	9.78	21.7	14.9	15.1	13.1	9.44	14
	MeOH_035	5.86	5.76	1.01	5.28	17.2	9.06	7.35
	MeOH_036	18.7	8.74	2.9	5.8	23.1	9.04	11.4
	MeOH_037	28.5	6.19	6.12	5.65	19.3	8.98	12.5
	MeOH_038	51.5	9.55	12.6	5.97	23.7	9.08	18.7
	MeOH_039	14.1	7.1	14.8	8.71	23.1	11.2	13.2
	MeOH_040	18.8	6.21	16.4	8.65	22.5	11.1	13.9
	MeOH_043	45.5	8.33	5.7	5.13	12.7	3.79	13.5
	MeOH_045	21.3	6.63	16.7	8.29	23.3	10.5	14.4
	MeOH_046	30	8.88	8.4	7.16	15.6	5.91	12.7
	MeOH_047	35.2	9.31	8.17	7.09	14.3	5.29	13.2
	MeOH_048	43.4	10.6	6.97	6.04	14.4	5.65	14.5
	MeOH_049	39.5	8.38	7.18	6.83	12.3	4.93	13.2
	MeOH_050	31.6	7.95	7.61	6.64	14.5	5.26	12.3
	MeOH_051	23.4	6.83	6.77	5.93	14.4	5.37	10.5
	MeOH_052	36	7.47	6.87	5.68	12.4	4.6	12.2
	MeOH_055	33.6	6.65	16.1	9.01	22.4	11.3	16.5
	MeOH_073	47.3	5.64	10.6	7.66	12.8	9.75	15.6
	MeOH_074	8.15	16.9	5.53	7.34	26.2	9.11	12.2
	MeOH_077	8.5	8.49	1.14	6.63	11	10	7.64
	MeOH_081	47.3	16	7.9	10.6	20.8	12.2	19.1
	MeOH_083	46.6	13.9	4.47	8.8	16.6	10	16.7

Table A10. Detailed MAPE values of the mechanistic model (NOED) corresponding to Table 4.

Dataset	Experiment	${\mathit{x}}_{{\mathbf{CH}}_3\mathbf{OH}}$	${\mathit{x}}_{\mathbf{CO}}$	${\mathit{x}}_{{\mathbf{CO}}_2}$	${\mathit{x}}_{{\mathbf{H}}_2}$	${\mathit{x}}_{{\mathbf{H}}_2\mathbf{O}}$	${\mathit{x}}_{{\mathbf{N}}_2}$	Total
Testing	MeOH_025	27.8	4.97	3.63	6.37	13.6	9.87	11
	MeOH_027	34.2	132	68.7	100	8.41	7.62	58.5
	MeOH_033	89.8	7.23	1.32	5.42	15.7	8.78	21.4
	MeOH_041	16.7	7.95	13.6	5.4	18.6	9.53	11.9
	MeOH_042	42.8	17.8	6.17	5.3	16.3	6.17	15.8
	MeOH_044	91	155	82.4	128	15.6	6.45	79.8
	MeOH_053	25.2	5.39	14.3	7.68	21.1	10.3	14
	MeOH_054	16	8.37	6.21	4.93	9.2	11	9.27
	MeOH_076	37.2	33.4	5.87	7.35	17.5	9.79	18.5
	MeOH_079	43.2	7.31	3.6	7.58	15	10.7	14.6
Training	MeOH_019	35.7	9.77	24.8	5.18	12.4	8.42	16.1
	MeOH_020	16.7	6.15	10.4	5.25	7.65	8.68	9.13
	MeOH_021	23.9	6.42	1.26	5.59	20.7	7.93	11
	MeOH_022	4.58	3.81	1.6	5.72	3.69	4.45	3.97
	MeOH_023	6.2	6.33	2.37	5.32	20.1	8.76	8.18
	MeOH_024	27.6	6.73	4.33	5.41	16.6	8.74	11.6
	MeOH_026	17	2.56	0.581	5.97	16.8	6.31	8.21
	MeOH_028	8.56	4.88	6.72	7.75	3.46	5.02	6.06
	MeOH_029	11.1	4.68	6.4	7.17	3.23	4.67	6.21
	MeOH_030	7.24	7.2	1.85	6.01	20.5	9.17	8.67
	MeOH_031	6.36	6.97	1.08	5.84	18.4	9.13	7.96
	MeOH_032	8.43	6.12	1.1	5.35	19	8.59	8.1
	MeOH_034	9.78	21.7	14.9	15.1	13.1	9.44	14
	MeOH_035	5.86	5.76	1.01	5.28	17.2	9.06	7.35
	MeOH_036	18.7	8.74	2.9	5.8	23.1	9.04	11.4
	MeOH_037	28.5	6.19	6.12	5.65	19.3	8.98	12.5
	MeOH_038	51.5	9.55	12.6	5.97	23.7	9.08	18.7
	MeOH_039	14.1	7.1	14.8	8.71	23.1	11.2	13.2
	MeOH_040	18.8	6.21	16.4	8.65	22.5	11.1	13.9
	MeOH_043	45.5	8.33	5.7	5.13	12.7	3.79	13.5
	MeOH_045	21.3	6.63	16.7	8.29	23.3	10.5	14.4
	MeOH_046	30	8.88	8.4	7.16	15.6	5.91	12.7
	MeOH_047	35.2	9.31	8.17	7.09	14.3	5.29	13.2
	MeOH_048	43.4	10.6	6.97	6.04	14.4	5.65	14.5
	MeOH_049	39.5	8.38	7.18	6.83	12.3	4.93	13.2
	MeOH_050	31.6	7.95	7.61	6.64	14.5	5.26	12.3
	MeOH_051	23.4	6.83	6.77	5.93	14.4	5.37	10.5
	MeOH_052	36	7.47	6.87	5.68	12.4	4.6	12.2
	MeOH_055	33.6	6.65	16.1	9.01	22.4	11.3	16.5
	MeOH_073	47.3	5.64	10.6	7.66	12.8	9.75	15.6
	MeOH_074	8.15	16.9	5.53	7.34	26.2	9.11	12.2
	MeOH_077	8.5	8.49	1.14	6.63	11	10	7.64
	MeOH_081	47.3	16	7.9	10.6	20.8	12.2	19.1
	MeOH_083	46.6	13.9	4.47	8.8	16.6	10	16.7

Appendix D.1. Hyperparameter Selection

As noted in Table 5, we initially selected the hybrid model based on the coefficient of determination $R^2$. Later on, we found that this measure was not suitable to clearly capture differences in performance (as now visible in Table 4) or even misleading ( e.g. in the case of the model discrepancy as seen in fig:parityimpact ). Hence, we switched to a more direct and relatable measure, the mean absolute percentage error (MAPE). Reevaluating the results of the hyperparameter search lead to a slightly different picture, which still included our choosen models in the top ten candidates, but ranked them differently.

Appendix D.2. Detailed Fitting Results

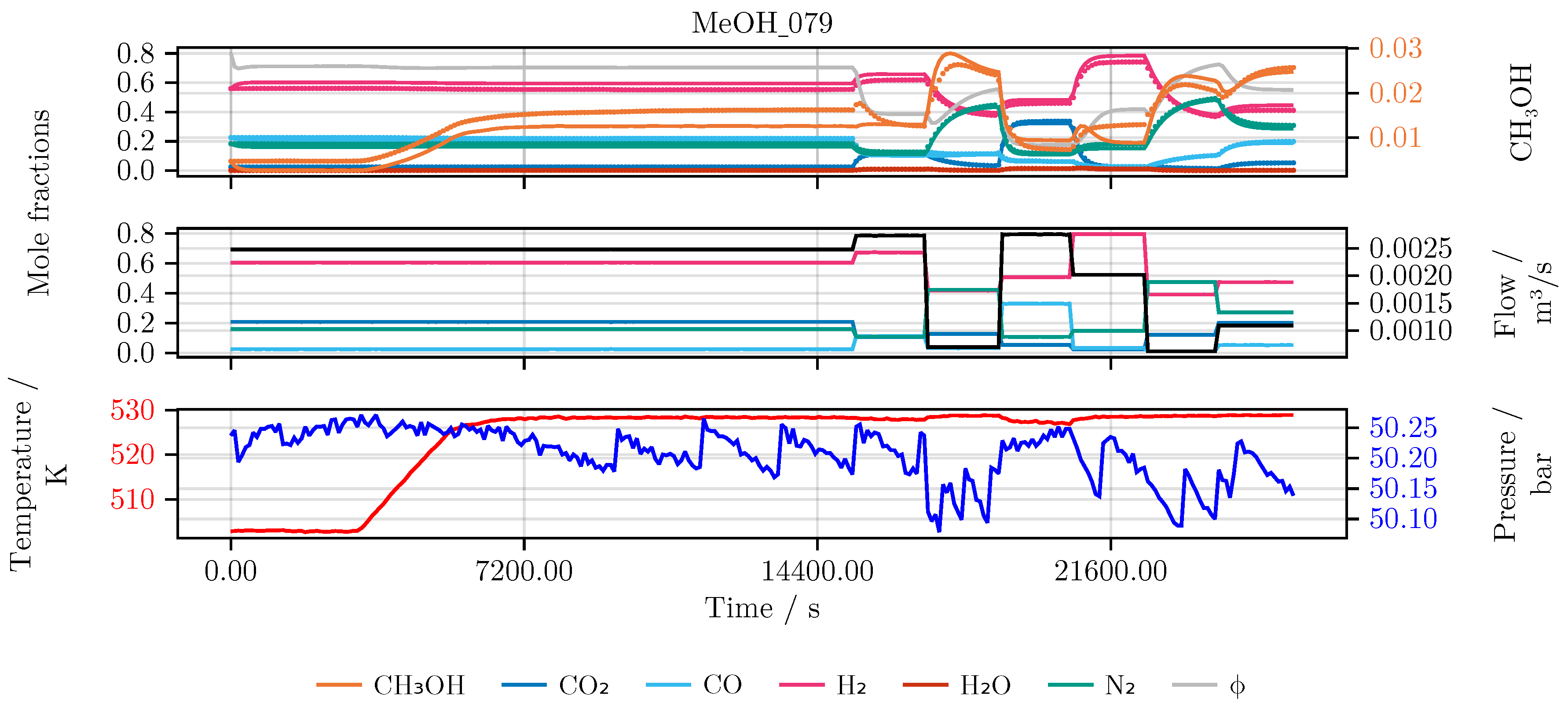
Figure A15. Trajecotry of MeOH_079 using hybrid model after hyperparameter search and first L-BFGS optimization over the training data set. (INIT)

Figure A15. Trajecotry of MeOH_079 using hybrid model after hyperparameter search and first L-BFGS optimization over the training data set. (INIT)

Figure A16. Parity plot of the hybrid model after hyperparameter search and first L-BFGS optimization over the training data set. (INIT)

Figure A16. Parity plot of the hybrid model after hyperparameter search and first L-BFGS optimization over the training data set. (INIT)

Figure A17. Parity plot of the hybrid model after hyperparameter search and first L-BFGS optimization over the test data. (INIT)

Figure A17. Parity plot of the hybrid model after hyperparameter search and first L-BFGS optimization over the test data. (INIT)

Figure A18. Trajecotry of MeOH_079 using hybrid model after adding experiment MeOH_083 and second L-BFGS optimization over the training data set. (OED)

Figure A18. Trajecotry of MeOH_079 using hybrid model after adding experiment MeOH_083 and second L-BFGS optimization over the training data set. (OED)

Figure A19. Parity plot of the hybrid model after adding experiment MeOH_083 and second L-BFGS optimization over the training data set. (OED)

Figure A19. Parity plot of the hybrid model after adding experiment MeOH_083 and second L-BFGS optimization over the training data set. (OED)

Figure A20. Parity plot of the fitted hybrid model after adding experiment MeOH_083 and second L-BFGS optimization over the test data set. (OED)

Figure A20. Parity plot of the fitted hybrid model after adding experiment MeOH_083 and second L-BFGS optimization over the test data set. (OED)

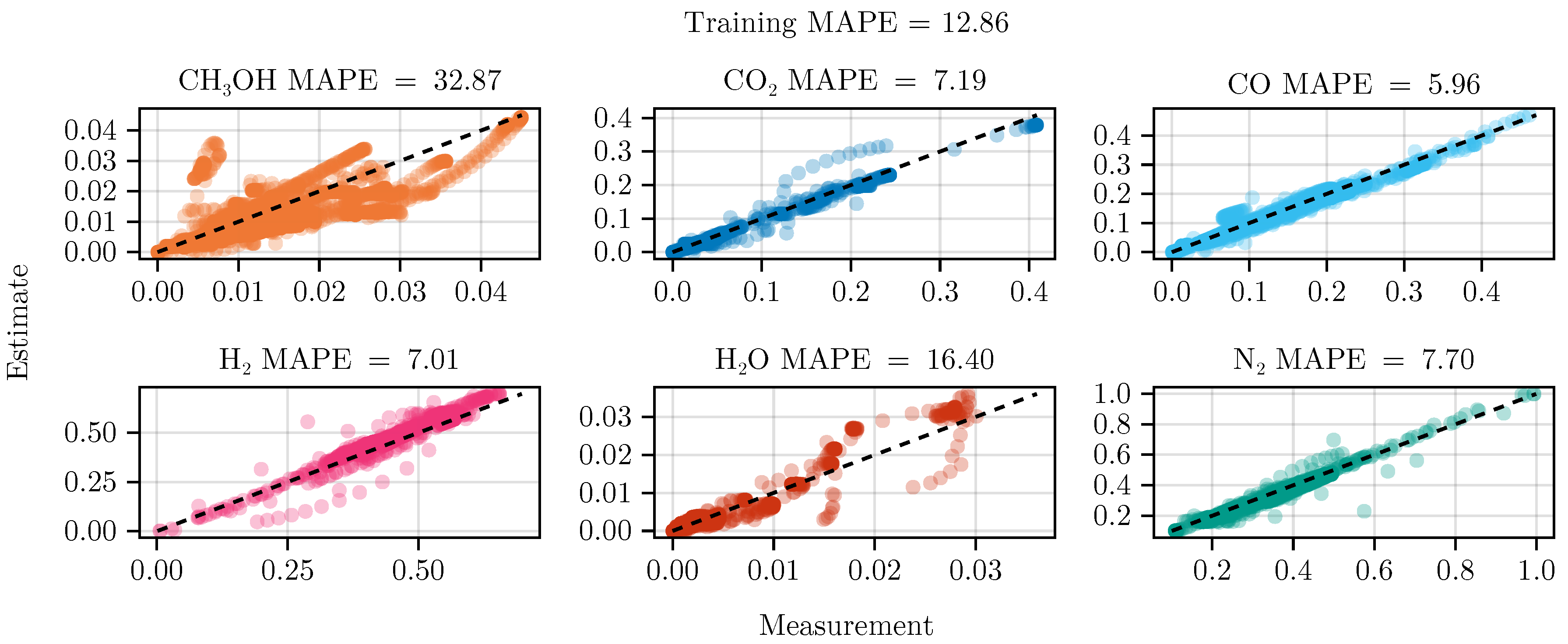
Figure A21. Trajecotry of MeOH_079 using hybrid model after second L-BFGS optimization over the training data set excluding optimal experimental designs. (NOED)

Figure A21. Trajecotry of MeOH_079 using hybrid model after second L-BFGS optimization over the training data set excluding optimal experimental designs. (NOED)

Figure A22. Parity plot of the hybrid model after second L-BFGS optimization over the training data set excluding optimal experimental designs. (NOED)

Figure A22. Parity plot of the hybrid model after second L-BFGS optimization over the training data set excluding optimal experimental designs. (NOED)

Figure A23. Parity plot of the hybrid model after second L-BFGS optimization over the test data set excluding optimal experimental designs. (NOED)

Figure A23. Parity plot of the hybrid model after second L-BFGS optimization over the test data set excluding optimal experimental designs. (NOED)

Table A11. Detailed MAPE values of the hybrid model after hyperparameter search

Dataset	Experiment	${\mathit{x}}_{{\mathbf{CH}}_3\mathbf{OH}}$	${\mathit{x}}_{\mathbf{CO}}$	${\mathit{x}}_{{\mathbf{CO}}_2}$	${\mathit{x}}_{{\mathbf{H}}_2}$	${\mathit{x}}_{{\mathbf{H}}_2\mathbf{O}}$	${\mathit{x}}_{{\mathbf{N}}_2}$	Total
Testing	MeOH_025	17.9	5.38	5.61	5.89	19.2	9.43	10.6
	MeOH_027	77.2	129	69	97.5	9.74	6.77	64.9
	MeOH_033	19.6	6.38	5.3	5.46	36.5	9.06	13.7
	MeOH_041	53.8	10.1	15.4	4.33	20	8.63	18.7
	MeOH_042	53.1	17	9.67	4.68	34.3	5.97	20.8
	MeOH_044	106	156	83.1	127	39.9	6.33	86.3
	MeOH_053	13.1	6	16.7	7.02	25.6	9.65	13
	MeOH_054	84.6	14.6	6.05	3.13	43.6	9.32	26.9
	MeOH_076	74	28.7	8.79	5.66	78.9	8.57	34.1
	MeOH_079	25.5	8.06	3.84	6.11	17.7	9.58	11.8
Training	MeOH_019	77.2	11.8	22.9	3.73	48.7	7.36	28.6
	MeOH_020	41.6	9.75	8.07	4.08	45.4	7.25	19.4
	MeOH_021	12.3	5.52	5.78	5.36	39.6	8.16	12.8
	MeOH_022	52.4	10.6	1.19	2.99	2.1	2.56	12
	MeOH_023	13.2	5.55	2.96	5.25	30	8.92	11
	MeOH_024	79.6	8.23	7.61	3.46	61.1	7.47	27.9
	MeOH_026	25.9	1.52	4.14	6.16	20.5	6.61	10.8
	MeOH_028	48	7.9	5.53	6.03	3.39	3.91	12.5
	MeOH_029	44.5	7.51	5.29	5.49	3.56	3.55	11.6
	MeOH_030	12.5	6.67	5.55	5.89	20.9	9.23	10.1
	MeOH_031	11.6	6.44	4.86	5.72	24.6	9.2	10.4
	MeOH_032	12.9	5.62	4.62	5.23	20.9	8.65	9.65
	MeOH_034	11.8	27.4	13.3	19	13.5	9.3	15.7
	MeOH_035	8.73	5.36	3.98	5.17	18.1	9.09	8.41
	MeOH_036	30.9	25.2	6.25	4.68	43.3	8.61	19.8
	MeOH_037	28	5.87	8.46	5.54	14.8	9	11.9
	MeOH_038	75.1	45.9	15.1	3.88	72	8.14	36.7
	MeOH_039	15.4	6.72	18.8	8.32	30.5	11.1	15.1
	MeOH_040	15.7	6.41	19.1	8.08	21.3	10.7	13.6
	MeOH_043	60.6	7.88	9.56	4.45	37.2	3.59	20.5
	MeOH_045	18.4	6.56	19.7	7.87	20.1	10.2	13.8
	MeOH_046	47.3	8.51	12.8	6.52	35.3	5.74	19.4
	MeOH_047	53.1	8.78	12.3	6.3	37	5.06	20.4
	MeOH_048	55.3	10.4	11	5.47	39.3	5.53	21.2
	MeOH_049	53.2	7.75	11	6.25	38.7	4.8	20.3
	MeOH_050	47.3	7.36	11.7	5.97	36.5	5.08	19
	MeOH_051	43.1	6.71	11	5.24	34.6	5.13	17.6
	MeOH_052	51.4	6.91	10.7	5.09	38.4	4.45	19.5
	MeOH_055	22.8	7.16	17.8	8.43	16.7	10.7	14
	MeOH_073	12.8	6.44	10.9	6.85	19.5	8.97	10.9
	MeOH_074	5.59	16.1	7.06	7.23	24.7	9.1	11.6
	MeOH_077	4.54	7.9	3.83	6.44	41.2	10.1	12.3
	MeOH_081	33.1	17	7.7	9.19	22.9	11.3	16.9
	MeOH_083	26.8	22.2	4.67	6.96	27.2	9.3	16.2

Table A11. Detailed MAPE values of the hybrid model after hyperparameter search

Dataset	Experiment	${\mathit{x}}_{{\mathbf{CH}}_3\mathbf{OH}}$	${\mathit{x}}_{\mathbf{CO}}$	${\mathit{x}}_{{\mathbf{CO}}_2}$	${\mathit{x}}_{{\mathbf{H}}_2}$	${\mathit{x}}_{{\mathbf{H}}_2\mathbf{O}}$	${\mathit{x}}_{{\mathbf{N}}_2}$	Total
Testing	MeOH_025	17.9	5.38	5.61	5.89	19.2	9.43	10.6
	MeOH_027	77.2	129	69	97.5	9.74	6.77	64.9
	MeOH_033	19.6	6.38	5.3	5.46	36.5	9.06	13.7
	MeOH_041	53.8	10.1	15.4	4.33	20	8.63	18.7
	MeOH_042	53.1	17	9.67	4.68	34.3	5.97	20.8
	MeOH_044	106	156	83.1	127	39.9	6.33	86.3
	MeOH_053	13.1	6	16.7	7.02	25.6	9.65	13
	MeOH_054	84.6	14.6	6.05	3.13	43.6	9.32	26.9
	MeOH_076	74	28.7	8.79	5.66	78.9	8.57	34.1
	MeOH_079	25.5	8.06	3.84	6.11	17.7	9.58	11.8
Training	MeOH_019	77.2	11.8	22.9	3.73	48.7	7.36	28.6
	MeOH_020	41.6	9.75	8.07	4.08	45.4	7.25	19.4
	MeOH_021	12.3	5.52	5.78	5.36	39.6	8.16	12.8
	MeOH_022	52.4	10.6	1.19	2.99	2.1	2.56	12
	MeOH_023	13.2	5.55	2.96	5.25	30	8.92	11
	MeOH_024	79.6	8.23	7.61	3.46	61.1	7.47	27.9
	MeOH_026	25.9	1.52	4.14	6.16	20.5	6.61	10.8
	MeOH_028	48	7.9	5.53	6.03	3.39	3.91	12.5
	MeOH_029	44.5	7.51	5.29	5.49	3.56	3.55	11.6
	MeOH_030	12.5	6.67	5.55	5.89	20.9	9.23	10.1
	MeOH_031	11.6	6.44	4.86	5.72	24.6	9.2	10.4
	MeOH_032	12.9	5.62	4.62	5.23	20.9	8.65	9.65
	MeOH_034	11.8	27.4	13.3	19	13.5	9.3	15.7
	MeOH_035	8.73	5.36	3.98	5.17	18.1	9.09	8.41
	MeOH_036	30.9	25.2	6.25	4.68	43.3	8.61	19.8
	MeOH_037	28	5.87	8.46	5.54	14.8	9	11.9
	MeOH_038	75.1	45.9	15.1	3.88	72	8.14	36.7
	MeOH_039	15.4	6.72	18.8	8.32	30.5	11.1	15.1
	MeOH_040	15.7	6.41	19.1	8.08	21.3	10.7	13.6
	MeOH_043	60.6	7.88	9.56	4.45	37.2	3.59	20.5
	MeOH_045	18.4	6.56	19.7	7.87	20.1	10.2	13.8
	MeOH_046	47.3	8.51	12.8	6.52	35.3	5.74	19.4
	MeOH_047	53.1	8.78	12.3	6.3	37	5.06	20.4
	MeOH_048	55.3	10.4	11	5.47	39.3	5.53	21.2
	MeOH_049	53.2	7.75	11	6.25	38.7	4.8	20.3
	MeOH_050	47.3	7.36	11.7	5.97	36.5	5.08	19
	MeOH_051	43.1	6.71	11	5.24	34.6	5.13	17.6
	MeOH_052	51.4	6.91	10.7	5.09	38.4	4.45	19.5
	MeOH_055	22.8	7.16	17.8	8.43	16.7	10.7	14
	MeOH_073	12.8	6.44	10.9	6.85	19.5	8.97	10.9
	MeOH_074	5.59	16.1	7.06	7.23	24.7	9.1	11.6
	MeOH_077	4.54	7.9	3.83	6.44	41.2	10.1	12.3
	MeOH_081	33.1	17	7.7	9.19	22.9	11.3	16.9
	MeOH_083	26.8	22.2	4.67	6.96	27.2	9.3	16.2

Table A12. Detailed MAPE values of the hybrid model (INIT) corresponding to Table 4.

Dataset	Experiment	${\mathit{x}}_{{\mathbf{CH}}_3\mathbf{OH}}$	${\mathit{x}}_{\mathbf{CO}}$	${\mathit{x}}_{{\mathbf{CO}}_2}$	${\mathit{x}}_{{\mathbf{H}}_2}$	${\mathit{x}}_{{\mathbf{H}}_2\mathbf{O}}$	${\mathit{x}}_{{\mathbf{N}}_2}$	Total
Testing	MeOH_025	8.13	6.29	3.93	5.55	11	8.95	7.32
	MeOH_027	47.8	131	68.7	99.2	14.1	7.17	61.3
	MeOH_033	15	6.51	4.57	5.46	27.8	9.03	11.4
	MeOH_041	20.3	5.75	14	5.94	11.9	10.2	11.3
	MeOH_042	14.2	16	7.58	6.63	10.1	6.76	10.2
	MeOH_044	41.2	157	82.9	131	10.4	7.39	71.7
	MeOH_053	5.48	6.93	14.6	6.76	13	9.22	9.34
	MeOH_054	28.4	7.36	6.84	5.33	11.7	11.4	11.8
	MeOH_076	31.1	23.9	5.03	7.46	13.9	9.87	15.2
	MeOH_079	15.8	7.39	3.21	6.54	15	9.78	9.62
Training	MeOH_019	25.4	7.36	23.6	5.82	21.8	9.05	15.5
	MeOH_020	22.7	7.81	10.4	4.54	8.11	7.89	10.2
	MeOH_021	15.8	5.88	3.92	5.38	17.6	8.07	9.44
	MeOH_022	26.2	7.12	1.15	4.38	10.3	3.47	8.78
	MeOH_023	4.01	6.02	1.3	5.18	11.1	8.74	6.06
	MeOH_024	32	4.72	5.38	5.55	9.04	8.78	10.9
	MeOH_026	12.3	2.63	2.29	5.68	5.45	6.15	5.75
	MeOH_028	20.7	6.21	5.33	7.09	13.3	4.52	9.51
	MeOH_029	18.6	5.89	5	6.5	14.3	4.16	9.08
	MeOH_030	2.8	7	4.16	5.85	7	9.11	5.99
	MeOH_031	1.92	6.77	3.45	5.68	9.97	9.07	6.14
	MeOH_032	3.29	5.94	3.32	5.19	7.59	8.53	5.64
	MeOH_034	8.59	21.1	15.4	15.3	7.97	9.49	13
	MeOH_035	2.44	5.62	2.97	5.12	7.69	8.98	5.47
	MeOH_036	19.5	15.3	4.66	5.51	6.72	8.97	10.1
	MeOH_037	20	6.09	7.74	5.51	6.58	8.91	9.13
	MeOH_038	43.5	26.5	13.3	5.69	9.09	9.02	17.9
	MeOH_039	16.8	7.8	16.1	8.09	10	10.7	11.6
	MeOH_040	14.4	7.7	16.8	7.66	11.6	10.1	11.4
	MeOH_043	11.5	4.67	7.07	6.65	8.68	4.85	7.23
	MeOH_045	11.1	7.49	17.6	7.62	10	9.84	10.6
	MeOH_046	10.6	6.4	9.97	8.08	9.31	6.61	8.5
	MeOH_047	7.77	6.51	9.58	8.01	8.44	5.97	7.71
	MeOH_048	17.3	9.58	8.37	7.09	7.34	6.17	9.31
	MeOH_049	9.56	6.13	8.53	7.63	7.1	5.62	7.43
	MeOH_050	6.17	5.8	9.01	7.43	8.68	5.88	7.16
	MeOH_051	9.81	5.24	8.04	6.52	9.2	5.87	7.45
	MeOH_052	8.06	5.56	8.11	6.51	6.94	5.2	6.73
	MeOH_055	12	8.05	16.1	8.12	14.6	10.3	11.5
	MeOH_073	11.5	7.07	10.7	6.49	15.9	8.57	10
	MeOH_074	3.76	16.4	4.34	7.32	11.5	9.08	8.73
	MeOH_077	8.3	8.17	1.81	6.5	20.4	10	9.2
	MeOH_081	20.5	20.4	6.84	9.51	17.2	11.4	14.3
	MeOH_083	16.1	15.3	3.85	7.21	17.8	9.23	11.6

Table A12. Detailed MAPE values of the hybrid model (INIT) corresponding to Table 4.

Dataset	Experiment	${\mathit{x}}_{{\mathbf{CH}}_3\mathbf{OH}}$	${\mathit{x}}_{\mathbf{CO}}$	${\mathit{x}}_{{\mathbf{CO}}_2}$	${\mathit{x}}_{{\mathbf{H}}_2}$	${\mathit{x}}_{{\mathbf{H}}_2\mathbf{O}}$	${\mathit{x}}_{{\mathbf{N}}_2}$	Total
Testing	MeOH_025	8.13	6.29	3.93	5.55	11	8.95	7.32
	MeOH_027	47.8	131	68.7	99.2	14.1	7.17	61.3
	MeOH_033	15	6.51	4.57	5.46	27.8	9.03	11.4
	MeOH_041	20.3	5.75	14	5.94	11.9	10.2	11.3
	MeOH_042	14.2	16	7.58	6.63	10.1	6.76	10.2
	MeOH_044	41.2	157	82.9	131	10.4	7.39	71.7
	MeOH_053	5.48	6.93	14.6	6.76	13	9.22	9.34
	MeOH_054	28.4	7.36	6.84	5.33	11.7	11.4	11.8
	MeOH_076	31.1	23.9	5.03	7.46	13.9	9.87	15.2
	MeOH_079	15.8	7.39	3.21	6.54	15	9.78	9.62
Training	MeOH_019	25.4	7.36	23.6	5.82	21.8	9.05	15.5
	MeOH_020	22.7	7.81	10.4	4.54	8.11	7.89	10.2
	MeOH_021	15.8	5.88	3.92	5.38	17.6	8.07	9.44
	MeOH_022	26.2	7.12	1.15	4.38	10.3	3.47	8.78
	MeOH_023	4.01	6.02	1.3	5.18	11.1	8.74	6.06
	MeOH_024	32	4.72	5.38	5.55	9.04	8.78	10.9
	MeOH_026	12.3	2.63	2.29	5.68	5.45	6.15	5.75
	MeOH_028	20.7	6.21	5.33	7.09	13.3	4.52	9.51
	MeOH_029	18.6	5.89	5	6.5	14.3	4.16	9.08
	MeOH_030	2.8	7	4.16	5.85	7	9.11	5.99
	MeOH_031	1.92	6.77	3.45	5.68	9.97	9.07	6.14
	MeOH_032	3.29	5.94	3.32	5.19	7.59	8.53	5.64
	MeOH_034	8.59	21.1	15.4	15.3	7.97	9.49	13
	MeOH_035	2.44	5.62	2.97	5.12	7.69	8.98	5.47
	MeOH_036	19.5	15.3	4.66	5.51	6.72	8.97	10.1
	MeOH_037	20	6.09	7.74	5.51	6.58	8.91	9.13
	MeOH_038	43.5	26.5	13.3	5.69	9.09	9.02	17.9
	MeOH_039	16.8	7.8	16.1	8.09	10	10.7	11.6
	MeOH_040	14.4	7.7	16.8	7.66	11.6	10.1	11.4
	MeOH_043	11.5	4.67	7.07	6.65	8.68	4.85	7.23
	MeOH_045	11.1	7.49	17.6	7.62	10	9.84	10.6
	MeOH_046	10.6	6.4	9.97	8.08	9.31	6.61	8.5
	MeOH_047	7.77	6.51	9.58	8.01	8.44	5.97	7.71
	MeOH_048	17.3	9.58	8.37	7.09	7.34	6.17	9.31
	MeOH_049	9.56	6.13	8.53	7.63	7.1	5.62	7.43
	MeOH_050	6.17	5.8	9.01	7.43	8.68	5.88	7.16
	MeOH_051	9.81	5.24	8.04	6.52	9.2	5.87	7.45
	MeOH_052	8.06	5.56	8.11	6.51	6.94	5.2	6.73
	MeOH_055	12	8.05	16.1	8.12	14.6	10.3	11.5
	MeOH_073	11.5	7.07	10.7	6.49	15.9	8.57	10
	MeOH_074	3.76	16.4	4.34	7.32	11.5	9.08	8.73
	MeOH_077	8.3	8.17	1.81	6.5	20.4	10	9.2
	MeOH_081	20.5	20.4	6.84	9.51	17.2	11.4	14.3
	MeOH_083	16.1	15.3	3.85	7.21	17.8	9.23	11.6

Table A13. Detailed MAPE values of the hybrid model (OED) corresponding to Table 4.

Dataset	Experiment	${\mathit{x}}_{{\mathbf{CH}}_3\mathbf{OH}}$	${\mathit{x}}_{\mathbf{CO}}$	${\mathit{x}}_{{\mathbf{CO}}_2}$	${\mathit{x}}_{{\mathbf{H}}_2}$	${\mathit{x}}_{{\mathbf{H}}_2\mathbf{O}}$	${\mathit{x}}_{{\mathbf{N}}_2}$	Total
Testing	MeOH_025	27.7	5.74	4.11	5.87	4.4	9.33	9.52
	MeOH_027	45	131	68.9	99.7	11.7	7.4	60.5
	MeOH_033	30.6	6.53	1.58	5.82	19.7	9.28	12.3
	MeOH_041	24.5	5.3	14.5	5.96	7.1	10.4	11.3
	MeOH_042	21.9	15.1	8.97	7.01	14.9	7	12.5
	MeOH_044	45.6	158	83.2	132	23.2	7.82	75
	MeOH_053	29.7	6.47	14.6	7.06	11.7	9.57	13.2
	MeOH_054	17.9	10.5	7.31	5.25	12.6	11.2	10.8
	MeOH_076	32.4	17.8	4.2	7.48	13.2	9.74	14.1
	MeOH_079	18.8	8.15	2.43	6.53	15.9	9.74	10.3
Training	MeOH_019	34.1	8.44	23	5.56	28.7	9.1	18.2
	MeOH_020	30.8	6.45	5.87	5.33	31.3	9.12	14.8
	MeOH_021	32.4	5.3	2.81	5.73	8.39	8.63	10.6
	MeOH_022	24.5	7.24	1.16	4.37	3.41	3.49	7.37
	MeOH_023	38.9	5.18	1.01	5.74	10.8	9.39	11.8
	MeOH_024	32.1	9.86	5.35	5.44	8.12	8.7	11.6
	MeOH_026	40.8	1.33	4.25	6.75	16.1	7.11	12.7
	MeOH_028	10.8	6.11	5.56	7.29	10.3	4.65	7.46
	MeOH_029	7.61	5.89	5.14	6.73	13.1	4.29	7.12
	MeOH_030	37.1	6.65	2.47	6.27	17.7	9.52	13.3
	MeOH_031	36.4	6.4	1.78	6.11	14.6	9.5	12.5
	MeOH_032	35.1	5.6	1.74	5.6	15.3	8.92	12
	MeOH_034	20.5	27.5	11.8	19.1	12.2	9.42	16.7
	MeOH_035	31.3	5.42	0.973	5.48	20.1	9.3	12.1
	MeOH_036	28.7	11.7	2.7	5.87	22.5	9.14	13.4
	MeOH_037	37	6	6.11	5.76	21.7	9.12	14.3
	MeOH_038	22.8	15.4	12.3	5.8	18.6	8.82	13.9
	MeOH_039	37.5	5.13	19.1	9.29	20	12.2	17.2
	MeOH_040	33.1	5.31	19.3	8.74	12.8	11.4	15.1
	MeOH_043	18.9	3.79	8.48	7.07	22.1	5.23	10.9
	MeOH_045	37.9	5.81	19	8.45	6.41	10.8	14.7
	MeOH_046	25.4	5.33	10.6	8.61	18.8	7.08	12.6
	MeOH_047	23.4	5.5	10.2	8.4	8.09	6.33	10.3
	MeOH_048	22.4	9.52	8.91	7.61	17.2	6.51	12
	MeOH_049	22.8	5.38	8.95	8.17	16.6	5.98	11.3
	MeOH_050	26	4.91	9.26	7.92	14.1	6.27	11.4
	MeOH_051	27.8	4.75	7.73	7.02	21	6.24	12.4
	MeOH_052	24.1	4.96	8.11	7.02	18.7	5.58	11.4
	MeOH_055	36.6	6.92	16.6	8.75	14.1	11	15.7
	MeOH_073	122	7.71	10.1	5.24	15.5	7.68	28.1
	MeOH_074	38	16.8	5.43	7.69	12.9	9.69	15.1
	MeOH_077	33.1	7.95	1.16	6.99	16.2	10.4	12.6
	MeOH_081	22.6	14.4	6.95	9.42	19.3	11.3	14
	MeOH_083	18.3	13	3.63	7.32	20	9.3	11.9

Table A13. Detailed MAPE values of the hybrid model (OED) corresponding to Table 4.

Dataset	Experiment	${\mathit{x}}_{{\mathbf{CH}}_3\mathbf{OH}}$	${\mathit{x}}_{\mathbf{CO}}$	${\mathit{x}}_{{\mathbf{CO}}_2}$	${\mathit{x}}_{{\mathbf{H}}_2}$	${\mathit{x}}_{{\mathbf{H}}_2\mathbf{O}}$	${\mathit{x}}_{{\mathbf{N}}_2}$	Total
Testing	MeOH_025	27.7	5.74	4.11	5.87	4.4	9.33	9.52
	MeOH_027	45	131	68.9	99.7	11.7	7.4	60.5
	MeOH_033	30.6	6.53	1.58	5.82	19.7	9.28	12.3
	MeOH_041	24.5	5.3	14.5	5.96	7.1	10.4	11.3
	MeOH_042	21.9	15.1	8.97	7.01	14.9	7	12.5
	MeOH_044	45.6	158	83.2	132	23.2	7.82	75
	MeOH_053	29.7	6.47	14.6	7.06	11.7	9.57	13.2
	MeOH_054	17.9	10.5	7.31	5.25	12.6	11.2	10.8
	MeOH_076	32.4	17.8	4.2	7.48	13.2	9.74	14.1
	MeOH_079	18.8	8.15	2.43	6.53	15.9	9.74	10.3
Training	MeOH_019	34.1	8.44	23	5.56	28.7	9.1	18.2
	MeOH_020	30.8	6.45	5.87	5.33	31.3	9.12	14.8
	MeOH_021	32.4	5.3	2.81	5.73	8.39	8.63	10.6
	MeOH_022	24.5	7.24	1.16	4.37	3.41	3.49	7.37
	MeOH_023	38.9	5.18	1.01	5.74	10.8	9.39	11.8
	MeOH_024	32.1	9.86	5.35	5.44	8.12	8.7	11.6
	MeOH_026	40.8	1.33	4.25	6.75	16.1	7.11	12.7
	MeOH_028	10.8	6.11	5.56	7.29	10.3	4.65	7.46
	MeOH_029	7.61	5.89	5.14	6.73	13.1	4.29	7.12
	MeOH_030	37.1	6.65	2.47	6.27	17.7	9.52	13.3
	MeOH_031	36.4	6.4	1.78	6.11	14.6	9.5	12.5
	MeOH_032	35.1	5.6	1.74	5.6	15.3	8.92	12
	MeOH_034	20.5	27.5	11.8	19.1	12.2	9.42	16.7
	MeOH_035	31.3	5.42	0.973	5.48	20.1	9.3	12.1
	MeOH_036	28.7	11.7	2.7	5.87	22.5	9.14	13.4
	MeOH_037	37	6	6.11	5.76	21.7	9.12	14.3
	MeOH_038	22.8	15.4	12.3	5.8	18.6	8.82	13.9
	MeOH_039	37.5	5.13	19.1	9.29	20	12.2	17.2
	MeOH_040	33.1	5.31	19.3	8.74	12.8	11.4	15.1
	MeOH_043	18.9	3.79	8.48	7.07	22.1	5.23	10.9
	MeOH_045	37.9	5.81	19	8.45	6.41	10.8	14.7
	MeOH_046	25.4	5.33	10.6	8.61	18.8	7.08	12.6
	MeOH_047	23.4	5.5	10.2	8.4	8.09	6.33	10.3
	MeOH_048	22.4	9.52	8.91	7.61	17.2	6.51	12
	MeOH_049	22.8	5.38	8.95	8.17	16.6	5.98	11.3
	MeOH_050	26	4.91	9.26	7.92	14.1	6.27	11.4
	MeOH_051	27.8	4.75	7.73	7.02	21	6.24	12.4
	MeOH_052	24.1	4.96	8.11	7.02	18.7	5.58	11.4
	MeOH_055	36.6	6.92	16.6	8.75	14.1	11	15.7
	MeOH_073	122	7.71	10.1	5.24	15.5	7.68	28.1
	MeOH_074	38	16.8	5.43	7.69	12.9	9.69	15.1
	MeOH_077	33.1	7.95	1.16	6.99	16.2	10.4	12.6
	MeOH_081	22.6	14.4	6.95	9.42	19.3	11.3	14
	MeOH_083	18.3	13	3.63	7.32	20	9.3	11.9

Table A14. Detailed MAPE values of the hybrid model (NOED) corresponding to Table 4.

Dataset	Experiment	${\mathit{x}}_{{\mathbf{CH}}_3\mathbf{OH}}$	${\mathit{x}}_{\mathbf{CO}}$	${\mathit{x}}_{{\mathbf{CO}}_2}$	${\mathit{x}}_{{\mathbf{H}}_2}$	${\mathit{x}}_{{\mathbf{H}}_2\mathbf{O}}$	${\mathit{x}}_{{\mathbf{N}}_2}$	Total
Testing	MeOH_025	27.7	5.74	4.11	5.87	4.4	9.33	9.52
	MeOH_027	45	131	68.9	99.7	11.7	7.4	60.5
	MeOH_033	30.6	6.53	1.58	5.82	19.7	9.28	12.3
	MeOH_041	24.5	5.3	14.5	5.96	7.1	10.4	11.3
	MeOH_042	21.9	15.1	8.97	7.01	14.9	7	12.5
	MeOH_044	45.6	158	83.2	132	23.2	7.82	75
	MeOH_053	29.7	6.47	14.6	7.06	11.7	9.57	13.2
	MeOH_054	17.9	10.5	7.31	5.25	12.6	11.2	10.8
	MeOH_076	32.4	17.8	4.2	7.48	13.2	9.74	14.1
	MeOH_079	18.8	8.15	2.43	6.53	15.9	9.74	10.3
Training	MeOH_019	34.1	8.44	23	5.56	28.7	9.1	18.2
	MeOH_020	30.8	6.45	5.87	5.33	31.3	9.12	14.8
	MeOH_021	32.4	5.3	2.81	5.73	8.39	8.63	10.6
	MeOH_022	24.5	7.24	1.16	4.37	3.41	3.49	7.37
	MeOH_023	38.9	5.18	1.01	5.74	10.8	9.39	11.8
	MeOH_024	32.1	9.86	5.35	5.44	8.12	8.7	11.6
	MeOH_026	40.8	1.33	4.25	6.75	16.1	7.11	12.7
	MeOH_028	10.8	6.11	5.56	7.29	10.3	4.65	7.46
	MeOH_029	7.61	5.89	5.14	6.73	13.1	4.29	7.12
	MeOH_030	37.1	6.65	2.47	6.27	17.7	9.52	13.3
	MeOH_031	36.4	6.4	1.78	6.11	14.6	9.5	12.5
	MeOH_032	35.1	5.6	1.74	5.6	15.3	8.92	12
	MeOH_034	20.5	27.5	11.8	19.1	12.2	9.42	16.7
	MeOH_035	31.3	5.42	0.973	5.48	20.1	9.3	12.1
	MeOH_036	28.7	11.7	2.7	5.87	22.5	9.14	13.4
	MeOH_037	37	6	6.11	5.76	21.7	9.12	14.3
	MeOH_038	22.8	15.4	12.3	5.8	18.6	8.82	13.9
	MeOH_039	37.5	5.13	19.1	9.29	20	12.2	17.2
	MeOH_040	33.1	5.31	19.3	8.74	12.8	11.4	15.1
	MeOH_043	18.9	3.79	8.48	7.07	22.1	5.23	10.9
	MeOH_045	37.9	5.81	19	8.45	6.41	10.8	14.7
	MeOH_046	25.4	5.33	10.6	8.61	18.8	7.08	12.6
	MeOH_047	23.4	5.5	10.2	8.4	8.09	6.33	10.3
	MeOH_048	22.4	9.52	8.91	7.61	17.2	6.51	12
	MeOH_049	22.8	5.38	8.95	8.17	16.6	5.98	11.3
	MeOH_050	26	4.91	9.26	7.92	14.1	6.27	11.4
	MeOH_051	27.8	4.75	7.73	7.02	21	6.24	12.4
	MeOH_052	24.1	4.96	8.11	7.02	18.7	5.58	11.4
	MeOH_055	36.6	6.92	16.6	8.75	14.1	11	15.7
	MeOH_073	122	7.71	10.1	5.24	15.5	7.68	28.1
	MeOH_074	38	16.8	5.43	7.69	12.9	9.69	15.1
	MeOH_077	33.1	7.95	1.16	6.99	16.2	10.4	12.6
	MeOH_081	22.6	14.4	6.95	9.42	19.3	11.3	14
	MeOH_083	18.3	13	3.63	7.32	20	9.3	11.9

Table A14. Detailed MAPE values of the hybrid model (NOED) corresponding to Table 4.

Dataset	Experiment	${\mathit{x}}_{{\mathbf{CH}}_3\mathbf{OH}}$	${\mathit{x}}_{\mathbf{CO}}$	${\mathit{x}}_{{\mathbf{CO}}_2}$	${\mathit{x}}_{{\mathbf{H}}_2}$	${\mathit{x}}_{{\mathbf{H}}_2\mathbf{O}}$	${\mathit{x}}_{{\mathbf{N}}_2}$	Total
Testing	MeOH_025	27.7	5.74	4.11	5.87	4.4	9.33	9.52
	MeOH_027	45	131	68.9	99.7	11.7	7.4	60.5
	MeOH_033	30.6	6.53	1.58	5.82	19.7	9.28	12.3
	MeOH_041	24.5	5.3	14.5	5.96	7.1	10.4	11.3
	MeOH_042	21.9	15.1	8.97	7.01	14.9	7	12.5
	MeOH_044	45.6	158	83.2	132	23.2	7.82	75
	MeOH_053	29.7	6.47	14.6	7.06	11.7	9.57	13.2
	MeOH_054	17.9	10.5	7.31	5.25	12.6	11.2	10.8
	MeOH_076	32.4	17.8	4.2	7.48	13.2	9.74	14.1
	MeOH_079	18.8	8.15	2.43	6.53	15.9	9.74	10.3
Training	MeOH_019	34.1	8.44	23	5.56	28.7	9.1	18.2
	MeOH_020	30.8	6.45	5.87	5.33	31.3	9.12	14.8
	MeOH_021	32.4	5.3	2.81	5.73	8.39	8.63	10.6
	MeOH_022	24.5	7.24	1.16	4.37	3.41	3.49	7.37
	MeOH_023	38.9	5.18	1.01	5.74	10.8	9.39	11.8
	MeOH_024	32.1	9.86	5.35	5.44	8.12	8.7	11.6
	MeOH_026	40.8	1.33	4.25	6.75	16.1	7.11	12.7
	MeOH_028	10.8	6.11	5.56	7.29	10.3	4.65	7.46
	MeOH_029	7.61	5.89	5.14	6.73	13.1	4.29	7.12
	MeOH_030	37.1	6.65	2.47	6.27	17.7	9.52	13.3
	MeOH_031	36.4	6.4	1.78	6.11	14.6	9.5	12.5
	MeOH_032	35.1	5.6	1.74	5.6	15.3	8.92	12
	MeOH_034	20.5	27.5	11.8	19.1	12.2	9.42	16.7
	MeOH_035	31.3	5.42	0.973	5.48	20.1	9.3	12.1
	MeOH_036	28.7	11.7	2.7	5.87	22.5	9.14	13.4
	MeOH_037	37	6	6.11	5.76	21.7	9.12	14.3
	MeOH_038	22.8	15.4	12.3	5.8	18.6	8.82	13.9
	MeOH_039	37.5	5.13	19.1	9.29	20	12.2	17.2
	MeOH_040	33.1	5.31	19.3	8.74	12.8	11.4	15.1
	MeOH_043	18.9	3.79	8.48	7.07	22.1	5.23	10.9
	MeOH_045	37.9	5.81	19	8.45	6.41	10.8	14.7
	MeOH_046	25.4	5.33	10.6	8.61	18.8	7.08	12.6
	MeOH_047	23.4	5.5	10.2	8.4	8.09	6.33	10.3
	MeOH_048	22.4	9.52	8.91	7.61	17.2	6.51	12
	MeOH_049	22.8	5.38	8.95	8.17	16.6	5.98	11.3
	MeOH_050	26	4.91	9.26	7.92	14.1	6.27	11.4
	MeOH_051	27.8	4.75	7.73	7.02	21	6.24	12.4
	MeOH_052	24.1	4.96	8.11	7.02	18.7	5.58	11.4
	MeOH_055	36.6	6.92	16.6	8.75	14.1	11	15.7
	MeOH_073	122	7.71	10.1	5.24	15.5	7.68	28.1
	MeOH_074	38	16.8	5.43	7.69	12.9	9.69	15.1
	MeOH_077	33.1	7.95	1.16	6.99	16.2	10.4	12.6
	MeOH_081	22.6	14.4	6.95	9.42	19.3	11.3	14
	MeOH_083	18.3	13	3.63	7.32	20	9.3	11.9

Appendix I.1. Optimal Experimental Design as Optimal Control

As described in [28] we formulate the optimal experimental design problem as the following optimal control problem:

u, x0, x (F(tf)-1)objective]eq:OEDOjective problem]eq:OEDProblem 0 =f(x, x, q, t, u),constraint]cons:OEDDynamics y =h(x, q, t, u),constraint]cons:OEDObserved 0 =fx G + fx G + fp,constraint]cons:OEDSensitivityDynamics F =i = 1ny (hxi G)T (hxi G ),constraint]cons:OEDFisherDynamics x(t0) =x0,constraint]cons:OEDx0 G(t0) =x0q,constraint]cons:OEDG0 F(t0) =0,constraint]cons:OEDF0 0c(x,q,t,u)constraint]cons:OEDgeneralCons uUconstraint]cons:OEDParamDoms

In () a suitable criterion based on the variance-covariance matrix $F^{-1}\in {\mathbb{R}}^{\left|\mathcal{Q}\right|\times \left|\mathcal{Q}\right|}$ of the unknown or uncertain parameters $q\in \mathcal{Q}$ is minimized. To this end, different criteria $\varphi :{\mathbb{R}}^{\left|\mathcal{Q}\right|\times \left|\mathcal{Q}\right|}\mapsto \mathbb{R}$ have been proposed, typically related to the volume of the confidence ellipsoid of the associated parameters p. The most commonly used criteria are the A-Criterion (trace of $F^{-1}$), the D-Criterion (determinant of $F^{-1}$), and the E-Criterion (maximum eigenvalue of $F^{-1}$). The degrees of freedom are controls $u\in \mathcal{U}$ and potentially also the initial conditions $x_0$ on the differential states. The dynamics of the original DAE system are incorporated in . The dynamics of the Fisher information matrix F is given by the weighted sum of observability Gramians $h_x^i\left(x\right)G,i=1,\cdots ,\left|\mathcal{Y}\right|$ for each observed function in . Here $G\in {\mathbb{R}}^{\left|\mathcal{X}\right|\times \left|\mathcal{Q}\right|}$ denotes the forward sensitivities of the states x with respect to the parameters q as given in . Also general constraints $c:\mathcal{X}\times \mathcal{Q}\times \mathbb{R}\times \mathcal{U}\mapsto {\mathbb{R}}^{n_c}$ may be present to model path constraints in .

Given the (), we need to solve an augmented system of differential equations $f^{\prime }\left({\dot{x}}^{\prime },x^{\prime },q,t,u\right)=0$ with $x^{\prime }\in {\mathcal{X}}^{\prime },\left|{\mathcal{X}}^{\prime }\right|=\left|\mathcal{X}\right|+\left|\mathcal{G}\right|+\left|\mathcal{F}\right|$ states. Using the fact that F is positive semidefinite and symmetric, we only need to add $\left|\mathcal{F}\right|={\displaystyle \frac{\left|\mathcal{Q}\right|\left(\right|\mathcal{Q}|+1)}{2}}$ state variables to model its dynamics, which in total leads to $\left|{\mathcal{X}}^{\prime }\right|=\left|\mathcal{X}\right|+\left|\mathcal{X}\right|·\left|\mathcal{Q}\right|+{\displaystyle \frac{\left|\mathcal{Q}\right|\left(\right|\mathcal{Q}|+1)}{2}}$ states, i.e., the size of the augmented system scales quadratically with the number of parameters $\left|\mathcal{Q}\right|$.

Appendix I.2. OED for Physical Parameters

After a first re-calibration of the mechanistic model described in Appendix C, we computed four optimal experimental designs for different subsets of model parameters in order to collect insightful data to reduce parameter uncertainty. The specific parameters for which we compute experimental designs are the two parameters in the Arrhenius equation of each of the three elementary reactions, i.e., CO and CO₂-hydrogenation and RWGS reaction, and the two rate constants $k_1^{+},k_2^{+}$ in the kinetic equation for the state $\varphi$.

The solutions to the four experimental design problems are illustrated in fig:oedbeta12,fig:oedbeta34,fig:oedbeta56,fig:oedk12.

In the optimal design for the CO hydrogenation (Figure A14) no CO₂ is present in the feed. Thus, the CO hydrogenation is the only reaction in this experiment yielding specific information for this reaction kinetics. The design for the CO₂ hydrogenation (Figure A15) is an interesting result. Switching between one feed containing the reactants CO₂ and H₂ of the desired reaction and another feed completely without both was suggested. Thus, a broad range of reactant concentrations is included in the experiment. In the RWGS design (Figure A16) no CO is present in the feed, forcing the reverse path of the reaction. Interestingly, in the first time period of the experiment all carbon species are purged out of the reactor with N₂ and H₂. In the design for the reversible conversion of active catalytic sites (Figure A17) first a low reduction potential via a low hydrogen concentration (and no CO) is applied which is later on increased in the experiment to influence the state $\varphi$. All in all, the optimal experiments are qualitatively meaningful with regard to their design purpose, but nevertheless not trivial in their specific quantitative design.

Figure A24. Experimental design for estimating parameters in Arrhenius equation of the $CO$ hydrogenation. The temperature was determined as $T=257$ °C.

Figure A24. Experimental design for estimating parameters in Arrhenius equation of the $CO$ hydrogenation. The temperature was determined as $T=257$ °C.

Figure A25. As in fig:oedbeta12, but for the $C{O}_2$ hydrogenation. The temperature was determined as $T=233$ °C.

Figure A25. As in fig:oedbeta12, but for the $C{O}_2$ hydrogenation. The temperature was determined as $T=233$ °C.

Figure A26. As in fig:oedbeta12, but for the RWGS reaction. The temperature was determined as $T=227$ °C.

Figure A26. As in fig:oedbeta12, but for the RWGS reaction. The temperature was determined as $T=227$ °C.

Figure A27. As in fig:oedbeta12, but for the kinetic equation for the differential state $\varphi$. The temperature was determined as $T=227$ °C.

Figure A27. As in fig:oedbeta12, but for the kinetic equation for the differential state $\varphi$. The temperature was determined as $T=227$ °C.

Appendix I.3. OED for Hybrid Model

After training the hybrid model on the collected experimental data, we computed an additional experimental design to collect insightful data for further training of the embedded neural network. We identified the most important weights and biases of the network by decomposing the Fisher information matrix in a singular value decomposition which we truncated to the two largest singular values. In contrast to the previous experimental designs, for this experiment we chose a discretization parameter of $\Delta t=600$s, while the other options, bounds and initial values remained the same. The obtained solution is illustrated in fig:oedhybrid.