GravitationalWaves and Higgs-Like Potential from Alena Tensor

1. Introduction

Gravitational waves are a well-understood and researched issue [1], and it seems that the area of this research will develop dynamically both in theoretical understanding [2,3] and methods of waves detection [4,5]. While there is much evidence that General Relativity is (so far) the best description of relativistic gravity, the analysis of gravitational waves provides further evidence and is an important area of research, providing significant information about physical systems. The ability to describe gravitational waves is also an important requirement for alternative to GR theories [6,7,8] and the theories of quantum gravity [9].

Alena Tensor is in the early stages of research. It is a recently discovered class of energy-momentum tensors that allows for equivalent description and analysis of physical systems in flat spacetime (with fields and forces) and in curved spacetime (using Einstein Field Equations) proposing the overall equivalence of the curved path and the geodesic. In this method it is assumed that the metric tensor is not a feature of spacetime, but only a method of its mathematical description. In previous publications [10,11,12] it was already shown that this approach allows for a unified description of a physical system (curvilinear, classical and quantum) ensuring compliance with GR and QM equations. Due to this property, the Alena Tensor seems to be a useful tool for studying unification problems, quantum gravity and many other applications in physics.

Many researchers try to reproduce GR equations in flat spacetime or vice versa [13,14] also many researchers try to incorporate electromagnetism into GR, connecting it in many ways with the geometry of spacetime [15,16,17,18,19,20,21,22]. There are known such approaches on the basis of differential geometry [23,24,24], based on field equations [25,26] as well as promising analyses of spinor fields [27] or helpful approximations for a weak field [28]. For this reason, the Alena Tensor should be viewed as a useful tool that can help in the development of many different approaches or, potentially, as an independent theory requiring theoretical and experimental verification. Therefore it seems worth checking whether the this approach ensures the existence of gravitational waves and what their interpretation is.

Another important reason for writing this article is the fact that although the Alena Tensor equations provide consistency with the Einstein Field Equations in curved spacetime, the description of curvilinear solutions provided by this approach has not been sufficiently discussed in the literature so far. The description of gravitational waves, due to the required mathematical apparatus, will allow to deepen knowledge of this approach and to narrow down the classes of GR solutions that are consistent with it. Such a description will not provide full knowledge about unification, because full unification is not a task for one article and will probably require many years of cooperation of the scientific community. However, this article has the potential to take another step towards unification using the Alena Tensor, providing theoretical tools and hints for further research on unification using this approach.

In this paper it will be analyzed the possibility of describing gravitational waves using the Alena Tensor. Due to the fact that research on this approach is a relatively young field, to facilitate the analysis of the article, the next section summarizes the results obtained so far and introduces the necessary notation. All computationally difficult equations and graphs can be found in the attached supplementary material as computational notebook.

In the Results section, at first it will be shown that the use of the Alena Tensor leads to the decomposition of the electromagnetic field stress-energy tensor into components dependent on two null vectors. Next, the general form of the metrics for curved spacetime described by the Alena Tensor will be obtained, the Riemann and Weyl tensors will be calculated and presented for an example field configuration. It will also be shown that the correct operation of the Alena Tensor requires the existence of the Higgs field. The article also presents tables and graphs illustrating the obtained results (Higgs field, Weyl tensor components, Newman-Penrose scalars) and it was shown, that the analysis of the equations lead to the conclusions contained in the abstract.

Although at the first moment the paradigm shift proposed by this approach may seem incomprehensible, the author hopes that the reader will trust the scientific method, which encourages us to calculate and check everything based on the correctness of the results obtained.

2. Organizing and Interpreting the Alena Tensor Previous Results for Electromagnetism

To provide an introduction to Alena Tensor approach, one may first systematize and organize the conclusions drawn from previous research on as systems with only electromagnetic field. In the last section, the possibility of generalizing this approach to all gauge fields will be discussed.

2.1. Transforming a Curved Path into a Geodesic

It is worth starting the analysis with a postulate concerning the field invariant, which follows directly from Equation (28) in [11]. Considering a system with only an electromagnetic field as an example, denoting the electromagnetic field as $F^{\mu \nu }$ and denoting the metric tensor by means of which the physical system is analyzed as $g^{\mu \nu }$, one may denote the invariant of this field as $\Lambda$. Let this field invariant be defined dually as follows

$$\Lambda \equiv {\displaystyle \frac{1}{4}}{\displaystyle \frac{1}{{\mu }_o}}{F}^{\mu \nu }{g}_{\mu \alpha }{F}^{\alpha \beta }{g}_{\beta \nu }\equiv {\Lambda }_o{\mathbb{k}}^2;\mathbb{k}\equiv {\mathbb{k}}^{\mu \nu }{g}_{\mu \nu }$$

(1)

where ${\Lambda }_o$ is some unknown constant and where ${\mathbb{k}}^{\mu \nu }$, as raised in [11], in this approach is a metric tensor describing a curved spacetime in which all motion occurs along geodesics. By making variation on $-\Lambda$ with respect to metric $g^{\mu \nu }$ (Hilbert’s method) one obtains the energy-momentum tensor of the electromagnetic field denoted as ${{\rm Y}}^{\mu \nu }$, which can be expressed dually as

$${{\rm Y}}^{\mu \nu }\equiv {\displaystyle \frac{1}{{\mu }_o}}{F}^{\mu \alpha }{g}_{\alpha \beta }{F}^{\nu \beta }-\Lambda g^{\mu \nu }=\Lambda \left({\displaystyle \frac{4}{\mathbb{k}}}{\mathbb{k}}^{\mu \nu }-g^{\mu \nu }\right)$$

(2)

As can be seen, such approach establishes a relationship between the field and the metric tensor ${\mathbb{k}}^{\mu \nu }$ and in the spacetime described by the metric tensor $g^{\mu \nu }\to {\mathbb{k}}^{\mu \nu }$, one obtains $\mathbb{k}=4$. The value of $\Lambda$ becomes thus constant only for such field configuration, therefore in the limit for $g^{\mu \nu }\to {\mathbb{k}}^{\mu \nu }$ electromagnetic field tensor ${{\rm Y}}^{\mu \nu }$ vanishes, maintaining continuity of function. This is quite important, because most calculations in curved spacetime are performed under the assumption that the variation of the constant $\Lambda$ does not vanish. This is indeed true, with one exception, where the constancy follows precisely from the limit.

In this way one obtains a generalized description of the field stress-energy tensor ${{\rm Y}}^{\alpha \beta }$ which has the following properties

• in flat spacetime ${{\rm Y}}^{\alpha \beta }$ is the usual, classical energy-momentum tensor of the electromagnetic field
• its trace vanishes in any spacetime, regardless of the considered metric tensor $g^{\alpha \beta }$
• in spacetime for which $g^{\alpha \beta }={\mathbb{k}}^{\alpha \beta }$ the entire tensor ${{\rm Y}}^{\alpha \beta }$ vanishes
• ${\mathbb{k}}^{\alpha \beta }{\mathbb{k}}_{\alpha \beta }=4$ which is expected property of the metric tensor (it was already shown in [11] that ${\mathbb{k}}^{\alpha \beta }$ indeed may be considered as metric tensor for curved spacetime).

Such approach also means that every field stress-energy tensor could naturally satisfy the Israel junction condition for hypersurface [29]. For example, in electromagnetism this provides the possibility of viewing ${{\rm Y}}^{\alpha \beta }$ as a certain hyperspace, where $\Lambda {\displaystyle \frac{4}{\mathbb{k}}}{\mathbb{k}}^{\mu \nu }$ actually describes a discontinuity, eg. ${\displaystyle \frac{1}{{\mu }_o}}{F}_{\alpha }^{\mu }{\partial }^{\nu }{A}^{\alpha }-{\displaystyle \frac{1}{{\mu }_o}}{F}_{\alpha }^{\mu }{\partial }^{\alpha }{A}^{\nu }$, so the system could satisfy the holographic principle [30] and the entire volume dynamics could be described by the surface theory and vice-versa. It will be shown later that such a perception of ${{\rm Y}}^{\alpha \beta }$ may be a simple explanation for Alena Tensor.

The second important postulate underlying the Alena Tensor is an amendment to continuum mechanics introduced in Equation (11) of [11]. Assuming ${\varrho }_o$ as rest mass density, four-momentum density is defined as $\varrho U^{\alpha }\equiv {\varrho }_o\gamma U^{\alpha }$ what takes into account motion and Lorentz contraction of the volume. Total four-force density acting on matter is therefore defined as

$$f^{\nu }\equiv {\partial }_{\mu }\varrho U^{\mu }{U}^{\nu }=\varrho U^{\mu }{\partial }_{\mu }{U}^{\nu }=\varrho {\displaystyle \frac{d{U}^{\nu }}{d\tau }}$$

(3)

As shown in [11], the above amendment thus introduces a natural property concerning curved spacetime

$$\begin{array}{c}\hfill {\partial }_{\alpha }\varrho U^{\alpha }=0\to U_{,\alpha }^{\alpha }=-{\displaystyle \frac{d\gamma }{dt}}\to U_{;\alpha }^{\alpha }=0\end{array}$$

(4)

$$\begin{array}{c}\hfill U^{\alpha }{U}_{;\alpha }^{\beta }=0\to {\displaystyle \frac{D{U}^{\beta }}{D\tau }}=0;{\left(\varrho U^{\alpha }{U}^{\beta }\right)}_{;\alpha }=0\end{array}$$

(5)

The above property means that the field is indeed not needed in curved spacetime and can only manifest itself through curvature. This also means that the four-currents $J^{\mu }$ have the form ${\rho }_o\gamma U^{\mu }$ where ${\rho }_o$ denotes the rest density of the transferred charge, which ensures the continuity equation.

The final postulate that explains the results obtained so far is the assumption that the density of matter is not a value independent of the field, but is in fact a manifestation of the existence of the field, and without fields, matter does not exist. This assumption is consistent with the general idea of Quantum Mechanics, in which particles are de facto quanta of the field and it was also raised in [11]. In the system with only electromagnetic field one may thus define rest matter density linking it to electric susceptibility ${\chi }_e$ as

$$-\varrho c^2\equiv {\chi }_e\Lambda$$

(6)

where one may recall from [10] other coefficients related to the electromagnetic field

• relative permittivity ${\epsilon }_r=1+{\chi }_e$
• relative permeability ${\mu }_r={\displaystyle \frac{1}{{\epsilon }_r}}$
• volume magnetic susceptibility $\chi ={\mu }_r-1$

This approach allows to associate the momentum density with a certain four-current $\stackrel{\varrho }{J^{\mu }}\equiv {\chi }_e{U}^{\mu }$ what makes it dependent on the metric $c^2{\chi }_e^2=\stackrel{\varrho }{J^{\mu }}{g}_{\mu \nu }\stackrel{\varrho }{J^{\nu }}$.

Defining the Lagrangian density for the system as

$${\mathcal{L}}_{\mathcal{H}}\equiv {\epsilon }_r\Lambda =\Lambda -\varrho c^2=\Lambda (1+{\chi }_e)$$

(7)

and making variations with respect to the metric (Hilbert’s method), using the three postulates mentioned earlier, one obtains Alena Tensor $T^{\alpha \beta }$ for the system

$$T^{\alpha \beta }=\varrho U^{\alpha }{U}^{\beta }-{\displaystyle \frac{1}{{\mu }_r}}{{\rm Y}}^{\alpha \beta }$$

(8)

where $T^{\alpha \beta }$ is energy-momentum tensor of the system, which can be analyzed independently of the $g_{\alpha \beta }$ used for analysis. Its vanishing four-divergence can be considered both in flat spacetime and in curved spacetime. One may therefore denote the four-force densities due to the field ${\partial }_{\alpha }{\displaystyle \frac{1}{{\mu }_r}}{{\rm Y}}^{\alpha \beta }\equiv {\displaystyle \frac{1}{{\mu }_r}}{f}_{em}^{\beta }+f_{gr}^{\beta }$ in flat spacetime, where

• $f_{em}^{\beta }$ is the density of the electromagnetic four-force
• $f_{gr}^{\beta }={{\rm Y}}^{\alpha \beta }{\partial }_{\alpha }{\displaystyle \frac{1}{{\mu }_r}}$ was shown in [10] as related to the presence of gravity in the system.

and where vanishing four-divergence of $T^{\alpha \beta }$ in flat spacetime results from the balance of the four-force densities

$$0={\partial }_{\alpha }{T}^{\alpha \beta }=f^{\beta }-{\displaystyle \frac{1}{{\mu }_r}}{f}_{em}^{\beta }-f_{gr}^{\beta }$$

(9)

In curved spacetime ($g^{\mu \nu }={\mathbb{k}}^{\mu \nu }$) one obtains ${\displaystyle \frac{1}{{\mu }_r}}{{\rm Y}}^{\alpha \beta }=0\to T^{\alpha \beta }=\varrho U^{\alpha }{U}^{\beta }$ thus the forces due to the field are replaced by Christoffel symbols of the second kind corresponding to curvature related to the metric tensor defined by the filed according to (2) and (4).

The reasoning carried out above for electromagnetism is universal and creates possibility to consider dually also energy-momentum tensors associated with all gauge fields, what will be shown further.

2.2. Connection with Continuum Mechanics, GR and QFT/QM

In the sense of Continuum Mechanics, ${\displaystyle \frac{1}{{\mu }_r}}{f}_{em}^{\mu }={\displaystyle \frac{1}{{\mu }_r}}{\partial }_{\nu }{{\rm Y}}^{\mu \nu }$ may be considered as a density of the volume four-forces, while the $f_{gr}^{\mu }={{\rm Y}}^{\mu \nu }{\partial }_{\nu }{\displaystyle \frac{1}{{\mu }_r}}$ may be considered as a density of surface four-forces, related to hyperspace described by ${{\rm Y}}^{\alpha \beta }$, where surface waves are driven by the gradient of the pressure. To make the Alena Tensor consistent with Continuum Mechanics in flat spacetime, it is thus enough to define negative pressure p as in [11], $p\equiv -{\mathcal{L}}_{\mathcal{H}}$. Such substitution yields

$$\varrho U^{\alpha }{U}^{\beta }-T^{\alpha \beta }=p{\eta }^{\alpha \beta }-c^2\varrho {\displaystyle \frac{4}{\mathbb{k}}}{\mathbb{k}}^{\alpha \beta }+\Lambda {\displaystyle \frac{4}{\mathbb{k}}}{\mathbb{k}}^{\alpha \beta }$$

(10)

where ${\eta }^{\alpha \beta }$ is the metric tensor of flat Minkowski spacetime. Introducing deviatoric stress tensor ${\Pi }^{\alpha \beta }\equiv -c^2\varrho {\displaystyle \frac{4}{\mathbb{k}}}{\mathbb{k}}^{\alpha \beta }$ one obtains relativistic equivalence of Cauchy momentum equation (convective form) in which only $f_{em}^{\alpha }$ appears as a pure volume force (body force)

$$f^{\alpha }={\partial }^{\alpha }p+{\partial }_{\beta }{\Pi }^{\alpha \beta }+f_{em}^{\alpha }$$

(11)

One may therefore construct a Lagrangian ${\mathcal{L}}_{\sigma }$ whose variation provides the tensor ${\sigma }^{\mu \nu }$ responsible for the four-force density $f_{\sigma }^{\alpha }$ understood as

$$f_{\sigma }^{\alpha }\equiv {\partial }^{\alpha }p+{\partial }_{\beta }{\Pi }^{\alpha \beta }={\chi }_e{f}_{em}^{\alpha }+f_{gr}^{\alpha }={\partial }_{\beta }\left({\chi }_e{{\rm Y}}^{\alpha \beta }\right)$$

(12)

It may be obtained with the use of the interpolating path method based on path parameter $\lambda$, where the $g_{\mu \nu }$ is the target metric, thus $g_{\mu \nu }\left(0\right)={\eta }_{\mu \nu },g_{\mu \nu }\left(1\right)=g_{\mu \nu }$. Using this method one obtains that

$${\mathcal{L}}_{\sigma }=-{\int }_0^{1}d\lambda {\chi }_e\left[g_{\mu \nu }\left(\lambda \right)\right]{\displaystyle \frac{d}{d\lambda }}\left(\sqrt{-g\left(\lambda \right)}\Lambda [g_{\mu \nu }\left(\lambda \right),{\mathbb{k}}_{\mu \nu }]\right)$$

(13)

The variation of the integral gives

$$\delta {\mathcal{L}}_{\sigma }=-{\int }_0^{1}d\lambda {\chi }_e{\displaystyle \frac{d}{d\lambda }}\left({\displaystyle \frac{\delta (\sqrt{-g}\Lambda )}{\delta g_{\rho \sigma }}}\delta g_{\rho \sigma }\right)$$

(14)

Assuming that at the end of the path $\delta g_{\mu \nu }\left(0\right)=0$, the remaining contribution is for $\lambda =1$, thus

$$\delta {\mathcal{L}}_{\sigma }=-{\chi }_e\left[g_{\mu \nu }\right]\delta (\sqrt{-g}\Lambda );{\sigma }^{\mu \nu }={\chi }_e\left[g_{\mu \nu }\right]{{\rm Y}}^{\mu \nu }$$

(15)

As one may notice, ${\mathcal{L}}_{\sigma }$ integrates along the deformation path and reflects the total deformation effect, which can be identified with the effective ”surface forces” at the boundary of the metric space. Therefore ${\sigma }^{\mu \nu }$ tensor, created with ${\mathcal{L}}_{\sigma }$ by variation over the metric gives the spacetime equivalent of the Cauchy tensor, which gives a local description of the energy-momentum and stress flows. Its spatial part ${\sigma }^{ij}$ on the surface t=const can be thus identified as the equivalent of the Cauchy tensor of mechanical stresses. In this perspective, Lagrangian ${\mathcal{L}}_{field}\equiv {\mathcal{L}}_{\sigma }-\Lambda$ is responsible for all forces due to the field ${\displaystyle \frac{1}{{\mu }_r}}{{\rm Y}}^{\alpha \beta }$, and Lagrangian ${\mathcal{L}}_{matt}\equiv {\mathcal{L}}_{\sigma }-\varrho c^2$ is responsible for $\varrho U^{\alpha }{U}^{\beta }$. This reflects the classical division into the Lagrangian of matter and fields, although in this approach the existence of matter is also a consequence of the existence of the fields, and ${\mathcal{L}}_H={\mathcal{L}}_{matt}-{\mathcal{L}}_{field}$ because the four-divergences of the tensors resulting from them cancel each other out.

The above also provides a connection to General Relativity in curved spacetime. For this purpose, one may introduce the following tensors, which can be analyzed in both flat and curved spacetime

$$\begin{array}{c}\hfill R^{\alpha \beta }\equiv 2\varrho U^{\alpha }{U}^{\beta }-p{g}^{\alpha \beta };G^{\alpha \beta }\equiv R^{\alpha \beta }-{\displaystyle \frac{R}{2}}{\displaystyle \frac{4}{\mathbb{k}}}{\mathbb{k}}^{\alpha \beta }\end{array}$$

(16)

$$\begin{array}{c}\hfill R\equiv R^{\alpha \beta }{g}_{\alpha \beta }=2\Lambda -2p\end{array}$$

(17)

Above allows to rewrite Alena Tensor making variations with respect to the metric on following Lagrangian density $2{\mathcal{L}}_{\mathcal{H}}+{\mathcal{L}}_{\sigma }={\mathcal{L}}_{matt}+{\displaystyle \frac{1}{2}}R$ to obtain

$$\begin{array}{c}\hfill G^{\alpha \beta }+\Lambda g^{\alpha \beta }=2T^{\alpha \beta }+{\sigma }^{\alpha \beta }\end{array}$$

(18)

As can be seen, the tensor $(G^{\alpha \beta }+\Lambda g^{\alpha \beta })$ may be constructed with the use of Hilbert’s method (for any $g^{\alpha \beta }$), however $G^{\alpha \beta }$ alone and $\Lambda g^{\alpha \beta }$ cannot be constructed this way, because it is impossible to construct such a tensor in a general way by forcing an additional trace of $\Lambda g^{\alpha \beta }$ in the prior Lagrangians. The only spacetime in which Hilbert’s method allows the derivation of $G^{\alpha \beta }$ alone is curved spacetime ($g^{\mu \nu }={\mathbb{k}}^{\mu \nu }$), where $\Lambda$ is constant, it is therefore possible to correct the obtained tensors with a Lagrangian constructed from a constant.

Analyzing the above equation in curved spacetime ($g^{\alpha \beta }={\mathbb{k}}^{\alpha \beta }$), one obtains simplifications

$$G^{\alpha \beta }+\Lambda g^{\alpha \beta }=2T^{\alpha \beta }=2\varrho U^{\alpha }{U}^{\beta };G^{\alpha \beta }=R^{\alpha \beta }-{\displaystyle \frac{1}{2}}R{g}^{\alpha \beta }$$

(19)

thus above can be interpreted in curved spacetime as the main equation of General Relativity up to the constant ${\displaystyle \frac{4\pi G}{c^4}}$ where $G^{\alpha \beta }$ and $R^{\alpha \beta }$ can be interpreted in curved spacetime, respectively, as Einstein curvature tensor and Ricci tensor both with an accuracy of ${\displaystyle \frac{4\pi G}{c^4}}$ constant. However, in this approach R is not a source Lagrangian density for tensor $G^{\alpha \beta }$.

Denoting in general case

$$2{\displaystyle \frac{\delta \frac{1}{2}R}{\delta g_{\alpha \beta }}}\equiv \varrho U^{\alpha }{U}^{\beta }-2{\mathcal{R}}^{\alpha \beta }$$

(20)

one may rewrite (18) as

$$\begin{array}{c}\hfill G^{\alpha \beta }+\Lambda g^{\alpha \beta }=2\varrho U^{\alpha }{U}^{\beta }-\left(2{\mathcal{R}}^{\alpha \beta }-{\displaystyle \frac{1}{2}}R{g}^{\alpha \beta }\right)\to {\mathcal{R}}^{\alpha \beta }{g}_{\alpha \beta }=R\end{array}$$

(21)

where the trace of ${\mathcal{R}}^{\alpha \beta }$ must give R, since the whole term in the brackets describes the field

$$\begin{array}{c}\hfill \left(2{\mathcal{R}}^{\alpha \beta }-{\displaystyle \frac{1}{2}}R{g}^{\alpha \beta }\right)={\sigma }^{\alpha \beta }-2{\displaystyle \frac{1}{{\mu }_r}}{{\rm Y}}^{\alpha \beta }=\left({\chi }_e-{\displaystyle \frac{2}{{\mu }_r}}\right){{\rm Y}}^{\alpha \beta }\end{array}$$

(22)

thus must have vanishing trace and the whole term vanish in curved spacetime. For this reason in curved spacetime $G^{\alpha \beta }$ and $R^{\alpha \beta }$ must be related to ${\mathcal{R}}^{\alpha \beta }$ and R plays the role of invariant of this field tensor.

Indeed, analyzing the $G^{\alpha \beta }$ tensor in flat spacetime ($g^{\alpha \beta }={\eta }^{\alpha \beta }$) one can notice, that it is related to the non-body forces seen in the description of the Cauchy momentum equation

$${\partial }_{\beta }{G}^{\alpha \beta }={\partial }_{\beta }{\sigma }^{\alpha \beta }={\partial }^{\alpha }p+{\partial }_{\beta }{\Pi }^{\alpha \beta }=f_{gr}^{\alpha }+f_{rr}^{\alpha }$$

(23)

which means that in the Alena Tensor analysis method gravity is not a body force, and as shown in [10] in above

• $f_{rr}^{\alpha }={\chi }_e{f}_{em}^{\alpha }$ is the density of the radiation reaction four-force
• $f_{gr}^{\alpha }=\varrho \left({\displaystyle \frac{d\varphi }{d\tau }}{U}^{\alpha }-c^2{\partial }^{\alpha }\varphi \right)$ is density of the four-force related to gravity, where
• $\varphi =-ln\left({\mu }_r\right)$ is related to the effective potential in the system with gravity.

It can be calculated that $f_{gr}^{\alpha }$ vanishes in two cases:

• $\overrightarrow{u}={\overrightarrow{u}}_{ff}\equiv -c{\displaystyle \frac{\nabla \varphi }{{\partial }^0\varphi }}$ - which turns out to be the case of free fall
• ${\partial }^{\alpha }\varphi =0$ which occurs in the case of circular orbits

Neglecting the electromagnetic force and the radiation reaction force, using the above equation one can reproduce the motion of bodies in the effective potential obtained from the solutions of General Relativity. Such a description has already been done for the Schwarzschild metric [10] for

$$\varphi +c_o\equiv \sqrt{{\displaystyle \frac{E^2}{m^2{c}^4}}-{\left({\displaystyle \frac{1}{c}}{\displaystyle \frac{dr}{d\tau }}\right)}^2}=\sqrt{\left(1-{\displaystyle \frac{r_s}{r}}\right)\left(1+{\displaystyle \frac{L^2}{r^2}}\right)}$$

(24)

where $c_o$ is a certain constant. The solutions obtained in this way enforce the existence of gravitational waves due to time-varying $\varphi$ (except for free fall and circular orbits).

In the above description, gravity itself is not a force, because the above description is based on an effective potential. However, one can see a similarity to Newton’s classical equations for the stationary case with a stationary observer, for which $f_{gr}^{\alpha }$ can be approximated by Newton’s gravitational force with the opposite sign. Thus for stationary observer $f_{gr}^{\alpha }$ represents a force that must exist to keep a stationary observer suspended above the source of gravity in fixed place.

The description of gravity obtained from Alena Tensor is surprisingly consistent with current knowledge both in flat and curved spacetime, despite the fact that gravity itself in this description in flat spacetime is not a force, and the force $f_{gr}^{\alpha }$ is not a body force but is related to surface forces on some hyperspace.

The Alena Tensor constructed in presented way according to [10,12] may be also represented in flat spacetime as a symmetric Noether tensor using the obtained properties of the electromagnetic field. Denoting ${\mathcal{L}}_{\mathcal{N}}$ as the Lagrangian for computing the Noether tensor, Alena Tensor may be simplified in flat spacetime to

$$\begin{array}{c}\hfill T^{\alpha \beta }=\Lambda {\eta }^{\alpha \beta }-{\displaystyle \frac{1}{{\mu }_o}}{F}^{\alpha \gamma }{\partial }^{\beta }{A}_{\gamma };{\mathcal{L}}_{\mathcal{N}}=T^{00}=-\Lambda \end{array}$$

(25)

$$\begin{array}{c}\hfill \chi T^{\alpha \beta }={\partial }_{\gamma }{\displaystyle \frac{1}{{\mu }_o}}{F}^{\alpha \gamma }{A}^{\beta }\end{array}$$

(26)

where $A^{\beta }$ is known four-potential ensuring required symmetry of such Noether tensor, which allows analysis in classical field theory and quantum theories. Obtained canonical four-momentum $H^{\alpha }\equiv -{\displaystyle \frac{1}{c}}\int T^{\alpha 0}{d}^{3}x$ provides $0=H_{,\alpha }^{\alpha }=H^{\alpha }{H}_{\alpha }$ and to consider charged particles one may use

$${\partial }^{\alpha }{H}^{\mu }{X}_{\mu }=H^{\alpha }={\mu }_r{P}^{\alpha }+q{\mathcal{E}}^{\alpha };-L={\displaystyle \frac{m{c}^2}{\gamma }}-W_{pv}$$

(27)

where $P^{\alpha }$ is four-momentum, $W_{pv}=-\int p{d}^{3}x$ is pressure-volume work, and where $q{\mathcal{E}}^{\alpha }$ and $-{\mu }_r{P}^{\alpha }$ are in fact two gauges of electromagnetic four-potential, and mentioned previously four-potential $q{A}^{\beta }=-{\mu }_r{P}^{\alpha }$ where $\left({\mu }_r-1\right)P^{\alpha }$ is responsible for the force associated with gravity and radiation reaction force. It was also shown that canonical four-momentum $H^{\mu }$ may be expressed as

$$H^{\mu }=P^{\mu }+W^{\mu }=-{\displaystyle \frac{\gamma L}{c^2}}{U}^{\mu }+{\mathbb{S}}^{\mu }$$

(28)

where ${\mathbb{S}}^{\mu }$ due to its property ${\mathbb{S}}^{\mu }{U}_{\mu }=0$, seems to be some description of rotation or spin, and where $W^{\mu }$ describes the transport of energy due to the field.

The quantum picture obtained from the Alena Tensor [10,12] for the system with electromagnetic field leads to the conclusion that gravity and the radiation reaction force have always been present in Quantum Mechanics and Quantum Field Theory. This conclusion follows from the fact that the quantum equations obtained from the Alena Tensor for the system with electromagnetic field [10] are actually the three main quantum equations currently used:

• simplified Dirac equation for QED:
  ${\mathcal{L}}_{QED}={\displaystyle \frac{1}{4{\mu }_o}}{F}^{\alpha \beta }{F}_{\alpha \beta }={\displaystyle \frac{1}{2{\mu }_o}}{F}^{0\gamma }{\partial }^0{A}_{\gamma }={\displaystyle \frac{1}{2}}\overline{\Psi }\left(i\hslash c\neg D-m{c}^2\right)\Psi$
• Klein-Gordon equation,
• equivalent of the Schrödinger equation: $ic\hslash {\partial }^0\psi =-{\displaystyle \frac{{\hslash }^2}{m\left(\gamma +\frac{1}{\gamma }\right)}}{\nabla }^2\psi +cq{\widehat{A}}^0\psi$

where ${\widehat{A}}^{\alpha }$ is another gauge of electromagnetic four-potential, and where the last equation in the limit of small energies (Lorentz factor $\gamma \approx 1$) turns into the classical Schrödinger equation considered for charged particles.

The above results make the Alena Tensor a useful tool for the analysis of physical systems with fields, allowing modeling phenomena in flat spacetime, curved spacetime, and in the quantum image using a single, mathematically consistent apparatus.

2.3. Possible Generalizations to All Gauge Fields

Alena Tensor could be generalized to all gauge fields, which would open up the possibility of further investigation of physical systems using this approach.

A quite natural generalization of the Alena Tensor to the remaining fields seems to be the creation of a tensor $O^{\mu \nu \alpha \beta }$ in terms of the gauge field tensors ${\mathbb{F}}_A^{\mu \nu }$ for each gauge group A, with associated tensor $Q^{\nu \beta }$ and its trace Q, as

$$O^{\mu \nu \alpha \beta }\equiv \sum _A{\mathbb{F}}_A^{\mu \nu }\otimes {\mathbb{F}}_A^{\alpha \beta };Q^{\nu \beta }\equiv O^{\mu \nu \alpha \beta }{\eta }_{\mu \alpha };Q\equiv Q^{\nu \beta }{\eta }_{\nu \beta }$$

(29)

and then constructing a generalized field tensor $F^{\mu \nu \alpha \beta }$ with a vanishing trace by subtracting the trace part

$$F^{\mu \nu \alpha \beta }\equiv O^{\mu \nu \alpha \beta }-{\displaystyle \frac{1}{2}}\left({\eta }^{\mu [\alpha }{Q}^{\beta ]\nu }-{\eta }^{\nu [\alpha }{Q}^{\beta ]\mu }\right)+{\displaystyle \frac{1}{6}}Q{\eta }^{\mu [\alpha }{\eta }^{\beta ]\nu }$$

(30)

thanks to which it has properties analogous to the Weyl tensor (antisymmetry, pair symmetry, vanishing trace $F^{\mu \nu \alpha \beta }{\eta }_{\mu \alpha }{\eta }_{\nu \beta }=0$). Building on the above field tensor, the stress-energy tensor ${{\rm Y}}^{\mu \nu }$ for such generalized field, as

$${{\rm Y}}^{\mu \nu }\equiv F^{\mu \gamma \alpha \beta }{F}_{\gamma \alpha \beta }^{\nu }-{\eta }^{\mu \nu }{\displaystyle \frac{1}{4}}{F}^{\sigma \gamma \alpha \beta }{F}_{\sigma \gamma \alpha \beta }$$

(31)

and assuming that the equations of motion for the gauge fields A are satisfied, one obtains gauge four-currents $J_A^{\nu }\equiv D_{\mu }{\mathbb{F}}_A^{\mu \nu }$. Therefore, one obtains the total density of the Yang-Mills four-forces [31,32]$f^{\nu }$ acting in the system, as

$$f^{\nu }={\partial }_{\mu }{{\rm Y}}^{\mu \nu }=\sum _A{J}_A^{\alpha }{\mathbb{F}}_{A\alpha }^{\nu }+f_{non-linear}^{\nu }$$

(32)

where $f_{non-linear}^{\nu }$ describes the self-interactions of gauge fields in a non-Abelian theory [33]. It could allow to define the Alena Tensor analogously as in (8) but for ${{\rm Y}}^{\mu \nu }$ defined in (31) and to obtain a consistent classical, quantum and curvilinear descriptions for such physical system.

It can be calculated that the Yang-Mills Lagrangian density is given by the expression ${\mathcal{L}}_{YM}=-{\displaystyle \frac{1}{4}}Q$, where

$$Q=Q^{\nu \beta }{\eta }_{\nu \beta }=\sum _A{\mathbb{F}}_A^{\mu \nu }{\mathbb{F}}_{\mu \nu }^A,$$

(33)

so Q is the sum of the contributions of the individual gauge fields. Since

$$O^{\mu \nu \alpha \beta }{O}_{\mu \nu \alpha \beta }=\sum _{A,B}{\mathbb{F}}_A^{\mu \nu }{\mathbb{F}}_{\mu \nu }^A{\mathbb{F}}_B^{\alpha \beta }{\mathbb{F}}_{\alpha \beta }^B,$$

(34)

also includes inserts from trace parts, therfore it seems that according to the conclusions reached so far using the Alena Tensor (7), the Lagrangian density of the system for the Hilbert’s method could be, actually, ${\mathcal{L}}_H={\displaystyle \frac{1}{4}}{F}^{\mu \nu \alpha \beta }{F}_{\mu \nu \alpha \beta }·e^{\varphi }$, where $e^{\varphi }$ plays a role similar to ${\epsilon }_r={\displaystyle \frac{1}{{\mu }_r}}$ in electromagnetism and where ${\chi }_m\equiv e^{\varphi }-1$ is responsible for the four-current associated with matter, similarly as seen in (6).

Such approach would provide a field energy density "cleaned" from trace contributions in the Yang-Mills theory, what can be seen after performing calculations as

$$F^{\mu \nu \alpha \beta }{F}_{\mu \nu \alpha \beta }=O^{\mu \nu \alpha \beta }{O}_{\mu \nu \alpha \beta }-Q^{\nu \beta }{Q}_{\nu \beta }$$

(35)

Deriving the energy-momentum tensor $T^{\mu \nu }$ for the system using the variational method on $\Lambda ={\Lambda }_o{\mathbb{k}}^2={\displaystyle \frac{1}{4}}{F}^{\mu \nu \alpha \beta }{F}_{\mu \nu \alpha \beta }$ where $\mathbb{k}\equiv {\mathbb{k}}^{\mu \nu }{g}_{\mu \nu }$ as in (1) one would obtain Alena Tensor created exactly as before, but for all gauge fields where the field stress-energy tensor has dual representation and vanish in curved spacetime.

Deriving the Noether tensor $T^{\mu \nu }$ for the system from $-{\displaystyle \frac{1}{4}}{F}^{\mu \nu \alpha \beta }{F}_{\mu \nu \alpha \beta }$ one also obtains

$$-T^{\mu \nu }={{\rm Y}}^{\mu \nu }-\left(F^{\mu \gamma \alpha \beta }{F}_{\nu }^{\gamma \alpha \beta }-\sum _A{F}^{\mu \rho \alpha \beta }{\mathbb{F}}_{\alpha \beta }^A{\partial }^{\nu }{\mathbb{A}}_{\rho }^A\right)$$

(36)

where the term in brackets, will be hereinafter referred to as $\Delta$. Following the conclusions from [10,12] seen in (25) one may also assume, that, similarly to electromagnetism, it gives

$$\sum _A{J}_A^{\mu }{\mathbb{A}}_A^{\nu }=-e^{-\varphi }\varrho U^{\mu }{U}^{\nu }\to \sum _A{J}_A^{\mu }{\mathbb{A}}_{A\mu }=-e^{-\varphi }\varrho c^2$$

(37)

where $e^{\varphi }=1-{\displaystyle \frac{\varrho c^2}{F^{\mu \nu \alpha \beta }{F}_{\mu \nu \alpha \beta }}}=1+{\chi }_m$ which is de facto the definition of a matter current coupled to the gauge field potentials with the factor $e^{-\varphi }$ (similarly to the minimal coupling in the gauge theory with matter). Therefore

$$\Delta =\sum _A{F}^{\left(\mu \gamma \alpha \beta \right)}{\mathbb{F}}_{\alpha \beta }^A\left({\partial }^{\nu )}{\mathbb{A}}_{\gamma }^A-{\partial }_{\gamma }{\mathbb{A}}^{\nu )A}\right)=e^{-\varphi }\varrho U^{\mu }{U}^{\nu }-(e^{-\varphi }-1)T^{\mu \nu }$$

(38)

This would ensure correct Alena Tensor equations for the physical system also in Noether approach, which, as for electromagnetism, leads to the same result

$$T^{\mu \nu }=\varrho U^{\mu }{U}^{\nu }-e^{\varphi }{{\rm Y}}^{\mu \nu }$$

(39)

with expected trace for the stress-energy tensor for the system $(T^{\mu \nu }{g}_{\mu \nu }=\varrho c^2)$, the existence of gravity and the radiation reaction force as in (23). It also allows switching to a curvilinear description the same way as described in (18-19) and provides all other benefits from the application of the Alena Tensor.

The above description, of course, does not yet constitute proof of the validity of the Alena Tensor approach. It was introduced to facilitate future research and to demonstrate the potential generalizability of this approach across all gauge fields. The unification, as an extremely broad topic, is certainly not feasible by one person within a single article. Therefore, the only chance for developing this idea is the involvement of the scientific community and further research.

3. Results

Narrowing the discussion to spacetime with only electromagnetic field, described in a way provided by Alena Tensor using notation introduced in Section 2, one may reverse the reasoning presented in introduction and consider the field as a manifestation of a propagating perturbation of the curvature of spacetime which in flat spacetime is just interpreted as a field. For this purpose, one may define a certain perturbation $h^{\alpha \beta }$ of the metric tensor ${\mathbb{k}}^{\alpha \beta }$ that describes the deviation from flat spacetime, and also define its trace h as

$$h^{\alpha \beta }\equiv {\mathbb{k}}^{\alpha \beta }-{\eta }^{\alpha \beta };h=h^{\alpha \beta }{\eta }_{\alpha \beta }=\mathbb{k}-4$$

(40)

The stress-energy tensor of the electromagnetic field in flat spacetime can be thus represented as follows

$${\displaystyle \frac{\mathbb{k}}{4\Lambda }}{{\rm Y}}^{\alpha \beta }=h^{\alpha \beta }-{\displaystyle \frac{h}{4}}{\eta }^{\alpha \beta }$$

(41)

As one can see in the above, considering gravitational waves in the Alena Tensor is natural and does not require classical linearization. This would mean that gravitational waves in Alena Tensor approach are de facto a propagating disturbance of the energy-momentum tensor for the field (in the case analyzed, the electromagnetic field energy-momentum tensor).

Denoting the pressure amplitude ${\mathcal{P}}_o$ and ${\overline{h}}^{\alpha \beta }$ one obtains

$${\mathcal{P}}_o\equiv {\displaystyle \frac{4\Lambda }{\mathbb{k}}};{\overline{h}}^{\alpha \beta }\equiv h^{\alpha \beta }-{\displaystyle \frac{h}{4}}{\eta }^{\alpha \beta }\to {{\rm Y}}^{\alpha \beta }={\mathcal{P}}_o{\overline{h}}^{\alpha \beta }$$

(42)

which shows that the energy-momentum tensor of the field may be also interpreted as propagating vacuum pressure waves with tensor amplitude.

To provide an analysis of the above equation for gravitational waves and the analysis of the resulting classes of metrics, a representation using null-vectors will be useful. Therefore, in the next few steps it will be shown that Alena Tensor allows representing the energy-momentum tensor of the electromagnetic field with the use of two null-vectors.

3.1. Decomposition of the Electromagnetic Field Using Null Vectors

To demonstrate the division of the electromagnetic tensor into null vectors, it is necessary to carry out a rather tedious mathematical deduction. At first step one may recall equation (28) and define new four-vector $B^{\mu }$ obtaining

$$B^{\mu }\equiv -{\displaystyle \frac{\gamma L}{c^2}}{U}^{\mu }-{\mathbb{S}}^{\mu };H^{\mu }=-{\displaystyle \frac{\gamma L}{c^2}}{U}^{\mu }+{\mathbb{S}}^{\mu }$$

(43)

Since it is know from previous publications, that $H^{\mu }{H}_{\mu }=0$ and $U^{\mu }{\mathbb{S}}_{\mu }=0$, therefore above definition also yields $B^{\mu }{B}_{\mu }=0$. This property allows to represent $U^{\mu }$ and ${\mathbb{S}}^{\mu }$ using two null-vectors $H^{\mu }$ and $B^{\mu }$ as follows

$$H^{\alpha }-B^{\alpha }=2{\mathbb{S}}^{\mu };H^{\alpha }+B^{\alpha }=-{\displaystyle \frac{2\gamma L}{c^2}}{U}^{\alpha }\to H^{\alpha }{B}_{\alpha }={\displaystyle \frac{2{\gamma }^2{L}^2}{c^2}}$$

(44)

thus

$$H^{\alpha }{B}^{\beta }+B^{\alpha }{H}^{\beta }={\displaystyle \frac{2H^{\mu }{B}_{\mu }}{c^2}}{U}^{\alpha }{U}^{\beta }-\left(H^{\alpha }{H}^{\beta }+B^{\alpha }{B}^{\beta }\right)$$

(45)

Next, one may define auxiliary parameter $\alpha$ as

$$\alpha \equiv {\displaystyle \frac{B^0}{H^0}}+{\displaystyle \frac{2H^{\mu }{B}_{\mu }}{H^{0}mc\gamma }}$$

(46)

and subtract the linear combination of $H^{\alpha }$ and $B^{\alpha }$ from both sides

$$\begin{array}{c}\hfill H^{\alpha }{B}^{\beta }+B^{\alpha }{H}^{\beta }-\alpha H^{\alpha }{H}^{\beta }-{\displaystyle \frac{H^0}{B^0}}{B}^{\alpha }{B}^{\beta }=\end{array}$$

(47)

$$\begin{array}{c}\hfill ={\displaystyle \frac{2H^{\mu }{B}_{\mu }}{c^2}}{U}^{\alpha }{U}^{\beta }-\left(\left[1+\alpha \right]H^{\alpha }{H}^{\beta }+\left[1+{\displaystyle \frac{H^0}{B^0}}\right]B^{\alpha }{B}^{\beta }\right)\end{array}$$

(48)

Next, using $H\equiv c{H}^0$ for simplicity, one may recall from [10] coefficients related to the electromagnetic field

• relative permeability ${\mu }_r={\displaystyle \frac{\Lambda }{-p}}={\displaystyle \frac{H}{W_{pv}}}=e^{-\varphi }$
• volume magnetic susceptibility $\chi ={\mu }_r-1={\displaystyle \frac{\varrho c^2}{-p}}={\displaystyle \frac{m{c}^2\gamma }{W_{pv}}}$
• relative permittivity ${\epsilon }_r={\displaystyle \frac{1}{{\mu }_r}}={\displaystyle \frac{-p}{\Lambda }}={\displaystyle \frac{W_{pv}}{H}}$
• electric susceptibility ${\chi }_e={\epsilon }_r-1=-{\displaystyle \frac{\varrho c^2}{\Lambda }}=-{\displaystyle \frac{m{c}^2\gamma }{H}}=-\chi {\epsilon }_r$

and notice, that one obtains Alena Tensor $T^{\alpha \beta }$ as

$$\begin{array}{c}\hfill {\displaystyle \frac{{\mu }_r}{\Lambda }}{T}^{\alpha \beta }={\displaystyle \frac{\chi }{2H^{\mu }{B}_{\mu }}}\left(H^{\alpha }{B}^{\beta }+B^{\alpha }{H}^{\beta }-\alpha H^{\alpha }{H}^{\beta }-{\displaystyle \frac{H^0}{B^0}}{B}^{\alpha }{B}^{\beta }\right)=\end{array}$$

(49)

$$\begin{array}{c}\hfill ={\displaystyle \frac{\chi }{c^2}}{U}^{\alpha }{U}^{\beta }-{\displaystyle \frac{\chi }{2H^{\mu }{B}_{\mu }}}\left(\left[1+\alpha \right]H^{\alpha }{H}^{\beta }+\left[1+{\displaystyle \frac{H^0}{B^0}}\right]B^{\alpha }{B}^{\beta }\right)\end{array}$$

(50)

where electromagnetic stress-energy tensor is equal to

$${\displaystyle \frac{1}{\Lambda }}{{\rm Y}}^{\alpha \beta }={\displaystyle \frac{\chi }{2H^{\mu }{B}_{\mu }}}\left(\left[1+\alpha \right]H^{\alpha }{H}^{\beta }+\left[1+{\displaystyle \frac{H^0}{B^0}}\right]B^{\alpha }{B}^{\beta }\right)$$

(51)

and where $T^{0\beta }$ actually simplifies, as shown in introduction, to

$${\displaystyle \frac{{\mu }_r}{\Lambda }}{T}^{0\beta }=-{\displaystyle \frac{{\mu }_r}{H^0}}{H}^{\beta }$$

(52)

Completing the definition of the first invariant of the electromagnetic field tensor $\Lambda$, one may define the second invariant $I_{\perp }$ by electric $\overrightarrow{E}$ and magnetic $\overrightarrow{B}$ fields as

$$I_{\perp }\equiv {\displaystyle \frac{1}{c{\mu }_o}}\overrightarrow{E}\overrightarrow{B}$$

(53)

where it is known [34], that

$${{\rm Y}}^{\alpha \beta }{{\rm Y}}_{\alpha \beta }=4\left({\Lambda }^2+I_{\perp }^2\right)=4\left({{\rm Y}}^{0\beta }{{\rm Y}}_{0\beta }\right)$$

(54)

Therefore from (51) one obtains simplifications

$$B^0={\displaystyle \frac{H^{\mu }{B}_{\mu }}{4H^0}}={\displaystyle \frac{{\gamma }^2{L}^2}{2cH}}\to \alpha ={\displaystyle \frac{B^0}{H^0}}\left(1-{\displaystyle \frac{8}{{\chi }_e}}\right)\to {\displaystyle \frac{1}{H^0}}+{\displaystyle \frac{1}{B^0}}={\displaystyle \frac{4c}{-L}}$$

(55)

and by defining a useful auxiliary variable $\phi$ one gets

$$e^{\phi }\equiv {\displaystyle \frac{-\gamma L}{\sqrt{2}H}}\to \gamma ={\displaystyle \frac{1}{\sqrt{2}}}cosh\left(\phi \right)\to e^{2\phi }={\displaystyle \frac{B^0}{H^0}}$$

(56)

Finally, defining for simplicity as below

$$e^{\theta }sinh\left(\theta \right)\equiv {\displaystyle \frac{-L}{m{c}^2\gamma }};I_o^2\equiv 1+{\displaystyle \frac{I_{\perp }^2}{{\Lambda }^2}}$$

(57)

then calculating from (51) and (54)

$$I_o^2={\chi }^2{\gamma }^2\left(1-{\displaystyle \frac{2L}{m{c}^2\gamma }}\right)={\chi }^2{\gamma }^2{e}^{2\theta }\to \sqrt{2}{\mu }_r{e}^{\phi }={\displaystyle \frac{-\gamma L}{W_{pv}}}=I_{o}sinh\left(\theta \right)$$

(58)

and expressing ${\mu }_r={\displaystyle \frac{H}{W_{pv}}}=e^{-\varphi }$, one gets further useful expressions

$${\displaystyle \frac{I_o}{\sqrt{2}}}={\displaystyle \frac{e^{\phi -\varphi }}{sinh\left(\theta \right)}};\chi \gamma =I_o{e}^{-\theta }$$

(59)

To simplify further analysis, one may also normalize four-vectors $H^{\mu }$ and $B^{\mu }$ using (55) as follows

$$a^{\mu }\equiv {\displaystyle \frac{1}{H^0}}{H}^{\mu };b^{\mu }\equiv {\displaystyle \frac{1}{B^0}}{B}^{\mu }\to a^{\mu }{b}_{\mu }=4$$

(60)

where $a^{\mu }$ (not $h^{\mu }$) was introduced to avoid confusion related to the previously defined perturbation $h^{\alpha \beta }$. After few calculations using previously derived relationships in (51)

$${\displaystyle \frac{\chi }{8H^0{B}^0}}[1+\alpha ]{\left(H^0\right)}^2={\displaystyle \frac{\chi }{8}}\left(-{\displaystyle \frac{4c{H}^0}{L}}-{\displaystyle \frac{8}{{\chi }_e}}\right)={\mu }_r\left(1-{\displaystyle \frac{m{c}^2\gamma }{2L}}\right)$$

(61)

$${\displaystyle \frac{\chi }{8H^0{B}^0}}\left[1+{\displaystyle \frac{H^0}{B^0}}\right]{\left(B^0\right)}^2=-{\displaystyle \frac{\chi c{B}^0}{2L}}=\chi {\gamma }^2+{\mu }_r{\displaystyle \frac{m{c}^2\gamma }{2L}}$$

(62)

one may now rewrite the electromagnetic field tensor ${{\rm Y}}^{\alpha \beta }$ as

$${{\rm Y}}^{\alpha \beta }={\mu }_r\Lambda \left(1+{\displaystyle \frac{1}{2e^{\theta }sinh\left(\theta \right)}}\right)a^{\alpha }{a}^{\beta }+\Lambda \left(\chi {\gamma }^2-{\displaystyle \frac{{\mu }_r}{2e^{\theta }sinh\left(\theta \right)}}\right)b^{\alpha }{b}^{\beta }$$

(63)

As shown in [10] element ${\mu }_r\Lambda$ is responsible for electric field energy density carried by light, where $\Lambda \chi {\gamma }^2$ was shown as describing energy density of magnetic moment and was linked to charged matter in motion. The element ${\displaystyle \frac{{\mu }_r}{2e^{\theta }sinh\left(\theta \right)}}$ is a new term and part of equation related to this term may be expressed as ${\mathbb{S}}^{\alpha \beta }$ with help of (59) as

$${\mathbb{S}}^{\alpha \beta }\equiv {\displaystyle \frac{{\mu }_r}{2e^{\theta }sinh\left(\theta \right)}}\left(a^{\alpha }{a}^{\beta }-b^{\alpha }{b}^{\beta }\right)={\displaystyle \frac{I_o}{2\sqrt{2}}}{e}^{-(\theta +\phi )}\left(a^{\alpha }{a}^{\beta }-b^{\alpha }{b}^{\beta }\right)$$

(64)

Since ${\mathbb{S}}^{\alpha \beta }$ does not actually carry energy but only momentum, it can be associated with some description of spin field effects by analogy to (44). Using (55), (56) (59) and (62), electromagnetic field tensor ${{\rm Y}}^{\alpha \beta }$ may be, however, expressed in more useful form. Since

$${\mu }_r\left(1+{\displaystyle \frac{1}{2e^{\theta }sinh\left(\theta \right)}}\right)={\displaystyle \frac{I_o}{2\sqrt{2}}}{e}^{\theta -\phi };-{\displaystyle \frac{\chi c{B}^0}{2L}}={\displaystyle \frac{I_o}{2\sqrt{2}}}{e}^{\phi -\theta }$$

(65)

thus

$${\displaystyle \frac{1}{\Lambda }}{{\rm Y}}^{\alpha \beta }={\displaystyle \frac{I_o}{2\sqrt{2}}}{e}^{\theta -\phi }{a}^{\alpha }{a}^{\beta }+{\displaystyle \frac{I_o}{2\sqrt{2}}}{e}^{\phi -\theta }{b}^{\alpha }{b}^{\beta }$$

(66)

As one may notice, (60) also allows to simplify (43) by introducing $-e^{\phi }{s}^{\mu }\equiv {\displaystyle \frac{1}{H^0}}{\mathbb{S}}^{\mu }$

$$a^{\mu }=e^{\phi }\left({\displaystyle \frac{\sqrt{2}}{c}}{U}^{\mu }-s^{\mu }\right);b^{\mu }=e^{-\phi }\left({\displaystyle \frac{\sqrt{2}}{c}}{U}^{\mu }+s^{\mu }\right)$$

(67)

what using (56) yields

$$s^0=sinh\phi ;\overrightarrow{s}\overrightarrow{s}=1+{cosh}^2\phi ;s^{\mu }{s}_{\mu }=-2e^{2\phi }$$

(68)

and therefore allows to analyze the system using hyperbolic (and trigonometric) functions

$$\begin{array}{c}\hfill {\displaystyle \frac{a^{\mu }+b^{\mu }}{2}}={\displaystyle \frac{\sqrt{2}}{c}}cosh\phi U^{\mu }-sinh\phi s^{\mu }\end{array}$$

(69)

$$\begin{array}{c}\hfill {\displaystyle \frac{a^{\mu }-b^{\mu }}{2}}={\displaystyle \frac{\sqrt{2}}{c}}sinh\phi U^{\mu }-cosh\phi s^{\mu }\end{array}$$

(70)

$$\begin{array}{c}\hfill a^{\alpha }{a}^{\beta }=e^{2\phi }\left({\displaystyle \frac{2}{c^2}}{U}^{\alpha }{U}^{\beta }+s^{\alpha }{s}^{\beta }-{\displaystyle \frac{\sqrt{2}}{c}}\left[U^{\alpha }{s}^{\beta }+s^{\alpha }{U}^{\beta }\right]\right)\end{array}$$

(71)

$$\begin{array}{c}\hfill {\displaystyle \frac{\sqrt{2}}{c}}{U}^{\mu }={\displaystyle \frac{e^{-\phi }}{2}}{a}^{\mu }+{\displaystyle \frac{e^{\phi }}{2}}{b}^{\mu }\end{array}$$

(72)

One may thus denote normalized Alena Tensor in flat spacetime as $K^{\alpha \beta }$ with help of (49) and above as follows

$$K^{\mu \nu }\equiv {\displaystyle \frac{T^{\mu \nu }}{\Lambda }}={\displaystyle \frac{-{\chi }_e}{8}}\left(a^{\mu }{b}^{\nu }+b^{\mu }{a}^{\nu }-\left[1-{\displaystyle \frac{8}{{\chi }_e}}\right]a^{\mu }{a}^{\nu }-b^{\mu }{b}^{\nu }\right)$$

(73)

and notice, that it may be presented after simple calculations using (67) - (71) as

$$K^{\mu \nu }={\displaystyle \frac{-{\chi }_e}{c^2}}{U}^{\alpha }{U}^{\beta }-\left(\left[1-{\displaystyle \frac{{\chi }_e}{8}}(1+e^{-2\phi })\right]a^{\mu }{a}^{\nu }+\left[-{\displaystyle \frac{{\chi }_e}{8}}(1+e^{2\phi })\right]b^{\mu }{b}^{\nu }\right)$$

(74)

Since the expression in the brackets must be equal to ${\displaystyle \frac{1}{{\mu }_r}}{\displaystyle \frac{1}{\Lambda }}{{\rm Y}}^{\alpha \beta }$, thus

$${\displaystyle \frac{1}{\Lambda }}{{\rm Y}}^{\alpha \beta }=\left[{\mu }_r+{\displaystyle \frac{\chi }{8}}(1+e^{-2\phi })\right]a^{\mu }{a}^{\nu }+\left[{\displaystyle \frac{\chi }{8}}(1+e^{2\phi })\right]b^{\mu }{b}^{\nu }$$

(75)

Therefore, according to (63), (64) there must occur ${\displaystyle \frac{I_o}{2\sqrt{2}}}{e}^{-(\theta +\phi )}={\displaystyle \frac{\chi }{8}}(1+e^{-2\phi })$. Indeed, with help of (56) and (59) one obtains

$${\displaystyle \frac{I_o}{2\sqrt{2}}}{e}^{-\theta }={\displaystyle \frac{\chi }{8}}(e^{\phi }+e^{-\phi })={\displaystyle \frac{\chi }{4}}cosh\phi ={\displaystyle \frac{\chi }{2\sqrt{2}}}·{\displaystyle \frac{cosh\phi }{\sqrt{2}}}={\displaystyle \frac{1}{2\sqrt{2}}}·\chi \gamma ={\displaystyle \frac{I_o}{2\sqrt{2}}}{e}^{-\theta }$$

(76)

and the same equality may be calculated for ${\displaystyle \frac{\chi }{8}}(1+e^{2\phi })={\displaystyle \frac{I_o}{2\sqrt{2}}}{e}^{\phi -\theta }$ what confirms compliance with (66). Since $\theta$ is merely auxiliary variable (used only to highlight certain relationships) and thanks to simple algebraic transformations may be expressed in terms of $\phi$

$$2\sqrt{2}H{e}^{\phi }=m{c}^2{e}^{\theta }sinh\left(\theta \right){cosh}^2\left(\phi \right)\to -{\displaystyle \frac{8}{{\chi }_e}}=\left(e^{2\theta }-1\right)\left(e^{-2\phi }+1\right)$$

(77)

one may thus further simplify the description of the system. This shows that further, in-depth analysis of the system is also possible, however, modeling and simplifying the description of the electromagnetic field or searching for elementary particles that provide stable solutions requires a separate article (probably several articles). From the perspective of describing gravitational waves, other elements of the description are crucial, which will be discussed next.

Finally, one may notice, that property $a^{\mu }{b}_{\mu }=4$ in (60) requires analysis in a complex basis. An example of such a basis are four-vectors

$$a^{\mu }\left(\sigma \right)\equiv \left(\begin{array}{c}1\\ isinh\left(i\sigma \right)\\ cosh\left(i\sigma \right)\\ 0\end{array}\right),b^{\mu }\left(\sigma \right)\equiv \left(\begin{array}{c}1\\ i\left(2\sqrt{2}cosh\left(i\sigma \right)-3sinh\left(i\sigma \right)\right)\\ -3cosh\left(i\sigma \right)+2\sqrt{2}sinh\left(i\sigma \right)\\ 0\end{array}\right)$$

(78)

where the angle $\sigma$ was introduced to facilitate further analysis. The null basis product is a simple consequence of equation (54) as a consequence of taking only the electromagnetic field into account in the analysis. Since reality requires other fields (e.g. electroweak), it can be assumed that changing ${{\rm Y}}^{\alpha \beta }\to {\overline{{\rm Y}}}^{\alpha \beta }$ into the field tensor corresponding to reality, would probably provide ${\overline{{\rm Y}}}^{\alpha \beta }{\overline{{\rm Y}}}_{\alpha \beta }=2\left({\overline{{\rm Y}}}^{0\beta }{\overline{{\rm Y}}}_{0\beta }\right)\to a^{\mu }{b}_{\mu }=2$, which then makes it possible to assume a basis in real numbers. However, since in this paper it is considered the Alena Tensor with the electromagnetic field only, the basis (78) will be retained for further analysis as an example, especially since the transition to the generalized field in the discussed approach is a fairly simple procedure.

A cursory examination shows that this basis describes the electromagnetic field very well indeed. It has a good representation in conformal geometry (null vectors correspond to points on the equator of the Penrose sphere), where the propagation directions are perpendicular to the time axis (purely spatial), ideal for describing a circularly or elliptically polarized wave in the direction of Poyting vector $\overrightarrow{z}\equiv (0,0,2i\sqrt{2})$, where $a^{\mu }{b}_{\mu }=4$ represents the constant phase relation between the electric and magnetic fields. The proposed basis naturally enters the Newman–Penrose formalism, allows for a full spinor representation of the electromagnetic field, where $\sigma$ is a typical massless wave, satisfies the wave equation $\square \sigma =0$, and since it provides a spin-helicity of +/- 1, it is well suited for further analysis in the QFT framework as a photon wave representation, describing a single-particle state. However, detailed analysis of these issues is beyond the scope of this article.

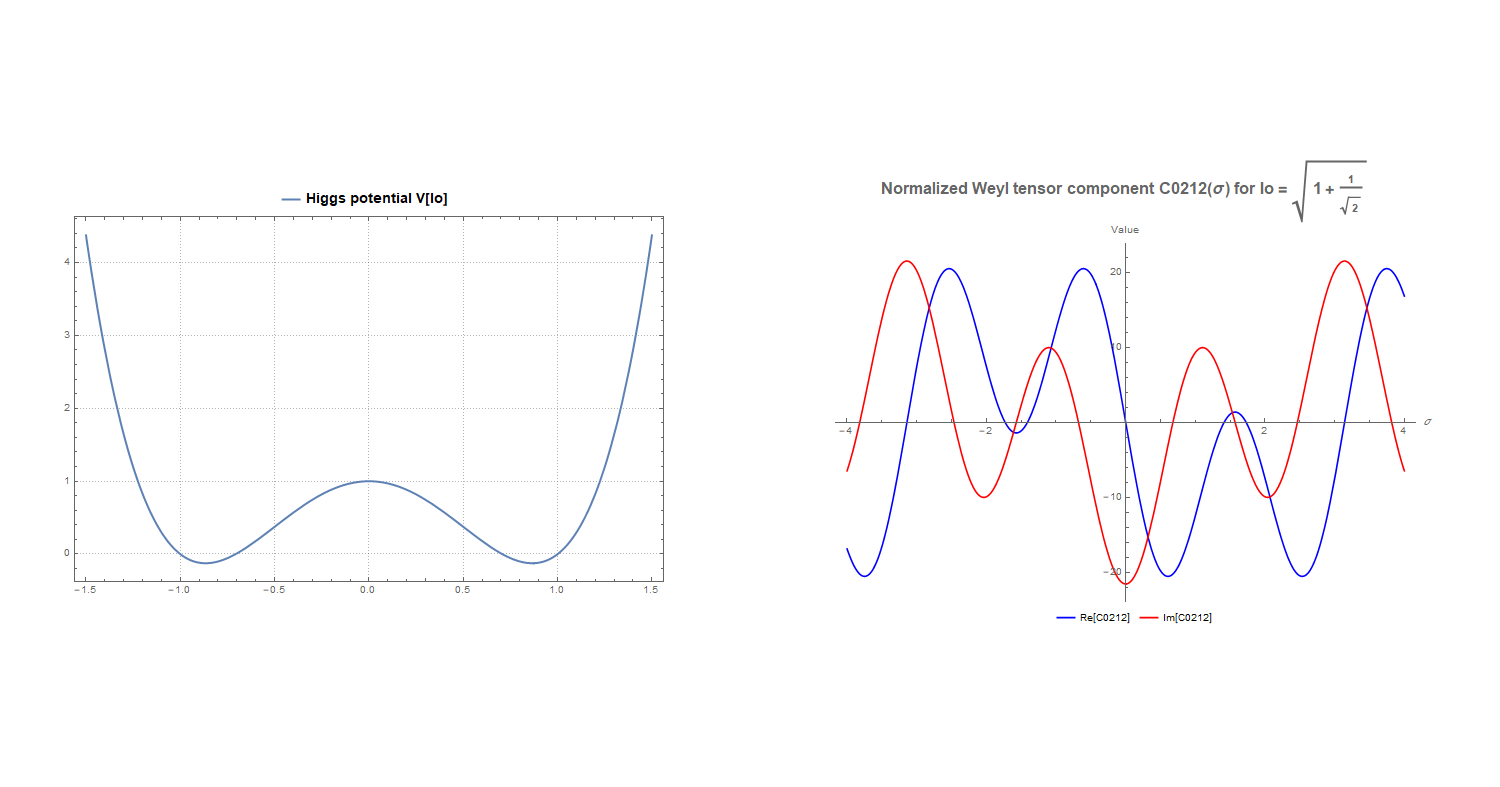
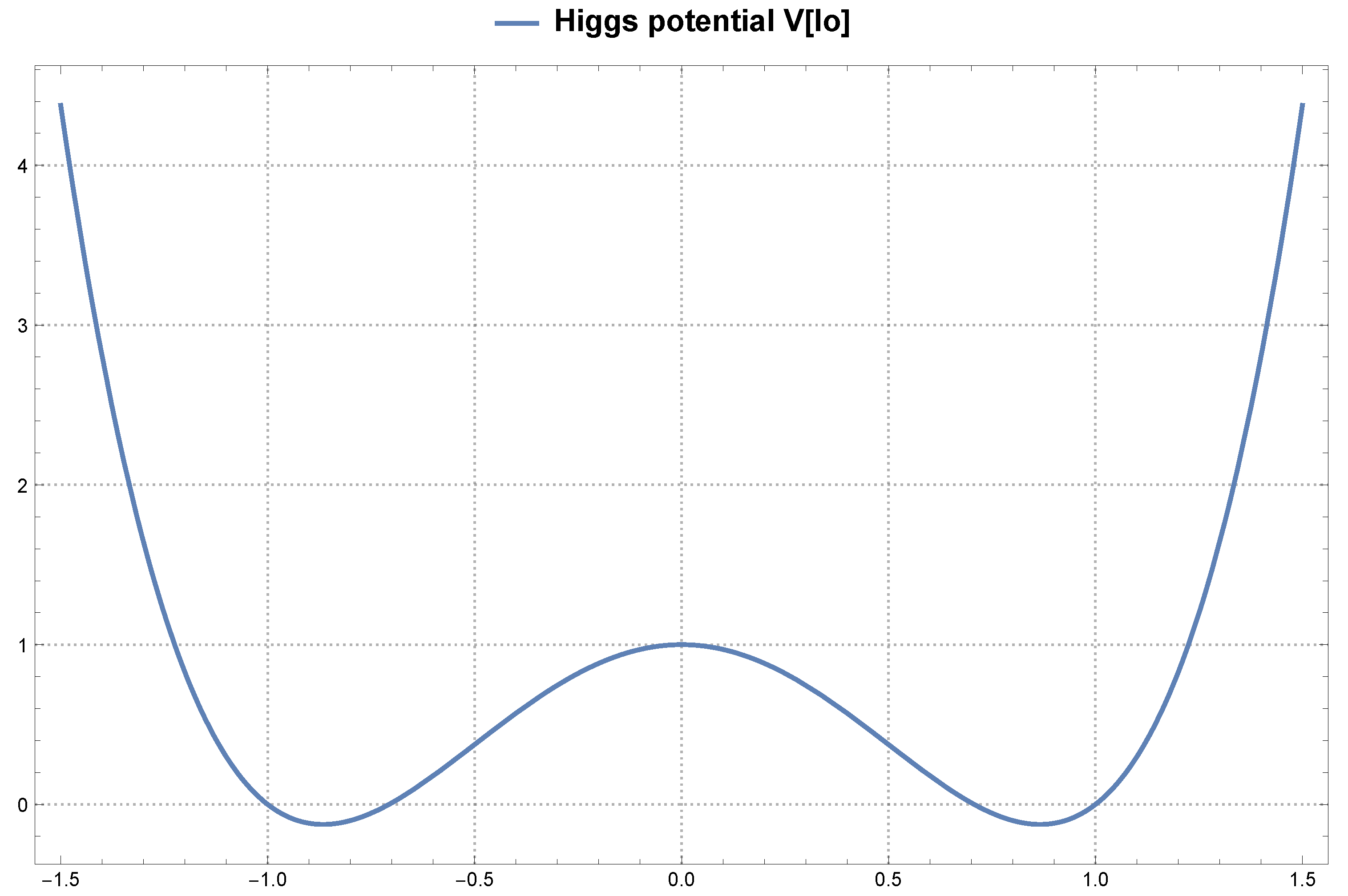
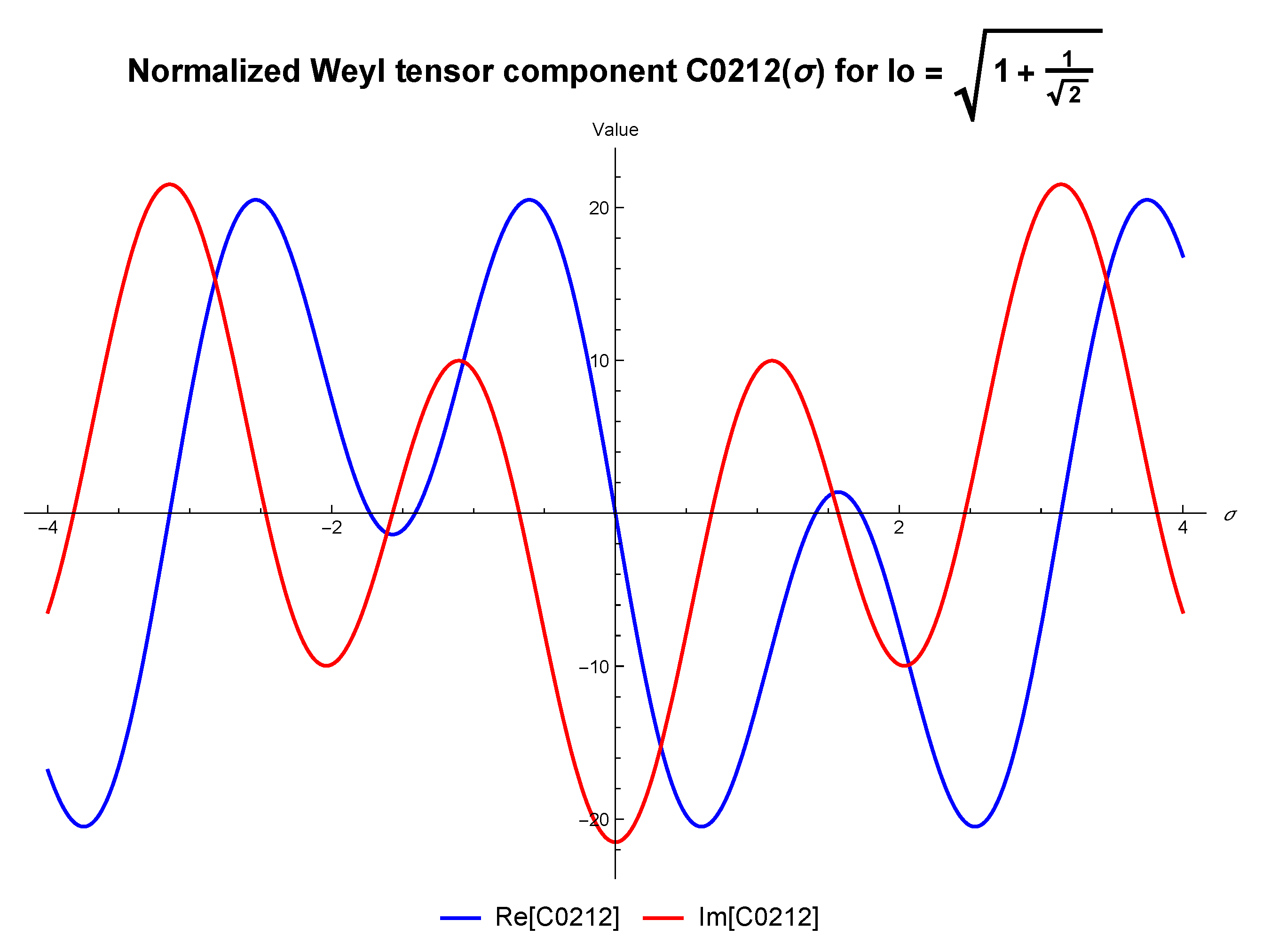
3.2. Covariant Metric, Higgs Potential, Riemann Tensor, Weyl Tensor and Gravitational Waves

Substituting (63) into (41) using (59) and using Alena Tensor properties one gets expression for metric ${\mathbb{k}}^{\alpha \beta }$ describing the system in curved spacetime

$${\mathbb{k}}^{\alpha \beta }={\displaystyle \frac{\mathbb{k}}{4}}\left({\displaystyle \frac{I_o}{2\sqrt{2}}}{e}^{\theta -\phi }{a}^{\alpha }{a}^{\beta }+{\displaystyle \frac{I_o}{2\sqrt{2}}}{e}^{\phi -\theta }{b}^{\alpha }{b}^{\beta }+{\eta }^{\alpha \beta }\right)$$

(79)

To avoid confusion when inverting the metric, it is useful to adopt the notations ${\mathbb{k}}_{\alpha \beta }\left(\eta \right)\equiv {\mathbb{k}}^{\mu \nu }{\eta }_{\alpha \mu }{\eta }_{\beta \nu }$ and just ${\mathbb{k}}_{\alpha \beta }$ for the actual covariant metric. It turns out that using properties of metrics, one may find a general solution for the inverted metric ${\mathbb{k}}_{\alpha \beta }$. Summarizing the key properties one obtains

$${\mathbb{k}}^{\alpha \beta }{\eta }_{\alpha \beta }={\mathbb{k}}_{\alpha \beta }{\eta }^{\alpha \beta }=\mathbb{k};{\mathbb{k}}^{\alpha \beta }{\mathbb{k}}_{\alpha \beta }=4;det\left({\mathbb{k}}^{\alpha \beta }\right)det\left({\mathbb{k}}_{\alpha \beta }\right)=1;{\mathbb{k}}_{\alpha \mu }{\mathbb{k}}^{\mu \beta }={\delta }_{\alpha }^{\beta }$$

(80)

where in the last condition it is enough to check the index (0,0), because the null vectors are normalized ($a^0=1;b^0=1$). To simplify the calculations, it is easiest to define auxiliary variable q and start from anstaz with unknown $A,B,C,D$ in

$$e^{-q}\equiv {\displaystyle \frac{\mathbb{k}}{4}};{\mathbb{k}}_{\mu \nu }\equiv {\displaystyle \frac{A}{I_o}}{\displaystyle \frac{e^{\theta -\phi }}{\sqrt{2}}}{a}_{\mu }{a}_{\nu }+{\displaystyle \frac{B}{I_o}}{\displaystyle \frac{e^{\phi -\theta }}{\sqrt{2}}}{b}_{\mu }{b}_{\nu }-C\left(a_{\mu }{b}_{\nu }+b_{\mu }{a}_{\nu }\right)+D{\eta }_{\mu \nu }$$

(81)

By eliminating the subsequent variables to provide equations (80), one obtains covariant metric in the form

$${\mathbb{k}}_{\mu \nu }\equiv {\displaystyle \frac{sinh\left(q\right)}{I_o}}{\displaystyle \frac{e^{\theta -\phi }}{\sqrt{2}}}{a}_{\mu }{a}_{\nu }+{\displaystyle \frac{sinh\left(q\right)}{I_o}}{\displaystyle \frac{e^{\phi -\theta }}{\sqrt{2}}}{b}_{\mu }{b}_{\nu }-sinh\left(q\right)\left(a_{\mu }{b}_{\nu }+b_{\mu }{a}_{\nu }\right)+e^q{\eta }_{\mu \nu }$$

(82)

where invariants of electromagnetic field turns out to be related to the trace

$${\displaystyle \frac{I_{\perp }^2}{{\Lambda }^2}}={\displaystyle \frac{1}{e^{2q}-2}}\to I_o=\sqrt{{\displaystyle \frac{e^{2q}-1}{e^{2q}-2}}};det\left({\mathbb{k}}_{\alpha \beta }\right)=e^{2q}\left(e^{2q}-2\right)$$

(83)

which means that the trace $\mathbb{k}$ is also invariant. The supplementary material contains equations confirming the correctness of the derivation.

Using arc $⌢$ for simplicity, to emphasize the change to curvilinear description (since values in curvilinear description may be different), one may notice, that considered in curved spacetime trace $\stackrel{⌢}{\mathbb{k}}=4$ yields $\stackrel{⌢}{q}=0$. Therefore, the transition to curved spacetime can be understood as solutions with imaginary magnetic field $\overrightarrow{B}\to i\overrightarrow{B}$. It is also worth notice, that for the null basis example (78), the above metric seems to describe a gravitational wave in conformal geometry, where ${\displaystyle \frac{\mathbb{k}}{4}}=e^{-q}$ plays the role of a conformal factor ${\Omega }^{-2}$. Further analysis in this direction should allow to isolate both the polarization and the relation of $\mathbb{k}$ to the Ricci scalar by classical relation $R={\Omega }^{-2}\left(\tilde{R}-6\tilde{\square }log\Omega \right)$.

Expressing $U^{\mu }$ by null-vectors as in (71) and requesting $U^{\alpha }{U}^{\beta }{\mathbb{k}}_{\alpha \beta }=c^2$ one obtains ugly expression linking $cosh(\phi +\theta )$ and q (due to the complexity of the calculations and the result, it is shown in the attached supplementary material with calculations).

$$cosh(\theta +\phi )={\displaystyle \frac{cosh\left(q\right)-3sinh\left(q\right)-1}{2\sqrt{-\frac{1}{coth\left(q\right)-3}}(cosh\left(q\right)-3sinh\left(q\right))}}$$

(84)

However, substituting q as the $I_o$ function according to (83)

$$q=log\sqrt{2-{\displaystyle \frac{1}{1-I_o^2}}}$$

(85)

and denoting $V\equiv 1+2I_o^4-3I_o^2$, it appears that this ugly expression (84) actually expresses following dependence

$$cosh(\theta +\phi )={\displaystyle \frac{1+\sqrt{V}}{\sqrt{2}{I}_o}}\to V=1+2I_o^2{cosh}^2(\theta +\phi )-2\sqrt{2}{I}_{o}cosh(\theta +\phi )$$

(86)

where V is the classical Higgs potential and the broken symmetry in the system can be interpreted as an apparent mismatch of coefficients related to $cosh(\phi +\theta )$. The Figure 1 shows the classic "Mexican sombrero" potential $V\left(I_o\right)$. Since $cosh(\phi +\theta )$ is related in equation (64) to the angle describing the spin, this means that in this solution the spin effect of the field is described by invariant angle (depends only on $I_o$) and, according to (83) it is closely related to the trace of the metric and, consequently, to the Ricci scalar in the curvilinear description and thus to spacetime curvature. This also at least means that to obtain correct results in curved spacetime in the Alena Tensor model, the Higgs-like potential is needed.

Since this paper considers a system with only electromagnetic field, the above described broken symmetry should be considered more as a consequence of the Higgs field in electromagnetism (equivalent to the Abelian mechanism and broken U(1) symmetry) visible in the curvilinear description within GR. However, the above result may contribute to a better understanding of the description of the Higgs field action within the GR containing electromagnetism and connections of the Higgs potential with curvature and spin seen in obtained result. Perhaps it will also help to extend Alena Tensor description to the electroweak field, which will allow to compare the quantum and curvilinear images, which, however, deserves a separate article.

For $I_o=\sqrt{1+{\displaystyle \frac{1}{\sqrt{2}}}}$ the whole metric becomes significantly simplified and symmetric

$$I_o=\sqrt{1+{\displaystyle \frac{1}{\sqrt{2}}}}\to V=I_o^2\to q=ln\left(\sqrt{2}{I}_o\right)\to {\displaystyle \frac{sinh\left(q\right)}{\sqrt{2}{I}_o}}={\displaystyle \frac{I_o}{2\sqrt{2}}}$$

(87)

which means that it may be assumed that adopting the above value leads to some significant and physically important solution of the equations for the system.

Using hyperbolic identities and expressing

$$cosh(\theta +\phi )=cosh\left(\theta \right)cosh\left(\phi \right)+sinh\left(\theta \right)sinh\left(\phi \right)=e^{-\theta }cosh\left(\phi \right)+e^{\phi }sinh\left(\theta \right)$$

(88)

then using (59) one obtains

$$\chi {\gamma }^2+{\mu }_r{e}^{2\phi }={\displaystyle \frac{1+\sqrt{V}}{2}}\to V={\left(2{\gamma }^2\chi +2{\mu }_r{e}^{2\phi }-1\right)}^2$$

(89)

which allows for further analysis of the Higgs potential. For example, using (63) and (68), the relation between electromagnetic energy density ${{\rm Y}}^{00}$, angle $\phi$ and spin four-vector ${\mathbb{S}}^{\mu }$ zero component is therefore

$${\displaystyle \frac{1}{\Lambda }}{{\rm Y}}^{00}={\mu }_r+\chi {\gamma }^2={\displaystyle \frac{1+\sqrt{V}}{2}}-2{\mu }_r{e}^{\phi }sinh\left(\phi \right)={\displaystyle \frac{1+\sqrt{V}}{2}}+{\displaystyle \frac{2c{\mathbb{S}}^0}{W_{pv}}}$$

(90)

Above also explains the origin of $\phi$ and the connection of spin and Lagrangian with the energy density of the electromagnetic field. Since, according to the considered Alena Tensor approach, in curved spacetime the energy density expressed by ${{\rm Y}}^{00}$ must vanish (the entire stress-energy tensor of the electromagnetic field vanishes), this means, that $\phi$ and thus $\gamma$ in curved spacetime becomes invariant, which allows to analyze the transition to curved spacetime.

One may now consider what value the Alena Tensor takes in curved spacetime. To do this, it is easiest to analyze the behavior of $K^{\mu \nu }$. As one may calculate, the determinant of this tensor is 0 and the matrix rank is 2, but, as described in the introduction, it degenerates to $\stackrel{⌢}{K^{\mu \nu }}={\displaystyle \frac{-\stackrel{⌢}{{\chi }_e}}{c^2}}{U}^{\alpha }{U}^{\beta }$ in curved spacetime. It can be seen that in the Alena Tensor approach the metric follows from propagation. However, in curved spacetime the electromagnetic field according to this approach should vanish, remaining present only in the metric and determining geodetic. This can be achieved by degenerating vectors $a^{\mu }$ and $b^{\mu }$ to a single vector in curved spacetime $\stackrel{⌢}{a^{\mu }}=\stackrel{⌢}{b^{\mu }}$. However, in such situation the equation (71) forces this vector to be the four-velocity, divided by the Lorenz factor

$$\stackrel{⌢}{a^{\mu }}=\stackrel{⌢}{b^{\mu }}\to U^{\mu }={\displaystyle \frac{c}{\sqrt{2}}}\left({\displaystyle \frac{e^{-\phi }}{2}}\stackrel{⌢}{a^{\mu }}+{\displaystyle \frac{e^{\phi }}{2}}\stackrel{⌢}{a^{\mu }}\right)=c\gamma \stackrel{⌢}{a^{\mu }}\to \stackrel{⌢}{a^{\mu }}={\displaystyle \frac{1}{c\gamma }}{U}^{\mu }$$

(91)

which degenerates $\stackrel{⌢}{K^{\mu \nu }}$ from (73) to the form

$$\stackrel{⌢}{a^{\mu }}=\stackrel{⌢}{b^{\mu }}={\displaystyle \frac{1}{c\gamma }}{U}^{\mu }\to \stackrel{⌢}{K^{\mu \nu }}=-\stackrel{⌢}{a^{\mu }}\stackrel{⌢}{a^{\nu }}=-{\displaystyle \frac{1}{c^2{\gamma }^2}}{U}^{\mu }{U}^{\nu }\to \stackrel{⌢}{{\chi }_e}={\displaystyle \frac{1}{{\gamma }^2}}$$

(92)

As can be easily verified, the exact above relation of variables leads to the vanishing field stress-energy tensor in (75) upon transition to curved spacetime.

Since the metric is known and $U^{\mu }$ may be expressed by values of $a^{\mu }$, $b^{\mu }$ in flat spacetime thanks to (71) this allows to easy obtain the normalized Einstein tensor and Ricci tensor (normalized by $\Lambda$) using the equation (19). According to the notation used in (19) one obtains

$${\displaystyle \frac{1}{\Lambda }}{R}^{\mu \nu }=2\stackrel{⌢}{K^{\mu \nu }}+\left(1+{\displaystyle \frac{1}{{\gamma }^2}}\right){\mathbb{k}}^{\mu \nu };{\displaystyle \frac{1}{\Lambda }}{G}^{\mu \nu }=2\stackrel{⌢}{K^{\mu \nu }}-{\mathbb{k}}^{\mu \nu }$$

(93)

where Ricci scalar R (normalized according to notation used) may be calculated as ${\displaystyle \frac{1}{\Lambda }}R=4+{\displaystyle \frac{2}{{\gamma }^2}}$.

The described system seems to be Petrov type D or II [35], although to be sure, the Weyl tensor should be calculated. This does not seem possible for the general case (without auxiliary assumptions about symmetries), but one could simplify the obtained description considerably, based on the following observation. One may notice, that the vanishing Lorentz factor $\gamma$ in $\stackrel{⌢}{K^{\alpha \beta }}$ can be interpreted as an important suggestion for the description of motion in curved spacetime. Such motion would correspond to a stream of particles moving without dilation, a strictly ordered flow without local perturbations, resembling a perfect, infinitely stiff fluid. This means that $\stackrel{⌢}{K^{\alpha \beta }}$ should be the Killing tensor and the system should have hidden symmetry (similar to the Carter constant in Kerr solutions).

As shown previously, product of the basis is in considered case $a^{\mu }{b}_{\mu }=4$, which means that null vectors have global significance for spacetime geometry, thus Killing tensor should have a strong connection with propagation along null vectors (it is not a random symmetry, but a deep feature of spacetime) and this would mean the existence of special wave surfaces, e.g. electromagnetic waves and/or gravitational radiation. This would be also a clear indication that spacetime belongs to the Petrov D or II class and is associated with wave propagation solutions.

Also, the analysis of obtained equations drive to conclusion, that energy (energy density) is not something external to geometry in Alena Tensor approach, but energy is defined by the geometry of spacetime itself. This is a result in the spirit of General Relativity, but it goes even deeper: metric ${\mathbb{k}}^{\mu \nu }$ depends on $e^{\phi }$, but at the same time ${\displaystyle \frac{1}{\gamma \left(\phi \right)}}$ depends on the metric because it is trace of $\stackrel{⌢}{K^{\alpha \beta }}$ in this metric. The system itself defines its own energy through the structure of the field, which is similar to the idea of Self-consistent Field [36] - where the field and the source are inseparable, or Emergent Gravity [37,38] - where energy, gravity and geometry arise from a common structure, or Induced Geometry [39] - where energy comes from deformation of spacetime itself, as e.g. in Sakharov’s theory [40]. It seems impossible to "decree" energy in Alena Tensor, but it must be calculated from geometry and the system works as a closed causal cycle.

The dependence for $\stackrel{⌢}{K^{\alpha \beta }}$ of its norm and trace in curved spacetime (the norm is the square of the trace) is a key property for null space and suggests that $\stackrel{⌢}{K^{\alpha \beta }}$ describes isometries related to null wave propagation, similar to pp-wave [41] and Robinson-Trautman solutions [42], what is actually expected in considered approach based on electromagnetic stress-energy tensor and result (79). This would also mean that the Killing tensor is directly related to the energy distribution in spacetime as expected, similar to other GR solutions (eg. Kerr solution), and lead to a rather groundbreaking but also expected result in the context of the discussed approach, that the Killing tensor directly determines the Einstein tensor in main GR equation.

Since $\stackrel{⌢}{K^{\alpha \beta }}$ is simply the Alena Tensor (stress-energy tensor for the system) divided by $\Lambda$, it gives correct conserved values in the Noether formalism (conserved density of energy and momentum). From the definition of the Alena Tensor as the energy-momentum tensor for the system it also follows that $\stackrel{⌢}{K^{\mu \nu }}$ is symmetric and ${\nabla }_{\mu }\stackrel{⌢}{K^{\mu \nu }}$ vanishes.

Since ${\stackrel{⌢}{K}}_{\alpha \beta }{U}^{\alpha }{U}^{\beta }=-{\displaystyle \frac{c^2}{{\gamma }^2}}$ this implies that along a geodesic parametrized by proper time $\tau$, its total derivative vanishes.

$${\displaystyle \frac{d}{d\tau }}\left({\stackrel{⌢}{K}}_{\alpha \beta }{U}^{\alpha }{U}^{\beta }\right)=0=U^{\lambda }{\nabla }_{\lambda }{\stackrel{⌢}{K}}_{\alpha \beta }{U}^{\alpha }{U}^{\beta }$$

(94)

Using the symmetry of ${\stackrel{⌢}{K}}_{\mu \nu }$ one may note that

$$U^{\alpha }{U}^{\mu }{U}^{\nu }{\nabla }_{\alpha }{\stackrel{⌢}{K}}_{\mu \nu }=U^{\alpha }{U}^{\mu }{U}^{\nu }{\nabla }_{(\alpha }{\stackrel{⌢}{K}}_{\mu \nu )}$$

(95)

Therefore, the condition

$$\left({\nabla }_{(\alpha }{\stackrel{⌢}{K}}_{\mu \nu )}\right)U^{\alpha }{U}^{\mu }{U}^{\nu }=0\to {\nabla }_{(\alpha }{\stackrel{⌢}{K}}_{\mu \nu )}=0$$

(96)

holds for arbitrary tangent vectors $U^{\mu }$, and it indeed follows that ${\nabla }_{(\alpha }{\stackrel{⌢}{K}}_{\mu \nu )}=0$. Therefore normalized Alena Tensor is Killing tensor for considered system.

In this way Alena Tensor theory, in curved spacetime, becomes equivalent to some specific case of General Relativity equation expressed in the following form

$${\nabla }_{(\mu }{\stackrel{⌢}{K}}_{\alpha \beta )}=0\to {\displaystyle \frac{4\pi G}{c^4}}{G}_{\alpha \beta }+\Lambda {\mathbb{k}}_{\alpha \beta }=2\Lambda {\stackrel{⌢}{K}}_{\alpha \beta }$$

(97)

where according to (19) in the above equation ${\displaystyle \frac{4\pi G}{c^4}}{G}_{\alpha \beta }$ is the classical Einstein tensor in commonly used notation ${\displaystyle \frac{4\pi G}{c^4}}{G}_{\alpha \beta }=G_{\alpha \beta }^{*}$ (classical Einstein tensor).

Thanks to the above, since the Weyl tensor is defined as the part of the Riemann tensor that does not depend on the Ricci tensor, this implies that since Killing tensor determines the Einstein tensor, and the Einstein tensor determines the Ricci tensor, then one could calculate the Weyl tensor by extracting the part of the curvature that does not contain the Ricci tensor. This would also mean that the Christoffel symbols can be expressed as a function of the Killing and Einstein tensors, and the Riemann tensor can be written directly as a function of the Ricci and Killing tensors.

For the considered system with only electromagnetism (two null vectors in metric), one may therefore construct a general Weyl tensor ansatz $C^{\mu \nu \alpha \beta }$, which must contain only components that do not become zero when the trace part is subtracted from the Riemann tensor. It should be of the form

$$C^{\mu \nu \alpha \beta }\equiv c_1{\Sigma }^{\mu \nu \alpha \beta }+c_2{P}^{\mu \nu \alpha \beta }+c_3{Q}^{\mu \nu \alpha \beta }$$

(98)

where

$$\begin{array}{ccc}\hfill {\Sigma }^{\mu \nu \alpha \beta }& =& a^{\mu }{b}^{\nu }{a}^{\alpha }{b}^{\beta }-a^{\mu }{b}^{\nu }{b}^{\alpha }{a}^{\beta }-b^{\mu }{a}^{\nu }{a}^{\alpha }{b}^{\beta }+b^{\mu }{a}^{\nu }{b}^{\alpha }{a}^{\beta }\hfill \end{array}$$

(99)

$$\begin{array}{ccc}\hfill P^{\mu \nu \alpha \beta }& =& a^{\mu }{a}^{\nu }{b}^{\alpha }{b}^{\beta }-b^{\mu }{b}^{\nu }{a}^{\alpha }{a}^{\beta }\hfill \end{array}$$

(100)

$$\begin{array}{ccc}\hfill Q^{\mu \nu \alpha \beta }& =& a^{\mu }{b}^{\nu }{\eta }^{\alpha \beta }-a^{\alpha }{b}^{\beta }{\eta }^{\mu \nu }\hfill \end{array}$$

(101)

It is easy to check that the above tensors are linearly independent and form the basis for the representation of any Weyl tensor in the system under consideration. Analysis of their behavior indicates that

• ${\Sigma }^{\mu \nu \alpha \beta }$ is responsible for "pure" directional propagation, e.g. a gravitational wave propagating along null directions (purely conformal part of the Weyl tensor, described solely by null geometry),
• $P^{\mu \nu \alpha \beta }$ describes non-radiating, "axial" deformation of space, e.g. tidal sequences, consistent with mass motion without undulations,
• $Q^{\mu \nu \alpha \beta }$ describes conformal distortion of the background metric itself.

The coefficients $c_1$, $c_2$, $c_3$ are not known a priori, but one may determine them with help of Riemann tensor. To obtain Riemann tensor $R^{\mu \nu \alpha \beta }$ in the system under consideration, it is enough to assume the following ansatz

$$\begin{array}{c}\hfill R^{\mu \nu \alpha \beta }\equiv A_1\left({\mathbb{k}}^{\mu \alpha }{\mathbb{k}}^{\nu \beta }-{\mathbb{k}}^{\mu \beta }{\mathbb{k}}^{\nu \alpha }\right)+\end{array}$$

(102)

$$\begin{array}{c}\hfill +A_2\left(\stackrel{⌢}{K^{\mu \alpha }}{\mathbb{k}}^{\nu \beta }-\stackrel{⌢}{K^{\mu \beta }}{\mathbb{k}}^{\nu \alpha }-\stackrel{⌢}{K^{\nu \alpha }}{\mathbb{k}}^{\mu \beta }+\stackrel{⌢}{K^{\nu \beta }}{\mathbb{k}}^{\mu \alpha }\right)\end{array}$$

(103)

It has the following justification

• The Riemann tensor satisfies the known algebraic symmetries: $R_{\mu \nu \alpha \beta }=-R_{\nu \mu \alpha \beta }=-R_{\mu \nu \beta \alpha },R_{\mu \nu \alpha \beta }=R_{\alpha \beta \mu \nu },R_{\mu \left[\nu \alpha \beta \right]}=0$. The above ansatz satisfies them automatically.
• There are only two tensor objects available in the system: the metric ${\mathbb{k}}_{\mu \nu }$ and the Killing tensor ${\stackrel{⌢}{K}}_{\mu \nu }=-{\displaystyle \frac{1}{c^2{\gamma }^2}}{U}_{\mu }{U}_{\nu }$. The Riemann tensor must be constructed exclusively from them.
• The first term with $A_1$ corresponds to the geometry of a spacetime with constant curvature, as in de Sitter spacetime: $R_{\left(\mathrm{constant}\mathrm{curvature}\right)}^{\mu \nu \alpha \beta }\sim {\mathbb{k}}^{\mu \alpha }{\mathbb{k}}^{\nu \beta }-{\mathbb{k}}^{\mu \beta }{\mathbb{k}}^{\nu \alpha }$
• The second term with $A_2$ is the minimal geometrically correct extension that takes into account the presence of non-null energy (represented by $\stackrel{⌢}{K^{\mu \nu }}$). Its construction provides correct symmetries and enables the reproduction of a non-null Ricci tensor $R^{\nu \beta }=R_{\mu }^{\mu \nu \beta }$
• Other possible combinations (e.g. $\stackrel{⌢}{K}\otimes \stackrel{⌢}{K}$) are linearly dependent or asymmetric with respect to the required properties of the Riemann tensor, and do not provide new information in the case under consideration.
• The whole creates the most general fourth-order tensor with Riemann symmetries, which can be constructed from available geometric objects.

Computing the contraction of the above Riemann tensor anstaz with ${\mathbb{k}}_{\mu \alpha }$ one gets

$${\mathbb{k}}_{\mu \alpha }{R}^{\mu \nu \alpha \beta }=3A_1{\mathbb{k}}^{\nu \beta }+A_2\left(2\stackrel{⌢}{K^{\nu \beta }}-{\displaystyle \frac{1}{{\gamma }^2}}{\mathbb{k}}^{\nu \beta }\right)$$

(104)

Since normalized Ricci tensor $R^{\alpha \beta }$ is known (93), therefore considering for simplicity above Riemann tensor anstaz as normalized, one gets

$$A_1={\displaystyle \frac{1}{3}}\left(1+{\displaystyle \frac{2}{{\gamma }^2}}\right);A_2=1$$

(105)

Such normalized form is convenient to use because it allows one to easily obtain both: classical tensors (multiplication by the cosmological constant $\Lambda *$) and tensors in the Alena Tensor notation (multiplication by field invariant $\Lambda$).

Next, one may consider normalized trace part of the Riemann tensor $S^{\mu \nu \alpha \beta }$, which provides the necessary symmetries and the vanishing trace in the Weyl tensor. For this to be satisfied, trace part must have the following, classical [43] form (where Ricci tensor $R^{\nu \beta }$ is considered for simplicity also as normalized):

$$\begin{array}{c}\hfill S^{\mu \nu \alpha \beta }={\displaystyle \frac{1}{2}}\left({\mathbb{k}}^{\mu \alpha }{R}^{\nu \beta }-{\mathbb{k}}^{\mu \beta }{R}^{\nu \alpha }-{\mathbb{k}}^{\nu \alpha }{R}^{\mu \beta }+{\mathbb{k}}^{\nu \beta }{R}^{\mu \alpha }\right)\end{array}$$

(106)

$$\begin{array}{c}\hfill -{\displaystyle \frac{1}{6}}R\left({\mathbb{k}}^{\mu \alpha }{\mathbb{k}}^{\nu \beta }-{\mathbb{k}}^{\mu \beta }{\mathbb{k}}^{\nu \alpha }\right)=\end{array}$$

(107)

$$\begin{array}{c}\hfill {\displaystyle \frac{1}{2}}[{\mathbb{k}}^{\mu \alpha }\left(2\stackrel{⌢}{K^{\beta \nu }}+\left(1+{\displaystyle \frac{1}{{\gamma }^2}}\right){\mathbb{k}}^{\beta \nu }\right)-{\mathbb{k}}^{\mu \beta }\left(2\stackrel{⌢}{K^{\alpha \nu }}+\left(1+{\displaystyle \frac{1}{{\gamma }^2}}\right){\mathbb{k}}^{\alpha \nu }\right)\end{array}$$

(108)

$$\begin{array}{c}\hfill -{\mathbb{k}}^{\nu \alpha }\left(2\stackrel{⌢}{K^{\beta \mu }}+\left(1+{\displaystyle \frac{1}{{\gamma }^2}}\right){\mathbb{k}}^{\beta \mu }\right)+{\mathbb{k}}^{\nu \beta }\left(2\stackrel{⌢}{K^{\alpha \mu }}+\left(1+{\displaystyle \frac{1}{{\gamma }^2}}\right){\mathbb{k}}^{\alpha \mu }\right)]\end{array}$$

(109)

$$\begin{array}{c}\hfill -{\displaystyle \frac{1}{3}}\left(2+{\displaystyle \frac{1}{{\gamma }^2}}\right)\left({\mathbb{k}}^{\mu \alpha }{\mathbb{k}}^{\nu \beta }-{\mathbb{k}}^{\mu \beta }{\mathbb{k}}^{\nu \alpha }\right)\end{array}$$

(110)

Since all terms related to $\stackrel{⌢}{K^{\mu \nu }}$ reduce after grouping the components in $C^{\mu \nu \alpha \beta }=R^{\mu \nu \alpha \beta }-S^{\mu \nu \alpha \beta }$, one obtains normalized Weyl tensor in generalized form for the system under consideration

$$\begin{array}{c}\hfill C^{\mu \nu \alpha \beta }=R^{\mu \nu \alpha \beta }-S^{\mu \nu \alpha \beta }=\end{array}$$

(111)

$$\begin{array}{c}\hfill \left(1+{\displaystyle \frac{1}{{\gamma }^2}}\right)\left({\mathbb{k}}^{\mu \alpha }{\mathbb{k}}^{\nu \beta }-{\mathbb{k}}^{\mu \beta }{\mathbb{k}}^{\nu \alpha }\right)\end{array}$$

(112)

$$\begin{array}{c}\hfill -{\displaystyle \frac{1}{2}}\left(1+{\displaystyle \frac{1}{{\gamma }^2}}\right)\left({\mathbb{k}}^{\mu \alpha }{\mathbb{k}}^{\beta \nu }-{\mathbb{k}}^{\mu \beta }{\mathbb{k}}^{\alpha \nu }+{\mathbb{k}}^{\nu \alpha }{\mathbb{k}}^{\beta \mu }-{\mathbb{k}}^{\nu \beta }{\mathbb{k}}^{\alpha \mu }\right)\end{array}$$

(113)

Trace of above Weyl tensor disappears and it has all the expected symmetries. Substituting the metric known from (79), one obtains the coefficients postulated in the anstaz (98) and as one may notice from non-zero coefficient $c_1$, gravitational waves exist in the system.

$$\begin{array}{ccc}\hfill c_1& =& \left(1+{\displaystyle \frac{1}{{\gamma }^2}}\right){\displaystyle \frac{I_o^2}{8}}{e}^{-2q}\hfill \end{array}$$

(114)

$$\begin{array}{ccc}\hfill c_2& =& \left(1+{\displaystyle \frac{1}{{\gamma }^2}}\right){\displaystyle \frac{I_o^2}{4}}{e}^{-2q}sinh\left(2\theta -2\phi \right)\hfill \end{array}$$

(115)

$$\begin{array}{ccc}\hfill c_3& =& \left(1+{\displaystyle \frac{1}{{\gamma }^2}}\right){\displaystyle \frac{I_o}{\sqrt{2}}}{e}^{-2q}sinh\left(\theta -\phi \right)\hfill \end{array}$$

(116)

One can also demonstrate the existence of gravitational waves using classical analysis using the Weyl tensor components and Newman-Penrose formalism [44]. Having calculated the above-mentioned tensors and sample basis (78), one may notice, that four-vector $a^{\mu }\left(\sigma \right)$ is purely real. One may thus construct a Newman-Penrose tetrad around it, fitting to the geometry of the system, as follows

$$\begin{array}{ccc}\hfill l^{\mu }& \equiv & a^{\mu }\left(\sigma \right)\hfill \end{array}$$

(117)

$$\begin{array}{ccc}\hfill n^{\mu }& \equiv & {\displaystyle \frac{1-sin\sigma }{{cos}^2\sigma }}\left(1,1,0,0\right)\hfill \end{array}$$

(118)

$$\begin{array}{ccc}\hfill m^{\mu }& \equiv & {\displaystyle \frac{1}{\sqrt{2}\left(cos\frac{\sigma }{2}+sin\frac{\sigma }{2}\right)}}\left(-{\displaystyle \frac{icos\sigma }{1+sin\sigma }},-{\displaystyle \frac{icos\sigma }{1+sin\sigma }},-i,1\right)\hfill \end{array}$$

(119)

$$\begin{array}{ccc}\hfill {\overline{m}}^{\mu }& \equiv & {\displaystyle \frac{cos\frac{\sigma }{2}+sin\frac{\sigma }{2}}{\sqrt{2}}}\left({\displaystyle \frac{icos\sigma }{1+sin\sigma }},{\displaystyle \frac{icos\sigma }{1+sin\sigma }},i,1\right)\hfill \end{array}$$

(120)

The above four-vectors satisfy all the tetrad requirements and lead to only two non-zero NP scalars

$$\begin{array}{ccc}\hfill {\Psi }_3& =& 8C_1\left[(i\sqrt{2}-1)sin\left({\displaystyle \frac{\sigma }{2}}\right)-(i\sqrt{2}+1)cos\left({\displaystyle \frac{\sigma }{2}}\right)\right]\hfill \end{array}$$

(121)

$$\begin{array}{ccc}\hfill {\Psi }_4& =& 4C_1\left[1-2i\sqrt{2}cos\left(\sigma \right)-3sin\left(\sigma \right)\right]\hfill \end{array}$$

(122)

what is confirmed in the supplementary materials. Scalar ${\Psi }_3$ can be zeroed by a rotation around $n^{\mu }$ without modifying ${\Psi }_4$ and the system under consideration with sample $a^{\mu }\left(\sigma \right),b^{\mu }\left(\sigma \right)$ is thus Petrov type III or N. However, taking into account the non-zero Ricci tensor and the Bel criteria, considered spacetime must be Petrov type III, since due $C^{\mu \nu \alpha \beta }$ is built from reversible metric (111), thus there does not exist any vector ${\xi }_{\beta }$ satisfying $C^{\mu \nu \alpha \beta }{\xi }_{\beta }=0$.

Therefore, finally, spacetime described by Alena Tensor with only electromagnetic field may be interpreted as a certain form of the Kundt solution with dust [45] and for sample $a^{\mu }\left(\sigma \right),b^{\mu }\left(\sigma \right)$ it is Petrov type III, similar to described in [46,47]. One may also notice, that additional fields added to the Alena Tensor depending on the new null directions should break the obtained degeneracy leading to the general Petrov type I case.

One may also substitute an example basis (78) into Weyl tensor to analyze its values. Table 1 presents the values of the key components of the Weyl tensor in this basis.

Table 1. Component values of the Weyl tensor.

Component	Value
$C^{0212}$	${\displaystyle \frac{i(16C_1-5C_2)cos\left(\sigma \right)-7i{C}_{2}cos\left(3\sigma \right)}{\sqrt{2}}}+8C_{1}sin\left(\sigma \right)-20C_2{cos}^2\sigma sin\left(\sigma \right)$
$C^{1313}$	0
$C^{0202}$	$4C_1\left(1+3cos\left(2\sigma \right)-2i\sqrt{2}sin\left(2\sigma \right)\right)$
$C^{1010}$	$4C_1\left(1-3cos\left(2\sigma \right)+2i\sqrt{2}sin\left(2\sigma \right)\right)$
$C^{2323}$	0
$C^{1213}$	0
$C^{1323}$	0

Table 1. Component values of the Weyl tensor.

Component	Value
$C^{0212}$	${\displaystyle \frac{i(16C_1-5C_2)cos\left(\sigma \right)-7i{C}_{2}cos\left(3\sigma \right)}{\sqrt{2}}}+8C_{1}sin\left(\sigma \right)-20C_2{cos}^2\sigma sin\left(\sigma \right)$
$C^{1313}$	0
$C^{0202}$	$4C_1\left(1+3cos\left(2\sigma \right)-2i\sqrt{2}sin\left(2\sigma \right)\right)$
$C^{1010}$	$4C_1\left(1-3cos\left(2\sigma \right)+2i\sqrt{2}sin\left(2\sigma \right)\right)$
$C^{2323}$	0
$C^{1213}$	0
$C^{1323}$	0

One may then solve the system of equations (59, 77, 86) presenting the results only as a function of $I_o$ and $\sigma$. Due to the complex relationships between variables, analytical solution and obtained results are presented in supplementary file. Weyl tensor component values were calculated for the value $I_o=\sqrt{1+{\displaystyle \frac{1}{\sqrt{2}}}}$ adopted for the analysis (87) and for chosen solution $\phi \left(I_o\right),\theta \left(I_o\right)$. The Figure 2 below clearly shows the wave nature of the $C^{0212}$ component of the Weyl tensor, presenting the result of the calculations performed. Obtained Weyl tensor component $C^{0212}$ seems to encode the variation of some curvature field along the propagating direction $\sigma$.

Gravitational waves are often modeled using Gaussian impulse as in [48], but this can also be done using the dependence of ${\Psi }_4$ on $\sigma$. One may therefore show in Figure 3 the deformation effects for an example arrangement of test particles on a circle. In the supplementary materials there are calculations and a gif file presenting animation of this distortion. This animation reveals the typical quadrupolar nature of spacetime distortions induced by gravitational waves (characteristic twisting and stretching).

The above Weyl tensor components are actually normalized. One may thus present the main GR equation in the Alena Tensor notation (19) and represent it using the vacuum pressure $2p_{\Lambda }\equiv {\displaystyle \frac{\Lambda c^4}{4\pi G}}=\Lambda$ as follows

$$G^{\alpha \beta }+2p_{\Lambda }{\mathbb{k}}^{\alpha \beta }=2T^{\alpha \beta }=2\Lambda \stackrel{⌢}{K^{\alpha \beta }}=4p_{\Lambda }\stackrel{⌢}{K^{\alpha \beta }}$$

(123)

Since the obtained Weyl tensor is normalized (by $\Lambda$) this means that the interpretation from (42) that gravitational waves in the Alena Tensor approach are in fact propagating vacuum pressure disturbances also seems to be correct.

It is also worth noting that the obtained metric term $e^{-q}{\eta }^{\alpha \beta }={\displaystyle \frac{\mathbb{k}}{4}}{\eta }^{\alpha \beta }$ can in principle be interpreted as a vacuum energy contribution (effective cosmological constant) as in [49,50] playing the role of a metric scaling factor, as e.g. described in [51].

Additionally, one may invoke the scalar field $\varphi$ associated with the presence of matter, where $e^{\varphi }={\displaystyle \frac{1}{{\mu }_r}}$. It is known from 2.2 that $e^{\varphi }$ is responsible for the presence of sources and in their absence ${\mu }_r=1$. Therefore, interpreting whole ${{\rm Y}}^{\alpha \beta }$ as the wave amplitude tensor one would get representation ${\displaystyle \frac{1}{{\mu }_r}}{{\rm Y}}^{\alpha \beta }={\mathcal{P}}_o{\overline{h}}^{\alpha \beta }{e}^{\varphi }$ which would also allow to search for $e^{\varphi }$ as a certain wave function.

This approach allows for two simplifications related to the analysis of gravitational waves. Considering the force $f_{gr}^{\alpha }$ responsible for effects related to gravity as shown in (24) and extracting the acceleration ${\mathcal{A}}^{\alpha }$ from it, one gets

$$\varrho {\mathcal{A}}^{\alpha }\equiv f_{gr}^{\alpha }=\varrho \left({\displaystyle \frac{d\varphi }{d\tau }}{U}^{\alpha }-c^2{\partial }^{\alpha }\varphi \right)\to c^2\square \varphi ={\gamma }^2{\displaystyle \frac{d^2\varphi }{d{t}^2}}-{\partial }_{\alpha }{\mathcal{A}}^{\alpha }$$

(124)

since according amendment from [11] ${\partial }_{\alpha }\gamma U^{\alpha }=0$.

As shown in [10], $\varphi$ is directly related to the effective potential in gravitational systems which can be calculated from the GR equations. This would allow searching for propagating changes of the effective potential itself ($\square \varphi =0$) similarly as was postulated in [52]. It would significantly simplify both the calculations and perhaps the methods of detecting gravitational waves, for example, using the approach discussed in [53].

One can for example consider the dispersion of gravitational waves using the postulated relationship between gravitational potential and $\gamma$ given in simplification as

$$e^{\varphi }=1-{\displaystyle \frac{\gamma }{n}}\to \varphi =ln\left(1-{\displaystyle \frac{\gamma }{n}}\right)$$

(125)

where in analysis for particular gravitational system n may be assumed as constant and $\gamma$ depends on the four positions. Assuming a wave solution $\varphi \equiv \Theta e^{i(\overrightarrow{k}\overrightarrow{x}-\omega t)}$ one obtains the dispersion relation

$${\omega }^2={\displaystyle \frac{c^2}{1+{\gamma }^2}}\left(k^2-{\displaystyle \frac{1}{c^2\varphi }}{\partial }_{\alpha }{\mathcal{A}}^{\alpha }\right)$$

(126)

The relationship $\gamma \left(x^{\mu }\right)$ means that $\omega \left(k\right)$ is a function of position and can lead to local dispersion $\omega =\omega (k;x^{\mu })$. The lack of dispersion therefore forces the source (four-acceleration four-divergence) to adjust itself to maintain wave propagation at the same wave speed for all frequencies

$${\partial }_{\alpha }{\mathcal{A}}^{\alpha }=\left[c^2-(1+{\gamma }^2)v_{wave}^2\right]k^2\varphi$$

(127)

which acts as a kind of geometric compensation and for $v_{wave}=c$ it simplifies to ${\partial }_{\alpha }{\mathcal{A}}^{\alpha }=-{\gamma }^2{c}^2{k}^2\varphi$.

Other solutions would affect

• the local phase and group velocity of the wave: $v_{ph},v_{gr}$,
• the amplitude and time course of $\varphi \left(t\right)$,
• possible distortion of the wave shape (blurring, flattening, dispersion tail).

The $\varphi$ function therefore acts as a carrier of dynamic information about the gravitational wave, its amplitude, phase, and local course.

The last possible simplification results from the possibility of analyzing only the Poynting four-vector ${{\rm Y}}^{\alpha 0}$ as ${\displaystyle \frac{1}{{\mu }_r}}{{\rm Y}}^{\alpha 0}={\mathcal{P}}_o{\overline{h}}^{\alpha 0}{e}^{\varphi }$ which might also help simplify the calculations and search for experimental proof for the Alena Tensor approach.

4. Conclusion and Discussion

As shown in the above article, the Alena Tensor ensures the existence of gravitational waves and allows their physical interpretation, providing key tools for their further analysis including the ability to calculate and visualize Weyl tensor components. The obtained decomposition of the electromagnetic field stress-energy tensor (79) allows for further analysis of metrics for curved spacetimes (e.g. extending obtained solution for other fields) and also to use the proposed null basis for further Alena Tensor development in the framework of conformal geometry, the NP formalism and the description of photons in QFT. It also seems reasonable to generalize above results for all known fields or to non-linear electromagnetism (using e.g. approach presented in [54]) and search for a description of elementary particles that could provide relatively stable solutions to the obtained equations, perhaps also taking into account new approaches, such as those proposed in [55].

A discussion of the main conclusions of the article is grouped into three key sections below.

4.1. Conclusions About GR and Gravitational Waves

As this article clearly shows, Alena Tensor narrows the class of available GR solutions. In this mathematical framework

• The cosmological constant is indeed constant in curved spacetime.
• The energy-momentum tensor of the system in curved spacetime becomes the Killing tensor.
• The available metrics take on a specific form (2+ null vectors and a background metric). Although the paper presents the metric only for a system with electromagnetism and gravity, the Alena Tensor model enforces this metric arrangement in general case.
• The resulting Riemann tensor describes the general case, ensures the formation of the Ricci tensor in contraction, and allows for the derivation of the Weyl tensor.

It is worth noting that the obtained non-zero form of the Weyl tensor $C^{\mu \nu \alpha \beta }$ (111) built on the basis of the metric tensor ${\mathbb{k}}^{\mu \nu }$ used for curvilinear description, given as $C^{\mu \nu \alpha \beta }=\left(1+{\displaystyle \frac{1}{{\gamma }^2}}\right)\left[{\mathbb{k}}^{\mu [\alpha }{\mathbb{k}}^{\nu \beta ]}-{\displaystyle \frac{1}{2}}\left({\mathbb{k}}^{\mu [\alpha }{\mathbb{k}}^{\beta ]\nu }+{\mathbb{k}}^{\nu [\alpha }{\mathbb{k}}^{\beta ]\mu }\right)\right]$ will not change regardless of the fields considered and no matter how many null vectors the metric consists of (assuming more complex fields than electromagnetism). This Weyl tensor has also an important property: for any tetrad considered in curved spacetime, all NP scalars become zero, and they remain non-zero only for tetrads constructed on the background Minkowski metric. This means that gravitational waves derived from Alena Tensor are undetectable for curvilinear observers in their local frame of reference and can be detected only against the background of the Minkowski metric. Therefore, according to the postulate (41), gravitational waves are not "local fluctuations" of curvature but global effects of the difference of geometry with respect to a flat background, similar to postulated in [56,57]. This result has a rather intuitive interpretation and means that, according to the equivalence principle, observers in curved spacetime do not experience gravity in any form, including gravitational waves, because their tetrad "co-curves" with the geometry.

The obtained form of the Weyl tensor can thus be treated as a formal geometry of the equivalence principle and as a requirement for every physically possible solution of GR, which would, however, require a separate proof. This direction of further research also seems very important, because it would provide a formal justification for the fact that the measurability of gravity is relational, not absolute, and also offers a new way of considering quantum gravity: not so much as field fluctuations, but as fluctuations of the geometric background with respect to the algebraically defined Weyl tensor. This result is of particular importance e.g. in the context of Penrose’s Weyl curvature hypothesis [58], developed in e.g. [59,60]. The discussion about what gravity is [61] remains open, and Alena Tensor joins this discussion.

The connection between Alena Tensor and the Killing tensor obtained in this paper reveals a deep, nonlinear connection between the matter distribution and the geometry and symmetries of spacetime. These results show that the matter distribution in this approach is not arbitrary, but precisely tuned to the geometry and hidden symmetries of spacetime, which allows for their further analysis in the language of Killing tensors and conformal Weyl curvature. This also explains why in flat spacetime $T^{\alpha \beta }$ is Noether tensor and in curved spacetime, tensor $T^{\alpha \beta }$ turns into the Killing tensor, requesting, that translational symmetries in ${\eta }^{\alpha \beta }$ turn into isometries of Killing vectors in ${\mathbb{k}}^{\alpha \beta }$.

The obtained results regarding gravitational waves are qualitative in nature, as it is difficult to provide quantitative experimental verification for sources understood as a consequence of the existence of an electromagnetic field alone. The Alena Tensor model, unlike other models, links the GR results to the fields under consideration, treating matter solely as a consequence of the fields’ existence. This requires extending the model to all gauge fields to make realistic predictions, since generalization of the Alena Tensor to other fields (e.g. electroweak) may correct some results, providing the possibility of experimental verification of the predictions for more realistic sources. However, certain conclusions can be drawn that may allow experimental verification of the obtained results.

The obtained picture of Kundt spacetime with dust would suggest, that in gravitational waves for sources that can be treated simplistically as the result of the existence of an electromagnetic field alone, one should be able to observe effects related to non-zero ${\Psi }_3$ (visible twisted components). The obtained x and + polarizations resulting from the Weyl tensor values (121) are consistent with the general conclusions of GR and LIGO Virgo data [62]. Because the waveform depends strictly on the source dynamics, it cannot be analyzed without additional assumptions about the sources introduced into the metric. This does not seem possible for such simplified sources as those discussed here and requires generalization of the Alena Tensor to other gauge fields.

The dispersions of gravitational waves was discussed in the description of the equation (125). Since the Alena Tensor allows for an equivalent description of gravity in curved (GR) and flat spacetime (a four-force based on gravitational potential $\varphi$ ensuring compliance with the equivalence principle) one may simplify calculations. It appears, that gravitational waves propagating without dispersion with the velocity $v_{wave}=c$ require that the system satisfies the relation

$${\partial }_{\alpha }{\mathcal{A}}^{\alpha }=-{\gamma }^2{c}^2{k}^2\varphi$$

(128)

where ${\partial }_{\alpha }{\mathcal{A}}^{\alpha }$ is the four-divergence of the acceleration related to gravitational source. If the above equation is not satisfied (the source does not provide geometric compensation) then other wave velocities and dispersions are possible. It also shows that $\varphi$ acts as a carrier of dynamic information about the gravitational wave, its amplitude, phase, and local course.

4.2. Possible Directions of Further Unification

As discussed in Section 2.3, the Alena Tensor could be generalized to all gauge fields, but this requires further research. The research on gravity and electromagnetism carried out in this article according to the approach of Alena Tensor shows that, surprisingly, it naturally forces the existence of the Higgs-like potential and this potential turns out to be necessary to even consider curved spacetime. The spontaneously appearing faithful reproduction of the Higgs potential may of course be a completely coincidental result, but it may also be an indication that the proposed approach is worth further investigation and development for other fields (electroweak, strong or more general solutions), to obtain complete picture of unification.

This direction of research seems to be particularly important. For example, the unification of gravity with electroweak interactions has been analyzed so far, among others, in the context of symmetry breaking and gauge geometry [63,64], through the prism of the influence of gravity on the global properties of quantum vacuum [65,66], analogies between spin-gravity coupling and the Higgs mechanism [67] or analysis of chiral fermions and CPT symmetry in the presence of curvature [68,69]. It seems that the approach considered in the article best fits into the last of these research directions, due to the possibility of analyzing the structure of the Weyl curvature, the potential asymmetry of gravitational waves (related to ${\Psi }_3$) and because it actually touches upon chirality in the spatial and propagation sense, although not directly in the fermion sense.

An equally interesting research direction seems to be the use of the smooth transition between classical, quantum and curvilinear descriptions provided by the Alena Tensor to reanalyze existing studies, such as [70].

4.3. Conclusions on Energy Conservation in Energy-Momentum Tensors

It is also worth raising the issue of the energy conservation in the Alena Tensor. As it follows from chapter 2, this approach ensures local conservation of energy and momentum, because the four-divergence of the tensor describing matter cancels the four-divergence of the field tensors. Additionally, for electromagnetism, the Alena Tensor turned out to be a symmetric, canonical Noether tensor with vanishing four-divergence. A similar result can be expected after extending the Alena Tensor to all gauge fields, because this approach provides a conclusion, that the cosmological constant is actually constant, which strengthens the argument for conservation of energy. Although, obviously, another scenario should also be considered, especially in the context of the dark sector.

It was e.g. shown in [71] that violating conservation of energy can generate effects corresponding to dark energy, making such approaches attractive for cosmology. Similarly, in scalar-tensor theories in the Einstein framework [72], the coupling of the dilaton to matter causes energy not to be conserved locally, justifying a reinterpretation of the field as effective. Also approaches based on non-commutative structures, such as [73], introduce non-classical position operators, which result in four-momentum fluctuations and energy can transfer between geometric dimensions, formally manifested as a nonzero divergence of the energy-momentum tensor.

As shown in [74], many nonconservative theories rely on geometric coupling, e.g., $f(R,T)$ or a modified metric structure, resulting in ${\nabla }_{\mu }{T}^{\mu \nu }\ne 0$. In particular, Rastall theory [75,76] introduces a dependence of the four-divergence on the gradient of the Ricci scalar ${\nabla }_{\mu }{T}^{\mu \nu }=\lambda {\nabla }^{\nu }R$, resulting in effective energy creation or annihilation depending on the local curvature. This approach enables flexible modeling of dark energy and dark matter, and therefore provides a better fit to cosmological data. Violating the energy conservation principle while maintaining the metric, modifies the behavior of matter, but does not generate causality violations and ensures formal convergence with effective and entropy theories.

In diffusion models [77], the ${\nabla }_{\mu }{T}^{\mu \nu }\ne 0$ describe entropy fluctuations, enabling consideration of thermodynamic mechanisms of energy flow. Similar mechanisms occur in wave collapse theories in quantum mechanics [78], where random perturbations to the system’s state lead to a constant exchange of energy with the background. Thanks to such approach, violation of local conservation of energy and momentum is not an artifact of a flawed theory, but a deliberate extension of the classical framework, leading to new conclusions about the nature of energy, gravity, and cosmological evolution.

In [79] a wide class of modified gravity theories is discussed, including scalar-tensor or $f(R,T)$ theories, where additional geometric components coupled to matter appear. In many models, the matter divergence is locally nonzero, but by influencing the metric it is possible to conserve some form of global energy in an effective sense, and global boundary conditions (e.g., asymptotic flatness) determine whether a total conserved energy can be defined. E.g., the model described in [80] is based on the general relativistic thermodynamics equation (Gibbs–Duhem) and allows for fluctuations in entropy, temperature, and interactions. The lack of local conservation thus translates into a global impact: thermodynamic actions can model dark energy and the expansion of the Universe. An important consequence is that total energy is not conserved globally, which has key cosmological implications, e.g., extending the age of the Universe through non-conservative dynamics.

Also in the context of unimodular gravity, the authors show that a local violation of a conservation law, even a very small one, can generate the effect of an effective cosmological constant. If energy is not conserved locally, a global effect (e.g., a positive accelerating influence) can be interpreted as a source of dark energy, directly linking local divergence to global cosmological observations.

In light of the above review, in addition to generalizing to other fields, it is worth considering a potential modifications of the Alena Tensor, adapting it to non-conserved energy-momentum frameworks. This would open up additional possibilities for analyzing non-classical solutions and new directions of reasoning contained in these publications, which could also increase the unification potential of the Alena Tensor.

In conclusion, it remains an open question whether the Alena Tensor is a correct way to describe physical systems, but this paper shows that it exhibits many properties that are expected from such a description, including the existence of gravitational waves whose behavior and description agrees with GR. The author hopes that the results obtained in this article will facilitate further use of discussed approach as a tool that can help develop many different concepts. It seems that its further analysis may provide useful descriptions of the transformation between curved and flat spacetime and bring new insights that will contribute to a better understanding of issues related to the broadly understood unification of physical theories.

5. Statements

All data that support the findings of this study are included within the article (and any supplementary files).

During the preparation of this work the author did not use generative AI or AI-assisted technologies.

Author did not receive support from any organization for the submitted work.

Author have no relevant financial or non-financial interests to disclose.