1. Introduction
In recent years, Permanent Magnet Synchronous Motor (PMSM) has attracted extensive attention [
1] and application in fields such as household appliances, new energy vehicles [
2,
3], and industrial machinery [
4,
5,
6,
7] due to its excellent characteristics like high power density, high efficiency, and wide speed regulation range. The high-performance control of the PMSM is particularly important. To achieve high-performance PMSM servo control systems, to facilitate high-precision torque, speed, and position control, it is necessary to obtain accurate key parameters such as stator resistance,
dq-axis inductance, permanent magnet flux linkage, moment of inertia, viscous damping coefficient, and Coulomb friction, for designing excellent controllers [
8,
9]. Controllers commonly used in engineering, whether it is proportional-integral (PI) controller or modern controllers derived from modern control theory, all rely on motor parameters. For example, the design of the current loop controller parameters is directly related to resistance and inductance [
10], the parameters of the speed loop and position loop controllers are directly related to the mechanical parameters and permanent magnet flux linkage [
11,
12,
13]. The controller under parameter mismatch will cause the system response to be slower or larger overshoot, and due to the strong non-linearity friction torque when the speed crosses zero, the system will exhibit low-speed “creep” phenomenon. All of the above will greatly affect the control performance and tracking performance of the permanent magnet servo control system. Therefore, the study on parameter identification of PMSM is of significant importance for improving its control performance and meeting the demands in various fields [
14].
Regarding the electrical parameters of PMSM, they can be mainly divided into offline identification and online identification. The offline electrical parameter identification methods mainly include finite element analysis and experimental measurement, in which the finite element analysis mainly used for motor design, but the influence of processing technology, etc., will bring some errors. The experimental measurement method can measure the current motor parameters accurately, but it is not conducive to the accurate identification of motor parameters under various operating conditions. Online electrical parameter identification methods mainly include recursive least squares method [
15], model reference adaptive, extended Kalman filter, affine projection algorithm [
16] and intelligent algorithms, etc. Recursive Least Square (RLS), due to its simple principle and easy to implement, is widely used in parameter identification. The accuracy of the model reference adaptive algorithm depends on the model accuracy and adaptation rate. However, when the identified parameters are many, the design of the adaptation rate is difficult. The extended Kalman filter, can suppress noise interference, but when the identified parameters are many, the computation is large. Affine projection algorithm, the computation is less than RLS, but the convergence speed is slower than RLS. Intelligent algorithms used in parameter identification mainly include particle swarm optimization algorithm [
17] and neural network [
18], their convergence speeds are fast, but the computation is large.
For the mechanical parameter identification of PMSM, similarly, they are mainly divided into offline identification [
19,
20,
21,
22] and online identification [
23,
24]. Offline mechanical parameter identification algorithm does not need to consider whether the application scenario is limited, and more researches exist. It mainly includes signal injection method [
19,
20], extended state observer method [
21], and sliding mode observer method [
22], etc. In signal injection methods, Papers [
19,
20] utilize the orthogonality of the cosine function and the symmetry of friction torque about speed, integrate the mechanical equation within a specific semi-period range of triangular function, and identify the system’s moment of inertia, viscous damping coefficient and Coulomb friction coefficient. However, the above methods all involve the integration of force to position, that is, parameter identification results depend on the tracking effect of the predetermined position trajectory. The operation of the algorithm needs real-time adjustment of the speed controller parameters, improving speed trajectory tracking effect, to enhance the identification accuracy. This leads to a long identification time, complicated algorithm implementation. Paper [
20] identifies the three mechanical parameters without using a speed loop, by injecting a linearly increasing current to stimulate the system, comparing the actual rotor speed response and theoretical response, obtaining the moment of inertia and the Coulomb friction coefficient. According to the natural decay situation of the speed, the viscous damping coefficient can be obtained. Due to the rank deficient problem, two successive current stimuli are needed in the identification process, and the algorithm implementation is complicated; the implementation of this scheme requires the storage of speed response data, and the algorithm occupies a large storage space. Paper [
21] designs an extended state observer, based on the Lyapunov stability theory to tune the observer parameters, and excites the system with a forward sine speed, obtaining more accurate identification results. But the algorithm control logic is complex, and calculation is large. Paper [
22] applies a parallel sliding mode observer network to identify the three mechanical parameters of the servo system, and obtains good identification results under square wave speed excitation. Paper [
25] points out that the excitatory effect of the high-order sliding mode algorithm on the unmodeled states of the system is significant, affecting the normal operation of the system and producing considerable negative impacts on the identification results. Papers [
19,
20] and [
21,
22] all involve speed loop control; on the premise of no prior information about the moment of inertia, the initial convergence situation and identification effect of the algorithm are not good. Online mechanical parameter identification algorithms usually need to adopt position control mode, they are restricted by the application scenario, and specific identification algorithms need to be designed for online identification. Paper [
23], based on the traditional fixed-period integral moment of inertia identification method, proposed a variable-period moment of inertia identification method, overcoming the problems of poor identification results under irregular and slowly changing speed. However, this algorithm requires more zero-crossing speed cases, limiting the scope of application. Paper [
24] addresses the problem of large range changes in system moment of inertia affecting normal system operation by treating the torque change caused by moment of inertia change equivalent to load torque disturbance, and effective suppression is achieved by designing a two-degree-of-freedom speed controller, obtaining excellent experimental results. Both Papers [
23,
24] did not carry out identification of friction coefficients such as viscous damping coefficient and Coulomb friction coefficient, which is not conducive to zero and low-speed operation of the system.
This article proposes a complete parameter identification algorithm based on signal injection for PMSM. Injecting a single high frequency voltage excitation, not using Fast Fourier Transform (FFT), but adopting a novel function amplitude and frequency extraction algorithm to acquire resistance and dq-axis inductance parameters. Based on the results of electrical parameter identification, a current loop is designed, and a constant current excitation is applied to the system. According to the electromechanical torque and speed response, the system’s three mechanical parameters and magnetic linkage parameters can be obtained. The identification precision of this complete parameter identification algorithm is independent of the system’s response to any particular signal. The algorithm is simple, effective, easy to implement, and requires a small amount of microcontroller memory. Both simulation results and experimental results have validated the scientific and validity of the proposed algorithm.
2. Mathematical Model of PMSM
Neglecting the eddy current loss and hysteresis loss of the PMSM, assuming that the excitation magnetic field generated by the permanent magnet and the armature reaction magnetic field generated by the stator winding are uniformly distributed in the air gap, then the voltage equation of the PMSM in the synchronous rotating d-q coordinate system is:
ud and
uq are the voltage components of the motor on the d and q axes, respectively;
id and
iq are the current components of the motor on the
d and
q axes, respectively;
p is the differentiation operator;
Rs is the resistance of the motor’s stator winding;
Ld and
Lq are
dq axis inductance;
ωe is the angular velocity of the motor;
ψf is the magnetic flux linkage of the motor rotor’s permanent magnet.
The electromagnetic torque equation and mechanical motion equation of PMSM are as below.
where,
Te represents electromagnetic torque;
pn is the pole pairs number;
ωm is the mechanical angular velocity of the motor;
J,
Bm,
Cm are respectively the moment of inertia, viscous damping coefficient and Coulomb friction coefficient of the servo system;
TL is the load torque of the servo system. Considering the significant role of permanent magnet flux linkage
ψf in the electro-mechanical energy conversion of PMSM, this paper will present parameter identification related to
ψf in the mechanical parameters identification algorithm.
4. Mechanical Parameter Identification Algorithm Based on Constant Current Excitation
To avoid the dependence of the mechanical parameter identification algorithm on the speed loop, and thus on the selection of the prior value of the system rotational inertia. This paper will present a mechanical parameter identification algorithm based on a constant current excitation, which can not only identify the rotational inertia, viscous damping coefficient, and Coulomb friction coefficient, but also obtain the magnitude of the permanent magnet flux linkage parameters. The algorithm is simple, efficient, and easy to implement, and the entire algorithm execution time does not exceed 3 seconds to complete.
Under no-load conditions in PMSM drive system, that is, the load torque
TL = 0. Based on the results of electrical parameter identification in the previous section, the parameter tuning of the current loop PI controller can be realized.
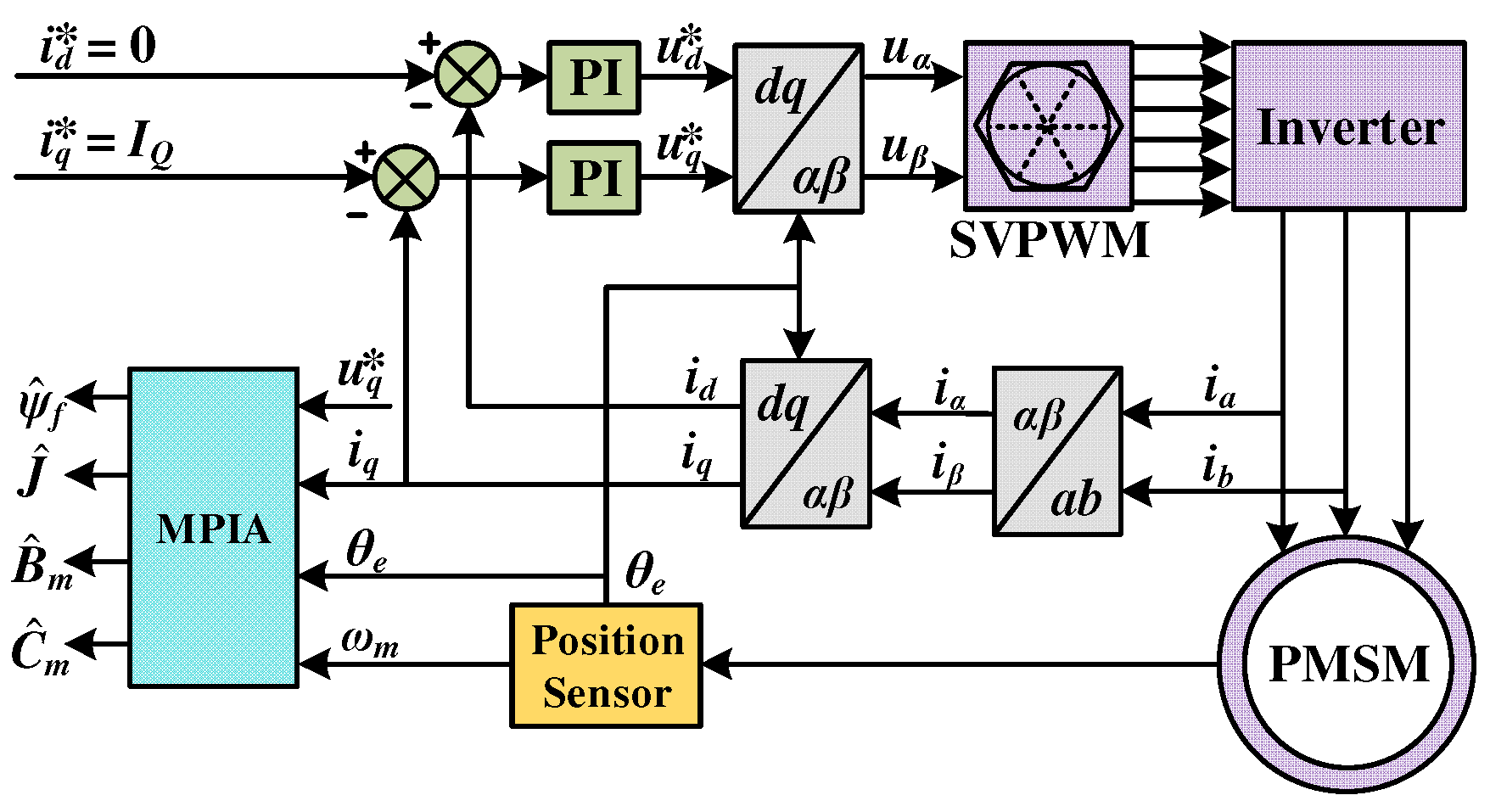
Figure 2 shows the control block diagram of the system’s mechanical parameter identification algorithm. The following current excitation is applied to the system.
where
and
represent current excitation signals;
IQ is the constant value stimulating the PMSM drive system. To fully stimulate the system, this paper sets
IQ as the rated current
IN, but it is important to note that this is not a prerequisite condition.
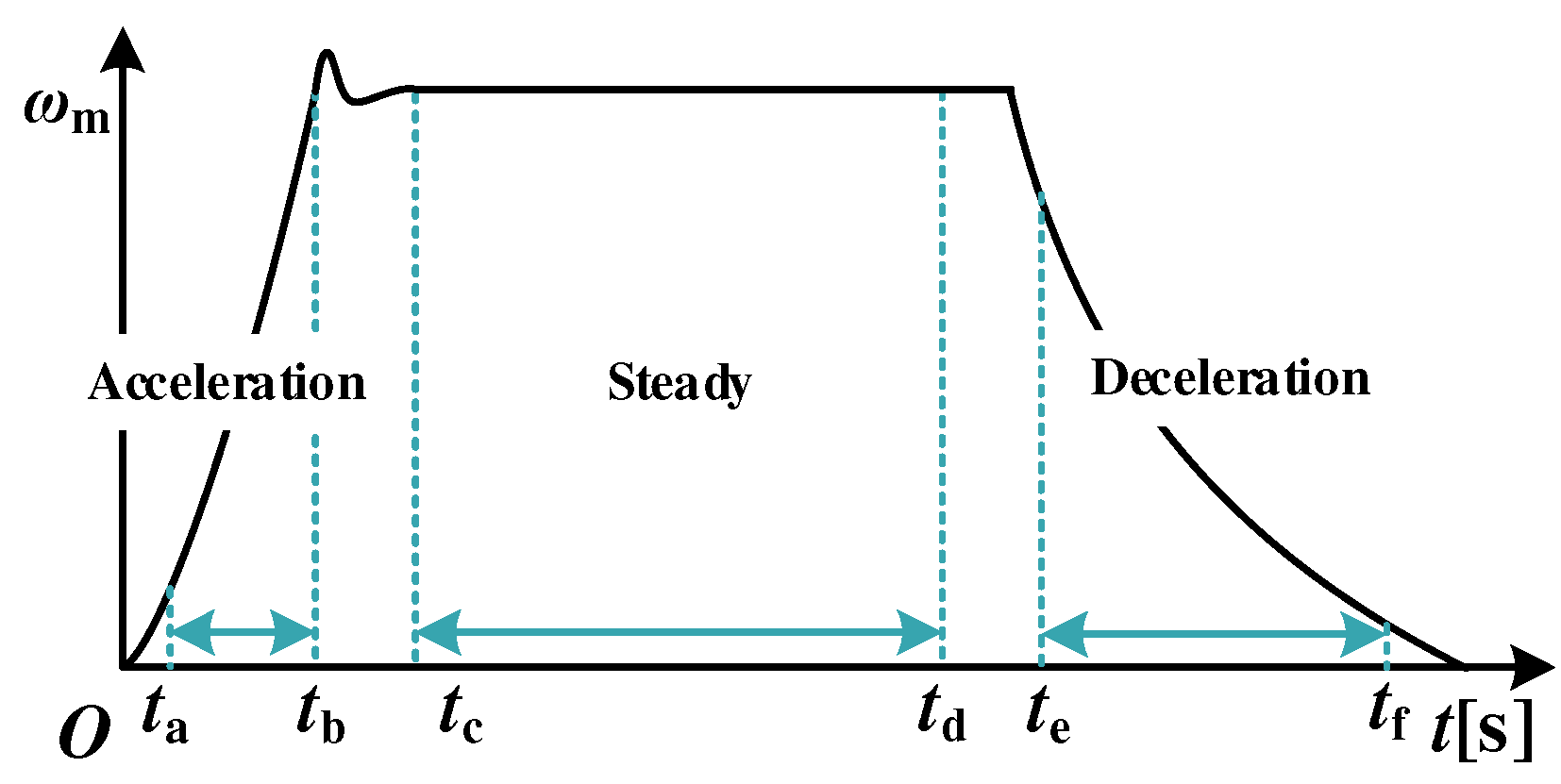
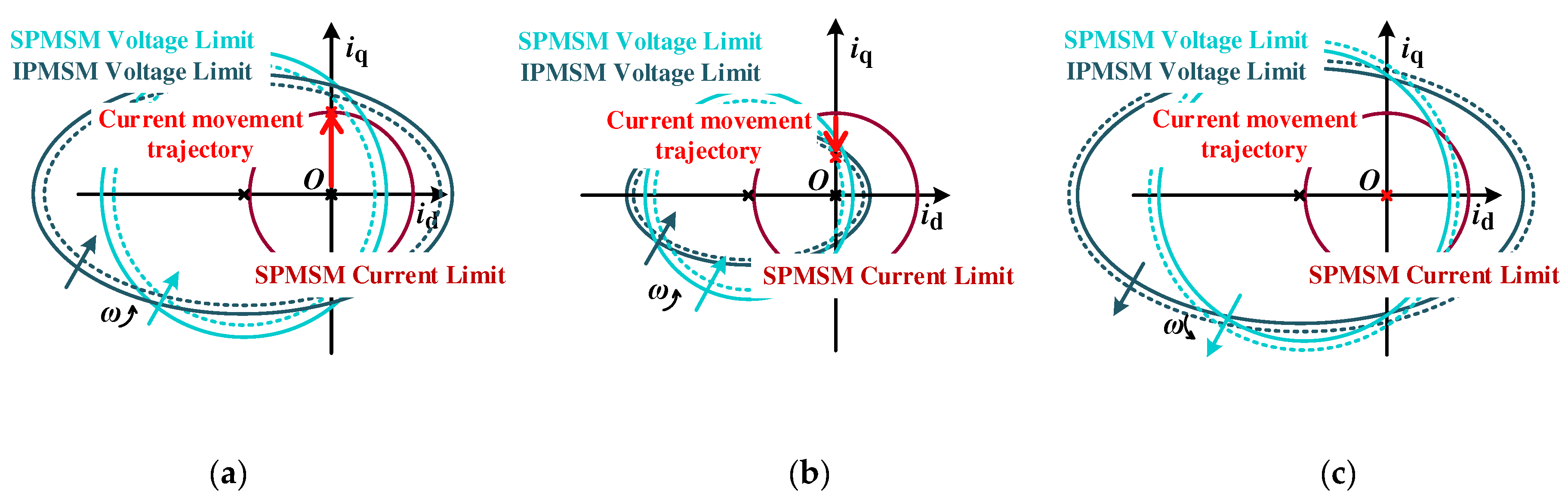
The whole identification process includes three stages: the acceleration stage, constant speed stage, and deceleration stage. In the acceleration phase, the current PI of the drive system will quickly reach the limit value, and the rotor will start to accelerate in rotation. Then, as the speed increases, the voltage limit circle begins to shrink, and the actual q-axis current will decrease accordingly until the electromagnetic torque is exactly equal to the friction torque, and the system speed remains stable, which is the constant speed stage. After maintaining a brief constant speed operation, the inverter six switches are immediately forced off, and due to the PMSM losing power, the rotor naturally decelerates to zero, which is known as the deceleration stage.
Figure 3 provides a schematic diagram of the rotor’s speed response in these three stages, and
Figure 4 provides a schematic diagram of the voltage and current limit circles and the current working point changes during different stages of the mechanical parameter identification algorithm.
During the steady-state operation process and considering that the system adopts the
id = 0 control strategy, the q-axis voltage equation of the system is as follows.
Considering the noise pollution in the drive system, this paper uses an integral operator to identify the magnetic linkage of the permanent magnet, with the identification values as follows.
Integrating the mechanical equation (3) of the PMSM drive system over the time [
t1,
t2], we can obtain
From the above analysis, it can be concluded that if the system rotational speed is always positive, then
Among them,
ωm(
t)
=
ωm (
t2)-
ωm (
t1),
θm(
t)
=
θm (
t2)-
θm (
t1),
t=
t2-
t1. According to the acceleration phase (
ta,
tb), the uniform speed phase (
tc,
td) and the deceleration phase (
te,
tf), these three phases, combined with equation (26), it can be concluded.
The mechanical parameter identification results can be obtained from equation (27), as shown in the following formula:
Among them, J, Bm and Cm with a hat are the identified values of moment of inertia, viscous damping coefficient and Coulomb friction coefficient respectively.
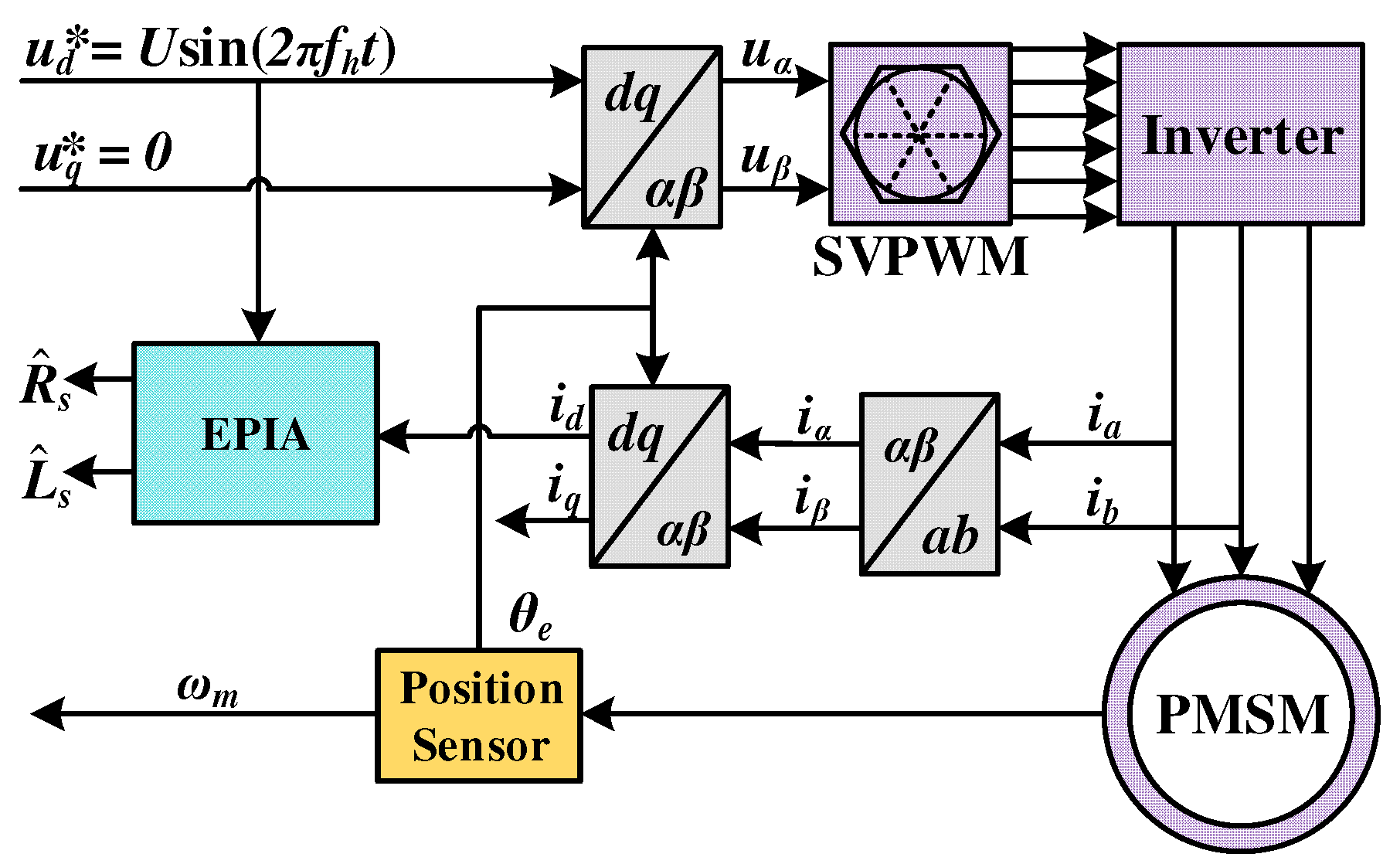
Figure 1.
Electric parameter identification system control block diagram.
Figure 1.
Electric parameter identification system control block diagram.
Figure 2.
Mechanical parameter identification system control block diagram.
Figure 2.
Mechanical parameter identification system control block diagram.
Figure 3.
Schematic diagram of rotor speed response in the process of mechanical parameter identification.
Figure 3.
Schematic diagram of rotor speed response in the process of mechanical parameter identification.
Figure 4.
Schematic diagram of speed response in the process of mechanical parameter identification. (a) Acceleration stage; (b) Steady stage; (c) Deceleration stage.
Figure 4.
Schematic diagram of speed response in the process of mechanical parameter identification. (a) Acceleration stage; (b) Steady stage; (c) Deceleration stage.
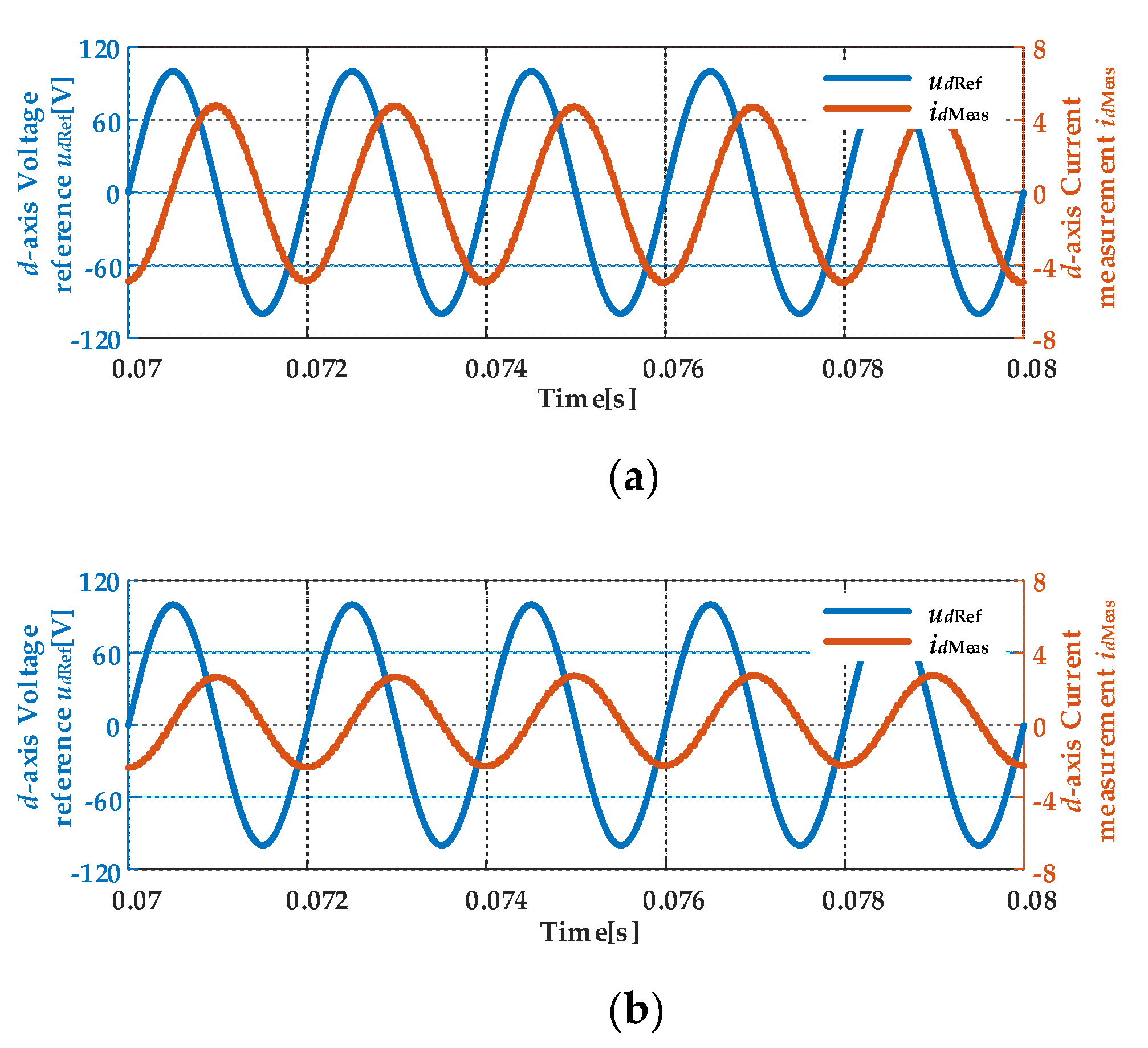
Figure 5.
Figure 5.Dq axis voltage reference values and current measurement curve. (a) D-axis; (b) Q-axis.
Figure 5.
Figure 5.Dq axis voltage reference values and current measurement curve. (a) D-axis; (b) Q-axis.
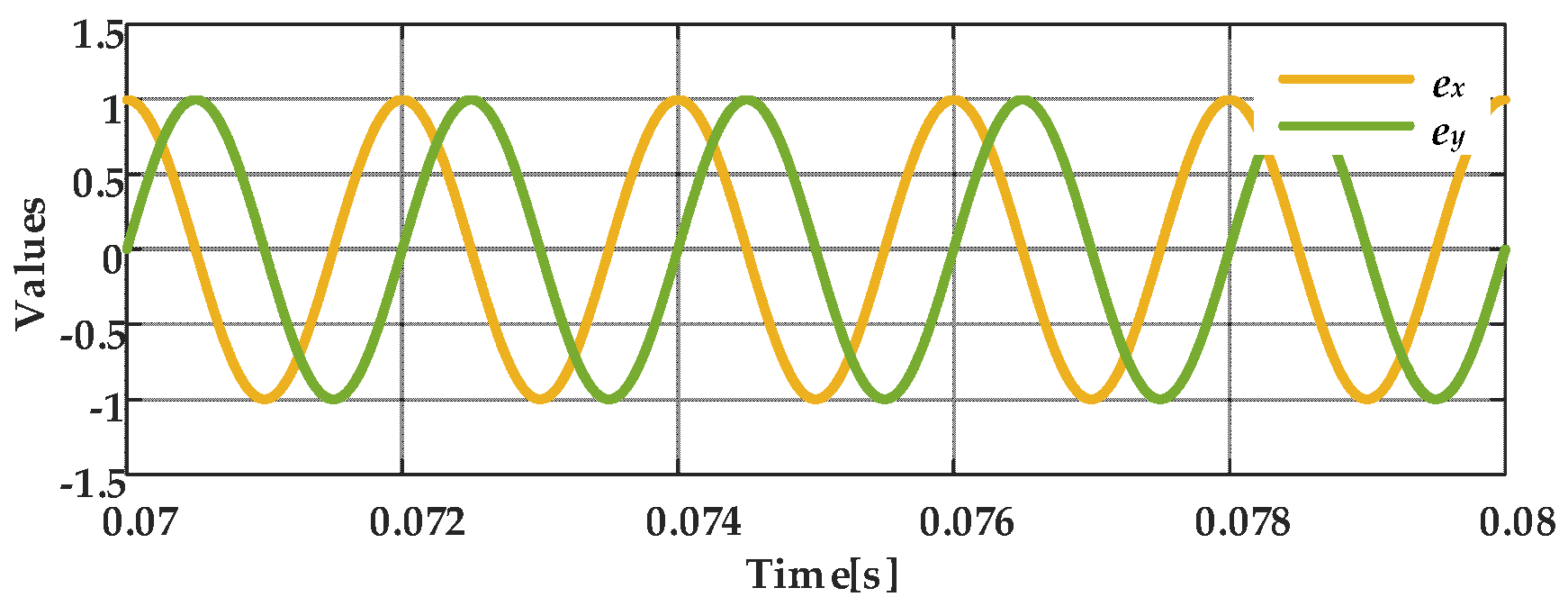
Figure 6.
Base functions ex and ey.
Figure 6.
Base functions ex and ey.
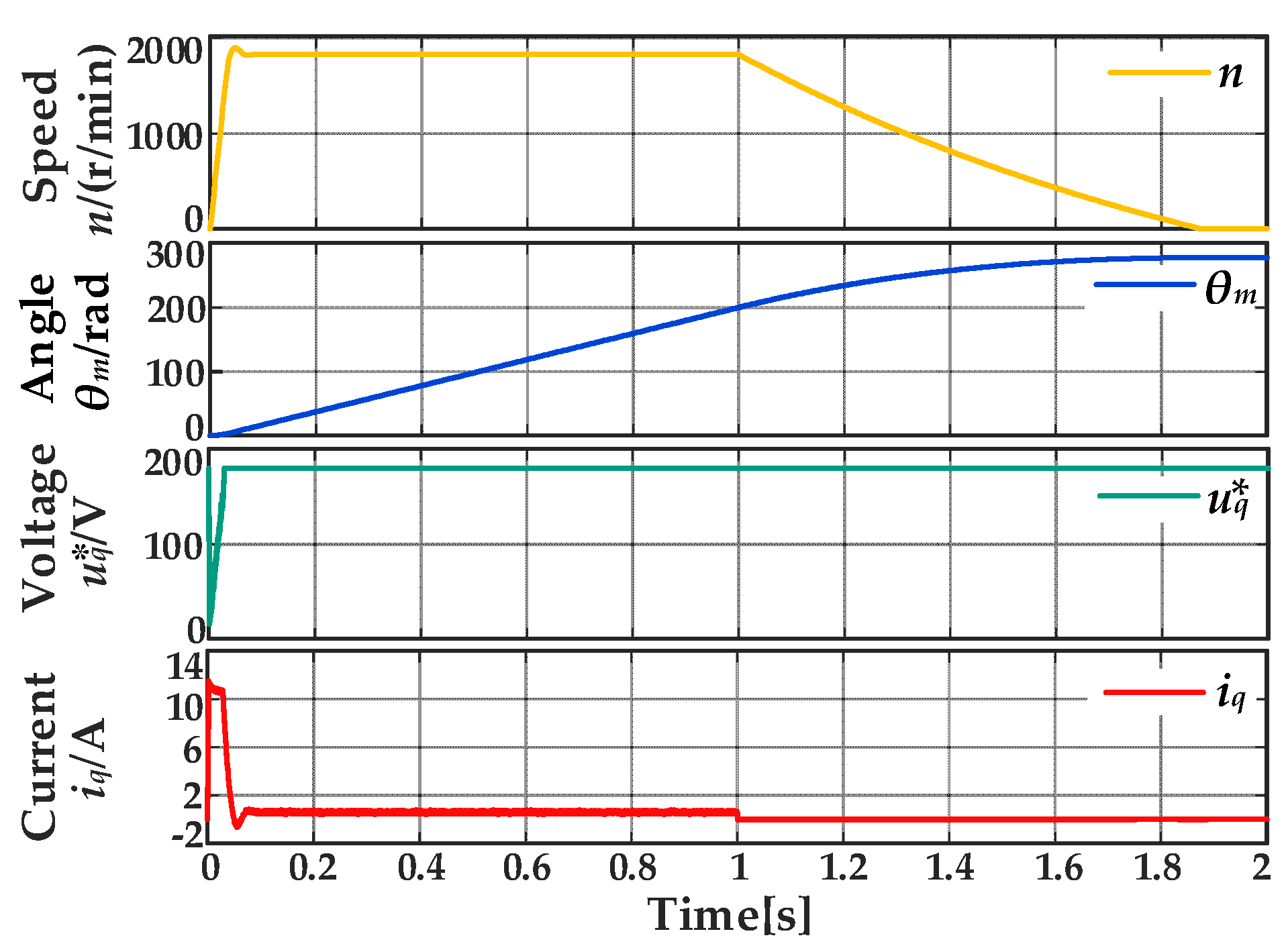
Figure 7.
The changing curve of relevant variables during the process of mechanical parameter identification.
Figure 7.
The changing curve of relevant variables during the process of mechanical parameter identification.
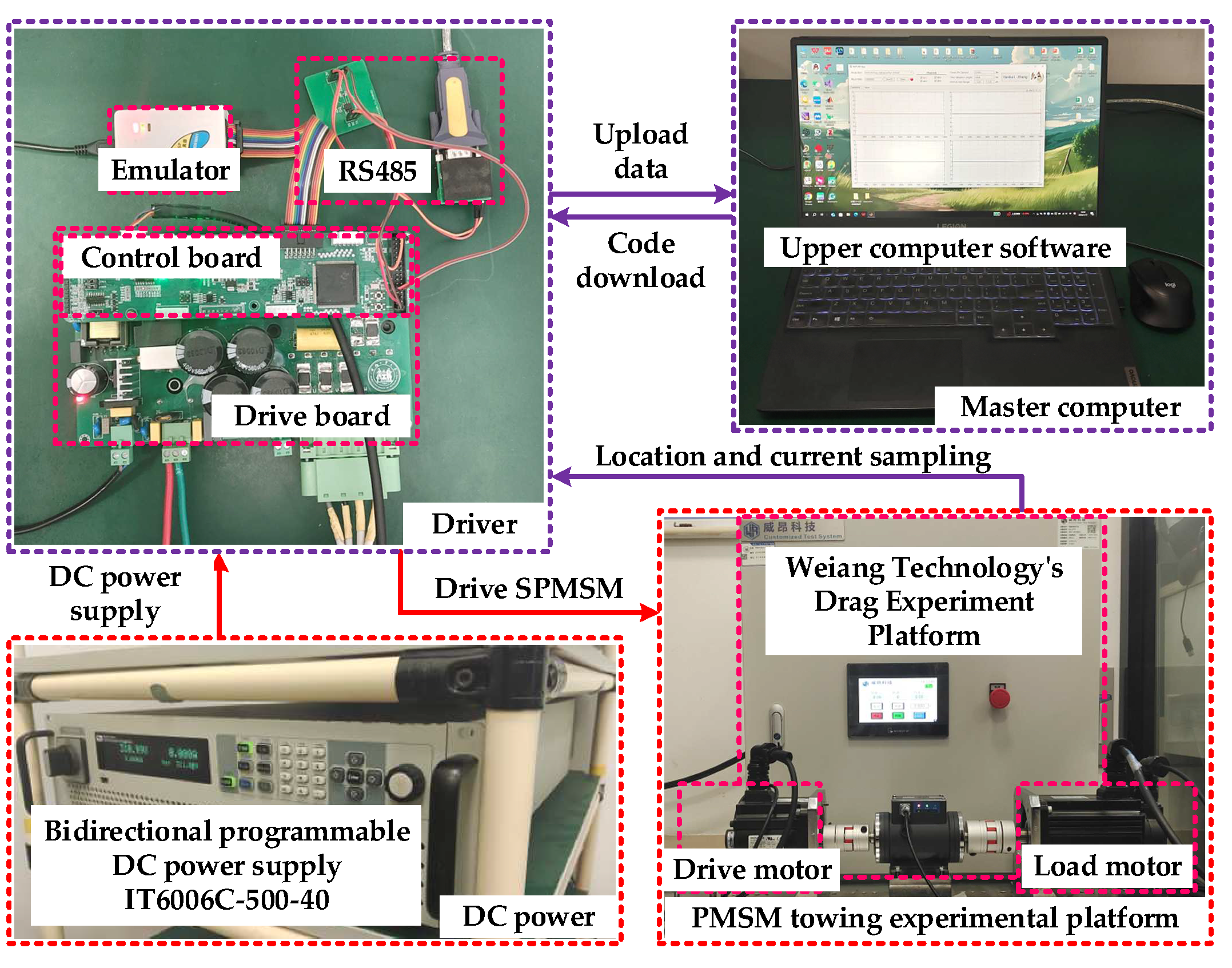
Figure 8.
TMS320F28335-based drive system experimental platform.
Figure 8.
TMS320F28335-based drive system experimental platform.
Figure 9.
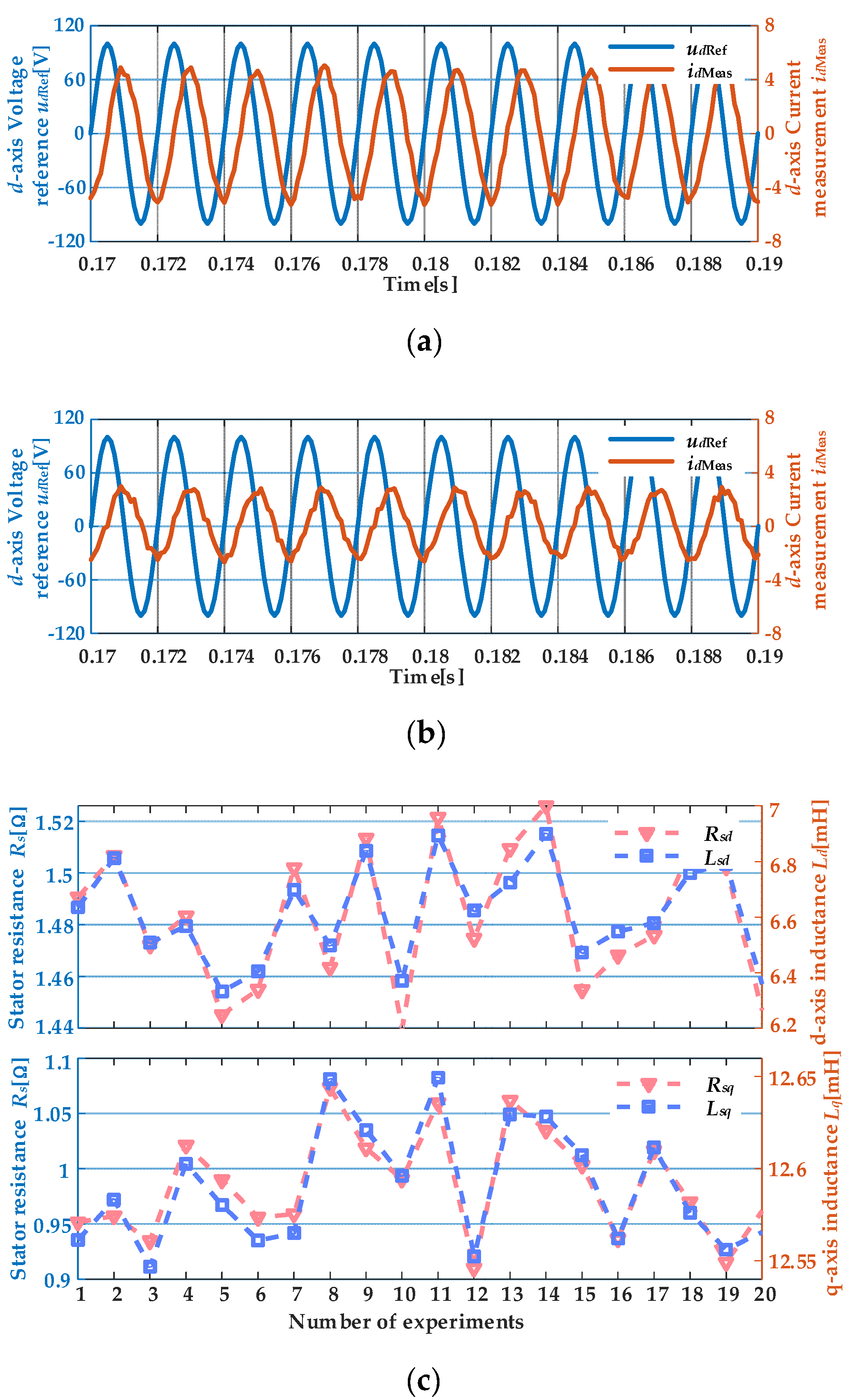
Waveform of electrical parameter identification algorithm experiment. (a) D-axis voltage reference value and current measurement value; (b) Q-axis voltage reference value and current measurement value; (c) Results of 20 identification experiments of Rs and Ldq.
Figure 9.
Waveform of electrical parameter identification algorithm experiment. (a) D-axis voltage reference value and current measurement value; (b) Q-axis voltage reference value and current measurement value; (c) Results of 20 identification experiments of Rs and Ldq.
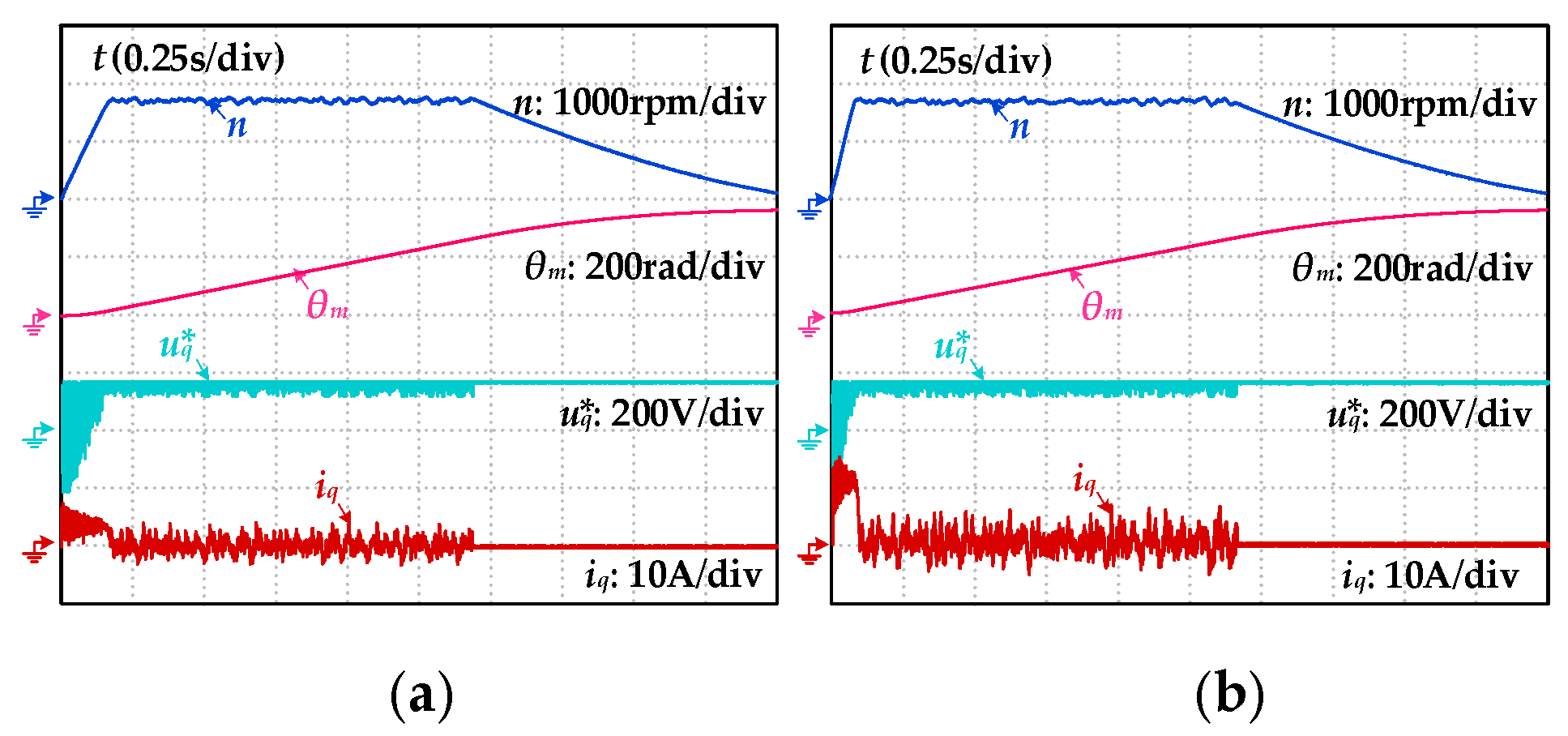
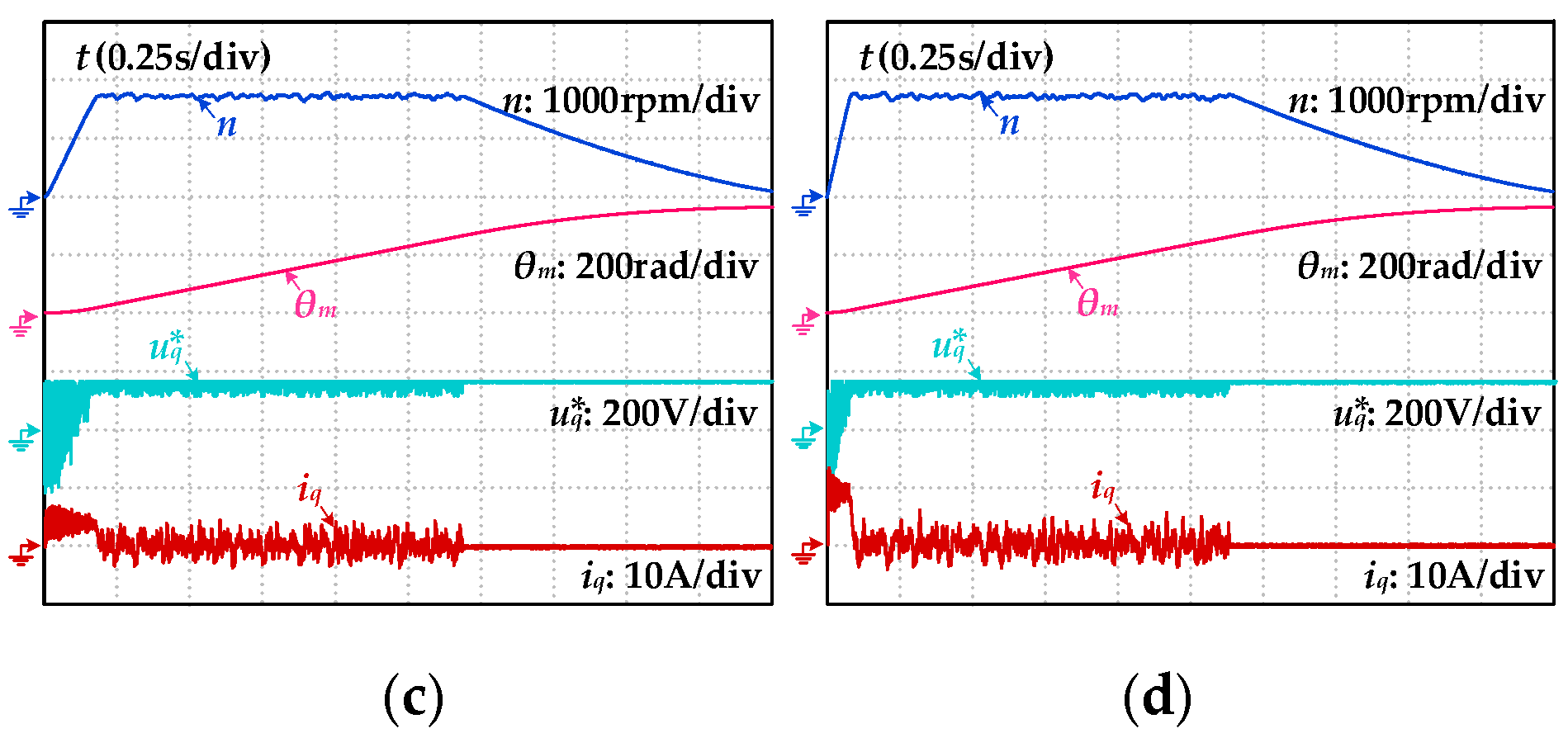
Figure 10.
System response under different current loop bandwidths and different current intensities stimulation. (a) fc=500Hz, = 0.5IN; (b) fc=500Hz, = 1.0IN; (c) fc=1000Hz, = 0.5IN; (d) fc=1000Hz, = 1.0IN.
Figure 10.
System response under different current loop bandwidths and different current intensities stimulation. (a) fc=500Hz, = 0.5IN; (b) fc=500Hz, = 1.0IN; (c) fc=1000Hz, = 0.5IN; (d) fc=1000Hz, = 1.0IN.
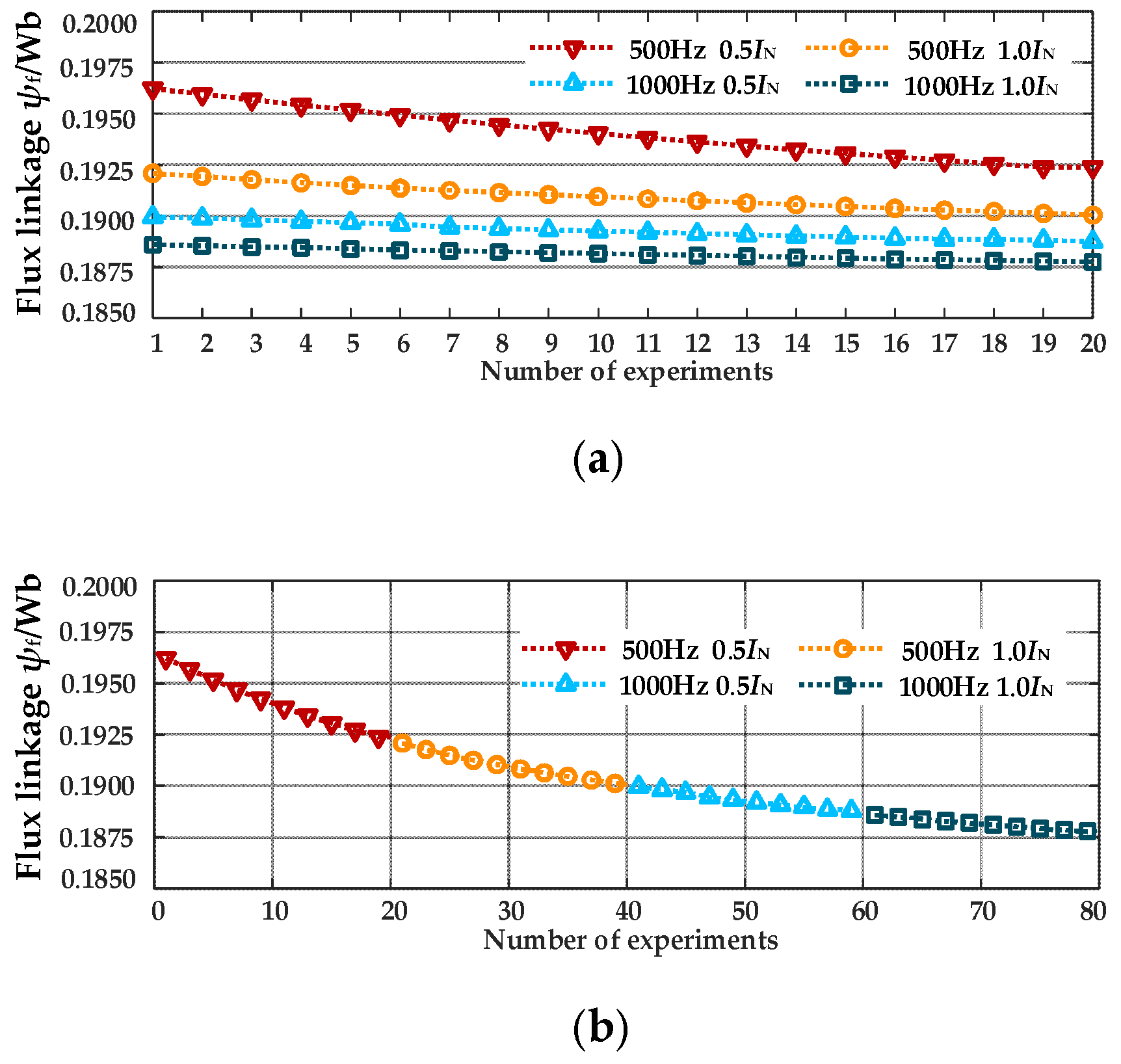
Figure 11.
Recognition result of permanent magnet flux ψf. (a) Experimental results of magnetic chain identification under different conditions; (b) Results of the 80 magnetic flux linkage identification experiments.
Figure 11.
Recognition result of permanent magnet flux ψf. (a) Experimental results of magnetic chain identification under different conditions; (b) Results of the 80 magnetic flux linkage identification experiments.
Figure 12.
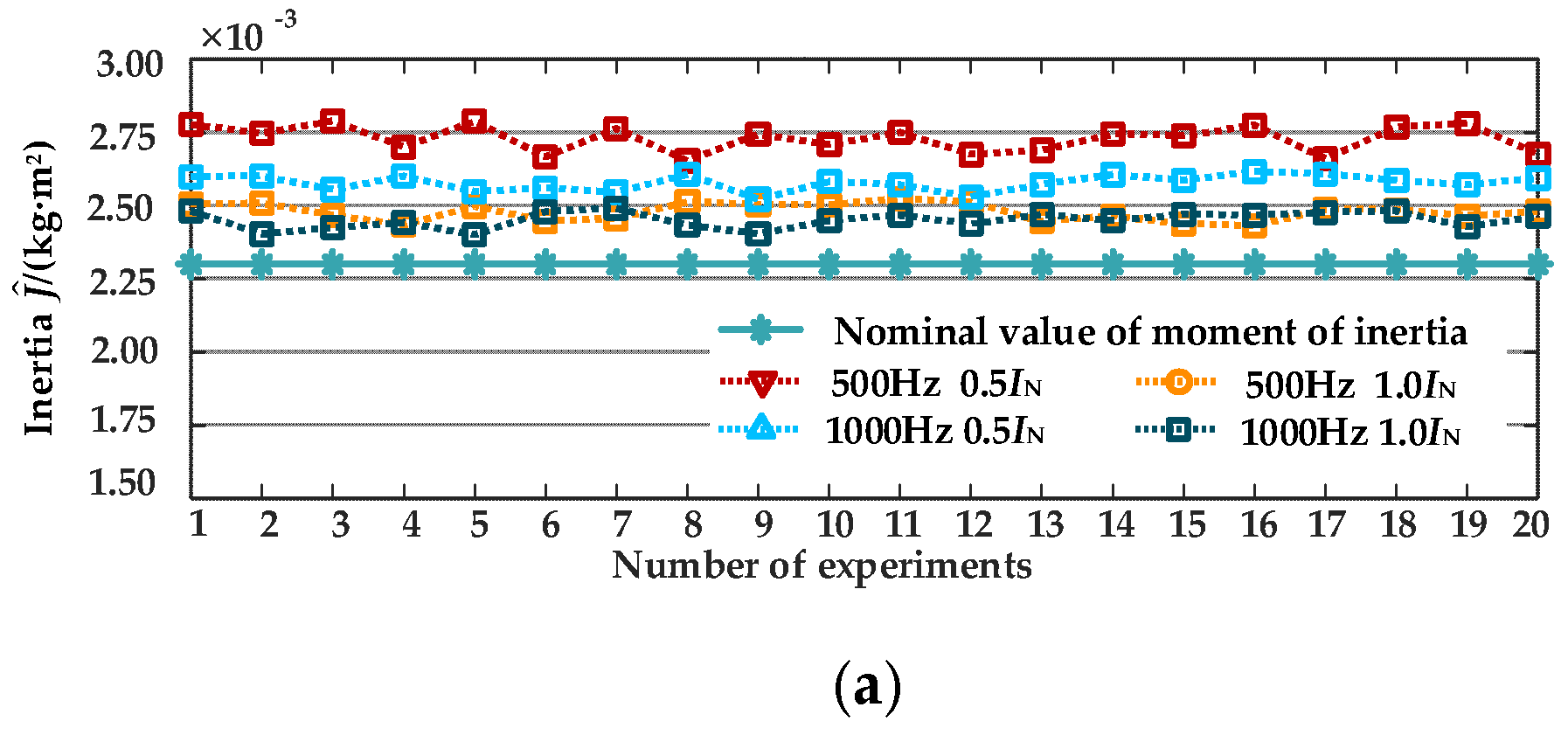
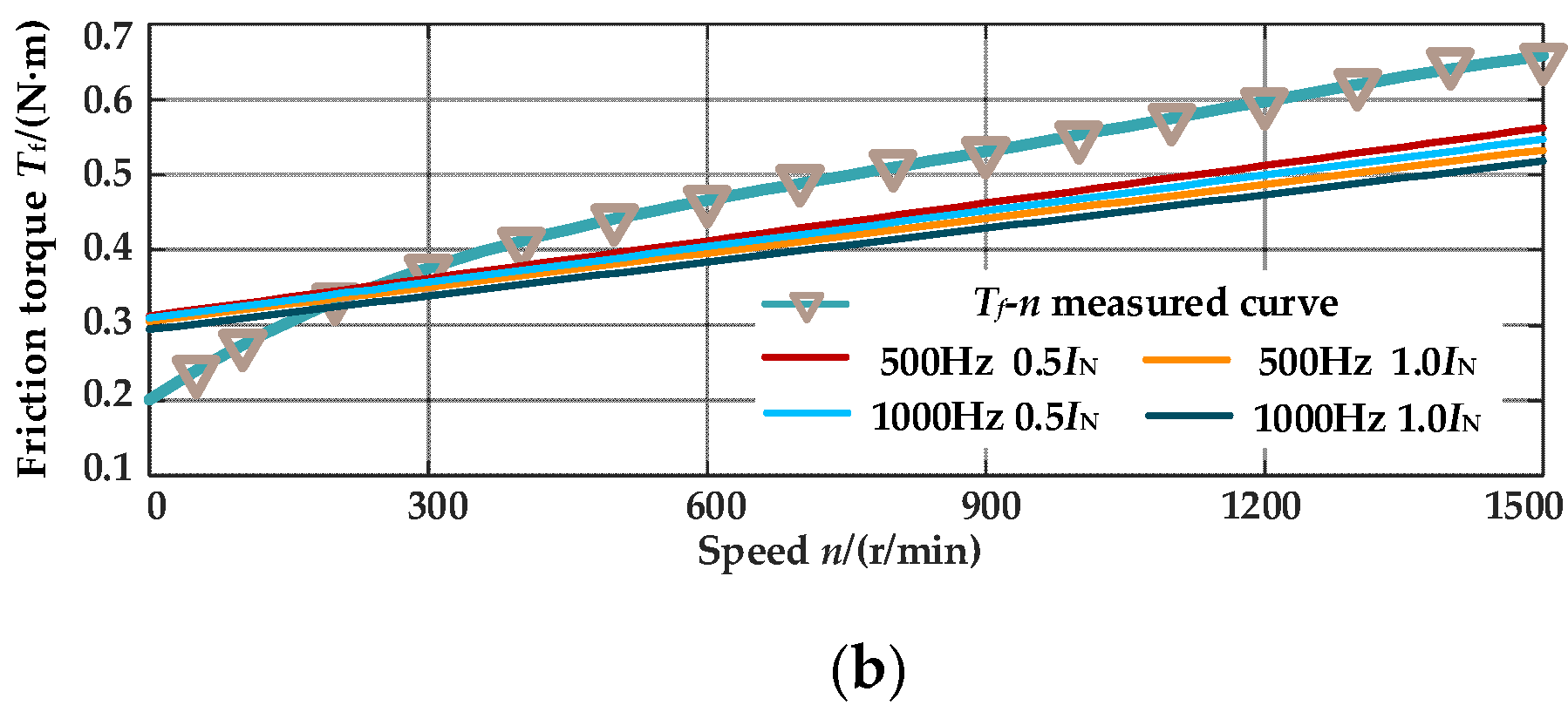
Identification results of J, Bm, and Cm mechanical parameters. (a) Experimental results of inertia identification under different conditions; (b) Identification experiment results of viscous damping and Coulomb friction under different conditions.
Figure 12.
Identification results of J, Bm, and Cm mechanical parameters. (a) Experimental results of inertia identification under different conditions; (b) Identification experiment results of viscous damping and Coulomb friction under different conditions.
Table 1.
Related parameters of PMSM drive system.
Table 1.
Related parameters of PMSM drive system.
| Parameters |
Values |
| Direct current bus voltage Udc/V |
311 |
| Stator resistance Rs/Ω |
1.508 |
| Stator inductance Ld/mH |
6.6571 |
| Stator inductance Lq/mH |
12.8436 |
| Permanent magnet flux linkage ψf/Wb |
0.175 |
| Number of pole pairs pn
|
5 |
| Rated voltage UN/V |
220 |
| Rated current IN/A |
8 |
| Rated speed n/(r/min) |
1500 |
| Moment of inertia J/(kg·m2) |
0.0023 |
| Viscous damping coefficient Bm/(N·m·s/rad) |
0.002 |
| Coulomb friction coefficient Cm/(N·m) |
0.35 |
Table 2.
Simulation Results of Electrical Parameter Identification Algorithm.
Table 2.
Simulation Results of Electrical Parameter Identification Algorithm.
| Project |
Actual Value |
Identified Value |
Relative Error σ
|
| Stator Resistance Rs/Ω |
1.508 |
1.41855 |
-5.93168% |
| d-axis inductance Ld/mH |
6.6571 |
6.59177 |
-0.981290% |
| q-axis inductance Lq/mH |
12.8436 |
12.75555 |
-0.685547% |
Table 3.
Simulation Results of Mechanical Parameter Identification Algorithm.
Table 3.
Simulation Results of Mechanical Parameter Identification Algorithm.
| Project |
Actual Value |
Identified Value |
Relative Error σ
|
| Magnet Flux ψf/Wb |
0.1750 |
0.176216 |
0.695069% |
| Rotational Inertia J/(kg·m2) |
0.0023 |
0.0023006 |
0.026919% |
| Viscous Damping Bm/(N·m·s/rad) |
0.0020 |
0.0019989 |
-0.059131% |
| Coulomb Friction Cm/(N·m) |
0.3500 |
0.3502411 |
0.068883% |