Global Plasma Model in DC Dual Stage Gridded Ion Thrusters

1. Introduction

In recent years, the use of electric propulsion for space applications is undergoing rapid development, related to very accurate and low thrust requirements for precise satellite control in scientific and civil missions [1]. Electric Propulsion (EP) is a propulsion technology in which electricity is exploited to create thrust with high exhaust velocities. Despite low thrust levels, in the order of millinewtons and reaching a maximum of 1 N, EPs are able to achieve excellent performances, 10-20 times greater than the conventional thrusters [2]. Moreover, EP requires the use of small amounts of propellants for its successful operation and returns high exhaust velocities on the order of ${10}^2$ $\mathrm{k}$$\mathrm{m}$/$\mathrm{s}$ for heavy propellants such as Xenon and ${10}^3$ $\mathrm{k}$$\mathrm{m}$/$\mathrm{s}$ for light ones such as Helium [3].

Electric thrusters are classified according to the method of acceleration employed to produce thrust and can be classified into three categories [4]:

• Electrothermal systems include all techniques regarding the electrical heating and expansion of a propellant gas in order to convert its thermal energy to kinetic energy. There exist different types of Electrothermal Thrusters depending on the way the propellant flow is heated. The flow can either pass over an electrically heated solid surface (Resistojet), or through an arc discharge, (Arcjet), otherwise it can be heated by high-frequency excitation. The achievable exhaust velocity, 3.5-20 $\mathrm{k}$$\mathrm{m}$/$\mathrm{s}$ [5], which is an important value in terms of fuel efficiency, depends both on the maximum tolerable temperature by the chamber surfaces and the nozzle and on the propellant thermodynamic and kinetic properties;
• Electrostatic systems regard the branch of propulsion in which the propellant is ionized and accelerated by electrostatic forces and characterized by low thrusts and high specific impulses. The most common use of electric forces on a propellant flow is in an ion thruster, where a beam of positive ions is accelerated by an electrostatic field. The obtainable thrust only depends on the exhaust velocity, 20-40 $\mathrm{k}$$\mathrm{m}$/$\mathrm{s}$ [5], the mass of the ion, and the total ion flux;
• Electromagnetic systems accelerate ionized gas by means of their interaction with electric and magnetic fields. They are promising in terms of high exhaust velocities, 20-30 $\mathrm{k}$$\mathrm{m}$/$\mathrm{s}$ [5], and high mass flows.

A comparison of thrust-to-power ratio and specific impulse for these three major categories is provided in Figure 1 for completeness.

Among the outlined categories of electric thrusters, the electrostatic systems are the most fully developed concept in EP. These engines include the Gridded Ion Thrusters (GITs), which are a well-established technology that have proven to be a suitable and efficient alternative to conventional propulsion systems. They enable a wide range of missions, such as facing the problem of the drag compensation in Very Low Earth Orbit (VLEO), due to the high specific impulses and low thrust profiles they provide [2].

GITs main components are two hollow cathodes, two or three grids (i.e. the Optic System), and a discharge chamber, in which the propellant is ionized to generate and confine plasma (Figure 2). The discharge chamber consists of a cathode, an anode and magnets for plasma confinement. The hollow cathode emits electrons through a thermionic process, where heat causes the cathode to release electrons. These electrons collide with neutral propellant atoms, ionizing them and forming plasma, the basis of the thruster’s operation. To optimize ionization, various magnetic field configurations are employed along the anode wall, in order to lengthen the electron mean free path, thereby increasing collision frequency and ionization probability. Among the existing different types of magnetic confinement, the ring cusp magnetic field, generated by permanent magnets, has emerged as the most effective configuration [3]. At the discharge chamber’s exit, two or three perforated grids shape the ion beam. The extraction and acceleration of ions from plasma by GITs involves the use of these grids, whose potential difference establishes the electrostatic forces needed to generate the thrust. The first electrode of the optical system is the screen grid which is held at a high positive potential, while the second one, the acceleration grid, is set at a significantly negative potential that further accelerates the ions. The last and optional electrode, the deceleration grid, is needed to mitigate erosion on the acceleration grid by shielding it from ion bombardment and removing erosion phenomena, such as pits-and-grooves; however, it also increases the thruster complexity [6]. To neutralize the ion beam and prevent spacecraft charging, a smaller hollow cathode, the neutralizer, is placed outside the chamber, close to its exit. This counteracts the Ion Backstream phenomenon, ensuring efficient thrust generation and safeguarding satellite’s electric neutrality [3]. The outputs of the GITs are very good in terms of efficiency and specific impulse: the first reaches values between 60 % and 80 %, the latter is characterized by values between 2000 $\mathrm{s}$ and 10000 $\mathrm{s}$ [3]. However, GITs present an intrinsic trade-off between maximum extractable current density and specific impulse, which limits the maximum achievable thrust, usually of the order of a few Newtons, for a given specific impulse.

In conventional GITs, the extraction and acceleration process occurs in a single stage, imposing a constraint on the acceleration potential of the grids so as to limit excessive electric field penetration within the discharge chamber. This penetration leads to a curvature of the plasma sheath, which is bigger as the beam potential increases. It results in an increment of the extracted ion beamlet divergence until significant impingement occurs on the acceleration and deceleration grids, leading to excessive grid erosion, performance degradation and limitation of thruster lifetime. To avoid these effects, the grid acceleration potential is limited to maximum values of 5 $\mathrm{k}$$\mathrm{V}$, being able to achieve specific impulse to <10000 $\mathrm{s}$, thrust density to <$0.5$ $\mathrm{m}$$\mathrm{N}$/cm² and power density to <20 $\mathrm{W}$/cm² with Xenon propellant [7,8].

To overcome this limitation, D. Fearn proposed a solution [9] inspired by the United Kingdom Atomic Energy Authority (UKAEA) Culham Laboratory’s Controlled Thermonuclear Reactor (CTR), a multi-stage ion optics system, initially designed for high-energy injections into tokamaks [11,12,13,29]. The CTR design is based on a 4-grid optical system that allows extremely high acceleration potentials and, therefore, high ion velocities with light gases, such as hydrogen. This configuration allows the decoupling of the extraction and acceleration process, effectively creating a dual-stage system, as shown in Figure 2. It is achieved through the introduction of an additional electrode, the extraction grid, placed between screen and acceleration grid. From this concept, then, originates the idea of a DSGIT, which, theoretically, enables improved performance and overcomes the limitations of the classic GIT architecture (Figure 2). Thus, the dual stage system results in improved specific impulse, thrust density and thrust, as well as beam divergence (reduced to values of $2^{\circ }$-$6^{\circ }$ compared to ${12}^{\circ }$-${15}^{\circ }$ in conventional GIT systems) at the expense of higher input power [14].

Fearn’s idea paved the way for the scientific community, encouraging them to investigate and make improvements on this technology. The first attempt, conducted jointly by the European Space Agency (ESA), Australia and Great Britain, allowed to develop a prototype of Dual Stage 4-Grid (DS4G), powered by Xenon and with a radio frequency source. This new technology allows to obtain a specific impulse of 14500 $\mathrm{s}$, a beam divergence angle of about $5^{\circ }$ and beam energies up to 80 $\mathrm{k}$$\mathrm{V}$. These parameters, comparable to those found in fusion devices, are accomplished with an active grid diameter of only 2 cm [7,9,15]. The University of Southampton and Mars Space Ltd. are working on the design of a DS4G ion thruster with a Kaufman ion source, whose many theoretical research and numerical simulation reports are available but not the experimental ones [16,17,18,19]. Theoretical research and numerical simulation of the DS4G ionic optical systems was also conducted by the Lanzhou Institute of Physics in 2015, and the prototype was developed in 2017 [20,21]. This study presents the decoupling mechanism of ion extraction and acceleration processes of the DS4G optical system by experiment and simulation.

Coletti et al. [17] proposed a modified design of the DS4G, known as the Dual-Stage 3-Grid (DS3G), which removes the deceleration grid to reduce thruster complexity while preserving erosion control. Experimental tests have shown that the DS3G has a significantly longer operating life (≈ 50000 $\mathrm{h}$) than conventional grid ion thrusters (≈ 25000 $\mathrm{h}$) due to reduced erosion and power losses. These results were confirmed by a study conducted by Bramer [22], using Particle In Cell (PIC) code, which revealed that the slight performance improvement of the DS4G over the DS3G does not justify the increased complexity introduced by the deceleration grid.

The current research activity has focused on the development of a Global Plasma Model (GPM) for Direct Current Dual Stage Gridded Ion Thruster (DC-DSGIT). The methodology, similarly to the models presented in Ref. [23,24], begins with either input power or thrust, combines analytical formulas, that describe the underlying physics of DC-DSGIT and employs a curve-fitting approach based upon open literature data from similar ion thrusters. In the curve fitting part, an educated guess is made about the thrust/diameter-total efficiency curve of DC-DSGITs (i.e. conventional GIT curve is used), given the lack of data in the literature. The model is able to calculate both performances (e.g. specific impulse, efficiency) and operative parameters (e.g. voltages, magnetic field intensity and propellant flow rates).

The paper is organized as follows: the description of the model is in Chapter 2; the results that validate the model is shown and discussed in Chapter 3; the conclusions are drawn in Chapter 4.

2. Global Plasma Model for DC-DSGITs

2.1. Definition and assumptions

The model for DC-DSGIT takes in input the chamber diameter, either the power or the thrust and the propellant. Figure 3 shows a flow chart illustrating the main parts, inputs and outputs of the model.

Additionally, the GPM is characterized by some Degrees of Fredoom (DoF) set by considering the operating life, efficiency and complexity:

1.

The discharge voltage $V_d$ is set at 28 $\mathrm{V}$ to minimize the erosion of the screen grid [25];

2.

The cathode drop voltage, $V_c$, is adopted by keeping the primary electron voltage, $V_k$, below the second ionization potential, $U_{+}^2$ (e.g. for Xenon ≈ 20 $\mathrm{V}$) [23]. At the same time, must have a high enough value to increase ionization-to-excitation ratio [26,27].

3.

Regarding the optics system, the grid geometry in Ref. [20] is selected for small DSGITs, while for large ones conventional T6 ion thruster grids are chosen [8];

4.

For the discharge chamber length, a typical value for medium-low-power Gridded Ion Thruster is chosen (i.e. $L=D$) [28];

5.

The extraction stage voltage drop, $\Delta V_{ext}$, is set at 1000 $\mathrm{V}$ because it has been experimentally demonstrated that this value achieves high specific impulses. At the same time, it enables a high degree of beam collimation, thereby minimizing grid erosion [18,22];

6.

The beam divergence angle $\theta$ is set around $5^{\circ }$ [15,18,20] .

The model can be run in two different ways: the first one consists in taking thrust (or power) or the size of the discharge chamber in input, in order to determine the performance of the thruster; the second one involves setting thrust (or power) requirements that the thruster must meet and, through an iterative procedure, it is possible to determine the minimum size. Using the analytical Equations discussed in the next sections, the magnetic field and the corresponding design parameters can be calculated. The Table 1 summarizes the input, output and degrees of freedom of the developed tool.

2.2. Curve Fitting Approach

This part of the model allows for the calculation of such important performance parameters such as efficiencies and thrust (or power), Figure 3.

The main performances, under different operating conditions, are collected from the open literature [15,22] to build useful interpolating curves that can be used to easily get these data. Following Refs. [23,24], these curves are the thrust/diameter-total efficiency and the power density-thrust density curves.

Due to the novelty of the technology there is few total efficiency data, thus only the power density-thrust density curve has been built (e.g. Figure 4). Therefore, to cover the gap, the validity of the thrust/diameter-total efficiency curve, obtained for conventional GIT [23], was supposed. This hypothesis is validated by the fact that the total efficiency estimate using this interpolating curve provides relatively low errors (on average less than 4-8%) compared to the few available data regarding DSGITs.

The curve in Figure 4 shows a power-type law between the power density and the thrust density for DSGIT Xenon-fed that can be explained in a simple way by Equation (1), in which ${\displaystyle \frac{T}{A}}$ represents the thrust density in $\mathrm{m}$$\mathrm{N}$/$\mathrm{m}$² and ${\displaystyle \frac{P_{\mathrm{in}}}{A}}$ the power density in $\mathrm{k}$$\mathrm{W}$/$\mathrm{m}$² .

$${\displaystyle \frac{T}{A}}=670.3821{\left({\displaystyle \frac{P_{\mathrm{in}}}{A}}\right)}^{0.4806}-1276.6$$

(1)

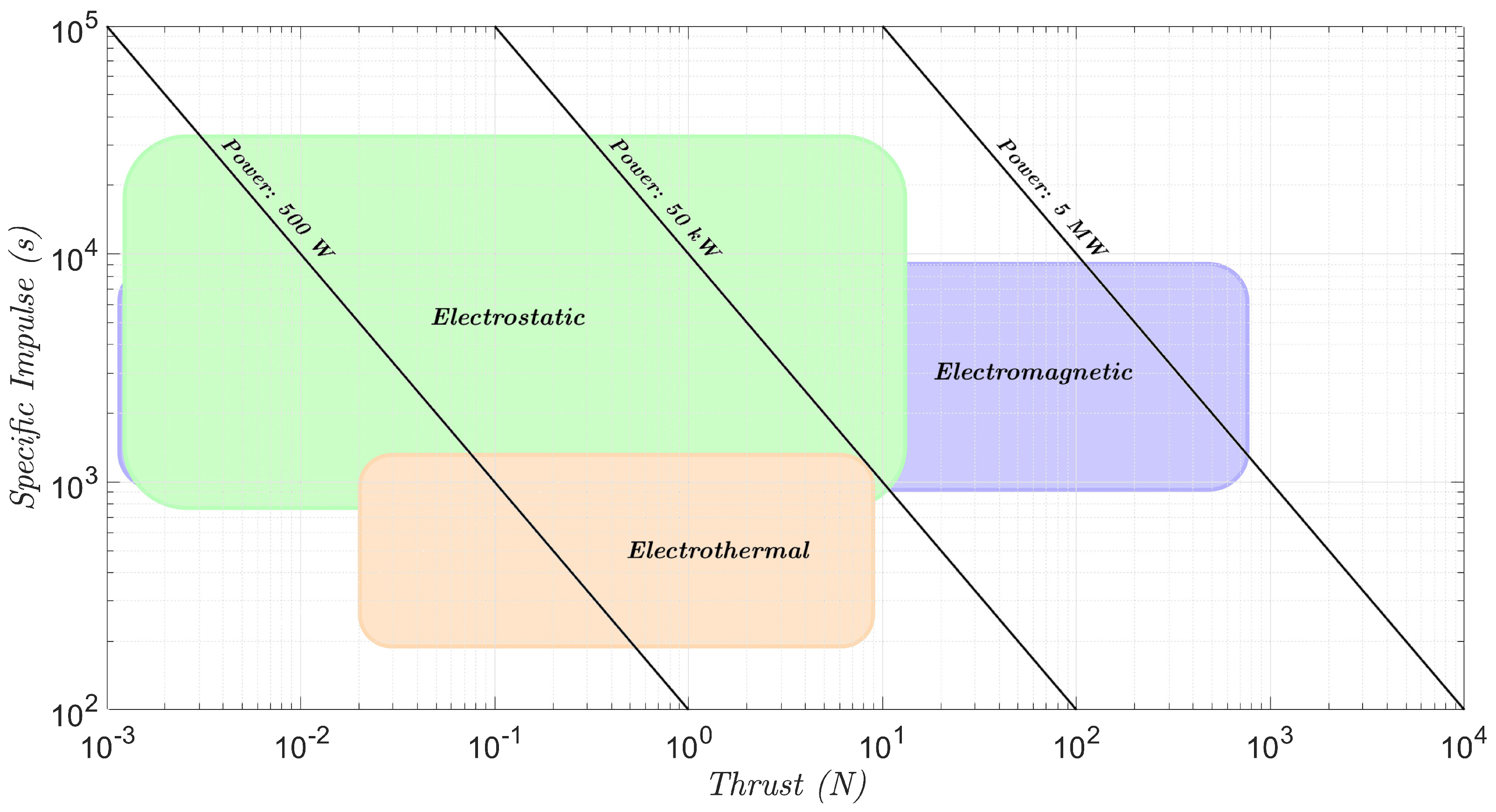
2.3. Ion Optic System Modeling

Ion acceleration and thrust production in a GIT occur through the use of electro-polarized grids. The design of such grids results from a trade-off between lifetime, size, and performance. In general, the main factor turns out to be durability, since ion thrusters must operate for months or years. The aim of the grids is to extract ions from the plasma and accelerate them, while minimizing the impacts of ions on the shielding grid and the loss of neutral atoms out of the chamber, in order to maximize the mass utilization efficiency, as described in the following sections.

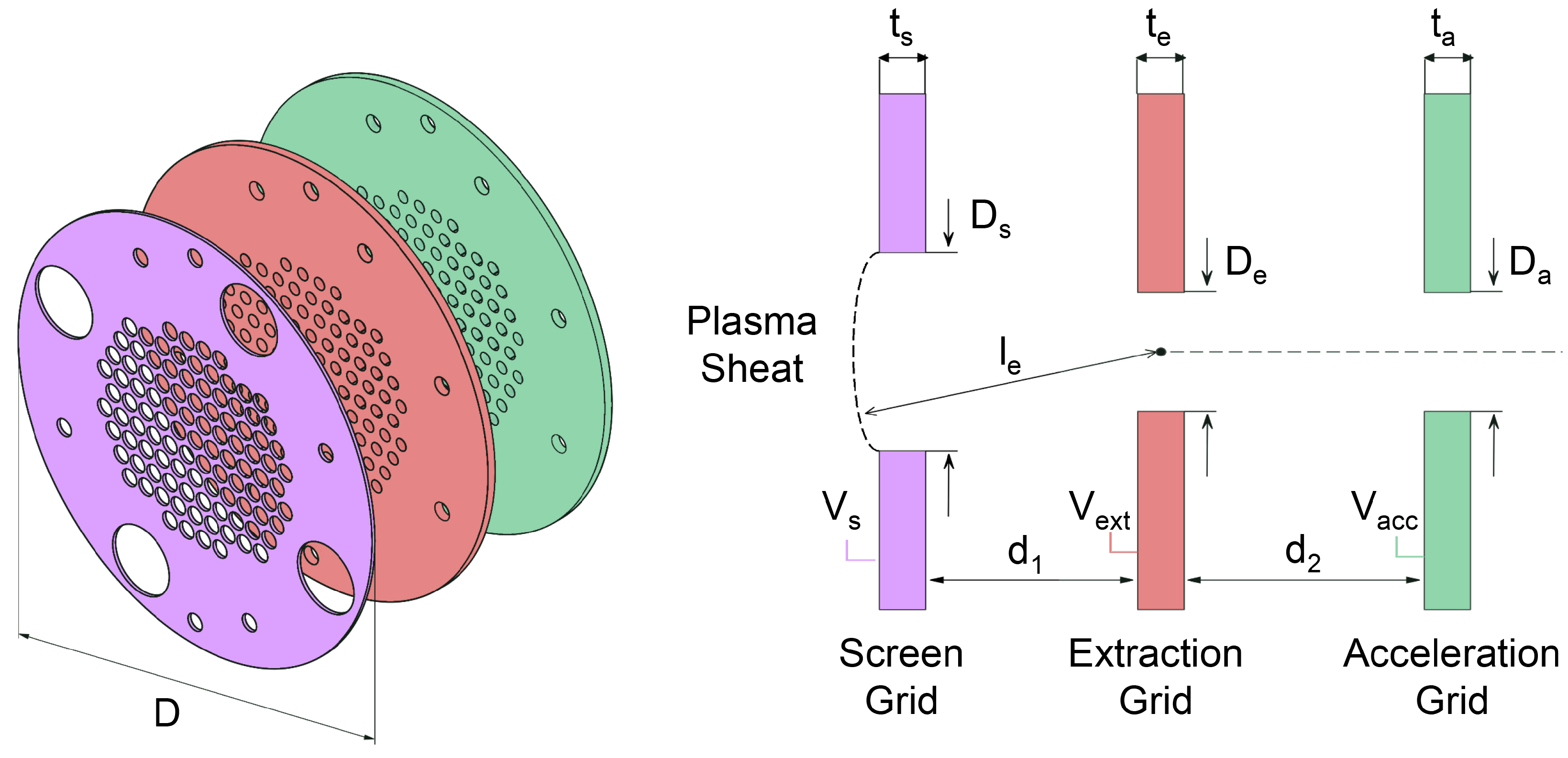
The main parameters that define the grid geometry are the grid thickness, distance between grids, the diameter and number of holes. These parameters are expressed considering the confinement of neutrals and the minimization of impacts between ions and accelerating grid. In particular, one of the advantages of a Dual-Stage ion optics system is the possibility of obtaining highly focused ion beams with rather low divergence values. In DSGITs, although the extraction and acceleration processes occur in different regions (in the first and second grid gaps, respectively), if a well-collimated jet is desired, the magnitude of the acceleration process will influence the requirements of the extraction process in terms of the optimal perveance ratio ${\displaystyle \frac{P}{P_{max}}}$ (Equations 7, Equations 8). This effect can be easily understood by representing the grids as electrical lenses. An electrode separating two regions with different electric field strengths is equivalent to an electrostatic lens with focal length f explicated in Equation (2).

$$f={\displaystyle \frac{4V}{E_{ext}-E_{acc}}}$$

(2)

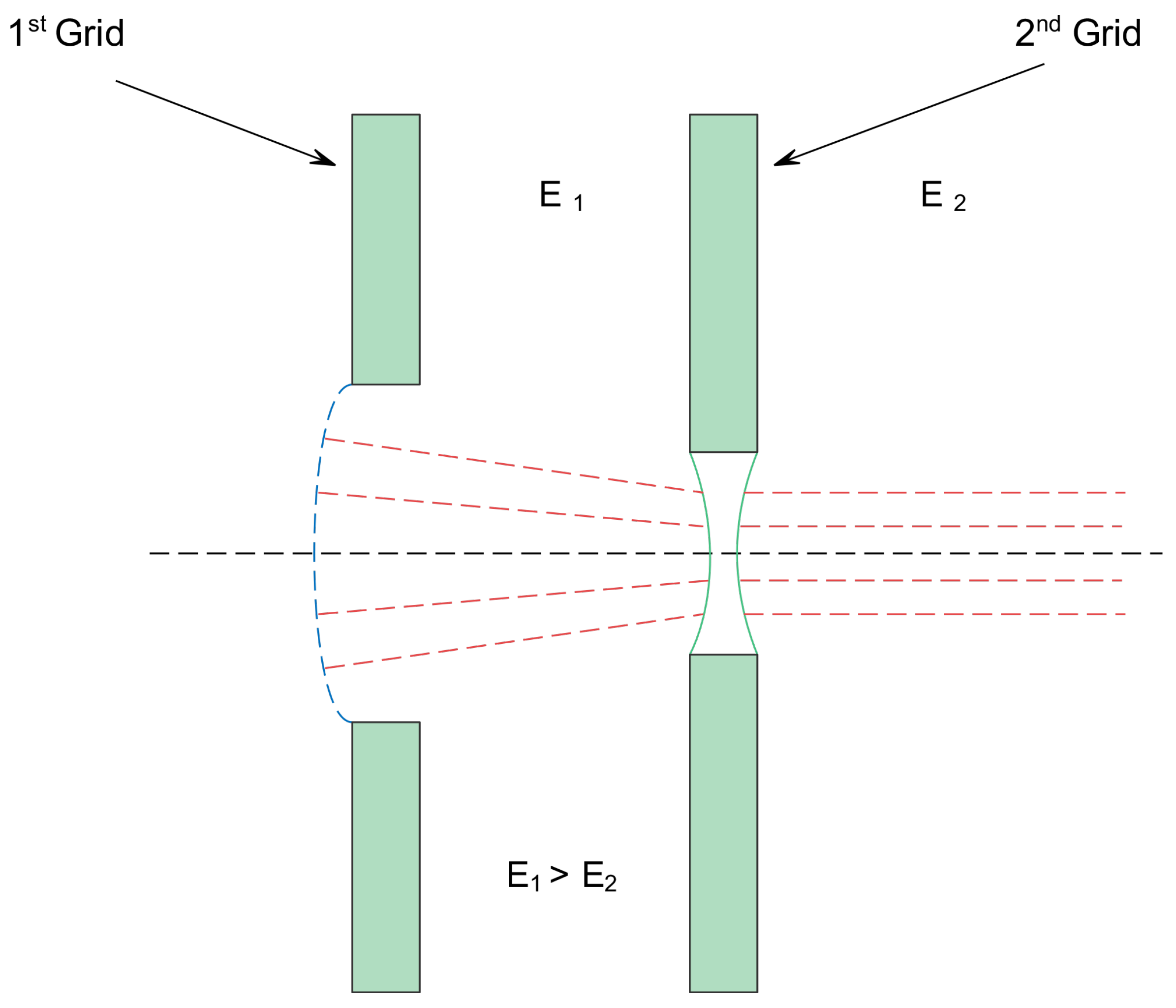
In Equation (2), V is the ion energy at the position of the grids, while $E_{ext}$ and $E_{acc}$ are the electric fields in the extraction and acceleration gaps, respectively. Consequently, using Equation (2), it can be seen that in a conventional GIT extraction system, as visible in Figure 5, the divergent lens is the second grid that balances the effect of sheath shape, ideally producing a perfectly collimated ion beam.

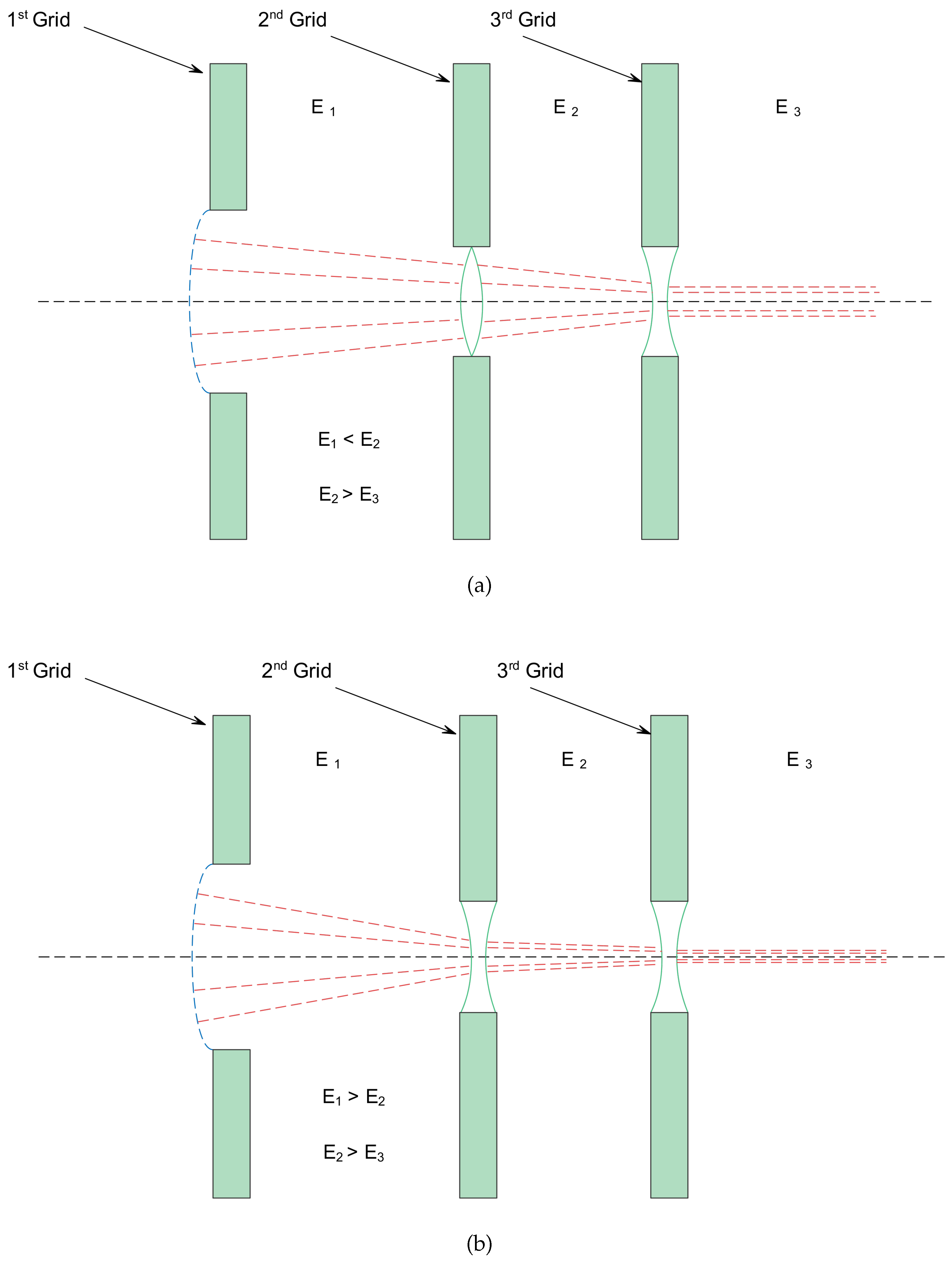
In a dual stage system, the lens corresponding to the second grid can be convergent or divergent according to the relative electric field strength in the first and second gaps, as shown in Figure 6. When the electric field in the first gap, $E_1$, is weaker than the one in the second gap, $E_2$, the lens is convergent and a flatter shape of the plasma sheath can be tolerated (compared with a conventional extraction system), leading to higher perveance values and, therefore, higher extracted current densities. Instead, if the field in the first gap, $E_1$, is stronger than the one in the second gap, $E_2$, the second grid corresponds to a divergent lens. This results in the plasma sheath having to penetrate more into the plasma to have more convergent ion trajectories so as to compensate for the presence of two divergent lenses. As a consequence, there is a reduction in perveance and, therefore, a reduction in the total extracted current.

The change in the optimal perveance can be investigated as a function of the ratio $\Gamma$ between the voltage drop applied to the acceleration stage, $\Delta V_{acc}$, and the voltage drop applied to the extraction stage, $\Delta V_{ext}$, as can be seen in Equation (4). For this purpose, the four-grid ion optics model developed in Ref. [29] is used; this analytical model, based on the theory of linear optics, allows the calculation of the divergence of the ion beam as a function of grid geometry and applied voltages. 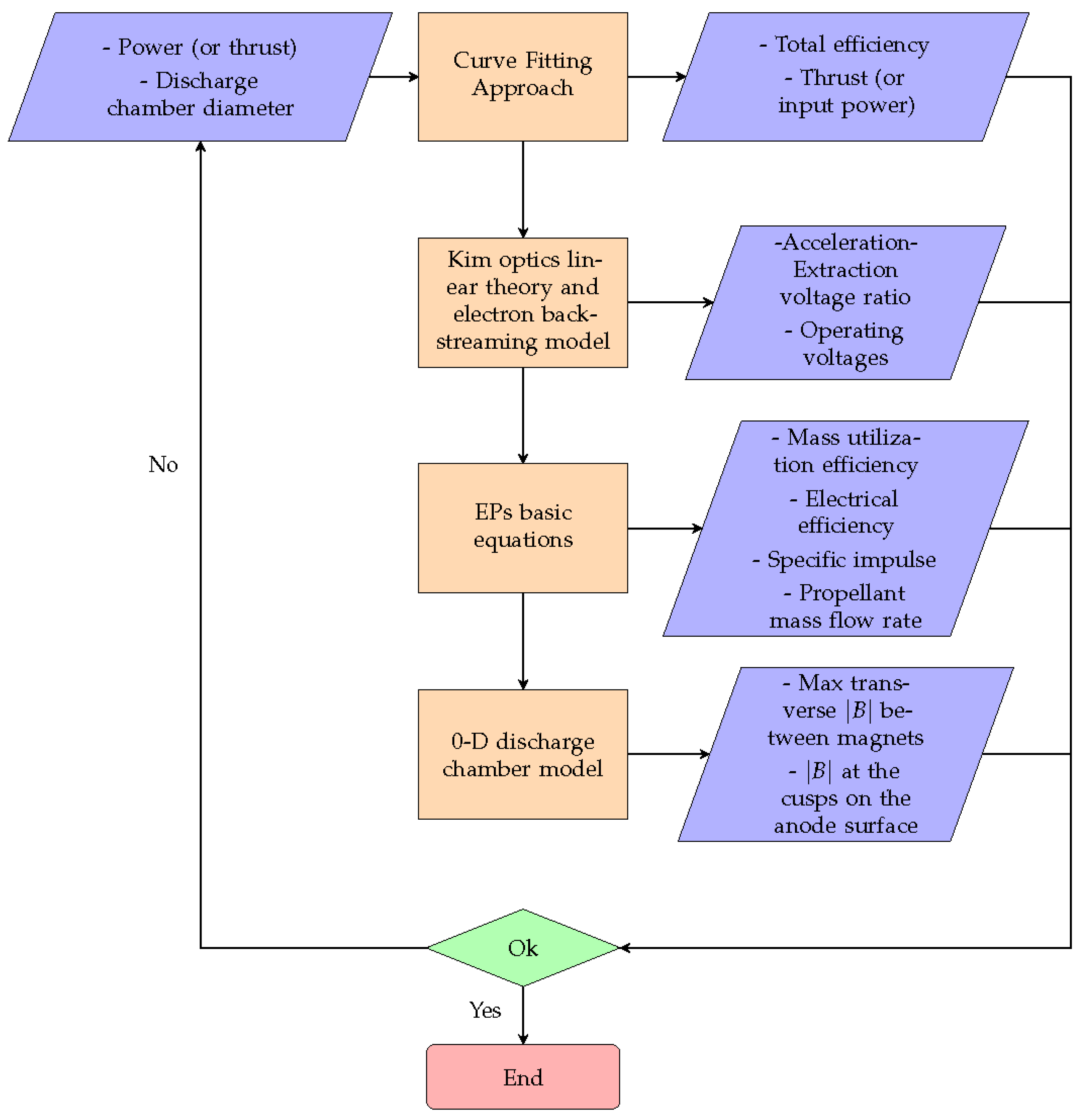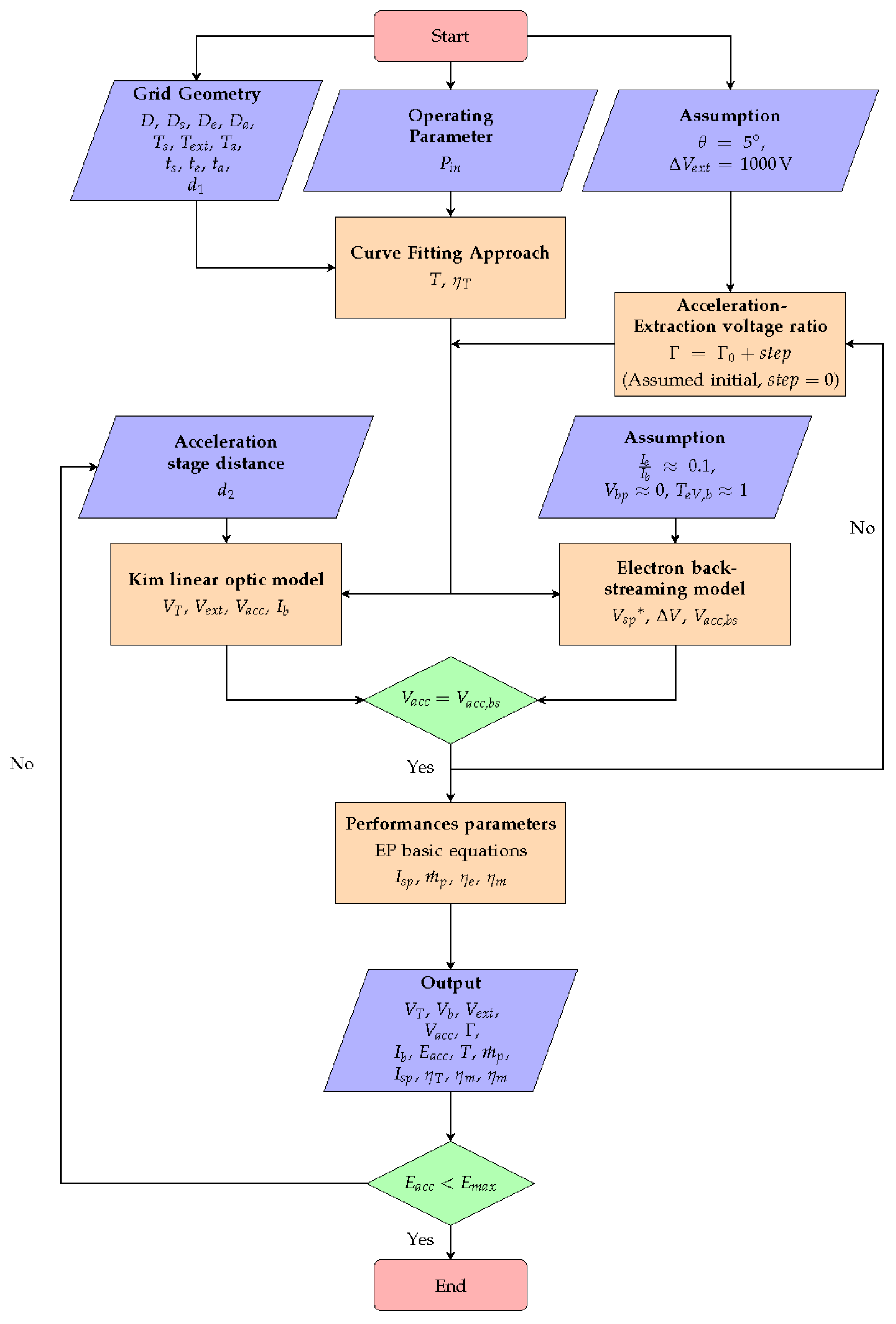Figure 7 represents the flowchart showing the logic of ion optics’ parameters determination.

The linear optics model proposed in Ref. [29], hence, allows the beam divergence to be defined by Equation (3).

$$\begin{array}{cc}\hfill {\theta }_{DSGIT}& =0.62S\left[{\displaystyle \frac{P}{P_{max}}}-0.4{\displaystyle \frac{D_e}{D_s}}{\displaystyle \frac{{\Gamma }^2}{\lambda \left(1+\Gamma \right)}}+0.53{\displaystyle \frac{D_e}{D_s}}-1\right]\hfill \\ \hfill & +0.31S{\displaystyle \frac{P}{P_{max}}}\left[1+{\displaystyle \frac{t_e}{t_s}}+0.35{\displaystyle \frac{D_e}{D_s}}\left(\lambda +{\displaystyle \frac{t_a+t_e}{d_1}}\right){\left(1+0.5\Gamma \right)}^{-1.5}\right]\hfill \end{array}$$

(3)

In Equation (3), $\Gamma$ is the ratio of the acceleration voltage $\Delta V_{acc}$ to the extraction voltage $\Delta V_{ext}$, $\lambda$ the ratio of the acceleration gap to the extraction gap and S the ratio of the screen grid aperture radius to the extraction gap.

$$\Gamma ={\displaystyle \frac{\Delta V_{acc}}{\Delta V_{ext}}}={\displaystyle \frac{V_{ext}-V_{acc}}{V_s-V_{ext}}}$$

(4)

$$\lambda ={\displaystyle \frac{d_2}{d_1}}$$

(5)

$$S={\displaystyle \frac{D_s}{2d_1}}$$

(6)

Given the grid geometry in Figure 8, using Equation (3), and varying $\Gamma$, it is possible to obtain the optimal perveance ratio (${\displaystyle \frac{P}{P_{max}}}$) to produce a beam jet with almost zero divergence.

To be able to understand the ion extraction process and its influence on a GIT performance and lifetime, the perveance of an extraction system is defined in Equation (7).

$$P={\displaystyle \frac{I}{{\Delta V_{ext}}^{\frac{3}{2}}}}$$

(7)

Where I is the extraction current and $\Delta V_{ext}$ is the extraction voltage drop ($\Delta V_{ext}=V_s-V_{ext}$). The perveance results to be strongly related to space charge effects on the extraction of a ionic current and its maximum value is governed by the Child-Langmuir equation, reported in Equation (8).

$$P_{max}={\displaystyle \frac{\pi }{9}}{\epsilon }_0\sqrt{{\displaystyle \frac{2e}{M}}}{\left({\displaystyle \frac{D_s}{d_1}}\right)}^2$$

(8)

Consequently, in Equation (8) $P_{max}$ refers to the Child-Langmuir limit perveance, while ${\epsilon }_0$, e and M are, respectively, the vacuum dielectric constant, the electron charge and the mass of the extracted ions, $D_s$ is the first grid aperture diameter and $d_1$ the gap between the first two grids of the extraction system. Assuming a constant extraction voltage $\Delta V_{ext}$ ($=1000\mathrm{V}$), the lower the specific impulse $I_{sp}$ is, the lower the optimal work perveance and the extracted current are. In particular, the optimal value of ${\displaystyle \frac{P}{P_{max}}}$ for a Dual Stage ion engine decreases below the one of a conventional GIT for values of $\Gamma$ less than 0.7-1.5. This reduction in working perveance could be balanced by reducing the ratio $\lambda$ between the distance of the first and second stages. However, decreasing the value of $\lambda$ means either increasing the gap of the first stage, causing a decrease in the maximum perveance $P_{max}$, or decreasing the grid spacing in the acceleration stage. It should be noted, however, how the minimum grid gap is limited by the maximum electric field $E_{max}$ (≈ 4 $\mathrm{k}$$\mathrm{V}$/$\mathrm{m}$$\mathrm{m}$ for Molybdenum) that can be applied between two grids before the arcing occurs [30]. These two limitations discussed above are applied in the identical manner to both extraction stage (screen and extraction grid) and acceleration stage (extraction and acceleration grid), so it is possible to verify the value of the relative electric fields by Equations (9) and (10).

$$E_{ext}={\displaystyle \frac{\Delta V_{ext}}{l_e}}$$

(9)

$$E_{acc}={\displaystyle \frac{\Delta V_{acc}}{d_2+\left(\frac{t_e+t_a}{2}\right)}}$$

(10)

The parameter $l_e$ in Equation (9) is the sheath thickness or gap equivalent of the extraction stage which can be defined by Equation (11).

$$l_e=\sqrt{{\left(d_1+t_s+{\displaystyle \frac{t_e}{2}}\right)}^2+{\displaystyle \frac{D_s^2}{4}}}$$

(11)

It should be noted from the Equation (12) that the maximum current density of the extractable beam is found to be related to the electric field in the extraction stage gap $E_{ext}$.

$$J_{max}={\displaystyle \frac{4{\epsilon }_0}{9}}\sqrt{{\displaystyle \frac{2e}{M}}}{\displaystyle \frac{E_{ext}^2}{\sqrt{\Delta V_{ext}}}}$$

(12)

The thrust density is likewise proportional to the electric field of the DSGIT extraction stage, as can be observed from Equation (13).

$${\displaystyle \frac{T}{A}}={\displaystyle \frac{8{\epsilon }_0}{9}}{E}_{ext}^2\gamma T_s\sqrt{{\displaystyle \frac{V_T}{\Delta V_{ext}}}}$$

(13)

In Equation (13), the term $V_T$ is the ion acceleration potential in the dual stage system, which corresponds to the difference between the beam voltage $V_b$ and twice the absolute value of the acceleration grid potential $|V_{acc}|$.

$$V_T=\Delta V_{ext}+\Delta V_{acc}+\left|V_{acc}\right|=V_b+2\left|V_{acc}\right|$$

(14)

Hence, given the thrust density ${\displaystyle \frac{T}{A}}$ and the ratio of voltages $\Gamma$, it is possible to obtain the extraction grid voltage $V_{ext}$ and the screen grid voltage $V_s(\approx V_b)$, respectively.

$$V_{ext}=V_{acc}+\Delta V_{acc}$$

(15)

$$V_b\approx V_{ext}+\Delta V_{ext}$$

(16)

The acceleration grid voltage, calculated by the voltage ratio $\Gamma$ and the potential difference of the extraction stage $V_{ext}$, must be compared iteratively in order to determine the optimal value of perveance with analytical model of electron backstreaming for ion thrusters [3,31]. This analytical model, shown in Equation (17), enables the explication of the backstreaming limit, coinciding with the minimum potential of the acceleration grid, which allows the backstreaming current to be reduced to a specific percentage of the beam current ${\displaystyle \frac{I_e}{I_b}}(\mathrm{i}.\mathrm{e}.,0.1\%)$.

$$V_{acc,bs}={\displaystyle \frac{V_{sp}^{*}-\Delta V-B{V}_b}{1-B}}$$

(17)

In Equation (17), ${V_{sp}}^{*}$ is the minimum local potential (or “saddle-point” voltage) required for the electronic backstreaming limit. It is quantified in terms of the ratio of the backstreaming current to the beam current. The term $\Delta V$ represents the potential difference between the beam axis and acceleration aperture wall, while B is a geometric factor that considers the acceleration grid geometry, as shown in Equation (20).

$$V_{sp}^{*}=V_{bp}+T_{eV,b}ln\left[2{\displaystyle \frac{I_e}{I_b}}\sqrt{{\displaystyle \frac{\pi m}{M}}\left({\displaystyle \frac{V_b-V_{bp}}{T_{eV,b}}}\right)}\right]$$

(18)

$$\Delta V={\displaystyle \frac{I_b}{4\pi {\epsilon }_0}}\sqrt{{\displaystyle \frac{M}{2e(V_b-V_{sp}^{*})}}}\left[{\displaystyle \frac{1}{2}}-ln\left({\displaystyle \frac{2R_b}{D_a}}\right)\right]$$

(19)

$$B={\displaystyle \frac{D_a}{2\pi (l_e+l_a)}}\left[1-{\displaystyle \frac{2t_a}{D_a}}{tan}^{-1}\left({\displaystyle \frac{D_a}{2t_a}}\right)\right]e^{-{\displaystyle \frac{t_a}{D_a}}}$$

(20)

In Equation (18), $V_{bp}$ corresponds to the plasma potential into the beam, which, as a first approximation, can be set equal to 0 $\mathrm{V}$; $T_{eV,b}$ is the beam plasma electronic temperature in eV (usually of the order of 1-2 eV). In Equation (19), $R_b$ represents the beam diameter obtained through the analytical model developed in Ref. [29]. With this model the beam radius can be estimated along the ion beam trajectory.

$$R_b=\rho (1+k_c)+{\displaystyle \frac{2(U^{0.5}-1)}{\Gamma \rho d_2}}\left[{\displaystyle \frac{k}{d_1}}-{\displaystyle \frac{1+k_c}{f_1}}\right]$$

(21)

In Equation (21), $R_b$ is the radius of the ion beam at the exit of the last grid and $\rho$ is the radius of the initial beam. In Equations (22)-(24) are reported, respectively, the U term, related to the Acceleration-Extraction voltage ratio $\Gamma$, $k_c$ corresponding to the measurement of boundary curvature and $f_1$ to the effect of plasma boundary curvature in extraction stage [30].

$$U=\Gamma +1$$

(22)

$$k_c={\displaystyle \frac{1}{0.8}}\left(\sqrt{{\displaystyle \frac{P}{P_{max}}}}-1\right)$$

(23)

$${\displaystyle \frac{1}{f_1}}={\displaystyle \frac{\Gamma }{4d_2}}-{\displaystyle \frac{1-0.2k_c}{3d_1}}+{\displaystyle \frac{d_2}{9d_1^2}}\left[{\displaystyle \frac{2}{\Gamma }}-{\displaystyle \frac{4(U^{1.5}-1)}{3{\Gamma }^2}}\right](1-0.4k_c)$$

(24)

The comparison of the acceleration grid voltage, obtained from Equations (4) and (17), allows to determine the optimal value of perveance, ${\displaystyle \frac{P}{P_{max}}}$, and the ratio of voltages, $\Gamma$, for a given input power and a fixed value of beam divergence.

2.4. Performances Calculation

Once the grid voltages have been obtained by Kim’s linear optics model [29] and the electron backstreaming model [31], it is possible, through the general equations of electric propulsion, to determine the performances of the thruster.

The curve-fitting approach has enabled the determination of the main performance parameters, such as thrust T (or input power $P_{in}$) and total efficiency ${\eta }_T$. In GITs there are different energy loss mechanisms that can be summarized in three main coefficients ${\eta }_m$, ${\eta }_e$ and ${\eta }_T$. The first is the mass utilization efficiency ${\eta }_m$, which takes into account the amount of neutrals that escape from the discharge chamber without being ionized and can be expressed by using Equation (25).

$${\eta }_m={\displaystyle \frac{{\dot{m}}_i}{{\dot{m}}_p}}={\displaystyle \frac{I_{b}M}{{\dot{m}}_{p}e}}={\displaystyle \frac{g{I}_{sp}}{\gamma \sqrt{\frac{2e{V}_T}{M}}}}$$

(25)

In Equation (25), ${\dot{m}}_p$ is the total propellant mass flux and ${\dot{m}}_i$ is the mass flux of ions, thus the mass utilization efficiency represents the fraction of the total ionized propellant flux. This expression is valid in the case of singly ionized particles, but in the presence of many multi-ionized particles, Equation (25) must be redefined with a correction factor. Sometimes it is useful to define a discharge chamber propellant utilization efficiency ${\eta }_{md}$ by dividing ${\dot{m}}_i$ by the fraction of propellant injected into the chamber, as shown in Equation (26).

$${\eta }_{md}={\eta }_m{\displaystyle \frac{{\dot{m}}_p}{{\dot{m}}_p-{\dot{m}}_n}}$$

(26)

In Equation (26), ${\dot{m}}_n$ represents the neutralizer propellant flow rate outside the chamber and is assumed, as a first approximation, around 10% of the total mass flow rate of the thruster, ${\dot{m}}_p$. The second efficiency is the electrical one ${\eta }_e$, defined in Equation (27) as the ratio of the beam power to the total input power.

$${\eta }_e={\displaystyle \frac{P_b}{P_{in}}}={\displaystyle \frac{I_b{V}_b}{P_{in}}}$$

(27)

Equation (29) provides the last efficiency, the total thruster one ${\eta }_T$, denoted as the jet power divided by the total power. In this expression $\gamma$ is a correction factor related to beam divergence and double ionization in the thruster; its value can be estimated experimentally with Equation (28) or by codes that calculate the beam divergence and consider the propellant multi-ionization.

$$\gamma =cos\theta$$

(28)

$${\eta }_T={\displaystyle \frac{P_{jet}}{P_{in}}}={\gamma }^2{\eta }_e{\eta }_m$$

(29)

Combining the previous relations Equation (30) can be easily obtained. It can be observed that, for a given input power and total efficiency, an increase in specific impulse results in a decrease in thrust of the same amount.

$${\displaystyle \frac{T}{P_{in}}}={\displaystyle \frac{2{\gamma }^2{\eta }_e{\eta }_m}{g{I}_{sp}}}={\displaystyle \frac{2}{g}}{\displaystyle \frac{{\eta }_T}{I_{sp}}}$$

(30)

As Equation (30) shows, a trade-off between thrust and specific impulse must be achieved in the development of an ion thruster, thus the efficiency needs to be increased. It is also important to compute the power loss in Equation (31), which is not exactly an efficiency but still represents a power loss.

$${\eta }_d={\displaystyle \frac{P_d}{I_b}}\approx {\displaystyle \frac{I_d{V}_d}{I_b}}$$

(31)

The discharge loss ${\eta }_d$ indicates the cost of ion production, specifically it represents the power required to generate unit ion beam current. Since it is a power loss, it should be as small as possible. In Equation (32), it is reported the discharge current $I_d$, produced inside the discharge chamber, in which it can be seen the dependence on net beam voltage $V_b$, discharge voltage $V_d$ and electrical efficiency ${\eta }_e$.

$$I_d=I_b{\displaystyle \frac{V_b}{V_d}}{\displaystyle \frac{1-{\eta }_e}{{\eta }_e}}$$

(32)

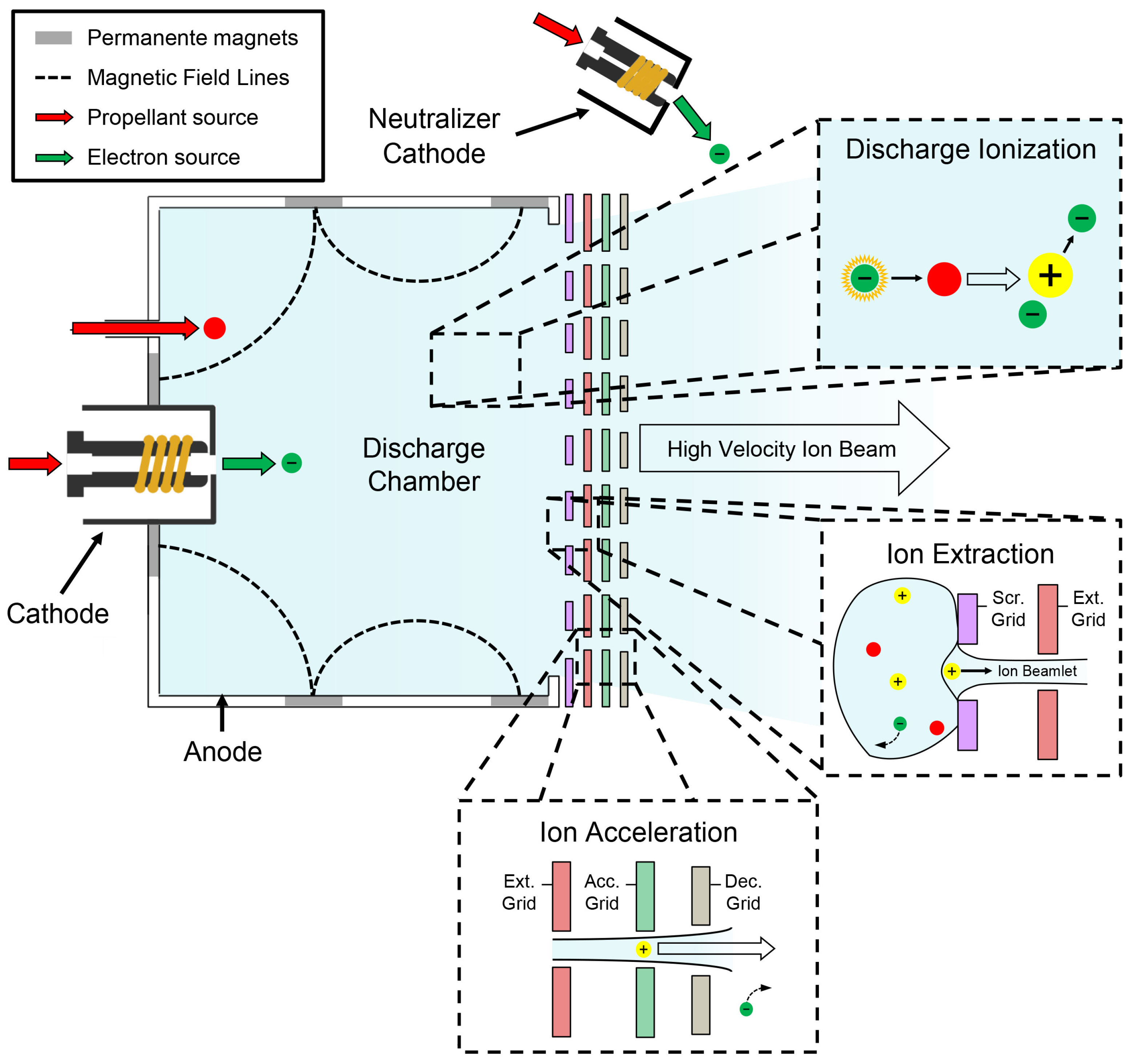
2.5. Discharge Chamber Model

Analytical equations, derived from Goebel and Katz 0-D model [3], allow the determination of the maximum transverse magnetic field between magnetic rings and magnetic field strength in the cusps along the anode wall. These values are used to size magnets arranged in a ring cusp magnetic field configuration, which is one of the most effective solutions for electron and ion confinement [32,33].

In the model, a homogeneous plasma is assumed within the volume confined by the magnetic field, an assumption that is generally valid except for the area near the cathode plume. Therefore, the predictions of the model is expected to deviate only marginally from the experimental results.

The main equations are given by the power balance in the discharge chamber and in the overall thruster expressed respectively in Equations (33) and (34).

$$P_{in,c}=P_{out,c}$$

(33)

$$P_{in,t}=P_{out,t}$$

(34)

In Equation (33), the term $P_{in,c}$ represents the power in the discharge chamber. This power, as shown in Equation (35), depends on the current emitted by the hollow cathode and the voltage to which the electrons inside it are subjected. The second term, $P_{out,c}$, given by Equation (36), represents the output power of the ionization chamber, considering the phenomena of ion production and neutral excitation, as well as electrode losses, related to the power $P_{in,c}$. Equation (34) considers the energy balance of the entire thruster, where $P_{in,t}$ represents the input power of the thruster, assumed to be the model DoF. On the other hand, $P_{out,t}$, defined in Equation (37), includes not only the power required for the ionization chamber, but also the power destined for the electrodes.

$$P_{in,c}=I_e{V}_k=I_e(V_d-V_c+V_p+\varphi )$$

(35)

$$\begin{array}{cc}\hfill P_{out,c}& =I_p{U}^{+}+I^{*}{U}^{*}+I_s(V_d+V_p+\varphi )+I_k(V_d+V_p+\varphi )\hfill \\ \hfill & +(I_b+I_{ia})(V_p+\varphi )+I_a{ϵ}_e+I_L(V_d-V_c+V_p+\varphi )\hfill \end{array}$$

(36)

$$\begin{array}{cc}\hfill P_{out,t}& =I_b(V_b+\Delta V_{ext})+I_p{U}^{+}+I^{*}{U}^{*}+I_s(V_d+V_p+\varphi )\hfill \\ \hfill & +(I_b+I_{ia})(V_p+\varphi )+I_a{ϵ}_e+I_L(V_d-V_c+V_p+\varphi )\hfill \end{array}$$

(37)

In Equation (35), $I_e$ is the electron current, $V_d$ the discharge voltage, $V_c$ the cathode voltage drop, $\varphi$ the sheath potential relative to the anode wall, $V_p$ the plasma potential drop related to the electron temperature $T_{eV}$ (see Equation (38)).

$$V_p={\displaystyle \frac{T_{eV}}{2}}$$

(38)

In Equations (36) and (37), the first term $I_p{U}_{+}$ represents the power to produce ions, where $I_p$ is the ion production rate and $U_{+}$ is the ionization potential. The second term $I^{*}{U}^{*}$ refers to the power to excite neutrals, where $I^{*}$ is the neutral excitation rate and $U^{*}$ is the average excitation potential ($U_{+}$ and $U^{*}$, for Xenon, are respectively $12.5$ eV and 10 eV). As for the production rate of ions $I_p$ and the neutral excitation rate $I^{*}$ are described respectively in Equations (39) and (40).

$$I_p=n_0{n}_{e}e\langle {\sigma }_{+}{v}_e\rangle V+n_0{n}_{p}e\langle {\sigma }_{+}{v}_p\rangle V$$

(39)

$$I^{*}=n_0{n}_{e}e\langle {\sigma }_{*}{v}_e\rangle V+n_0{n}_{p}e\langle {\sigma }_{*}{v}_p\rangle V$$

(40)

In these last two Equations, $n_0$ is the neutral density, $n_e$ the electron density, $n_p$ the primary electron density, e the electron charge and V the plasma volume inside the discharge chamber. The first terms within the brackets, $\langle {\sigma }_{+}{v}_e\rangle$ in Equation (39) and $\langle {\sigma }_{*}{v}_e\rangle$ in Equation (40), represent respectively the ionization and the excitation reaction rate coefficients, i.e., the cross section averaged over the Maxwellian electron velocity distribution function.

The second terms within the brackets, $\langle {\sigma }_{+}{v}_p\rangle$ and $\langle {\sigma }_{*}{v}_p\rangle$, are respectively the ionization and excitation cross section averaged over the primary electron velocity, depending on the electron temperature. By assuming mono-energetic electrons, the second term in brackets can be expressed as a product of the cross section $\sigma$ and the primary velocity $v_p$, considered constant [3].

In the case of DSGIT Xenon-fed:

• The ionization and excitation reaction coefficients expressed as a function of electronic temperature, can be computed by the fits reported in Ref. [3];
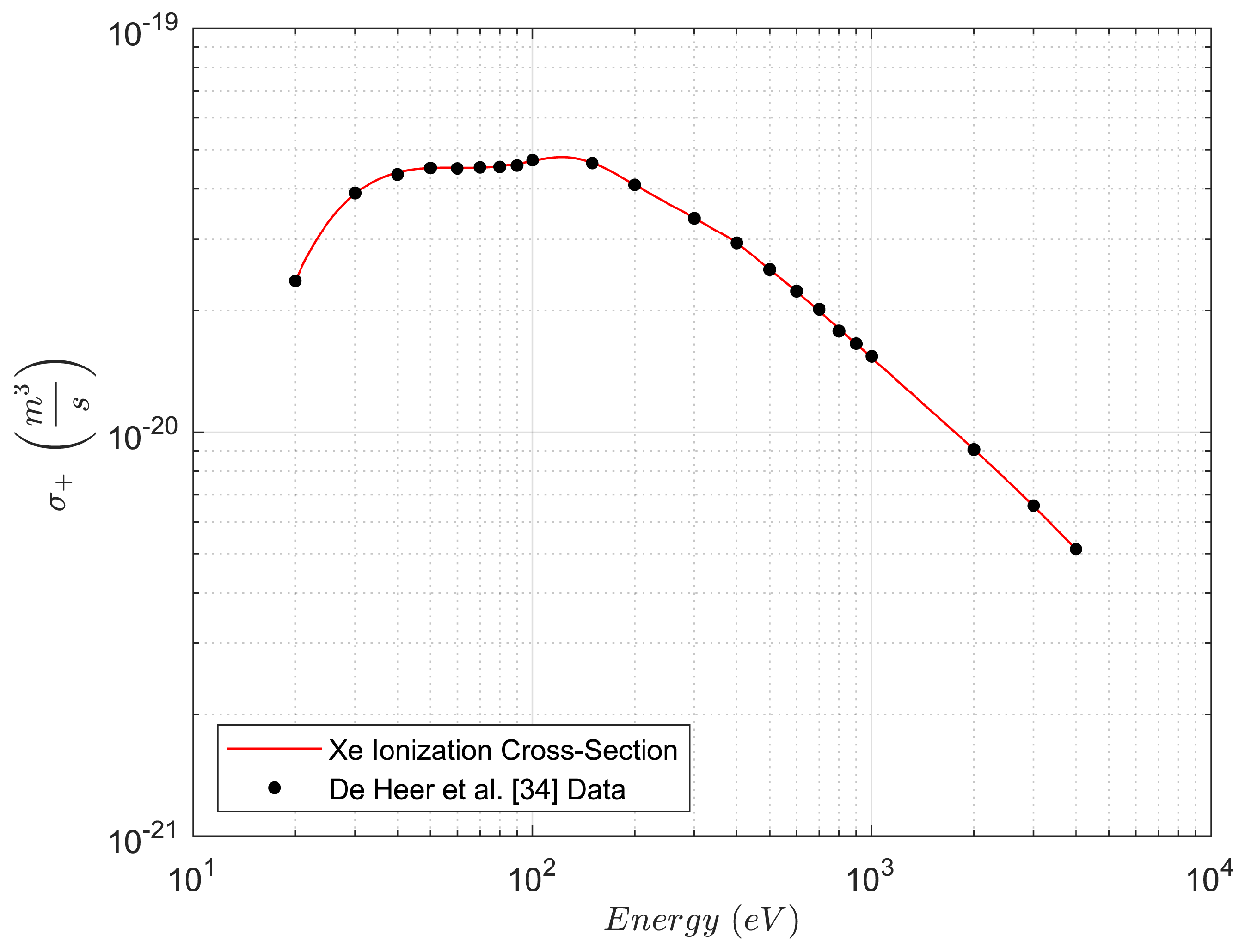
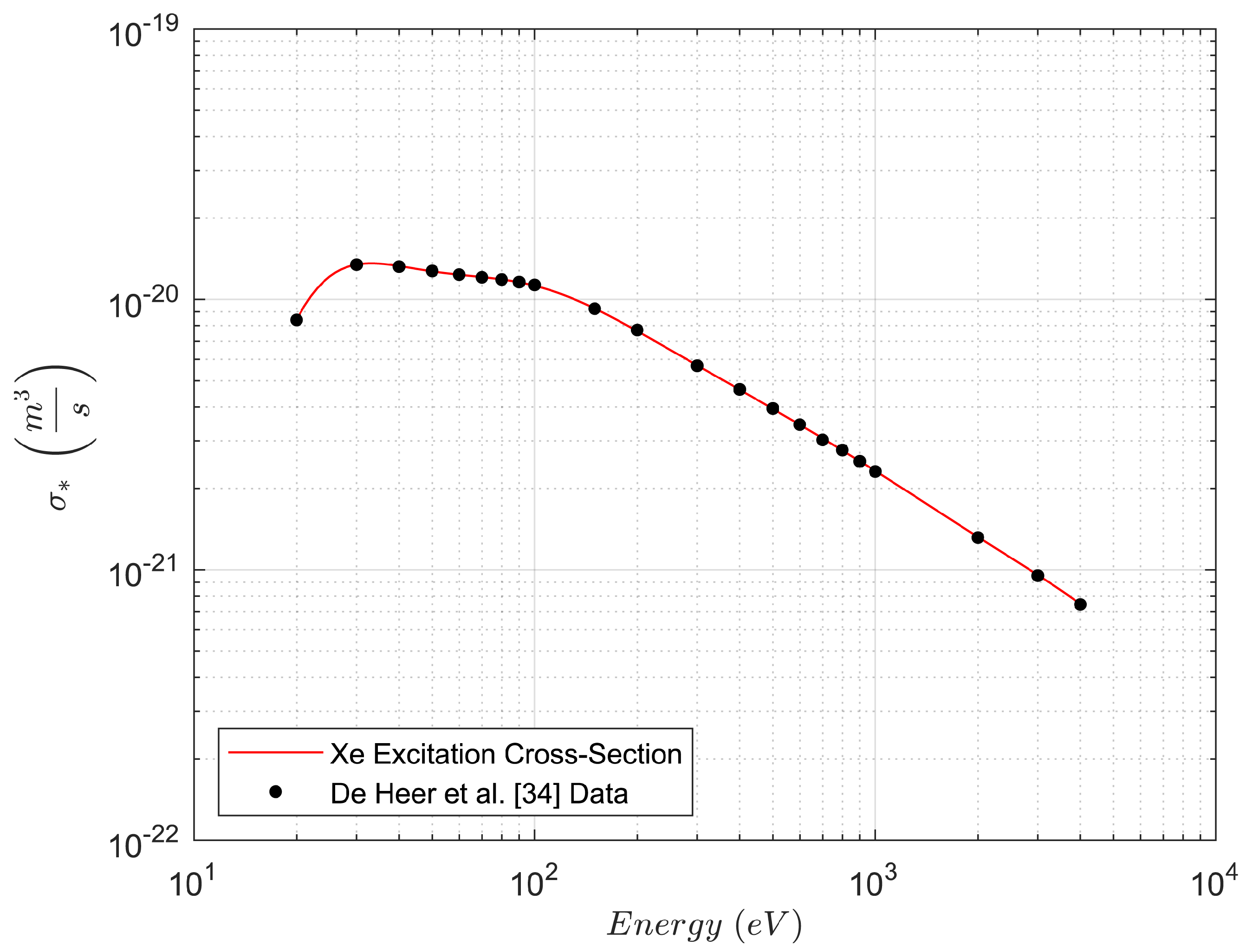
• Ionization and excitation cross-sections are obtained as a function of the primary electron energy $V_k$. Equation (41) is a seventh-order Gaussian fit, derived from the study of De Heer et al. [34] and using the coefficients given in Table 2 and Table 3. These curve fits, shown in Figure 9 and Figure 10, are in accordance with experimental data, yielding an R-squared value of 1, and operate in the energy range 20-4000 eV.

For the calculation hereinafter, the energy of the primary electron, $V_k$, is set to 20 eV, thus the values of cross sections are calculated at the same energy level, E, by using Equation (41).

$$log\sigma =\sum _{n=1}^7{a}_n{e}^{-{\left({\displaystyle \frac{E-b_n}{c_n}}\right)}^2},E=log{V}_k$$

(41)

The remaining terms in the Equations (36) and (37), describe the power lost to the electrodes and to the anode wall due to ions recombination and electrons loss. $I_s$ the ions on the screen grid, $I_k$ the ions back to the cathode, $I_b$ the ions beam current, $I_{ia}$ the ion current lost to the anode, $I_a$ the electron current from the plasma that go to the anode, $I_L$ the primary electron current lost to the anode and ${ϵ}_e$ the plasma electron energy lost to the wall, expressed as $2T_{eV}+\varphi$. Furthermore, in the Equation (37), $V_b$ corresponds to the ion beam voltage and $\Delta V_{ext}$ to the potential drop in the extraction stage. The term $\Delta V_{ext}$ is added, compared with the conventional GIT equations [3], in the power balance of the overall thruster to consider the decoupling effect of the extraction and acceleration process in the DSGIT.

As concerns the currents, they have to satisfy the balance Equations (42)-(45).

$$I_a=I_d+I_{ia}-I_L$$

(42)

$$I_e=I_d-I_s-I_k$$

(43)

$$I_p=I_{ia}+I_b+I_s$$

(44)

$$I_p=I_a+I_b+I_L-I_e$$

(45)

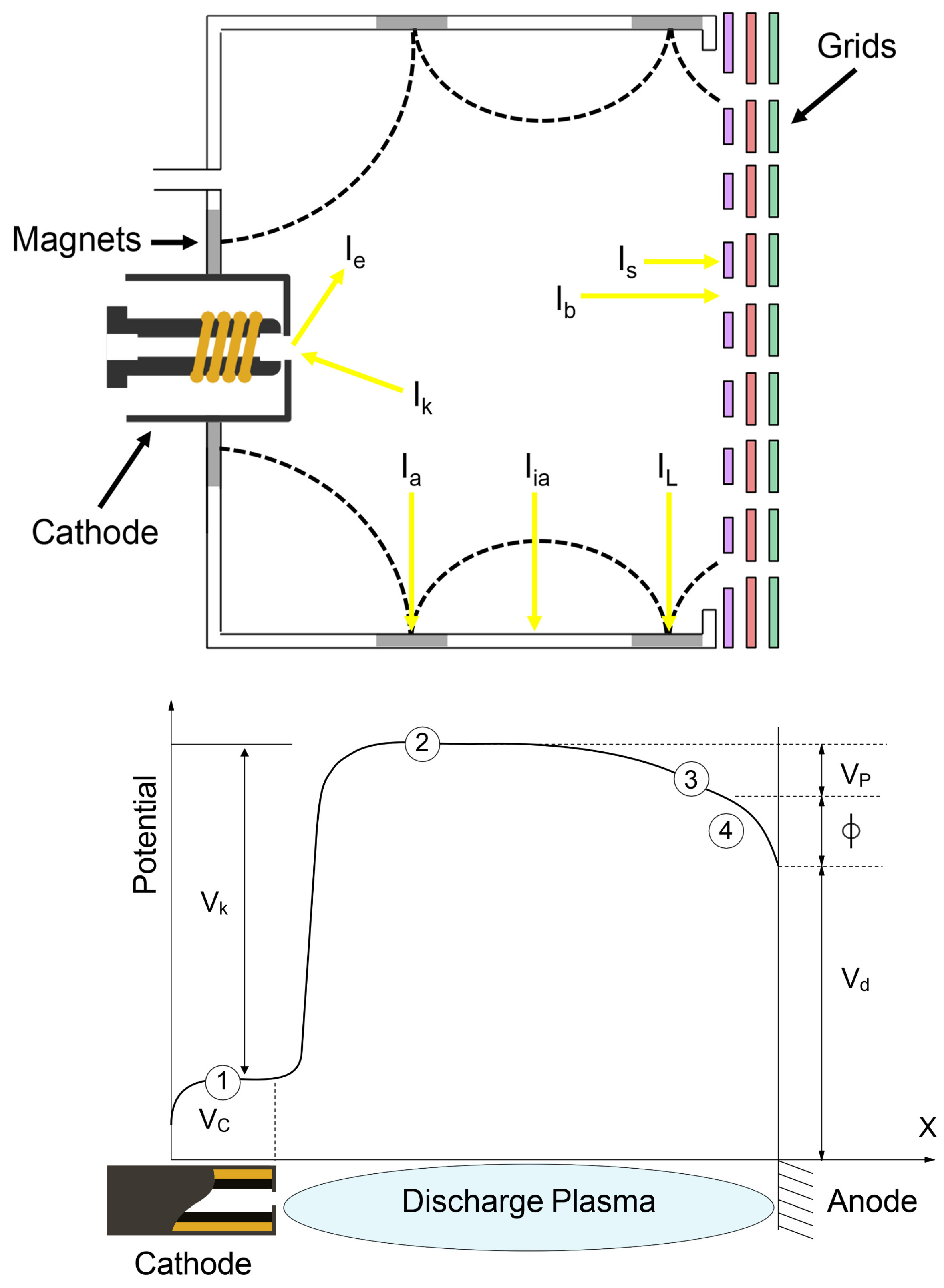
Regarding magnetic confinement, it is decided to focus on the currents $I_L$, $I_a$ and $I_{ia}$, found in Equations (42)-(45), due to their dependence on the magnetic field. Equations (42) and (43) represent the conservation of particles flowing to the anode and the current emitted from the hollow cathode, respectively, while Equations (44) and (45) express the rate of ion production. The $I_k$ term is put equal to zero, given the negligible values it generally assumes.

Figure 11 shows the defined currents and potentials in the discharge chamber.

Equation (46) allows to define the primary electron current lost directly to the anode wall at the cusps of the magnetic field, since the magnetic field lines are perpendicular to the surface.

$$I_L=n_{p}e{v}_p{A}_p$$

(46)

The term $n_p$ is the primary electron density, $v_p$ the primary electron velocity and $A_p$ the loss area at anode expressed in the Equation (47).

$$A_p=2r_p{L}_c$$

(47)

As reported in Equation (48), $L_c$ is the total length of the magnetic cusps in the azimuthal direction given by the sum of the single length of the cusps.

$$L_c=\pi D{N}_{cusp}$$

(48)

The value $r_p$ is the Larmor radius shown in the Equation (49) and influenced by $B_{cusp}$, which is the magnetic field strength at the cusp of the anode wall.

$$r_p={\displaystyle \frac{m{v}_p}{e{B}_{cusp}}}$$

(49)

As can be seen, $r_p$ and $B_{cusp}$ are inversely proportional, thus the higher the magnetic field, the lower the loss area; therefore, the probability, P, that a primary electron undergoes a collision without being lost at the anode is higher, in agreement with the Equation (50).

$$P=1-e^{-{\displaystyle \frac{n_0\sigma \overline{V}}{A_p}}}$$

(50)

The term $n_0$ is the neutral density, $\sigma$ the total inelastic collision cross-section for the primary electrons and V the discharge chamber volume. Typically, most of the electrons lost at the anode magnetic cusps are plasma electrons, the so-called secondary electrons. The plasma electrons current lost to the anode magnetic cusps can be expressed by the Equation (51).

$$I_a={\displaystyle \frac{1}{4}}\sqrt{{\displaystyle \frac{8k{T}_e}{\pi m}}}e{n}_e{A}_a{e}^{-{\displaystyle \frac{e\varphi }{k{T}_e}}}$$

(51)

In this expression, $n_e$ is the electron density in the plasma, $T_e$ the electron temperature, m the electron mass, $\varphi$ the anode sheath potential and $A_a$ a hybrid anode area reported in Equation (52).

$$A_a=4r_h{L}_c=4\sqrt{r_e{r}_i}{L}_c$$

(52)

In Equation (52), $r_h$ represents the hybrid Larmor radius, which depends on the magnetic field strength B at the magnetic cusps on the anode wall; while $r_e$ and $r_i$ are respectively the electron Larmor radius and the ion Larmor radius, explicated in the Equations (53) and (54).

$$r_e={\displaystyle \frac{m{v}_e}{e{B}_{cusp}}}$$

(53)

$$r_i={\displaystyle \frac{M{v}_i}{e{B}_{cusp}}}$$

(54)

The ion current to the anode wall is expressed in the Equation 55, where $A_{as}$ is the total surface area of the anode exposed to the plasma and $f_c$ the confinement factor.

$$I_{ia}={\displaystyle \frac{1}{2}}{n}_{i}e\sqrt{{\displaystyle \frac{k{T}_e}{M}}}{A}_{as}{f}_c$$

(55)

The factor $f_c$ is related to the presence of magnetized electrons that influence the motion of ions, causing a reduction of the Bohm current toward the wall area between the cusps.

$$f_c={\displaystyle \frac{v_i}{v_{Bohm}}}$$

(56)

The confinement factor $f_c$ corresponds to the ratio of the transverse ion velocity $v_i$ to the Bohm velocity $v_{Bohm}$, as reported in Equation (56). Furthermore, it depends primarily on the magnetic field configuration since the transverse ion velocity $v_i$ is expressed, as seen in Equation (57), as a function of the maximum transverse magnetic field $B_t$. The latter induces a reduction in the expected ion flux to the anode, which also directly affects the ion velocity. As a result, ions are conserved because those that do not flow to the anode wall, due to the transverse magnetic field, impact toward the grids, i.e. in a region of no confinement.

$$v_i={\displaystyle \frac{1}{2}}\sqrt{{\left[{\displaystyle \frac{el}{M{\mu }_e}}\left(1+{\mu }_e^2{B}_t^2-{\displaystyle \frac{{\nu }_{ei}}{{\nu }_e}}\right)\right]}^2+{\displaystyle \frac{4k{T}_e}{M}}}-\left[{\displaystyle \frac{el}{M{\mu }_e}}\left(1+{\mu }_e^2{B}_t^2-{\displaystyle \frac{{\nu }_{ei}}{{\nu }_e}}\right)\right]$$

(57)

In Equation (57), ${\nu }_{ei}$ represents the electron-ion collision frequency, ${\nu }_e$ is the sum of the electron-neutral collision frequency ${\nu }_{en}$ and the electron-ion one ${\nu }_{ei}$, ${\mu }_e$ the electron mobility and l the diffusion length. The latter term, corresponding to the transverse location of the maximum magnetic field magnitude between magnets, in the case of the ring cusp magnetic field, can be determined with good approximation as $0.29d$, where d is the distance of the magnets.

Equations (58)-(60) describe the collision frequencies and electron mobility.

$${\nu }_{ei}={\displaystyle \frac{e^{5/2}}{16\pi {ϵ}_0^2\sqrt{m}}}{\displaystyle \frac{n_e}{T_{eV}^{1.5}}}\left(23-0.5ln\left({\displaystyle \frac{{10}^{-6}{n}_e}{T_{eV}^3}}\right)\right)$$

(58)

$${\nu }_{en}={\sigma }_{en}{n}_0\sqrt{{\displaystyle \frac{8k{T}_e}{\pi m}}}$$

(59)

$${\mu }_e={\displaystyle \frac{e}{m{\nu }_e}}$$

(60)

The term ${\sigma }_{en}$ represents the Average Maxwellian inelastic cross-section, i.e. the measure of the probability of a particle interaction in a gas or plasma. This cross-section is determined as a function of the electronic temperature $T_{eV}$ and depends on the selected propellant. Curve fits valid in the electronic temperature range 0.1-100 eV, can be found in Ref. [35] .

3. Results

3.1. Validation

For the validation of the model, Ref. [15] has been selected because it deals with the preliminary design of DSGITs for different mission classes and reports the highest number of data to compare with. Particularly those referring to the following missions have been selected: Infra-structure to Earth-Moon L1 in Table 4 and Table 5 and NEO NEP in Table 6, Table 7 and Table 8. Each one has several mission levels, thus only a few of them are randomly chosen to make the comparison, e.g., for Infra-structure to Earth-Moon L1, mission level 1 and 2.

In each simulation, the power and discharge chamber diameter have been used as inputs to the model. Xenon has been used as propellant. As regarding the OS, in Table 4 and in Table 6, Table 7 and Table 8 the comparison is made using the grids in Ref. [8], while in Table 5 and Table 9 those in Ref. [20].

The performances and working parameters predicted by the model, Table 4, Table 5, Table 6, Table 7 and Table 8, compared to those reported in Ref. [15], show differences which are, for the most of the parameters, lower than 5 %, even if one parameter for each test case can exceed this value, reaching also value close to 10 %.

Specifically, regarding the results of the simulation of the NEO NEP Mission Level 1, reported in Table 6, the highest difference is about the value of $V_{acc}$, i.e. $5.02$ %. This can be attributed to the dependence of this parameter on the $V_{ext}$ and $V_t$, as in Equation 14. The differences of these parameters with respect the data reported in open literature, are probably due to the thrust obtained by the curve fitting approach. In general, it can be seen that in all Table 4, Table 5, Table 6, Table 7, Table 8 and Table 9 the acceleration grid voltage has the highest difference among the working parameters, due to its dependence on the total acceleration voltage and on the extraction grid voltage.

This is true except for Table 5 and Table 9, where it can be seen that the specific impulse $I_{sp}$ and the total propellant mass flow rate ${\dot{m}}_p$, related to the total efficiency ${\eta }_T$, have errors up to a maximum of 9 % and 10 %, respectively. This highlights that the educated guess, applied to total thruster efficiency, allows for more accurate values as the diameter increases, as seen in Table 4 and Table 6, Table 7 and Table 8, to a similar trend with respect to that of conventional GITs.

3.2. GIT vs DSGIT

The previous section has dealt with the validation of the model that has involved high power thruster (25-50 kW). In this section the model has been applied to show the advantages of DSGIT against GIT, in low power range (i.e. 1 $\mathrm{k}$$\mathrm{W}$). Particularly a DSGIT was designed to match the thrust and the power of NSTAR (Throttle level 5, TH5) [37], a well studied and characterized ion thruster.

Table 10 clearly shows how the DS technology is promising: with ten times smaller thruster, hundred times thrust and power density can be achieved. Moreover, the specific impulse and the total efficiency are increased by 25 %. Obviously thermal analysis would be necessary to verify if such high power on such small thruster could be managed.

4. Conclusions

The paper has described a Global Plasma Model able to compute the performances and the main working parameters of a Direct Current Dual Stage Gridded Ion Thruster, a promising Electric Propulsion architecture.

The model makes use of a curve-fitting approach, the classic performance definition for Gridded Ion Thruster, a linear Optic System model and a plasma model for the ionization chamber. It takes as input the discharge chamber diameter and the thrust or the total power; it is assumed a cylindrical ionization chamber with the length equal to its diameter; the extraction and discharge voltages are set respectively to 1000 V and 28V. The grid geometry can be arbitrary assigned as well as the divergence beam angle. The main assumption of the model is that the thrust/diameter-total efficiency curve, used in the curve-fitting approach, obtained for conventional GIT, is supposed to be valid for Dual Stage Thrusters, too.

The results of the validation tests, conducted on the data available in open literature, regarding high power DSGIT (25-50kW), and get by means of a preliminary design tool, has shown the reliability of the model. Except for very few parameters the differences are below 5 %. Perhaps, the usage of thrust/diameter-total efficiency curve built by using specifically experimental data regarding DSGITs, would improve predictions’ accuracy.

The model has been proved to be used for the design of new thrusters, too. As example, a 1kW DSGIT, with the same thrust and power of NSTAR, was designed. A diameter ten times lower (3cm vs. 30cm) has resulted, leading to hundred times higher power/thrust density; moreover the specific impulse and the total efficiency have been increased by 25 %.